| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
Б. Томпсон
4.2.1. Получение голограмм
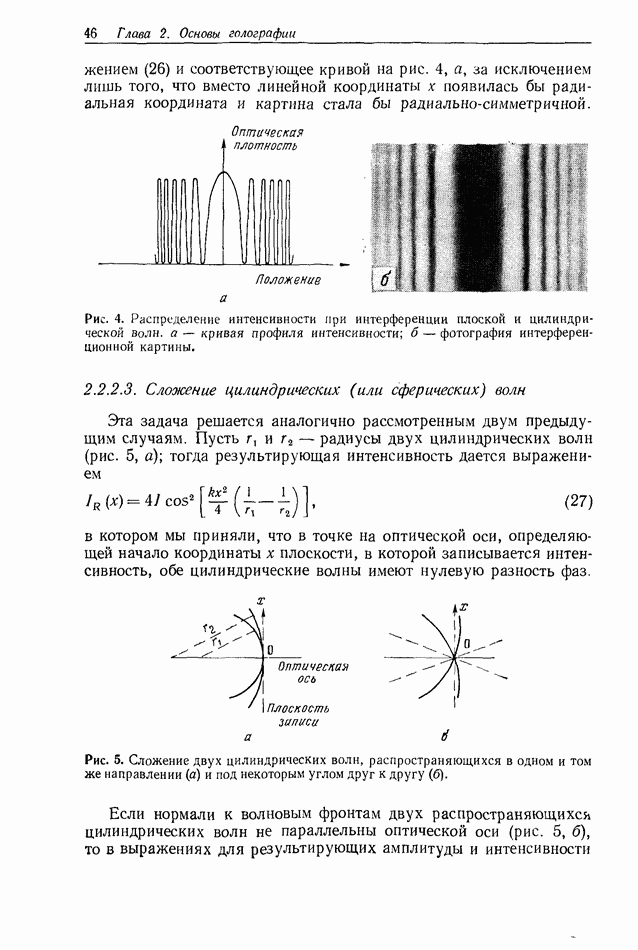
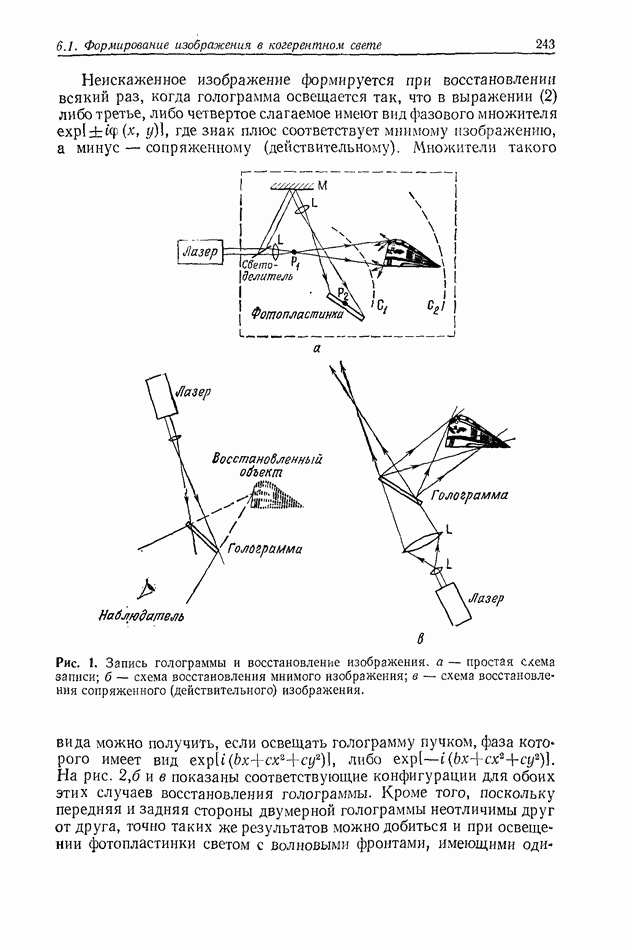
Было установлено, что характер голограммы и до некоторой степени свойства получаемого с ее помощью изображения зависят от фактически регистрируемого на ней дифрагированного поля,
связанного с объектом или сигналом, представляющим интерес. Важный класс голограмм представляют собой голограммы, получаемые по осевой схеме, в которой объект должен быть достаточно прозрачным, чтобы пропустить необходимое количество недифрагированного света для создания когерентного фона. Кроме того, плоскость регистрации голограммы в рассматриваемом случае находится в дальней зоне дифракции голографируемого объекта. Таким образом, эта голограмма есть не что иное, как запись интерференционной картины, образованной дифракцией Фраунгофера на объекте, формируемой в дальней зоне, и коллинеарным когерентным фоном.

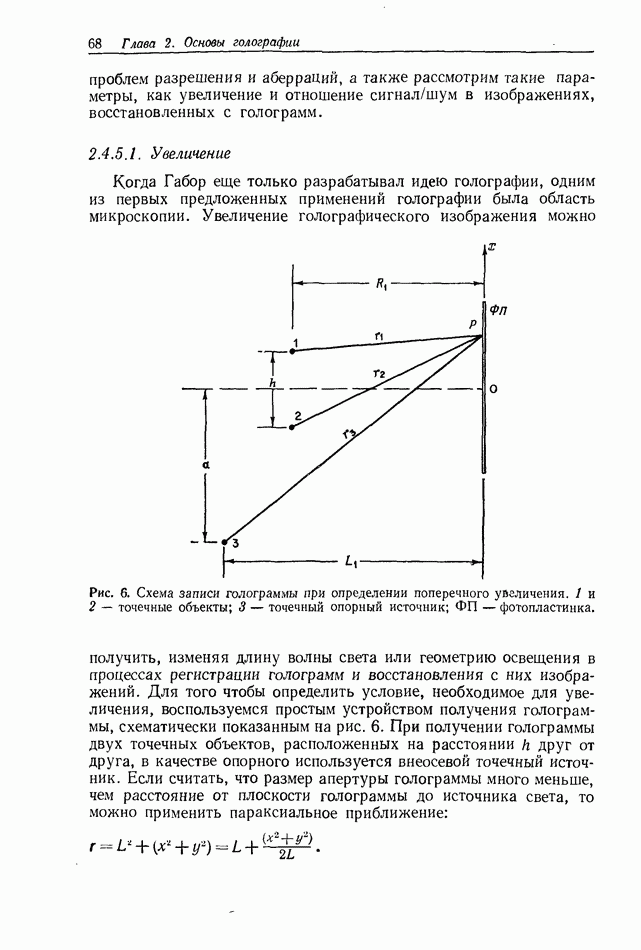
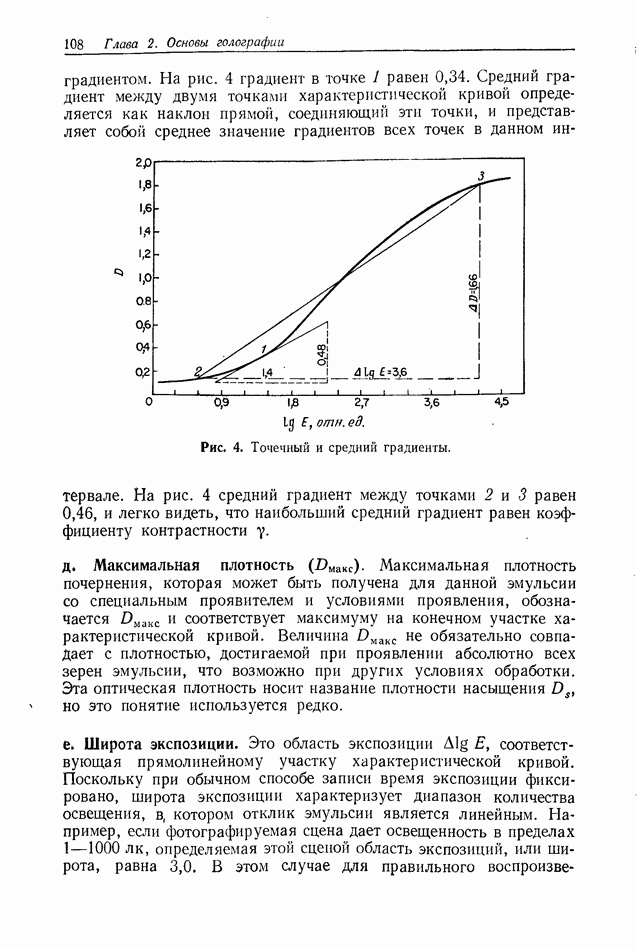
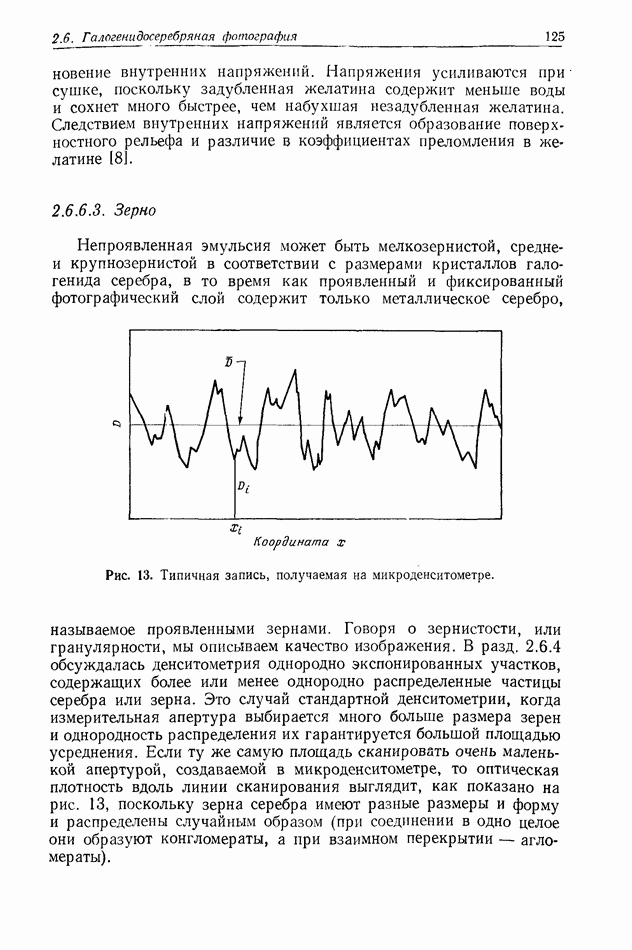
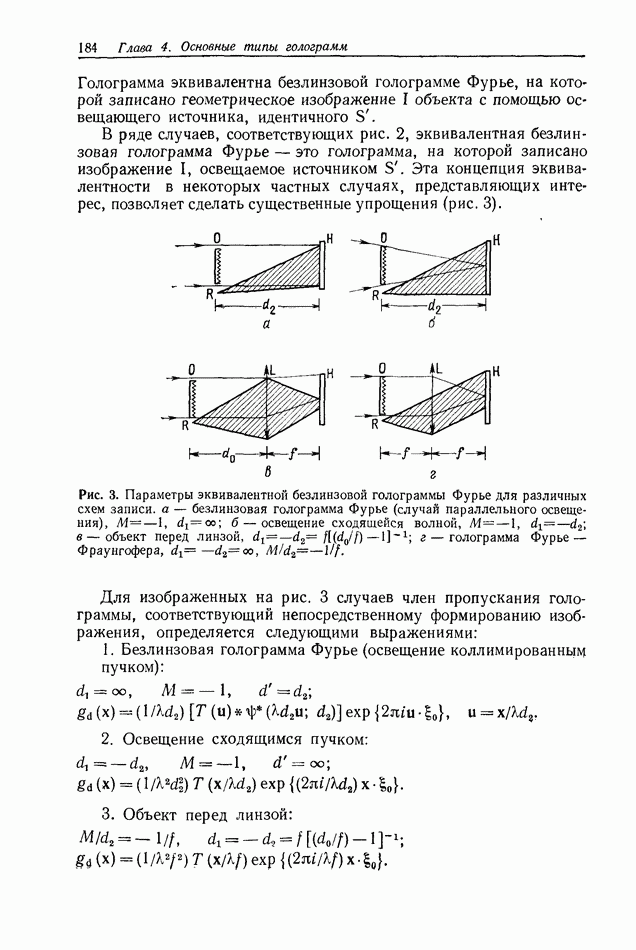
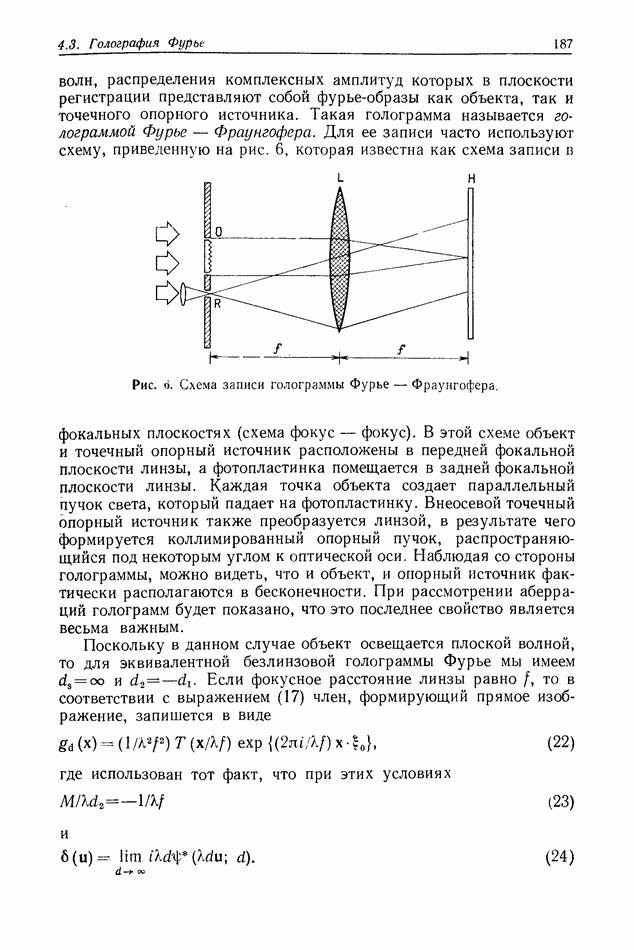
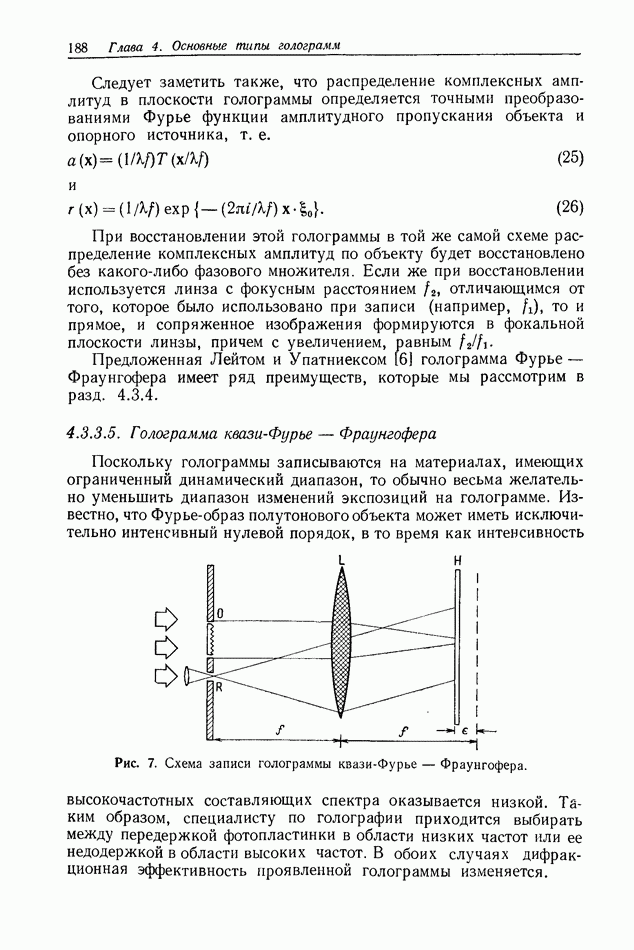
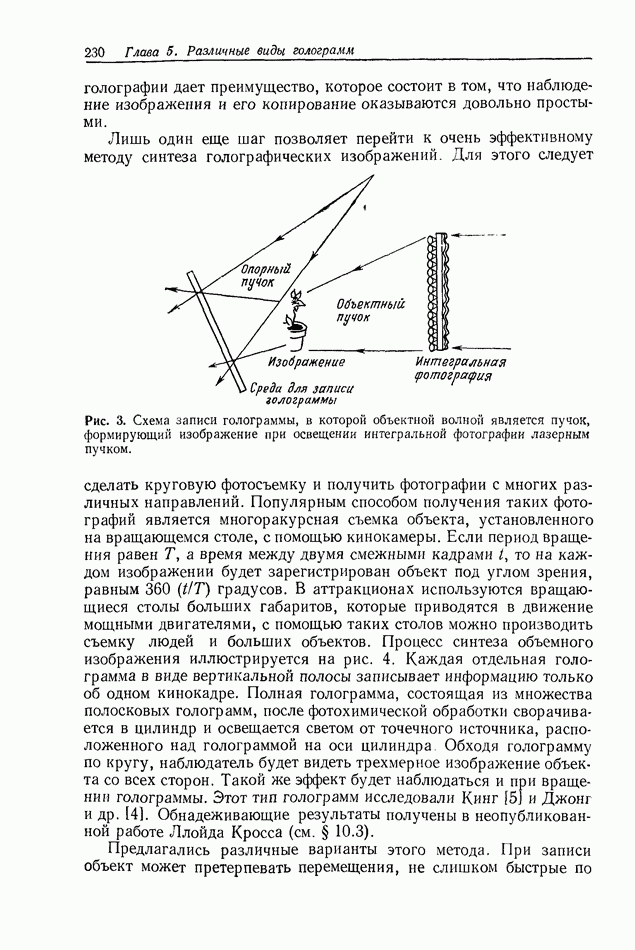
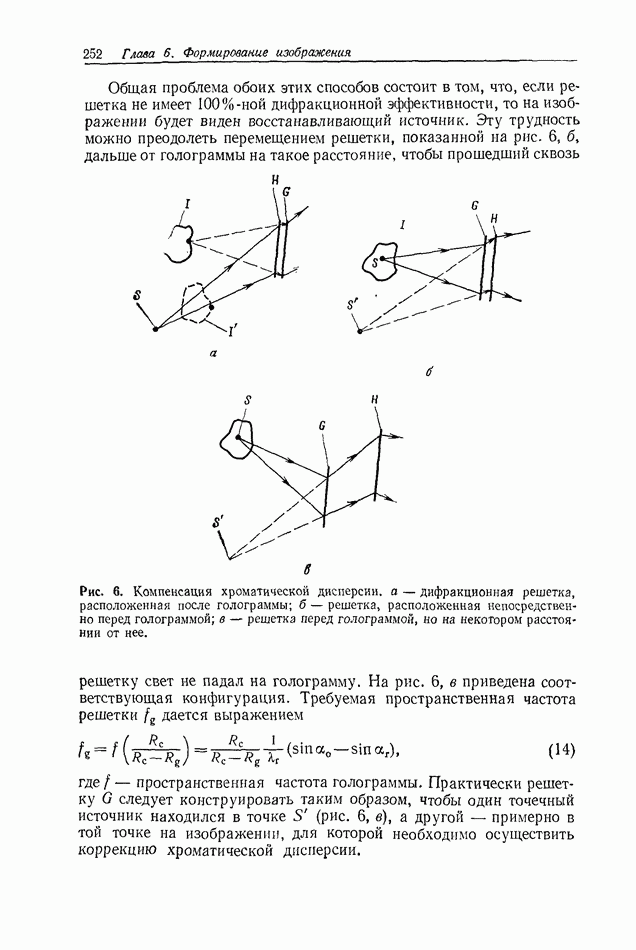
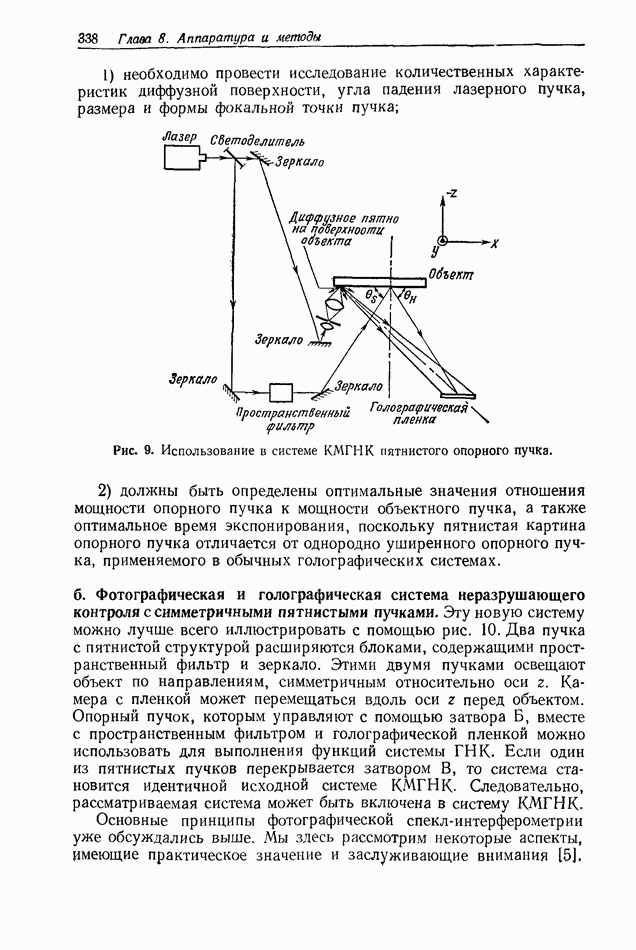
Рис. 1. Схематическое представление формирования голограммы Фраунгофера.
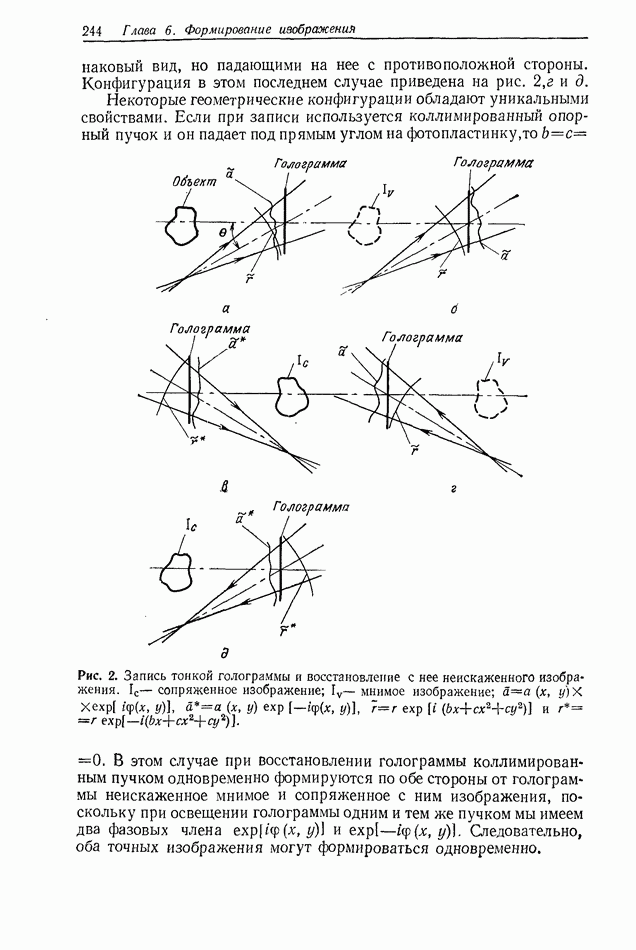
Этот тип голограмм предложили Томпсон [4] и Паррент и Томпсон [3] для решения конкретной задачи анализа размеров частиц. В дальнейшем теоретический аспект рассматриваемого голографического процесса рассматривался в работе [1], а недавно Тайлер и Томпсон [71 вновь занялись его подробной теорией. В то же время применение голографии Фраунгофера для решения важных проблем привело к значительно более глубокому пониманию самой голографии Фраунгофера (см., например, [5, 61).
Таким образом, при записи голограммы объект помещается в плоскости  и освещается коллимированным пучком когерентного света (мы используем здесь для простоты рассмотрения коллимированный пучок, однако можно применять и неколлимированный пучок, но при выполнении условий для дальней зоны). Записывается голограмма в плоскости
и освещается коллимированным пучком когерентного света (мы используем здесь для простоты рассмотрения коллимированный пучок, однако можно применять и неколлимированный пучок, но при выполнении условий для дальней зоны). Записывается голограмма в плоскости  отстоящей от объекта на расстояние
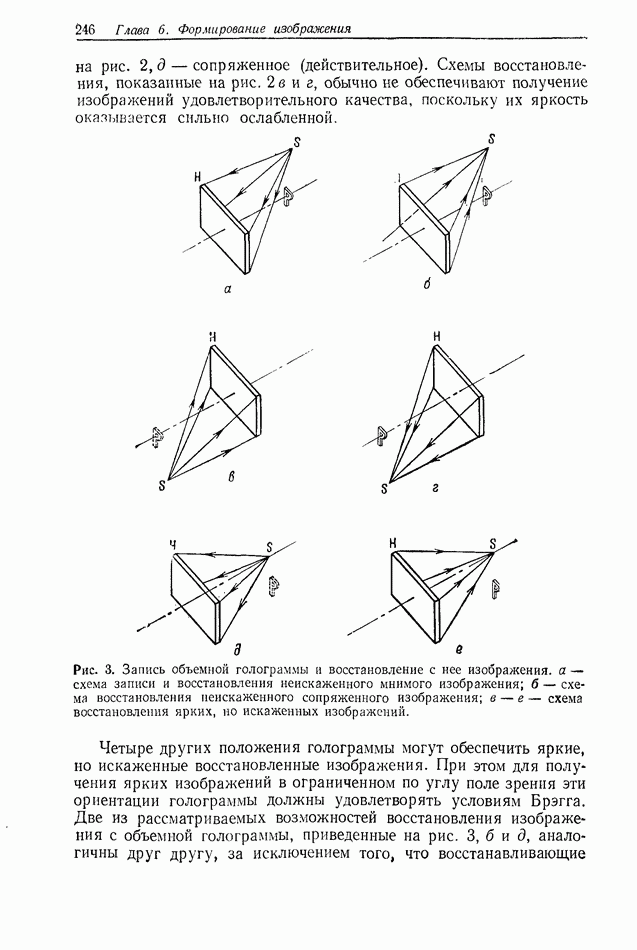
отстоящей от объекта на расстояние  (рис. 1). Будем полагать, что объект описывается распределением амплитудного пропускания
(рис. 1). Будем полагать, что объект описывается распределением амплитудного пропускания  и освещается волной с единичной амплитудой и длиной волны
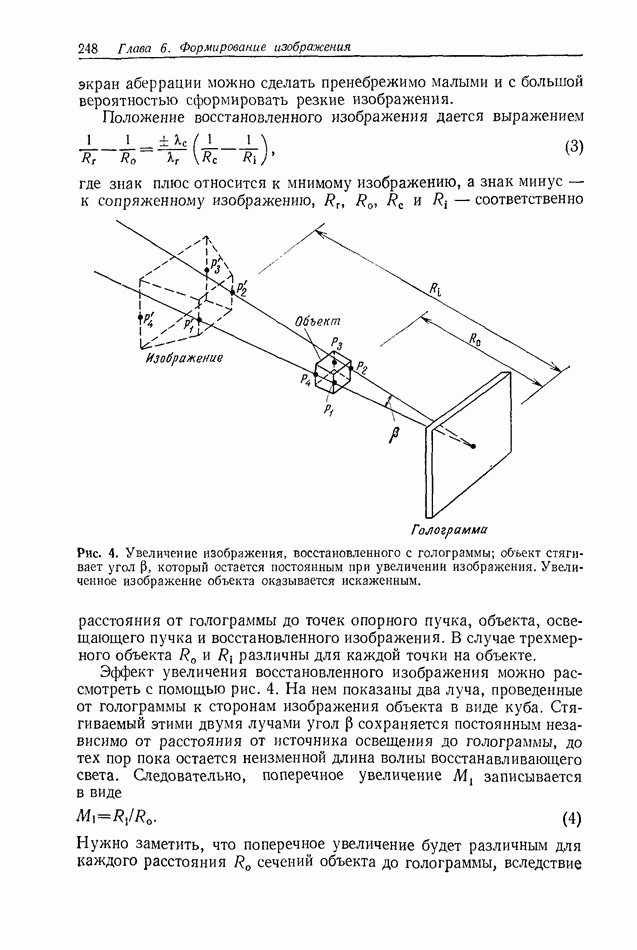
и освещается волной с единичной амплитудой и длиной волны  (Мы здесь будем следовать рассмотрению, приведенному Тайлером и Томпсоном
(Мы здесь будем следовать рассмотрению, приведенному Тайлером и Томпсоном  При этом распределение комплексных амплитуд поля в плоскости регистрации
При этом распределение комплексных амплитуд поля в плоскости регистрации  определяется, согласно принципу Гюйгенса — Френеля, выражением
определяется, согласно принципу Гюйгенса — Френеля, выражением

При выполнении условия дальней зоны распределение интенсивности на голограмме запишется в виде

где  соответственно действительные и мнимые части,
соответственно действительные и мнимые части,  фурье-образ распределения амплитуд на объекте, определяемый следующим образом:
фурье-образ распределения амплитуд на объекте, определяемый следующим образом:

Для примера будем полагать, что объект представляет собой проволоку диаметром 2а. В этом случае задача облегчается и сводится к одномерному случаю (условие дальней зоны выполняется только для одного направления). Теперь распределение амплитуд на объекте будет  и выражение (2) принимает вид
и выражение (2) принимает вид

где

В заключение следует заметить, что амплитудное пропускание полученной голограммы описывается выражением

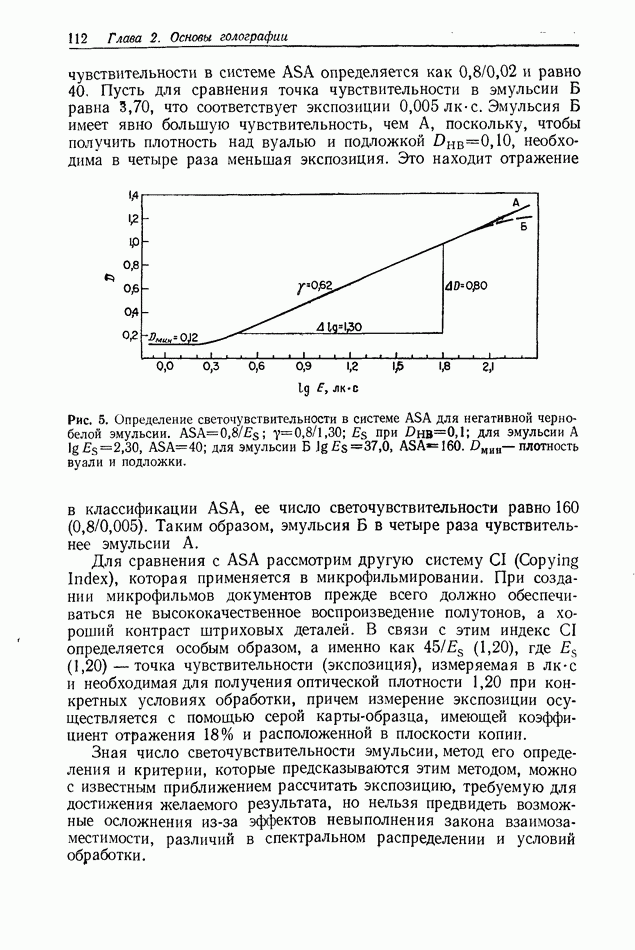
На рис. 2 приведена голограмма Фраунгофера проволоки диаметром  которая была получена при освещении светом аргонового лазера с
которая была получена при освещении светом аргонового лазера с  при
при  см. Голограмма записывалась на фотопластинке Кодак
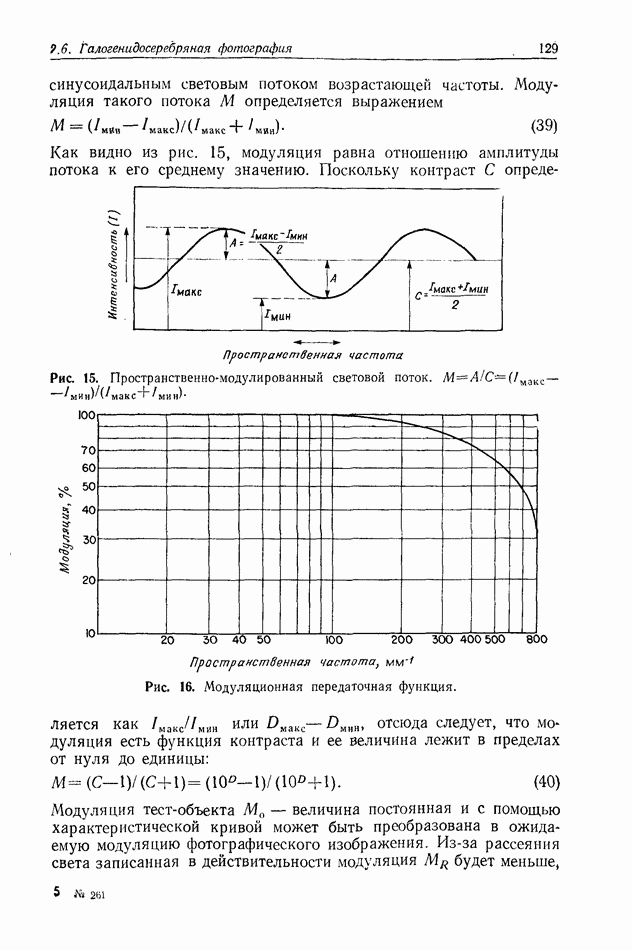
см. Голограмма записывалась на фотопластинке Кодак  на рис. 2, а приведен ее позитивный отпечаток. На рис. 2, б показана микроденситограмма сечения голограммы, а на рис. 2, в приведено распределение
на рис. 2, а приведен ее позитивный отпечаток. На рис. 2, б показана микроденситограмма сечения голограммы, а на рис. 2, в приведено распределение
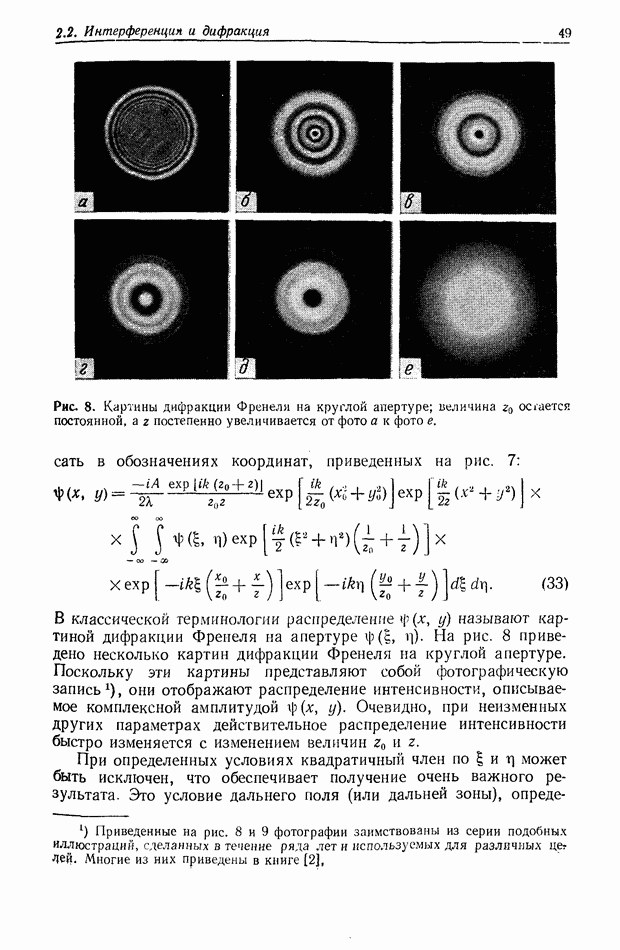
интенсивности, вычисленное по формуле (6) с помощью ЭВМ. Интересно отметить, что кривую, приведенную на рис. 2, в, можно было бы получить, рассмотрев полную апертурную функцию как отдельную функцию и затем выполнив расчет соответствующей картины дифракции Френеля для всего поля. Например, аналогичный график можно найти во многих учебниках, в которых рассматривается дифракция Френеля (см., например, [2]). Разумеется, при этом остается незамеченным тот факт, что эта дифракционная картина есть голограмма, и это приводит к потере физического понимания явления.

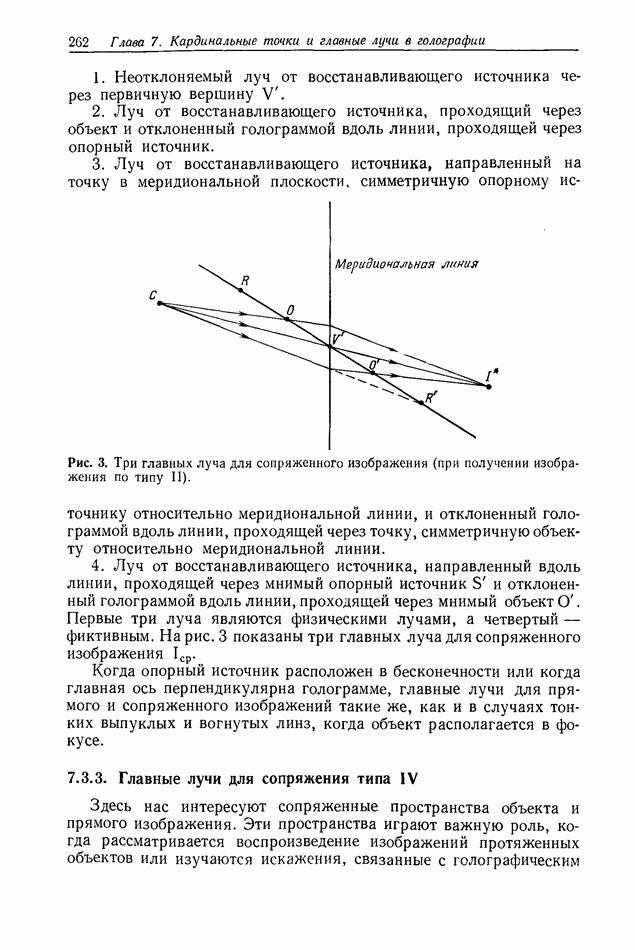
Рис. 2. Голограмма Фраунгофера проволоки диаметром  полученная на расстоянии
полученная на расстоянии  см от объекта при использовании света с длиной волны
см от объекта при использовании света с длиной волны  позитивный отпечаток части голограммы; б - микроденситограмма сечения голограммы; в — кривая, вычисленная на ЭВМ по формуле (6). Согласно [7].
позитивный отпечаток части голограммы; б - микроденситограмма сечения голограммы; в — кривая, вычисленная на ЭВМ по формуле (6). Согласно [7].
4.2.2. Формирование изображения
При восстановлении голограмма освещается плоской монохроматической волной единичной амплитуды, и в плоскости  на расстоянии
на расстоянии  от голограммы формируется действительное изображение объекта. (Можно учесть влияние записи и восстановления с использованием сферических волн, если допустить, что значения
от голограммы формируется действительное изображение объекта. (Можно учесть влияние записи и восстановления с использованием сферических волн, если допустить, что значения  могут быть различными.) Распределение амплитуд поля
могут быть различными.) Распределение амплитуд поля  в восстановленном изображении имеет вид
в восстановленном изображении имеет вид
(см. скан)
где  . С помощью этого выражения можно затем вычислить распределение интенсивности в изображении,
. С помощью этого выражения можно затем вычислить распределение интенсивности в изображении,
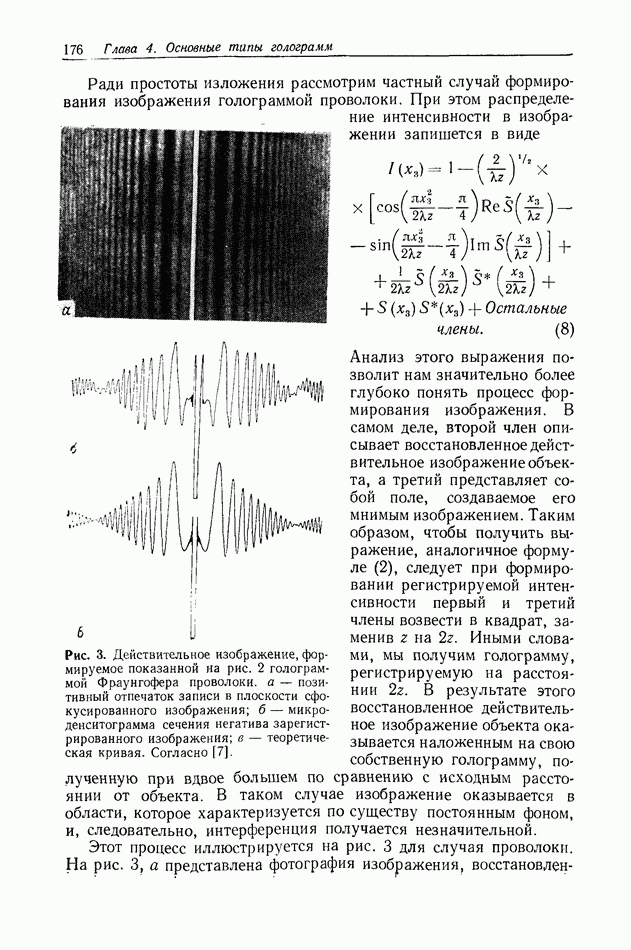
Ради простоты изложения рассмотрим частный случай формирования изображения голограммой проволоки. При этом распределение интенсивности в изображении запишется в виде

Анализ этого выражения позволит нам значительно более глубоко понять процесс формирования изображения. В самом деле, второй член описывает восстановленное действительное изображение объекта, а третий представляет собой поле, создаваемое его мнимым изображением. Таким образом, чтобы получить выражение, аналогичное формуле (2), следует при формировании регистрируемой интенсивности первый и третий члены возвести в квадрат, заменив  на
на  Иными словами, мы получим голограмму, регистрируемую на расстоянии
Иными словами, мы получим голограмму, регистрируемую на расстоянии  В результате этого восстановленное действительное изображение объекта оказывается наложенным на свою собственную голограмму, полученную при вдвое большем по сравнению с исходным расстоянии от объекта. В таком случае изображение оказывается в области, которое характеризуется по существу постоянным фоном, и, следовательно, интерференция получается незначительной.
В результате этого восстановленное действительное изображение объекта оказывается наложенным на свою собственную голограмму, полученную при вдвое большем по сравнению с исходным расстоянии от объекта. В таком случае изображение оказывается в области, которое характеризуется по существу постоянным фоном, и, следовательно, интерференция получается незначительной.
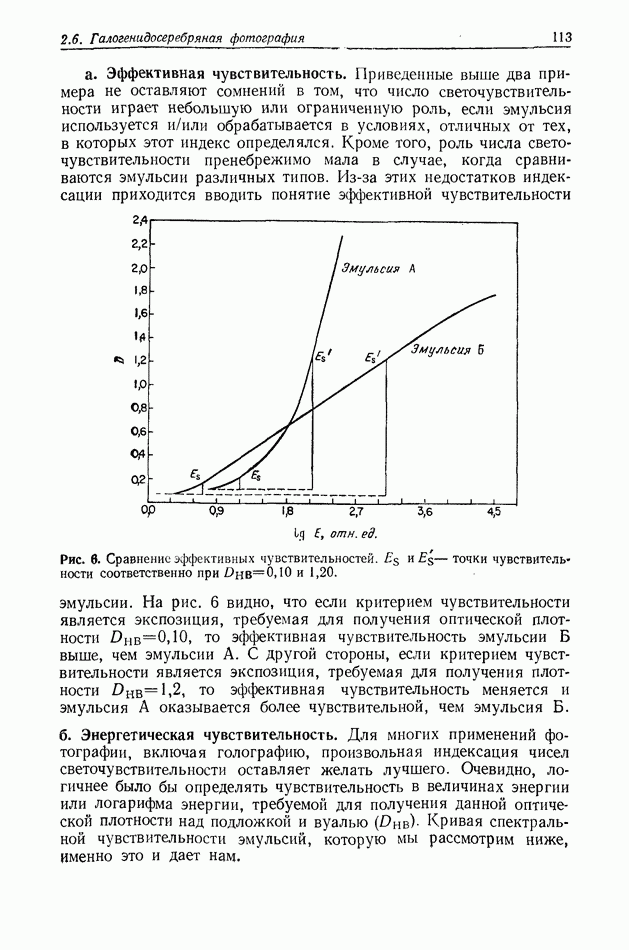
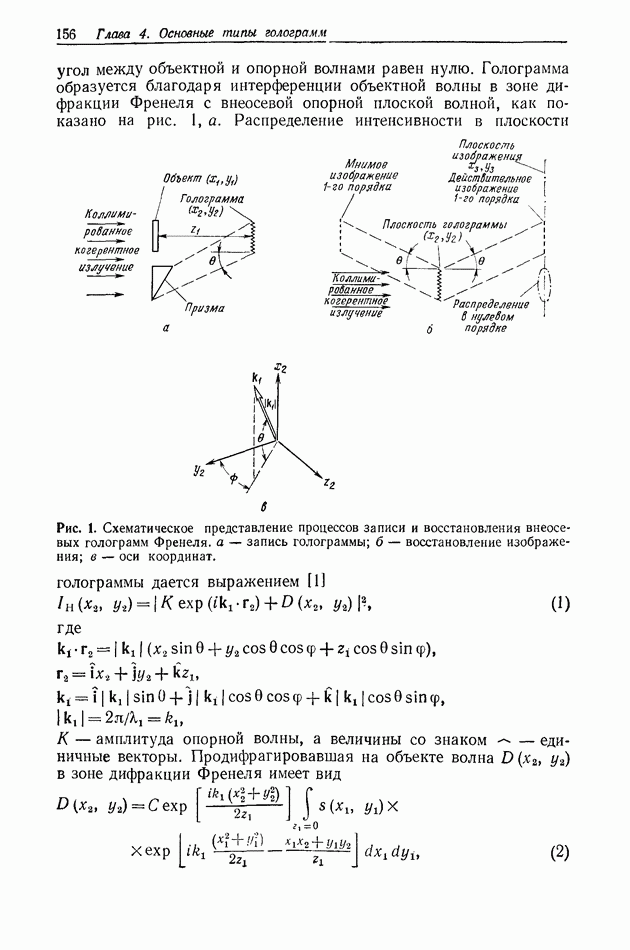
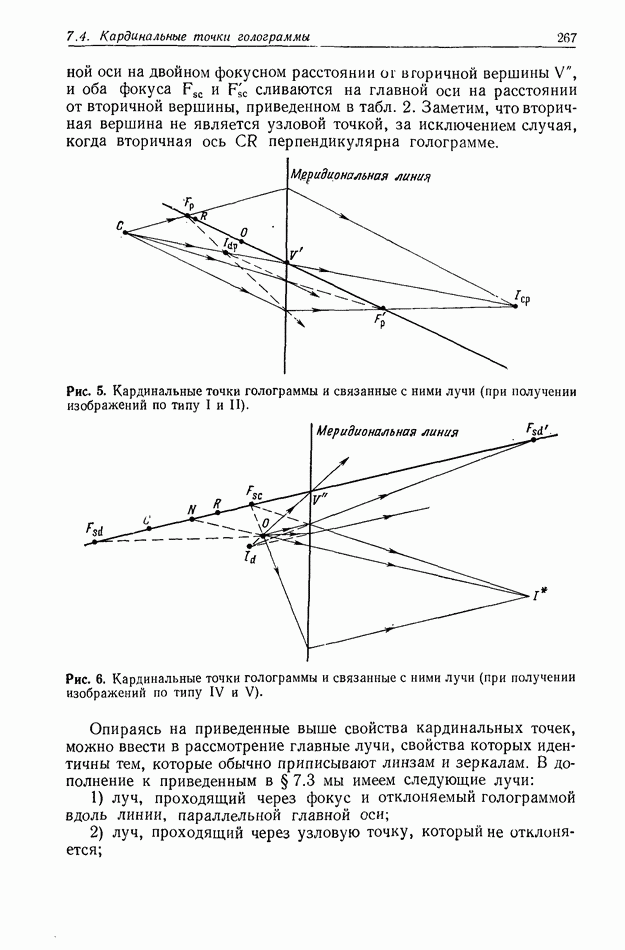
Этот процесс иллюстрируется на рис. 3 для случая проволоки. На рис. 3, а представлена фотография изображения,

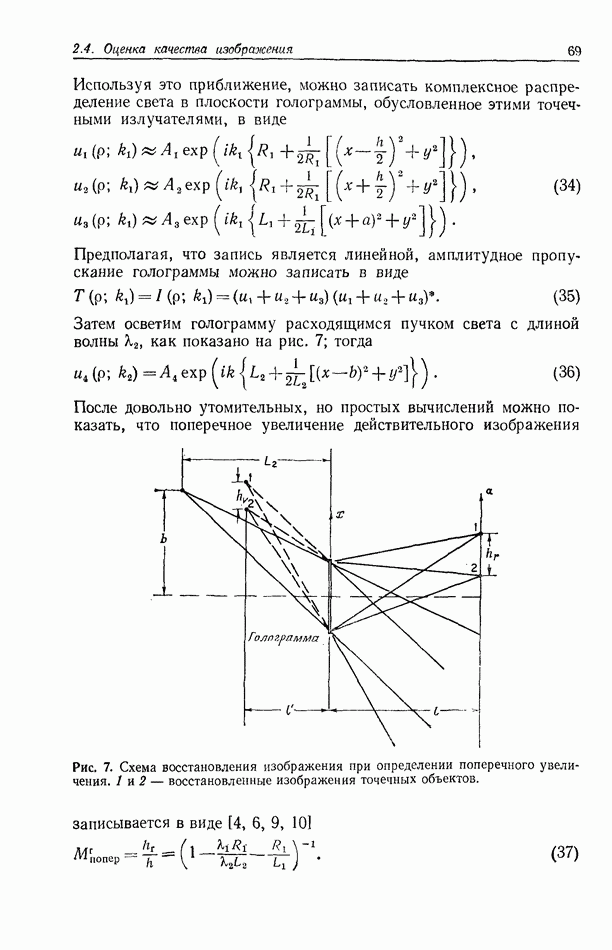
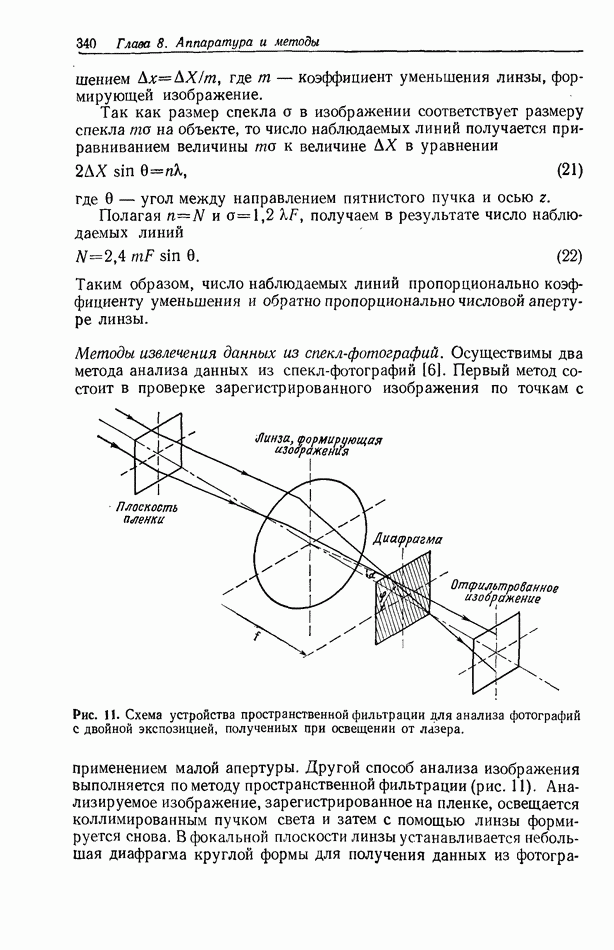
Рис. 3. Действительное изображение, формируемое показанной на рис. 2 голограммой Фраунгофера проволоки, а — позитивный отпечаток записи в плоскости сфокусированного изображения; б - микроденситограмма сечения негатива зарегистрированного изображения; в — теоретическая кривая. Согласно [7].
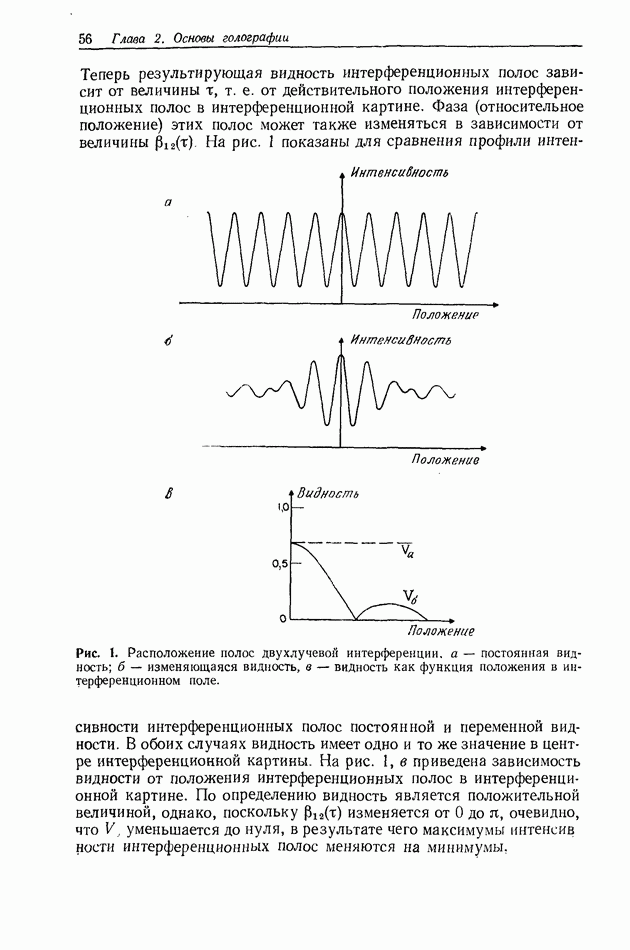
восстановленного с голограммы, приведенной на рис. 2, а. Это изображение имеет весьма хорошее качество и наблюдается вместе с голограммой, образованной мнимым изображением, которая довольно отчетливо видна на окружающем фоне. Для сравнения на рис. 3, б и в показаны соответственно микроденситограммы горизонтального сечения изображения, приведенного на рис. 3, а, и теоретическая кривая, полученная с помощью ЭВМ.
4.2.3. Свойства голограмм Фраунгофера
Голограммы, приведенные в § 1.2 в качестве примеров голограмм Френеля с осевым опорным пучком, на самом деле являются голограммами Фраунгофера, что объясняется характером выбранного объекта. В частности, случай 1 относится к точечному объекту. Разумеется, в этом случае изображение не может не находиться в дальней зоне. Изображение такого точечного объекта, формируемое голограммой, является мерой импульсного отклика всей системы. Поскольку в примере используется фотопленка большого размера, вид функции импульсного отклика будет определяться пределом разрешения среды и/или недостаточно хорошей когерентностью освещающего пучка. В случае 3, рассмотренным в § 1.2, исследуется влияние конечных размеров регистрирующей среды, и, поскольку рассматриваемый объект снова точечный, полученные результаты непосредственно применимы к голограммам Фраунгофера.
Приведенные в табл. 1 § 4.1 результаты для осевой голографической системы Френеля применимы и для осевых голограмм Фраунгофера, рассматриваемых в настоящем параграфе. Важное отличие, однако, состоит в том, что в голограммах Фраунгофера поля обоих сопряженных восстановленных изображений не интерферируют в значительной степени друг с другом, как в случае осевой голограммы Френеля. Благодаря этому голография Фраунгофера нашла большое практическое применение, тогда как осевая голография Френеля по существу не используется.

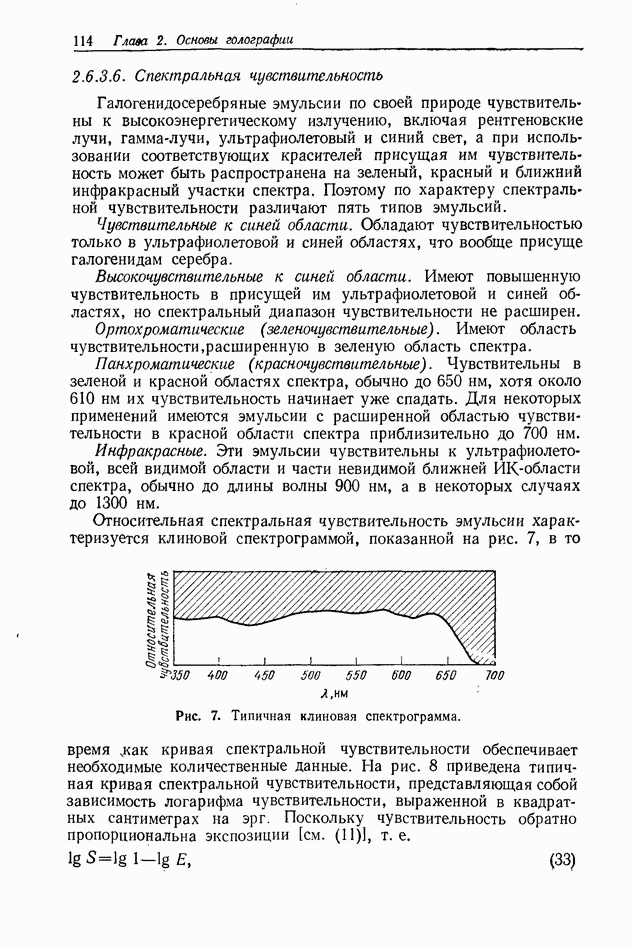
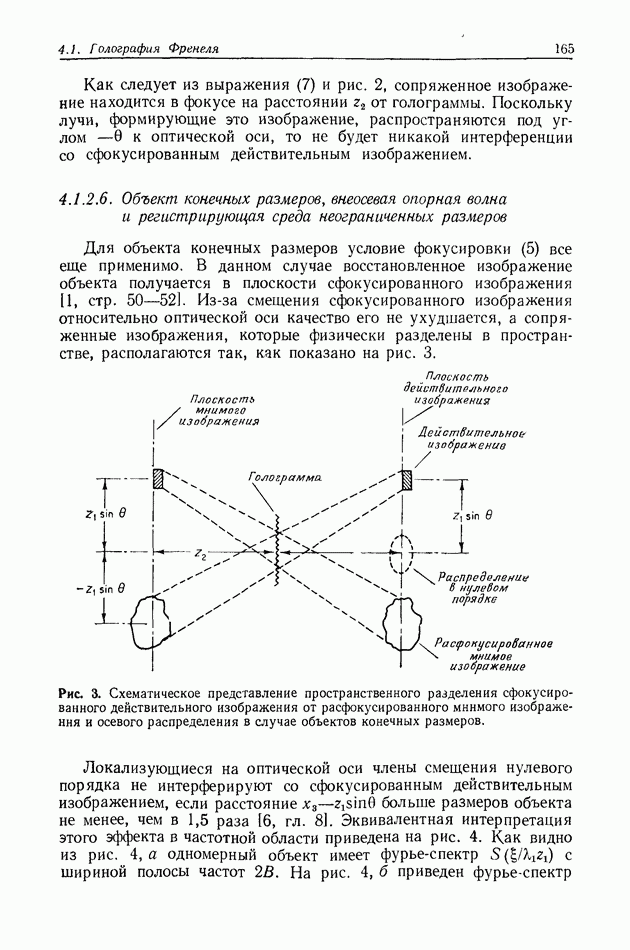
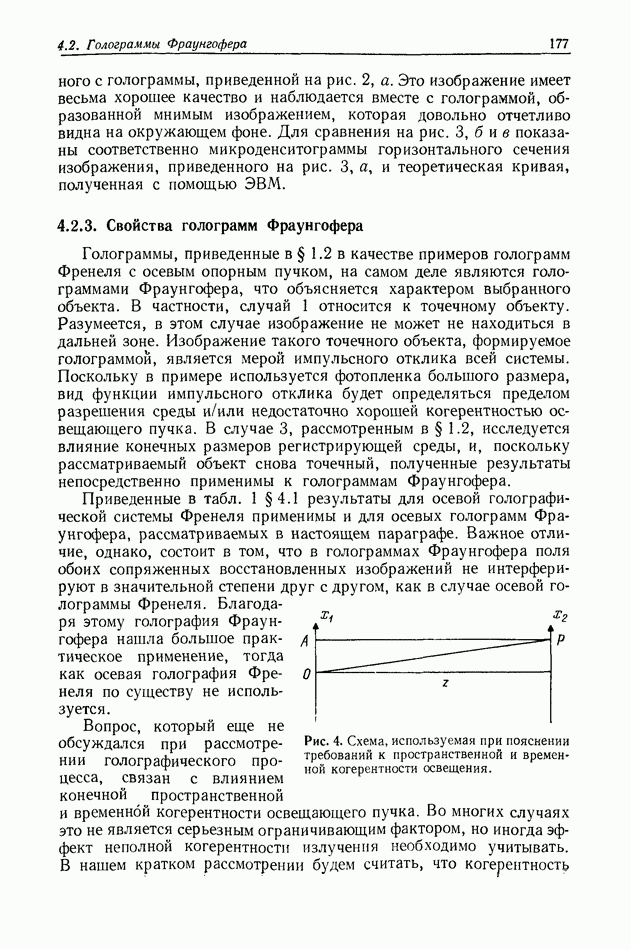
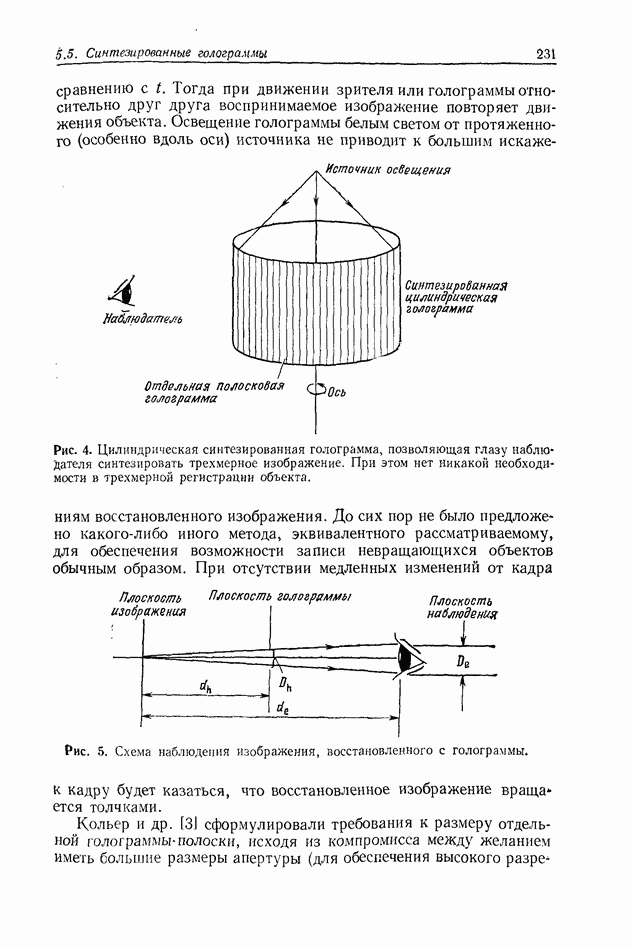
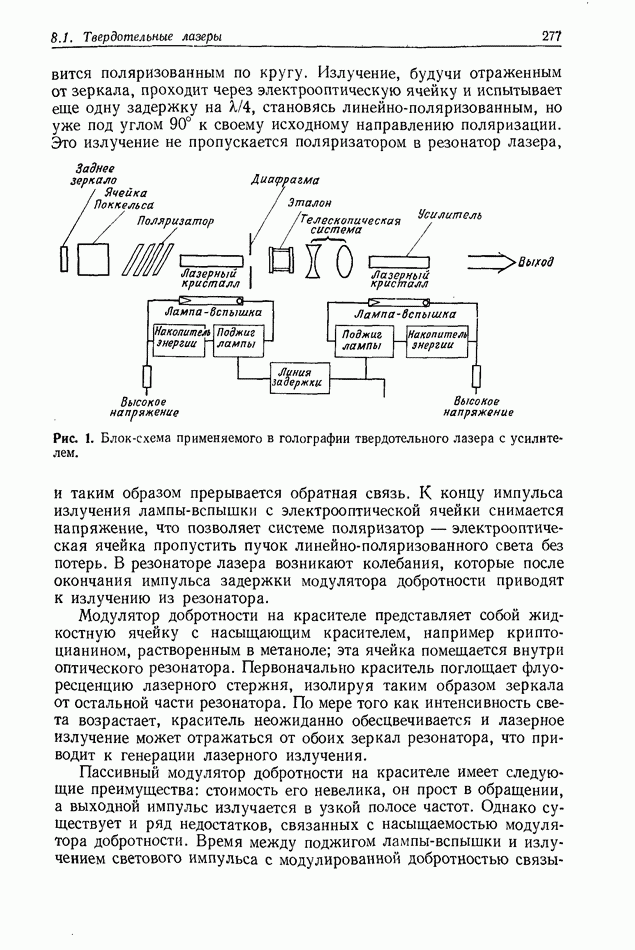
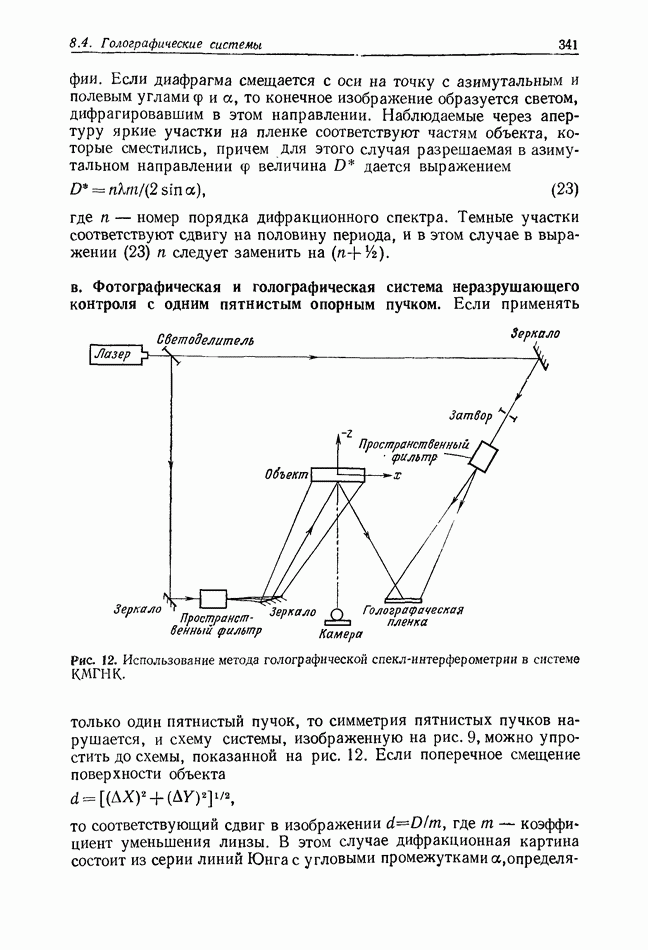
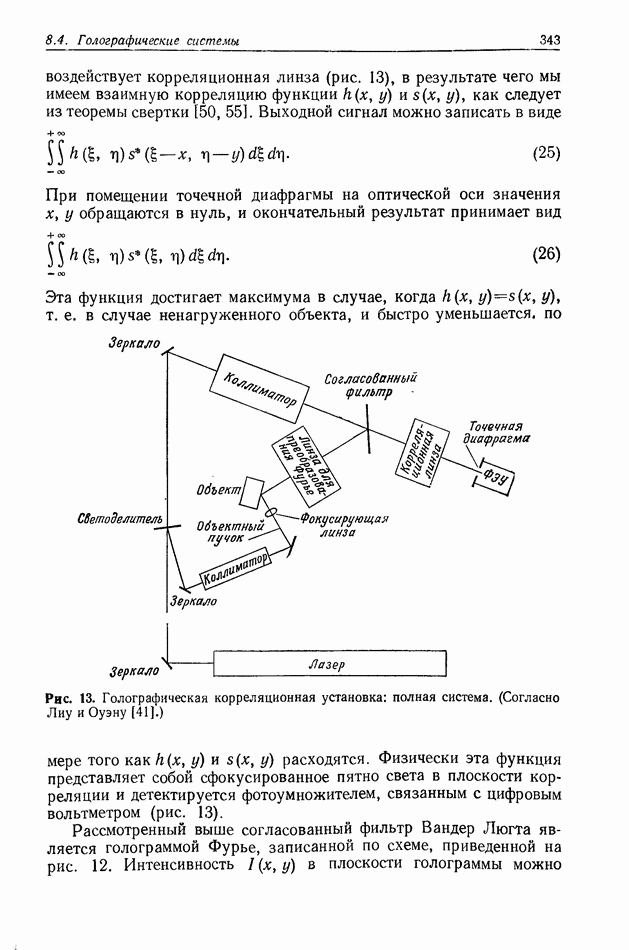
Рис. 4. Схема, используемая при пояснении требований к пространственной и временной когерентности освещения.
Вопрос, который еще не обсуждался при рассмотрении голографического процесса, связан с влиянием конечной пространственной и временной когерентности освещающего пучка. Во многих случаях это не является серьезным ограничивающим фактором, но иногда эффект неполной когерентности излучения необходимо учитывать. В нашем кратком рассмотрении будем считать, что когерентность
накладывает некоторые ограничения на голографический процесс. Предположим, что для обеспечения требуемого разрешения голограмма должна записываться в окрестности точки  (рис. 4). Оптический путь составляющих света, продифрагировавших на объекте, расположенном вокруг точки 0, приблизительно равен
(рис. 4). Оптический путь составляющих света, продифрагировавших на объекте, расположенном вокруг точки 0, приблизительно равен  В точке
В точке  дифрагированный свет интерферирует с недифрагированным, приходящим из точки А, расположенной в плоскости объекта. Следовательно, для получения хорошей интерференционной картины в точке
дифрагированный свет интерферирует с недифрагированным, приходящим из точки А, расположенной в плоскости объекта. Следовательно, для получения хорошей интерференционной картины в точке  свет в точках
свет в точках  и А должен иметь высокую пространственную когерентность. Временная когерентность интерферирующих пучков определяется разностью хода, приобретаемой пучками при достижении точки
и А должен иметь высокую пространственную когерентность. Временная когерентность интерферирующих пучков определяется разностью хода, приобретаемой пучками при достижении точки  (т. е.
(т. е.  ). Эта разность хода должна быть в пределах длины когерентности используемого излучения, Для практических целей голографическую систему следует проектировать таким образом, чтобы пространственная и временная когерентности интерферирующих пучков не представляли собой ограничивающих факторов.
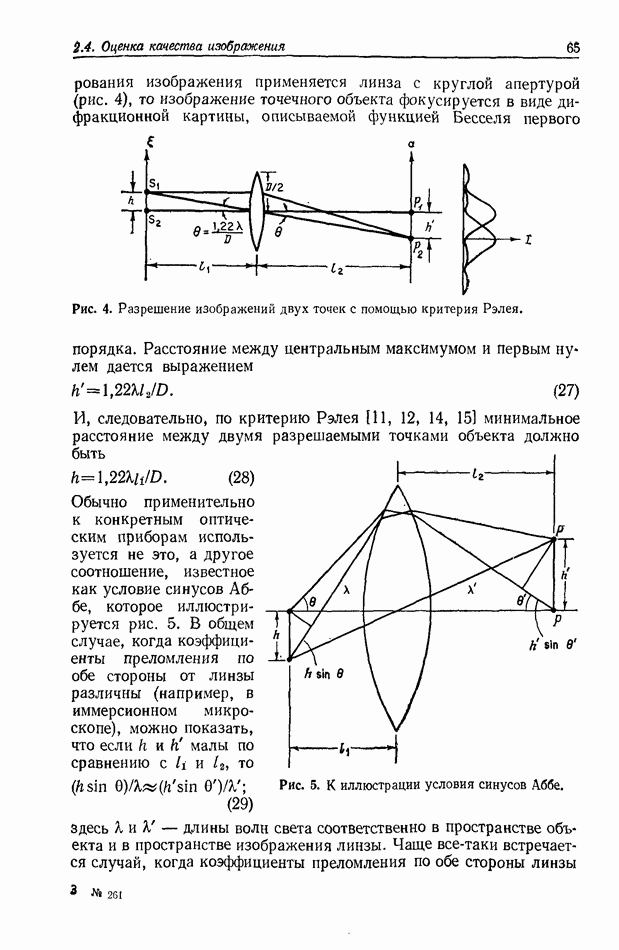
). Эта разность хода должна быть в пределах длины когерентности используемого излучения, Для практических целей голографическую систему следует проектировать таким образом, чтобы пространственная и временная когерентности интерферирующих пучков не представляли собой ограничивающих факторов.
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
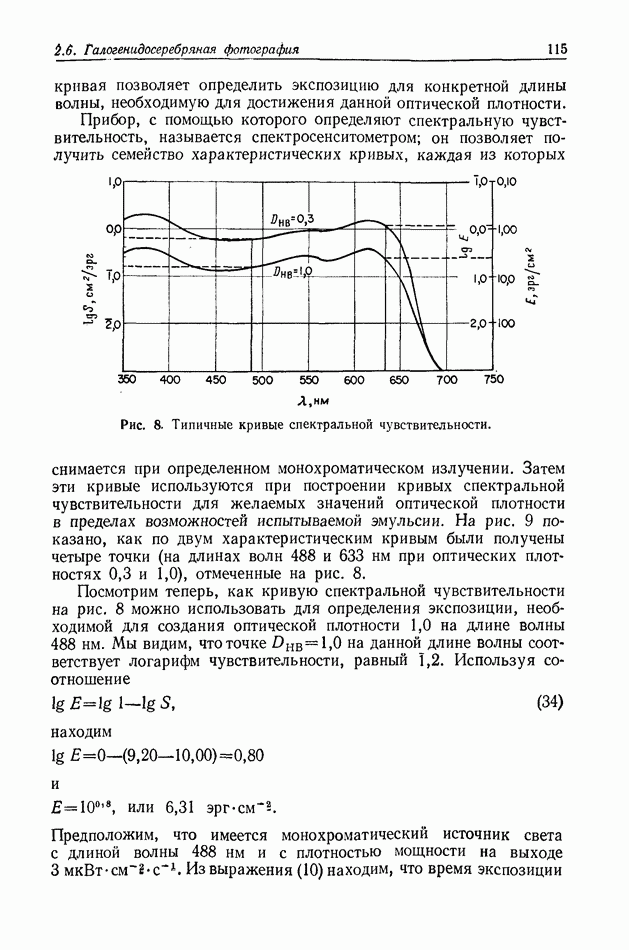
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
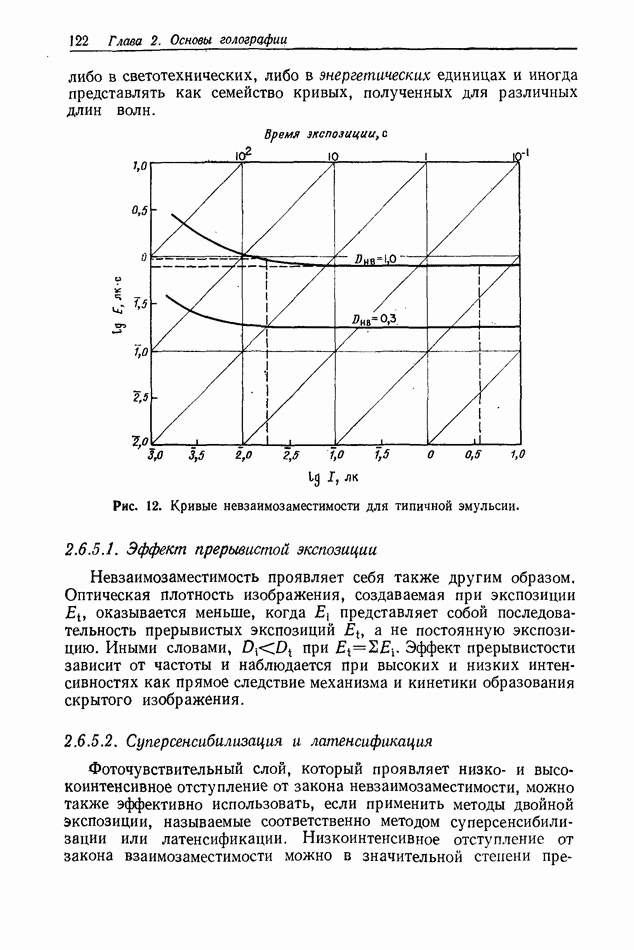
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
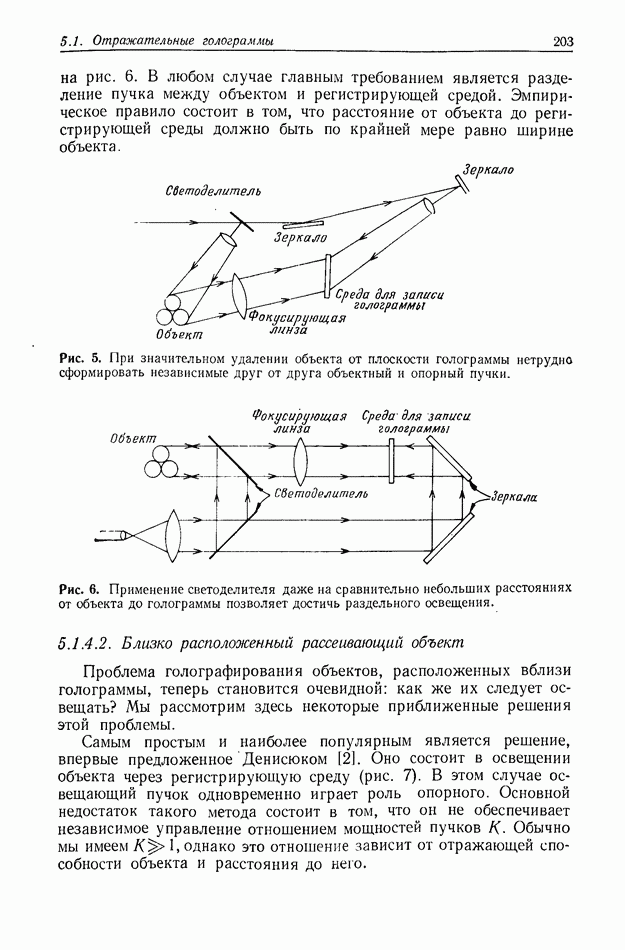
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
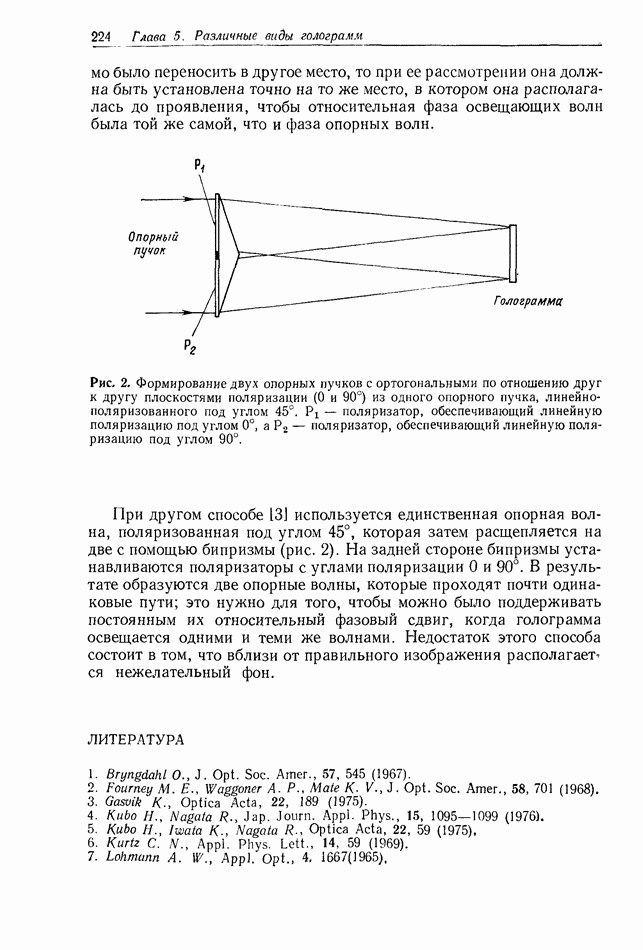
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
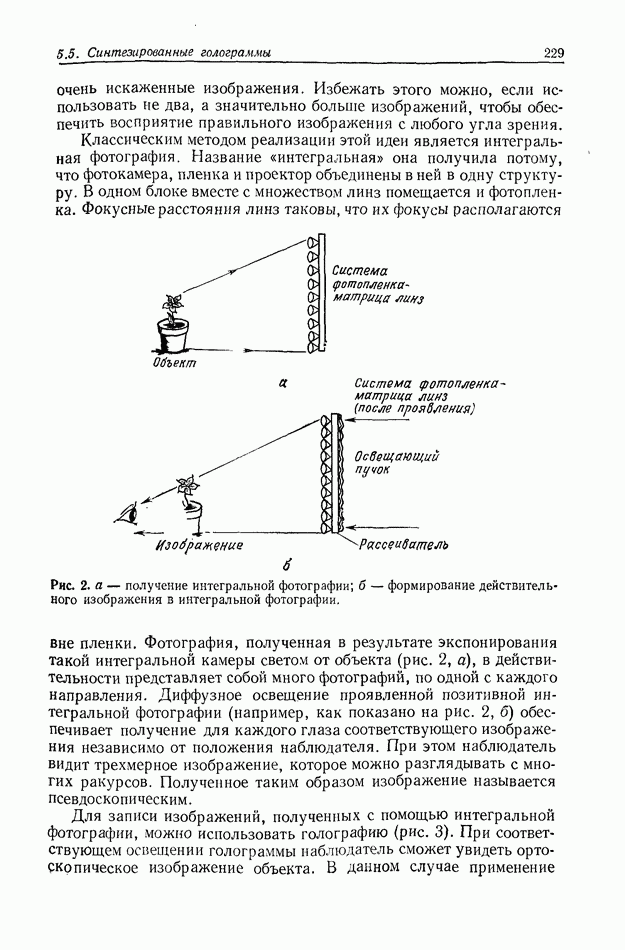
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
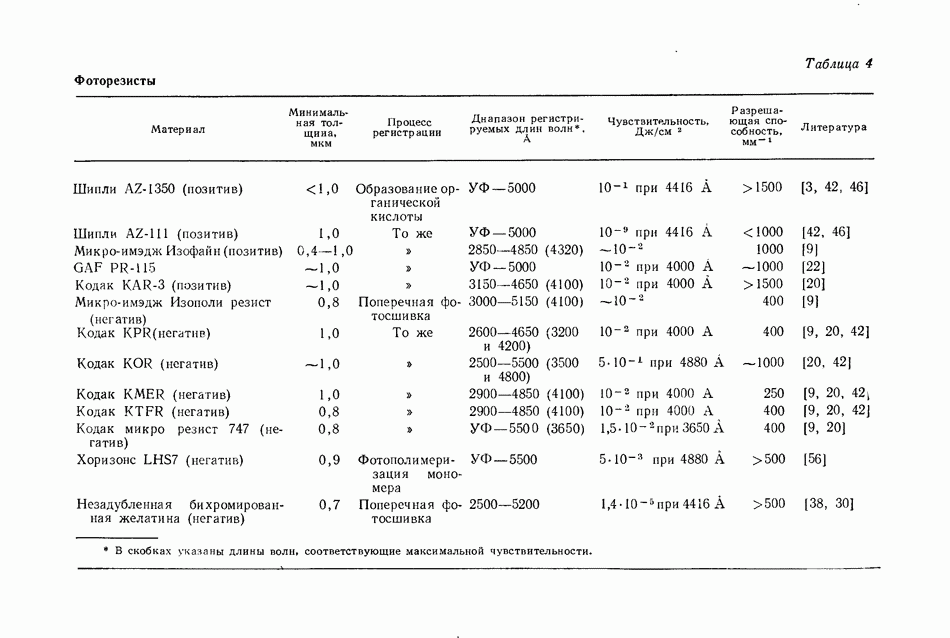
- 8.3.5. Фоторезисты
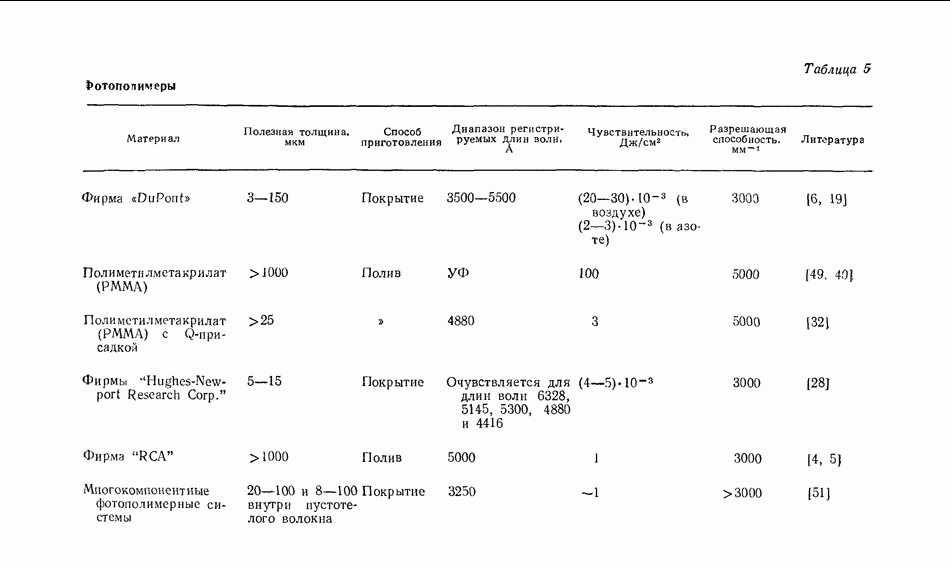
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
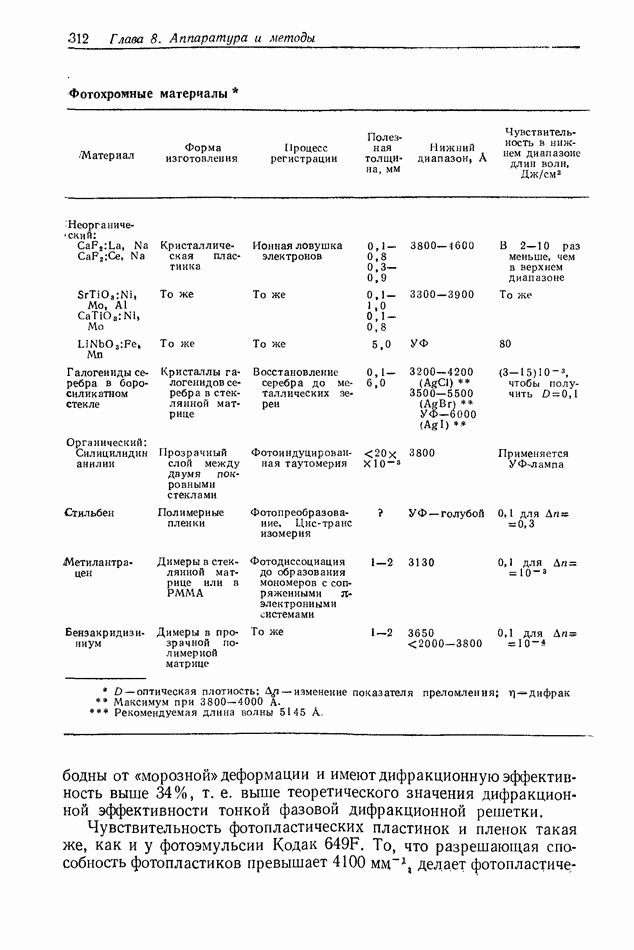
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
- 8.4.5. Голографическая корреляция
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
- 8.4.7. Голография движущихся объектов
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение