| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.1.5. Преобразование Гильберта
Пара уравнений

и

определяет соответственно прямое и обратное преобразования Гильберта 125]. В отличие от других функций и их преобразований, которые определяются в сопряженных областях, здесь  являются функциями от
являются функциями от  Между
Между  существует несимметрично-обратное соотношение (обратное, если исключить знак минус); говорят, что
существует несимметрично-обратное соотношение (обратное, если исключить знак минус); говорят, что
 сопряжена с
сопряжена с  сопряжена
сопряжена  Функцию
Функцию  иногда называют функцией квадратуры, соответствующей
иногда называют функцией квадратуры, соответствующей 
Очевидно, что прямое и обратное преобразования Гильберта представляют собой операции свертки соответственно с  Это приводит к особенно простому соотношению между
Это приводит к особенно простому соотношению между  в пространстве координат преобразования Фурье. Если фурье-образами этих функций являются
в пространстве координат преобразования Фурье. Если фурье-образами этих функций являются  и
и  то
то  связана с
связана с  соотношением
соотношением

где функция  принимает значения 1 при
принимает значения 1 при  и —1 при
и —1 при 
Преобразование Гильберта представляет собой полезную аналитическую операцию, которая связывает любую вещественную функцию  с комплексной функцией
с комплексной функцией  Можно показать, что спектр этой последней функции является односторонним фурье-спектром (нулем при
Можно показать, что спектр этой последней функции является односторонним фурье-спектром (нулем при  а во всем остальном тождествен спектру функции
а во всем остальном тождествен спектру функции  во многом также связаны между собой функции
во многом также связаны между собой функции  Таким образом, с помощью преобразования Гильберта принцип фазорного анализа обобщается и на немонохроматические сигналы.
Таким образом, с помощью преобразования Гильберта принцип фазорного анализа обобщается и на немонохроматические сигналы.
Это преобразование играет также важную роль при описании спектров временных сетей и фильтров, которые должны иметь однозначные импульсные характеристики. Поскольку на импульсные характеристики оптических систем не накладывается ограничений, в оптических исследованиях такой метод, к сожалению, не нашел себе применения. Тем не менее, используя преобразование Гильберта, можно изучать некоторые оптические методы, например шлирен-метод воспроизведения фазовых объектов путем введения теневого ножа для вырезания части оптического спектра [13].
2.1.5.1. Соотношения в случае преобразования Гильберта
Если преобразование Гильберта связывает функции  то оно связывает также следующие пары:
то оно связывает также следующие пары: 

Преобразованием Гильберта свертки  являются также
являются также  Кроме того, справедливы следующие соотношения:
Кроме того, справедливы следующие соотношения:

2.1.5.2. Некоторые пары преобразования Гильберта

Другие пары преобразования Гильберта можно найти в работе Брэйсуэлла [5], в которой также подробно рассматривается само преобразование. В работе Титчмарша [25, гл. 5] имеется больше математических подробностей.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
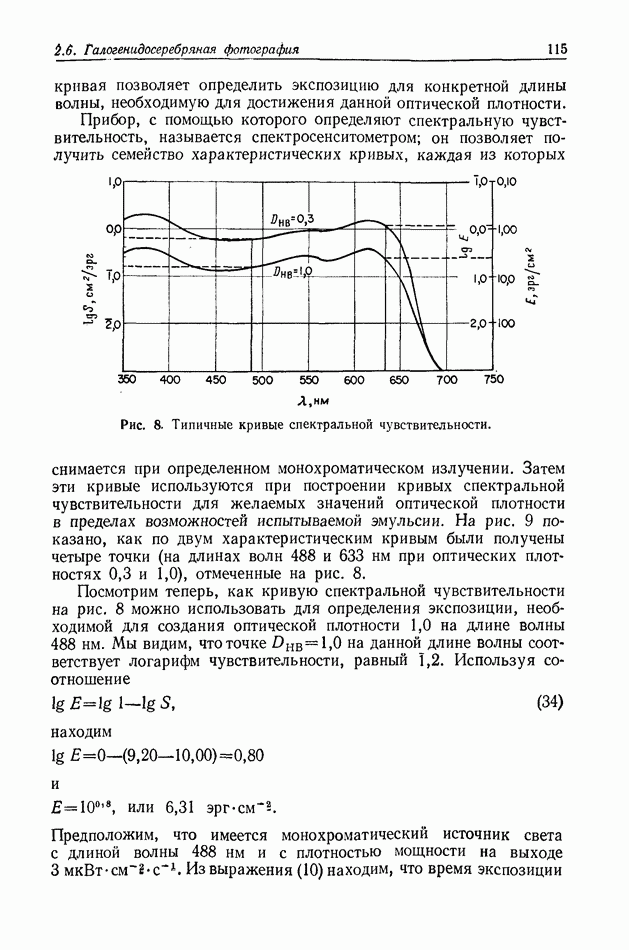
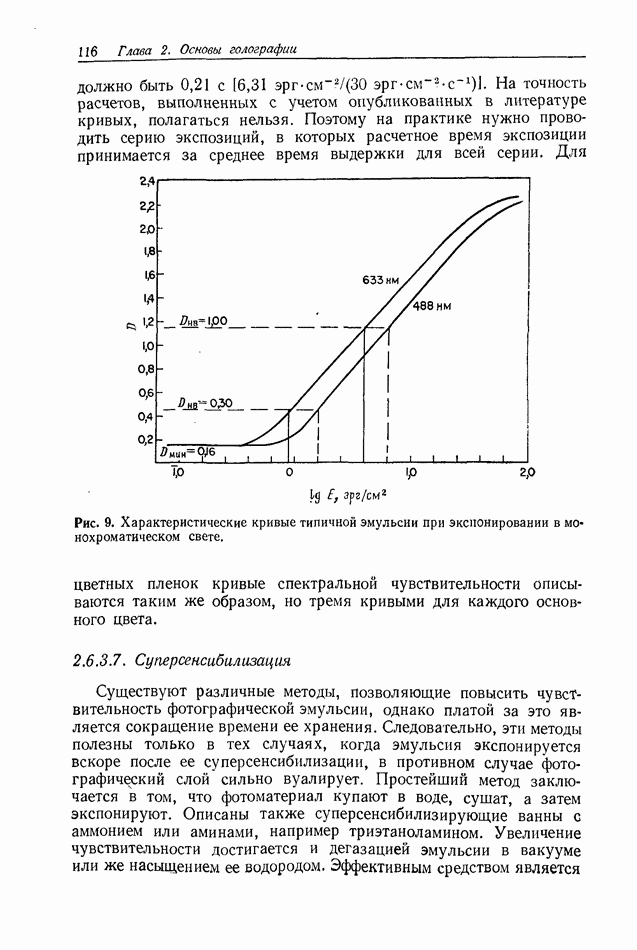
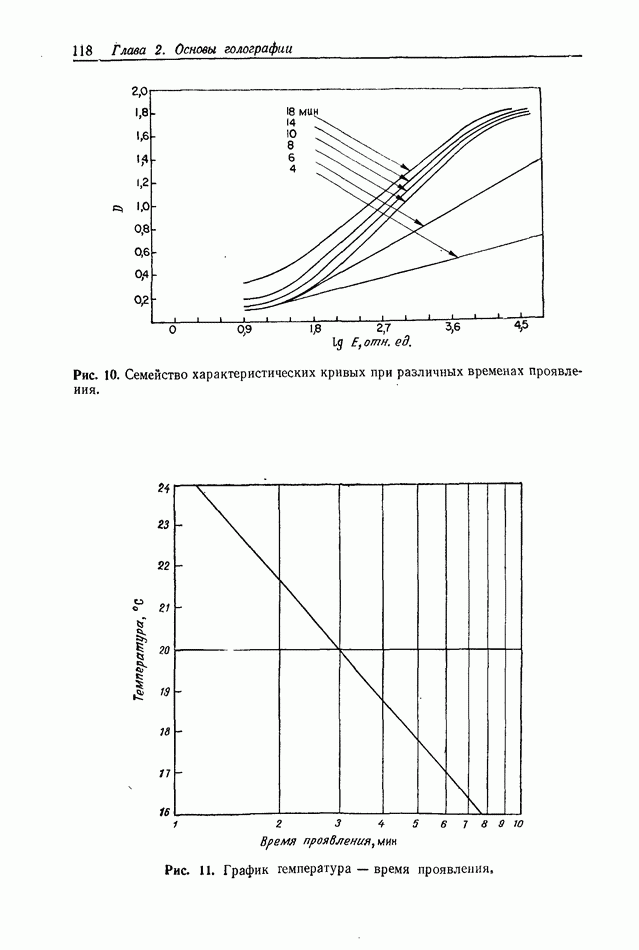
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
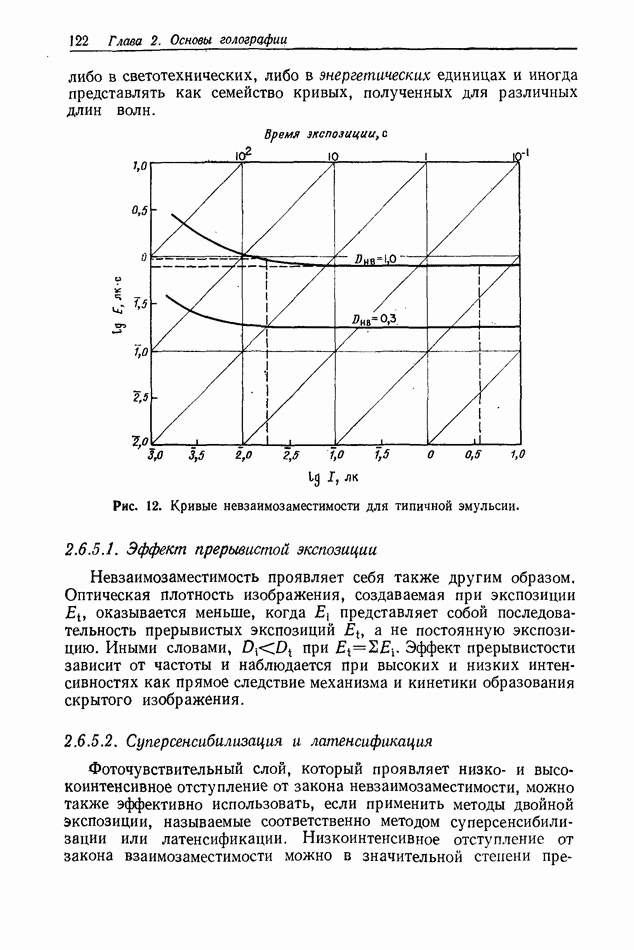
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
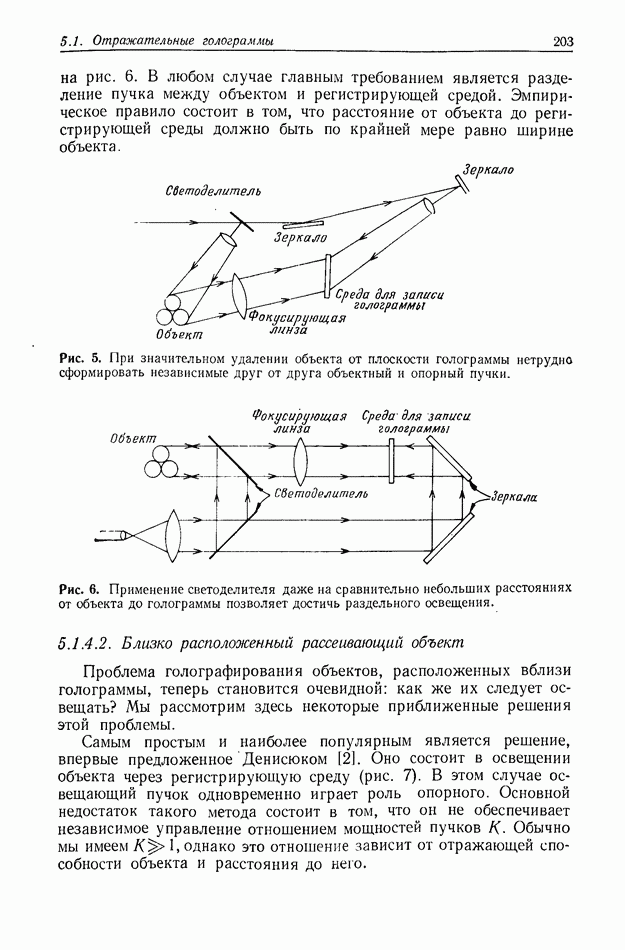
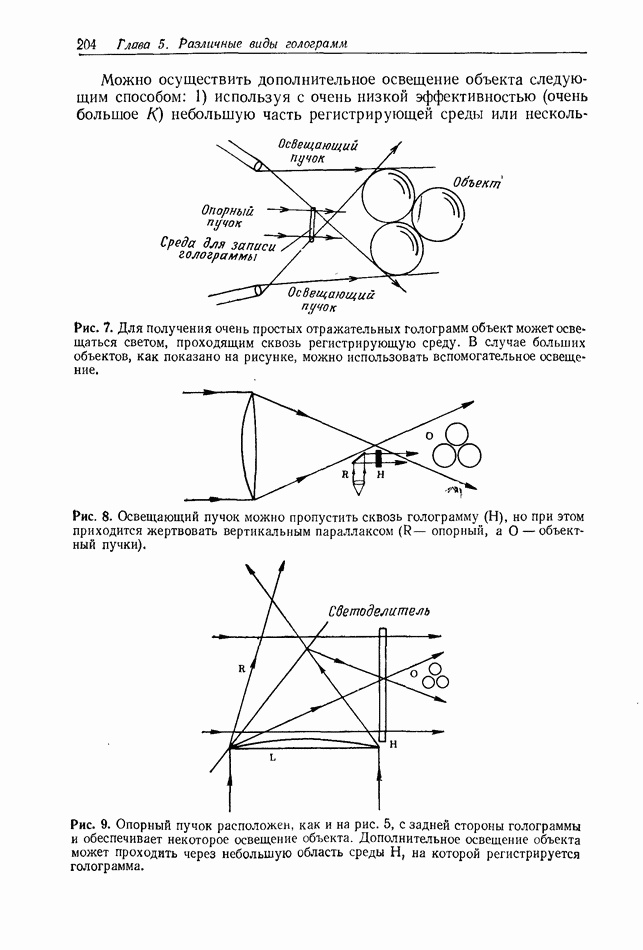
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
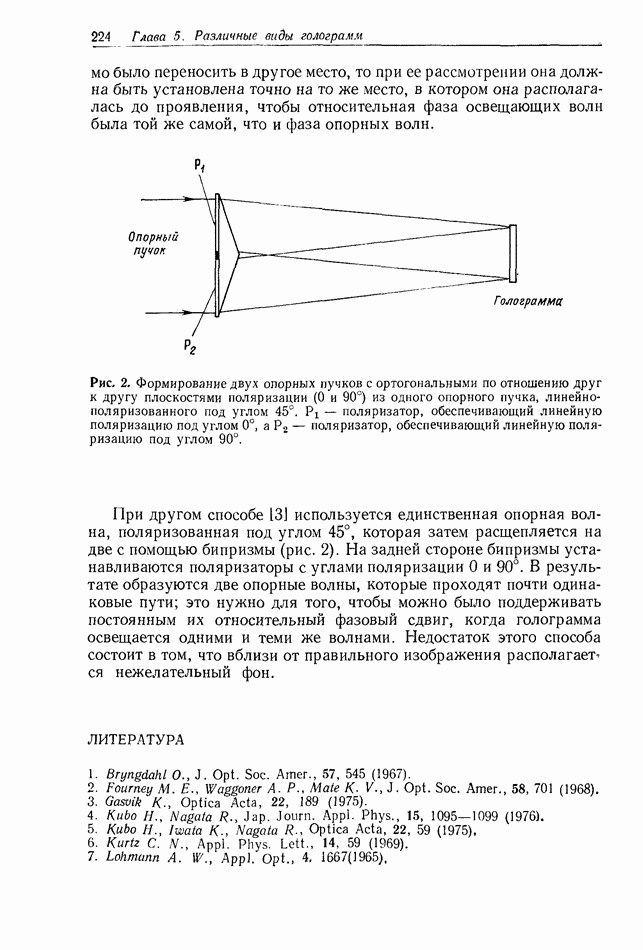
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
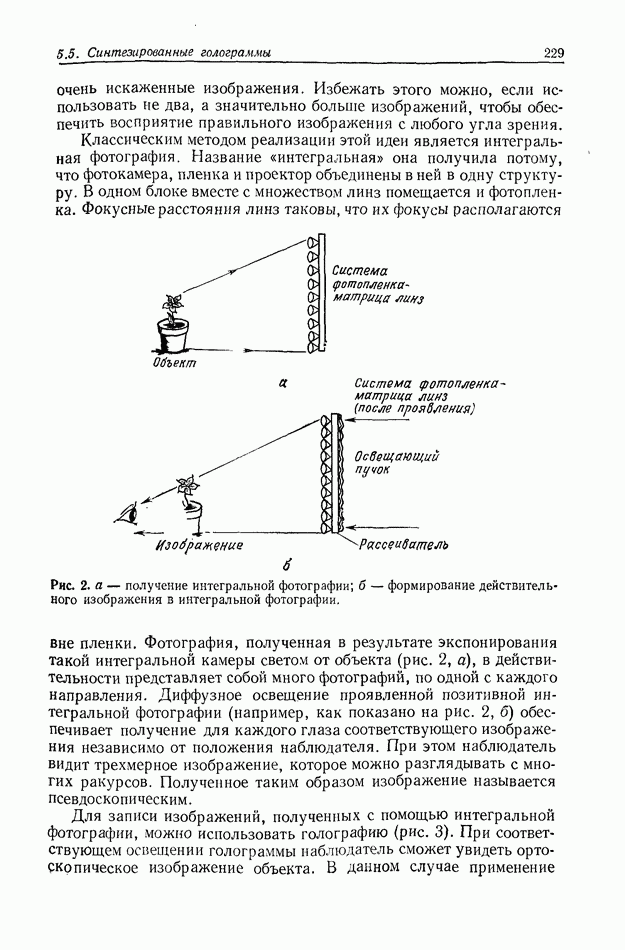
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
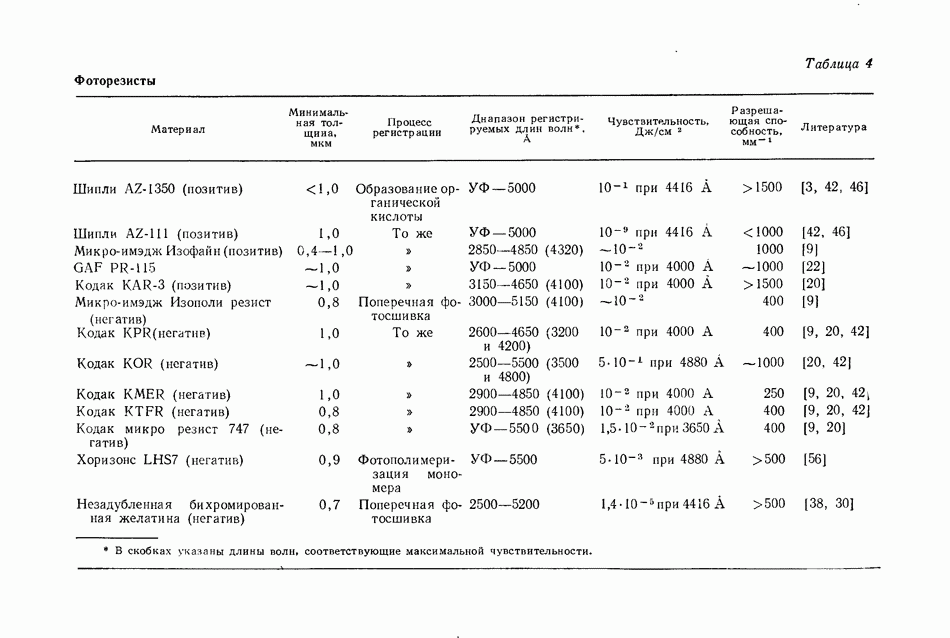
- 8.3.5. Фоторезисты
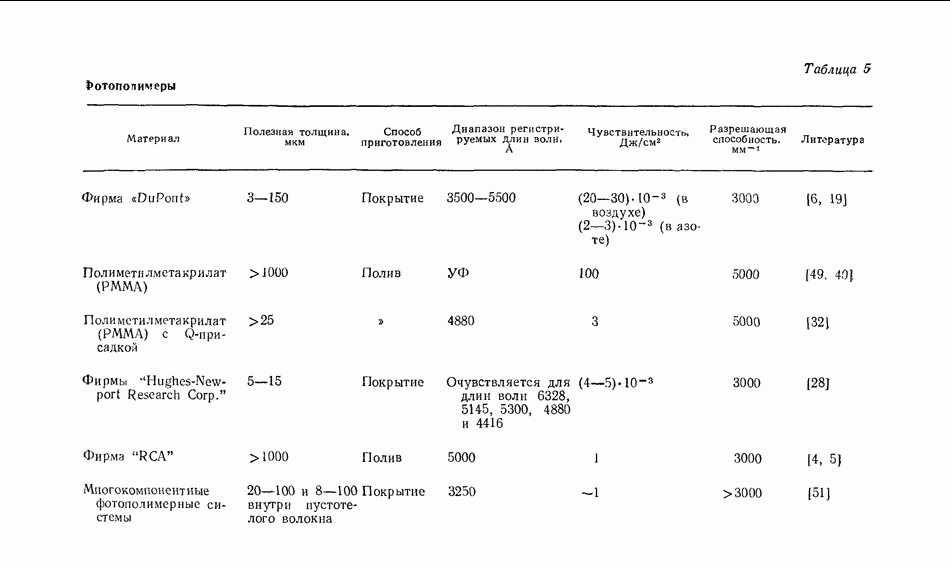
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
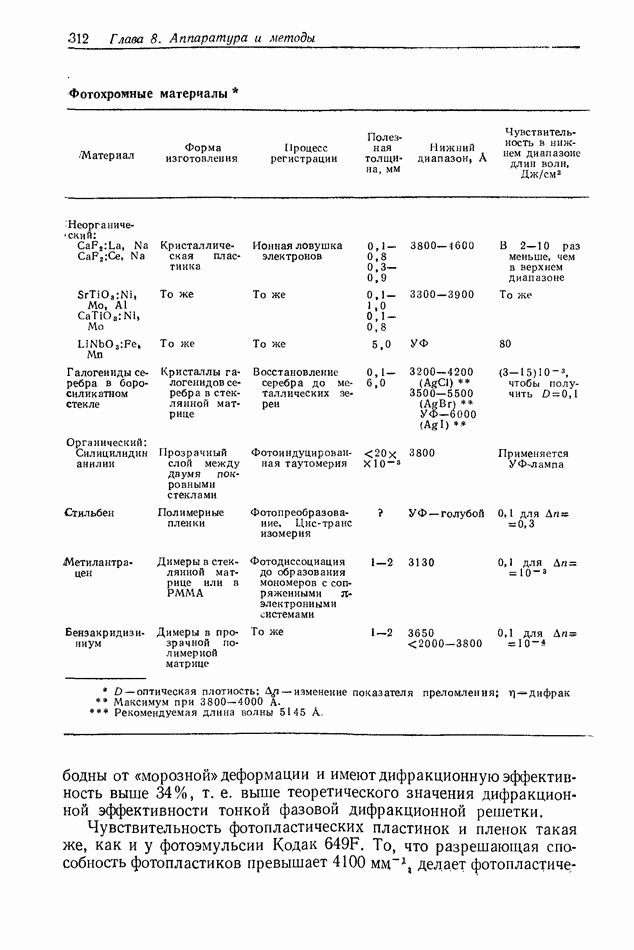
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
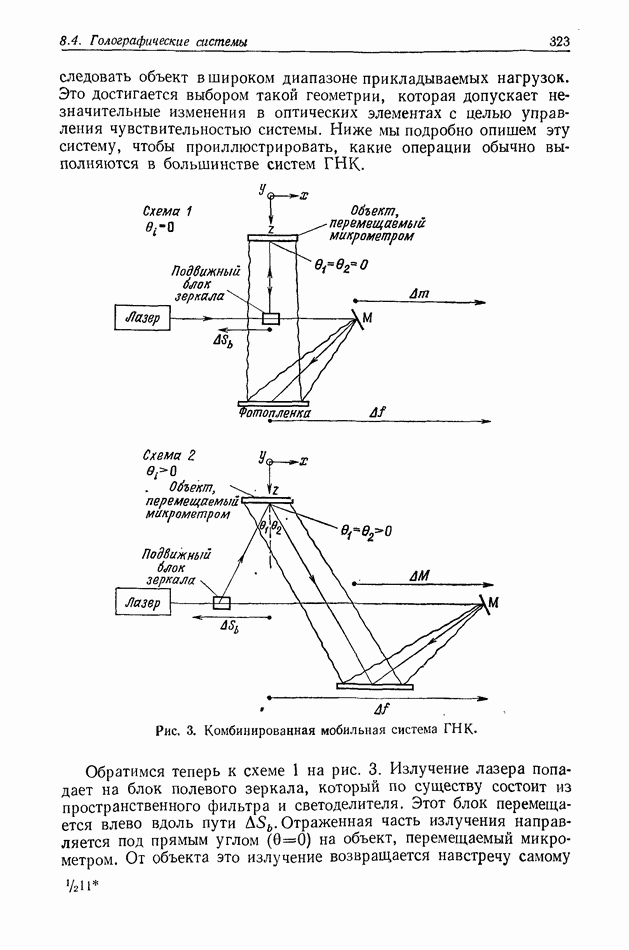
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
- 8.4.5. Голографическая корреляция
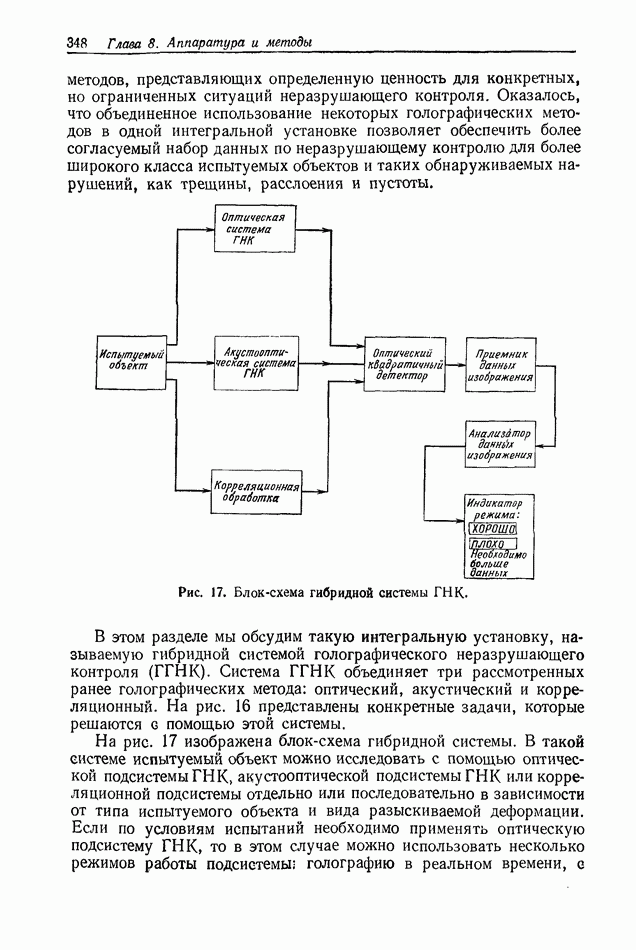
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
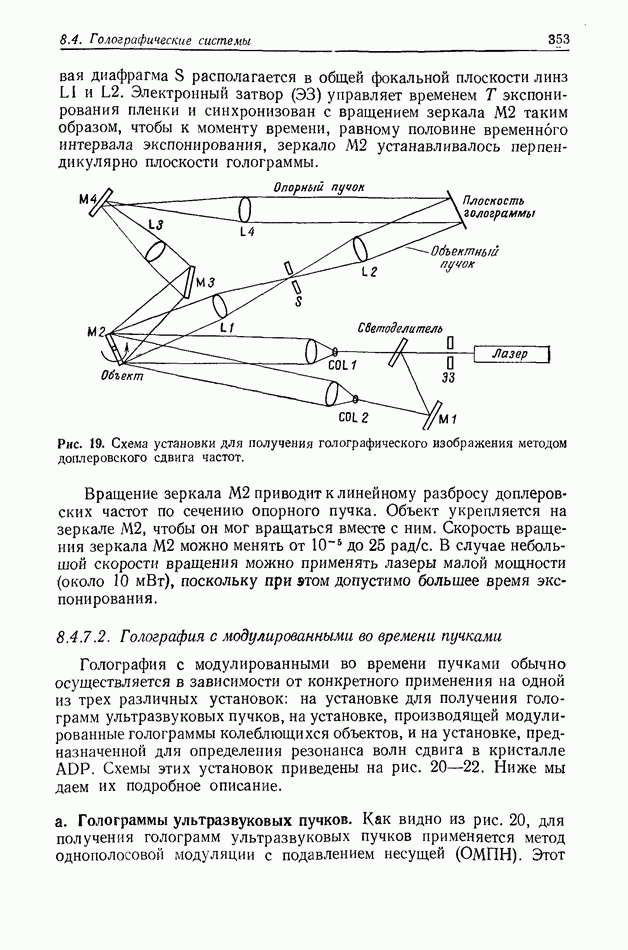
- 8.4.7. Голография движущихся объектов
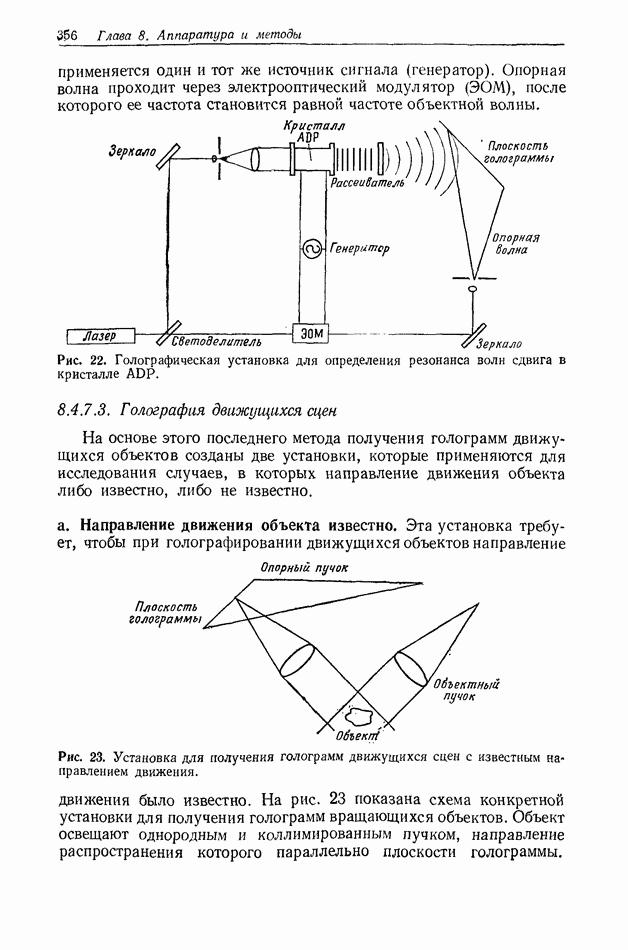
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение