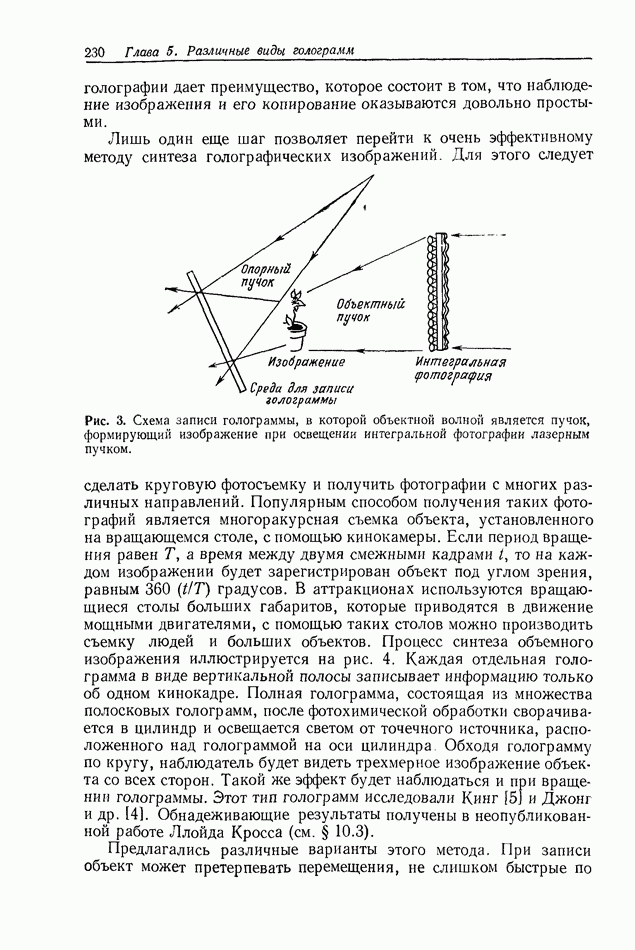
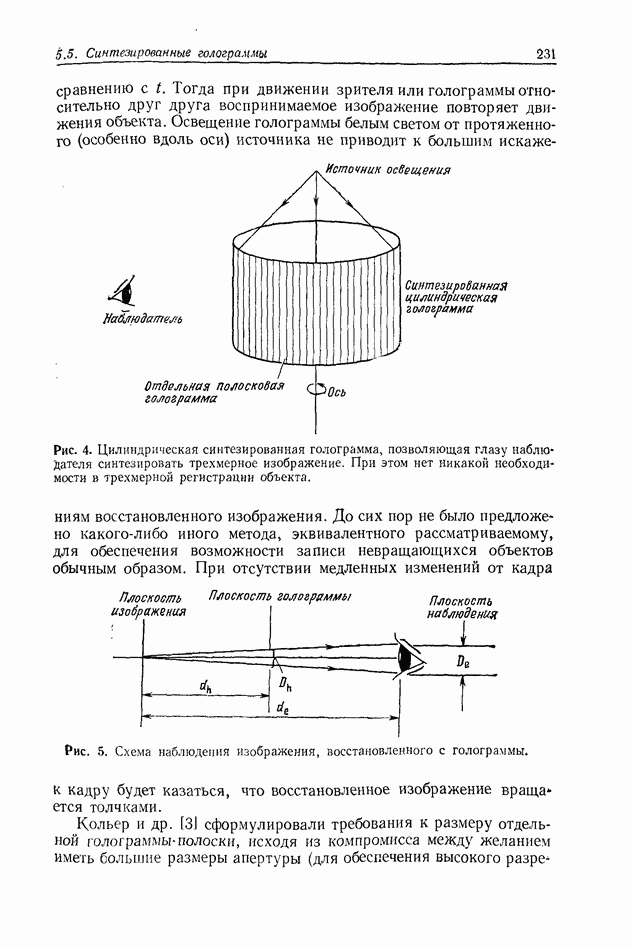
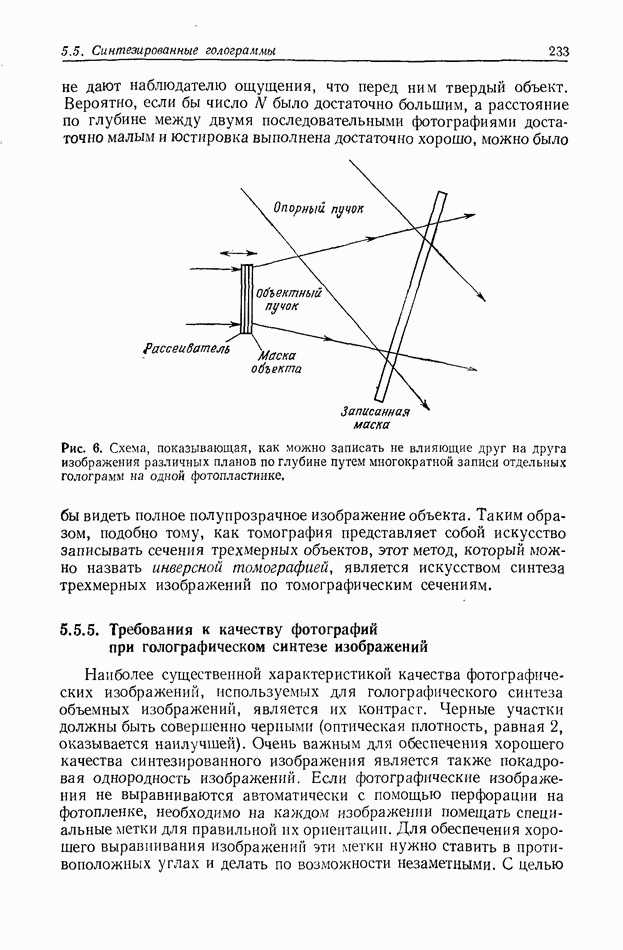
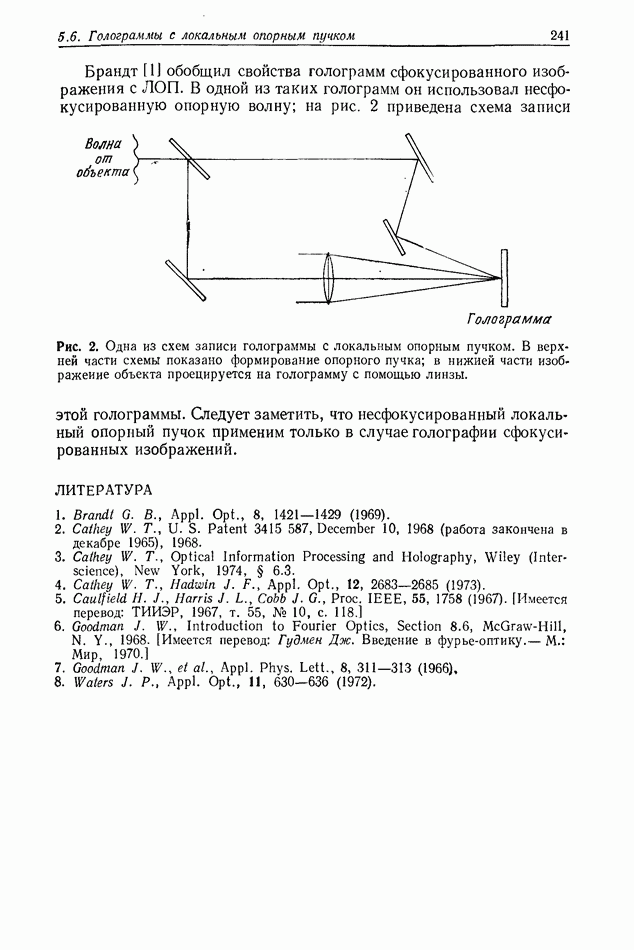
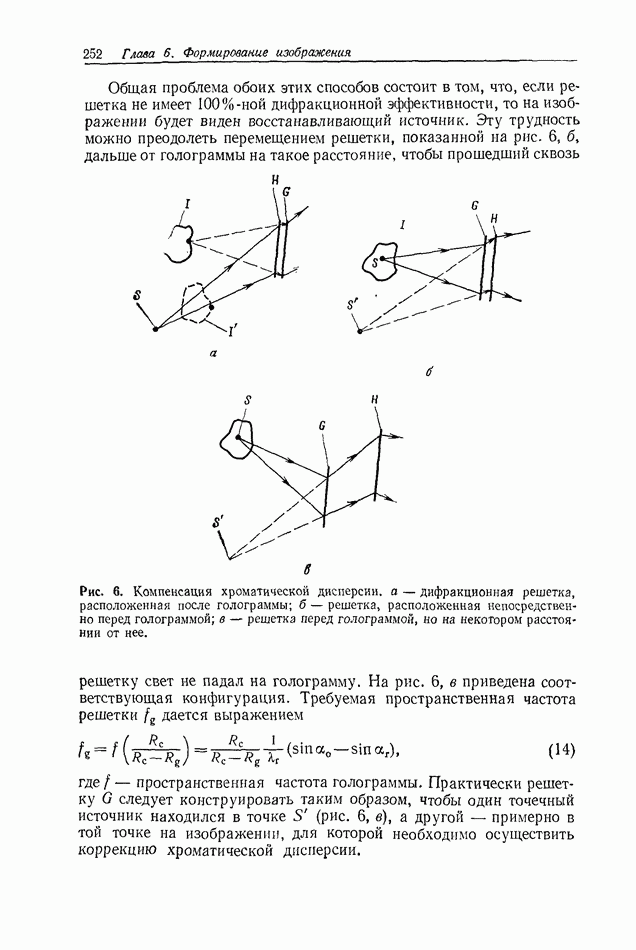
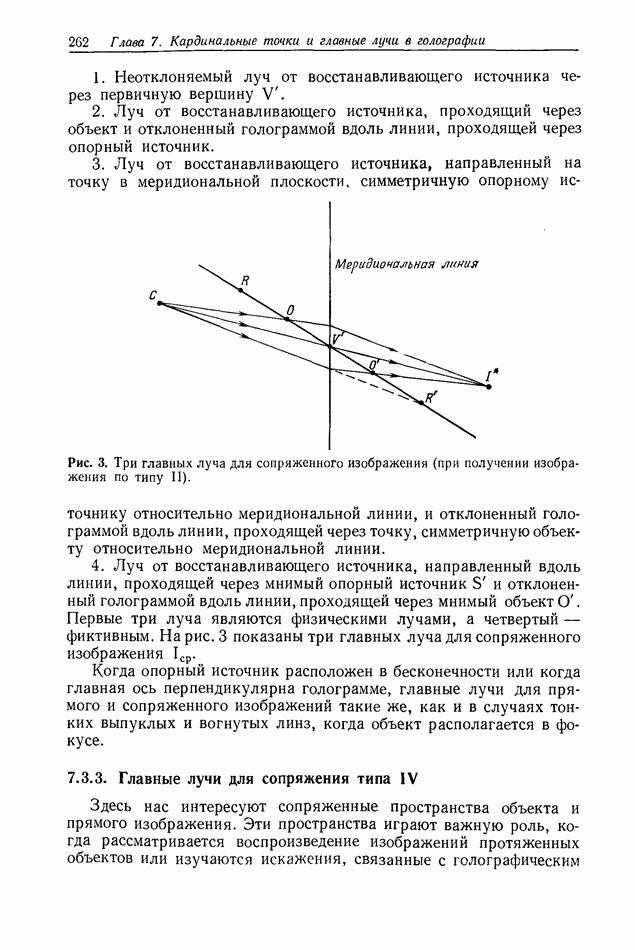
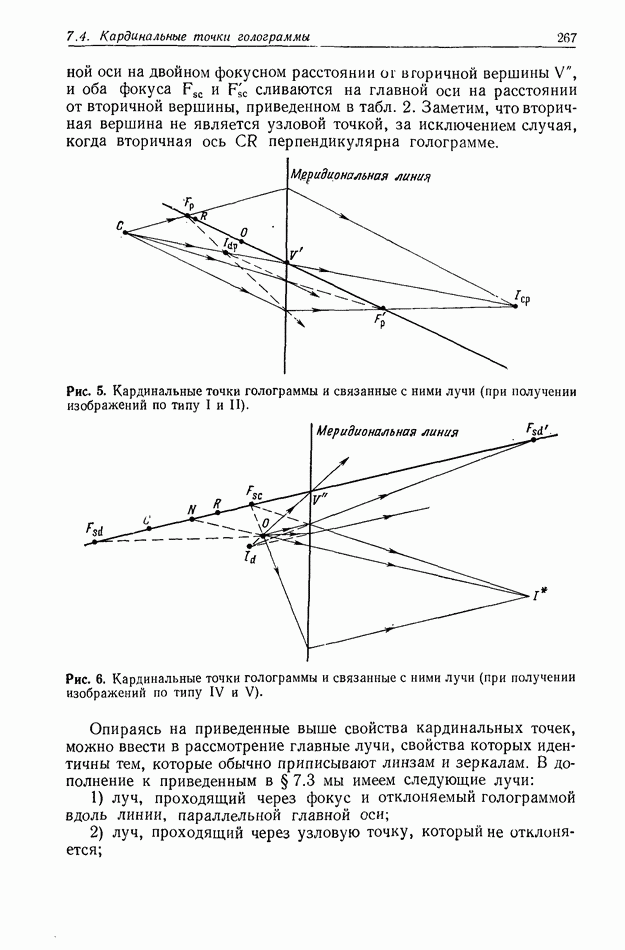
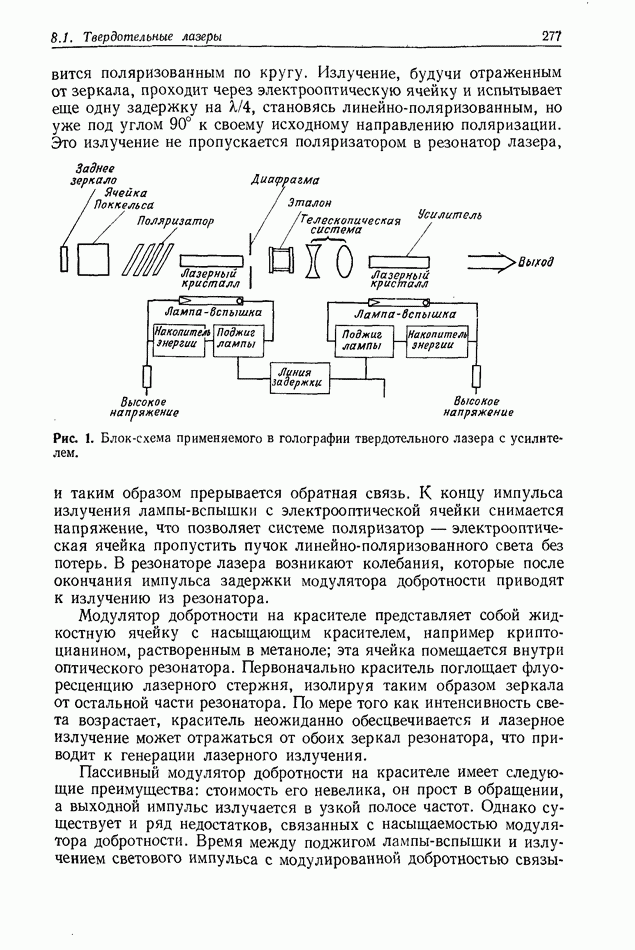
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
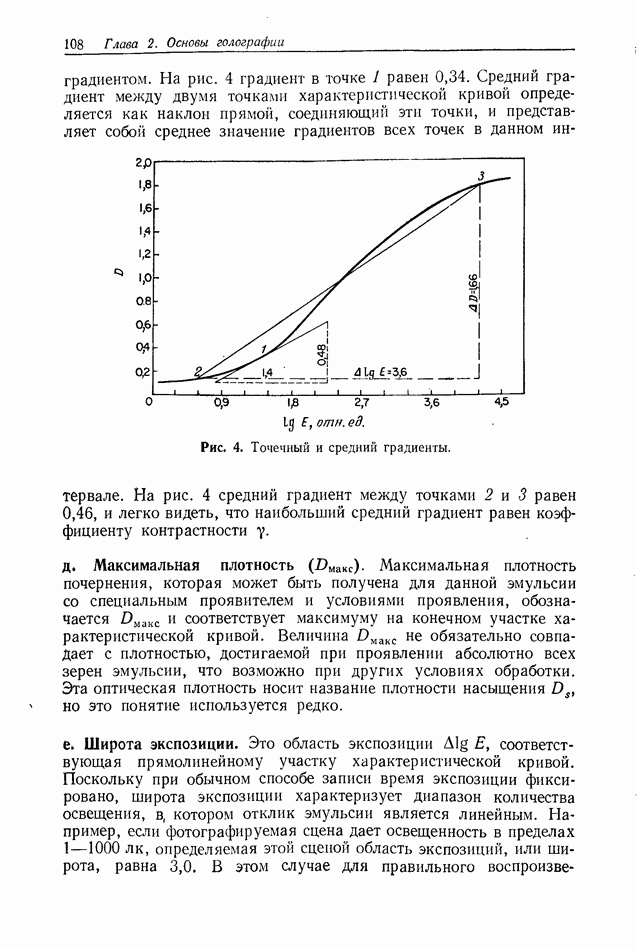
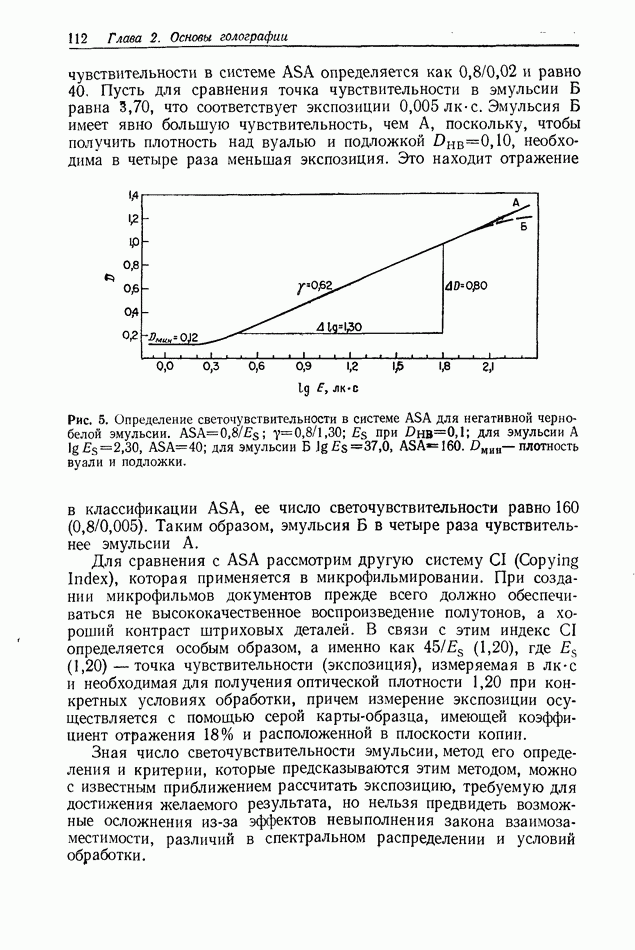
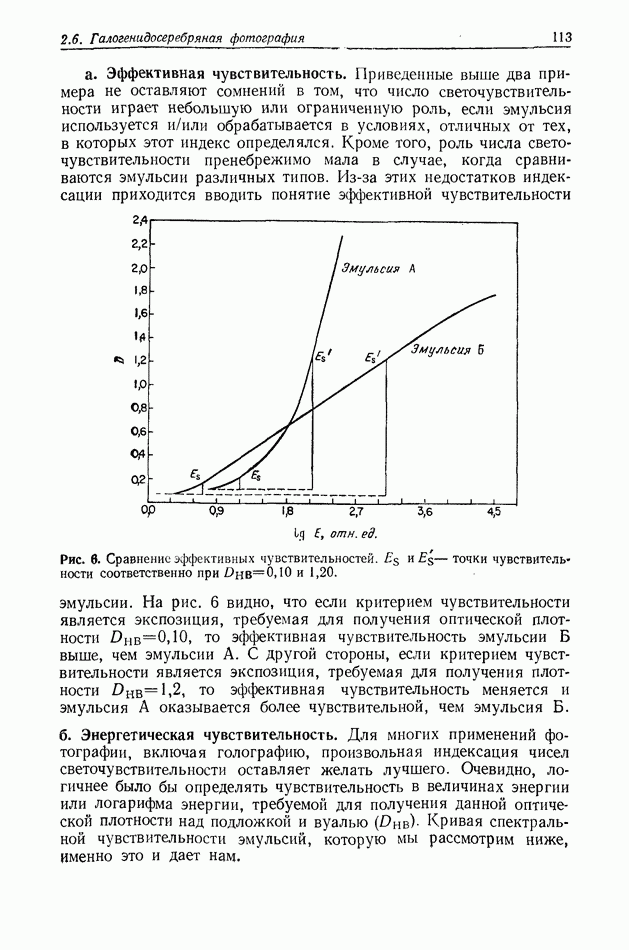
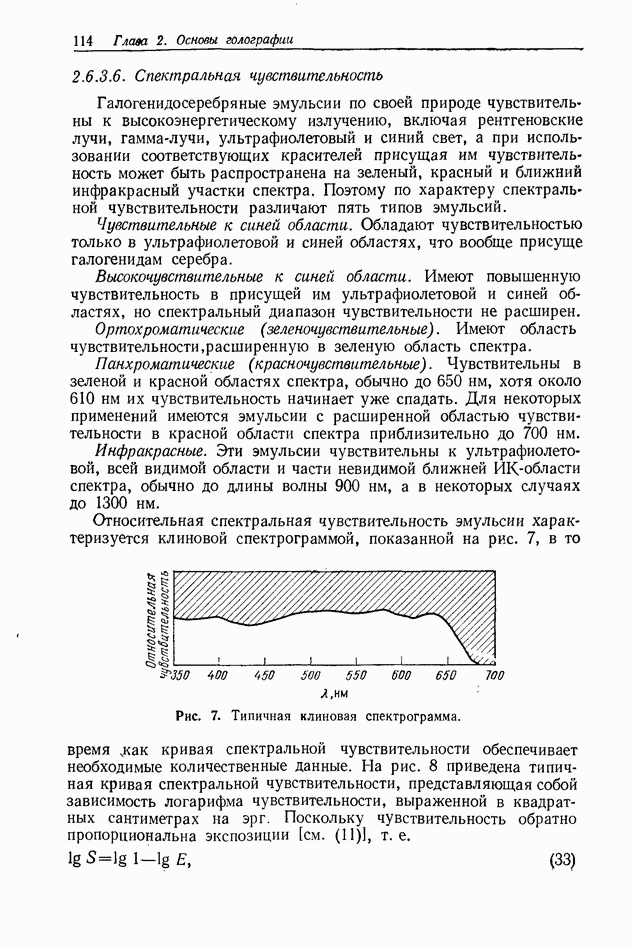
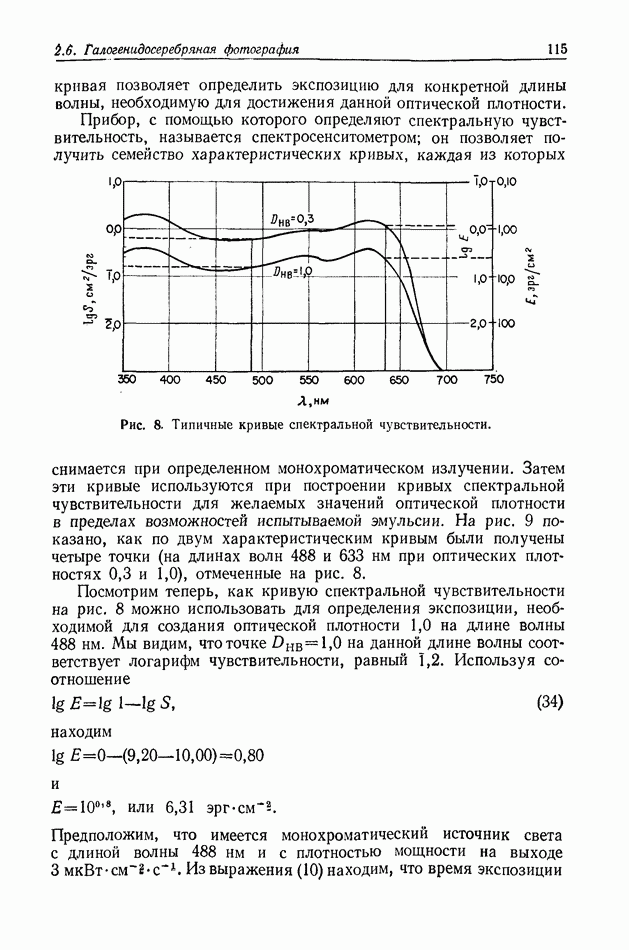
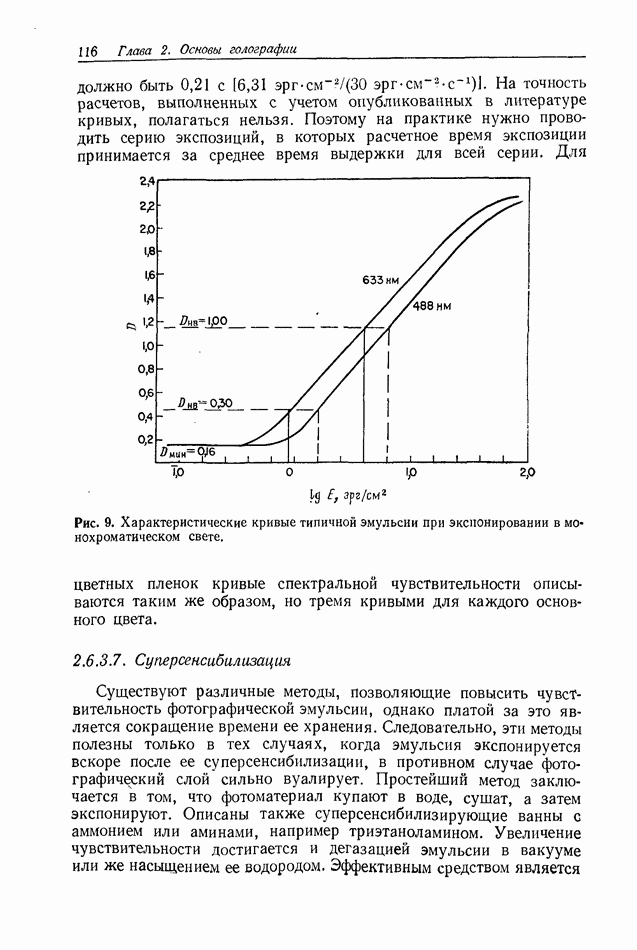
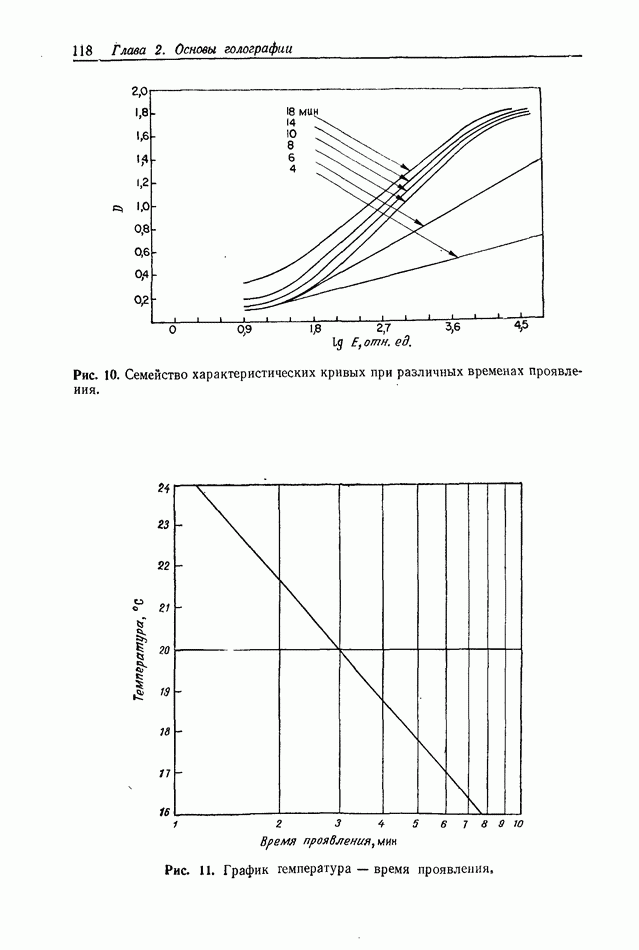
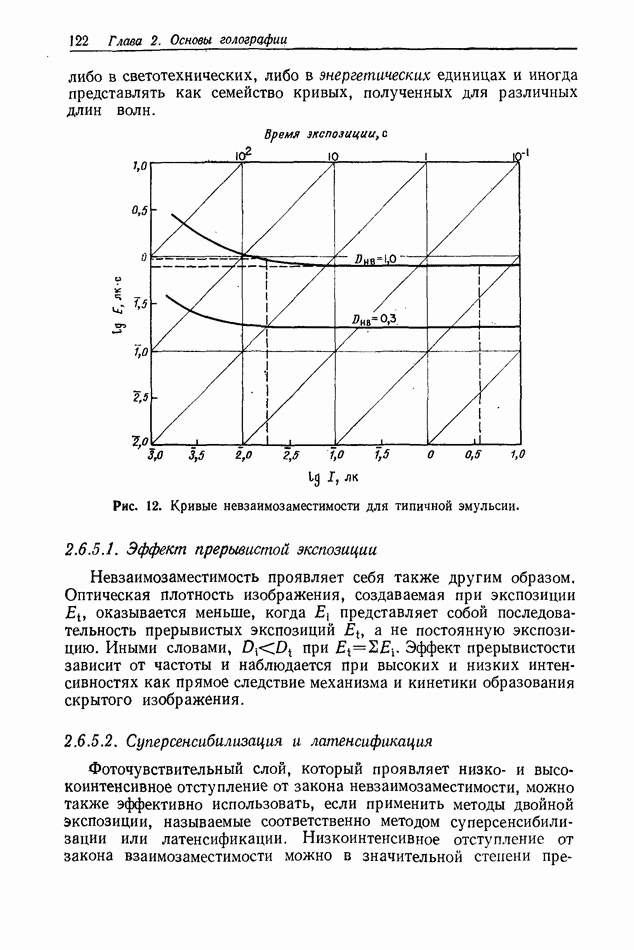
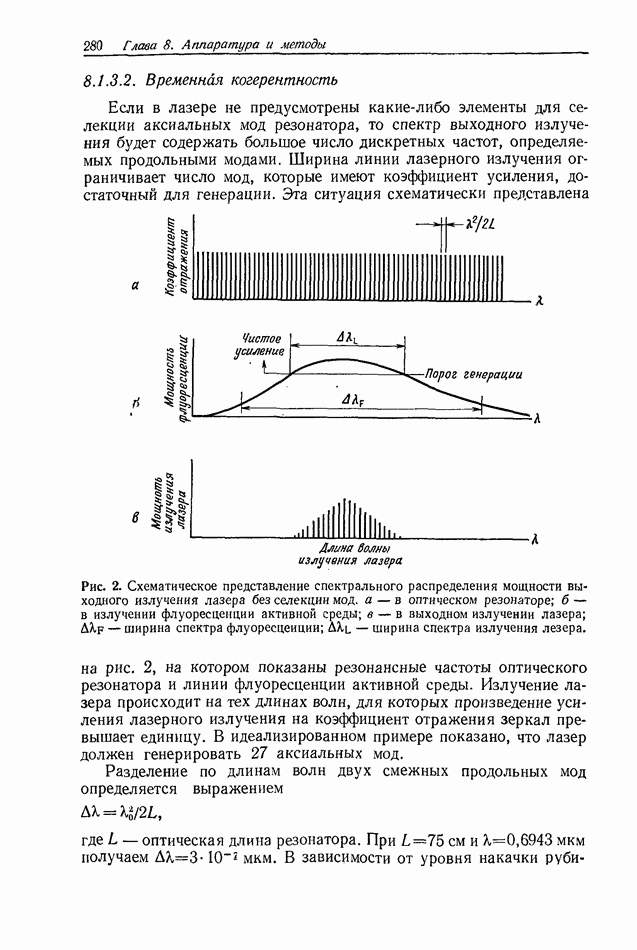
2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
Ф. Юу, Э. Тэй
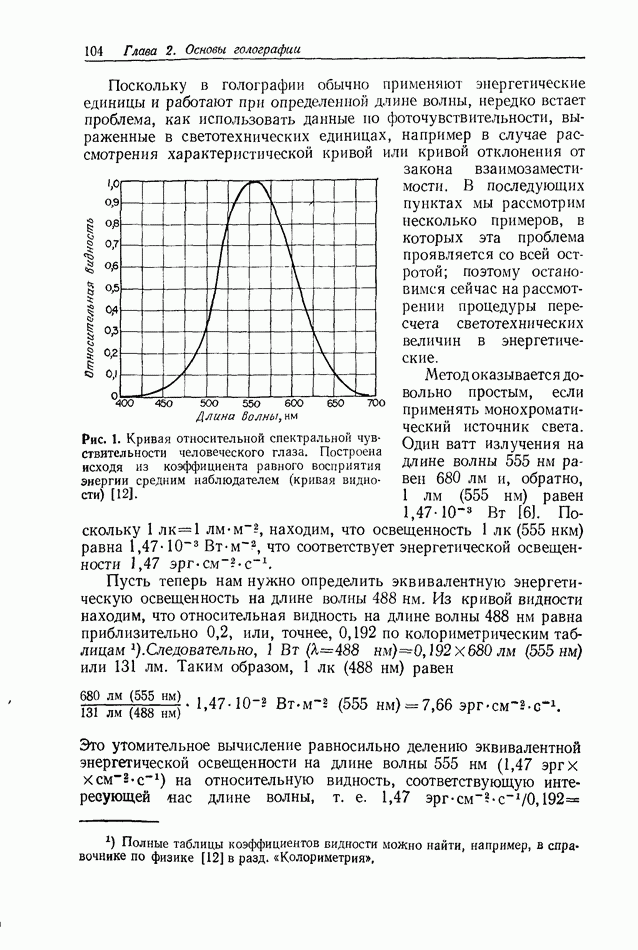
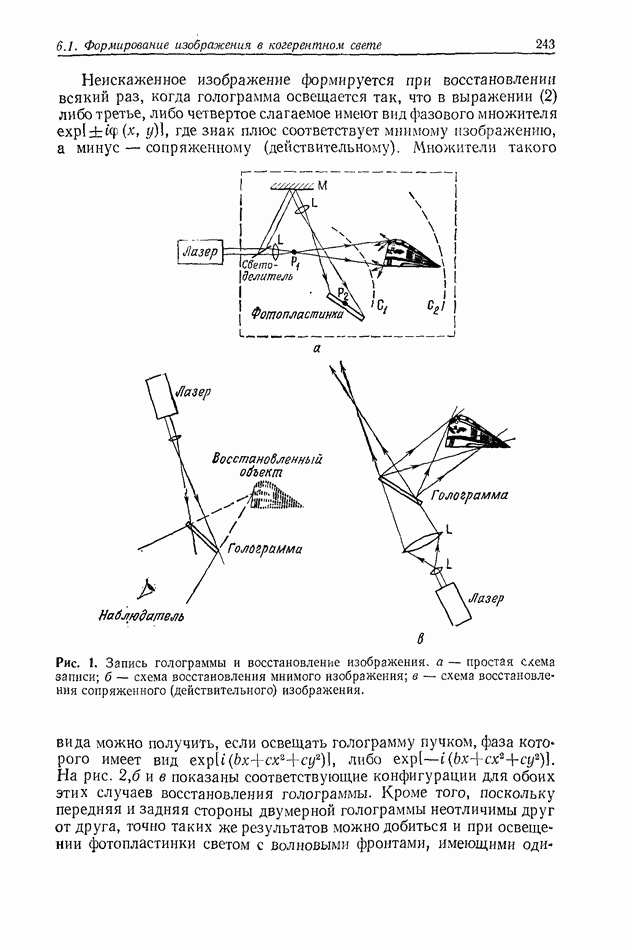
Формирование голографических изображений подробно обсуждается в гл. 6 и 7. Прежде чем производить оценку качества голографических изображений, по-видимому, полезно сначала дать краткое описание процесса формирования изображения обычными оптическими системами (использующими сферические линзы), а также некоторых параметров, применяемых для описания изображений.
2.4.1. Формирование изображения
Предположим, что мы имеем две плоскости, расположенные на расстоянии  друг от друга, и что комплексное распределение света в плоскости
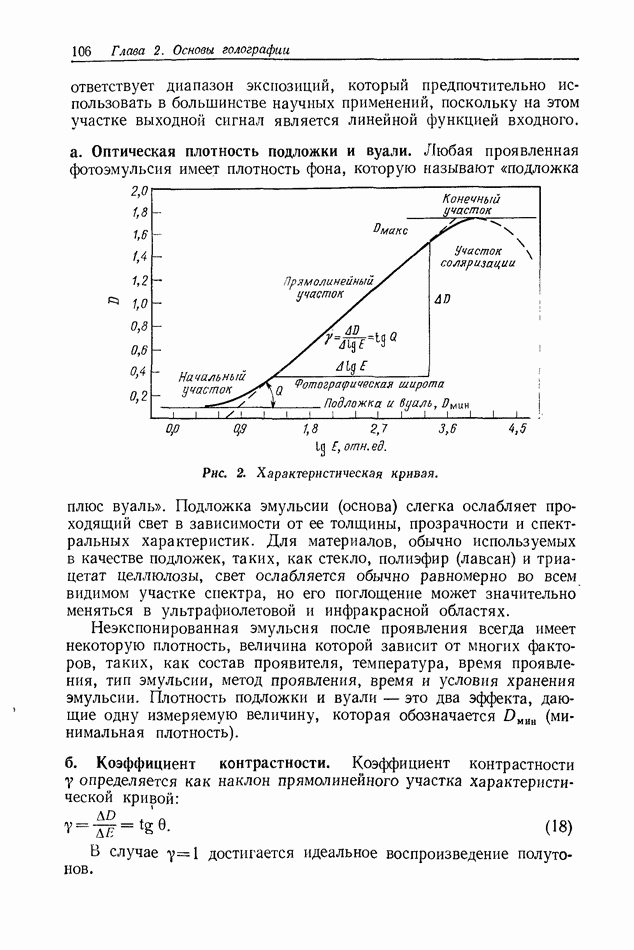
друг от друга, и что комплексное распределение света в плоскости  описывается функцией
описывается функцией  (рис. 1). Это световое поле распространяется от плоскости
(рис. 1). Это световое поле распространяется от плоскости  к плоскости
к плоскости  В плоскости
В плоскости
 комплексное распределение света можно вычислить с помощью принципа Гюйгенса [17, 7, 2, 3, 16, 8, 51:
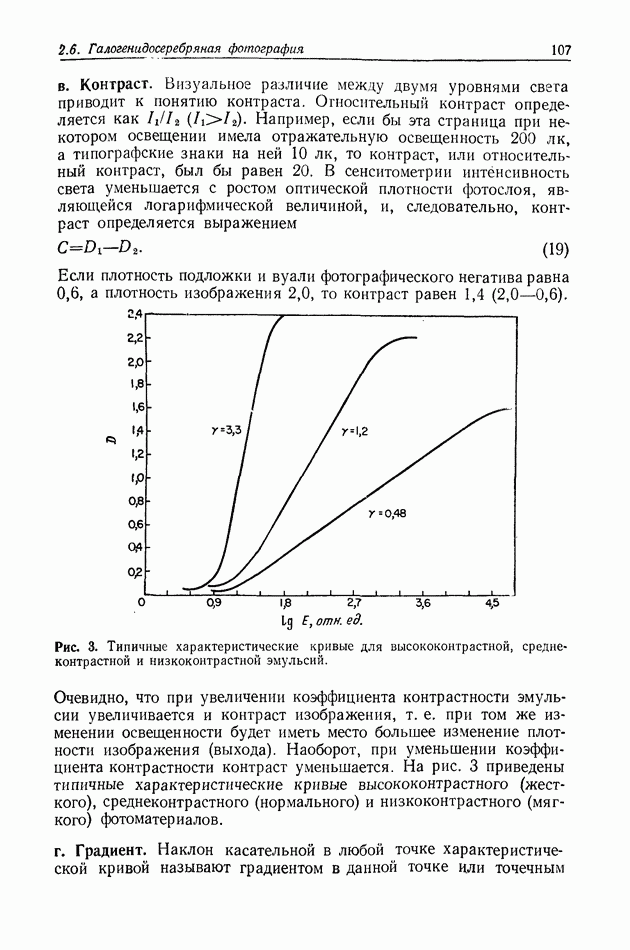
комплексное распределение света можно вычислить с помощью принципа Гюйгенса [17, 7, 2, 3, 16, 8, 51:

где  поверхность интегрирования, С — произвольная постоянная и
поверхность интегрирования, С — произвольная постоянная и  волновое число.
волновое число.

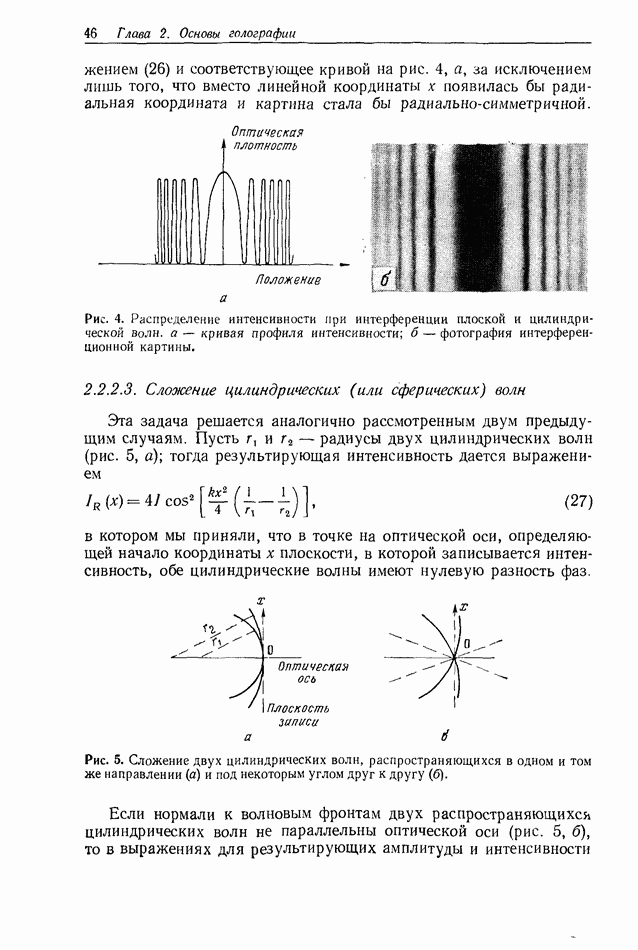
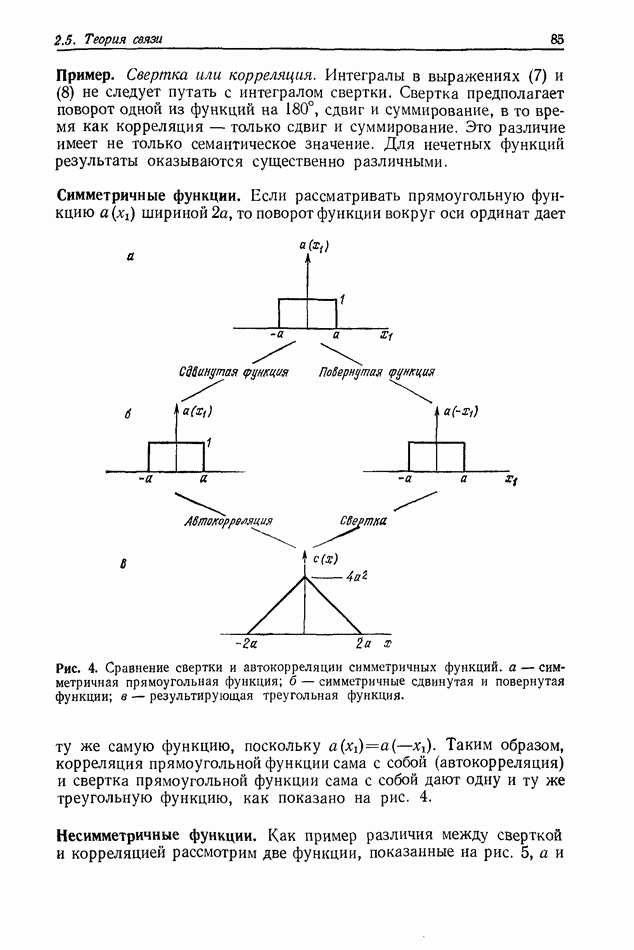
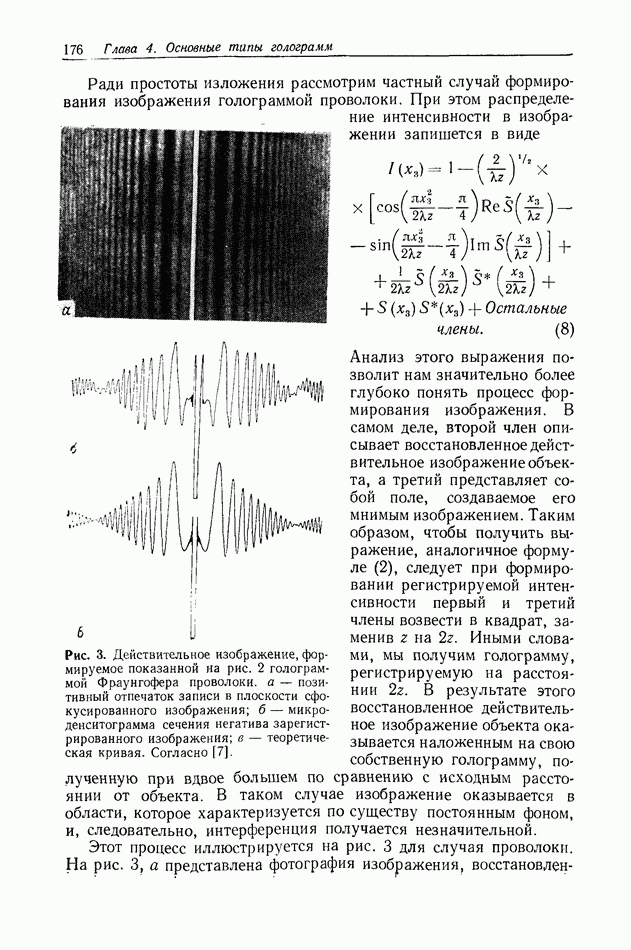
Рис. 1. Распространение комплексного светового поля.
Если I велико по сравнению с размерами плоскостей  то уравнение (1) принимает вид
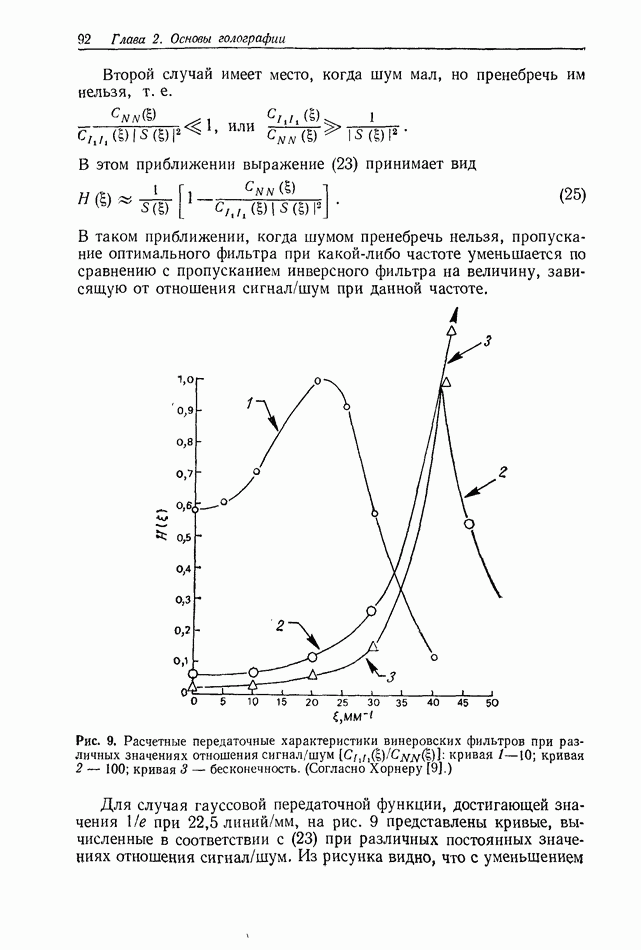
то уравнение (1) принимает вид

Это уравнение можно записать в виде свертки

где  пространственный импульсный отклик,
пространственный импульсный отклик,  входная и выходная плоскости линейной системы. Поскольку положительная линза преобразует плоскую волну в сходящийся сферический волновой фронт, можно показать, что такая линза выполняет фазовое преобразование [171:
входная и выходная плоскости линейной системы. Поскольку положительная линза преобразует плоскую волну в сходящийся сферический волновой фронт, можно показать, что такая линза выполняет фазовое преобразование [171:

здесь  фокусное расстояние линзы. Рассмотрим простую систему формирования изображения (рис. 2). Световое поле в выходной плоскости
фокусное расстояние линзы. Рассмотрим простую систему формирования изображения (рис. 2). Световое поле в выходной плоскости  можно записать как
можно записать как

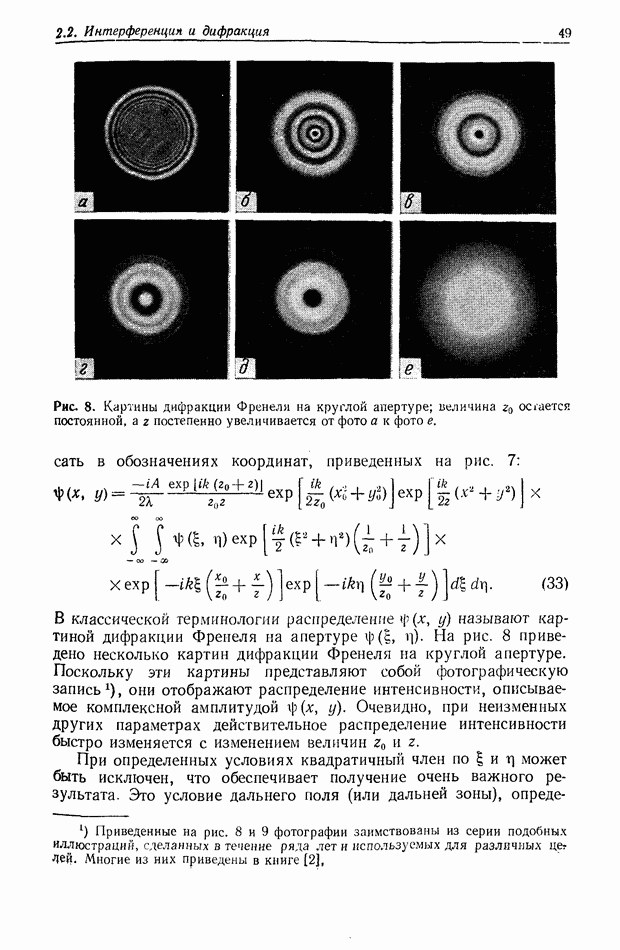
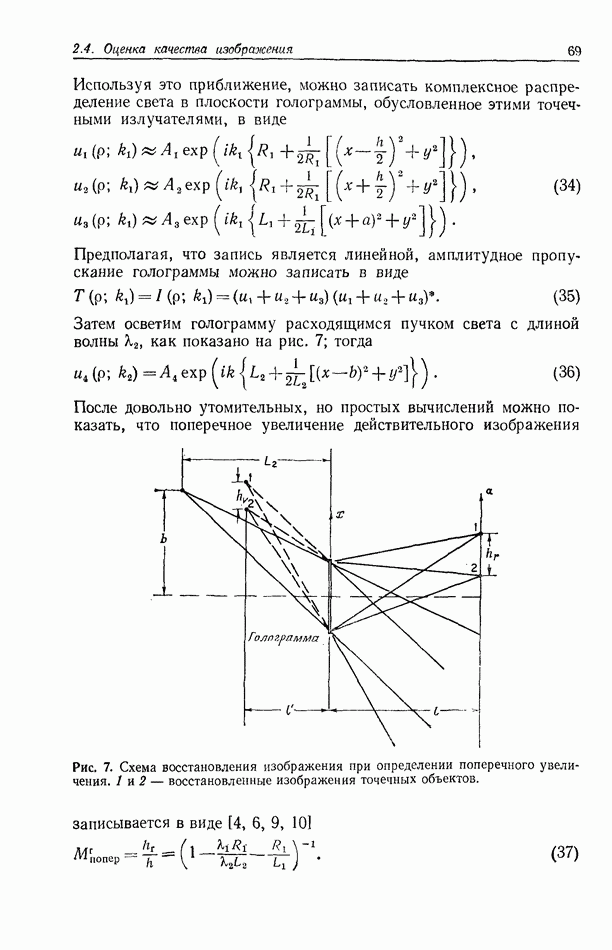
где  соответствующие импульсные отклики. Во входной и выходной плоскостях световые поля связаны между собой прямым соотношением
соответствующие импульсные отклики. Во входной и выходной плоскостях световые поля связаны между собой прямым соотношением


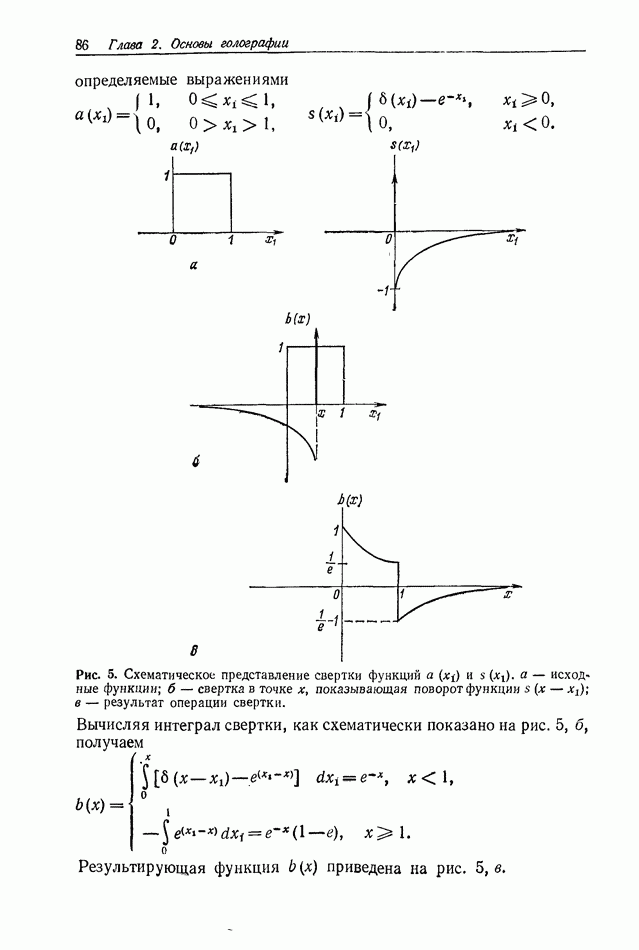
Рис. 2. Схема простой системы формирования изображения.
где

Мы замечаем, что члены уравнения, содержащие фазовые множители

не зависят от координат  Можно показать, что в общем случае этими двумя фазовыми членами пренебрегают, так как обычно изображения наблюдают или регистрируют в виде распределения интенсивности. Следовательно, импульсный отклик системы упрощается [7]:
Можно показать, что в общем случае этими двумя фазовыми членами пренебрегают, так как обычно изображения наблюдают или регистрируют в виде распределения интенсивности. Следовательно, импульсный отклик системы упрощается [7]:

Предположим, что выполнено следующее условие:

где  фокусное расстояние линзы. При этом выражение для импульсного отклика принимает еще более простой вид:
фокусное расстояние линзы. При этом выражение для импульсного отклика принимает еще более простой вид:

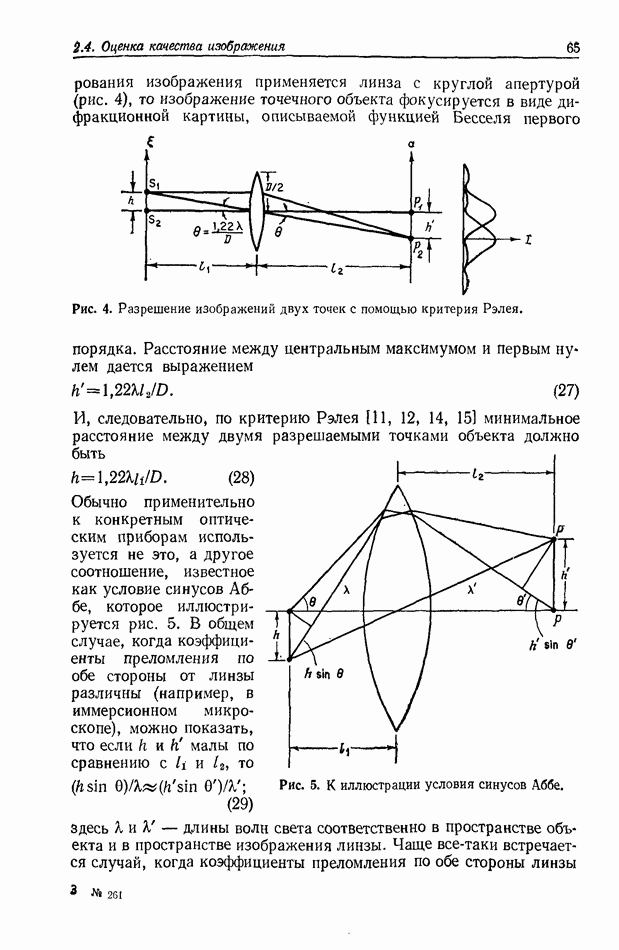
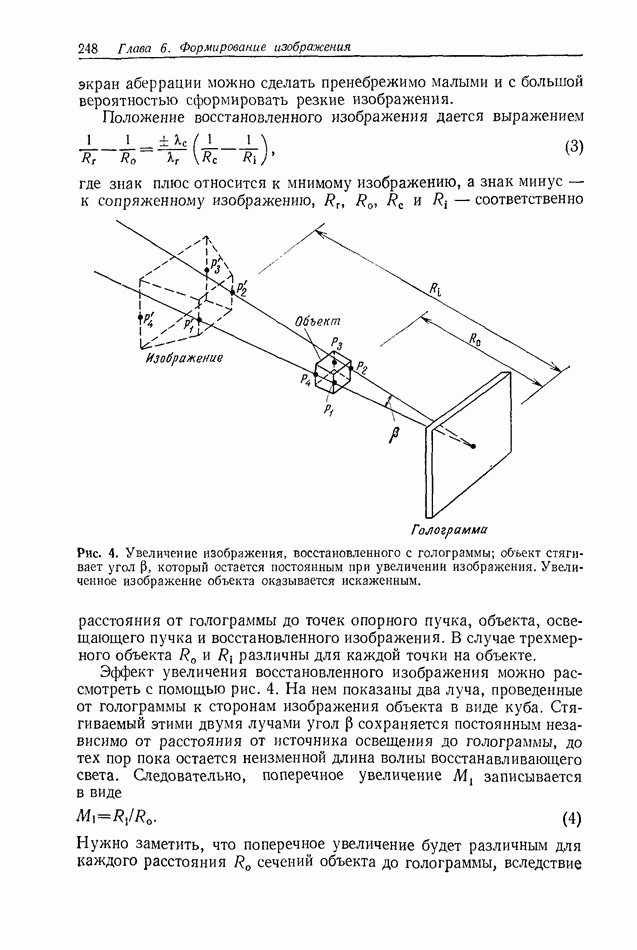
Уравнение (10) представляет собой хорошо известное уравнение линзы. Если распределение света от объекта рассматривать как результат сложения света от многих точечных излучателей,
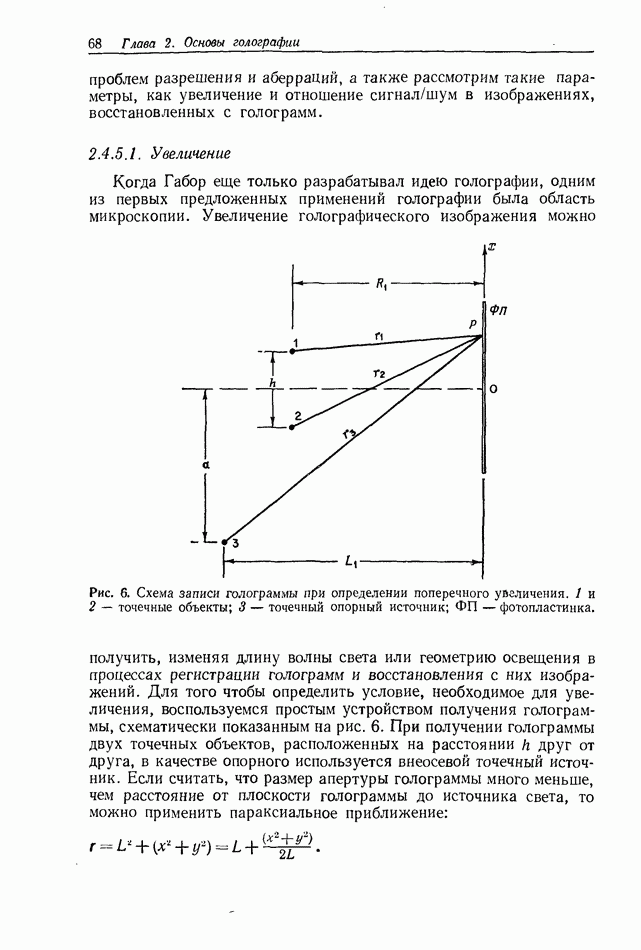
находящихся на поверхности объекта, то уравнение линзы описывает условие, при котором световое поле будет сходиться и воспроизводить изображения точечных объектов в выходной плоскости. Следовательно, уравнение (11) описывает распределение света в плоскости изображения, а отношение  является поперечным увеличением.
является поперечным увеличением.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
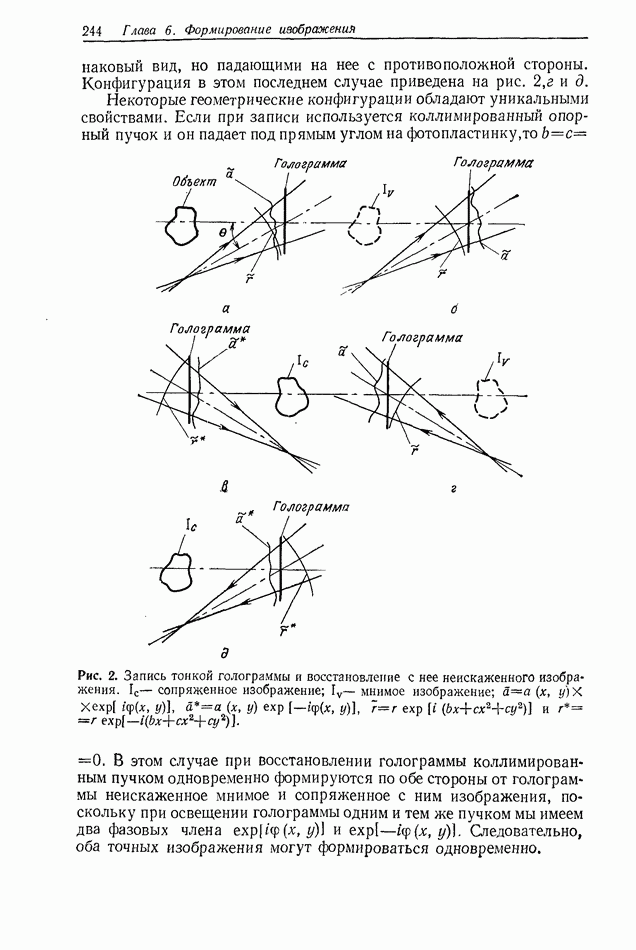
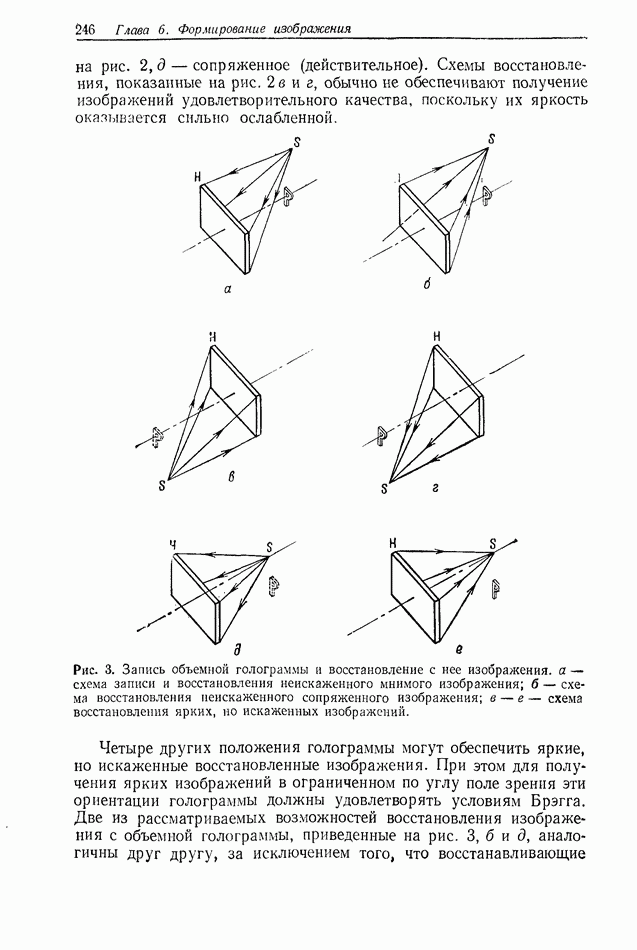
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
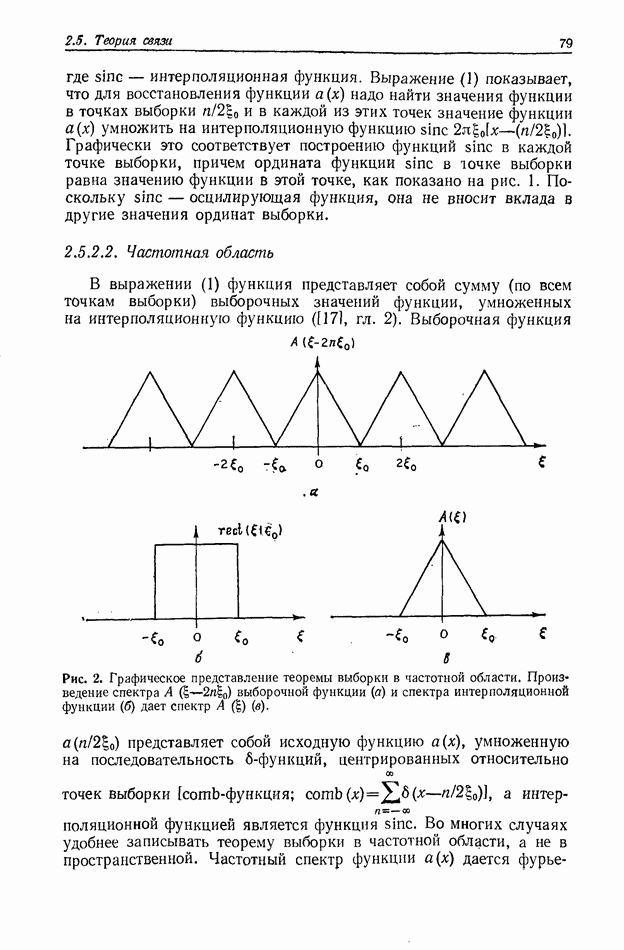
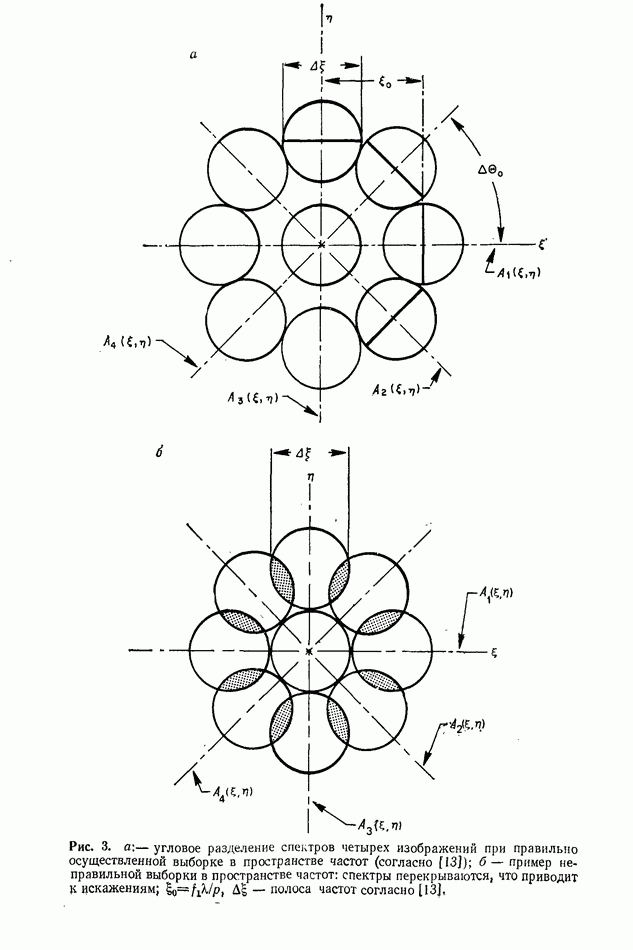
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
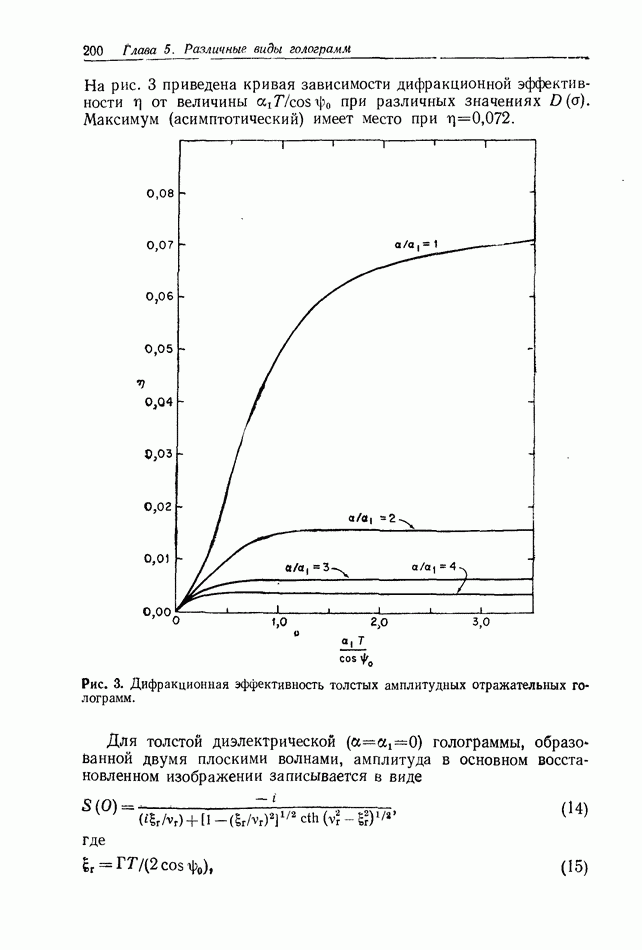
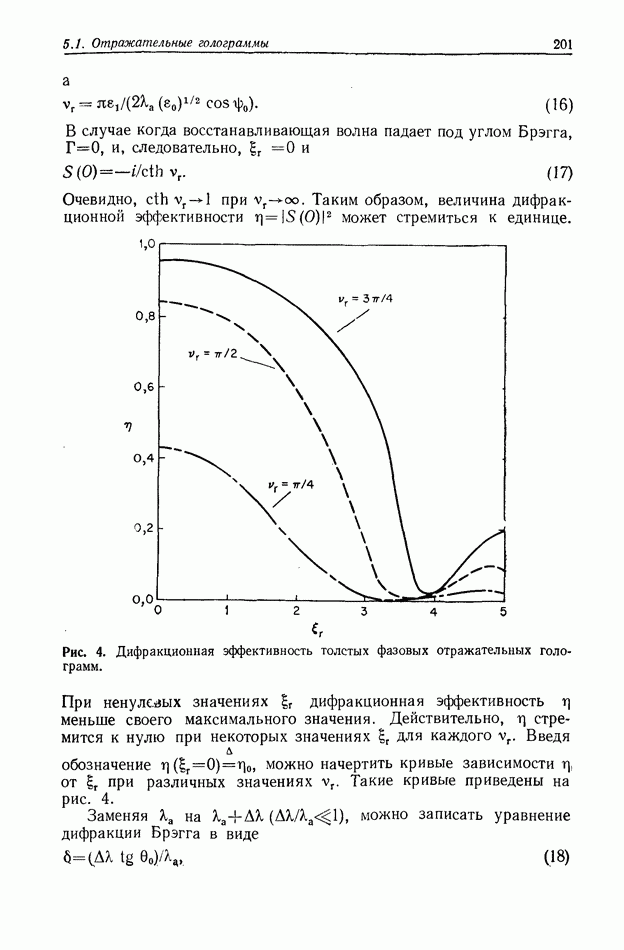
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
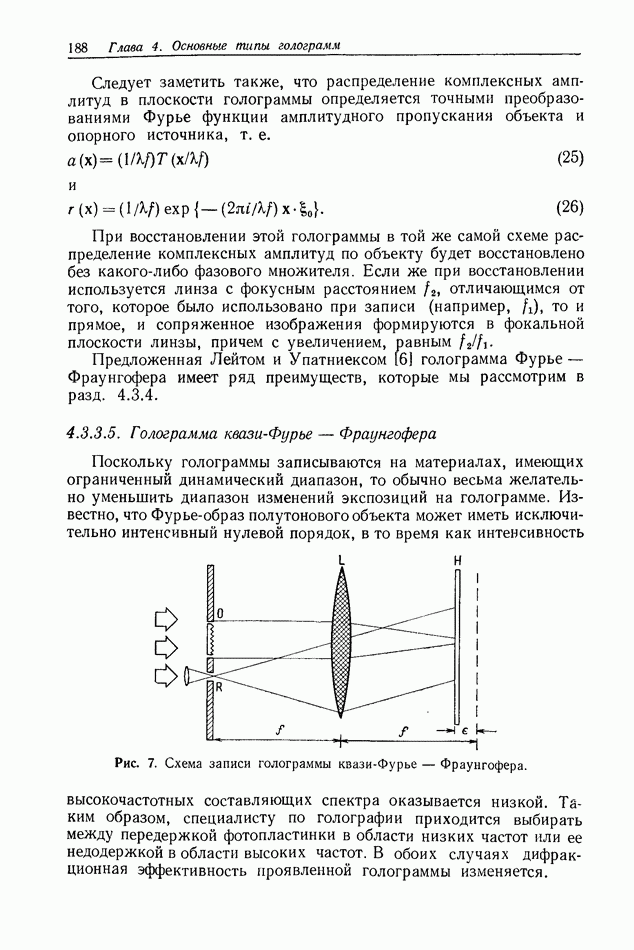
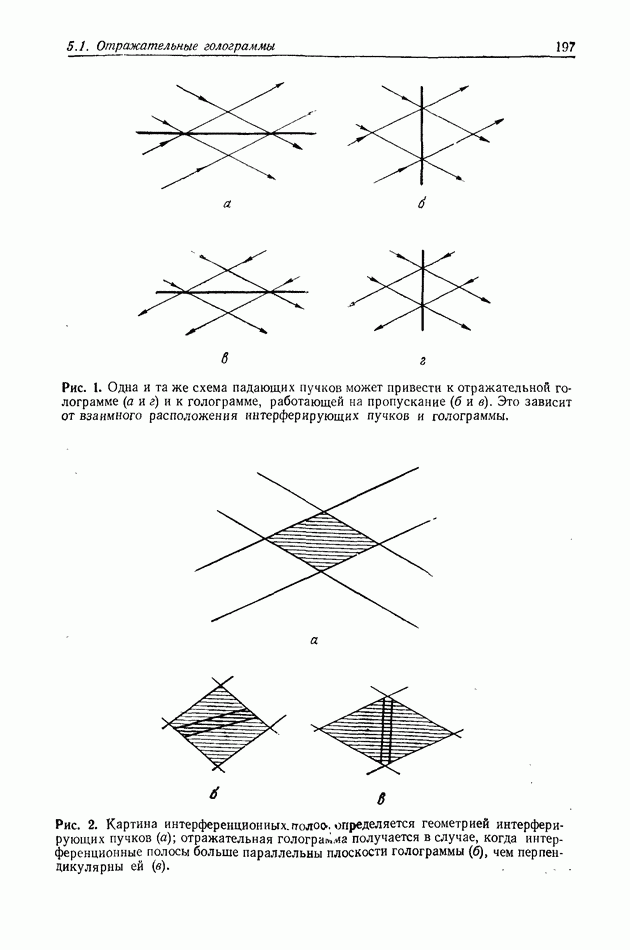
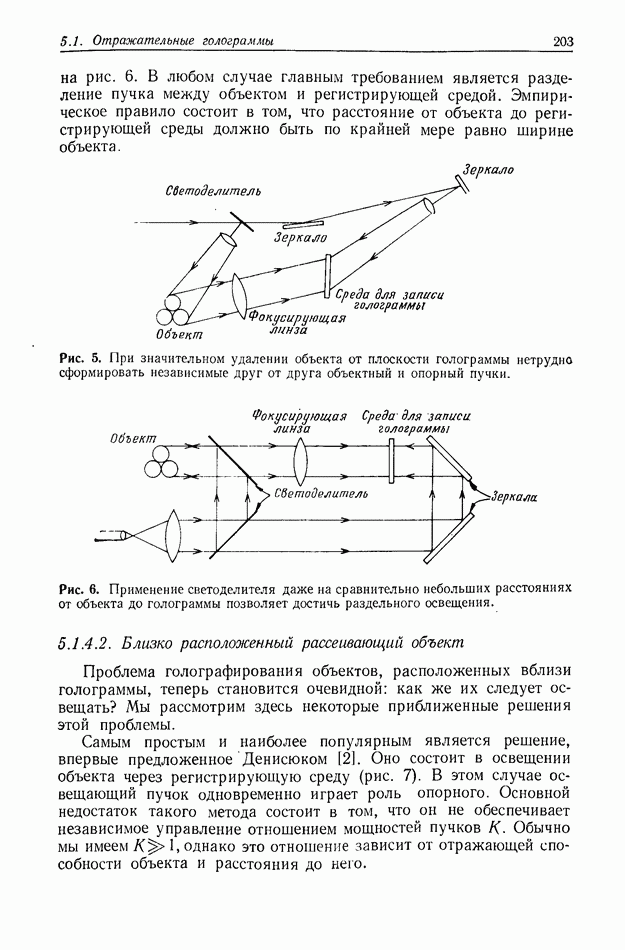
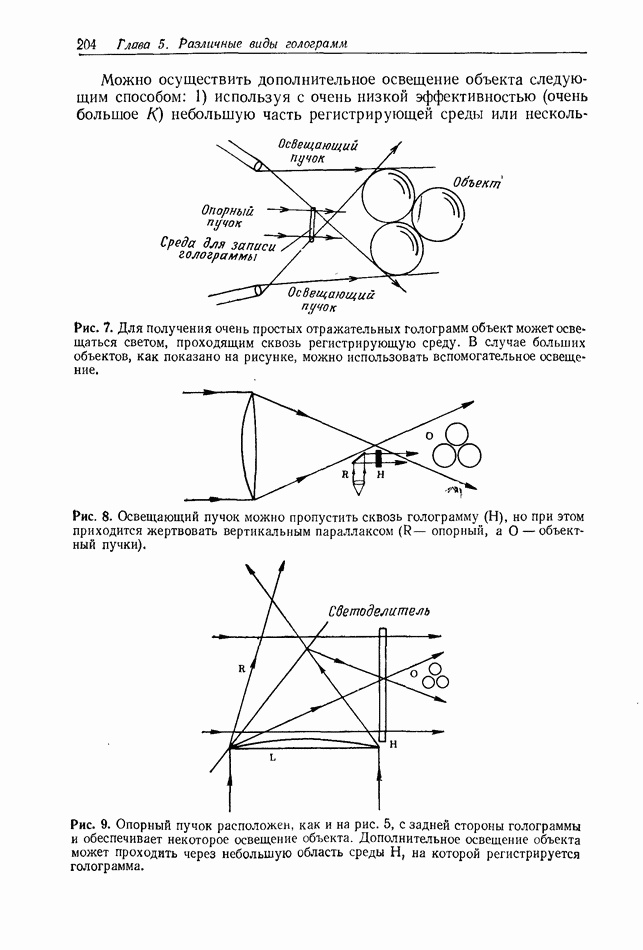
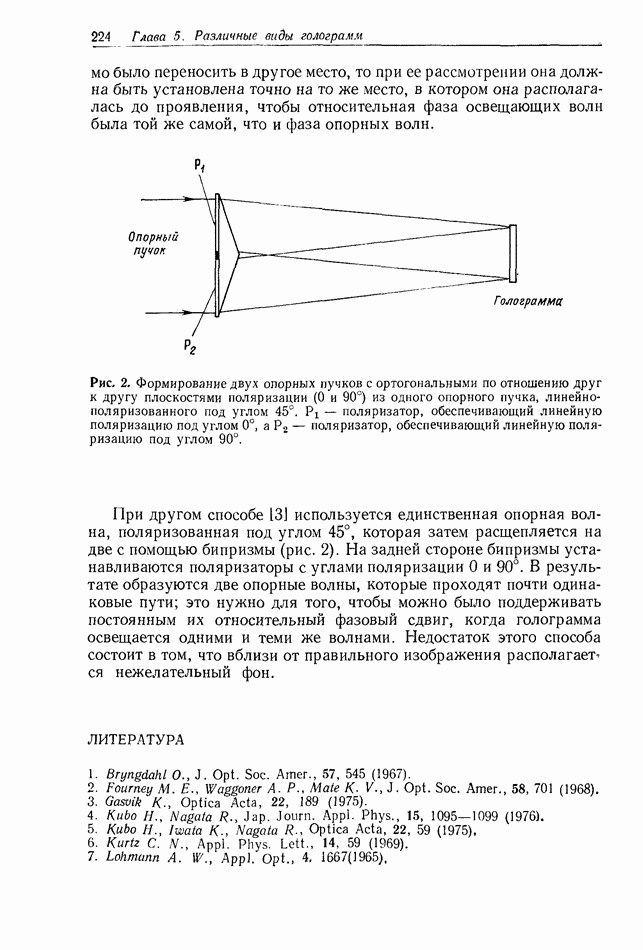
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
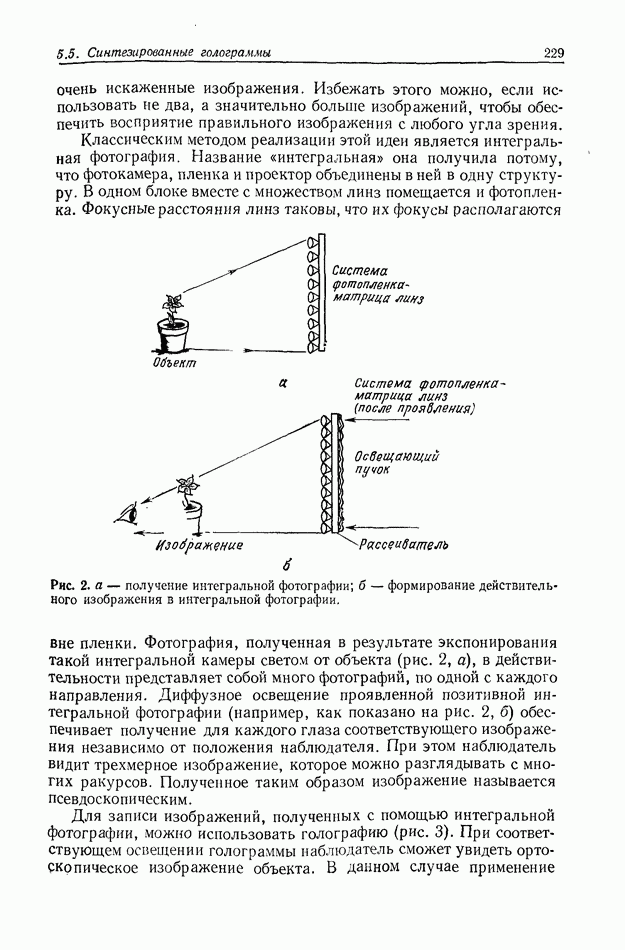
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
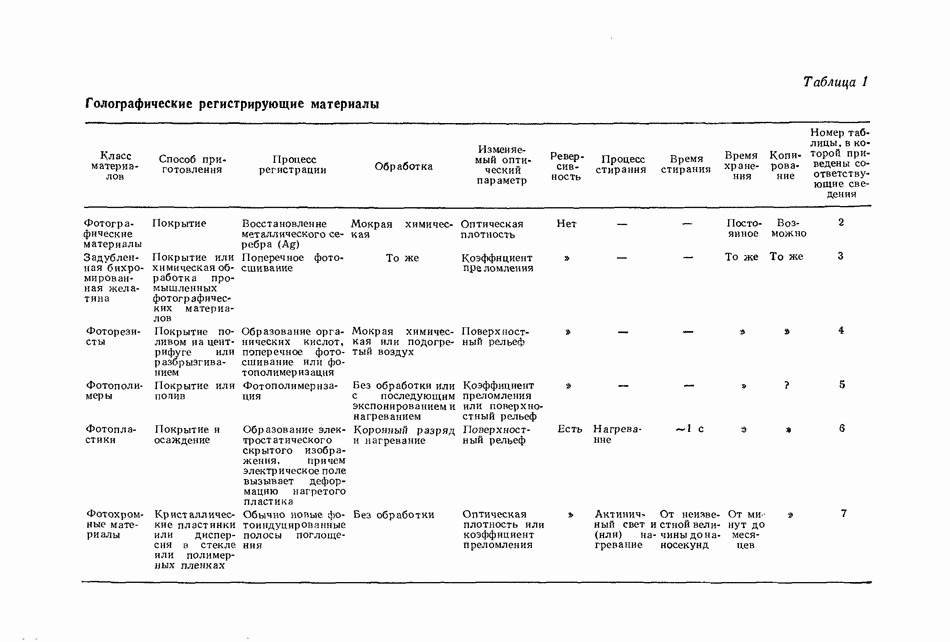
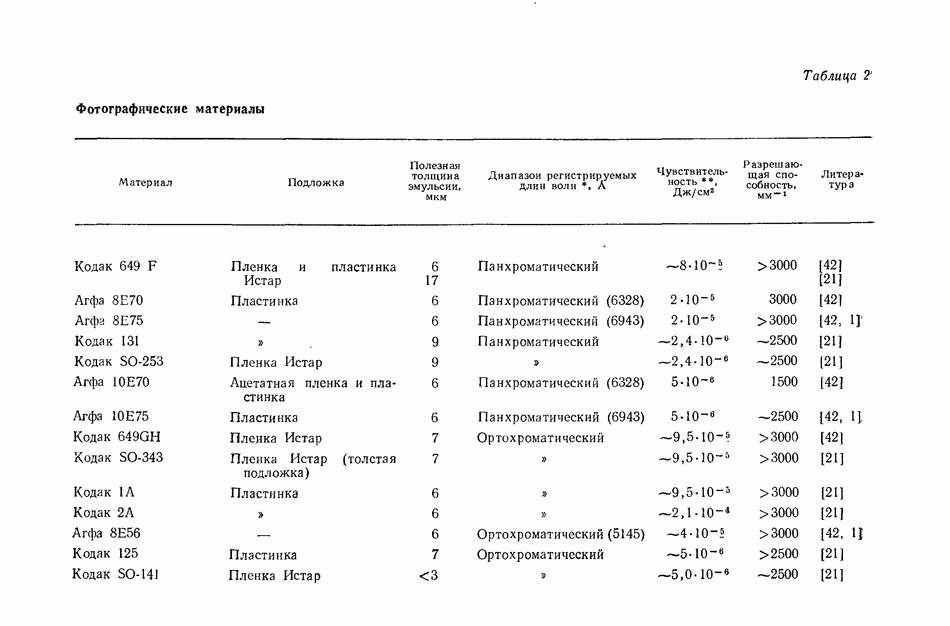
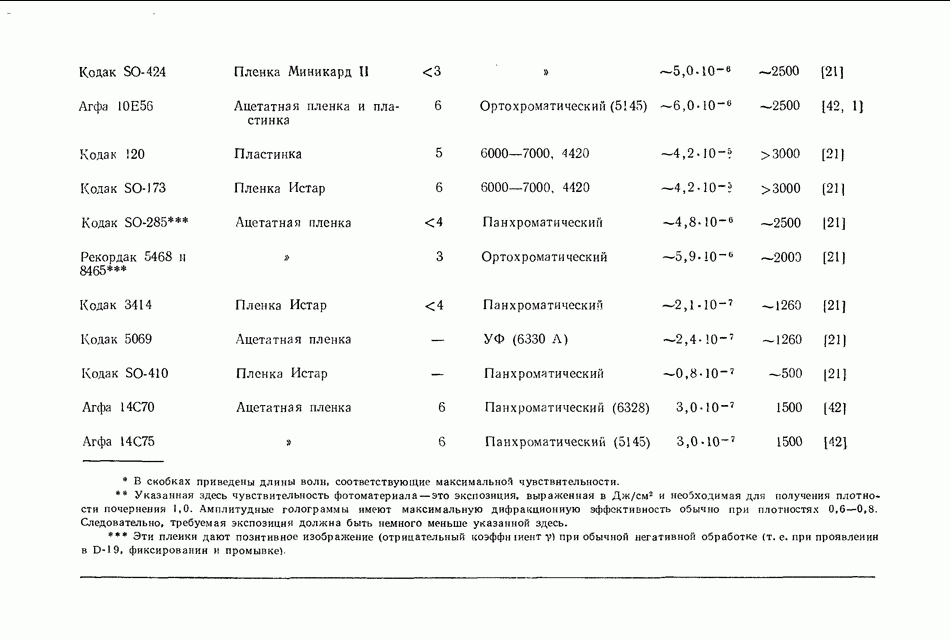
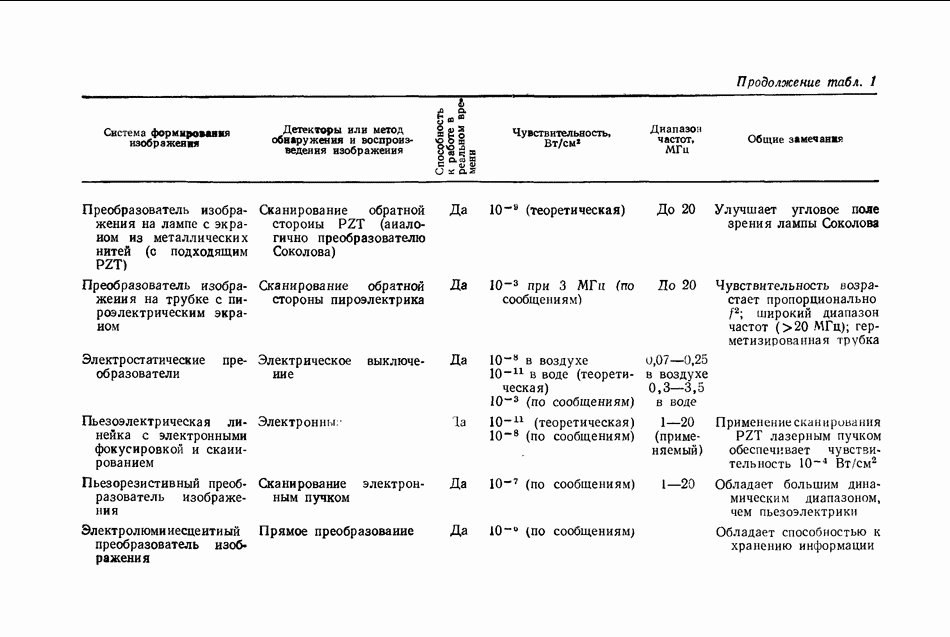
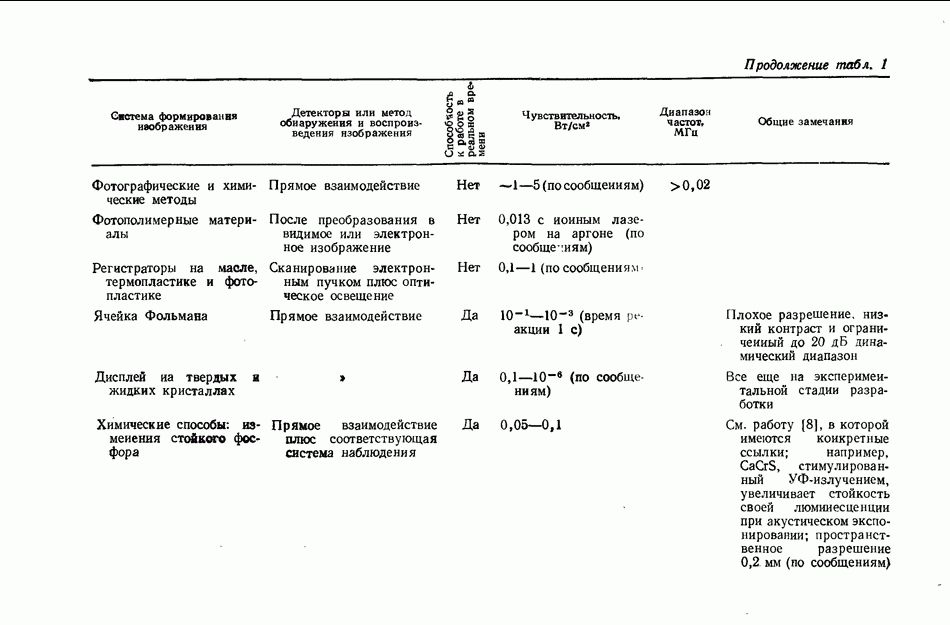
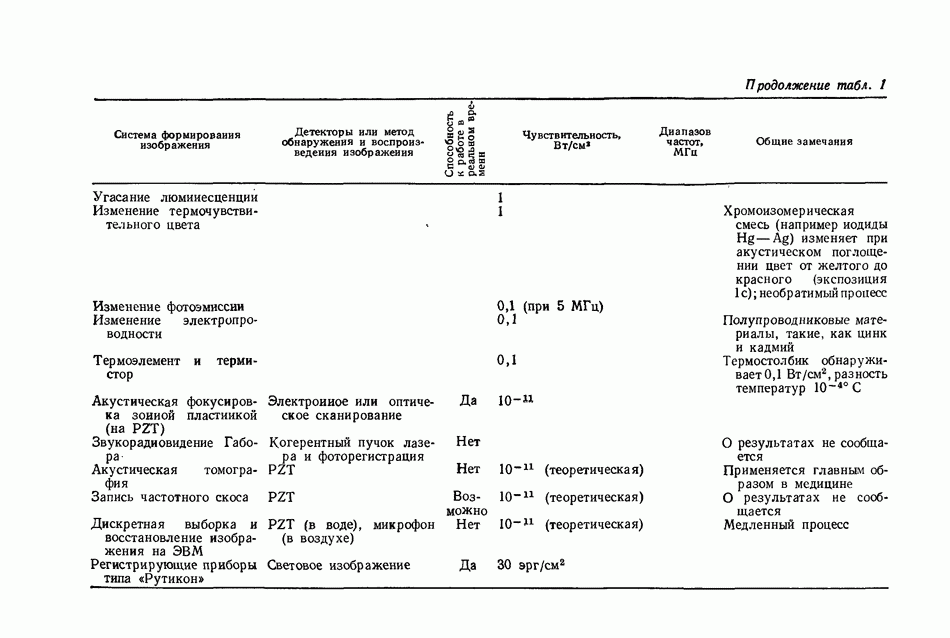
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
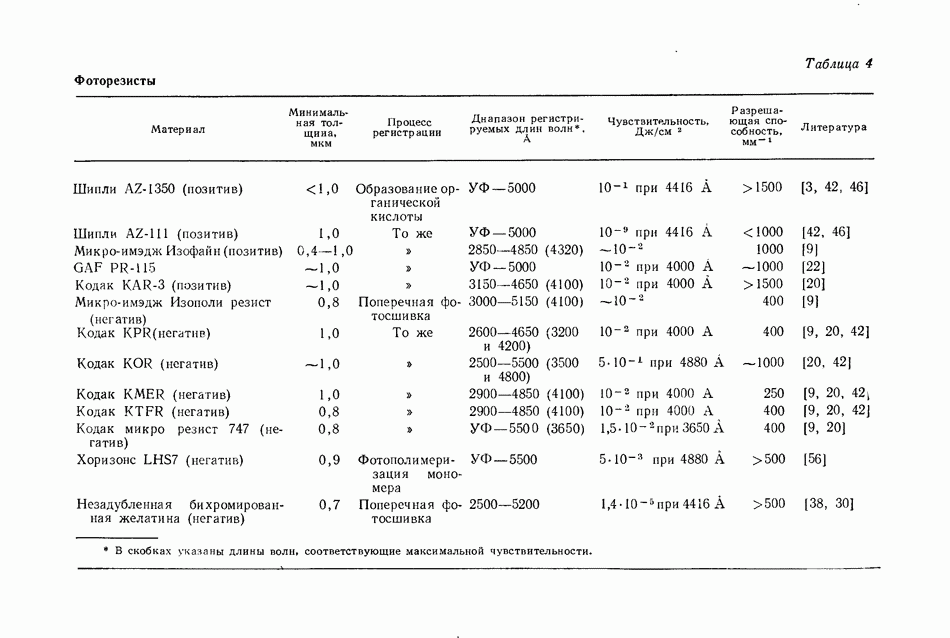
- 8.3.5. Фоторезисты
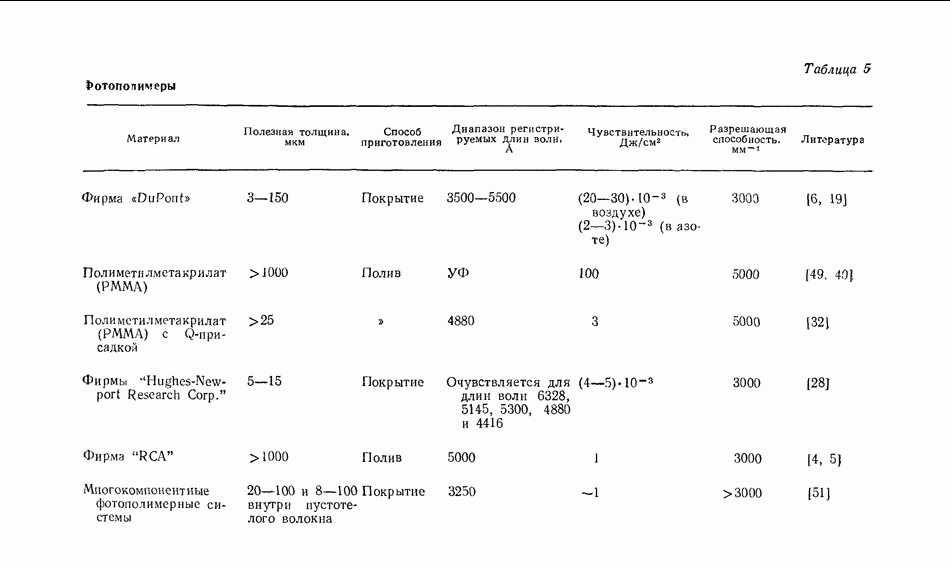
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
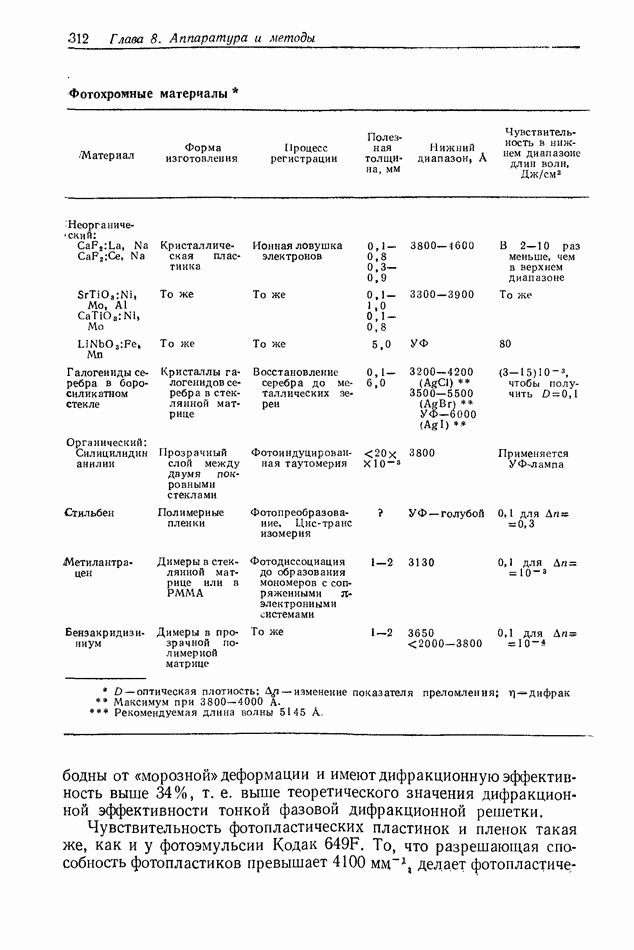
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
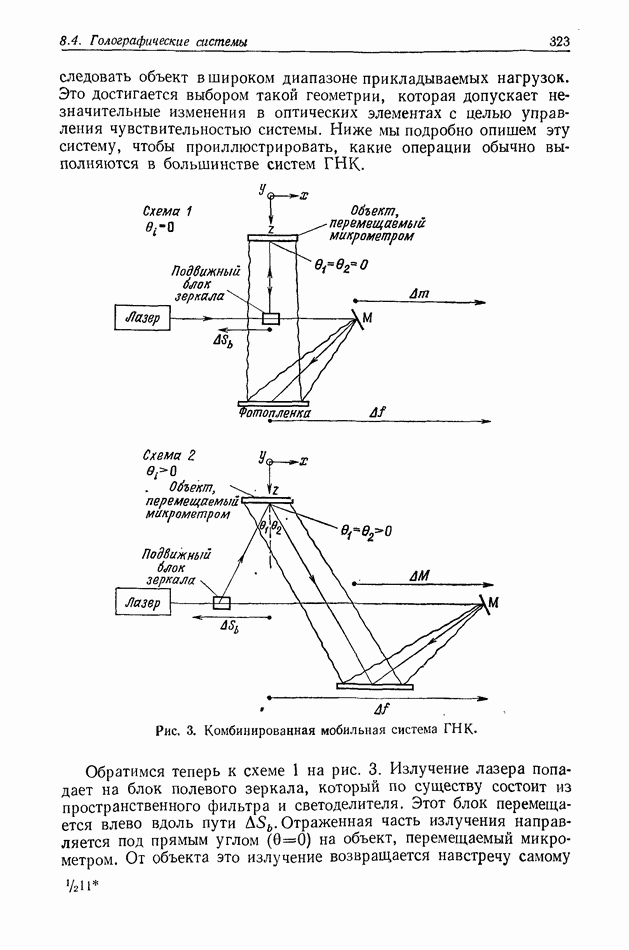
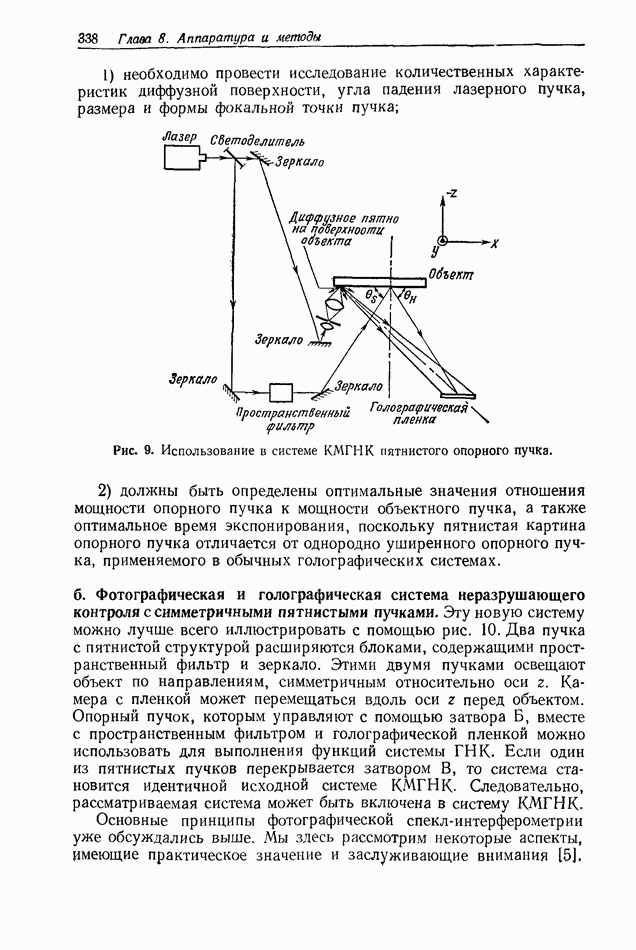
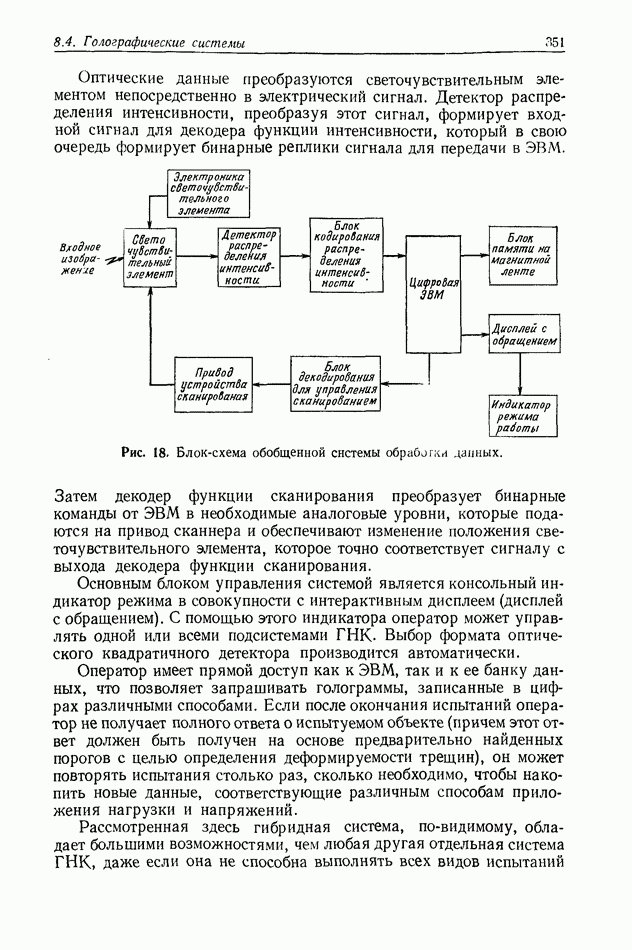
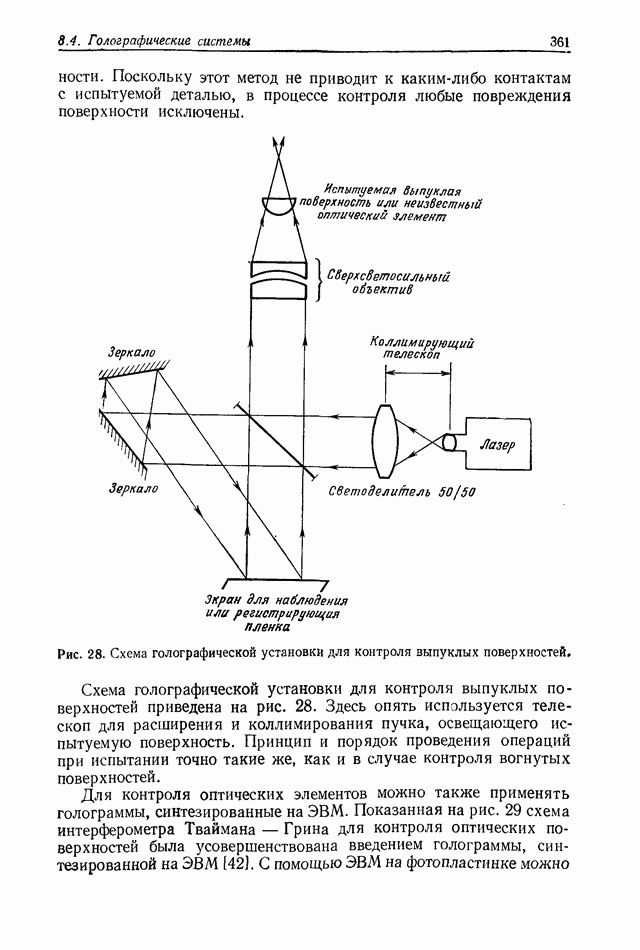
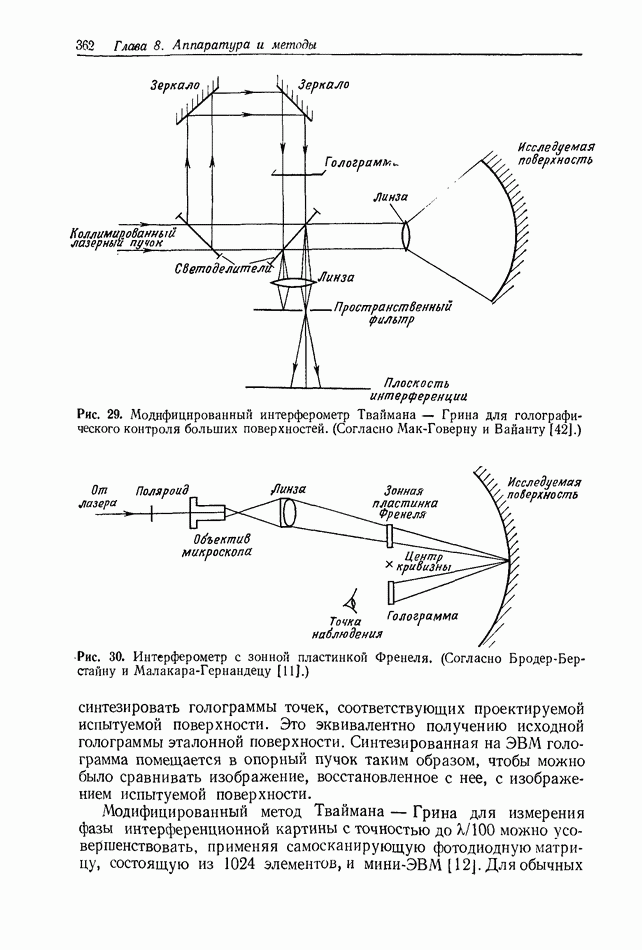
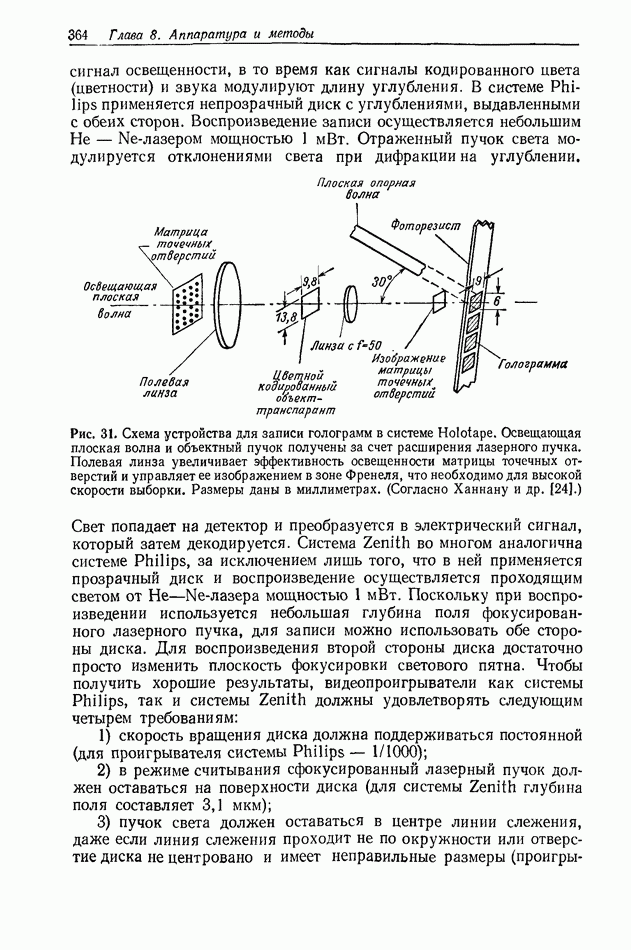
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
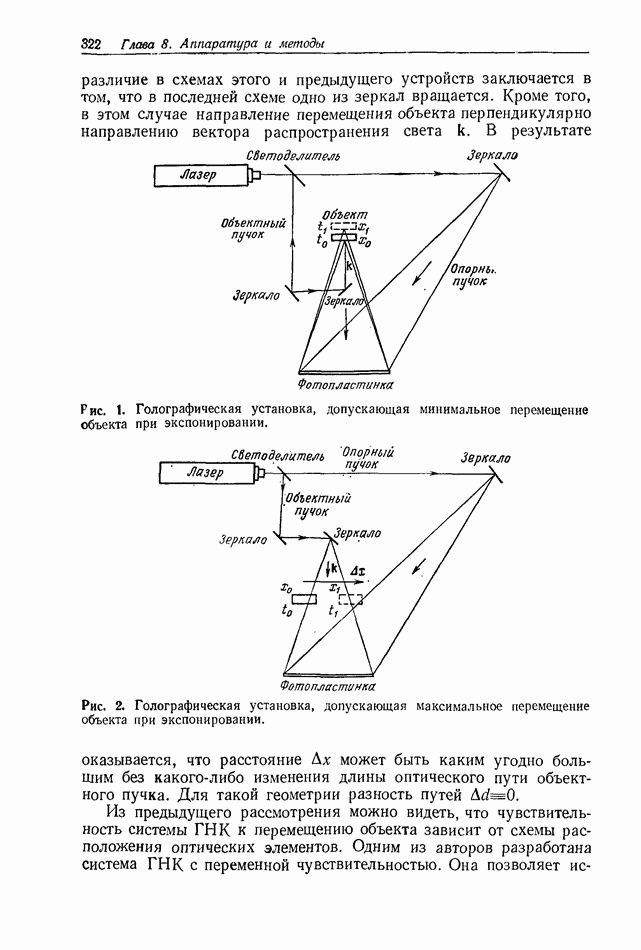
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
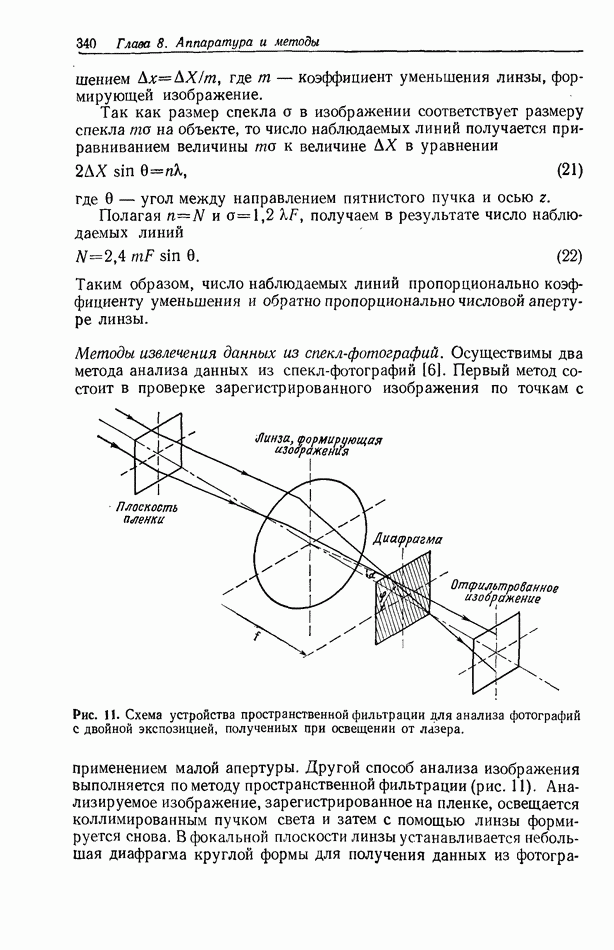
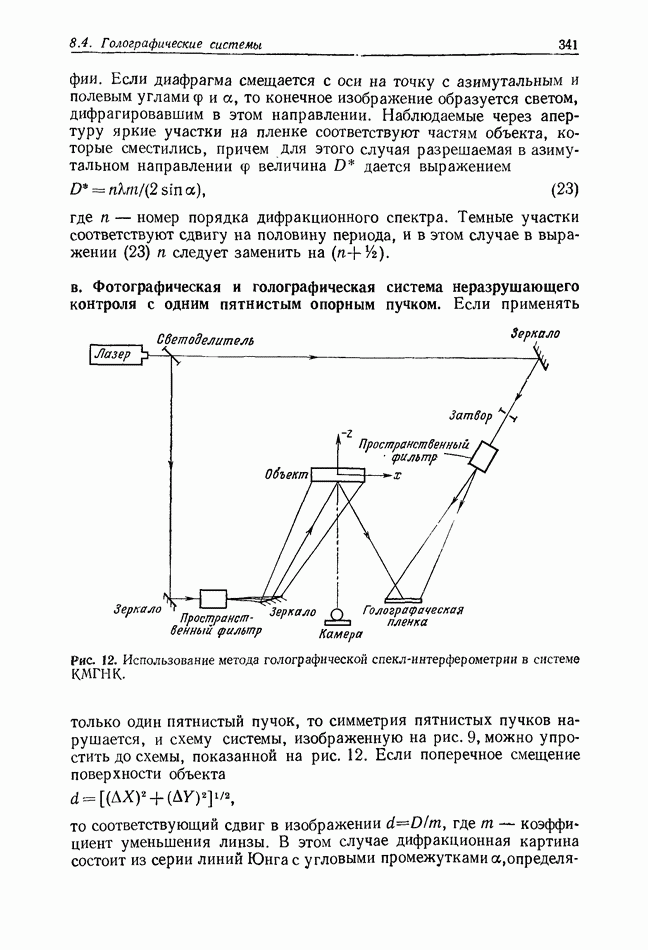
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
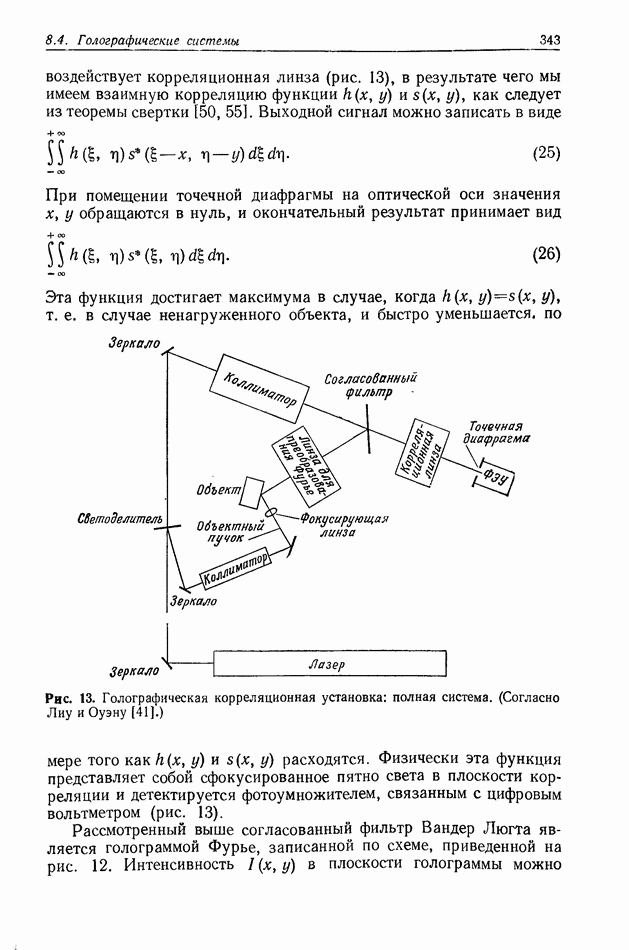
- 8.4.5. Голографическая корреляция
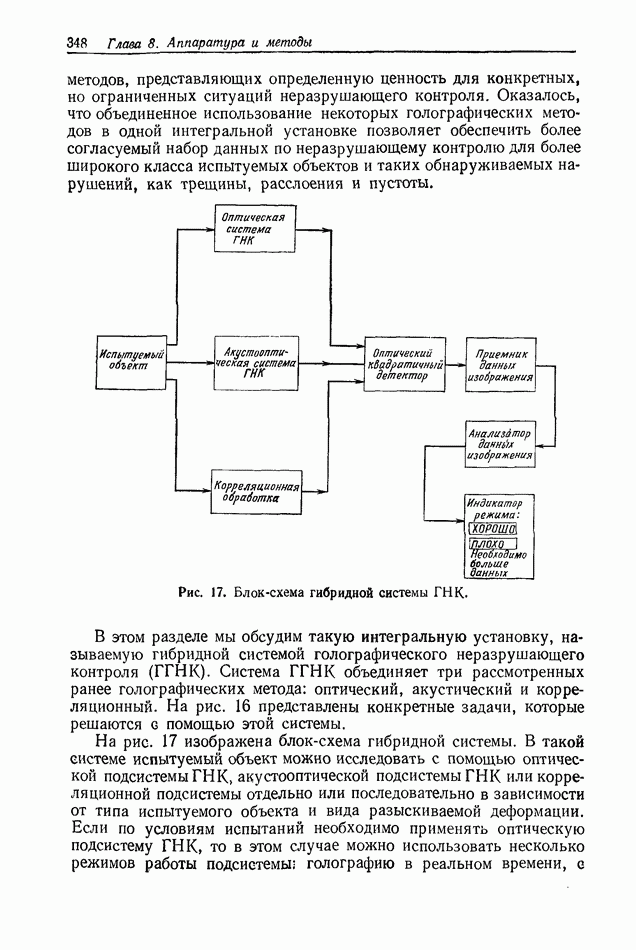
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
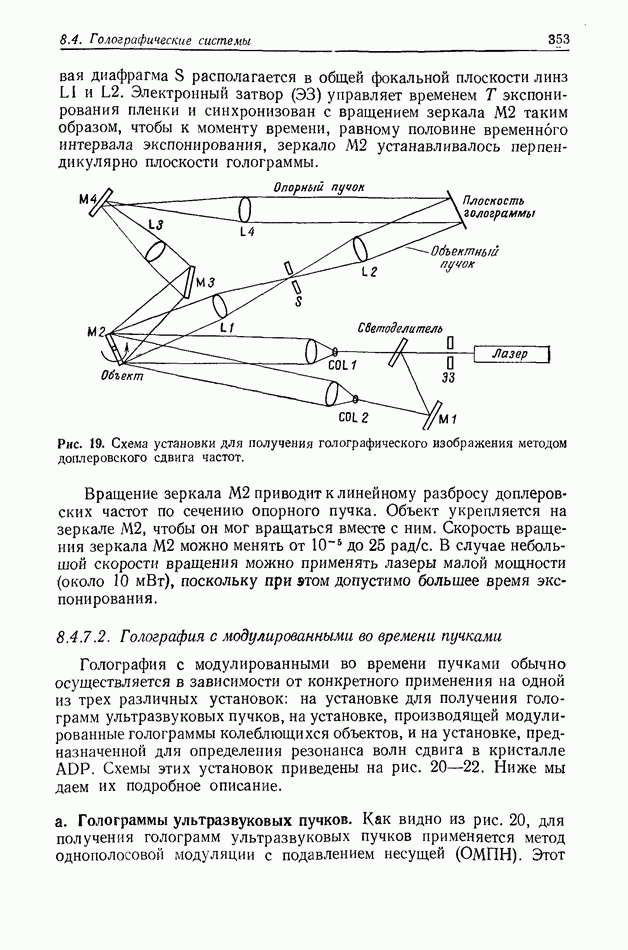
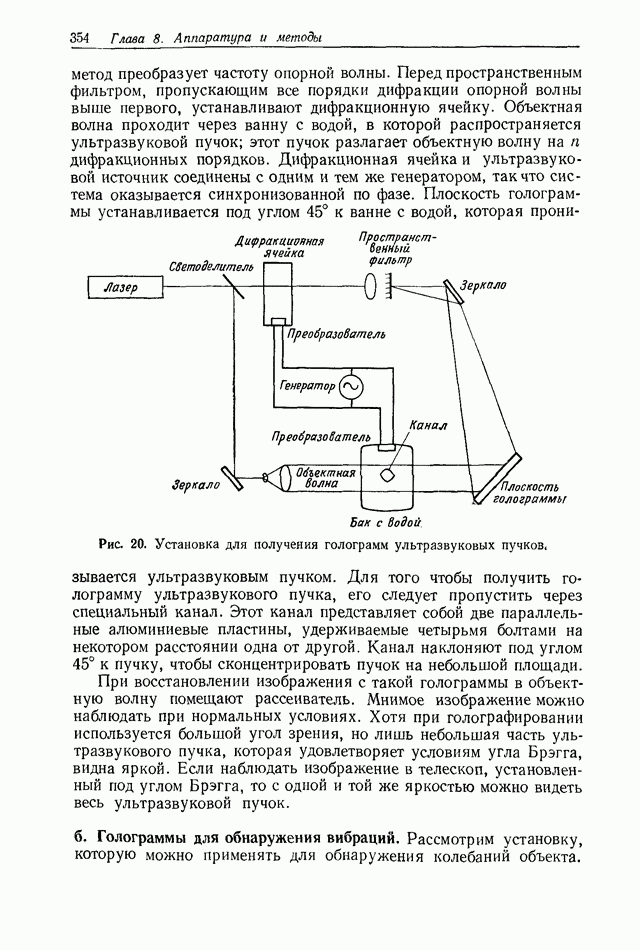
- 8.4.7. Голография движущихся объектов
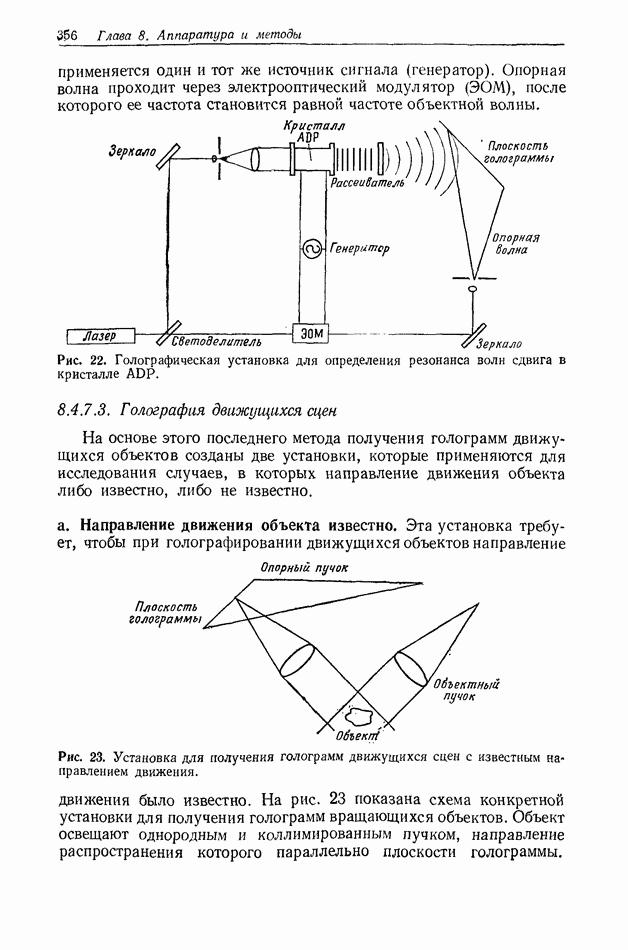
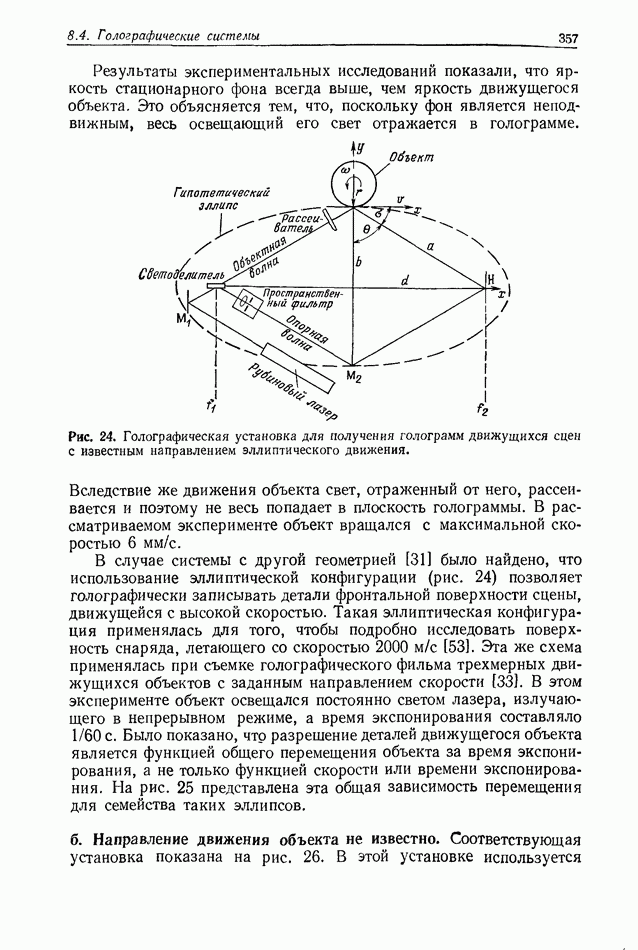
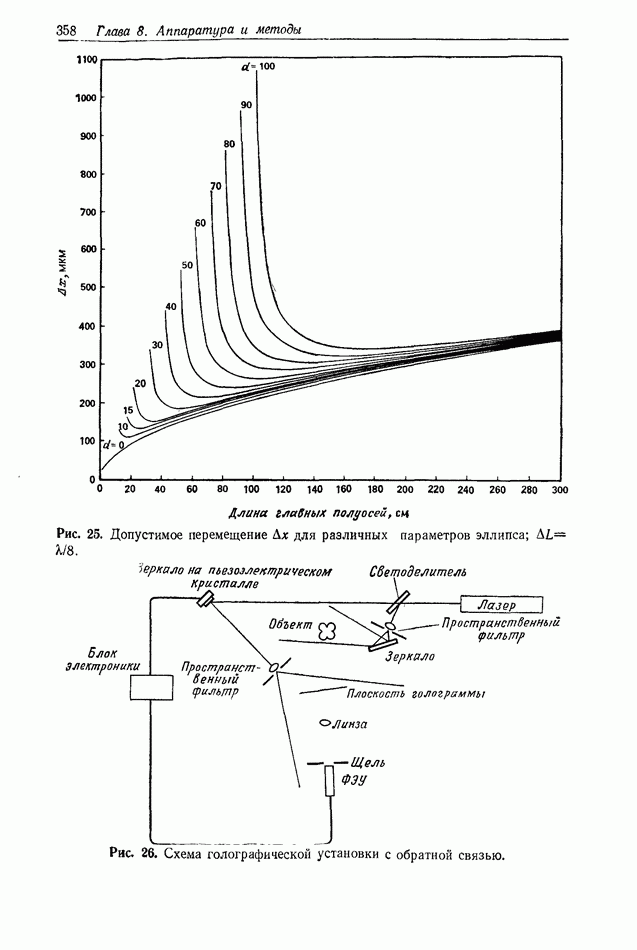
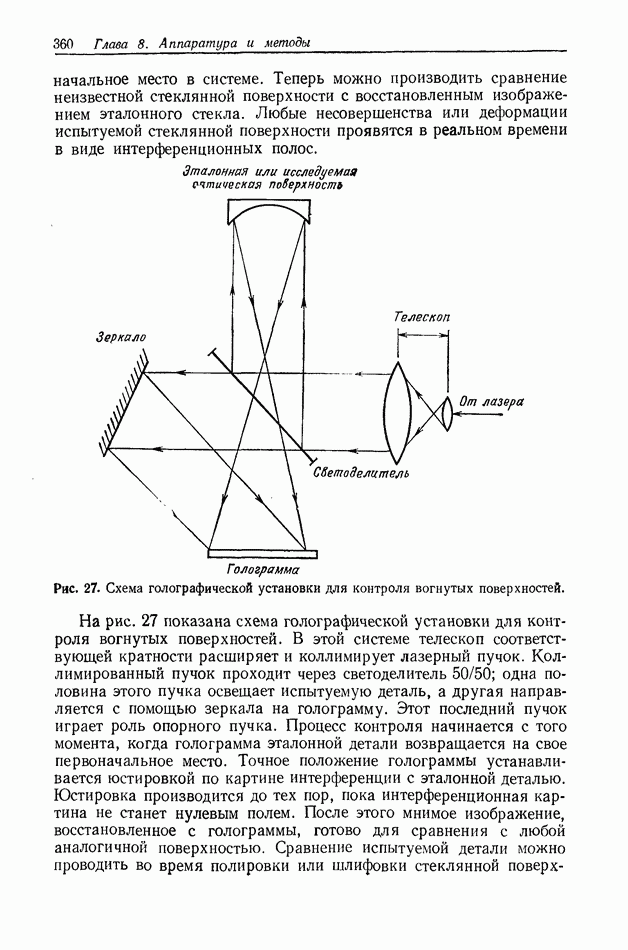
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение