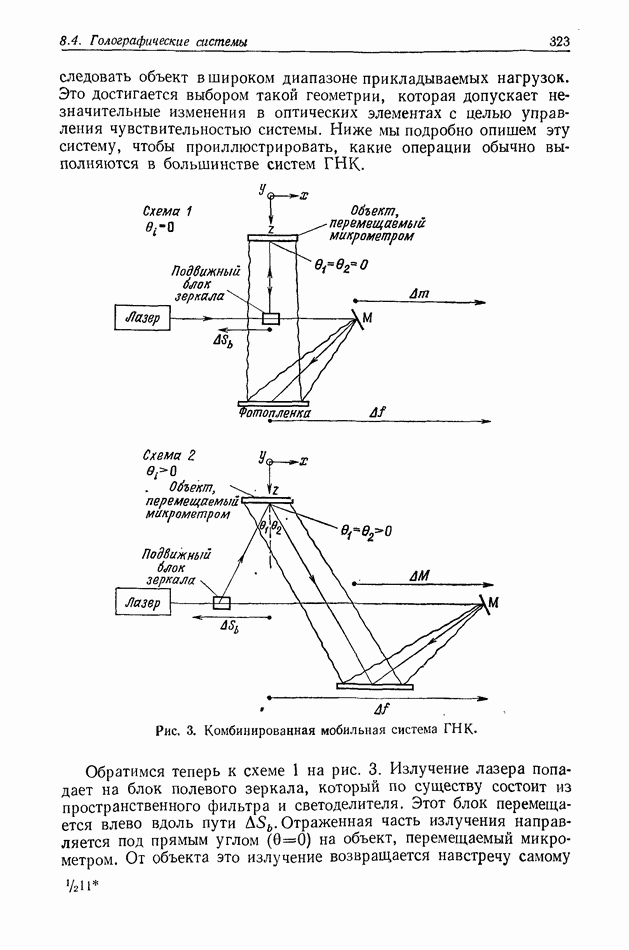
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5.2. Теорема выборки (или теорема отсчетов)
2.5.2.1. Пространственная область
Теорема выборки ([14], приложение А) представляет собой способ подгонки кривых при определении функций с конечным спектром, симметричным относительно нулевой частоты. Если функция, записываемая в виде выборки отдельных значений, действительно имеет ограниченную полосу частот, то, согласно теореме выборки, эта функция будет точно описываться выборкой.
Теорема. Если спектр одномерной функции  не содержит частот выше, чем
не содержит частот выше, чем  то функция полностью определена заданием ее ординат в дискретных точках пространственной области, отстоящих друг от друга на расстояние
то функция полностью определена заданием ее ординат в дискретных точках пространственной области, отстоящих друг от друга на расстояние 

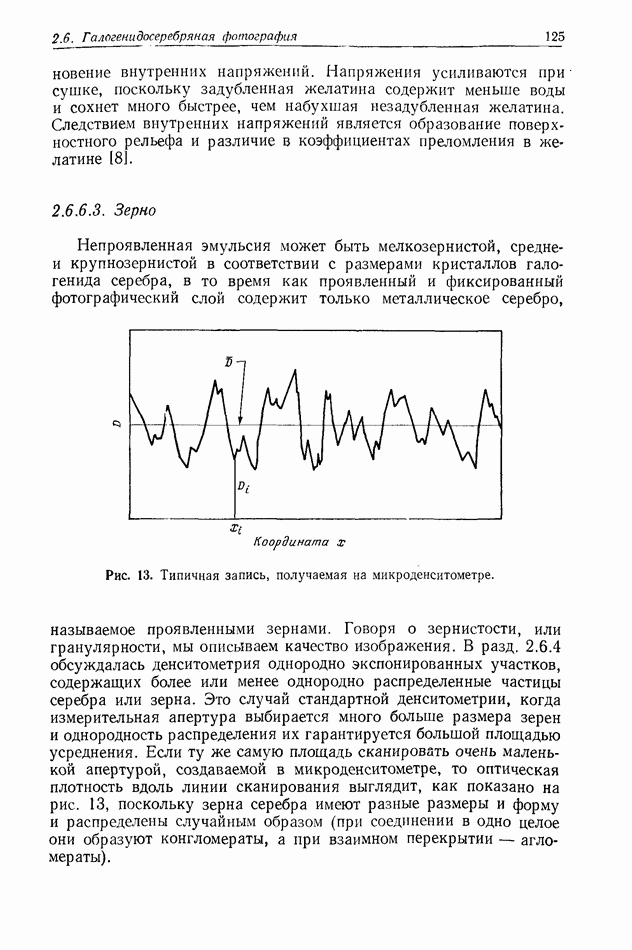
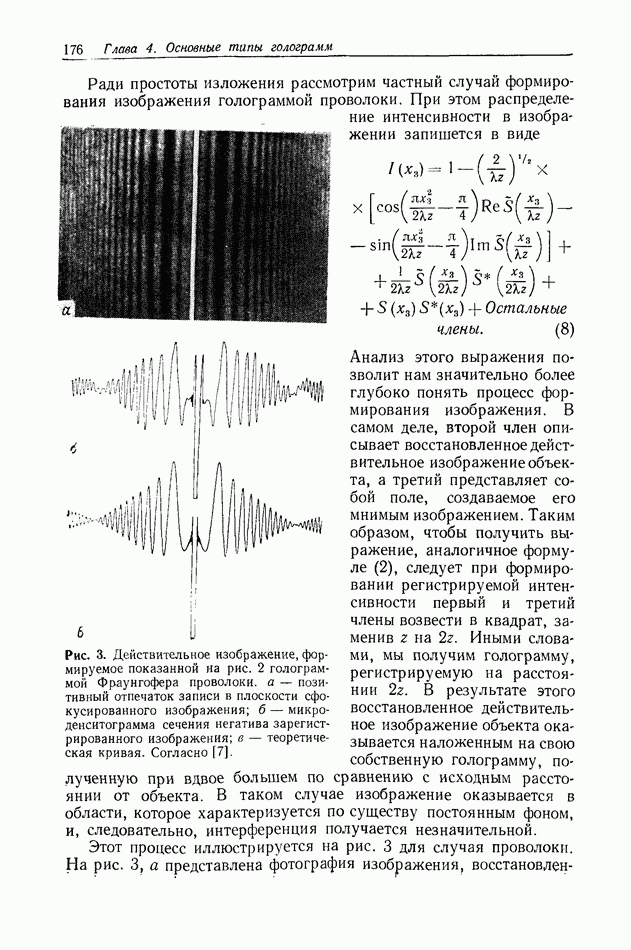
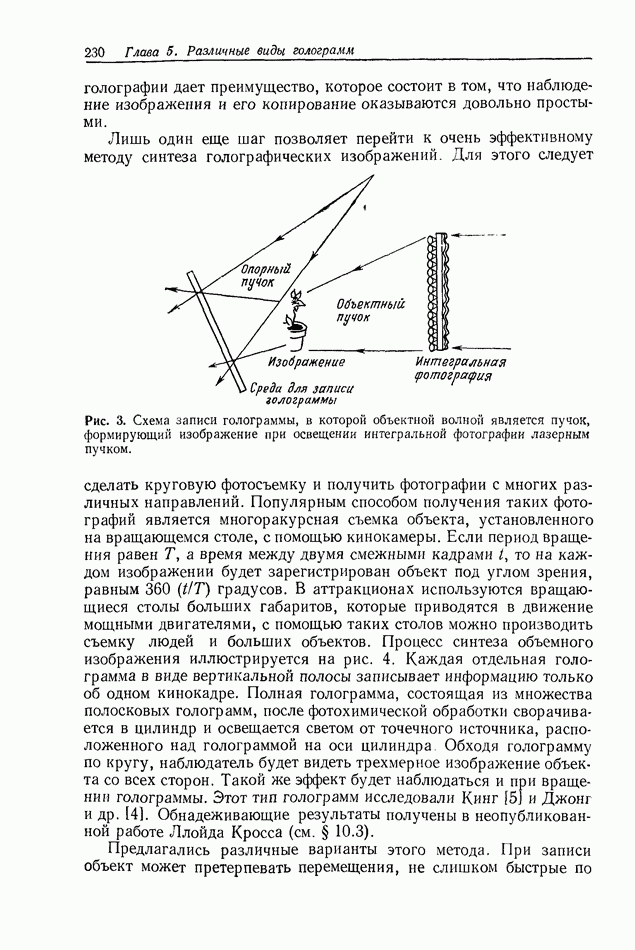
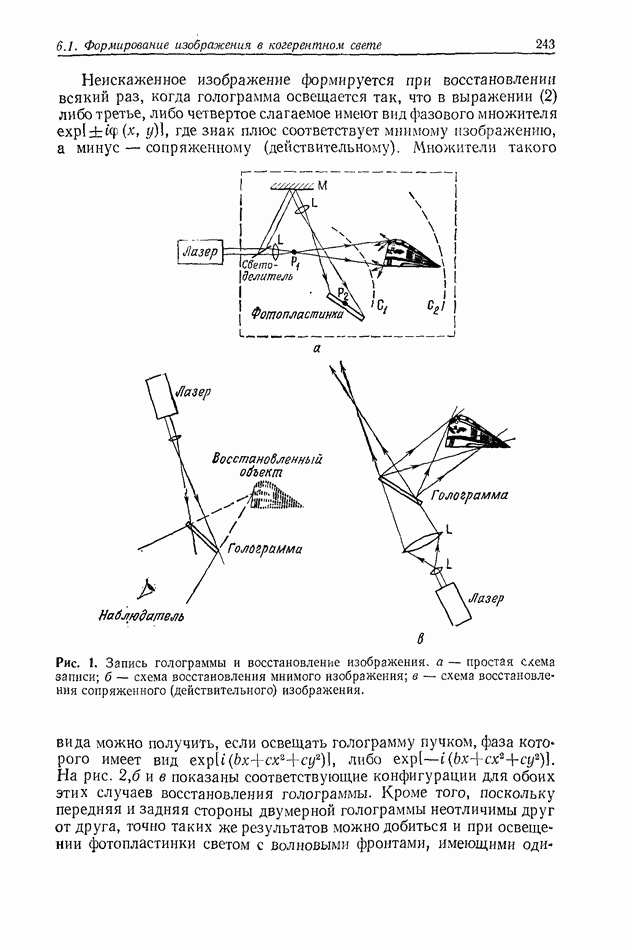
Рис. 1. Графическое представление теоремы выборки в пространственной области,
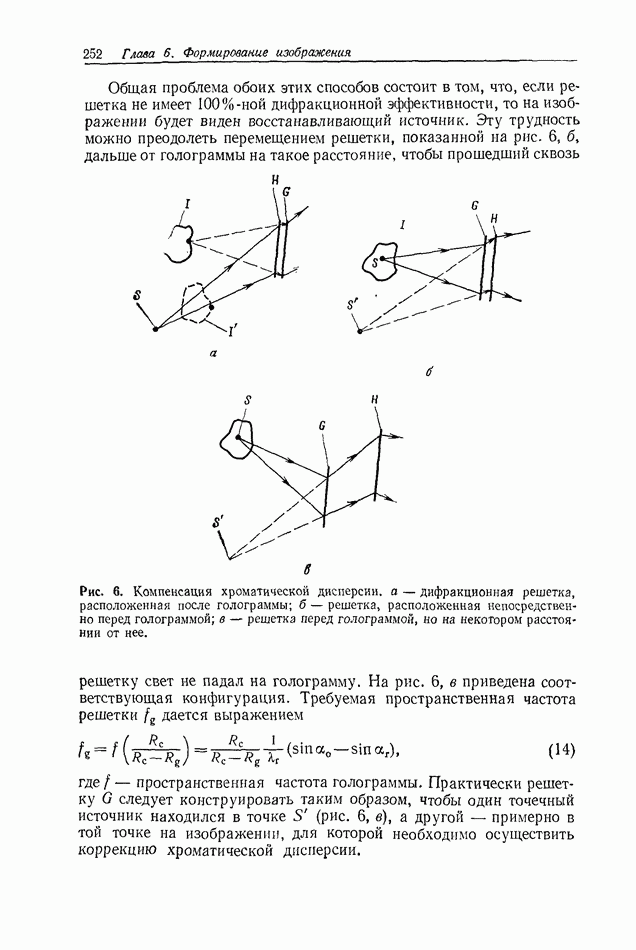
Например, в оптике функция  может быть изображением объекта, ограниченным передаточной характеристикой линзы, или же фотографическим изображением, ограниченным передаточной характеристикой фотоматериала, имеющего конечное разрешение.
может быть изображением объекта, ограниченным передаточной характеристикой линзы, или же фотографическим изображением, ограниченным передаточной характеристикой фотоматериала, имеющего конечное разрешение.
В одномерном случае теорема выборки дается выражением 00

где  интерполяционная функция. Выражение (1) показывает, что для восстановления функции
интерполяционная функция. Выражение (1) показывает, что для восстановления функции  надо найти значения функции в точках выборки
надо найти значения функции в точках выборки  и в каждой из этих точек значение функции
и в каждой из этих точек значение функции  умножить на интерполяционную функцию
умножить на интерполяционную функцию  Графически это соответствует построению функций
Графически это соответствует построению функций  в каждой точке выборки, причем ордината функции
в каждой точке выборки, причем ордината функции  в ючке выборки равна значению функции в этой точке, как показано на рис. 1. Поскольку
в ючке выборки равна значению функции в этой точке, как показано на рис. 1. Поскольку  осцилирующая функция, она не вносит вклада в другие значения ординат выборки.
осцилирующая функция, она не вносит вклада в другие значения ординат выборки.
2.5.2.2, Частотная область
В выражении (1) функция представляет собой сумму (по всем точкам выборки) выборочных значений функции, умноженных на интерполяционную функцию ([17], гл. 2).

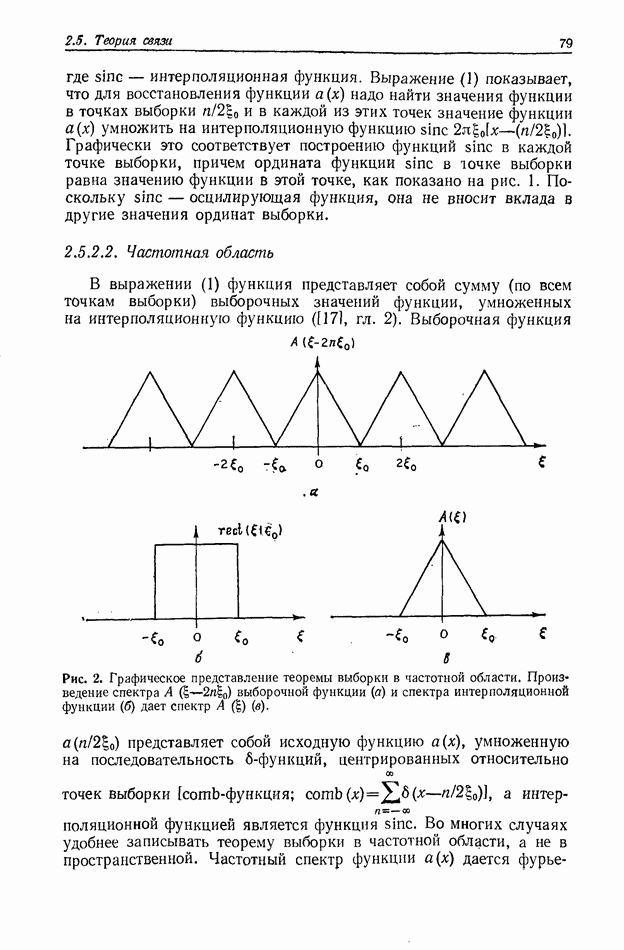
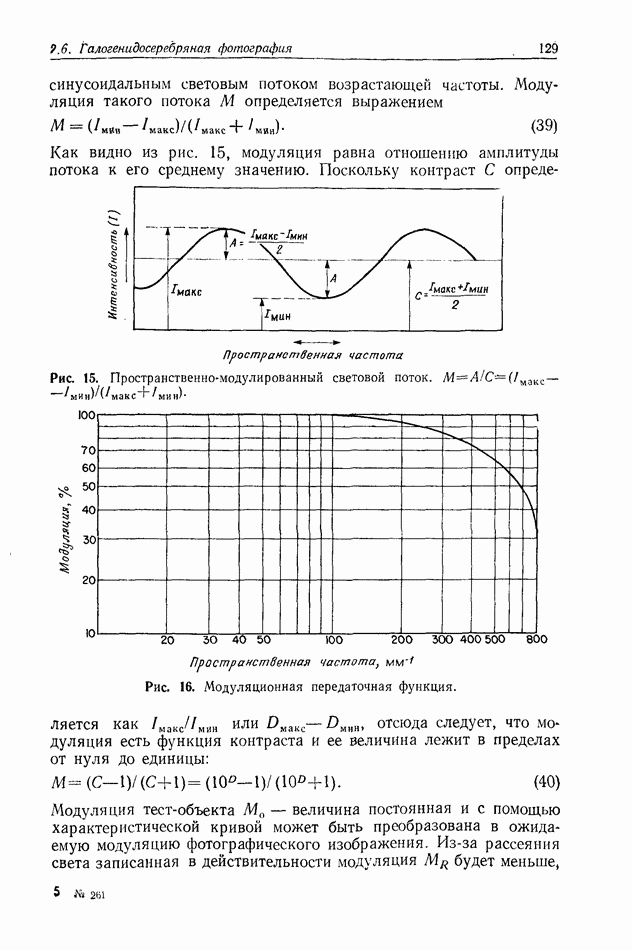
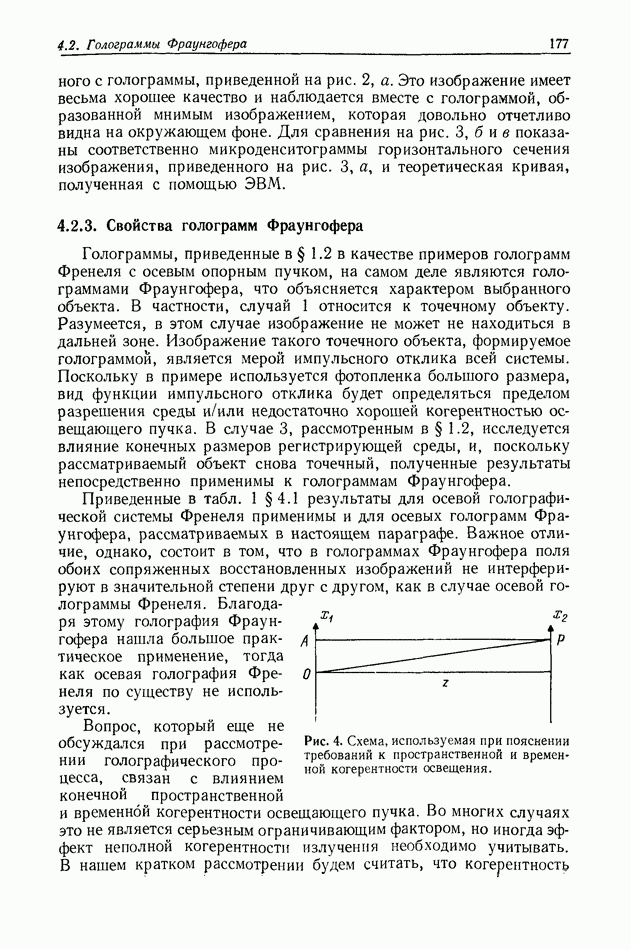
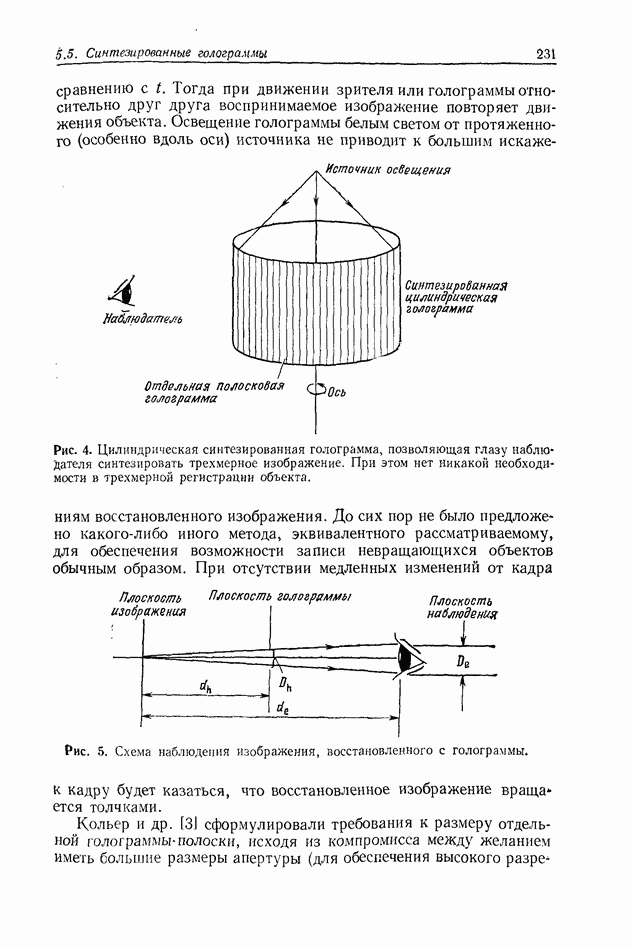
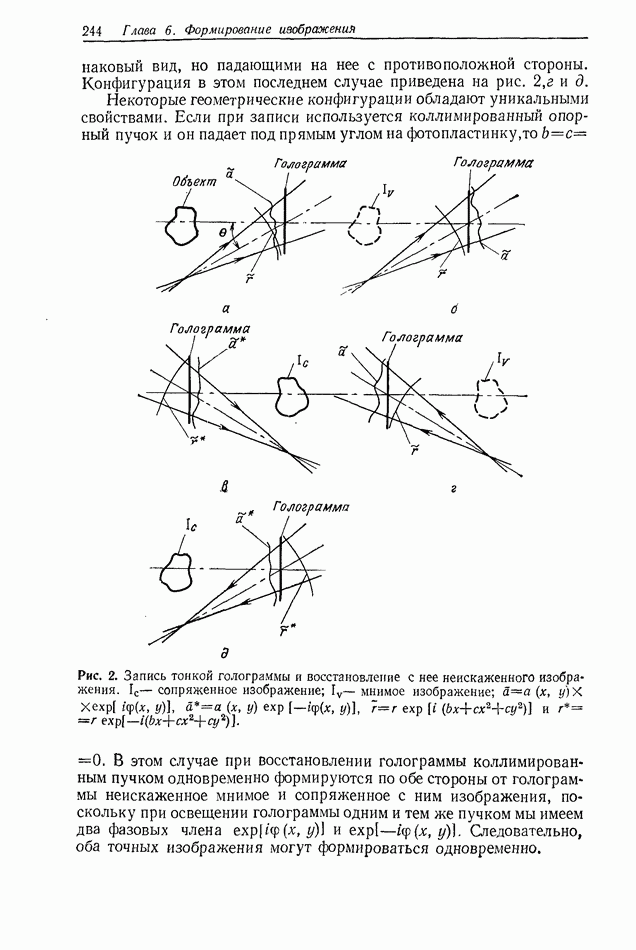
Рис. 2. Графическое представление теоремы выборки в частотной области. Произведение спектра  выборочной функции (а) и спектра интерполяционной функции (б) дает спектр
выборочной функции (а) и спектра интерполяционной функции (б) дает спектр  (в).
(в).
Выборочная функция  представляет собой исходную функцию
представляет собой исходную функцию  умноженную на последовательность
умноженную на последовательность  -функций, центрированных относительно точек выборки
-функций, центрированных относительно точек выборки  -функция;
-функция;  а интерполяционной функцией является функция
а интерполяционной функцией является функция  Во многих случаях удобнее записывать теорему выборки в частотной области, а не в пространственной. Частотный спектр функции
Во многих случаях удобнее записывать теорему выборки в частотной области, а не в пространственной. Частотный спектр функции  дается
дается
фурье-образом выражения (1); при этом выборочная функция состоит из набора  -функций. Спектр Фурье
-функций. Спектр Фурье  функции
функции  представляет собой произведение периодического спектра выборочной функции и прямоугольной функции
представляет собой произведение периодического спектра выборочной функции и прямоугольной функции  размер которой равен полосе частот
размер которой равен полосе частот  функции
функции  Функция
Функция  ведет себя как линейный фильтр; из спектра выборочной функции она выделяет спектр объекта и обеспечивает неискаженное восстановление объекта. Это иллюстрируется графически на рис. 2.
ведет себя как линейный фильтр; из спектра выборочной функции она выделяет спектр объекта и обеспечивает неискаженное восстановление объекта. Это иллюстрируется графически на рис. 2.
2.5.2.3. Критерий выборки и произведение пространства на ширину полосы частот
Для того чтобы в выражении (1) правильно восстановить функцию  координаты выборки должны удовлетворять условию
координаты выборки должны удовлетворять условию

где  расстояние между точками выборок в пространственной области. Выполнение этого условия гарантирует, что периодические спектры на рис. 2, а не будут перекрываться. Если интервал выборки
расстояние между точками выборок в пространственной области. Выполнение этого условия гарантирует, что периодические спектры на рис. 2, а не будут перекрываться. Если интервал выборки  меньше чем
меньше чем  то спектры на рис. 2, а дальше отстоят друг от друга, и функция может быть восстановлена, хотя для этого приходится использовать большее число точек выборки. Если интервал выборки
то спектры на рис. 2, а дальше отстоят друг от друга, и функция может быть восстановлена, хотя для этого приходится использовать большее число точек выборки. Если интервал выборки  больше
больше  то спектры на рис. 2, а перекрываются, и функция не может быть восстановлена полностью.
то спектры на рис. 2, а перекрываются, и функция не может быть восстановлена полностью.
На практике суммирование в выражении (1) осуществляется не в бесконечных пределах от  до
до  а от
а от  до
до  т. е. в
т. е. в  точках выборки. Более того, условие (2) справедливо для каждой точки выборки.
точках выборки. Более того, условие (2) справедливо для каждой точки выборки.
Произведение  т. е. полного числа точек выборки на полосу частот функции (которая определяет интервал выборки), называют одномерным произведением пространства на ширину полосы частот рассматриваемой части функции.
т. е. полного числа точек выборки на полосу частот функции (которая определяет интервал выборки), называют одномерным произведением пространства на ширину полосы частот рассматриваемой части функции.
2.5.2.4. Двумерная теорема выборки
Теорему выборки нетрудно обобщить и на двумерный случай. Для двумерного случая в прямоугольной системе координат выражение (1) принимает вид

где  граничные частоты соответственно по осям
граничные частоты соответственно по осям  фурье-образа функции
фурье-образа функции  . В случае двумерных функций с осевой симметрией при выборке используют функции Бесселя первого рода;
. В случае двумерных функций с осевой симметрией при выборке используют функции Бесселя первого рода;
при этом мы имеем [7]

где 
2.5.2.5. Примеры
Хорошо известными процессами, в которых используются принципы выборки, являются полутоновая обработка фотографий, передача и воспроизведение факсимиле и телевизионных изображений. В этих применениях совместно используют электронные и оптические принципы, которые позволяют при ограниченной полосе частот получить оптимальное воспроизведение информации.
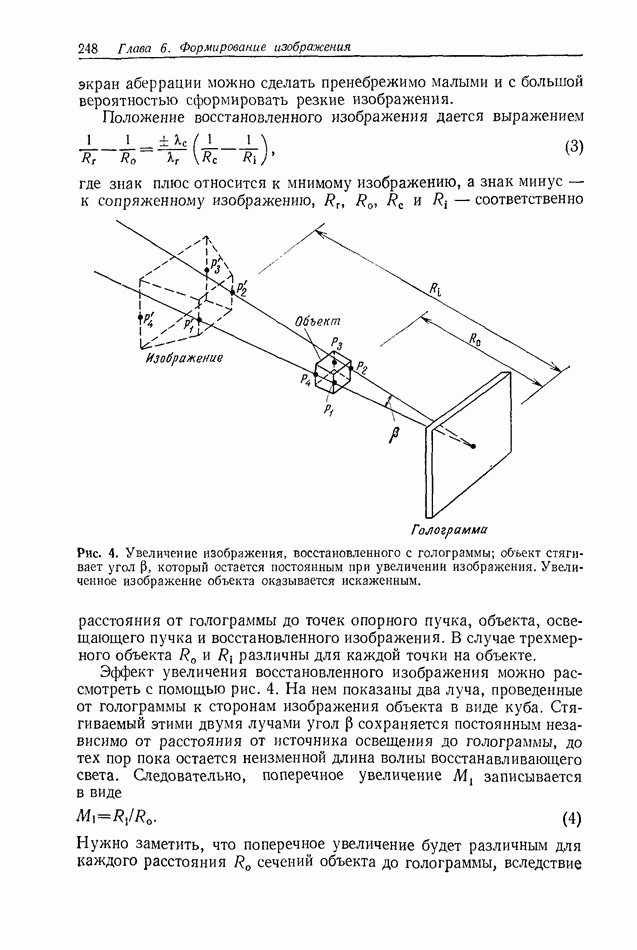
К другим примерам, в которых выборка используется как основной процесс, можно отнести электрооптические сканирующие системы [2, 4]. В этом случае входная информация на фотопленке имеет дополнительное ограничение по частоте благодаря апертуре дифракционно-ограниченной оптической сканирующей системы. Интервал выборки в пространственной области обратно пропорционален ширине полосы частот системы (как и в случае линзы с квадратной апертурой):

где d - апертура,  фокусное расстояние линзы. Размеры апертуры можно менять, в то время как скорость сканирования сохраняется постоянной; таким образом, количество поступающей информации обусловливается размерами апертуры. Интервал электронной выборки определяется выражением (5) и скоростью сканирования.
фокусное расстояние линзы. Размеры апертуры можно менять, в то время как скорость сканирования сохраняется постоянной; таким образом, количество поступающей информации обусловливается размерами апертуры. Интервал электронной выборки определяется выражением (5) и скоростью сканирования.
Теорема выборки используется также при модуляционной записи изображений [13]. В этом процессе полоса частот изображения ограничивается линзой и выборка осуществляется с помощью дифракционной решетки, причем интервал выборки задается периодом решетки.
Для записи нескольких изображений на одном участке фотоматериала можно использовать принцип угловой модуляции. В промежутке между экспонированием решетка поворачивается на угол

где  полоса частот отдельного изображения, а
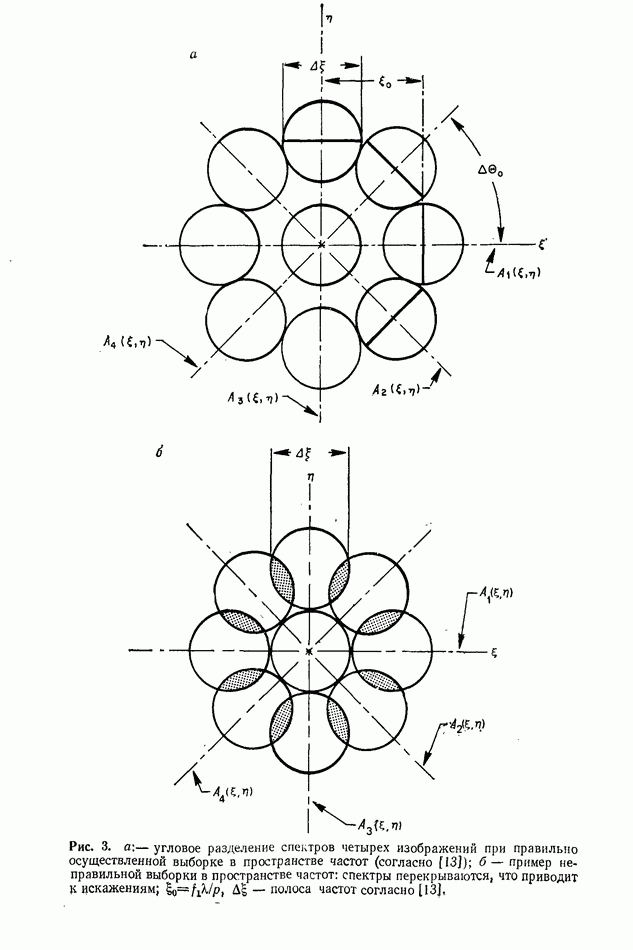
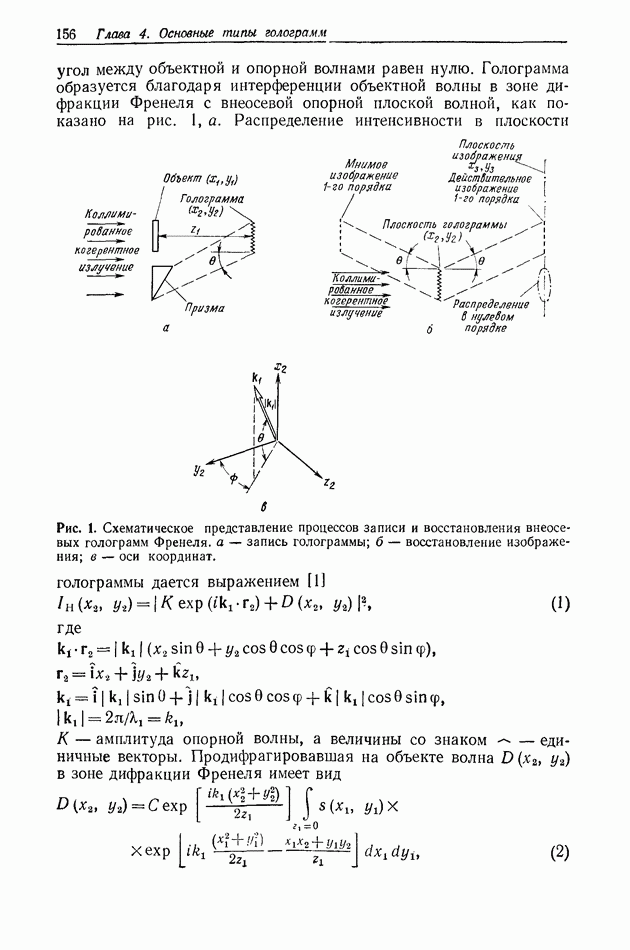
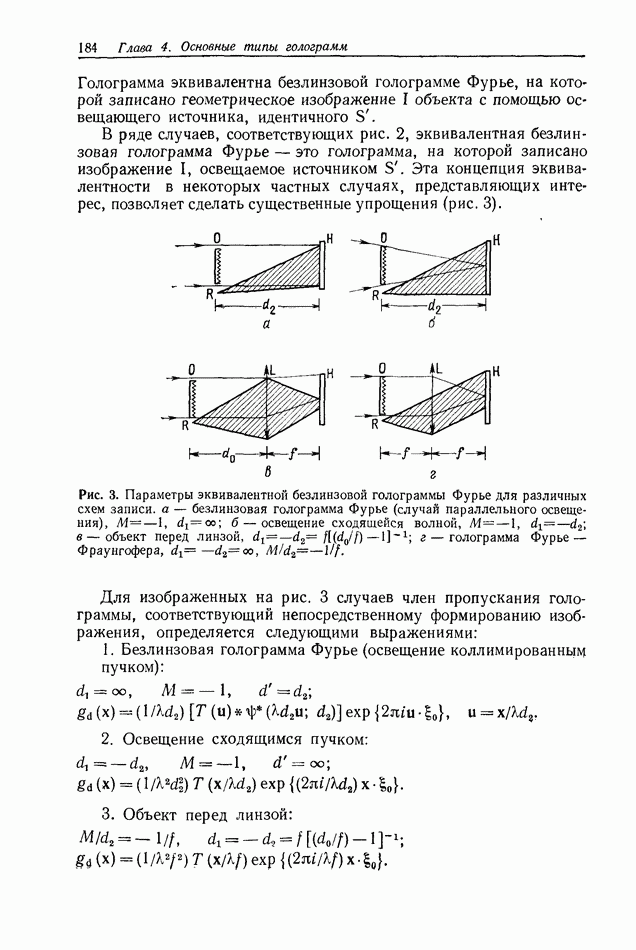
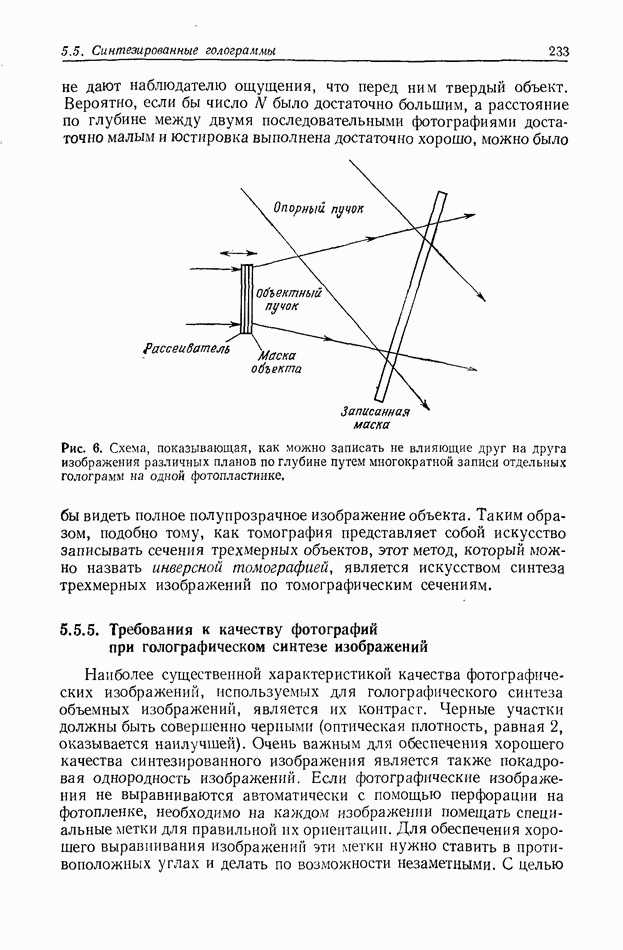
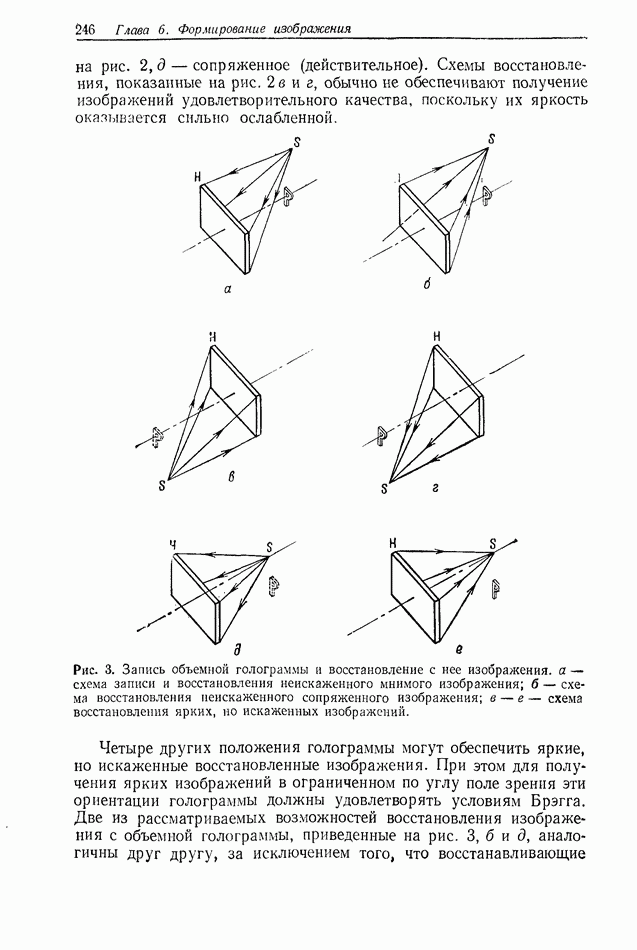
полоса частот отдельного изображения, а  частота выборки. Угол, определяемый выражением (6), обеспечивает пространственное разделение спектров изображения, как показано на рис. 3, а. Записанные таким образом изображения можно раздельно
частота выборки. Угол, определяемый выражением (6), обеспечивает пространственное разделение спектров изображения, как показано на рис. 3, а. Записанные таким образом изображения можно раздельно

(кликните для просмотра скана)
восстановить в когерентной оптической системе, устанавливая в частотной плоскости оптической системы фильтр-маску, который выделяет спектр, соответствующий изображению.
Если интервал выборки взят слишком большим, то при восстановлении изображения возникает определенное искажение, связанное с перекрытием спектров, как показано на рис. 3, б.
В плоскости восстановления искажение выделенного фильтром изображения обусловлено присутствием высокочастотных компонент спектров от соседних изображений.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
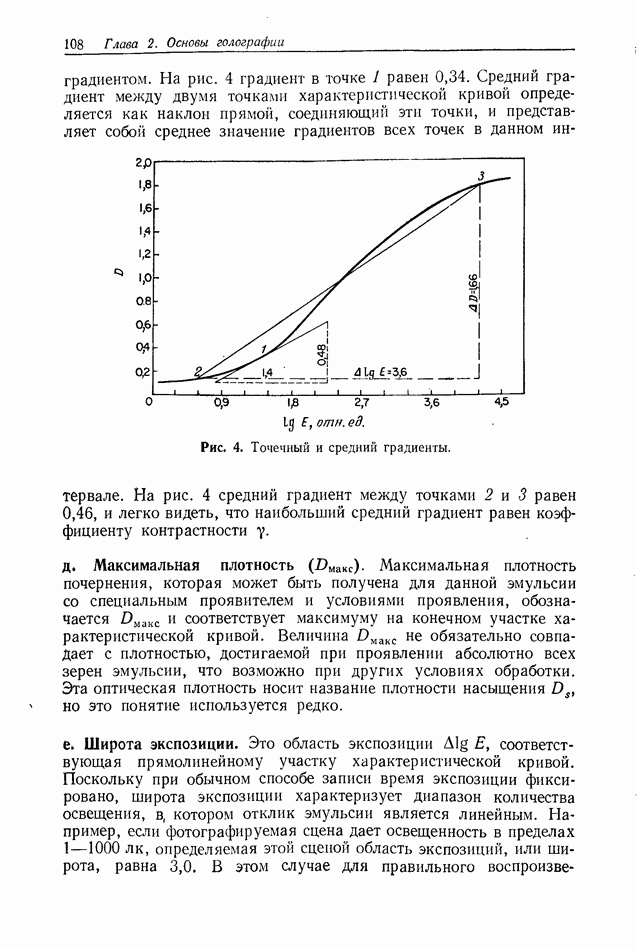
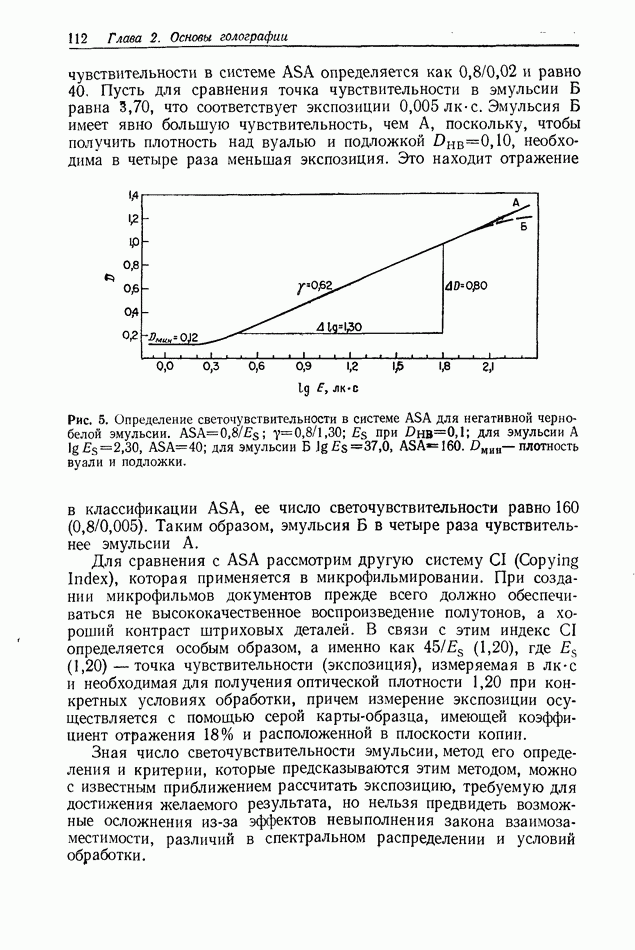
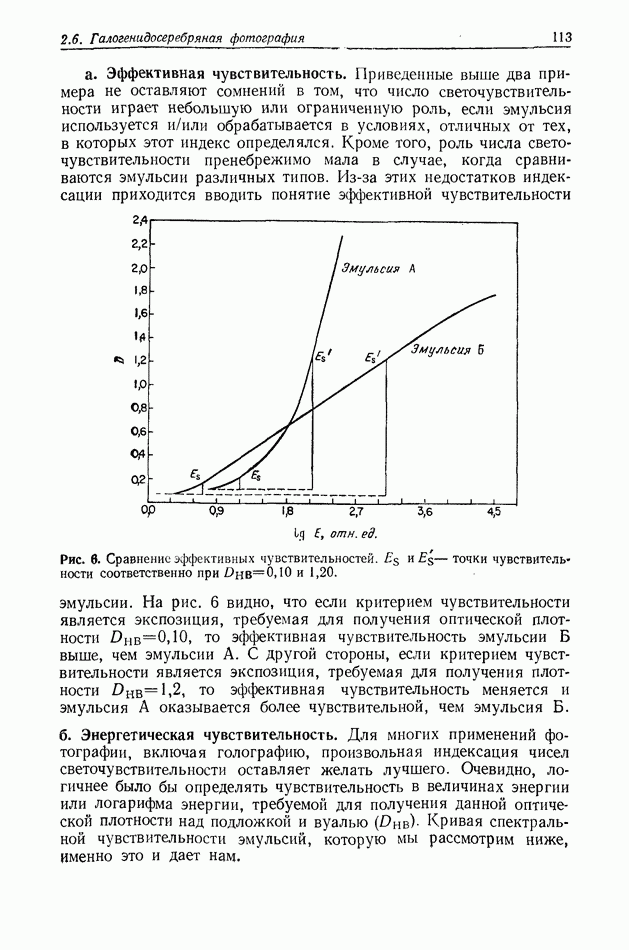
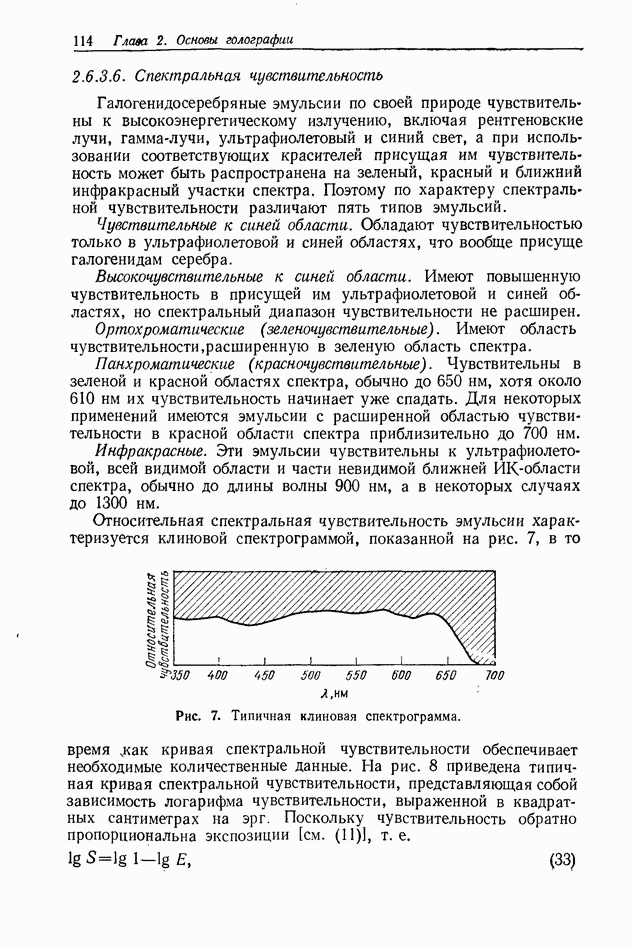
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
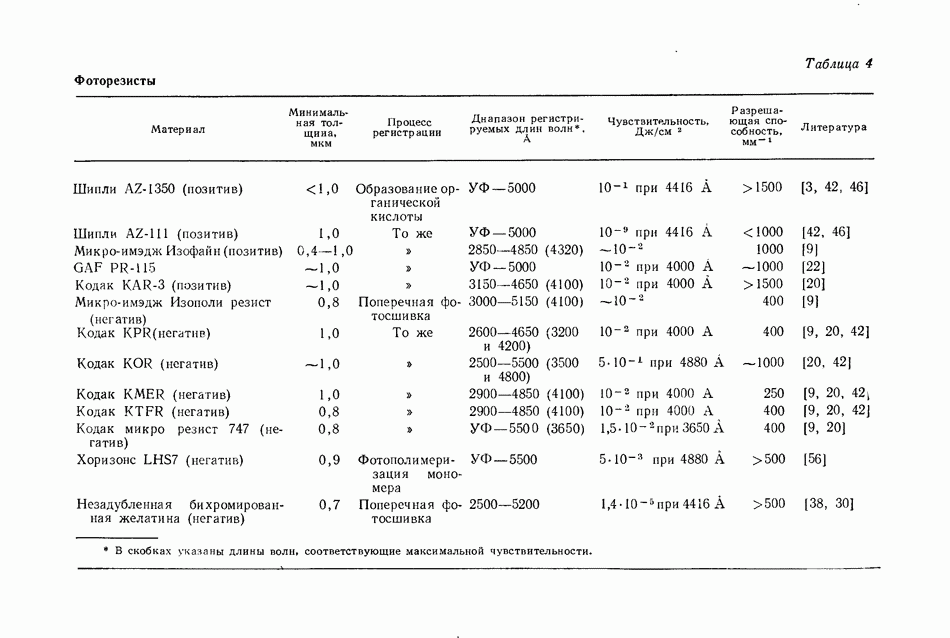
- 8.3.5. Фоторезисты
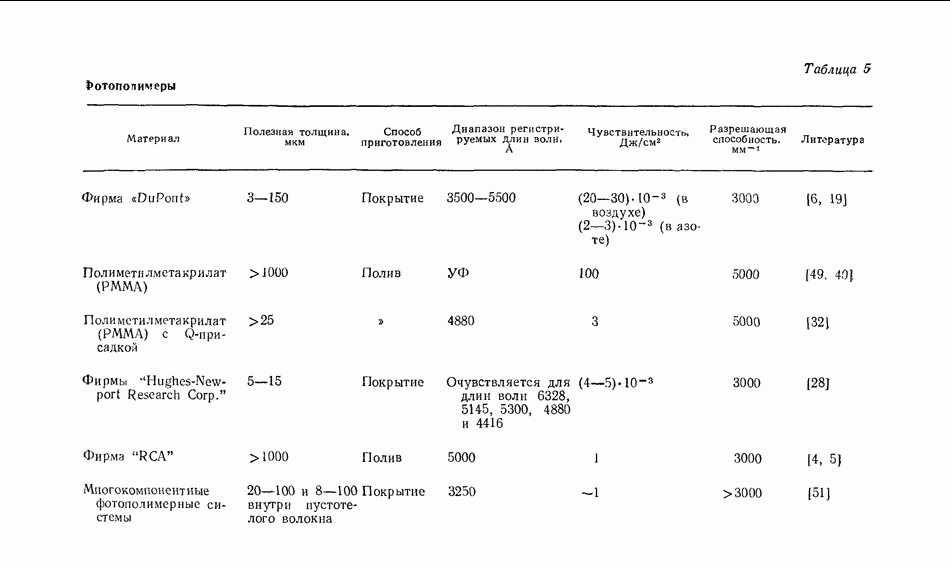
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
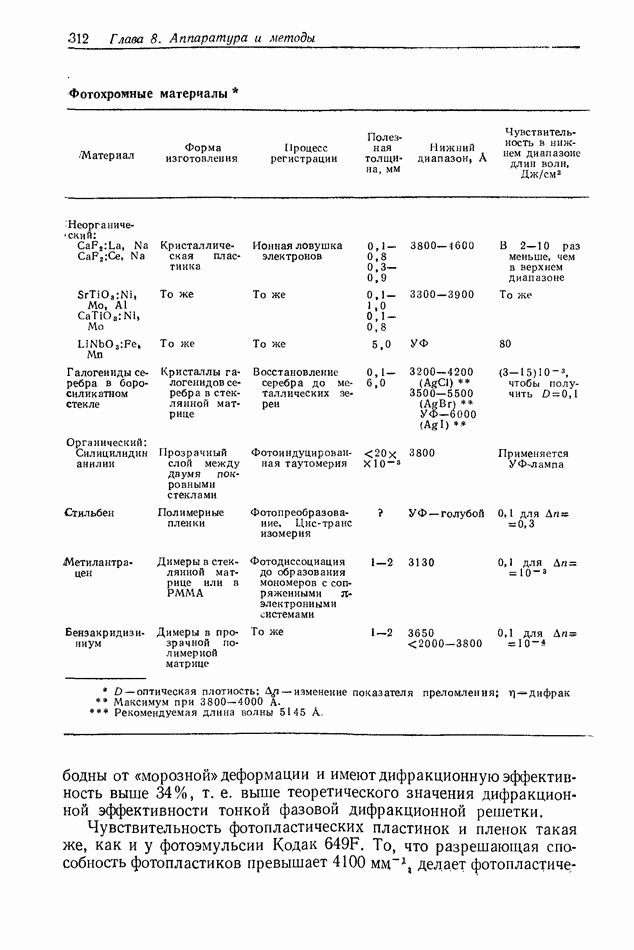
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
- 8.4.5. Голографическая корреляция
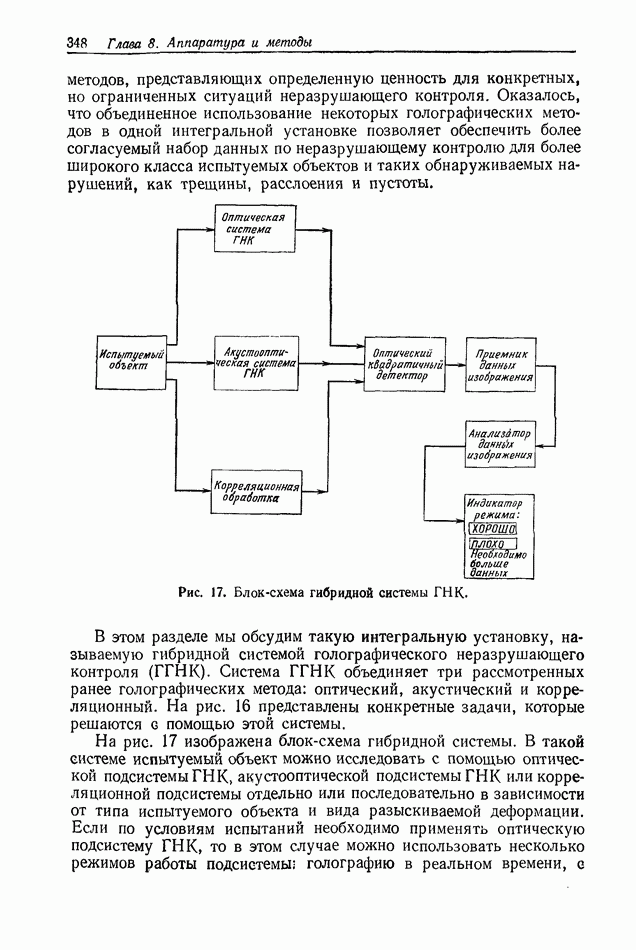
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
- 8.4.7. Голография движущихся объектов
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение