| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
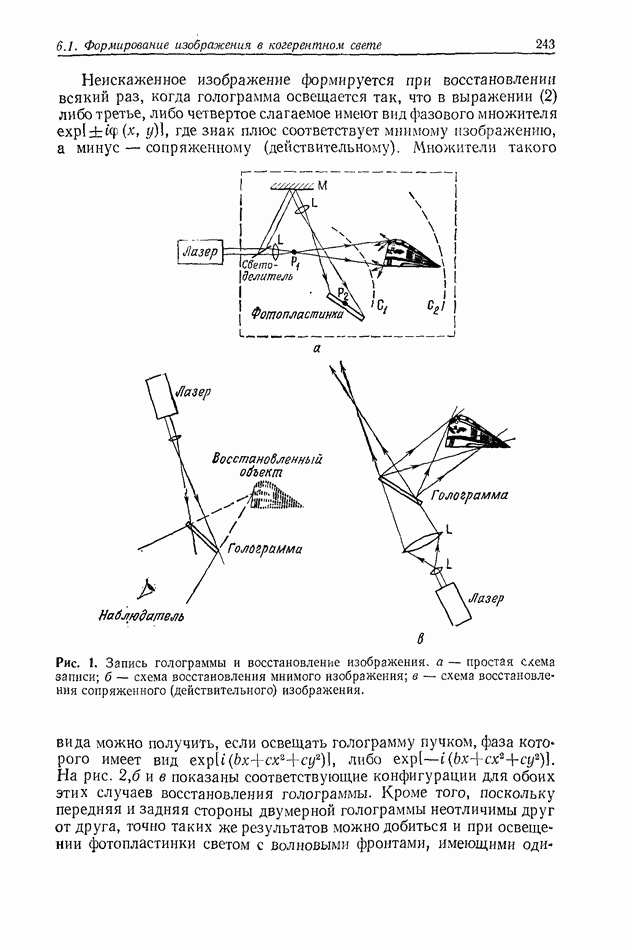
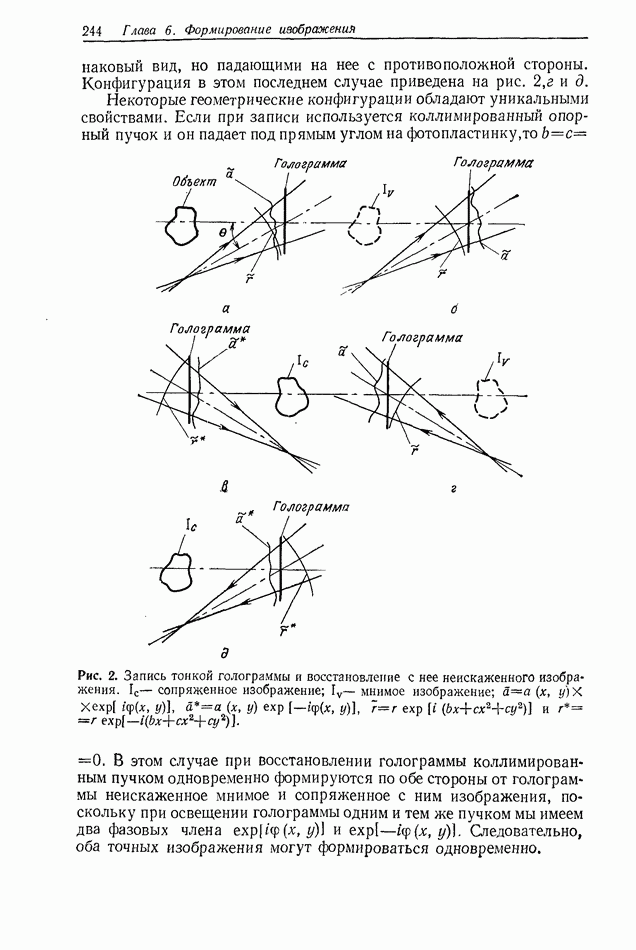
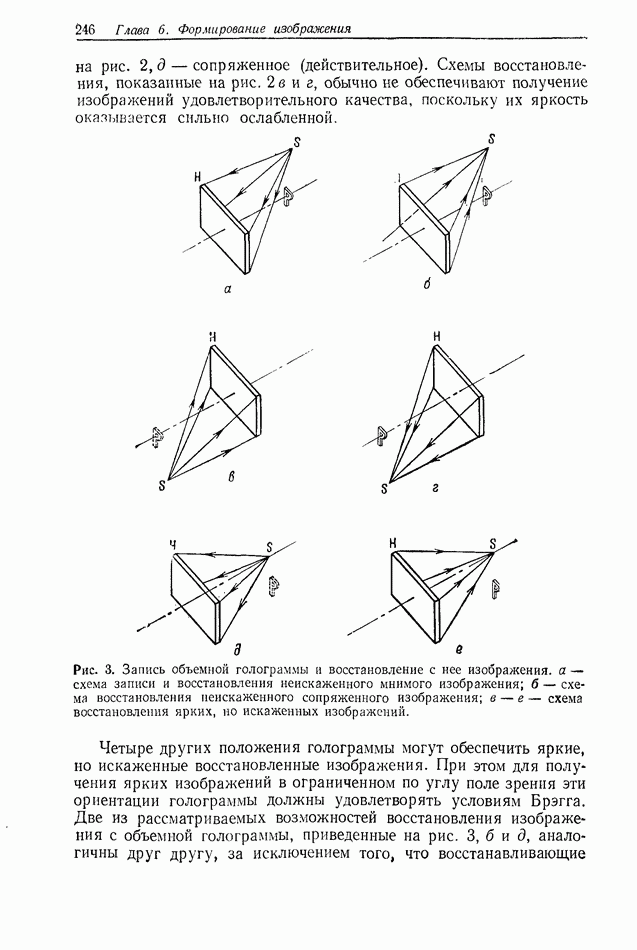
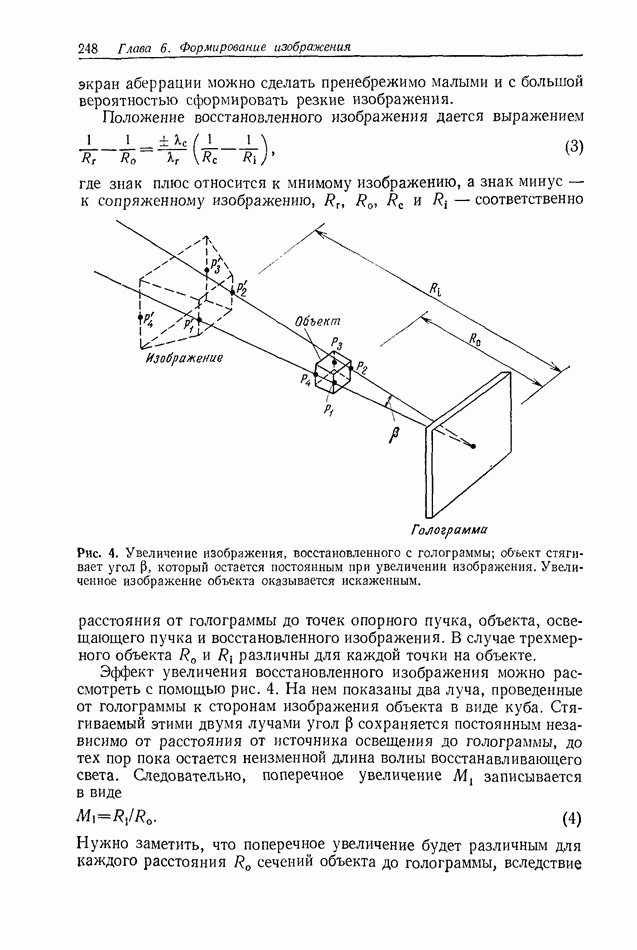
Результаты, рассмотренные в предыдущем разделе, описывают ситуацию, в которой свет исходит из двух идеальных точечных Источников. В действительности точечные источники представляют
собой обычно отверстия (апертуры) конечных размеров. Теперь следовало бы задать вопрос о том, какое влияние оказывают эти конечные апертуры, т. е. как когерентный свет распространяется через отверстие.
В начале разд. 2.2.2 мы привели волновое уравнение в виде (176), описывающее распространение комплексной амплитуды, а также записали выражения для плоской и сферической волн.

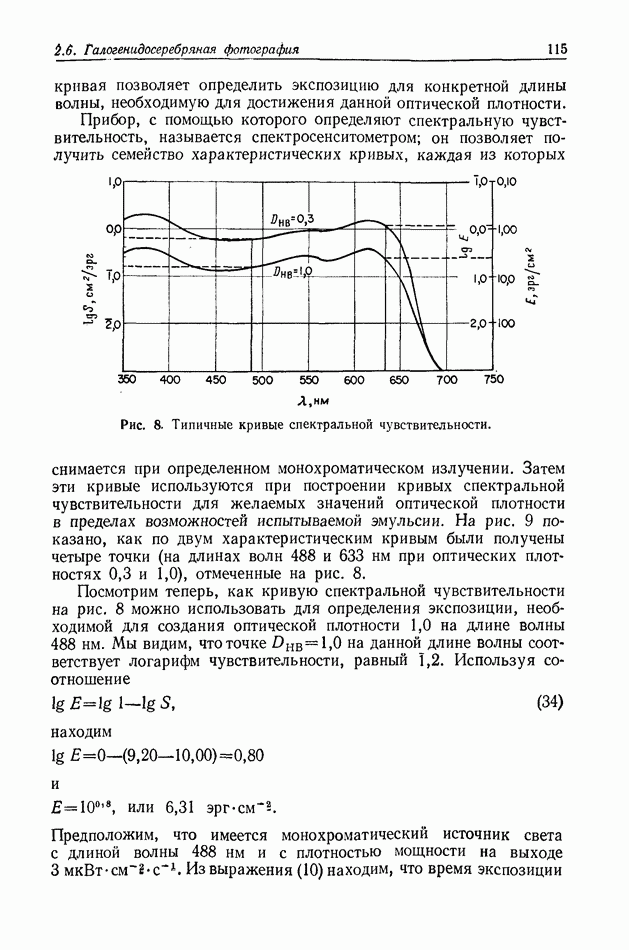
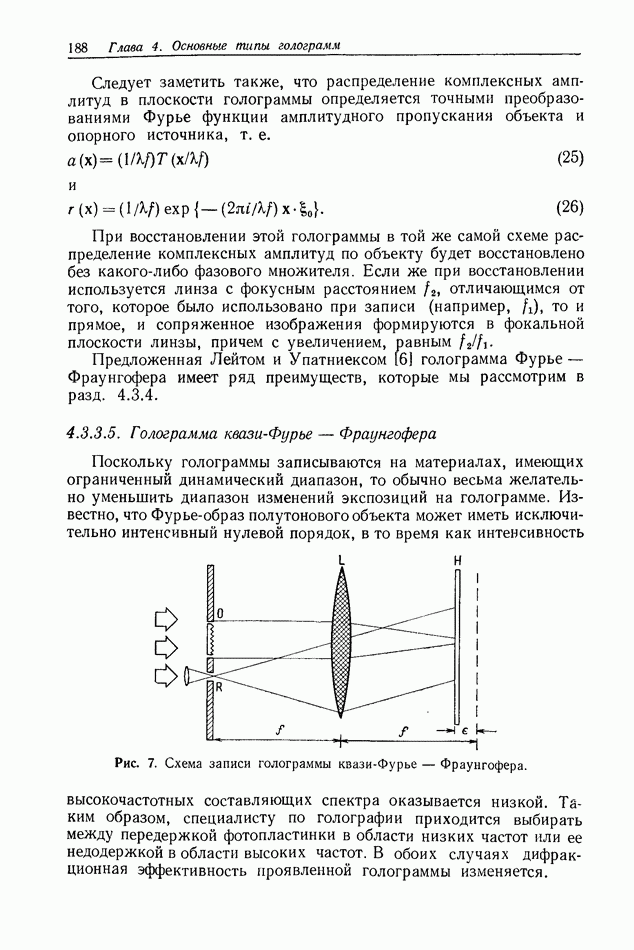
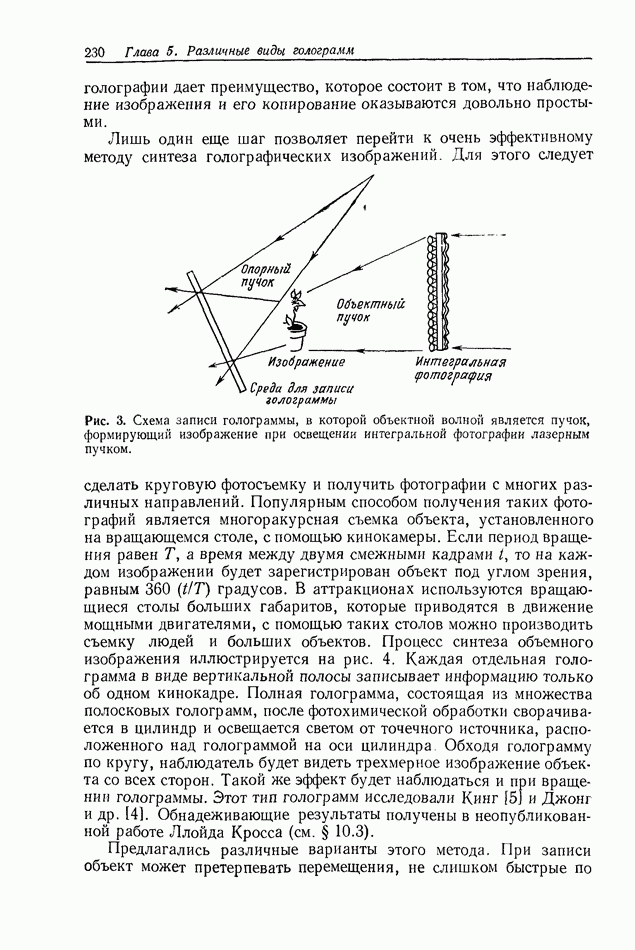
Рис. 7. к определению координат при прохождении света через отверстие произвольной формы.
Теперь мы хотим применить эти решения в задаче о распространении света через отверстие. На рис. 7 показана интересующая нас система с соответствующими координатами. Свет от очень маленького источника (который можно считать точечным), расположенного в точке  на плоскости
на плоскости  освещает плоскость апертуры
освещает плоскость апертуры  и затем распространяется к плоскости наблюдения
и затем распространяется к плоскости наблюдения  Найдем значение комплексной амплитуды в точке
Найдем значение комплексной амплитуды в точке  плоскости
плоскости  Если углы малы, то дифракцию можно описать следующим интегралом:
Если углы малы, то дифракцию можно описать следующим интегралом:

где А — постоянная,  расстояния, указанные на рис.
расстояния, указанные на рис.  элементарная площадка в плоскости апертуры в некоторой произвольной точке
элементарная площадка в плоскости апертуры в некоторой произвольной точке  Выражение (32) представляет собой дифракционную формулу Кирхгофа для случая скалярной волны и подробно рассмотрено во многих учебниках (например, [11). Однако его физический смысл можно легко объяснить следующим образом: точечный источник, расположенный в точке
Выражение (32) представляет собой дифракционную формулу Кирхгофа для случая скалярной волны и подробно рассмотрено во многих учебниках (например, [11). Однако его физический смысл можно легко объяснить следующим образом: точечный источник, расположенный в точке  излучает сферическую волну
излучает сферическую волну  и заполняет ею всю апертуру, которая в свою очередь вырезает часть сферической волны. В апертуре каждая точка волнового фронта становится новым источником расходящихся сферических волн вида
и заполняет ею всю апертуру, которая в свою очередь вырезает часть сферической волны. В апертуре каждая точка волнового фронта становится новым источником расходящихся сферических волн вида  затем берется интеграл по всем таким точкам
затем берется интеграл по всем таким точкам  в плоскости апертуры. Формулу (32) можно теперь
в плоскости апертуры. Формулу (32) можно теперь

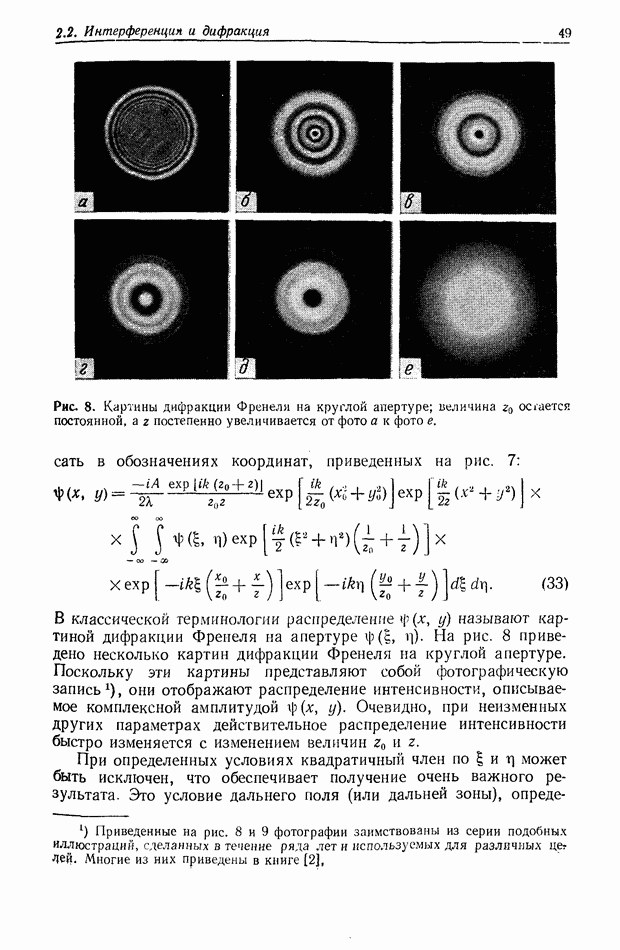
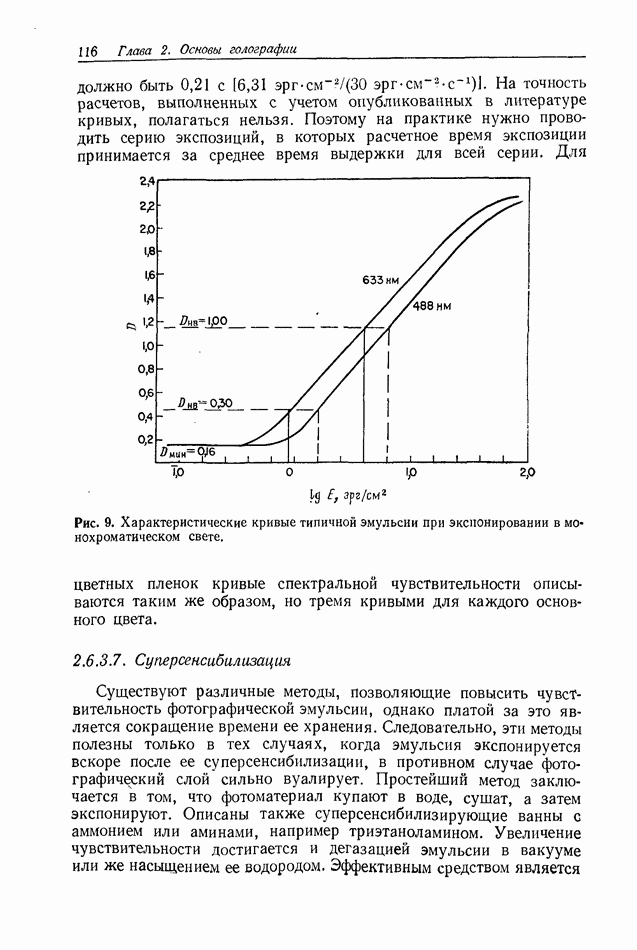
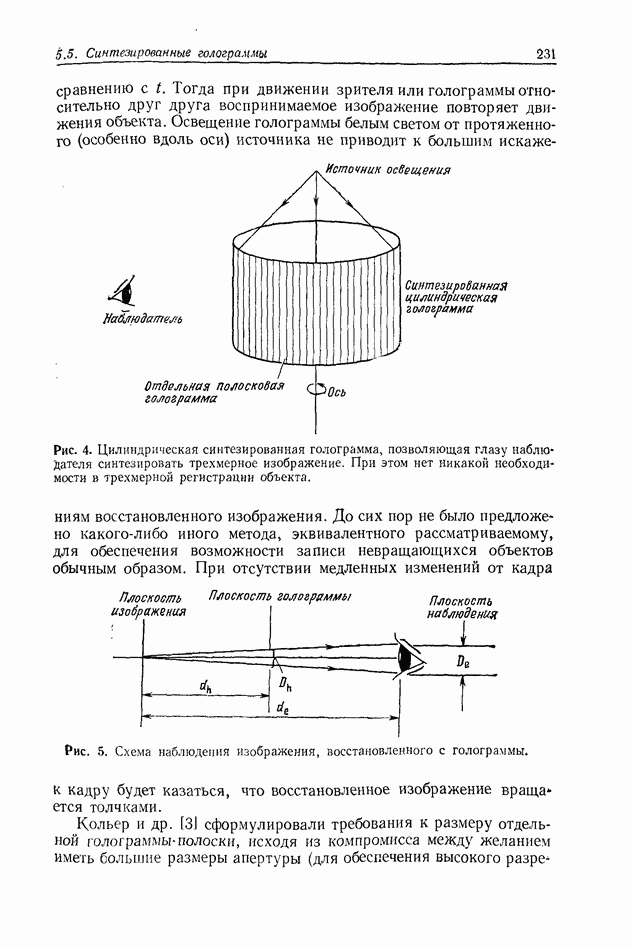
Рис. 8. Картины дифракции Френеля на круглой апертуре; величина  остается постоянной, а
остается постоянной, а  постепенно увеличивается от фото а к фото
постепенно увеличивается от фото а к фото 
переписать в обозначениях координат, приведенных на рис. 7:

В классической терминологии распределение  называют картиной дифракции Френеля на апертуре
называют картиной дифракции Френеля на апертуре  На рис. 8 приведено несколько картин дифракции Френеля на круглой апертуре. Поскольку эти картины представляют собой фотографическую запись, они отображают распределение интенсивности, описываемое комплексной амплитудой
На рис. 8 приведено несколько картин дифракции Френеля на круглой апертуре. Поскольку эти картины представляют собой фотографическую запись, они отображают распределение интенсивности, описываемое комплексной амплитудой  Очевидно, при неизменных Других параметрах действительное распределение интенсивности быстро изменяется с изменением величин
Очевидно, при неизменных Других параметрах действительное распределение интенсивности быстро изменяется с изменением величин 
При определенных условиях квадратичный член по  может быть исключен, что обеспечивает получение очень важного результата. Это условие дальнего поля (или дальней зоны),
может быть исключен, что обеспечивает получение очень важного результата. Это условие дальнего поля (или дальней зоны),
определяемое парой следующих неравенств:

При выполнении этих условий интересующие нас расстояния  по существу оказываются бесконечно большими. Таким образом, комплексную амплитуду можно записать в виде
по существу оказываются бесконечно большими. Таким образом, комплексную амплитуду можно записать в виде

где  а постоянная С содержит множество постоянных и фазовых членов, не входящих в интеграл. Однако эти фазовые члены имеют определенное значение при голографической записи, и о них не следует забывать.
а постоянная С содержит множество постоянных и фазовых членов, не входящих в интеграл. Однако эти фазовые члены имеют определенное значение при голографической записи, и о них не следует забывать.
Выражение (35) описывает дифракцию Фраунгофера, в которой имеет место постоянная функциональная связь между апертурной функцией  и полем
и полем  . В данном случае
. В данном случае  образуют пару функций, связанных преобразованием Фурье. Таким образом, в классической дифракции Фраунгофера распределение комплексных амплитуд есть фурье-образ апертурной функции.
образуют пару функций, связанных преобразованием Фурье. Таким образом, в классической дифракции Фраунгофера распределение комплексных амплитуд есть фурье-образ апертурной функции.
Часто экспериментальные значения величин, удовлетворяющих выполнению неравенств (34), достигаются освещением апертуры светом от точечного источника, удаленного на бесконечность (или использованием коллимированного пучка, формируемого линзой). При этих условиях выражение (35) для дифракции Фраунгофера принимает вид

при этом предполагается, что точечный источник расположен на оптической оси и, следовательно, квадратичный член по  обращается в нуль.
обращается в нуль.
Картину дифракции Фраунгофера можно также отобразить с помощью линзы, дающей изображение дальнего поля. Поскольку это поле находится на бесконечности, картина дифракции Фраунгофера локализуется в фокальной плоскости линзы. Кроме того, если апертурная функция расположена в передней фокальной плоскости линзы, обращается в нуль и квадратичный член по х и у. Таким образом, распределение комплексных амплитуд запишется в виде


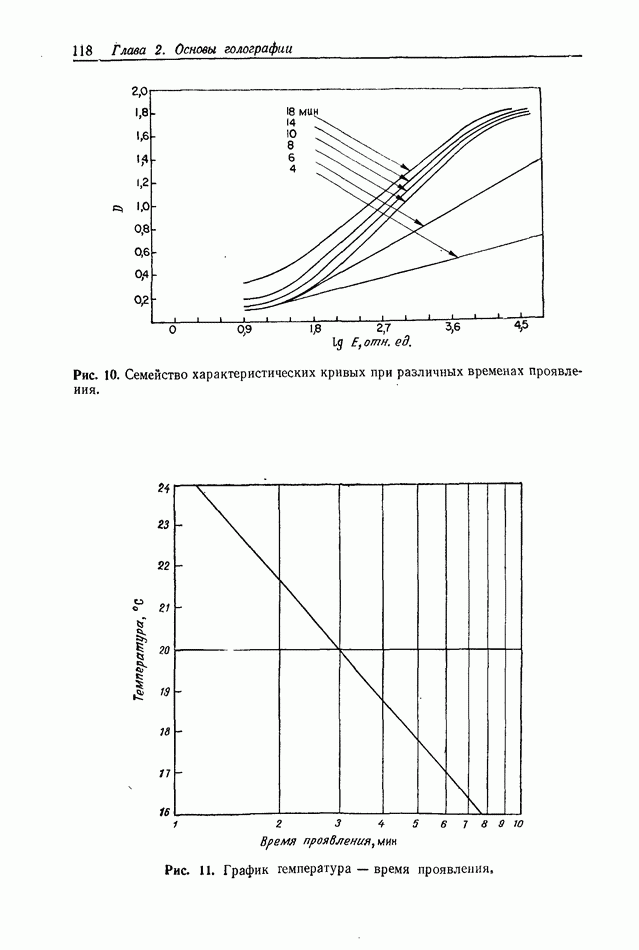
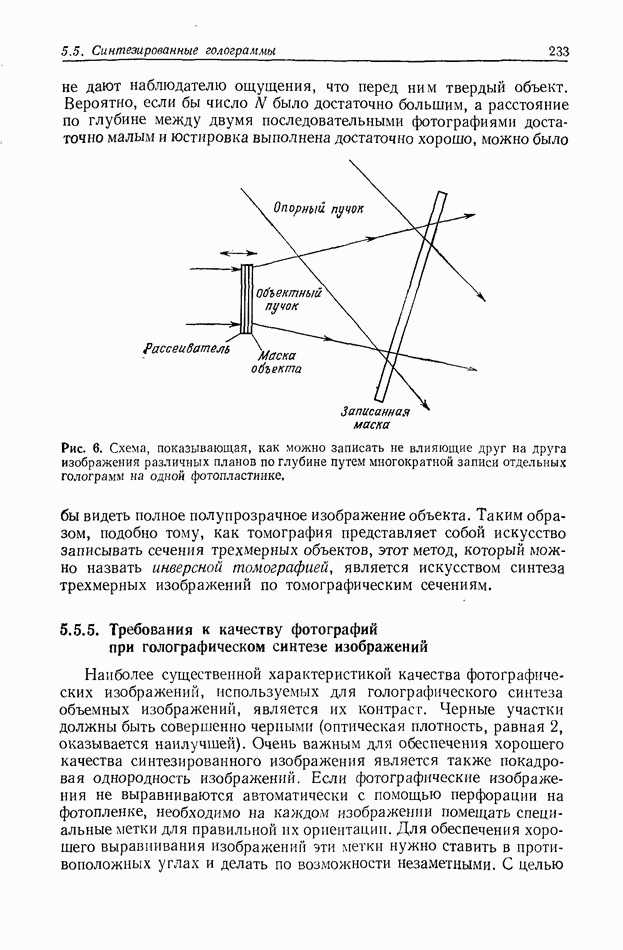
Рис. 9. Картины дифракции Фраунгофера на некоторых апертурах, показанных под каждым фото.
где  фокусное расстояние линзы,
фокусное расстояние линзы,  постоянная. Очевидно, что смещение плоскости наблюдения из фокальной плоскости приводит к появлению дифракции Френеля.
постоянная. Очевидно, что смещение плоскости наблюдения из фокальной плоскости приводит к появлению дифракции Френеля.
Целесообразно рассмотреть выражение (37) для некоторых конкретных функций  В одних случаях решения можно получить аналитически в компактном виде, в других же интегрирование должно выполняться численными методами. Хорошо известны играющие важную роль соотношения, которые описывают дифракцию на прямоугольной апертуре высотой
В одних случаях решения можно получить аналитически в компактном виде, в других же интегрирование должно выполняться численными методами. Хорошо известны играющие важную роль соотношения, которые описывают дифракцию на прямоугольной апертуре высотой  и шириной 2а. При этом распределение комплексных амплитуд в картине дифракции Фраунгофера дается выражением
и шириной 2а. При этом распределение комплексных амплитуд в картине дифракции Фраунгофера дается выражением

где  Чтобы в начале координат функция
Чтобы в начале координат функция  была равна единице, т. е.
была равна единице, т. е.  выражение (38) часто нормируют, однако при этом можно потерять информацию о том, что в постоянный сомножитель входит площадь дифрагирующей апертуры. Нули функции
выражение (38) часто нормируют, однако при этом можно потерять информацию о том, что в постоянный сомножитель входит площадь дифрагирующей апертуры. Нули функции  равномерно распределены вдоль осей
равномерно распределены вдоль осей  и отстоят друг от друга на расстояниях соответственно
и отстоят друг от друга на расстояниях соответственно  На рис. 9, а показана фотографическая запись распределения
На рис. 9, а показана фотографическая запись распределения
интенсивности в картине дифракции Фраунгофера на прямоугольной апертуре вместе с самой апертурой. Взаимное соотношение между апертурой и дифракционной картиной очевидно. Особенностью здесь является то, что картина симметрична относительно обеих осей и имеется ряд непрерывных линий нулевой интенсивности, пересекающих ее в двух взаимно перпендикулярных направлениях. В результате этого образуются изолированные площадки интенсивности, в пределах каждой из которых фаза постоянна, однако при переходе интенсивности через нуль фаза меняется на 180°. Таким образом, в данном поле присутствуют лишь два значения фазы, что обусловлено симметрией апертурной функции (она обладает центральной симметрией). И наоборот, апертуры, не имеющие центральной симметрии, такие, как треугольная апертура (рис. 9, в), имеют преобразования Фурье с непрерывно изменяющейся фазой от  до
до  рад. К тому же картина дифракции от треугольной апертуры не может быть описана аналитически в компактном виде.
рад. К тому же картина дифракции от треугольной апертуры не может быть описана аналитически в компактном виде.
Картина дифракции от круглой апертуры диаметром 2а обладает круговой симметрией и описывается аналитически в радиальных координатах  следующим образом:
следующим образом:

где  функция Бесселя первого рода первого порядка. Поскольку круглая апертура также обладает центральной симметрией, то в пределах центрального диска фаза однородна и равна 0, а фаза колец меняется, принимая поочередно значения
функция Бесселя первого рода первого порядка. Поскольку круглая апертура также обладает центральной симметрией, то в пределах центрального диска фаза однородна и равна 0, а фаза колец меняется, принимая поочередно значения  и т. д.
и т. д.
Мы можем вернуться теперь к случаю двулучевой интерференции, описываемой формулой (30), когда два интерферирующих пучка образованы двумя круглыми апертурами с радиусом а, разделенными расстоянием  В этом случае интенсивность
В этом случае интенсивность  не остается больше постоянной, но благодаря дифракции на круглой апертуре оказывается пространственно-распределенной:
не остается больше постоянной, но благодаря дифракции на круглой апертуре оказывается пространственно-распределенной:

Это распределение иллюстрируется на рис. 9, д. Такой же результат можно было бы получить в дальней зоне, но при этом  нужно заменить на
нужно заменить на  Следует заметить, что результирующее преобразование равно произведению. [Поскольку выражение (40) представляет собой произведение двух возведенных в квадрат функций, распределение комплексных амплитуд равно произведению этих двух функций.] Таким образом, это служит напоминанием того, что фурье-образ произведения равен свертке фурье-образов отдельных сомножителей, и, следовательно, апертурная функция оказывается представимой в виде свертки. Это свертка между самой апертурной функцией круглой апертуры и функцией вида
Следует заметить, что результирующее преобразование равно произведению. [Поскольку выражение (40) представляет собой произведение двух возведенных в квадрат функций, распределение комплексных амплитуд равно произведению этих двух функций.] Таким образом, это служит напоминанием того, что фурье-образ произведения равен свертке фурье-образов отдельных сомножителей, и, следовательно, апертурная функция оказывается представимой в виде свертки. Это свертка между самой апертурной функцией круглой апертуры и функцией вида  которая определяет взаимное расположение круглых апертур. Выражение
которая определяет взаимное расположение круглых апертур. Выражение
апертурной функции в таком виде поучительно в том смысле, что позволяет непосредственно написать результат, представленный формулой (40).
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
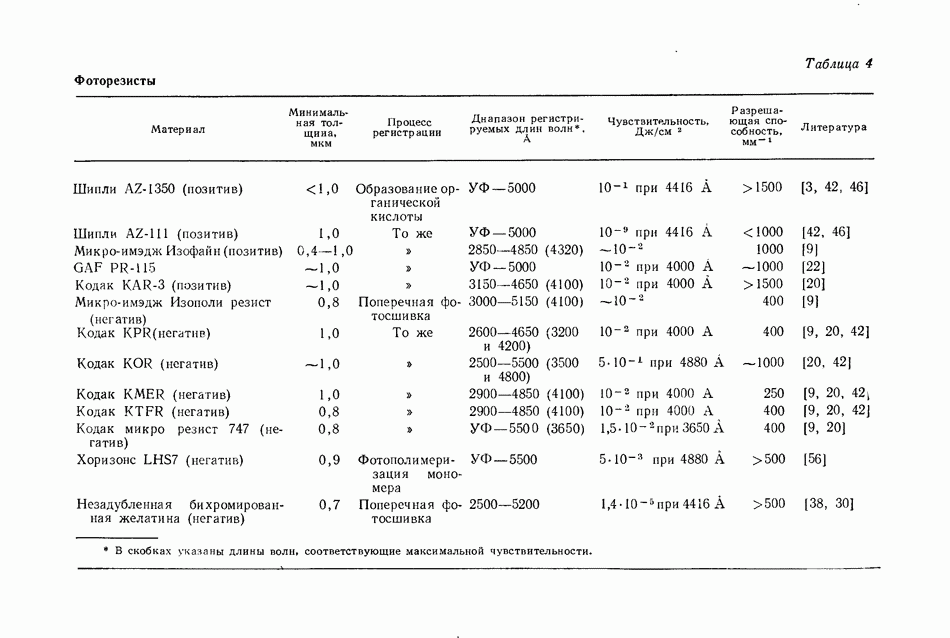
- 8.3.5. Фоторезисты
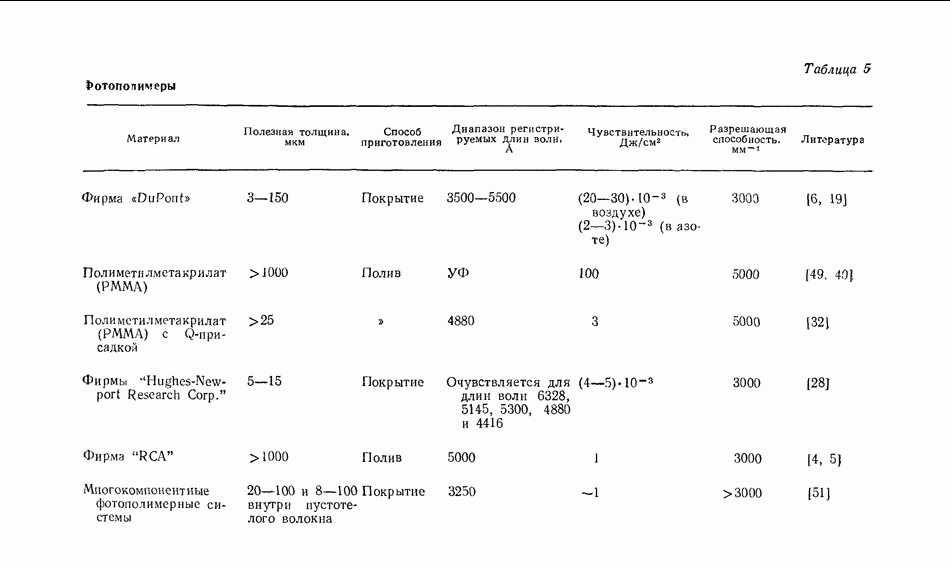
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
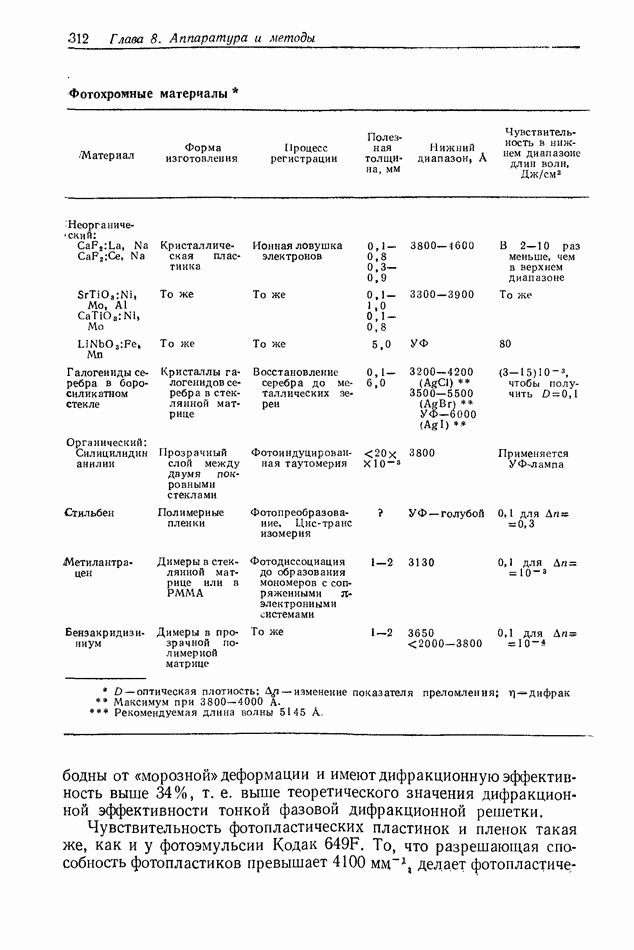
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
- 8.4.5. Голографическая корреляция
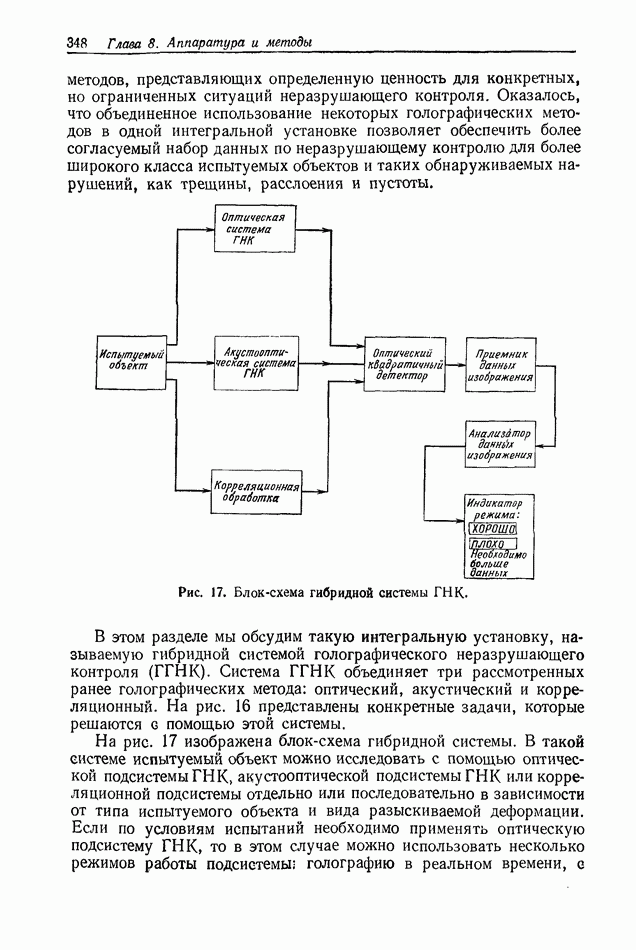
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
- 8.4.7. Голография движущихся объектов
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение