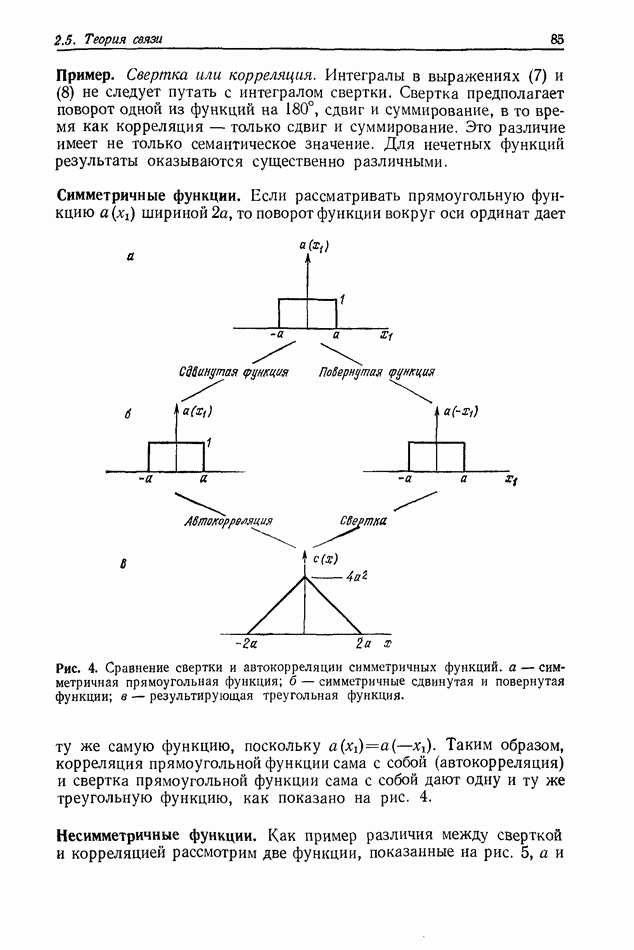
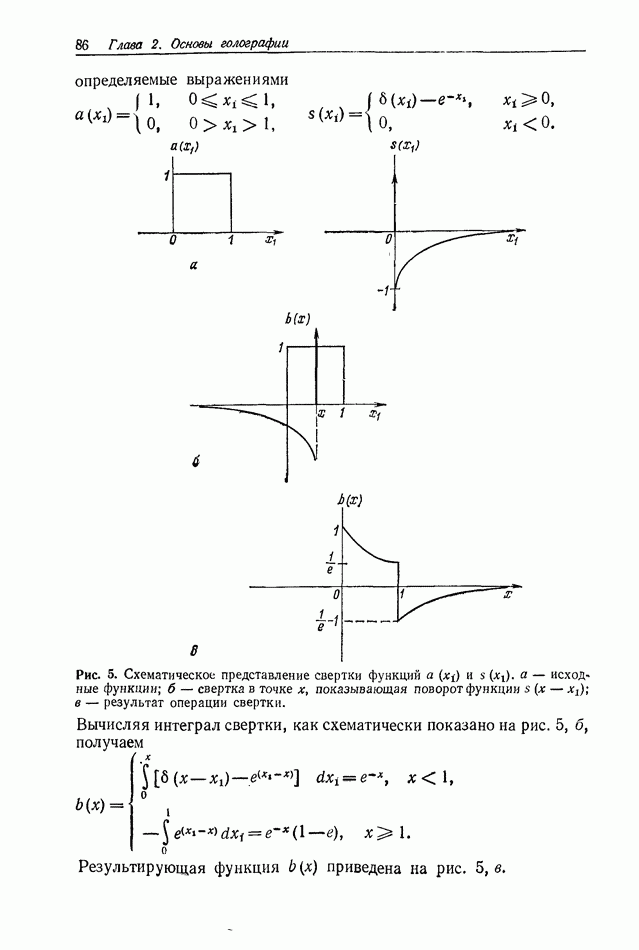
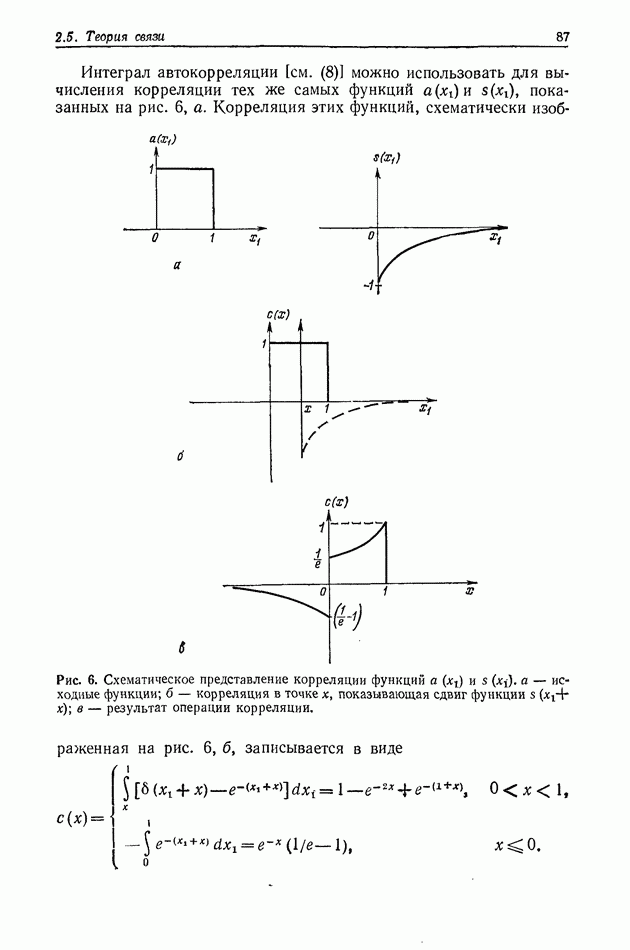
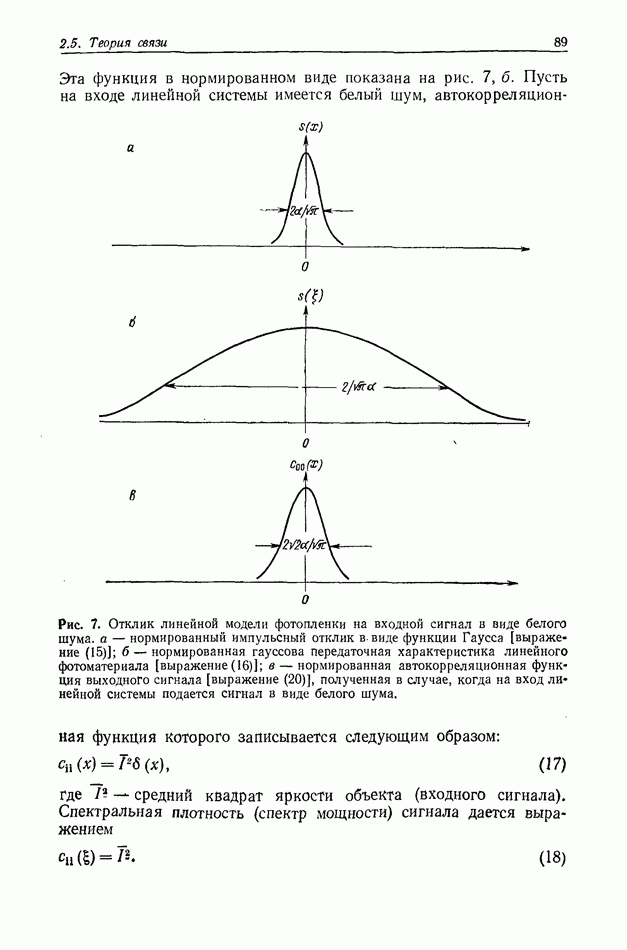
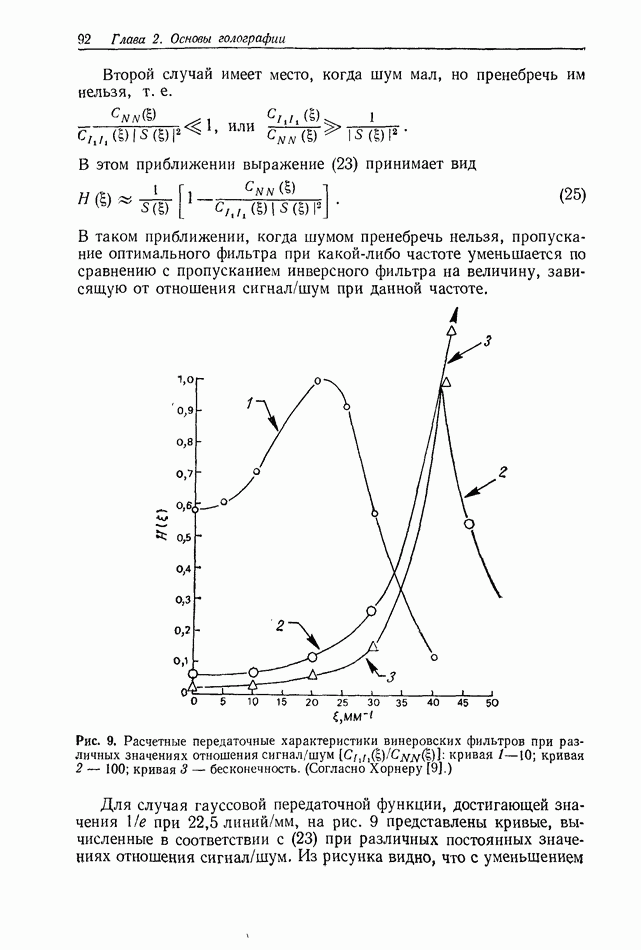
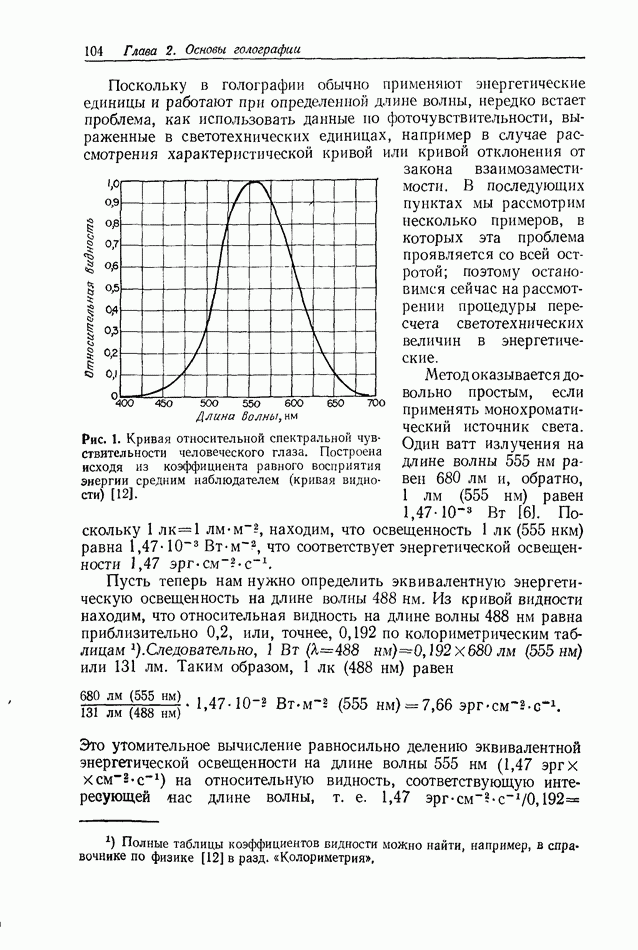
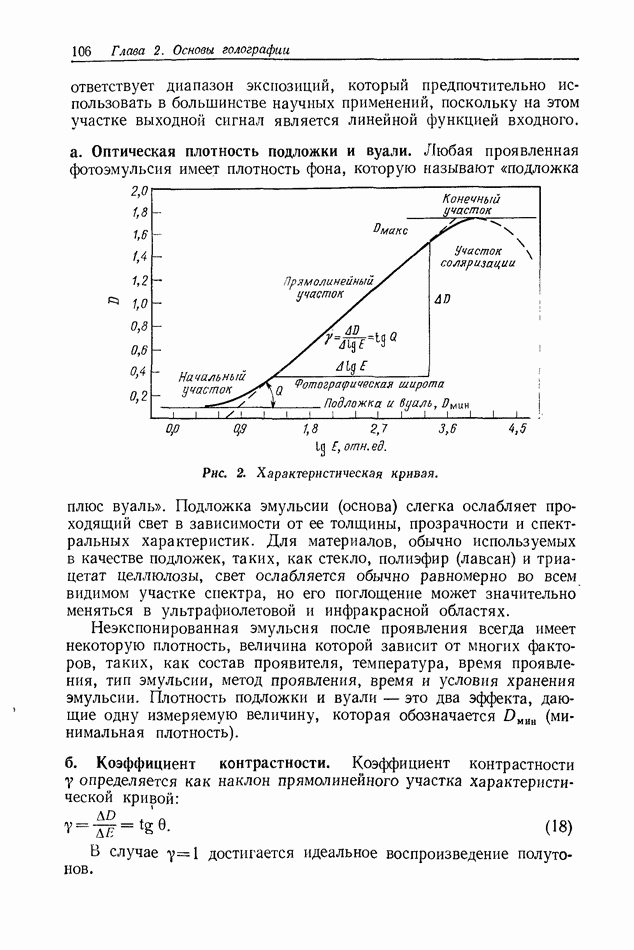
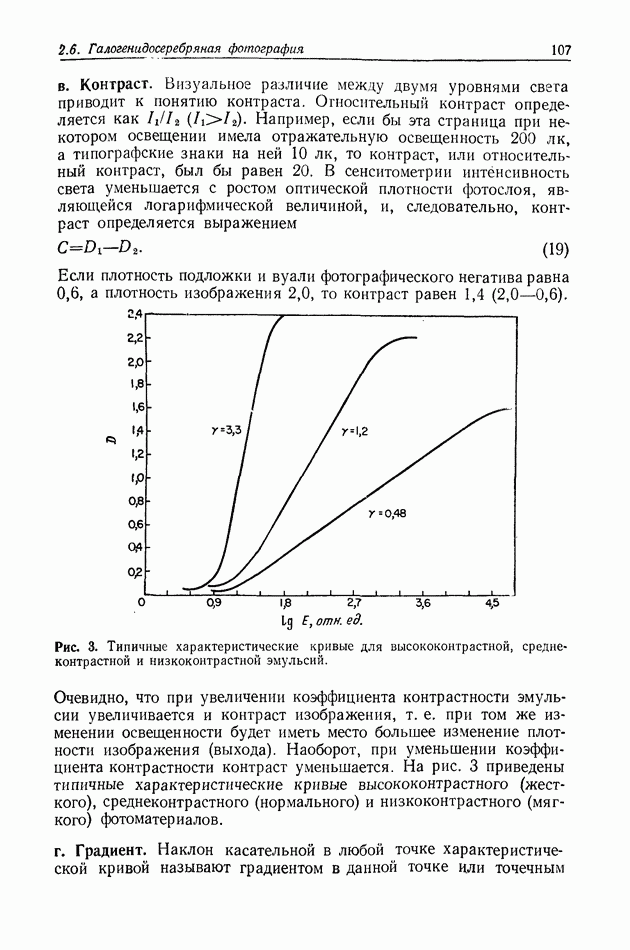
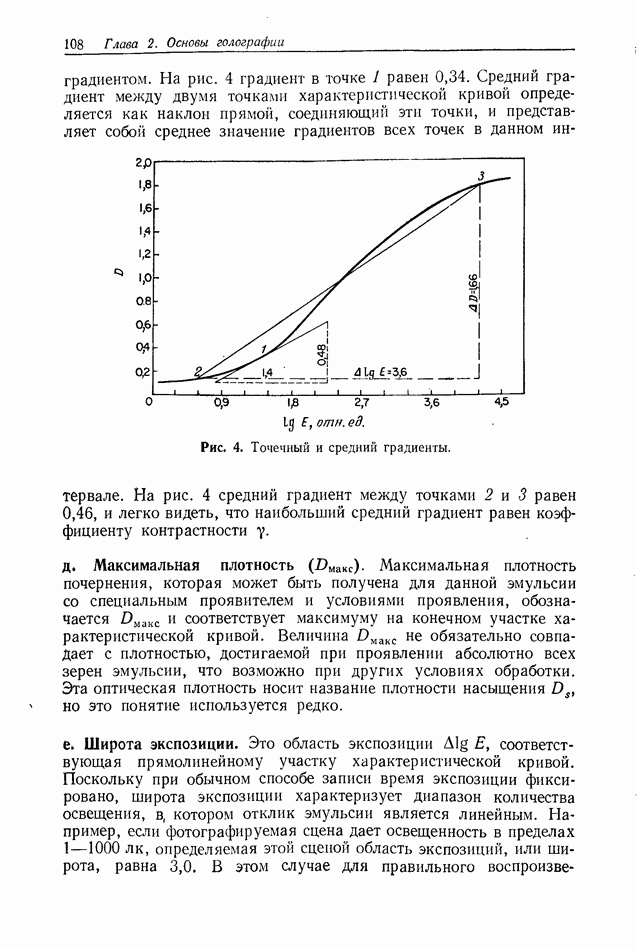
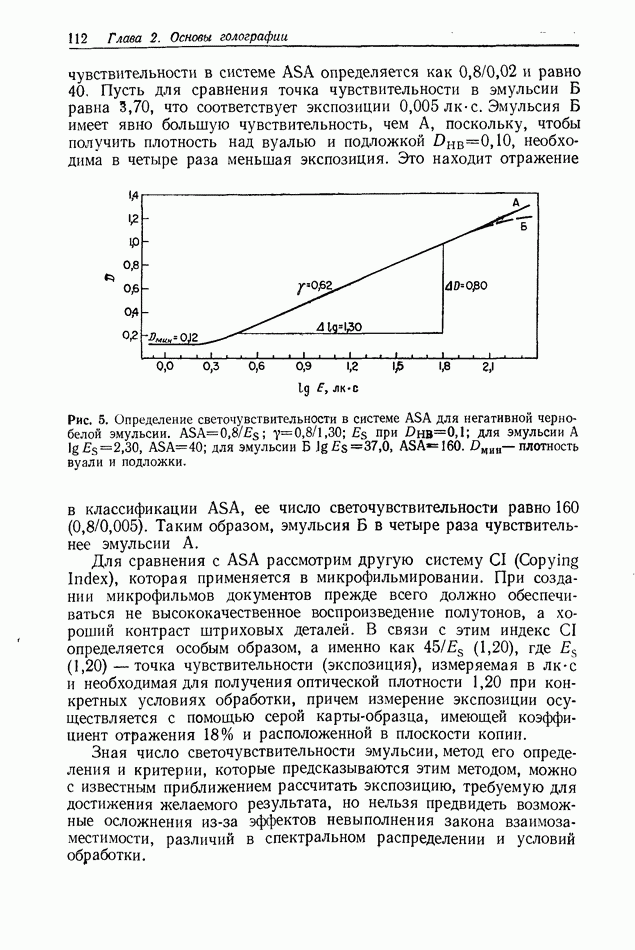
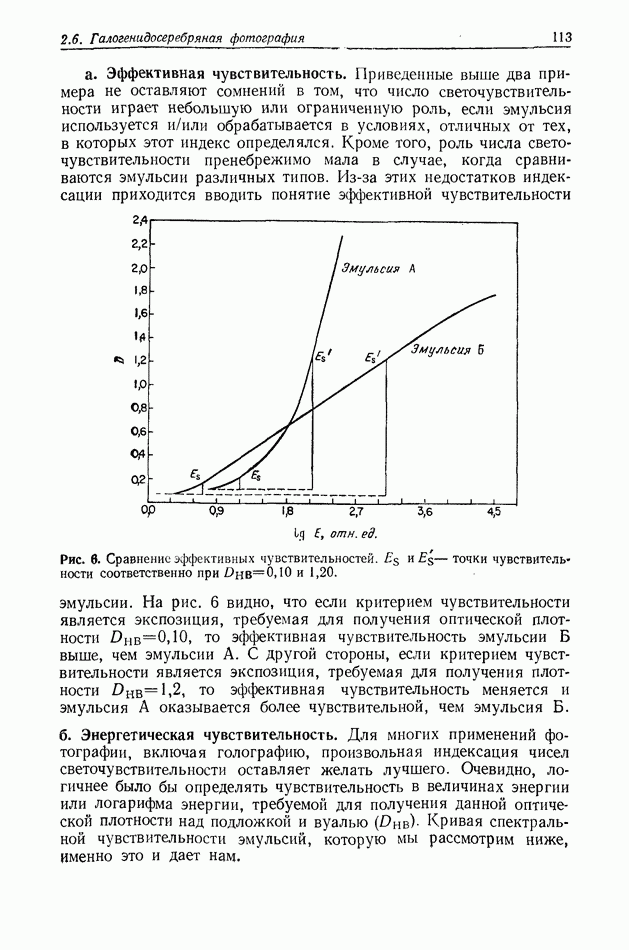
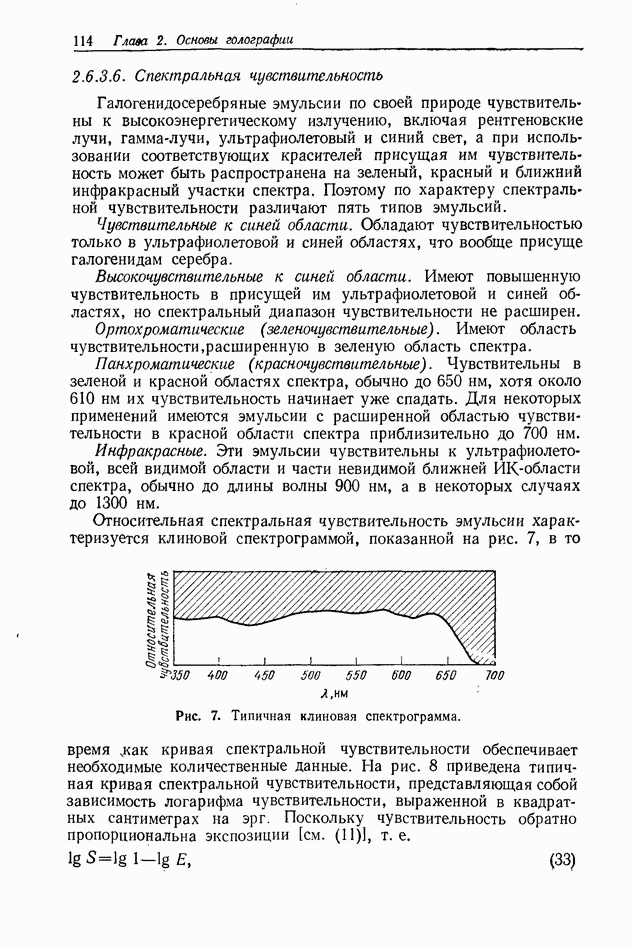
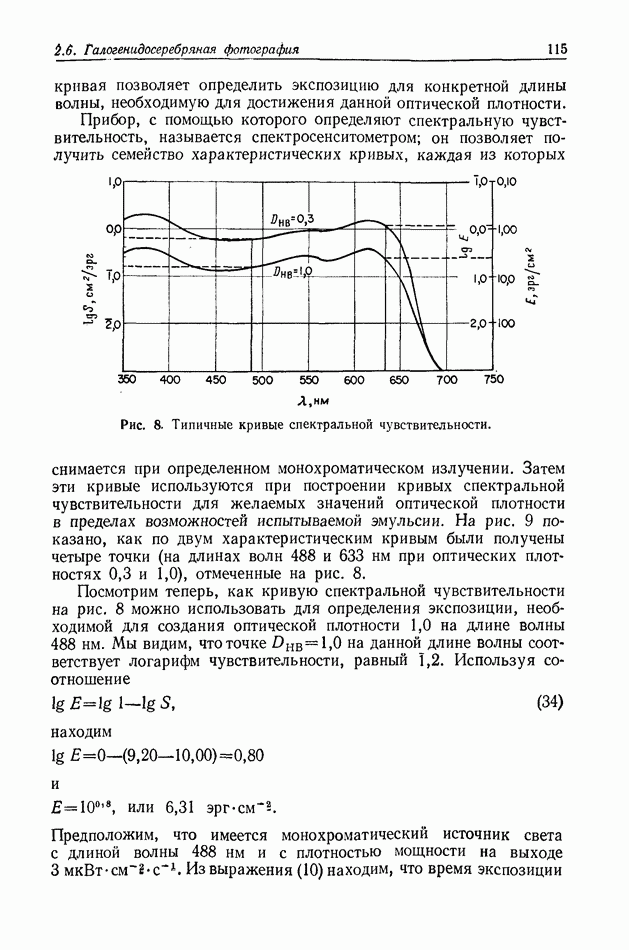
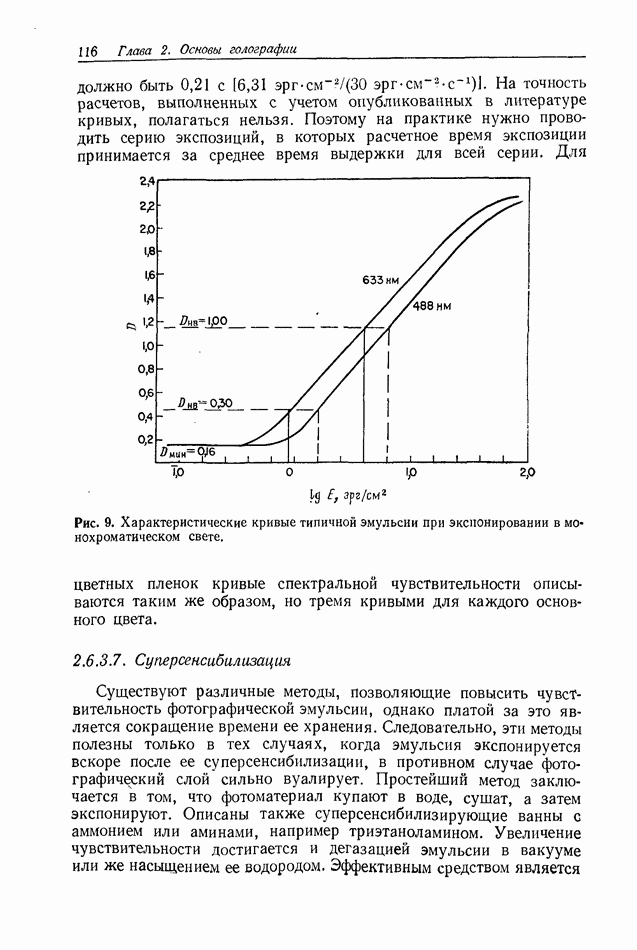
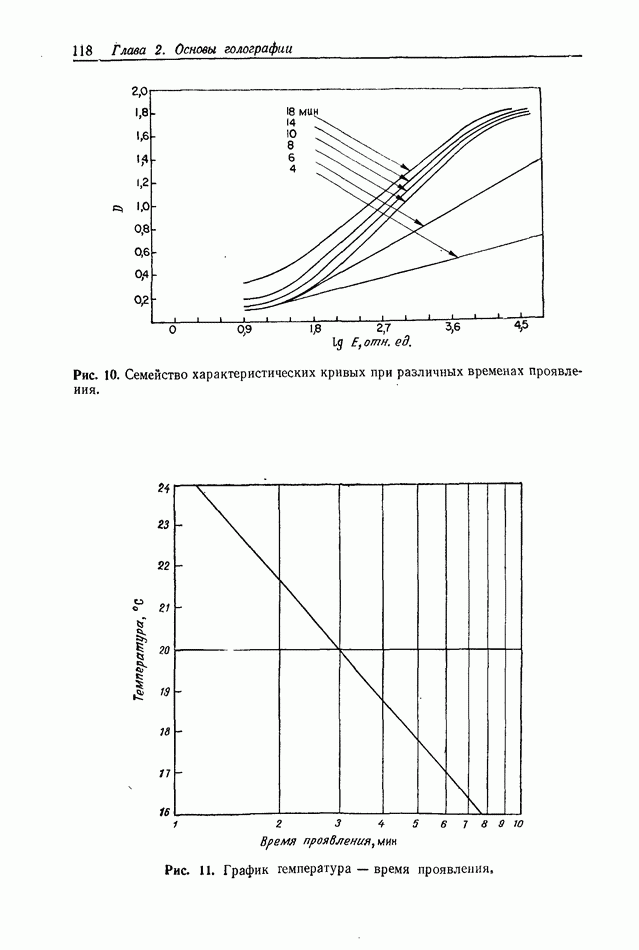
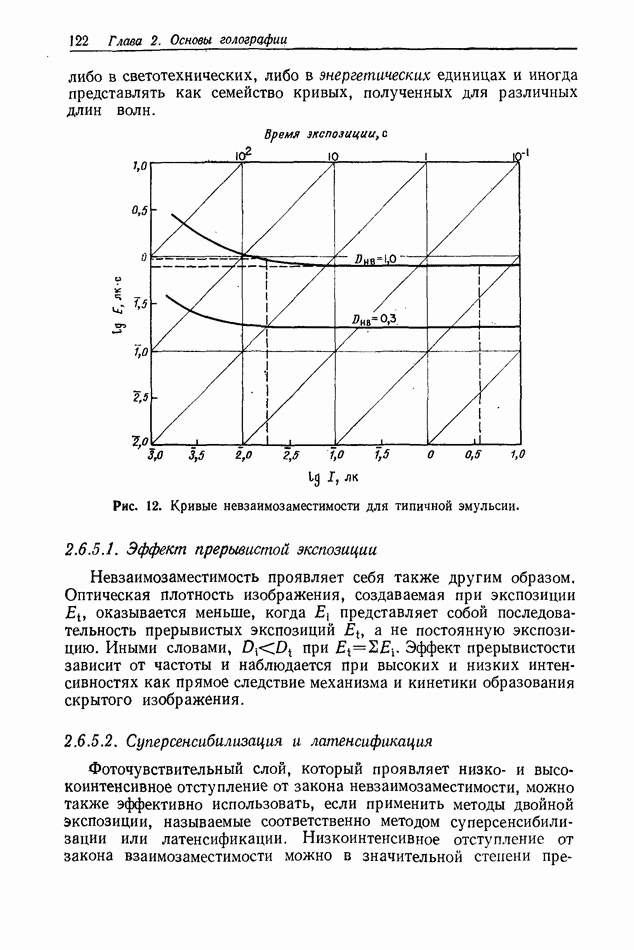
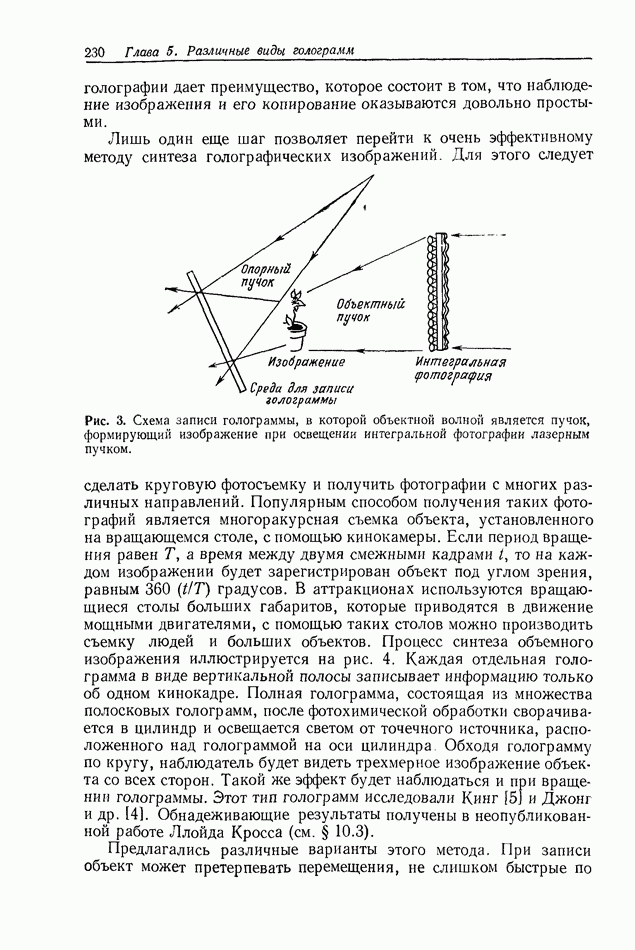
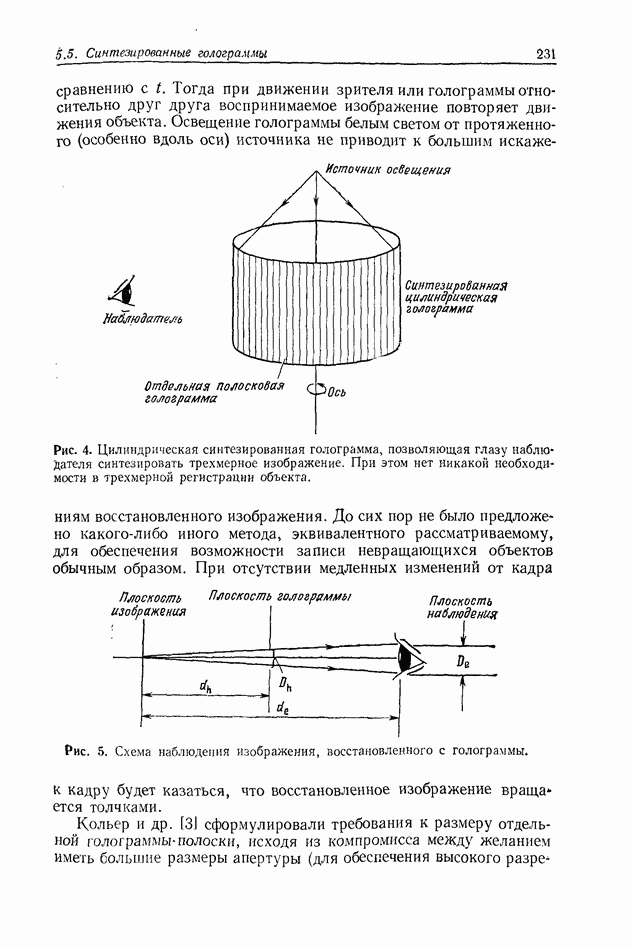
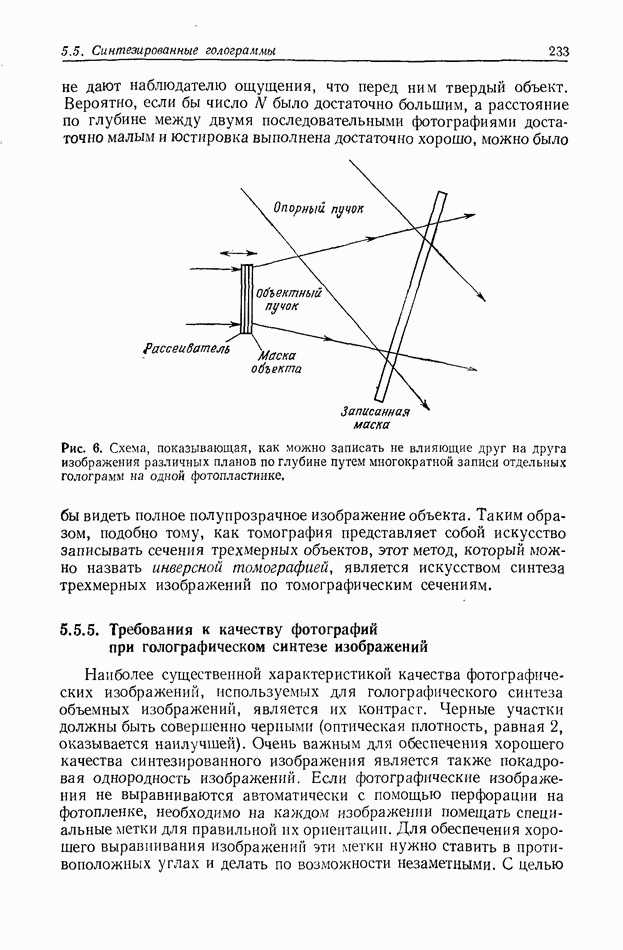
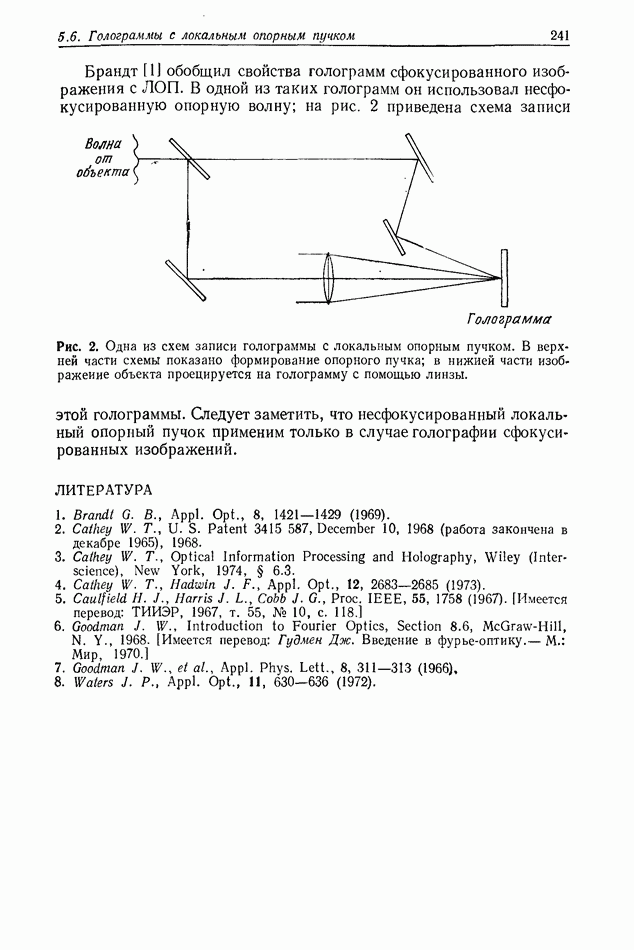
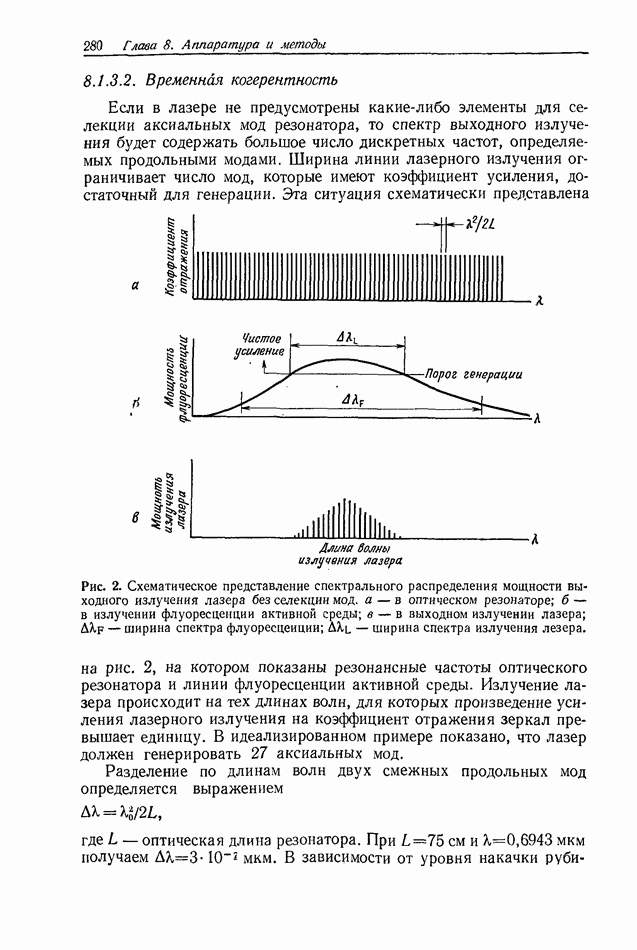
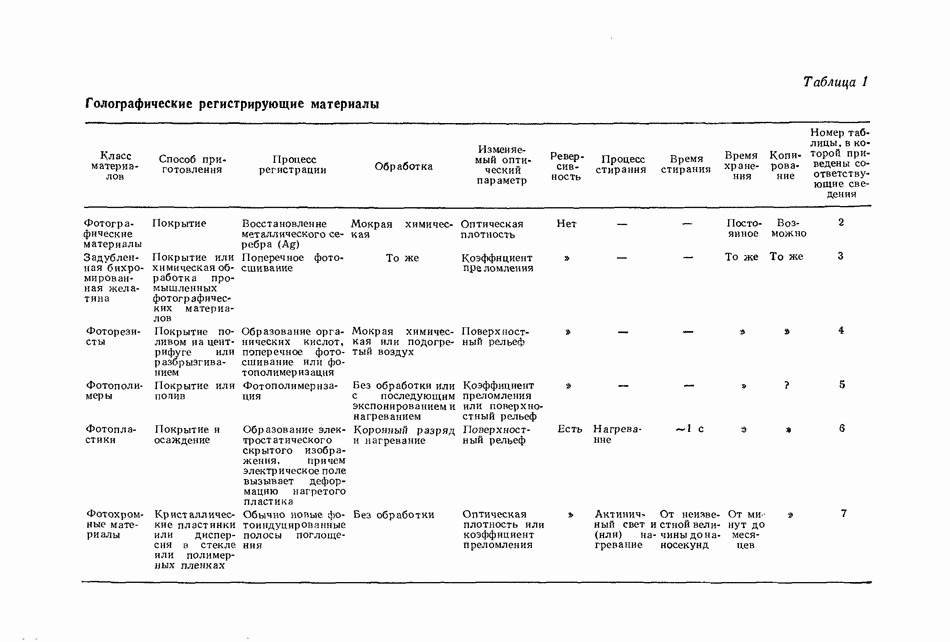
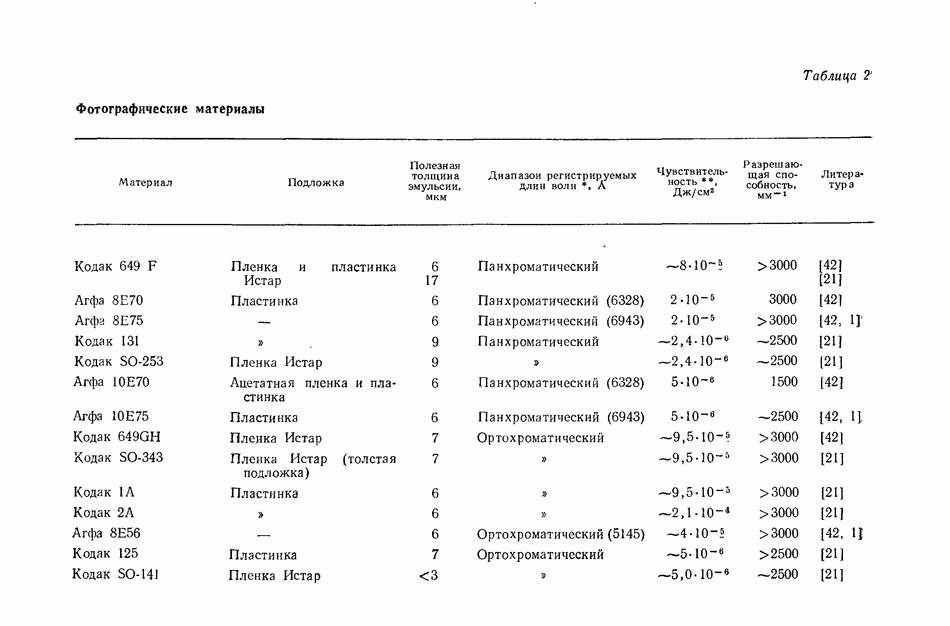
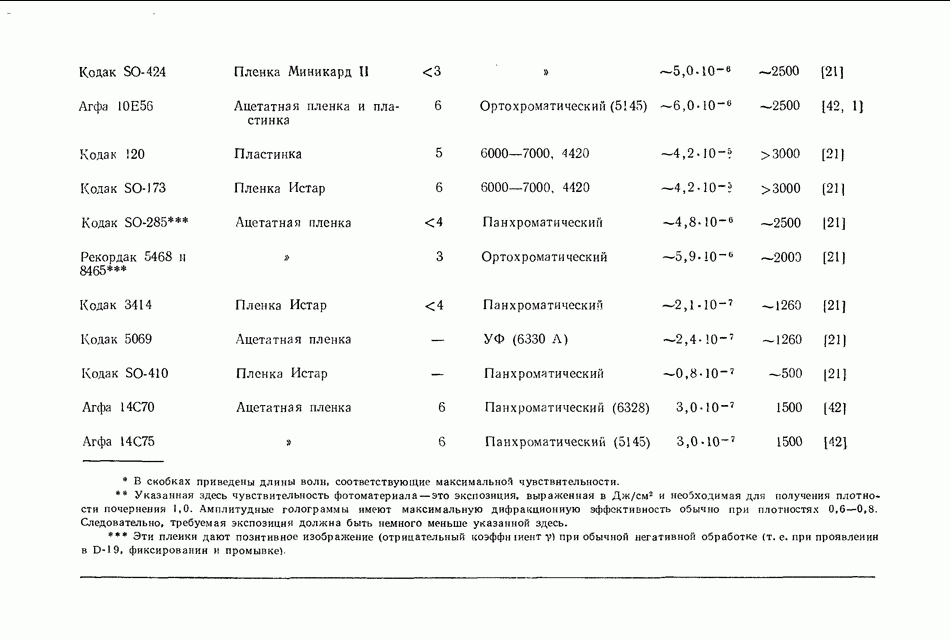
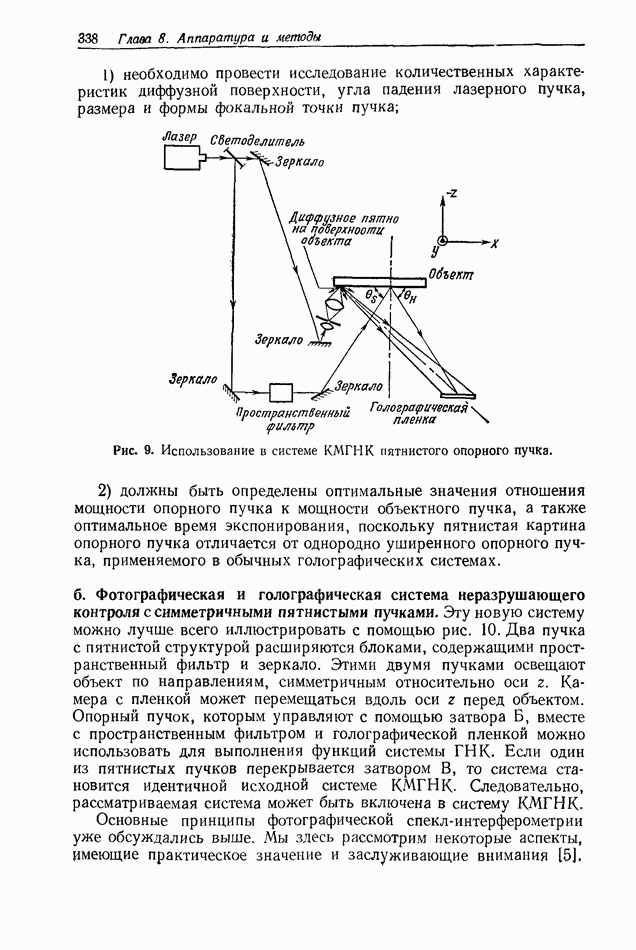
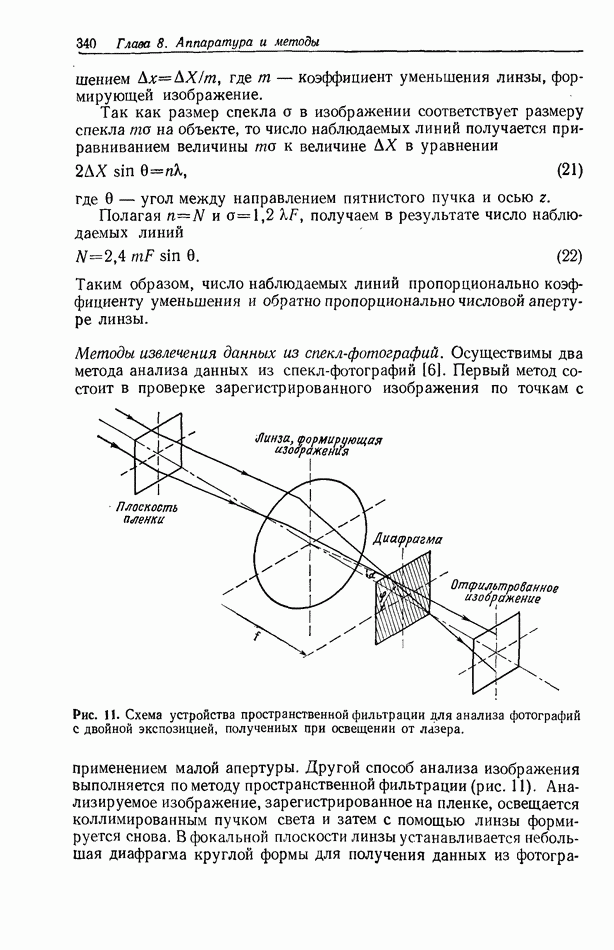
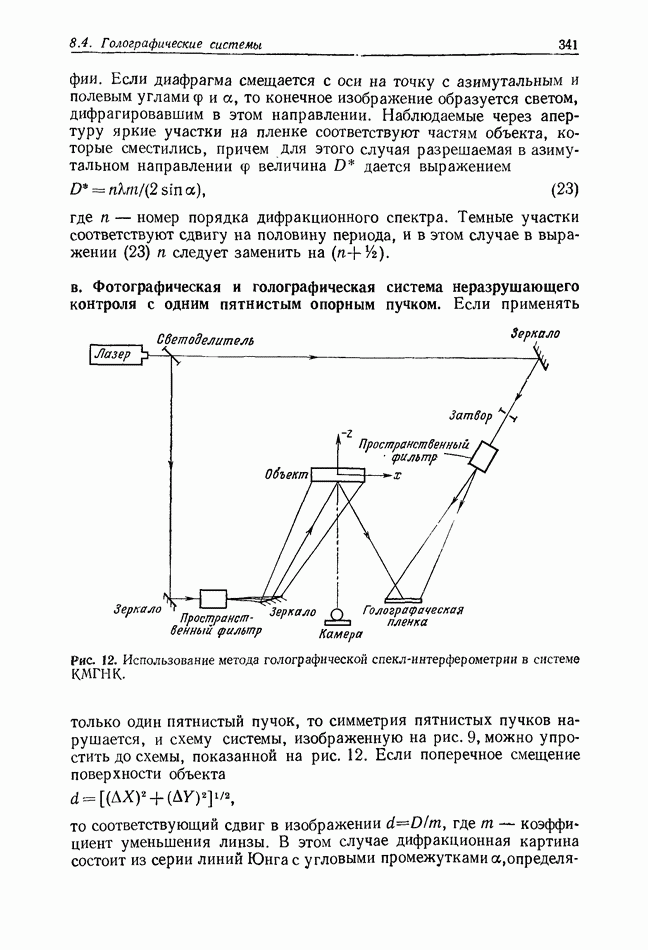
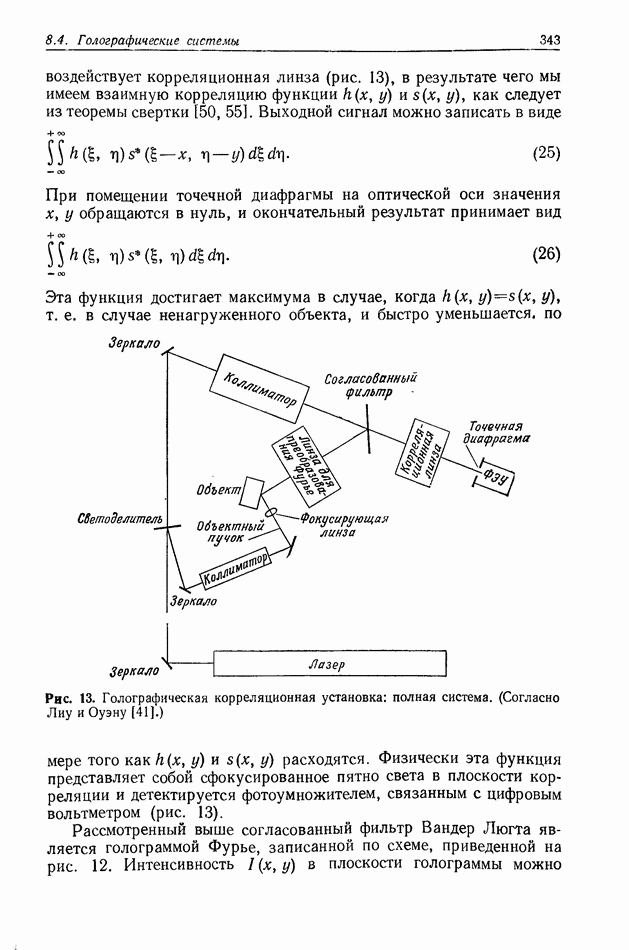
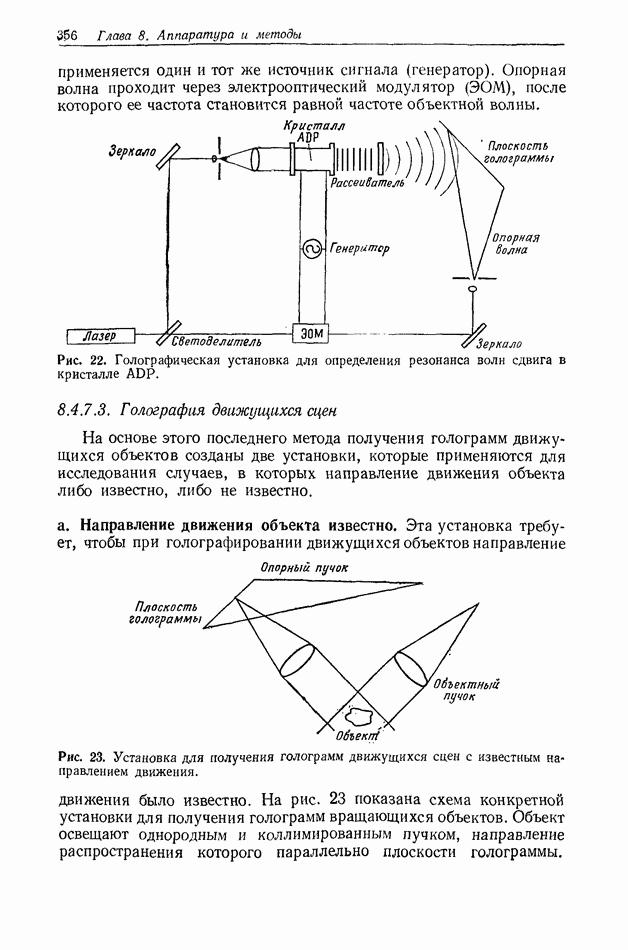
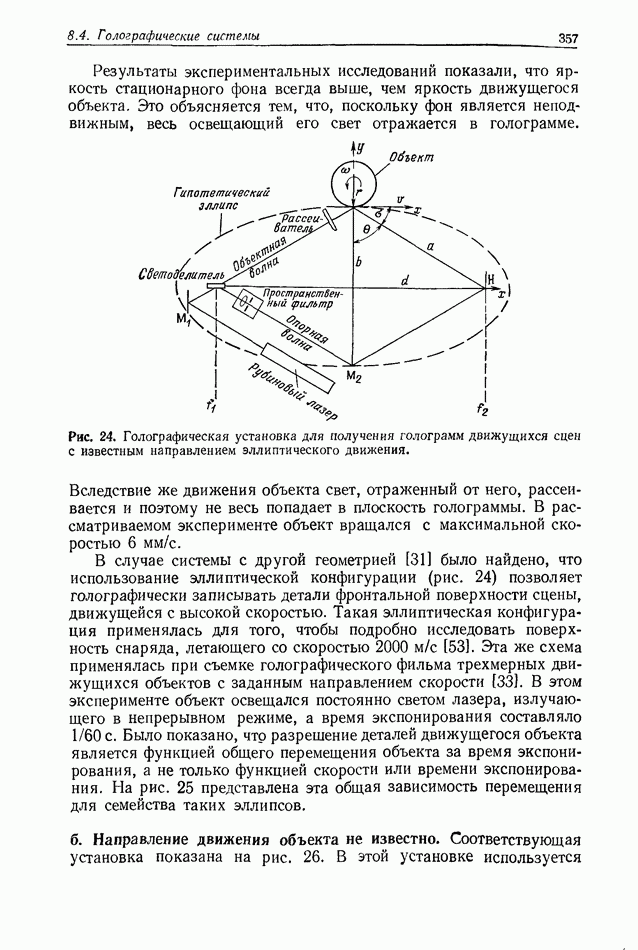
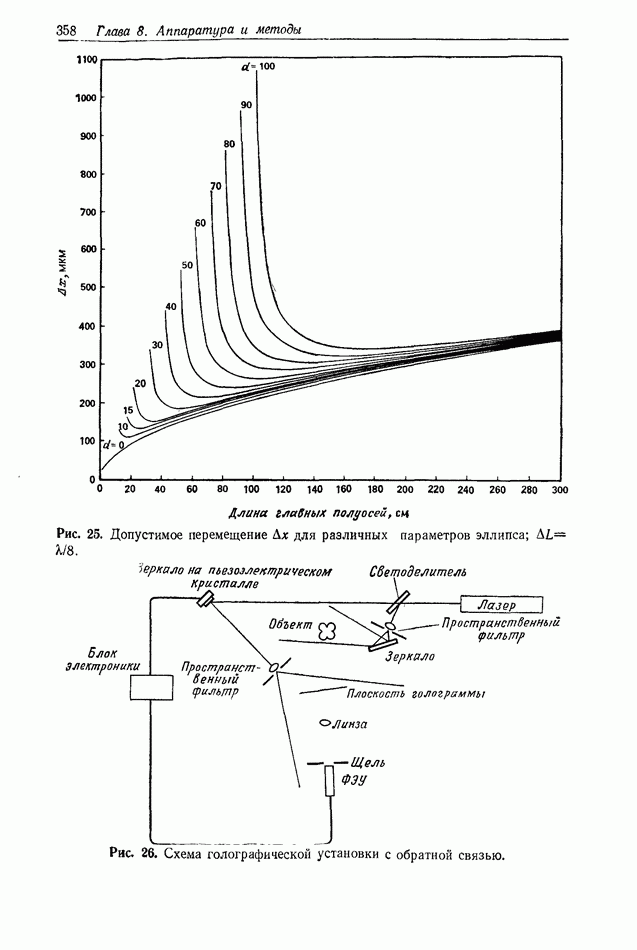
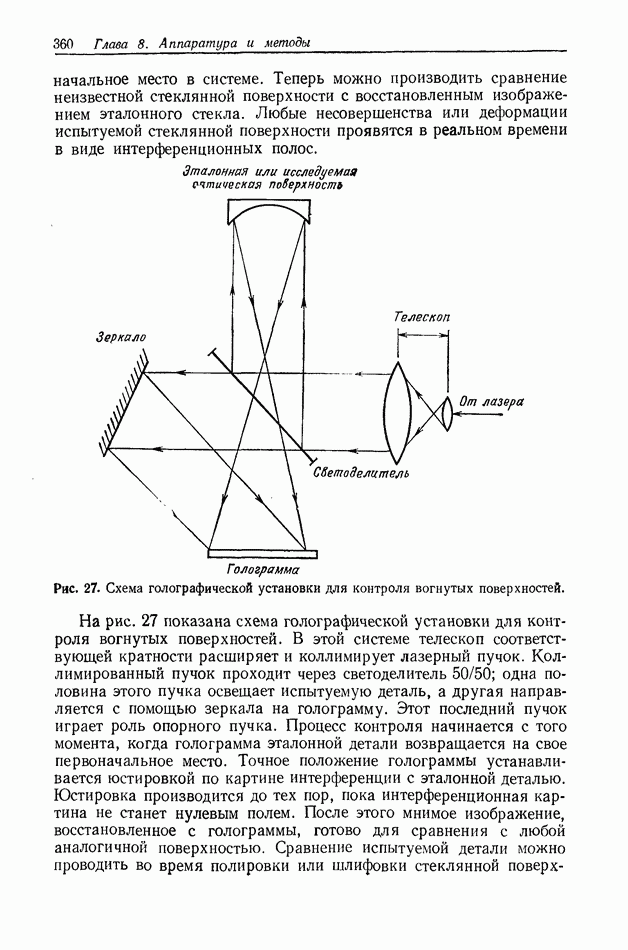
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 2. ОСНОВЫ ГОЛОГРАФИИ
2.1. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
К. Датта
Интегральным преобразованием функции  является другая функция
является другая функция  которая записывается в виде
которая записывается в виде

где  некоторая функция от
некоторая функция от  называемая ядром преобразования. Использование интегрального преобразования
называемая ядром преобразования. Использование интегрального преобразования  вместо
вместо  представляет собой обычный прием при решении физических задач, в которых проще обращаться с функцией
представляет собой обычный прием при решении физических задач, в которых проще обращаться с функцией  чем с
чем с  В оптике для анализа голографических систем и систем формирования изображения широко применяется метод преобразования Фурье [с ядром вида
В оптике для анализа голографических систем и систем формирования изображения широко применяется метод преобразования Фурье [с ядром вида 
В последнее время многие из таких преобразований стали играть все большую роль при исследовании оптических систем. Каждое из преобразований целесообразно использовать в связи с каким-то конкретным режимом работы системы, который трудно исследовать прямыми методами или методом преобразования Фурье. Некоторые из этих преобразований позволяют получать результаты более просто и с более высокой точностью даже в тех случаях, когда систему можно адекватно изучать прямым методом или методом Фурье.
В данном параграфе мы рассмотрим и определим многие из таких преобразований, а также приведем ряд теорем и результатов, связанных с применением этих преобразований. Кроме того, мы дадим перечень пар оригинал — образ для наиболее часто используемых функций в каждом преобразовании. Применяя одну или несколько приведенных нами теорем, можно получить любые другие пары оригинала и его образа.
Многие из интегральных преобразований тесно связаны с преобразованием Фурье и, следовательно, друг с другом. Некоторые такие соотношения приводятся в литературе и иногда помогают решить задачи, связанные с одним из преобразований при использовании результатов, справедливых для другого преобразования. Здесь мы умышленно не затронули вопрос о дискретных аналогах некоторых из этих преобразований, а также целого ряда других дискретных преобразований, которые применяются главным образом в цифровой обработке дискретной выборки данных [1].
Следует заметить, что, согласно данному выше определению, все интегральные преобразования могут рассматриваться как линейные операторы, действующие на функцию  с целью получения
с целью получения  Следовательно, все преобразования, приводимые ниже, являются линейными. Кроме того, учитывая то, что преобразования должны быть применимыми на практике, мы рассмотрим лишь те из них, для которых существует обратное преобразование вида
Следовательно, все преобразования, приводимые ниже, являются линейными. Кроме того, учитывая то, что преобразования должны быть применимыми на практике, мы рассмотрим лишь те из них, для которых существует обратное преобразование вида 

В специальных случаях ядра прямого и обратного преобразований могут быть одинаковыми, при этом в том и другом случае функция и ее образ будут связаны симметричными соотношениями.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
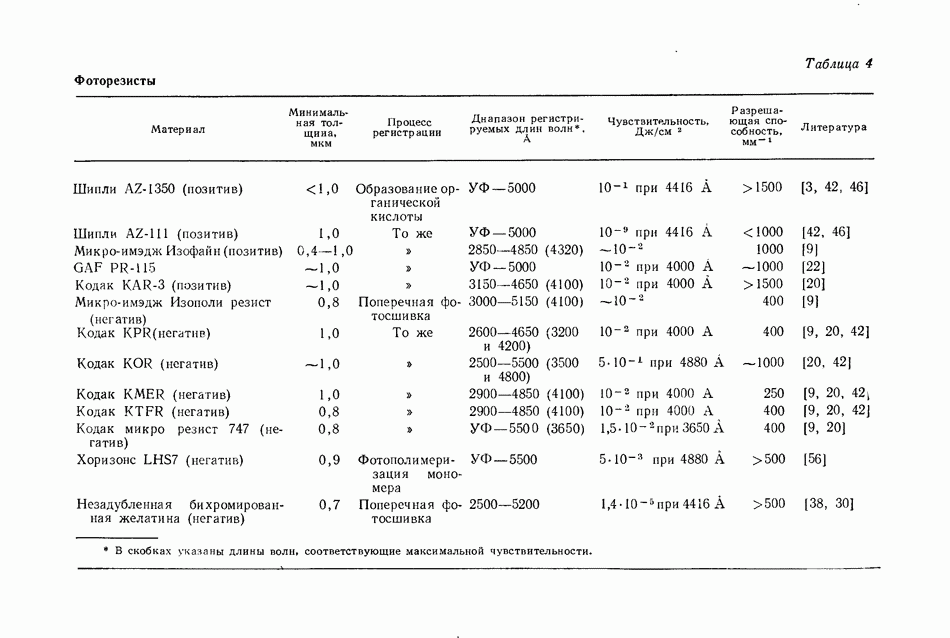
- 8.3.5. Фоторезисты
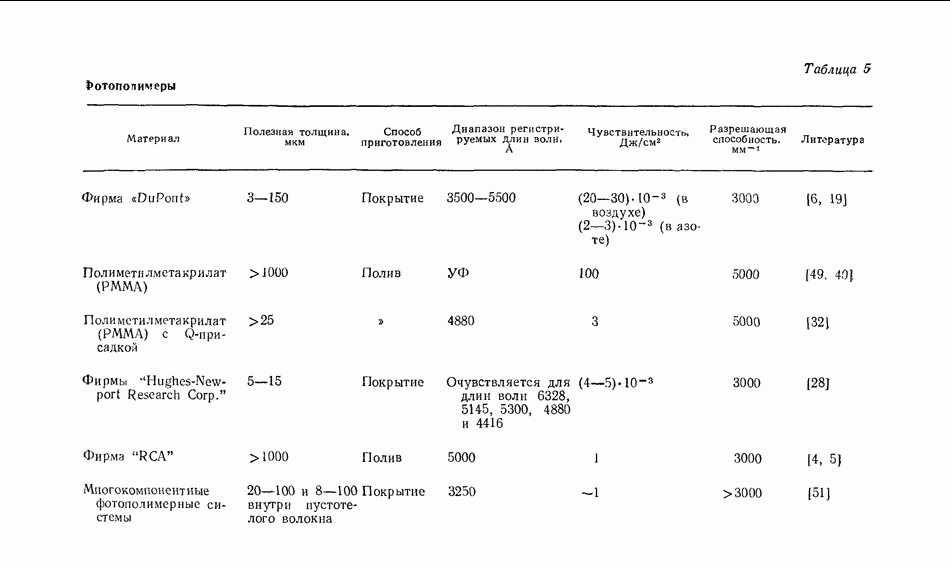
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
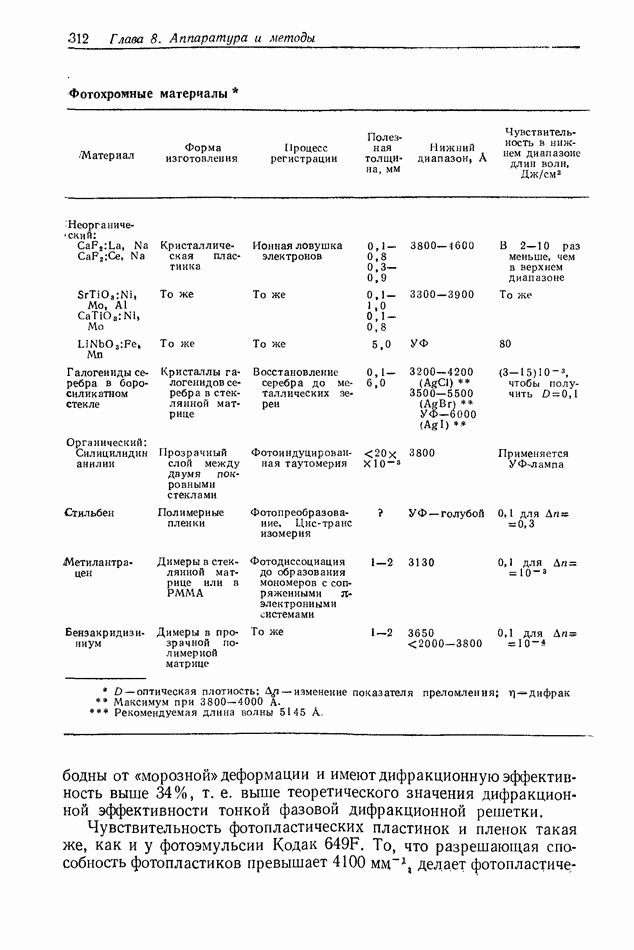
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
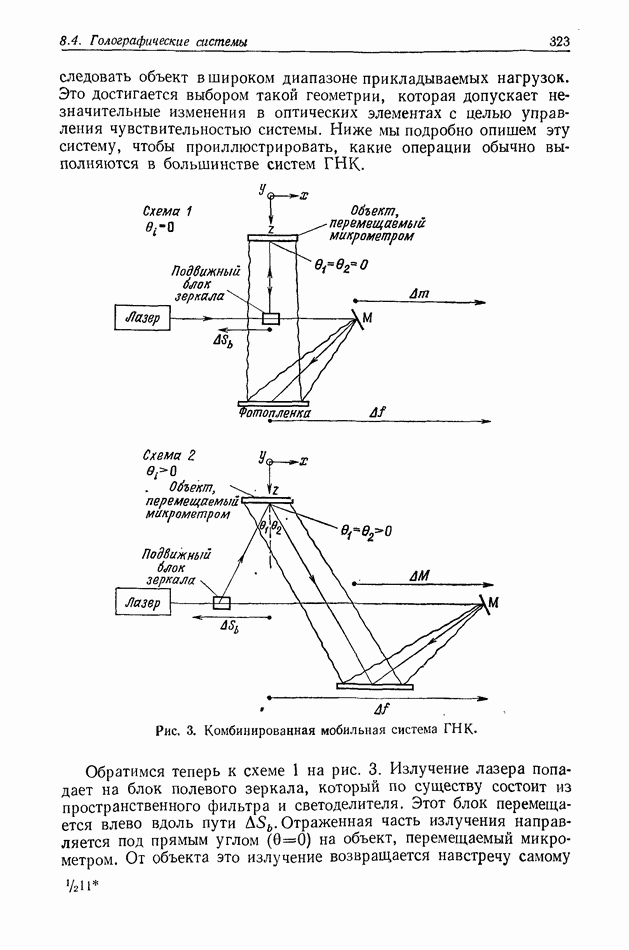
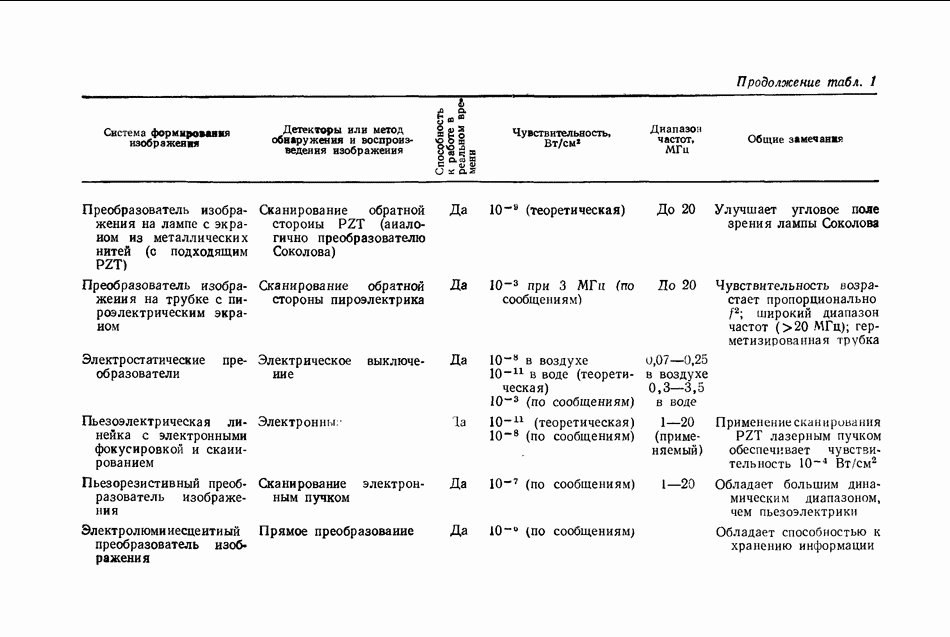
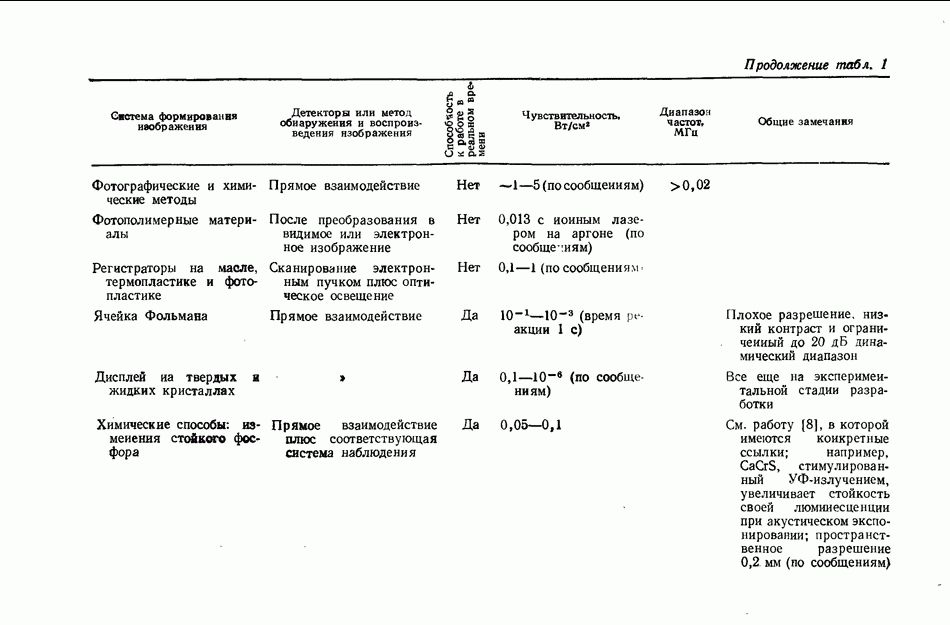
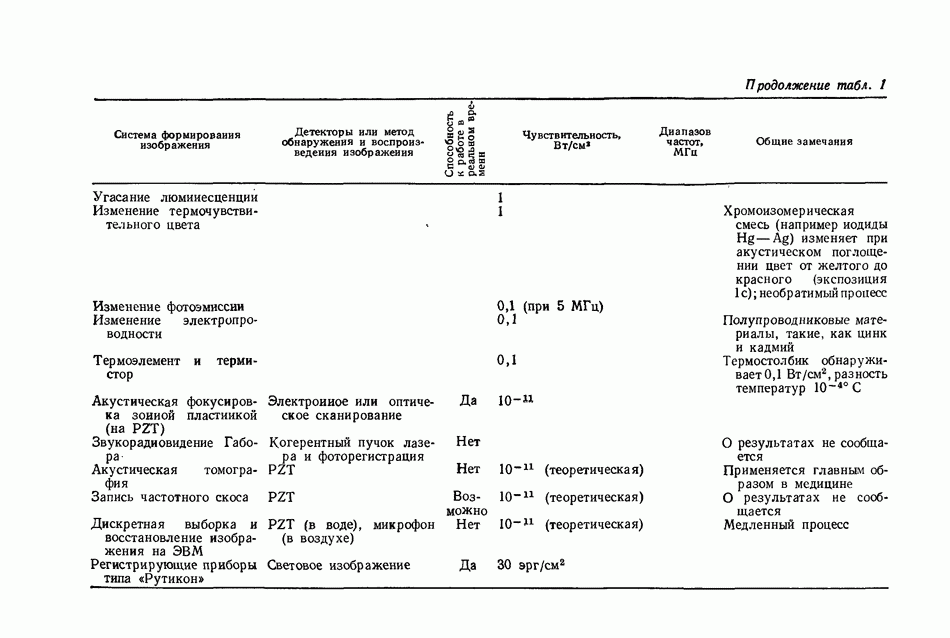
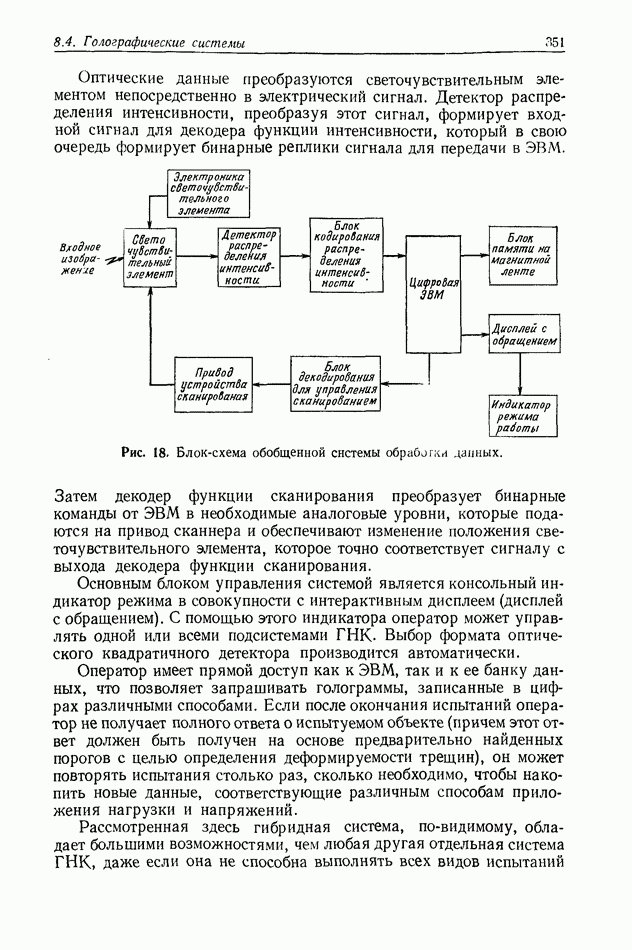
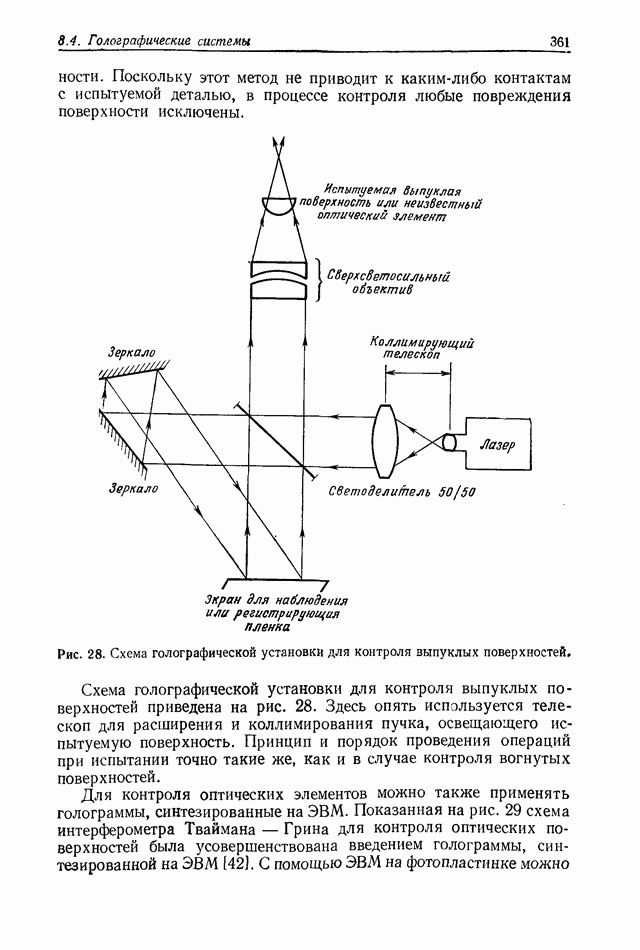
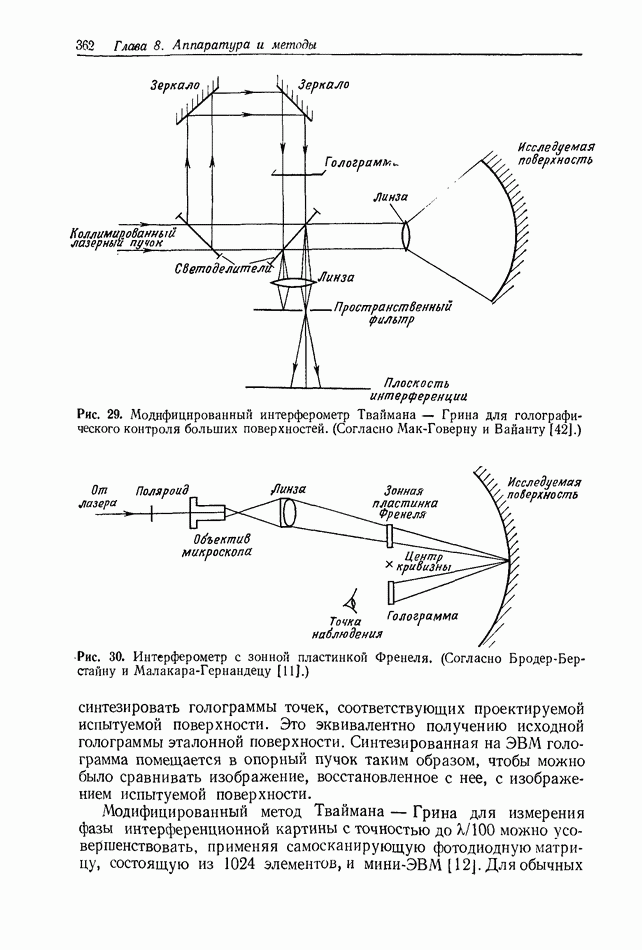
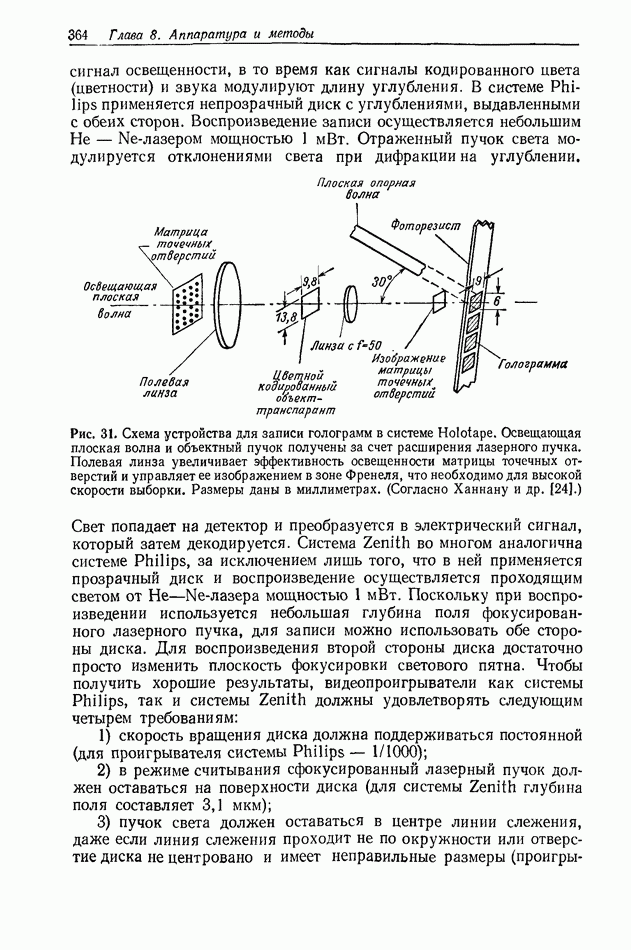
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
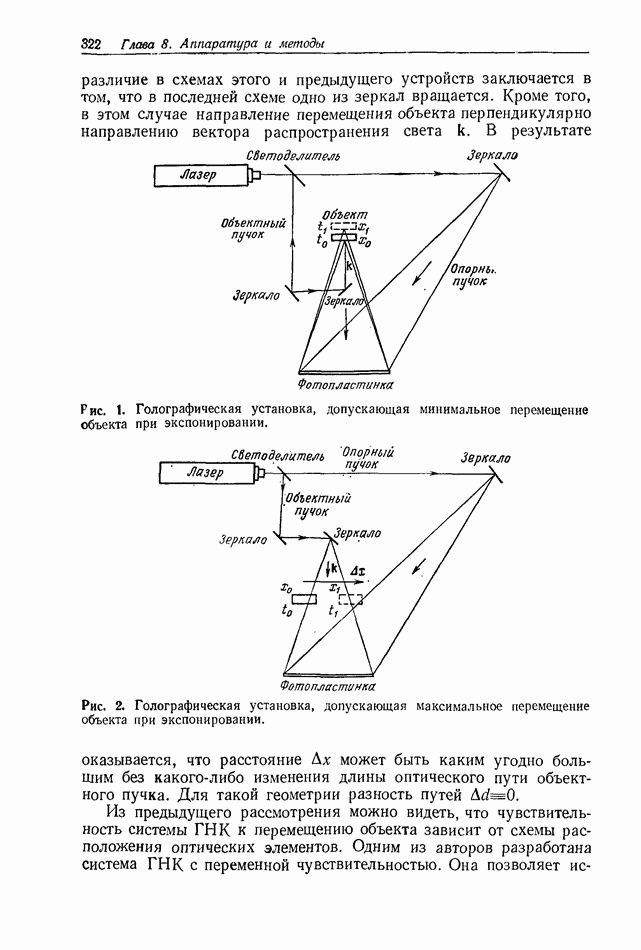
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
- 8.4.5. Голографическая корреляция
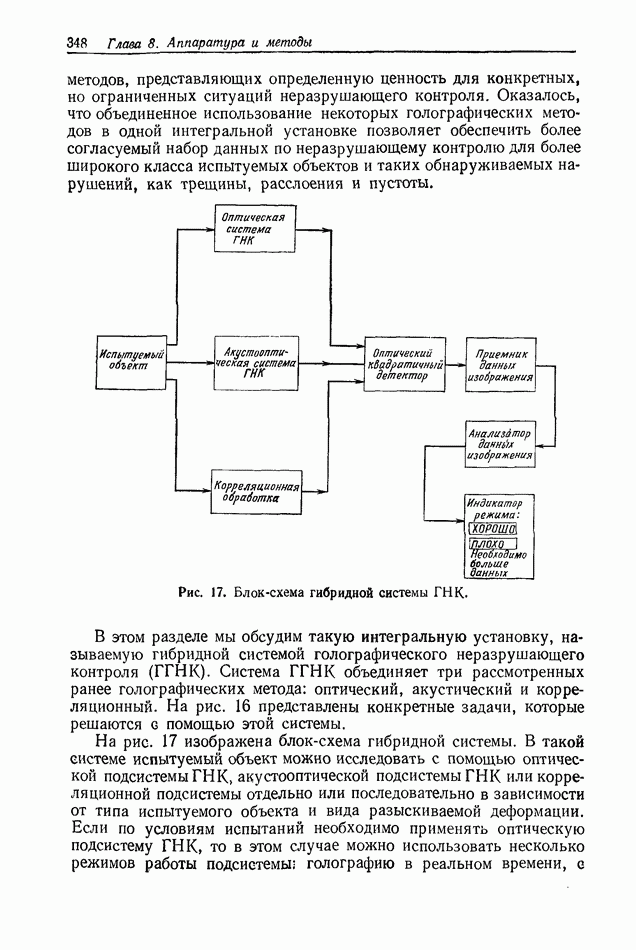
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
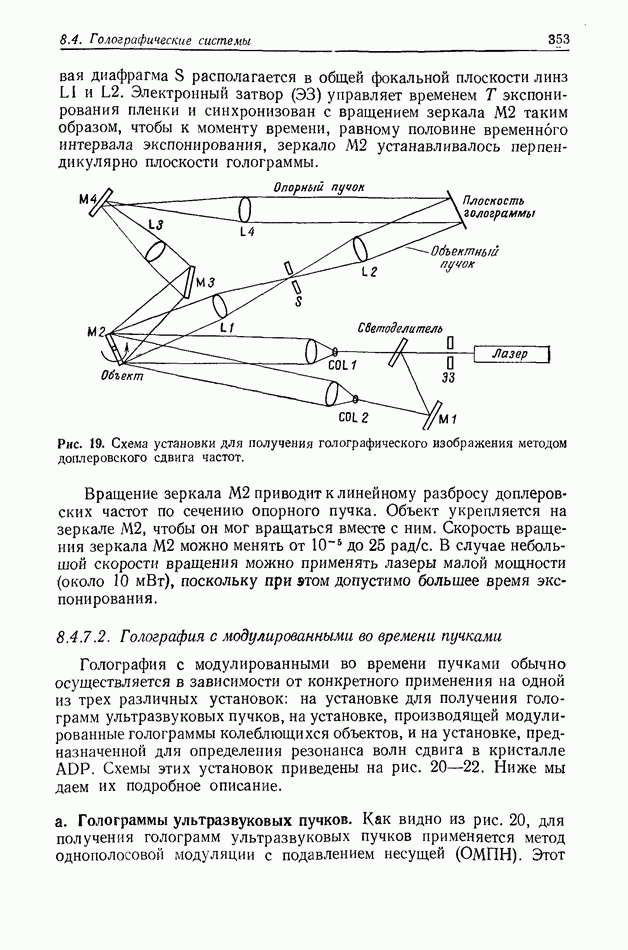
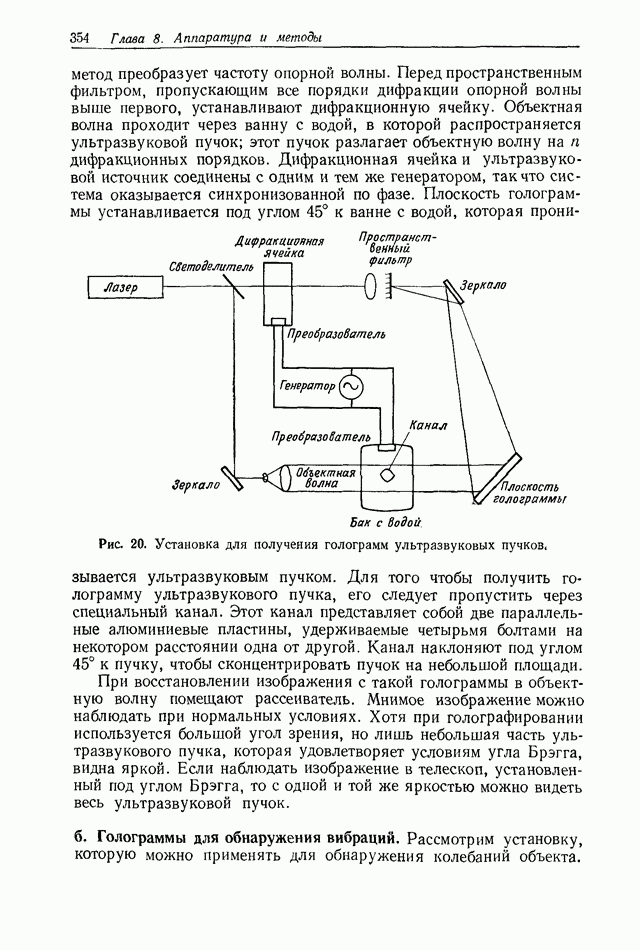
- 8.4.7. Голография движущихся объектов
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение