| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.1.4. Преобразование Френеля
Преобразование Френеля [15, 21] играет важную роль при описании свободного распространения когерентных оптических полей и при анализе дифракции в условиях, менее ограниченных, чем те, которые требуются для преобразования Фурье. Преобразование Френеля в своем основном виде можно определить следующим образом [201:

Мы видим, что это просто свертка функции  с экспоненциальной фазовой функцией
с экспоненциальной фазовой функцией  Обратное преобразование записывается также в виде свертки:
Обратное преобразование записывается также в виде свертки:

Аналогично можно определить двумерные прямое и обратное преобразования Френеля:

Преобразование Френеля тесно связано с преобразованием Фурье. Разложением ядра преобразования Френеля можно показать, что функции  связаны друг с другом преобразованием Фурье. Наоборот, если
связаны друг с другом преобразованием Фурье. Наоборот, если  пары преобразования Фурье, то можно показать, что пара
пары преобразования Фурье, то можно показать, что пара  связана преобразованием Френеля. В этих выражениях умножение на квадратичный фазовый множитель аналогично виду преобразования, осуществляемого тонкой линзой над комплексной амплитудой падающего на нее светового поля [14, гл. 5]. То, что распространение электромагнитного поля между линзами можно описать, с помощью преобразования Френеля (или свертки с фазовым множителем), позволяет изучать свойства когерентных оптических процессоров, в которых основными операциями являются умножение и свертка [7], на основе алгебраических соотношений. Преобразование Френеля применяется также при исследовании голограмм Френеля и анализе систем воспроизведения с апертурами, кодированными зонной пластинкой.
связана преобразованием Френеля. В этих выражениях умножение на квадратичный фазовый множитель аналогично виду преобразования, осуществляемого тонкой линзой над комплексной амплитудой падающего на нее светового поля [14, гл. 5]. То, что распространение электромагнитного поля между линзами можно описать, с помощью преобразования Френеля (или свертки с фазовым множителем), позволяет изучать свойства когерентных оптических процессоров, в которых основными операциями являются умножение и свертка [7], на основе алгебраических соотношений. Преобразование Френеля применяется также при исследовании голограмм Френеля и анализе систем воспроизведения с апертурами, кодированными зонной пластинкой.
Поскольку операция преобразования Френеля включает в себя свертку с функцией  то для любого анализа, связанного с преобразованиями Френеля, полезно знать свойства этой функции. В вышеприведенных выражениях параметр
то для любого анализа, связанного с преобразованиями Френеля, полезно знать свойства этой функции. В вышеприведенных выражениях параметр  в большинстве случаев интерпретируется как кривизна сферических волновых фронтов. Обобщая это представление, комплексные значения
в большинстве случаев интерпретируется как кривизна сферических волновых фронтов. Обобщая это представление, комплексные значения  можно представить себе как значения комплексной кривизны волнового фронта (т. е. сферический волновой фронт с гауссовым профилем интенсивности).
можно представить себе как значения комплексной кривизны волнового фронта (т. е. сферический волновой фронт с гауссовым профилем интенсивности).
Свойства двумерной функции  рассмотрены Кэти [10, приложение 2]; их описание можно найти также в работе Карлсона и Франсуа [7].
рассмотрены Кэти [10, приложение 2]; их описание можно найти также в работе Карлсона и Франсуа [7].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
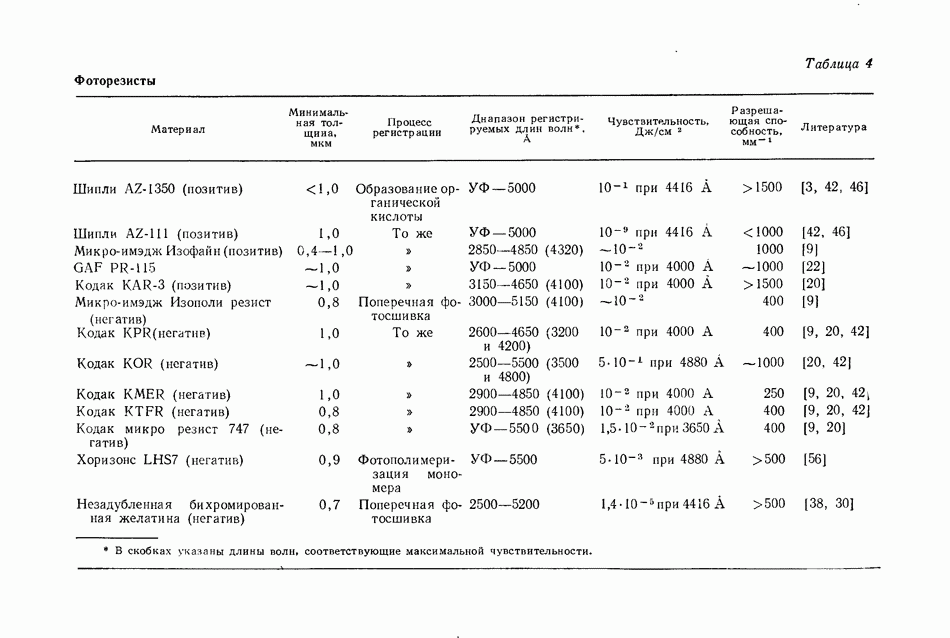
- 8.3.5. Фоторезисты
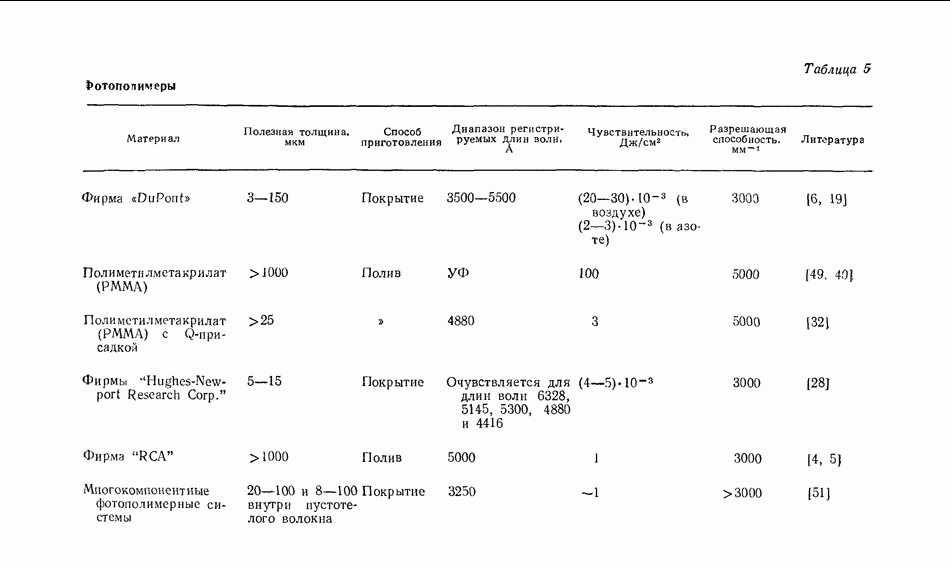
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
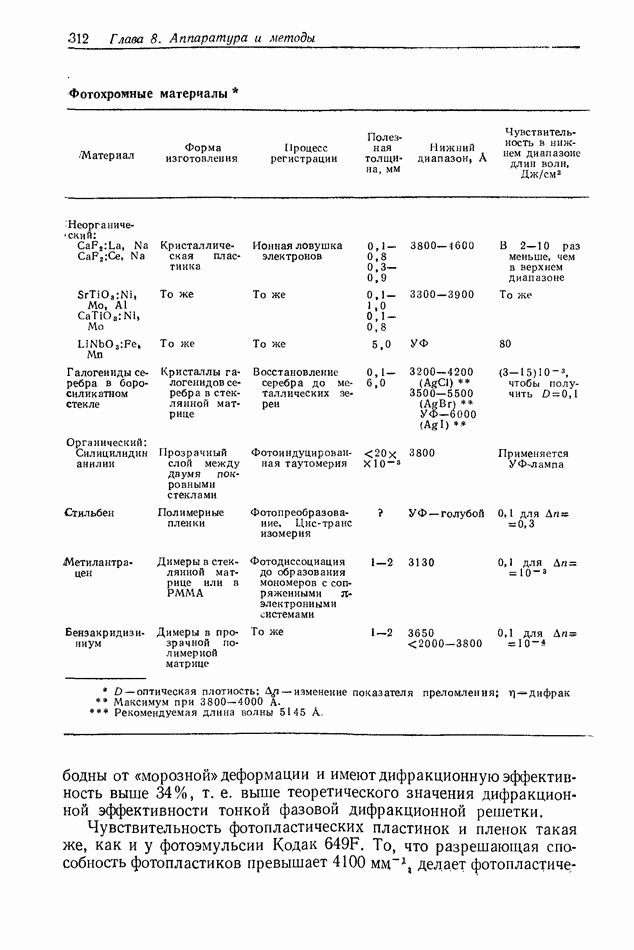
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
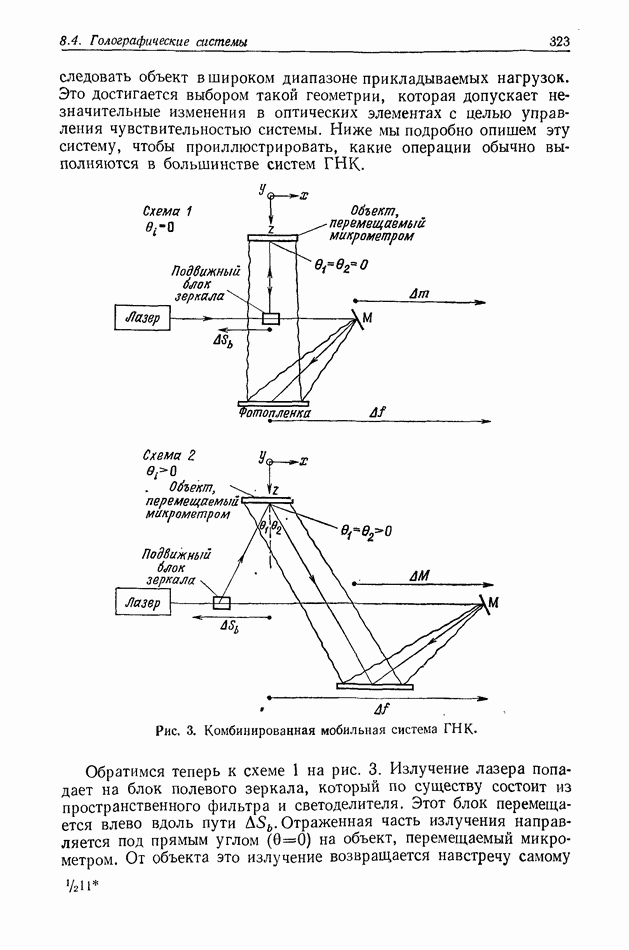
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
- 8.4.5. Голографическая корреляция
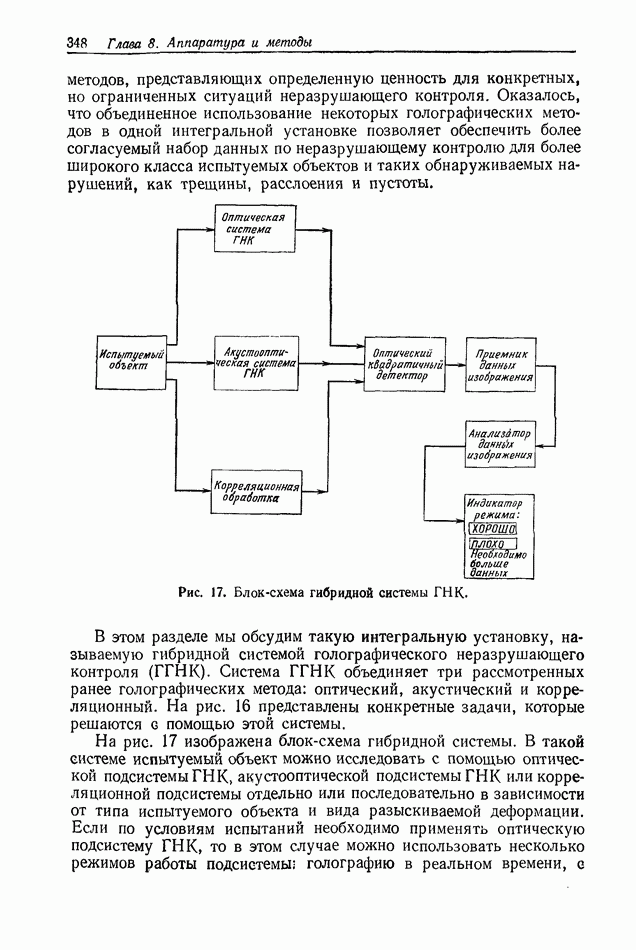
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
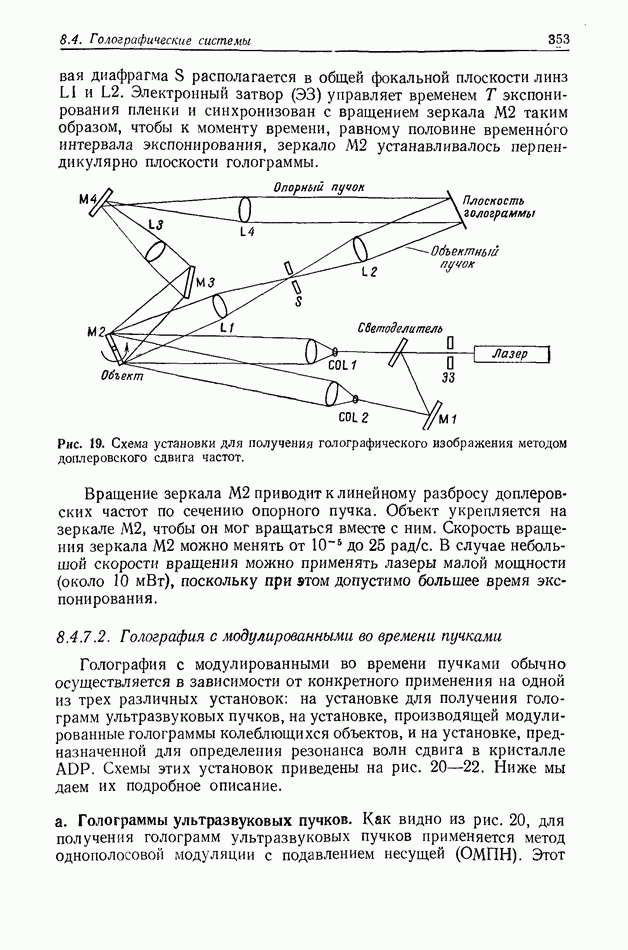
- 8.4.7. Голография движущихся объектов
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение