| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.3.5. Дифракция и интерференция частично-когерентного света
В разд. 2.2.4 рассматривалась дифракция Фраунгофера при прохождении когерентного света через два круглых отверстия диаметром 2а, расположенных на расстоянии  друг от друга [см. выражение (40) в § 2.21. Если свет в каждом из отверстий действительно когерентный, но между отверстиями он не является полностью когерентным, то выражение (40) из § 2.2 запишется в виде
друг от друга [см. выражение (40) в § 2.21. Если свет в каждом из отверстий действительно когерентный, но между отверстиями он не является полностью когерентным, то выражение (40) из § 2.2 запишется в виде

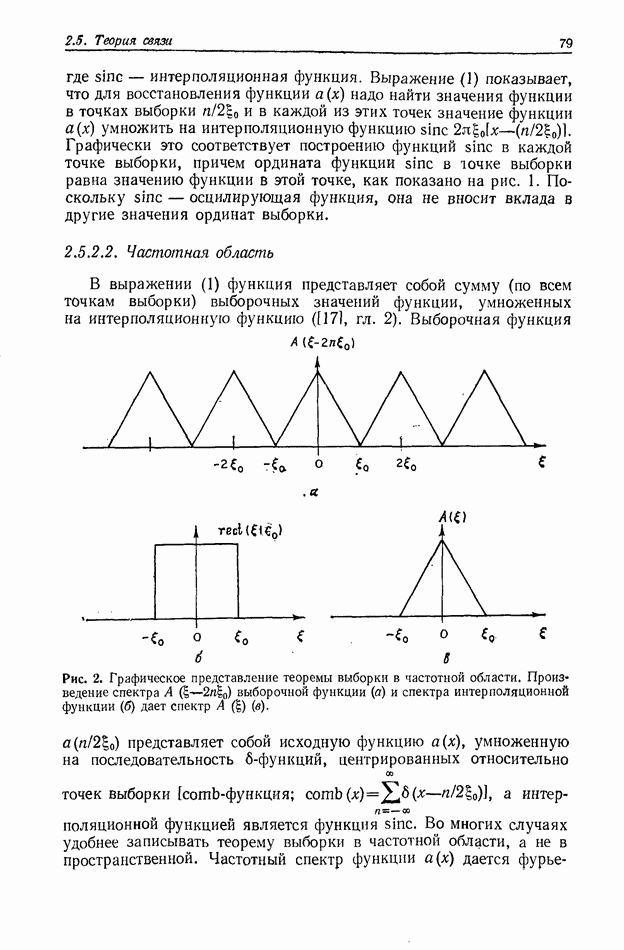
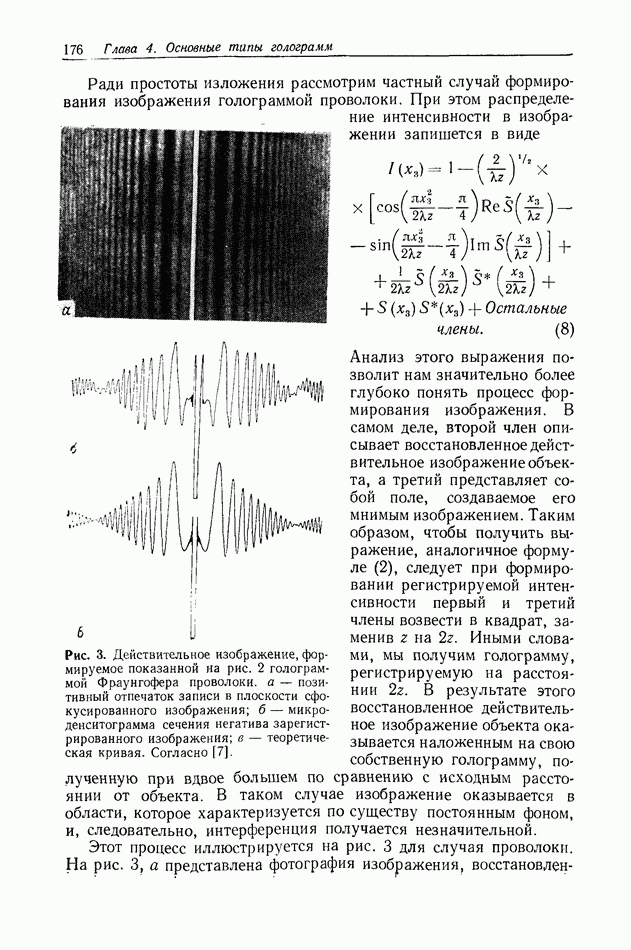
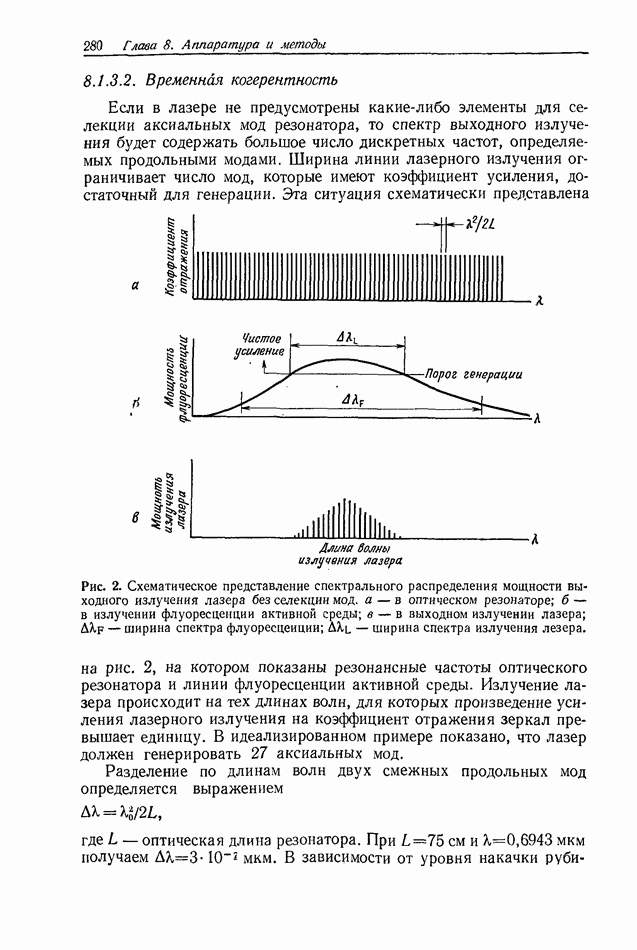
На рис. 2 показана типичная картина таких интерференционных полос, содержащихся внутри центрального максимума огибающей функции, которая представляет собой дифракционную картину на круглых отверстиях. Интерференционные полосы, пересекающие эту картину, действительно появляются и имеют видность, величина которой зависит от их положения в интерференционном поле.
Эту картину дифракции Фраунгофера можно также представить себе как свертку полностью когерентного отклика с образом функции некогерентного источника и функцией его спектрального распределения.
Распространение функции когерентности можно описать

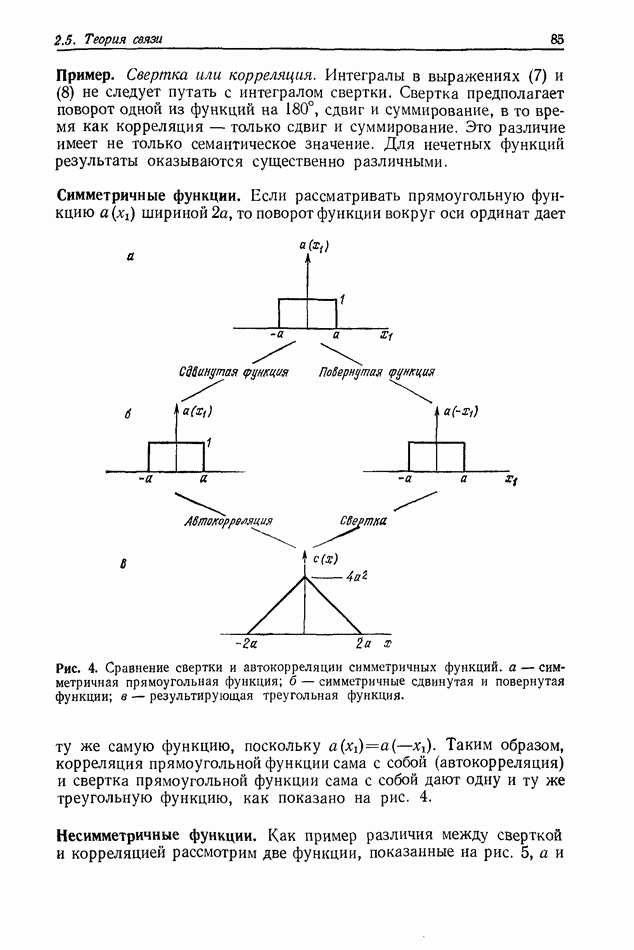
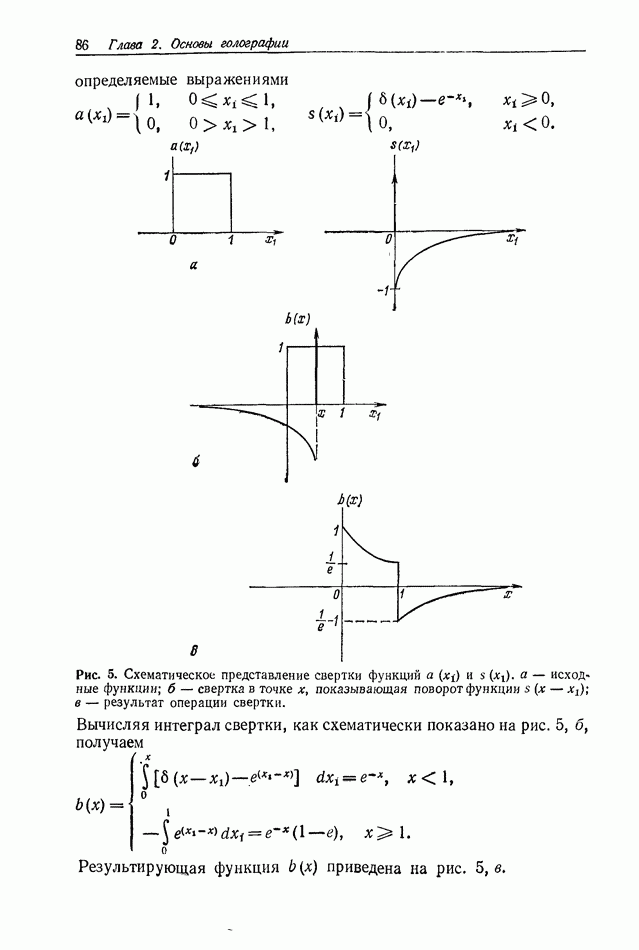
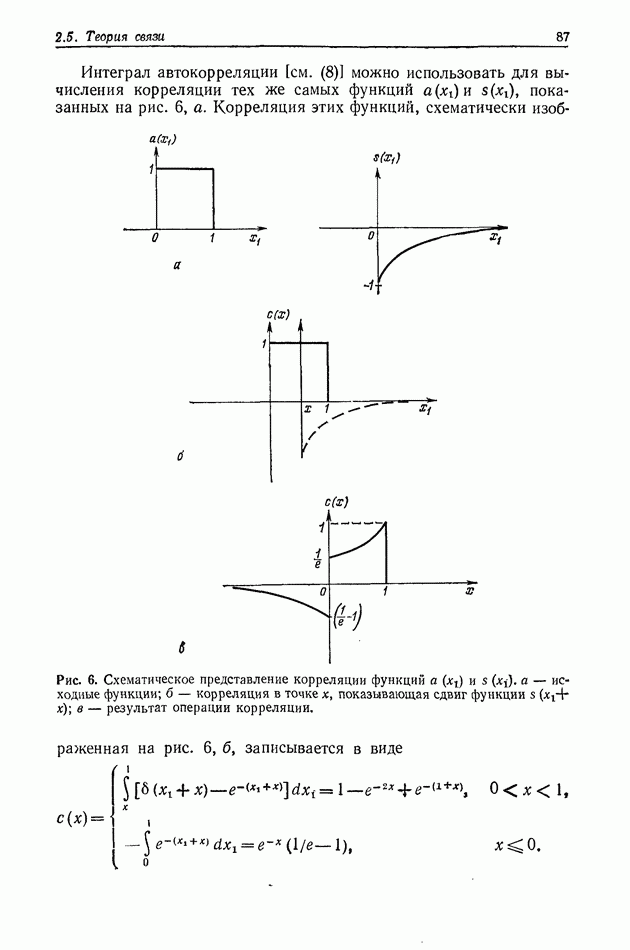
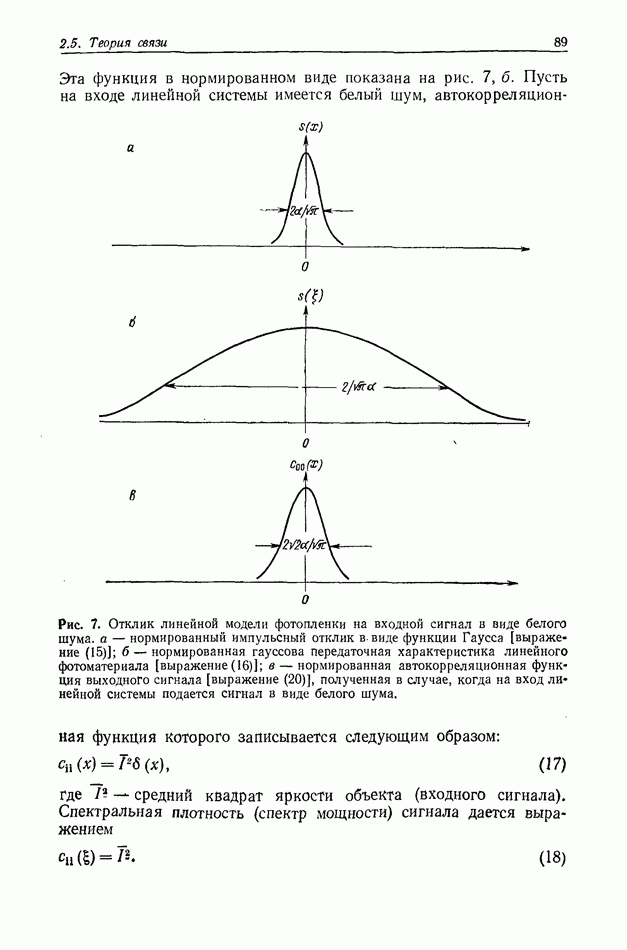
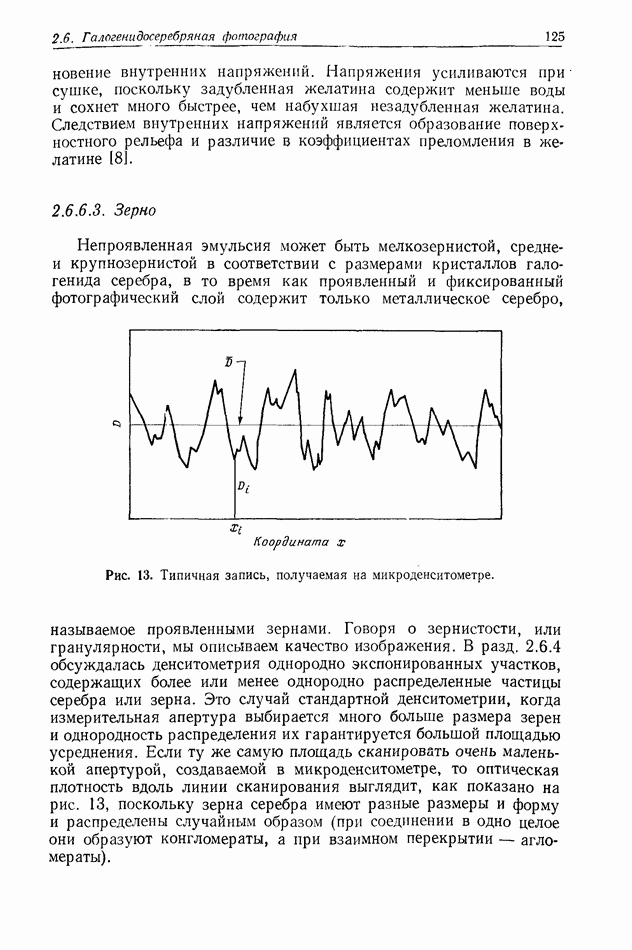
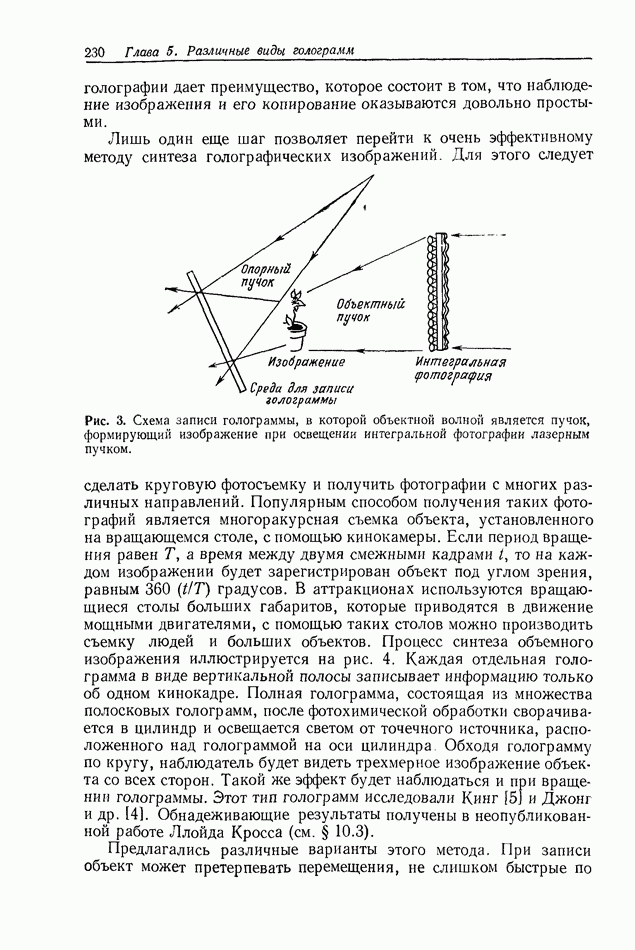
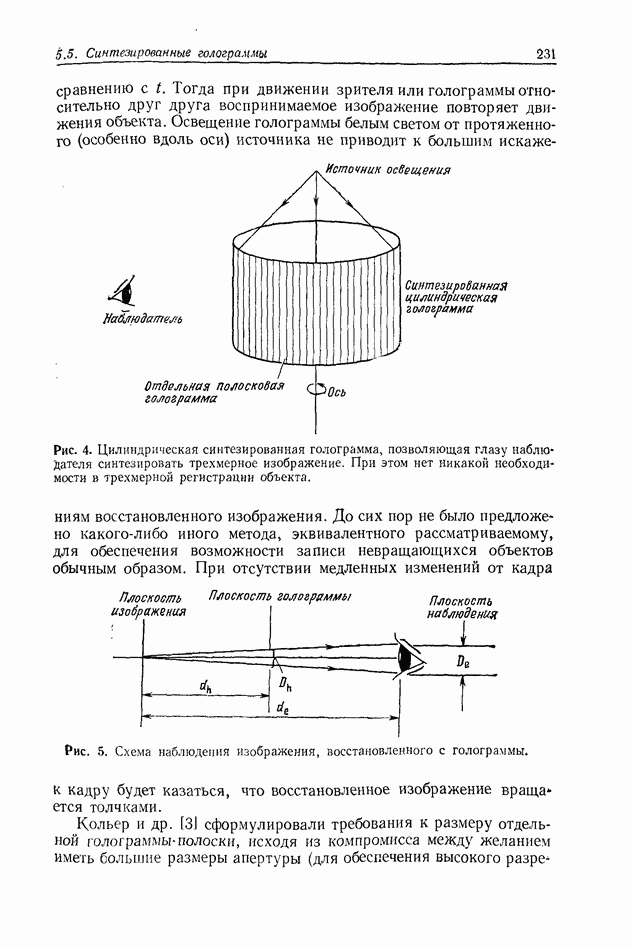
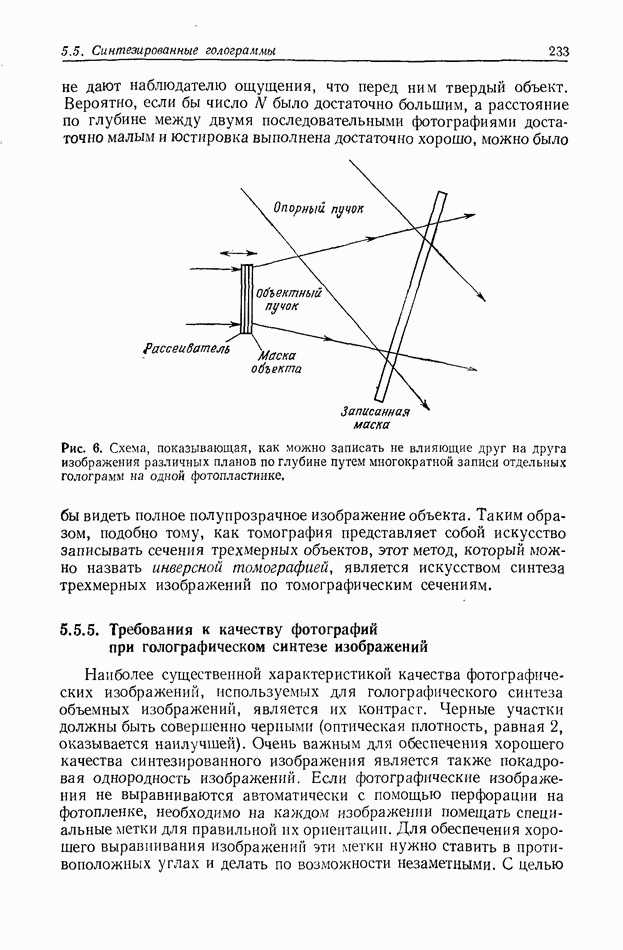
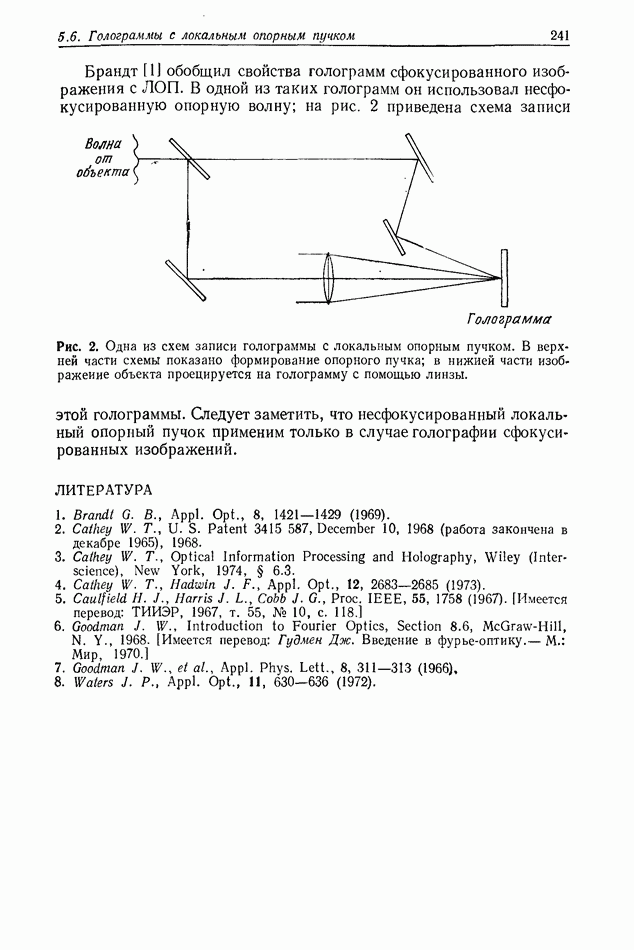
Рис. 2. Дифракционная картина от двух круглых отверстий, образованная частично-когерентным светом,
уравнениями, аналогичными волновым уравнениям, которые описывают распространение функций  и В частности, распространение функции взаимной когерентности дается парой волновых уравнений
и В частности, распространение функции взаимной когерентности дается парой волновых уравнений

В квазимонохроматическом пределе это уравнение сводится к двум уравнениям Гельмгольца:

Последнее уравнение играет очень важную роль, так как оно представляет собой обобщение на случай распространения комплексной амплитуды. Например, если мы имеем оптическое поле, характеризуемое взаимной интенсивностью  то в плоскости
то в плоскости  расположенной на расстоянии z от плоскости падения, взаимная интенсивность дается выражением
расположенной на расстоянии z от плоскости падения, взаимная интенсивность дается выражением

где  расстояние от точки до точки
расстояние от точки до точки  расстояние от точки
расстояние от точки  до точки
до точки  Используя приближение малых углов, выражение (24) можно упростить и провести анализ подобно тому, как это было сделано в разд. 2.2.4. Кроме того, если падающее поле некогерентно, можно вывести выражение (19).
Используя приближение малых углов, выражение (24) можно упростить и провести анализ подобно тому, как это было сделано в разд. 2.2.4. Кроме того, если падающее поле некогерентно, можно вывести выражение (19).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ОСНОВЫ ГОЛОГРАФИИ
- 2.1.1. Преобразование Фурье
- 2.1.2. Преобразование Лапласа
- 2.1.3. Преобразование Фурье — Бесселя
- 2.1.4. Преобразование Френеля
- 2.1.5. Преобразование Гильберта
- 2.1.6. Преобразование Меллина
- 2.1.7. Преобразование Абеля
- 2.2. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
- 2.2.2. Сложение двух когерентных волн
- 2.2.3. Интерференция двух пучков
- 2.2.4. Распространение когерентного света — дифракция Френеля и Фраунгофера
- 2.3. ЧАСТИЧНО-КОГЕРЕНТНЫЙ СВЕТ
- 2.3.1. Сложение двух частично-когерентных квазимонохроматических полей
- 2.3.2. Интерференция двух частично-когерентных квазимонохроматических пучков
- 2.3.3. Интерференция двух частично-когерентных полихроматических пучков
- 2.3.4. Пространственная и временная когерентность
- 2.3.5. Дифракция и интерференция частично-когерентного света
- 2.4. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ
- 2.4.2. Формирование изображения в когерентном и некогерентном свете
- 2.4.3. Предел разрешения
- 2.4.4. Аберрации
- 2.4.5. Голографические изображения
- 2.4.6. Голографические аберрации
- 2.4.7. Отношение сигнал/шум
- 2.4.8. Заключение
- 2.5. ТЕОРИЯ СВЯЗИ
- 2.5.2. Теорема выборки (или теорема отсчетов)
- 2.5.3. Статистическое описание случайных сигналов
- 2.5.4. Выводы
- 2.6. ГАЛОГЕНИДОСЕРЕБРЯНАЯ ФОТОГРАФИЯ
- 2.6.2. Галогенидосеребряный фотографический процесс
- 2.6.3. Сенситометрия
- 2.6.4. Денситометрия
- 2.6.5. Взаимозаместимость
- 2.6.6. Характеристики изображения
- 2.6.7. Влияние изменения окружающей среды на стабильность пространственных параметров слоя
- 2.6.8. Характеристики сохраняемости фотоматериалов
- 2.6.9. Словарь терминов
- Глава 3. КЛАССИФИКАЦИЯ ГОЛОГРАММ
- 3.2. РЕГИСТРИРУЮЩИЕ СРЕДЫ И ИХ ПРИМЕНЕНИЕ
- 3.3. РЕГИСТРИРУЕМЫЕ ПАРАМЕТРЫ ОБЪЕКТНОЙ ВОЛНЫ
- 3.4. МОДУЛИРУЕМЫЕ ПАРАМЕТРЫ
- 3.5. КОНФИГУРАЦИЯ
- 3.6. СВОЙСТВА ИСТОЧНИКОВ
- 3.7. ОПИСАНИЕ ГОЛОГРАММЫ
- Глава 4. ОСНОВНЫЕ ТИПЫ ГОЛОГРАММ
- 4.1. ГОЛОГРАФИЯ ФРЕНЕЛЯ
- 4.2. ГОЛОГРАММЫ ФРАУНГОФЕРА
- 4.3. ГОЛОГРАФИЯ ФУРЬЕ
- 4.3.4. Свойства голограмм Фурье
- Глава 5. РАЗЛИЧНЫЕ ВИДЫ ГОЛОГРАММ
- 5.1. ОТРАЖАТЕЛЬНЫЕ ГОЛОГРАММЫ
- 5.2. МУЛЬТИПЛЕКСНЫЕ ГОЛОГРАММЫ
- 5.3. ЦВЕТНЫЕ ГОЛОГРАММЫ
- 5.4. ПОЛЯРИЗАЦИОННЫЕ ГОЛОГРАММЫ
- 5.5. СИНТЕЗИРОВАННЫЕ ГОЛОГРАММЫ
- 5.6. ГОЛОГРАММЫ С ЛОКАЛЬНЫМ ОПОРНЫМ ПУЧКОМ
- Глава 6. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ
- 6.1. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В КОГЕРЕНТНОМ СВЕТЕ
- 6.2. ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЯ В ЧАСТИЧНО-КОГЕРЕНТНОМ СВЕТЕ
- 6.3. ОЦЕНКА ЯРКОСТИ ВОССТАНОВЛЕННОГО ИЗОБРАЖЕНИЯ
- Глава 7. КАРДИНАЛЬНЫЕ ТОЧКИ И ГЛАВНЫЕ ЛУЧИ В ГОЛОГРАФИИ
- 7.2. ГОЛОГРАФИЧЕСКИЕ УРАВНЕНИЯ ОПТИЧЕСКИХ ЛУЧЕЙ
- 7.3. ГЛАВНЫЕ ТОЧКИ ГОЛОГРАММ
- 7.4. КАРДИНАЛЬНЫЕ ТОЧКИ ГОЛОГРАММЫ
- 7.5. УРАВНЕНИЯ СОПРЯЖЕНИЯ
- 7.6. ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ТИПАМ ГОЛОГРАММ
- Глава 8. АППАРАТУРА И МЕТОДЫ
- 8.1. ТВЕРДОТЕЛЬНЫЕ ЛАЗЕРЫ
- 8.1.2. Рубиновый и Nd:YAG-лазеры
- 8.1.3. Главные конструктивные характеристики лазеров для голографии
- 8.2. ГАЗОВЫЕ ЛАЗЕРЫ
- 8.2.2. Когерентные свойства газовых лазеров
- 8.2.3. Когерентные свойства коммерческих лазеров
- 8.2.4. Диапазон длин волн выходного излучения газовых лазеров
- 8.2.5. Диапазон мощностей выходного излучения
- 8.2.6. Срок службы и стоимость
- 8.3. РЕГИСТРИРУЮЩИЕ СРЕДЫ
- 8.3.3. Галогенидосеребряные эмульсии
- 8.3.4. Задубленная бихромированная желатина
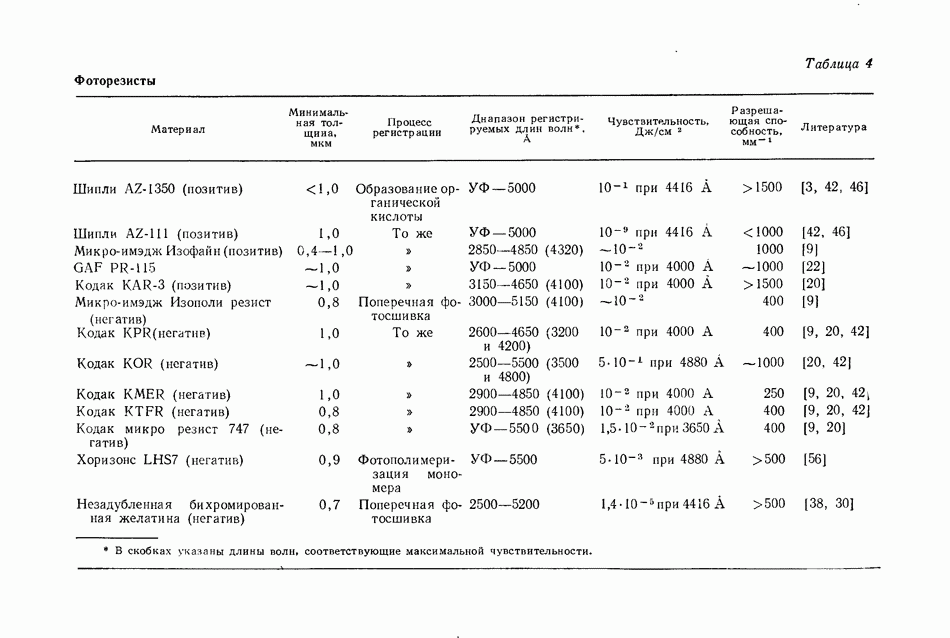
- 8.3.5. Фоторезисты
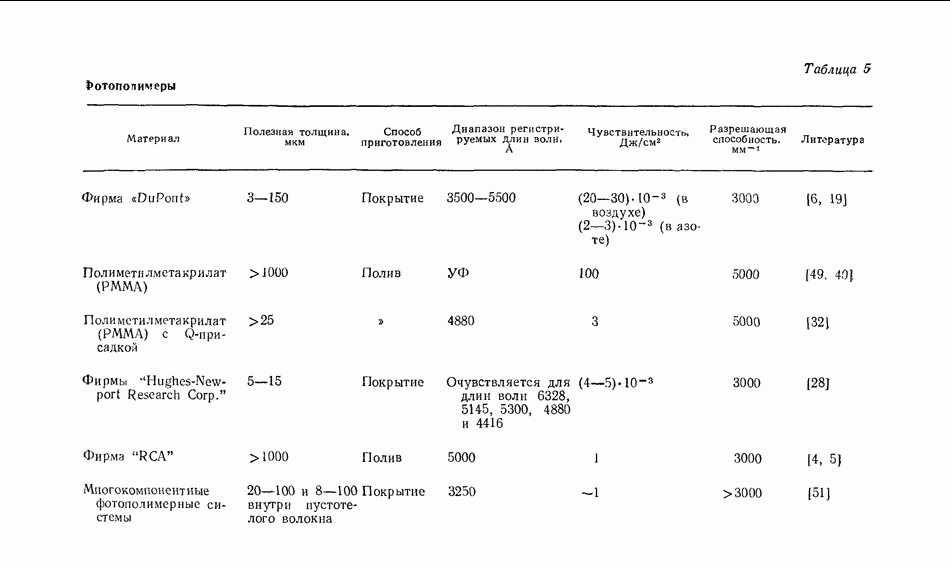
- 8.3.6. Фотополимеры
- 8.3.7. Фотопластики
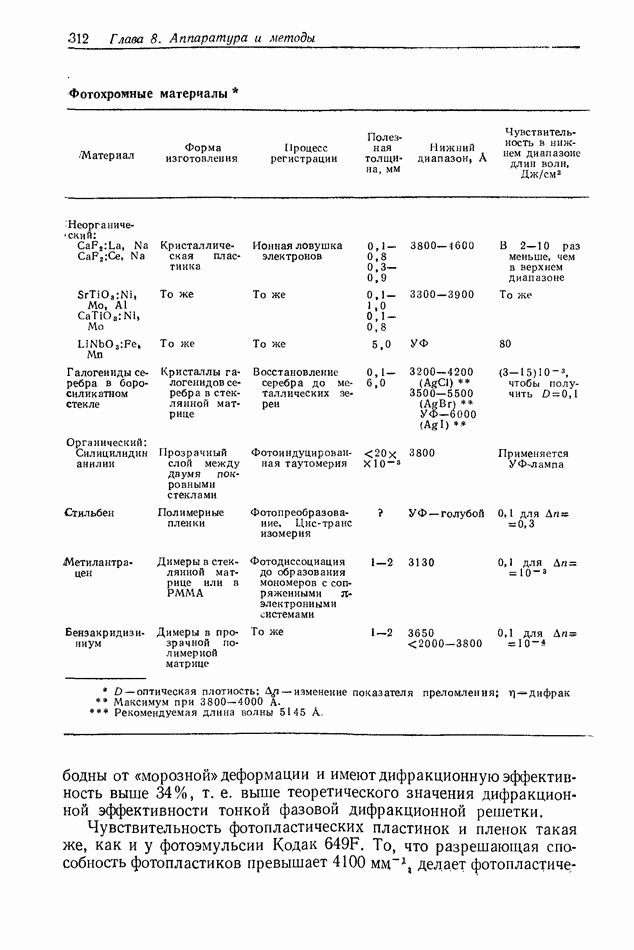
- 8.3.8. Фотохромные материалы
- 8.3.9. Прозрачные электрофотографические пленки
- 8.4. ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
- 8.4.2. Описание комбинированной мобильной установки ГНК; система с переменной чувствительностью
- 8.4.3. Акустооптический голографический неразрушающий контроль
- 8.4.4. Неразрушающий контроль с применением голографии спеклов
- 8.4.5. Голографическая корреляция
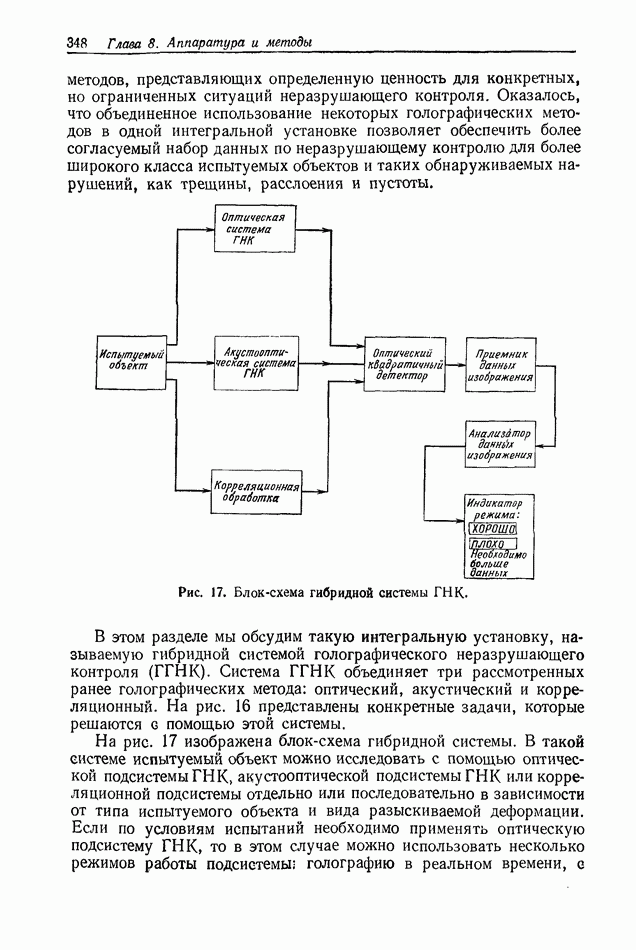
- 8.4.6. Гибридная система ГНК с автоматической обработкой данных
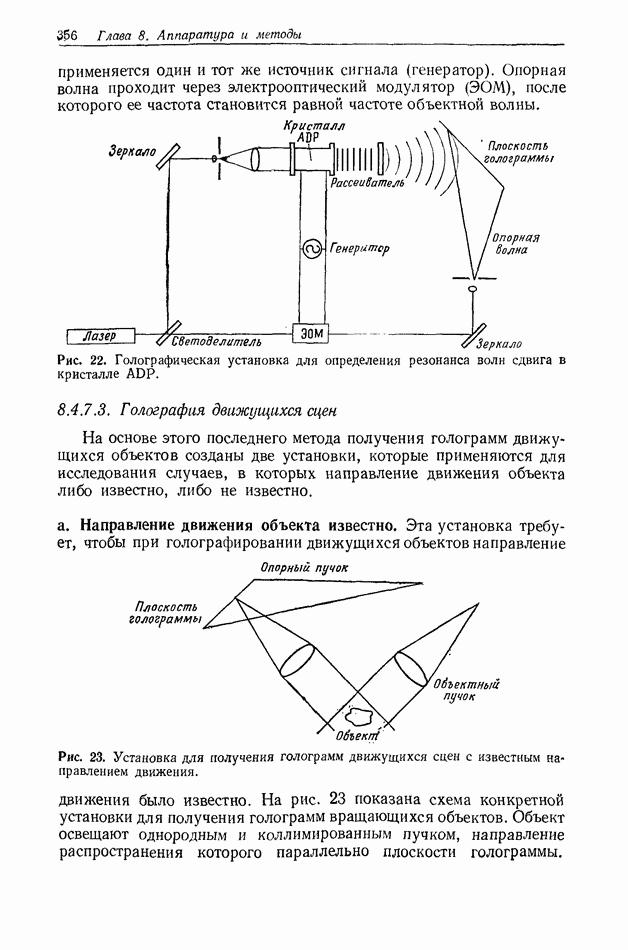
- 8.4.7. Голография движущихся объектов
- 8.4.7.3. Голография движущихся сцен
- 8.4.8. Другие голографические системы
- 8.4.9. Заключение