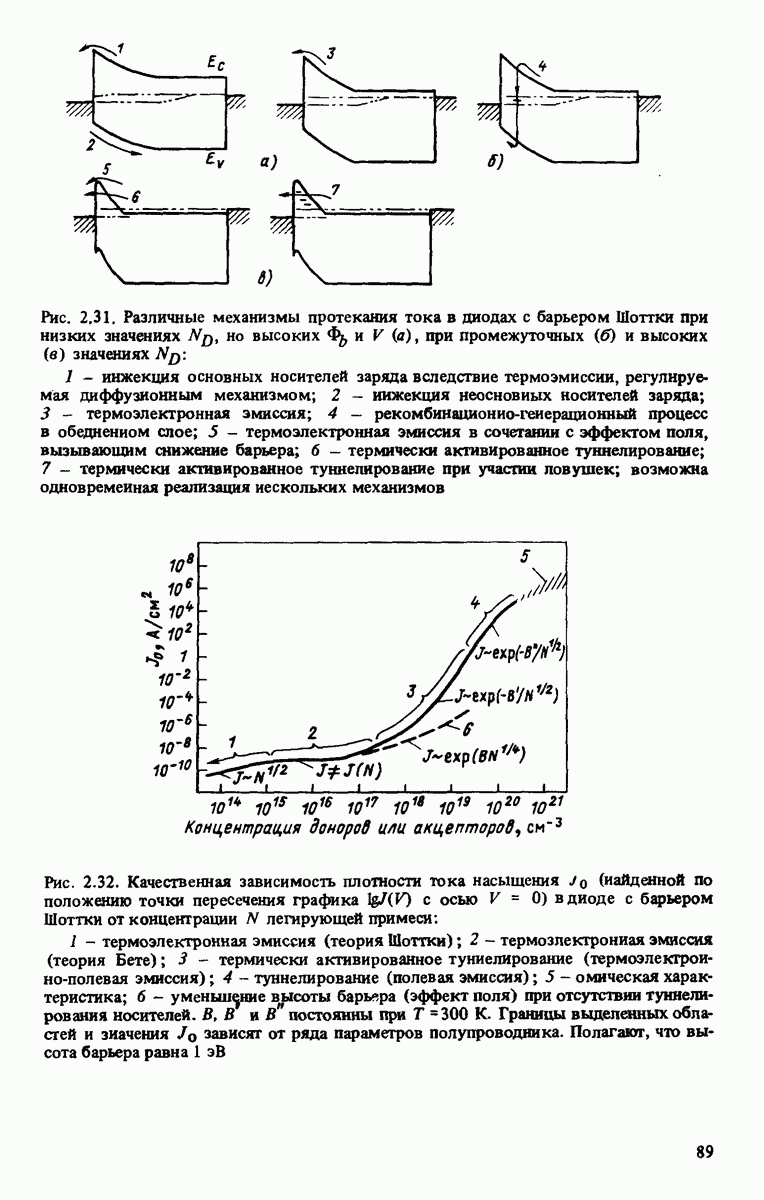
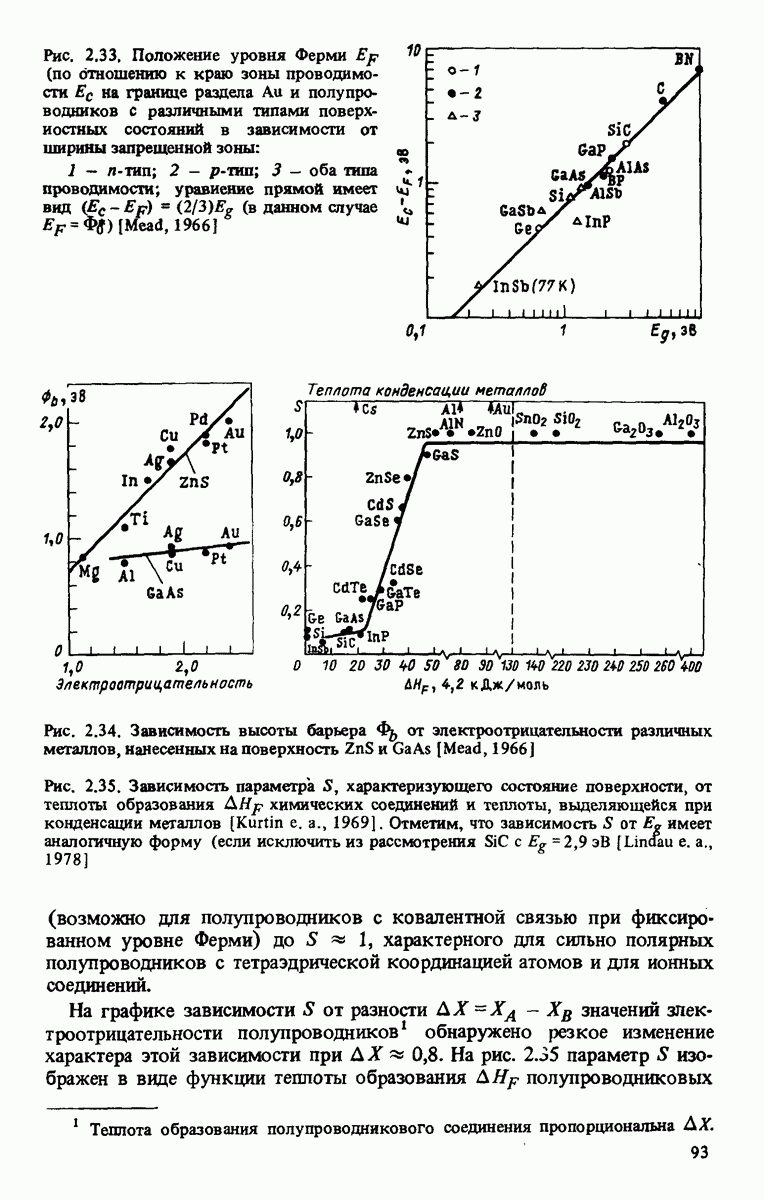
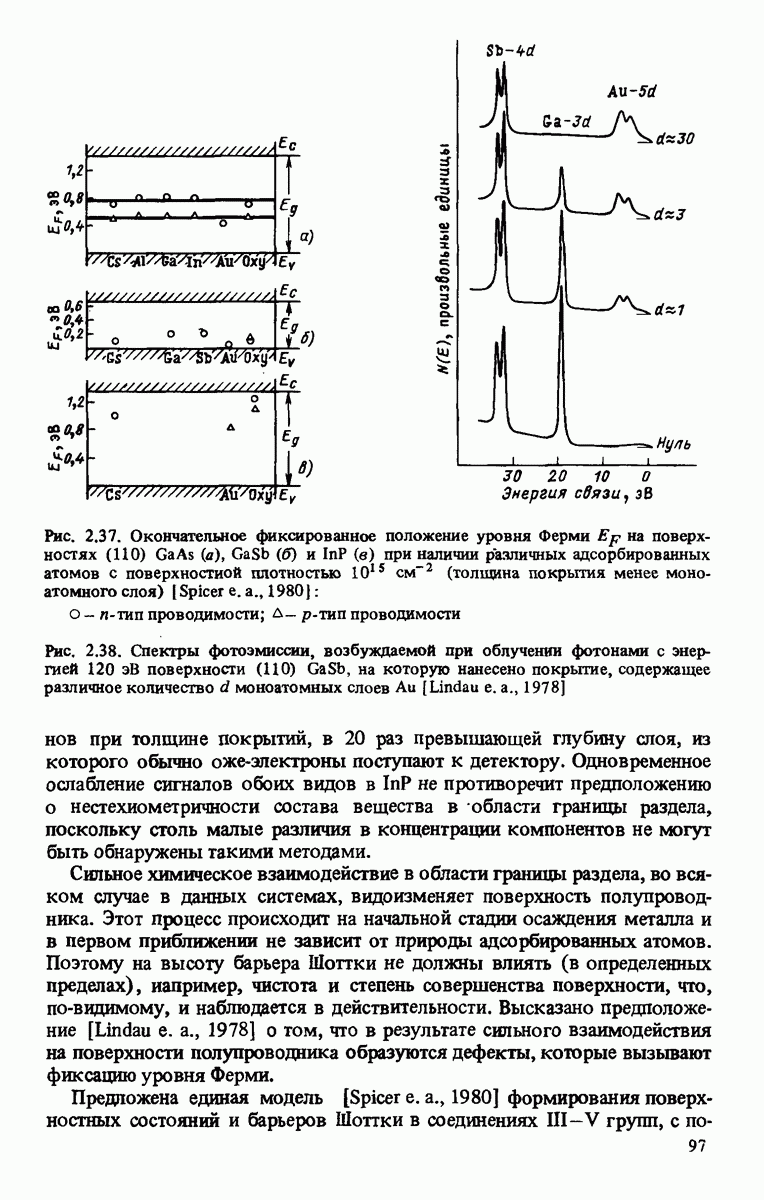
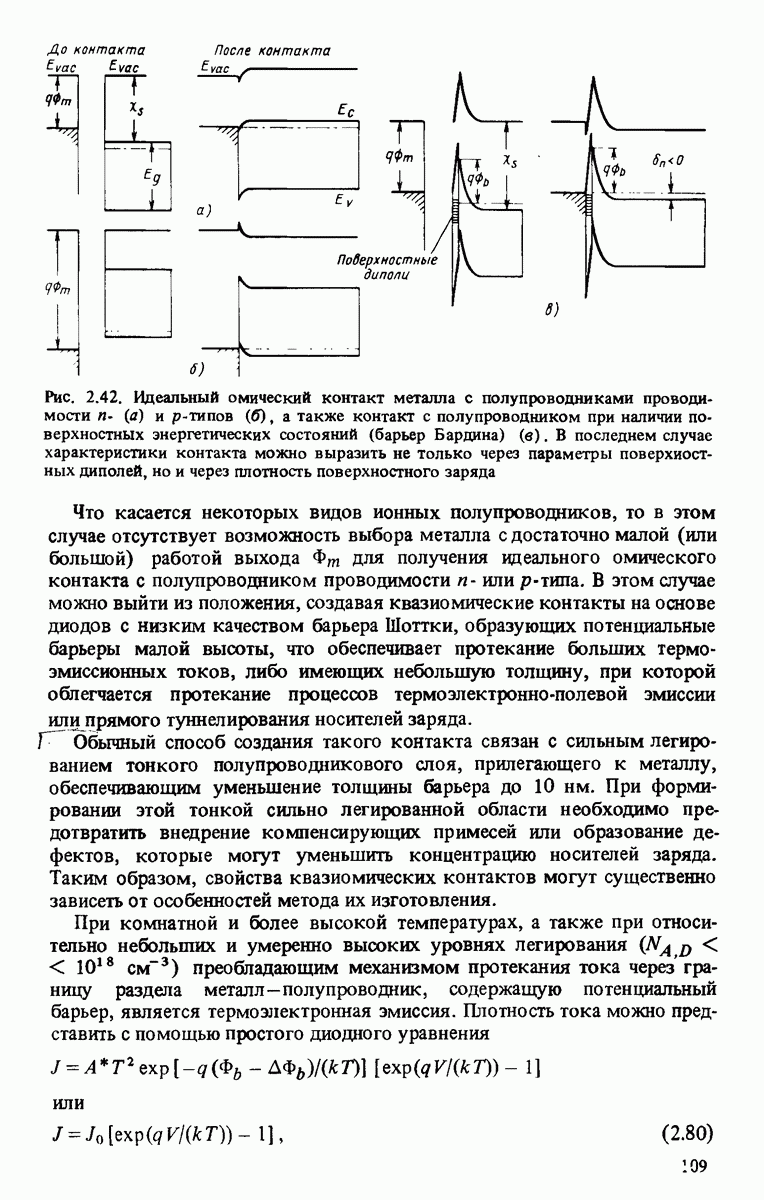
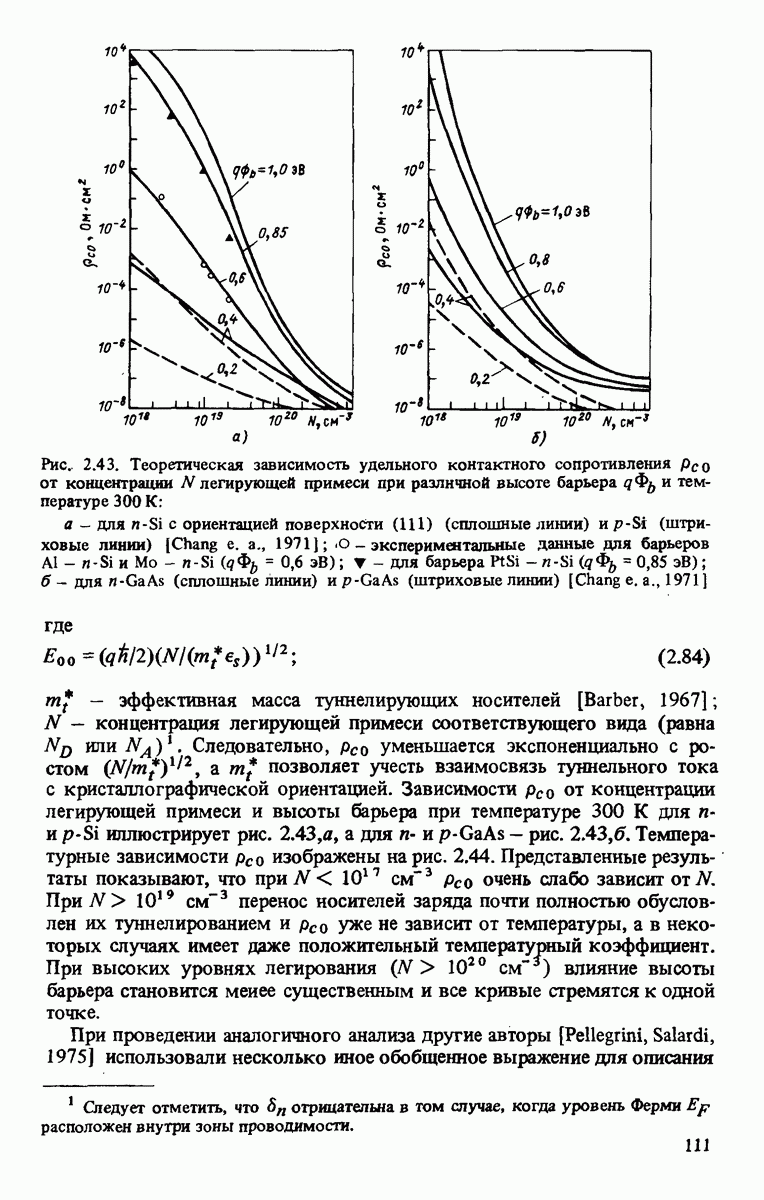
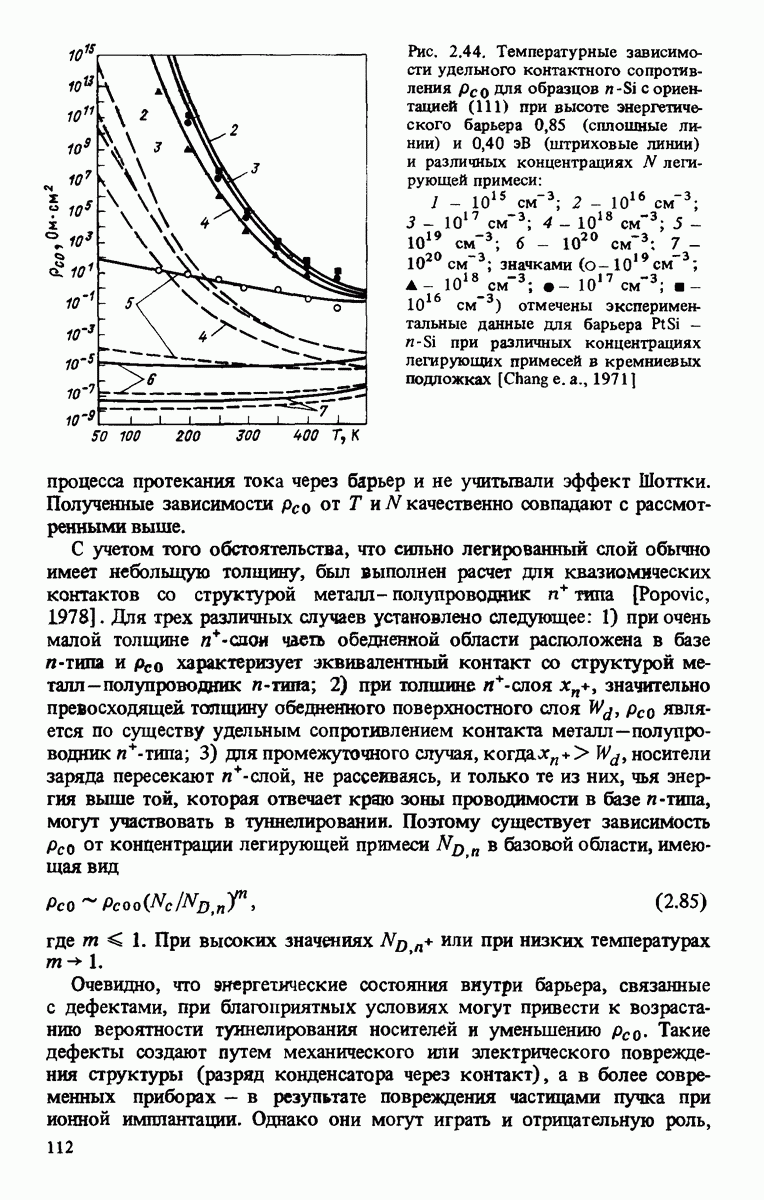
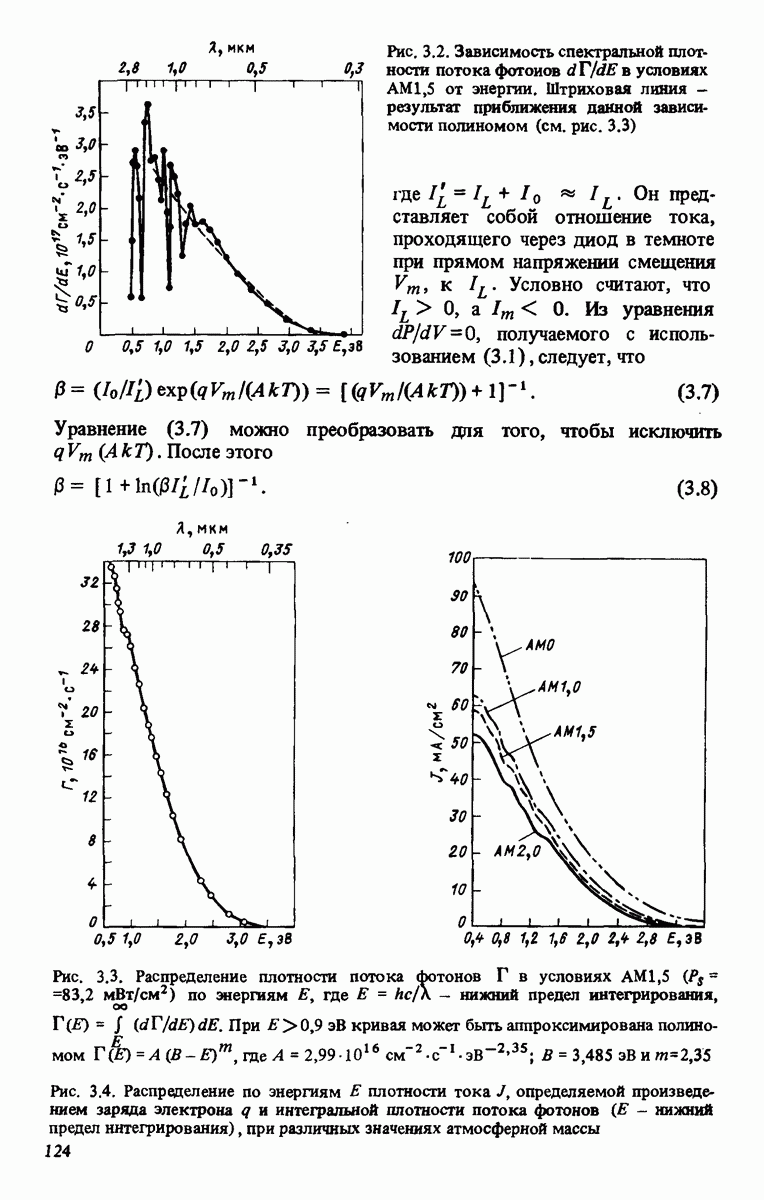
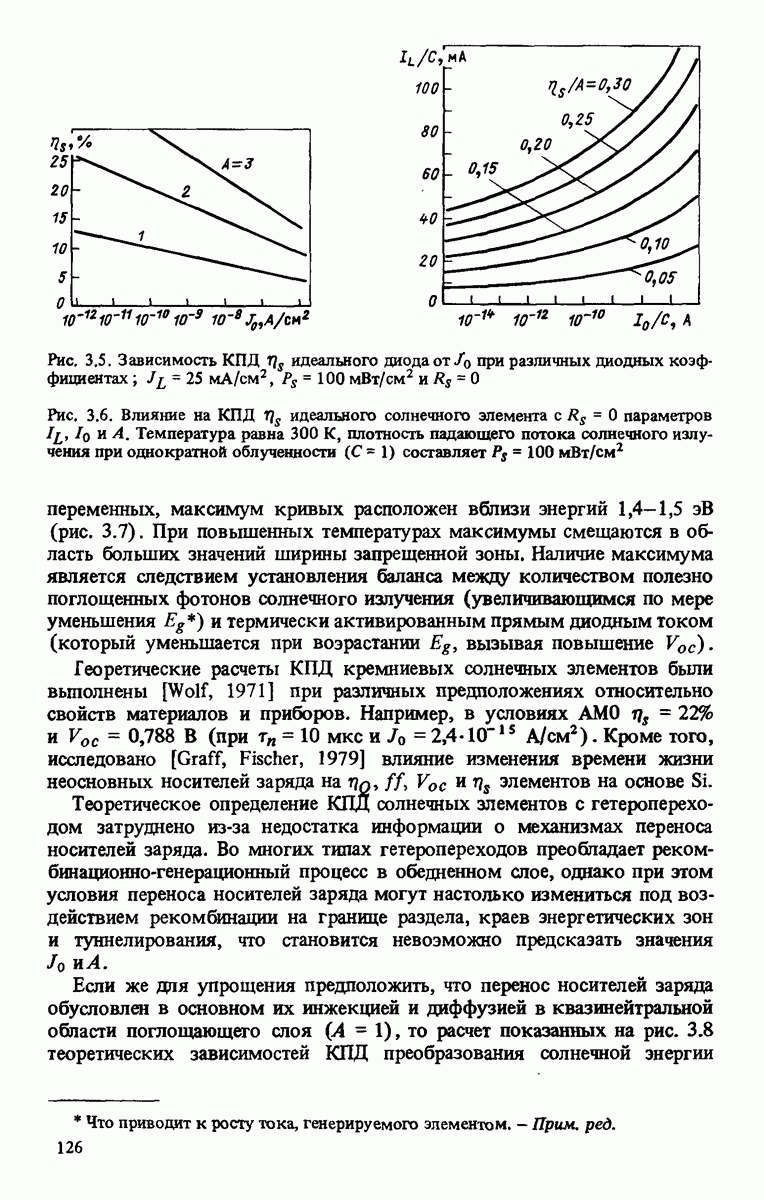
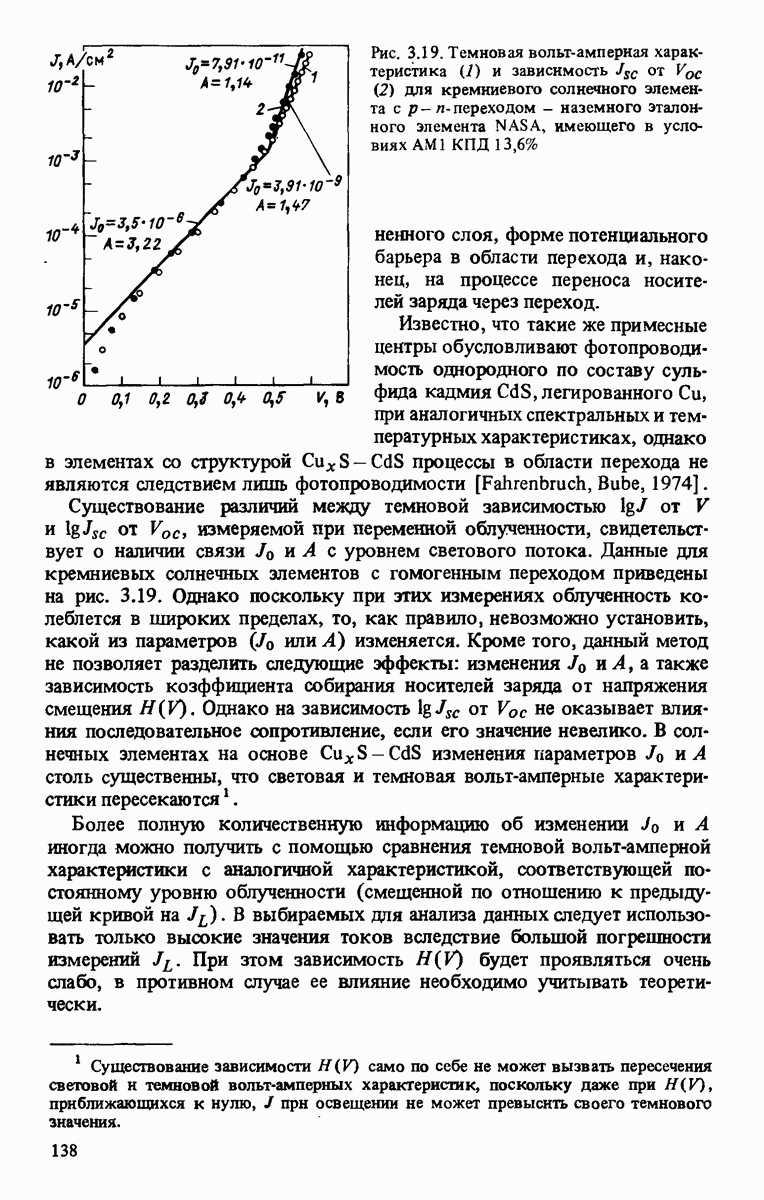
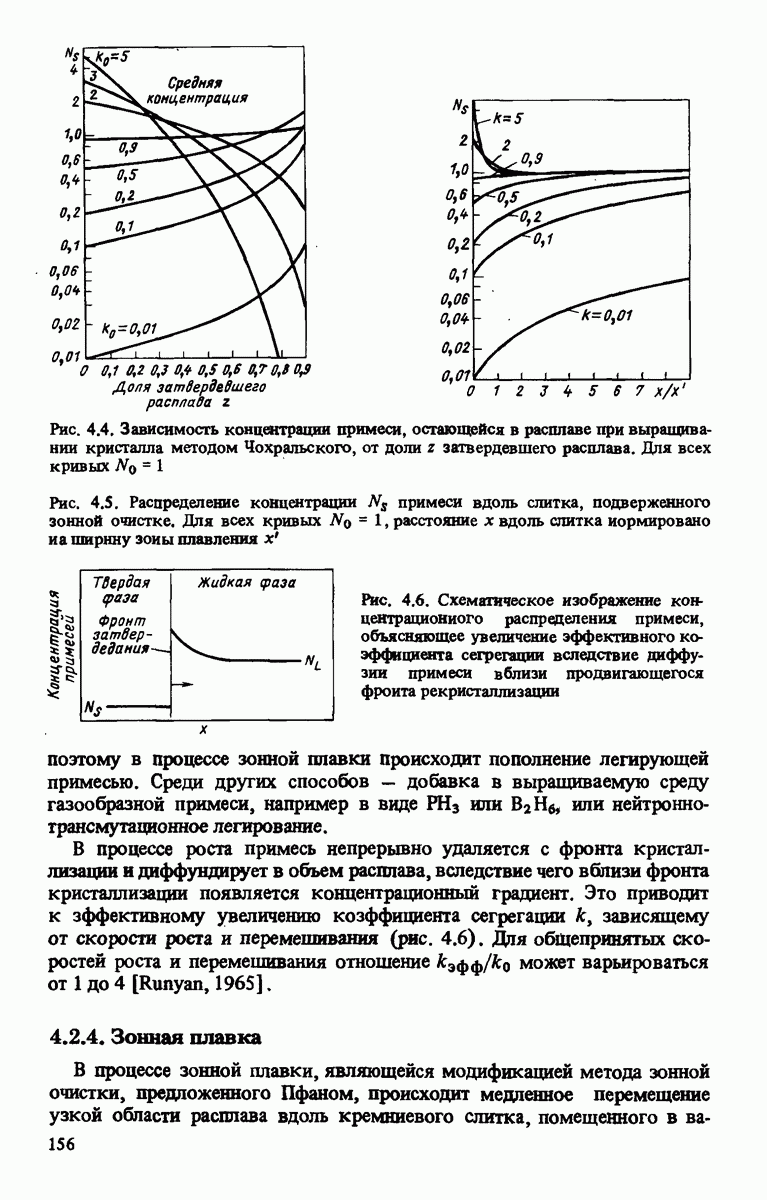
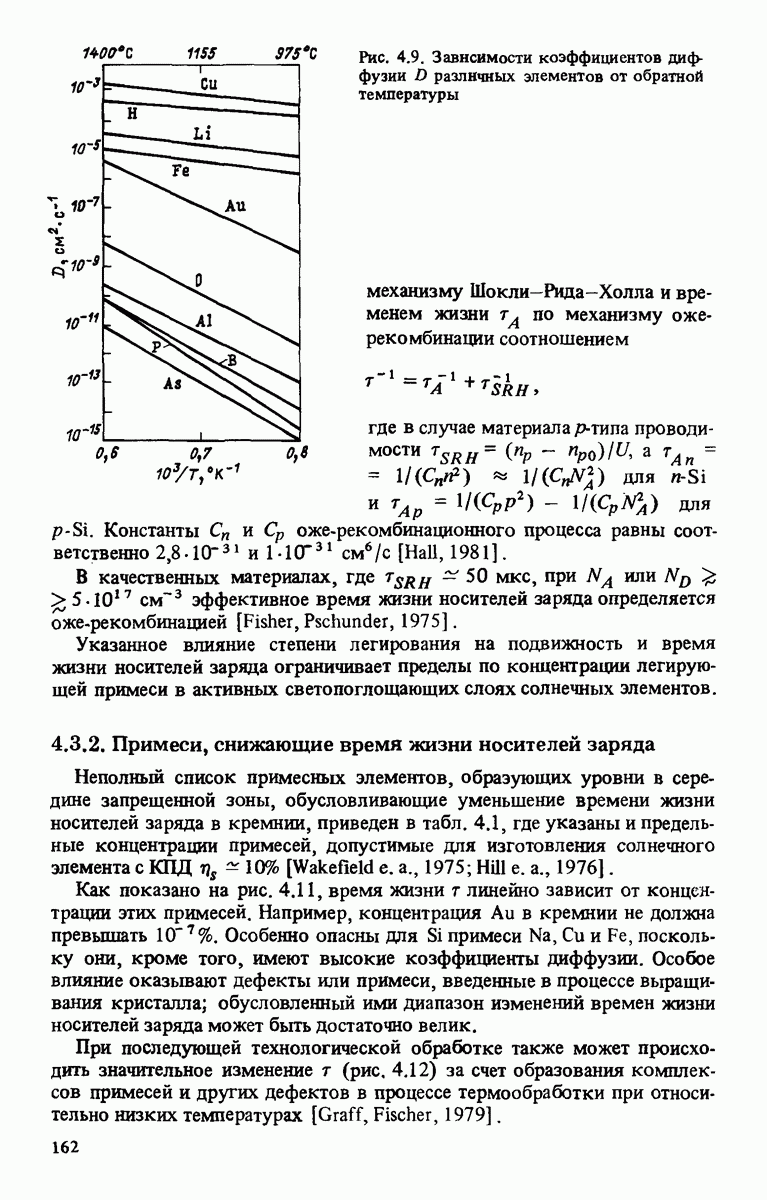
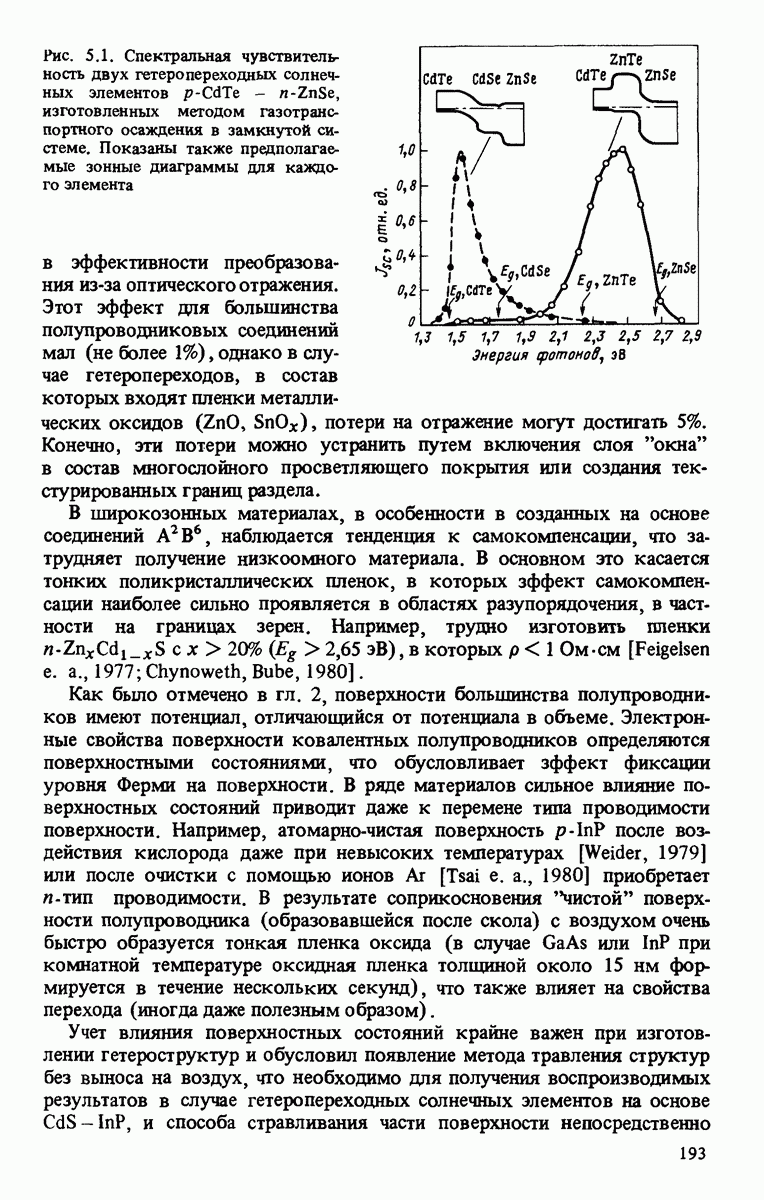
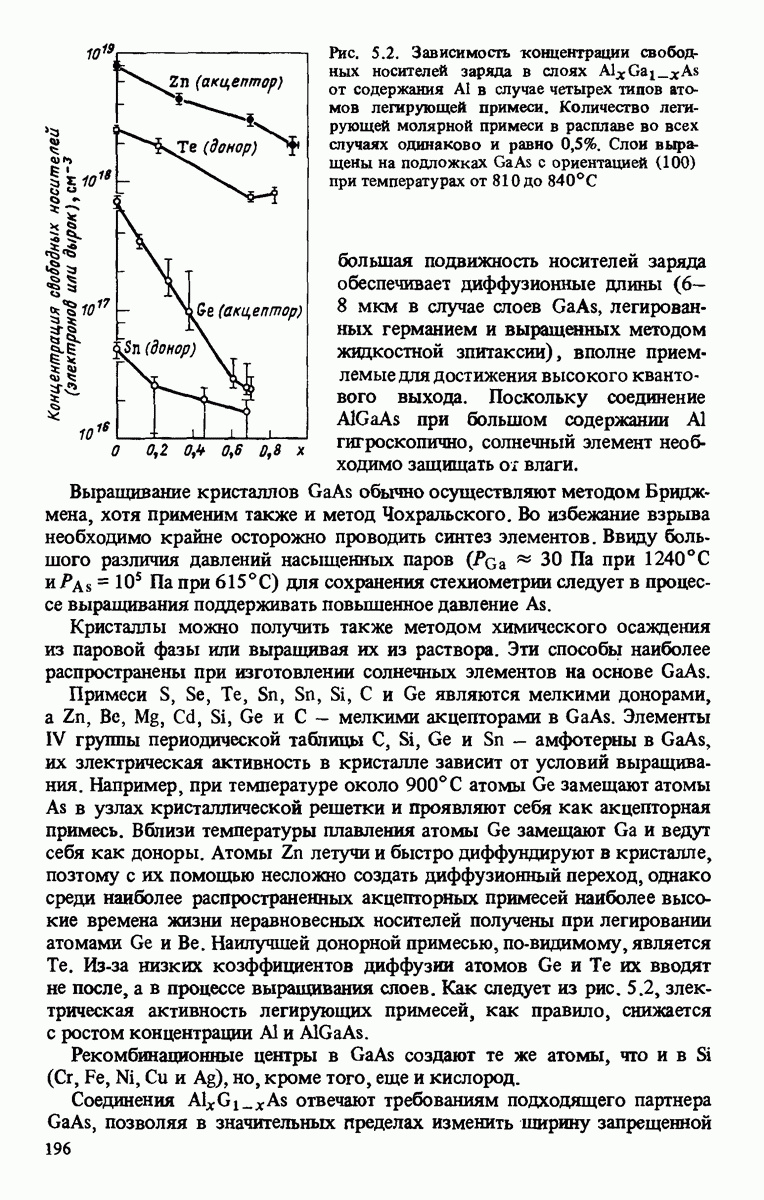
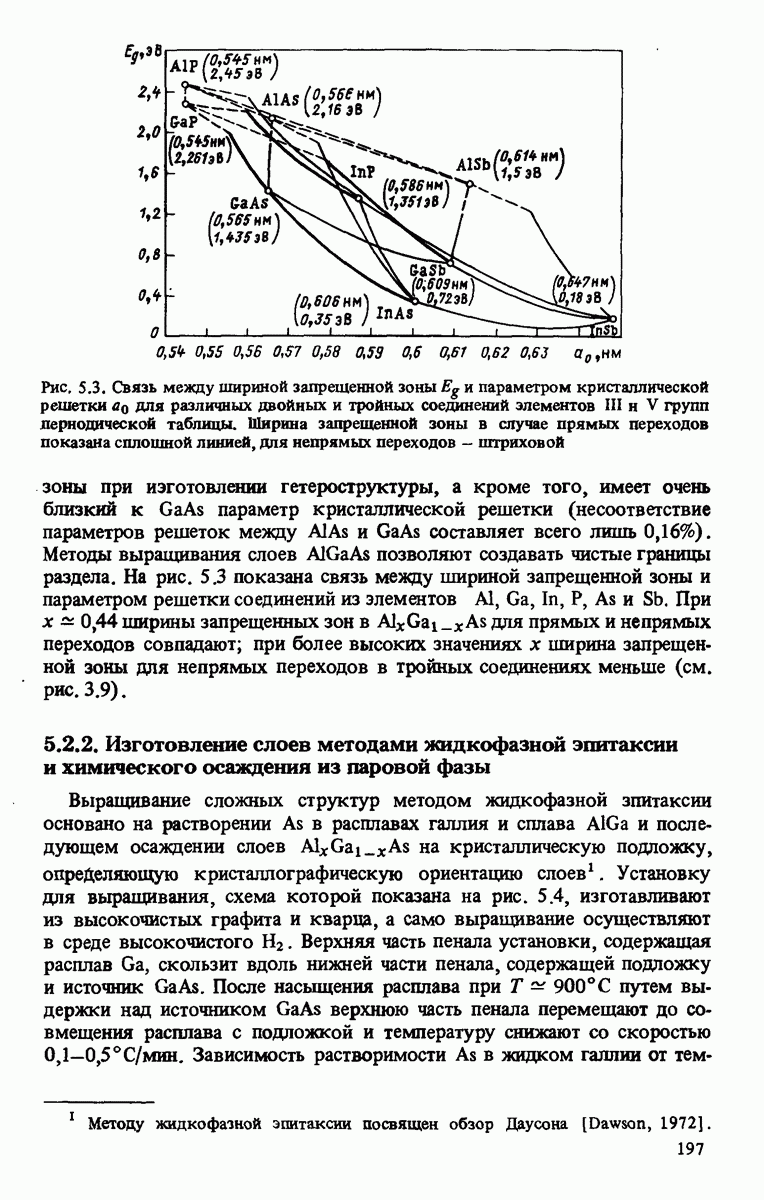
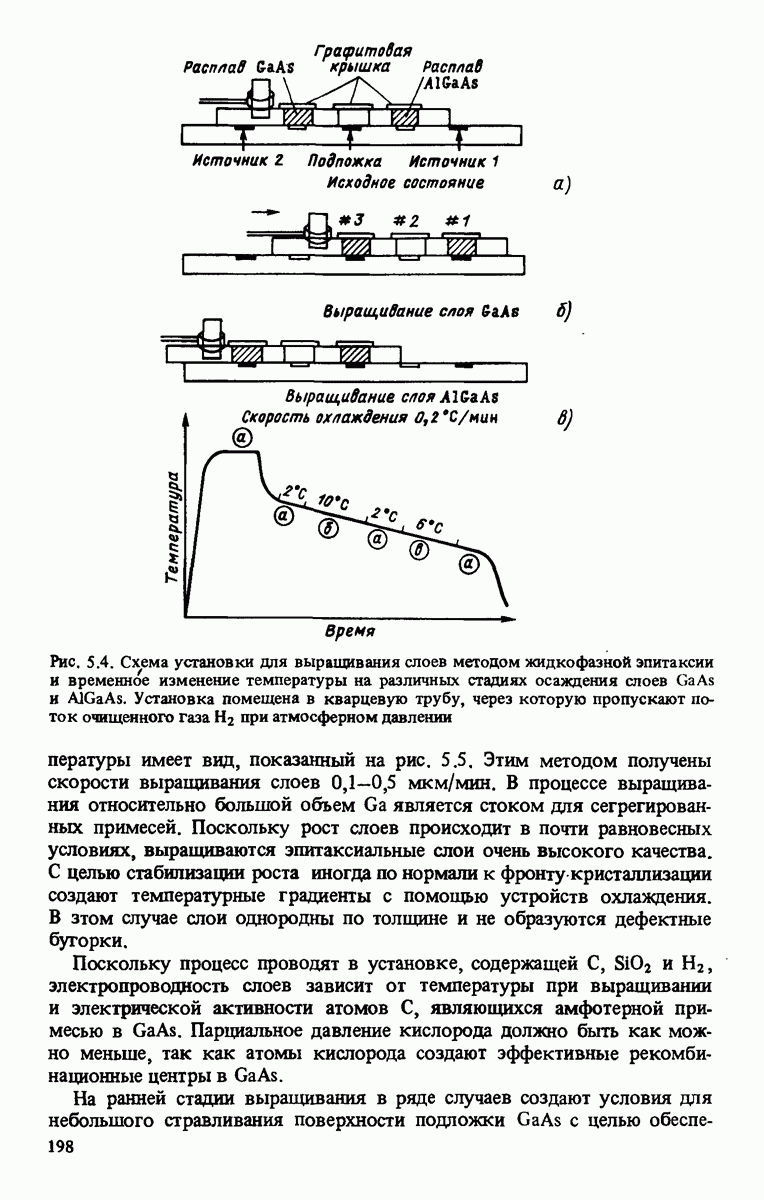
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5.6. Термическая активация и туннелирование
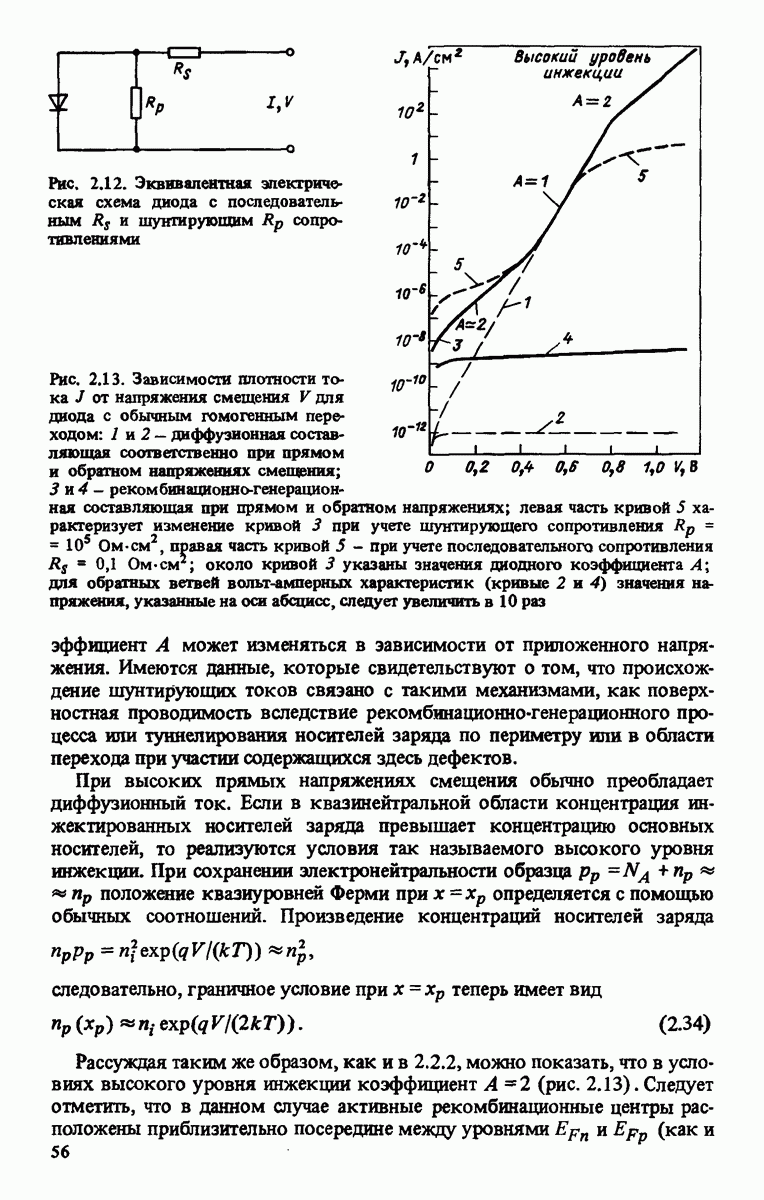
Во многих гетеропереходах одновременно реализуются два (или даже несколько) механизма переноса носителей заряда: туннелирование с последующей рекомбинацией (было рассмотрено ранее) и термическая активация, приводящая к повышению энергии носителей до уровня, при котором прозрачность барьера повышается или становится возможным их прямой переход на рекомбинационные центры в области границы раздела. Таким образом, по мере понижения температуры наклон кривой  сначала изменяется обратно пропорционально температуре, как это происходит при термической активации, а затем перестает зависеть от Т, что свидетельствует о протекании туннельного тока. В обоих случаях основная доля носителей рекомбинирует на границе раздела. С помощью такой комбинированной модели были объяснены [Lindquist, Bube, 1972] особенности протекания тока при прямом напряжении смещения в солнечных элементах с гетеропереходом
сначала изменяется обратно пропорционально температуре, как это происходит при термической активации, а затем перестает зависеть от Т, что свидетельствует о протекании туннельного тока. В обоих случаях основная доля носителей рекомбинирует на границе раздела. С помощью такой комбинированной модели были объяснены [Lindquist, Bube, 1972] особенности протекания тока при прямом напряжении смещения в солнечных элементах с гетеропереходом  на основе монокристаллическо-го сульфида кадмия. Другим примером структуры служит солнечный элемент с гетеропереходом
на основе монокристаллическо-го сульфида кадмия. Другим примером структуры служит солнечный элемент с гетеропереходом  исследование которого показало [Mitchell е. а., 1977], что при
исследование которого показало [Mitchell е. а., 1977], что при  темновой диодный ток, обусловленный в основном туннелированием носителей, отвечает (2.51) с
темновой диодный ток, обусловленный в основном туннелированием носителей, отвечает (2.51) с  При
При  . К преобладает рекомбинационный механизм протекания тока в соответствии с (2.41), в котором
. К преобладает рекомбинационный механизм протекания тока в соответствии с (2.41), в котором  а энергия активации
а энергия активации  для
для  равна 0,59 эВ. При отсутствии напряжения смещения ширина обедненного слоя в этой структуре, сосредоточенного в основном в
равна 0,59 эВ. При отсутствии напряжения смещения ширина обедненного слоя в этой структуре, сосредоточенного в основном в  составляет 0,19 мкм.
составляет 0,19 мкм.
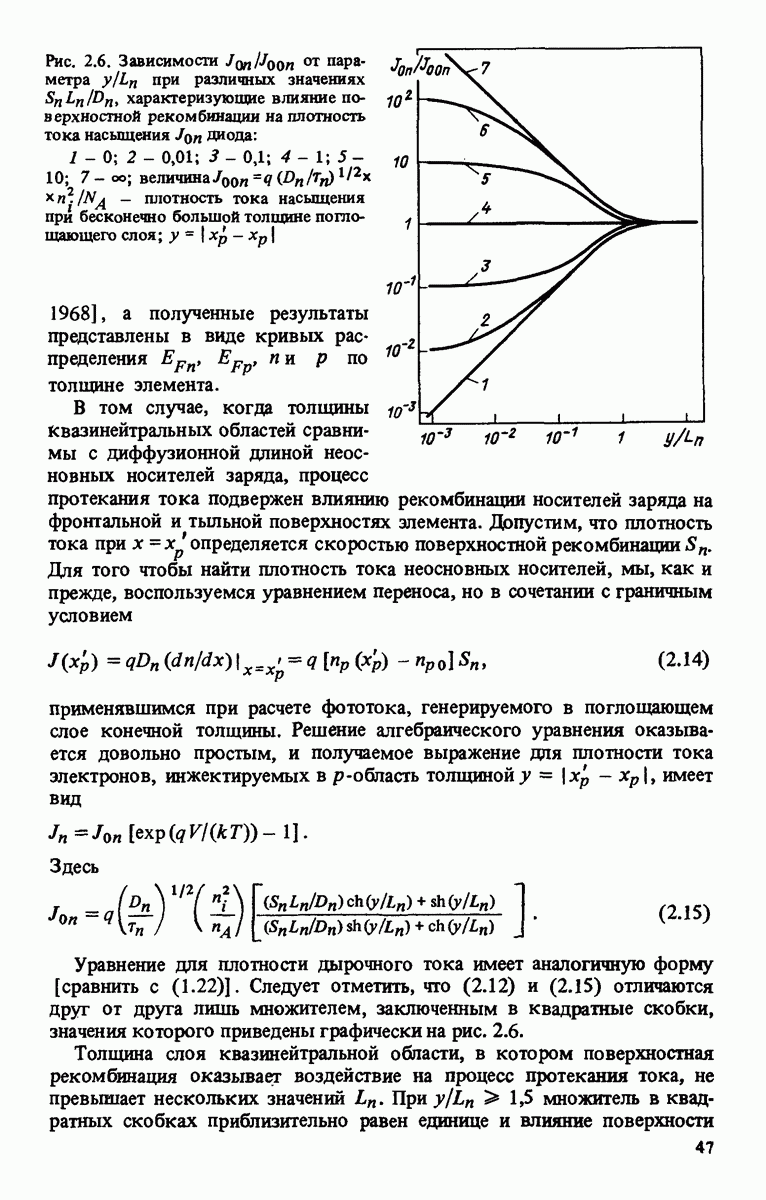
Существует аналогия между гетеропереходами, характеризующимися большими значениями  (при которых поверхностная рекомбинация не является процессом, ограничивающим протекание тока), и барьерами Шоттки, где эффективная скорость поверхностной рекомбинации бесконечно велика. Для описания термически стимулированного туннелирования (называемого также термоэлектронной полевой эмиссией) в барьерах Шоттки разработаны различные модели [Stratton, 1962; Padovani, Stratton, 1966; Chang, Sze, 1970; Crowell, Rideout, 1969], которым посвящены обзоры Rhoderick, 1974; Padovani, 1971. Протекающий через барьер ток равен интегралу произведения падающего потока электронов и квантовомеханического коэффициента прозрачности барьера (т. е. вероятности туннелирования), каждый из множителей является функцией энергии.
(при которых поверхностная рекомбинация не является процессом, ограничивающим протекание тока), и барьерами Шоттки, где эффективная скорость поверхностной рекомбинации бесконечно велика. Для описания термически стимулированного туннелирования (называемого также термоэлектронной полевой эмиссией) в барьерах Шоттки разработаны различные модели [Stratton, 1962; Padovani, Stratton, 1966; Chang, Sze, 1970; Crowell, Rideout, 1969], которым посвящены обзоры Rhoderick, 1974; Padovani, 1971. Протекающий через барьер ток равен интегралу произведения падающего потока электронов и квантовомеханического коэффициента прозрачности барьера (т. е. вероятности туннелирования), каждый из множителей является функцией энергии.

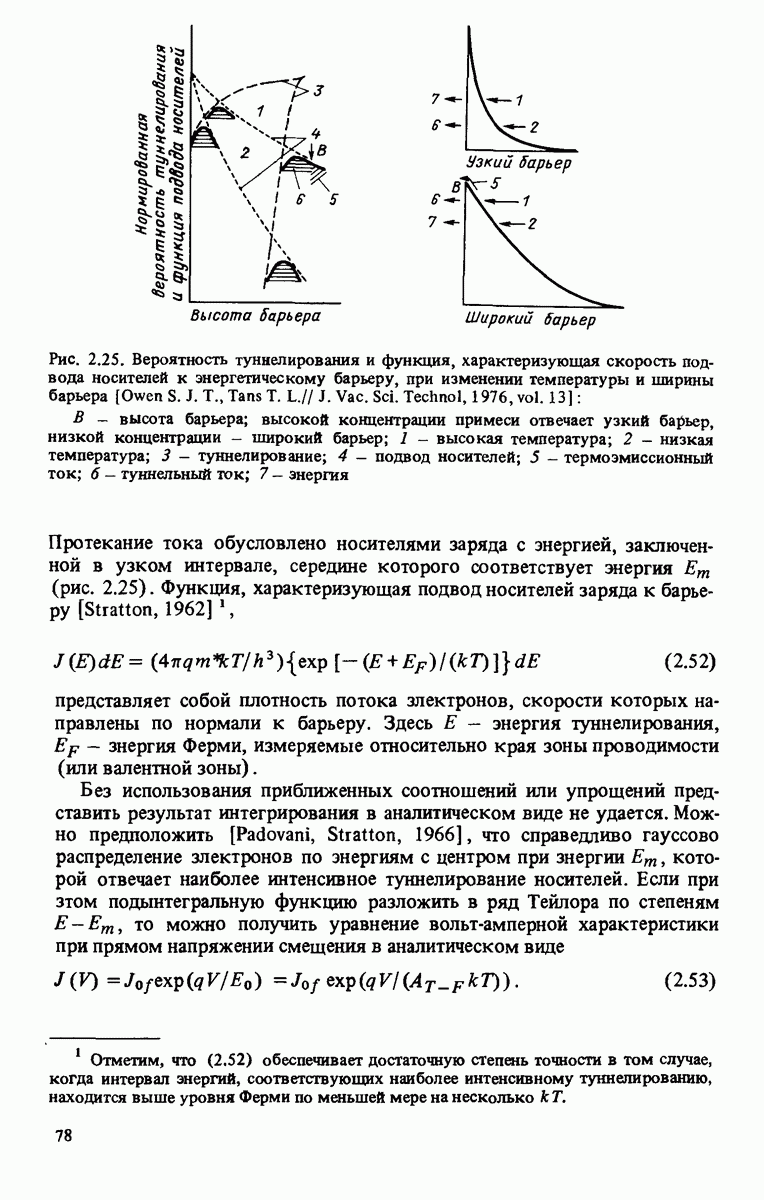
Рис. 2.25. Вероятность туннелирования и функция, характеризующая скорость подвода носителей к энергетическому барьеру, при изменении температуры и ширины барьера [Owen S. J. Т., Tans Т. L. // J. Vac. Sci. Technol, 1976, vol. 13]: В - высота барьера; высокой концентрации примеси отвечает узкий барьер, низкой концентрации - широкий барьер; 1 - высокая температура; 2 - низкая температура; 3 - туннелирование; 4 - подвод носителей; 5 - термоэмиссионный ток; б - туннельный ток; 7 - энергия
Протекание тока обусловлено носителями заряда с энергией, заключенной в узком интервале, середине которого соответствует энергия  (рис. 2.25). Функция, характеризующая подвод носителей заряда к барьеру [Stratton, 1962]
(рис. 2.25). Функция, характеризующая подвод носителей заряда к барьеру [Stratton, 1962]

представляет собой плотность потока электронов, скорости которых направлены по нормали к барьеру. Здесь Е - энергия туннелирования,  — энергия Ферми, измеряемые относительно края зоны проводимости (или валентной зоны).
— энергия Ферми, измеряемые относительно края зоны проводимости (или валентной зоны).
Без использования приближенных соотношений или упрощений представить результат интегрирования в аналитическом виде не удается. Можно предположить [Padovani, Stratton, 1966], что справедливо гауссово распределение электронов по энергиям с центром при энергии  которой отвечает наиболее интенсивное туннелирование носителей. Если при этом подынтегральную функцию разложить в ряд Тейлора по степеням
которой отвечает наиболее интенсивное туннелирование носителей. Если при этом подынтегральную функцию разложить в ряд Тейлора по степеням  то можно получить уравнение вольт-амперной характеристики при прямом напряжении смещения в аналитическом виде
то можно получить уравнение вольт-амперной характеристики при прямом напряжении смещения в аналитическом виде


Рис. 2.26. Отношение энергии  отвечающей максимуму тока, протекающего через барьер Шоттки или над ним, к высоте Е энергетического барьера при различных значениях параметра
отвечающей максимуму тока, протекающего через барьер Шоттки или над ним, к высоте Е энергетического барьера при различных значениях параметра  и соответствующих концентрациях доноров
и соответствующих концентрациях доноров  при
при  и распределение энергии
и распределение энергии  по ширине
по ширине  барьера, имеющего параболическую форму (б). Отметим, что в
барьера, имеющего параболическую форму (б). Отметим, что в  механизм переноса носителей заряда, обусловленный термоэлектроннополевой эмиссией, реализуется в узком диапазоне концентраций легирующей примеси. При рассмотрении
механизм переноса носителей заряда, обусловленный термоэлектроннополевой эмиссией, реализуется в узком диапазоне концентраций легирующей примеси. При рассмотрении  шкала
шкала  существенно смещается относительно
существенно смещается относительно  и значение
и значение  при котором реализуется этот механизм переноса [Rideout, 1975), соответствует середине области концентраций: I - поле: II - термоэмиссия-поле; III - термоэмиссня
при котором реализуется этот механизм переноса [Rideout, 1975), соответствует середине области концентраций: I - поле: II - термоэмиссия-поле; III - термоэмиссня
При рассмотрении барьера Шоттки

При фиксированном значении  величина
величина  о представляет собой высоту потенциального барьера треугольной формы, для которого вероятность туннелирования носителей через его основание равна
о представляет собой высоту потенциального барьера треугольной формы, для которого вероятность туннелирования носителей через его основание равна  [см. (2.49) ]. С учетом упрощений предыдущие выражения справедливы лишь при
[см. (2.49) ]. С учетом упрощений предыдущие выражения справедливы лишь при  На рис. 2.26 показаны области, которым отвечают различные механизмы протекания тока (в их основе лежат полевая, термоэлектронно-полевая и термоэлектронная эмиссии). Данные представлены в виде зависимости энергии
На рис. 2.26 показаны области, которым отвечают различные механизмы протекания тока (в их основе лежат полевая, термоэлектронно-полевая и термоэлектронная эмиссии). Данные представлены в виде зависимости энергии  соответствующей максимуму туннельного тока, от параметра
соответствующей максимуму туннельного тока, от параметра  При прямом смещении
При прямом смещении  имеет вид
имеет вид


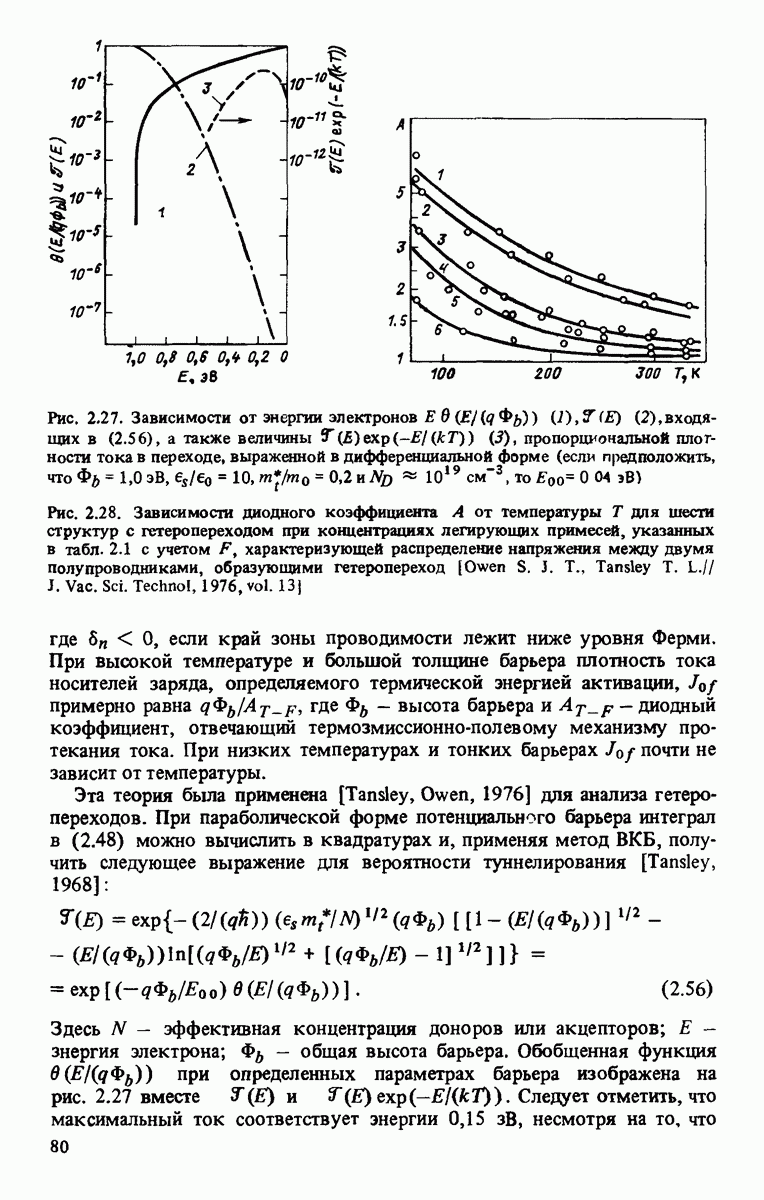
Рис. 2.27. Зависимости от энергии электронов Е в  в (2.56), а также величины
в (2.56), а также величины  пропорциональной плотности тока в переходе, выраженной в дифференциальной форме (если предположить, что
пропорциональной плотности тока в переходе, выраженной в дифференциальной форме (если предположить, что  эВ,
эВ,  то
то 

Рис. 2.28. Зависимости диодного коэффициента А от температуры Т для шести структур с гетеропереходом при концентрациях легирующих примесей, указанных в табл. 2.1 с учетом F, характеризующей распределение напряжения между двумя полупроводниками, образующими гетеропереход [Owen S. J. Т., Tansley Т. L.// J. Vac. Sci. Techno!, 1976, vol. 13]
где  если край зоны проводимости лежит ниже уровня Ферми. При высокой температуре и большой толщине барьера плотность тока носителей заряда, определяемого термической энергией активации,
если край зоны проводимости лежит ниже уровня Ферми. При высокой температуре и большой толщине барьера плотность тока носителей заряда, определяемого термической энергией активации,  примерно равна
примерно равна  где
где  - высота барьера и
- высота барьера и  — диодный коэффициент, отвечающий термозмиссионно-полевому механизму протекания тока. При низких температурах и тонких барьерах
— диодный коэффициент, отвечающий термозмиссионно-полевому механизму протекания тока. При низких температурах и тонких барьерах  почти не зависит от температуры.
почти не зависит от температуры.
Эта теория была применена [Tansley, Owen, 1976] для анализа гетеропереходов. При параболической форме потенциального барьера интеграл в (2.48) можно вычислить в квадратурах и, применяя метод ВКБ, получить следующее выражение для вероятности туннелирования [Tansley, 1968]:

Здесь N — эффективная концентрация доноров или акцепторов; Е - энергия электрона;  - общая высота барьера. Обобщенная функция
- общая высота барьера. Обобщенная функция  при определенных параметрах барьера изображена на рис. 2.27 вместе
при определенных параметрах барьера изображена на рис. 2.27 вместе  Следует отметить, что максимальный ток соответствует энергии
Следует отметить, что максимальный ток соответствует энергии  несмотря на то, что
несмотря на то, что
Таблица 2.1. Концентрации легирующих примесей и распределение приложенного напряжения в гетеропереходах

в этом случае вероятность туннелирования чрезвычайно мала (менее  ). С учетом (2.56) и (2.52) для плотности потока электронов посредством интегрирования численными методами произведения
). С учетом (2.56) и (2.52) для плотности потока электронов посредством интегрирования численными методами произведения  была найдена [Tansley, Owen, 1976] плотность полного тока в переходе
была найдена [Tansley, Owen, 1976] плотность полного тока в переходе  Для нахождения эквивалентного диодного коэффициента асимметричного перехода выражение
Для нахождения эквивалентного диодного коэффициента асимметричного перехода выражение  входящее в (2.53), следует умножить на параметр, характеризующий распределение напряжения в асимметричном переходе. Так, для
входящее в (2.53), следует умножить на параметр, характеризующий распределение напряжения в асимметричном переходе. Так, для  -гетероструктуры, в которой протекание тока ограничено процессом туннелирования электронов через обедненный слой
-гетероструктуры, в которой протекание тока ограничено процессом туннелирования электронов через обедненный слой  -типа, эквивалентный диодный коэффициент
-типа, эквивалентный диодный коэффициент  можно представить в виде [Tansley, Owen, 1976]
можно представить в виде [Tansley, Owen, 1976]

Как следует из рис. 2.28, расчетные и экспериментальные температурные зависимости  для гетеропереходов, образованных
для гетеропереходов, образованных  в сочетании с
в сочетании с  (концентрации легирующих примесей в этих материалах приведены в табл. 2.1), с высокой точностью согласуются между собой.
(концентрации легирующих примесей в этих материалах приведены в табл. 2.1), с высокой точностью согласуются между собой.
Аналогичный подход был применен для описания процесса протекания тока в солнечных элементах с гетеропереходом  [Aranovich е. а., 1980]. Поскольку в данном случае использовали вырожденный
[Aranovich е. а., 1980]. Поскольку в данном случае использовали вырожденный  диффузионный потенциал приходится в основном на слой
диффузионный потенциал приходится в основном на слой  . Авторы следовали ранее высказанному предположейию [Padovani,
. Авторы следовали ранее высказанному предположейию [Padovani,
1971] о том, что наличие внутри обедненного слоя большого количества глубоких акцепторных уровней может вызвать значительное сужение обедненного слоя, что делает возможным туннелирование носителей. Наличие в этих диодах глубоких уровней энергетических состояний привело к появлению зависимости вольт-амперной характеристики от облученности элементов и продолжительности их экспозиции. Обнаружена отчетливо выраженная взаимосвязь между значением  и плотностью состояний на поверхности раздела (зависящей от условий процесса изготовления)
и плотностью состояний на поверхности раздела (зависящей от условий процесса изготовления)  , которая влияет на высоту барьера, а также зависимость параметра диода
, которая влияет на высоту барьера, а также зависимость параметра диода  от эффективной концентрации акцепторов в обедненном слое
от эффективной концентрации акцепторов в обедненном слое 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 1. УРАВНЕНИЕ ПЕРЕНОСА
- 1.2. ОСНОВНЫЕ СОСТАВЛЯЮЩИЕ УРАВНЕНИЯ ПЕРЕНОСА
- 1.3. ВЫВОД УРАВНЕНИЯ ПЕРЕНОСА
- 1.4. РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА
- 1.5. СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- 1.6. ИЗМЕРЕНИЕ ВРЕМЕНИ ЖИЗНИ И ДИФФУЗИОННОЙ ДЛИНЫ НЕОСНОВНЫХ НОСИТЕЛЕЙ ЗАРЯДА
- Глава 2. ЭЛЕКТРОННО-ДЫРОЧНЫЕ ПЕРЕХОДЫ
- 2.2. ГОМОГЕННЫЕ ПЕРЕХОДЫ
- 2.2.2. Диффузионный механизм протекания тока в гомопереходах с p- и n-областями бесконечно большой и конечной толщины
- 2.2.3. Положение квазиуровней Ферми в обедненном слое
- 2.2.4. Рекомбинационно-генерационный процесс в обедненном слое
- 2.2.5. Вольт-амперные характеристики элементов с гомогенным переходом при различных механизмах переноса носителей заряда
- 2.2.6. Трехмерные объемные эффекты в гомогенных переходах
- 2.2.7. Модификации структуры солнечного элемента с гомогенным переходом
- 2.3. ГЕТЕРОПЕРЕХОДЫ
- 2.3.1. Основная модель
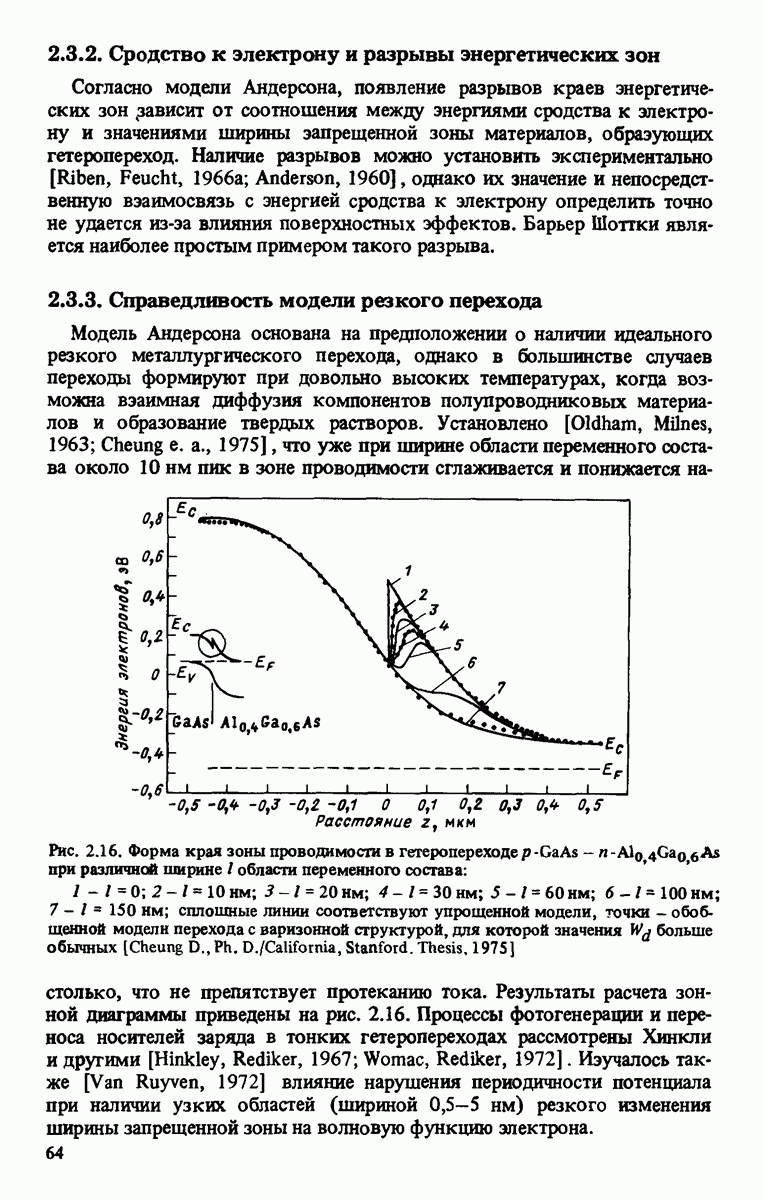
- 2.3.2. Сродство к электрону и разрывы энергетических зон
- 2.3.3. Справедливость модели резкого перехода
- 2.4. УСОВЕРШЕНСТВОВАННЫЕ МОДЕЛИ ГЕТЕРОПЕРЕХОДА
- 2.4.2. Влияние поверхностных состояний на электрические свойства гетеропереходов
- 2.4.3. Диполи на границе раздела
- 2.5. МОДЕЛИ КИНЕТИЧЕСКИХ ЯВЛЕНИЙ В ГЕТЕРОПЕРЕХОДАХ
- 2.5.2. Рекомбинация и генерация носителей в обедненном слое
- 2.5.3. Прямая рекомбинация носителей заряда через состояния на границе раздела, определяемая высотой барьера Шоттки
- 2.5.4. Протекание тока, обусловленное рекомбинацией носителей заряда на границе раздела
- 2.5.5. Туннелирование носителей
- 2.5.6. Термическая активация и туннелирование
- 2.5.7. Гетероструктуры
- 2.6. БАРЬЕРЫ ШОТТКИ, СТРУКТУРЫ МЕТАЛЛ-ДИЭЛЕКТРИК-ПОЛУПРОВОДНИК И ПОЛУПРОВОДНИК-ДИЭЛЕКТРИК-ПОЛУПРОВОДНИК
- 2.6.1. Исходная модель барьера Шоттки
- 2.6.2. Высота барьера
- 2.6.3. Происхождение состояний на поверхности и границе раздела
- 2.6.4. Приборы со структурой металл—диэлектрик—полупроводник
- 2.6.5. Структуры полупроводник—диэлектрик—полупроводник
- 2.7. ОМИЧЕСКИЕ КОНТАКТЫ
- Глава 3. РАСЧЕТ КПД ПРЕОБРАЗОВАНИЯ СОЛНЕЧНОЙ ЭНЕРГИИ
- 3.1. ИДЕАЛЬНЫЙ СОЛНЕЧНЫЙ ЭЛЕМЕНТ ПРИ НАЛИЧИИ ОСВЕЩЕНИЯ
- 3.2. ВЛИЯНИЕ ПОСЛЕДОВАТЕЛЬНОГО И ШУНТИРУЮЩЕГО СОПРОТИВЛЕНИЙ
- 3.2.2. Модели с распределенными сопротивлениями
- 3.2.3. Физические явления, обусловливающие последовательное и шунтирующее сопротивления
- 3.3. ДРУГИЕ СПОСОБЫ АНАЛИЗА ЭФФЕКТИВНОСТИ ПРЕОБРАЗОВАНИЯ СОЛНЕЧНОЙ ЭНЕРГИИ
- 3.4. ВЛИЯНИЕ ТЕМПЕРАТУРЫ И ОБЛУЧЕННОСТИ НА КПД СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 3.4.2. Тепловые характеристики
- 3.4.3. Эффекты, связанные с высоким уровнем облученности
- 3.5. АНАЛИЗ ПОТЕРЬ ЭНЕРГИИ
- Глава 4. КРЕМНИЕВЫЕ СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ
- 4.2. ВЫРАЩИВАНИЕ МОНОКРИСТАЛЛИЧЕСКОГО КРЕМНИЯ
- 4.2.2. Выращивание кристаллов методом Чохральского
- 4.2.3. Сегрегация примесей
- 4.2.4. Зонная плавка
- 4.2.5. Другие методы выращивания
- 4.3. ДЕФЕКТНОСТЬ, ЛЕГИРОВАНИЕ И ВРЕМЯ ЖИЗНИ НОСИТЕЛЕЙ ЗАРЯДА
- 4.3.2. Примеси, снижающие время жизни носителей заряда
- 4.3.3. Введение легирующей примеси путем диффузии
- 4.3.4. Другие способы легирования
- 4.4. ТЕХНОЛОГИЯ И ПАРАМЕТРЫ ТИПИЧНЫХ КРЕМНИЕВЫХ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 4.4.2. Этапы изготовления
- 4.4.3. Электрические параметры
- 4.4.4. Текстурированный элемент
- 4.5. ОПТИМИЗАЦИЯ КОНСТРУКЦИИ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 4.5.2. Увеличение КПД с помощью электрических полей
- 4.5.3. Оптимизация элементов обычной конструкции
- 4.6. НОВЫЕ ПУТИ СОЗДАНИЯ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 4.6.2. Тандемный солнечный элемент
- 4.6.3. Тонкие солнечные элементы
- 4.6.4. Другие направления
- 4.7. ЭКОНОМИКА И НОВЫЕ ИДЕИ
- Глава 5. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ С ГЕТЕРОПЕРЕХОДАМИ И ГЕТЕРОСТРУКТУРАМИ
- 5.2. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ НА ОСНОВЕ СТРУКТУР AlGaAs С ГЕТЕРОФАЗНОЙ ГРАНИЦЕЙ РАЗДЕЛА
- 5.2.2. Изготовление слоев методами жидкофазной эпитаксии и химического осаждения из паровой фазы
- 5.2.3. Наиболее распространенная структура солнечного элемента на основе GaAs и ее предварительная оптимизация
- 5.2.4. Концентраторные солнечные элементы AlGaAs — GaAs
- 5.2.5. Солнечные элементы на основе GaAs для космических энергетических установок
- 5.2.6. Арсенид-галлиевые солнечные элементы с переменной шириной зоны и барьерами Шоттки
- 5.3. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ НА ОСНОВЕ lnP
- 5.4. ЗАКЛЮЧЕНИЕ
- Глава 6. ТОНКИЕ ПОЛИКРИСТАЛЛИЧЕСКИЕ ПЛЕНКИ ДЛЯ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 6.2. ПЕРЕНОС ЭЛЕКТРИЧЕСКОГО ЗАРЯДА В ПОЛИКРИСТАЛЛИЧЕСКИХ ПЛЕНКАХ
- 6.2.2. Границы между зернами в поликристаллических пленках
- 6.2.3. Электропроводность поликристаллических материалов
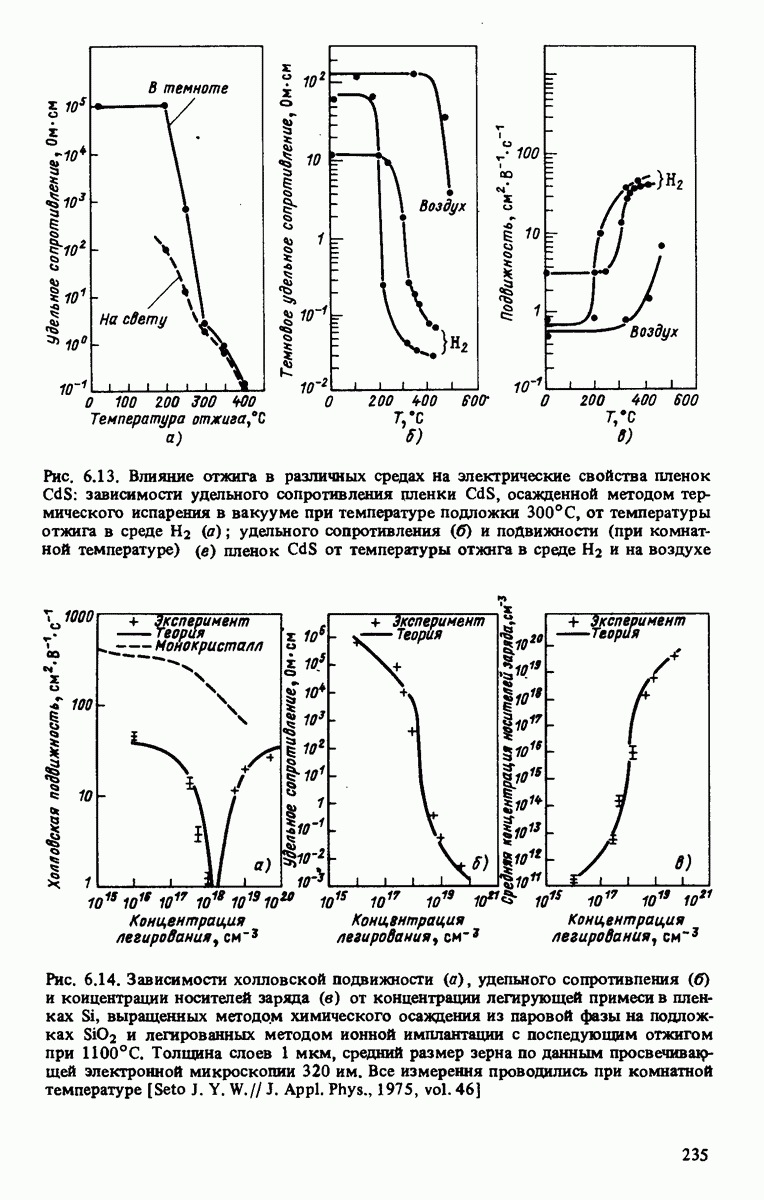
- 6.2.4. Электропроводность различных поликристаллических пленок
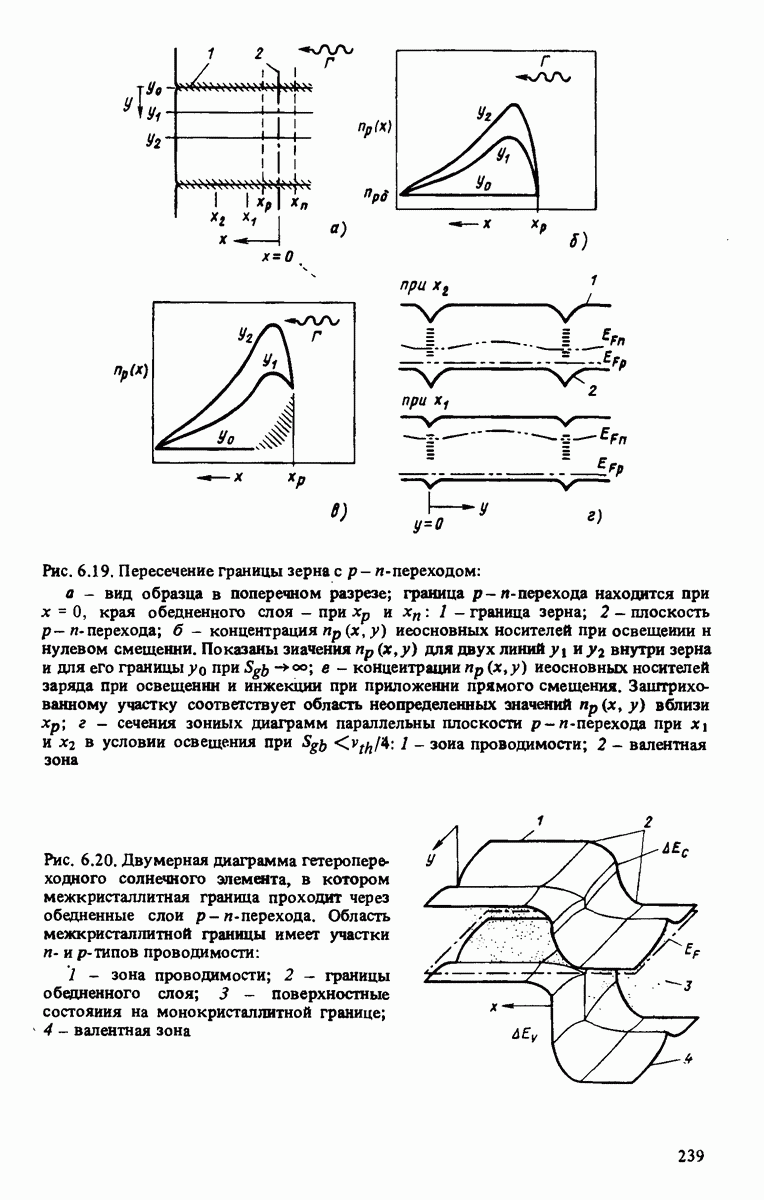
- 6.3. ВЛИЯНИЕ МЕЖКРИСТАЛЛИТНЫХ ГРАНИЦ В СОЛНЕЧНЫХ ЭЛЕМЕНТАХ С ПОЛИКРИСТАЛЛИЧЕСКИМИ СЛОЯМИ
- 6.3.1. Исследования рекомбинации на межкрнсталлитных границах в бикристалле и поликристалле с большим размером кристаллитов
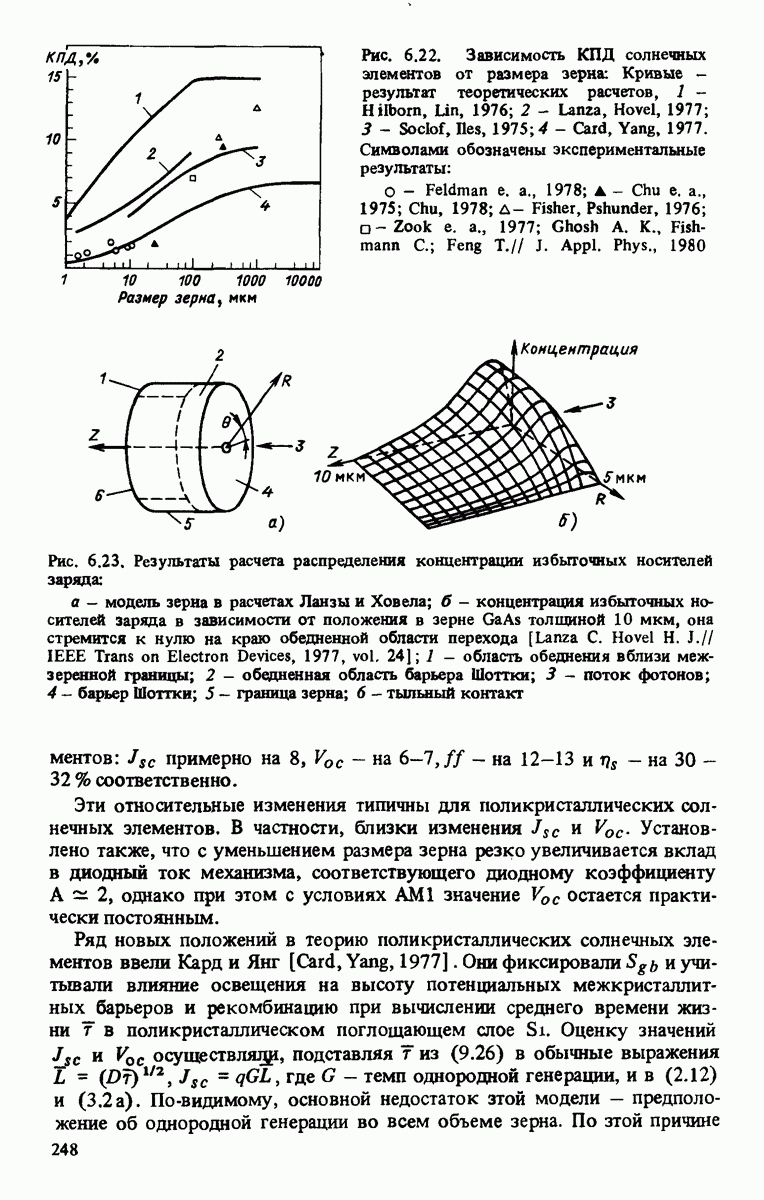
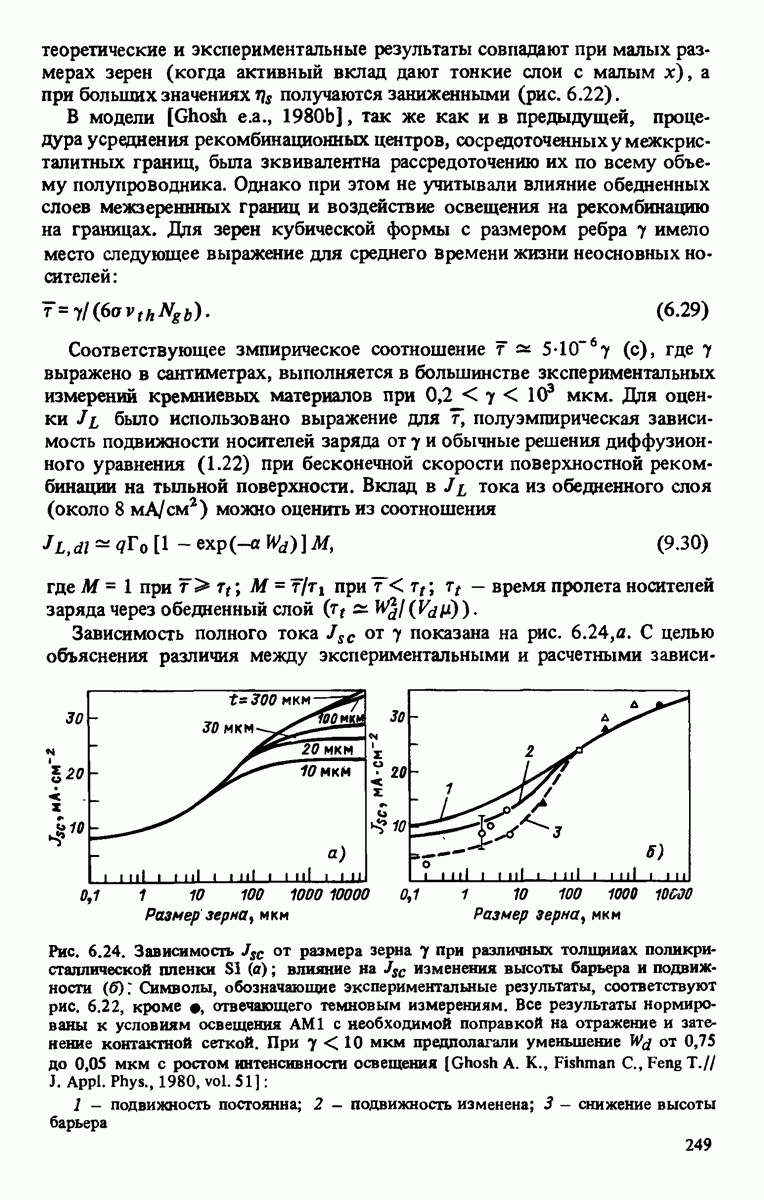
- 6.3.2. Теоретические исследования поликристаллических солнечных элементов
- 6.3.3. Снижение рекомбинации на межкристаллитной границе
- 6.4. Заключение
- СПИСОК ЛИТЕРАТУРЫ