2.6.2. Высота барьера

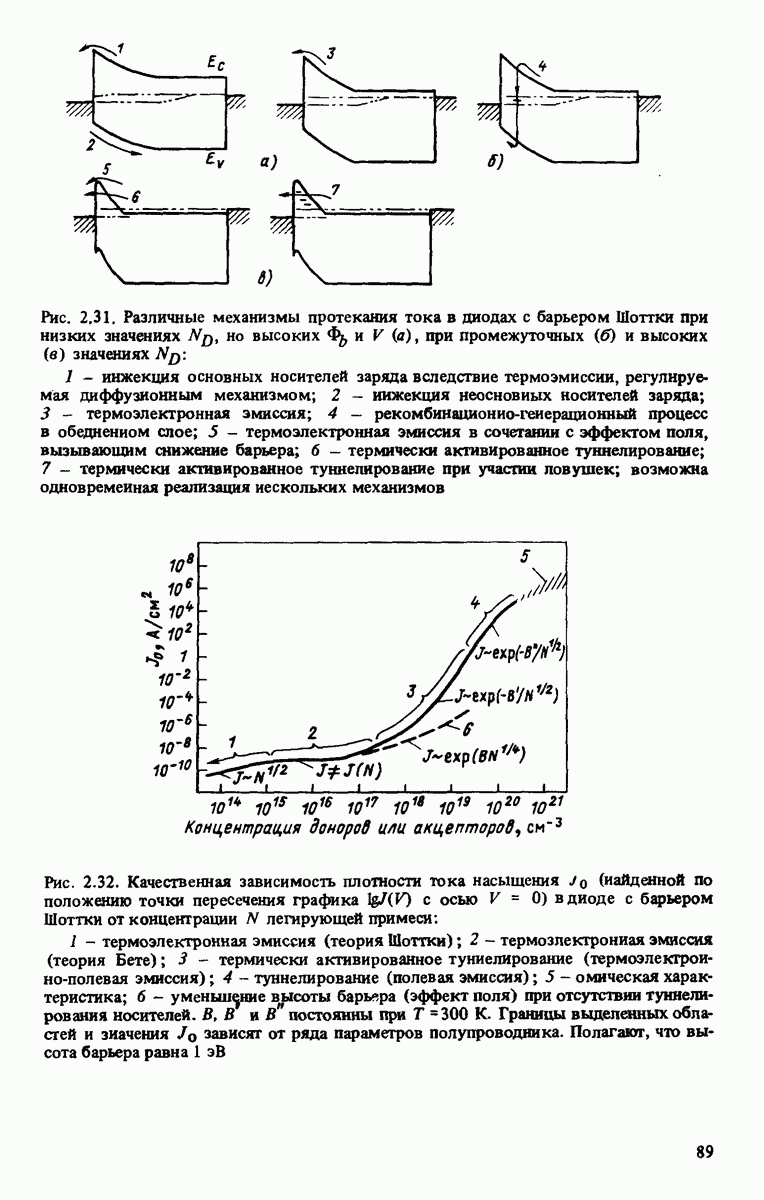
Наиболее важным результатом, полученным при анализе процесса протекания тока в структурах с барьером Шоттки, является выявление зависимости от высоты барьера Высота барьера определяет значения напряжения холостого хода в солнечных элементах. Если свойства поверхности раздела не влияют на то ее значение находится непосредственно с помощью соотношения

где — разность потенциалов, соответствующая работе выхода металла; — энергия сродства к электрону в полупроводнике (рис. 2.29). Однако экспериментально определяемые значения высоты барьера ниже получаемых согласно (2.69). На практике почти не зависит от вида металла, используемого в сочетаниях с полупроводниками, имеющими ковалентную связь, такими, как и большинство соединений III—V групп периодической системы элементов.

При возрастании доли ионной связи в полупроводниках зависимость Ф, от проявляется более ярко и оказывается даже не линейной, как следует из (2.69). Отсутствие зависимости экспериментально определяемых значений от вида металла отражает постоянство уровня Ферми при нанесении металлических слоев в обычных условиях, что характерно для фиксированного положения при наличии состояний на границе раздела.

Отсутствие точного совпадения измеренных значений высоты барьера в структурах на основе металла и полупроводника с ковалентной связью

и значений, рассчитанных с помощью (2.69), было обнаружено уже достаточно давно при изучении структур металл—полупроводник.

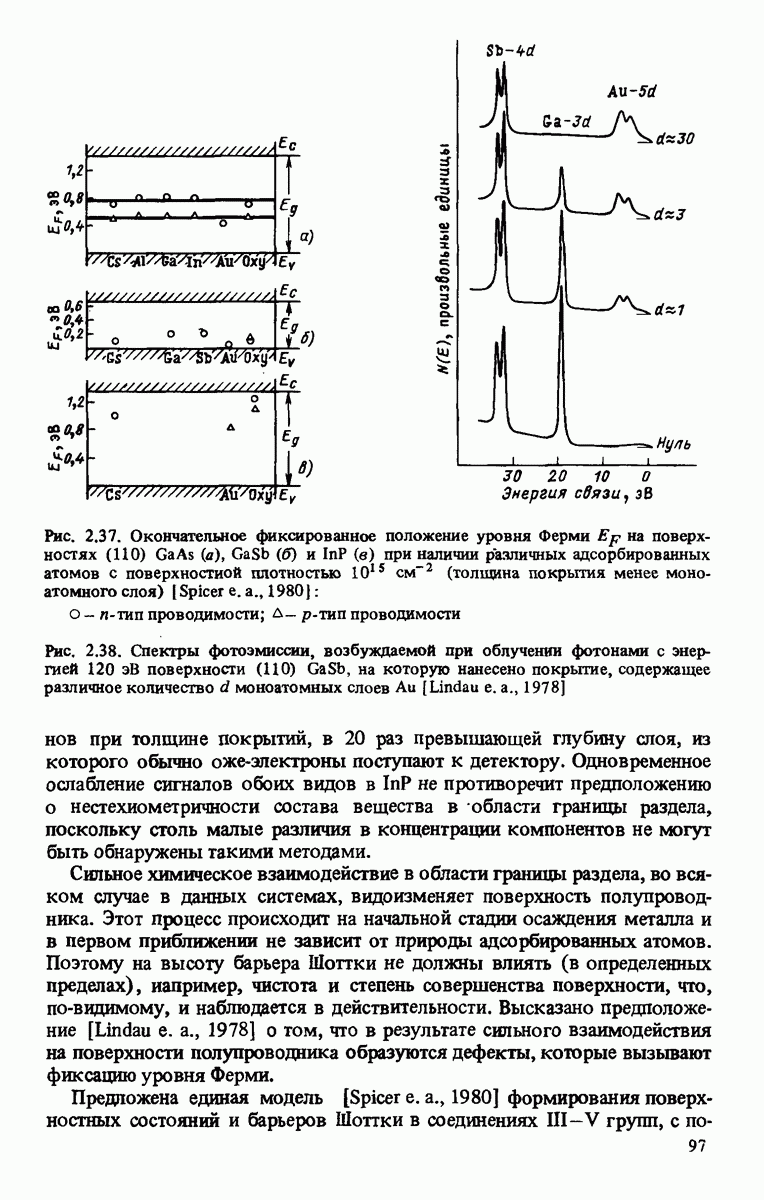
Высказывалось предположение [Bardeen, 1947] о том, что фиксированное положение уровня Ферми обусловлено собственными состояниями на поверхности полупроводника, а приведение ее впоследствии в контакт с металлом обеспечивает эффекты лишь второго порядка. По мнению Хейне [Heine, 1965], характерные для полупроводников локализованные состояния, строго говоря, не могут существовать на границе раздела металл—полупроводник, однако возможно появление виртуальных резонансных (металлоподобных) поверхностных состояний, наличием которых и объясняются наблюдаемые эффекты. Изучению свойств границы раздела посвящены многочисленные экспериментальные и теоретические исследования, и значительная их часть (возможно, за исключением исследований, проводившихся в последние годы) связана с изучением собственных поверхностных состояний. Результаты этих работ представлены в кратком, но полном обзоре Линдау [Lindau е. а., 1978].

Высоту барьера можно измерить несколькими методами:

1) по значению пороговой энергии фотонов при возбуждении тока, обусловленного внутренней фотоэмиссией и направленного из металла в полупроводник;

2) по результатам измерений зависимости от полагая, что реализуется либо термо эмиссионный, либо диффузионный механизм ограничения тока (2.60) или

3) по результатам измерений емкостных характеристик перехода, экстраполируя зависимость от V к точке

4) с помощью фотоэмиссионной спектроскопии (с использованием излучения дальнего ультрафиолетового диапазона), измеряя изгиб зон по отношению к глубоким уровням вблизи валентной зоны.

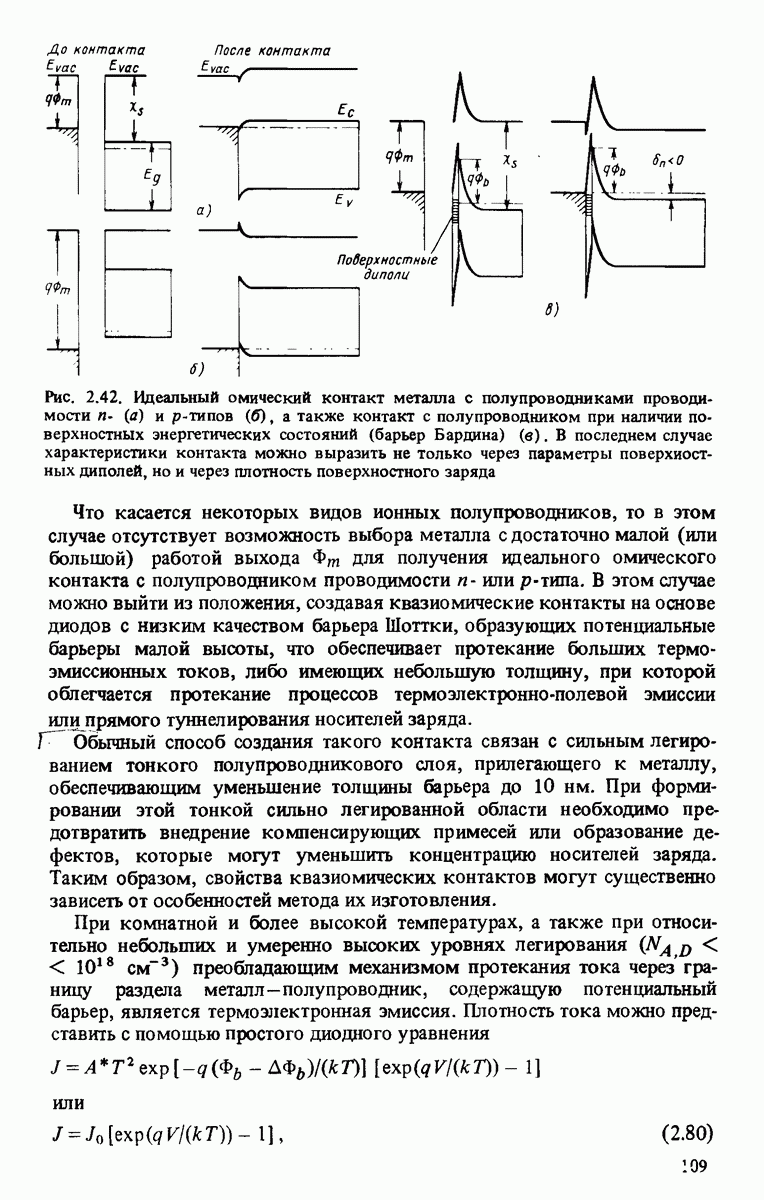
Эффекты, определяющие высоту барьера на макроскопическом уровне могут быть представлены как результат влияния суммарного заряда на границе раздела или диполей на «истинные» значения работы выхода металла и полупроводника. Это традиционный подход к решению данной проблемы, применяемый специалистами в области полупроводниковых приборов. С помощью простой модели, в которой предполагалось, что состояния, существующие в области границыраздела, распределены равномерно по поверхности полупроводника, изолированной от металла очень тонким слоем диэлектрика, получено [Crowell, Sze, 1966а] следующее выражение для высоты барьера:

Здесь — соответственно диэлектрическая проницаемость и толщина промежуточного слоя; — плотность состояний на границе раздела, — положение уровня Ферми по отношению к краю валентной зоны при отсутствии металла; обычно можно пренебречь. Если, например, в структуре металл—полупроводник

-типа , то и

В данном случае уровень Ферми фиксирован поверхностными состояниями и высота барьера не зависит от вида металла, а полностью определяется свойствами границы раздела. Этот случай известен под названием предела Бардина. Если то и

в соответствии с (2.70). Данный случай известен как предел Шоттки.

Обычно для обработки экспериментальных данных (при рассмотрении определенного полупроводника) используют соотношение

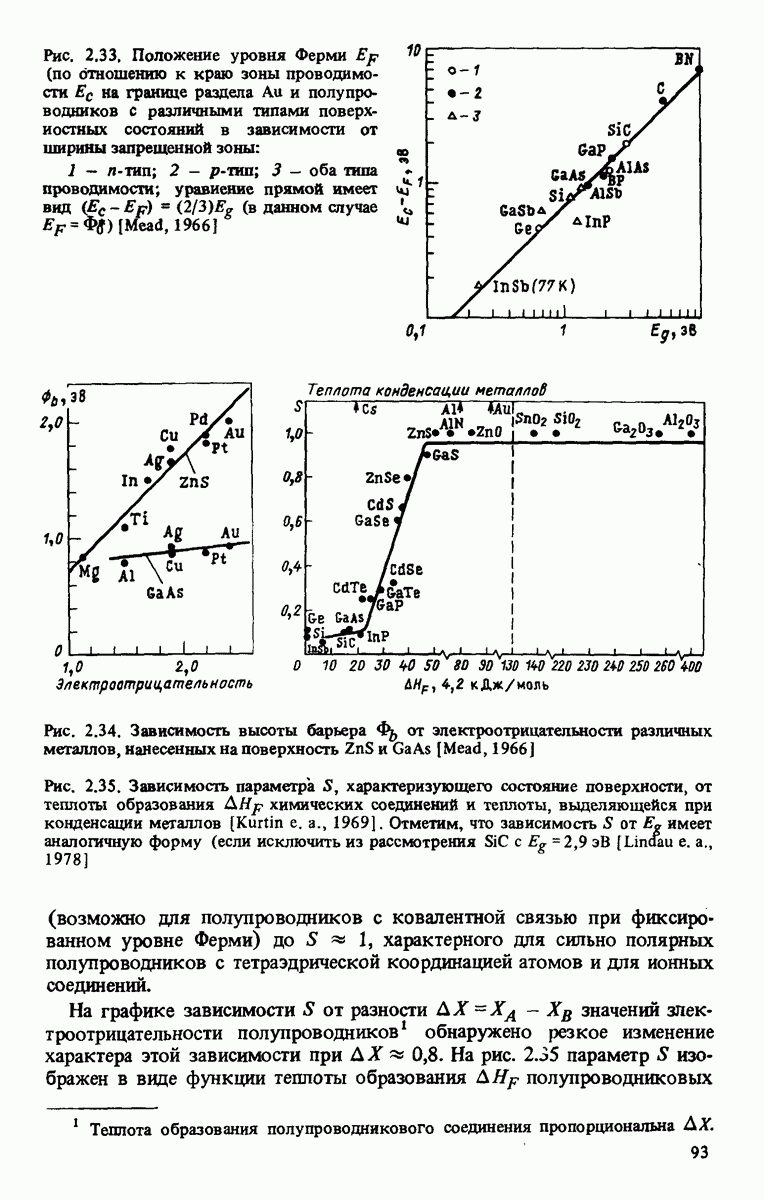
С помощью экспериментально найденных значений постоянных а и b можно затем вычислить и Ф. Подобные данные для различных полупроводников с ковалентной связью, представленные на рис. 2.33, свидетельствуют о том, что фиксированное положение уровня Ферми отвечает энергии (по отношению к краю зоны проводимости) — это известное правило двух третей.

Зависимость реальной высоты барьера от значений работы выхода металла и полупроводника также представляют в линейной форме

где S характеризует состояние поверхности. Случай соответствует пределу Шоттки, тогда как отвечает полной стабилизации уровня Ферми и отсутствию зависимости от работы выхода металла. Поскольку связана линейной зависимостью с электроотрицательностью последнее уравнение после преобразования можно представить в виде

Удобство его применения заключается в том, что входящая в него злектроотрицательность является более стабильным по сравнению с работой выхода металла параметром, экспериментальное значение которого существенно зависит от состояния поверхности.

В известной работе Куртина [Kurtin е. а., 1969], представлены обширные справочные данные по экспериментальным значениям . Установлено, что параметр S, характеризующий состояние поверхности и определяемый посредством представления экспериментальных данных в виде зависимости (2.75), как это показано на рис. 2.34, изменяется от

Рис. 2.33. Положение уровня Ферми отношению к краю зоны проводимости на границе раздела и полупроводников с различными типами поверхностных состояний в зависимости от ширины запрещенной зоны: 1 — -тип; 2 - -тип; 3 — оба типа проводимости; уравнение прямой имеет вид данном случае

Рис. 2.34. Зависимость высоты барьера от электроотрицательности различных металлов, нанесенных на поверхность [Mead, 1966]

Рис. 2.35. Зависимость параметра S, характеризующего состояние поверхности, от теплоты образования химических соединений и теплоты, выделяющейся при конденсации металлов [Kurtin е. а., 1969]. Отметим, что зависимость S от имеет аналогичную форму (если исключить из рассмотрения эВ [Linaau е. а., 1978] (возможно для полупроводников с ковалентной связью при фиксированном уровне Ферми) до характерного для сильно полярных полупроводников с тетраэдрической координацией атомов и для ионных соединений.

На графике зависимости S от разности значений злектроотрицательности полупроводников обнаружено резкое изменение характера этой зависимости при На рис. 2.35 параметр S изображен в виде функции теплоты образования полупроводниковых

соединений. Этот параметр (связанный с ) более удобен при рассмотрении вопросов, касающихся химических свойств границы раздела.

Заслуживают внимания и две другие особенности Во-первых, при измерении параметров материалов, содержащих носители заряда обоих типов, с целью определения как так и установлено, что для разнообразных сочетаний полупроводников и металлов (если только один из контактов не является омическим, когда невозможно измерить эквивалентное значение ). Этот результат согласуется как с (2.71), так и с (2.72). Таким образом, можно приближенно считать, что высота барьера не зависит от уровня легирования.

Во-вторых, показано, что при формировании барьеров на основе и различных полупроводниковых соединений III - V и II - VI групп периодической системы максимальная энергия края валентной зоны на границе раздела зависит лишь от анионной составляющей соединения [McCaldin е. а., 1976]. Выбор обусловлен его низкой химической активностью. Так, разность значений высоты барьера в структурах равна разности ширины запрещенной зоны Величина же изгиба зон в каждом случае такова, что независимо от природы катионной составляющей энергия края валентной зоны данного полупроводникового соединения на контакте с приблизительно одинакова. Эти результаты справедливы для ряда соединений .