6.2.3. Электропроводность поликристаллических материалов

Межкристаллитные потенциальные барьеры являются препятствием для прохождения носителей заряда в поликристаллических слоях и в ряде случаев значительно снижают подвижность носителей по сравнению с монокристаллическими материалами. В пленках, толщина которых сравнима с размером зерен, межзеренные потенциальные барьеры оказывают более существенное влияние на проводимость в плоскости, параллельной пленке, чем поперек нее. Если тонкая пленка, входящая в состав гетеропереходного солнечного элемента, покрыта проводящим слоем и, следовательно,

электрический ток может проходить поперек нее вдоль столбчатых кристаллитов, поликристалличность в этом случае не играет существенной роли. Однако если линии собираемого тока проходят вдоль пленки, вклад межзеренных барьеров в последовательное сопротивление солнечного элемента становится весьма существенным.

Даже когда высота потенциального барьера на границе зерен практически равна нулю (как, например, на границе когерентных двойников), такая граница тем не менее может оказаться диффузно рассеивающей поверхностью. Для невырожденного полупроводника справедлива следующая упрощенная модель. Если длина свободного пробега носителей заряда между столкновениями с границами зерен равна у тогда время между ними составляет примерно где Поскольку то в итоге для подвижности носителей заряда получается выражение

Таким образом, подвижность должна зависеть от температуры по закону При мкм и из (6.6) следует, что . Таким образом, при средних размерах зерен их границы с нулевым потенциальным барьером практически не влияют на проводимость.

Однако в большинстве поликристаллических материалов потенциальные барьеры на межзеренных границах достаточно велики и оказывают существенное, а во многих случаях доминирующее влияние на перенос носителей заряда. В качестве иллюстрации будет рассмотрен перенос носителей заряда вдоль пленки с поперечными межзеренными границами. При этом предположим, что: 1) обедненная область не захватывает целиком зерна; 2) рассеянием в этой области можно пренебречь (приближение Бете в диодной теории Шоттки); 3) перенос заряда вдоль межзеренных границ можно не учитывать, и задача поэтому сводится к одномерному случаю; 4) значение остается постоянным при подаче внешнего смещения. Падение напряжения Д V на каждом зерне определяется из соотношения

где - удельное объемное сопротивление зерна (рис. 6.6). Падение напряжения на всей пленке (длина которой )

где — число зерен вдоль пленки. Если ввести понятие об эффективной подвижности носителей в пленке, то выражение для падения напряжения на всей пленке можно переписать в виде

Рис. 6.6. Одномерная зонная энергетическая модель поликристаллического материала при подаче на него внешнего электрического смешения. Показан случай, когда большая часть падения напряжения Д V на отдельной межкристаллитной границе приходится на обратносмещенную (левую) сторону каждого барьера и, следовательно,

При анализе падения напряжения Д V на межзеренной границе используют диаметрально противоположные модели. В первой из них плотность поверхностных состояний не изменяется при приложении относительно небольших напряжений смешения, а во второй предполагаемое увеличение с ростом внешнего напряжения, при котором высота потенциального барьера остается фиксированной вблизи значения, соответствует нулевому смещению, вплоть до невысоких значений напряжений. При малом падении напряжения () на каждой отдельной межзеренной границе обе модели дают одинаковые результаты. Этому случаю отвечает режим работы высокоэффективного солнечного элемента с очень низким последовательным сопротивлением. Ввиду информативной ценности исследований проводимости через межзеренную границу при более высоких напряжениях далее будут кратко рассмотрены обе модели.

Модель, предполагающая постоянство Если плотность заполненных зарядом поверхностных состояний не зависит от приложенного напряжения, из условия сохранения заряда следует, что падение напряжения V является суммой по обе стороны потенциального межзеренного барьера, причем

При барьер полностью пропадает ( условие плоских зон); определяется в зтом случае подвижностью носителей заряда внутри зерна. При внешних напряжениях, соответствующих условию и учитывая термоэмиссионный механизм прохождения носителей заряда через барьер, получим вольт-амперную характеристику межзеренной границы в виде [Taylor е. а., 1952; Tarng, 1978; Korsh, Muller, 1978]

При выводе зтого выражения сделано предположение, что носители заряда проходят через границу без рассеяния и, в частности, не вступают в равновесное взаимодействие с поверхностными состояниями на межзеренной

Рис. 6.7. Потенциальные барьеры на отдельной межкристаллитной границе в случае приложения внешнего смещения константа и отсутствует рассеяние заряда на межкристаллитной границе; б — и носители заряда термапизуются на межкрнсталлитных состояниях

границе. В поликристаллическом материале с большим числом межкристаллитных границ падение напряжения на одной границе мало, Их и, следовательно,

Модель, допускающая рост при увеличении напряжения смещения. Согласно этой модели [Mueller, 1961; Pike, Seager, 1979; Seager, Castner, 1978; Baccarani e. a., 1978] носители заряда проходят через первую часть барьера, термализуются на поверхностных состояниях на границе зерна, а затем по термоэмиссионному механизму преодолевают вторую часть обратносмещенного барьера (рис. 6.7,б). В этом случае значение определяющее высоту барьера, возрастает при увеличении смещения, и большая часть напряжения падает на обратносмещенном барьере. Учитывая относительные падения напряжения на встречновключенных диодах Шоттки при прохождении через них одинакового тока, легко показать, что при средних значениях смещений.

Точное соотношение между V, и можно получить, решив уравнение Пуассона с учетом вида функции заполнения зарядом поверхностных состояний зависящей от При малых смещениях ток снова определяется по (6.11). При средних смещениях высоту барьера определяет возросшее значение и ток становится равным току насыщения обратносмещенного диода или сублинейно зависит от напряжения смещения. В ряде случаев барьеры выдерживают напряжения до 100 В. При достаточно высоких напряжениях потенциальный барьер исчезает и наблюдается экспоненциальная зависимость тока от напряжения. С помощью указанной модели по зависимости удалось определить распределение состояний на границе зерен (рис. 6.4) для бикристалла

Вновь возвращаясь к расчету подвижности носителей заряда при слабых полях в поликристаллических слоях с зернами, частично обедненными носителями, подставим (6.11) в (6.8) и, предполагая, что получим

Если подвижность определяется главным образом барьерами на границе зерен, тогда

Наконец, если подставить значение А и учесть, что то выражение для примет вид

соответствующий выражению дня подвижности в поликристаллических материалах в теории Петрица [Petritz, 1956,1958].

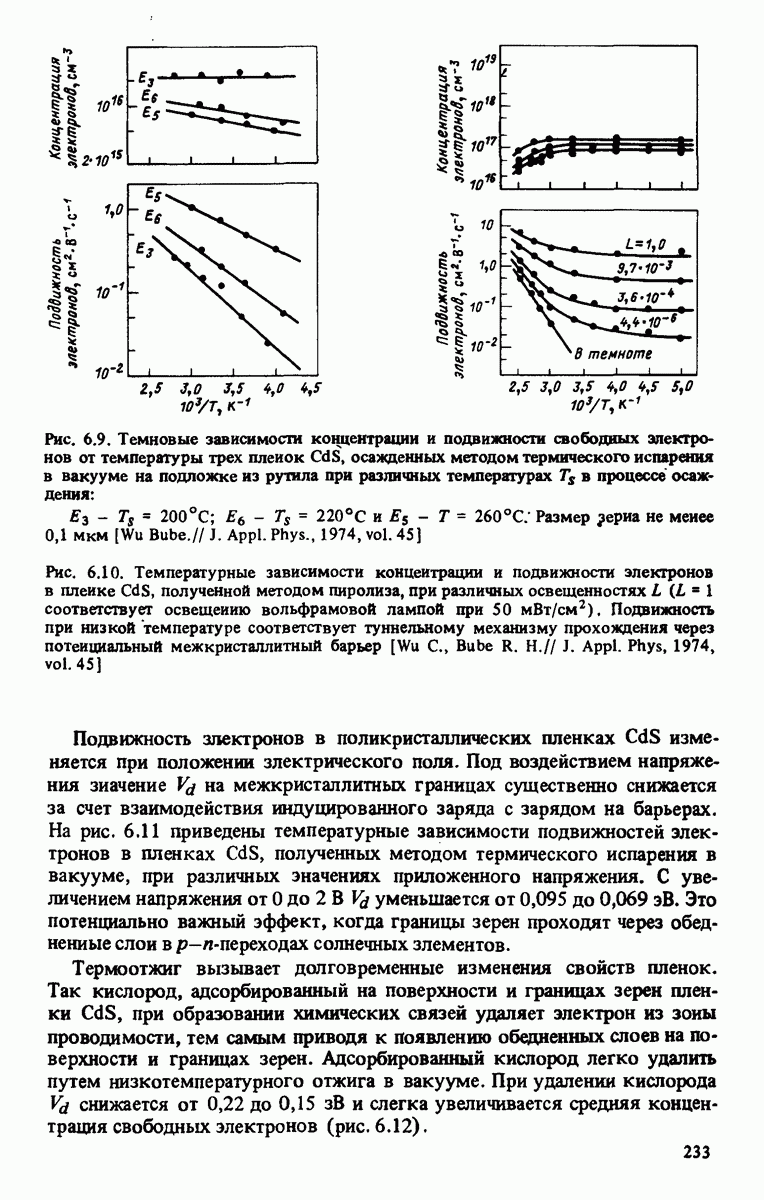
При больших концентрациях носителей заряда высота и ширина барьеров снижаются и необходимо учитывать эффект туннелирования, в особенности при низких температурах. Относительный вклад механизмов термоэлектронной эмиссии и туннелирования в подвижность зарядов в поликристаллических слоях был рассмотрен в ряде работ [Martinez, Piqueras, 1980; Wu, Bube, 1974].

Исходя из измерений температурной зависимости проводимости поликристаллических слоев по наклону графика ln а от 1/7 можно определить значение энергии активации связанной с высотой потенциального барьера между кристаллитами. Полагая, что и высота потенциального барьера фиксирована состояниями на границе зерна, (6.13) легко преобразуется к виду

и, следовательно, для частично обедненных зерен

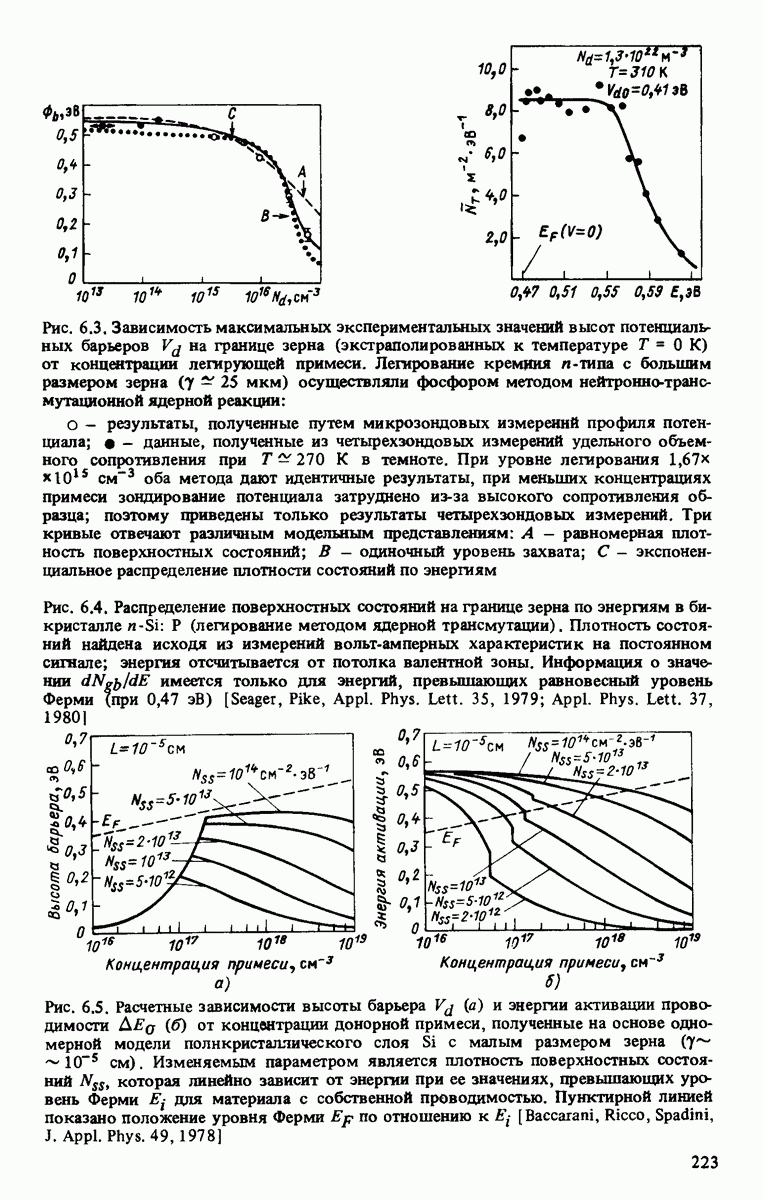
При отсутствии сведений о виде функции в ряде случаев предполагают ее равной нулю или аналогичной температурной зависимости ширины запрещенной зоны полупроводника [Миейег, 1961]. Различие между энергией активации и высотой барьера показано на рис. 6.5.

Результаты экспериментальных измерений эффективных подвижностей в поликристаллических образцах соответствуют экспоненциальной зависимости (6.13) или (6.14), однако, как правило, значения А в раз меньше чем в случае переходов монокристаллический полупроводник-металл

Значение холловских измерений в поликристаллических пленках можно показать, обратившись к основным соотношениям. При (пренебрегая эффектами рассеяния носителей заряда на границах зерен) индуцированное холловское поле направлено противоположно силе магнитной индукции действующей на движущиеся основные носители заряда,

где напряженность поля в В/см, в см/с. Дрейфовая скорость носителей заряда Поскольку определяется главным образом потенциальными барьерами на границе зерен, не влияющими на подвижность внутри зерна, соотношение не является адекватным описанием происходящих процессов. Плотность тока J одинакова во всем слое (проводимостью вдоль границ зерен пренебрегаем), поэтому соотношение удобнее и из него следует, что

где — концентрация носителей заряда внутри зерен. Тогда подвижность, найденная из соотношения является эффективной подвижностью , соответствующей (6.14).

При холловских измерениях в поликристаллических образцах в условиях интенсивного солнечного освещения, устраняющего влияние межкристаллических барьеров на проводимость, установлено, что концентрация основных носителей заряда, вычисленная по (6.16), совпадает со значением, полученным при темновых холловских измерениях [Maruska е. а., 1980] , что указывает на возможность использования этой процедуры нахождения эффективной подвижности, по крайней мере в указанных режимах. Когда толщина обедненной области сравнима с размером зерна, полезность холловских измерений сомнительна [Volger, 1950; Petritz, 1958; Blount е. а., 1970; Kamins, 1971].

Ряд авторов предлагали более полные модели переноса заряда в тонких поликристаллических слоях, однако в последние годы большинство из них относилось к исследованиям варисторов, электролюминесцентных устройств и фоторезисторов.

Рис. 6.8. Расчетные зависимости контактной разности потенциалов на межкристаллитных границах в от плотности состояний на границе и концентрации легирования : а - при солнечном освещении ; насыщение связано с условием на межзеренной границе б - темновые условия [Card Yang// IEEE Trans, on Electron Devices, 1977, vol. 24]

Была развита модель темновой проводимости, рассматривающая движение носителей заряда с тепловыми скоростями и учитывающая различные распределения ловушек (рис. 6.3) [Seager, Castner, 1978; Pike, Seager, 1979]. Было установлено соответствие между расчетом и измерениями в бикристаллах и крупнозернистых поликристаллических пластинах. Рассмотрен случай, при котором область обеднения целиком заполняет зерно [Baccarani е. а., 1978; Seto, 1975]. В рамках этой модели предсказано скачкообразное изменение энергии активации проводимости от условия частичного обеднения к полному обеднению кристаллита (рис. 6.5, б).

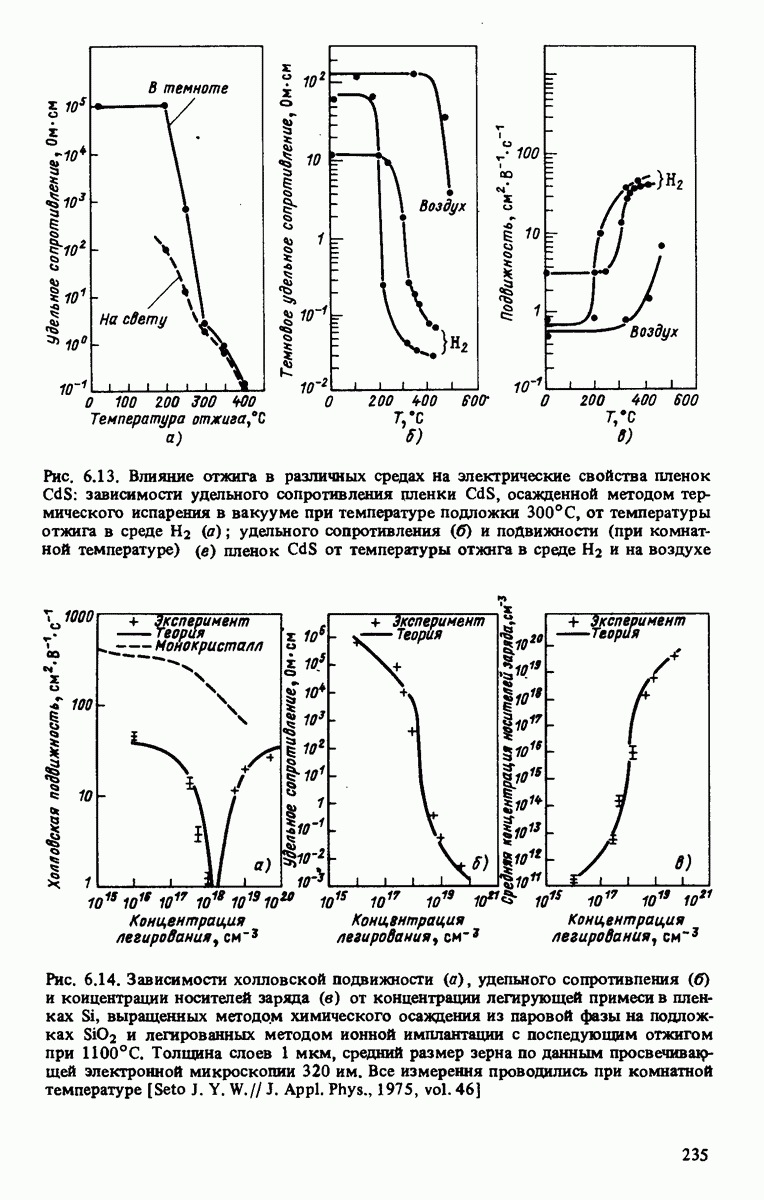
При концентрациях легирования, соответствующих переходу от условия частичного обеднения к полному обеднению кристаллита свободными носителями заряда, наблюдался резкий минимум эффективной подвижности (см. рис. 6.14, a) [Seto, 1975;Cowher, Sedgwick, 1972], непосредственно связанный с максимальным значением высоты барьера (рис. 6.5, а). Модель Бакарани и Сето [Baccarani е. а., 1978; Seto, 1975] была успешно применена для объяснения экспериментальных результатов в случае поликристаллических слоев выращенных методом химического осаждения паровой фазы, исходя из наличия непрерывного распределения ловушек в запрещенной зоне. Все измерения проводились на свету.

При интерпретации измерений на свету в рамках рекомбинационной модели Шокли—Рида—Холла контактная разность потенциалов снижается до значений (рис. 6.8), при которых ее влияние на проводимость значительно ослабляется [Card, Yang, 1977]. Это и другие исследования поликристаллических образцов в условиях освещения будут рассмотрены далее, поскольку высота потенциальных барьеров существенным образом зависит от характера рекомбинационных процессов.

При особых обстоятельствах могут оказаться существенными другие источники эффектов рассеяния в поликристаллических тонких пленках. Среди них деформация [Dexter, Seitz, 1952] и (или) рассеяние на заряженных

дефектах, например дислокациях; рассеяние, обусловленное механическими напряжениями, возникающими из-за различия коэффициентов теплового расширения пленки и подложки и дефектами упаковки [Kazmerski, 1972], которые можно рассматривать как потенциальные барьеры наподобие межкрнсталлитных барьеров.

В темновых условиях проводимость поликристаллических пленок ограничивается в большинстве случаев барьерами на межкрнсталлитных границах. Освещение снижает потенциалы границ и приводит к существенному увеличению проводимости образцов иногда сводя на нет влияние барьеров между зернами. При освещении определяющим становится механизм рекомбинации, однако в общем случае учет влияния рекомбинации на перенос носителей заряда требует решения трехмерной задачи.