| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.1. ИДЕАЛЬНЫЙ СОЛНЕЧНЫЙ ЭЛЕМЕНТ ПРИ НАЛИЧИИ ОСВЕЩЕНИЯ
Здесь будет выведено соотношение для КПД идеального элемента при условии, что выполняется принцип суперпозиции. Эта модель применима при следующих условиях.
1. В диапазоне облученностей, не превосходящих значение  при которых предполагается использовать элементы, зависимость
при которых предполагается использовать элементы, зависимость  от V и угол наклона графика
от V и угол наклона графика  от V не меняются при вариациях
от V не меняются при вариациях  и длины волны света, вследствие чего кривые зависимости
и длины волны света, вследствие чего кривые зависимости  от
от  и темно-вой зависимости
и темно-вой зависимости  от V совпадают.
от V совпадают.
2.  не является функцией напряжения смещения.
не является функцией напряжения смещения.
3.  , т. е. потери мощности на сопротивлениях отсутствуют.
, т. е. потери мощности на сопротивлениях отсутствуют.
Для определения плотности полного фототока интегрируют произведение  (или
(или  ) и спектральной плотности потока фотонов солнечного излучения
) и спектральной плотности потока фотонов солнечного излучения 

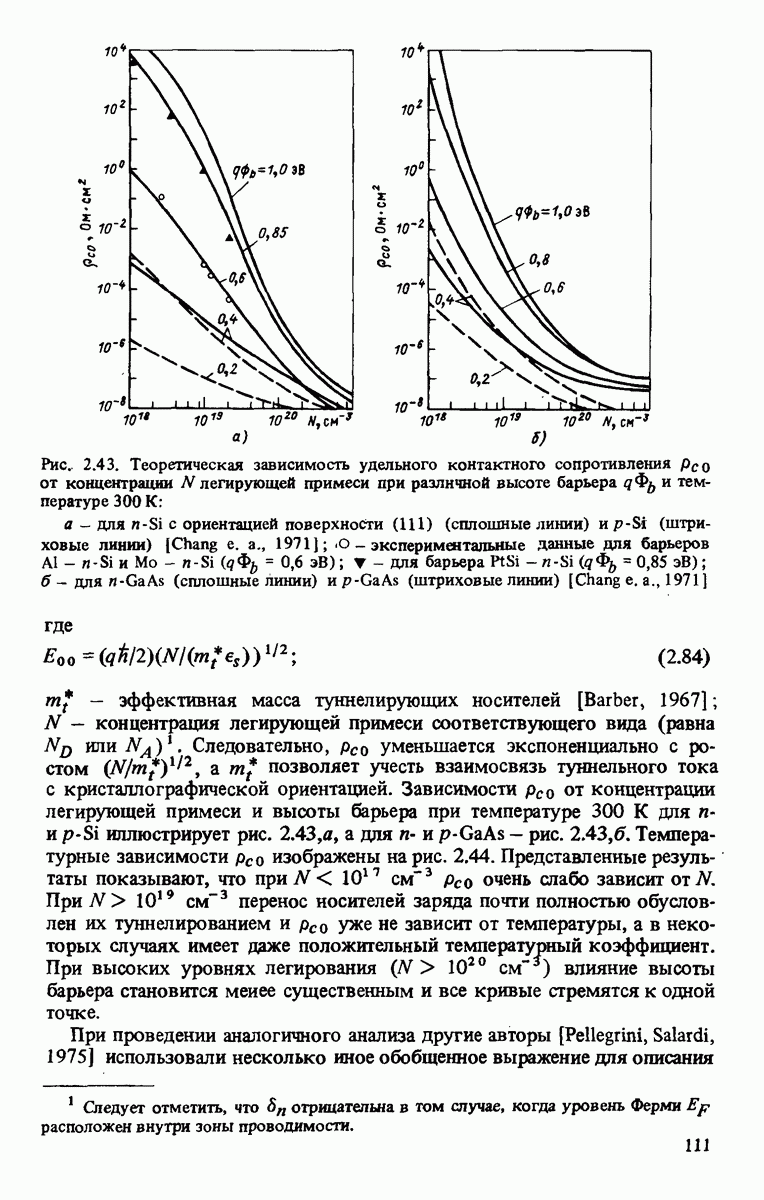
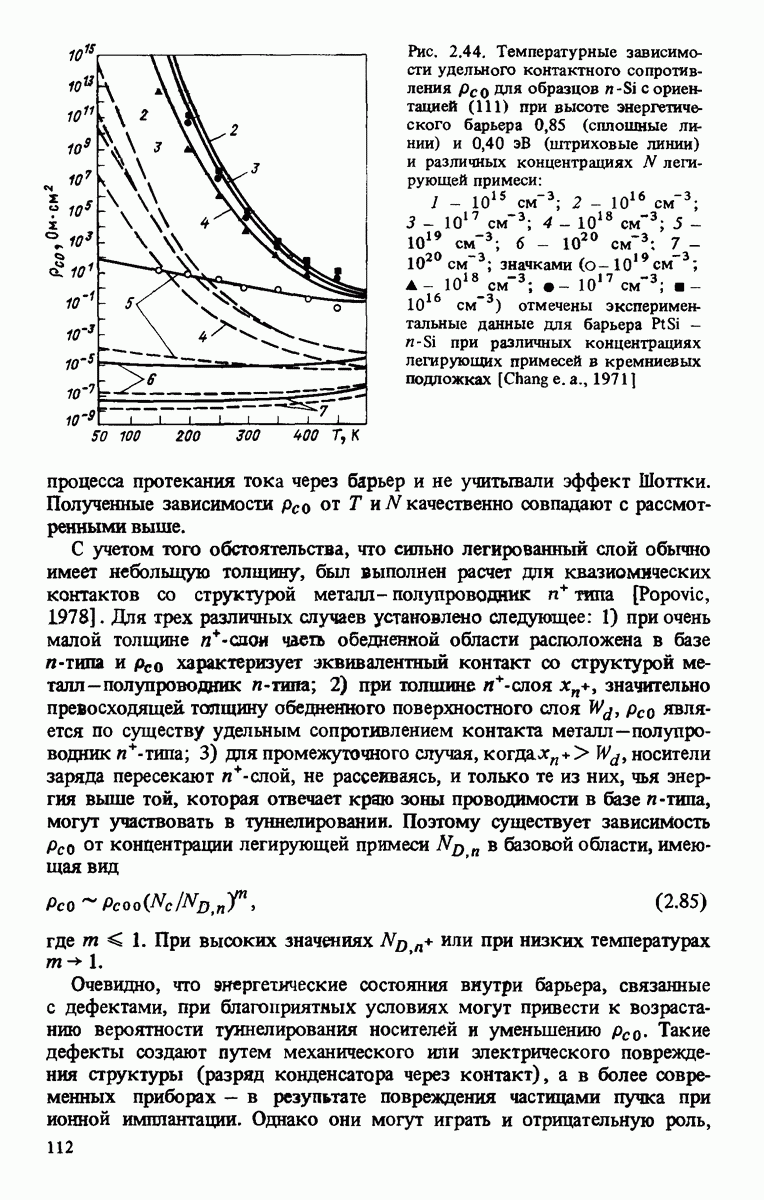
Отметим, что коэффициент собирания носителей заряда также может быть функцией облученности. Распределение спектральной плотности потока фотонов по энергиям в условиях  приведено на рис. 3.2. Представленные на рис. 3.3 и 3.4 интегральные значения плотности потока фотонов полезны для выполнения оценочных расчетов. Если предположить, ЧТО
приведено на рис. 3.2. Представленные на рис. 3.3 и 3.4 интегральные значения плотности потока фотонов полезны для выполнения оценочных расчетов. Если предположить, ЧТО  то
то

Удельная мощность, вырабатываемая солнечным элементом,  (см. рис. 3.1). Для определения ее максимального значения
(см. рис. 3.1). Для определения ее максимального значения  что эквивалентно), хотя оно и не может быть найдено точно, оптимизируют зависимость
что эквивалентно), хотя оно и не может быть найдено точно, оптимизируют зависимость  Методом итераций
Методом итераций  можно определить с любой необходимой степенью точности; эта процедура рассмотрена ниже.
можно определить с любой необходимой степенью точности; эта процедура рассмотрена ниже.
Поскольку площадь активной светопоглощающей поверхности  солнечного элемента, как правило, меньше общей площади
солнечного элемента, как правило, меньше общей площади  диода, используемые в дальнейшем параметры удобно представить в виде функций токов
диода, используемые в дальнейшем параметры удобно представить в виде функций токов

В точке вольт-амперной характеристики, соответствующей максимальной мощности  производная
производная  Введем параметр
Введем параметр  равный согласно определению
равный согласно определению


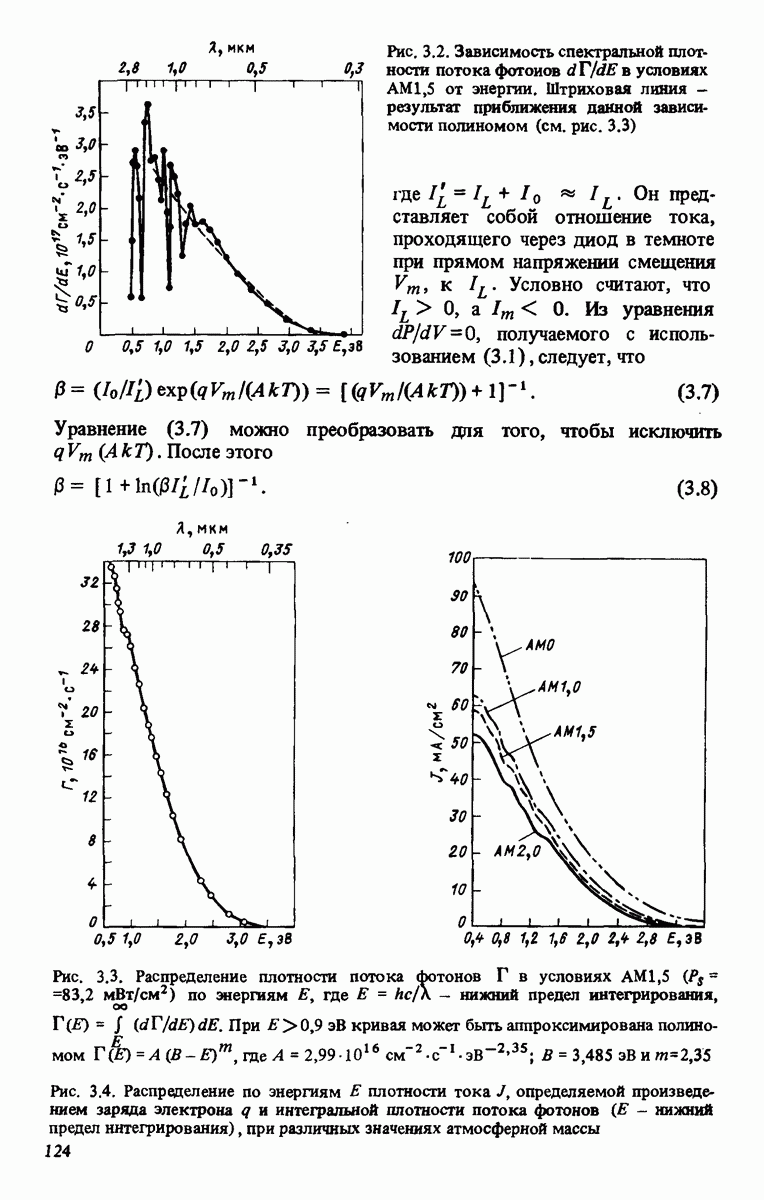
Рис. 3.2. Зависимость спектральной плотности потока фотонов  в условиях
в условиях  от энергии. Штриховая линия - результат приближения данной зависимости полиномом (см. рис. 3.3)
от энергии. Штриховая линия - результат приближения данной зависимости полиномом (см. рис. 3.3)
где  . Он представляет собой отношение тока, проходящего через диод в темноте при прямом напряжении смещения
. Он представляет собой отношение тока, проходящего через диод в темноте при прямом напряжении смещения  к
к  . Условно считают, что
. Условно считают, что  Из уравнения
Из уравнения  получаемого с использованием (3.1), следует, что
получаемого с использованием (3.1), следует, что

Уравнение (3.7) можно преобразовать для того, чтобы исключить  . После этого
. После этого


Рис. 3.3. Распределение плотности потока Лотонов Г в условиях  по энергиям Е, где
по энергиям Е, где  — нижний предел интегрирования,
— нижний предел интегрирования,  При
При  эВ кривая может быть аппроксимирована полиномом
эВ кривая может быть аппроксимирована полиномом 

Рис. 3.4. Распределение по энергиям Е плотности тока J, определяемой произведением заряда электрона q и интегральной плотности потока фотонов (Е - нижний предел интегрирования), при различных значениях атмосферной массы
Лишь с помощью нескольких итераций можно найти Р с точностью до четвертой значащей цифры. Для высококачественных элементов значения  будут меняться в диапазоне от 0,04 до 0,10. Максимальная мощность, выраженная непосредственно через Р, имеет вид
будут меняться в диапазоне от 0,04 до 0,10. Максимальная мощность, выраженная непосредственно через Р, имеет вид

а коэффициент заполнения вольт-амперной характеристики, получаемый в результате деления  на
на  (поскольку
(поскольку  при
при  равен
равен

Из этого соотношения следует, что в идеальном солнечном элементе, где отсутствуют потери мощности на сопротивлении, коэффициент заполнения не является функцией диодного коэффициента А, который можно рассматривать в зтом случае как параметр, изменяющий масштаб шкалы напряжений. Помимо этого,  и, следовательно,
и, следовательно,  прямо пропорциональны А.
прямо пропорциональны А.
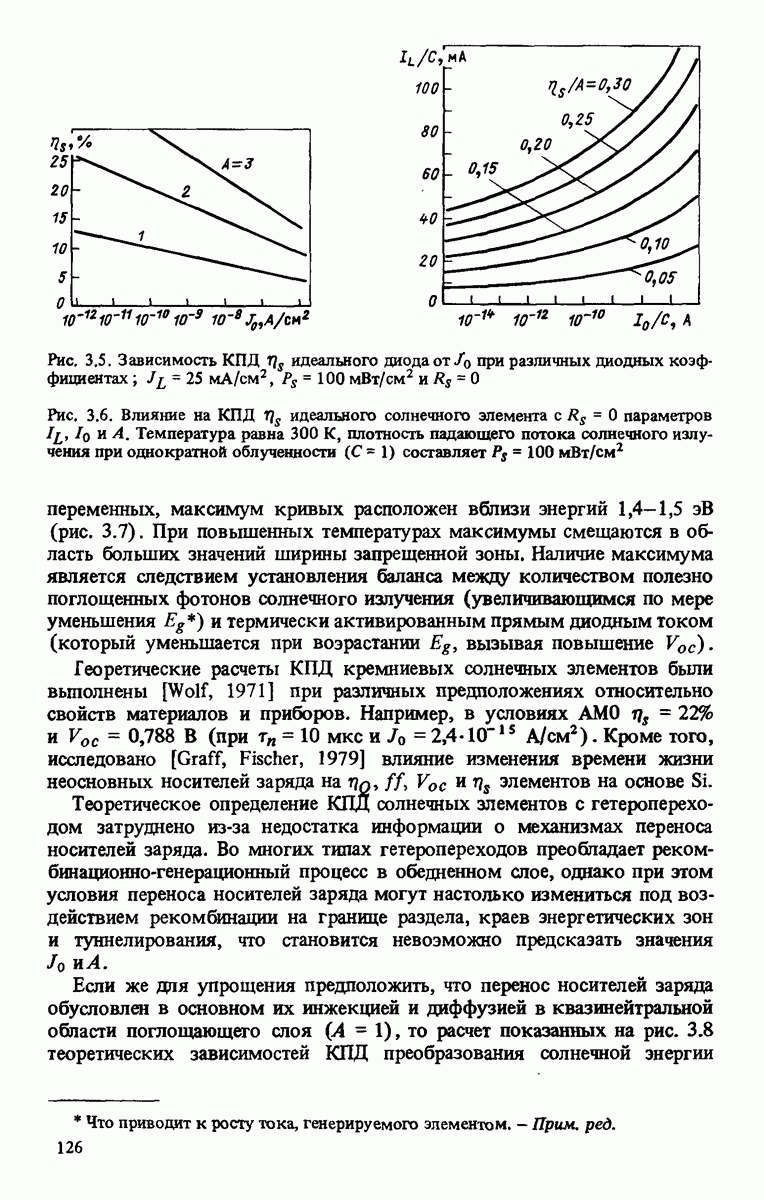
Значения  такого идеального диода приведены на рис. 3.5. В более общем виде взаимосвязь между фотоэлектрическими параметрами показана на рис. 3.6, где принимается во внимание также и коэффициент концентрации солнечного излучения.
такого идеального диода приведены на рис. 3.5. В более общем виде взаимосвязь между фотоэлектрическими параметрами показана на рис. 3.6, где принимается во внимание также и коэффициент концентрации солнечного излучения.
Из анализа приведенных зависимостей можно заключить, что наиболее эффективный способ повышения —  увеличение А или уменьшение
увеличение А или уменьшение  Однако
Однако  возрастает почти экспоненциально при повышении А. Кривые постоянных значений
возрастает почти экспоненциально при повышении А. Кривые постоянных значений  рассчитанные с помощью (3.9), иллюстрируют эту взаимосвязь, а также показывают, что получение предельно высоких значений
рассчитанные с помощью (3.9), иллюстрируют эту взаимосвязь, а также показывают, что получение предельно высоких значений  представляет собой более сложную задачу, требующую не только простого снижения
представляет собой более сложную задачу, требующую не только простого снижения  или увеличения А.
или увеличения А.
Анализ фотоэлектрических свойств элементов не будет полным, если не высказать по меньшей мере общих соображений относительно их предельного теоретического КПД. Соотношение между теоретическим КПД солнечных элементов с гомопереходом и шириной запрещенной зоны полупроводника установлено несколькими исследователями, например, [Prince, 1955; Loferski, 1956; Wolf, 1960], рассматривавшими материалы, обладавшие до некоторой степени идеальными свойствами, и идеализированные модели переходов. Несмотря на то что предсказываемые значения  в определенной мере зависят от параметров, выбранных в качестве
в определенной мере зависят от параметров, выбранных в качестве

Рис. 3.5, Зависимость КПД  идеального диода
идеального диода  при различных диодных коэффициентах
при различных диодных коэффициентах 

Рис. 3.6. Влияние на КПД  идеального солнечного элемента с
идеального солнечного элемента с  параметров
параметров  и А. Температура равна 300 К, плотность падающего потока солнечного излучения при однократной облученности
и А. Температура равна 300 К, плотность падающего потока солнечного излучения при однократной облученности  составляет
составляет 
переменных, максимум кривых расположен вблизи энергий  эВ (рис. 3.7). При повышенных температурах максимумы смещаются в область больших значений ширины запрещенной зоны. Наличие максимума является следствием установления баланса между количеством полезно поглощенных фотонов солнечного излучения (увеличивающимся по мере уменьшения
эВ (рис. 3.7). При повышенных температурах максимумы смещаются в область больших значений ширины запрещенной зоны. Наличие максимума является следствием установления баланса между количеством полезно поглощенных фотонов солнечного излучения (увеличивающимся по мере уменьшения  и термически активированным прямым диодным током (который уменьшается при возрастании
и термически активированным прямым диодным током (который уменьшается при возрастании  вызывая повышение
вызывая повышение  ).
).
Теоретические расчеты КПД кремниевых солнечных элементов были выполнены [Wolf, 1971] при различных предположениях относительно свойств материалов и приборов. Например, в условиях  (при
(при  ). Кроме того, исследовано [Graff, Fischer, 1979] влияние изменения времени жизни неосновных носителей заряда на
). Кроме того, исследовано [Graff, Fischer, 1979] влияние изменения времени жизни неосновных носителей заряда на  элементов на основе
элементов на основе 
Теоретическое определение КПД солнечных элементов с гетеропереходом затруднено из-за недостатка информации о механизмах переноса носителей заряда. Во многих типах гетеропереходов преобладает рекомбинационно-генерационный процесс в обедненном слое, однако при этом условия переноса носителей заряда могут настолько измениться под воздействием рекомбинации на границе раздела, краев энергетических зон и туннелирования, что становится невозможно предсказать значения  и А.
и А.
Если же для упрощения предположить, что перенос носителей заряда обусловлен в основном их инжекцией и диффузией в квазинейтральной области поглощающего слоя  то расчет показанных на рис. 3.8 теоретических зависимостей КПД преобразования солнечной энергии
то расчет показанных на рис. 3.8 теоретических зависимостей КПД преобразования солнечной энергии

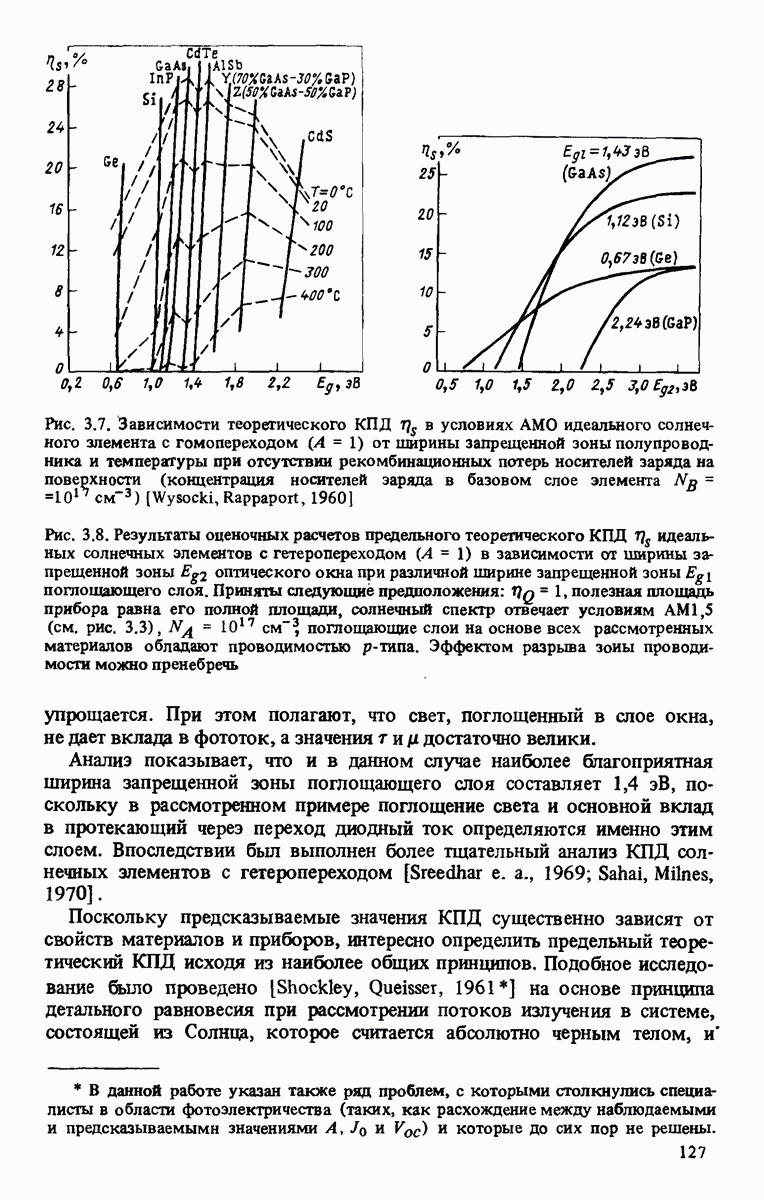
Рис. 3.7. Зависимости теоретического КПД  в условиях АМО идеального солнечного элемента с гомопереходом
в условиях АМО идеального солнечного элемента с гомопереходом  от ширины запрещенной зоны полупроводника и температуры при отсутствии рекомбинационных потерь носителей заряда на поверхности (концентрация носителей заряда в базовом слое элемента
от ширины запрещенной зоны полупроводника и температуры при отсутствии рекомбинационных потерь носителей заряда на поверхности (концентрация носителей заряда в базовом слое элемента 

Рис. 3.8. Результаты оценочных расчетов предельного теоретического КПД  идеальных солнечных элементов с гетеропереходом
идеальных солнечных элементов с гетеропереходом  в зависимости от ширины запрещенной зоны
в зависимости от ширины запрещенной зоны  оптического окна при различной ширине запрещенной зоны
оптического окна при различной ширине запрещенной зоны  поглощающего слоя. Приняты следующие предположения:
поглощающего слоя. Приняты следующие предположения:  полезная площадь прибора равна его полной площади, солнечный спектр отвечает условиям AM 1,5 (см. рис. 3.3),
полезная площадь прибора равна его полной площади, солнечный спектр отвечает условиям AM 1,5 (см. рис. 3.3),  поглощающие слои на основе всех рассмотренных материалов обладают проводимостью
поглощающие слои на основе всех рассмотренных материалов обладают проводимостью  -типа. Эффектом разрыва зоиы проводимости можно пренебречь
-типа. Эффектом разрыва зоиы проводимости можно пренебречь
упрощается. При этом полагают, что свет, поглощенный в слое окна, не дает вклада в фототок, а значения  достаточно велики.
достаточно велики.
Анализ показывает, что и в данном случае наиболее благоприятная ширина запрещенной зоны поглощающего слоя составляет 1,4 эВ, поскольку в рассмотренном примере поглощение света и основной вклад в протекающий через переход диодный ток определяются именно этим слоем. Впоследствии был выполнен более тщательный анализ КПД солнечных элементов с гетеропереходом [Sreedhar е. а., 1969; Sahai, Milnes, 1970].
Поскольку предсказываемые значения КПД существенно зависят от свойств материалов и приборов, интересно определить предельный теоретический КПД исходя из наиболее общих принципов. Подобное исследование было проведено [Shockley, Queisser, 1961] на основе принципа детального равновесия при рассмотрении потоков излучения в системе, состоящей из Солнца, которое считается абсолютно черным телом, 
солнечного элемента, и в предположении, что каждый фотон (проникающий в элемент) с энергией  создает единичный заряд q при напряжении
создает единичный заряд q при напряжении  . Полагая также, что коэффициент концентрации солнечного света равен единице и в полупроводнике происходит только излуча-тельная рекомбинация носителей заряда в результате межзонных переходов, авторы определили КПД
. Полагая также, что коэффициент концентрации солнечного света равен единице и в полупроводнике происходит только излуча-тельная рекомбинация носителей заряда в результате межзонных переходов, авторы определили КПД  удовлетворяющий принципу детального равновесия и соответствующий оптимальной ширине запрещенной зоны 1,1 эВ. (Это значение энергии чрезвычайно близко к ширине запрещенной зоны
удовлетворяющий принципу детального равновесия и соответствующий оптимальной ширине запрещенной зоны 1,1 эВ. (Это значение энергии чрезвычайно близко к ширине запрещенной зоны  одного из наиболее распространенных химических элементов.)
одного из наиболее распространенных химических элементов.)
Вопрос о предельном КПД обсуждался также и другими авторами [Mathers, 1977; Landsberg, 1977; De  На основе перечисленных предположений [Shockley, Queisser, 1961] было показано
На основе перечисленных предположений [Shockley, Queisser, 1961] было показано  что для единичного солнечного элемента при теоретически максимальном коэффициенте концентрации солнечного излучения
что для единичного солнечного элемента при теоретически максимальном коэффициенте концентрации солнечного излучения  предельный КПД, удовлетворяющий принципу детального равновесия,
предельный КПД, удовлетворяющий принципу детального равновесия,  При неограниченном количестве элементов в каскадной структуре предельный КПД
При неограниченном количестве элементов в каскадной структуре предельный КПД  при
при  при
при 
С учетом условий, необходимых для получения КПД цикла Карно, было найдено [Rose, 1960] предельное напряжение холостого хода  ), где
), где  — температура солнечного элемента,
— температура солнечного элемента,  - температура черного тела, излучение которого падает на элемент. Согласно этому соотношению для кремниевого солнечного элемента
- температура черного тела, излучение которого падает на элемент. Согласно этому соотношению для кремниевого солнечного элемента  .
.
Подразумевалось, что система элемент—радиатор обратима, потери фотонов в ней отсутствуют (при максимальной концентрации излучения) и в элементе поглощается почти монохроматическое излучение с энергией  Полученные результаты [Shockley, Queisser, 1961] показывают, что предельное значение
Полученные результаты [Shockley, Queisser, 1961] показывают, что предельное значение  (авторы использовали для
(авторы использовали для  ; если же считать, что
; если же считать, что  , то
, то  ).
).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 1. УРАВНЕНИЕ ПЕРЕНОСА
- 1.2. ОСНОВНЫЕ СОСТАВЛЯЮЩИЕ УРАВНЕНИЯ ПЕРЕНОСА
- 1.3. ВЫВОД УРАВНЕНИЯ ПЕРЕНОСА
- 1.4. РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА
- 1.5. СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- 1.6. ИЗМЕРЕНИЕ ВРЕМЕНИ ЖИЗНИ И ДИФФУЗИОННОЙ ДЛИНЫ НЕОСНОВНЫХ НОСИТЕЛЕЙ ЗАРЯДА
- Глава 2. ЭЛЕКТРОННО-ДЫРОЧНЫЕ ПЕРЕХОДЫ
- 2.2. ГОМОГЕННЫЕ ПЕРЕХОДЫ
- 2.2.2. Диффузионный механизм протекания тока в гомопереходах с p- и n-областями бесконечно большой и конечной толщины
- 2.2.3. Положение квазиуровней Ферми в обедненном слое
- 2.2.4. Рекомбинационно-генерационный процесс в обедненном слое
- 2.2.5. Вольт-амперные характеристики элементов с гомогенным переходом при различных механизмах переноса носителей заряда
- 2.2.6. Трехмерные объемные эффекты в гомогенных переходах
- 2.2.7. Модификации структуры солнечного элемента с гомогенным переходом
- 2.3. ГЕТЕРОПЕРЕХОДЫ
- 2.3.1. Основная модель
- 2.3.2. Сродство к электрону и разрывы энергетических зон
- 2.3.3. Справедливость модели резкого перехода
- 2.4. УСОВЕРШЕНСТВОВАННЫЕ МОДЕЛИ ГЕТЕРОПЕРЕХОДА
- 2.4.2. Влияние поверхностных состояний на электрические свойства гетеропереходов
- 2.4.3. Диполи на границе раздела
- 2.5. МОДЕЛИ КИНЕТИЧЕСКИХ ЯВЛЕНИЙ В ГЕТЕРОПЕРЕХОДАХ
- 2.5.2. Рекомбинация и генерация носителей в обедненном слое
- 2.5.3. Прямая рекомбинация носителей заряда через состояния на границе раздела, определяемая высотой барьера Шоттки
- 2.5.4. Протекание тока, обусловленное рекомбинацией носителей заряда на границе раздела
- 2.5.5. Туннелирование носителей
- 2.5.6. Термическая активация и туннелирование
- 2.5.7. Гетероструктуры
- 2.6. БАРЬЕРЫ ШОТТКИ, СТРУКТУРЫ МЕТАЛЛ-ДИЭЛЕКТРИК-ПОЛУПРОВОДНИК И ПОЛУПРОВОДНИК-ДИЭЛЕКТРИК-ПОЛУПРОВОДНИК
- 2.6.1. Исходная модель барьера Шоттки
- 2.6.2. Высота барьера
- 2.6.3. Происхождение состояний на поверхности и границе раздела
- 2.6.4. Приборы со структурой металл—диэлектрик—полупроводник
- 2.6.5. Структуры полупроводник—диэлектрик—полупроводник
- 2.7. ОМИЧЕСКИЕ КОНТАКТЫ
- Глава 3. РАСЧЕТ КПД ПРЕОБРАЗОВАНИЯ СОЛНЕЧНОЙ ЭНЕРГИИ
- 3.1. ИДЕАЛЬНЫЙ СОЛНЕЧНЫЙ ЭЛЕМЕНТ ПРИ НАЛИЧИИ ОСВЕЩЕНИЯ
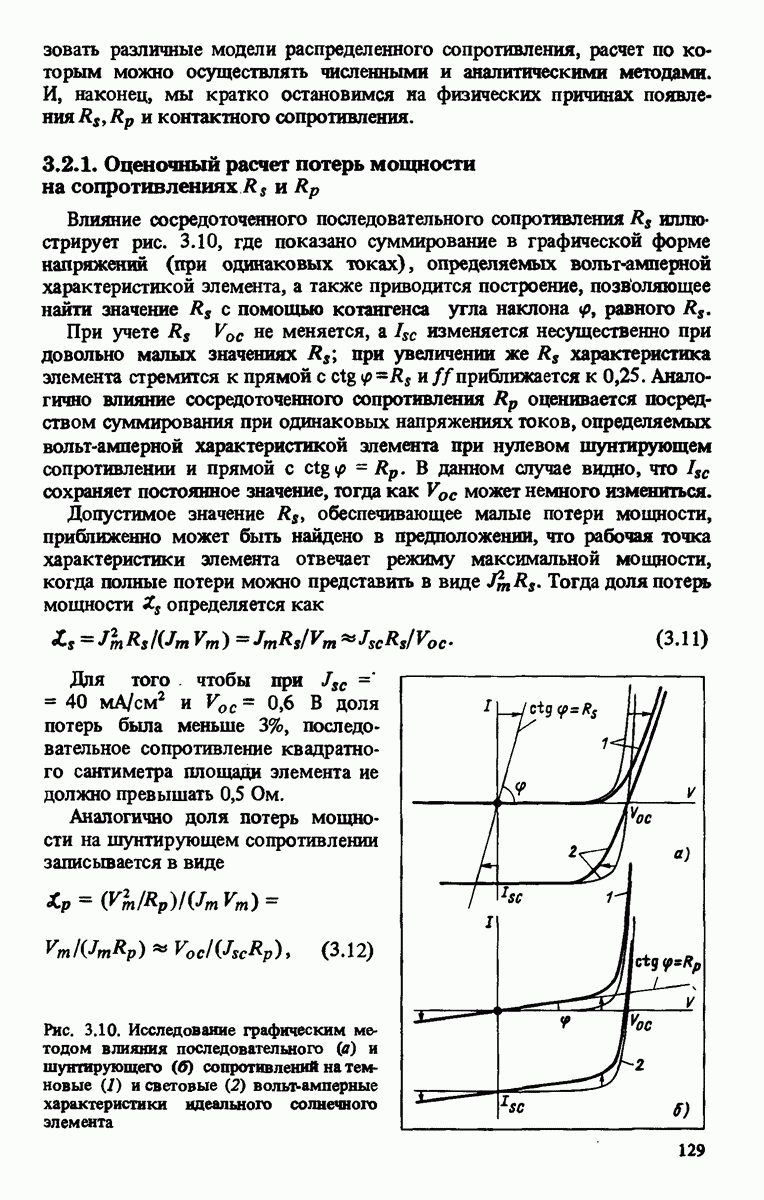
- 3.2. ВЛИЯНИЕ ПОСЛЕДОВАТЕЛЬНОГО И ШУНТИРУЮЩЕГО СОПРОТИВЛЕНИЙ
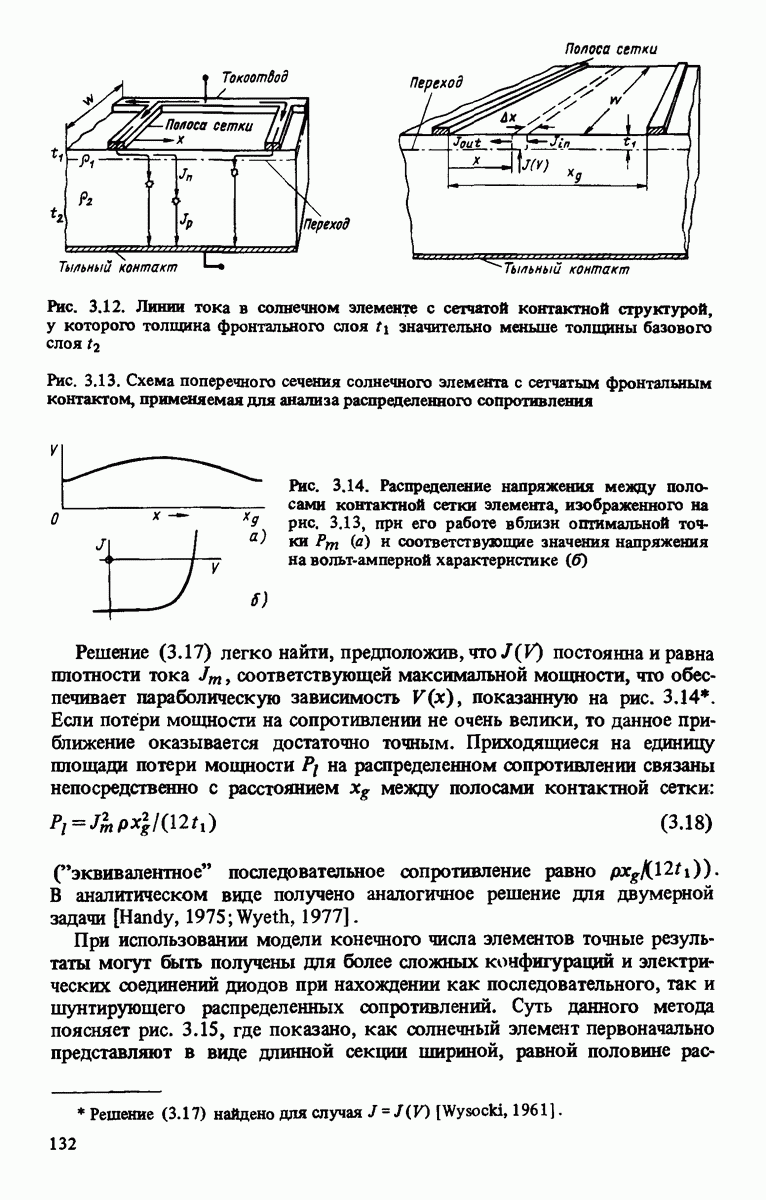
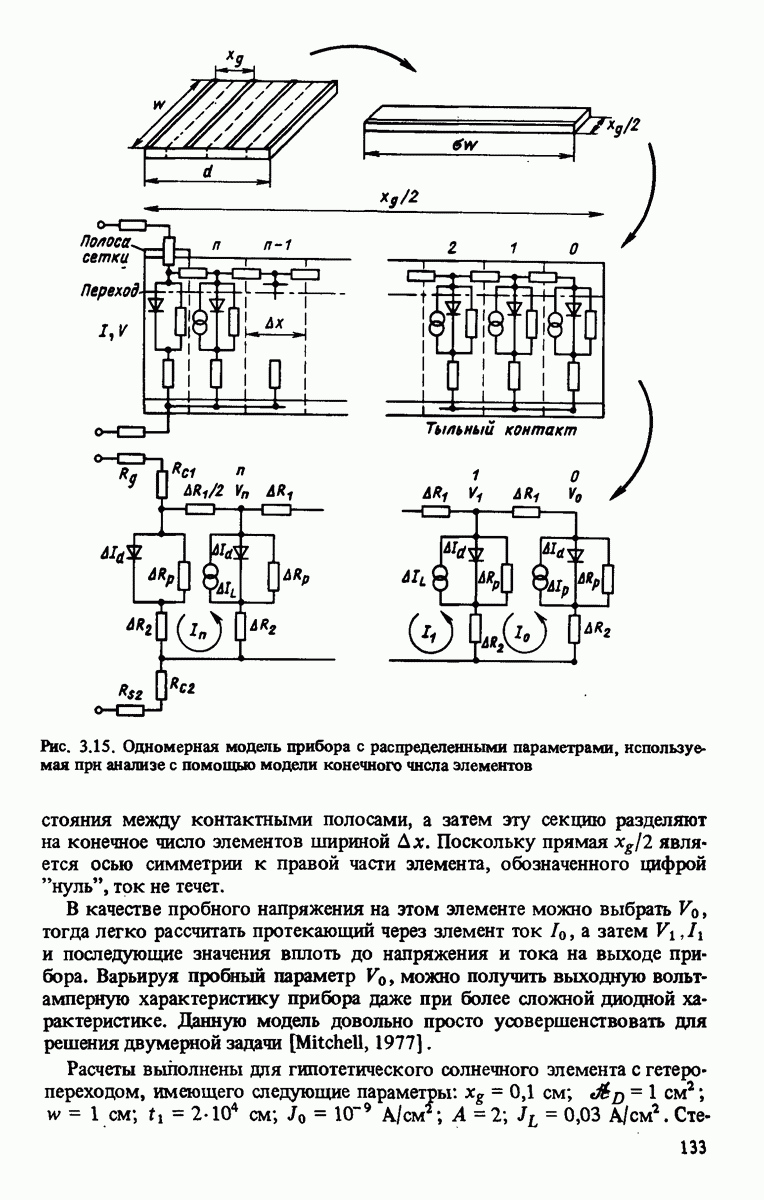
- 3.2.2. Модели с распределенными сопротивлениями
- 3.2.3. Физические явления, обусловливающие последовательное и шунтирующее сопротивления
- 3.3. ДРУГИЕ СПОСОБЫ АНАЛИЗА ЭФФЕКТИВНОСТИ ПРЕОБРАЗОВАНИЯ СОЛНЕЧНОЙ ЭНЕРГИИ
- 3.4. ВЛИЯНИЕ ТЕМПЕРАТУРЫ И ОБЛУЧЕННОСТИ НА КПД СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 3.4.2. Тепловые характеристики
- 3.4.3. Эффекты, связанные с высоким уровнем облученности
- 3.5. АНАЛИЗ ПОТЕРЬ ЭНЕРГИИ
- Глава 4. КРЕМНИЕВЫЕ СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ
- 4.2. ВЫРАЩИВАНИЕ МОНОКРИСТАЛЛИЧЕСКОГО КРЕМНИЯ
- 4.2.2. Выращивание кристаллов методом Чохральского
- 4.2.3. Сегрегация примесей
- 4.2.4. Зонная плавка
- 4.2.5. Другие методы выращивания
- 4.3. ДЕФЕКТНОСТЬ, ЛЕГИРОВАНИЕ И ВРЕМЯ ЖИЗНИ НОСИТЕЛЕЙ ЗАРЯДА
- 4.3.2. Примеси, снижающие время жизни носителей заряда
- 4.3.3. Введение легирующей примеси путем диффузии
- 4.3.4. Другие способы легирования
- 4.4. ТЕХНОЛОГИЯ И ПАРАМЕТРЫ ТИПИЧНЫХ КРЕМНИЕВЫХ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 4.4.2. Этапы изготовления
- 4.4.3. Электрические параметры
- 4.4.4. Текстурированный элемент
- 4.5. ОПТИМИЗАЦИЯ КОНСТРУКЦИИ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 4.5.2. Увеличение КПД с помощью электрических полей
- 4.5.3. Оптимизация элементов обычной конструкции
- 4.6. НОВЫЕ ПУТИ СОЗДАНИЯ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 4.6.2. Тандемный солнечный элемент
- 4.6.3. Тонкие солнечные элементы
- 4.6.4. Другие направления
- 4.7. ЭКОНОМИКА И НОВЫЕ ИДЕИ
- Глава 5. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ С ГЕТЕРОПЕРЕХОДАМИ И ГЕТЕРОСТРУКТУРАМИ
- 5.2. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ НА ОСНОВЕ СТРУКТУР AlGaAs С ГЕТЕРОФАЗНОЙ ГРАНИЦЕЙ РАЗДЕЛА
- 5.2.2. Изготовление слоев методами жидкофазной эпитаксии и химического осаждения из паровой фазы
- 5.2.3. Наиболее распространенная структура солнечного элемента на основе GaAs и ее предварительная оптимизация
- 5.2.4. Концентраторные солнечные элементы AlGaAs — GaAs
- 5.2.5. Солнечные элементы на основе GaAs для космических энергетических установок
- 5.2.6. Арсенид-галлиевые солнечные элементы с переменной шириной зоны и барьерами Шоттки
- 5.3. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ НА ОСНОВЕ lnP
- 5.4. ЗАКЛЮЧЕНИЕ
- Глава 6. ТОНКИЕ ПОЛИКРИСТАЛЛИЧЕСКИЕ ПЛЕНКИ ДЛЯ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 6.2. ПЕРЕНОС ЭЛЕКТРИЧЕСКОГО ЗАРЯДА В ПОЛИКРИСТАЛЛИЧЕСКИХ ПЛЕНКАХ
- 6.2.2. Границы между зернами в поликристаллических пленках
- 6.2.3. Электропроводность поликристаллических материалов
- 6.2.4. Электропроводность различных поликристаллических пленок
- 6.3. ВЛИЯНИЕ МЕЖКРИСТАЛЛИТНЫХ ГРАНИЦ В СОЛНЕЧНЫХ ЭЛЕМЕНТАХ С ПОЛИКРИСТАЛЛИЧЕСКИМИ СЛОЯМИ
- 6.3.1. Исследования рекомбинации на межкрнсталлитных границах в бикристалле и поликристалле с большим размером кристаллитов
- 6.3.2. Теоретические исследования поликристаллических солнечных элементов
- 6.3.3. Снижение рекомбинации на межкристаллитной границе
- 6.4. Заключение
- СПИСОК ЛИТЕРАТУРЫ