| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.3.1. Исследования рекомбинации на межкрнсталлитных границах в бикристалле и поликристалле с большим размером кристаллитов
При освещении фотогенерированные неосновные носители увлекаются к межкристаллитным границам электрическими полями в обедненных областях, окружающих эти границы. Поскольку в начальный момент времени избыточное число основных носителей в области максимума потенциального барьера на межкристаллитной границе мало, неосновные захватываются на пограничных состояниях, тем самым уменьшая полный заряд и снижая высоту потенциальных барьеров.
Стационарное состояние достигается тогда, когда концентрация основных носителей на участке максимума потенциального барьера становится настолько большой, что выполняется соотношение  (в случае полупроводникового материала
(в случае полупроводникового материала  -типа проводимости, где
-типа проводимости, где  — скорости поверхностной рекомбинации электронов и дырок на межкристаллитной границе). Число заполненных зарядами пограничных состояний
— скорости поверхностной рекомбинации электронов и дырок на межкристаллитной границе). Число заполненных зарядами пограничных состояний  и, следовательно,
и, следовательно,  резко изменяется при солнечном освещении.
резко изменяется при солнечном освещении.
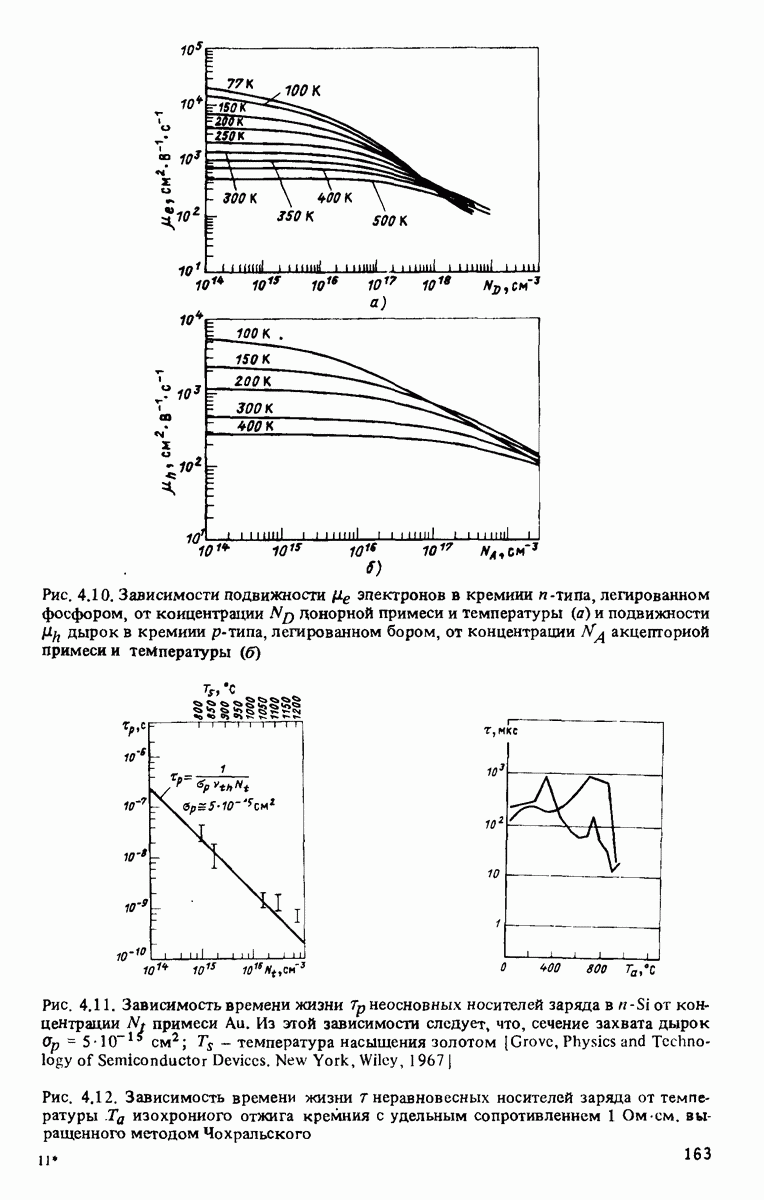
Безотносительно к солнечным элементам рекомбинационные процессы на межкрнсталлитных границах исследовали в течение продолжительного периода. Шокли провел расчет времени спада избыточной концентрации носителей заряда после выключения светового источника однородной генерации в случае нитевидного полупроводникового кристалла, имеющего скорость поверхностной рекомбинации  , коэффициент диффузии Ли время жизни
, коэффициент диффузии Ли время жизни  [Shockley, 1950].
[Shockley, 1950].
Рассматривая фактически случай прямоугольного бруска с размерами сечения  и бесконечной длиной
и бесконечной длиной  Решением двумерного кинетического уравнения является сумма собственных функций, каждый последующий член которой имеет меньшее значение характеристического времени жизни. После выключения источника, вызывающего фотогенерацию, слагаемые с большими номерами быстро уменьшаются и остается лишь член с наибольшим характеристическим временем, соответствующий собственным значениям
Решением двумерного кинетического уравнения является сумма собственных функций, каждый последующий член которой имеет меньшее значение характеристического времени жизни. После выключения источника, вызывающего фотогенерацию, слагаемые с большими номерами быстро уменьшаются и остается лишь член с наибольшим характеристическим временем, соответствующий собственным значениям  которые приближенно можно считать «временем жизни» фотогенерированных носителей в нитевидном кристалле:
которые приближенно можно считать «временем жизни» фотогенерированных носителей в нитевидном кристалле:

где

Если  - тогда
- тогда

При малых 

Из этих соотношений следует, что время жизни  определяется наименьшим размером нитевидного кристаллита. Поскольку эти формулы соответствуют не начальным участкам переходного процесса после выключения однородного светового возбуждения, значения
определяется наименьшим размером нитевидного кристаллита. Поскольку эти формулы соответствуют не начальным участкам переходного процесса после выключения однородного светового возбуждения, значения  определенные таким способом, могут не совпадать со значениями Т и L для стационарного случая с неоднородным возбуждением.
определенные таким способом, могут не совпадать со значениями Т и L для стационарного случая с неоднородным возбуждением.
Шокли выполнил аналогичные расчеты при анализе прохождения тока через смещенный  -переход в нитевид ном кристалле (с инжекцией в направлении
-переход в нитевид ном кристалле (с инжекцией в направлении  с одного конца кристаллита) и установил, что подстановка значения
с одного конца кристаллита) и установил, что подстановка значения  из (6.22) в обычное диодное уравнение [например, (2.13)] дает разумные результаты при условии, что
из (6.22) в обычное диодное уравнение [например, (2.13)] дает разумные результаты при условии, что  мало, т.е.
мало, т.е.  [Shockley, 1949]. В поликристаллических солнечных элементах это условие, как правило, невыполнимо. При больших значениях
[Shockley, 1949]. В поликристаллических солнечных элементах это условие, как правило, невыполнимо. При больших значениях  решение представляет собой полную сумму членов ряда, поскольку они медленно спадают со временем. Слой обеднения, примыкающий к границе кристаллита, в обоих случаях не учитывают.
решение представляет собой полную сумму членов ряда, поскольку они медленно спадают со временем. Слой обеднения, примыкающий к границе кристаллита, в обоих случаях не учитывают.
В других работах основное внимание уделялось экспериментальному определению свойств межкрнсталлитных границ в бикристаллах [Vogel е.а., 1954; Pearson, 1949; Morrison, 1956; Werthiem, Pearson, 1957]. В одной из моделей [Vogel ел., 1954] близко расположенные дислокационные ядра на малоугловых межзеренных границах рассматривали как слой рекомбинации  . В экспериментах с линеаризованными границами (т.е. с границами с настолько малыми углами, что расстояния между дислокациями составляют около микрометра) в
. В экспериментах с линеаризованными границами (т.е. с границами с настолько малыми углами, что расстояния между дислокациями составляют около микрометра) в  с помощью оптического зондирования (в условиях, близких к тепловым) было обнаружено, что
с помощью оптического зондирования (в условиях, близких к тепловым) было обнаружено, что  см/с.
см/с.
Обзор ранних работ [Sosnowski, 1959], посвященных бикристаллам  показал, что высокоугловые межзеренные границы имеют значительно большие высоты барьеров
показал, что высокоугловые межзеренные границы имеют значительно большие высоты барьеров  и повышенную фотоэлектрическую активность и вместе с тем, как ни странно, меньшие скорости поверхностной рекомбинации. По сравнению с малоугловыми вдоль высокоугловых границ в
и повышенную фотоэлектрическую активность и вместе с тем, как ни странно, меньшие скорости поверхностной рекомбинации. По сравнению с малоугловыми вдоль высокоугловых границ в  сильнее проводимость, и концентрация заряда на них такова, что пограничная область
сильнее проводимость, и концентрация заряда на них такова, что пограничная область  -типа становится вырожденной. Для объяснения экспериментально наблюдавшихся значений
-типа становится вырожденной. Для объяснения экспериментально наблюдавшихся значений  была предложена модель рекомбинации на линеаризованных и двойниковых границах в
была предложена модель рекомбинации на линеаризованных и двойниковых границах в  не учитывающая, однако никаких эффектов, связанных с электрическими полями вблизи потенциальных барьеров. Полный теоретический анализ всех типов межзеренных границ был проведен Матаре [Matare, 1971] как со структурной, так и с электронной
не учитывающая, однако никаких эффектов, связанных с электрическими полями вблизи потенциальных барьеров. Полный теоретический анализ всех типов межзеренных границ был проведен Матаре [Matare, 1971] как со структурной, так и с электронной
точек зрения. Экспериментальные результаты, в особенности по электронным свойствам, относятся главным образом к 
Рекомбинацию в  -переходах, изготовленных в бикристаллах
-переходах, изготовленных в бикристаллах  исследовали на шлифах методом тока, наведенного электронным пучком [Daud ел., 1978]. Эффективная диффузионная длина
исследовали на шлифах методом тока, наведенного электронным пучком [Daud ел., 1978]. Эффективная диффузионная длина  вблизи межкристаллитной границы составляла около 2 мкм и почти линейно возрастала при удалении от нее, пока не становилась постоянной и равной по значению для монокристалла
вблизи межкристаллитной границы составляла около 2 мкм и почти линейно возрастала при удалении от нее, пока не становилась постоянной и равной по значению для монокристалла  мкм. Протяженность области по обе стороны от межкристаллитной границы, в которой
мкм. Протяженность области по обе стороны от межкристаллитной границы, в которой  примерно
примерно  т.е. значительно превосходит ширину обедненной области
т.е. значительно превосходит ширину обедненной области  .
.
Рекомбинацию на границах зерен в крупнозеренных поликристаллических материалах изучали методами оптического и электронно-лучевого сканирования [Inoue е.а., 1981; Hanoka, 1980Н; Itoh е.а., 1978]. Например, в  была установлена связь между кристаллографической ориентацией границ зереи и их рекомбинационными свойствами.
была установлена связь между кристаллографической ориентацией границ зереи и их рекомбинационными свойствами.
До сих пор обсуждали исследования, проводимые в темновых условиях (или в условиях локального светового зондирования), когда рекомбинационные свойства, как правило, можно описать с помощью постоянного параметра  на зависящего от концентрации носителей заряда. Влияние освещения на потенциальный барьер и рекомбинации на межкристаллитной границе учитывали в рамках модели Шокли-Рида—Холла [Card, Yang, 1977]. При освещении материала
на зависящего от концентрации носителей заряда. Влияние освещения на потенциальный барьер и рекомбинации на межкристаллитной границе учитывали в рамках модели Шокли-Рида—Холла [Card, Yang, 1977]. При освещении материала  -типа фотогенериро-ванные дырки нейтрализуют отрицательно заряженные состояния на межзеренной границе и снижают высоту потенциального барьера до тех пор, пока не уравновесятся рекомбинационные токи электронов и дырок. В приближении постоянства
-типа фотогенериро-ванные дырки нейтрализуют отрицательно заряженные состояния на межзеренной границе и снижают высоту потенциального барьера до тех пор, пока не уравновесятся рекомбинационные токи электронов и дырок. В приближении постоянства  во всем обедненном слое и равенства рекомбинационных сечений захвата электронов и дырок
во всем обедненном слое и равенства рекомбинационных сечений захвата электронов и дырок  — равновесие наступает, когда неравновесные концентрации
— равновесие наступает, когда неравновесные концентрации  на межкристаллитной границе становятся равны друг другу.
на межкристаллитной границе становятся равны друг другу.
При этом темп рекомбинации максимален. Основной вклад в рекомбинационный ток дают состояния, находящиеся между уровнями  поэтому для темпа рекомбинации справедливо соотношение
поэтому для темпа рекомбинации справедливо соотношение

где  — тепловая скорость;
— тепловая скорость;  — плотность распределения поверхностных состояний на межзеренной границе,
— плотность распределения поверхностных состояний на межзеренной границе,  На основе этого получена связь между
На основе этого получена связь между  в условиях освещения
в условиях освещения  (рис. 6.8) [см. также Hwang е.а., 1981 ].
(рис. 6.8) [см. также Hwang е.а., 1981 ].
Концентрация дырок на межкристаллитной границе увеличивается в присутствии остаточного барьера, поэтому скорость поверхностной рекомбинации  на краю обедненного слоя вблизи границы зерна
на краю обедненного слоя вблизи границы зерна

В результате темп рекомбинации на межзеренной границе

нелинейно зависит от  . Член
. Член  в рассматриваемом случае почти не влияет на линейность. Однако экспоненциальная зависимость высоты барьера от интенсивности облучения может обусловить более высокую степень нелинейности, поскольку Vdgb также зависит от
в рассматриваемом случае почти не влияет на линейность. Однако экспоненциальная зависимость высоты барьера от интенсивности облучения может обусловить более высокую степень нелинейности, поскольку Vdgb также зависит от  Таким образом, в области солнечного элемента с более высоким уровнем возбуждения [большая концентрация
Таким образом, в области солнечного элемента с более высоким уровнем возбуждения [большая концентрация  и малое значение
и малое значение  темп рекомбинации меньше, чем на участках, где этот уровень ниже [малая концентрация
темп рекомбинации меньше, чем на участках, где этот уровень ниже [малая концентрация  , большое значение
, большое значение  Поскольку
Поскольку  зависит от уровня легирования
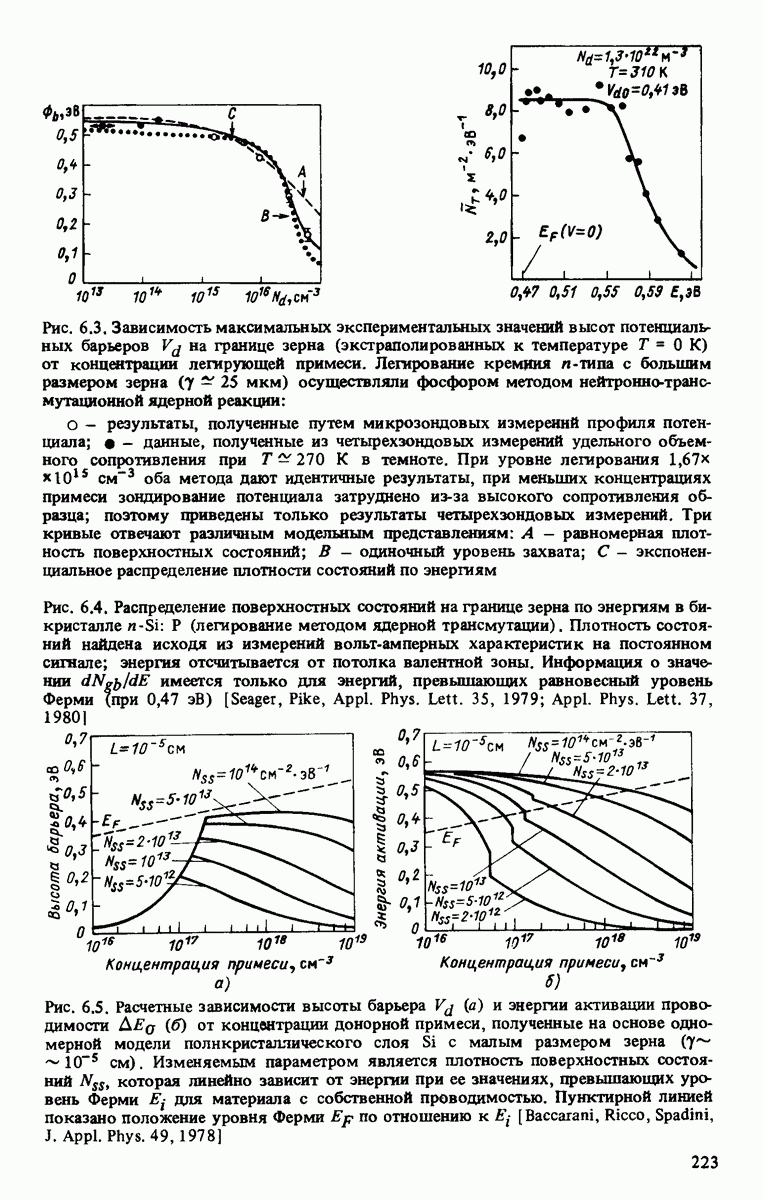
зависит от уровня легирования  (рис. 6.3 и
(рис. 6.3 и  ), существует связь между
), существует связь между  при больших значениях
при больших значениях 
Кардом и Янгом [Card, Yang, 1977], был проведен расчет среднего времени жизни  неосновных носителей заряда для столбчатых кристаллитов с квадратным поперечным сечением
неосновных носителей заряда для столбчатых кристаллитов с квадратным поперечным сечением  в предположении однородной генерации вдоль сечения и длины кристаллитов. Предполагали также, что рекомбинационные центры однородно распределены по всему объему поликристаллического материала, причем их эффективность увеличивается пропорционально напряженности электрического поля обедненного слоя вблизи межкристаллитной границы. В этом случае для
в предположении однородной генерации вдоль сечения и длины кристаллитов. Предполагали также, что рекомбинационные центры однородно распределены по всему объему поликристаллического материала, причем их эффективность увеличивается пропорционально напряженности электрического поля обедненного слоя вблизи межкристаллитной границы. В этом случае для  получается выражение
получается выражение

Для материала  -типа проводимости связь между
-типа проводимости связь между  показана на рис. 6.21.
показана на рис. 6.21.
Глубокий теоретический анализ солнечных элементов с поликристаллическими слоями дан в работе Фоссума и Линдхольма [Fossum, Lind-holm, 1980а]. В работе отмечен ряд важных обстоятельств, касающихся зависимости  от освещения. Для малых занчений
от освещения. Для малых занчений  когда
когда  постоянны во всей обедненной области, окружающей границу зерен, для темпа рекомбинации получено выражение
постоянны во всей обедненной области, окружающей границу зерен, для темпа рекомбинации получено выражение

где  — рекомбинационные сечения захвата электронов и дырок пустыми рекомбинационными центрами.
— рекомбинационные сечения захвата электронов и дырок пустыми рекомбинационными центрами.
Этот результат справедлив лишь при условии достаточно высокого уровня возбуждения, при котором  и тем самым обоснованы некоторые допущения в модели Шокли—Рида—Холла. Результат аналогичен (6.23), в нем лишь фигурируют
и тем самым обоснованы некоторые допущения в модели Шокли—Рида—Холла. Результат аналогичен (6.23), в нем лишь фигурируют  а не
а не 

Рис. 6.21. Расчетные зависимости среднего времени жизни Г неосновных носителей заряда в поликристалле  от размера d кристаллитов и плотности пограничных состояний
от размера d кристаллитов и плотности пограничных состояний  при
при  Резкий начальный спад Тсвязан с увеличением
Резкий начальный спад Тсвязан с увеличением  свету) при росте
свету) при росте  и среднего времени жизни Т неосновных носителей заряда от
и среднего времени жизни Т неосновных носителей заряда от  и размера кристаллитов при
и размера кристаллитов при 
При высокой интенсивности освещения результаты совпадают, так как  . Из (6.27) следует, что темп рекомбинации при сильном освещении слабо или вовсе не зависит от высоты потенциального барьера
. Из (6.27) следует, что темп рекомбинации при сильном освещении слабо или вовсе не зависит от высоты потенциального барьера 
При низком уровне инжекции в поглощающем слое  -типа
-типа  внутри зерна, поэтому
внутри зерна, поэтому  и выражение для эффективной скорости поверхностной рекомбинации на границе зерна можно переписать в виде
и выражение для эффективной скорости поверхностной рекомбинации на границе зерна можно переписать в виде

где  — концентрация носителей на границе обедненного слоя при освещении. В этом случае, как и в модели Карда и Янга, значение
— концентрация носителей на границе обедненного слоя при освещении. В этом случае, как и в модели Карда и Янга, значение  уменьшается с ростом уровня возбуждения и увеличивается с ростом уровня легирования.
уменьшается с ростом уровня возбуждения и увеличивается с ростом уровня легирования.
При решении уравнения переноса заряда (6.28) представляет собой нелинейное граничное условие, зависящее от уровня инжекции. Однако при ее высоких уровнях 
Кроме того, когда произведение  настолько велико, что в обедненной области
настолько велико, что в обедненной области  высота потенциального барьера фиксируется при темновом значении,
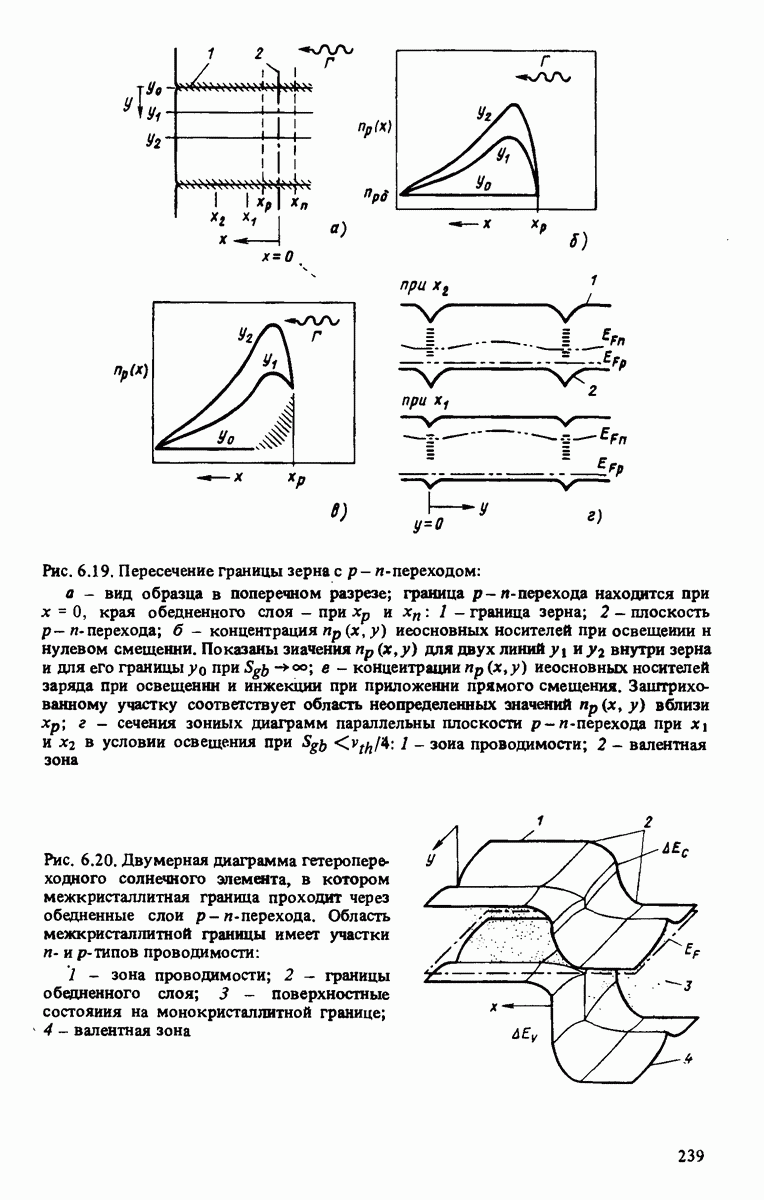
высота потенциального барьера фиксируется при темновом значении,  . В обоих случаях граничное условие становится линейным. Выражения (6.24) и (6.28) в значительной степени уменьшают неопределенность в описании переноса заряда на пересечении межкристаллитной границы и границы обедненной области (рис. 6.19, в), пренебрегая проводимостью вдоль межкристаллитной границы.
. В обоих случаях граничное условие становится линейным. Выражения (6.24) и (6.28) в значительной степени уменьшают неопределенность в описании переноса заряда на пересечении межкристаллитной границы и границы обедненной области (рис. 6.19, в), пренебрегая проводимостью вдоль межкристаллитной границы.
Теория рекомбинации на одиночной межкристаллитной границе в бикристалле  в широком диапазоне интенсивностей освещения предложена Сигером [Seager, 1981]. Основываясь на принципе детального равновесия [Hall, 1952; Shockley, Read, 1952] при рассмотрении поверхностной рекомбинации, Сигер объединил полученные результаты с выводами
в широком диапазоне интенсивностей освещения предложена Сигером [Seager, 1981]. Основываясь на принципе детального равновесия [Hall, 1952; Shockley, Read, 1952] при рассмотрении поверхностной рекомбинации, Сигер объединил полученные результаты с выводами
предложенной им ранее модели проводимости и емкости межзеренных границ в Si [Pike, Seager, 1979].
При этом предполагали [Seager, 1981], что: концентрации носителей заряда и токи лимитируются механизмами термоэлектронной эмиссии через межкристаллитные барьеры; в рекомбинационных процессах участвуют те же состояния, которые ответственны за захват заряда, контролирующий Vjgb; все состояния на межкристаллитной границе имеют одиночный энергетический уровень; соблюдено условие однородного возбуждения и низкого уровня инжекции  захват и эмиссия носителей заряда не зависят от интенсивности освещения.
захват и эмиссия носителей заряда не зависят от интенсивности освещения.
Одно из основных отличий теории Сигера от ранее рассмотренных [Card, Yang, 1977; Fossum, Lindholm, 1980a,b] — возможность изменения квазиуровней Ферми в объединенном слое межкристаллитной области. При не сильно ограничивающих предположениях с помощью этой теории удалось получить соотношение между высотой барьера  при освещении, интенсивностью освещения Г, концентрацией доноров
при освещении, интенсивностью освещения Г, концентрацией доноров  сечением рекомбинации а для дырок и высотой барьера в темноте. На основании решения трансцендентного уравнения были сделаны следующие выводы:
сечением рекомбинации а для дырок и высотой барьера в темноте. На основании решения трансцендентного уравнения были сделаны следующие выводы:
1. Высокие потенциальные барьеры на межкристаллитных границах чувствительны даже к очень слабым интенсивностям освещения, в то время как барьеры с малым значением  практически не зависят от освещенности.
практически не зависят от освещенности.
2. При больших  , (около 0,4 эВ) освещение приводит к значительному изменению высоты барьера, в первом приближении не зависящему от рекомбинационного сечения захвата
, (около 0,4 эВ) освещение приводит к значительному изменению высоты барьера, в первом приближении не зависящему от рекомбинационного сечения захвата  дырок при
дырок при 
3. При малых  (не более
(не более  ) выражение для эффективной скорости поверхностной рекомбинации имеет вид
) выражение для эффективной скорости поверхностной рекомбинации имеет вид

из которого следует, что быстро уменьшается при уменьшении
Vdgb. Например, при  солнца
солнца  в случае
в случае 

4. Значение  не зависит от интенсивности освещения при малых
не зависит от интенсивности освещения при малых  (не более
(не более  ), однако при Vdgb
), однако при Vdgb  эВ
эВ  уменьшается, если освещенность выше уровня примерно 0,3 солнца.
уменьшается, если освещенность выше уровня примерно 0,3 солнца.
5. При малых  и высоких уровнях освещения (более 3 солнц), квазиуровень Ферми дырок становится практически одинаковым во всем обедненном слое, как и предполагалось в ранее рассмотренных работах [Card, Yang, 1977; Fossum, Lindholm, 1980 a,b].
и высоких уровнях освещения (более 3 солнц), квазиуровень Ферми дырок становится практически одинаковым во всем обедненном слое, как и предполагалось в ранее рассмотренных работах [Card, Yang, 1977; Fossum, Lindholm, 1980 a,b].
Расчеты Сигера хорошо согласуются с измерениями на образцах  легированных нейтронно-трансмутационным методом, во всем исследовавшемся диапазоне интенсивностей света (от темновых до световых измерений при интенсивностях до 0,3 солнца).
легированных нейтронно-трансмутационным методом, во всем исследовавшемся диапазоне интенсивностей света (от темновых до световых измерений при интенсивностях до 0,3 солнца).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 1. УРАВНЕНИЕ ПЕРЕНОСА
- 1.2. ОСНОВНЫЕ СОСТАВЛЯЮЩИЕ УРАВНЕНИЯ ПЕРЕНОСА
- 1.3. ВЫВОД УРАВНЕНИЯ ПЕРЕНОСА
- 1.4. РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА
- 1.5. СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- 1.6. ИЗМЕРЕНИЕ ВРЕМЕНИ ЖИЗНИ И ДИФФУЗИОННОЙ ДЛИНЫ НЕОСНОВНЫХ НОСИТЕЛЕЙ ЗАРЯДА
- Глава 2. ЭЛЕКТРОННО-ДЫРОЧНЫЕ ПЕРЕХОДЫ
- 2.2. ГОМОГЕННЫЕ ПЕРЕХОДЫ
- 2.2.2. Диффузионный механизм протекания тока в гомопереходах с p- и n-областями бесконечно большой и конечной толщины
- 2.2.3. Положение квазиуровней Ферми в обедненном слое
- 2.2.4. Рекомбинационно-генерационный процесс в обедненном слое
- 2.2.5. Вольт-амперные характеристики элементов с гомогенным переходом при различных механизмах переноса носителей заряда
- 2.2.6. Трехмерные объемные эффекты в гомогенных переходах
- 2.2.7. Модификации структуры солнечного элемента с гомогенным переходом
- 2.3. ГЕТЕРОПЕРЕХОДЫ
- 2.3.1. Основная модель
- 2.3.2. Сродство к электрону и разрывы энергетических зон
- 2.3.3. Справедливость модели резкого перехода
- 2.4. УСОВЕРШЕНСТВОВАННЫЕ МОДЕЛИ ГЕТЕРОПЕРЕХОДА
- 2.4.2. Влияние поверхностных состояний на электрические свойства гетеропереходов
- 2.4.3. Диполи на границе раздела
- 2.5. МОДЕЛИ КИНЕТИЧЕСКИХ ЯВЛЕНИЙ В ГЕТЕРОПЕРЕХОДАХ
- 2.5.2. Рекомбинация и генерация носителей в обедненном слое
- 2.5.3. Прямая рекомбинация носителей заряда через состояния на границе раздела, определяемая высотой барьера Шоттки
- 2.5.4. Протекание тока, обусловленное рекомбинацией носителей заряда на границе раздела
- 2.5.5. Туннелирование носителей
- 2.5.6. Термическая активация и туннелирование
- 2.5.7. Гетероструктуры
- 2.6. БАРЬЕРЫ ШОТТКИ, СТРУКТУРЫ МЕТАЛЛ-ДИЭЛЕКТРИК-ПОЛУПРОВОДНИК И ПОЛУПРОВОДНИК-ДИЭЛЕКТРИК-ПОЛУПРОВОДНИК
- 2.6.1. Исходная модель барьера Шоттки
- 2.6.2. Высота барьера
- 2.6.3. Происхождение состояний на поверхности и границе раздела
- 2.6.4. Приборы со структурой металл—диэлектрик—полупроводник
- 2.6.5. Структуры полупроводник—диэлектрик—полупроводник
- 2.7. ОМИЧЕСКИЕ КОНТАКТЫ
- Глава 3. РАСЧЕТ КПД ПРЕОБРАЗОВАНИЯ СОЛНЕЧНОЙ ЭНЕРГИИ
- 3.1. ИДЕАЛЬНЫЙ СОЛНЕЧНЫЙ ЭЛЕМЕНТ ПРИ НАЛИЧИИ ОСВЕЩЕНИЯ
- 3.2. ВЛИЯНИЕ ПОСЛЕДОВАТЕЛЬНОГО И ШУНТИРУЮЩЕГО СОПРОТИВЛЕНИЙ
- 3.2.2. Модели с распределенными сопротивлениями
- 3.2.3. Физические явления, обусловливающие последовательное и шунтирующее сопротивления
- 3.3. ДРУГИЕ СПОСОБЫ АНАЛИЗА ЭФФЕКТИВНОСТИ ПРЕОБРАЗОВАНИЯ СОЛНЕЧНОЙ ЭНЕРГИИ
- 3.4. ВЛИЯНИЕ ТЕМПЕРАТУРЫ И ОБЛУЧЕННОСТИ НА КПД СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 3.4.2. Тепловые характеристики
- 3.4.3. Эффекты, связанные с высоким уровнем облученности
- 3.5. АНАЛИЗ ПОТЕРЬ ЭНЕРГИИ
- Глава 4. КРЕМНИЕВЫЕ СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ
- 4.2. ВЫРАЩИВАНИЕ МОНОКРИСТАЛЛИЧЕСКОГО КРЕМНИЯ
- 4.2.2. Выращивание кристаллов методом Чохральского
- 4.2.3. Сегрегация примесей
- 4.2.4. Зонная плавка
- 4.2.5. Другие методы выращивания
- 4.3. ДЕФЕКТНОСТЬ, ЛЕГИРОВАНИЕ И ВРЕМЯ ЖИЗНИ НОСИТЕЛЕЙ ЗАРЯДА
- 4.3.2. Примеси, снижающие время жизни носителей заряда
- 4.3.3. Введение легирующей примеси путем диффузии
- 4.3.4. Другие способы легирования
- 4.4. ТЕХНОЛОГИЯ И ПАРАМЕТРЫ ТИПИЧНЫХ КРЕМНИЕВЫХ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 4.4.2. Этапы изготовления
- 4.4.3. Электрические параметры
- 4.4.4. Текстурированный элемент
- 4.5. ОПТИМИЗАЦИЯ КОНСТРУКЦИИ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 4.5.2. Увеличение КПД с помощью электрических полей
- 4.5.3. Оптимизация элементов обычной конструкции
- 4.6. НОВЫЕ ПУТИ СОЗДАНИЯ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 4.6.2. Тандемный солнечный элемент
- 4.6.3. Тонкие солнечные элементы
- 4.6.4. Другие направления
- 4.7. ЭКОНОМИКА И НОВЫЕ ИДЕИ
- Глава 5. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ С ГЕТЕРОПЕРЕХОДАМИ И ГЕТЕРОСТРУКТУРАМИ
- 5.2. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ НА ОСНОВЕ СТРУКТУР AlGaAs С ГЕТЕРОФАЗНОЙ ГРАНИЦЕЙ РАЗДЕЛА
- 5.2.2. Изготовление слоев методами жидкофазной эпитаксии и химического осаждения из паровой фазы
- 5.2.3. Наиболее распространенная структура солнечного элемента на основе GaAs и ее предварительная оптимизация
- 5.2.4. Концентраторные солнечные элементы AlGaAs — GaAs
- 5.2.5. Солнечные элементы на основе GaAs для космических энергетических установок
- 5.2.6. Арсенид-галлиевые солнечные элементы с переменной шириной зоны и барьерами Шоттки
- 5.3. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ НА ОСНОВЕ lnP
- 5.4. ЗАКЛЮЧЕНИЕ
- Глава 6. ТОНКИЕ ПОЛИКРИСТАЛЛИЧЕСКИЕ ПЛЕНКИ ДЛЯ СОЛНЕЧНЫХ ЭЛЕМЕНТОВ
- 6.2. ПЕРЕНОС ЭЛЕКТРИЧЕСКОГО ЗАРЯДА В ПОЛИКРИСТАЛЛИЧЕСКИХ ПЛЕНКАХ
- 6.2.2. Границы между зернами в поликристаллических пленках
- 6.2.3. Электропроводность поликристаллических материалов
- 6.2.4. Электропроводность различных поликристаллических пленок
- 6.3. ВЛИЯНИЕ МЕЖКРИСТАЛЛИТНЫХ ГРАНИЦ В СОЛНЕЧНЫХ ЭЛЕМЕНТАХ С ПОЛИКРИСТАЛЛИЧЕСКИМИ СЛОЯМИ
- 6.3.1. Исследования рекомбинации на межкрнсталлитных границах в бикристалле и поликристалле с большим размером кристаллитов
- 6.3.2. Теоретические исследования поликристаллических солнечных элементов
- 6.3.3. Снижение рекомбинации на межкристаллитной границе
- 6.4. Заключение
- СПИСОК ЛИТЕРАТУРЫ