| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3-12. Электромагнитная индукция
а) Электродвижущая смла, наведенная в проводе
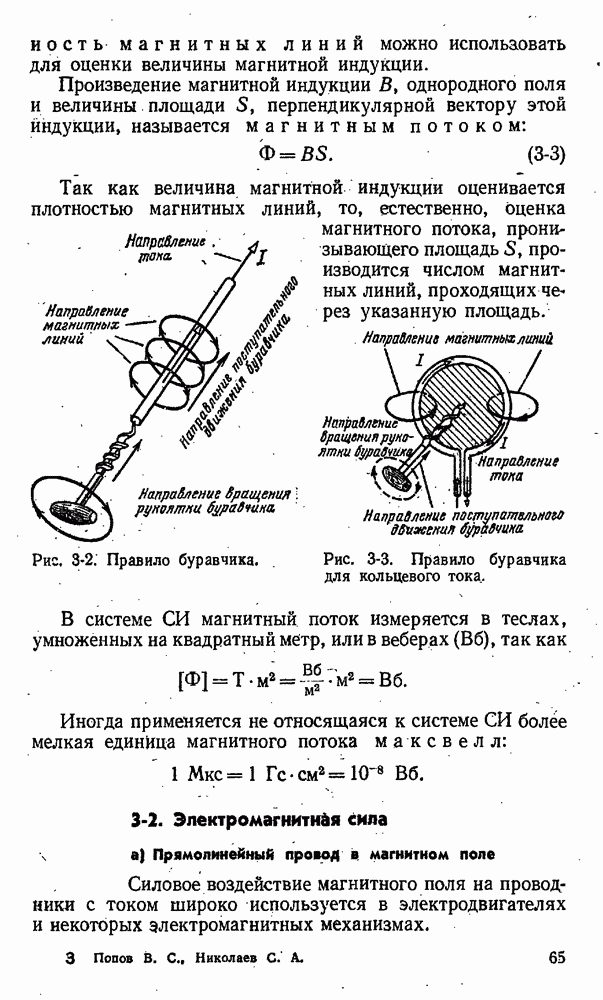
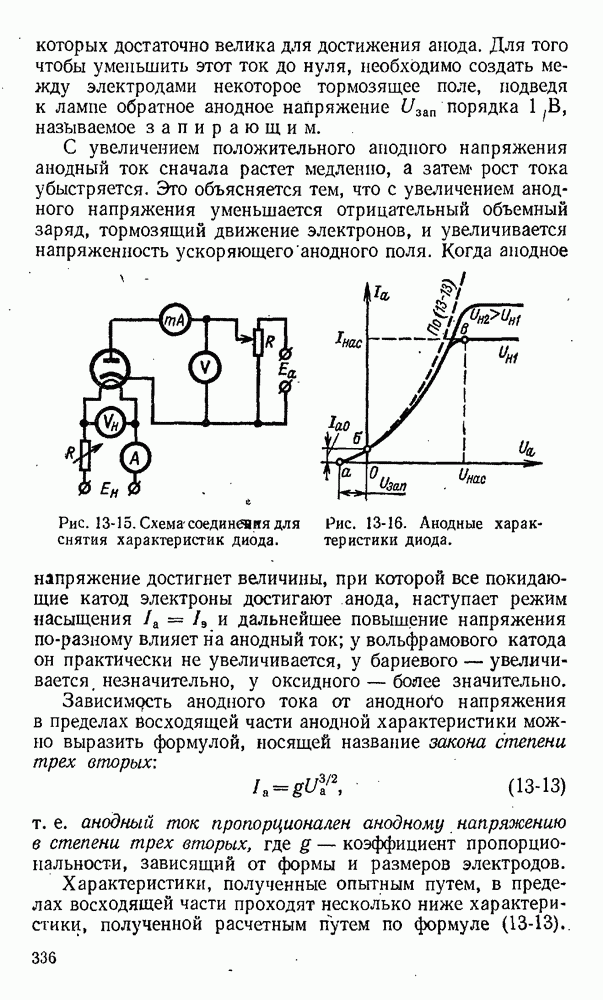
При движении провода с постоянной скоростью v с той же скоростью будут, перемещаться свободные электроны и положительные ионы провода. Если провод движется в однородном поле перпендикулярно магнитным линиям (рис. 3-22), то на каждую заряженную частицу будет действовать электромагнитная сила (§ 3-1 и 3-2), направление которой определяется правилом левой руки. Под действием этих: сил электроны будут перемещаться на один конец провода, создавая на нем отрицательный заряд, а на другом конце провода недостаток электронов вызовет положительный заряд.

Рис. 3-22. Движение провода в магнитном поле.
Разделение зарядов прекратится, если электромагнитные силы уравновесятся электрическими силами притяжения разноименных зарядов. Так, в результате работы электромагнитных сил в. проводнике возникает э. д. с., которую называют э. д. с. электромагнитной индукции, а само явление — электромагнитной индукцией. В этом случае механическая энергия, затраченная на движение проводника, преобразуется в электрическую. Явление электромагнитной индукции было открыто в. 1831 г. английским физиком М. Фарадеем.
На концах незамкнутого провода напряжение U равно э. д. с. электромагнитной индукции Е, таким образом (1-3);

но так как  , а сила, действующая на электрон (3-6),
, а сила, действующая на электрон (3-6),  , то
, то

Следовательно, наведенная (индуктированная) в проводе э. д. с. электромагнитной индукции пропорциональна величине магнитной индукции поля, в котором движется проводник, длине провода и Скорости его движения в направлении, перпендикулярном магнитным линиям. Это первая формулировка закона электромагнитной индукции.
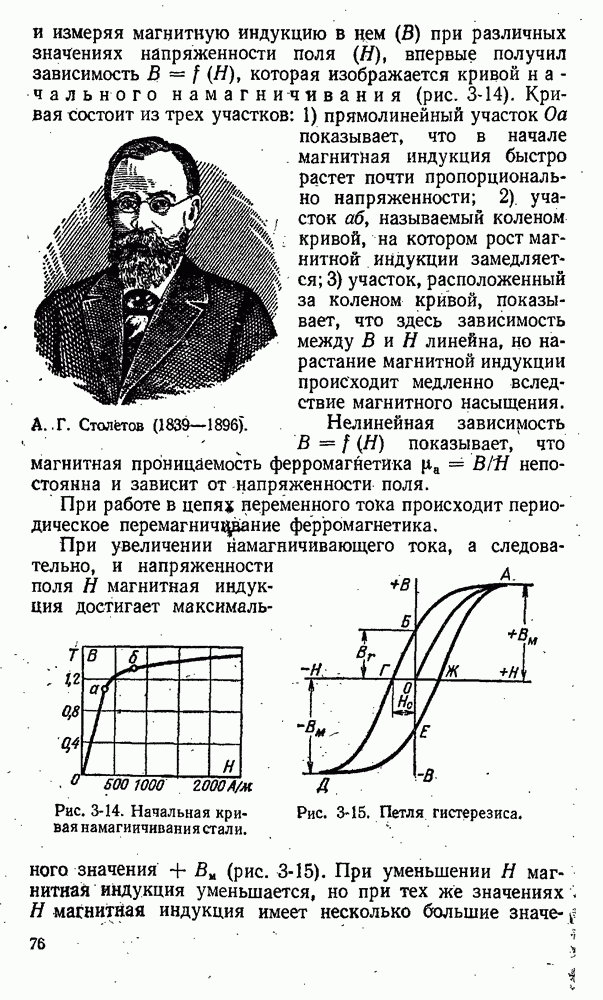
Направление наведенной э. д. с. определяется правилом правой руки.
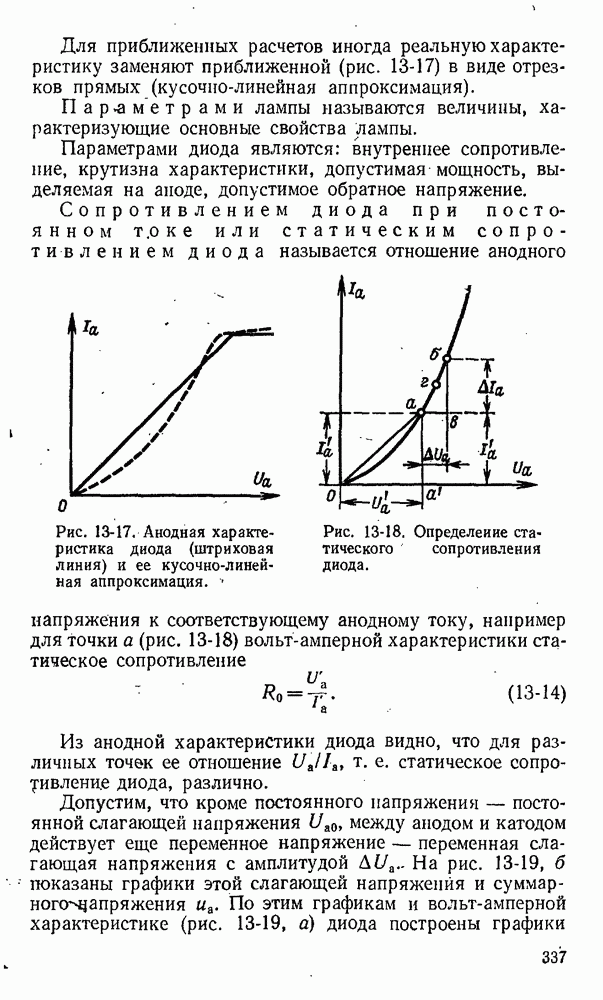
Ладонь правой руки располагают так, чтобы магнитные линии входили в нее, отогнутый под прямым углом большой палец совмещают с направлением движения проводника, тогда вытянутые четыре пальца укажут направление индуктированной э. д. с. (рис. 3-23).
При движении проводника в плоскости, расположенной под углом а к вектору магнитной индукции, э. д. с. определяется только слагающей скорости, нормальной к вектору магнитной индукции, т. е.  а, следовательно,
а, следовательно,

При перемещении проводника со скоростью  в плоскости, нормальной к магнитным линиям поля, наведенная в нем э. д. с.
в плоскости, нормальной к магнитным линиям поля, наведенная в нем э. д. с.


Рис. 3-23. Правило правой руки.
Учитывая, что произведение В и площади  равно магнитному потоку
равно магнитному потоку  пересеченному проводником за время
пересеченному проводником за время  наведенная в нем э. д. с.
наведенная в нем э. д. с.

Следовательно, наведенная э. д. с. равна скорости пересечения проводником магнитного пбтока.
б) Электродвижущая сила, наведенная в контуре
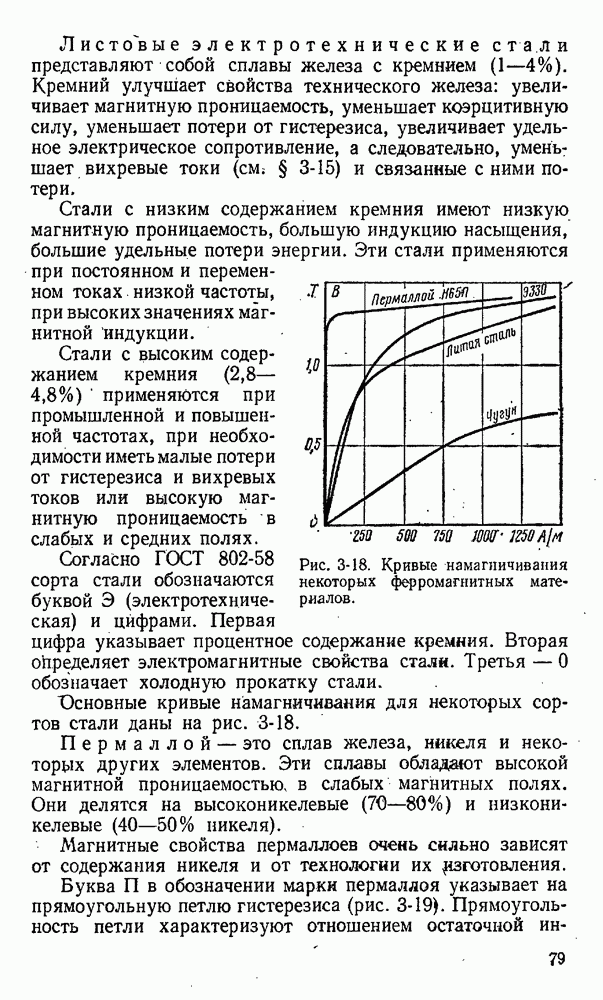
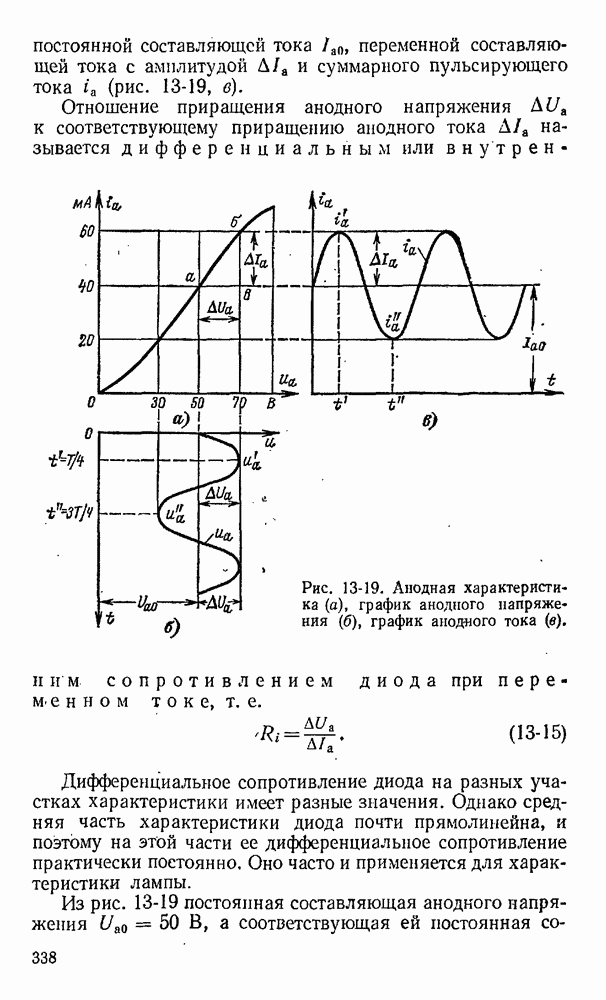
При движении контура (рис. 3-24). в неоднородном магнитном поле в плоскости, нормальной к магнитным линиям (на рис. 3-24 показаны крестиками), в направлении, указанном стрелкой, в сторонах контура 1 и 2 наводятся э. д. с.  . Направления этих э. д. с., найденные по правилу правой руки, показаны стрелками. В сторонах контура 3 и 4 э. д. с. не наводятся, так как они не пересекают магнитного поля.
. Направления этих э. д. с., найденные по правилу правой руки, показаны стрелками. В сторонах контура 3 и 4 э. д. с. не наводятся, так как они не пересекают магнитного поля.
Обозначив  потоки, пересеченные соответственно сторонами контура 1 и 2 за время
потоки, пересеченные соответственно сторонами контура 1 и 2 за время  , напишем величины э. д. с. (3-26):
, напишем величины э. д. с. (3-26):

В результате движения контура за время  пересеченный магнитный поток
пересеченный магнитный поток  окажется внутри контура, а поток
окажется внутри контура, а поток  за пределами контура (рис. 3-24). Так как положительное направление э. д. с. связано правилом буравчика с направлением магнитного потока, то направление
за пределами контура (рис. 3-24). Так как положительное направление э. д. с. связано правилом буравчика с направлением магнитного потока, то направление  будет положительным, а
будет положительным, а  — отрицательным. Таким образом, наведенная в контуре э. д. с.
— отрицательным. Таким образом, наведенная в контуре э. д. с.

При другой форме записи, при которой элементарные приращения потока и времени  и
и  заменены бесконечно малыми приращениями Ф и dt, получим для произвольного момента времени выражение э. д. с., наводимой в контуре:
заменены бесконечно малыми приращениями Ф и dt, получим для произвольного момента времени выражение э. д. с., наводимой в контуре:


Рис. 3-24. Движение контура в магнитном поле.
Из полученного выражения следует, что э. д. с. электромагнитной индукции, наведенная в контуре, равна скорости уменьшения магнитного потока, пронизыеающего контур. Это вторая формулировка закона Электромагнитной индукции.
Опытом установлено, что безразлично, происходит ли это изменение потока при движении контура в магнитном поле или в результате нарастания или убывания магнитного потока, пронизывающего неподвижный контур.
Если контур состоит из w последовательно соединенных витков, то индуктированная э. д. с. будет:

Произведение числа витков и пронизывающего их магнитного потока называется потокосцеплением:

следовательно, индуктированная э. д. с.

равна скорости уменьшения потокосцепления.
При движении контура в направлении, указанном на рис. 3-24, магнитный поток, пронизывающий контур, уменьшается, т. е. приращение его отрицательно  , так как
, так как  .
.
Следовательно, э. д. с. (3-28) положительна и направлена по ходу часовой стрелки. Так же направлен и ток, вызванный этой э. д. с. Магнитный поток, созданный этим током, имеет то же направление, что и уменьшающийся магнитный поток, в чем легко убедиться, применив правило буравчика. Следовательно, убывание потека, пронизывающего контур, вызывает появление э. д. с. и тока, магнитный поток которого стремится противодействовать убыванию магнитного потока.
При движении контура в обратном направлении поток, пронизывающий контур, увеличивается ( ) и э. д. с. (по 3-28) отрицательна и направлена против хода часовой стрелки.
) и э. д. с. (по 3-28) отрицательна и направлена против хода часовой стрелки.

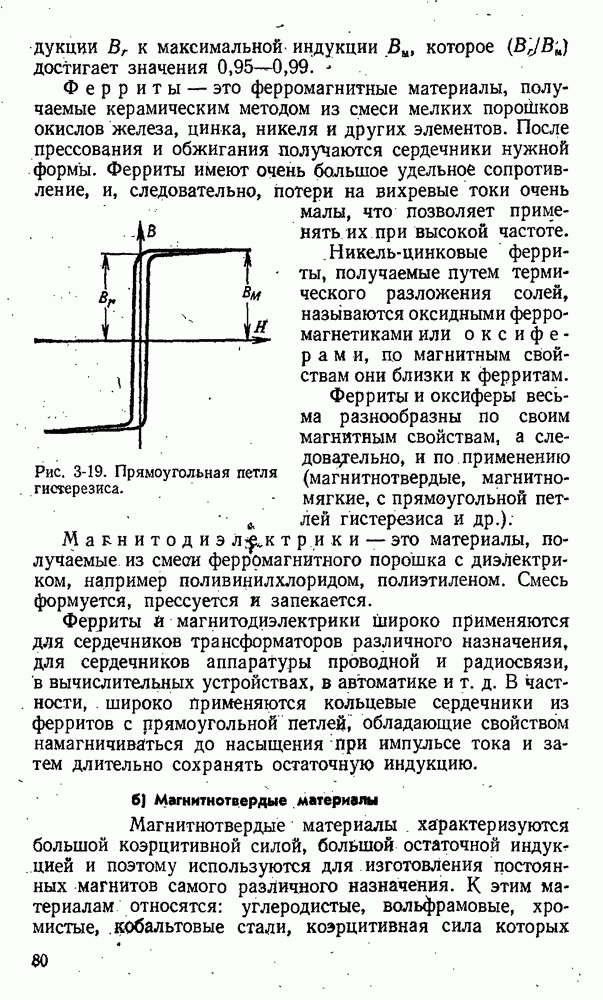
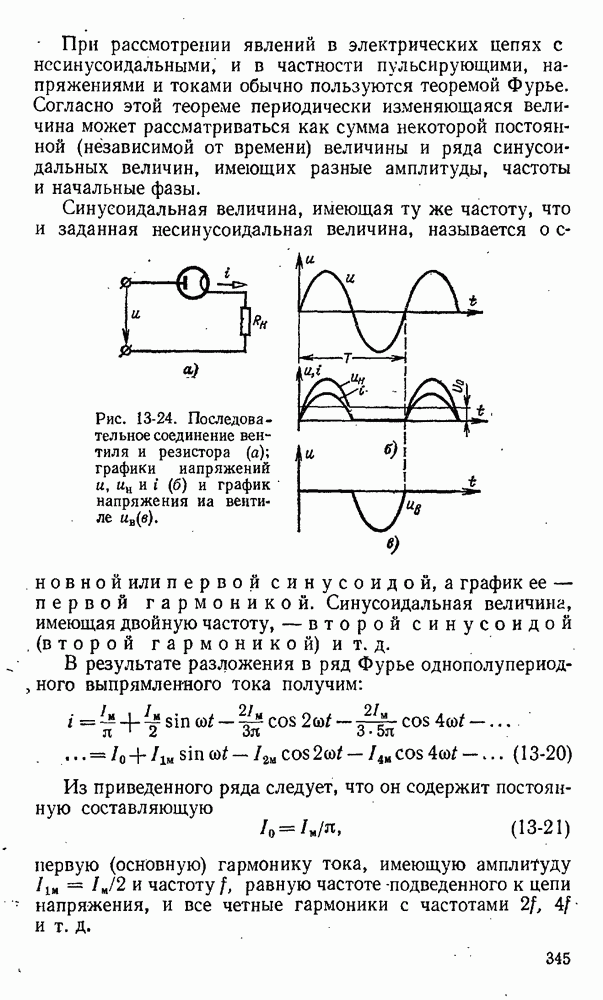
Рис. 3-25. Ток, индуктированный в кольце.
Так же направлен и вызванный ею ток. Магнитный поток, - созданный этим током, направлен встречно возрастающему магнитному потоку контура.
Следовательно, возрастание потока контура приводит к появлению э. д. с. и тока, магнитный поток которого стремится противодействовать увеличению потока контура.
Из сказанного следует: направление наведенной э. д. с. всегда таково, что вызванный ею ток противодействует причине появления э. д. с. Это положение было установлено русским академиком Э. X. Ленцем в 1833 г. и носит название закона Ленца.
При увеличении тока в катушке электромагнита (рис. 3-25) или при сближении кольца и электромагнита увеличивается магнитный поток, пронизывающий кольцо, и в нем наводятся э. д. с. и ток i. По закону Ленца направление магнитного потока, созданного током i в кольце, противоположно направлению потока электромагнита, следовательно, направление индуктированного тока i легко определяется по правилу буравчика.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- Часть первая. Общая электротехника
- 1-1. Основные понятия
- 1-2. Электрическое напряжение. Потенциал
- 1-3. Электропроводность
- 1-4. Электрическая емкость. Конденсаторы
- 1-5. Соединение конденсаторов
- 1-6. Энергия электрического поля
- 1-8. Электроизоляционные материалы
- Глава вторая. Электрические цепи постоянного тока
- 2-1. Электрический ток
- 2-2. Электрическая цепь и ее элементы
- 2-3. Закон Ома
- 2-4. Электрические сопротивление и проводимость
- 2-5. Зависимость сопротивления от температуры
- 2-6. Проводниковые материалы
- 2-7. Работа и мощность
- 2-8. Преобразование электрической энергии в тепловую
- 2-9. Электрическая нагрузка проводов и защита их от перегрузки
- 2-10. Потеря напряжения в проводах
- 2-11. Первый закон Кирхгофа
- 2-12. Последовательное соединение сопротивлений — приемников энергии
- 2-13. Параллельное соединение сопротивлений — приемников энергии
- 2-14. Смешенное соединение сопротивлений
- 2-15. Два режима работы источника питания
- 2-16. Второй закон Кирхгофа
- 2-17. Расчет сложных цепей
- 2-18. Химические источники питания
- 2-19. Соединение химических источников питания
- 2-20. Нелинейные электрические цепи
- 2-21. Лабораторная работа. Потеря напряжения в линии
- Глава третья. Электромагнетизм
- 3-1. Магнитное поле тока. Магнитная индукция. Магнитный поток
- 3-2. Электромагнитная сила
- 3-3. Взаимодействие параллельных проводов с токами
- 3-4. Магнитная проницаемость
- 3-5. Напряженность магнитного поля. Магнитное напряжение
- 3-6. Закон полного тока
- 3-7. Магнитное поле катушки с током
- 3-8. Ферромагнетики, их намагничивание и перемагничивание
- 3-9. Ферромагнитные материалы
- 3-10. Магнитная цепь и ее расчет
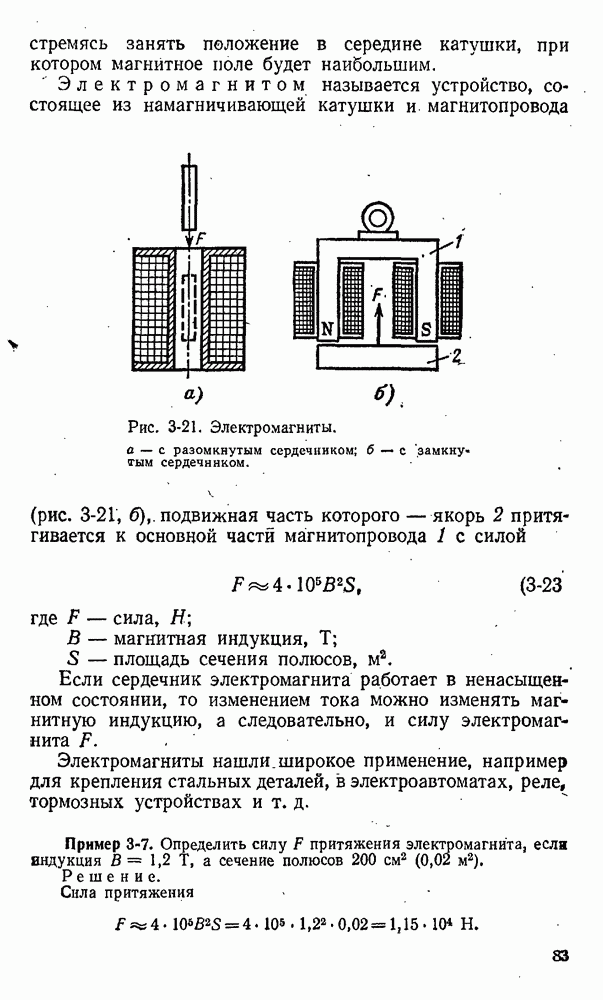
- 3-11. Электромагниты
- 3-12. Электромагнитная индукция
- 3-13. Принцип работы электрического генератора
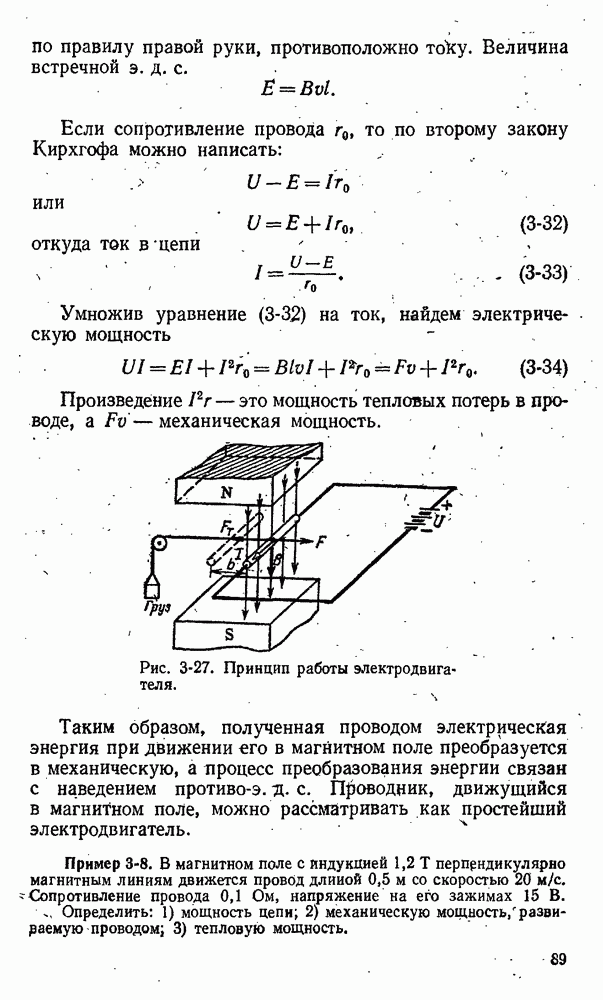
- 3-14. Принцип работы электродвигателя
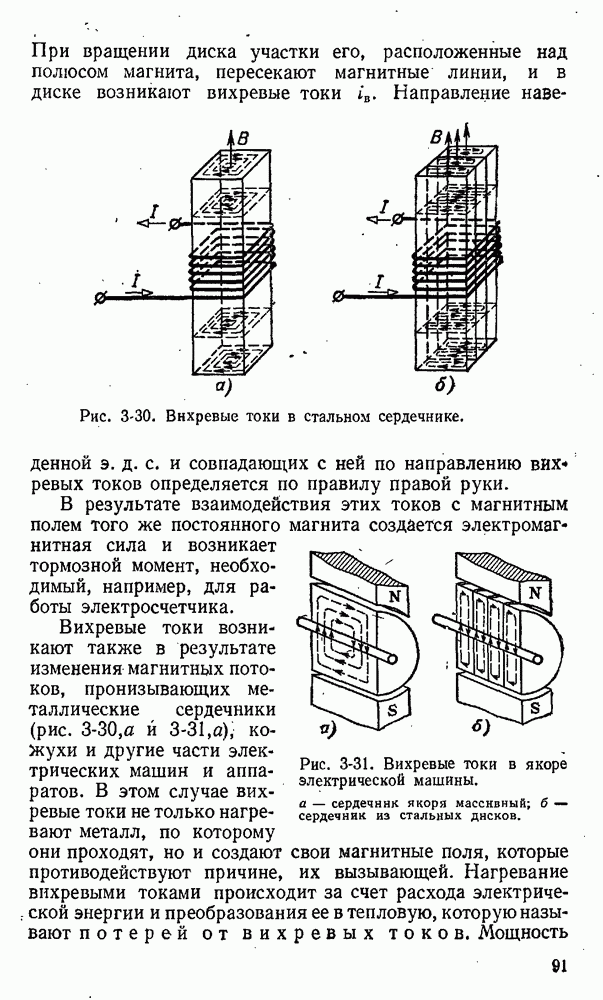
- 3-15. Вихревые токи
- 3-16. Индуктивность. Электродвижущая сила самоиндукции
- 3-17. Энергия магнитного поля
- 3-18. Взаимная индуктивность
- Глава четвертая. Электрические машины постоянного тока
- 4-1. Назначение машин постоянного тока
- 4-2. Устройство машины постоянного тока
- 4-3. Принцип работы машины постоянного тока
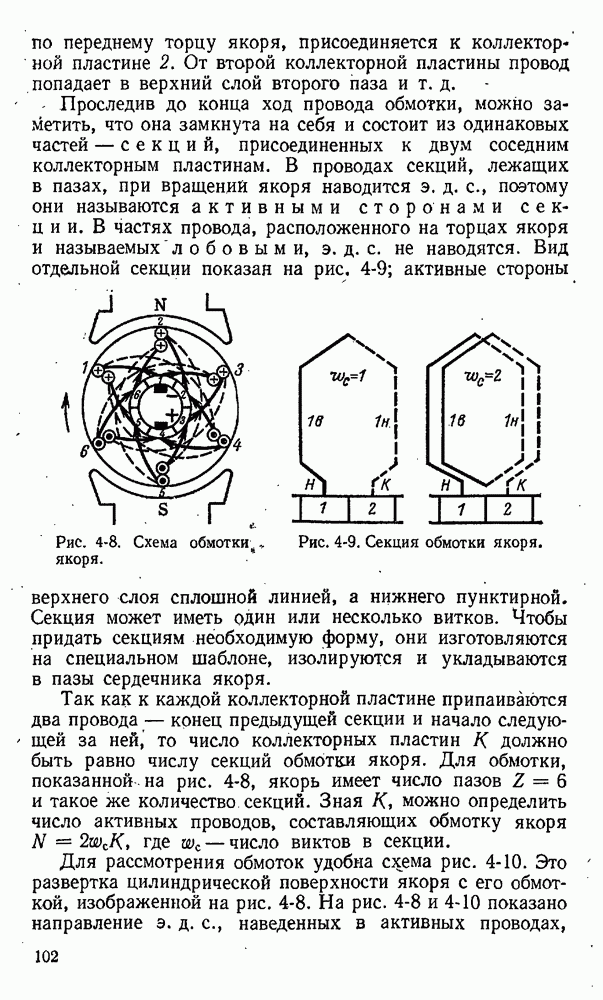
- 4-4. Устройство обмотки якоря
- 4-5. Электродвижущая сила обмотки якоря
- 4-6. Электромагнитный момент на валу машины
- 4-7. Механическая мощность машины постоянного тока
- 4-8. Реакция якоря машины постоянного тока
- 4-9. Коммутация тока
- 4-10. Понятие о номинальных данных и характеристиках электрических машин
- 4-11. Генератор с независимым возбуждением
- 4-12. Генератор с параллельным возбуждением
- 4-13. Генератор со смешанным возбуждением
- 4-14. Электродвигатели постоянного тока
- 4-15. Электродвигатель с параллельным возбуждением
- 4-16. Электродвигатель с независимым возбуждением
- 4-17. Электродвигатели с. последовательным и со смешанным возбуждением
- 4-18. Потери и коэффициент полезного действия
- 4-19. Лабораторная работа. Электродвигатель с параллельным возбуждением
- 4-20. Лабораторная работа. Генератор с параллельным возбуждением
- Главе пятая. Основные понятия, относящиеся к переменным токам
- 5-1. Переменный ток
- 5-2. Получение синусоидальной э. д. с.
- 5-3. Сдвиг фаз
- 5-4. Действующие значения тока и напряжения
- 5-5. Векторная диаграмма
- Глава шестая. Цепи переменного тока
- 6-1. Особенности цепей переменного тока
- 6-2. Цепь с сопротивлением
- 6-3. Цепь с индуктивностью
- 6-4. Цепь с активным сопротивлением и индуктивностью
- 6-5. Неразветвленная цепь с активными сопротивлениями и индуктивностями
- 6-6. Разветвленная цепь с активными сопротивлениями и индуктивностями
- 6-7. Цепь с емкостью
- 6-8. Колебательный контур
- 6-9. Резонанс напряжений
- 6-10. Резонанс токов
- 6-11. Коэффициент мощности
- 6-12. Активная и реактивная энергия
- 6-13. Лабораторная работа. Цепь переменного тока с активным сопротивлением, индуктивностью и емкостью
- 6-14. Лабораторная работа. Параллельное соединение катушки и конденсатора
- Глава седьмая. Трехфазные цепи
- 7-1. Трехфазные системы
- 7-2. Соединение обмоток генератора звездой
- 7-3. Соединение обмоток генератора треугольником
- 7-4. Соединение приемников энергии звездой
- 7-5. Соединение приемников энергии треугольником
- 7-6. Лабораторная работа. Трехфазные цепи
- Глава восьмая. Электротехнические измерения и приборы
- 8-1. Основные понятия
- 8-2. Классификация электроизмерительных приборов
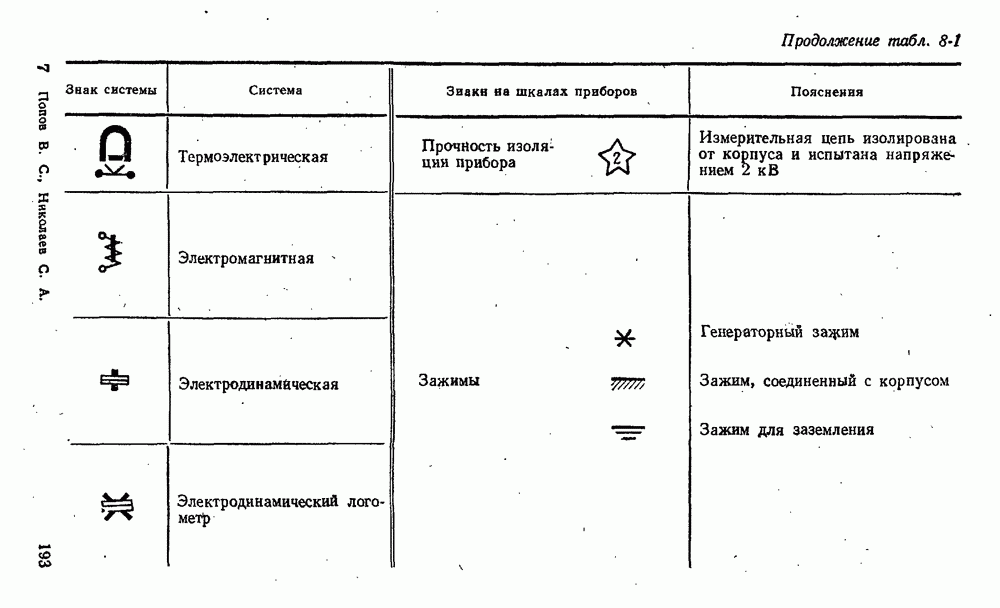
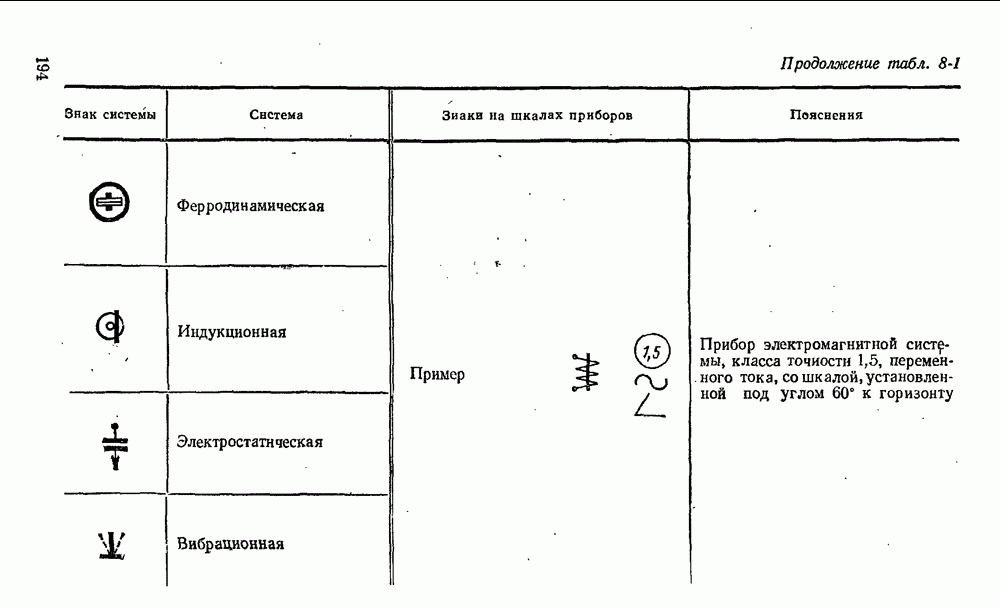
- 8-3. Измерительные механизмы приборов
- 8-4. Измерение тока и напряжения
- 8-5. Измерение мощности
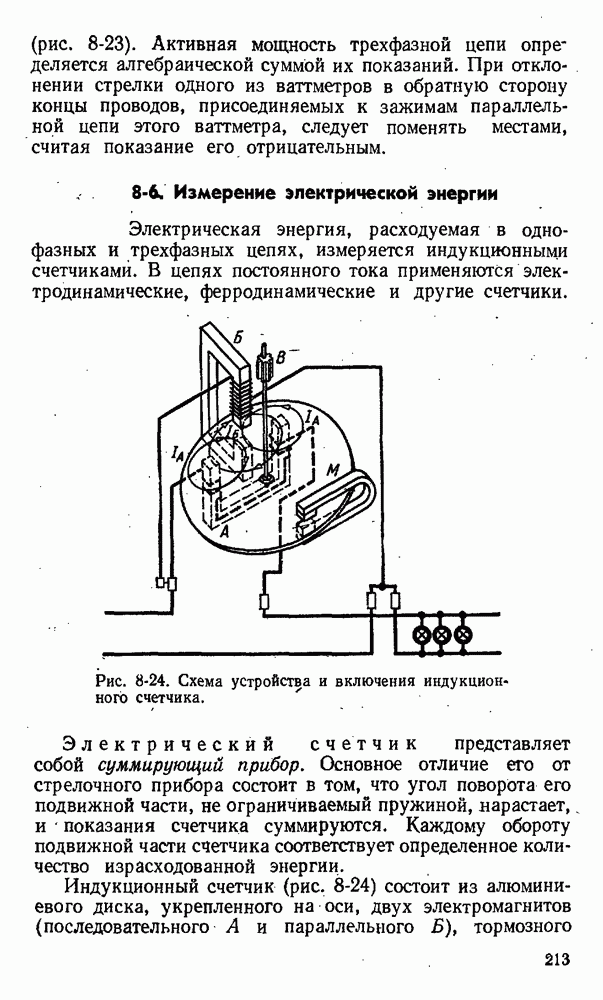
- 8-6. Измерение электрической энергии
- 8-7. Измерение сопротивлений
- 8-8. Измерение неэлектрических величин электрическими методами
- 8-9. Лабораторная работа. Измерение сопротивлений
- 8-10. Лабораторная работа. Поверка индукционного счетчика
- 8-11. Лабораторная работа. Измерение мощности в трехфазной цепи
- Глава девятая. Трансформаторы
- 9-1. Назначение трансформаторов
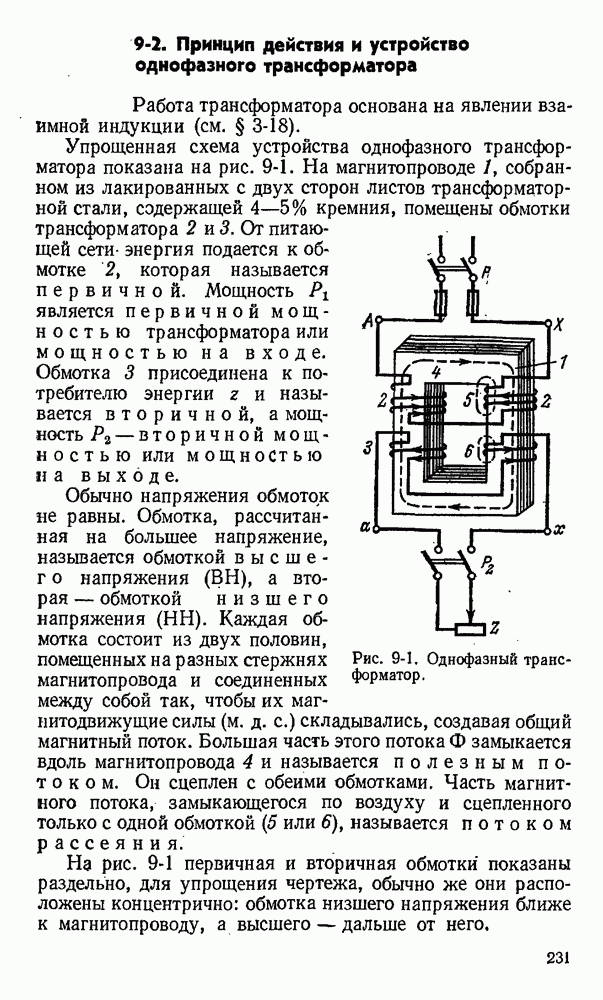
- 9-2. Принцип действия и устройство однофазного трансформатора
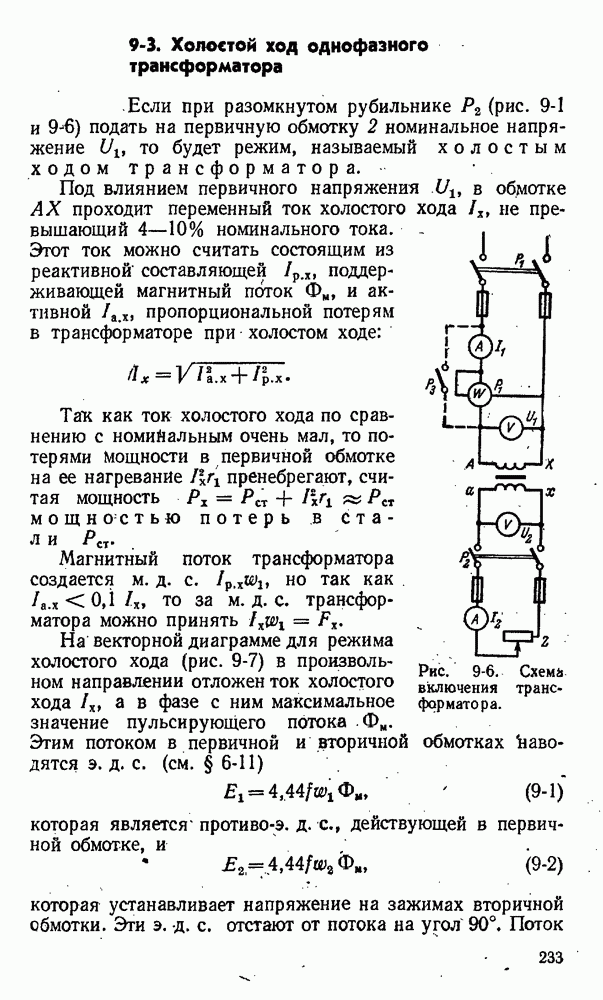
- 9-3. Холостой ход однофазного трансформатора
- 9-4. Работа нагруженного трансформатора и диаграмма магнитодвижущих сил (м. д. с.)
- 9-5. Изменение напряжения трансформатора при нагрузке
- 9-6. Мощность потерь в обмотках нагруженного трансформатора
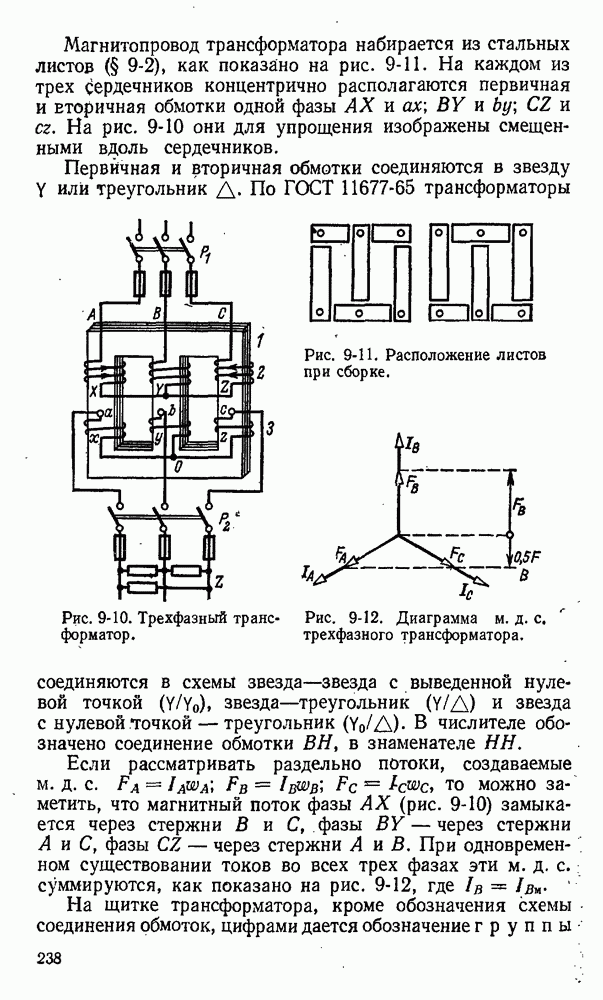
- 9-7. Трехфазный трансформатор
- 9-8. Регулирование напряжения трансформаторов
- 9-9. Автотрансформаторы
- 9-10. Трансформаторы для дуговой электросварки
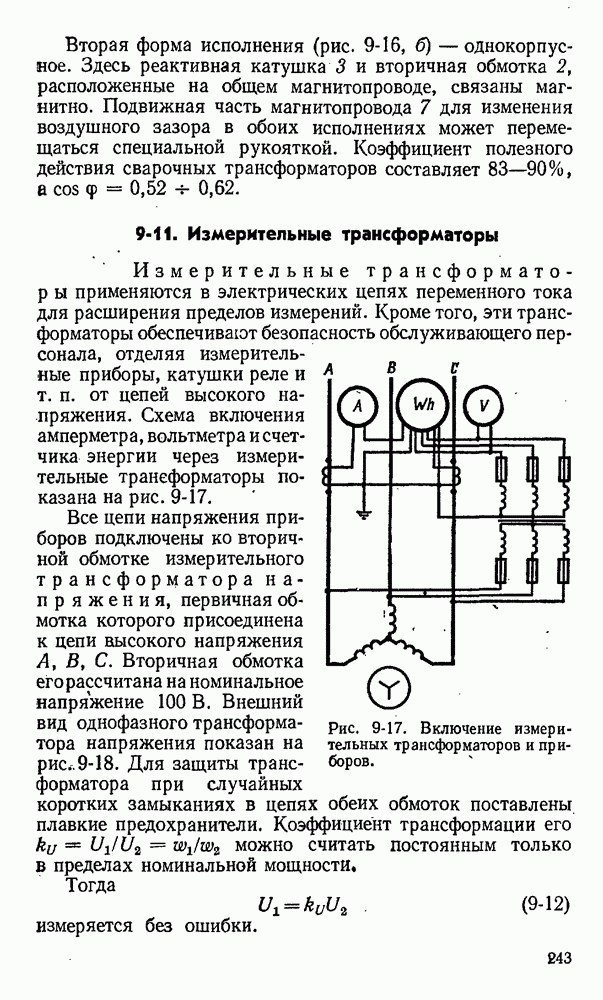
- 9-11. Измерительные трансформаторы
- 9-12. Коэффициент полезного действия трансформатора
- 9-13. Нагрев и охлаждение трансформаторов
- 9-14. Лабораторная работа. Однофазный трансформатор
- Глава десятая. Электрические машины переменного тока
- 10-1. Назначение машин переменного тока. Асинхронные электродвигатели
- 10-2. Получение вращающегося магнитного поля
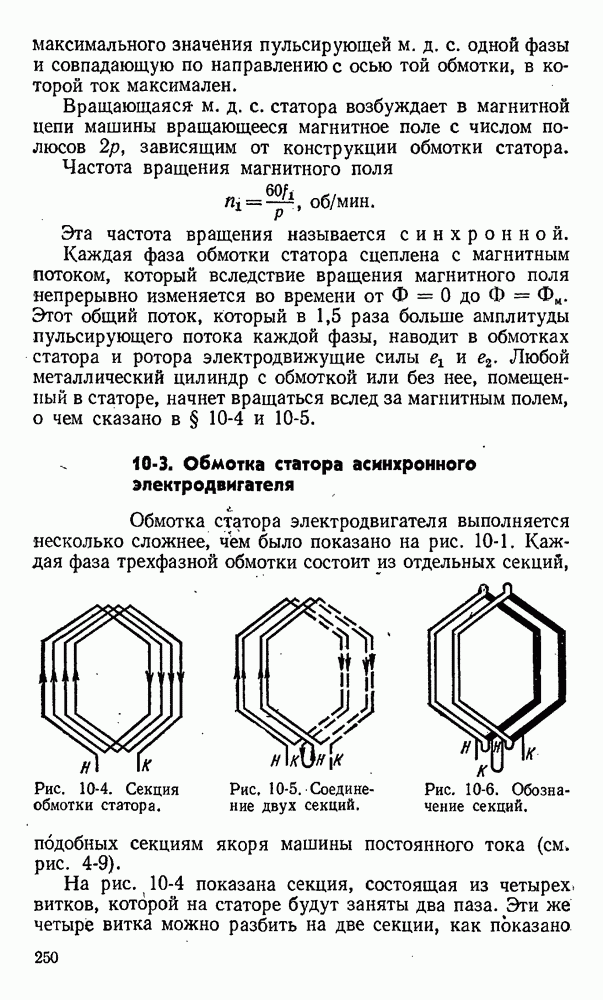
- 10-3. Обмотка статора асинхронного электродвигателя
- 10-4. Обмотка ротора асинхронного двигателя
- 10-5. Принцип действия асинхронного двигателя
- 10-6. Электродвижущие силы в обмотках статора и ротора
- 10-7. Сопротивления обмотки ротора
- 10-8. Токи в обмотке ротора
- 10-9. Вращающий момент двигателя
- 10-10. Пуск в ход асинхронных двигателей
- 10-11. Регулирование частоты вращения асинхронного двигателя
- 10-12. Однофазный асинхронный двигатель
- 10-13. Потери и к. п. д. асинхронного двигателя
- 10-14. Синхронные машины
- 10-15. Универсальный коллекторный двигатель
- 10-16. Лабораторная работа. Трехфазный асинхронный электродвигатель
- Глава одиннадцатая. Электропривод и аппаратура управления
- 11-1. Система электропривода
- 11-2. Нагрев и охлаждение электрических машин
- 11-3. Выбор мощности двигателя при продолжительном режиме
- 11-4. Выбор мощности двигателя при кратковременном режиме
- 11-5. Выбор мощности двигателя при повторно-кратковременном режиме
- 11-6. Рубильники
- 11-7. Пакетные выключатели
- 11-8. Реостаты для пуска и регулирования электродвигателей
- 11-9. Контроллеры
- 11-10. Плавкие предохранители
- 11-11. Автоматические воздушные выключатели
- 11-12. Контакторы
- 11-13. Реле
- 11-14. Схема управления асинхронным двигателем с помощью реверсивного магнитного пускателя
- 11-15. Схема включения двухскоростного асинхронного двигателя
- 11-16. Автоматический пуск асинхронного двигателя с кольцами
- 11-17. Автоматический пуск двигателя постоянного тока с параллельным возбуждением
- 11-18. Лабораторная работа. Сборка и проверка работы схемы релейноконтакторного управления трехфазным асинхронным двигателем с короткозамкнутым ротором
- Глава двенадцатая. Передача и распределение электрической энергии
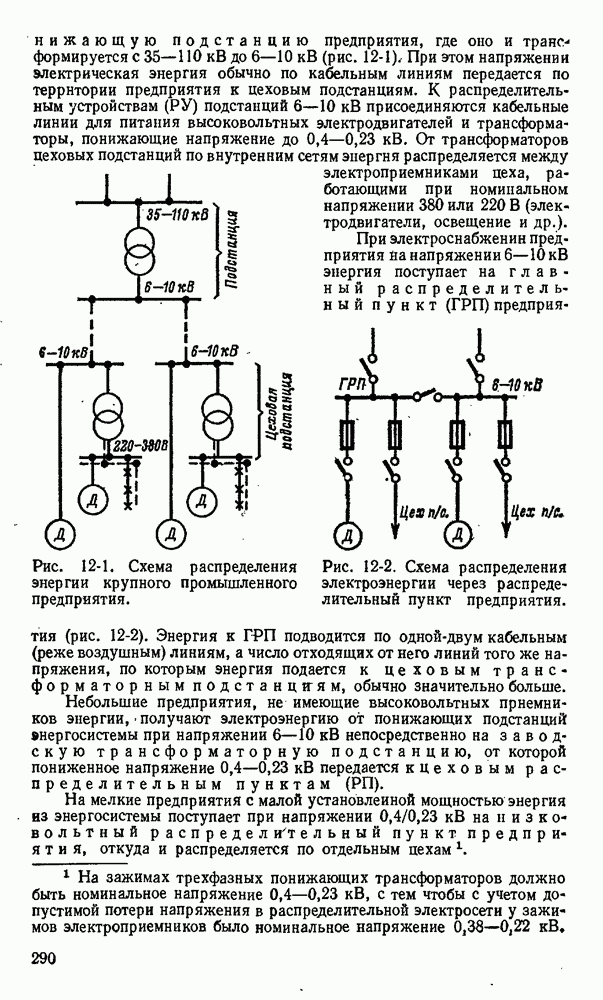
- 12-1. Схемы электроснабжения промышленных предприятий.
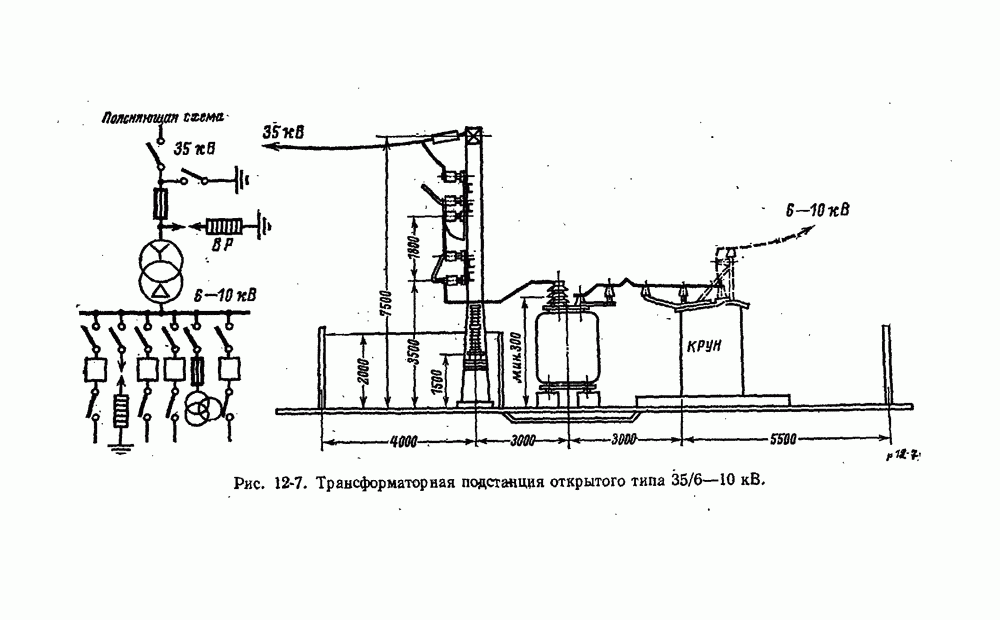
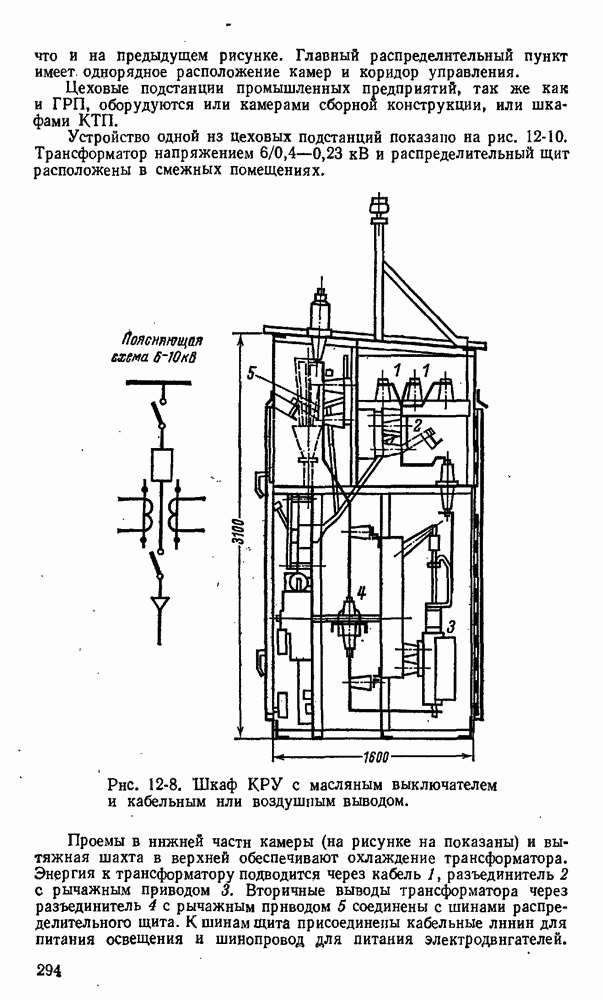
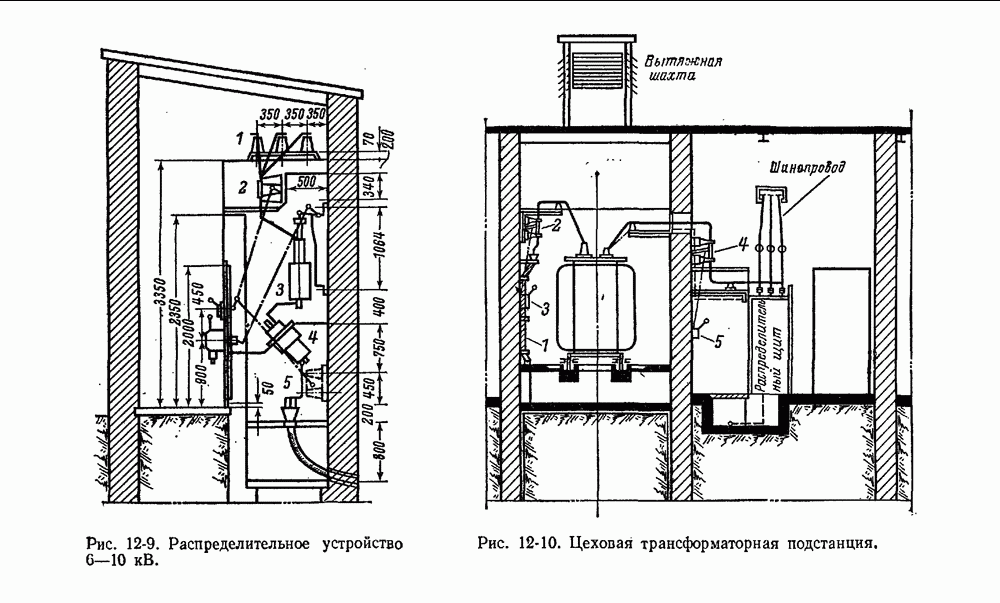
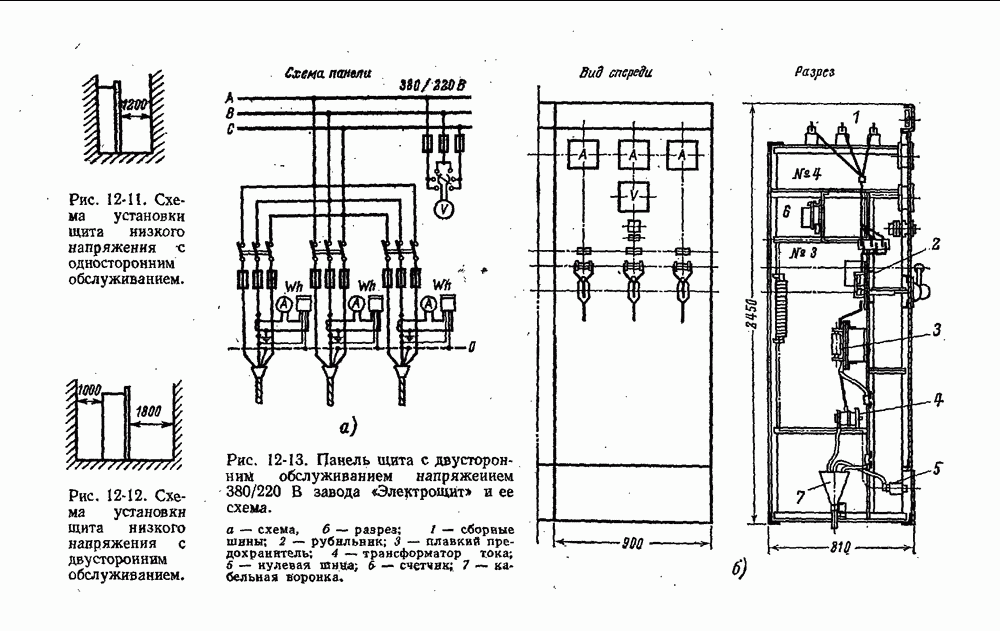
- 12-2. Трансформаторные подстанции и распределительные устройства промышленных предприятий
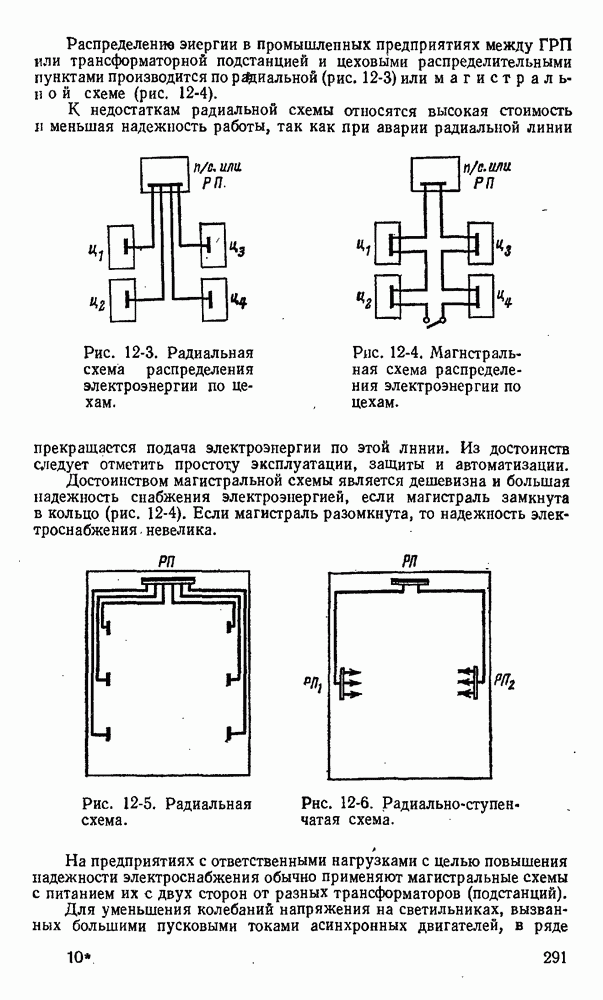
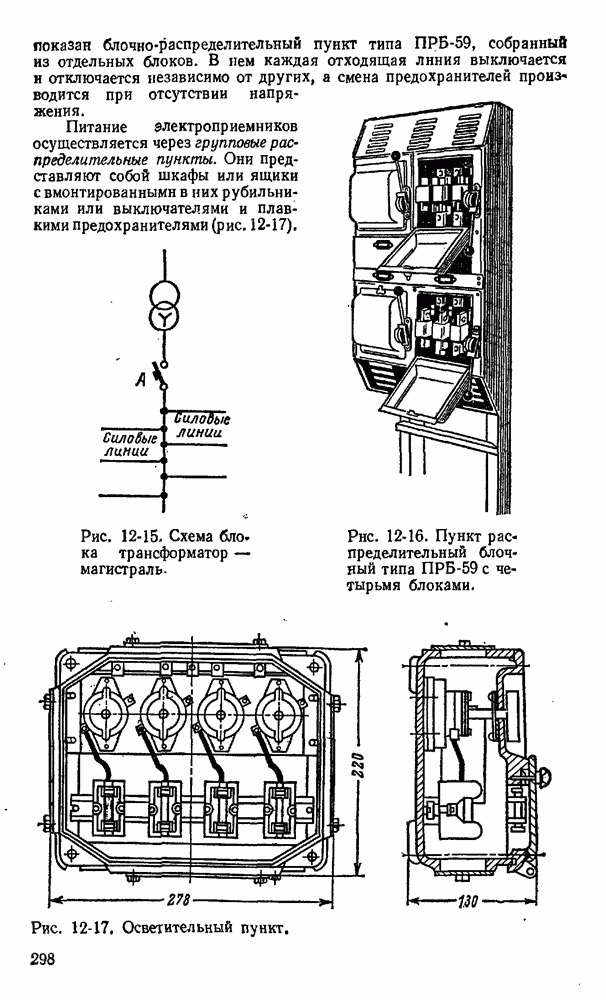
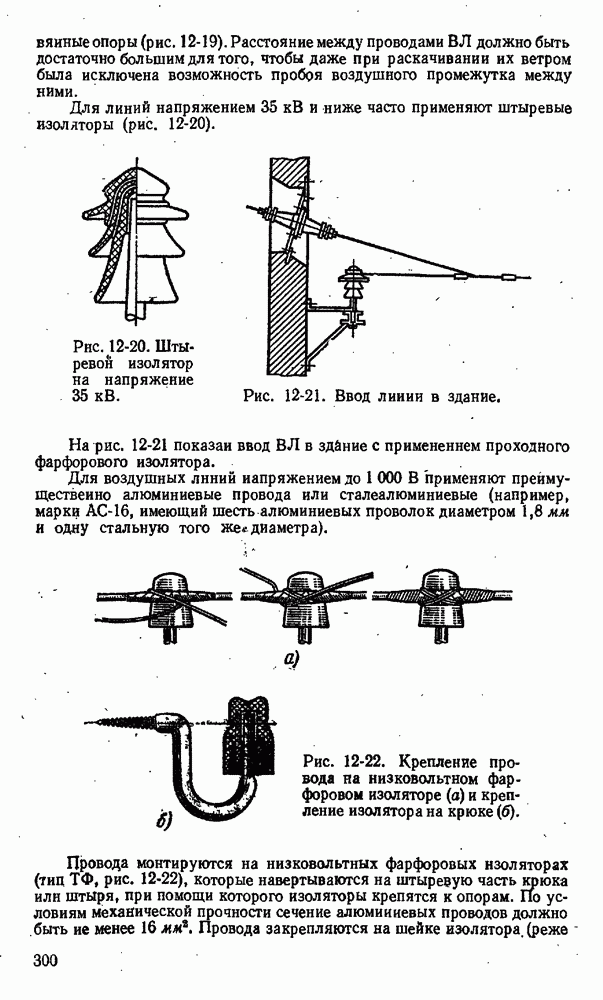
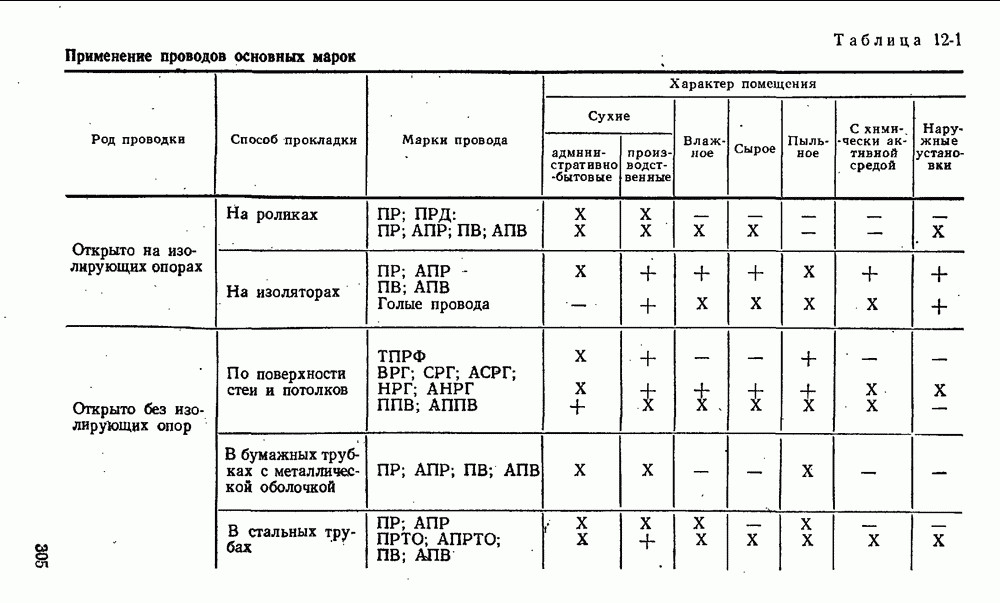
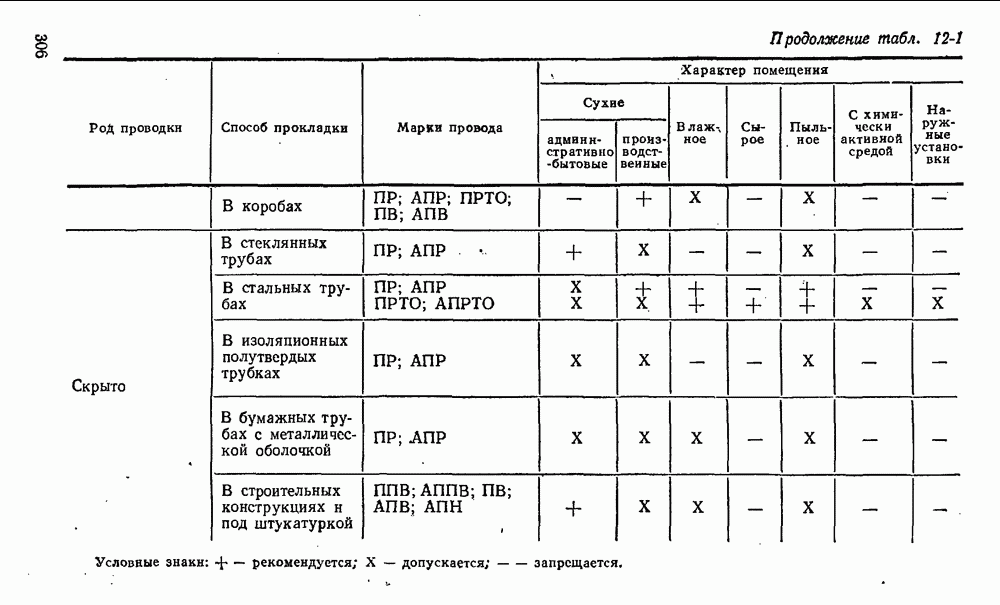
- 12-3. Электрические сети промышленных предприятий
- 12-4. Защитное заземление
- Часть вторая. Основы промышленной электроники
- 13-1. Классификация и применение электронных приборов
- 13-2. Движение электронов в электрическом поле
- 13-3. Движение электронов в магнитном поле
- 13-4. Электронная эмиссия
- 13-5. Катоды электровакуумных приборов
- 13-6. Двухэлектродные электронные лампы — диоды
- 13-7. Применение двухэлектродных ламп
- Глава четырнадцатая. Трехэлектродные лампы. Четырех- и пятиэлектродные лампы. Усилители
- 14-1. Устройство и принцип работы триода
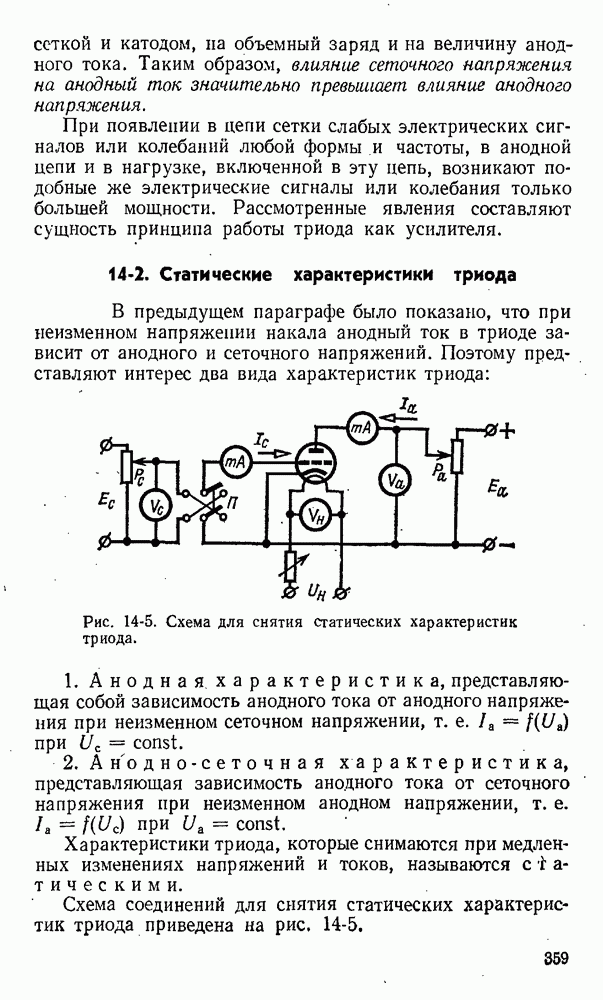
- 14-2. Статические характеристики триода
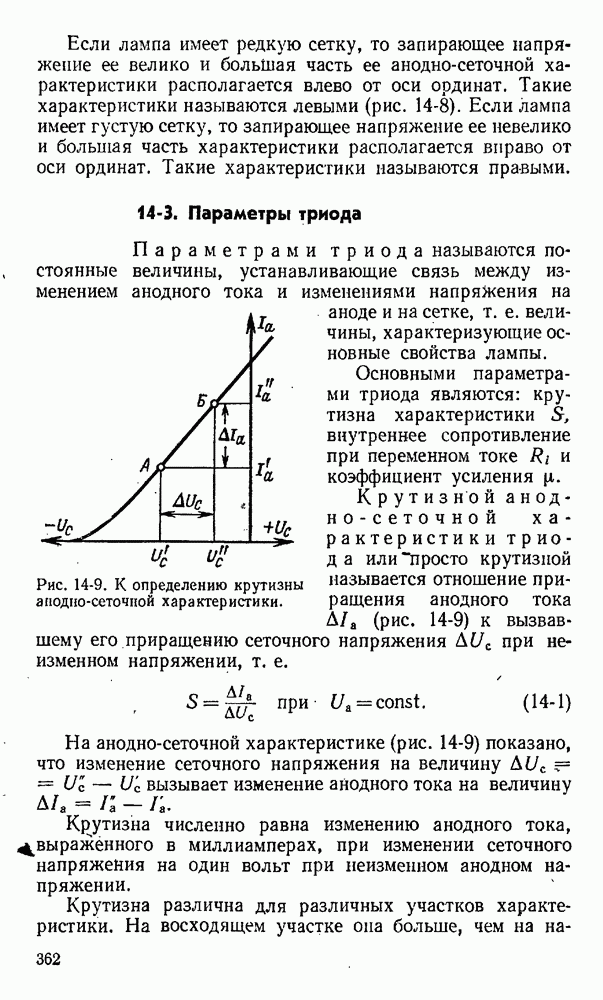
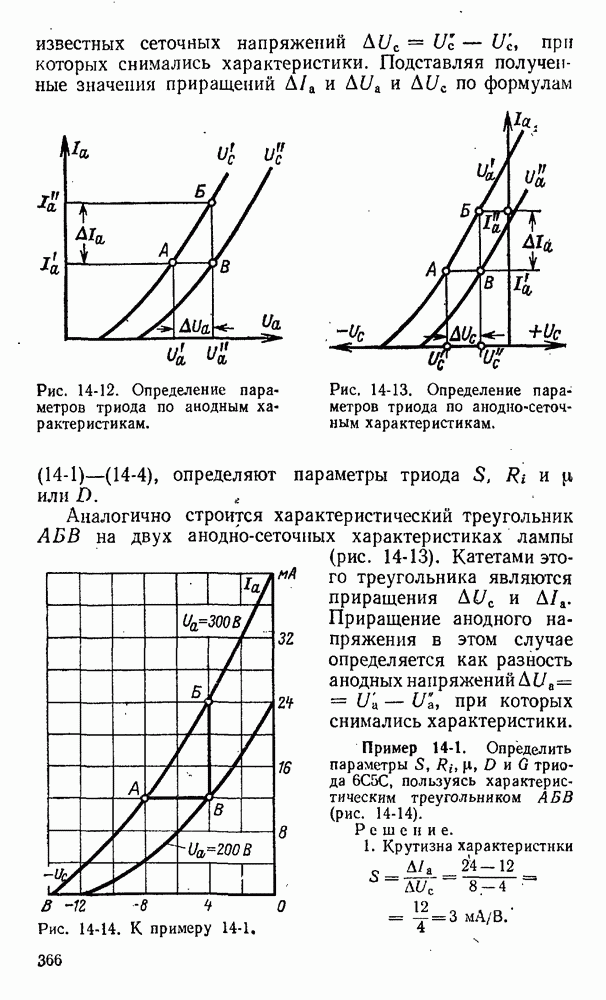
- 14-3. Параметры триода
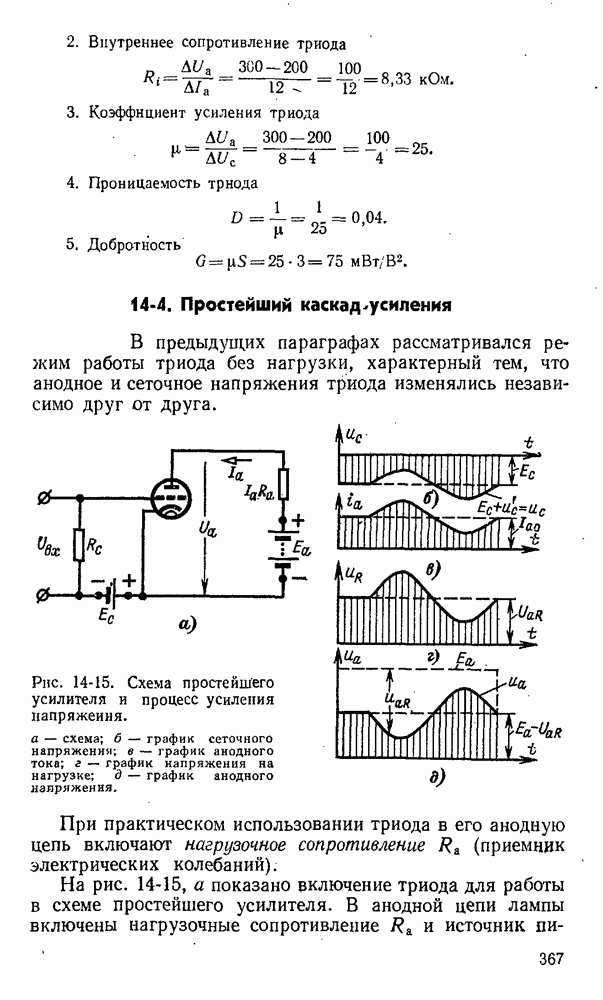
- 14-4. Простейший каскад усиления
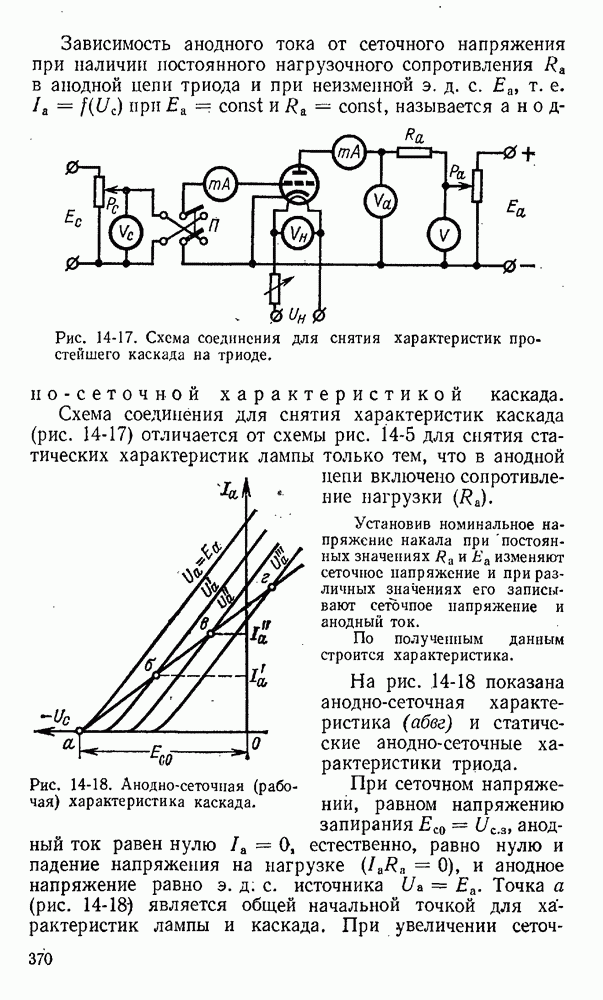
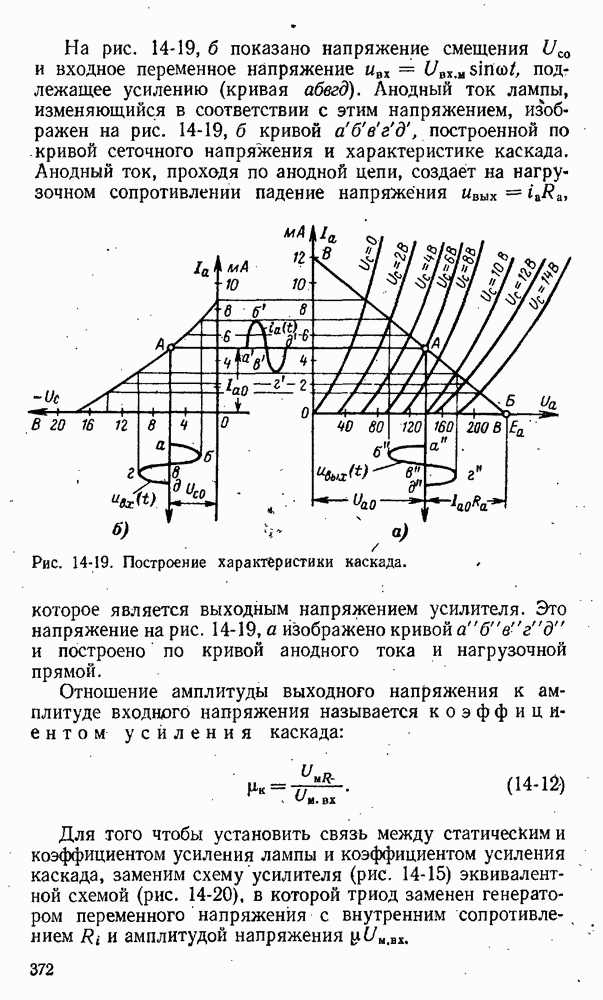
- 14-5. Характеристики и параметры простейшего каскада усиления
- 14-6. Типы триодов
- 14-7. Четырехэлектродные лампы — тетроды
- 14-8. Пятиэлектродные лампы — пентоды
- 14-9. Комбинированные и многосеточные лампы. Типы ламп
- 14-10. Общие понятия, относящиеся к усилителям
- 14-11. Режимы работы усилителей
- 14-12. Многокаскадные ламповые усилители
- 14-13. Обратная связь в усилителях
- 14-14. Лабораторная работа. Снятие анодных и анодно-сеточных характеристик триода и определение по ним статических параметров
- 14-15. Лабораторная работа. Снятие частотных характеристик усилителя напряжения низкой частоты
- Глава пятнадцатая. Газоразрядные приборы и их применение
- 15-1. Виды газового разряда и его вольт-амперная характеристика
- 15-2. Ионные приборы с несамостоятельным дуговым разрядом
- 15-3. Приборы с тлеющим разрядом
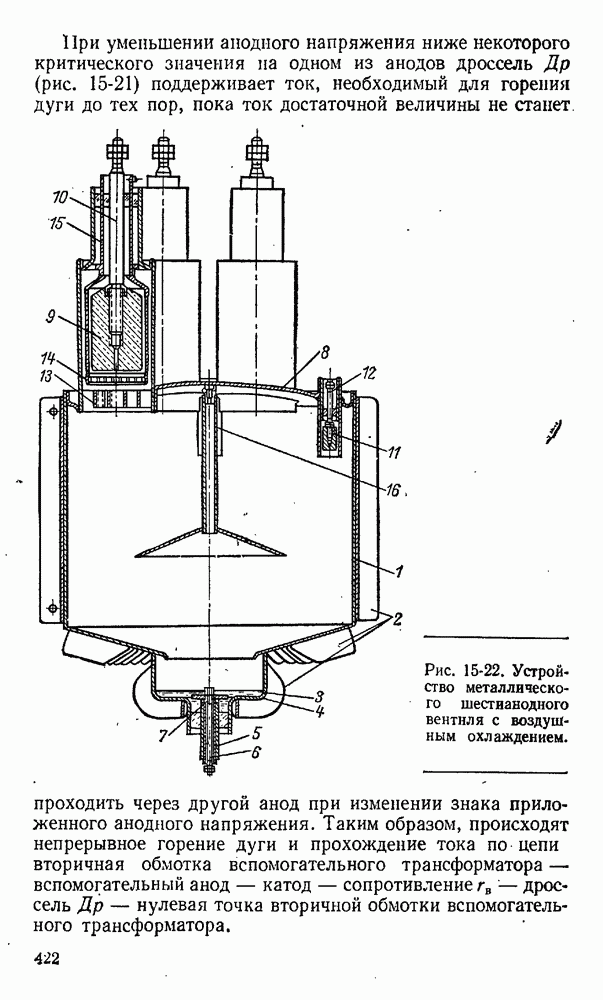
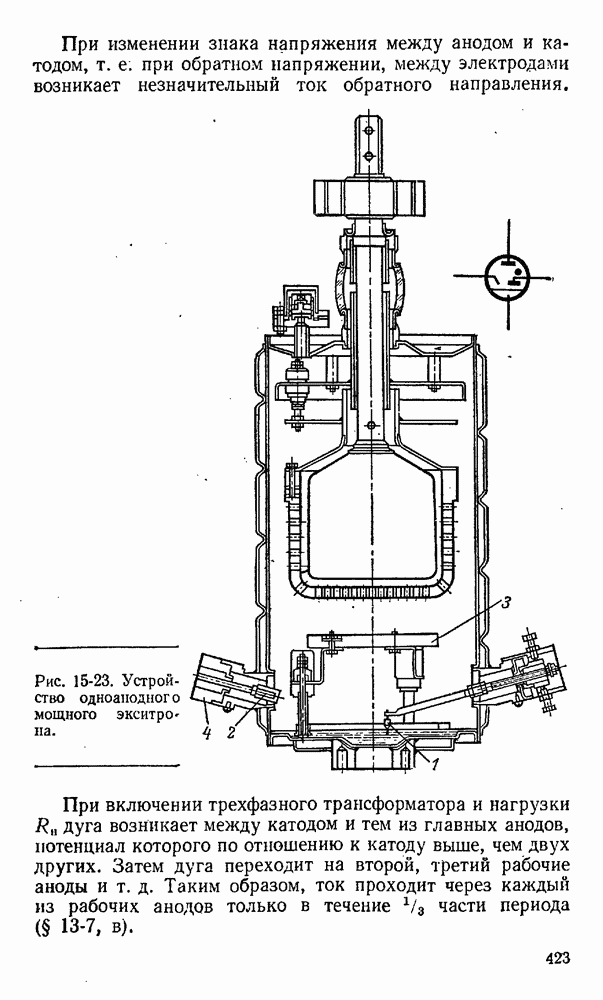
- 15-4. Ионные приборы с самостоятельным дуговым разрядом
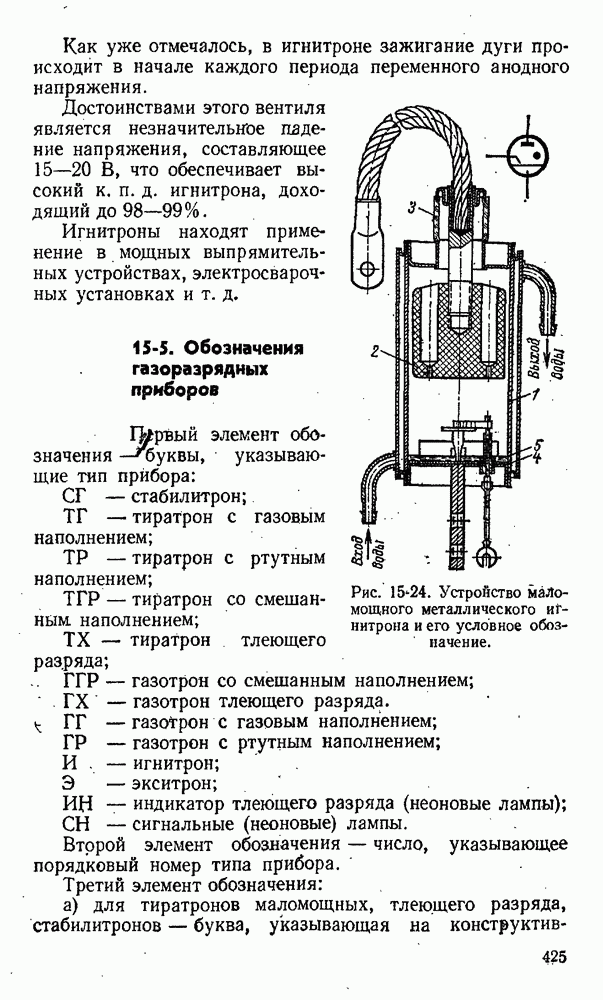
- 15-5. Обозначения газоразрядных приборов
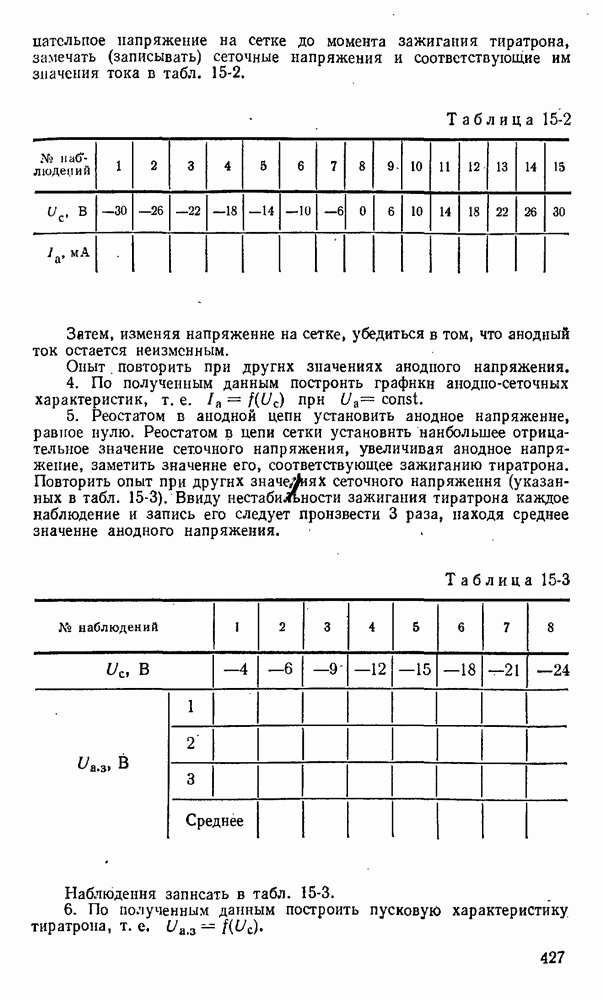
- 15-6. Лабораторная работа. Снятие анодносеточных и пусковых характеристик тиратрона
- Глава шестнадцатая. Электронные генераторы. Осциллографы
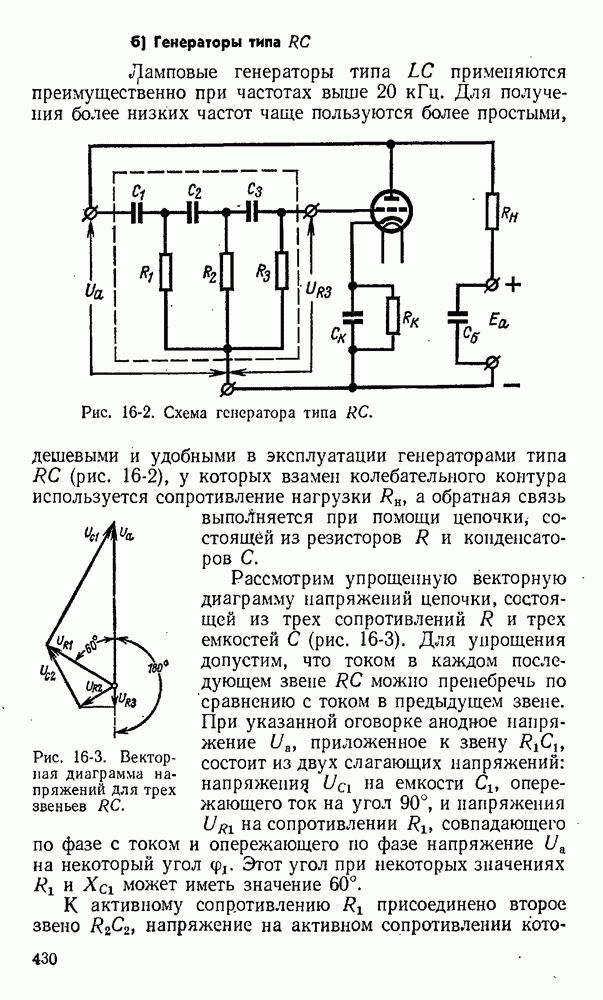
- 16-1. Генераторы синусоидальных напряжений
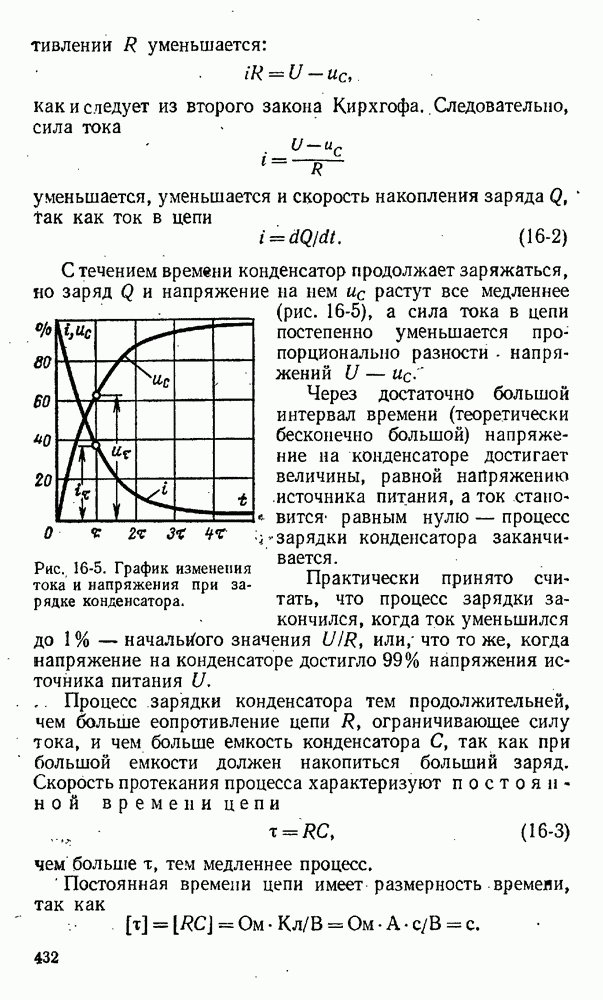
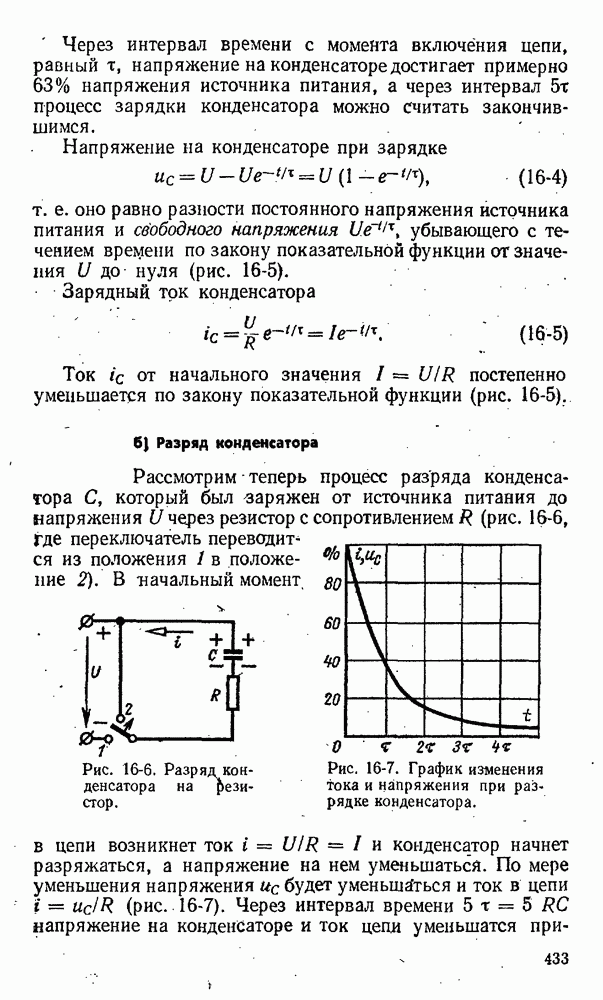
- 16-2. Зарядка и разряд конденсатора
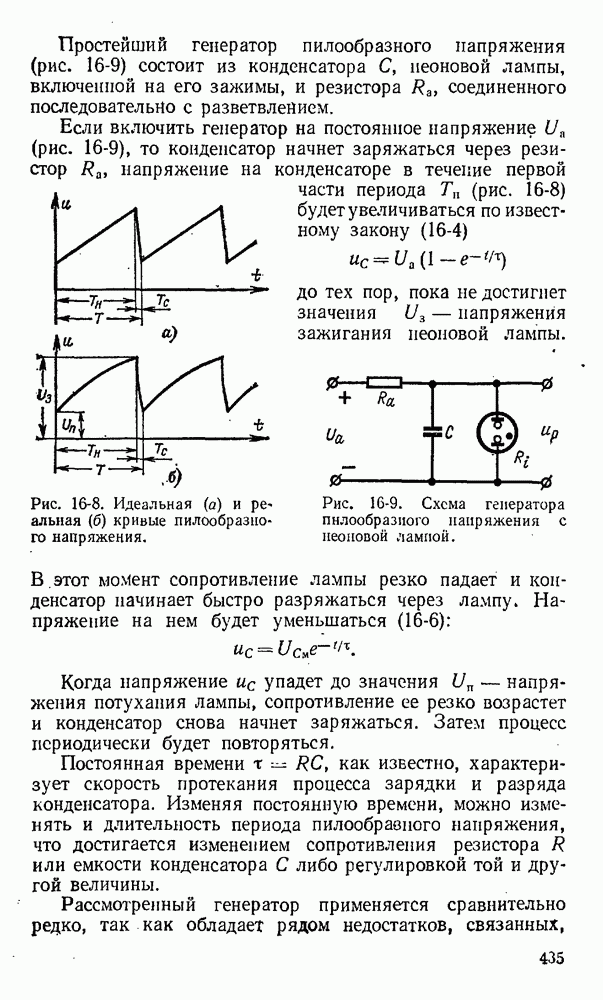
- 16-3. Релаксационные генераторы (генераторы пилообразного напряжения)
- 16-4. Мультивибраторы
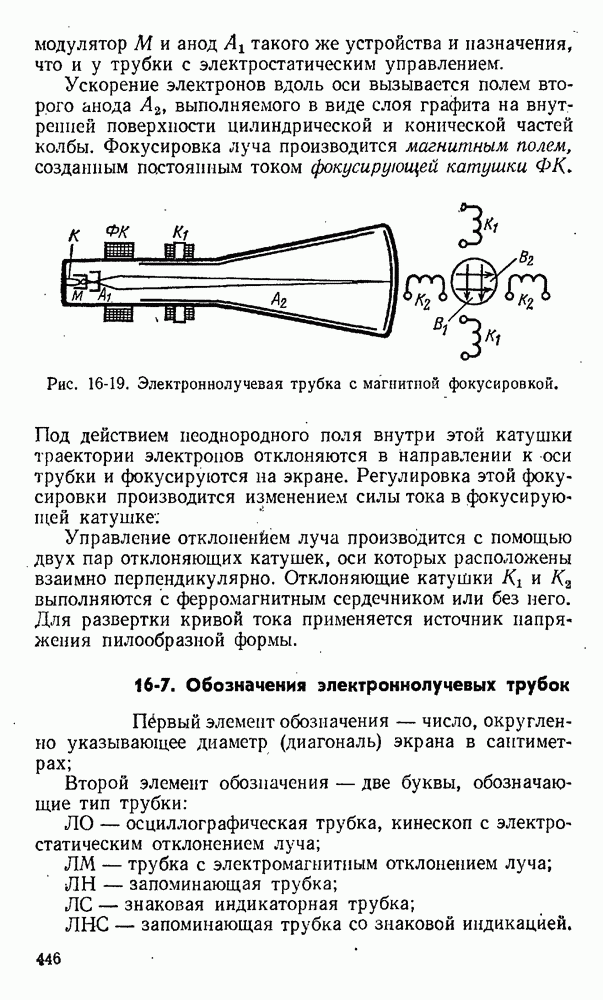
- 16-5. Электроннолучевые трубки
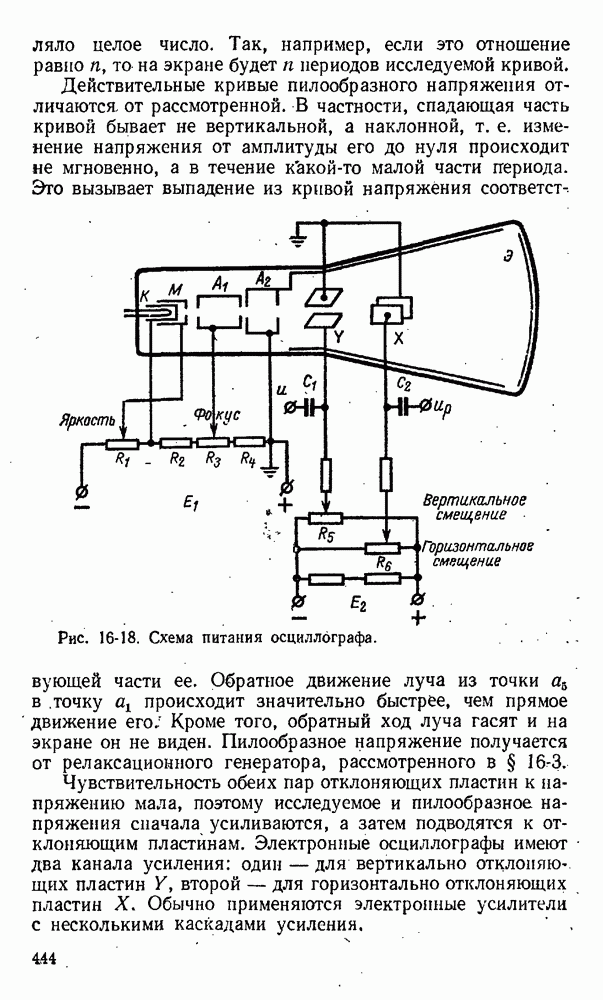
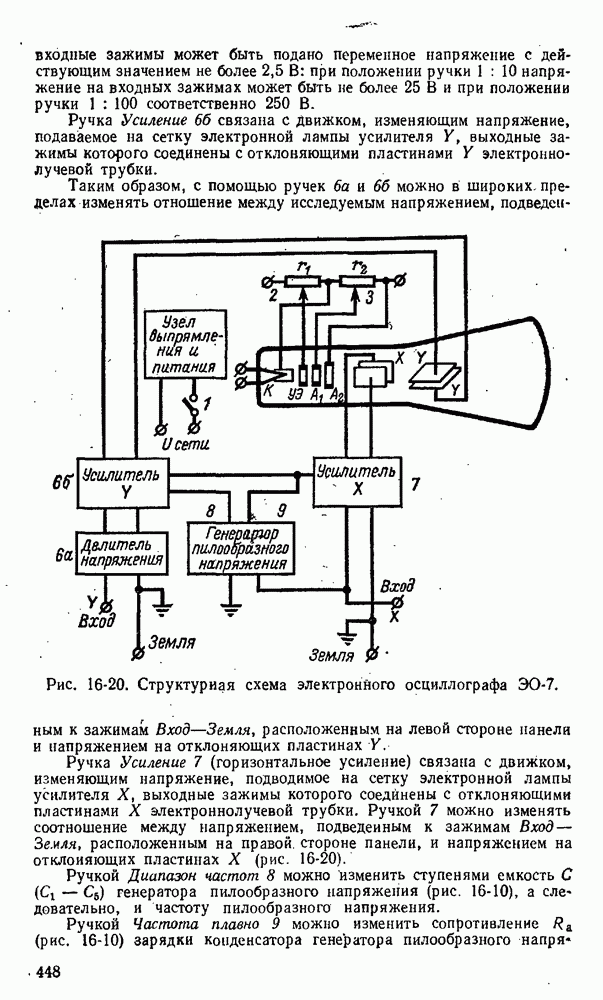
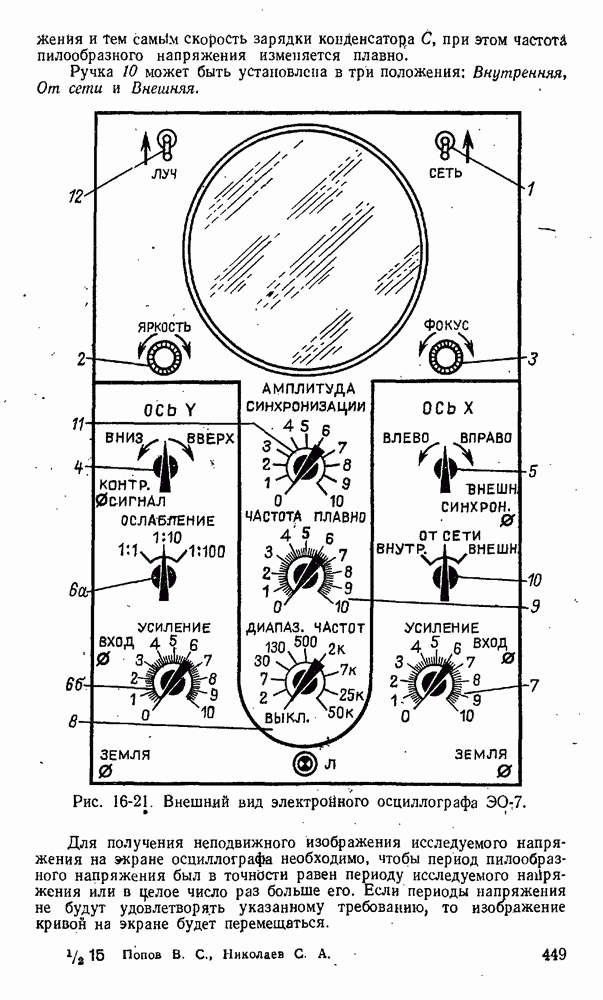
- 16-6. Электроннолучевой осциллограф
- 16-7. Обозначения электроннолучевых трубок
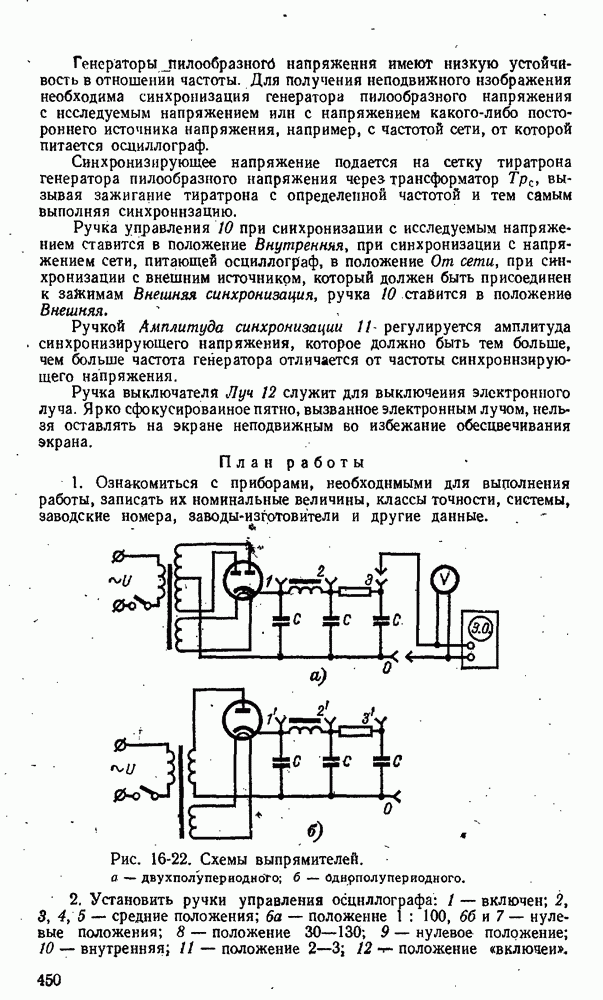
- 16-8. Лабораторная работа. Экспериментальное, определение кривых напряжений в схемах выпрямителей
- Глава семнадцатая. Полупроводниковые приборы и их применение
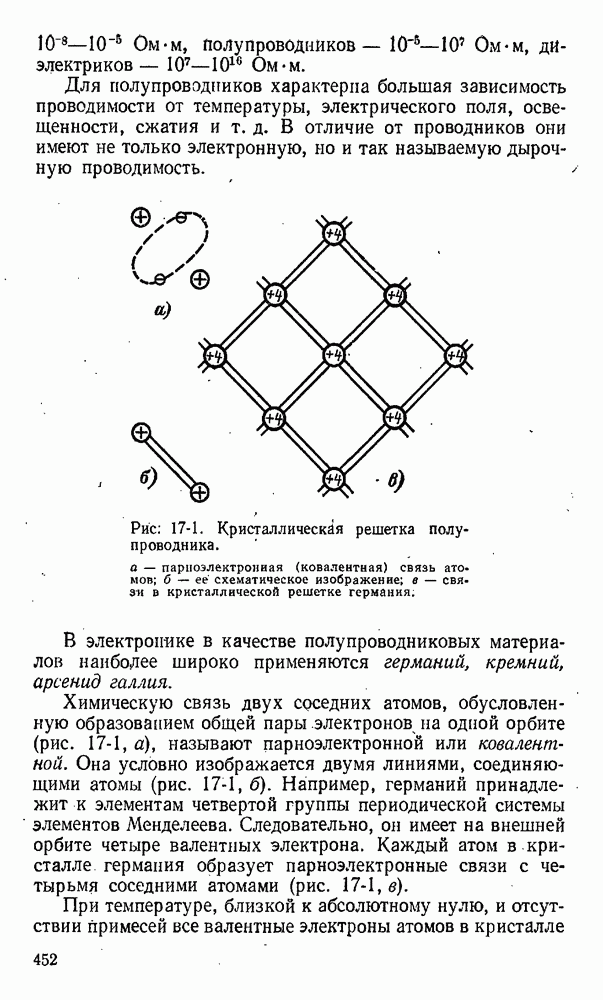
- 17-1. Собственная электропроводность полупроводников
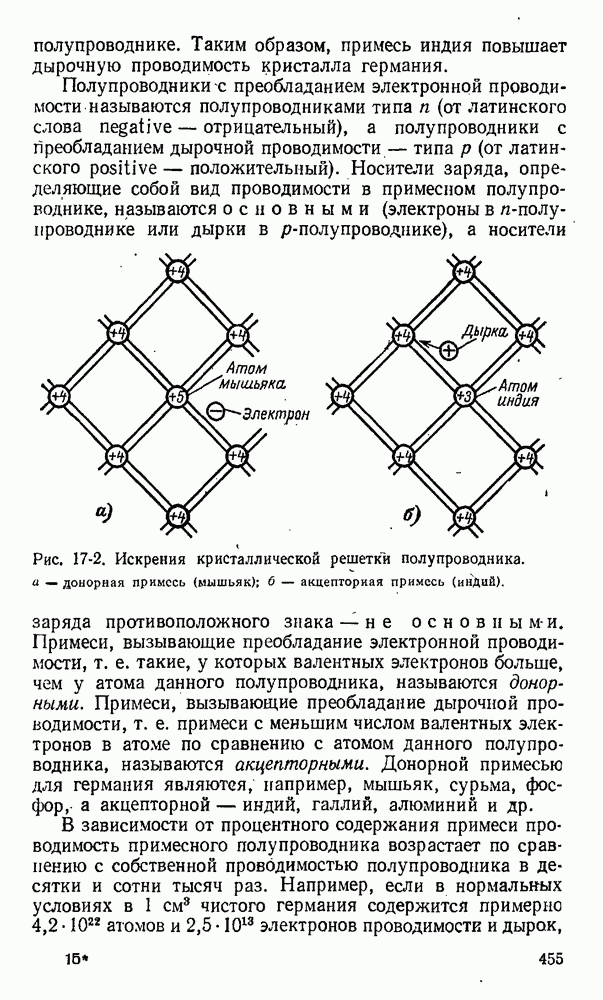
- 17-2. Примесная электропроводность полупроводников
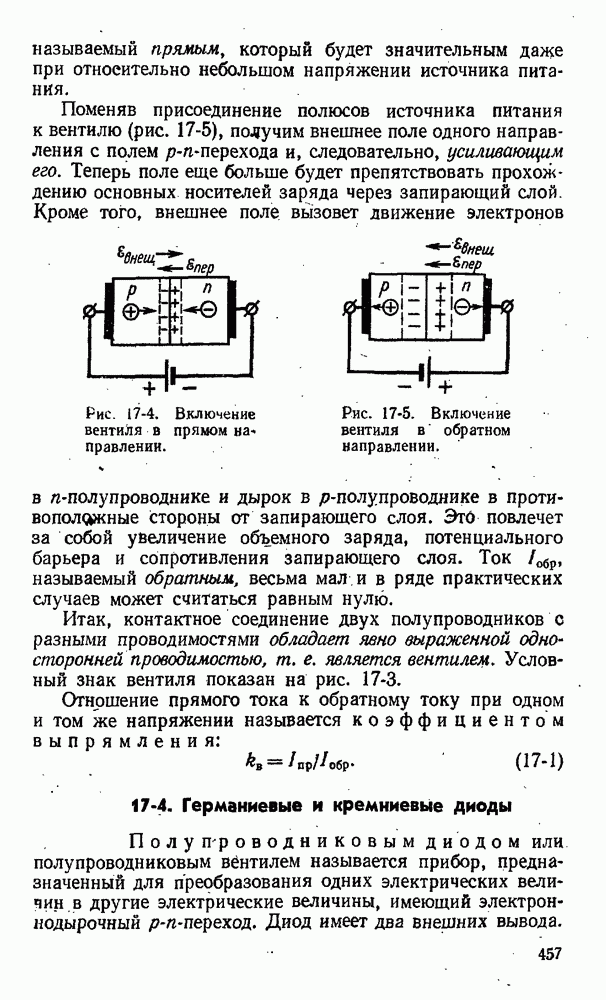
- 17-3. Полупроводниковый вентиль
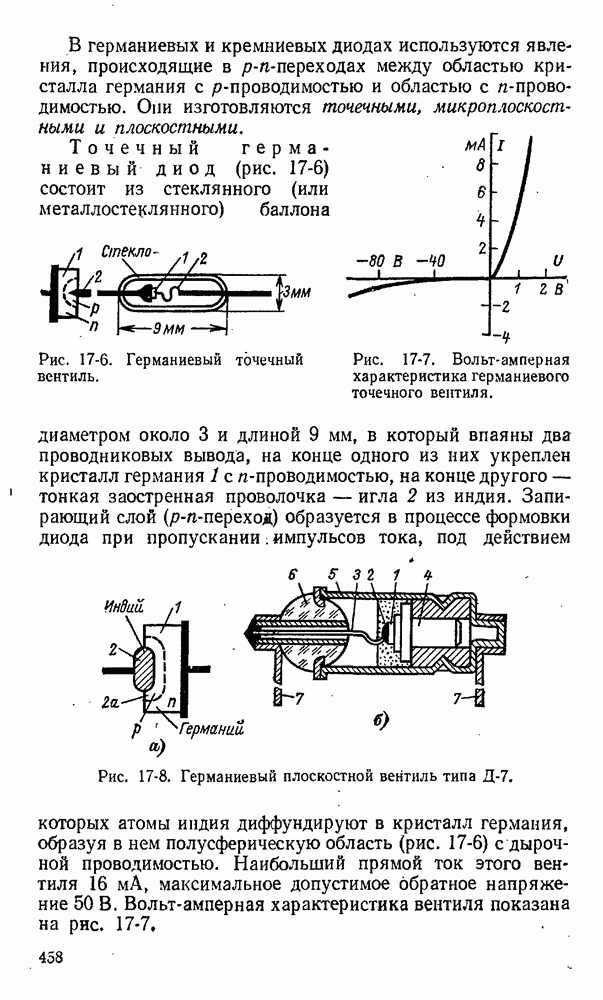
- 17-4. Германиевые и кремниевые диоды
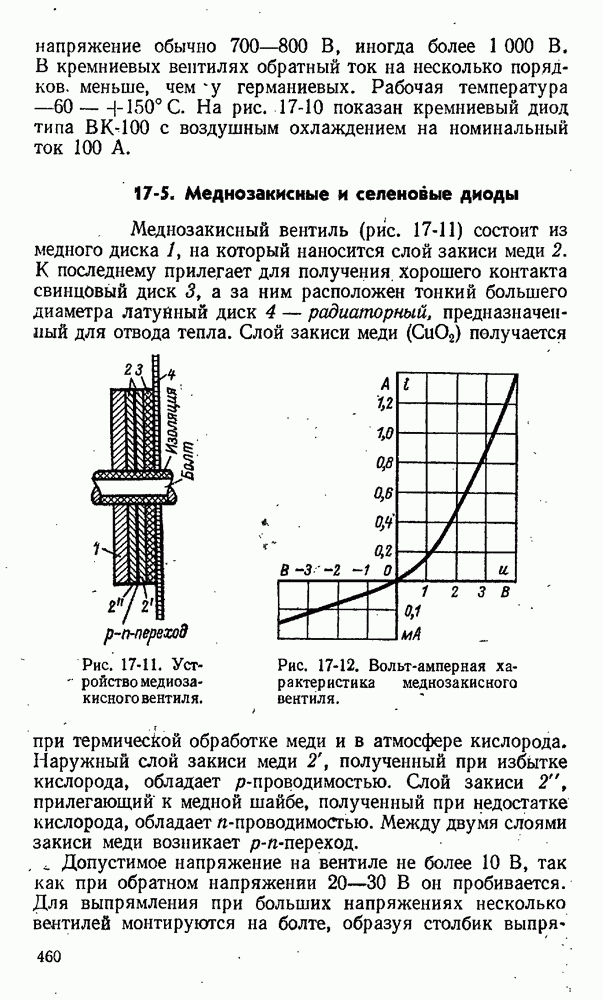
- 17-5. Меднозакисные и селеновые диоды
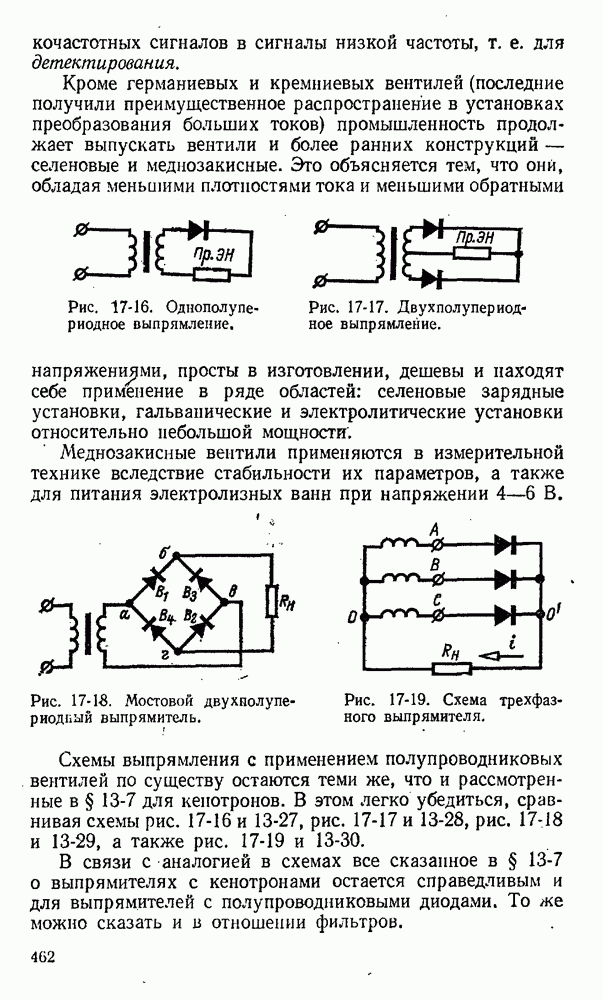
- 17-6. Применение полупроводниковых вентилей и схемы выпрямителей
- 17-7. Обозначения полупроводниковых диодов
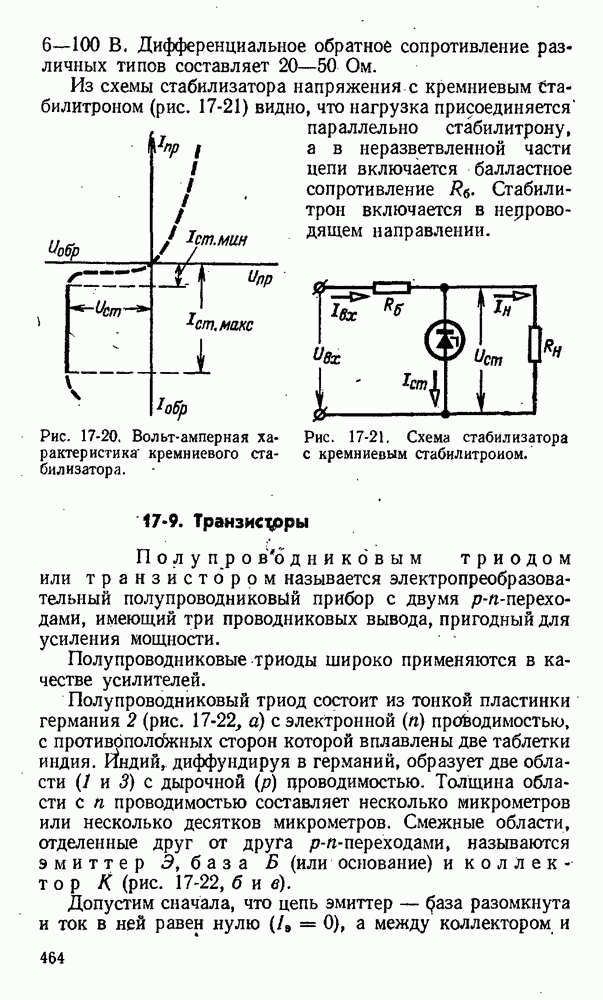
- 17-8. Кремниевые стабилитроны (опорные диоды)
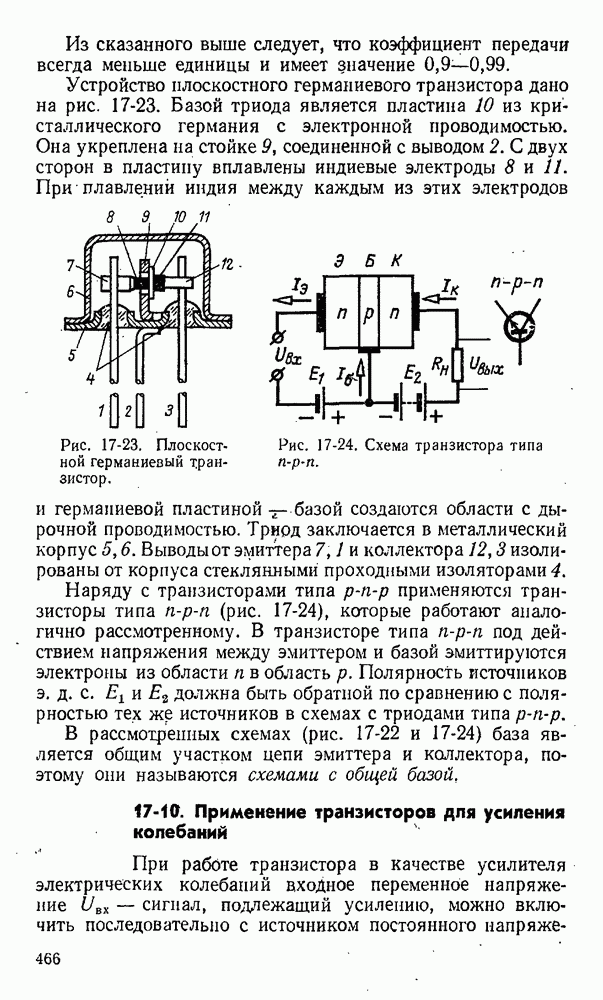
- 17-9. Транзисторы
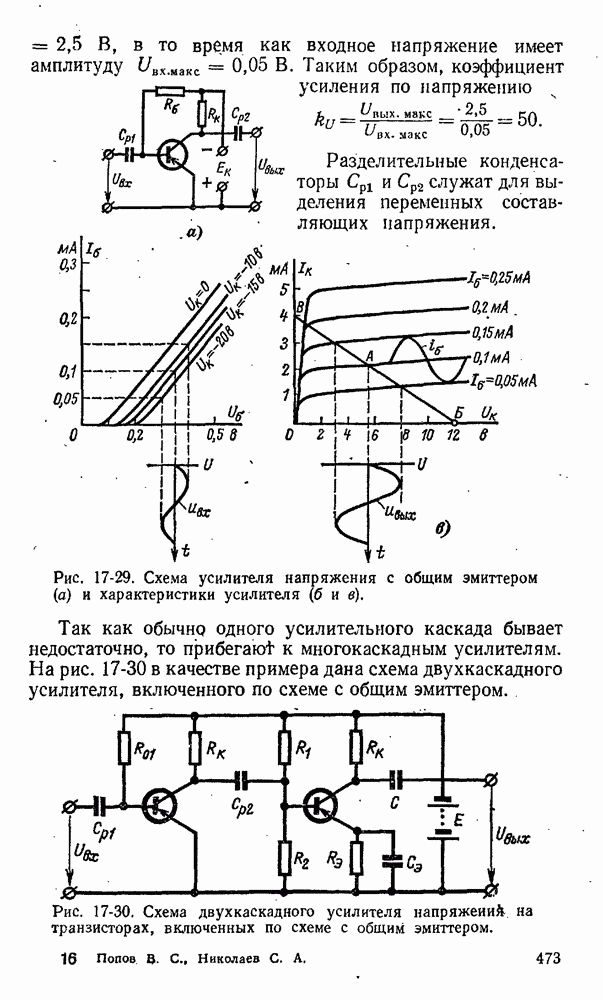
- 17-10. Применение транзисторов для усиления колебаний
- 17-11. Схемы включения и характеристики транзисторов
- 17-12. Обозначения полупроводниковых триодов
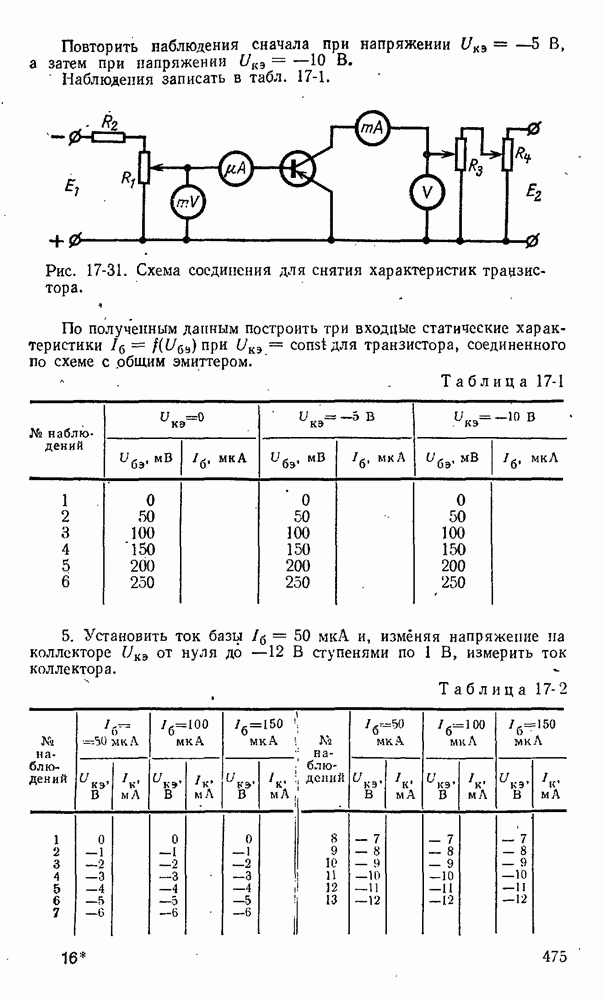
- 17-13. Лабораторная работа. Снятие характеристик транзистора
- Глава восемнадцатая. Фотоэлектронные приборы и электронные реле
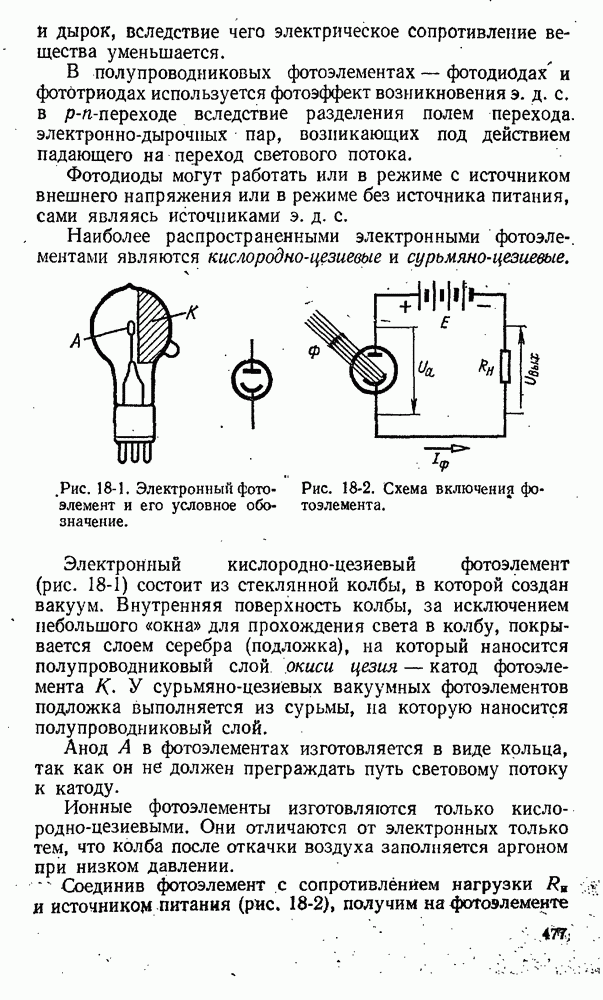
- 18-1. Фотоэлементы с внешним фотоэффектом
- 18-2. Фоторезисторы
- 18-3. Полупроводниковые фотоэлементы
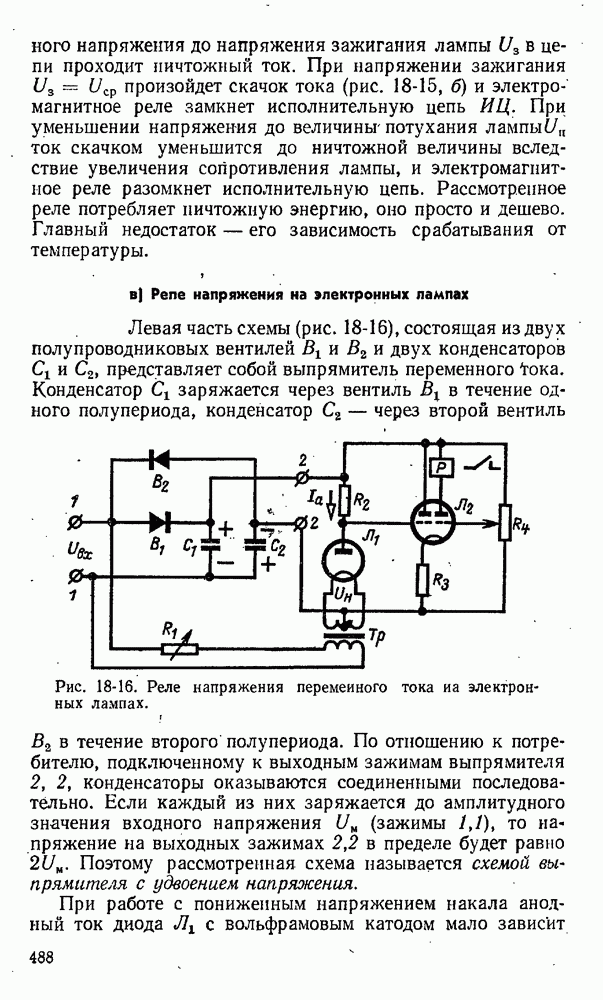
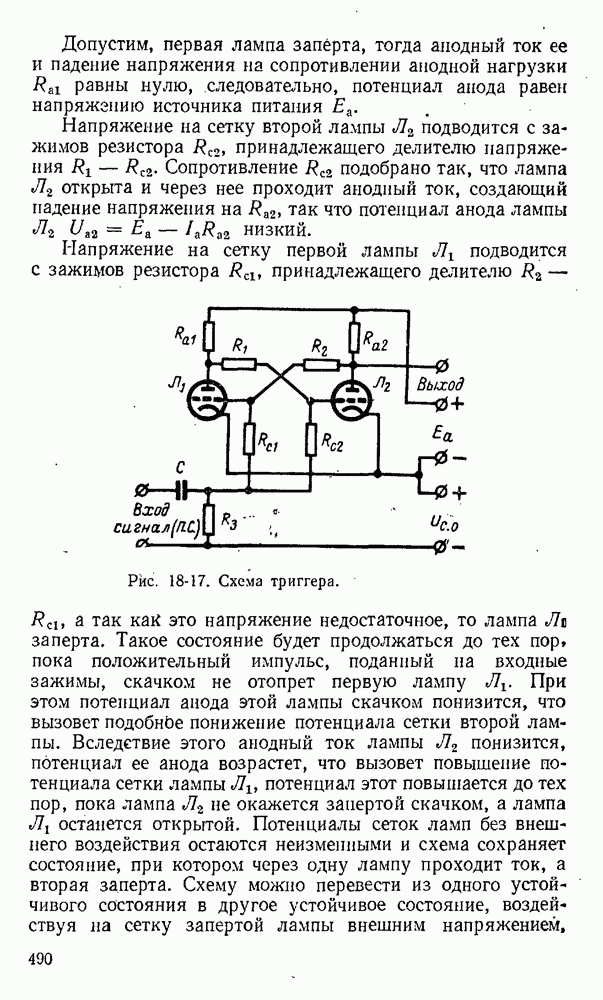
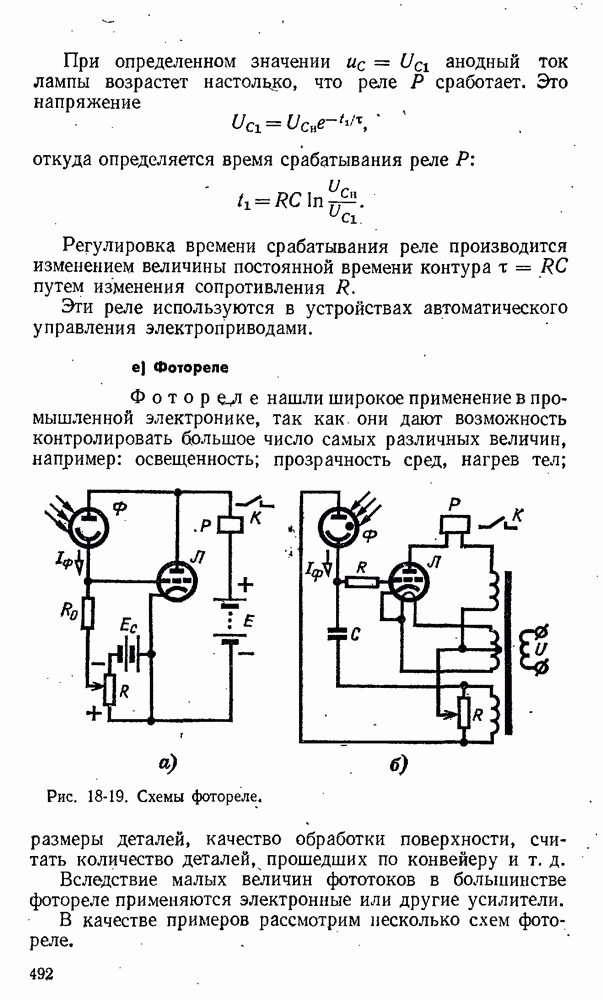
- 18-4. Электронные и ионные реле
- 18-5. Лабораторная работа. Электронное реле — триггер