| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ФИЗИЧЕСКОЕ СОСТОЯНИЕ ХРОМОСФЕРЫ. ВОЛНОВЫЕ ДВИЖЕНИЯ В АТМОСФЕРЕ СОЛНЦА
В спектре солнечной хромосферы, кроме повторения линий фраунгоферова спектра в обращенном виде, наблюдается несколько новых эмиссионных линий. Об одной из них мы уже говорили, это линия  гелия, существование которой в хромосфере несколько странно: ведь хромосфера, как более высокий слой, должна быть холоднее фотосферы, а для возбуждения того верхнего уровня атома Не, переход с которого дает линию
гелия, существование которой в хромосфере несколько странно: ведь хромосфера, как более высокий слой, должна быть холоднее фотосферы, а для возбуждения того верхнего уровня атома Не, переход с которого дает линию  нужна энергия, встречающаяся лишь у частиц при температуре около 200 000 К. Еще более странно присутствие в спектре хромосферы линий ионизованного гелия, так как ионизационный потенциал Не равен 24,5 эВ, а для наблюдаемой в хромосфере линии гелия
нужна энергия, встречающаяся лишь у частиц при температуре около 200 000 К. Еще более странно присутствие в спектре хромосферы линий ионизованного гелия, так как ионизационный потенциал Не равен 24,5 эВ, а для наблюдаемой в хромосфере линии гелия  нужна энергия возбуждения до 50 эВ!
нужна энергия возбуждения до 50 эВ!
Другой особенностью хромосферы является ее большая протяженность. Газ в состоянии гидростатического равновесия подчиняется дифференциальному условию

утверждающему, что при изменении высоты на  давление убывает на
давление убывает на  равное массе элемента объема
равное массе элемента объема  причем р — плотность вещества, a g — ускорение силы тяжести.
причем р — плотность вещества, a g — ускорение силы тяжести.
Сочетая уравнение (4.1) с уравнением идеального газа

где  — универсальная газовая постоянная, а
— универсальная газовая постоянная, а  — молекулярная масса, легко найдем для изотермического слоя или тонкого слоя, в котором можно считать Т и g постоянными, так называемое барометрическое уравнение
— молекулярная масса, легко найдем для изотермического слоя или тонкого слоя, в котором можно считать Т и g постоянными, так называемое барометрическое уравнение

в котором  есть давление на уровне h = 0. Мы видим, что газовое давление в атмосфере при неизменной температуре должно убывать экспоненциально, причем величина Я, вытекающая из равенства
есть давление на уровне h = 0. Мы видим, что газовое давление в атмосфере при неизменной температуре должно убывать экспоненциально, причем величина Я, вытекающая из равенства

определяет высоту однородной атмосферы, потому что если бы атмосфера была одинаковой плотности  , то давление ее оказалось бы равным
, то давление ее оказалось бы равным  в том случае, когда высота ее равнялась бы
в том случае, когда высота ее равнялась бы  т. е. введенной нами величине
т. е. введенной нами величине  .
.
Вместе с тем  определяет так называемую шкалу высот в атмосфере, так как согласно (4.3) плотность (или давление) бывает в е раз при возрастании высоты на величину
определяет так называемую шкалу высот в атмосфере, так как согласно (4.3) плотность (или давление) бывает в е раз при возрастании высоты на величину  .
.
На Солнце g очень велико, поэтому  мало даже для самого легкого газа — водорода. В этом случае по формуле (4.4) определяется
мало даже для самого легкого газа — водорода. В этом случае по формуле (4.4) определяется  при
при  км. Именно поэтому мы смогли без труда объяснить резкий край у Солнца. Но у хромосферы наблюдения дают для водорода
км. Именно поэтому мы смогли без труда объяснить резкий край у Солнца. Но у хромосферы наблюдения дают для водорода  км. Если бы теоретическое значение
км. Если бы теоретическое значение  реально соблюдалось, то на протяжении 1200 км яркость хромосферы должна была уменьшиться в
реально соблюдалось, то на протяжении 1200 км яркость хромосферы должна была уменьшиться в  раз, а фактически она уменьшается не более чем в
раз, а фактически она уменьшается не более чем в  раз, вся же хромосфера прослеживается до высот в 6—7 раз выше. Еще разительнее расхождение у CaII. Хромосфера в лучах CaII видна выше всего, а между тем по формуле (4.4) для
раз, вся же хромосфера прослеживается до высот в 6—7 раз выше. Еще разительнее расхождение у CaII. Хромосфера в лучах CaII видна выше всего, а между тем по формуле (4.4) для  высота однородной атмосферы должна быть еще в 40 раз меньше, чем у водорода. Действительное значение
высота однородной атмосферы должна быть еще в 40 раз меньше, чем у водорода. Действительное значение  у металлов — порядка 200—400 км.
у металлов — порядка 200—400 км.
Такое расхождение между теорией и наблюдениями может быть отчасти объяснено тем, что на самом деле хромосфера не изотермична, но становится горячее с высотой. Это предположение может объяснить и перевозбуждение атомов в хромосфере. Однако во многих отношениях разумнее предположить, что в хромосфере рядом существуют горячие и холодные элементы, делающие ее среднюю температуру много выше 5000 К. Иначе невозможно понять одновременное присутствие в спектре хромосферы линий HeII и бальмеровской серии водорода.

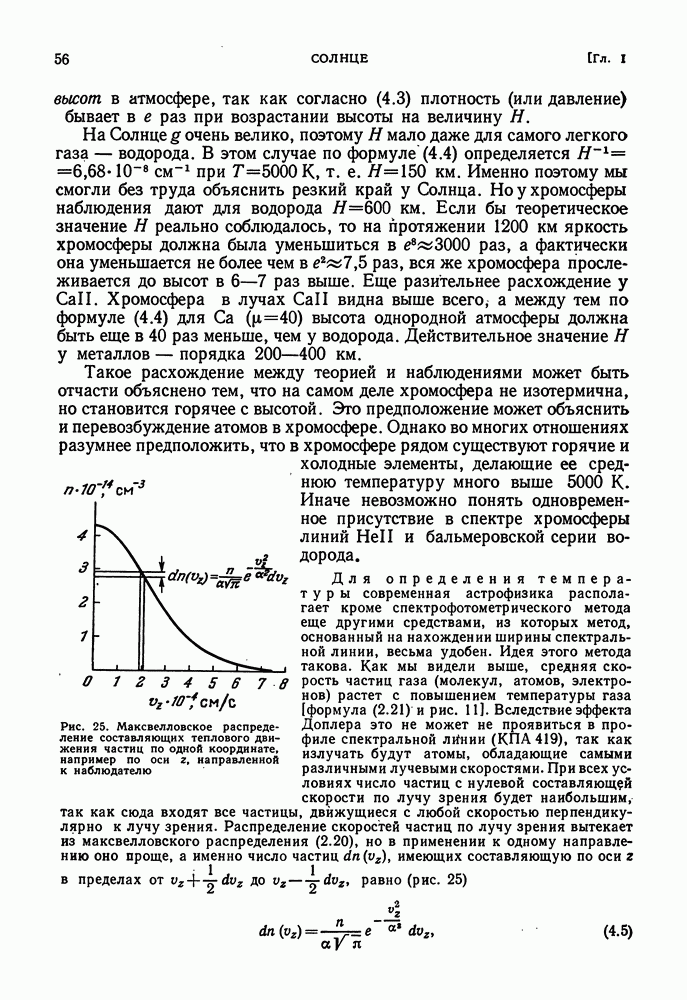
Рис. 25. Максвелловское распределение составляющих теплового движения частиц по одной координате, например по оси z, направленной к наблюдателю
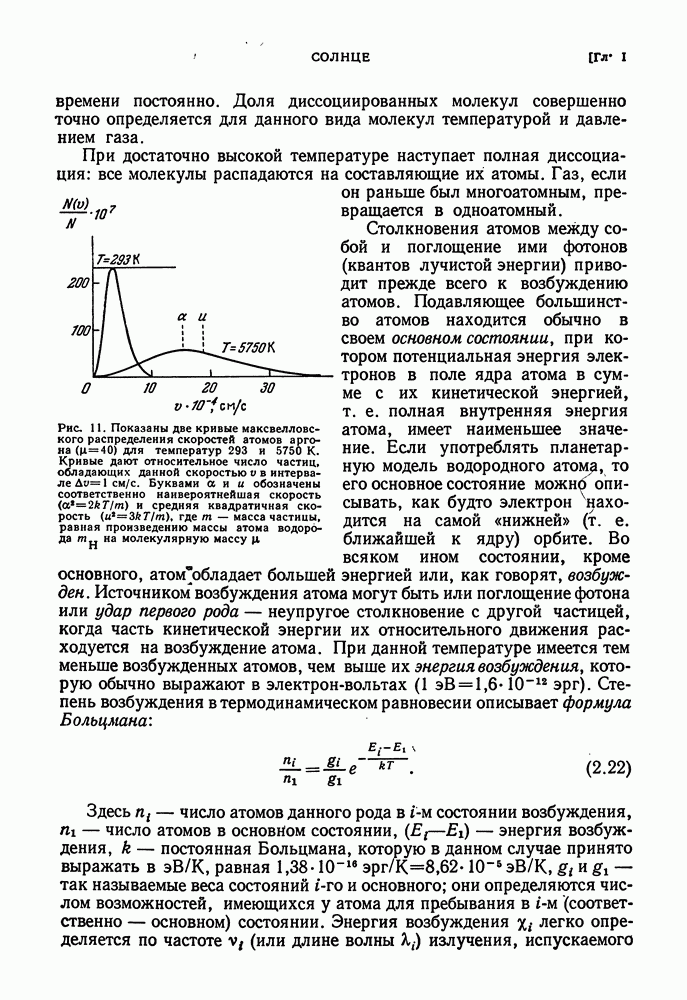
Для определения температуры современная астрофизика располагает кроме спектрофотометрического метода еще другими средствами, из которых метод, основанный на нахождении ширины спектральной линии, весьма удобен. Идея этого метода такова. Как мы видели выше, средняя скорость частиц газа (молекул, атомов, электронов) растет с повышением температуры газа (формула (2.21) и рис. 111. Вследствие эффекта Доплера это не может не проявиться в профиле спектральной лйнии (КПА 419), так как излучать будут атомы, обладающие самыми различными лучевыми скоростями. При всех условиях число частиц с нулевой составляющей скорости по лучу зрения будет наибольшим, так как сюда входят все частицы, движущиеся с любой скоростью перпендикулярно к лучу зрения. Распределение скоростей частиц по лучу зрения вытекает из максвелловского распределения (2.20), но в применении к одному направлению оно проще, а именно число частиц  имеющих составляющую по оси
имеющих составляющую по оси  в пределах от
в пределах от  до
до  , равно (рис. 25)
, равно (рис. 25)

где  определяется из (2.21) как наивероятнейшая скорость движения частиц. Это распределение показано на рис. 25 для положительных скоростей
определяется из (2.21) как наивероятнейшая скорость движения частиц. Это распределение показано на рис. 25 для положительных скоростей  . Кривая должна быть дополнена распределением для отрицательных скоростей — такой же кривой, симметричной относительно
. Кривая должна быть дополнена распределением для отрицательных скоростей — такой же кривой, симметричной относительно  .
.
Соответственно, если каждый атом изучает чрезвычайно тонкую спектральную линию (т. е. она имеет очень малую ширину в шкале длин волн  ), то при изучении ее движущимися атомами (так же, как и при поглощении) она расширится и ее профиль воспроизведет распределение по лучевым скоростям (по
), то при изучении ее движущимися атомами (так же, как и при поглощении) она расширится и ее профиль воспроизведет распределение по лучевым скоростям (по  -координате) излучающих (или поглощающих) частиц. Именно, распределение интенсивности в линии должно подчиняться формуле
-координате) излучающих (или поглощающих) частиц. Именно, распределение интенсивности в линии должно подчиняться формуле

Здесь  обозначает количество энергии, содержащейся в интервале длин волн от до
обозначает количество энергии, содержащейся в интервале длин волн от до  — длину волны центра линии. Переход от (4.5) к (4.6) осуществляется с помощью основной формулы принципа Доплера — Физо
— длину волны центра линии. Переход от (4.5) к (4.6) осуществляется с помощью основной формулы принципа Доплера — Физо

(КПА 481), в которой под  , следует понимать отклонение
, следует понимать отклонение  от центральной длины волны под влиянием движения по лучу зрения со скоростью
от центральной длины волны под влиянием движения по лучу зрения со скоростью  .
.
Обычно из наблюдений выводят полуширину линии, т. е. значение  , соответствующее половинной интенсивности, так что
, соответствующее половинной интенсивности, так что

Есть много других факторов, расширяющих спектральные линии, в особенности, когда число излучающих (поглощающих) атомов велико. Об этом мы будем говорить в главе II. Близко к рассмотренному случаю лежит тоже доплеровское расширение, но происходящее вследствие макроскопических движений газовых масс. Когда газ находится в состоянии систематического движения, это приводит лишь к простому смещению спектральной линии как целого (ср. определение лучевой скорости вращения Солнца). Но при беспорядочных бурных движениях турбулентного характера, когда крупные и мелкие турбулентные ячейки движутся совершенно хаотически, произойдет расширение спектральных линий, которое отличается от расширения вследствие теплового движения атомов тем, что оно не зависит от атомной (молекулярной) массы элемента, производящего линию, втовремя как в формуле (2.21) имеем  (см. §2).
(см. §2).
В этом случае определение температуры по формуле (2.21) теряет смысл, да и приводит оно к неприемлемым результатам. Действительно, ширина многих линий в спектре средней и верхней хромосферы такова, что позволяет заключить о турбулентных скоростях до 15—20 км/с. Если же определяемую из ширины хромосферных линий скорость в формуле (2.21) интерпретировать как а, т. е. как к  , то в применении к таким атомам, как, например,
, то в применении к таким атомам, как, например,  , это даст температуру 500—700 тыс. Кельвинов, что в применении к хромосфере выглядит совершенно неправдоподобно. В спектре некоторых звезд наблюдаются иногда несравненно ббльшие ширины линий, которые указывают либо на турбулентные скорости в 50—70 км/с, либо на температуры свыше полу миллиона Кельвинов; последнее противоречит наблюдаемому спектру звезды.
, это даст температуру 500—700 тыс. Кельвинов, что в применении к хромосфере выглядит совершенно неправдоподобно. В спектре некоторых звезд наблюдаются иногда несравненно ббльшие ширины линий, которые указывают либо на турбулентные скорости в 50—70 км/с, либо на температуры свыше полу миллиона Кельвинов; последнее противоречит наблюдаемому спектру звезды.
Возвращаясь к вопросу о температуре хромосферы, следует отметить, что нижняя хромосфера более или менее однородна и имеет  .
.
Но на высоте, большей 3—4 тыс км, появляются спикулы — горячие струи, температура которых достигает 15 000 К. Тут же, рядом со спикулами, происходит очень быстрый переход к очень горячей солнечной короне, когда на протяжении 50 000 км температура повышается сперва до нескольких сотен тысяч Кельвинов, а затем до миллиона. При этом электронная концентрация в газе изменяется очень мало — всего на один порядок. Это — так называемая солнечная переходная зона. Таким образом, в хромосфере существуют холодные и горячие массы, а это свидетельствует об очень бурном перемешивании, делающем химический состав всей хромосферы однородным. Наблюдаемые различия высоты, которой достигают эмиссионные линии разных элементов, можно объяснить их разным количественным содержанием, изменениями ионизации и возбуждения. Остается объяснить источник нагрева и перегрева хромосферы.
Для этого нужно обратиться к явлениям конвективного перемешивания, которое начинается на большой глубине и уже в фотосфере проявляется в виде грануляции. Соответствующие им конвективные ячейки, поднимаясь выше, несут с собой тепло, поток которого в фотосфере мал сравнительно с теплом, переносимым путем излучения. Движения гранул сопровождаются мелкими турбулентными движениями.
При этом возникают местные нарушения равновесия, которые в виде упругих возмущений распространяются в форме горизонтальных и вертикальных волн. Такие акустические волны встречаются с различными значениями плотности и температуры, и тогда скорость их распространения, длины волн, скорость движения газовых масс в колебательных движениях изменяются. Может возрасти амплитуда колебаний настолько, что движение газа становится сверхзвуковым. Может оказаться запрещенным дальнейшее распространение колебаний, определяется поверхность, от которой волны отражаются, так что возникают стоячие волны.
Конечно, эта очень сложная картина движений может иметь множество последствий, доступных и недоступных наблюдению. Таковы, например, пятиминутные вертикальные колебания в фотосфере, амплитуда которых достигает ±25 км при максимальных скоростях 250 км/с. Волны эти временами затухают или изменяют фазу на 180°, но сохраняют когерентность на протяжении от 1000 (гранулы) до 50 000 км.
Акустические волны очень долгого периода (десятки минут) не могут существовать на Солнце, но оказываются возможными так называемые гравитационные волны, т. е. такие, в которых колебания поддерживаются не упругими силами, а силой тяжести (например, волны на поверхности морей и океанов). Они могут иметь глобальный характер пульсации поверхностной зоны Солнца, включая глубинную конвективную зону его (см. главу IV).
Поскольку с высотой плотность падает, скорость частиц в волне возрастает, и если она превзойдет скорость распространения звуковых волн (а с падением температуры последняя уменьшается), то образуется ударная волна, приводящая к быстрой диссипации энергии, вызывающей нагревание масс газа.
Вначале, до высоты около 2—3 тыс. км, этот нагрев незначителен, так как очень много тепла уходит на ионизацию водорода, нос достижением больших высот нагревание пойдет очень быстро, пока температура не поднимется настолько, что станет возможной массовая ионизация гелия, что опять задержит повышение температуры. В то же время падение плотности в присутствии магнитных полей на большой высоте может привести к тому, что и в магнитогидродинамических волнах скорость движения газа превзойдет звуковую, так что и они будут быстро затухать, нагревая плазму. Хромосферные спикулы с их высокой температурой могут представлять собой пути распространения затухающих волн. Значительному нагреву на большой высоте спикул и аморфной хромосферы (до 20 000 К) способствует то, что сильно разреженный газ очень медленно охлаждается, так как взаимные столкновения частиц, которые приводят к их возбуждению и высвечиванию этого возбуждения, достаточно редки. Протуберанцы совсем не обладают столь высокой температурой, потому что их вещество более плотно.

Рис. 26. Примерная схема строения хромосферы по де Ягеру. Указаны значения температуры и логарифма электронной концентрации на разной высоте h
Заметим, что схема распределения температуры в хромосфере (так же как указание электронной концентрации в ней), показанная на рис. 26, получает подтверждение из радионаблюдений Солнца, о чем мы будем говорить в следующем параграфе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ГЛАВА I. СОЛНЦЕ
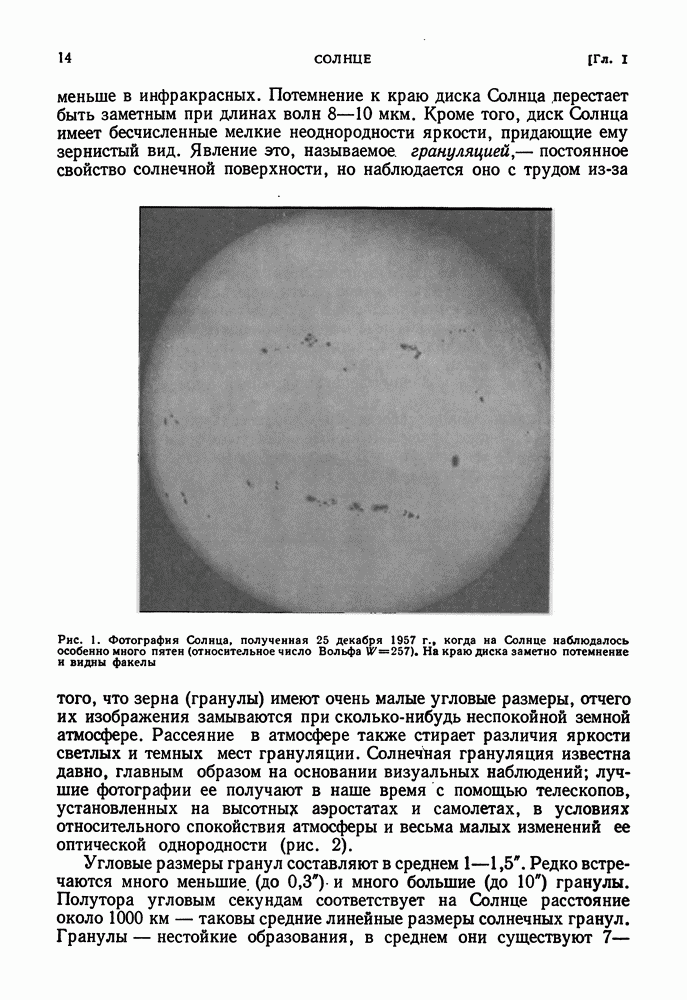
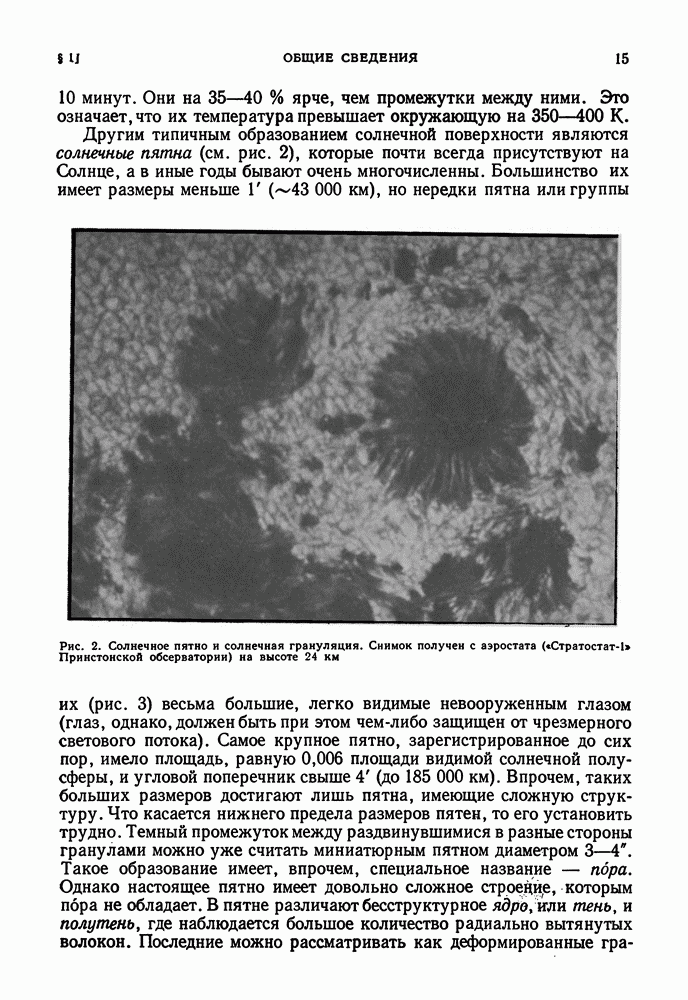
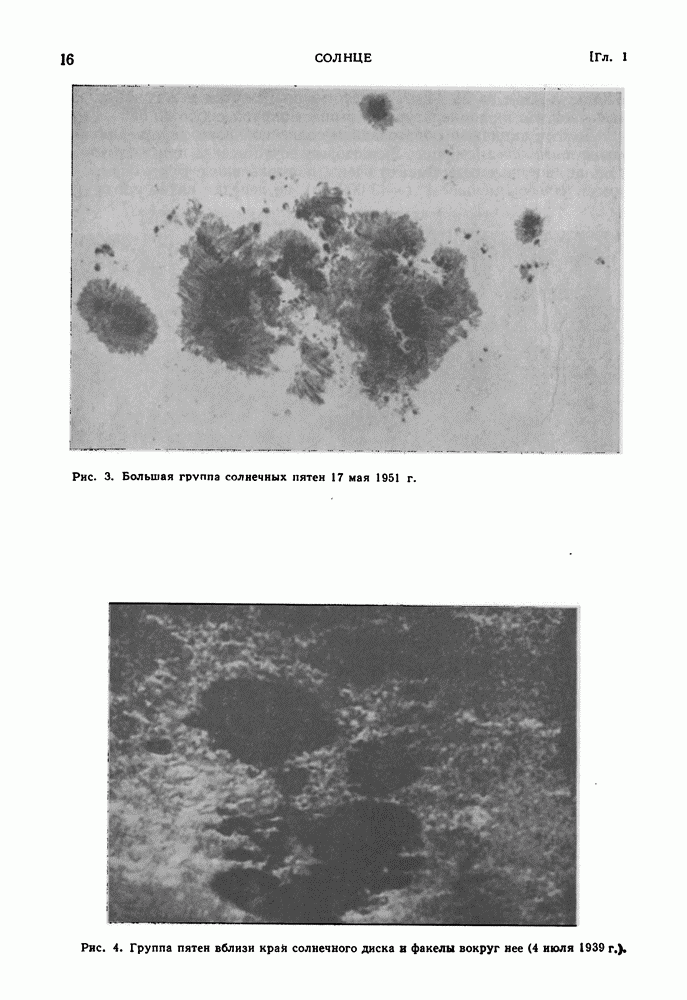
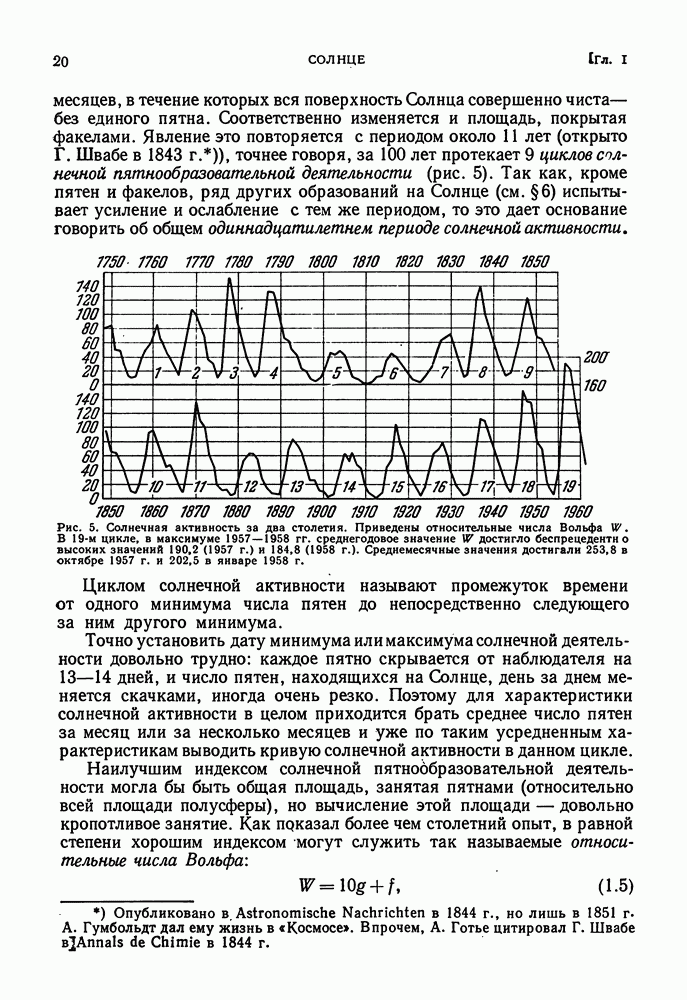
- ВНЕШНИЙ ВИД СОЛНЦА. ФОТОСФЕРА
- ВРАЩЕНИЕ СОЛНЦА
- ПЕРИОДИЧНОСТЬ СОЛНЕЧНОЙ ПЯТНООБРАЗОВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
- § 2. ЭЛЕМЕНТЫ ТЕОРИИ СОЛНЕЧНОЙ АТМОСФЕРЫ
- УРАВНЕНИЕ ЛУЧИСТОГО РАВНОВЕСИЯ И ЕГО ПРИБЛИЖЕННОЕ РЕШЕНИЕ
- МОДЕЛЬ СОЛНЕЧНОЙ АТМОСФЕРЫ
- КОНВЕКЦИЯ В СОЛНЕЧНОЙ АТМОСФЕРЕ
- ИОНИЗАЦИЯ СОЛНЕЧНОГО ВЕЩЕСТВА
- СОЛНЕЧНАЯ ПЛАЗМА И ЕЕ ВЗАИМОДЕЙСТВИЕ С МАГНИТНЫМИ ПОЛЯМИ
- § 3. СОЛНЕЧНЫЙ СПЕКТР. ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА
- ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА. КАЧЕСТВЕННЫЙ АНАЛИЗ
- КОЛИЧЕСТВЕННЫЙ ХИМИЧЕСКИЙ АНАЛИЗ СОЛНЕЧНОЙ АТМОСФЕРЫ
- § 4. ВЕРХНЯЯ АТМОСФЕРА СОЛНЦА
- ОБРАЩАЮЩИЙ СЛОЙ И ХРОМОСФЕРА. ПРИЧИНА ИХ ВИДИМОСТИ ЗА ПРЕДЕЛАМИ СОЛНЕЧНОГО ДИСКА
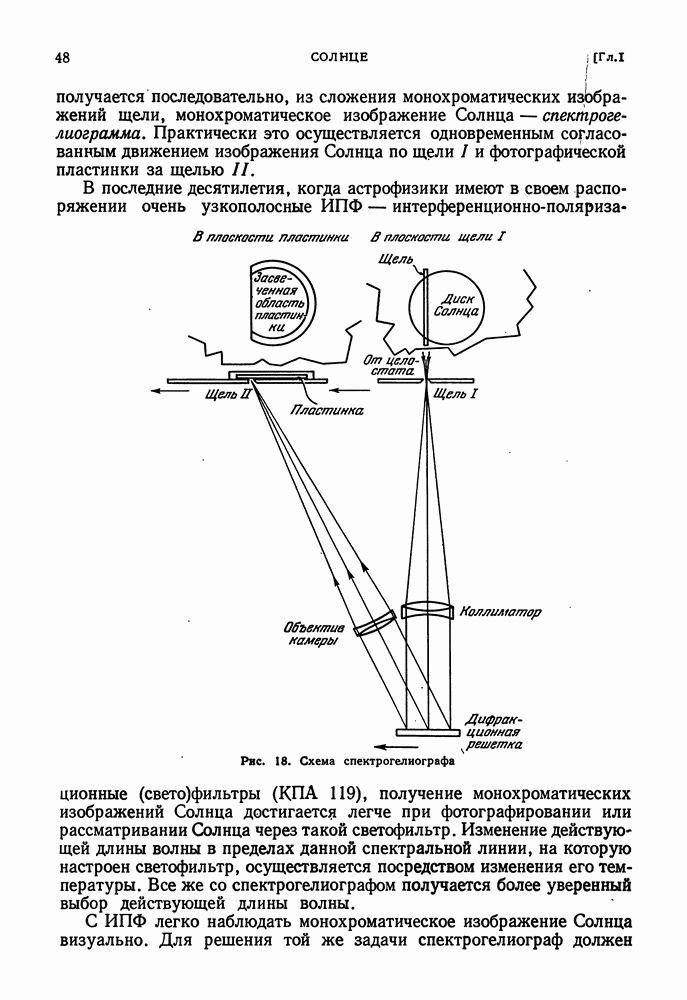
- НАБЛЮДЕНИЯ ХРОМОСФЕРЫ НА ДИСКЕ СОЛНЦА. СПЕКТРОГЕЛИОГРАФ
- ХРОМОСФЕРНЫЕ ФАКЕЛЫ, ФЛОККУЛЫ И ВОЛОКНА. СПИКУЛЫ
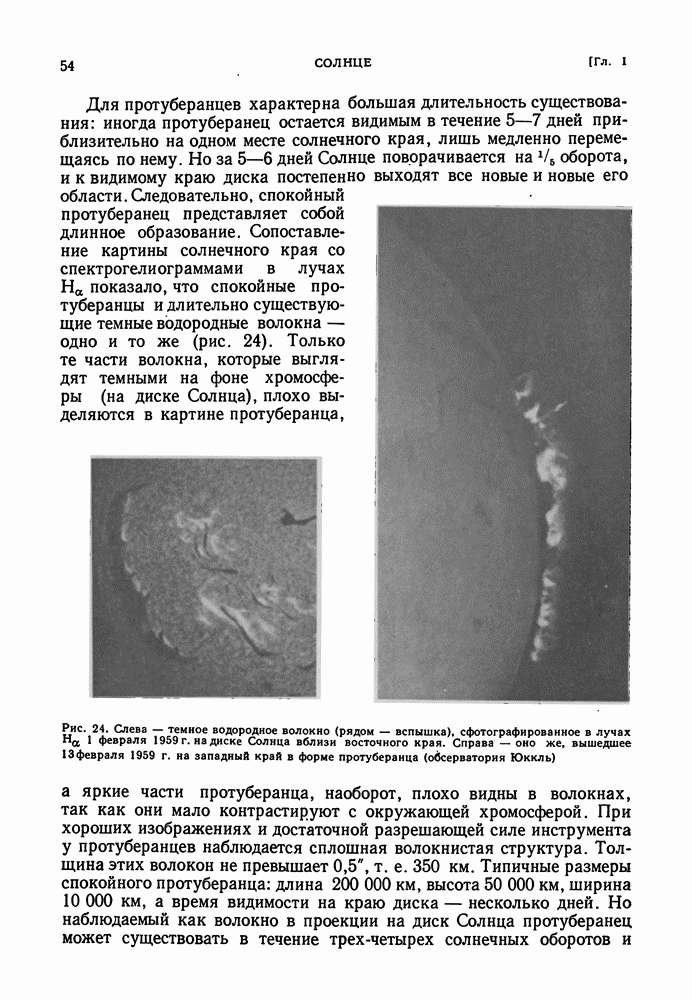
- ПРОТУБЕРАНЦЫ
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ ХРОМОСФЕРЫ. ВОЛНОВЫЕ ДВИЖЕНИЯ В АТМОСФЕРЕ СОЛНЦА
- § 5. СОЛНЕЧНАЯ КОРОНА
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ КОРОНЫ
- ЭМИССИОННЫЙ СПЕКТР КОРОНЫ И ЕГО ИНТЕРПРЕТАЦИЯ
- РАДИОИЗЛУЧЕНИЕ КОРОНЫ И ХРОМОСФЕРЫ
- НЕПРЕРЫВНОЕ ИЗЛУЧЕНИЕ КОРОНЫ. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ И ТЕМПЕРАТУРЫ В ХРОМОСФЕРЕ И КОРОНЕ
- § 6. НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ НА СОЛНЦЕ
- ОБНАРУЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ НА СОЛНЦЕ
- СОЛНЕЧНЫЕ ПЯТНА И ИХ МАГНИТНЫЕ ПОЛЯ
- ПРИРОДА СОЛНЕЧНЫХ ПЯТЕН. АКТИВНЫЕ ОБЛАСТИ НА СОЛНЦЕ. СУПЕРГРАНУЛЯЦИЯ
- ПРОТУБЕРАНЦЫ
- ПРОЯВЛЕНИЕ СОЛНЕЧНОЙ АКТИВНОСТИ В КОРОНЕ
- СОЛНЕЧНЫЕ ВСПЫШКИ
- СПОРАДИЧЕСКОЕ РАДИОИЗЛУЧЕНИЕ СОЛНЦА
- КОРПУСКУЛЯРНОЕ ИЗЛУЧЕНИЕ СОЛНЦА
- § 7. СВЯЗЬ МЕЖДУ СОЛНЕЧНЫМИ И ЗЕМНЫМИ ЯВЛЕНИЯМИ
- ПОЛЯРНЫЕ СИЯНИЯ
- ВЕРХНЯЯ АТМОСФЕРА ЗЕМЛИ. ИОНОСФЕРА. ВОЗДЕЙСТВИЕ НА НИХ СОЛНЦА
- ЯВЛЕНИЯ НА ЗЕМЛЕ, ПРОИСХОДЯЩИЕ ВО ВРЕМЯ ПЕРИОДОВ ПОВЫШЕННОЙ СОЛНЕЧНОЙ АКТИВНОСТИ
- РАДИАЦИОННЫЕ ПОЯСА ЗЕМЛИ
- ДВИЖЕНИЕ КОРПУСКУЛЯРНЫХ потоков В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- СОЛНЕЧНЫЙ ВЕТЕР И МАГНИТОСФЕРА ЗЕМЛИ
- ЗАДАЧИ К ГЛАВЕ I
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ I
- ГЛАВА III. ЗВЕЗДНЫЕ АТМОСФЕРЫ
- § 8. СПЕКТРЫ ЗВЕЗД
- РАЗЛИЧИЯ В СПЕКТРАХ ГИГАНТОВ И КАРЛИКОВ
- ВЛИЯНИЕ РАЗНЫХ ФИЗИЧЕСКИХ ФАКТОРОВ НА ВИД И ИНТЕНСИВНОСТЬ СПЕКТРАЛЬНЫХ ЛИНИЙ
- СПЕКТРАЛЬНЫЕ ПАРАЛЛАКСЫ И ДВУМЕРНАЯ СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ
- § 9. МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. ХИМИЧЕСКИЙ СОСТАВ ЗВЕЗД
- МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. СРЕДНИЙ ХИМИЧЕСКИЙ СОСТАВ АТМОСФЕР ЗВЕЗД
- УКЛОНЕНИЯ ХИМИЧЕСКОГО СОСТАВА ЗВЕЗД ОТ СРЕДНЕГО
- СПЕКТРЫ БЕЛЫХ КАРЛИКОВ
- ЗВЕЗДЫ ПОНИЖЕННОЙ СВЕТИМОСТИ
- МАГНИТНЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- ВЛИЯНИЕ ВРАЩЕНИЯ ЗВЕЗДЫ НА ЕЕ СПЕКТР
- ЭФФЕКТ ТУРБУЛЕНТНОСТИ
- § 10. ВЗАИМНЫЕ СВЯЗИ МЕЖДУ ВНЕШНИМИ ХАРАКТЕРИСТИКАМИ ЗВЕЗД
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА
- СВЯЗЬ МЕЖДУ ПОЛОЖЕНИЕМ ЗВЕЗДЫ НА ДИАГРАММЕ Г — Р И ЕЕ ДВИЖЕНИЕМ В ГАЛАКТИКЕ
- ЗВЕЗДЫ СФЕРИЧЕСКОЙ И ПЛОСКОЙ СОСТАВЛЯЮЩИХ. РАЗЛИЧИЕ ИХ ДИАГРАММ Г — Р
- РАЗНООБРАЗИЕ СВЕТИМОСТЕЙ И РАЗМЕРОВ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ II
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ II
- ГЛАВА III. ДВОЙНЫЕ ЗВЕЗДЫ И МАССЫ ЗВЕЗД
- ВИЗУАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- НЕВИДИМЫЕ СПУТНИКИ ЗВЕЗД
- СПЕКТРАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- ШИРОКИЕ И ТЕСНЫЕ ПАРЫ
- ЗАТМЕННЫЕ ИЛИ ФОТОМЕТРИЧЕСКИЕ ДВОЙНЫЕ ЗВЕЗДЫ
- § 12. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ ХАРАКТЕРИСТИК ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- КРИВАЯ ЛУЧЕВЫХ СКОРОСТЕЙ И ЭЛЕМЕНТЫ ОРБИТЫ СПЕКТРАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- ОПРЕДЕЛЕНИЕ МАСС КОМПОНЕНТ СПЕКТРАЛЬНО-ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ФОТОМЕТРИЧЕСКОЙ ОРБИТЫ
- ОПРЕДЕЛЕНИЕ ЭКСЦЕНТРИСИТЕТА ОРБИТЫ У ЗАТМЕННОЙ ДВОЙНОЙ ВРАЩЕНИЕ ЛИНИИ АПСИД
- ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ КОМПОНЕНТ ФОТОМЕТРИЧЕСКИХ ДВОЙНЫХ ЗВЕЗД
- ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОЙ ТЕМПЕРАТУРЫ ЗАТМЕННЫХ ДВОЙНЫХ ЗВЕЗД
- § 13. МАССЫ И ДРУГИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВОЙНЫХ ЗВЕЗД. ЗАКОН МАССА — СВЕТИМОСТЬ
- § 14. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВЕЗД В ДВОЙНЫХ СИСТЕМАХ
- РАЗНЫЕ ТИПЫ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- КОНТАКТНЫЕ СИСТЕМЫ
- ТРИ ТИПА ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- ОСЕВОЕ ВРАЩЕНИЕ КОМПОНЕНТ В ТЕСНЫХ ПАРАХ
- ГАЗОВЫЕ ПОТОКИ В ТЕСНЫХ ПАРАХ
- МНОГОЧИСЛЕННОСТЬ ДВОЙНЫХ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ III
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ III
- ГЛАВА IV. ВНУТРЕННЕЕ СТРОЕНИЕ ЗВЕЗД
- ОБЩИЕ СООБРАЖЕНИЯ. СОСТОЯНИЕ ВЕЩЕСТВА В НЕДРАХ ЗВЕЗД
- ЛУЧИСТОЕ ДАВЛЕНИЕ В ЗВЕЗДАХ
- ЛУЧИСТЫЙ И КОНВЕКТИВНЫЙ ПЕРЕНОС ТЕПЛА ВНУТРИ ЗВЕЗДЫ
- ГОМОЛОГИЧЕСКИЕ КОНФИГУРАЦИИ
- ПОЛИТРОПНЫЕ МОДЕЛИ ЗВЕЗД
- § 16. ЛУЧЕИСПУСКАНИЕ ЗВЕЗДЫ
- ИСТОЧНИКИ НЕПРОЗРАЧНОСТИ ЗВЕЗДНОГО ВЕЩЕСТВА
- ЗАВИСИМОСТЬ ЛУЧЕИСПУСКАНИЯ ЗВЕЗДЫ ОТ ИСТОЧНИКОВ ЭНЕРГИИ И НЕПРОЗРАЧНОСТИ
- § 17. ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ГРАВИТАЦИОННОЕ СЖАТИЕ
- ТЕРМОЯДЕРНЫЕ ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ПРОТОН-ПРОТОННАЯ РЕАКЦИЯ
- УГЛЕРОДНО-АЗОТНЫЙ ЦИКЛ
- ТРАНСФОРМАЦИЯ ГЕЛИЯ В ЗВЕЗДАХ
- § 18. ЗВЕЗДНЫЕ МОДЕЛИ
- БЕЛЫЕ КАРЛИКИ
- НЕЙТРОННЫЕ ЗВЕЗДЫ. ПУЛЬСАРЫ
- ПРОВЕРКА ТЕОРИИ ПО ВРАЩЕНИЮ ЛИНИИ АПСИД В ТЕСНЫХ СИСТЕМАХ И ПО СОЛНЕЧНЫМ ПУЛЬСАЦИЯМ
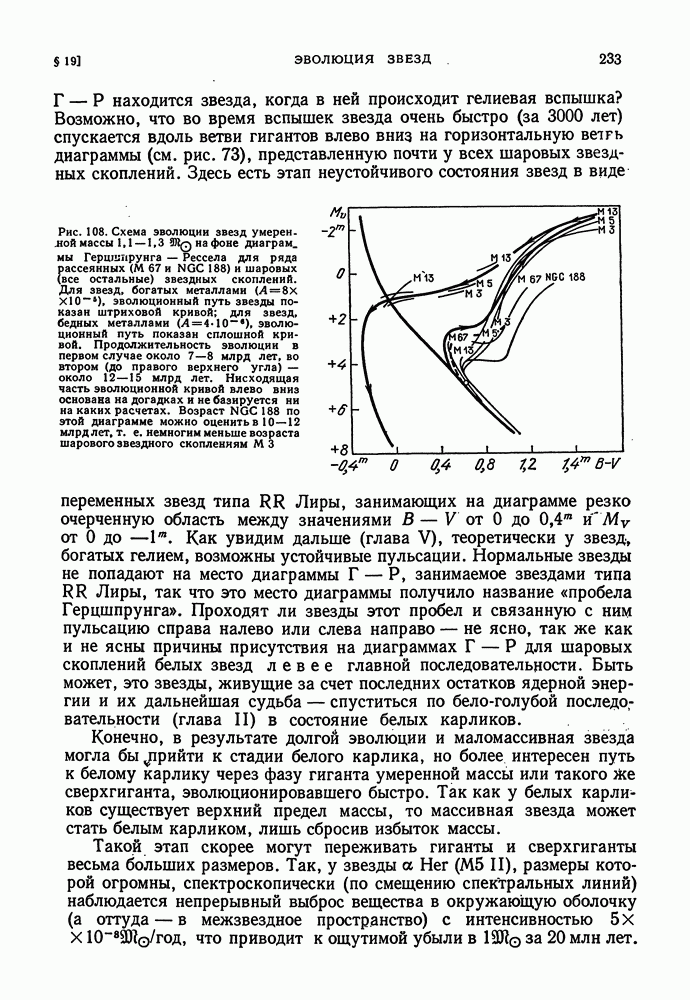
- § 19. ЭВОЛЮЦИЯ ЗВЕЗД
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЭВОЛЮЦИЯ ЗВЕЗД
- КОНТРАКЦИОННАЯ ФАЗА ЗВЕЗДНОЙ ЭВОЛЮЦИИ
- ЭВОЛЮЦИЯ ЗВЕЗД НА ТЕРМОЯДЕРНОЙ ОСНОВЕ
- ЭВОЛЮЦИЯ К КРАСНЫМ ГИГАНТАМ
- ДАЛЬНЕЙШАЯ ЭВОЛЮЦИЯ ЗВЕЗДЫ
- § 20. ЭВОЛЮЦИЯ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
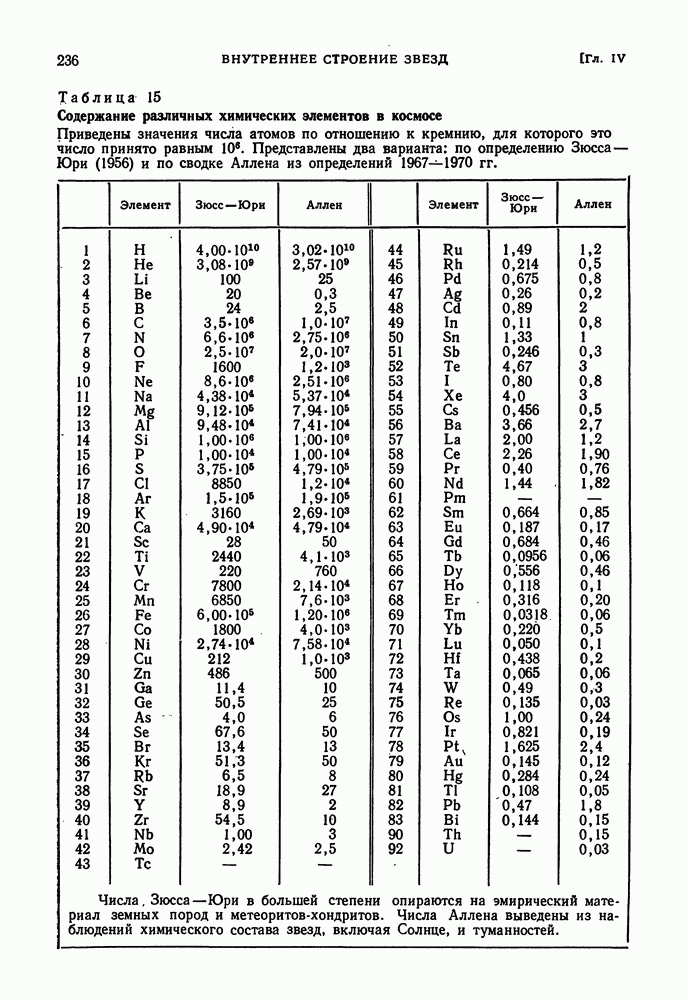
- СОВРЕМЕННАЯ РАСПРОСТРАНЕННОСТЬ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ ВО ВСЕЛЕННОЙ
- ТЕРМОЯДЕРНЫЕ РЕАКЦИИ С ОБРАЗОВАНИЕМ ЭЛЕМЕНТОВ БОЛЕЕ ТЯЖЕЛЫХ, ЧЕМ 12С
- ЗВЕЗДЫ РАЗНОГО ВОЗРАСТА И ИХ ХИМИЧЕСКИЙ СОСТАВ
- ЗАДАЧИ К ГЛАВЕ IV
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ IV
- ГЛАВА V. НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ
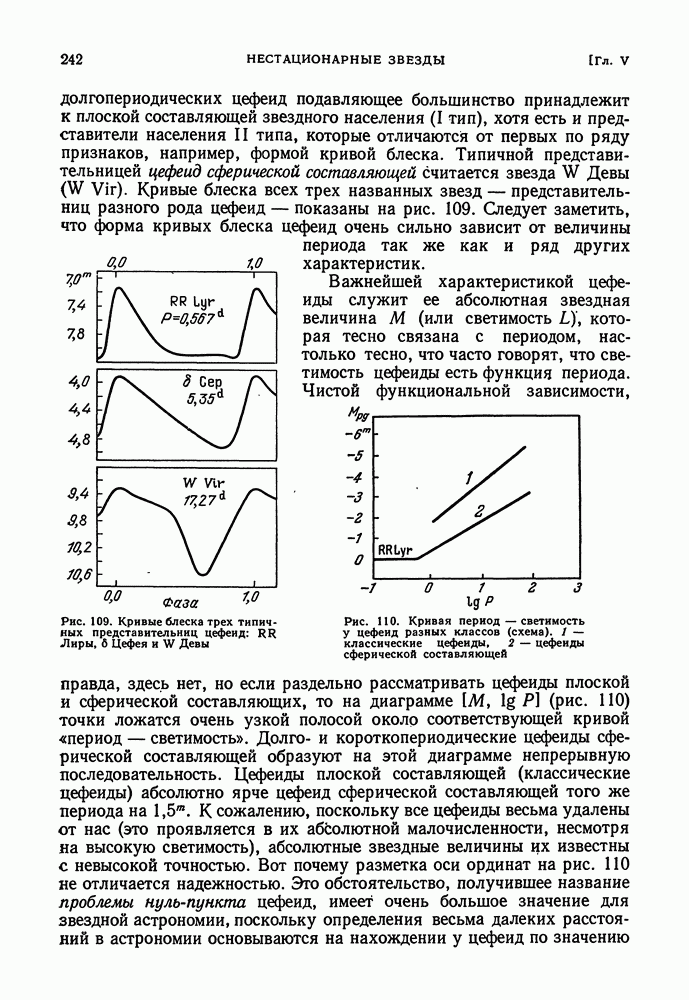
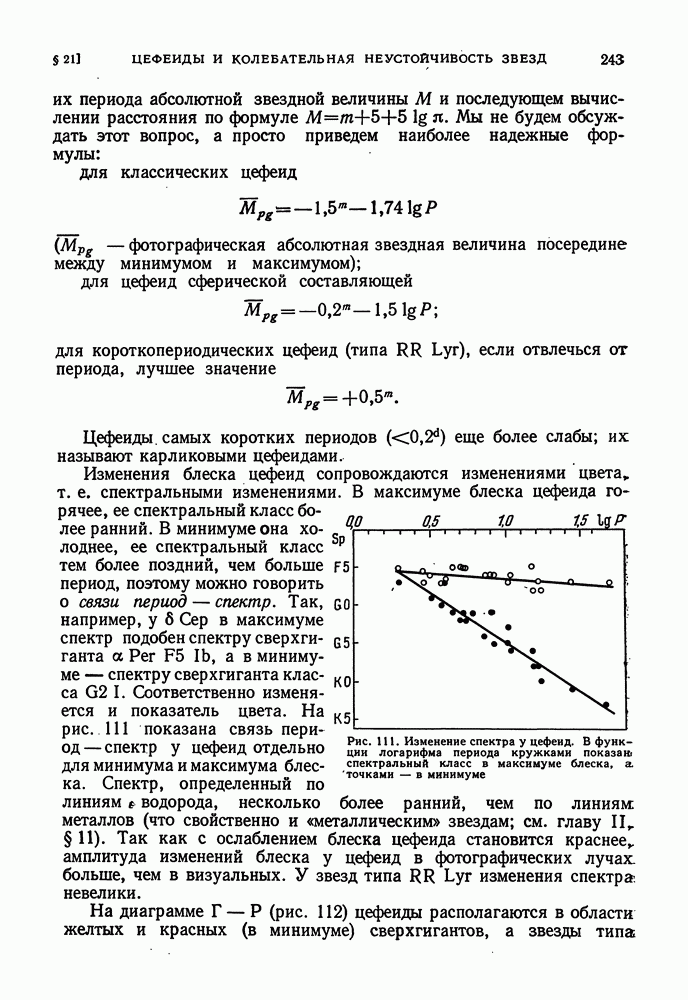
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦЕФЕИД
- ПУЛЬСАЦИИ ЦЕФЕИД
- ГИПОТЕЗА РАДИАЛЬНЫХ АДИАБАТИЧЕСКИХ ПУЛЬСАЦИЙ И ЕЕ ЗАТРУДНЕНИЯ
- НОВЫЕ ПРЕДСТАВЛЕНИЯ О КОЛЕБАТЕЛЬНЫХ ПРОЦЕССАХ У ЦЕФЕИД
- ЗВЕЗДЫ ТИПА b БОЛЬШОГО ПСА
- ЗВЕЗДЫ ТИПА RV ТЕЛЬЦА И МИРЫ КИТА
- § 22. ВЫНОС ВЕЩЕСТВА С ПОВЕРХНОСТИ ЗВЕЗД
- ГАЗОВЫЕ ОБОЛОЧКИ И КОЛЬЦА ВОКРУГ ЗВЕЗД
- ЗВЕЗДЫ ВОЛЬФА — РАЙЕ
- § 23. ВРАЩЕНИЕ ЗВЕЗД И ОБМЕН ВЕЩЕСТВА ВНУТРИ ДВОЙНЫХ СИСТЕМ
- ВРАЩЕНИЕ ЗВЕЗД РАЗНЫХ ТИПОВ
- ЭВОЛЮЦИОННЫЕ ИЗМЕНЕНИЯ СКОРОСТИ ВРАЩЕНИЯ ЗВЕЗД
- ПРОИСХОЖДЕНИЕ ВРАЩЕНИЯ ЗВЕЗД
- ОБМЕН ВЕЩЕСТВА ВНУТРИ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ. АККРЕЦИЯ. ЭВОЛЮЦИОННЫЕ СЛЕДСТВИЯ
- § 24. НОВЫЕ И СВЕРХНОВЫЕ ЗВЕЗДЫ
- СВЕТИМОСТЬ, АМПЛИТУДЫ ВСПЫШЕК И ЧИСЛО НОВЫХ ЗВЕЗД
- СПЕКТРАЛЬНЫЕ ИЗМЕНЕНИЯ У НОВЫХ ЗВЕЗД
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ ВО ВРЕМЯ ВСПЫШКИ НОВОЙ ЗВЕЗДЫ
- ДВОЙСТВЕННОСТЬ НОВЫХ ЗВЕЗД
- СВЕРХНОВЫЕ ЗВЕЗДЫ
- ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ ЗВЕЗД. КРАБОВИДНАЯ ТУМАННОСТЬ. ПУЛЬСАРЫ
- § 25. КАРЛИКОВЫЕ ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ДРУГИЕ СЛУЧАИ НЕСТАЦИОНАРНОСТИ: РЕНТГЕНОВСКИЕ ЗВЕЗДЫ
- ЗВЕЗДЫ ТИПА U БЛИЗНЕЦОВ. СИМБИОТИЧЕСКИЕ ЗВЕЗДЫ
- ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ТИПА UV КИТА
- ЗВЕЗДЫ ТИПОВ Т ТЕЛЬЦА, RW ВОЗНИЧЕГО И ТОРИОНА
- НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ В РЕНТГЕНОВСКОМ ДИАПАЗОНЕ
- ЗАДАЧИ К ГЛАВЕ V
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ V
- ГЛАВА VI. ДИФФУЗНОЕ ВЕЩЕСТВО В ПРОСТРАНСТВЕ
- ВЫСОКАЯ СПОСОБНОСТЬ ПЫЛИ ЗАДЕРЖИВАТЬ ПРОХОДЯЩИЙ СВЕТ
- ЗАВИСИМОСТЬ ОСЛАБЛЕНИЯ СВЕТА ПЫЛЬЮ ОТ ДЛИНЫ ВОЛНЫ
- ПРАКТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ОБЩЕГО ОСЛАБЛЕНИЯ СВЕТА в ЗАДАННОМ НАПРАВЛЕНИИ
- ОБЛАЧНАЯ СТРУКТУРА ПЫЛЕВОЙ СРЕДЫ В ГАЛАКТИКЕ
- РАСПРЕДЕЛЕНИЕ МЕЖЗВЕЗДНОЙ ПЫЛИ В ГАЛАКТИКЕ
- СВЕТЛЫЕ ПЫЛЕВЫЕ ТУМАННОСТИ
- СВЕТОВОЕ ДАВЛЕНИЕ НА ПЫЛЕВЫЕ ЧАСТИЦЫ
- МЕЖЗВЕЗДНАЯ ПОЛЯРИЗАЦИЯ СВЕТА ЗВЕЗД
- ОРИЕНТИРОВАНИЕ МЕЖЗВЕЗДНЫХ ПЫЛЕВЫХ ЧАСТИЦ МАГНИТНЫМИ ПОЛЯМИ
- § 27. ГАЗОВАЯ СОСТАВЛЯЮЩАЯ МЕЖЗВЕЗДНОЙ СРЕДЫ
- МЕЖЗВЕЗДНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ Са, Na И ДРУГИХ ЭЛЕМЕНТОВ И МОЛЕКУЛ
- ГАЗОВЫЙ ГАЛАКТИЧЕСКИЙ СУБСТРАТ
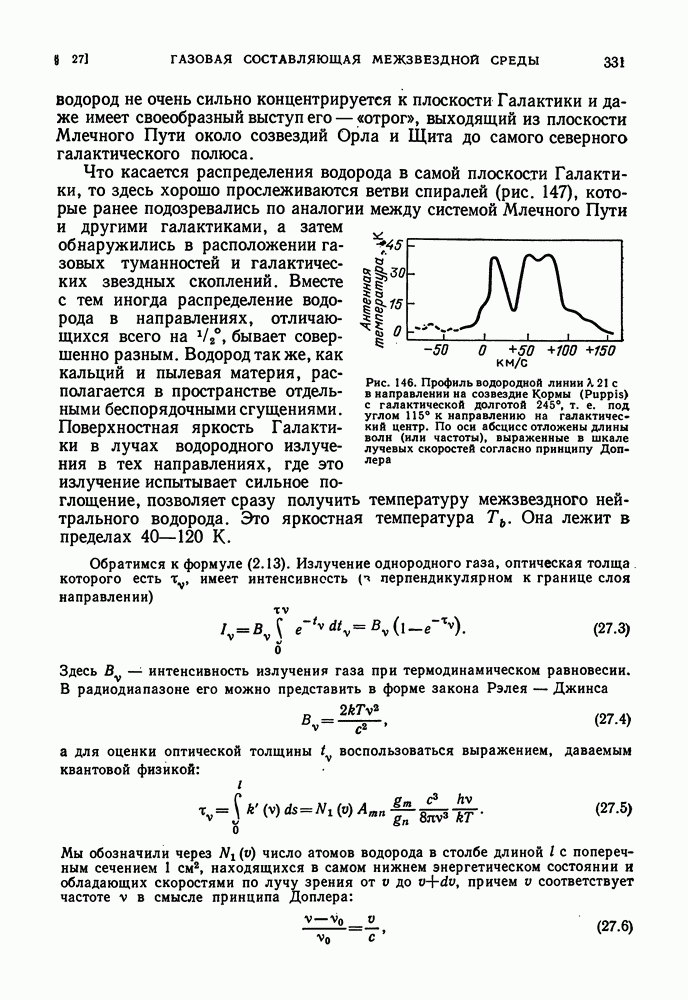
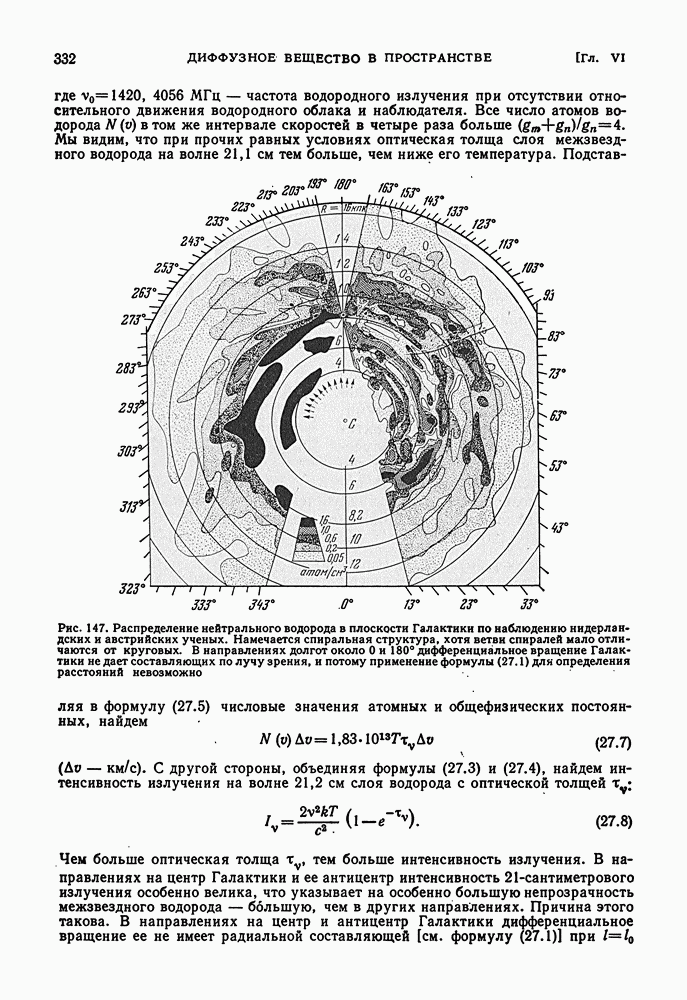
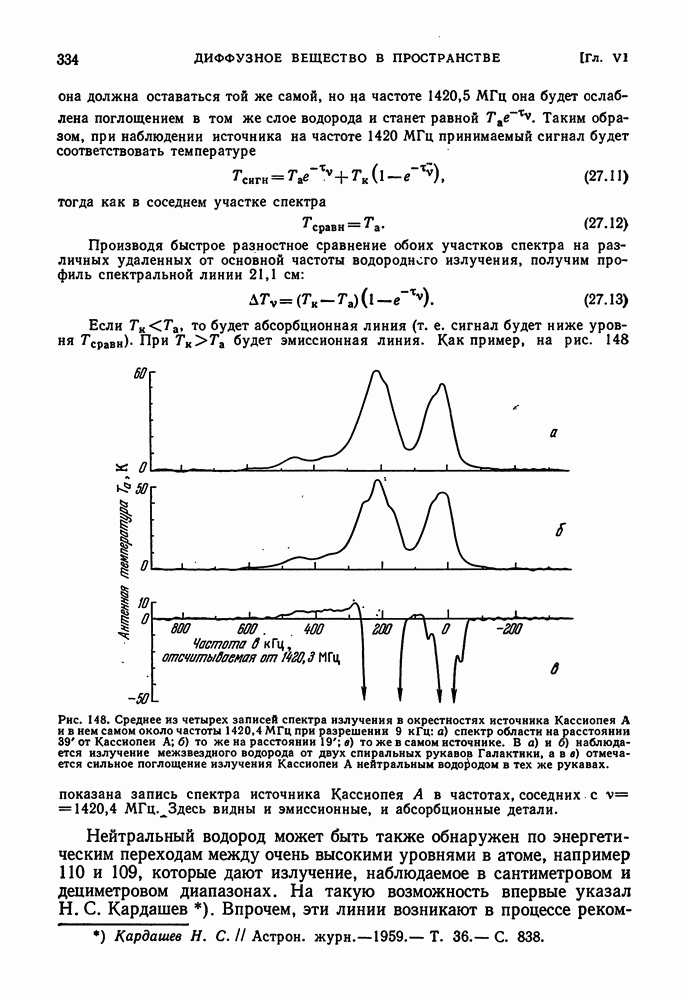
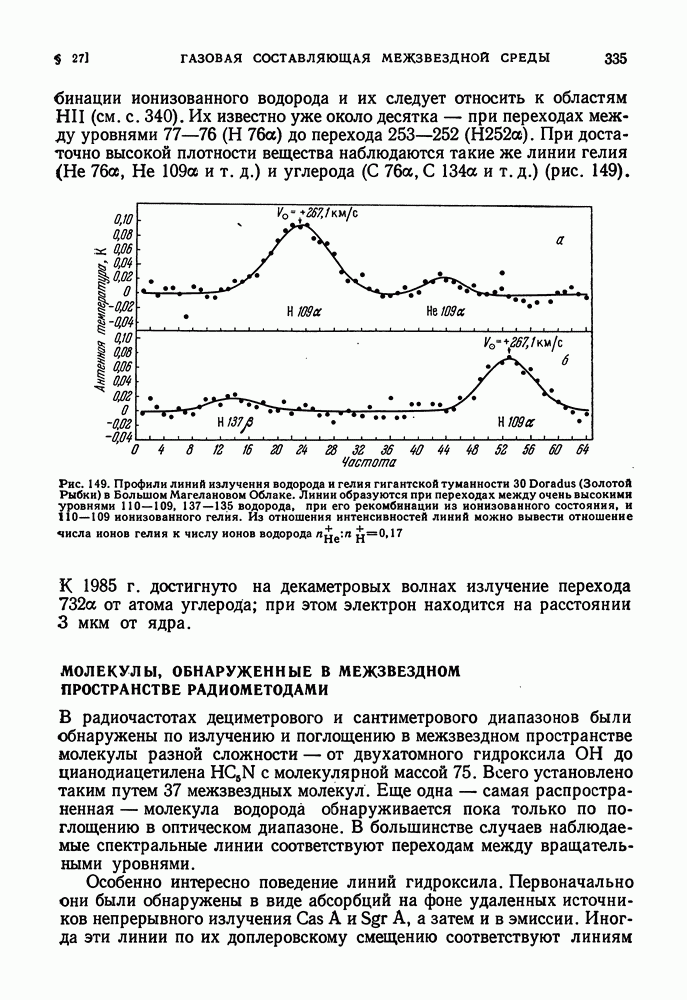
- ИЗЛУЧЕНИЕ МЕЖЗВЕЗДНОГО НЕЙТРАЛЬНОГО ВОДОРОДА НА ВОЛНЕ 21 см
- МОЛЕКУЛЫ, ОБНАРУЖЕННЫЕ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ РАДИОМЕТОДАМИ
- ОТНОСИТЕЛЬНАЯ РОЛЬ ГАЗА И ПЫЛИ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭЛЕКТРОНЫ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ. ОБЛАСТИ HII И HI
- § 28. ГАЗОВЫЕ ТУМАННОСТИ
- ПЛАНЕТАРНЫЕ ТУМАННОСТИ
- ФЛУОРЕСЦЕНЦИЯ ВЕЩЕСТВА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ТЕМПЕРАТУРЫ ЯДЕР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЗАПРЕЩЕННЫЕ ЛИНИИ В СПЕКТРАХ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЭЛЕКТРОННЫЕ ТЕМПЕРАТУРЫ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- НЕПРЕРЫВНЫЙ СПЕКТР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ. ИХ МАССЫ
- РАСШИРЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ПОЛЕ ЛАЙМАНОВСКОГО ИЗЛУЧЕНИЯ В ПЛАНЕТАРНЫХ ТУМАННОСТЯХ
- ГРАНИЦА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ЯДРА ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ПРОИСХОЖДЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ДИФФУЗНЫЕ ГАЗОВЫЕ ТУМАННОСТИ
- ОБЛАСТИ HII И ИХ РАЗМЕРЫ
- ВЗАИМОДЕЙСТВИЕ ГАЗА И ИЗЛУЧЕНИЯ ГОРЯЧЕЙ ЗВЕЗДЫ. ДВИЖЕНИЯ ВНУТРИ ГАЗОВОЙ ТУМАННОСТИ
- РАДИОИЗЛУЧЕНИЕ ГАЗОВЫХ ТУМАННОСТЕЙ
- КРАБОВИДНАЯ ТУМАННОСТЬ — ИСТОЧНИК РАДИОИЗЛУЧЕНИЯ ТЕЛЕЦ А
- ТОРМОЗНОЕ ИЗЛУЧЕНИЕ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ КАК ИСТОЧНИК СВЕЧЕНИЯ КРАБОВИДНОЙ ТУМАННОСТИ
- КРАБОВИДНАЯ И НЕКОТОРЫЕ ДРУГИЕ ТУМАННОСТИ КАК ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ В ПУЛЬСАРАХ
- § 29. ФИЗИЧЕСКОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА В ГАЛАКТИКЕ
- ТЕМПЕРАТУРА ТЕЛА, ПОМЕЩЕННОГО В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭНЕРГЕТИЧЕСКИЙ БАЛАНС У ЧАСТИЦ МЕЖЗВЕЗДНОЙ СРЕДЫ
- РАДИОИЗЛУЧЕНИЕ ИЗ МЕЖЗВЕЗДНОГО ПРОСТРАНСТВА ГАЛАКТИКИ
- КОСМИЧЕСКИЕ ЛУЧИ В ГАЛАКТИКЕ
- МАГНИТНЫЕ ПОЛЯ В ГАЛАКТИКЕ
- КОНДЕНСАЦИИ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА И ЗВЕЗДООБРАЗОВАНИЕ
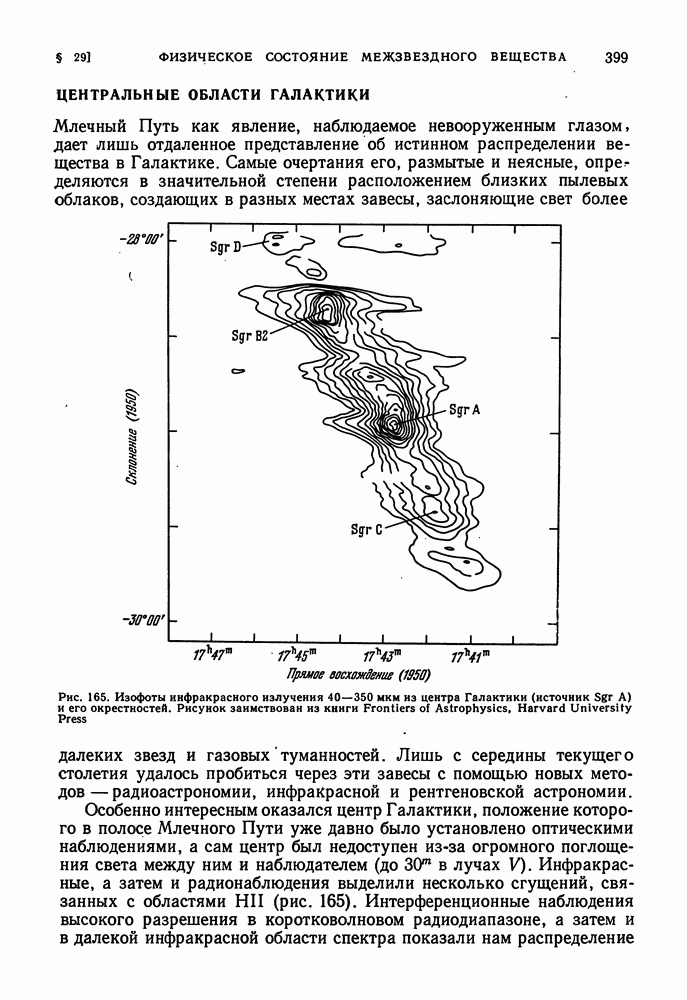
- ЦЕНТРАЛЬНЫЕ ОБЛАСТИ ГАЛАКТИКИ
- ОСОБЕННОСТИ РАСПОЛОЖЕНИЯ И ДВИЖЕНИЯ ГАЗОВЫХ МАСС В ГАЛАКТИКЕ
- МЕЖЗВЕЗДНЫЙ ГАЗ В ГАЛАКТИКЕ (РЕЗЮМЕ). АКТИВНОСТЬ ЯДРА ГАЛАКТИКИ
- ЗАДАЧИ К ГЛАВЕ VI
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VI
- ГЛАВА VII. ГАЛАКТИКИ И МЕТАГАЛАКТИКА
- § 30. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
- КЛАССИФИКАЦИЯ ГАЛАКТИК- ОБЩИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
- ВРАЩЕНИЕ ГАЛАКТИК. ИХ МАССЫ
- КРАСНОЕ СМЕЩЕНИЕ В СПЕКТРАХ ГАЛАКТИК
- ЗАКОН ХАББЛА. ПОСТОЯННАЯ ХАББЛА
- СТРУКТУРА МЕТАГАЛАКТИКИ. СКОПЛЕНИЕ ГАЛАКТИК-ГРУППЫ ГАЛАКТИК
- ЗВЕЗДООБРАЗОВАНИЕ В ГАЛАКТИКАХ
- НЕВИДИМОЕ ВЕЩЕСТВО В ГАЛАКТИКАХ И ИХ СКОПЛЕНИЯХ
- § 31. РАДИОГАЛАКТИКИ И НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ В ГАЛАКТИКАХ
- РАДИОИЗЛУЧЕНИЕ НОРМАЛЬНЫХ ГАЛАКТИК
- РАДИОГАЛАКТИКИ
- ГАЛАКТИКИ СЕЙФЕРТА
- АКТИВНЫЕ ГАЛАКТИКИ И ПРИЗНАКИ ВЗРЫВА В НИХ
- КВАЗАРЫ И РОДСТВЕННЫЕ ИМ ОБЪЕКТЫ
- СПЕКТРАЛЬНЫЙ ИНДЕКС РАДИОИЗЛУЧЕНИЯ. ВОЗРАСТ РАДИОГАЛАКТИК
- ОБЩИЕ ЗАПАСЫ ЭНЕРГИИ В ГАЛАКТИКАХ
- § 32. ГАЛАКТИКИ И КОСМОЛОГИЯ
- ЗАДАЧИ К ГЛАВЕ VII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VII
- ГЛАВА VIII. СОЛНЕЧНАЯ СИСТЕМА. ПЛАНЕТЫ И ИХ СПУТНИКИ
- § 33. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ПЛАНЕТ
- ФОТОМЕТРИЧЕСКИЙ АНАЛИЗ ПЛАНЕТНЫХ ПОВЕРХНОСТЕЙ И АТМОСФЕРЫ
- ПОЛЯРИМЕТРИЯ ПЛАНЕТ
- СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЛАНЕТНЫХ АТМОСФЕР
- СПЕКТРАЛЬНОЕ ОПРЕДЕЛЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ
- ПЛАНЕТНЫЕ ТЕМПЕРАТУРЫ. ТЕОРИЯ. РОЛЬ АТМОСФЕРЫ
- РАЗЛИЧНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЛАНЕТНЫХ ТЕМПЕРАТУР
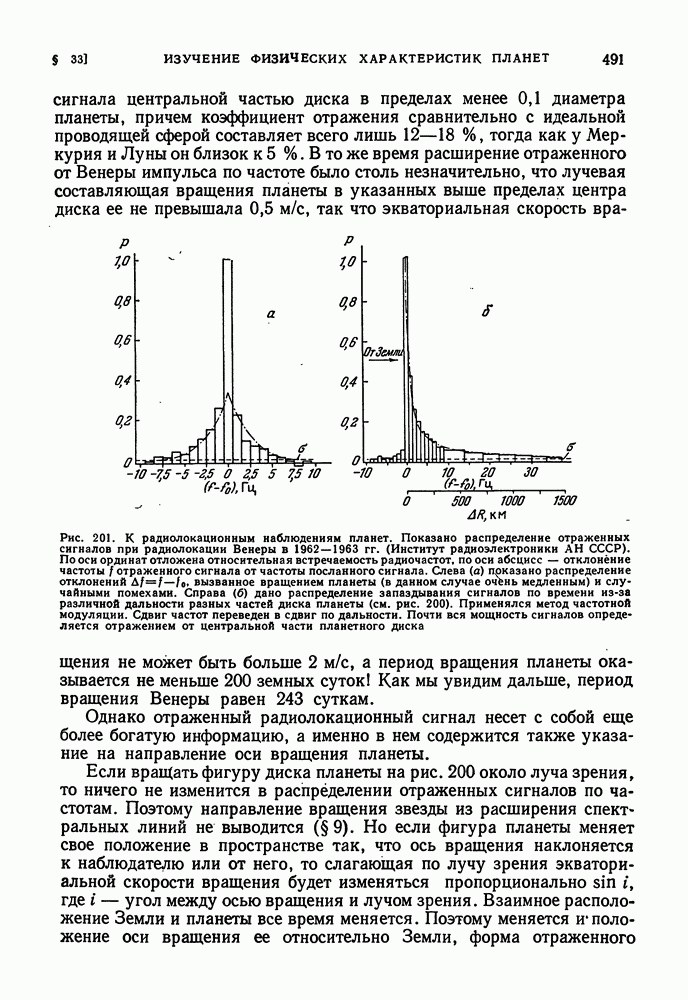
- РАДИОЛОКАЦИОННЫЕ МЕТОДЫ ИЗУЧЕНИЯ ПЛАНЕТ
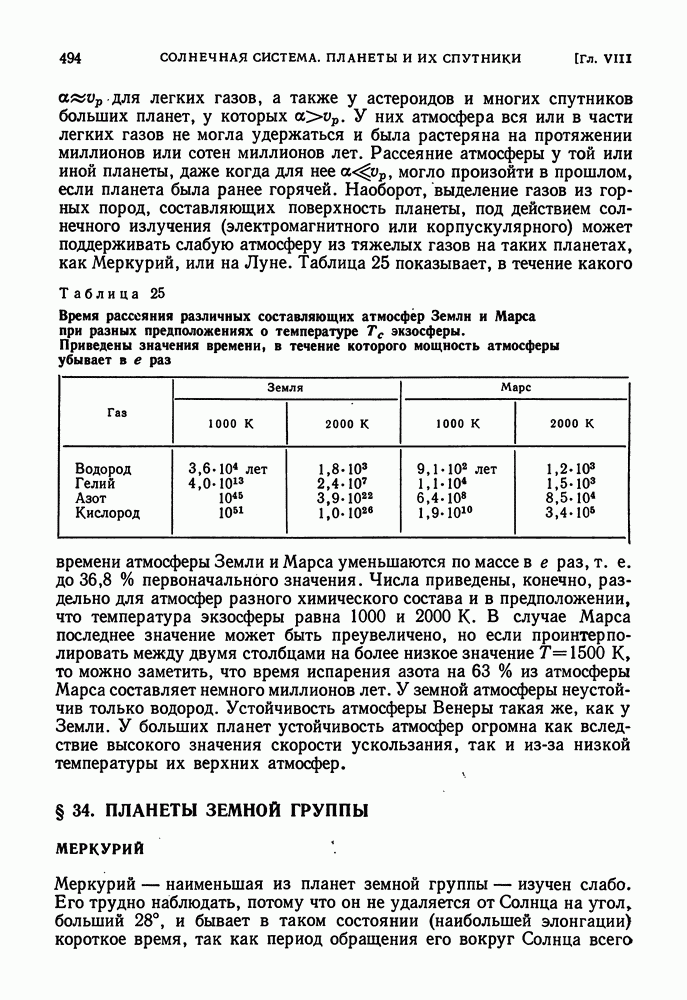
- УСТОЙЧИВОСТЬ ПЛАНЕТНЫХ АТМОСФЕР ВО ВРЕМЕНИ
- § 34. ПЛАНЕТЫ ЗЕМНОЙ ГРУППЫ
- МЕРКУРИЙ
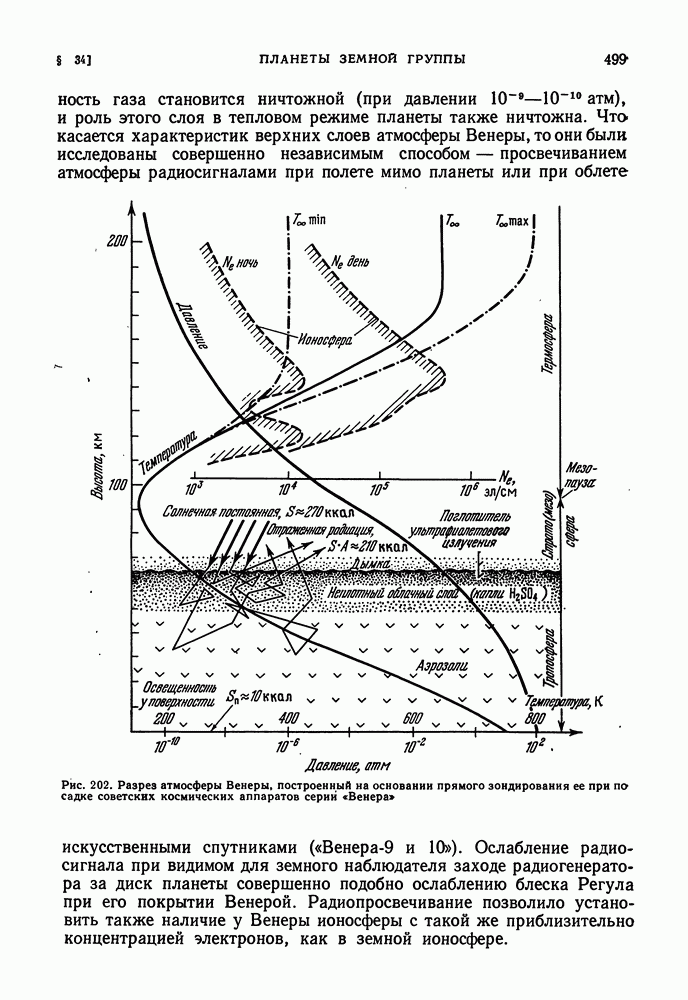
- ВЕНЕРА. ТЕМПЕРАТУРА. ПАРНИКОВАЯ МОДЕЛЬ АТМОСФЕРЫ. ВРАЩЕНИЕ
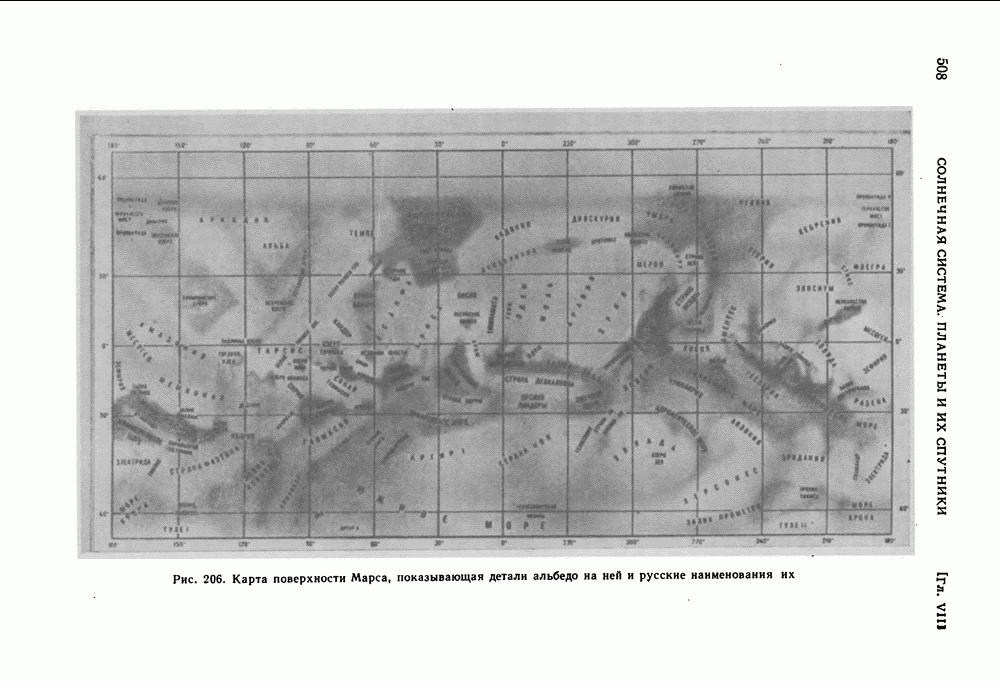
- МАРС. ОСОБЕННОСТИ ЕГО ПОВЕРХНОСТИ. ИХ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ
- АТМОСФЕРА МАРСА
- ТЕМПЕРАТУРА МАРСА
- ВОДА НА МАРСЕ. ЖИЗНЬ НА МАРСЕ?
- МАЛЫЕ ПЛАНЕТЫ
- § 35. ЛУНА
- АТМОСФЕРА ЛУНЫ
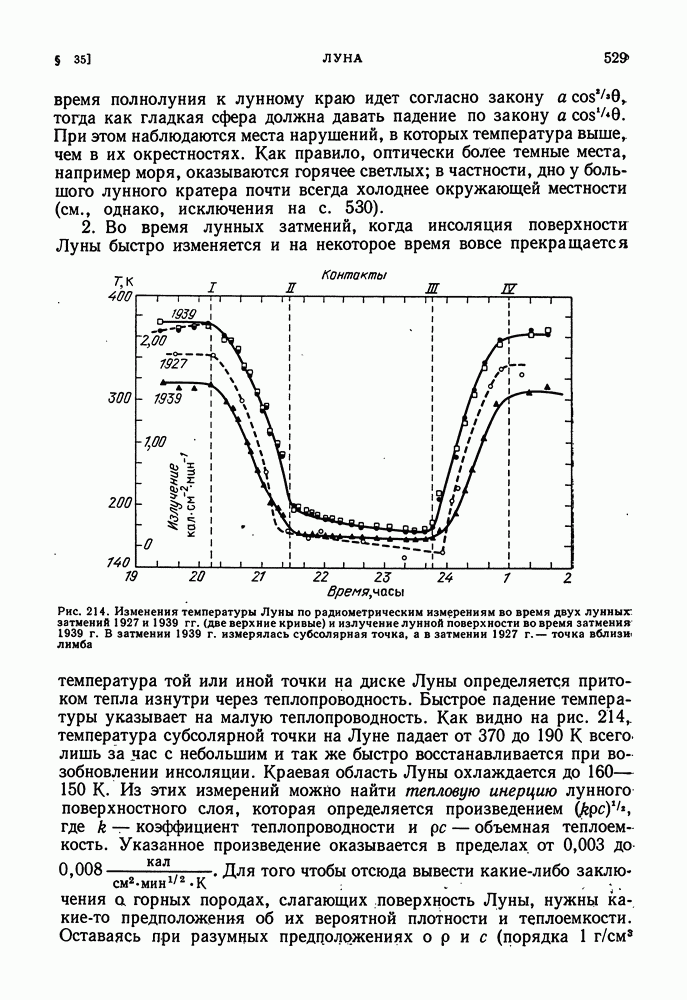
- ТЕМПЕРАТУРНЫЙ РЕЖИМ НА ЛУНЕ
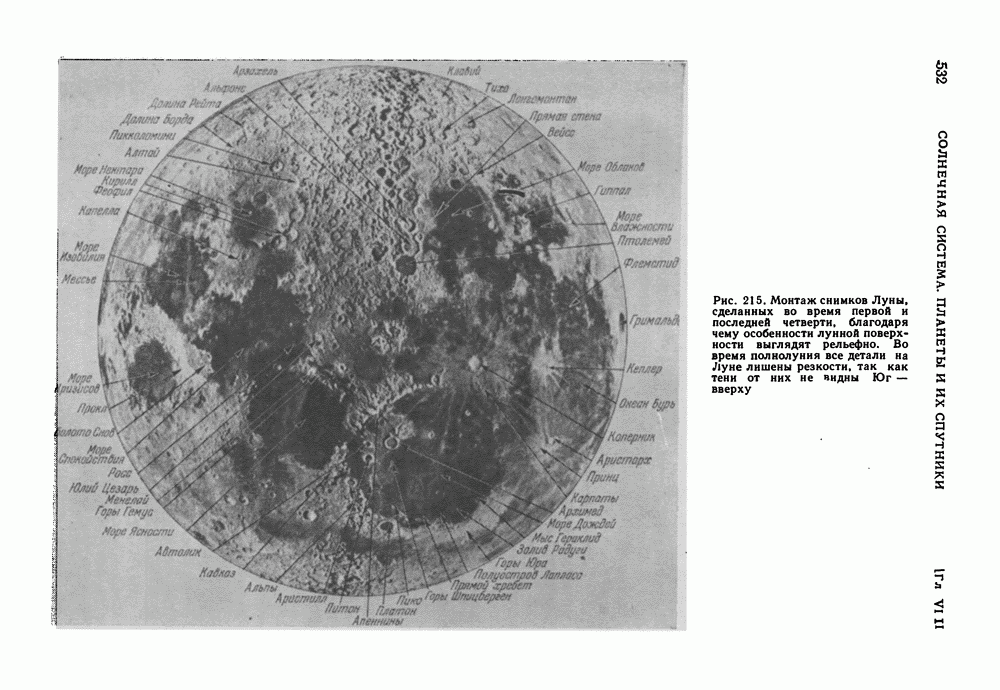
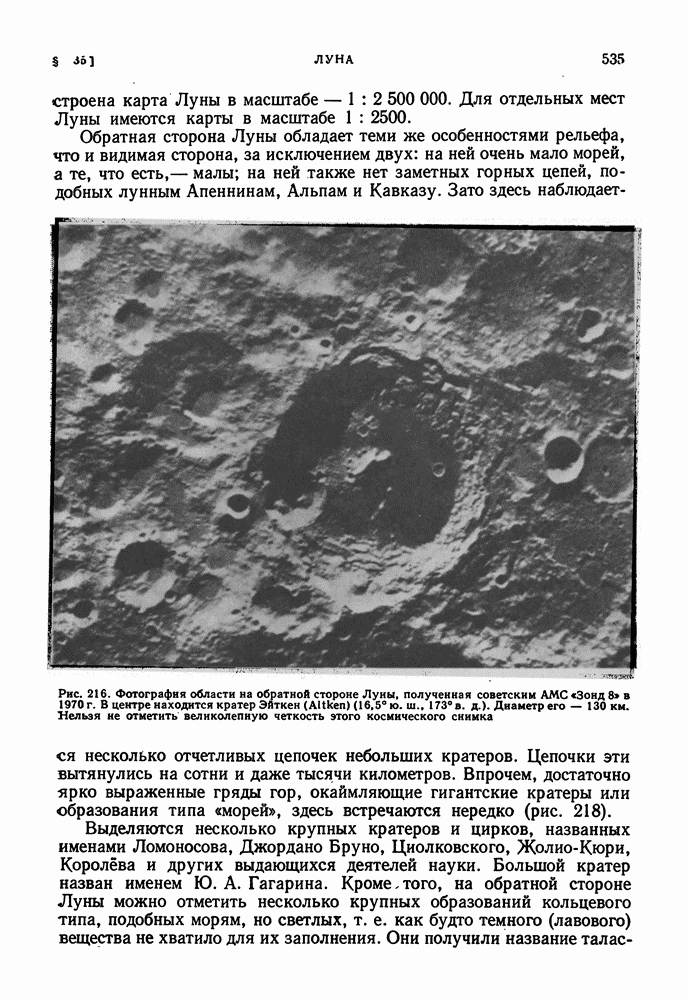
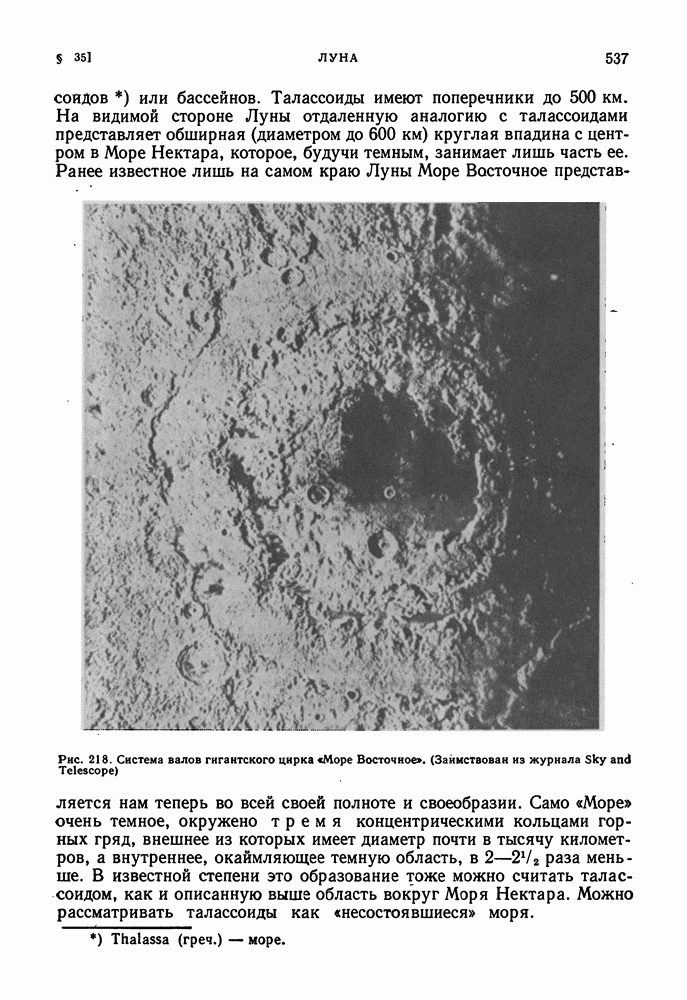
- МОРФОЛОГИЯ ЛУННОЙ ПОВЕРХНОСТИ
- ВНУТРЕННЕЕ СТРОЕНИЕ ЛУНЫ
- ОБРАЗОВАНИЕ СОВРЕМЕННОГО ЛУННОГО ЛАНДШАФТА
- § 36. ВНЕШНИЕ ПЛАНЕТЫ СОЛНЕЧНОЙ СИСТЕМЫ
- ЮПИТЕР
- САТУРН
- УРАН И НЕПТУН
- ПЛУТОН
- ЗАДАЧИ К ГЛАВЕ VIII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VIII
- ГЛАВА IX. СОЛНЕЧНАЯ СИСТЕМА. КОМЕТЫ И МАЛЫЕ ТЕЛА СОЛНЕЧНОЙ СИСТЕМЫ
- ОБЩАЯ ХАРАКТЕРИСТИКА КОМЕТ
- ОБРАЗОВАНИЕ КОМЕТНЫХ ФОРМ
- МЕХАНИЧЕСКАЯ ТЕОРИЯ КОМЕТНЫХ ФОРМ
- СПЕКТРЫ КОМЕТ
- БЛЕСК КОМЕТЫ И ЕГО ИЗМЕНЕНИЯ
- ДАВЛЕНИЕ СВЕТА НА КОМЕТНЫЕ ЧАСТИЦЫ
- СОЛНЕЧНАЯ АКТИВНОСТЬ КАК ИСТОЧНИК ВОЗНИКНОВЕНИЯ КОМЕТНЫХ ФОРМ
- РАСПАД КОМЕТ. ПРОИСХОЖДЕНИЕ КОМЕТ
- КОМЕТА ГАЛЛЕЯ В 1986 г.
- § 38. МЕТЕОРЫ
- ОБЩИЕ ХАРАКТЕРИСТИКИ МЕТЕОРОВ. СПОСОБЫ ИХ НАБЛЮДЕНИЯ
- МЕТЕОРНЫЕ ПОТОКИ И СПОРАДИЧЕСКИЕ МЕТЕОРЫ
- ЯВЛЕНИЯ ПРИ ВТОРЖЕНИИ МЕТЕОРНОГО ТЕЛА В ЗЕМНУЮ АТМОСФЕРУ
- РАДИОЛОКАЦИОННЫЕ НАБЛЮДЕНИЯ МЕТЕОРОВ
- МАССЫ МЕТЕОРНЫХ ТЕЛ
- МЕТЕОРИТЫ И ИХ КЛАССИФИКАЦИЯ
- ВОЗРАСТ МЕТЕОРИТОВ
- МЕТЕОРИТНЫЕ КРАТЕРЫ И ВОРОНКИ
- ТУНГУССКИЙ МЕТЕОРИТ
- § 39. МЕТЕОРНОЕ И ПЫЛЕВОЕ ВЕЩЕСТВО В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
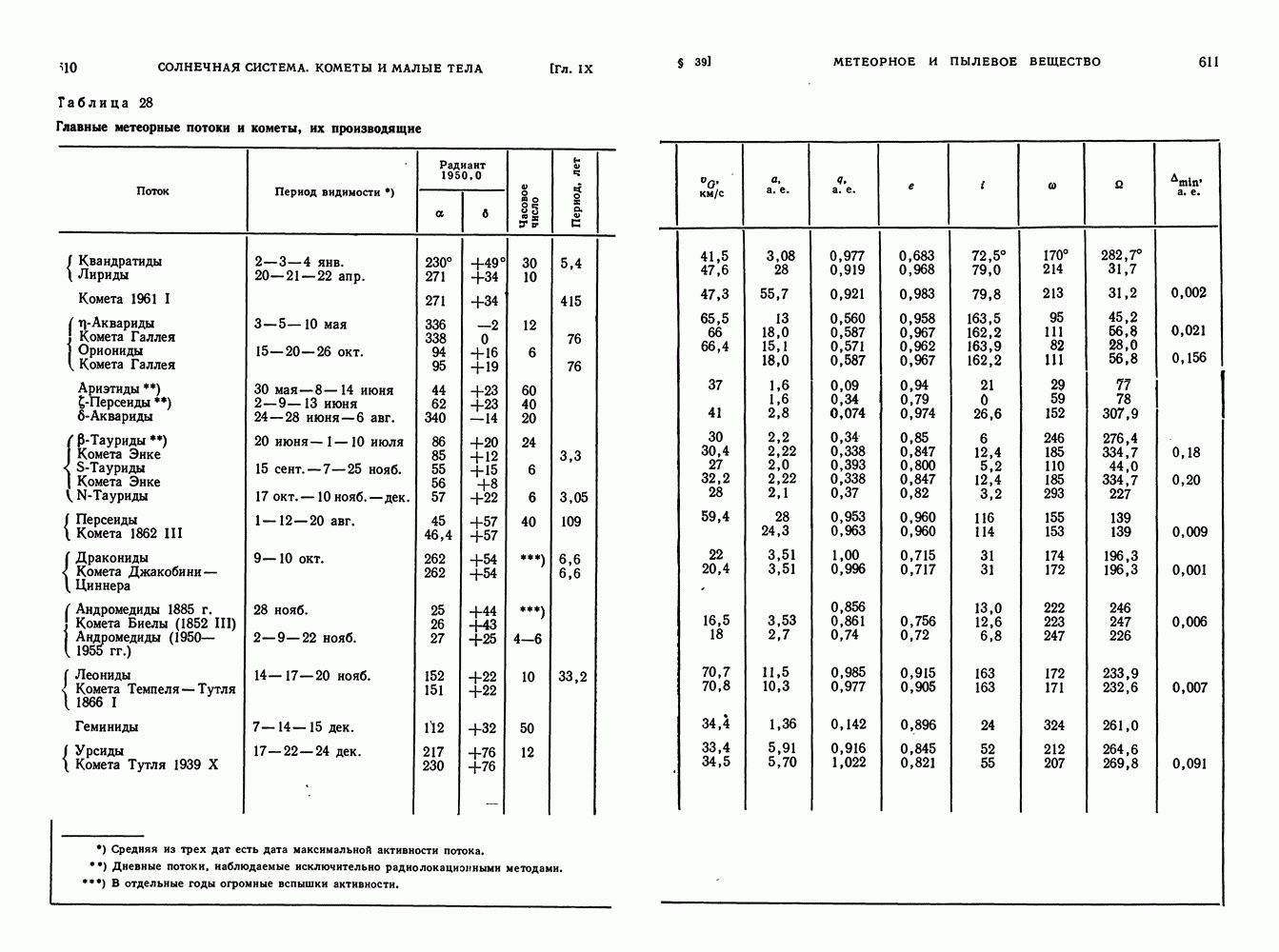
- МЕТЕОРНЫЕ РОИ И СВЯЗЬ ИХ С КОМЕТАМИ
- МИКРОМЕТЕОРИТЫ
- МЕТЕОРНОЕ ВЕЩЕСТВО ВОКРУГ ЗЕМЛИ
- ЗОДИАКАЛЬНЫЙ СВЕТ
- ПЫЛЕВАЯ И ГАЗОВАЯ СОСТАВЛЯЮЩИЕ В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- ДВИЖЕНИЕ МАЛОЙ ЧАСТИЦЫ В ПОЛЕ ТЯГОТЕНИЯ И ИЗЛУЧЕНИЯ СОЛНЦА
- ПРОТИВОСИЯНИЕ
- ЗАДАЧИ К ГЛАВЕ IX