| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ПОЛИТРОПНЫЕ МОДЕЛИ ЗВЕЗД
Одной из таких общих моделей, разработанных с исчерпывающей полнотой, является политропная модель, рассмотренная Риттером, а затем Эмденом в начале XX столетия. Политропные модели полагают в основу следующий закон изменений упругости газа р в зависимости от плотности р:
 (15.39)
(15.39)
Это — уравнение политропы. Формально оно не отличается от уравнения адиабаты (15.34), но, в отличие от последнего, в нем постоянный показатель k не есть отношение  а может быть любой положительной величиной (в том числе и величиной
а может быть любой положительной величиной (в том числе и величиной  ). Постоянство k выражает лишь один факт — политропные изменения вещества звезды происходят так, что теплоемкость его неизменна. Удобно представить k таким образом:
). Постоянство k выражает лишь один факт — политропные изменения вещества звезды происходят так, что теплоемкость его неизменна. Удобно представить k таким образом:

и тогда n называют показателем политропии. Практические значения для нашей теории имеют только значения n в пределах
 (15.41)
(15.41)
n = 0 соответствует однородному шару, а  — изотермическому; при
— изотермическому; при  газовый шар имеет бесконечно большие размеры. Шар из идеального одноатомного газа в конвективном равновесии имеет адиабатическое значение
газовый шар имеет бесконечно большие размеры. Шар из идеального одноатомного газа в конвективном равновесии имеет адиабатическое значение  или
или  . Газовый шар в лучистом равновесии имеет показатель политропии
. Газовый шар в лучистом равновесии имеет показатель политропии  , но из этого не следует, что истинная структура звезды заключена между политропными структурами
, но из этого не следует, что истинная структура звезды заключена между политропными структурами  , так как политропные структуры вообще представляют лишь формальное приближение к структуре звезды — они совершенно обходят вопрос о поддержании звездного лучеиспускания. Тем не менее характеристики газовых шаров
, так как политропные структуры вообще представляют лишь формальное приближение к структуре звезды — они совершенно обходят вопрос о поддержании звездного лучеиспускания. Тем не менее характеристики газовых шаров  в общем правильно указывают на порядок величин центральной плотности, температуры и давления.
в общем правильно указывают на порядок величин центральной плотности, температуры и давления.
В частности, центральная плотность  относится к средней р при различных классах политроиии следующим образом:
относится к средней р при различных классах политроиии следующим образом:

С возрастанием класса политропии возрастает и центральная температура, но не столь быстро. Конечно, она зависит от массы звезды и ее радиуса.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ГЛАВА I. СОЛНЦЕ
- ВНЕШНИЙ ВИД СОЛНЦА. ФОТОСФЕРА
- ВРАЩЕНИЕ СОЛНЦА
- ПЕРИОДИЧНОСТЬ СОЛНЕЧНОЙ ПЯТНООБРАЗОВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
- § 2. ЭЛЕМЕНТЫ ТЕОРИИ СОЛНЕЧНОЙ АТМОСФЕРЫ
- УРАВНЕНИЕ ЛУЧИСТОГО РАВНОВЕСИЯ И ЕГО ПРИБЛИЖЕННОЕ РЕШЕНИЕ
- МОДЕЛЬ СОЛНЕЧНОЙ АТМОСФЕРЫ
- КОНВЕКЦИЯ В СОЛНЕЧНОЙ АТМОСФЕРЕ
- ИОНИЗАЦИЯ СОЛНЕЧНОГО ВЕЩЕСТВА
- СОЛНЕЧНАЯ ПЛАЗМА И ЕЕ ВЗАИМОДЕЙСТВИЕ С МАГНИТНЫМИ ПОЛЯМИ
- § 3. СОЛНЕЧНЫЙ СПЕКТР. ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА
- ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА. КАЧЕСТВЕННЫЙ АНАЛИЗ
- КОЛИЧЕСТВЕННЫЙ ХИМИЧЕСКИЙ АНАЛИЗ СОЛНЕЧНОЙ АТМОСФЕРЫ
- § 4. ВЕРХНЯЯ АТМОСФЕРА СОЛНЦА
- ОБРАЩАЮЩИЙ СЛОЙ И ХРОМОСФЕРА. ПРИЧИНА ИХ ВИДИМОСТИ ЗА ПРЕДЕЛАМИ СОЛНЕЧНОГО ДИСКА
- НАБЛЮДЕНИЯ ХРОМОСФЕРЫ НА ДИСКЕ СОЛНЦА. СПЕКТРОГЕЛИОГРАФ
- ХРОМОСФЕРНЫЕ ФАКЕЛЫ, ФЛОККУЛЫ И ВОЛОКНА. СПИКУЛЫ
- ПРОТУБЕРАНЦЫ
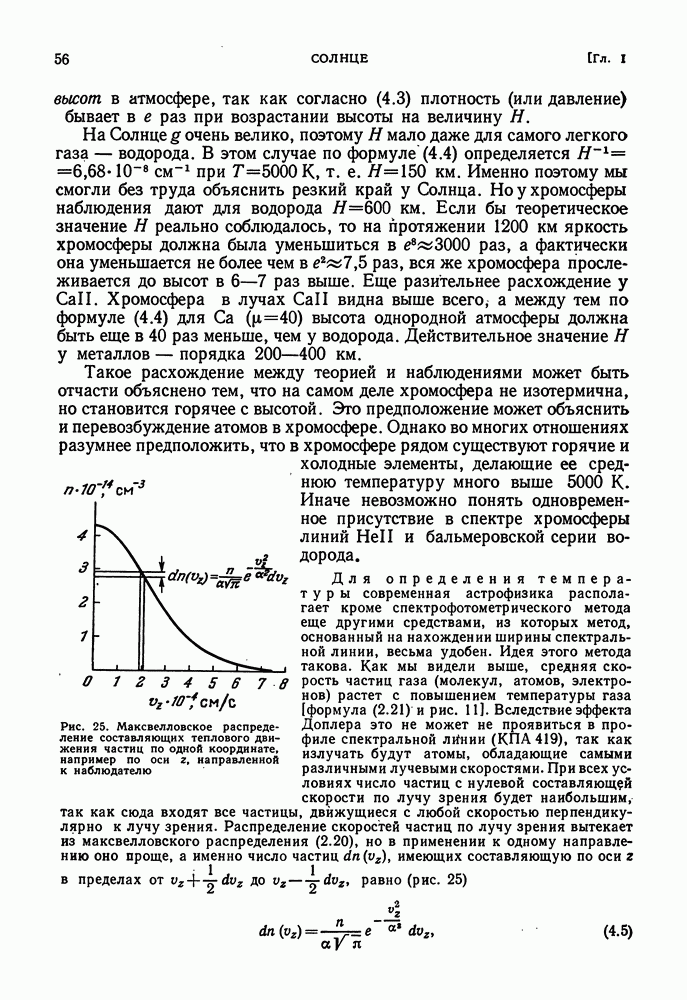
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ ХРОМОСФЕРЫ. ВОЛНОВЫЕ ДВИЖЕНИЯ В АТМОСФЕРЕ СОЛНЦА
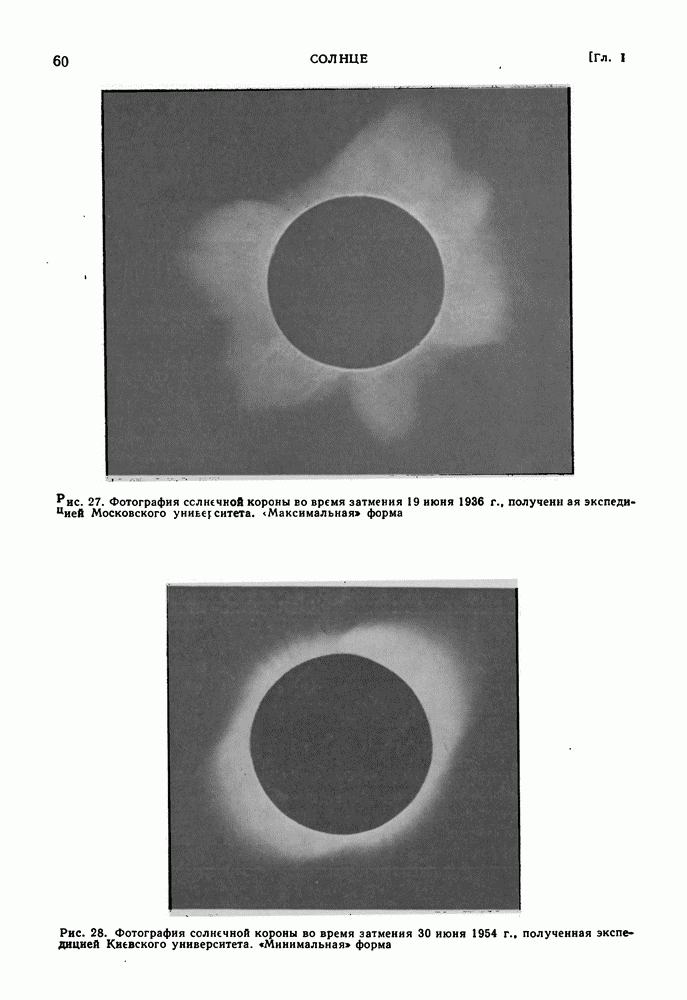
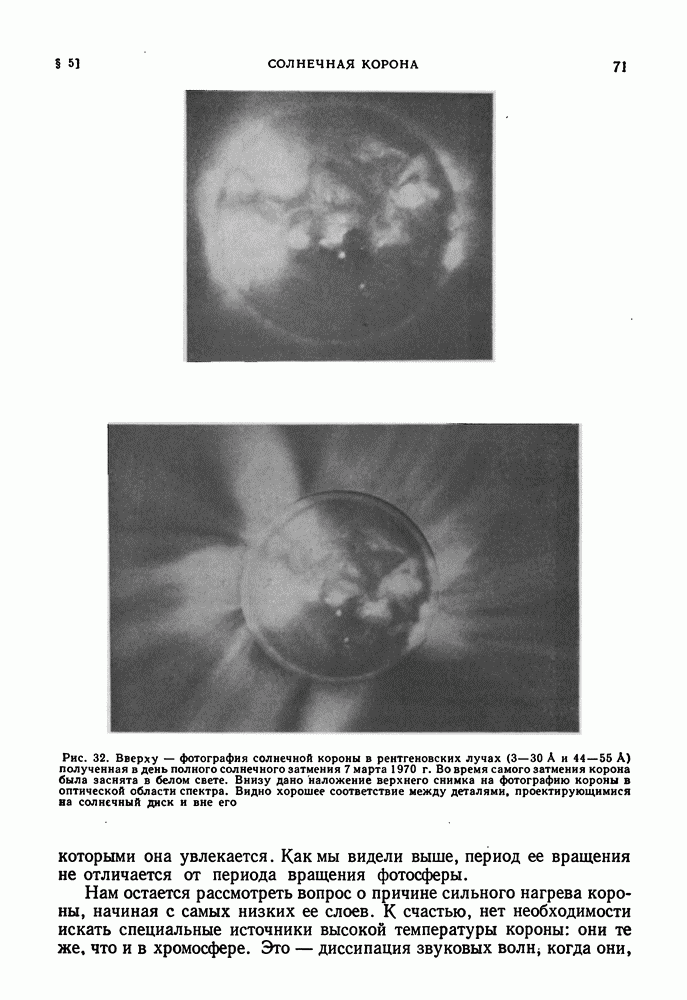
- § 5. СОЛНЕЧНАЯ КОРОНА
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ КОРОНЫ
- ЭМИССИОННЫЙ СПЕКТР КОРОНЫ И ЕГО ИНТЕРПРЕТАЦИЯ
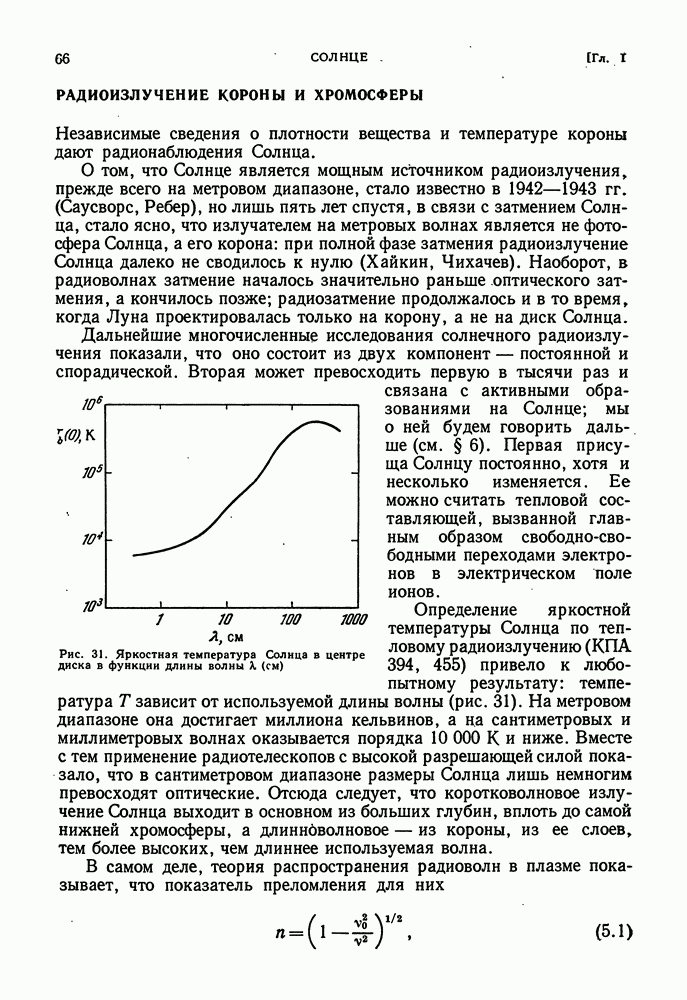
- РАДИОИЗЛУЧЕНИЕ КОРОНЫ И ХРОМОСФЕРЫ
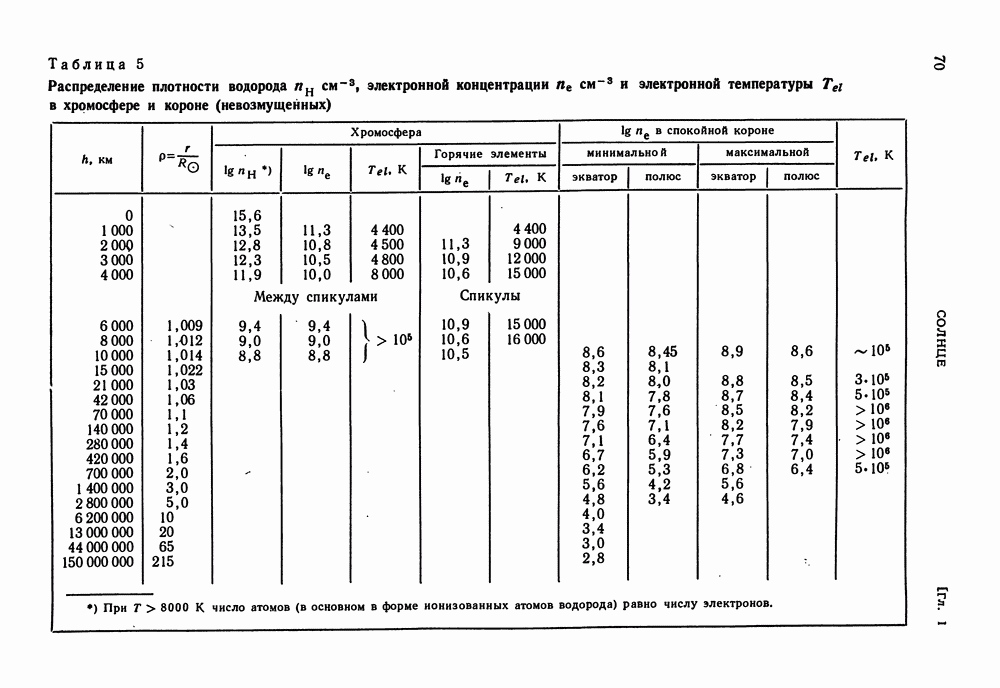
- НЕПРЕРЫВНОЕ ИЗЛУЧЕНИЕ КОРОНЫ. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ И ТЕМПЕРАТУРЫ В ХРОМОСФЕРЕ И КОРОНЕ
- § 6. НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ НА СОЛНЦЕ
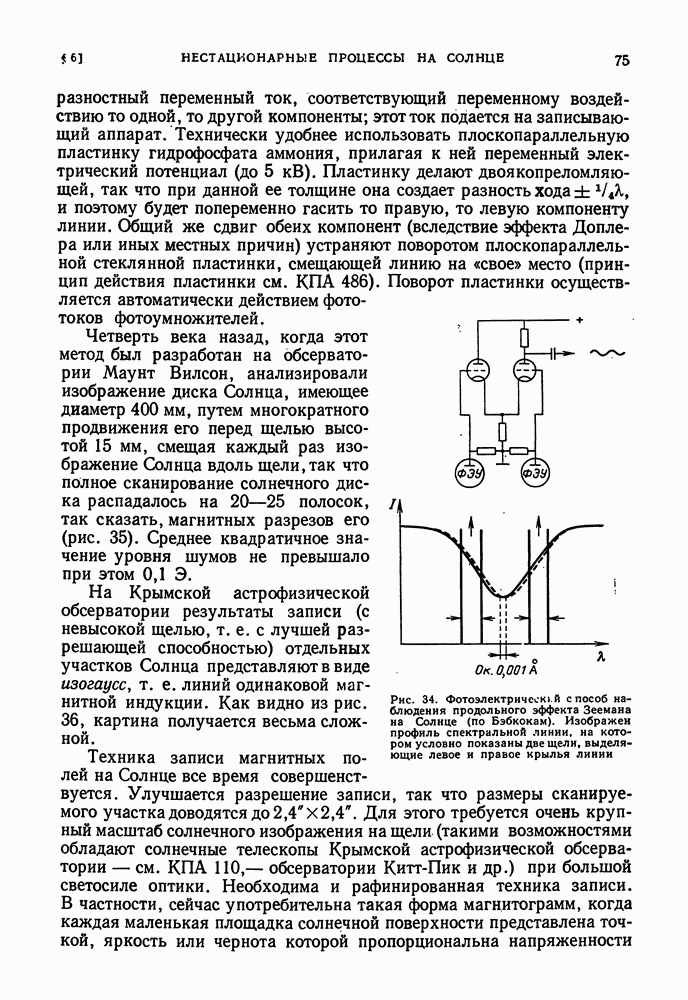
- ОБНАРУЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ НА СОЛНЦЕ
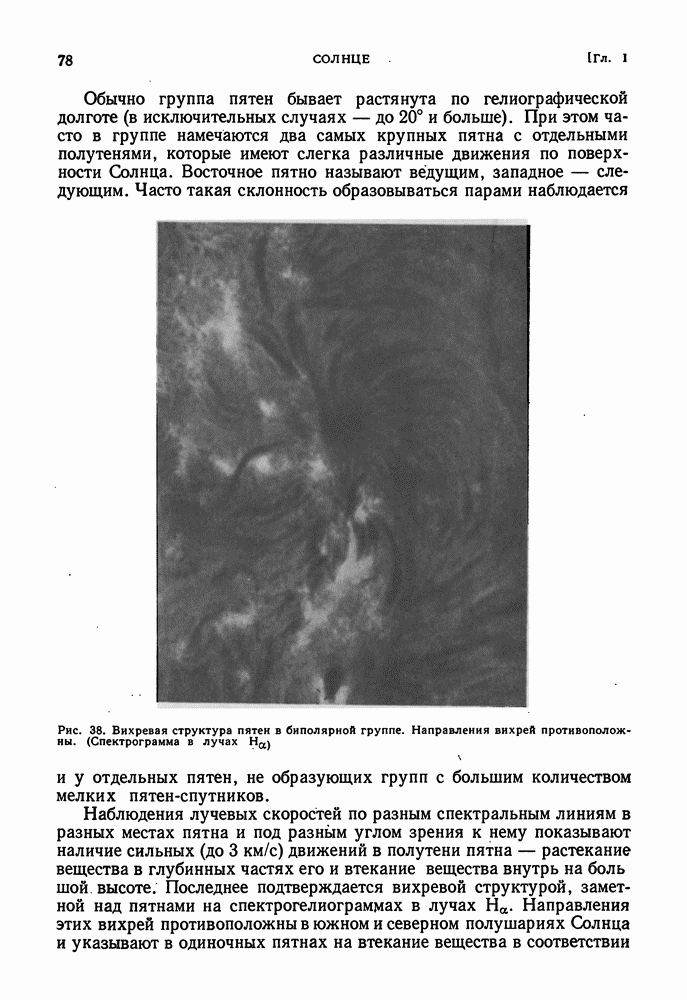
- СОЛНЕЧНЫЕ ПЯТНА И ИХ МАГНИТНЫЕ ПОЛЯ
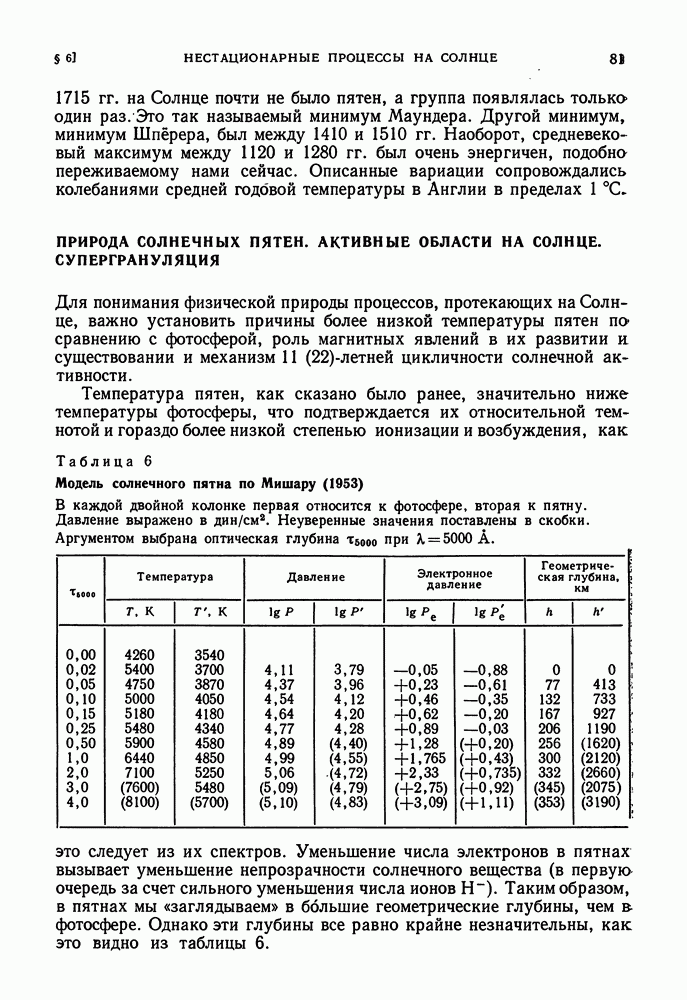
- ПРИРОДА СОЛНЕЧНЫХ ПЯТЕН. АКТИВНЫЕ ОБЛАСТИ НА СОЛНЦЕ. СУПЕРГРАНУЛЯЦИЯ
- ПРОТУБЕРАНЦЫ
- ПРОЯВЛЕНИЕ СОЛНЕЧНОЙ АКТИВНОСТИ В КОРОНЕ
- СОЛНЕЧНЫЕ ВСПЫШКИ
- СПОРАДИЧЕСКОЕ РАДИОИЗЛУЧЕНИЕ СОЛНЦА
- КОРПУСКУЛЯРНОЕ ИЗЛУЧЕНИЕ СОЛНЦА
- § 7. СВЯЗЬ МЕЖДУ СОЛНЕЧНЫМИ И ЗЕМНЫМИ ЯВЛЕНИЯМИ
- ПОЛЯРНЫЕ СИЯНИЯ
- ВЕРХНЯЯ АТМОСФЕРА ЗЕМЛИ. ИОНОСФЕРА. ВОЗДЕЙСТВИЕ НА НИХ СОЛНЦА
- ЯВЛЕНИЯ НА ЗЕМЛЕ, ПРОИСХОДЯЩИЕ ВО ВРЕМЯ ПЕРИОДОВ ПОВЫШЕННОЙ СОЛНЕЧНОЙ АКТИВНОСТИ
- РАДИАЦИОННЫЕ ПОЯСА ЗЕМЛИ
- ДВИЖЕНИЕ КОРПУСКУЛЯРНЫХ потоков В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- СОЛНЕЧНЫЙ ВЕТЕР И МАГНИТОСФЕРА ЗЕМЛИ
- ЗАДАЧИ К ГЛАВЕ I
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ I
- ГЛАВА III. ЗВЕЗДНЫЕ АТМОСФЕРЫ
- § 8. СПЕКТРЫ ЗВЕЗД
- РАЗЛИЧИЯ В СПЕКТРАХ ГИГАНТОВ И КАРЛИКОВ
- ВЛИЯНИЕ РАЗНЫХ ФИЗИЧЕСКИХ ФАКТОРОВ НА ВИД И ИНТЕНСИВНОСТЬ СПЕКТРАЛЬНЫХ ЛИНИЙ
- СПЕКТРАЛЬНЫЕ ПАРАЛЛАКСЫ И ДВУМЕРНАЯ СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ
- § 9. МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. ХИМИЧЕСКИЙ СОСТАВ ЗВЕЗД
- МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. СРЕДНИЙ ХИМИЧЕСКИЙ СОСТАВ АТМОСФЕР ЗВЕЗД
- УКЛОНЕНИЯ ХИМИЧЕСКОГО СОСТАВА ЗВЕЗД ОТ СРЕДНЕГО
- СПЕКТРЫ БЕЛЫХ КАРЛИКОВ
- ЗВЕЗДЫ ПОНИЖЕННОЙ СВЕТИМОСТИ
- МАГНИТНЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- ВЛИЯНИЕ ВРАЩЕНИЯ ЗВЕЗДЫ НА ЕЕ СПЕКТР
- ЭФФЕКТ ТУРБУЛЕНТНОСТИ
- § 10. ВЗАИМНЫЕ СВЯЗИ МЕЖДУ ВНЕШНИМИ ХАРАКТЕРИСТИКАМИ ЗВЕЗД
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА
- СВЯЗЬ МЕЖДУ ПОЛОЖЕНИЕМ ЗВЕЗДЫ НА ДИАГРАММЕ Г — Р И ЕЕ ДВИЖЕНИЕМ В ГАЛАКТИКЕ
- ЗВЕЗДЫ СФЕРИЧЕСКОЙ И ПЛОСКОЙ СОСТАВЛЯЮЩИХ. РАЗЛИЧИЕ ИХ ДИАГРАММ Г — Р
- РАЗНООБРАЗИЕ СВЕТИМОСТЕЙ И РАЗМЕРОВ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ II
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ II
- ГЛАВА III. ДВОЙНЫЕ ЗВЕЗДЫ И МАССЫ ЗВЕЗД
- ВИЗУАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- НЕВИДИМЫЕ СПУТНИКИ ЗВЕЗД
- СПЕКТРАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- ШИРОКИЕ И ТЕСНЫЕ ПАРЫ
- ЗАТМЕННЫЕ ИЛИ ФОТОМЕТРИЧЕСКИЕ ДВОЙНЫЕ ЗВЕЗДЫ
- § 12. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ ХАРАКТЕРИСТИК ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- КРИВАЯ ЛУЧЕВЫХ СКОРОСТЕЙ И ЭЛЕМЕНТЫ ОРБИТЫ СПЕКТРАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- ОПРЕДЕЛЕНИЕ МАСС КОМПОНЕНТ СПЕКТРАЛЬНО-ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ФОТОМЕТРИЧЕСКОЙ ОРБИТЫ
- ОПРЕДЕЛЕНИЕ ЭКСЦЕНТРИСИТЕТА ОРБИТЫ У ЗАТМЕННОЙ ДВОЙНОЙ ВРАЩЕНИЕ ЛИНИИ АПСИД
- ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ КОМПОНЕНТ ФОТОМЕТРИЧЕСКИХ ДВОЙНЫХ ЗВЕЗД
- ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОЙ ТЕМПЕРАТУРЫ ЗАТМЕННЫХ ДВОЙНЫХ ЗВЕЗД
- § 13. МАССЫ И ДРУГИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВОЙНЫХ ЗВЕЗД. ЗАКОН МАССА — СВЕТИМОСТЬ
- § 14. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВЕЗД В ДВОЙНЫХ СИСТЕМАХ
- РАЗНЫЕ ТИПЫ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- КОНТАКТНЫЕ СИСТЕМЫ
- ТРИ ТИПА ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- ОСЕВОЕ ВРАЩЕНИЕ КОМПОНЕНТ В ТЕСНЫХ ПАРАХ
- ГАЗОВЫЕ ПОТОКИ В ТЕСНЫХ ПАРАХ
- МНОГОЧИСЛЕННОСТЬ ДВОЙНЫХ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ III
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ III
- ГЛАВА IV. ВНУТРЕННЕЕ СТРОЕНИЕ ЗВЕЗД
- ОБЩИЕ СООБРАЖЕНИЯ. СОСТОЯНИЕ ВЕЩЕСТВА В НЕДРАХ ЗВЕЗД
- ЛУЧИСТОЕ ДАВЛЕНИЕ В ЗВЕЗДАХ
- ЛУЧИСТЫЙ И КОНВЕКТИВНЫЙ ПЕРЕНОС ТЕПЛА ВНУТРИ ЗВЕЗДЫ
- ГОМОЛОГИЧЕСКИЕ КОНФИГУРАЦИИ
- ПОЛИТРОПНЫЕ МОДЕЛИ ЗВЕЗД
- § 16. ЛУЧЕИСПУСКАНИЕ ЗВЕЗДЫ
- ИСТОЧНИКИ НЕПРОЗРАЧНОСТИ ЗВЕЗДНОГО ВЕЩЕСТВА
- ЗАВИСИМОСТЬ ЛУЧЕИСПУСКАНИЯ ЗВЕЗДЫ ОТ ИСТОЧНИКОВ ЭНЕРГИИ И НЕПРОЗРАЧНОСТИ
- § 17. ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ГРАВИТАЦИОННОЕ СЖАТИЕ
- ТЕРМОЯДЕРНЫЕ ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ПРОТОН-ПРОТОННАЯ РЕАКЦИЯ
- УГЛЕРОДНО-АЗОТНЫЙ ЦИКЛ
- ТРАНСФОРМАЦИЯ ГЕЛИЯ В ЗВЕЗДАХ
- § 18. ЗВЕЗДНЫЕ МОДЕЛИ
- БЕЛЫЕ КАРЛИКИ
- НЕЙТРОННЫЕ ЗВЕЗДЫ. ПУЛЬСАРЫ
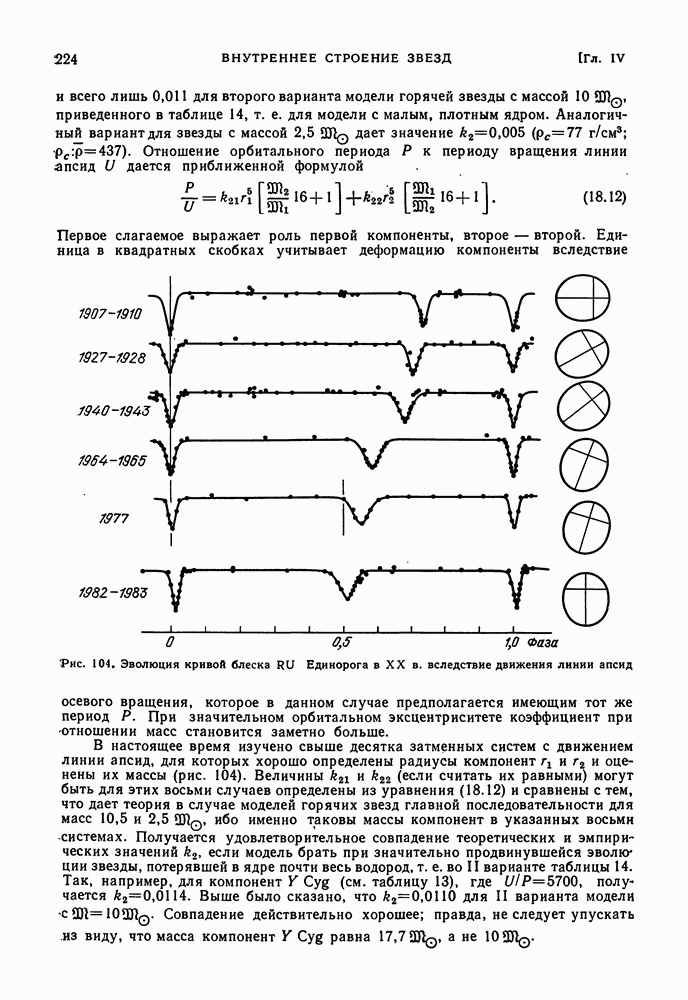
- ПРОВЕРКА ТЕОРИИ ПО ВРАЩЕНИЮ ЛИНИИ АПСИД В ТЕСНЫХ СИСТЕМАХ И ПО СОЛНЕЧНЫМ ПУЛЬСАЦИЯМ
- § 19. ЭВОЛЮЦИЯ ЗВЕЗД
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЭВОЛЮЦИЯ ЗВЕЗД
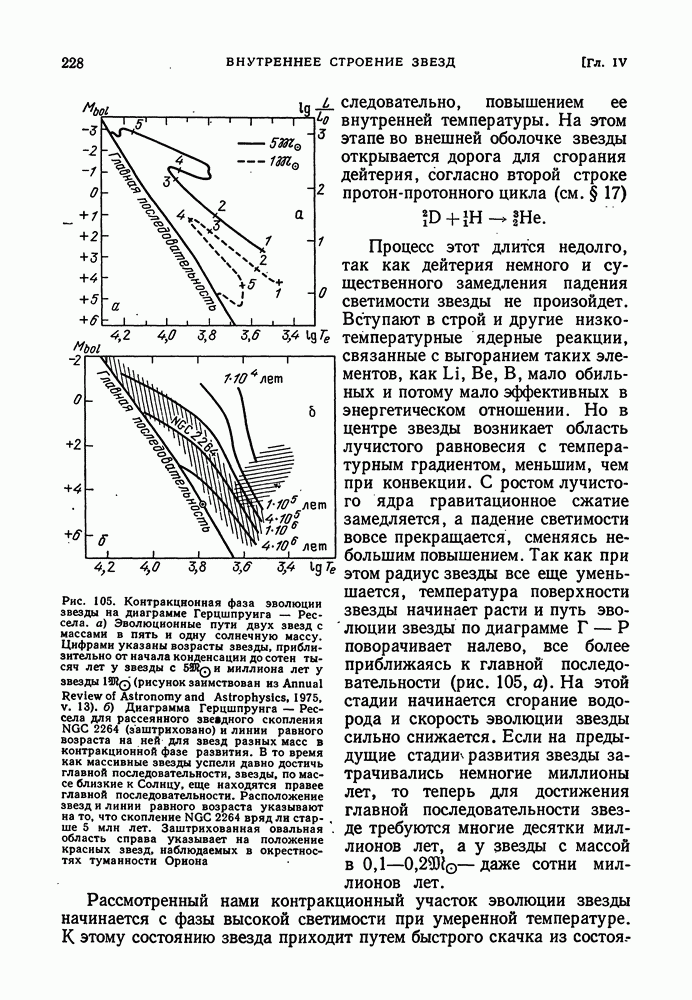
- КОНТРАКЦИОННАЯ ФАЗА ЗВЕЗДНОЙ ЭВОЛЮЦИИ
- ЭВОЛЮЦИЯ ЗВЕЗД НА ТЕРМОЯДЕРНОЙ ОСНОВЕ
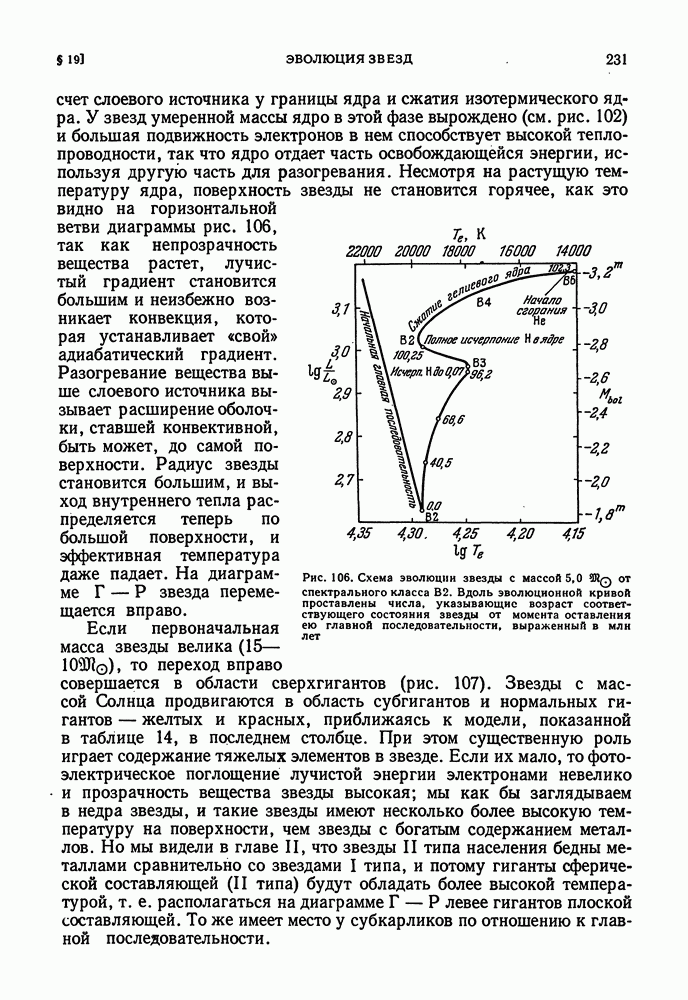
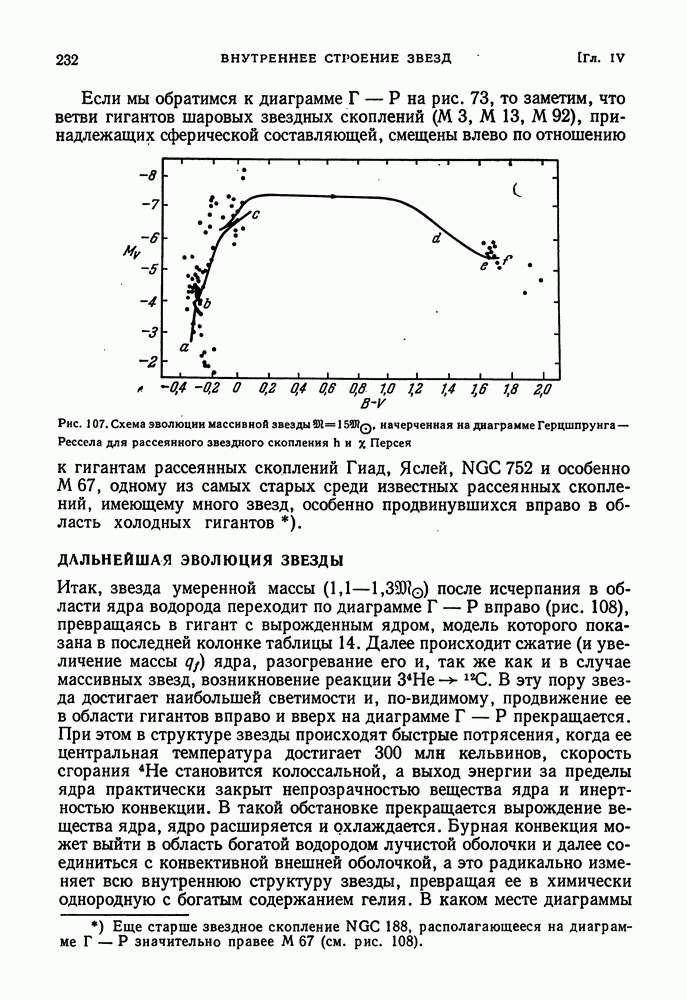
- ЭВОЛЮЦИЯ К КРАСНЫМ ГИГАНТАМ
- ДАЛЬНЕЙШАЯ ЭВОЛЮЦИЯ ЗВЕЗДЫ
- § 20. ЭВОЛЮЦИЯ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- СОВРЕМЕННАЯ РАСПРОСТРАНЕННОСТЬ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ ВО ВСЕЛЕННОЙ
- ТЕРМОЯДЕРНЫЕ РЕАКЦИИ С ОБРАЗОВАНИЕМ ЭЛЕМЕНТОВ БОЛЕЕ ТЯЖЕЛЫХ, ЧЕМ 12С
- ЗВЕЗДЫ РАЗНОГО ВОЗРАСТА И ИХ ХИМИЧЕСКИЙ СОСТАВ
- ЗАДАЧИ К ГЛАВЕ IV
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ IV
- ГЛАВА V. НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ
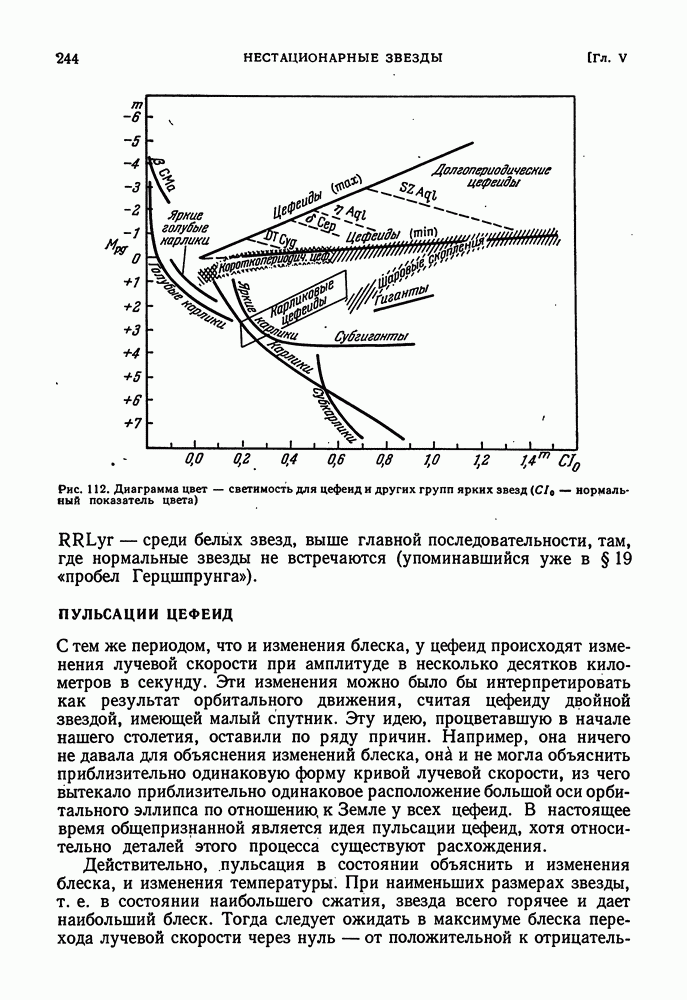
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦЕФЕИД
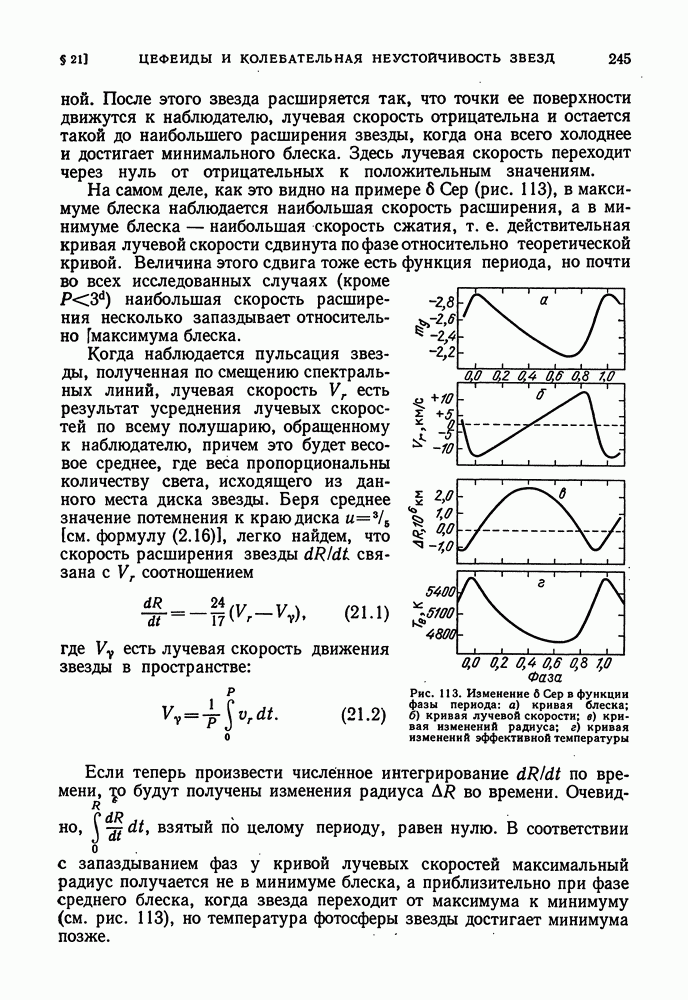
- ПУЛЬСАЦИИ ЦЕФЕИД
- ГИПОТЕЗА РАДИАЛЬНЫХ АДИАБАТИЧЕСКИХ ПУЛЬСАЦИЙ И ЕЕ ЗАТРУДНЕНИЯ
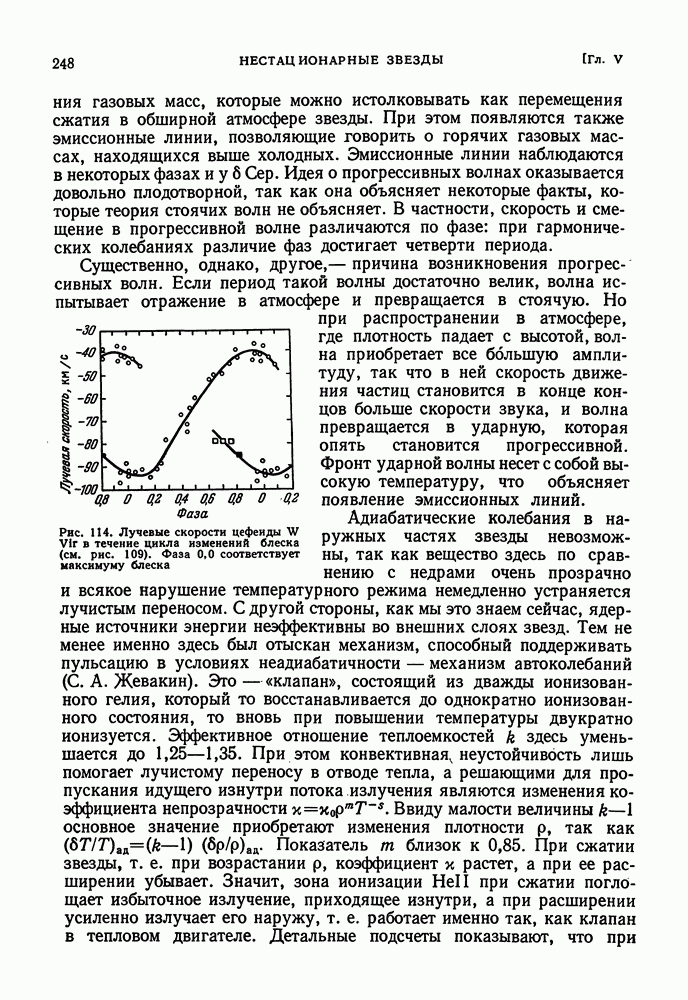
- НОВЫЕ ПРЕДСТАВЛЕНИЯ О КОЛЕБАТЕЛЬНЫХ ПРОЦЕССАХ У ЦЕФЕИД
- ЗВЕЗДЫ ТИПА b БОЛЬШОГО ПСА
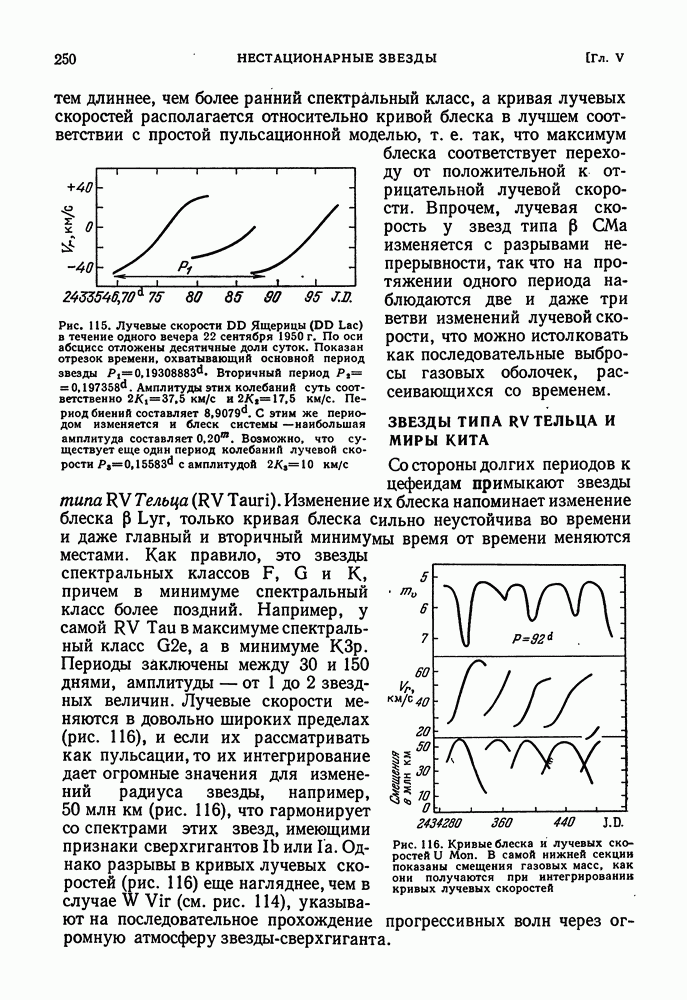
- ЗВЕЗДЫ ТИПА RV ТЕЛЬЦА И МИРЫ КИТА
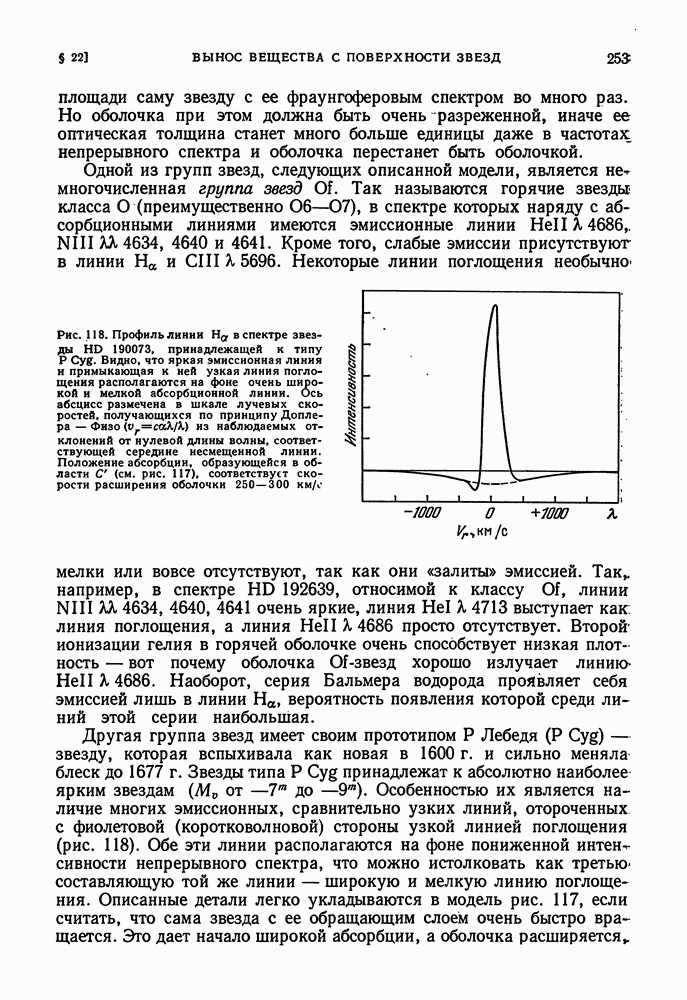
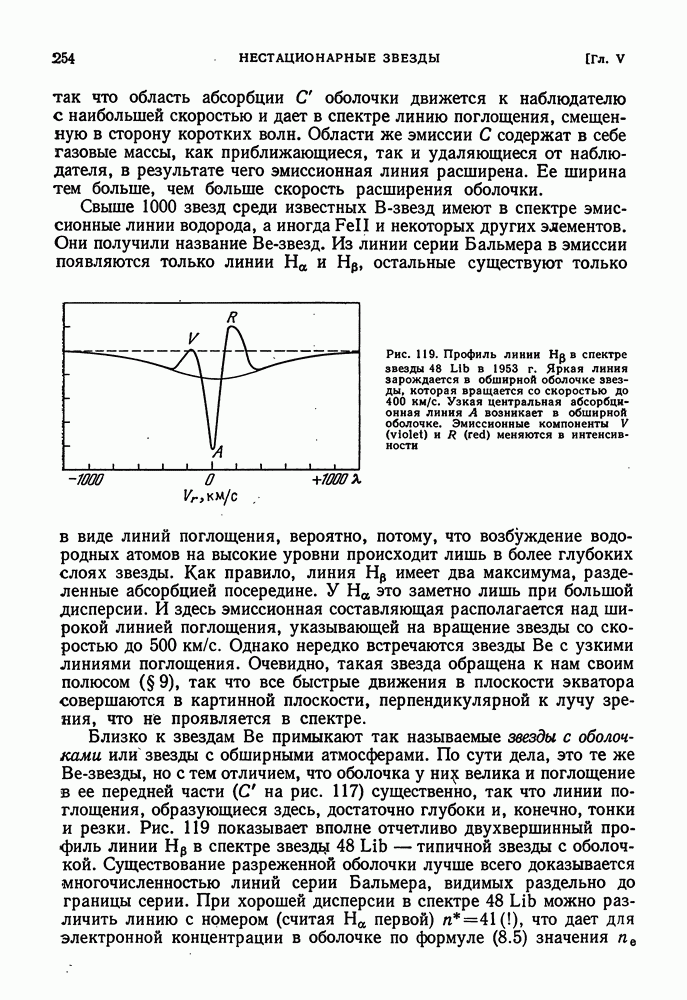
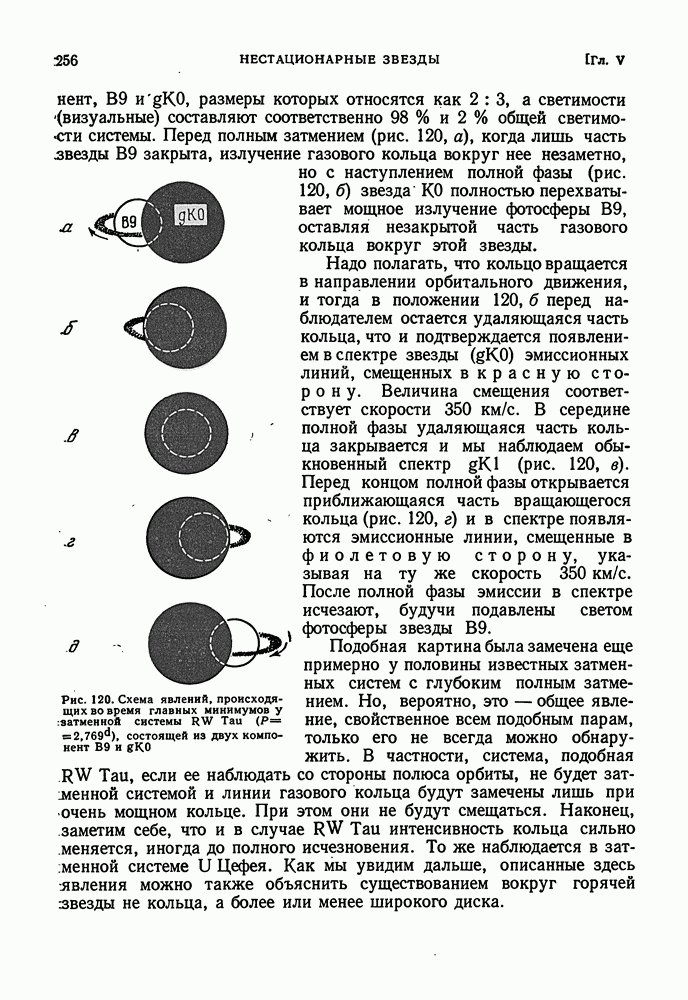
- § 22. ВЫНОС ВЕЩЕСТВА С ПОВЕРХНОСТИ ЗВЕЗД
- ГАЗОВЫЕ ОБОЛОЧКИ И КОЛЬЦА ВОКРУГ ЗВЕЗД
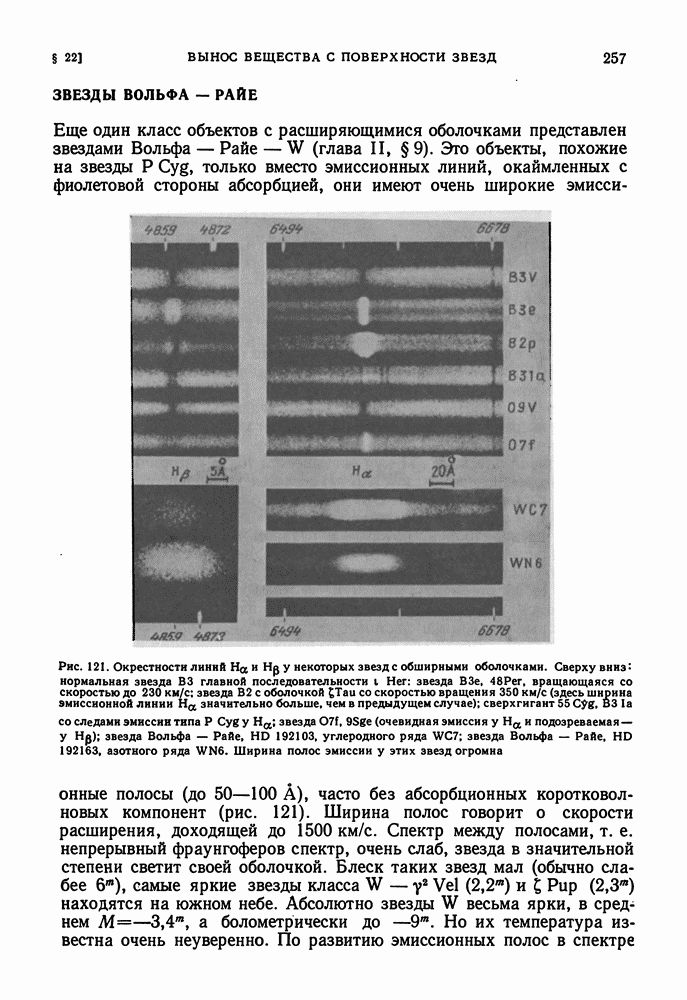
- ЗВЕЗДЫ ВОЛЬФА — РАЙЕ
- § 23. ВРАЩЕНИЕ ЗВЕЗД И ОБМЕН ВЕЩЕСТВА ВНУТРИ ДВОЙНЫХ СИСТЕМ
- ВРАЩЕНИЕ ЗВЕЗД РАЗНЫХ ТИПОВ
- ЭВОЛЮЦИОННЫЕ ИЗМЕНЕНИЯ СКОРОСТИ ВРАЩЕНИЯ ЗВЕЗД
- ПРОИСХОЖДЕНИЕ ВРАЩЕНИЯ ЗВЕЗД
- ОБМЕН ВЕЩЕСТВА ВНУТРИ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ. АККРЕЦИЯ. ЭВОЛЮЦИОННЫЕ СЛЕДСТВИЯ
- § 24. НОВЫЕ И СВЕРХНОВЫЕ ЗВЕЗДЫ
- СВЕТИМОСТЬ, АМПЛИТУДЫ ВСПЫШЕК И ЧИСЛО НОВЫХ ЗВЕЗД
- СПЕКТРАЛЬНЫЕ ИЗМЕНЕНИЯ У НОВЫХ ЗВЕЗД
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ ВО ВРЕМЯ ВСПЫШКИ НОВОЙ ЗВЕЗДЫ
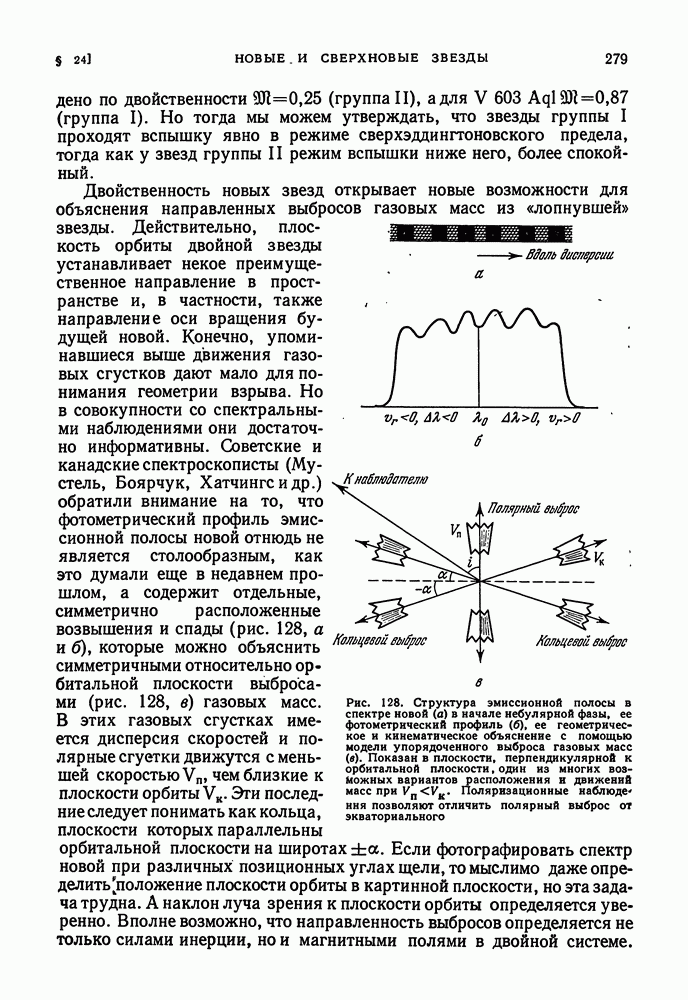
- ДВОЙСТВЕННОСТЬ НОВЫХ ЗВЕЗД
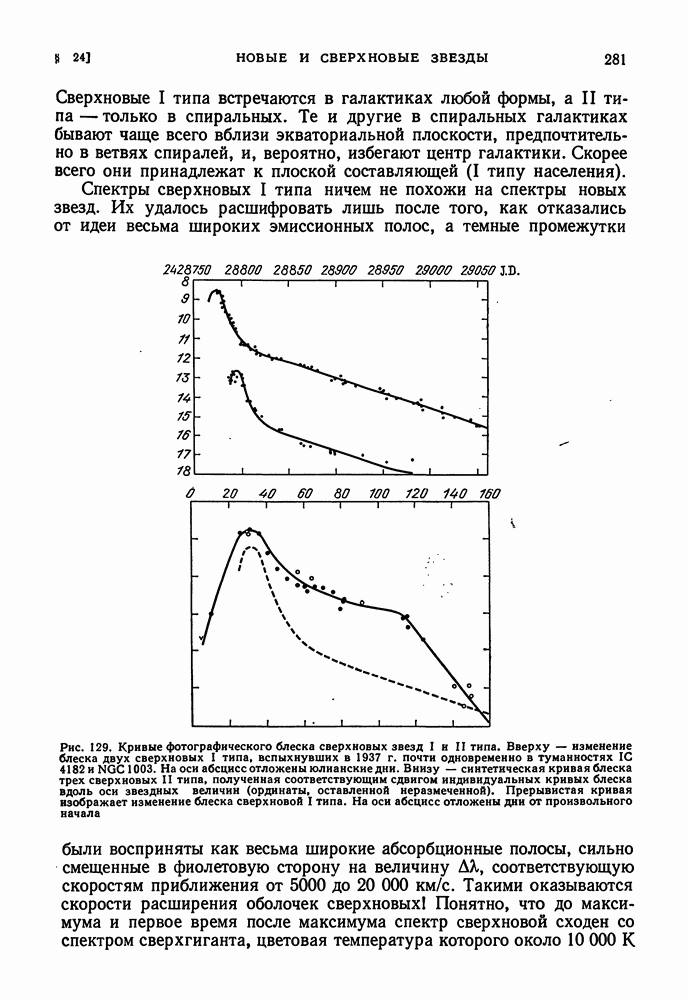
- СВЕРХНОВЫЕ ЗВЕЗДЫ
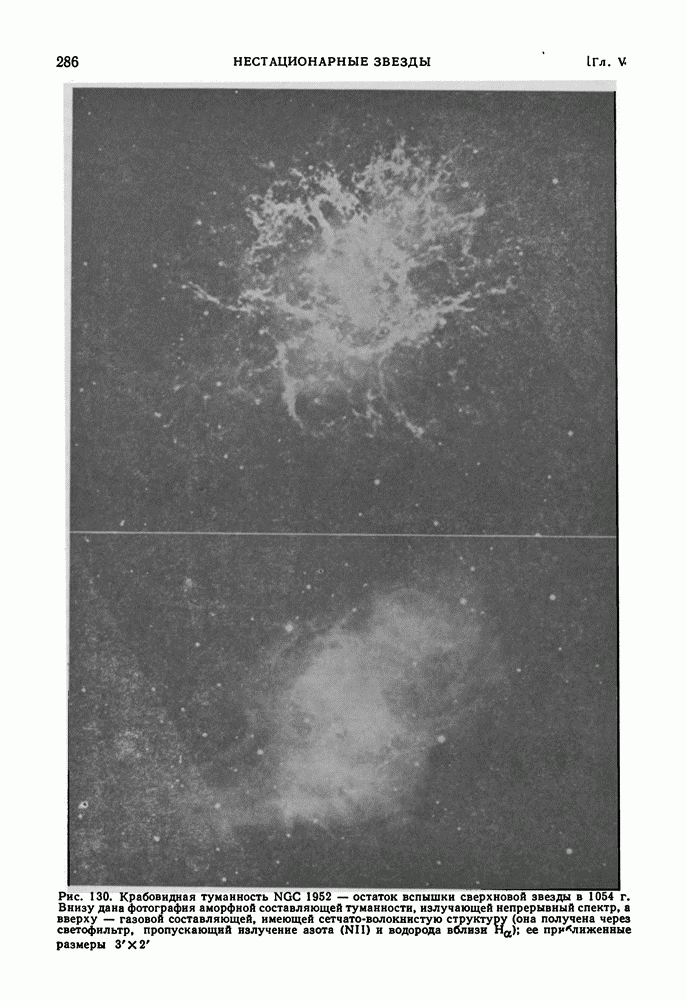
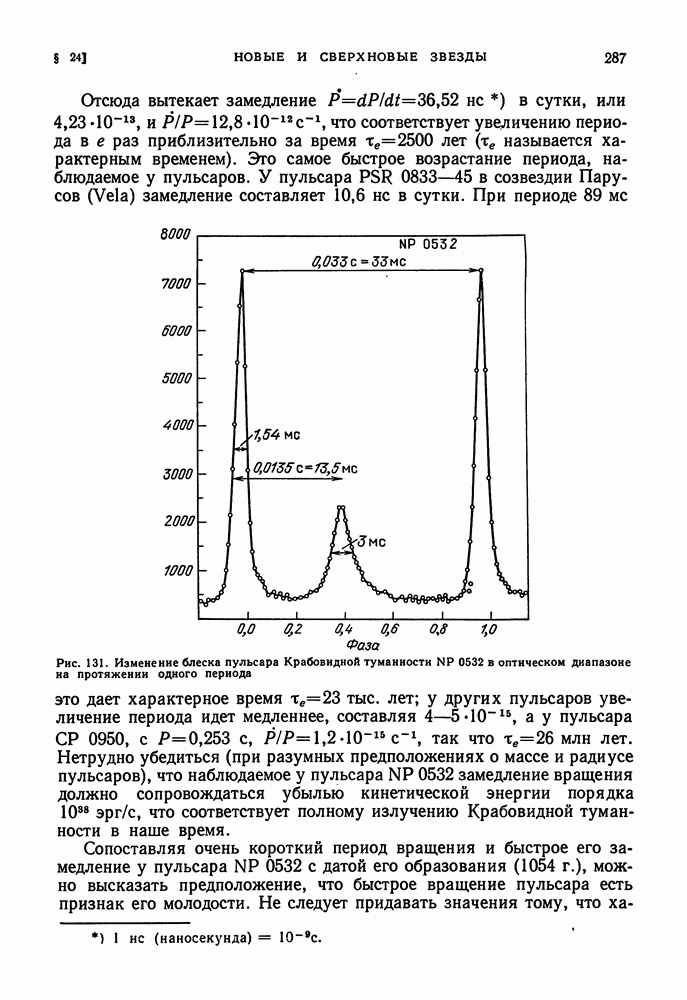
- ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ ЗВЕЗД. КРАБОВИДНАЯ ТУМАННОСТЬ. ПУЛЬСАРЫ
- § 25. КАРЛИКОВЫЕ ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ДРУГИЕ СЛУЧАИ НЕСТАЦИОНАРНОСТИ: РЕНТГЕНОВСКИЕ ЗВЕЗДЫ
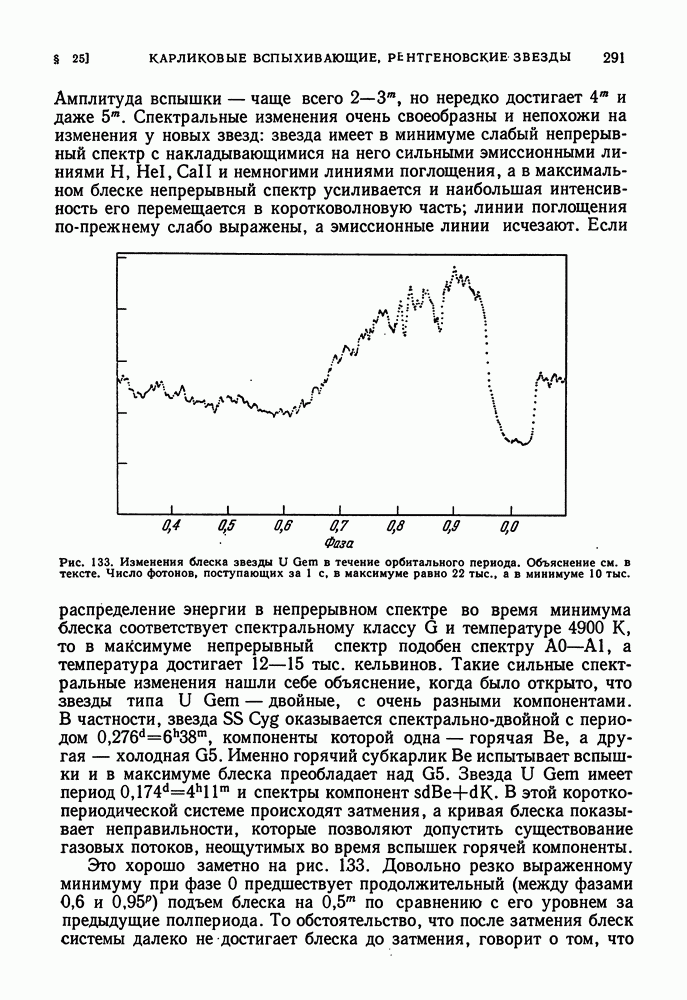
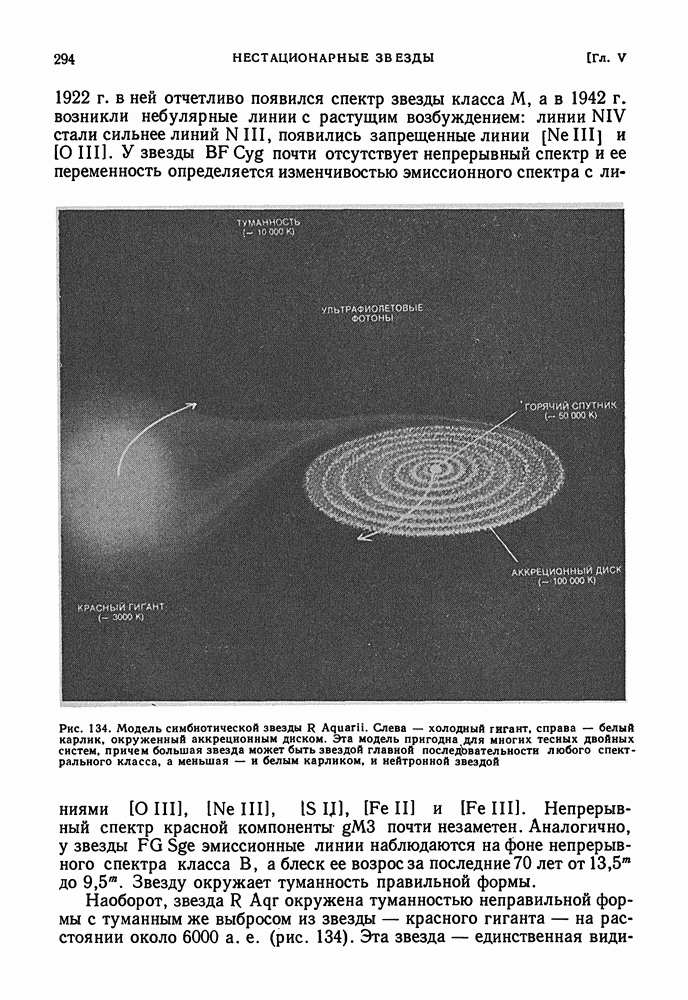
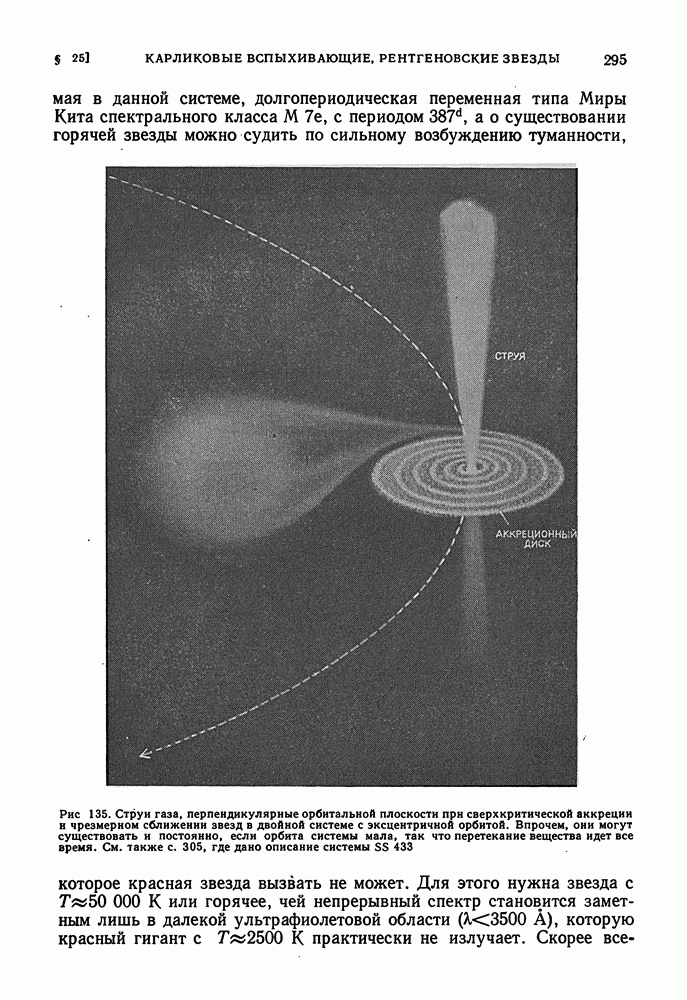
- ЗВЕЗДЫ ТИПА U БЛИЗНЕЦОВ. СИМБИОТИЧЕСКИЕ ЗВЕЗДЫ
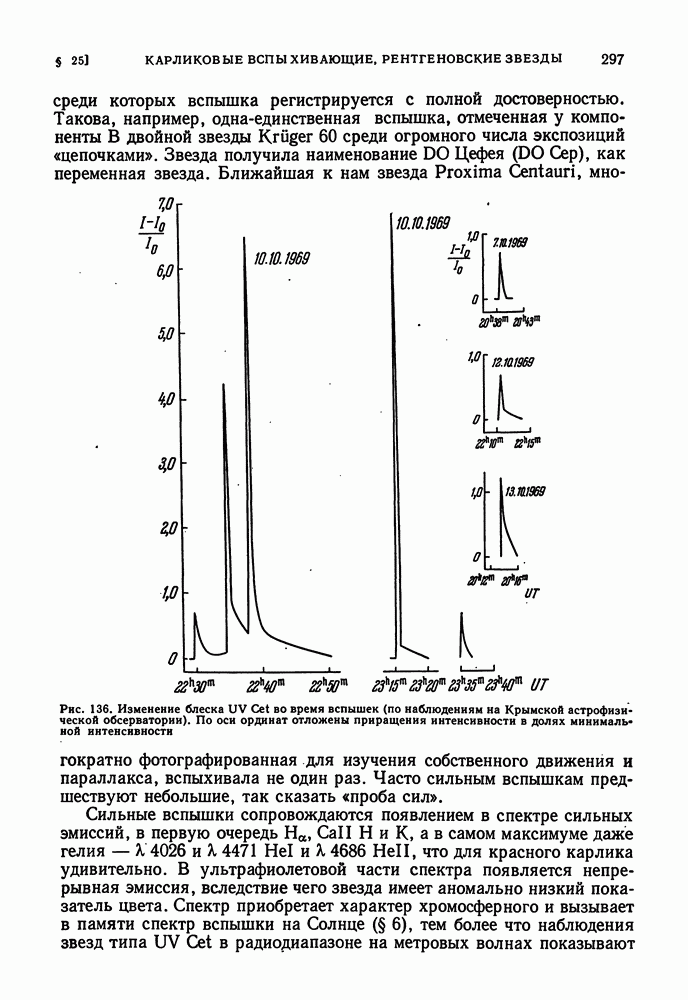
- ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ТИПА UV КИТА
- ЗВЕЗДЫ ТИПОВ Т ТЕЛЬЦА, RW ВОЗНИЧЕГО И ТОРИОНА
- НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ В РЕНТГЕНОВСКОМ ДИАПАЗОНЕ
- ЗАДАЧИ К ГЛАВЕ V
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ V
- ГЛАВА VI. ДИФФУЗНОЕ ВЕЩЕСТВО В ПРОСТРАНСТВЕ
- ВЫСОКАЯ СПОСОБНОСТЬ ПЫЛИ ЗАДЕРЖИВАТЬ ПРОХОДЯЩИЙ СВЕТ
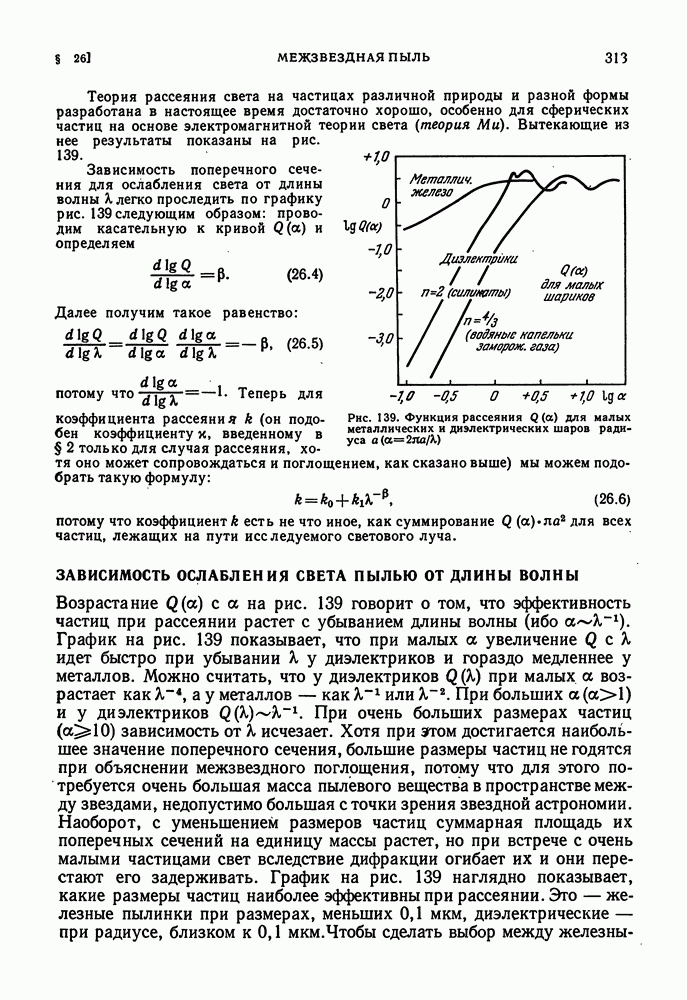
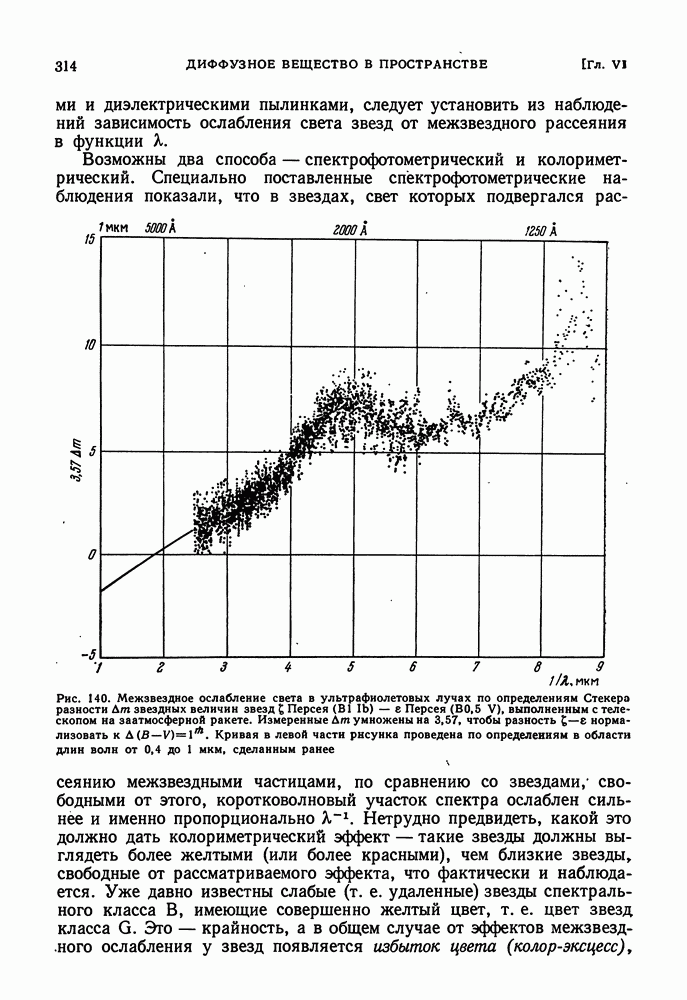
- ЗАВИСИМОСТЬ ОСЛАБЛЕНИЯ СВЕТА ПЫЛЬЮ ОТ ДЛИНЫ ВОЛНЫ
- ПРАКТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ОБЩЕГО ОСЛАБЛЕНИЯ СВЕТА в ЗАДАННОМ НАПРАВЛЕНИИ
- ОБЛАЧНАЯ СТРУКТУРА ПЫЛЕВОЙ СРЕДЫ В ГАЛАКТИКЕ
- РАСПРЕДЕЛЕНИЕ МЕЖЗВЕЗДНОЙ ПЫЛИ В ГАЛАКТИКЕ
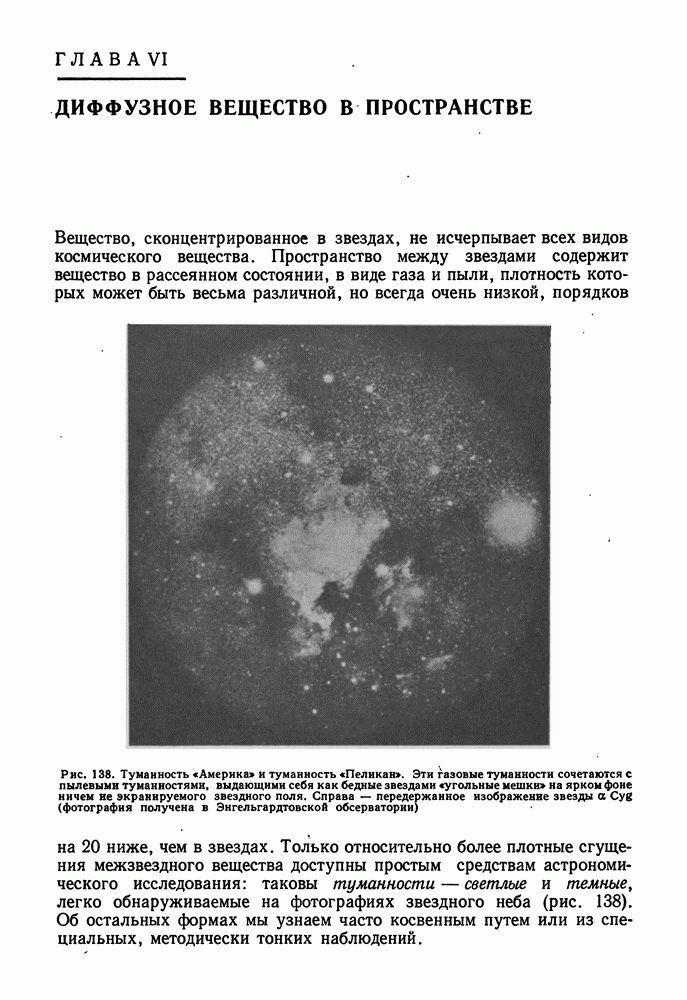
- СВЕТЛЫЕ ПЫЛЕВЫЕ ТУМАННОСТИ
- СВЕТОВОЕ ДАВЛЕНИЕ НА ПЫЛЕВЫЕ ЧАСТИЦЫ
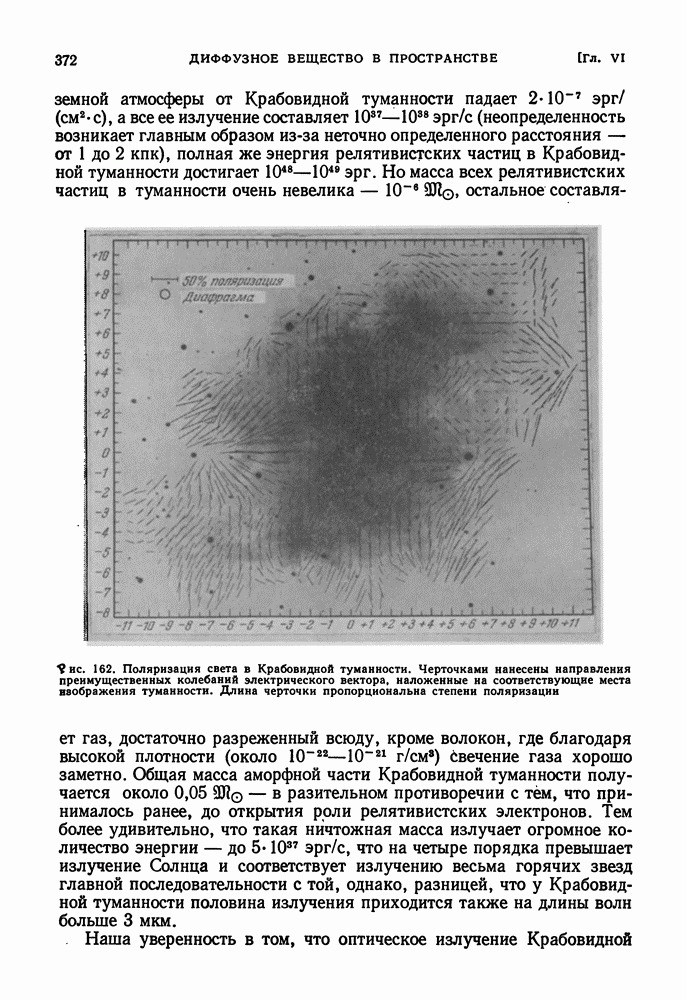
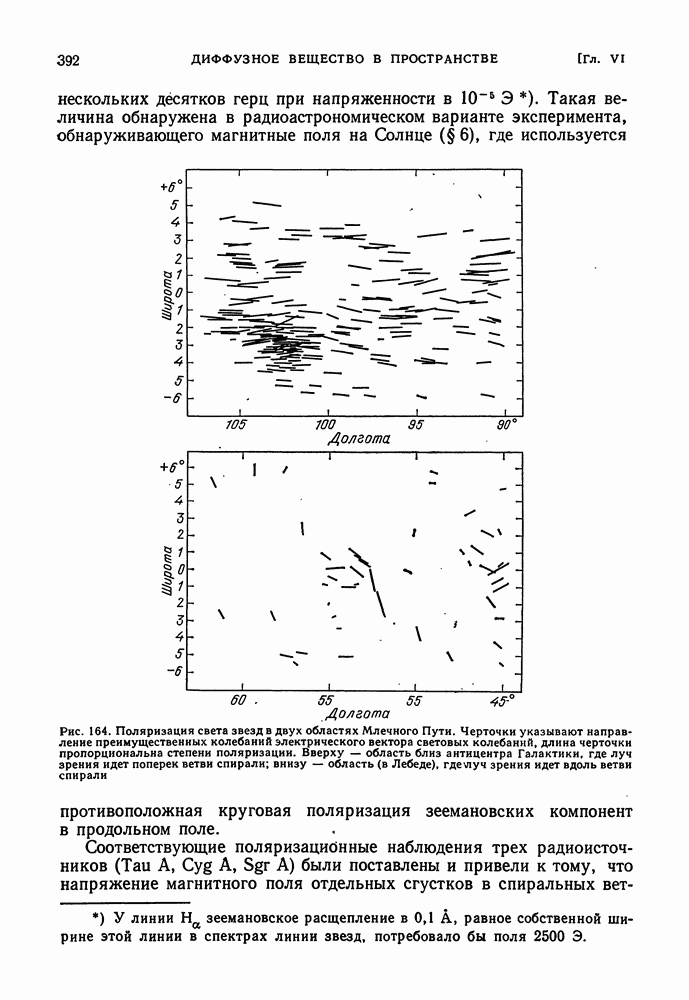
- МЕЖЗВЕЗДНАЯ ПОЛЯРИЗАЦИЯ СВЕТА ЗВЕЗД
- ОРИЕНТИРОВАНИЕ МЕЖЗВЕЗДНЫХ ПЫЛЕВЫХ ЧАСТИЦ МАГНИТНЫМИ ПОЛЯМИ
- § 27. ГАЗОВАЯ СОСТАВЛЯЮЩАЯ МЕЖЗВЕЗДНОЙ СРЕДЫ
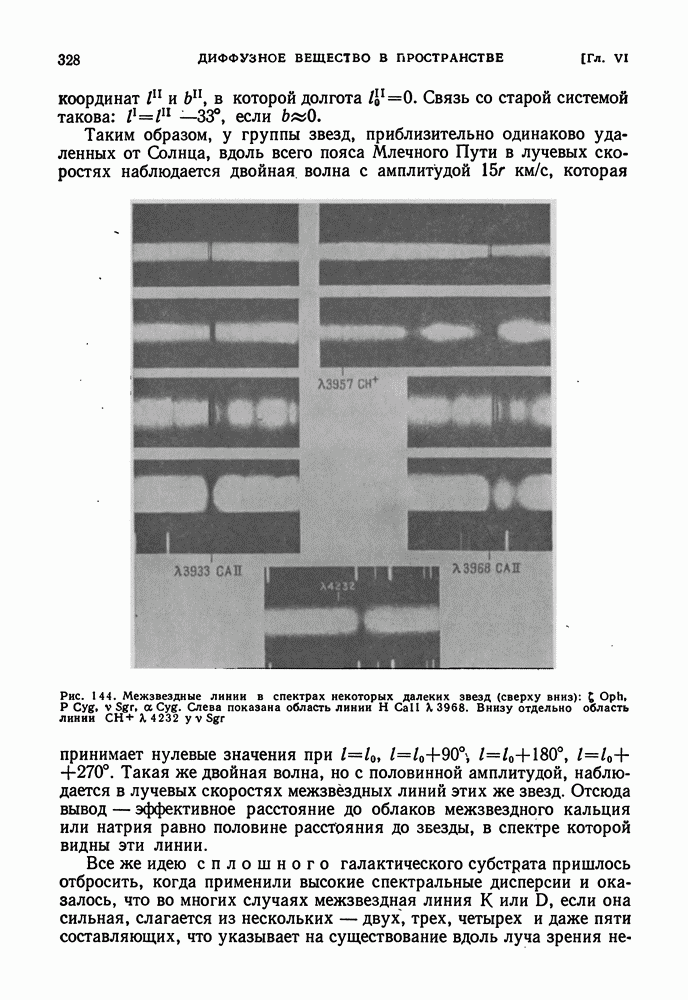
- МЕЖЗВЕЗДНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ Са, Na И ДРУГИХ ЭЛЕМЕНТОВ И МОЛЕКУЛ
- ГАЗОВЫЙ ГАЛАКТИЧЕСКИЙ СУБСТРАТ
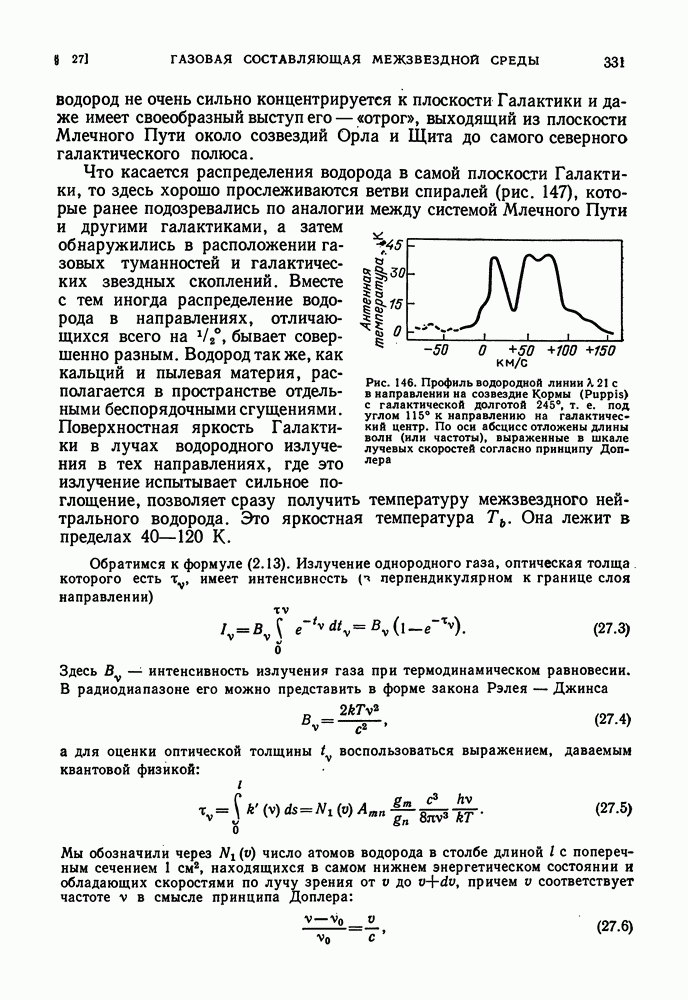
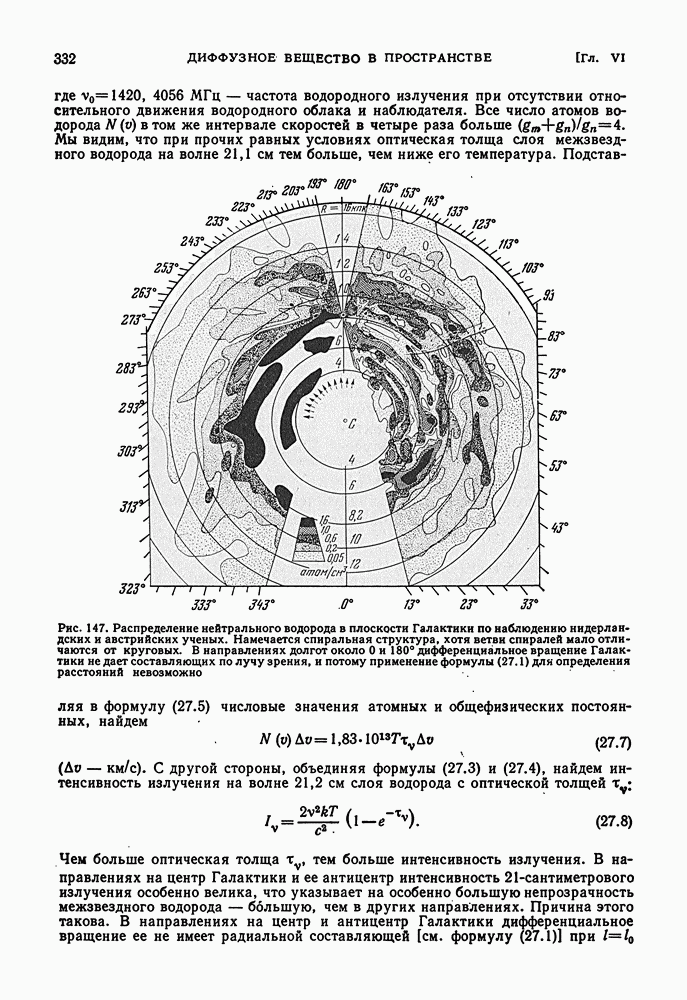
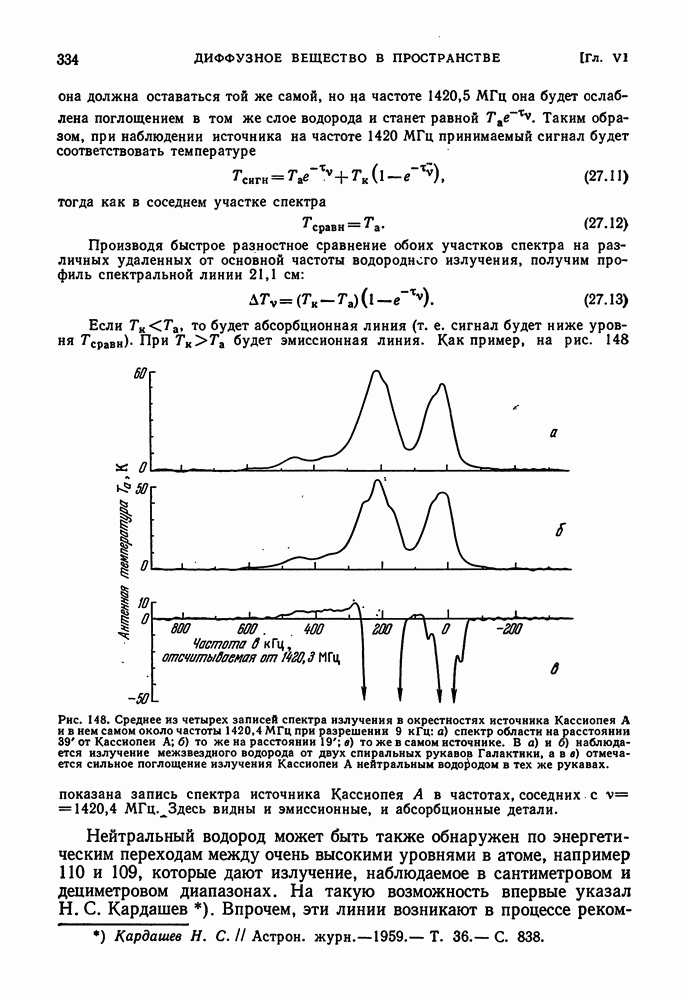
- ИЗЛУЧЕНИЕ МЕЖЗВЕЗДНОГО НЕЙТРАЛЬНОГО ВОДОРОДА НА ВОЛНЕ 21 см
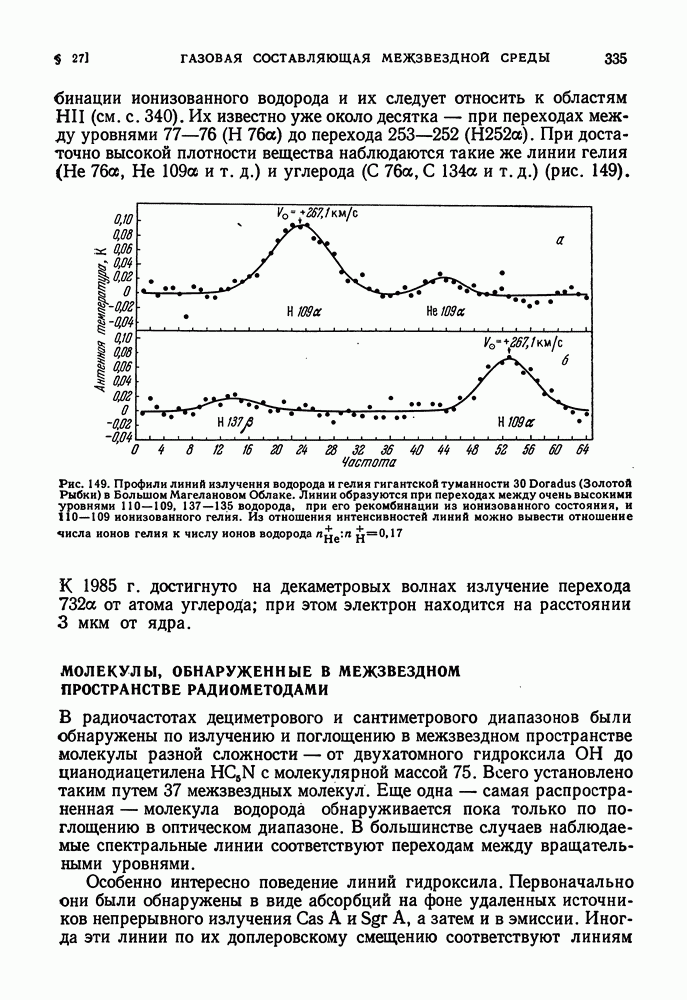
- МОЛЕКУЛЫ, ОБНАРУЖЕННЫЕ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ РАДИОМЕТОДАМИ
- ОТНОСИТЕЛЬНАЯ РОЛЬ ГАЗА И ПЫЛИ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭЛЕКТРОНЫ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ. ОБЛАСТИ HII И HI
- § 28. ГАЗОВЫЕ ТУМАННОСТИ
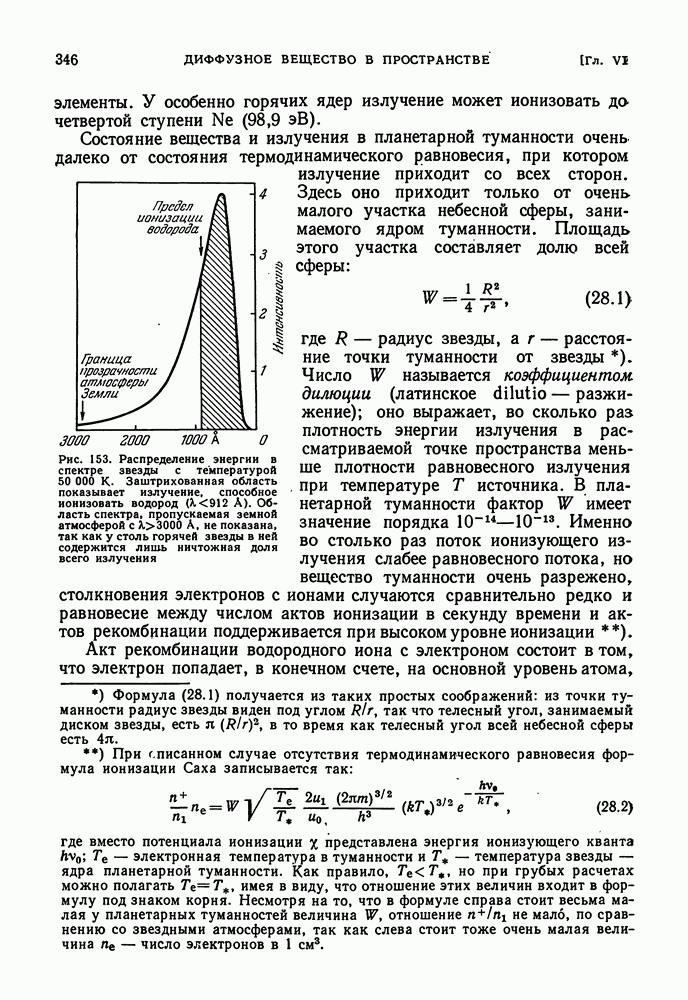
- ПЛАНЕТАРНЫЕ ТУМАННОСТИ
- ФЛУОРЕСЦЕНЦИЯ ВЕЩЕСТВА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ТЕМПЕРАТУРЫ ЯДЕР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЗАПРЕЩЕННЫЕ ЛИНИИ В СПЕКТРАХ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЭЛЕКТРОННЫЕ ТЕМПЕРАТУРЫ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- НЕПРЕРЫВНЫЙ СПЕКТР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ. ИХ МАССЫ
- РАСШИРЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
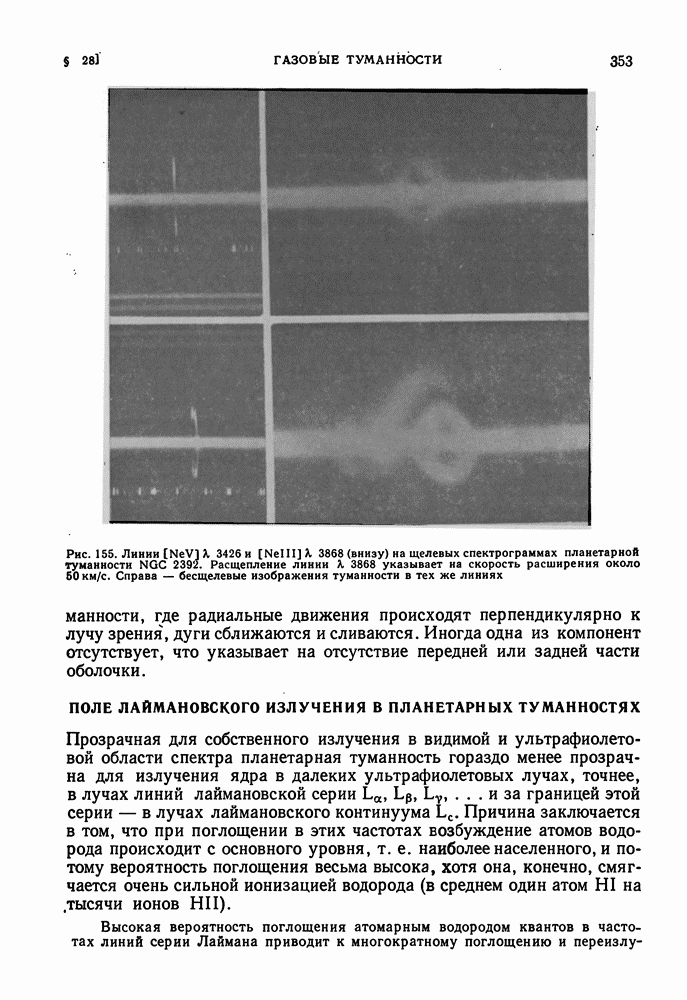
- ПОЛЕ ЛАЙМАНОВСКОГО ИЗЛУЧЕНИЯ В ПЛАНЕТАРНЫХ ТУМАННОСТЯХ
- ГРАНИЦА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ЯДРА ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
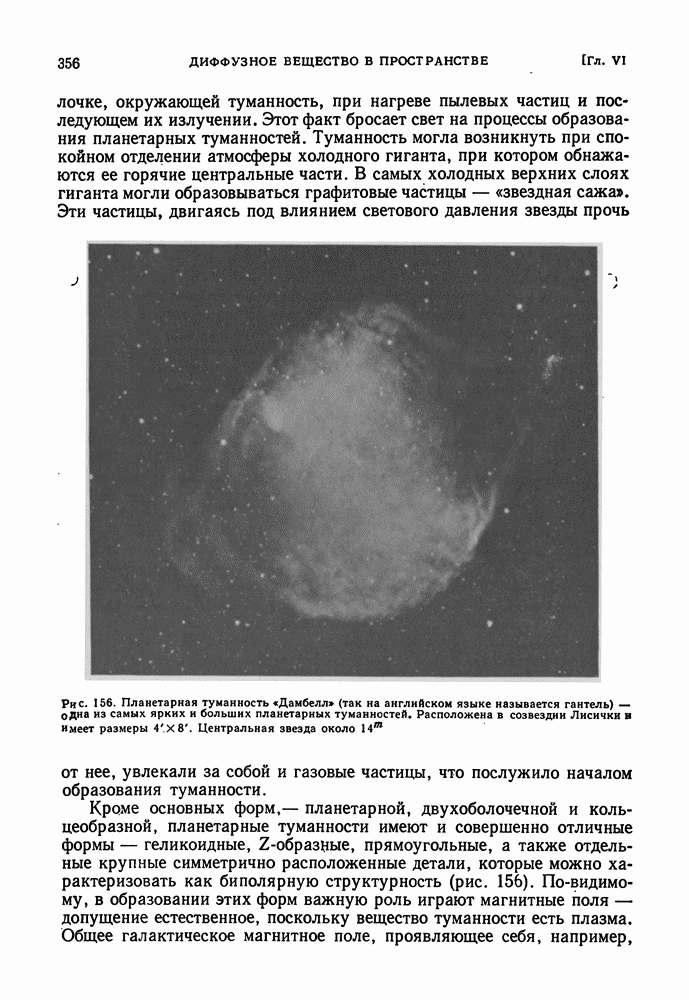
- ПРОИСХОЖДЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
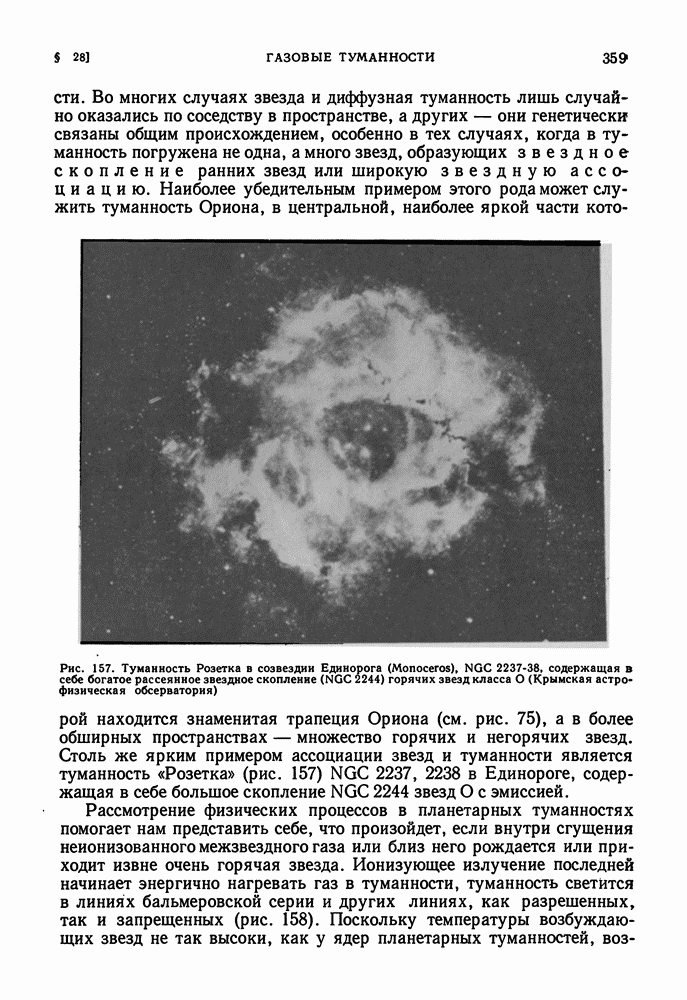
- ДИФФУЗНЫЕ ГАЗОВЫЕ ТУМАННОСТИ
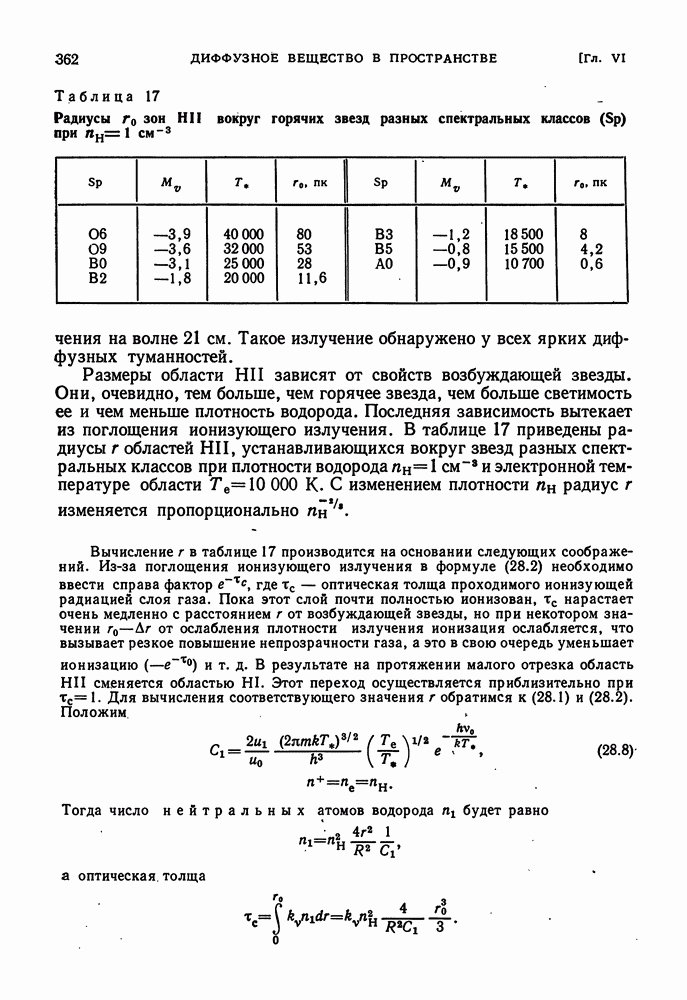
- ОБЛАСТИ HII И ИХ РАЗМЕРЫ
- ВЗАИМОДЕЙСТВИЕ ГАЗА И ИЗЛУЧЕНИЯ ГОРЯЧЕЙ ЗВЕЗДЫ. ДВИЖЕНИЯ ВНУТРИ ГАЗОВОЙ ТУМАННОСТИ
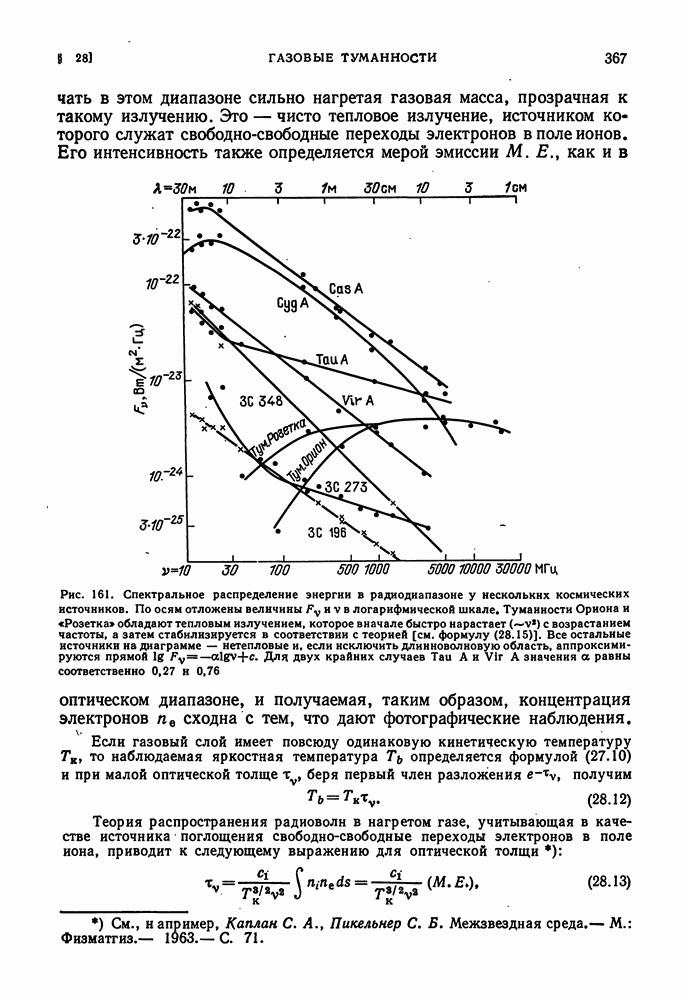
- РАДИОИЗЛУЧЕНИЕ ГАЗОВЫХ ТУМАННОСТЕЙ
- КРАБОВИДНАЯ ТУМАННОСТЬ — ИСТОЧНИК РАДИОИЗЛУЧЕНИЯ ТЕЛЕЦ А
- ТОРМОЗНОЕ ИЗЛУЧЕНИЕ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ КАК ИСТОЧНИК СВЕЧЕНИЯ КРАБОВИДНОЙ ТУМАННОСТИ
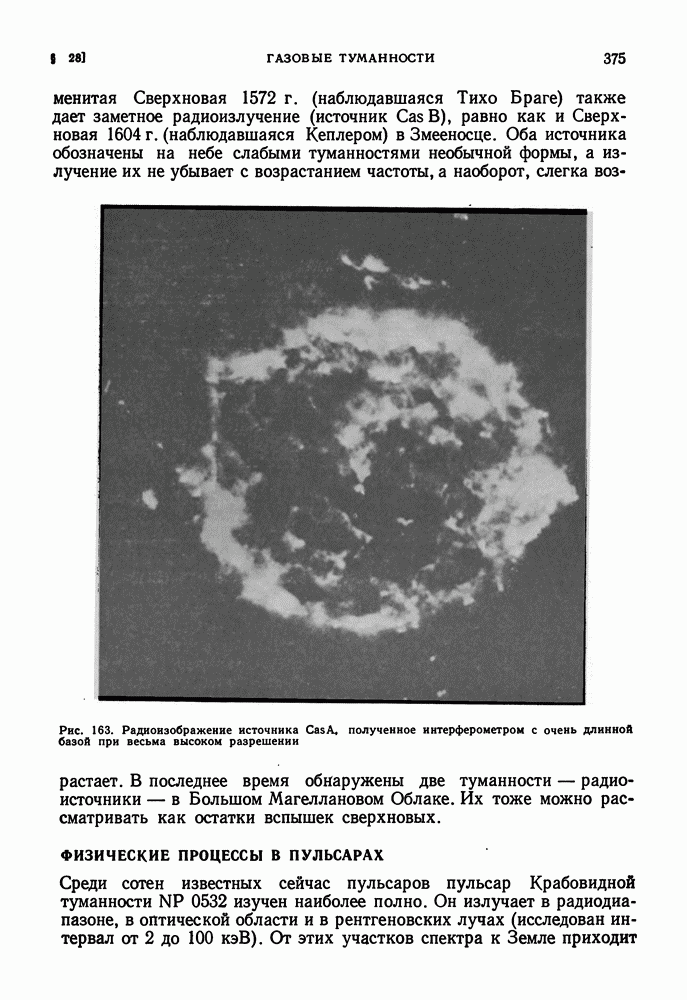
- КРАБОВИДНАЯ И НЕКОТОРЫЕ ДРУГИЕ ТУМАННОСТИ КАК ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ В ПУЛЬСАРАХ
- § 29. ФИЗИЧЕСКОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА В ГАЛАКТИКЕ
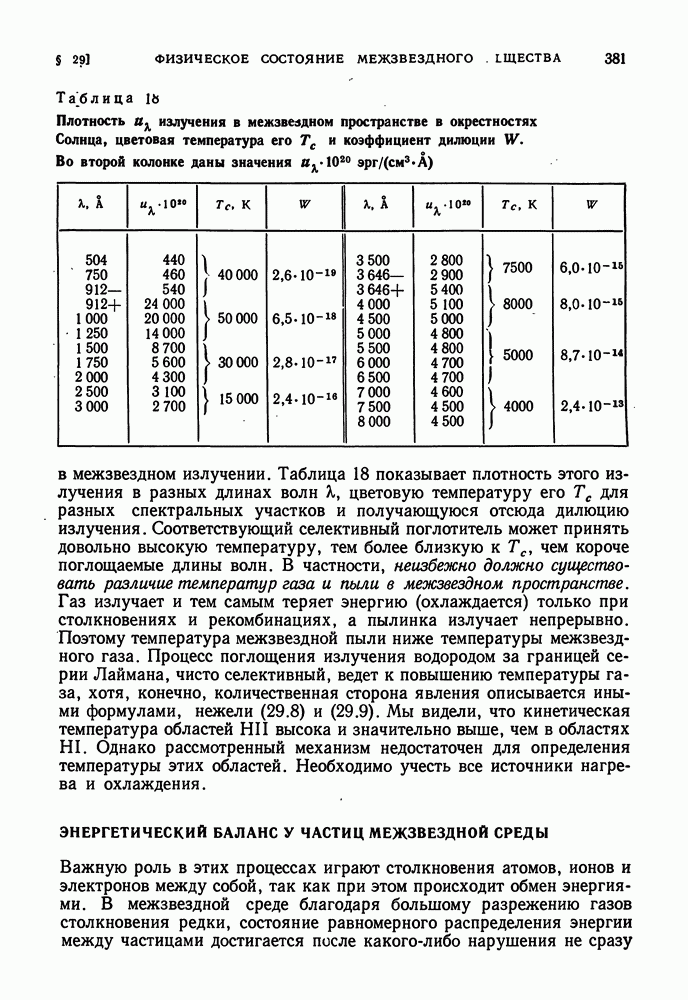
- ТЕМПЕРАТУРА ТЕЛА, ПОМЕЩЕННОГО В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭНЕРГЕТИЧЕСКИЙ БАЛАНС У ЧАСТИЦ МЕЖЗВЕЗДНОЙ СРЕДЫ
- РАДИОИЗЛУЧЕНИЕ ИЗ МЕЖЗВЕЗДНОГО ПРОСТРАНСТВА ГАЛАКТИКИ
- КОСМИЧЕСКИЕ ЛУЧИ В ГАЛАКТИКЕ
- МАГНИТНЫЕ ПОЛЯ В ГАЛАКТИКЕ
- КОНДЕНСАЦИИ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА И ЗВЕЗДООБРАЗОВАНИЕ
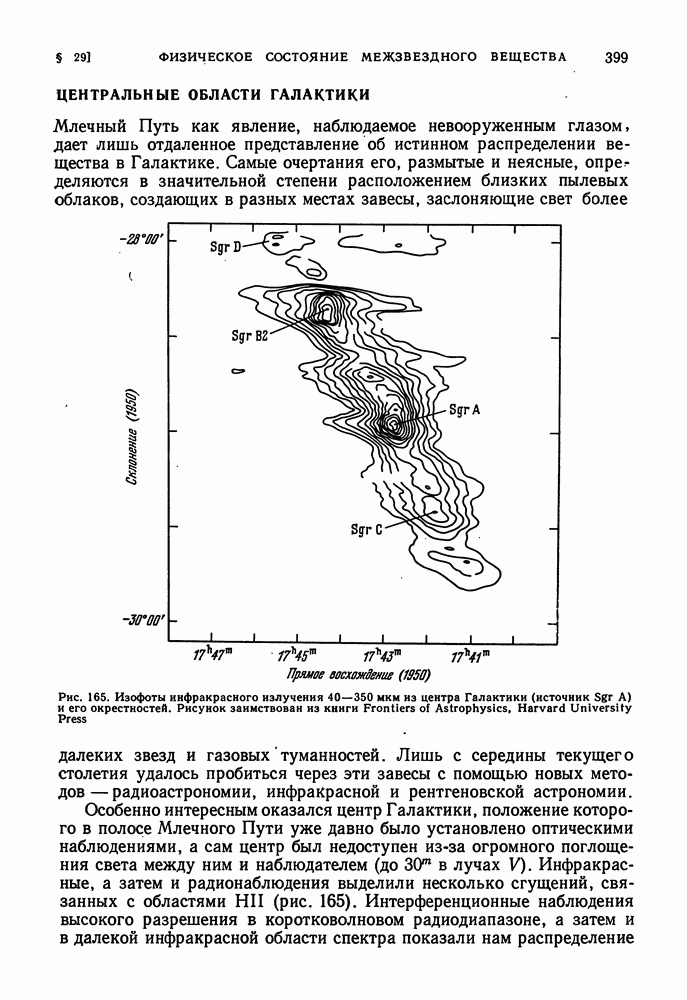
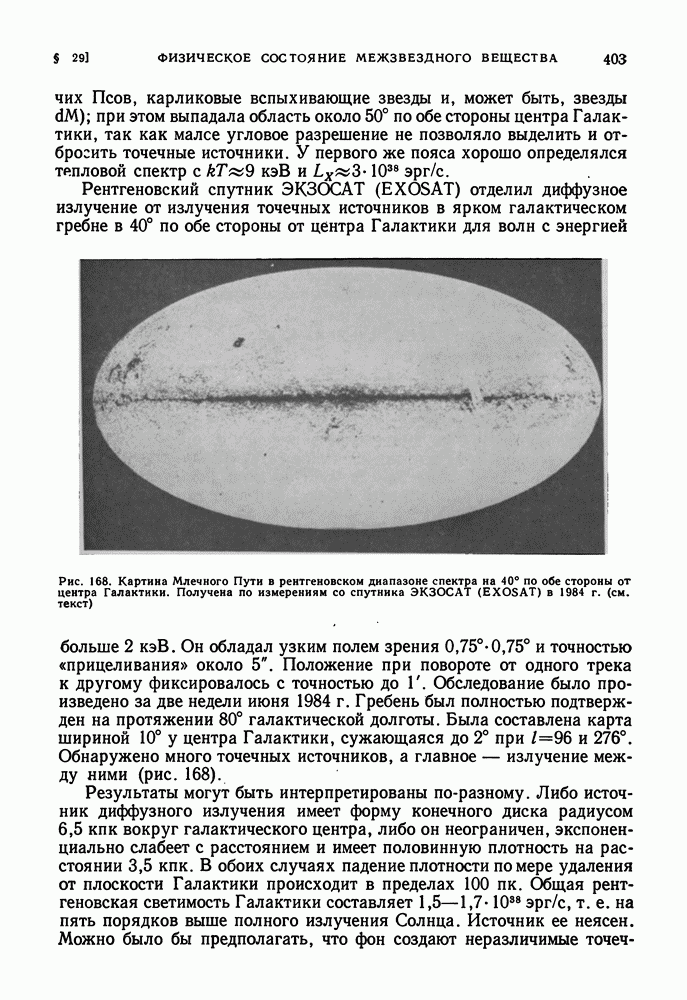
- ЦЕНТРАЛЬНЫЕ ОБЛАСТИ ГАЛАКТИКИ
- ОСОБЕННОСТИ РАСПОЛОЖЕНИЯ И ДВИЖЕНИЯ ГАЗОВЫХ МАСС В ГАЛАКТИКЕ
- МЕЖЗВЕЗДНЫЙ ГАЗ В ГАЛАКТИКЕ (РЕЗЮМЕ). АКТИВНОСТЬ ЯДРА ГАЛАКТИКИ
- ЗАДАЧИ К ГЛАВЕ VI
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VI
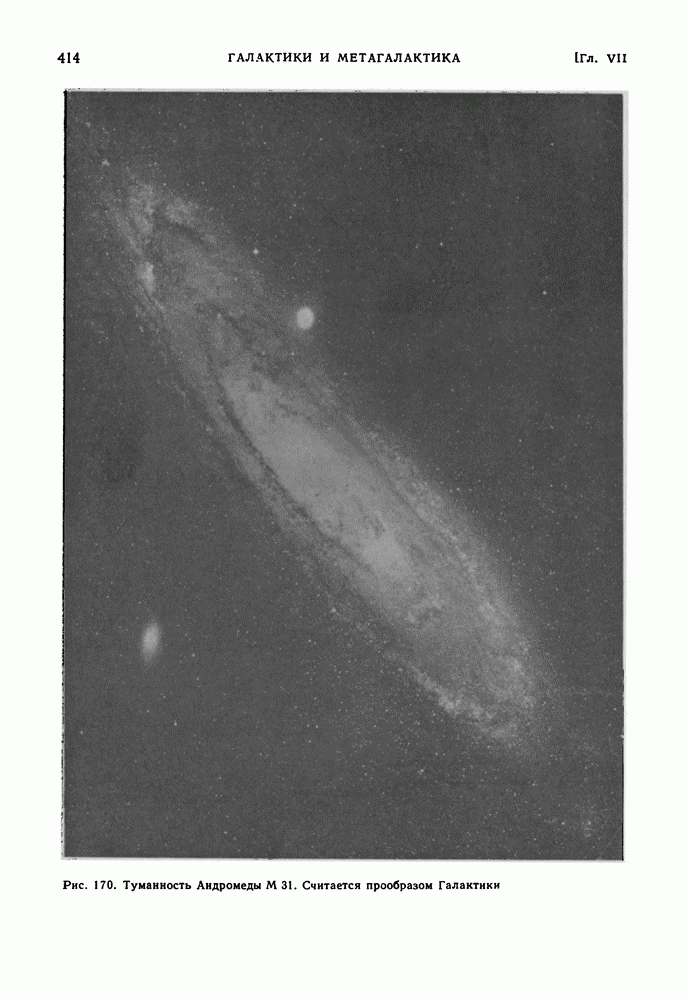
- ГЛАВА VII. ГАЛАКТИКИ И МЕТАГАЛАКТИКА
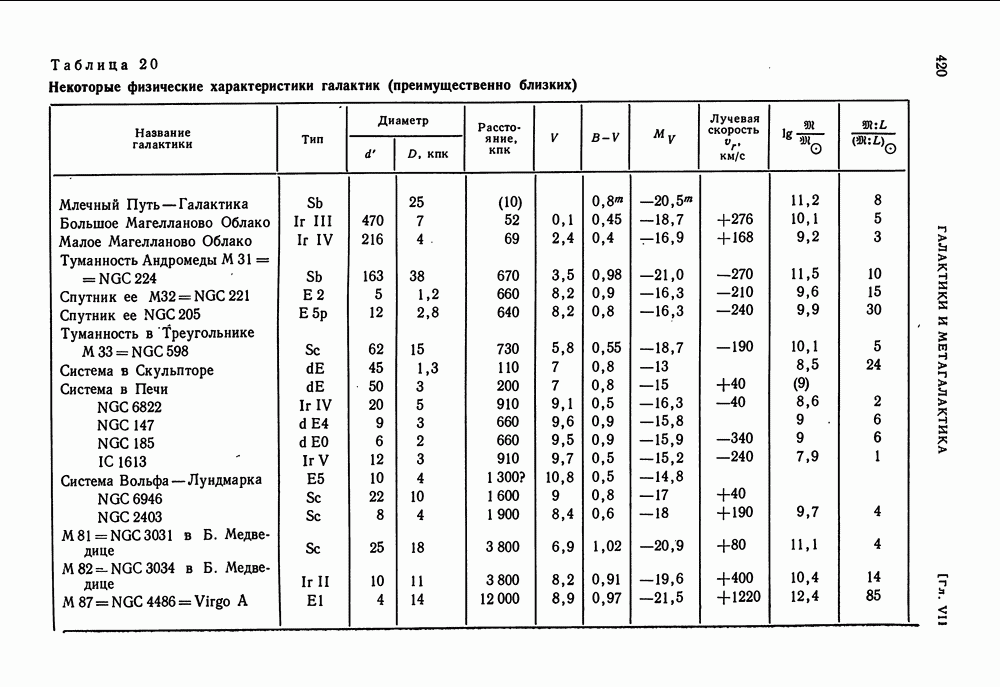
- § 30. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
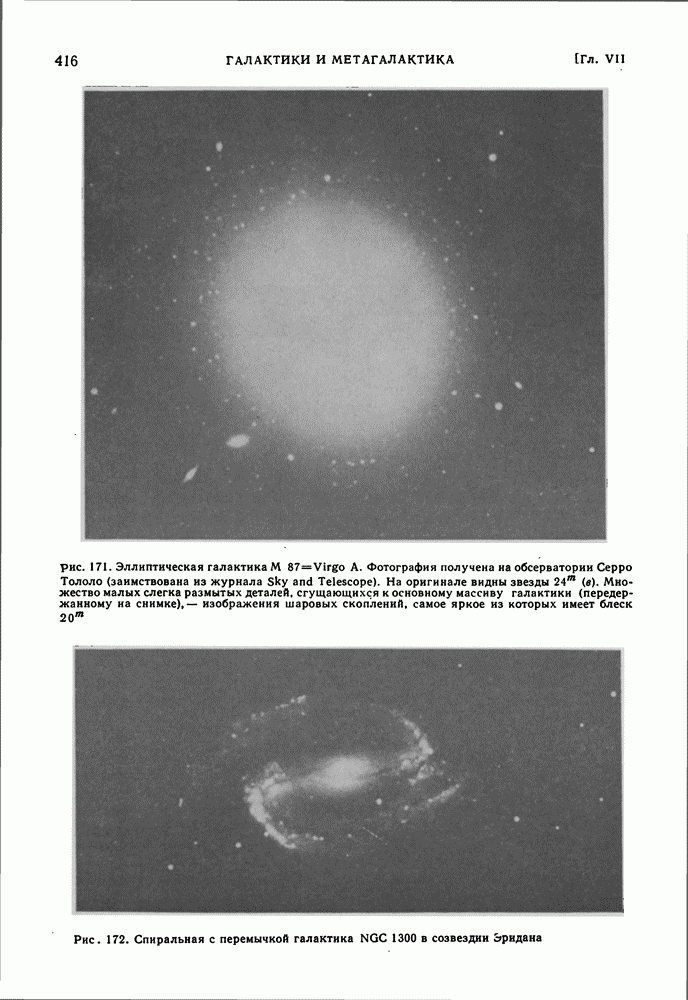
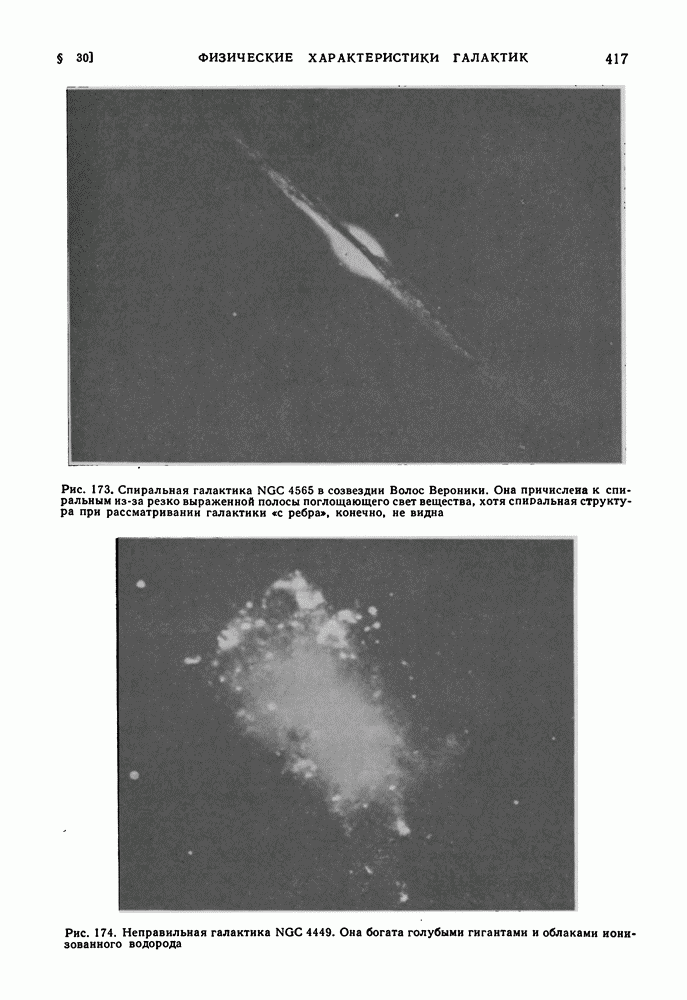
- КЛАССИФИКАЦИЯ ГАЛАКТИК- ОБЩИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
- ВРАЩЕНИЕ ГАЛАКТИК. ИХ МАССЫ
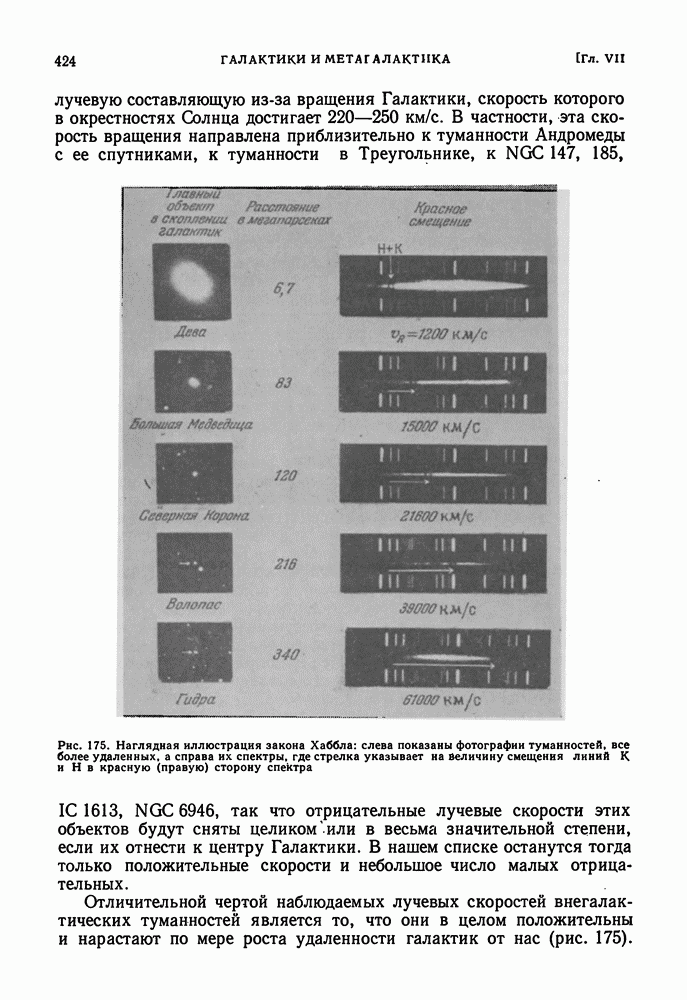
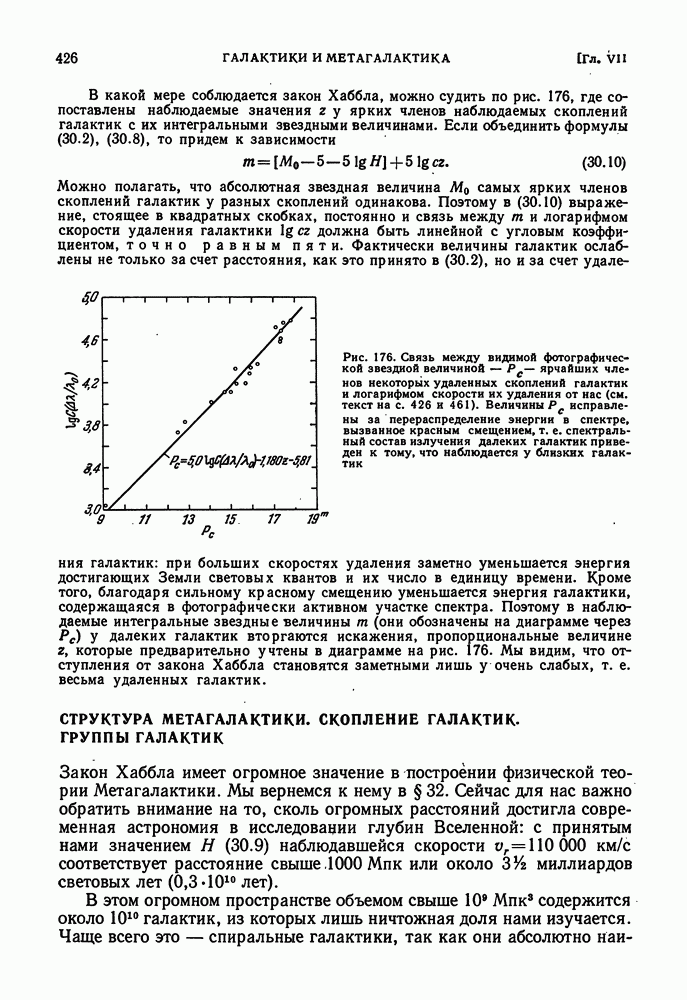
- КРАСНОЕ СМЕЩЕНИЕ В СПЕКТРАХ ГАЛАКТИК
- ЗАКОН ХАББЛА. ПОСТОЯННАЯ ХАББЛА
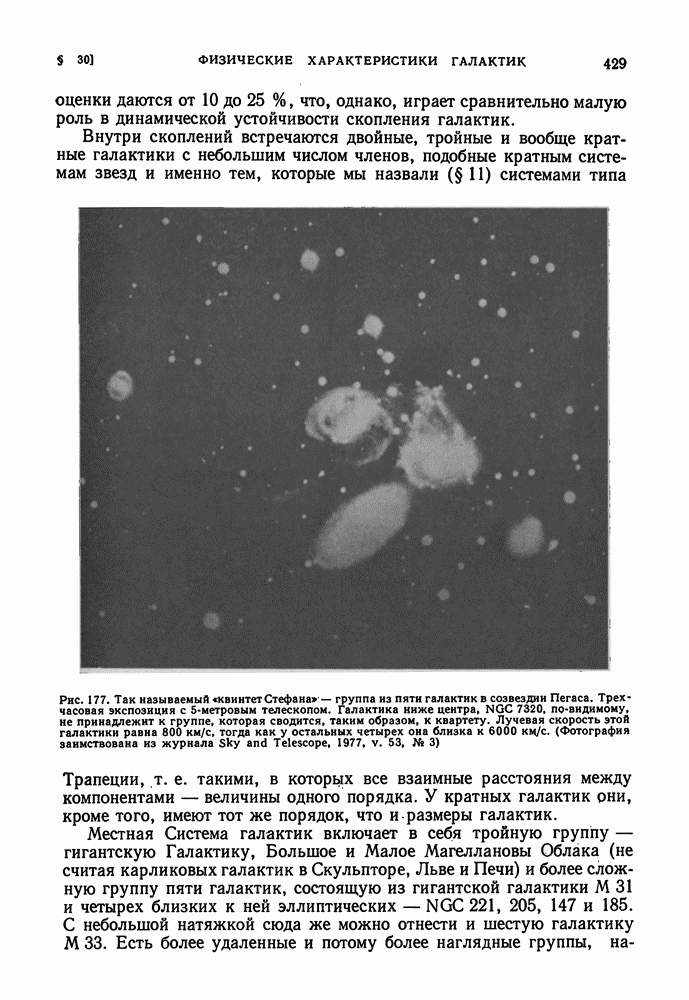
- СТРУКТУРА МЕТАГАЛАКТИКИ. СКОПЛЕНИЕ ГАЛАКТИК-ГРУППЫ ГАЛАКТИК
- ЗВЕЗДООБРАЗОВАНИЕ В ГАЛАКТИКАХ
- НЕВИДИМОЕ ВЕЩЕСТВО В ГАЛАКТИКАХ И ИХ СКОПЛЕНИЯХ
- § 31. РАДИОГАЛАКТИКИ И НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ В ГАЛАКТИКАХ
- РАДИОИЗЛУЧЕНИЕ НОРМАЛЬНЫХ ГАЛАКТИК
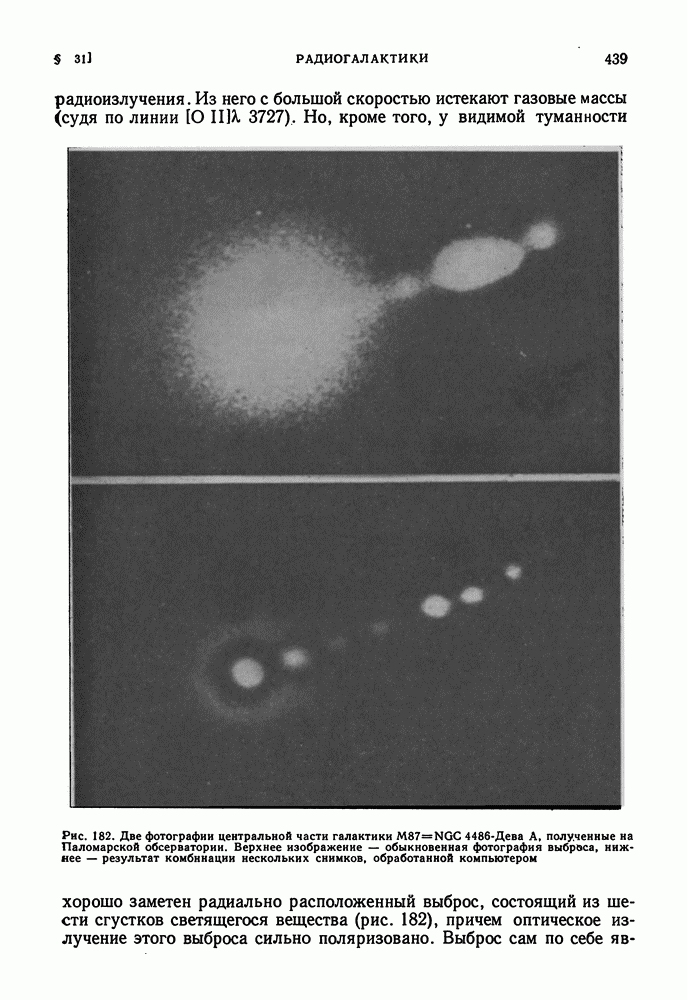
- РАДИОГАЛАКТИКИ
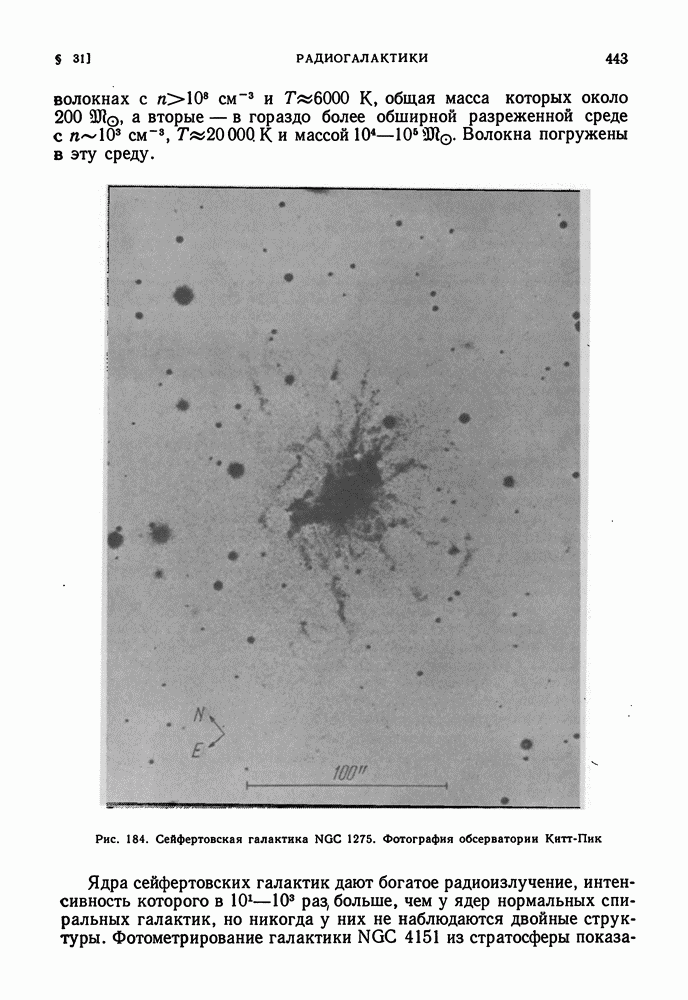
- ГАЛАКТИКИ СЕЙФЕРТА
- АКТИВНЫЕ ГАЛАКТИКИ И ПРИЗНАКИ ВЗРЫВА В НИХ
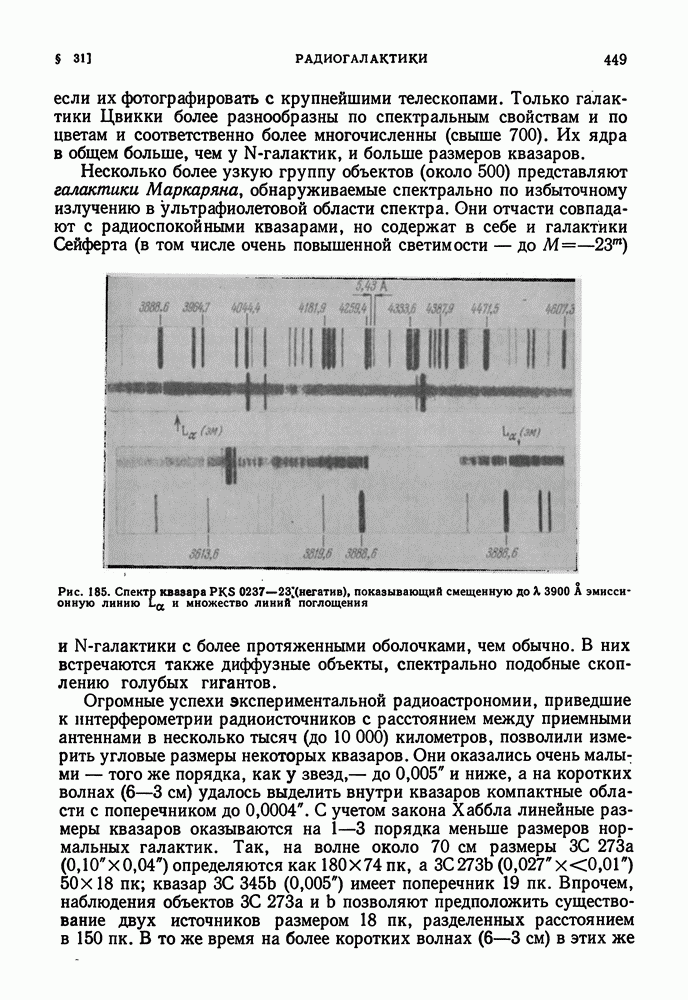
- КВАЗАРЫ И РОДСТВЕННЫЕ ИМ ОБЪЕКТЫ
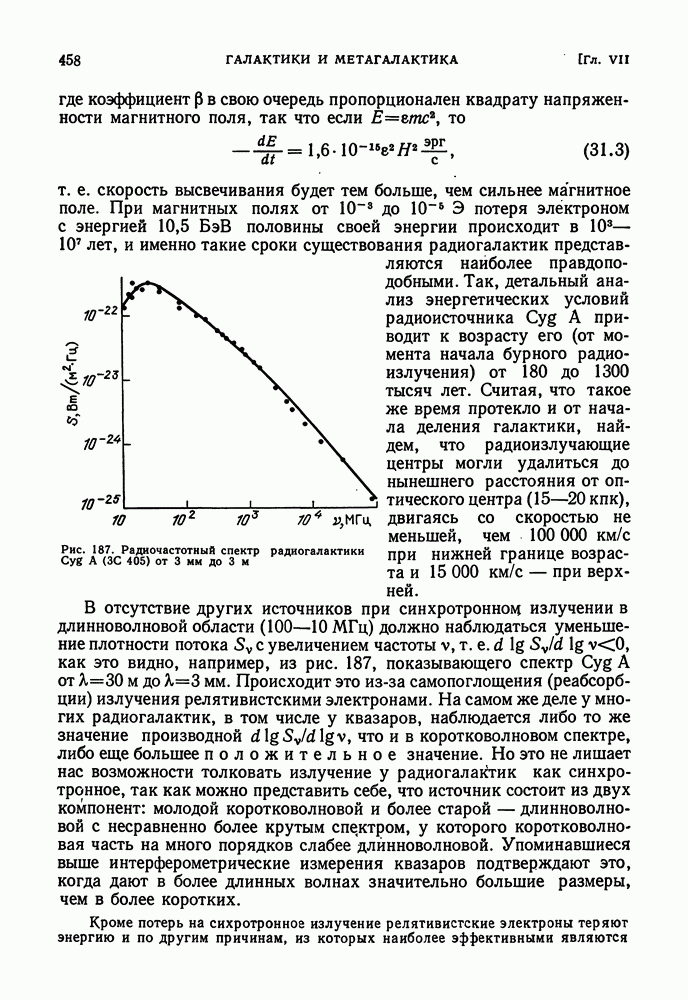
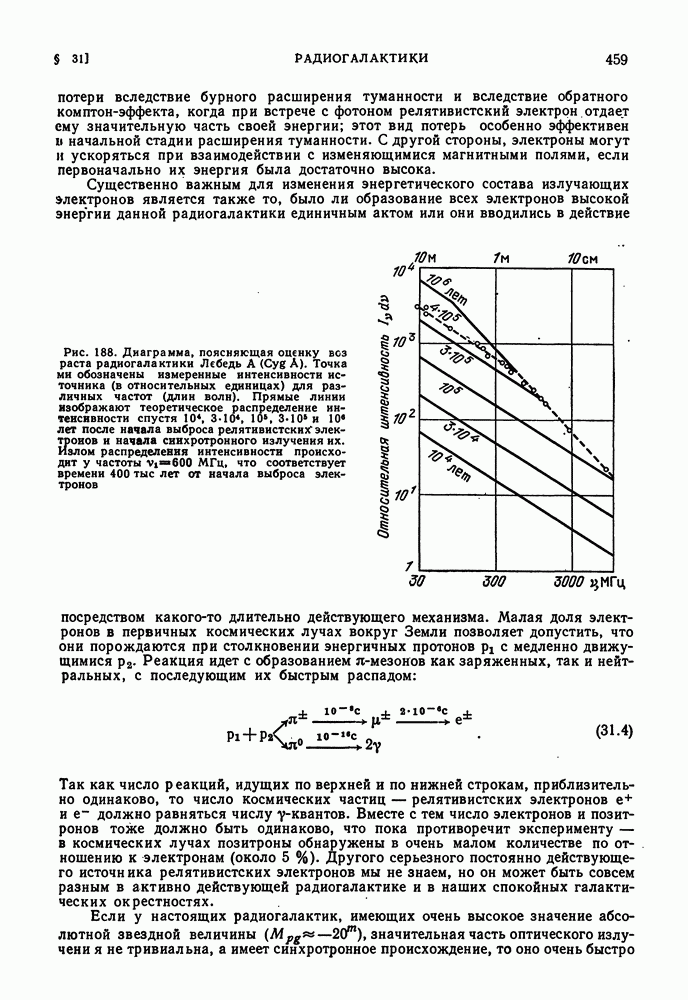
- СПЕКТРАЛЬНЫЙ ИНДЕКС РАДИОИЗЛУЧЕНИЯ. ВОЗРАСТ РАДИОГАЛАКТИК
- ОБЩИЕ ЗАПАСЫ ЭНЕРГИИ В ГАЛАКТИКАХ
- § 32. ГАЛАКТИКИ И КОСМОЛОГИЯ
- ЗАДАЧИ К ГЛАВЕ VII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VII
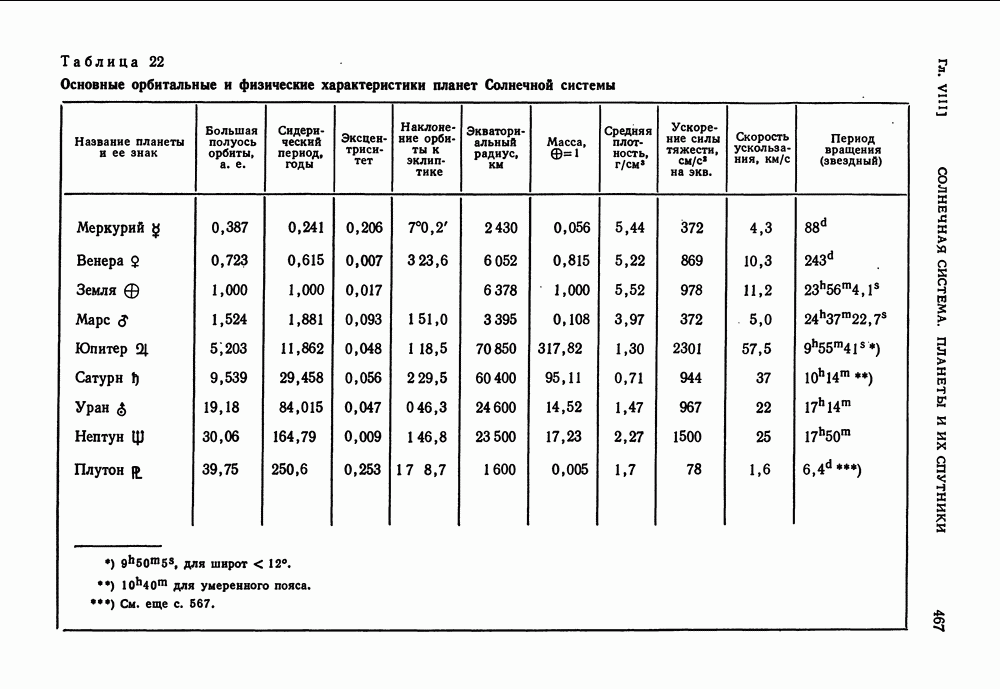
- ГЛАВА VIII. СОЛНЕЧНАЯ СИСТЕМА. ПЛАНЕТЫ И ИХ СПУТНИКИ
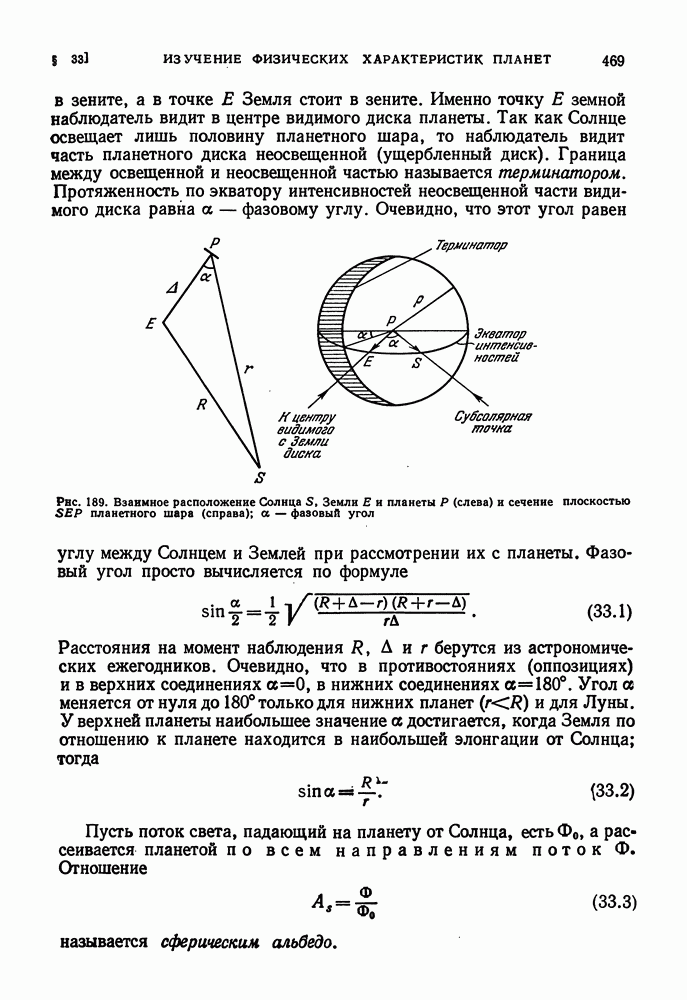
- § 33. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ПЛАНЕТ
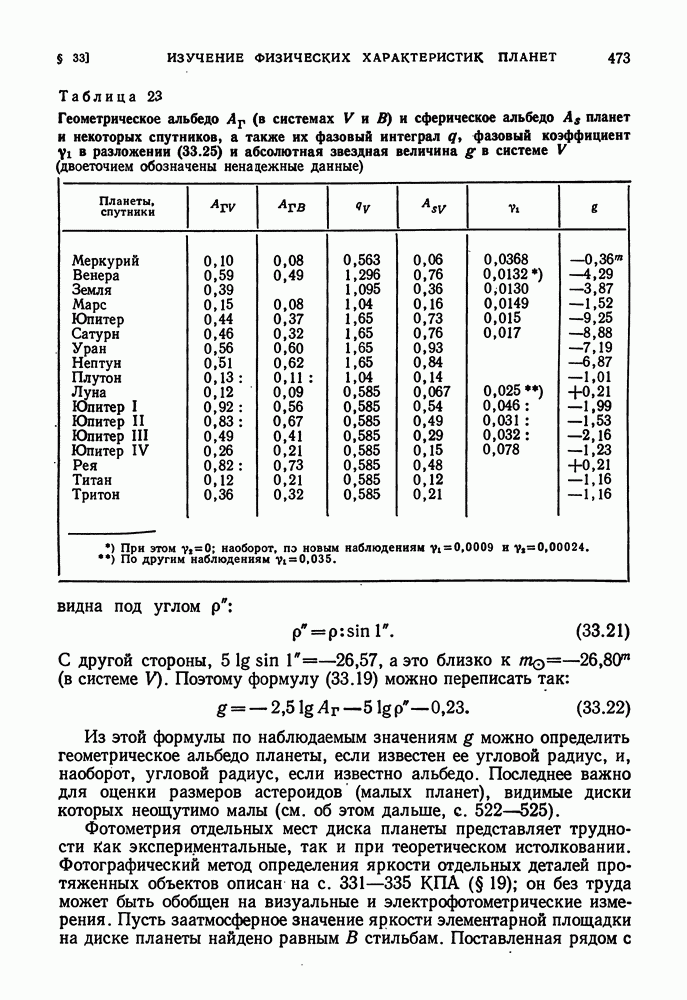
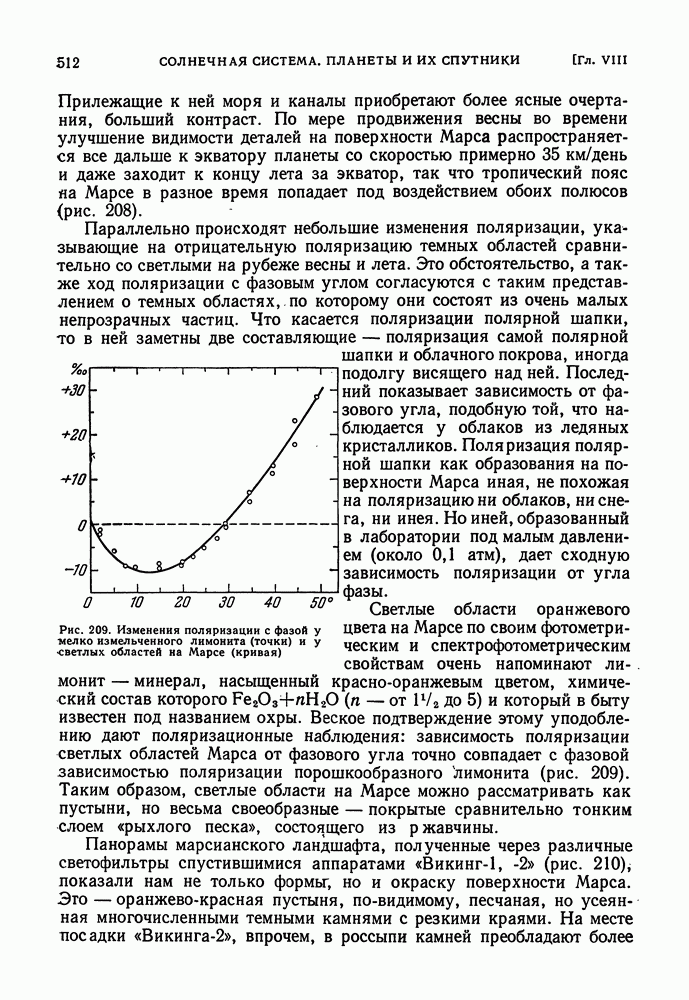
- ФОТОМЕТРИЧЕСКИЙ АНАЛИЗ ПЛАНЕТНЫХ ПОВЕРХНОСТЕЙ И АТМОСФЕРЫ
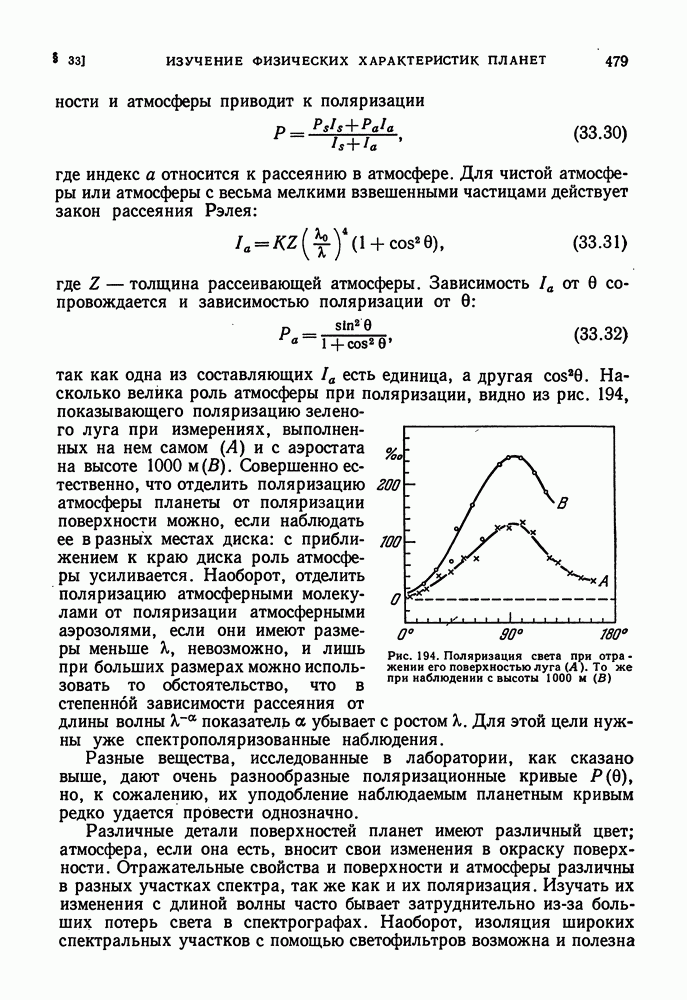
- ПОЛЯРИМЕТРИЯ ПЛАНЕТ
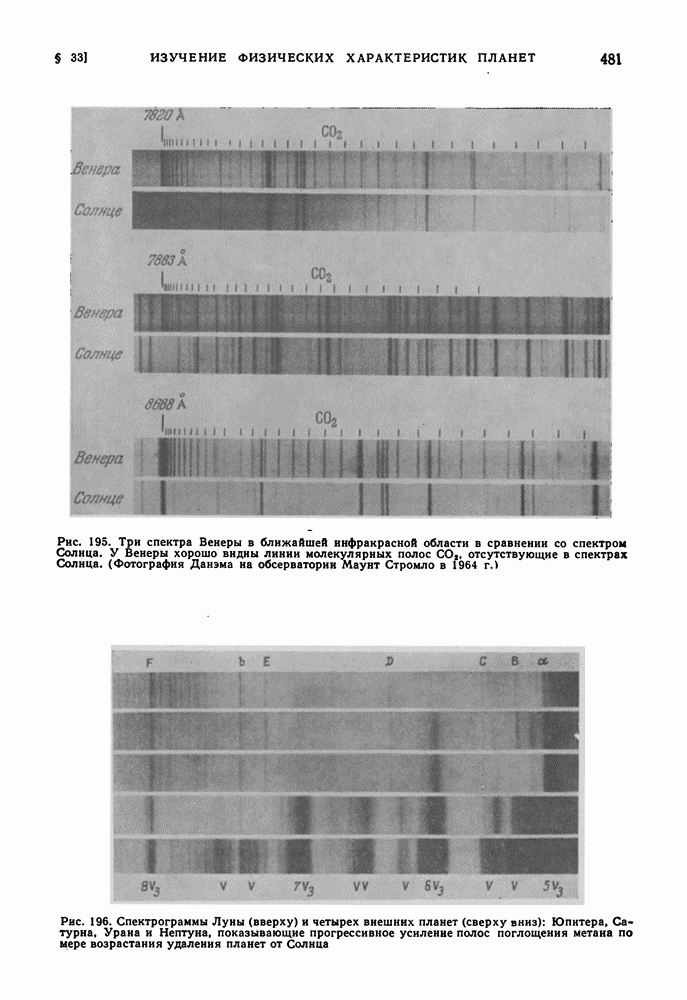
- СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЛАНЕТНЫХ АТМОСФЕР
- СПЕКТРАЛЬНОЕ ОПРЕДЕЛЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ
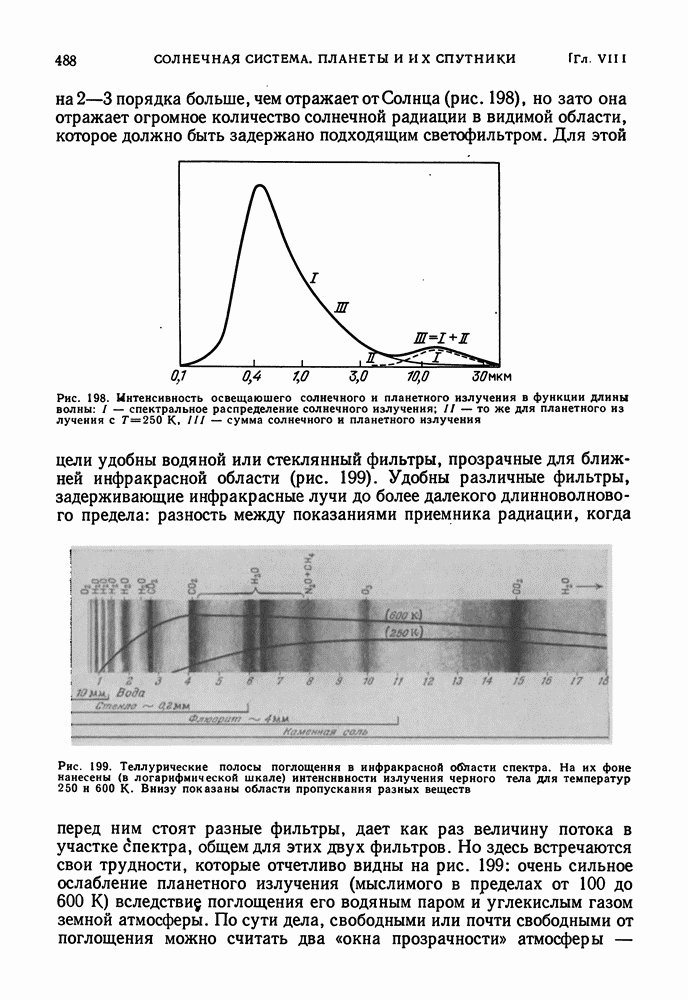
- ПЛАНЕТНЫЕ ТЕМПЕРАТУРЫ. ТЕОРИЯ. РОЛЬ АТМОСФЕРЫ
- РАЗЛИЧНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЛАНЕТНЫХ ТЕМПЕРАТУР
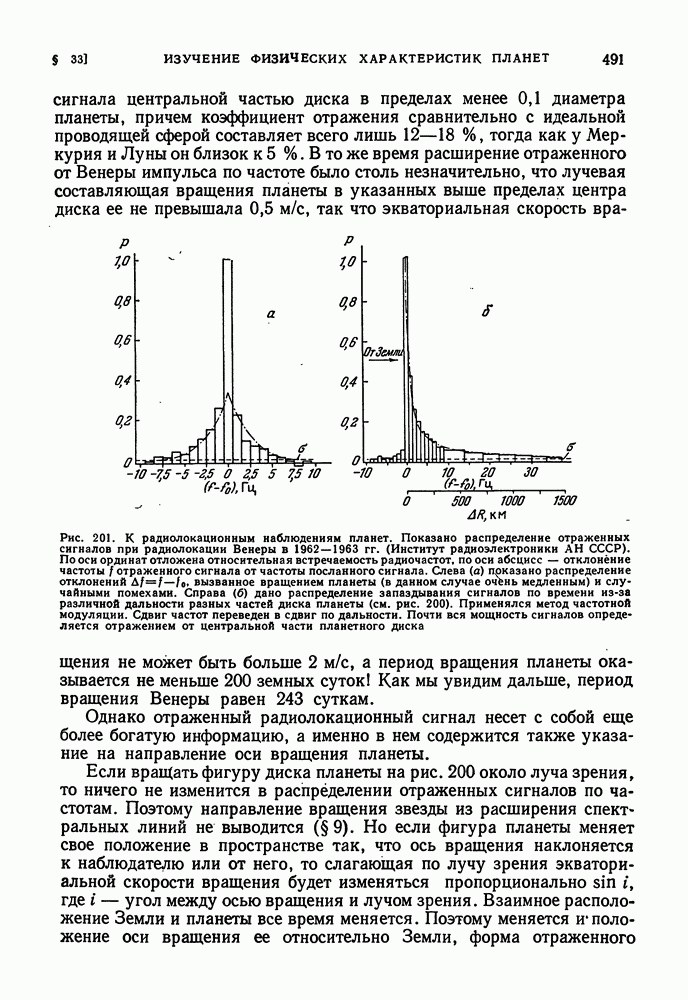
- РАДИОЛОКАЦИОННЫЕ МЕТОДЫ ИЗУЧЕНИЯ ПЛАНЕТ
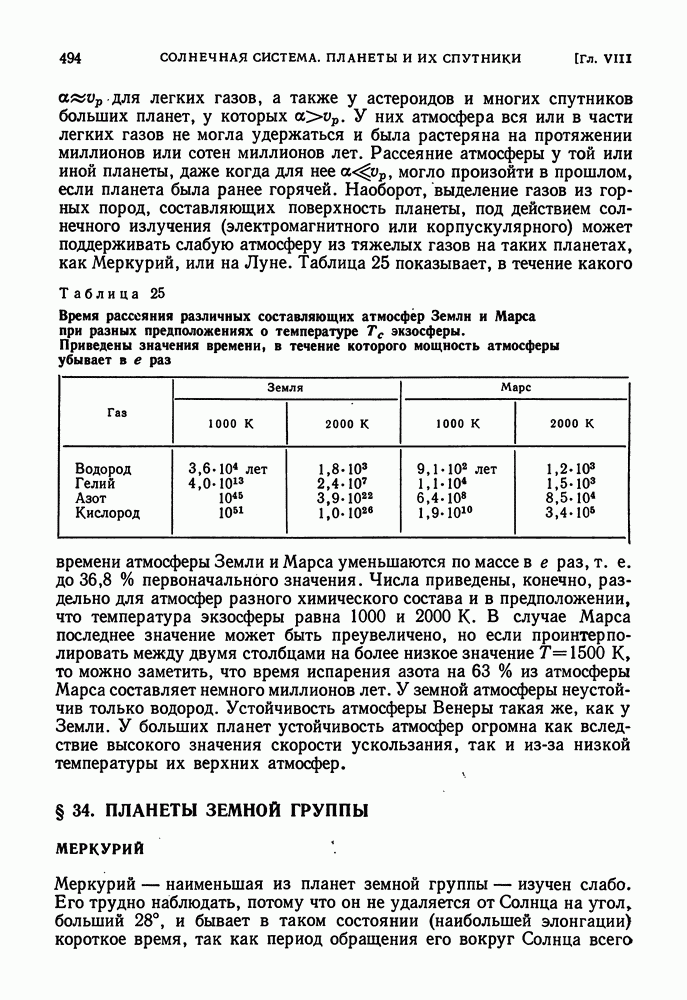
- УСТОЙЧИВОСТЬ ПЛАНЕТНЫХ АТМОСФЕР ВО ВРЕМЕНИ
- § 34. ПЛАНЕТЫ ЗЕМНОЙ ГРУППЫ
- МЕРКУРИЙ
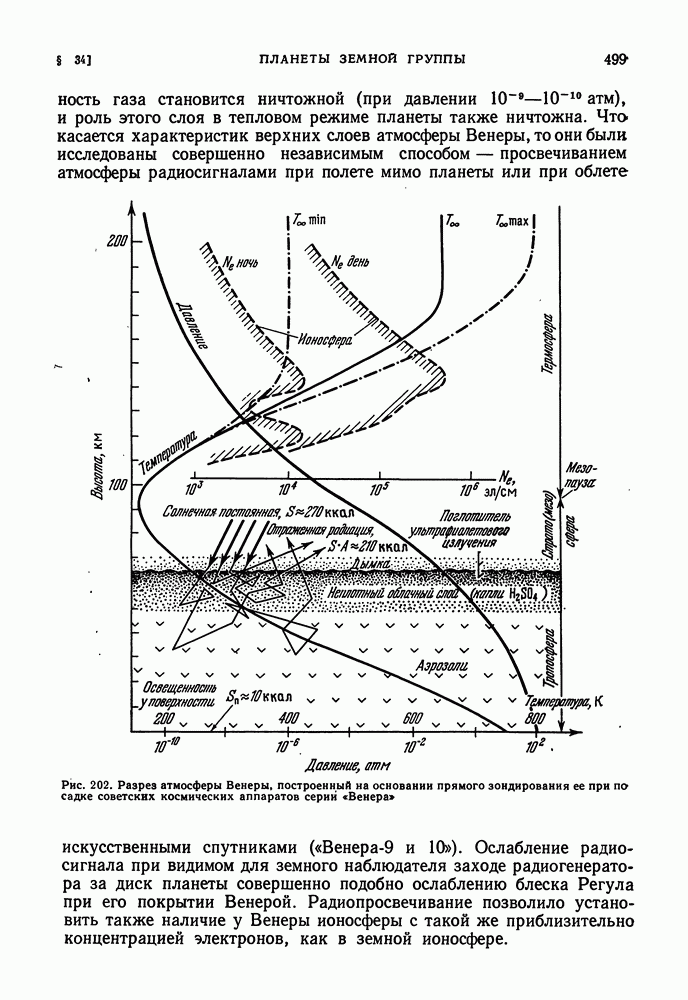
- ВЕНЕРА. ТЕМПЕРАТУРА. ПАРНИКОВАЯ МОДЕЛЬ АТМОСФЕРЫ. ВРАЩЕНИЕ
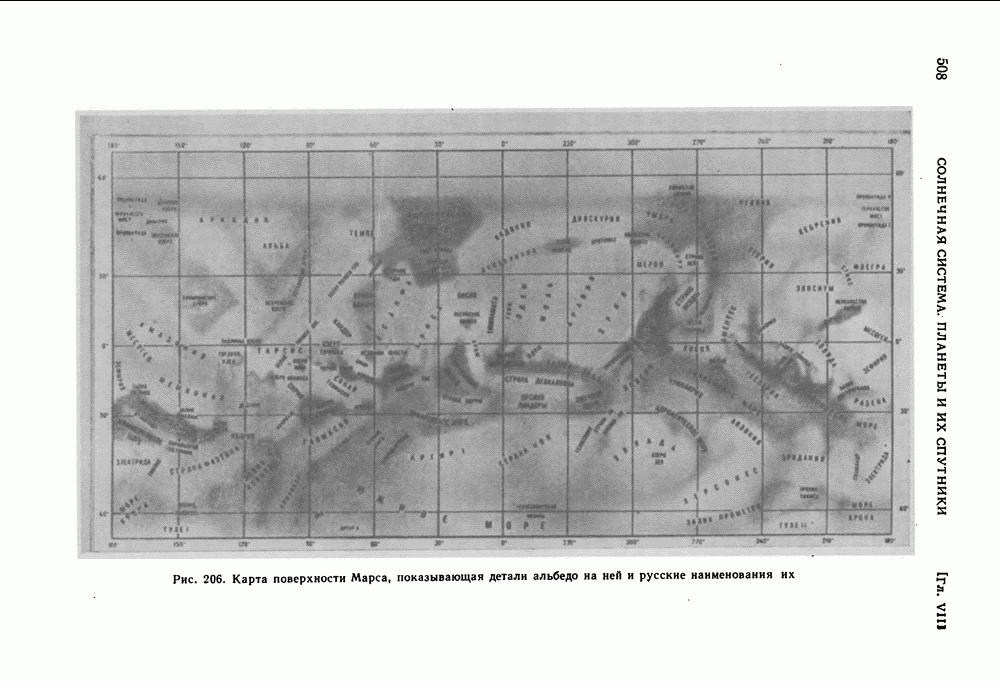
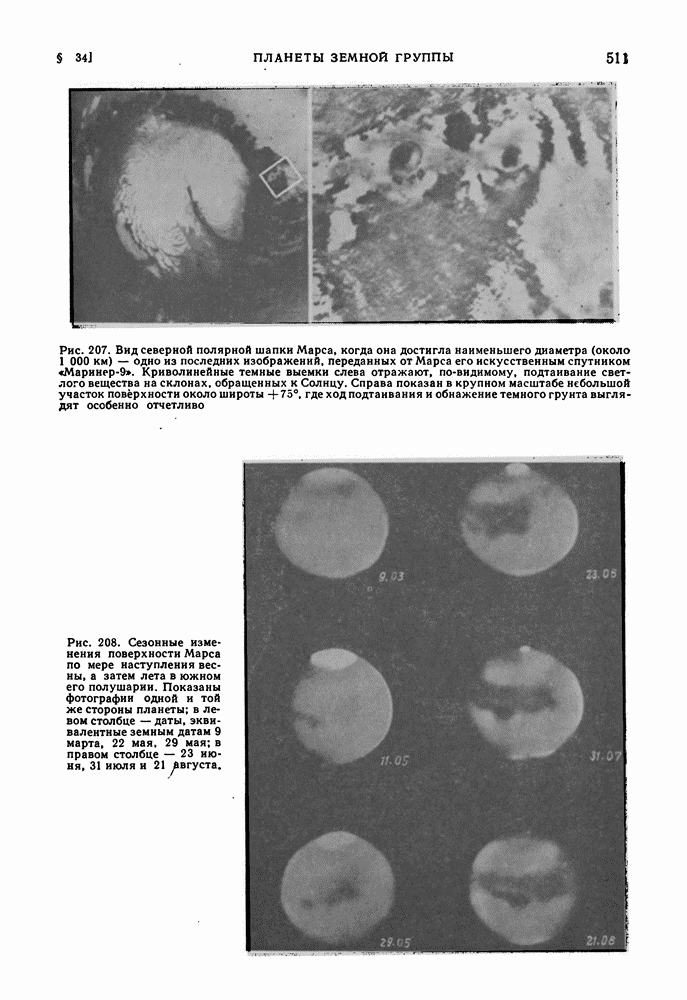
- МАРС. ОСОБЕННОСТИ ЕГО ПОВЕРХНОСТИ. ИХ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ
- АТМОСФЕРА МАРСА
- ТЕМПЕРАТУРА МАРСА
- ВОДА НА МАРСЕ. ЖИЗНЬ НА МАРСЕ?
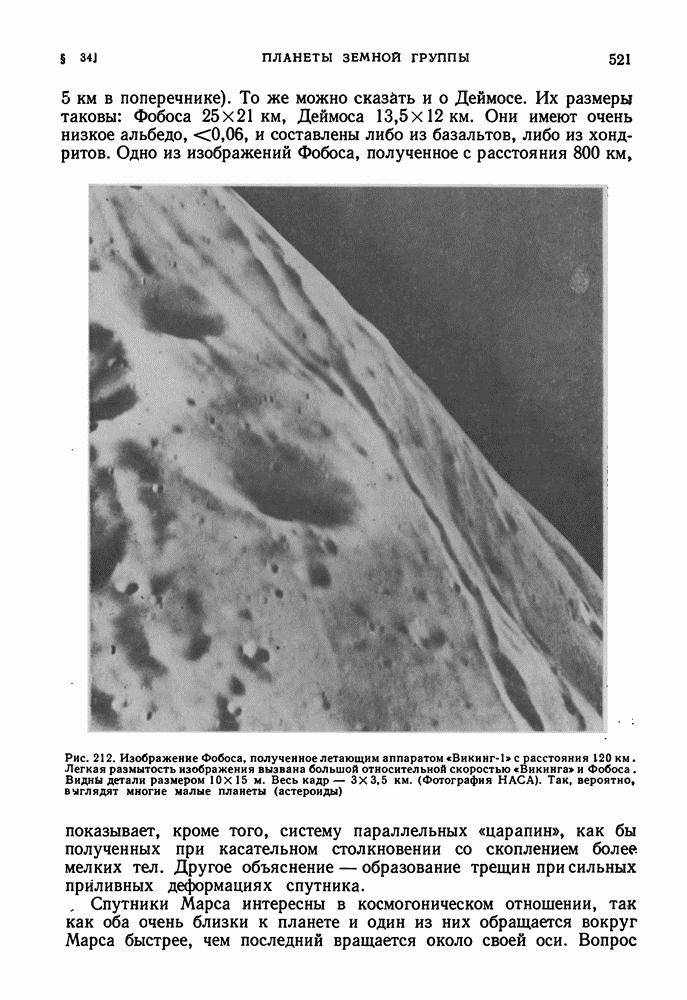
- МАЛЫЕ ПЛАНЕТЫ
- § 35. ЛУНА
- АТМОСФЕРА ЛУНЫ
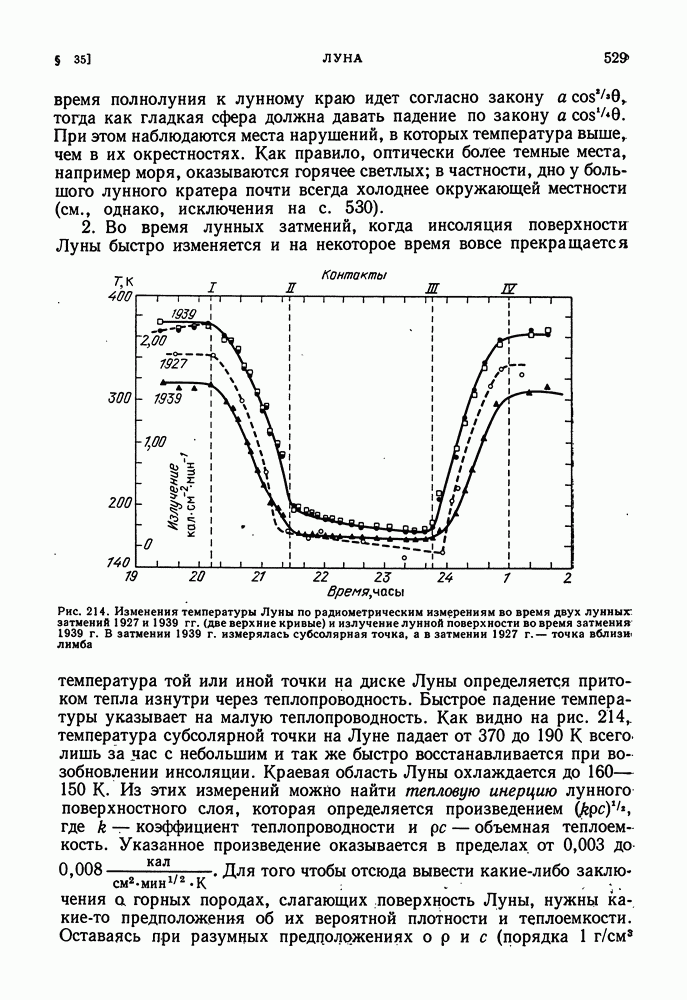
- ТЕМПЕРАТУРНЫЙ РЕЖИМ НА ЛУНЕ
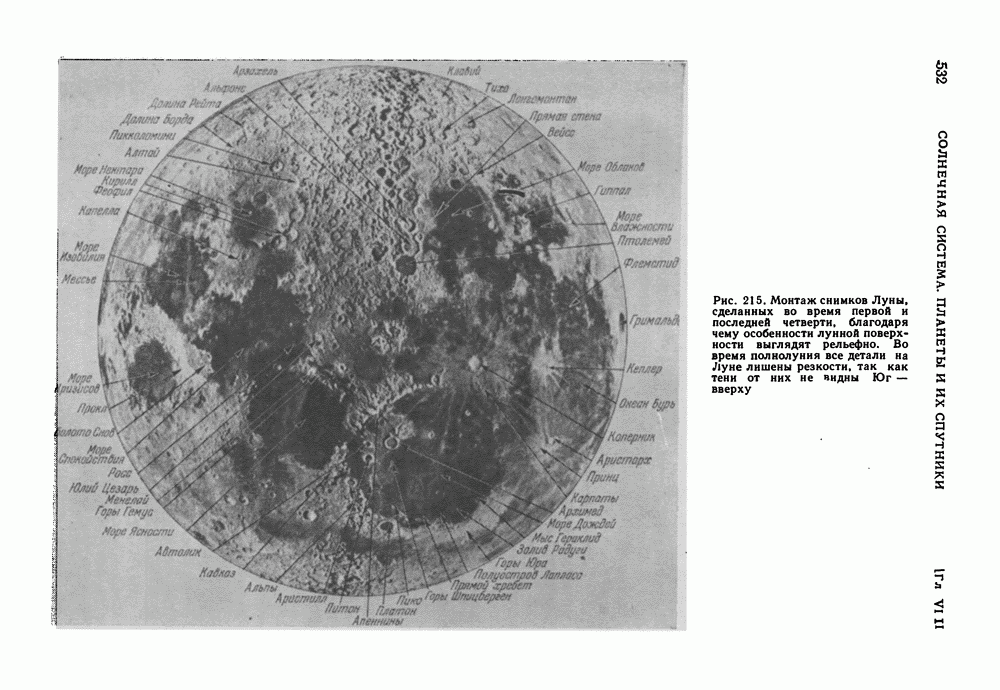
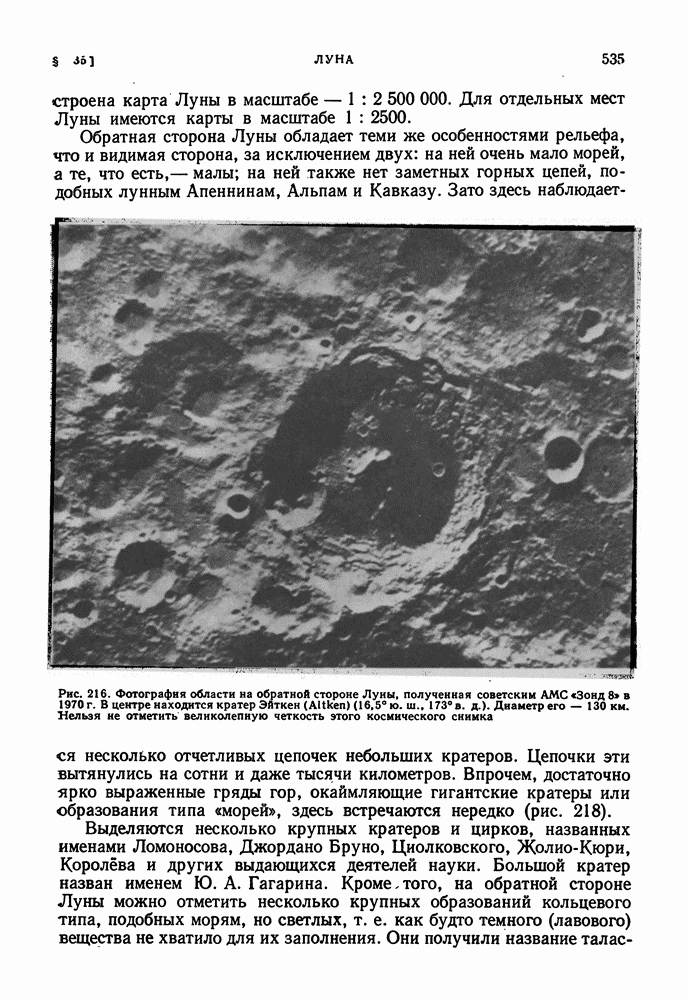
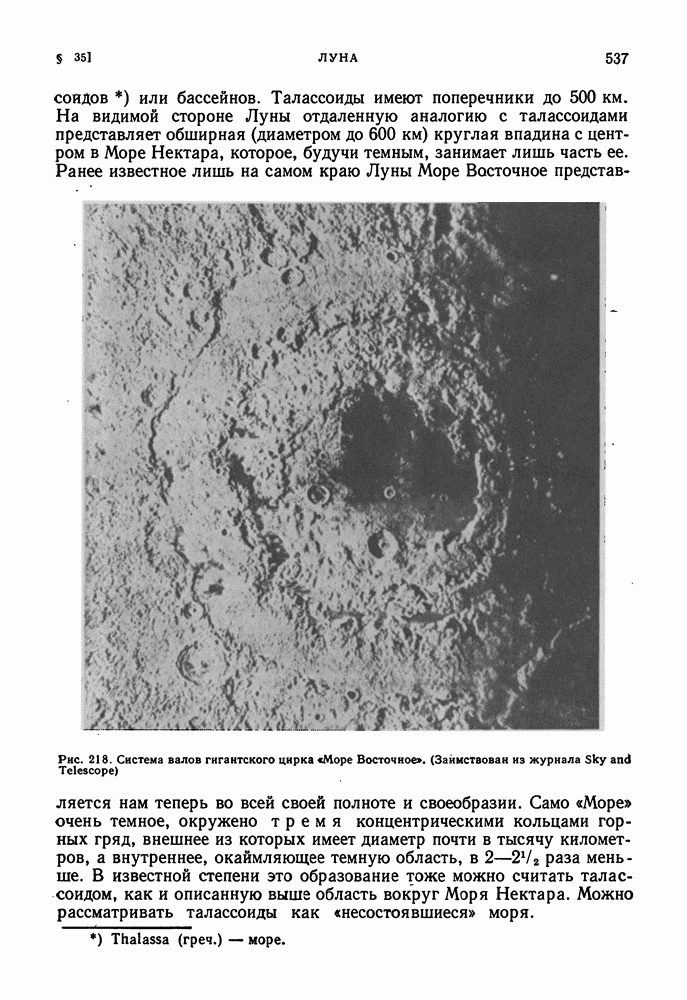
- МОРФОЛОГИЯ ЛУННОЙ ПОВЕРХНОСТИ
- ВНУТРЕННЕЕ СТРОЕНИЕ ЛУНЫ
- ОБРАЗОВАНИЕ СОВРЕМЕННОГО ЛУННОГО ЛАНДШАФТА
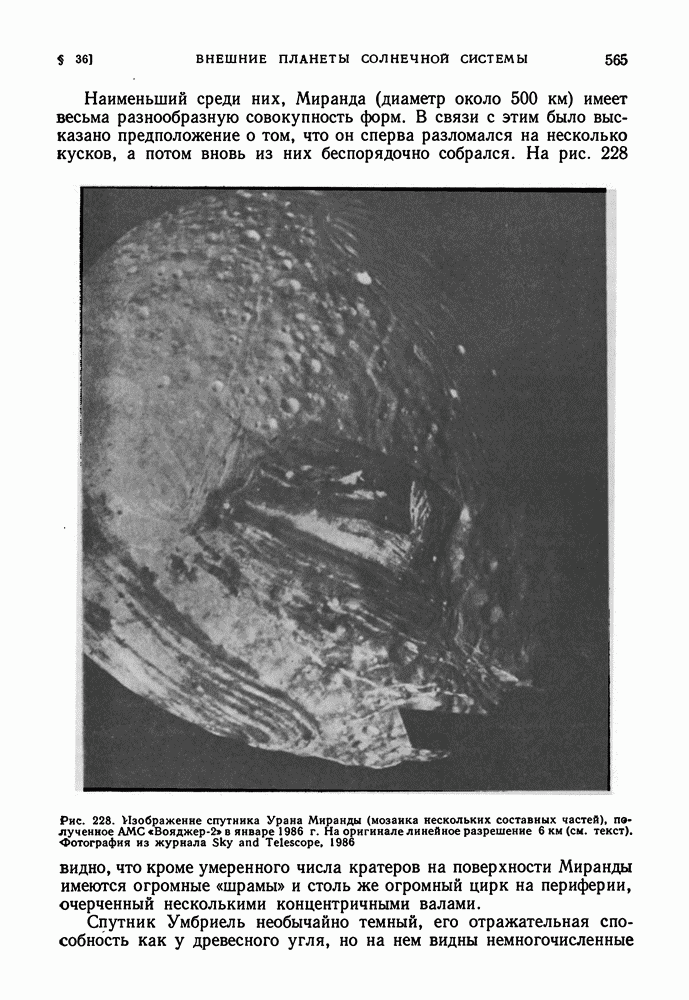
- § 36. ВНЕШНИЕ ПЛАНЕТЫ СОЛНЕЧНОЙ СИСТЕМЫ
- ЮПИТЕР
- САТУРН
- УРАН И НЕПТУН
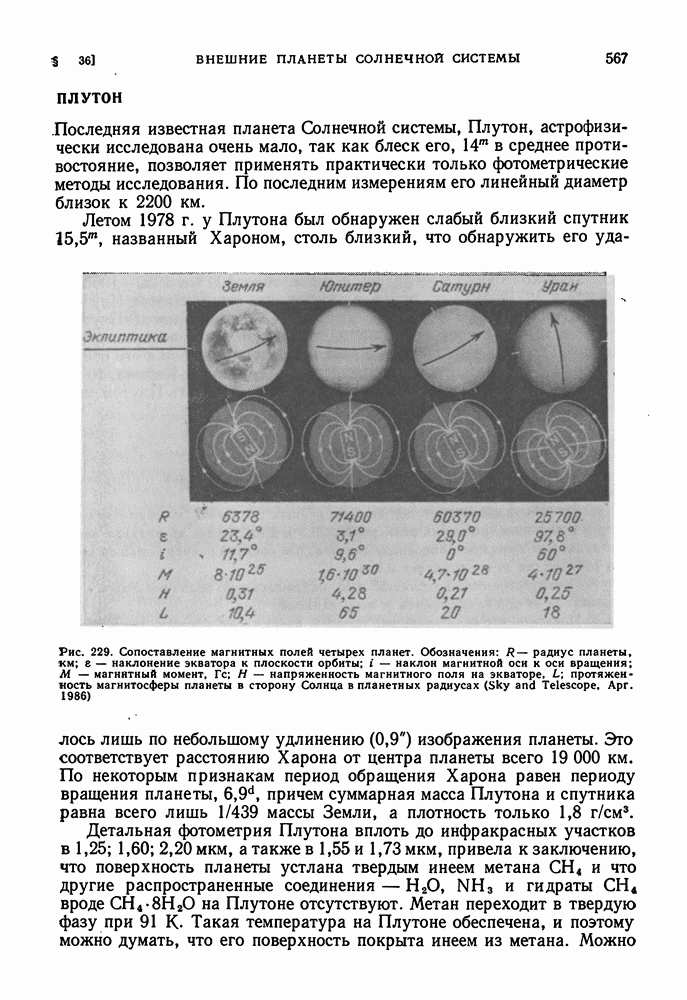
- ПЛУТОН
- ЗАДАЧИ К ГЛАВЕ VIII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VIII
- ГЛАВА IX. СОЛНЕЧНАЯ СИСТЕМА. КОМЕТЫ И МАЛЫЕ ТЕЛА СОЛНЕЧНОЙ СИСТЕМЫ
- ОБЩАЯ ХАРАКТЕРИСТИКА КОМЕТ
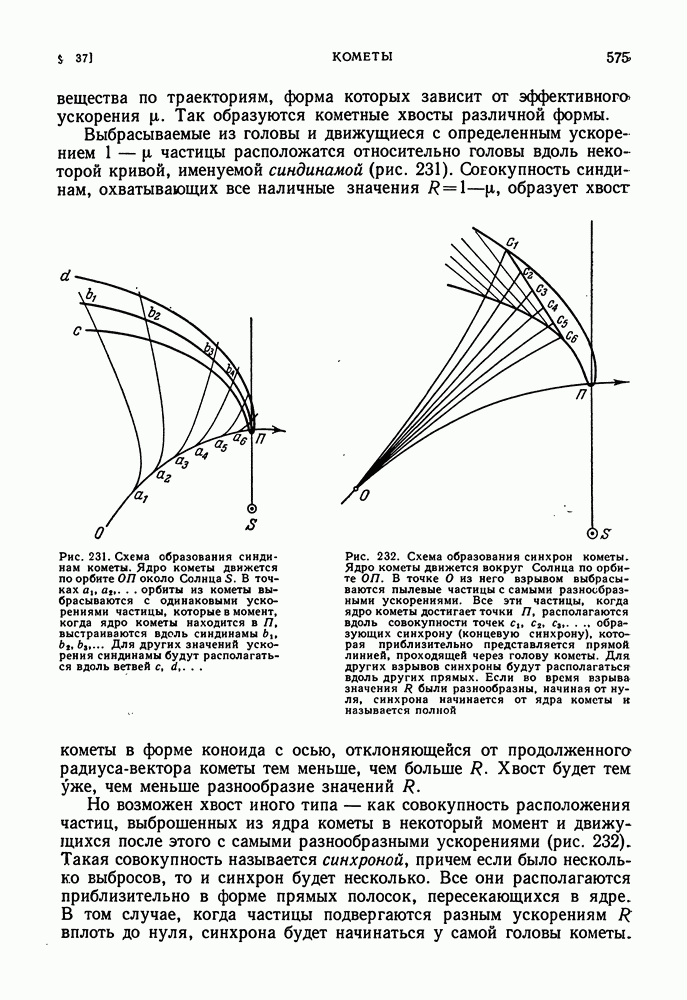
- ОБРАЗОВАНИЕ КОМЕТНЫХ ФОРМ
- МЕХАНИЧЕСКАЯ ТЕОРИЯ КОМЕТНЫХ ФОРМ
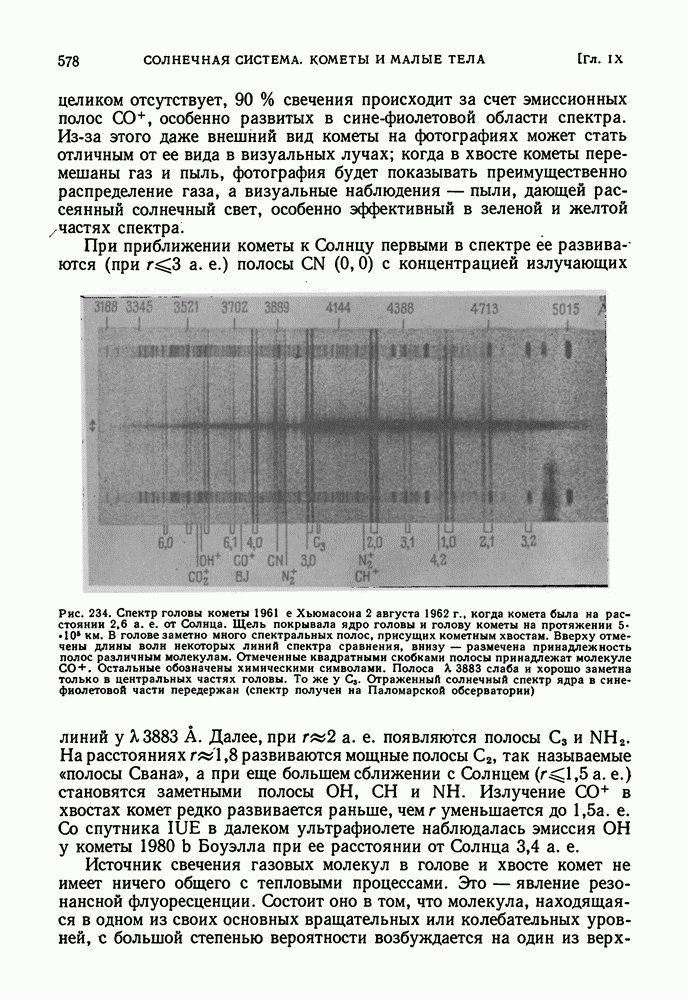
- СПЕКТРЫ КОМЕТ
- БЛЕСК КОМЕТЫ И ЕГО ИЗМЕНЕНИЯ
- ДАВЛЕНИЕ СВЕТА НА КОМЕТНЫЕ ЧАСТИЦЫ
- СОЛНЕЧНАЯ АКТИВНОСТЬ КАК ИСТОЧНИК ВОЗНИКНОВЕНИЯ КОМЕТНЫХ ФОРМ
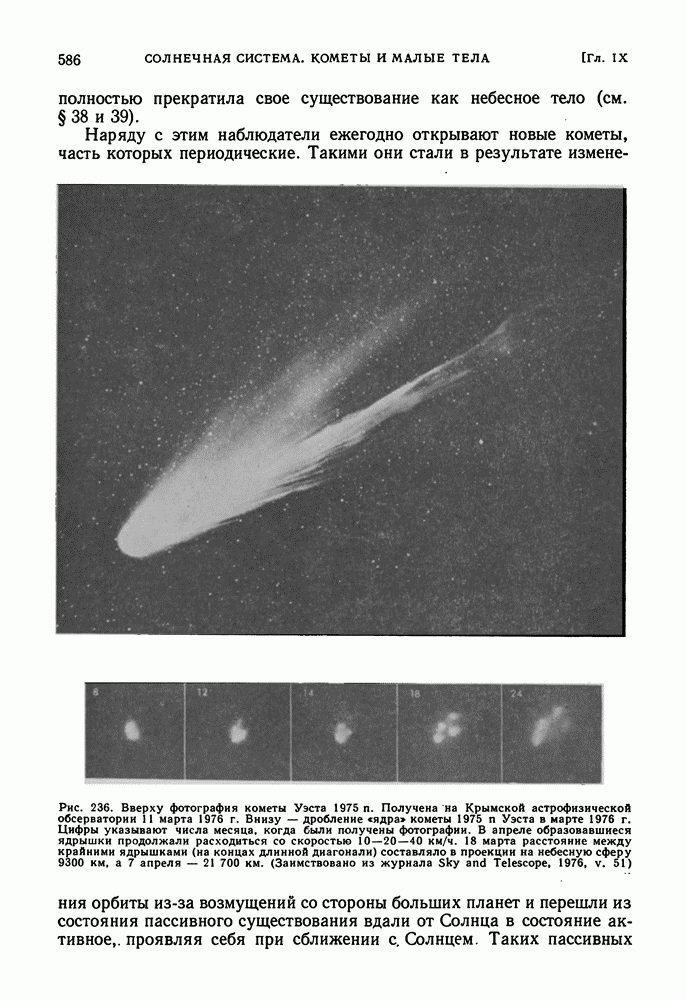
- РАСПАД КОМЕТ. ПРОИСХОЖДЕНИЕ КОМЕТ
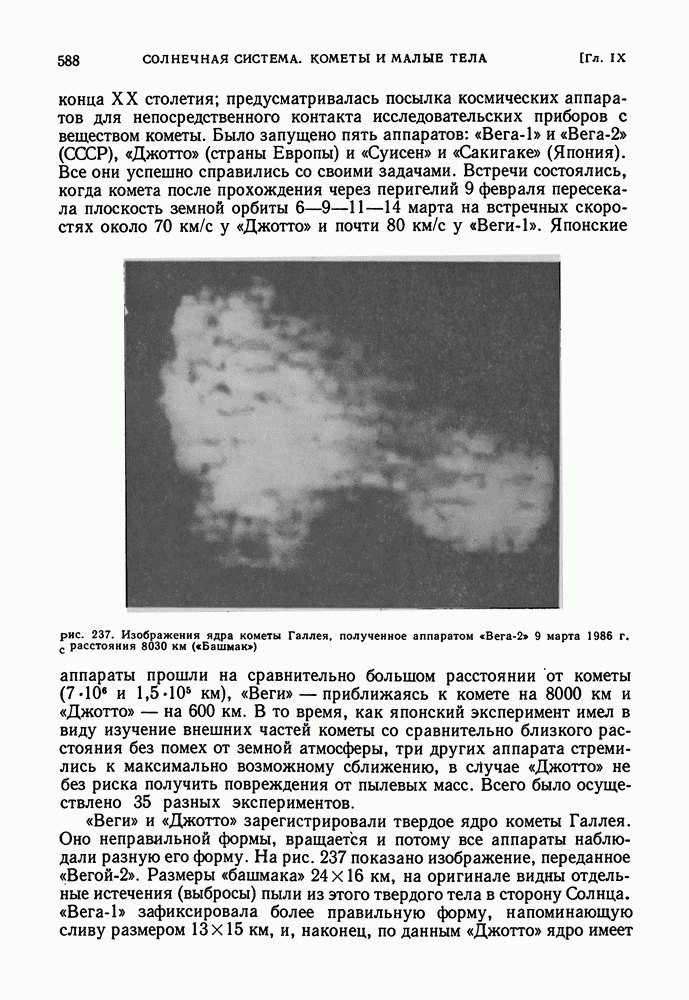
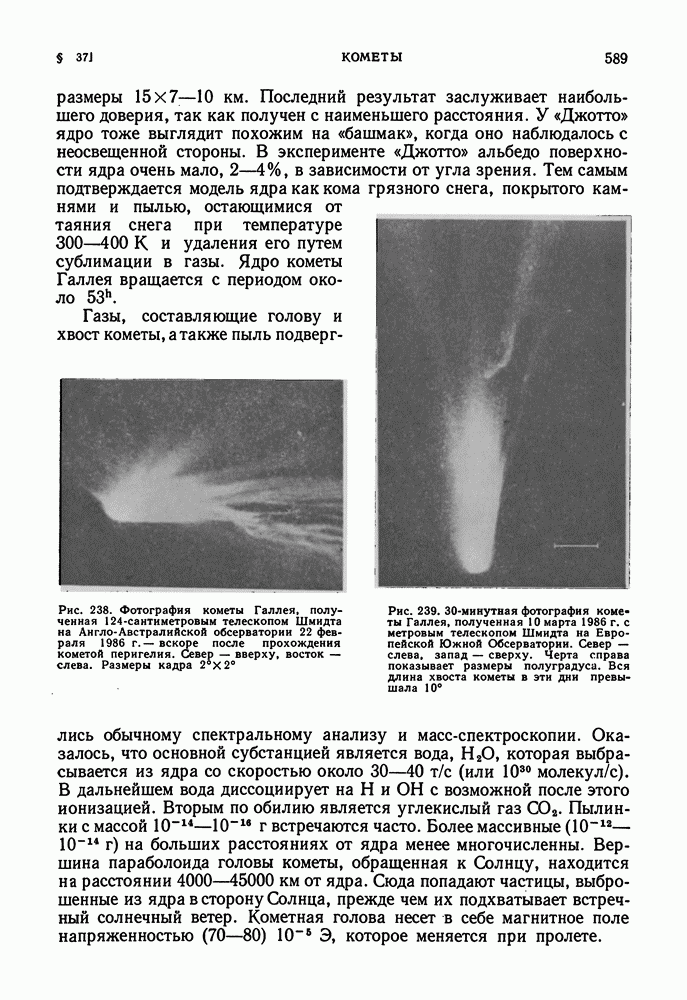
- КОМЕТА ГАЛЛЕЯ В 1986 г.
- § 38. МЕТЕОРЫ
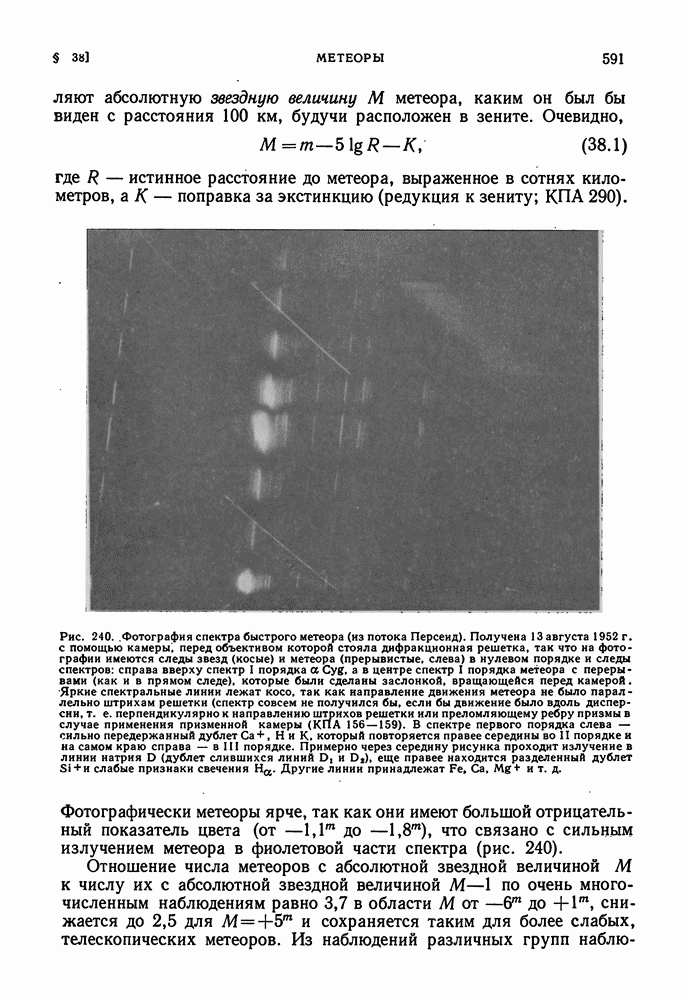
- ОБЩИЕ ХАРАКТЕРИСТИКИ МЕТЕОРОВ. СПОСОБЫ ИХ НАБЛЮДЕНИЯ
- МЕТЕОРНЫЕ ПОТОКИ И СПОРАДИЧЕСКИЕ МЕТЕОРЫ
- ЯВЛЕНИЯ ПРИ ВТОРЖЕНИИ МЕТЕОРНОГО ТЕЛА В ЗЕМНУЮ АТМОСФЕРУ
- РАДИОЛОКАЦИОННЫЕ НАБЛЮДЕНИЯ МЕТЕОРОВ
- МАССЫ МЕТЕОРНЫХ ТЕЛ
- МЕТЕОРИТЫ И ИХ КЛАССИФИКАЦИЯ
- ВОЗРАСТ МЕТЕОРИТОВ
- МЕТЕОРИТНЫЕ КРАТЕРЫ И ВОРОНКИ
- ТУНГУССКИЙ МЕТЕОРИТ
- § 39. МЕТЕОРНОЕ И ПЫЛЕВОЕ ВЕЩЕСТВО В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
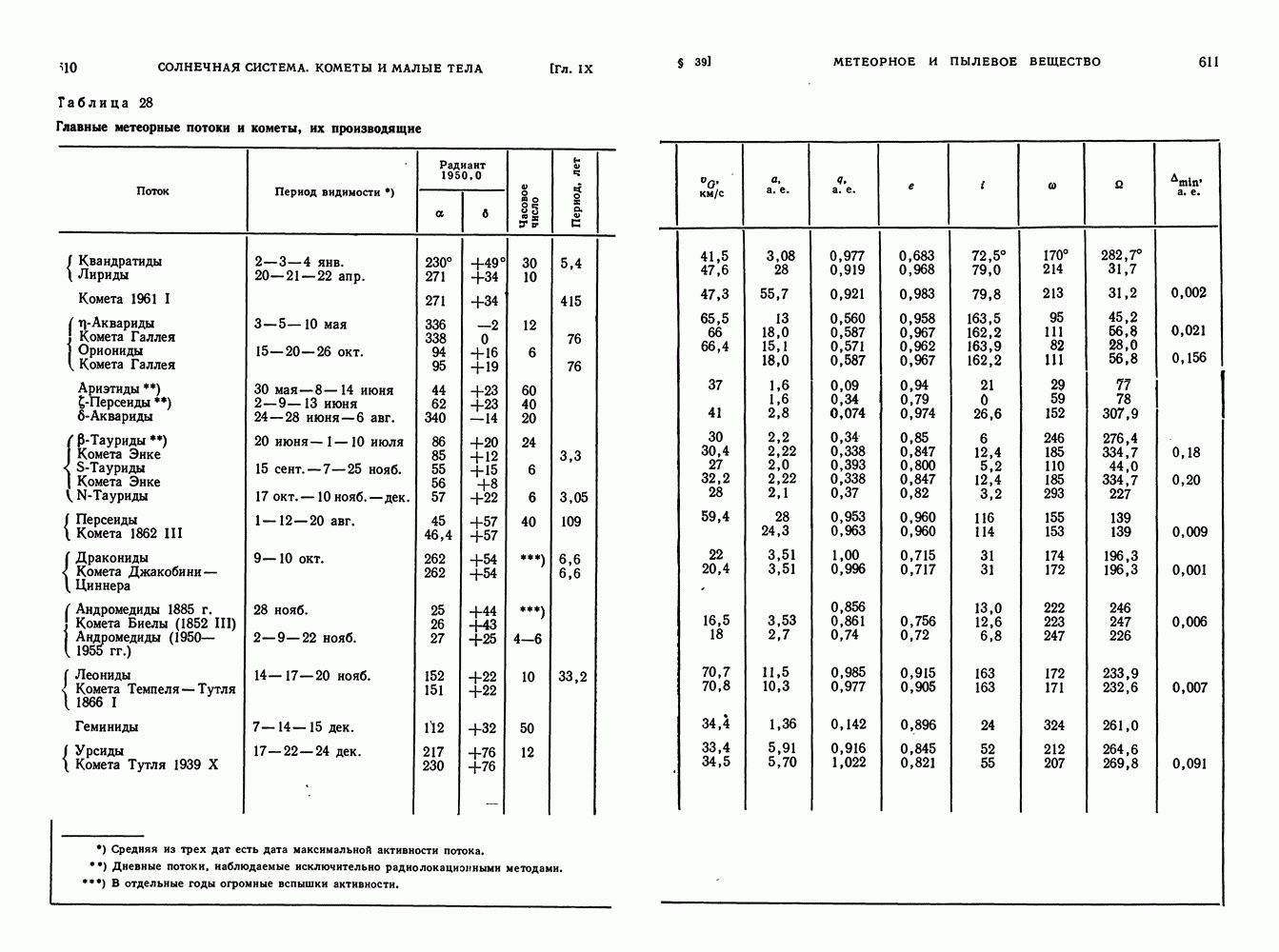
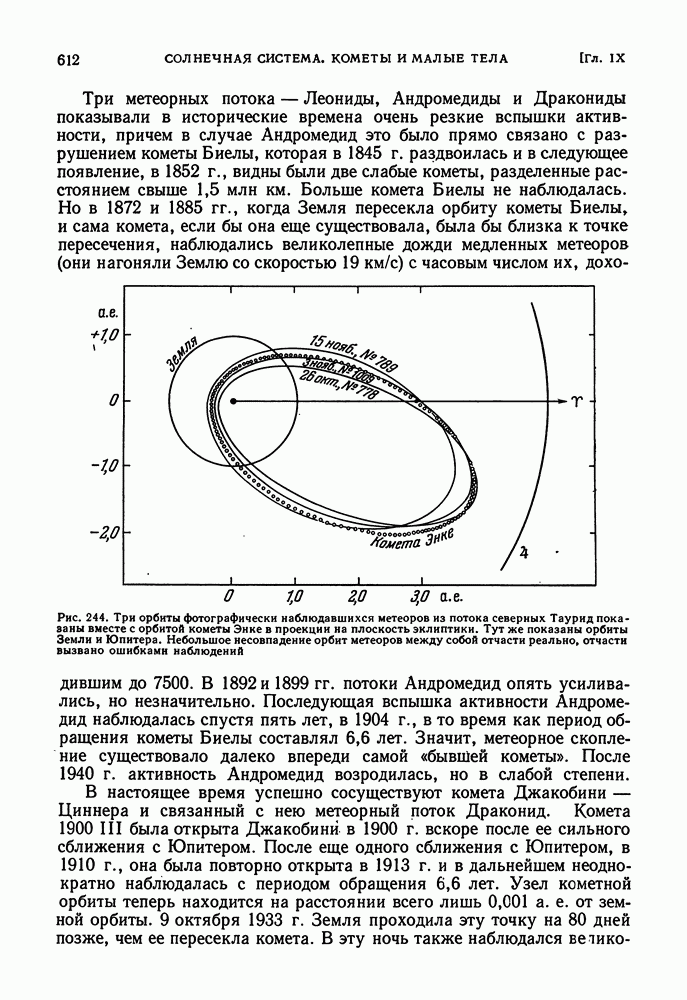
- МЕТЕОРНЫЕ РОИ И СВЯЗЬ ИХ С КОМЕТАМИ
- МИКРОМЕТЕОРИТЫ
- МЕТЕОРНОЕ ВЕЩЕСТВО ВОКРУГ ЗЕМЛИ
- ЗОДИАКАЛЬНЫЙ СВЕТ
- ПЫЛЕВАЯ И ГАЗОВАЯ СОСТАВЛЯЮЩИЕ В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- ДВИЖЕНИЕ МАЛОЙ ЧАСТИЦЫ В ПОЛЕ ТЯГОТЕНИЯ И ИЗЛУЧЕНИЯ СОЛНЦА
- ПРОТИВОСИЯНИЕ
- ЗАДАЧИ К ГЛАВЕ IX