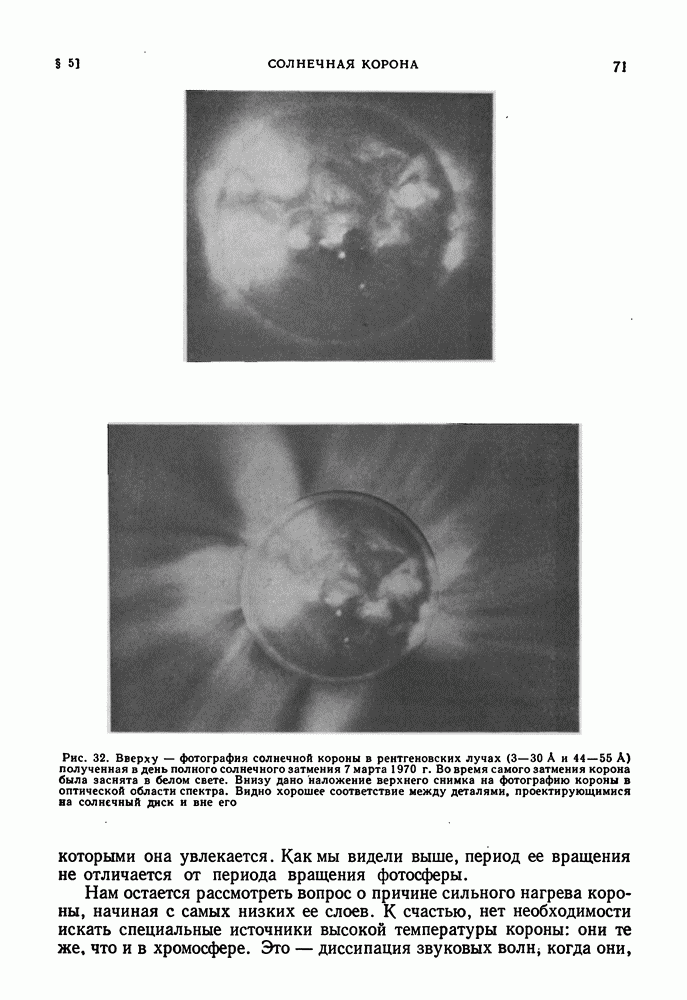
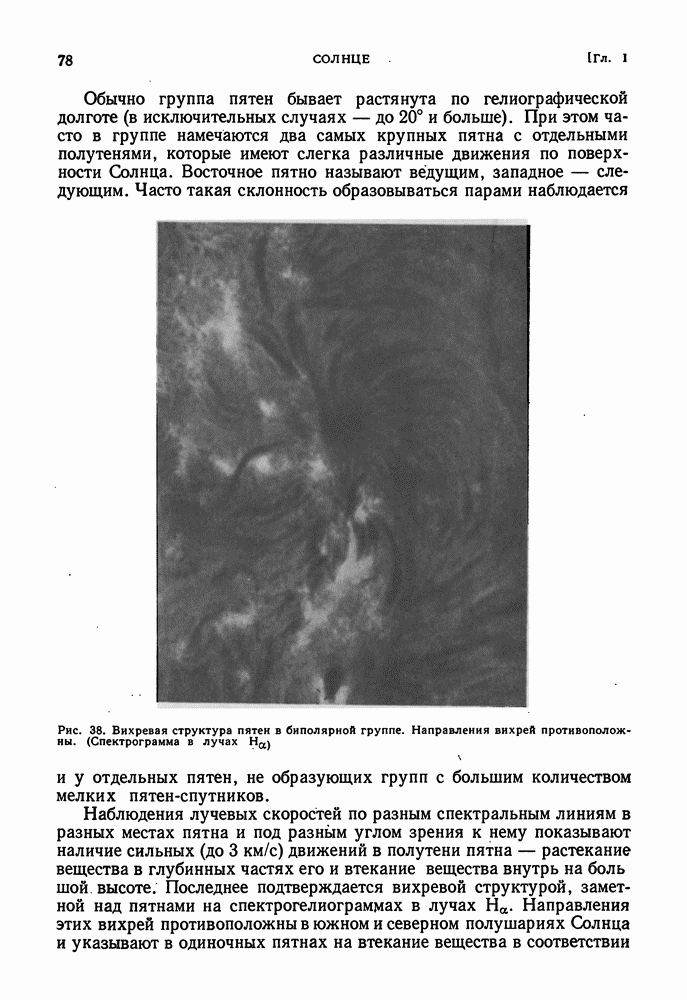
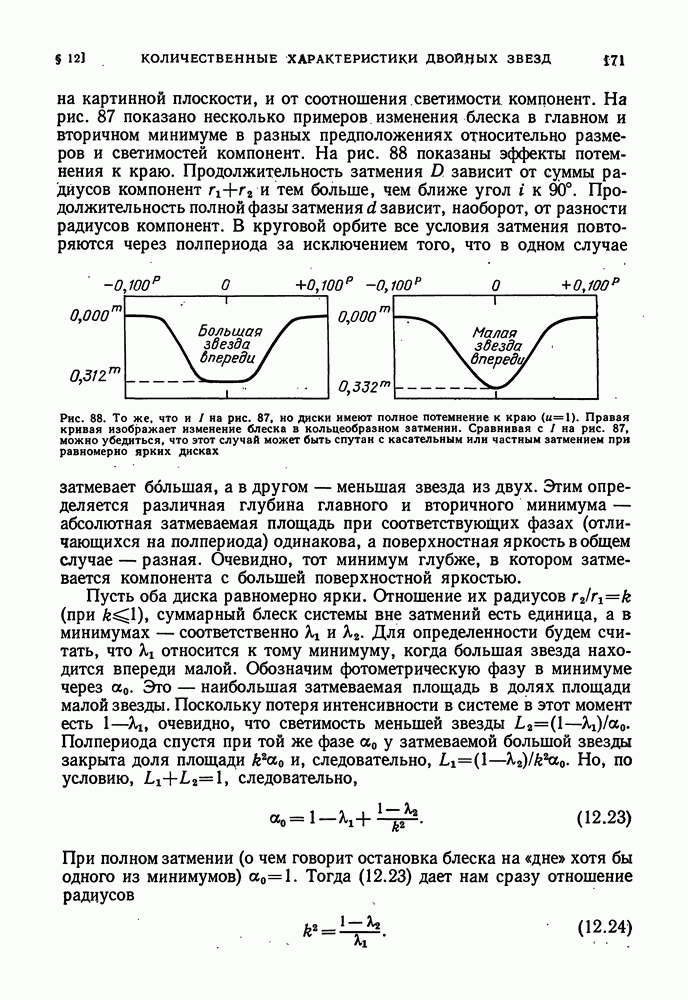
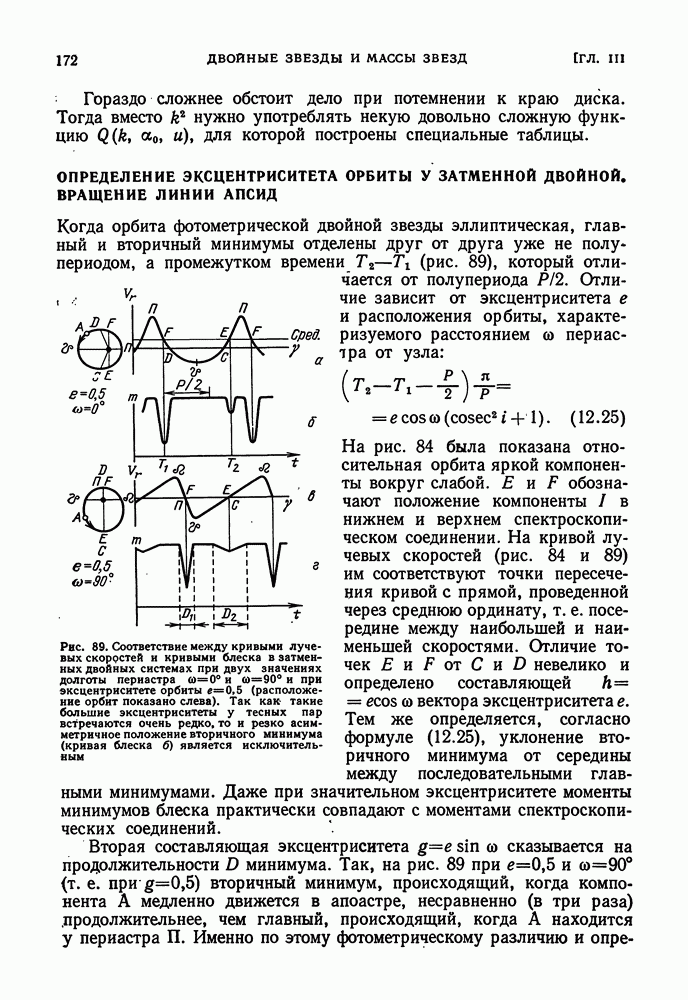
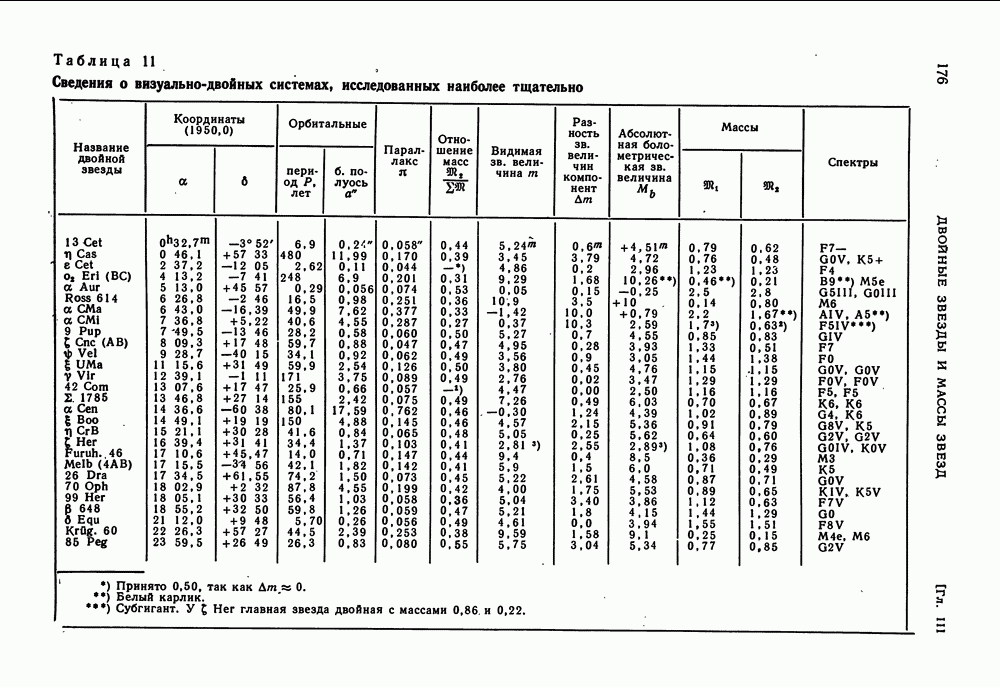
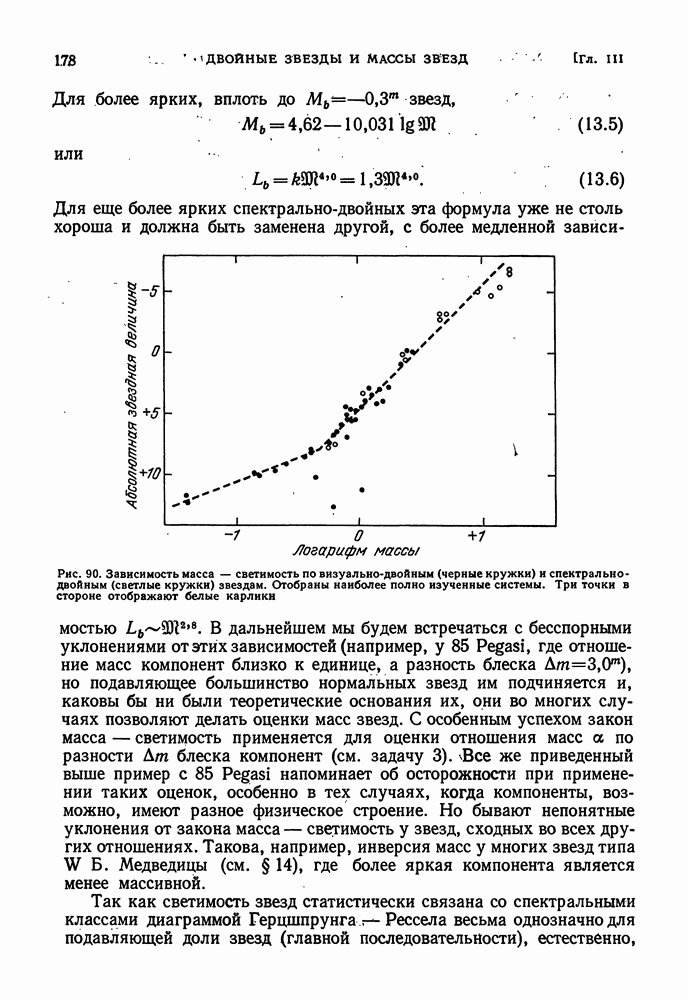
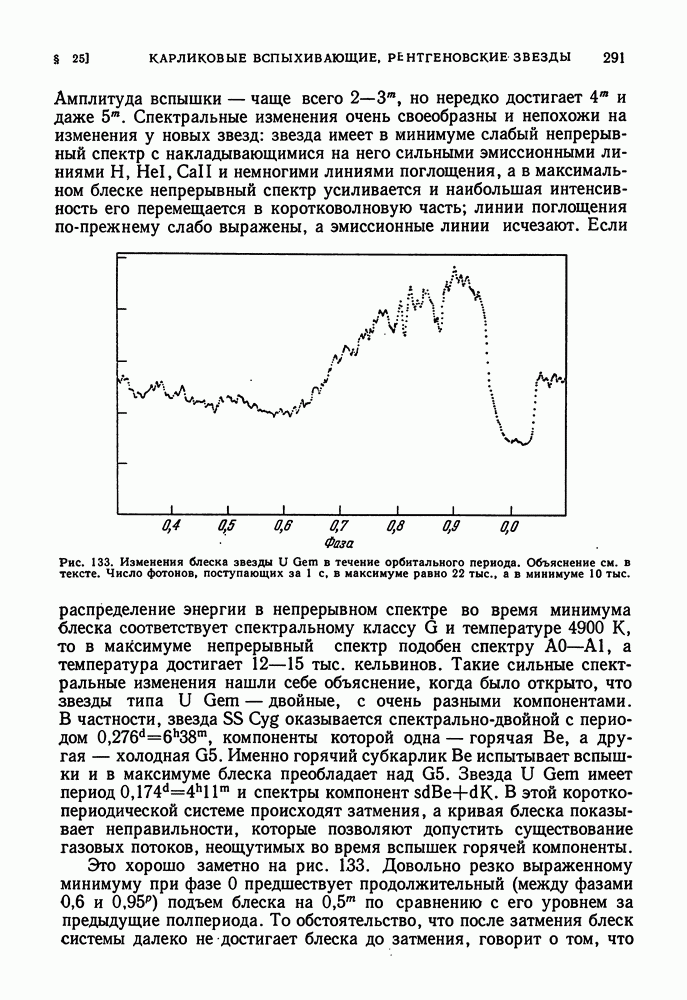
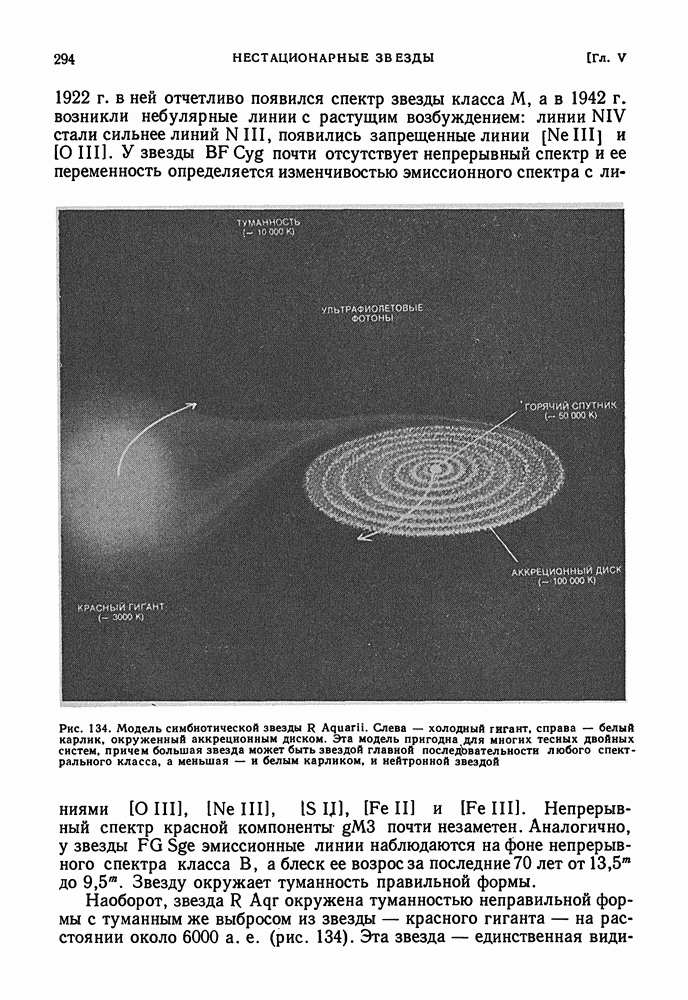
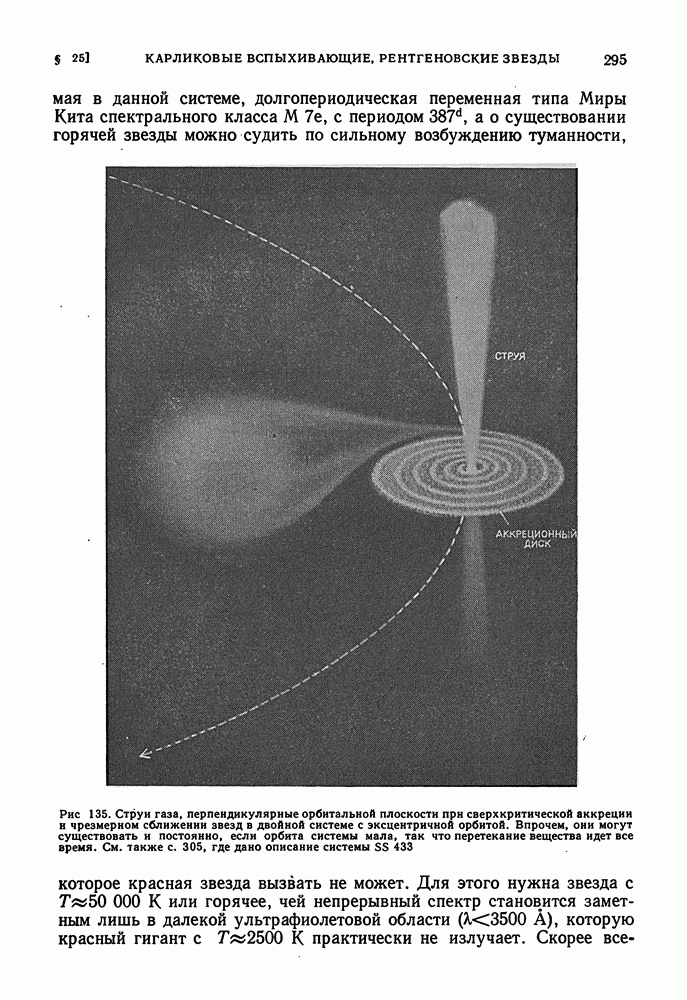
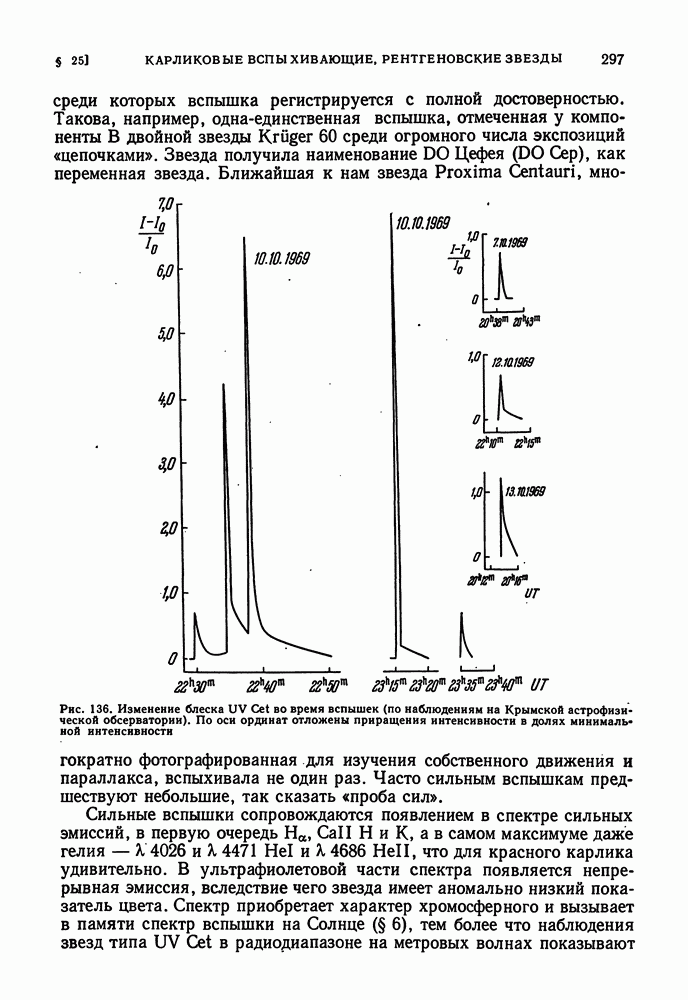
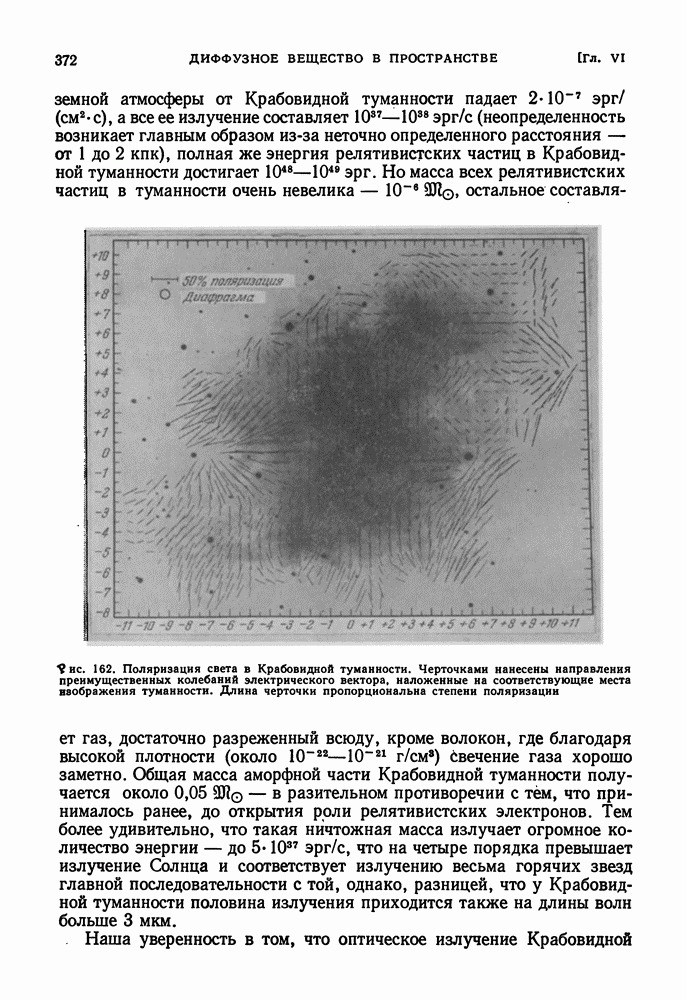
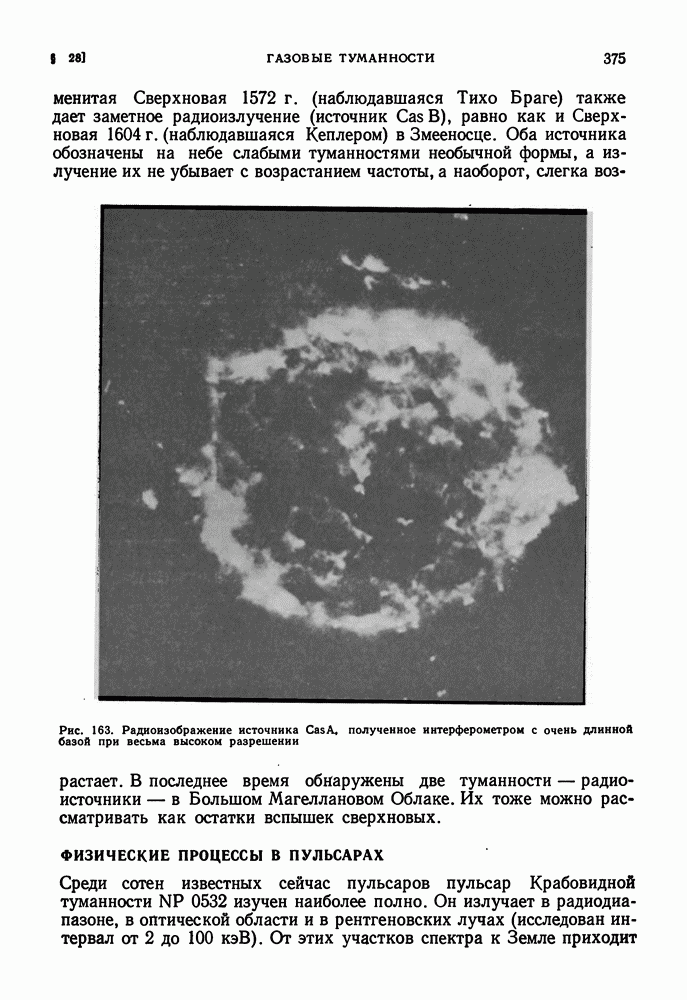
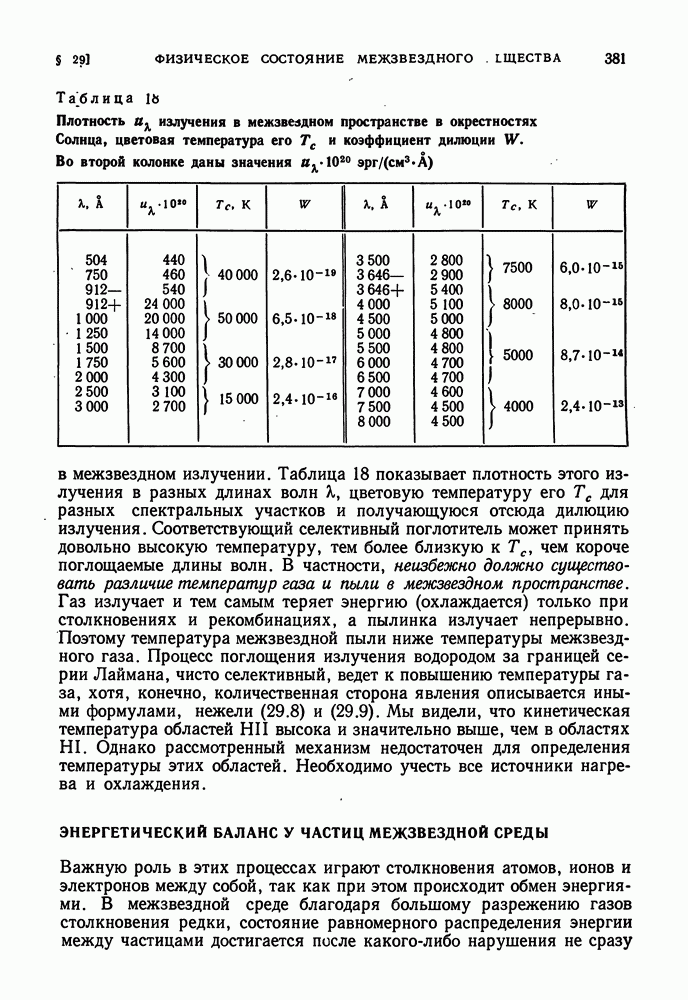
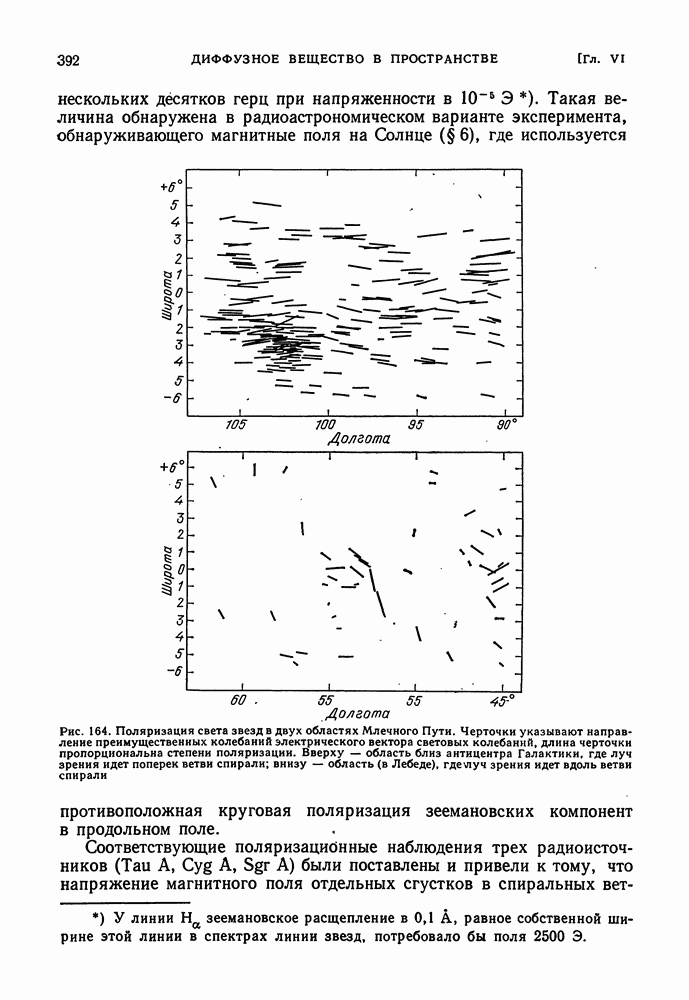
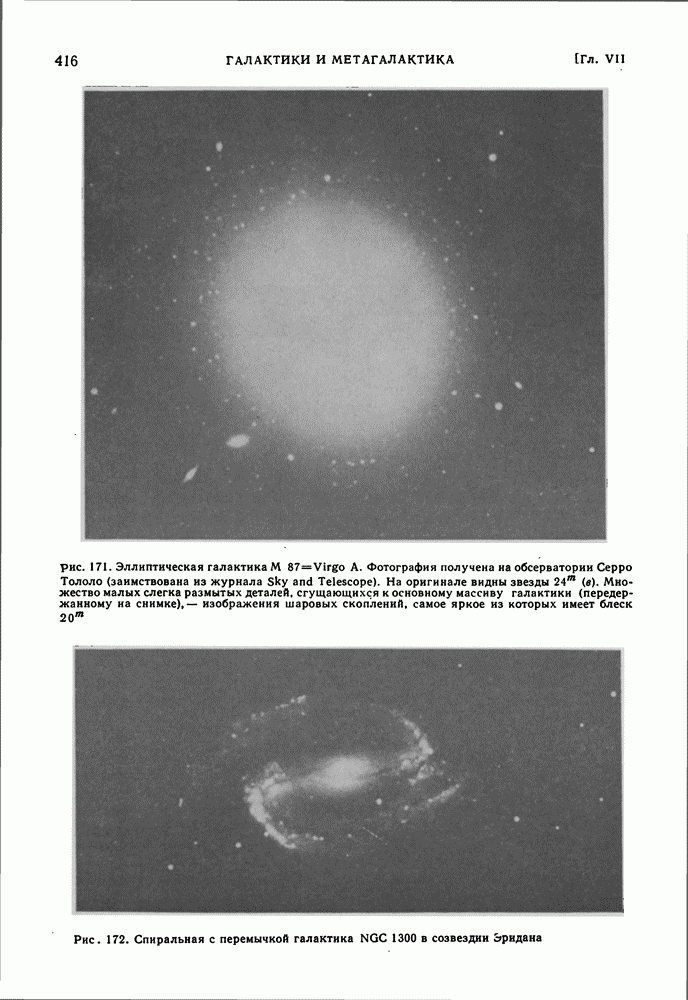
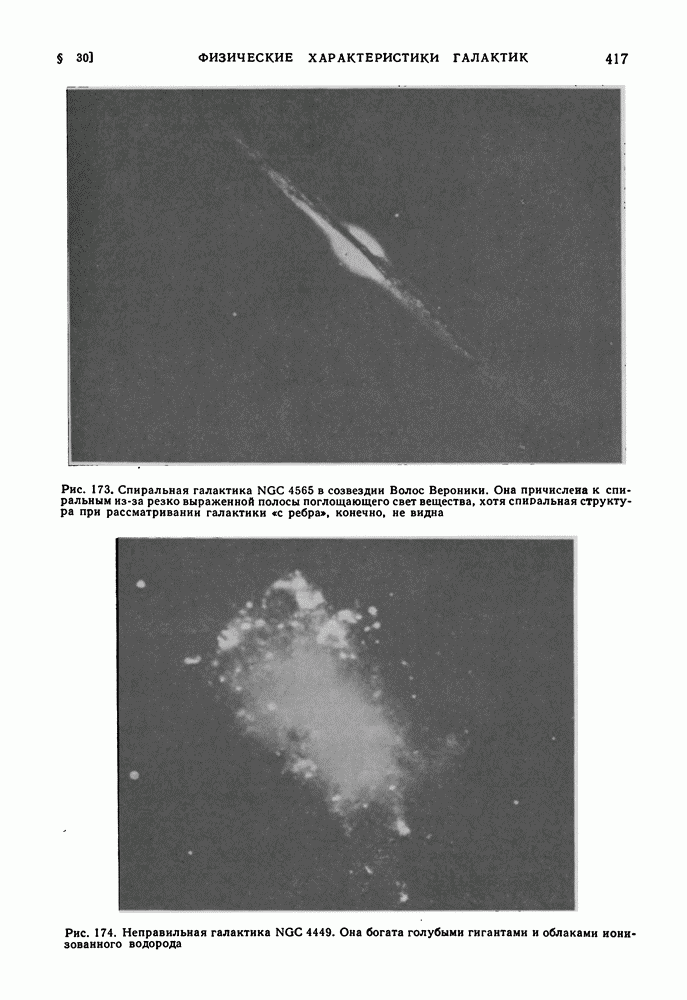
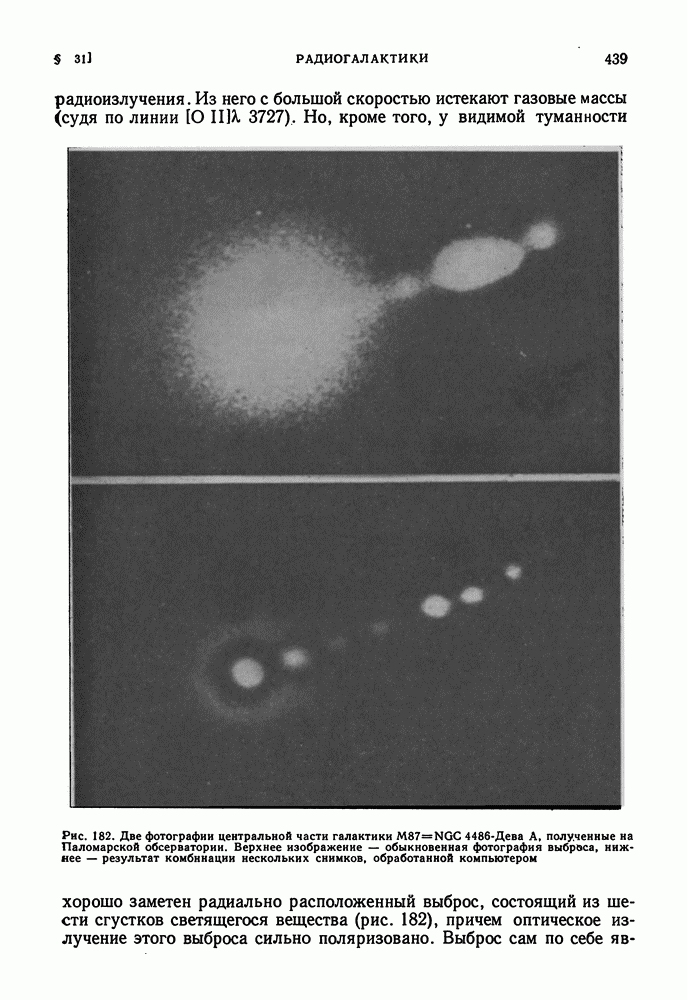
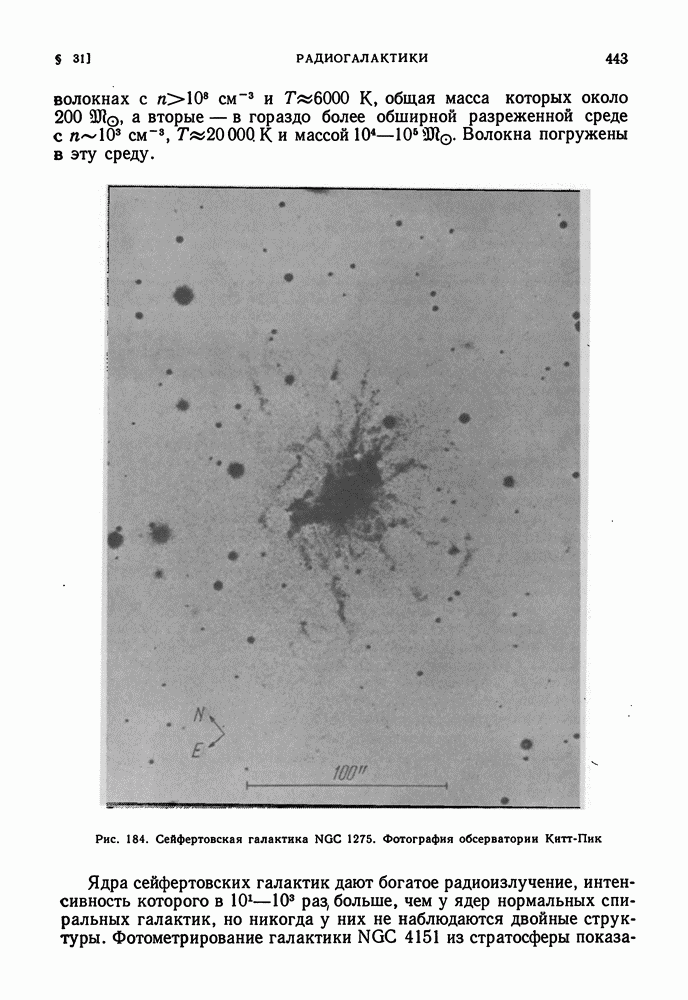
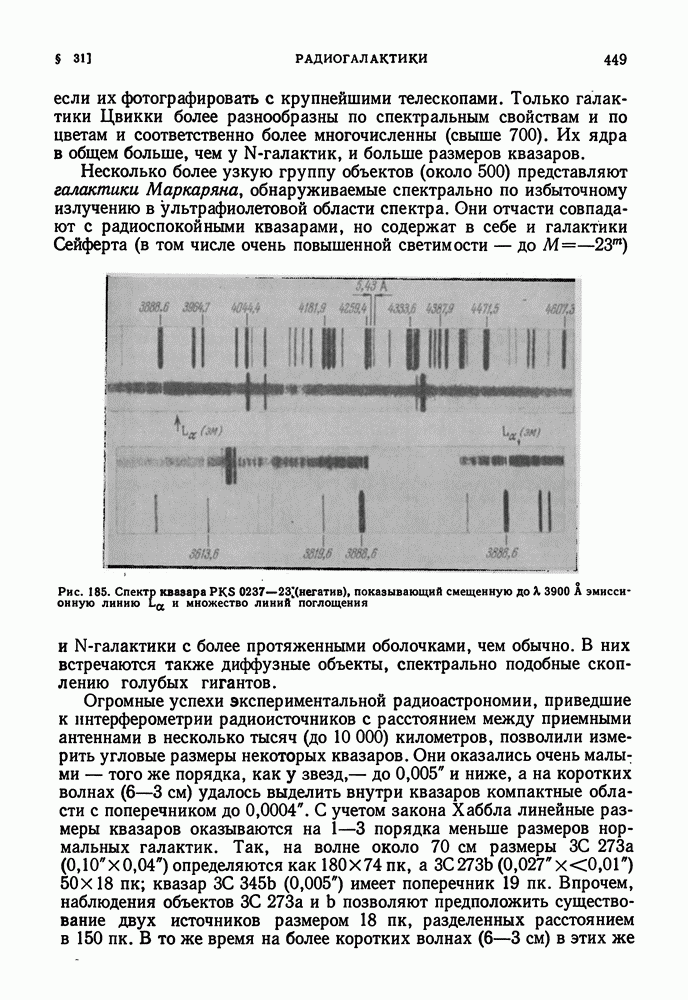
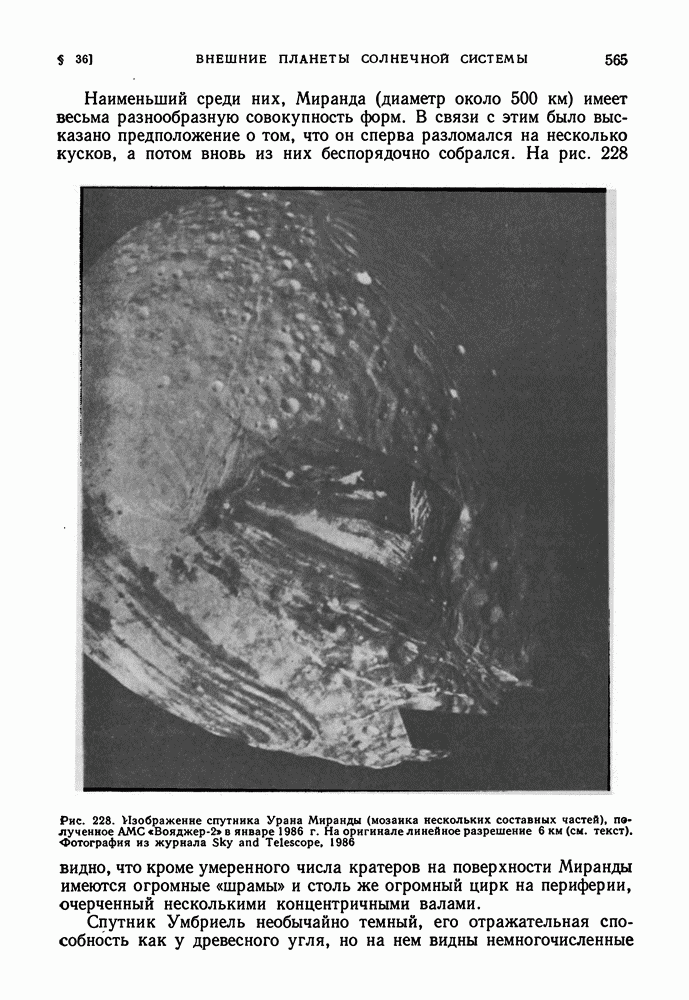
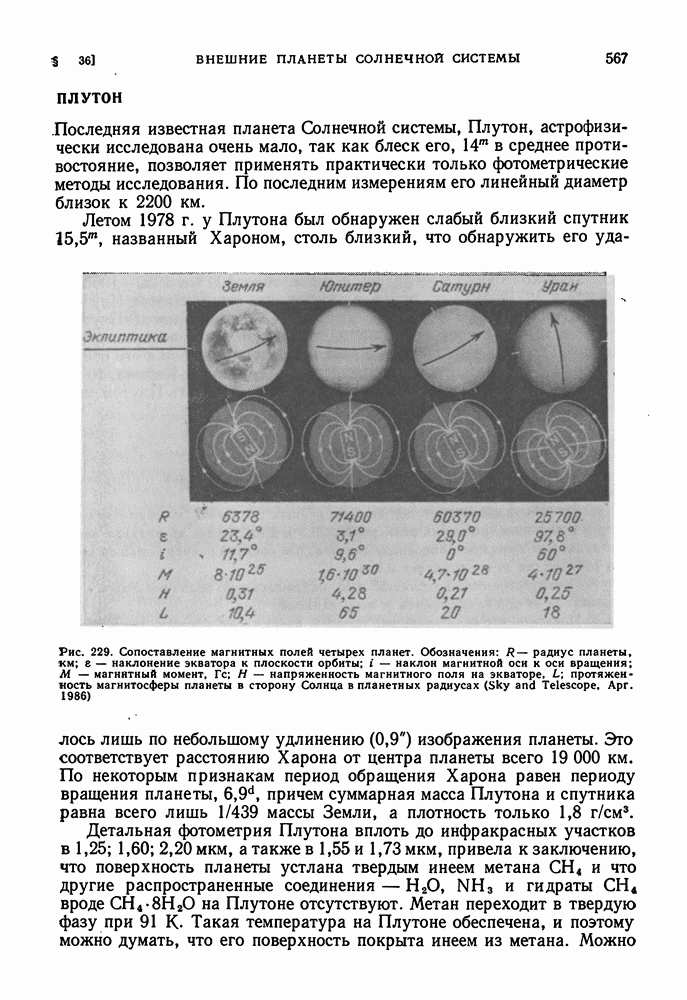
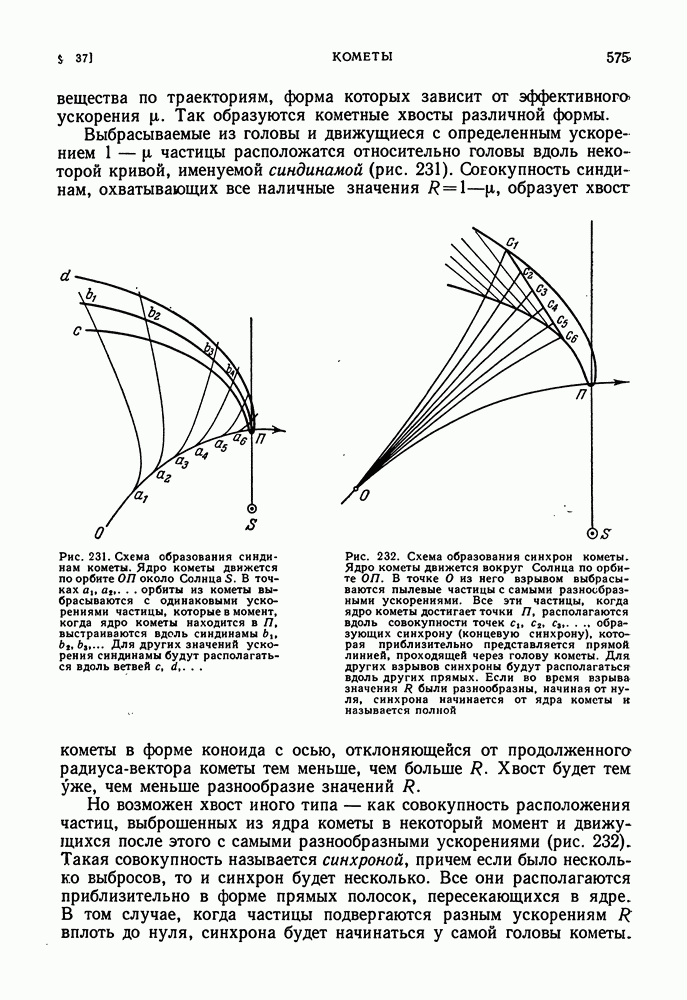
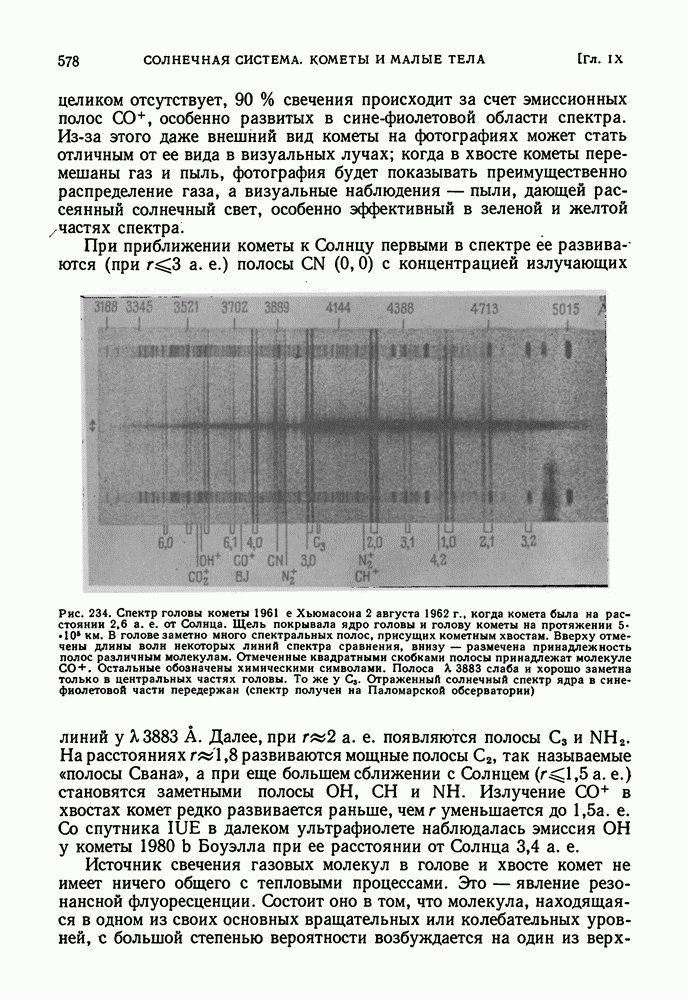
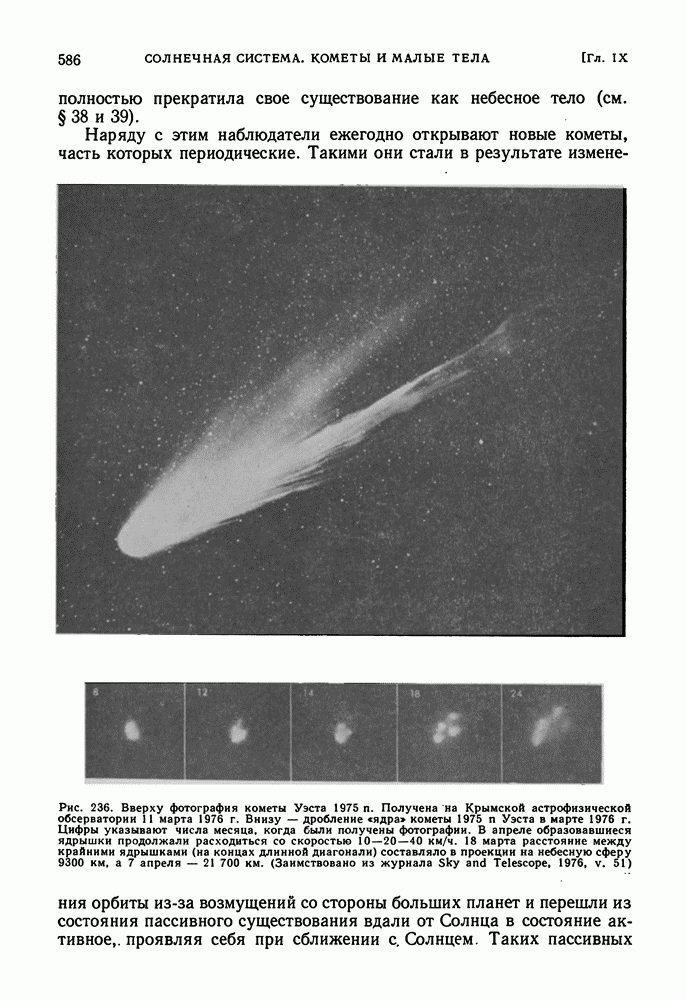
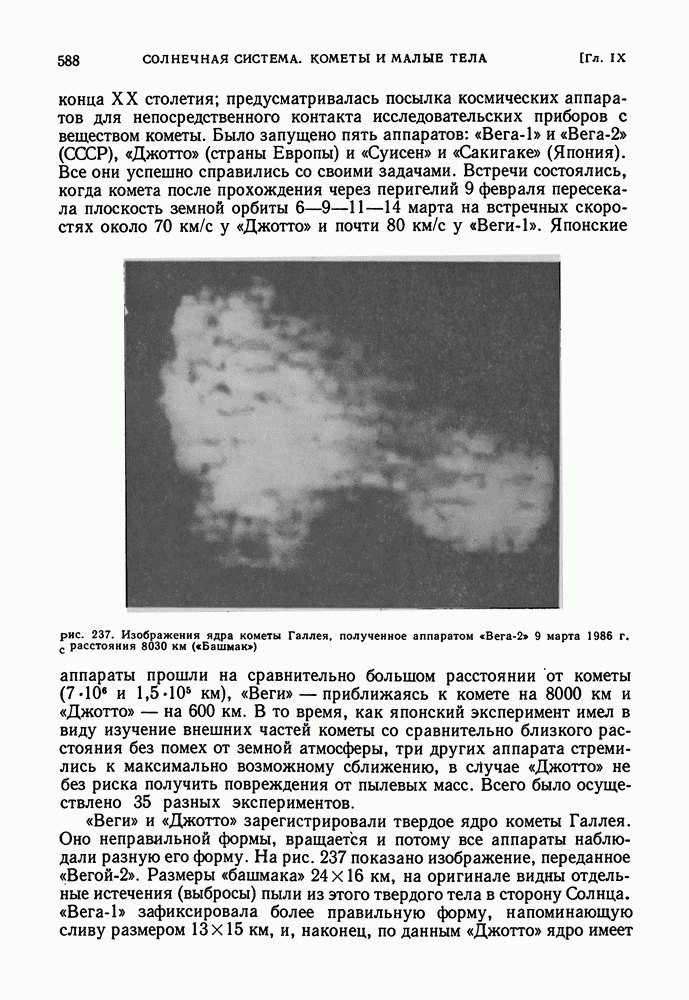
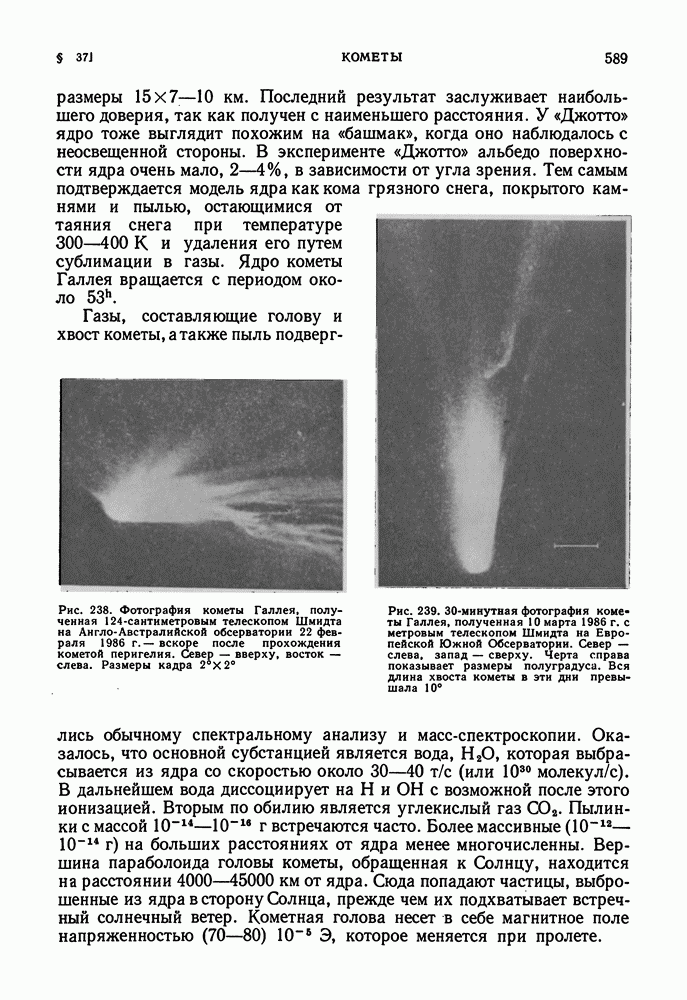
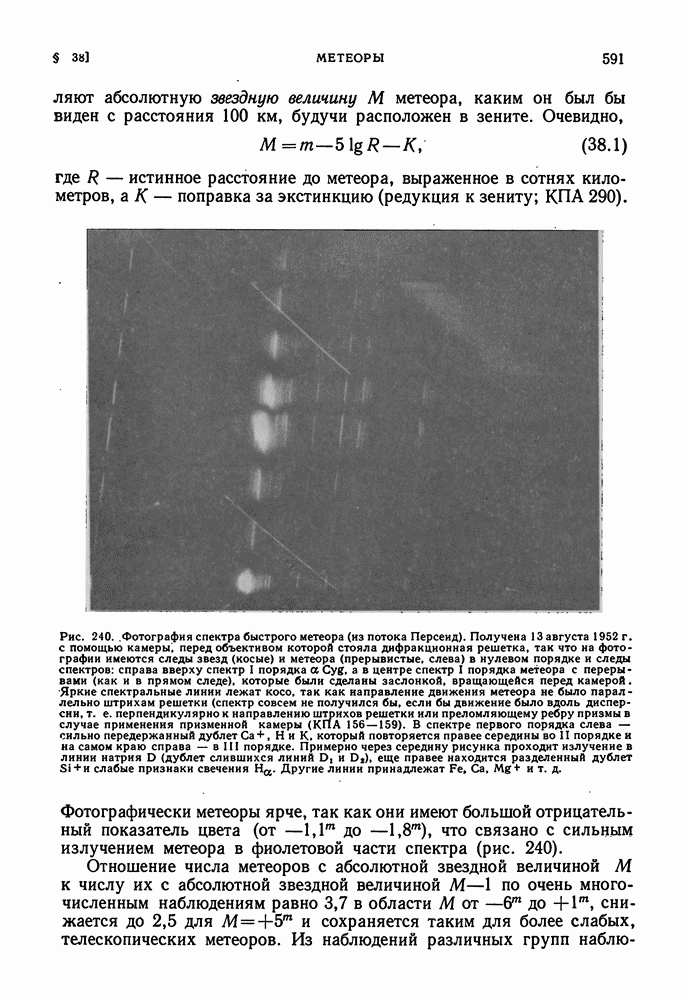
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
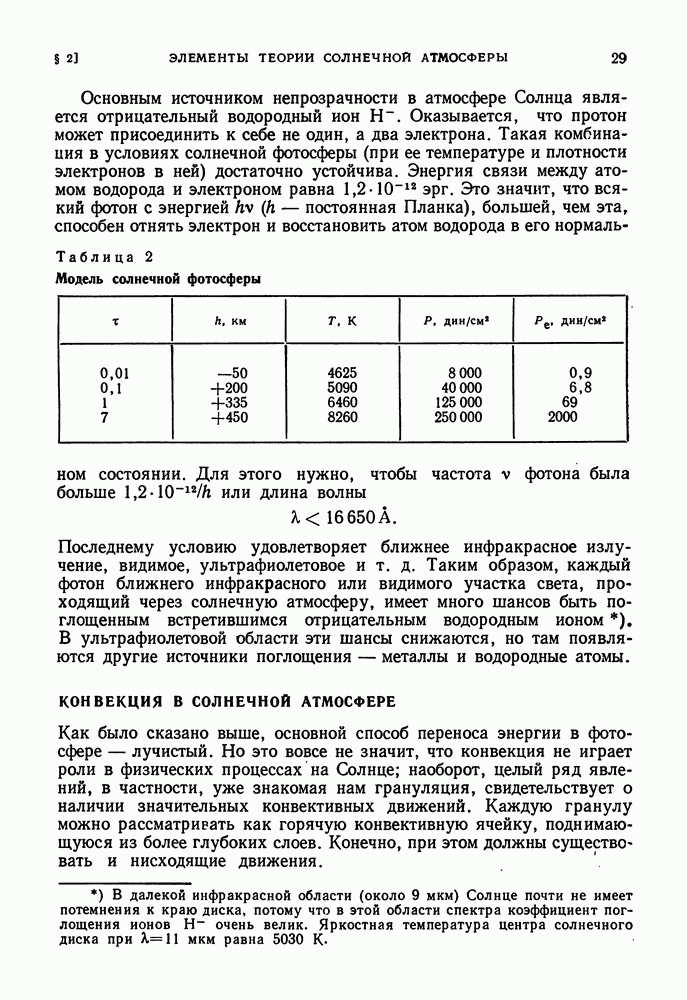
ГЛАВА IV. ВНУТРЕННЕЕ СТРОЕНИЕ ЗВЕЗД
§ 15. УСЛОВИЯ РАВНОВЕСИЯ ВНУТРИ ЗВЕЗДЫ
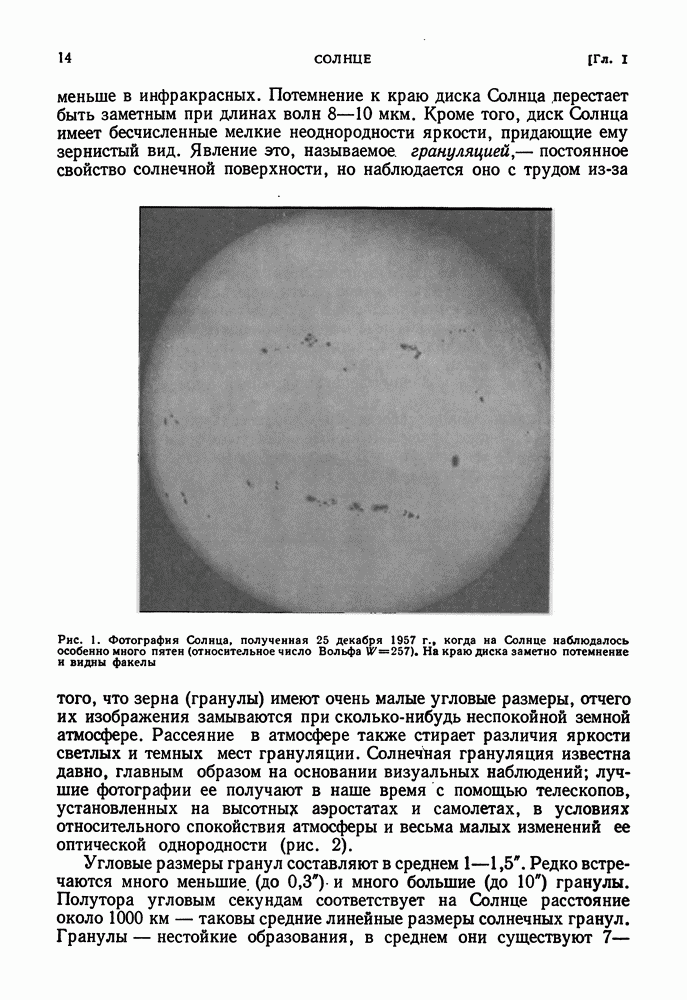
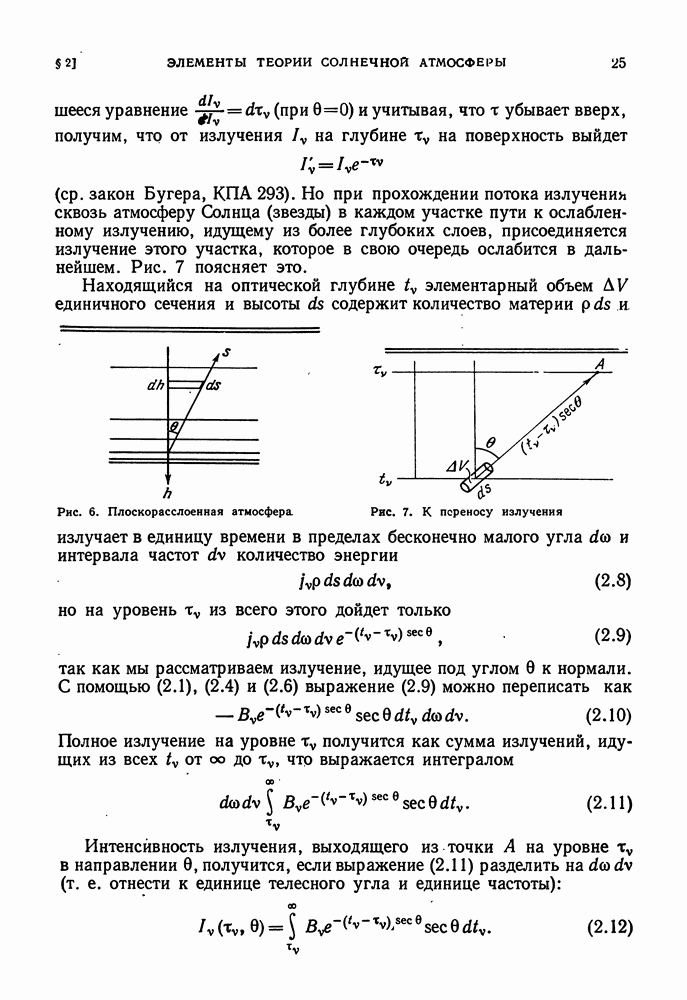
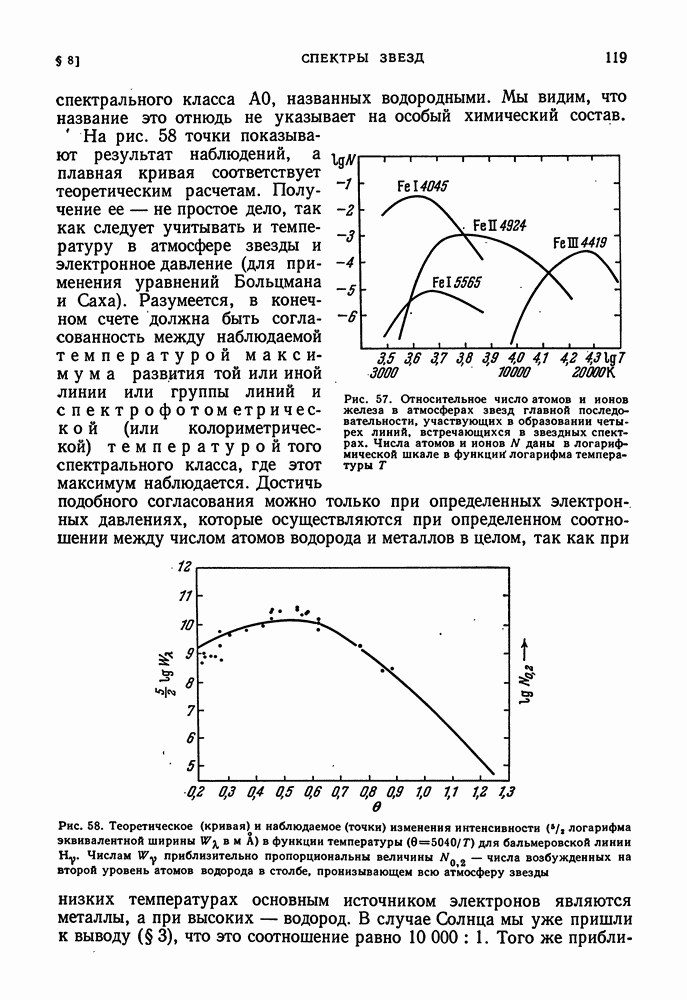
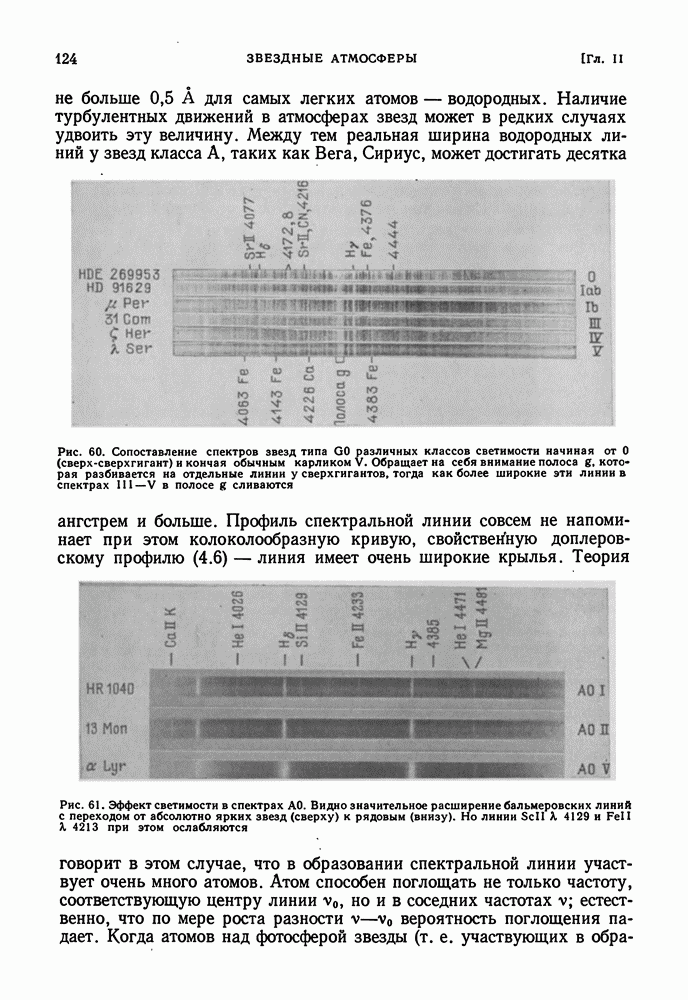
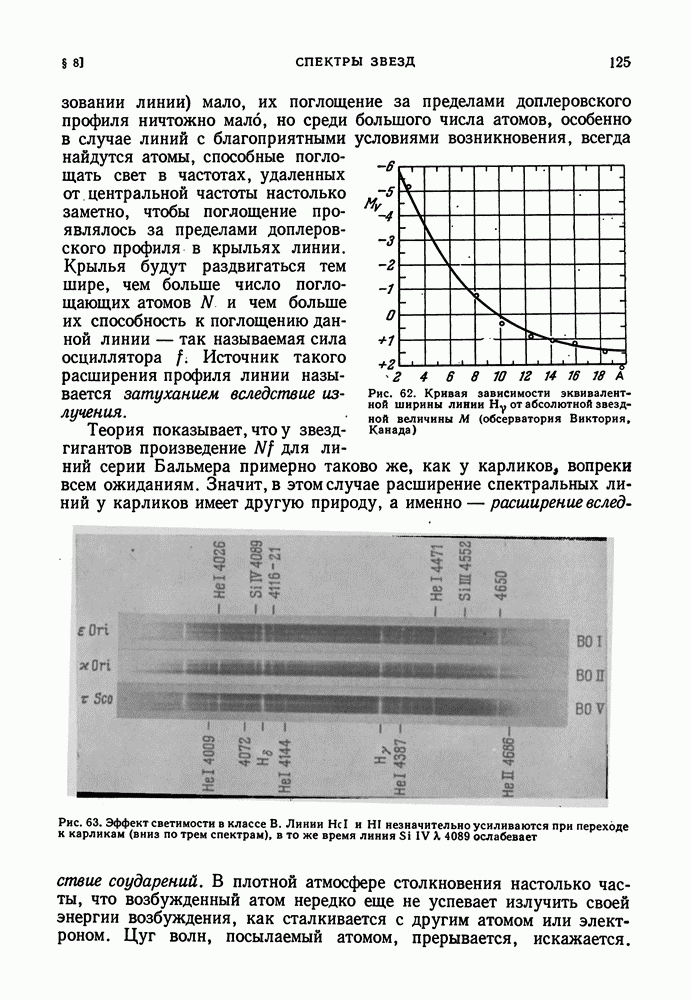
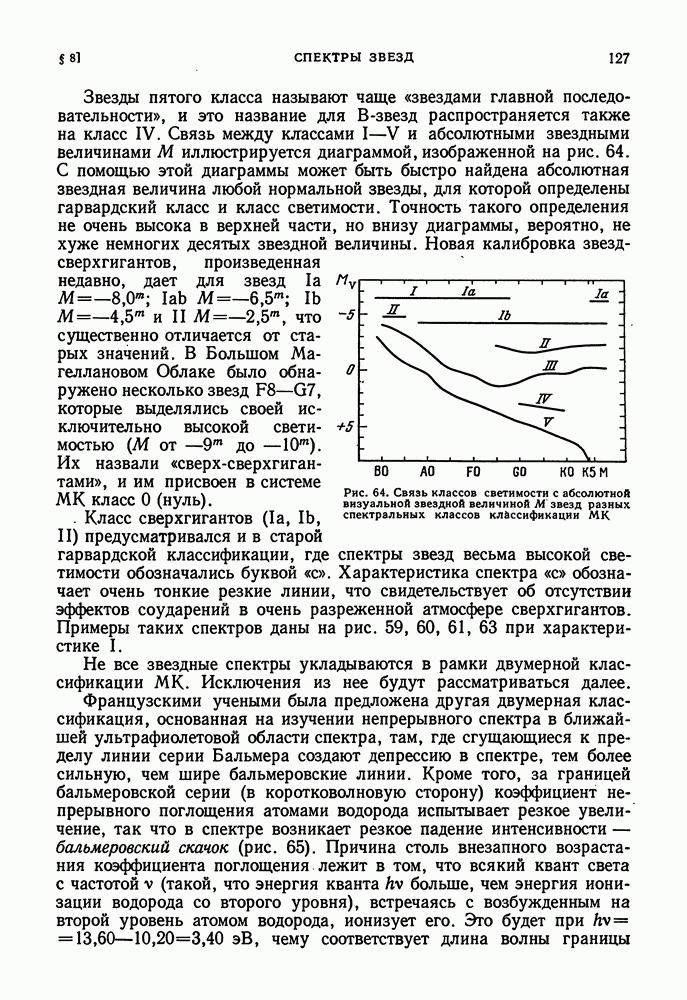
Нашим наблюдениям доступны только самые внешние слои звезды. Представление о внутреннем строении звезды можно составить лишь с помощью теоретических рассуждений, основанных на общих физических законах. Правильность наших представлений может быть проверена по совпадению теоретических значений интегральных характеристик звезды — массы светимости L и радиуса R — с наблюдаемыми.
ОБЩИЕ СООБРАЖЕНИЯ. СОСТОЯНИЕ ВЕЩЕСТВА В НЕДРАХ ЗВЕЗД
Мы будем рассматривать простейший случай: стационарную невращающуюся звезду. Такая звезда, в силу соображений симметрии, имеет сферическую форму. Каждый ее элемент находится в состоянии гидростатического равновесия. Выберем внутри звезды на расстоянии  от центра сферический слой бесконечно малой толщины
от центра сферический слой бесконечно малой толщины 

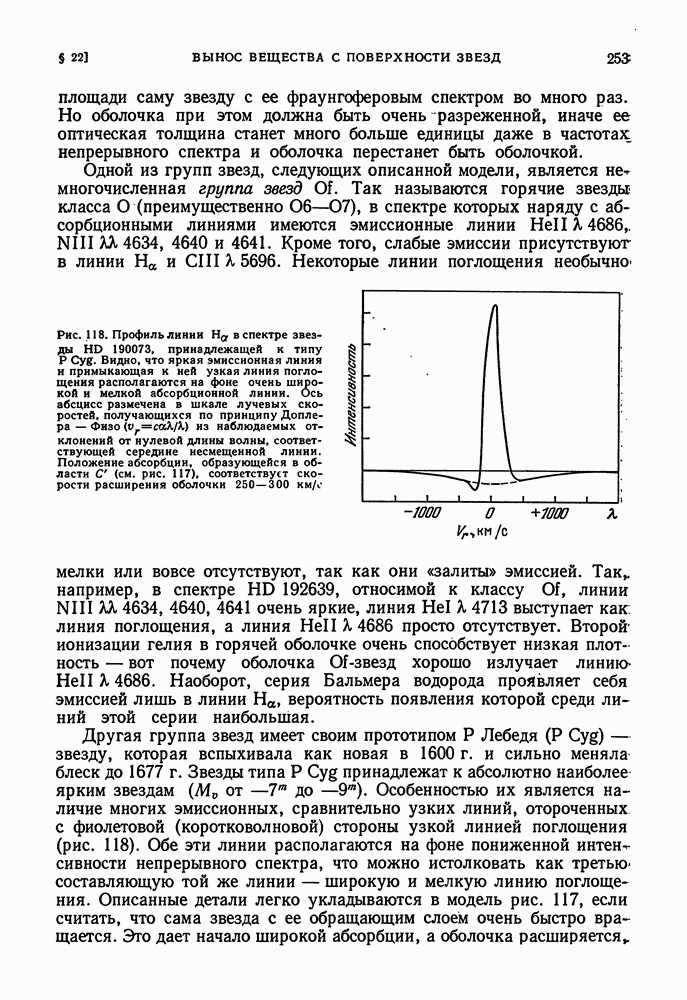
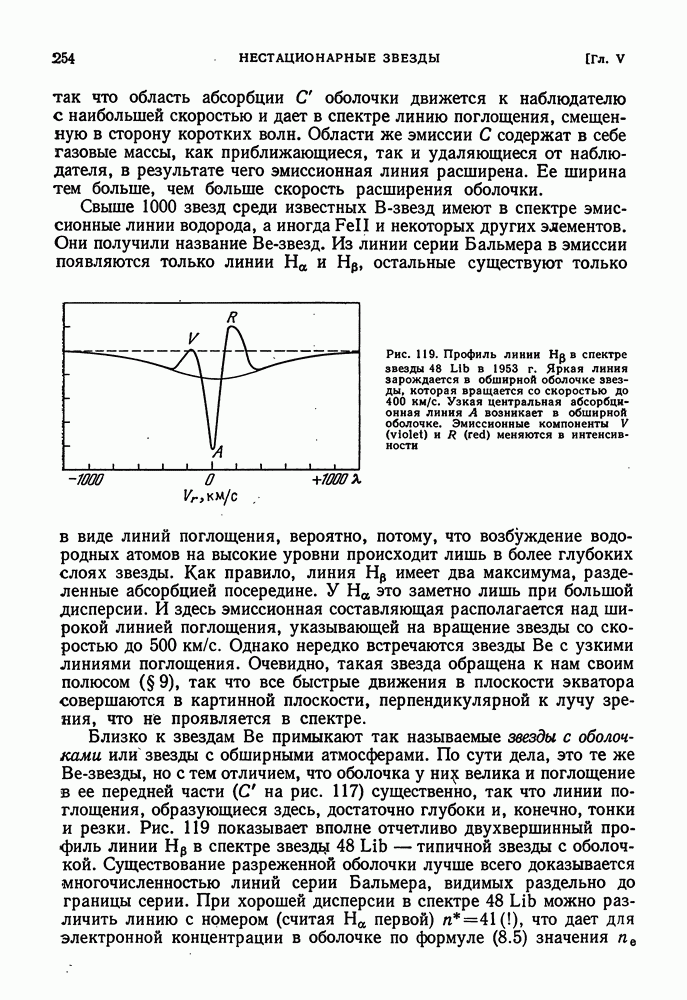
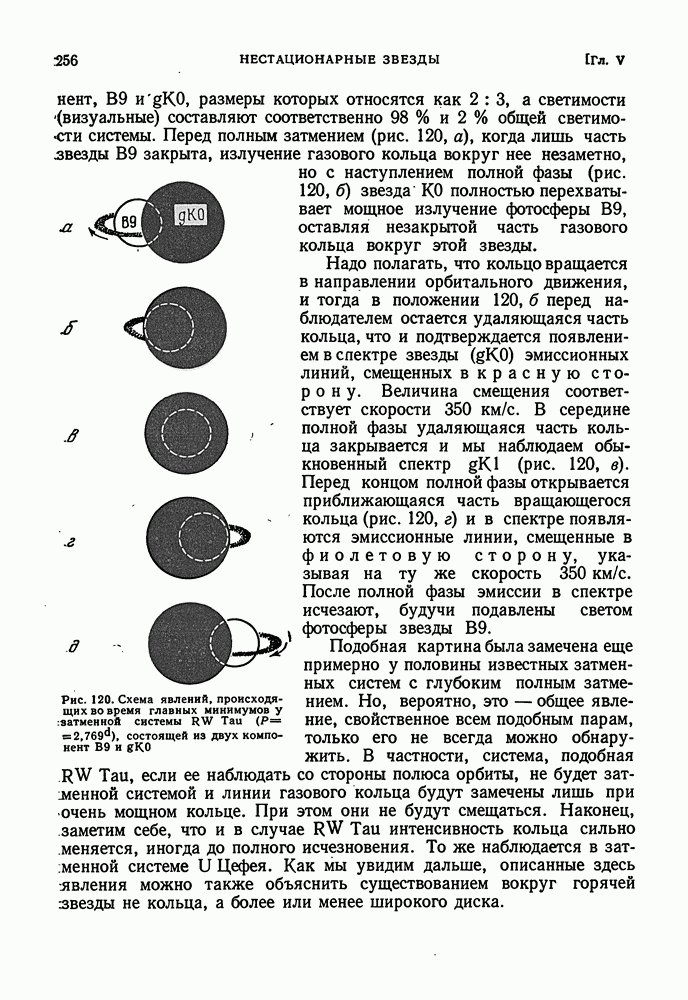
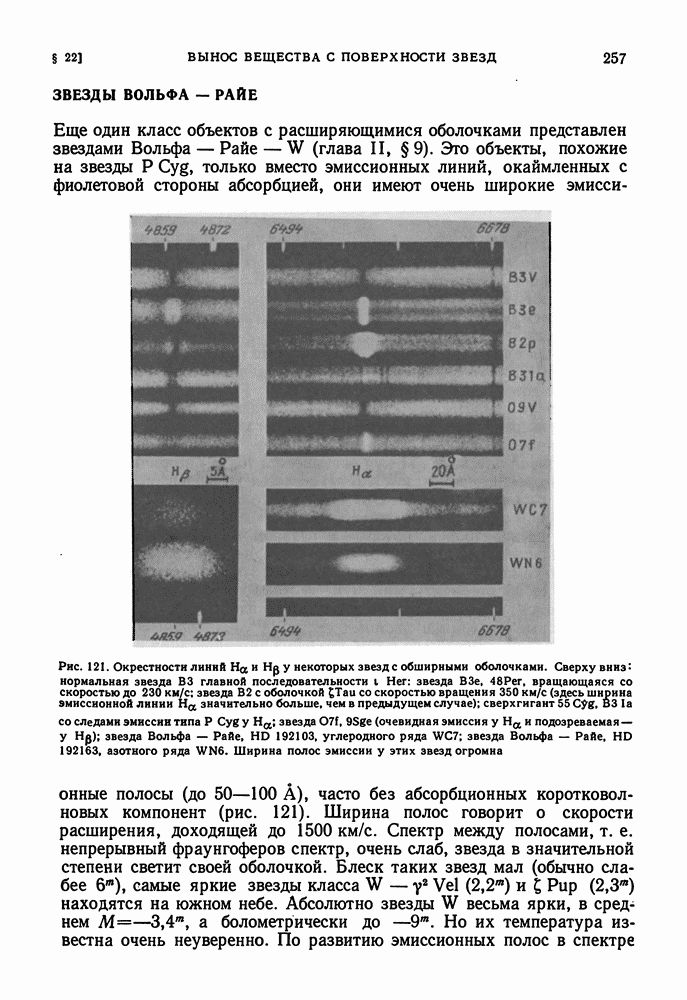
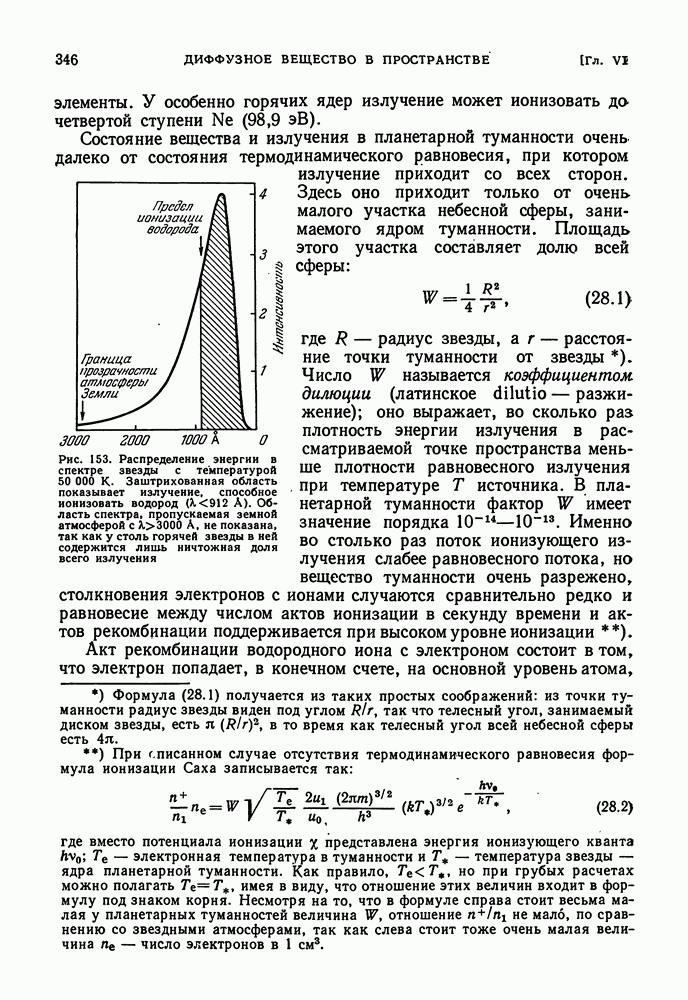
Рис. 100. К внутреннему строению звезды
На внутренней стороне этого  слоя давление вышележащих слоев
слоя давление вышележащих слоев  но р, а на внешней —
но р, а на внешней —  (очевидно,
(очевидно,  Разность
Разность  по абсолютной величине равна весу жидкости (газа) в столбике высотой
по абсолютной величине равна весу жидкости (газа) в столбике высотой  и площадью
и площадью  т. е.
т. е.  где р — плотность жидкости, a g — ускорение силы тяжести. Итак,
где р — плотность жидкости, a g — ускорение силы тяжести. Итак,

Что касается величин g и р, то они являются функциями расстояния от центра  , и модель звезды была бы наполовину построена, если бы был известен вид функции
, и модель звезды была бы наполовину построена, если бы был известен вид функции  Величину g определяем на основании доказанной еще Ньютоном теоремы: внутри материального шара при тяжение зависит только от массы той части шара, по отношению к которой притягиваемая точка является внешней, т. е. если обозначить массу, сосредоточенную внутри шара с радиусом
Величину g определяем на основании доказанной еще Ньютоном теоремы: внутри материального шара при тяжение зависит только от массы той части шара, по отношению к которой притягиваемая точка является внешней, т. е. если обозначить массу, сосредоточенную внутри шара с радиусом  , через
, через  то
то

где G — постоянная тяготения. Для определения величины  , имеем дифференциальное соотношение
, имеем дифференциальное соотношение
 (15.3)
(15.3)
откуда следует

Масса всей звезды определится, очевидно, равенством

Уже в наблюдаемых нами внешних слоях звезды температура настолько высока, что вещество находится в газообразном состоянии; при еще более высокой температуре недра звезды могут быть только газовыми. Звезду можно представлять себе, таким образом, как динамическую систему, состоящую из колоссального числа частиц: атомов ионов, электронов, протонов, нейтронов, позитронов,  -квантов и атомных ядер. Если число этих частиц есть N и средняя скорость движения частиц
-квантов и атомных ядер. Если число этих частиц есть N и средняя скорость движения частиц  , то согласно формуле (2.19) полная кинетическая энергия всей массы газа будет
, то согласно формуле (2.19) полная кинетическая энергия всей массы газа будет

где  — средняя молекулярная масса вещества звезды, Т — ее средняя температура. Применим к нашей системе теорему о вириале
— средняя молекулярная масса вещества звезды, Т — ее средняя температура. Применим к нашей системе теорему о вириале  , гласящую, что в стационарной динамической системе потенциальная энергия равна по абсолютной величине удвоенной кинетической энергии:
, гласящую, что в стационарной динамической системе потенциальная энергия равна по абсолютной величине удвоенной кинетической энергии:

Потенциальная энергия газового неоднородного шара равна

где С — константа, учитывающая распределение плотности внутри звезды. Для однородной звезды  , и С растет с ростом степени сосредоточения вещества в центре звезды. Из трех последних формул следует (с применением равенства
, и С растет с ростом степени сосредоточения вещества в центре звезды. Из трех последних формул следует (с применением равенства  ):
):

Подставляя сюда числовые значения постоянных и принимая промежуточное значение константы  , найдем, что средняя температура звезды равна
, найдем, что средняя температура звезды равна
 (15.10)
(15.10)
Для Солнца это дает  , а для звезды, такой как компонента
, а для звезды, такой как компонента  (см. таблицу 13), в четыре раза больше.
(см. таблицу 13), в четыре раза больше.
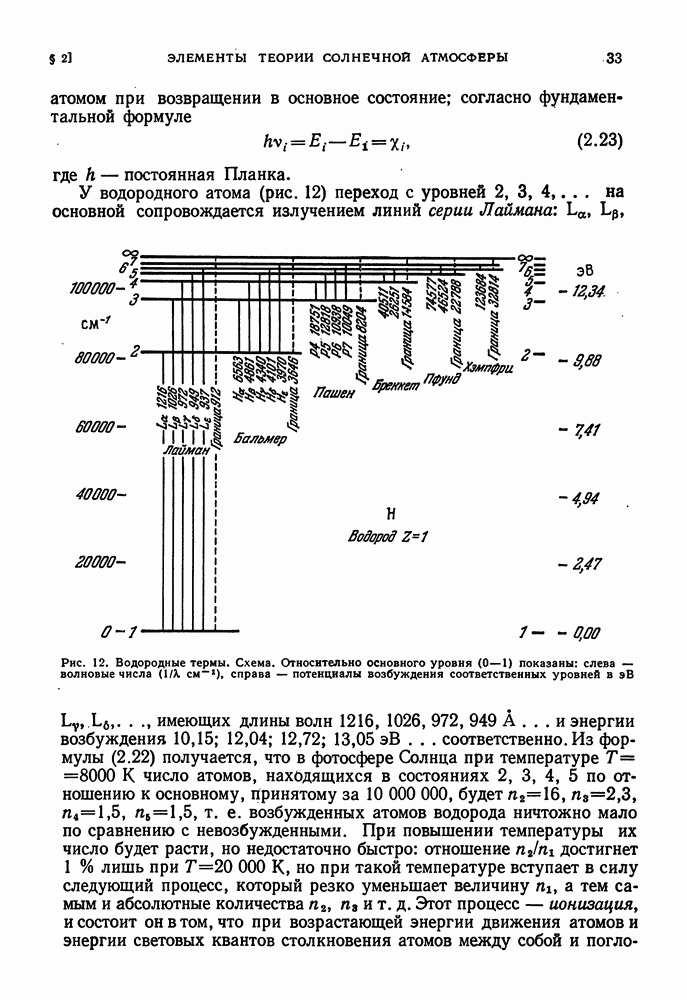
Конечно, при температуре порядка  все вещество звезды находится в состоянии очень сильной ионизации. Не только водород и гелий, но и атомы многих тяжелых элементов лишены почти всех своих электронов. Это позволяет довольно уверенно определить молекулярную массу звездного вещества. Действительно, пусть X — масса водорода в 1 г вещества, Y — масса гелия и Z=(1—X—Y) — масса всех остальных так называемых тяжелых элементов, начиная с углерода (
все вещество звезды находится в состоянии очень сильной ионизации. Не только водород и гелий, но и атомы многих тяжелых элементов лишены почти всех своих электронов. Это позволяет довольно уверенно определить молекулярную массу звездного вещества. Действительно, пусть X — масса водорода в 1 г вещества, Y — масса гелия и Z=(1—X—Y) — масса всех остальных так называемых тяжелых элементов, начиная с углерода ( — несущественны по своей малочисленности). При полной ионизации один атом Н дает две частицы, т. е. молекулярная масса становится равной
— несущественны по своей малочисленности). При полной ионизации один атом Н дает две частицы, т. е. молекулярная масса становится равной  ; для Не, распадающегося на три частицы,
; для Не, распадающегося на три частицы,  ; для тяжелых элементов приблизительно справедливо соотношение
; для тяжелых элементов приблизительно справедливо соотношение  между атомной массой А и атомным номером Z (это Z, конечно, не совпадает с введенным выше). Но атом с атомным номером Z при полной ионизации распадается на
между атомной массой А и атомным номером Z (это Z, конечно, не совпадает с введенным выше). Но атом с атомным номером Z при полной ионизации распадается на  частиц, т. е. тогда
частиц, т. е. тогда  . Так, например, для Na, имеющего 11 электронов, т. е.
. Так, например, для Na, имеющего 11 электронов, т. е.  , после полной ионизации становится
, после полной ионизации становится  для
для  и для
и для  .
.
Для данной смеси газов X, Y и (1—X—Y) в недрах звезды средняя молекулярная масса получается тогда равной
 (15.11)
(15.11)
или
 (15.12)
(15.12)
При значительном преобладании водорода в космическом веществе разумной предварительной оценкой будет  , и тогда
, и тогда  . Если принять Х=0,5 и Y=0,5, то
. Если принять Х=0,5 и Y=0,5, то  .
.
При таком значении  средняя температура Солнца оказывается около 8 млн Кельвинов, а у компоненты
средняя температура Солнца оказывается около 8 млн Кельвинов, а у компоненты  — свыше 30 млн Кельвинов.
— свыше 30 млн Кельвинов.
Газ при такой температуре имеет огромную упругость, способную противостоять давлению вышележащих слоев. Мы можем сопоставить упругость газа при температуре Т и среднее давление в звезде. Последнее мы можем определить как среднее, взвешенное по массе соответствующих слоев:

Интегрируем по частям:

Но  , так как
, так как  при
при  при
при  . К остающемуся интегралу применим (15.1) и (15.2). Это приведет нас к формуле
. К остающемуся интегралу применим (15.1) и (15.2). Это приведет нас к формуле

воспользоваться которой мы не можем, не зная  . Но мы можем найти нижний предел среднего давления р, если заменим под интегралом
. Но мы можем найти нижний предел среднего давления р, если заменим под интегралом  его максимальным значением R. Тогда получим неравенство
его максимальным значением R. Тогда получим неравенство

Переходя к числовым значениям, найдем

Максимальное значение р, которое достигается в центре, может быть получено на основании следующих соображений: оно будет наибольшим из возможных, если вещество будет возможно ближе подтянуто к центру, т. е. когда звезда однородна с плотностью  — центральной плотностью действительной звезды. В этом случае
— центральной плотностью действительной звезды. В этом случае
 (15.17)
(15.17)
Здесь значение радиуса однородной звезды R такое, что
 (15.18)
(15.18)
Итак, у действительной звезды давление  не может быть больше, чем по формуле (15.17). Исключая отсюда
не может быть больше, чем по формуле (15.17). Исключая отсюда  с помощью (15.18), найдем неравенство
с помощью (15.18), найдем неравенство
 (15.19)
(15.19)
Минимальное значение давления в центре находим без труда, интегрируя выражение
 (15.20)
(15.20)
получаемое из формул (15.1)—(15.3), в пределах от  до 0, если положить под интегралом R вместо
до 0, если положить под интегралом R вместо  . Это дает нам неравенство
. Это дает нам неравенство

или, со значениями коэффициентов:

Хотя давление во внутренних областях звезды огромно, далеко зашедшая ионизация вещества позволяет газу сохранять свойства идеального газа  , уравнение состояния которого
, уравнение состояния которого
 (15.23)
(15.23)
где  — универсальная газовая постоянная. Действительно, среднему давлению в Солнце в 300 млн атмосфер соответствует вполне умеренная средняя плотность 1,4 г/см3, но у более массивных звезд давление растет быстро, особенно, если звезда малых размеров, и тогда растет плотность. Газ остается идеальным, пока плотность не превзойдет предельную, определяемую равенством
— универсальная газовая постоянная. Действительно, среднему давлению в Солнце в 300 млн атмосфер соответствует вполне умеренная средняя плотность 1,4 г/см3, но у более массивных звезд давление растет быстро, особенно, если звезда малых размеров, и тогда растет плотность. Газ остается идеальным, пока плотность не превзойдет предельную, определяемую равенством
 (15.24)
(15.24)
после чего он становится вырожденным. Последняя формула дает очень высокую границу, приблизительно 1500 г/см3 при температуре  , которая оказывается непревзойденной у большинства звезд даже в центре их. Исключение составляют белые карлики. В них вещество вследствие очень высокой плотности (см. еще § 18) переходит в состояние вырожденного электронного газа, уравнение состояния которого
, которая оказывается непревзойденной у большинства звезд даже в центре их. Исключение составляют белые карлики. В них вещество вследствие очень высокой плотности (см. еще § 18) переходит в состояние вырожденного электронного газа, уравнение состояния которого
 (15.25)
(15.25)
т. е. давление не зависит от температуры
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ГЛАВА I. СОЛНЦЕ
- ВНЕШНИЙ ВИД СОЛНЦА. ФОТОСФЕРА
- ВРАЩЕНИЕ СОЛНЦА
- ПЕРИОДИЧНОСТЬ СОЛНЕЧНОЙ ПЯТНООБРАЗОВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
- § 2. ЭЛЕМЕНТЫ ТЕОРИИ СОЛНЕЧНОЙ АТМОСФЕРЫ
- УРАВНЕНИЕ ЛУЧИСТОГО РАВНОВЕСИЯ И ЕГО ПРИБЛИЖЕННОЕ РЕШЕНИЕ
- МОДЕЛЬ СОЛНЕЧНОЙ АТМОСФЕРЫ
- КОНВЕКЦИЯ В СОЛНЕЧНОЙ АТМОСФЕРЕ
- ИОНИЗАЦИЯ СОЛНЕЧНОГО ВЕЩЕСТВА
- СОЛНЕЧНАЯ ПЛАЗМА И ЕЕ ВЗАИМОДЕЙСТВИЕ С МАГНИТНЫМИ ПОЛЯМИ
- § 3. СОЛНЕЧНЫЙ СПЕКТР. ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА
- ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА. КАЧЕСТВЕННЫЙ АНАЛИЗ
- КОЛИЧЕСТВЕННЫЙ ХИМИЧЕСКИЙ АНАЛИЗ СОЛНЕЧНОЙ АТМОСФЕРЫ
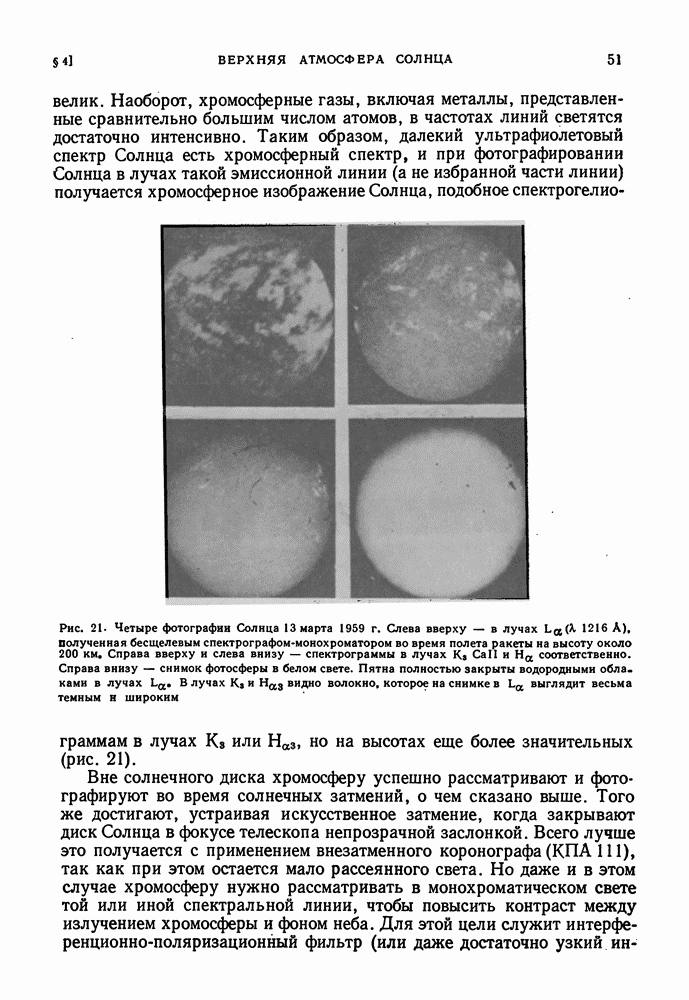
- § 4. ВЕРХНЯЯ АТМОСФЕРА СОЛНЦА
- ОБРАЩАЮЩИЙ СЛОЙ И ХРОМОСФЕРА. ПРИЧИНА ИХ ВИДИМОСТИ ЗА ПРЕДЕЛАМИ СОЛНЕЧНОГО ДИСКА
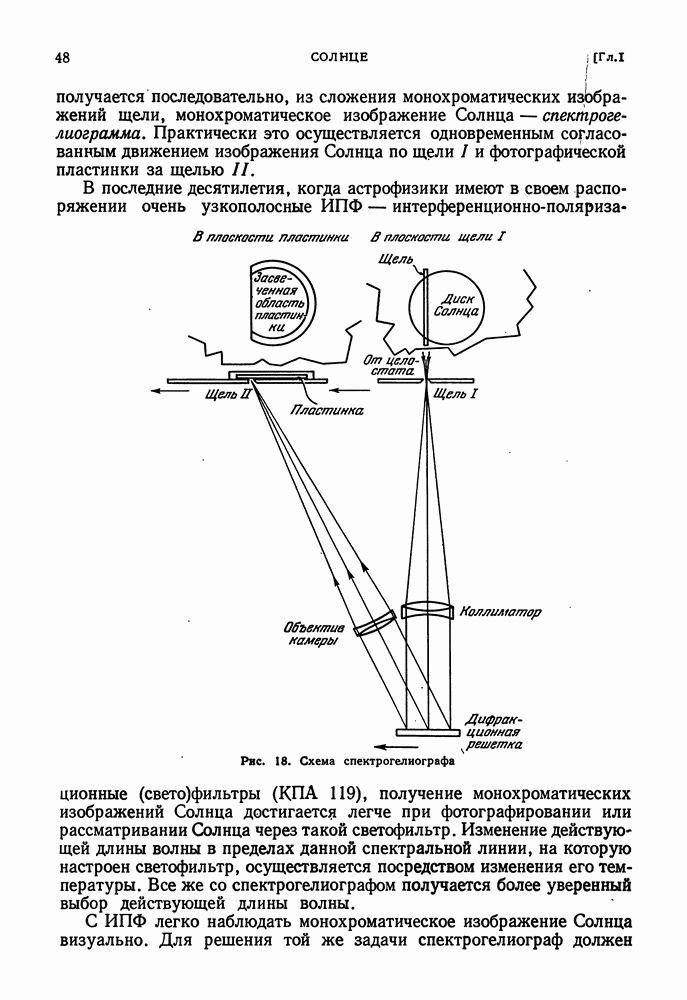
- НАБЛЮДЕНИЯ ХРОМОСФЕРЫ НА ДИСКЕ СОЛНЦА. СПЕКТРОГЕЛИОГРАФ
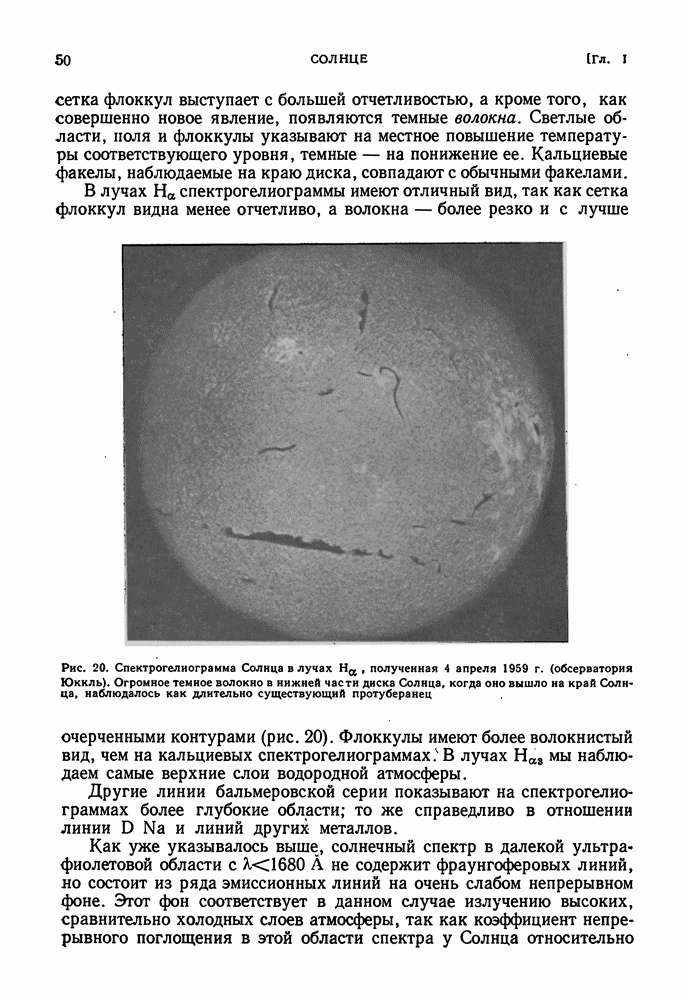
- ХРОМОСФЕРНЫЕ ФАКЕЛЫ, ФЛОККУЛЫ И ВОЛОКНА. СПИКУЛЫ
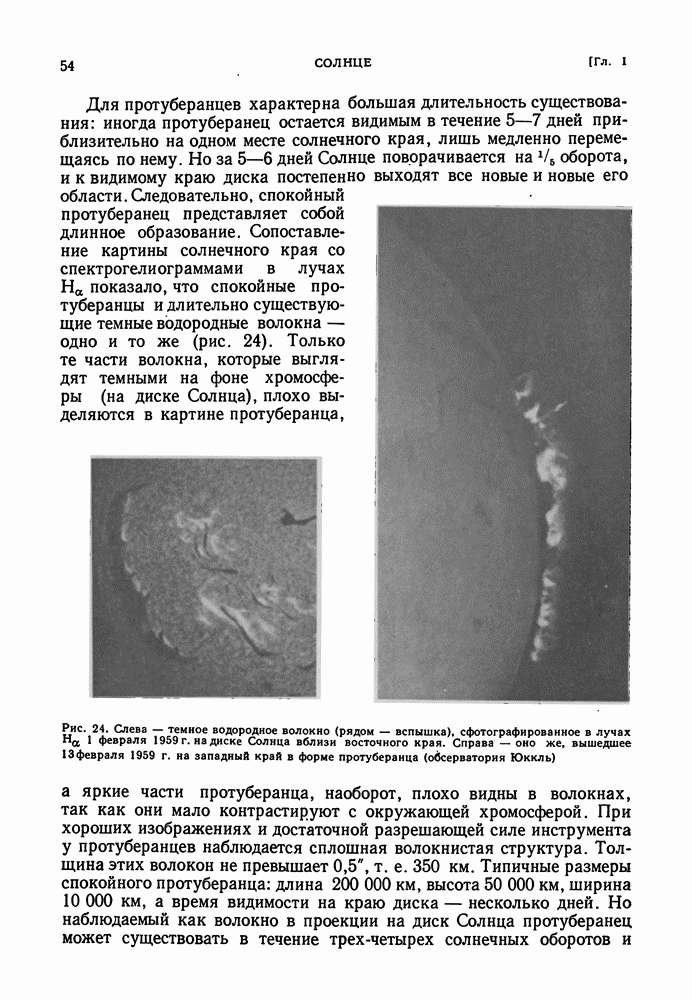
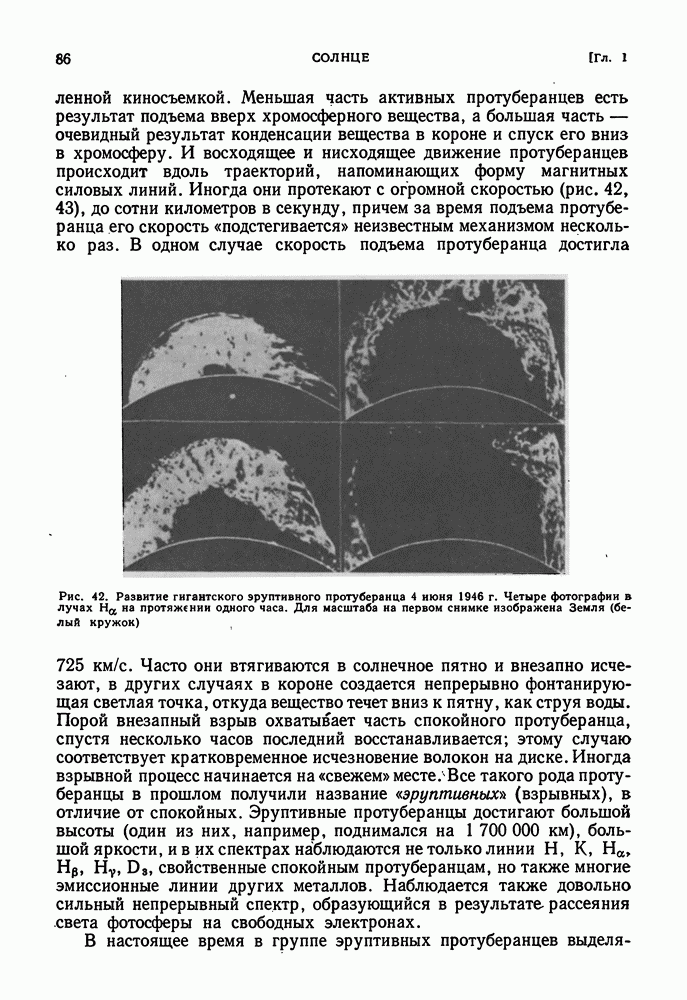
- ПРОТУБЕРАНЦЫ
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ ХРОМОСФЕРЫ. ВОЛНОВЫЕ ДВИЖЕНИЯ В АТМОСФЕРЕ СОЛНЦА
- § 5. СОЛНЕЧНАЯ КОРОНА
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ КОРОНЫ
- ЭМИССИОННЫЙ СПЕКТР КОРОНЫ И ЕГО ИНТЕРПРЕТАЦИЯ
- РАДИОИЗЛУЧЕНИЕ КОРОНЫ И ХРОМОСФЕРЫ
- НЕПРЕРЫВНОЕ ИЗЛУЧЕНИЕ КОРОНЫ. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ И ТЕМПЕРАТУРЫ В ХРОМОСФЕРЕ И КОРОНЕ
- § 6. НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ НА СОЛНЦЕ
- ОБНАРУЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ НА СОЛНЦЕ
- СОЛНЕЧНЫЕ ПЯТНА И ИХ МАГНИТНЫЕ ПОЛЯ
- ПРИРОДА СОЛНЕЧНЫХ ПЯТЕН. АКТИВНЫЕ ОБЛАСТИ НА СОЛНЦЕ. СУПЕРГРАНУЛЯЦИЯ
- ПРОТУБЕРАНЦЫ
- ПРОЯВЛЕНИЕ СОЛНЕЧНОЙ АКТИВНОСТИ В КОРОНЕ
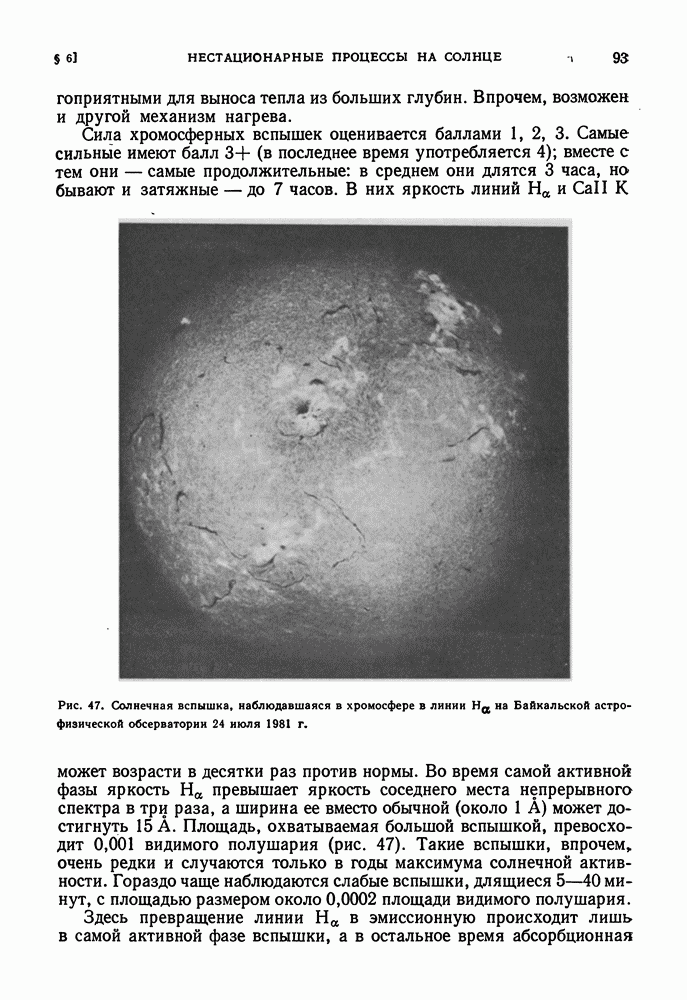
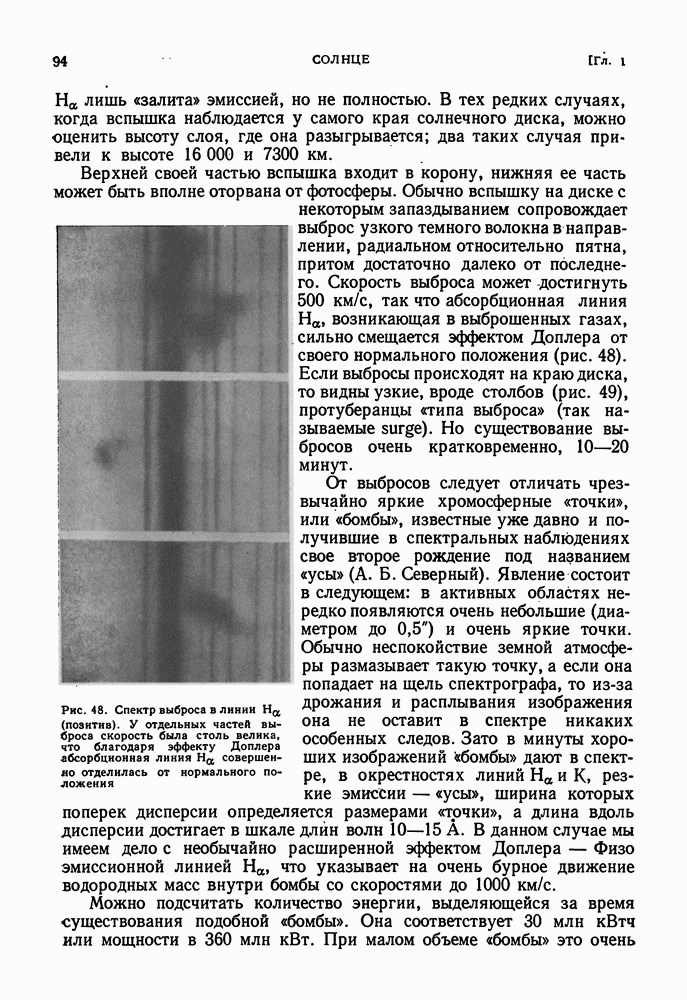
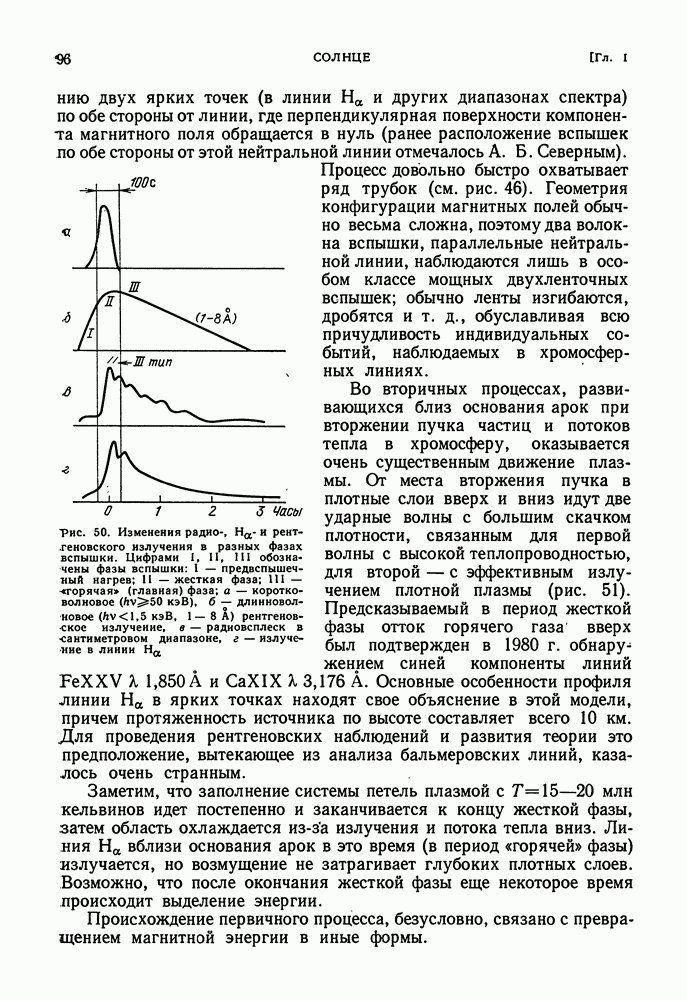
- СОЛНЕЧНЫЕ ВСПЫШКИ
- СПОРАДИЧЕСКОЕ РАДИОИЗЛУЧЕНИЕ СОЛНЦА
- КОРПУСКУЛЯРНОЕ ИЗЛУЧЕНИЕ СОЛНЦА
- § 7. СВЯЗЬ МЕЖДУ СОЛНЕЧНЫМИ И ЗЕМНЫМИ ЯВЛЕНИЯМИ
- ПОЛЯРНЫЕ СИЯНИЯ
- ВЕРХНЯЯ АТМОСФЕРА ЗЕМЛИ. ИОНОСФЕРА. ВОЗДЕЙСТВИЕ НА НИХ СОЛНЦА
- ЯВЛЕНИЯ НА ЗЕМЛЕ, ПРОИСХОДЯЩИЕ ВО ВРЕМЯ ПЕРИОДОВ ПОВЫШЕННОЙ СОЛНЕЧНОЙ АКТИВНОСТИ
- РАДИАЦИОННЫЕ ПОЯСА ЗЕМЛИ
- ДВИЖЕНИЕ КОРПУСКУЛЯРНЫХ потоков В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- СОЛНЕЧНЫЙ ВЕТЕР И МАГНИТОСФЕРА ЗЕМЛИ
- ЗАДАЧИ К ГЛАВЕ I
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ I
- ГЛАВА III. ЗВЕЗДНЫЕ АТМОСФЕРЫ
- § 8. СПЕКТРЫ ЗВЕЗД
- РАЗЛИЧИЯ В СПЕКТРАХ ГИГАНТОВ И КАРЛИКОВ
- ВЛИЯНИЕ РАЗНЫХ ФИЗИЧЕСКИХ ФАКТОРОВ НА ВИД И ИНТЕНСИВНОСТЬ СПЕКТРАЛЬНЫХ ЛИНИЙ
- СПЕКТРАЛЬНЫЕ ПАРАЛЛАКСЫ И ДВУМЕРНАЯ СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ
- § 9. МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. ХИМИЧЕСКИЙ СОСТАВ ЗВЕЗД
- МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. СРЕДНИЙ ХИМИЧЕСКИЙ СОСТАВ АТМОСФЕР ЗВЕЗД
- УКЛОНЕНИЯ ХИМИЧЕСКОГО СОСТАВА ЗВЕЗД ОТ СРЕДНЕГО
- СПЕКТРЫ БЕЛЫХ КАРЛИКОВ
- ЗВЕЗДЫ ПОНИЖЕННОЙ СВЕТИМОСТИ
- МАГНИТНЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- ВЛИЯНИЕ ВРАЩЕНИЯ ЗВЕЗДЫ НА ЕЕ СПЕКТР
- ЭФФЕКТ ТУРБУЛЕНТНОСТИ
- § 10. ВЗАИМНЫЕ СВЯЗИ МЕЖДУ ВНЕШНИМИ ХАРАКТЕРИСТИКАМИ ЗВЕЗД
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА
- СВЯЗЬ МЕЖДУ ПОЛОЖЕНИЕМ ЗВЕЗДЫ НА ДИАГРАММЕ Г — Р И ЕЕ ДВИЖЕНИЕМ В ГАЛАКТИКЕ
- ЗВЕЗДЫ СФЕРИЧЕСКОЙ И ПЛОСКОЙ СОСТАВЛЯЮЩИХ. РАЗЛИЧИЕ ИХ ДИАГРАММ Г — Р
- РАЗНООБРАЗИЕ СВЕТИМОСТЕЙ И РАЗМЕРОВ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ II
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ II
- ГЛАВА III. ДВОЙНЫЕ ЗВЕЗДЫ И МАССЫ ЗВЕЗД
- ВИЗУАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- НЕВИДИМЫЕ СПУТНИКИ ЗВЕЗД
- СПЕКТРАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- ШИРОКИЕ И ТЕСНЫЕ ПАРЫ
- ЗАТМЕННЫЕ ИЛИ ФОТОМЕТРИЧЕСКИЕ ДВОЙНЫЕ ЗВЕЗДЫ
- § 12. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ ХАРАКТЕРИСТИК ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- КРИВАЯ ЛУЧЕВЫХ СКОРОСТЕЙ И ЭЛЕМЕНТЫ ОРБИТЫ СПЕКТРАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- ОПРЕДЕЛЕНИЕ МАСС КОМПОНЕНТ СПЕКТРАЛЬНО-ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ФОТОМЕТРИЧЕСКОЙ ОРБИТЫ
- ОПРЕДЕЛЕНИЕ ЭКСЦЕНТРИСИТЕТА ОРБИТЫ У ЗАТМЕННОЙ ДВОЙНОЙ ВРАЩЕНИЕ ЛИНИИ АПСИД
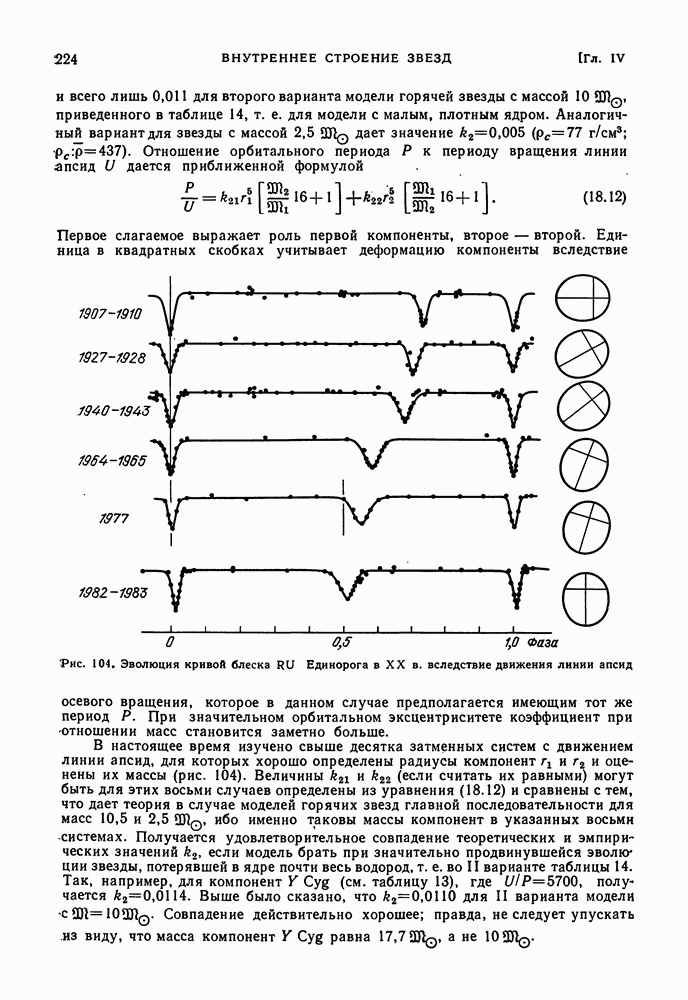
- ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ КОМПОНЕНТ ФОТОМЕТРИЧЕСКИХ ДВОЙНЫХ ЗВЕЗД
- ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОЙ ТЕМПЕРАТУРЫ ЗАТМЕННЫХ ДВОЙНЫХ ЗВЕЗД
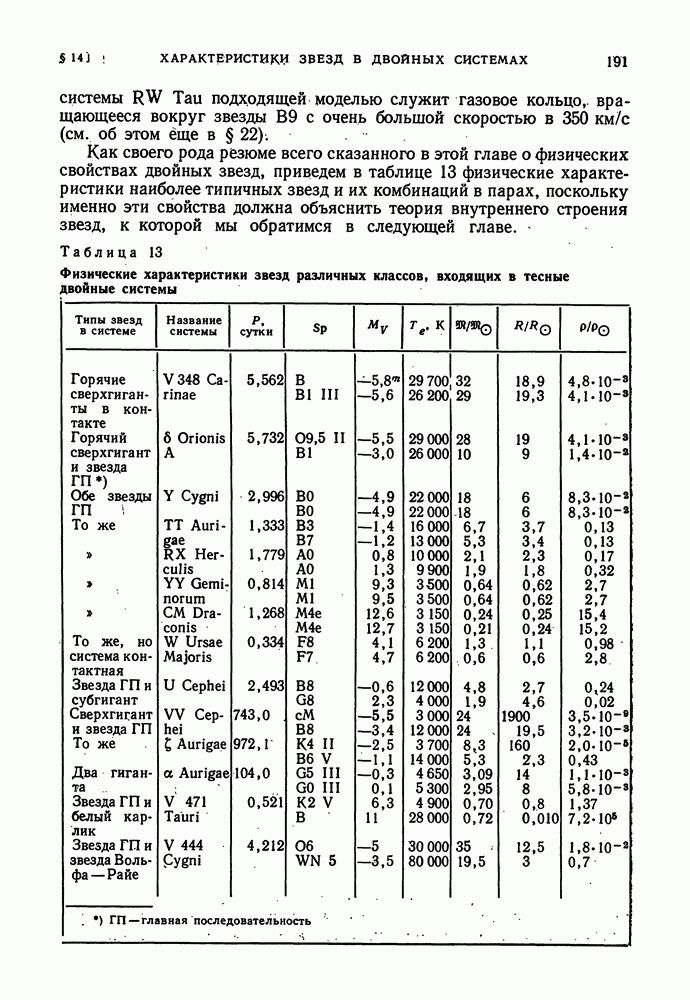
- § 13. МАССЫ И ДРУГИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВОЙНЫХ ЗВЕЗД. ЗАКОН МАССА — СВЕТИМОСТЬ
- § 14. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВЕЗД В ДВОЙНЫХ СИСТЕМАХ
- РАЗНЫЕ ТИПЫ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- КОНТАКТНЫЕ СИСТЕМЫ
- ТРИ ТИПА ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- ОСЕВОЕ ВРАЩЕНИЕ КОМПОНЕНТ В ТЕСНЫХ ПАРАХ
- ГАЗОВЫЕ ПОТОКИ В ТЕСНЫХ ПАРАХ
- МНОГОЧИСЛЕННОСТЬ ДВОЙНЫХ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ III
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ III
- ГЛАВА IV. ВНУТРЕННЕЕ СТРОЕНИЕ ЗВЕЗД
- ОБЩИЕ СООБРАЖЕНИЯ. СОСТОЯНИЕ ВЕЩЕСТВА В НЕДРАХ ЗВЕЗД
- ЛУЧИСТОЕ ДАВЛЕНИЕ В ЗВЕЗДАХ
- ЛУЧИСТЫЙ И КОНВЕКТИВНЫЙ ПЕРЕНОС ТЕПЛА ВНУТРИ ЗВЕЗДЫ
- ГОМОЛОГИЧЕСКИЕ КОНФИГУРАЦИИ
- ПОЛИТРОПНЫЕ МОДЕЛИ ЗВЕЗД
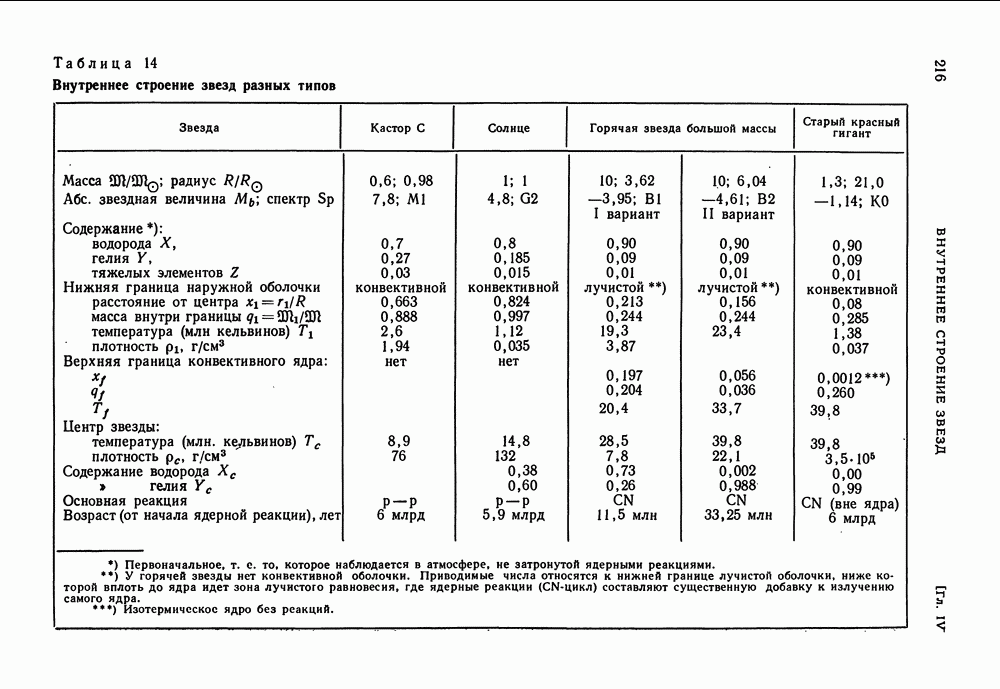
- § 16. ЛУЧЕИСПУСКАНИЕ ЗВЕЗДЫ
- ИСТОЧНИКИ НЕПРОЗРАЧНОСТИ ЗВЕЗДНОГО ВЕЩЕСТВА
- ЗАВИСИМОСТЬ ЛУЧЕИСПУСКАНИЯ ЗВЕЗДЫ ОТ ИСТОЧНИКОВ ЭНЕРГИИ И НЕПРОЗРАЧНОСТИ
- § 17. ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ГРАВИТАЦИОННОЕ СЖАТИЕ
- ТЕРМОЯДЕРНЫЕ ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ПРОТОН-ПРОТОННАЯ РЕАКЦИЯ
- УГЛЕРОДНО-АЗОТНЫЙ ЦИКЛ
- ТРАНСФОРМАЦИЯ ГЕЛИЯ В ЗВЕЗДАХ
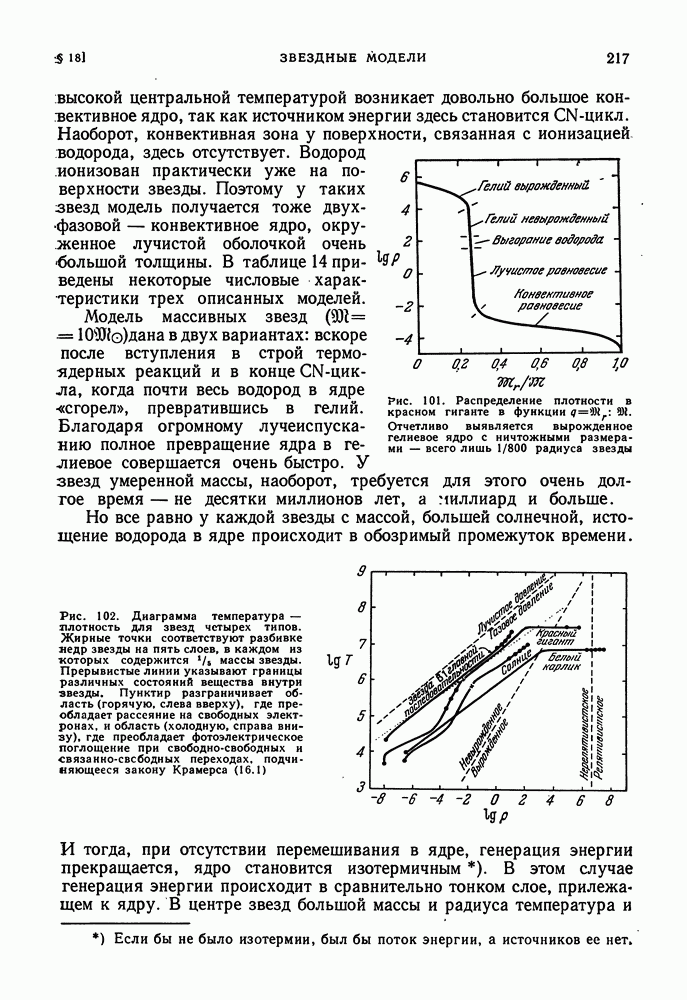
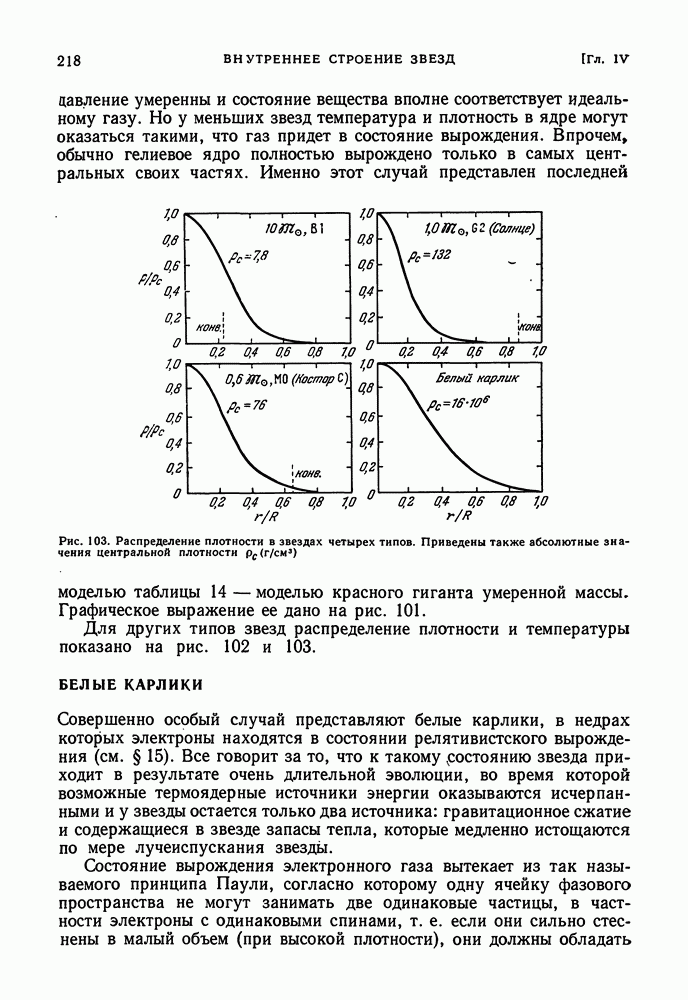
- § 18. ЗВЕЗДНЫЕ МОДЕЛИ
- БЕЛЫЕ КАРЛИКИ
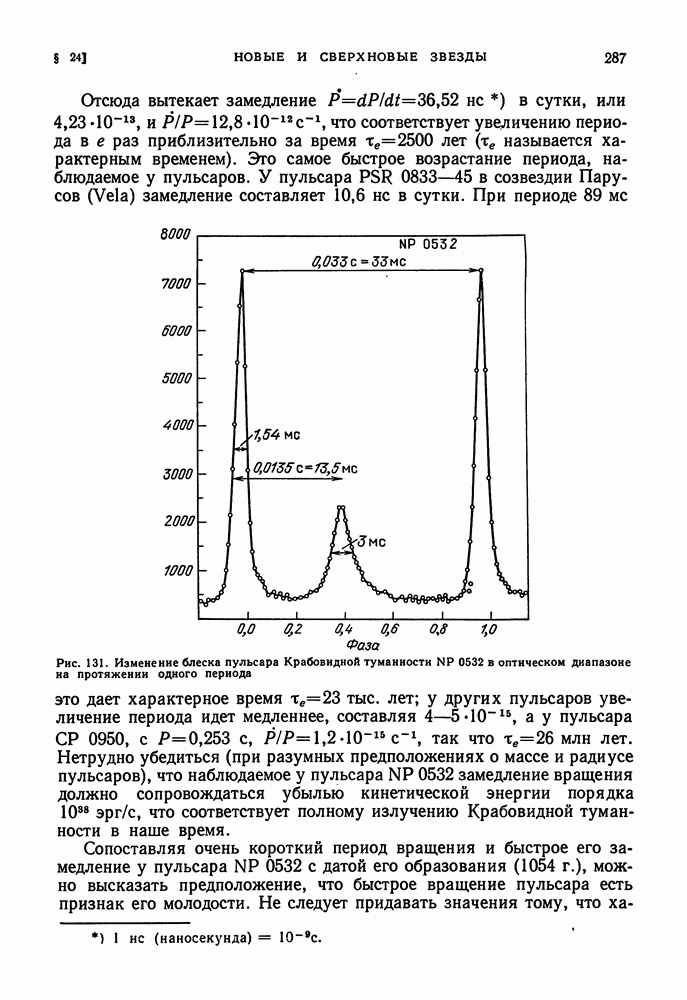
- НЕЙТРОННЫЕ ЗВЕЗДЫ. ПУЛЬСАРЫ
- ПРОВЕРКА ТЕОРИИ ПО ВРАЩЕНИЮ ЛИНИИ АПСИД В ТЕСНЫХ СИСТЕМАХ И ПО СОЛНЕЧНЫМ ПУЛЬСАЦИЯМ
- § 19. ЭВОЛЮЦИЯ ЗВЕЗД
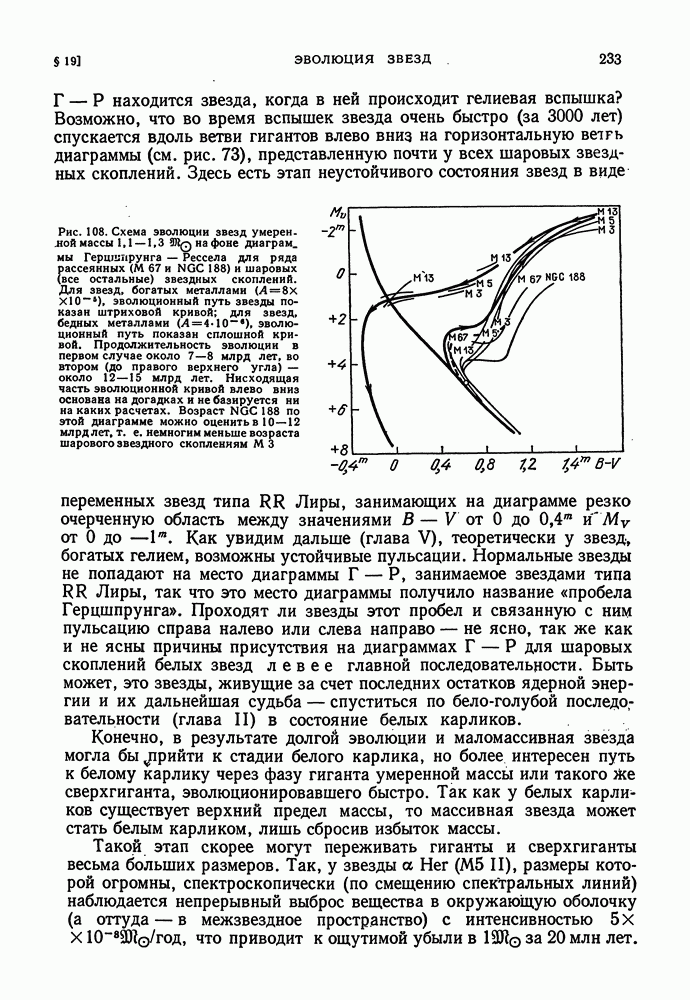
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЭВОЛЮЦИЯ ЗВЕЗД
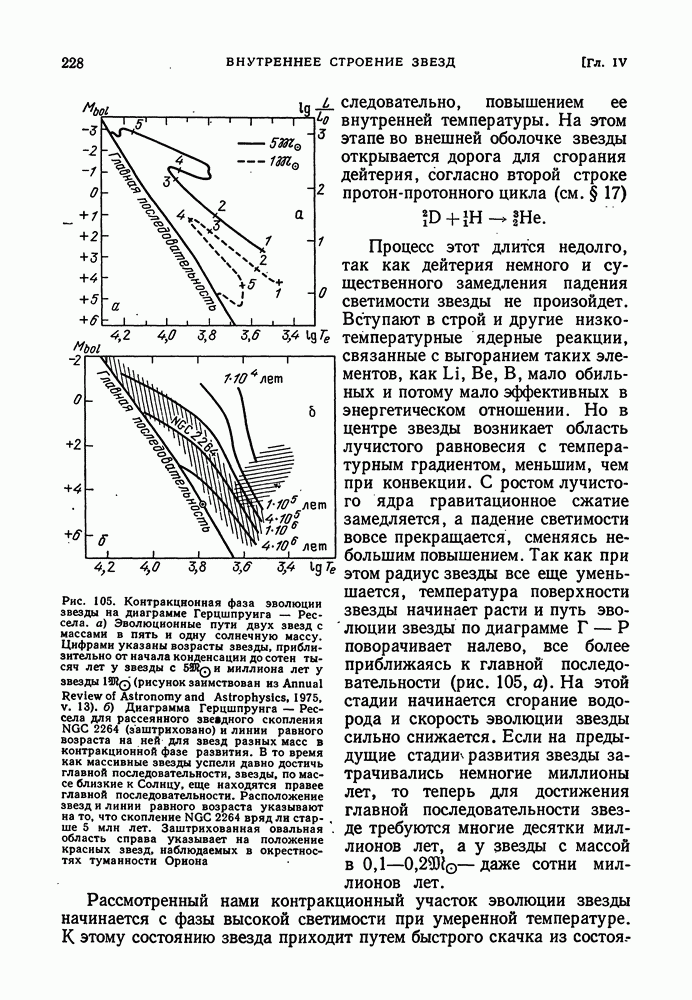
- КОНТРАКЦИОННАЯ ФАЗА ЗВЕЗДНОЙ ЭВОЛЮЦИИ
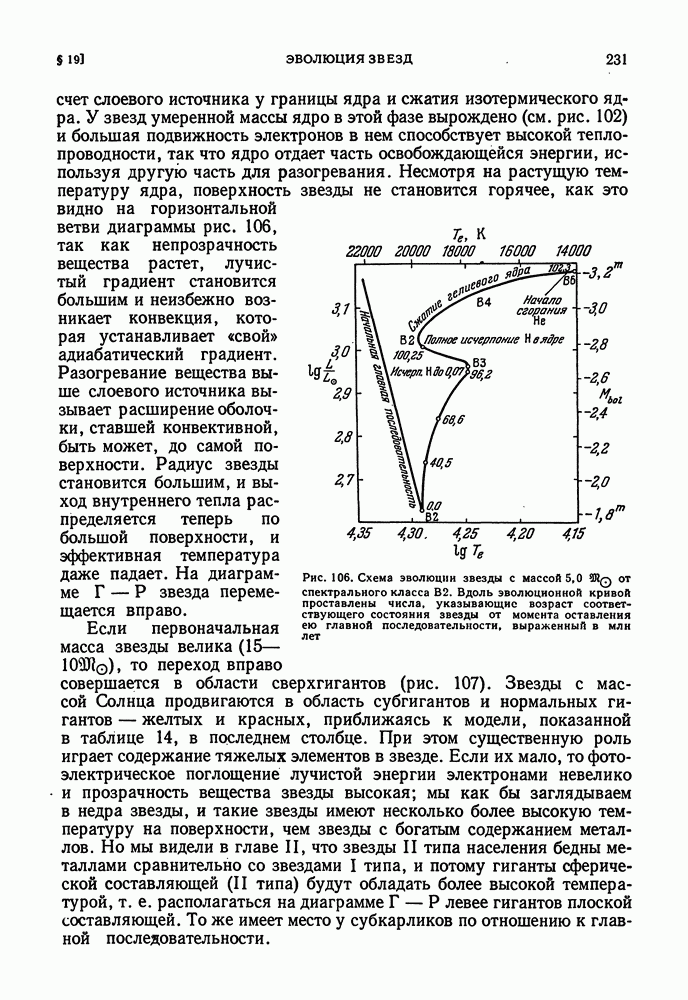
- ЭВОЛЮЦИЯ ЗВЕЗД НА ТЕРМОЯДЕРНОЙ ОСНОВЕ
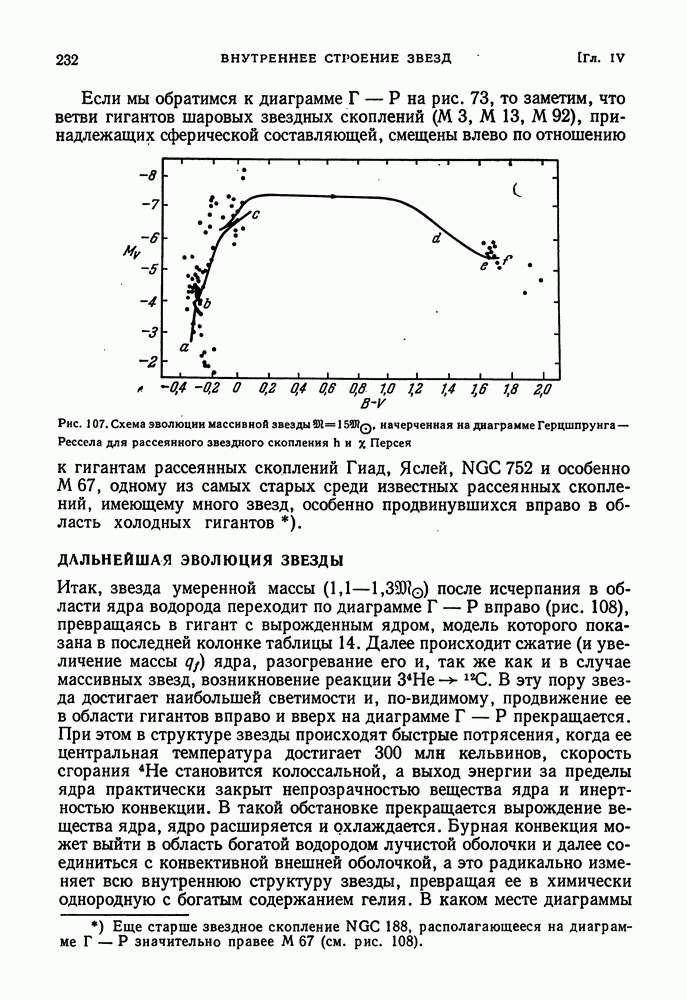
- ЭВОЛЮЦИЯ К КРАСНЫМ ГИГАНТАМ
- ДАЛЬНЕЙШАЯ ЭВОЛЮЦИЯ ЗВЕЗДЫ
- § 20. ЭВОЛЮЦИЯ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
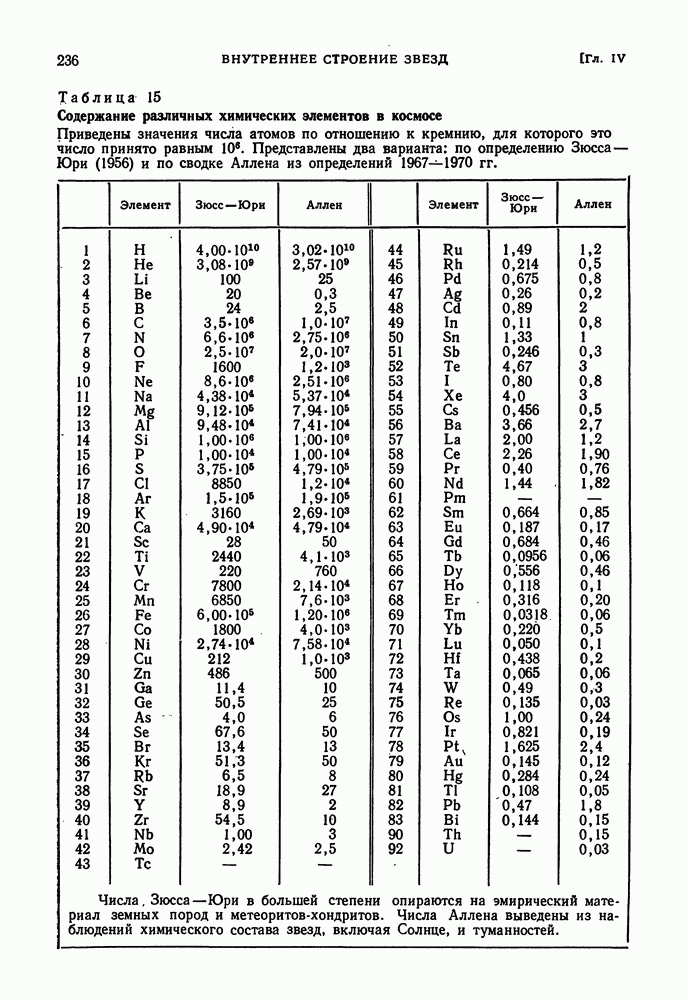
- СОВРЕМЕННАЯ РАСПРОСТРАНЕННОСТЬ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ ВО ВСЕЛЕННОЙ
- ТЕРМОЯДЕРНЫЕ РЕАКЦИИ С ОБРАЗОВАНИЕМ ЭЛЕМЕНТОВ БОЛЕЕ ТЯЖЕЛЫХ, ЧЕМ 12С
- ЗВЕЗДЫ РАЗНОГО ВОЗРАСТА И ИХ ХИМИЧЕСКИЙ СОСТАВ
- ЗАДАЧИ К ГЛАВЕ IV
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ IV
- ГЛАВА V. НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ
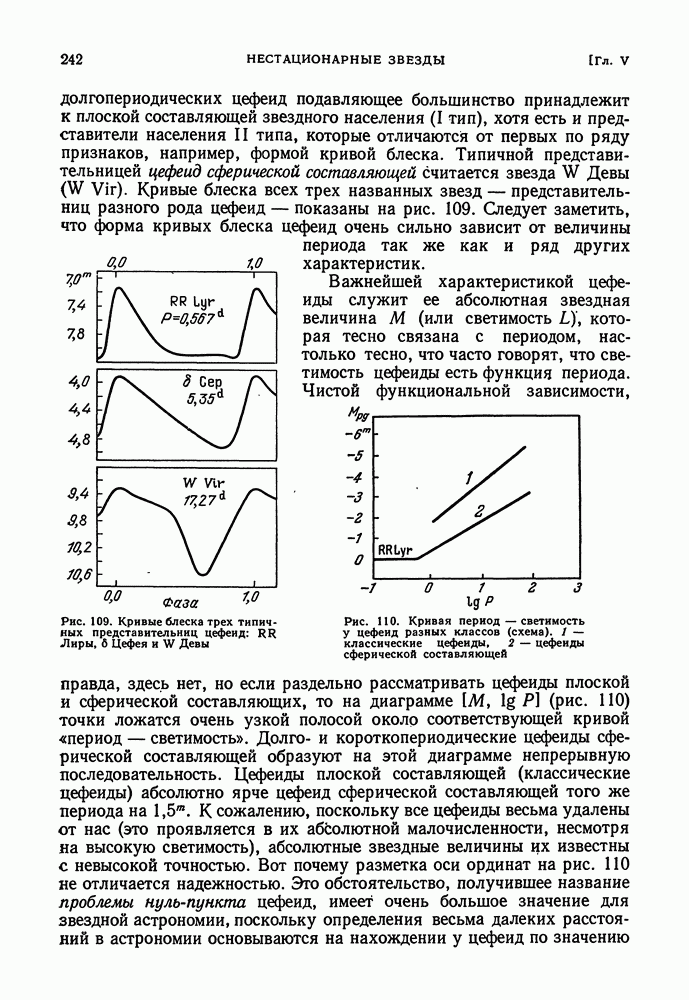
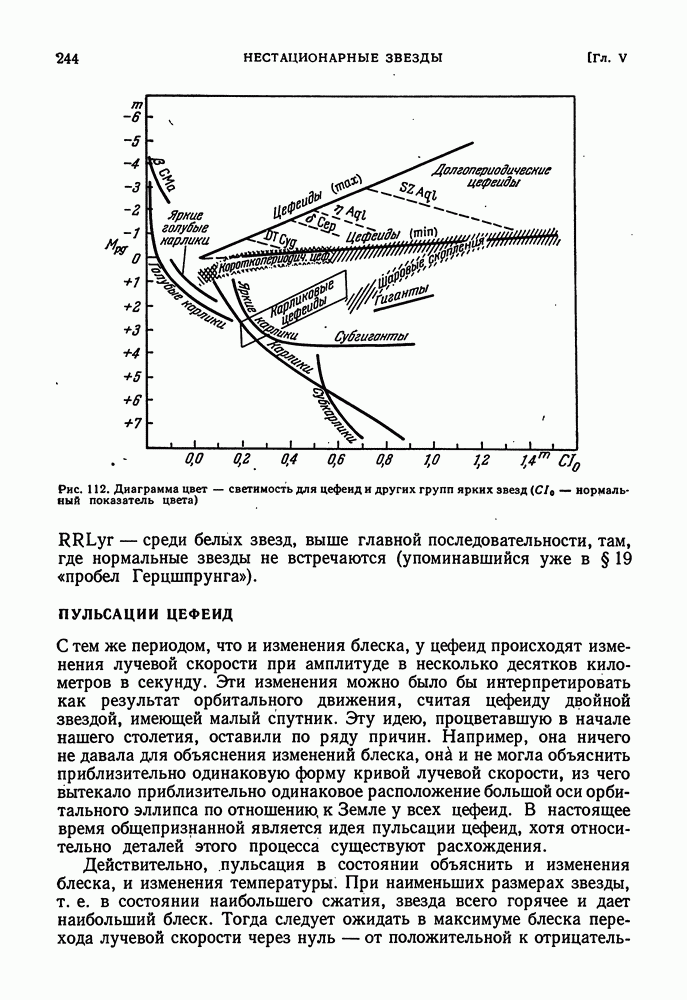
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦЕФЕИД
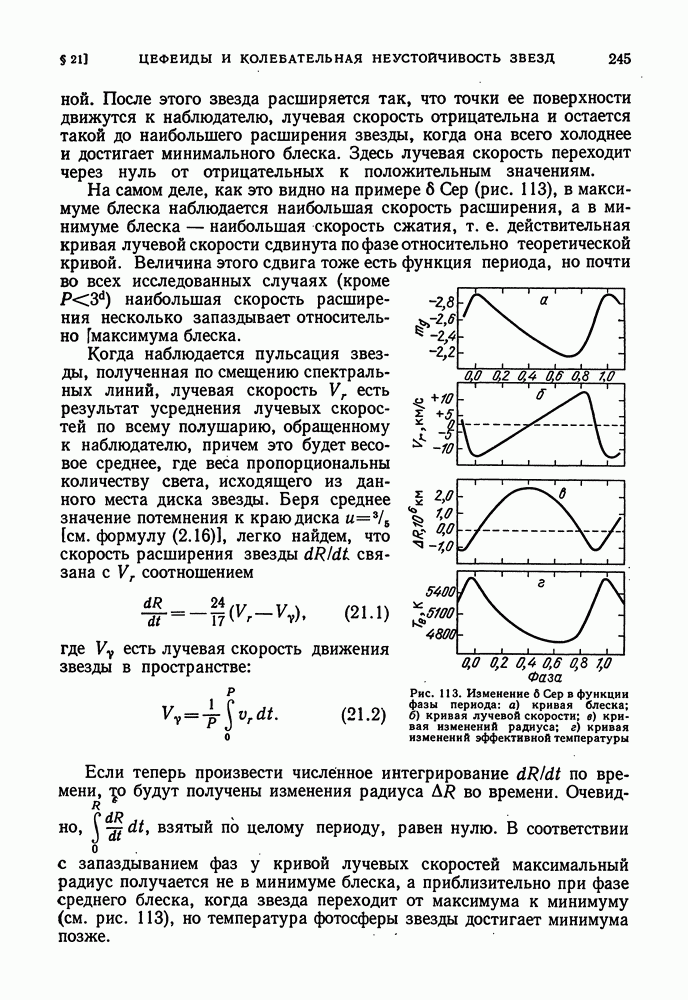
- ПУЛЬСАЦИИ ЦЕФЕИД
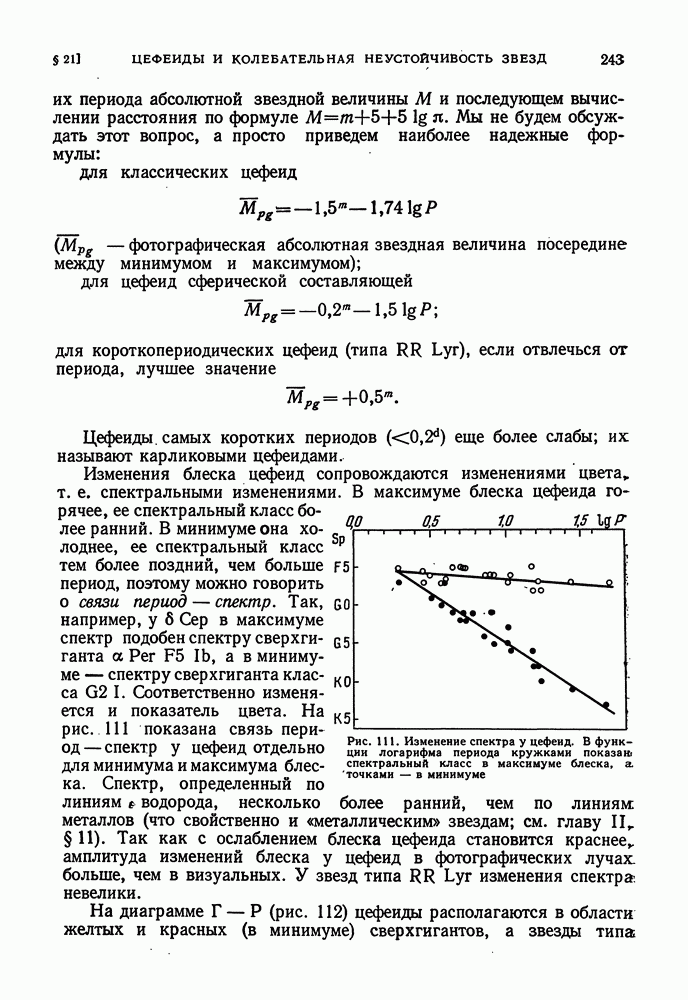
- ГИПОТЕЗА РАДИАЛЬНЫХ АДИАБАТИЧЕСКИХ ПУЛЬСАЦИЙ И ЕЕ ЗАТРУДНЕНИЯ
- НОВЫЕ ПРЕДСТАВЛЕНИЯ О КОЛЕБАТЕЛЬНЫХ ПРОЦЕССАХ У ЦЕФЕИД
- ЗВЕЗДЫ ТИПА b БОЛЬШОГО ПСА
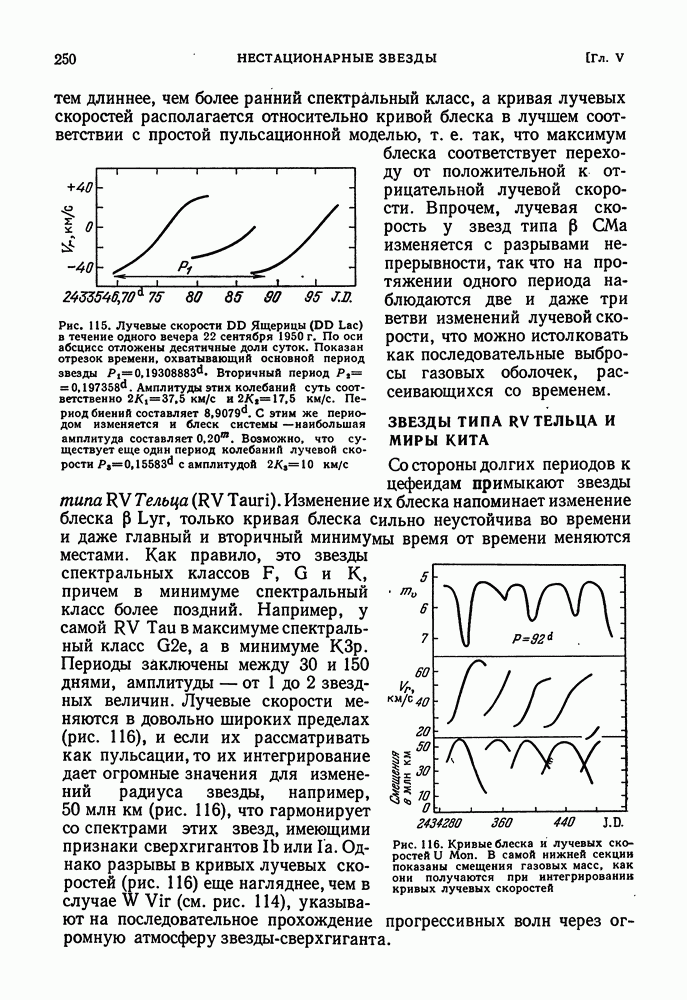
- ЗВЕЗДЫ ТИПА RV ТЕЛЬЦА И МИРЫ КИТА
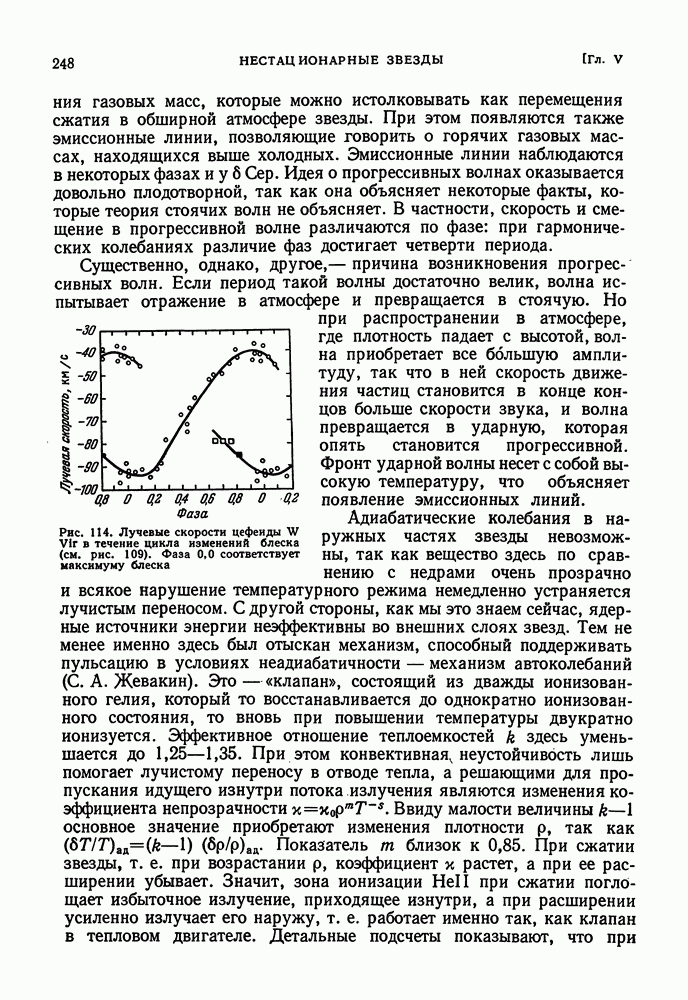
- § 22. ВЫНОС ВЕЩЕСТВА С ПОВЕРХНОСТИ ЗВЕЗД
- ГАЗОВЫЕ ОБОЛОЧКИ И КОЛЬЦА ВОКРУГ ЗВЕЗД
- ЗВЕЗДЫ ВОЛЬФА — РАЙЕ
- § 23. ВРАЩЕНИЕ ЗВЕЗД И ОБМЕН ВЕЩЕСТВА ВНУТРИ ДВОЙНЫХ СИСТЕМ
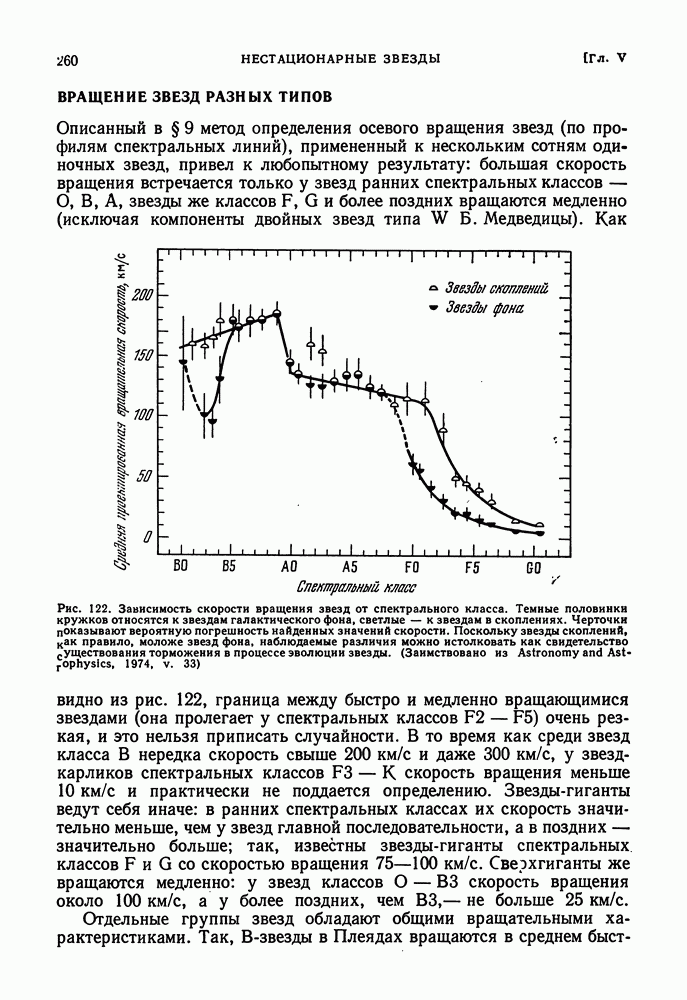
- ВРАЩЕНИЕ ЗВЕЗД РАЗНЫХ ТИПОВ
- ЭВОЛЮЦИОННЫЕ ИЗМЕНЕНИЯ СКОРОСТИ ВРАЩЕНИЯ ЗВЕЗД
- ПРОИСХОЖДЕНИЕ ВРАЩЕНИЯ ЗВЕЗД
- ОБМЕН ВЕЩЕСТВА ВНУТРИ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ. АККРЕЦИЯ. ЭВОЛЮЦИОННЫЕ СЛЕДСТВИЯ
- § 24. НОВЫЕ И СВЕРХНОВЫЕ ЗВЕЗДЫ
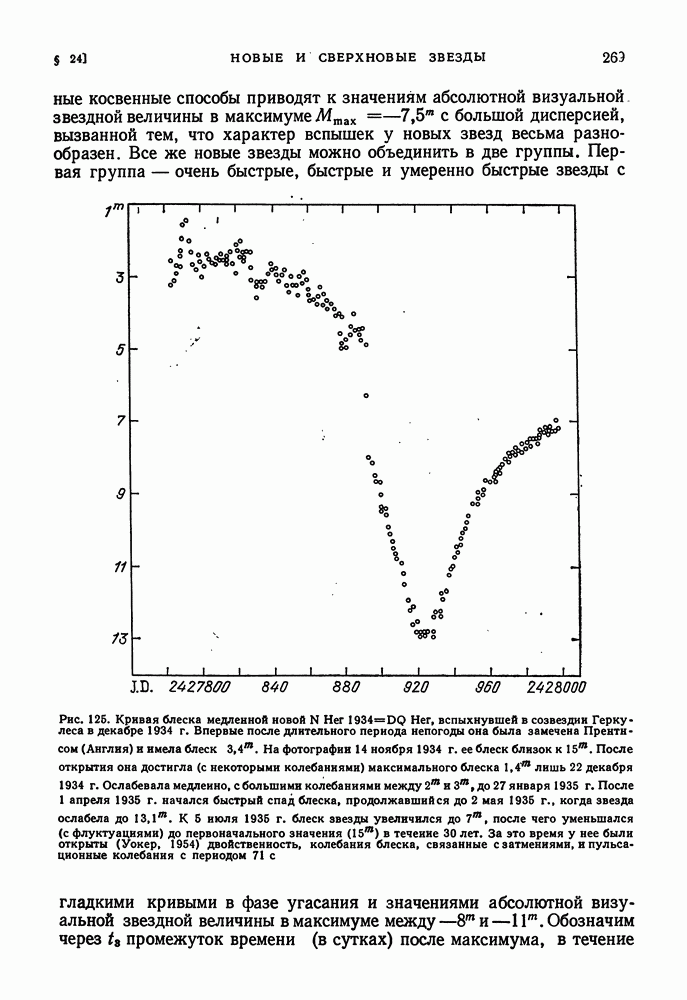
- СВЕТИМОСТЬ, АМПЛИТУДЫ ВСПЫШЕК И ЧИСЛО НОВЫХ ЗВЕЗД
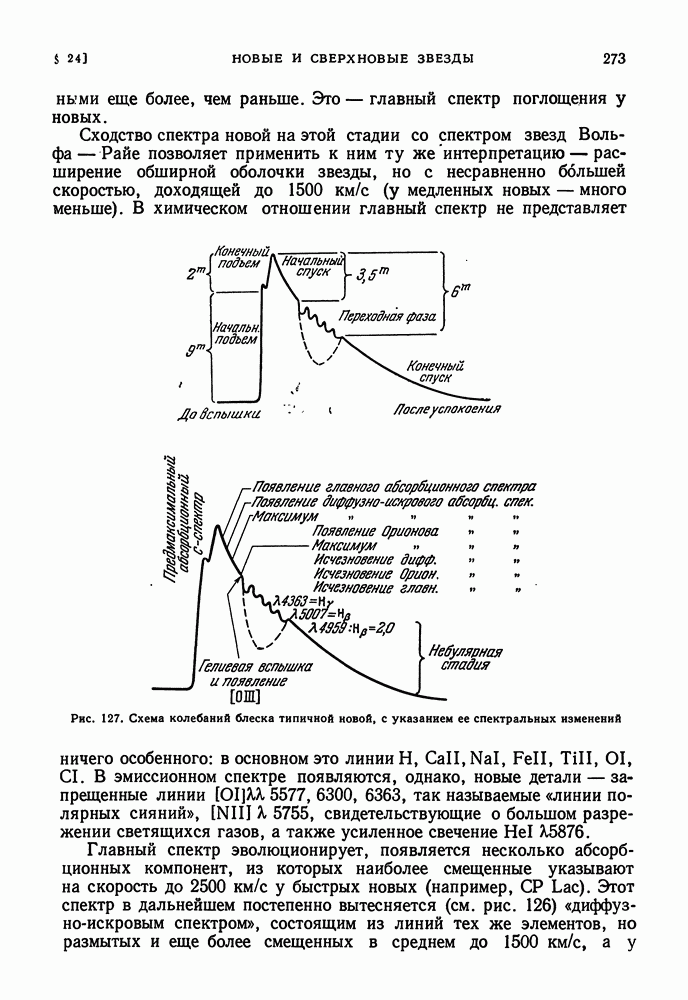
- СПЕКТРАЛЬНЫЕ ИЗМЕНЕНИЯ У НОВЫХ ЗВЕЗД
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ ВО ВРЕМЯ ВСПЫШКИ НОВОЙ ЗВЕЗДЫ
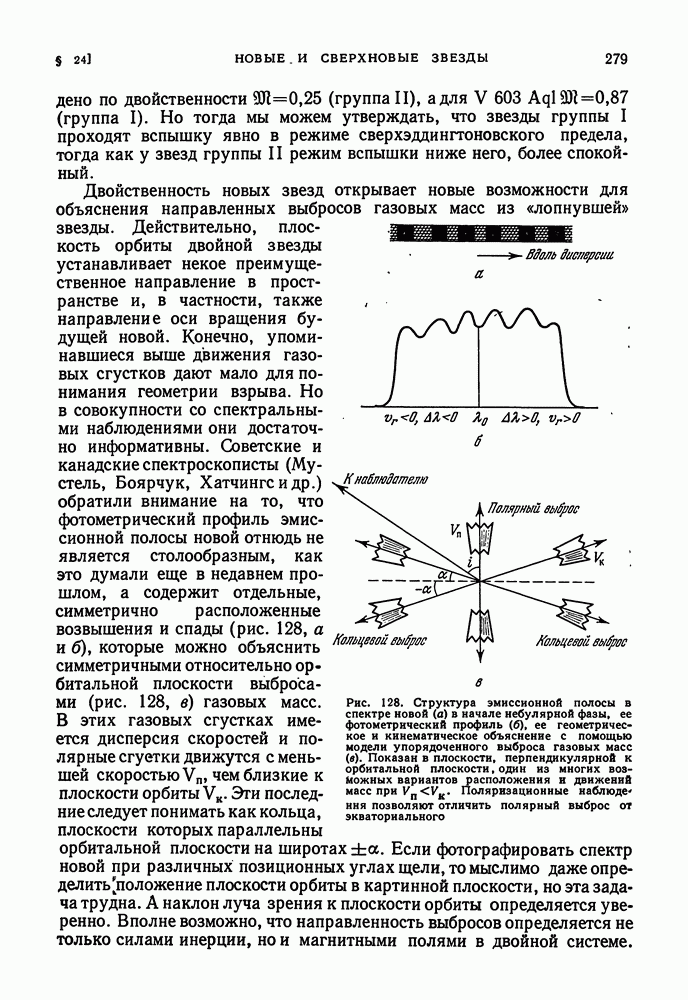
- ДВОЙСТВЕННОСТЬ НОВЫХ ЗВЕЗД
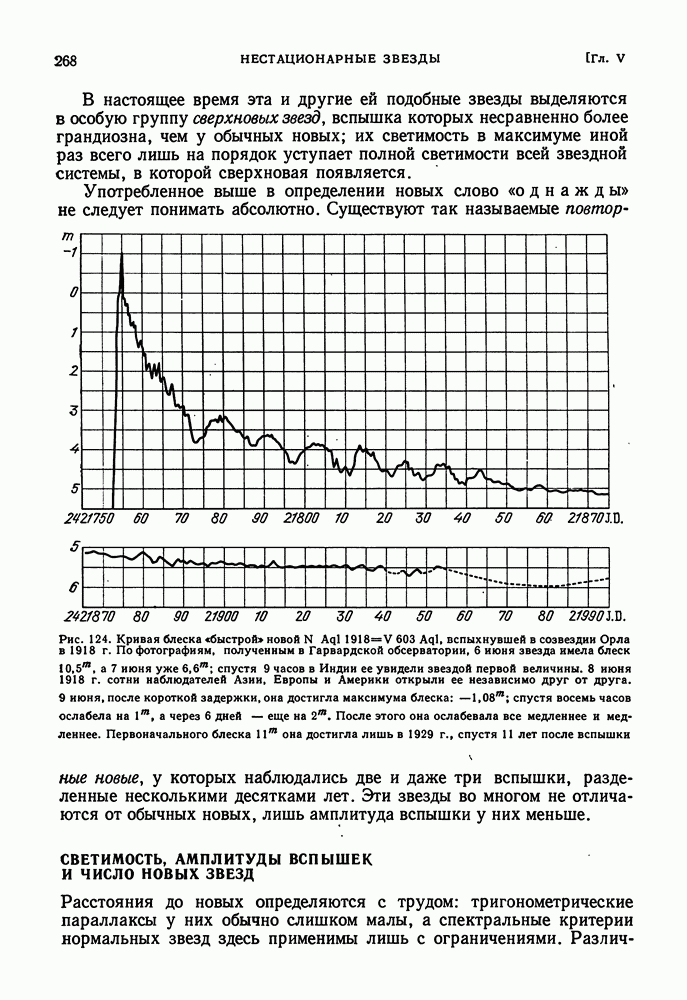
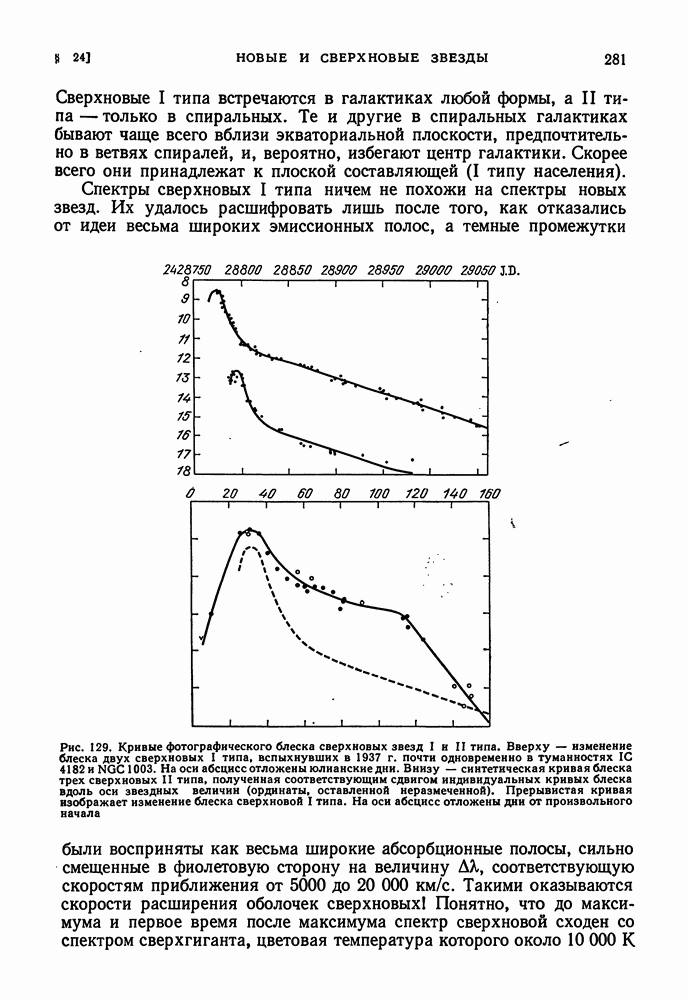
- СВЕРХНОВЫЕ ЗВЕЗДЫ
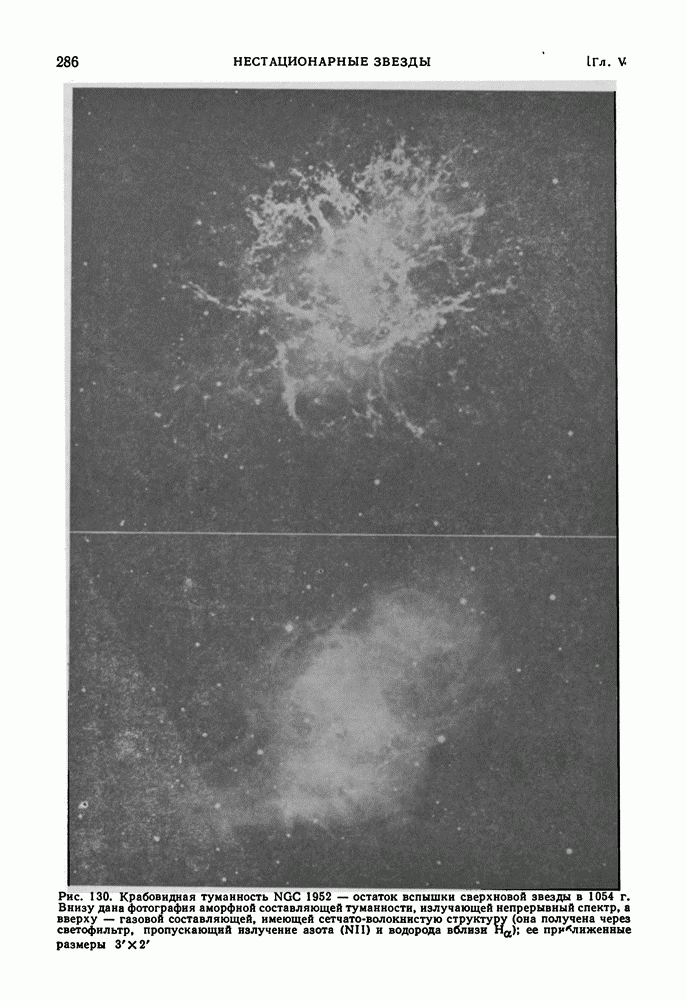
- ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ ЗВЕЗД. КРАБОВИДНАЯ ТУМАННОСТЬ. ПУЛЬСАРЫ
- § 25. КАРЛИКОВЫЕ ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ДРУГИЕ СЛУЧАИ НЕСТАЦИОНАРНОСТИ: РЕНТГЕНОВСКИЕ ЗВЕЗДЫ
- ЗВЕЗДЫ ТИПА U БЛИЗНЕЦОВ. СИМБИОТИЧЕСКИЕ ЗВЕЗДЫ
- ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ТИПА UV КИТА
- ЗВЕЗДЫ ТИПОВ Т ТЕЛЬЦА, RW ВОЗНИЧЕГО И ТОРИОНА
- НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ В РЕНТГЕНОВСКОМ ДИАПАЗОНЕ
- ЗАДАЧИ К ГЛАВЕ V
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ V
- ГЛАВА VI. ДИФФУЗНОЕ ВЕЩЕСТВО В ПРОСТРАНСТВЕ
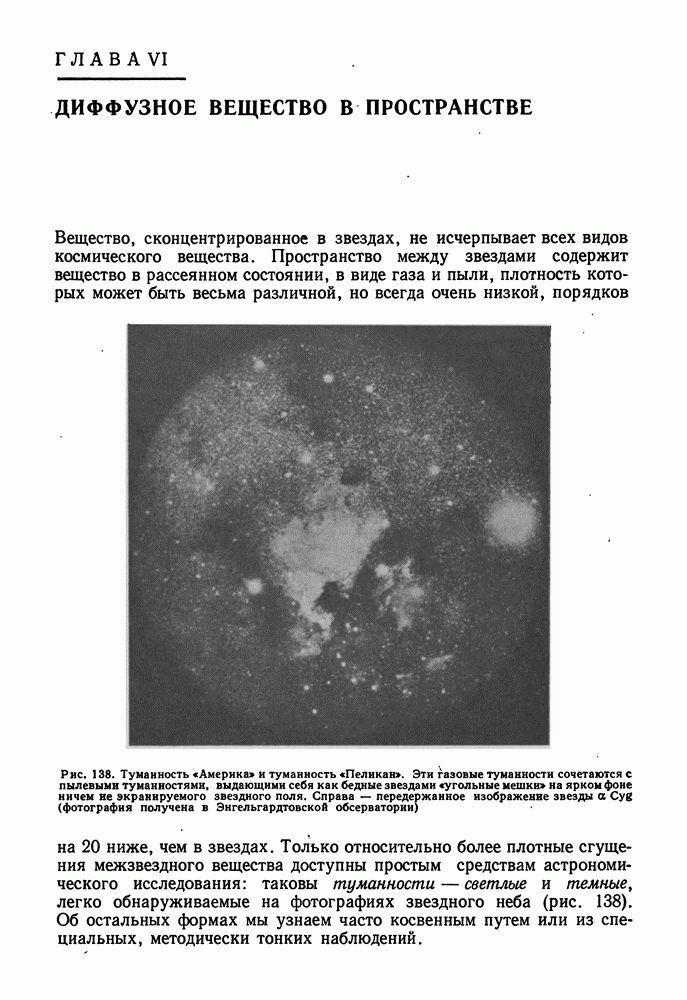
- ВЫСОКАЯ СПОСОБНОСТЬ ПЫЛИ ЗАДЕРЖИВАТЬ ПРОХОДЯЩИЙ СВЕТ
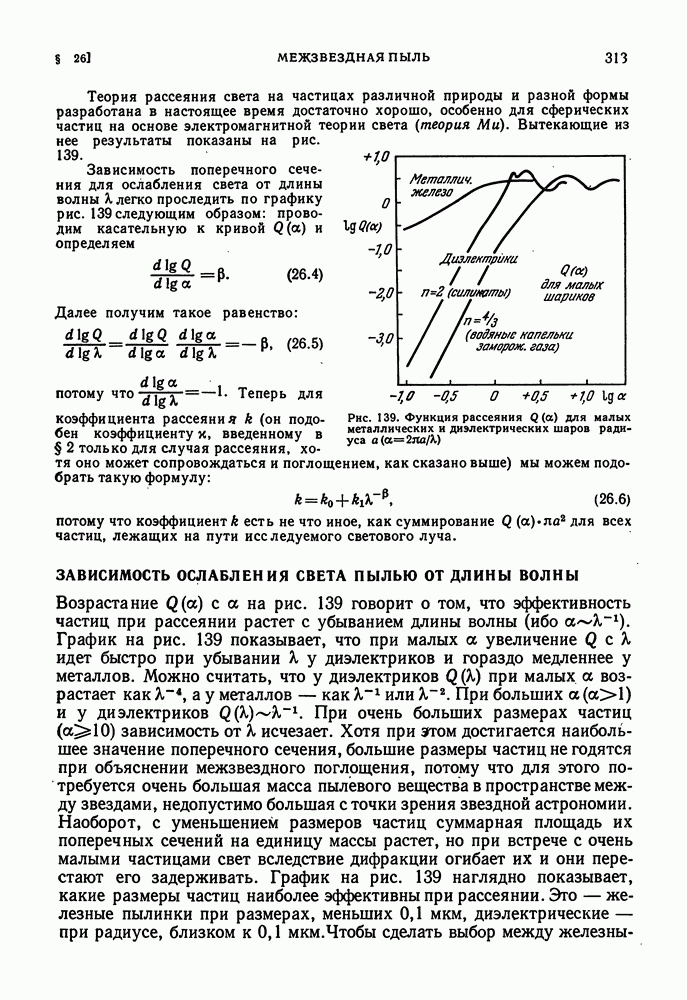
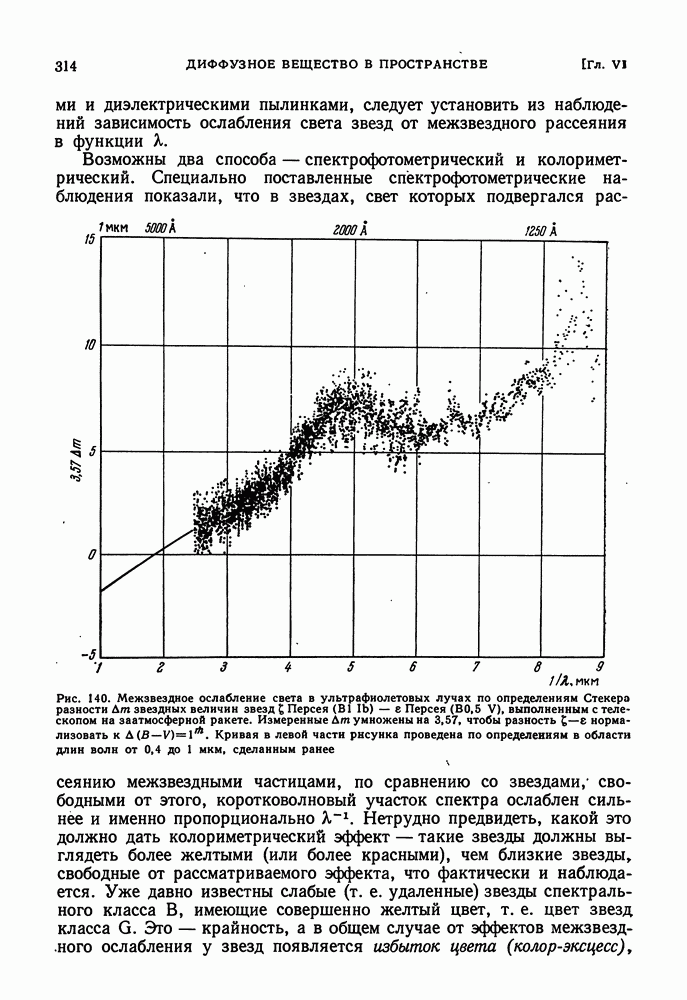
- ЗАВИСИМОСТЬ ОСЛАБЛЕНИЯ СВЕТА ПЫЛЬЮ ОТ ДЛИНЫ ВОЛНЫ
- ПРАКТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ОБЩЕГО ОСЛАБЛЕНИЯ СВЕТА в ЗАДАННОМ НАПРАВЛЕНИИ
- ОБЛАЧНАЯ СТРУКТУРА ПЫЛЕВОЙ СРЕДЫ В ГАЛАКТИКЕ
- РАСПРЕДЕЛЕНИЕ МЕЖЗВЕЗДНОЙ ПЫЛИ В ГАЛАКТИКЕ
- СВЕТЛЫЕ ПЫЛЕВЫЕ ТУМАННОСТИ
- СВЕТОВОЕ ДАВЛЕНИЕ НА ПЫЛЕВЫЕ ЧАСТИЦЫ
- МЕЖЗВЕЗДНАЯ ПОЛЯРИЗАЦИЯ СВЕТА ЗВЕЗД
- ОРИЕНТИРОВАНИЕ МЕЖЗВЕЗДНЫХ ПЫЛЕВЫХ ЧАСТИЦ МАГНИТНЫМИ ПОЛЯМИ
- § 27. ГАЗОВАЯ СОСТАВЛЯЮЩАЯ МЕЖЗВЕЗДНОЙ СРЕДЫ
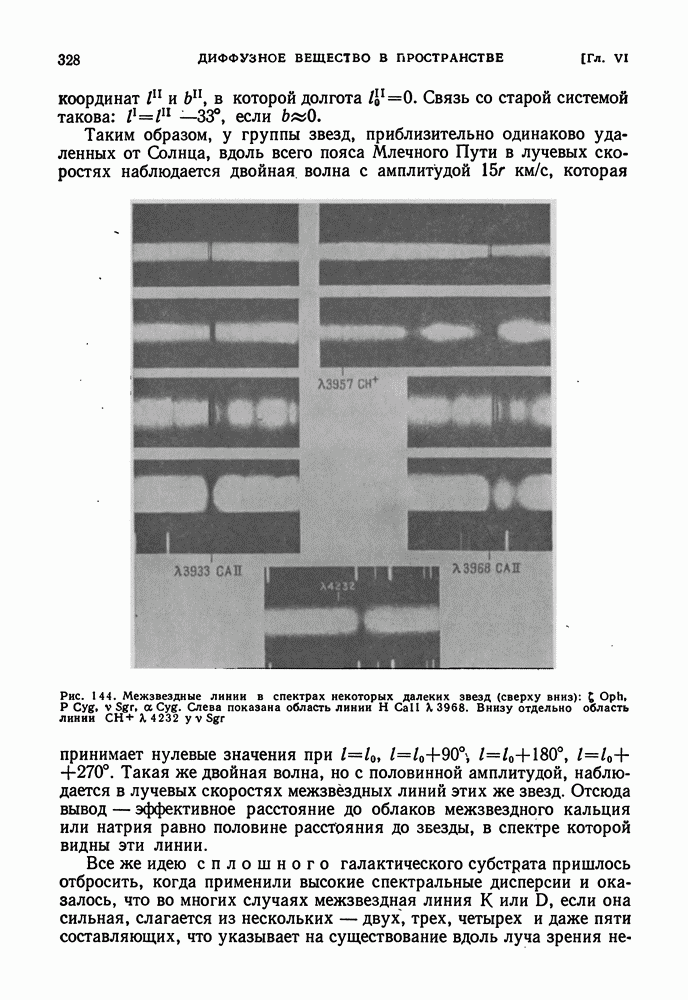
- МЕЖЗВЕЗДНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ Са, Na И ДРУГИХ ЭЛЕМЕНТОВ И МОЛЕКУЛ
- ГАЗОВЫЙ ГАЛАКТИЧЕСКИЙ СУБСТРАТ
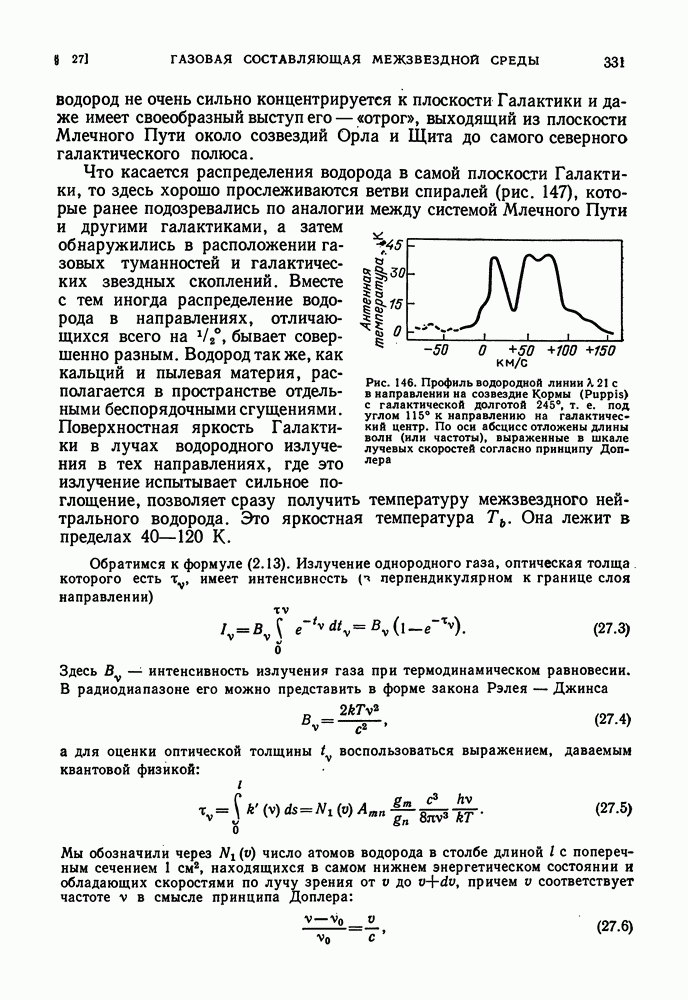
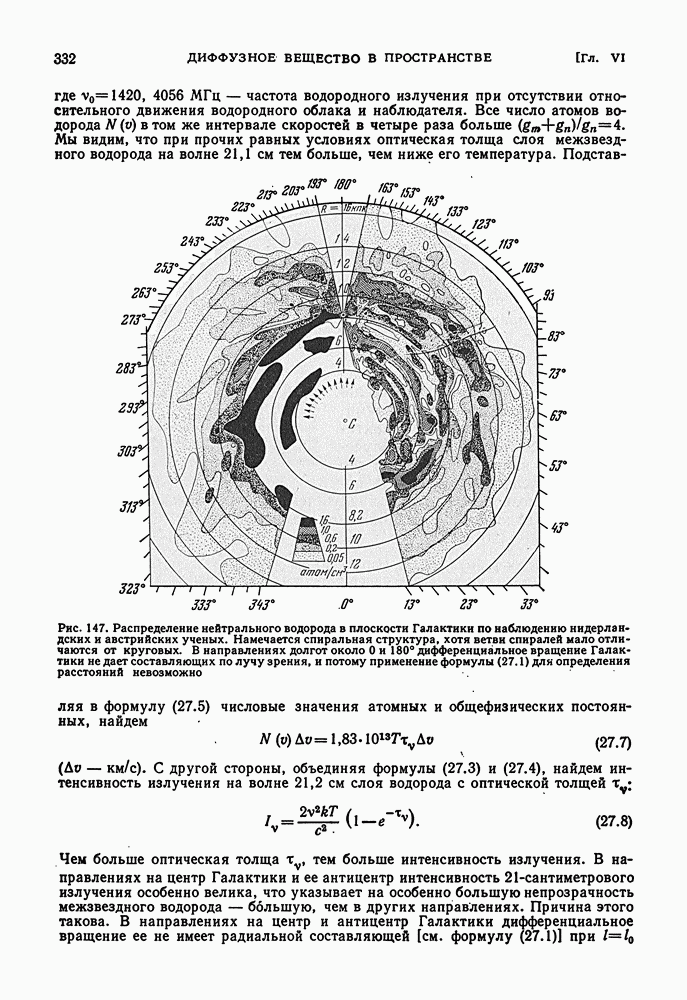
- ИЗЛУЧЕНИЕ МЕЖЗВЕЗДНОГО НЕЙТРАЛЬНОГО ВОДОРОДА НА ВОЛНЕ 21 см
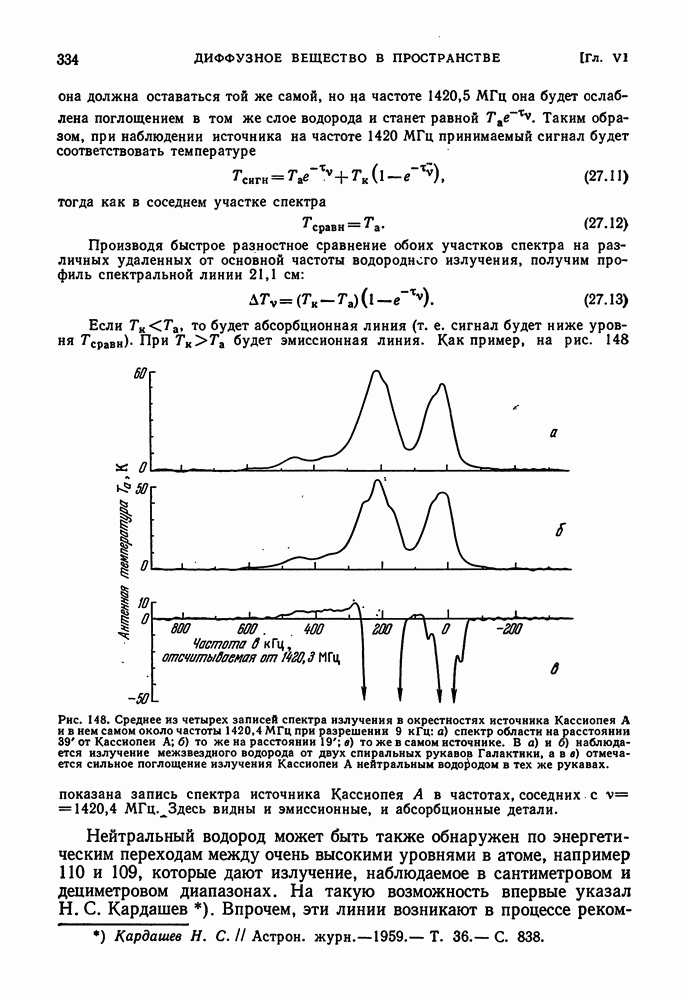
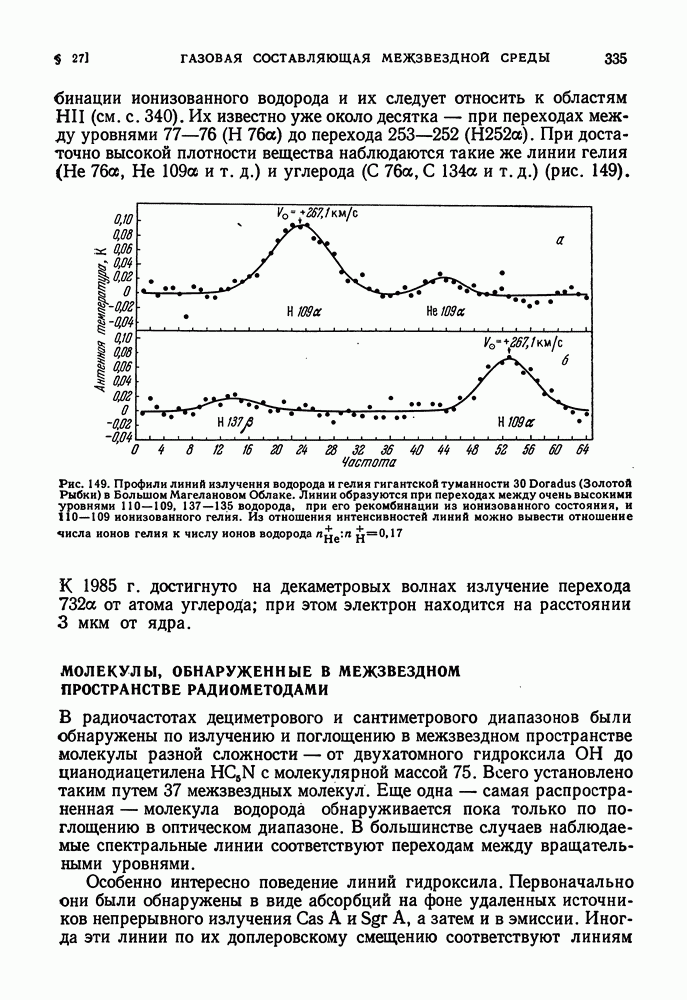
- МОЛЕКУЛЫ, ОБНАРУЖЕННЫЕ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ РАДИОМЕТОДАМИ
- ОТНОСИТЕЛЬНАЯ РОЛЬ ГАЗА И ПЫЛИ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭЛЕКТРОНЫ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ. ОБЛАСТИ HII И HI
- § 28. ГАЗОВЫЕ ТУМАННОСТИ
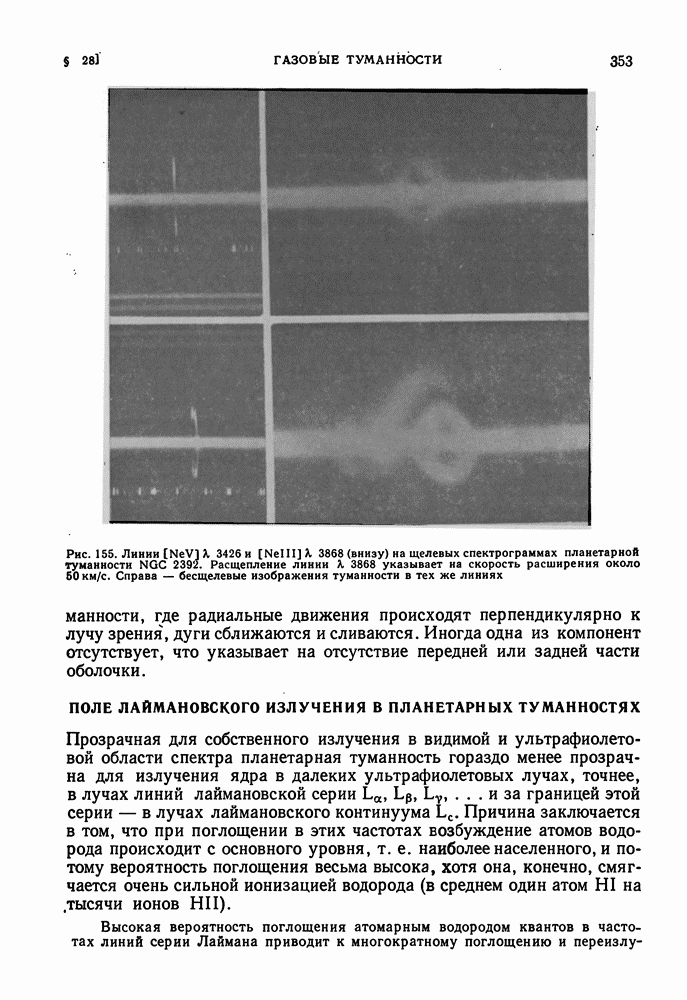
- ПЛАНЕТАРНЫЕ ТУМАННОСТИ
- ФЛУОРЕСЦЕНЦИЯ ВЕЩЕСТВА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ТЕМПЕРАТУРЫ ЯДЕР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЗАПРЕЩЕННЫЕ ЛИНИИ В СПЕКТРАХ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЭЛЕКТРОННЫЕ ТЕМПЕРАТУРЫ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- НЕПРЕРЫВНЫЙ СПЕКТР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ. ИХ МАССЫ
- РАСШИРЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ПОЛЕ ЛАЙМАНОВСКОГО ИЗЛУЧЕНИЯ В ПЛАНЕТАРНЫХ ТУМАННОСТЯХ
- ГРАНИЦА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ЯДРА ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
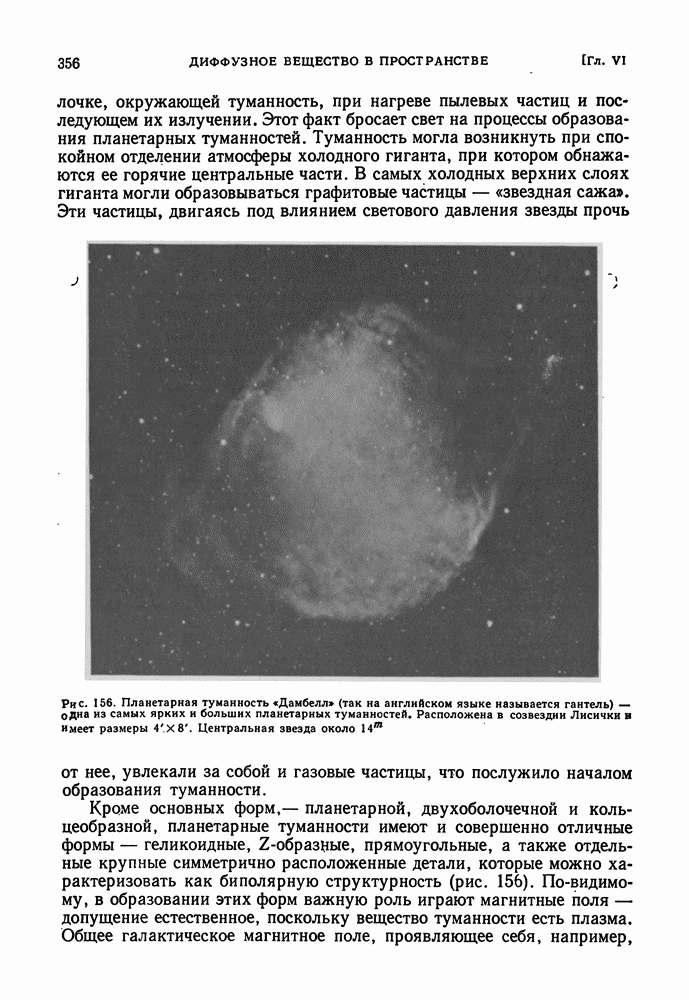
- ПРОИСХОЖДЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ДИФФУЗНЫЕ ГАЗОВЫЕ ТУМАННОСТИ
- ОБЛАСТИ HII И ИХ РАЗМЕРЫ
- ВЗАИМОДЕЙСТВИЕ ГАЗА И ИЗЛУЧЕНИЯ ГОРЯЧЕЙ ЗВЕЗДЫ. ДВИЖЕНИЯ ВНУТРИ ГАЗОВОЙ ТУМАННОСТИ
- РАДИОИЗЛУЧЕНИЕ ГАЗОВЫХ ТУМАННОСТЕЙ
- КРАБОВИДНАЯ ТУМАННОСТЬ — ИСТОЧНИК РАДИОИЗЛУЧЕНИЯ ТЕЛЕЦ А
- ТОРМОЗНОЕ ИЗЛУЧЕНИЕ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ КАК ИСТОЧНИК СВЕЧЕНИЯ КРАБОВИДНОЙ ТУМАННОСТИ
- КРАБОВИДНАЯ И НЕКОТОРЫЕ ДРУГИЕ ТУМАННОСТИ КАК ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ В ПУЛЬСАРАХ
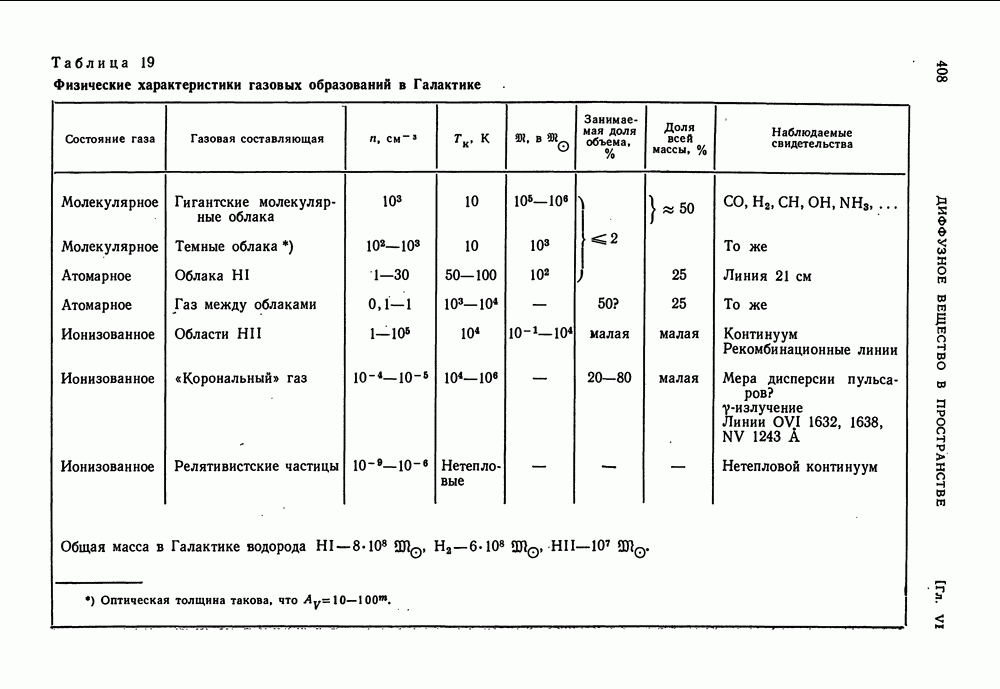
- § 29. ФИЗИЧЕСКОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА В ГАЛАКТИКЕ
- ТЕМПЕРАТУРА ТЕЛА, ПОМЕЩЕННОГО В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭНЕРГЕТИЧЕСКИЙ БАЛАНС У ЧАСТИЦ МЕЖЗВЕЗДНОЙ СРЕДЫ
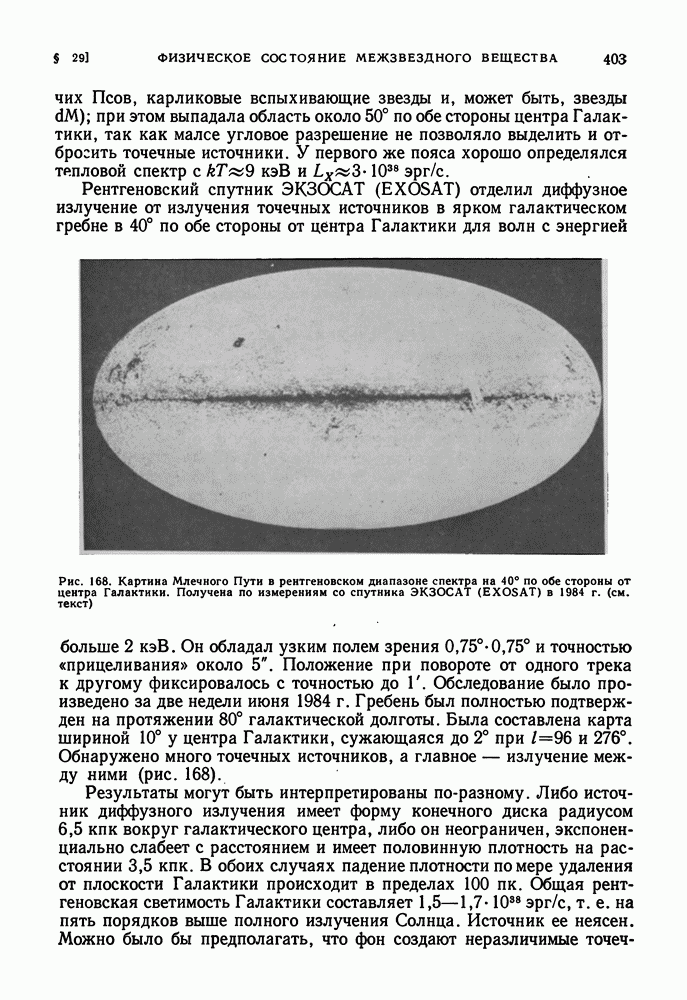
- РАДИОИЗЛУЧЕНИЕ ИЗ МЕЖЗВЕЗДНОГО ПРОСТРАНСТВА ГАЛАКТИКИ
- КОСМИЧЕСКИЕ ЛУЧИ В ГАЛАКТИКЕ
- МАГНИТНЫЕ ПОЛЯ В ГАЛАКТИКЕ
- КОНДЕНСАЦИИ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА И ЗВЕЗДООБРАЗОВАНИЕ
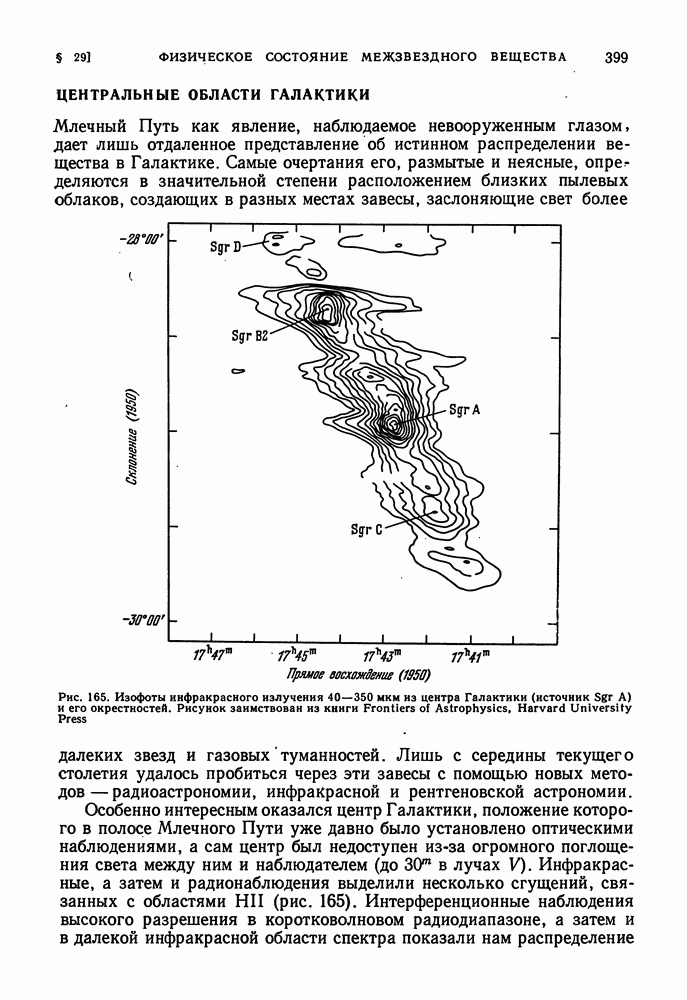
- ЦЕНТРАЛЬНЫЕ ОБЛАСТИ ГАЛАКТИКИ
- ОСОБЕННОСТИ РАСПОЛОЖЕНИЯ И ДВИЖЕНИЯ ГАЗОВЫХ МАСС В ГАЛАКТИКЕ
- МЕЖЗВЕЗДНЫЙ ГАЗ В ГАЛАКТИКЕ (РЕЗЮМЕ). АКТИВНОСТЬ ЯДРА ГАЛАКТИКИ
- ЗАДАЧИ К ГЛАВЕ VI
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VI
- ГЛАВА VII. ГАЛАКТИКИ И МЕТАГАЛАКТИКА
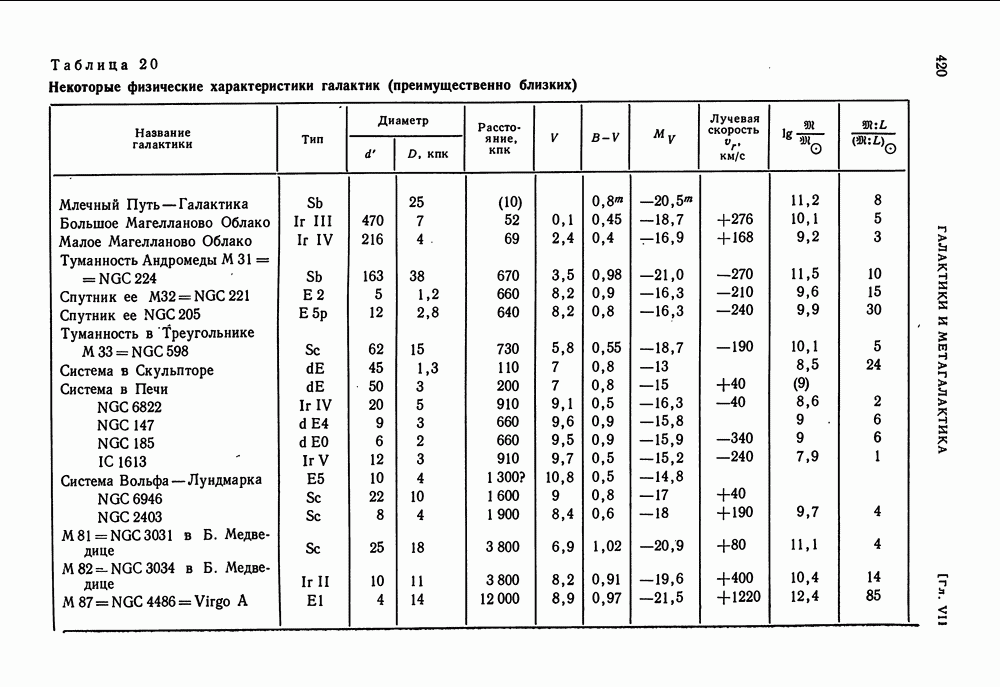
- § 30. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
- КЛАССИФИКАЦИЯ ГАЛАКТИК- ОБЩИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
- ВРАЩЕНИЕ ГАЛАКТИК. ИХ МАССЫ
- КРАСНОЕ СМЕЩЕНИЕ В СПЕКТРАХ ГАЛАКТИК
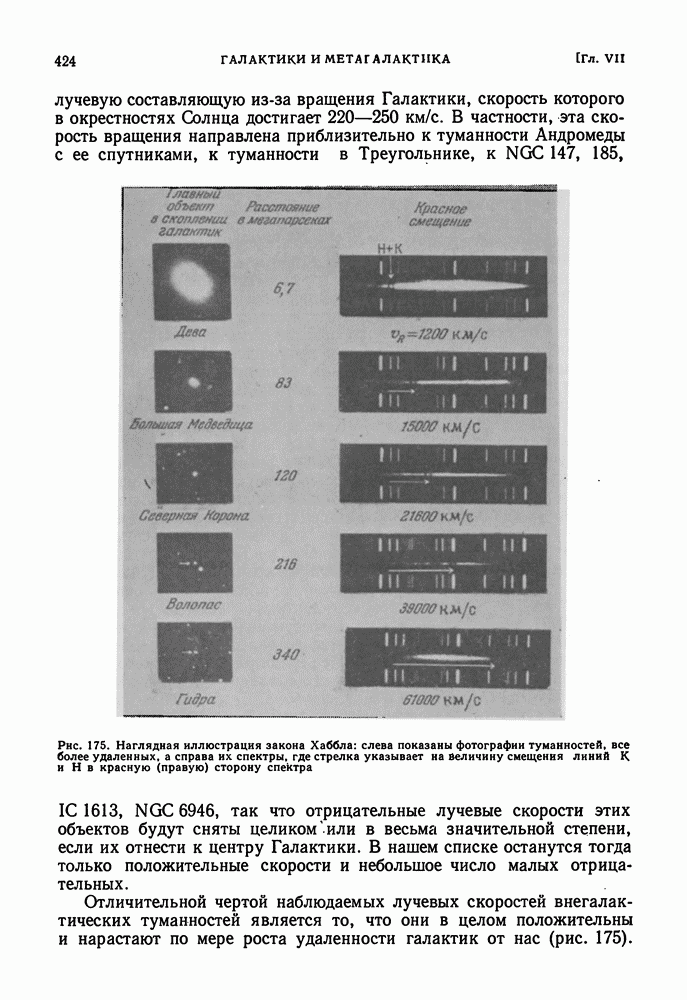
- ЗАКОН ХАББЛА. ПОСТОЯННАЯ ХАББЛА
- СТРУКТУРА МЕТАГАЛАКТИКИ. СКОПЛЕНИЕ ГАЛАКТИК-ГРУППЫ ГАЛАКТИК
- ЗВЕЗДООБРАЗОВАНИЕ В ГАЛАКТИКАХ
- НЕВИДИМОЕ ВЕЩЕСТВО В ГАЛАКТИКАХ И ИХ СКОПЛЕНИЯХ
- § 31. РАДИОГАЛАКТИКИ И НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ В ГАЛАКТИКАХ
- РАДИОИЗЛУЧЕНИЕ НОРМАЛЬНЫХ ГАЛАКТИК
- РАДИОГАЛАКТИКИ
- ГАЛАКТИКИ СЕЙФЕРТА
- АКТИВНЫЕ ГАЛАКТИКИ И ПРИЗНАКИ ВЗРЫВА В НИХ
- КВАЗАРЫ И РОДСТВЕННЫЕ ИМ ОБЪЕКТЫ
- СПЕКТРАЛЬНЫЙ ИНДЕКС РАДИОИЗЛУЧЕНИЯ. ВОЗРАСТ РАДИОГАЛАКТИК
- ОБЩИЕ ЗАПАСЫ ЭНЕРГИИ В ГАЛАКТИКАХ
- § 32. ГАЛАКТИКИ И КОСМОЛОГИЯ
- ЗАДАЧИ К ГЛАВЕ VII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VII
- ГЛАВА VIII. СОЛНЕЧНАЯ СИСТЕМА. ПЛАНЕТЫ И ИХ СПУТНИКИ
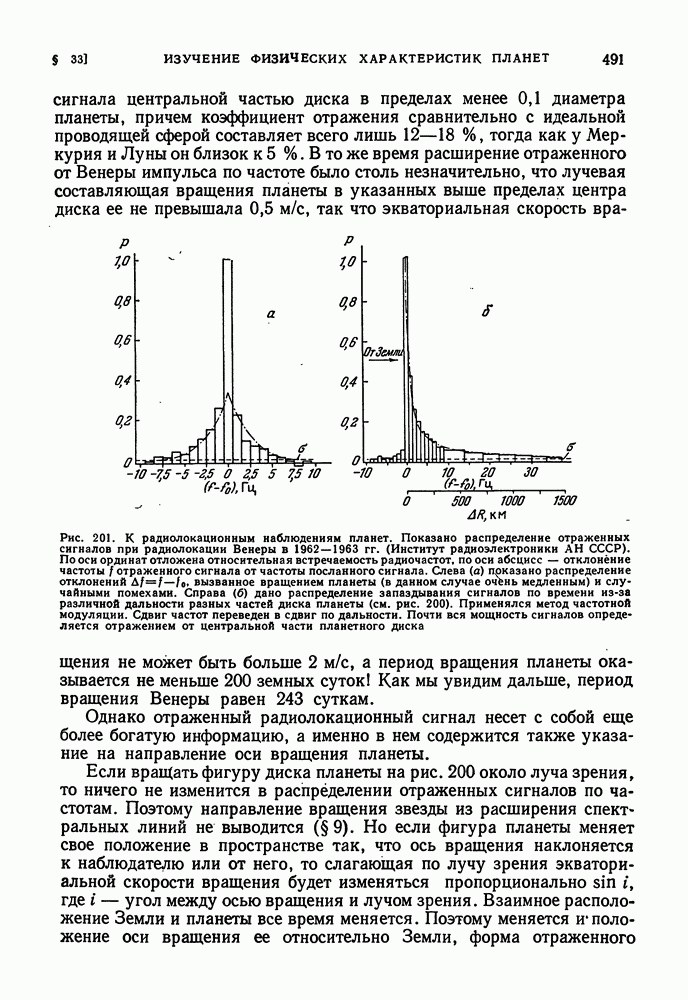
- § 33. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ПЛАНЕТ
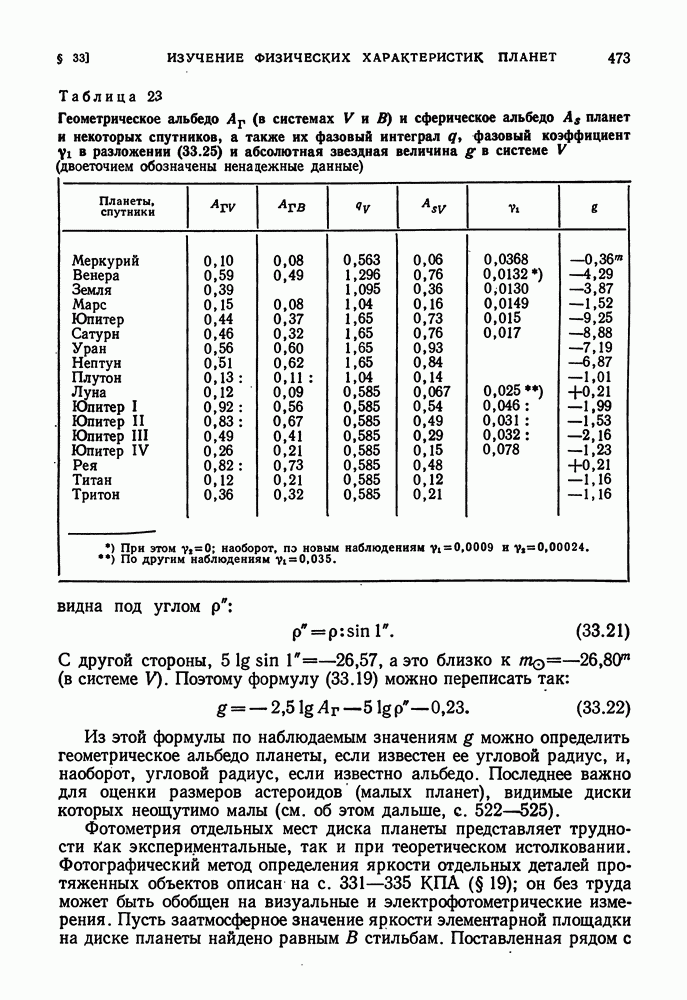
- ФОТОМЕТРИЧЕСКИЙ АНАЛИЗ ПЛАНЕТНЫХ ПОВЕРХНОСТЕЙ И АТМОСФЕРЫ
- ПОЛЯРИМЕТРИЯ ПЛАНЕТ
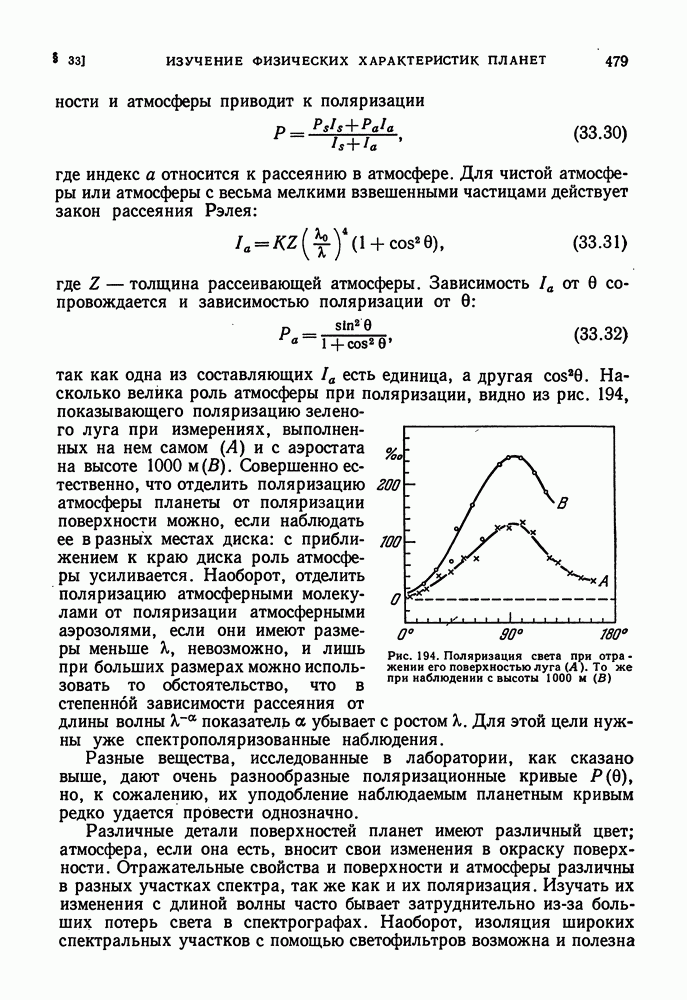
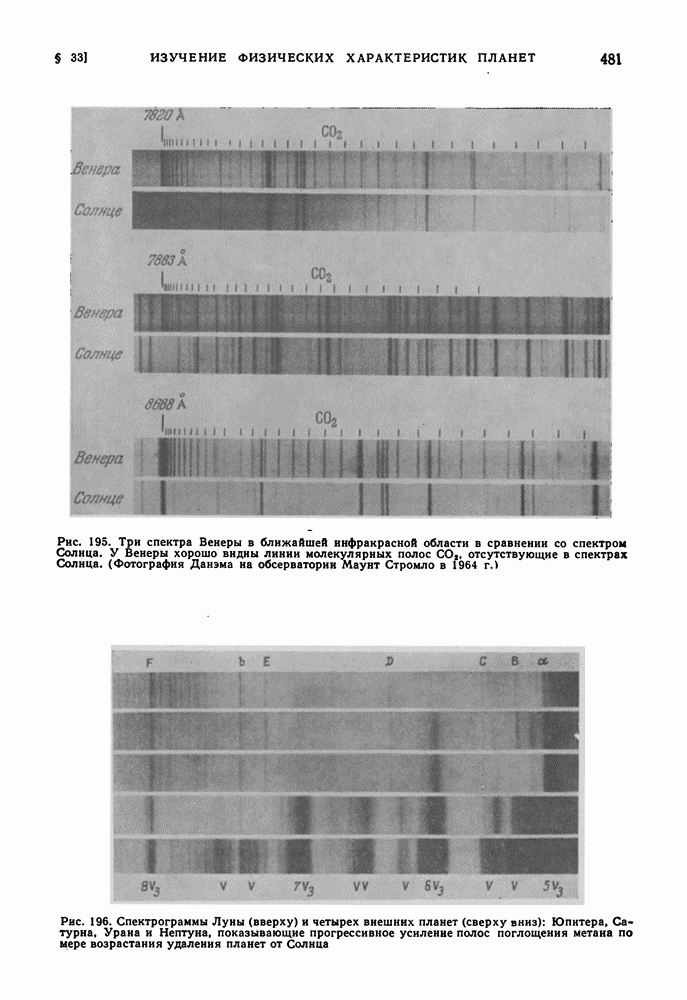
- СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЛАНЕТНЫХ АТМОСФЕР
- СПЕКТРАЛЬНОЕ ОПРЕДЕЛЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ
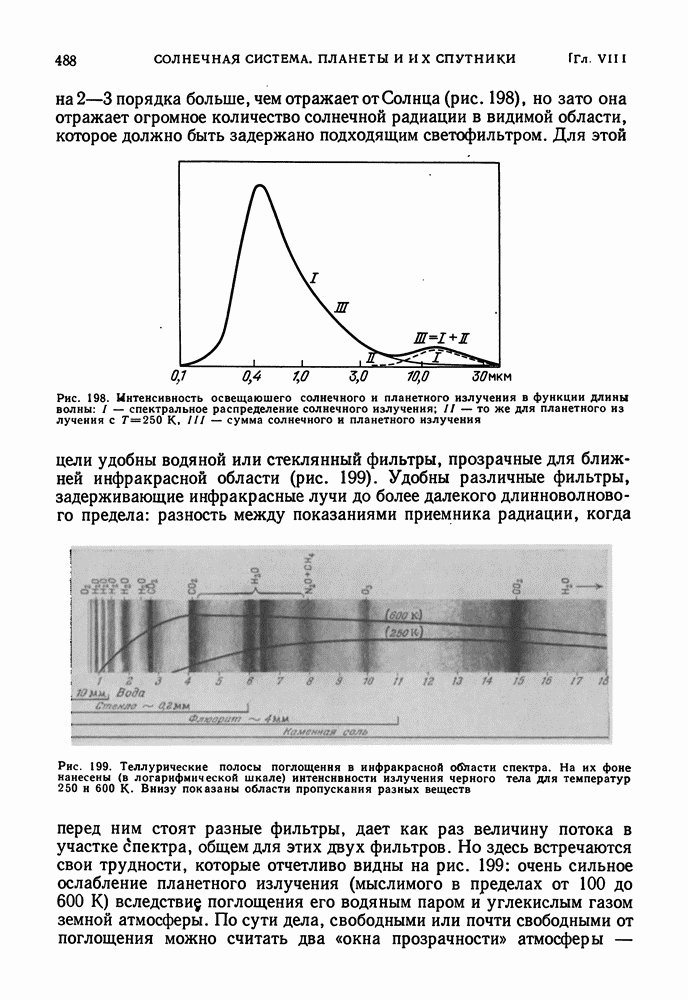
- ПЛАНЕТНЫЕ ТЕМПЕРАТУРЫ. ТЕОРИЯ. РОЛЬ АТМОСФЕРЫ
- РАЗЛИЧНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЛАНЕТНЫХ ТЕМПЕРАТУР
- РАДИОЛОКАЦИОННЫЕ МЕТОДЫ ИЗУЧЕНИЯ ПЛАНЕТ
- УСТОЙЧИВОСТЬ ПЛАНЕТНЫХ АТМОСФЕР ВО ВРЕМЕНИ
- § 34. ПЛАНЕТЫ ЗЕМНОЙ ГРУППЫ
- МЕРКУРИЙ
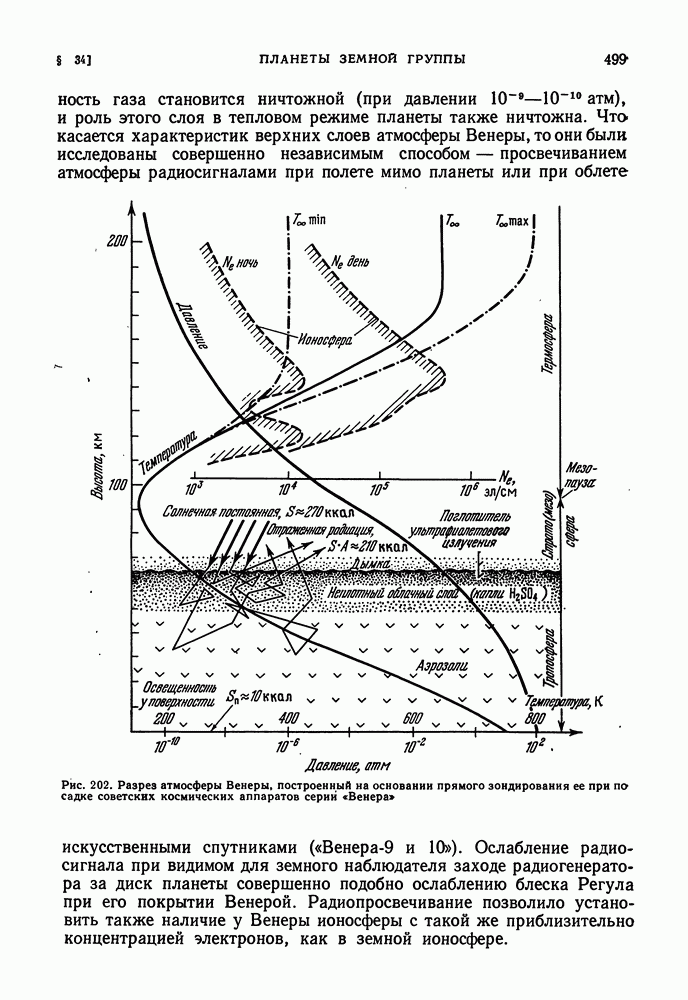
- ВЕНЕРА. ТЕМПЕРАТУРА. ПАРНИКОВАЯ МОДЕЛЬ АТМОСФЕРЫ. ВРАЩЕНИЕ
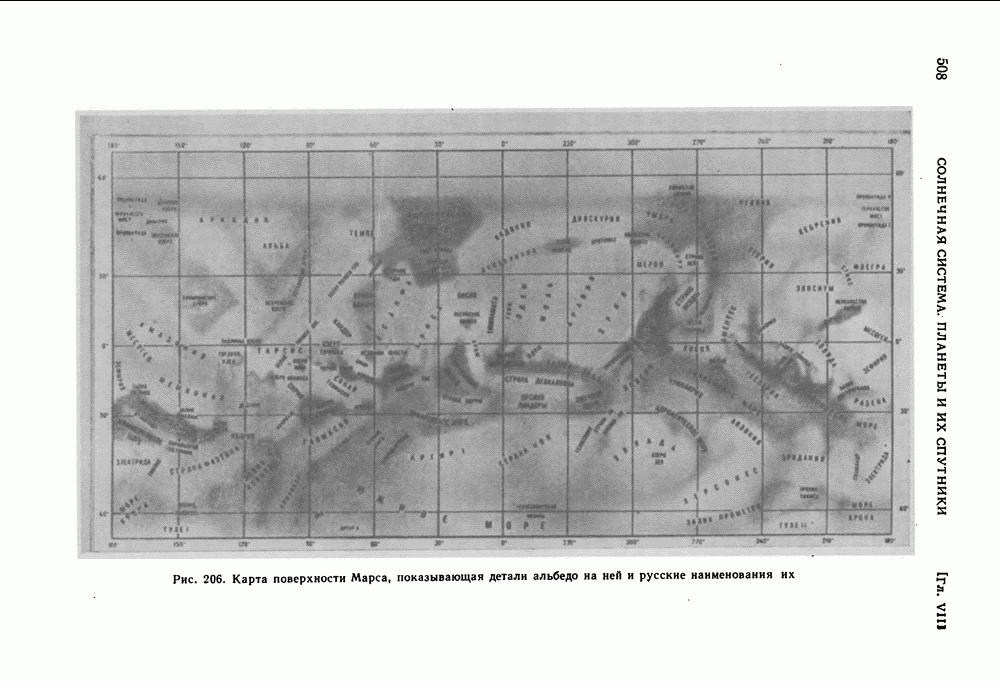
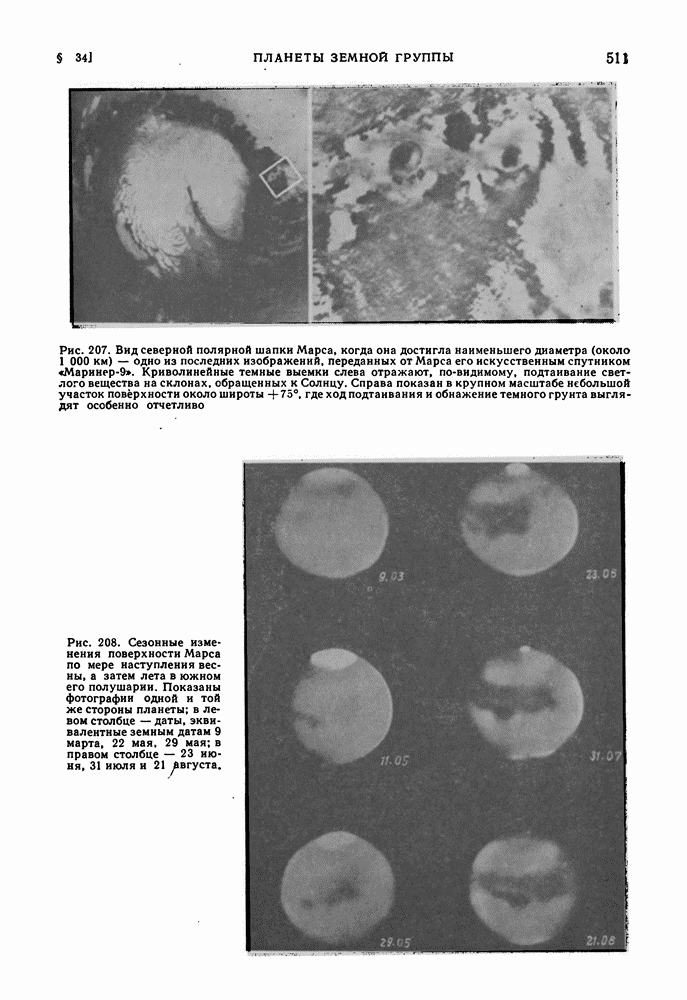
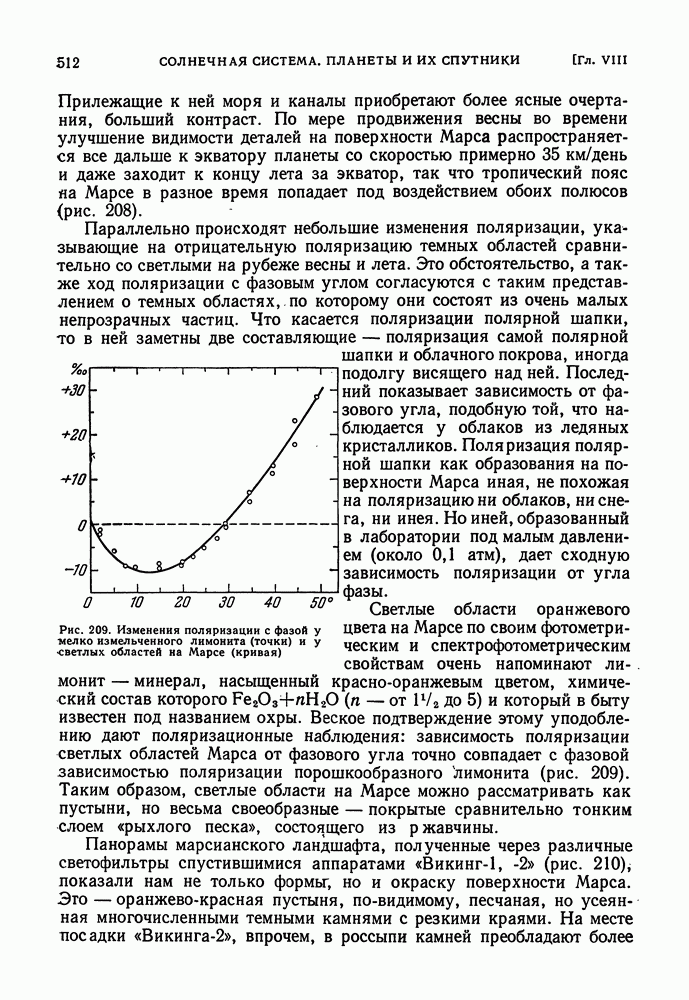
- МАРС. ОСОБЕННОСТИ ЕГО ПОВЕРХНОСТИ. ИХ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ
- АТМОСФЕРА МАРСА
- ТЕМПЕРАТУРА МАРСА
- ВОДА НА МАРСЕ. ЖИЗНЬ НА МАРСЕ?
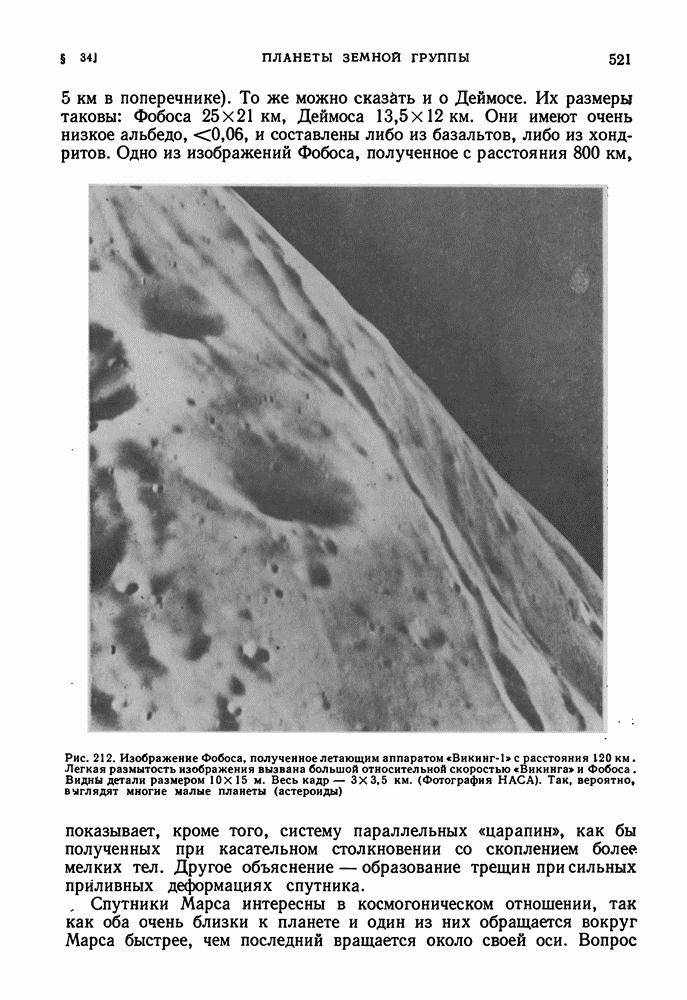
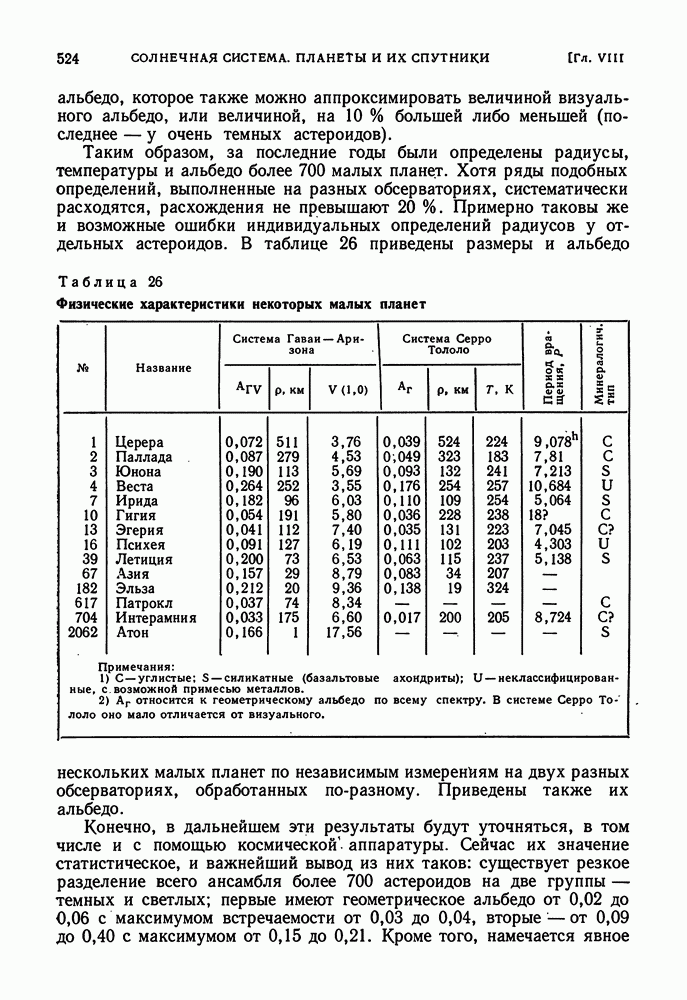
- МАЛЫЕ ПЛАНЕТЫ
- § 35. ЛУНА
- АТМОСФЕРА ЛУНЫ
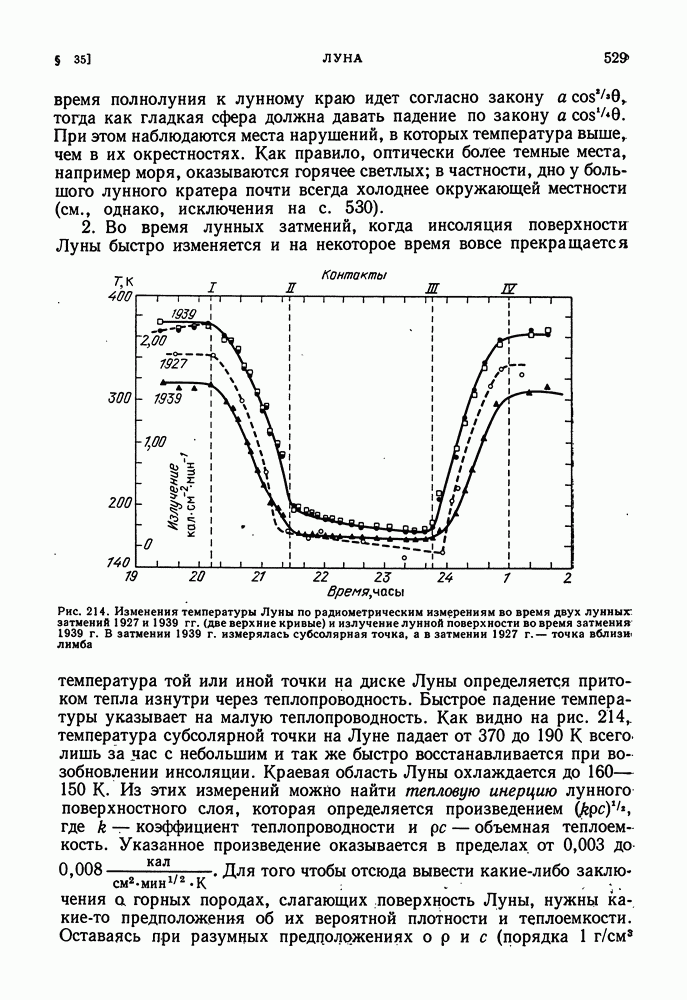
- ТЕМПЕРАТУРНЫЙ РЕЖИМ НА ЛУНЕ
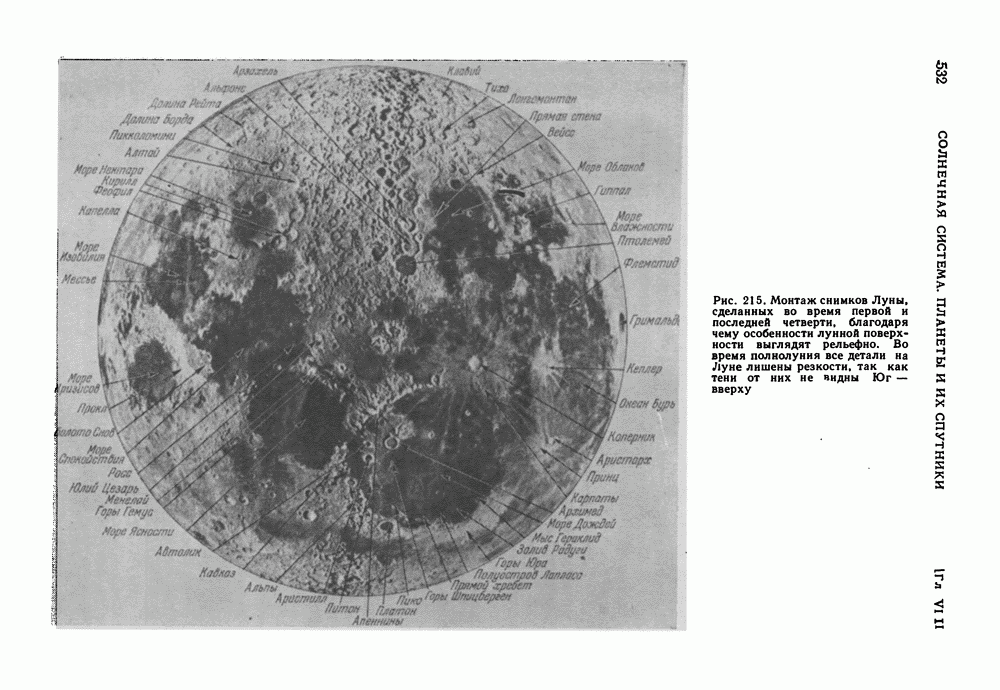
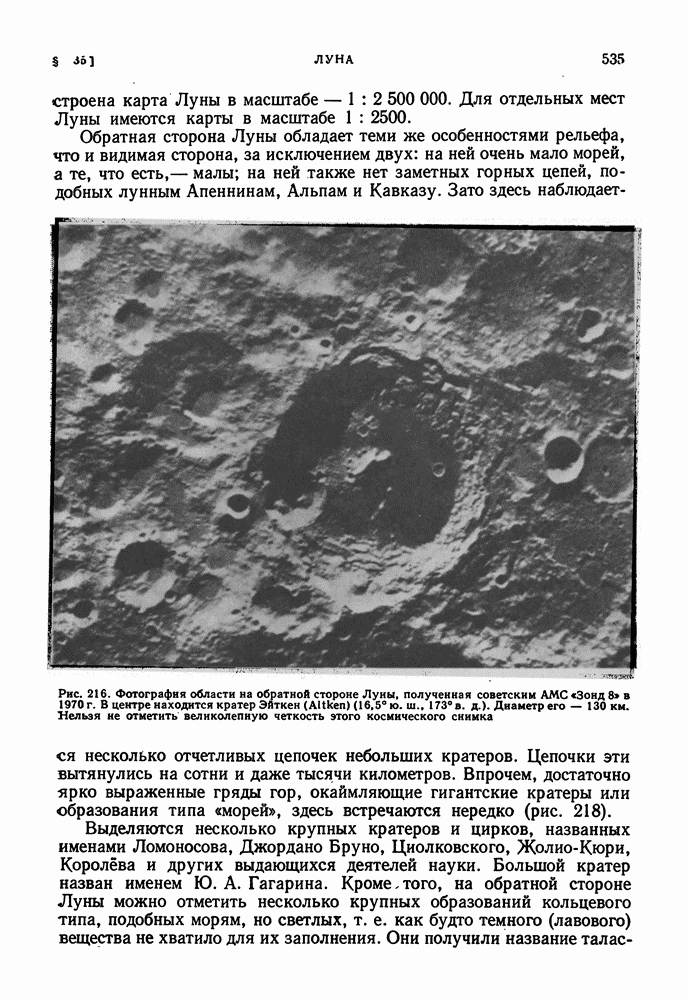
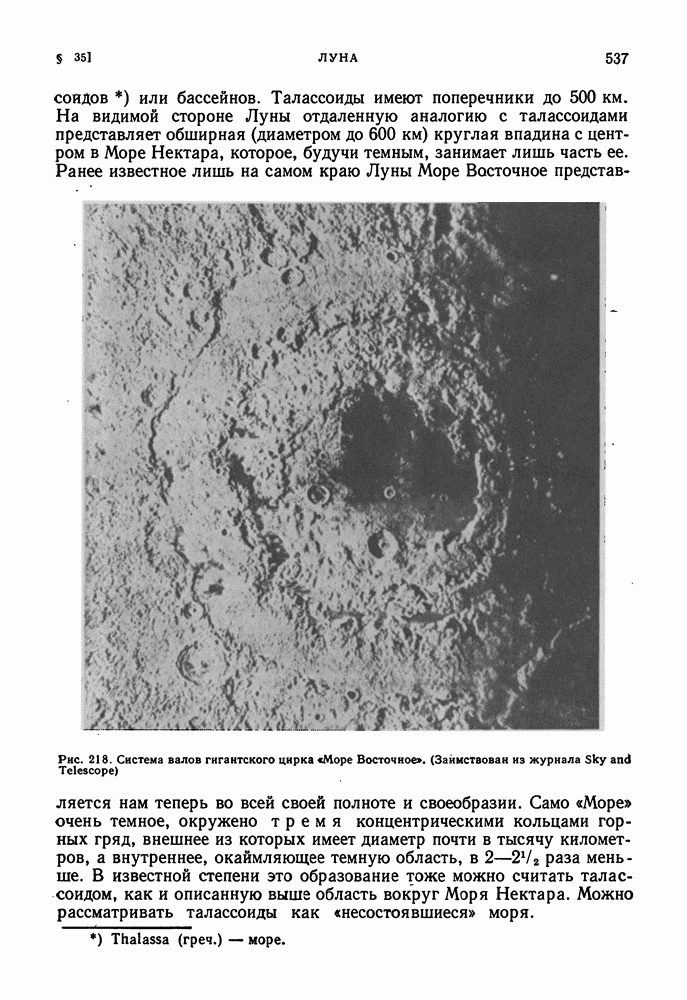
- МОРФОЛОГИЯ ЛУННОЙ ПОВЕРХНОСТИ
- ВНУТРЕННЕЕ СТРОЕНИЕ ЛУНЫ
- ОБРАЗОВАНИЕ СОВРЕМЕННОГО ЛУННОГО ЛАНДШАФТА
- § 36. ВНЕШНИЕ ПЛАНЕТЫ СОЛНЕЧНОЙ СИСТЕМЫ
- ЮПИТЕР
- САТУРН
- УРАН И НЕПТУН
- ПЛУТОН
- ЗАДАЧИ К ГЛАВЕ VIII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VIII
- ГЛАВА IX. СОЛНЕЧНАЯ СИСТЕМА. КОМЕТЫ И МАЛЫЕ ТЕЛА СОЛНЕЧНОЙ СИСТЕМЫ
- ОБЩАЯ ХАРАКТЕРИСТИКА КОМЕТ
- ОБРАЗОВАНИЕ КОМЕТНЫХ ФОРМ
- МЕХАНИЧЕСКАЯ ТЕОРИЯ КОМЕТНЫХ ФОРМ
- СПЕКТРЫ КОМЕТ
- БЛЕСК КОМЕТЫ И ЕГО ИЗМЕНЕНИЯ
- ДАВЛЕНИЕ СВЕТА НА КОМЕТНЫЕ ЧАСТИЦЫ
- СОЛНЕЧНАЯ АКТИВНОСТЬ КАК ИСТОЧНИК ВОЗНИКНОВЕНИЯ КОМЕТНЫХ ФОРМ
- РАСПАД КОМЕТ. ПРОИСХОЖДЕНИЕ КОМЕТ
- КОМЕТА ГАЛЛЕЯ В 1986 г.
- § 38. МЕТЕОРЫ
- ОБЩИЕ ХАРАКТЕРИСТИКИ МЕТЕОРОВ. СПОСОБЫ ИХ НАБЛЮДЕНИЯ
- МЕТЕОРНЫЕ ПОТОКИ И СПОРАДИЧЕСКИЕ МЕТЕОРЫ
- ЯВЛЕНИЯ ПРИ ВТОРЖЕНИИ МЕТЕОРНОГО ТЕЛА В ЗЕМНУЮ АТМОСФЕРУ
- РАДИОЛОКАЦИОННЫЕ НАБЛЮДЕНИЯ МЕТЕОРОВ
- МАССЫ МЕТЕОРНЫХ ТЕЛ
- МЕТЕОРИТЫ И ИХ КЛАССИФИКАЦИЯ
- ВОЗРАСТ МЕТЕОРИТОВ
- МЕТЕОРИТНЫЕ КРАТЕРЫ И ВОРОНКИ
- ТУНГУССКИЙ МЕТЕОРИТ
- § 39. МЕТЕОРНОЕ И ПЫЛЕВОЕ ВЕЩЕСТВО В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
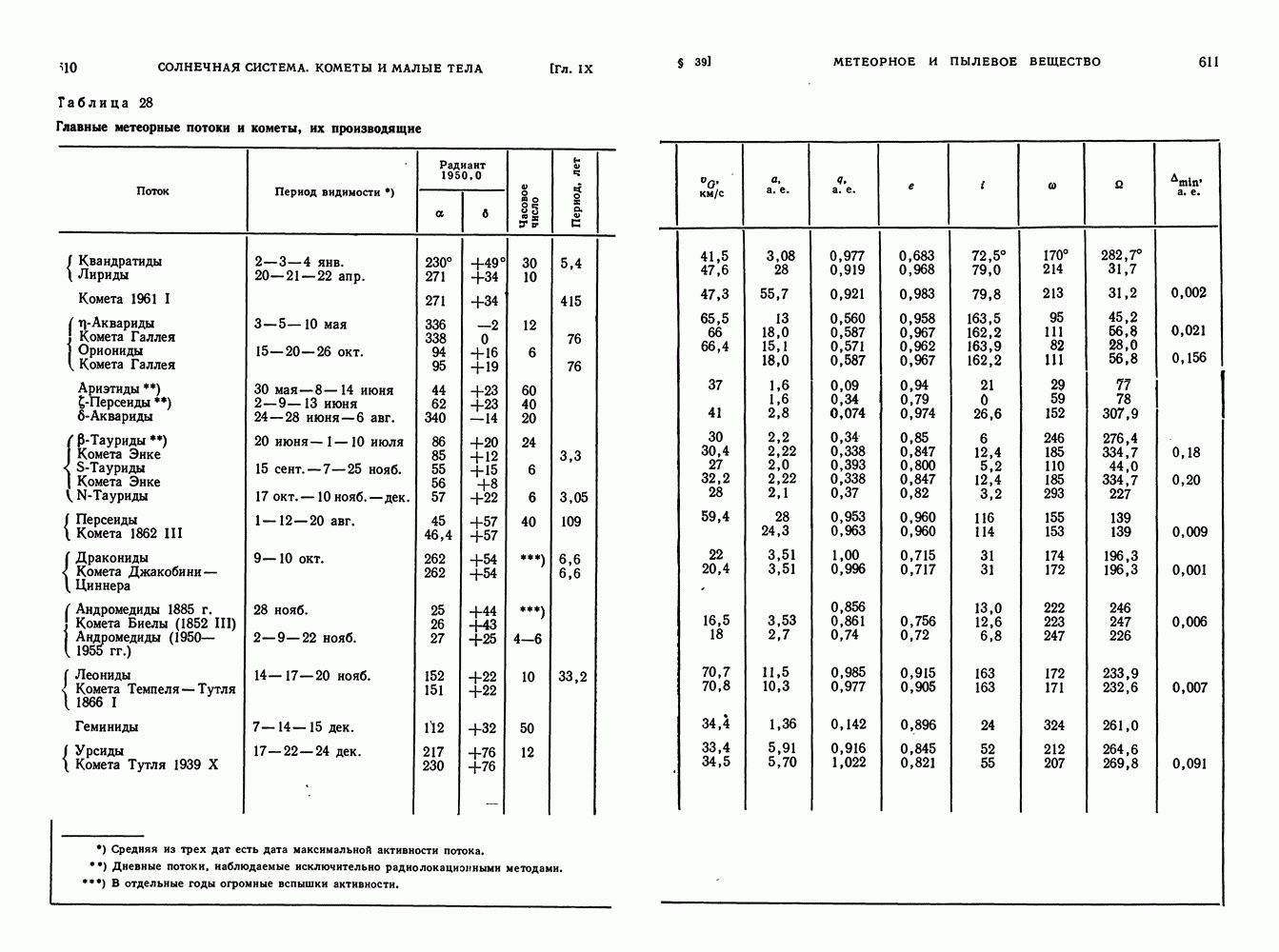
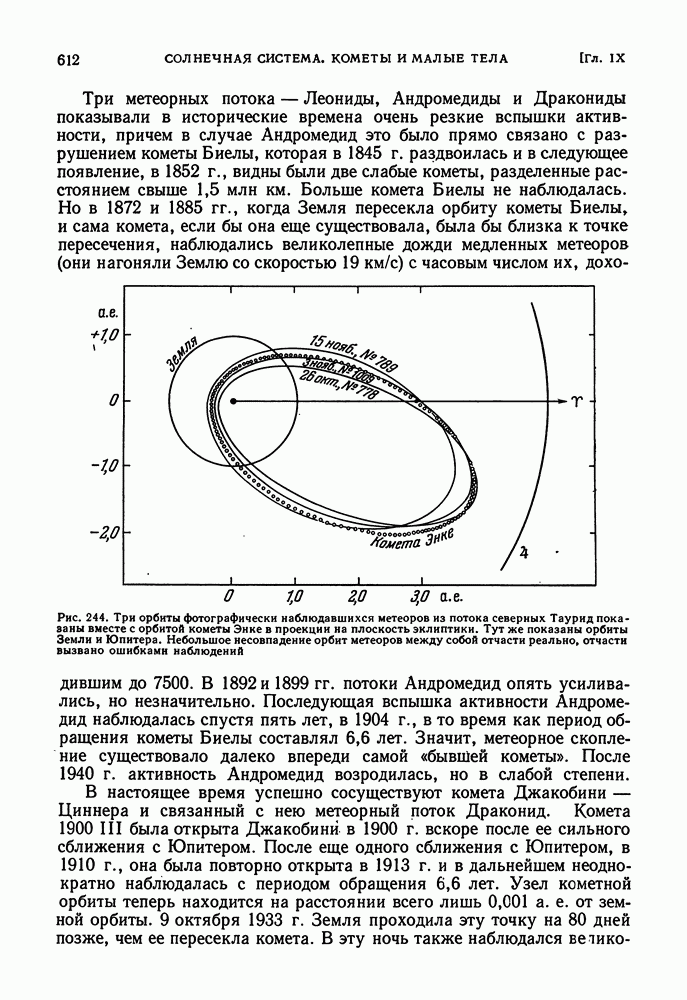
- МЕТЕОРНЫЕ РОИ И СВЯЗЬ ИХ С КОМЕТАМИ
- МИКРОМЕТЕОРИТЫ
- МЕТЕОРНОЕ ВЕЩЕСТВО ВОКРУГ ЗЕМЛИ
- ЗОДИАКАЛЬНЫЙ СВЕТ
- ПЫЛЕВАЯ И ГАЗОВАЯ СОСТАВЛЯЮЩИЕ В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- ДВИЖЕНИЕ МАЛОЙ ЧАСТИЦЫ В ПОЛЕ ТЯГОТЕНИЯ И ИЗЛУЧЕНИЯ СОЛНЦА
- ПРОТИВОСИЯНИЕ
- ЗАДАЧИ К ГЛАВЕ IX