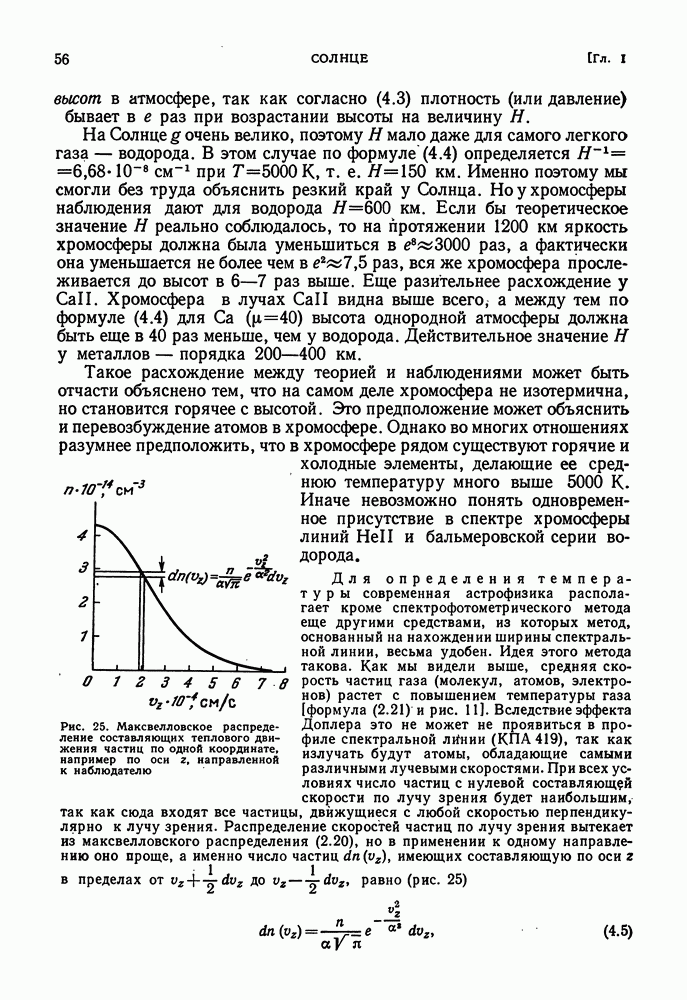
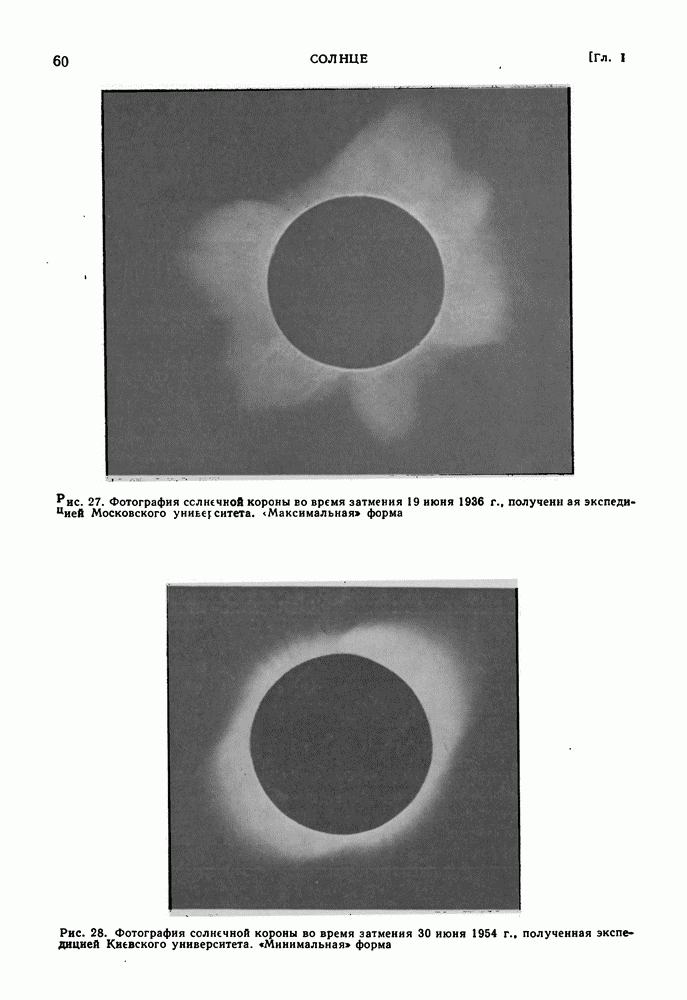
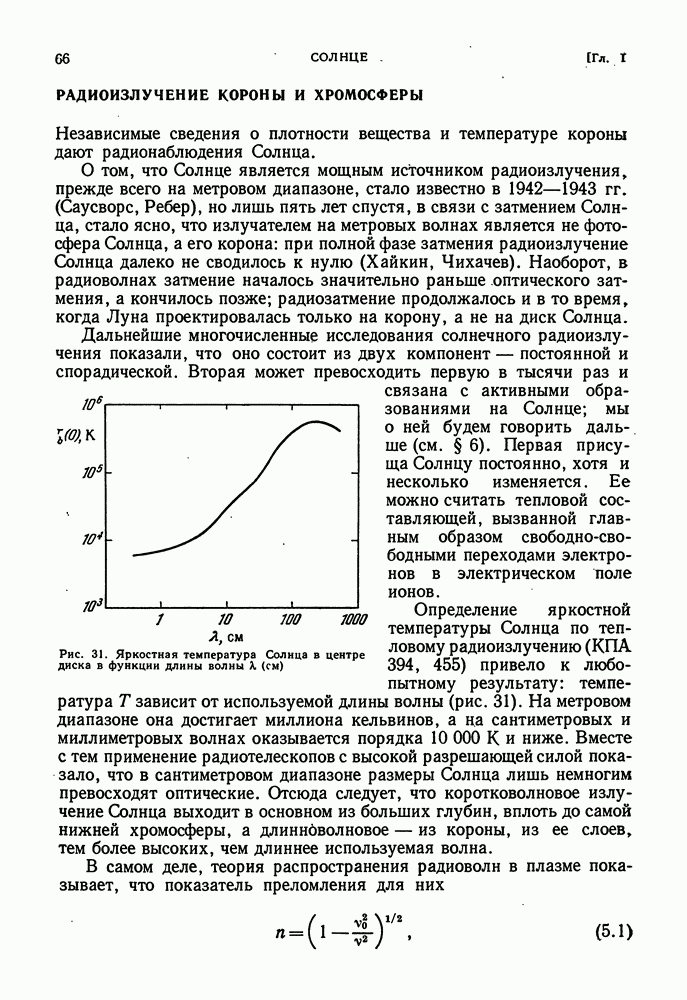
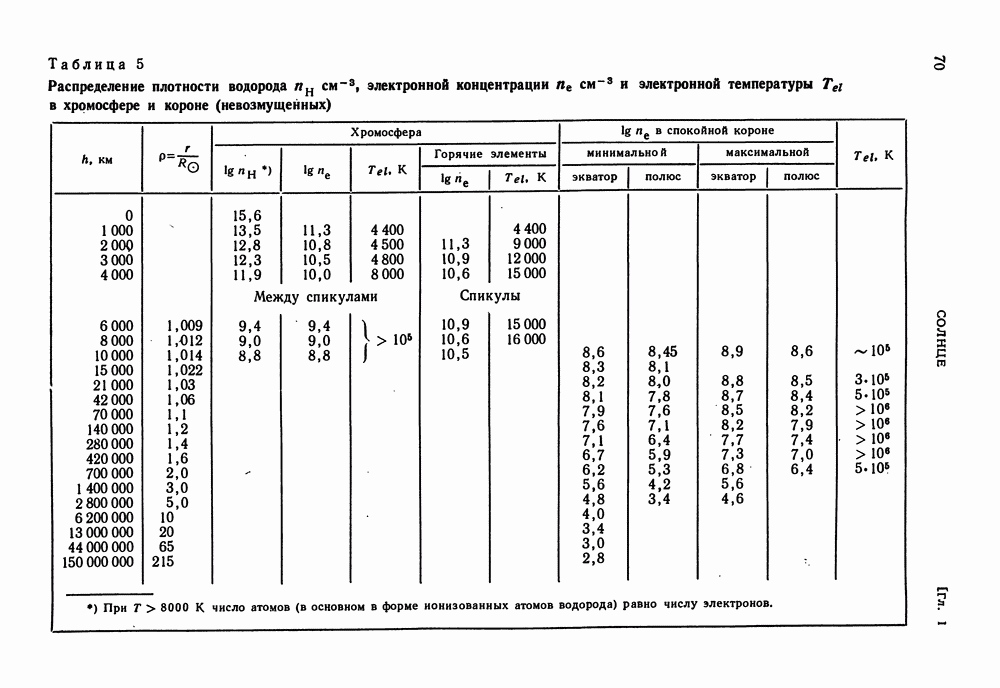
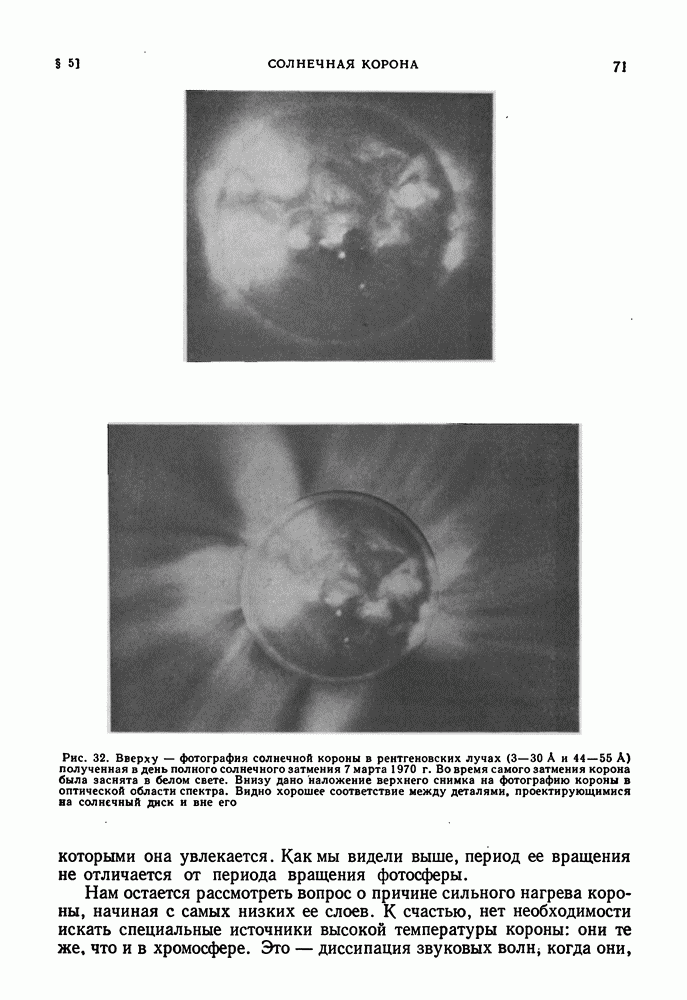
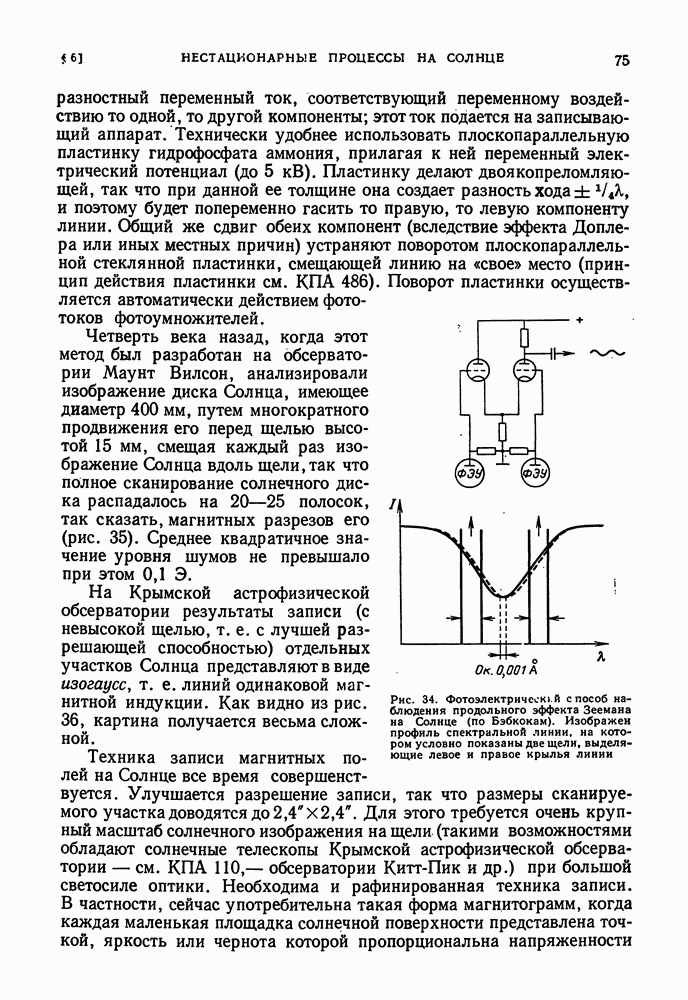
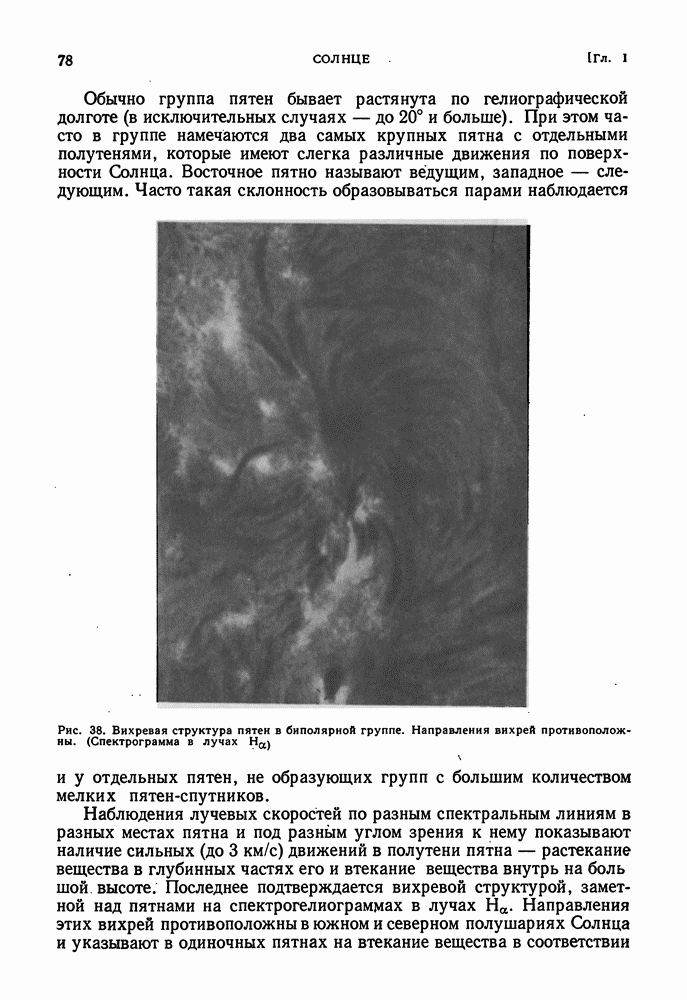
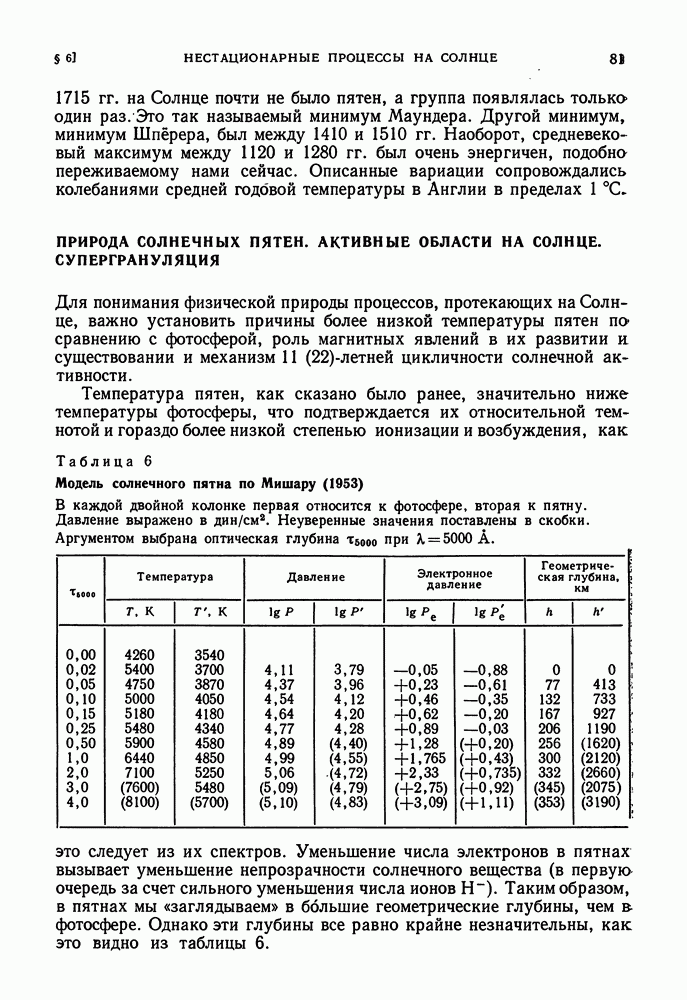
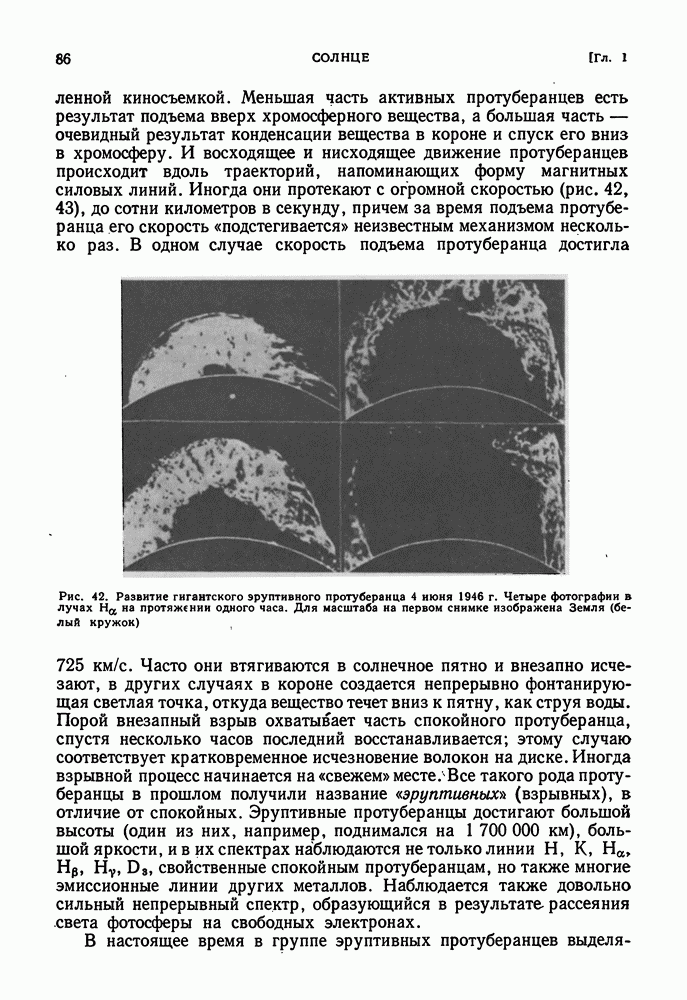
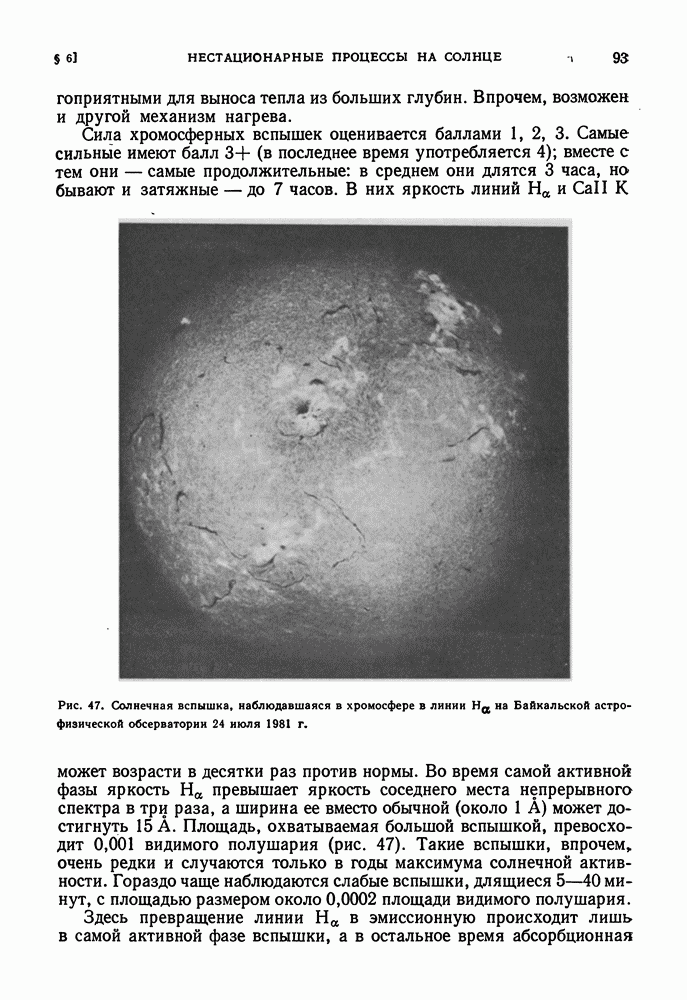
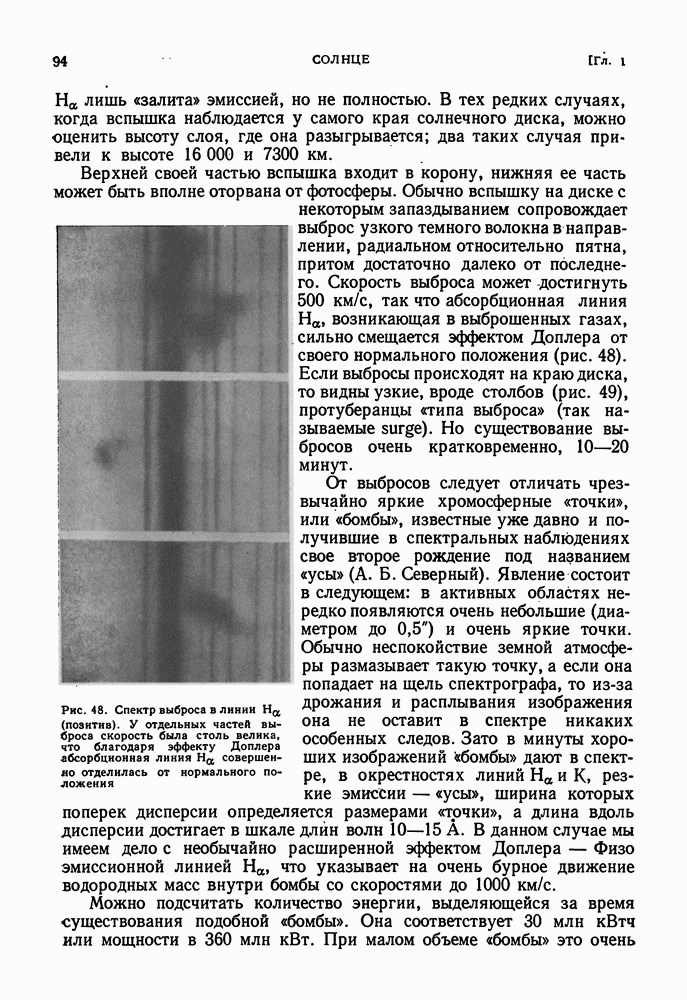
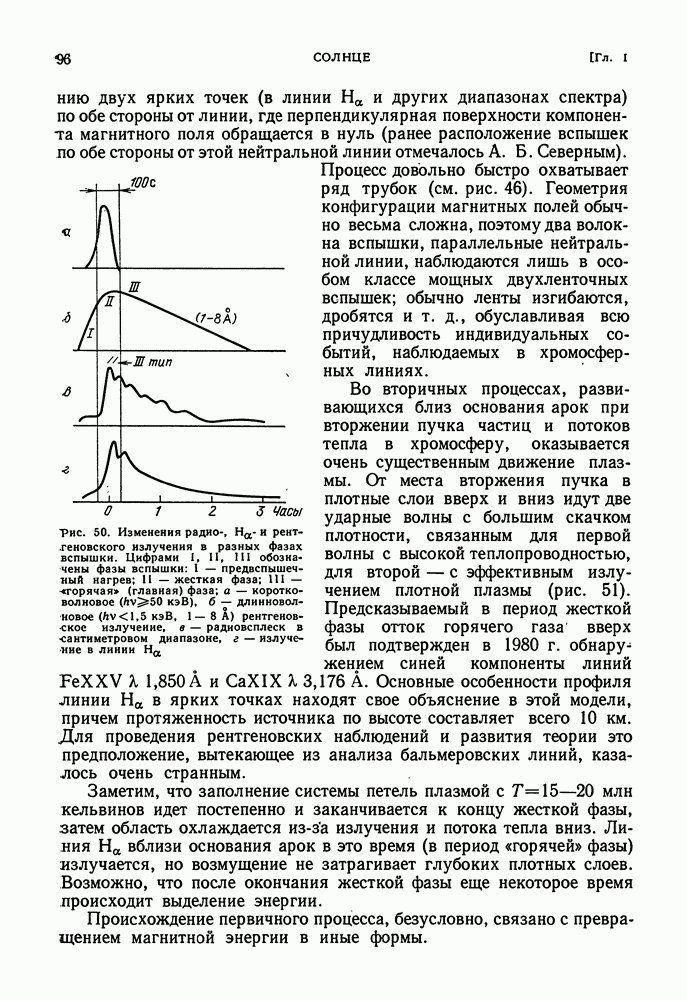
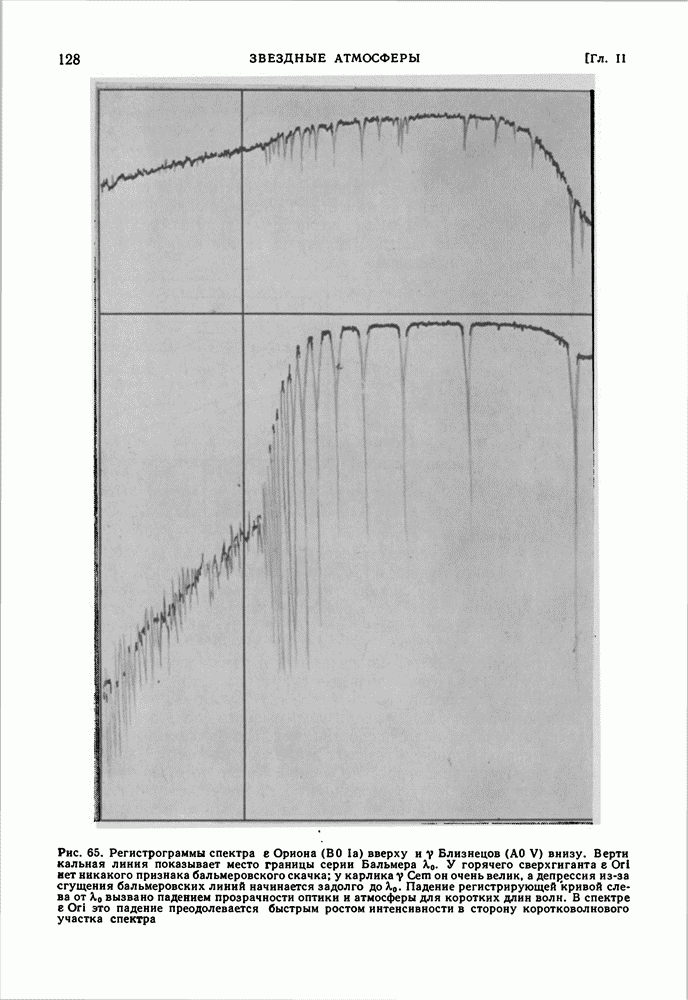
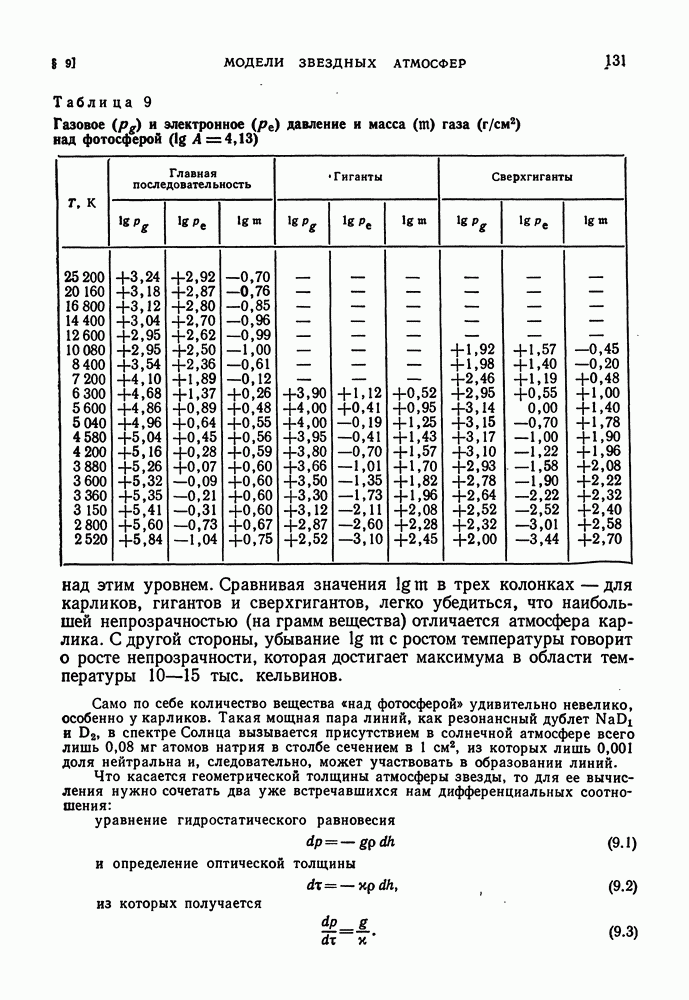
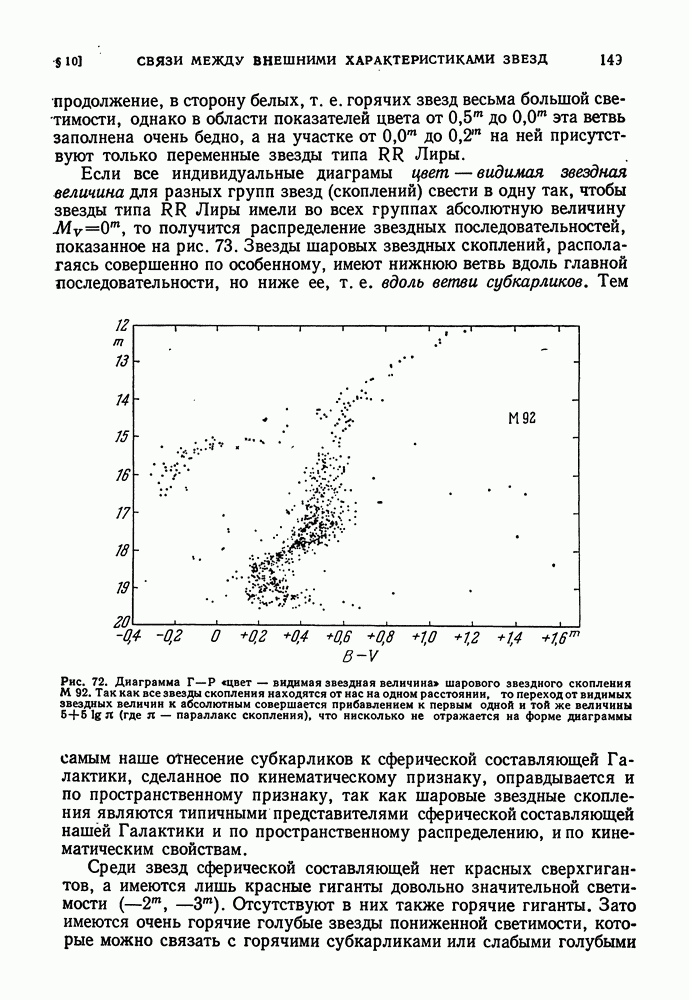
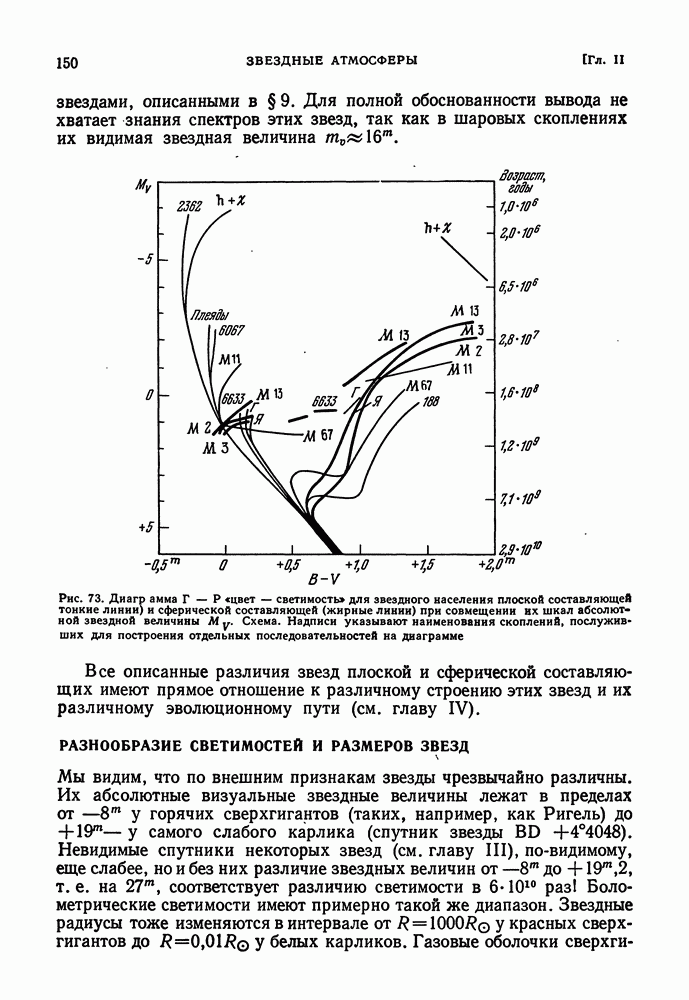
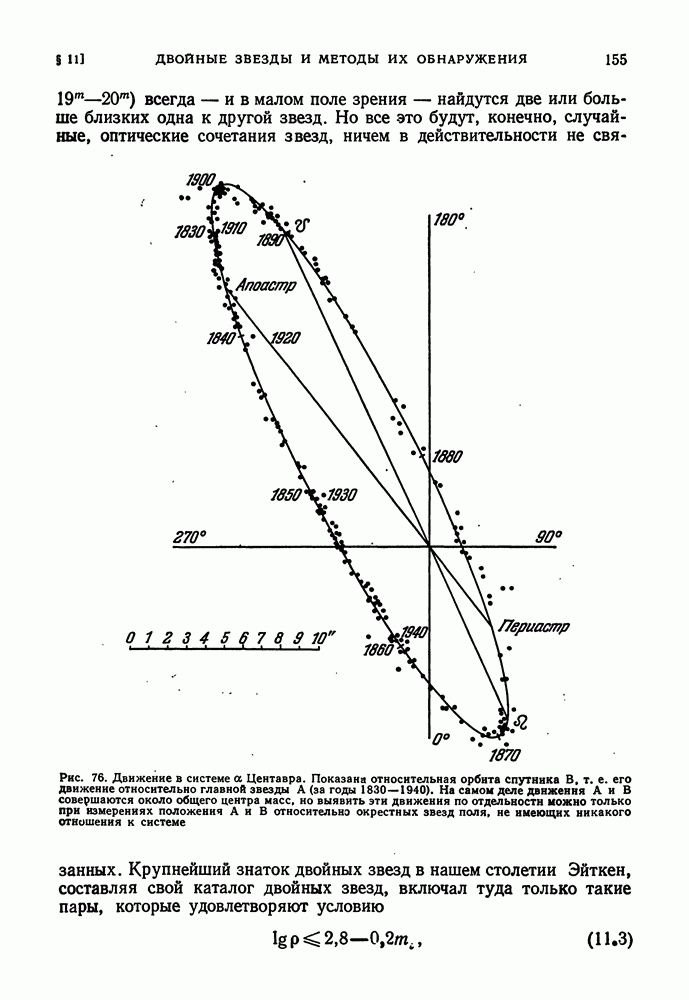
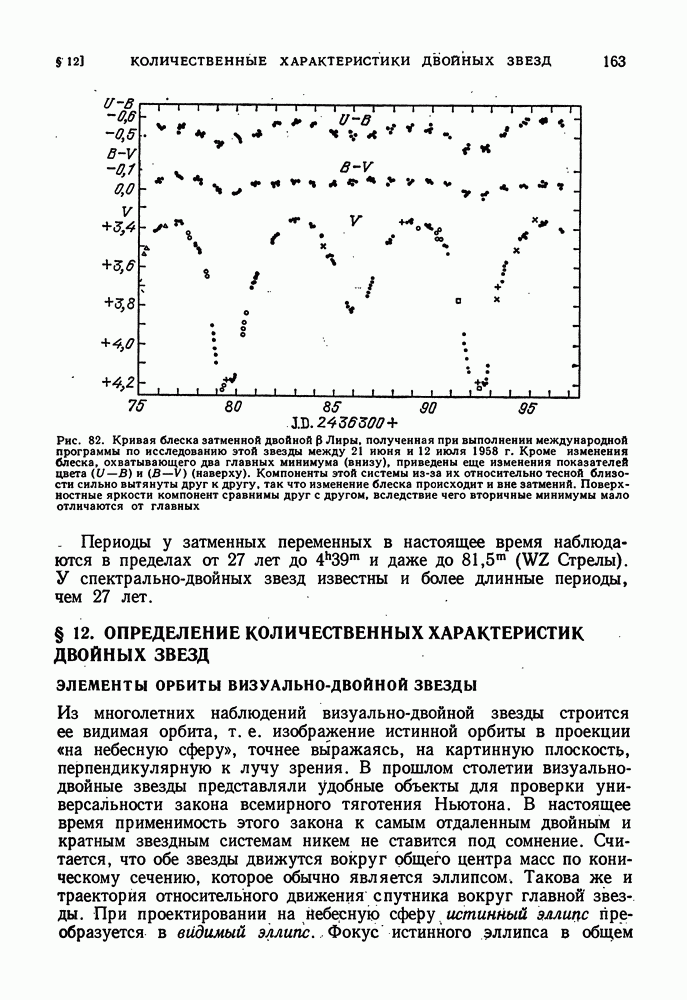
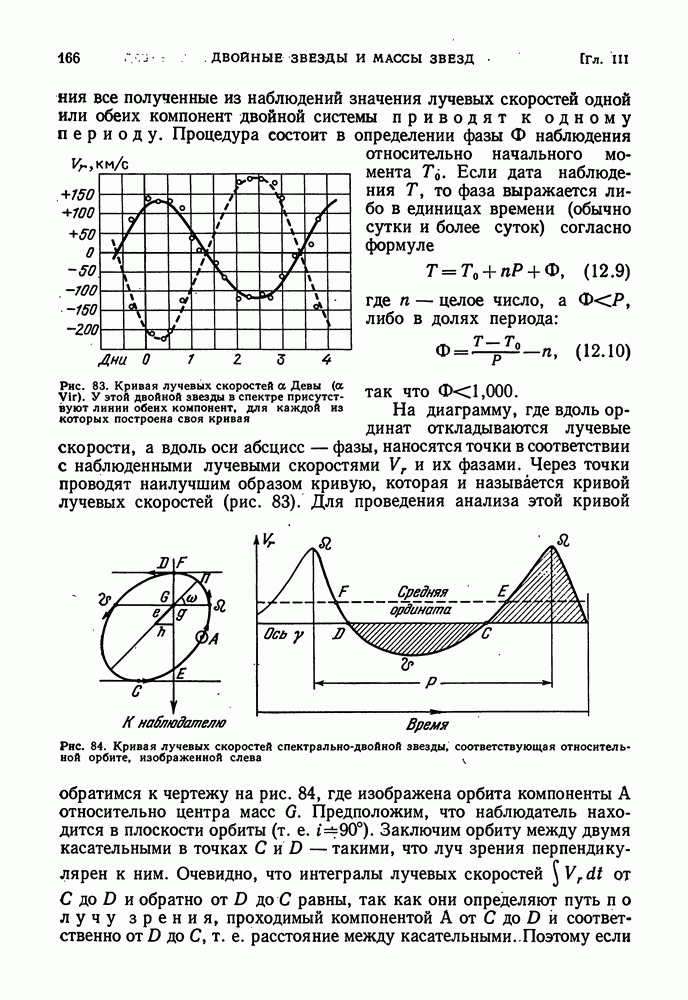
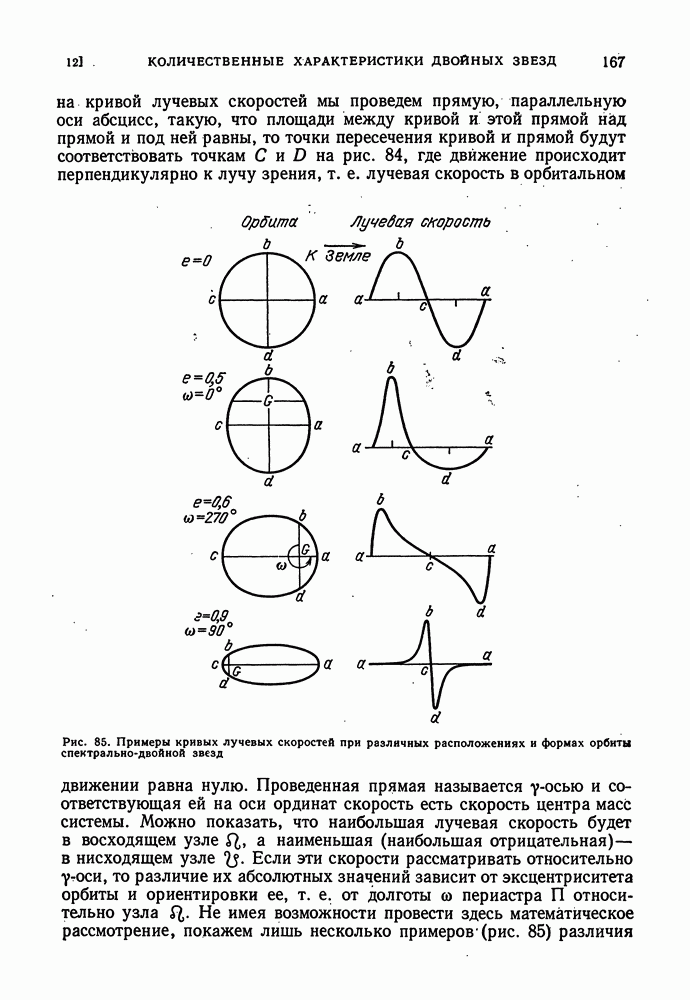
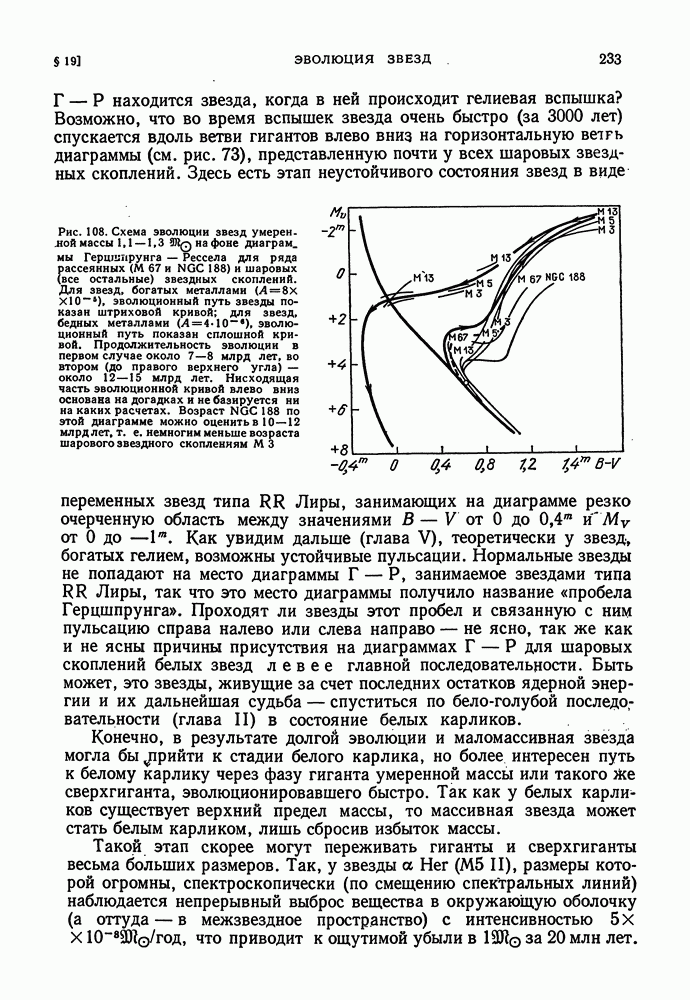
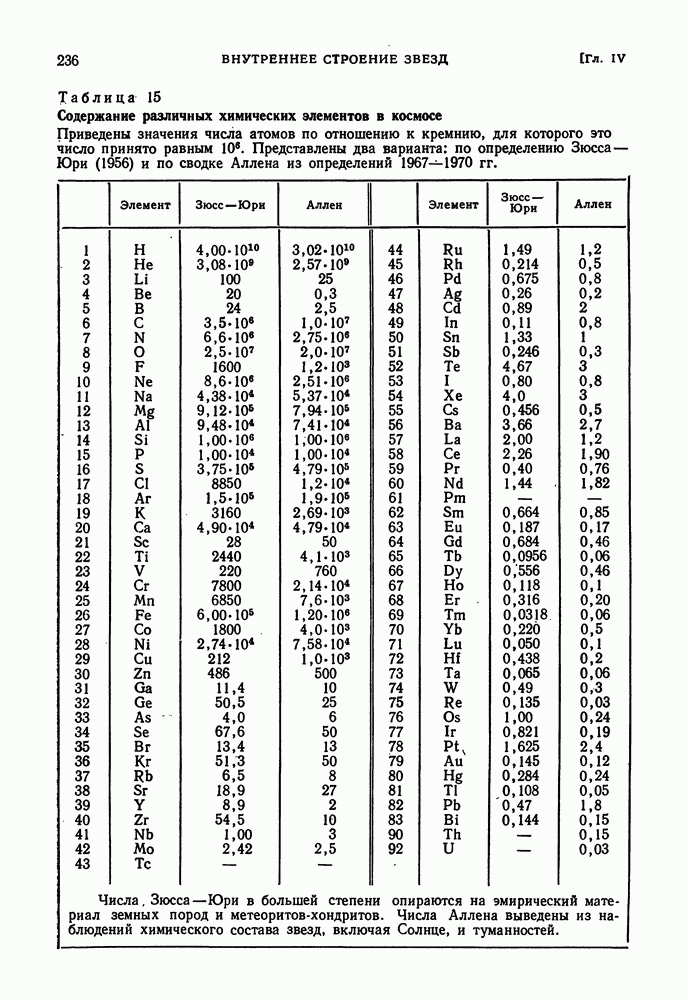
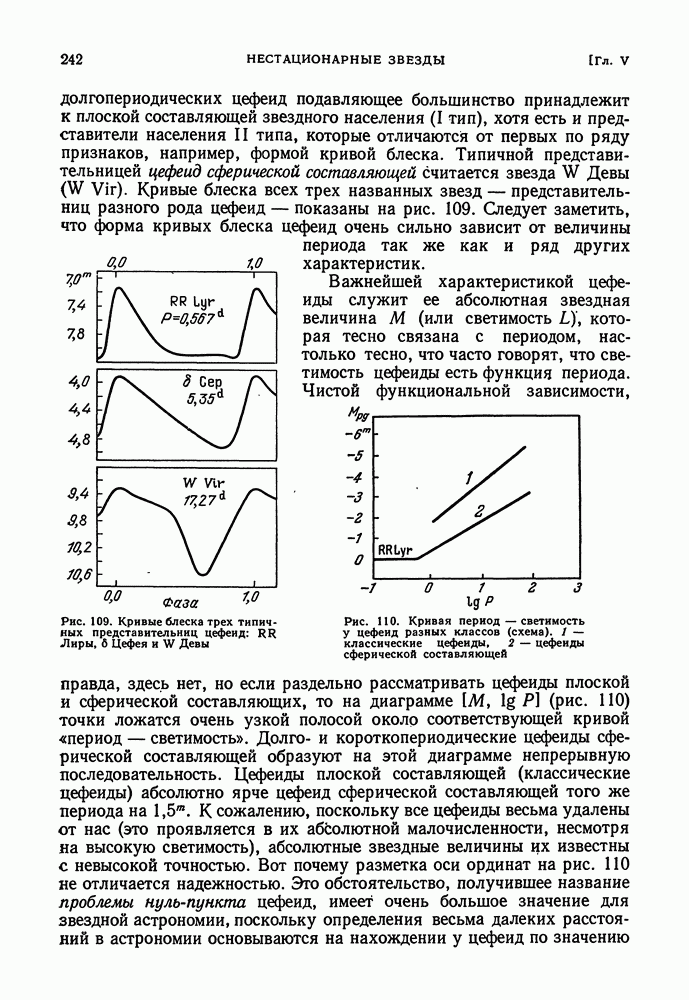
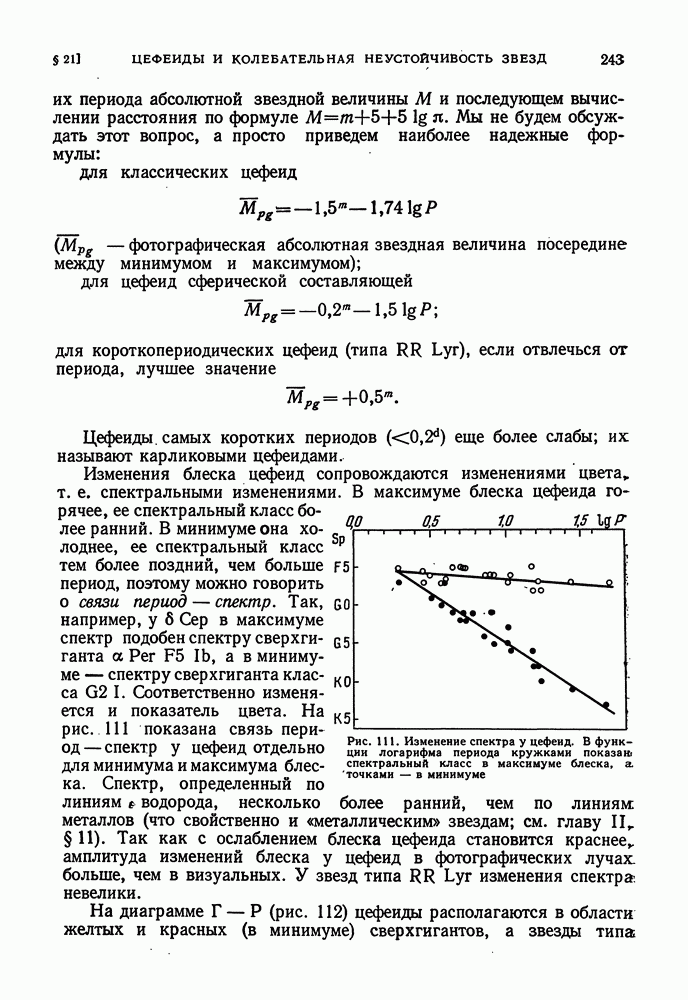
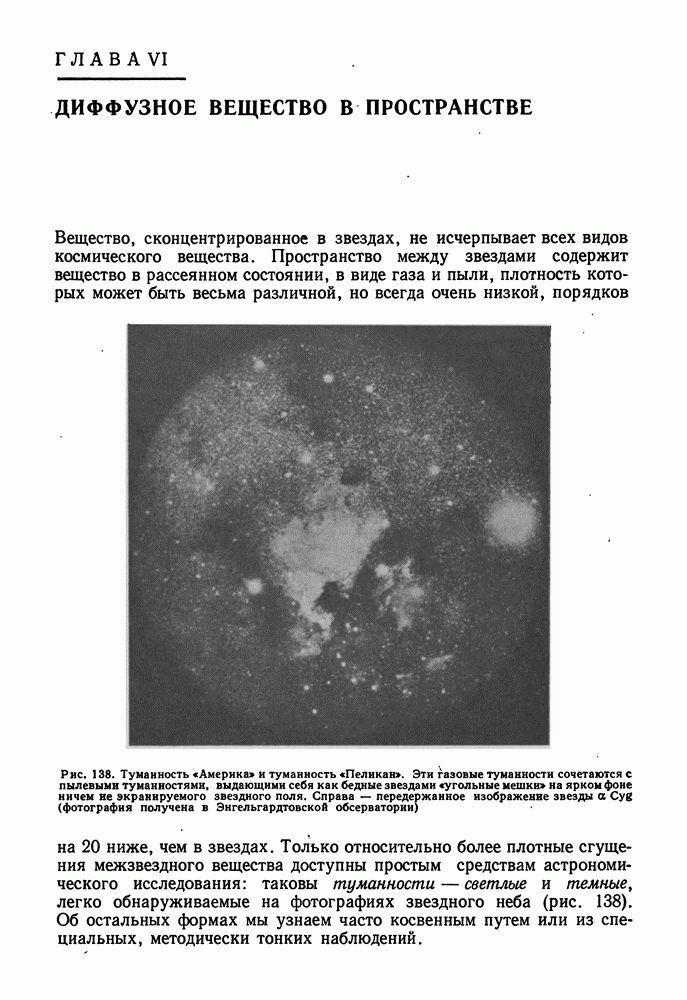
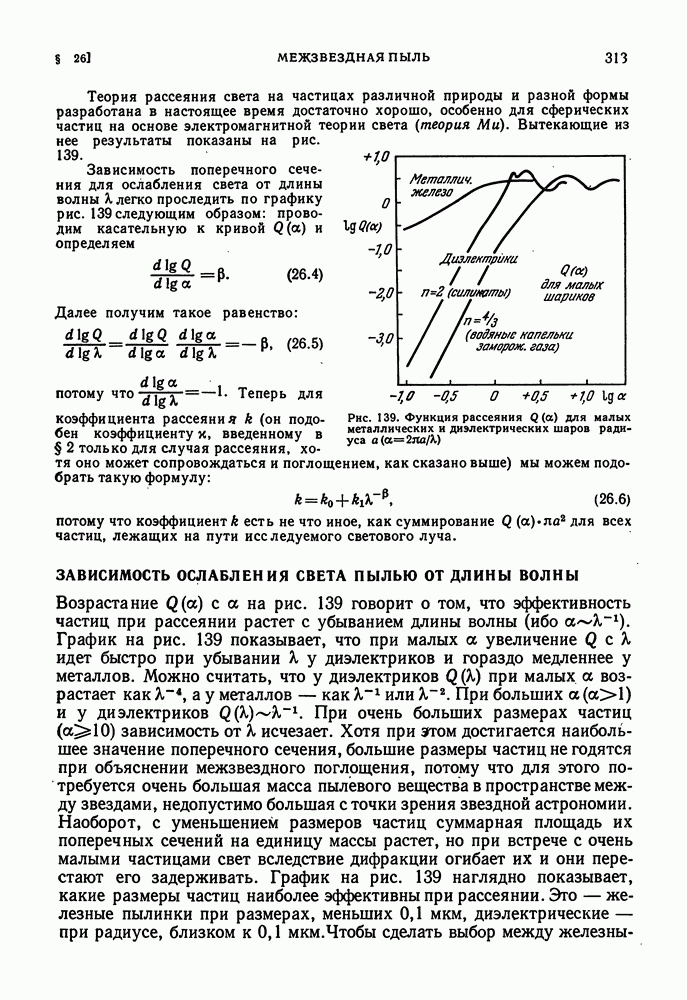
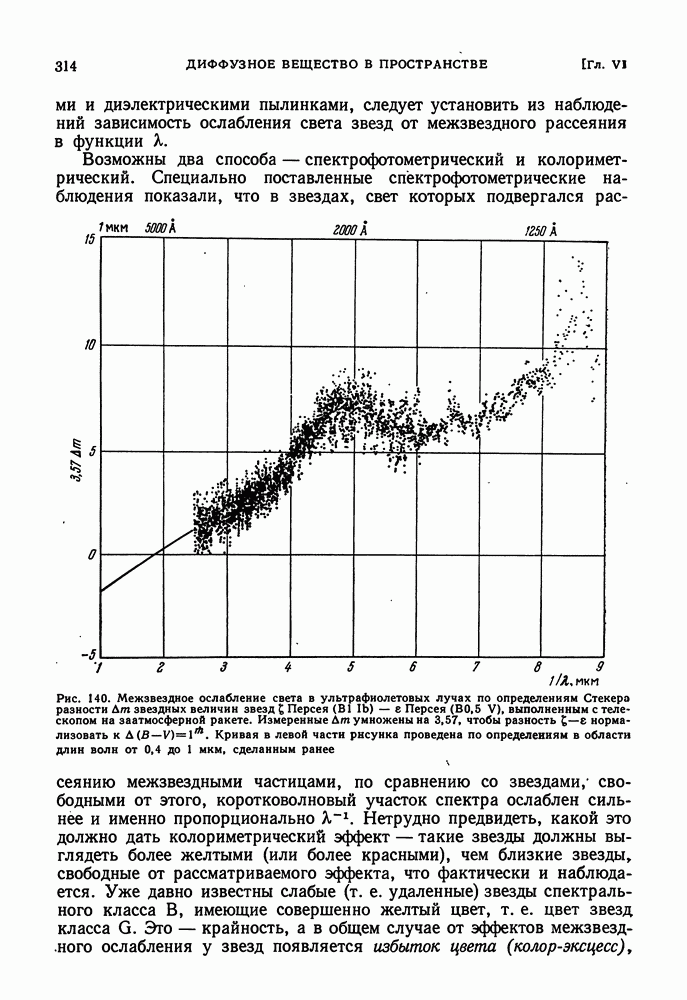
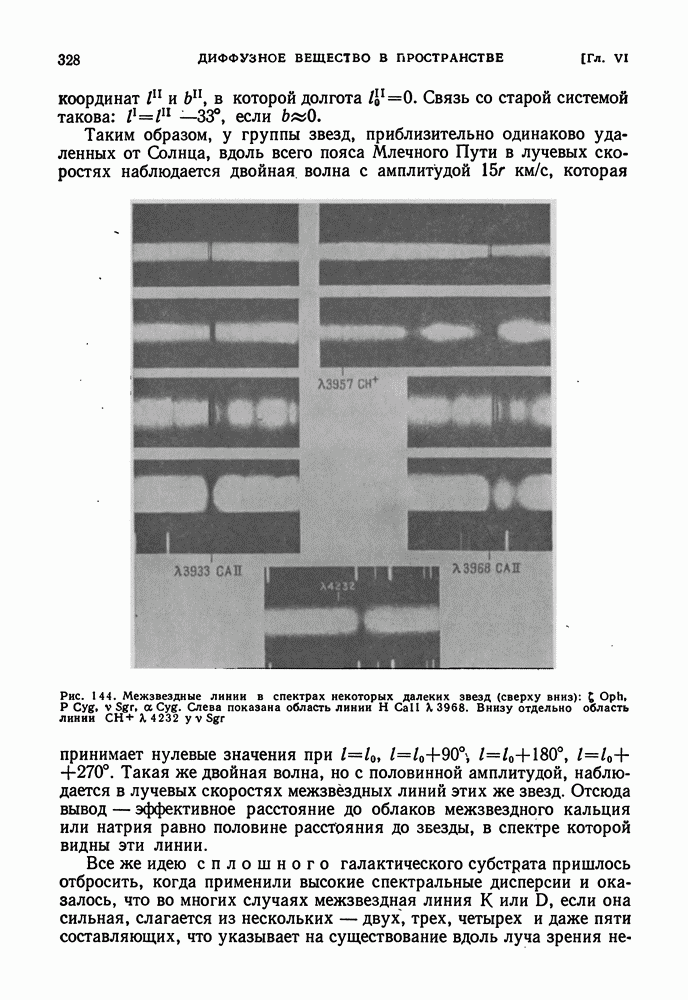
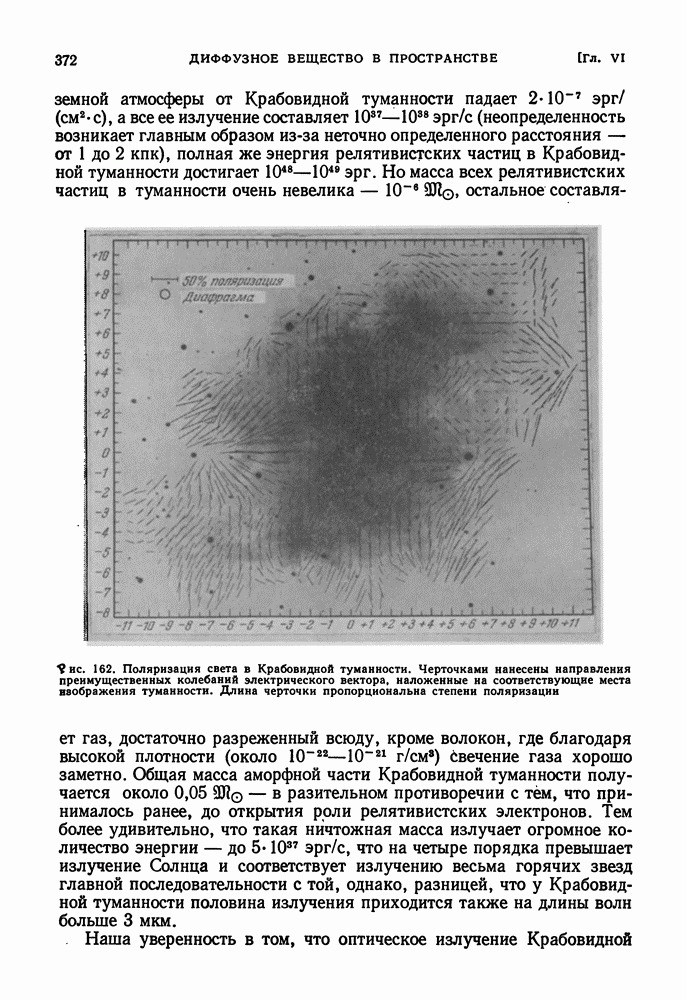
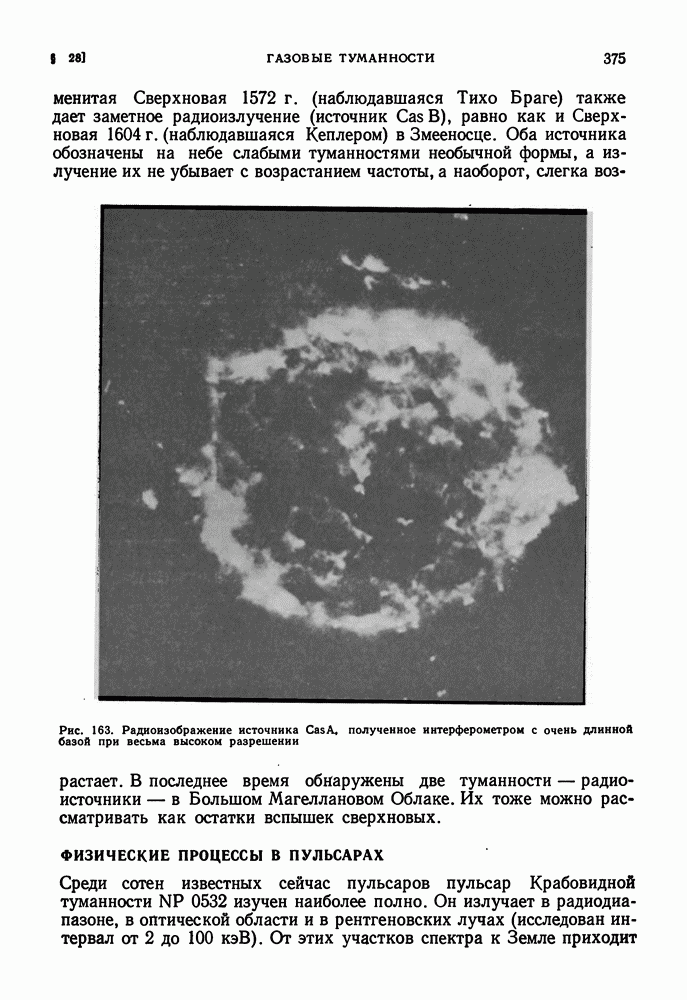
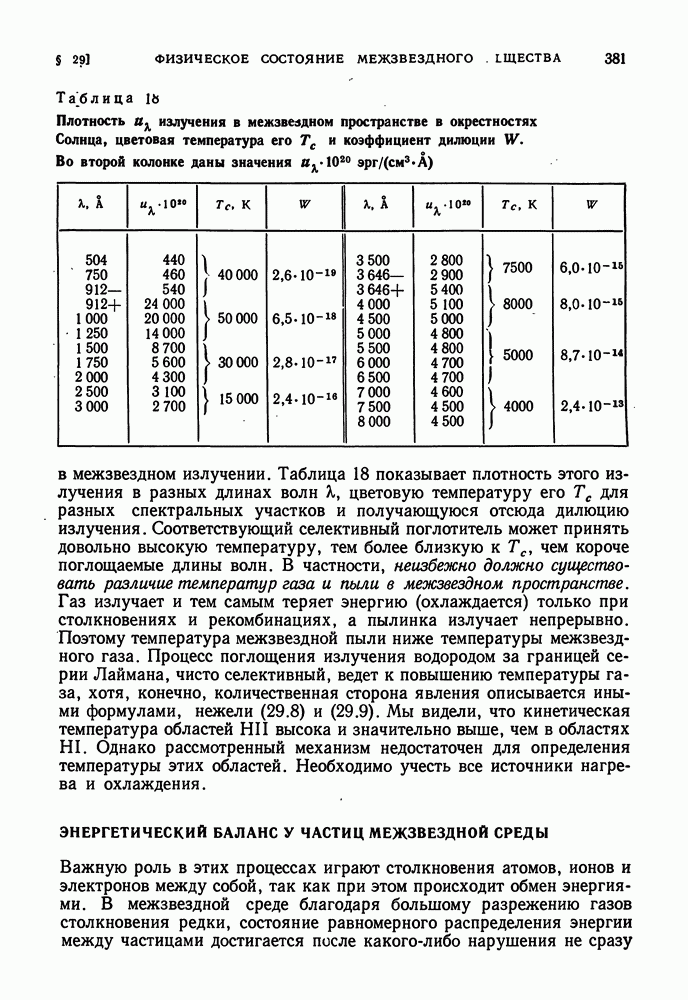
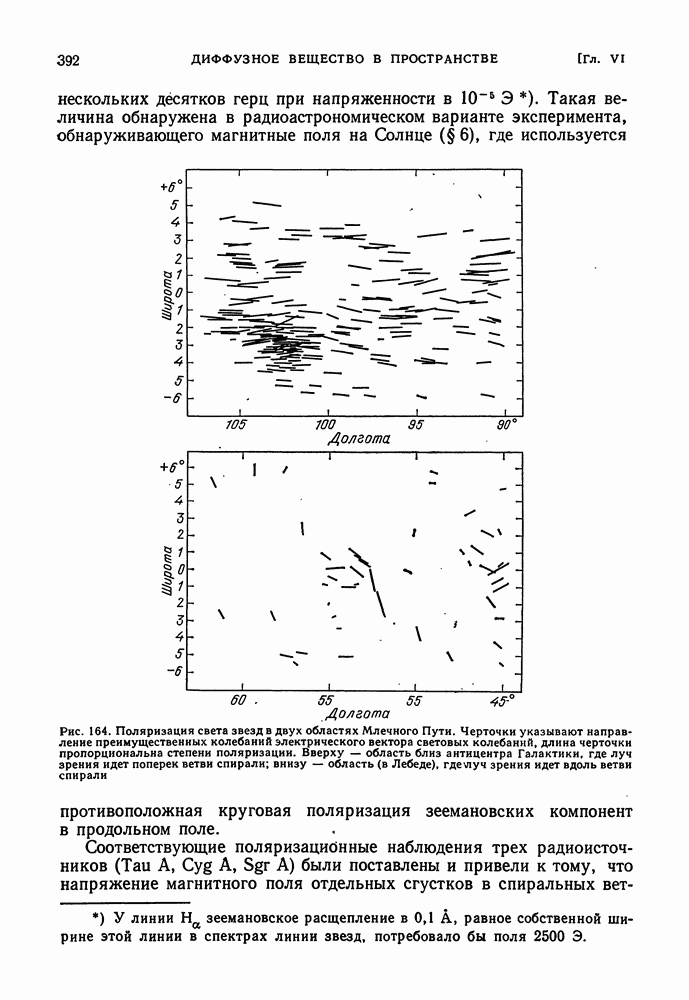
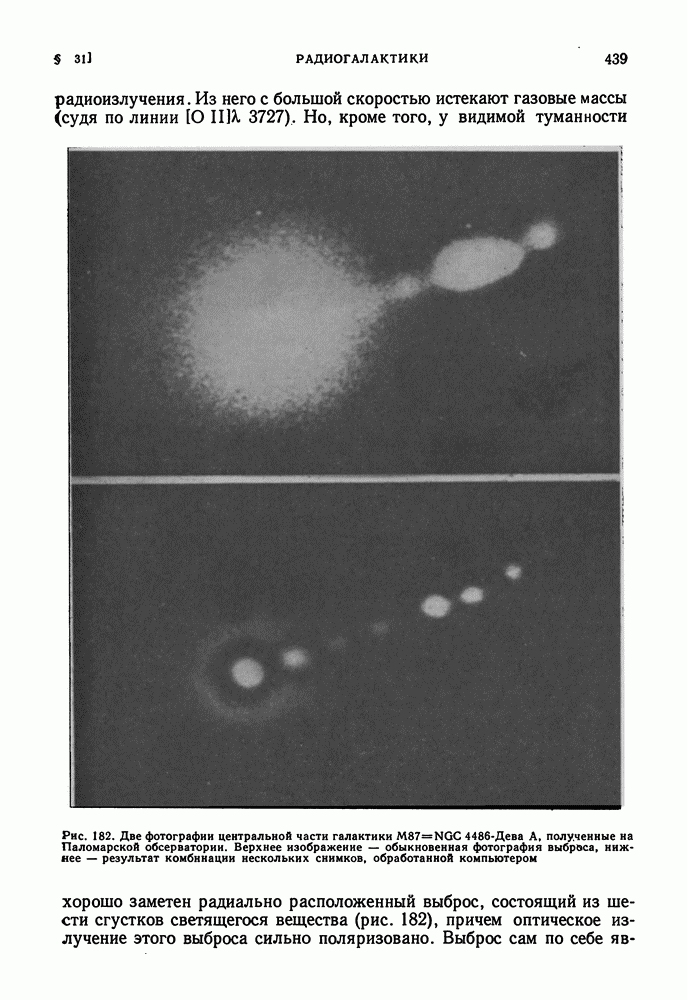
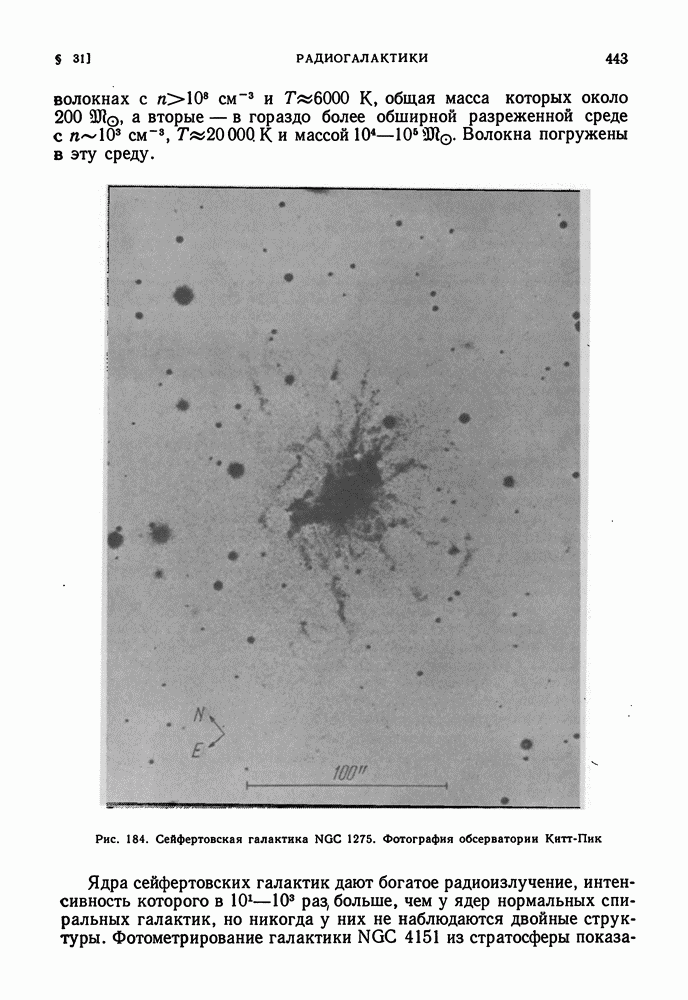
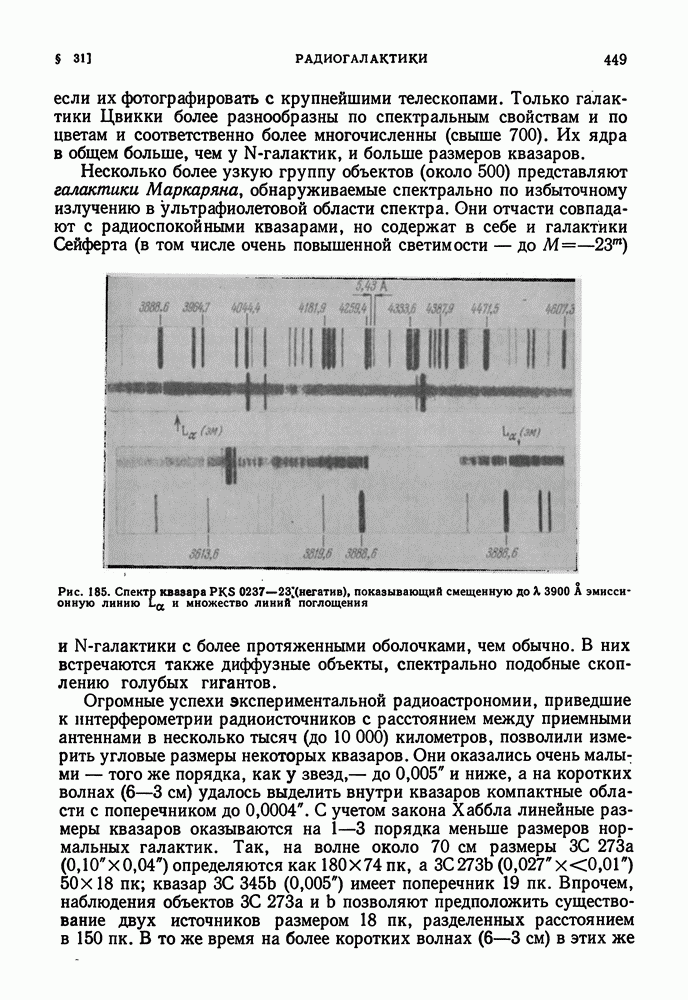
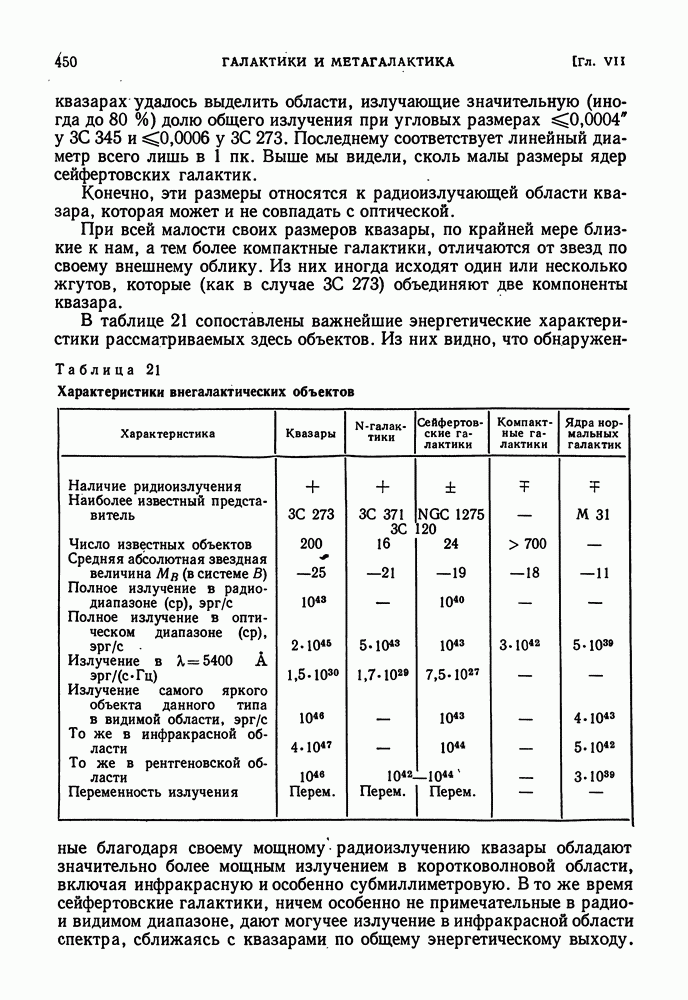
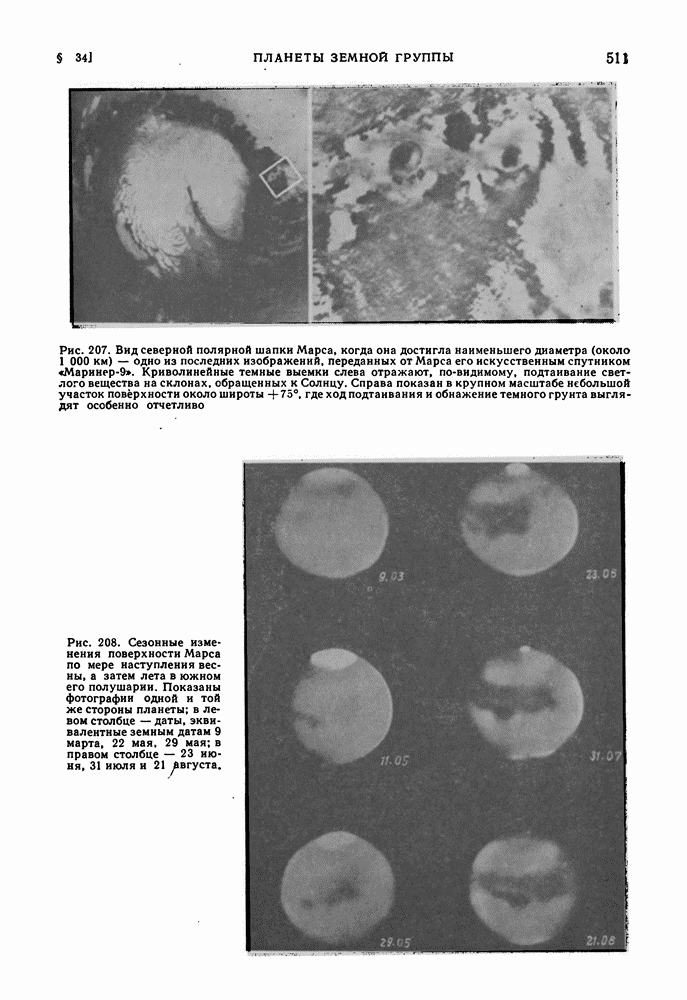
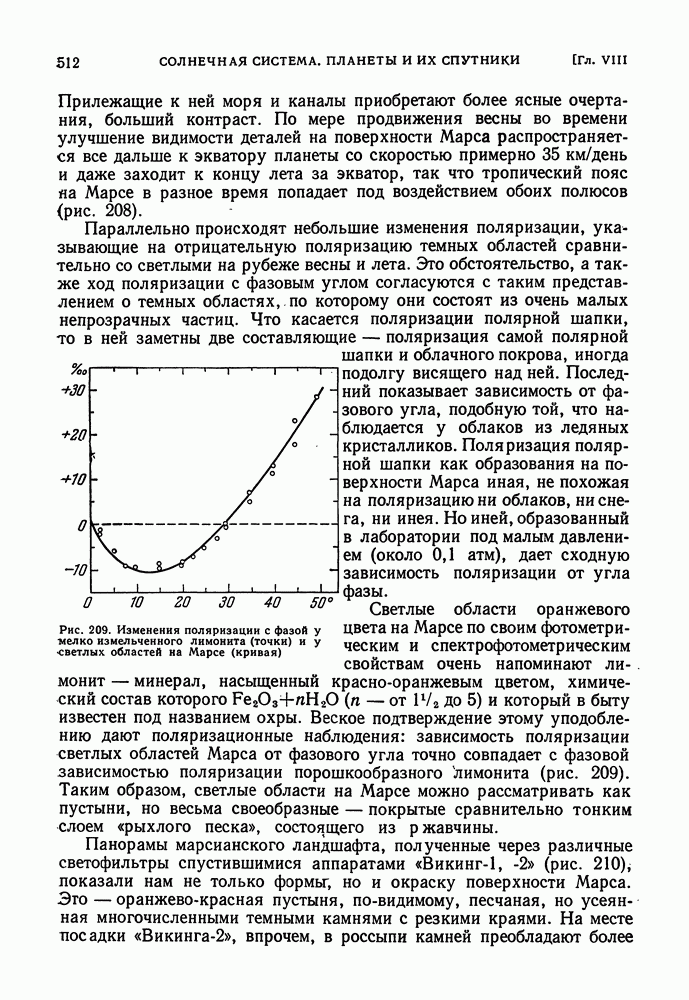
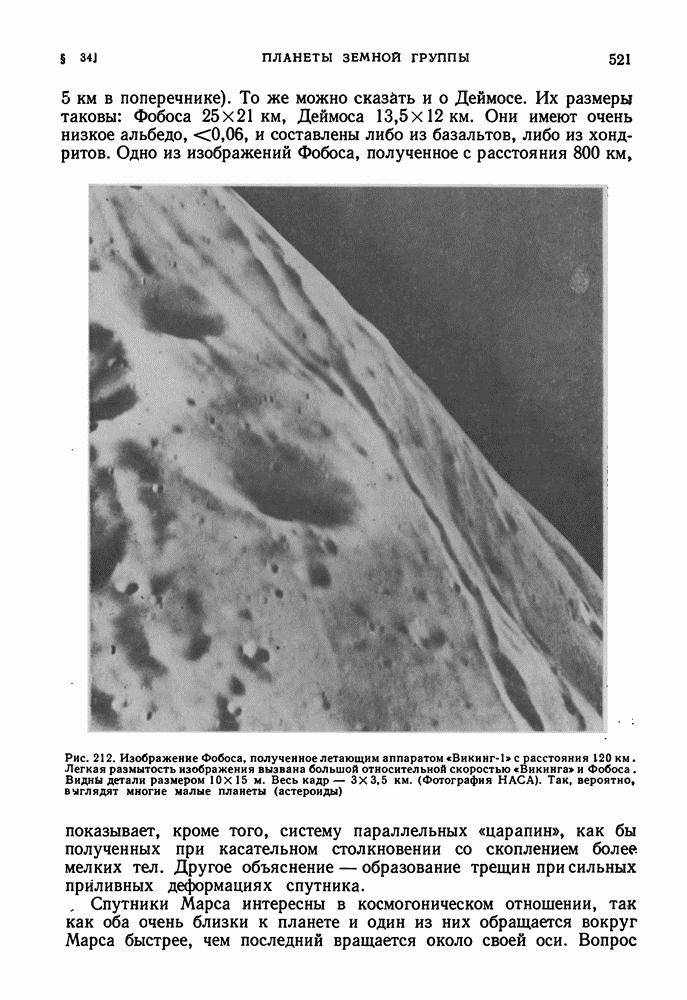
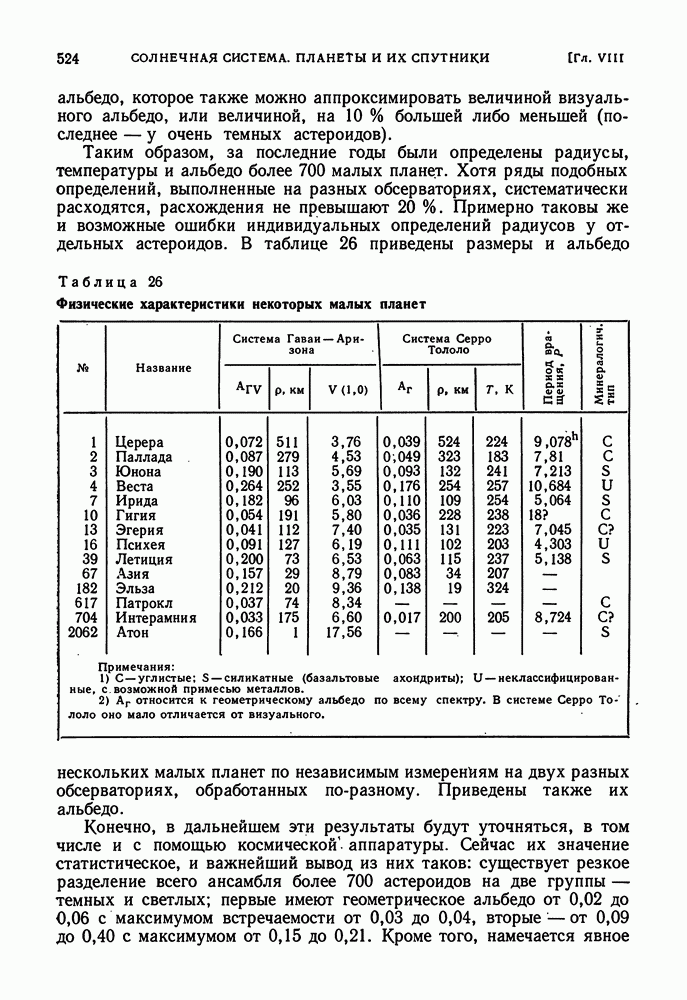
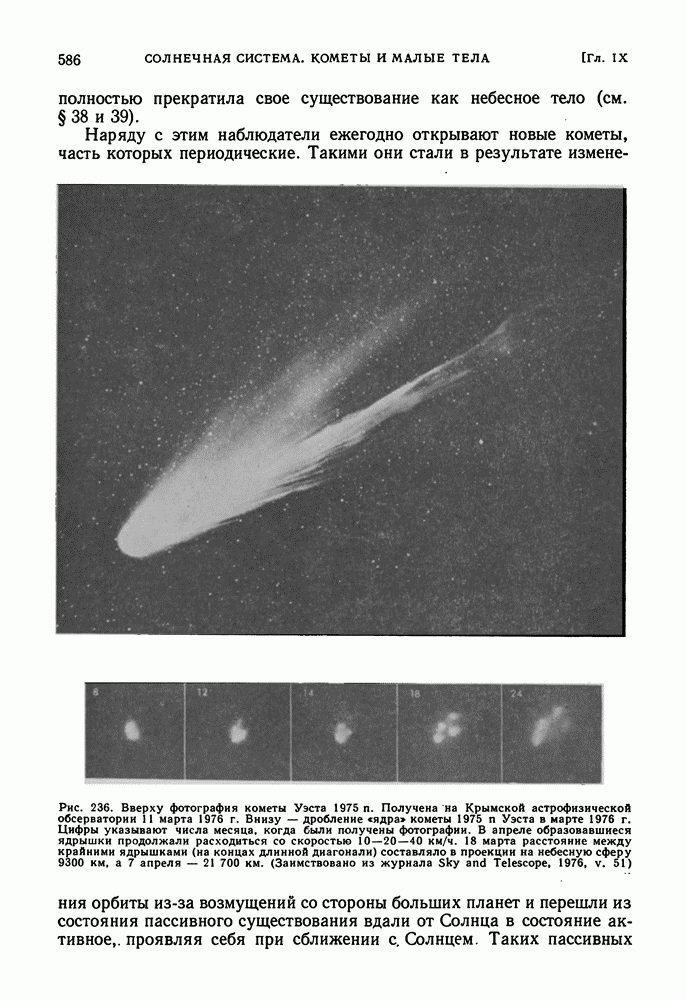
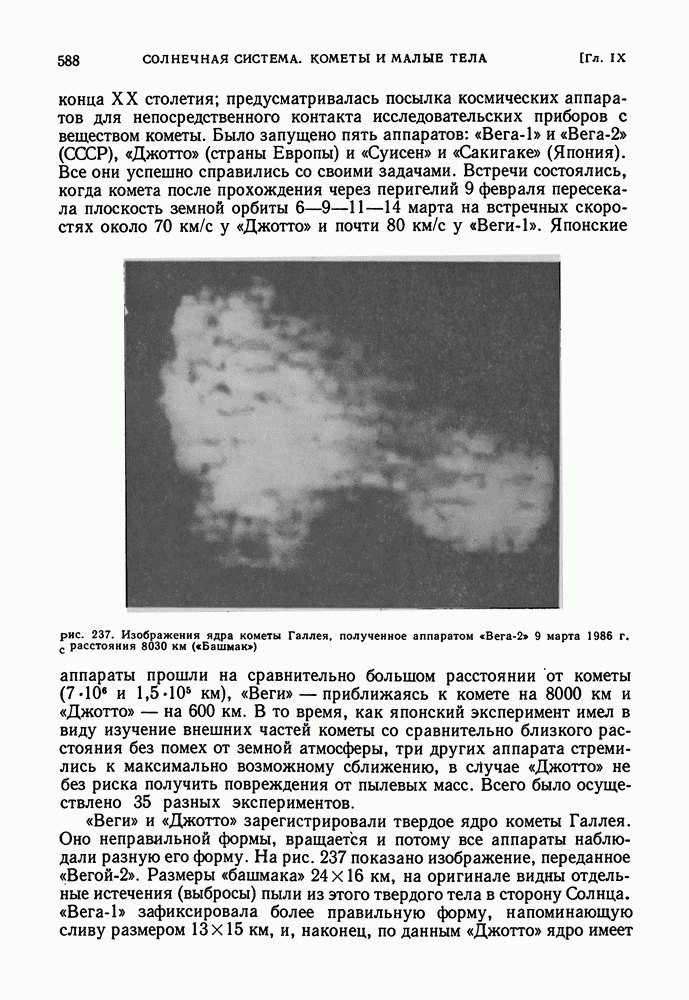
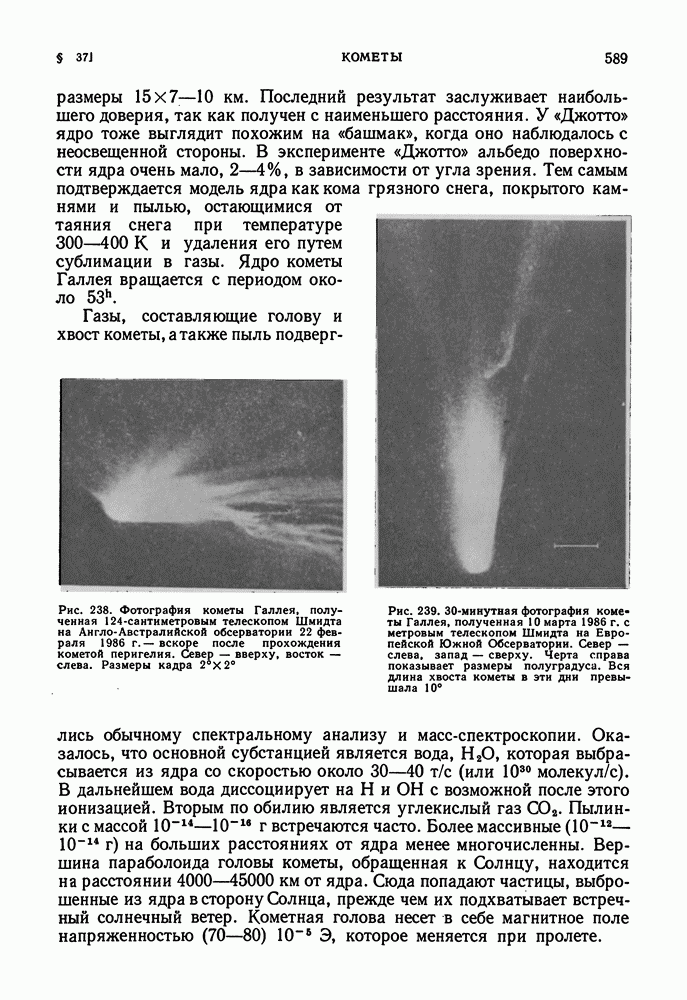
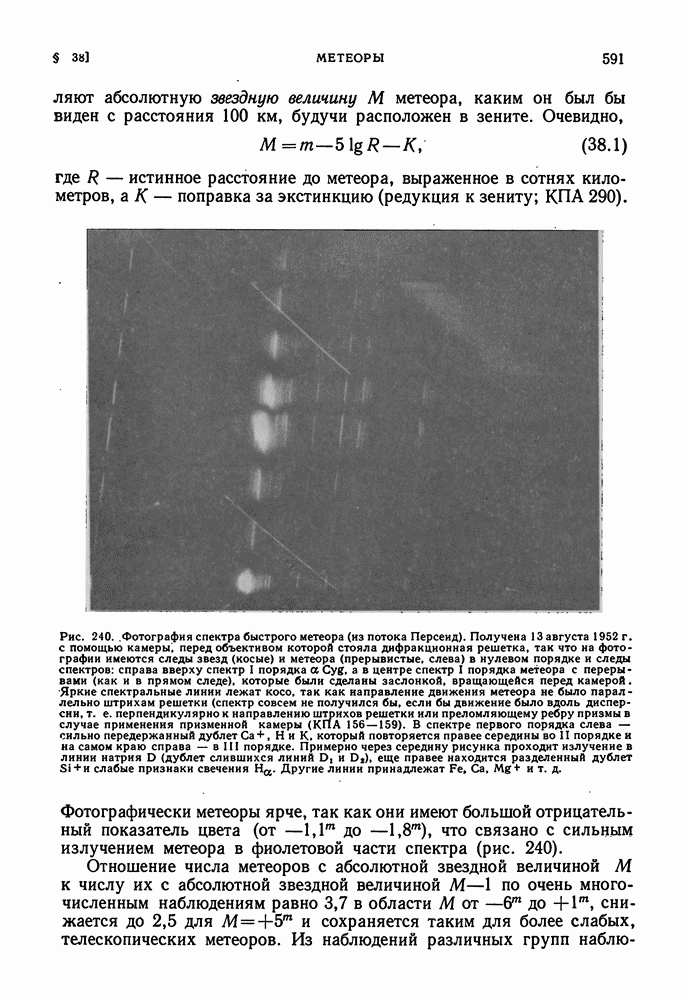
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 17. ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
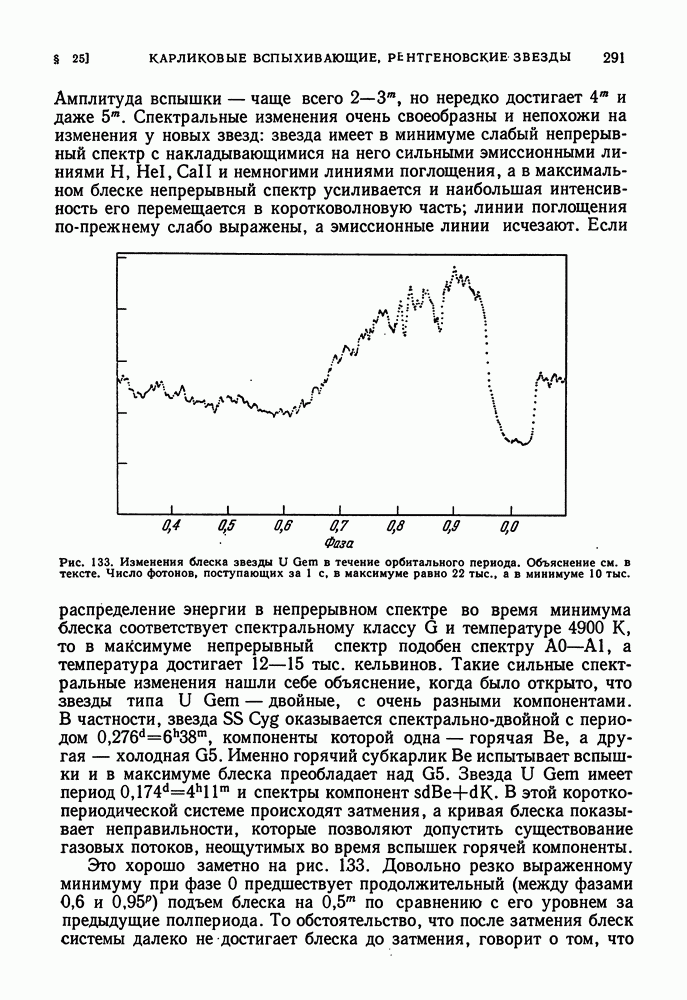
Главная компонента затменной двойной  имеет абсолютную визуальную величину
имеет абсолютную визуальную величину  ; болометрическая поправка, соответствующая ее спектру
; болометрическая поправка, соответствующая ее спектру  около
около  , так что
, так что  : у Солнца
: у Солнца  излучает энергии больше, чем Солнце, в 2,5121484 = 860 000 раз, но масса ее в 19 раз больше солнечной и потому на 1 г вещества она излучает в 45 000 раз больше, чем Солнце. У Солнца на 1 г массы приходится излучение
излучает энергии больше, чем Солнце, в 2,5121484 = 860 000 раз, но масса ее в 19 раз больше солнечной и потому на 1 г вещества она излучает в 45 000 раз больше, чем Солнце. У Солнца на 1 г массы приходится излучение  . Подобным же образом находим, что компонента В визуально-двойной звезды Kruger 60 излучает на 1 г вещества в 80 раз меньше, чем Солнце, т. е. для нее
. Подобным же образом находим, что компонента В визуально-двойной звезды Kruger 60 излучает на 1 г вещества в 80 раз меньше, чем Солнце, т. е. для нее  . Еще меньше удельное лучеиспускание у Сириуса В — белого карлика:
. Еще меньше удельное лучеиспускание у Сириуса В — белого карлика:  . Между тем средняя температура Т звезды меняется у тех же звезд (кроме, может быть, белого карлика) несравненно меньше (см. с. 196). Трудно наперед допустить, что во всех трех случаях механизм генерации энергии одинаков, но если уж он один и тот же, то, очевидно, он очень чувствителен к изменениям физических условий внутри звезды, в частности, температуры. Из различных возможных видов генерации энергии в звездах имеют значение два следующих:
. Между тем средняя температура Т звезды меняется у тех же звезд (кроме, может быть, белого карлика) несравненно меньше (см. с. 196). Трудно наперед допустить, что во всех трех случаях механизм генерации энергии одинаков, но если уж он один и тот же, то, очевидно, он очень чувствителен к изменениям физических условий внутри звезды, в частности, температуры. Из различных возможных видов генерации энергии в звездах имеют значение два следующих:
а) гравитационное сжатие,
б) термоядерные процессы.
ГРАВИТАЦИОННОЕ СЖАТИЕ
Если разреженный шар сжимается, то его потенциальная энергия убывает [см. (15.8)]; эта убыль идет на увеличение кинетической энергии частиц шара, т. е. на увеличение температуры, когда шар — газовый (см. (15.9)).
Внутренняя тепловая энергия идеального газа, достигшего температуры  равна
равна  на 1 г. Для всей звезды это будет
на 1 г. Для всей звезды это будет

Интеграл равен  . Подставляя сюда вместо
. Подставляя сюда вместо  выражение его из (15.9), в котором
выражение его из (15.9), в котором  , и присоединяя из (15.8) выражение для потенциальной энергии
, и присоединяя из (15.8) выражение для потенциальной энергии  , без труда получим
, без труда получим

Полная энергия

Для одноатомного газа  и, следовательно, пренебрегая у звезды давлением излучения (для которого
и, следовательно, пренебрегая у звезды давлением излучения (для которого  ), будем иметь
), будем иметь

т. е. полная энергия равна половине потенциальной и ее изменение составляет лишь половину изменения потенциальной энергии.
Достаточно широкая по применимости политропная модель имеет потенциальную энергию

Здесь n — класс политропии (при  энергия становится положительной, т. е. шар имеет бесконечно большие размеры) и для конвективной модели
энергия становится положительной, т. е. шар имеет бесконечно большие размеры) и для конвективной модели 

а для стандартной модели

Скорость изменения энергии  очевидно, следует отождествить со светимостью звезды в стадии сжатия:
очевидно, следует отождествить со светимостью звезды в стадии сжатия:

Отсюда

Как видно из равенства (17.4). изменения полной энергии, которые мы приравниваем в (17.8) светимости, составляют лишь половину изменения потенциальной энергии звезды. Другая половина идет на разогревание ее.
Если подставить в правую часть (17.9) вместо L лучеиспускание Солнца, а вместо  и R — массу и радиус Солнца, то будем иметь
и R — массу и радиус Солнца, то будем иметь
 (17.10)
(17.10)
Отнесясь формально к последнему расчету, мы можем сказать, что если предполагать Солнце сжимающимся, то при нынешних характеристиках Солнца для возмещения потери тепла лучеиспусканием радиуса Солнца «хватит» всего лишь на  лет. По существу, мы должны сказать, что при гравитационном сжатии Солнце изменяется существенным образом за 25 млн лет. Но геологическая история Земли учит нас, что Солнце более или менее неизменно облучает Землю около 3 млрд лет и, следовательно, указанная временная шкала порядка 20 млн лет, так называемая контракционная шкала времени Кельвина — Гельмгольца, для объяснения современной эволюции Солнца не годится. Она вполне подходит для эволюции конденсирующихся звезд при их разогревании во время сжатия, пока разогрев не стал настолько сильным, что вступили в строй термоядерные реакции.
лет. По существу, мы должны сказать, что при гравитационном сжатии Солнце изменяется существенным образом за 25 млн лет. Но геологическая история Земли учит нас, что Солнце более или менее неизменно облучает Землю около 3 млрд лет и, следовательно, указанная временная шкала порядка 20 млн лет, так называемая контракционная шкала времени Кельвина — Гельмгольца, для объяснения современной эволюции Солнца не годится. Она вполне подходит для эволюции конденсирующихся звезд при их разогревании во время сжатия, пока разогрев не стал настолько сильным, что вступили в строй термоядерные реакции.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ГЛАВА I. СОЛНЦЕ
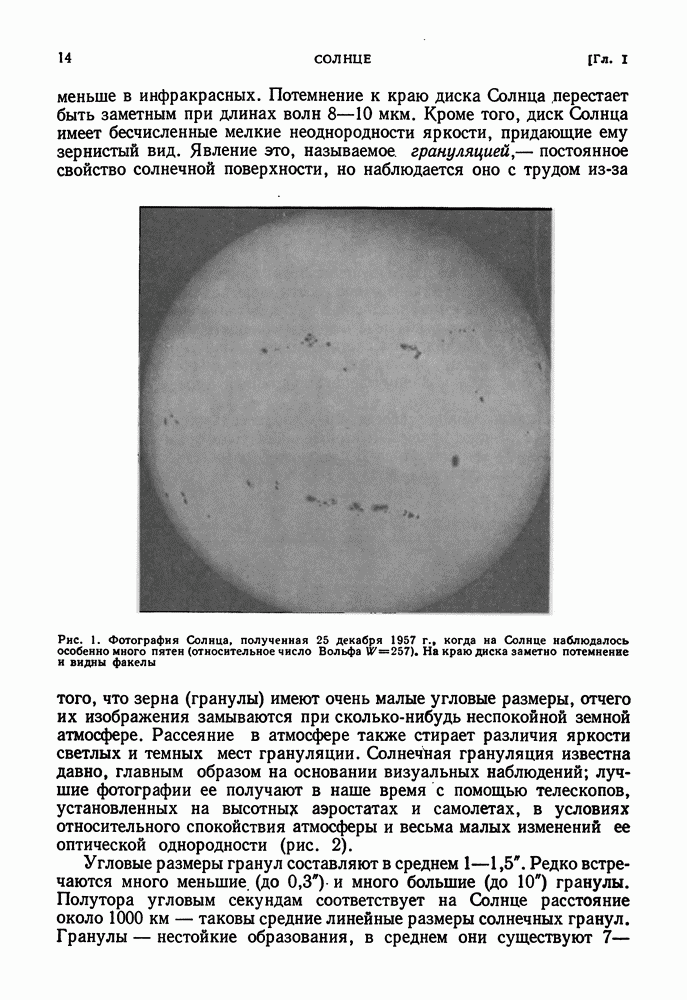
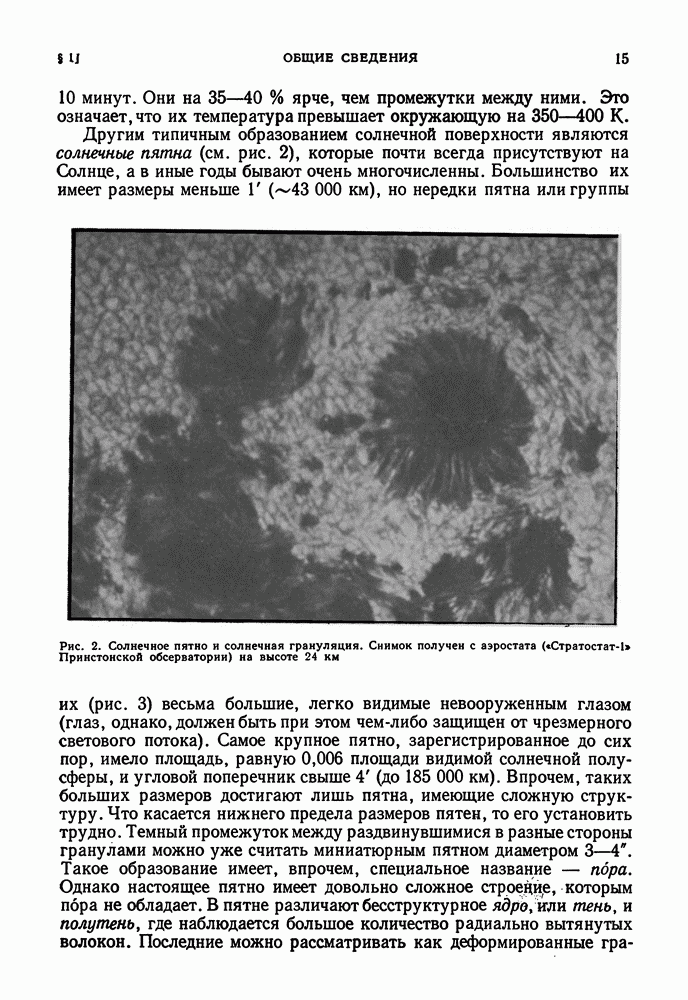
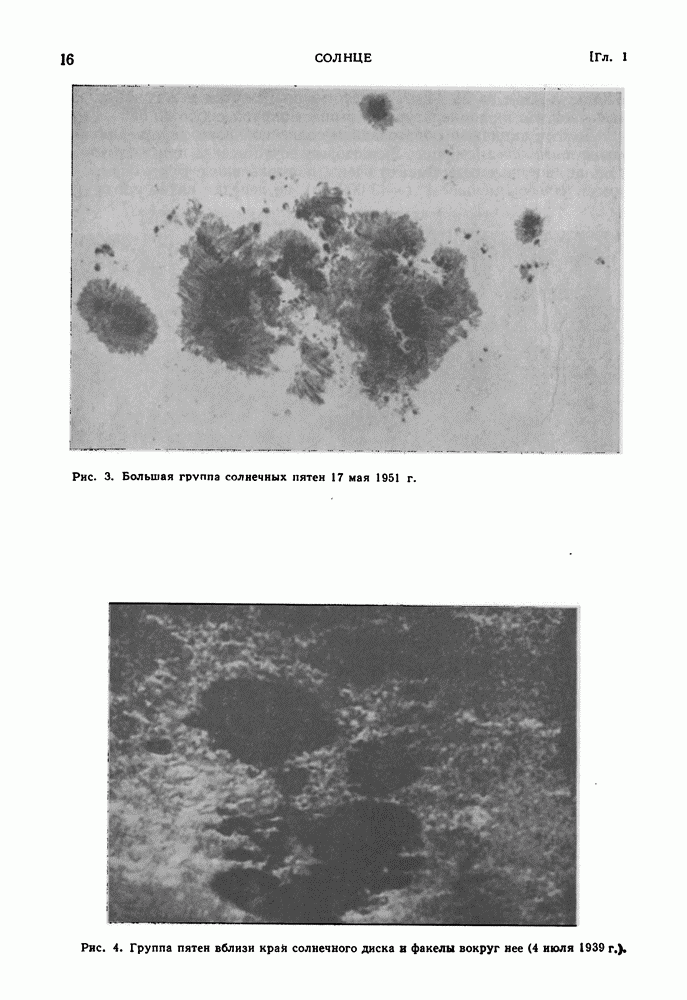
- ВНЕШНИЙ ВИД СОЛНЦА. ФОТОСФЕРА
- ВРАЩЕНИЕ СОЛНЦА
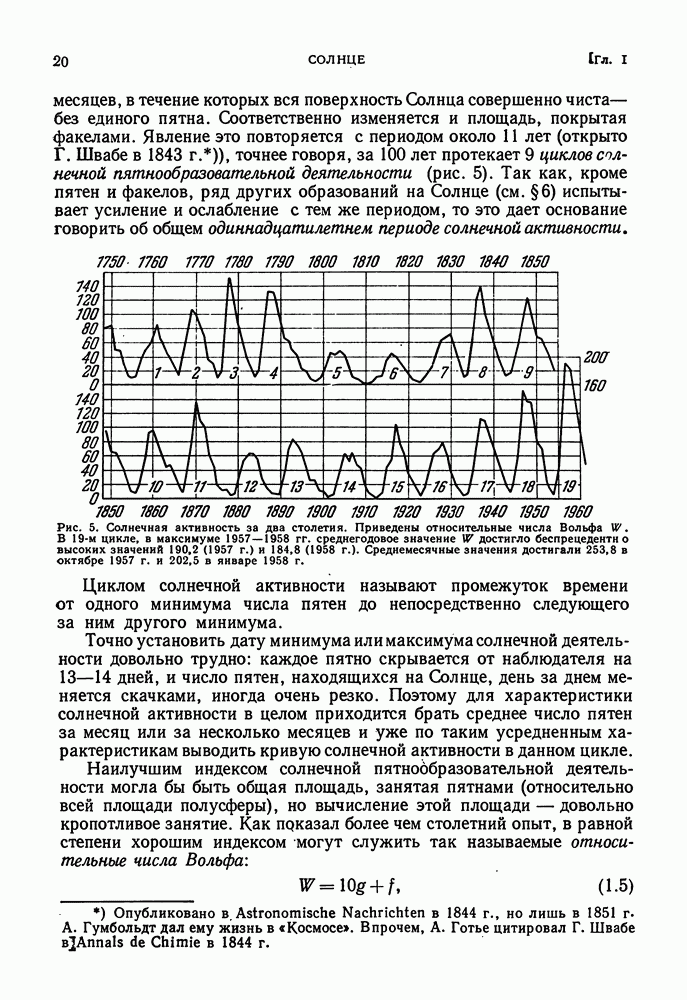
- ПЕРИОДИЧНОСТЬ СОЛНЕЧНОЙ ПЯТНООБРАЗОВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
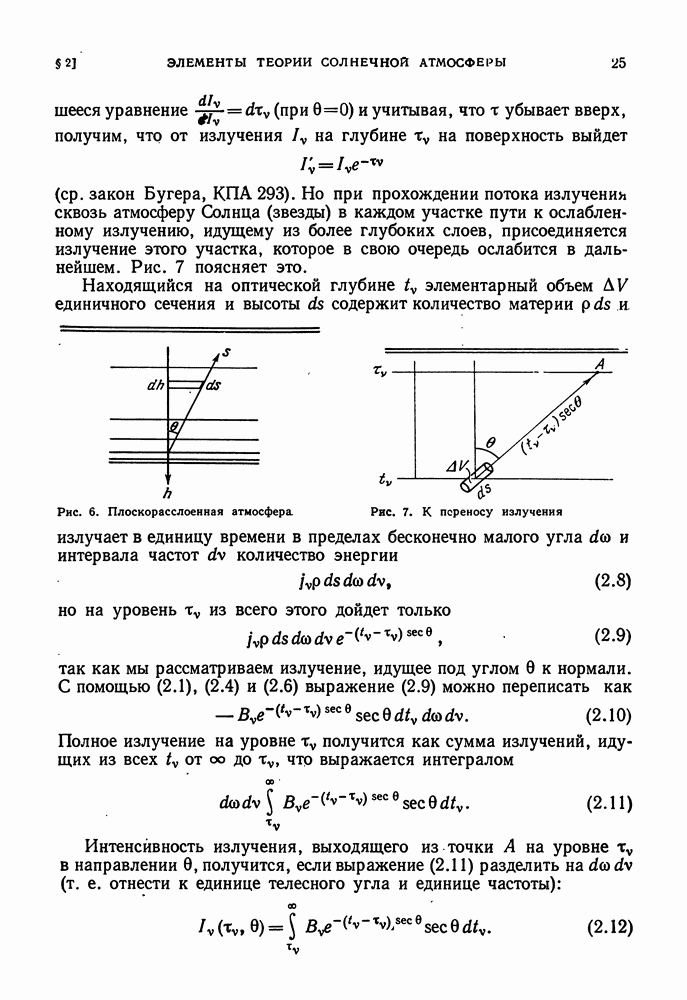
- § 2. ЭЛЕМЕНТЫ ТЕОРИИ СОЛНЕЧНОЙ АТМОСФЕРЫ
- УРАВНЕНИЕ ЛУЧИСТОГО РАВНОВЕСИЯ И ЕГО ПРИБЛИЖЕННОЕ РЕШЕНИЕ
- МОДЕЛЬ СОЛНЕЧНОЙ АТМОСФЕРЫ
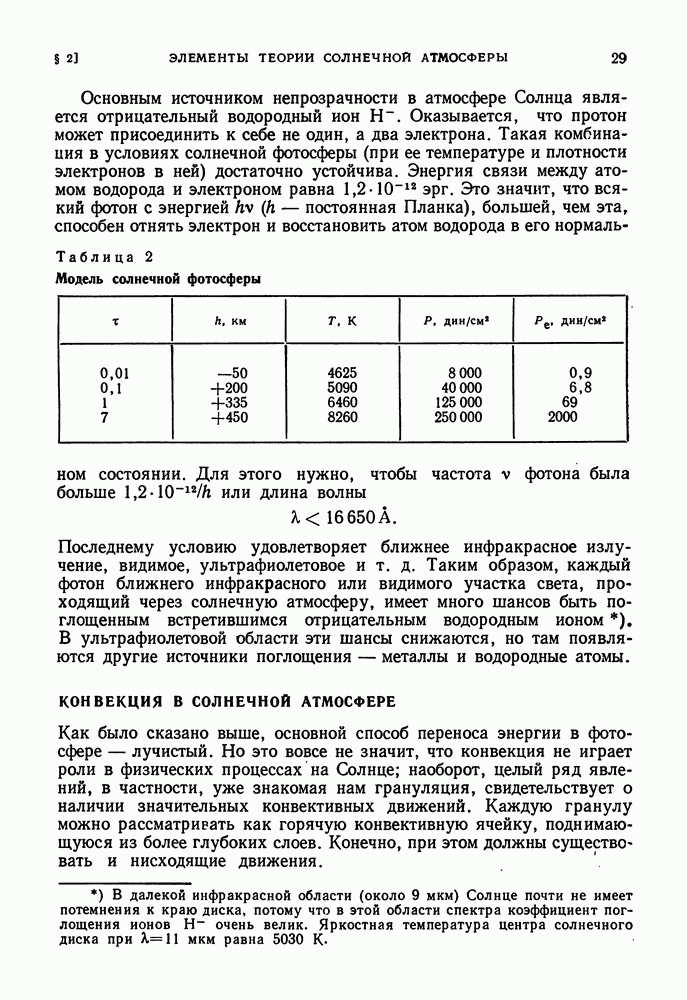
- КОНВЕКЦИЯ В СОЛНЕЧНОЙ АТМОСФЕРЕ
- ИОНИЗАЦИЯ СОЛНЕЧНОГО ВЕЩЕСТВА
- СОЛНЕЧНАЯ ПЛАЗМА И ЕЕ ВЗАИМОДЕЙСТВИЕ С МАГНИТНЫМИ ПОЛЯМИ
- § 3. СОЛНЕЧНЫЙ СПЕКТР. ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА
- ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА. КАЧЕСТВЕННЫЙ АНАЛИЗ
- КОЛИЧЕСТВЕННЫЙ ХИМИЧЕСКИЙ АНАЛИЗ СОЛНЕЧНОЙ АТМОСФЕРЫ
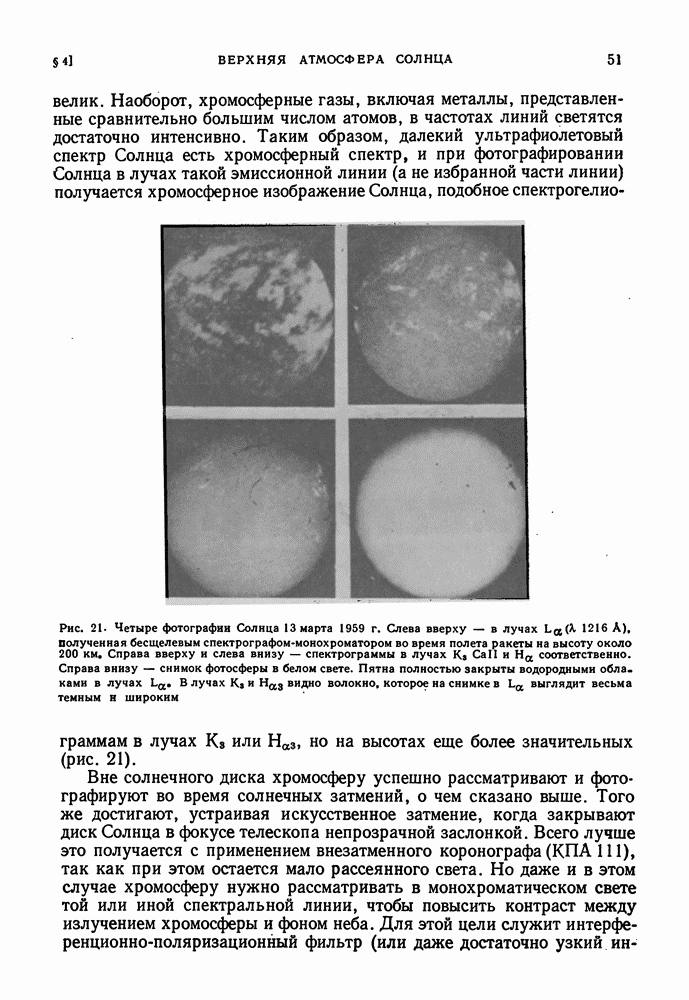
- § 4. ВЕРХНЯЯ АТМОСФЕРА СОЛНЦА
- ОБРАЩАЮЩИЙ СЛОЙ И ХРОМОСФЕРА. ПРИЧИНА ИХ ВИДИМОСТИ ЗА ПРЕДЕЛАМИ СОЛНЕЧНОГО ДИСКА
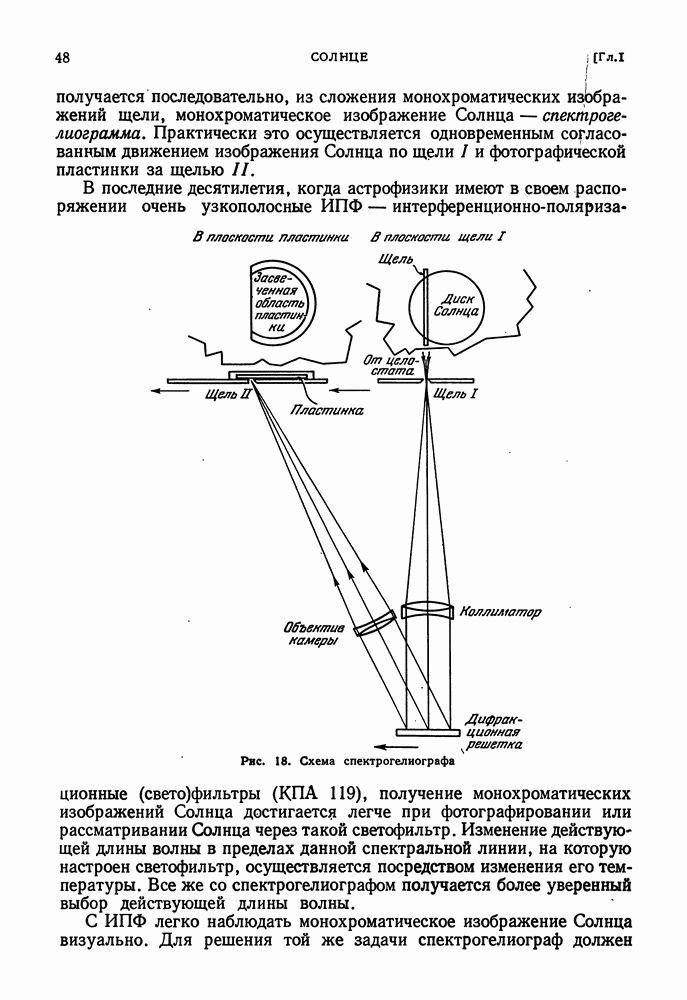
- НАБЛЮДЕНИЯ ХРОМОСФЕРЫ НА ДИСКЕ СОЛНЦА. СПЕКТРОГЕЛИОГРАФ
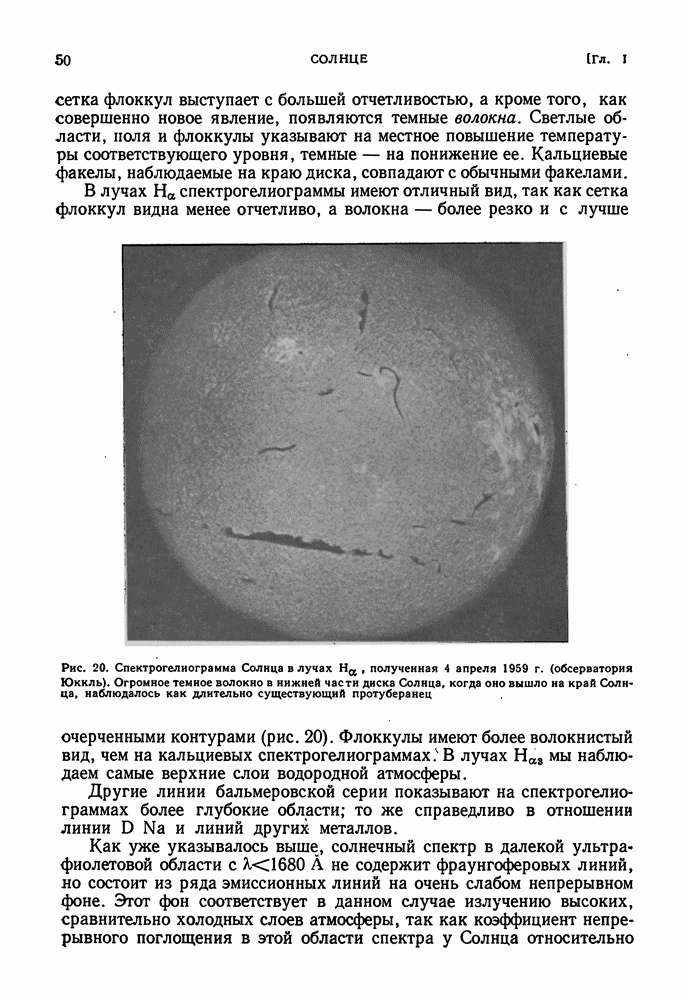
- ХРОМОСФЕРНЫЕ ФАКЕЛЫ, ФЛОККУЛЫ И ВОЛОКНА. СПИКУЛЫ
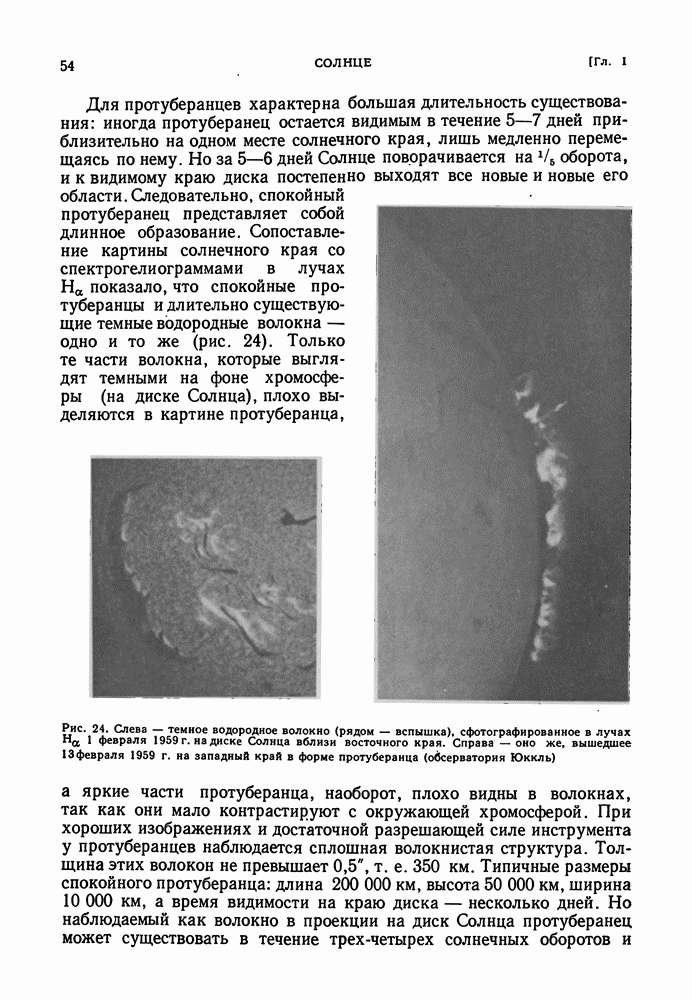
- ПРОТУБЕРАНЦЫ
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ ХРОМОСФЕРЫ. ВОЛНОВЫЕ ДВИЖЕНИЯ В АТМОСФЕРЕ СОЛНЦА
- § 5. СОЛНЕЧНАЯ КОРОНА
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ КОРОНЫ
- ЭМИССИОННЫЙ СПЕКТР КОРОНЫ И ЕГО ИНТЕРПРЕТАЦИЯ
- РАДИОИЗЛУЧЕНИЕ КОРОНЫ И ХРОМОСФЕРЫ
- НЕПРЕРЫВНОЕ ИЗЛУЧЕНИЕ КОРОНЫ. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ И ТЕМПЕРАТУРЫ В ХРОМОСФЕРЕ И КОРОНЕ
- § 6. НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ НА СОЛНЦЕ
- ОБНАРУЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ НА СОЛНЦЕ
- СОЛНЕЧНЫЕ ПЯТНА И ИХ МАГНИТНЫЕ ПОЛЯ
- ПРИРОДА СОЛНЕЧНЫХ ПЯТЕН. АКТИВНЫЕ ОБЛАСТИ НА СОЛНЦЕ. СУПЕРГРАНУЛЯЦИЯ
- ПРОТУБЕРАНЦЫ
- ПРОЯВЛЕНИЕ СОЛНЕЧНОЙ АКТИВНОСТИ В КОРОНЕ
- СОЛНЕЧНЫЕ ВСПЫШКИ
- СПОРАДИЧЕСКОЕ РАДИОИЗЛУЧЕНИЕ СОЛНЦА
- КОРПУСКУЛЯРНОЕ ИЗЛУЧЕНИЕ СОЛНЦА
- § 7. СВЯЗЬ МЕЖДУ СОЛНЕЧНЫМИ И ЗЕМНЫМИ ЯВЛЕНИЯМИ
- ПОЛЯРНЫЕ СИЯНИЯ
- ВЕРХНЯЯ АТМОСФЕРА ЗЕМЛИ. ИОНОСФЕРА. ВОЗДЕЙСТВИЕ НА НИХ СОЛНЦА
- ЯВЛЕНИЯ НА ЗЕМЛЕ, ПРОИСХОДЯЩИЕ ВО ВРЕМЯ ПЕРИОДОВ ПОВЫШЕННОЙ СОЛНЕЧНОЙ АКТИВНОСТИ
- РАДИАЦИОННЫЕ ПОЯСА ЗЕМЛИ
- ДВИЖЕНИЕ КОРПУСКУЛЯРНЫХ потоков В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- СОЛНЕЧНЫЙ ВЕТЕР И МАГНИТОСФЕРА ЗЕМЛИ
- ЗАДАЧИ К ГЛАВЕ I
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ I
- ГЛАВА III. ЗВЕЗДНЫЕ АТМОСФЕРЫ
- § 8. СПЕКТРЫ ЗВЕЗД
- РАЗЛИЧИЯ В СПЕКТРАХ ГИГАНТОВ И КАРЛИКОВ
- ВЛИЯНИЕ РАЗНЫХ ФИЗИЧЕСКИХ ФАКТОРОВ НА ВИД И ИНТЕНСИВНОСТЬ СПЕКТРАЛЬНЫХ ЛИНИЙ
- СПЕКТРАЛЬНЫЕ ПАРАЛЛАКСЫ И ДВУМЕРНАЯ СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ
- § 9. МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. ХИМИЧЕСКИЙ СОСТАВ ЗВЕЗД
- МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. СРЕДНИЙ ХИМИЧЕСКИЙ СОСТАВ АТМОСФЕР ЗВЕЗД
- УКЛОНЕНИЯ ХИМИЧЕСКОГО СОСТАВА ЗВЕЗД ОТ СРЕДНЕГО
- СПЕКТРЫ БЕЛЫХ КАРЛИКОВ
- ЗВЕЗДЫ ПОНИЖЕННОЙ СВЕТИМОСТИ
- МАГНИТНЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- ВЛИЯНИЕ ВРАЩЕНИЯ ЗВЕЗДЫ НА ЕЕ СПЕКТР
- ЭФФЕКТ ТУРБУЛЕНТНОСТИ
- § 10. ВЗАИМНЫЕ СВЯЗИ МЕЖДУ ВНЕШНИМИ ХАРАКТЕРИСТИКАМИ ЗВЕЗД
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА
- СВЯЗЬ МЕЖДУ ПОЛОЖЕНИЕМ ЗВЕЗДЫ НА ДИАГРАММЕ Г — Р И ЕЕ ДВИЖЕНИЕМ В ГАЛАКТИКЕ
- ЗВЕЗДЫ СФЕРИЧЕСКОЙ И ПЛОСКОЙ СОСТАВЛЯЮЩИХ. РАЗЛИЧИЕ ИХ ДИАГРАММ Г — Р
- РАЗНООБРАЗИЕ СВЕТИМОСТЕЙ И РАЗМЕРОВ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ II
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ II
- ГЛАВА III. ДВОЙНЫЕ ЗВЕЗДЫ И МАССЫ ЗВЕЗД
- ВИЗУАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- НЕВИДИМЫЕ СПУТНИКИ ЗВЕЗД
- СПЕКТРАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- ШИРОКИЕ И ТЕСНЫЕ ПАРЫ
- ЗАТМЕННЫЕ ИЛИ ФОТОМЕТРИЧЕСКИЕ ДВОЙНЫЕ ЗВЕЗДЫ
- § 12. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ ХАРАКТЕРИСТИК ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- КРИВАЯ ЛУЧЕВЫХ СКОРОСТЕЙ И ЭЛЕМЕНТЫ ОРБИТЫ СПЕКТРАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- ОПРЕДЕЛЕНИЕ МАСС КОМПОНЕНТ СПЕКТРАЛЬНО-ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ФОТОМЕТРИЧЕСКОЙ ОРБИТЫ
- ОПРЕДЕЛЕНИЕ ЭКСЦЕНТРИСИТЕТА ОРБИТЫ У ЗАТМЕННОЙ ДВОЙНОЙ ВРАЩЕНИЕ ЛИНИИ АПСИД
- ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ КОМПОНЕНТ ФОТОМЕТРИЧЕСКИХ ДВОЙНЫХ ЗВЕЗД
- ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОЙ ТЕМПЕРАТУРЫ ЗАТМЕННЫХ ДВОЙНЫХ ЗВЕЗД
- § 13. МАССЫ И ДРУГИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВОЙНЫХ ЗВЕЗД. ЗАКОН МАССА — СВЕТИМОСТЬ
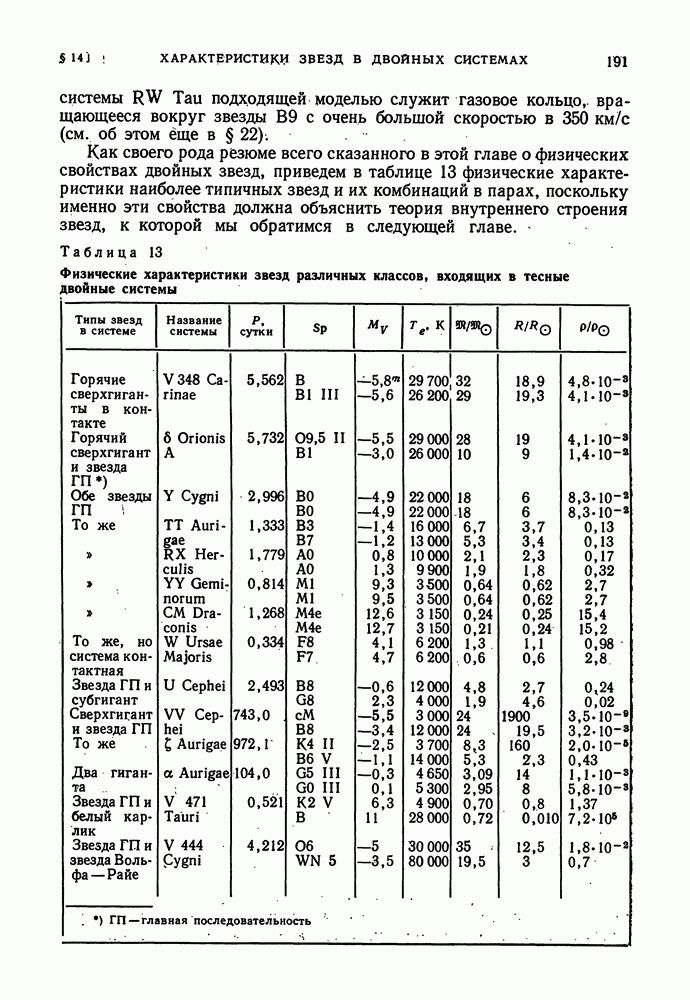
- § 14. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВЕЗД В ДВОЙНЫХ СИСТЕМАХ
- РАЗНЫЕ ТИПЫ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- КОНТАКТНЫЕ СИСТЕМЫ
- ТРИ ТИПА ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- ОСЕВОЕ ВРАЩЕНИЕ КОМПОНЕНТ В ТЕСНЫХ ПАРАХ
- ГАЗОВЫЕ ПОТОКИ В ТЕСНЫХ ПАРАХ
- МНОГОЧИСЛЕННОСТЬ ДВОЙНЫХ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ III
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ III
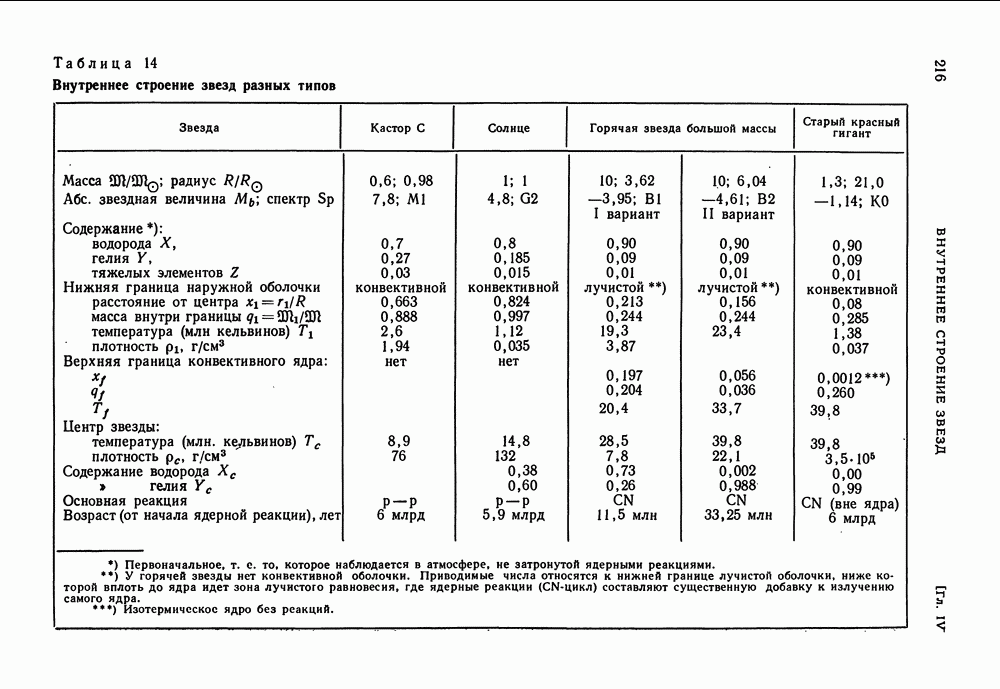
- ГЛАВА IV. ВНУТРЕННЕЕ СТРОЕНИЕ ЗВЕЗД
- ОБЩИЕ СООБРАЖЕНИЯ. СОСТОЯНИЕ ВЕЩЕСТВА В НЕДРАХ ЗВЕЗД
- ЛУЧИСТОЕ ДАВЛЕНИЕ В ЗВЕЗДАХ
- ЛУЧИСТЫЙ И КОНВЕКТИВНЫЙ ПЕРЕНОС ТЕПЛА ВНУТРИ ЗВЕЗДЫ
- ГОМОЛОГИЧЕСКИЕ КОНФИГУРАЦИИ
- ПОЛИТРОПНЫЕ МОДЕЛИ ЗВЕЗД
- § 16. ЛУЧЕИСПУСКАНИЕ ЗВЕЗДЫ
- ИСТОЧНИКИ НЕПРОЗРАЧНОСТИ ЗВЕЗДНОГО ВЕЩЕСТВА
- ЗАВИСИМОСТЬ ЛУЧЕИСПУСКАНИЯ ЗВЕЗДЫ ОТ ИСТОЧНИКОВ ЭНЕРГИИ И НЕПРОЗРАЧНОСТИ
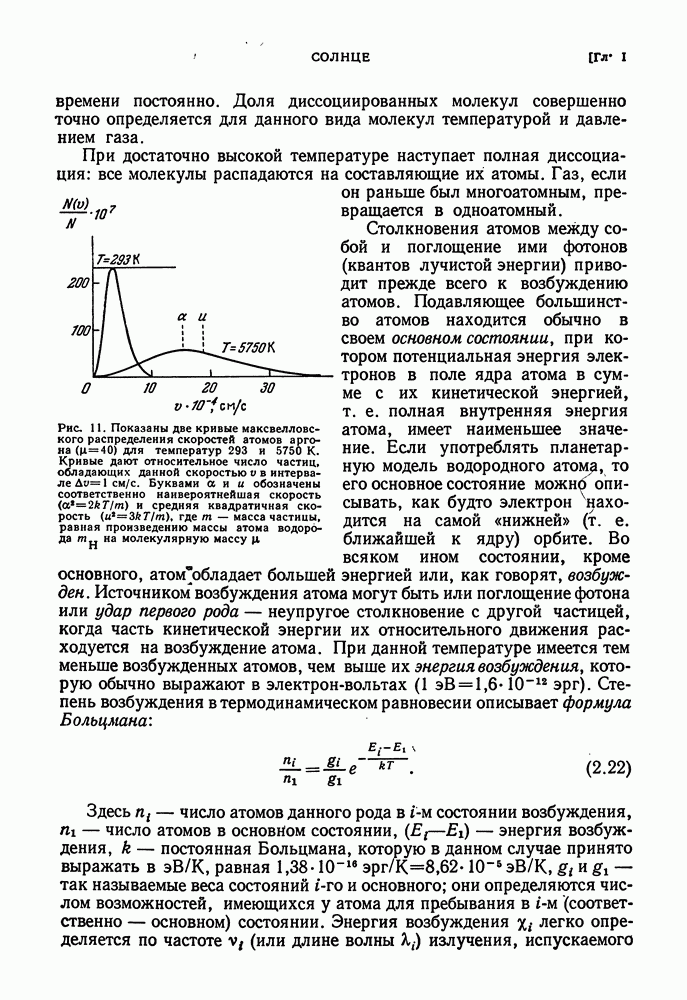
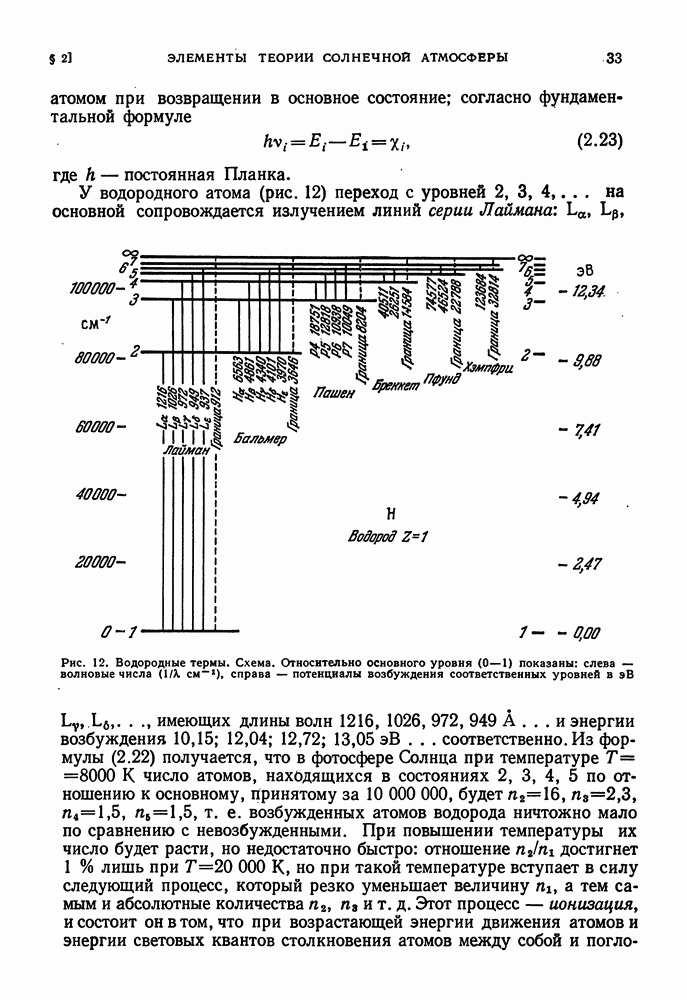
- § 17. ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ГРАВИТАЦИОННОЕ СЖАТИЕ
- ТЕРМОЯДЕРНЫЕ ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ПРОТОН-ПРОТОННАЯ РЕАКЦИЯ
- УГЛЕРОДНО-АЗОТНЫЙ ЦИКЛ
- ТРАНСФОРМАЦИЯ ГЕЛИЯ В ЗВЕЗДАХ
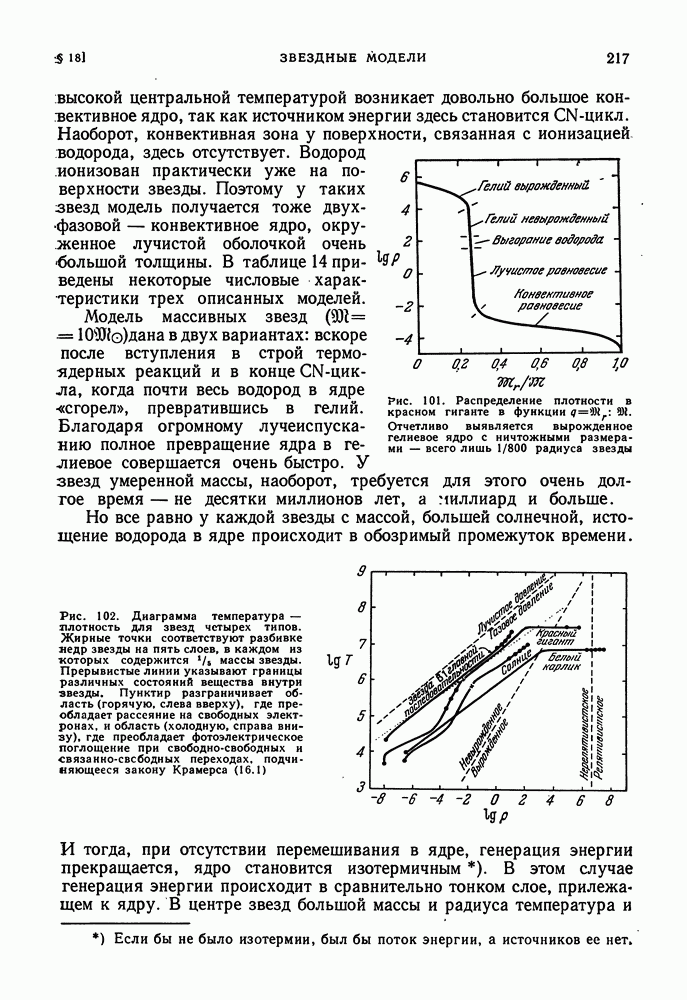
- § 18. ЗВЕЗДНЫЕ МОДЕЛИ
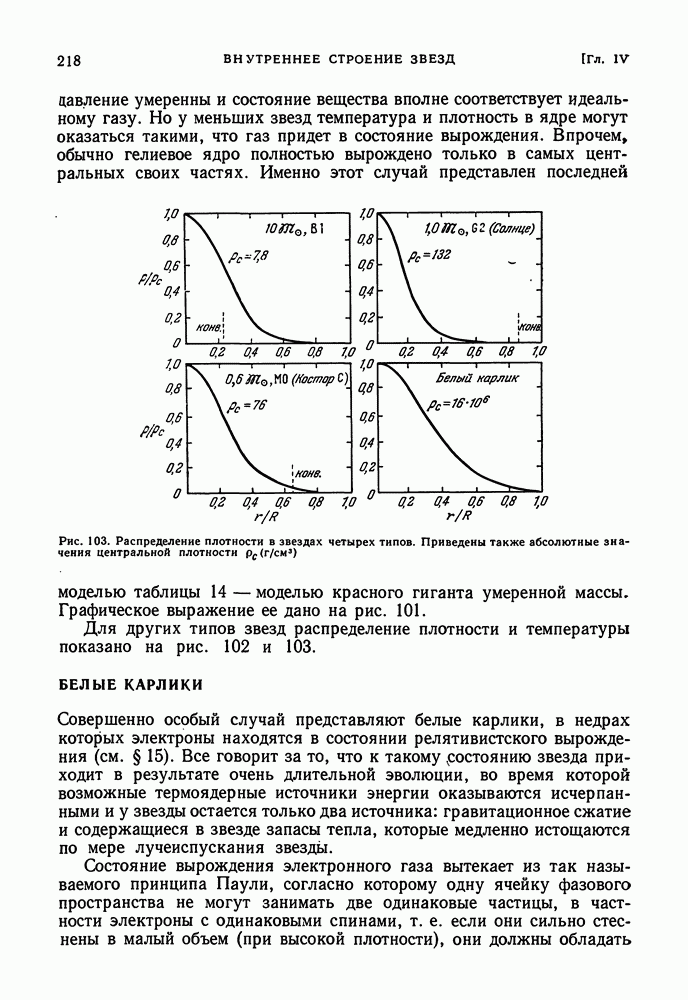
- БЕЛЫЕ КАРЛИКИ
- НЕЙТРОННЫЕ ЗВЕЗДЫ. ПУЛЬСАРЫ
- ПРОВЕРКА ТЕОРИИ ПО ВРАЩЕНИЮ ЛИНИИ АПСИД В ТЕСНЫХ СИСТЕМАХ И ПО СОЛНЕЧНЫМ ПУЛЬСАЦИЯМ
- § 19. ЭВОЛЮЦИЯ ЗВЕЗД
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЭВОЛЮЦИЯ ЗВЕЗД
- КОНТРАКЦИОННАЯ ФАЗА ЗВЕЗДНОЙ ЭВОЛЮЦИИ
- ЭВОЛЮЦИЯ ЗВЕЗД НА ТЕРМОЯДЕРНОЙ ОСНОВЕ
- ЭВОЛЮЦИЯ К КРАСНЫМ ГИГАНТАМ
- ДАЛЬНЕЙШАЯ ЭВОЛЮЦИЯ ЗВЕЗДЫ
- § 20. ЭВОЛЮЦИЯ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- СОВРЕМЕННАЯ РАСПРОСТРАНЕННОСТЬ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ ВО ВСЕЛЕННОЙ
- ТЕРМОЯДЕРНЫЕ РЕАКЦИИ С ОБРАЗОВАНИЕМ ЭЛЕМЕНТОВ БОЛЕЕ ТЯЖЕЛЫХ, ЧЕМ 12С
- ЗВЕЗДЫ РАЗНОГО ВОЗРАСТА И ИХ ХИМИЧЕСКИЙ СОСТАВ
- ЗАДАЧИ К ГЛАВЕ IV
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ IV
- ГЛАВА V. НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦЕФЕИД
- ПУЛЬСАЦИИ ЦЕФЕИД
- ГИПОТЕЗА РАДИАЛЬНЫХ АДИАБАТИЧЕСКИХ ПУЛЬСАЦИЙ И ЕЕ ЗАТРУДНЕНИЯ
- НОВЫЕ ПРЕДСТАВЛЕНИЯ О КОЛЕБАТЕЛЬНЫХ ПРОЦЕССАХ У ЦЕФЕИД
- ЗВЕЗДЫ ТИПА b БОЛЬШОГО ПСА
- ЗВЕЗДЫ ТИПА RV ТЕЛЬЦА И МИРЫ КИТА
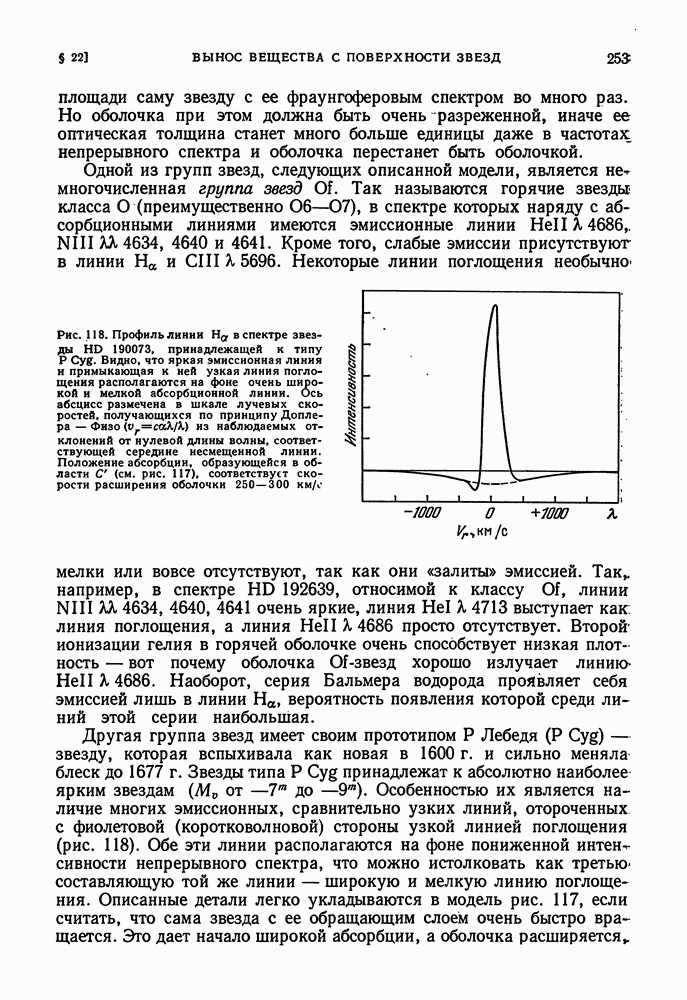
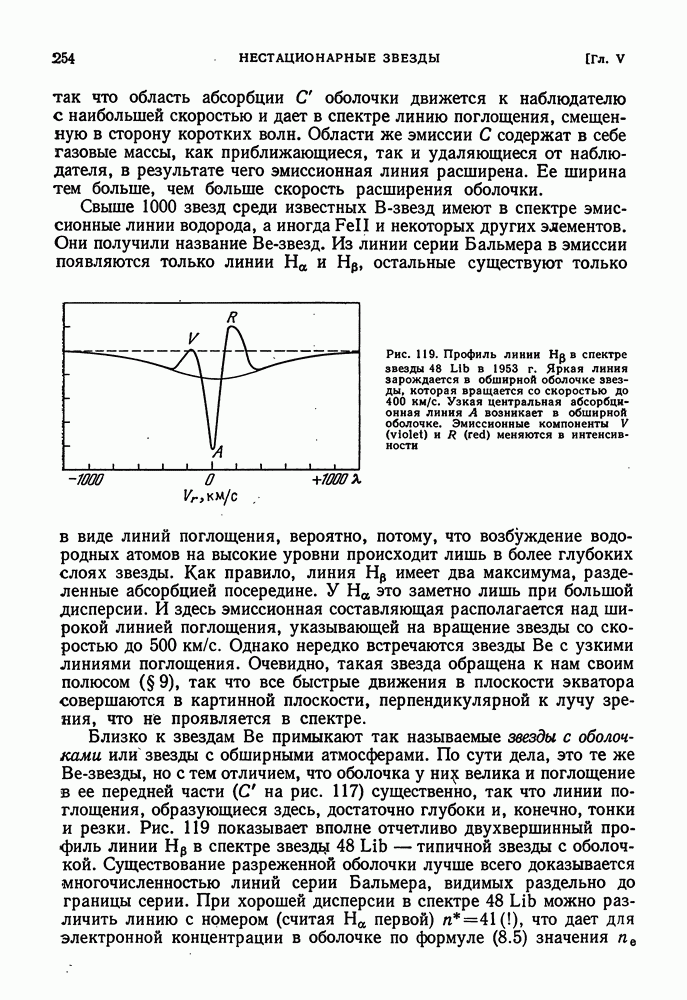
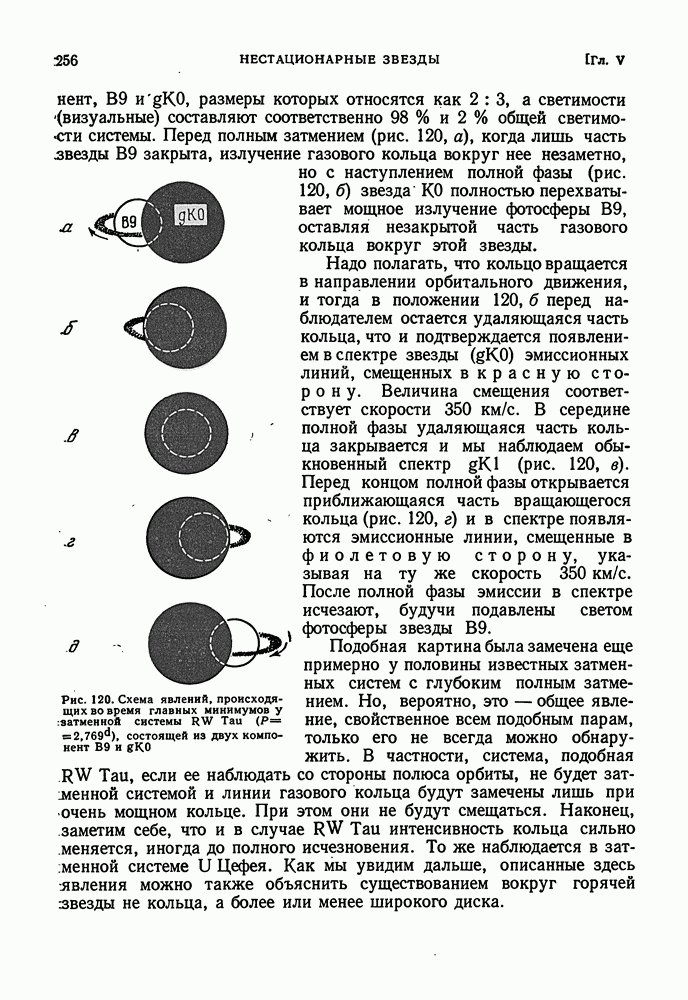
- § 22. ВЫНОС ВЕЩЕСТВА С ПОВЕРХНОСТИ ЗВЕЗД
- ГАЗОВЫЕ ОБОЛОЧКИ И КОЛЬЦА ВОКРУГ ЗВЕЗД
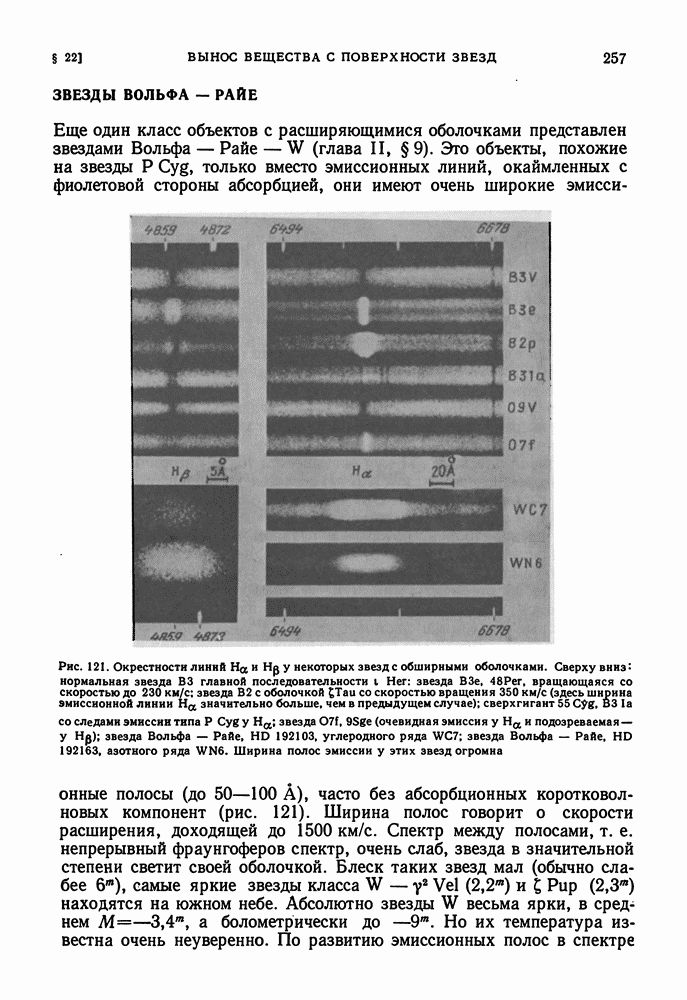
- ЗВЕЗДЫ ВОЛЬФА — РАЙЕ
- § 23. ВРАЩЕНИЕ ЗВЕЗД И ОБМЕН ВЕЩЕСТВА ВНУТРИ ДВОЙНЫХ СИСТЕМ
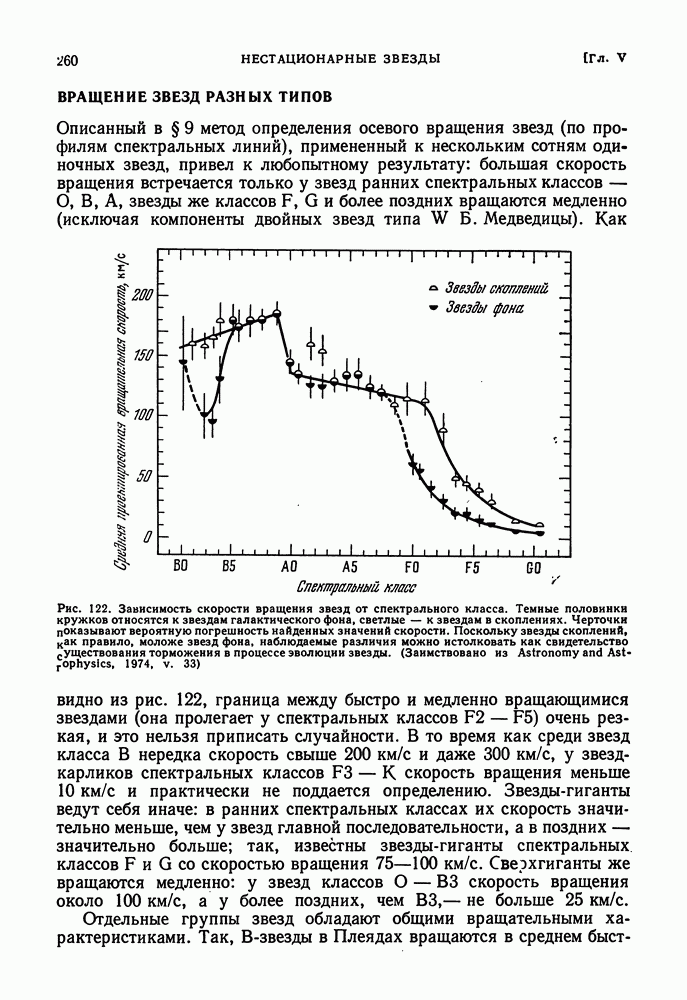
- ВРАЩЕНИЕ ЗВЕЗД РАЗНЫХ ТИПОВ
- ЭВОЛЮЦИОННЫЕ ИЗМЕНЕНИЯ СКОРОСТИ ВРАЩЕНИЯ ЗВЕЗД
- ПРОИСХОЖДЕНИЕ ВРАЩЕНИЯ ЗВЕЗД
- ОБМЕН ВЕЩЕСТВА ВНУТРИ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ. АККРЕЦИЯ. ЭВОЛЮЦИОННЫЕ СЛЕДСТВИЯ
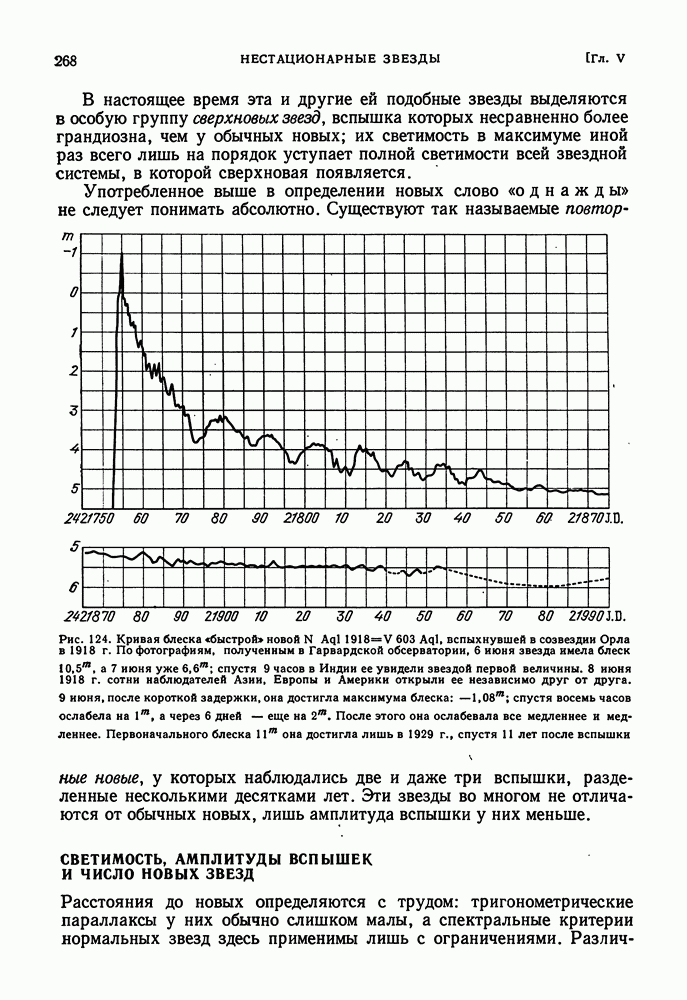
- § 24. НОВЫЕ И СВЕРХНОВЫЕ ЗВЕЗДЫ
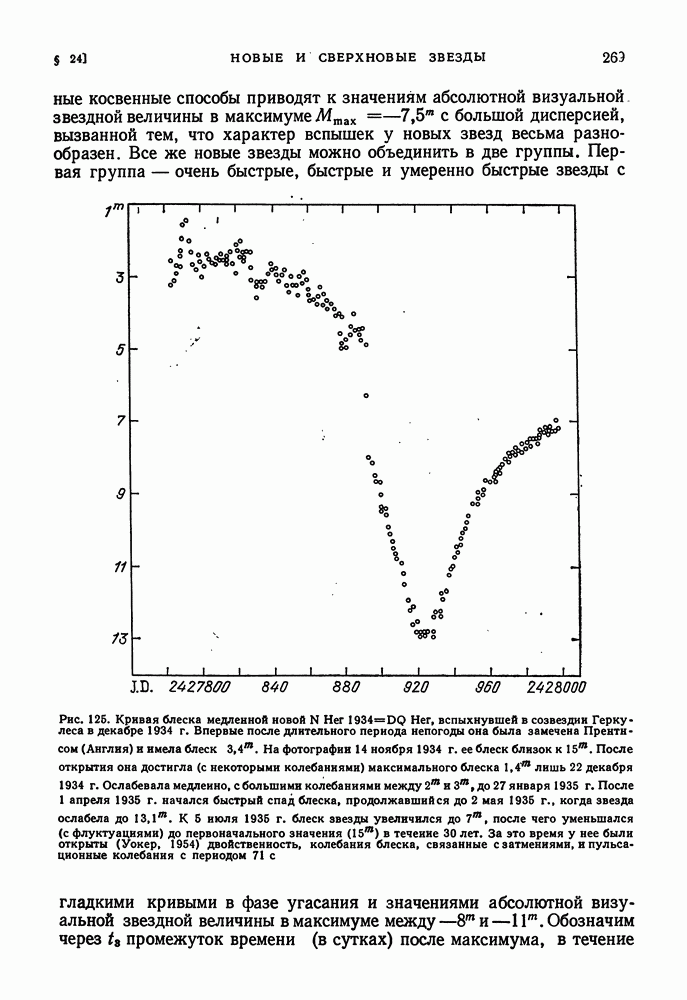
- СВЕТИМОСТЬ, АМПЛИТУДЫ ВСПЫШЕК И ЧИСЛО НОВЫХ ЗВЕЗД
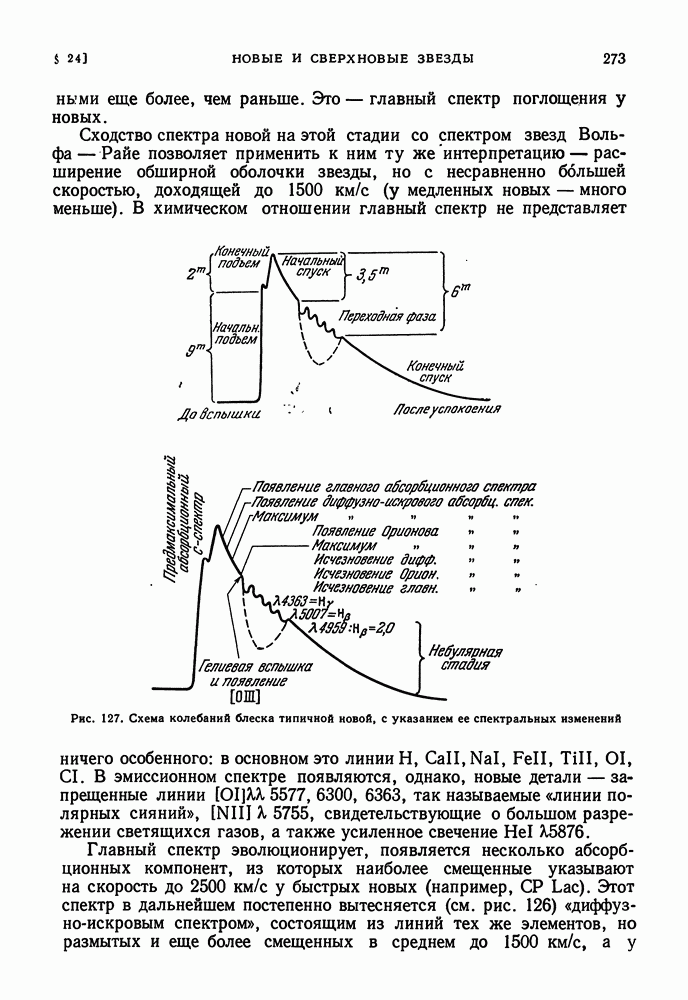
- СПЕКТРАЛЬНЫЕ ИЗМЕНЕНИЯ У НОВЫХ ЗВЕЗД
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ ВО ВРЕМЯ ВСПЫШКИ НОВОЙ ЗВЕЗДЫ
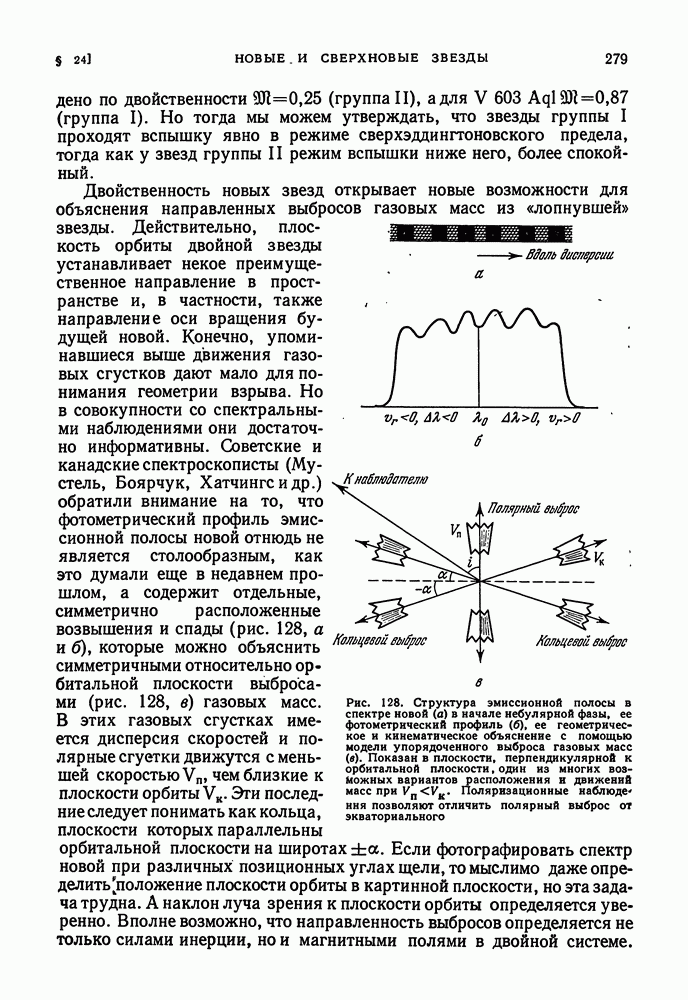
- ДВОЙСТВЕННОСТЬ НОВЫХ ЗВЕЗД
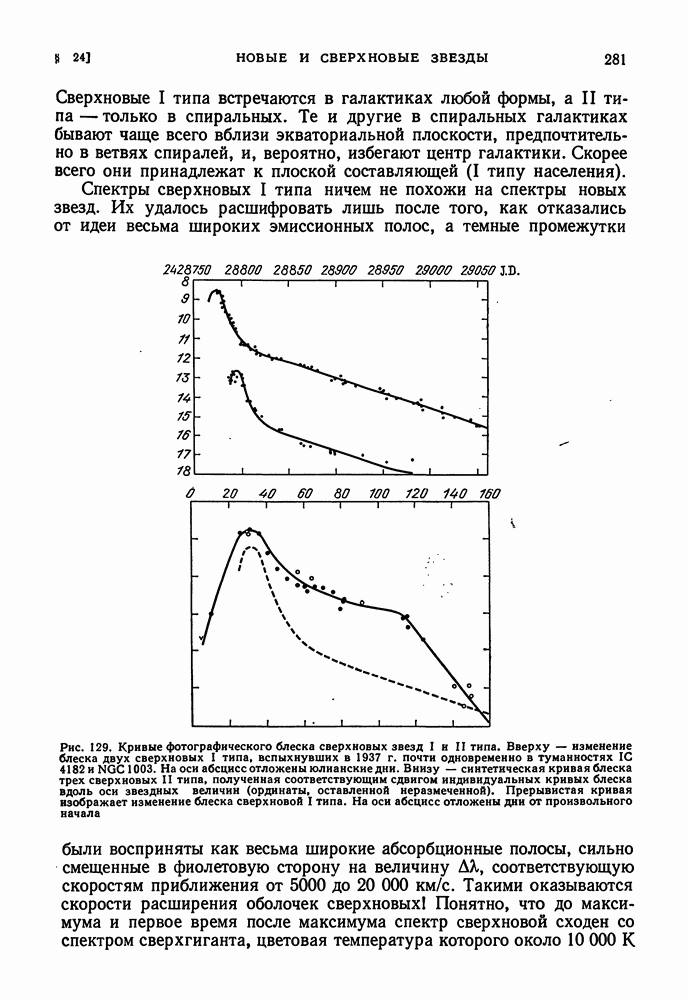
- СВЕРХНОВЫЕ ЗВЕЗДЫ
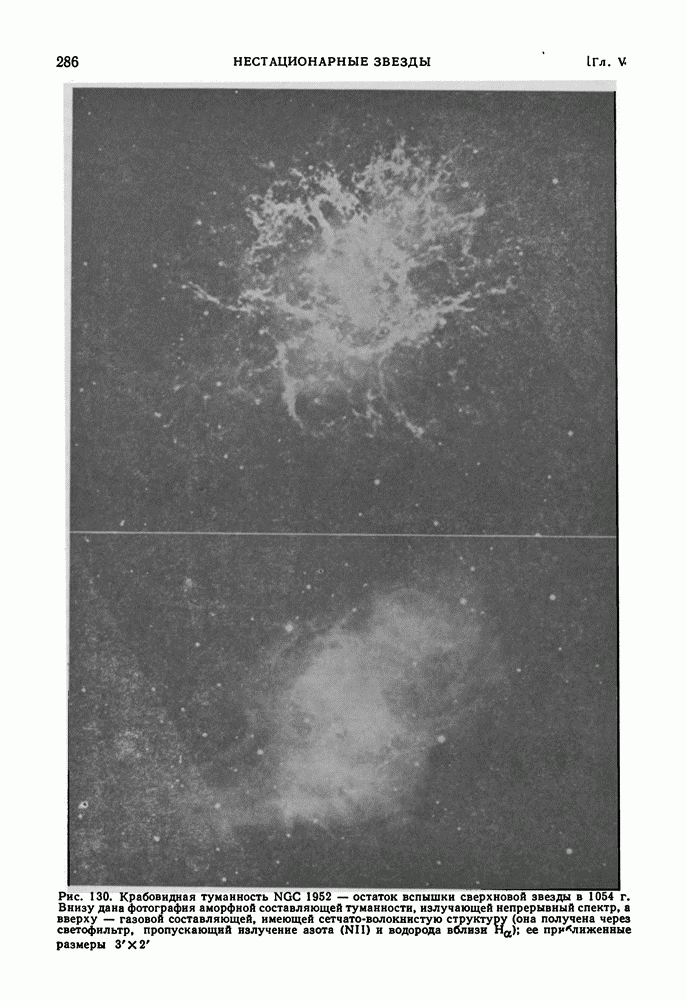
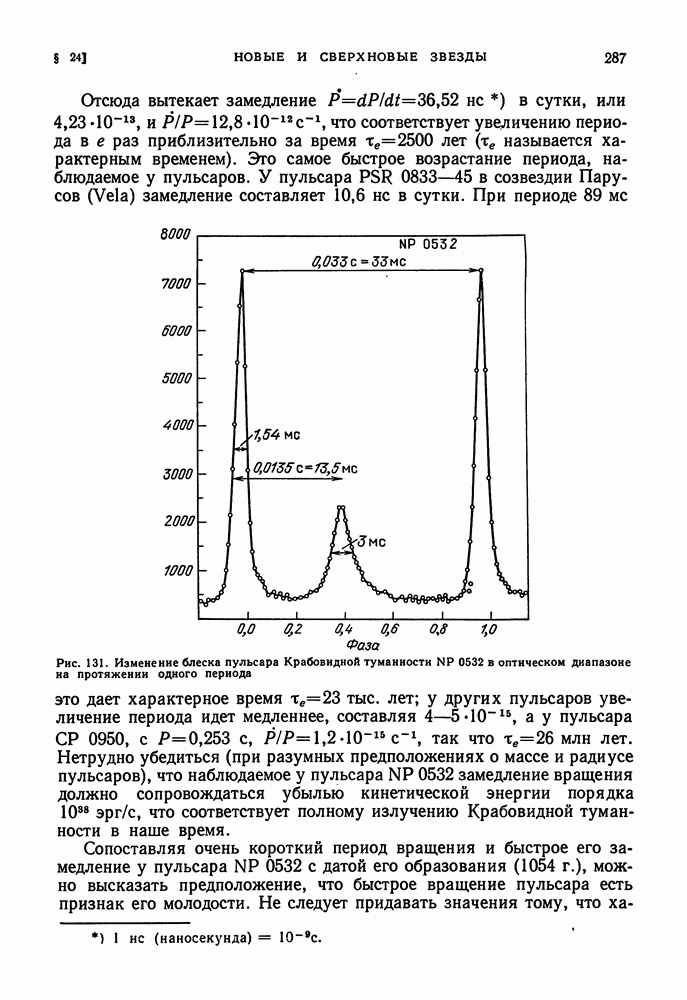
- ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ ЗВЕЗД. КРАБОВИДНАЯ ТУМАННОСТЬ. ПУЛЬСАРЫ
- § 25. КАРЛИКОВЫЕ ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ДРУГИЕ СЛУЧАИ НЕСТАЦИОНАРНОСТИ: РЕНТГЕНОВСКИЕ ЗВЕЗДЫ
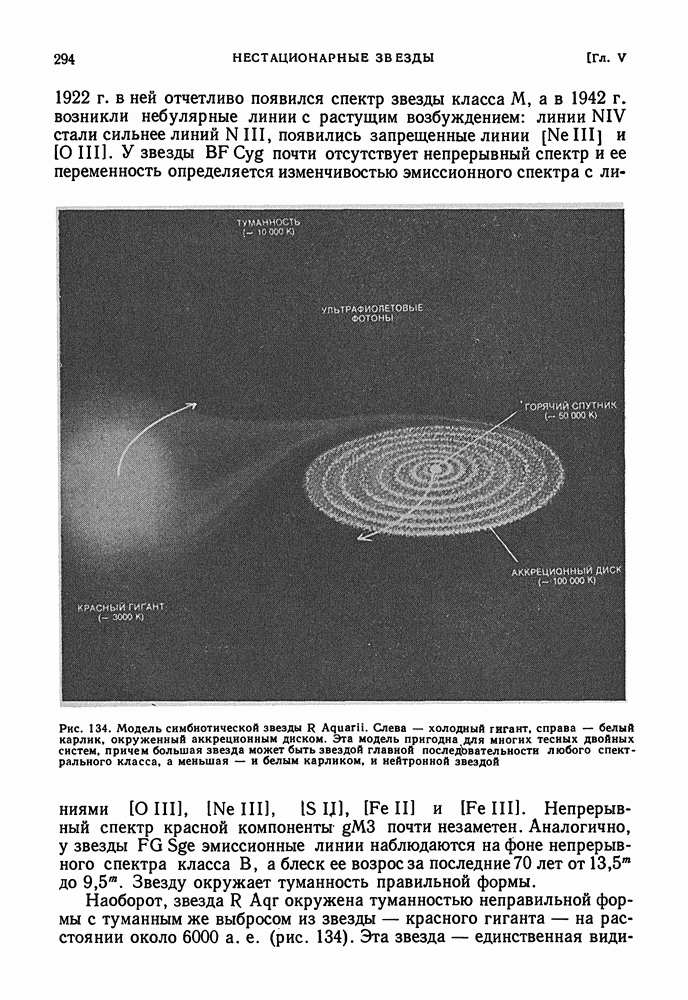
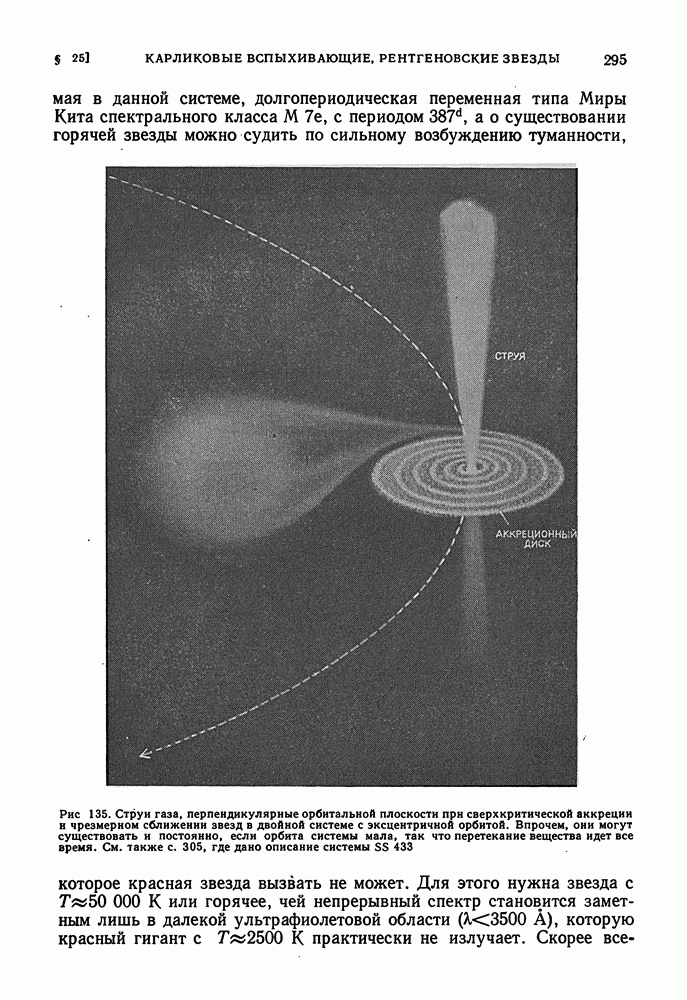
- ЗВЕЗДЫ ТИПА U БЛИЗНЕЦОВ. СИМБИОТИЧЕСКИЕ ЗВЕЗДЫ
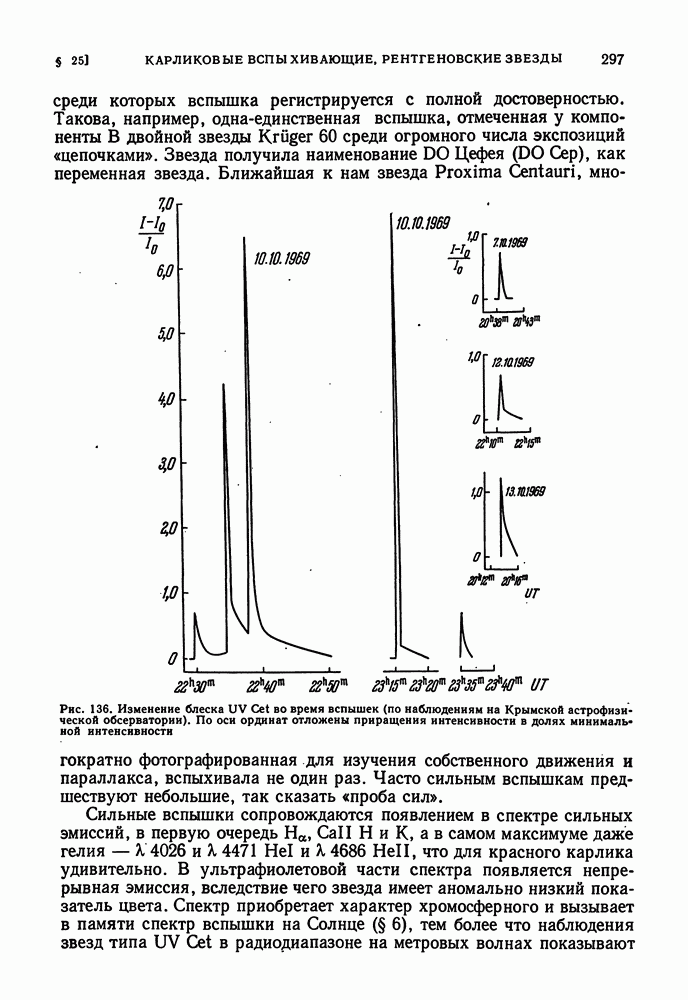
- ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ТИПА UV КИТА
- ЗВЕЗДЫ ТИПОВ Т ТЕЛЬЦА, RW ВОЗНИЧЕГО И ТОРИОНА
- НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ В РЕНТГЕНОВСКОМ ДИАПАЗОНЕ
- ЗАДАЧИ К ГЛАВЕ V
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ V
- ГЛАВА VI. ДИФФУЗНОЕ ВЕЩЕСТВО В ПРОСТРАНСТВЕ
- ВЫСОКАЯ СПОСОБНОСТЬ ПЫЛИ ЗАДЕРЖИВАТЬ ПРОХОДЯЩИЙ СВЕТ
- ЗАВИСИМОСТЬ ОСЛАБЛЕНИЯ СВЕТА ПЫЛЬЮ ОТ ДЛИНЫ ВОЛНЫ
- ПРАКТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ОБЩЕГО ОСЛАБЛЕНИЯ СВЕТА в ЗАДАННОМ НАПРАВЛЕНИИ
- ОБЛАЧНАЯ СТРУКТУРА ПЫЛЕВОЙ СРЕДЫ В ГАЛАКТИКЕ
- РАСПРЕДЕЛЕНИЕ МЕЖЗВЕЗДНОЙ ПЫЛИ В ГАЛАКТИКЕ
- СВЕТЛЫЕ ПЫЛЕВЫЕ ТУМАННОСТИ
- СВЕТОВОЕ ДАВЛЕНИЕ НА ПЫЛЕВЫЕ ЧАСТИЦЫ
- МЕЖЗВЕЗДНАЯ ПОЛЯРИЗАЦИЯ СВЕТА ЗВЕЗД
- ОРИЕНТИРОВАНИЕ МЕЖЗВЕЗДНЫХ ПЫЛЕВЫХ ЧАСТИЦ МАГНИТНЫМИ ПОЛЯМИ
- § 27. ГАЗОВАЯ СОСТАВЛЯЮЩАЯ МЕЖЗВЕЗДНОЙ СРЕДЫ
- МЕЖЗВЕЗДНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ Са, Na И ДРУГИХ ЭЛЕМЕНТОВ И МОЛЕКУЛ
- ГАЗОВЫЙ ГАЛАКТИЧЕСКИЙ СУБСТРАТ
- ИЗЛУЧЕНИЕ МЕЖЗВЕЗДНОГО НЕЙТРАЛЬНОГО ВОДОРОДА НА ВОЛНЕ 21 см
- МОЛЕКУЛЫ, ОБНАРУЖЕННЫЕ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ РАДИОМЕТОДАМИ
- ОТНОСИТЕЛЬНАЯ РОЛЬ ГАЗА И ПЫЛИ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭЛЕКТРОНЫ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ. ОБЛАСТИ HII И HI
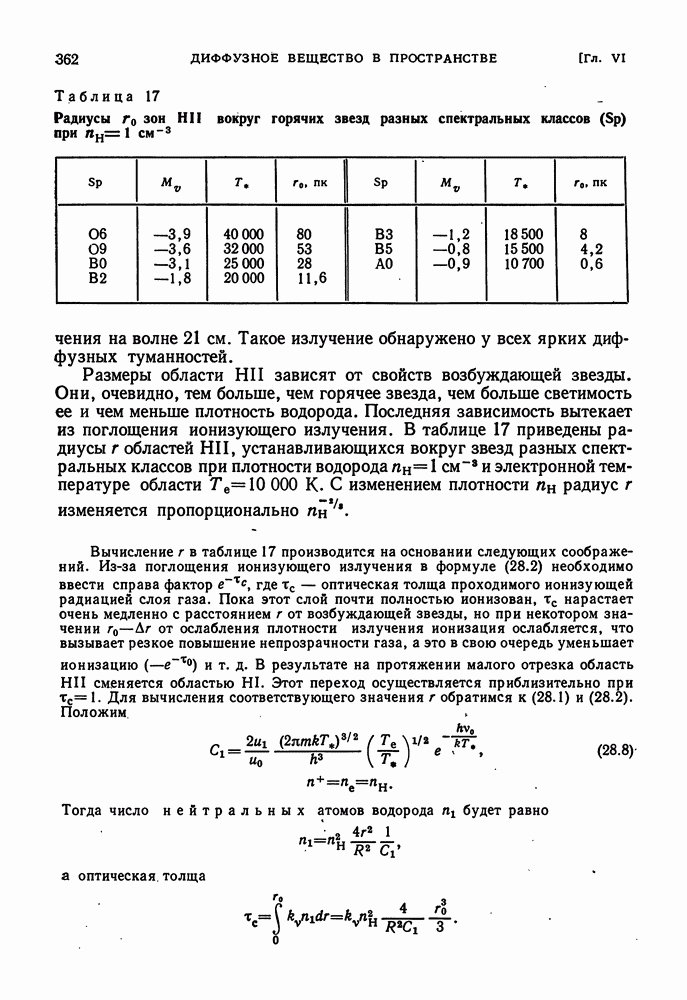
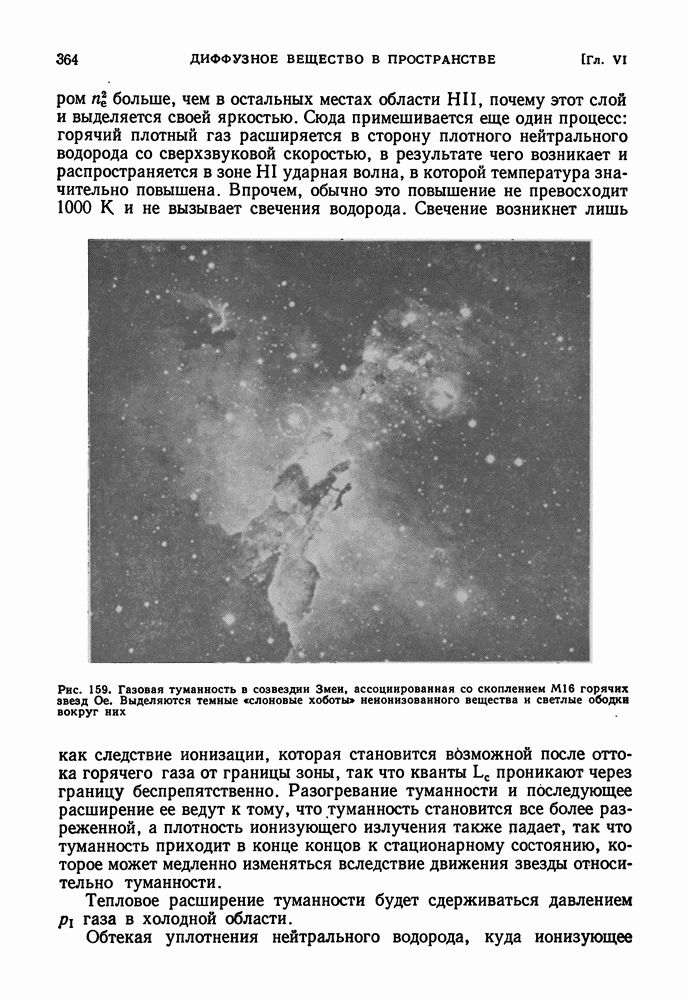
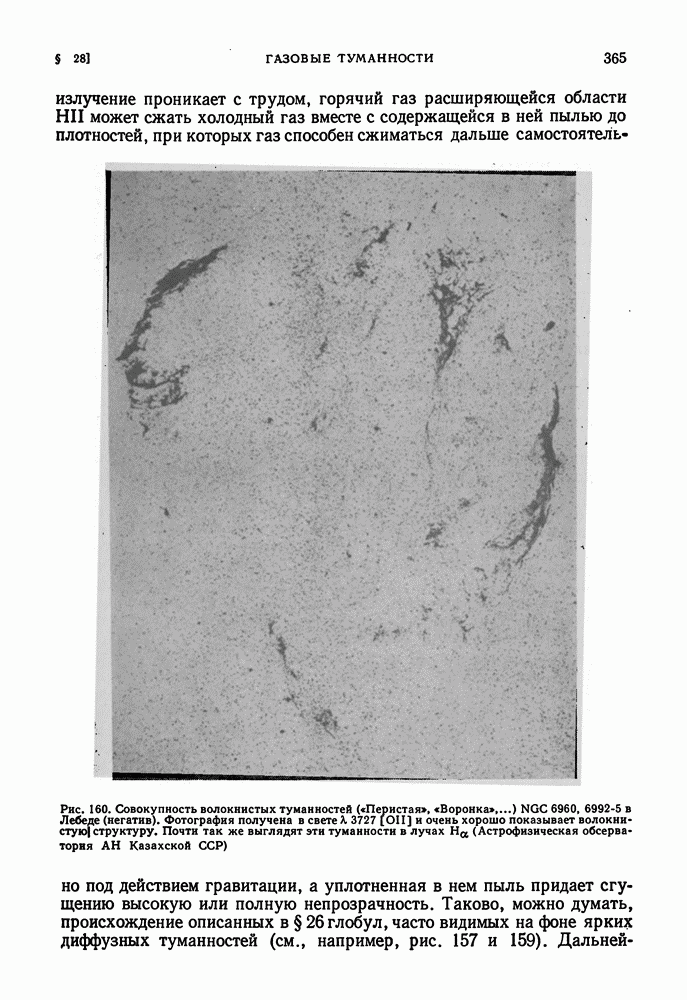
- § 28. ГАЗОВЫЕ ТУМАННОСТИ
- ПЛАНЕТАРНЫЕ ТУМАННОСТИ
- ФЛУОРЕСЦЕНЦИЯ ВЕЩЕСТВА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ТЕМПЕРАТУРЫ ЯДЕР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЗАПРЕЩЕННЫЕ ЛИНИИ В СПЕКТРАХ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЭЛЕКТРОННЫЕ ТЕМПЕРАТУРЫ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- НЕПРЕРЫВНЫЙ СПЕКТР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ. ИХ МАССЫ
- РАСШИРЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ПОЛЕ ЛАЙМАНОВСКОГО ИЗЛУЧЕНИЯ В ПЛАНЕТАРНЫХ ТУМАННОСТЯХ
- ГРАНИЦА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ЯДРА ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ПРОИСХОЖДЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ДИФФУЗНЫЕ ГАЗОВЫЕ ТУМАННОСТИ
- ОБЛАСТИ HII И ИХ РАЗМЕРЫ
- ВЗАИМОДЕЙСТВИЕ ГАЗА И ИЗЛУЧЕНИЯ ГОРЯЧЕЙ ЗВЕЗДЫ. ДВИЖЕНИЯ ВНУТРИ ГАЗОВОЙ ТУМАННОСТИ
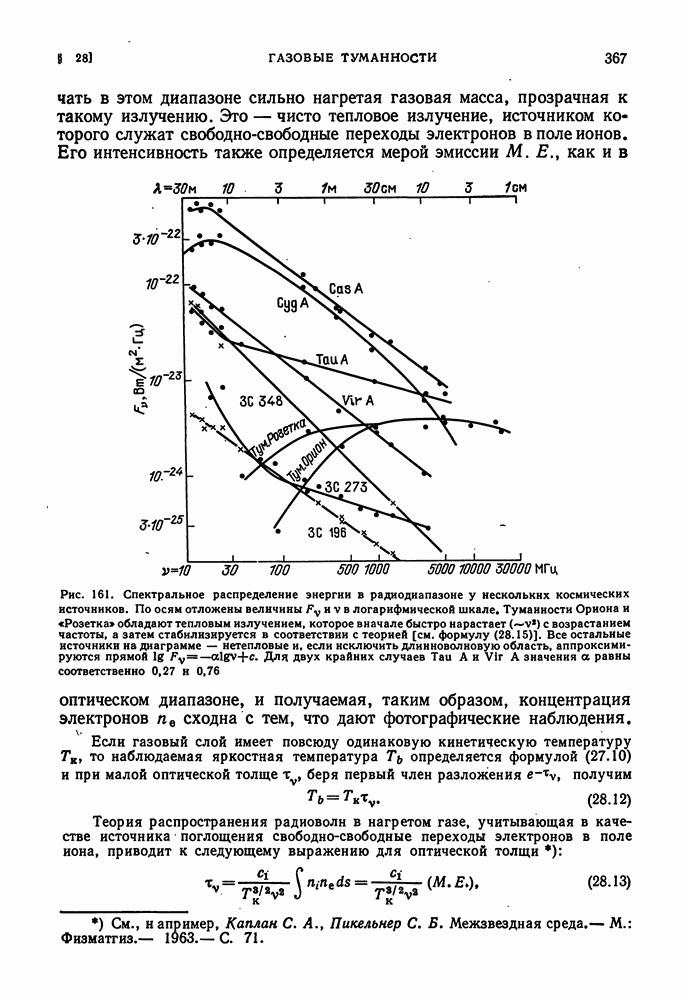
- РАДИОИЗЛУЧЕНИЕ ГАЗОВЫХ ТУМАННОСТЕЙ
- КРАБОВИДНАЯ ТУМАННОСТЬ — ИСТОЧНИК РАДИОИЗЛУЧЕНИЯ ТЕЛЕЦ А
- ТОРМОЗНОЕ ИЗЛУЧЕНИЕ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ КАК ИСТОЧНИК СВЕЧЕНИЯ КРАБОВИДНОЙ ТУМАННОСТИ
- КРАБОВИДНАЯ И НЕКОТОРЫЕ ДРУГИЕ ТУМАННОСТИ КАК ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ В ПУЛЬСАРАХ
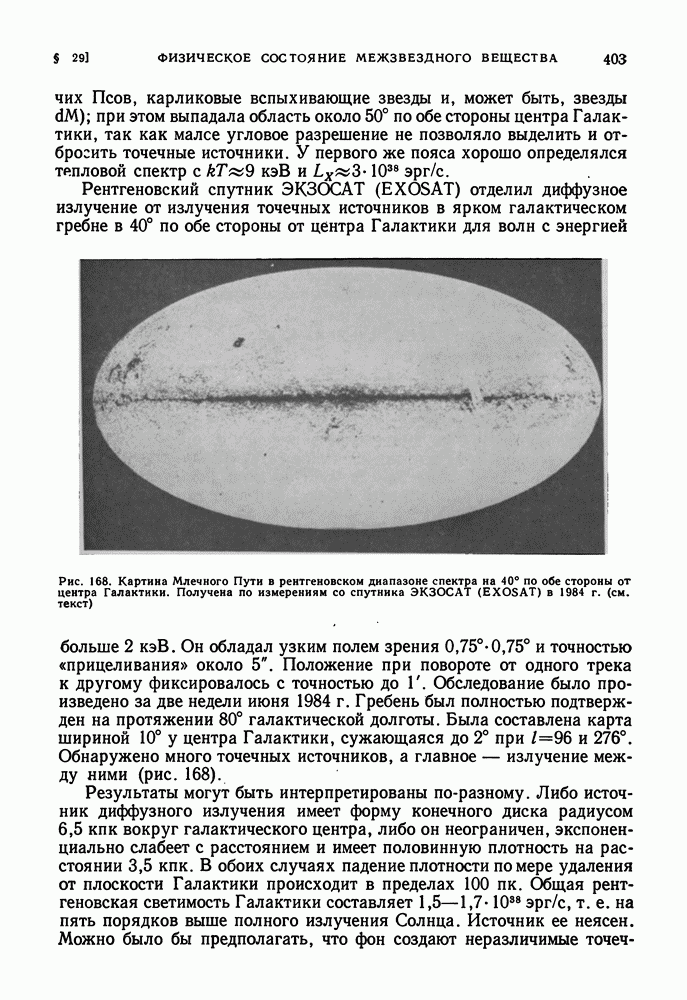
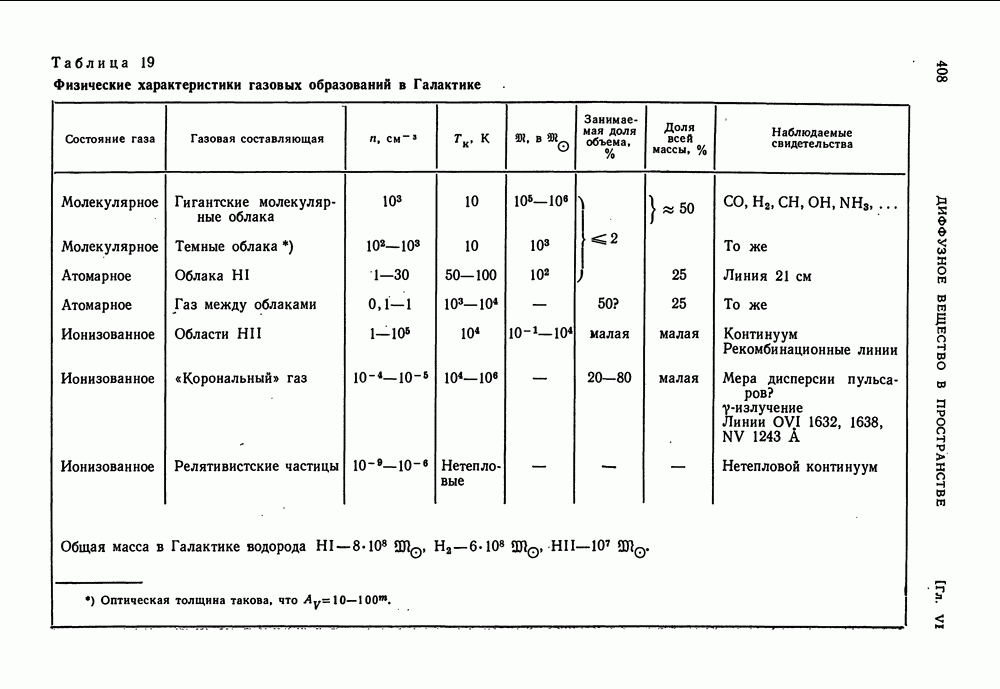
- § 29. ФИЗИЧЕСКОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА В ГАЛАКТИКЕ
- ТЕМПЕРАТУРА ТЕЛА, ПОМЕЩЕННОГО В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭНЕРГЕТИЧЕСКИЙ БАЛАНС У ЧАСТИЦ МЕЖЗВЕЗДНОЙ СРЕДЫ
- РАДИОИЗЛУЧЕНИЕ ИЗ МЕЖЗВЕЗДНОГО ПРОСТРАНСТВА ГАЛАКТИКИ
- КОСМИЧЕСКИЕ ЛУЧИ В ГАЛАКТИКЕ
- МАГНИТНЫЕ ПОЛЯ В ГАЛАКТИКЕ
- КОНДЕНСАЦИИ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА И ЗВЕЗДООБРАЗОВАНИЕ
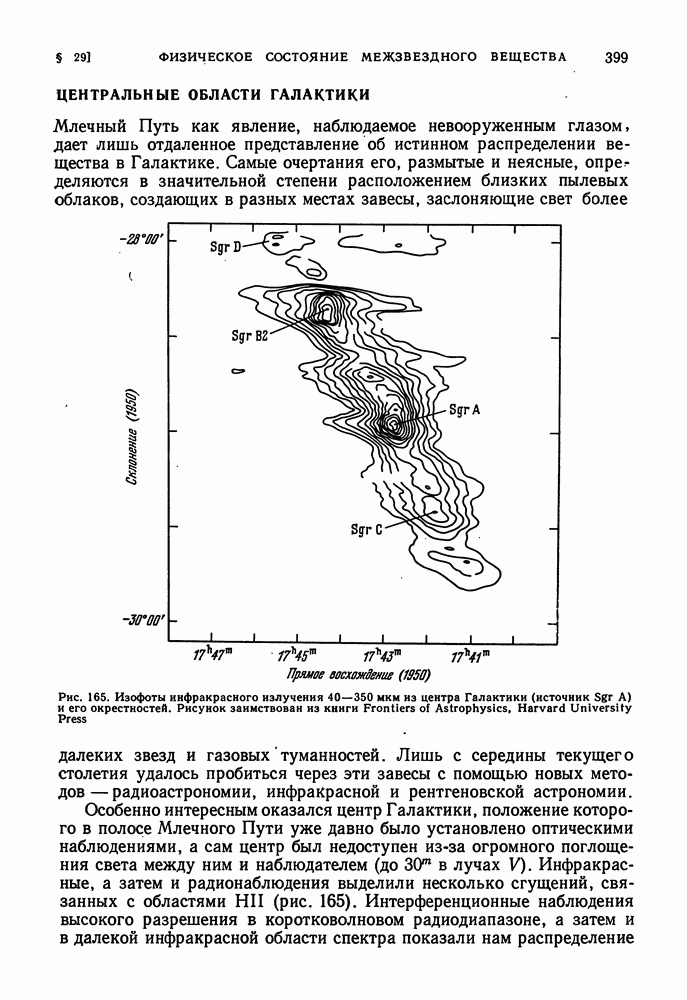
- ЦЕНТРАЛЬНЫЕ ОБЛАСТИ ГАЛАКТИКИ
- ОСОБЕННОСТИ РАСПОЛОЖЕНИЯ И ДВИЖЕНИЯ ГАЗОВЫХ МАСС В ГАЛАКТИКЕ
- МЕЖЗВЕЗДНЫЙ ГАЗ В ГАЛАКТИКЕ (РЕЗЮМЕ). АКТИВНОСТЬ ЯДРА ГАЛАКТИКИ
- ЗАДАЧИ К ГЛАВЕ VI
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VI
- ГЛАВА VII. ГАЛАКТИКИ И МЕТАГАЛАКТИКА
- § 30. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
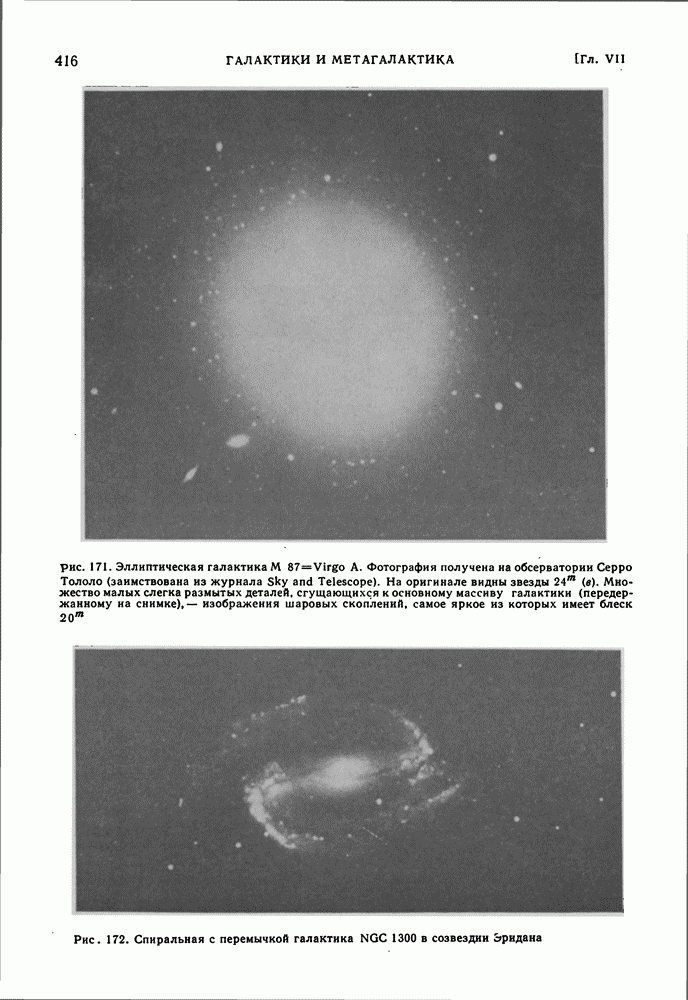
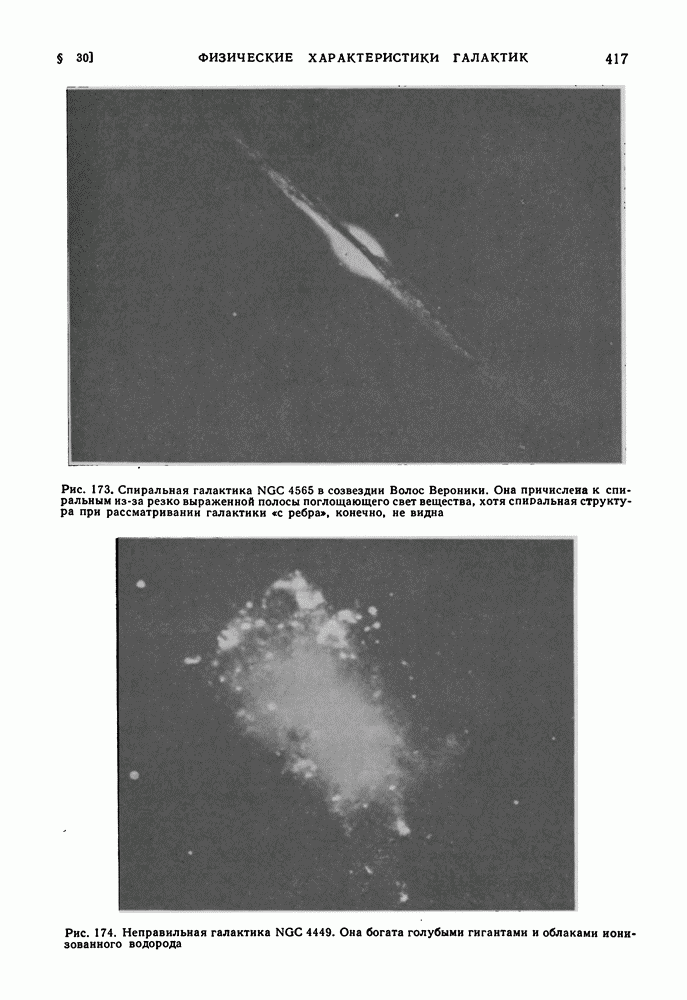
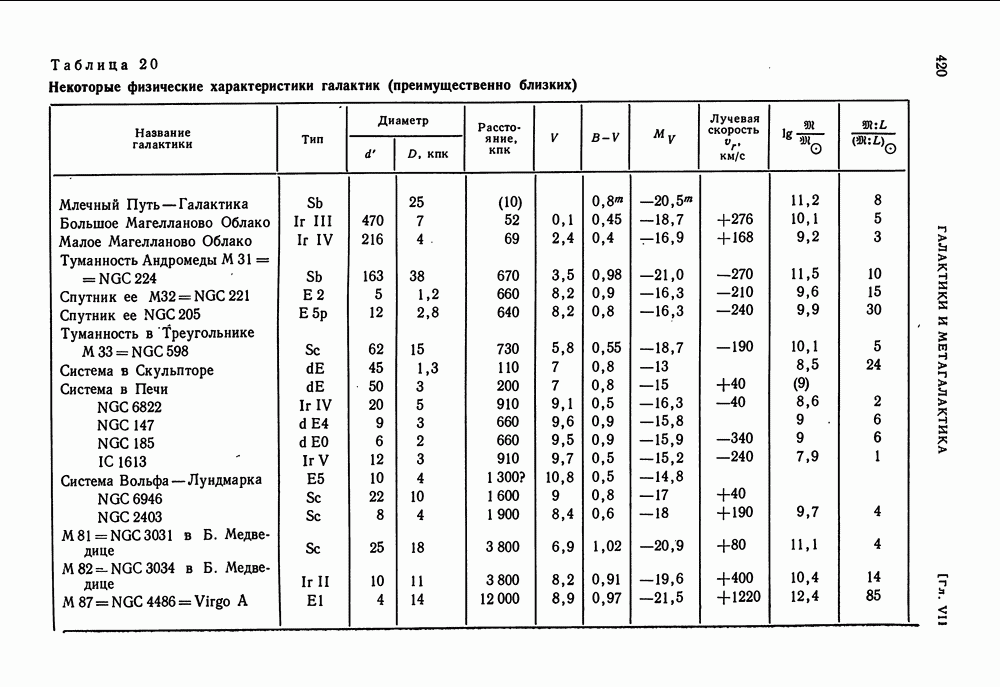
- КЛАССИФИКАЦИЯ ГАЛАКТИК- ОБЩИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
- ВРАЩЕНИЕ ГАЛАКТИК. ИХ МАССЫ
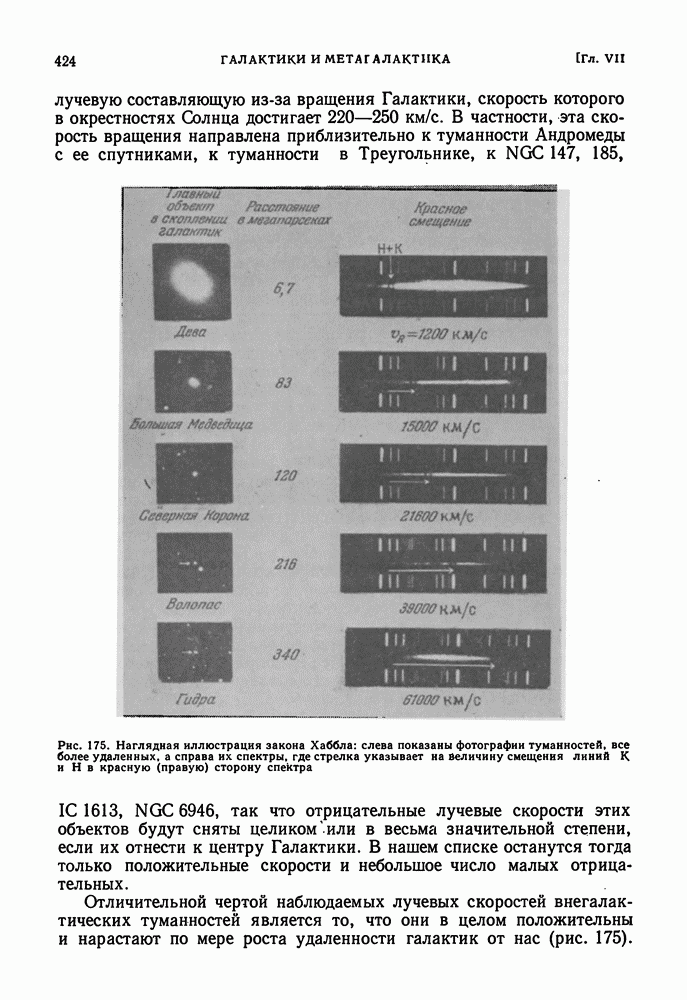
- КРАСНОЕ СМЕЩЕНИЕ В СПЕКТРАХ ГАЛАКТИК
- ЗАКОН ХАББЛА. ПОСТОЯННАЯ ХАББЛА
- СТРУКТУРА МЕТАГАЛАКТИКИ. СКОПЛЕНИЕ ГАЛАКТИК-ГРУППЫ ГАЛАКТИК
- ЗВЕЗДООБРАЗОВАНИЕ В ГАЛАКТИКАХ
- НЕВИДИМОЕ ВЕЩЕСТВО В ГАЛАКТИКАХ И ИХ СКОПЛЕНИЯХ
- § 31. РАДИОГАЛАКТИКИ И НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ В ГАЛАКТИКАХ
- РАДИОИЗЛУЧЕНИЕ НОРМАЛЬНЫХ ГАЛАКТИК
- РАДИОГАЛАКТИКИ
- ГАЛАКТИКИ СЕЙФЕРТА
- АКТИВНЫЕ ГАЛАКТИКИ И ПРИЗНАКИ ВЗРЫВА В НИХ
- КВАЗАРЫ И РОДСТВЕННЫЕ ИМ ОБЪЕКТЫ
- СПЕКТРАЛЬНЫЙ ИНДЕКС РАДИОИЗЛУЧЕНИЯ. ВОЗРАСТ РАДИОГАЛАКТИК
- ОБЩИЕ ЗАПАСЫ ЭНЕРГИИ В ГАЛАКТИКАХ
- § 32. ГАЛАКТИКИ И КОСМОЛОГИЯ
- ЗАДАЧИ К ГЛАВЕ VII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VII
- ГЛАВА VIII. СОЛНЕЧНАЯ СИСТЕМА. ПЛАНЕТЫ И ИХ СПУТНИКИ
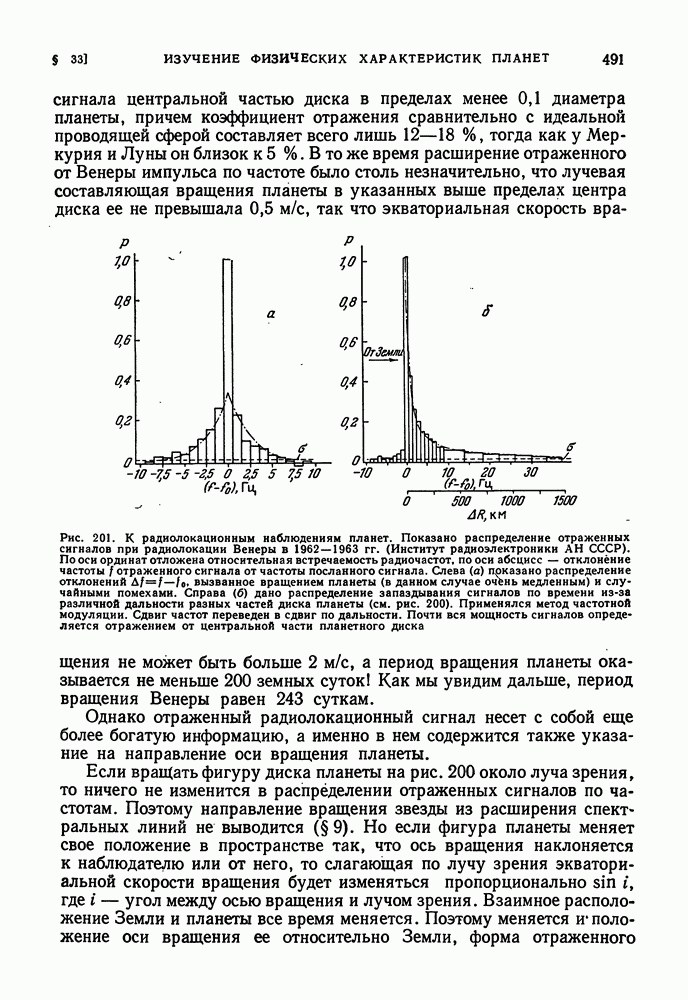
- § 33. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ПЛАНЕТ
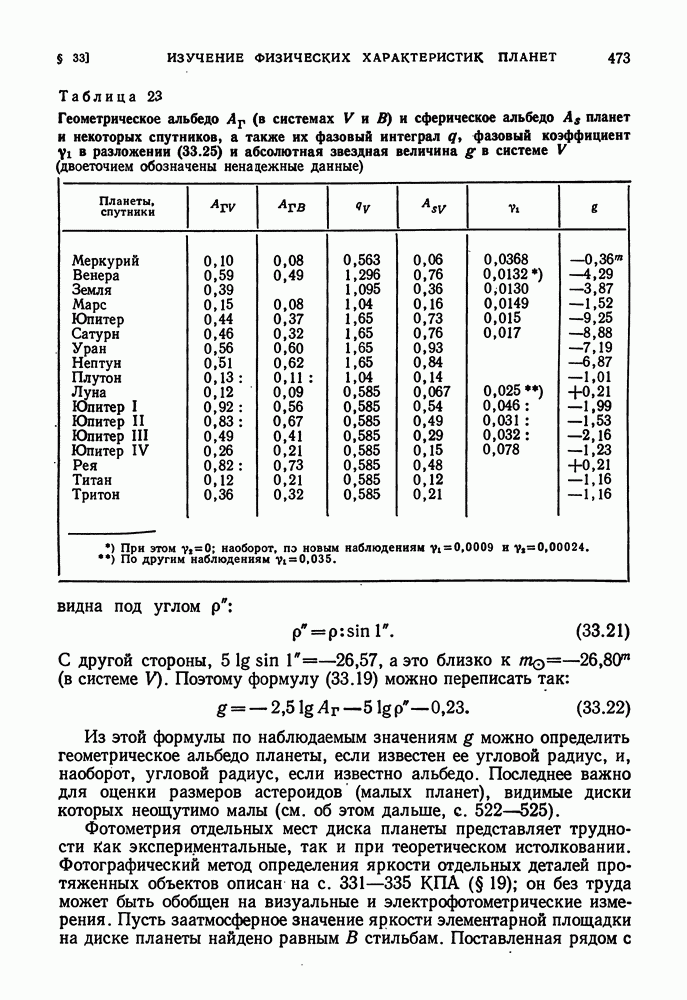
- ФОТОМЕТРИЧЕСКИЙ АНАЛИЗ ПЛАНЕТНЫХ ПОВЕРХНОСТЕЙ И АТМОСФЕРЫ
- ПОЛЯРИМЕТРИЯ ПЛАНЕТ
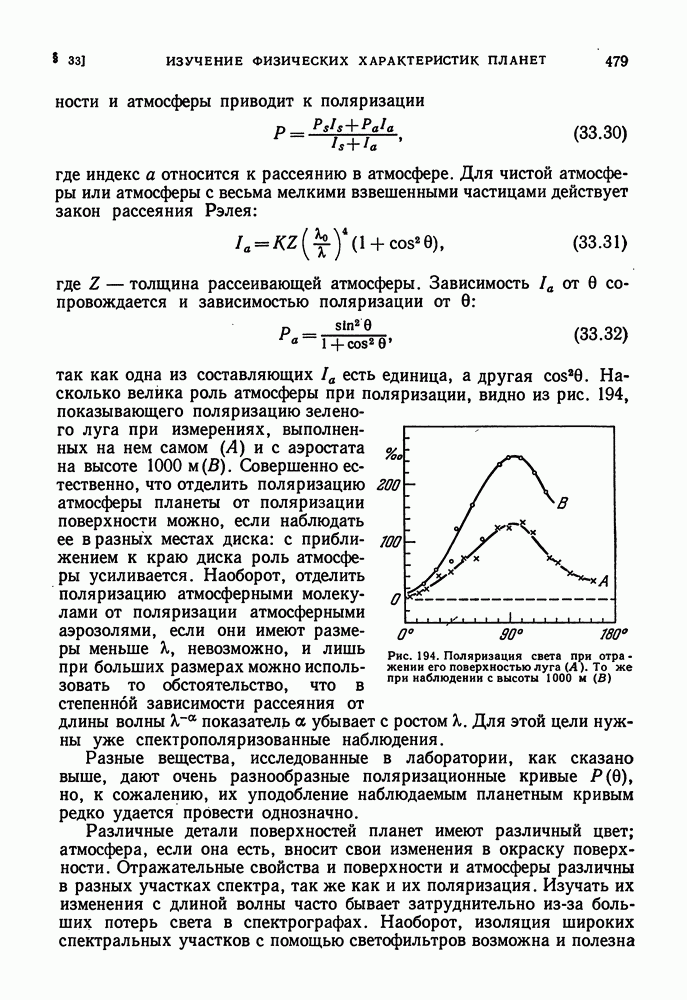
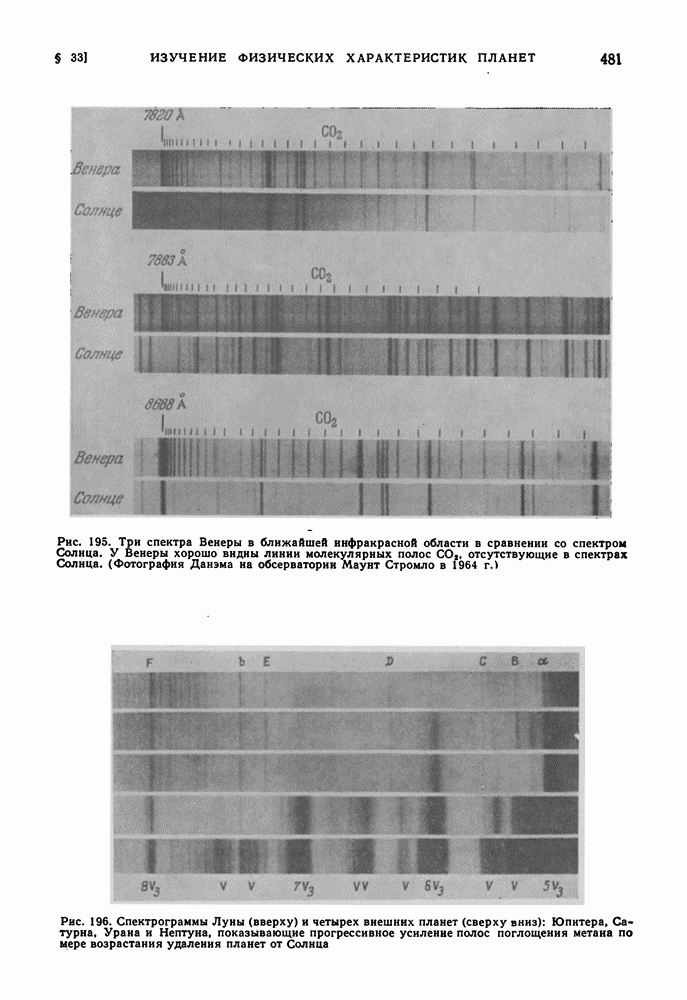
- СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЛАНЕТНЫХ АТМОСФЕР
- СПЕКТРАЛЬНОЕ ОПРЕДЕЛЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ
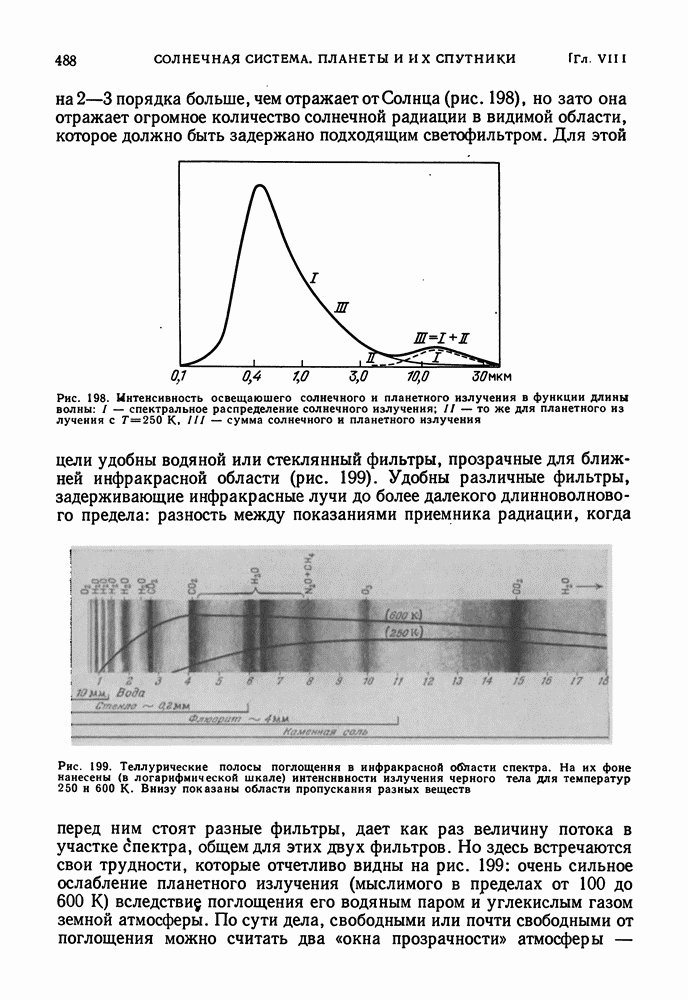
- ПЛАНЕТНЫЕ ТЕМПЕРАТУРЫ. ТЕОРИЯ. РОЛЬ АТМОСФЕРЫ
- РАЗЛИЧНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЛАНЕТНЫХ ТЕМПЕРАТУР
- РАДИОЛОКАЦИОННЫЕ МЕТОДЫ ИЗУЧЕНИЯ ПЛАНЕТ
- УСТОЙЧИВОСТЬ ПЛАНЕТНЫХ АТМОСФЕР ВО ВРЕМЕНИ
- § 34. ПЛАНЕТЫ ЗЕМНОЙ ГРУППЫ
- МЕРКУРИЙ
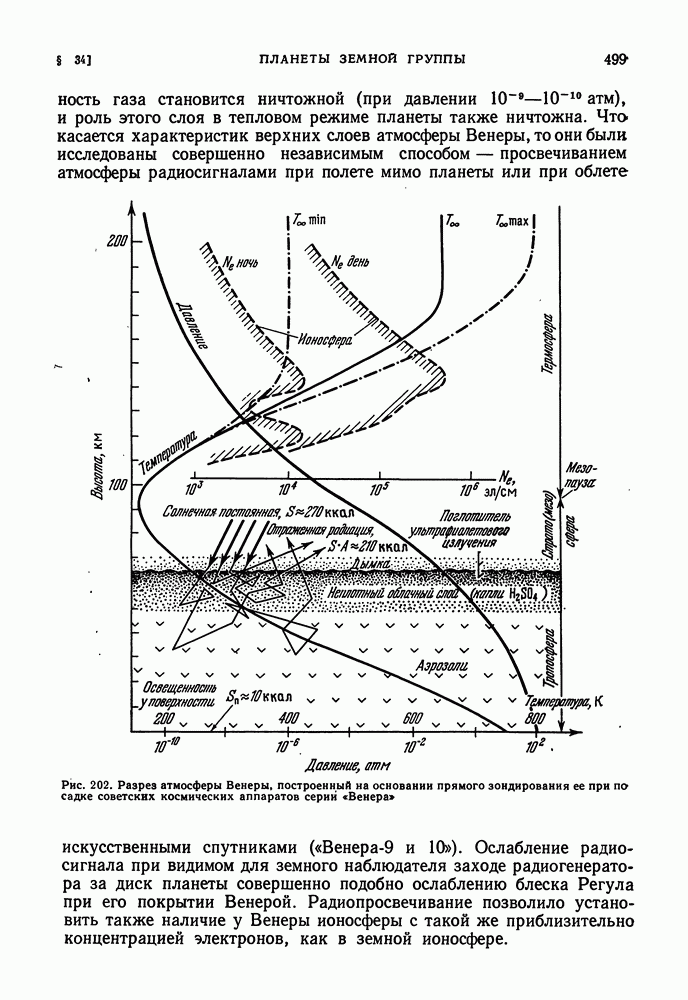
- ВЕНЕРА. ТЕМПЕРАТУРА. ПАРНИКОВАЯ МОДЕЛЬ АТМОСФЕРЫ. ВРАЩЕНИЕ
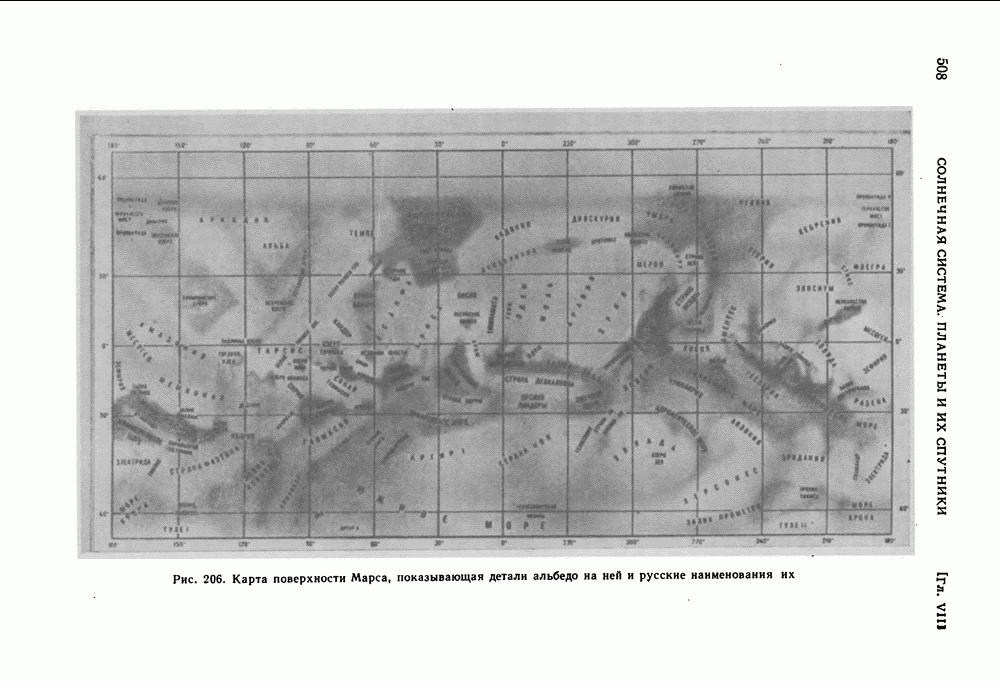
- МАРС. ОСОБЕННОСТИ ЕГО ПОВЕРХНОСТИ. ИХ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ
- АТМОСФЕРА МАРСА
- ТЕМПЕРАТУРА МАРСА
- ВОДА НА МАРСЕ. ЖИЗНЬ НА МАРСЕ?
- МАЛЫЕ ПЛАНЕТЫ
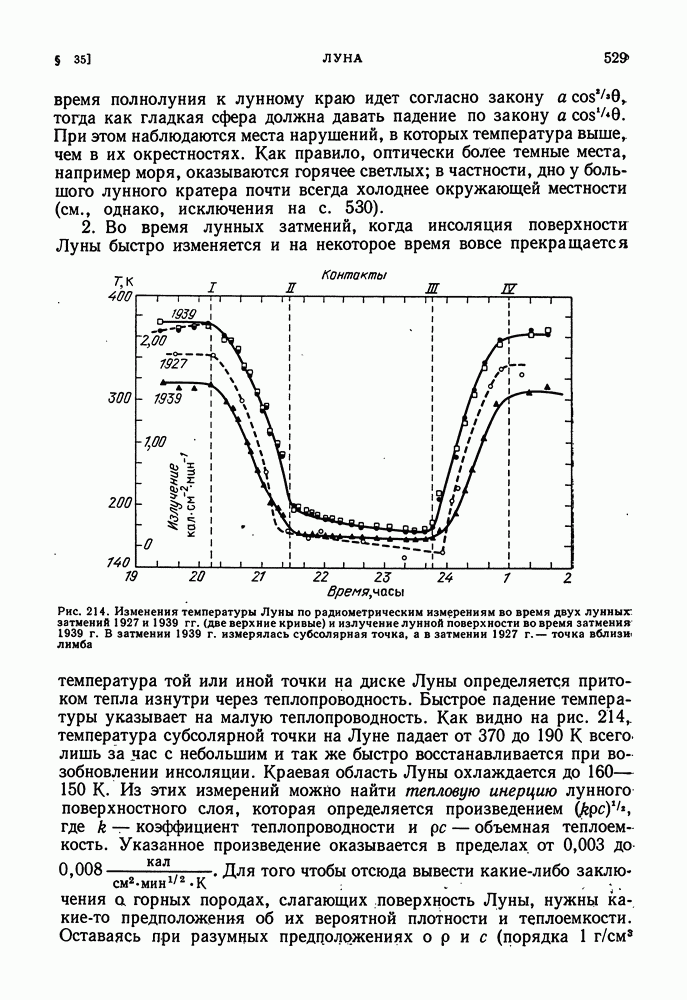
- § 35. ЛУНА
- АТМОСФЕРА ЛУНЫ
- ТЕМПЕРАТУРНЫЙ РЕЖИМ НА ЛУНЕ
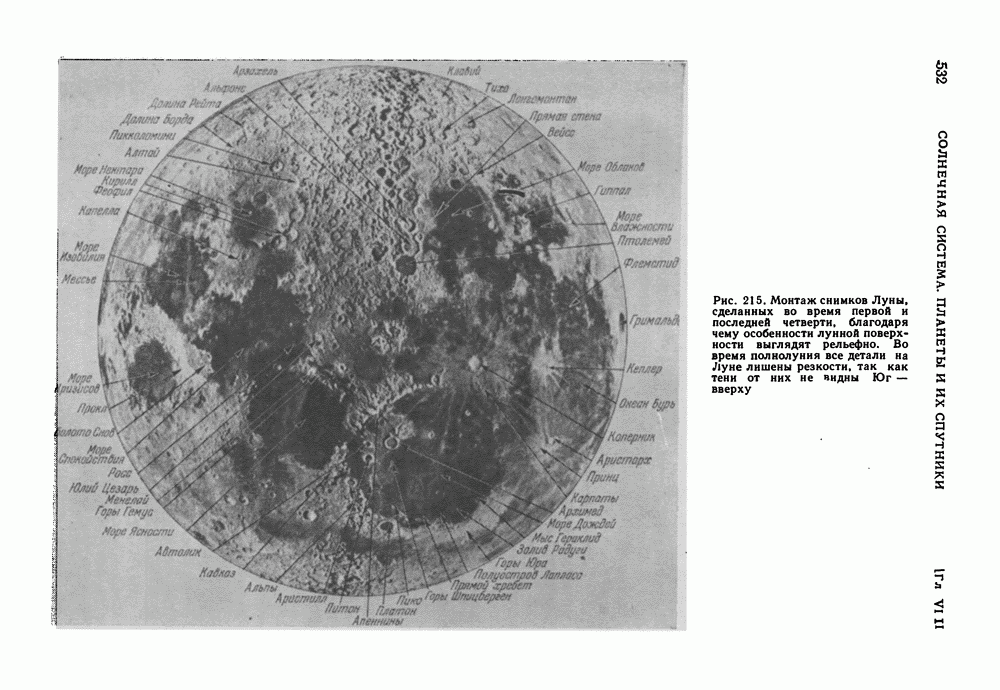
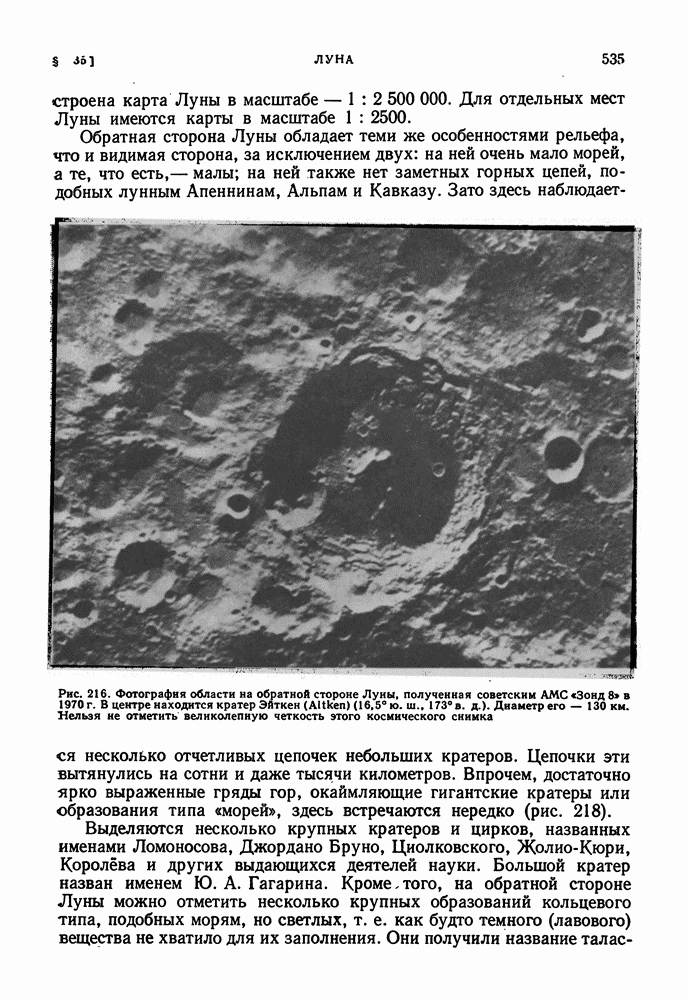
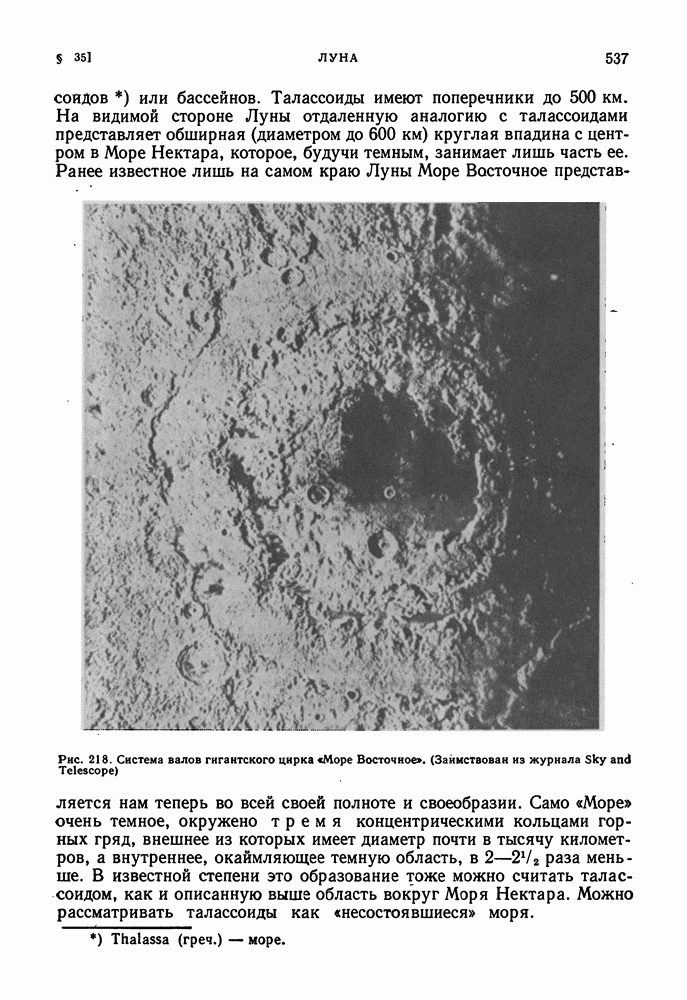
- МОРФОЛОГИЯ ЛУННОЙ ПОВЕРХНОСТИ
- ВНУТРЕННЕЕ СТРОЕНИЕ ЛУНЫ
- ОБРАЗОВАНИЕ СОВРЕМЕННОГО ЛУННОГО ЛАНДШАФТА
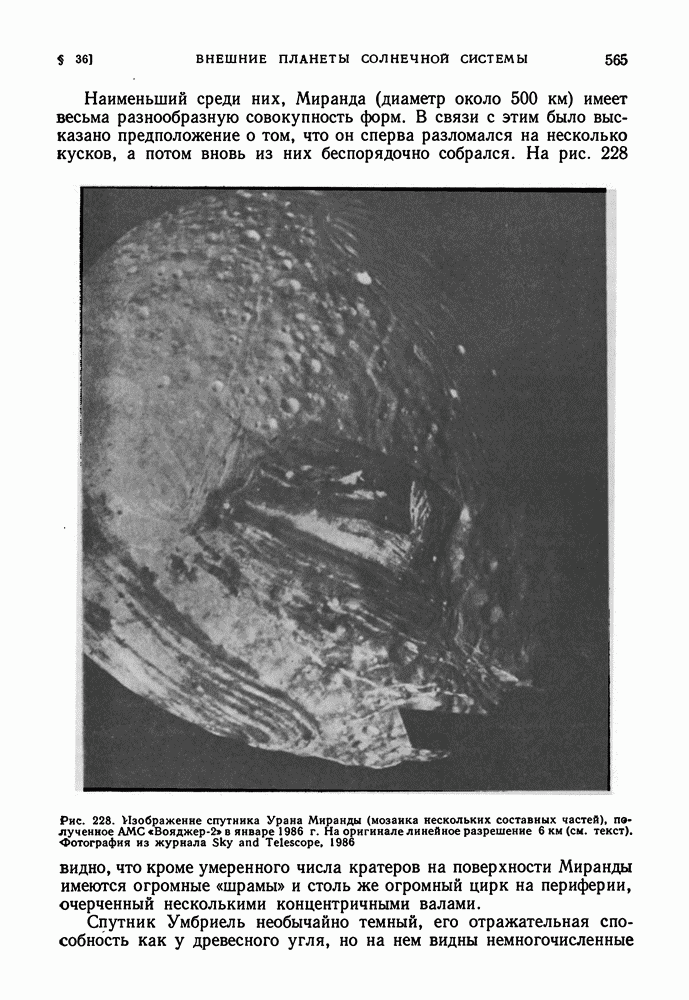
- § 36. ВНЕШНИЕ ПЛАНЕТЫ СОЛНЕЧНОЙ СИСТЕМЫ
- ЮПИТЕР
- САТУРН
- УРАН И НЕПТУН
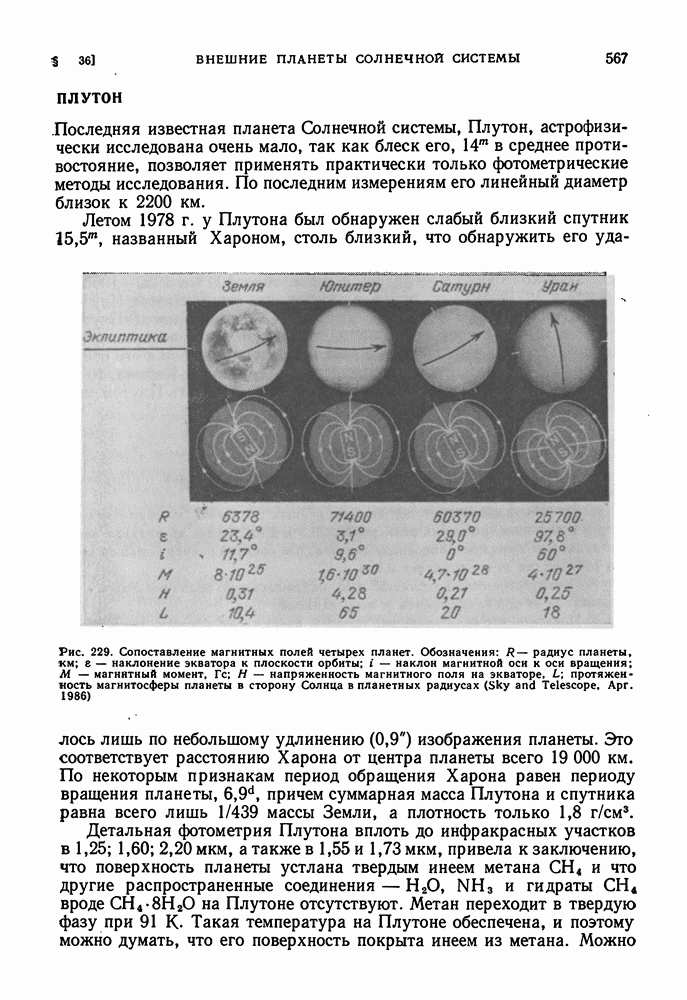
- ПЛУТОН
- ЗАДАЧИ К ГЛАВЕ VIII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VIII
- ГЛАВА IX. СОЛНЕЧНАЯ СИСТЕМА. КОМЕТЫ И МАЛЫЕ ТЕЛА СОЛНЕЧНОЙ СИСТЕМЫ
- ОБЩАЯ ХАРАКТЕРИСТИКА КОМЕТ
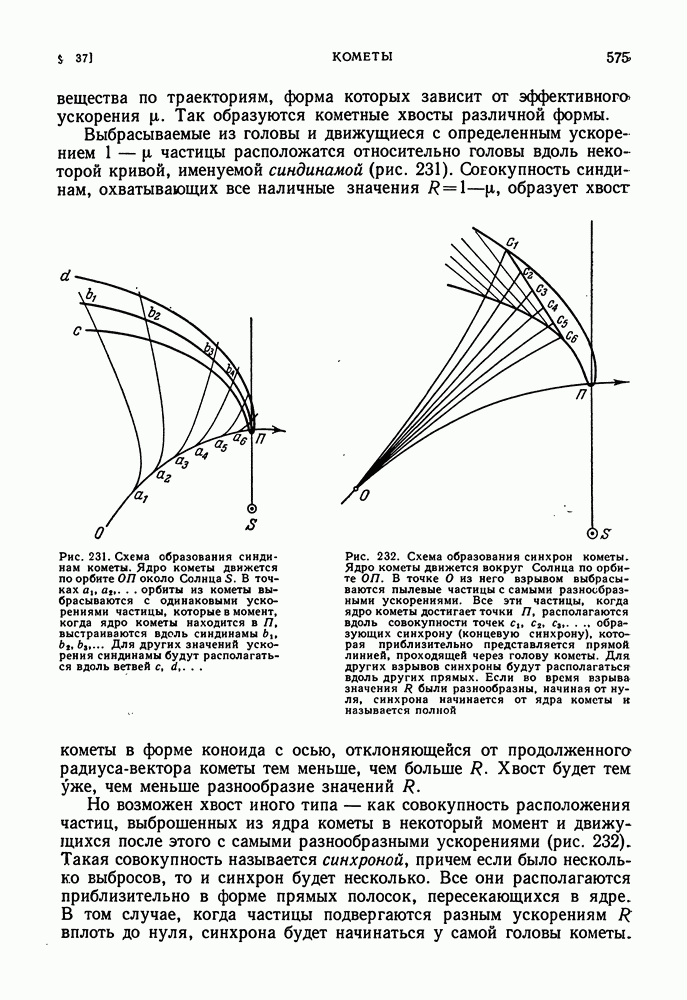
- ОБРАЗОВАНИЕ КОМЕТНЫХ ФОРМ
- МЕХАНИЧЕСКАЯ ТЕОРИЯ КОМЕТНЫХ ФОРМ
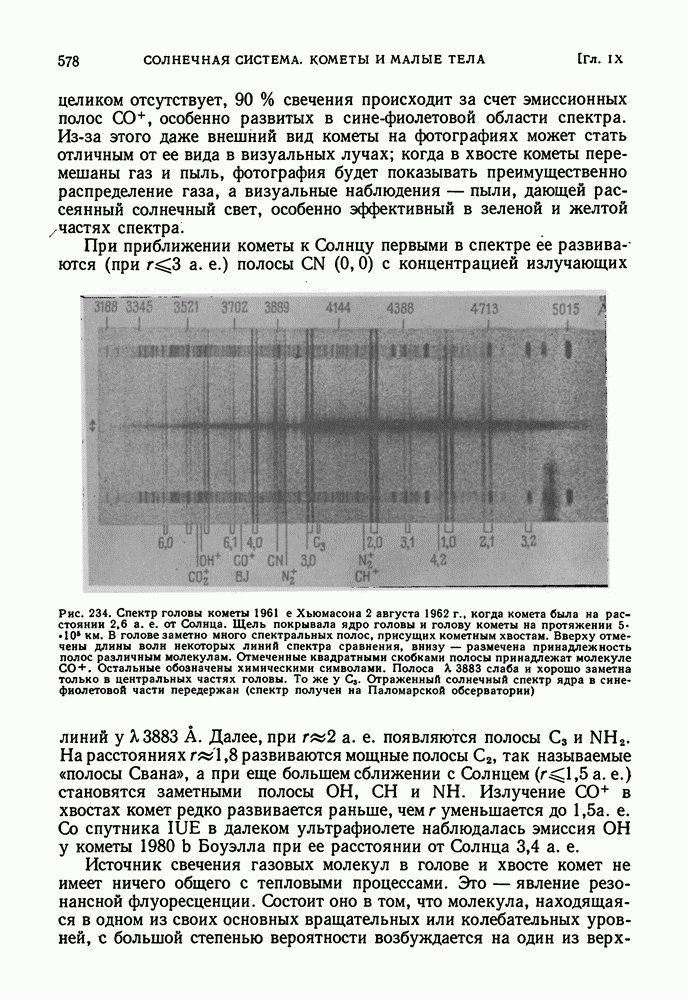
- СПЕКТРЫ КОМЕТ
- БЛЕСК КОМЕТЫ И ЕГО ИЗМЕНЕНИЯ
- ДАВЛЕНИЕ СВЕТА НА КОМЕТНЫЕ ЧАСТИЦЫ
- СОЛНЕЧНАЯ АКТИВНОСТЬ КАК ИСТОЧНИК ВОЗНИКНОВЕНИЯ КОМЕТНЫХ ФОРМ
- РАСПАД КОМЕТ. ПРОИСХОЖДЕНИЕ КОМЕТ
- КОМЕТА ГАЛЛЕЯ В 1986 г.
- § 38. МЕТЕОРЫ
- ОБЩИЕ ХАРАКТЕРИСТИКИ МЕТЕОРОВ. СПОСОБЫ ИХ НАБЛЮДЕНИЯ
- МЕТЕОРНЫЕ ПОТОКИ И СПОРАДИЧЕСКИЕ МЕТЕОРЫ
- ЯВЛЕНИЯ ПРИ ВТОРЖЕНИИ МЕТЕОРНОГО ТЕЛА В ЗЕМНУЮ АТМОСФЕРУ
- РАДИОЛОКАЦИОННЫЕ НАБЛЮДЕНИЯ МЕТЕОРОВ
- МАССЫ МЕТЕОРНЫХ ТЕЛ
- МЕТЕОРИТЫ И ИХ КЛАССИФИКАЦИЯ
- ВОЗРАСТ МЕТЕОРИТОВ
- МЕТЕОРИТНЫЕ КРАТЕРЫ И ВОРОНКИ
- ТУНГУССКИЙ МЕТЕОРИТ
- § 39. МЕТЕОРНОЕ И ПЫЛЕВОЕ ВЕЩЕСТВО В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- МЕТЕОРНЫЕ РОИ И СВЯЗЬ ИХ С КОМЕТАМИ
- МИКРОМЕТЕОРИТЫ
- МЕТЕОРНОЕ ВЕЩЕСТВО ВОКРУГ ЗЕМЛИ
- ЗОДИАКАЛЬНЫЙ СВЕТ
- ПЫЛЕВАЯ И ГАЗОВАЯ СОСТАВЛЯЮЩИЕ В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- ДВИЖЕНИЕ МАЛОЙ ЧАСТИЦЫ В ПОЛЕ ТЯГОТЕНИЯ И ИЗЛУЧЕНИЯ СОЛНЦА
- ПРОТИВОСИЯНИЕ
- ЗАДАЧИ К ГЛАВЕ IX