| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 33. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ПЛАНЕТ
ФОТОМЕТРИЧЕСКИЙ АНАЛИЗ ПЛАНЕТНЫХ ПОВЕРХНОСТЕЙ И АТМОСФЕРЫ
Широкую характеристику планеты дают фотометрические наблюдения. Даже качественные наблюдения этого рода позволяют судить, например, о наличии или отсутствииатмосферы планеты.
Так, если отвлечься от очень тонких эффектов, на Луне все детали, как в центре диска, так и на краю его, всегда видны одинаково четко и резко. Наоборот, на Марсе часто бывают затуманены, порой до полной невидимости, хорошо известные детали поверхности планеты. На самом краю его диска детали вообще не видны и диск имеет большую яркость в центре, чем на периферии. Все это — явные свидетельства в пользу существования на Марсе атмосферы: мы рассматриваем поверхность планеты на краю планетного диска под очень косым углом и сквозь значительную толщу атмосферы. Сказанное подтверждается и при наблюдениях покрытий звезд. Когда диск Луны при ее движении среди неподвижных звезд надвигается и закрывает ту или другую из них, блеск звезды нисколько не ослабевает до последнего момента мгновенного исчезновения за лунным краем. Наоборот, у Марса (так же, как у Венеры, Юпитера, Сатурна) звезда задолго до геометрического покрытия начинает «угасать», так как при этом ее свет достигает нас после того как прошел через планетную атмосферу (см. об этом подробнее дальше, с. 497).
Для того чтобы качественное высказывание («есть», «нет» атмосферы) заменить количественным — о плотности атмосферы и ее простирании, — необходимы фотометрические измерения. Простейшими являются измерения общего блеска планеты с оценкой отношения отраженного и падающего на планету света. Как известно (КПА 193), это отношение называется альбедо. Альбедо ортотропной поверхности (КПА 192) теоретически и практически определяется очень просто, но применение этого понятия к сферическому телу планеты, освещаемой Солнцем сбоку, оказывается трудным и неудобным. Более удобно понятие сферического альбедо, к рассмотрению которого мы сейчас и перейдем.
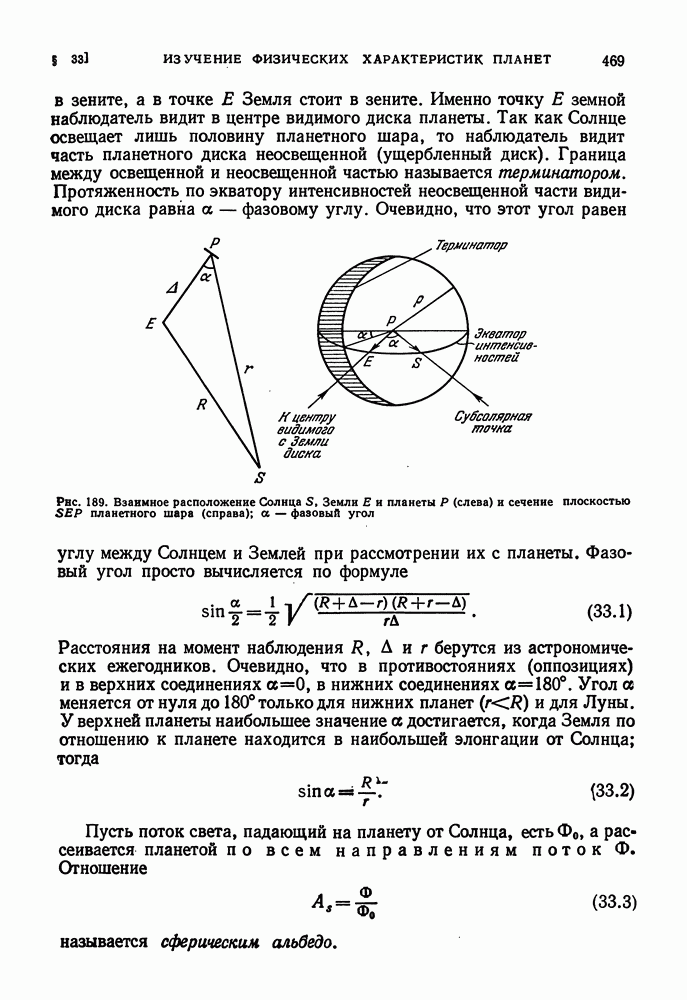
Будем для простоты считать фигуру планеты сферической. Пусть расположение Солнца S, планеты  Земли Е будет таким, как показано на рис. 189 слева. Здесь А — геоцентрическое расстояние планеты, r — ее гелиоцентрическое расстояние и R — гелиоцентрическое расстояние Земли. Плоскость PSE пересекается с поверхностью планетного шара по большому кругу, именуемому экватором интенсивности.
Земли Е будет таким, как показано на рис. 189 слева. Здесь А — геоцентрическое расстояние планеты, r — ее гелиоцентрическое расстояние и R — гелиоцентрическое расстояние Земли. Плоскость PSE пересекается с поверхностью планетного шара по большому кругу, именуемому экватором интенсивности.
В точке S — субсолярной (подсолнечной) точке — Солнце стоит в зените, а в точке Е Земля стоит в зените. Именно точку Е земной наблюдатель видит в центре видимого диска планеты. Так как Солнце освещает лишь половину планетного шара, то наблюдатель видит часть планетного диска неосвещенной (ущербленный диск). Граница между освещенной и неосвещенной частью называется терминатором. Протяженность по экватору интенсивностей неосвещенной части видимого диска равна а — фазовому углу.

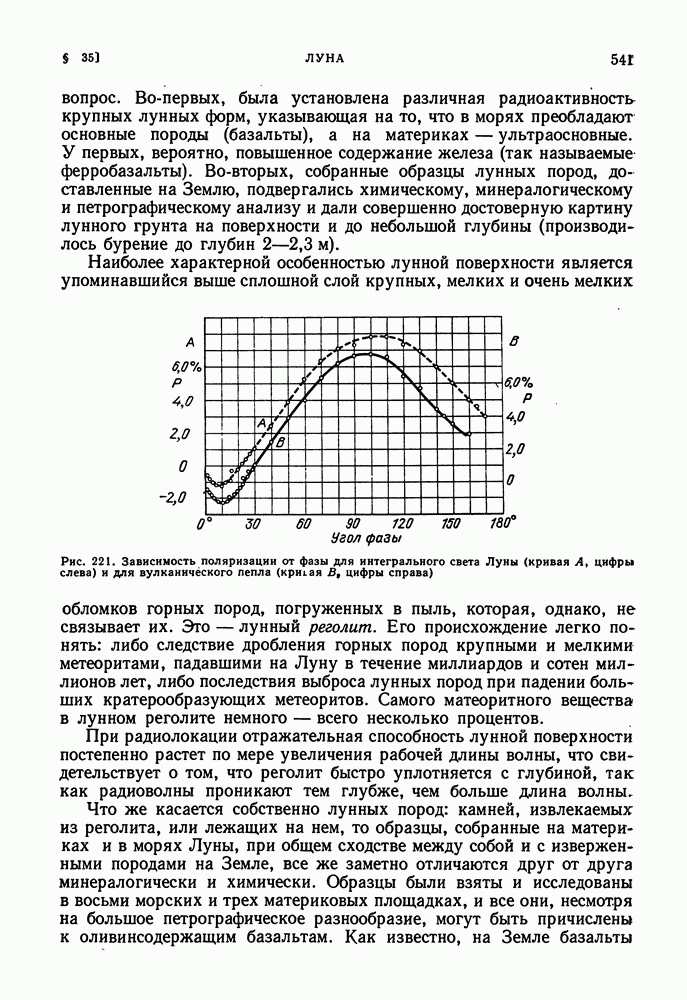
Рис. 189. Взаимное расположение Солнца S. Земли Е и планеты Р (слева) и сеченне плоскостью SEP планетного шара (справа); а — фазовый угол
Очевидно, что этот угол равен углу между Солнцем и Землей при рассмотрении их с планеты. Фазовый угол просто вычисляется по формуле

Расстояния на момент наблюдения  берутся из астрономических ежегодников. Очевидно, что в противостояниях (оппозициях) и в верхних соединениях а=0, в нижних соединениях а=180°. Угол а меняется от нуля до 180° только для нижних планет
берутся из астрономических ежегодников. Очевидно, что в противостояниях (оппозициях) и в верхних соединениях а=0, в нижних соединениях а=180°. Угол а меняется от нуля до 180° только для нижних планет  и для Луны. У верхней планеты наибольшее значение а достигается, когда Земля по отношению к планете находится в наибольшей элонгации от Солнца; тогда
и для Луны. У верхней планеты наибольшее значение а достигается, когда Земля по отношению к планете находится в наибольшей элонгации от Солнца; тогда

Пусть поток света, падающий на планету от Солнца, есть  , а рассеивается планетой по всем направлениям поток Ф. Отношение
, а рассеивается планетой по всем направлениям поток Ф. Отношение

называется сферическим альбедо.
Пусть  — внеатмосферная освещенность Земли Солнцем при
— внеатмосферная освещенность Земли Солнцем при  (
( ; см. КПА 196). Тогда освещенность Солнцем планеты будет в
; см. КПА 196). Тогда освещенность Солнцем планеты будет в  раз меньше (
раз меньше ( как и
как и  , выражают в тех же единицах, что и R). Если р — радиус планеты (выраженный в сантиметрах), то площадь диска ее есть
, выражают в тех же единицах, что и R). Если р — радиус планеты (выраженный в сантиметрах), то площадь диска ее есть  и, следовательно, весь поток, падающий на планету, равен
и, следовательно, весь поток, падающий на планету, равен


Рис. 190. К расчету освещения планеты Солнцем
Внеатмосферная освещенность Земли планетой равна L. Согласно формуле (10.8) КПА сила света планеты есть

Построим у центра планеты конус с осью, направленной на Солнце и с полууглом растворения а, а затем такой же конус с полууглом  (рис. 190). Пространство между этими конусами определит нам элементарный телесный угол
(рис. 190). Пространство между этими конусами определит нам элементарный телесный угол

Элементарный поток в этом телесном угле есть

Чтобы подставить сюда значение  , заметим, что в выражении (33.5) величину L можно представить себе с помощью (33.4) как
, заметим, что в выражении (33.5) величину L можно представить себе с помощью (33.4) как

где Г — коэффициент пропорциональности, устанавливающий, какую долю падающего потока планета рассеивает по физическим причинам, а  учитывает геометрические причины, связанные с изменением светящей в сторону Земли освещенной площади планеты. Функция
учитывает геометрические причины, связанные с изменением светящей в сторону Земли освещенной площади планеты. Функция  называется фазовой функцией планеты. Теперь мы можем написать
называется фазовой функцией планеты. Теперь мы можем написать

Подставив (33.9 и (33.6) в (33.7), найдем после интегрирования
 (33.10)
(33.10)
и поэтому сферическое альбедо равно
 (33.11)
(33.11)
Фактор  называют геометрическим альбедо:
называют геометрическим альбедо:
 (33.12)
(33.12)
 есть отношение действительного блеска планеты при
есть отношение действительного блеска планеты при  к блеску абсолютно белого диска того же радиуса и расположенного на том же расстоянии, перпендикулярно к солнечным лучам, а множитель
к блеску абсолютно белого диска того же радиуса и расположенного на том же расстоянии, перпендикулярно к солнечным лучам, а множитель
 (33.13)
(33.13)
называется фазовым интегралом. Итак,
 (33.14)
(33.14)
Величину  легко определяют из наблюдений планеты во время противостояний или верхних соединений, когда а=0 и принимают
легко определяют из наблюдений планеты во время противостояний или верхних соединений, когда а=0 и принимают  . Тогда по (33.8)
. Тогда по (33.8)
 (33.15)
(33.15)
и, следовательно,

Здесь дробь  есть угловой радиус планеты, выраженный в радианах; его можно заменить через
есть угловой радиус планеты, выраженный в радианах; его можно заменить через  . Радиус
. Радиус  диска планеты, выраженный в секундах дуги, дается в Ежегодниках, как и r (в астрономических единицах). Пусть звездная величина
диска планеты, выраженный в секундах дуги, дается в Ежегодниках, как и r (в астрономических единицах). Пусть звездная величина  планеты в оппозиции (в верхнем соединении) измерена. Та же величина для Солнца есть
планеты в оппозиции (в верхнем соединении) измерена. Та же величина для Солнца есть  . Логарифмируя (33.16), найдем
. Логарифмируя (33.16), найдем
 (33.17)
(33.17)
Что касается фазового интеграла, то его нетрудно найти, наблюдая планету при разных значениях фазового угла а. Действительно, прологарифмировав обе части формулы (33.8) и умножив их на — 2,5, слева получим та (планеты) плюс константа, а справа  дает нам
дает нам  + константа (та же). Таким образом, при фазе
+ константа (та же). Таким образом, при фазе  блеск планеты
блеск планеты
 (33.18)
(33.18)
Выделим отсюда величину
 (33.19)
(33.19)
которая представляет собой звездную величину планеты при  . Величина g называется абсолютной звездной величиной планеты. В последнее время ее чаще об означают V(1,0) или В (1,0), если она относится к фотографическим определениям. После того как
. Величина g называется абсолютной звездной величиной планеты. В последнее время ее чаще об означают V(1,0) или В (1,0), если она относится к фотографическим определениям. После того как  найдено из наблюдений в оппозицию, g может быть вычислено, и при измеренном
найдено из наблюдений в оппозицию, g может быть вычислено, и при измеренном  можно найти
можно найти  с помощью формулы (33.18).
с помощью формулы (33.18).
Для нижней планеты и Луны таким образом можно определить значения  для ряда значений
для ряда значений  , после чего вычислить фазовый интеграл q. Для внешних планет это сделать труднее, так как для них, в соответствии с (33.2), а не превосходит 48° у Mapca, 11° у Юпитера, а у Сатурна и последующих планет еще меньше. Рессел из наблюдений нижних планет нашел, что довольно точно соблюдается равенство
, после чего вычислить фазовый интеграл q. Для внешних планет это сделать труднее, так как для них, в соответствии с (33.2), а не превосходит 48° у Mapca, 11° у Юпитера, а у Сатурна и последующих планет еще меньше. Рессел из наблюдений нижних планет нашел, что довольно точно соблюдается равенство
 (33.20)
(33.20)
Этой эмпирической формулой можно воспользоваться в случае Марса, но для всех более удаленных планет значения  приходится экстраполировать до значения
приходится экстраполировать до значения  , т. е. очень далеко от наблюдаемых значений
, т. е. очень далеко от наблюдаемых значений  .
.
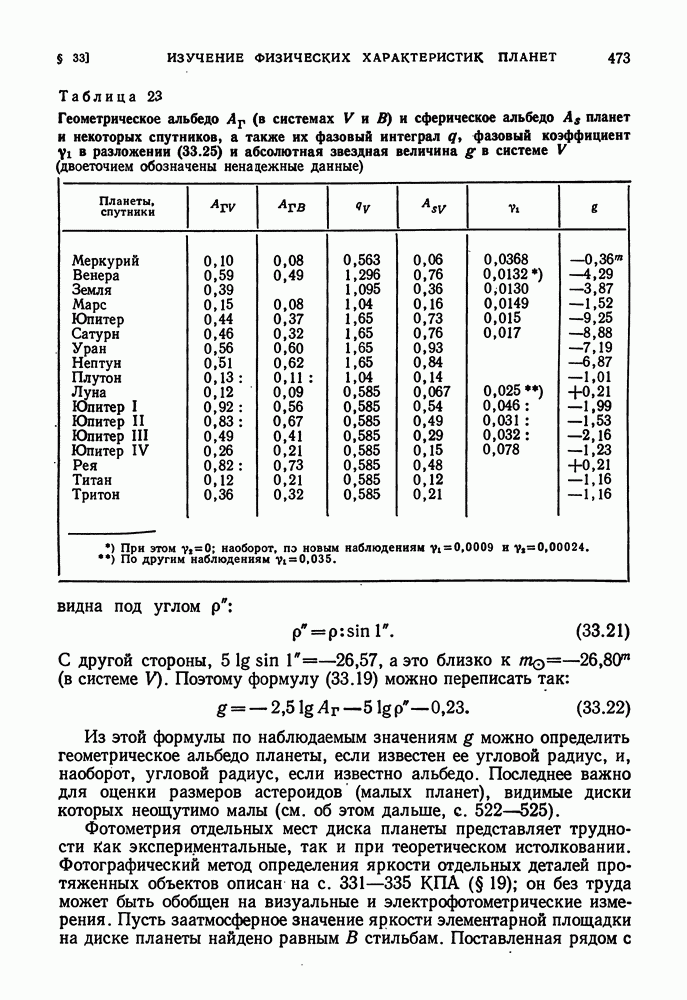
Сводка значений геометрического и сферического альбедо для планет и некоторых спутников (у которых можно определить  приведена в таблице 23.
приведена в таблице 23.
Заметим себе, что геометрическое альбедо у шара с идеально белой ортотропной поверхностью (КПА 192) равно 2/3 (так как периферические части диска освещаются под очень косым углом). Если планета светит только отраженным светом, то, очевидно,  не может быть больше этого значения, что и подтверждается таблицей 23, за исключением одного случая, где очень высокое значение r У двух спутников Юпитера и спутника Сатурна Реи не очень надежно и нуждается в подтверждении. Значения фазового интеграла q для четырех планет-гигантов приняты равными 1,65; может быть, это значение слегка завышено. Наоборот, значение
не может быть больше этого значения, что и подтверждается таблицей 23, за исключением одного случая, где очень высокое значение r У двух спутников Юпитера и спутника Сатурна Реи не очень надежно и нуждается в подтверждении. Значения фазового интеграла q для четырех планет-гигантов приняты равными 1,65; может быть, это значение слегка завышено. Наоборот, значение  , уверенно выведенное из наблюдений Луны, распространено на другие спутники, вероятно, не всегда с достаточным основанием; в частности, у Титана q может быть вдвое большим.
, уверенно выведенное из наблюдений Луны, распространено на другие спутники, вероятно, не всегда с достаточным основанием; в частности, у Титана q может быть вдвое большим.
Альбедо Земли получено из наблюдений пепельного света Луны. Сравнение яркости дневной и ночной сторон Луны дает возможность сразу сравнить блеск Земли с блеском Солнца  , так как пепельный свет Луны есть рассеянный лунной поверхностью свет освещающей ее Земли. Значение
, так как пепельный свет Луны есть рассеянный лунной поверхностью свет освещающей ее Земли. Значение  у Земли очень сильно зависит от облачности на ней и может возрасти на 50% и больше в те сезоны, когда значительная часть поверхности Земли покрыта облаками.
у Земли очень сильно зависит от облачности на ней и может возрасти на 50% и больше в те сезоны, когда значительная часть поверхности Земли покрыта облаками.
Конечно, альбедо сильно зависит от длины волны падающего света из-за цветовых различий на поверхности планеты и из-за различной способности планетной атмосферы поглощать и рассеивать свет разных длин волн. Так, например, у Марса  меняется от 0,047 при
меняется от 0,047 при  нм до 0,30 при
нм до 0,30 при  . Наоборот, у Урана и Нептуна альбедо резко падает от голубой к инфракрасной области спектра. Это результат сильного поглощения света молекулами метана
. Наоборот, у Урана и Нептуна альбедо резко падает от голубой к инфракрасной области спектра. Это результат сильного поглощения света молекулами метана  , обильного в атмосферах названных планет.
, обильного в атмосферах названных планет.
Если отвлечься от такого поглощения, то можно заключить из обозрения данных таблицы 23, что высокая отражательная способность встречается у тех планет, которые обладают атмосферами. Самые низкие альбедо найдены у Луны и у Меркурия, у которых визуальные наблюдения не дают никаких признаков атмосферы.
Вернемся к формуле (33.19). Так как р в ней должно быть выражено в астрономических единицах, то с расстояния в 1 а. е. планета видна под углом  :
:
Таблица 23. Геометрическое альбедо  (в системах V и В) и сферическое альбедо
(в системах V и В) и сферическое альбедо  планет и некоторых спутников, а также их фазовый интеграл
планет и некоторых спутников, а также их фазовый интеграл  , фазовый коэффициент
, фазовый коэффициент  в разложении (33.25) и абсолютная звездная величина g в системе V (двоеточием обозначены ненадежные данные)
в разложении (33.25) и абсолютная звездная величина g в системе V (двоеточием обозначены ненадежные данные)

 (33.21)
(33.21)
С другой стороны,  , а это близко к
, а это близко к  (в системе V). Поэтому формулу (33.19) можно переписать так:
(в системе V). Поэтому формулу (33.19) можно переписать так:
 (33.22)
(33.22)
Из этой формулы по наблюдаемым значениям g можно определить геометрическое альбедо планеты, если известен ее угловой радиус, и, наоборот, угловой радиус, если известно альбедо. Последнее важно для оценки размеров астероидов (малых планет), видимые диски которых неощутимо малы (см. об этом дальше, с. 522—525).
Фотометрия отдельных мест диска планеты представляет трудности Как экспериментальные, так и при теоретическом истолковании. Фотографический метод определения яркости отдельных деталей протяженных объектов описан на с. 331—335 КПА (§ 19); он без труда может быть обобщен на визуальные и электрофотометрические измерения. Пусть заатмосферное значение яркости элементарной площадки на диске планеты найдено равным В стильбам.
Поставленная рядом с нею параллельно ей идеально белая ортотропная поверхность имела бы яркость
 (33-23)
(33-23)
(множитель  , где i — угол падения света, мы опускаем, так как он одинаков для обеих площадок). Тогда отражательная способность планетной поверхности может быть представлена отношением
, где i — угол падения света, мы опускаем, так как он одинаков для обеих площадок). Тогда отражательная способность планетной поверхности может быть представлена отношением
 (33.24)
(33.24)

Рис. 191. К условиям диффузного отражения (рассеяния) света, падающего на площадку а
Различные поверхности в зависимости от степени гладкости очень по-разному рассеивают свет в разных направлениях. У поверхности не идеально матовой яркость В зависит от угла рассеивания (рассматривания площадки)  и даже от угла падения освещающего света i. Поэтому величина R, называемая коэффициентом яркости поверхности, есть вообще функция
и даже от угла падения освещающего света i. Поэтому величина R, называемая коэффициентом яркости поверхности, есть вообще функция  и i и даже азимута 9 (рис. 191) направления рассеивания:
и i и даже азимута 9 (рис. 191) направления рассеивания:  . Так, например, глянцевитые или зеркалящие поверхности обладают повышенным рассеиванием в направлении
. Так, например, глянцевитые или зеркалящие поверхности обладают повышенным рассеиванием в направлении  . Чтобы не усложнять чрезмерно рассеивательную характеристику поверхности, за R принимают значение, выводимое при рассматривании поверхности в том же направлении, в котором она освещается, т. е.
. Чтобы не усложнять чрезмерно рассеивательную характеристику поверхности, за R принимают значение, выводимое при рассматривании поверхности в том же направлении, в котором она освещается, т. е.  . Такой коэффициент отражения называется светлотой. Условие
. Такой коэффициент отражения называется светлотой. Условие  осуществляется при наблюдениях планеты в противостоянии или верхнем соединении. При этом устраняется влияние теней, возникающих от мелких и крупных неровностей при боковом освещении. Для многих земных образований светлота определена в разных спектральных участках при разных углах освещения. Выборка из этих определений приводится в таблице 24. При отсутствии у планеты атмосферы, определение светлоты отдельных ее участков и сравнение со светлотой образований, встречающихся на Земле, может служить основанием для догадок о природе деталей поверхности планеты, особенно если параллельно проведены цветовые определения, т. е. сравниваются коэффициенты R в разных длинах волн.
осуществляется при наблюдениях планеты в противостоянии или верхнем соединении. При этом устраняется влияние теней, возникающих от мелких и крупных неровностей при боковом освещении. Для многих земных образований светлота определена в разных спектральных участках при разных углах освещения. Выборка из этих определений приводится в таблице 24. При отсутствии у планеты атмосферы, определение светлоты отдельных ее участков и сравнение со светлотой образований, встречающихся на Земле, может служить основанием для догадок о природе деталей поверхности планеты, особенно если параллельно проведены цветовые определения, т. е. сравниваются коэффициенты R в разных длинах волн.
Разумеется, догадки подобного рода должны высказываться очень осторожно. Так, многие темные места на Луне имеют ту же светлоту, что распаханный чернозем или кокс. Но ни то, ни другое вещество не могут представлять лунную поверхность, лишенную жизни.
Возможность подобных сравнений отпадает в том случае, когда планета имеет атмосферу, потому что атмосфера рассеивает (и поглощает) солнечное излучение как прямое, так и рассеянное поверхностью планеты.
Количественный анализ фотометрических эффектов, вносимых атмосферой, относится к числу труднейших задач теоретической фотометрии и, разумеется, не может быть сделан здесь, за исключением самых общих замечаний.
Таблица 24. Светлота R (см. (33.24)) некоторых поверхностей, встречающихся на Земле, а также метеоритов (визуально)

Трудность задачи состоит в том, что свет, рассеиваемый в атмосфере молекулами газов или неоднородностями их распределения, или, наконец, взвешенными в атмосфере твердыми и жидкими мелкими частицами — аэрозолями, после первого рассеяния испытывает повторное рассеяние второго, третьего и т. д. порядка, в результате чего каждая точка поверхности планеты освещается не только прямыми солнечными лучами, но и всем небосводом, распределение яркости по которому зависит от того, как атмосфера рассеивает свет в разных направлениях. Один атмосферный эффект нетрудно предугадать. Вместо узко направленного параллельного пучка солнечных лучей каждое место поверхности планеты освещено еще со всех сторон небосводом, и это рассеянное излучение сильнее у мощной атмосферы. Когда нет атмосферы, неровности поверхности планеты сильно снижают среднюю яркость ее действием густых теней, занимающих тем большую площадь, чем больше фазовый угол а освещения планеты Солнцем. Освещение атмосферой смягчает тени и поэтому зависимость полного блеска от угла фазы также смягчается.
Обычно звездную величину планеты представляют в виде
 (33.25)
(33.25)
Коэффициент  называется фазовым коэффициентом. Как правило, он самый большой из всех коэффициентов у и характеризует зависимость
называется фазовым коэффициентом. Как правило, он самый большой из всех коэффициентов у и характеризует зависимость  в первую очередь.
в первую очередь.
Из таблицы 23 видно, что этот коэффициент наибольший у планеты Меркурий и у Луны, достоверно лишенных атмосферы, и наименьший у планет с мощной атмосферой — Венеры, Земли, Юпитера, Сатурна. То, что он мал у Марса, имеющего слабую атмосферу, говорит о том, что поверхность Марса очень гладкая (речь идет о микрорельефе). Наоборот, большие значения  у спутников Юпитера указывают как будто на отсутствие атмосфер.
у спутников Юпитера указывают как будто на отсутствие атмосфер.

Рис. 192. Различные виды индииатрис рассеяния (сечение пространственной индикатрисы плоскостью, содержащей направление падающего луча), а — рэлеевское рассеяние очень малыми частицами; б — рассеяние более крупными частицами; в — индикатриса по измерениям рассеяния в чистом воздухе у поверхности Земли; г — рассеяние земной атмосферой, выведенное из распределения яркости по небесному своду; д — индикатриса рассеяния в слоистых облаках; е — индикатриса рассеяния атмосферы Венеры, полученная В. В. Соболевым из фазовой кривой для Венеры
Рассеивающую способность атмосферы характеризует индикатриса рассеяния. Так называется функция  , выражающая вероятность рассеяния кванта света в направлении, составляющем угол
, выражающая вероятность рассеяния кванта света в направлении, составляющем угол  с направлением распространения света (см. рис. 191). Сама вероятность рассеяния в пределах телесного угла
с направлением распространения света (см. рис. 191). Сама вероятность рассеяния в пределах телесного угла  есть
есть

и очевидно, что функция  должна удовлетворять условию
должна удовлетворять условию

Наглядно индикатрису рассеяния удобно представлять графически в виде полярной диаграммы, соединяя концы векторов, направленных по разным направлениям  и имеющих длину, пропорциональную
и имеющих длину, пропорциональную  . Несколько таких индикатрис показано на рис. 192.
. Несколько таких индикатрис показано на рис. 192.
Очень малые частицы рассеивают по закону Рэлея (КПА 299). В этом случае индикатриса выражается формулой
 (33.27)
(33.27)
а графически выглядит как симметричная фигура, вытянутая вдоль направлений  или сжатая при
или сжатая при  (рис. 192, а).
(рис. 192, а).
Для простоты расчетов функцию (33.27) иногда аппроксимируют сферической индикатрисой  . Такая аппроксимация не годится для представления рассеяния более крупными частицами, сравнимыми по размерам с длиной волны падающего света, так как в этом случае имеется очень большое рассеяние «вперед» при
. Такая аппроксимация не годится для представления рассеяния более крупными частицами, сравнимыми по размерам с длиной волны падающего света, так как в этом случае имеется очень большое рассеяние «вперед» при  , пример чего можно видеть на рис. 192, б. Теория позволяет предсказать вид фазовой функции, величину альбедо и степень потемнения к краю у диска планеты для разных индикатрис рассеяния и в разных предположениях об относительной роли поглощения и рассеяния при экстинкции света в планетной атмосфере. Наоборот, индикатрису рассеяния можно получить по наблюдаемым
, пример чего можно видеть на рис. 192, б. Теория позволяет предсказать вид фазовой функции, величину альбедо и степень потемнения к краю у диска планеты для разных индикатрис рассеяния и в разных предположениях об относительной роли поглощения и рассеяния при экстинкции света в планетной атмосфере. Наоборот, индикатрису рассеяния можно получить по наблюдаемым  и потемнению к краю. Затруднения здесь вносит отражение от самой поверхности планеты — подстилающей поверхности. Если эти две составляющие удается разделить, то при правильном определении физической природы рассеивающего агента (чистый газ, частицы больших или малых размеров) можно сделать правильное заключение и о мощности атмосферы вплоть до значения атмосферного давления у ее основания. Однако правильное решение получить бывает трудно.
и потемнению к краю. Затруднения здесь вносит отражение от самой поверхности планеты — подстилающей поверхности. Если эти две составляющие удается разделить, то при правильном определении физической природы рассеивающего агента (чистый газ, частицы больших или малых размеров) можно сделать правильное заключение и о мощности атмосферы вплоть до значения атмосферного давления у ее основания. Однако правильное решение получить бывает трудно.
Возвращаясь к рис. 192, замечаем, что индикатрисы рассеяния земной атмосферы также вытянуты «вперед», что вызвано взвешенными в атмосфере аэрозолями. Вытянутость особенно велика при рассеянии света на крупных капельках воды, составляющих слоистые облака. Она велика при рассеянии в атмосфере Венеры, что, конечно, говорит о наличии в ней взвешенных крупных частиц. Неточность фотометрических наблюдений Венеры вблизи ее нижних соединений, когда  не позволила установить индикатрису для углов
не позволила установить индикатрису для углов  .
.
Пример трудностей, возникающих при интерпретации фотометрических наблюдений на дисках планет с малой атмосферой, дает Марс, для которого разные метода дают весьма различные результаты (см. с. 513—515).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ГЛАВА I. СОЛНЦЕ
- ВНЕШНИЙ ВИД СОЛНЦА. ФОТОСФЕРА
- ВРАЩЕНИЕ СОЛНЦА
- ПЕРИОДИЧНОСТЬ СОЛНЕЧНОЙ ПЯТНООБРАЗОВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
- § 2. ЭЛЕМЕНТЫ ТЕОРИИ СОЛНЕЧНОЙ АТМОСФЕРЫ
- УРАВНЕНИЕ ЛУЧИСТОГО РАВНОВЕСИЯ И ЕГО ПРИБЛИЖЕННОЕ РЕШЕНИЕ
- МОДЕЛЬ СОЛНЕЧНОЙ АТМОСФЕРЫ
- КОНВЕКЦИЯ В СОЛНЕЧНОЙ АТМОСФЕРЕ
- ИОНИЗАЦИЯ СОЛНЕЧНОГО ВЕЩЕСТВА
- СОЛНЕЧНАЯ ПЛАЗМА И ЕЕ ВЗАИМОДЕЙСТВИЕ С МАГНИТНЫМИ ПОЛЯМИ
- § 3. СОЛНЕЧНЫЙ СПЕКТР. ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА
- ХИМИЧЕСКИЙ СОСТАВ СОЛНЦА. КАЧЕСТВЕННЫЙ АНАЛИЗ
- КОЛИЧЕСТВЕННЫЙ ХИМИЧЕСКИЙ АНАЛИЗ СОЛНЕЧНОЙ АТМОСФЕРЫ
- § 4. ВЕРХНЯЯ АТМОСФЕРА СОЛНЦА
- ОБРАЩАЮЩИЙ СЛОЙ И ХРОМОСФЕРА. ПРИЧИНА ИХ ВИДИМОСТИ ЗА ПРЕДЕЛАМИ СОЛНЕЧНОГО ДИСКА
- НАБЛЮДЕНИЯ ХРОМОСФЕРЫ НА ДИСКЕ СОЛНЦА. СПЕКТРОГЕЛИОГРАФ
- ХРОМОСФЕРНЫЕ ФАКЕЛЫ, ФЛОККУЛЫ И ВОЛОКНА. СПИКУЛЫ
- ПРОТУБЕРАНЦЫ
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ ХРОМОСФЕРЫ. ВОЛНОВЫЕ ДВИЖЕНИЯ В АТМОСФЕРЕ СОЛНЦА
- § 5. СОЛНЕЧНАЯ КОРОНА
- ФИЗИЧЕСКОЕ СОСТОЯНИЕ КОРОНЫ
- ЭМИССИОННЫЙ СПЕКТР КОРОНЫ И ЕГО ИНТЕРПРЕТАЦИЯ
- РАДИОИЗЛУЧЕНИЕ КОРОНЫ И ХРОМОСФЕРЫ
- НЕПРЕРЫВНОЕ ИЗЛУЧЕНИЕ КОРОНЫ. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ И ТЕМПЕРАТУРЫ В ХРОМОСФЕРЕ И КОРОНЕ
- § 6. НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ НА СОЛНЦЕ
- ОБНАРУЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ НА СОЛНЦЕ
- СОЛНЕЧНЫЕ ПЯТНА И ИХ МАГНИТНЫЕ ПОЛЯ
- ПРИРОДА СОЛНЕЧНЫХ ПЯТЕН. АКТИВНЫЕ ОБЛАСТИ НА СОЛНЦЕ. СУПЕРГРАНУЛЯЦИЯ
- ПРОТУБЕРАНЦЫ
- ПРОЯВЛЕНИЕ СОЛНЕЧНОЙ АКТИВНОСТИ В КОРОНЕ
- СОЛНЕЧНЫЕ ВСПЫШКИ
- СПОРАДИЧЕСКОЕ РАДИОИЗЛУЧЕНИЕ СОЛНЦА
- КОРПУСКУЛЯРНОЕ ИЗЛУЧЕНИЕ СОЛНЦА
- § 7. СВЯЗЬ МЕЖДУ СОЛНЕЧНЫМИ И ЗЕМНЫМИ ЯВЛЕНИЯМИ
- ПОЛЯРНЫЕ СИЯНИЯ
- ВЕРХНЯЯ АТМОСФЕРА ЗЕМЛИ. ИОНОСФЕРА. ВОЗДЕЙСТВИЕ НА НИХ СОЛНЦА
- ЯВЛЕНИЯ НА ЗЕМЛЕ, ПРОИСХОДЯЩИЕ ВО ВРЕМЯ ПЕРИОДОВ ПОВЫШЕННОЙ СОЛНЕЧНОЙ АКТИВНОСТИ
- РАДИАЦИОННЫЕ ПОЯСА ЗЕМЛИ
- ДВИЖЕНИЕ КОРПУСКУЛЯРНЫХ потоков В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- СОЛНЕЧНЫЙ ВЕТЕР И МАГНИТОСФЕРА ЗЕМЛИ
- ЗАДАЧИ К ГЛАВЕ I
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ I
- ГЛАВА III. ЗВЕЗДНЫЕ АТМОСФЕРЫ
- § 8. СПЕКТРЫ ЗВЕЗД
- РАЗЛИЧИЯ В СПЕКТРАХ ГИГАНТОВ И КАРЛИКОВ
- ВЛИЯНИЕ РАЗНЫХ ФИЗИЧЕСКИХ ФАКТОРОВ НА ВИД И ИНТЕНСИВНОСТЬ СПЕКТРАЛЬНЫХ ЛИНИЙ
- СПЕКТРАЛЬНЫЕ ПАРАЛЛАКСЫ И ДВУМЕРНАЯ СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ
- § 9. МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. ХИМИЧЕСКИЙ СОСТАВ ЗВЕЗД
- МОДЕЛИ ЗВЕЗДНЫХ АТМОСФЕР. СРЕДНИЙ ХИМИЧЕСКИЙ СОСТАВ АТМОСФЕР ЗВЕЗД
- УКЛОНЕНИЯ ХИМИЧЕСКОГО СОСТАВА ЗВЕЗД ОТ СРЕДНЕГО
- СПЕКТРЫ БЕЛЫХ КАРЛИКОВ
- ЗВЕЗДЫ ПОНИЖЕННОЙ СВЕТИМОСТИ
- МАГНИТНЫЕ ПЕРЕМЕННЫЕ ЗВЕЗДЫ
- ВЛИЯНИЕ ВРАЩЕНИЯ ЗВЕЗДЫ НА ЕЕ СПЕКТР
- ЭФФЕКТ ТУРБУЛЕНТНОСТИ
- § 10. ВЗАИМНЫЕ СВЯЗИ МЕЖДУ ВНЕШНИМИ ХАРАКТЕРИСТИКАМИ ЗВЕЗД
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА
- СВЯЗЬ МЕЖДУ ПОЛОЖЕНИЕМ ЗВЕЗДЫ НА ДИАГРАММЕ Г — Р И ЕЕ ДВИЖЕНИЕМ В ГАЛАКТИКЕ
- ЗВЕЗДЫ СФЕРИЧЕСКОЙ И ПЛОСКОЙ СОСТАВЛЯЮЩИХ. РАЗЛИЧИЕ ИХ ДИАГРАММ Г — Р
- РАЗНООБРАЗИЕ СВЕТИМОСТЕЙ И РАЗМЕРОВ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ II
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ II
- ГЛАВА III. ДВОЙНЫЕ ЗВЕЗДЫ И МАССЫ ЗВЕЗД
- ВИЗУАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- НЕВИДИМЫЕ СПУТНИКИ ЗВЕЗД
- СПЕКТРАЛЬНО-ДВОЙНЫЕ ЗВЕЗДЫ
- ШИРОКИЕ И ТЕСНЫЕ ПАРЫ
- ЗАТМЕННЫЕ ИЛИ ФОТОМЕТРИЧЕСКИЕ ДВОЙНЫЕ ЗВЕЗДЫ
- § 12. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ ХАРАКТЕРИСТИК ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ОРБИТЫ ВИЗУАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- КРИВАЯ ЛУЧЕВЫХ СКОРОСТЕЙ И ЭЛЕМЕНТЫ ОРБИТЫ СПЕКТРАЛЬНО-ДВОЙНОЙ ЗВЕЗДЫ
- ОПРЕДЕЛЕНИЕ МАСС КОМПОНЕНТ СПЕКТРАЛЬНО-ДВОЙНЫХ ЗВЕЗД
- ЭЛЕМЕНТЫ ФОТОМЕТРИЧЕСКОЙ ОРБИТЫ
- ОПРЕДЕЛЕНИЕ ЭКСЦЕНТРИСИТЕТА ОРБИТЫ У ЗАТМЕННОЙ ДВОЙНОЙ ВРАЩЕНИЕ ЛИНИИ АПСИД
- ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ КОМПОНЕНТ ФОТОМЕТРИЧЕСКИХ ДВОЙНЫХ ЗВЕЗД
- ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОЙ ТЕМПЕРАТУРЫ ЗАТМЕННЫХ ДВОЙНЫХ ЗВЕЗД
- § 13. МАССЫ И ДРУГИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВОЙНЫХ ЗВЕЗД. ЗАКОН МАССА — СВЕТИМОСТЬ
- § 14. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВЕЗД В ДВОЙНЫХ СИСТЕМАХ
- РАЗНЫЕ ТИПЫ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- КОНТАКТНЫЕ СИСТЕМЫ
- ТРИ ТИПА ТЕСНЫХ ДВОЙНЫХ СИСТЕМ
- ОСЕВОЕ ВРАЩЕНИЕ КОМПОНЕНТ В ТЕСНЫХ ПАРАХ
- ГАЗОВЫЕ ПОТОКИ В ТЕСНЫХ ПАРАХ
- МНОГОЧИСЛЕННОСТЬ ДВОЙНЫХ ЗВЕЗД
- ЗАДАЧИ К ГЛАВЕ III
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ III
- ГЛАВА IV. ВНУТРЕННЕЕ СТРОЕНИЕ ЗВЕЗД
- ОБЩИЕ СООБРАЖЕНИЯ. СОСТОЯНИЕ ВЕЩЕСТВА В НЕДРАХ ЗВЕЗД
- ЛУЧИСТОЕ ДАВЛЕНИЕ В ЗВЕЗДАХ
- ЛУЧИСТЫЙ И КОНВЕКТИВНЫЙ ПЕРЕНОС ТЕПЛА ВНУТРИ ЗВЕЗДЫ
- ГОМОЛОГИЧЕСКИЕ КОНФИГУРАЦИИ
- ПОЛИТРОПНЫЕ МОДЕЛИ ЗВЕЗД
- § 16. ЛУЧЕИСПУСКАНИЕ ЗВЕЗДЫ
- ИСТОЧНИКИ НЕПРОЗРАЧНОСТИ ЗВЕЗДНОГО ВЕЩЕСТВА
- ЗАВИСИМОСТЬ ЛУЧЕИСПУСКАНИЯ ЗВЕЗДЫ ОТ ИСТОЧНИКОВ ЭНЕРГИИ И НЕПРОЗРАЧНОСТИ
- § 17. ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ГРАВИТАЦИОННОЕ СЖАТИЕ
- ТЕРМОЯДЕРНЫЕ ИСТОЧНИКИ ЗВЕЗДНОЙ ЭНЕРГИИ
- ПРОТОН-ПРОТОННАЯ РЕАКЦИЯ
- УГЛЕРОДНО-АЗОТНЫЙ ЦИКЛ
- ТРАНСФОРМАЦИЯ ГЕЛИЯ В ЗВЕЗДАХ
- § 18. ЗВЕЗДНЫЕ МОДЕЛИ
- БЕЛЫЕ КАРЛИКИ
- НЕЙТРОННЫЕ ЗВЕЗДЫ. ПУЛЬСАРЫ
- ПРОВЕРКА ТЕОРИИ ПО ВРАЩЕНИЮ ЛИНИИ АПСИД В ТЕСНЫХ СИСТЕМАХ И ПО СОЛНЕЧНЫМ ПУЛЬСАЦИЯМ
- § 19. ЭВОЛЮЦИЯ ЗВЕЗД
- ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЭВОЛЮЦИЯ ЗВЕЗД
- КОНТРАКЦИОННАЯ ФАЗА ЗВЕЗДНОЙ ЭВОЛЮЦИИ
- ЭВОЛЮЦИЯ ЗВЕЗД НА ТЕРМОЯДЕРНОЙ ОСНОВЕ
- ЭВОЛЮЦИЯ К КРАСНЫМ ГИГАНТАМ
- ДАЛЬНЕЙШАЯ ЭВОЛЮЦИЯ ЗВЕЗДЫ
- § 20. ЭВОЛЮЦИЯ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- СОВРЕМЕННАЯ РАСПРОСТРАНЕННОСТЬ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ ВО ВСЕЛЕННОЙ
- ТЕРМОЯДЕРНЫЕ РЕАКЦИИ С ОБРАЗОВАНИЕМ ЭЛЕМЕНТОВ БОЛЕЕ ТЯЖЕЛЫХ, ЧЕМ 12С
- ЗВЕЗДЫ РАЗНОГО ВОЗРАСТА И ИХ ХИМИЧЕСКИЙ СОСТАВ
- ЗАДАЧИ К ГЛАВЕ IV
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ IV
- ГЛАВА V. НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦЕФЕИД
- ПУЛЬСАЦИИ ЦЕФЕИД
- ГИПОТЕЗА РАДИАЛЬНЫХ АДИАБАТИЧЕСКИХ ПУЛЬСАЦИЙ И ЕЕ ЗАТРУДНЕНИЯ
- НОВЫЕ ПРЕДСТАВЛЕНИЯ О КОЛЕБАТЕЛЬНЫХ ПРОЦЕССАХ У ЦЕФЕИД
- ЗВЕЗДЫ ТИПА b БОЛЬШОГО ПСА
- ЗВЕЗДЫ ТИПА RV ТЕЛЬЦА И МИРЫ КИТА
- § 22. ВЫНОС ВЕЩЕСТВА С ПОВЕРХНОСТИ ЗВЕЗД
- ГАЗОВЫЕ ОБОЛОЧКИ И КОЛЬЦА ВОКРУГ ЗВЕЗД
- ЗВЕЗДЫ ВОЛЬФА — РАЙЕ
- § 23. ВРАЩЕНИЕ ЗВЕЗД И ОБМЕН ВЕЩЕСТВА ВНУТРИ ДВОЙНЫХ СИСТЕМ
- ВРАЩЕНИЕ ЗВЕЗД РАЗНЫХ ТИПОВ
- ЭВОЛЮЦИОННЫЕ ИЗМЕНЕНИЯ СКОРОСТИ ВРАЩЕНИЯ ЗВЕЗД
- ПРОИСХОЖДЕНИЕ ВРАЩЕНИЯ ЗВЕЗД
- ОБМЕН ВЕЩЕСТВА ВНУТРИ ТЕСНЫХ ДВОЙНЫХ СИСТЕМ. АККРЕЦИЯ. ЭВОЛЮЦИОННЫЕ СЛЕДСТВИЯ
- § 24. НОВЫЕ И СВЕРХНОВЫЕ ЗВЕЗДЫ
- СВЕТИМОСТЬ, АМПЛИТУДЫ ВСПЫШЕК И ЧИСЛО НОВЫХ ЗВЕЗД
- СПЕКТРАЛЬНЫЕ ИЗМЕНЕНИЯ У НОВЫХ ЗВЕЗД
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ ВО ВРЕМЯ ВСПЫШКИ НОВОЙ ЗВЕЗДЫ
- ДВОЙСТВЕННОСТЬ НОВЫХ ЗВЕЗД
- СВЕРХНОВЫЕ ЗВЕЗДЫ
- ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ ЗВЕЗД. КРАБОВИДНАЯ ТУМАННОСТЬ. ПУЛЬСАРЫ
- § 25. КАРЛИКОВЫЕ ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ДРУГИЕ СЛУЧАИ НЕСТАЦИОНАРНОСТИ: РЕНТГЕНОВСКИЕ ЗВЕЗДЫ
- ЗВЕЗДЫ ТИПА U БЛИЗНЕЦОВ. СИМБИОТИЧЕСКИЕ ЗВЕЗДЫ
- ВСПЫХИВАЮЩИЕ ЗВЕЗДЫ ТИПА UV КИТА
- ЗВЕЗДЫ ТИПОВ Т ТЕЛЬЦА, RW ВОЗНИЧЕГО И ТОРИОНА
- НЕСТАЦИОНАРНЫЕ ЗВЕЗДЫ В РЕНТГЕНОВСКОМ ДИАПАЗОНЕ
- ЗАДАЧИ К ГЛАВЕ V
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ V
- ГЛАВА VI. ДИФФУЗНОЕ ВЕЩЕСТВО В ПРОСТРАНСТВЕ
- ВЫСОКАЯ СПОСОБНОСТЬ ПЫЛИ ЗАДЕРЖИВАТЬ ПРОХОДЯЩИЙ СВЕТ
- ЗАВИСИМОСТЬ ОСЛАБЛЕНИЯ СВЕТА ПЫЛЬЮ ОТ ДЛИНЫ ВОЛНЫ
- ПРАКТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ОБЩЕГО ОСЛАБЛЕНИЯ СВЕТА в ЗАДАННОМ НАПРАВЛЕНИИ
- ОБЛАЧНАЯ СТРУКТУРА ПЫЛЕВОЙ СРЕДЫ В ГАЛАКТИКЕ
- РАСПРЕДЕЛЕНИЕ МЕЖЗВЕЗДНОЙ ПЫЛИ В ГАЛАКТИКЕ
- СВЕТЛЫЕ ПЫЛЕВЫЕ ТУМАННОСТИ
- СВЕТОВОЕ ДАВЛЕНИЕ НА ПЫЛЕВЫЕ ЧАСТИЦЫ
- МЕЖЗВЕЗДНАЯ ПОЛЯРИЗАЦИЯ СВЕТА ЗВЕЗД
- ОРИЕНТИРОВАНИЕ МЕЖЗВЕЗДНЫХ ПЫЛЕВЫХ ЧАСТИЦ МАГНИТНЫМИ ПОЛЯМИ
- § 27. ГАЗОВАЯ СОСТАВЛЯЮЩАЯ МЕЖЗВЕЗДНОЙ СРЕДЫ
- МЕЖЗВЕЗДНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ Са, Na И ДРУГИХ ЭЛЕМЕНТОВ И МОЛЕКУЛ
- ГАЗОВЫЙ ГАЛАКТИЧЕСКИЙ СУБСТРАТ
- ИЗЛУЧЕНИЕ МЕЖЗВЕЗДНОГО НЕЙТРАЛЬНОГО ВОДОРОДА НА ВОЛНЕ 21 см
- МОЛЕКУЛЫ, ОБНАРУЖЕННЫЕ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ РАДИОМЕТОДАМИ
- ОТНОСИТЕЛЬНАЯ РОЛЬ ГАЗА И ПЫЛИ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭЛЕКТРОНЫ В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ. ОБЛАСТИ HII И HI
- § 28. ГАЗОВЫЕ ТУМАННОСТИ
- ПЛАНЕТАРНЫЕ ТУМАННОСТИ
- ФЛУОРЕСЦЕНЦИЯ ВЕЩЕСТВА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ТЕМПЕРАТУРЫ ЯДЕР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЗАПРЕЩЕННЫЕ ЛИНИИ В СПЕКТРАХ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ЭЛЕКТРОННЫЕ ТЕМПЕРАТУРЫ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- НЕПРЕРЫВНЫЙ СПЕКТР ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ. ИХ МАССЫ
- РАСШИРЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ПОЛЕ ЛАЙМАНОВСКОГО ИЗЛУЧЕНИЯ В ПЛАНЕТАРНЫХ ТУМАННОСТЯХ
- ГРАНИЦА ПЛАНЕТАРНОЙ ТУМАННОСТИ
- ЯДРА ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ПРОИСХОЖДЕНИЕ ПЛАНЕТАРНЫХ ТУМАННОСТЕЙ
- ДИФФУЗНЫЕ ГАЗОВЫЕ ТУМАННОСТИ
- ОБЛАСТИ HII И ИХ РАЗМЕРЫ
- ВЗАИМОДЕЙСТВИЕ ГАЗА И ИЗЛУЧЕНИЯ ГОРЯЧЕЙ ЗВЕЗДЫ. ДВИЖЕНИЯ ВНУТРИ ГАЗОВОЙ ТУМАННОСТИ
- РАДИОИЗЛУЧЕНИЕ ГАЗОВЫХ ТУМАННОСТЕЙ
- КРАБОВИДНАЯ ТУМАННОСТЬ — ИСТОЧНИК РАДИОИЗЛУЧЕНИЯ ТЕЛЕЦ А
- ТОРМОЗНОЕ ИЗЛУЧЕНИЕ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ КАК ИСТОЧНИК СВЕЧЕНИЯ КРАБОВИДНОЙ ТУМАННОСТИ
- КРАБОВИДНАЯ И НЕКОТОРЫЕ ДРУГИЕ ТУМАННОСТИ КАК ОСТАТКИ ВСПЫШЕК СВЕРХНОВЫХ
- ФИЗИЧЕСКИЕ ПРОЦЕССЫ В ПУЛЬСАРАХ
- § 29. ФИЗИЧЕСКОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА В ГАЛАКТИКЕ
- ТЕМПЕРАТУРА ТЕЛА, ПОМЕЩЕННОГО В МЕЖЗВЕЗДНОМ ПРОСТРАНСТВЕ
- ЭНЕРГЕТИЧЕСКИЙ БАЛАНС У ЧАСТИЦ МЕЖЗВЕЗДНОЙ СРЕДЫ
- РАДИОИЗЛУЧЕНИЕ ИЗ МЕЖЗВЕЗДНОГО ПРОСТРАНСТВА ГАЛАКТИКИ
- КОСМИЧЕСКИЕ ЛУЧИ В ГАЛАКТИКЕ
- МАГНИТНЫЕ ПОЛЯ В ГАЛАКТИКЕ
- КОНДЕНСАЦИИ МЕЖЗВЕЗДНОГО ВЕЩЕСТВА И ЗВЕЗДООБРАЗОВАНИЕ
- ЦЕНТРАЛЬНЫЕ ОБЛАСТИ ГАЛАКТИКИ
- ОСОБЕННОСТИ РАСПОЛОЖЕНИЯ И ДВИЖЕНИЯ ГАЗОВЫХ МАСС В ГАЛАКТИКЕ
- МЕЖЗВЕЗДНЫЙ ГАЗ В ГАЛАКТИКЕ (РЕЗЮМЕ). АКТИВНОСТЬ ЯДРА ГАЛАКТИКИ
- ЗАДАЧИ К ГЛАВЕ VI
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VI
- ГЛАВА VII. ГАЛАКТИКИ И МЕТАГАЛАКТИКА
- § 30. ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
- КЛАССИФИКАЦИЯ ГАЛАКТИК- ОБЩИЕ ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИК
- ВРАЩЕНИЕ ГАЛАКТИК. ИХ МАССЫ
- КРАСНОЕ СМЕЩЕНИЕ В СПЕКТРАХ ГАЛАКТИК
- ЗАКОН ХАББЛА. ПОСТОЯННАЯ ХАББЛА
- СТРУКТУРА МЕТАГАЛАКТИКИ. СКОПЛЕНИЕ ГАЛАКТИК-ГРУППЫ ГАЛАКТИК
- ЗВЕЗДООБРАЗОВАНИЕ В ГАЛАКТИКАХ
- НЕВИДИМОЕ ВЕЩЕСТВО В ГАЛАКТИКАХ И ИХ СКОПЛЕНИЯХ
- § 31. РАДИОГАЛАКТИКИ И НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ В ГАЛАКТИКАХ
- РАДИОИЗЛУЧЕНИЕ НОРМАЛЬНЫХ ГАЛАКТИК
- РАДИОГАЛАКТИКИ
- ГАЛАКТИКИ СЕЙФЕРТА
- АКТИВНЫЕ ГАЛАКТИКИ И ПРИЗНАКИ ВЗРЫВА В НИХ
- КВАЗАРЫ И РОДСТВЕННЫЕ ИМ ОБЪЕКТЫ
- СПЕКТРАЛЬНЫЙ ИНДЕКС РАДИОИЗЛУЧЕНИЯ. ВОЗРАСТ РАДИОГАЛАКТИК
- ОБЩИЕ ЗАПАСЫ ЭНЕРГИИ В ГАЛАКТИКАХ
- § 32. ГАЛАКТИКИ И КОСМОЛОГИЯ
- ЗАДАЧИ К ГЛАВЕ VII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VII
- ГЛАВА VIII. СОЛНЕЧНАЯ СИСТЕМА. ПЛАНЕТЫ И ИХ СПУТНИКИ
- § 33. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ПЛАНЕТ
- ФОТОМЕТРИЧЕСКИЙ АНАЛИЗ ПЛАНЕТНЫХ ПОВЕРХНОСТЕЙ И АТМОСФЕРЫ
- ПОЛЯРИМЕТРИЯ ПЛАНЕТ
- СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЛАНЕТНЫХ АТМОСФЕР
- СПЕКТРАЛЬНОЕ ОПРЕДЕЛЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ
- ПЛАНЕТНЫЕ ТЕМПЕРАТУРЫ. ТЕОРИЯ. РОЛЬ АТМОСФЕРЫ
- РАЗЛИЧНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЛАНЕТНЫХ ТЕМПЕРАТУР
- РАДИОЛОКАЦИОННЫЕ МЕТОДЫ ИЗУЧЕНИЯ ПЛАНЕТ
- УСТОЙЧИВОСТЬ ПЛАНЕТНЫХ АТМОСФЕР ВО ВРЕМЕНИ
- § 34. ПЛАНЕТЫ ЗЕМНОЙ ГРУППЫ
- МЕРКУРИЙ
- ВЕНЕРА. ТЕМПЕРАТУРА. ПАРНИКОВАЯ МОДЕЛЬ АТМОСФЕРЫ. ВРАЩЕНИЕ
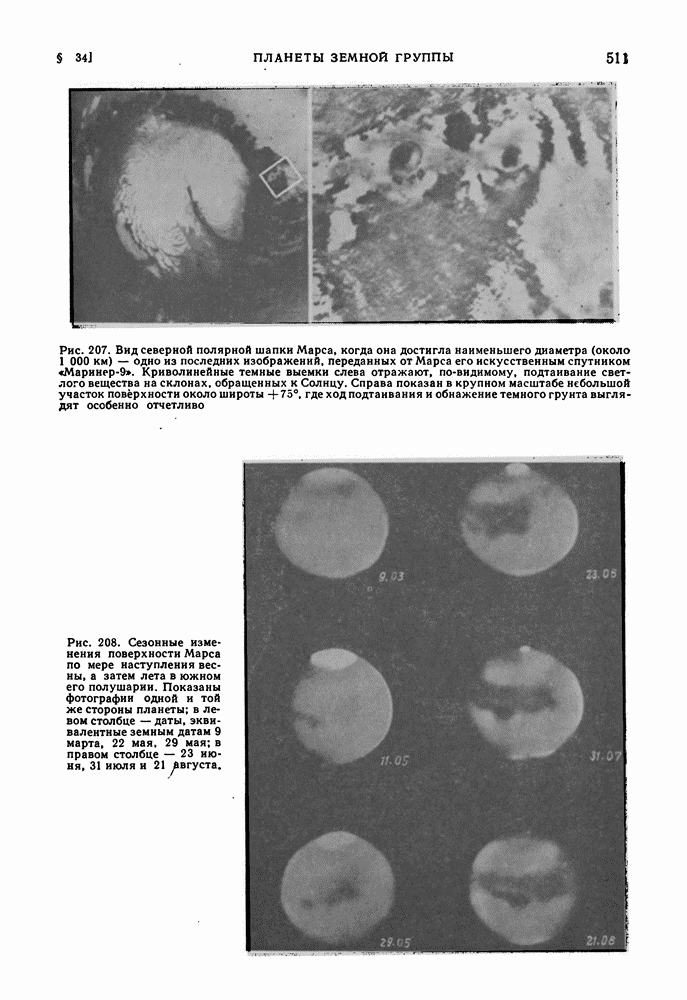
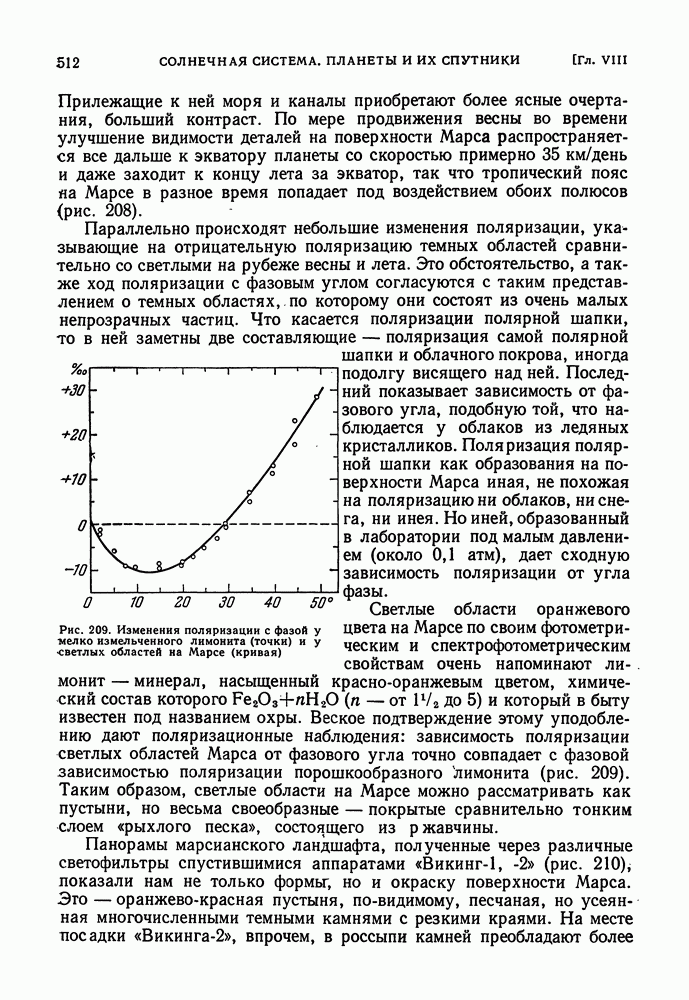
- МАРС. ОСОБЕННОСТИ ЕГО ПОВЕРХНОСТИ. ИХ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ
- АТМОСФЕРА МАРСА
- ТЕМПЕРАТУРА МАРСА
- ВОДА НА МАРСЕ. ЖИЗНЬ НА МАРСЕ?
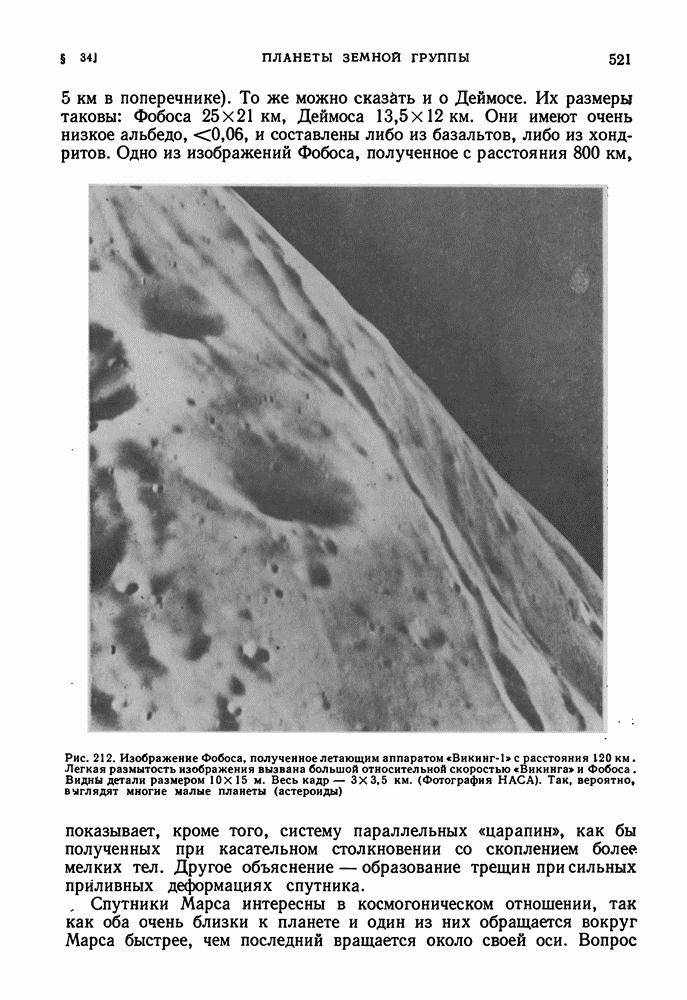
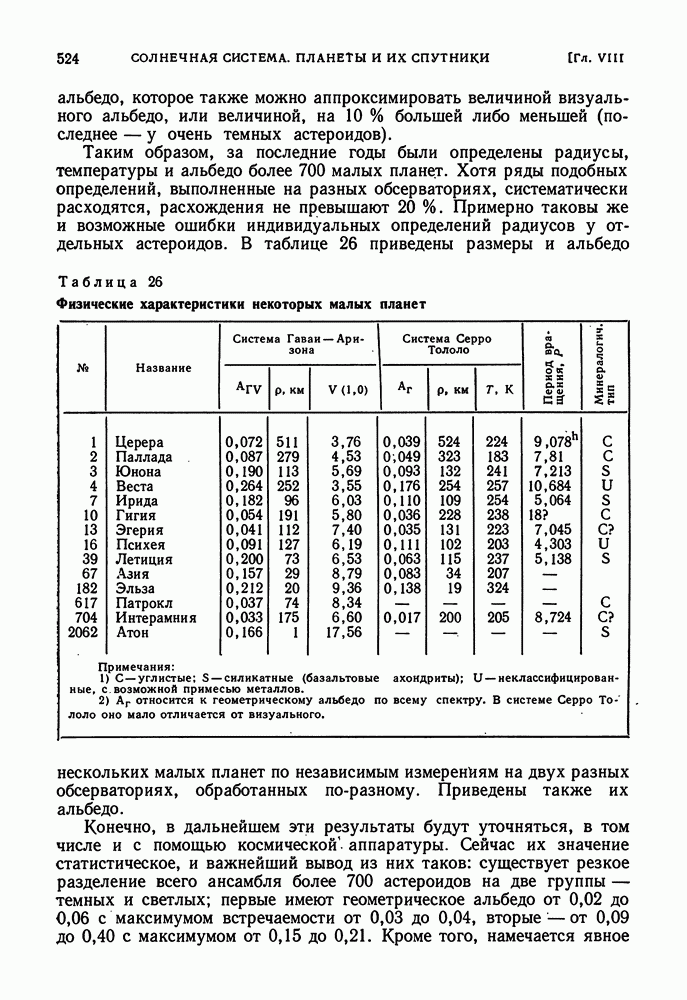
- МАЛЫЕ ПЛАНЕТЫ
- § 35. ЛУНА
- АТМОСФЕРА ЛУНЫ
- ТЕМПЕРАТУРНЫЙ РЕЖИМ НА ЛУНЕ
- МОРФОЛОГИЯ ЛУННОЙ ПОВЕРХНОСТИ
- ВНУТРЕННЕЕ СТРОЕНИЕ ЛУНЫ
- ОБРАЗОВАНИЕ СОВРЕМЕННОГО ЛУННОГО ЛАНДШАФТА
- § 36. ВНЕШНИЕ ПЛАНЕТЫ СОЛНЕЧНОЙ СИСТЕМЫ
- ЮПИТЕР
- САТУРН
- УРАН И НЕПТУН
- ПЛУТОН
- ЗАДАЧИ К ГЛАВЕ VIII
- СПИСОК ЛИТЕРАТУРЫ К ГЛАВЕ VIII
- ГЛАВА IX. СОЛНЕЧНАЯ СИСТЕМА. КОМЕТЫ И МАЛЫЕ ТЕЛА СОЛНЕЧНОЙ СИСТЕМЫ
- ОБЩАЯ ХАРАКТЕРИСТИКА КОМЕТ
- ОБРАЗОВАНИЕ КОМЕТНЫХ ФОРМ
- МЕХАНИЧЕСКАЯ ТЕОРИЯ КОМЕТНЫХ ФОРМ
- СПЕКТРЫ КОМЕТ
- БЛЕСК КОМЕТЫ И ЕГО ИЗМЕНЕНИЯ
- ДАВЛЕНИЕ СВЕТА НА КОМЕТНЫЕ ЧАСТИЦЫ
- СОЛНЕЧНАЯ АКТИВНОСТЬ КАК ИСТОЧНИК ВОЗНИКНОВЕНИЯ КОМЕТНЫХ ФОРМ
- РАСПАД КОМЕТ. ПРОИСХОЖДЕНИЕ КОМЕТ
- КОМЕТА ГАЛЛЕЯ В 1986 г.
- § 38. МЕТЕОРЫ
- ОБЩИЕ ХАРАКТЕРИСТИКИ МЕТЕОРОВ. СПОСОБЫ ИХ НАБЛЮДЕНИЯ
- МЕТЕОРНЫЕ ПОТОКИ И СПОРАДИЧЕСКИЕ МЕТЕОРЫ
- ЯВЛЕНИЯ ПРИ ВТОРЖЕНИИ МЕТЕОРНОГО ТЕЛА В ЗЕМНУЮ АТМОСФЕРУ
- РАДИОЛОКАЦИОННЫЕ НАБЛЮДЕНИЯ МЕТЕОРОВ
- МАССЫ МЕТЕОРНЫХ ТЕЛ
- МЕТЕОРИТЫ И ИХ КЛАССИФИКАЦИЯ
- ВОЗРАСТ МЕТЕОРИТОВ
- МЕТЕОРИТНЫЕ КРАТЕРЫ И ВОРОНКИ
- ТУНГУССКИЙ МЕТЕОРИТ
- § 39. МЕТЕОРНОЕ И ПЫЛЕВОЕ ВЕЩЕСТВО В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- МЕТЕОРНЫЕ РОИ И СВЯЗЬ ИХ С КОМЕТАМИ
- МИКРОМЕТЕОРИТЫ
- МЕТЕОРНОЕ ВЕЩЕСТВО ВОКРУГ ЗЕМЛИ
- ЗОДИАКАЛЬНЫЙ СВЕТ
- ПЫЛЕВАЯ И ГАЗОВАЯ СОСТАВЛЯЮЩИЕ В МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
- ДВИЖЕНИЕ МАЛОЙ ЧАСТИЦЫ В ПОЛЕ ТЯГОТЕНИЯ И ИЗЛУЧЕНИЯ СОЛНЦА
- ПРОТИВОСИЯНИЕ
- ЗАДАЧИ К ГЛАВЕ IX