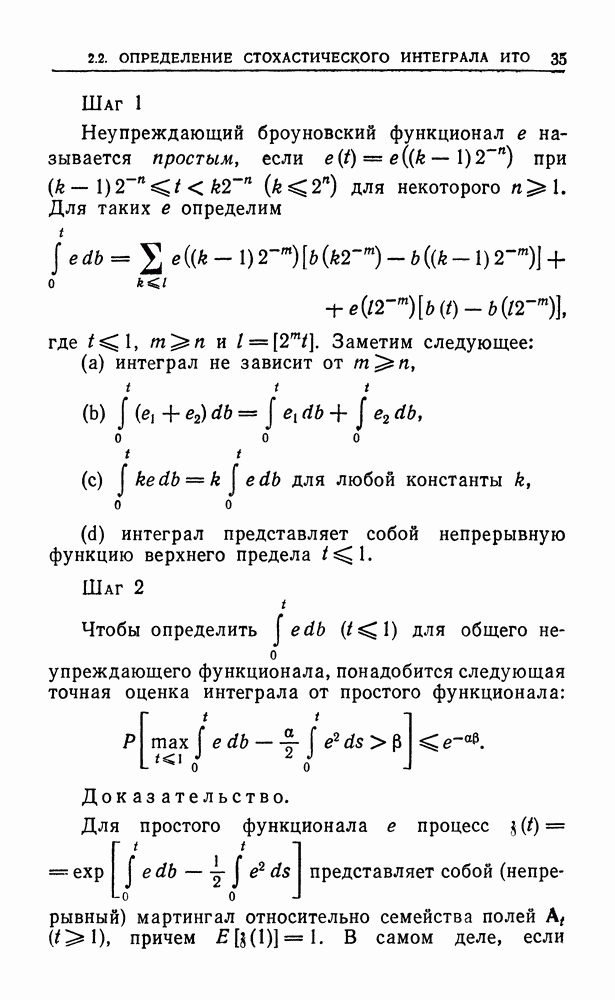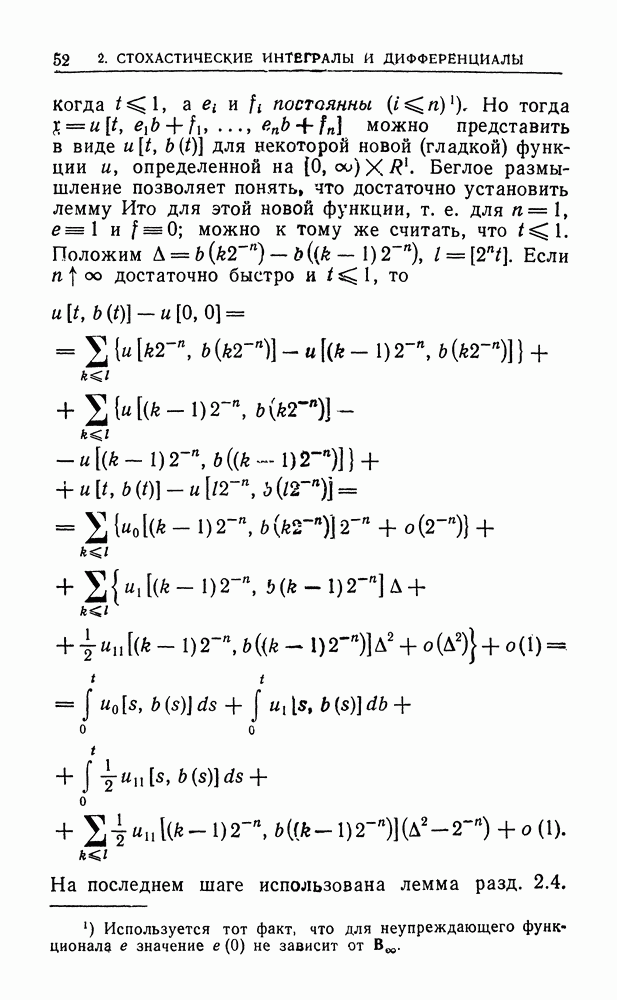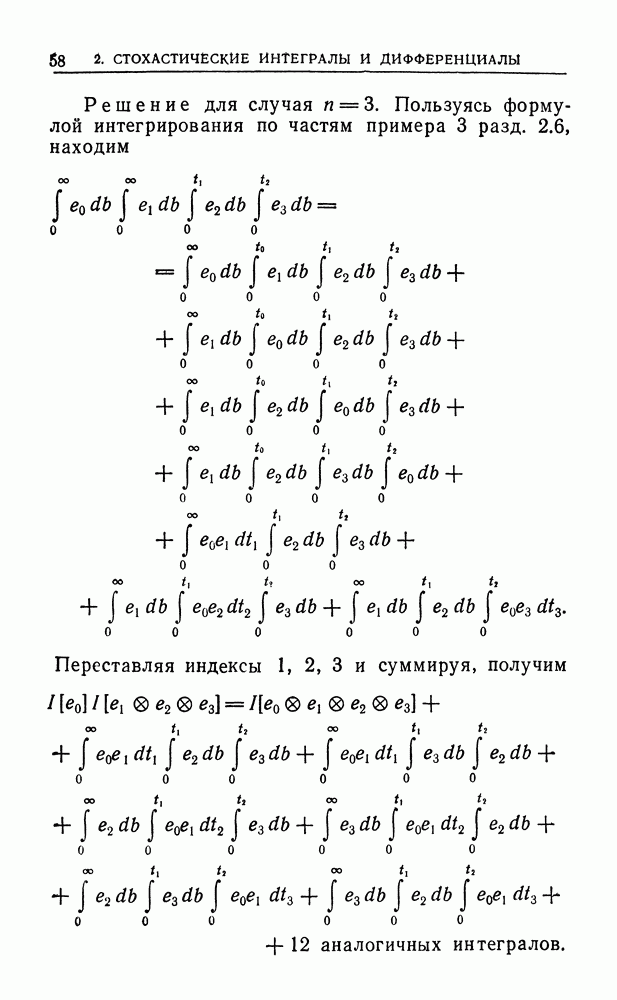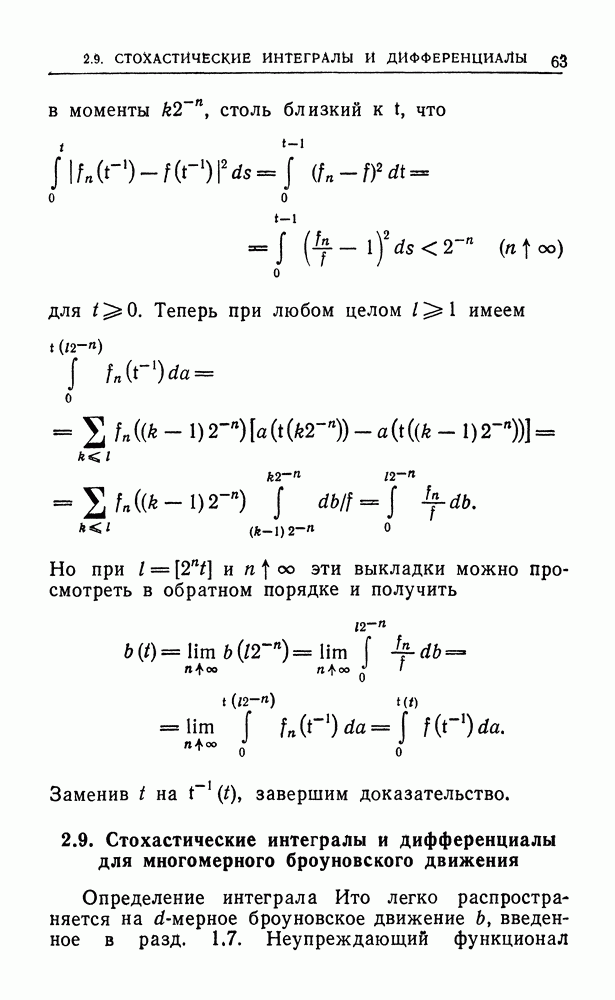| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Лемма Вейля
Мы сейчас докажем лемму Вейля, уже использованную нами в разд. 3.6. Учитывая это, читатель может при желании перейти сразу к разд. 4.3.
Рассмотрим эллиптический оператор  определенный на многообразии
определенный на многообразии  как в разд. 4.1. Пусть
как в разд. 4.1. Пусть  оператор, формально сопряженный с
оператор, формально сопряженный с  относительно элемента объема
относительно элемента объема 

для финитных  Лемма Вейля утверждает, что если
Лемма Вейля утверждает, что если  — (формальная) плотность распределения масс на пространстве
— (формальная) плотность распределения масс на пространстве  и если
и если

для какой-то функции  и любой финитной
и любой финитной  то и допускает модификацию, принадлежащую
то и допускает модификацию, принадлежащую  Модифицированная функция удовлетворяет уравнению
Модифицированная функция удовлетворяет уравнению  в обычном смысле. Так как доказательство сильно упрощается в том случае, когда
в обычном смысле. Так как доказательство сильно упрощается в том случае, когда  не зависят от
не зависят от  то легче всего и начать с этого специального случая. Наше доказательство представляет собой некоторое упрощение доказательства Ниренберга.
то легче всего и начать с этого специального случая. Наше доказательство представляет собой некоторое упрощение доказательства Ниренберга.
Шаг 1.
Введем пространство  формальных тригонометрических сумм:
формальных тригонометрических сумм:

у которых  сопряжено с
сопряжено с  и
и

Будем рассматривать  как (формальную) функцию на
как (формальную) функцию на  -мерном торе
-мерном торе  и отметим некоторые простые факты, которые пригодятся нам в дальнейшем:
и отметим некоторые простые факты, которые пригодятся нам в дальнейшем:

(2)  есть ограниченный оператор из
есть ограниченный оператор из  .
.
(3)  есть ограниченный оператор из
есть ограниченный оператор из  для любой
для любой  причем константы
причем константы  зависят от
зависят от  но не зависят от
но не зависят от  .
.
Доказательство (1).
Это можно предоставить читателю.
Доказательство (2).
Оператор  определяется сначала на
определяется сначала на  а потом замыкается. Оценка для
а потом замыкается. Оценка для  становится очевидной, если написать формальную сумму для
становится очевидной, если написать формальную сумму для  где
где 
Доказательство (3).
Оператор  определяется сначала в
определяется сначала в  а потом, как и раньше, замыкается; поэтому достаточно оценить
а потом, как и раньше, замыкается; поэтому достаточно оценить  для
для  Но для таких
Но для таких 

и поскольку  то из оценки для некоторого
то из оценки для некоторого  следует оценка для
следует оценка для 

Это завершает доказательство для 0. Переходя к случаю —  заметим, что
заметим, что  естественным образом сопряжены, причем оператор, двойственный к умножению
естественным образом сопряжены, причем оператор, двойственный к умножению  представляет собой умножение на ту же функцию
представляет собой умножение на ту же функцию  так что
так что  Далее,
Далее,  является дифференциальным оператором порядка 1 с коэффициентами из
является дифференциальным оператором порядка 1 с коэффициентами из  поэтому вследствие (2) он задает ограниченное отображение
поэтому вследствие (2) он задает ограниченное отображение 
 Оператор
Оператор  есть изометрическое отображение
есть изометрическое отображение  на
на  и поэтому
и поэтому

является ограниченным отображением  Отсюда следует (3) для
Отсюда следует (3) для 

Шаг 2
В силу утверждений (2) и (3) шага 1 можно рассматривать эллиптический оператор  на
на  как ограниченное отображение
как ограниченное отображение  Цель этого шага — доказать априорную оценку
Цель этого шага — доказать априорную оценку

где константы зависят от  но не зависят от
но не зависят от  Можно выразить
Можно выразить  через глобальные координаты на
через глобальные координаты на  Так как часть
Так как часть  порядок которой 1, задает ограниченное отображение
порядок которой 1, задает ограниченное отображение  при доказательстве можно предположить, что эта часть
при доказательстве можно предположить, что эта часть  отсутствует, т. е. что
отсутствует, т. е. что  Как всегда, достаточно доказать оценку для
Как всегда, достаточно доказать оценку для 
Доказательство для случая постоянных коэффициентов.
Пусть у наименьшее собственное значение матрицы  составленной из (старших) коэффициентов оператора
составленной из (старших) коэффициентов оператора  Тогда
Тогда

В последнем неравенстве мы используем тот факт, что  Этим установлена требуемая оценка с коэффициентами
Этим установлена требуемая оценка с коэффициентами 
Доказательство для случая переменных коэффициентов.
Пусть  минимум наименьшего собственного значения матрицы, составленной из (старших) коэффициентов оператора
минимум наименьшего собственного значения матрицы, составленной из (старших) коэффициентов оператора  Возьмем
Возьмем  настолько малым, чтобы в шаре радиуса
настолько малым, чтобы в шаре радиуса  можно было заменить
можно было заменить  на
на  с постоянными коэффициентами и наименьшим собственным значением у, сохраняя (старшие) коэффициенты оператора
с постоянными коэффициентами и наименьшим собственным значением у, сохраняя (старшие) коэффициенты оператора  по модулю
по модулю  По только что полученной оценке
По только что полученной оценке

где  вне шара радиуса
вне шара радиуса  Но, с другой стороны,
Но, с другой стороны,

поэтому

Представив функцию, тождественно равную 1, в виде конечной суммы таких функций  получим
получим

Шаг 3
Теперь можно доказать лемму Вейля для  с помощью априорной оценки из шага 2.
с помощью априорной оценки из шага 2.
Утверждение ее состоит в том, что если  - (формальная) плотность распределения масс на
- (формальная) плотность распределения масс на  и если
и если

для некоторой  и любой финитной
и любой финитной  то можно изменить и так, чтобы
то можно изменить и так, чтобы  после этой модификации
после этой модификации  в обычном смысле.
в обычном смысле.
Доказательство.
Так как это утверждение локально, то достаточно доказать его на некоторой карте  Модифицировав локальные координаты
Модифицировав локальные координаты  на
на  так, чтобы тор
так, чтобы тор  «сидел внутри»
«сидел внутри»  подберем финитные
подберем финитные  так, чтобы
так, чтобы

и пусть  эллиптический оператор на
эллиптический оператор на  совпадающий с
совпадающий с  на
на  Рассмотрим
Рассмотрим  как элемент пространства
как элемент пространства  при
при  Выражение
Выражение  можно рассматривать как результат действия дифференциального оператора порядка 1 с коэффициентами из
можно рассматривать как результат действия дифференциального оператора порядка 1 с коэффициентами из  на
на  поэтому из априорной оценки шага 2 получим
поэтому из априорной оценки шага 2 получим

т. e.  , Повторяя эту оценку, находим
, Повторяя эту оценку, находим

Остальное ясно.
Шаг 4.
Теперь можно доказать лемму Вейля для  почти тем же способом. Введем пространство
почти тем же способом. Введем пространство  формальных сумм
формальных сумм

где  сопряжены и
сопряжены и

и будем рассматривать  как (формальную) функцию на
как (формальную) функцию на  Отображение
Отображение  есть ограниченный оператор из в где
есть ограниченный оператор из в где  определяется, как и в шаге 2. Априорная оценка
определяется, как и в шаге 2. Априорная оценка

доказывается почти так же, как раньше. Можно предполагать, что  не содержит членов, порядок которых 1. Тогда
не содержит членов, порядок которых 1. Тогда

так что между  нет интерференции. Остальная часть доказательства аналогична эллиптическому случаю.
нет интерференции. Остальная часть доказательства аналогична эллиптическому случаю.
Предупреждение: отныне под  понимается эллиптический оператору причем
понимается эллиптический оператору причем  означает оператор, сопряженный с
означает оператор, сопряженный с  относительно элемента объема
относительно элемента объема 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. БРОУНОВСКОЕ ДВИЖЕНИЕ
- 1.1. Гауссовские семейства
- 1.2. Построение броуновского движения
- 1.8. Простейшие свойства броуновского движения
- 1.4. Неравенство для мартингалов
- 1.5. Закон повторного логарифма
- 1.6. Модуль Леви
- 1.7. Многомерное броуновское движение
- 2. СТОХАСТИЧЕСКИЕ ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЫ
- 2.1. Винеровское определение стохастического интеграла
- 2.2. Определение стохастического интеграла Ито
- 2.3. Простейшие свойства стохастического интеграла
- 2.4. Вычисление одного стохастического интеграла
- 2.5. Замена времени
- 2.6. Стохастические дифференциалы и лемма Ито
- 2.7. Решение простейшего стохастического дифференциального уравнения
- 2.8. Стохастические дифференциалы при замене времени
- 2.9. Стохастические интегралы и дифференциалы для многомерного броуновского движения
- 3. СТОХАСТИЧЕСКИЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ (ОДНОМЕРНЫЙ СЛУЧАЙ)
- 3.2. Решение уравнения dx=e(x)db+f(x)dt для случая коэффициентов ограниченного наклона
- 3.3. Решение уравнения dx=e(x)db+f(x)dt для общих коэффициентов класса
- 3.4. Метод Ламперти
- 3.5. Прямое уравнение
- 3.6. Феллеровский критерий взрыва
- 3.7. Формула Камерона — Мартина
- 3.8. Броуновское локальное время
- 3.9. Отражающие экраны
- 3.10. Некоторые сингулярные уравнения
- 4. СТОХАСТИЧЕСКИЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ (МНОГОМЕРНЫЙ СЛУЧАЙ)
- 4.2. Лемма Вейля
- 4.3. Диффузионные процессы на многообразии
- 4.4. Взрывы и гармонические функции
- 4.5. Критерий взрывов Хасьминского
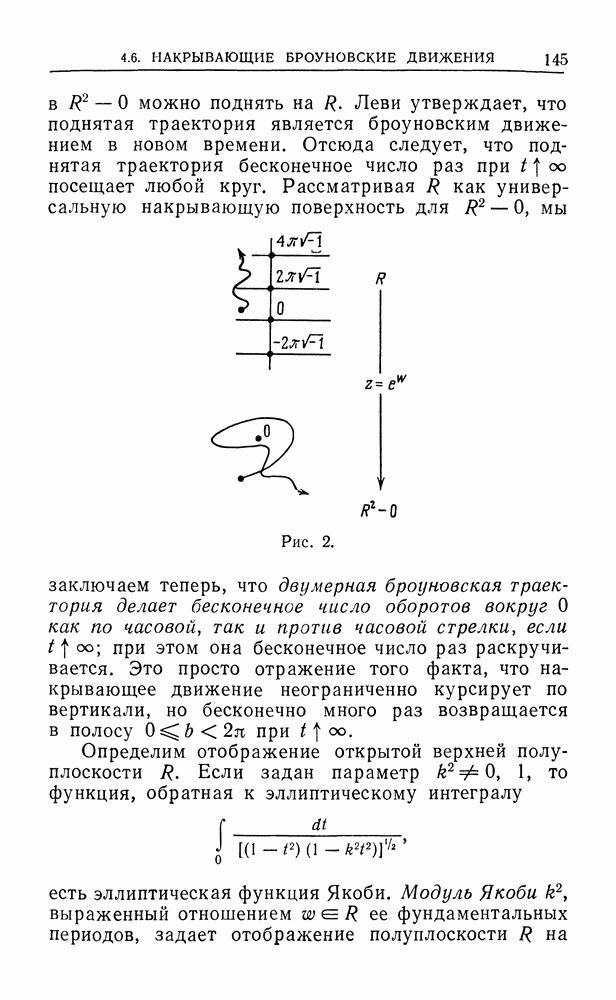
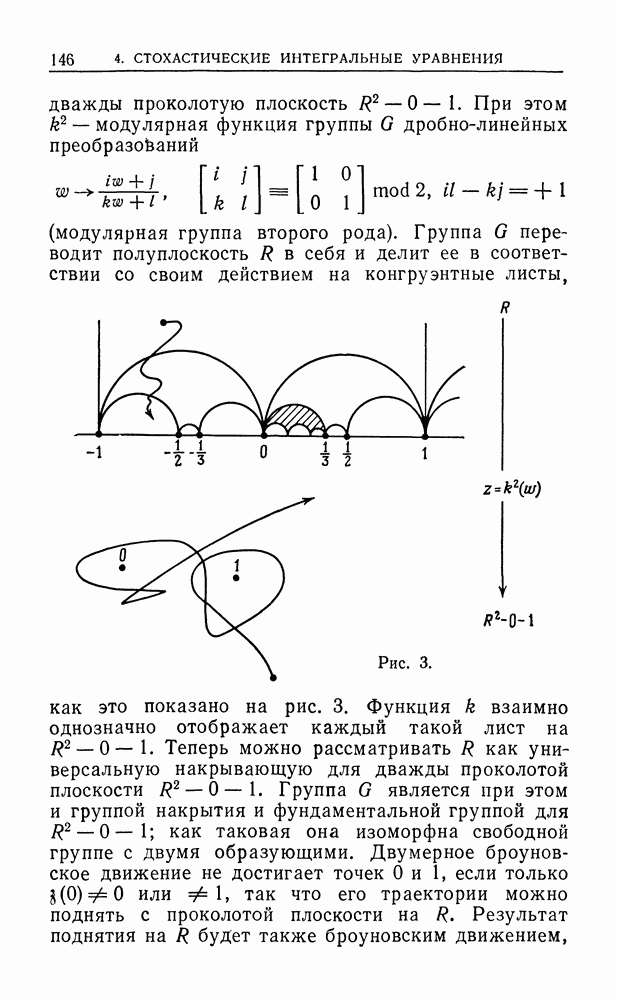
- 4.6. Накрывающие броуновские движения
- 4.7. Броуновское движение на группе Ли
- 4.8. Вложение
- 4.9. Броуновское движение на симметрических матрицах
- 4.10. Броуновское движение с косым отражением
- УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
- Список литературы