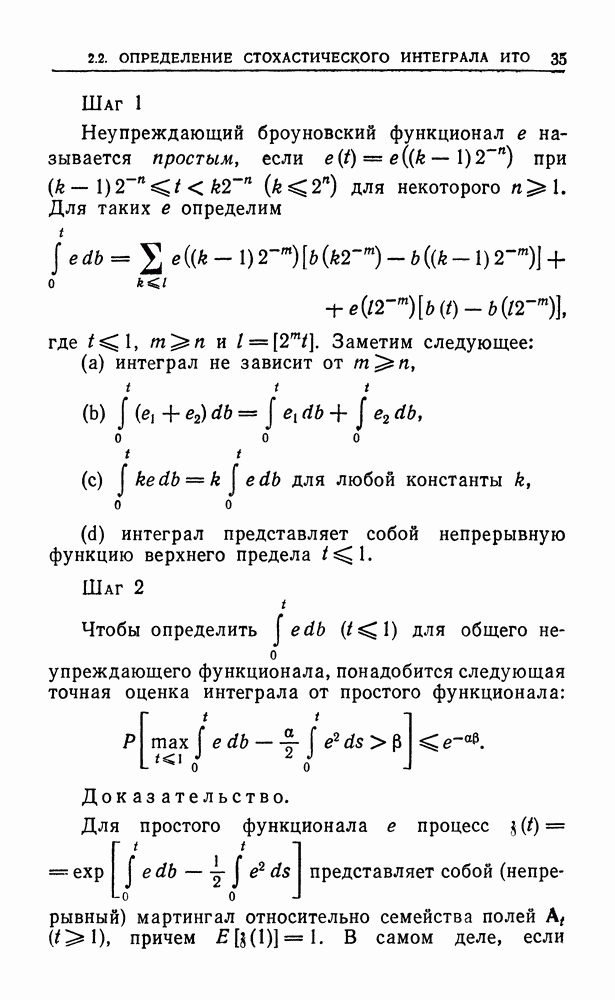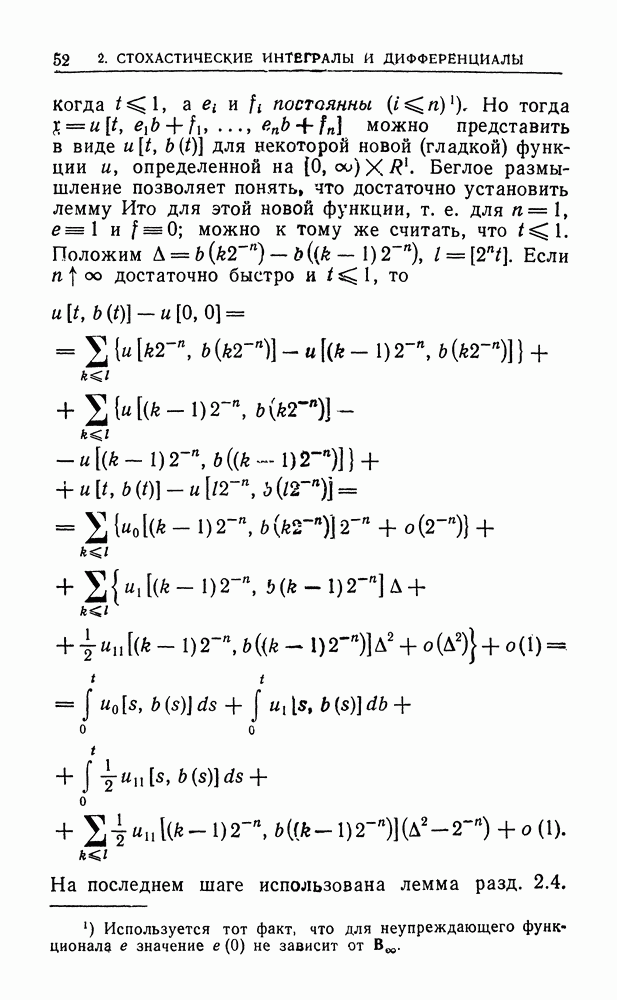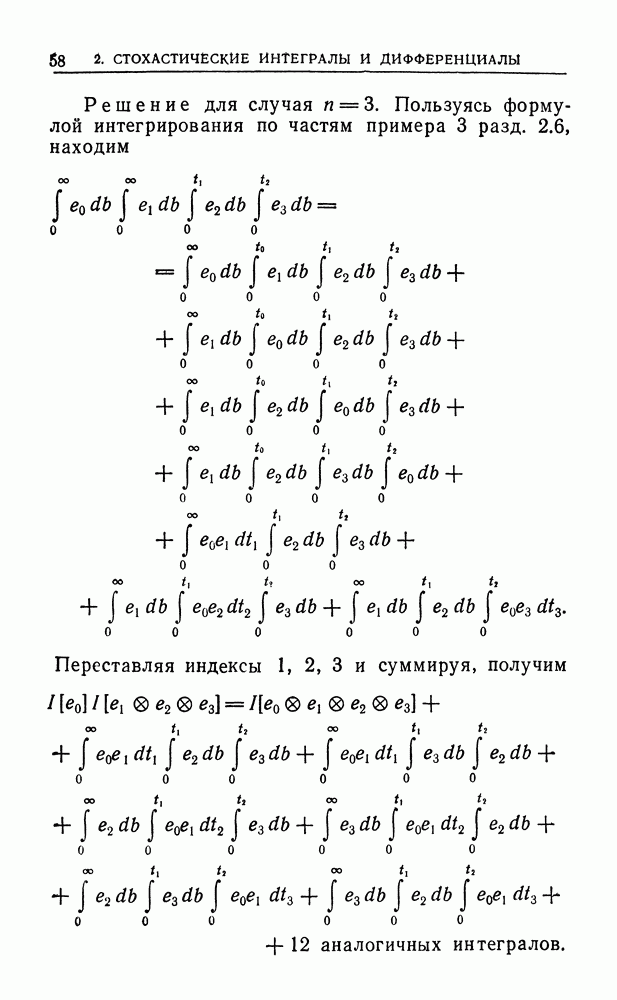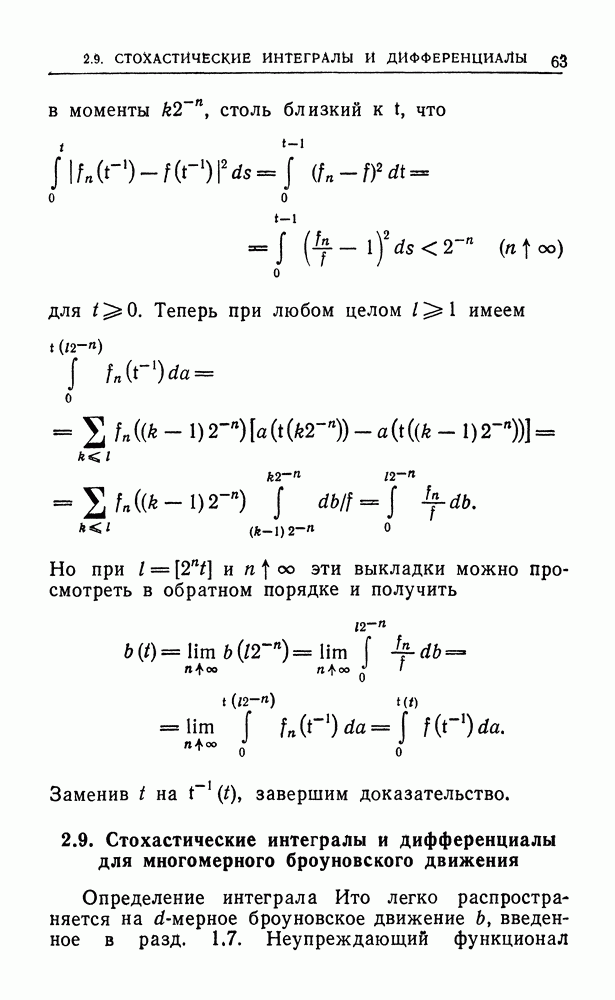| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.6. Накрывающие броуновские движения
Используя лемму  можно дать изящное доказательство результата Леви, состоящего в том, что двумерная броуновская траектория конформно инвариантна]). Последнее означает, что если
можно дать изящное доказательство результата Леви, состоящего в том, что двумерная броуновская траектория конформно инвариантна]). Последнее означает, что если  стандартное броуновское движение в
стандартное броуновское движение в  отличная от постоянной аналитическая функция, определенная в содержащей
отличная от постоянной аналитическая функция, определенная в содержащей  области
области  то до момента
то до момента  первого выхода процесса
первого выхода процесса  из
из  процесс
процесс  также представляет собой броуновское движение с новым временем
также представляет собой броуновское движение с новым временем 
Специально отметим, что если  риманова поверхность над
риманова поверхность над  то броуновскую траекторию
то броуновскую траекторию  можно поднять на
можно поднять на  обращая проекцию
обращая проекцию  и на каждой карте поверхности
и на каждой карте поверхности  с локальными координатами
с локальными координатами  эта накрывающая траектория играет роль соответствующего стандартного броуновского движения
эта накрывающая траектория играет роль соответствующего стандартного броуновского движения  протекающего во времени
протекающего во времени 
Доказательство.
Воспользуемся уравнениями Коши-Римана  и тем обстоятельством, что
и тем обстоятельством, что  Применив лемму
Применив лемму  получим
получим

Положим  тогда
тогда  неупреждающий функционал от
неупреждающий функционал от  так что
так что  некоторое новое броуновское стандартное движение. Итак,
некоторое новое броуновское стандартное движение. Итак,  причем
причем  неупреждающий функционал от
неупреждающий функционал от  Несколько обобщив правило замены времени разд. 2.5, можно показать теперь, что до момента
Несколько обобщив правило замены времени разд. 2.5, можно показать теперь, что до момента 

также есть броуновское движение, чем и завершим доказательство.
Конформная инвариантность, помимо самостоятельного интереса, находит занятные приложения к задаче о скручивании двумерной броуновской траектории. Этот вопрос будет обсужден ниже. При этом понадобятся некоторые сведения о группах накрытий, модулярных группах второго рода и модуле Якоби  Соответствующую информацию можно найти у Ленера [1] и Вейля [1]. Кроме этого, нужно также знать, что двумерная броуновская траектория бесконечное число раз при
Соответствующую информацию можно найти у Ленера [1] и Вейля [1]. Кроме этого, нужно также знать, что двумерная броуновская траектория бесконечное число раз при  посещает каждый круг.
посещает каждый круг.
Доказательство.
Проколотая сфера  отображается с помощью стереографической проекции
отображается с помощью стереографической проекции

на плоскость  Сферическое броуновское движение
Сферическое броуновское движение  управляется оператором
управляется оператором  имеющим в сферических координатах вид
имеющим в сферических координатах вид

В силу конформности стереографической проекции процесс  представляет собой (локально) броуновское движение в новом времени. Если
представляет собой (локально) броуновское движение в новом времени. Если  то
то  так что 5 не может достигнуть южного полюса
так что 5 не может достигнуть южного полюса  при
при  Поскольку оператор
Поскольку оператор  перестановочен со сферическими вращениями, то
перестановочен со сферическими вращениями, то  не может достигнуть и северного полюса (0, 0, 1). Но это значит, что при
не может достигнуть и северного полюса (0, 0, 1). Но это значит, что при  проекция
проекция  при 0 вполне определена. Тот факт, что при
при 0 вполне определена. Тот факт, что при  процесс I бесконечное число раз посещает любой кружок на сфере, немедленно находит отражение в том, что процесс
процесс I бесконечное число раз посещает любой кружок на сфере, немедленно находит отражение в том, что процесс  бесконечное число раз достигает любого круга на плоскости.
бесконечное число раз достигает любого круга на плоскости.
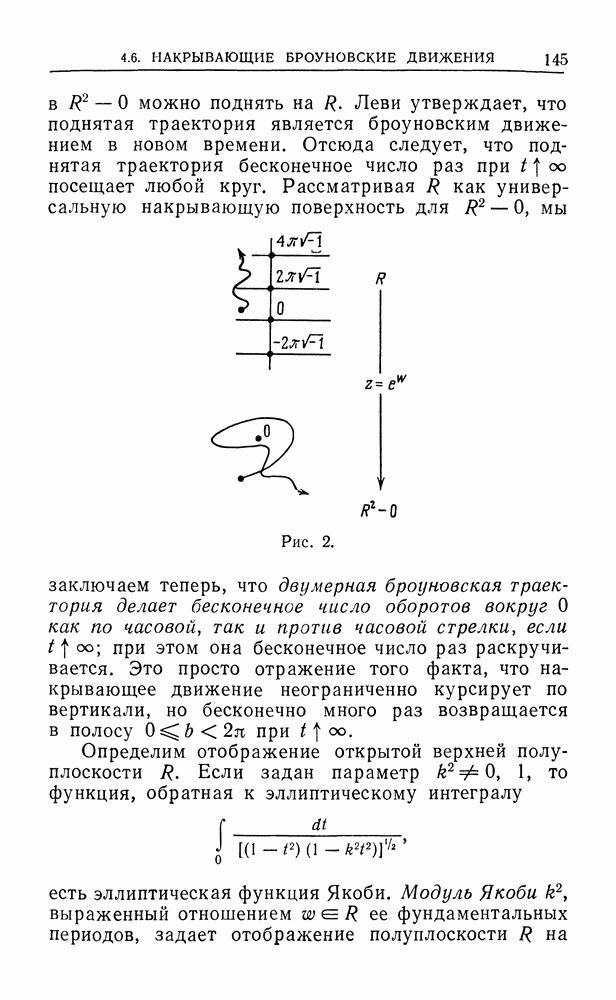
Рассмотрим риманову поверхность  функции
функции  как плоскость, разделенную на горизонтальные полосы ширины
как плоскость, разделенную на горизонтальные полосы ширины  с проекцией
с проекцией  отображающей каждую полосу на проколотую плоскость
отображающей каждую полосу на проколотую плоскость  (рис. 2). Поверхность
(рис. 2). Поверхность  можно рассматривать как универсальную накрывающую для
можно рассматривать как универсальную накрывающую для  Вследствие этого группа накрытия изоморфна
Вследствие этого группа накрытия изоморфна  фундаментальной группе области
фундаментальной группе области  Поскольку броуновское движение
Поскольку броуновское движение  на плоскости никогда не достигает 0, если
на плоскости никогда не достигает 0, если  то броуновское движение
то броуновское движение
в  можно поднять на
можно поднять на  Леви утверждает, что поднятая траектория является броуновским движением в новом времени. Отсюда следует, что поднятая траектория бесконечное число раз при
Леви утверждает, что поднятая траектория является броуновским движением в новом времени. Отсюда следует, что поднятая траектория бесконечное число раз при  посещает любой круг.
посещает любой круг.

Рис. 2.
Рассматривая  как универсальную накрывающую поверхность для
как универсальную накрывающую поверхность для  мы заключаем теперь, что двумерная броуновская траектория делает бесконечное число оборотов вокруг О как по часовой, так и против часовой стрелки, если
мы заключаем теперь, что двумерная броуновская траектория делает бесконечное число оборотов вокруг О как по часовой, так и против часовой стрелки, если  при этом она бесконечное число раз раскручивается. Это просто отражение того факта, что накрывающее движение неограниченно курсирует по вертикали, но бесконечно много раз возвращается в полосу
при этом она бесконечное число раз раскручивается. Это просто отражение того факта, что накрывающее движение неограниченно курсирует по вертикали, но бесконечно много раз возвращается в полосу  при
при 
Определим отображение открытой верхней полуплоскости  Если задан параметр
Если задан параметр  то функция, обратная к эллиптическому интегралу
то функция, обратная к эллиптическому интегралу

есть эллиптическая функция Якоби. Модуль Якоби  выраженный отношением
выраженный отношением  ее фундаментальных периодов, задает отображение полуплоскости
ее фундаментальных периодов, задает отображение полуплоскости  на
на
дважды проколотую плоскость  При этом
При этом  модулярная функция группы
модулярная функция группы  дробно-линейных преобразований
дробно-линейных преобразований

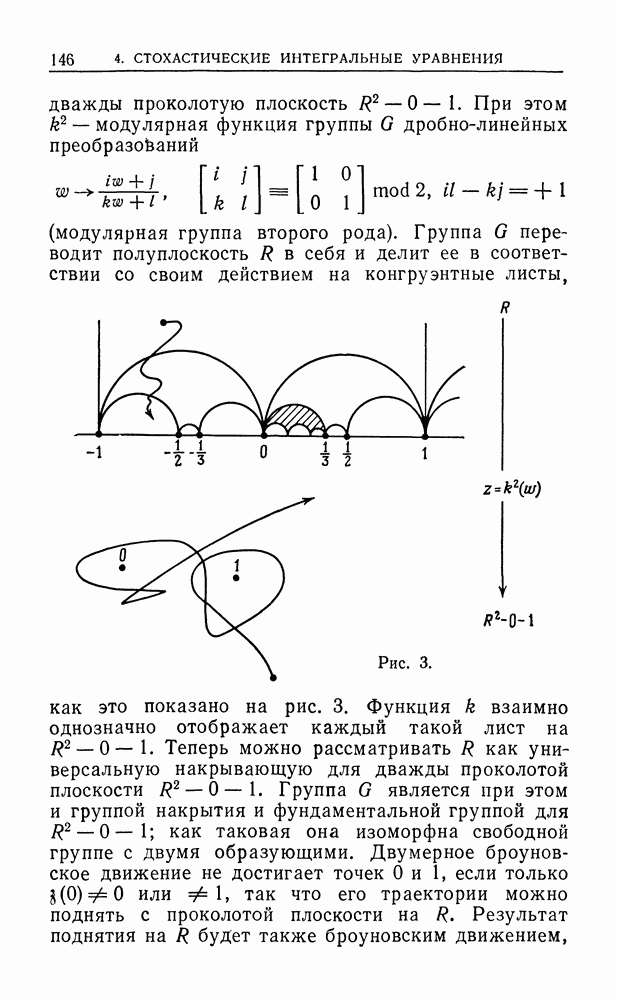
(модулярная группа второго рода). Группа  переводит полуплоскость
переводит полуплоскость  в себя и делит ее в соответствии со своим действием на конгруэнтные листы, как это показано на рис. 3.
в себя и делит ее в соответствии со своим действием на конгруэнтные листы, как это показано на рис. 3.

Рис. 3.
Функция  взаимно однозначно отображает каждый такой лист на
взаимно однозначно отображает каждый такой лист на  Теперь можно рассматривать
Теперь можно рассматривать  как универсальную накрывающую для дважды проколотой плоскости
как универсальную накрывающую для дважды проколотой плоскости  Группа
Группа  является при этом и группой накрытия и фундаментальной группой для
является при этом и группой накрытия и фундаментальной группой для  как таковая она изоморфна свободной группе с двумя образующими. Двумерное броуновское движение не достигает точек 0 и 1, если только
как таковая она изоморфна свободной группе с двумя образующими. Двумерное броуновское движение не достигает точек 0 и 1, если только  или
или  так что его траектории можно поднять с проколотой плоскости на
так что его траектории можно поднять с проколотой плоскости на  Результат поднятия на
Результат поднятия на  будет также броуновским движением,
будет также броуновским движением,
но в новом времени. Поскольку  полуплоскость, то при
полуплоскость, то при  накрывающее движение стремится к границе
накрывающее движение стремится к границе  Из того что каждый лист полуплоскости
Из того что каждый лист полуплоскости  соответствует какому-то элементу фундаментальной группы
соответствует какому-то элементу фундаментальной группы  нетрудно вывести, что в отличие от случая плоскости, проколотой один раз, картина закручивания броуновской траектории вокруг точек 0 и 1 становится при
нетрудно вывести, что в отличие от случая плоскости, проколотой один раз, картина закручивания броуновской траектории вокруг точек 0 и 1 становится при  все более и более сложной и, начиная с некоторого момента, траектория никогда не раскрутится.
все более и более сложной и, начиная с некоторого момента, траектория никогда не раскрутится.
Рассмотрим риманову поверхность  накрывающую
накрывающую  и имеющую в качестве группы накрытия коммутативную группу с двумя образующими
и имеющую в качестве группы накрытия коммутативную группу с двумя образующими  Поверхность
Поверхность  можно реализовать как риманову поверхность функции
можно реализовать как риманову поверхность функции  и тогда ее возможно описать как счетное число копий римановой поверхности функции
и тогда ее возможно описать как счетное число копий римановой поверхности функции  соединенных между собой в точках
соединенных между собой в точках  логарифмического ветвления. Группа
логарифмического ветвления. Группа  это попросту группа
это попросту группа  сделанная коммутативной, точнее,
сделанная коммутативной, точнее,  изоморфна факторгруппе
изоморфна факторгруппе  по ее коммутанту. Можно отождествить
по ее коммутанту. Можно отождествить  с группой гомологий
с группой гомологий  многообразия
многообразия  Поднимем броуновскую траекторию с
Поднимем броуновскую траекторию с  на
на  Теорема Леви утверждает, что это поднятие представляет собой броуновское движение на
Теорема Леви утверждает, что это поднятие представляет собой броуновское движение на  происходящее в новом времени. Но это броуновское движение посещает при
происходящее в новом времени. Но это броуновское движение посещает при  каждый кружок на
каждый кружок на  бесконечно много раз (доказательство приводится ниже), так что при закручивании плоской броуновской траектории вокруг точек 0 и 1 она бесконечное число раз при
бесконечно много раз (доказательство приводится ниже), так что при закручивании плоской броуновской траектории вокруг точек 0 и 1 она бесконечное число раз при  «распутывается» с точки зрения целочисленных гомологий.
«распутывается» с точки зрения целочисленных гомологий.
Доказательство бесконечно частого посещения броуновским движением любого круга на  при
при 
Пусть  коммутант группы
коммутант группы  Точка 1—1 переходит под действием коммутатора
Точка 1—1 переходит под действием коммутатора

в точку, которая сходится при  Если первый множитель
Если первый множитель  пробегает
пробегает  взаимно просты,
взаимно просты,  четно,
четно,  нечетно), то дроби
нечетно), то дроби  всюду плотны на границе
всюду плотны на границе  Группа
Группа  действует из
действует из  Это так называемая основная модулярная группа первого рода, и по теореме Пуанкаре получим
Это так называемая основная модулярная группа первого рода, и по теореме Пуанкаре получим

Рассмотрим теперь стандартное броуновское движение  протекающее во времени
протекающее во времени  обратном к функционалу
обратном к функционалу  Ясно, что величина
Ясно, что величина  определена до момента
определена до момента  где
где  время первого выхода
время первого выхода  процесса
процесса  из
из  Последний интеграл бесконечен, так как
Последний интеграл бесконечен, так как

Но тогда проекция процесса на  является броуновским движением, происходящим в новом времени, которое определяется как функция
является броуновским движением, происходящим в новом времени, которое определяется как функция  Среднее время пребывания процесса в области
Среднее время пребывания процесса в области
 с индикатором
с индикатором  задается формулой
задается формулой

Из инвариантности элемента объема  относительно действия группы
относительно действия группы  непосредственно следует, что среднее время, которое процесс
непосредственно следует, что среднее время, которое процесс  проводит в проекции круга
проводит в проекции круга  равно
равно

Так как процесс совпадает с точностью до замены времени с плоским броуновским движением, поднятым с  на
на  то осталось проверить, что посещает бесконечно много раз при
то осталось проверить, что посещает бесконечно много раз при  каждый круг в
каждый круг в  Убедиться в этом не составит труда, если вспомнить, что среднее время пребывания
Убедиться в этом не составит труда, если вспомнить, что среднее время пребывания  в круге бесконечно и что процесс начинается заново в каждый момент достижения. В самом деле, пусть
в круге бесконечно и что процесс начинается заново в каждый момент достижения. В самом деле, пусть 
замкнутый круг, расположенный в большем круге В  последовательные моменты достижения процессом
последовательные моменты достижения процессом  множества
множества  после пребывания в
после пребывания в  Обозначим через
Обозначим через  функции
функции  и
и

начальной точки  ; тогда полное среднее время пребывания в
; тогда полное среднее время пребывания в  представляется в виде
представляется в виде

Если внешний круг В достаточно мал, то функция  ограничена на
ограничена на  Это легко получить, опуская процесс
Это легко получить, опуская процесс  на
на  Функция а гармонична вне
Функция а гармонична вне  поэтому из расходимости ряда следует, что
поэтому из расходимости ряда следует, что  Отсюда
Отсюда  в некоторой точке окружности
в некоторой точке окружности  и в результате
и в результате  Доказательство закончено.
Доказательство закончено.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. БРОУНОВСКОЕ ДВИЖЕНИЕ
- 1.1. Гауссовские семейства
- 1.2. Построение броуновского движения
- 1.8. Простейшие свойства броуновского движения
- 1.4. Неравенство для мартингалов
- 1.5. Закон повторного логарифма
- 1.6. Модуль Леви
- 1.7. Многомерное броуновское движение
- 2. СТОХАСТИЧЕСКИЕ ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЫ
- 2.1. Винеровское определение стохастического интеграла
- 2.2. Определение стохастического интеграла Ито
- 2.3. Простейшие свойства стохастического интеграла
- 2.4. Вычисление одного стохастического интеграла
- 2.5. Замена времени
- 2.6. Стохастические дифференциалы и лемма Ито
- 2.7. Решение простейшего стохастического дифференциального уравнения
- 2.8. Стохастические дифференциалы при замене времени
- 2.9. Стохастические интегралы и дифференциалы для многомерного броуновского движения
- 3. СТОХАСТИЧЕСКИЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ (ОДНОМЕРНЫЙ СЛУЧАЙ)
- 3.2. Решение уравнения dx=e(x)db+f(x)dt для случая коэффициентов ограниченного наклона
- 3.3. Решение уравнения dx=e(x)db+f(x)dt для общих коэффициентов класса
- 3.4. Метод Ламперти
- 3.5. Прямое уравнение
- 3.6. Феллеровский критерий взрыва
- 3.7. Формула Камерона — Мартина
- 3.8. Броуновское локальное время
- 3.9. Отражающие экраны
- 3.10. Некоторые сингулярные уравнения
- 4. СТОХАСТИЧЕСКИЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ (МНОГОМЕРНЫЙ СЛУЧАЙ)
- 4.2. Лемма Вейля
- 4.3. Диффузионные процессы на многообразии
- 4.4. Взрывы и гармонические функции
- 4.5. Критерий взрывов Хасьминского
- 4.6. Накрывающие броуновские движения
- 4.7. Броуновское движение на группе Ли
- 4.8. Вложение
- 4.9. Броуновское движение на симметрических матрицах
- 4.10. Броуновское движение с косым отражением
- УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
- Список литературы