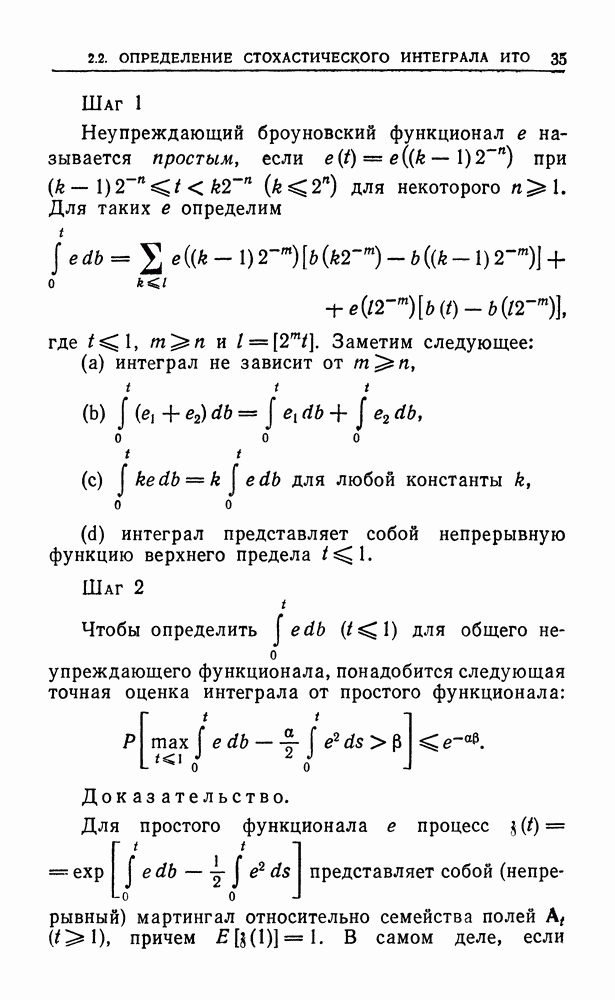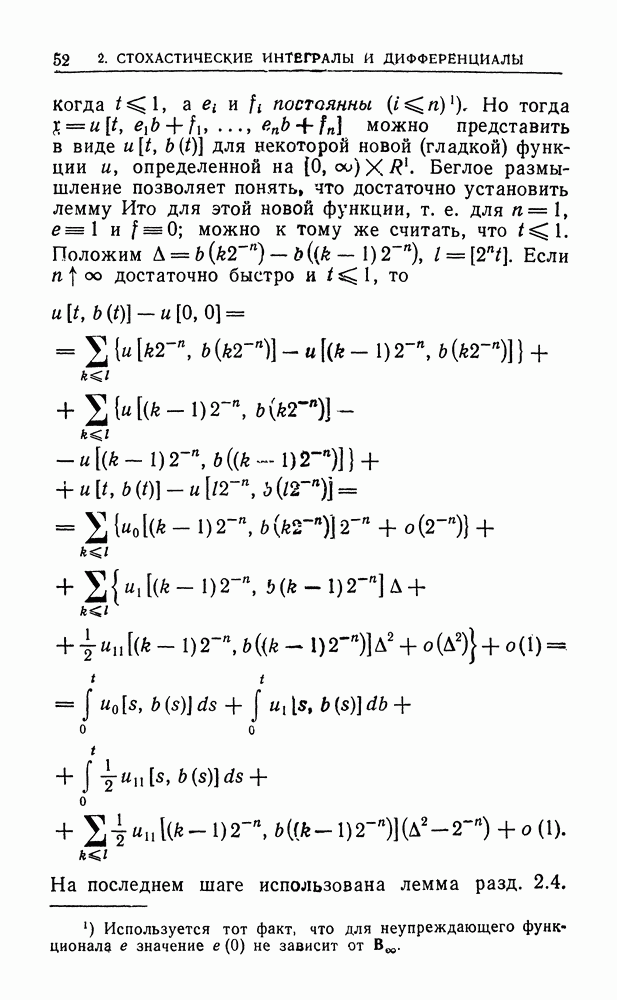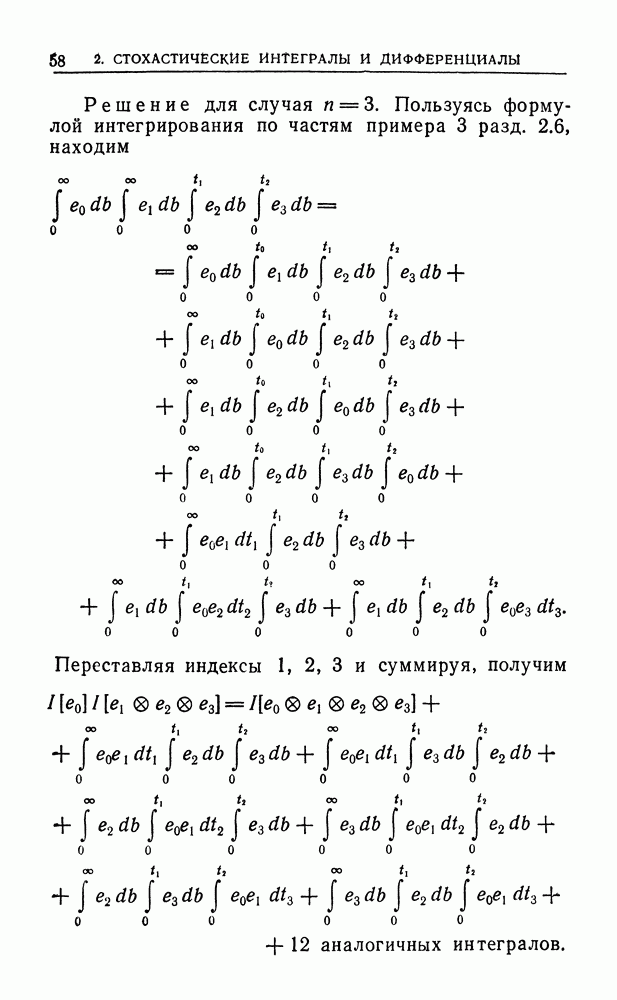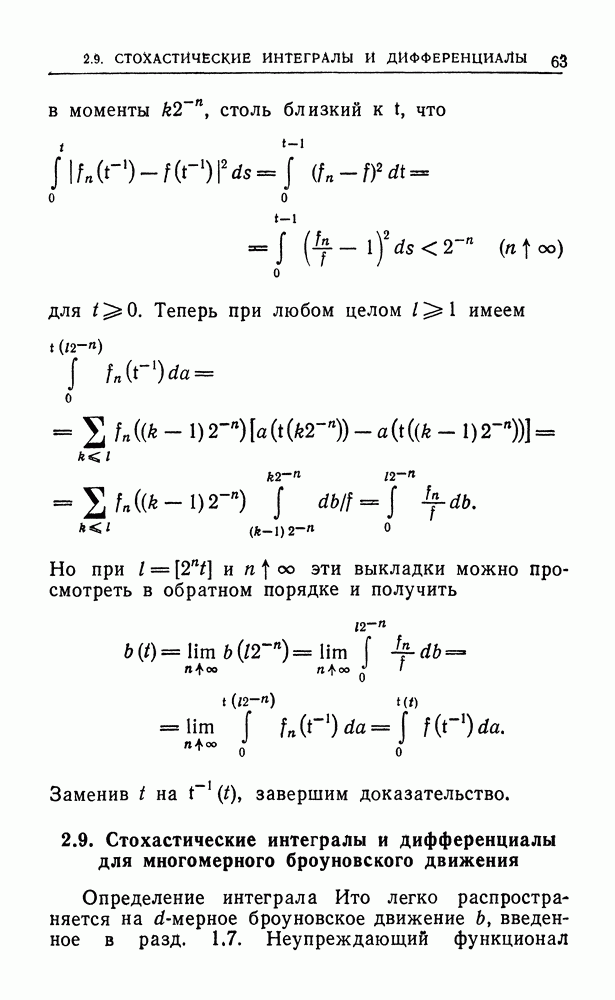| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.8. Вложение
Пусть заданы постоянные матрица  и вектор
и вектор  и стандартное
и стандартное  -мерное броуновское движение
-мерное броуновское движение  Рассмотрим процесс
Рассмотрим процесс  как (косое) броуновское движение на алгебре Ли А группы
как (косое) броуновское движение на алгебре Ли А группы  т. е. отождествим точки не
т. е. отождествим точки не 
Проверим следующее предложение: если

то так называемый мультипликативный интеграл 

существует и определяет левоинвариантное броуновское движение на группе  управляемое оператором
управляемое оператором 
Шаг 1
Теорема  устанавливает, что А допускает при некотором
устанавливает, что А допускает при некотором  точное представление как подалгебра Ли алгебры
точное представление как подалгебра Ли алгебры  с обычной операцией коммутирования. Классическая экспоненциальная сумма
с обычной операцией коммутирования. Классическая экспоненциальная сумма  отображает эту точную копию А на некоторую подгруппу Ли общей линейной группы
отображает эту точную копию А на некоторую подгруппу Ли общей линейной группы  Построенная подгруппа локально изоморфна
Построенная подгруппа локально изоморфна  хотя глобально это, возможно, и не так. Но конструкция вложения локальна, так что доказательство можно проводить в предположении, что
хотя глобально это, возможно, и не так. Но конструкция вложения локальна, так что доказательство можно проводить в предположении, что  точно вкладывается в
точно вкладывается в  как подгруппа Ли.
как подгруппа Ли.
Введем в  норму
норму  не смешивая ее с нормой
не смешивая ее с нормой  линейного оператора а,
линейного оператора а,
действующего в  Мы часто будем пользоваться следующими неравенствами:
Мы часто будем пользоваться следующими неравенствами:

Предупреждение: для того чтобы последующие формулы выглядели более четко, транспонирование элемента  как оператора в
как оператора в  будем обозначать а.
будем обозначать а.
Шаг 2
Мультипликативное представление для предполагает, что в обертывающей алгебре  выполнено соотношение
выполнено соотношение 
Сейчас будет доказано,  задача имеет единственное неупреждающее решение
задача имеет единственное неупреждающее решение  такое, что
такое, что 
Доказательство единственности.
Рассмотрим разность 1) двух неупреждающих решений, и пусть броуновский момент остановки  определяется как наименьшая из двух величин
определяется как наименьшая из двух величин  Применение леммы Ито к процессу приводит к представлению
Применение леммы Ито к процессу приводит к представлению 

где  Используя оценки, отмеченные в шаге 1, нетрудно вывести, что
Используя оценки, отмеченные в шаге 1, нетрудно вывести, что  и что справедлива оценка
и что справедлива оценка

Отсюда заключаем, что  Доказательство завершается предельным переходом при
Доказательство завершается предельным переходом при 
Доказательство существования.
По аналогии с разд. 2.7 определим  как сумму ряда
как сумму ряда  где
где  при
при  Точно так же, как только что при оценке выражения
Точно так же, как только что при оценке выражения  докажем, что
докажем, что

Используя, как и в разд. 2.7, мартингальное неравенство и первую лемму Бореля — Кантелли, находим, что сумма для  сходится экспоненциально быстро к решению уравнения
сходится экспоненциально быстро к решению уравнения 
Шаг 3
Положим по определению  если
если 
Докажем, что при любом 

Доказательство.
Норма  оценивается сверху выражением
оценивается сверху выражением  Так как
Так как  то нетрудно доказать, что среднее
то нетрудно доказать, что среднее  ограничено при
ограничено при  для каждого
для каждого  и что
и что  также ограничено, причем
также ограничено, причем

Но при  справа стоит общий член сходящегося ряда и доказательство завершается ссылкой на первую лемму Бореля — Кантелли.
справа стоит общий член сходящегося ряда и доказательство завершается ссылкой на первую лемму Бореля — Кантелли.
Шаг 4
Докажем, что при любом 

Доказательство.
Определим  где
где  Используя модули Леви (разд. 1.6), их обобщение для стохастических интегралов (разд. 2.5) и оценку предыдущего шага, можно показать, что при
Используя модули Леви (разд. 1.6), их обобщение для стохастических интегралов (разд. 2.5) и оценку предыдущего шага, можно показать, что при  с точностью до величин, не превосходящих
с точностью до величин, не превосходящих  выполняется неравенство
выполняется неравенство

где  Так как последние суммы
Так как последние суммы  образуют мартингал, то последовательность
образуют мартингал, то последовательность  субмартингал. Пользуясь оценкой шага 3:
субмартингал. Пользуясь оценкой шага 3:  и независимостью величин
и независимостью величин  и
и  находим, что
находим, что

Но при  это общий член сходящегося ряда, так что все прочее следует из первой леммы Бореля — Кантелли.
это общий член сходящегося ряда, так что все прочее следует из первой леммы Бореля — Кантелли.
Шаг 5
Докажем, что при любом 

Доказательство.
Имеем  где —
где —  Согласно шагу 4, последнее выражение при
Согласно шагу 4, последнее выражение при  не превосходит по величине
не превосходит по величине  Введем в рассмотрение броуновский момент
Введем в рассмотрение броуновский момент  определенный как первый момент
определенный как первый момент  такой, что
такой, что  или
или  (Если ни одно из этих двух событий не произошло при
(Если ни одно из этих двух событий не произошло при  то полагаем
то полагаем  ) В силу результатов шагов
) В силу результатов шагов  при
при  Пусть
Пусть  Величину
Величину  можно оценить, как и в шаге 2:
можно оценить, как и в шаге 2:

В результате для  получается при 1 верхняя оценка:
получается при 1 верхняя оценка:  Теперь обычный мартингальный прием, примененный к субмартингалу
Теперь обычный мартингальный прием, примененный к субмартингалу

показывает, что

Аналогичную оценку

доказать еще проще. Отсюда и следует нужный результат.
Шаг 6
Предел  существует и для невырожденной матрицы
существует и для невырожденной матрицы  он представляет собой левоинвариантное движение на группе
он представляет собой левоинвариантное движение на группе  управляемое оператором
управляемое оператором 
Доказательство.
Из результата шага 5 немедленно следует, что при  мультипликативный интеграл
мультипликативный интеграл  существует; читатель без труда проверит, что конструкцию можно распространить и на случай
существует; читатель без труда проверит, что конструкцию можно распространить и на случай  Ясно также, что — левоинвариантное броуновское движение. Осталось доказать последнее утверждение. Но, как легко видеть, для финитной функции и
Ясно также, что — левоинвариантное броуновское движение. Осталось доказать последнее утверждение. Но, как легко видеть, для финитной функции и  при
при  с точностью до величины, не превосходящей
с точностью до величины, не превосходящей 

 член этого ряда вычисляется при
член этого ряда вычисляется при  Нетрудно показать, что при
Нетрудно показать, что при  последнее выражение стремится к
последнее выражение стремится к

Но это значит, что на каждой карте  с локальными координатами
с локальными координатами  процесс
процесс  является решением уравнения
является решением уравнения  В этой окрестности
В этой окрестности  служат локальными коэффициентами оператора
служат локальными коэффициентами оператора  Тем самым мы можем отождествить с левоинвариантным броуновским движением на группе
Тем самым мы можем отождествить с левоинвариантным броуновским движением на группе  управляемым оператором
управляемым оператором  Доказательство закончено.
Доказательство закончено.
Простой, но любопытный пример вложения получается, если рассмотреть движение трехмерного шара, катящегося без скольжения по плоскости  в то время как его центр совершает стандартное двумерное броуновское движение
в то время как его центр совершает стандартное двумерное броуновское движение  на плоскости
на плоскости  Здесь
Здесь  инфинитезимальные вращения
инфинитезимальные вращения

порождают А, и экспоненциальное отображение переводит  в поворот против часовой стрелки на угол
в поворот против часовой стрелки на угол  вокруг оси
вокруг оси  как уже отмечалось в разд. 4.8.
как уже отмечалось в разд. 4.8.

Рис. 4.
Так как броуновская частица движется из  (точка 1 рис. 4) в
(точка 1 рис. 4) в  (точка 2
(точка 2
рис. 4), то шар за то же время испытывает приблизительно поворот  на угол
на угол  (против часовой стрелки) вокруг оси
(против часовой стрелки) вокруг оси  как показано на рис. 4. Поэтому к моменту
как показано на рис. 4. Поэтому к моменту  шар претерпевает вращение, в точности равное соответствующему мультипликативному интегралу; именно, (левое) броуновское движение на
шар претерпевает вращение, в точности равное соответствующему мультипликативному интегралу; именно, (левое) броуновское движение на  управляется оператором
управляется оператором 
Задача 1. Докажите, что движение  северного полюса катящегося шара есть сферическая диффузия, управляемая оператором
северного полюса катящегося шара есть сферическая диффузия, управляемая оператором

Решение. Так как  то
то  коммутирует с подгруппой
коммутирует с подгруппой  вращений вокруг северного полюса
вращений вокруг северного полюса  Поэтому
Поэтому  есть диффузия на сфере
есть диффузия на сфере  Для завершения доказательства достаточно вычислить результат действия
Для завершения доказательства достаточно вычислить результат действия  оператора
оператора  на
на  , рассматривая функцию
, рассматривая функцию  как элемент пространства
как элемент пространства  зависящий только от классов смежности
зависящий только от классов смежности 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. БРОУНОВСКОЕ ДВИЖЕНИЕ
- 1.1. Гауссовские семейства
- 1.2. Построение броуновского движения
- 1.8. Простейшие свойства броуновского движения
- 1.4. Неравенство для мартингалов
- 1.5. Закон повторного логарифма
- 1.6. Модуль Леви
- 1.7. Многомерное броуновское движение
- 2. СТОХАСТИЧЕСКИЕ ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЫ
- 2.1. Винеровское определение стохастического интеграла
- 2.2. Определение стохастического интеграла Ито
- 2.3. Простейшие свойства стохастического интеграла
- 2.4. Вычисление одного стохастического интеграла
- 2.5. Замена времени
- 2.6. Стохастические дифференциалы и лемма Ито
- 2.7. Решение простейшего стохастического дифференциального уравнения
- 2.8. Стохастические дифференциалы при замене времени
- 2.9. Стохастические интегралы и дифференциалы для многомерного броуновского движения
- 3. СТОХАСТИЧЕСКИЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ (ОДНОМЕРНЫЙ СЛУЧАЙ)
- 3.2. Решение уравнения dx=e(x)db+f(x)dt для случая коэффициентов ограниченного наклона
- 3.3. Решение уравнения dx=e(x)db+f(x)dt для общих коэффициентов класса
- 3.4. Метод Ламперти
- 3.5. Прямое уравнение
- 3.6. Феллеровский критерий взрыва
- 3.7. Формула Камерона — Мартина
- 3.8. Броуновское локальное время
- 3.9. Отражающие экраны
- 3.10. Некоторые сингулярные уравнения
- 4. СТОХАСТИЧЕСКИЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ (МНОГОМЕРНЫЙ СЛУЧАЙ)
- 4.2. Лемма Вейля
- 4.3. Диффузионные процессы на многообразии
- 4.4. Взрывы и гармонические функции
- 4.5. Критерий взрывов Хасьминского
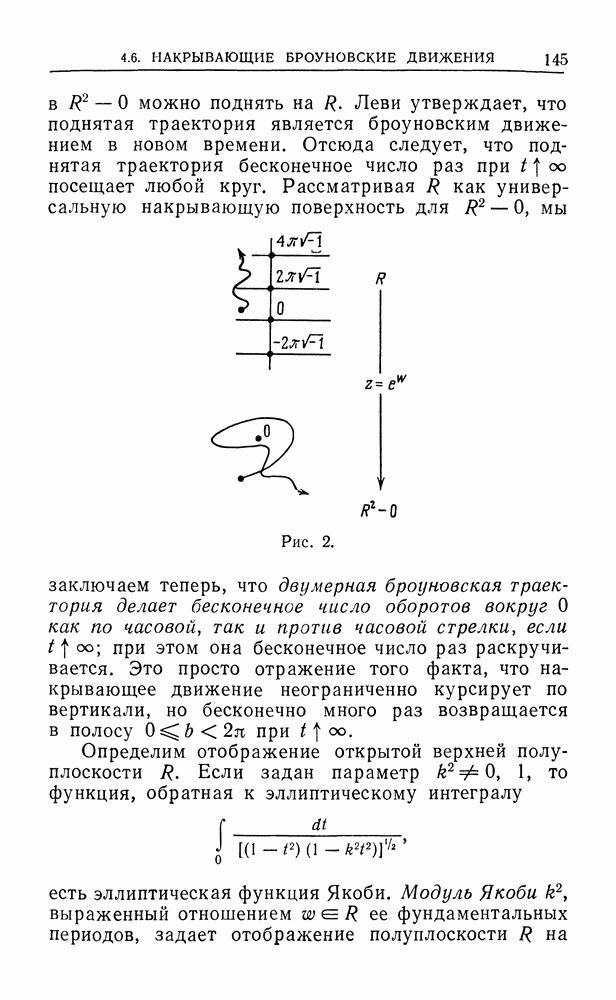
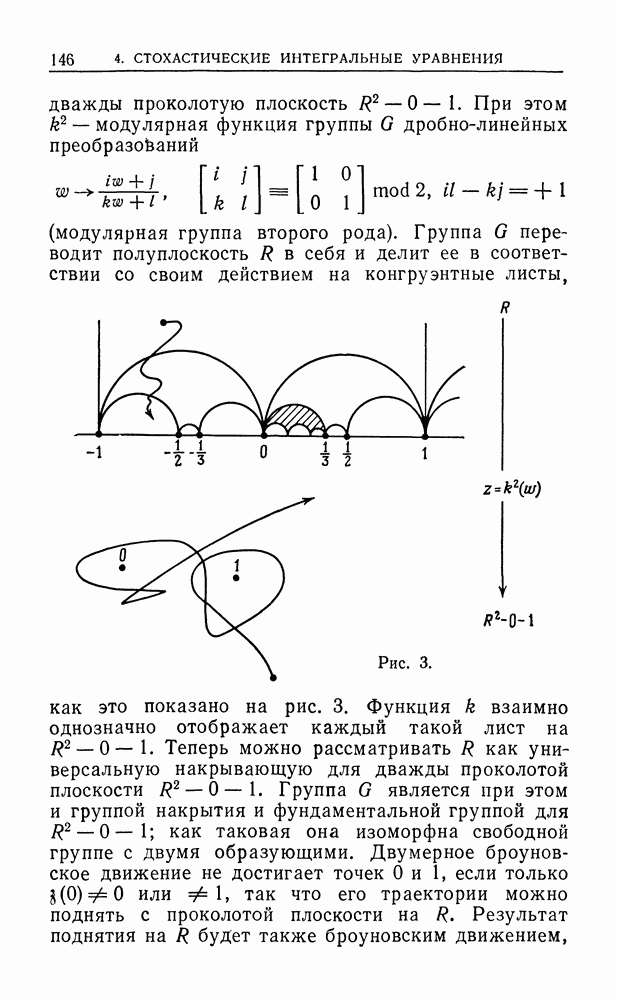
- 4.6. Накрывающие броуновские движения
- 4.7. Броуновское движение на группе Ли
- 4.8. Вложение
- 4.9. Броуновское движение на симметрических матрицах
- 4.10. Броуновское движение с косым отражением
- УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
- Список литературы