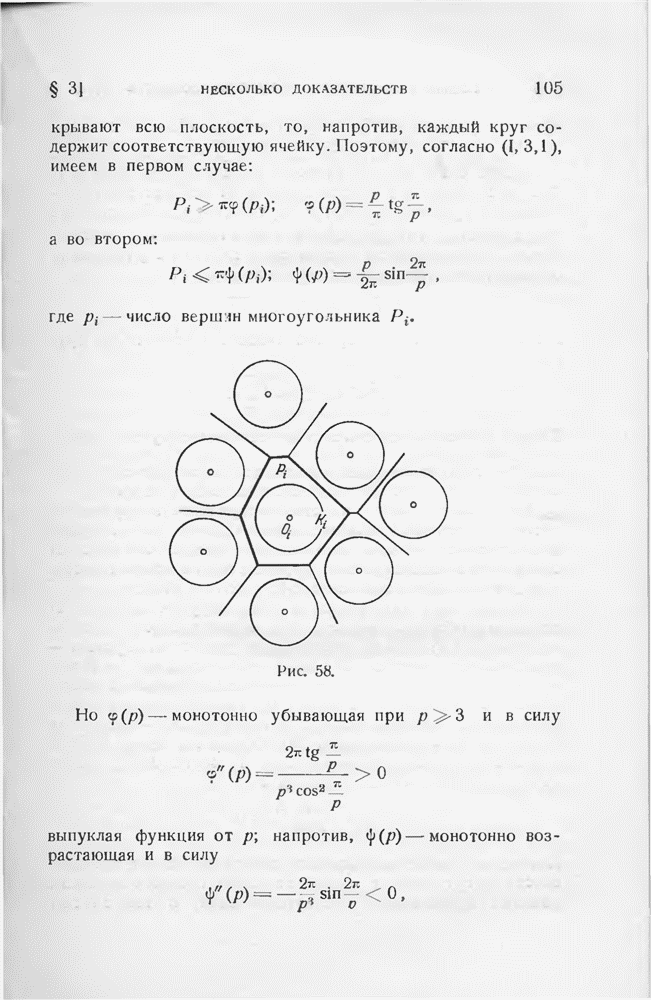| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Одно экстремальное свойство эллипса
Докажем следующую теорему:
Пусть Т — выпуклая фигура и  — вписанный
— вписанный  -угольник наибольшей площади. Тогда
-угольник наибольшей площади. Тогда

причем равенство достигается только в том случае, когда Т есть эллипс.
Таким образом, из всех выпуклых фигур эллипс наименее точно может быть заменен вписанным  -угольником (если точность приближения выпуклой области вписанным
-угольником (если точность приближения выпуклой области вписанным  -угольником оценивать отношением площадей). Замечательно при этом, что в этой задаче экстремальная область не зависит от значения я; в двойственной задаче об описанных
-угольником оценивать отношением площадей). Замечательно при этом, что в этой задаче экстремальная область не зависит от значения я; в двойственной задаче об описанных  -угольниках это обстоятельство уже не будет иметь места.
-угольниках это обстоятельство уже не будет иметь места.
Для доказательства выберем прямоугольную систему координат х, у так, чтобы концы наибольшей хорды Т имели координаты (-1,0) и (1,0). В этой координатной системе кривую динию К, ограничивающую Т, можно представить системой уравнений

где  — непрерывная, положительная функция t с периодом
— непрерывная, положительная функция t с периодом  .
.
Впишем теперь в кривую линию К многоугольник, вершины которого находятся в точках К, определяемых значениями параметра  Площадь этого
Площадь этого  -угольника будет равна:
-угольника будет равна:

Если теперь положим

то получим:

Так как интегральное среднее величины  равно
равно

то заведомо найдется такое значение  , что
, что  , что и доказывает неравенство (1).
, что и доказывает неравенство (1).
Теперь покажем, что знак равенства в (1) достигается только для эллипса.
Если  не постоянно, то в силу непрерывности
не постоянно, то в силу непрерывности  найдется такое значение
найдется такое значение  для которого
для которого 
Однако  как это было впервые показано Сасом [2), может быть постоянным и в том случае, когда
как это было впервые показано Сасом [2), может быть постоянным и в том случае, когда  не является постоянным. Покажем, что в этом случае
не является постоянным. Покажем, что в этом случае  не представляет собой вписанный
не представляет собой вписанный  -угольник наибольшей площади.
-угольник наибольшей площади.
Предположим, что многоугольник  ни при каком значении t не может быть увеличен. Тогда Т имеет в каждой вершине
ни при каком значении t не может быть увеличен. Тогда Т имеет в каждой вершине  опорную прямую, которая параллельна прямой, соединяющей обе смежные вершины многоугольника. Отсюда следует, что кривая линия К имеет непрерывно изменяющуюся касательную и что [36]
опорную прямую, которая параллельна прямой, соединяющей обе смежные вершины многоугольника. Отсюда следует, что кривая линия К имеет непрерывно изменяющуюся касательную и что [36]

Следовательно,  имеет в этом случае непрерывную производную ограниченной вариации. Если разложим
имеет в этом случае непрерывную производную ограниченной вариации. Если разложим  в ряд Фурье:
в ряд Фурье:

то дифференцирование даст:

Отсюда по теореме единственности Кантора из теории тригонометрических рядов следует, что  для
для  , т. е. что
, т. е. что

Так как  , то это возможно, только если
, то это возможно, только если  , т. е. если кривая К - эллипс.
, т. е. если кривая К - эллипс.
Повторим кратко еще раз построение, использованное выше. Наибольшую хорду кривой К принимаем за диаметр круга, в который вписан правильный  -угольник. Затем проектируем вершины правильного
-угольник. Затем проектируем вершины правильного  -угольника перпендикулярно к наибольшей хорде на кривую К, при этом мы приходим к
-угольника перпендикулярно к наибольшей хорде на кривую К, при этом мы приходим к  -угольнику, вписанному в кривую. Если построенные таким образом
-угольнику, вписанному в кривую. Если построенные таким образом  -угольники не все равновелики, то среди них имеется такой, площадь
-угольники не все равновелики, то среди них имеется такой, площадь  которого больше
которого больше  чем
чем  . Если же все эти
. Если же все эти  -угольники равновелики, то площадь каждого из них равна
-угольники равновелики, то площадь каждого из них равна  . В этом последнем случае либо среди рассмотренных
. В этом последнем случае либо среди рассмотренных  -угольников имеется по крайней мере один, площадь которого можно увеличить сдвигом одной из вершин вдоль кривой, либо кривая К есть эллипс.
-угольников имеется по крайней мере один, площадь которого можно увеличить сдвигом одной из вершин вдоль кривой, либо кривая К есть эллипс.
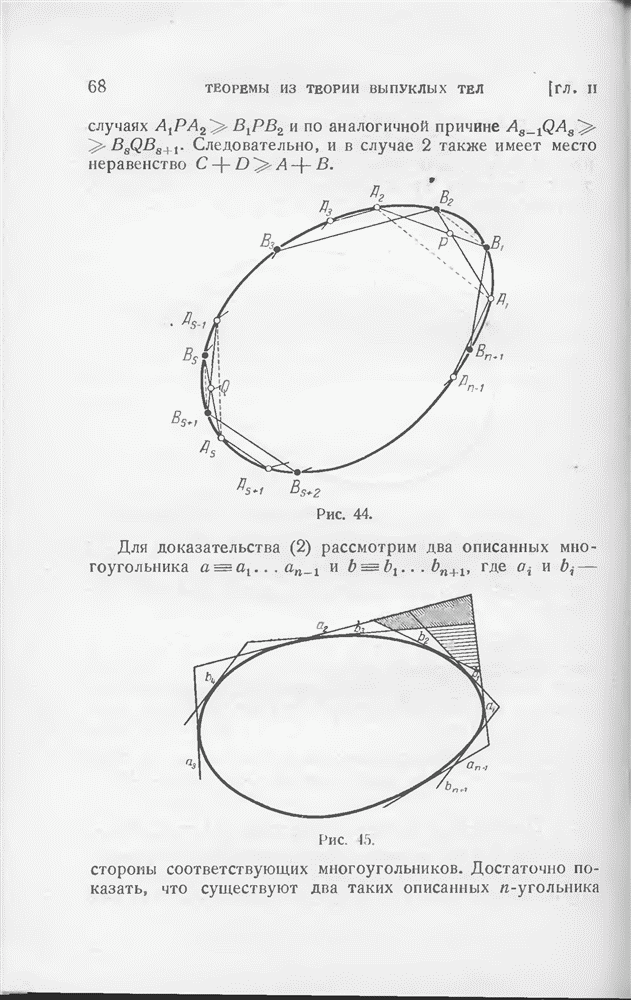
Рассмотрим теперь аналогичную задачу, относящуюся к описанным многоугольникам: для какой из равновеликих выпуклых фигур  площадь
площадь  описанного
описанного  -угольника наименьшей площади достигает максимума?
-угольника наименьшей площади достигает максимума?
Неравенство  которое означало бы, что и тут экстремальная фигура является эллипсом, в общем случае не имеет места. Так, например, для единичного квадрата из
которое означало бы, что и тут экстремальная фигура является эллипсом, в общем случае не имеет места. Так, например, для единичного квадрата из  , что больше, чем
, что больше, чем 
Можно доказать, что для  экстремальной фигурой является квадрат (или, более обще, параллелограмм, который аффинно тождествен с квадратом)
экстремальной фигурой является квадрат (или, более обще, параллелограмм, который аффинно тождествен с квадратом)  Для
Для  экстремальные фигуры не известны, однако мы знаем, что для больших значений
экстремальные фигуры не известны, однако мы знаем, что для больших значений  они приближенно могут быть заменены эллипсами. А именно, имеет место следующая теорема:
они приближенно могут быть заменены эллипсами. А именно, имеет место следующая теорема:
Пусть Т — выпуклия фигура, граничная кривая которой содержит две равные диаметрально противоположные дуги окружности периметра L (радиуса общей длины  (здесь мы считаем, что
(здесь мы считаем, что  ). Тогда вокруг фигуры Т можно описать
). Тогда вокруг фигуры Т можно описать  -угольник
-угольник  площади
площади

Эта теорема позволяет предположить, что экстремальные кривые для  при подходящем «аффинном нормировании» довольно быстро будут сходиться к кругу.
при подходящем «аффинном нормировании» довольно быстро будут сходиться к кругу.
Представим снова граничную кривую К фигуры Т системой уравнений (2), так чтобы точки  совпадали с серединами фигурирующих в теореме дуг окружности, и рассмотрим описанный
совпадали с серединами фигурирующих в теореме дуг окружности, и рассмотрим описанный  -угольник
-угольник  точки соприкосновения сторон которого с К определяются значениями
точки соприкосновения сторон которого с К определяются значениями  параметра. Покажем, что
параметра. Покажем, что

Рассмотрим для этого правильный  -угольник, описанный около круга
-угольник, описанный около круга

точки соприкосновения сторон которого с кругом определяются значениями  параметра, и спроектируем каждую сторону перпендикулярно к оси
параметра, и спроектируем каждую сторону перпендикулярно к оси  на соответствующую сторону
на соответствующую сторону  Таким образом, получаем я отрезков, касающихся кривой К. Дополняем эти отрезки до замкнутой ломаной, соединив соответствующие точки отрезками, перпендикулярными к оси
Таким образом, получаем я отрезков, касающихся кривой К. Дополняем эти отрезки до замкнутой ломаной, соединив соответствующие точки отрезками, перпендикулярными к оси  . Правая часть выписанного выше неравенства представляет собой не что иное, как площадь ограниченного этой ломаной многоугольника, заключающего
. Правая часть выписанного выше неравенства представляет собой не что иное, как площадь ограниченного этой ломаной многоугольника, заключающего  внутри себя
внутри себя  .
.
Теперь имеем:

откуда и следует неравенство (3).
В случае произвольной выпуклой фигуры это рассуждение не проходит, так как рассмотренная ломанная в общем случае не является простой замкнутой ломаной и, с другой стороны,  может выйти за пределы многоугольника, ограниченного этой ломаной.
может выйти за пределы многоугольника, ограниченного этой ломаной.
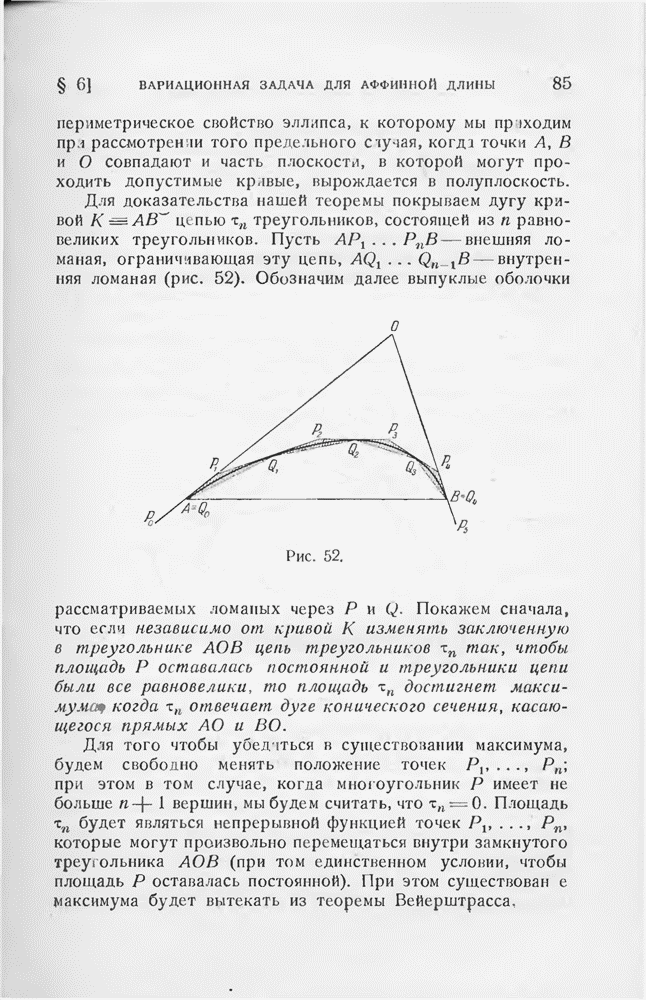
Аналогичные задачи, относящиеся не к площади, а к периметру, не решены ни для описанных, ни для вписанных многоугольников Поэтому представляет определенный интерес следующая точная оценка, относящаяся к задаче об одновременном приближении выпуклой кривой вписанными и описанными  -угольниками: каждую выпуклую кривую можно заключить между вписанным
-угольниками: каждую выпуклую кривую можно заключить между вписанным  -угольником периметра
-угольником периметра  и описанным
и описанным  -угольником периметра
-угольником периметра  такими, что
такими, что

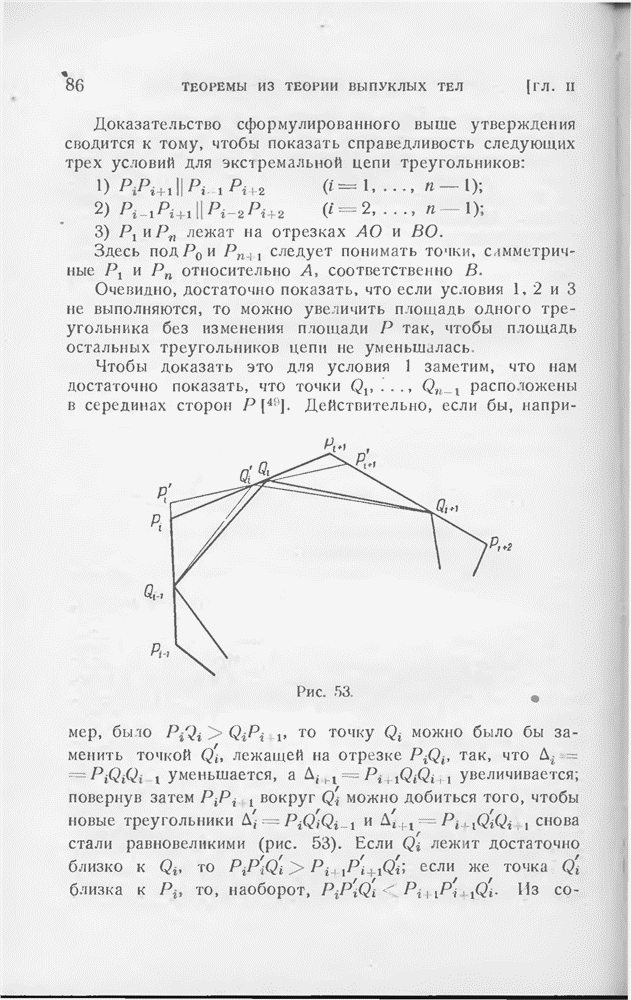
Рассмотрим произвольный правильный  -угольник, содержащий внутри себя нашу кривую, сдвинем параллельно все его стороны до соприкосновения с кривой. Таким образом, мы получим равноугольный описанный
-угольник, содержащий внутри себя нашу кривую, сдвинем параллельно все его стороны до соприкосновения с кривой. Таким образом, мы получим равноугольный описанный  -угольник. Если соединить соседние точки соприкосновения, то мы получим вписанный
-угольник. Если соединить соседние точки соприкосновения, то мы получим вписанный  -угольник. Мы утверждаем, что для рассматриваемой пары
-угольник. Мы утверждаем, что для рассматриваемой пары  -угольников достигается неравенство (4). Пусть А и В — две смежные вершины вписанного
-угольников достигается неравенство (4). Пусть А и В — две смежные вершины вписанного  -угольника и С — точка пересечения соответствующих касательных. Зафиксируем вершины А и В треугольника ABC и будем изменять С так, чтобы величина угла АСВ (равная —
-угольника и С — точка пересечения соответствующих касательных. Зафиксируем вершины А и В треугольника ABC и будем изменять С так, чтобы величина угла АСВ (равная —  не менялась; при этом сумма
не менялась; при этом сумма  достигает максимума, когда
достигает максимума, когда  Отсюда вытекает, что
Отсюда вытекает, что

Если просуммировать все подобные неравенства, то получим:  что и требовалось доказать.
что и требовалось доказать.
Аналогичная теорема для площади читается следующим образом: для каждой выпуклой фигуры можно указать такие вписанный  -угольник
-угольник  и описанный
и описанный  -угольник
-угольник  что
что

Доказательство этого неравенства (представляющееся, впрочем, чрезмерно сложным) будет приведено в § 6.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ АВТОРА
- ГЛАВА I. НЕСКОЛЬКО ТЕОРЕМ ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ
- § 1. Выпуклые фигуры
- § 2. Аффинное преобразование и полярное преобразование
- § 3. Экстремальные свойства правильных многоугольников
- § 4. Изопериметрическая задача
- § 5. Некоторые неравенства, относящиеся к треугольнику
- § 6. Теорема Эйлера о многогранниках
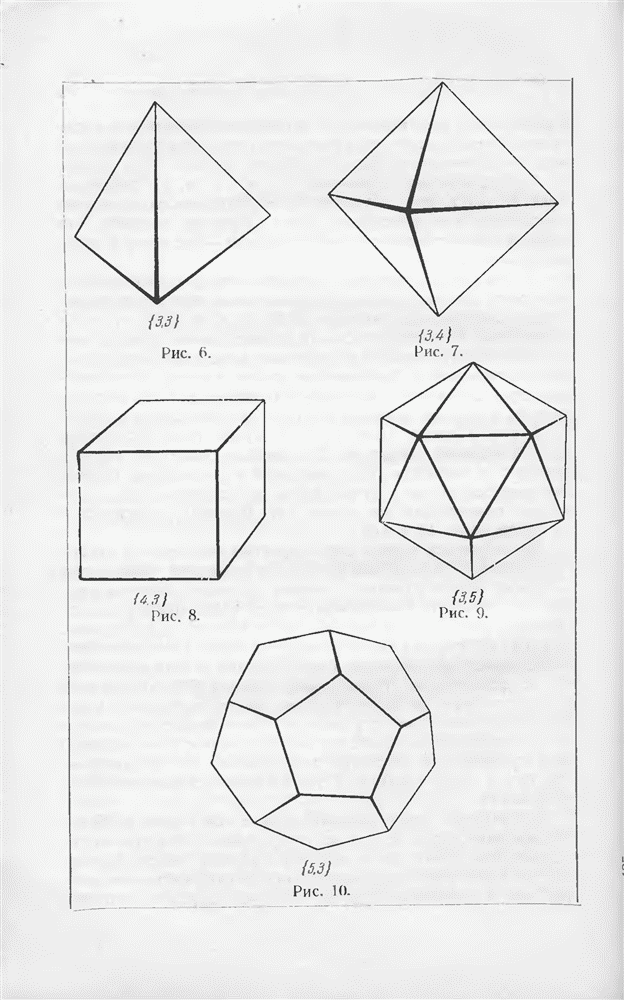
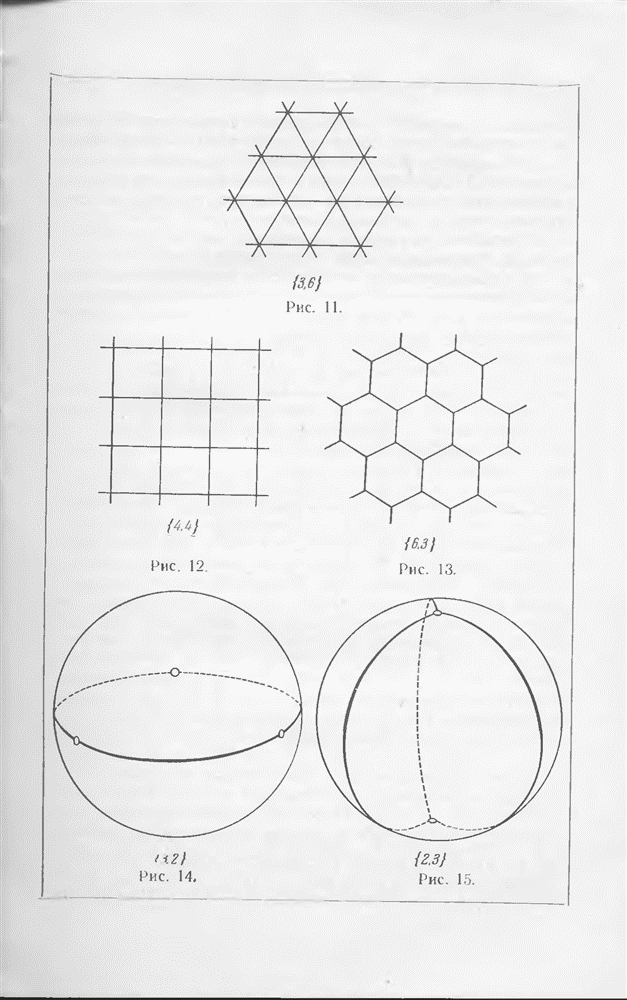
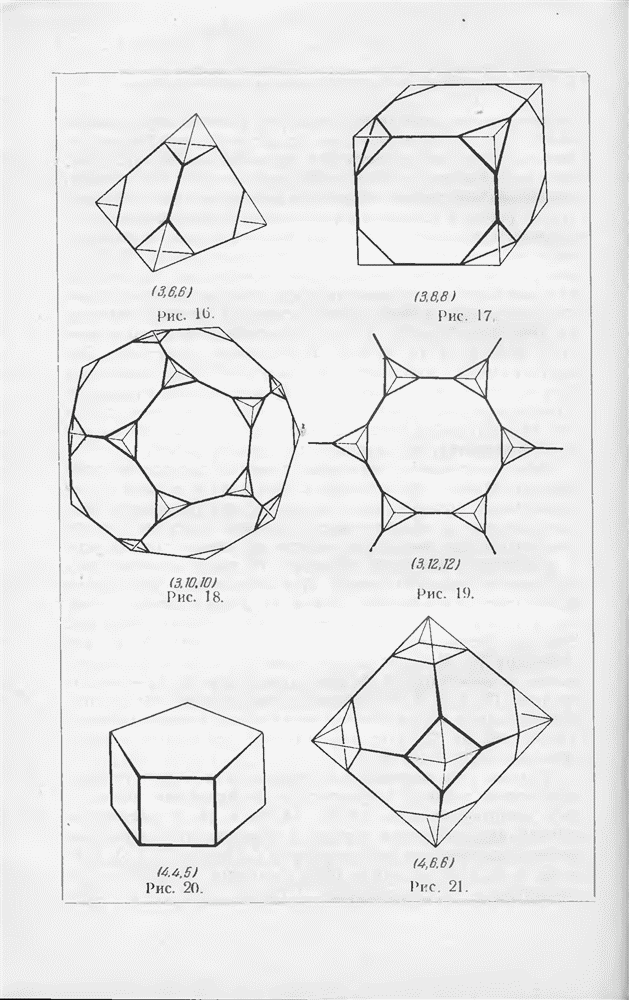
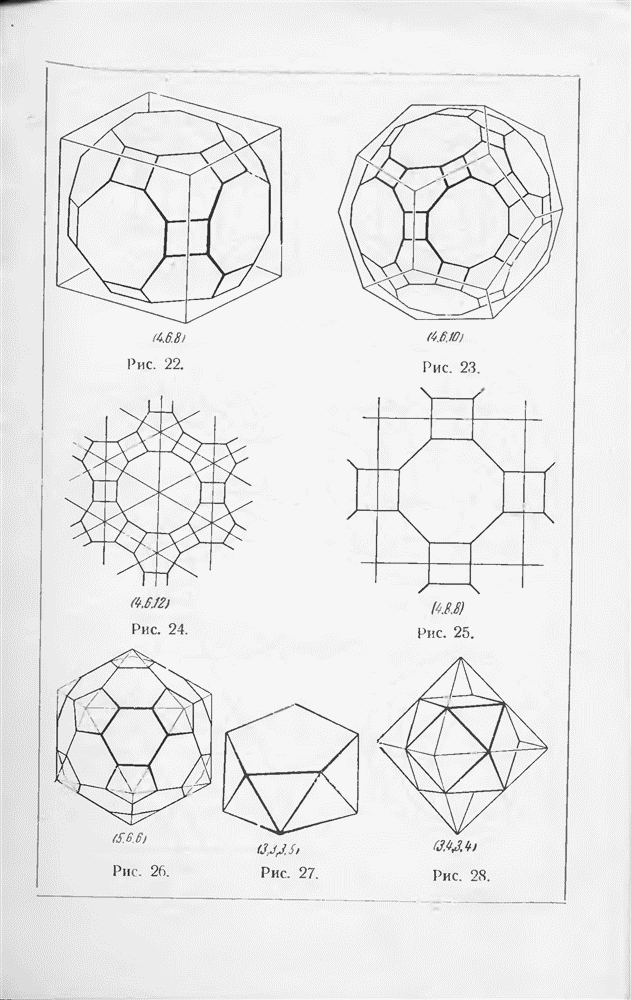
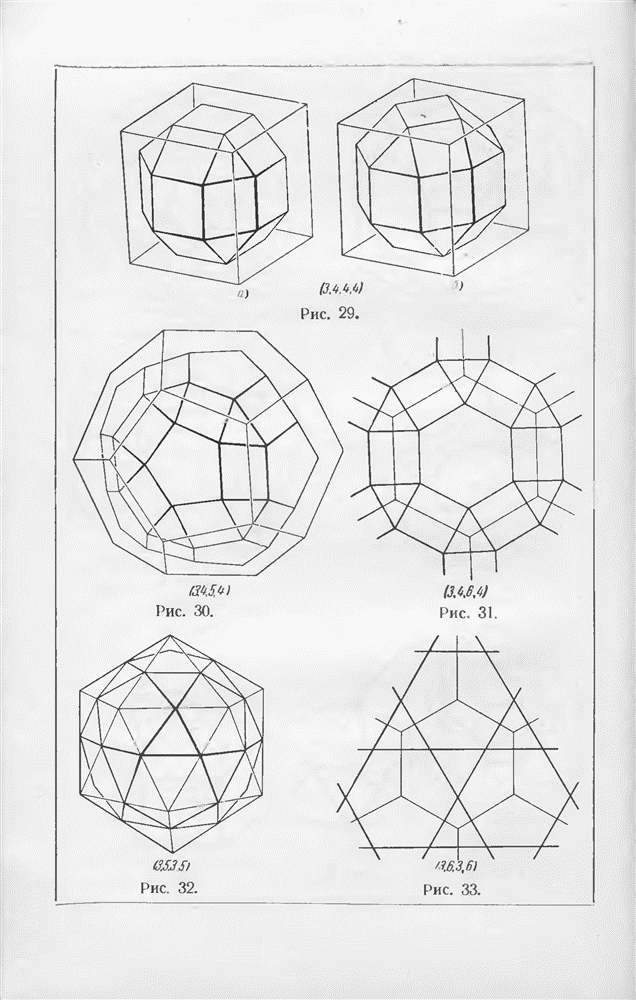
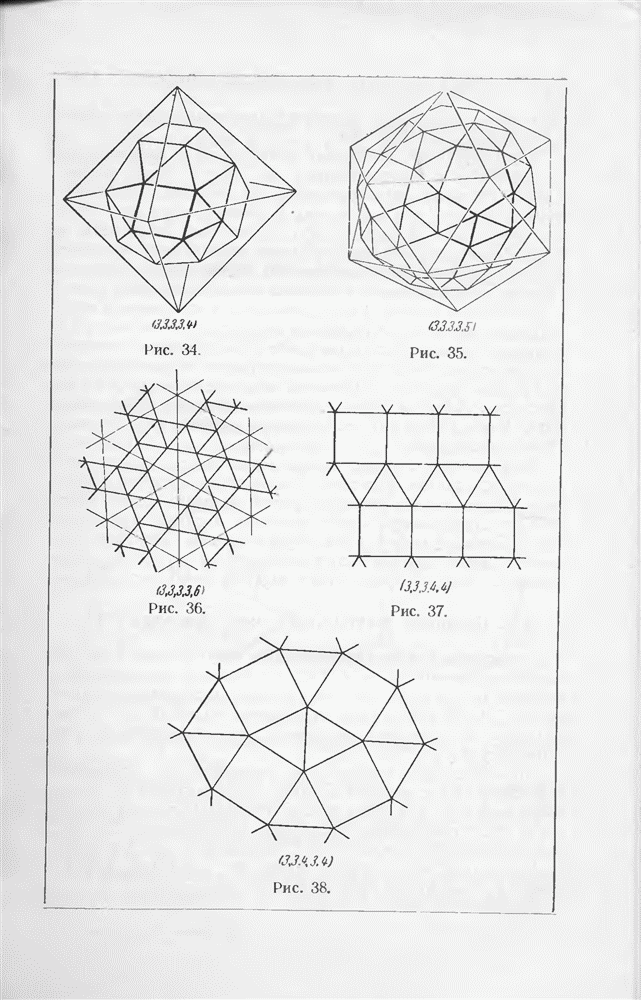
- § 7. Правильные и полуправильные многогранники
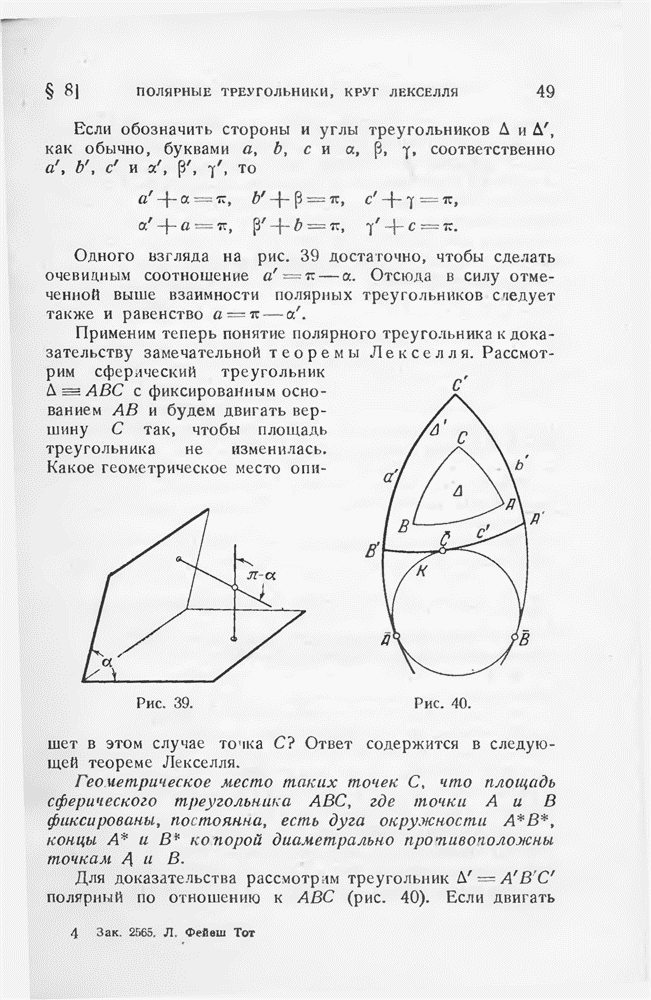
- § 8. Полярные треугольники, круг Лекселля
- § 9. Некоторые тождества из векторной алгебры
- § 10. Некоторые формулы сферической тригонометрии
- § 11. Исторические замечания
- ГЛАВА II. ТЕОРЕМЫ ИЗ ТЕОРИИ ВЫПУКЛЫХ ТЕЛ
- § 1. «Теорема выбора» Бляшке
- § 2. Неравенство Иенсена
- § 3. Теоремы Доукера
- § 4. Одно экстремальное свойство эллипса
- § 5. Об аффинной длине
- § 6. Вариационная задача для аффинной длины
- § 7. Основные факты интегральной геометрии
- § 8. Исторические замечания
- ГЛАВА III. ЗАДАЧА ЗАПОЛНЕНИЯ И ЗАДАЧА ПОКРЫТИЯ ДЛЯ СЛУЧАЯ ПЛОСКОСТИ
- § 1. Плотность системы фигур
- § 2. Задачи о плотнейшем заполнении плоскости кругами и о редчайшем покрытии плоскости кругами
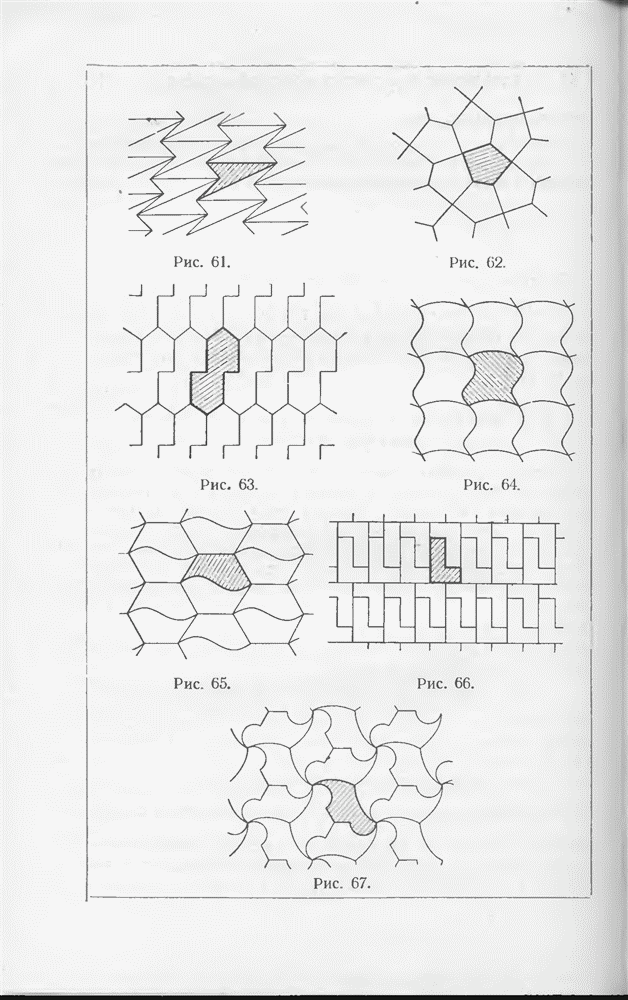
- § 3. Несколько доказательств
- § 4. Заполнение и покрытие выпуклой области равными кругами
- § 5. Разбиение выпуклой области на выпуклые подобласти
- § 6. Заполнение выпуклой области кругами n различных размеров
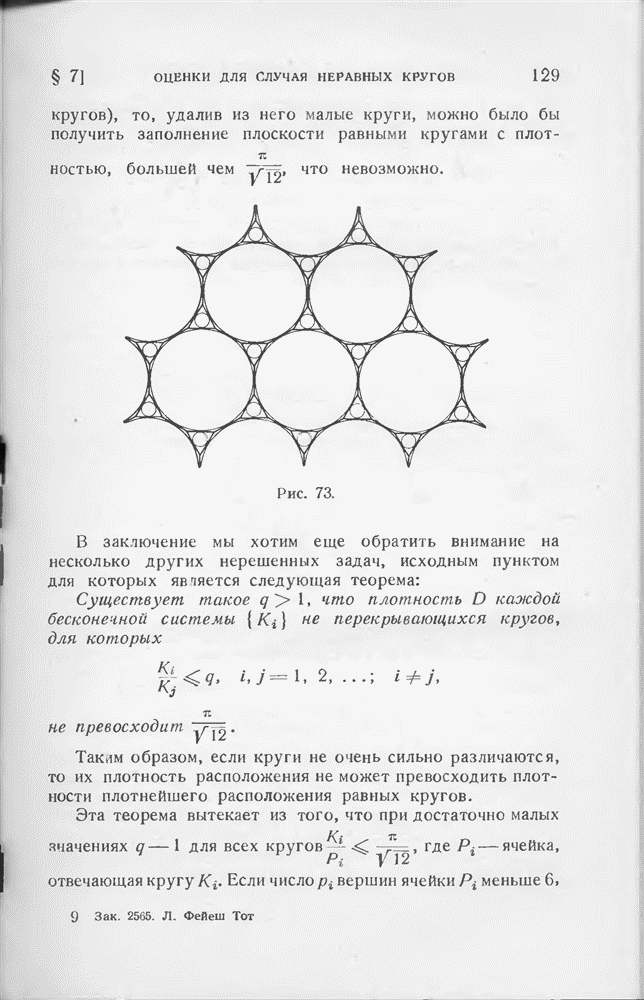
- § 7. Оценки для случая неравных кругов
- § 8. Дальнейшие теоремы о покрытии кругами
- § 9. Разбиение выпуклого шестиугольника на выпуклые многоугольники
- § 10. Заполнение и покрытие выпуклого шестиугольника равными выпуклыми фигурами
- § 11. Одна задача о заполнении выпуклыми фигурами, связанная с понятием аффинной длины
- § 12. О формуле осреднения
- § 13. Исторические замечания
- ГЛАВА IV. ЭКОНОМИЧНОСТЬ ЗАПОЛНЕНИЯ и ПОКРЫТИЯ ФИГУРАМИ ДАННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
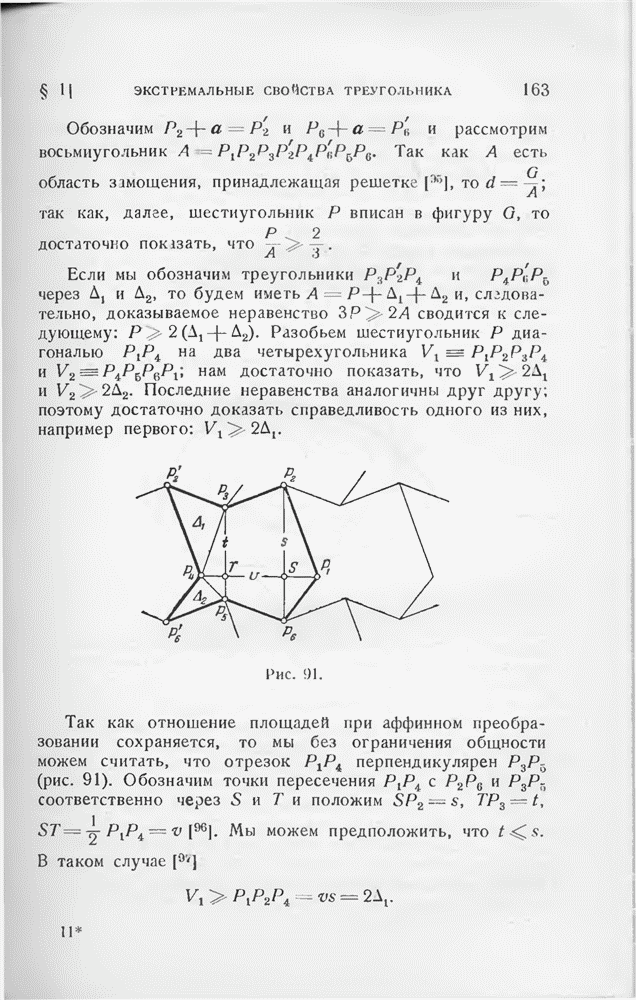
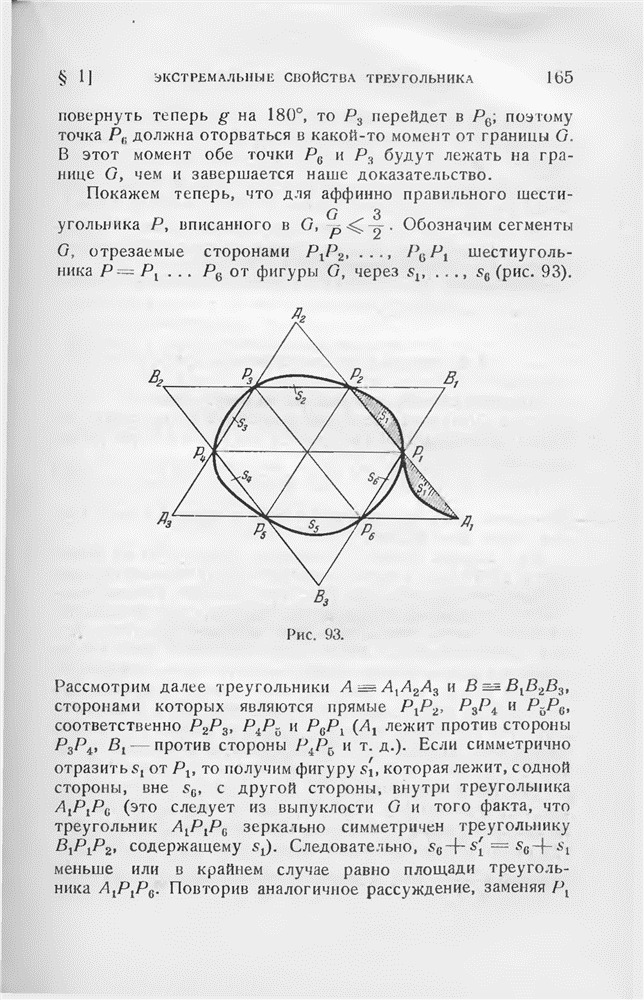
- § 1. Экстремальные свойства треугольника
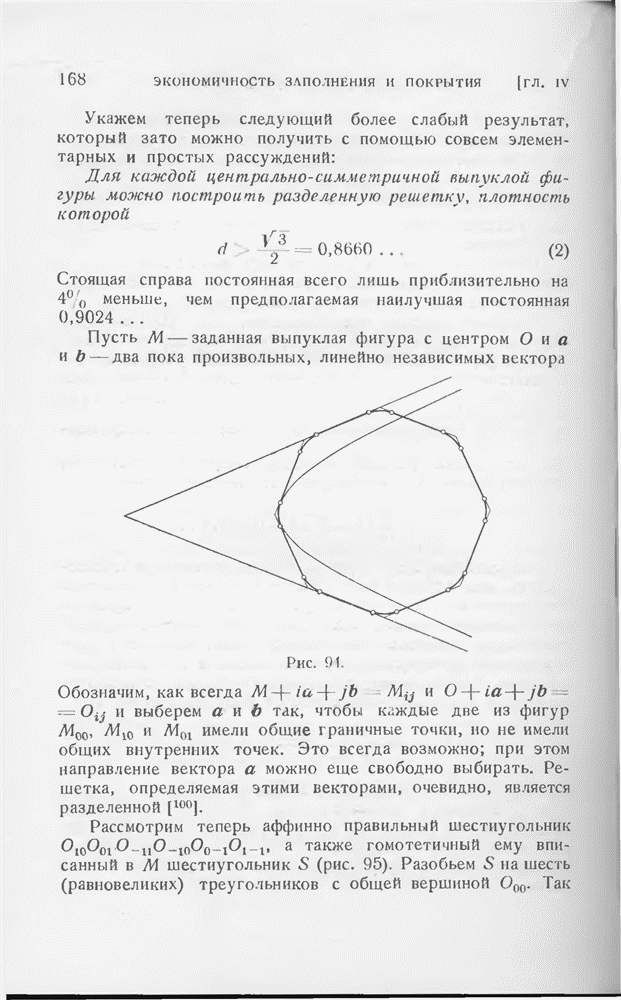
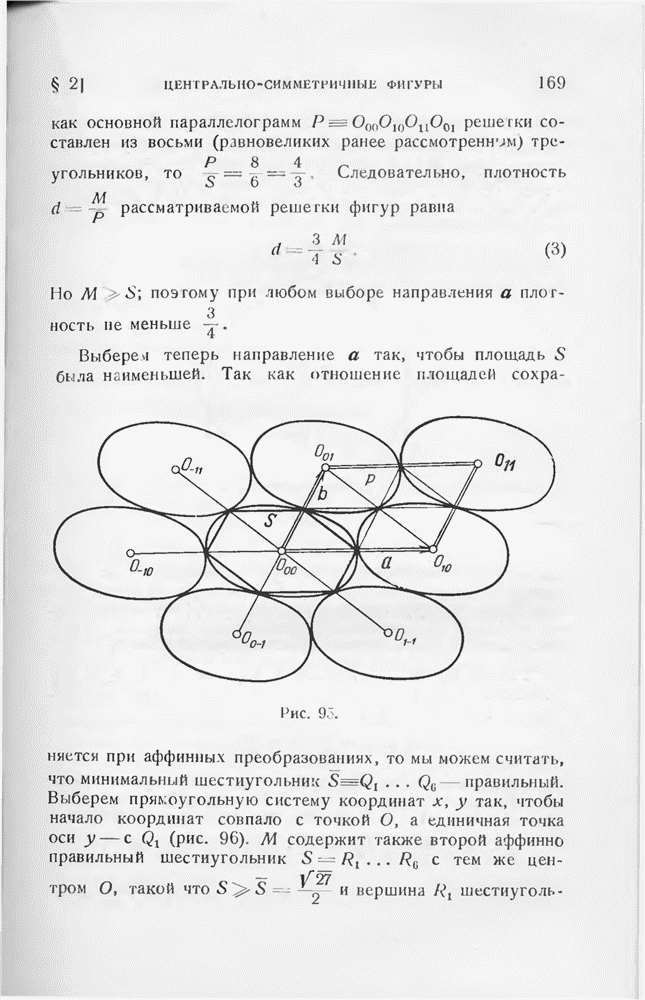
- § 2. Центрально-симметричные фигуры
- § 3. Экономичность заполнения и покрытия фигурами данной последовательности
- § 4. Покрытие разрезанными на куски выпуклыми фигурами
- § 5. Исторические замечания
- ГЛАВА V. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
- § 1. Заполнение и покрытие сферы равными кругами
- § 2. Некоторые другие доказательства
- § 3. Приближение шара многогранниками
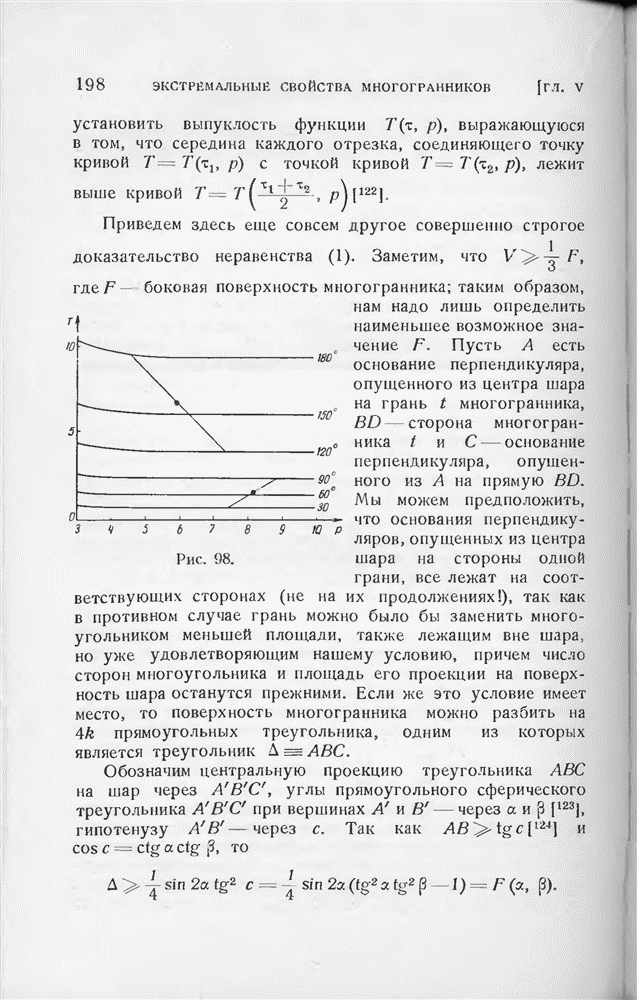
- § 4. Объем описанного многогранника
- § 5. Объем вписанного многогранника
- § 6. Неравенства, связывающие радиусы вписанного и описанного шаров выпуклого многогранника
- § 7. Изопериметрическая задача для многогранников
- § 8. Одно общее неравенство
- § 9. О кратчайшей сети, разбивающей сферу на равновеликие выпуклые части
- § 10. О сумме длин ребер многогранника
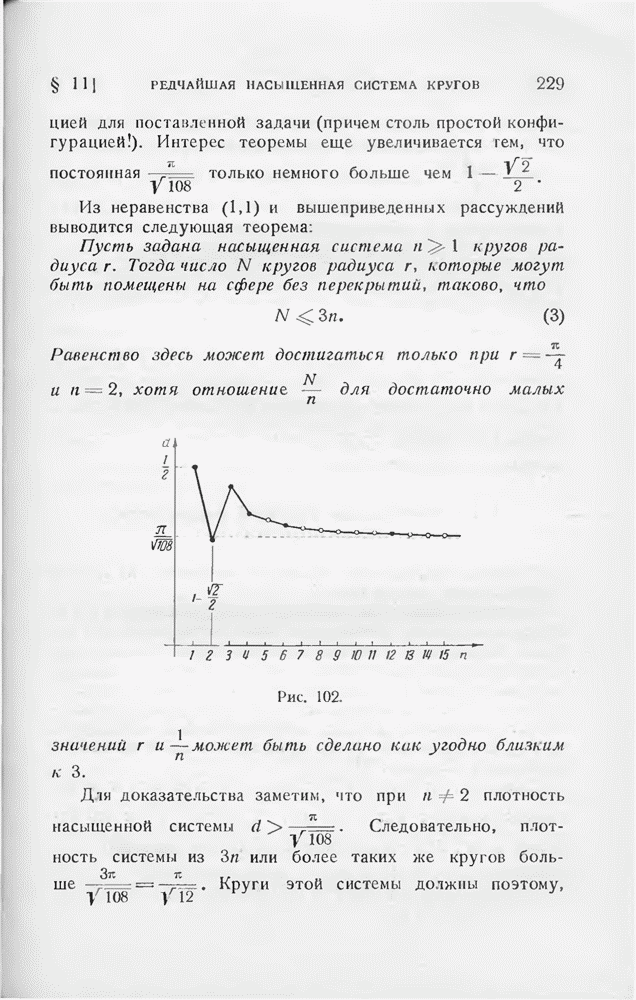
- § 11. Редчайшая насыщенная система сферических кругов
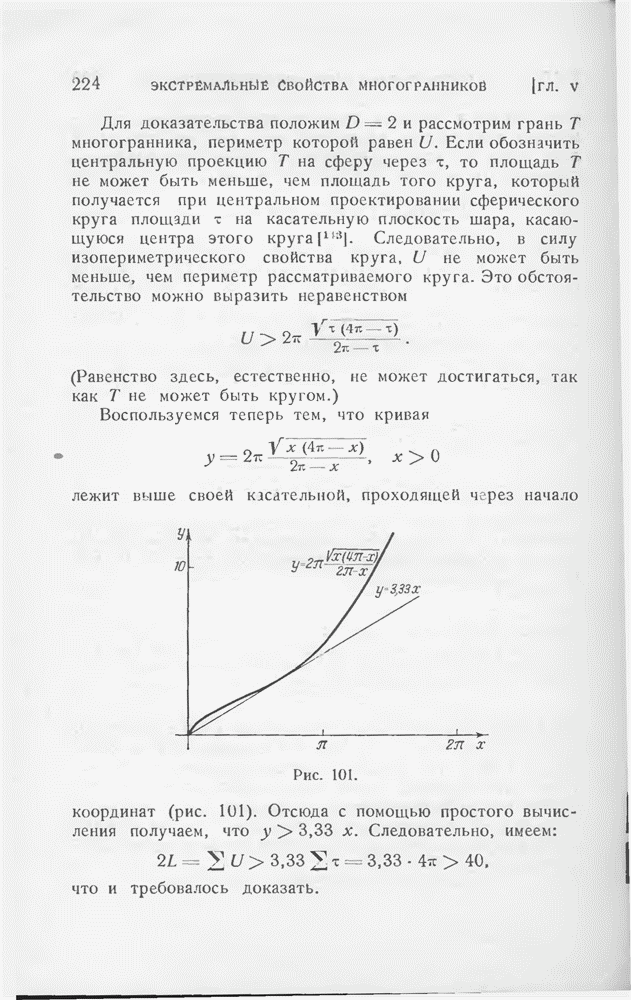
- § 12. Приближение выпуклой поверхности многогранниками
- § 13. Исторические замечания
- ГЛАВА VI. НЕПРАВИЛЬНЫЕ РАСПОЛОЖЕНИЯ НА СФЕРЕ
- § 1. Граф, отвечающий заданной системе точек
- § 2. Максимальная фигура для n = 7
- § 3. Максимальная фигура для n = 8 и n = 9
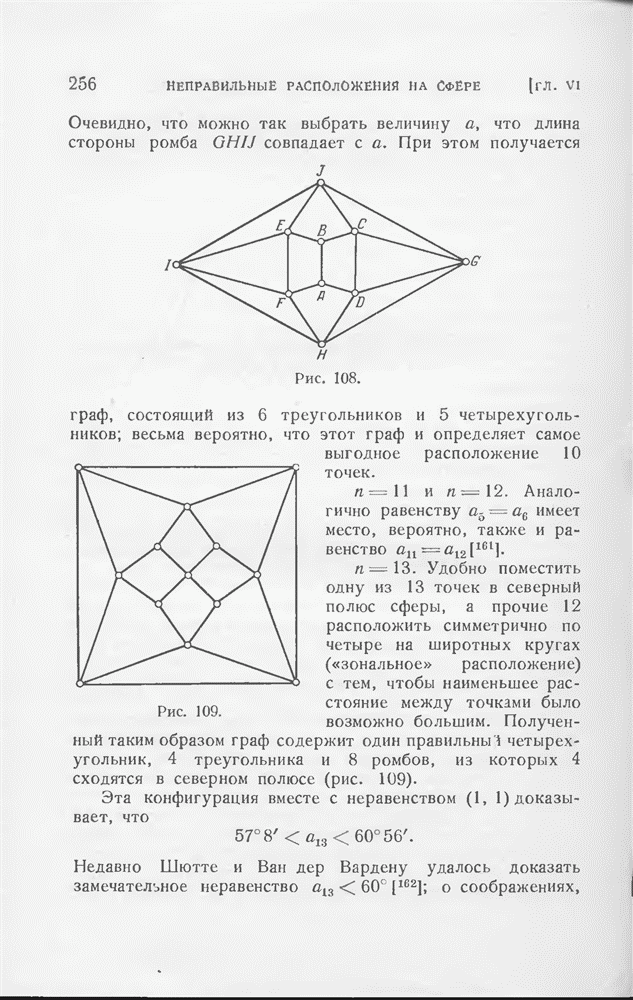
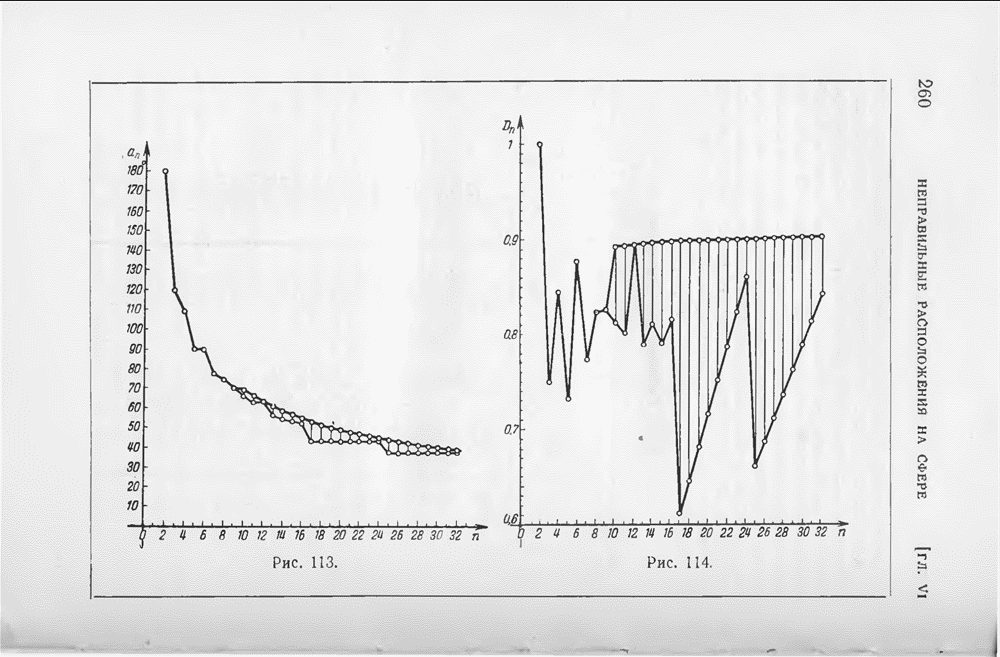
- § 4. Несколько расположений более чем 9 точек
- § 5. Таблица результатов
- § 6. Исторические замечания
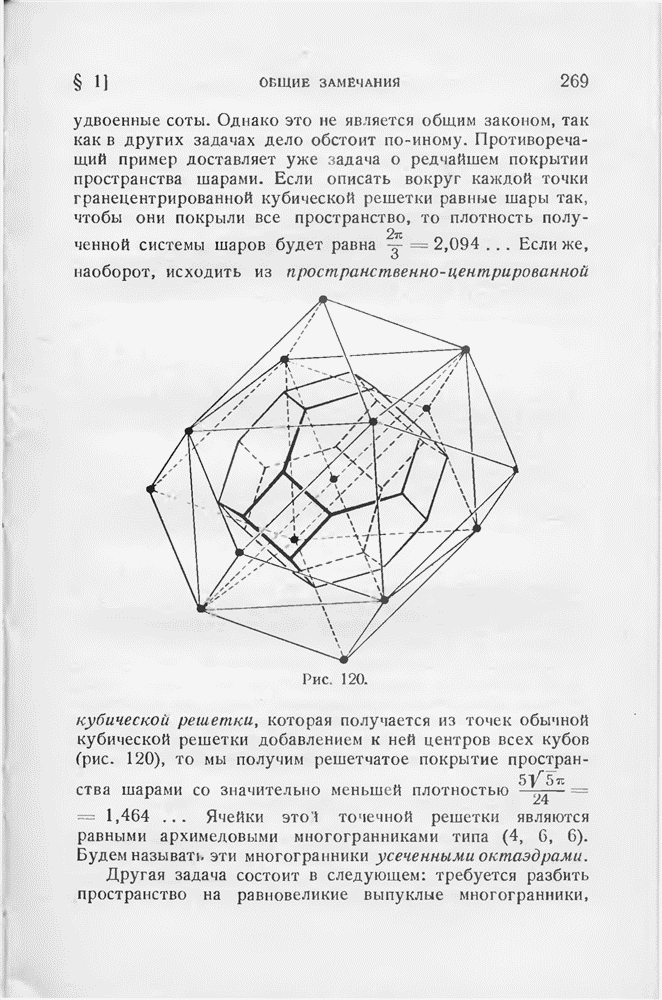
- ГЛАВА VII. РАСПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ
- § 2. Задача о теснейшей упаковке шаров
- § 3. Об одном экстремальном разбиении пространства
- § 4. Формула осреднения для пространства
- § 5. Исторические замечания
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ПРИЛОЖЕНИЕ I. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ, КАСАЮЩИЕСЯ РАСПОЛОЖЕНИЙ В n-МЕРНОМ ПРОСТРАНСТВЕ
- ПРИЛОЖЕНИЕ II. НЕСКОЛЬКО ОПРЕДЕЛЕНИЙ РАЗМЕРНОСТИ
- БИБЛИОГРАФИЯ