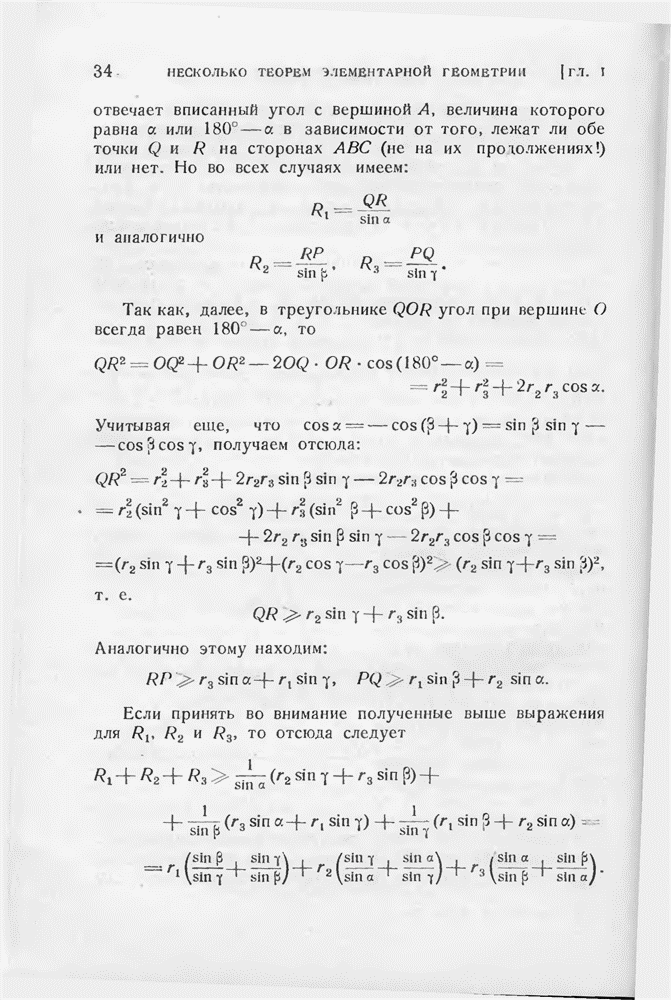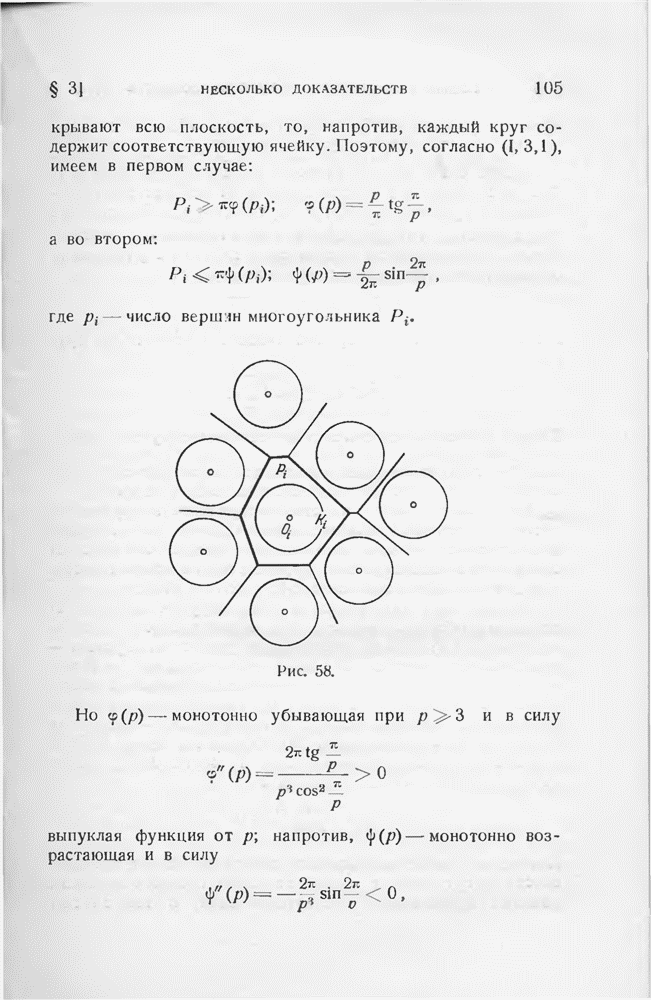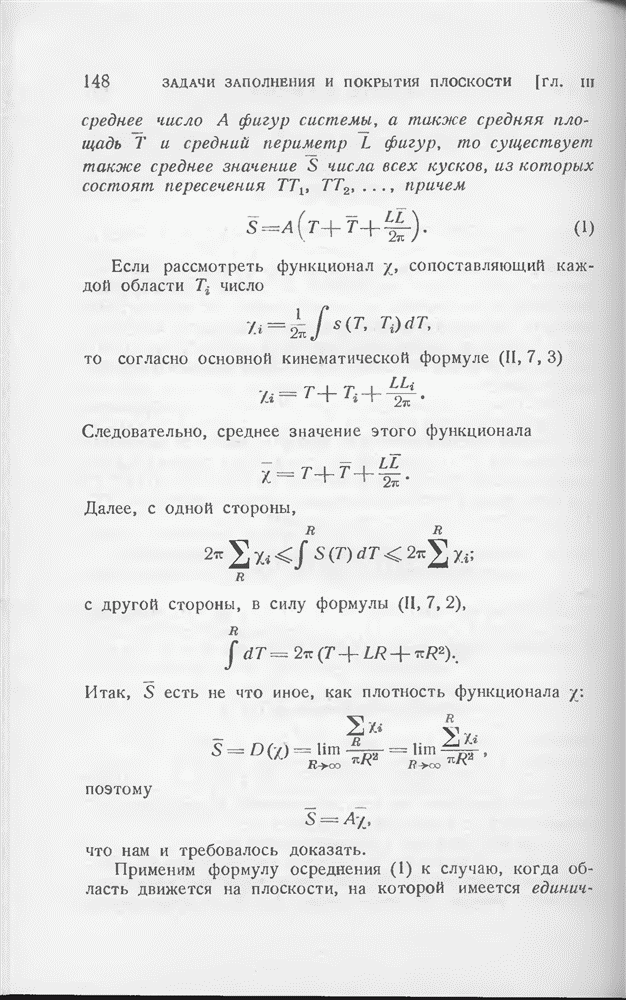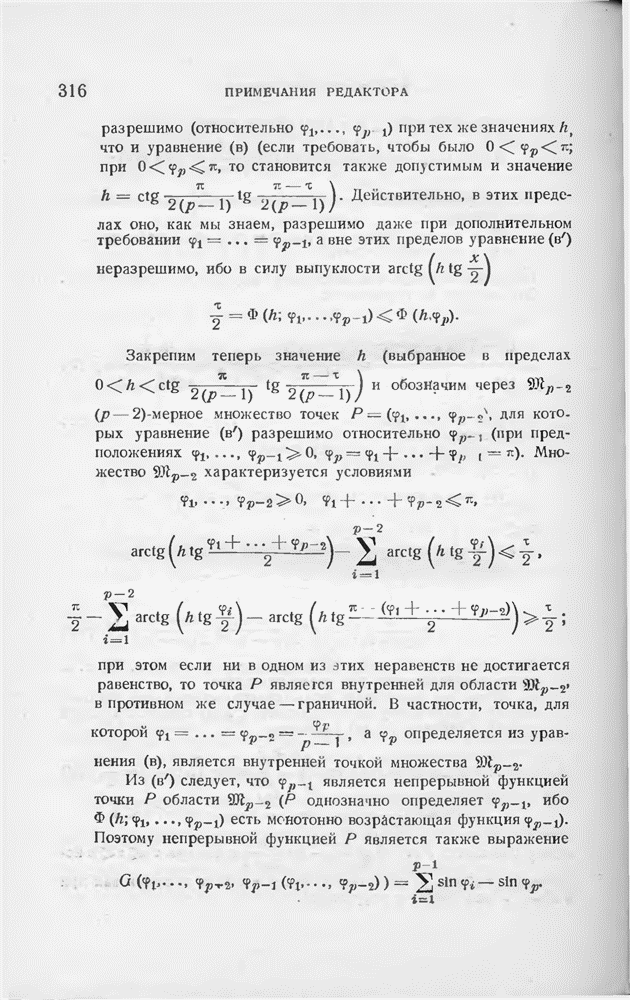| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
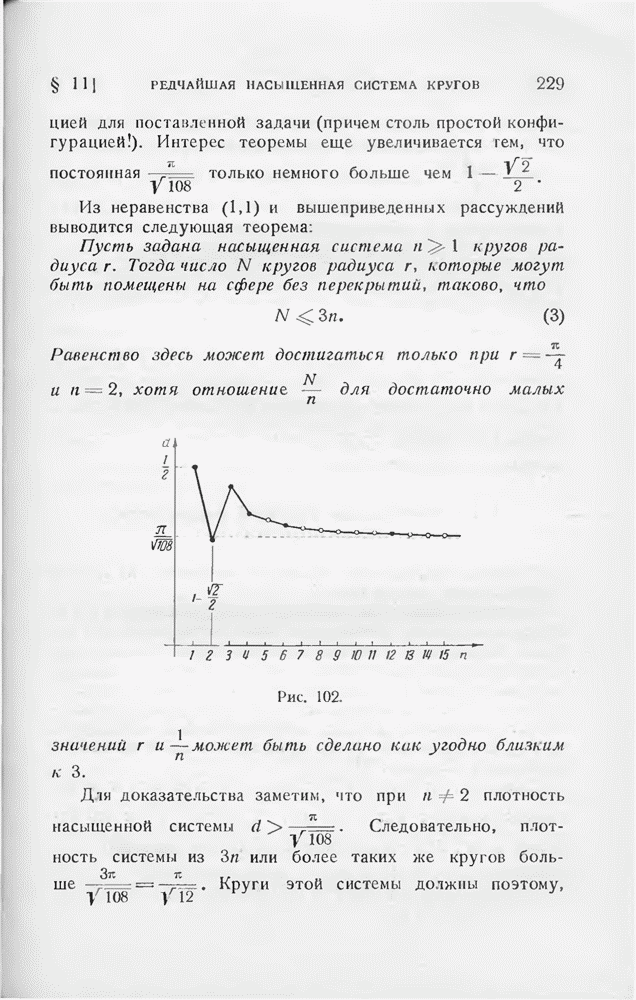
§ 2. Некоторые другие доказательства
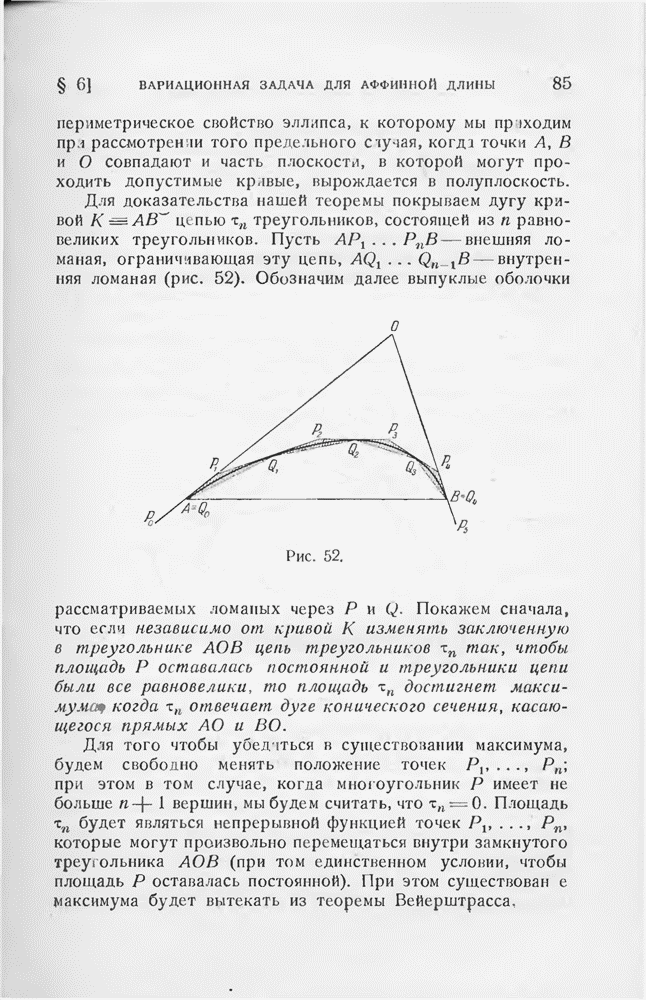
Собранные в этом параграфе доказательства тех же неравенств (1,1) и (1,2) принципиально проще, так как они не опираются на неравенство Иенсена.
Докажем прежде всего следующее предложение, эквивалентное неравенству (1,1):
Среди  точек единичной сферы всегда можно найти две такие, расстояние между которыми
точек единичной сферы всегда можно найти две такие, расстояние между которыми

Для сферического расстояния между теми же точками из (1) вытекает оценка
 (2)
(2)
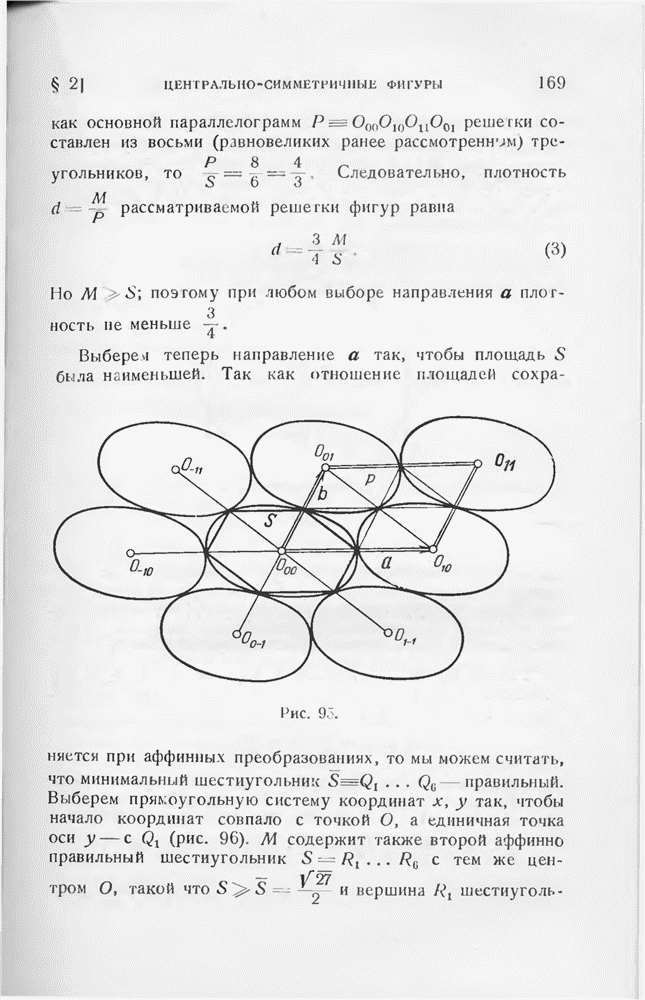
Правая часть последнего неравенства представляет собой не что иное, как длину  стороны равностороннего сферического треугольника площади —
стороны равностороннего сферического треугольника площади — 
Доказательство основывается на следующей лемме:
Пусть АВ наименьшая сторона сферического треугольника  равносторонний треугольник. Если
равносторонний треугольник. Если  то радиус сферической окружности, описанной вокруг Д, больше, чем АВ.
то радиус сферической окружности, описанной вокруг Д, больше, чем АВ.
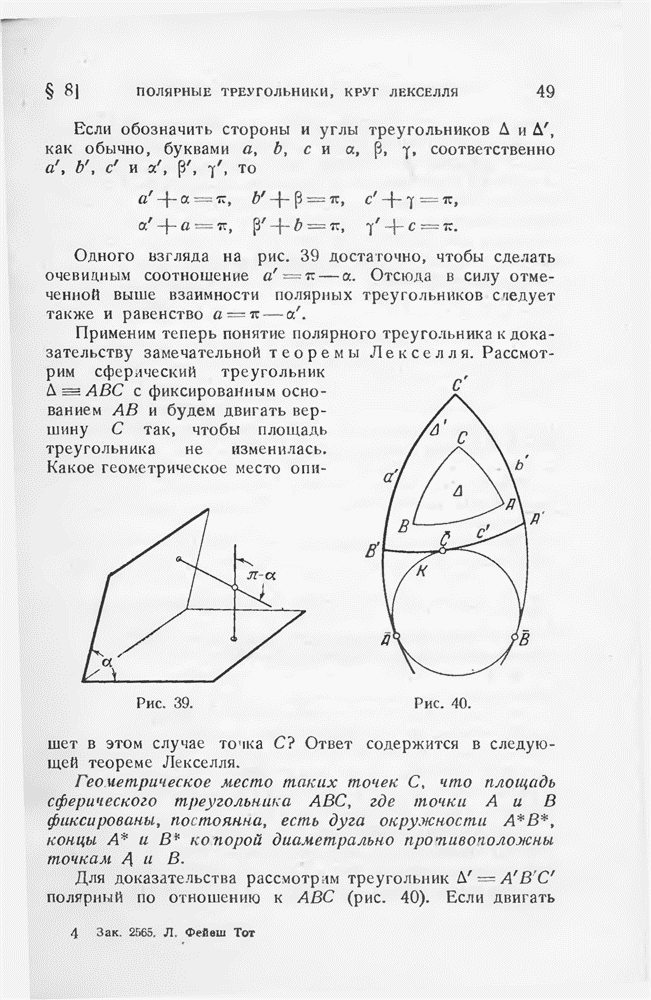
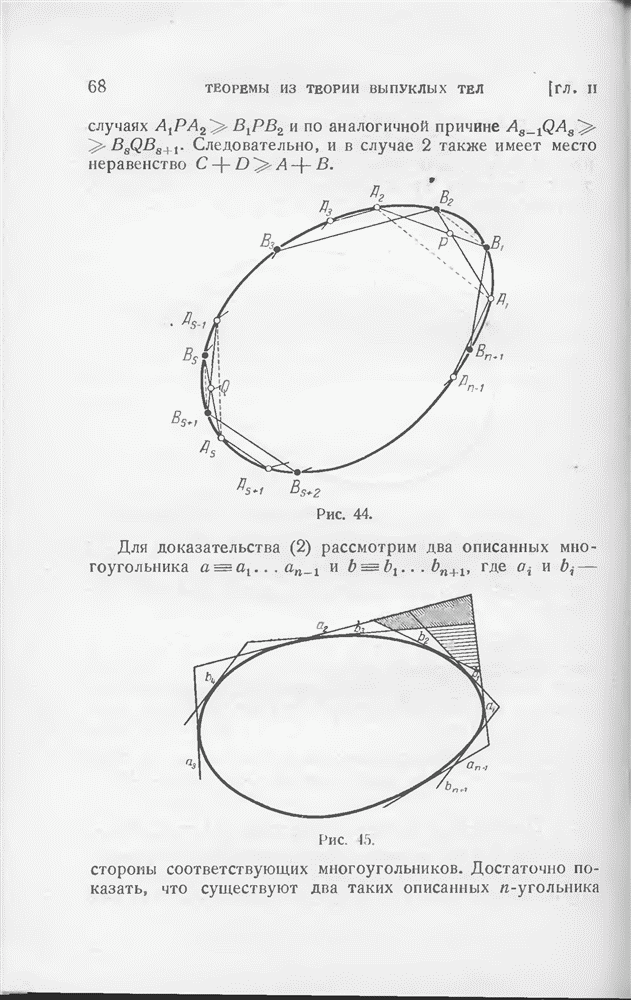
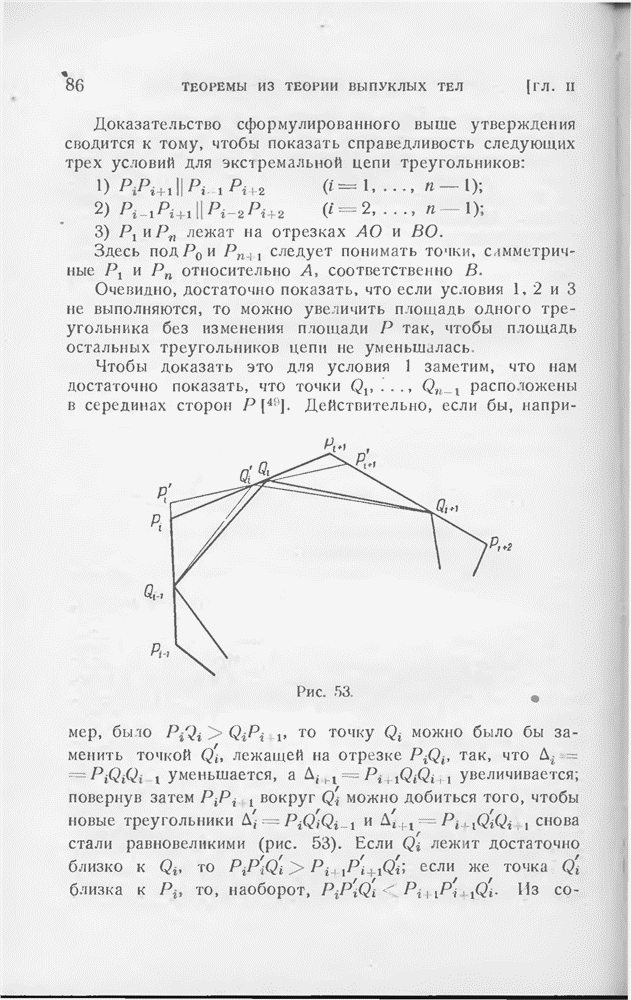
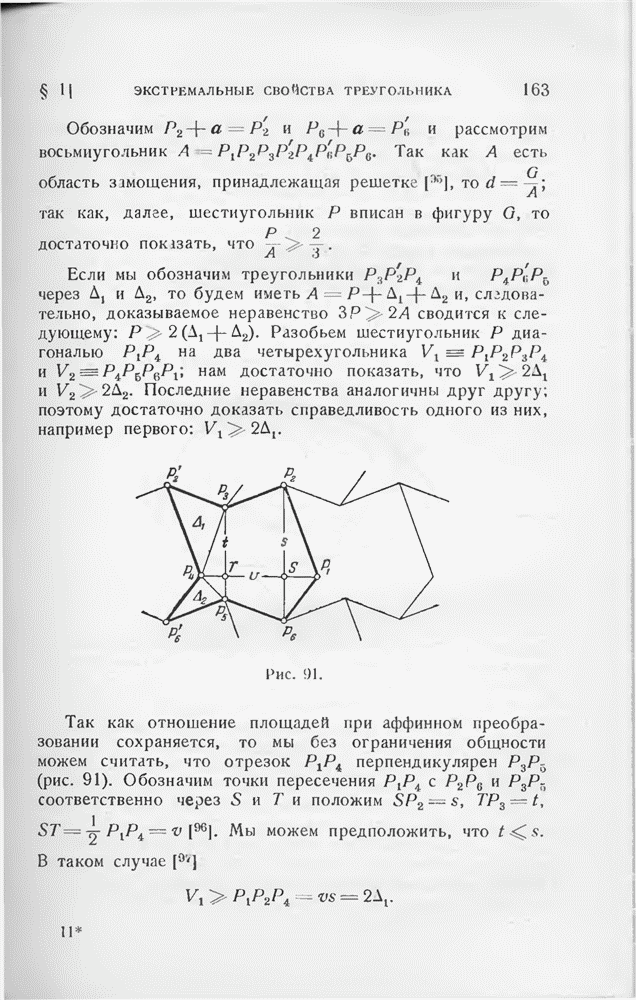
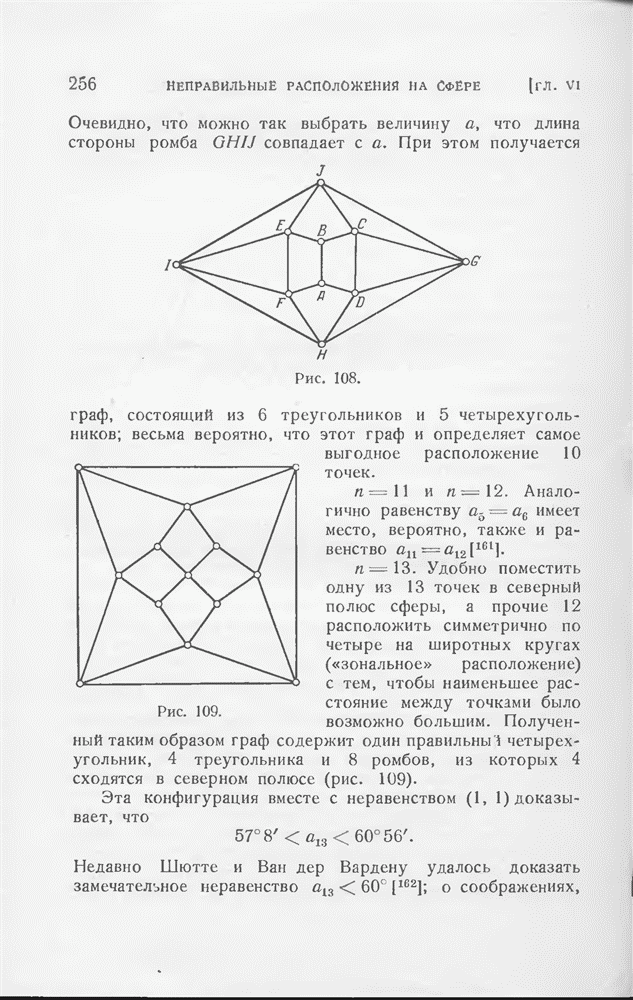
Для доказательства предположим, что С и С лежат по одну сторону от большой окружности АВ и рассмотрим окружности а, b и с радиуса АВ с центрами А, В и  далее обозначим отличную от А точку пересечения кругов
далее обозначим отличную от А точку пересечения кругов  и с через А и отличную от В точку пересечения кругов а и с через В (рис. 97). Треугольники ABA, АВВ и ABC равновелики
и с через А и отличную от В точку пересечения кругов а и с через В (рис. 97). Треугольники ABA, АВВ и ABC равновелики  ; поэтому дуга круга АВС, лежащая «выше» большого круга АВ, явчяетсн геометрическим местом вершин равносторонних треугольников с основанием АВ (ср. § 8 гл. I). Согласно нашему предположению С лежит выше большого круга АВ и ниже круга Лекселля АВС. Так как С лежит вне кругов а и b, то С должна лежать и вне с, что и доказывает наше утверждение.
; поэтому дуга круга АВС, лежащая «выше» большого круга АВ, явчяетсн геометрическим местом вершин равносторонних треугольников с основанием АВ (ср. § 8 гл. I). Согласно нашему предположению С лежит выше большого круга АВ и ниже круга Лекселля АВС. Так как С лежит вне кругов а и b, то С должна лежать и вне с, что и доказывает наше утверждение.
Предположим теперь снова, что  и что точки
и что точки  не лежат на одной полусфере. Тогда выпуклая оболочка Н этих точек содержит центр О сферы. Далее можно предположить, что многогранник Н имеет только треугольные грани, так как каждую не треугольную грань всегда можно разложить на треугольники; в таком случге число граней Н будет равно
не лежат на одной полусфере. Тогда выпуклая оболочка Н этих точек содержит центр О сферы. Далее можно предположить, что многогранник Н имеет только треугольные грани, так как каждую не треугольную грань всегда можно разложить на треугольники; в таком случге число граней Н будет равно  Рассмотрим сеть линий на сфере, которая получается, если спроектировать
Рассмотрим сеть линий на сфере, которая получается, если спроектировать

Рис. 97.
все ребра многогранника Н из центра О сферы на ее поверхность. Эта сеть линий разбивает поверхность сферы на ряд сферических треугольников; пусть  - наименьший из них. Если бы неравенство (2) не выполнялось, т. е. наименьшее из измеренных по сфере расстояний между двумя из наших точек, а следовательно, и каждая сторона А, было бы больше
- наименьший из них. Если бы неравенство (2) не выполнялось, т. е. наименьшее из измеренных по сфере расстояний между двумя из наших точек, а следовательно, и каждая сторона А, было бы больше  , то в силу неравенства
, то в силу неравенства  и доказанной леммы также и радиус круга, описанного вокруг А, был бы больше чем
и доказанной леммы также и радиус круга, описанного вокруг А, был бы больше чем  . Но так как круг, описанный около А, не содержит внутри себя ни одной из точек
. Но так как круг, описанный около А, не содержит внутри себя ни одной из точек  нашей системы, то эту систему точек можно дополнить еще одной точкой — центром
нашей системы, то эту систему точек можно дополнить еще одной точкой — центром  описанного круга без того, чтобы наименьшее расстояние пары точек стало меньше или равно
описанного круга без того, чтобы наименьшее расстояние пары точек стало меньше или равно 
Это пополнение числа точек можно таким же образом продолжить и далее. Но так как число точек, наименьшее расстояние между двумя из которых больше  очевидно, ограничено, то после конечного числа шагов мы придем к противоречию.
очевидно, ограничено, то после конечного числа шагов мы придем к противоречию.
Обратимся теперь к неравенству (1,2), которое при  можно сформулировать также следуюцим образом.
можно сформулировать также следуюцим образом.
Если выпуклый многогранник с  вершинами или с
вершинами или с  гранями заключается внутри шарового слоя, ограниченного концентрическими сферами радиусов
гранями заключается внутри шарового слоя, ограниченного концентрическими сферами радиусов  и R, то
и R, то

Так как многогранник с  вершинами полярным преобразованием переводится в многогранник с
вершинами полярным преобразованием переводится в многогранник с  гранями, то в этой теореме утверждения о том, что многогранник имеет
гранями, то в этой теореме утверждения о том, что многогранник имеет  вершин, и о том, что он имеет
вершин, и о том, что он имеет  граней, эквивалентны между собой. Наше утверждение, относящееся к случаю
граней, эквивалентны между собой. Наше утверждение, относящееся к случаю  -гранника, связано с задачей о покрытии сферы в силу того, что плоскости, отрезающие от сферы К покрывающие поверхность К (сферические) круги
-гранника, связано с задачей о покрытии сферы в силу того, что плоскости, отрезающие от сферы К покрывающие поверхность К (сферические) круги  ограничивают
ограничивают  -гранник, содержащийся внутри К. То что круги
-гранник, содержащийся внутри К. То что круги  не слишком малы, равносильно тому, что радиус
не слишком малы, равносильно тому, что радиус  концентрического с К шара, заключающегося внутри
концентрического с К шара, заключающегося внутри  -гранника, не слишком велик; наоборот, по величине сферических кругов, а следовательно, и по плотности покрытия можно судить о радиусе
-гранника, не слишком велик; наоборот, по величине сферических кругов, а следовательно, и по плотности покрытия можно судить о радиусе  [
[ ].
].
Докажем (3) для многогранника  вершинами. Без ограничения общности можно считать, что
вершинами. Без ограничения общности можно считать, что  . Далее предположим, что Р имеет только треугольные грани. Так как число треугольных граней равно
. Далее предположим, что Р имеет только треугольные грани. Так как число треугольных граней равно  , то сферическая сеть, получающаяся проектированием ребер Р из центра шара К на его поверхность, содержит по крайней мере один треугольник площади, не меньшей чем
, то сферическая сеть, получающаяся проектированием ребер Р из центра шара К на его поверхность, содержит по крайней мере один треугольник площади, не меньшей чем  радиус о (сферической) окружности, описанной вокруг этого треугольника, не меньше, чем радиус окружности, описанной вокруг равностороннего треугольника площади
радиус о (сферической) окружности, описанной вокруг этого треугольника, не меньше, чем радиус окружности, описанной вокруг равностороннего треугольника площади 
Отсюда следует, что наименьшее из расстояний рассматриваемых треугольных граней от центра шара, а значит, также и величина  , не превосходит
, не превосходит  что и доказывает неравенство (3).
что и доказывает неравенство (3).
Это рассуждение, по-видимому, представляет собой самое простое доказательство неравенства (1,2).
Приведем, наконец, еще одно доказательство неравенств (1,1) и (1,2). Отметим на сфере точки  минимальное расстояние (сферическое) о между которыми равно стороне равностороннего треугольника
минимальное расстояние (сферическое) о между которыми равно стороне равностороннего треугольника  , и обозначим радиус описанной вокруг
, и обозначим радиус описанной вокруг  окружности через
окружности через  , а угол А — через
, а угол А — через  Опишем вокруг каждой точки
Опишем вокруг каждой точки  круг
круг  радиуса
радиуса  . Так как никакая часть поверхности сферы не будет при этом покрыта более чем двумя кругами, то площадь части поверхности, покрытой кругами, равна
. Так как никакая часть поверхности сферы не будет при этом покрыта более чем двумя кругами, то площадь части поверхности, покрытой кругами, равна

где сумма распространена по всем возможным комбинациям  Но число отличных от нуля пересечений
Но число отличных от нуля пересечений  не может превосходить наибольшего возможного числа ребер выпуклого
не может превосходить наибольшего возможного числа ребер выпуклого  -гранника в силу (1, 6, 4), равного
-гранника в силу (1, 6, 4), равного  . С другой стороны,
. С другой стороны,  не может превосходить пересечения двух кругов, расстояние между центрами которых равно о. Следовательно, имеем
не может превосходить пересечения двух кругов, расстояние между центрами которых равно о. Следовательно, имеем 

Так как, далее, площадь части поверхности шара, покрытой кругами, не может превосходить  то
то

то есть

что и доказывает неравенство (2), а следоватетьно и (1,1).
Чтобы получить аналогичное доказательство неравенства (1,2), предположим, что круги  полностью покрывают поверхность сферы радиуса единица, и будем исходить из равенства
полностью покрывают поверхность сферы радиуса единица, и будем исходить из равенства

где

есть часть поверхности шара, покрытая по крайне мере дважды кругами 
Здесь сумма распространяется по чем тройкам индексов I, j, k, для которых треугольник  представляет собой грань выпуклой оболочки центров
представляет собой грань выпуклой оболочки центров  кругов. Это соотношение соответствует равенству (111,4,3). Однако приведенное ниже доказательство проще того, которое было изложено в гл. III, так как здесь покрываемая область не имеет края.
кругов. Это соотношение соответствует равенству (111,4,3). Однако приведенное ниже доказательство проще того, которое было изложено в гл. III, так как здесь покрываемая область не имеет края.
Если изменять круги  так, чтобы они продолжали иметь общую точку, то, совершенно аналогично случаю плоскости, достигнет минимума в том случае, когда пересечение
так, чтобы они продолжали иметь общую точку, то, совершенно аналогично случаю плоскости, достигнет минимума в том случае, когда пересечение  стягивается в точку и треугольник
стягивается в точку и треугольник  становится равносторонним. Следовательно, имеем
становится равносторонним. Следовательно, имеем 

Так как, далее, число  равно
равно  , то
, то

то есть

чем и завершается доказательство.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ АВТОРА
- ГЛАВА I. НЕСКОЛЬКО ТЕОРЕМ ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ
- § 1. Выпуклые фигуры
- § 2. Аффинное преобразование и полярное преобразование
- § 3. Экстремальные свойства правильных многоугольников
- § 4. Изопериметрическая задача
- § 5. Некоторые неравенства, относящиеся к треугольнику
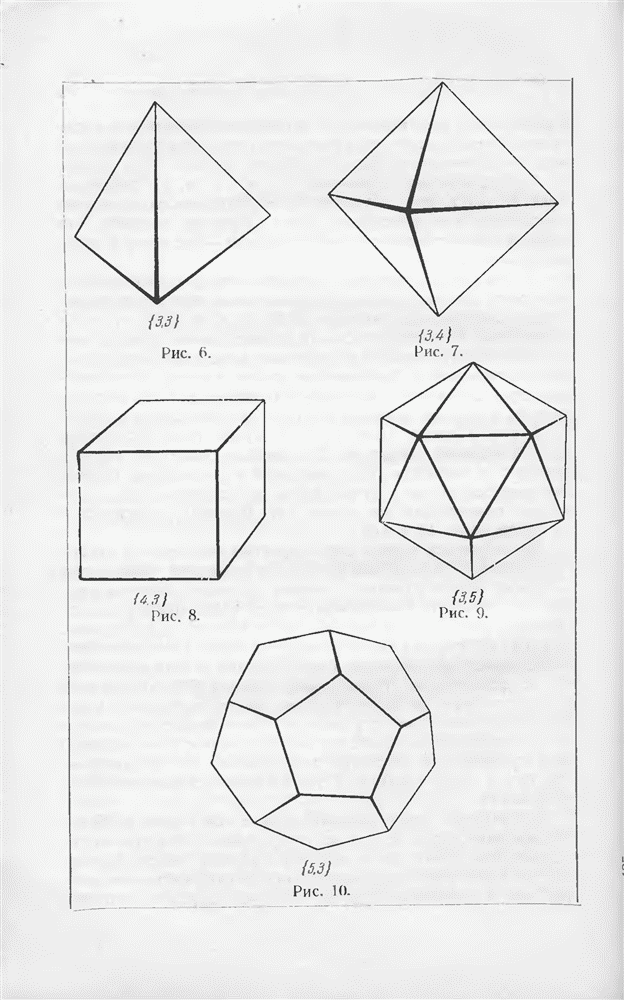
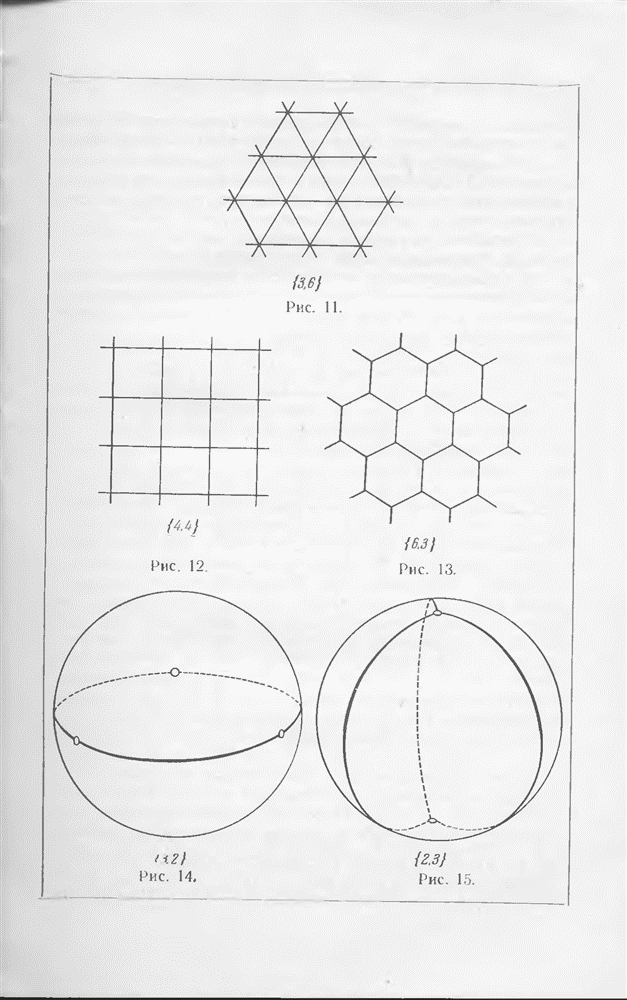
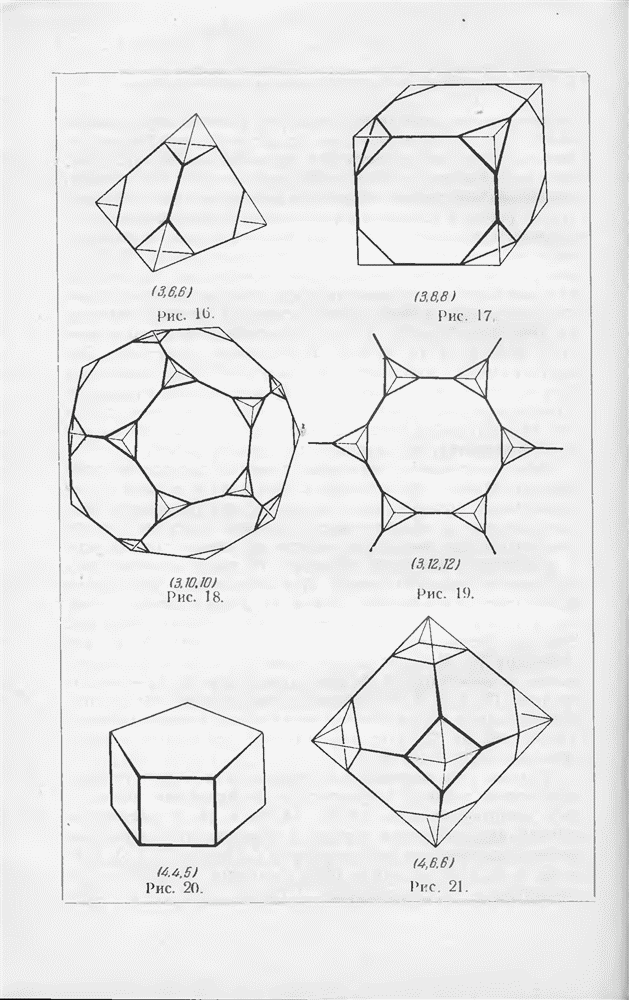
- § 6. Теорема Эйлера о многогранниках
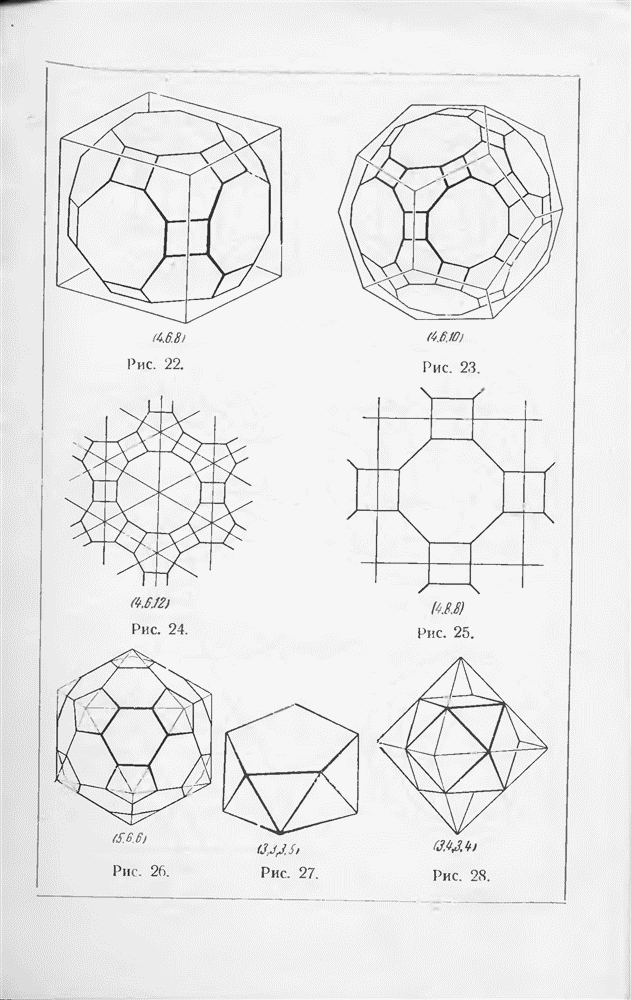
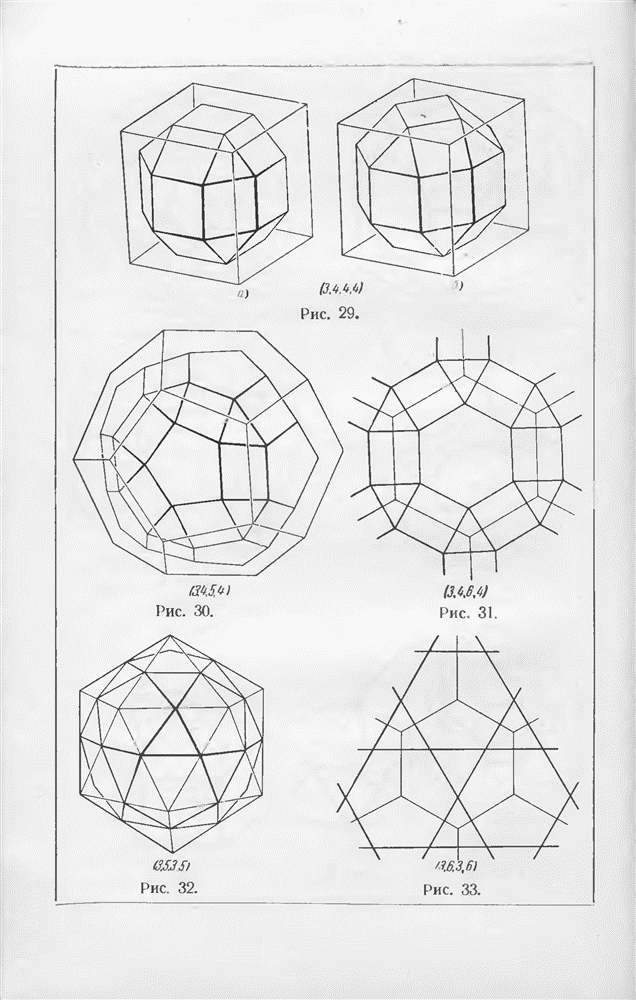
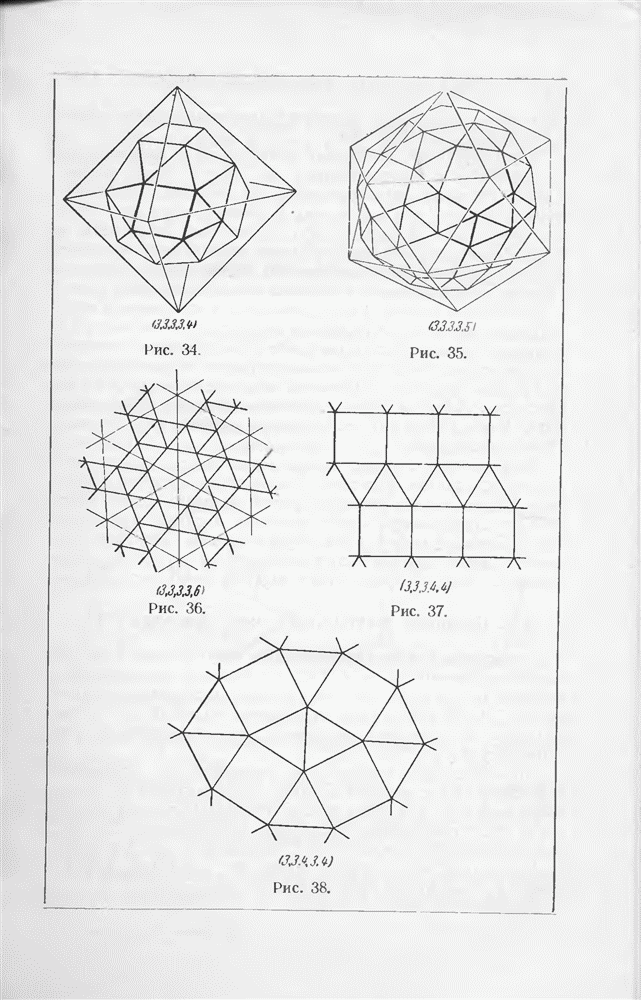
- § 7. Правильные и полуправильные многогранники
- § 8. Полярные треугольники, круг Лекселля
- § 9. Некоторые тождества из векторной алгебры
- § 10. Некоторые формулы сферической тригонометрии
- § 11. Исторические замечания
- ГЛАВА II. ТЕОРЕМЫ ИЗ ТЕОРИИ ВЫПУКЛЫХ ТЕЛ
- § 1. «Теорема выбора» Бляшке
- § 2. Неравенство Иенсена
- § 3. Теоремы Доукера
- § 4. Одно экстремальное свойство эллипса
- § 5. Об аффинной длине
- § 6. Вариационная задача для аффинной длины
- § 7. Основные факты интегральной геометрии
- § 8. Исторические замечания
- ГЛАВА III. ЗАДАЧА ЗАПОЛНЕНИЯ И ЗАДАЧА ПОКРЫТИЯ ДЛЯ СЛУЧАЯ ПЛОСКОСТИ
- § 1. Плотность системы фигур
- § 2. Задачи о плотнейшем заполнении плоскости кругами и о редчайшем покрытии плоскости кругами
- § 3. Несколько доказательств
- § 4. Заполнение и покрытие выпуклой области равными кругами
- § 5. Разбиение выпуклой области на выпуклые подобласти
- § 6. Заполнение выпуклой области кругами n различных размеров
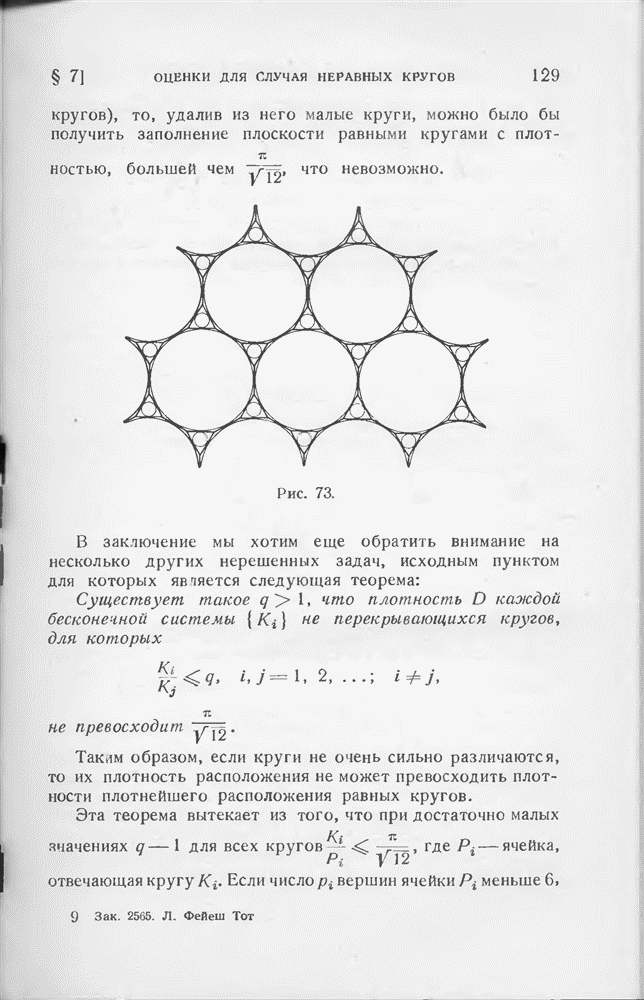
- § 7. Оценки для случая неравных кругов
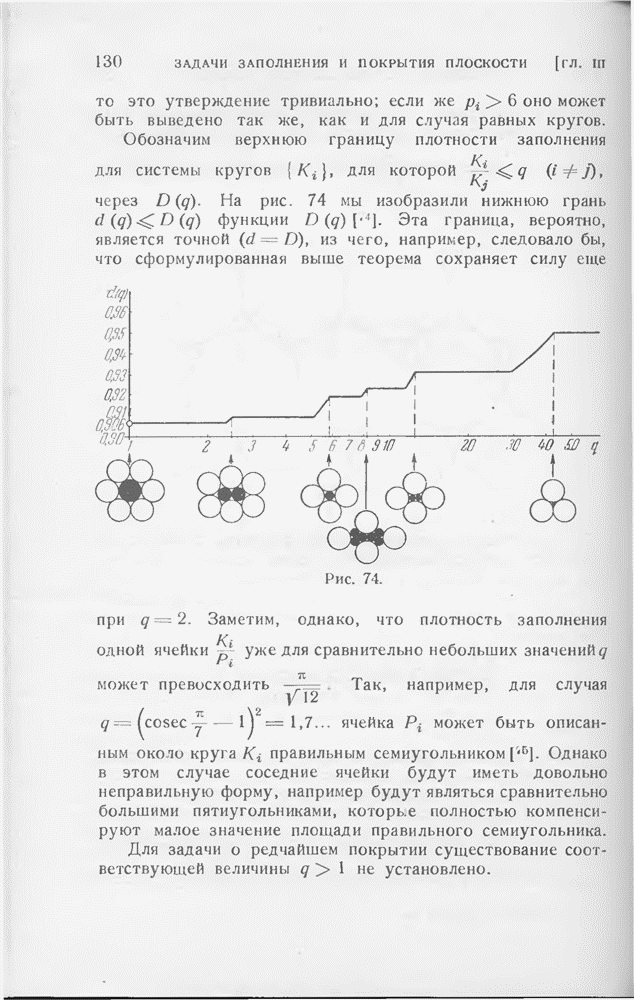
- § 8. Дальнейшие теоремы о покрытии кругами
- § 9. Разбиение выпуклого шестиугольника на выпуклые многоугольники
- § 10. Заполнение и покрытие выпуклого шестиугольника равными выпуклыми фигурами
- § 11. Одна задача о заполнении выпуклыми фигурами, связанная с понятием аффинной длины
- § 12. О формуле осреднения
- § 13. Исторические замечания
- ГЛАВА IV. ЭКОНОМИЧНОСТЬ ЗАПОЛНЕНИЯ и ПОКРЫТИЯ ФИГУРАМИ ДАННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 1. Экстремальные свойства треугольника
- § 2. Центрально-симметричные фигуры
- § 3. Экономичность заполнения и покрытия фигурами данной последовательности
- § 4. Покрытие разрезанными на куски выпуклыми фигурами
- § 5. Исторические замечания
- ГЛАВА V. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
- § 1. Заполнение и покрытие сферы равными кругами
- § 2. Некоторые другие доказательства
- § 3. Приближение шара многогранниками
- § 4. Объем описанного многогранника
- § 5. Объем вписанного многогранника
- § 6. Неравенства, связывающие радиусы вписанного и описанного шаров выпуклого многогранника
- § 7. Изопериметрическая задача для многогранников
- § 8. Одно общее неравенство
- § 9. О кратчайшей сети, разбивающей сферу на равновеликие выпуклые части
- § 10. О сумме длин ребер многогранника
- § 11. Редчайшая насыщенная система сферических кругов
- § 12. Приближение выпуклой поверхности многогранниками
- § 13. Исторические замечания
- ГЛАВА VI. НЕПРАВИЛЬНЫЕ РАСПОЛОЖЕНИЯ НА СФЕРЕ
- § 1. Граф, отвечающий заданной системе точек
- § 2. Максимальная фигура для n = 7
- § 3. Максимальная фигура для n = 8 и n = 9
- § 4. Несколько расположений более чем 9 точек
- § 5. Таблица результатов
- § 6. Исторические замечания
- ГЛАВА VII. РАСПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ
- § 2. Задача о теснейшей упаковке шаров
- § 3. Об одном экстремальном разбиении пространства
- § 4. Формула осреднения для пространства
- § 5. Исторические замечания
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ПРИЛОЖЕНИЕ I. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ, КАСАЮЩИЕСЯ РАСПОЛОЖЕНИЙ В n-МЕРНОМ ПРОСТРАНСТВЕ
- ПРИЛОЖЕНИЕ II. НЕСКОЛЬКО ОПРЕДЕЛЕНИЙ РАЗМЕРНОСТИ
- БИБЛИОГРАФИЯ