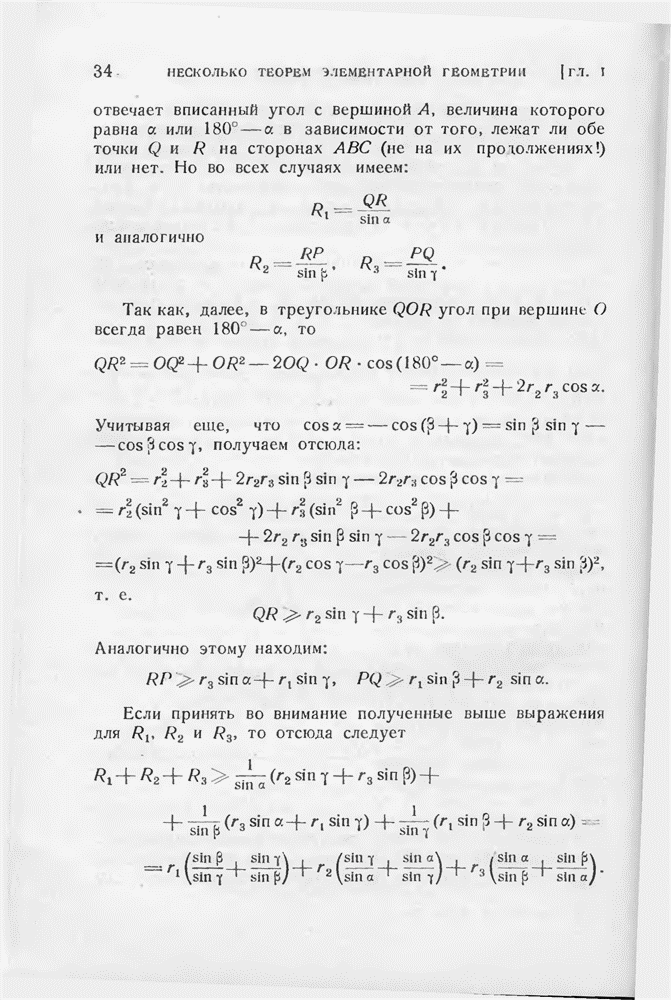| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Изопериметрическая задача
Какая из плоских фигур одинакового периметра (такие фигуры мы будем называть изопериметрическими), имеет наибольшую площадь? Решением этой классической задачи, называемой изопериметрической задачей, является круг.
По-другому это можно выразить так; если L есть периметр плоской фигуры F, то

причем равенство достигается только в случае круга.
Из этой основной задачи можно получить множество других задач; для этого надо только наложить на рассматриваемые фигуры те или иные дополнительные условия. Ниже мы рассмотрим изопериметрическую задачу для  -угольника. Другими словами, мы рассмотрим совокупность всех многоугольников одного периметра, имеющих не более
-угольника. Другими словами, мы рассмотрим совокупность всех многоугольников одного периметра, имеющих не более  вершин, и зададимся вопросом о том, какой из этих многоугольников имеет наибольшую площадь.
вершин, и зададимся вопросом о том, какой из этих многоугольников имеет наибольшую площадь.
Мы набросаем здесь сначала косвенное доказательство того, что наилучшим  -угольником в этой задаче является правильный. Это доказательство имеет то преимущество, что оно легко переносится также и на аналогичную задачу сферической геометрии.
-угольником в этой задаче является правильный. Это доказательство имеет то преимущество, что оно легко переносится также и на аналогичную задачу сферической геометрии.
Очевидно, что мы можем с самого начала ограничиться лишь выпуклыми многоугольниками, так как при замене невыпуклого многоугольника его выпуклой оболочкой периметр уменьшается, а площадь, напротив того, увеличивается; так же и число вершин многоугольника при этом уменьшается. После того как (в силу теоремы Вейерштрасса!) установлено существование наилучшего  -угольника Р, можно легко показать, что в каждой вершине Р биссектриса внешнего угла параллельна прямой, соединяющей две вершины многоугольника, смежные с рассматриваемой; действительно, в противном случае Р можно было бы улучшить при помощи подходящего сдвига соответствующей вершины. Отсюда следует, что стороны наилучшего
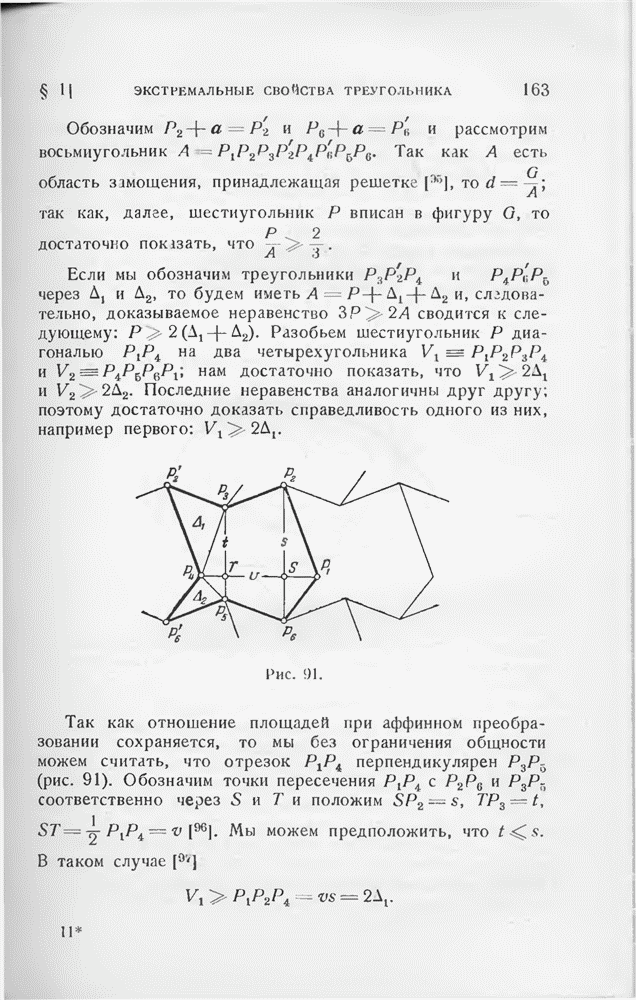
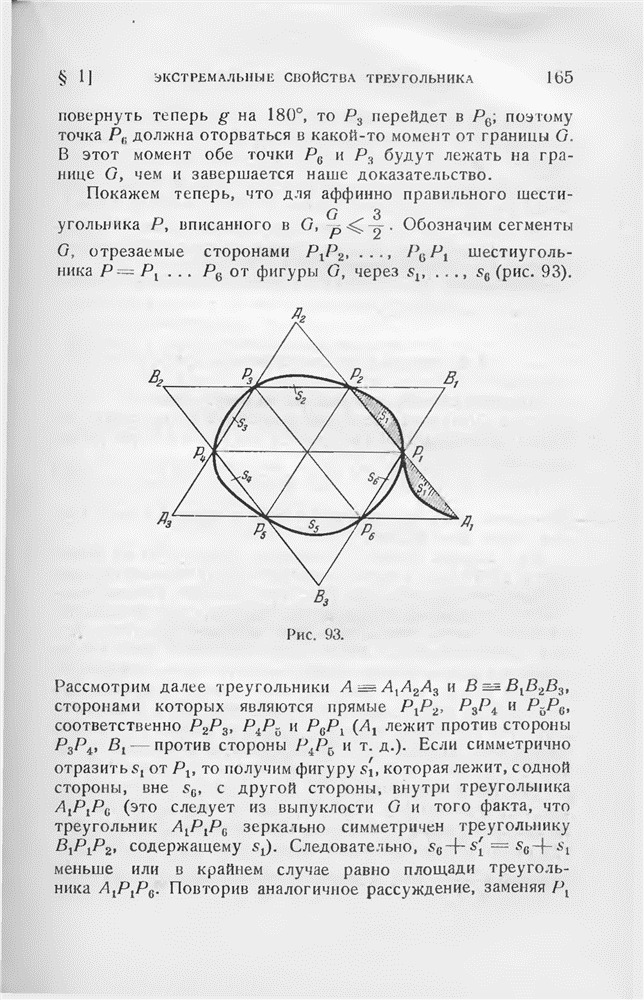
-угольника Р, можно легко показать, что в каждой вершине Р биссектриса внешнего угла параллельна прямой, соединяющей две вершины многоугольника, смежные с рассматриваемой; действительно, в противном случае Р можно было бы улучшить при помощи подходящего сдвига соответствующей вершины. Отсюда следует, что стороны наилучшего  -угольника должны быть равной длины. Легко также усмотреть, что круг, который касается стороны АВ многоугольника Р и продолжений двух смежных с АВ сторон, должен касаться отрезка АВ в его середине. Отсюда следует, что углы Р также должны быть равны, что и доказывает наше утверждение.
-угольника должны быть равной длины. Легко также усмотреть, что круг, который касается стороны АВ многоугольника Р и продолжений двух смежных с АВ сторон, должен касаться отрезка АВ в его середине. Отсюда следует, что углы Р также должны быть равны, что и доказывает наше утверждение.
Полученный результат можно выразить неравенством

где  -периметр и
-периметр и  -плошадь любого
-плошадь любого  -угольника; равенство в (2) достигается только для случая правильного
-угольника; равенство в (2) достигается только для случая правильного  -угольника.
-угольника.
Нижеследующее прямое доказательство даст нам важное усиление этого результата. Пусть F — произвольно заданный выпуклый  -угольник периметра L, радиус вписанного круга которого равен
-угольник периметра L, радиус вписанного круга которого равен  . Рассмотрим тот описанный вокруг единичного круга
. Рассмотрим тот описанный вокруг единичного круга  -угольник
-угольник  направления внешних нормалей к сторонам которого совпадают с направлениями внешних нормалей к соответствующим сторонам
направления внешних нормалей к сторонам которого совпадают с направлениями внешних нормалей к соответствующим сторонам  -угольника F. Мы покажем, что
-угольника F. Мы покажем, что

Это неравенство можно преобразовать следующим образом:

Отсюда вытекает следующее замечательное неравенство, впервые доказанное Люилье:

причем равенство имеет место только для многоугольника, описанного около круга; оно означает, что среди выпуклых многоугольников, имеющих заданные направления внешних нормалей к сторонам, многоугольники, описанные около круга, имеют наименьшую величину отношения 
Обозначим углы между внешними нормалями к смежным сторонам многоугольника через  тогда
тогда 

Следовательно, неравенство Люилье можно записать следующим образом:

Далее, из (3) следует (так как  )
)

или, что эквивалентно этому,

Из этого усиленного изопериметрического неравенства вытекает справедливость аналогичного неравенства (в котором лишь знак  следует заменить на для произвольной выпуклой фигуры, отсюда непосредственно следует, что в первоначальном изопериметрическом неравенстве (1) равенство может достигаться только для круга.
следует заменить на для произвольной выпуклой фигуры, отсюда непосредственно следует, что в первоначальном изопериметрическом неравенстве (1) равенство может достигаться только для круга.
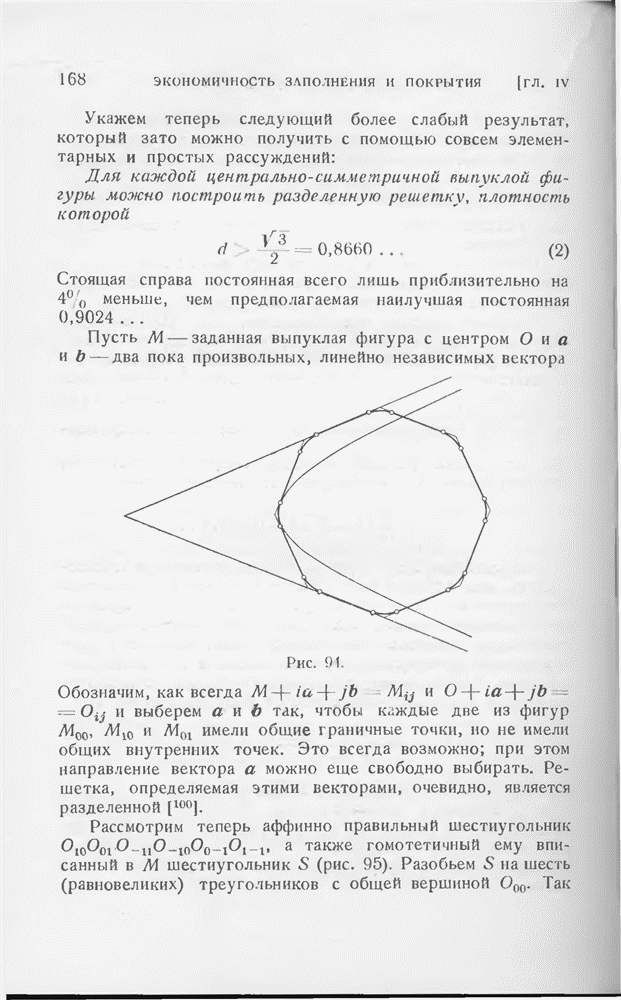
Для доказательства (3) сдвинем каждую сторону многоугольника параллельно самой себе внутрь на расстояние  и обозначим многоугольник, образованный полученными прямыми через
и обозначим многоугольник, образованный полученными прямыми через 

Рис. 3.
Исследуем, как изменяется многоугольник  который можно назвать внутренней параллельной оболочкой F (ср. выше, стр. 18), когда а растет от 0 до
который можно назвать внутренней параллельной оболочкой F (ср. выше, стр. 18), когда а растет от 0 до  (рис. 3).
(рис. 3).
Для малых значений а углы  двигаются по внутренним биссектрисам многоугольника
двигаются по внутренним биссектрисам многоугольника  каждая сторона
каждая сторона  при этом уменьшается и при определенном значении а она стягивается в точку. Начиная с этого «критического» значения а,
при этом уменьшается и при определенном значении а она стягивается в точку. Начиная с этого «критического» значения а,  будет уже иметь меньшее число сторон; наконец, для значения
будет уже иметь меньшее число сторон; наконец, для значения  многоугольник
многоугольник  стянется в «ядро» многоугольника F, которое есть не что иное, как множество центров вписанных кругов F и, следовательно, вообще говоря, представтяет собой точку, хотя в некоторых особых случаях (например, в случае прямоугольника) может являться также и отрезком.
стянется в «ядро» многоугольника F, которое есть не что иное, как множество центров вписанных кругов F и, следовательно, вообще говоря, представтяет собой точку, хотя в некоторых особых случаях (например, в случае прямоугольника) может являться также и отрезком.
Многоугольники  отвечающие «критическим» значениям а, разбизают совокупность параллельных оболочек
отвечающие «критическим» значениям а, разбизают совокупность параллельных оболочек  на отдельные пласты. Многоугольники, принадлежащие одному и тому же пласту, имеют одинаковое число сторон. Пусть
на отдельные пласты. Многоугольники, принадлежащие одному и тому же пласту, имеют одинаковое число сторон. Пусть  — два многоугольника одного и того же пласта:
— два многоугольника одного и того же пласта:  Обозначим численные характеристики многоугольников
Обозначим численные характеристики многоугольников  теми же буквами, что и для F, но с соответствующими индексами; тогда мы будем иметь
теми же буквами, что и для F, но с соответствующими индексами; тогда мы будем иметь 

Отсюда следует

и стало быть, величина  для всех многоугольников одного пласта будет одна и та же.
для всех многоугольников одного пласта будет одна и та же.
Заметим теперь, что  есть ступенчатая возрастающая функция а. Внутри птаста эта функция
есть ступенчатая возрастающая функция а. Внутри птаста эта функция  остается постоянной; когда мы переход
остается постоянной; когда мы переход  от одного пласта к следующему пласту, то одна сторона многоугольника
от одного пласта к следующему пласту, то одна сторона многоугольника  пропадает и, значит, величина
пропадает и, значит, величина  увеличивается. Так как, далее, F, L и
увеличивается. Так как, далее, F, L и  суть непрерывные функции а, то
суть непрерывные функции а, то  есть ступенчатая убывающая функция от а. Так как величина функции для а
есть ступенчатая убывающая функция от а. Так как величина функции для а  т. е. для «ядра» равна нулю, то для исходного многоугольника F она не может быть отрицательной. Это и доказывает наше утверждение.
т. е. для «ядра» равна нулю, то для исходного многоугольника F она не может быть отрицательной. Это и доказывает наше утверждение.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ АВТОРА
- ГЛАВА I. НЕСКОЛЬКО ТЕОРЕМ ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ
- § 1. Выпуклые фигуры
- § 2. Аффинное преобразование и полярное преобразование
- § 3. Экстремальные свойства правильных многоугольников
- § 4. Изопериметрическая задача
- § 5. Некоторые неравенства, относящиеся к треугольнику
- § 6. Теорема Эйлера о многогранниках
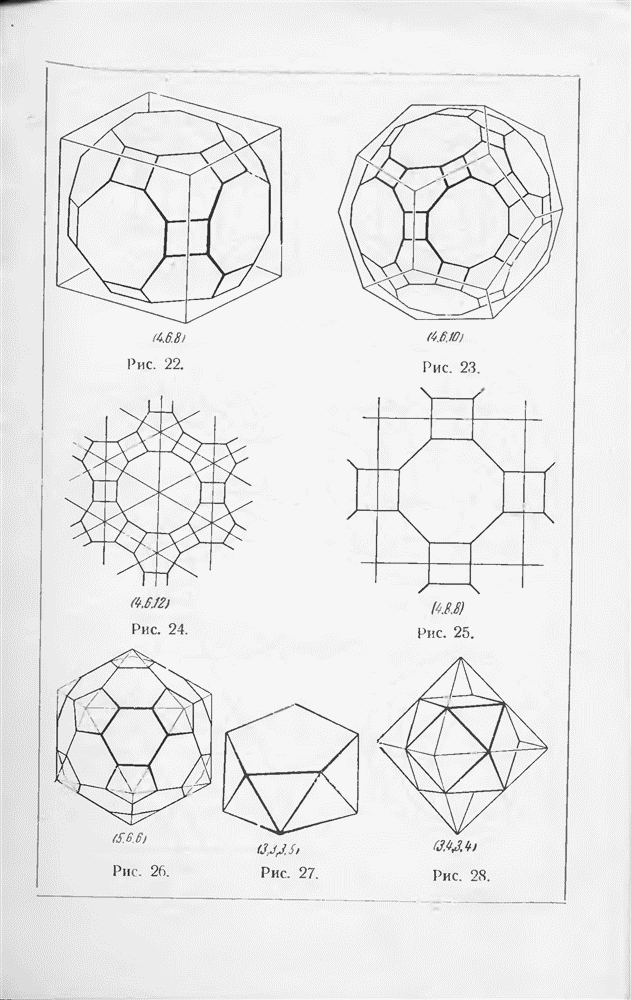
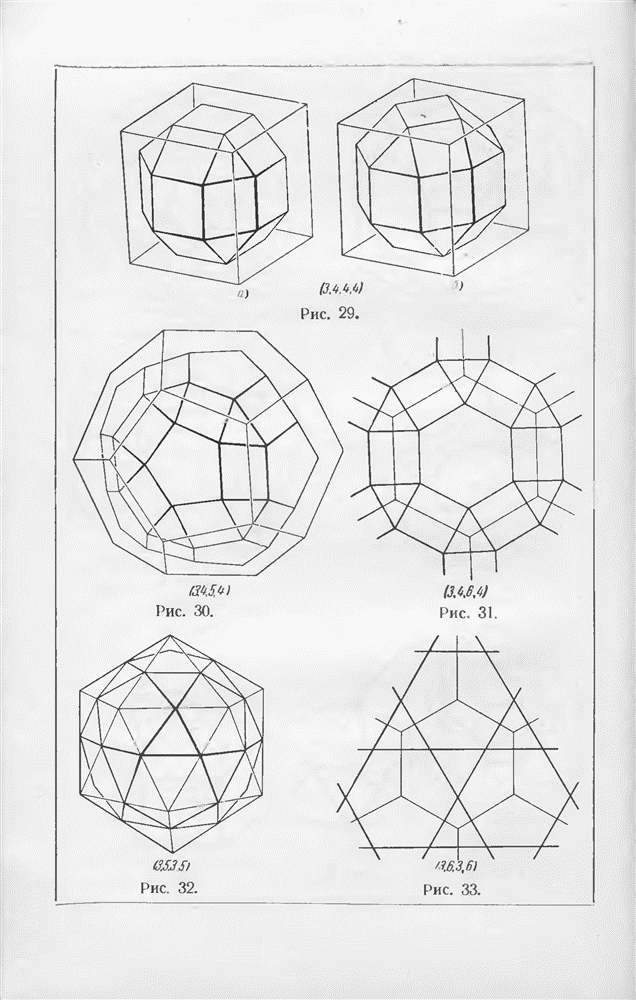
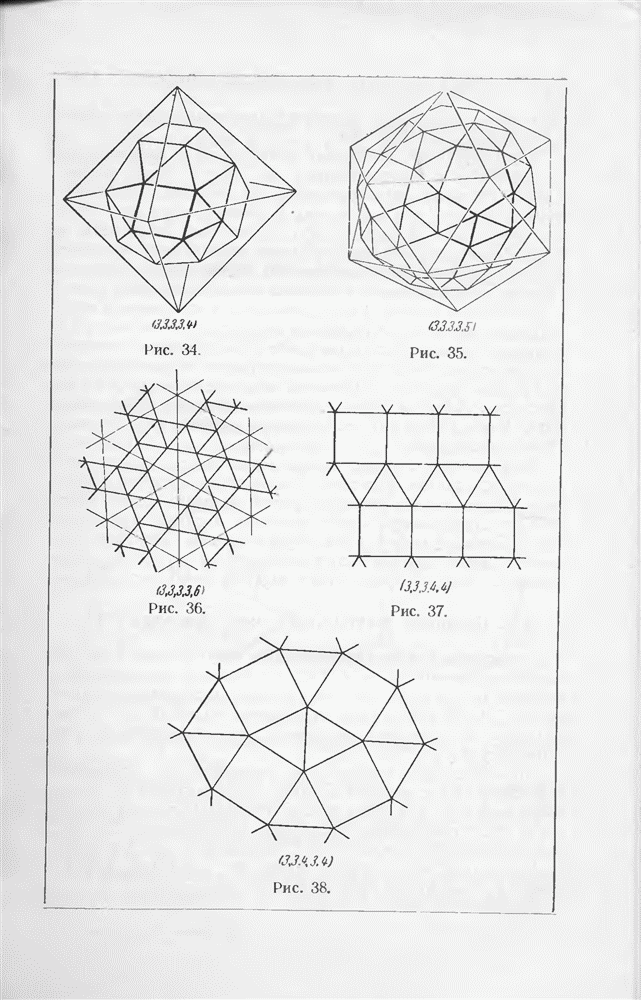
- § 7. Правильные и полуправильные многогранники
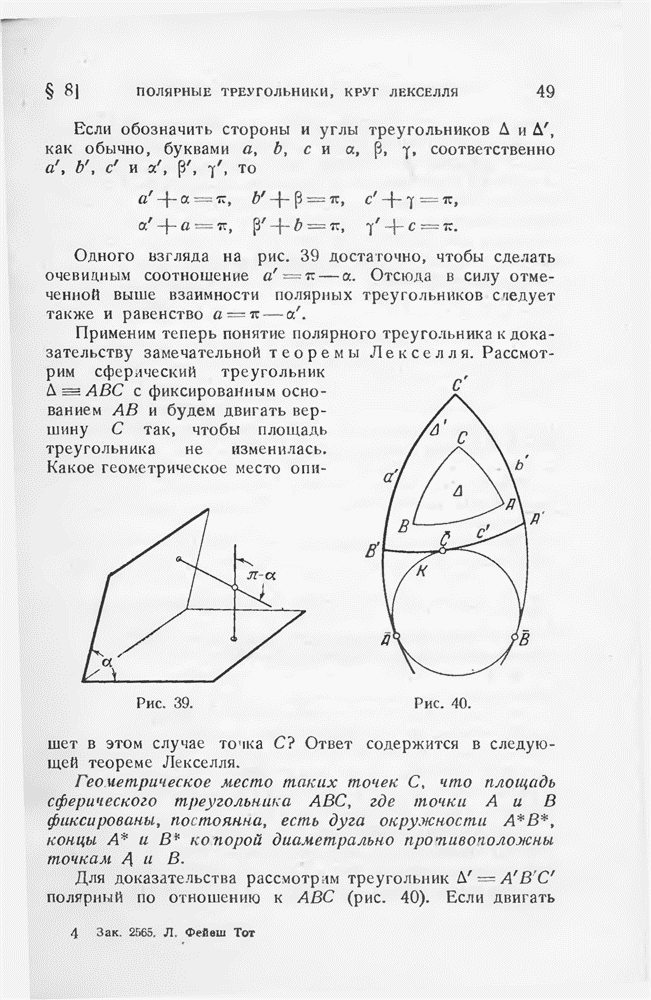
- § 8. Полярные треугольники, круг Лекселля
- § 9. Некоторые тождества из векторной алгебры
- § 10. Некоторые формулы сферической тригонометрии
- § 11. Исторические замечания
- ГЛАВА II. ТЕОРЕМЫ ИЗ ТЕОРИИ ВЫПУКЛЫХ ТЕЛ
- § 1. «Теорема выбора» Бляшке
- § 2. Неравенство Иенсена
- § 3. Теоремы Доукера
- § 4. Одно экстремальное свойство эллипса
- § 5. Об аффинной длине
- § 6. Вариационная задача для аффинной длины
- § 7. Основные факты интегральной геометрии
- § 8. Исторические замечания
- ГЛАВА III. ЗАДАЧА ЗАПОЛНЕНИЯ И ЗАДАЧА ПОКРЫТИЯ ДЛЯ СЛУЧАЯ ПЛОСКОСТИ
- § 1. Плотность системы фигур
- § 2. Задачи о плотнейшем заполнении плоскости кругами и о редчайшем покрытии плоскости кругами
- § 3. Несколько доказательств
- § 4. Заполнение и покрытие выпуклой области равными кругами
- § 5. Разбиение выпуклой области на выпуклые подобласти
- § 6. Заполнение выпуклой области кругами n различных размеров
- § 7. Оценки для случая неравных кругов
- § 8. Дальнейшие теоремы о покрытии кругами
- § 9. Разбиение выпуклого шестиугольника на выпуклые многоугольники
- § 10. Заполнение и покрытие выпуклого шестиугольника равными выпуклыми фигурами
- § 11. Одна задача о заполнении выпуклыми фигурами, связанная с понятием аффинной длины
- § 12. О формуле осреднения
- § 13. Исторические замечания
- ГЛАВА IV. ЭКОНОМИЧНОСТЬ ЗАПОЛНЕНИЯ и ПОКРЫТИЯ ФИГУРАМИ ДАННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 1. Экстремальные свойства треугольника
- § 2. Центрально-симметричные фигуры
- § 3. Экономичность заполнения и покрытия фигурами данной последовательности
- § 4. Покрытие разрезанными на куски выпуклыми фигурами
- § 5. Исторические замечания
- ГЛАВА V. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
- § 1. Заполнение и покрытие сферы равными кругами
- § 2. Некоторые другие доказательства
- § 3. Приближение шара многогранниками
- § 4. Объем описанного многогранника
- § 5. Объем вписанного многогранника
- § 6. Неравенства, связывающие радиусы вписанного и описанного шаров выпуклого многогранника
- § 7. Изопериметрическая задача для многогранников
- § 8. Одно общее неравенство
- § 9. О кратчайшей сети, разбивающей сферу на равновеликие выпуклые части
- § 10. О сумме длин ребер многогранника
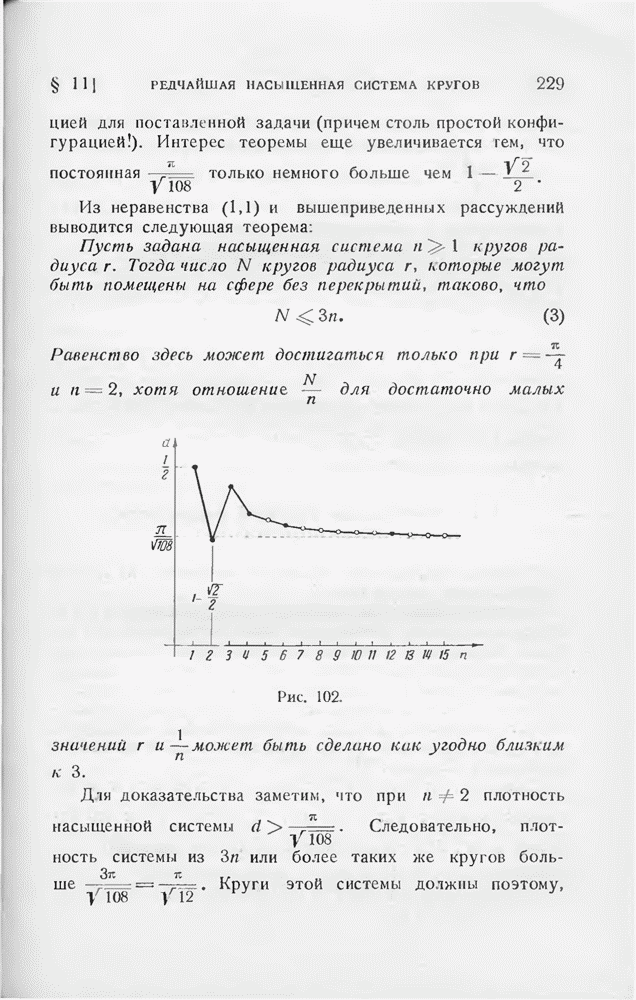
- § 11. Редчайшая насыщенная система сферических кругов
- § 12. Приближение выпуклой поверхности многогранниками
- § 13. Исторические замечания
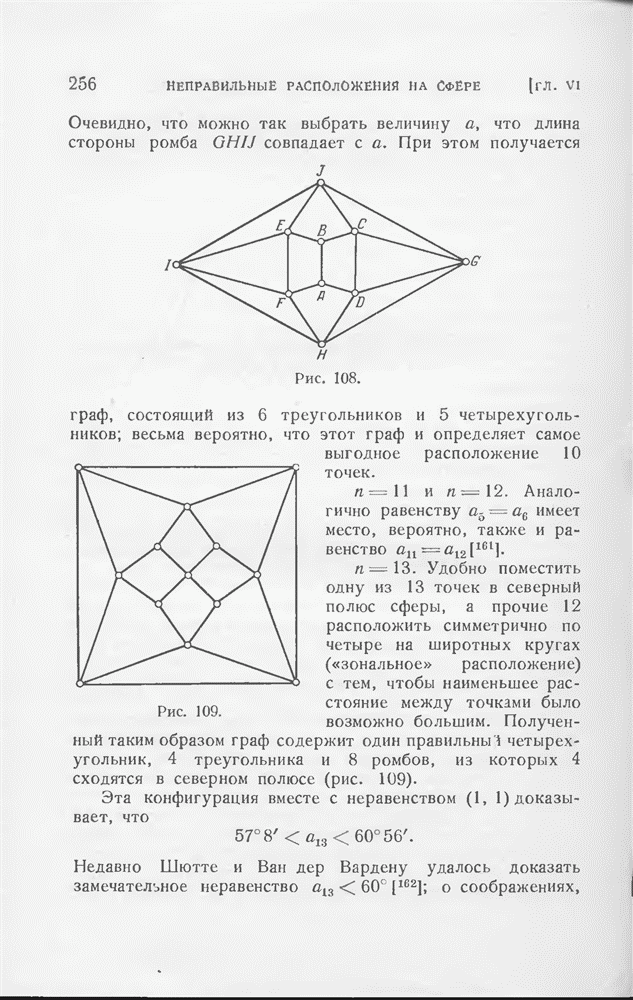
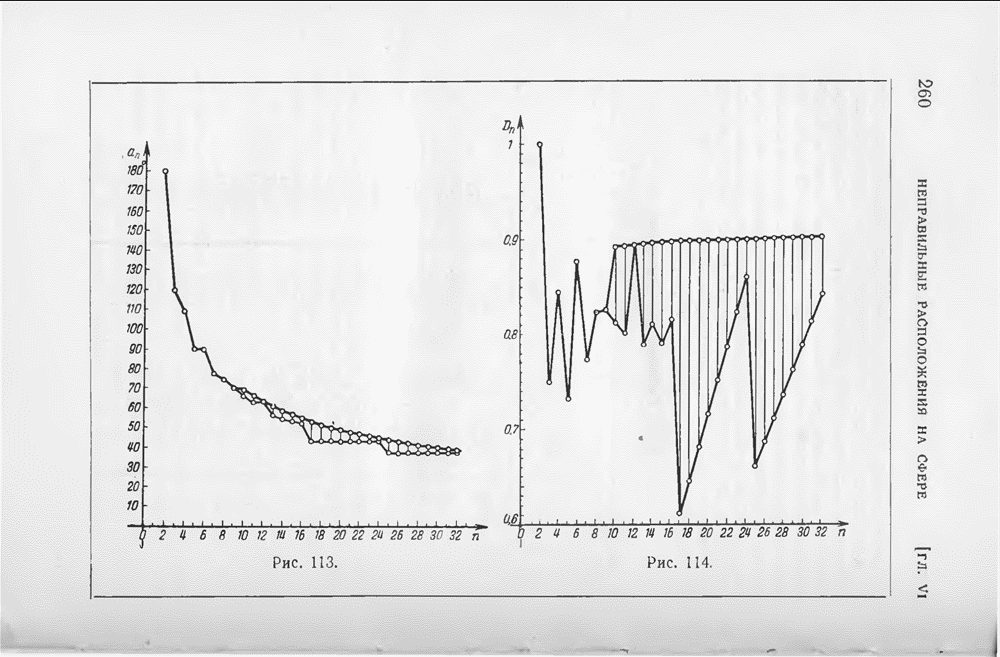
- ГЛАВА VI. НЕПРАВИЛЬНЫЕ РАСПОЛОЖЕНИЯ НА СФЕРЕ
- § 1. Граф, отвечающий заданной системе точек
- § 2. Максимальная фигура для n = 7
- § 3. Максимальная фигура для n = 8 и n = 9
- § 4. Несколько расположений более чем 9 точек
- § 5. Таблица результатов
- § 6. Исторические замечания
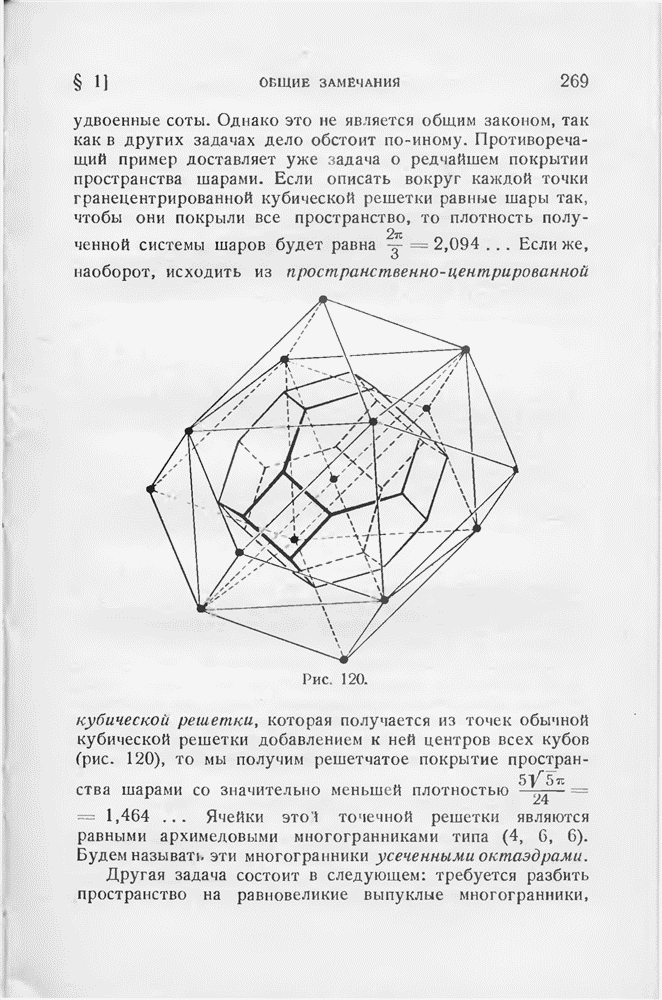
- ГЛАВА VII. РАСПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ
- § 2. Задача о теснейшей упаковке шаров
- § 3. Об одном экстремальном разбиении пространства
- § 4. Формула осреднения для пространства
- § 5. Исторические замечания
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ПРИЛОЖЕНИЕ I. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ, КАСАЮЩИЕСЯ РАСПОЛОЖЕНИЙ В n-МЕРНОМ ПРОСТРАНСТВЕ
- ПРИЛОЖЕНИЕ II. НЕСКОЛЬКО ОПРЕДЕЛЕНИЙ РАЗМЕРНОСТИ
- БИБЛИОГРАФИЯ