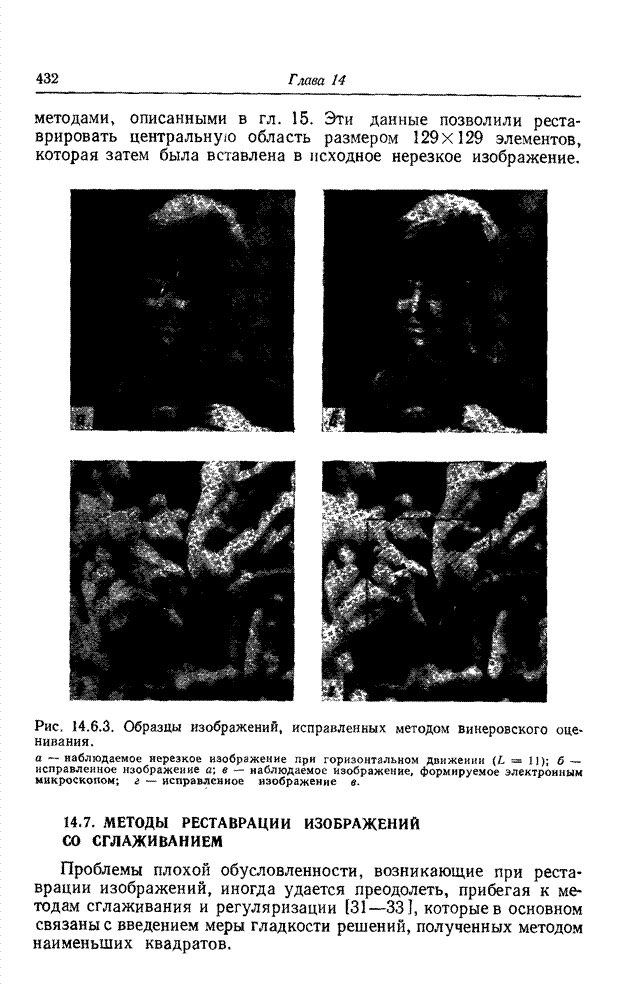
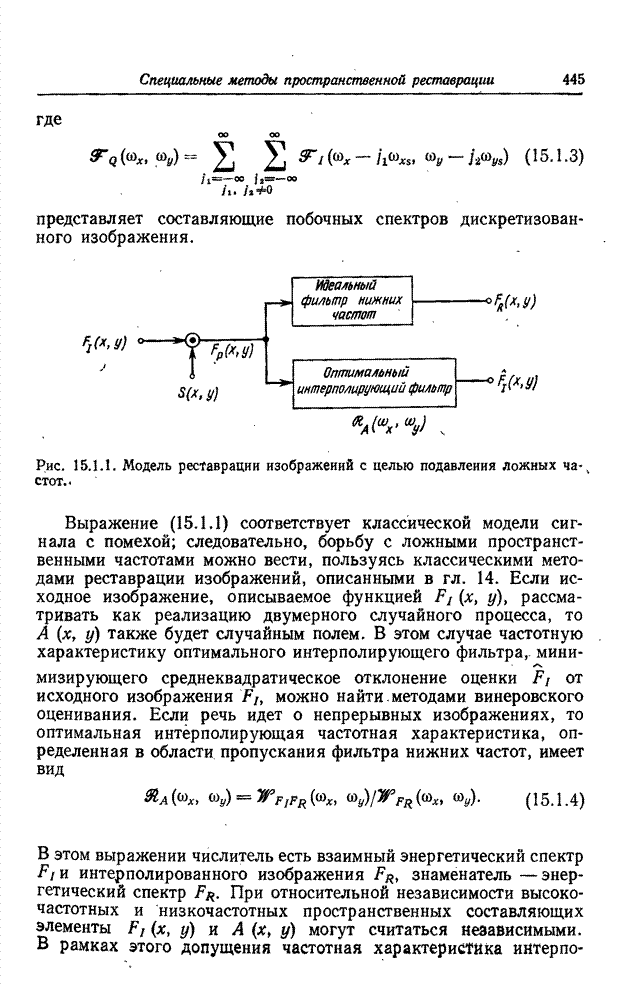
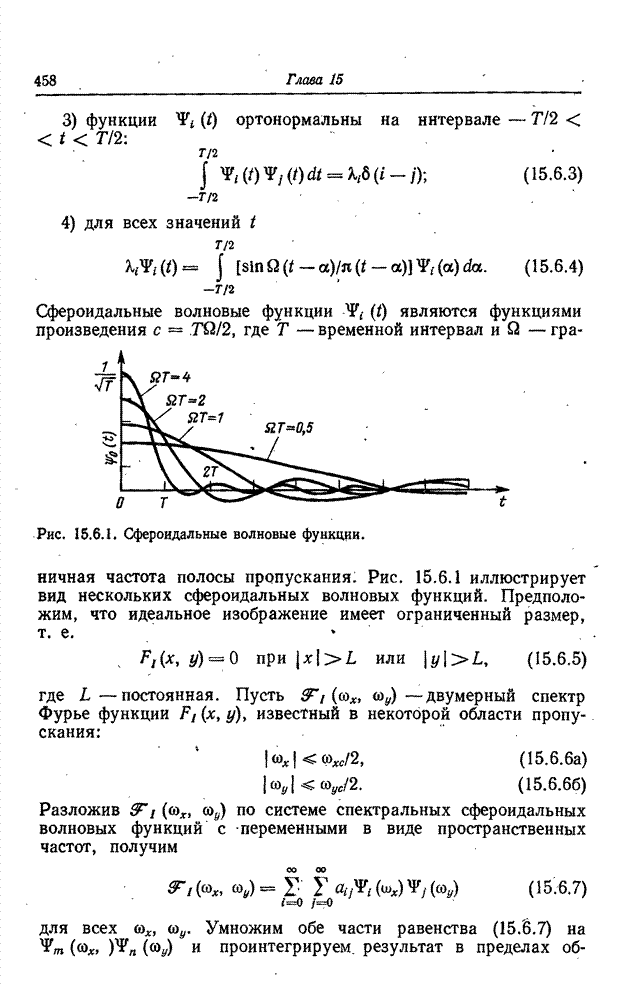
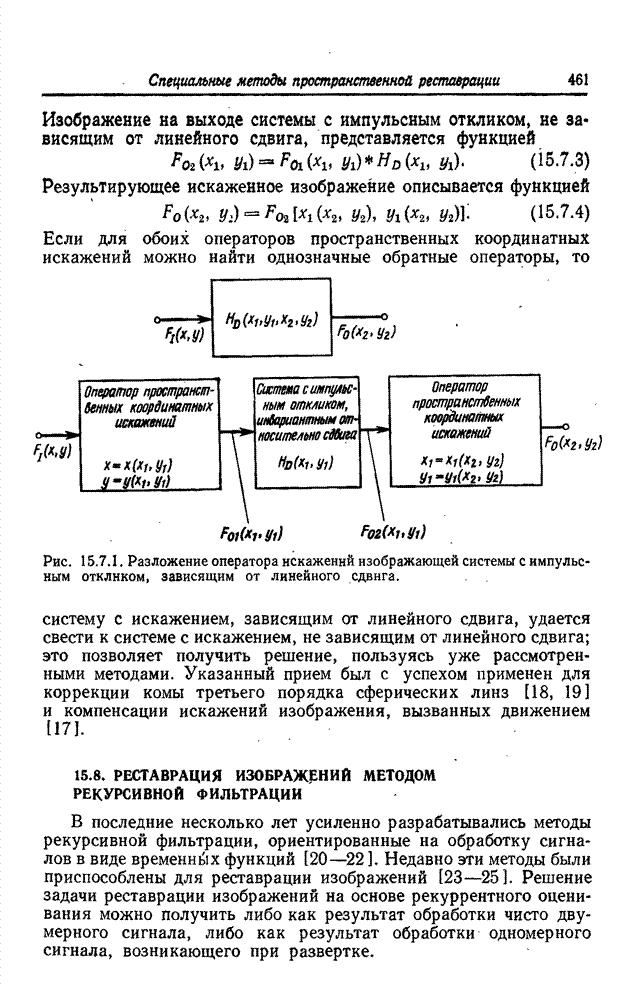
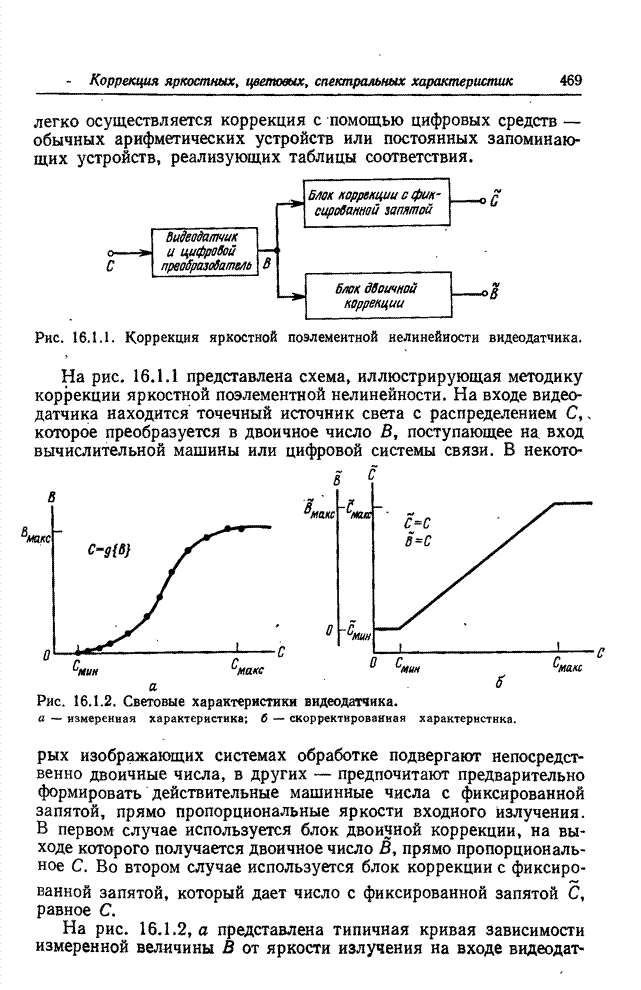
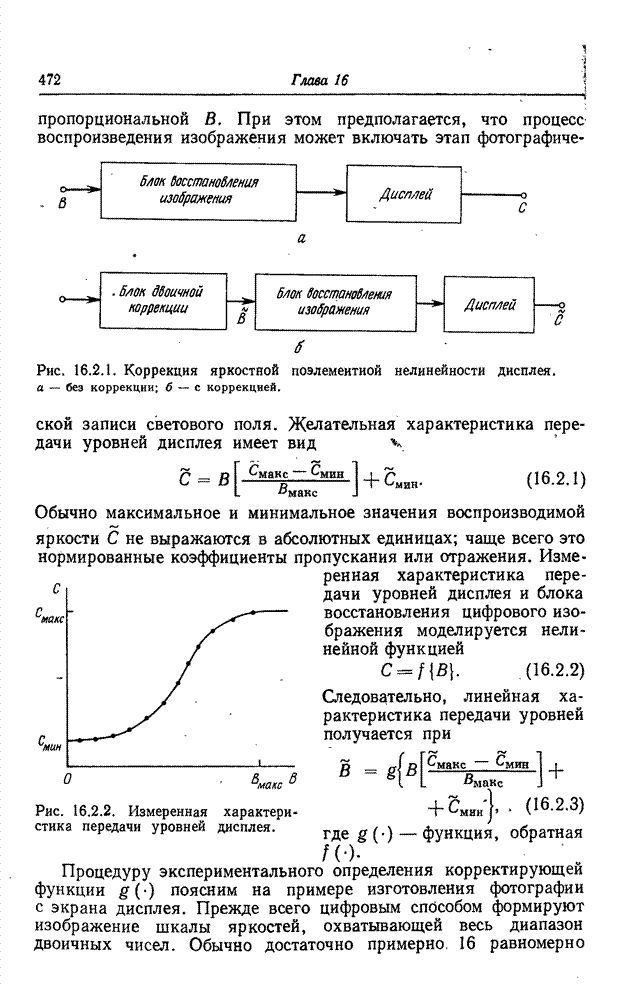
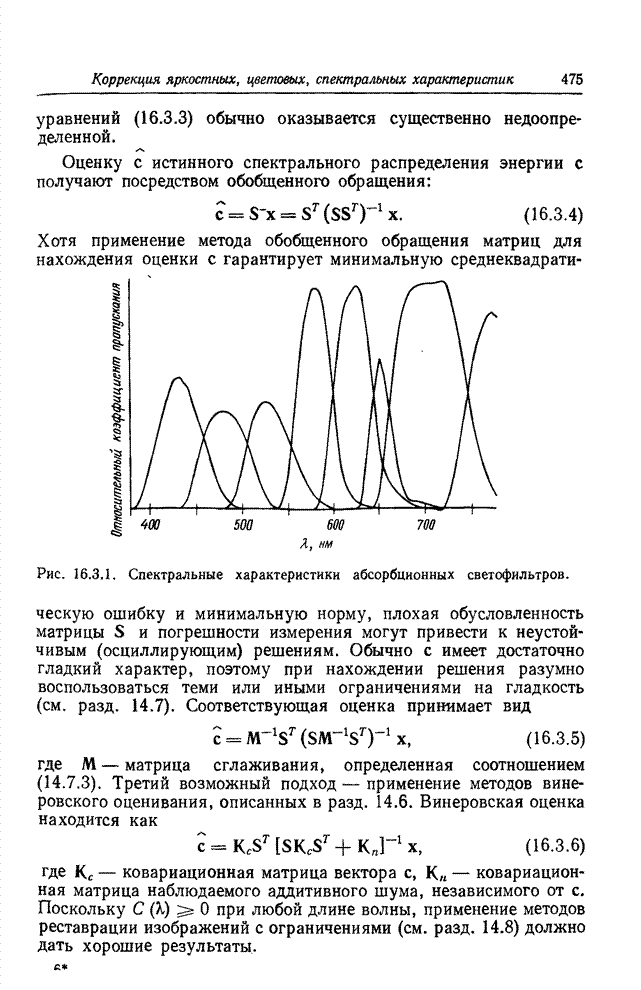
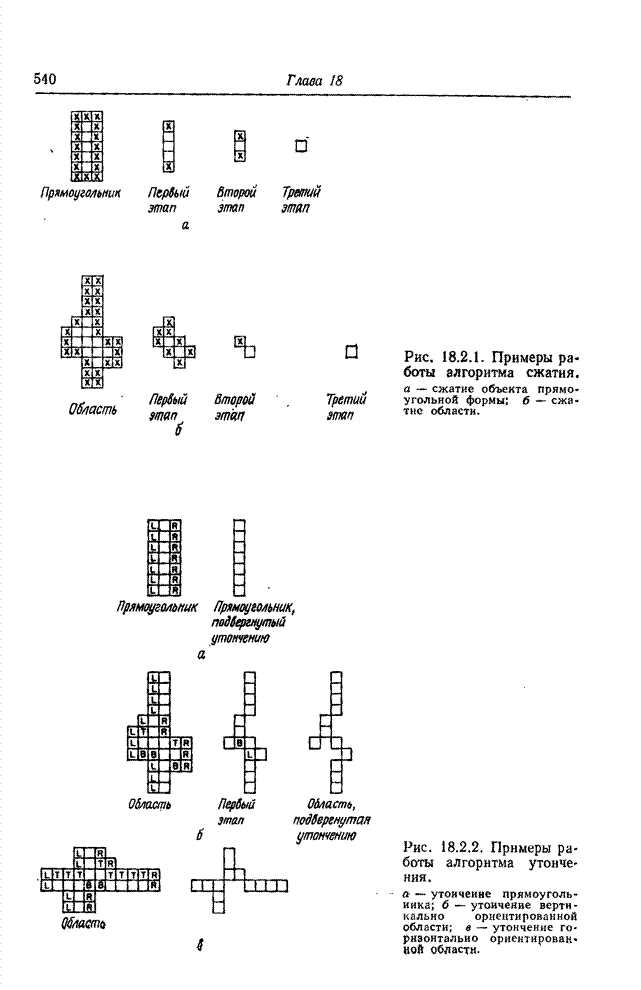
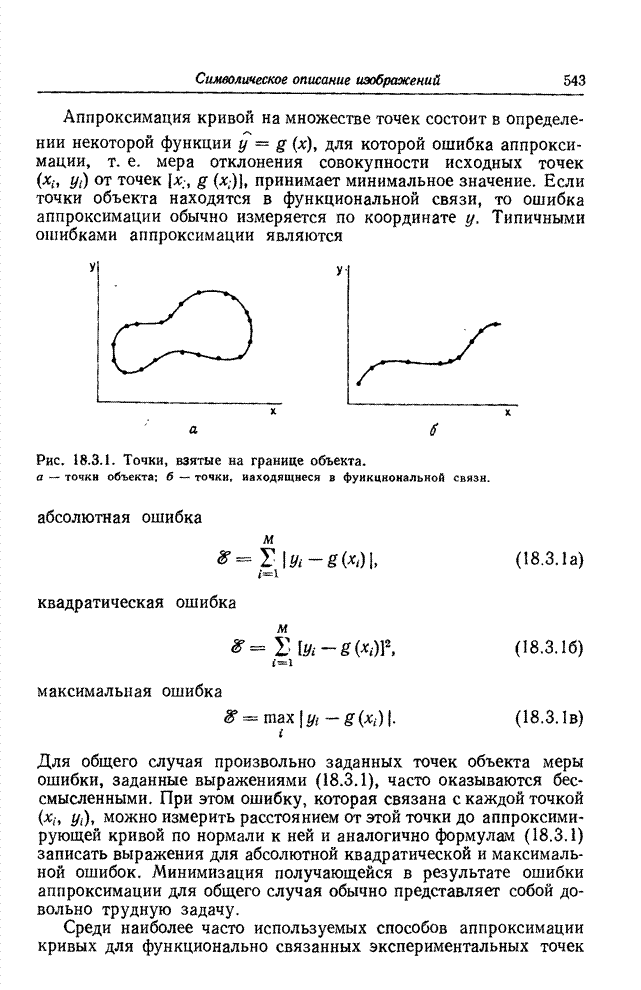
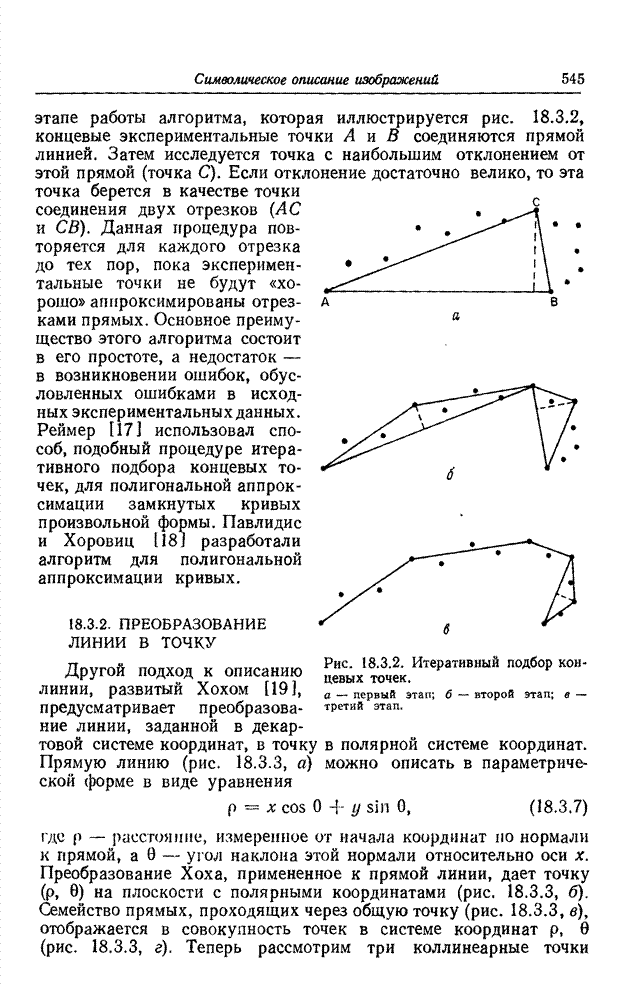
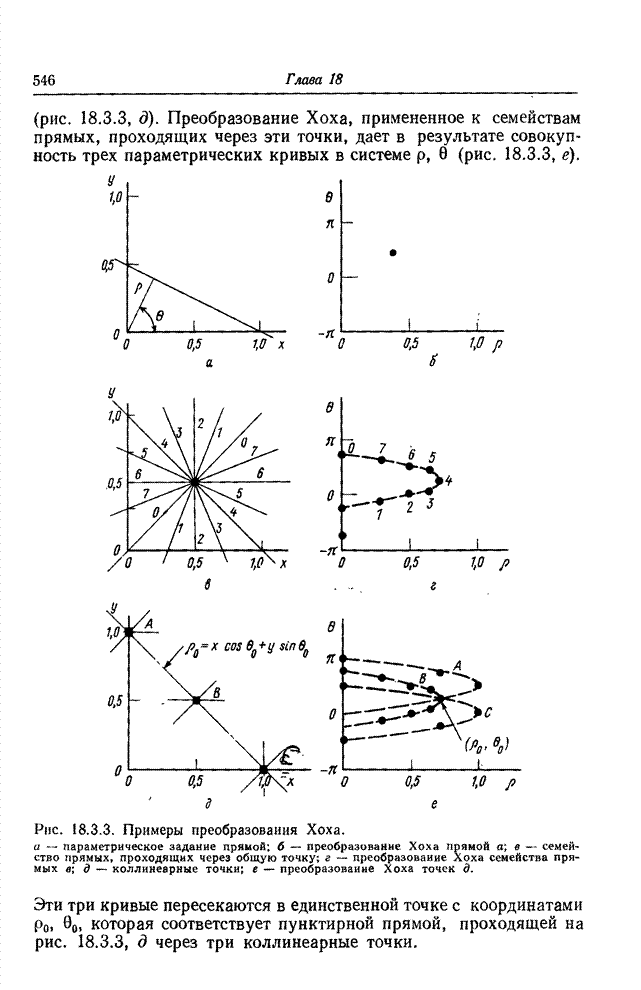
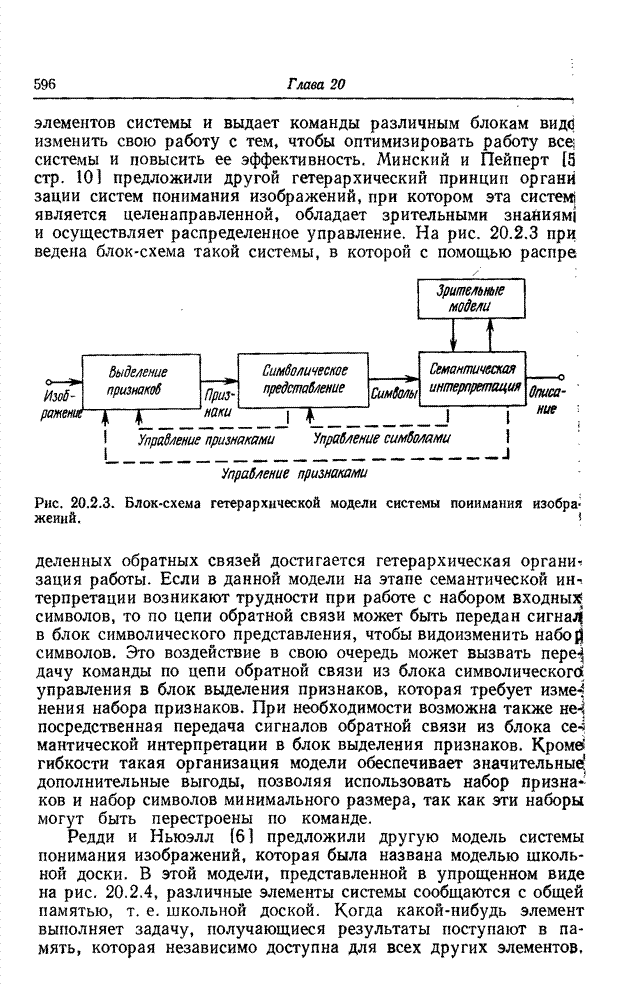
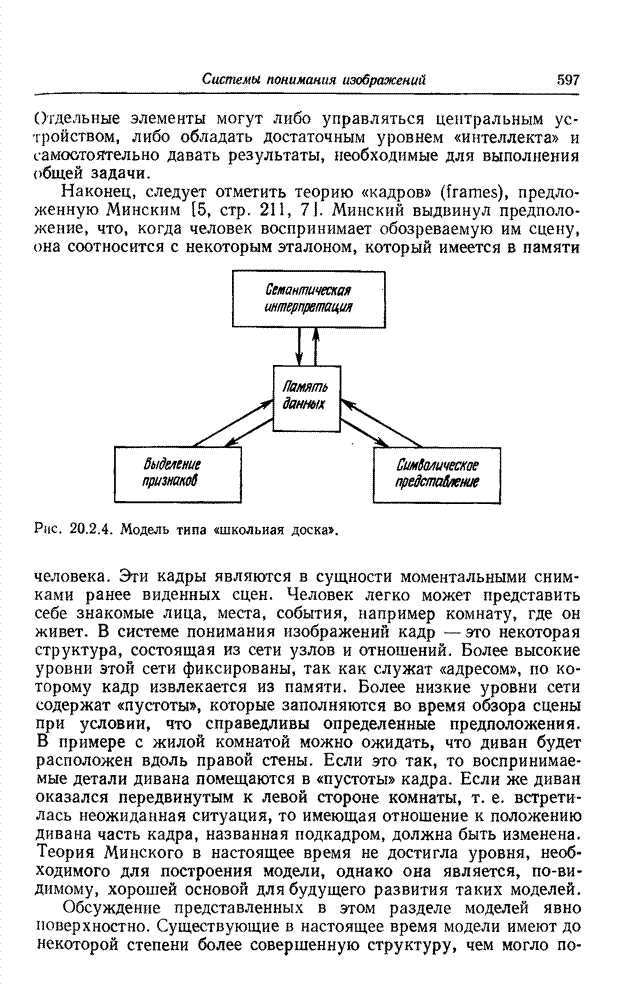
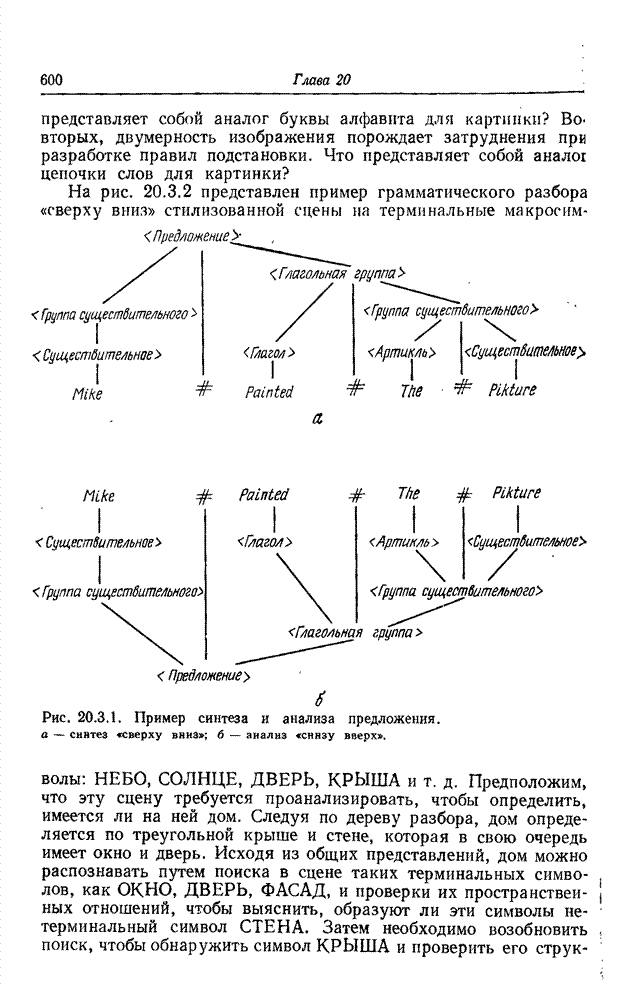
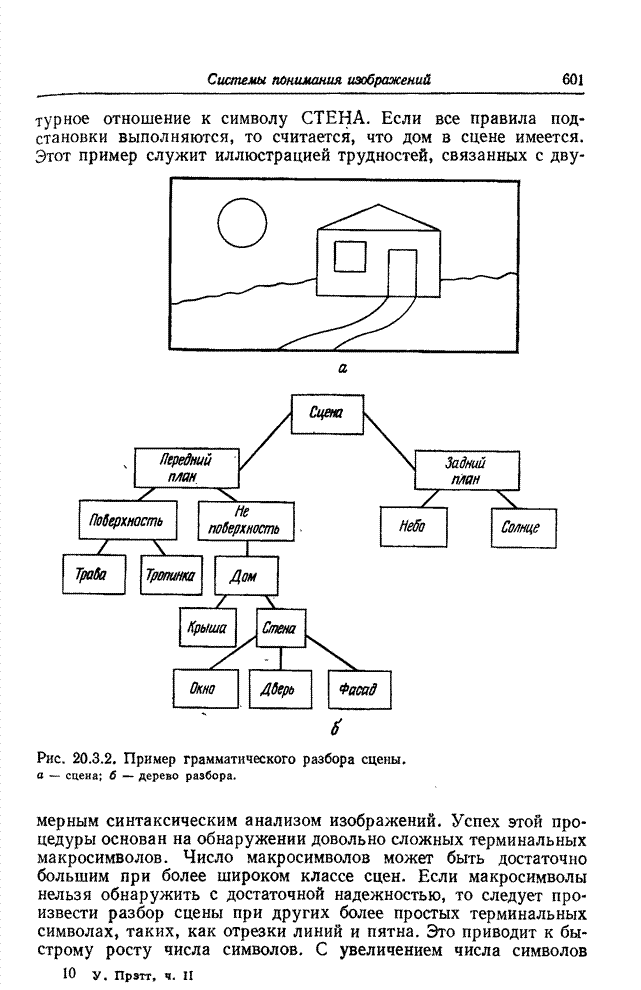
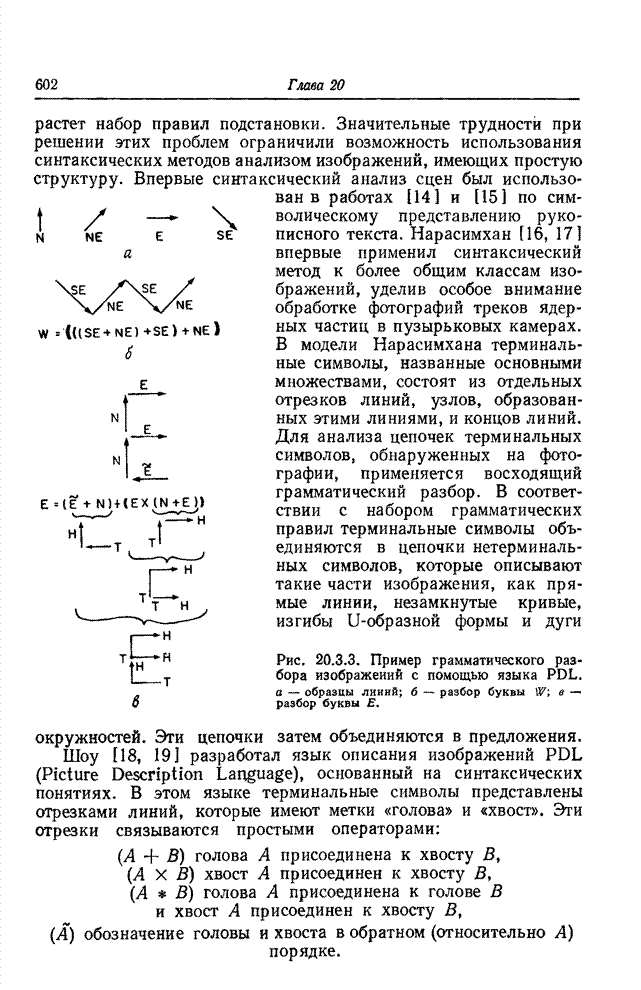
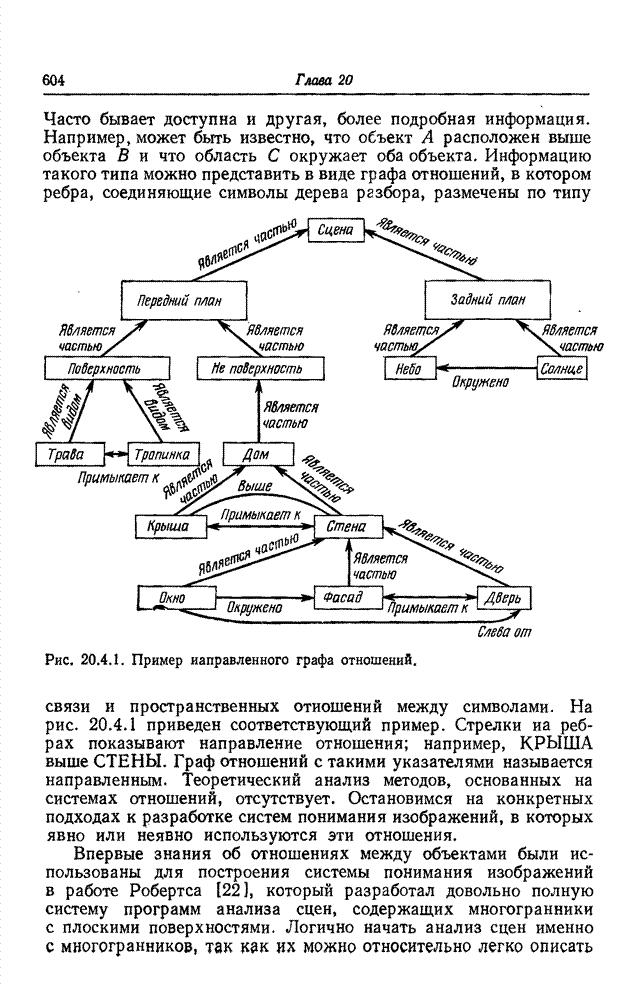
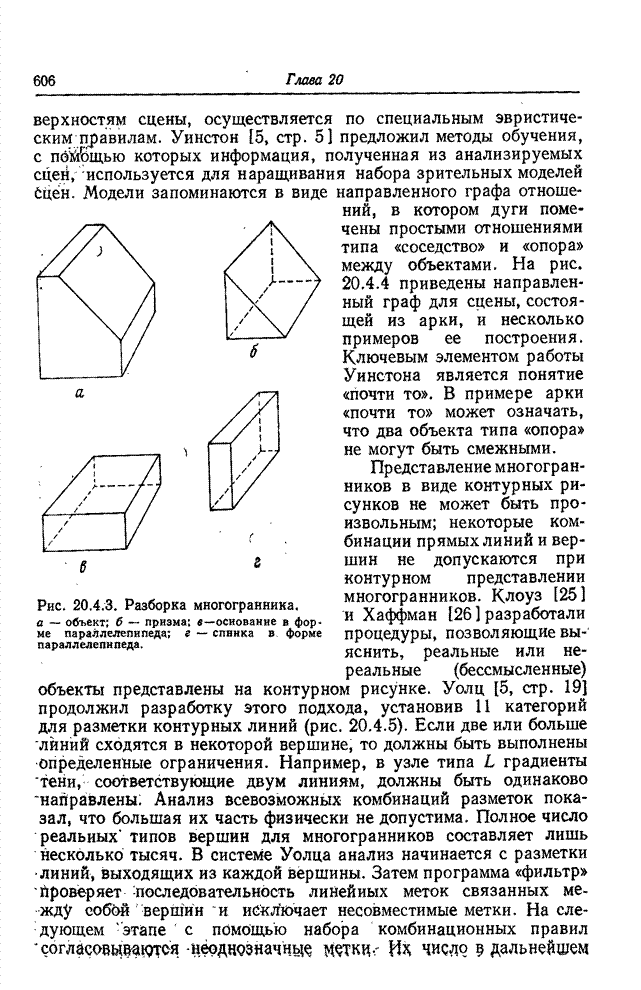
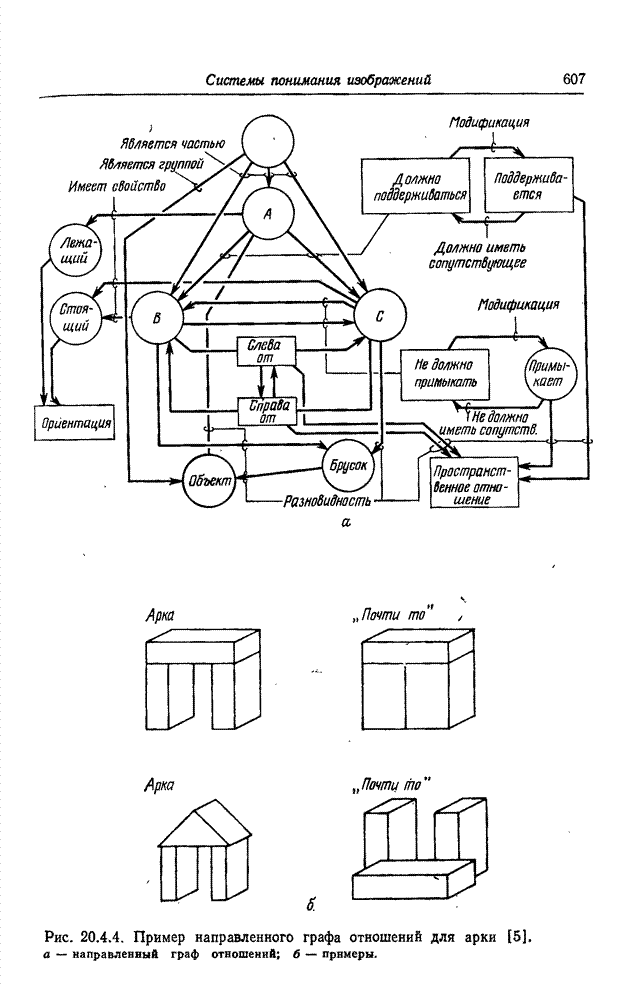
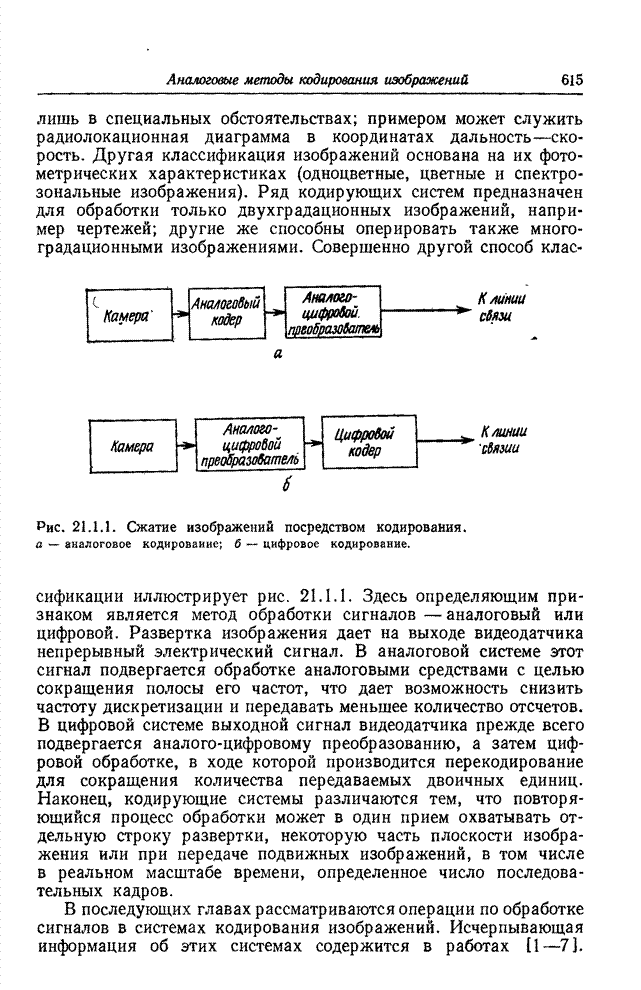
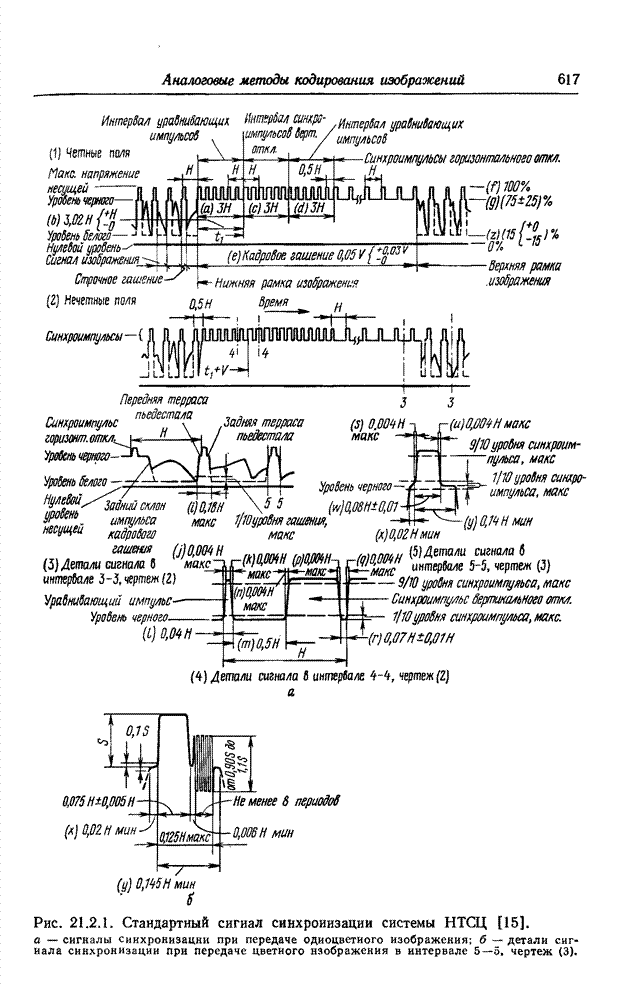
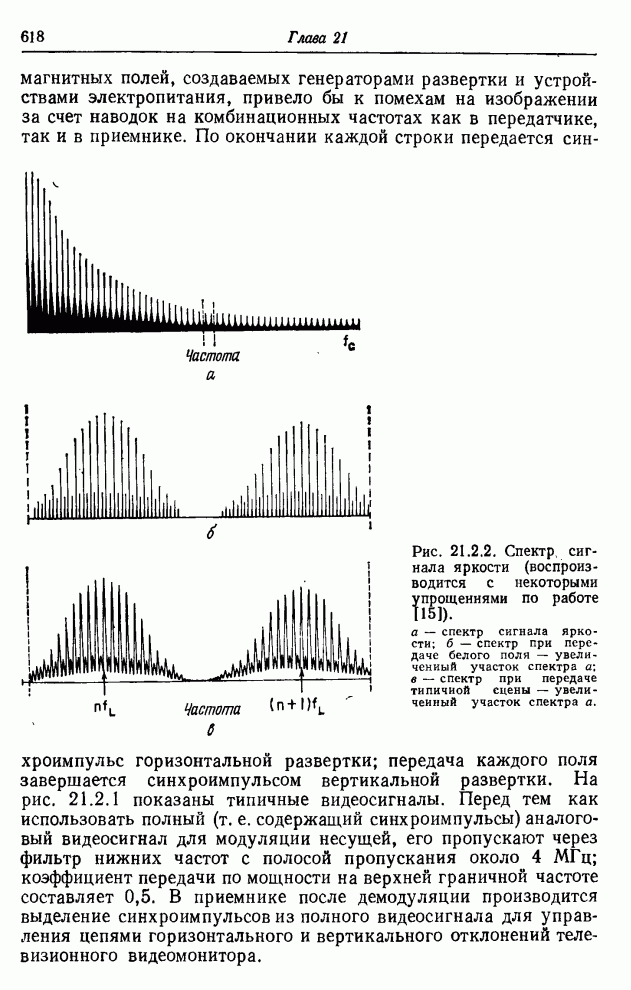
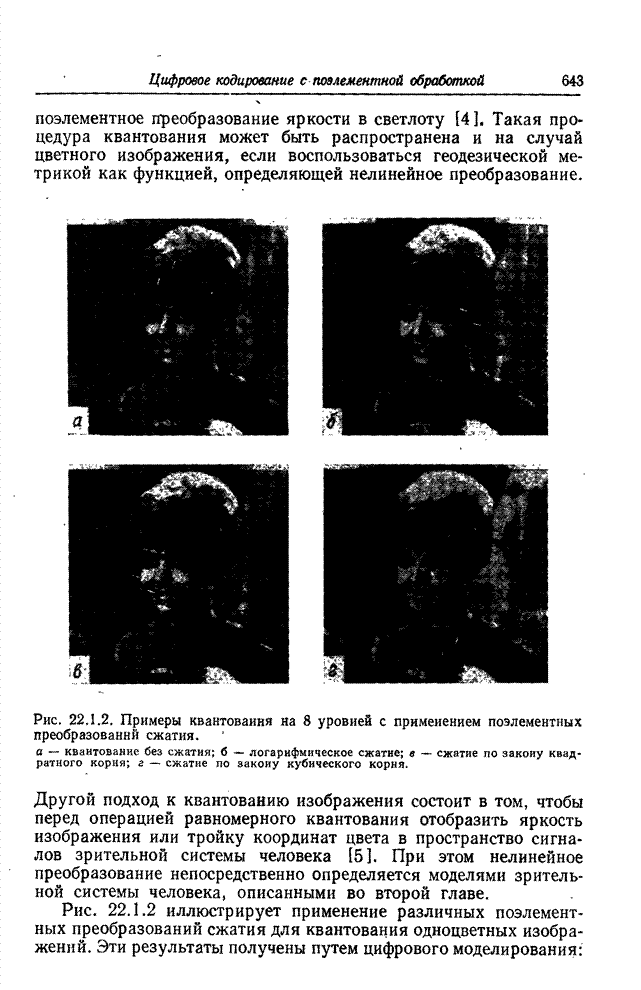
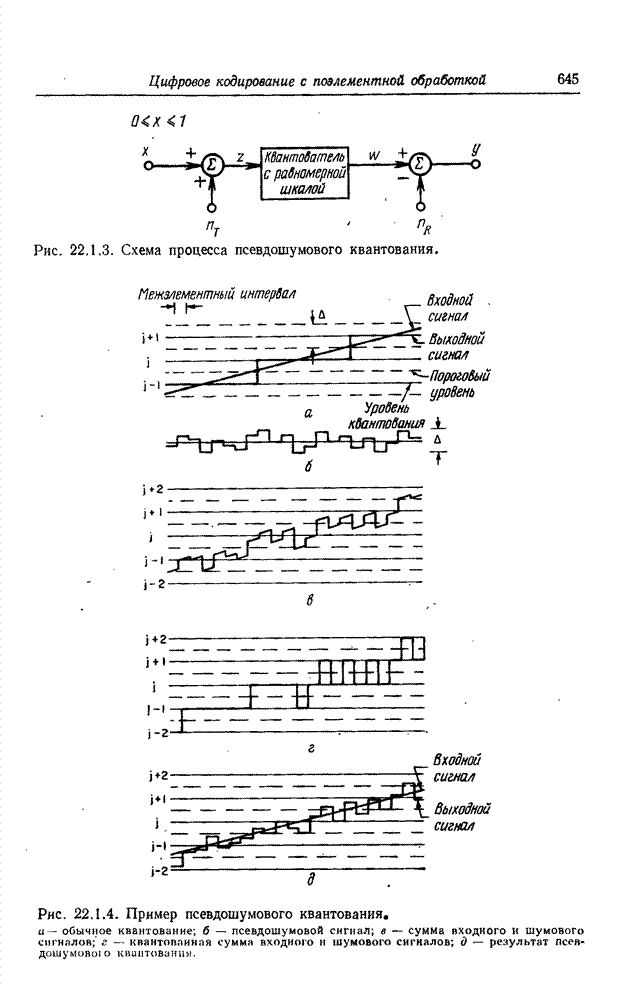
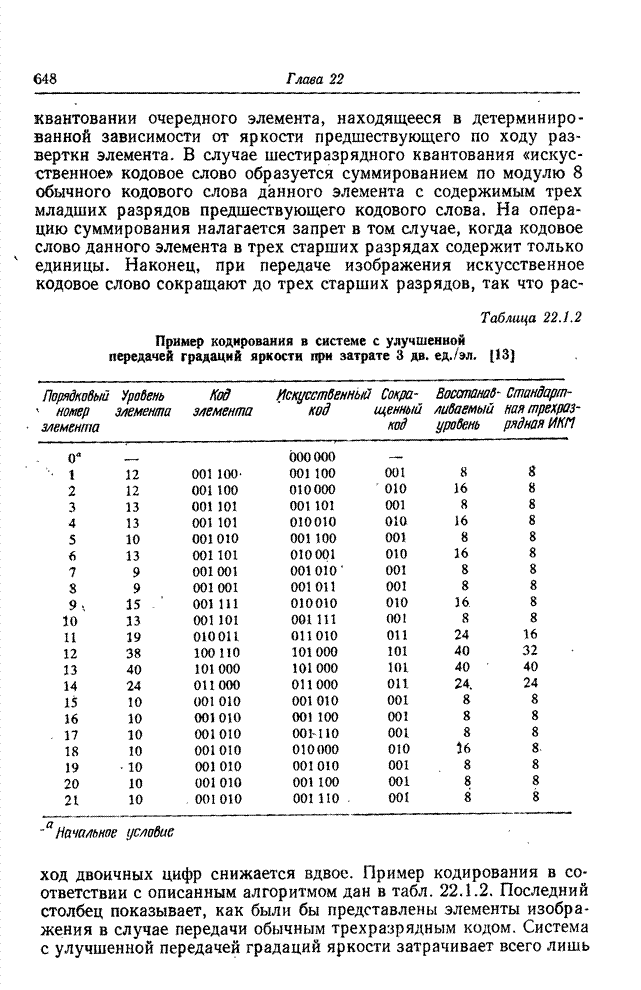
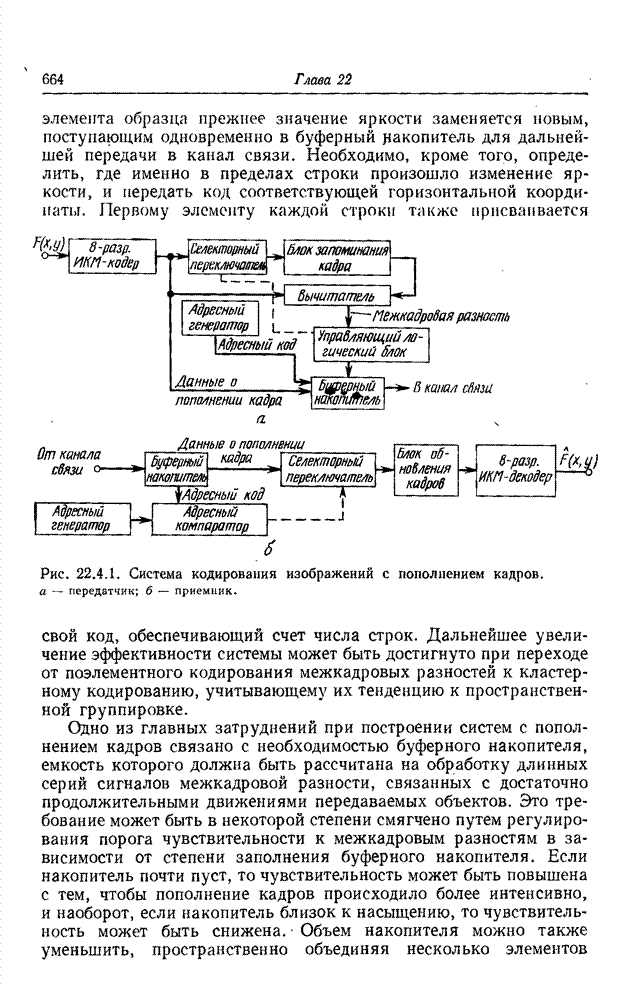
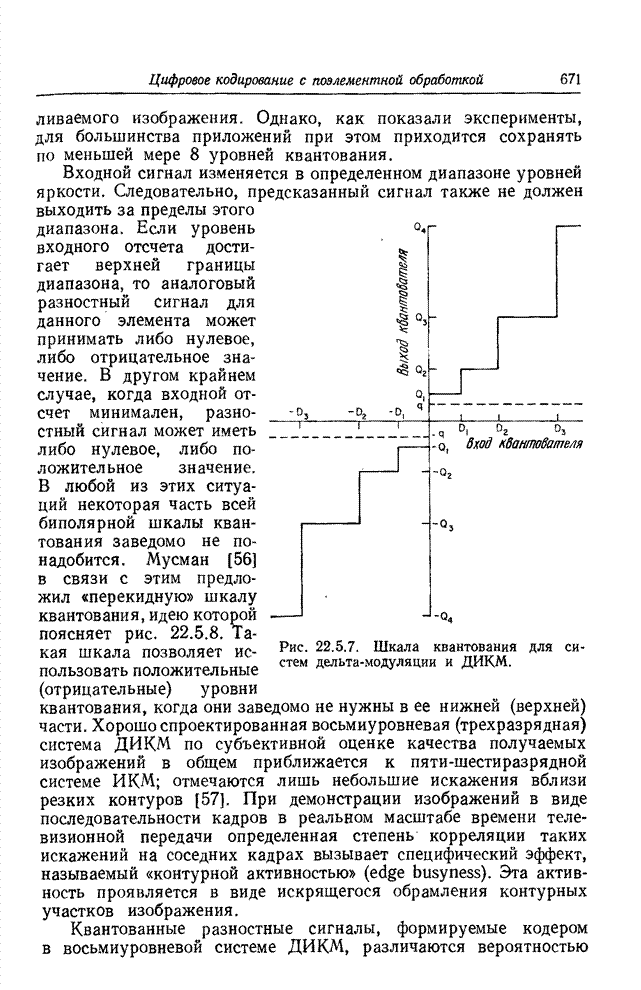
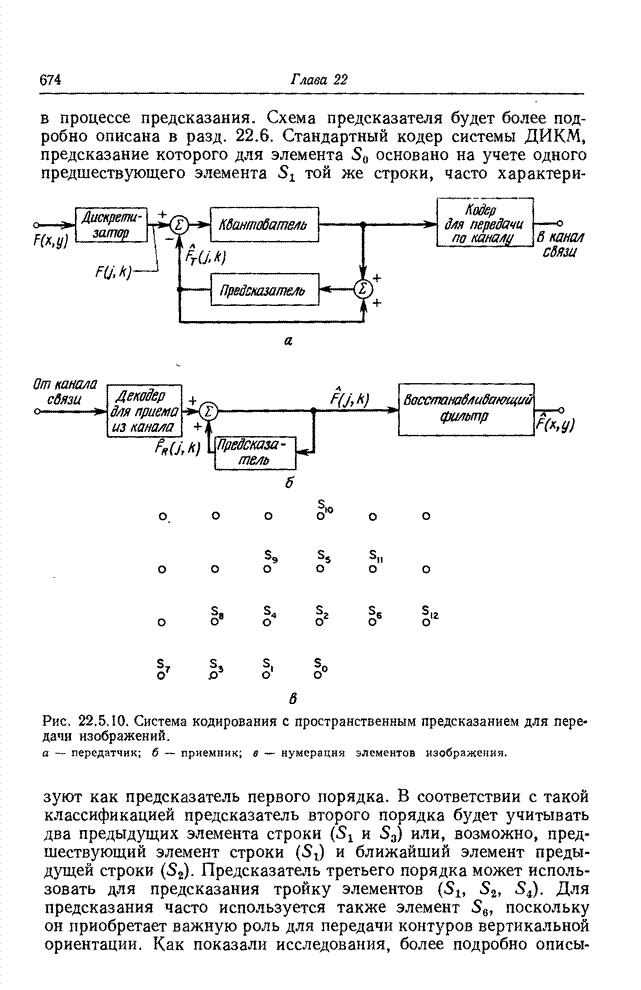
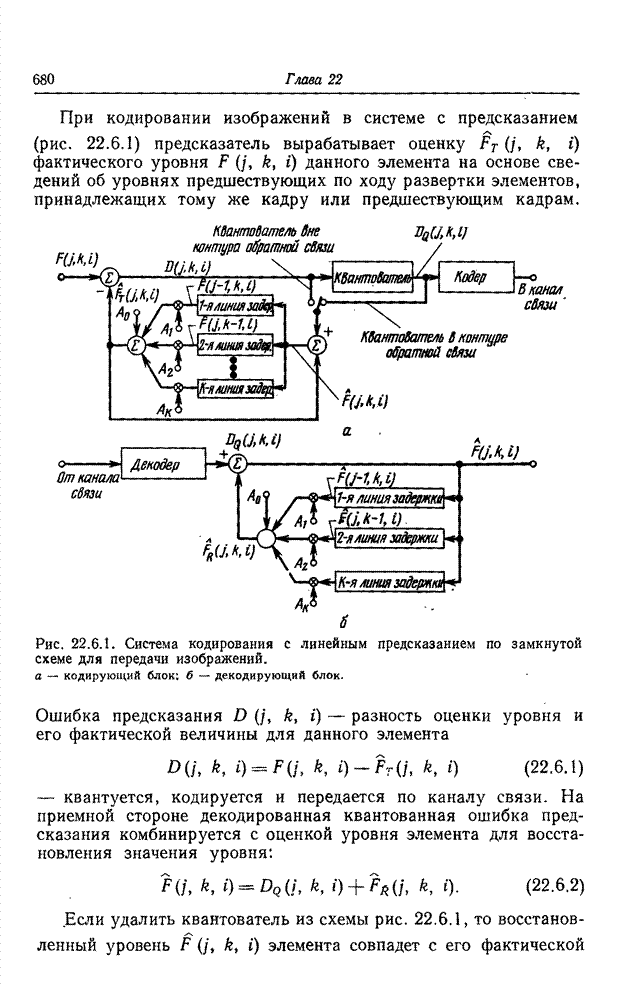
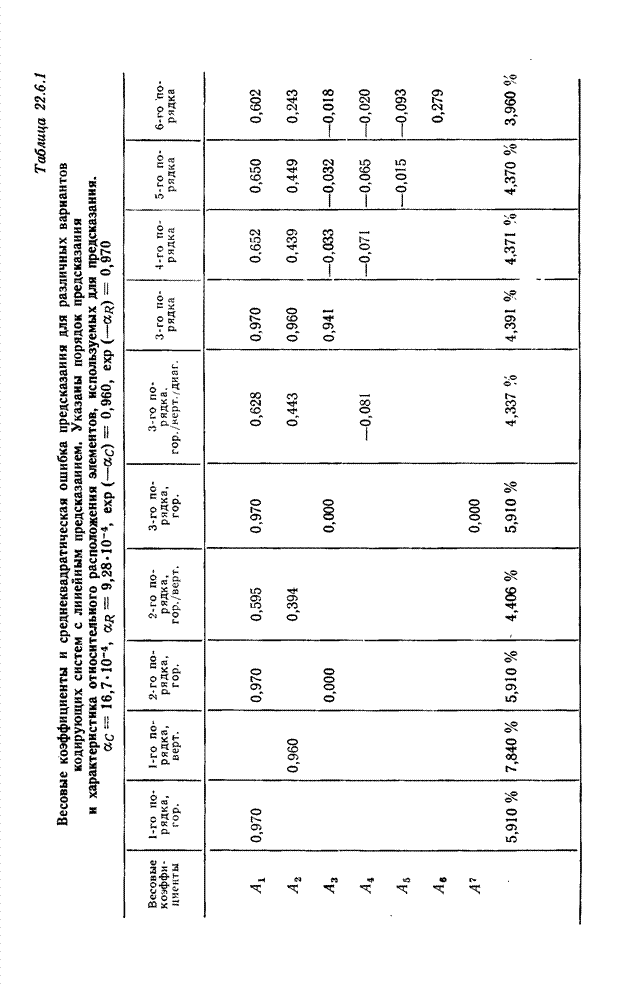
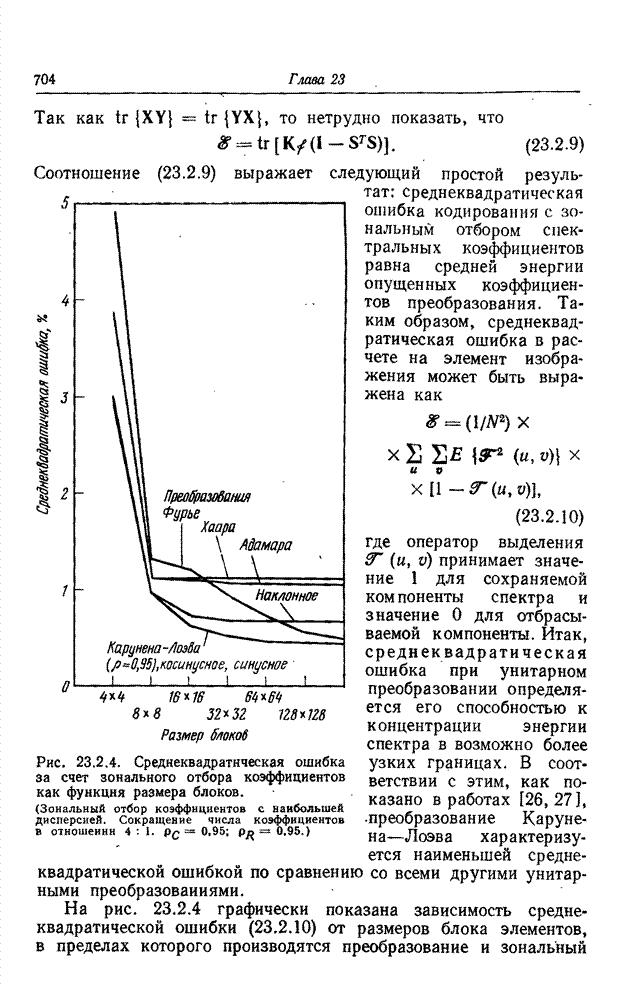
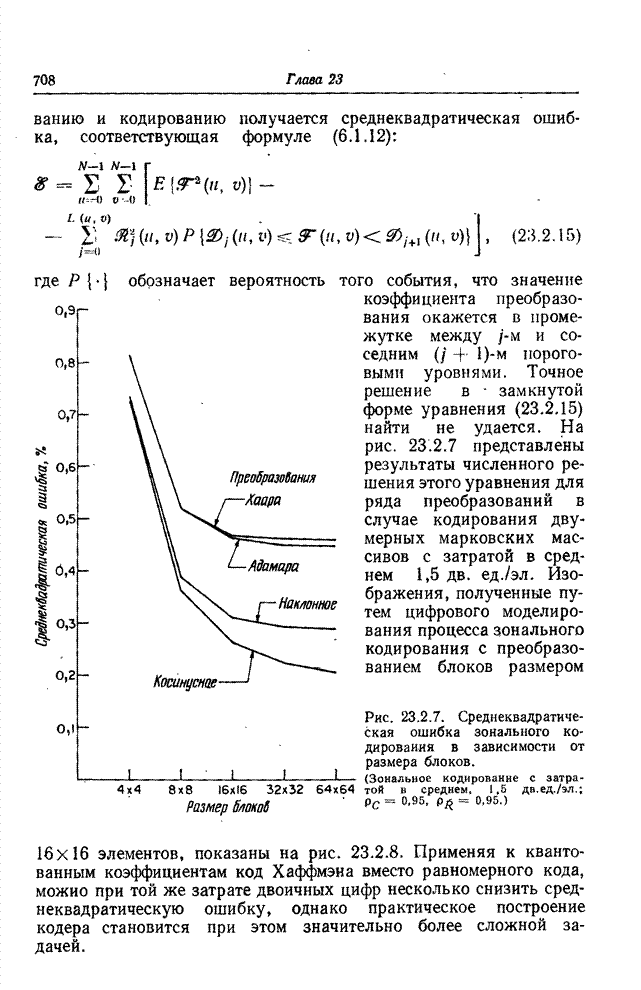
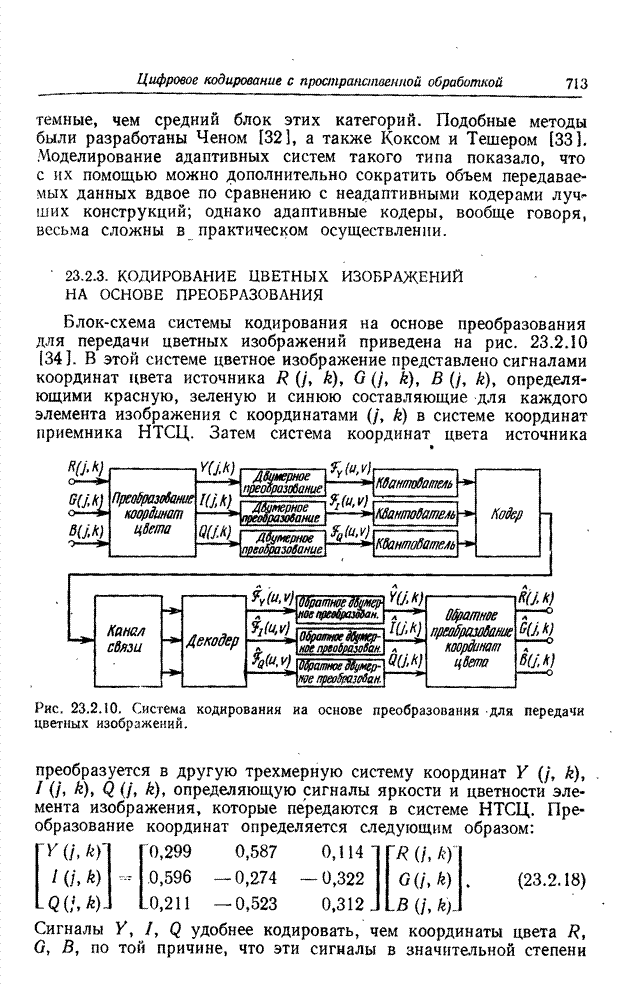
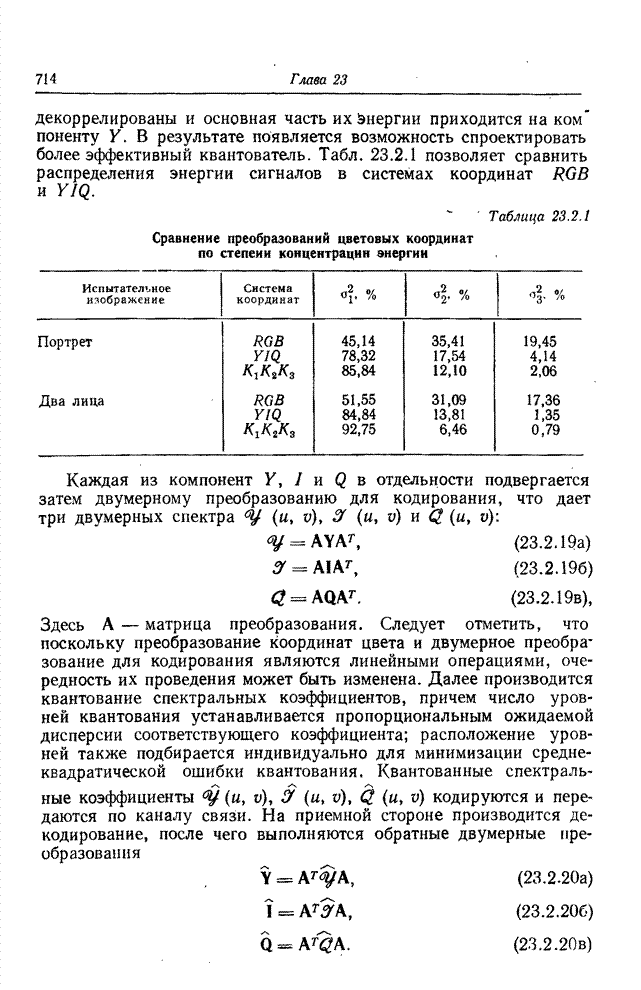
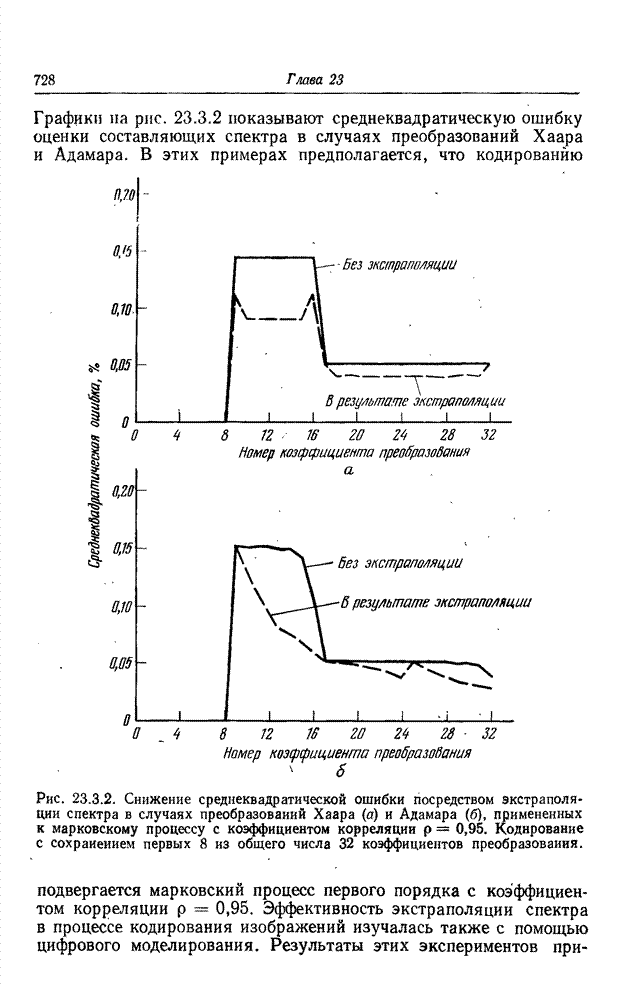
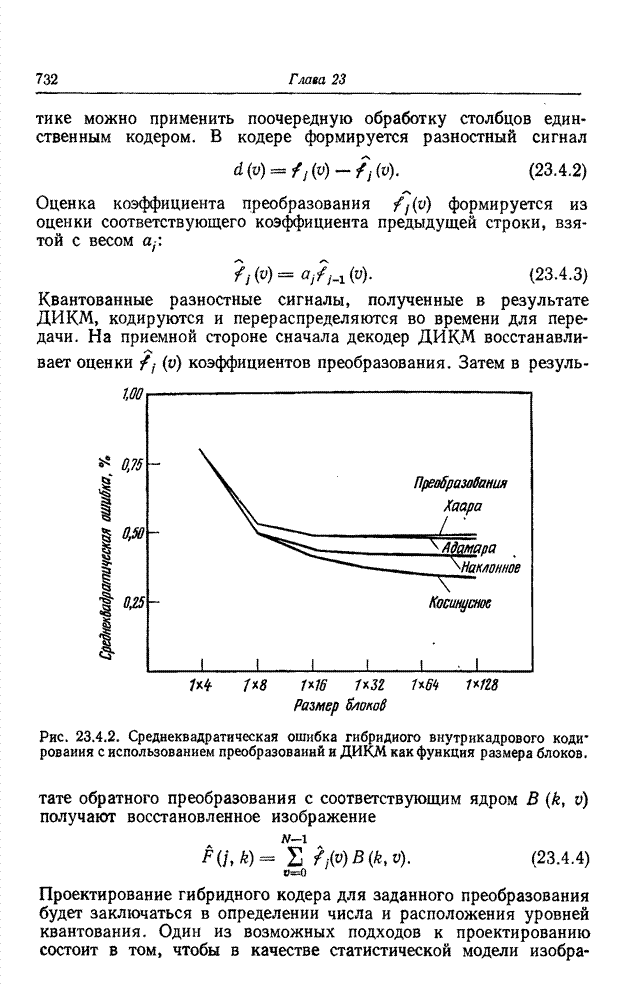
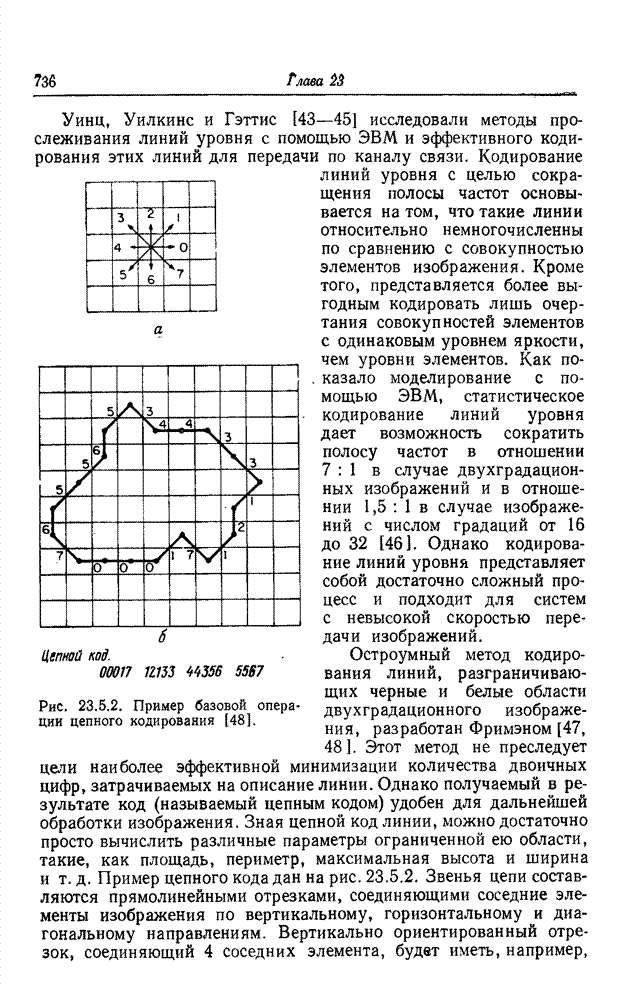
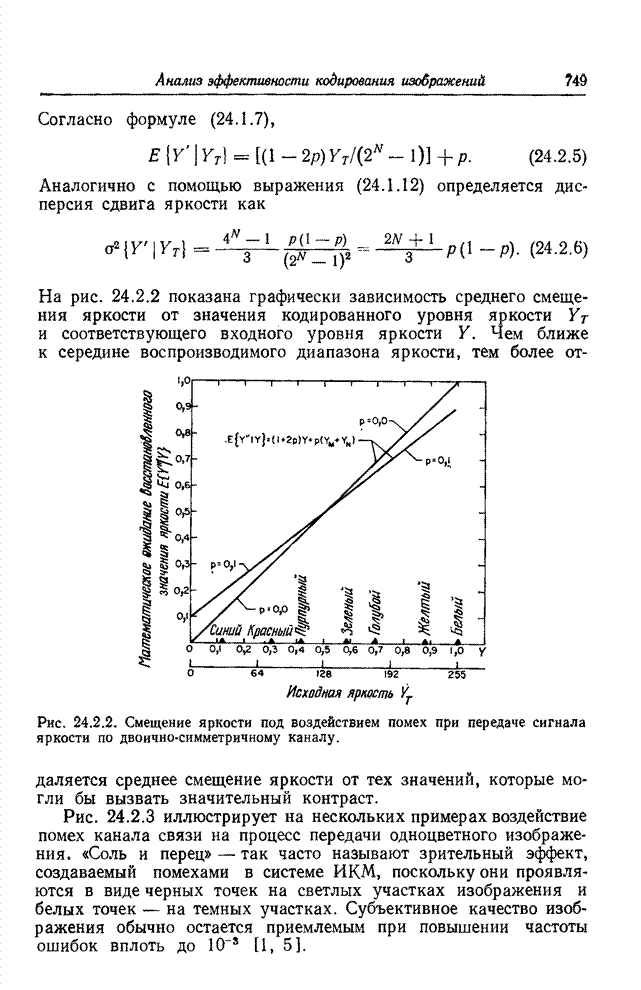
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
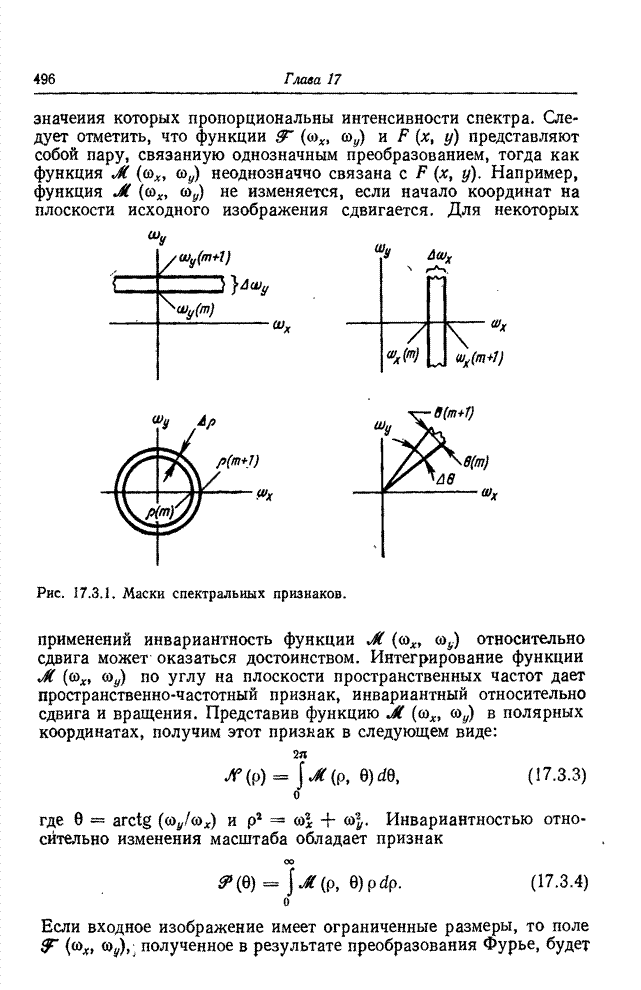
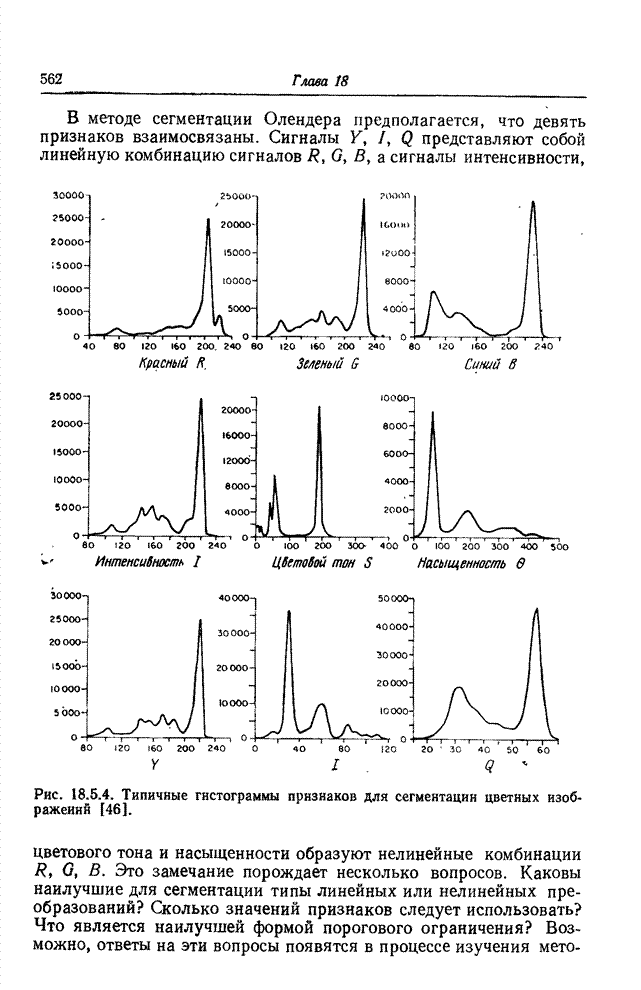
22.3.1. КОДИРОВАНИЕ ДЛИН СЕРИЙ; ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ [32-36]
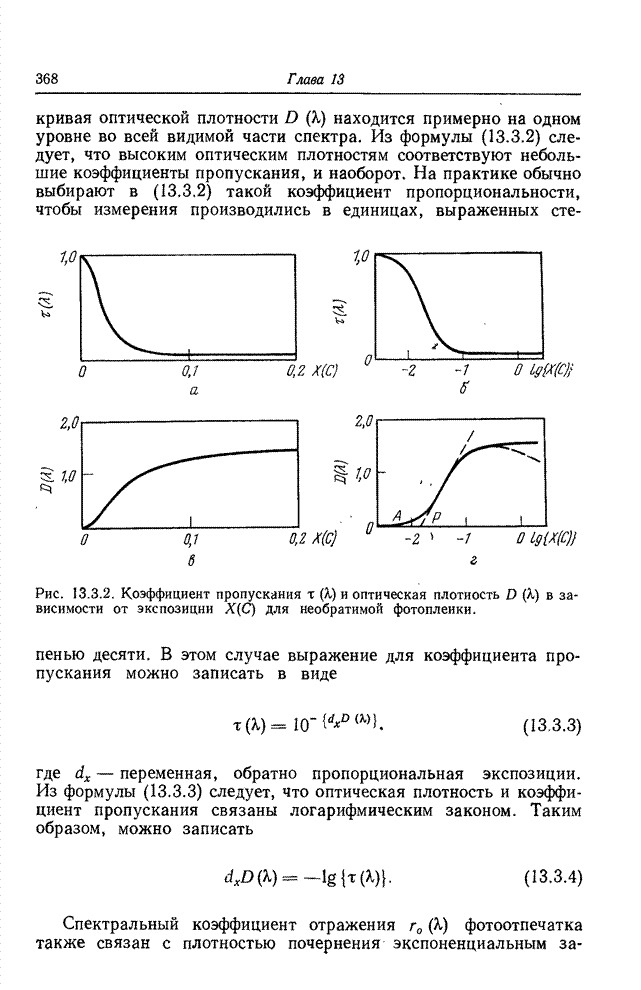
Простая, но достаточно точная модель процесса
кодирования длин серий получается в предположении, что обнаружение перепада
яркости на данном элементе изображения есть независимое событие. Пусть
вероятность обнаружения перепада ![]() одинакова для всех элементов, a
одинакова для всех элементов, a ![]() обозначает длину серии, т. е. число составляющих
ее элементов (
обозначает длину серии, т. е. число составляющих
ее элементов (![]() соответствует двум перепадам, следующим подряд). Распределение вероятностей
длин серий представляет собой геометрическое распределение
соответствует двум перепадам, следующим подряд). Распределение вероятностей
длин серий представляет собой геометрическое распределение
![]() , (22.3.1)
, (22.3.1)
где ![]() . Длина серии составляет в среднем
. Длина серии составляет в среднем
![]() . (22.3.2)
. (22.3.2)
Энтропия распределения вероятностей длин серий определяется как
 . (22.3.3)
. (22.3.3)
Предположим теперь, что максимально возможная длина
серий ограничена величиной ![]() элементов. При этом распределение
вероятностей длин серий примет следующий вид:
элементов. При этом распределение
вероятностей длин серий примет следующий вид:
![]() ,
, ![]() (22.3.4)
(22.3.4)
Средняя длина серий составит теперь
 , (22.3.5)
, (22.3.5)
а энтропия распределения вероятностей длин серий будет равна
![]() (22.3.6)
(22.3.6)

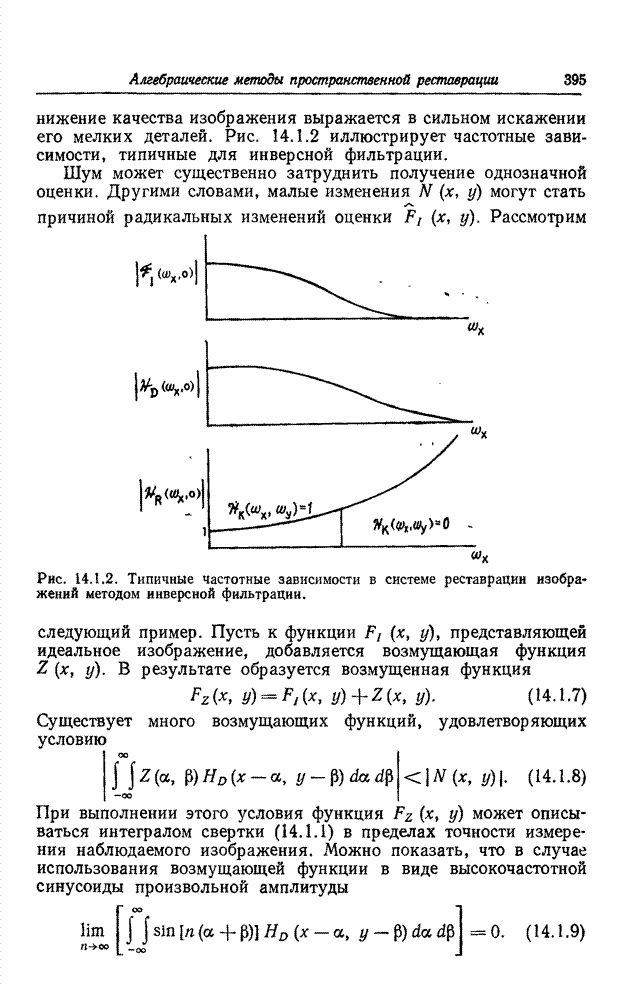
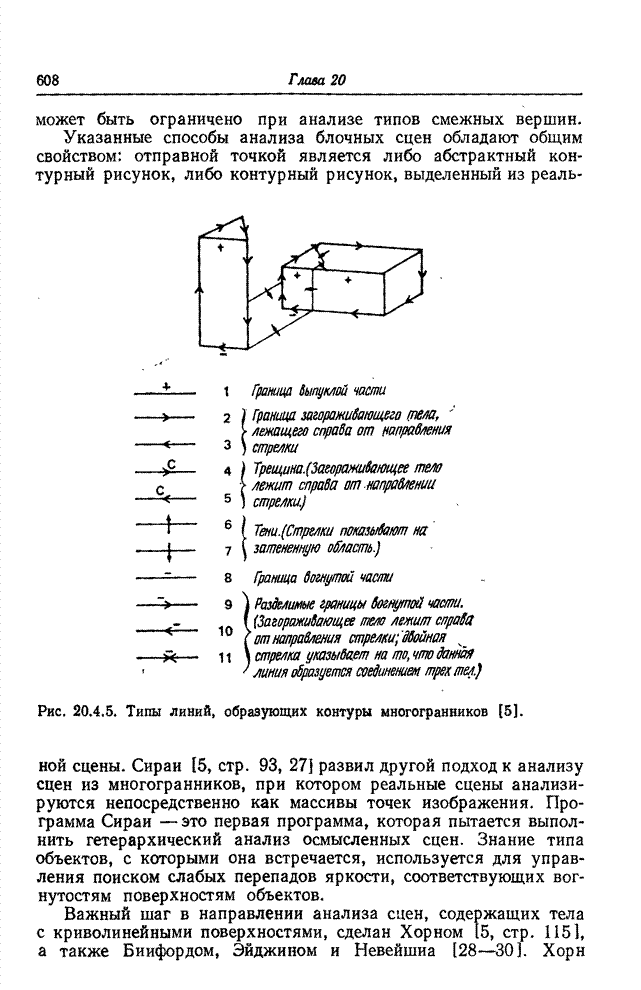
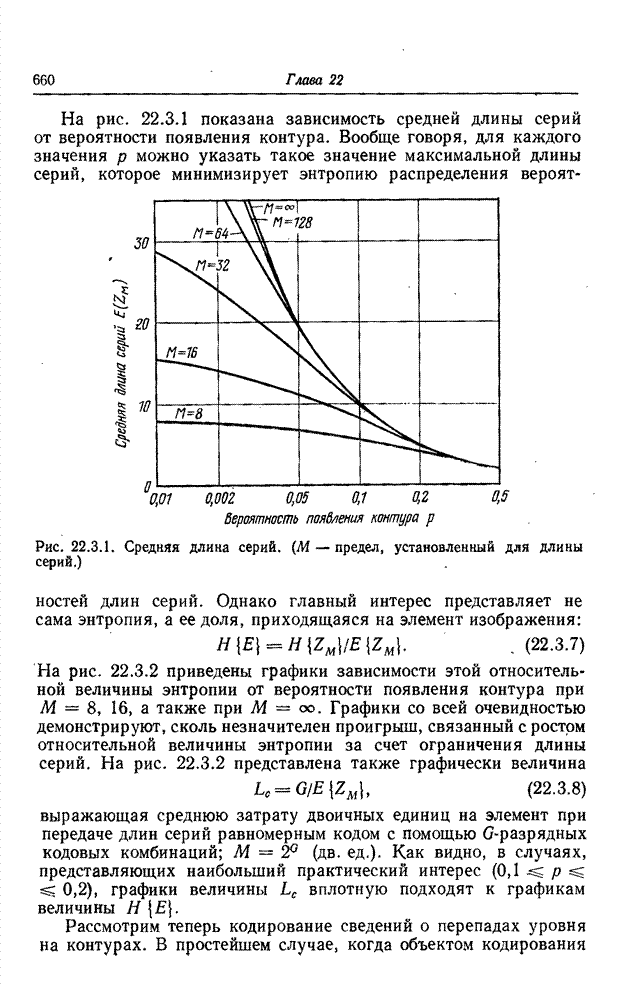
Рис. 22.3.1. Средняя
длина серий. (![]() — предел, установленный для длины серий.)
— предел, установленный для длины серий.)
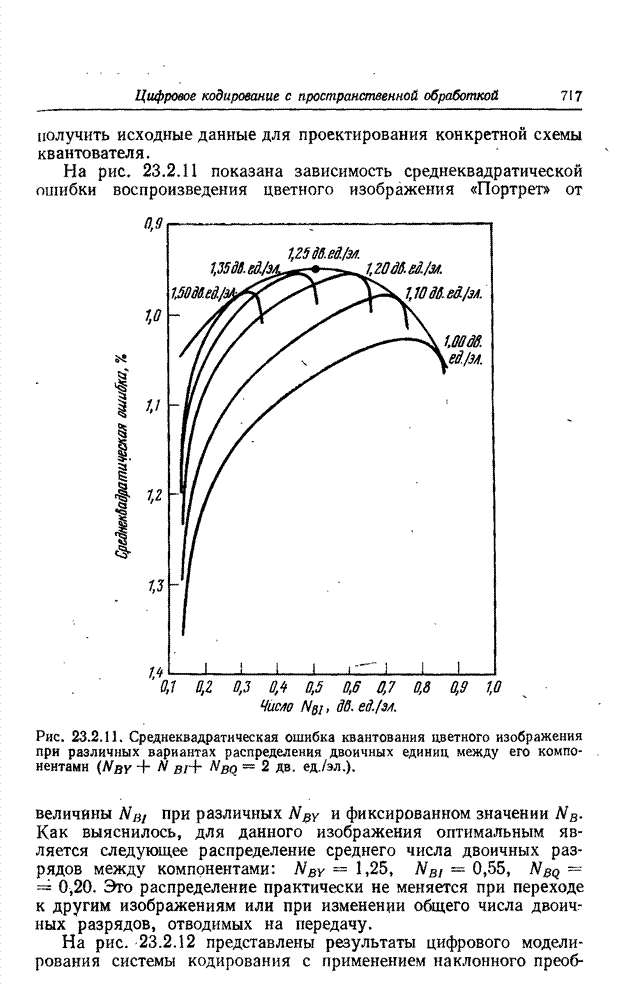
На рис. 22.3.1 показана зависимость средней длины
серий от вероятности появления контура. Вообще говоря, для каждого значения ![]() можно указать
такое значение максимальной длины серий, которое минимизирует энтропию
распределения вероятностей длин серий. Однако главный интерес представляет не
сама энтропия, а ее доля, приходящаяся на элемент изображения:
можно указать
такое значение максимальной длины серий, которое минимизирует энтропию
распределения вероятностей длин серий. Однако главный интерес представляет не
сама энтропия, а ее доля, приходящаяся на элемент изображения:
![]() (22.3.7)
(22.3.7)
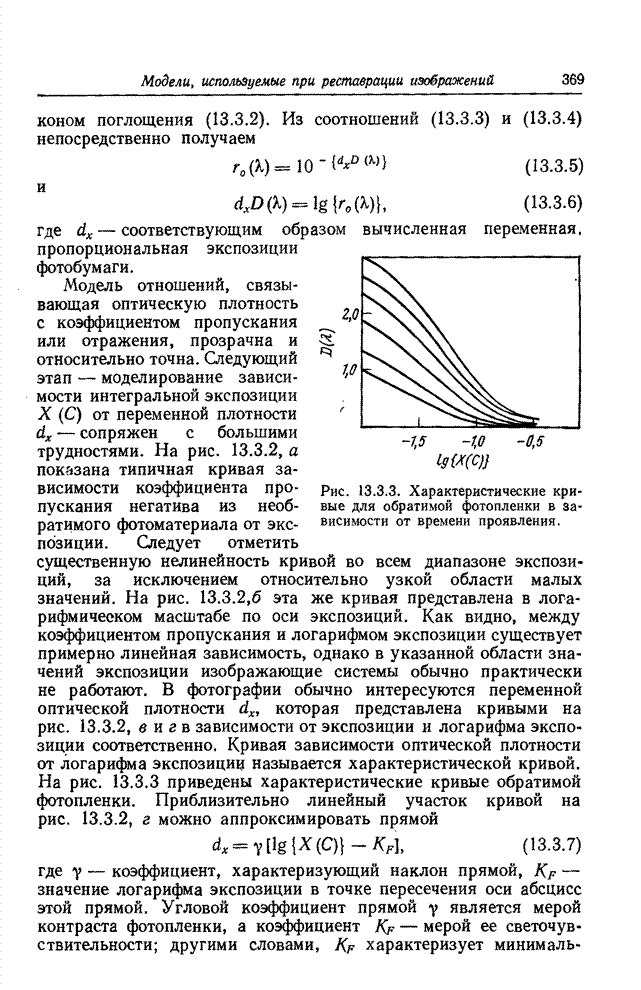
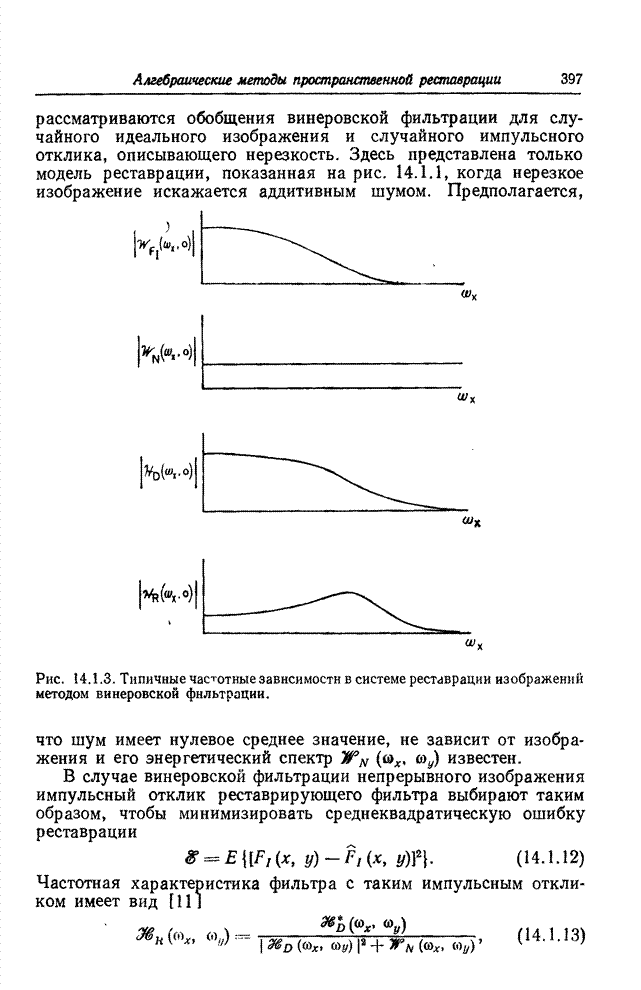
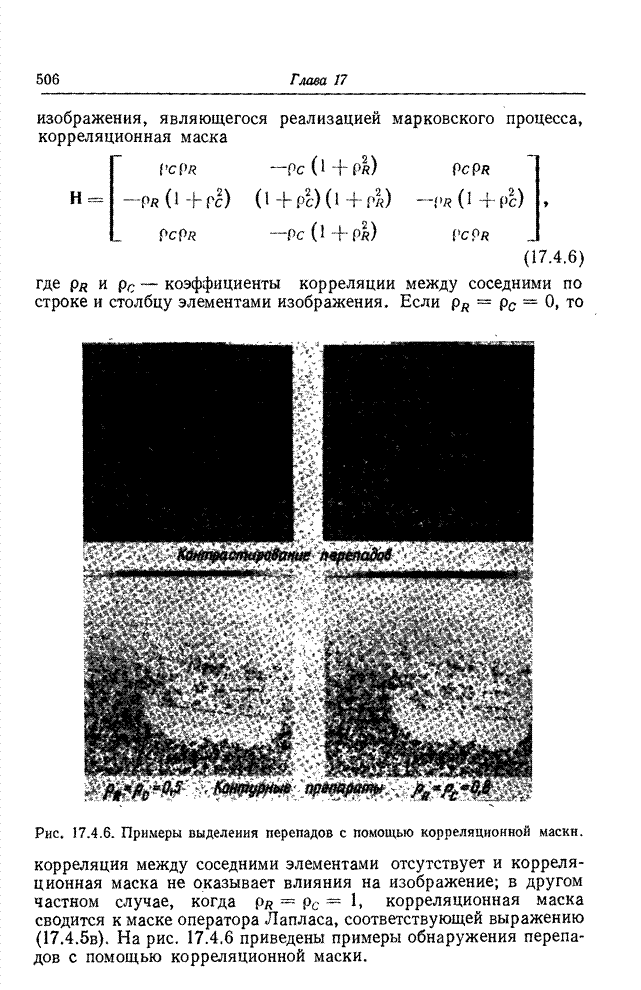
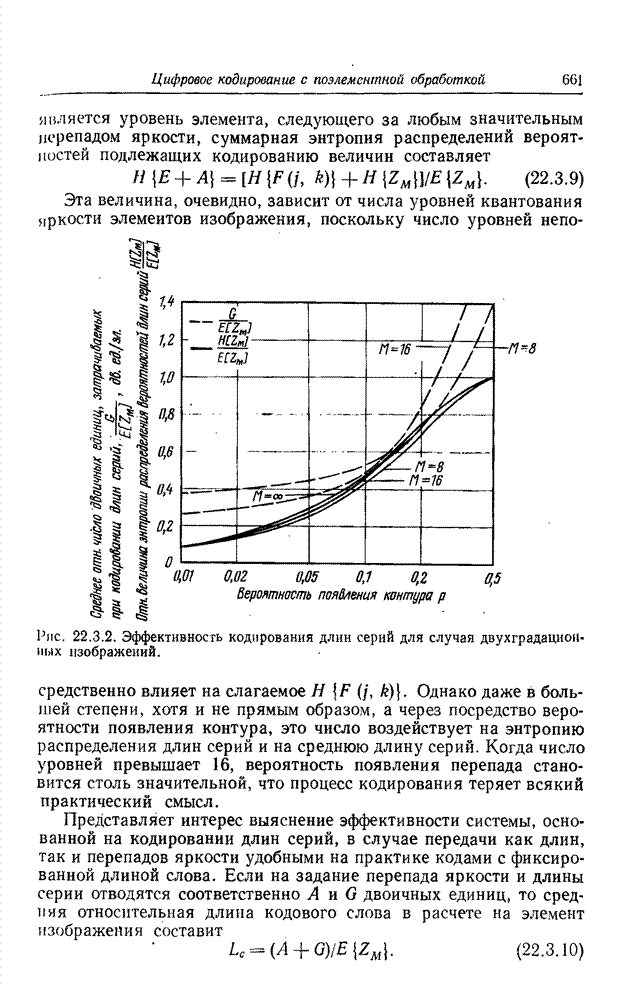
На рис. 22.3.2 приведены графики зависимости этой
относительной величины энтропии от вероятности появления контура при ![]() , а также при
, а также при ![]() . Графики со всей
очевидностью демонстрируют, сколь незначителен проигрыш, связанный с ростом
относительной величины энтропии за счет ограничения длины серий. На рис. 22.3.2
представлена также графически величина
. Графики со всей
очевидностью демонстрируют, сколь незначителен проигрыш, связанный с ростом
относительной величины энтропии за счет ограничения длины серий. На рис. 22.3.2
представлена также графически величина
![]() (22.3.8)
(22.3.8)
выражающая среднюю затрату двоичных единиц на элемент
при передаче длин серий равномерным кодом с помощью ![]() -разрядных кодовых
комбинаций;
-разрядных кодовых
комбинаций; ![]() (дв.
ед.). Как видно, в случаях, представляющих наибольший практический интерес
(дв.
ед.). Как видно, в случаях, представляющих наибольший практический интерес![]() , графики величины
, графики величины ![]() вплотную подходят к графикам величины
вплотную подходят к графикам величины ![]() .
.
Рассмотрим теперь кодирование сведений о перепадах уровня на контурах. В простейшем случае, когда объектом кодирования является уровень элемента, следующего за любым значительным перепадом яркости, суммарная энтропия распределений вероятностей подлежащих кодированию величин составляет
![]() . (22.3.9)
. (22.3.9)

Рис. 22.3.2. Эффективность кодирования длин серий для случая двухградационных изображений.
Эта
величина, очевидно, зависит от числа уровней квантования яркости элементов
изображения, поскольку число уровней непосредственно влияет на слагаемое ![]() . Однако даже в большей степени, хотя
и не прямым образом, а через посредство вероятности появления контура, это
число воздействует на энтропию распределения длин серий и на среднюю длину
серий. Когда число уровней превышает 16, вероятность появления перепада становится
столь значительной, что процесс кодирования теряет всякий практический смысл.
. Однако даже в большей степени, хотя
и не прямым образом, а через посредство вероятности появления контура, это
число воздействует на энтропию распределения длин серий и на среднюю длину
серий. Когда число уровней превышает 16, вероятность появления перепада становится
столь значительной, что процесс кодирования теряет всякий практический смысл.
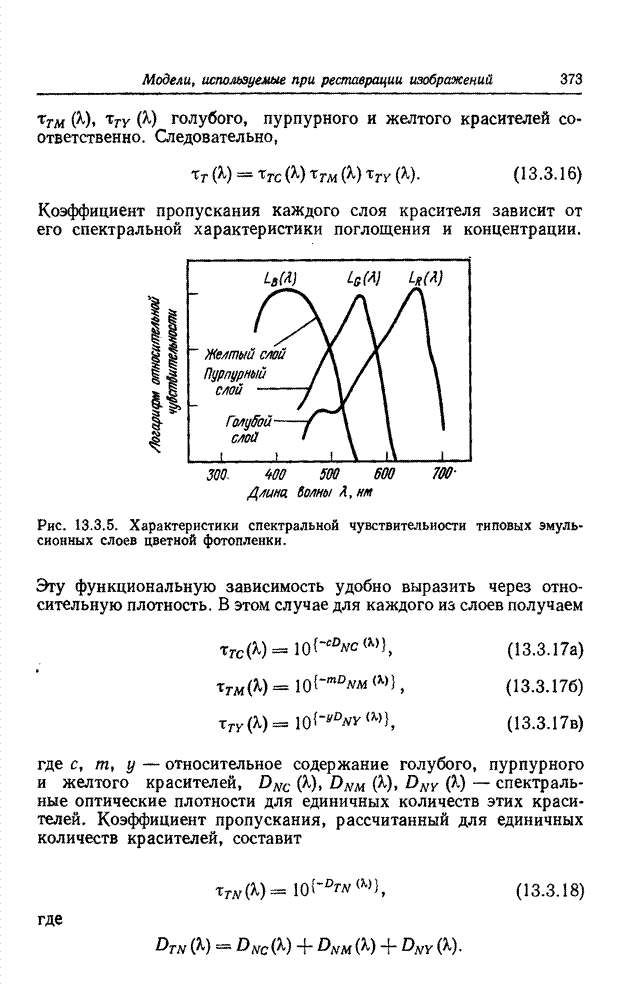
Представляет
интерес выяснение эффективности системы, основанной на кодировании длин серий,
в случае передачи как длин, так и перепадов яркости удобными на практике кодами
с фиксированной длиной слова. Если на задание перепада яркости и длины серии отводятся
соответственно ![]() и
и ![]() двоичных единиц, то средняя относительная длина
кодового слова в расчете на элемент изображения составит
двоичных единиц, то средняя относительная длина
кодового слова в расчете на элемент изображения составит
![]() . (22.3.10)
. (22.3.10)
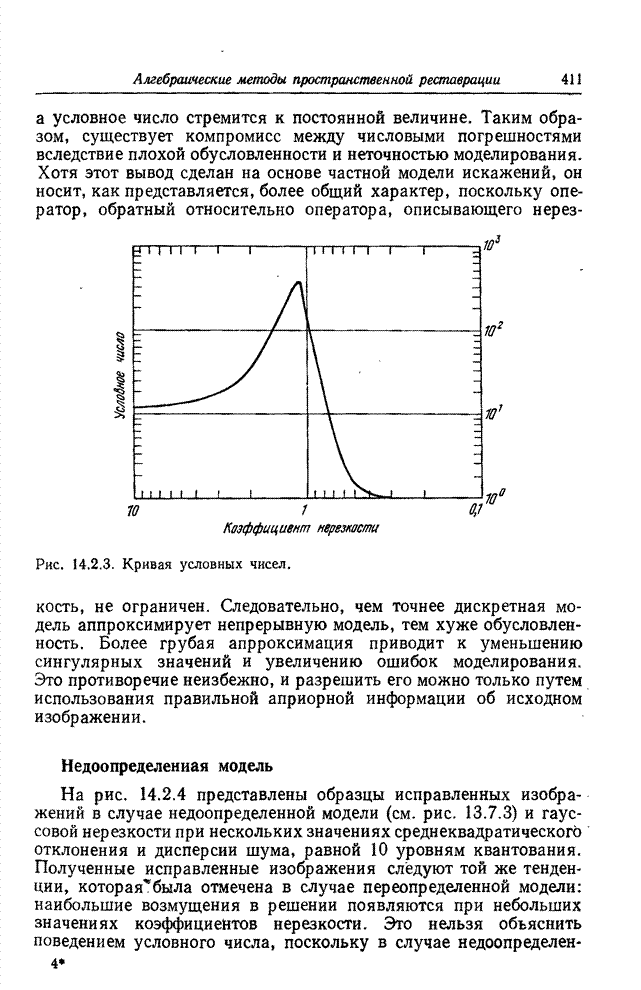
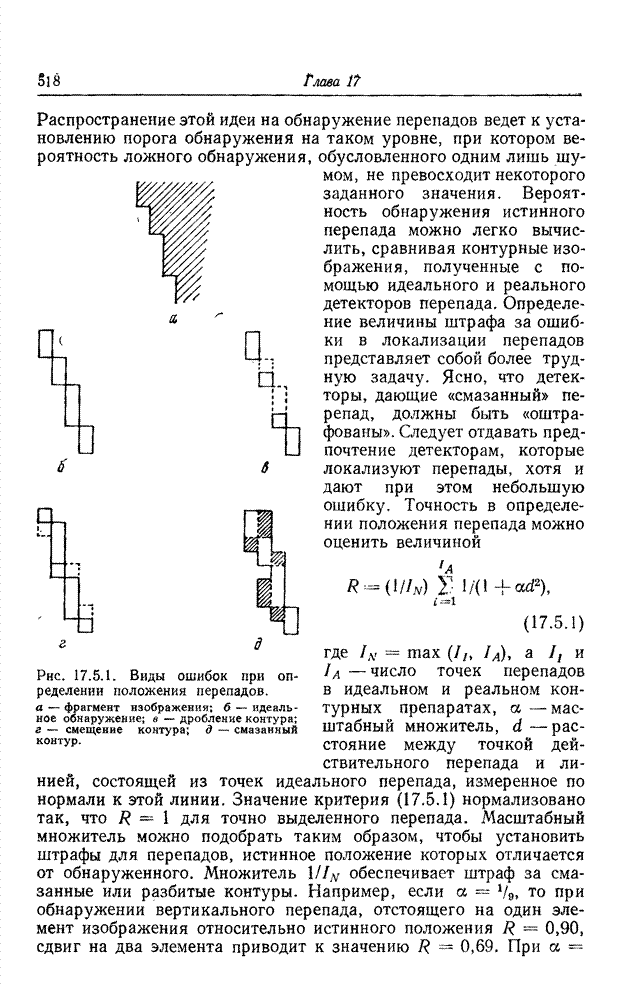
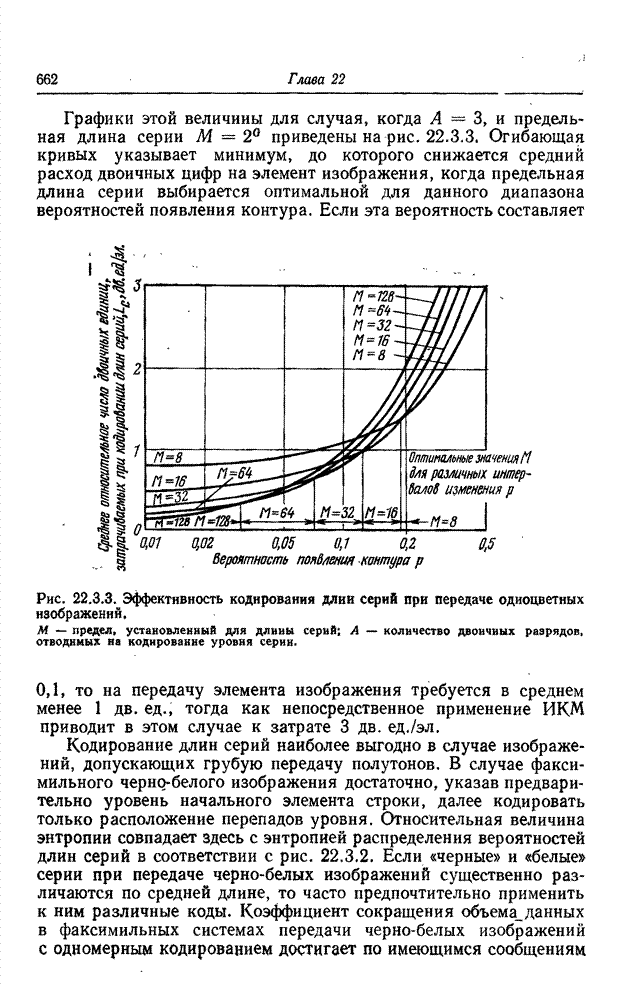
Графики этой величины для случая, когда ![]() , и предельная
длина серии
, и предельная
длина серии ![]() приведены на рис. 22.3.3. Огибающая
кривых указывает минимум, до которого снижается средний расход двоичных цифр на
элемент изображения, когда предельная длина серии выбирается оптимальной для
данного диапазона вероятностей появления контура. Если эта вероятность
составляет 0,1, то на передачу элемента изображения требуется в среднем менее 1
дв. ед., тогда как непосредственное применение ИКМ приводит в этом случае к
затрате 3 дв. ед./эл.
приведены на рис. 22.3.3. Огибающая
кривых указывает минимум, до которого снижается средний расход двоичных цифр на
элемент изображения, когда предельная длина серии выбирается оптимальной для
данного диапазона вероятностей появления контура. Если эта вероятность
составляет 0,1, то на передачу элемента изображения требуется в среднем менее 1
дв. ед., тогда как непосредственное применение ИКМ приводит в этом случае к
затрате 3 дв. ед./эл.

Рис. 22.3.3. Эффективность кодирования длин серий при передаче
одноцветных изображений: ![]() — предел, установленный для длины серий;
— предел, установленный для длины серий; ![]() — количество
двоичных разрядов, отводимых на кодирование уровня серии.
— количество
двоичных разрядов, отводимых на кодирование уровня серии.
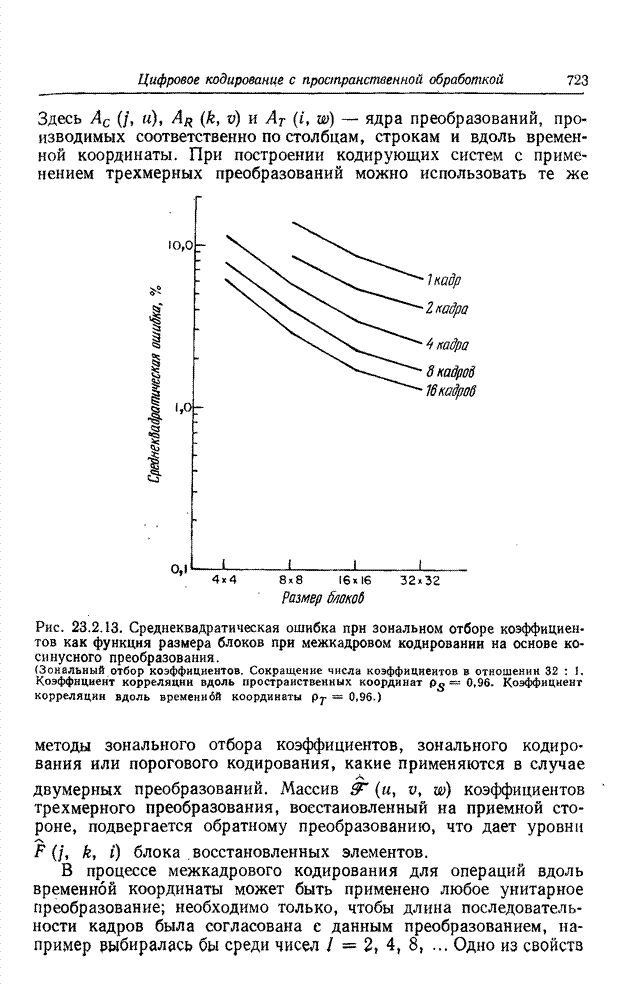
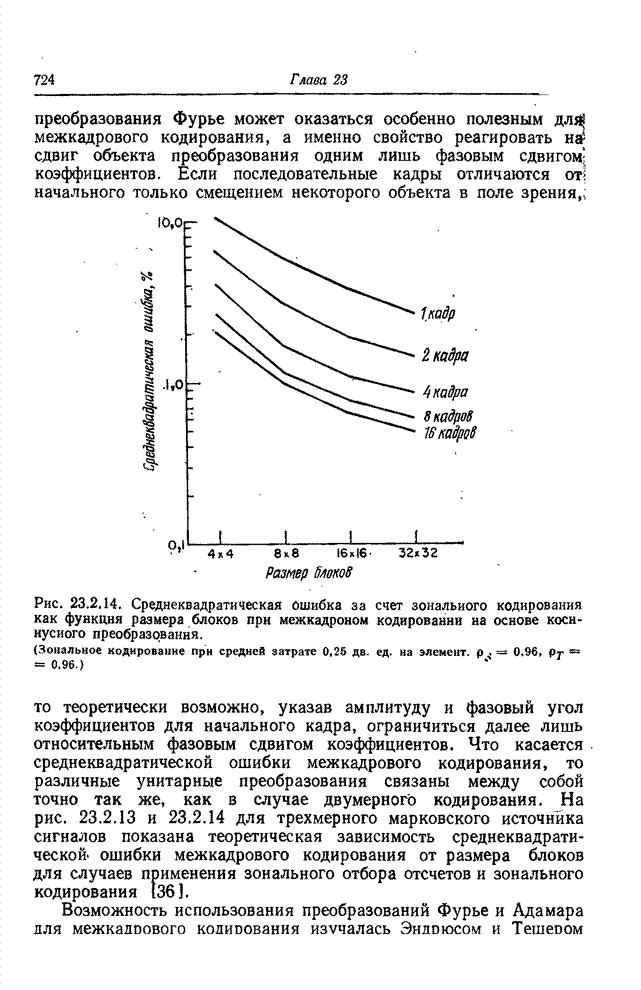
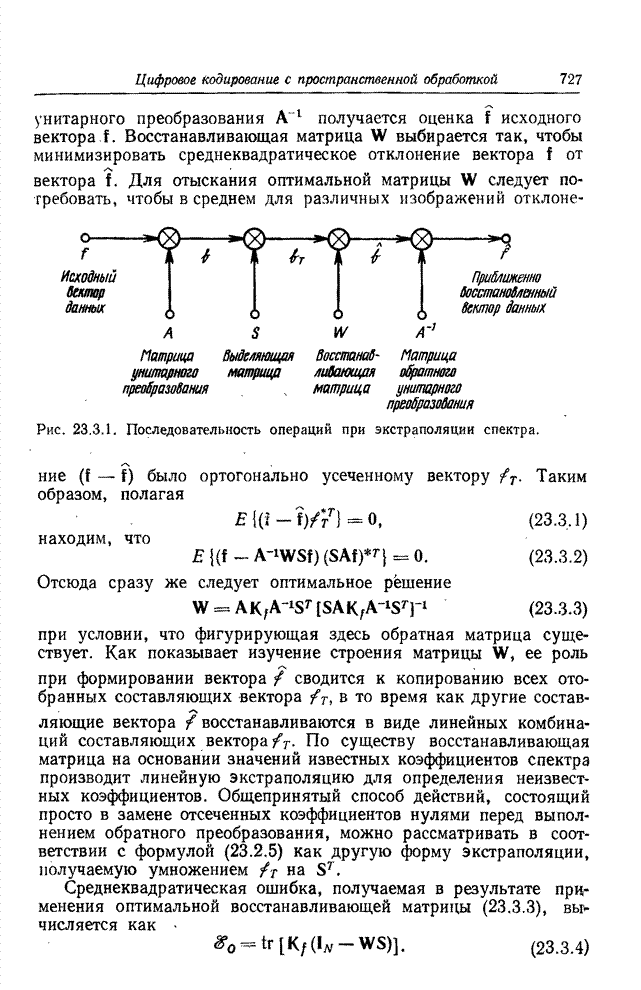
Кодирование длин серий наиболее выгодно в случае изображений, допускающих грубую передачу полутонов. В случае факсимильного черно-белого изображения достаточно, указав предварительно уровень начального элемента строки, далее кодировать только расположение перепадов уровня. Относительная величина энтропии совпадает здесь с энтропией распределения вероятностей длин серий в соответствии с рис. 22.3.2. Если «черные» и «белые» серии при передаче черно-белых изображений существенно различаются по средней длине, то часто предпочтительно применить к ним различные коды. Коэффициент сокращения объема данных в факсимильных системах передачи черно-белых изображений с одномерным кодированием достигает по имеющимся сообщениям величины 5:1. Обобщения метода кодирования длин серий, связанные с переходом к двум пространственным переменным [37—39], доводят это отношение до 10: 1.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Часть 4. РЕСТАВРАЦИЯ И УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
- Глава 12. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
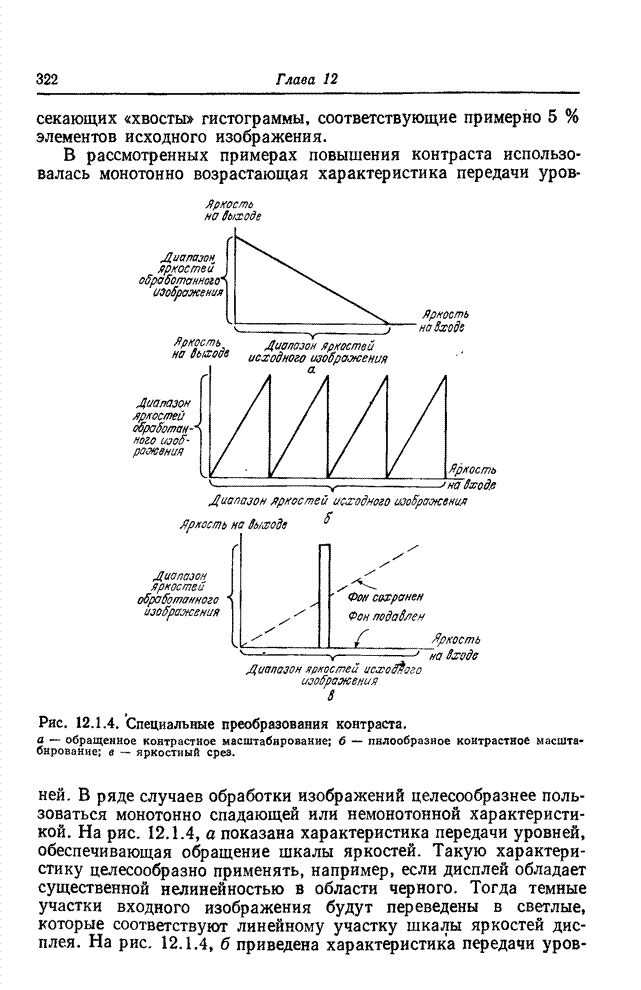
- 12.1. ИЗМЕНЕНИЕ КОНТРАСТА
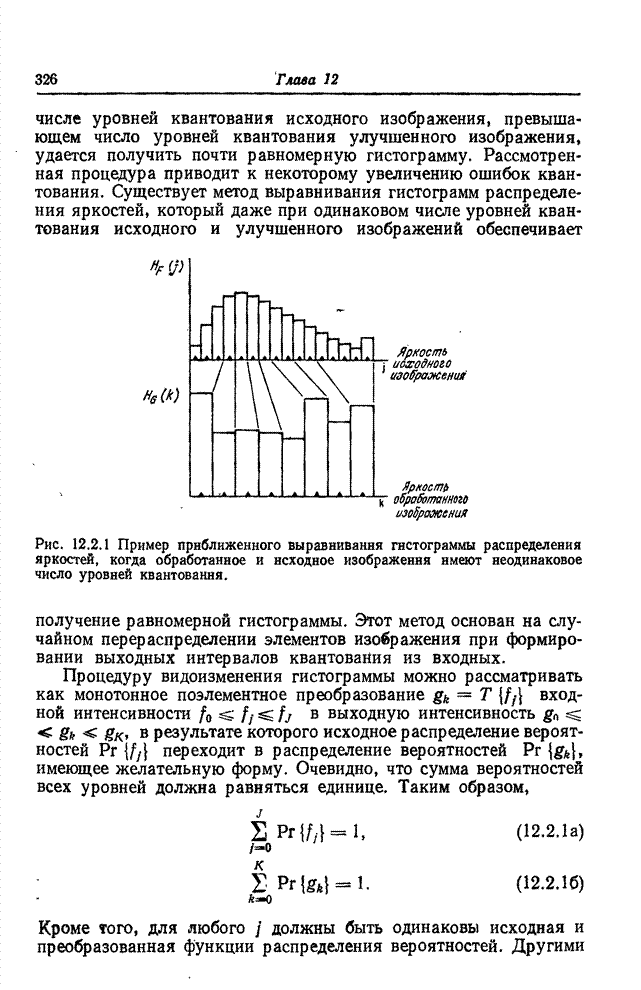
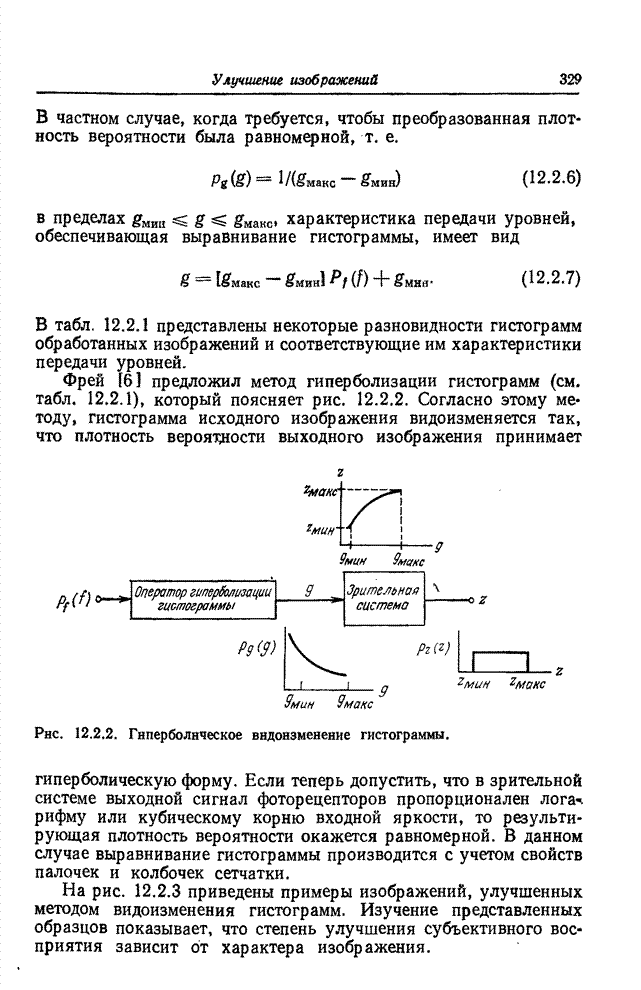
- 12.2. ВИДОИЗМЕНЕНИЕ ГИСТОГРАММ
- 12.3. ПОДАВЛЕНИЕ ШУМОВ
- 12.4. ПОДЧЕРКИВАНИЕ ГРАНИЦ
- 12.5. ОБРАБОТКА ИЗОБРАЖЕНИЙ С ПРЕОБРАЗОВАНИЕМ
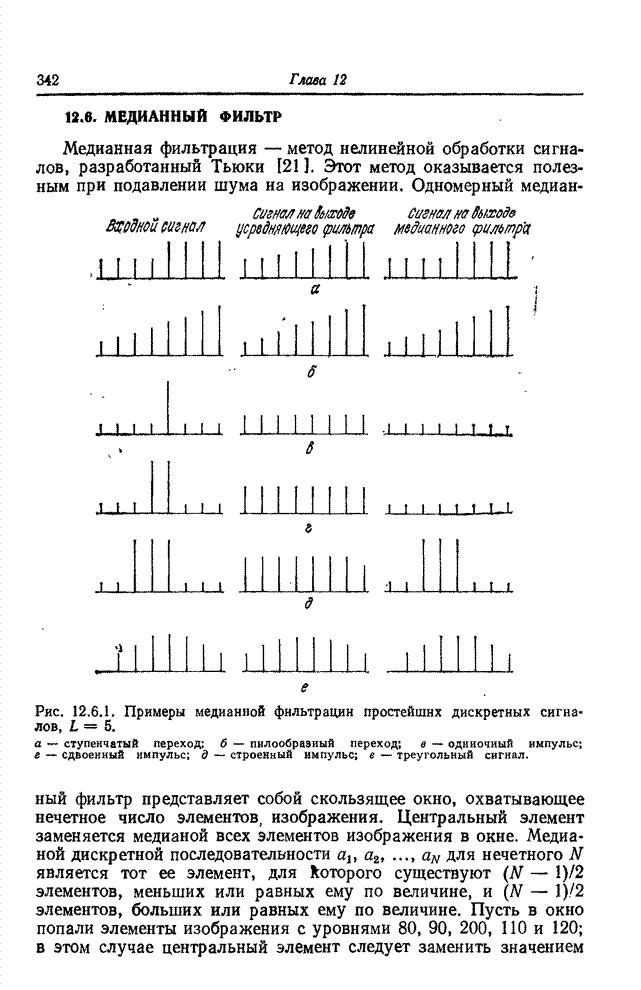
- 12.6. МЕДИАННЫЙ ФИЛЬТР
- 12.7. ЛОЖНЫЕ ЦВЕТА
- 12.8. ПСЕВДОЦВЕТА
- 12.9. УЛУЧШЕНИЕ СПЕКТРОЗОНАЛЬНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 13. МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.1. ОБОБЩЕННЫЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.2. МОДЕЛИ ОПТИЧЕСКИХ СИСТЕМ
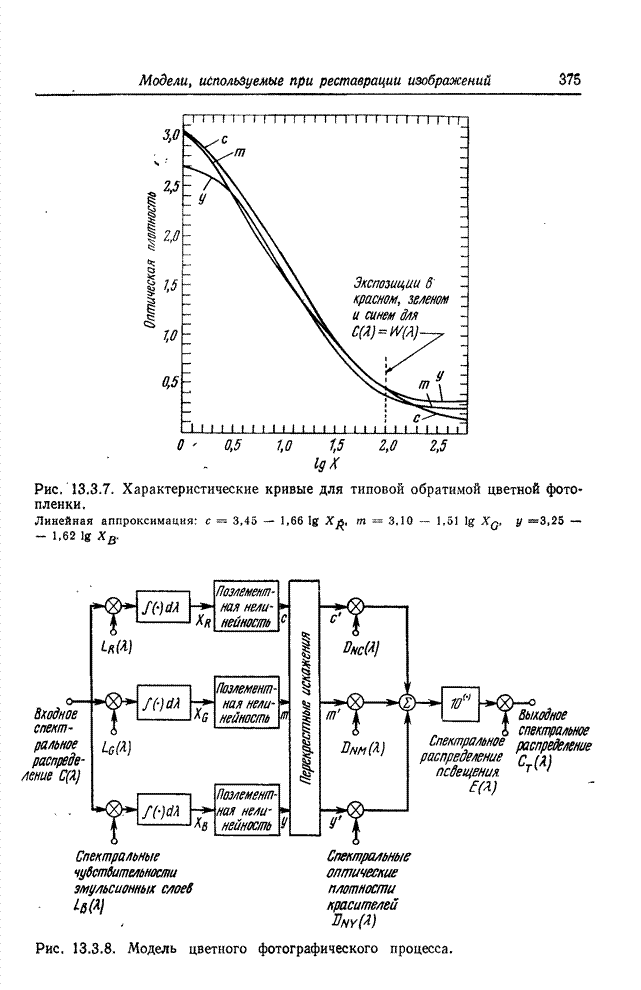
- 13.3. МОДЕЛИ ФОТОГРАФИЧЕСКИХ ПРОЦЕССОВ
- 13.3.1. ОДНОЦВЕТНАЯ ФОТОГРАФИЯ
- 13.3.2. ЦВЕТНАЯ ФОТОГРАФИЯ
- 13.4. МОДЕЛИ ЦИФРОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- 13.5. МОДЕЛЬ ДИСПЛЕЯ
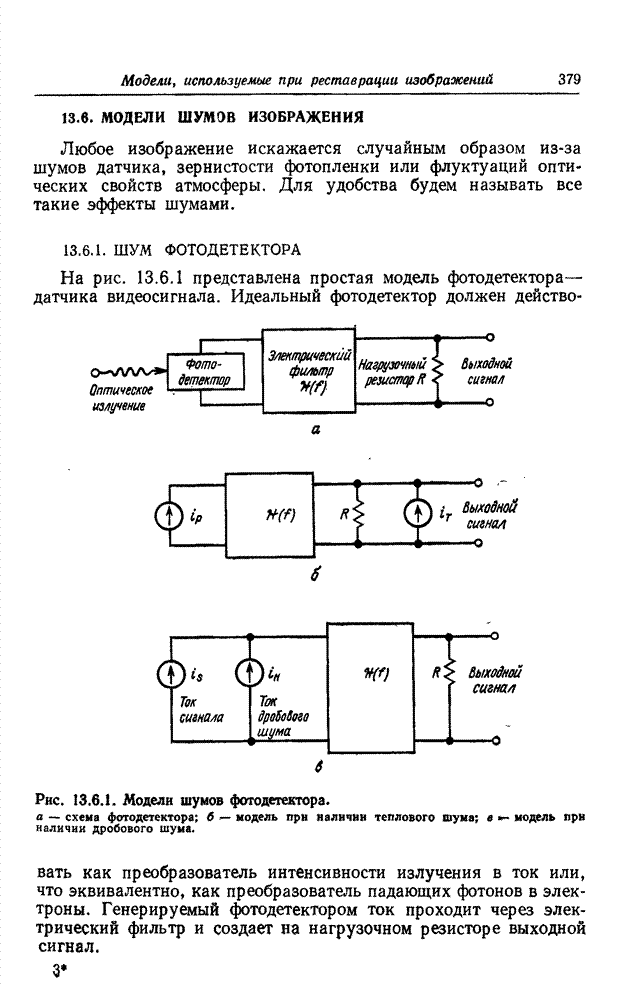
- 13.6. МОДЕЛИ ШУМОВ ИЗОБРАЖЕНИЯ
- 13.6.1. ШУМ ФОТОДЕТЕКТОРА
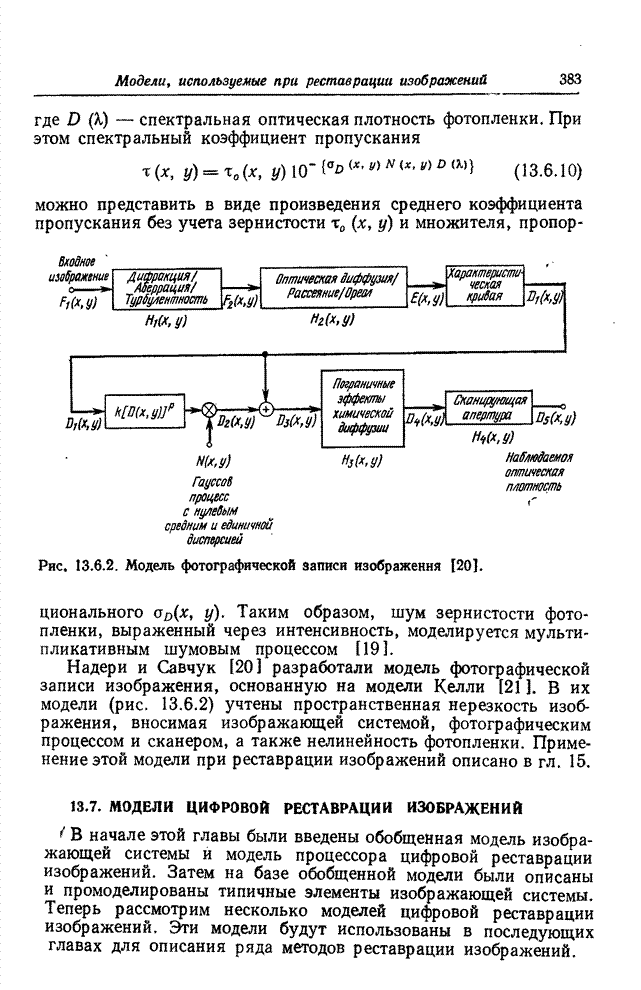
- 13.6.2. ШУМ ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
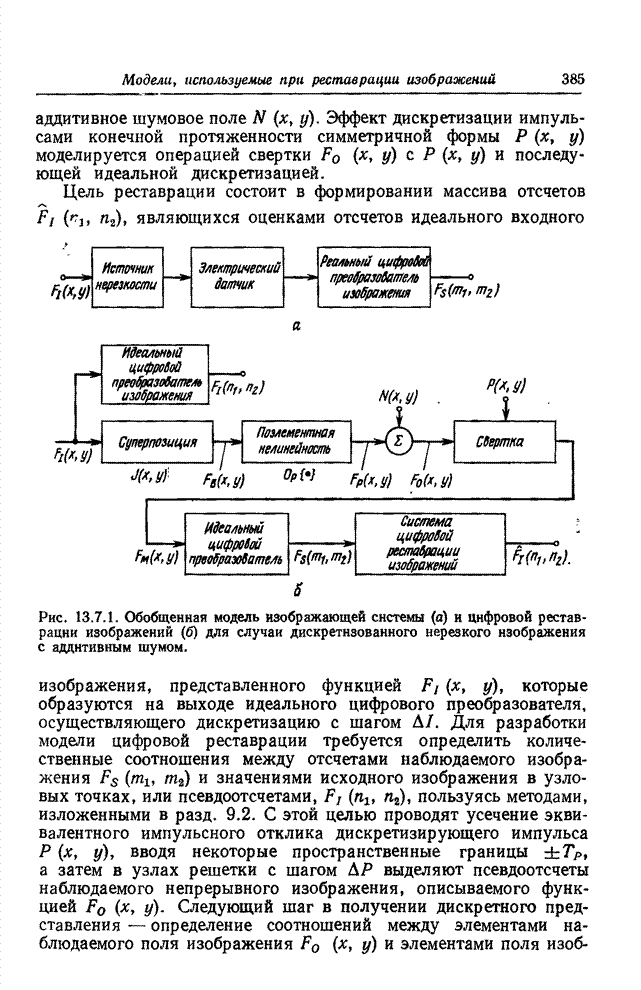
- 13.7. МОДЕЛИ ЦИФРОВОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 14. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 14.1. МЕТОДЫ ПРОСТРАНСТВЕННОЙ ФИЛЬТРАЦИИ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 14.1.1. ИНВЕРСНАЯ ФИЛЬТРАЦИЯ
- 14.1.2. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И АДДИТИВНЫЙ ШУМ
- 14.1.3. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНОЕ ИЗОБРАЖЕНИЕ
- 14.1.4. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНАЯ НЕРЕЗКОСТЬ
- 14.1.5. ФИЛЬТРЫ НА ОСНОВЕ ПАРАМЕТРИЧЕСКИХ ОЦЕНОК
- 14.1.6. ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 4.2. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.2.1. РЕСТАВРАЦИЯ НЕРЕЗКИХ ИЗОБРАЖЕНИЙ
- 14.2.2. РЕСТАВРАЦИЯ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ ПРИ НАЛИЧИИ ШУМА
- 14.3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.3.1. АЛГОРИТМ ДЛЯ ПЕРЕОПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.3.2. АЛГОРИТМ ДЛЯ НЕДООПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.4. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ С ИСПОЛЬЗОВАНИЕМ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- 14.5. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕГРЕССИИ
- 14.6. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ВИНЕРОВСКОГО ОЦЕНИВАНИЯ
- 14.6.1. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В ОБЩЕМ СЛУЧАЕ
- 14.6.2. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В СЛУЧАЕ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ С ШУМОМ
- 14.7. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ СО СГЛАЖИВАНИЕМ
- 14.8. МЕТОДЫ РЕСТАВРАЦИИ С ИСПОЛЬЗОВАНИЕМ ОГРАНИЧЕНИЙ
- 14.9. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
- ЛИТЕРАТУРА
- Глава 15. CПЕЦИАЛЬНЫЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 15.1. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮ ПОДАВЛЕНИЯ ОШИБОК НАЛОЖЕНИЯ СПЕКТРОВ
- 15.2. КОРРЕКЦИЯ ОШИБОК ИНТЕРПОЛЯЦИИ
- 15.3. КОРРЕКЦИЯ ГЕОМЕТРИЧЕСКИХ ИСКАЖЕНИЙ
- 15.4. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ГОМОМОРФНОЙ ФИЛЬТРАЦИИ
- 15.5. СЛЕПАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ
- 15.5.1. МЕТОДЫ НА ОСНОВЕ ПРЯМЫХ ИЗМЕРЕНИЙ
- 15.5.2. МЕТОДЫ НА ОСНОВЕ КОСВЕННОГО ОЦЕНИВАНИЯ
- 15.6. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ СПЕКТРА
- 15.7. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННО-ЗАВИСИМЫМИ ИСКАЖЕНИЯМИ
- 15.8. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕКУРСИВНОЙ ФИЛЬТРАЦИИ
- 15.9. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮОСЛАБЛЕНИЯ ШУМА ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- ЛИТЕРАТУРА
- Глава 16. КОРРЕКЦИЯ ЯРКОСТНЫХ, ЦВЕТОВЫХ И СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗОБРАЖАЮЩИХ СИСТЕМ
- 16.1. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ВИДЕОДАТЧИКОВ
- 16.2. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ДИСПЛЕЕВ
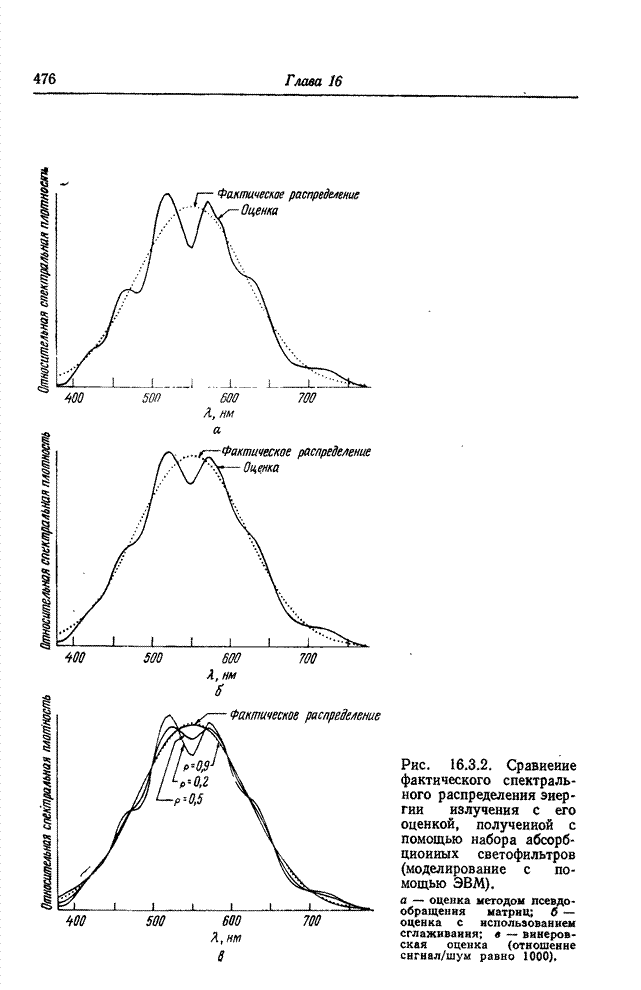
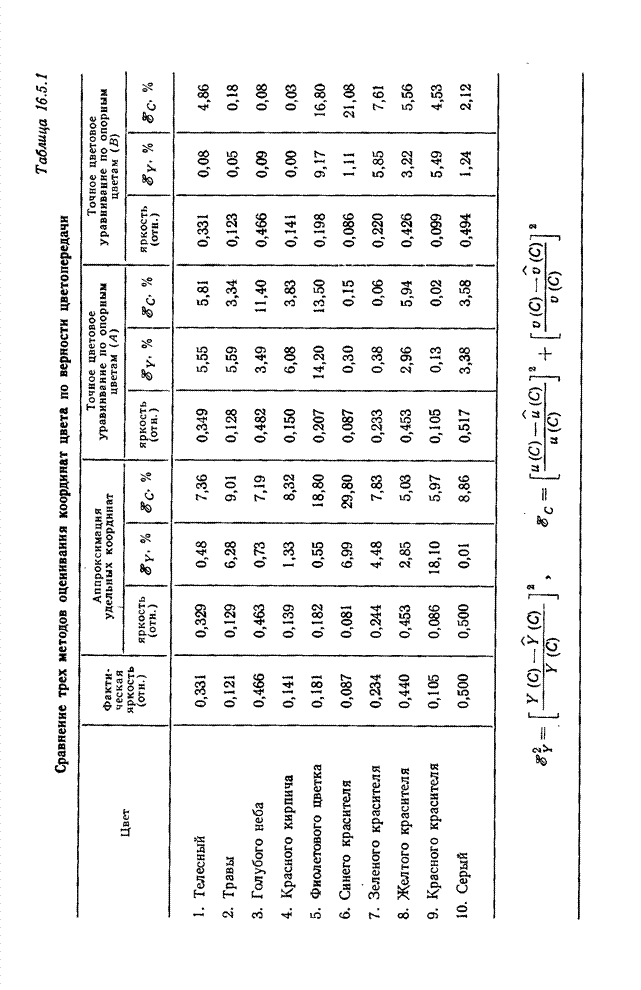
- 16.3. ОЦЕНИВАНИЕ СПЕКТРАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ИЗЛУЧЕНИЯ
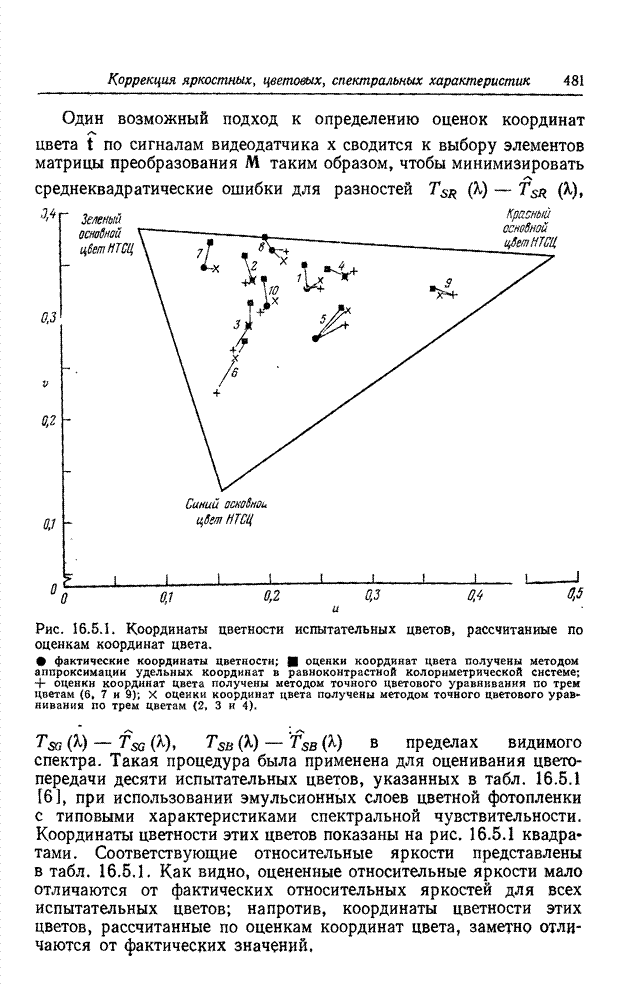
- 16.4. КОРРЕКЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ВИДЕОДАТЧИКОВ И ДИСПЛЕЕВ
- 16.5. ОЦЕНИВАНИЕ КООРДИНАТ СВЕТА ВИДЕОДАТЧИКОВ
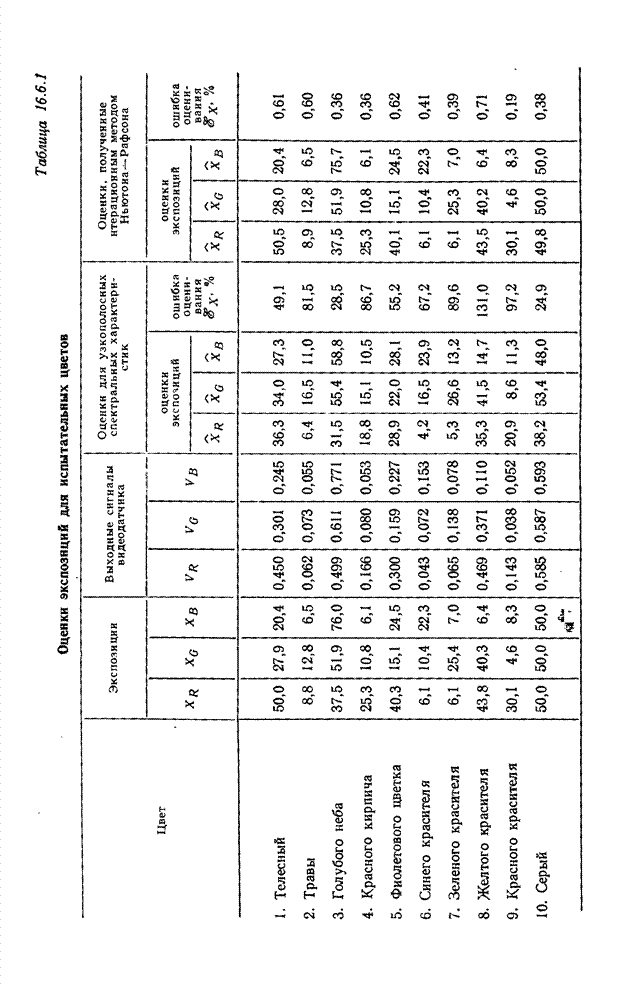
- 16.6. ОЦЕНИВАНИЕ ЭКСПОЗИЦИЙ ЦВЕТНОЙ ФОТОПЛЕНКИ
- 16.7. КОМПЕНСАЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ ЦВЕТНЫХ ДИСПЛЕЕВ
- ЛИТЕРАТУРА
- Часть 5. АНАЛИЗ ИЗОБРАЖЕНИЙ
- Глава 17. ВЫДЕЛЕНИЕ ПРИЗНАКОВ ИЗОБРАЖЕНИЯ
- 17.1. ЯРКОСТНЫЕ ПРИЗНАКИ
- 17.2. ГИСТОГРАММНЫЕ ПРИЗНАКИ
- 17.3. ПРОСТРАНСТВЕННО-СПЕКТРАЛЬНЫЕ ПРИЗНАКИ
- 17.4. КОНТУРНЫЕ ПРИЗНАКИ
- 17.4.1. ЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.2. НЕЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.3. МЕТОДЫ АППРОКСИМАЦИИ ПЕРЕПАДОВ ЯРКОСТИ
- 17.4.4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ
- 17.5. ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ ЯРКОСТИ
- 17.6. ЦВЕТОВЫЕ КОНТУРЫ
- 17.7. ПРИЗНАКИ ПЯТНА И ЛИНИИ
- 17.8. ТЕКСТУРНЫЕ ПРИЗНАКИ
- 17.9. СИНТЕЗ ТЕКСТУР
- ЛИТЕРАТУРА
- Глава 18. СИМВОЛИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
- 18.1. СВЯЗНОСТЬ
- 18.2. СЖАТИЕ, УТОНЧЕНИЕ И ПОСТРОЕНИЕ ОСТОВА
- 18.3. ОПИСАНИЕ ЛИНИЙ
- 18.3.1. АППРОКСИМАЦИЯ КРИВЫХ
- 18.3.2. ПРЕОБРАЗОВАНИЕ ЛИНИИ В ТОЧКУ
- 18.4. ОПИСАНИЕ ФОРМЫ
- 18.4.1. МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.2. ТОПОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.3. АНАЛИТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.5. СЕГМЕНТАЦИЯ ПО ЯРКОСТИ
- 18.5.1. ПОРОГОВОЕ ОГРАНИЧЕНИЕ ПО ЯРКОСТИ
- 18.5.2. МНОГОМЕРНОЕ ПОРОГОВОЕ ОГРАНИЧЕНИЕ
- 18.5.3. НАРАЩИВАНИЕ ОБЛАСТЕЙ
- 18.6. КОНТУРНАЯ СЕГМЕНТАЦИЯ
- 18.7. ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ
- 18.8. СЕГМЕНТАЦИЯ ФОРМЫ
- ЛИТЕРАТУРА
- Глава 19. ОБНАРУЖЕНИЕ ОБЪЕКТОВ И СОВМЕЩЕНИЕ (ПРИВЯЗКА) ИЗОБРАЖЕНИЙ
- 19.1. СОПОСТАВЛЕНИЕ С ЭТАЛОНОМ
- 19.2. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ ДЕТЕРМИНИРОВАННЫХ ПОЛЕЙ
- 19.3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ СЛУЧАЙНЫХ ПОЛЕЙ
- 19.4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
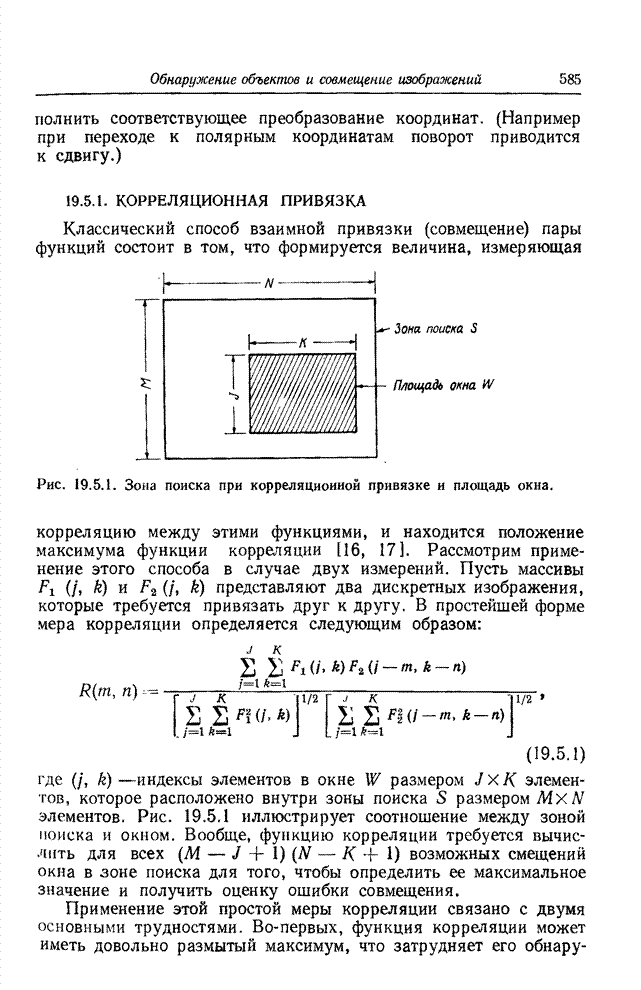
- 19.5. ПРИВЯЗКА ИЗОБРАЖЕНИЙ
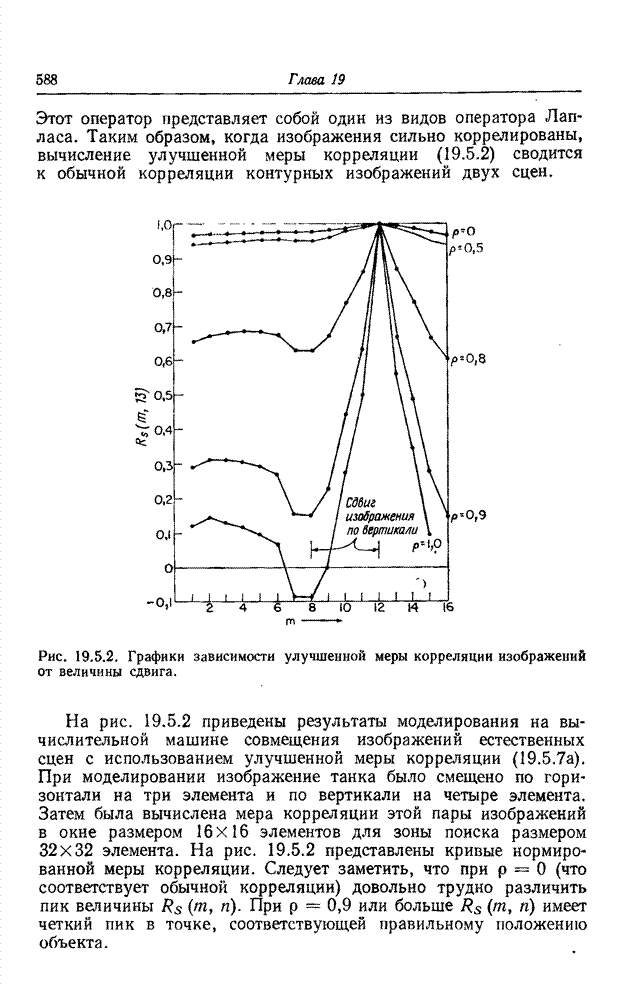
- 19.5.1. КОРРЕЛЯЦИОННАЯ ПРИВЯЗКА
- 19.5.2. ПОСЛЕДОВАТЕЛЬНАЯ ПРИВЯЗКА
- ЛИТЕРАТУРА
- Глава 20. СИСТЕМЫ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
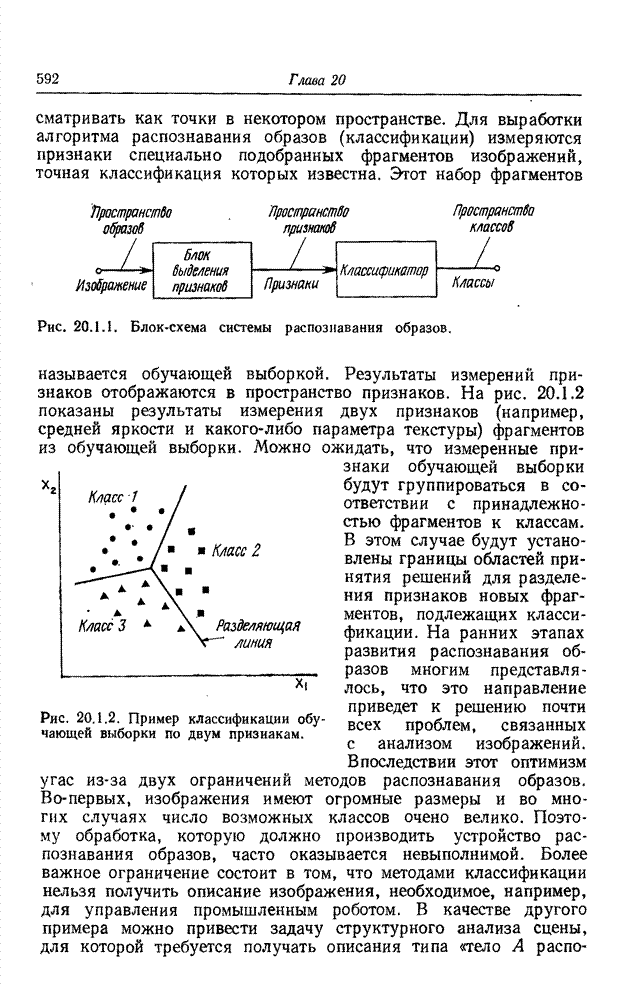
- 20.1. СИСТЕМЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 20.2. МОДЕЛИ СИСТЕМ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.3. СИНТАКСИЧЕСКИЕ МЕТОДЫ
- 20.4. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ОТНОШЕНИЯ МЕЖДУ ОБЪЕКТАМИ
- ЛИТЕРАТУРА
- Часть 6. Кодирование изображений
- Глава 21. АНАЛОГОВЫЕ МЕТОДЫ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.1. КЛАССИФИКАЦИЯ МЕТОДОВ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.2. СИСТЕМЫ ВЕЩАТЕЛЬНОГО ТЕЛЕВИДЕНИЯ
- 21.2.1. СИСТЕМА НТСЦ [13-15]
- 21.2.2. СИСТЕМА СЕКАМ [17]
- 21.2.3.СИСТЕМА ПАЛ
- 21.3. МОДУЛЯЦИОННЫЕ МЕТОДЫ СОКРВЩЕНИЯ ПОЛОСЫ ЧАСТОТЫ
- 21.4.УМЕНЬШЕНИЕ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ И ЧАСТОТЫ КАДРОВ
- 21.4.1. УМЕНЬШЕНИЕ ПРОСТРАНСТВЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
- 21.4.2. УМЕНЬШЕНИЕ ЧАСТОТЫ КАДРОВ
- 21.5. МЕТОДЫ ВРЕМЕННОГО ПЕРЕМЕЖЕНИЯ
- 21.5.1. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ СТРОК
- 21.5.2. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ ЭЛЕМЕНТОВ
- 21.6. РАЗВЕРТКА С ПЕРЕМЕННОЙ СКОРОСТЬЮ
- 21.7. МУЛЬТИПЛЕКСНЫЕ МЕТОДЫ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Глава 22. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПОЭЛЕМЕНТНОЙ ОБРАБОТКОЙ
- 22.1. СИСТЕМЫ КОДИРОВАНИЯ С ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИЕЙ
- 22.1.1. КВАНТОВАНИЕ СО СЖАТИЕМ ДИАПАЗОНА ЯРКОСТЕЙ
- 22.1.2. ПСЕВДОШУМОВОЕ КВАНТОВАНИЕ
- 22.1.3. КВАНТОВАНИЕ С УЛУЧШЕННОЙ ПЕРЕДАЧЕЙ ГРАДАЦИЙ ЯРКОСТИ
- 22.1.4. СИСТЕМА С ГРУБОЙ-ТОНКОЙ ШКАЛОЙ КВАНТОВАНИЯ
- 22.1.5. КВАНТОВАНИЕ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ
- 22.2. СТАТИСТИЧЕСКИЕ МЕТОДЫ КОДИРОВАНИЯ
- 22.2.1. ПОЭЛЕМЕНТНОЕ СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- 22.2.2. КОДИРОВАНИЕ С УЧЕТОМ ПРЕДШЕСТВУЮЩЕГО ЭЛЕМЕНТА
- 22.3. КОДИРОВАНИЕ СЕРИЙ
- 22.3.1. КОДИРОВАНИЕ ДЛИН СЕРИЙ; ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ [32-36]
- 22.3.2. КОДИРОВАНИЕ РАЗРЯДНЫХ ПЛОСКОСТЕЙ
- 22.4. КОДИРОВАНИЕ С ПОПОЛНЕНИЕМ КАДРОВ
- 22.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ
- 22.5.1. ДЕЛЬТА-МОДУЛЯЦИЯ
- 22.5.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ
- 22.5.3. КОДЕРЫ С ПРОСТРАНСТВЕННЫМ ПРЕДСКАЗАНИЕМ
- 22.5.4. АДАПТИВНЫЕ КОДЕРЫ С ПРЕДСКАЗАНИЕМ
- 22.5.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ ПРИМЕНИТЕЛЬНО К ЦВЕТНЫМ ИЗОБРАЖЕНИЯМ
- 22.5.6. ДИФФЕРЕНЦИАЛЬНОЕ МЕЖКАДРОВОЕ КОДИРОВАНИЕ
- 22.6. ПРОЕКТИРОВАНИЕ СИСТЕМ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ДЛЯ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 23. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННОЙ ОБРАБОТКОЙ
- 23.1. ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ КОДИРОВАНИЯ
- 23.1.1. ИНТЕРПОЛЯЦИЯ НА ПЕРЕДАЮЩЕЙ СТОРОНЕ
- 23.1.2. ИНТЕРПОЛЯЦИЯ НА ПРИЕМНОЙ СТОРОНЕ
- 23.2. КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.1. КОДИРОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.2. АДАПТИВНОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.3. КОДИРОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.4. МЕЖКАДРОВОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.3. УМЕНЬШЕНИЕ ОШИБОК КВАНТОВАНИЯ ПРИ КОДИРОВАНИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.4. ГИБРИДНОЕ КОДИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ И ДИКМ
- 23.5. КОДИРОВАНИЕ ПРИЗНАКОВ
- 23.5.1. КОДИРОВАНИЕ ЛИНИЙ УРОВНЯ
- 23.5.2. КОДИРОВАНИЕ КОНТУРОВ
- 23.5.3. КОДИРОВАНИЕ ТЕКСТУР
- 23.6. КОДИРОВАНИЕ С ПОМОЩЬЮ НАБОРА СИМВОЛОВ
- 23.6.1. КОДИРОВАНИЕ БЛОКОВ ПО СЛОВАРЮ ОБРАЗОВ
- 23.6.2. КОДИРОВАНИЕ НА ОСНОВЕ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- ЛИТЕРАТУРА
- Глава 24. АНАЛИЗ ЭФФЕКТИВНОСТИ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 24.1. СТАТИСТИЧЕСКИЕ МОДЕЛИ КАНАЛА СВЯЗИ КАК ИСТОЧНИКА ПОМЕХ [1-4]
- 24.2. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ
- 24.3. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ [4]
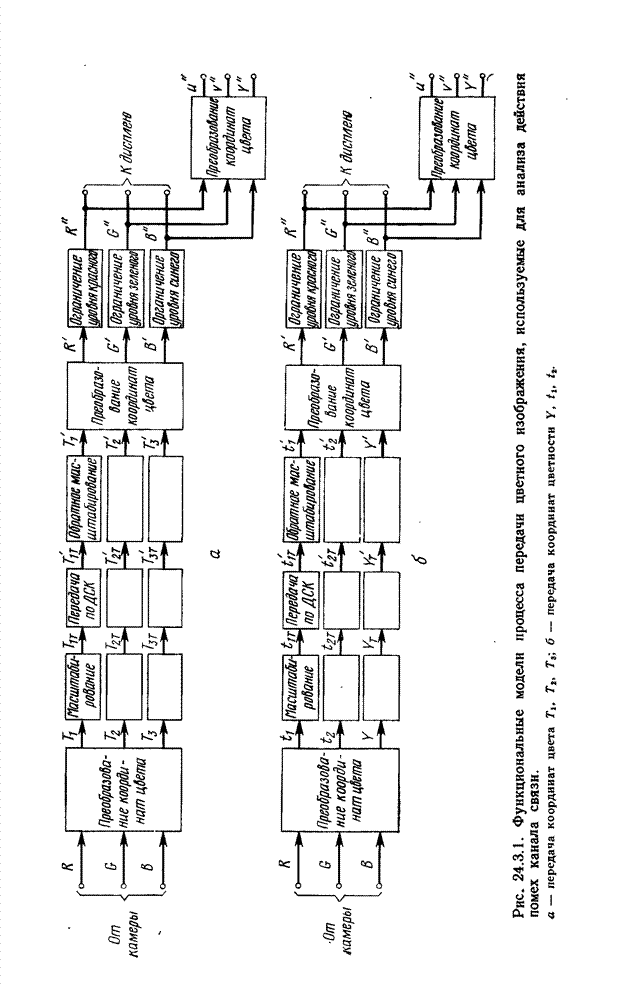
- 24.3.1. ПЕРЕДАЧА КООРДИНАТ ЦВЕТА
- 24.3.2. ПЕРЕДАЧА ЯРКОСТИ И КООРДИНАТ ЦВЕТНОСТИ
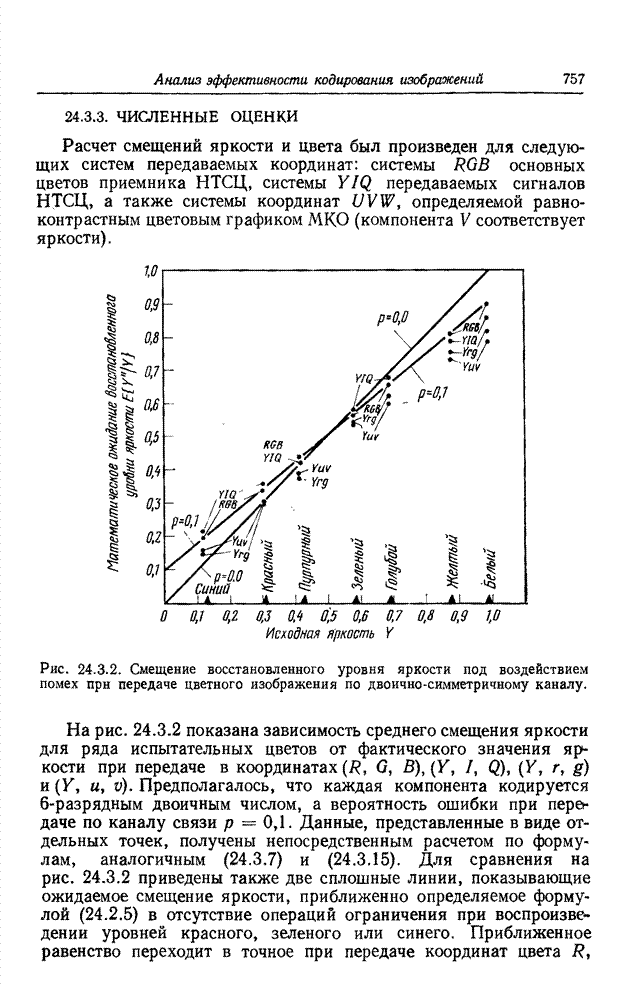
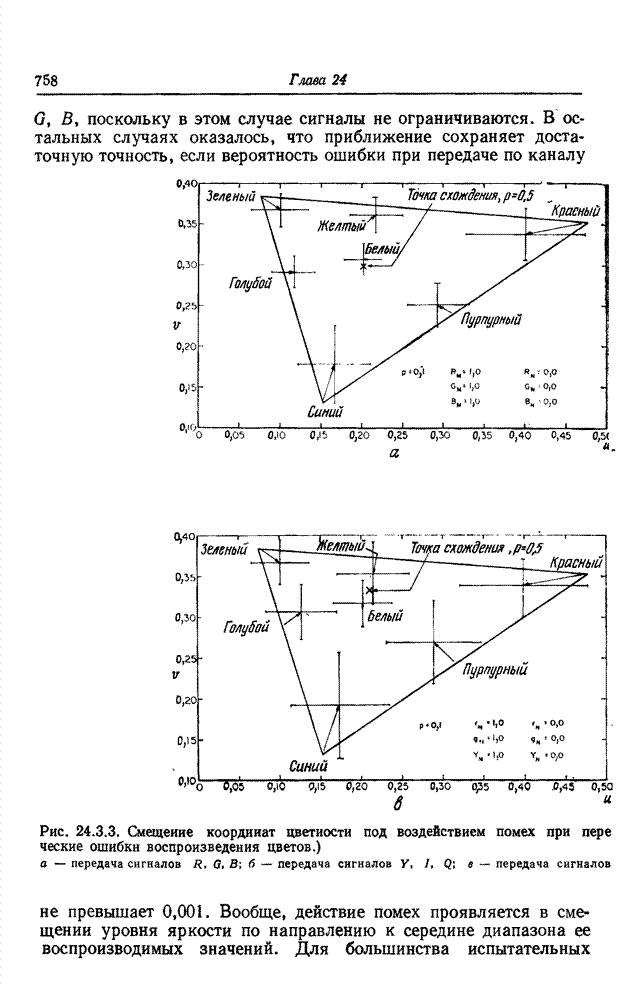
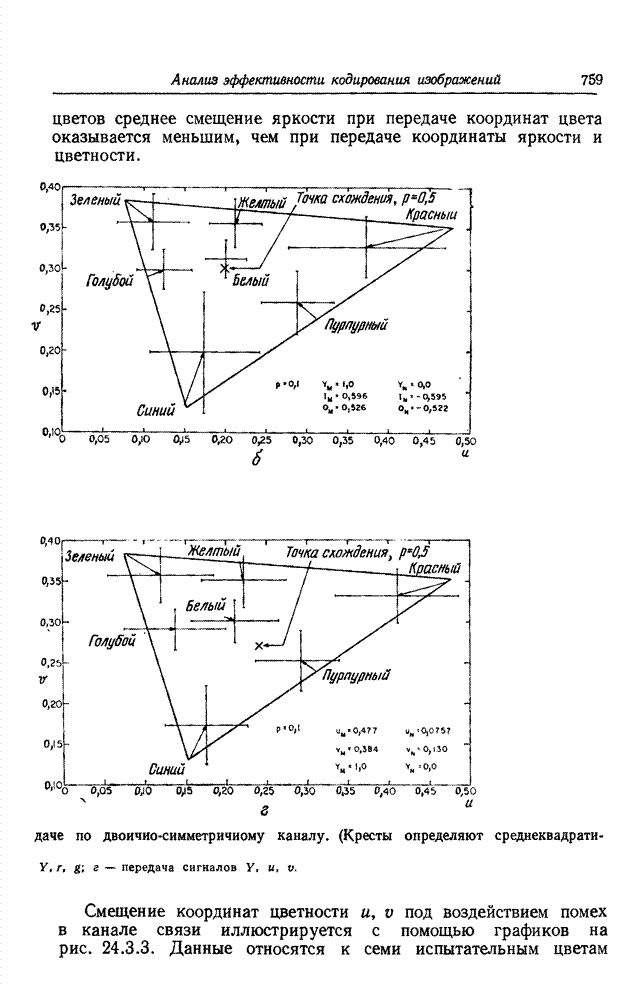
- 24.3.3. ЧИСЛЕННЫЕ ОЦЕНКИ
- 24.4. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ ДИКМ
- 24.5. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ КОДИРОВАНИЯ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
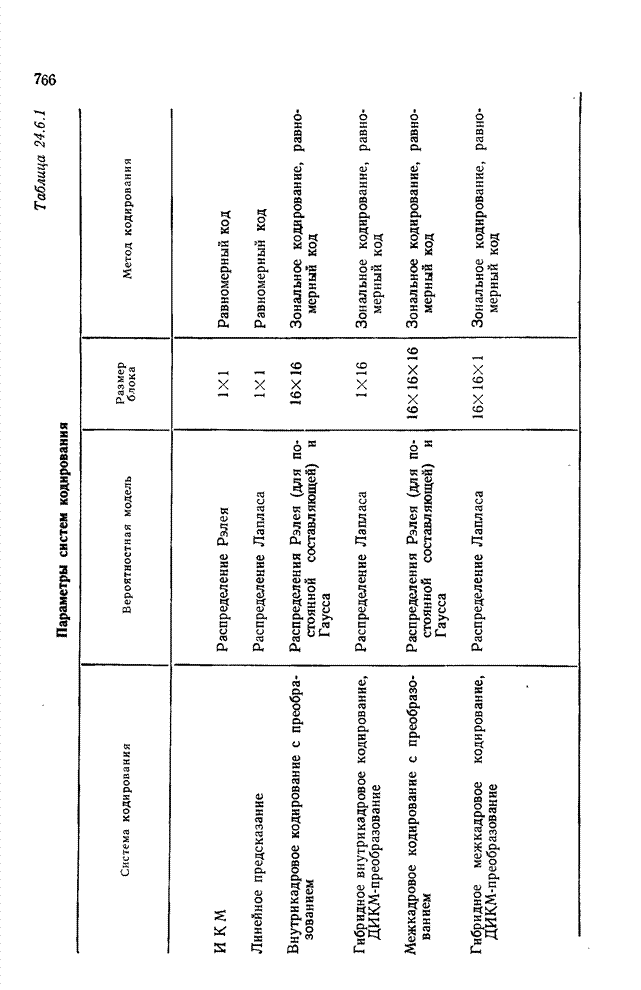
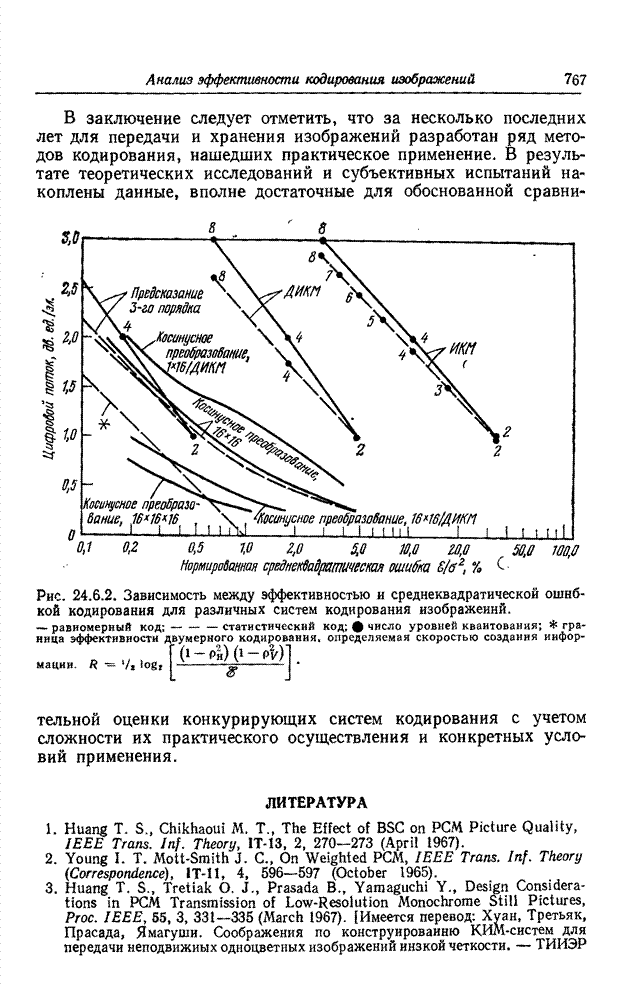
- 24.6. СРАВНЕНИЕ РАЗЛИЧНЫХ МЕТОДОВ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Приложение 1. ОСНОВНАЯ ЛИТЕРАТУРА
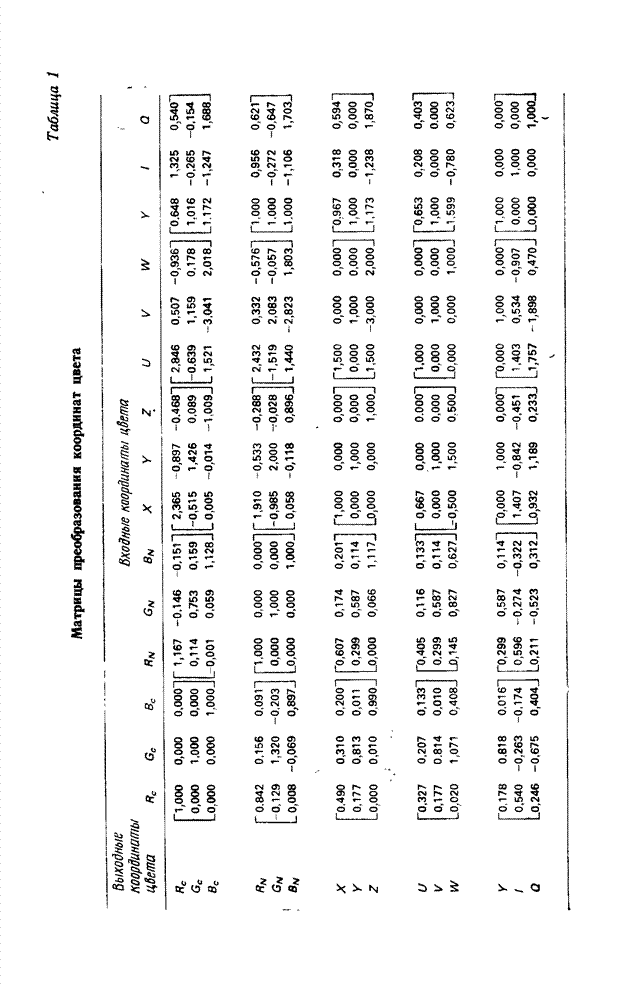
- Приложение 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА И ЦВЕТНОСТИ
- Приложение 3. СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА