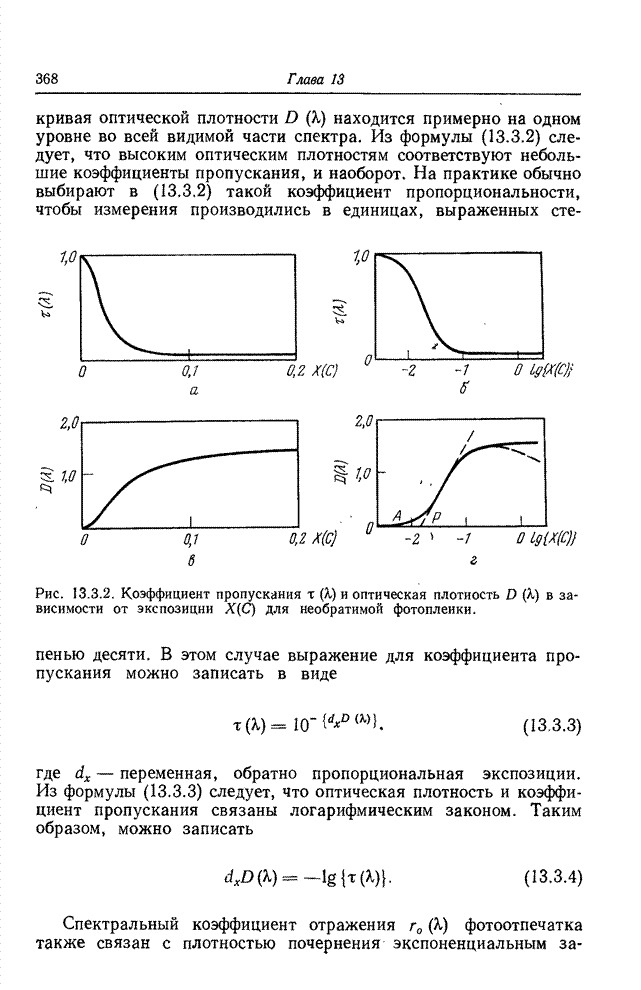
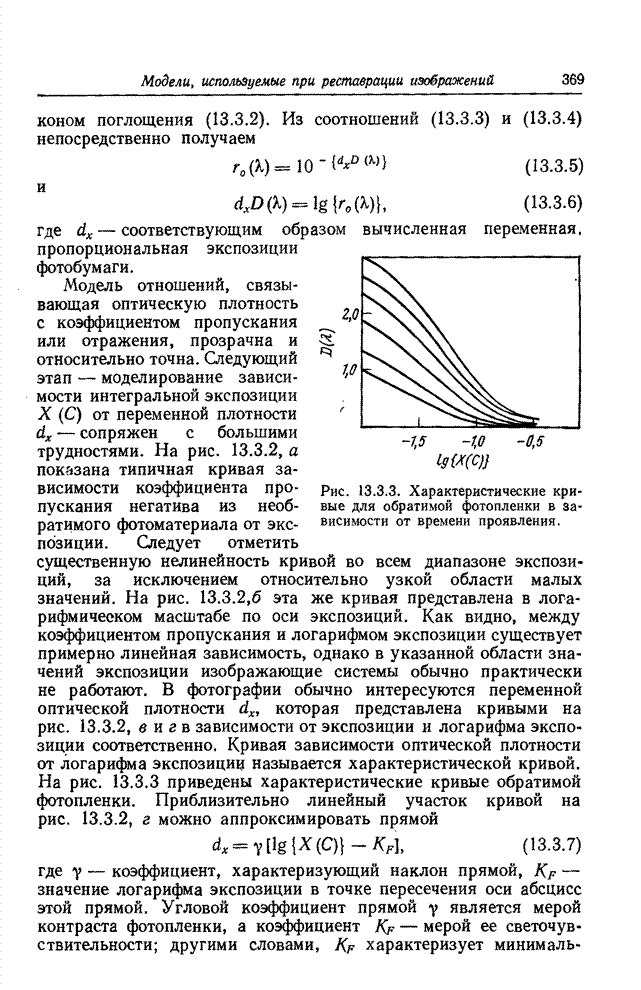
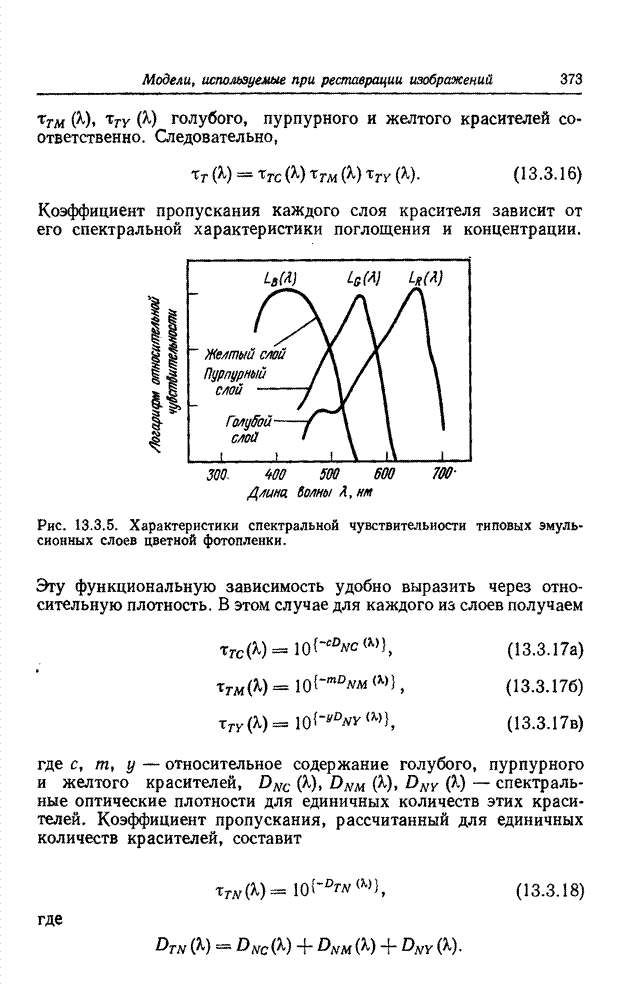
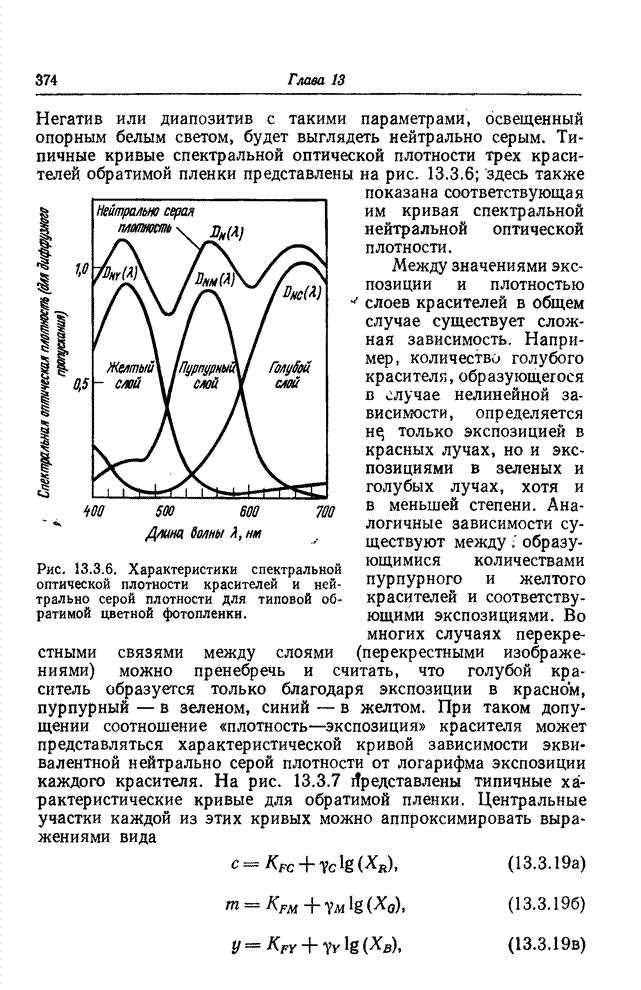
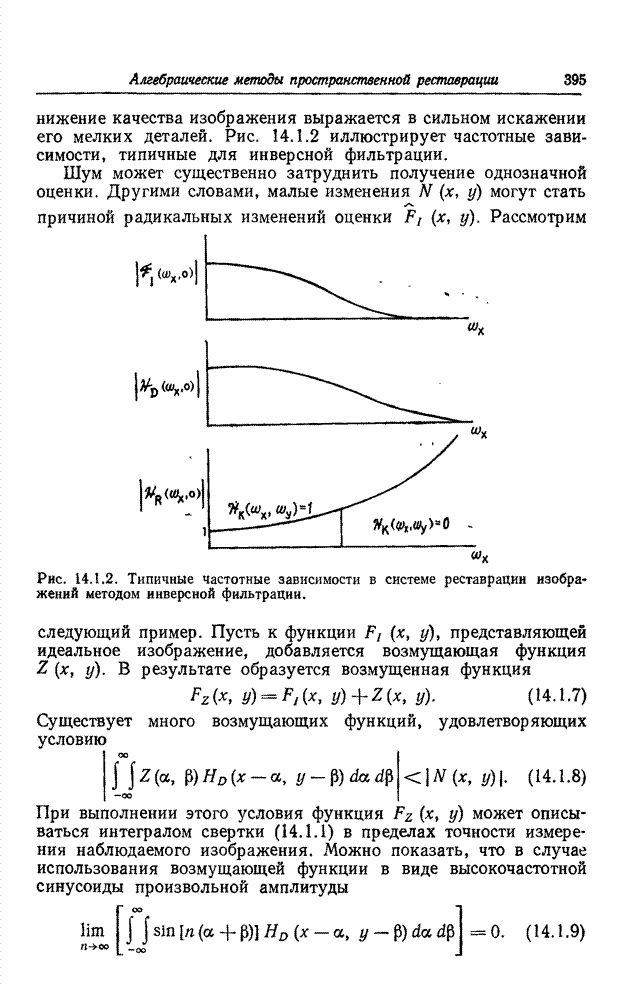
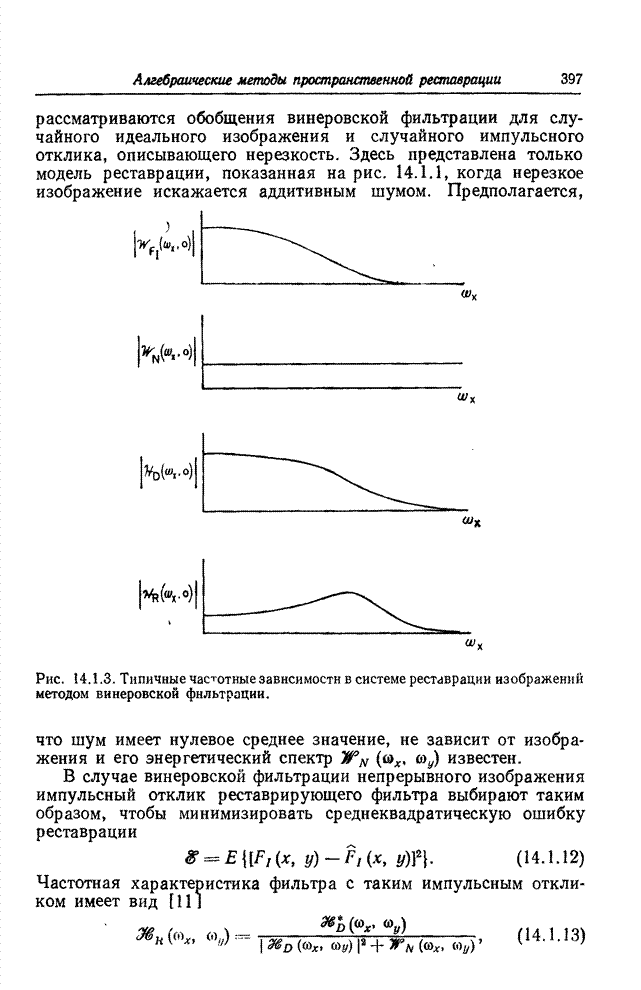
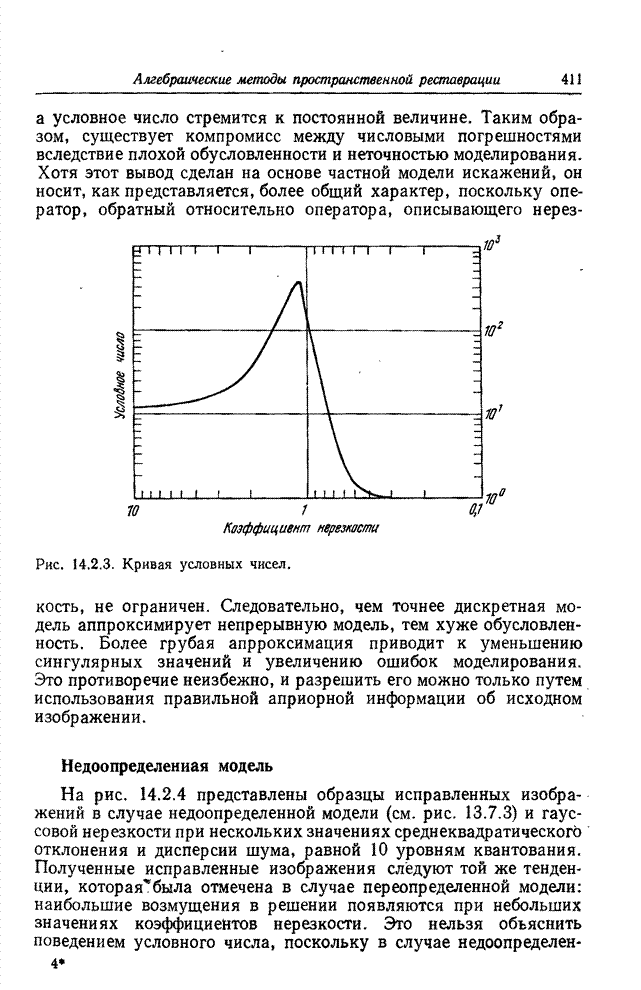
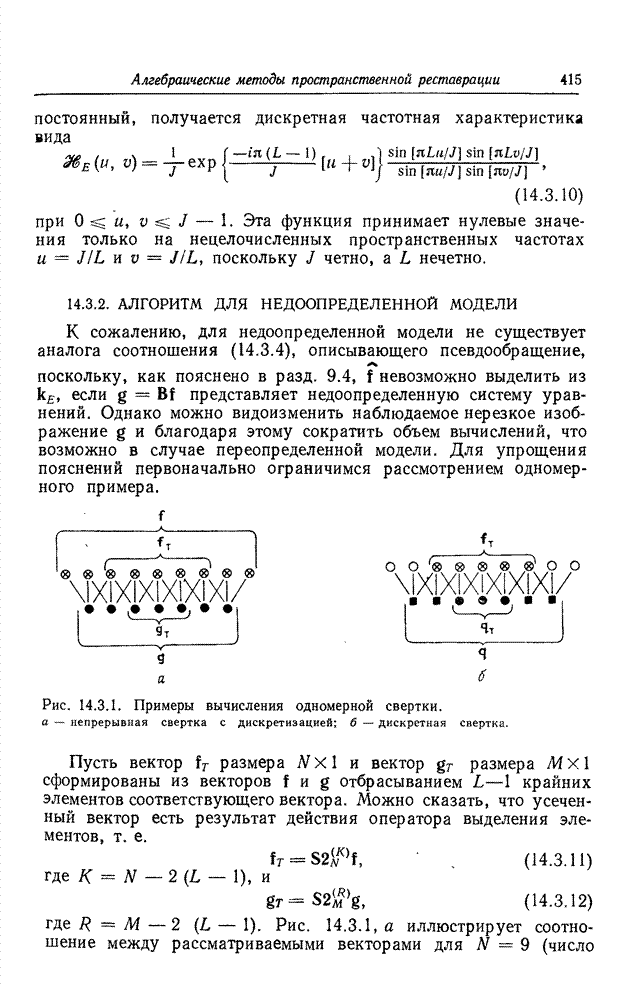
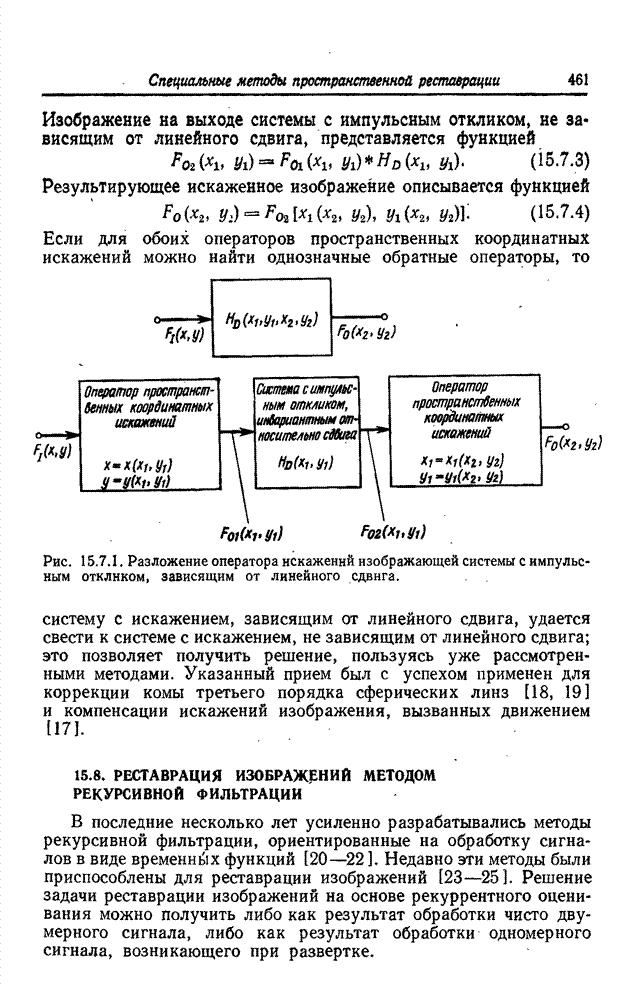
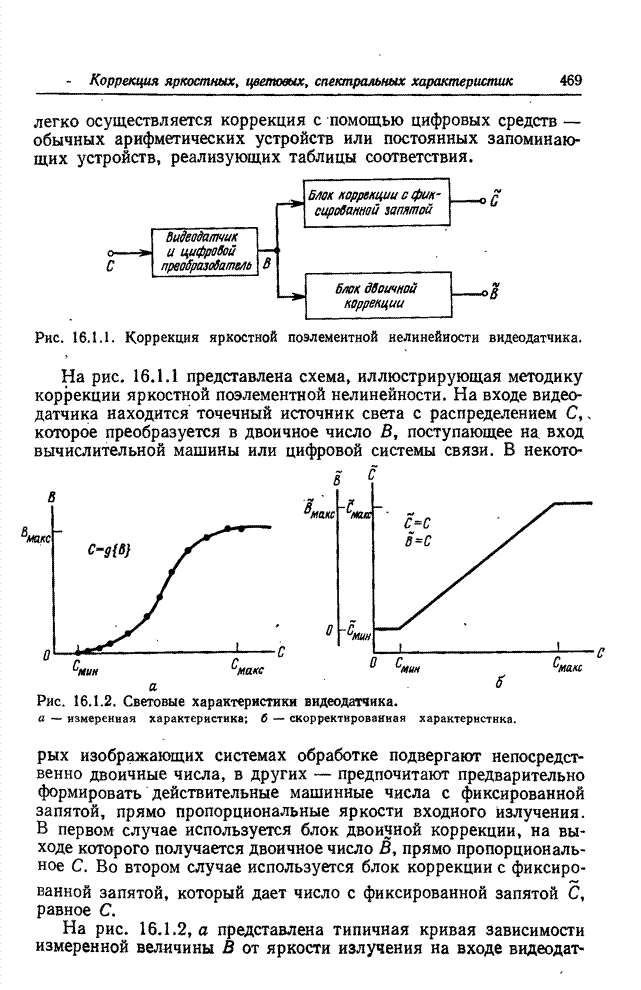
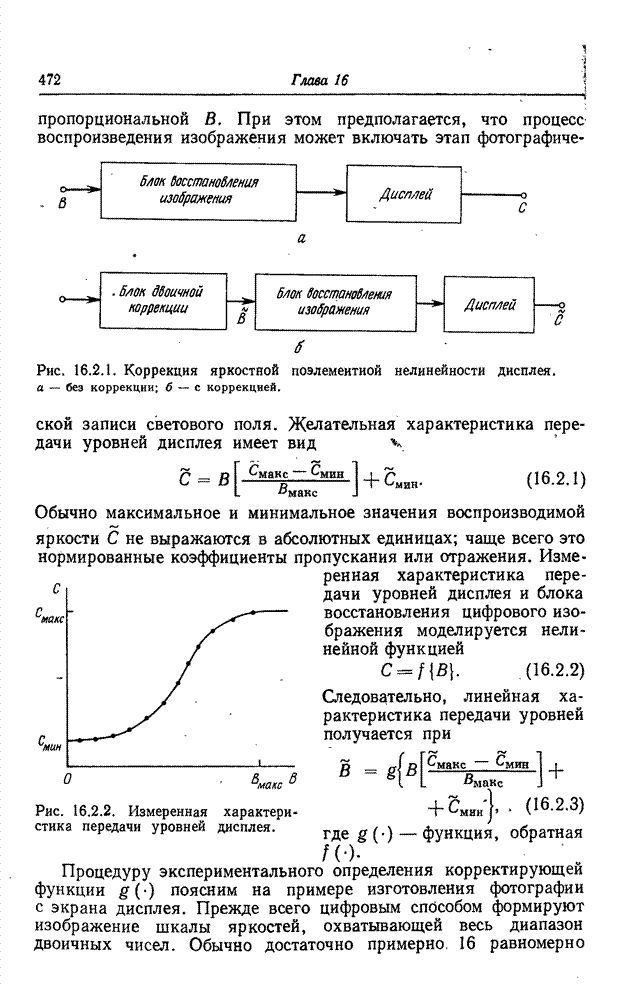
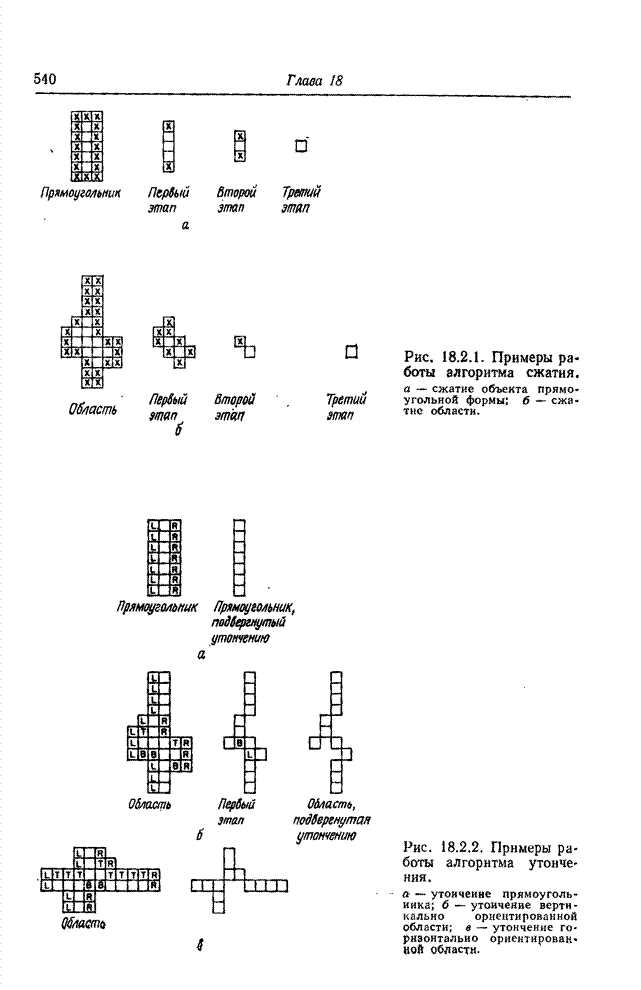
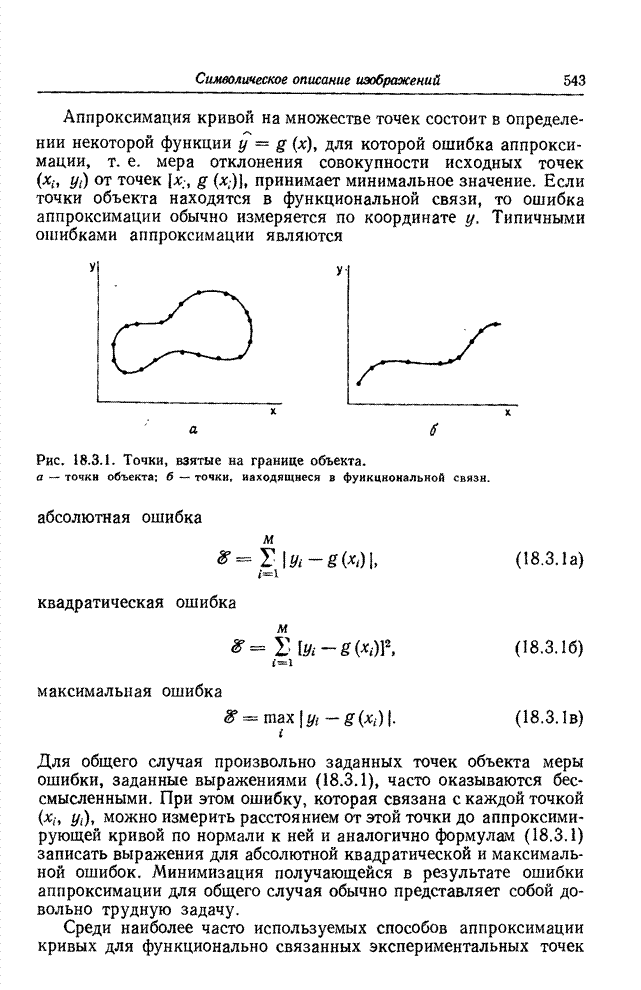
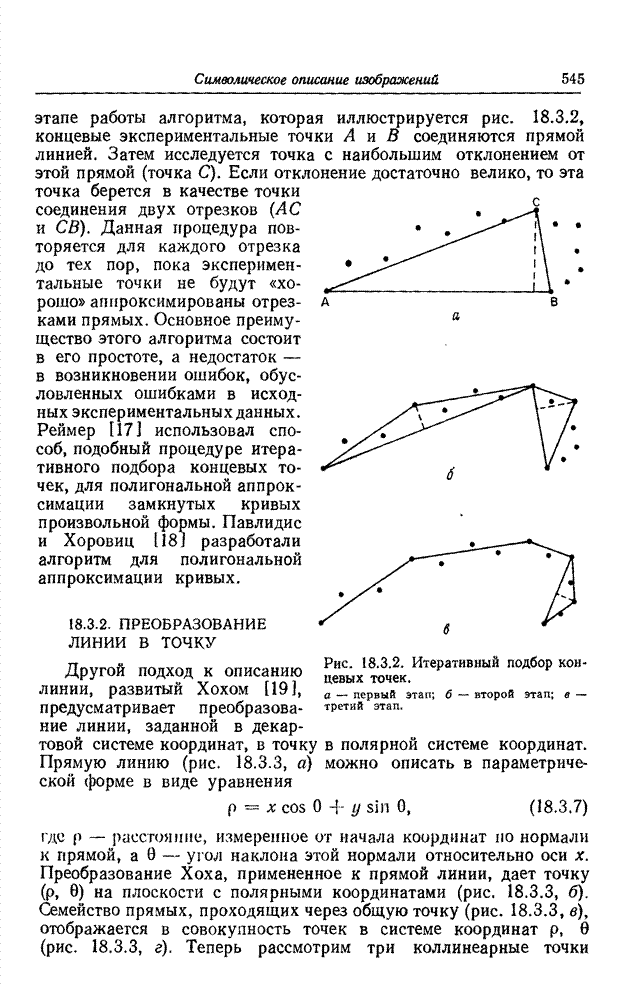
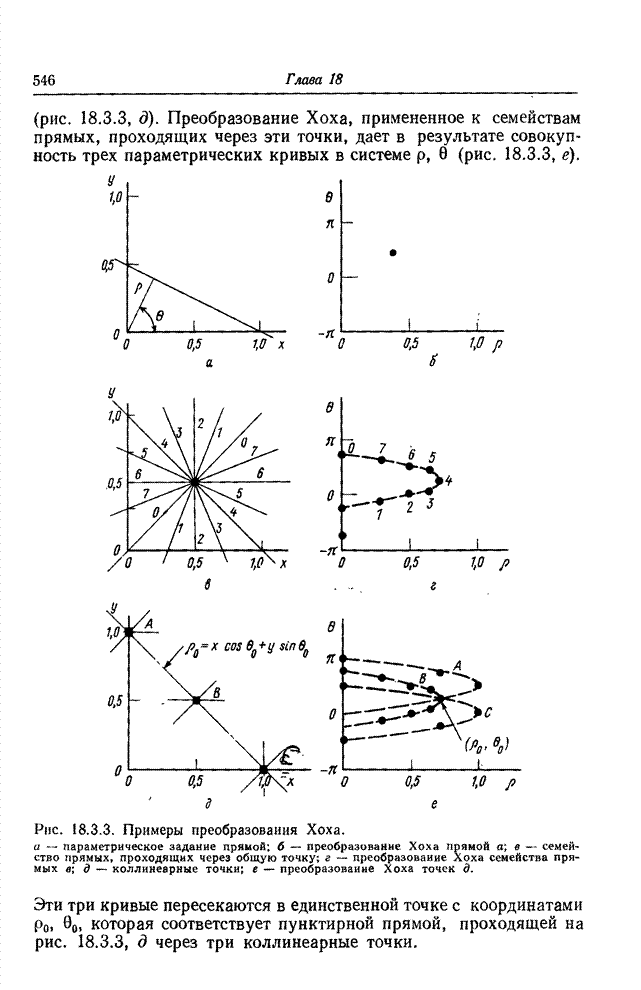
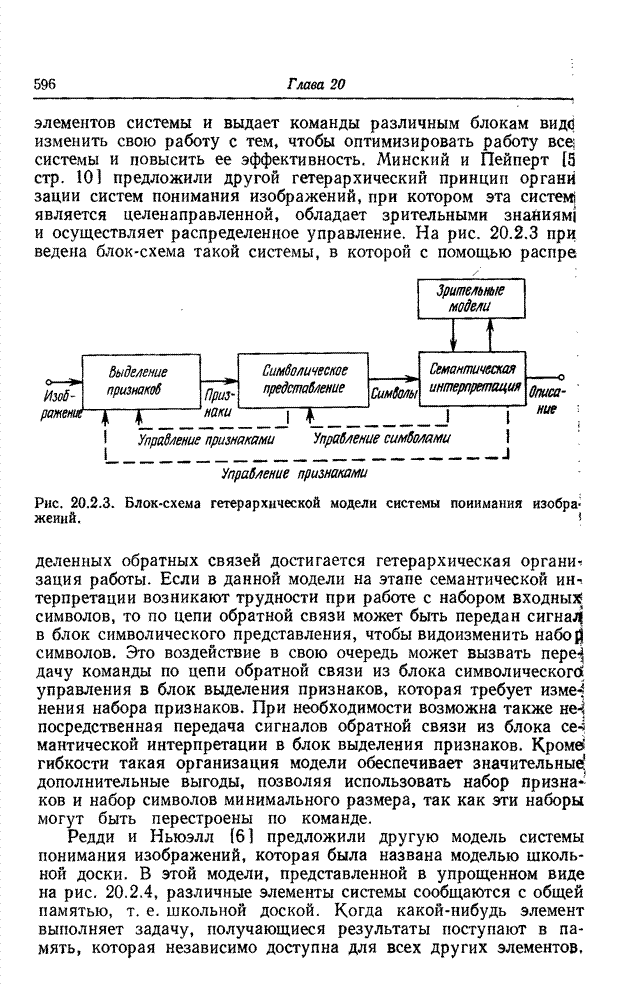
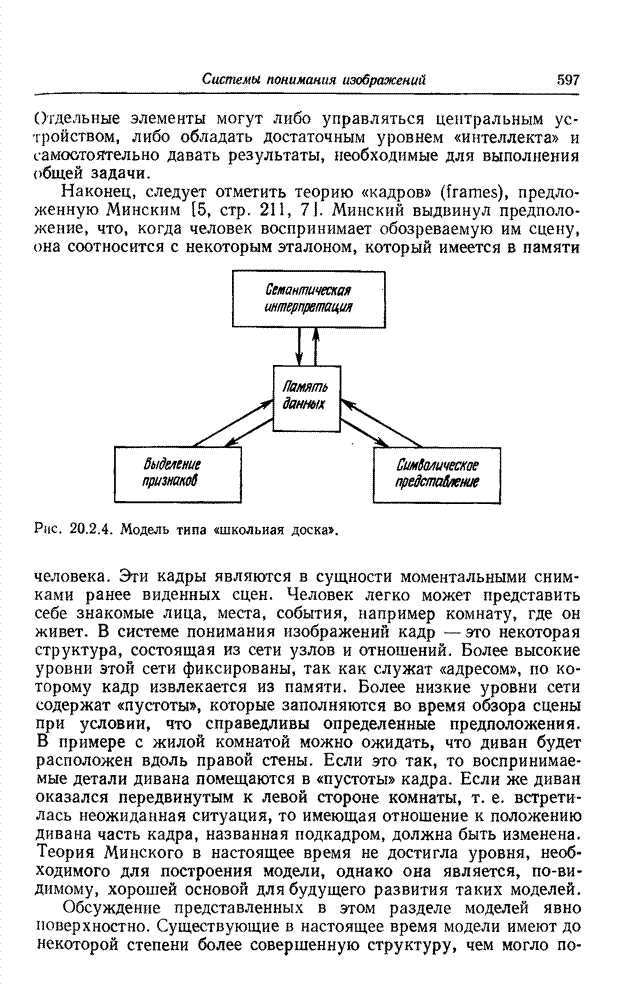
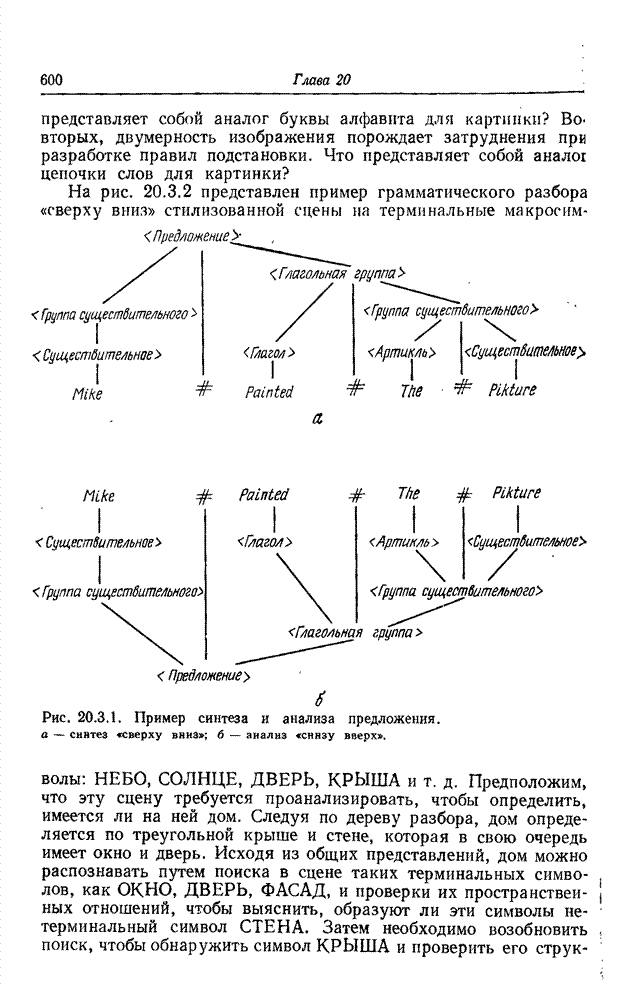
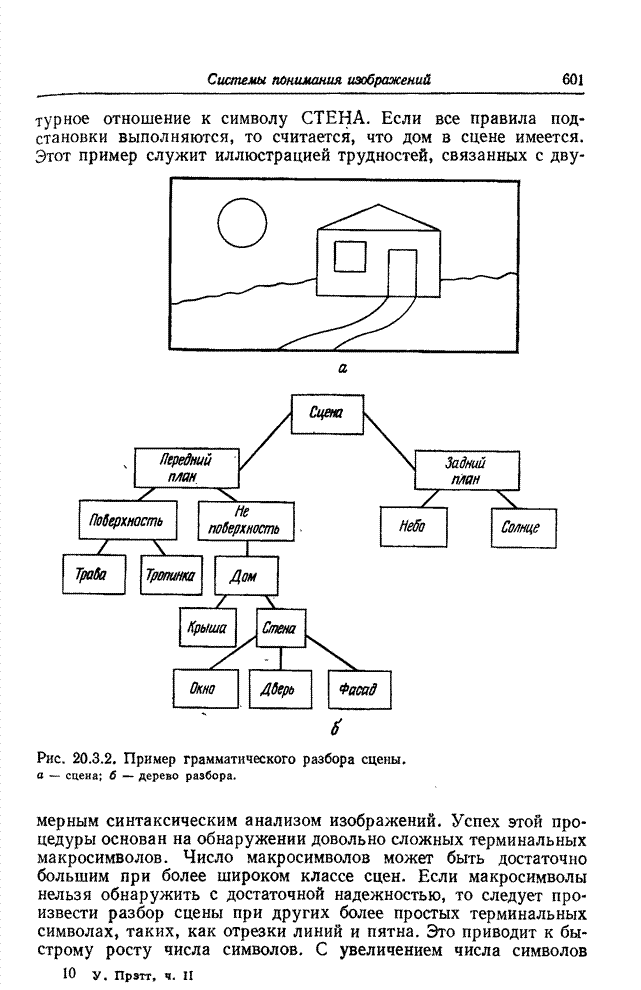
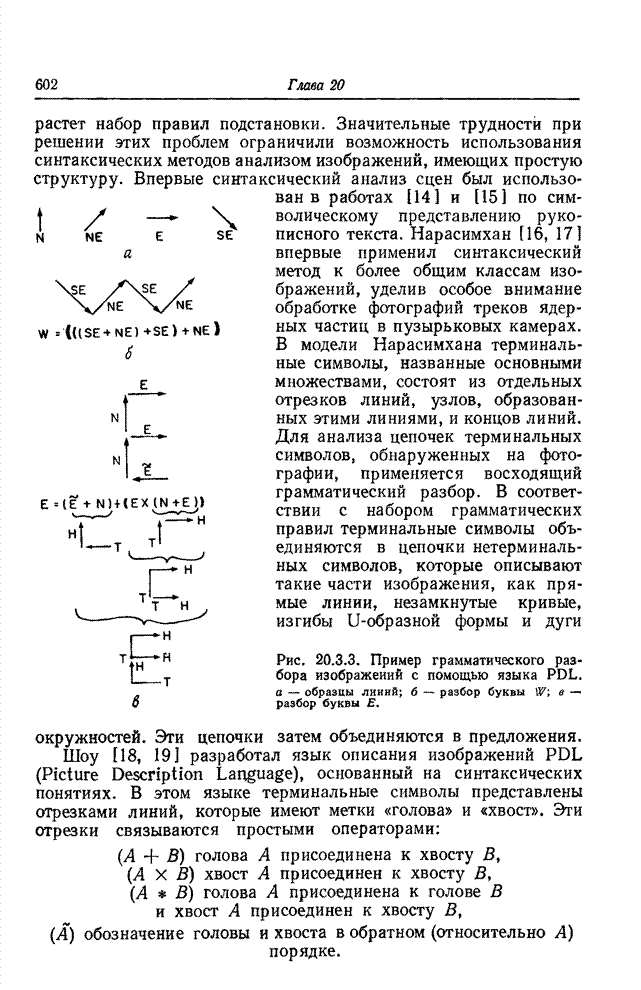
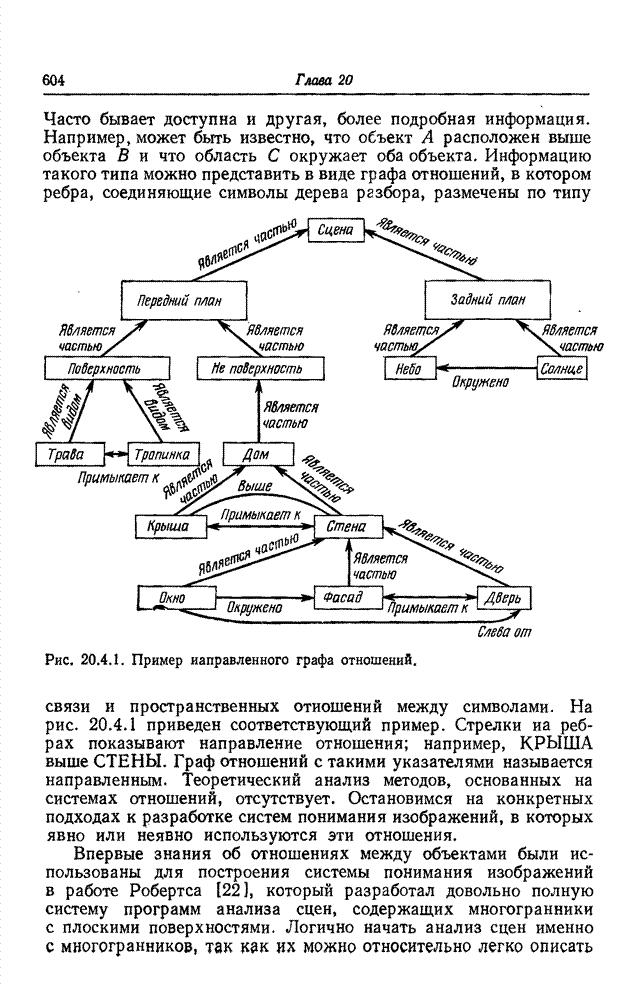
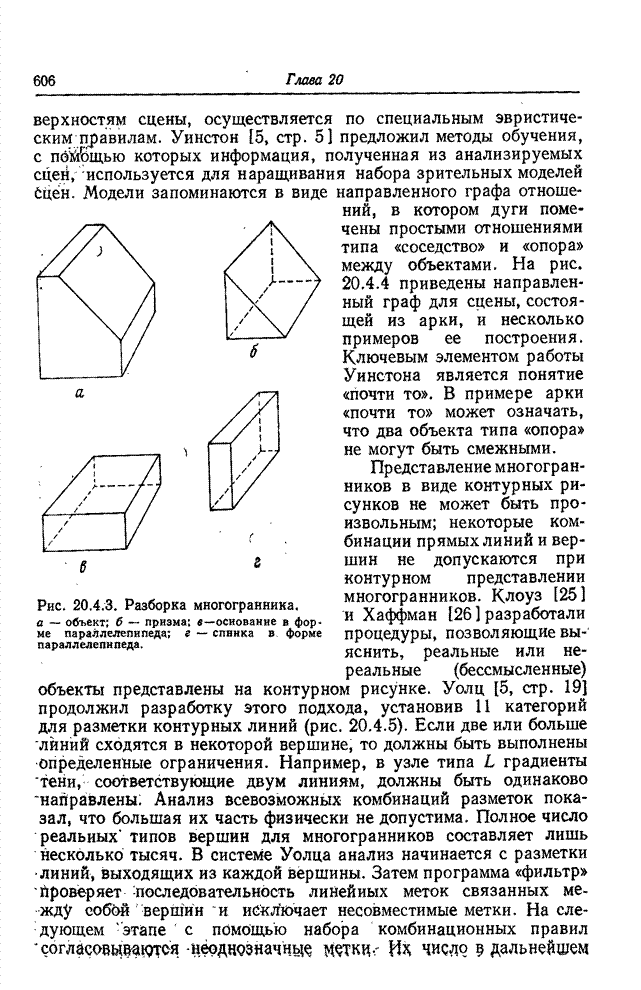
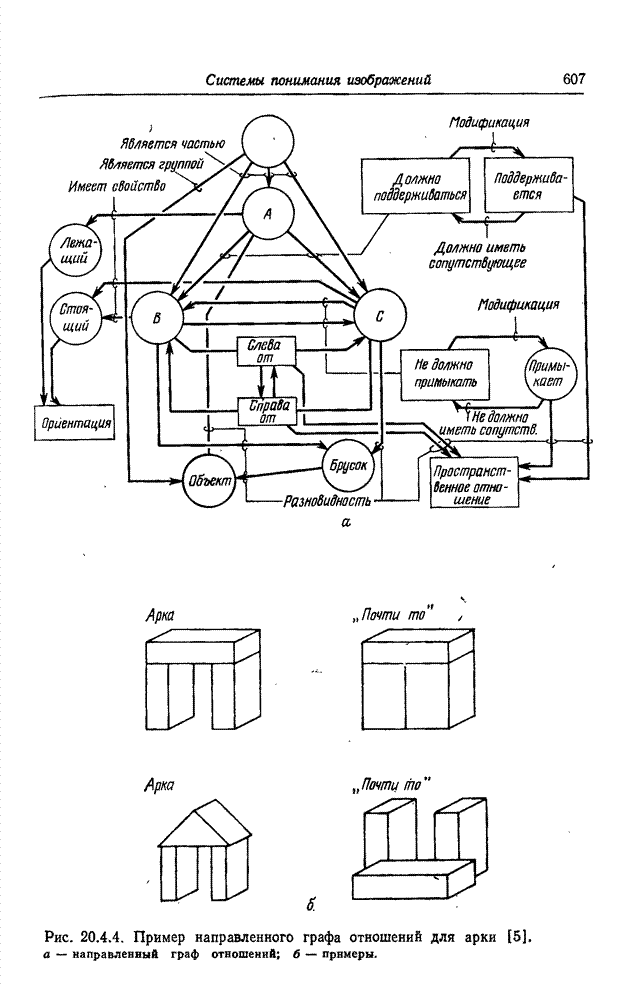
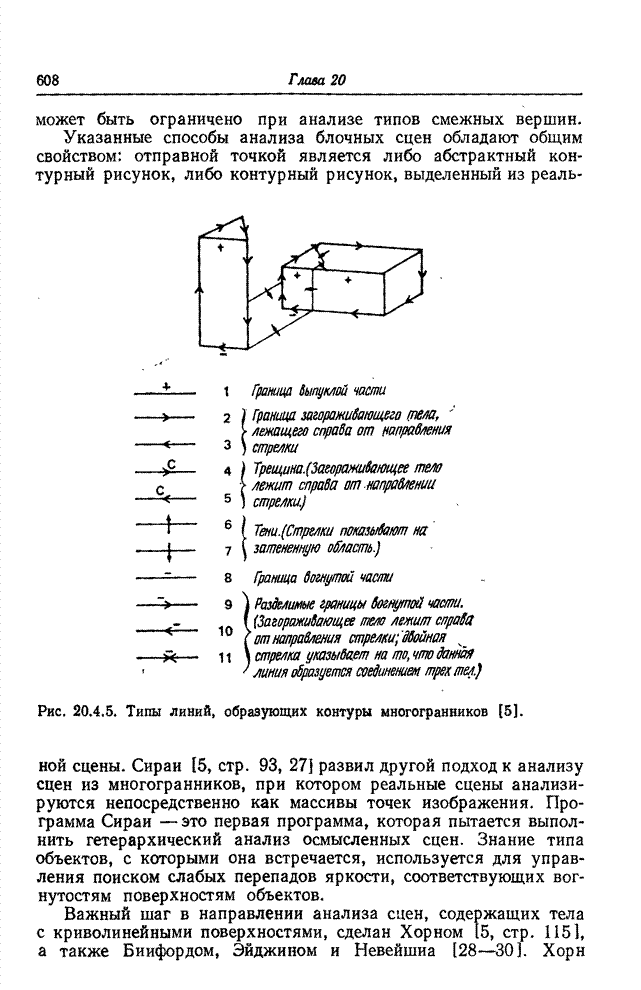
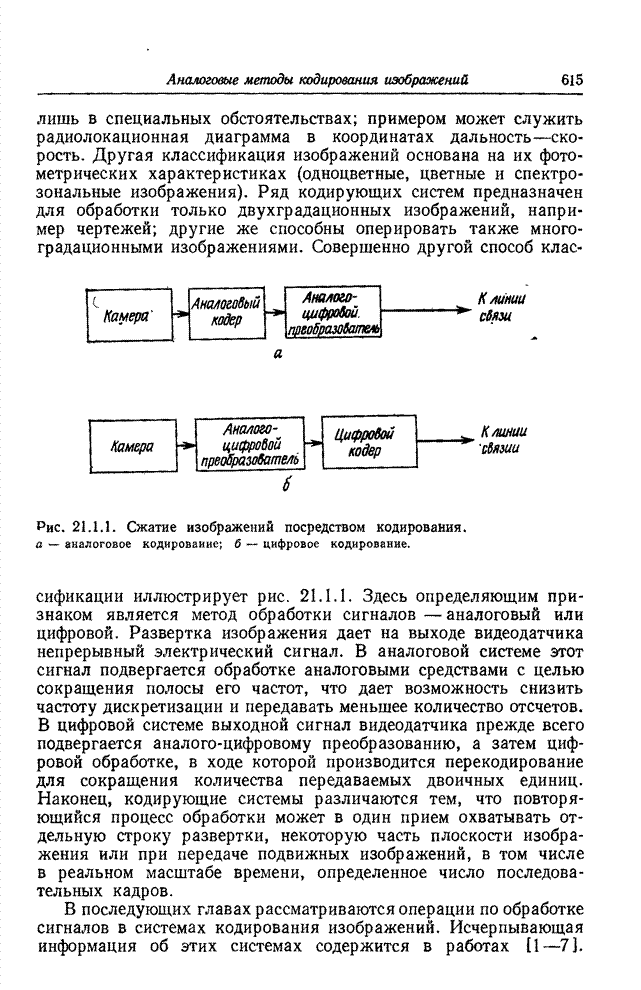
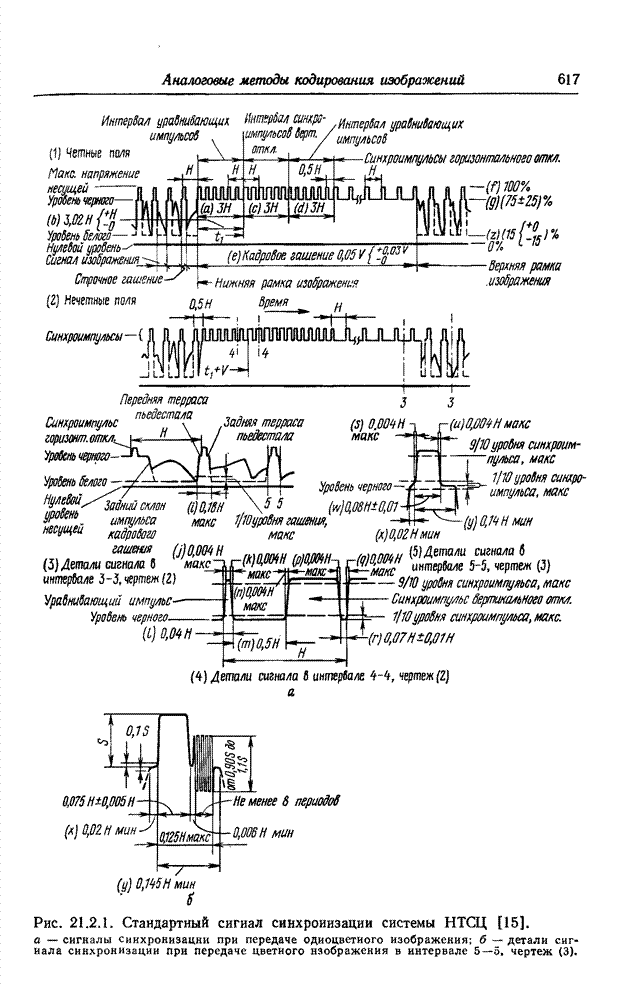
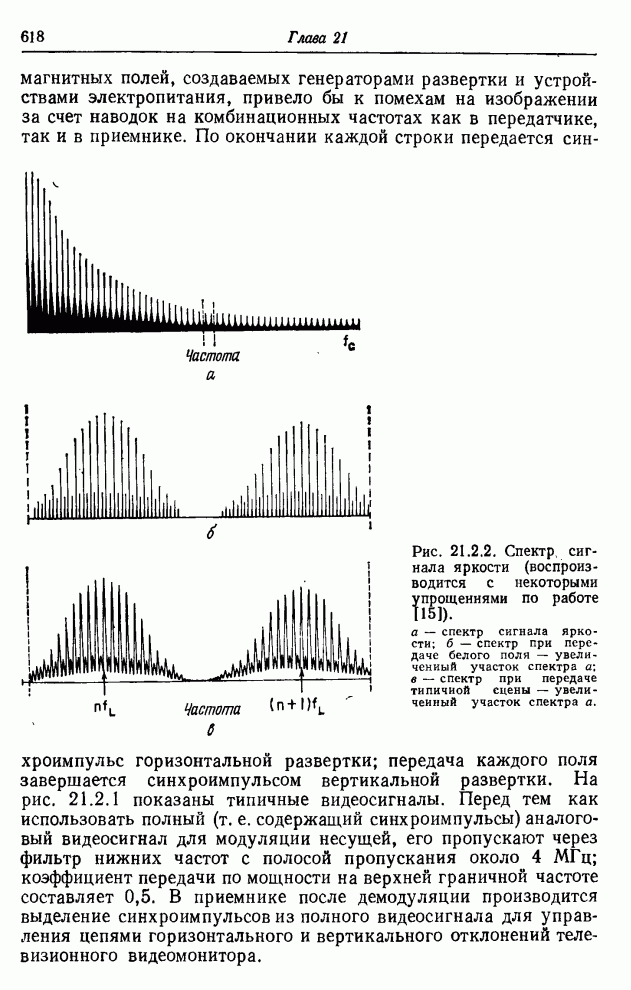
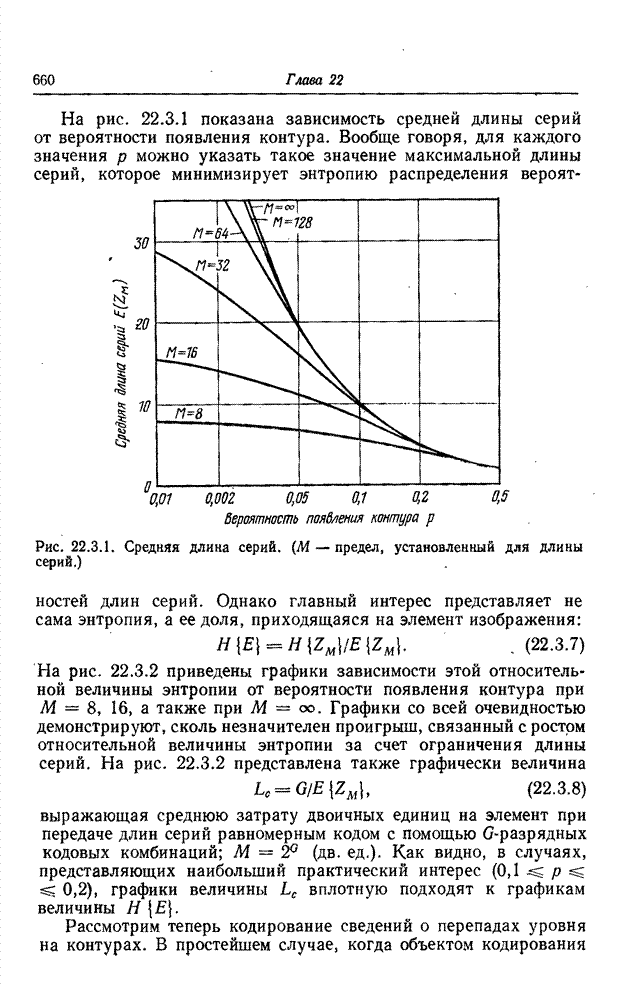
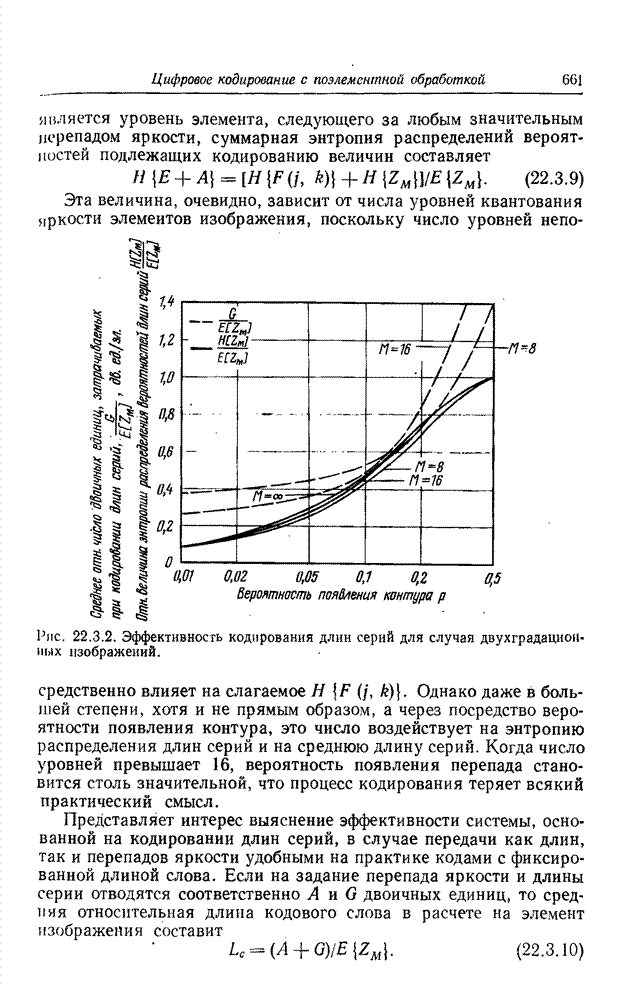
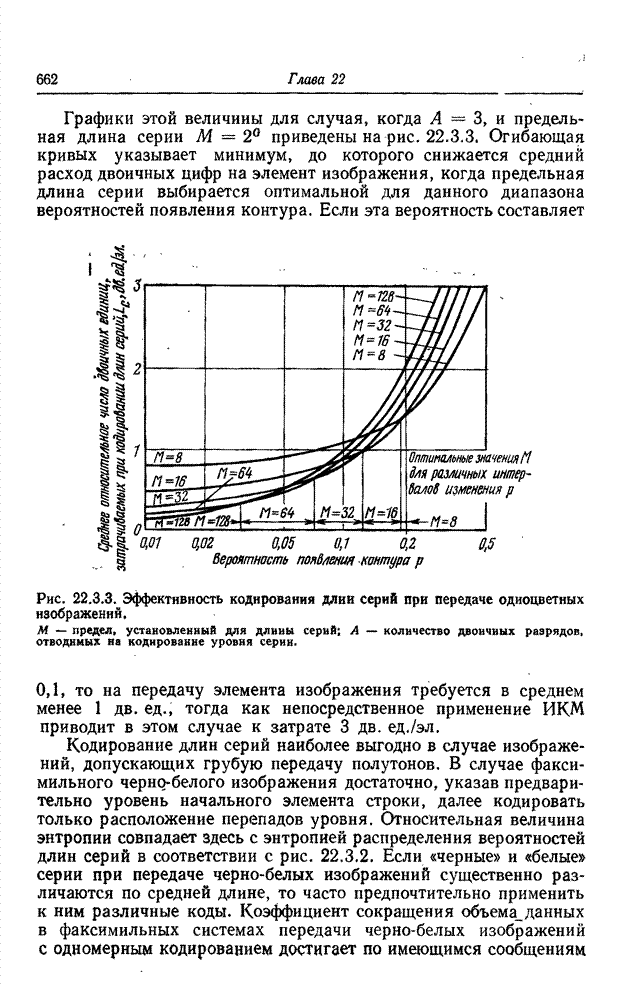
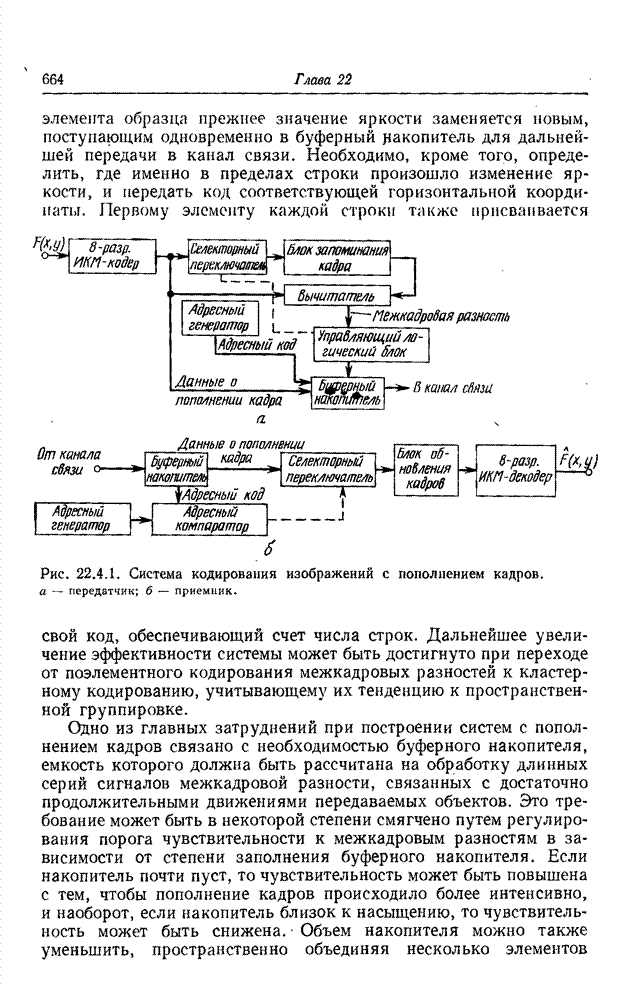
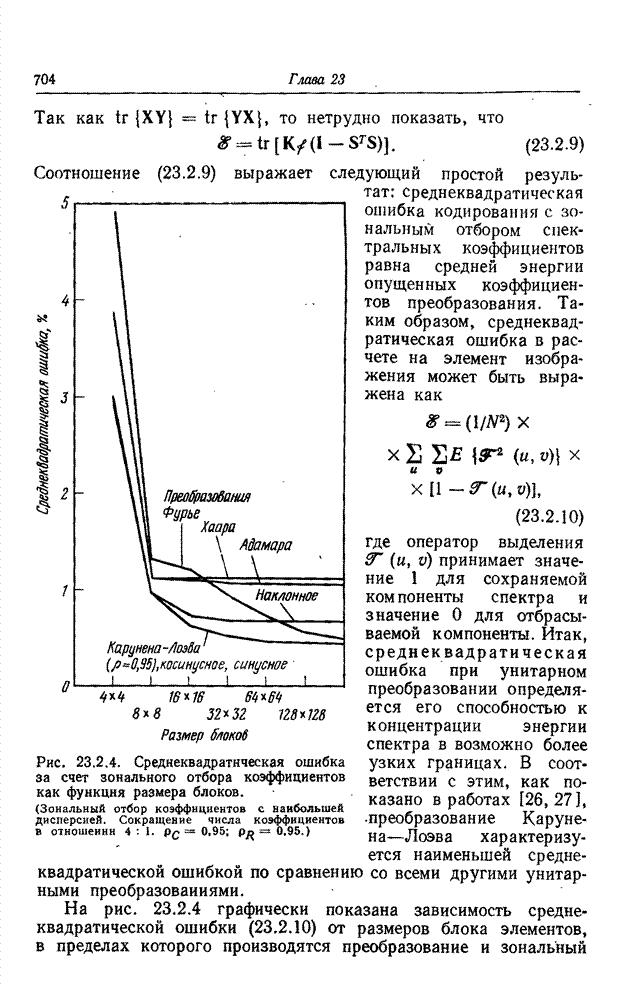
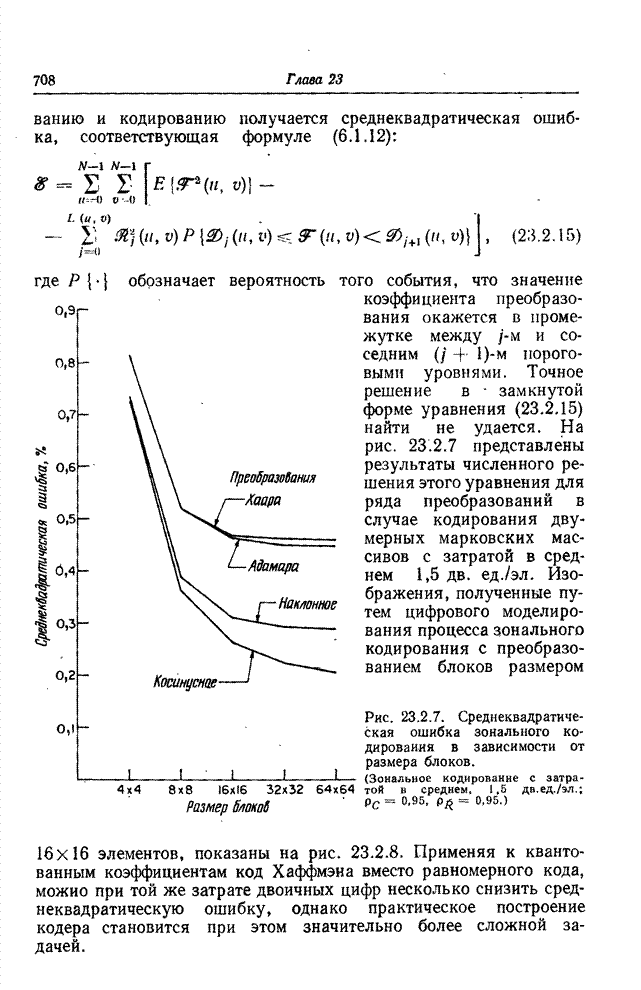
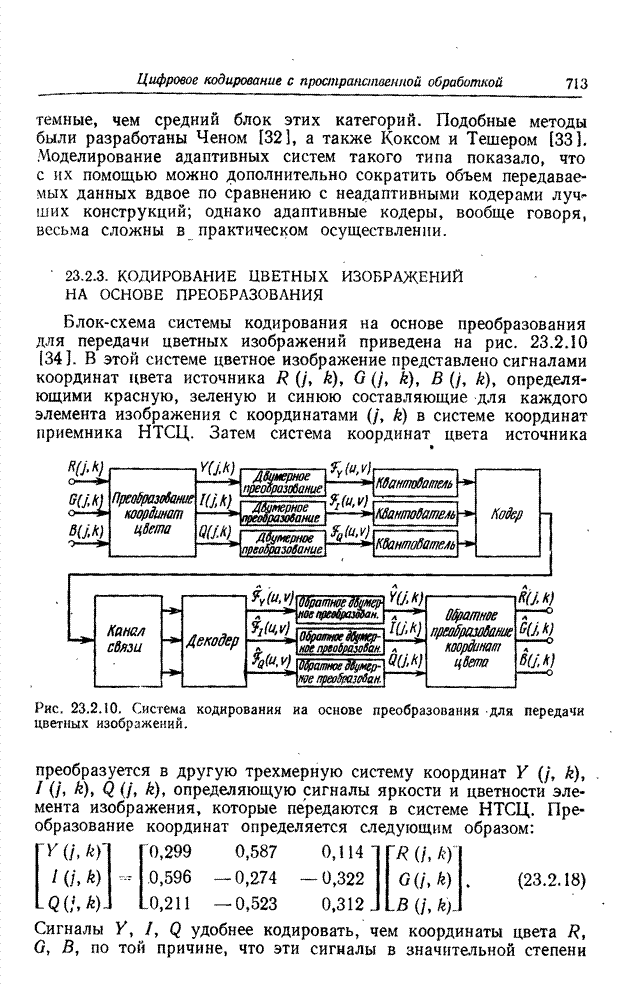
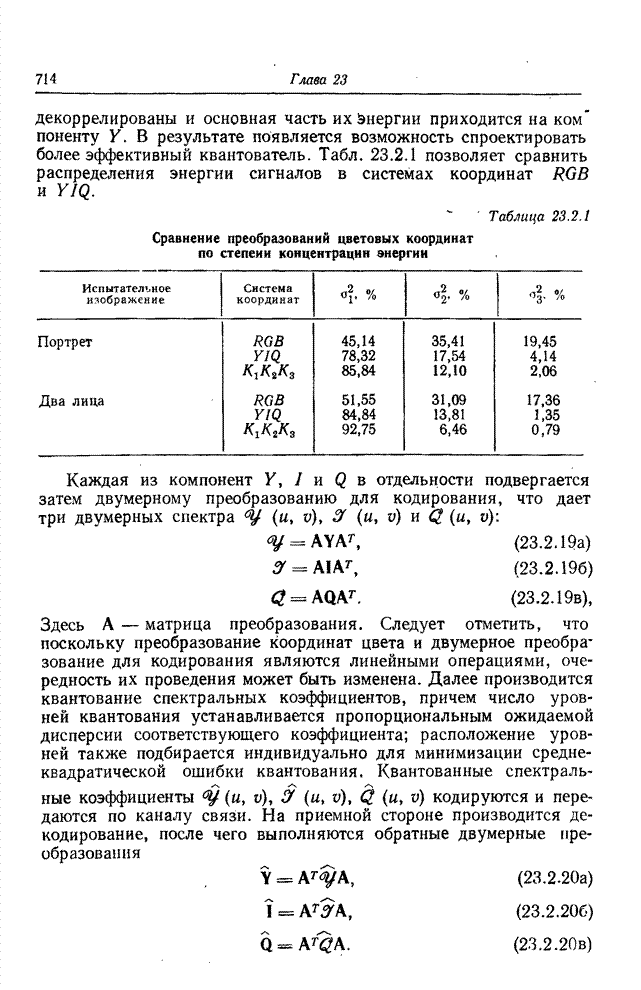
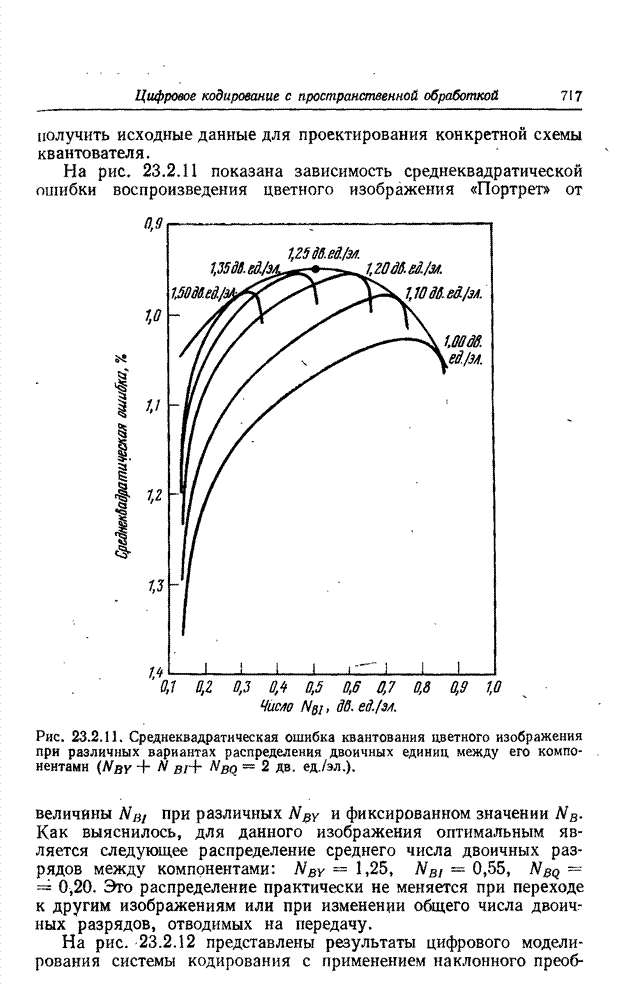
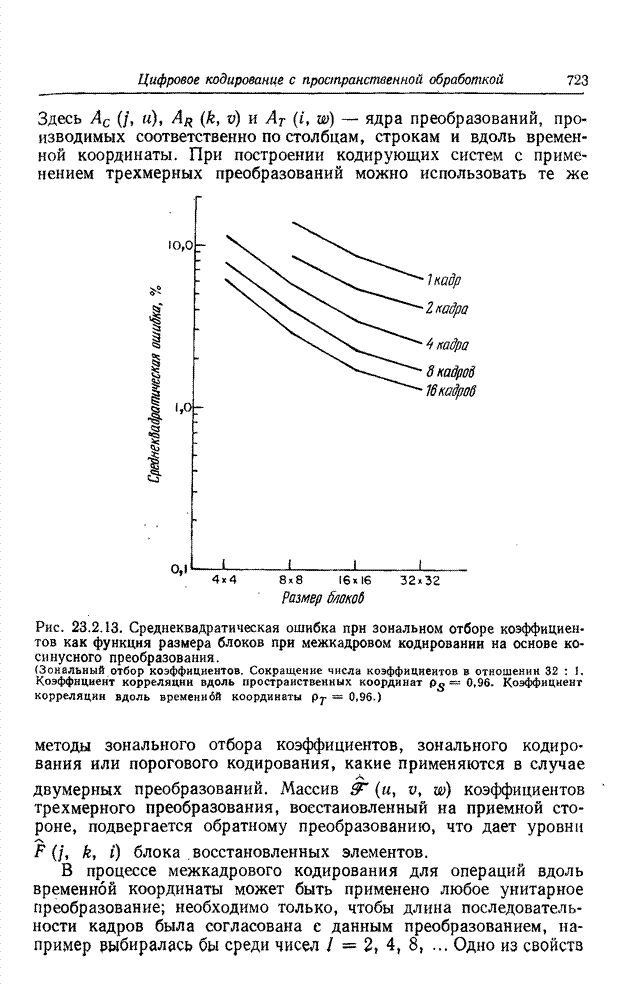
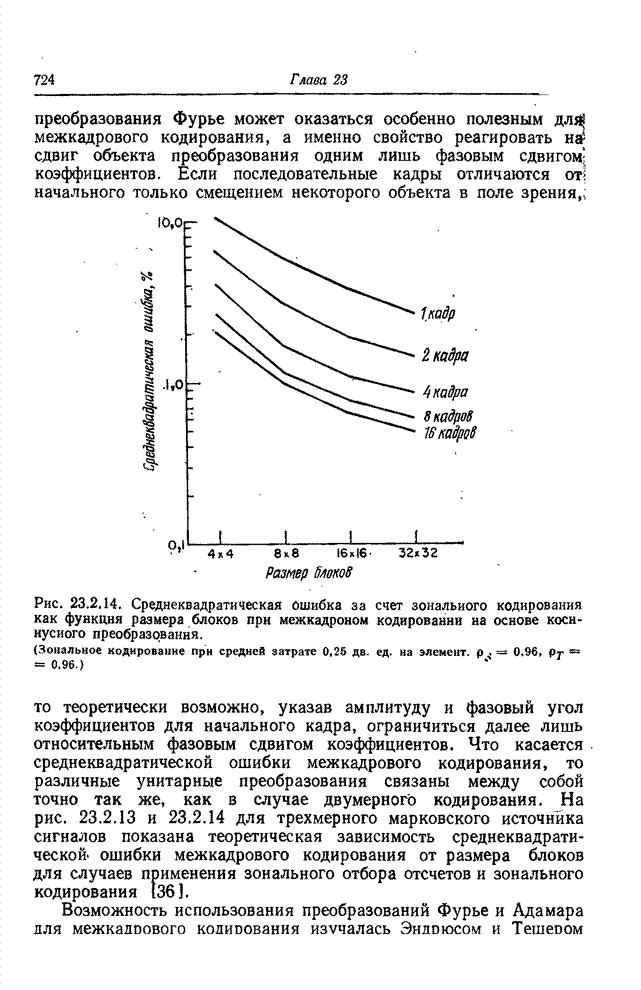
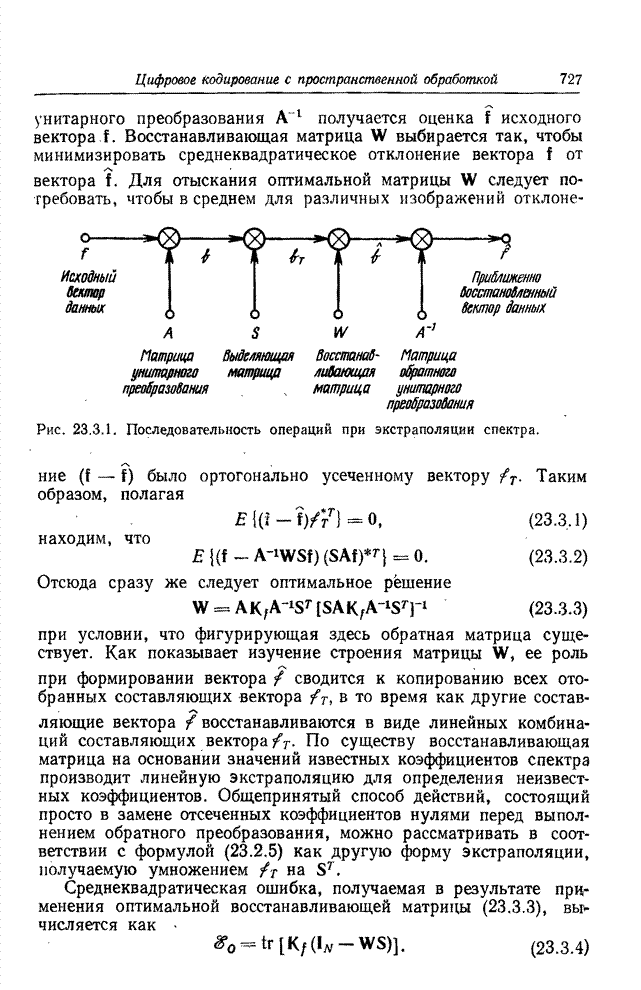
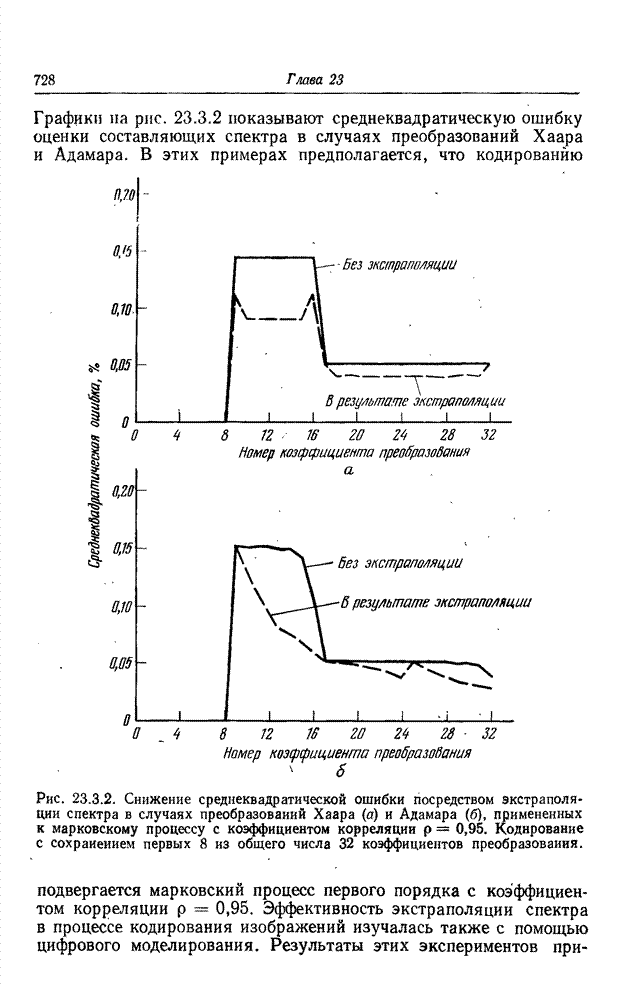
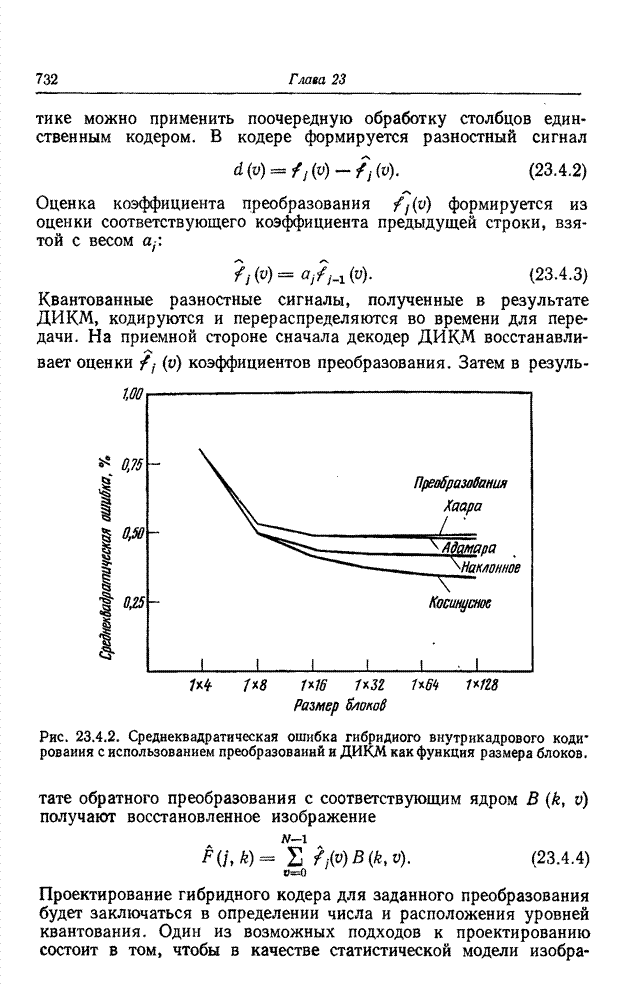
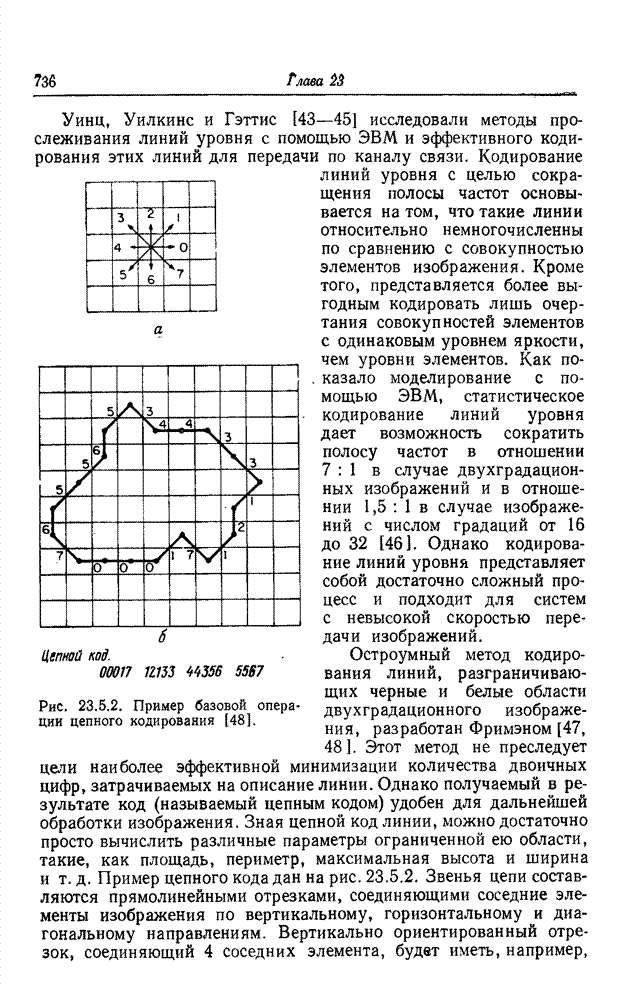
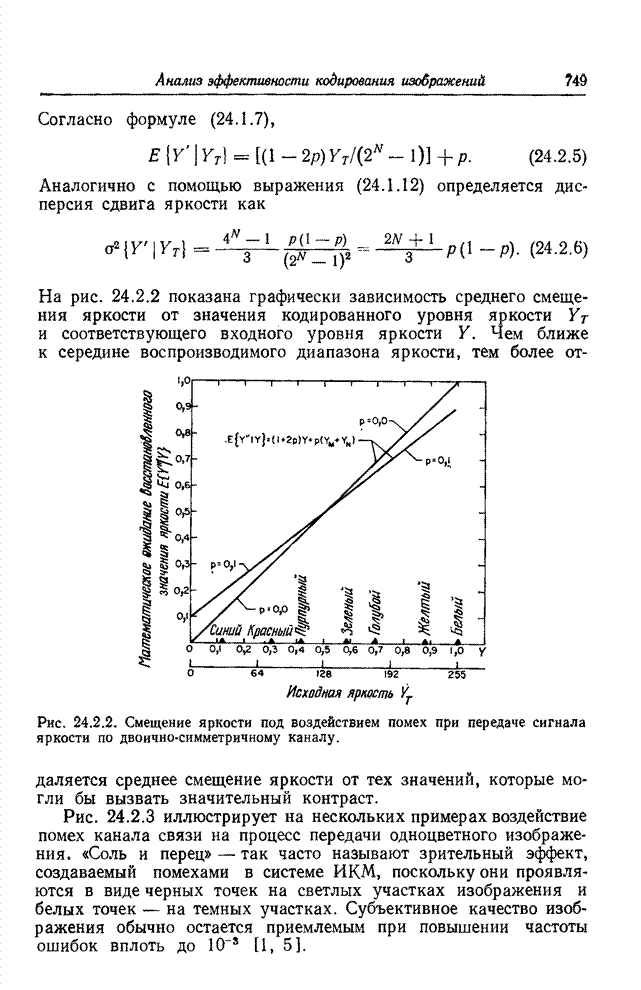
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
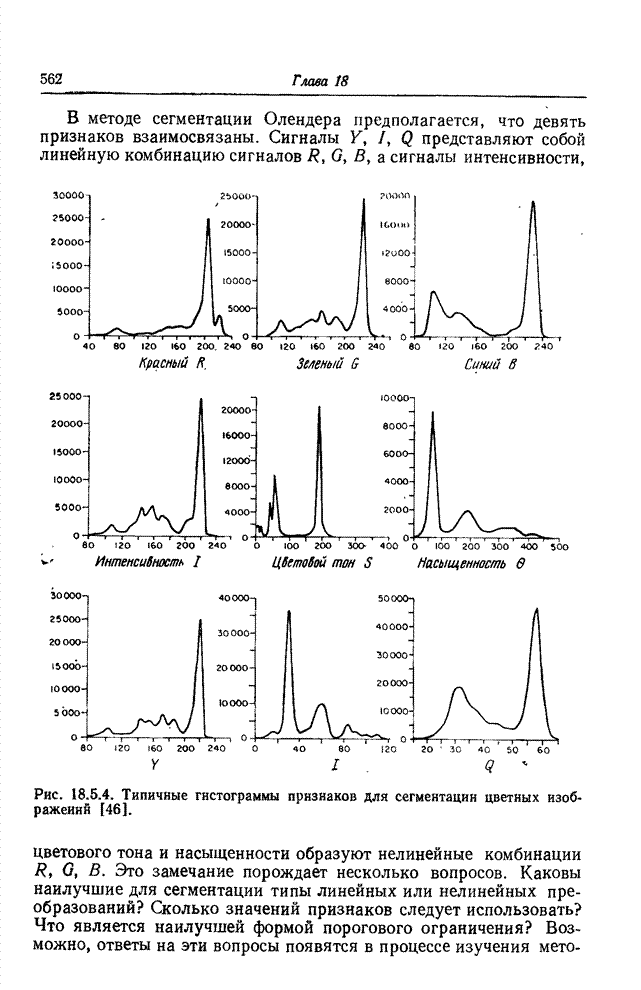
16.3. ОЦЕНИВАНИЕ СПЕКТРАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ИЗЛУЧЕНИЯ
При решении многих задач
реставрации цветных и спектрозональных изображений должна быть найдена оценка
спектрального распределения энергии излучения ![]() по серии наблюдаемых величин
по серии наблюдаемых величин
![]() , (16.3.1)
, (16.3.1)
где ![]() - спектральная характеристика
спектрозонального светофильтра, используемого для получения
- спектральная характеристика
спектрозонального светофильтра, используемого для получения ![]() -й величины,
-й величины, ![]() . Член
. Член ![]() представляет
аддитивный шум или неопределенность измерения. Методы оценивания, описанные в
гл. 14, позволяют найти решение и в рассматриваемом случае [4]. Первый шаг
заключается в получении дискретного представления интеграла, что приводит к
векторному уравнению
представляет
аддитивный шум или неопределенность измерения. Методы оценивания, описанные в
гл. 14, позволяют найти решение и в рассматриваемом случае [4]. Первый шаг
заключается в получении дискретного представления интеграла, что приводит к
векторному уравнению
![]() , (16.3.2)
, (16.3.2)
где ![]() и
и ![]() - векторы, составленные из
- векторы, составленные из ![]() отсчетов функций
отсчетов функций ![]() и
и ![]() соответственно.
Совокупность
соответственно.
Совокупность ![]() наблюдаемых
изображений можно представить вектором размера
наблюдаемых
изображений можно представить вектором размера ![]() :
:
![]() , (16.3.3)
, (16.3.3)
где вектор ![]() находится в
находится в ![]() -м столбце матрицы
-м столбце матрицы ![]() . Чтобы уменьшить
погрешность численного интегрирования до разумных пределов, увеличивают число
узловых точек. При этом система уравнений (16.3.3) обычно оказывается
существенно недоопределенной.
. Чтобы уменьшить
погрешность численного интегрирования до разумных пределов, увеличивают число
узловых точек. При этом система уравнений (16.3.3) обычно оказывается
существенно недоопределенной.
Оценку ![]() истинного спектрального
распределения энергии
истинного спектрального
распределения энергии ![]() получают посредством обобщенного
обращения:
получают посредством обобщенного
обращения:
![]() . (16.3.4)
. (16.3.4)

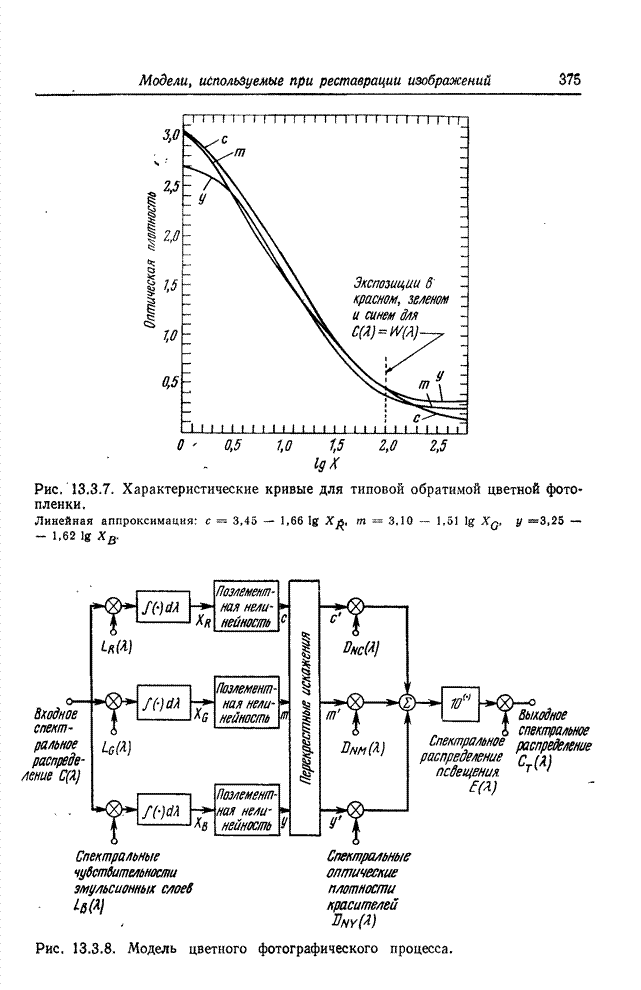
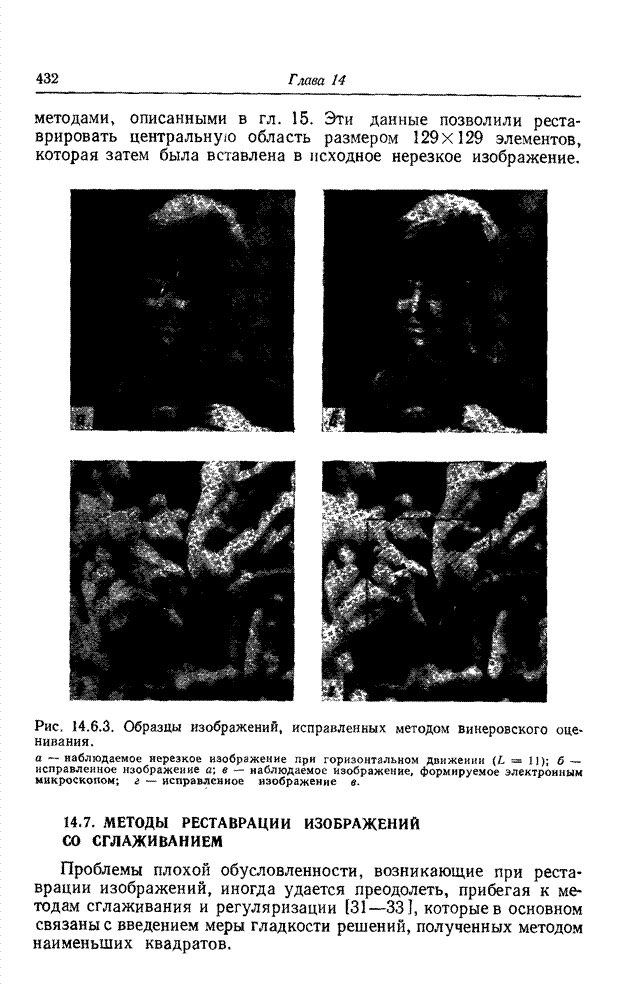
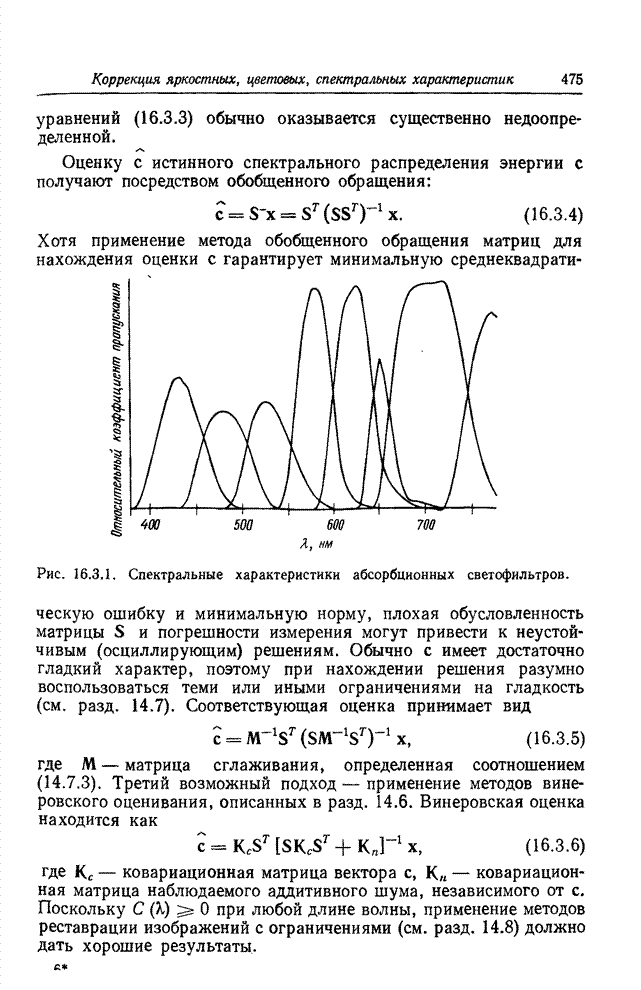
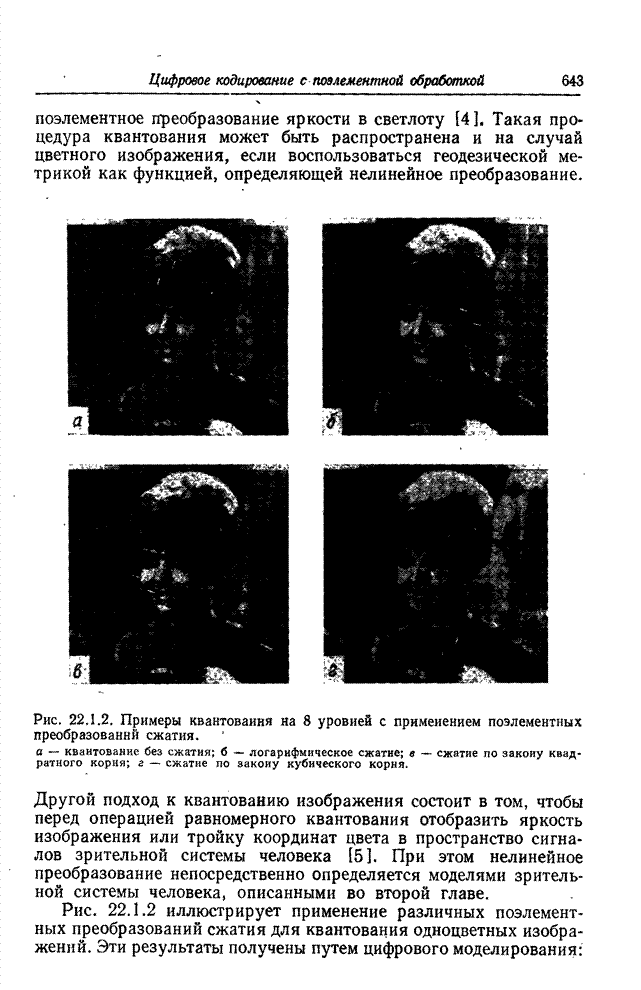
Рис. 16.3.1. Спектральные характеристики абсорбционных светофильтров.
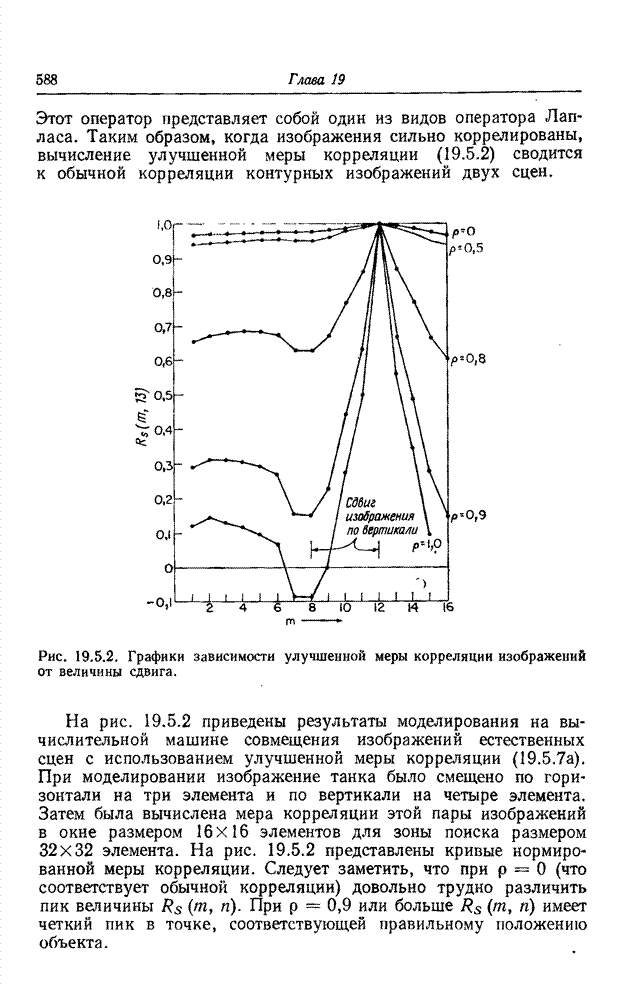
Хотя применение метода
обобщенного обращения матриц для нахождения оценки ![]() гарантирует минимальную
среднеквадратическую ошибку и минимальную норму, плохая обусловленность матрицы
гарантирует минимальную
среднеквадратическую ошибку и минимальную норму, плохая обусловленность матрицы
![]() и
погрешности измерения могут привести к неустойчивым (осциллирующим) решениям.
Обычно
и
погрешности измерения могут привести к неустойчивым (осциллирующим) решениям.
Обычно ![]() имеет
достаточно гладкий характер, поэтому при нахождении решения разумно
воспользоваться теми или иными ограничениями на гладкость (см. разд. 14.7).
Соответствующая оценка принимает вид
имеет
достаточно гладкий характер, поэтому при нахождении решения разумно
воспользоваться теми или иными ограничениями на гладкость (см. разд. 14.7).
Соответствующая оценка принимает вид
![]() , (16.3.5)
, (16.3.5)
где ![]() - матрица сглаживания, определенная
соотношением (14.7.3). Третий возможный подход - применение методов винеровского
оценивания, описанных в разд. 14.6. Винеровская оценка находится как
- матрица сглаживания, определенная
соотношением (14.7.3). Третий возможный подход - применение методов винеровского
оценивания, описанных в разд. 14.6. Винеровская оценка находится как
![]() , (16.3.6)
, (16.3.6)
где ![]() - ковариационная матрица вектора
- ковариационная матрица вектора ![]() ,
, ![]() - ковариационная
матрица наблюдаемого аддитивного шума, независимого от
- ковариационная
матрица наблюдаемого аддитивного шума, независимого от ![]() . Поскольку
. Поскольку ![]() при любой длине,
применение методов реставрации изображений с ограничениями (см. разд. 14.8)
должно дать хорошие результаты.
при любой длине,
применение методов реставрации изображений с ограничениями (см. разд. 14.8)
должно дать хорошие результаты.

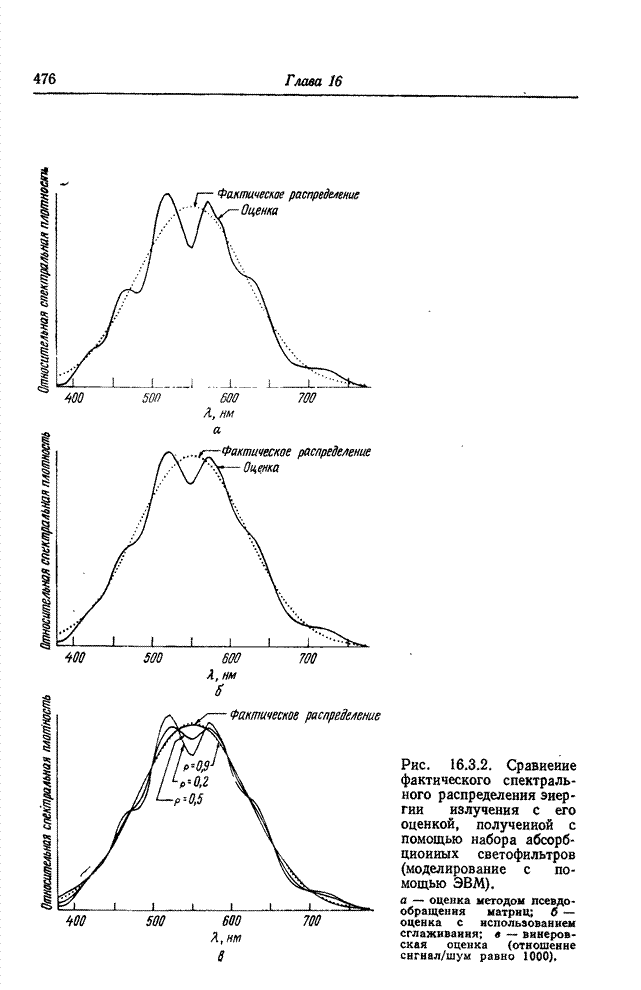
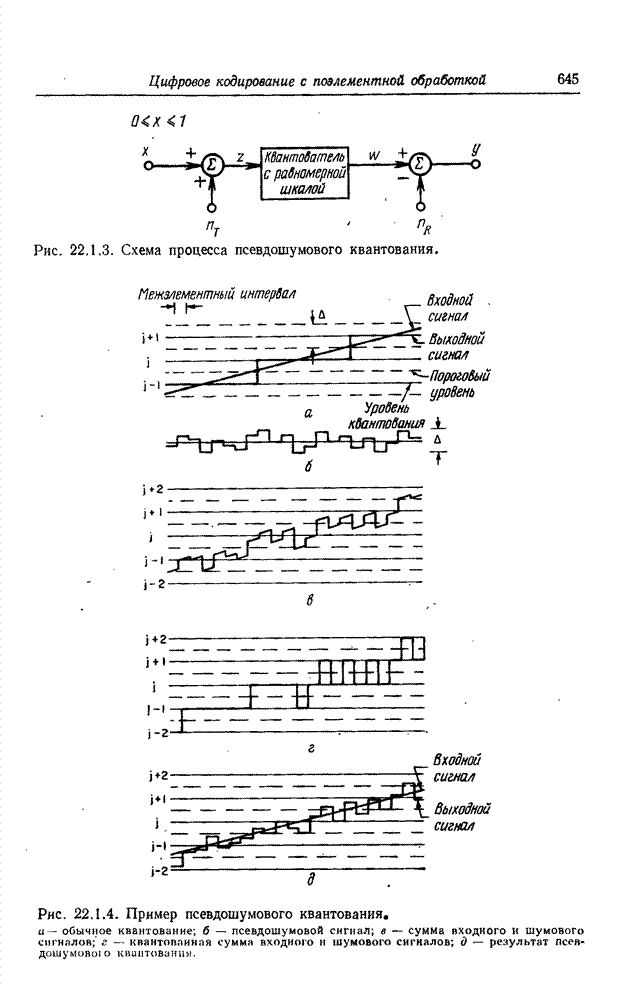
Рис. 16.3.2. Сравнение фактического спектрального распределения энергии излучения с его оценкой, полученной с помощью набора абсорбционных светофильтров (моделирование с помощью ЭВМ): а - оценка методом псевдообращения матриц; б - оценка с использованием сглаживания; в - винеровская оценка (отношение сигнал/шум равно 1000).
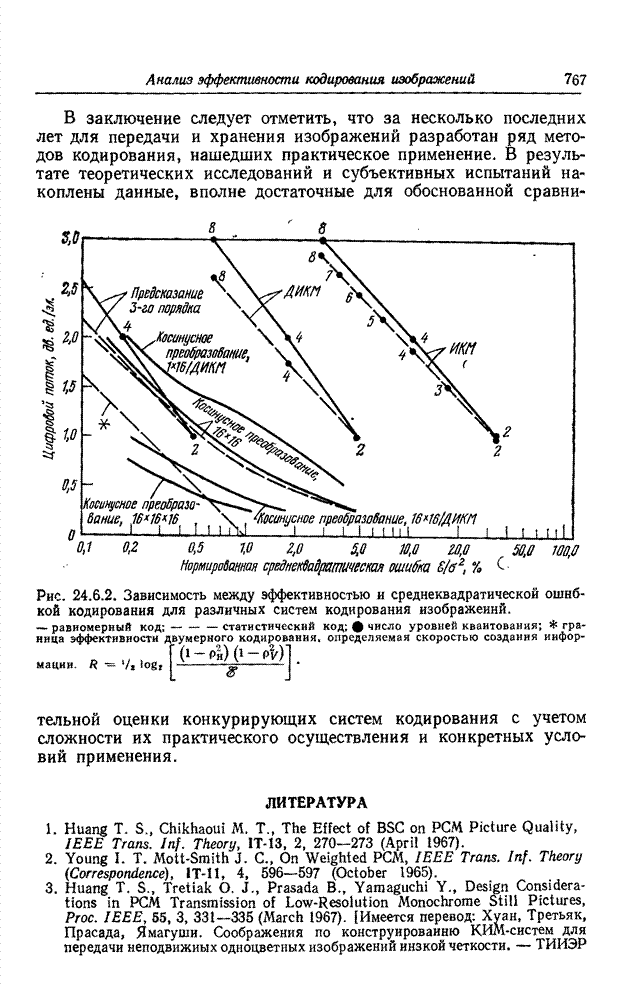
Для сравнения указанных методов
оценивания был проведен эксперимент, в котором с помощью ЭВМ моделировались
измерения гауссова спектрального распределения энергии излучения с помощью
набора различных светофильтров. На рис. 16.3.1 показаны спектральные
характеристики этих светофильтров. Результаты измерений использовались в
качестве спектрозональных наблюдаемых величин (16.3.1), по которым находилась
оценка распределения ![]() . Рис. 16.3.2 иллюстрирует
эффективность трех методов оценивания: посредством псевдообращения матриц, с
использованием сглаживания и винеровского. Винеровская оценка получена при
допущениях, что шум белый, а распределение
. Рис. 16.3.2 иллюстрирует
эффективность трех методов оценивания: посредством псевдообращения матриц, с
использованием сглаживания и винеровского. Винеровская оценка получена при
допущениях, что шум белый, а распределение ![]() - реализация марковского процесса.
Эксперименты показали, что минимальную среднеквадратическую ошибку аппроксимации
исходного распределения
- реализация марковского процесса.
Эксперименты показали, что минимальную среднеквадратическую ошибку аппроксимации
исходного распределения ![]() оценкой
оценкой ![]() обеспечивает метод винеровского
оценивания при коэффициенте корреляции марковского процесса
обеспечивает метод винеровского
оценивания при коэффициенте корреляции марковского процесса ![]() и отношении сигнал/шум,
равном 1000.
и отношении сигнал/шум,
равном 1000.
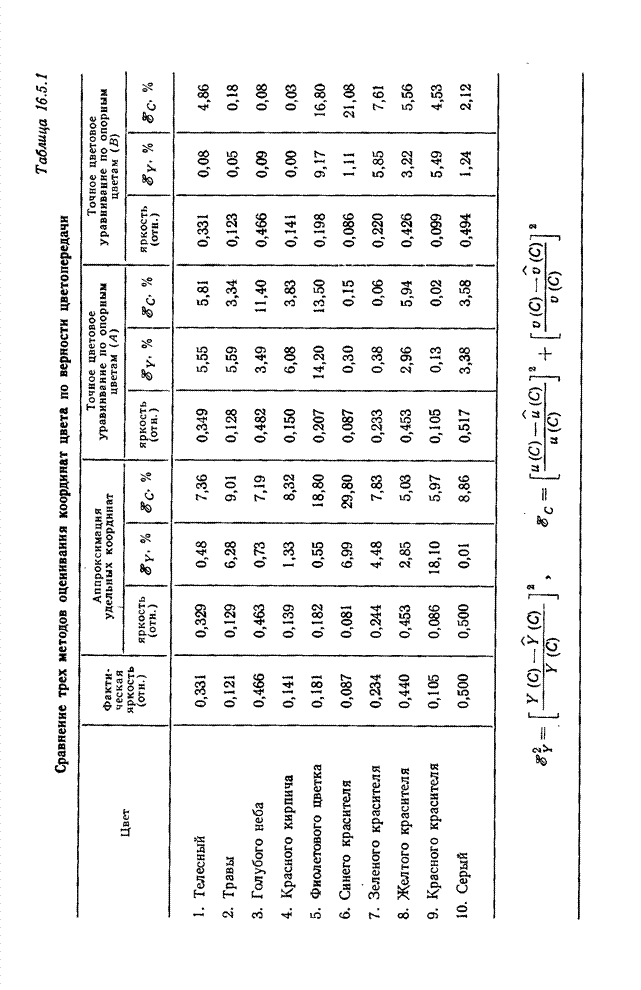
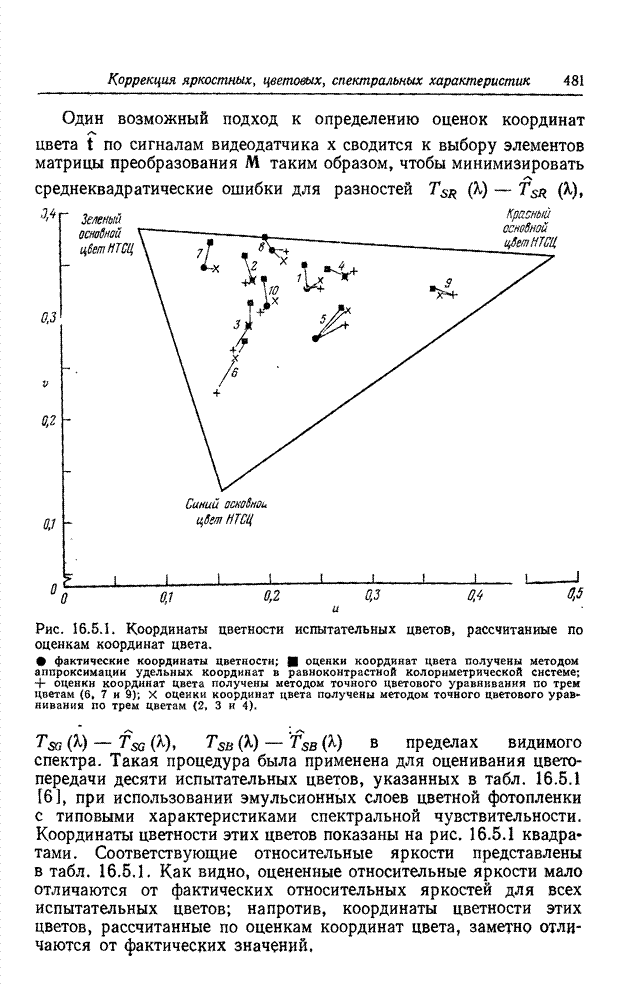
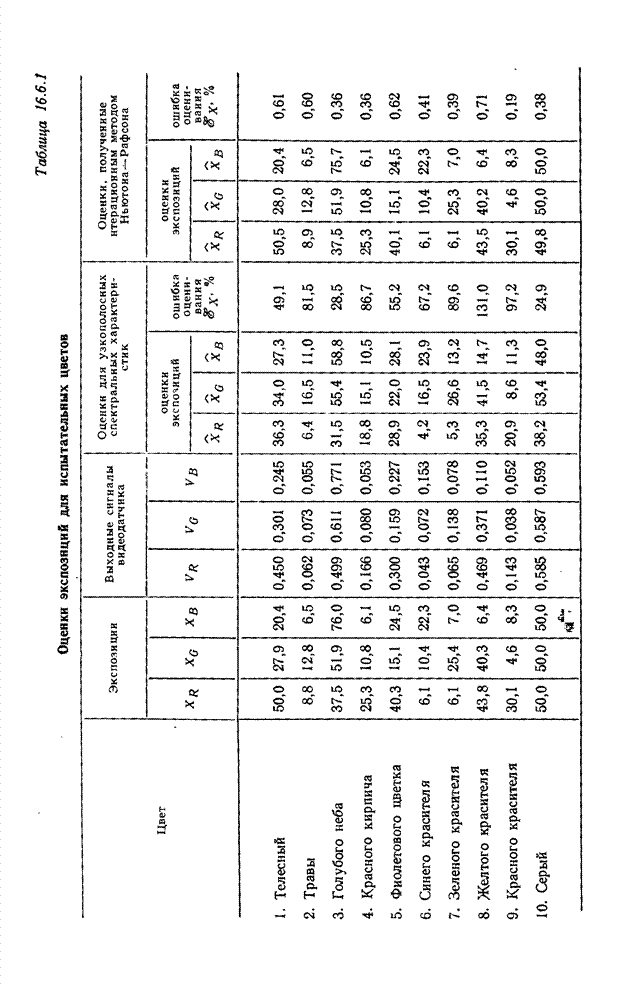
В работе [4] рассмотрен пример спектральной калибровки датчика цветового видеосигнала методом оценивания спектрального распределения энергии излучения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Часть 4. РЕСТАВРАЦИЯ И УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
- Глава 12. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
- 12.1. ИЗМЕНЕНИЕ КОНТРАСТА
- 12.2. ВИДОИЗМЕНЕНИЕ ГИСТОГРАММ
- 12.3. ПОДАВЛЕНИЕ ШУМОВ
- 12.4. ПОДЧЕРКИВАНИЕ ГРАНИЦ
- 12.5. ОБРАБОТКА ИЗОБРАЖЕНИЙ С ПРЕОБРАЗОВАНИЕМ
- 12.6. МЕДИАННЫЙ ФИЛЬТР
- 12.7. ЛОЖНЫЕ ЦВЕТА
- 12.8. ПСЕВДОЦВЕТА
- 12.9. УЛУЧШЕНИЕ СПЕКТРОЗОНАЛЬНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 13. МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.1. ОБОБЩЕННЫЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.2. МОДЕЛИ ОПТИЧЕСКИХ СИСТЕМ
- 13.3. МОДЕЛИ ФОТОГРАФИЧЕСКИХ ПРОЦЕССОВ
- 13.3.1. ОДНОЦВЕТНАЯ ФОТОГРАФИЯ
- 13.3.2. ЦВЕТНАЯ ФОТОГРАФИЯ
- 13.4. МОДЕЛИ ЦИФРОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- 13.5. МОДЕЛЬ ДИСПЛЕЯ
- 13.6. МОДЕЛИ ШУМОВ ИЗОБРАЖЕНИЯ
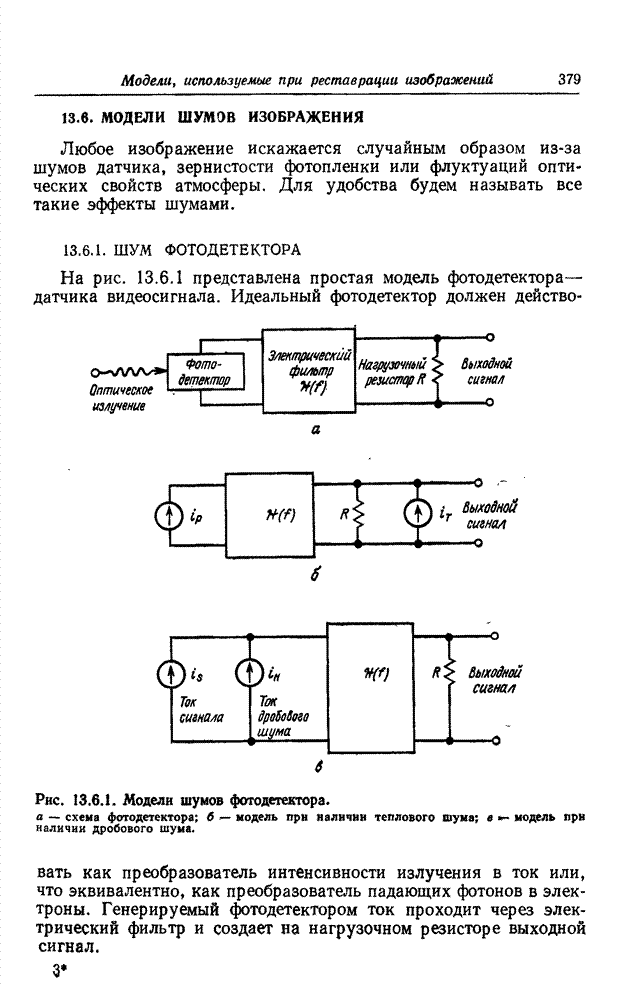
- 13.6.1. ШУМ ФОТОДЕТЕКТОРА
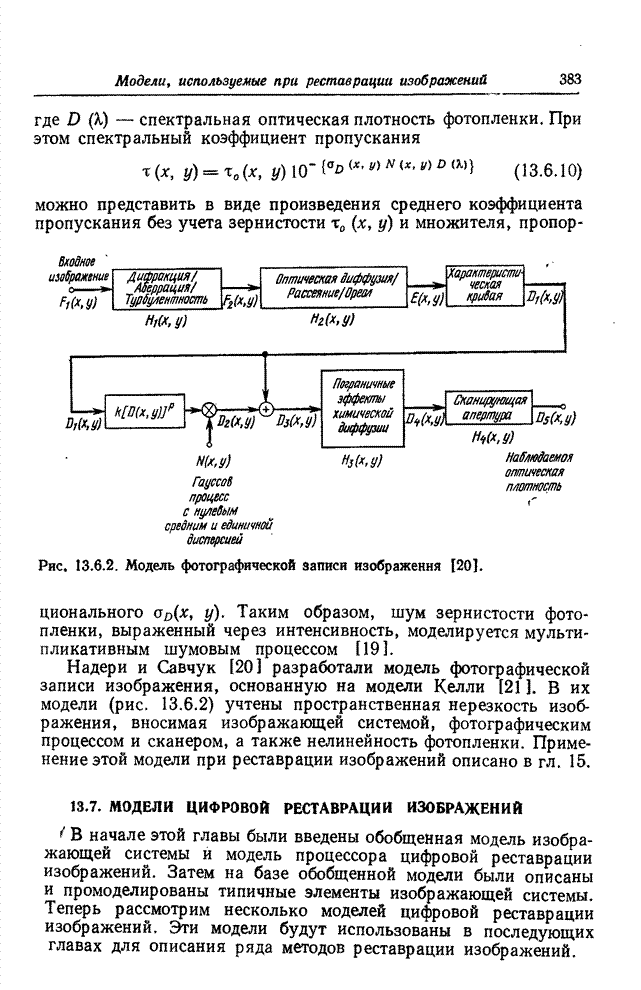
- 13.6.2. ШУМ ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
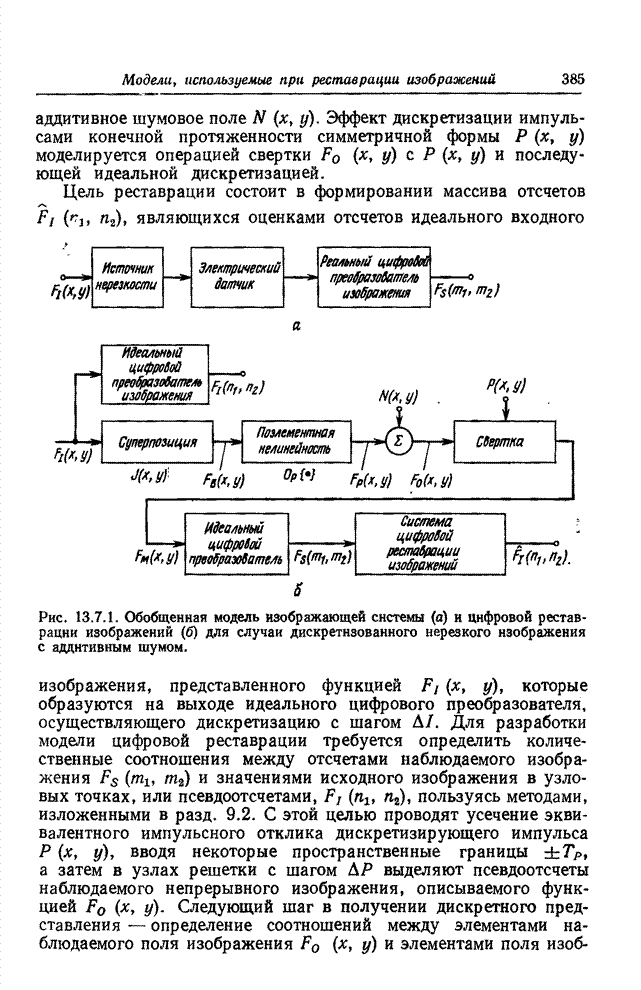
- 13.7. МОДЕЛИ ЦИФРОВОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 14. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 14.1. МЕТОДЫ ПРОСТРАНСТВЕННОЙ ФИЛЬТРАЦИИ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 14.1.1. ИНВЕРСНАЯ ФИЛЬТРАЦИЯ
- 14.1.2. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И АДДИТИВНЫЙ ШУМ
- 14.1.3. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНОЕ ИЗОБРАЖЕНИЕ
- 14.1.4. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНАЯ НЕРЕЗКОСТЬ
- 14.1.5. ФИЛЬТРЫ НА ОСНОВЕ ПАРАМЕТРИЧЕСКИХ ОЦЕНОК
- 14.1.6. ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 4.2. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.2.1. РЕСТАВРАЦИЯ НЕРЕЗКИХ ИЗОБРАЖЕНИЙ
- 14.2.2. РЕСТАВРАЦИЯ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ ПРИ НАЛИЧИИ ШУМА
- 14.3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.3.1. АЛГОРИТМ ДЛЯ ПЕРЕОПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.3.2. АЛГОРИТМ ДЛЯ НЕДООПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.4. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ С ИСПОЛЬЗОВАНИЕМ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- 14.5. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕГРЕССИИ
- 14.6. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ВИНЕРОВСКОГО ОЦЕНИВАНИЯ
- 14.6.1. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В ОБЩЕМ СЛУЧАЕ
- 14.6.2. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В СЛУЧАЕ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ С ШУМОМ
- 14.7. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ СО СГЛАЖИВАНИЕМ
- 14.8. МЕТОДЫ РЕСТАВРАЦИИ С ИСПОЛЬЗОВАНИЕМ ОГРАНИЧЕНИЙ
- 14.9. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
- ЛИТЕРАТУРА
- Глава 15. CПЕЦИАЛЬНЫЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 15.1. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮ ПОДАВЛЕНИЯ ОШИБОК НАЛОЖЕНИЯ СПЕКТРОВ
- 15.2. КОРРЕКЦИЯ ОШИБОК ИНТЕРПОЛЯЦИИ
- 15.3. КОРРЕКЦИЯ ГЕОМЕТРИЧЕСКИХ ИСКАЖЕНИЙ
- 15.4. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ГОМОМОРФНОЙ ФИЛЬТРАЦИИ
- 15.5. СЛЕПАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ
- 15.5.1. МЕТОДЫ НА ОСНОВЕ ПРЯМЫХ ИЗМЕРЕНИЙ
- 15.5.2. МЕТОДЫ НА ОСНОВЕ КОСВЕННОГО ОЦЕНИВАНИЯ
- 15.6. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ СПЕКТРА
- 15.7. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННО-ЗАВИСИМЫМИ ИСКАЖЕНИЯМИ
- 15.8. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕКУРСИВНОЙ ФИЛЬТРАЦИИ
- 15.9. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮОСЛАБЛЕНИЯ ШУМА ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- ЛИТЕРАТУРА
- Глава 16. КОРРЕКЦИЯ ЯРКОСТНЫХ, ЦВЕТОВЫХ И СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗОБРАЖАЮЩИХ СИСТЕМ
- 16.1. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ВИДЕОДАТЧИКОВ
- 16.2. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ДИСПЛЕЕВ
- 16.3. ОЦЕНИВАНИЕ СПЕКТРАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 16.4. КОРРЕКЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ВИДЕОДАТЧИКОВ И ДИСПЛЕЕВ
- 16.5. ОЦЕНИВАНИЕ КООРДИНАТ СВЕТА ВИДЕОДАТЧИКОВ
- 16.6. ОЦЕНИВАНИЕ ЭКСПОЗИЦИЙ ЦВЕТНОЙ ФОТОПЛЕНКИ
- 16.7. КОМПЕНСАЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ ЦВЕТНЫХ ДИСПЛЕЕВ
- ЛИТЕРАТУРА
- Часть 5. АНАЛИЗ ИЗОБРАЖЕНИЙ
- Глава 17. ВЫДЕЛЕНИЕ ПРИЗНАКОВ ИЗОБРАЖЕНИЯ
- 17.1. ЯРКОСТНЫЕ ПРИЗНАКИ
- 17.2. ГИСТОГРАММНЫЕ ПРИЗНАКИ
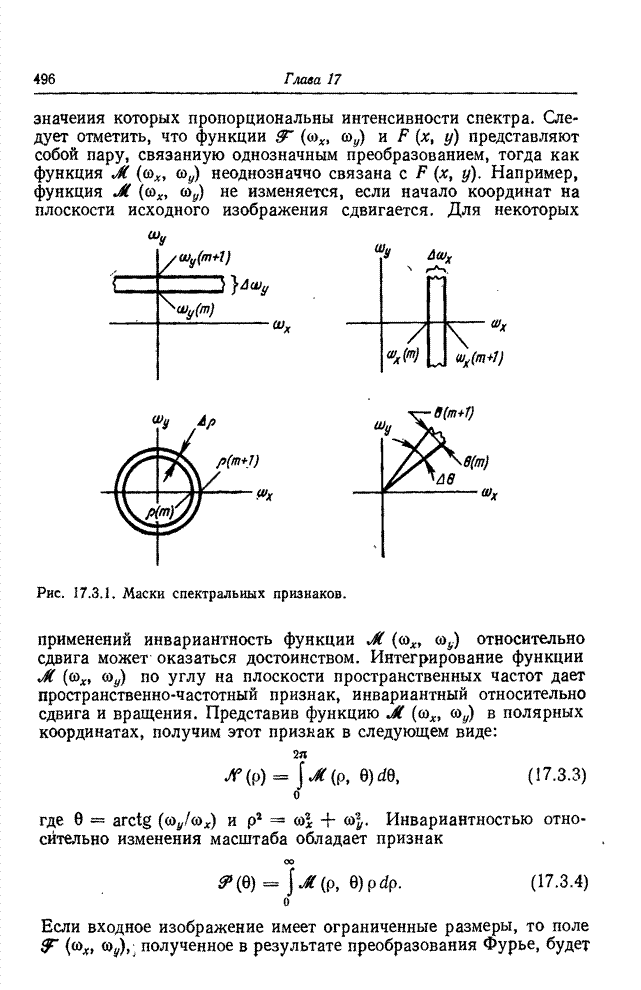
- 17.3. ПРОСТРАНСТВЕННО-СПЕКТРАЛЬНЫЕ ПРИЗНАКИ
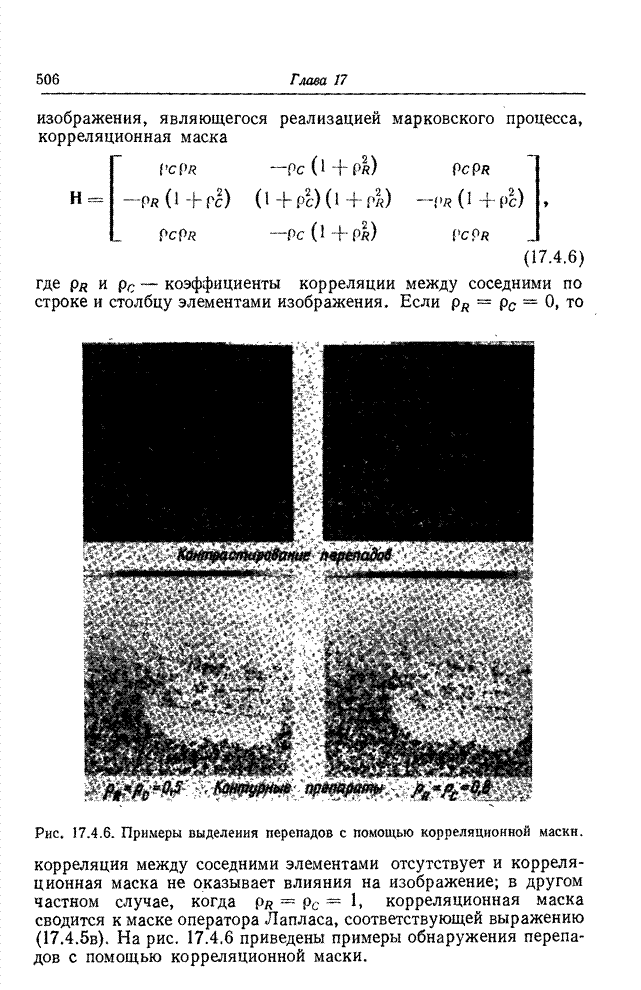
- 17.4. КОНТУРНЫЕ ПРИЗНАКИ
- 17.4.1. ЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.2. НЕЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.3. МЕТОДЫ АППРОКСИМАЦИИ ПЕРЕПАДОВ ЯРКОСТИ
- 17.4.4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ
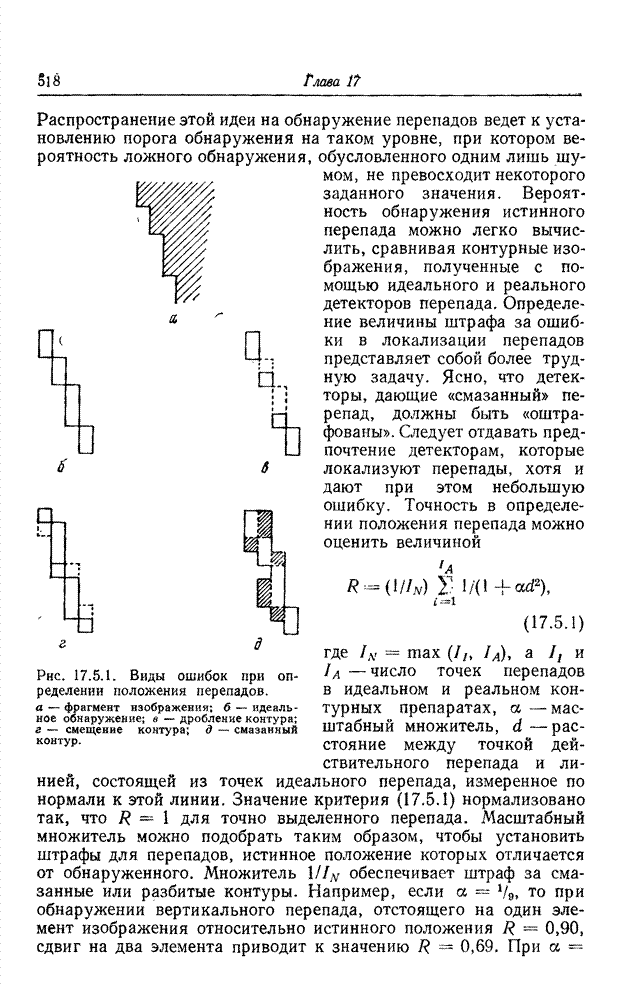
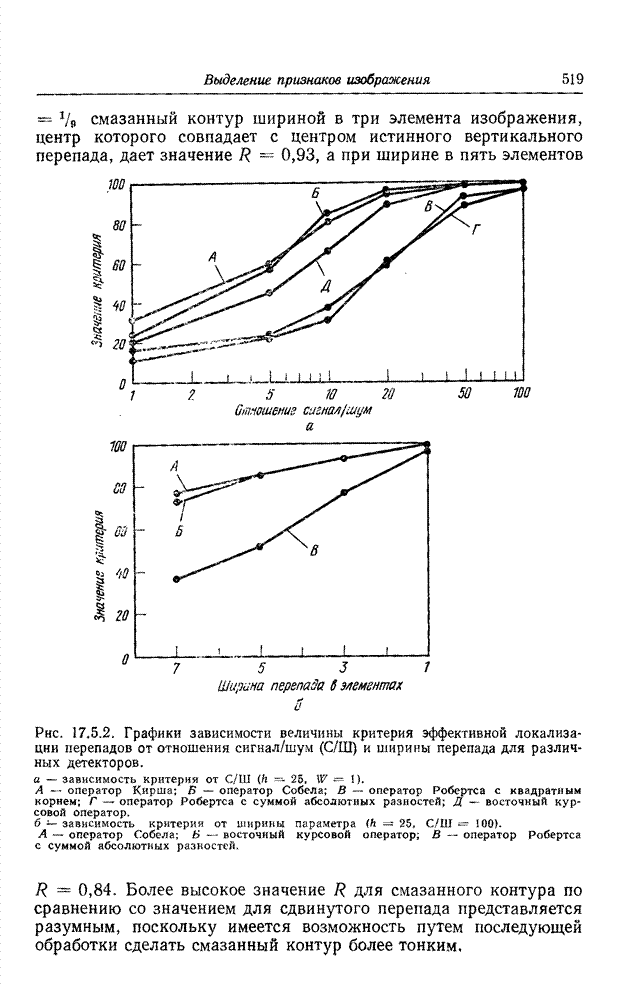
- 17.5. ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ ЯРКОСТИ
- 17.6. ЦВЕТОВЫЕ КОНТУРЫ
- 17.7. ПРИЗНАКИ ПЯТНА И ЛИНИИ
- 17.8. ТЕКСТУРНЫЕ ПРИЗНАКИ
- 17.9. СИНТЕЗ ТЕКСТУР
- ЛИТЕРАТУРА
- Глава 18. СИМВОЛИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
- 18.1. СВЯЗНОСТЬ
- 18.2. СЖАТИЕ, УТОНЧЕНИЕ И ПОСТРОЕНИЕ ОСТОВА
- 18.3. ОПИСАНИЕ ЛИНИЙ
- 18.3.1. АППРОКСИМАЦИЯ КРИВЫХ
- 18.3.2. ПРЕОБРАЗОВАНИЕ ЛИНИИ В ТОЧКУ
- 18.4. ОПИСАНИЕ ФОРМЫ
- 18.4.1. МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.2. ТОПОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.3. АНАЛИТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.5. СЕГМЕНТАЦИЯ ПО ЯРКОСТИ
- 18.5.1. ПОРОГОВОЕ ОГРАНИЧЕНИЕ ПО ЯРКОСТИ
- 18.5.2. МНОГОМЕРНОЕ ПОРОГОВОЕ ОГРАНИЧЕНИЕ
- 18.5.3. НАРАЩИВАНИЕ ОБЛАСТЕЙ
- 18.6. КОНТУРНАЯ СЕГМЕНТАЦИЯ
- 18.7. ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ
- 18.8. СЕГМЕНТАЦИЯ ФОРМЫ
- ЛИТЕРАТУРА
- Глава 19. ОБНАРУЖЕНИЕ ОБЪЕКТОВ И СОВМЕЩЕНИЕ (ПРИВЯЗКА) ИЗОБРАЖЕНИЙ
- 19.1. СОПОСТАВЛЕНИЕ С ЭТАЛОНОМ
- 19.2. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ ДЕТЕРМИНИРОВАННЫХ ПОЛЕЙ
- 19.3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ СЛУЧАЙНЫХ ПОЛЕЙ
- 19.4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
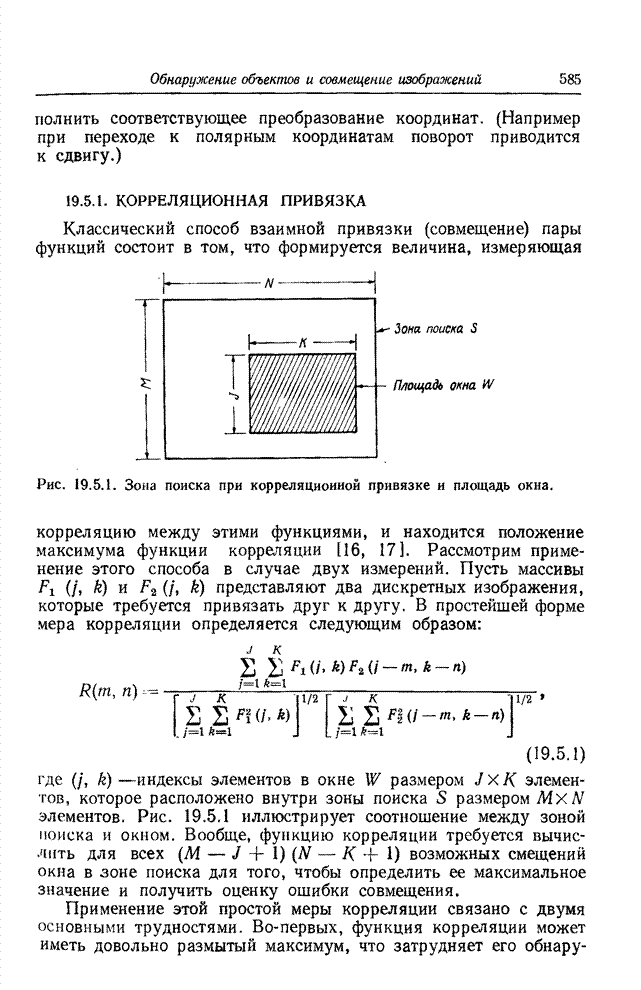
- 19.5. ПРИВЯЗКА ИЗОБРАЖЕНИЙ
- 19.5.1. КОРРЕЛЯЦИОННАЯ ПРИВЯЗКА
- 19.5.2. ПОСЛЕДОВАТЕЛЬНАЯ ПРИВЯЗКА
- ЛИТЕРАТУРА
- Глава 20. СИСТЕМЫ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
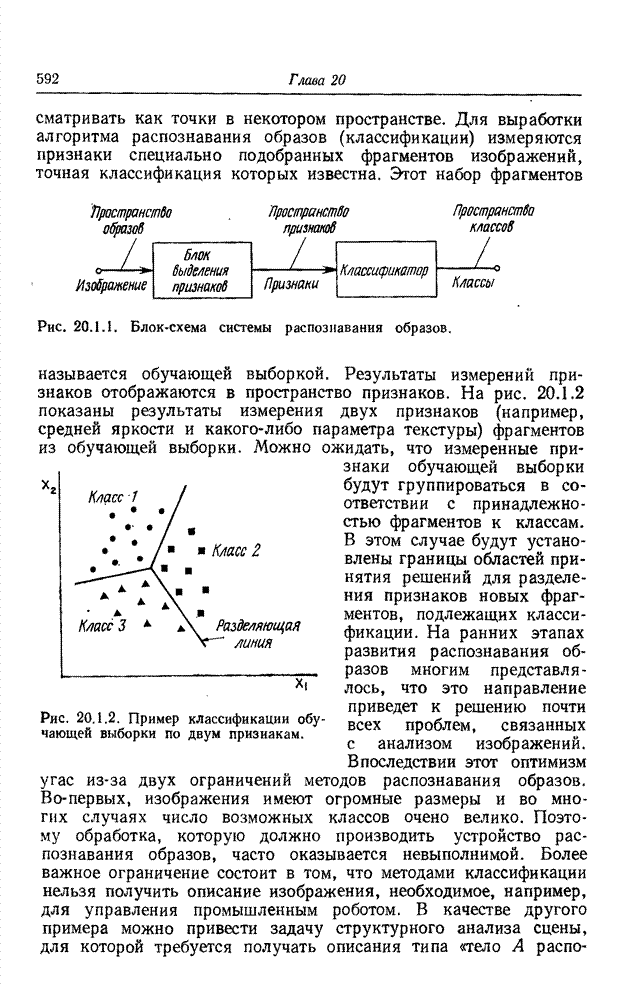
- 20.1. СИСТЕМЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 20.2. МОДЕЛИ СИСТЕМ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.3. СИНТАКСИЧЕСКИЕ МЕТОДЫ
- 20.4. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ОТНОШЕНИЯ МЕЖДУ ОБЪЕКТАМИ
- ЛИТЕРАТУРА
- Часть 6. Кодирование изображений
- Глава 21. АНАЛОГОВЫЕ МЕТОДЫ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.1. КЛАССИФИКАЦИЯ МЕТОДОВ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.2. СИСТЕМЫ ВЕЩАТЕЛЬНОГО ТЕЛЕВИДЕНИЯ
- 21.2.1. СИСТЕМА НТСЦ [13-15]
- 21.2.2. СИСТЕМА СЕКАМ [17]
- 21.2.3.СИСТЕМА ПАЛ
- 21.3. МОДУЛЯЦИОННЫЕ МЕТОДЫ СОКРВЩЕНИЯ ПОЛОСЫ ЧАСТОТЫ
- 21.4.УМЕНЬШЕНИЕ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ И ЧАСТОТЫ КАДРОВ
- 21.4.1. УМЕНЬШЕНИЕ ПРОСТРАНСТВЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
- 21.4.2. УМЕНЬШЕНИЕ ЧАСТОТЫ КАДРОВ
- 21.5. МЕТОДЫ ВРЕМЕННОГО ПЕРЕМЕЖЕНИЯ
- 21.5.1. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ СТРОК
- 21.5.2. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ ЭЛЕМЕНТОВ
- 21.6. РАЗВЕРТКА С ПЕРЕМЕННОЙ СКОРОСТЬЮ
- 21.7. МУЛЬТИПЛЕКСНЫЕ МЕТОДЫ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Глава 22. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПОЭЛЕМЕНТНОЙ ОБРАБОТКОЙ
- 22.1. СИСТЕМЫ КОДИРОВАНИЯ С ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИЕЙ
- 22.1.1. КВАНТОВАНИЕ СО СЖАТИЕМ ДИАПАЗОНА ЯРКОСТЕЙ
- 22.1.2. ПСЕВДОШУМОВОЕ КВАНТОВАНИЕ
- 22.1.3. КВАНТОВАНИЕ С УЛУЧШЕННОЙ ПЕРЕДАЧЕЙ ГРАДАЦИЙ ЯРКОСТИ
- 22.1.4. СИСТЕМА С ГРУБОЙ-ТОНКОЙ ШКАЛОЙ КВАНТОВАНИЯ
- 22.1.5. КВАНТОВАНИЕ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ
- 22.2. СТАТИСТИЧЕСКИЕ МЕТОДЫ КОДИРОВАНИЯ
- 22.2.1. ПОЭЛЕМЕНТНОЕ СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- 22.2.2. КОДИРОВАНИЕ С УЧЕТОМ ПРЕДШЕСТВУЮЩЕГО ЭЛЕМЕНТА
- 22.3. КОДИРОВАНИЕ СЕРИЙ
- 22.3.1. КОДИРОВАНИЕ ДЛИН СЕРИЙ; ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ [32-36]
- 22.3.2. КОДИРОВАНИЕ РАЗРЯДНЫХ ПЛОСКОСТЕЙ
- 22.4. КОДИРОВАНИЕ С ПОПОЛНЕНИЕМ КАДРОВ
- 22.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ
- 22.5.1. ДЕЛЬТА-МОДУЛЯЦИЯ
- 22.5.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ
- 22.5.3. КОДЕРЫ С ПРОСТРАНСТВЕННЫМ ПРЕДСКАЗАНИЕМ
- 22.5.4. АДАПТИВНЫЕ КОДЕРЫ С ПРЕДСКАЗАНИЕМ
- 22.5.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ ПРИМЕНИТЕЛЬНО К ЦВЕТНЫМ ИЗОБРАЖЕНИЯМ
- 22.5.6. ДИФФЕРЕНЦИАЛЬНОЕ МЕЖКАДРОВОЕ КОДИРОВАНИЕ
- 22.6. ПРОЕКТИРОВАНИЕ СИСТЕМ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ДЛЯ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 23. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННОЙ ОБРАБОТКОЙ
- 23.1. ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ КОДИРОВАНИЯ
- 23.1.1. ИНТЕРПОЛЯЦИЯ НА ПЕРЕДАЮЩЕЙ СТОРОНЕ
- 23.1.2. ИНТЕРПОЛЯЦИЯ НА ПРИЕМНОЙ СТОРОНЕ
- 23.2. КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.1. КОДИРОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.2. АДАПТИВНОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.3. КОДИРОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.4. МЕЖКАДРОВОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.3. УМЕНЬШЕНИЕ ОШИБОК КВАНТОВАНИЯ ПРИ КОДИРОВАНИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.4. ГИБРИДНОЕ КОДИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ И ДИКМ
- 23.5. КОДИРОВАНИЕ ПРИЗНАКОВ
- 23.5.1. КОДИРОВАНИЕ ЛИНИЙ УРОВНЯ
- 23.5.2. КОДИРОВАНИЕ КОНТУРОВ
- 23.5.3. КОДИРОВАНИЕ ТЕКСТУР
- 23.6. КОДИРОВАНИЕ С ПОМОЩЬЮ НАБОРА СИМВОЛОВ
- 23.6.1. КОДИРОВАНИЕ БЛОКОВ ПО СЛОВАРЮ ОБРАЗОВ
- 23.6.2. КОДИРОВАНИЕ НА ОСНОВЕ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- ЛИТЕРАТУРА
- Глава 24. АНАЛИЗ ЭФФЕКТИВНОСТИ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 24.1. СТАТИСТИЧЕСКИЕ МОДЕЛИ КАНАЛА СВЯЗИ КАК ИСТОЧНИКА ПОМЕХ [1-4]
- 24.2. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ
- 24.3. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ [4]
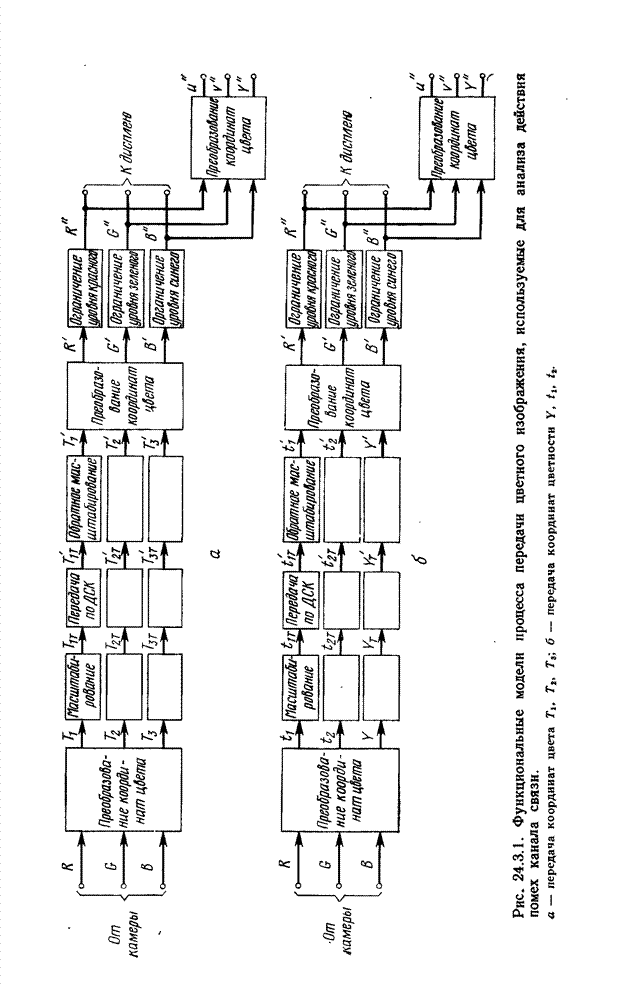
- 24.3.1. ПЕРЕДАЧА КООРДИНАТ ЦВЕТА
- 24.3.2. ПЕРЕДАЧА ЯРКОСТИ И КООРДИНАТ ЦВЕТНОСТИ
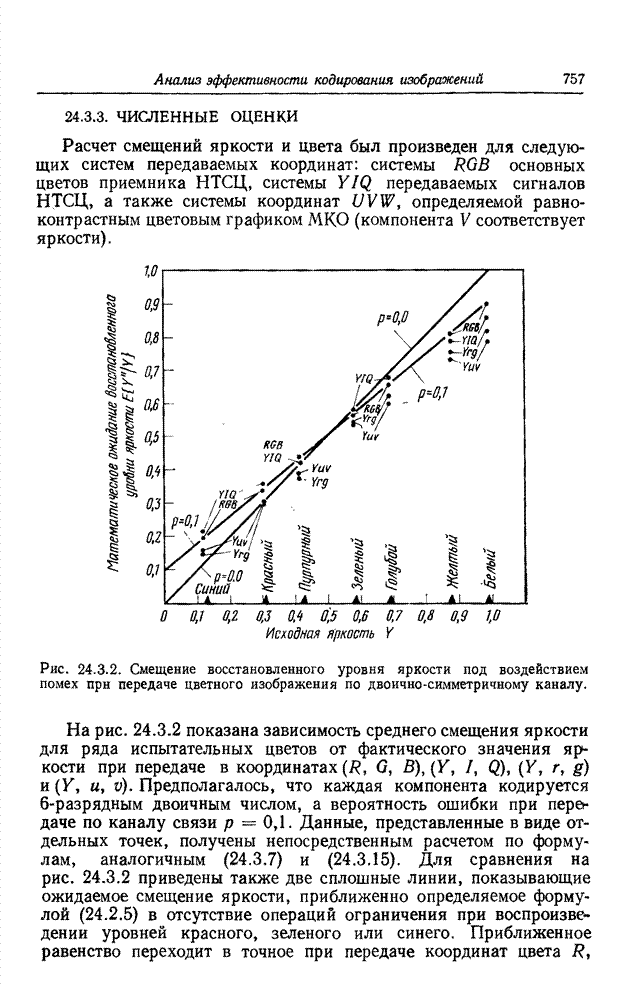
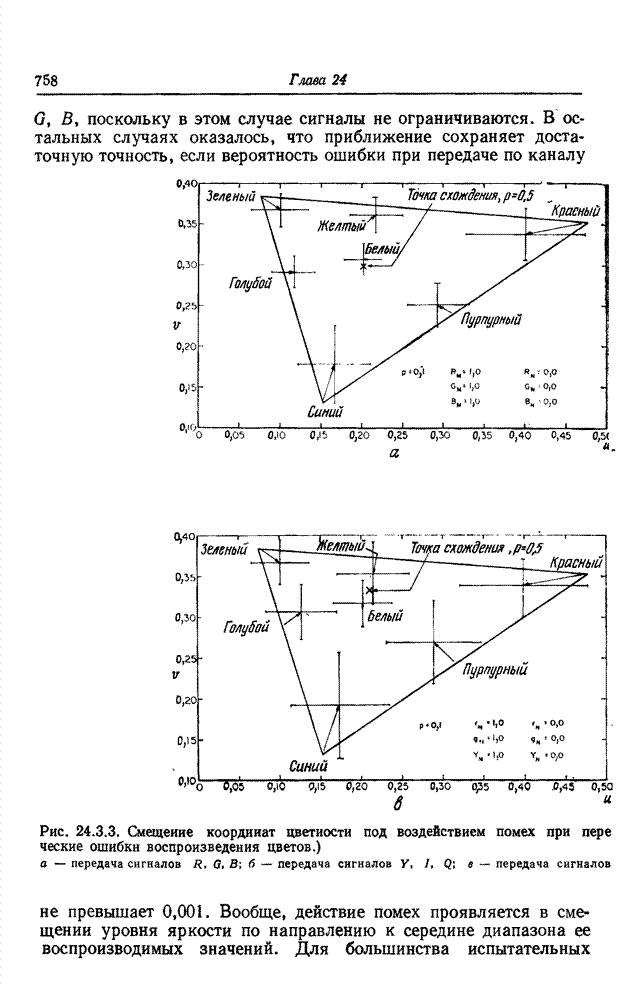
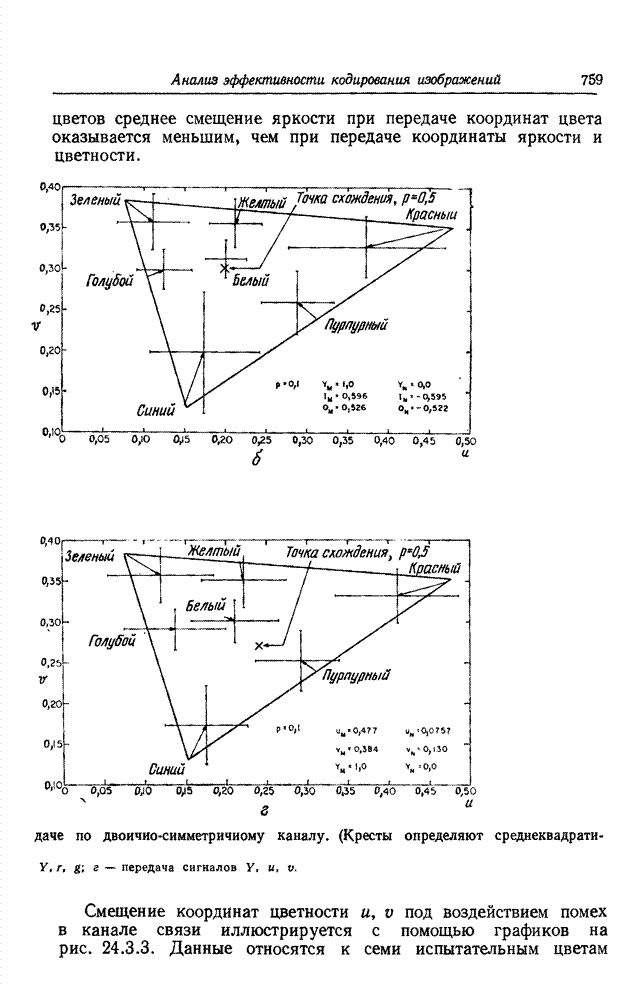
- 24.3.3. ЧИСЛЕННЫЕ ОЦЕНКИ
- 24.4. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ ДИКМ
- 24.5. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ КОДИРОВАНИЯ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
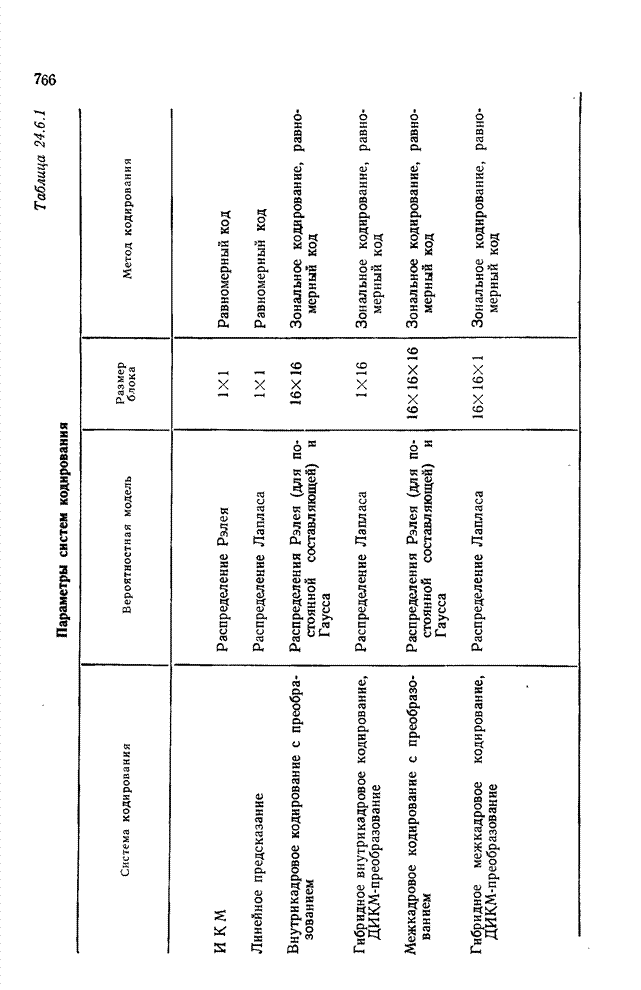
- 24.6. СРАВНЕНИЕ РАЗЛИЧНЫХ МЕТОДОВ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Приложение 1. ОСНОВНАЯ ЛИТЕРАТУРА
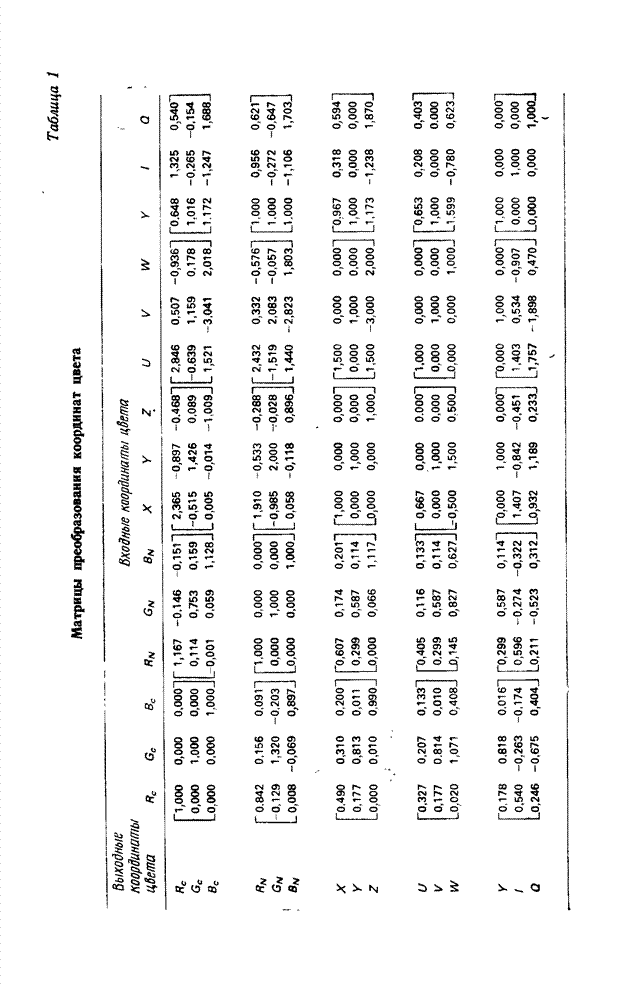
- Приложение 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА И ЦВЕТНОСТИ
- Приложение 3. СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА