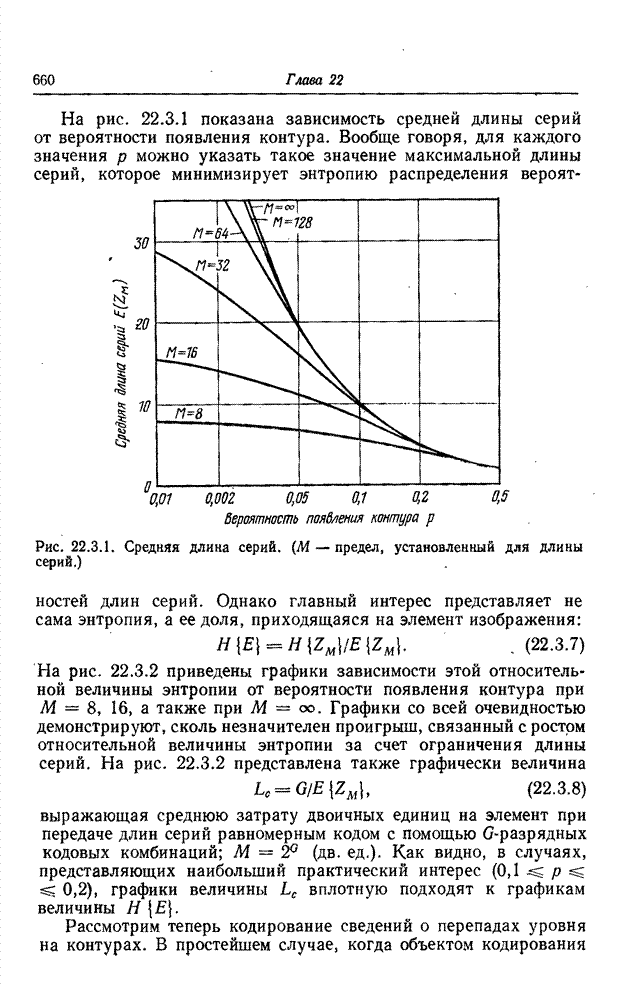
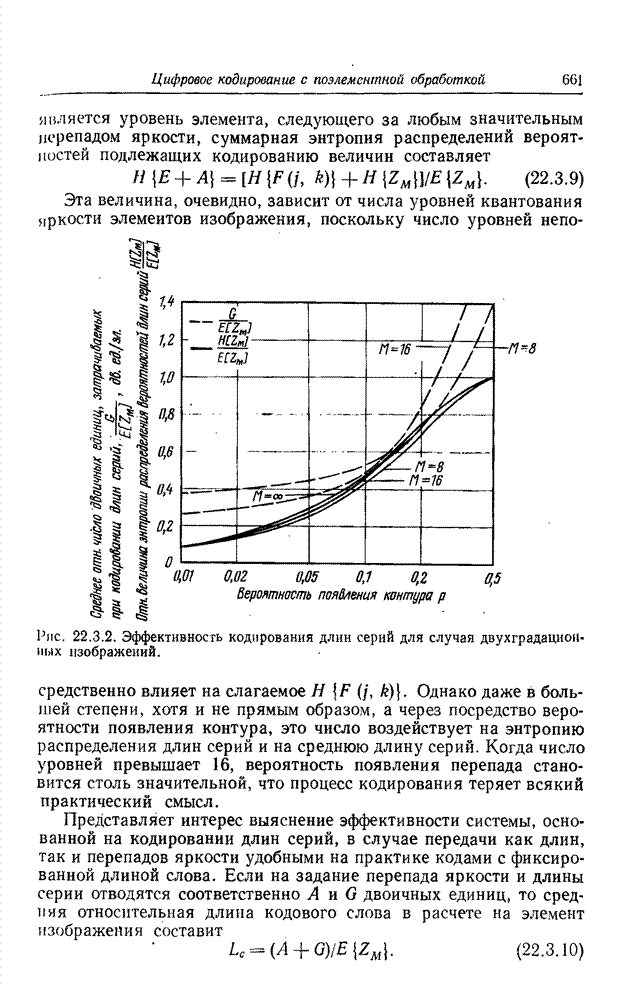
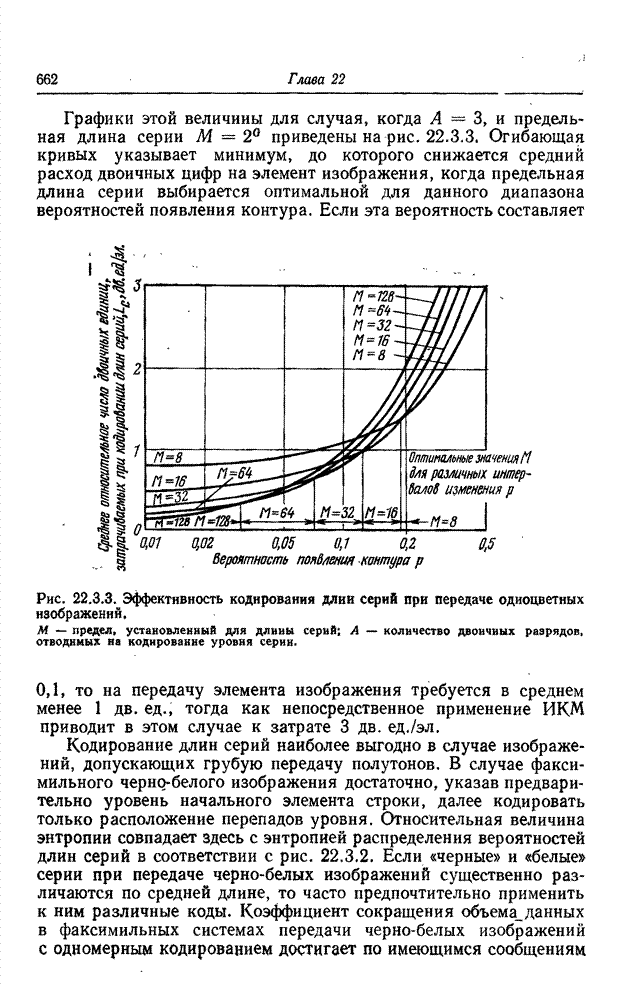
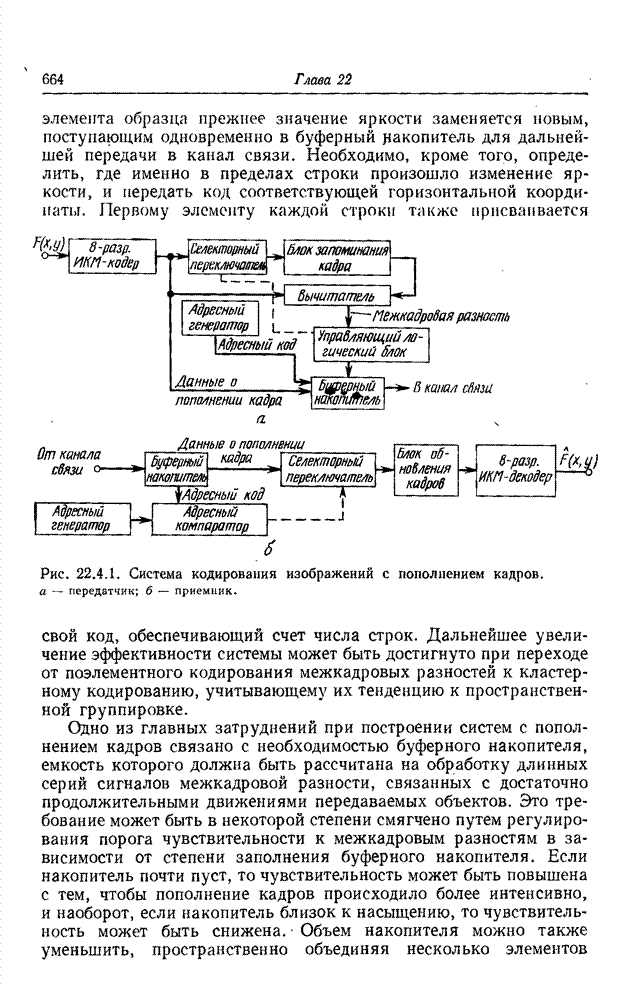
| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
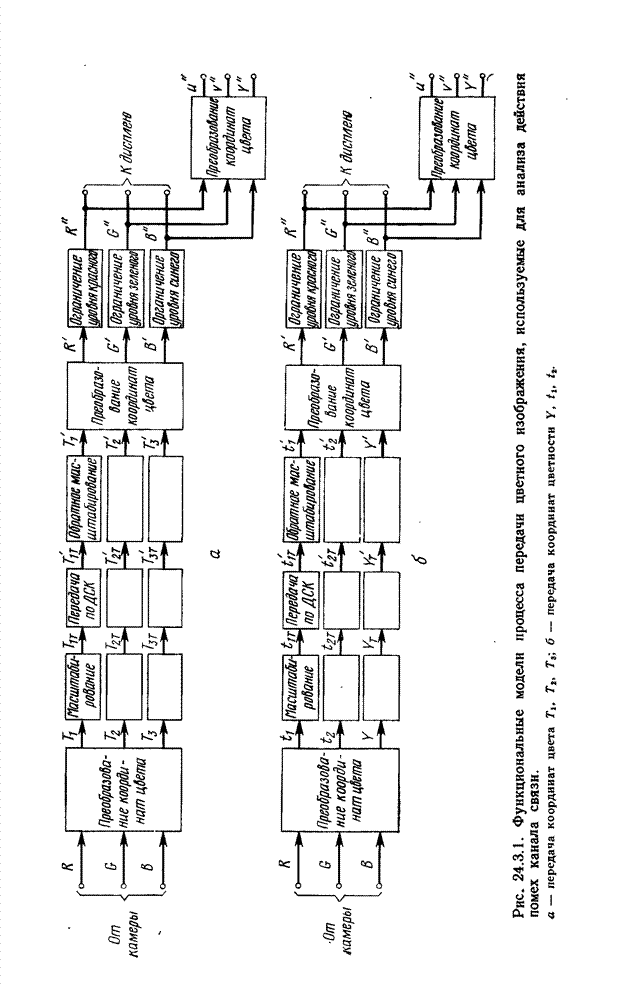
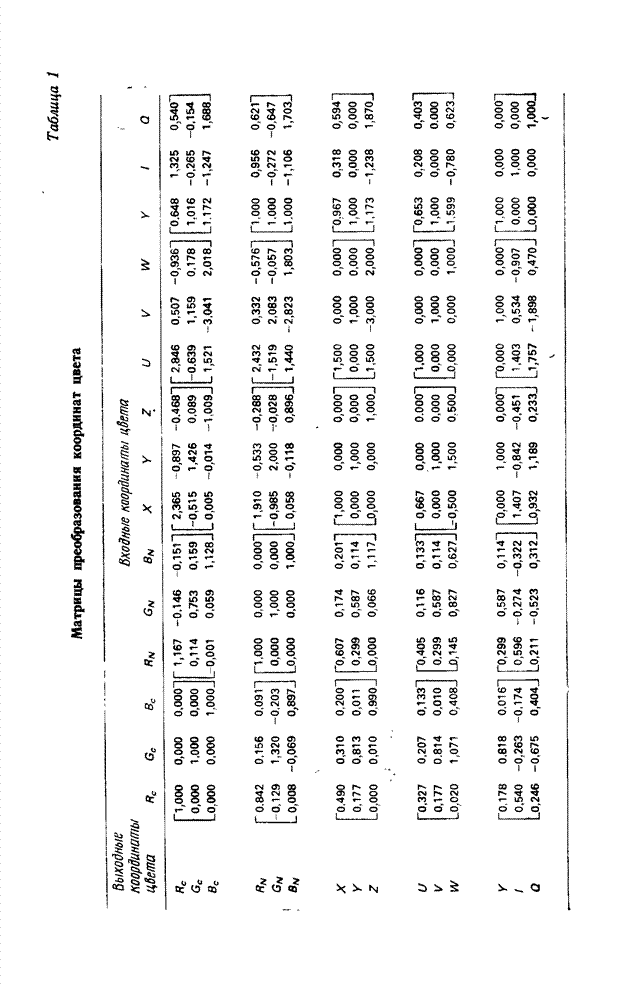
24.3.1. ПЕРЕДАЧА КООРДИНАТ ЦВЕТА
В
системе, показанной на рис. 24.3.1, а, нормированные первичные координаты цвета
![]() ,
значения каждой из которых заключены в интервале
,
значения каждой из которых заключены в интервале ![]() , подвергаются линейному
преобразованию для формирования передаваемых сигналов цвета
, подвергаются линейному
преобразованию для формирования передаваемых сигналов цвета
 , (24.3.1)
, (24.3.1)
причем
коэффициенты ![]() фиксированы.
Каждая из компонент
фиксированы.
Каждая из компонент ![]() с диапазоном изменения от
с диапазоном изменения от ![]() до
до ![]() подвергается
затем в процессе равномерного квантования масштабированию и округлению до
целого числа:
подвергается
затем в процессе равномерного квантования масштабированию и округлению до
целого числа:
![]() . (24.3.2)
. (24.3.2)
Принятая
компонента ![]() сигнала
цвета в результате обратной операции масштабирования принимает значение
сигнала
цвета в результате обратной операции масштабирования принимает значение
![]() . (24.3.3)
. (24.3.3)
Далее
производится преобразование координат цвета, дающее принятые координаты цвета ![]() . Помехи в канале
связи могут привести к расширению диапазона изменения этих величин по сравнению
с интервалом
. Помехи в канале
связи могут привести к расширению диапазона изменения этих величин по сравнению
с интервалом ![]() ,
воспроизводимым дисплеем. Поэтому необходимо ввести ограничение с тем, чтобы
диапазон изменения координат цвета
,
воспроизводимым дисплеем. Поэтому необходимо ввести ограничение с тем, чтобы
диапазон изменения координат цвета ![]() , полученных на выходе ограничителей,
соответствовал физически воспроизводимым цветам.
, полученных на выходе ограничителей,
соответствовал физически воспроизводимым цветам.
Схема
на рис. 24.3.1 преобразует координаты цвета ![]() , поступающие на дисплей, в
координаты яркости
, поступающие на дисплей, в
координаты яркости ![]() и цветности
и цветности ![]() :
:
![]() , (24.3.4)
, (24.3.4)
![]() , (24.3.5)
, (24.3.5)
![]() , (24.3.6)
, (24.3.6)
где
![]() и
и ![]() - постоянные,
определяющие это преобразование.
- постоянные,
определяющие это преобразование.
Смещение
цветов под воздействием помех определяется затем путем вычисления условных
моментов для ![]() и
и
![]() . Условный
момент
. Условный
момент ![]() -го
порядка величины
-го
порядка величины ![]() относительно переданных компонент
относительно переданных компонент ![]() может быть
непосредственно вычислен по формуле
может быть
непосредственно вычислен по формуле
 . (24.3.7)
. (24.3.7)
Аналогичные
выражения получаются для ![]() и
и ![]() .
.
Условные
распределения ![]() могут
быть рассчитаны в соответствии с формулой (24.1.3), а значение функции
могут
быть рассчитаны в соответствии с формулой (24.1.3), а значение функции ![]() , стоящей под
знаками сумм (и аналогично
, стоящей под
знаками сумм (и аналогично ![]() или
или ![]() ), может быть определено для любой
комбинации значений ее переменных
), может быть определено для любой
комбинации значений ее переменных ![]() . К сожалению, при больших
. К сожалению, при больших ![]() прямое вычисление
условных моментов связано со значительными затратами времени.
прямое вычисление
условных моментов связано со значительными затратами времени.
В
случае канала с малой вероятностью ошибок условные распределения вероятностей ![]() характеризуются
небольшим разбросом относительно своих средних. В этом случае вероятность того,
что принятые координаты цвета
характеризуются
небольшим разбросом относительно своих средних. В этом случае вероятность того,
что принятые координаты цвета ![]() выйдут за установленные для них
пределы, будет достаточно мала. Поэтому можно приближенно найти условные
средние для
выйдут за установленные для них
пределы, будет достаточно мала. Поэтому можно приближенно найти условные
средние для ![]() и
и
![]() [5,
стр. 212], пренебрегая операцией ограничения и выражая
[5,
стр. 212], пренебрегая операцией ограничения и выражая ![]() (аналогично
(аналогично ![]() ) и
) и ![]() непосредственно
через принятые значения переменных
непосредственно
через принятые значения переменных ![]() . Таким образом,
. Таким образом,
![]() , (24.3.8)
, (24.3.8)
![]() , (24.3.9)
, (24.3.9)
![]() , (24.3.10)
, (24.3.10)
где

Здесь
![]() и
и ![]() - постоянные
преобразования координат цвета
- постоянные
преобразования координат цвета ![]() в равноконтрастные координаты цвета.
Разложение функций
в равноконтрастные координаты цвета.
Разложение функций ![]() и
и ![]() в ряд Тейлора в окрестности их
среднего значения с сохранением в разложении членов до второго порядка
включительно дает приближенно средние значения координат цветности и яркости
восстановленного элемента изображения. Таким образом,
в ряд Тейлора в окрестности их
среднего значения с сохранением в разложении членов до второго порядка
включительно дает приближенно средние значения координат цветности и яркости
восстановленного элемента изображения. Таким образом,
 (24.3.11)
(24.3.11)
и
![]() , (24.3.12)
, (24.3.12)
где
![]() и
и ![]() - условное
среднее и условная дисперсия
- условное
среднее и условная дисперсия ![]() -й компоненты на выходе канала связи -
определяются выражениями (24.1.7) и (24.1.12).
-й компоненты на выходе канала связи -
определяются выражениями (24.1.7) и (24.1.12).
Аналогично
получаются выражения для условных дисперсий ![]() и
и ![]() :
:
 (24.3.13)
(24.3.13)
и
![]() . (24.3.14)
. (24.3.14)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Часть 4. РЕСТАВРАЦИЯ И УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
- Глава 12. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
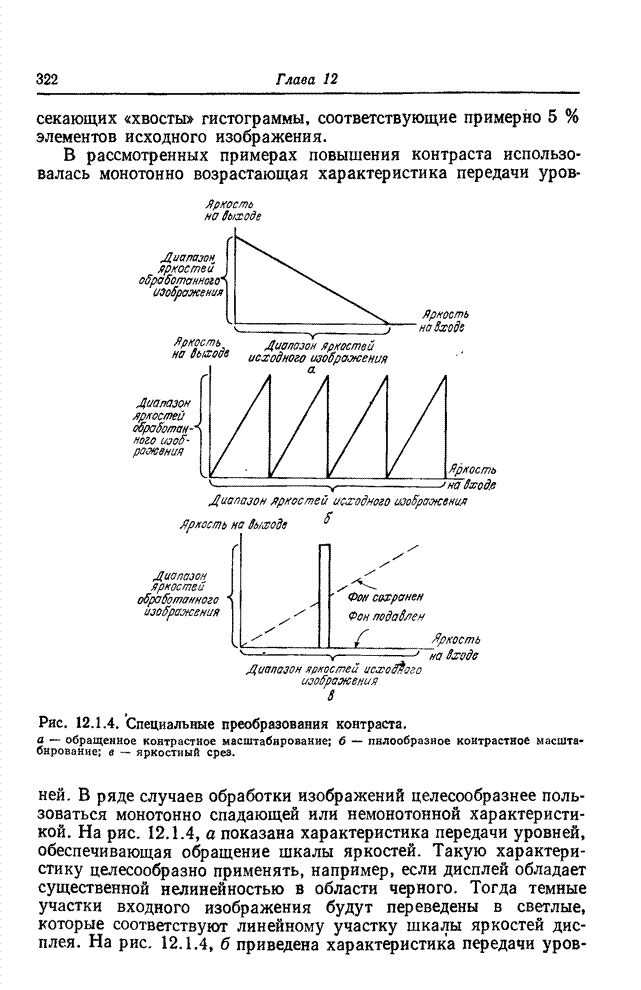
- 12.1. ИЗМЕНЕНИЕ КОНТРАСТА
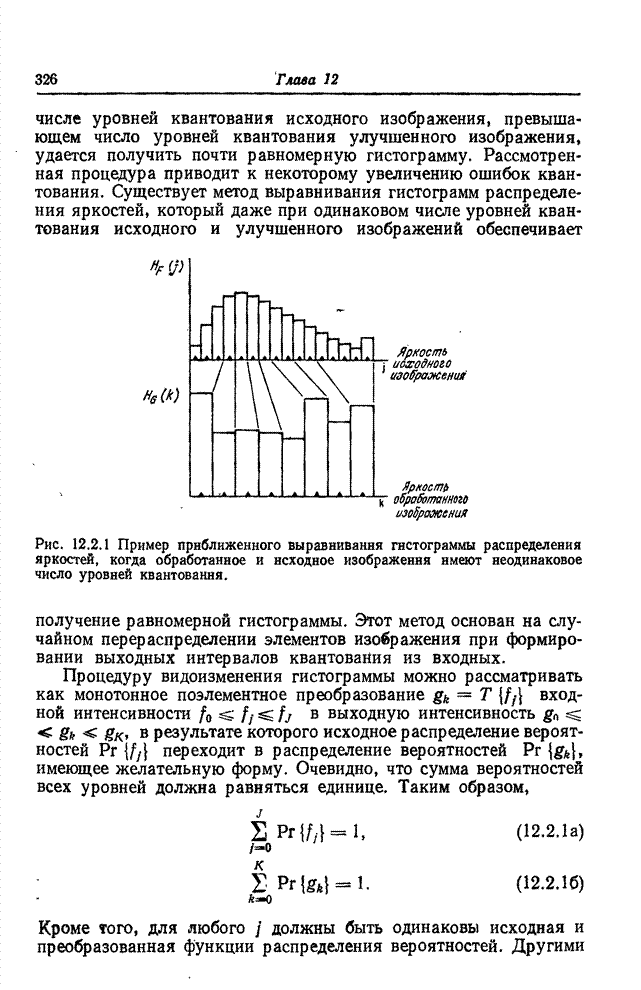
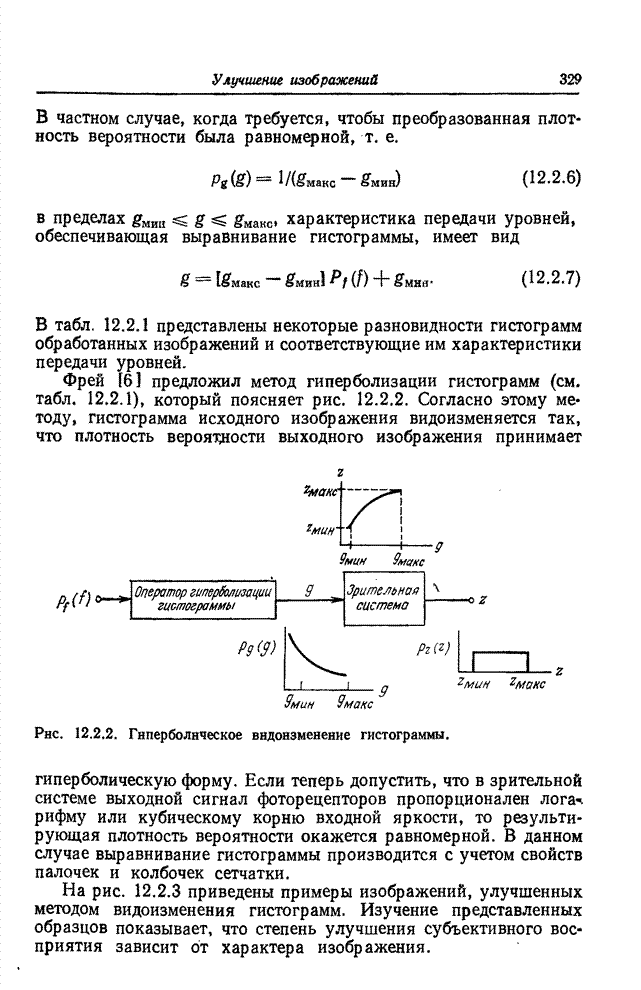
- 12.2. ВИДОИЗМЕНЕНИЕ ГИСТОГРАММ
- 12.3. ПОДАВЛЕНИЕ ШУМОВ
- 12.4. ПОДЧЕРКИВАНИЕ ГРАНИЦ
- 12.5. ОБРАБОТКА ИЗОБРАЖЕНИЙ С ПРЕОБРАЗОВАНИЕМ
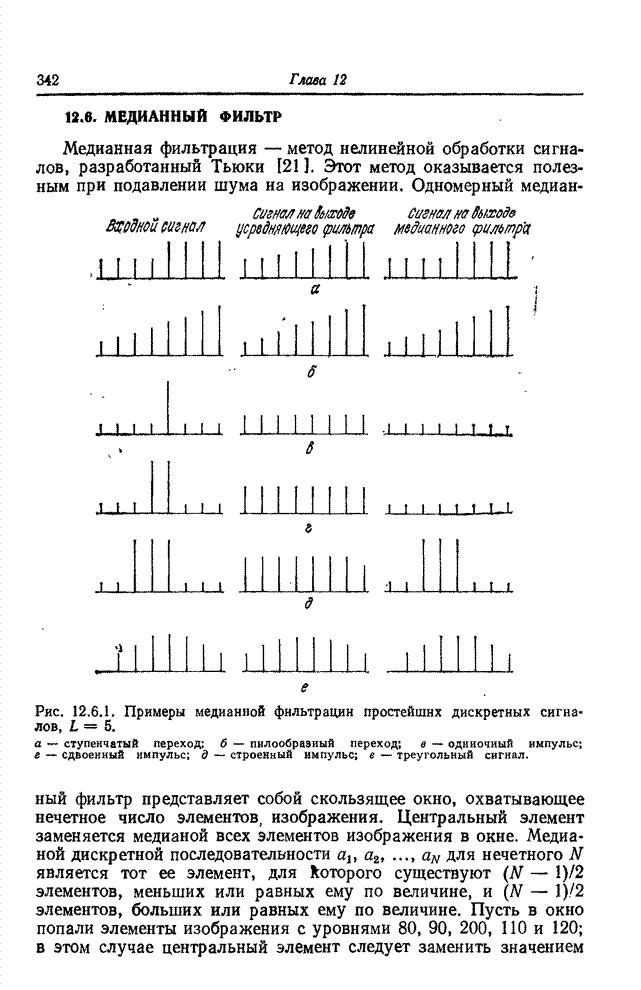
- 12.6. МЕДИАННЫЙ ФИЛЬТР
- 12.7. ЛОЖНЫЕ ЦВЕТА
- 12.8. ПСЕВДОЦВЕТА
- 12.9. УЛУЧШЕНИЕ СПЕКТРОЗОНАЛЬНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 13. МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.1. ОБОБЩЕННЫЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.2. МОДЕЛИ ОПТИЧЕСКИХ СИСТЕМ
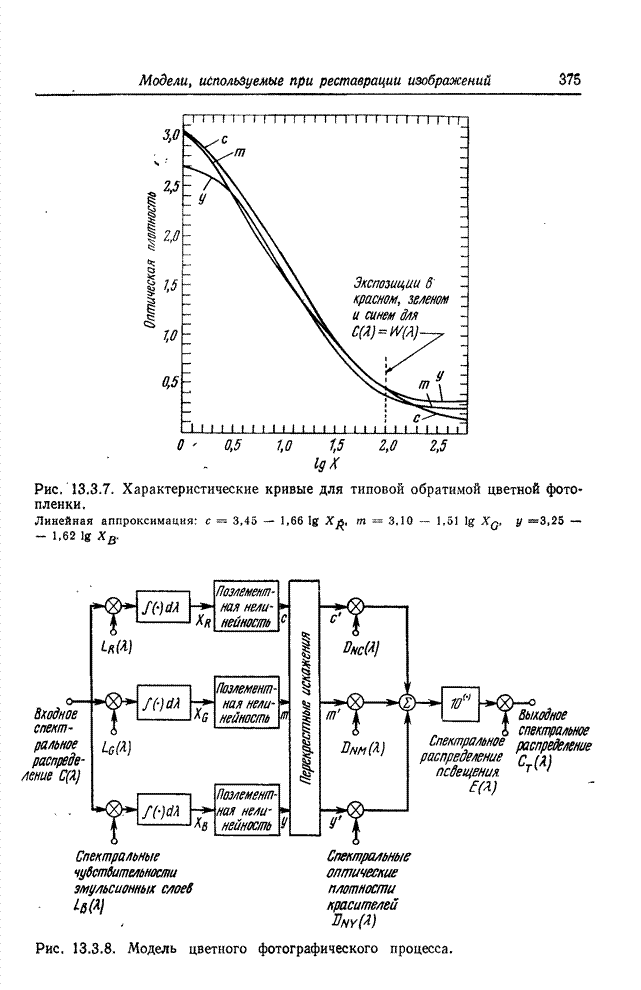
- 13.3. МОДЕЛИ ФОТОГРАФИЧЕСКИХ ПРОЦЕССОВ
- 13.3.1. ОДНОЦВЕТНАЯ ФОТОГРАФИЯ
- 13.3.2. ЦВЕТНАЯ ФОТОГРАФИЯ
- 13.4. МОДЕЛИ ЦИФРОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- 13.5. МОДЕЛЬ ДИСПЛЕЯ
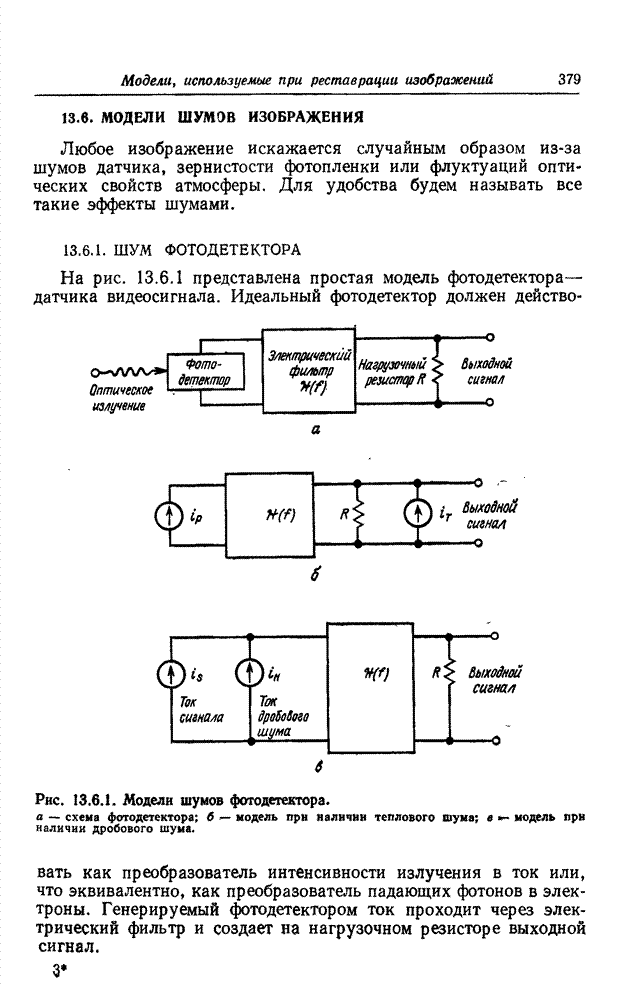
- 13.6. МОДЕЛИ ШУМОВ ИЗОБРАЖЕНИЯ
- 13.6.1. ШУМ ФОТОДЕТЕКТОРА
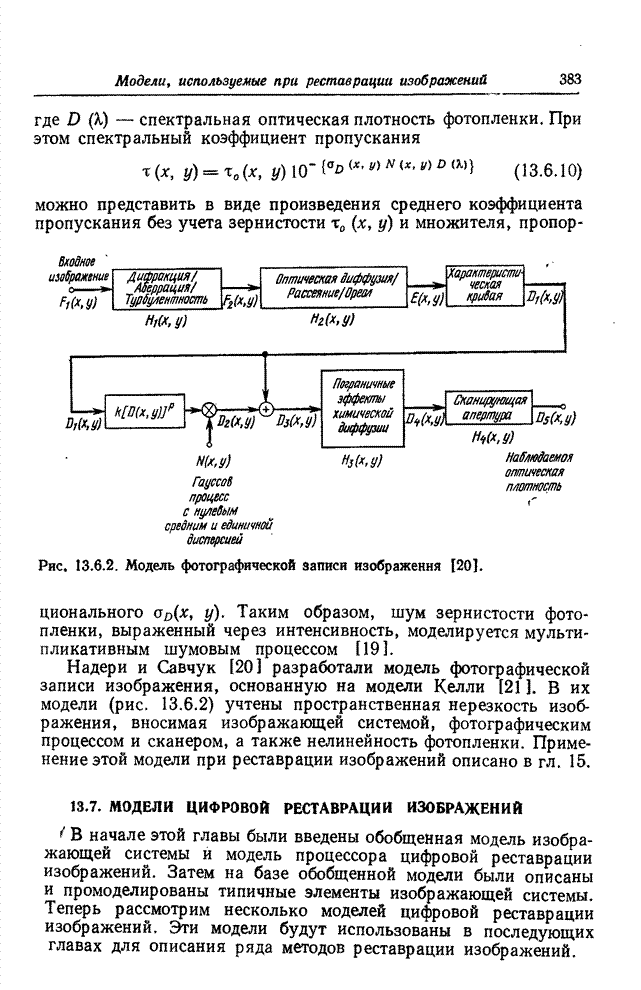
- 13.6.2. ШУМ ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
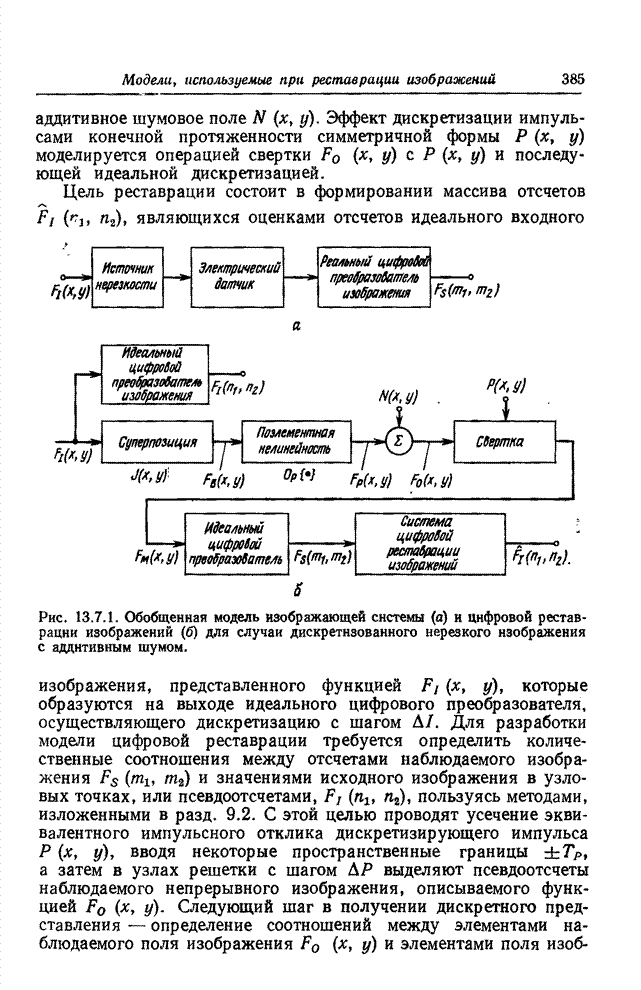
- 13.7. МОДЕЛИ ЦИФРОВОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 14. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 14.1. МЕТОДЫ ПРОСТРАНСТВЕННОЙ ФИЛЬТРАЦИИ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 14.1.1. ИНВЕРСНАЯ ФИЛЬТРАЦИЯ
- 14.1.2. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И АДДИТИВНЫЙ ШУМ
- 14.1.3. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНОЕ ИЗОБРАЖЕНИЕ
- 14.1.4. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНАЯ НЕРЕЗКОСТЬ
- 14.1.5. ФИЛЬТРЫ НА ОСНОВЕ ПАРАМЕТРИЧЕСКИХ ОЦЕНОК
- 14.1.6. ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 4.2. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.2.1. РЕСТАВРАЦИЯ НЕРЕЗКИХ ИЗОБРАЖЕНИЙ
- 14.2.2. РЕСТАВРАЦИЯ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ ПРИ НАЛИЧИИ ШУМА
- 14.3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.3.1. АЛГОРИТМ ДЛЯ ПЕРЕОПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.3.2. АЛГОРИТМ ДЛЯ НЕДООПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.4. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ С ИСПОЛЬЗОВАНИЕМ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- 14.5. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕГРЕССИИ
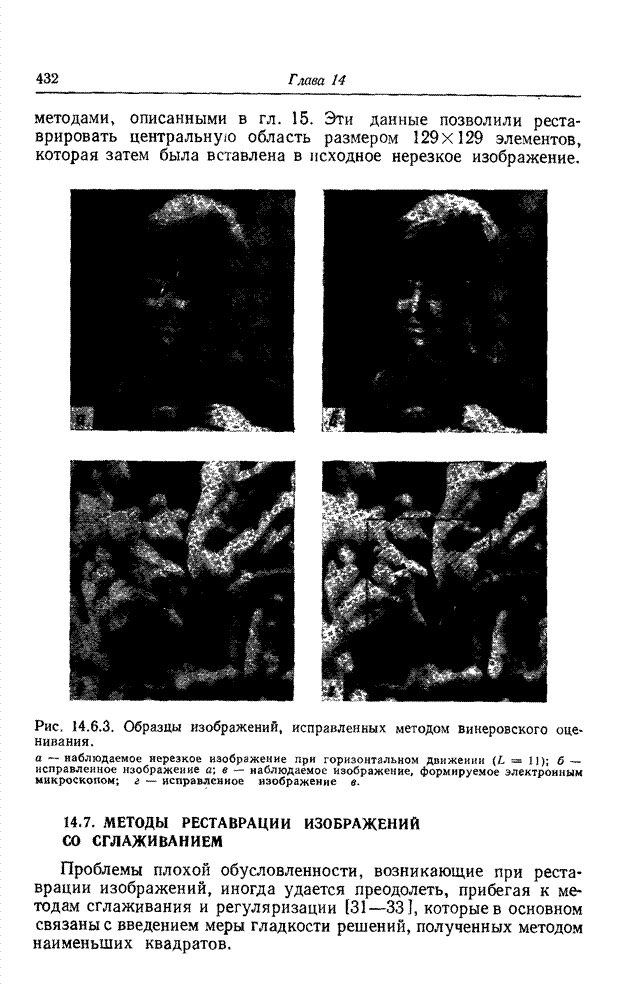
- 14.6. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ВИНЕРОВСКОГО ОЦЕНИВАНИЯ
- 14.6.1. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В ОБЩЕМ СЛУЧАЕ
- 14.6.2. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В СЛУЧАЕ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ С ШУМОМ
- 14.7. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ СО СГЛАЖИВАНИЕМ
- 14.8. МЕТОДЫ РЕСТАВРАЦИИ С ИСПОЛЬЗОВАНИЕМ ОГРАНИЧЕНИЙ
- 14.9. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
- ЛИТЕРАТУРА
- Глава 15. CПЕЦИАЛЬНЫЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
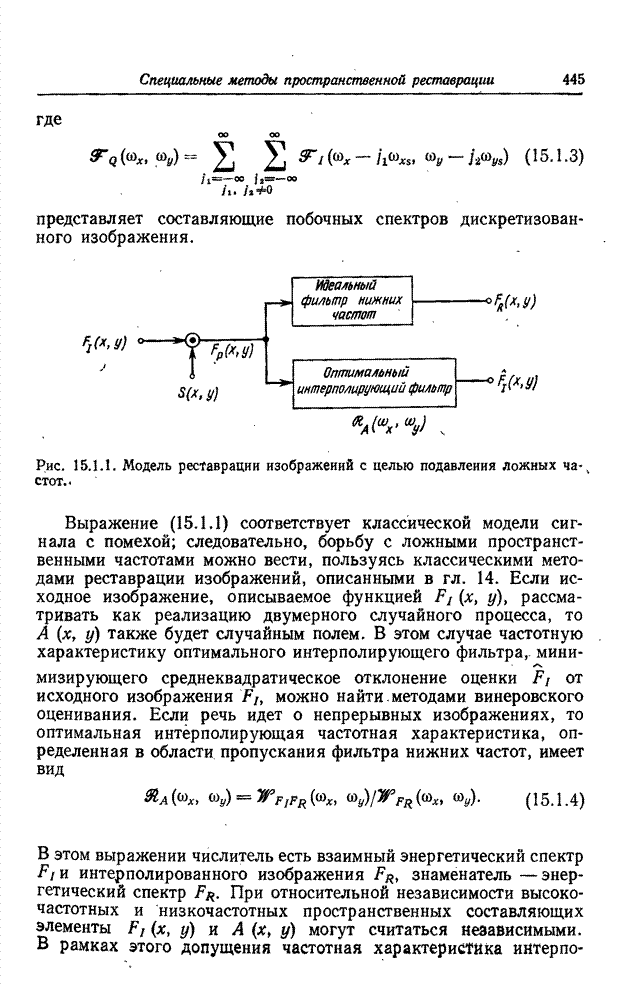
- 15.1. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮ ПОДАВЛЕНИЯ ОШИБОК НАЛОЖЕНИЯ СПЕКТРОВ
- 15.2. КОРРЕКЦИЯ ОШИБОК ИНТЕРПОЛЯЦИИ
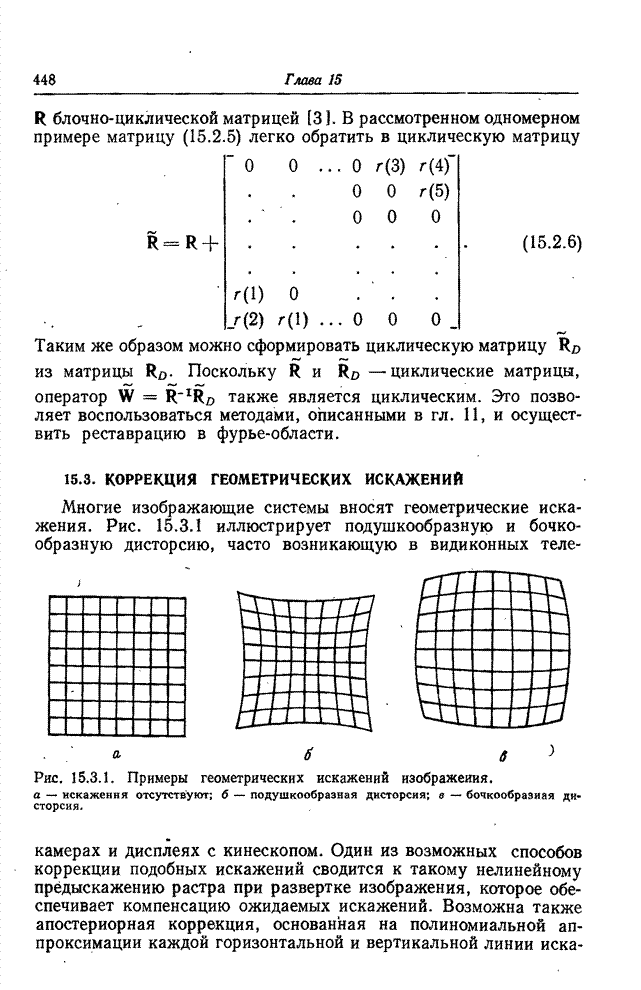
- 15.3. КОРРЕКЦИЯ ГЕОМЕТРИЧЕСКИХ ИСКАЖЕНИЙ
- 15.4. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ГОМОМОРФНОЙ ФИЛЬТРАЦИИ
- 15.5. СЛЕПАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ
- 15.5.1. МЕТОДЫ НА ОСНОВЕ ПРЯМЫХ ИЗМЕРЕНИЙ
- 15.5.2. МЕТОДЫ НА ОСНОВЕ КОСВЕННОГО ОЦЕНИВАНИЯ
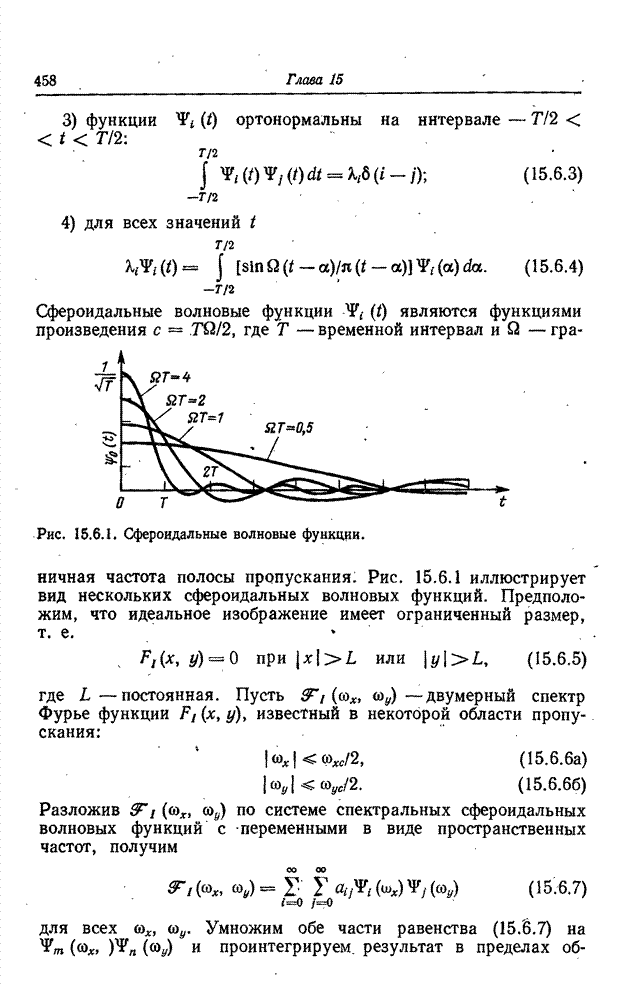
- 15.6. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ СПЕКТРА
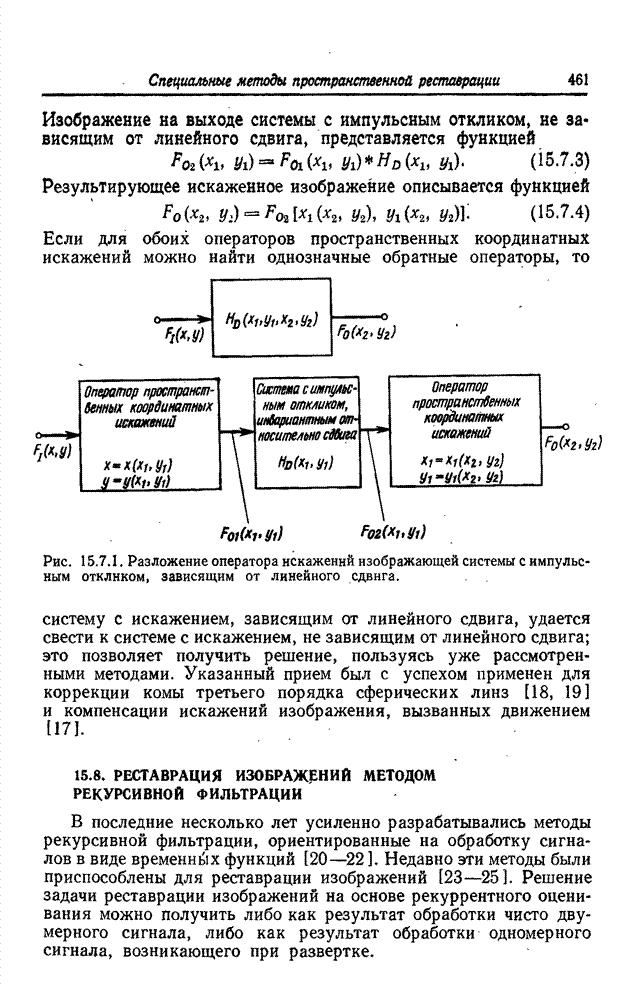
- 15.7. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННО-ЗАВИСИМЫМИ ИСКАЖЕНИЯМИ
- 15.8. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕКУРСИВНОЙ ФИЛЬТРАЦИИ
- 15.9. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮОСЛАБЛЕНИЯ ШУМА ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- ЛИТЕРАТУРА
- Глава 16. КОРРЕКЦИЯ ЯРКОСТНЫХ, ЦВЕТОВЫХ И СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗОБРАЖАЮЩИХ СИСТЕМ
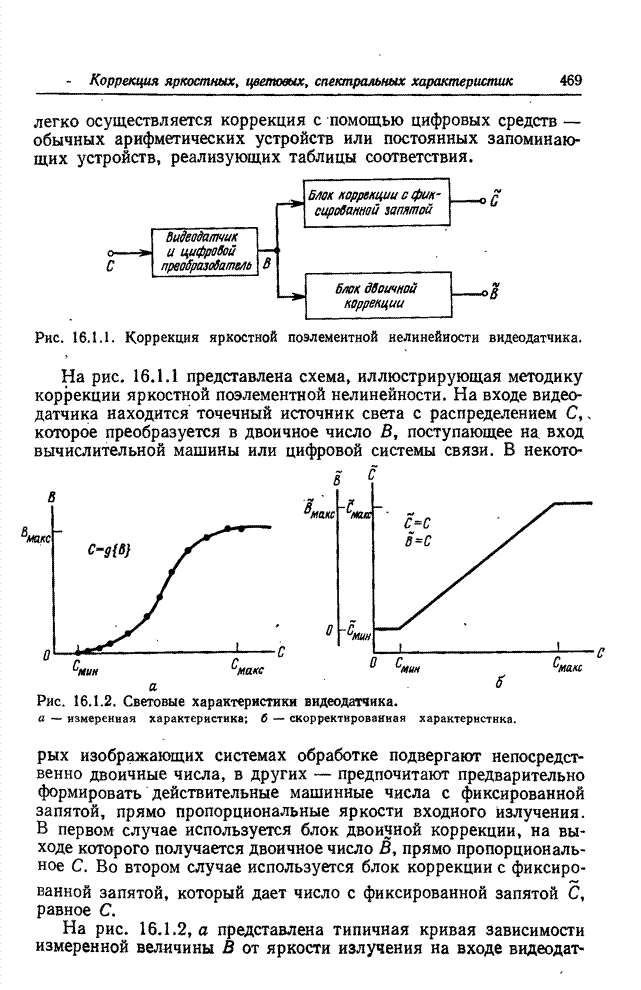
- 16.1. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ВИДЕОДАТЧИКОВ
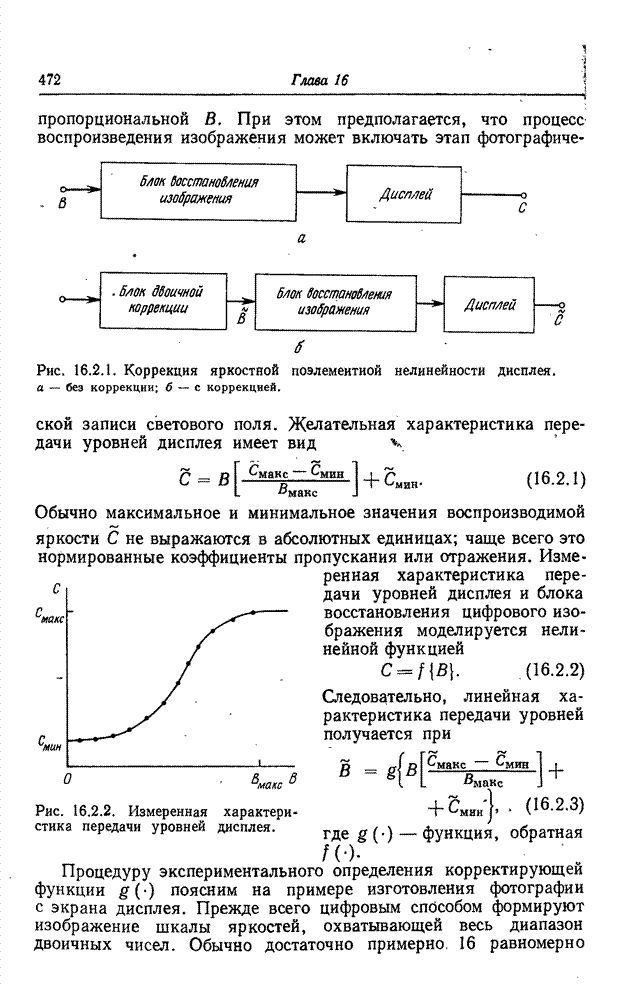
- 16.2. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ДИСПЛЕЕВ
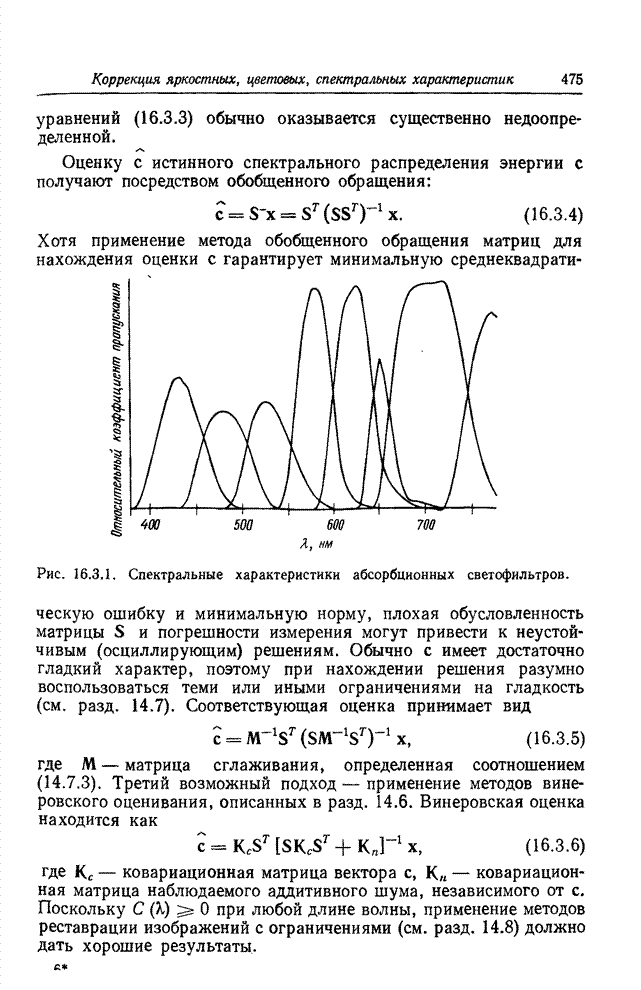
- 16.3. ОЦЕНИВАНИЕ СПЕКТРАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 16.4. КОРРЕКЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ВИДЕОДАТЧИКОВ И ДИСПЛЕЕВ
- 16.5. ОЦЕНИВАНИЕ КООРДИНАТ СВЕТА ВИДЕОДАТЧИКОВ
- 16.6. ОЦЕНИВАНИЕ ЭКСПОЗИЦИЙ ЦВЕТНОЙ ФОТОПЛЕНКИ
- 16.7. КОМПЕНСАЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ ЦВЕТНЫХ ДИСПЛЕЕВ
- ЛИТЕРАТУРА
- Часть 5. АНАЛИЗ ИЗОБРАЖЕНИЙ
- Глава 17. ВЫДЕЛЕНИЕ ПРИЗНАКОВ ИЗОБРАЖЕНИЯ
- 17.1. ЯРКОСТНЫЕ ПРИЗНАКИ
- 17.2. ГИСТОГРАММНЫЕ ПРИЗНАКИ
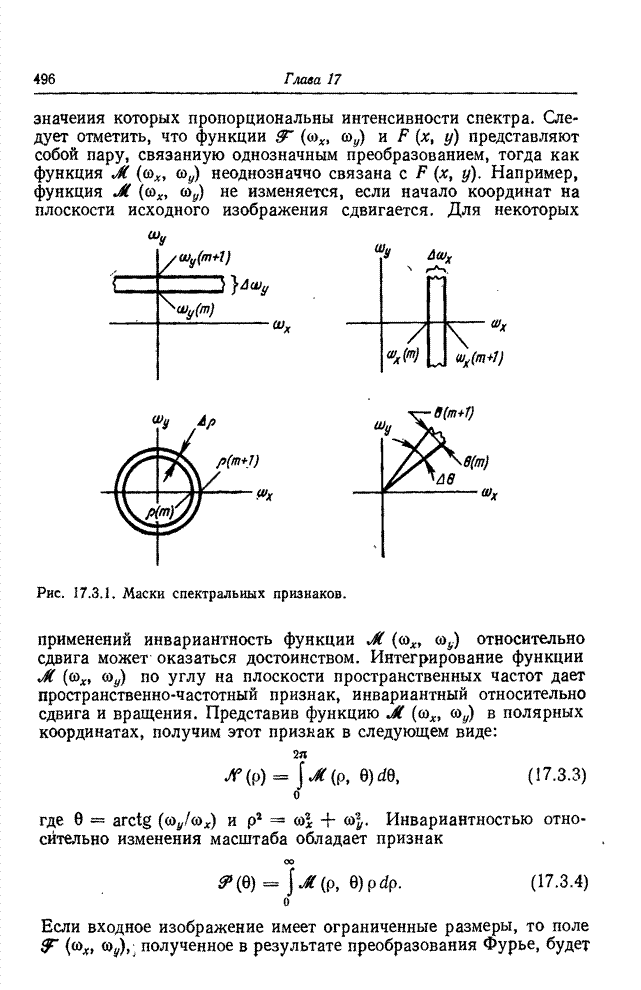
- 17.3. ПРОСТРАНСТВЕННО-СПЕКТРАЛЬНЫЕ ПРИЗНАКИ
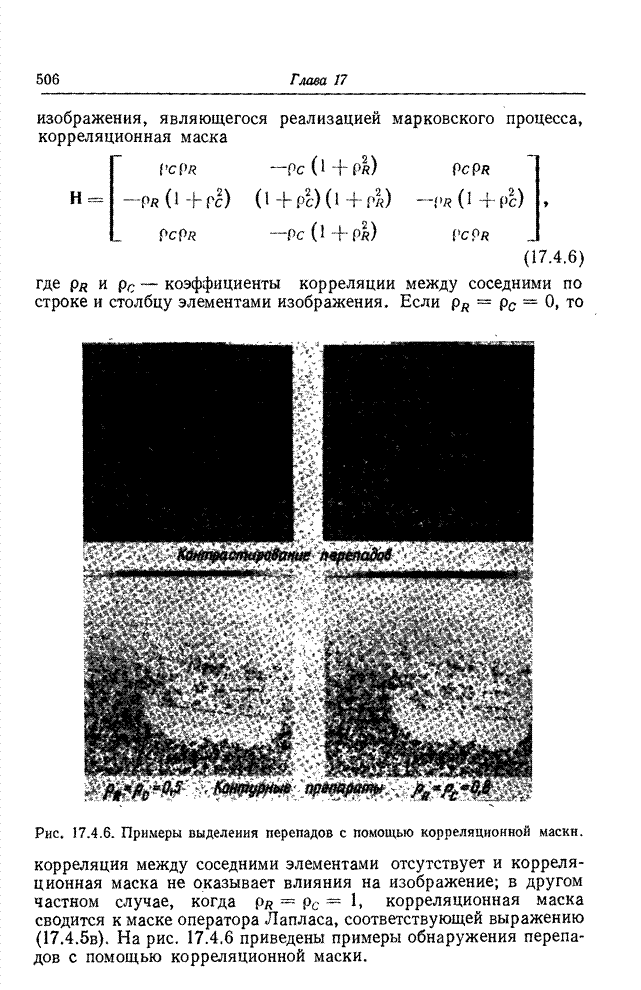
- 17.4. КОНТУРНЫЕ ПРИЗНАКИ
- 17.4.1. ЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.2. НЕЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.3. МЕТОДЫ АППРОКСИМАЦИИ ПЕРЕПАДОВ ЯРКОСТИ
- 17.4.4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ
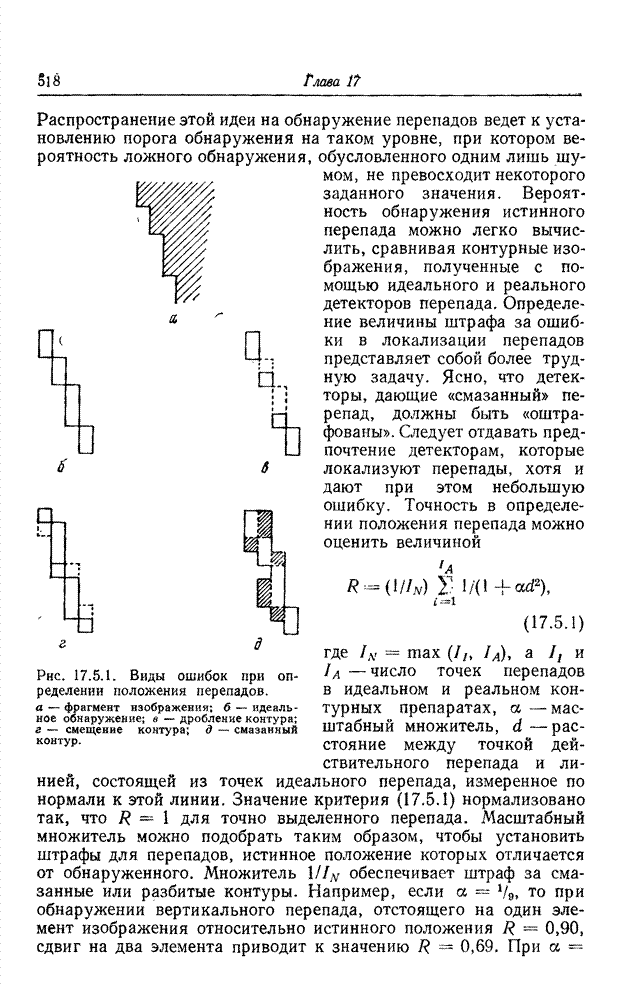
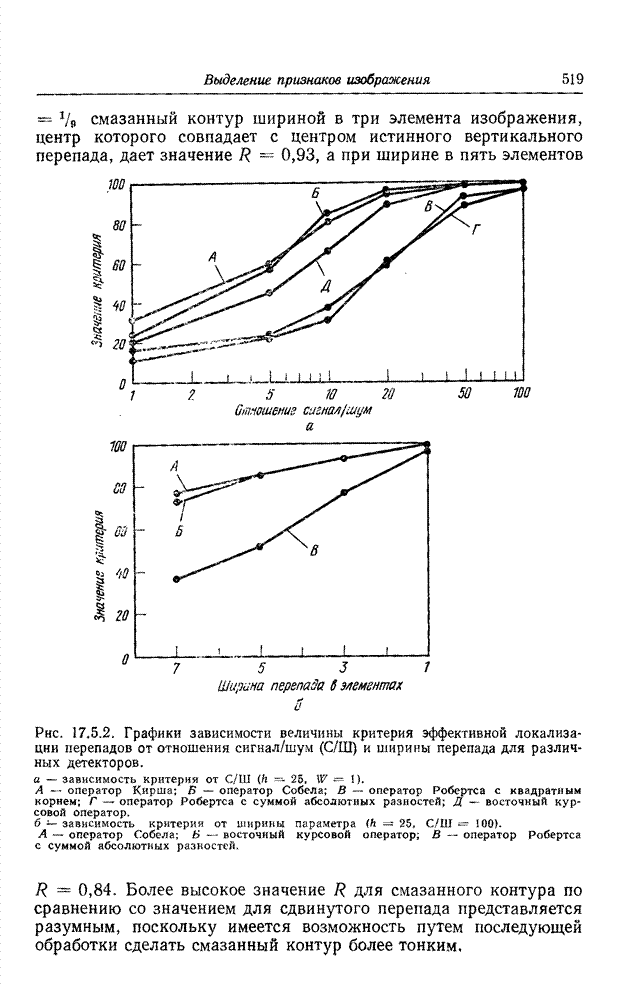
- 17.5. ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ ЯРКОСТИ
- 17.6. ЦВЕТОВЫЕ КОНТУРЫ
- 17.7. ПРИЗНАКИ ПЯТНА И ЛИНИИ
- 17.8. ТЕКСТУРНЫЕ ПРИЗНАКИ
- 17.9. СИНТЕЗ ТЕКСТУР
- ЛИТЕРАТУРА
- Глава 18. СИМВОЛИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
- 18.1. СВЯЗНОСТЬ
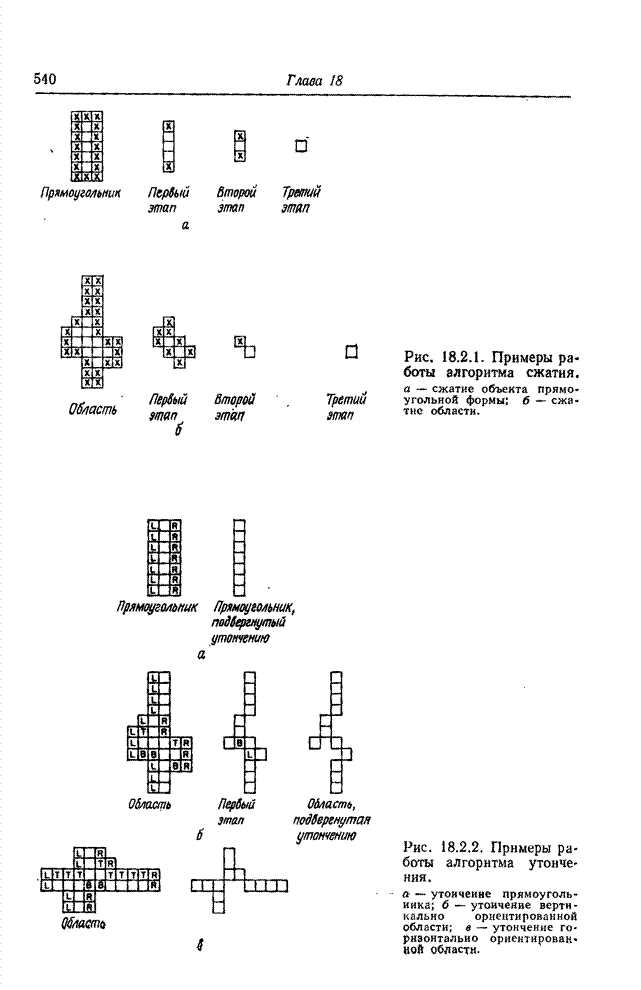
- 18.2. СЖАТИЕ, УТОНЧЕНИЕ И ПОСТРОЕНИЕ ОСТОВА
- 18.3. ОПИСАНИЕ ЛИНИЙ
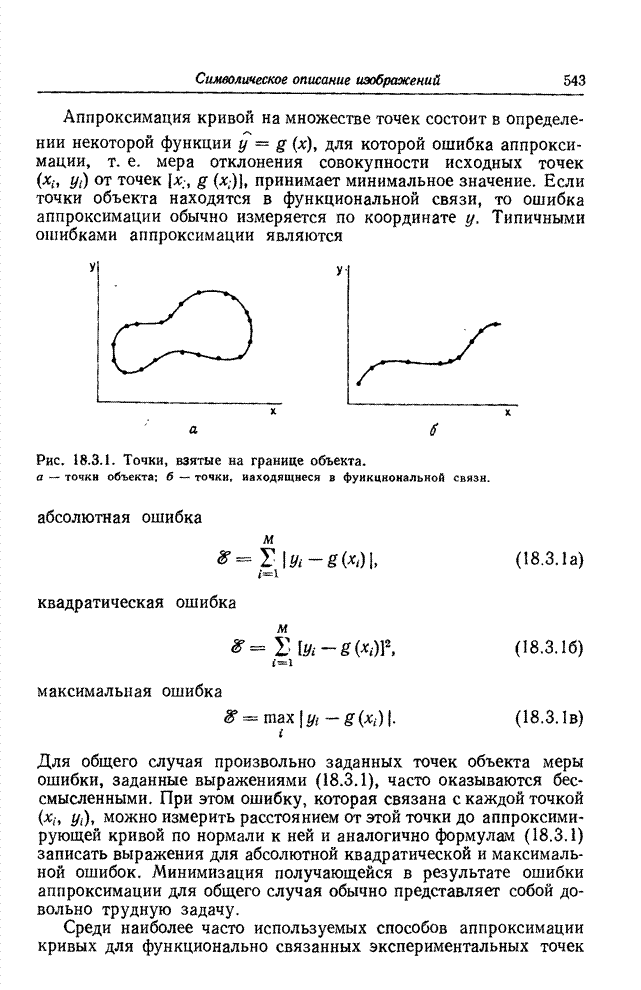
- 18.3.1. АППРОКСИМАЦИЯ КРИВЫХ
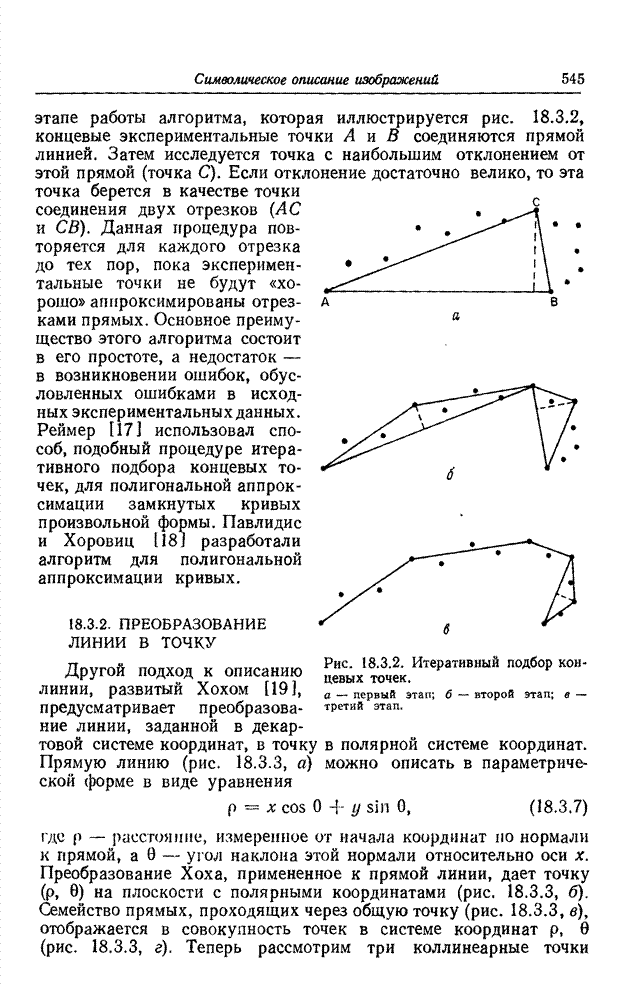
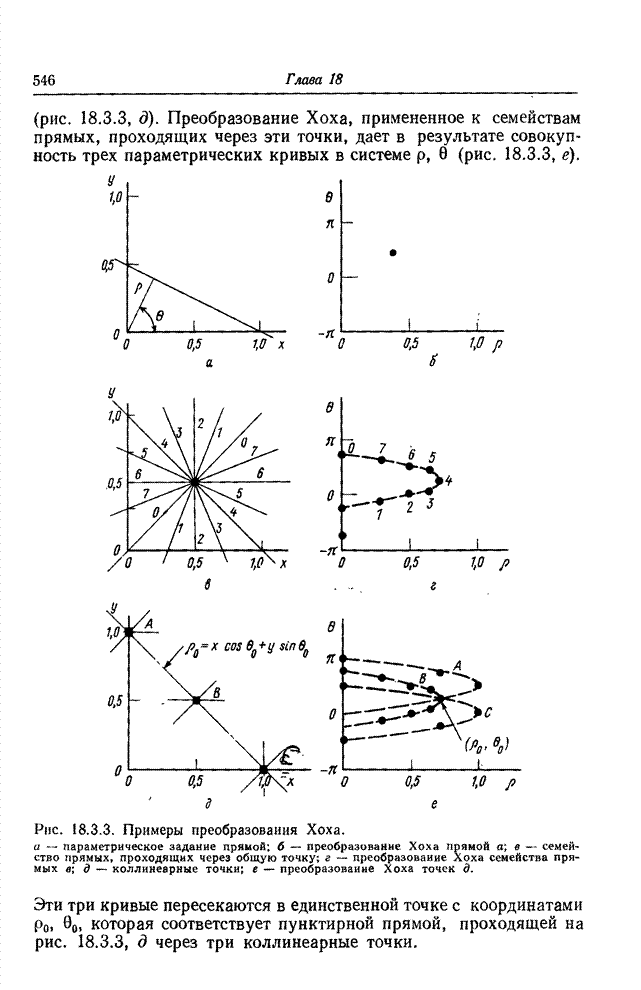
- 18.3.2. ПРЕОБРАЗОВАНИЕ ЛИНИИ В ТОЧКУ
- 18.4. ОПИСАНИЕ ФОРМЫ
- 18.4.1. МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.2. ТОПОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.3. АНАЛИТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.5. СЕГМЕНТАЦИЯ ПО ЯРКОСТИ
- 18.5.1. ПОРОГОВОЕ ОГРАНИЧЕНИЕ ПО ЯРКОСТИ
- 18.5.2. МНОГОМЕРНОЕ ПОРОГОВОЕ ОГРАНИЧЕНИЕ
- 18.5.3. НАРАЩИВАНИЕ ОБЛАСТЕЙ
- 18.6. КОНТУРНАЯ СЕГМЕНТАЦИЯ
- 18.7. ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ
- 18.8. СЕГМЕНТАЦИЯ ФОРМЫ
- ЛИТЕРАТУРА
- Глава 19. ОБНАРУЖЕНИЕ ОБЪЕКТОВ И СОВМЕЩЕНИЕ (ПРИВЯЗКА) ИЗОБРАЖЕНИЙ
- 19.1. СОПОСТАВЛЕНИЕ С ЭТАЛОНОМ
- 19.2. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ ДЕТЕРМИНИРОВАННЫХ ПОЛЕЙ
- 19.3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ СЛУЧАЙНЫХ ПОЛЕЙ
- 19.4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 19.5. ПРИВЯЗКА ИЗОБРАЖЕНИЙ
- 19.5.1. КОРРЕЛЯЦИОННАЯ ПРИВЯЗКА
- 19.5.2. ПОСЛЕДОВАТЕЛЬНАЯ ПРИВЯЗКА
- ЛИТЕРАТУРА
- Глава 20. СИСТЕМЫ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.1. СИСТЕМЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 20.2. МОДЕЛИ СИСТЕМ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.3. СИНТАКСИЧЕСКИЕ МЕТОДЫ
- 20.4. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ОТНОШЕНИЯ МЕЖДУ ОБЪЕКТАМИ
- ЛИТЕРАТУРА
- Часть 6. Кодирование изображений
- Глава 21. АНАЛОГОВЫЕ МЕТОДЫ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.1. КЛАССИФИКАЦИЯ МЕТОДОВ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.2. СИСТЕМЫ ВЕЩАТЕЛЬНОГО ТЕЛЕВИДЕНИЯ
- 21.2.1. СИСТЕМА НТСЦ [13-15]
- 21.2.2. СИСТЕМА СЕКАМ [17]
- 21.2.3.СИСТЕМА ПАЛ
- 21.3. МОДУЛЯЦИОННЫЕ МЕТОДЫ СОКРВЩЕНИЯ ПОЛОСЫ ЧАСТОТЫ
- 21.4.УМЕНЬШЕНИЕ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ И ЧАСТОТЫ КАДРОВ
- 21.4.1. УМЕНЬШЕНИЕ ПРОСТРАНСТВЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
- 21.4.2. УМЕНЬШЕНИЕ ЧАСТОТЫ КАДРОВ
- 21.5. МЕТОДЫ ВРЕМЕННОГО ПЕРЕМЕЖЕНИЯ
- 21.5.1. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ СТРОК
- 21.5.2. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ ЭЛЕМЕНТОВ
- 21.6. РАЗВЕРТКА С ПЕРЕМЕННОЙ СКОРОСТЬЮ
- 21.7. МУЛЬТИПЛЕКСНЫЕ МЕТОДЫ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Глава 22. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПОЭЛЕМЕНТНОЙ ОБРАБОТКОЙ
- 22.1. СИСТЕМЫ КОДИРОВАНИЯ С ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИЕЙ
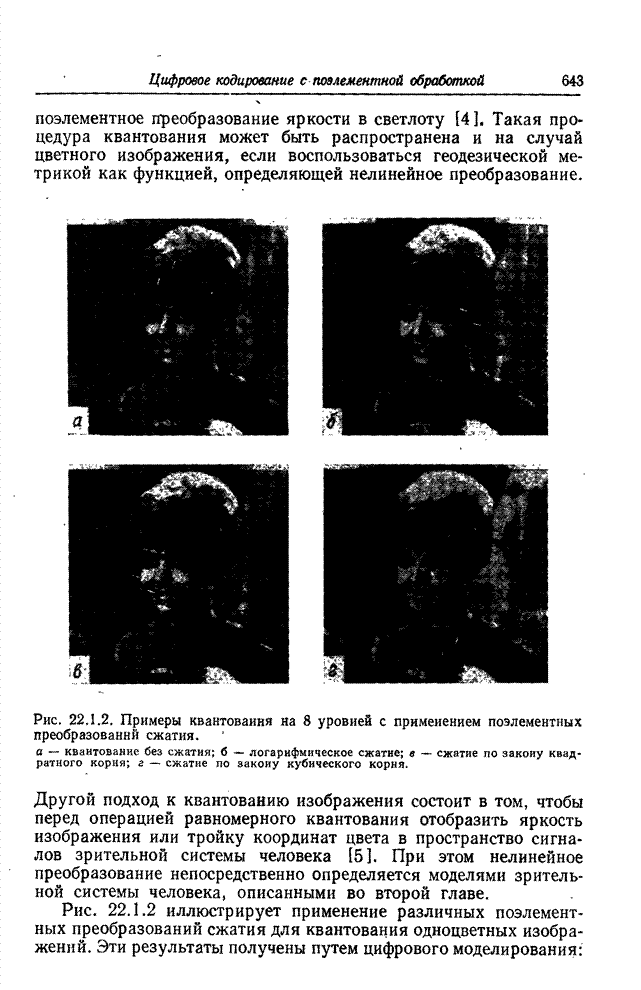
- 22.1.1. КВАНТОВАНИЕ СО СЖАТИЕМ ДИАПАЗОНА ЯРКОСТЕЙ
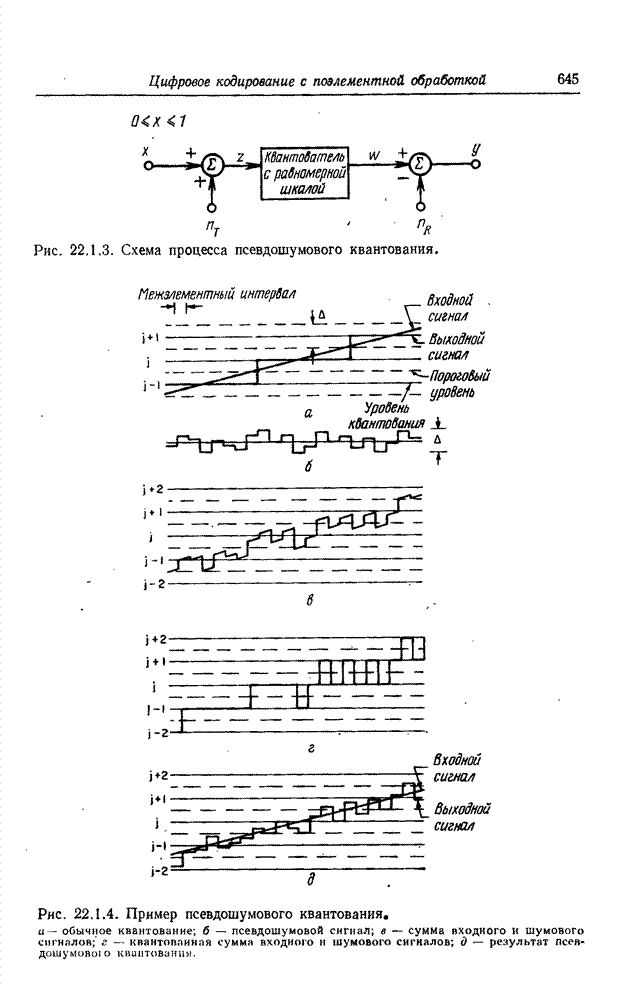
- 22.1.2. ПСЕВДОШУМОВОЕ КВАНТОВАНИЕ
- 22.1.3. КВАНТОВАНИЕ С УЛУЧШЕННОЙ ПЕРЕДАЧЕЙ ГРАДАЦИЙ ЯРКОСТИ
- 22.1.4. СИСТЕМА С ГРУБОЙ-ТОНКОЙ ШКАЛОЙ КВАНТОВАНИЯ
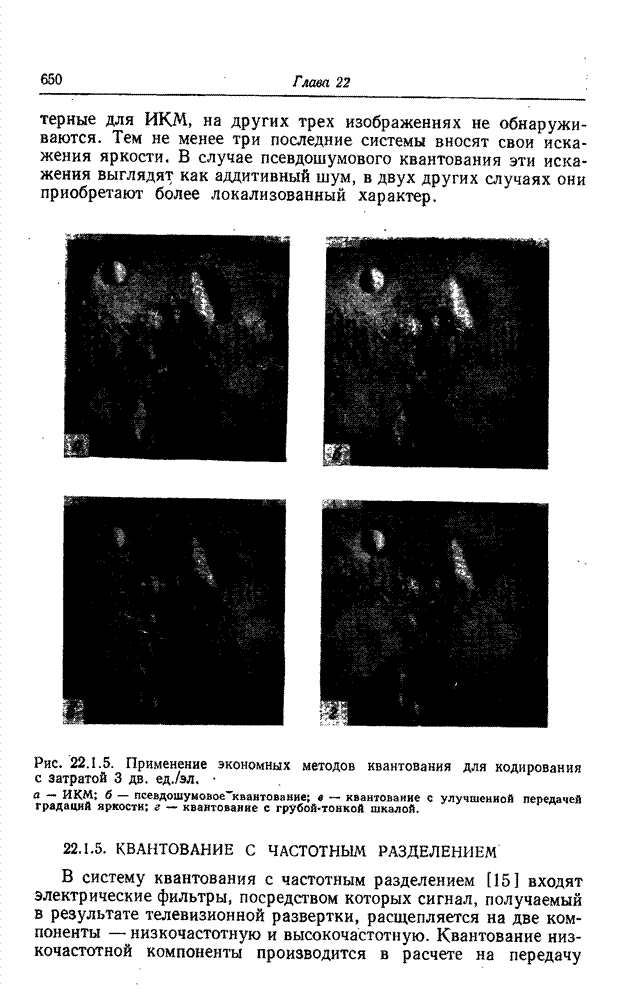
- 22.1.5. КВАНТОВАНИЕ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ
- 22.2. СТАТИСТИЧЕСКИЕ МЕТОДЫ КОДИРОВАНИЯ
- 22.2.1. ПОЭЛЕМЕНТНОЕ СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- 22.2.2. КОДИРОВАНИЕ С УЧЕТОМ ПРЕДШЕСТВУЮЩЕГО ЭЛЕМЕНТА
- 22.3. КОДИРОВАНИЕ СЕРИЙ
- 22.3.1. КОДИРОВАНИЕ ДЛИН СЕРИЙ; ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ [32-36]
- 22.3.2. КОДИРОВАНИЕ РАЗРЯДНЫХ ПЛОСКОСТЕЙ
- 22.4. КОДИРОВАНИЕ С ПОПОЛНЕНИЕМ КАДРОВ
- 22.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ
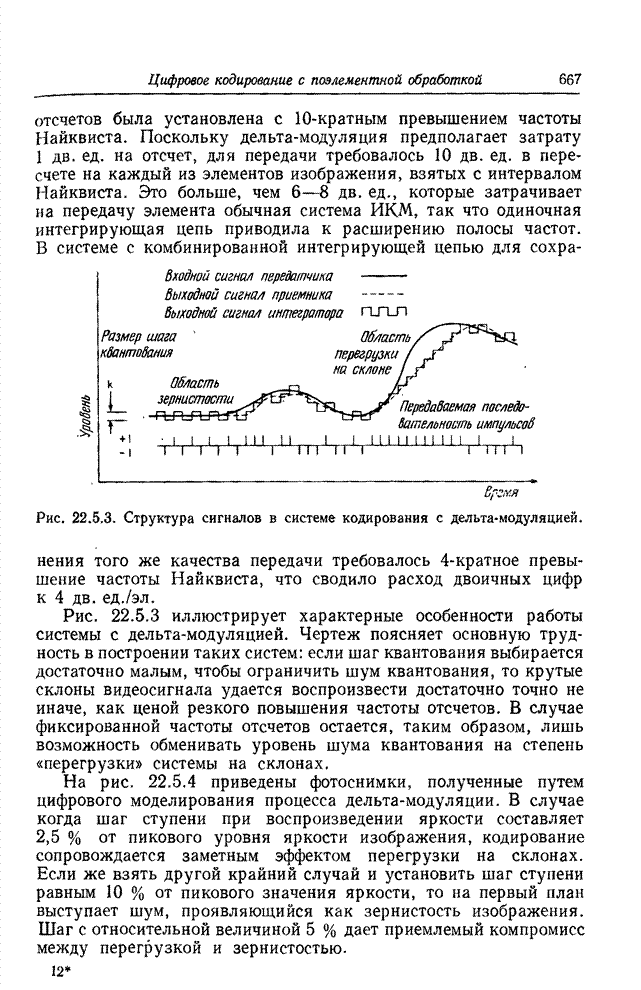
- 22.5.1. ДЕЛЬТА-МОДУЛЯЦИЯ
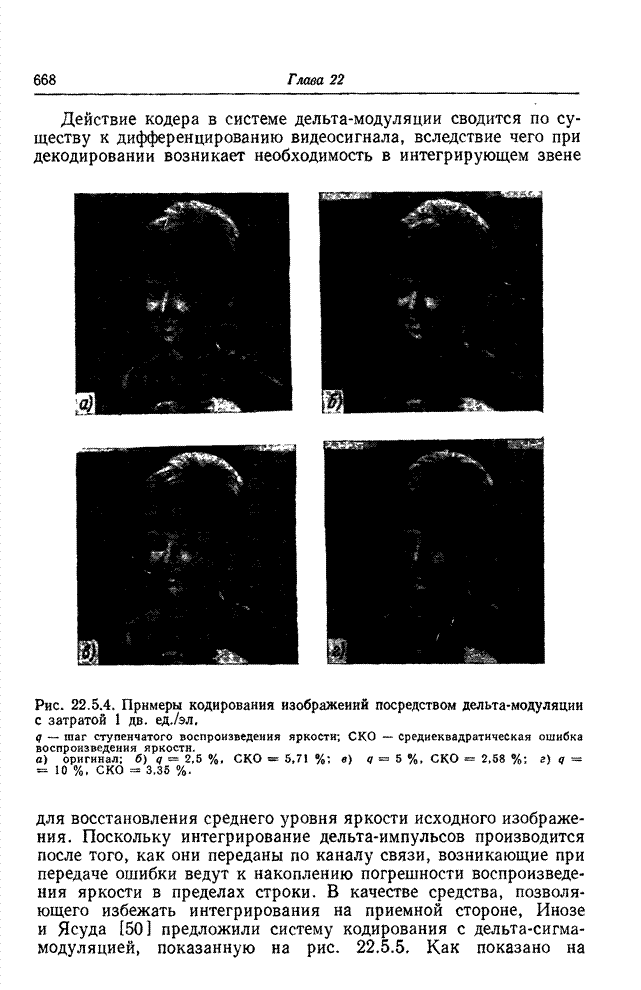
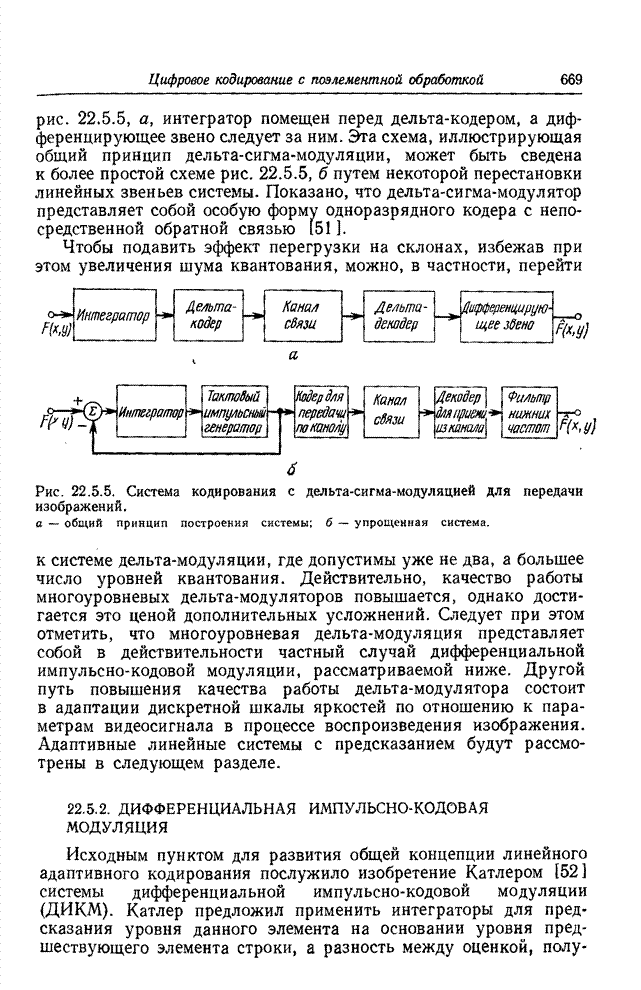
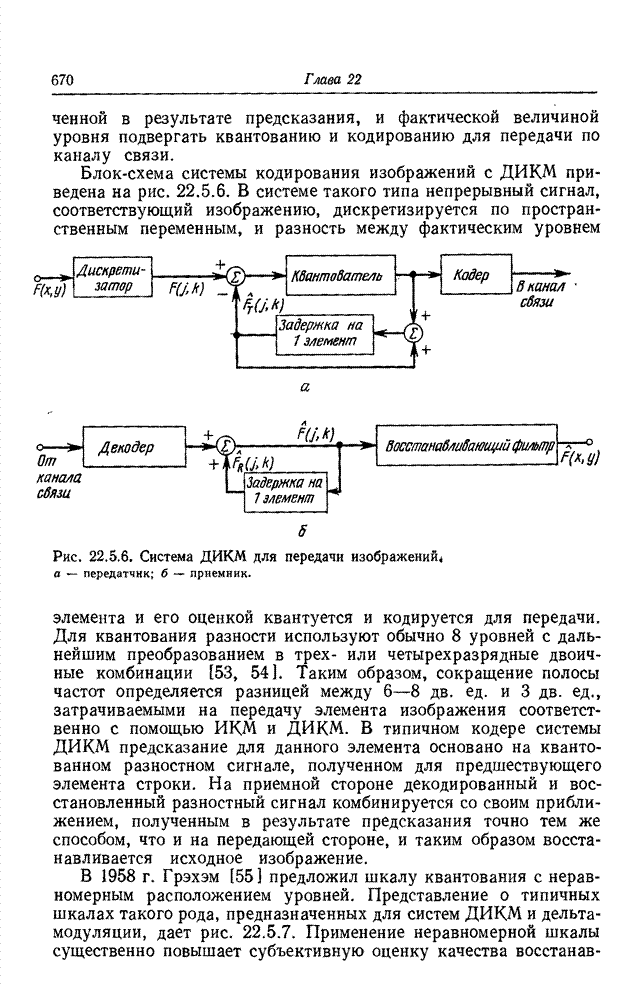
- 22.5.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ
- 22.5.3. КОДЕРЫ С ПРОСТРАНСТВЕННЫМ ПРЕДСКАЗАНИЕМ
- 22.5.4. АДАПТИВНЫЕ КОДЕРЫ С ПРЕДСКАЗАНИЕМ
- 22.5.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ ПРИМЕНИТЕЛЬНО К ЦВЕТНЫМ ИЗОБРАЖЕНИЯМ
- 22.5.6. ДИФФЕРЕНЦИАЛЬНОЕ МЕЖКАДРОВОЕ КОДИРОВАНИЕ
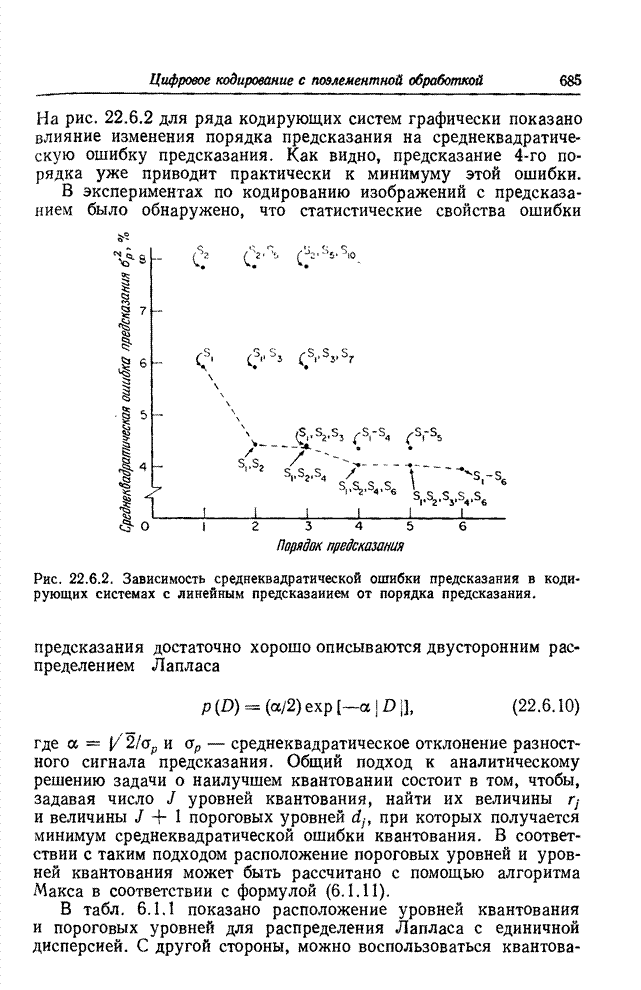
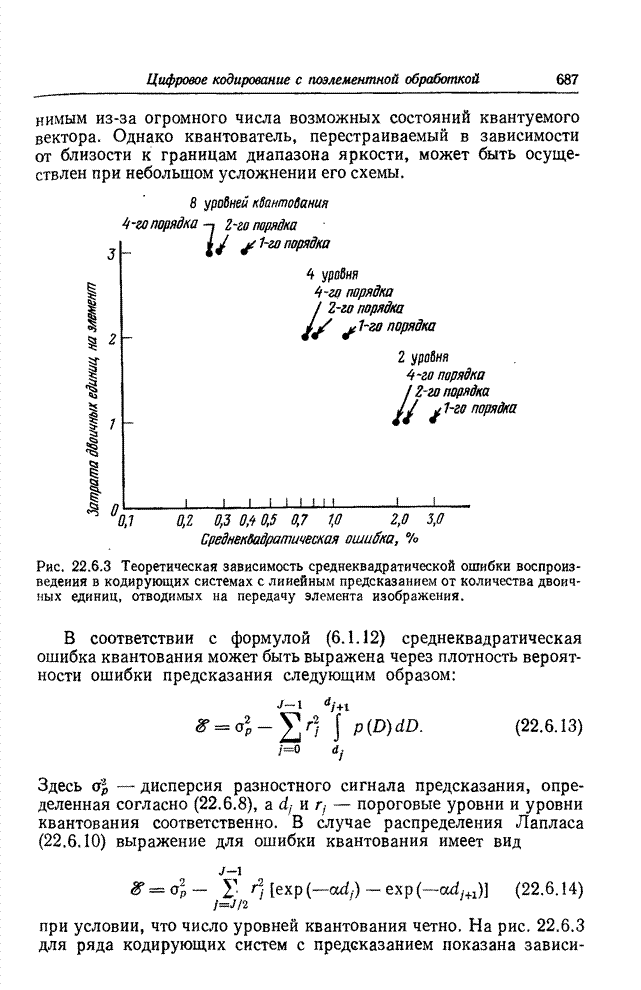
- 22.6. ПРОЕКТИРОВАНИЕ СИСТЕМ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ДЛЯ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 23. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННОЙ ОБРАБОТКОЙ
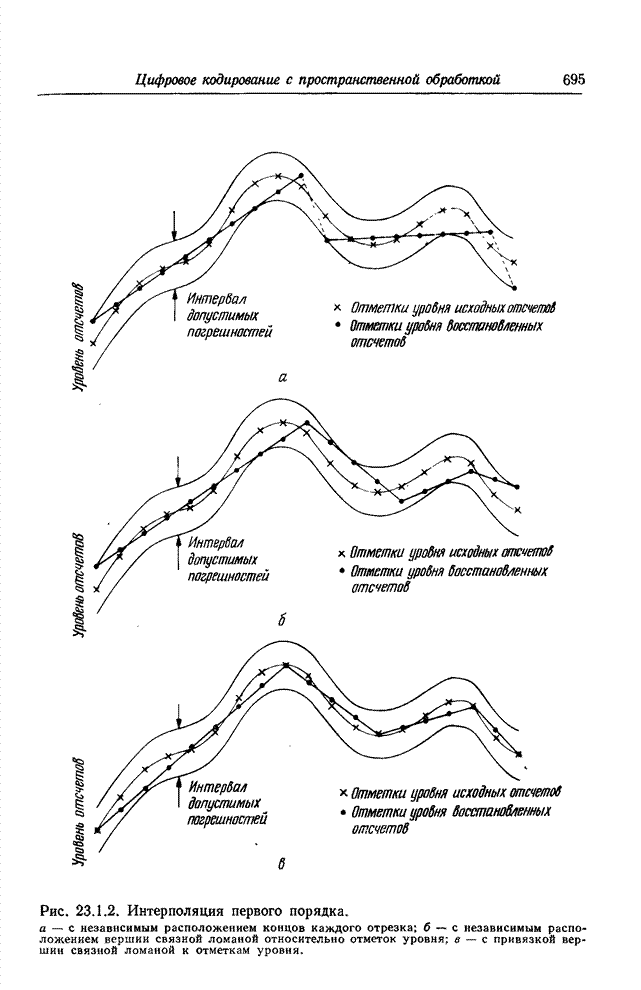
- 23.1. ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ КОДИРОВАНИЯ
- 23.1.1. ИНТЕРПОЛЯЦИЯ НА ПЕРЕДАЮЩЕЙ СТОРОНЕ
- 23.1.2. ИНТЕРПОЛЯЦИЯ НА ПРИЕМНОЙ СТОРОНЕ
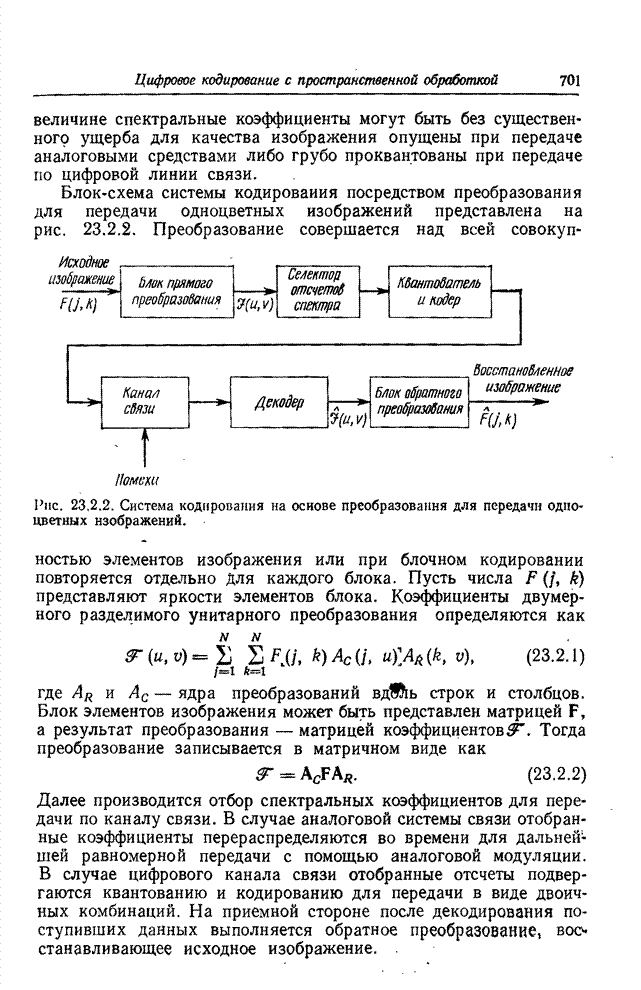
- 23.2. КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.1. КОДИРОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.2. АДАПТИВНОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.3. КОДИРОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.4. МЕЖКАДРОВОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.3. УМЕНЬШЕНИЕ ОШИБОК КВАНТОВАНИЯ ПРИ КОДИРОВАНИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.4. ГИБРИДНОЕ КОДИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ И ДИКМ
- 23.5. КОДИРОВАНИЕ ПРИЗНАКОВ
- 23.5.1. КОДИРОВАНИЕ ЛИНИЙ УРОВНЯ
- 23.5.2. КОДИРОВАНИЕ КОНТУРОВ
- 23.5.3. КОДИРОВАНИЕ ТЕКСТУР
- 23.6. КОДИРОВАНИЕ С ПОМОЩЬЮ НАБОРА СИМВОЛОВ
- 23.6.1. КОДИРОВАНИЕ БЛОКОВ ПО СЛОВАРЮ ОБРАЗОВ
- 23.6.2. КОДИРОВАНИЕ НА ОСНОВЕ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- ЛИТЕРАТУРА
- Глава 24. АНАЛИЗ ЭФФЕКТИВНОСТИ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 24.1. СТАТИСТИЧЕСКИЕ МОДЕЛИ КАНАЛА СВЯЗИ КАК ИСТОЧНИКА ПОМЕХ [1-4]
- 24.2. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ
- 24.3. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ [4]
- 24.3.1. ПЕРЕДАЧА КООРДИНАТ ЦВЕТА
- 24.3.2. ПЕРЕДАЧА ЯРКОСТИ И КООРДИНАТ ЦВЕТНОСТИ
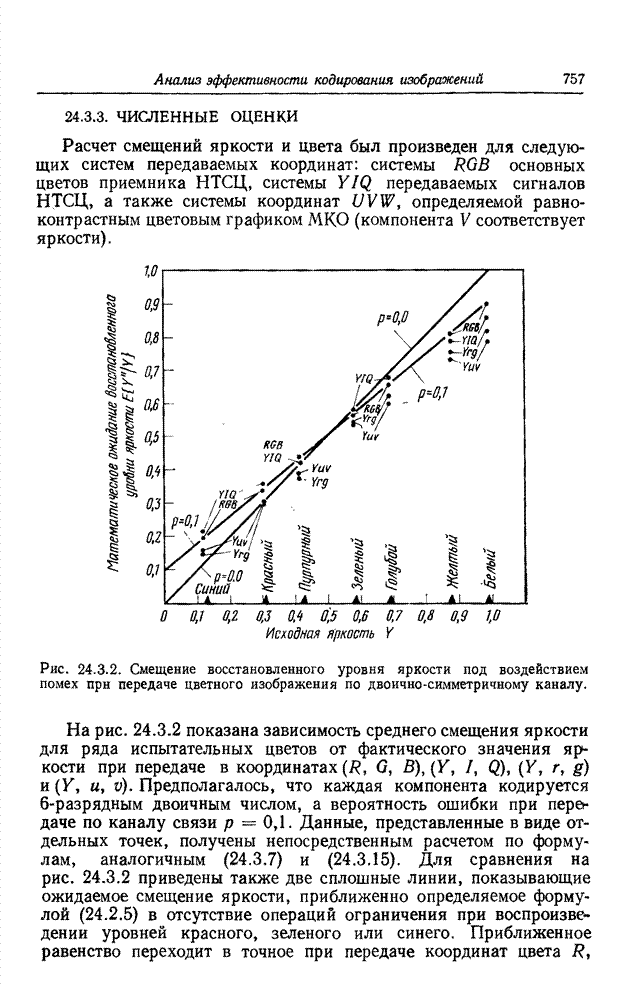
- 24.3.3. ЧИСЛЕННЫЕ ОЦЕНКИ
- 24.4. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ ДИКМ
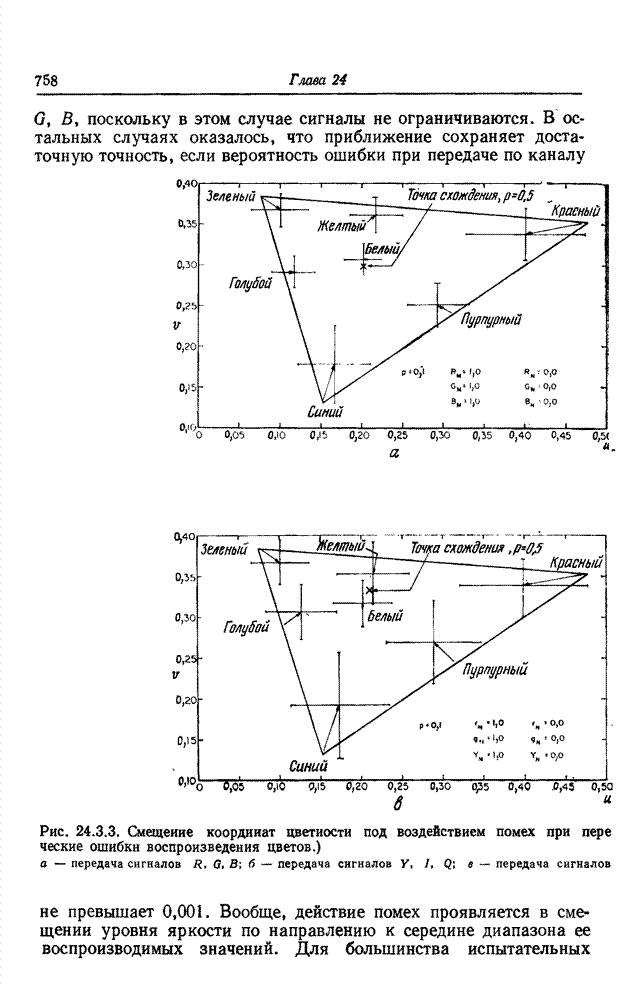
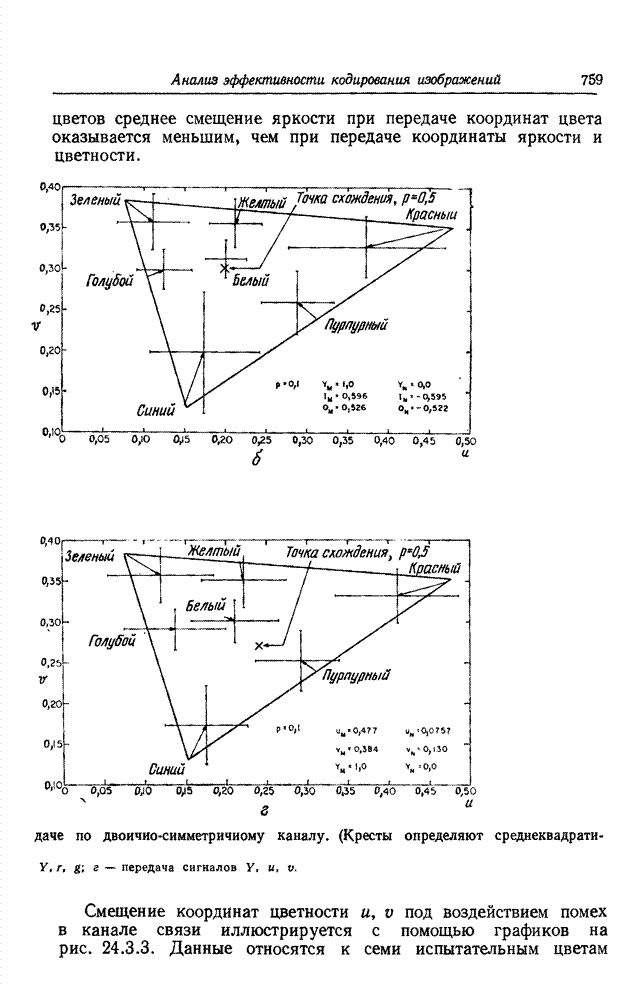
- 24.5. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ КОДИРОВАНИЯ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
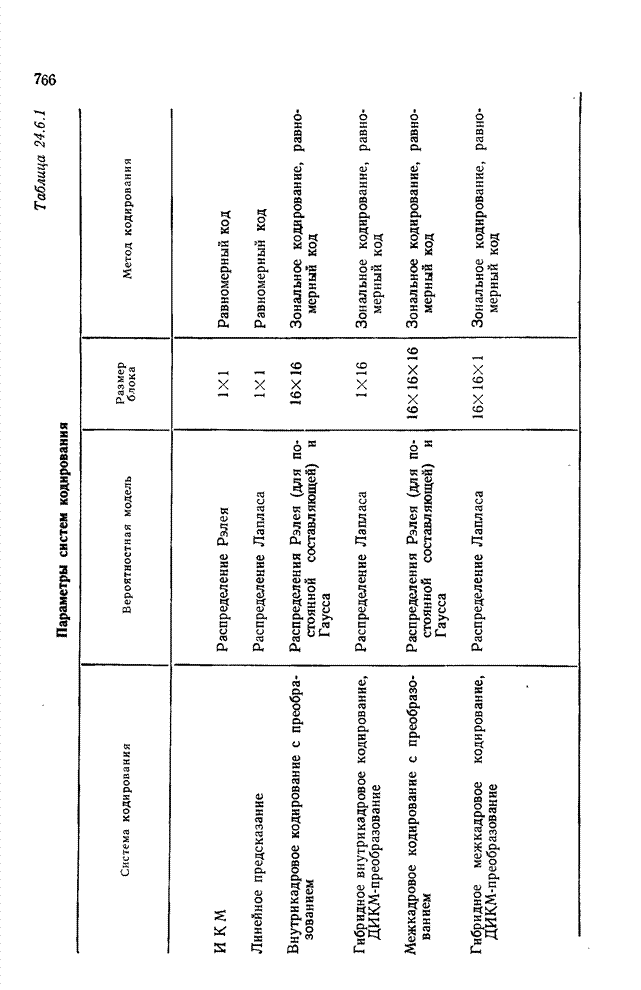
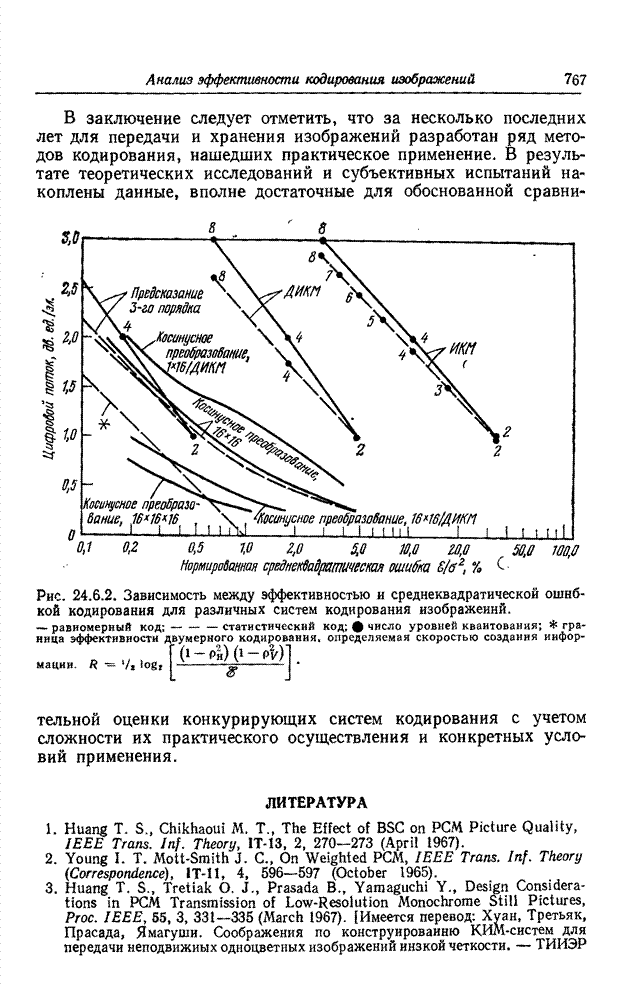
- 24.6. СРАВНЕНИЕ РАЗЛИЧНЫХ МЕТОДОВ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Приложение 1. ОСНОВНАЯ ЛИТЕРАТУРА
- Приложение 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА И ЦВЕТНОСТИ
- Приложение 3. СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА