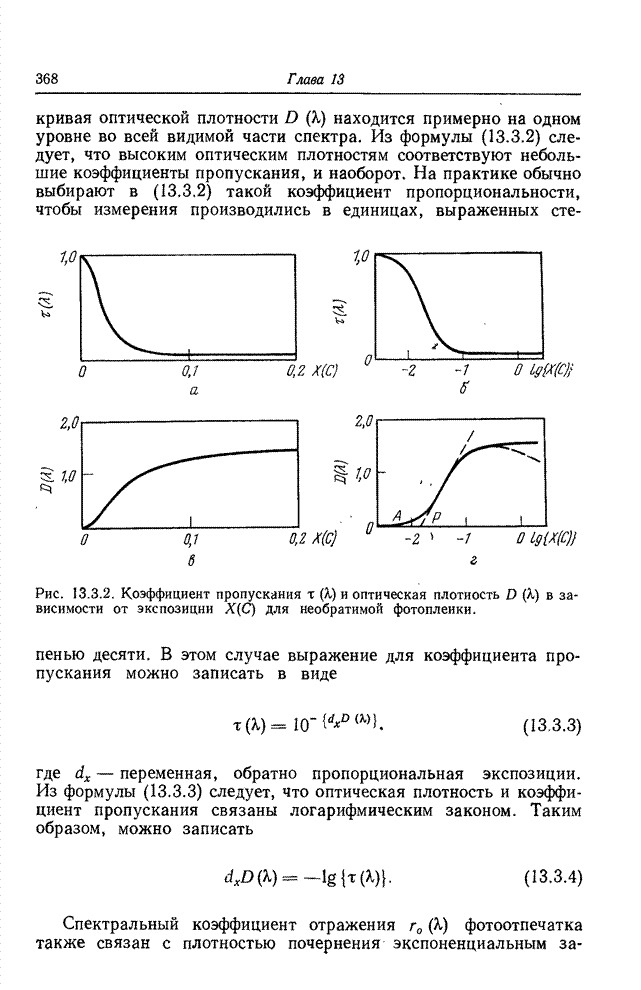
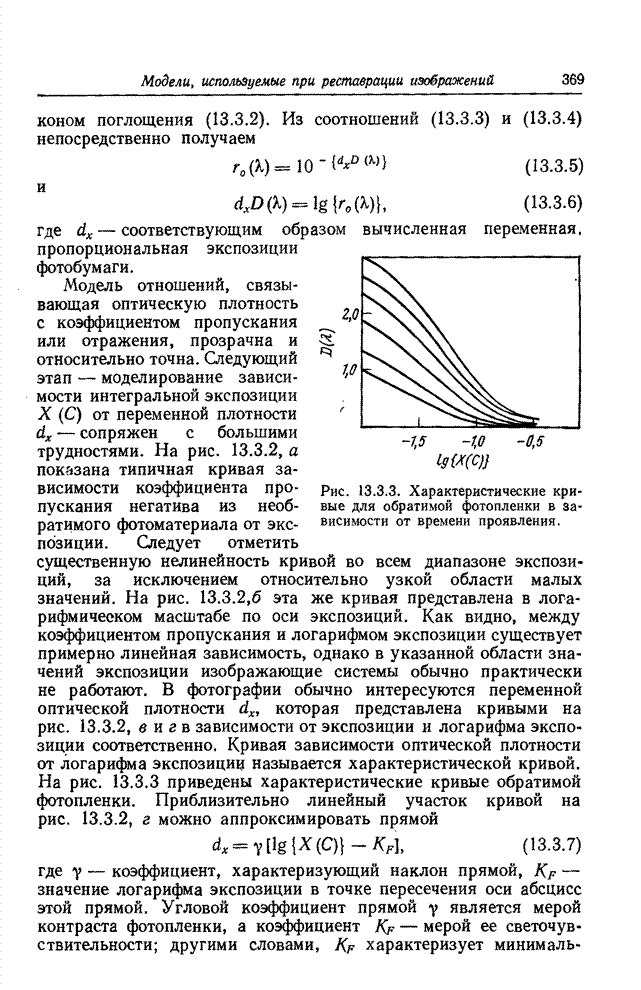
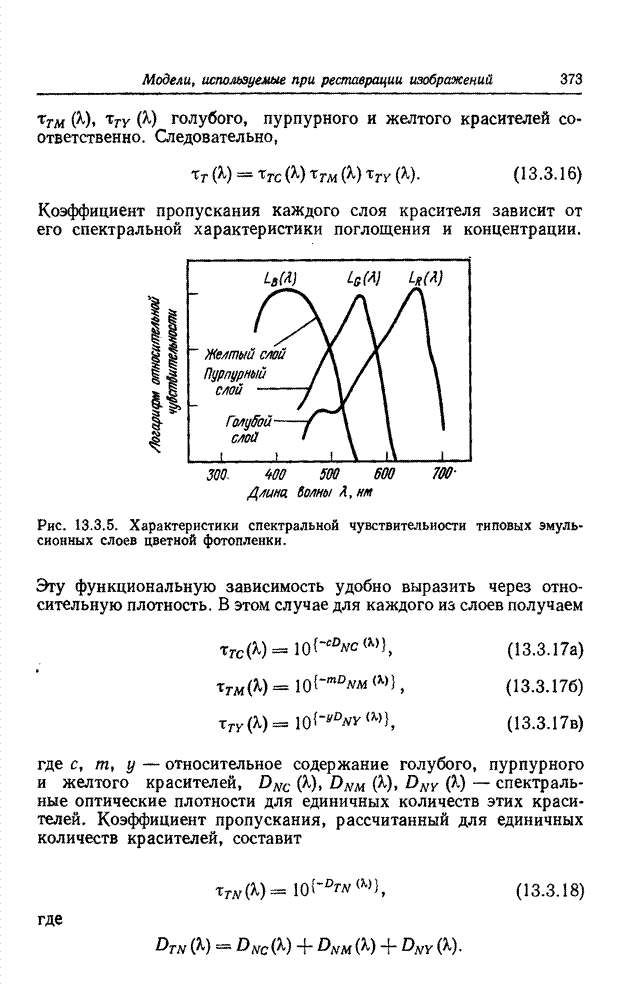
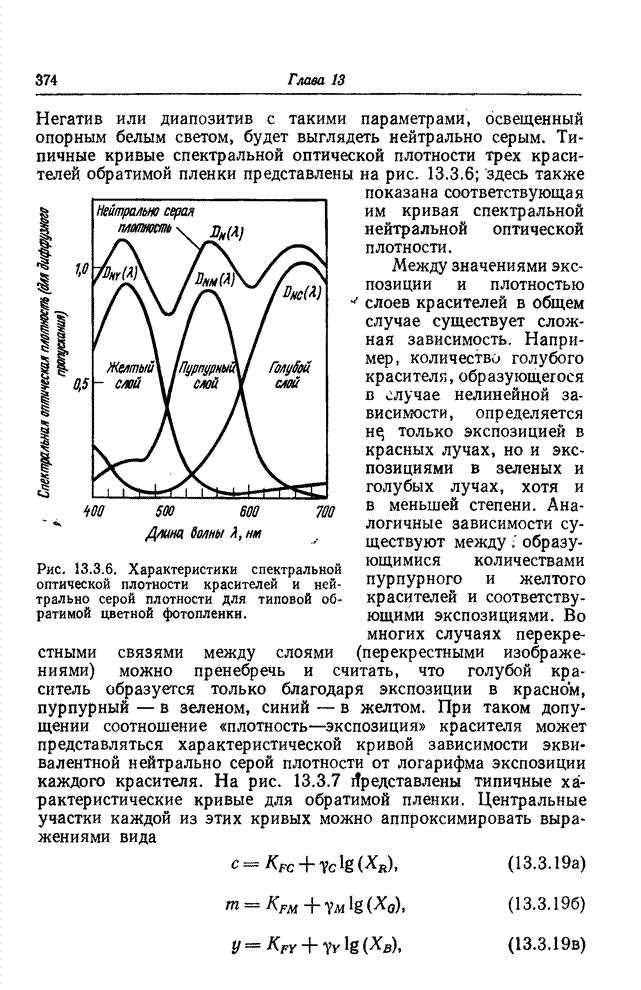
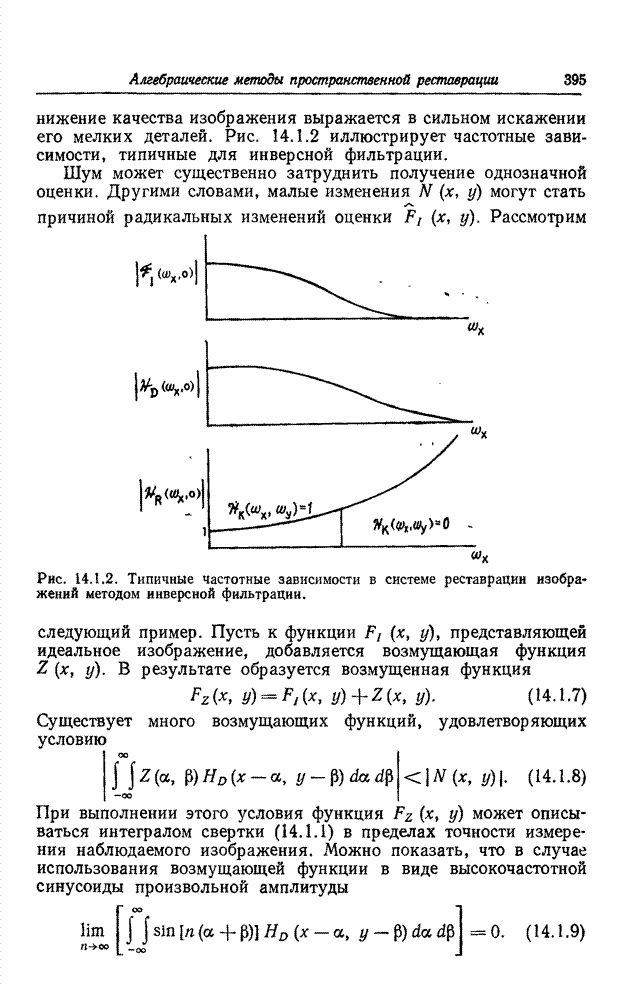
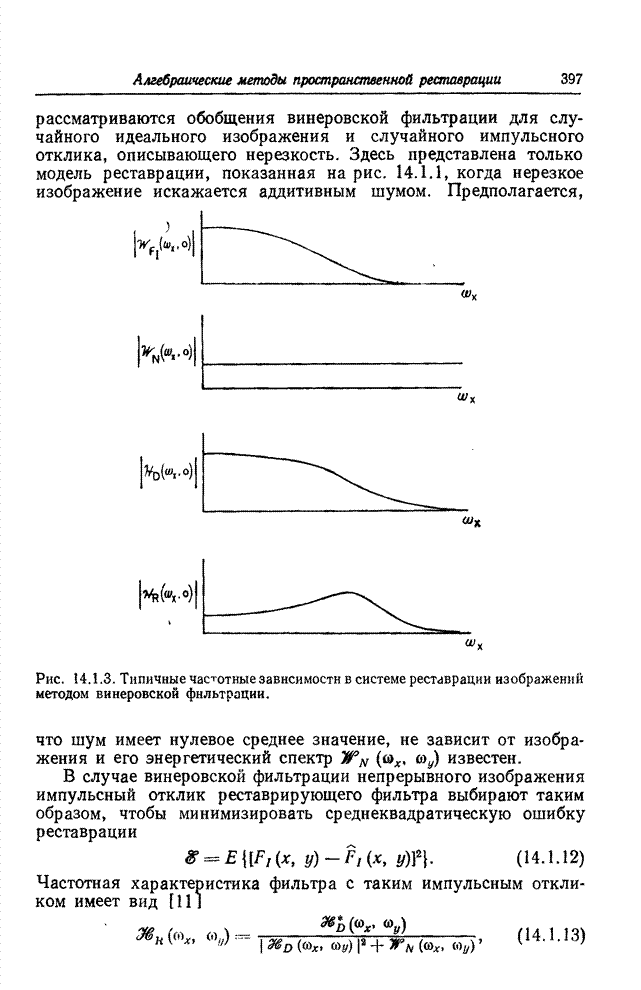
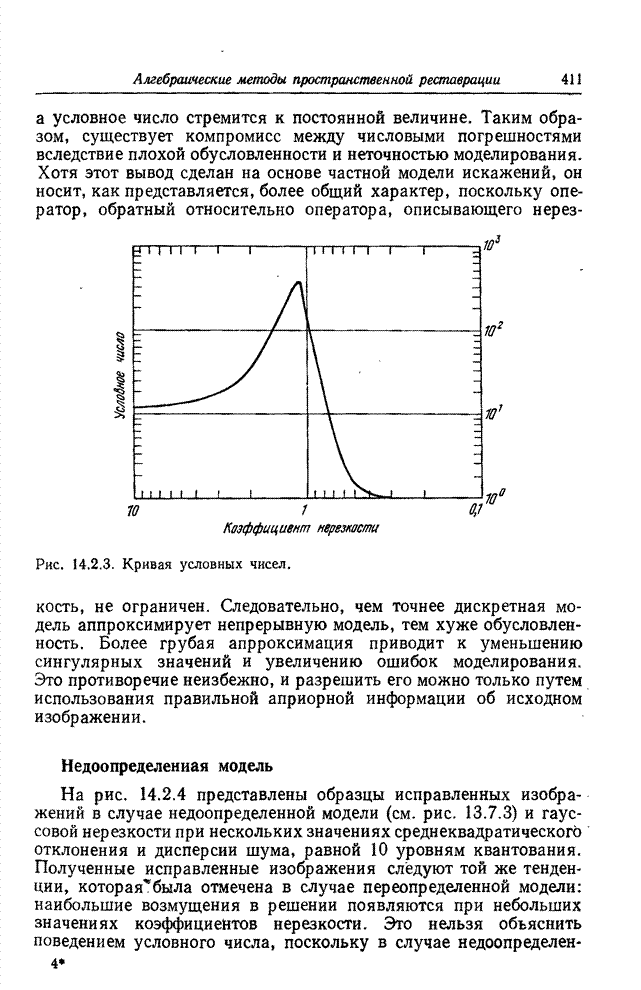
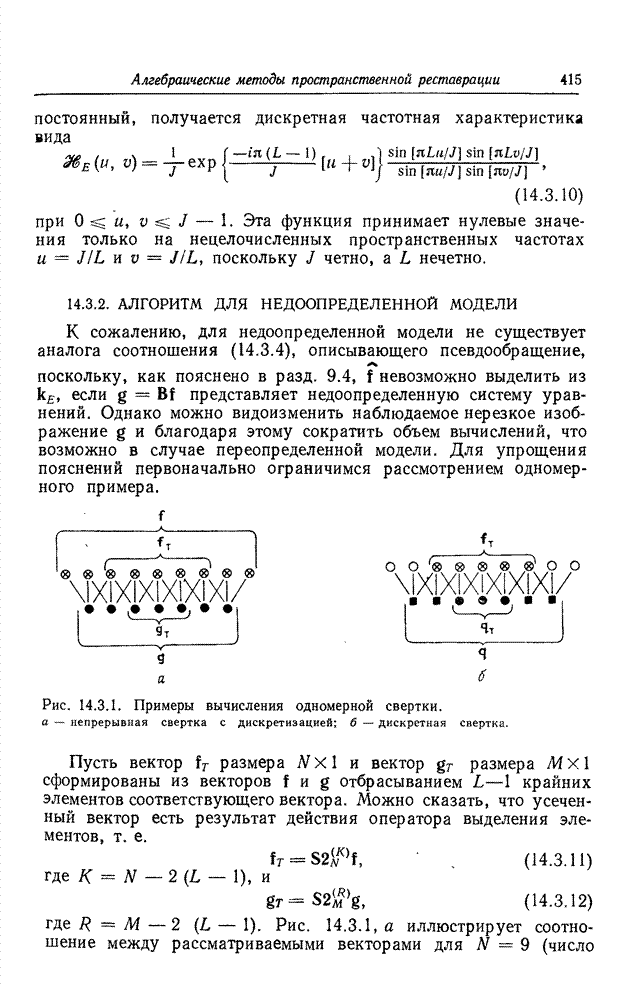
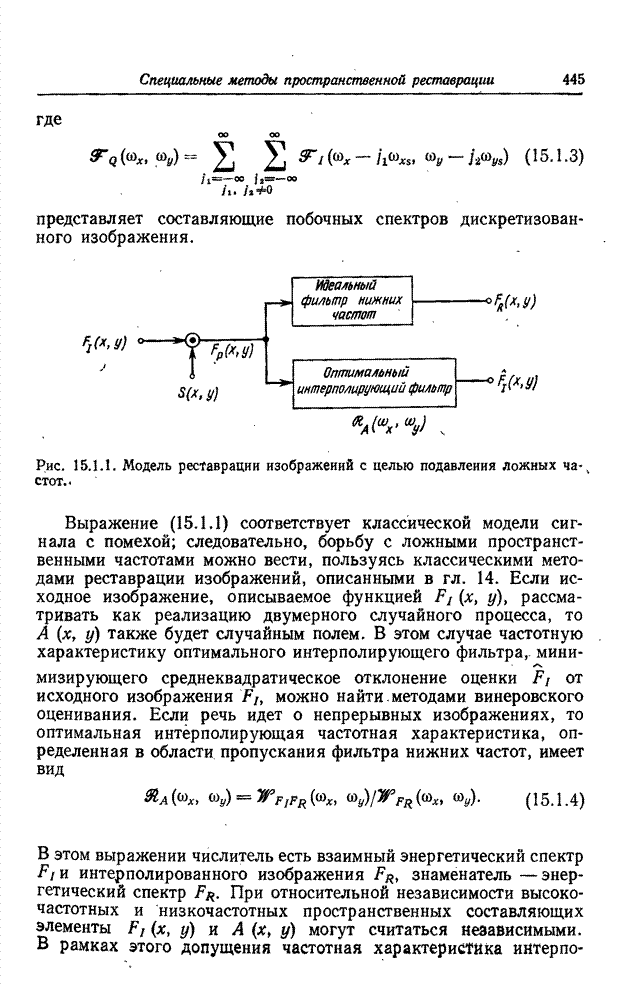
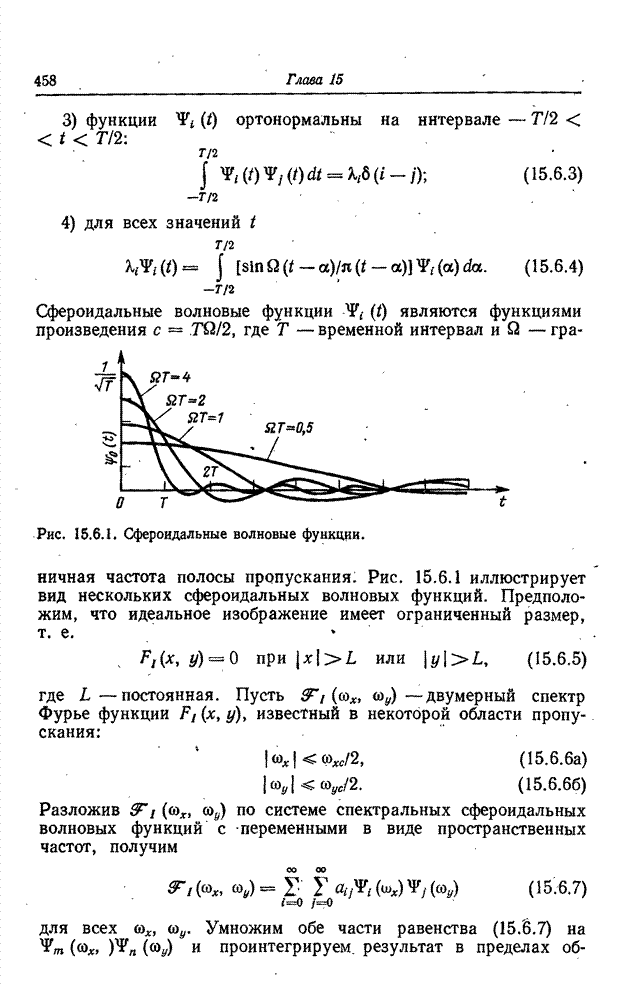
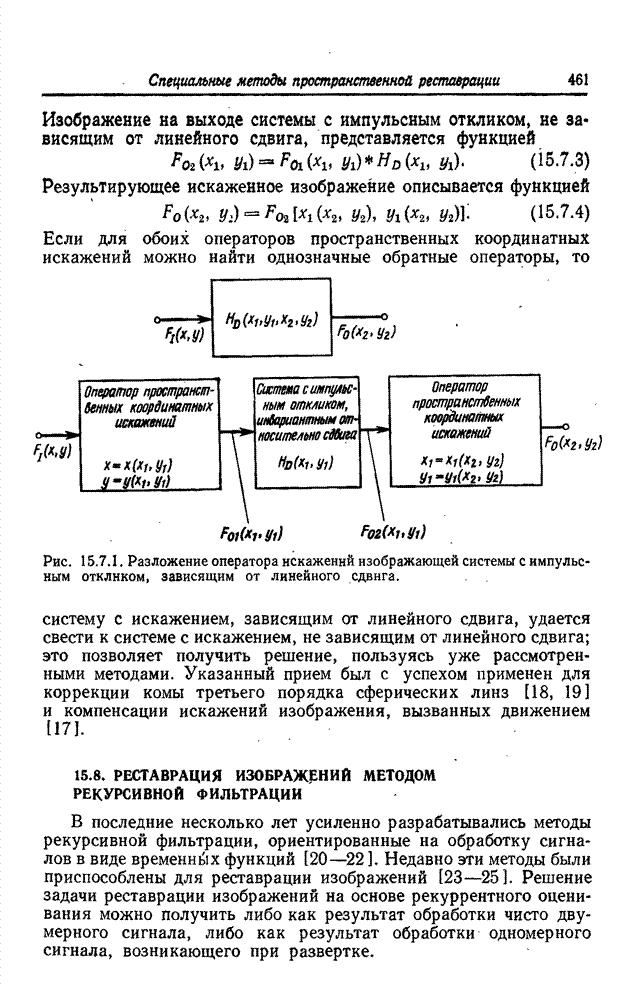
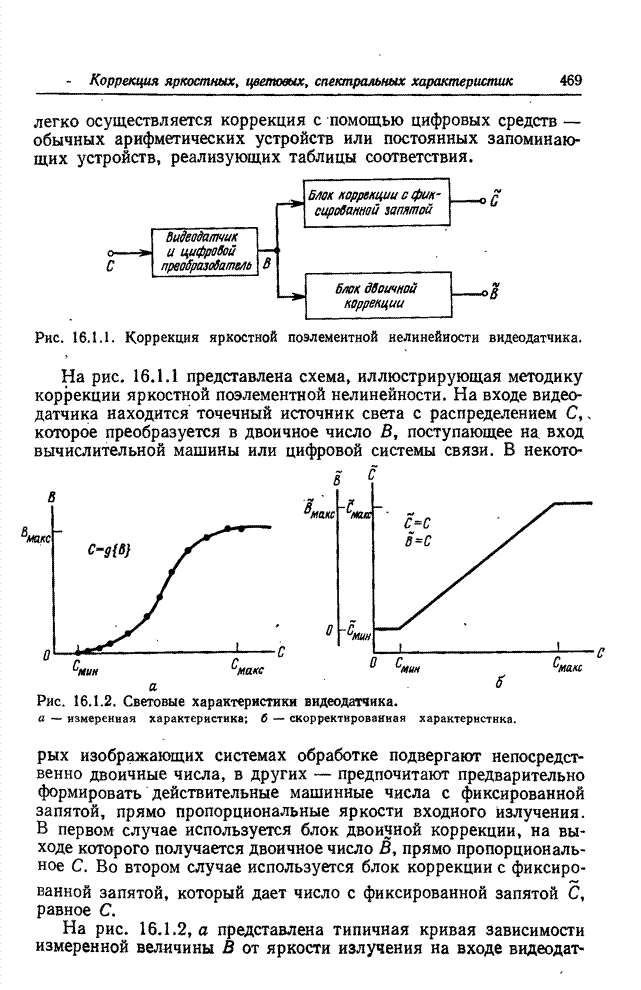
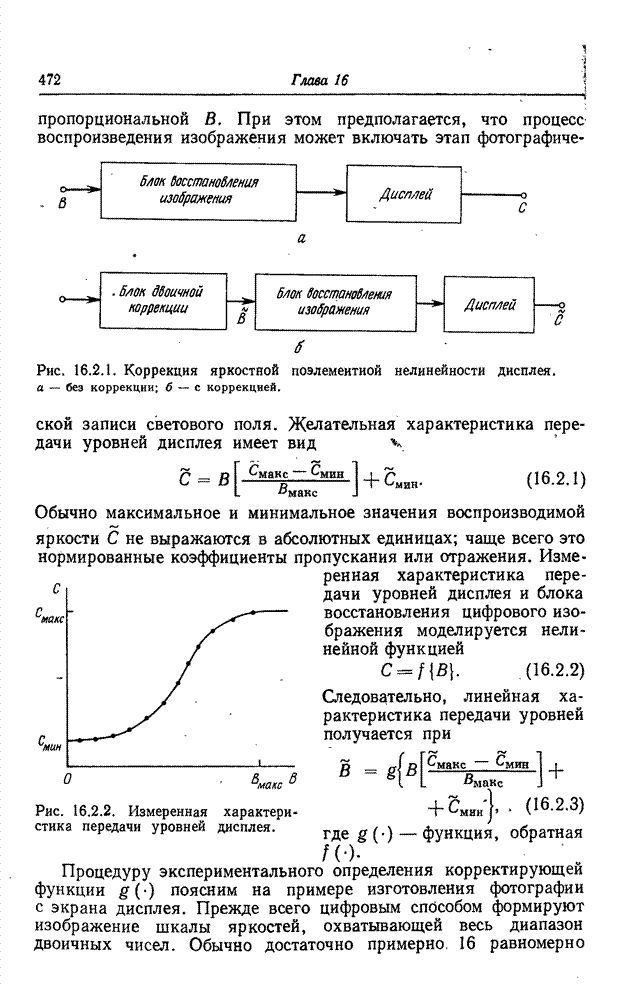
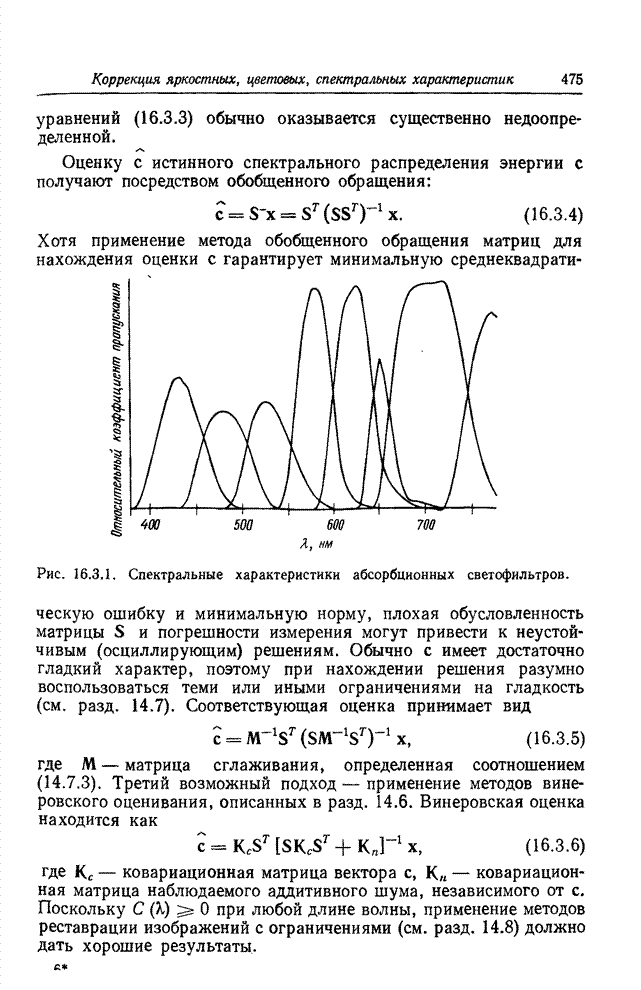
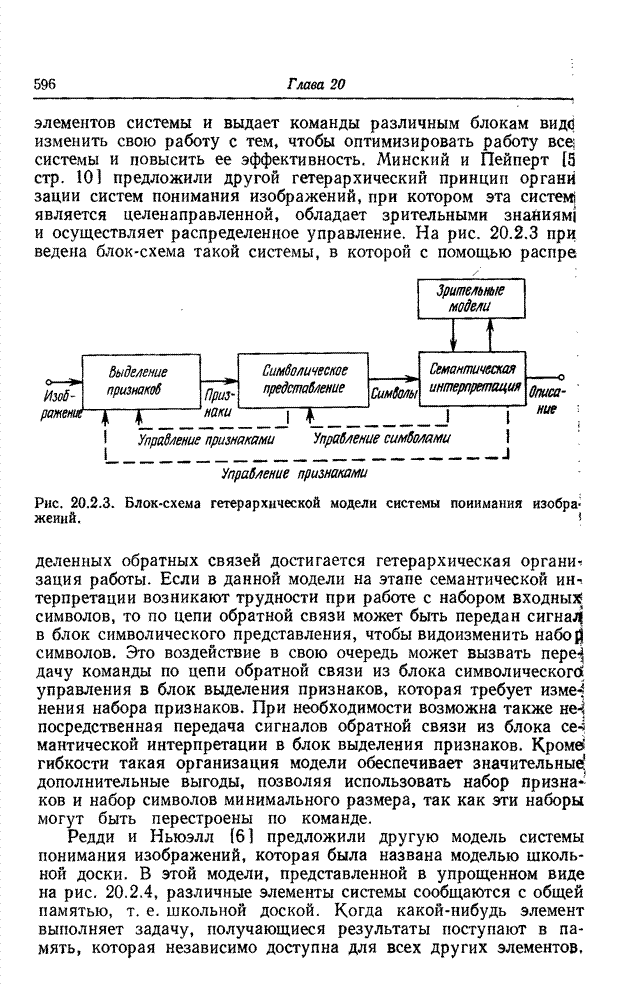
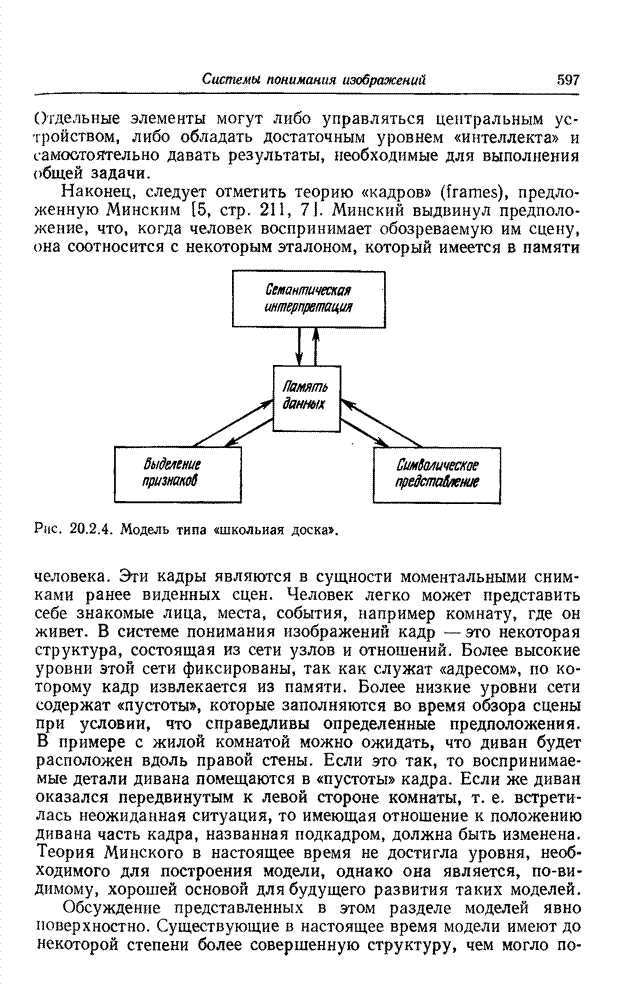
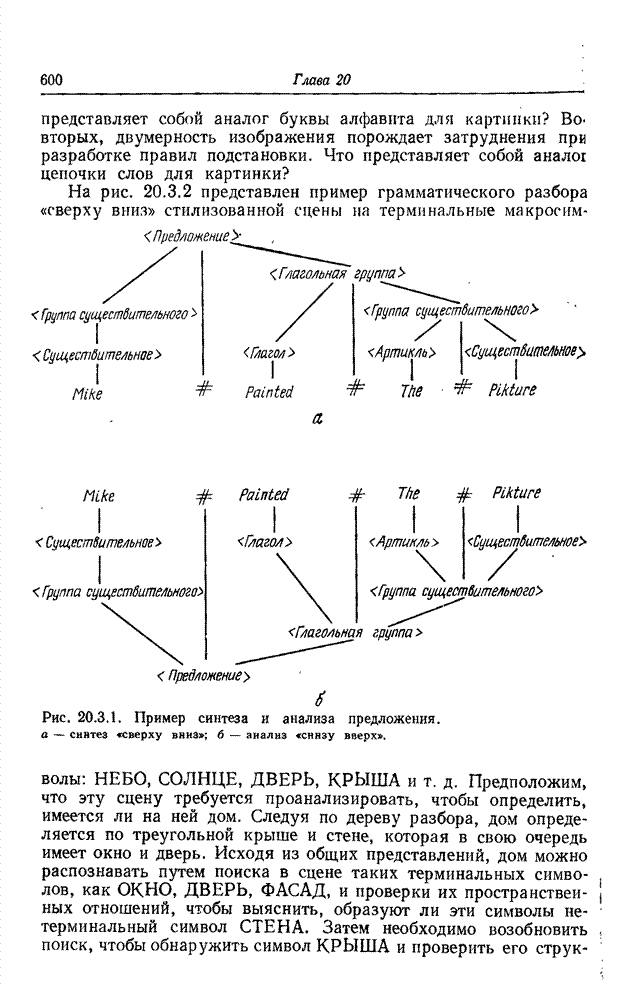
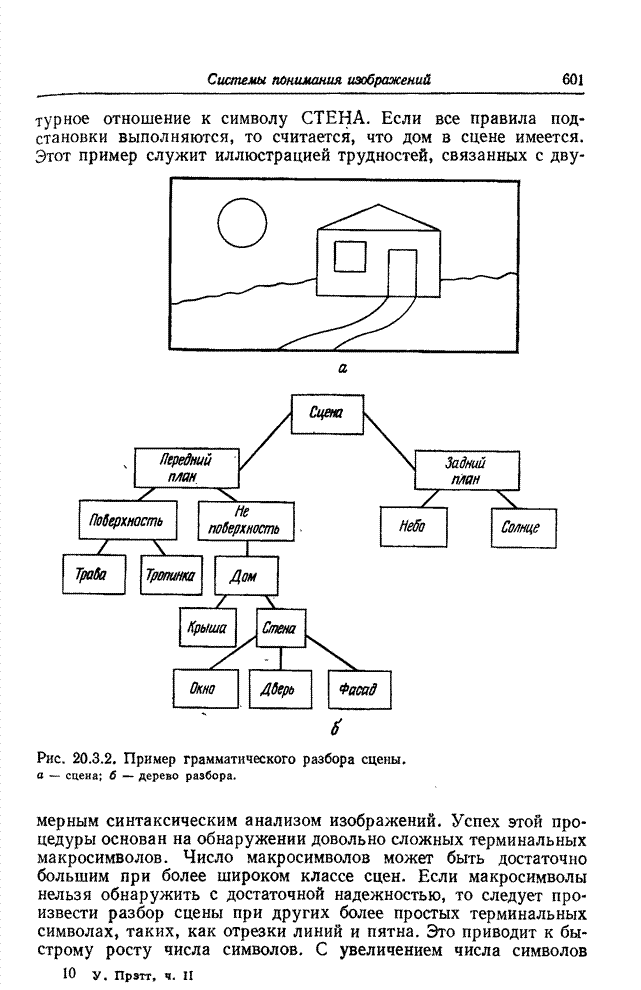
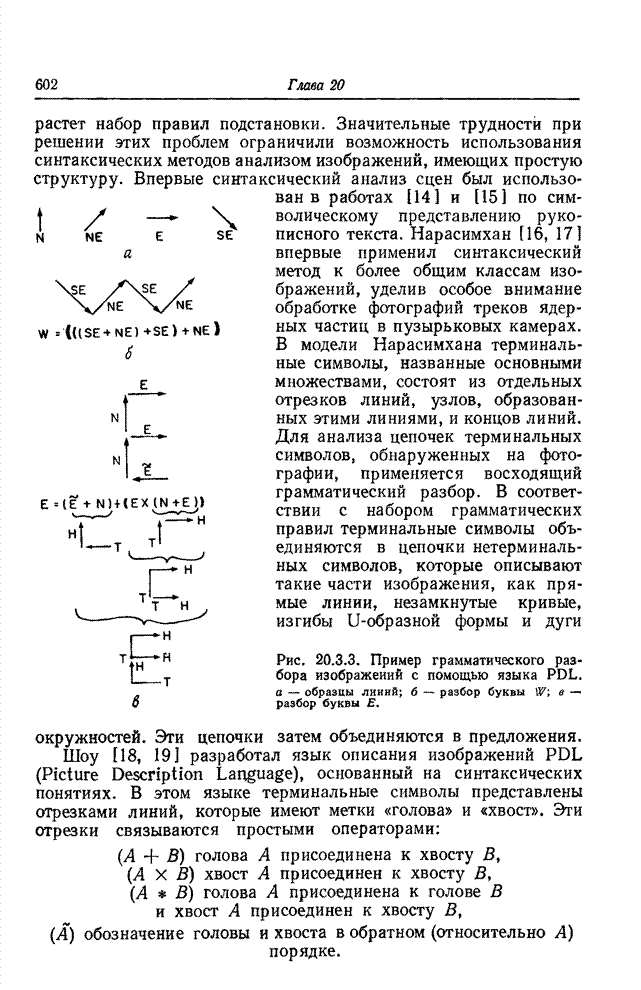
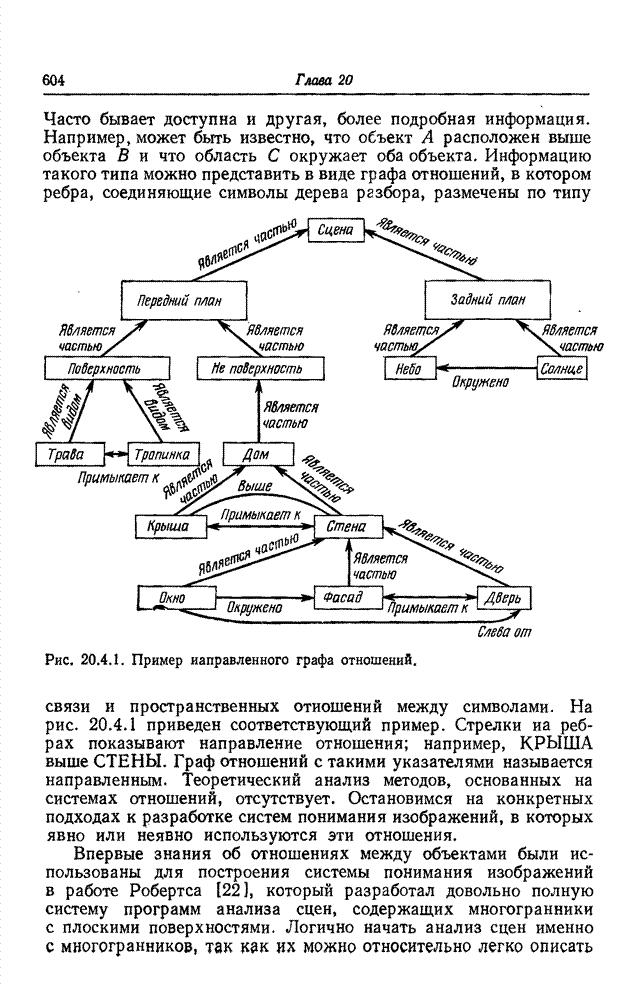
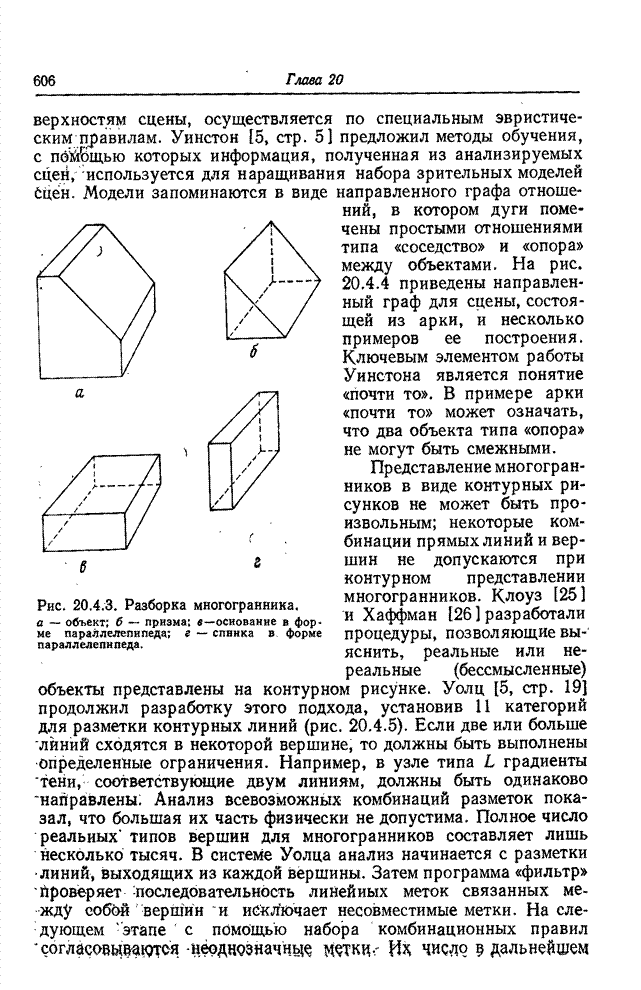
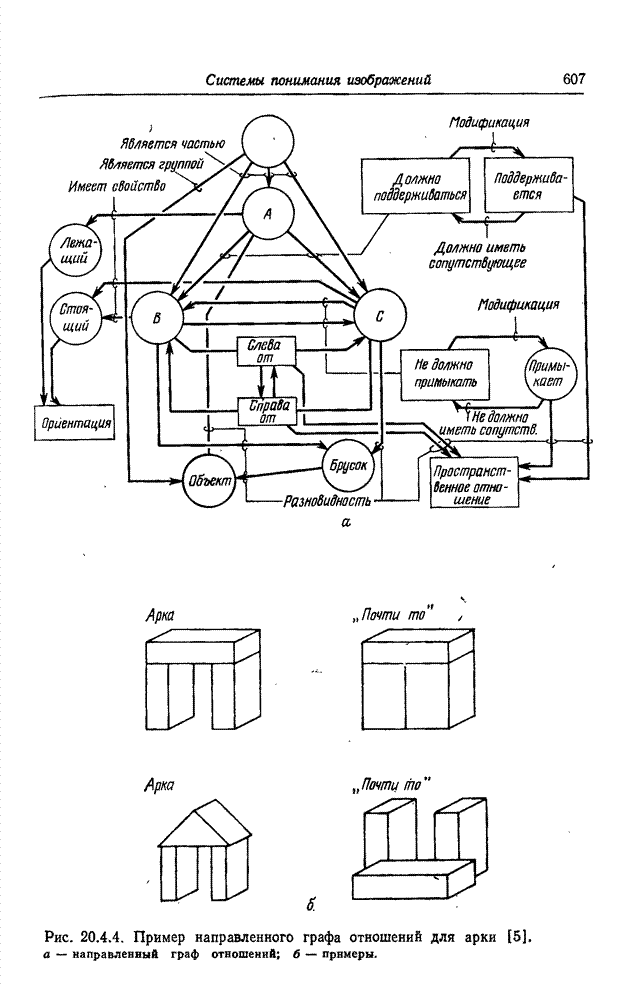
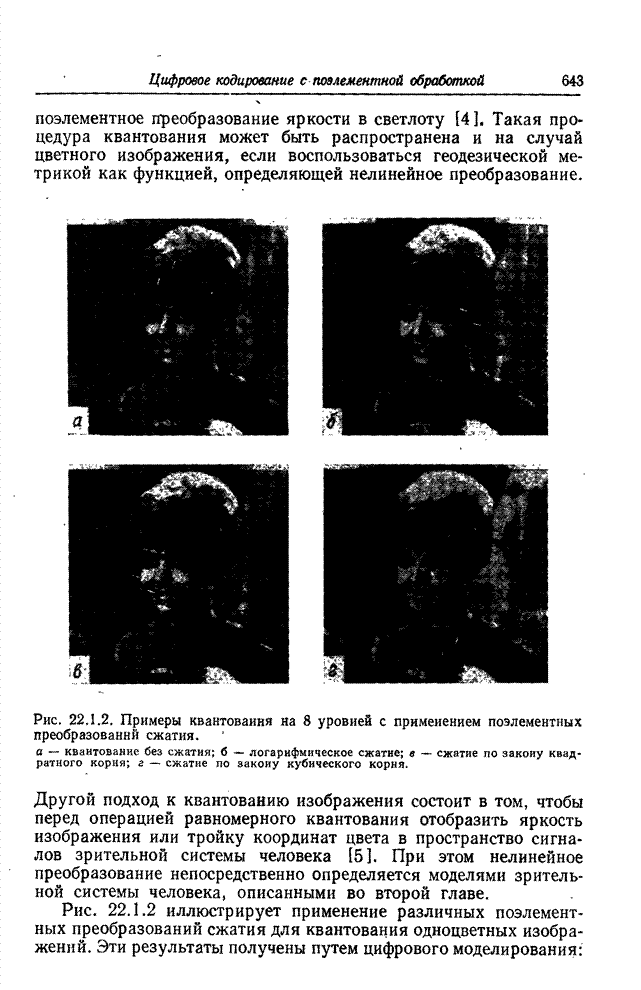
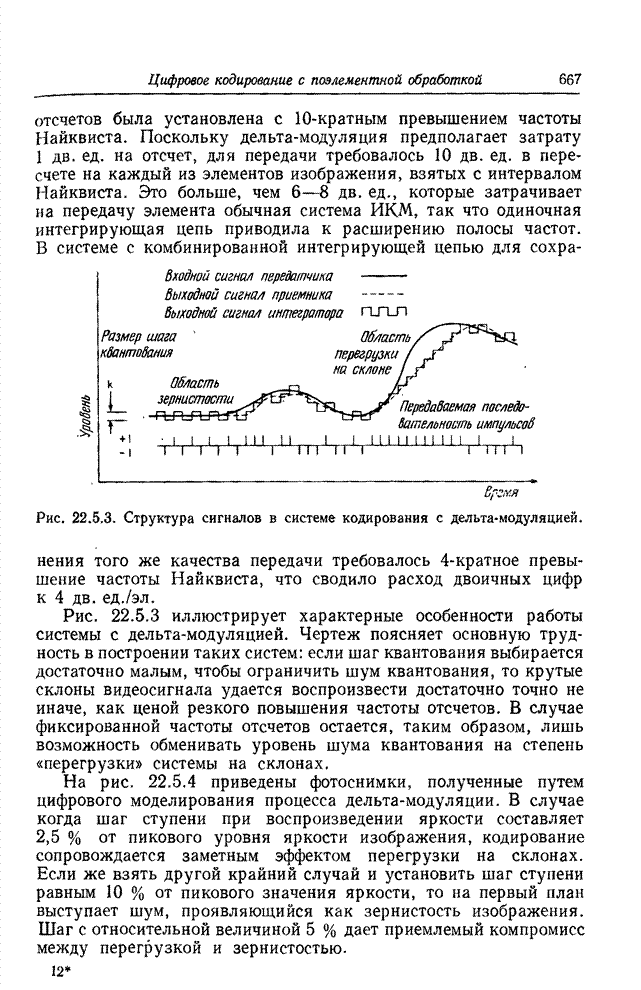
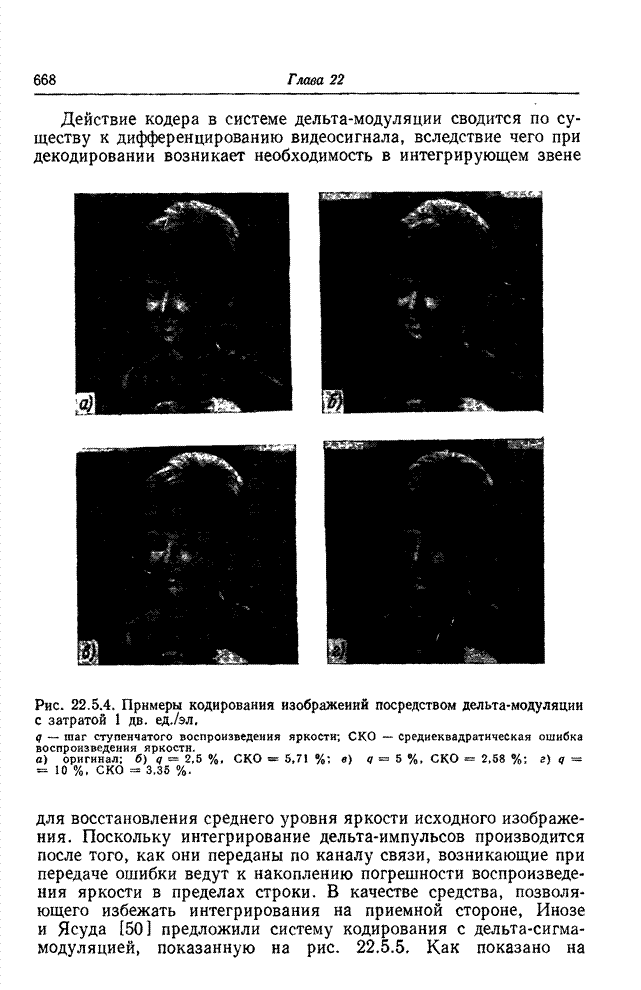
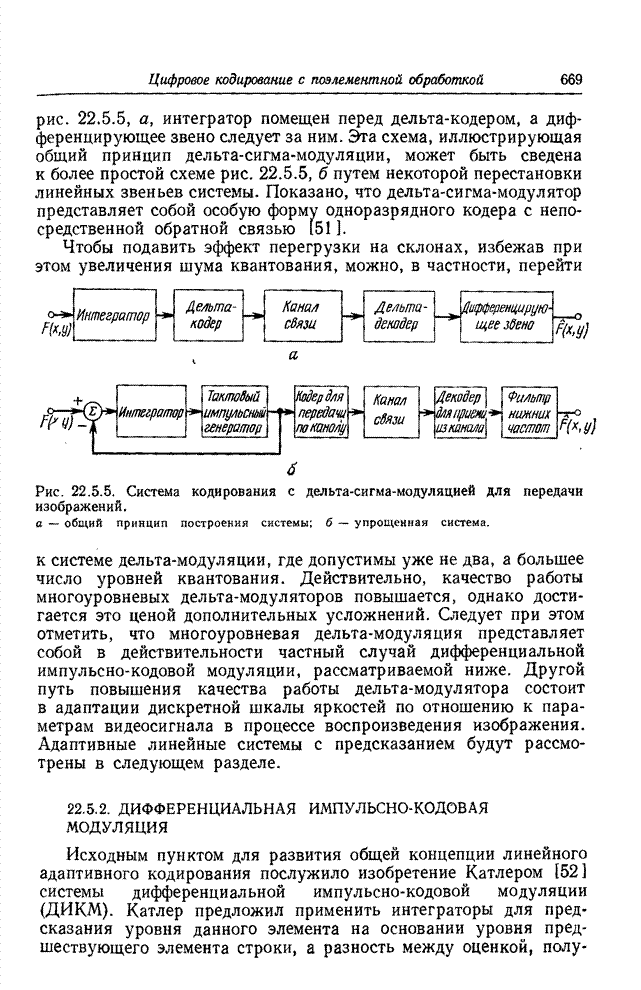
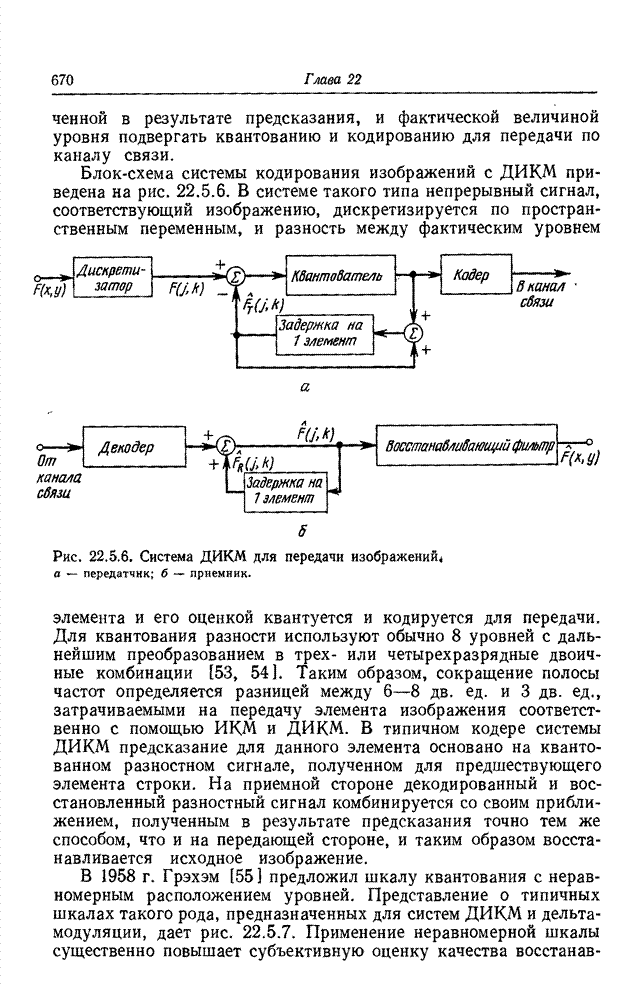
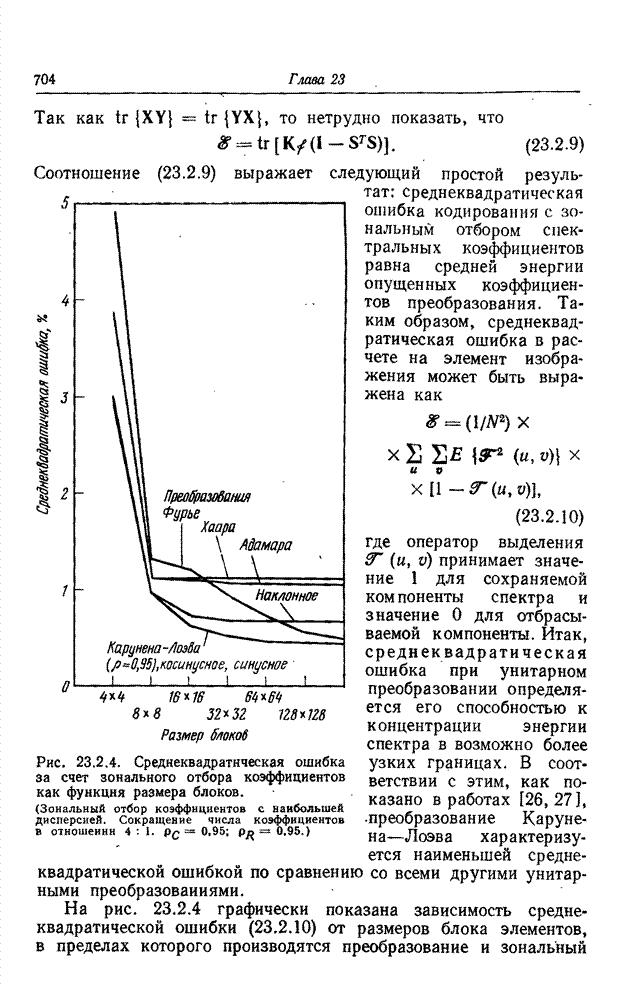
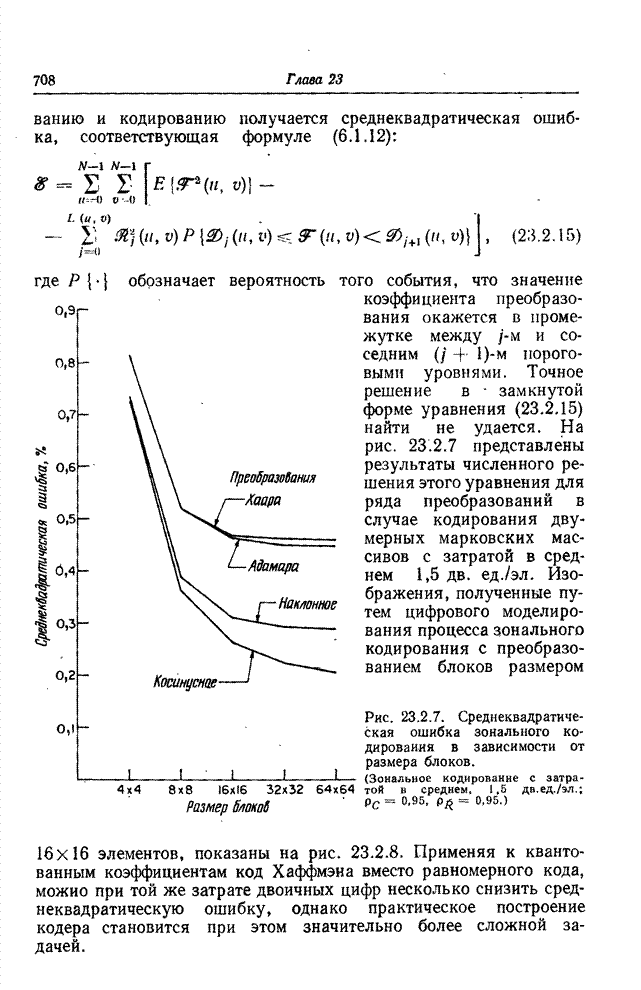
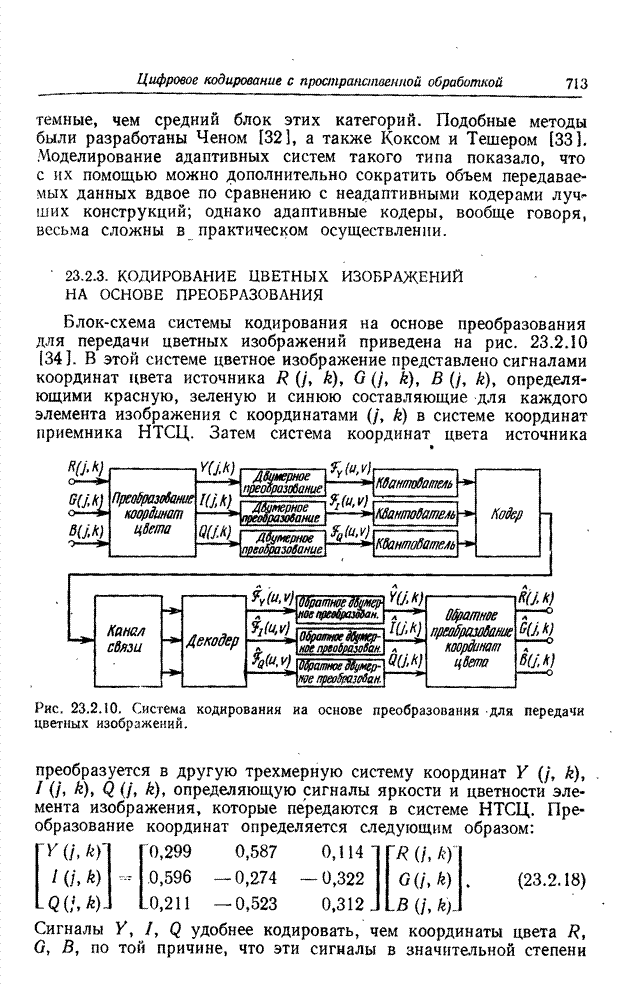
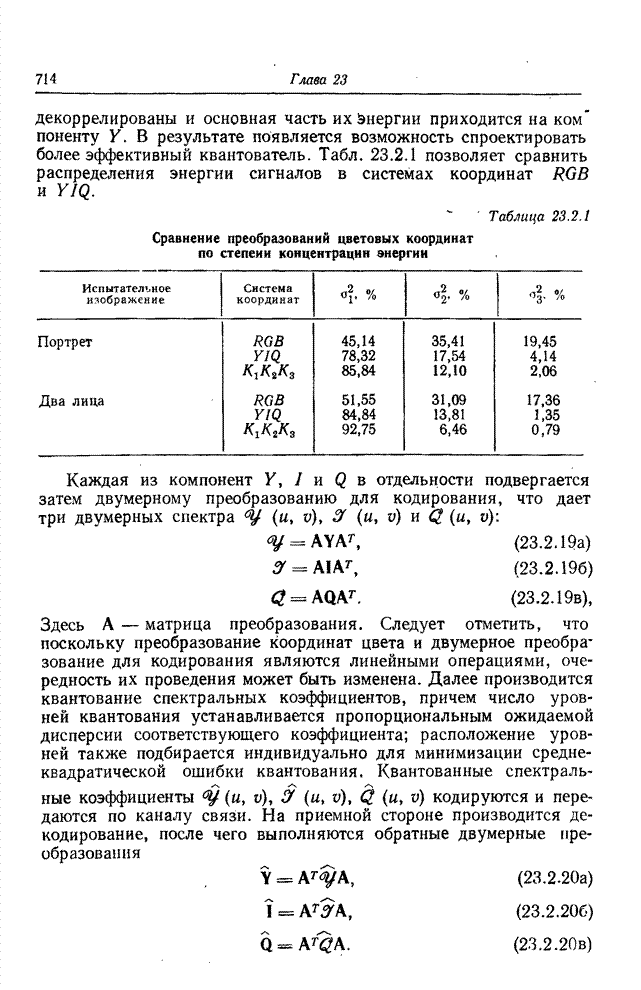
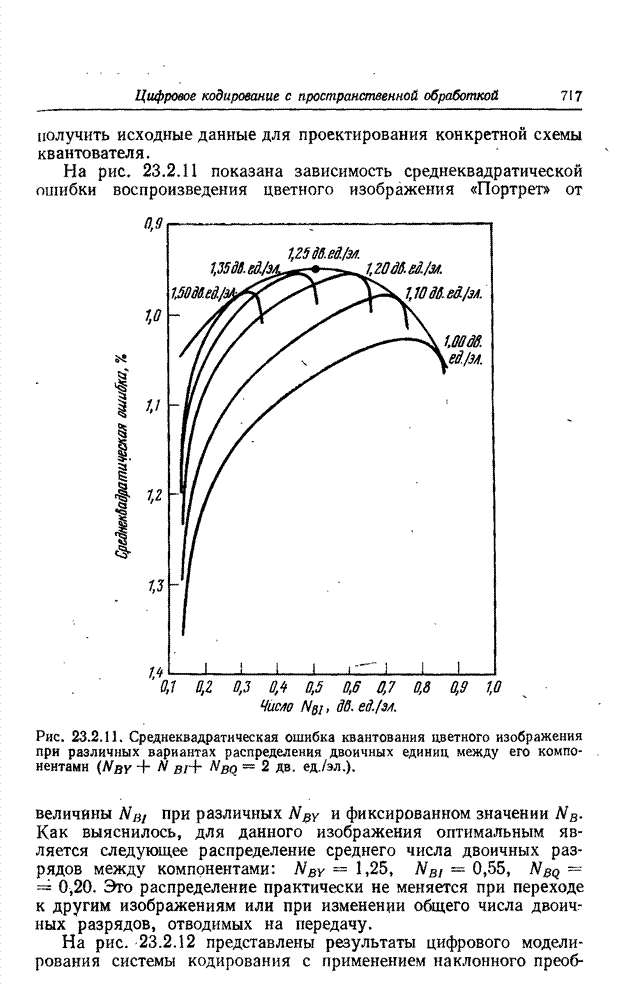
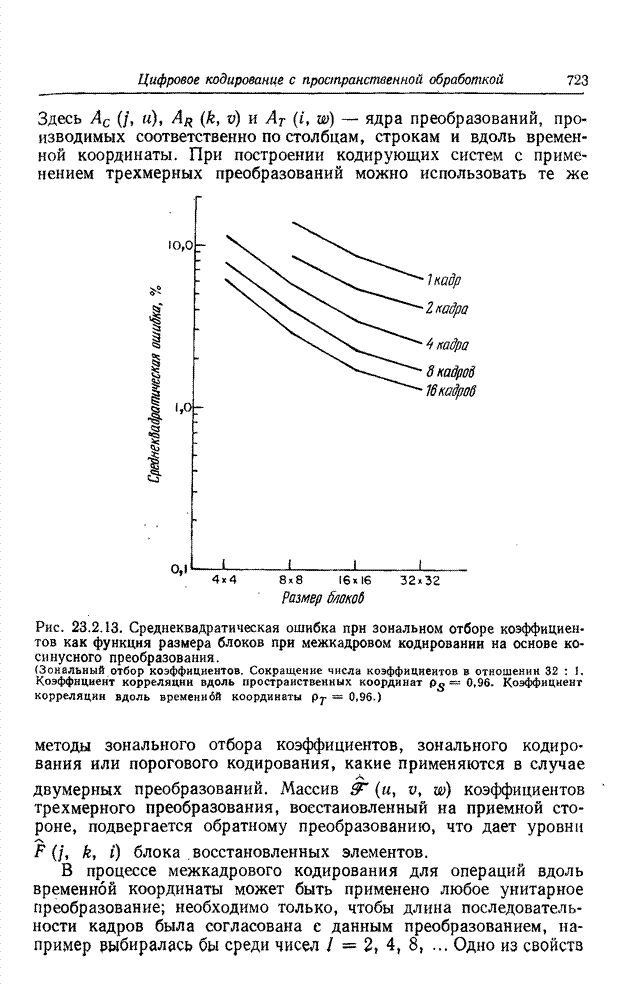
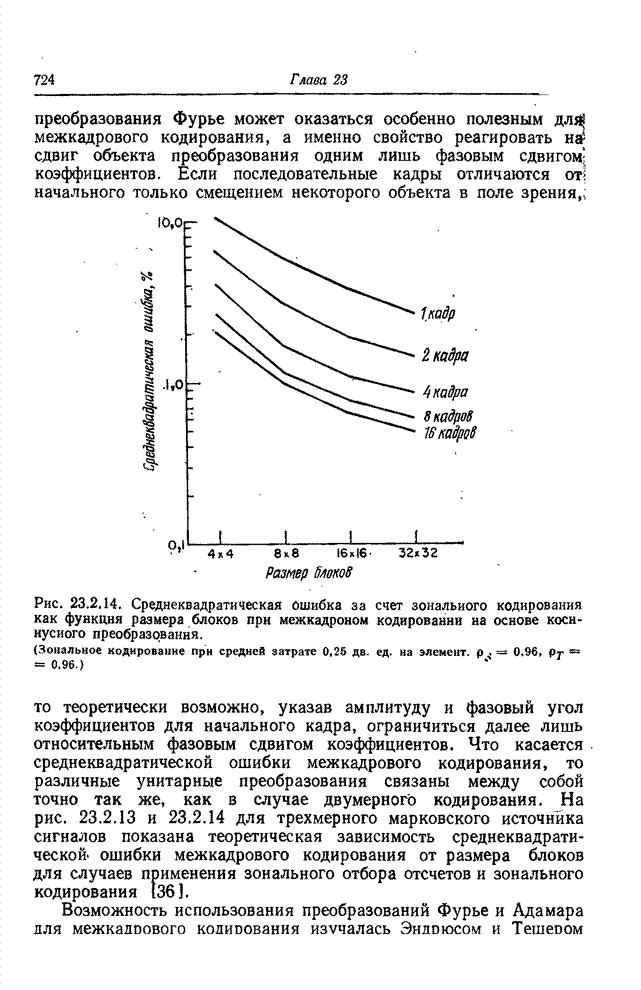
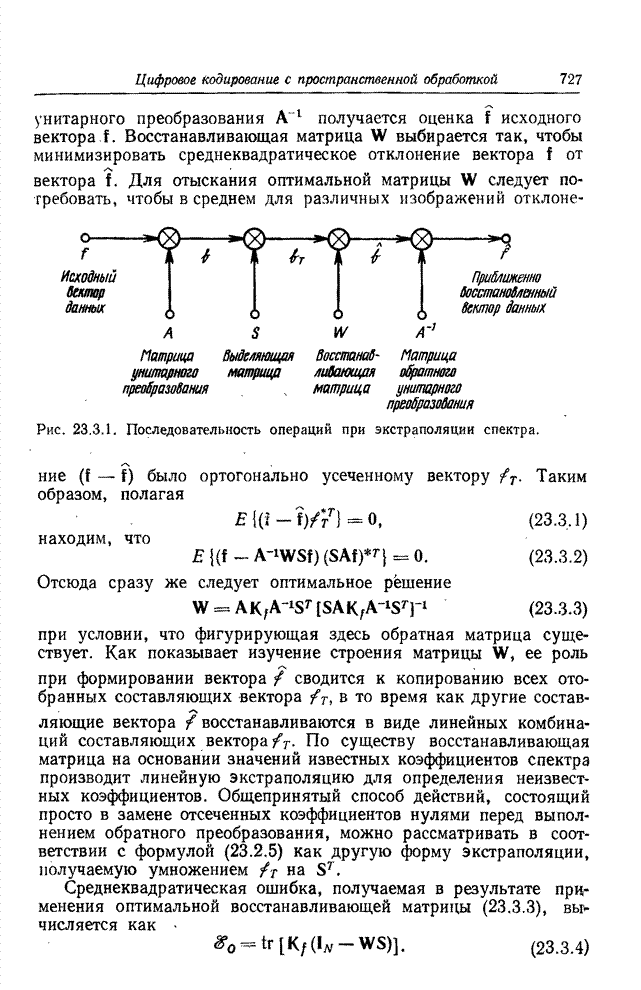
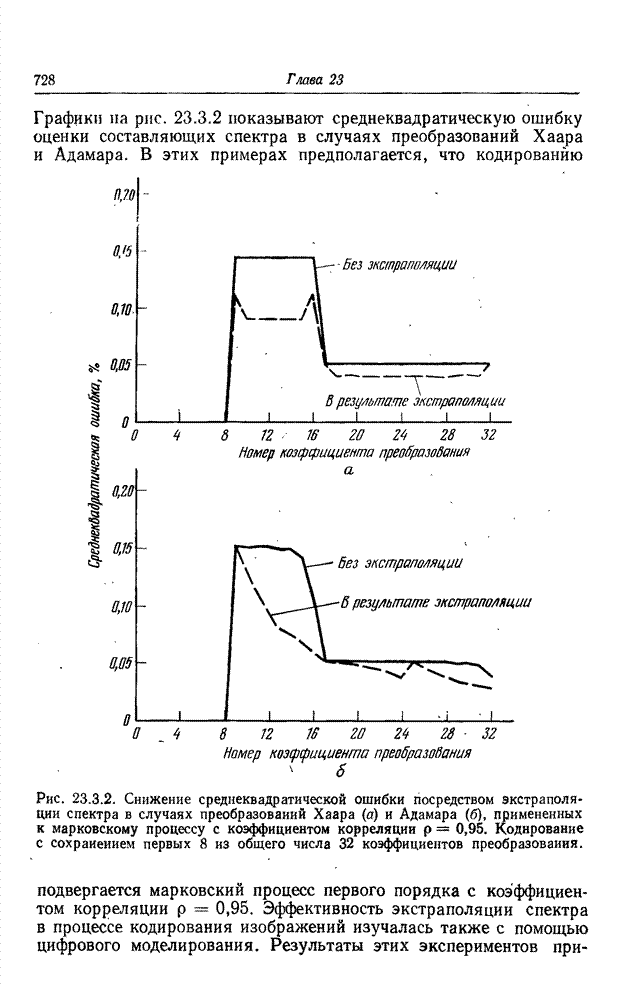
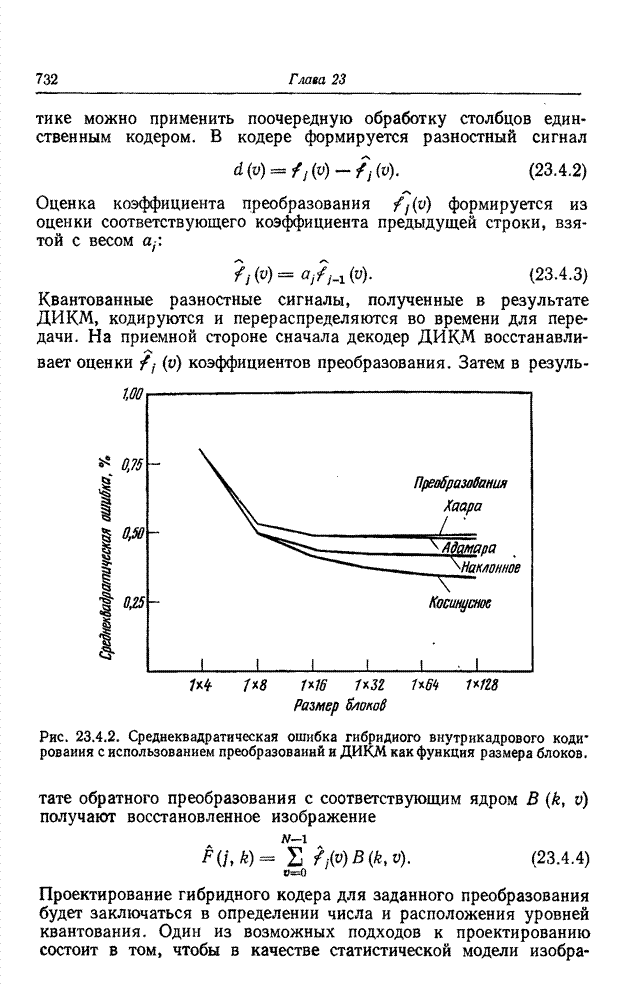
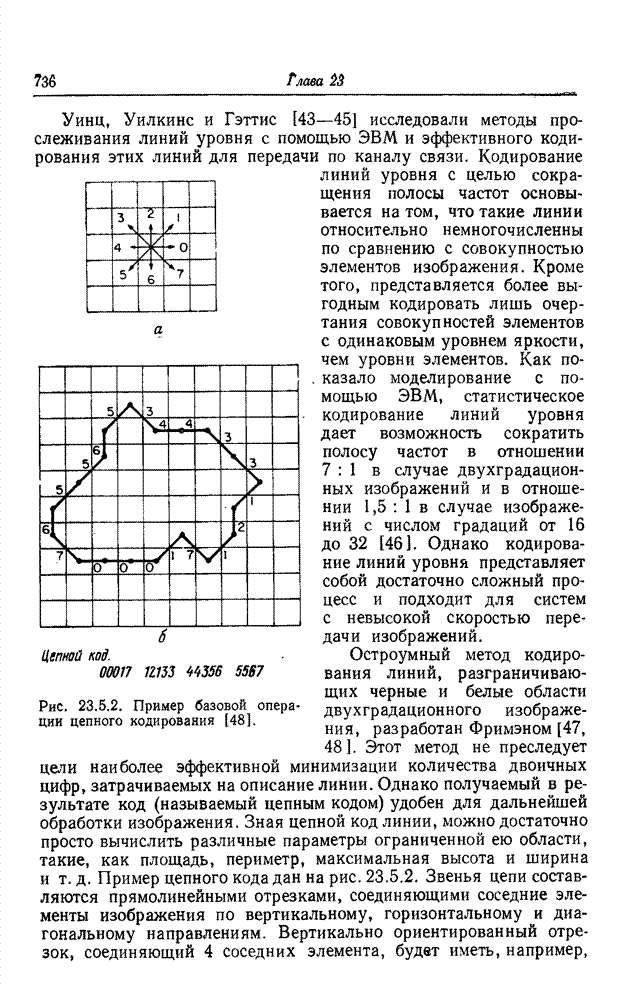
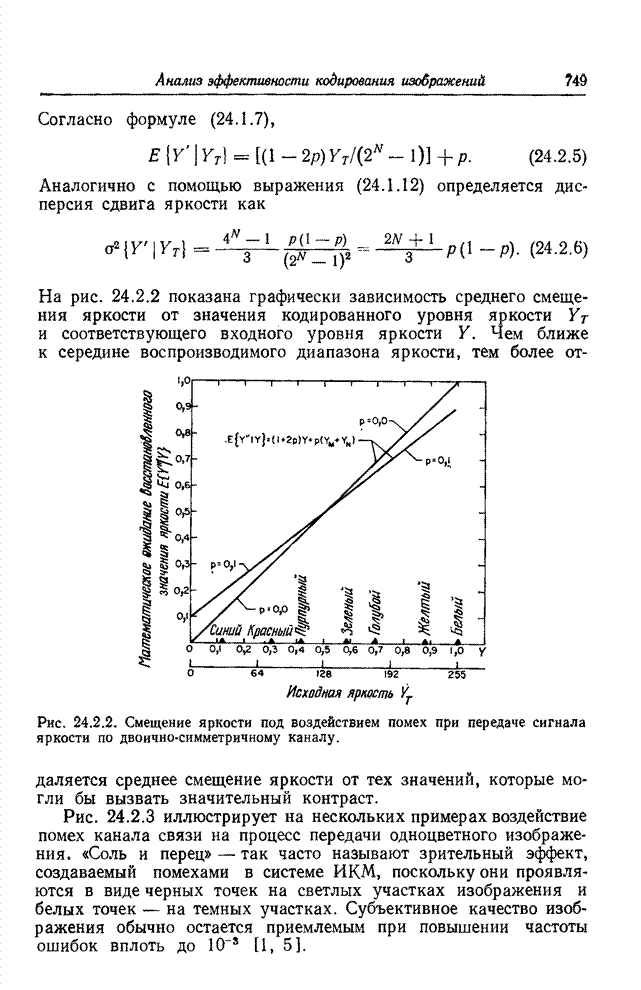
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
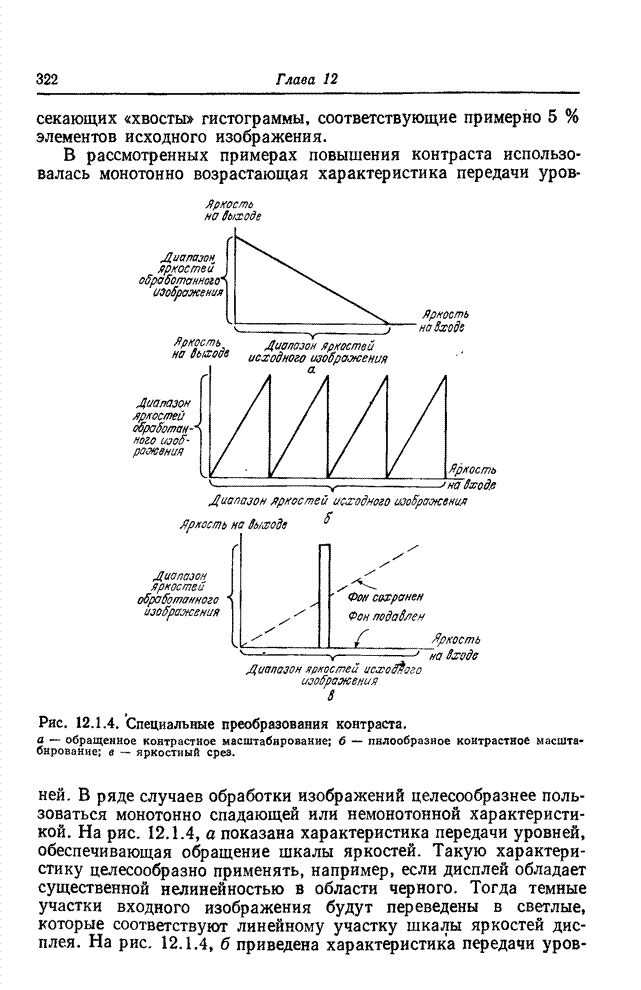
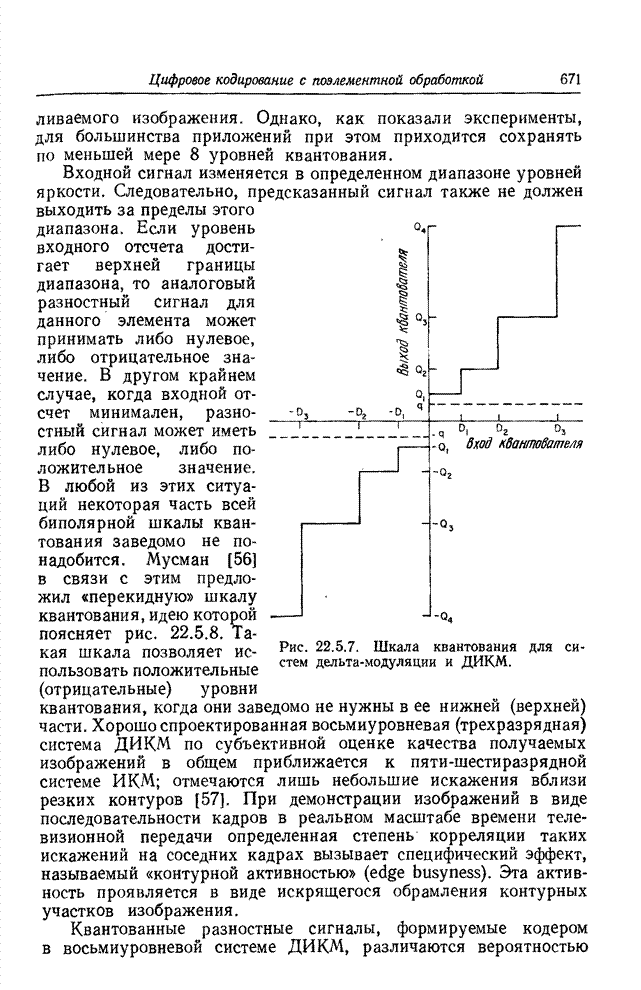
14.2. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
Иногда пространственные искажения удается промоделировать некоторой операцией в векторном пространстве над вектором псевдоотсчетов идеального изображения, результатом которой является вектор наблюдаемых отсчетов искаженного изображения; пространственную реставрацию цифровых изображений с таким искажением можно осуществить методом псевдообращения матриц, описанным в гл. 8 [19-21].
14.2.1. РЕСТАВРАЦИЯ НЕРЕЗКИХ ИЗОБРАЖЕНИЙ
Прежде всего применим псевдообращение с целью реставрации нерезкого изображения. Наблюдаемое изображение моделируется интегралом суперпозиции
 , (14.2.1)
, (14.2.1)
где
![]() и
и ![]() - функции,
представляющие идеальное и нерезкое изображения соответственно,
- функции,
представляющие идеальное и нерезкое изображения соответственно, ![]() - импульсный
отклик (который может быть пространственно-зависимым) изображающей системы,
вносящей нерезкость. Согласно формуле (13.7.6), дискретный эквивалент
соотношения (14:2.1) можно получить в виде матричного уравнения
- импульсный
отклик (который может быть пространственно-зависимым) изображающей системы,
вносящей нерезкость. Согласно формуле (13.7.6), дискретный эквивалент
соотношения (14:2.1) можно получить в виде матричного уравнения
![]() , (14.2.2)
, (14.2.2)
где
![]() - вектор
размера
- вектор
размера ![]()
![]() , учитывающий
, учитывающий ![]() реальных отсчетов
нерезкого изображения,
реальных отсчетов
нерезкого изображения, ![]() - вектор размера
- вектор размера ![]()
![]() , учитывающий
, учитывающий ![]() псевдоотсчетов
идеального изображения, а матрица
псевдоотсчетов
идеального изображения, а матрица ![]() размера
размера ![]() состоит из элементов, представляющих
собой отсчеты импульсного отклика. Если шаг реальных отсчетов совпадает с шагом
квадратурных сумм, то
состоит из элементов, представляющих
собой отсчеты импульсного отклика. Если шаг реальных отсчетов совпадает с шагом
квадратурных сумм, то ![]() , а система уравнений является
недоопределенной. Путем увеличения числа отсчетов нерезкого изображения можно обеспечить
, а система уравнений является
недоопределенной. Путем увеличения числа отсчетов нерезкого изображения можно обеспечить
![]() и даже
и даже ![]() . В любом из этих
двух случаев систему уравнений называют переопределенной. Систему такого рода
можно также получить, если некоторые компоненты вектора идеального изображения
выразить через априорные данные. Например, если известно, что идеальное
изображение содержит объект конечных размеров на черном фоне (с нулевой
яркостью), то компоненты
. В любом из этих
двух случаев систему уравнений называют переопределенной. Систему такого рода
можно также получить, если некоторые компоненты вектора идеального изображения
выразить через априорные данные. Например, если известно, что идеальное
изображение содержит объект конечных размеров на черном фоне (с нулевой
яркостью), то компоненты ![]() вне контура этого объекта можно
считать нулевыми.
вне контура этого объекта можно
считать нулевыми.
Задача
дискретной реставрации сводится к нахождению решения ![]() уравнения (14.2.2), такого,
что
уравнения (14.2.2), такого,
что
![]() . (14.2.3)
. (14.2.3)
Поскольку
вектор ![]() задается
реальными отсчетами, а элементы матрицы
задается
реальными отсчетами, а элементы матрицы ![]() определяются независимо моделью
системы, не гарантируется даже существование
определяются независимо моделью
системы, не гарантируется даже существование ![]() , удовлетворяющего условию (14.2.3).
Если система уравнений имеет решение, она называется совместной, если не имеет
- несовместной.
, удовлетворяющего условию (14.2.3).
Если система уравнений имеет решение, она называется совместной, если не имеет
- несовместной.
В гл. 8. было показано, что несовместность системы уравнений (14.2.2) можно выразить в виде
![]() , (14.2.4)
, (14.2.4)
где
![]() - вектор
ошибки, величина которой зависит от
- вектор
ошибки, величина которой зависит от ![]() . При несовместной системе уравнений
ищется решение
. При несовместной системе уравнений
ищется решение
![]() , (14.2.5)
, (14.2.5)
где
![]() -
линейный оператор, минимизирующий ошибку по критерию наименьших квадратов
-
линейный оператор, минимизирующий ошибку по критерию наименьших квадратов
![]() . (14.2.6)
. (14.2.6)
В
гл. 8 было показано, что эта ошибка минимальна, когда оператор ![]() выбирается равным
выбирается равным ![]() - обратной матрице
для
- обратной матрице
для ![]() , полученной
методом обращения по критерию наименьших квадратов. Такая обратная матрица не
обязательно является единственной. В той же главе доказывается, что оператор
обобщенного обращения
, полученной
методом обращения по критерию наименьших квадратов. Такая обратная матрица не
обязательно является единственной. В той же главе доказывается, что оператор
обобщенного обращения ![]() (особый случай обращения по критерию
наименьших квадратов) является единственным, минимизирует ошибку по критерию
наименьших квадратов и одновременно обеспечивает получение оценки с минимальной
нормой. Таким образом, сумма квадратов
(особый случай обращения по критерию
наименьших квадратов) является единственным, минимизирует ошибку по критерию
наименьших квадратов и одновременно обеспечивает получение оценки с минимальной
нормой. Таким образом, сумма квадратов ![]() минимальна при всех возможных
минимальна при всех возможных
оценках по критерию наименьших квадратов. Компенсация нерезкости методом обобщенного обращения матриц обеспечивает получение наименьшей яркости исправленного изображения.
Если система уравнений (14.2.2) является совместной, то условию (14.2.3) может удовлетворять одно или несколько решений. Обычно выбирается оценка, минимизирующая ошибку по критерию наименьших квадратов, которая определяется эквивалентными выражениями вида
![]() , (14.2.7а)
, (14.2.7а)
![]() . (14.2.7б)
. (14.2.7б)
Доказано,
что ошибка оценивания минимальна, если оценка получена методом обобщенного
обращения матриц ![]() .
В этом случае результирующая остаточная ошибка оценивания равна
.
В этом случае результирующая остаточная ошибка оценивания равна
![]() (14.2.8а)
(14.2.8а)
или
![]() . (14.2.8б)
. (14.2.8б)
При
![]() , естественно,
получаем идеальную оценку.
, естественно,
получаем идеальную оценку.
Таким образом, обобщенное обращение матриц дает оптимальное решение как для совместных, так и для несовместных систем уравнений. Как следует из формулы (8.3.5), обобщенная обратная матрица может быть представлена в виде
![]() , (14.2.9а)
, (14.2.9а)
если
матрица ![]() размера
размера
![]() имеет
ранг
имеет
ранг ![]() .
Если матрица
.
Если матрица ![]() имеет
ранг
имеет
ранг ![]() , то
, то
![]() . (14.2.9б)
. (14.2.9б)
В
случае совместной системы уравнений и ранга ![]() обобщенной обратной матрицы получаем
оценку
обобщенной обратной матрицы получаем
оценку
![]() , (14.2.10)
, (14.2.10)
которая,
очевидно, является идеальной. Однако во всех других случаях может появиться
остаточная ошибка оценивания. Очевидно, что для получения идеальной оценки
желательно иметь дело с переопределенной матрицей нерезкости ранга ![]() . К сожалению, этот
случай редко имеет место при реставрации изображений. Увеличение числа отсчетов
нерезкого изображения позволяет получить переопределенную систему уравнений
. К сожалению, этот
случай редко имеет место при реставрации изображений. Увеличение числа отсчетов
нерезкого изображения позволяет получить переопределенную систему уравнений ![]() , однако ранг
матрицы нерезкости чаще всего оказывается гораздо меньше
, однако ранг
матрицы нерезкости чаще всего оказывается гораздо меньше ![]() . Это объясняется тем, что с
увеличением плотности отсчетов возрастает линейная зависимость между строками
матрицы нерезкости. Единственный практический случай использования ранга
. Это объясняется тем, что с
увеличением плотности отсчетов возрастает линейная зависимость между строками
матрицы нерезкости. Единственный практический случай использования ранга ![]() обобщенной
обратной матрицы соответствует объекту реставрации с ограниченной и известной
протяженностью.
обобщенной
обратной матрицы соответствует объекту реставрации с ограниченной и известной
протяженностью.
Применение
обобщенного обращения матриц наталкивается на серьезные трудности, связанные с
их размером. Обобщенная обратная матрица - это матрица размера ![]() , где
, где ![]() - число отсчетов
изображения, подлежащих оцениванию, а
- число отсчетов
изображения, подлежащих оцениванию, а ![]() - число наблюдаемых отсчетов. При
использовании оператора обобщенного обращения (14.2.9) в случае изображений
большого размера возникают трудности, связанные с обеспечением достоверности
вычисления обобщенных обратных матриц и очень большим числом векторных перемножений
в (14.2.5). Если матрица нерезкости
- число наблюдаемых отсчетов. При
использовании оператора обобщенного обращения (14.2.9) в случае изображений
большого размера возникают трудности, связанные с обеспечением достоверности
вычисления обобщенных обратных матриц и очень большим числом векторных перемножений
в (14.2.5). Если матрица нерезкости ![]() разделима, т. е.
разделима, т. е.
![]() , (14.2.11)
, (14.2.11)
где
![]() и
и ![]() - операторы
«строчной» и «столбцовой» нерезкости, то можно уменьшить объем вычислений. В
этом случае обобщенная матрица разделима в том смысле, что
- операторы
«строчной» и «столбцовой» нерезкости, то можно уменьшить объем вычислений. В
этом случае обобщенная матрица разделима в том смысле, что
![]() , (14.2.12)
, (14.2.12)
где
![]() и
и ![]() - обобщенные
обратные матрицы для матриц
- обобщенные
обратные матрицы для матриц ![]() и
и ![]() . Таким образом, в случае разделимой
матрицы нерезкости оценку изображения можно получить, последовательно действуя
на все строки массива наблюдаемого изображения обобщенной обратной матрицей
строчной нерезкости, а затем обрабатывая каждый столбец массива обобщенной
обратной матрицей столбцовой нерезкости.
. Таким образом, в случае разделимой
матрицы нерезкости оценку изображения можно получить, последовательно действуя
на все строки массива наблюдаемого изображения обобщенной обратной матрицей
строчной нерезкости, а затем обрабатывая каждый столбец массива обобщенной
обратной матрицей столбцовой нерезкости.
Реставрацию методом псевдообращения изображений большого размера можно осуществить приближенно. При этом нерезкое изображение разбивается на малые фрагменты, реставрируемые независимо. Процедура пофрагментной реставрации изображений подобна процедуре пофрагментной фильтрации (см. разд. 11.3). Полезно предусматривать перекрытие фрагментов и использовать только центральные отсчеты в каждом реставрированном фрагменте, поскольку именно эти отсчеты обладают наименьшей неопределенностью. В разд. 14.3 описывается эффективный вычислительный алгоритм реставрации изображений методом псевдообращения матриц в случае пространственно-инвариантной нерезкости.
На
рис. 14.2.1 показаны нерезкие и исправленные изображения, иллюстрирующие
процедуру реставрации методом обобщенного обращения матриц, причем были
использованы модели искаженных изображений, представленные на рис. 13.7.3 и 13.7.4.
Наблюдаемые изображения не были повреждены шумом. Импульсный отклик нерезкости
имел гауссову форму (13.7.10) с ![]() . На рисунке, соответствующем случаю
переопределенной модели, воспроизведена только центральная реставрированная область
размером
. На рисунке, соответствующем случаю
переопределенной модели, воспроизведена только центральная реставрированная область
размером ![]() элементов,
увеличенная до размера
элементов,
увеличенная до размера ![]() элементов; нерезкое изображение имеет
размер
элементов; нерезкое изображение имеет
размер ![]() элементов.
Исправленное изображение визуально не отличается от исходного изображения,
однако изучение полученных числовых данных указывает на наличие вычислительных
ошибок округления. В случае недоопределенной модели также воспроизведена только
центральная область оценки размером
элементов.
Исправленное изображение визуально не отличается от исходного изображения,
однако изучение полученных числовых данных указывает на наличие вычислительных
ошибок округления. В случае недоопределенной модели также воспроизведена только
центральная область оценки размером ![]() элементов. Хотя исправленное
изображение выглядит как улучшенное нерезкое изображение, оно не идентично
исходному изображению.
элементов. Хотя исправленное
изображение выглядит как улучшенное нерезкое изображение, оно не идентично
исходному изображению.

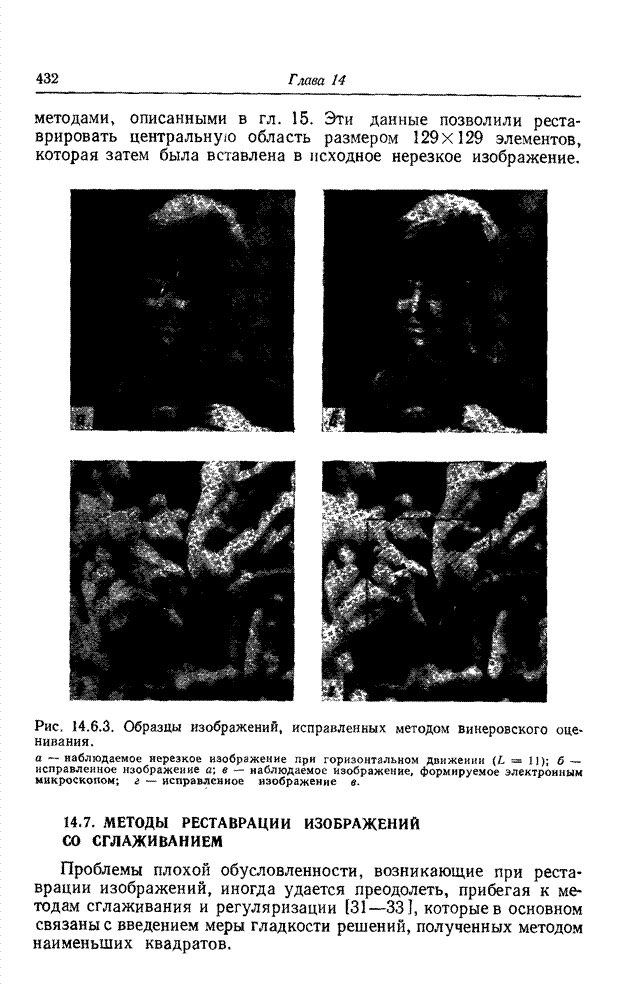
Рис. 14.2.1. Образцы испытательных изображений, исправленных методом псевдообращения матриц. Нерезкостъ внесена с помощью импульсного отклика гауссовой формы. Наблюдаемое изображение без шума.
а - случай переопределенной модели ![]() , нерезкое
изображение; б - исправленное изображение а; в - случай недоопределенной модели
, нерезкое
изображение; б - исправленное изображение а; в - случай недоопределенной модели
![]() , нерезкое
изображение, минимальная среднеквадратическая ошибка
, нерезкое
изображение, минимальная среднеквадратическая ошибка ![]() ; г - исправленное
изображение в
; г - исправленное
изображение в ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Часть 4. РЕСТАВРАЦИЯ И УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
- Глава 12. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
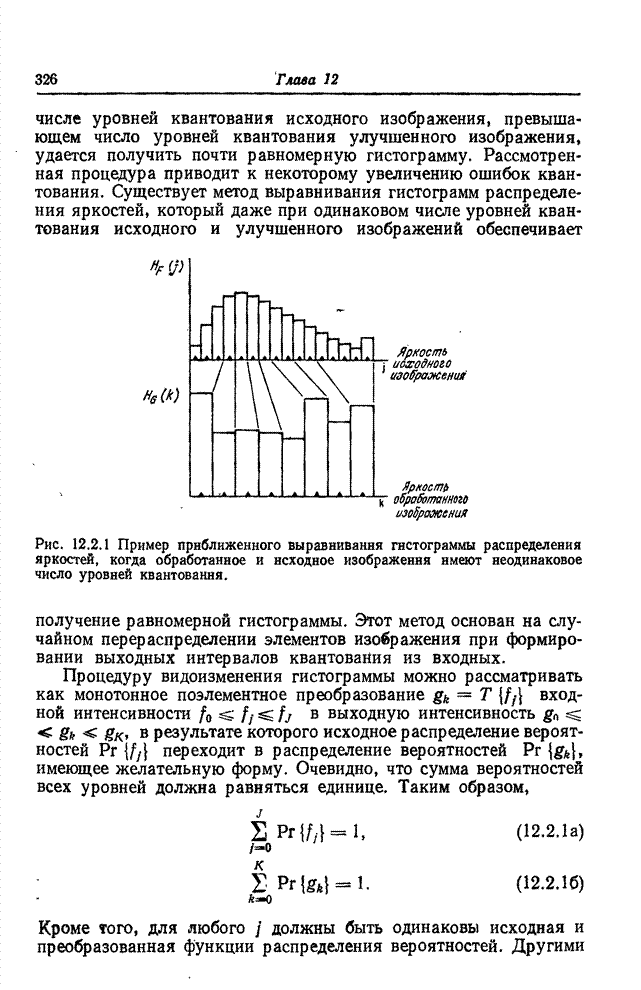
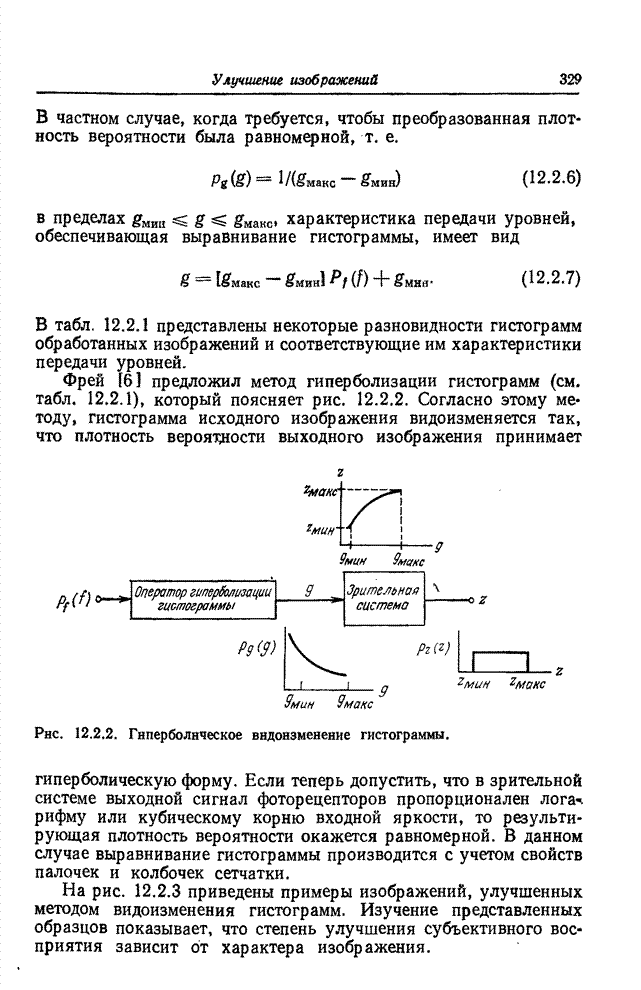
- 12.1. ИЗМЕНЕНИЕ КОНТРАСТА
- 12.2. ВИДОИЗМЕНЕНИЕ ГИСТОГРАММ
- 12.3. ПОДАВЛЕНИЕ ШУМОВ
- 12.4. ПОДЧЕРКИВАНИЕ ГРАНИЦ
- 12.5. ОБРАБОТКА ИЗОБРАЖЕНИЙ С ПРЕОБРАЗОВАНИЕМ
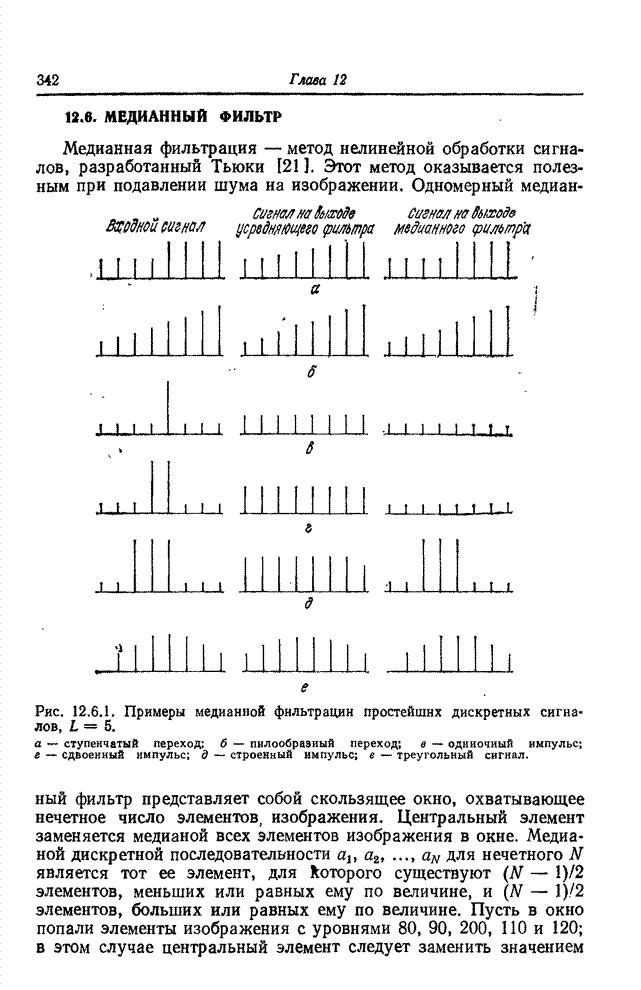
- 12.6. МЕДИАННЫЙ ФИЛЬТР
- 12.7. ЛОЖНЫЕ ЦВЕТА
- 12.8. ПСЕВДОЦВЕТА
- 12.9. УЛУЧШЕНИЕ СПЕКТРОЗОНАЛЬНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 13. МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.1. ОБОБЩЕННЫЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.2. МОДЕЛИ ОПТИЧЕСКИХ СИСТЕМ
- 13.3. МОДЕЛИ ФОТОГРАФИЧЕСКИХ ПРОЦЕССОВ
- 13.3.1. ОДНОЦВЕТНАЯ ФОТОГРАФИЯ
- 13.3.2. ЦВЕТНАЯ ФОТОГРАФИЯ
- 13.4. МОДЕЛИ ЦИФРОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- 13.5. МОДЕЛЬ ДИСПЛЕЯ
- 13.6. МОДЕЛИ ШУМОВ ИЗОБРАЖЕНИЯ
- 13.6.1. ШУМ ФОТОДЕТЕКТОРА
- 13.6.2. ШУМ ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- 13.7. МОДЕЛИ ЦИФРОВОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 14. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 14.1. МЕТОДЫ ПРОСТРАНСТВЕННОЙ ФИЛЬТРАЦИИ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 14.1.1. ИНВЕРСНАЯ ФИЛЬТРАЦИЯ
- 14.1.2. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И АДДИТИВНЫЙ ШУМ
- 14.1.3. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНОЕ ИЗОБРАЖЕНИЕ
- 14.1.4. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНАЯ НЕРЕЗКОСТЬ
- 14.1.5. ФИЛЬТРЫ НА ОСНОВЕ ПАРАМЕТРИЧЕСКИХ ОЦЕНОК
- 14.1.6. ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 4.2. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.2.1. РЕСТАВРАЦИЯ НЕРЕЗКИХ ИЗОБРАЖЕНИЙ
- 14.2.2. РЕСТАВРАЦИЯ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ ПРИ НАЛИЧИИ ШУМА
- 14.3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.3.1. АЛГОРИТМ ДЛЯ ПЕРЕОПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.3.2. АЛГОРИТМ ДЛЯ НЕДООПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.4. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ С ИСПОЛЬЗОВАНИЕМ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- 14.5. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕГРЕССИИ
- 14.6. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ВИНЕРОВСКОГО ОЦЕНИВАНИЯ
- 14.6.1. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В ОБЩЕМ СЛУЧАЕ
- 14.6.2. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В СЛУЧАЕ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ С ШУМОМ
- 14.7. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ СО СГЛАЖИВАНИЕМ
- 14.8. МЕТОДЫ РЕСТАВРАЦИИ С ИСПОЛЬЗОВАНИЕМ ОГРАНИЧЕНИЙ
- 14.9. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
- ЛИТЕРАТУРА
- Глава 15. CПЕЦИАЛЬНЫЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 15.1. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮ ПОДАВЛЕНИЯ ОШИБОК НАЛОЖЕНИЯ СПЕКТРОВ
- 15.2. КОРРЕКЦИЯ ОШИБОК ИНТЕРПОЛЯЦИИ
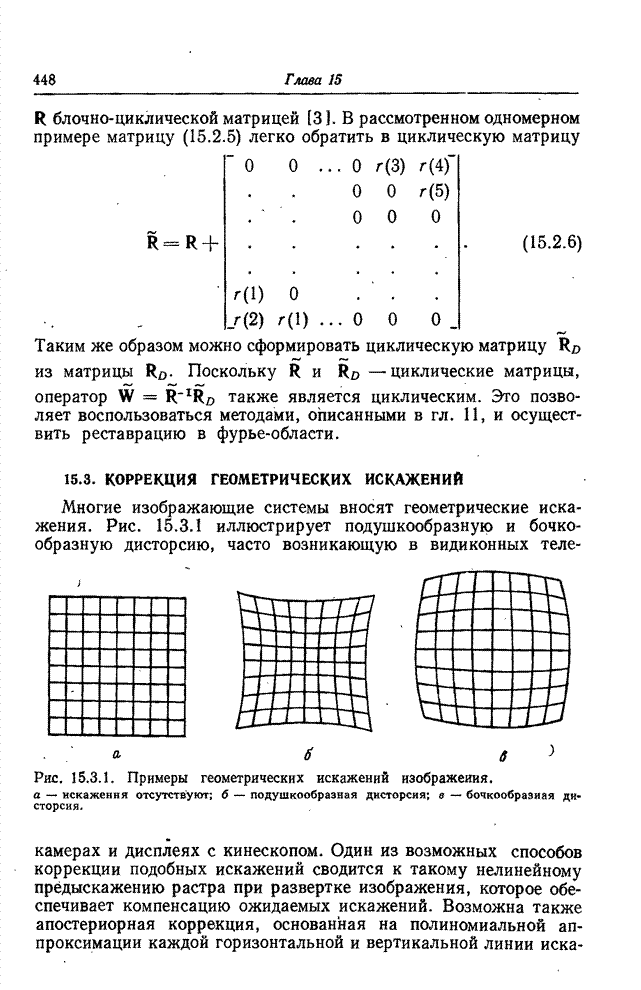
- 15.3. КОРРЕКЦИЯ ГЕОМЕТРИЧЕСКИХ ИСКАЖЕНИЙ
- 15.4. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ГОМОМОРФНОЙ ФИЛЬТРАЦИИ
- 15.5. СЛЕПАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ
- 15.5.1. МЕТОДЫ НА ОСНОВЕ ПРЯМЫХ ИЗМЕРЕНИЙ
- 15.5.2. МЕТОДЫ НА ОСНОВЕ КОСВЕННОГО ОЦЕНИВАНИЯ
- 15.6. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ СПЕКТРА
- 15.7. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННО-ЗАВИСИМЫМИ ИСКАЖЕНИЯМИ
- 15.8. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕКУРСИВНОЙ ФИЛЬТРАЦИИ
- 15.9. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮОСЛАБЛЕНИЯ ШУМА ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- ЛИТЕРАТУРА
- Глава 16. КОРРЕКЦИЯ ЯРКОСТНЫХ, ЦВЕТОВЫХ И СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗОБРАЖАЮЩИХ СИСТЕМ
- 16.1. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ВИДЕОДАТЧИКОВ
- 16.2. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ДИСПЛЕЕВ
- 16.3. ОЦЕНИВАНИЕ СПЕКТРАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 16.4. КОРРЕКЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ВИДЕОДАТЧИКОВ И ДИСПЛЕЕВ
- 16.5. ОЦЕНИВАНИЕ КООРДИНАТ СВЕТА ВИДЕОДАТЧИКОВ
- 16.6. ОЦЕНИВАНИЕ ЭКСПОЗИЦИЙ ЦВЕТНОЙ ФОТОПЛЕНКИ
- 16.7. КОМПЕНСАЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ ЦВЕТНЫХ ДИСПЛЕЕВ
- ЛИТЕРАТУРА
- Часть 5. АНАЛИЗ ИЗОБРАЖЕНИЙ
- Глава 17. ВЫДЕЛЕНИЕ ПРИЗНАКОВ ИЗОБРАЖЕНИЯ
- 17.1. ЯРКОСТНЫЕ ПРИЗНАКИ
- 17.2. ГИСТОГРАММНЫЕ ПРИЗНАКИ
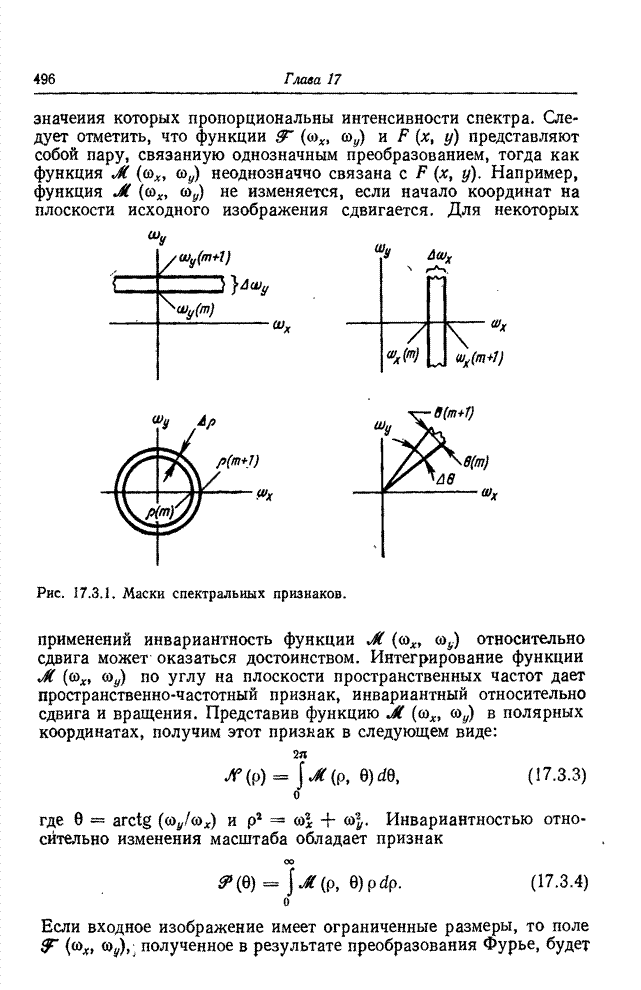
- 17.3. ПРОСТРАНСТВЕННО-СПЕКТРАЛЬНЫЕ ПРИЗНАКИ
- 17.4. КОНТУРНЫЕ ПРИЗНАКИ
- 17.4.1. ЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.2. НЕЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.3. МЕТОДЫ АППРОКСИМАЦИИ ПЕРЕПАДОВ ЯРКОСТИ
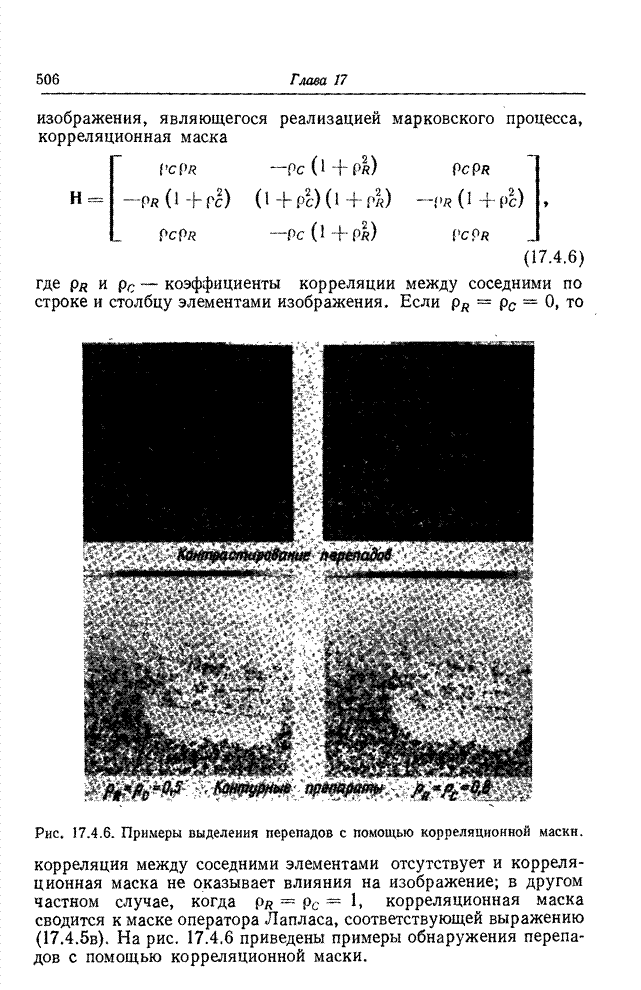
- 17.4.4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ
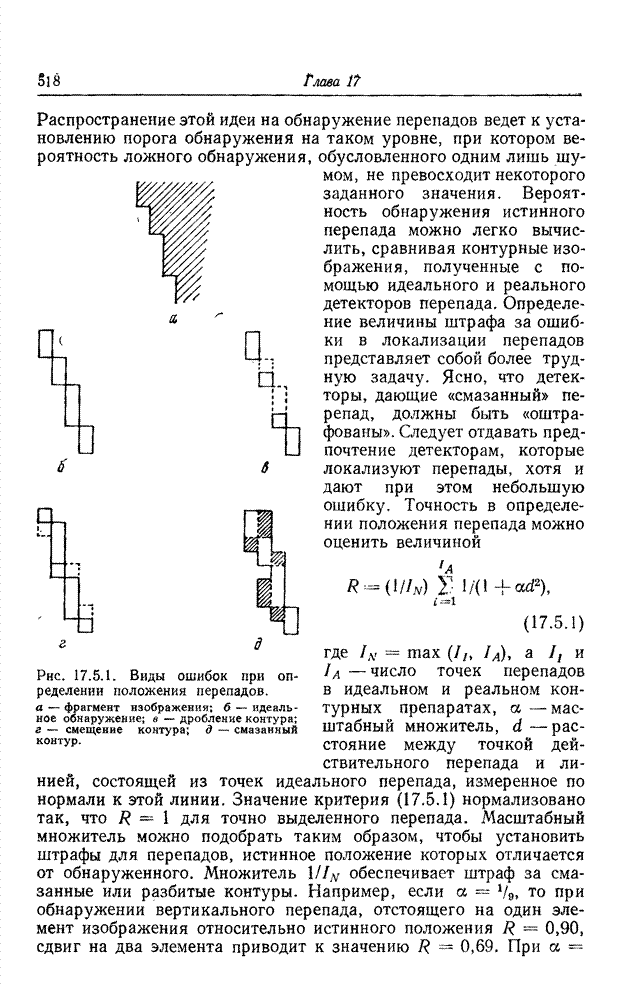
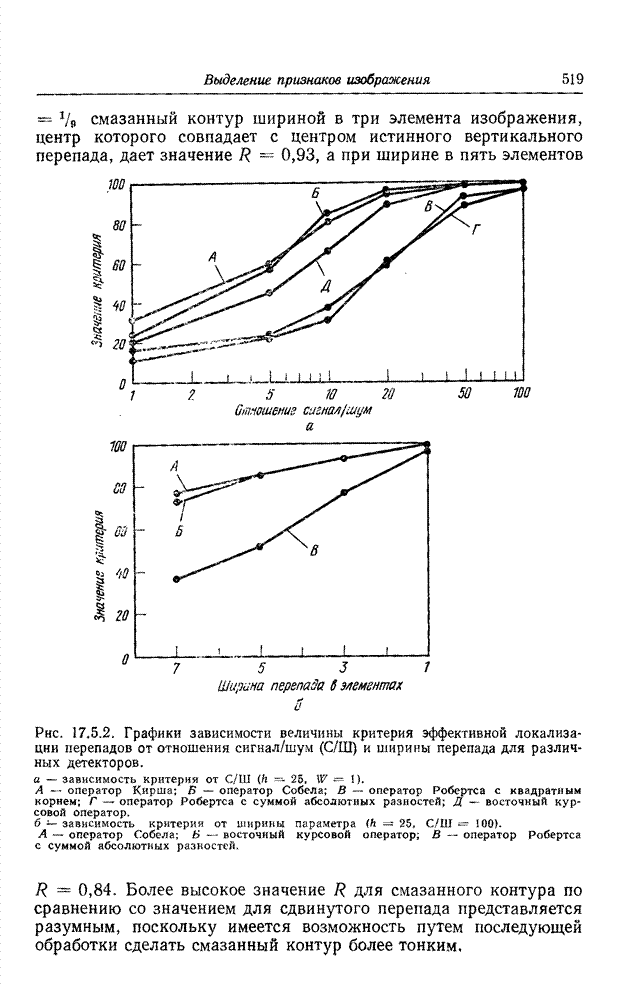
- 17.5. ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ ЯРКОСТИ
- 17.6. ЦВЕТОВЫЕ КОНТУРЫ
- 17.7. ПРИЗНАКИ ПЯТНА И ЛИНИИ
- 17.8. ТЕКСТУРНЫЕ ПРИЗНАКИ
- 17.9. СИНТЕЗ ТЕКСТУР
- ЛИТЕРАТУРА
- Глава 18. СИМВОЛИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
- 18.1. СВЯЗНОСТЬ
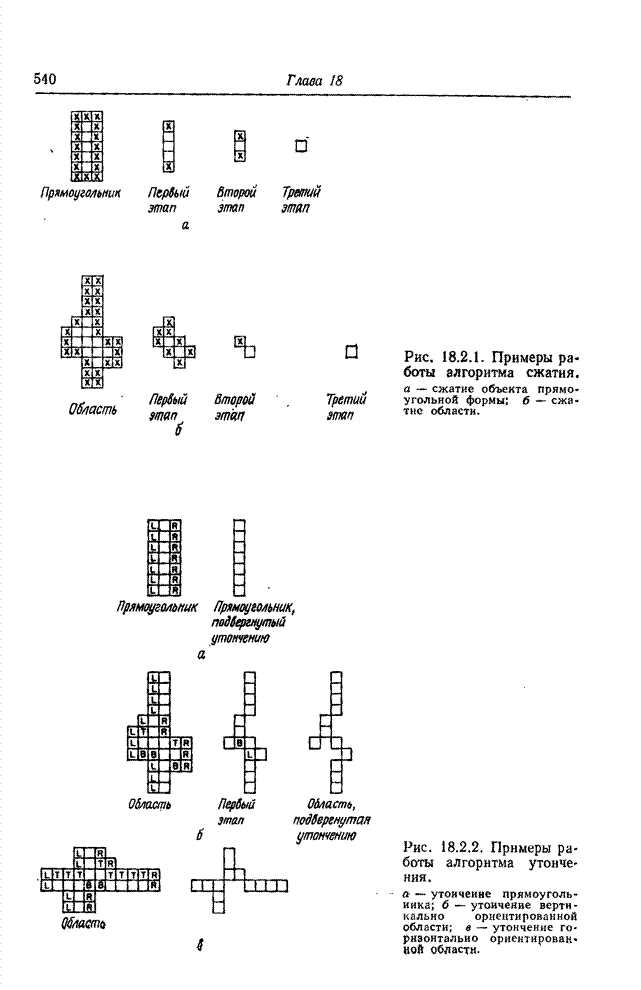
- 18.2. СЖАТИЕ, УТОНЧЕНИЕ И ПОСТРОЕНИЕ ОСТОВА
- 18.3. ОПИСАНИЕ ЛИНИЙ
- 18.3.1. АППРОКСИМАЦИЯ КРИВЫХ
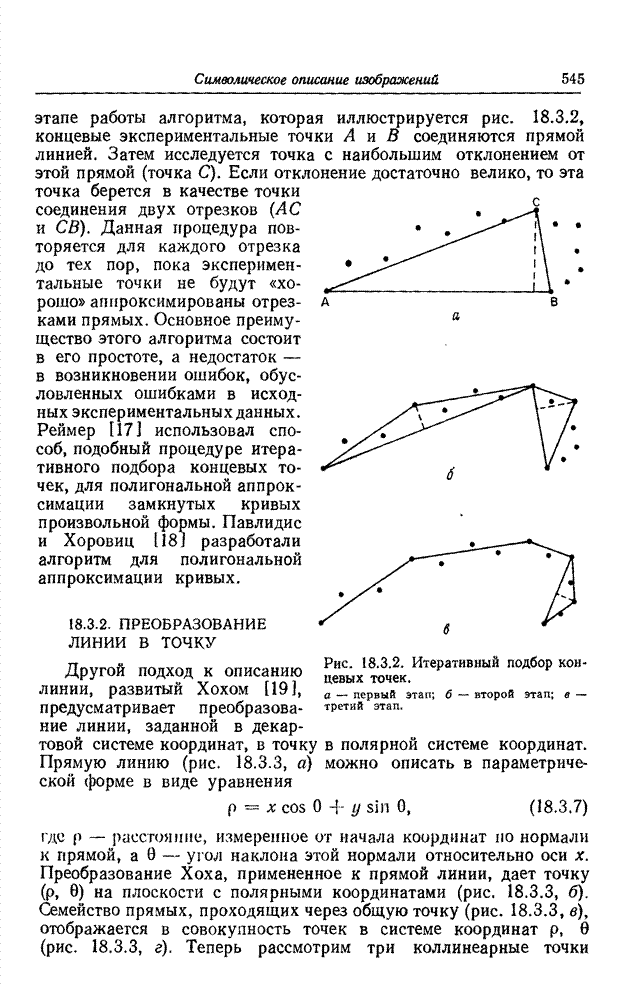
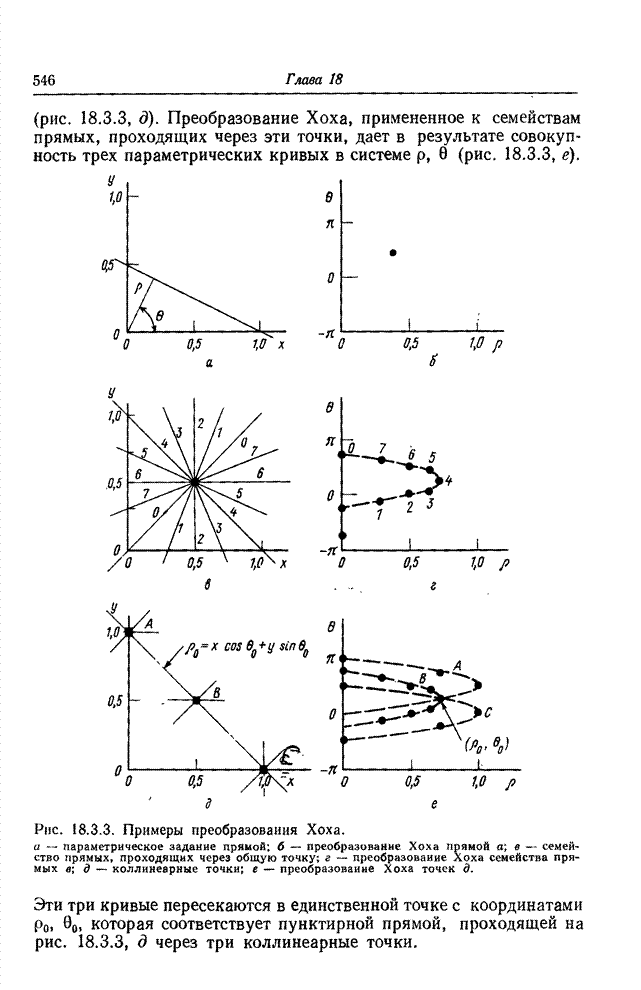
- 18.3.2. ПРЕОБРАЗОВАНИЕ ЛИНИИ В ТОЧКУ
- 18.4. ОПИСАНИЕ ФОРМЫ
- 18.4.1. МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.2. ТОПОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.3. АНАЛИТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
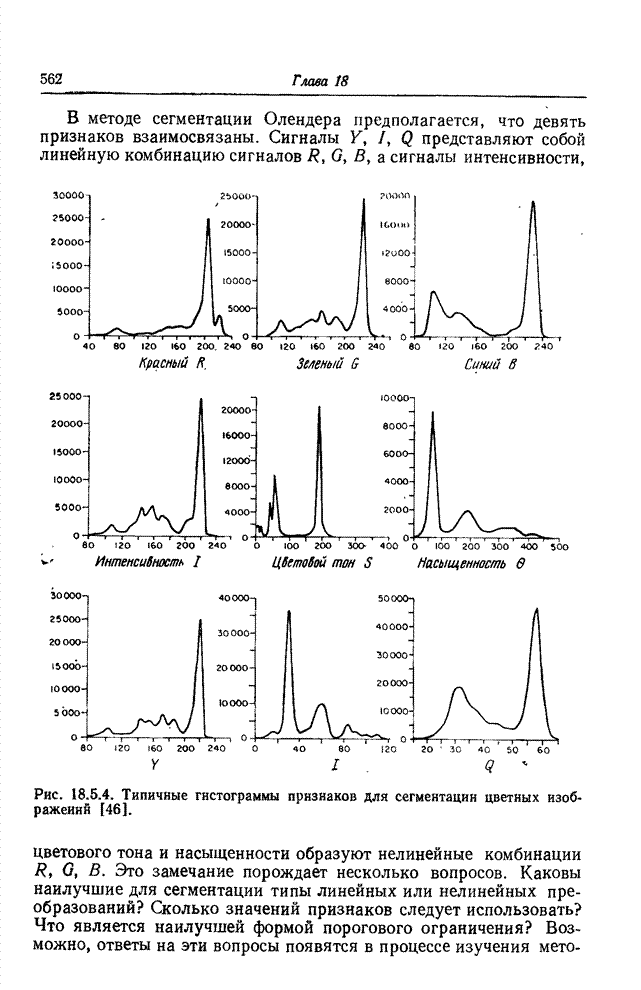
- 18.5. СЕГМЕНТАЦИЯ ПО ЯРКОСТИ
- 18.5.1. ПОРОГОВОЕ ОГРАНИЧЕНИЕ ПО ЯРКОСТИ
- 18.5.2. МНОГОМЕРНОЕ ПОРОГОВОЕ ОГРАНИЧЕНИЕ
- 18.5.3. НАРАЩИВАНИЕ ОБЛАСТЕЙ
- 18.6. КОНТУРНАЯ СЕГМЕНТАЦИЯ
- 18.7. ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ
- 18.8. СЕГМЕНТАЦИЯ ФОРМЫ
- ЛИТЕРАТУРА
- Глава 19. ОБНАРУЖЕНИЕ ОБЪЕКТОВ И СОВМЕЩЕНИЕ (ПРИВЯЗКА) ИЗОБРАЖЕНИЙ
- 19.1. СОПОСТАВЛЕНИЕ С ЭТАЛОНОМ
- 19.2. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ ДЕТЕРМИНИРОВАННЫХ ПОЛЕЙ
- 19.3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ СЛУЧАЙНЫХ ПОЛЕЙ
- 19.4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 19.5. ПРИВЯЗКА ИЗОБРАЖЕНИЙ
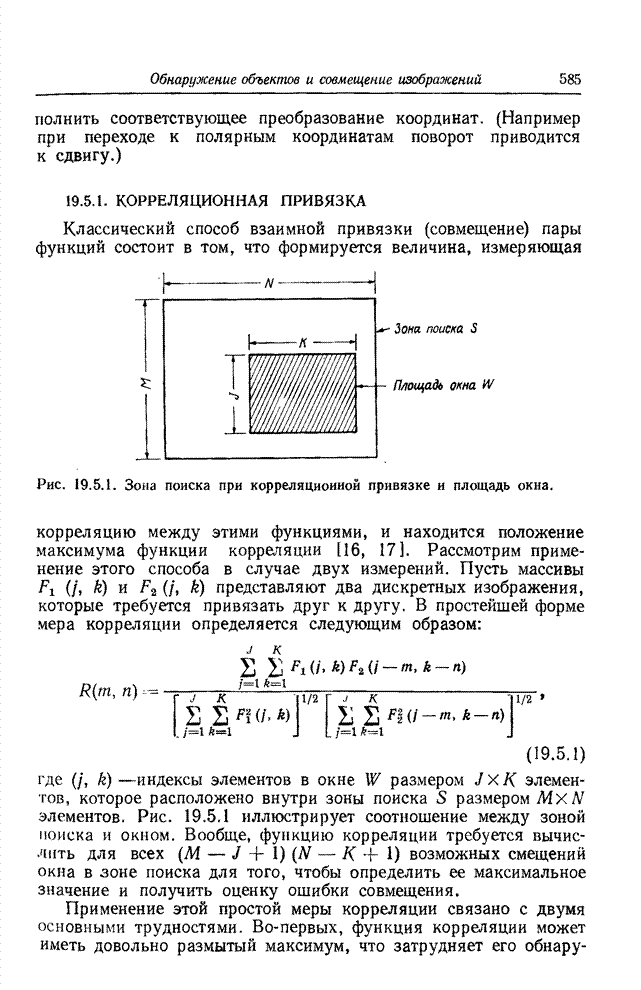
- 19.5.1. КОРРЕЛЯЦИОННАЯ ПРИВЯЗКА
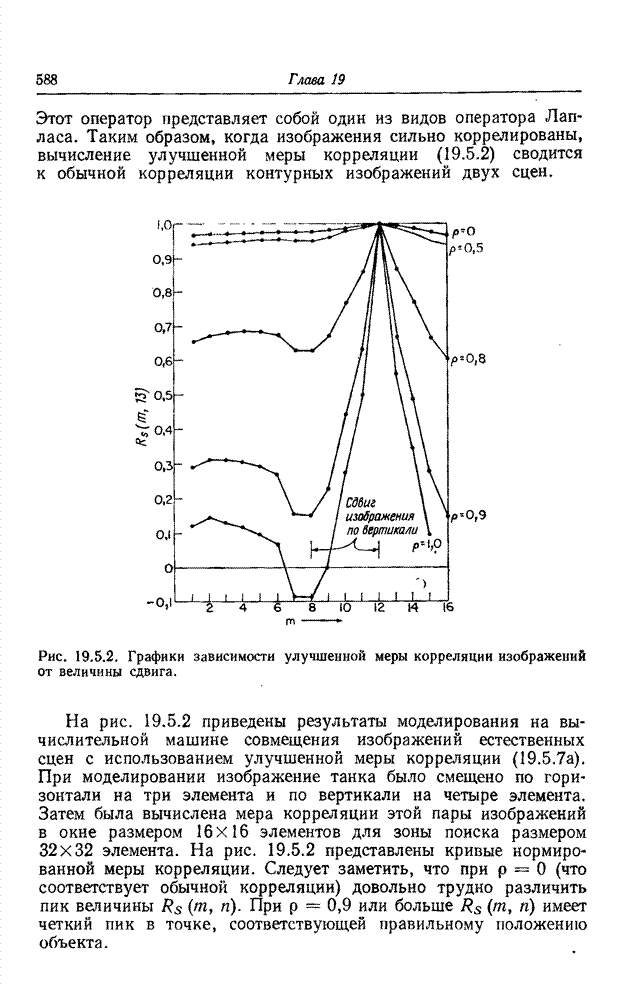
- 19.5.2. ПОСЛЕДОВАТЕЛЬНАЯ ПРИВЯЗКА
- ЛИТЕРАТУРА
- Глава 20. СИСТЕМЫ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
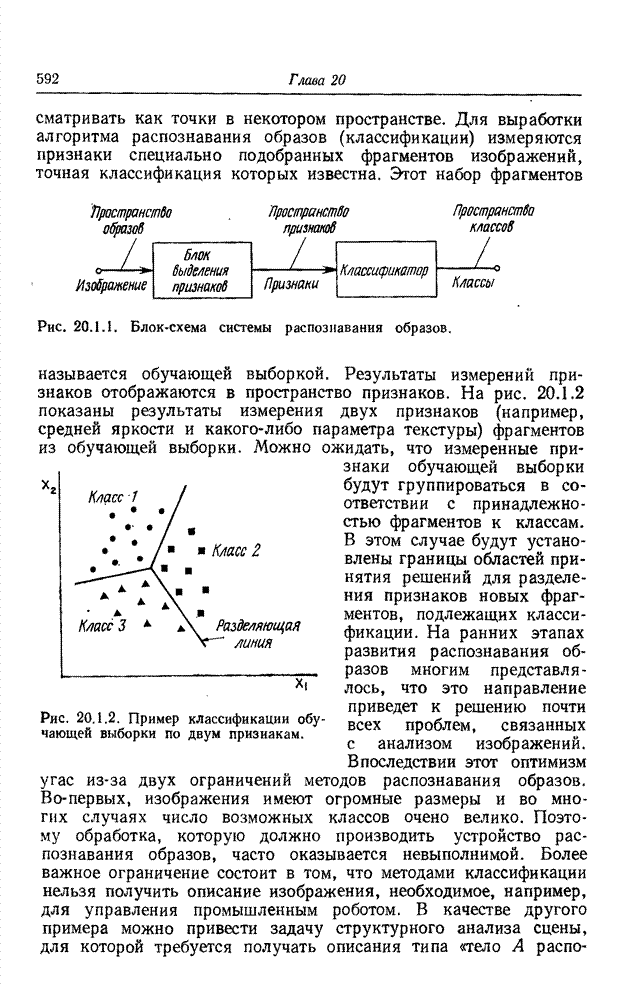
- 20.1. СИСТЕМЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 20.2. МОДЕЛИ СИСТЕМ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.3. СИНТАКСИЧЕСКИЕ МЕТОДЫ
- 20.4. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ОТНОШЕНИЯ МЕЖДУ ОБЪЕКТАМИ
- ЛИТЕРАТУРА
- Часть 6. Кодирование изображений
- Глава 21. АНАЛОГОВЫЕ МЕТОДЫ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.1. КЛАССИФИКАЦИЯ МЕТОДОВ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.2. СИСТЕМЫ ВЕЩАТЕЛЬНОГО ТЕЛЕВИДЕНИЯ
- 21.2.1. СИСТЕМА НТСЦ [13-15]
- 21.2.2. СИСТЕМА СЕКАМ [17]
- 21.2.3.СИСТЕМА ПАЛ
- 21.3. МОДУЛЯЦИОННЫЕ МЕТОДЫ СОКРВЩЕНИЯ ПОЛОСЫ ЧАСТОТЫ
- 21.4.УМЕНЬШЕНИЕ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ И ЧАСТОТЫ КАДРОВ
- 21.4.1. УМЕНЬШЕНИЕ ПРОСТРАНСТВЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
- 21.4.2. УМЕНЬШЕНИЕ ЧАСТОТЫ КАДРОВ
- 21.5. МЕТОДЫ ВРЕМЕННОГО ПЕРЕМЕЖЕНИЯ
- 21.5.1. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ СТРОК
- 21.5.2. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ ЭЛЕМЕНТОВ
- 21.6. РАЗВЕРТКА С ПЕРЕМЕННОЙ СКОРОСТЬЮ
- 21.7. МУЛЬТИПЛЕКСНЫЕ МЕТОДЫ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Глава 22. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПОЭЛЕМЕНТНОЙ ОБРАБОТКОЙ
- 22.1. СИСТЕМЫ КОДИРОВАНИЯ С ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИЕЙ
- 22.1.1. КВАНТОВАНИЕ СО СЖАТИЕМ ДИАПАЗОНА ЯРКОСТЕЙ
- 22.1.2. ПСЕВДОШУМОВОЕ КВАНТОВАНИЕ
- 22.1.3. КВАНТОВАНИЕ С УЛУЧШЕННОЙ ПЕРЕДАЧЕЙ ГРАДАЦИЙ ЯРКОСТИ
- 22.1.4. СИСТЕМА С ГРУБОЙ-ТОНКОЙ ШКАЛОЙ КВАНТОВАНИЯ
- 22.1.5. КВАНТОВАНИЕ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ
- 22.2. СТАТИСТИЧЕСКИЕ МЕТОДЫ КОДИРОВАНИЯ
- 22.2.1. ПОЭЛЕМЕНТНОЕ СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
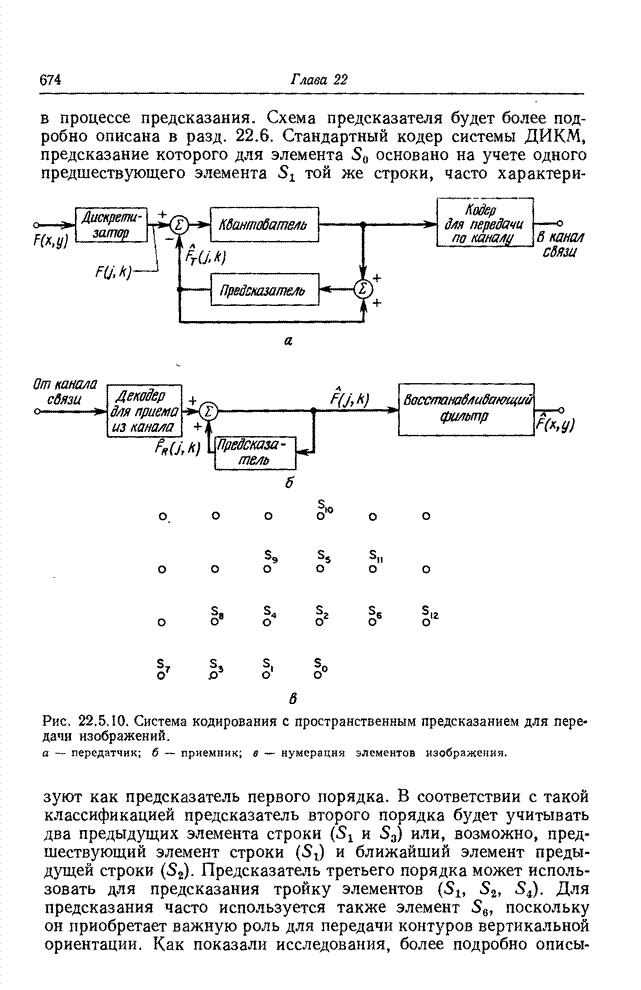
- 22.2.2. КОДИРОВАНИЕ С УЧЕТОМ ПРЕДШЕСТВУЮЩЕГО ЭЛЕМЕНТА
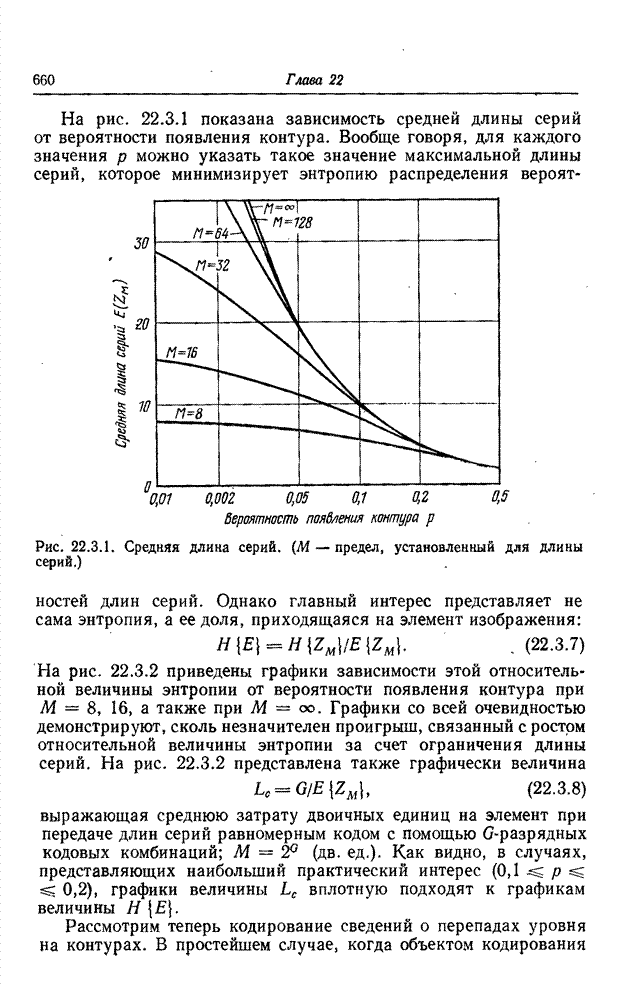
- 22.3. КОДИРОВАНИЕ СЕРИЙ
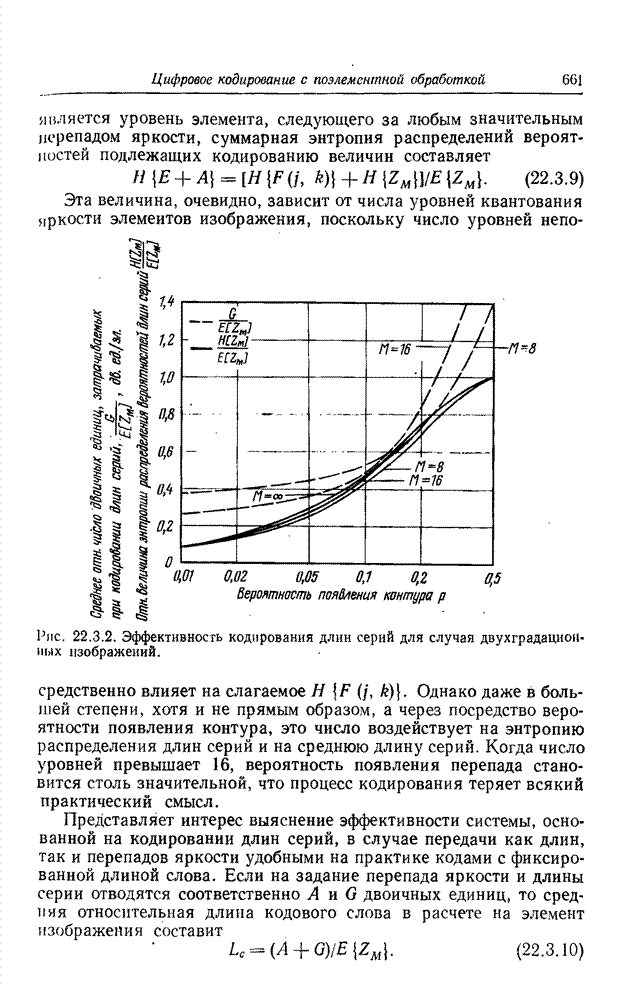
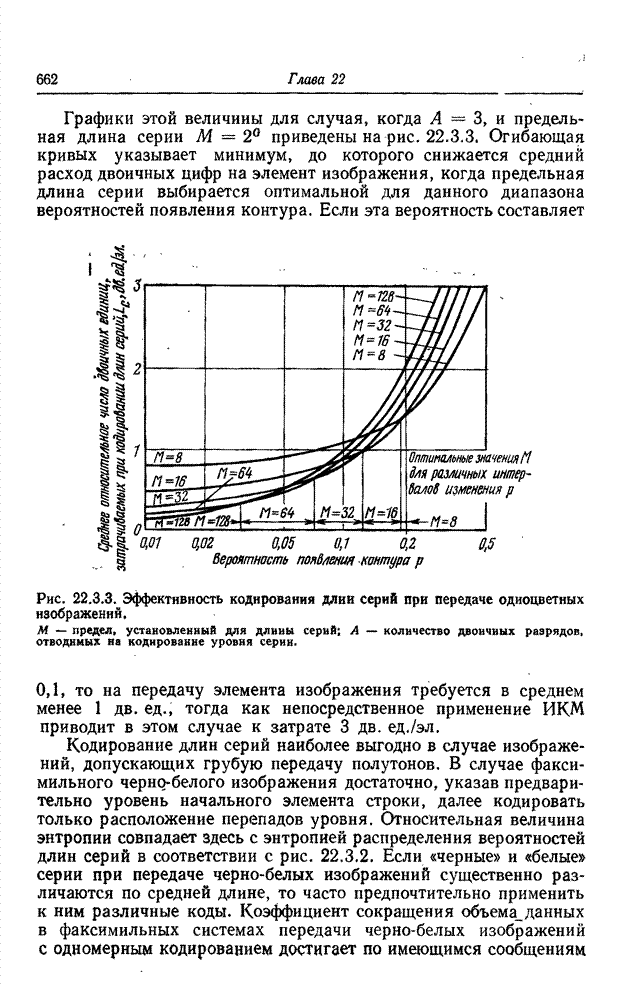
- 22.3.1. КОДИРОВАНИЕ ДЛИН СЕРИЙ; ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ [32-36]
- 22.3.2. КОДИРОВАНИЕ РАЗРЯДНЫХ ПЛОСКОСТЕЙ
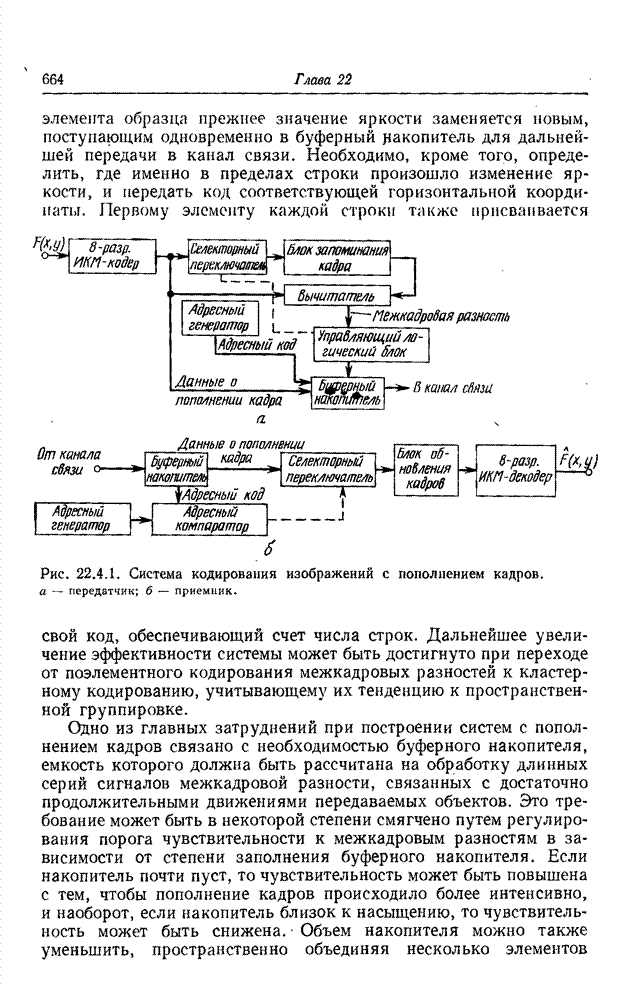
- 22.4. КОДИРОВАНИЕ С ПОПОЛНЕНИЕМ КАДРОВ
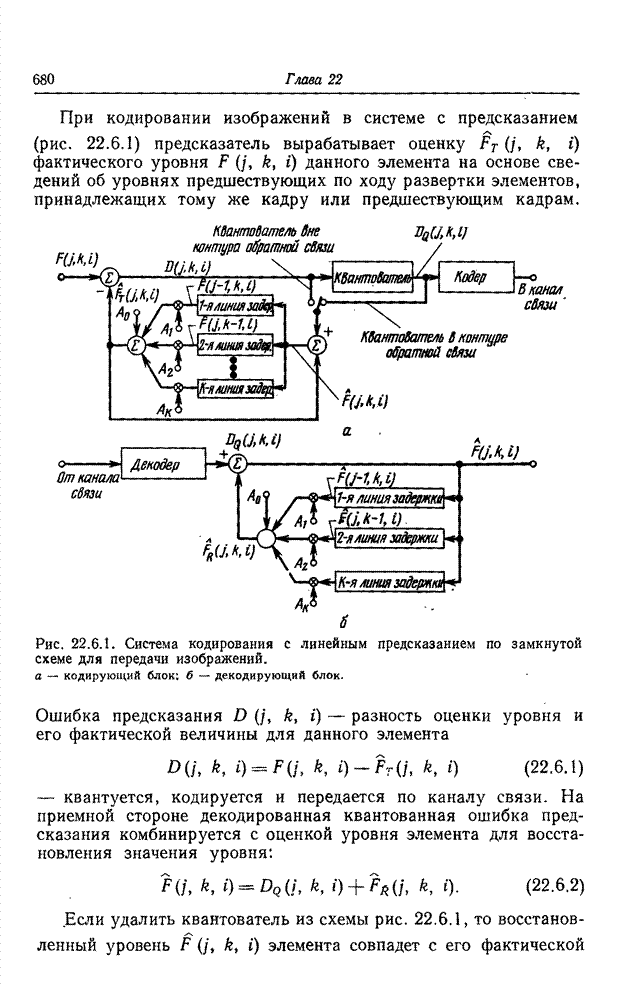
- 22.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ
- 22.5.1. ДЕЛЬТА-МОДУЛЯЦИЯ
- 22.5.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ
- 22.5.3. КОДЕРЫ С ПРОСТРАНСТВЕННЫМ ПРЕДСКАЗАНИЕМ
- 22.5.4. АДАПТИВНЫЕ КОДЕРЫ С ПРЕДСКАЗАНИЕМ
- 22.5.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ ПРИМЕНИТЕЛЬНО К ЦВЕТНЫМ ИЗОБРАЖЕНИЯМ
- 22.5.6. ДИФФЕРЕНЦИАЛЬНОЕ МЕЖКАДРОВОЕ КОДИРОВАНИЕ
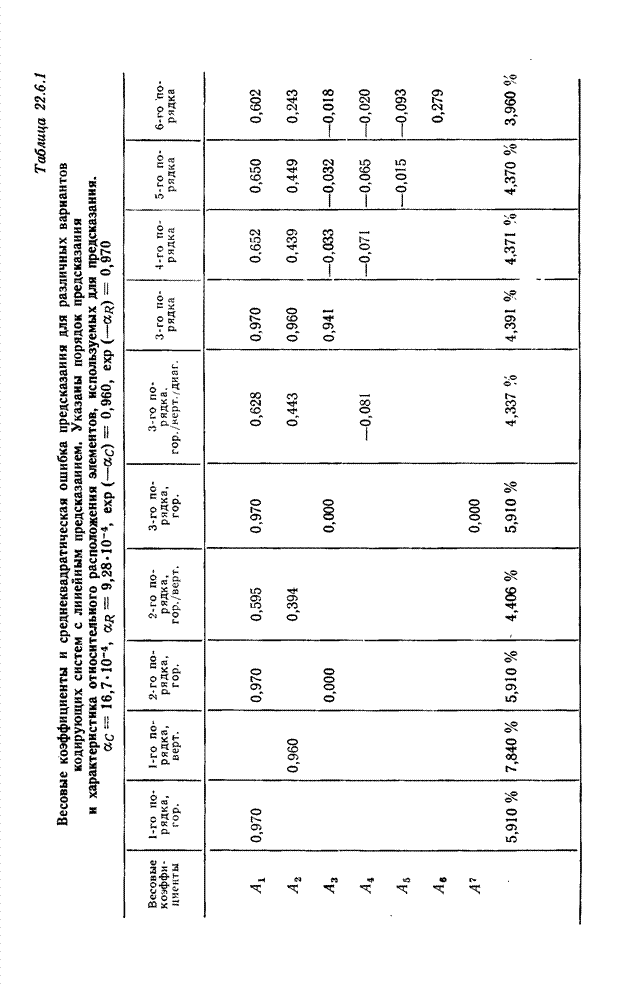
- 22.6. ПРОЕКТИРОВАНИЕ СИСТЕМ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ДЛЯ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 23. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННОЙ ОБРАБОТКОЙ
- 23.1. ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ КОДИРОВАНИЯ
- 23.1.1. ИНТЕРПОЛЯЦИЯ НА ПЕРЕДАЮЩЕЙ СТОРОНЕ
- 23.1.2. ИНТЕРПОЛЯЦИЯ НА ПРИЕМНОЙ СТОРОНЕ
- 23.2. КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.1. КОДИРОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.2. АДАПТИВНОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.3. КОДИРОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.4. МЕЖКАДРОВОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.3. УМЕНЬШЕНИЕ ОШИБОК КВАНТОВАНИЯ ПРИ КОДИРОВАНИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.4. ГИБРИДНОЕ КОДИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ И ДИКМ
- 23.5. КОДИРОВАНИЕ ПРИЗНАКОВ
- 23.5.1. КОДИРОВАНИЕ ЛИНИЙ УРОВНЯ
- 23.5.2. КОДИРОВАНИЕ КОНТУРОВ
- 23.5.3. КОДИРОВАНИЕ ТЕКСТУР
- 23.6. КОДИРОВАНИЕ С ПОМОЩЬЮ НАБОРА СИМВОЛОВ
- 23.6.1. КОДИРОВАНИЕ БЛОКОВ ПО СЛОВАРЮ ОБРАЗОВ
- 23.6.2. КОДИРОВАНИЕ НА ОСНОВЕ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- ЛИТЕРАТУРА
- Глава 24. АНАЛИЗ ЭФФЕКТИВНОСТИ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 24.1. СТАТИСТИЧЕСКИЕ МОДЕЛИ КАНАЛА СВЯЗИ КАК ИСТОЧНИКА ПОМЕХ [1-4]
- 24.2. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ
- 24.3. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ [4]
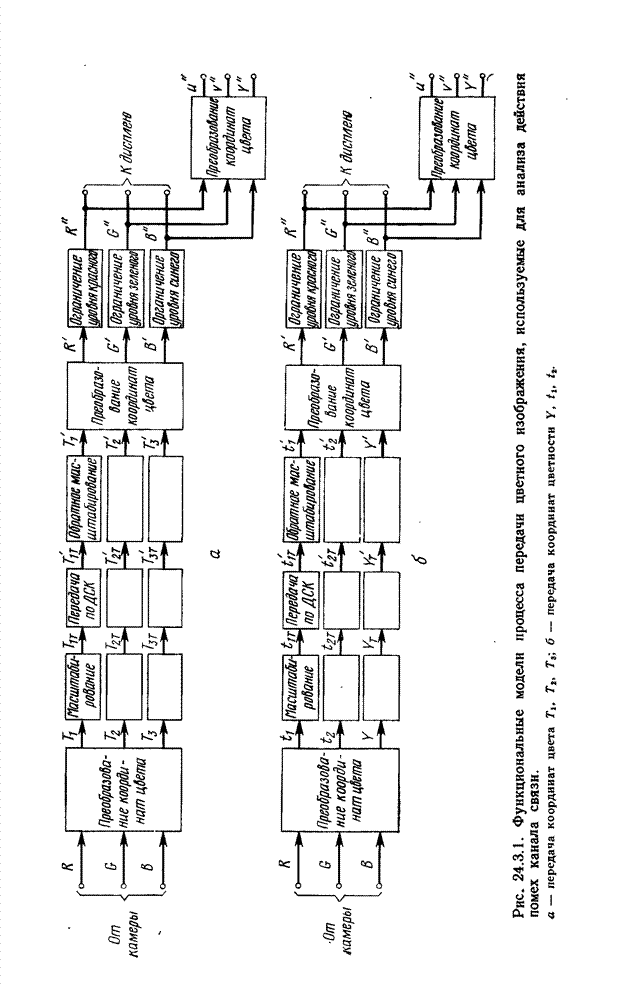
- 24.3.1. ПЕРЕДАЧА КООРДИНАТ ЦВЕТА
- 24.3.2. ПЕРЕДАЧА ЯРКОСТИ И КООРДИНАТ ЦВЕТНОСТИ
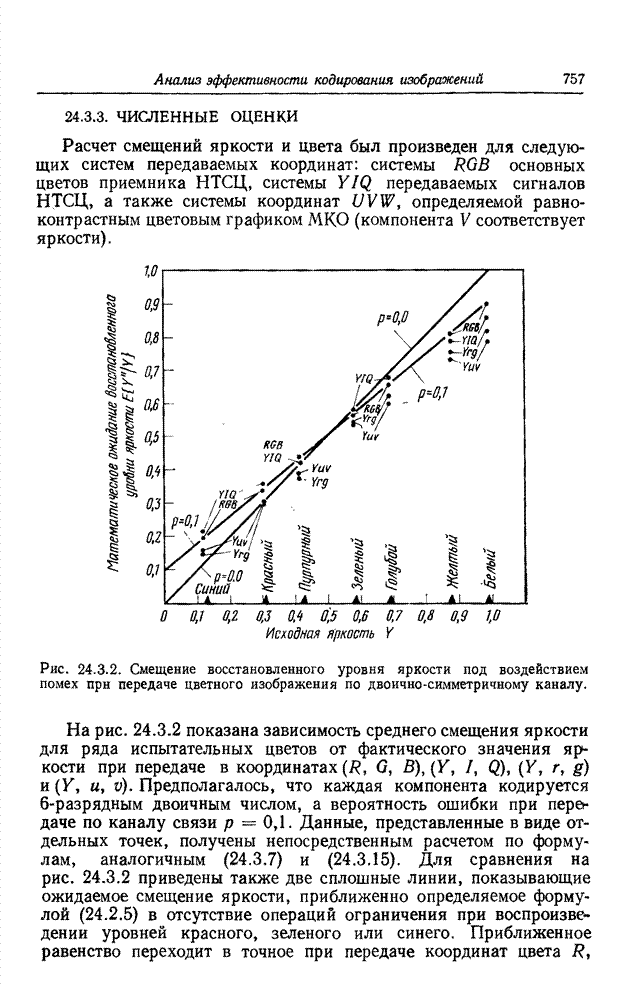
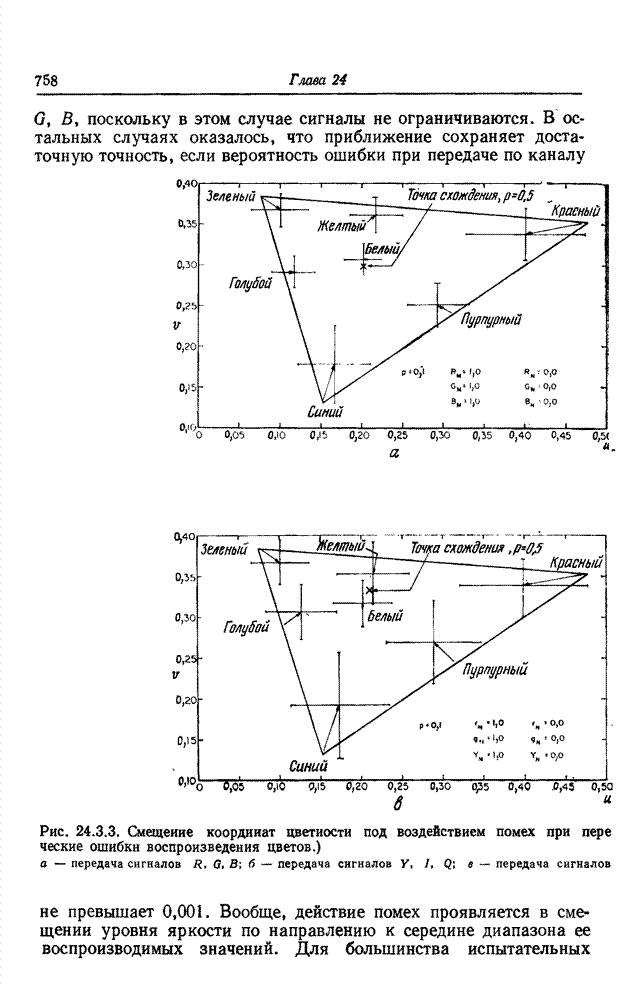
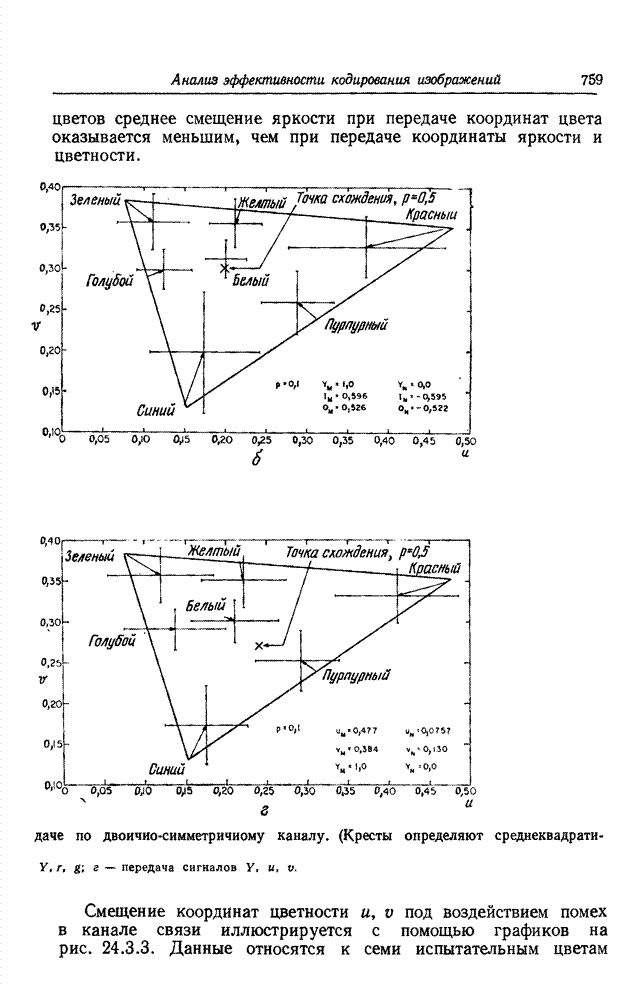
- 24.3.3. ЧИСЛЕННЫЕ ОЦЕНКИ
- 24.4. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ ДИКМ
- 24.5. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ КОДИРОВАНИЯ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
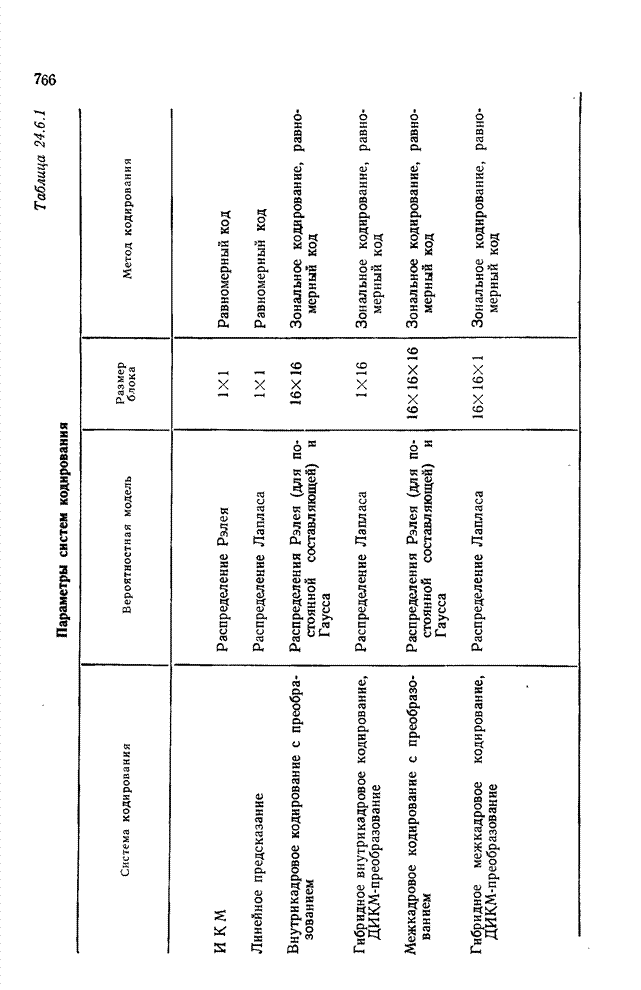
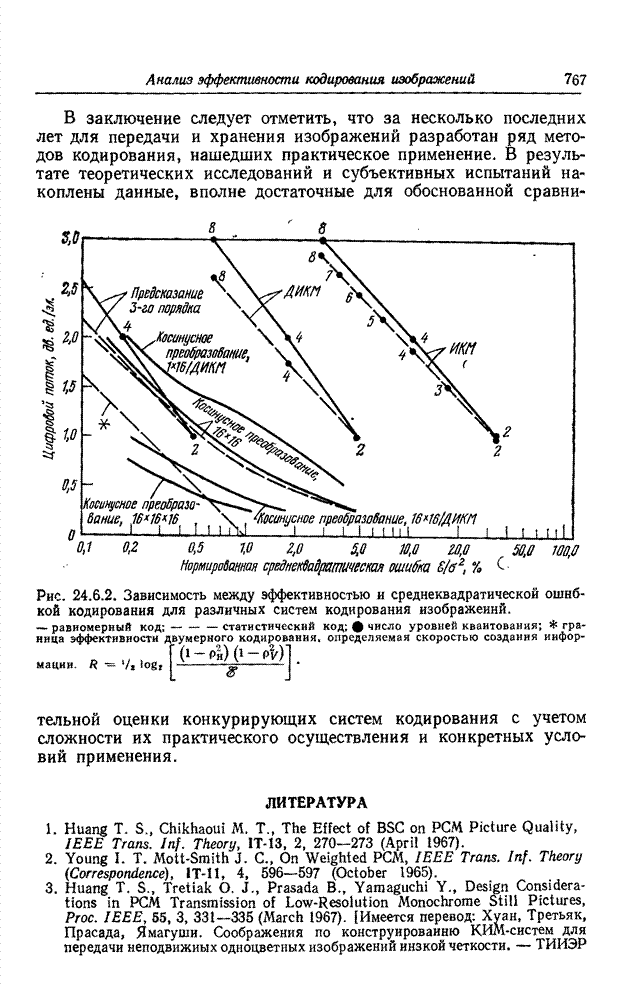
- 24.6. СРАВНЕНИЕ РАЗЛИЧНЫХ МЕТОДОВ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Приложение 1. ОСНОВНАЯ ЛИТЕРАТУРА
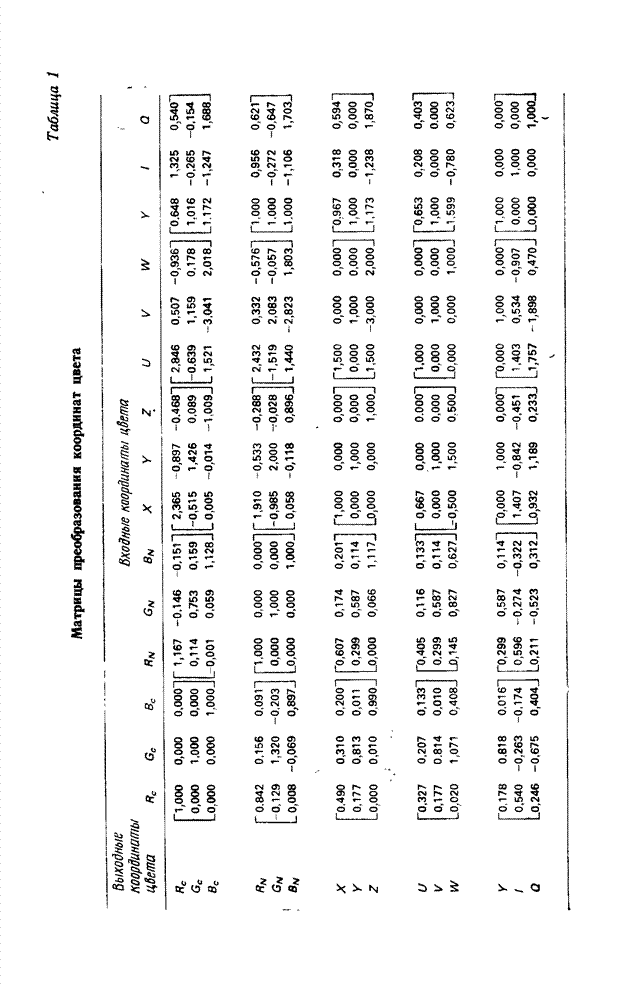
- Приложение 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА И ЦВЕТНОСТИ
- Приложение 3. СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА