| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
14.9. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
Большинство из рассмотренных в
этой главе методов реставрации изображений основано на использовании простой
модели нерезкого изображения, пораженного аддитивным шумом. Более того, почти
все эти методы разработаны для критериев наименьших квадратов или
среднеквадратической ошибки. Теперь рассмотрим более общий класс методов
реставрации изображений, основанных на теории статистического оценивания. Обращаясь
к формуле (13.7.2), запишем обобщенное векторное соотношение, связывающее
вектор наблюдаемого поля ![]() с векторами идеального изображения
с векторами идеального изображения ![]() и шума
и шума ![]() :
:
![]() , (14.9.1)
, (14.9.1)
где ![]() - обобщенная передаточная функция, моделирующая
поэлементные и пространственные искажения изображения. Для нахождения оценки
- обобщенная передаточная функция, моделирующая
поэлементные и пространственные искажения изображения. Для нахождения оценки ![]() по формуле (14.9.1)
можно воспользоваться двумя общими подходами, основанными на групповой и рекуррентной
обработке соответственно. Групповой процессор вычисляет оценку с
использованием одновременно всех элементов наблюдаемого поля
по формуле (14.9.1)
можно воспользоваться двумя общими подходами, основанными на групповой и рекуррентной
обработке соответственно. Групповой процессор вычисляет оценку с
использованием одновременно всех элементов наблюдаемого поля ![]() ; напротив,
рекуррентный процессор пользуется только теми элементами поля
; напротив,
рекуррентный процессор пользуется только теми элементами поля ![]() , которые
расположены в некоторой окрестности оцениваемого элемента. При сильной
корреляции элементов
, которые
расположены в некоторой окрестности оцениваемого элемента. При сильной
корреляции элементов ![]() групповой процессор вырабатывает
более точную оценку, поскольку он использует больше входных данных. Ниже
рассматриваются некоторые методы статистического оценивания [44—48],
потенциально применимые к модели реставрации изображений (14.9.1).
групповой процессор вырабатывает
более точную оценку, поскольку он использует больше входных данных. Ниже
рассматриваются некоторые методы статистического оценивания [44—48],
потенциально применимые к модели реставрации изображений (14.9.1).
Статистическая оценка самого общего вида минимизирует некоторый усредненный функционал ошибки, определенный как
![]() , (14.9.2)
, (14.9.2)
где ![]() - функция ошибки или стоимостная
функция,
- функция ошибки или стоимостная
функция, ![]() -
апостериорная плотность вероятности вектора идеального изображения
-
апостериорная плотность вероятности вектора идеального изображения ![]() при заданном
наблюдаемом векторе
при заданном
наблюдаемом векторе ![]() . Если в качестве функционала ошибки
используется среднеквадратическая ошибка (14.6.2), получаемая оптимальная
оценка называется бейесовской и имеет вид
. Если в качестве функционала ошибки
используется среднеквадратическая ошибка (14.6.2), получаемая оптимальная
оценка называется бейесовской и имеет вид
![]() , (14.9.3)
, (14.9.3)
т. е. она является условным математическим ожиданием вектора идеального изображения при заданном наблюдаемом векторе. Бейесовская оценка будет оптимальной и в случае применения многих других функционалов ошибки (например, абсолютной ошибки) при условии, что функционал ошибки обладает симметрией, а апостериорная плотность вероятности симметрична и одномодальна [48]. К сожалению, в случае нелинейной модели (14.9.1) наблюдаемого поля вычисление байесовской оценки (14.9.3) обычно связано с большими трудностями. Нараги [49]разработал алгоритм реставрации изображений, дающий приближение к оценке (14.9.3).
Другая распространенная
статистическая оценка - так называемая оценка максимума апостериорной
вероятности (МАВ), которая соответствует моде апостериорной плотности
вероятности ![]() .
Для нахождения моды не обязательно располагать информацией об апостериорной
плотности вероятности в явной форме. Теорема Бейеса позволяет выразить
апостериорную плотность условной вероятности через плотности безусловных вероятностей
.
Для нахождения моды не обязательно располагать информацией об апостериорной
плотности вероятности в явной форме. Теорема Бейеса позволяет выразить
апостериорную плотность условной вероятности через плотности безусловных вероятностей
![]() и
и ![]() и плотность
условной вероятности
и плотность
условной вероятности ![]() :
:
![]() . (14.9.4)
. (14.9.4)
Логарифмируя обе части равенства
(14.9.4) и дифференцируя результат по ![]() , получаем характеристическое
уравнение вида
, получаем характеристическое
уравнение вида
![]() , (14.9.5)
, (14.9.5)
которое требуется решить
относительно оценки ![]() при наличии подходящих моделей для
при наличии подходящих моделей для ![]() и
и ![]() . Большинство
найденных решений основано на гауссовых моделях для
. Большинство
найденных решений основано на гауссовых моделях для ![]() и
и ![]() . Хант [3] применил метод
МАВ – оценки для решений задач реставрации изображений при использовании модели
. Хант [3] применил метод
МАВ – оценки для решений задач реставрации изображений при использовании модели
![]() , (14.9.6)
, (14.9.6)
где ![]() матрица нерезкости,
матрица нерезкости, ![]() - известный
оператор поэлементной нелинейности, воздействующий на каждый элемент вектора
- известный
оператор поэлементной нелинейности, воздействующий на каждый элемент вектора ![]() . Приняв гауссову
модель, Хант представил (14.9.5) в рекуррентной форме, пригодной для вычисления
решений итеративными методами.
. Приняв гауссову
модель, Хант представил (14.9.5) в рекуррентной форме, пригодной для вычисления
решений итеративными методами.
Оценка наибольшего правдоподобия
есть такое значение ![]() , при котором апостериорная плотность
вероятности
, при котором апостериорная плотность
вероятности ![]() для
фактически наблюдаемого поля
для
фактически наблюдаемого поля ![]() максимальна. Математически такая
оценка определяется как
максимальна. Математически такая
оценка определяется как
![]() . (14.9.7)
. (14.9.7)
Если вектор идеального
изображения ![]() имеет
равномерное распределение, оценка наибольшего правдоподобия совпадает с
МАВ-оценкой.
имеет
равномерное распределение, оценка наибольшего правдоподобия совпадает с
МАВ-оценкой.
Методы статистических оценок должны дать хорошие результаты при решении задач реставрации изображений с нелинейными моделями наблюдаемых полей изображения. В таких случаях методы линейных оценок представляются неэффективными. Однако статистические методы реставрации изображений, известные в настоящее время, находят ограниченное применение из-за трудностей статистического моделирования и сложности практической реализации.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Часть 4. РЕСТАВРАЦИЯ И УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
- Глава 12. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
- 12.1. ИЗМЕНЕНИЕ КОНТРАСТА
- 12.2. ВИДОИЗМЕНЕНИЕ ГИСТОГРАММ
- 12.3. ПОДАВЛЕНИЕ ШУМОВ
- 12.4. ПОДЧЕРКИВАНИЕ ГРАНИЦ
- 12.5. ОБРАБОТКА ИЗОБРАЖЕНИЙ С ПРЕОБРАЗОВАНИЕМ
- 12.6. МЕДИАННЫЙ ФИЛЬТР
- 12.7. ЛОЖНЫЕ ЦВЕТА
- 12.8. ПСЕВДОЦВЕТА
- 12.9. УЛУЧШЕНИЕ СПЕКТРОЗОНАЛЬНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 13. МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.1. ОБОБЩЕННЫЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.2. МОДЕЛИ ОПТИЧЕСКИХ СИСТЕМ
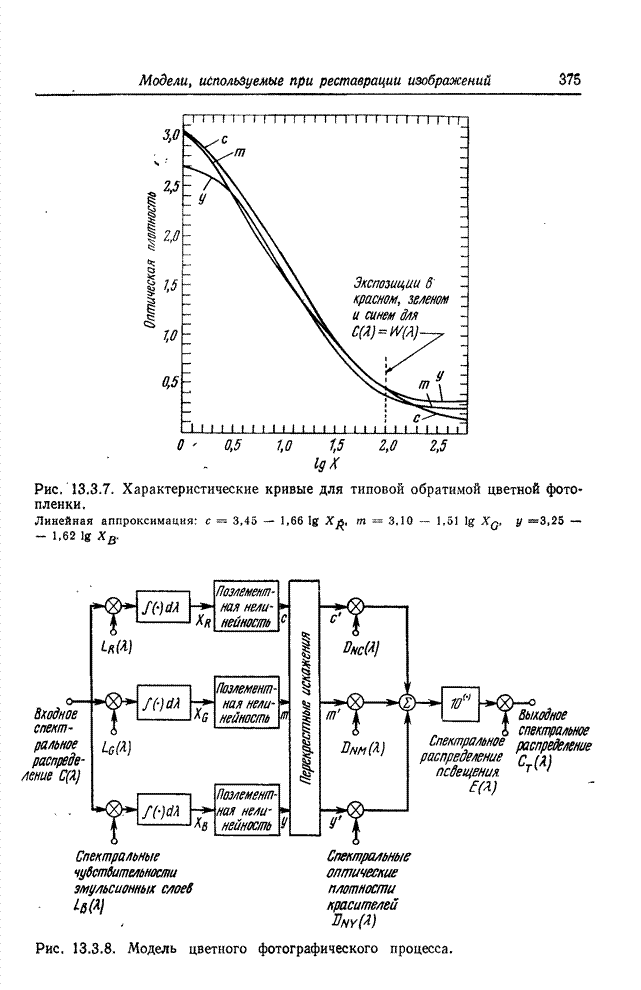
- 13.3. МОДЕЛИ ФОТОГРАФИЧЕСКИХ ПРОЦЕССОВ
- 13.3.1. ОДНОЦВЕТНАЯ ФОТОГРАФИЯ
- 13.3.2. ЦВЕТНАЯ ФОТОГРАФИЯ
- 13.4. МОДЕЛИ ЦИФРОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- 13.5. МОДЕЛЬ ДИСПЛЕЯ
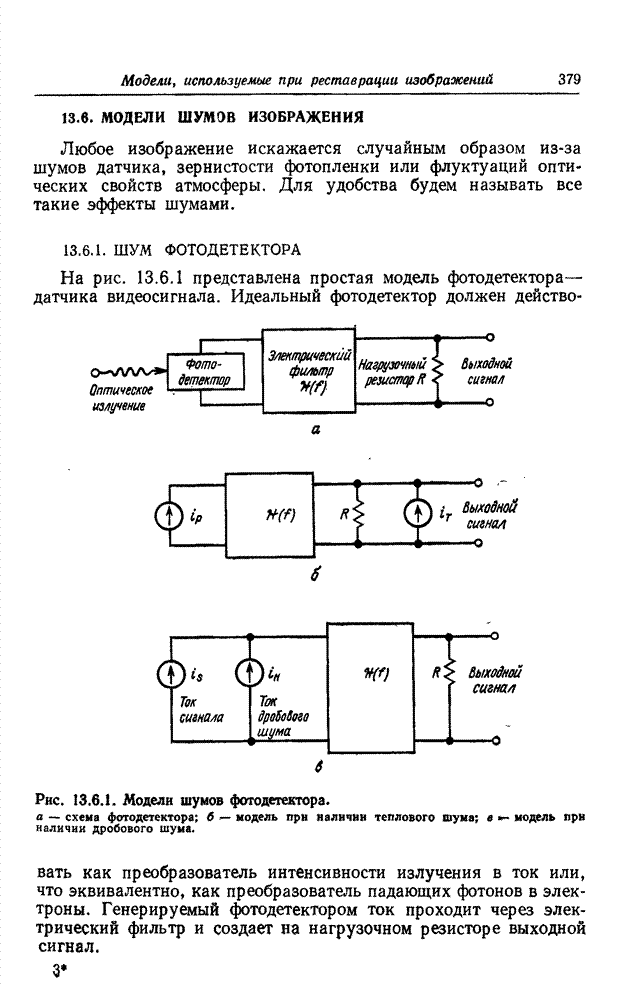
- 13.6. МОДЕЛИ ШУМОВ ИЗОБРАЖЕНИЯ
- 13.6.1. ШУМ ФОТОДЕТЕКТОРА
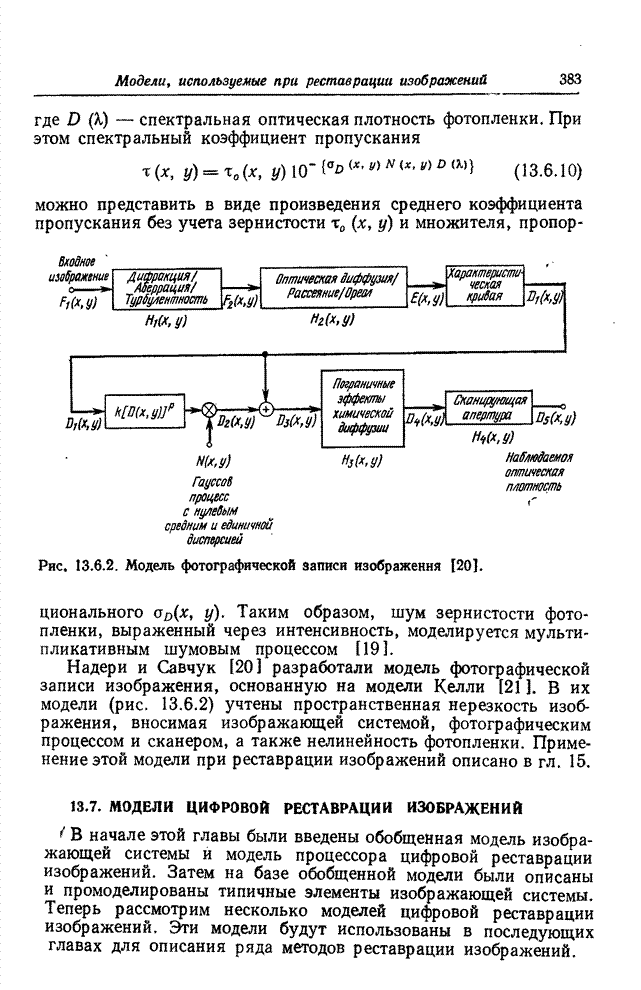
- 13.6.2. ШУМ ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
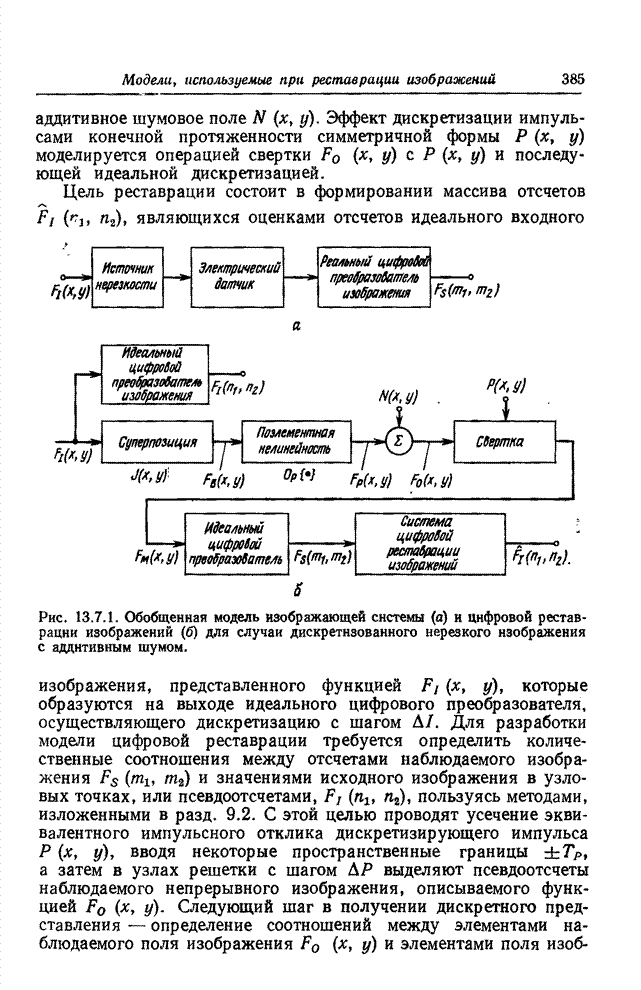
- 13.7. МОДЕЛИ ЦИФРОВОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 14. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 14.1. МЕТОДЫ ПРОСТРАНСТВЕННОЙ ФИЛЬТРАЦИИ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 14.1.1. ИНВЕРСНАЯ ФИЛЬТРАЦИЯ
- 14.1.2. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И АДДИТИВНЫЙ ШУМ
- 14.1.3. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНОЕ ИЗОБРАЖЕНИЕ
- 14.1.4. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНАЯ НЕРЕЗКОСТЬ
- 14.1.5. ФИЛЬТРЫ НА ОСНОВЕ ПАРАМЕТРИЧЕСКИХ ОЦЕНОК
- 14.1.6. ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 4.2. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.2.1. РЕСТАВРАЦИЯ НЕРЕЗКИХ ИЗОБРАЖЕНИЙ
- 14.2.2. РЕСТАВРАЦИЯ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ ПРИ НАЛИЧИИ ШУМА
- 14.3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.3.1. АЛГОРИТМ ДЛЯ ПЕРЕОПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.3.2. АЛГОРИТМ ДЛЯ НЕДООПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.4. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ С ИСПОЛЬЗОВАНИЕМ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- 14.5. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕГРЕССИИ
- 14.6. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ВИНЕРОВСКОГО ОЦЕНИВАНИЯ
- 14.6.1. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В ОБЩЕМ СЛУЧАЕ
- 14.6.2. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В СЛУЧАЕ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ С ШУМОМ
- 14.7. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ СО СГЛАЖИВАНИЕМ
- 14.8. МЕТОДЫ РЕСТАВРАЦИИ С ИСПОЛЬЗОВАНИЕМ ОГРАНИЧЕНИЙ
- 14.9. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
- ЛИТЕРАТУРА
- Глава 15. CПЕЦИАЛЬНЫЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 15.1. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮ ПОДАВЛЕНИЯ ОШИБОК НАЛОЖЕНИЯ СПЕКТРОВ
- 15.2. КОРРЕКЦИЯ ОШИБОК ИНТЕРПОЛЯЦИИ
- 15.3. КОРРЕКЦИЯ ГЕОМЕТРИЧЕСКИХ ИСКАЖЕНИЙ
- 15.4. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ГОМОМОРФНОЙ ФИЛЬТРАЦИИ
- 15.5. СЛЕПАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ
- 15.5.1. МЕТОДЫ НА ОСНОВЕ ПРЯМЫХ ИЗМЕРЕНИЙ
- 15.5.2. МЕТОДЫ НА ОСНОВЕ КОСВЕННОГО ОЦЕНИВАНИЯ
- 15.6. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ СПЕКТРА
- 15.7. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННО-ЗАВИСИМЫМИ ИСКАЖЕНИЯМИ
- 15.8. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕКУРСИВНОЙ ФИЛЬТРАЦИИ
- 15.9. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮОСЛАБЛЕНИЯ ШУМА ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- ЛИТЕРАТУРА
- Глава 16. КОРРЕКЦИЯ ЯРКОСТНЫХ, ЦВЕТОВЫХ И СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗОБРАЖАЮЩИХ СИСТЕМ
- 16.1. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ВИДЕОДАТЧИКОВ
- 16.2. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ДИСПЛЕЕВ
- 16.3. ОЦЕНИВАНИЕ СПЕКТРАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 16.4. КОРРЕКЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ВИДЕОДАТЧИКОВ И ДИСПЛЕЕВ
- 16.5. ОЦЕНИВАНИЕ КООРДИНАТ СВЕТА ВИДЕОДАТЧИКОВ
- 16.6. ОЦЕНИВАНИЕ ЭКСПОЗИЦИЙ ЦВЕТНОЙ ФОТОПЛЕНКИ
- 16.7. КОМПЕНСАЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ ЦВЕТНЫХ ДИСПЛЕЕВ
- ЛИТЕРАТУРА
- Часть 5. АНАЛИЗ ИЗОБРАЖЕНИЙ
- Глава 17. ВЫДЕЛЕНИЕ ПРИЗНАКОВ ИЗОБРАЖЕНИЯ
- 17.1. ЯРКОСТНЫЕ ПРИЗНАКИ
- 17.2. ГИСТОГРАММНЫЕ ПРИЗНАКИ
- 17.3. ПРОСТРАНСТВЕННО-СПЕКТРАЛЬНЫЕ ПРИЗНАКИ
- 17.4. КОНТУРНЫЕ ПРИЗНАКИ
- 17.4.1. ЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.2. НЕЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.3. МЕТОДЫ АППРОКСИМАЦИИ ПЕРЕПАДОВ ЯРКОСТИ
- 17.4.4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ
- 17.5. ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ ЯРКОСТИ
- 17.6. ЦВЕТОВЫЕ КОНТУРЫ
- 17.7. ПРИЗНАКИ ПЯТНА И ЛИНИИ
- 17.8. ТЕКСТУРНЫЕ ПРИЗНАКИ
- 17.9. СИНТЕЗ ТЕКСТУР
- ЛИТЕРАТУРА
- Глава 18. СИМВОЛИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
- 18.1. СВЯЗНОСТЬ
- 18.2. СЖАТИЕ, УТОНЧЕНИЕ И ПОСТРОЕНИЕ ОСТОВА
- 18.3. ОПИСАНИЕ ЛИНИЙ
- 18.3.1. АППРОКСИМАЦИЯ КРИВЫХ
- 18.3.2. ПРЕОБРАЗОВАНИЕ ЛИНИИ В ТОЧКУ
- 18.4. ОПИСАНИЕ ФОРМЫ
- 18.4.1. МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.2. ТОПОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.3. АНАЛИТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.5. СЕГМЕНТАЦИЯ ПО ЯРКОСТИ
- 18.5.1. ПОРОГОВОЕ ОГРАНИЧЕНИЕ ПО ЯРКОСТИ
- 18.5.2. МНОГОМЕРНОЕ ПОРОГОВОЕ ОГРАНИЧЕНИЕ
- 18.5.3. НАРАЩИВАНИЕ ОБЛАСТЕЙ
- 18.6. КОНТУРНАЯ СЕГМЕНТАЦИЯ
- 18.7. ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ
- 18.8. СЕГМЕНТАЦИЯ ФОРМЫ
- ЛИТЕРАТУРА
- Глава 19. ОБНАРУЖЕНИЕ ОБЪЕКТОВ И СОВМЕЩЕНИЕ (ПРИВЯЗКА) ИЗОБРАЖЕНИЙ
- 19.1. СОПОСТАВЛЕНИЕ С ЭТАЛОНОМ
- 19.2. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ ДЕТЕРМИНИРОВАННЫХ ПОЛЕЙ
- 19.3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ СЛУЧАЙНЫХ ПОЛЕЙ
- 19.4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 19.5. ПРИВЯЗКА ИЗОБРАЖЕНИЙ
- 19.5.1. КОРРЕЛЯЦИОННАЯ ПРИВЯЗКА
- 19.5.2. ПОСЛЕДОВАТЕЛЬНАЯ ПРИВЯЗКА
- ЛИТЕРАТУРА
- Глава 20. СИСТЕМЫ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.1. СИСТЕМЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 20.2. МОДЕЛИ СИСТЕМ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.3. СИНТАКСИЧЕСКИЕ МЕТОДЫ
- 20.4. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ОТНОШЕНИЯ МЕЖДУ ОБЪЕКТАМИ
- ЛИТЕРАТУРА
- Часть 6. Кодирование изображений
- Глава 21. АНАЛОГОВЫЕ МЕТОДЫ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.1. КЛАССИФИКАЦИЯ МЕТОДОВ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.2. СИСТЕМЫ ВЕЩАТЕЛЬНОГО ТЕЛЕВИДЕНИЯ
- 21.2.1. СИСТЕМА НТСЦ [13-15]
- 21.2.2. СИСТЕМА СЕКАМ [17]
- 21.2.3.СИСТЕМА ПАЛ
- 21.3. МОДУЛЯЦИОННЫЕ МЕТОДЫ СОКРВЩЕНИЯ ПОЛОСЫ ЧАСТОТЫ
- 21.4.УМЕНЬШЕНИЕ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ И ЧАСТОТЫ КАДРОВ
- 21.4.1. УМЕНЬШЕНИЕ ПРОСТРАНСТВЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
- 21.4.2. УМЕНЬШЕНИЕ ЧАСТОТЫ КАДРОВ
- 21.5. МЕТОДЫ ВРЕМЕННОГО ПЕРЕМЕЖЕНИЯ
- 21.5.1. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ СТРОК
- 21.5.2. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ ЭЛЕМЕНТОВ
- 21.6. РАЗВЕРТКА С ПЕРЕМЕННОЙ СКОРОСТЬЮ
- 21.7. МУЛЬТИПЛЕКСНЫЕ МЕТОДЫ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Глава 22. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПОЭЛЕМЕНТНОЙ ОБРАБОТКОЙ
- 22.1. СИСТЕМЫ КОДИРОВАНИЯ С ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИЕЙ
- 22.1.1. КВАНТОВАНИЕ СО СЖАТИЕМ ДИАПАЗОНА ЯРКОСТЕЙ
- 22.1.2. ПСЕВДОШУМОВОЕ КВАНТОВАНИЕ
- 22.1.3. КВАНТОВАНИЕ С УЛУЧШЕННОЙ ПЕРЕДАЧЕЙ ГРАДАЦИЙ ЯРКОСТИ
- 22.1.4. СИСТЕМА С ГРУБОЙ-ТОНКОЙ ШКАЛОЙ КВАНТОВАНИЯ
- 22.1.5. КВАНТОВАНИЕ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ
- 22.2. СТАТИСТИЧЕСКИЕ МЕТОДЫ КОДИРОВАНИЯ
- 22.2.1. ПОЭЛЕМЕНТНОЕ СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- 22.2.2. КОДИРОВАНИЕ С УЧЕТОМ ПРЕДШЕСТВУЮЩЕГО ЭЛЕМЕНТА
- 22.3. КОДИРОВАНИЕ СЕРИЙ
- 22.3.1. КОДИРОВАНИЕ ДЛИН СЕРИЙ; ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ [32-36]
- 22.3.2. КОДИРОВАНИЕ РАЗРЯДНЫХ ПЛОСКОСТЕЙ
- 22.4. КОДИРОВАНИЕ С ПОПОЛНЕНИЕМ КАДРОВ
- 22.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ
- 22.5.1. ДЕЛЬТА-МОДУЛЯЦИЯ
- 22.5.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ
- 22.5.3. КОДЕРЫ С ПРОСТРАНСТВЕННЫМ ПРЕДСКАЗАНИЕМ
- 22.5.4. АДАПТИВНЫЕ КОДЕРЫ С ПРЕДСКАЗАНИЕМ
- 22.5.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ ПРИМЕНИТЕЛЬНО К ЦВЕТНЫМ ИЗОБРАЖЕНИЯМ
- 22.5.6. ДИФФЕРЕНЦИАЛЬНОЕ МЕЖКАДРОВОЕ КОДИРОВАНИЕ
- 22.6. ПРОЕКТИРОВАНИЕ СИСТЕМ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ДЛЯ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 23. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННОЙ ОБРАБОТКОЙ
- 23.1. ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ КОДИРОВАНИЯ
- 23.1.1. ИНТЕРПОЛЯЦИЯ НА ПЕРЕДАЮЩЕЙ СТОРОНЕ
- 23.1.2. ИНТЕРПОЛЯЦИЯ НА ПРИЕМНОЙ СТОРОНЕ
- 23.2. КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.1. КОДИРОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.2. АДАПТИВНОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.3. КОДИРОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.4. МЕЖКАДРОВОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.3. УМЕНЬШЕНИЕ ОШИБОК КВАНТОВАНИЯ ПРИ КОДИРОВАНИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.4. ГИБРИДНОЕ КОДИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ И ДИКМ
- 23.5. КОДИРОВАНИЕ ПРИЗНАКОВ
- 23.5.1. КОДИРОВАНИЕ ЛИНИЙ УРОВНЯ
- 23.5.2. КОДИРОВАНИЕ КОНТУРОВ
- 23.5.3. КОДИРОВАНИЕ ТЕКСТУР
- 23.6. КОДИРОВАНИЕ С ПОМОЩЬЮ НАБОРА СИМВОЛОВ
- 23.6.1. КОДИРОВАНИЕ БЛОКОВ ПО СЛОВАРЮ ОБРАЗОВ
- 23.6.2. КОДИРОВАНИЕ НА ОСНОВЕ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- ЛИТЕРАТУРА
- Глава 24. АНАЛИЗ ЭФФЕКТИВНОСТИ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 24.1. СТАТИСТИЧЕСКИЕ МОДЕЛИ КАНАЛА СВЯЗИ КАК ИСТОЧНИКА ПОМЕХ [1-4]
- 24.2. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ
- 24.3. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ [4]
- 24.3.1. ПЕРЕДАЧА КООРДИНАТ ЦВЕТА
- 24.3.2. ПЕРЕДАЧА ЯРКОСТИ И КООРДИНАТ ЦВЕТНОСТИ
- 24.3.3. ЧИСЛЕННЫЕ ОЦЕНКИ
- 24.4. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ ДИКМ
- 24.5. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ КОДИРОВАНИЯ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 24.6. СРАВНЕНИЕ РАЗЛИЧНЫХ МЕТОДОВ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Приложение 1. ОСНОВНАЯ ЛИТЕРАТУРА
- Приложение 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА И ЦВЕТНОСТИ
- Приложение 3. СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА