| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.7. МОДЕЛИ ЦИФРОВОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
В начале этой главы были введены обобщенная модель изображающей системы и модель процессора цифровой реставрации изображений. Затем на базе обобщенной модели были описаны и промоделированы типичные элементы изображающей системы. Теперь рассмотрим несколько моделей цифровой реставрации изображений. Эти модели будут использованы в последующих главах для описания ряда методов реставрации изображений.
Процесс реставрации можно описать с помощью следующих выражений:
![]() , (13.7.1а)
, (13.7.1а)
![]() , (13.7.1б)
, (13.7.1б)
![]() . (13.7.1в)
. (13.7.1в)
Здесь
![]() - массив
наблюдаемых отсчетов изображения,
- массив
наблюдаемых отсчетов изображения, ![]() - массив элементов идеально
дискретизованного изображения,
- массив элементов идеально
дискретизованного изображения, ![]() - массив элементов идеально дискретизованной
оценки изображения,
- массив элементов идеально дискретизованной
оценки изображения, ![]() - массив компенсированных отсчетов на
выходе системы цифровой реставрации,
- массив компенсированных отсчетов на
выходе системы цифровой реставрации, ![]() - массивы отсчетов составляющих шума,
возникающих в различных элементах системы,
- массивы отсчетов составляющих шума,
возникающих в различных элементах системы, ![]() - обобщенные передаточные функции
изображающей системы, реставрирующего процессора и дисплея соответственно.
- обобщенные передаточные функции
изображающей системы, реставрирующего процессора и дисплея соответственно.
Соотношения (13.7.1) можно представить в эквивалентной векторной форме:
![]() , (13.7.2а)
, (13.7.2а)
![]() , (13.7.2б)
, (13.7.2б)
![]() , (13.7.2в)
, (13.7.2в)
где
![]() -
векторы, полученные разверткой по столбцам соответствующих массивов. В
последующих главах рассмотрены некоторые методы нахождения приближенных решений
(13.7.1) или (13.7.2). К сожалению, решения общего вида до сих пор не получены;
поэтому мы обратимся к частным решениям.
-
векторы, полученные разверткой по столбцам соответствующих массивов. В
последующих главах рассмотрены некоторые методы нахождения приближенных решений
(13.7.1) или (13.7.2). К сожалению, решения общего вида до сих пор не получены;
поэтому мы обратимся к частным решениям.
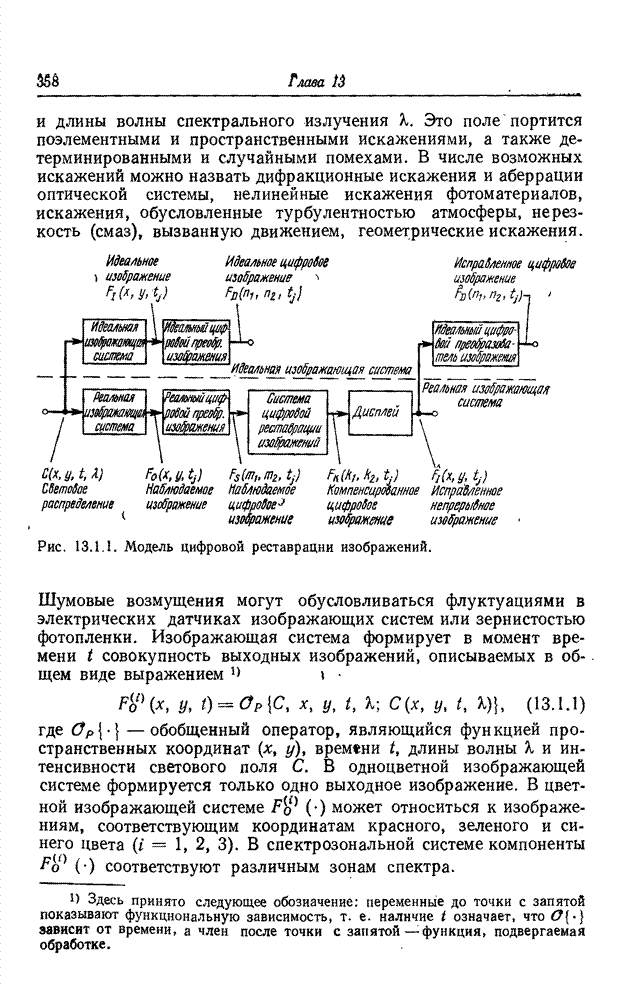
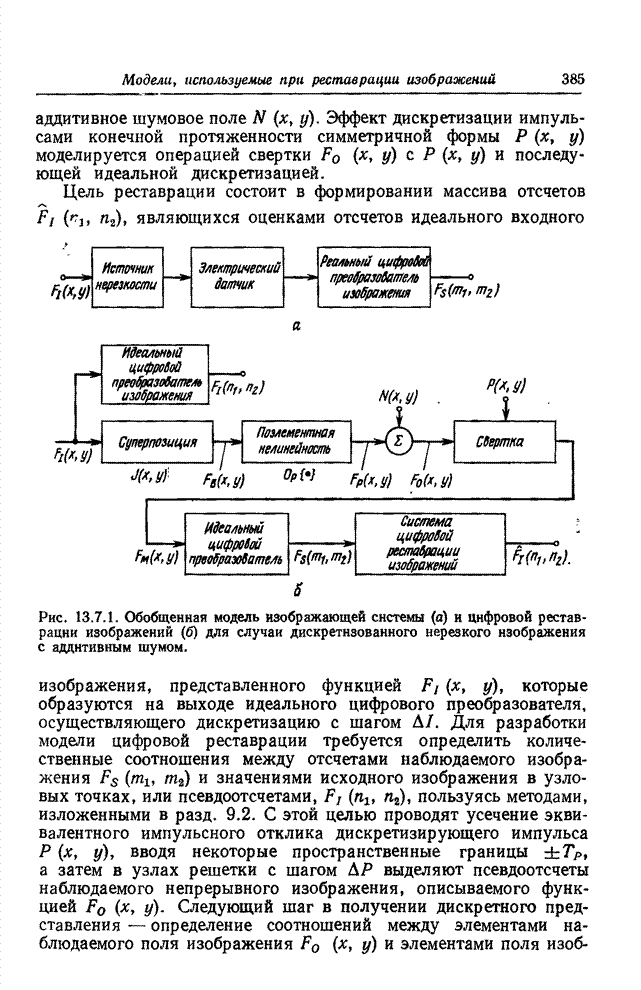
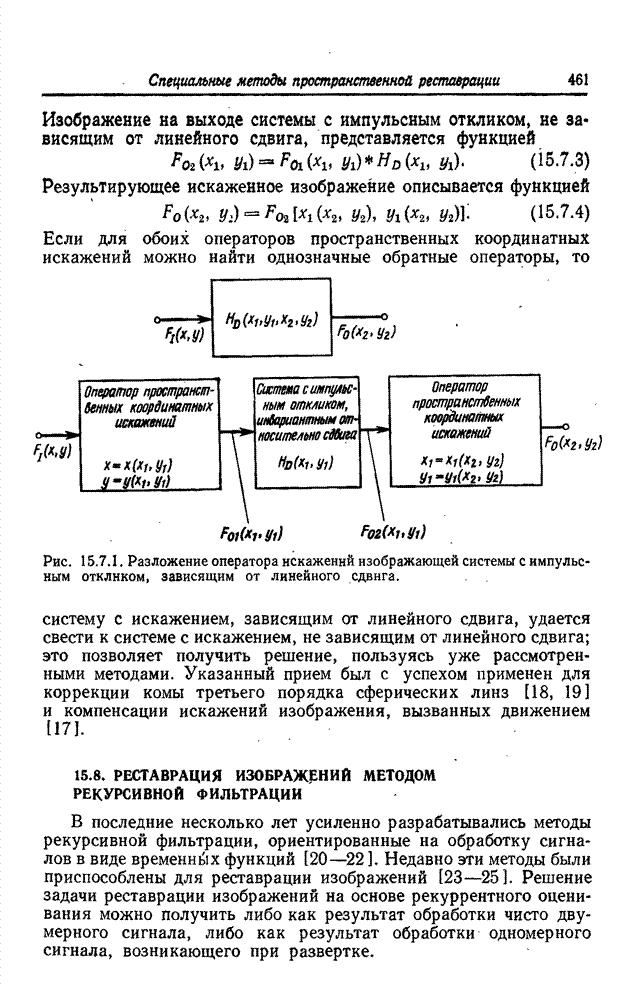
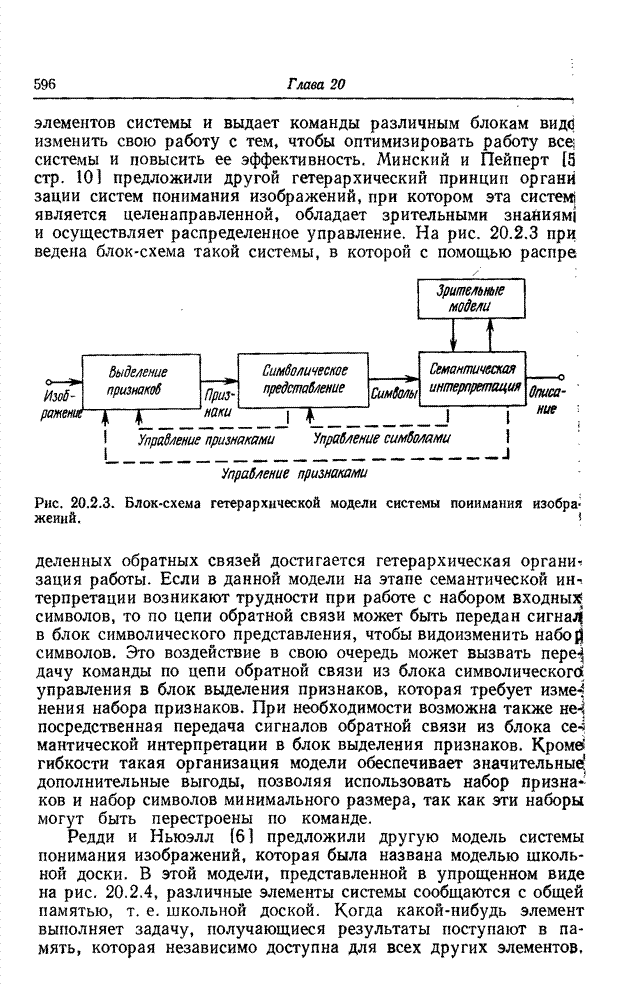
Модель, показанная на рис. 13.7.1, является наиболее общей моделью цифровой реставрации изображений, в которой изображение приобретает пространственные искажения, приводящие к ухудшению резкости, электрический датчик реагирует нелинейным образом на интенсивность входного излучения, а усилитель датчика вносит гауссов шум, не зависящий от изображения. Затем следует цифровой преобразователь, который также может увеличить нерезкость дискретизованного изображения в случае использования дискретизирующих импульсов конечной протяженности.

Рис. 13.7.1. Обобщенная модель изображающей системы (а) и цифровой реставрации изображений (б) для случая дискретизованного нерезкого изображения с аддитивным шумом.
Возникновение
нерезкости изображения можно промоделировать операцией суперпозиции с
импульсным откликом ![]() , который может быть пространственно-зависимым.
Предполагается, что нелинейная реакция датчика на изображение
, который может быть пространственно-зависимым.
Предполагается, что нелинейная реакция датчика на изображение ![]() имеет поэлементный
характер и что на выходе датчика имеется аддитивное шумовое поле
имеет поэлементный
характер и что на выходе датчика имеется аддитивное шумовое поле ![]() . Эффект
дискретизации импульсами конечной протяженности симметричной формы
. Эффект
дискретизации импульсами конечной протяженности симметричной формы ![]() моделируется
операцией свертки
моделируется
операцией свертки ![]() с
с ![]() и последующей идеальной
дискретизацией.
и последующей идеальной
дискретизацией.
Цель
реставрации состоит в формировании массива отсчетов ![]() , являющихся оценками
отсчетов идеального входного изображения, представленного функцией
, являющихся оценками
отсчетов идеального входного изображения, представленного функцией ![]() , которые
образуются на выходе идеального цифрового преобразователя, осуществляющего
дискретизацию с шагом
, которые
образуются на выходе идеального цифрового преобразователя, осуществляющего
дискретизацию с шагом ![]() . Для разработки модели цифровой
реставрации требуется определить количественные соотношения между отсчетами
наблюдаемого изображения
. Для разработки модели цифровой
реставрации требуется определить количественные соотношения между отсчетами
наблюдаемого изображения ![]() и значениями исходного изображения в
узловых точках, или псевдоотсчетами,
и значениями исходного изображения в
узловых точках, или псевдоотсчетами, ![]() , пользуясь методами, изложенными в
разд. 9.2. С этой целью проводят усечение эквивалентного импульсного отклика
дискретизирующего импульса
, пользуясь методами, изложенными в
разд. 9.2. С этой целью проводят усечение эквивалентного импульсного отклика
дискретизирующего импульса ![]() , вводя некоторые пространственные
границы
, вводя некоторые пространственные
границы ![]() ,
а затем в узлах решетки с шагом
,
а затем в узлах решетки с шагом ![]() выделяют псевдоотсчеты наблюдаемого
непрерывного изображения, описываемого функцией
выделяют псевдоотсчеты наблюдаемого
непрерывного изображения, описываемого функцией ![]() . Следующий шаг в получении
дискретного представления - определение соотношений между элементами
наблюдаемого поля изображения
. Следующий шаг в получении
дискретного представления - определение соотношений между элементами
наблюдаемого поля изображения ![]() и элементами поля изображения
и элементами поля изображения ![]() и шумового поля
и шумового поля ![]() . Последний шаг при
разработке модели цифровой реставрации изображений состоит в нахождении
дискретного эквивалента операции суперпозиции с использованием импульсного
отклика
. Последний шаг при
разработке модели цифровой реставрации изображений состоит в нахождении
дискретного эквивалента операции суперпозиции с использованием импульсного
отклика ![]() .
В рассмотренной модели существуют два потенциальных источника погрешностей:
усечение импульсных откликов
.
В рассмотренной модели существуют два потенциальных источника погрешностей:
усечение импульсных откликов ![]() и
и ![]() и интегрирование методом квадратурных
сумм. Чтобы можно было пренебречь погрешностями обоих видов, интервалы усечения
выбирают большими, а приращения
и интегрирование методом квадратурных
сумм. Чтобы можно было пренебречь погрешностями обоих видов, интервалы усечения
выбирают большими, а приращения ![]() и
и ![]() в квадратурных суммах берут малыми.
Конечно, при этом увеличиваются размеры массивов и, следовательно, возрастают
требования к объему памяти и мощности вычислительных средств. Более того, как
будет показано в дальнейшем, повышение точности дискретизации может даже
привести к неустойчивости вычислительного процесса реставрации!
в квадратурных суммах берут малыми.
Конечно, при этом увеличиваются размеры массивов и, следовательно, возрастают
требования к объему памяти и мощности вычислительных средств. Более того, как
будет показано в дальнейшем, повышение точности дискретизации может даже
привести к неустойчивости вычислительного процесса реставрации!
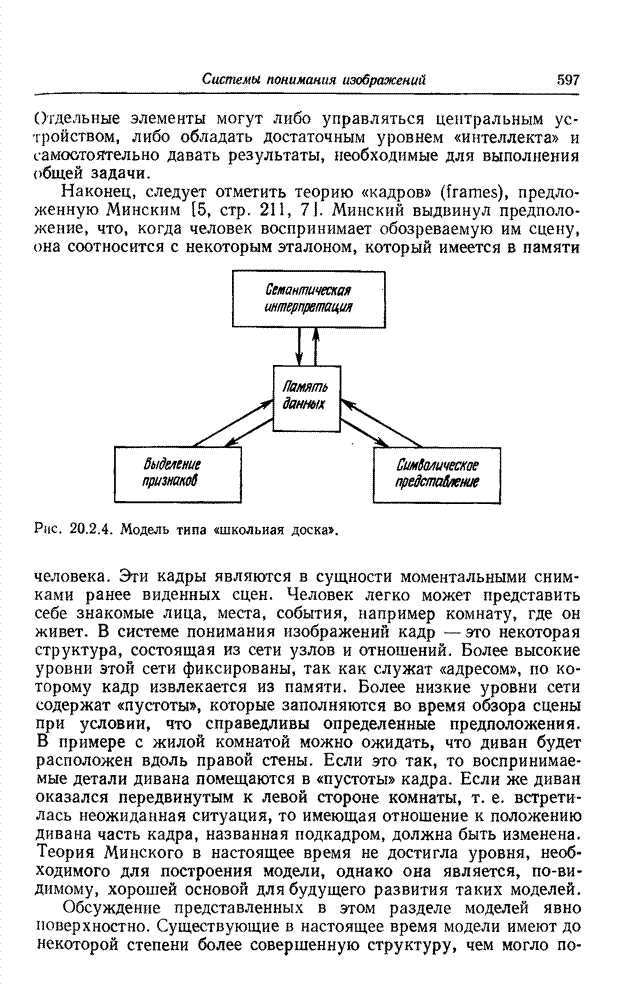
Важное
значение имеют относительные геометрические размеры различных массивов модели
реставрации изображений. Эти массивы образуют гнездо (рис. 13.7.2). Область
массива нерезкого изображения ![]() меньше области массива идеально
дискретизованного изображения
меньше области массива идеально
дискретизованного изображения ![]() на половину протяженности усеченного
импульсного отклика
на половину протяженности усеченного
импульсного отклика ![]() . Аналогично область массива
физических отсчетов
. Аналогично область массива
физических отсчетов ![]() меньше области массива наблюдаемых
элементов изображения
меньше области массива наблюдаемых
элементов изображения ![]() на половину протяженности усеченного
импульсного отклика
на половину протяженности усеченного
импульсного отклика ![]()

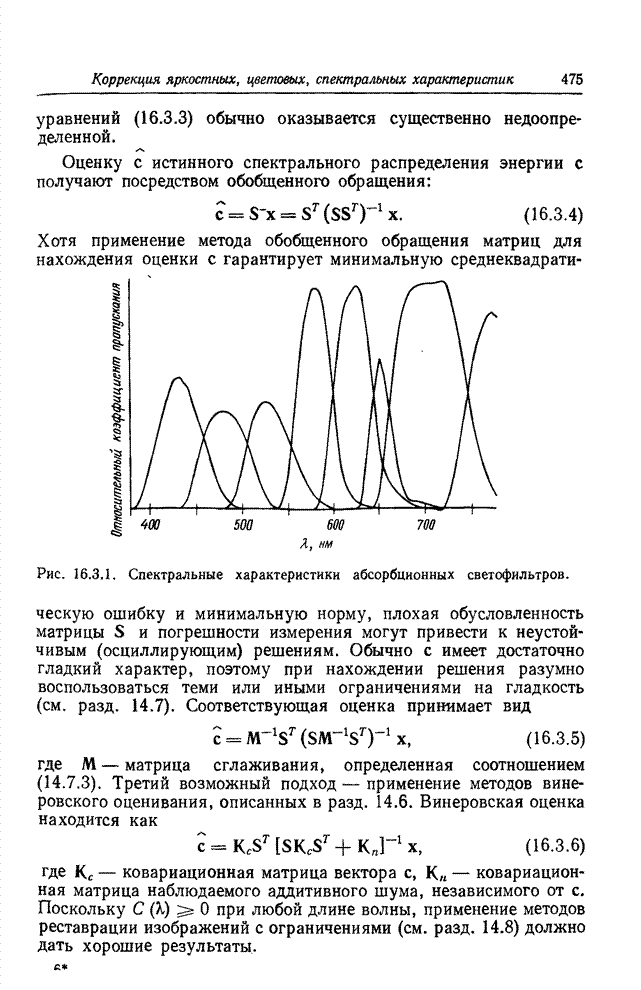
Рис. 13.7.2. Соотношение между различными массивами отсчетов изображения.
Чтобы можно было воспользоваться формальной структурой векторной алгебры при последующем анализе процедур реставрации изображений, образуем векторные эквиваленты различных массивов, используемых в реставрационной модели. Следуя методам разд. 9.2, и в этом случае изменим индексы массивов таким образом, чтобы в каждом из них первый элемент занял верхний левый угол.
Затем установим векторные соотношения между отдельными блоками модели, для чего произведем развертку столбцов указанных массивов.
В результате получим
![]() , (13.7.3а)
, (13.7.3а)
![]() , (13.7.3б)
, (13.7.3б)
![]() , (13.7.3в)
, (13.7.3в)
![]() , (13.7.3г)
, (13.7.3г)
где
![]() и
и ![]() - матрицы
нерезкости, содержащие отсчеты
- матрицы
нерезкости, содержащие отсчеты ![]() и
и ![]() соответственно. Нелинейная операция
(13.7.3в) определяется как поэлементное нелинейное преобразование. Таким
образом, имеем
соответственно. Нелинейная операция
(13.7.3в) определяется как поэлементное нелинейное преобразование. Таким
образом, имеем
![]() . (13.7.4)
. (13.7.4)
Из формул (13.7.3а) и (13.7.3г) можно получить соотношение, описывающее наблюдаемые физические отсчеты изображения, выраженные через математические псевдоотсчеты идеального изображения, следующего вида:
![]() . (13.7.5)
. (13.7.5)
Определим теперь некоторые специальные случаи для этого уравнения. Первый из них - отсутствие поэлементной нелинейности - соответствует равенству
![]() , (13.7.6)
, (13.7.6)
где
![]() и
и ![]() . Мы получили
классическую дискретную модель, содержащую систему линейных уравнений с
включением неопределенности измерения. Второй особый случай, который будет
рассматриваться позднее, соответствует условию пренебрежимо малой
пространственной нерезкости, вносимой цифровым преобразователем. В этом случае
можно записать
. Мы получили
классическую дискретную модель, содержащую систему линейных уравнений с
включением неопределенности измерения. Второй особый случай, который будет
рассматриваться позднее, соответствует условию пренебрежимо малой
пространственной нерезкости, вносимой цифровым преобразователем. В этом случае
можно записать
![]() , (13.7.7)
, (13.7.7)
где
![]() . Если
приращение в квадратурных суммах
. Если
приращение в квадратурных суммах ![]() взять равным шагу отсчетов
взять равным шагу отсчетов ![]() , то матрицы в
(13.7.6) и (13.7.7) примут особую форму:
, то матрицы в
(13.7.6) и (13.7.7) примут особую форму:
 , (13.7.8)
, (13.7.8)
где
![]() (13.7.9)
(13.7.9)
при ![]() и
и ![]() .
.
Для
проведения экспериментов по реставрации изображений с использованием моделей
(13.7.6) и (13.7.7) были сформированы два искусственных изображения [22].
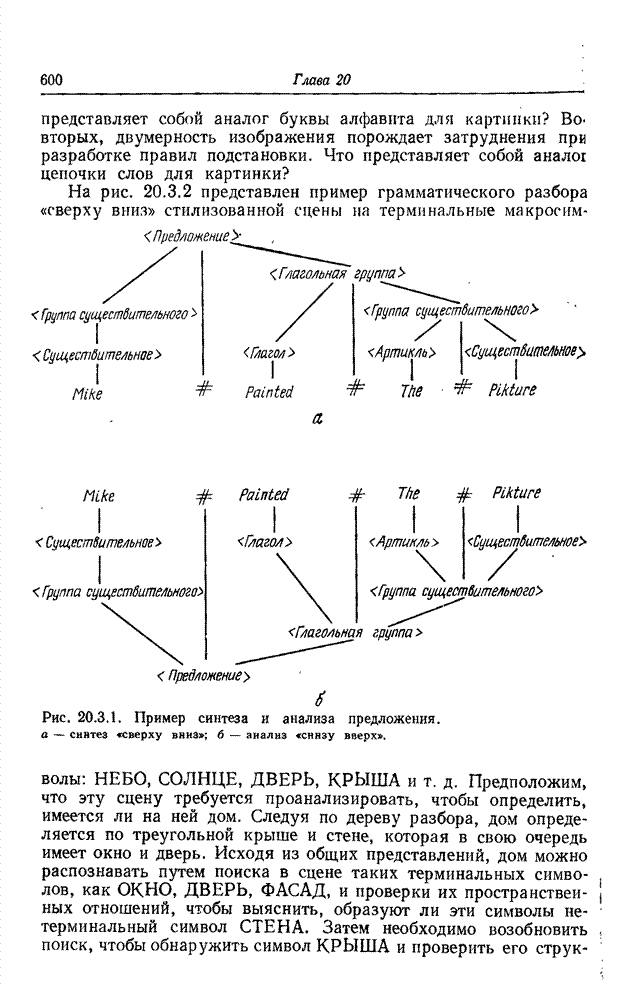
Исследования методов реставрации при недоопределении проводились с
использованием исходного изображения в виде квадрата размером ![]() элемента с уровнем
245, находящегося на фоне с уровнем 10 (рис. 13.7.3,а); полная шкала яркостей
охватывает уровни от -0 до 255. Функция рассеяния точки гауссовой формы, которую
иллюстрирует рис. 13.7.3,б, определяется выражением вида
элемента с уровнем
245, находящегося на фоне с уровнем 10 (рис. 13.7.3,а); полная шкала яркостей
охватывает уровни от -0 до 255. Функция рассеяния точки гауссовой формы, которую
иллюстрирует рис. 13.7.3,б, определяется выражением вида
 (13.7.10)
(13.7.10)
на
массиве размером ![]() элементов,
где
элементов,
где ![]() -
нормирующий коэффициент,
-
нормирующий коэффициент, ![]() и
и ![]() - коэффициенты пространственной
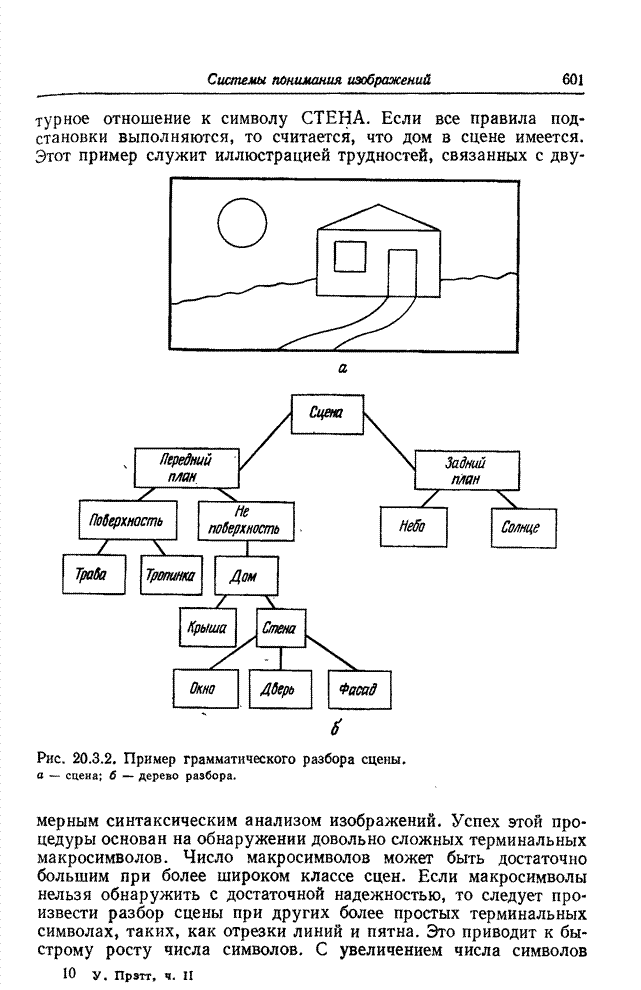
нерезкости. Исходное изображение, которое использовалось для исследования
методов реставрации при переопределении (рис. 13.7.4,а), имеет вид квадрата
размером
- коэффициенты пространственной
нерезкости. Исходное изображение, которое использовалось для исследования
методов реставрации при переопределении (рис. 13.7.4,а), имеет вид квадрата
размером ![]() элемента
с уровнем 245, расположенного в центре другого квадрата размером
элемента
с уровнем 245, расположенного в центре другого квадрата размером ![]() элементов с
уровнем 10 на фоне с нулевой яркостью. Это изображение может служить моделью реального
изображения в виде луны на фоне темного неба. Исходное изображение делалось
нерезким с помощью импульсного отклика размером
элементов с
уровнем 10 на фоне с нулевой яркостью. Это изображение может служить моделью реального
изображения в виде луны на фоне темного неба. Исходное изображение делалось
нерезким с помощью импульсного отклика размером ![]() элементов, показанного на рис.
13.7.4,б. Нерезкое изображение состоит из
элементов, показанного на рис.
13.7.4,б. Нерезкое изображение состоит из ![]() элементов. Предполагается, что
наблюдаются все
элементов. Предполагается, что
наблюдаются все ![]() элементов
и что имеется априорное знание об ограниченном размере исходного изображения,
состоящего из
элементов
и что имеется априорное знание об ограниченном размере исходного изображения,
состоящего из ![]() элементов.
Из этого следует, что многие элементы матрицы нерезкости (13.7.8) тождественно
равны нулю. Более того, обозначив через
элементов.
Из этого следует, что многие элементы матрицы нерезкости (13.7.8) тождественно
равны нулю. Более того, обозначив через ![]() просканированное по столбцам исходное
изображение размера
просканированное по столбцам исходное
изображение размера ![]() элементов
элементов ![]() , можно предложить следующую
векторную модель для
, можно предложить следующую
векторную модель для ![]() реально наблюдаемых элементов
реально наблюдаемых элементов ![]() :
:
![]() , (13.7.11)
, (13.7.11)
где
![]() -
матрица размера
-
матрица размера ![]()
 , (13.7.12)
, (13.7.12)
причем
![]() (13.7.13)
(13.7.13)
при
![]() и
и ![]() . Матрица
(13.7.12) представляет собой матрицу оператора конечной свертки
. Матрица
(13.7.12) представляет собой матрицу оператора конечной свертки ![]() -типа, введенного в
гл. 9. Сравнение структур матриц нерезкости (13.7.8) и (13.7.12) для
недоопределенной и переопределенной моделей показывает, что эти матрицы
являются транспонированными парами. Таким образом,
-типа, введенного в
гл. 9. Сравнение структур матриц нерезкости (13.7.8) и (13.7.12) для
недоопределенной и переопределенной моделей показывает, что эти матрицы
являются транспонированными парами. Таким образом, ![]() ; в особом случае
разделимости строк и столбцов можно записать
; в особом случае
разделимости строк и столбцов можно записать ![]() и
и ![]() .
.

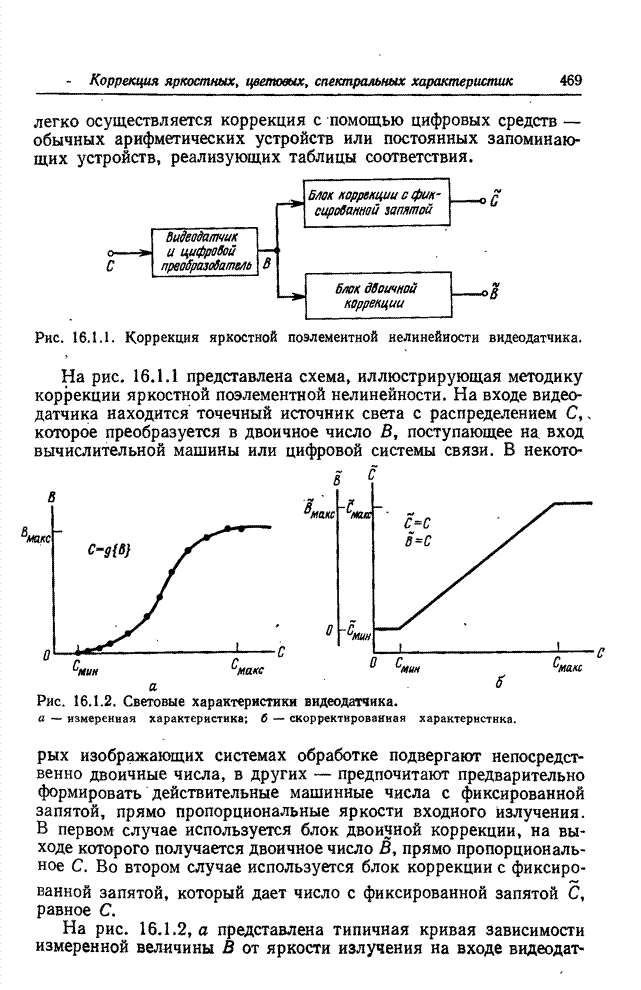
Рис. 13.7.3. Массивы изображения, использованные при исследовании недоопределенной модели.
а - исходное изображение; б - импульсный отклик; в - наблюдаемое изображение.

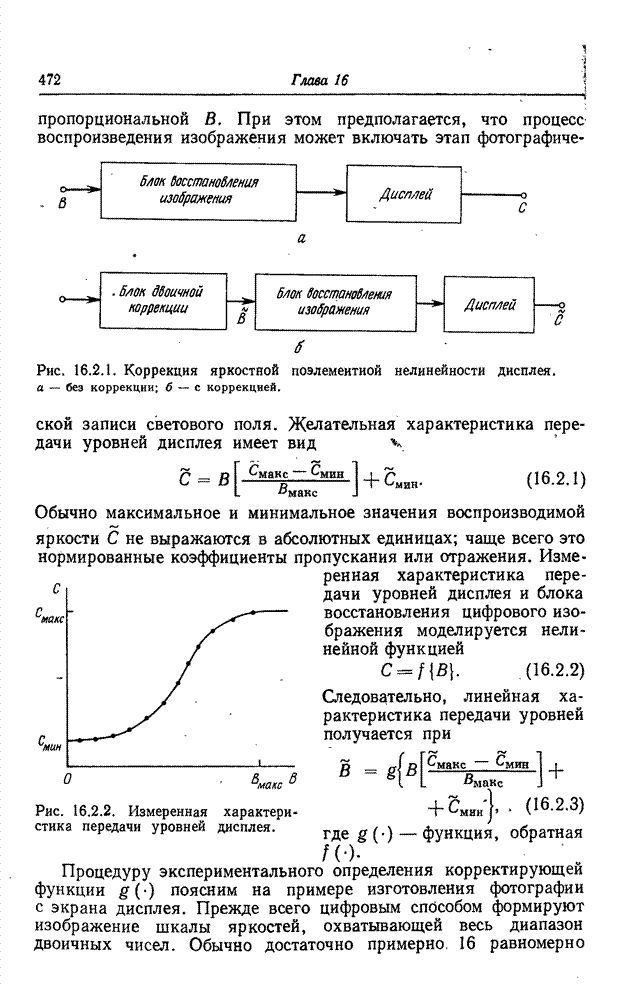
Рис. 13.7.4. Массивы изображения, использованные при исследовании переопределенной модели.
а - исходное изображение; б - импульсный отклик; в - наблюдаемое изображение.
В
машинных экспериментах по реставрации изображений наблюдаемые нерезкие
изображения для недоопределенной и переопределенной моделей были получены путем
умножения развернутых по столбцам матриц исходных изображений (рис. 13.7.3,а и
13.7.4,а) на матрицы нерезкости ![]() и
и ![]() соответственно. Аддитивный белый
гауссовый шум, добавляемый к нерезким изображениям, вырабатывался с помощью
генератора случайных чисел. Перед воспроизведением все реставрированные
изображения подвергались ограничению уровня (поэлементно), чтобы диапазон
уровней составил 0-255.
соответственно. Аддитивный белый
гауссовый шум, добавляемый к нерезким изображениям, вырабатывался с помощью
генератора случайных чисел. Перед воспроизведением все реставрированные
изображения подвергались ограничению уровня (поэлементно), чтобы диапазон
уровней составил 0-255.
| << Предыдущий параграф | Следующий параграф >> |
- Часть 4. РЕСТАВРАЦИЯ И УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
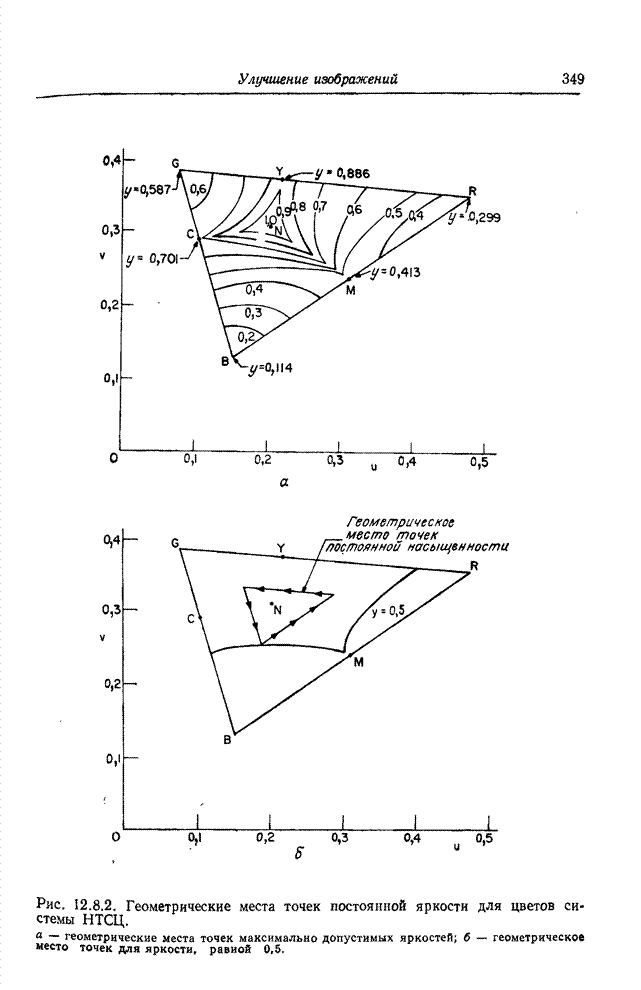
- Глава 12. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
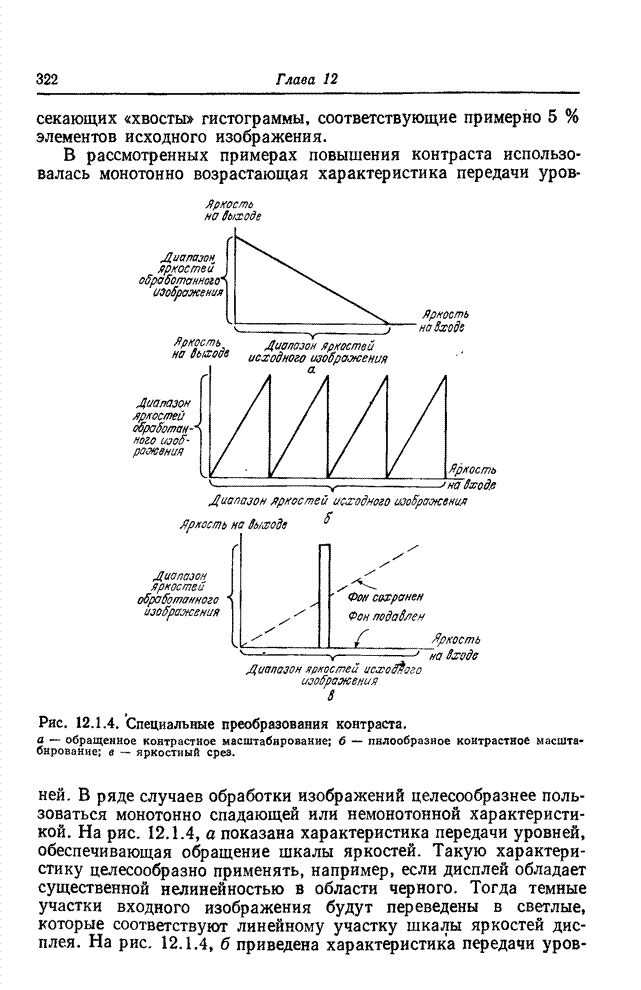
- 12.1. ИЗМЕНЕНИЕ КОНТРАСТА
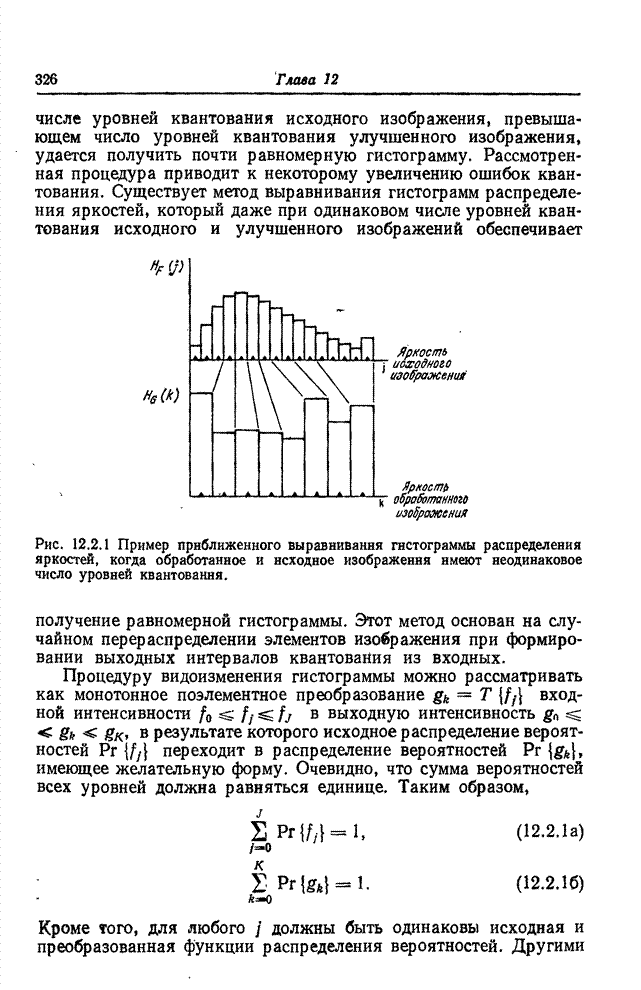
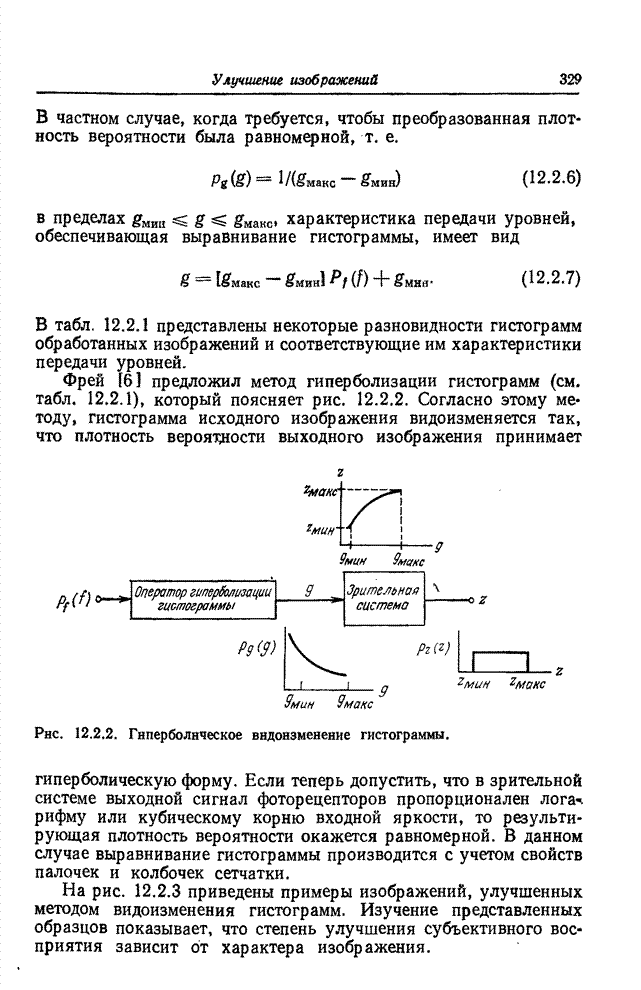
- 12.2. ВИДОИЗМЕНЕНИЕ ГИСТОГРАММ
- 12.3. ПОДАВЛЕНИЕ ШУМОВ
- 12.4. ПОДЧЕРКИВАНИЕ ГРАНИЦ
- 12.5. ОБРАБОТКА ИЗОБРАЖЕНИЙ С ПРЕОБРАЗОВАНИЕМ
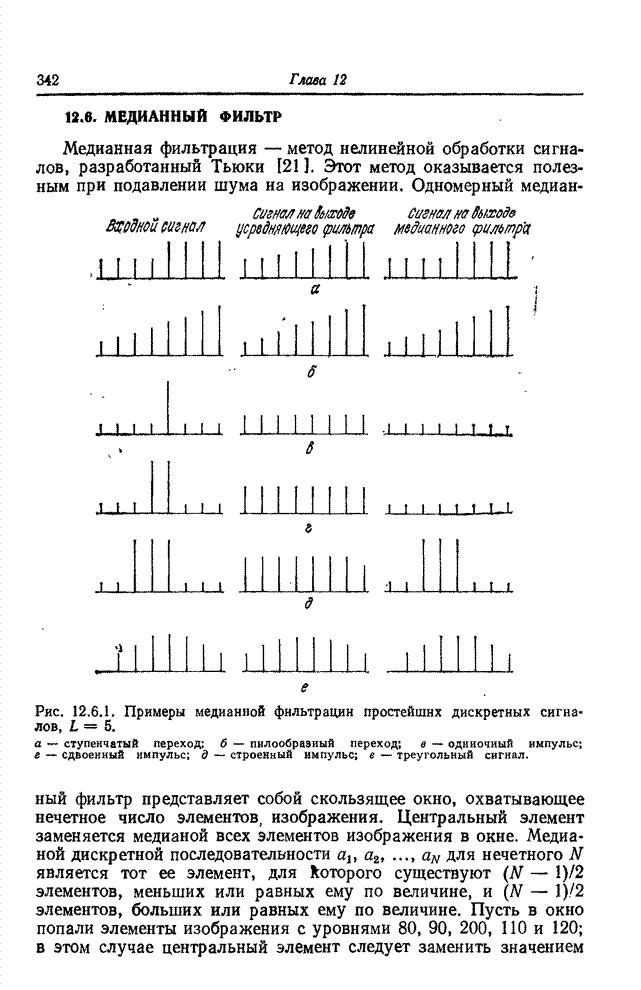
- 12.6. МЕДИАННЫЙ ФИЛЬТР
- 12.7. ЛОЖНЫЕ ЦВЕТА
- 12.8. ПСЕВДОЦВЕТА
- 12.9. УЛУЧШЕНИЕ СПЕКТРОЗОНАЛЬНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 13. МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.1. ОБОБЩЕННЫЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
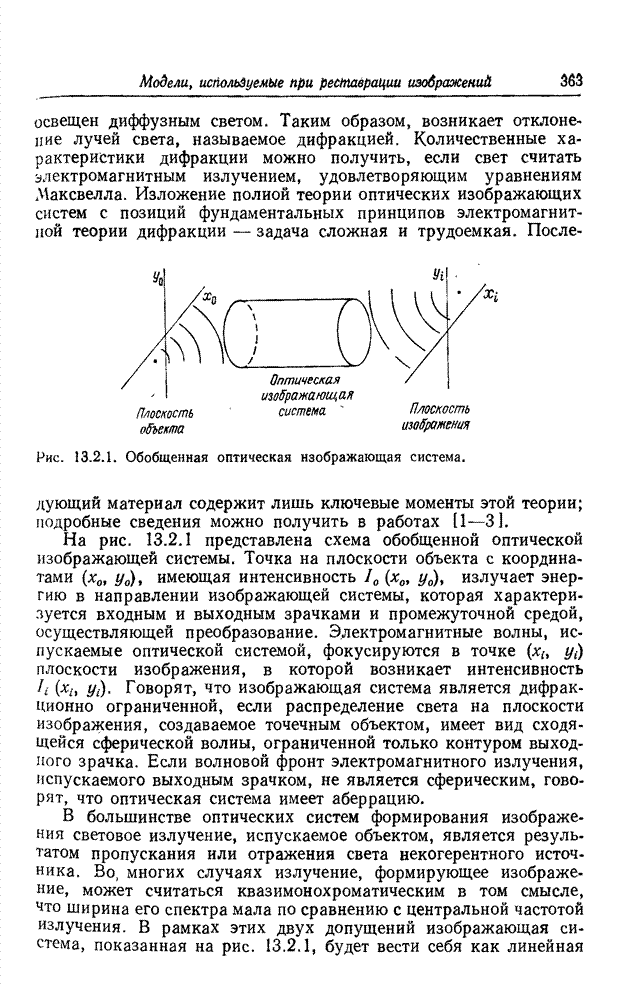
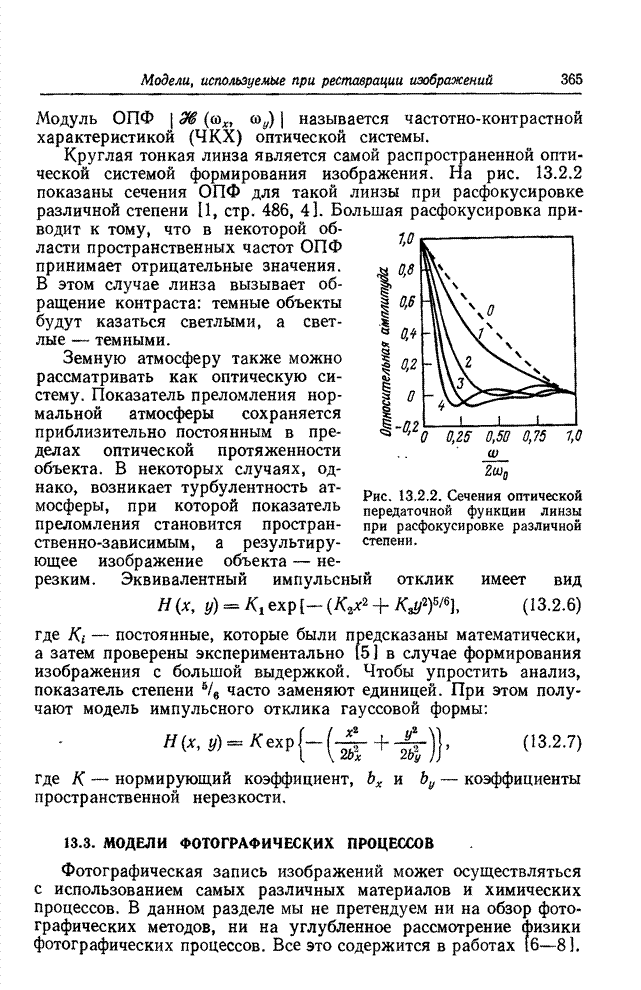
- 13.2. МОДЕЛИ ОПТИЧЕСКИХ СИСТЕМ
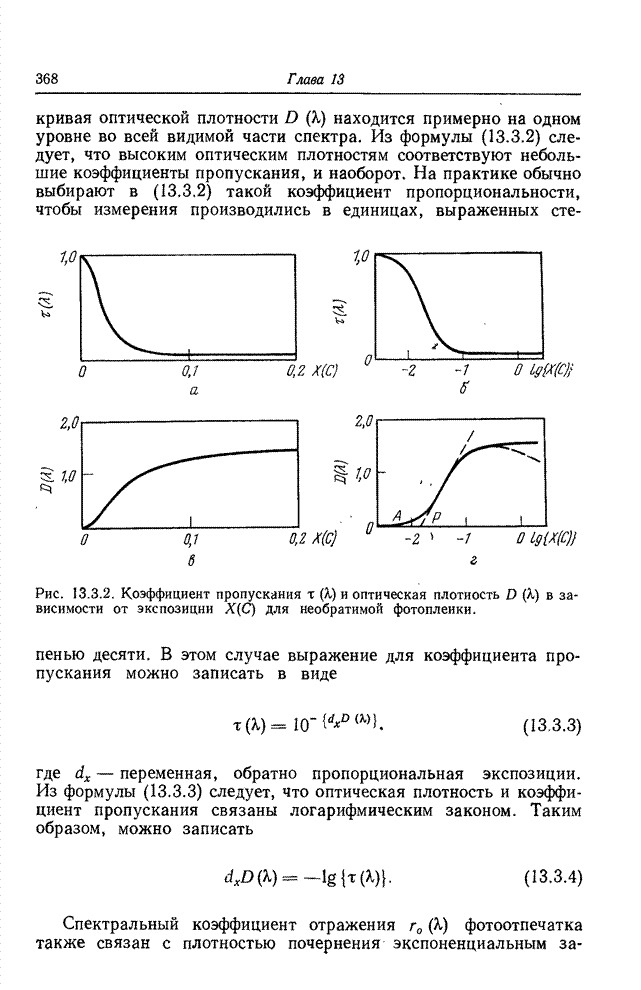
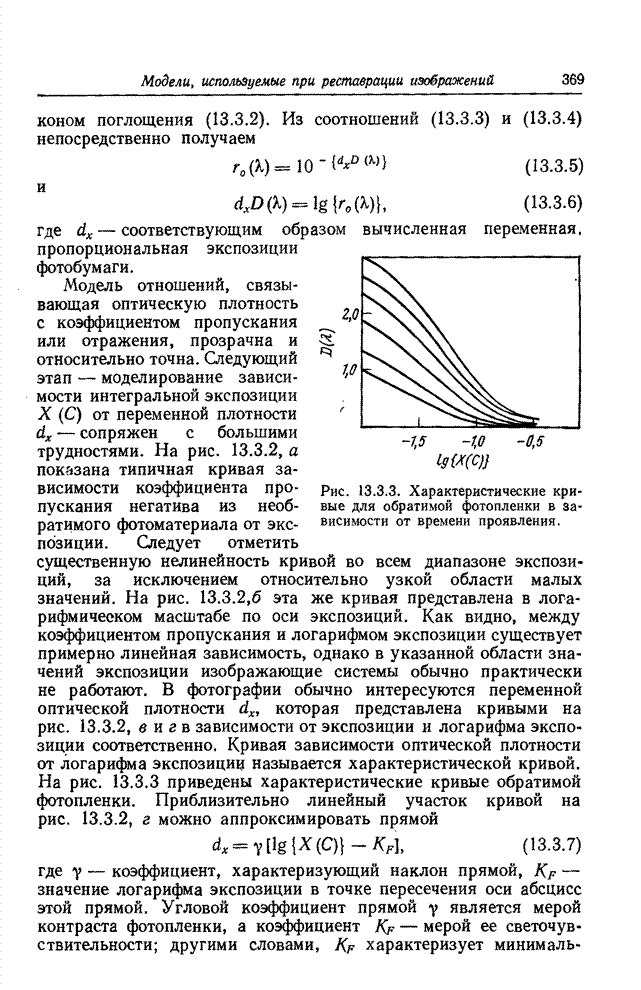
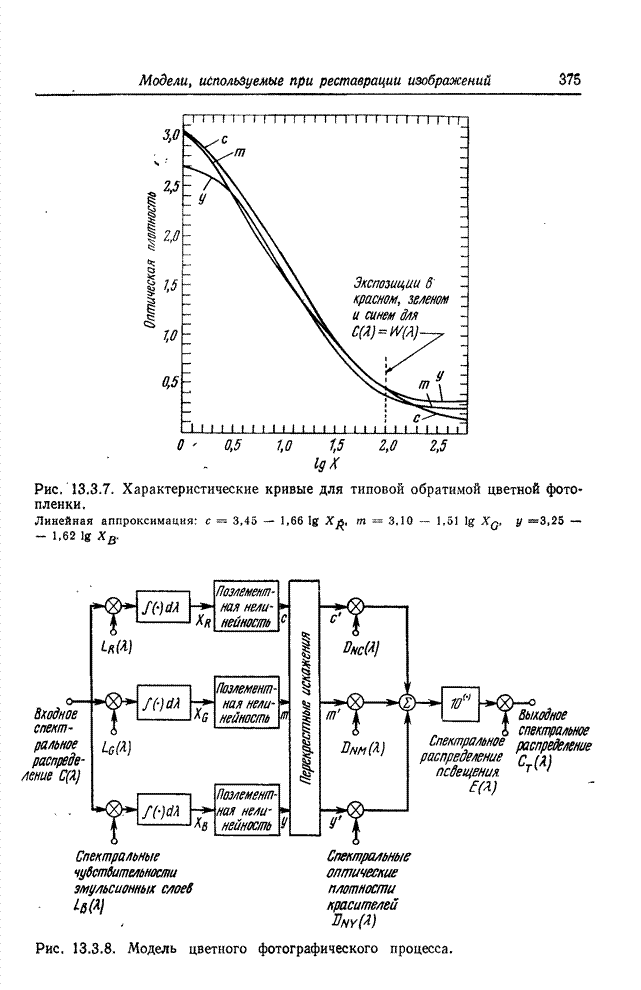
- 13.3. МОДЕЛИ ФОТОГРАФИЧЕСКИХ ПРОЦЕССОВ
- 13.3.1. ОДНОЦВЕТНАЯ ФОТОГРАФИЯ
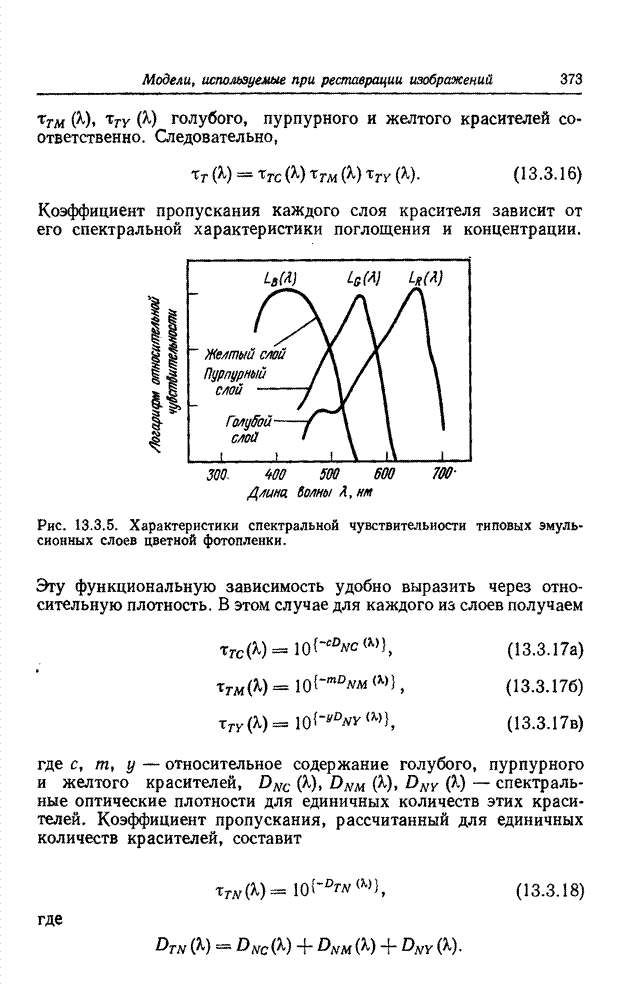
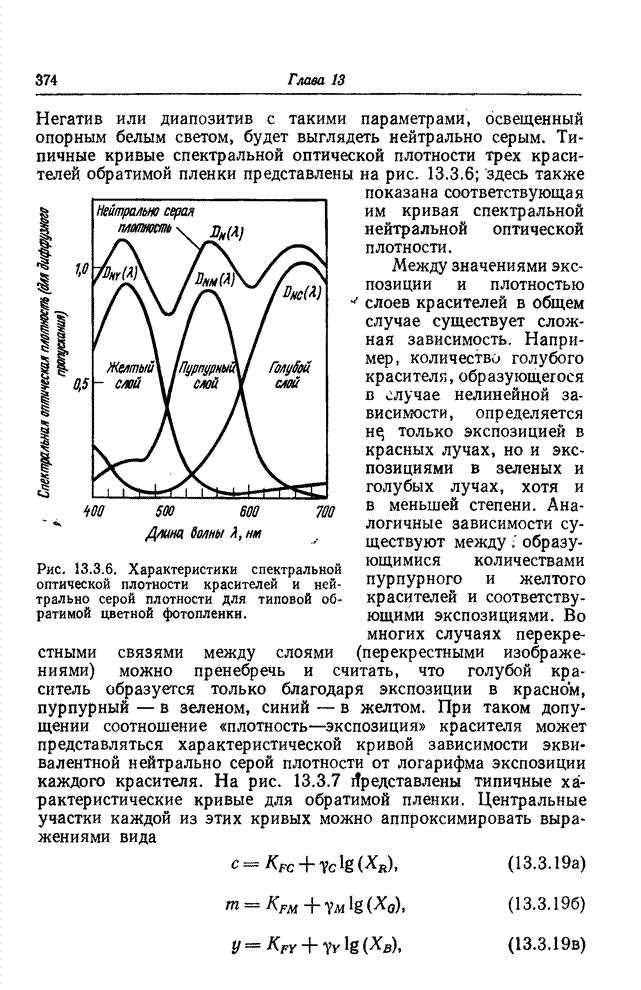
- 13.3.2. ЦВЕТНАЯ ФОТОГРАФИЯ
- 13.4. МОДЕЛИ ЦИФРОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- 13.5. МОДЕЛЬ ДИСПЛЕЯ
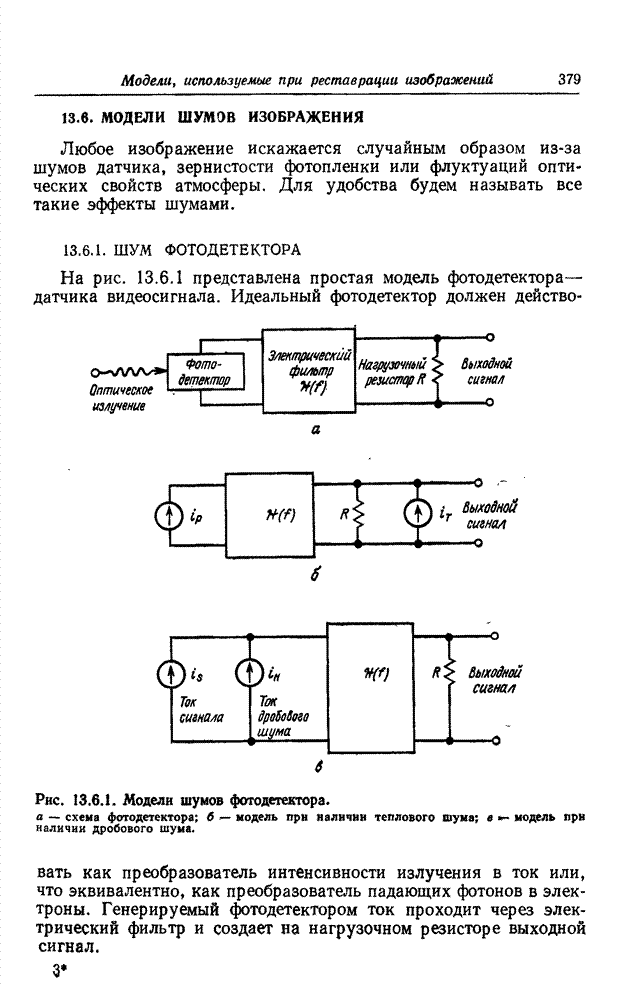
- 13.6. МОДЕЛИ ШУМОВ ИЗОБРАЖЕНИЯ
- 13.6.1. ШУМ ФОТОДЕТЕКТОРА
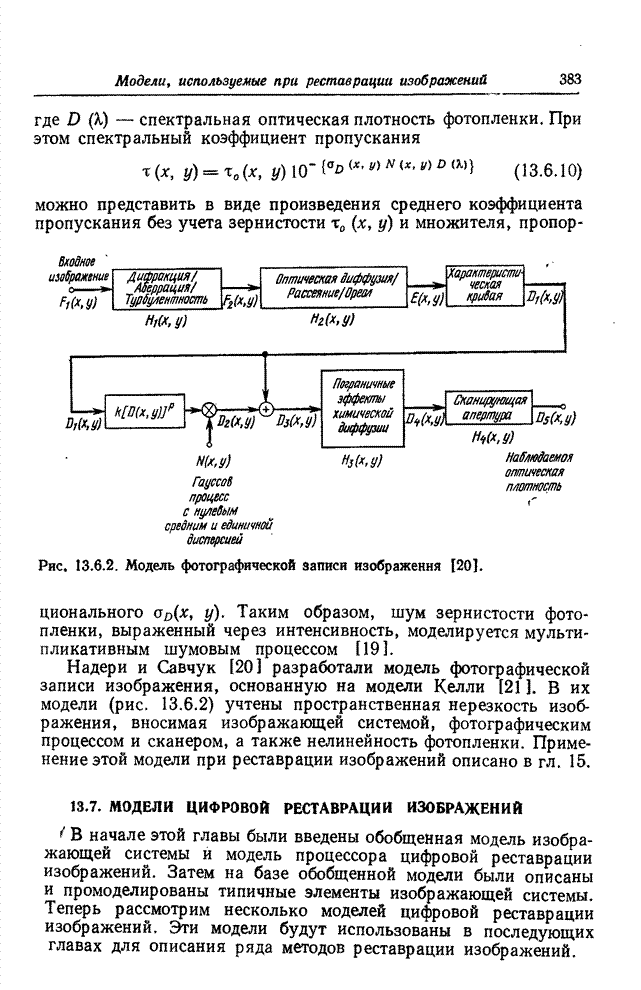
- 13.6.2. ШУМ ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- 13.7. МОДЕЛИ ЦИФРОВОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 14. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 14.1. МЕТОДЫ ПРОСТРАНСТВЕННОЙ ФИЛЬТРАЦИИ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 14.1.1. ИНВЕРСНАЯ ФИЛЬТРАЦИЯ
- 14.1.2. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И АДДИТИВНЫЙ ШУМ
- 14.1.3. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНОЕ ИЗОБРАЖЕНИЕ
- 14.1.4. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНАЯ НЕРЕЗКОСТЬ
- 14.1.5. ФИЛЬТРЫ НА ОСНОВЕ ПАРАМЕТРИЧЕСКИХ ОЦЕНОК
- 14.1.6. ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 4.2. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.2.1. РЕСТАВРАЦИЯ НЕРЕЗКИХ ИЗОБРАЖЕНИЙ
- 14.2.2. РЕСТАВРАЦИЯ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ ПРИ НАЛИЧИИ ШУМА
- 14.3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.3.1. АЛГОРИТМ ДЛЯ ПЕРЕОПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.3.2. АЛГОРИТМ ДЛЯ НЕДООПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.4. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ С ИСПОЛЬЗОВАНИЕМ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- 14.5. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕГРЕССИИ
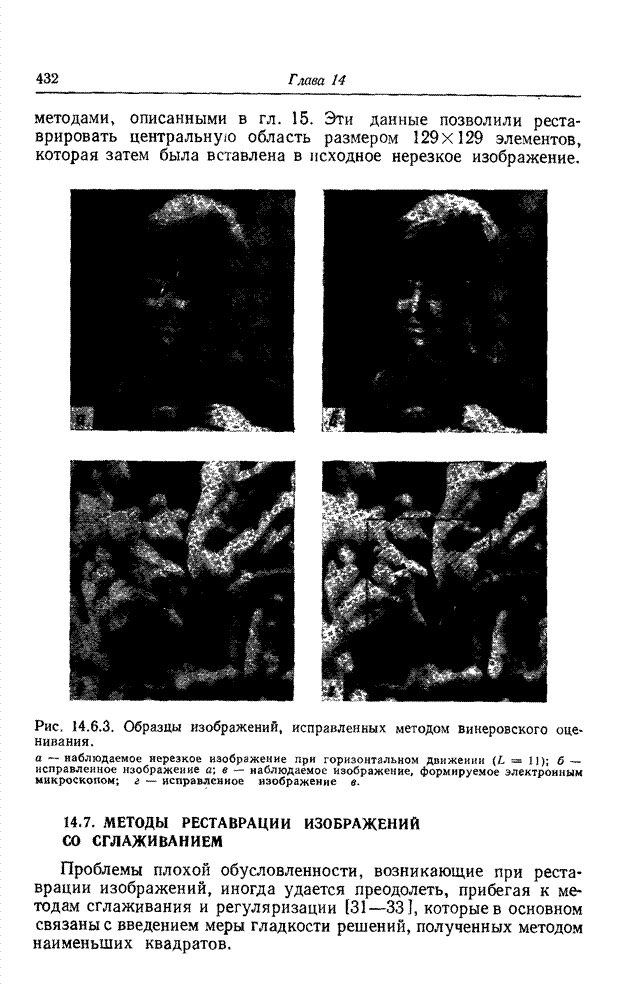
- 14.6. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ВИНЕРОВСКОГО ОЦЕНИВАНИЯ
- 14.6.1. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В ОБЩЕМ СЛУЧАЕ
- 14.6.2. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В СЛУЧАЕ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ С ШУМОМ
- 14.7. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ СО СГЛАЖИВАНИЕМ
- 14.8. МЕТОДЫ РЕСТАВРАЦИИ С ИСПОЛЬЗОВАНИЕМ ОГРАНИЧЕНИЙ
- 14.9. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
- ЛИТЕРАТУРА
- Глава 15. CПЕЦИАЛЬНЫЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
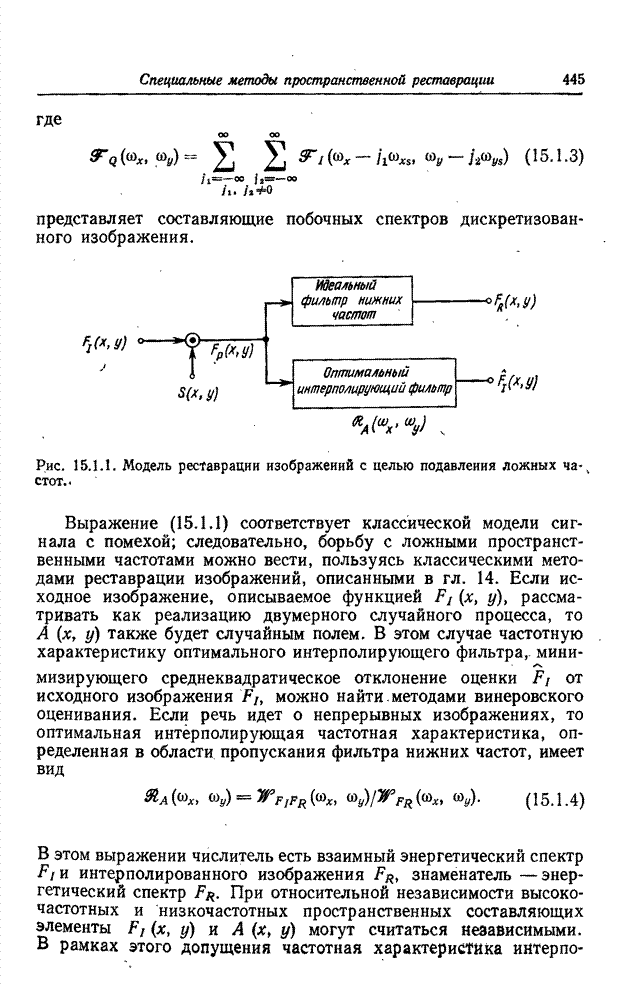
- 15.1. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮ ПОДАВЛЕНИЯ ОШИБОК НАЛОЖЕНИЯ СПЕКТРОВ
- 15.2. КОРРЕКЦИЯ ОШИБОК ИНТЕРПОЛЯЦИИ
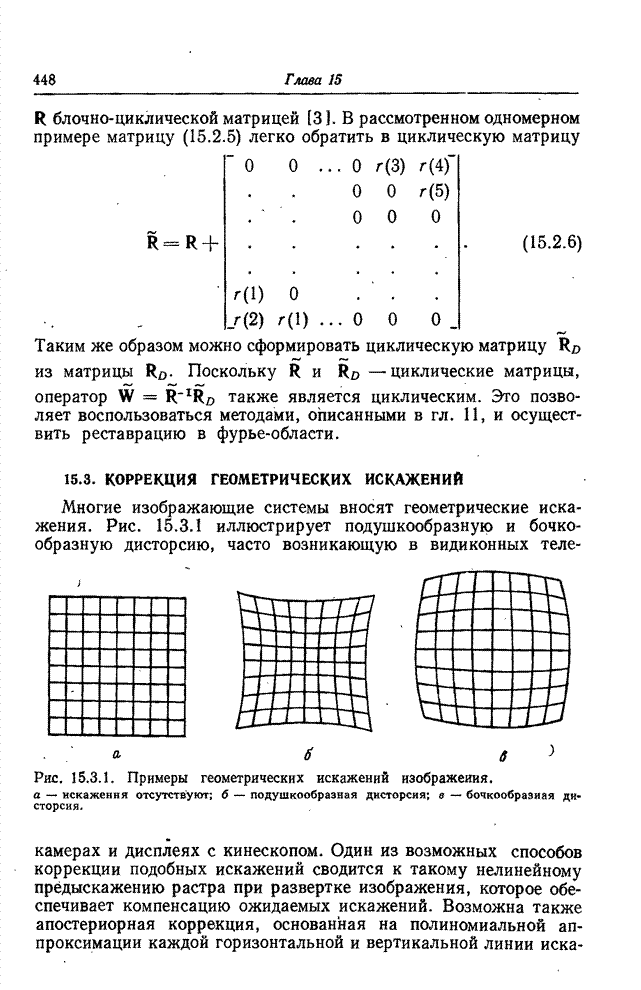
- 15.3. КОРРЕКЦИЯ ГЕОМЕТРИЧЕСКИХ ИСКАЖЕНИЙ
- 15.4. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ГОМОМОРФНОЙ ФИЛЬТРАЦИИ
- 15.5. СЛЕПАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ
- 15.5.1. МЕТОДЫ НА ОСНОВЕ ПРЯМЫХ ИЗМЕРЕНИЙ
- 15.5.2. МЕТОДЫ НА ОСНОВЕ КОСВЕННОГО ОЦЕНИВАНИЯ
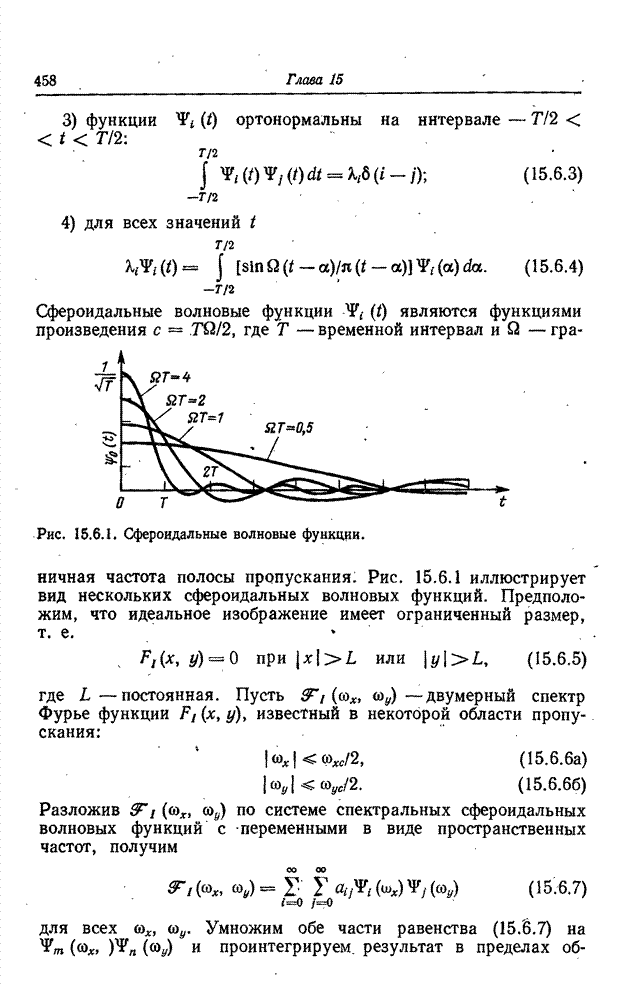
- 15.6. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ СПЕКТРА
- 15.7. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННО-ЗАВИСИМЫМИ ИСКАЖЕНИЯМИ
- 15.8. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕКУРСИВНОЙ ФИЛЬТРАЦИИ
- 15.9. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮОСЛАБЛЕНИЯ ШУМА ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- ЛИТЕРАТУРА
- Глава 16. КОРРЕКЦИЯ ЯРКОСТНЫХ, ЦВЕТОВЫХ И СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗОБРАЖАЮЩИХ СИСТЕМ
- 16.1. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ВИДЕОДАТЧИКОВ
- 16.2. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ДИСПЛЕЕВ
- 16.3. ОЦЕНИВАНИЕ СПЕКТРАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 16.4. КОРРЕКЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ВИДЕОДАТЧИКОВ И ДИСПЛЕЕВ
- 16.5. ОЦЕНИВАНИЕ КООРДИНАТ СВЕТА ВИДЕОДАТЧИКОВ
- 16.6. ОЦЕНИВАНИЕ ЭКСПОЗИЦИЙ ЦВЕТНОЙ ФОТОПЛЕНКИ
- 16.7. КОМПЕНСАЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ ЦВЕТНЫХ ДИСПЛЕЕВ
- ЛИТЕРАТУРА
- Часть 5. АНАЛИЗ ИЗОБРАЖЕНИЙ
- Глава 17. ВЫДЕЛЕНИЕ ПРИЗНАКОВ ИЗОБРАЖЕНИЯ
- 17.1. ЯРКОСТНЫЕ ПРИЗНАКИ
- 17.2. ГИСТОГРАММНЫЕ ПРИЗНАКИ
- 17.3. ПРОСТРАНСТВЕННО-СПЕКТРАЛЬНЫЕ ПРИЗНАКИ
- 17.4. КОНТУРНЫЕ ПРИЗНАКИ
- 17.4.1. ЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.2. НЕЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.3. МЕТОДЫ АППРОКСИМАЦИИ ПЕРЕПАДОВ ЯРКОСТИ
- 17.4.4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ
- 17.5. ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ ЯРКОСТИ
- 17.6. ЦВЕТОВЫЕ КОНТУРЫ
- 17.7. ПРИЗНАКИ ПЯТНА И ЛИНИИ
- 17.8. ТЕКСТУРНЫЕ ПРИЗНАКИ
- 17.9. СИНТЕЗ ТЕКСТУР
- ЛИТЕРАТУРА
- Глава 18. СИМВОЛИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
- 18.1. СВЯЗНОСТЬ
- 18.2. СЖАТИЕ, УТОНЧЕНИЕ И ПОСТРОЕНИЕ ОСТОВА
- 18.3. ОПИСАНИЕ ЛИНИЙ
- 18.3.1. АППРОКСИМАЦИЯ КРИВЫХ
- 18.3.2. ПРЕОБРАЗОВАНИЕ ЛИНИИ В ТОЧКУ
- 18.4. ОПИСАНИЕ ФОРМЫ
- 18.4.1. МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.2. ТОПОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.3. АНАЛИТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
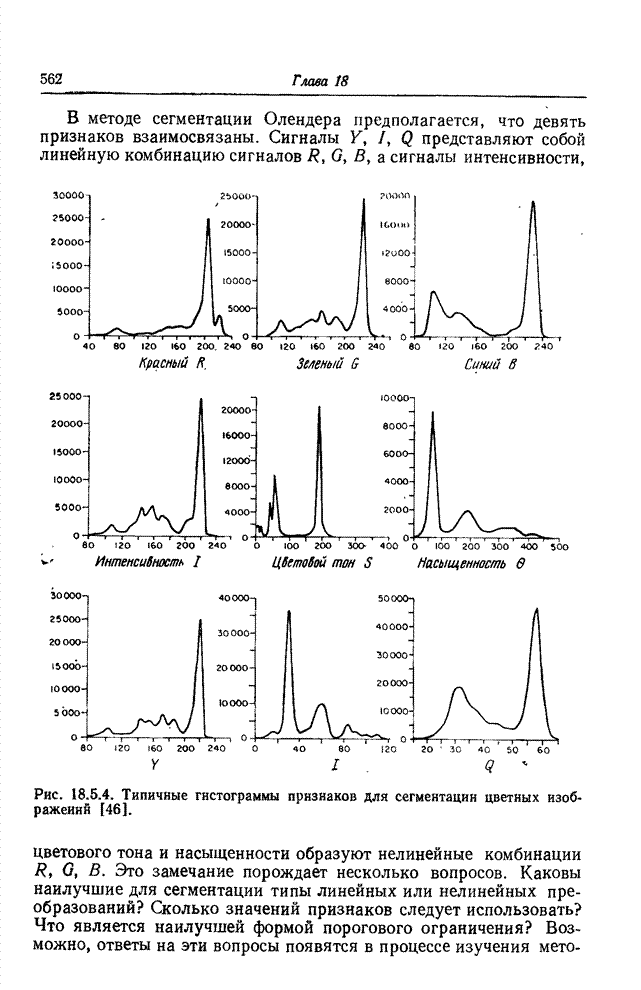
- 18.5. СЕГМЕНТАЦИЯ ПО ЯРКОСТИ
- 18.5.1. ПОРОГОВОЕ ОГРАНИЧЕНИЕ ПО ЯРКОСТИ
- 18.5.2. МНОГОМЕРНОЕ ПОРОГОВОЕ ОГРАНИЧЕНИЕ
- 18.5.3. НАРАЩИВАНИЕ ОБЛАСТЕЙ
- 18.6. КОНТУРНАЯ СЕГМЕНТАЦИЯ
- 18.7. ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ
- 18.8. СЕГМЕНТАЦИЯ ФОРМЫ
- ЛИТЕРАТУРА
- Глава 19. ОБНАРУЖЕНИЕ ОБЪЕКТОВ И СОВМЕЩЕНИЕ (ПРИВЯЗКА) ИЗОБРАЖЕНИЙ
- 19.1. СОПОСТАВЛЕНИЕ С ЭТАЛОНОМ
- 19.2. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ ДЕТЕРМИНИРОВАННЫХ ПОЛЕЙ
- 19.3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ СЛУЧАЙНЫХ ПОЛЕЙ
- 19.4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 19.5. ПРИВЯЗКА ИЗОБРАЖЕНИЙ
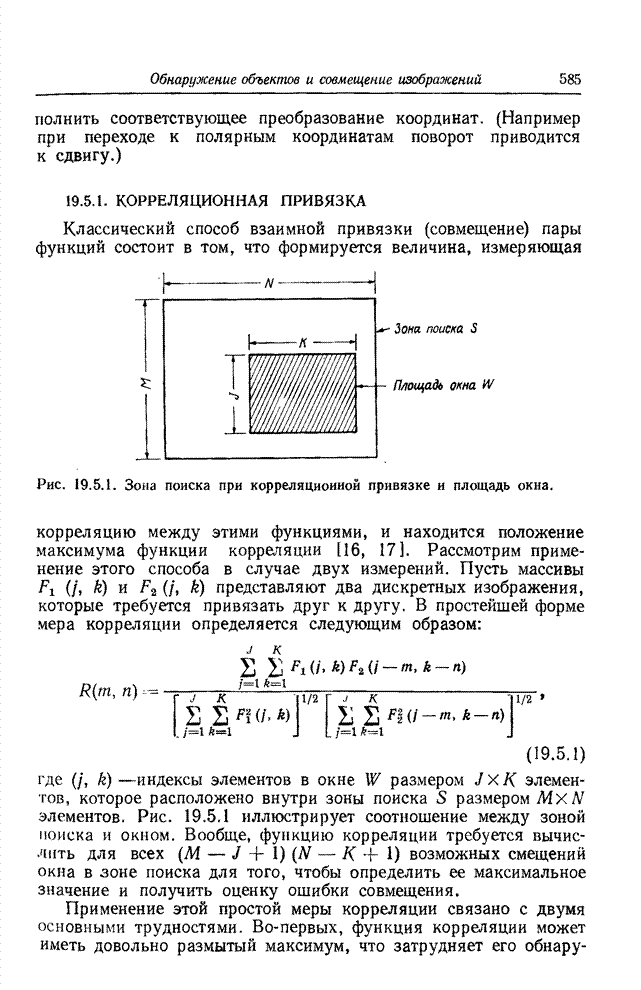
- 19.5.1. КОРРЕЛЯЦИОННАЯ ПРИВЯЗКА
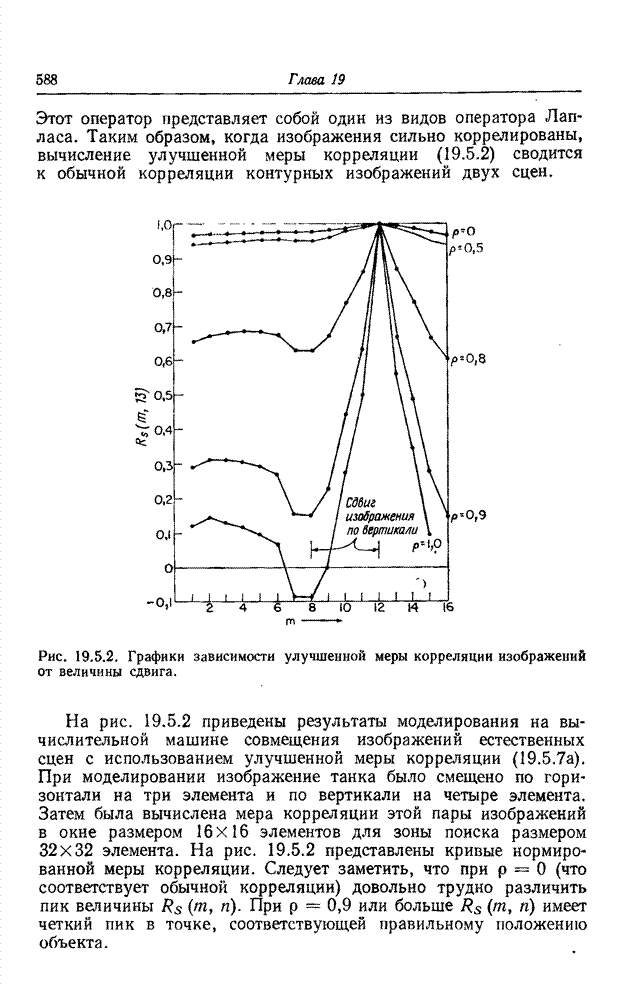
- 19.5.2. ПОСЛЕДОВАТЕЛЬНАЯ ПРИВЯЗКА
- ЛИТЕРАТУРА
- Глава 20. СИСТЕМЫ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
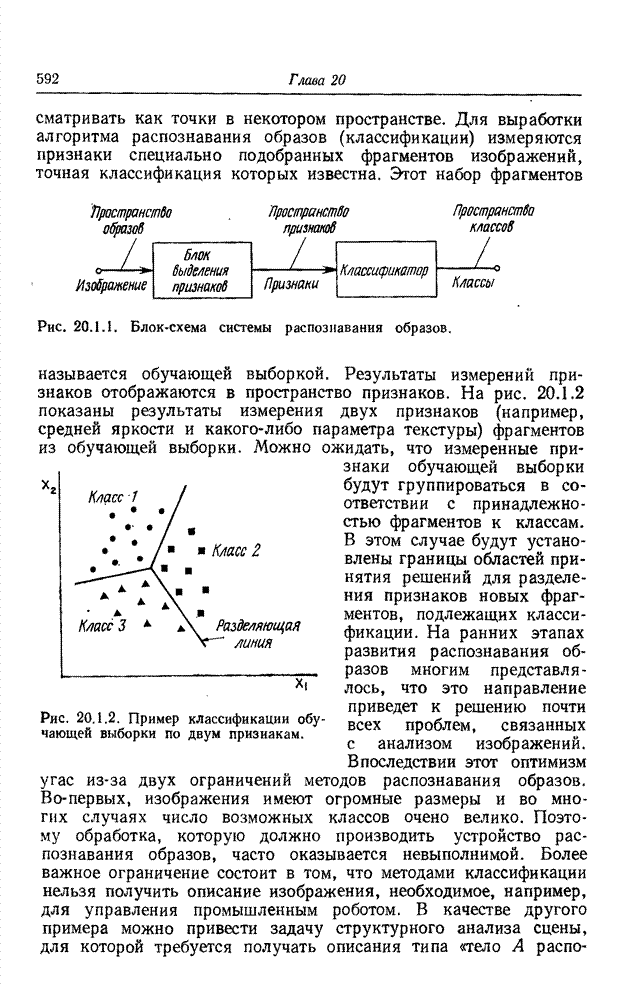
- 20.1. СИСТЕМЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 20.2. МОДЕЛИ СИСТЕМ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.3. СИНТАКСИЧЕСКИЕ МЕТОДЫ
- 20.4. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ОТНОШЕНИЯ МЕЖДУ ОБЪЕКТАМИ
- ЛИТЕРАТУРА
- Часть 6. Кодирование изображений
- Глава 21. АНАЛОГОВЫЕ МЕТОДЫ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.1. КЛАССИФИКАЦИЯ МЕТОДОВ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.2. СИСТЕМЫ ВЕЩАТЕЛЬНОГО ТЕЛЕВИДЕНИЯ
- 21.2.1. СИСТЕМА НТСЦ [13-15]
- 21.2.2. СИСТЕМА СЕКАМ [17]
- 21.2.3.СИСТЕМА ПАЛ
- 21.3. МОДУЛЯЦИОННЫЕ МЕТОДЫ СОКРВЩЕНИЯ ПОЛОСЫ ЧАСТОТЫ
- 21.4.УМЕНЬШЕНИЕ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ И ЧАСТОТЫ КАДРОВ
- 21.4.1. УМЕНЬШЕНИЕ ПРОСТРАНСТВЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
- 21.4.2. УМЕНЬШЕНИЕ ЧАСТОТЫ КАДРОВ
- 21.5. МЕТОДЫ ВРЕМЕННОГО ПЕРЕМЕЖЕНИЯ
- 21.5.1. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ СТРОК
- 21.5.2. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ ЭЛЕМЕНТОВ
- 21.6. РАЗВЕРТКА С ПЕРЕМЕННОЙ СКОРОСТЬЮ
- 21.7. МУЛЬТИПЛЕКСНЫЕ МЕТОДЫ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Глава 22. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПОЭЛЕМЕНТНОЙ ОБРАБОТКОЙ
- 22.1. СИСТЕМЫ КОДИРОВАНИЯ С ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИЕЙ
- 22.1.1. КВАНТОВАНИЕ СО СЖАТИЕМ ДИАПАЗОНА ЯРКОСТЕЙ
- 22.1.2. ПСЕВДОШУМОВОЕ КВАНТОВАНИЕ
- 22.1.3. КВАНТОВАНИЕ С УЛУЧШЕННОЙ ПЕРЕДАЧЕЙ ГРАДАЦИЙ ЯРКОСТИ
- 22.1.4. СИСТЕМА С ГРУБОЙ-ТОНКОЙ ШКАЛОЙ КВАНТОВАНИЯ
- 22.1.5. КВАНТОВАНИЕ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ
- 22.2. СТАТИСТИЧЕСКИЕ МЕТОДЫ КОДИРОВАНИЯ
- 22.2.1. ПОЭЛЕМЕНТНОЕ СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- 22.2.2. КОДИРОВАНИЕ С УЧЕТОМ ПРЕДШЕСТВУЮЩЕГО ЭЛЕМЕНТА
- 22.3. КОДИРОВАНИЕ СЕРИЙ
- 22.3.1. КОДИРОВАНИЕ ДЛИН СЕРИЙ; ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ [32-36]
- 22.3.2. КОДИРОВАНИЕ РАЗРЯДНЫХ ПЛОСКОСТЕЙ
- 22.4. КОДИРОВАНИЕ С ПОПОЛНЕНИЕМ КАДРОВ
- 22.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ
- 22.5.1. ДЕЛЬТА-МОДУЛЯЦИЯ
- 22.5.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ
- 22.5.3. КОДЕРЫ С ПРОСТРАНСТВЕННЫМ ПРЕДСКАЗАНИЕМ
- 22.5.4. АДАПТИВНЫЕ КОДЕРЫ С ПРЕДСКАЗАНИЕМ
- 22.5.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ ПРИМЕНИТЕЛЬНО К ЦВЕТНЫМ ИЗОБРАЖЕНИЯМ
- 22.5.6. ДИФФЕРЕНЦИАЛЬНОЕ МЕЖКАДРОВОЕ КОДИРОВАНИЕ
- 22.6. ПРОЕКТИРОВАНИЕ СИСТЕМ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ДЛЯ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 23. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННОЙ ОБРАБОТКОЙ
- 23.1. ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ КОДИРОВАНИЯ
- 23.1.1. ИНТЕРПОЛЯЦИЯ НА ПЕРЕДАЮЩЕЙ СТОРОНЕ
- 23.1.2. ИНТЕРПОЛЯЦИЯ НА ПРИЕМНОЙ СТОРОНЕ
- 23.2. КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.1. КОДИРОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.2. АДАПТИВНОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.3. КОДИРОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.4. МЕЖКАДРОВОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.3. УМЕНЬШЕНИЕ ОШИБОК КВАНТОВАНИЯ ПРИ КОДИРОВАНИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.4. ГИБРИДНОЕ КОДИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ И ДИКМ
- 23.5. КОДИРОВАНИЕ ПРИЗНАКОВ
- 23.5.1. КОДИРОВАНИЕ ЛИНИЙ УРОВНЯ
- 23.5.2. КОДИРОВАНИЕ КОНТУРОВ
- 23.5.3. КОДИРОВАНИЕ ТЕКСТУР
- 23.6. КОДИРОВАНИЕ С ПОМОЩЬЮ НАБОРА СИМВОЛОВ
- 23.6.1. КОДИРОВАНИЕ БЛОКОВ ПО СЛОВАРЮ ОБРАЗОВ
- 23.6.2. КОДИРОВАНИЕ НА ОСНОВЕ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- ЛИТЕРАТУРА
- Глава 24. АНАЛИЗ ЭФФЕКТИВНОСТИ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 24.1. СТАТИСТИЧЕСКИЕ МОДЕЛИ КАНАЛА СВЯЗИ КАК ИСТОЧНИКА ПОМЕХ [1-4]
- 24.2. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ
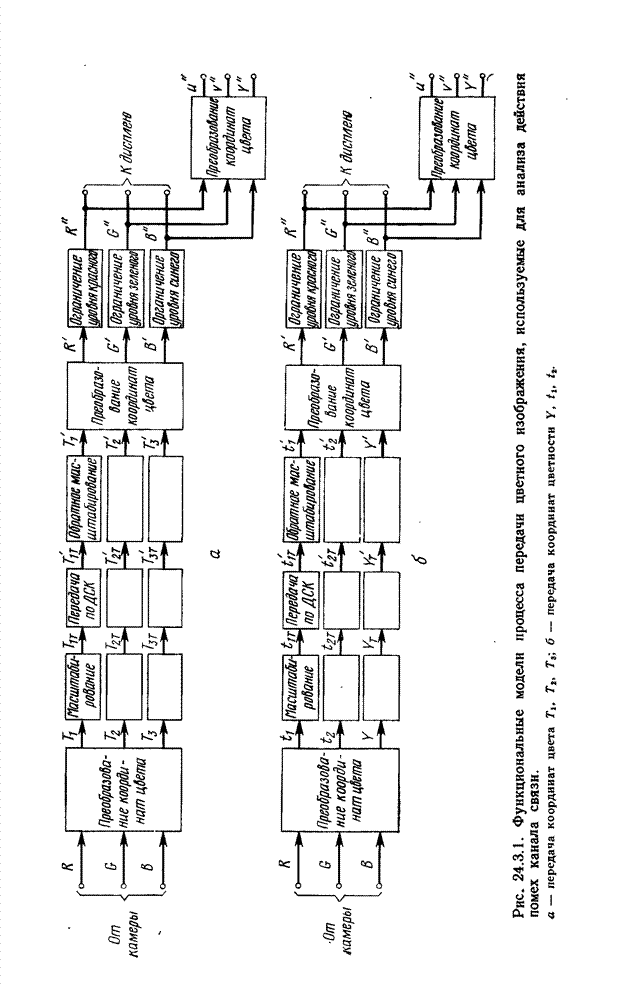
- 24.3. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ [4]
- 24.3.1. ПЕРЕДАЧА КООРДИНАТ ЦВЕТА
- 24.3.2. ПЕРЕДАЧА ЯРКОСТИ И КООРДИНАТ ЦВЕТНОСТИ
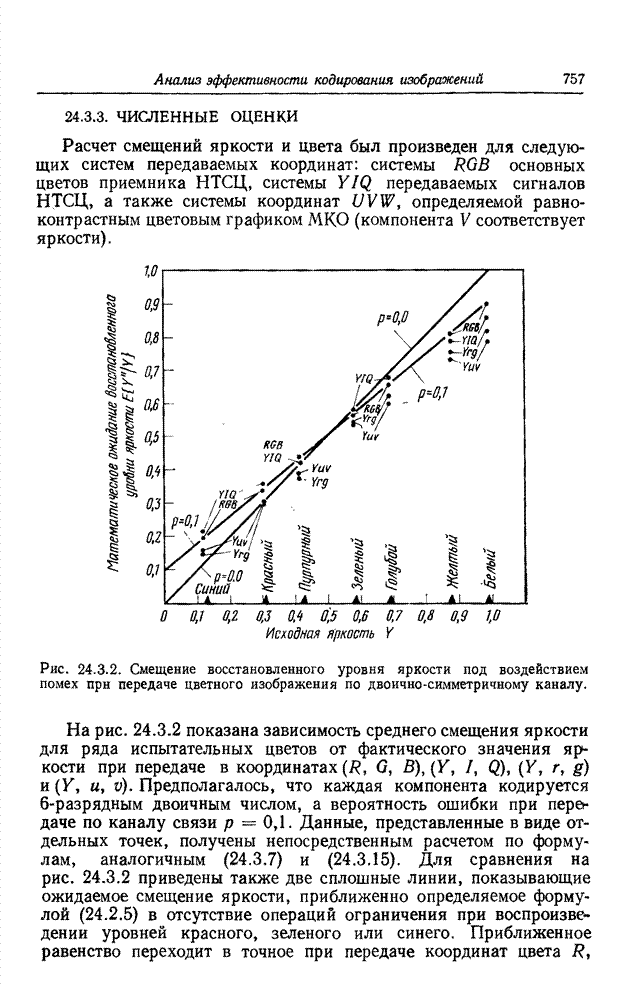
- 24.3.3. ЧИСЛЕННЫЕ ОЦЕНКИ
- 24.4. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ ДИКМ
- 24.5. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ КОДИРОВАНИЯ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 24.6. СРАВНЕНИЕ РАЗЛИЧНЫХ МЕТОДОВ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Приложение 1. ОСНОВНАЯ ЛИТЕРАТУРА
- Приложение 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА И ЦВЕТНОСТИ
- Приложение 3. СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА