| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14.8. МЕТОДЫ РЕСТАВРАЦИИ С ИСПОЛЬЗОВАНИЕМ ОГРАНИЧЕНИЙ
Для повышения качества исправленных изображений в моделях с плохой обусловленностью было предложено [19] вводить ограничения в виде равенств и ограничения в виде неравенств. Можно, например, задавать значения отдельных элементов, отношения отдельных элементов, сумму части или всех элементов или же предельно допустимые уровни элементов.
В переопределенной линейной модели могут использоваться ограничения в виде системы линейных уравнений
![]() , (14.8.1)
, (14.8.1)
где ![]() - заданная матрица размера
- заданная матрица размера ![]() ранга
ранга ![]() , описывающая
ограничения,
, описывающая
ограничения, ![]() -
оценка при наличии ограничений,
-
оценка при наличии ограничений, ![]() - известный вектор размера
- известный вектор размера ![]() . Минимизация
взвешенной ошибки
. Минимизация
взвешенной ошибки ![]() с учетом ограничений (14.8.1)
позволяет получить следующую оценку [28, стр. 100]:
с учетом ограничений (14.8.1)
позволяет получить следующую оценку [28, стр. 100]:
![]() , (14.8.2)
, (14.8.2)
где ![]() - решение без ограничений.
Ковариационная матрица оптимального решения определяется как
- решение без ограничений.
Ковариационная матрица оптимального решения определяется как
![]() , (14.8.3)
, (14.8.3)
где ![]() - (положительно
определенная) ковариационная матрица без ограничений. Можно показать, что
вторая матрица в выражении (14.8.3) является неотрицательно определенной
матрицей ранга
- (положительно
определенная) ковариационная матрица без ограничений. Можно показать, что
вторая матрица в выражении (14.8.3) является неотрицательно определенной
матрицей ранга ![]() .
Следовательно, каждый диагональный элемент матрицы
.
Следовательно, каждый диагональный элемент матрицы ![]() меньше или равен
соответствующему элементу
меньше или равен
соответствующему элементу ![]() , а дисперсия каждого элемента вектора
оценки с ограничениями меньше дисперсии соответствующего элемента вектора
оценки без ограничений. Однако это не означает, что оценка с ограничениями
всегда лучше оценки без ограничений. Более того, первая может оказаться
смещенной, вторая - нет. Смещение решения при наличии ограничений
, а дисперсия каждого элемента вектора
оценки с ограничениями меньше дисперсии соответствующего элемента вектора
оценки без ограничений. Однако это не означает, что оценка с ограничениями
всегда лучше оценки без ограничений. Более того, первая может оказаться
смещенной, вторая - нет. Смещение решения при наличии ограничений
![]() (14.8.4)
(14.8.4)
будет иметь нулевое значение
тогда и только тогда, когда ограничения удовлетворяются истинным вектором ![]() , т. е. тогда и
только тогда, когда
, т. е. тогда и
только тогда, когда ![]() . В этом случае система ограничений
может рассматриваться как совокупность дополнительных наблюдаемых полей, не
пораженных шумом. При решении задач реставрации изображений можно ввести
разумное ограничение, состоящее в том, что сумма значений элементов
исправленного изображения должна равняться некоторому усредненному значению,
например среднему уровню наблюдаемого изображения. Однако такое ограничение
оказывается не очень полезным для преодоления плохой обусловленности, так как
влияет только на одну степень свободы в векторном пространстве размерности
. В этом случае система ограничений
может рассматриваться как совокупность дополнительных наблюдаемых полей, не
пораженных шумом. При решении задач реставрации изображений можно ввести
разумное ограничение, состоящее в том, что сумма значений элементов
исправленного изображения должна равняться некоторому усредненному значению,
например среднему уровню наблюдаемого изображения. Однако такое ограничение
оказывается не очень полезным для преодоления плохой обусловленности, так как
влияет только на одну степень свободы в векторном пространстве размерности ![]() .
.
Часто доступна априорная информация в виде ограничений-неравенств, обусловливающих значения элементов изображения. Физика процесса формирования изображений такова, что элементы изображения должны иметь неотрицательные значения. Часто известна верхняя граница этих значений, поскольку при преобразовании изображений в цифровую форму на каждый элемент отводится конечное число двоичных разрядов. Кроме того, вводятся вполне очевидные ограничения по уровню, связанные с необходимостью подогнать контрастный диапазон реставрированного изображения к динамическому диапазону дисплея. Один из возможных подходов - линейное масштабирование контраста исправленного изображения с учетом заданного динамического диапазона дисплея. Прибегать к этой процедуре обычно нежелательно, поскольку появление даже нескольких элементов с ненормально высокой яркостью приводит к снижению контраста всего изображения. Следует также учитывать, что контрастное масштабирование обычно влияет на среднюю яркость исправленного изображения. Другой распространенный метод воспроизведения изображений предусматривает ограничение уровня элементов в случае превышения порогового уровня дисплея. Хотя этот метод превосходит метод контрастного масштабирования по субъективному качеству изображения, он может дать смещение оценки.
Если реставрация изображений должна осуществляться с априорно вводимыми ограничениями уровней элементов, то лучше всего учесть эти ограничения непосредственно при реставрации; введение ограничений после завершения процедуры реставрации дает худший результат. Известно несколько методов реставрации изображений с использованием ограничений в виде неравенств.
Рассмотрим общий случай
реставрации с ограничениями, когда вектор оценки ![]() должен удовлетворять неравенствам
должен удовлетворять неравенствам
![]() , (14.8.5)
, (14.8.5)
где ![]() и
и ![]() - векторы,
учитывающие верхний и нижний пределы ограничения оценки элементов. В случае
реставрации по критерию наименьших квадратов квадратическую ошибку следует
минимизировать с учетом ограничения (14.8.5). Такой подход приводит к задаче
квадратического программирования (19). При использовании абсолютной ошибки
задачу реставрации можно сформулировать как задачу линейного программирования [34,35].
- векторы,
учитывающие верхний и нижний пределы ограничения оценки элементов. В случае
реставрации по критерию наименьших квадратов квадратическую ошибку следует
минимизировать с учетом ограничения (14.8.5). Такой подход приводит к задаче
квадратического программирования (19). При использовании абсолютной ошибки
задачу реставрации можно сформулировать как задачу линейного программирования [34,35].



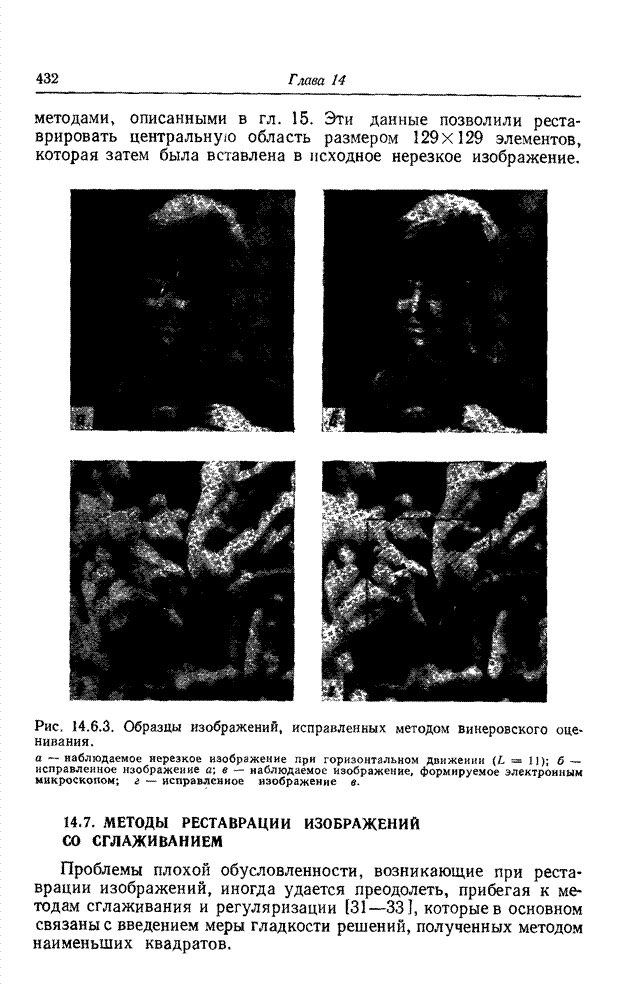
Рис. 14.8.1.
Сравнение изображений, реставрированных без ограничений и с ограничениями. Нерезкость
внесена с помощью импульсного отклика гауссовой формы ![]() . Случай переопределенной
модели
. Случай переопределенной
модели![]() . Наблюдаемое
изображение с шумом (дисперсия равна 10 уровням шкалы): а - нерезкое
изображение: б - изображение а, исправленное без ограничений; в - изображение а, исправленное с ограничениями в
виде неравенств.
. Наблюдаемое
изображение с шумом (дисперсия равна 10 уровням шкалы): а - нерезкое
изображение: б - изображение а, исправленное без ограничений; в - изображение а, исправленное с ограничениями в
виде неравенств.
Априорная информация, включающая ограничения в виде неравенств, может обеспечить существенное уменьшение неопределенности элементов исправленного изображения; однако, как и в случае использования ограничений-равенств, оценка может получить неизвестное смещение.
Рис. 14.8.1 иллюстрирует качество реставрации изображения с гауссовой нерезкостью, соответствующей переопределенной модели (см. гл. 13). Изображение на рис. 14.8.1, б реставрировано методом псевдообращения матриц, а изображение на рис. 14.8.1, в - с использованием ограничений-неравенств [19], требующих, чтобы яркость каждого элемента исправленного изображения находилась в диапазоне 0—255. Введение ограничений обеспечивает существенное повышение качества реставрации. К сожалению, решение задачи квадратического программирования, которое использовано в рассматриваемом примере, требует выполнения большого объема вычислений. Распространить принцип «грубой силы» на рассматриваемый метод не представляется возможным.
Предложен ряд способов улучшения метода реставрации изображений с использованием ограничений. Один простой подход, основанный на идее гомоморфной фильтрации, заключается в логарифмировании каждого наблюдаемого изображения. Потенцирование соответствующих оценок автоматически приводит к строго положительному результату. Берг [5, 36, 37] и Фриден [5, 38, 39] разработали методы реставрации с ограничением в виде условия положительности, основанные на принципе максимума энтропии, который впервые был применен для оценивания плотности вероятности по ее моментам. Метод Берга, дающий решение в замкнутой форме, при наличии шума иногда приводит к неустойчивым оценкам. Итеративный метод Фридена с успехом был применен для обработки одномерных сигналов и небольших изображений. Джанссон и др. [40] на основе результатов более ранней работы Ван Циттера [41] разработали итеративный метод реставрации, в котором используются итерационные уравнения вида [5, 40]
![]() ,
(14.8.6)
,
(14.8.6)
![]() , (14.8.7)
, (14.8.7)
где индекс ![]() указывает номер итерации, а
указывает номер итерации, а ![]() . Диагональная
матрица
. Диагональная
матрица ![]() определяется
как
определяется
как
 , (14.8.8)
, (14.8.8)
где ![]() - постоянная. Когда значение
элемента исправленного изображения приближается к верхнему или нижнему пределу
ограничения, соответствующий взвешивающий коэффициент
- постоянная. Когда значение
элемента исправленного изображения приближается к верхнему или нижнему пределу
ограничения, соответствующий взвешивающий коэффициент ![]() стремится к нулю, благодаря
чему обеспечивается устойчивость этого члена оценки. Метод дал хорошие
результаты при обработке одномерных сигналов. Хуанг и др. [42, 43] предложили
модифицированный метод для реставрации изображений с ограничениями — так
называемый метод проекций, предусматривающий итеративное решение системы
уравнений
стремится к нулю, благодаря
чему обеспечивается устойчивость этого члена оценки. Метод дал хорошие
результаты при обработке одномерных сигналов. Хуанг и др. [42, 43] предложили
модифицированный метод для реставрации изображений с ограничениями — так
называемый метод проекций, предусматривающий итеративное решение системы
уравнений ![]() численными
методами. На каждом этапе промежуточные оценки подвергаются ограничению по
уровню в соответствии с установленным динамическим диапазоном.
численными
методами. На каждом этапе промежуточные оценки подвергаются ограничению по
уровню в соответствии с установленным динамическим диапазоном.
Реставрация изображений с ограничениями - развивающаяся область исследований. Здесь ведутся настойчивые поиски эффективных вычислительных методов, минимизирующих ошибки оценивания при наличии дополнительных ограничений.
| << Предыдущий параграф | Следующий параграф >> |
- Часть 4. РЕСТАВРАЦИЯ И УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
- Глава 12. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
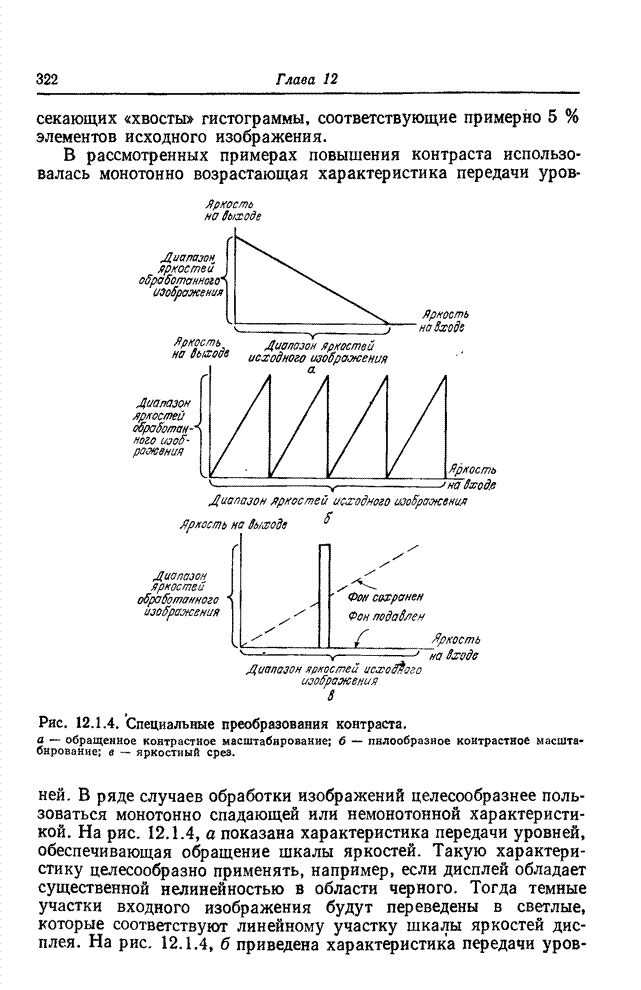
- 12.1. ИЗМЕНЕНИЕ КОНТРАСТА
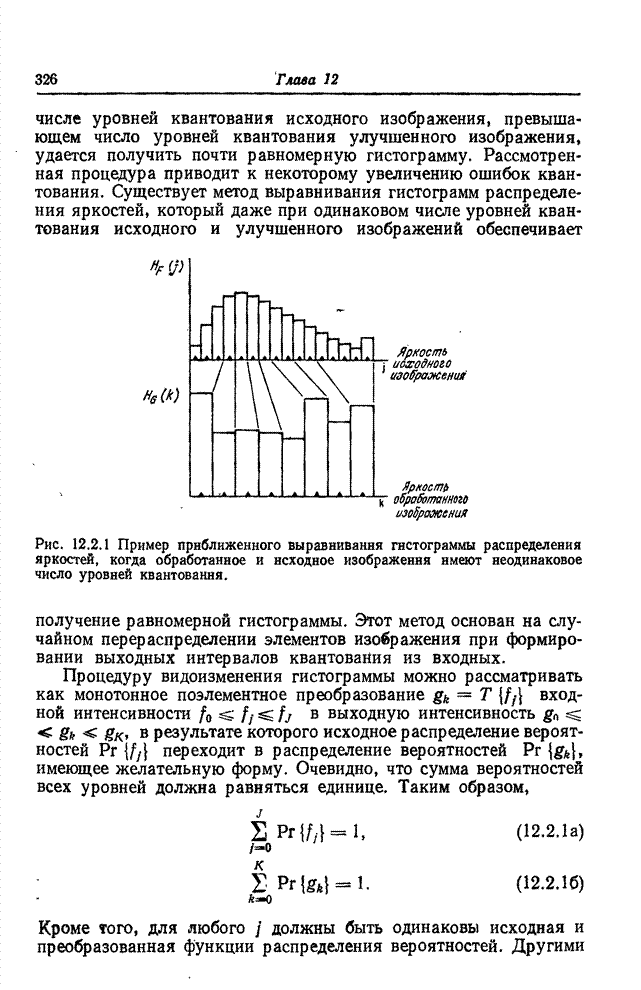
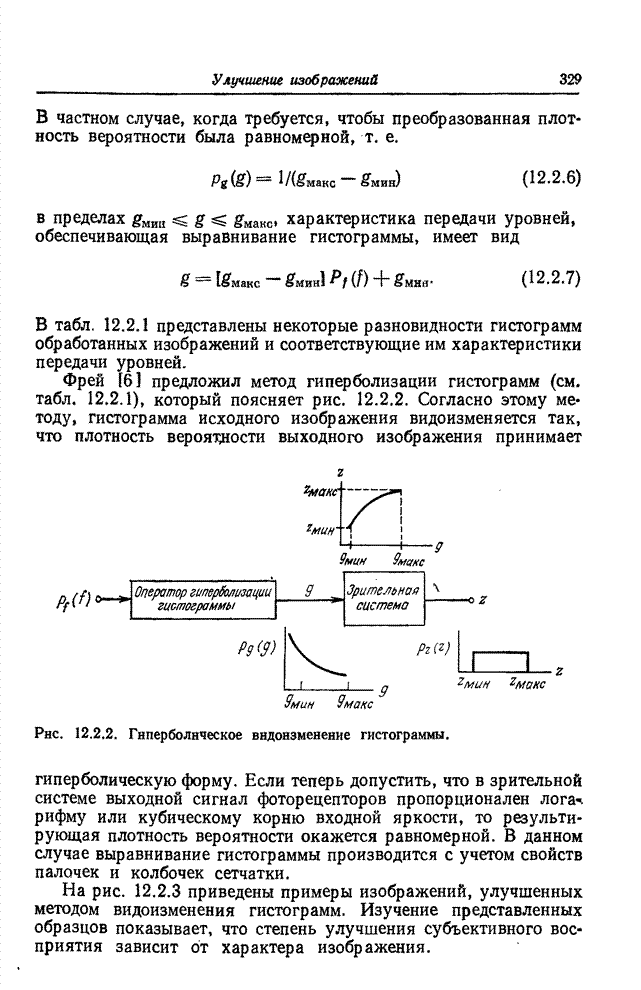
- 12.2. ВИДОИЗМЕНЕНИЕ ГИСТОГРАММ
- 12.3. ПОДАВЛЕНИЕ ШУМОВ
- 12.4. ПОДЧЕРКИВАНИЕ ГРАНИЦ
- 12.5. ОБРАБОТКА ИЗОБРАЖЕНИЙ С ПРЕОБРАЗОВАНИЕМ
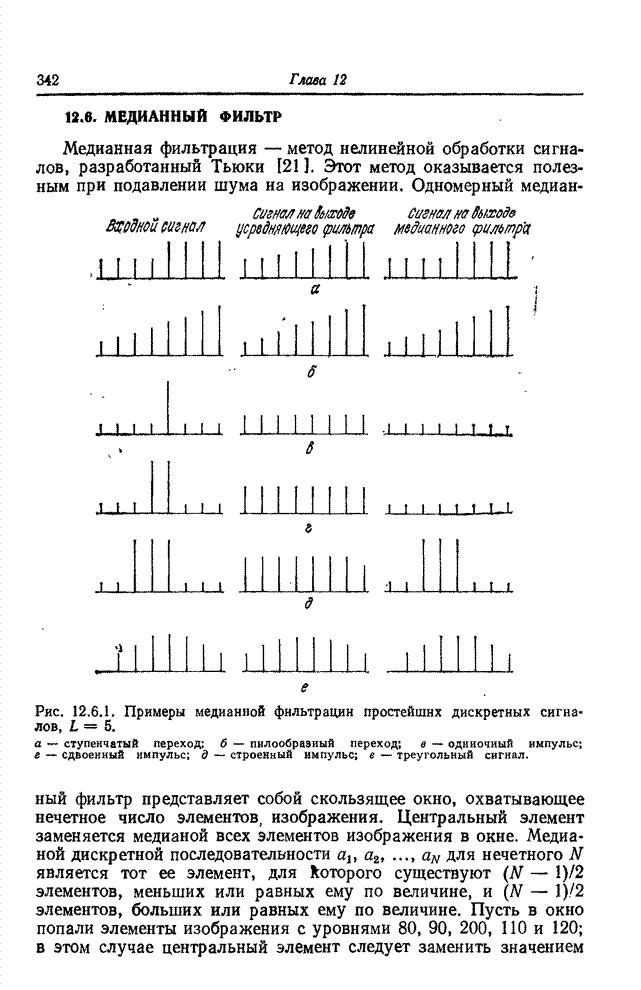
- 12.6. МЕДИАННЫЙ ФИЛЬТР
- 12.7. ЛОЖНЫЕ ЦВЕТА
- 12.8. ПСЕВДОЦВЕТА
- 12.9. УЛУЧШЕНИЕ СПЕКТРОЗОНАЛЬНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 13. МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.1. ОБОБЩЕННЫЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.2. МОДЕЛИ ОПТИЧЕСКИХ СИСТЕМ
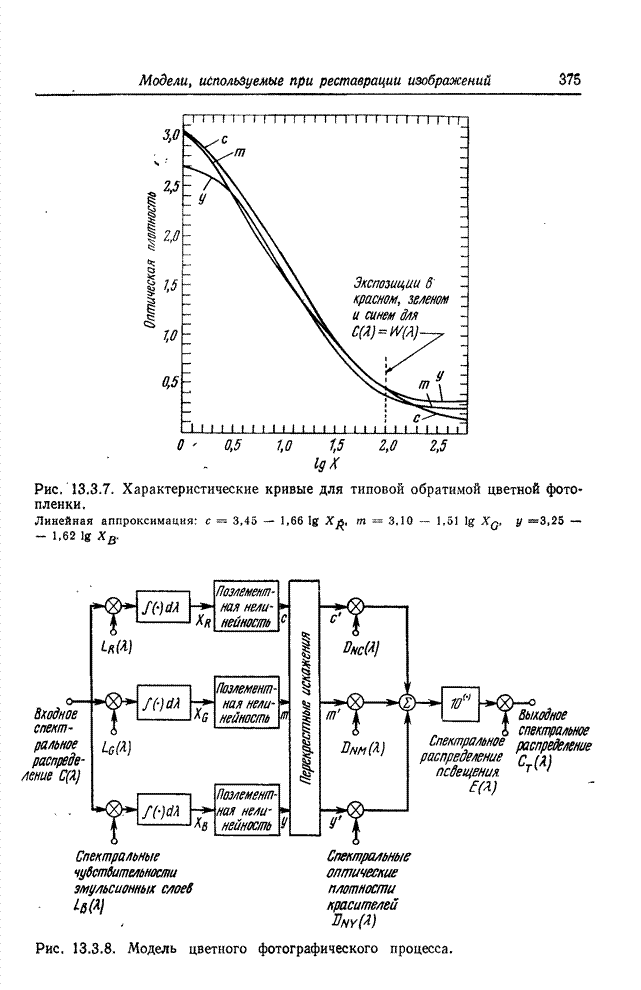
- 13.3. МОДЕЛИ ФОТОГРАФИЧЕСКИХ ПРОЦЕССОВ
- 13.3.1. ОДНОЦВЕТНАЯ ФОТОГРАФИЯ
- 13.3.2. ЦВЕТНАЯ ФОТОГРАФИЯ
- 13.4. МОДЕЛИ ЦИФРОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- 13.5. МОДЕЛЬ ДИСПЛЕЯ
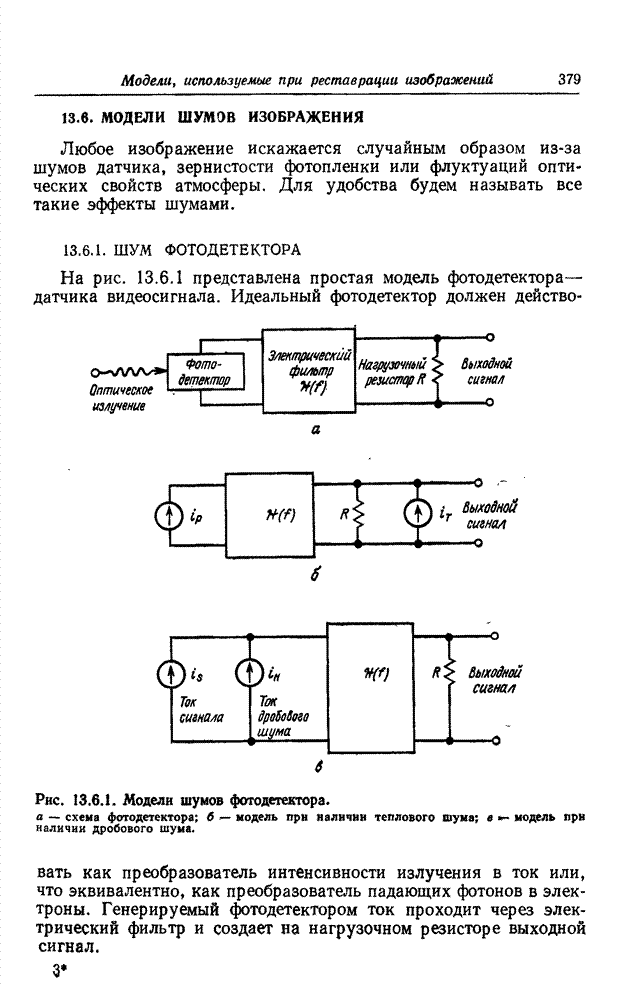
- 13.6. МОДЕЛИ ШУМОВ ИЗОБРАЖЕНИЯ
- 13.6.1. ШУМ ФОТОДЕТЕКТОРА
- 13.6.2. ШУМ ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
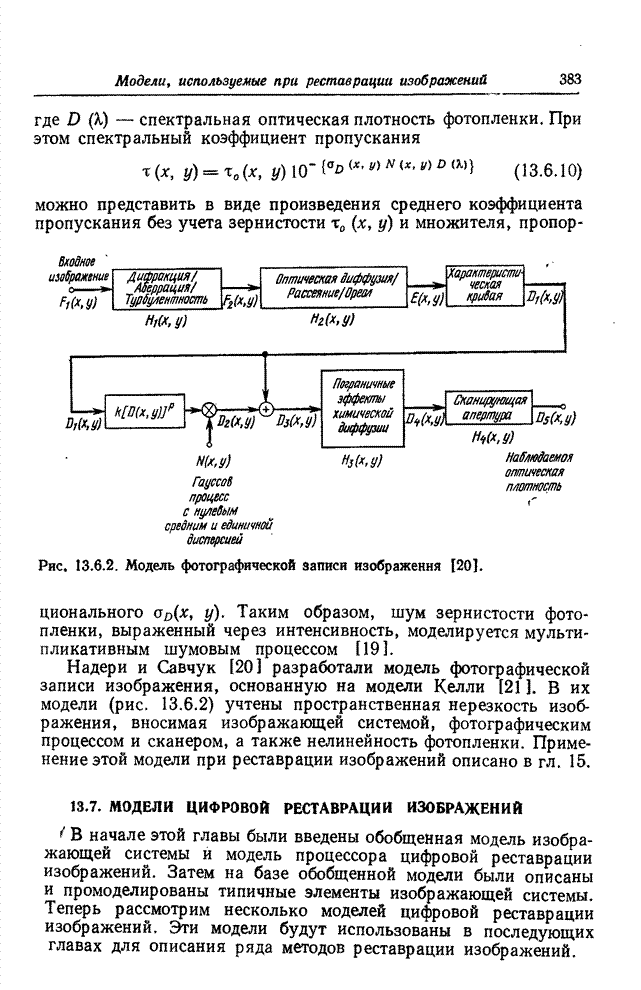
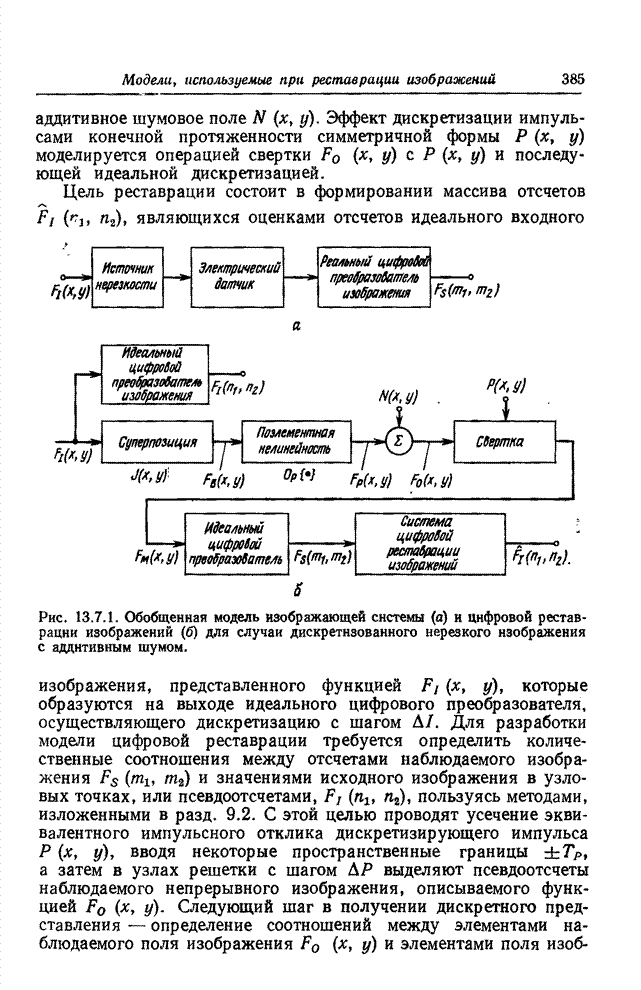
- 13.7. МОДЕЛИ ЦИФРОВОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 14. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 14.1. МЕТОДЫ ПРОСТРАНСТВЕННОЙ ФИЛЬТРАЦИИ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 14.1.1. ИНВЕРСНАЯ ФИЛЬТРАЦИЯ
- 14.1.2. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И АДДИТИВНЫЙ ШУМ
- 14.1.3. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНОЕ ИЗОБРАЖЕНИЕ
- 14.1.4. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНАЯ НЕРЕЗКОСТЬ
- 14.1.5. ФИЛЬТРЫ НА ОСНОВЕ ПАРАМЕТРИЧЕСКИХ ОЦЕНОК
- 14.1.6. ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 4.2. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.2.1. РЕСТАВРАЦИЯ НЕРЕЗКИХ ИЗОБРАЖЕНИЙ
- 14.2.2. РЕСТАВРАЦИЯ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ ПРИ НАЛИЧИИ ШУМА
- 14.3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.3.1. АЛГОРИТМ ДЛЯ ПЕРЕОПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.3.2. АЛГОРИТМ ДЛЯ НЕДООПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.4. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ С ИСПОЛЬЗОВАНИЕМ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- 14.5. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕГРЕССИИ
- 14.6. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ВИНЕРОВСКОГО ОЦЕНИВАНИЯ
- 14.6.1. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В ОБЩЕМ СЛУЧАЕ
- 14.6.2. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В СЛУЧАЕ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ С ШУМОМ
- 14.7. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ СО СГЛАЖИВАНИЕМ
- 14.8. МЕТОДЫ РЕСТАВРАЦИИ С ИСПОЛЬЗОВАНИЕМ ОГРАНИЧЕНИЙ
- 14.9. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
- ЛИТЕРАТУРА
- Глава 15. CПЕЦИАЛЬНЫЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 15.1. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮ ПОДАВЛЕНИЯ ОШИБОК НАЛОЖЕНИЯ СПЕКТРОВ
- 15.2. КОРРЕКЦИЯ ОШИБОК ИНТЕРПОЛЯЦИИ
- 15.3. КОРРЕКЦИЯ ГЕОМЕТРИЧЕСКИХ ИСКАЖЕНИЙ
- 15.4. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ГОМОМОРФНОЙ ФИЛЬТРАЦИИ
- 15.5. СЛЕПАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ
- 15.5.1. МЕТОДЫ НА ОСНОВЕ ПРЯМЫХ ИЗМЕРЕНИЙ
- 15.5.2. МЕТОДЫ НА ОСНОВЕ КОСВЕННОГО ОЦЕНИВАНИЯ
- 15.6. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ СПЕКТРА
- 15.7. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННО-ЗАВИСИМЫМИ ИСКАЖЕНИЯМИ
- 15.8. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕКУРСИВНОЙ ФИЛЬТРАЦИИ
- 15.9. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮОСЛАБЛЕНИЯ ШУМА ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- ЛИТЕРАТУРА
- Глава 16. КОРРЕКЦИЯ ЯРКОСТНЫХ, ЦВЕТОВЫХ И СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗОБРАЖАЮЩИХ СИСТЕМ
- 16.1. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ВИДЕОДАТЧИКОВ
- 16.2. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ДИСПЛЕЕВ
- 16.3. ОЦЕНИВАНИЕ СПЕКТРАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 16.4. КОРРЕКЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ВИДЕОДАТЧИКОВ И ДИСПЛЕЕВ
- 16.5. ОЦЕНИВАНИЕ КООРДИНАТ СВЕТА ВИДЕОДАТЧИКОВ
- 16.6. ОЦЕНИВАНИЕ ЭКСПОЗИЦИЙ ЦВЕТНОЙ ФОТОПЛЕНКИ
- 16.7. КОМПЕНСАЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ ЦВЕТНЫХ ДИСПЛЕЕВ
- ЛИТЕРАТУРА
- Часть 5. АНАЛИЗ ИЗОБРАЖЕНИЙ
- Глава 17. ВЫДЕЛЕНИЕ ПРИЗНАКОВ ИЗОБРАЖЕНИЯ
- 17.1. ЯРКОСТНЫЕ ПРИЗНАКИ
- 17.2. ГИСТОГРАММНЫЕ ПРИЗНАКИ
- 17.3. ПРОСТРАНСТВЕННО-СПЕКТРАЛЬНЫЕ ПРИЗНАКИ
- 17.4. КОНТУРНЫЕ ПРИЗНАКИ
- 17.4.1. ЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.2. НЕЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.3. МЕТОДЫ АППРОКСИМАЦИИ ПЕРЕПАДОВ ЯРКОСТИ
- 17.4.4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ
- 17.5. ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ ЯРКОСТИ
- 17.6. ЦВЕТОВЫЕ КОНТУРЫ
- 17.7. ПРИЗНАКИ ПЯТНА И ЛИНИИ
- 17.8. ТЕКСТУРНЫЕ ПРИЗНАКИ
- 17.9. СИНТЕЗ ТЕКСТУР
- ЛИТЕРАТУРА
- Глава 18. СИМВОЛИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
- 18.1. СВЯЗНОСТЬ
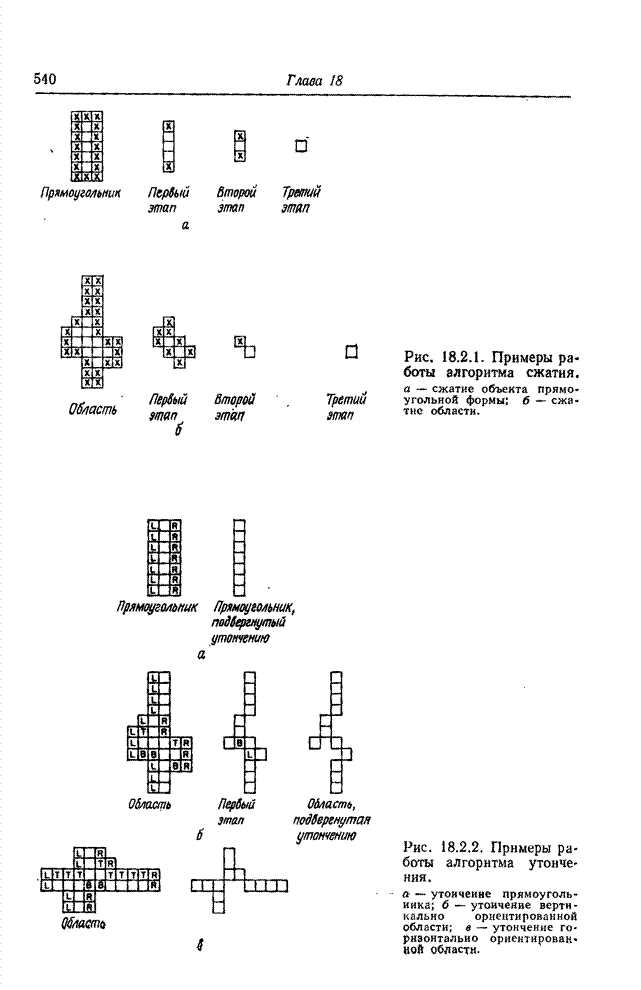
- 18.2. СЖАТИЕ, УТОНЧЕНИЕ И ПОСТРОЕНИЕ ОСТОВА
- 18.3. ОПИСАНИЕ ЛИНИЙ
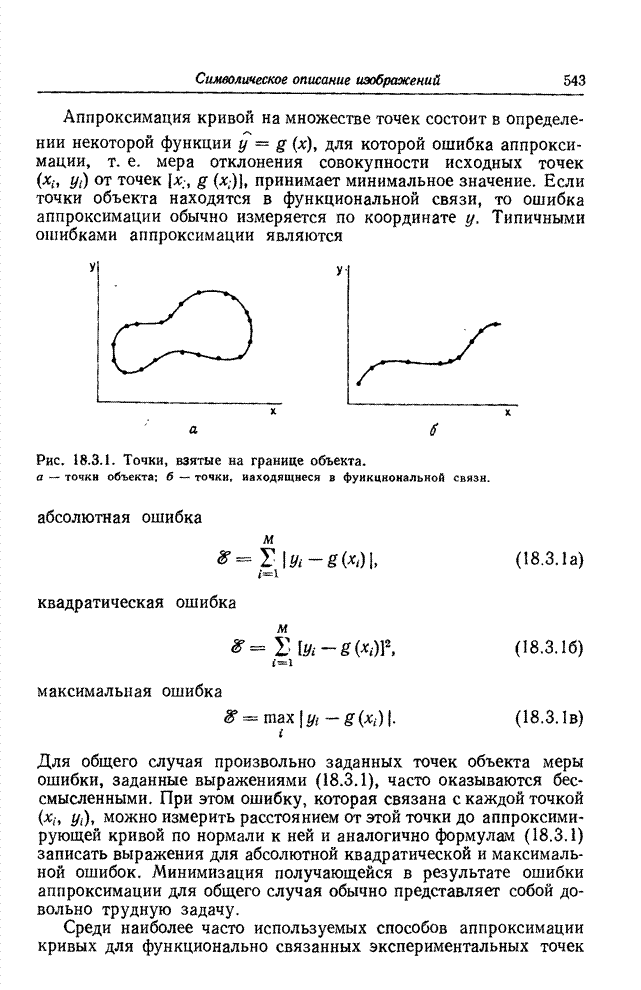
- 18.3.1. АППРОКСИМАЦИЯ КРИВЫХ
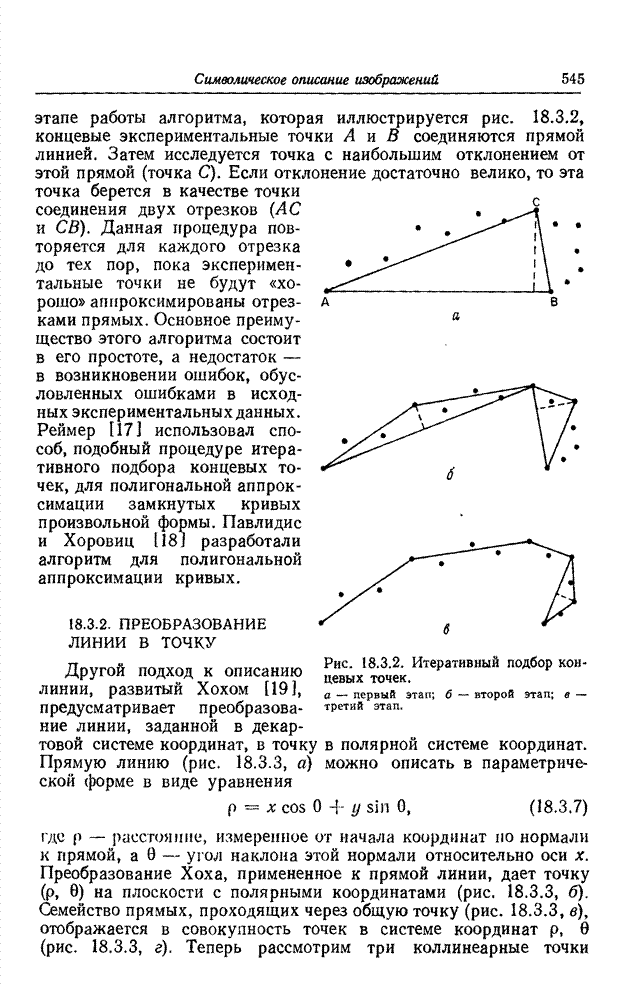
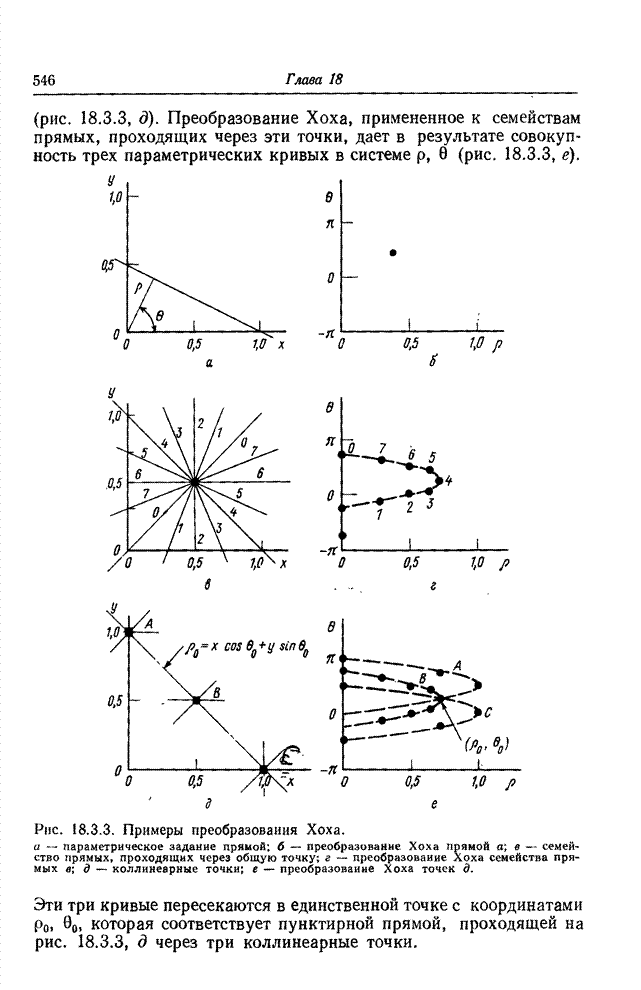
- 18.3.2. ПРЕОБРАЗОВАНИЕ ЛИНИИ В ТОЧКУ
- 18.4. ОПИСАНИЕ ФОРМЫ
- 18.4.1. МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.2. ТОПОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.3. АНАЛИТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.5. СЕГМЕНТАЦИЯ ПО ЯРКОСТИ
- 18.5.1. ПОРОГОВОЕ ОГРАНИЧЕНИЕ ПО ЯРКОСТИ
- 18.5.2. МНОГОМЕРНОЕ ПОРОГОВОЕ ОГРАНИЧЕНИЕ
- 18.5.3. НАРАЩИВАНИЕ ОБЛАСТЕЙ
- 18.6. КОНТУРНАЯ СЕГМЕНТАЦИЯ
- 18.7. ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ
- 18.8. СЕГМЕНТАЦИЯ ФОРМЫ
- ЛИТЕРАТУРА
- Глава 19. ОБНАРУЖЕНИЕ ОБЪЕКТОВ И СОВМЕЩЕНИЕ (ПРИВЯЗКА) ИЗОБРАЖЕНИЙ
- 19.1. СОПОСТАВЛЕНИЕ С ЭТАЛОНОМ
- 19.2. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ ДЕТЕРМИНИРОВАННЫХ ПОЛЕЙ
- 19.3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ СЛУЧАЙНЫХ ПОЛЕЙ
- 19.4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 19.5. ПРИВЯЗКА ИЗОБРАЖЕНИЙ
- 19.5.1. КОРРЕЛЯЦИОННАЯ ПРИВЯЗКА
- 19.5.2. ПОСЛЕДОВАТЕЛЬНАЯ ПРИВЯЗКА
- ЛИТЕРАТУРА
- Глава 20. СИСТЕМЫ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.1. СИСТЕМЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 20.2. МОДЕЛИ СИСТЕМ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
- 20.3. СИНТАКСИЧЕСКИЕ МЕТОДЫ
- 20.4. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ОТНОШЕНИЯ МЕЖДУ ОБЪЕКТАМИ
- ЛИТЕРАТУРА
- Часть 6. Кодирование изображений
- Глава 21. АНАЛОГОВЫЕ МЕТОДЫ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.1. КЛАССИФИКАЦИЯ МЕТОДОВ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.2. СИСТЕМЫ ВЕЩАТЕЛЬНОГО ТЕЛЕВИДЕНИЯ
- 21.2.1. СИСТЕМА НТСЦ [13-15]
- 21.2.2. СИСТЕМА СЕКАМ [17]
- 21.2.3.СИСТЕМА ПАЛ
- 21.3. МОДУЛЯЦИОННЫЕ МЕТОДЫ СОКРВЩЕНИЯ ПОЛОСЫ ЧАСТОТЫ
- 21.4.УМЕНЬШЕНИЕ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ И ЧАСТОТЫ КАДРОВ
- 21.4.1. УМЕНЬШЕНИЕ ПРОСТРАНСТВЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
- 21.4.2. УМЕНЬШЕНИЕ ЧАСТОТЫ КАДРОВ
- 21.5. МЕТОДЫ ВРЕМЕННОГО ПЕРЕМЕЖЕНИЯ
- 21.5.1. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ СТРОК
- 21.5.2. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ ЭЛЕМЕНТОВ
- 21.6. РАЗВЕРТКА С ПЕРЕМЕННОЙ СКОРОСТЬЮ
- 21.7. МУЛЬТИПЛЕКСНЫЕ МЕТОДЫ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Глава 22. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПОЭЛЕМЕНТНОЙ ОБРАБОТКОЙ
- 22.1. СИСТЕМЫ КОДИРОВАНИЯ С ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИЕЙ
- 22.1.1. КВАНТОВАНИЕ СО СЖАТИЕМ ДИАПАЗОНА ЯРКОСТЕЙ
- 22.1.2. ПСЕВДОШУМОВОЕ КВАНТОВАНИЕ
- 22.1.3. КВАНТОВАНИЕ С УЛУЧШЕННОЙ ПЕРЕДАЧЕЙ ГРАДАЦИЙ ЯРКОСТИ
- 22.1.4. СИСТЕМА С ГРУБОЙ-ТОНКОЙ ШКАЛОЙ КВАНТОВАНИЯ
- 22.1.5. КВАНТОВАНИЕ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ
- 22.2. СТАТИСТИЧЕСКИЕ МЕТОДЫ КОДИРОВАНИЯ
- 22.2.1. ПОЭЛЕМЕНТНОЕ СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- 22.2.2. КОДИРОВАНИЕ С УЧЕТОМ ПРЕДШЕСТВУЮЩЕГО ЭЛЕМЕНТА
- 22.3. КОДИРОВАНИЕ СЕРИЙ
- 22.3.1. КОДИРОВАНИЕ ДЛИН СЕРИЙ; ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ [32-36]
- 22.3.2. КОДИРОВАНИЕ РАЗРЯДНЫХ ПЛОСКОСТЕЙ
- 22.4. КОДИРОВАНИЕ С ПОПОЛНЕНИЕМ КАДРОВ
- 22.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ
- 22.5.1. ДЕЛЬТА-МОДУЛЯЦИЯ
- 22.5.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ
- 22.5.3. КОДЕРЫ С ПРОСТРАНСТВЕННЫМ ПРЕДСКАЗАНИЕМ
- 22.5.4. АДАПТИВНЫЕ КОДЕРЫ С ПРЕДСКАЗАНИЕМ
- 22.5.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ ПРИМЕНИТЕЛЬНО К ЦВЕТНЫМ ИЗОБРАЖЕНИЯМ
- 22.5.6. ДИФФЕРЕНЦИАЛЬНОЕ МЕЖКАДРОВОЕ КОДИРОВАНИЕ
- 22.6. ПРОЕКТИРОВАНИЕ СИСТЕМ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ДЛЯ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 23. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННОЙ ОБРАБОТКОЙ
- 23.1. ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ КОДИРОВАНИЯ
- 23.1.1. ИНТЕРПОЛЯЦИЯ НА ПЕРЕДАЮЩЕЙ СТОРОНЕ
- 23.1.2. ИНТЕРПОЛЯЦИЯ НА ПРИЕМНОЙ СТОРОНЕ
- 23.2. КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.1. КОДИРОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.2. АДАПТИВНОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.3. КОДИРОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.4. МЕЖКАДРОВОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.3. УМЕНЬШЕНИЕ ОШИБОК КВАНТОВАНИЯ ПРИ КОДИРОВАНИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.4. ГИБРИДНОЕ КОДИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ И ДИКМ
- 23.5. КОДИРОВАНИЕ ПРИЗНАКОВ
- 23.5.1. КОДИРОВАНИЕ ЛИНИЙ УРОВНЯ
- 23.5.2. КОДИРОВАНИЕ КОНТУРОВ
- 23.5.3. КОДИРОВАНИЕ ТЕКСТУР
- 23.6. КОДИРОВАНИЕ С ПОМОЩЬЮ НАБОРА СИМВОЛОВ
- 23.6.1. КОДИРОВАНИЕ БЛОКОВ ПО СЛОВАРЮ ОБРАЗОВ
- 23.6.2. КОДИРОВАНИЕ НА ОСНОВЕ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- ЛИТЕРАТУРА
- Глава 24. АНАЛИЗ ЭФФЕКТИВНОСТИ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 24.1. СТАТИСТИЧЕСКИЕ МОДЕЛИ КАНАЛА СВЯЗИ КАК ИСТОЧНИКА ПОМЕХ [1-4]
- 24.2. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ
- 24.3. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ [4]
- 24.3.1. ПЕРЕДАЧА КООРДИНАТ ЦВЕТА
- 24.3.2. ПЕРЕДАЧА ЯРКОСТИ И КООРДИНАТ ЦВЕТНОСТИ
- 24.3.3. ЧИСЛЕННЫЕ ОЦЕНКИ
- 24.4. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ ДИКМ
- 24.5. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ КОДИРОВАНИЯ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 24.6. СРАВНЕНИЕ РАЗЛИЧНЫХ МЕТОДОВ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Приложение 1. ОСНОВНАЯ ЛИТЕРАТУРА
- Приложение 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА И ЦВЕТНОСТИ
- Приложение 3. СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА