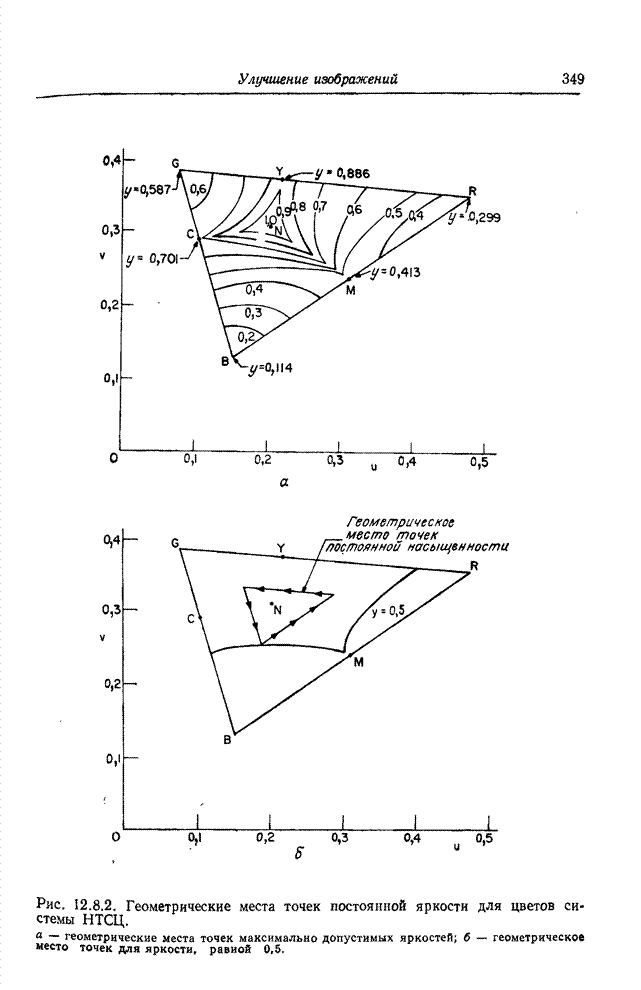
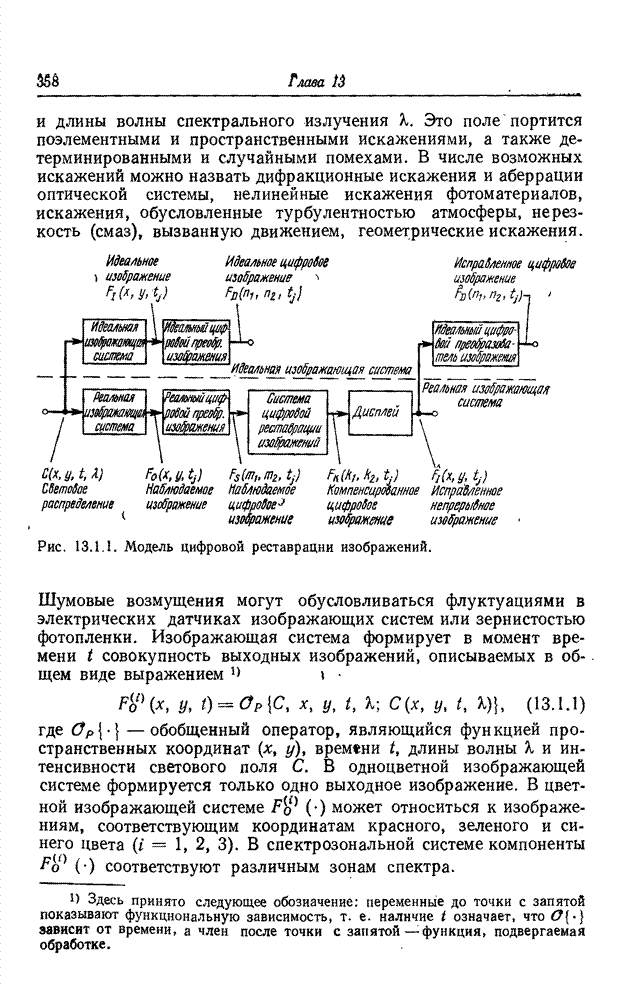
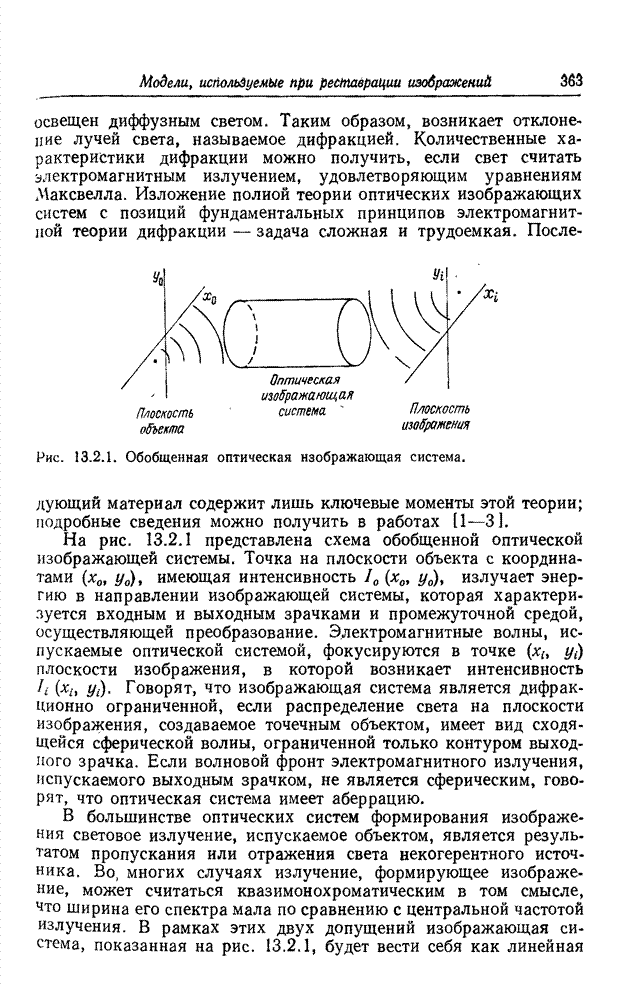
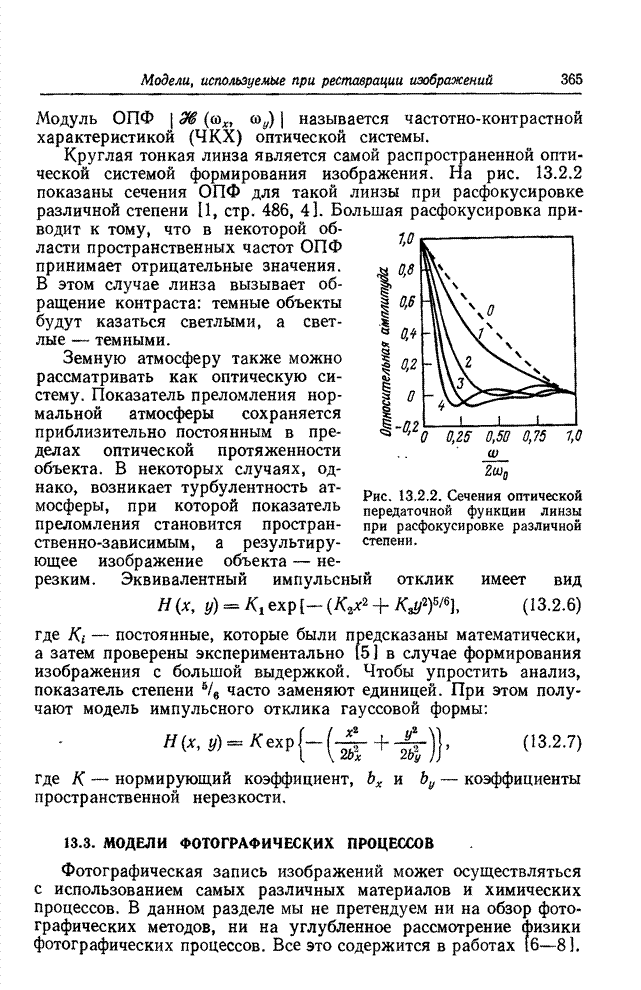
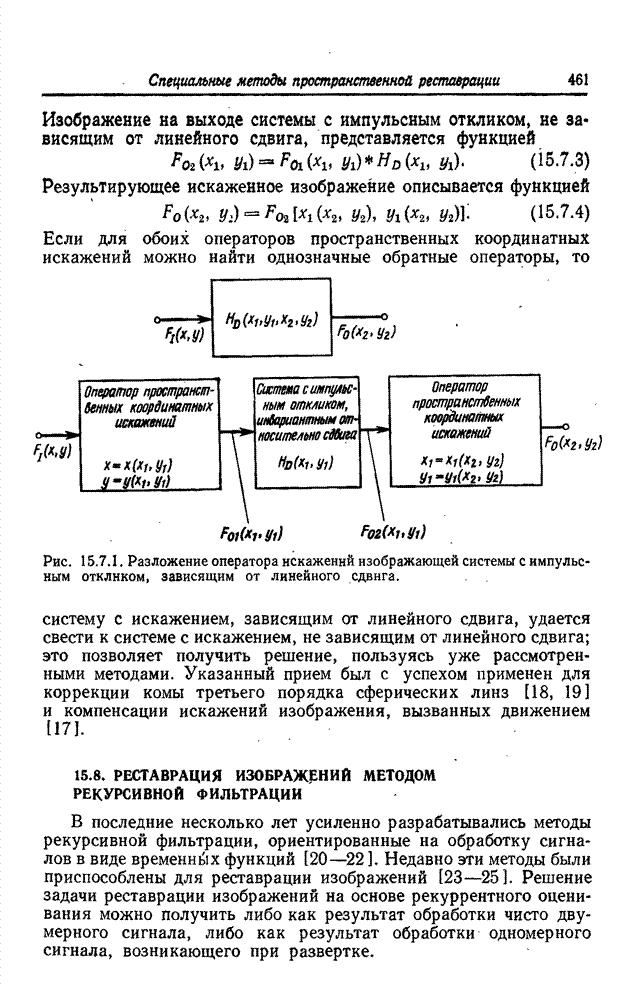
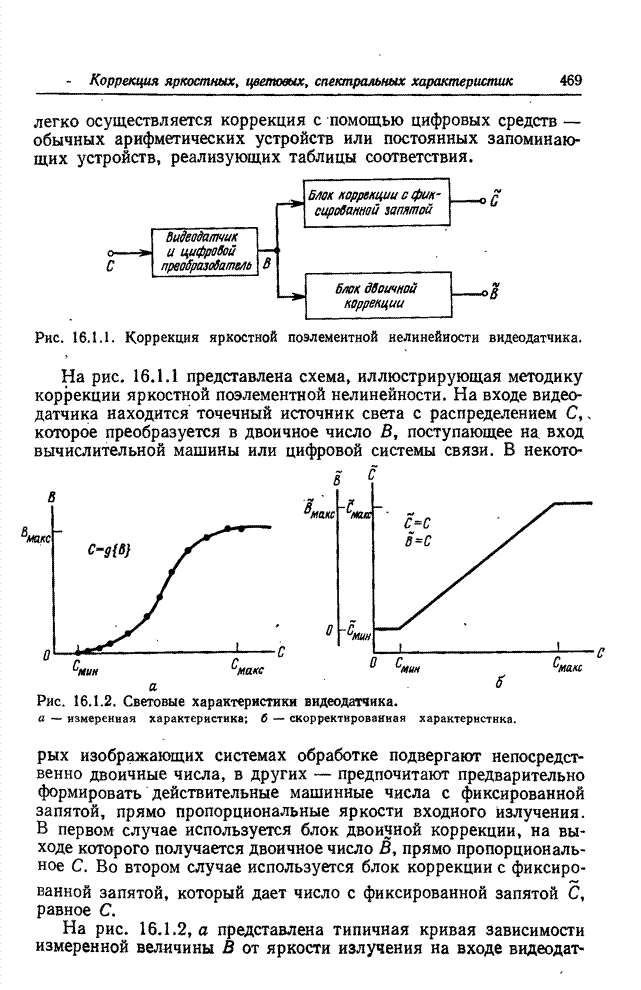
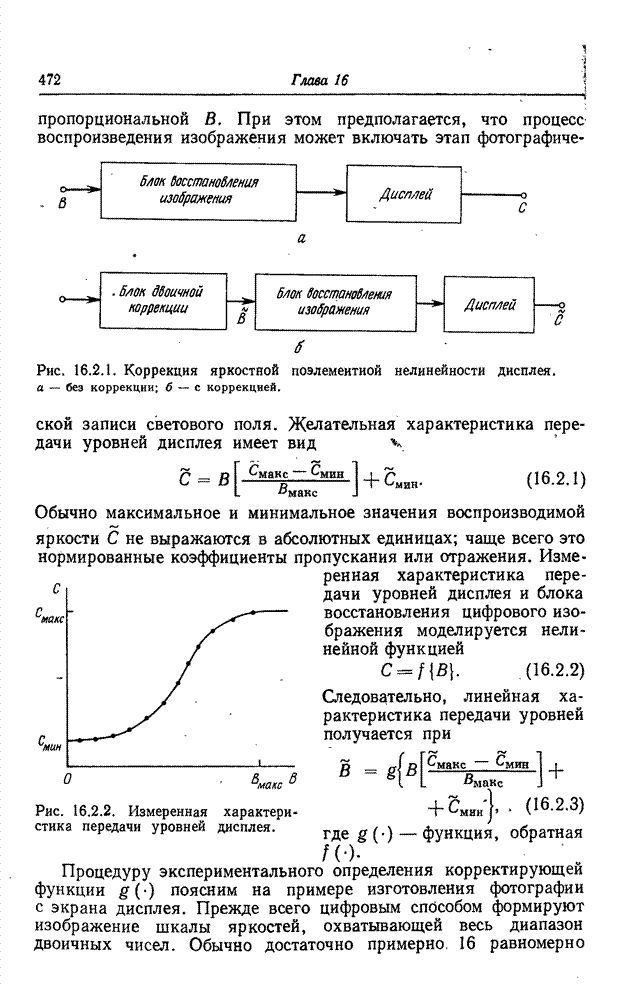
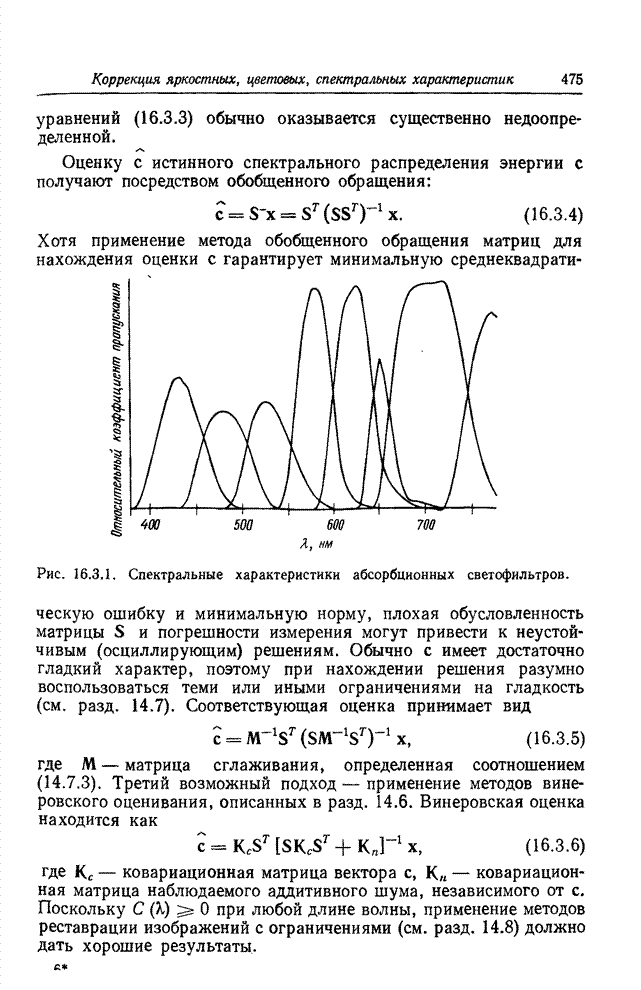
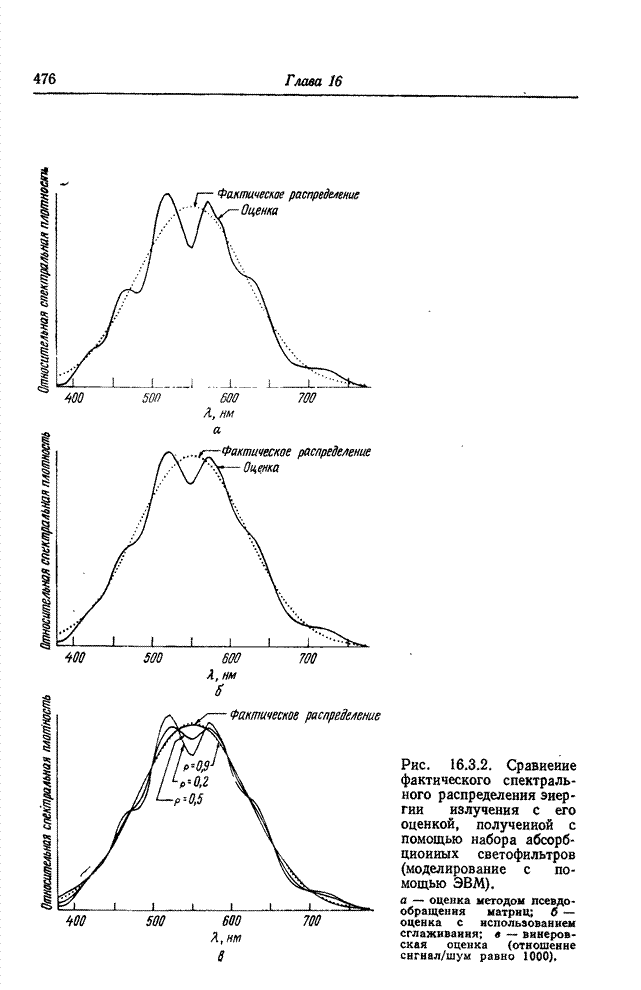
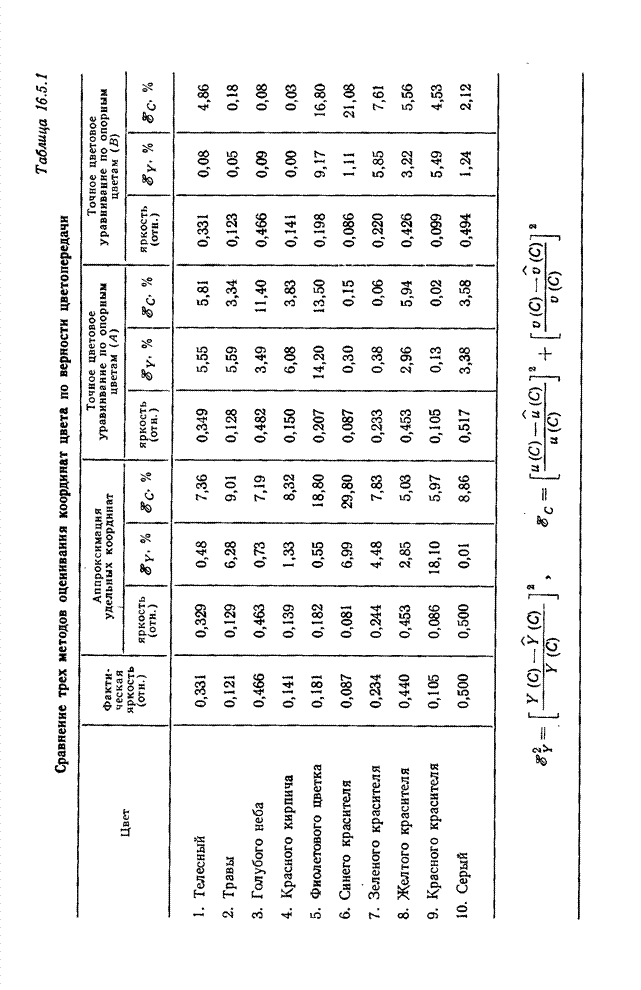
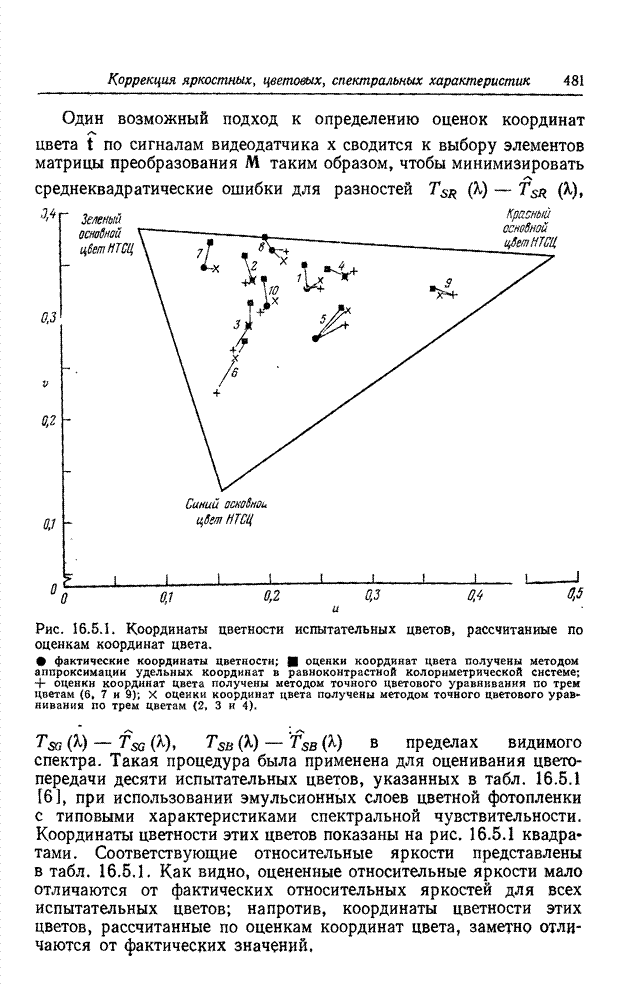
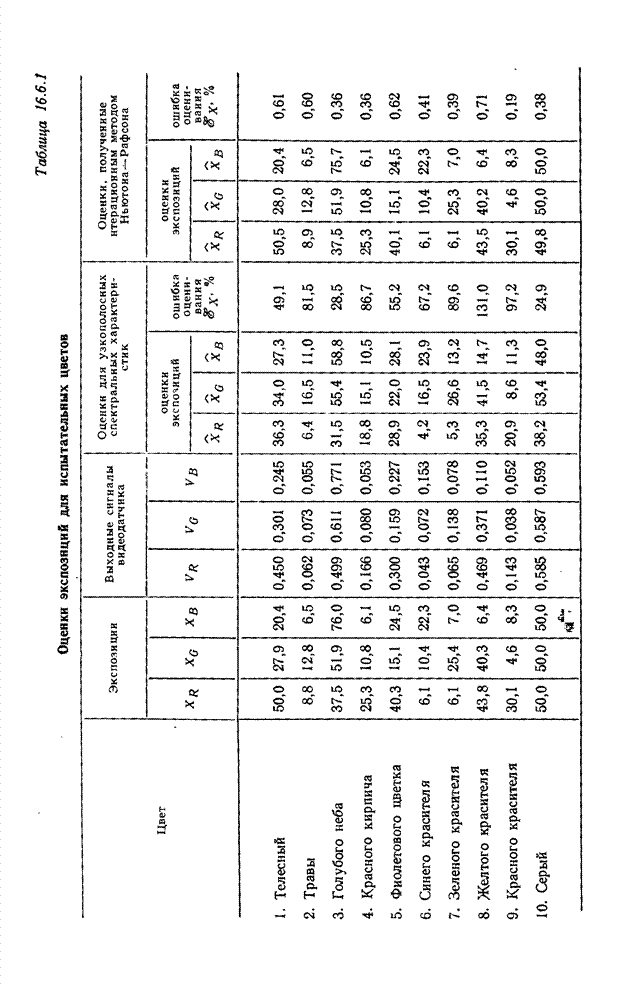
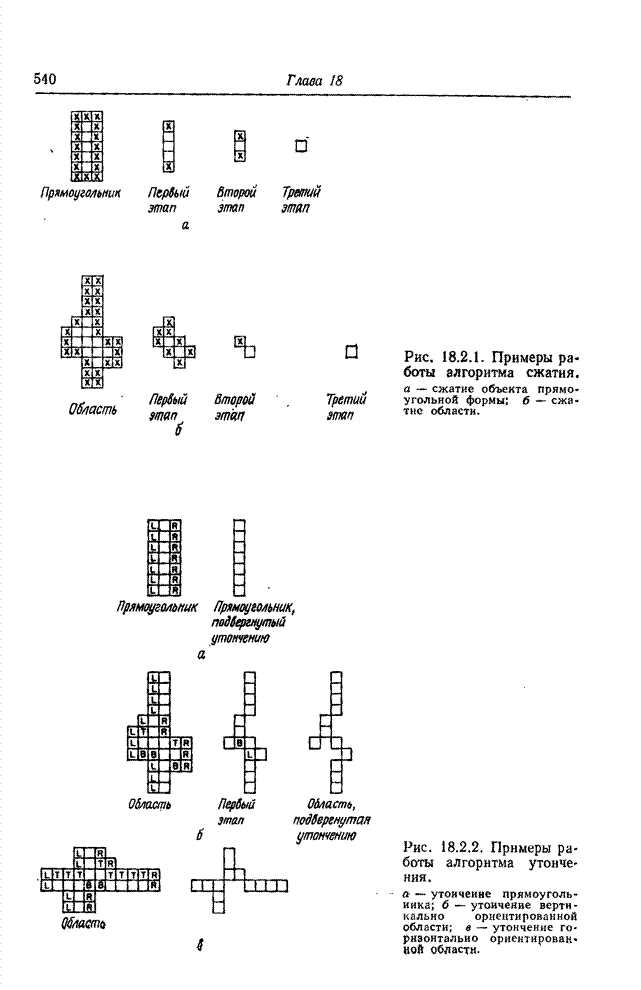
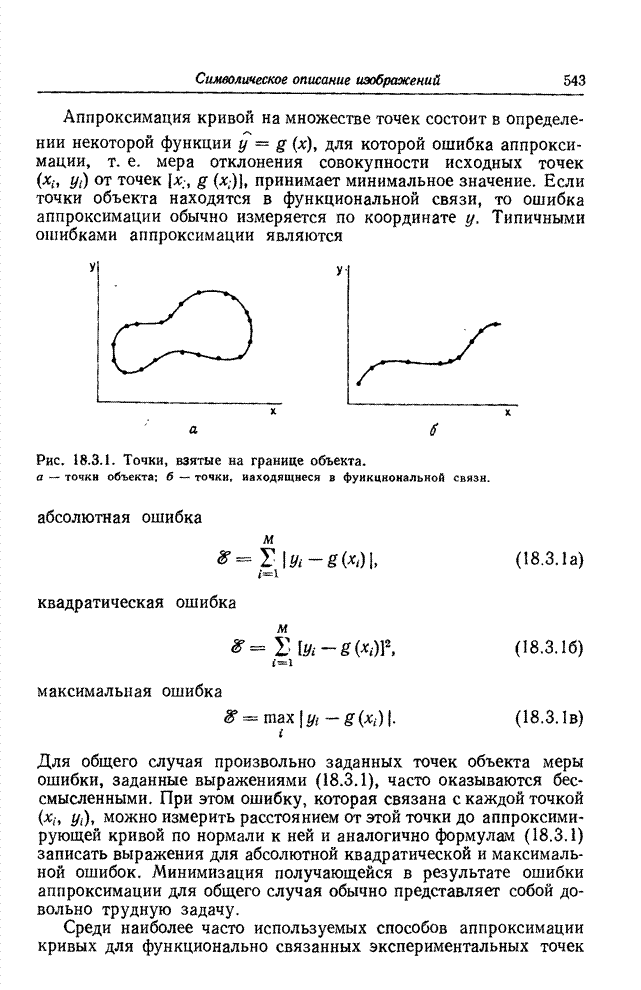
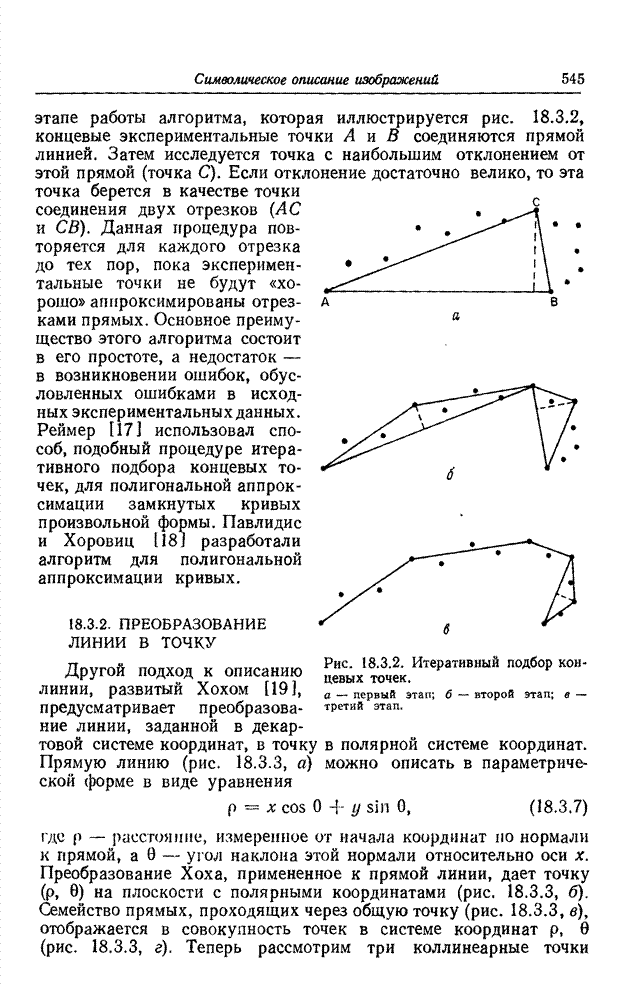
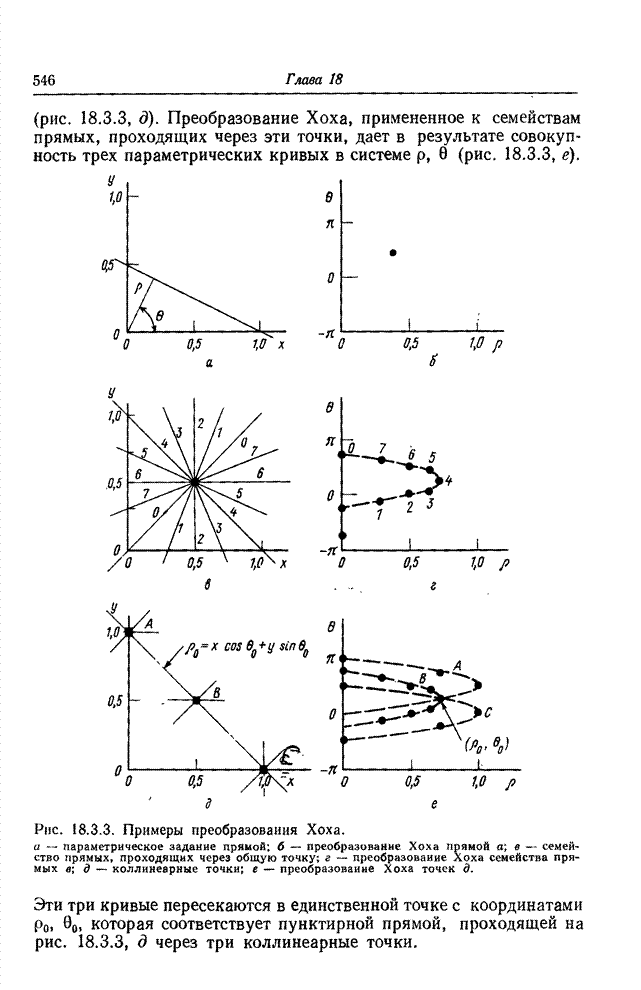
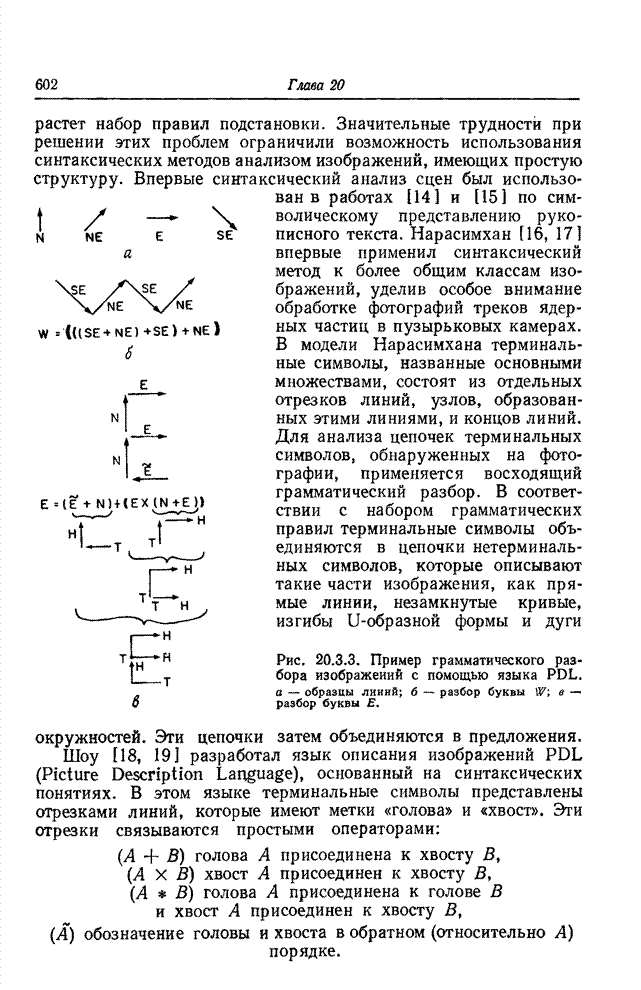
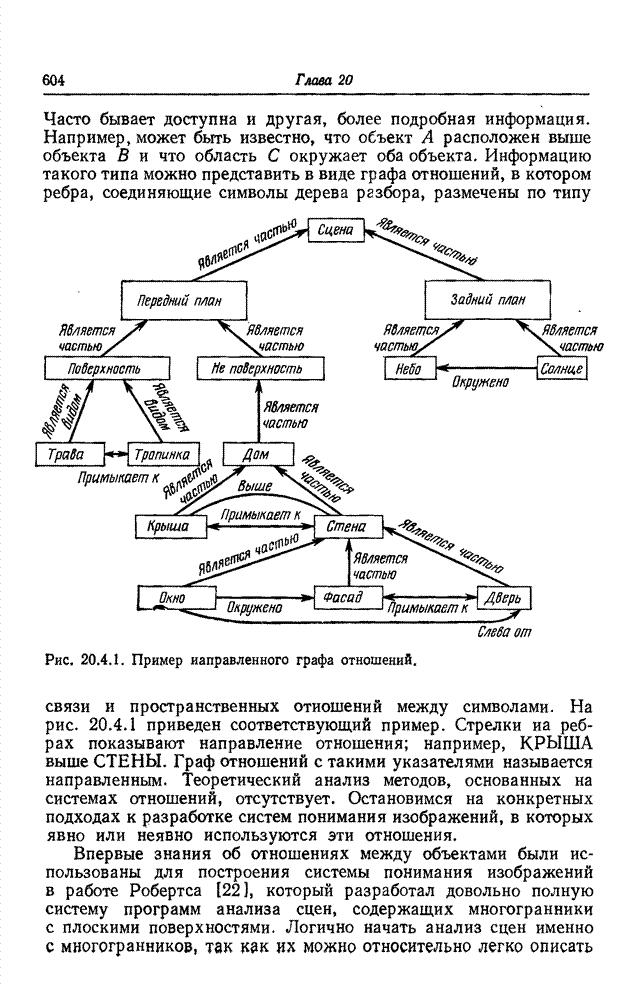
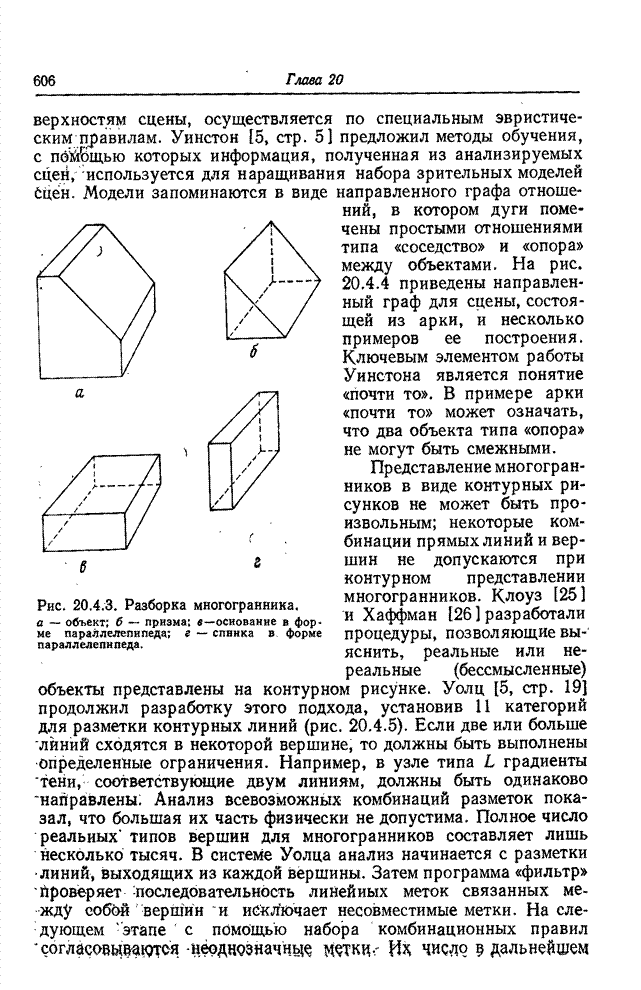
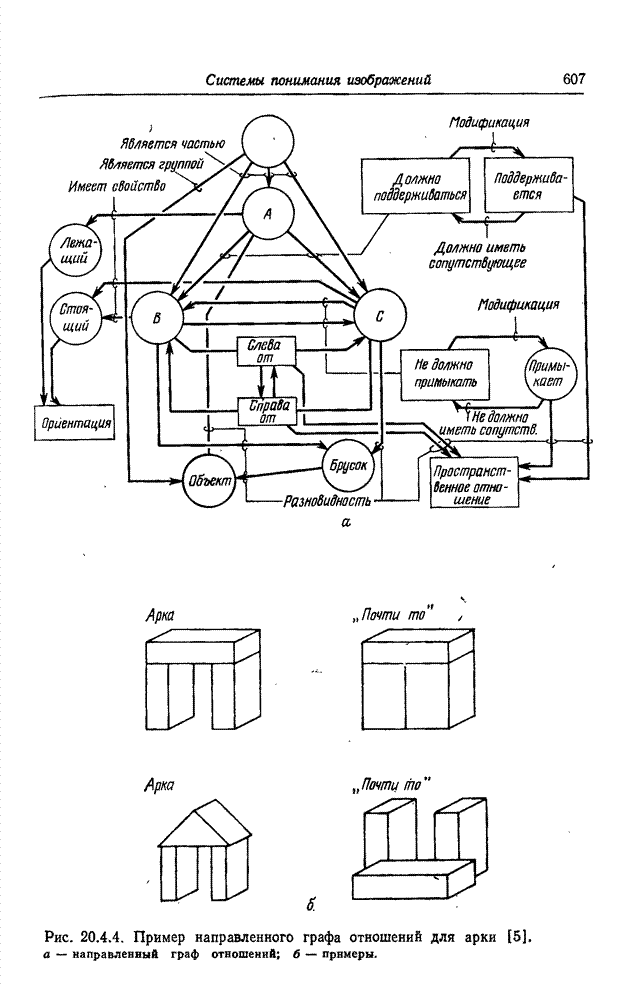
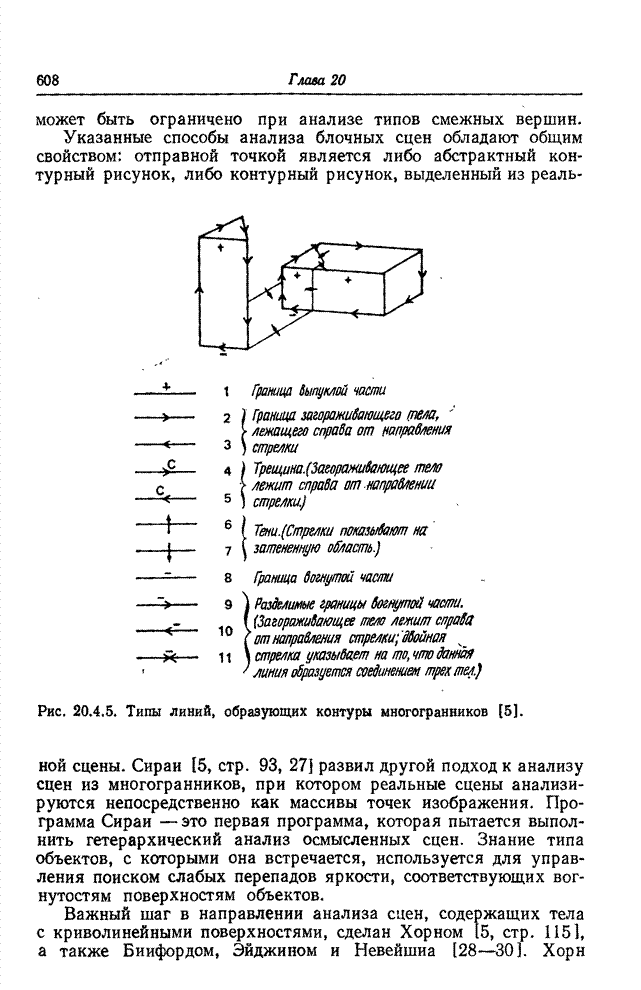
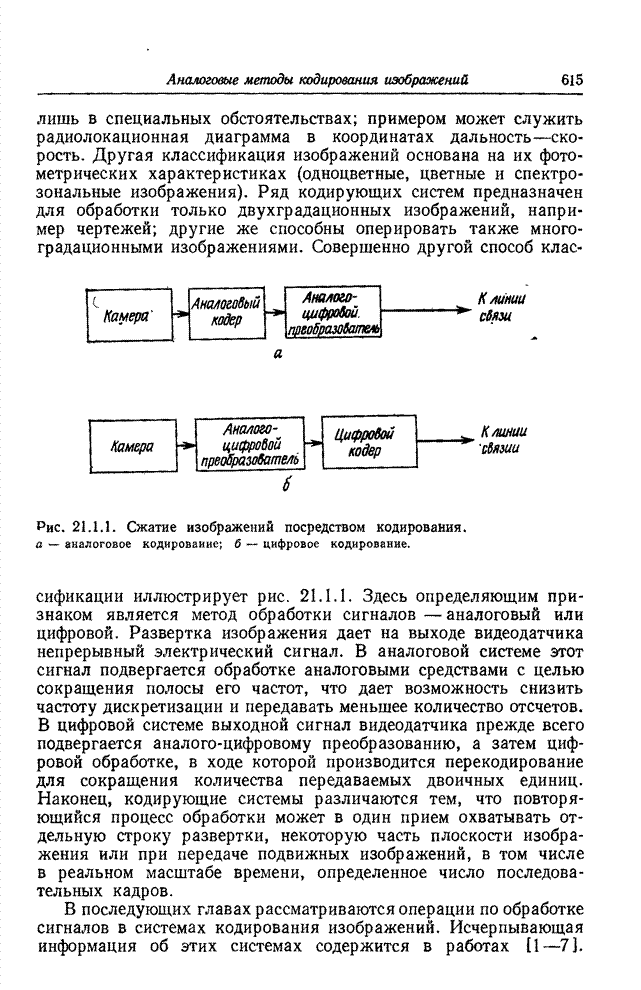
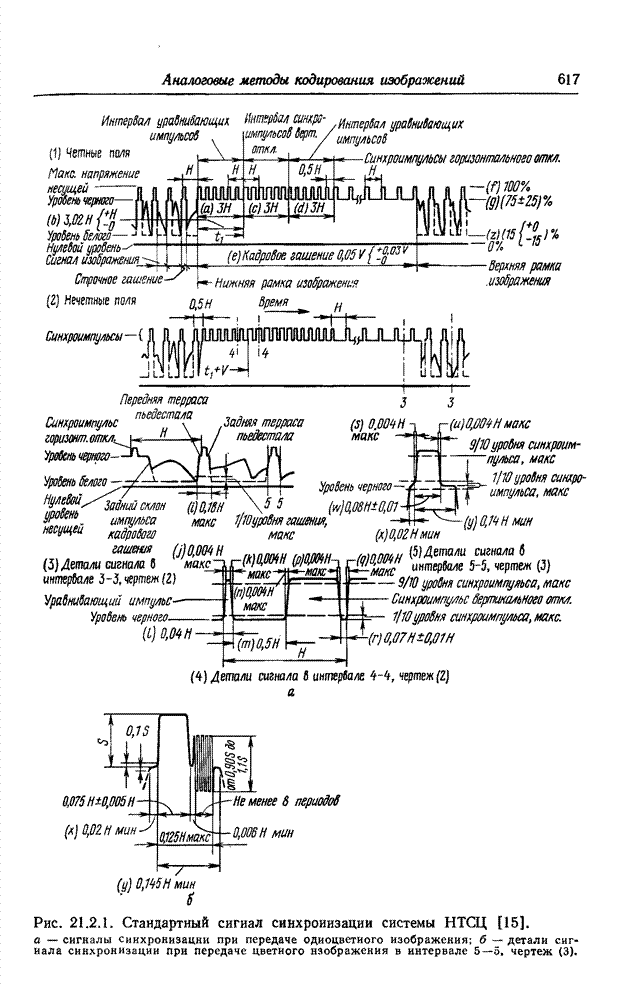
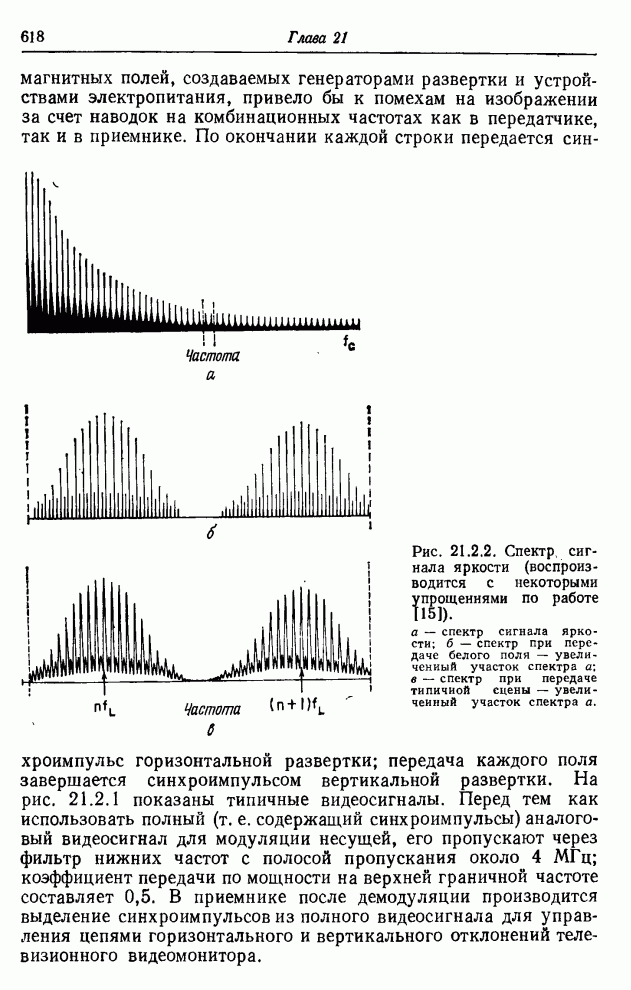
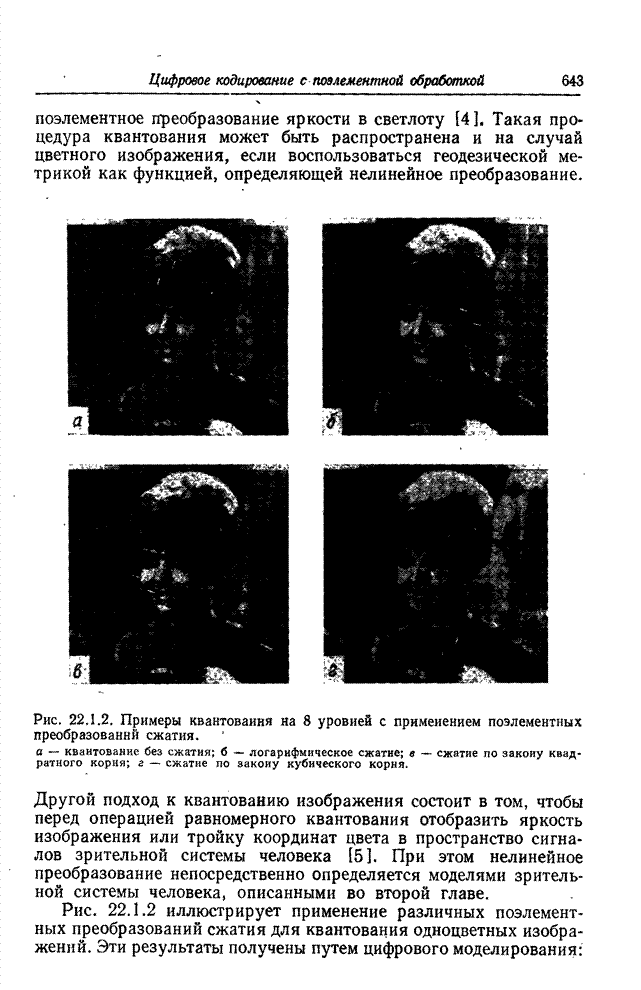
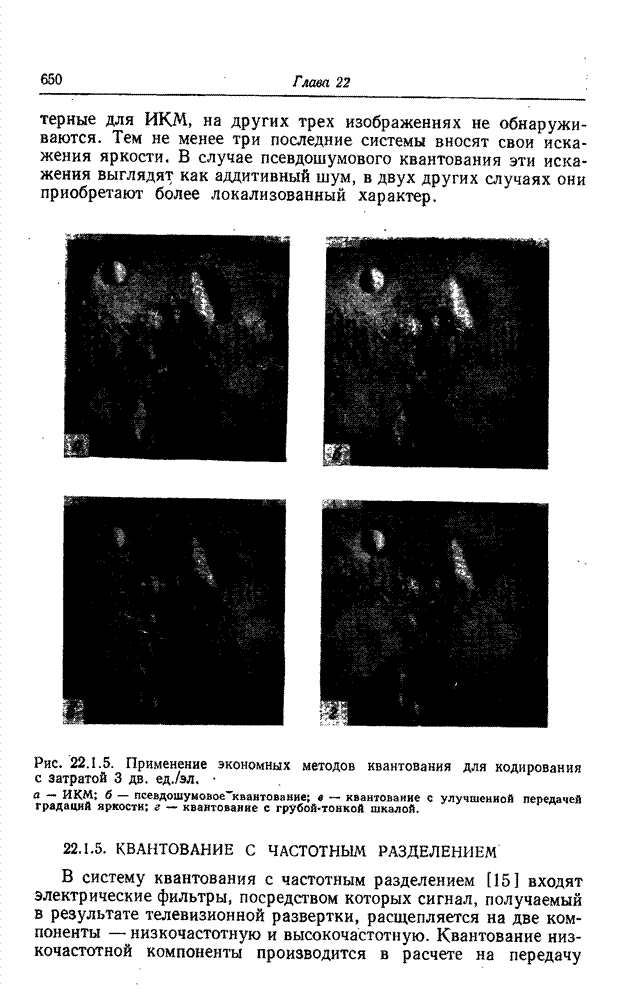
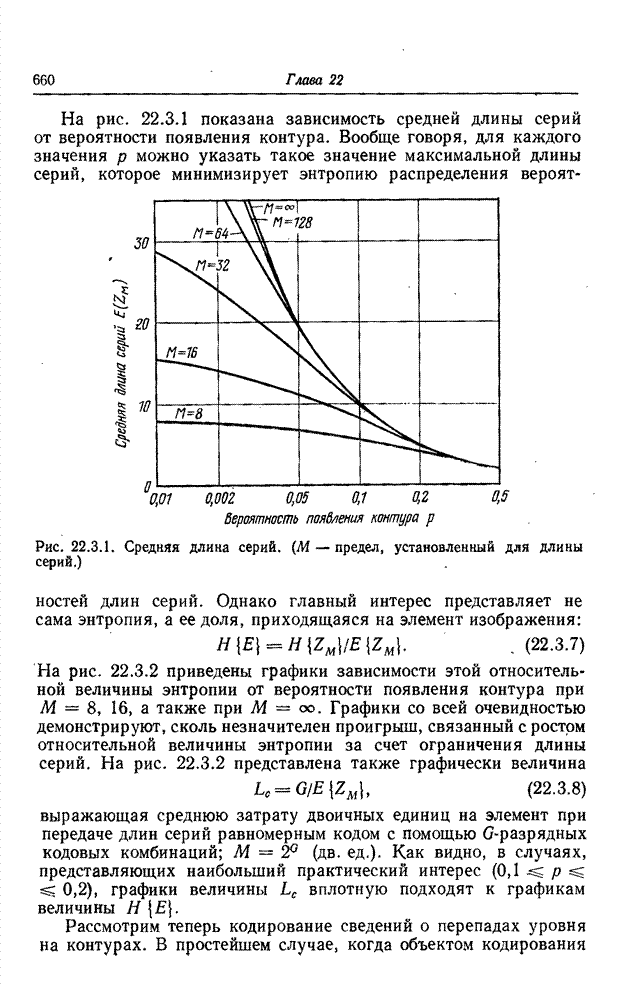
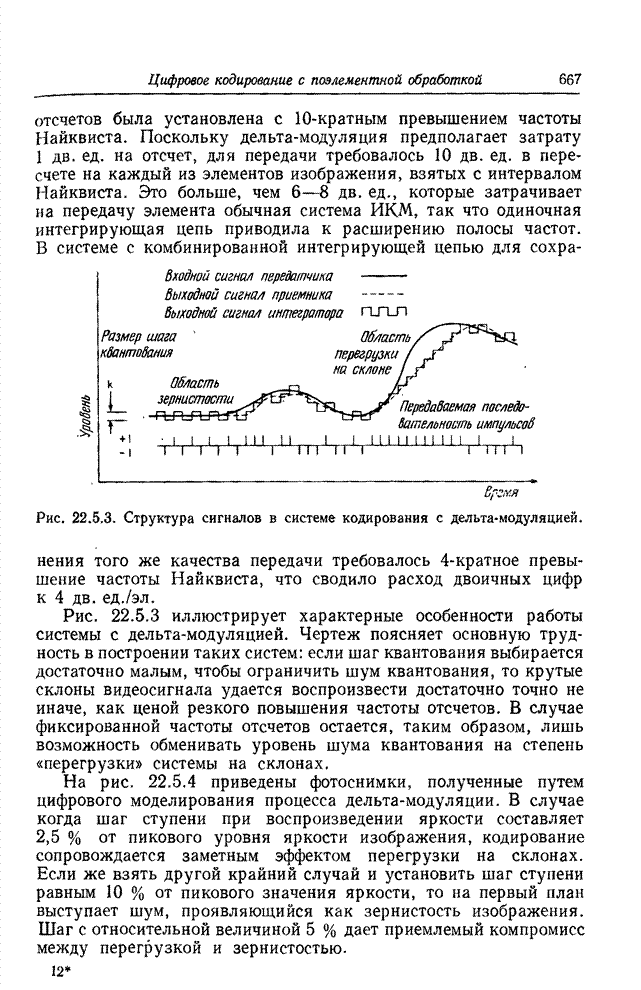
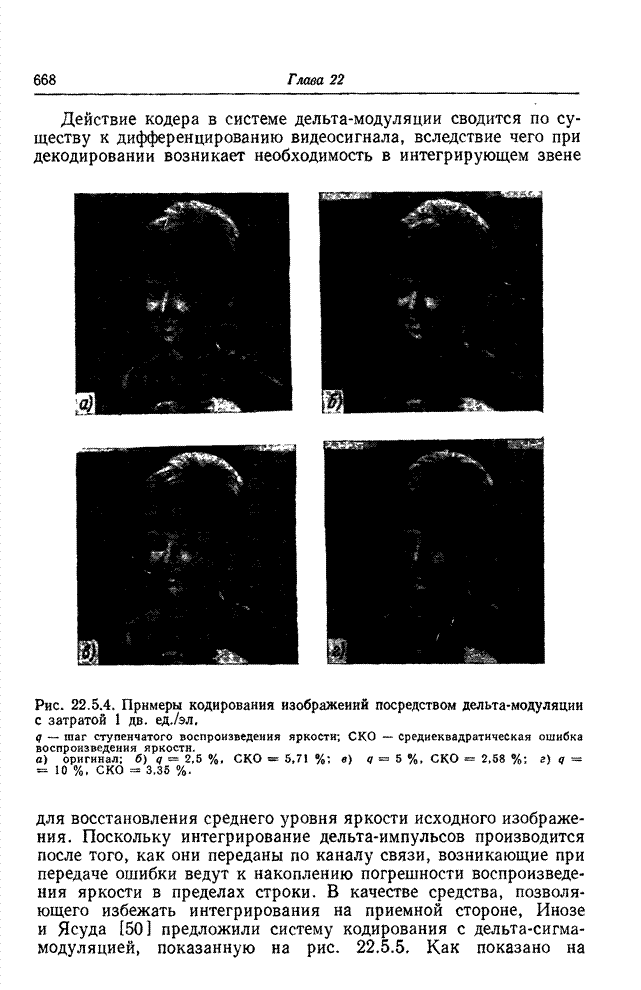
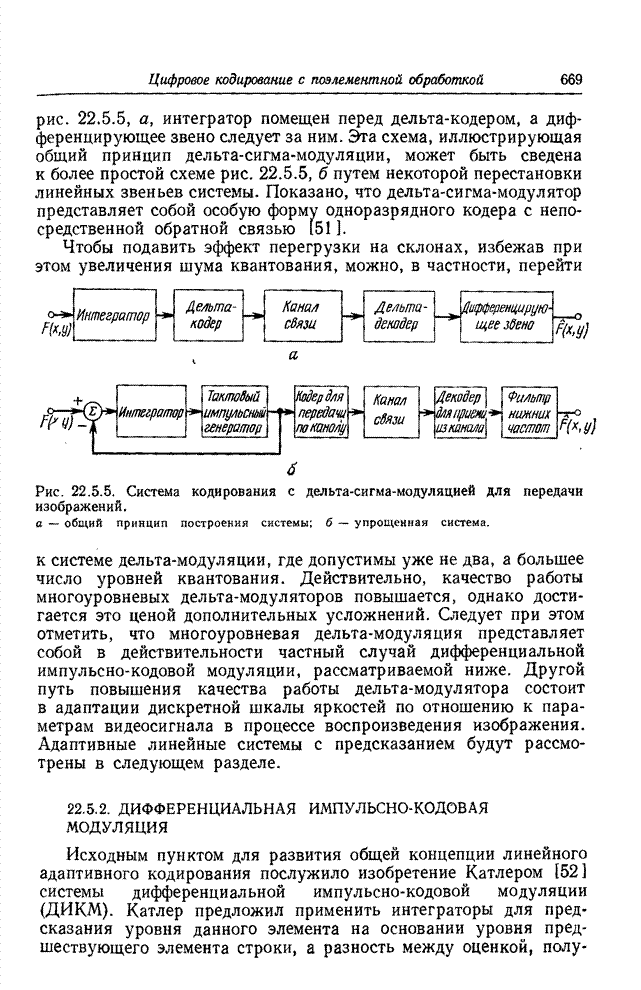
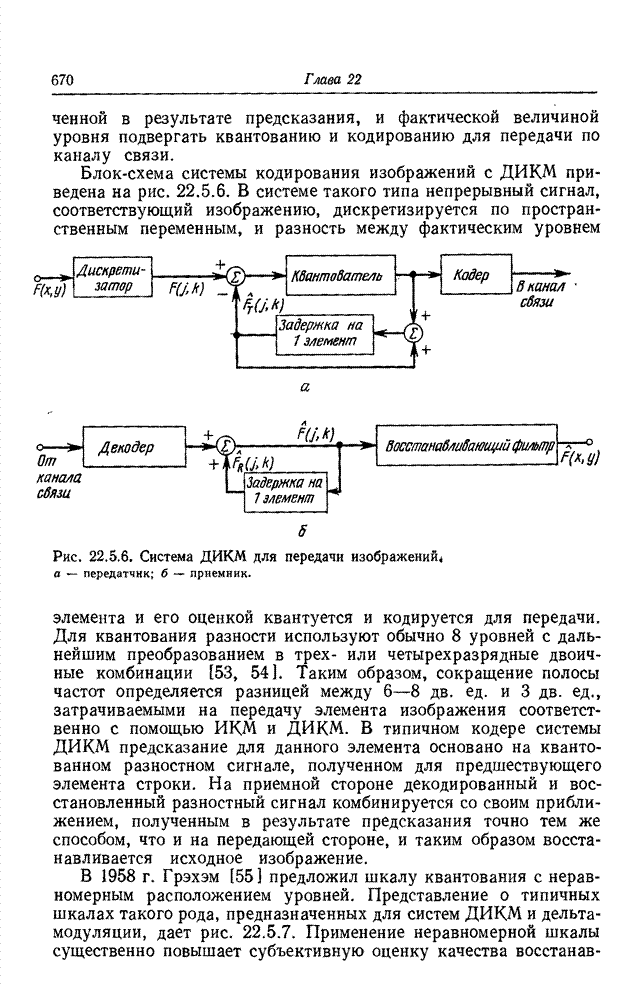
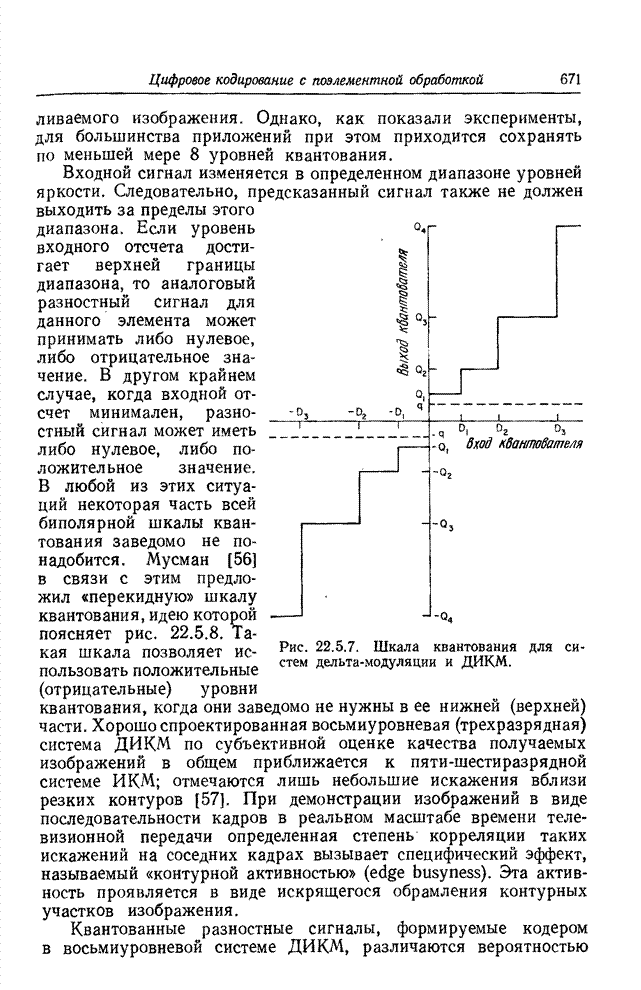
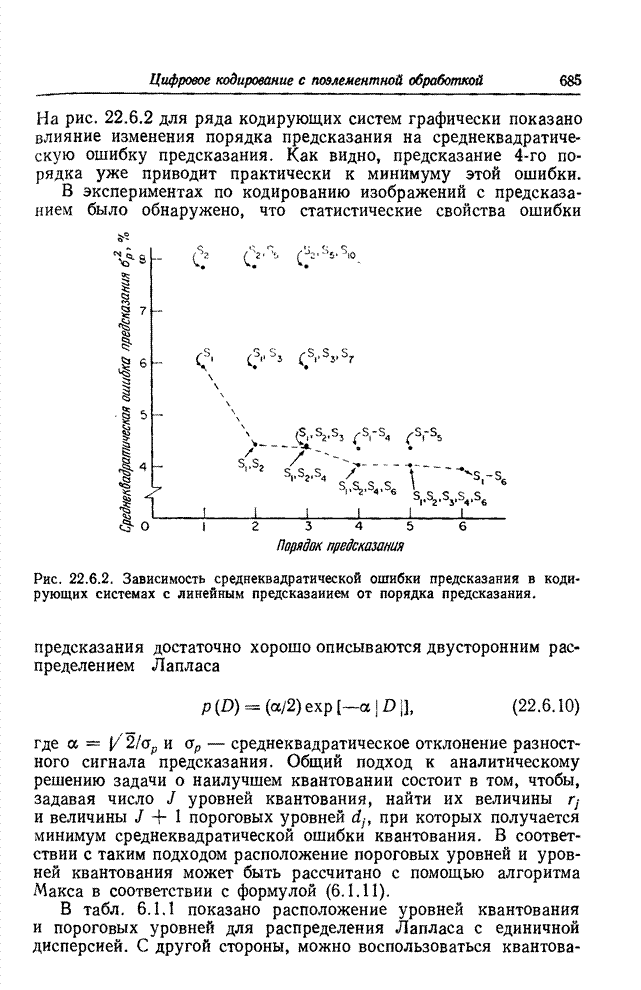
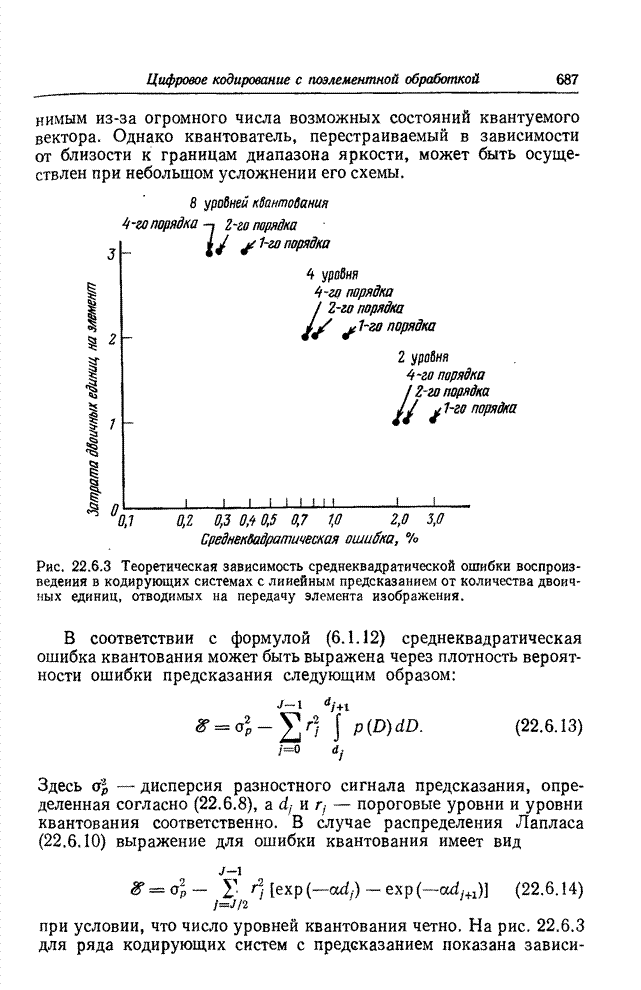
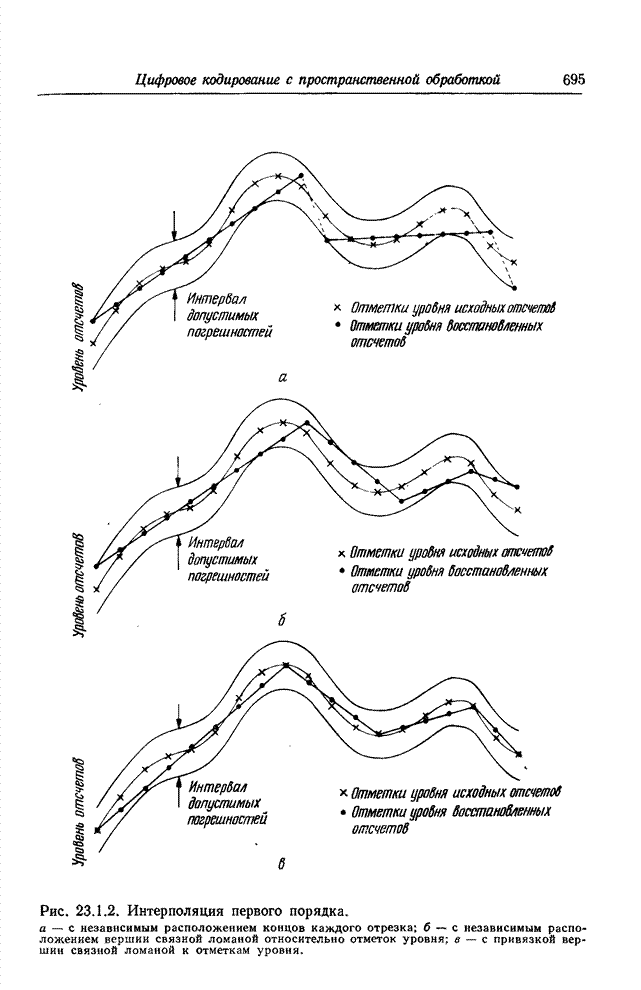
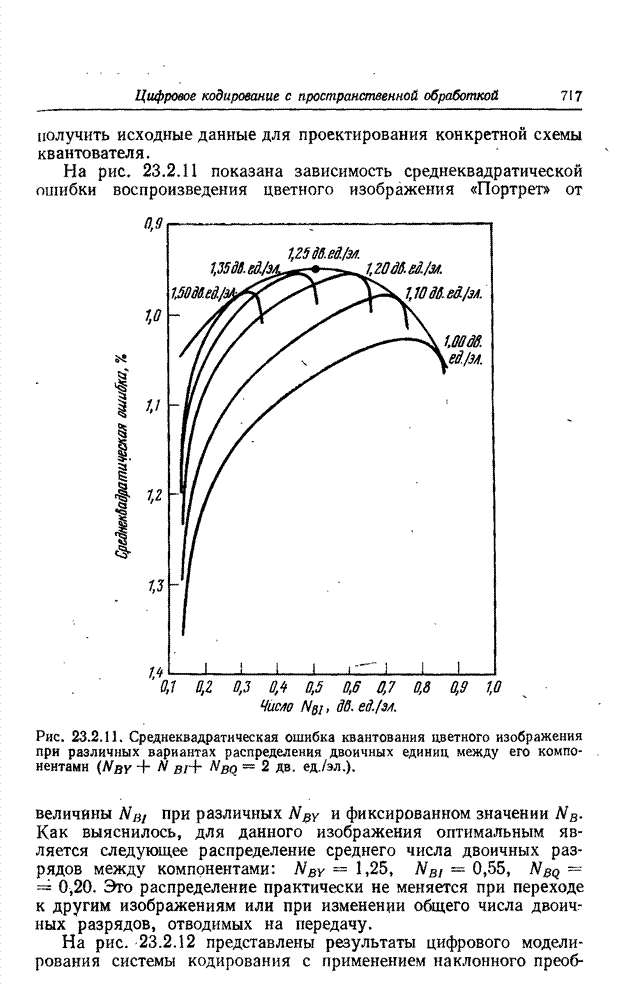
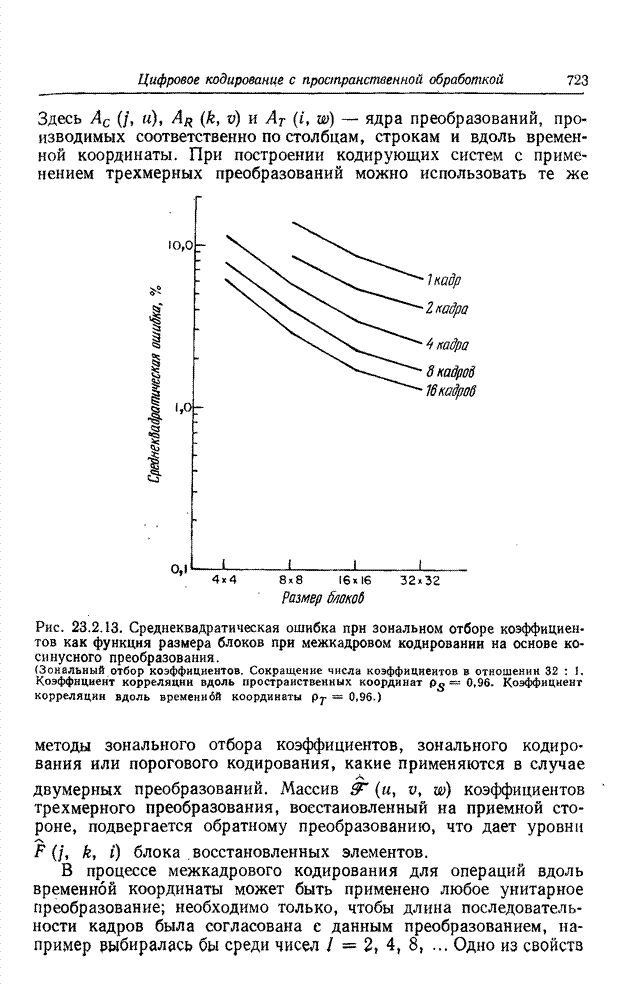
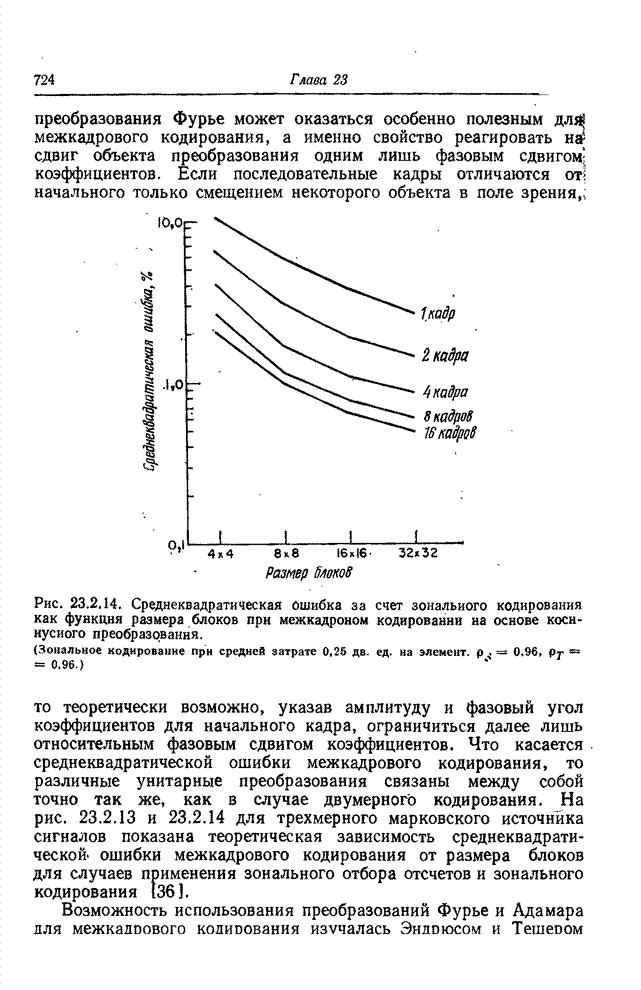
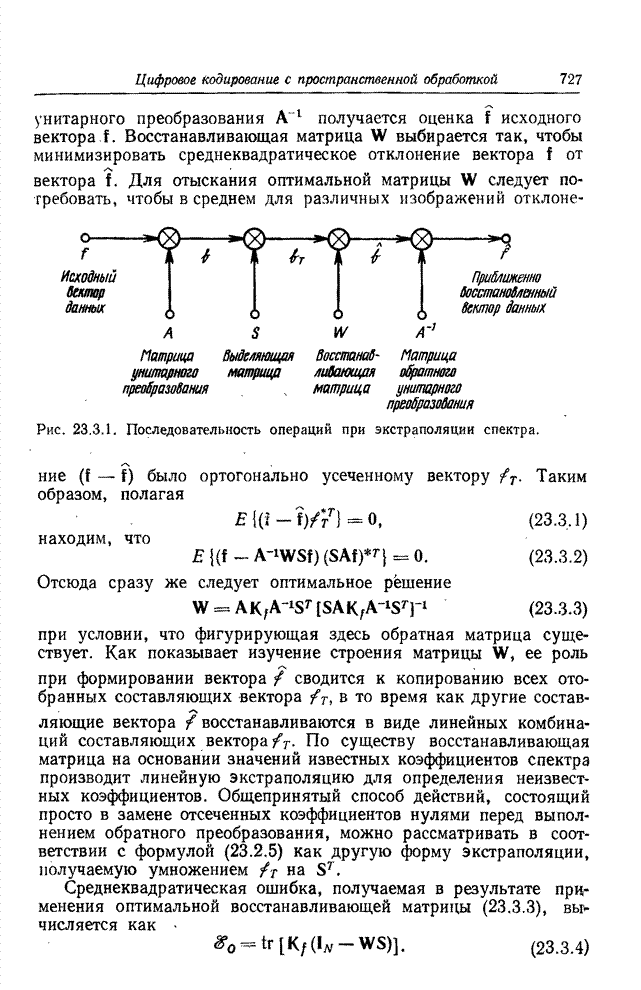
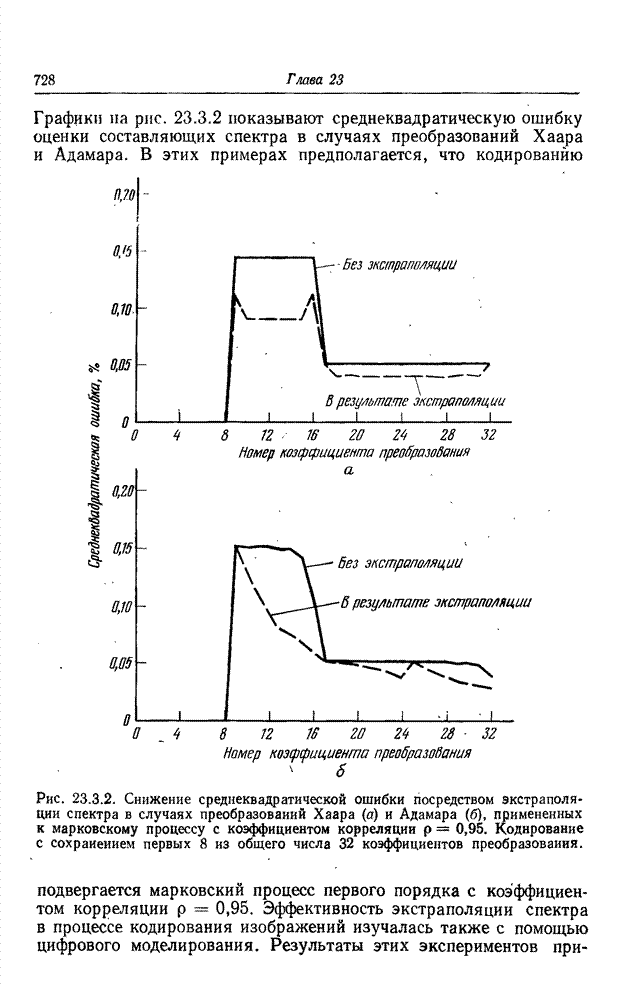
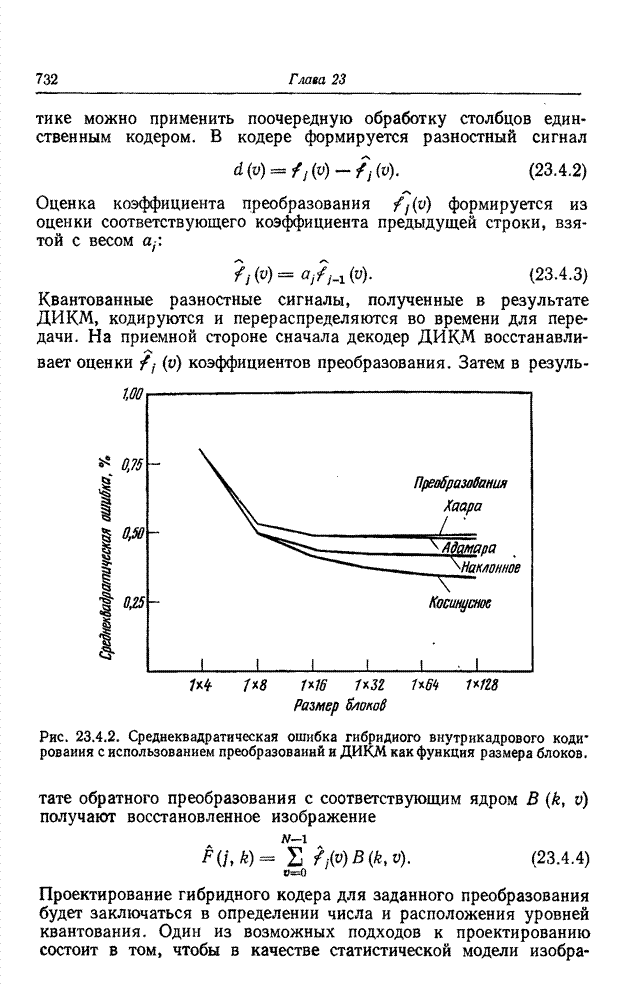
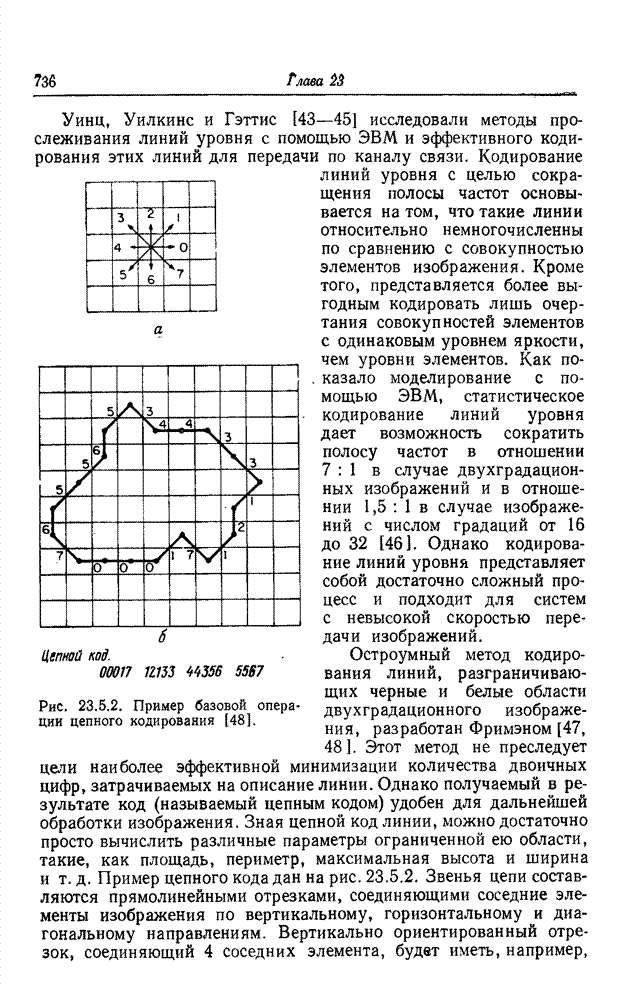
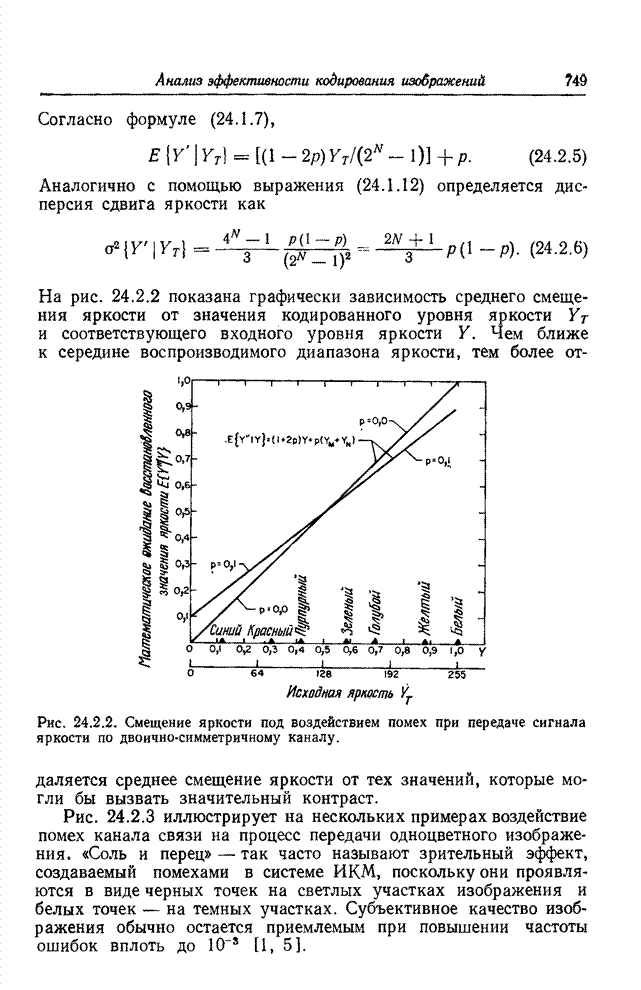
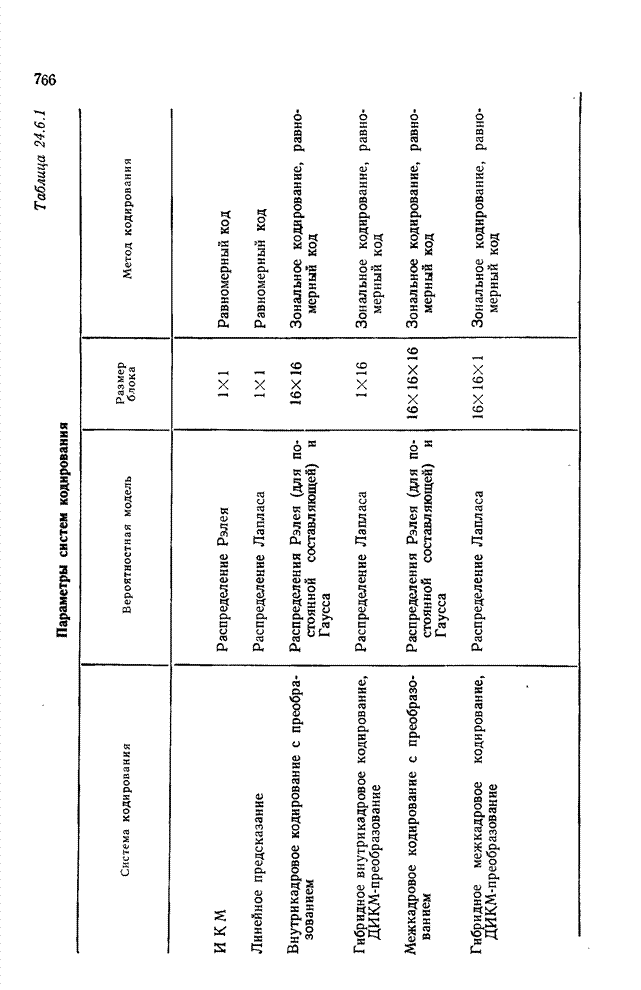
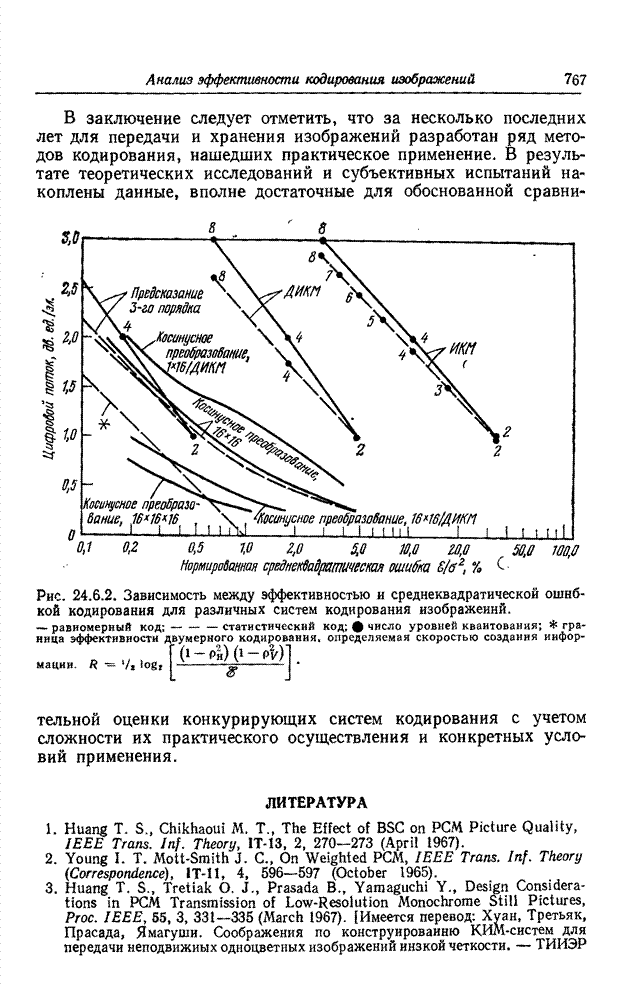
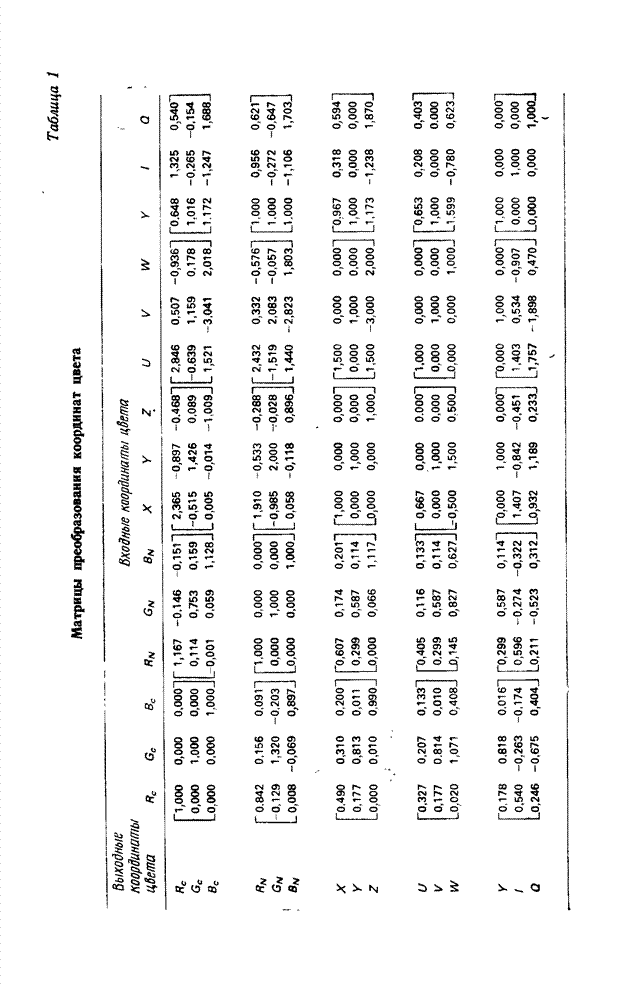
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
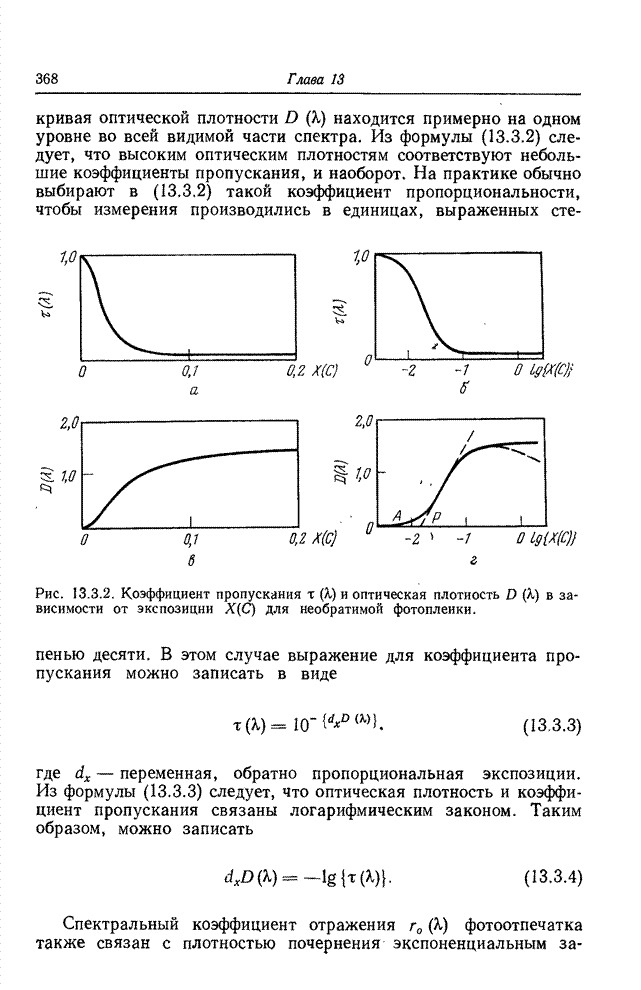
23.2. КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
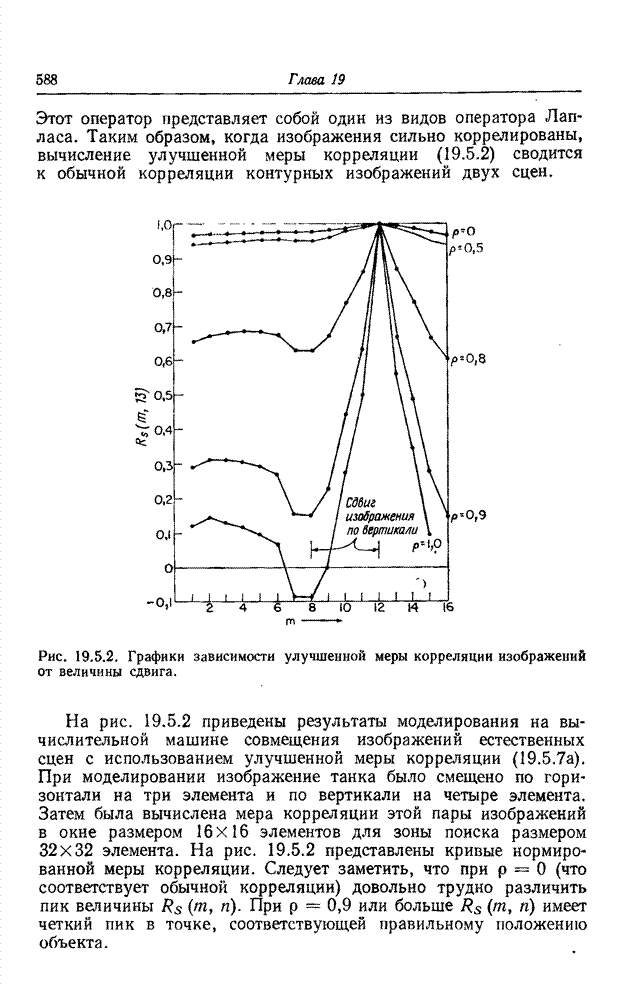
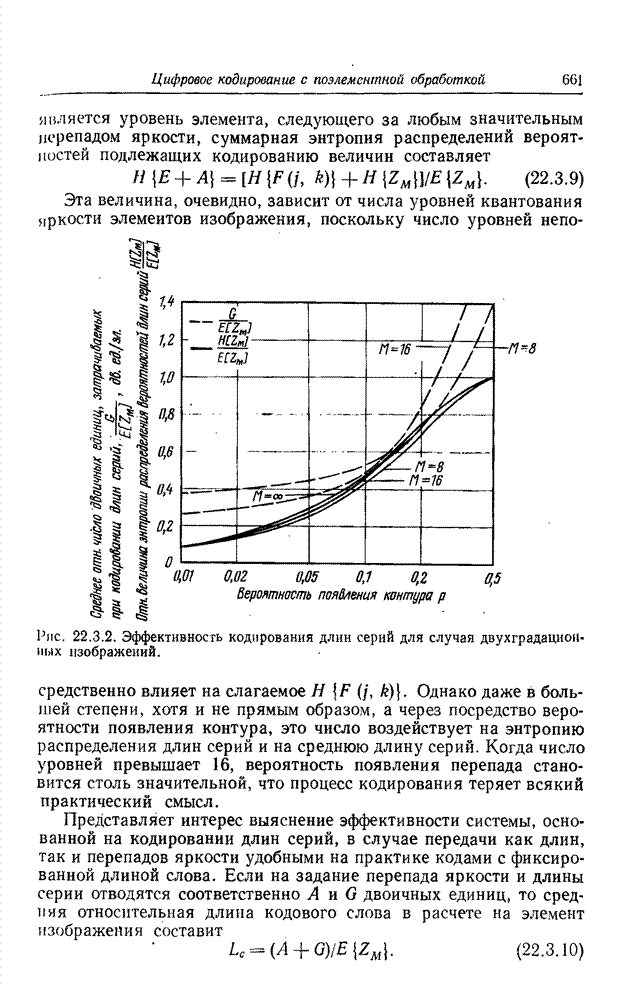
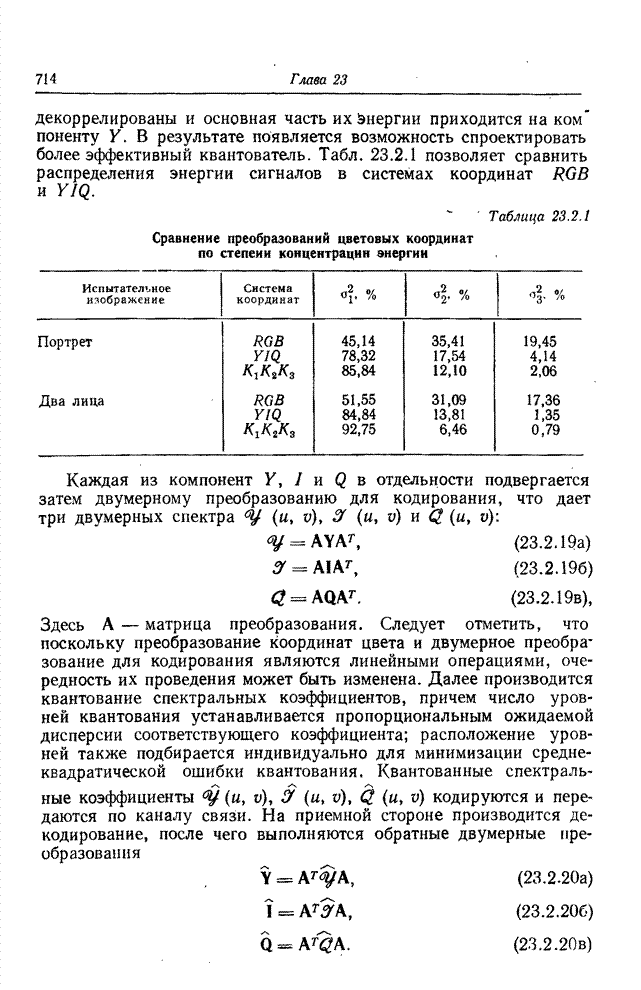
Кодирование на основе преобразования радикально отличается от классических методов кодирования, таких, как ИКМ, кодирование с предсказанием или с интерполяцией, которые применяются непосредственно к видеосигналу. Кодирование на основе преобразования — косвенный метод. Изображение подвергается унитарному математическому преобразованию; полученные в результате коэффициенты преобразования квантуются и кодируются для передачи по каналу связи. Этот метод утвердился как эффективное и практически удобное средство кодирования одноцветных, цветных и спектрозональных изображений, в том числе и в телевизионных системах, действующих в реальном масштабе времени.
23.2.1. КОДИРОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
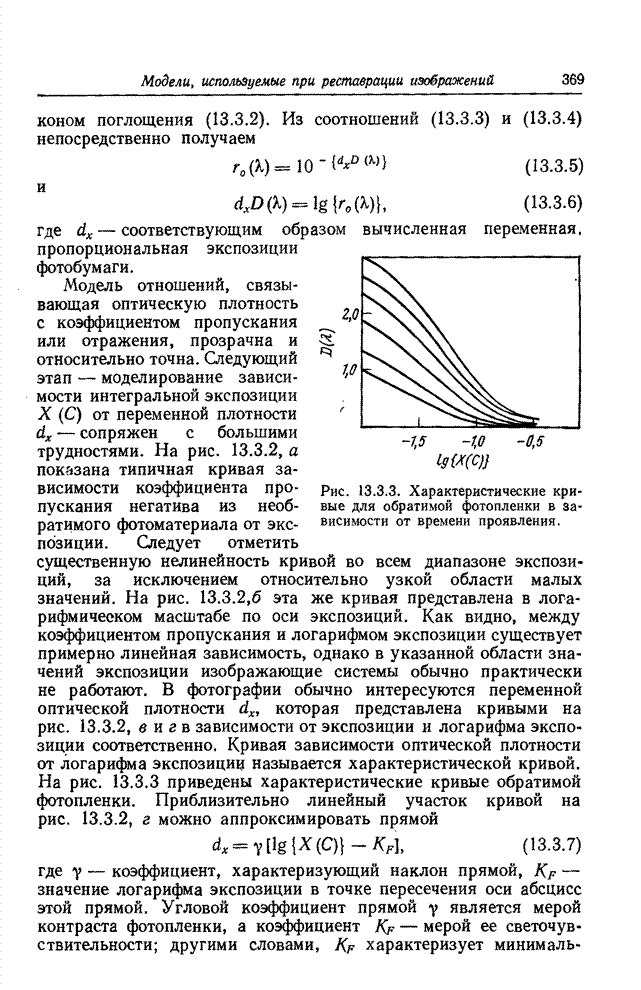
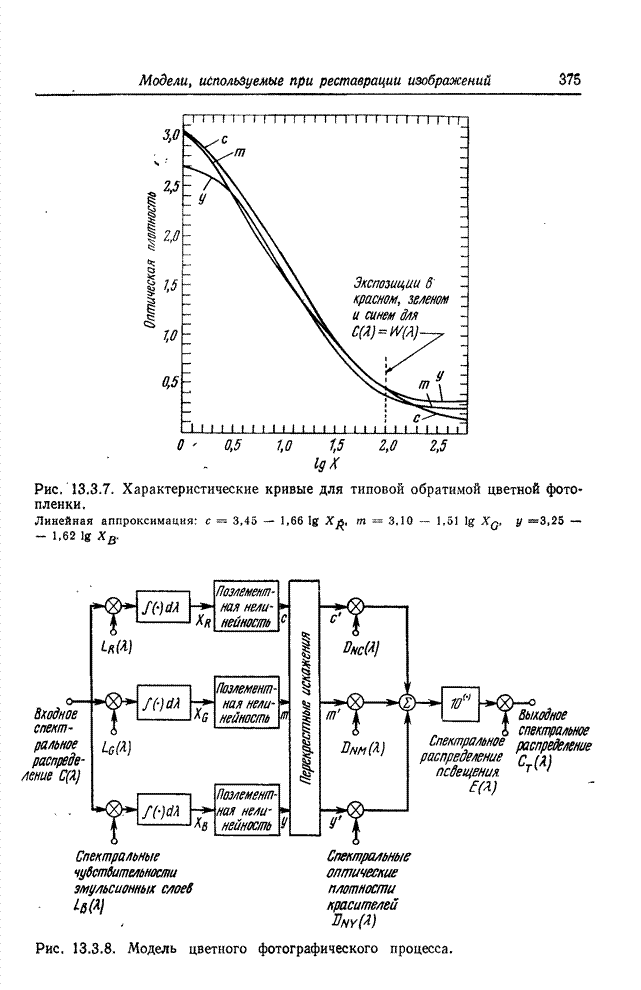
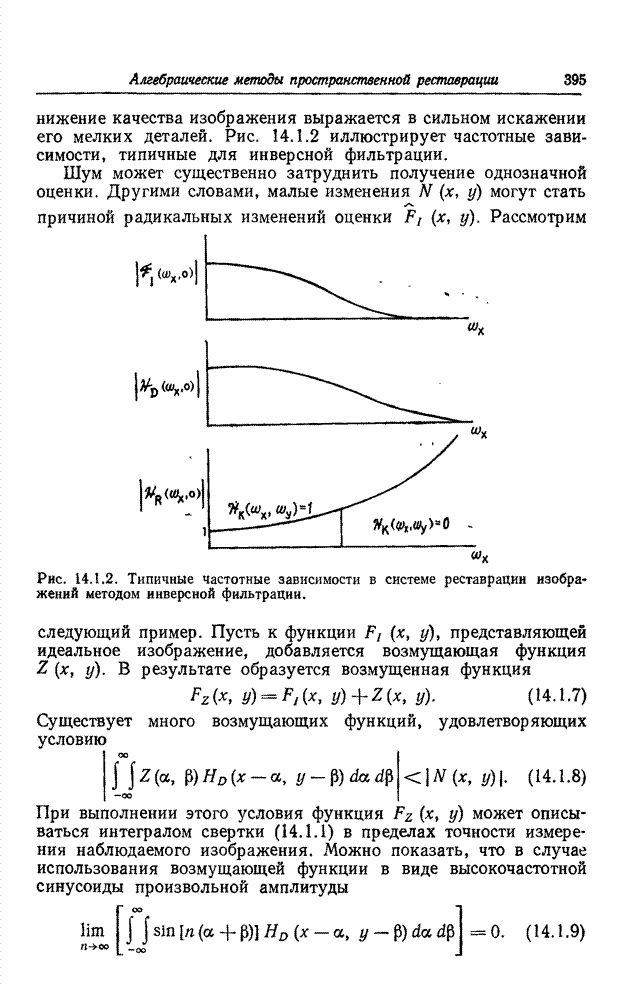
Идея замены одноцветного изображения как непосредственного объекта кодирования коэффициентами его двумерного преобразования Фурье была выдвинута в 1968 г. [11, 12]. Кодирование посредством преобразования Фурье основано на том, что для большинства изображений естественного происхождения значения многих коэффициентов преобразования сравнительно малы. Такие коэффициенты можно часто вообще отбросить или отвести на их кодирование малое число двоичных разрядов без риска сколько-нибудь значительных искажений изображения. В 1969 г. Прэтт, Эндрюс и Кэйн обнаружили, что во многих практических случаях можно резко сократить необходимый объем вычислительных операций, если вместо преобразования Фурье воспользоваться преобразованием Адамара [13—15]. После этого были предприняты исследования по кодированию изображений с применением дискретных преобразований Карунена—Лоэва [16] и Хаара [17, 18]. Преобразование Карунена—Лоэва, известное также как преобразование Хотеллинга, обеспечивает минимальную среднеквадратическую ошибку кодирования, но требует, к сожалению, знания статистических характеристик ансамбля передаваемых изображений, и к тому же для этого преобразования нет быстрого вычислительного алгоритма. С другой стороны, преобразование Хаара характеризуется в высшей степени эффективным алгоритмом вычисления, но приводит, как правило, к сравнительно большим погрешностям кодирования. В 1971 г. Шибата и Эномото [19] предложили так называемое наклонное ортогональное преобразование векторов из 4 или 8 компонент. «Наклонный» базисный вектор, представляющий собой дискретную пилообразную функцию, хорошо подходит для эффективного представления видеосигнала на участках строк с плавным изменением яркости. Вскоре после этого Прэтт, Чен и Уилч разработали обобщенный алгоритм наклонного преобразования векторов большой длины и двумерных массивов [20]. Как показал Ахмед, в применении к изображениям, для которых подходит марковская статистическая модель, косинусное преобразование, имеющее быстрый вычислительный алгоритм, приближается по эффективности к преобразованию Карунена—Лоэва [21]. Синусное преобразование с аналогичными свойствами предложила Джейн [22] Все преимущества кодирования одноцветных изображений с использованием преобразований вытекают в конечном счете из особенностей распределения энергии среди коэффициентов преобразования; благодаря этим особенностям двумерный спектр изображения более удобен для кодирования, чем изображение в исходном пространственном представлении [23]. Вследствие корреляционных связей между элементами естественного изображения энергия его спектра обнаруживает тенденцию концентрироваться в относительно небольшом числе отсчетов. Рис. 23.2.1 дает наглядное представление о двумерных спектрах изображения «Портрет», полученных в результате различных унитарных преобразований. В целях сокращения полосы частот малые по величине спектральные коэффициенты могут быть без существенного ущерба для качества изображения опущены при передаче аналоговыми средствами либо грубо проквантованы при передаче по цифровой линии связи.

Рис. 23.2.Двумерные спектры изображения «Портрет», 256х256 коэффициентов. Фотоснимки воспроизводят значения логарифмов коэффициентов: а - преобразование Фурье; б — преобразование Адамара; в – преобразование Хаара; г – наклонное преобразование; д — косинусное преобразование; е - синусное преобразование.

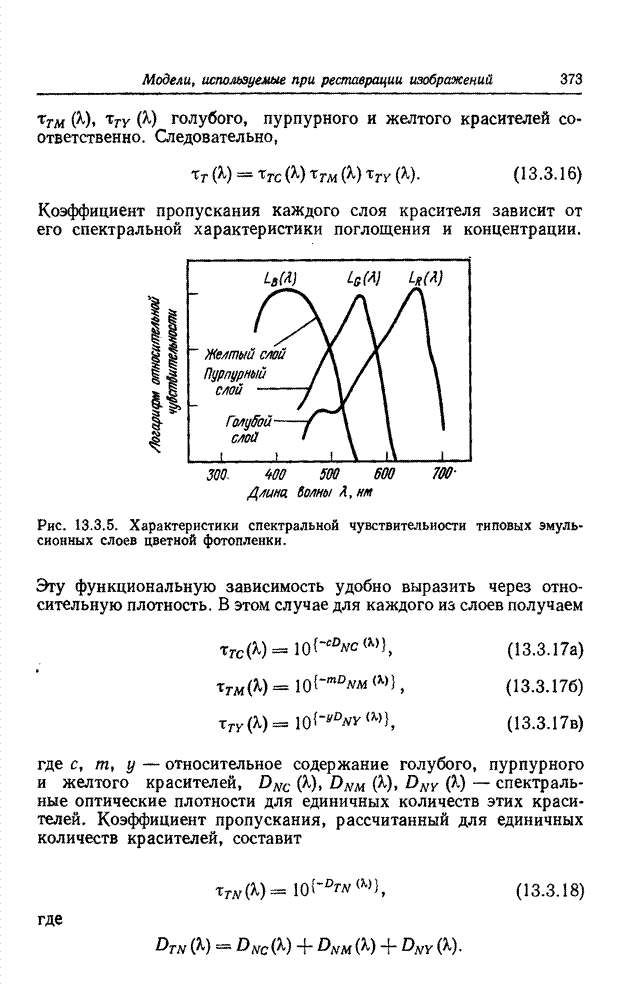
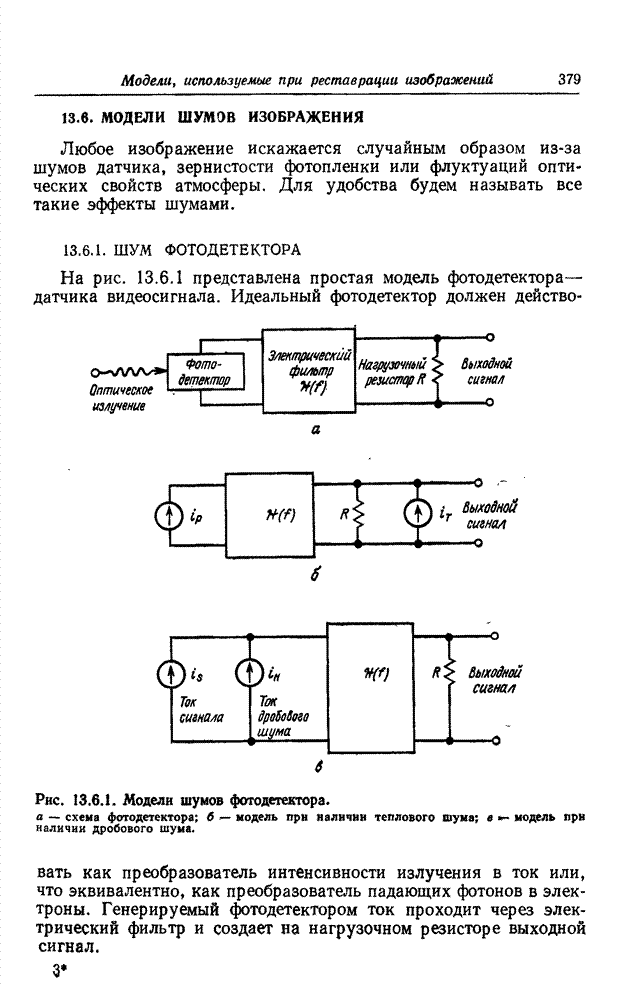
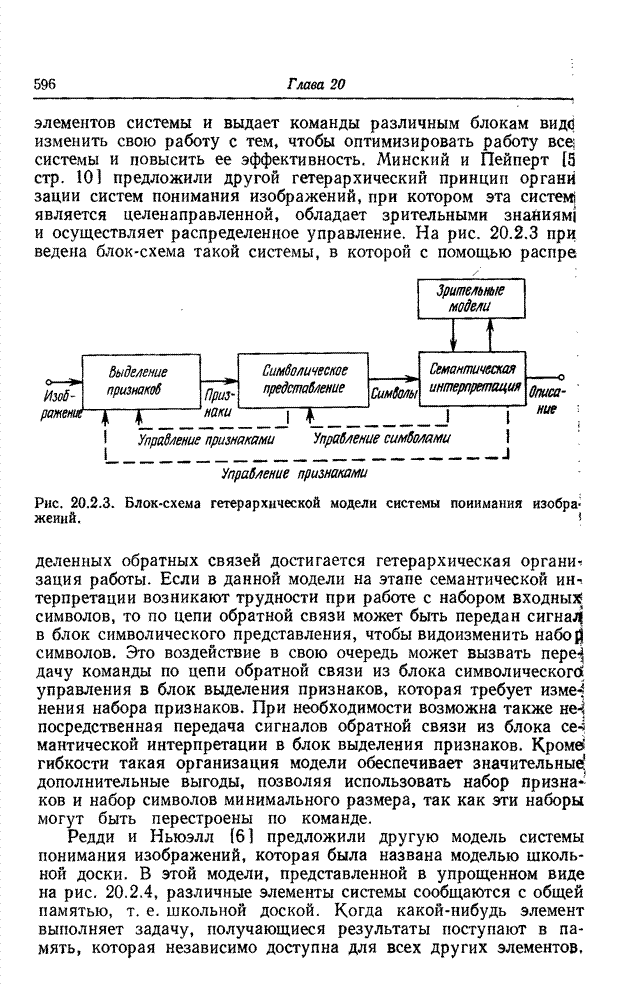
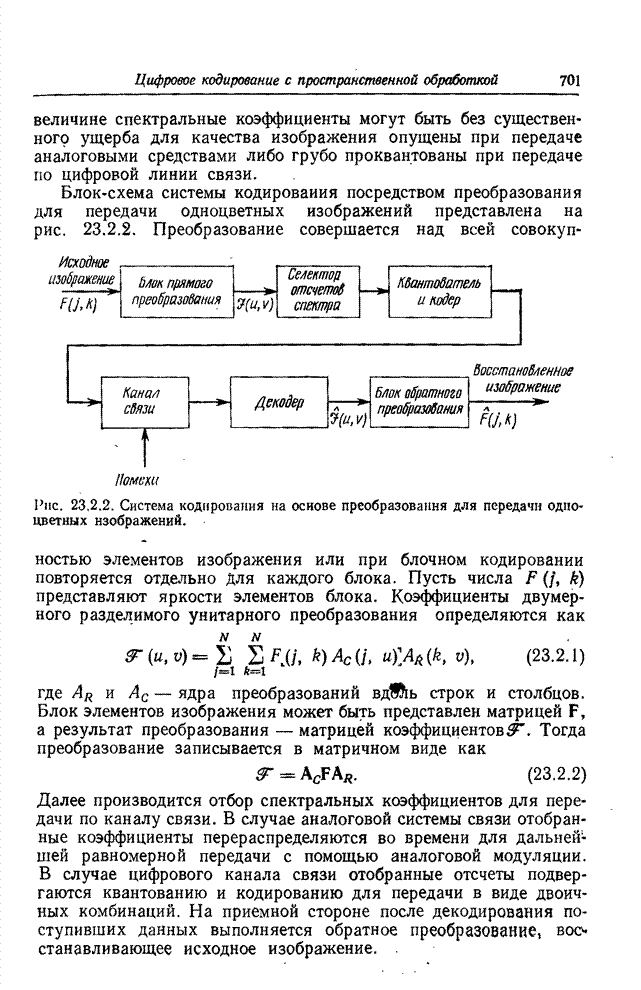
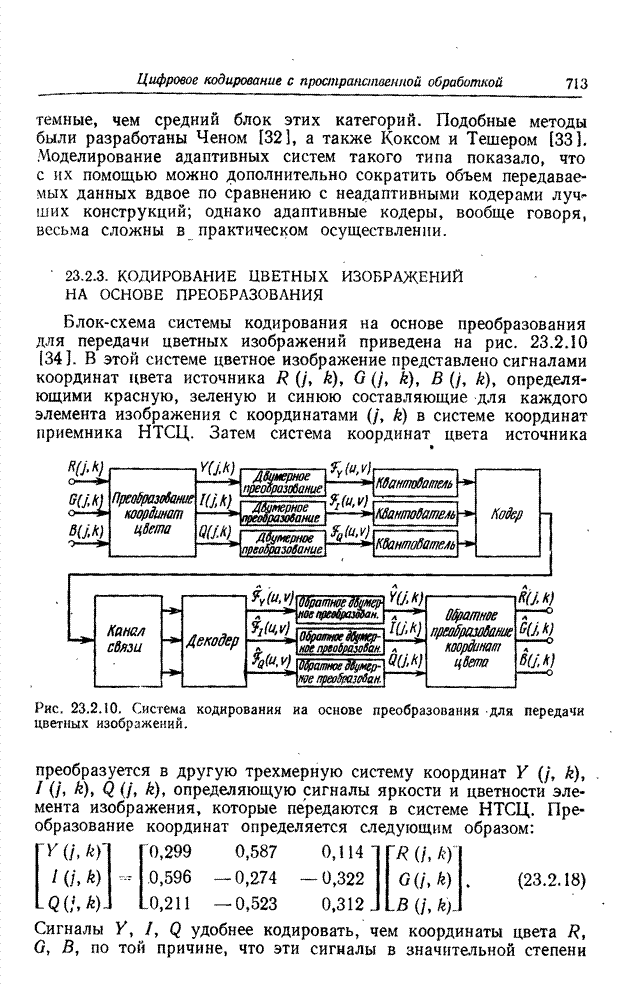
Рис. 23.2.2. Система кодирования на основе преобразования для передачи одноцветных изображений.
Блок-схема системы кодирования посредством
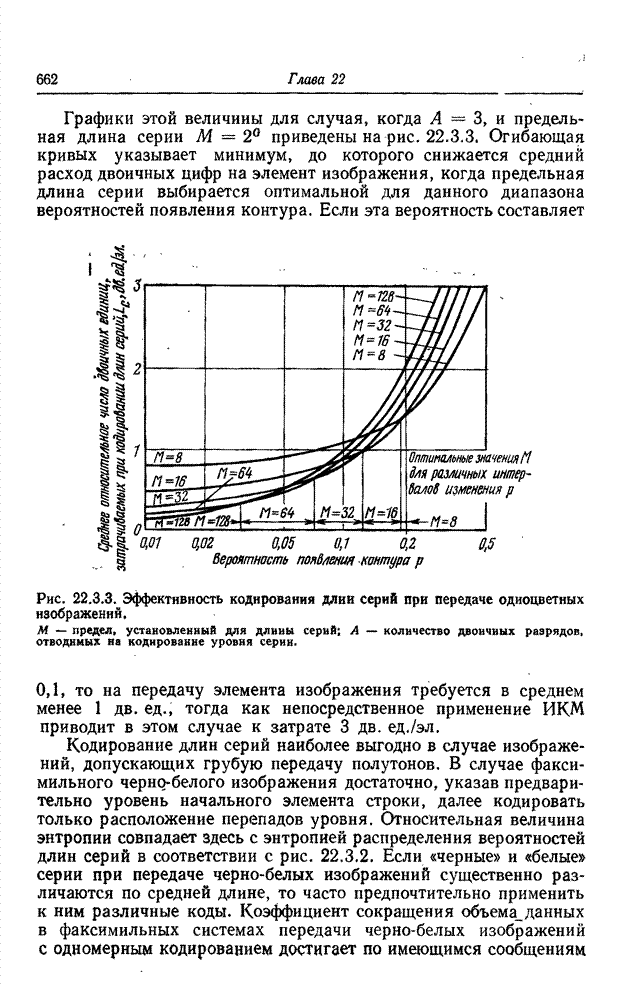
преобразования для передачи одноцветных изображений представлена на рис.
23.2.2. Преобразование совершается над всей совокупностью элементов изображения
или при блочном кодировании повторяется отдельно Для каждого блока. Пусть числа ![]() представляют яркости элементов блока. Коэффициенты
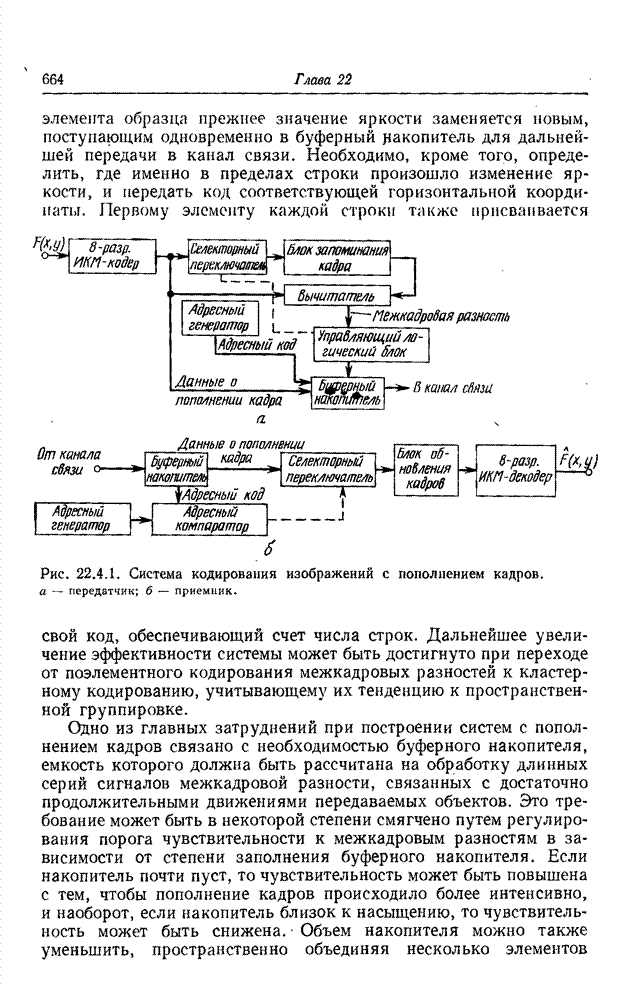
двумерного разделимого унитарного преобразования определяются как
представляют яркости элементов блока. Коэффициенты
двумерного разделимого унитарного преобразования определяются как
 (23.2.1)
(23.2.1)
где ![]() и
и ![]() — ядра преобразований вдоль строк и
столбцов. Блок элементов изображения может быть представлен матрицей
— ядра преобразований вдоль строк и
столбцов. Блок элементов изображения может быть представлен матрицей ![]() , а результат
преобразования — матрицей коэффициентов
, а результат
преобразования — матрицей коэффициентов ![]() . Тогда преобразование записывается в матричном виде
как
. Тогда преобразование записывается в матричном виде
как
![]() (23.2.2)
(23.2.2)
Далее производится отбор спектральных коэффициентов для передачи по каналу связи. В случае аналоговой системы связи отобранные коэффициенты перераспределяются во времени для дальнейшей равномерной передачи с помощью аналоговой модуляции. В случае цифрового канала связи отобранные отсчеты подвергаются квантованию и кодированию для передачи в виде двоичных комбинаций. На приемной стороне после декодирования поступивших данных выполняется обратное преобразование, восстанавливающее исходное изображение.
Существуют два способа отбора спектральных коэффициентов: зональный и пороговый [24]. Первый из них состоит в выделении совокупности коэффициентов, занимающих некоторые заранее очерченные, фиксированные области спектра, обычно соответствующие низкочастотным составляющим. По аналоговым линиям связи передаются значения коэффициентов, попавшие в зону отбора. При передаче по цифровым линиям связи значения отобранных коэффициентов квантуются и им присваиваются кодовые комбинации. Число уровней квантования берется пропорционально ожидаемой дисперсии соответствующего коэффициента. Второй способ отбора сохраняет лишь те коэффициенты, величина которых превышает заранее установленный порог. В связи с необходимостью сообщать при этом данные о расположении отобранных коэффициентов пороговый отбор применяется только для цифровой передачи.
Зональный отбор коэффициентов
Процесс зонального отбора в случае разделения спектра
на две зоны удобно описывать с помощью селекторной функции ![]() , принимающей значение 1 в
области расположения передаваемых спектральных коэффициентов и значение 0 за
пределами этой области. Восстановленное изображение будет теперь описываться
числами
, принимающей значение 1 в
области расположения передаваемых спектральных коэффициентов и значение 0 за
пределами этой области. Восстановленное изображение будет теперь описываться
числами
![]() (23.2.3)
(23.2.3)
Область передаваемых спектральных коэффициентов может
иметь различную конфигурацию, например прямоугольную, эллиптическую или
треугольную. Если следовать критерию среднеквадратической ошибки
воспроизведения, то, согласно теоретическим и экспериментальным исследованиям
[24], нужно придать
![]() значение 1 для тех коэффициентов,
которые имеют наибольшую дисперсию.
значение 1 для тех коэффициентов,
которые имеют наибольшую дисперсию.
Для теоретического анализа процесса зонального отбора
представим совокупность элементов всего изображения или его блока в виде ![]() -компонентного вектора
-компонентного вектора ![]() , рассматриваемого как реализация
случайного процесса с нулевым средним и известной ковариационной матрицей
, рассматриваемого как реализация
случайного процесса с нулевым средним и известной ковариационной матрицей ![]() [25]. Этот вектор
подвергается линейному преобразованию, заданному матрицей
[25]. Этот вектор
подвергается линейному преобразованию, заданному матрицей ![]() размера
размера ![]() .
. ![]() -компонентный вектор
-компонентный вектор ![]() обозначает результат одномерного
преобразования вектора
обозначает результат одномерного
преобразования вектора ![]() :
:
![]() (23.2.4)
(23.2.4)
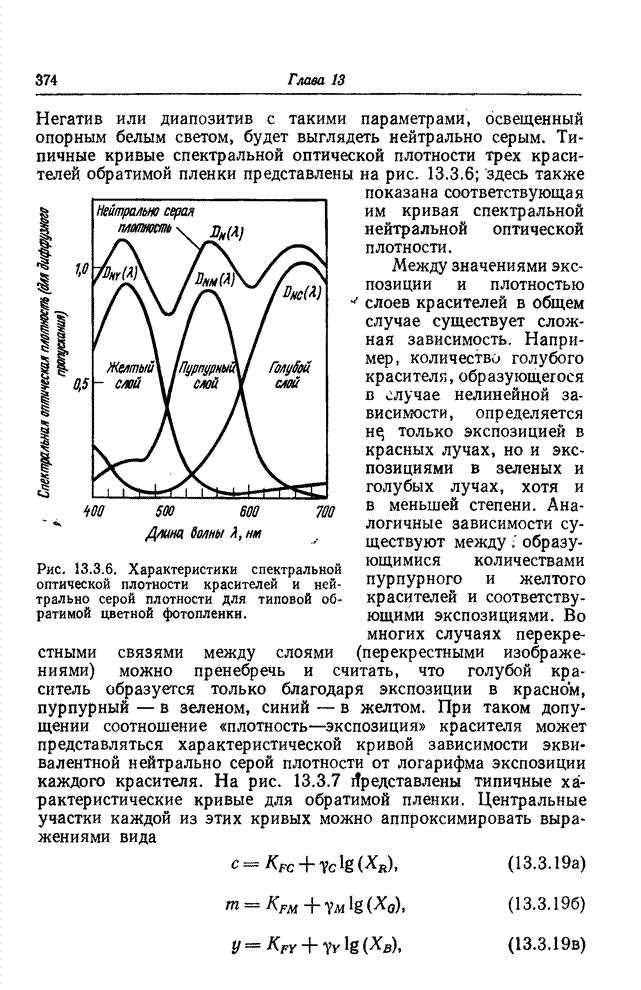
На рис. 23.2.3 приведена схема процесса вычисления и
отбора спектральных коэффициентов. Вектор![]() , состоящий из всех спектральных
компонент, подвергается воздействию матрицы
, состоящий из всех спектральных
компонент, подвергается воздействию матрицы ![]() размера
размера ![]()
![]() , выделяющей определенные компоненты вектора
, выделяющей определенные компоненты вектора ![]() . В результате
получается
. В результате
получается ![]() -компонентный
вектор
-компонентный
вектор ![]() . Матрица
. Матрица ![]() содержит только единицы и нули, и ее
единичный элемент с номером
содержит только единицы и нули, и ее
единичный элемент с номером ![]() переводит
переводит ![]() -ю компоненту вектора
-ю компоненту вектора ![]() в
в ![]() -ю компоненту вектора
-ю компоненту вектора ![]() . В кодирующей
системе типа показанной на рис. 23.2.3 вектор
. В кодирующей
системе типа показанной на рис. 23.2.3 вектор ![]() умножается затем на матрицу
умножается затем на матрицу ![]() размера
размера ![]() , в результате чего отобранным компонентам, составлявшим
вектор
, в результате чего отобранным компонентам, составлявшим
вектор ![]() ,
возвращаются их прежние номера, а все остальные компоненты заменяются нулями.
В конечном счете операция
,
возвращаются их прежние номера, а все остальные компоненты заменяются нулями.
В конечном счете операция ![]() лишь заменяет ненужные компоненты
вектора
лишь заменяет ненужные компоненты
вектора ![]() нулями.
Наконец, обратное унитарное преобразование
нулями.
Наконец, обратное унитарное преобразование ![]() дает восстановленный сигнал
дает восстановленный сигнал
![]() (23.2.5)
(23.2.5)

Рис. 23.2.3. Последовательность операций при зональном кодировании спектра.
Среднеквадратическое отклонение восстановленного сигнала от исходного равно
![]() (23.2.6)
(23.2.6)
Подстановка выражения (23.2.5) в (23.2.6) дает
![]() (23.2.7а)
(23.2.7а)
или
![]() (23.2.7б)
(23.2.7б)
если учесть, что в случае унитарных матриц связь между
корреляционной матрицей ![]() в пространственной области и корреляционной
матрицей
в пространственной области и корреляционной
матрицей ![]() в
спектральной области дается соотношением
в
спектральной области дается соотношением
![]() . (23.2.8)
. (23.2.8)
Так как ![]() , то нетрудно показать, что
, то нетрудно показать, что
![]() (23.2.9)
(23.2.9)

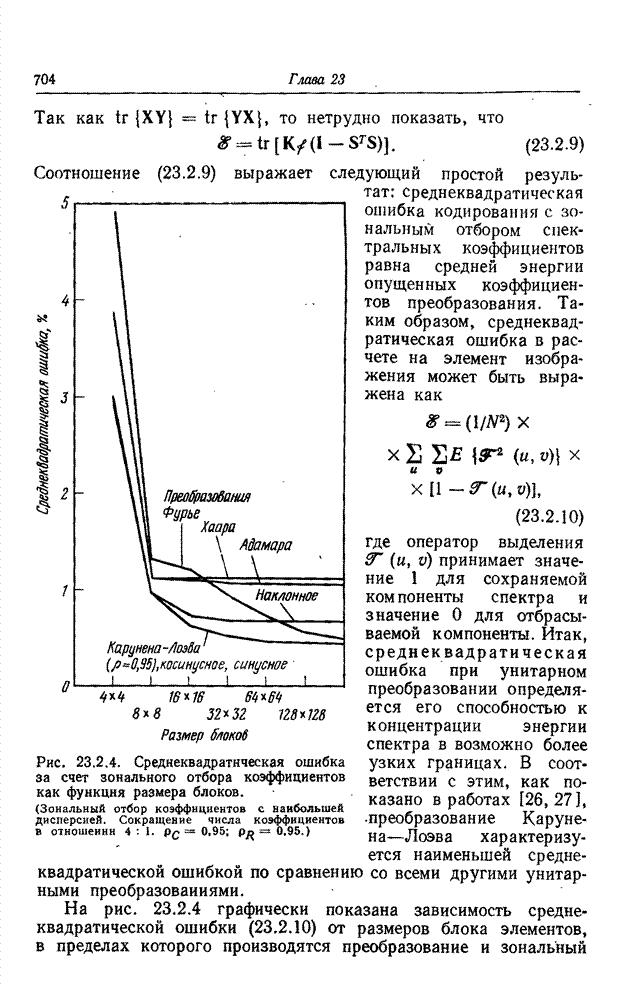
Рис.
23.2.4. Среднеквадратическая ошибка за счет зонального отбора коэффициентов как
функция размера блоков. (Зональный
отбор
коэффициентов с
наибольшей дисперсией.
Сокращение числа коэффициентов в отношении 4:1.
![]() ;
; ![]() .)
.)
Соотношение (23.2.9) выражает следующий простой результат: среднеквадратическая ошибка кодирования с зональным отбором спектральных коэффициентов равна средней энергии опущенных коэффициентов преобразования. Таким образом, среднеквадратическая ошибка в расчете на элемент изображения может быть выражена как
![]() , (23.2.10)
, (23.2.10)
где оператор выделения ![]() принимает значение 1 для
сохраняемой компоненты спектра и значение 0 для отбрасываемой компоненты.
Итак, среднеквадратическая ошибка при унитарном преобразовании определяется
его способностью к концентрации энергии спектра в возможно более узких
границах. В соответствии с этим, как показано в работах [26, 27], преобразование
Карунена—Лоэва характеризуется наименьшей среднеквадратической ошибкой по
сравнению со всеми другими унитарными преобразованиями.
принимает значение 1 для
сохраняемой компоненты спектра и значение 0 для отбрасываемой компоненты.
Итак, среднеквадратическая ошибка при унитарном преобразовании определяется
его способностью к концентрации энергии спектра в возможно более узких
границах. В соответствии с этим, как показано в работах [26, 27], преобразование
Карунена—Лоэва характеризуется наименьшей среднеквадратической ошибкой по
сравнению со всеми другими унитарными преобразованиями.

Рис. 23.2.5. Примеры кодирования с преобразованием блоков размером 16X16 элементов при зональном отборе отсчетов. Сокращение числа коэффициентов в отношении 4: 1.
а — преобразование Фурье; б — преобразование Адамара; о — преобразование Хаара; г — наклонное преобразование; д — косинусное преобразовании; е — преобразование Карунена—Лоэва.
На рис. 23.2.4 графически показана зависимость среднеквадратической ошибки (23.2.10) от размеров блока элементов, в пределах которого производятся преобразование и зональный отбор. Статистической моделью изображений служит при этом двумерный марковский процесс первого порядка. Отбиралось 25% коэффициентов, имеющих наибольшую дисперсию, а остальные коэффициенты опускались. Из рис. 23.2.4 видно, что наименьшая ошибка получается в случае преобразования Карунена— Лоэва. Для марковского процесса первого порядка практически такая же минимальная ошибка получается в случае четного косинусного преобразования и синусного преобразования. Можно заметить, что увеличение блока элементов сверх размера 16x16 не приводит к дальнейшему существенному снижению среднеквадратической ошибки. Исключением является лишь преобразование Фурье, при котором с увеличением размеров блока ошибка относительно медленно приближается к минимуму, характеризующему преобразование Карунена—Лоэва. На рис. 23.2.5 приведены результаты восстановления изображения по четвертой части спектральных компонент с наибольшей дисперсией, сохраненных в результате зонального отбора после преобразований блоков размером 16x16 элементов. Субъективные оценки качества изображений, получаемых с применением различных преобразований, достаточно хорошо согласуются с оценками среднеквадратической ошибки, приведенными на рис. 23.2.4.
Зональное кодирование
В системе зонального кодирования каждый блок
коэффициентов преобразования разделяется на ряд областей. Для каждой области
устанавливается набор уровней квантования, число которых выбирается
пропорционально средней дисперсии спектральных коэффициентов, принадлежащих
данной области. Если применяется равномерный код, отводящий ![]() двоичных разрядов для любого коэффициента данной
области, то соответствующее число уровней квантования составит
двоичных разрядов для любого коэффициента данной
области, то соответствующее число уровней квантования составит
![]() (23.2.11)
(23.2.11)
Для кодирования изображения потребуется в общей сложности
![]() (23.2.12)
(23.2.12)
двоичных единиц. Число двоичных разрядов ![]() , отводимых на каждый коэффициент, определяется либо в
соответствии с законом логарифма дисперсии (6.2.11), т.e. как
, отводимых на каждый коэффициент, определяется либо в
соответствии с законом логарифма дисперсии (6.2.11), т.e. как
![]() , (23.2.13)
, (23.2.13)
где ![]() обозначает
дисперсию коэффициента преобразования, либо с помощью последовательного
алгоритма распределения двоичных разрядов, описанного в гл. 6. Если для
обозначает
дисперсию коэффициента преобразования, либо с помощью последовательного
алгоритма распределения двоичных разрядов, описанного в гл. 6. Если для ![]() установлена малая величина, то в
результате квантования некоторым коэффициентам будут приписаны нулевые
значения, что равнозначно отсечению таких коэффициентов (подобно тому, как это
происходит при зональном отборе). Типичное распределение двоичных разрядов
между спектральными коэффициентами для блока размером 16x16 элементов показано
на рис. 23.2.6.
установлена малая величина, то в
результате квантования некоторым коэффициентам будут приписаны нулевые
значения, что равнозначно отсечению таких коэффициентов (подобно тому, как это
происходит при зональном отборе). Типичное распределение двоичных разрядов
между спектральными коэффициентами для блока размером 16x16 элементов показано
на рис. 23.2.6.
Оптимальная
шкала квантования, содержащая заданное число уровней, иначе говоря, расположение
пороговых уровней и уровней квантования, при котором получается минимальная
среднеквадратическая ошибка, определяется алгоритмом Макса (см. гл. 6). В
соответствии с формулой (6.1.11) отыскание пороговых уровней ![]() и уровней
квантования
и уровней
квантования ![]() сводится
к совместному решению уравнений
сводится
к совместному решению уравнений
![]() (23.2.14а)
(23.2.14а)
 (23.2.14б)
(23.2.14б)

Рис. 23.2.6. Типичное распределение двоичных единиц при зональном кодировании с преобразованием блоков размером 16X16 элементов; в среднем на элемент отводится 1,5 дв. ед.
где ![]() — плотность вероятности для
коэффициента, соответствующего пространственной частоте
— плотность вероятности для
коэффициента, соответствующего пространственной частоте![]() . Для коэффициента, определяющего постоянную
составляющую в разложении по данному базису, в качестве статистической модели
обычно используют распределение Рэлея (10.12.2). Для остальных коэффициентов
преобразования достаточно точной моделью служит гауссово распределение
(10.12.1). При таком подходе к квантованию и кодированию получается среднеквадратическая
ошибка, соответствующая формуле (6.1.12):
. Для коэффициента, определяющего постоянную
составляющую в разложении по данному базису, в качестве статистической модели
обычно используют распределение Рэлея (10.12.2). Для остальных коэффициентов
преобразования достаточно точной моделью служит гауссово распределение
(10.12.1). При таком подходе к квантованию и кодированию получается среднеквадратическая
ошибка, соответствующая формуле (6.1.12):
 (23.2.15)
(23.2.15)
где ![]() обозначает вероятность того события,
что значение коэффициента преобразования окажется в промежутке между
обозначает вероятность того события,
что значение коэффициента преобразования окажется в промежутке между ![]() -м и соседним
-м и соседним ![]() -м пороговыми
уровнями. Точное решение в замкнутой форме уравнения (23.2.15) найти не
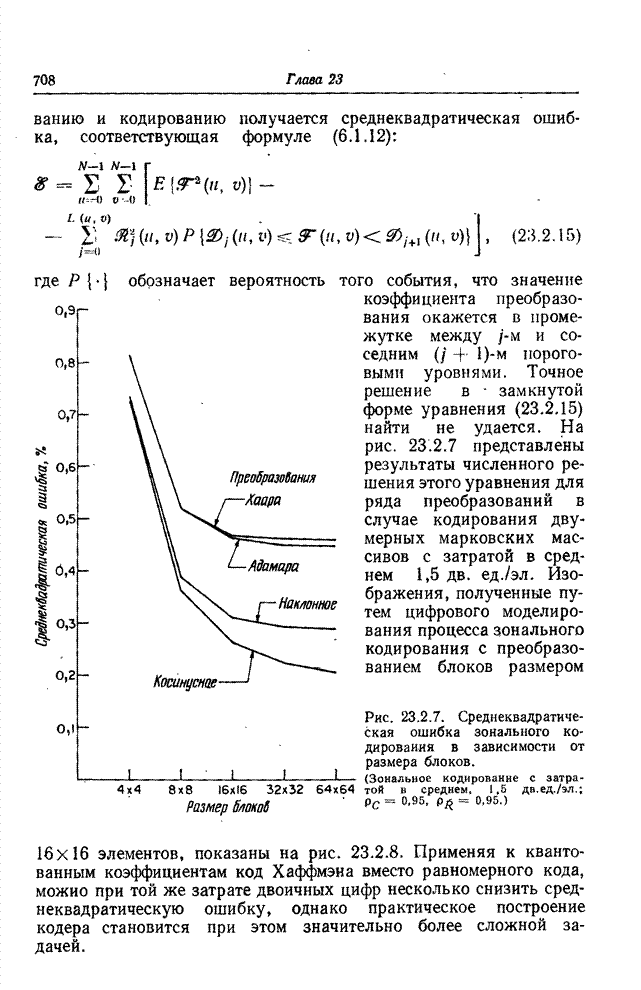
удается. На рис. 23.2.7 представлены результаты численного решения этого
уравнения для ряда преобразований в случае кодирования двумерных марковских
массивов с затратой в среднем 1,5 дв. ед./эл. Изображения, полученные путем
цифрового моделирования процесса зонального кодирования с преобразованием
блоков размером 16x16 элементов, показаны на рис. 23.2.8. Применяя к квантованным
коэффициентам код Хаффмэна вместо равномерного кода, можно при той же затрате
двоичных цифр несколько снизить среднеквадратическую ошибку, однако
практическое построение кодера становится при этом значительно более сложной
задачей.
-м пороговыми
уровнями. Точное решение в замкнутой форме уравнения (23.2.15) найти не
удается. На рис. 23.2.7 представлены результаты численного решения этого
уравнения для ряда преобразований в случае кодирования двумерных марковских
массивов с затратой в среднем 1,5 дв. ед./эл. Изображения, полученные путем
цифрового моделирования процесса зонального кодирования с преобразованием
блоков размером 16x16 элементов, показаны на рис. 23.2.8. Применяя к квантованным
коэффициентам код Хаффмэна вместо равномерного кода, можно при той же затрате
двоичных цифр несколько снизить среднеквадратическую ошибку, однако
практическое построение кодера становится при этом значительно более сложной
задачей.

Рис.
23.2.7. Среднеквадратическая ошибка зонального кодирования в зависимости от
размера блоков. (Зональное
кодирование с затратой
в среднем. 1,5 дв.ед./эл.; ![]() ;
; ![]() .)
.)

Рис. 23.2.8. Примеры зонального кодирования на основе преобразования блоков размером 16х16 элементов при средней затрате 1,5 дв. ед./эл.: а — оригинал; б — преобразование Адамара; в — преобразование Хаара; г — наклонное преобразование; д — косинусное преобразование; с — преобразование Карунена—Лоэва.
Пороговое кодирование
В системе порогового кодирования для всех спектральных коэффициентов, превышающих по величине заданный порог, устанавливается единая шкала квантования. При передаче значащих коэффициентов, прошедших пороговый отбор, необходимо указывать их местоположение. Простой, но достаточно эффективный метод кодирования позиций состоит в указании числа исключенных коэффициентов, разделяющих соседние значащие коэффициенты. Общей схеме кодирования длин серий применительно к данному случаю можно придать следующий вид:
1. Первому коэффициенту каждой строки, какова бы ни была его величина, всегда ставится в соответствие кодовое слово, определенная часть которого содержит только единицы или только нули. Эта часть служит маркером для строчной синхронизации и процессе передачи.
2. Второе и последующие кодовые слова в той части, которая отведена на передачу уровня, указывают квантованную величину соответствующего значащего коэффициента. В позиционной части указывается выраженное двоичным числом количество исключенных коэффициентов, отделяющих данный значащий коэффициент от предшествующего.
3. Если в пределах заранее установленной максимальной длины серии не встретился очередной значащий коэффициент, то обе части кодового слова заполняются только единицами или только нулями, чтобы указать появление серии максимальной длины.
Введение кодовой комбинации для строчной синхронизации позволяет обходиться без кодирования номера строки, а также ограничить распространение любой ошибки, возникшей при передаче по каналу связи, пределами соответствующей строки.

Рис.23.2.9. Примеры порогового кодирования на основе преобразования Адамара и наклонного преобразования для блоков размером 16х16 элементов: а — преобразование Адамара (2,0 дв ед./эл.); 6 — преобразование Адамара (1,15 дв. ед./эл); в — наклонное преобразование (2.0 дв. ед./эл.); г - наклонное преобразование (1,15 дв. ед./эл.).
Изображения, полученные путем цифрового моделирования
процесса порогового кодирования, показаны на рис. 23.2.9. Адаптивный характер
порогового кодирования обусловливает, как и следовало ожидать, некоторое
улучшение результатов по сравнению с более простым процессом зонального
кодирования Количество значащих коэффициентов, а тем самым и объем данных,
передаваемых обычной системой порогового кодирования, меняются от одного
изображения к другому. Для линий связи, предусматривающих передачу двоичных
цифр с постоянной скоростью, разработана специальная система порогового
кодирования [28]. В каждом блоке отбирается для передачи фиксированное количество ![]() наибольших коэффициентов. Тем самым для каждого блока
фактически устанавливается свой порог, обеспечивающий поддержание желаемой
скорости передачи.
наибольших коэффициентов. Тем самым для каждого блока
фактически устанавливается свой порог, обеспечивающий поддержание желаемой
скорости передачи.
| << Предыдущий параграф | Следующий параграф >> |
- Часть 4. РЕСТАВРАЦИЯ И УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
- Глава 12. УЛУЧШЕНИЕ ИЗОБРАЖЕНИЙ
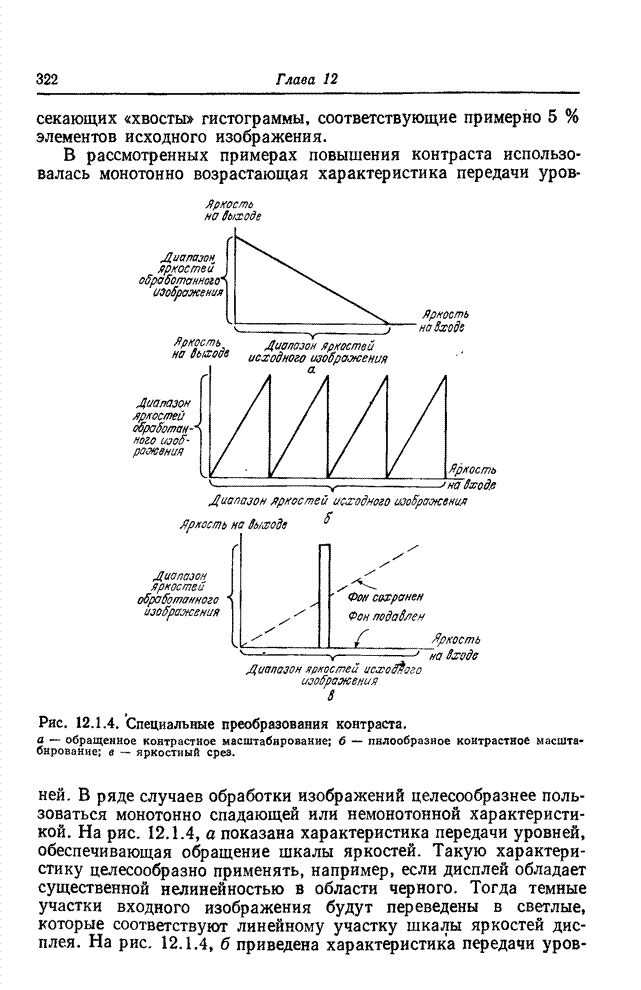
- 12.1. ИЗМЕНЕНИЕ КОНТРАСТА
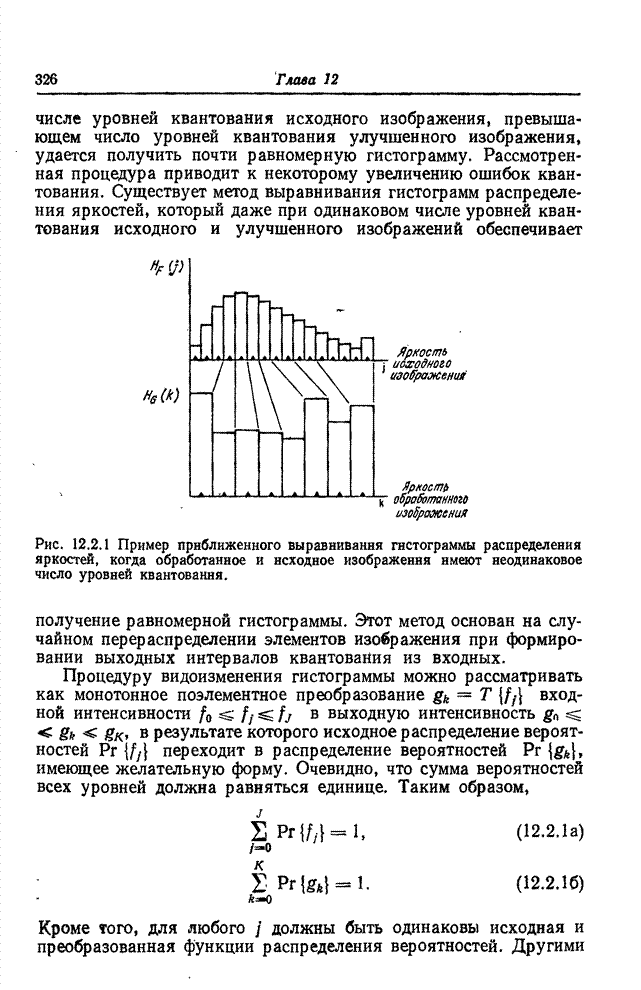
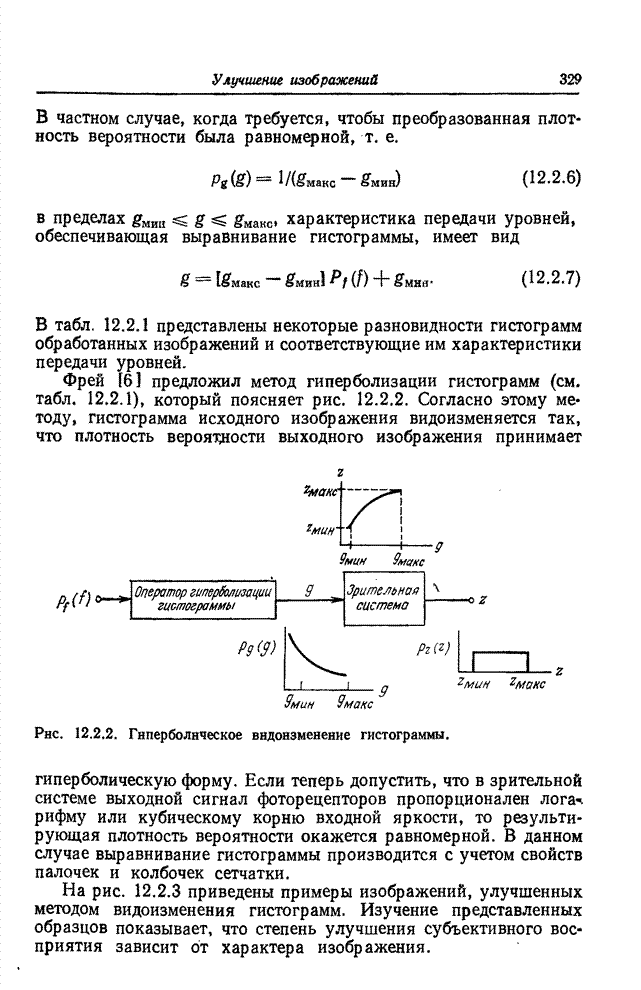
- 12.2. ВИДОИЗМЕНЕНИЕ ГИСТОГРАММ
- 12.3. ПОДАВЛЕНИЕ ШУМОВ
- 12.4. ПОДЧЕРКИВАНИЕ ГРАНИЦ
- 12.5. ОБРАБОТКА ИЗОБРАЖЕНИЙ С ПРЕОБРАЗОВАНИЕМ
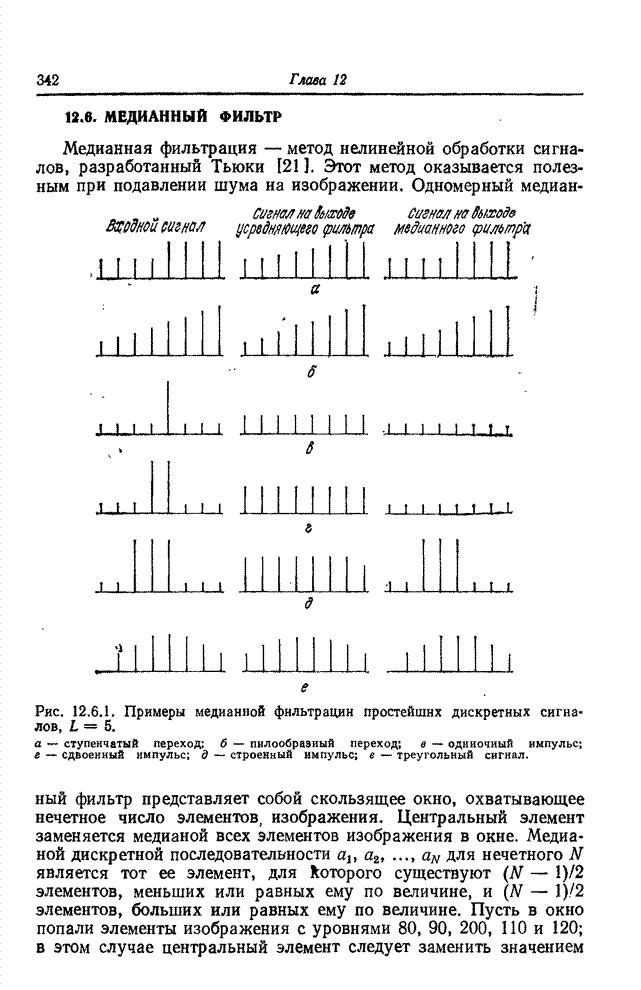
- 12.6. МЕДИАННЫЙ ФИЛЬТР
- 12.7. ЛОЖНЫЕ ЦВЕТА
- 12.8. ПСЕВДОЦВЕТА
- 12.9. УЛУЧШЕНИЕ СПЕКТРОЗОНАЛЬНЫХ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 13. МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.1. ОБОБЩЕННЫЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ПРИ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 13.2. МОДЕЛИ ОПТИЧЕСКИХ СИСТЕМ
- 13.3. МОДЕЛИ ФОТОГРАФИЧЕСКИХ ПРОЦЕССОВ
- 13.3.1. ОДНОЦВЕТНАЯ ФОТОГРАФИЯ
- 13.3.2. ЦВЕТНАЯ ФОТОГРАФИЯ
- 13.4. МОДЕЛИ ЦИФРОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- 13.5. МОДЕЛЬ ДИСПЛЕЯ
- 13.6. МОДЕЛИ ШУМОВ ИЗОБРАЖЕНИЯ
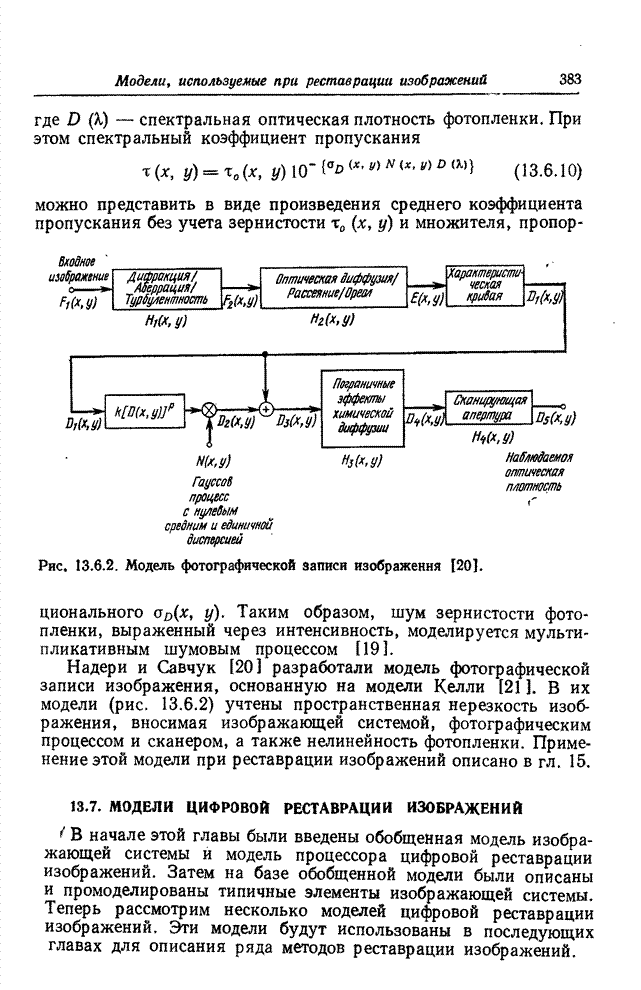
- 13.6.1. ШУМ ФОТОДЕТЕКТОРА
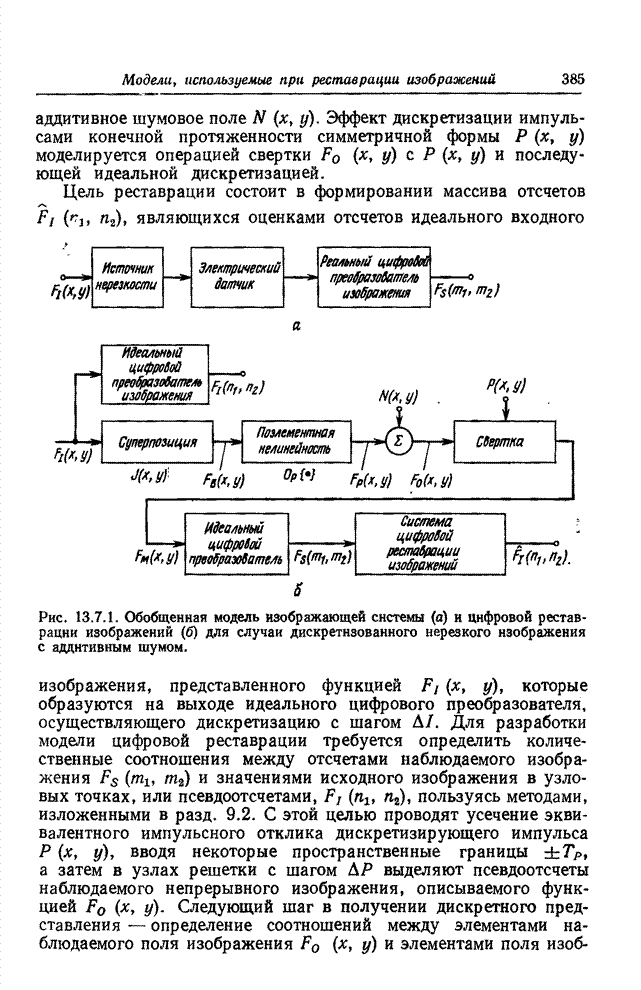
- 13.6.2. ШУМ ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- 13.7. МОДЕЛИ ЦИФРОВОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 14. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
- 14.1. МЕТОДЫ ПРОСТРАНСТВЕННОЙ ФИЛЬТРАЦИИ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
- 14.1.1. ИНВЕРСНАЯ ФИЛЬТРАЦИЯ
- 14.1.2. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И АДДИТИВНЫЙ ШУМ
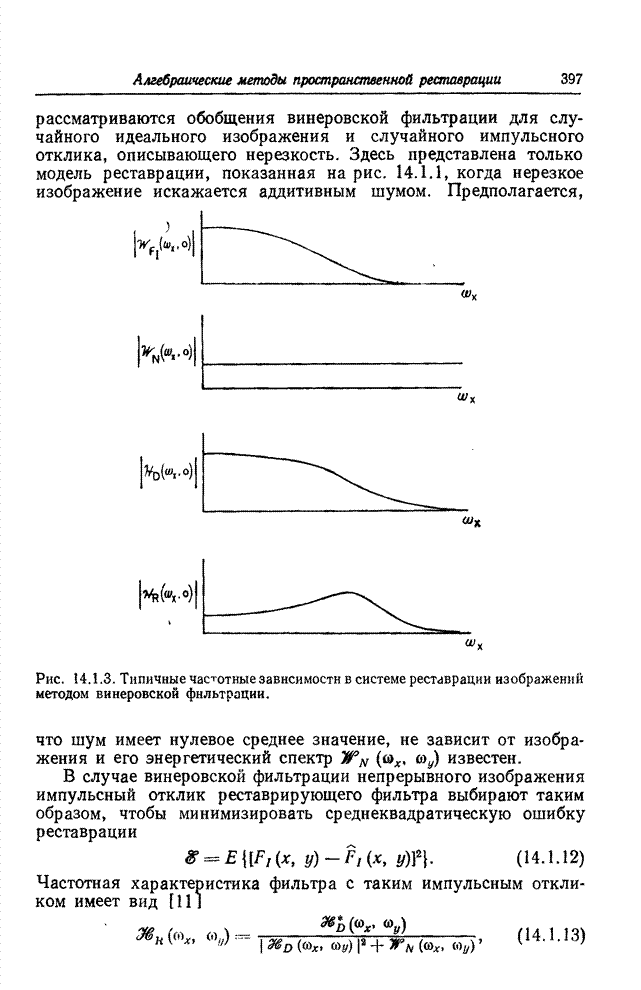
- 14.1.3. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНОЕ ИЗОБРАЖЕНИЕ
- 14.1.4. ВИНЕРОВСКАЯ ФИЛЬТРАЦИЯ И СЛУЧАЙНАЯ НЕРЕЗКОСТЬ
- 14.1.5. ФИЛЬТРЫ НА ОСНОВЕ ПАРАМЕТРИЧЕСКИХ ОЦЕНОК
- 14.1.6. ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
- 4.2. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
- 14.2.1. РЕСТАВРАЦИЯ НЕРЕЗКИХ ИЗОБРАЖЕНИЙ
- 14.2.2. РЕСТАВРАЦИЯ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ ПРИ НАЛИЧИИ ШУМА
- 14.3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ
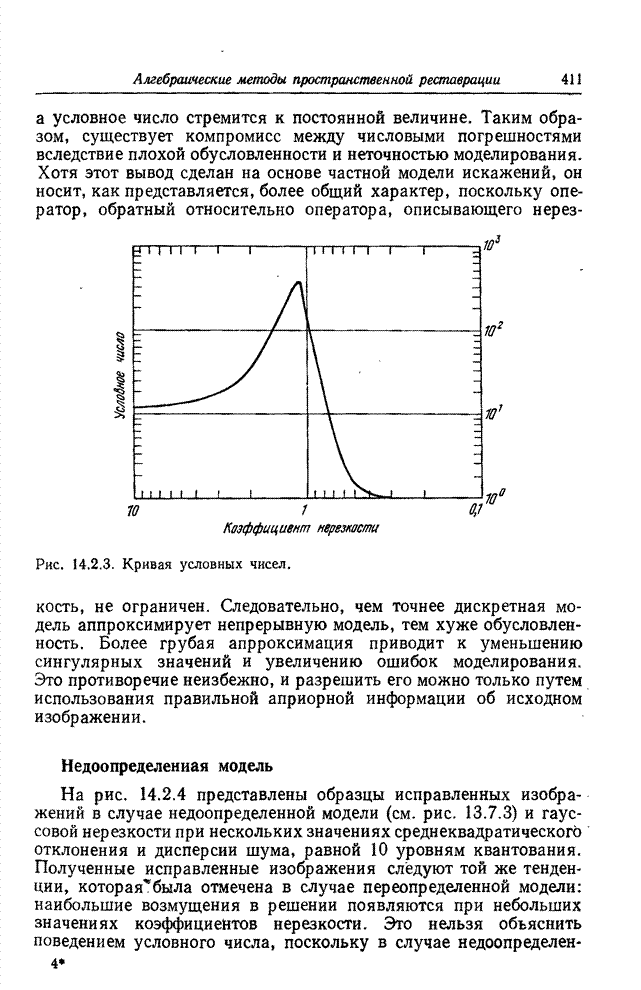
- 14.3.1. АЛГОРИТМ ДЛЯ ПЕРЕОПРЕДЕЛЕННОЙ МОДЕЛИ
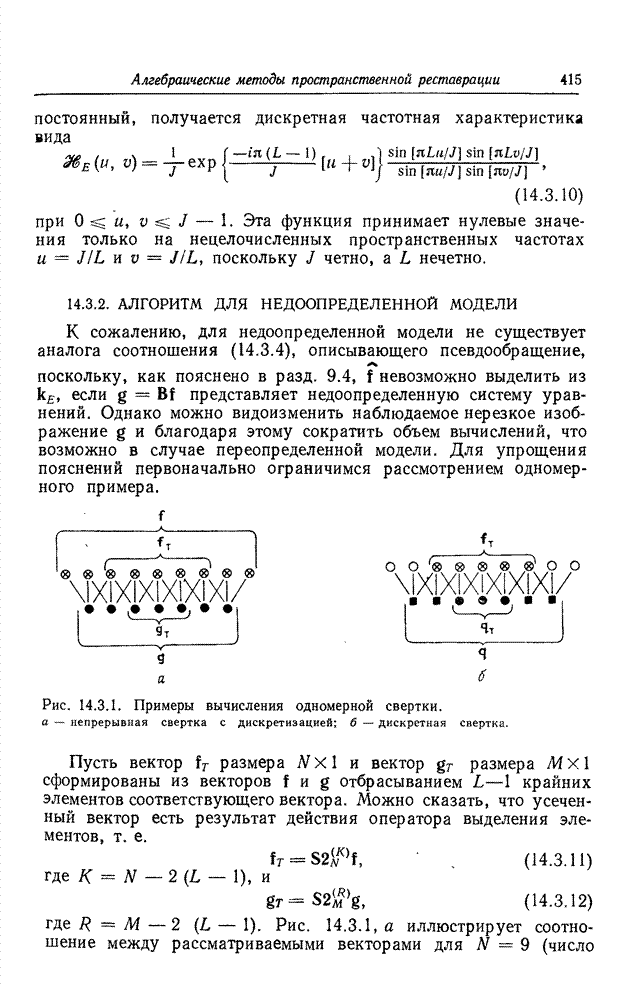
- 14.3.2. АЛГОРИТМ ДЛЯ НЕДООПРЕДЕЛЕННОЙ МОДЕЛИ
- 14.4. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ПСЕВДООБРАЩЕНИЯ МАТРИЦ С ИСПОЛЬЗОВАНИЕМ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- 14.5. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕГРЕССИИ
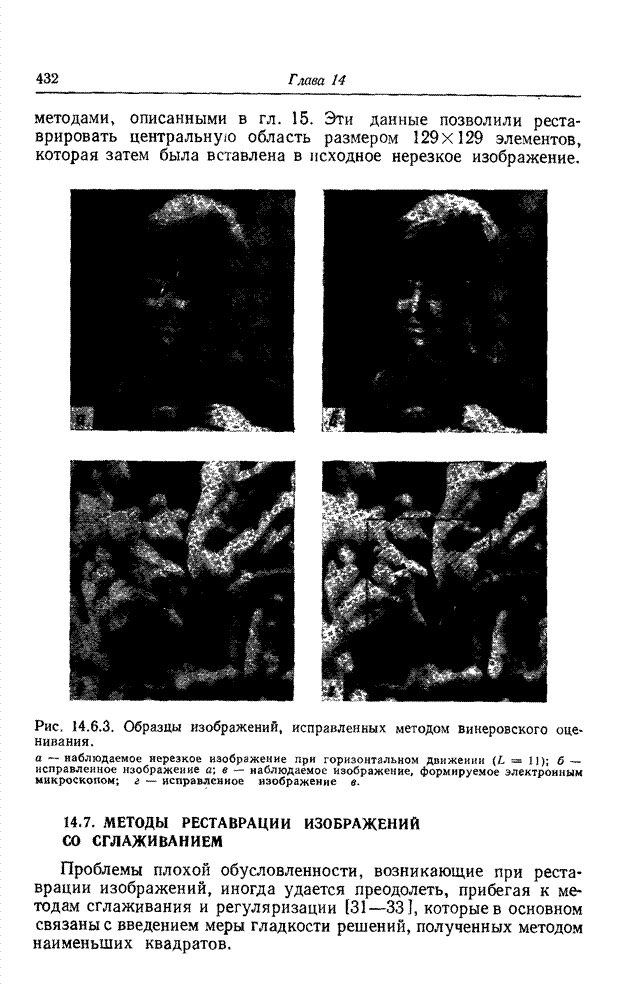
- 14.6. ПРОСТРАНСТВЕННАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ВИНЕРОВСКОГО ОЦЕНИВАНИЯ
- 14.6.1. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В ОБЩЕМ СЛУЧАЕ
- 14.6.2. ВИНЕРОВСКОЕ ОЦЕНИВАНИЕ В СЛУЧАЕ НЕРЕЗКОГО ИЗОБРАЖЕНИЯ С ШУМОМ
- 14.7. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ СО СГЛАЖИВАНИЕМ
- 14.8. МЕТОДЫ РЕСТАВРАЦИИ С ИСПОЛЬЗОВАНИЕМ ОГРАНИЧЕНИЙ
- 14.9. МЕТОДЫ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
- ЛИТЕРАТУРА
- Глава 15. CПЕЦИАЛЬНЫЕ МЕТОДЫ ПРОСТРАНСТВЕННОЙ РЕСТАВРАЦИИ ИЗОБРАЖЕНИЙ
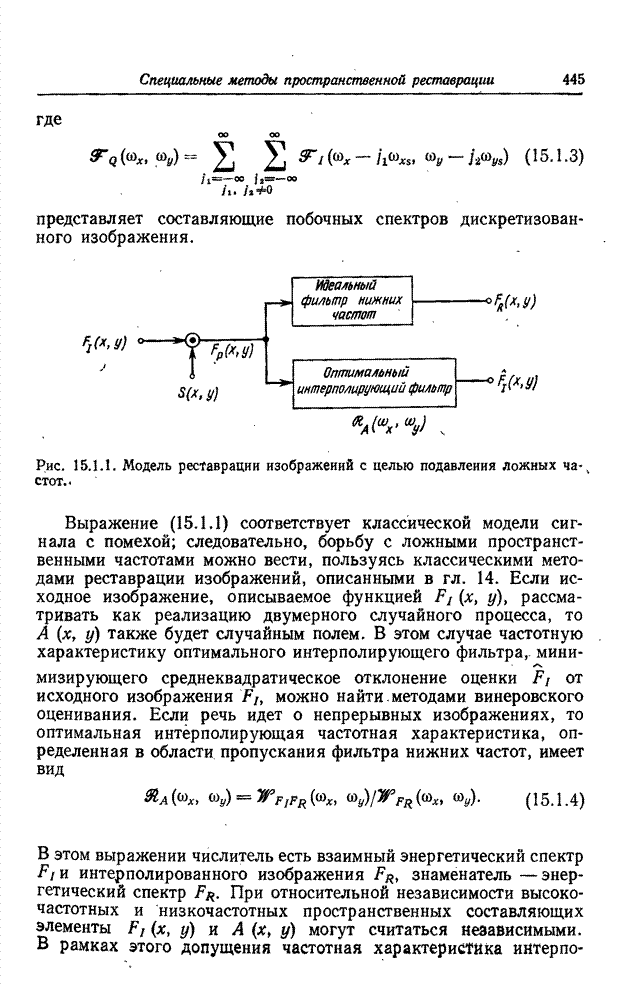
- 15.1. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮ ПОДАВЛЕНИЯ ОШИБОК НАЛОЖЕНИЯ СПЕКТРОВ
- 15.2. КОРРЕКЦИЯ ОШИБОК ИНТЕРПОЛЯЦИИ
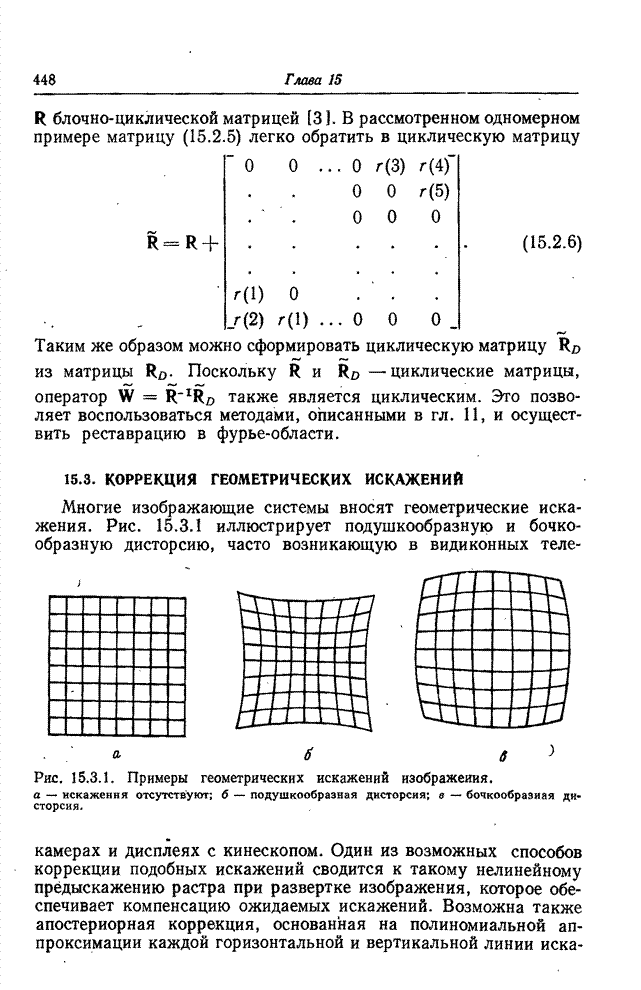
- 15.3. КОРРЕКЦИЯ ГЕОМЕТРИЧЕСКИХ ИСКАЖЕНИЙ
- 15.4. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ ГОМОМОРФНОЙ ФИЛЬТРАЦИИ
- 15.5. СЛЕПАЯ РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ
- 15.5.1. МЕТОДЫ НА ОСНОВЕ ПРЯМЫХ ИЗМЕРЕНИЙ
- 15.5.2. МЕТОДЫ НА ОСНОВЕ КОСВЕННОГО ОЦЕНИВАНИЯ
- 15.6. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ СПЕКТРА
- 15.7. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННО-ЗАВИСИМЫМИ ИСКАЖЕНИЯМИ
- 15.8. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ МЕТОДОМ РЕКУРСИВНОЙ ФИЛЬТРАЦИИ
- 15.9. РЕСТАВРАЦИЯ ИЗОБРАЖЕНИЙ С ЦЕЛЬЮОСЛАБЛЕНИЯ ШУМА ЗЕРНИСТОСТИ ФОТОПЛЕНКИ
- ЛИТЕРАТУРА
- Глава 16. КОРРЕКЦИЯ ЯРКОСТНЫХ, ЦВЕТОВЫХ И СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗОБРАЖАЮЩИХ СИСТЕМ
- 16.1. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ВИДЕОДАТЧИКОВ
- 16.2. КОРРЕКЦИЯ ЯРКОСТНОЙ ПОЭЛЕМЕНТНОЙ НЕЛИНЕЙНОСТИ ДИСПЛЕЕВ
- 16.3. ОЦЕНИВАНИЕ СПЕКТРАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 16.4. КОРРЕКЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ВИДЕОДАТЧИКОВ И ДИСПЛЕЕВ
- 16.5. ОЦЕНИВАНИЕ КООРДИНАТ СВЕТА ВИДЕОДАТЧИКОВ
- 16.6. ОЦЕНИВАНИЕ ЭКСПОЗИЦИЙ ЦВЕТНОЙ ФОТОПЛЕНКИ
- 16.7. КОМПЕНСАЦИЯ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ ЦВЕТНЫХ ДИСПЛЕЕВ
- ЛИТЕРАТУРА
- Часть 5. АНАЛИЗ ИЗОБРАЖЕНИЙ
- Глава 17. ВЫДЕЛЕНИЕ ПРИЗНАКОВ ИЗОБРАЖЕНИЯ
- 17.1. ЯРКОСТНЫЕ ПРИЗНАКИ
- 17.2. ГИСТОГРАММНЫЕ ПРИЗНАКИ
- 17.3. ПРОСТРАНСТВЕННО-СПЕКТРАЛЬНЫЕ ПРИЗНАКИ
- 17.4. КОНТУРНЫЕ ПРИЗНАКИ
- 17.4.1. ЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.2. НЕЛИНЕЙНЫЕ МЕТОДЫ КОНТРАСТИРОВАНИЯ
- 17.4.3. МЕТОДЫ АППРОКСИМАЦИИ ПЕРЕПАДОВ ЯРКОСТИ
- 17.4.4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ
- 17.5. ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ОБНАРУЖЕНИЯ ПЕРЕПАДОВ ЯРКОСТИ
- 17.6. ЦВЕТОВЫЕ КОНТУРЫ
- 17.7. ПРИЗНАКИ ПЯТНА И ЛИНИИ
- 17.8. ТЕКСТУРНЫЕ ПРИЗНАКИ
- 17.9. СИНТЕЗ ТЕКСТУР
- ЛИТЕРАТУРА
- Глава 18. СИМВОЛИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
- 18.1. СВЯЗНОСТЬ
- 18.2. СЖАТИЕ, УТОНЧЕНИЕ И ПОСТРОЕНИЕ ОСТОВА
- 18.3. ОПИСАНИЕ ЛИНИЙ
- 18.3.1. АППРОКСИМАЦИЯ КРИВЫХ
- 18.3.2. ПРЕОБРАЗОВАНИЕ ЛИНИИ В ТОЧКУ
- 18.4. ОПИСАНИЕ ФОРМЫ
- 18.4.1. МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.2. ТОПОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 18.4.3. АНАЛИТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
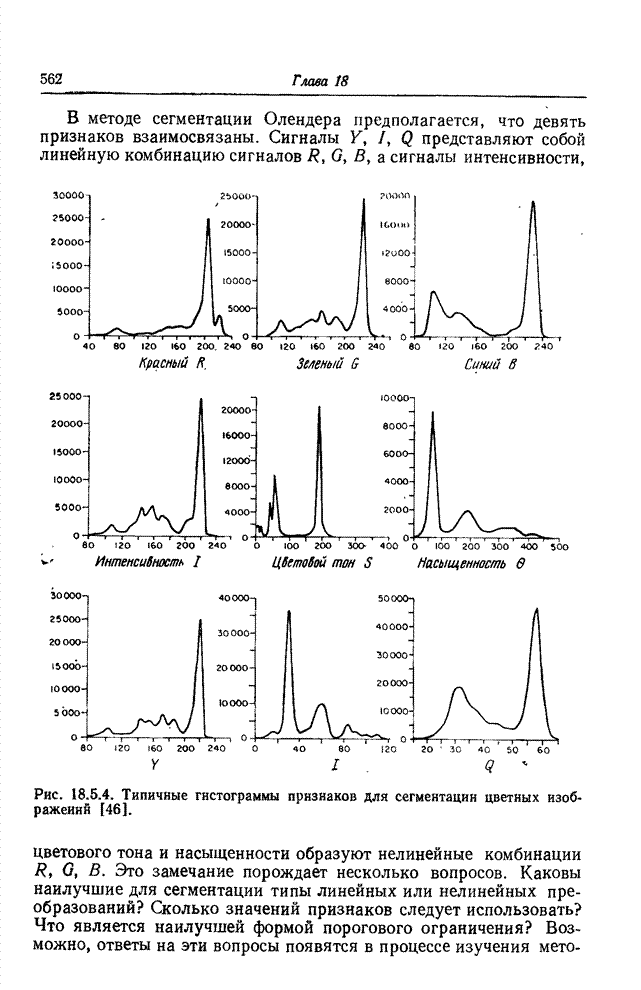
- 18.5. СЕГМЕНТАЦИЯ ПО ЯРКОСТИ
- 18.5.1. ПОРОГОВОЕ ОГРАНИЧЕНИЕ ПО ЯРКОСТИ
- 18.5.2. МНОГОМЕРНОЕ ПОРОГОВОЕ ОГРАНИЧЕНИЕ
- 18.5.3. НАРАЩИВАНИЕ ОБЛАСТЕЙ
- 18.6. КОНТУРНАЯ СЕГМЕНТАЦИЯ
- 18.7. ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ
- 18.8. СЕГМЕНТАЦИЯ ФОРМЫ
- ЛИТЕРАТУРА
- Глава 19. ОБНАРУЖЕНИЕ ОБЪЕКТОВ И СОВМЕЩЕНИЕ (ПРИВЯЗКА) ИЗОБРАЖЕНИЙ
- 19.1. СОПОСТАВЛЕНИЕ С ЭТАЛОНОМ
- 19.2. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ ДЕТЕРМИНИРОВАННЫХ ПОЛЕЙ
- 19.3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ СЛУЧАЙНЫХ ПОЛЕЙ
- 19.4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ
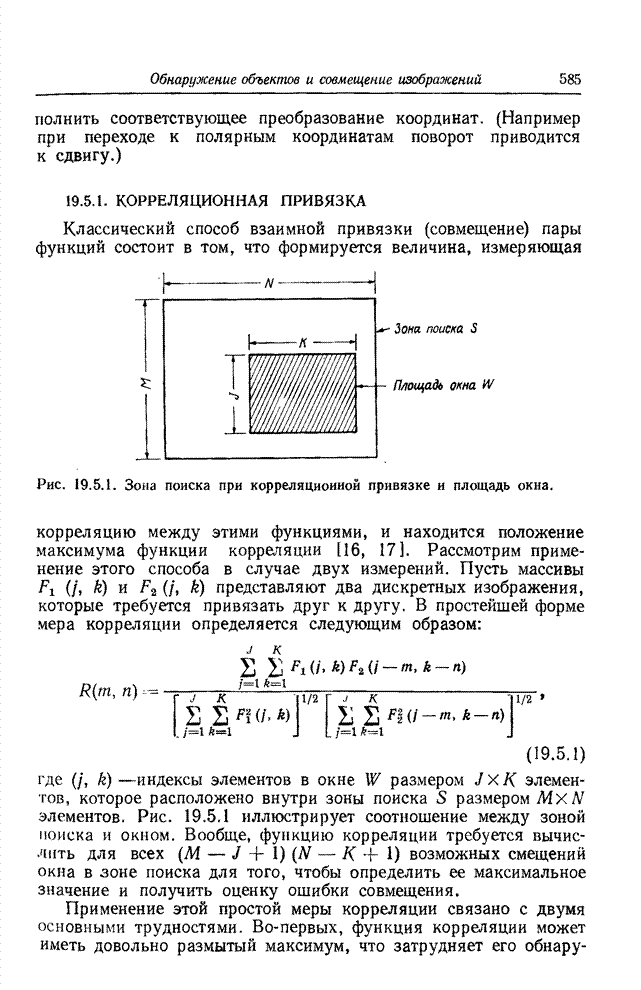
- 19.5. ПРИВЯЗКА ИЗОБРАЖЕНИЙ
- 19.5.1. КОРРЕЛЯЦИОННАЯ ПРИВЯЗКА
- 19.5.2. ПОСЛЕДОВАТЕЛЬНАЯ ПРИВЯЗКА
- ЛИТЕРАТУРА
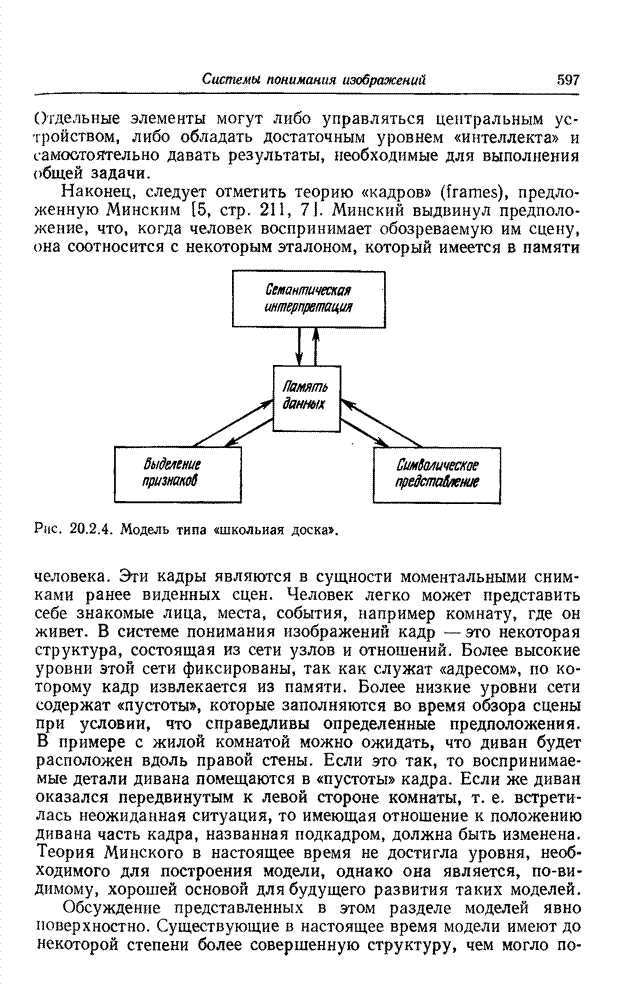
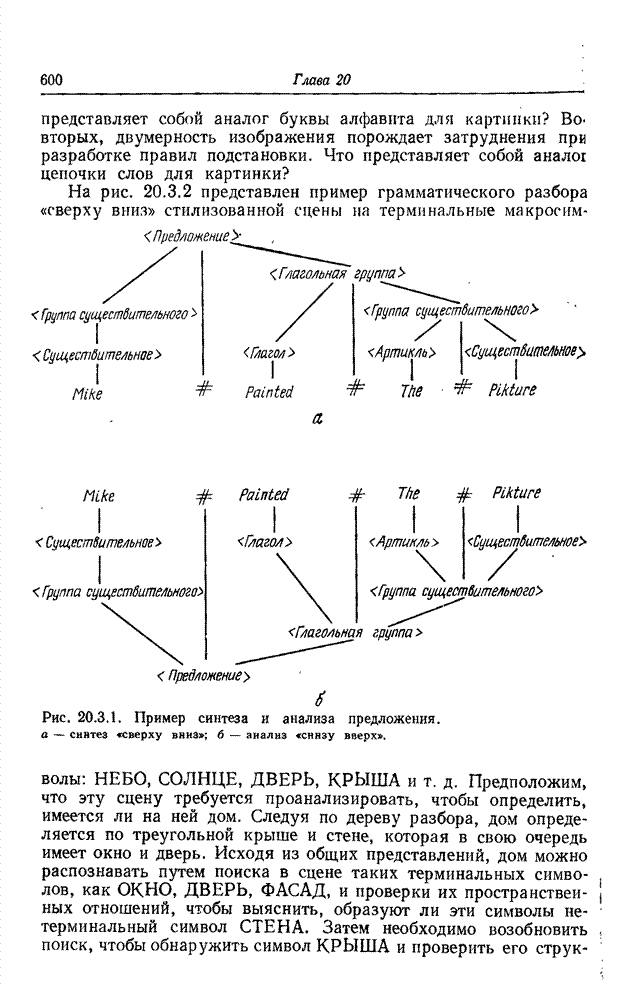
- Глава 20. СИСТЕМЫ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
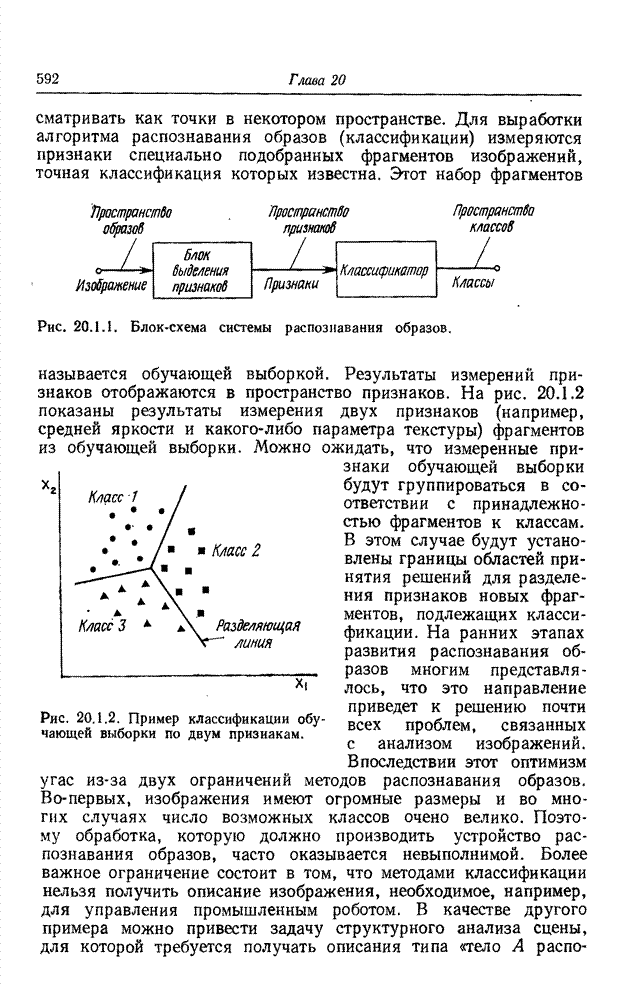
- 20.1. СИСТЕМЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 20.2. МОДЕЛИ СИСТЕМ ПОНИМАНИЯ ИЗОБРАЖЕНИЙ
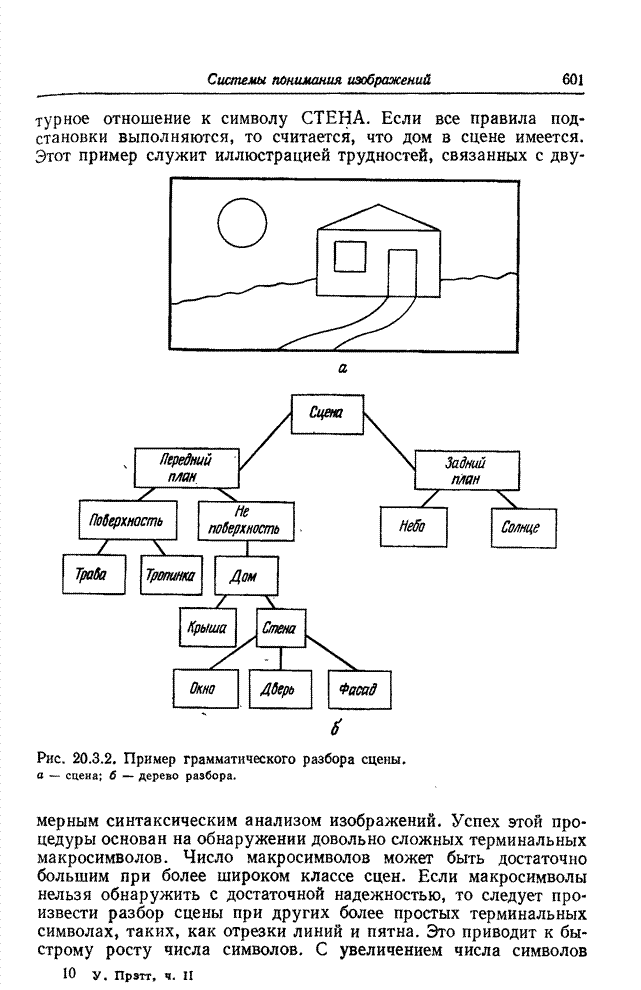
- 20.3. СИНТАКСИЧЕСКИЕ МЕТОДЫ
- 20.4. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ОТНОШЕНИЯ МЕЖДУ ОБЪЕКТАМИ
- ЛИТЕРАТУРА
- Часть 6. Кодирование изображений
- Глава 21. АНАЛОГОВЫЕ МЕТОДЫ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.1. КЛАССИФИКАЦИЯ МЕТОДОВ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 21.2. СИСТЕМЫ ВЕЩАТЕЛЬНОГО ТЕЛЕВИДЕНИЯ
- 21.2.1. СИСТЕМА НТСЦ [13-15]
- 21.2.2. СИСТЕМА СЕКАМ [17]
- 21.2.3.СИСТЕМА ПАЛ
- 21.3. МОДУЛЯЦИОННЫЕ МЕТОДЫ СОКРВЩЕНИЯ ПОЛОСЫ ЧАСТОТЫ
- 21.4.УМЕНЬШЕНИЕ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ И ЧАСТОТЫ КАДРОВ
- 21.4.1. УМЕНЬШЕНИЕ ПРОСТРАНСТВЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
- 21.4.2. УМЕНЬШЕНИЕ ЧАСТОТЫ КАДРОВ
- 21.5. МЕТОДЫ ВРЕМЕННОГО ПЕРЕМЕЖЕНИЯ
- 21.5.1. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ СТРОК
- 21.5.2. ПЕРЕДАЧА С ПЕРЕМЕЖЕНИЕМ ЭЛЕМЕНТОВ
- 21.6. РАЗВЕРТКА С ПЕРЕМЕННОЙ СКОРОСТЬЮ
- 21.7. МУЛЬТИПЛЕКСНЫЕ МЕТОДЫ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Глава 22. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПОЭЛЕМЕНТНОЙ ОБРАБОТКОЙ
- 22.1. СИСТЕМЫ КОДИРОВАНИЯ С ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИЕЙ
- 22.1.1. КВАНТОВАНИЕ СО СЖАТИЕМ ДИАПАЗОНА ЯРКОСТЕЙ
- 22.1.2. ПСЕВДОШУМОВОЕ КВАНТОВАНИЕ
- 22.1.3. КВАНТОВАНИЕ С УЛУЧШЕННОЙ ПЕРЕДАЧЕЙ ГРАДАЦИЙ ЯРКОСТИ
- 22.1.4. СИСТЕМА С ГРУБОЙ-ТОНКОЙ ШКАЛОЙ КВАНТОВАНИЯ
- 22.1.5. КВАНТОВАНИЕ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ
- 22.2. СТАТИСТИЧЕСКИЕ МЕТОДЫ КОДИРОВАНИЯ
- 22.2.1. ПОЭЛЕМЕНТНОЕ СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- 22.2.2. КОДИРОВАНИЕ С УЧЕТОМ ПРЕДШЕСТВУЮЩЕГО ЭЛЕМЕНТА
- 22.3. КОДИРОВАНИЕ СЕРИЙ
- 22.3.1. КОДИРОВАНИЕ ДЛИН СЕРИЙ; ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ [32-36]
- 22.3.2. КОДИРОВАНИЕ РАЗРЯДНЫХ ПЛОСКОСТЕЙ
- 22.4. КОДИРОВАНИЕ С ПОПОЛНЕНИЕМ КАДРОВ
- 22.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ
- 22.5.1. ДЕЛЬТА-МОДУЛЯЦИЯ
- 22.5.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ
- 22.5.3. КОДЕРЫ С ПРОСТРАНСТВЕННЫМ ПРЕДСКАЗАНИЕМ
- 22.5.4. АДАПТИВНЫЕ КОДЕРЫ С ПРЕДСКАЗАНИЕМ
- 22.5.5. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ ПРИМЕНИТЕЛЬНО К ЦВЕТНЫМ ИЗОБРАЖЕНИЯМ
- 22.5.6. ДИФФЕРЕНЦИАЛЬНОЕ МЕЖКАДРОВОЕ КОДИРОВАНИЕ
- 22.6. ПРОЕКТИРОВАНИЕ СИСТЕМ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ДЛЯ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- ЛИТЕРАТУРА
- Глава 23. ЦИФРОВОЕ КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ С ПРОСТРАНСТВЕННОЙ ОБРАБОТКОЙ
- 23.1. ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ КОДИРОВАНИЯ
- 23.1.1. ИНТЕРПОЛЯЦИЯ НА ПЕРЕДАЮЩЕЙ СТОРОНЕ
- 23.1.2. ИНТЕРПОЛЯЦИЯ НА ПРИЕМНОЙ СТОРОНЕ
- 23.2. КОДИРОВАНИЕ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.1. КОДИРОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.2. АДАПТИВНОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.3. КОДИРОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.2.4. МЕЖКАДРОВОЕ КОДИРОВАНИЕ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.3. УМЕНЬШЕНИЕ ОШИБОК КВАНТОВАНИЯ ПРИ КОДИРОВАНИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 23.4. ГИБРИДНОЕ КОДИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ И ДИКМ
- 23.5. КОДИРОВАНИЕ ПРИЗНАКОВ
- 23.5.1. КОДИРОВАНИЕ ЛИНИЙ УРОВНЯ
- 23.5.2. КОДИРОВАНИЕ КОНТУРОВ
- 23.5.3. КОДИРОВАНИЕ ТЕКСТУР
- 23.6. КОДИРОВАНИЕ С ПОМОЩЬЮ НАБОРА СИМВОЛОВ
- 23.6.1. КОДИРОВАНИЕ БЛОКОВ ПО СЛОВАРЮ ОБРАЗОВ
- 23.6.2. КОДИРОВАНИЕ НА ОСНОВЕ СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ
- ЛИТЕРАТУРА
- Глава 24. АНАЛИЗ ЭФФЕКТИВНОСТИ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 24.1. СТАТИСТИЧЕСКИЕ МОДЕЛИ КАНАЛА СВЯЗИ КАК ИСТОЧНИКА ПОМЕХ [1-4]
- 24.2. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ
- 24.3. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ИКМ [4]
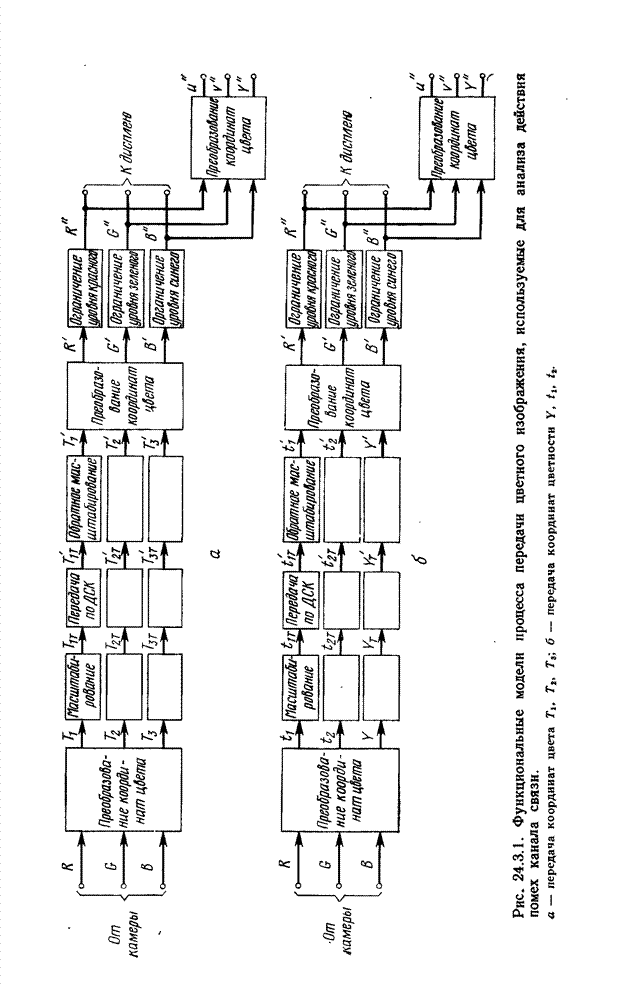
- 24.3.1. ПЕРЕДАЧА КООРДИНАТ ЦВЕТА
- 24.3.2. ПЕРЕДАЧА ЯРКОСТИ И КООРДИНАТ ЦВЕТНОСТИ
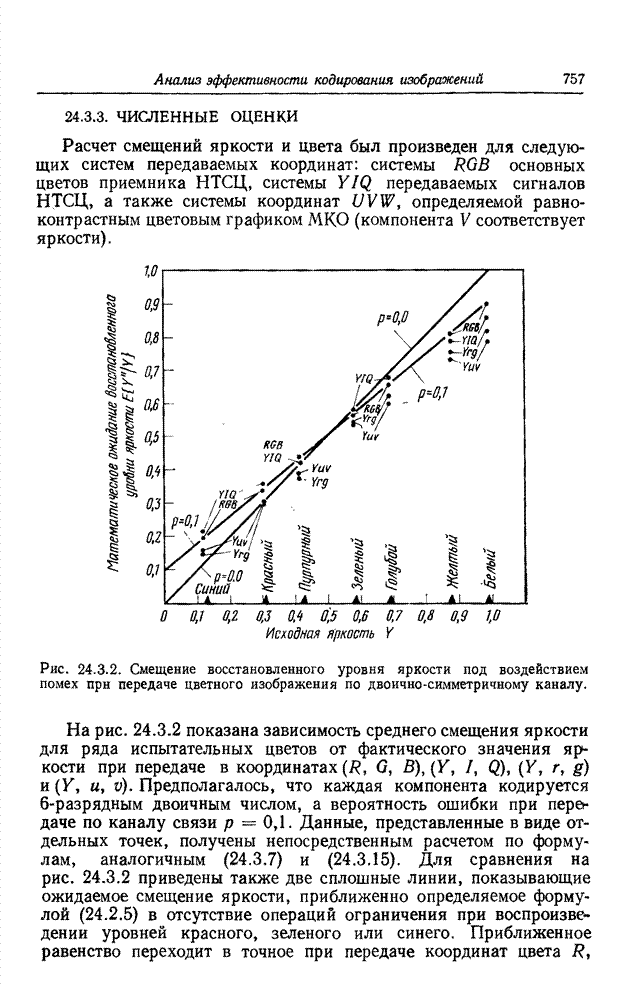
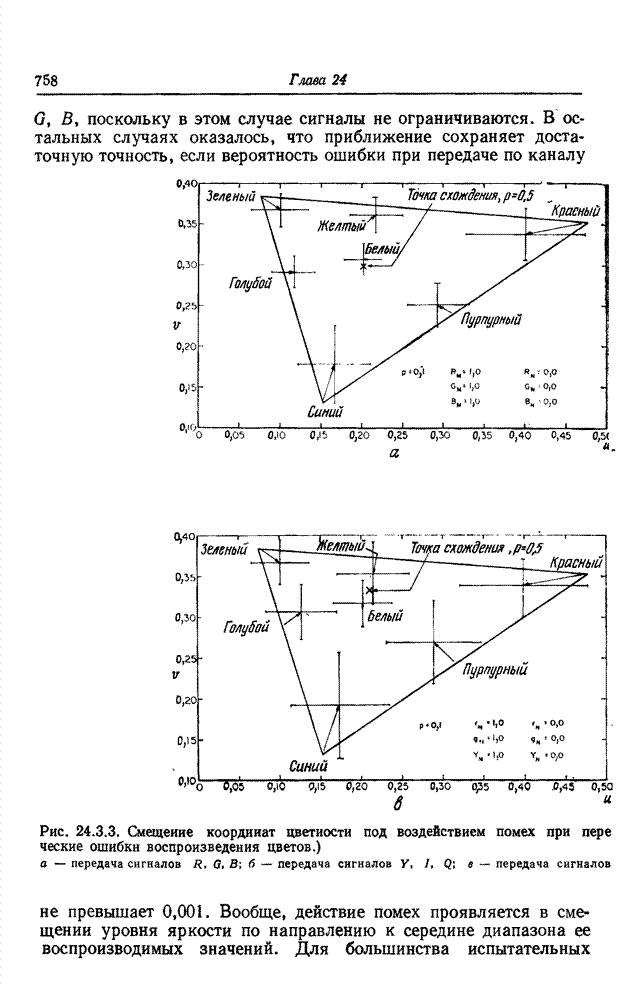
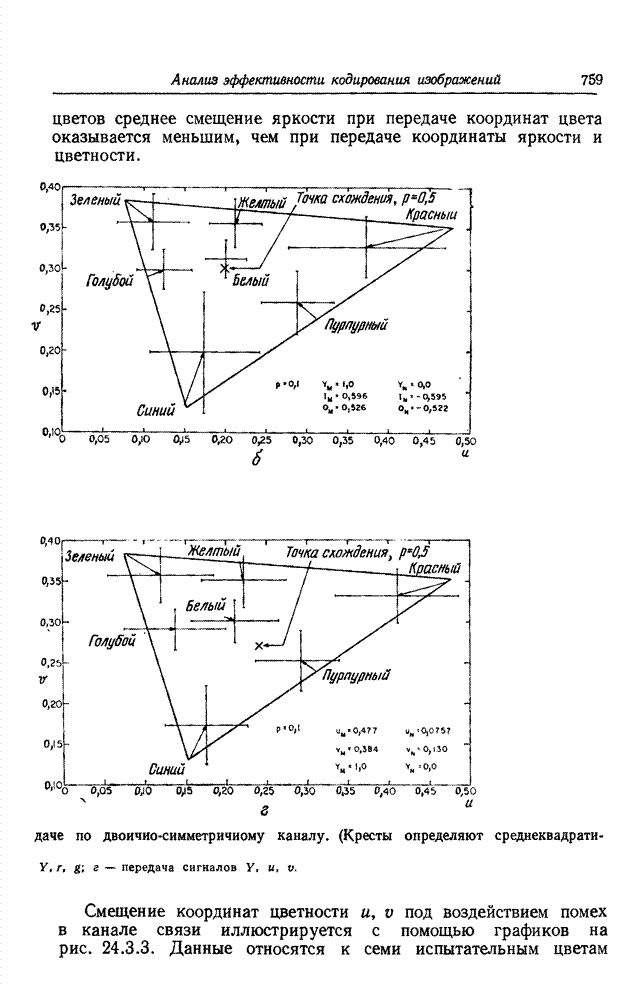
- 24.3.3. ЧИСЛЕННЫЕ ОЦЕНКИ
- 24.4. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ ДИКМ
- 24.5. ДЕЙСТВИЕ ПОМЕХ ПРИ ПЕРЕДАЧЕ ИЗОБРАЖЕНИЙ ПОСРЕДСТВОМ КОДИРОВАНИЯ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ
- 24.6. СРАВНЕНИЕ РАЗЛИЧНЫХ МЕТОДОВ КОДИРОВАНИЯ
- ЛИТЕРАТУРА
- Приложение 1. ОСНОВНАЯ ЛИТЕРАТУРА
- Приложение 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА И ЦВЕТНОСТИ
- Приложение 3. СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
- ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА