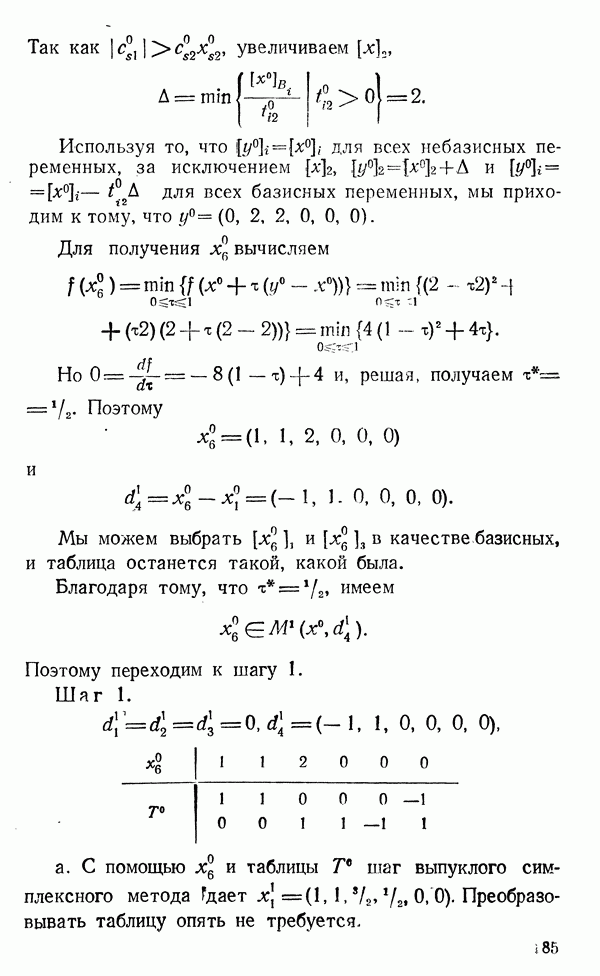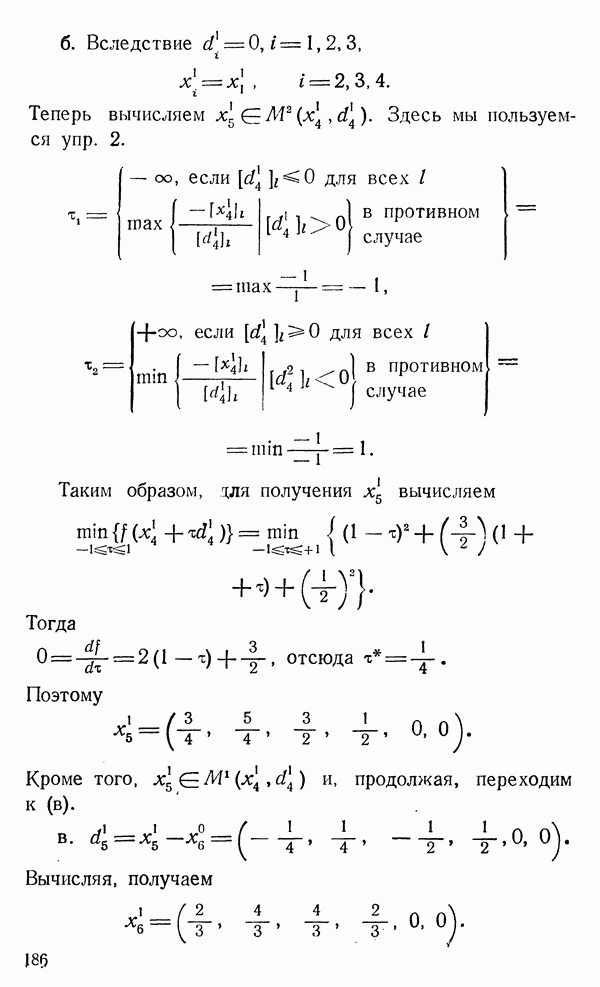| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3. ДВОЙСТВЕННАЯ ЗАДАЧА ГЕОМЕТРИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Чрезвычайно интересным и практически важным приложением теории двойственности является ее применение в ГП. Используя теорию двойственности, мы
сведем довольно сложную форму задачи ГП, выведенную в гл. 1., к эквивалентной задаче, решить которую намного легче.
Эквивалентная задача. В гл. 1 была выведена следующая задача ГП:

при условии 

где

 — переменные,
— переменные,  — фиксированный
— фиксированный  -мерный вектор,
-мерный вектор,  — фиксированная матрица размером
— фиксированная матрица размером 
Цель данного параграфа — показать, что решение этой задачи ГП при определенных условиях эквивалентно, решению следующей задачи:

при условиях  , где
, где

Здесь  — вектор, входящий в задачу
— вектор, входящий в задачу  Чтобы обеспечить непрерывность выражения
Чтобы обеспечить непрерывность выражения  в точке
в точке  мы принимаем, что
мы принимаем, что  Тогда функция
Тогда функция  непрерывна при
непрерывна при  .
.
Следует обратить внимание на то, что целевая функция  вогнута (упр. 3.2). Следовательно, задача (3.11) является задачей НЛП с вогнутой целевой функцией и линейными ограничениями и, как показано
вогнута (упр. 3.2). Следовательно, задача (3.11) является задачей НЛП с вогнутой целевой функцией и линейными ограничениями и, как показано
в гл. 8, решается значительно легче, чем задача (1.6) или (3.10).
Ниже показано, что, как только решена задача (3.11), оптимальные значения  в задачах (1.6) и (3.10) могут быть определены по известным оптимальным значениям
в задачах (1.6) и (3.10) могут быть определены по известным оптимальным значениям  с помощью соответствующих формул (упр. 3.3):
с помощью соответствующих формул (упр. 3.3):

Построение двойственной задачи ГП. Теперь необходимо показать, как из задачи (3.10) получить задачу (3.11). Прежде всего должна быть доказана выпуклость функций  Это позволит использовать теорию двойственности.
Это позволит использовать теорию двойственности.
Напомним, что, так как выпуклая функция представляет собой вогнутую функцию, взятую со знаком минус, функция будет выпуклой, если матрица Гесса из вторых частных производных положительно полуопределена. Матрица  положительно полуопределена, если для любого данного вектора
положительно полуопределена, если для любого данного вектора  или эквивалентно
или эквивалентно

Лемма 3.1. Пусть  Тогда
Тогда  выпуклая функция.
выпуклая функция.
Доказательство состоит в том, что будет показана непрерывность и положительная полуопределенность гессиана. Положим

Тогда

Поэтому для любых 

где последнее равенство следует из того, что если  то
то 
Следует обратить внимание на то, что

Поэтому

Отсюда

Следовательно,

Применяя лемму 3.1, убеждаемся, что функции  выпуклы. Перестроив вогнутую двойственную задачу гл. 2 для выпуклых функций,
выпуклы. Перестроив вогнутую двойственную задачу гл. 2 для выпуклых функций,
получим, что задача, двойственная к (3.10), принимает вид

при

Из уравнения  кроме того, после введения переменной
кроме того, после введения переменной  двойственная задача сводится к нахождению
двойственная задача сводится к нахождению

при

Теперь мы должны преобразовать задачу (3.13) к форме (3.11). Основная трудность в выполнении этого преобразования заключается в том, что не определен у, для которого  или эквивалентно, не определен
или эквивалентно, не определен  Поэтому данный случай требует специального рассмотрения.
Поэтому данный случай требует специального рассмотрения.
Предложение 3.2. Пусть  -допустимая точка для задачи (3.13). Тогда
-допустимая точка для задачи (3.13). Тогда

Доказательство. В силу того, что точка  допустима для задачи (3.13), имеем
допустима для задачи (3.13), имеем

Поэтому справедливо (а).
Чтобы доказать (б), суммируем (3.14)

Но  и поэтому справедливо (б). Утверждение (в) доказывается тем, что будет показано:
и поэтому справедливо (б). Утверждение (в) доказывается тем, что будет показано:

Если  по
по  и (3.15) удовлетворяется. Пусть
и (3.15) удовлетворяется. Пусть  тогда из
тогда из  Отсюда опять на основе (3.14) имеем
Отсюда опять на основе (3.14) имеем

Умножая на  и суммируя, получаем
и суммируя, получаем

Далее, применяя пункт (б) настоящего утверждения, получаем, что справедливо уравнение (3.15), следовательно, и (в).
Из предложения 3.2 вытекает, что мы можем записать двойственную задачу (3.13) в виде: найти  при
при 

где 
Следует обратить внимание на то, что задача (3.16) совпадает с задачей (3.11) во всем, за исключением ограничений

Теперь покажем, что в действительности эти ограничения излишни. Напомним, что согласно предположению о том, что  функция
функция  непрерывна при
непрерывна при 
Теорема 3.3. Пусть существует  такое, что
такое, что

Тогда, если  —оптимальная точка для задачи (3.16), то она оптимальна также и для задачи (3.11).
—оптимальная точка для задачи (3.16), то она оптимальна также и для задачи (3.11).
Доказательство. Не теряя общности, можно предположить, что

Обратите внимание также на то, что если точка 6 оптимальна для (3.16), то она допустима для задачи (3.11).
Теперь пусть  произвольная допустимая точка для задачи (3.11). Чтобы доказать теорему, мы должны показать, что
произвольная допустимая точка для задачи (3.11). Чтобы доказать теорему, мы должны показать, что  а (6), так как это означает, что точка
а (6), так как это означает, что точка  оптимальна для (3.11). Построим последовательность
оптимальна для (3.11). Построим последовательность 

Сначала установим, что точка  допустима для задачи (3.16). Согласно выбору точек
допустима для задачи (3.16). Согласно выбору точек  получаем
получаем

Полагая

и учитывая, что  можно определить
можно определить

Отсюда

так как согласно (3.22)

Тогда из (3.19) — (3.23) следует, что точка  допустима для задачи (3.16).
допустима для задачи (3.16).
В силу того, что 6 — оптимальная точка для задачи (3.16), а точка  допустима, получаем
допустима, получаем

Далее, переходя к пределу и замечая, что  а функция
а функция  и (8) непрерывна, получаем
и (8) непрерывна, получаем

Замечания. Теорема 3.3 утверждает, что некоторые из оптимальных точек задачи (3.11) являются оптимальными и для задачи (3.16). Требование существования  здесь может рассматриваться как условие регулярности.
здесь может рассматриваться как условие регулярности.
Используя теорему 3.3, мы можем обосновать утверждения, сделанные в первой части этого параграфа.
Именно при умеренных предположениях теория двойственности обеспечивает, что задача (3.10) и двойственная к ней задача (3.13) имеют решения и оптимальные значения целевых функций этих задач равны. Тогда, решив задачу (3.11), мы тем самым определим оптимальное значение целевой функции для задачи (3.13), а следовательно, и для задачи ГП.
Теорема 3.3 дает также следующее. Существует оптимальная точка  для задачи (3.16), именно
для задачи (3.16), именно  в теореме 3.3, которая является оптимальной и для задачи (3.11). При наличии этой точки
в теореме 3.3, которая является оптимальной и для задачи (3.11). При наличии этой точки  мы имеем
мы имеем
возможность определить оптимальные значения х и у для задачи  с помощью формулы
с помощью формулы

Эта формула представляет собой ограничения задачи (3.16), так что точки  удовлетворяют им.
удовлетворяют им.
Таким образом, при соответствующих предположениях, решая задачу (3.11) и определяя  , мы получаем решение задачи ГП.
, мы получаем решение задачи ГП.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава 1. ЗАДАЧА НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- 1.1. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- 1.2. ОБЛАСТИ ПРИМЕНЕНИЯ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- 1.3. ПОДРОБНЫЙ ПРИМЕР: ЗАДАЧА РЕГРЕССИИ ПРИ ОПРЕДЕЛЕНИИ ВЫБОРА ПОТРЕБИТЕЛЕМ
- 1.4. ГЕОМЕТРИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 1.5. ЗАДАЧА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- 1.6. ЗАДАЧА КВАДРАТИЧНОГО ПРОГРАММИРОВАНИЯ
- Глава 2. ИДЕНТИФИКАЦИЯ ОПТИМАЛЬНОЙ ТОЧКИ
- 2.2. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ ДЛЯ ЗАДАЧ БЕЗ ОГРАНИЧЕНИЙ
- 2.3. ВОГНУТОСТЬ, ВЫПУКЛОСТЬ, ПСЕВДОВОГНУТОСТЬ И КВАЗИВОГНУТОСТЬ
- 2.3.1. Некоторые важные следствия вогнутости в нелинейном программировании
- 2.4. НЕОБХОДИМЫЕ УСЛОВИЯ КУНА—ТАККЕРА
- 2.5. ДОСТАТОЧНОСТЬ И УСЛОВИЯ КУНА—ТАККЕРА
- 2.6. ФУНКЦИЯ ЛАГРАНЖА И ТЕОРИЯ ДВОЙСТВЕННОСТИ
- 2.6.1. Вычислительные формы двойственной задачи
- 2.7. СРАВНЕНИЕ ДОСТАТОЧНЫХ УСЛОВИЙ
- Глава 3. ПРИМЕНЕНИЕ УСЛОВИЙ КУНА—ТАККЕРА К ТЕОРИИ ДВОЙСТВЕННОСТИ
- 3.1. ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ФУНКЦИИ ЛАГРАНЖА И ТЕОРИЯ ДВОЙСТВЕННОСТИ
- 3.2. ИНТЕРПРЕТАЦИЯ МНОЖИТЕЛЕЙ В УСЛОВИЯХ КУНА-ТАККЕРА
- 3.3. ДВОЙСТВЕННАЯ ЗАДАЧА ГЕОМЕТРИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 3.4. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ И ПРИНЦИП МАКСИМУМА
- Глава 4. ПЕРВАЯ ТЕОРЕМА СХОДИМОСТИ
- 4.2. ОБОЗНАЧЕНИЯ
- 4.3. ИДЕЯ АЛГОРИТМА
- 4.4. СВОЙСТВА СХОДИМОСТИ
- 4.5. ТЕОРЕМА СХОДИМОСТИ
- 4.6. РАЗЛОЖЕНИЕ АЛГОРИТМИЧЕСКОГО ОТОБРАЖЕНИЯ
- Глава 5. ЗАДАЧИ БЕЗ ОГРАНИЧЕНИЙ
- 5.2. МЕТОДЫ ВОЗМОЖНЫХ НАПРАВЛЕНИЙ И ОТОБРАЖЕНИЯ М1 И D
- 5.3. ЗАМКНУТОСТЬ ОТОБРАЖЕНИЯ М1
- 5.4. АЛГОРИТМЫ ДЛЯ ЗАДАЧ БЕЗ ОГРАНИЧЕНИЙ
- 5.4.2. Модифицированный метод Ньютона
- 5.4.3. Циклический координатный спуск
- 5.4.4. Метод оптимизации второго порядка
- ПРИЛОЖЕНИЕ. ПРОЦЕДУРЫ ОДНОМЕРНОГО ПОИСКА
- Глава 6. СМЕШАННЫЕ АЛГОРИТМЫ И КВАДРАТИЧНЫЕ МЕТОДЫ УСКОРЕНИЯ СХОДИМОСТИ, ИСПОЛЬЗУЮЩИЕ СОПРЯЖЕННЫЕ НАПРАВЛЕНИЯ
- 6.1. СМЕШАННЫЕ АЛГОРИТМЫ И ИХ ИСПОЛЬЗОВАНИЕ ДЛЯ ПОВЫШЕНИЯ СКОРОСТИ СХОДИМОСТИ
- 6.2. СОПРЯЖЕННЫЕ НАПРАВЛЕНИЯ
- 6.3. МЕТОД ПОСТРОЕНИЯ СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ, ИСПОЛЬЗУЮЩИЙ ТОЛЬКО ЗНАЧЕНИЯ ФУНКЦИИ
- 6.4. МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ
- Глава 7. НЕПРЕРЫВНОСТЬ, КОМПАКТНОСТЬ И ЗАМКНУТОСТЬ
- 7.2. НЕПРЕРЫВНОСТЬ, КОМПАКТНОСТЬ И МАКСИМИЗАЦИЯ
- Глава 8. НЕКОТОРЫЕ МЕТОДЫ ДЛЯ ЗАДАЧ С ЛИНЕЙНЫМИ ОГРАНИЧЕНИЯМИ
- 8.2. ВЫПУКЛЫЙ СИМПЛЕКСНЫЙ МЕТОД
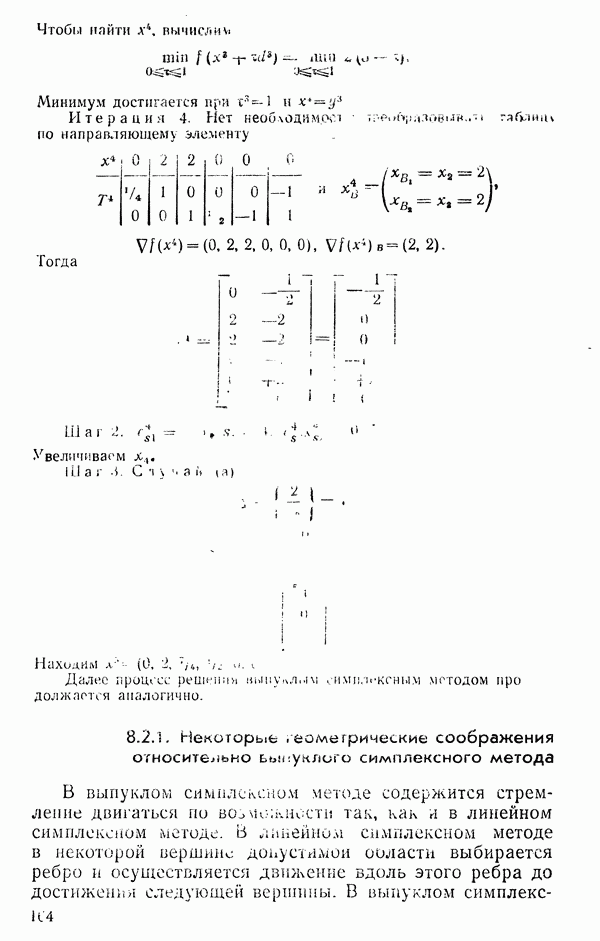
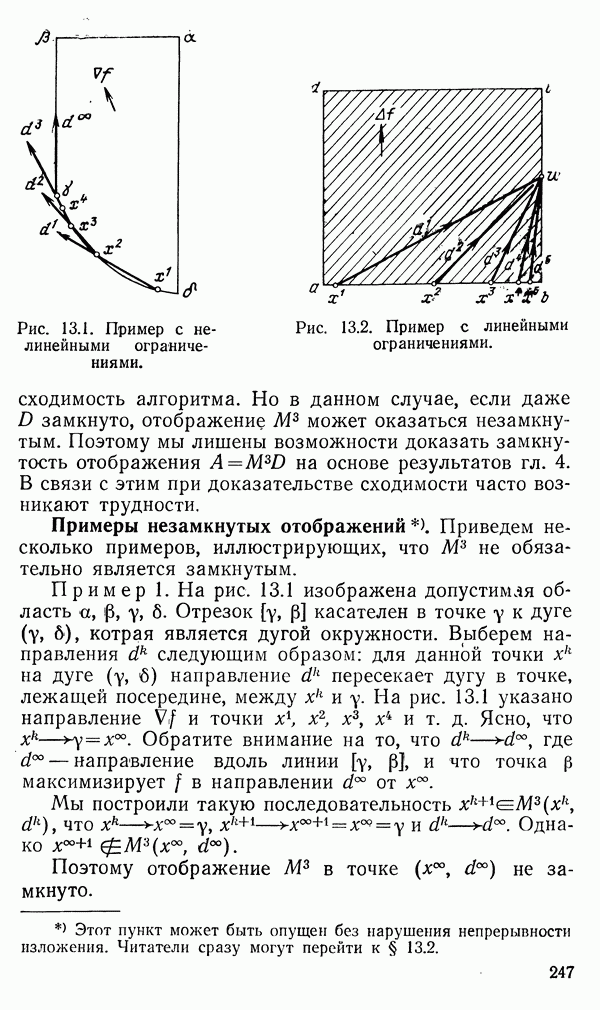
- 8.2.1. Некоторые геометрические соображения относительно выпуклого симплексного метода
- 8.3. МАКСИМИЗАЦИЯ ВОГНУТОЙ ФУНКЦИИ СУБОПТИМИЗАЦИЕЙ НА МНОГООБРАЗИЯХ
- Глава 9. МЕТОДЫ УСКОРЕНИЯ СХОДИМОСТИ И ЗАДАЧА КВАДРАТИЧНОГО ПРОГРАММИРОВАНИЯ
- 9.1.1. Пример алгоритма ВСМ-СН
- 9.2. МЕТОД СУБОПТИМИЗАЦИИ НА МНОГООБРАЗИЯХ ДЛЯ КВАДРАТИЧНОГО ПРОГРАММИРОВАНИЯ
- Глава 10. НЕКОТОРЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПРИМЕНЕНИЕМ К ТЕОРИИ ЛЯПУНОВА ДЛЯ РАЗНОСТНЫХ УРАВНЕНИЙ
- 10.2. АЛГОРИТМ ЛАГРАНЖА
- 10.3. ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
- 10.4. УСТОЙЧИВОСТЬ СИСТЕМ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ — ТЕОРИЯ ЛЯПУНОВА
- Глава 11. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ
- 11.2. АЛГОРИТМЫ
- 11.3. ТЕОРЕМЫ СХОДИМОСТИ
- Глава 12. МЕТОДЫ ШТРАФНЫХ ФУНКЦИЙ И БАРЬЕРОВ
- 12.2. МЕТОД ШТРАФНЫХ ФУНКЦИЙ
- 12.3. МЕТОД БАРЬЕРОВ
- Глава 13. МЕТОД ВОЗМОЖНЫХ НАПРАВЛЕНИЙ И ЯВЛЕНИЕ ЗАКЛИНИВАНИЯ
- 13.2. ЯВЛЕНИЕ ЗАКЛИНИВАНИЯ В МЕТОДЕ ВОЗМОЖНЫХ НАПРАВЛЕНИЙ
- 13.3. ТЕОРЕМА СХОДИМОСТИ ДЛЯ МЕТОДОВ ВОЗМОЖНЫХ НАПРАВЛЕНИЙ
- 13.4. МЕТОД r-ВОЗМУЩЕНИЙ
- Глава 14. АЛГОРИТМЫ ОТСЕЧЕНИЙ
- 14.2. ВОГНУТЫЙ АЛГОРИТМ ОТСЕЧЕНИЙ
- 14.3. АЛГОРИТМ ОПОРНОЙ ГИПЕРПЛОСКОСТИ
- 14.4. ДВОЙСТВЕННЫЙ МЕТОД ОТСЕЧЕНИЙ
- ПРИЛОЖЕНИЕ. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ ОБЩЕГО КУРСА МАТЕМАТИКИ И ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- СПИСОК ЛИТЕРАТУРЫ