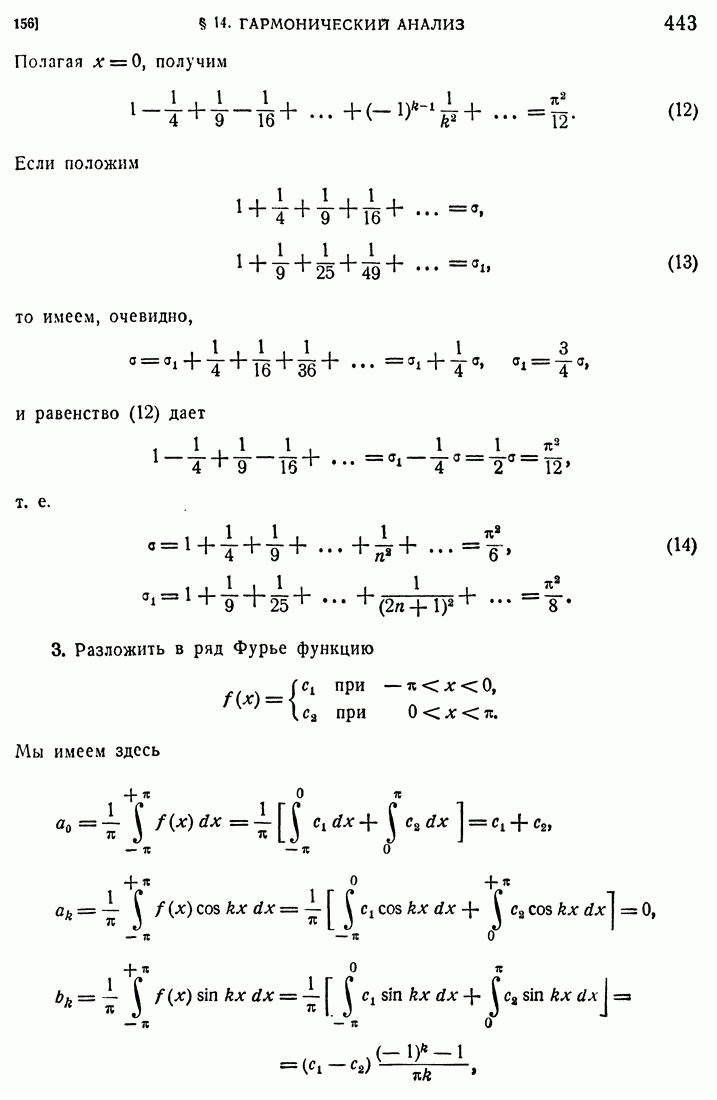| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
106. Интеграл Лебега.
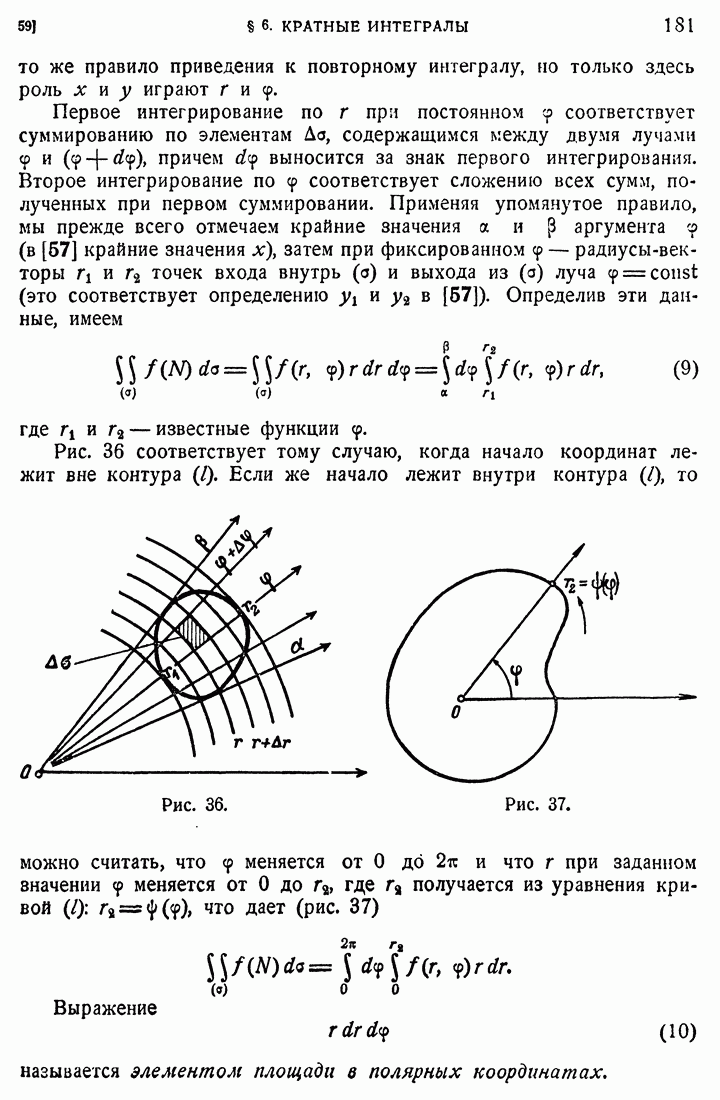
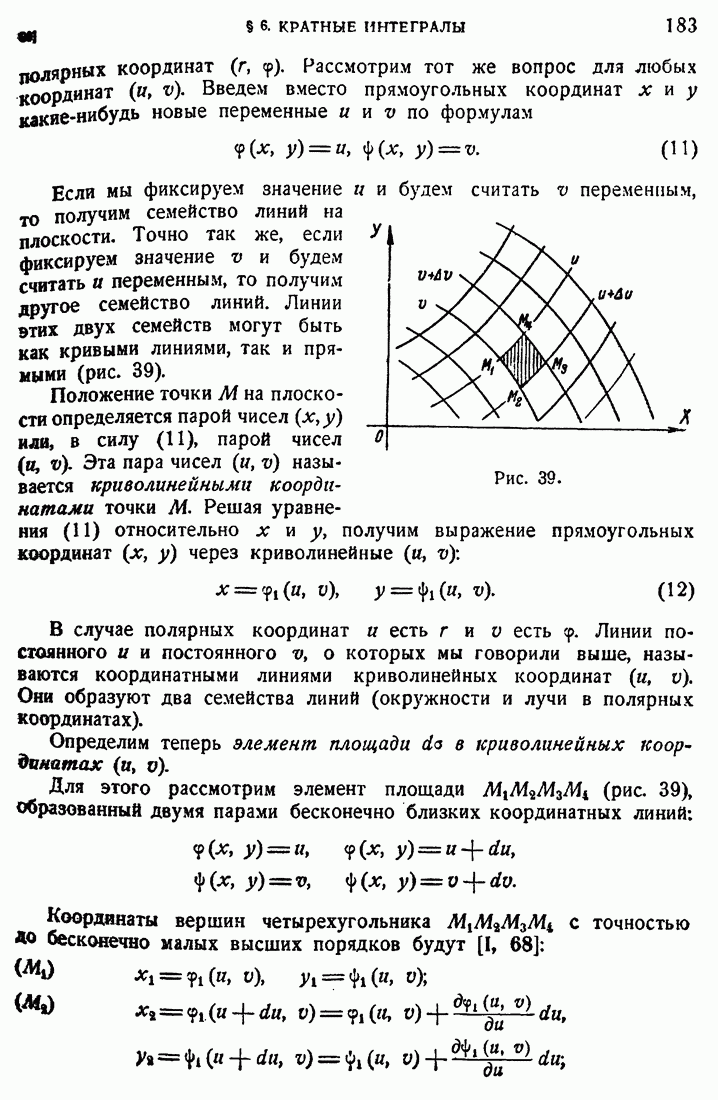
Переходим к определению интеграла Лебега. Пусть на измеримом множестве конечной меры Е задана ограниченная измеримая функция. Из ограниченности  следует существование такого числа
следует существование такого числа  что
что  при
при  Разбиваем Е на конечное число измеримых подмножеств попарно без общих точек:
Разбиваем Е на конечное число измеримых подмножеств попарно без общих точек:

и пусть  - точная нижняя и верхняя границы значений на Е. Составляем суммы
- точная нижняя и верхняя границы значений на Е. Составляем суммы 

где  обозначает подразделение (39). Эти суммы, очевидно, ограничены при любых подразделениях:
обозначает подразделение (39). Эти суммы, очевидно, ограничены при любых подразделениях:  Пусть
Пусть  точная верхняя граница
точная верхняя граница  точная нижняя граница
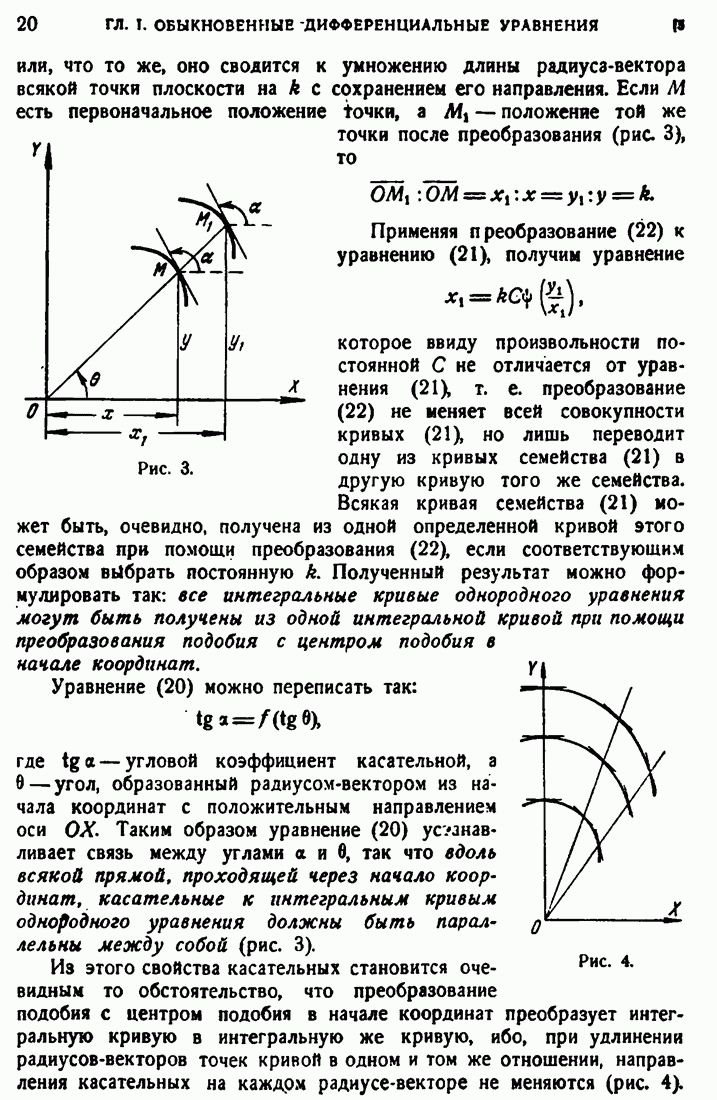
точная нижняя граница  при всевозможных
при всевозможных  .
.
Определение. Если  то говорят, что
то говорят, что  интегрируема по Е, и величину интеграла считают равной
интегрируема по Е, и величину интеграла считают равной 

Определенный таким образом интеграл называется интегралом Лебега. Отметим вид  подынтегрального выражения и тот факт, что мы пишем один знак интеграла во всех случаях: прямой, плоскости,
подынтегрального выражения и тот факт, что мы пишем один знак интеграла во всех случаях: прямой, плоскости,  -мерного пространства. В дальнейшем мы будем придерживаться этих обозначений. Только в
-мерного пространства. В дальнейшем мы будем придерживаться этих обозначений. Только в  при изложении вопроса о приведении кратного интеграла к последовательным квадратурам, мы будем записывать подынтегральное выражение в более подробной форме и знак интеграла при кратном интегрировании будем писать несколько раз. Так, например, для интеграла на плоскости можно писать
при изложении вопроса о приведении кратного интеграла к последовательным квадратурам, мы будем записывать подынтегральное выражение в более подробной форме и знак интеграла при кратном интегрировании будем писать несколько раз. Так, например, для интеграла на плоскости можно писать

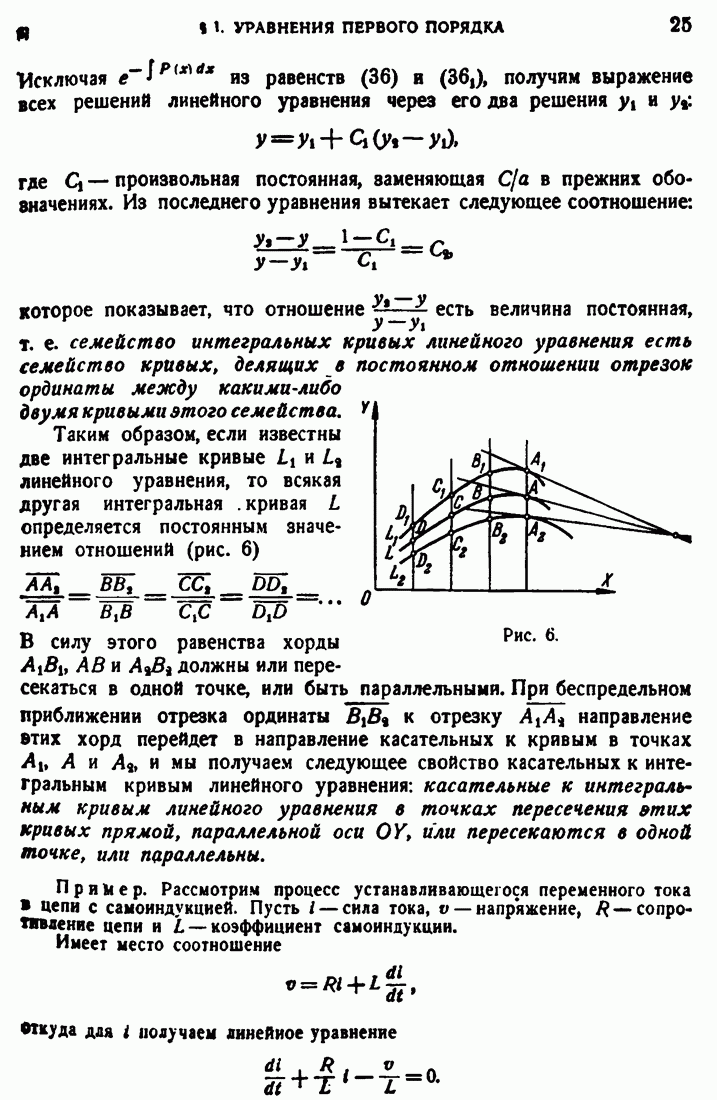
Введем понятие произведения подразделений [ср. I, 115-117]. Положим, что наряду с подразделением (39) мы имеем другое подразделение  ;
;

Произведением подразделений (41) и (42) называется подразделе  состоящее из всевозможных частичных множеств
состоящее из всевозможных частичных множеств  Эти последние не имеют попарно общих точек, но могут быть и пустыми. Подразделение
Эти последние не имеют попарно общих точек, но могут быть и пустыми. Подразделение

называем продолжением подразделения (39), если каждое  при надлежит только одному из
при надлежит только одному из  . При переходе от некоторого подразделения
. При переходе от некоторого подразделения  к его продолжению сумма
к его продолжению сумма  не убывает и
не убывает и  не воз растает. Если
не воз растает. Если  — два каких-либо подразделения, то откуда
— два каких-либо подразделения, то откуда  и, в частности [I, 115],
и, в частности [I, 115],

Кроме сумм (40), составим сумму

где  Имеем, очевидно,
Имеем, очевидно,

Теорема. Для равенства  необходимо и достаточно, чтобы существовала такая последовательность подразделений
необходимо и достаточно, чтобы существовала такая последовательность подразделений  которой
которой 
Доказываем достаточность. Если  , то из (43) следует, что
, то из (43) следует, что  .
.
Доказываем необходимость. Пусть  . По определению
. По определению  существуют такие последовательности подразделений
существуют такие последовательности подразделений  , что
, что  . Для последовательности подразделений
. Для последовательности подразделений  тем более
тем более  Но
Но  и, следовательно,
и, следовательно,  .
.
Доказанная теорема дает необходимое и достаточное условие интегрируемости  Отметим, что в подразделениях
Отметим, что в подразделениях  частичные множества не должны обязательно измельчаться, т. е. наибольший из их диаметров не должен обязательно стремиться к нулю.
частичные множества не должны обязательно измельчаться, т. е. наибольший из их диаметров не должен обязательно стремиться к нулю.
Если существует последовательность подразделений  для которой
для которой  , то
, то  и из (44) следует, что и
и из (44) следует, что и  при любом выборе точек
при любом выборе точек  из
из  Если
Если  суть продолжение
суть продолжение  то все сказанное выше имеет место и для
то все сказанное выше имеет место и для  Мы укажем сейчас такую последовательность подразделений
Мы укажем сейчас такую последовательность подразделений  что для любой ограниченной измеримой функции, определенной на множестве
что для любой ограниченной измеримой функции, определенной на множестве  конечной меры,
конечной меры,  откуда будет следовать интегрируемость такой функции. Пусть
откуда будет следовать интегрируемость такой функции. Пусть  — точные нижняя и верхняя границы значений
— точные нижняя и верхняя границы значений  на Е. Разобьем промежуток
на Е. Разобьем промежуток 
на частя

и определим следующим образом разбиение  множества Е на частичные множества:
множества Е на частичные множества:

Отсюда следует, что  и, таким образом,
и, таким образом,

и тем более

Образуем разность между крайними членами этого неравенства;

Пусть  наибольшая
наибольшая  разностей
разностей  . Имеем в силу того, что сумма
. Имеем в силу того, что сумма  равна
равна 

Если мы возьмем такую последовательность подразделений  для которых соответствующая величина
для которых соответствующая величина  при
при  , то разность между крайними членами неравенства (48) стремится к нулю, и, следовательно,
, то разность между крайними членами неравенства (48) стремится к нулю, и, следовательно,  интегрируема. Отметим, что условие
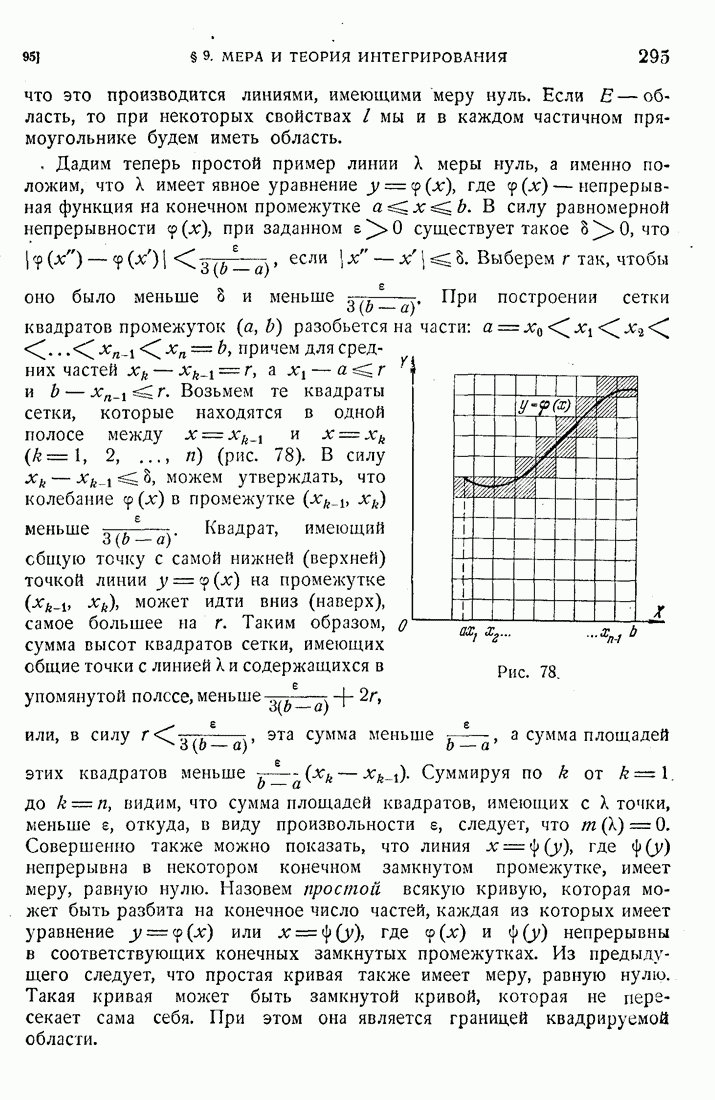
интегрируема. Отметим, что условие  при
при  сводится к беспредельному измельчению разбиения промежутка
сводится к беспредельному измельчению разбиения промежутка  изменения функции
изменения функции  Подразделение (46) множества Е называется обычно подразделением Лебега, а обе суммы, входящие в неравенство (47), соответствующими суммам и Лебега. Из сказанного выше следует
Подразделение (46) множества Е называется обычно подразделением Лебега, а обе суммы, входящие в неравенство (47), соответствующими суммам и Лебега. Из сказанного выше следует
Основная теорема. Всякая ограниченная, измеримая на измеримом множестве Е конечной меры функция  интегрируема по Е, и величина интеграла равна пределу сумм Лебега или сумм
интегрируема по Е, и величина интеграла равна пределу сумм Лебега или сумм  при любом выборе
при любом выборе  для подразделений Лебега при беспредельном измельчении промежутка
для подразделений Лебега при беспредельном измельчении промежутка  изменения функции.
изменения функции.
Суммы  будут иметь, как мы упоминали выше, тот же предел и для любых продолжений
будут иметь, как мы упоминали выше, тот же предел и для любых продолжений  подразделений
подразделений  о которых говорилось в теореме.
о которых говорилось в теореме.
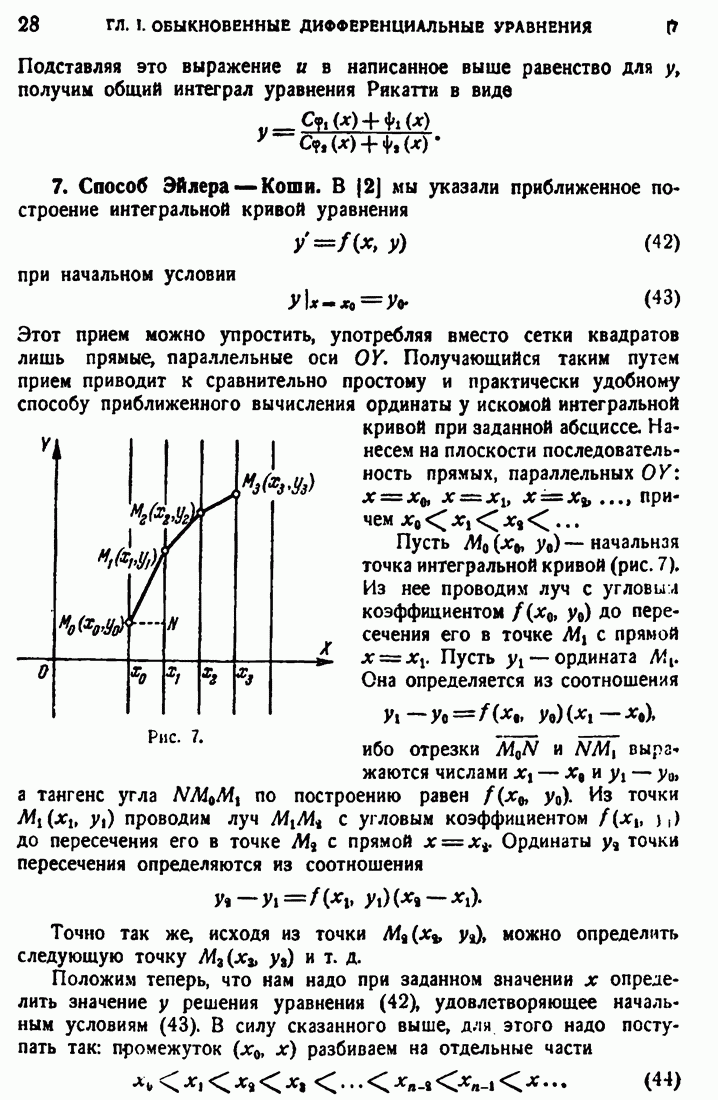
Пусть ограниченная функция  определена, например, на конечном замкнутом промежутке
определена, например, на конечном замкнутом промежутке  Как показал Лебег, для существования интеграла Римана от
Как показал Лебег, для существования интеграла Римана от  по
по  необходимо и достаточно, чтобы лебегова мера точек разрыва
необходимо и достаточно, чтобы лебегова мера точек разрыва  имела меру нуль. Из этого результата легко следует, что при этом
имела меру нуль. Из этого результата легко следует, что при этом  измерима на
измерима на  и ее интеграл Лебега по
и ее интеграл Лебега по  совпадает с интегралом Римана.
совпадает с интегралом Римана.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮ
- ГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Определение решения по начальному условию. Теорема существования и единственности.
- 3. Уравнения с отделяющимися переменными.
- 4. Примеры.
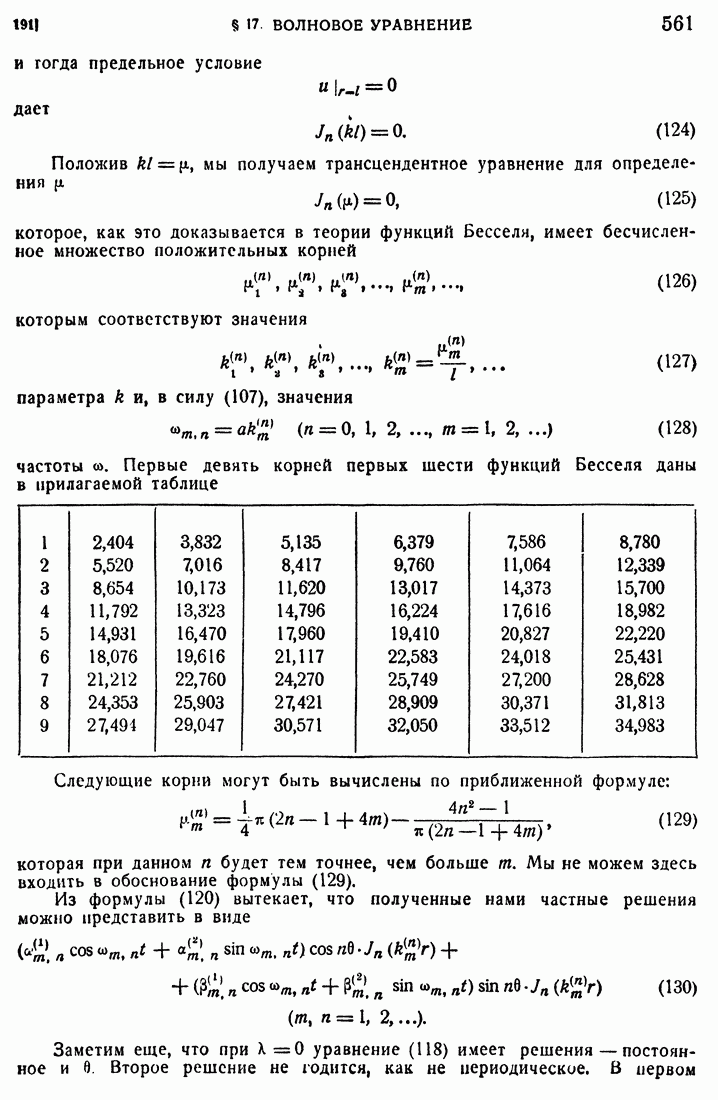
- 5. Однородное уравнение.
- 6. Линейные уравнения и уравнение Бернулли.
- 7. Способ Эйлера—Коши.
- 8. Применение степенных рядов.
- 9. Общий интеграл и особое решение.
- 10. Уравнения, не решенные относительно у’.
- 11. Уравнение Клеро.
- 12. Уравнение Лагранжа.
- 13. Огибающие семейства кривых и особые решения.
- 14. Изогональные траектории.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ И СИСТЕМЫ УРАВНЕНИЙ
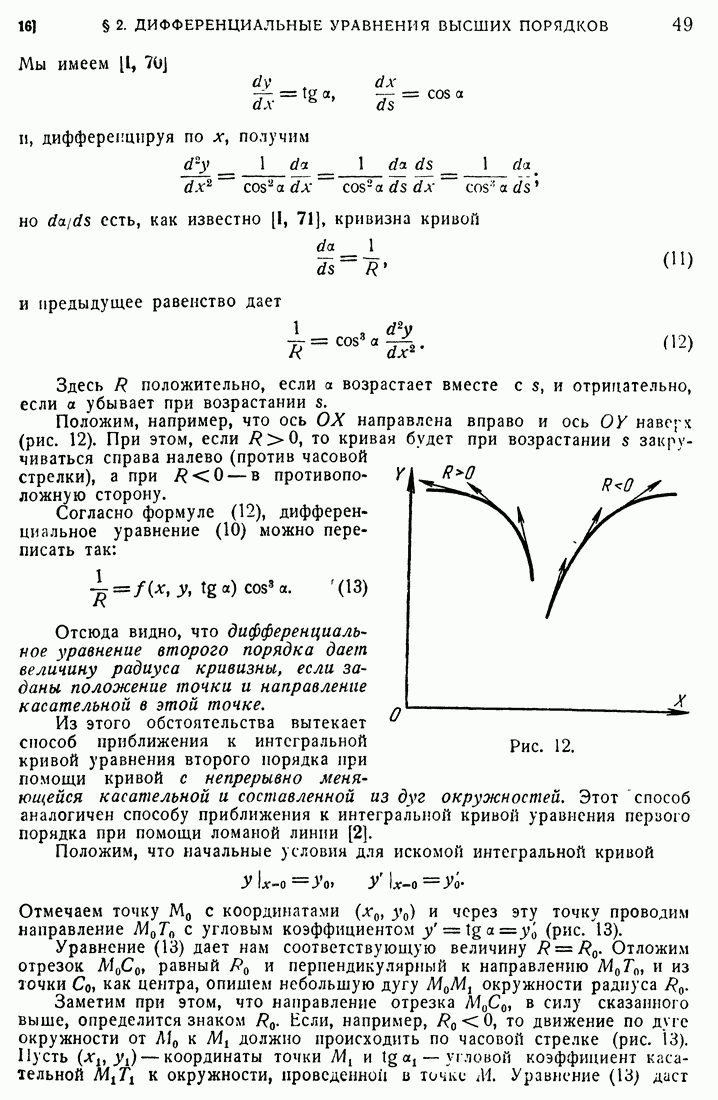
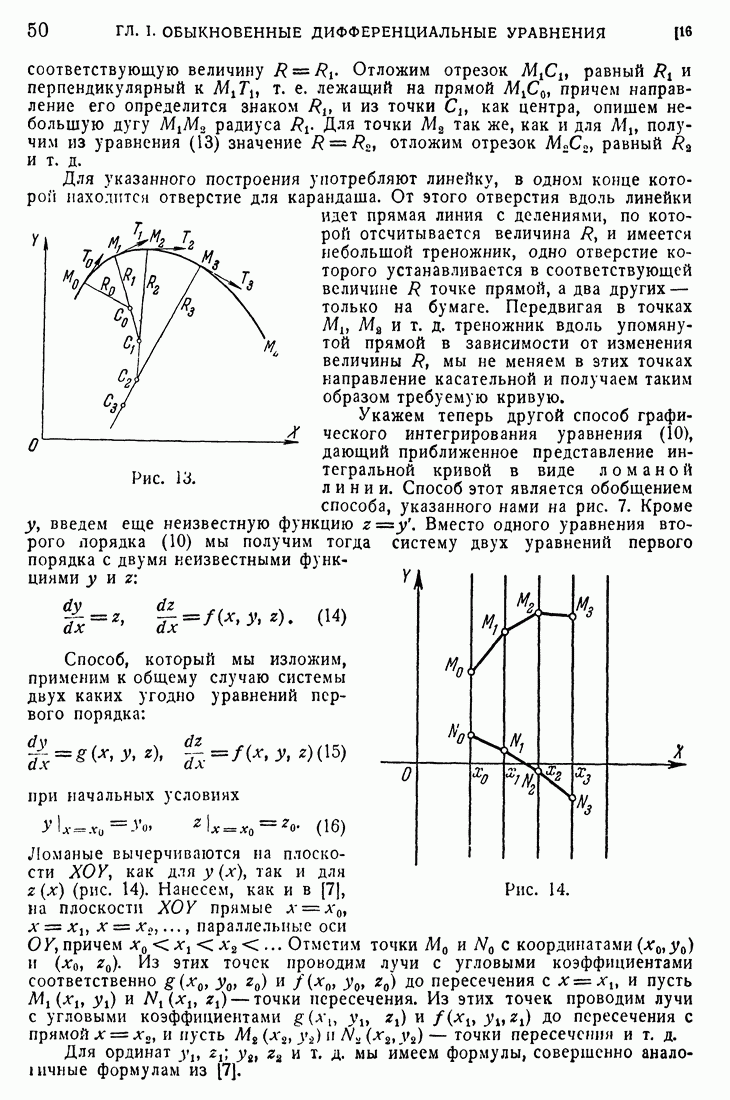
- 16. Графические способы интегрирования дифференциального уравнения второго порядка.
- 17. Уравнение у^(n)=f(x).
- 18. Понижение порядка дифференциального уравнения.
- 19. Системы обыкновенных дифференциальных уравнений.
- 20. Примеры.
- 21. Системы уравнений и уравнения высших порядков.
- 22. Линейные уравнения с частными производными.
- 23. Геометрическая интерпретация.
- 24. Примеры.
- ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 25. Линейные однородные уравнения второго порядка.
- 26. Линейные неоднородные уравнения второго порядка.
- 27. Линейные уравнения высших порядков.
- 28. Однородные уравнения второго порядка с постоянными коэффициентами.
- 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- 30. Частные случаи.
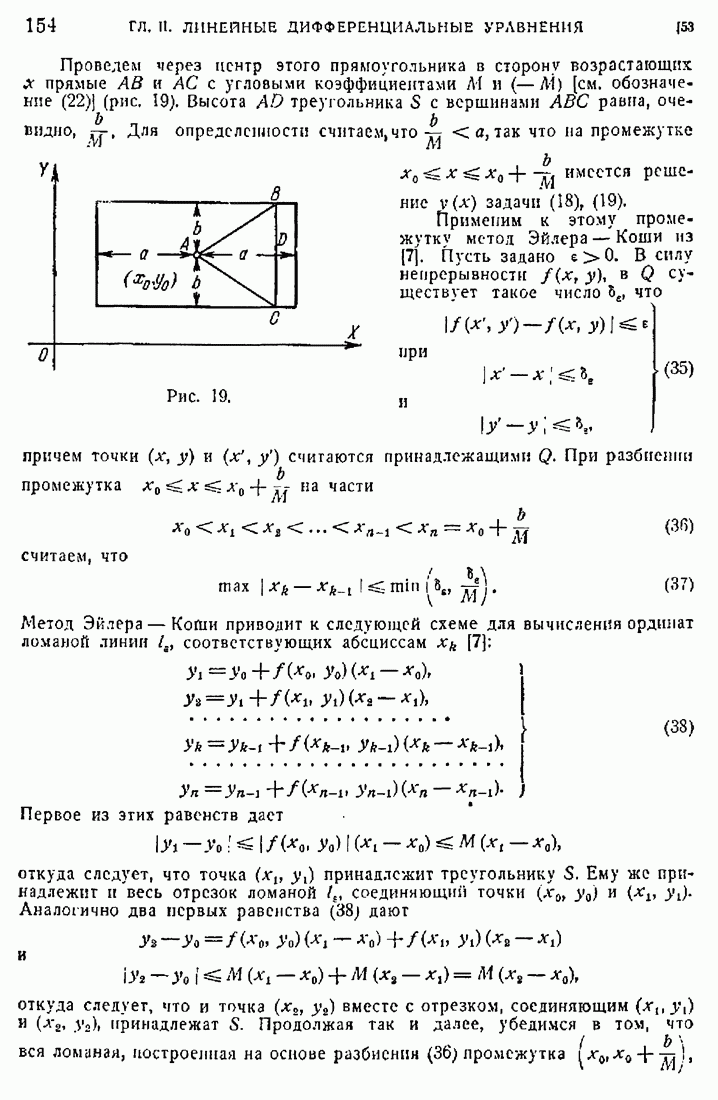
- 31. Корни решений и колеблющиеся решения
- 32. Линейные уравнения высших порядков с постоянными коэффициентами.
- 33. Линейные уравнения и колебательные явления.
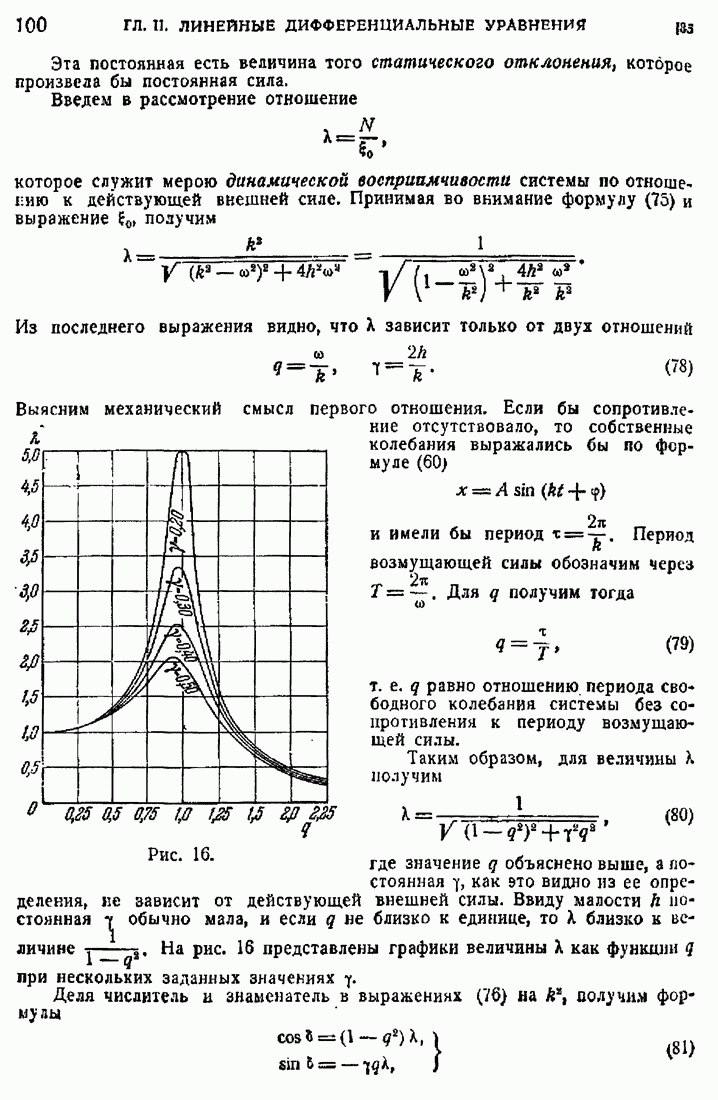
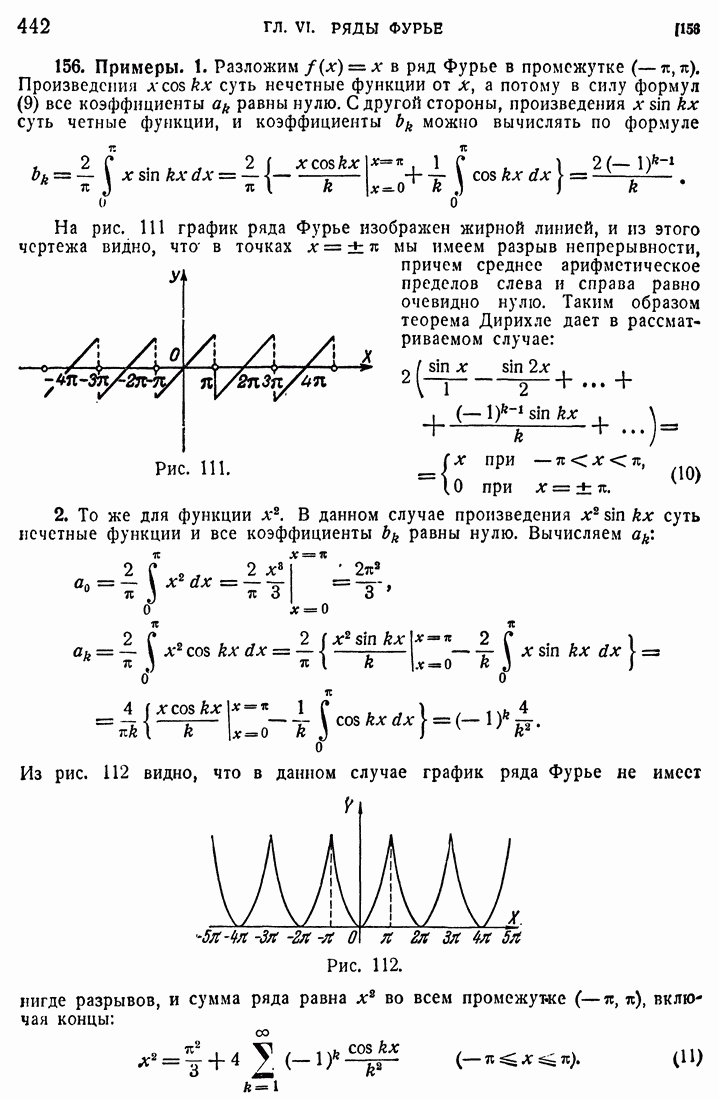
- 34. Собственные и вынужденные колебания.
- 35. Синусоидальная внешняя сила и резонанс.
- 36. Предельные задачи.
- 37. Примеры.
- 38. Символический метод.
- 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами.
- 40. Линейные неоднородные уравнения с постоянными коэффициентами.
- 41. Пример.
- 42 Уравнение Эйлера.
- 43. Системы линейных уравнений с постоянными коэффициентами.
- 44. Примеры
- § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
- 45. Интегрирование линейного уравнения с помощью степенного ряда
- 46. Примеры.
- 47. Разложение решения в обобщенный степенной ряд.
- 48. Уравнение Бесселя
- 49. Уравнения, приводящиеся к уравнению Бесселя
- § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 50. Метод последовательных приближений для линейных уравнений.
- 51. Случай нелинейного уравнения.
- 52. Дополнения к теореме существования и единственности.
- 53. Сходимость метода Эйлера — Коши.
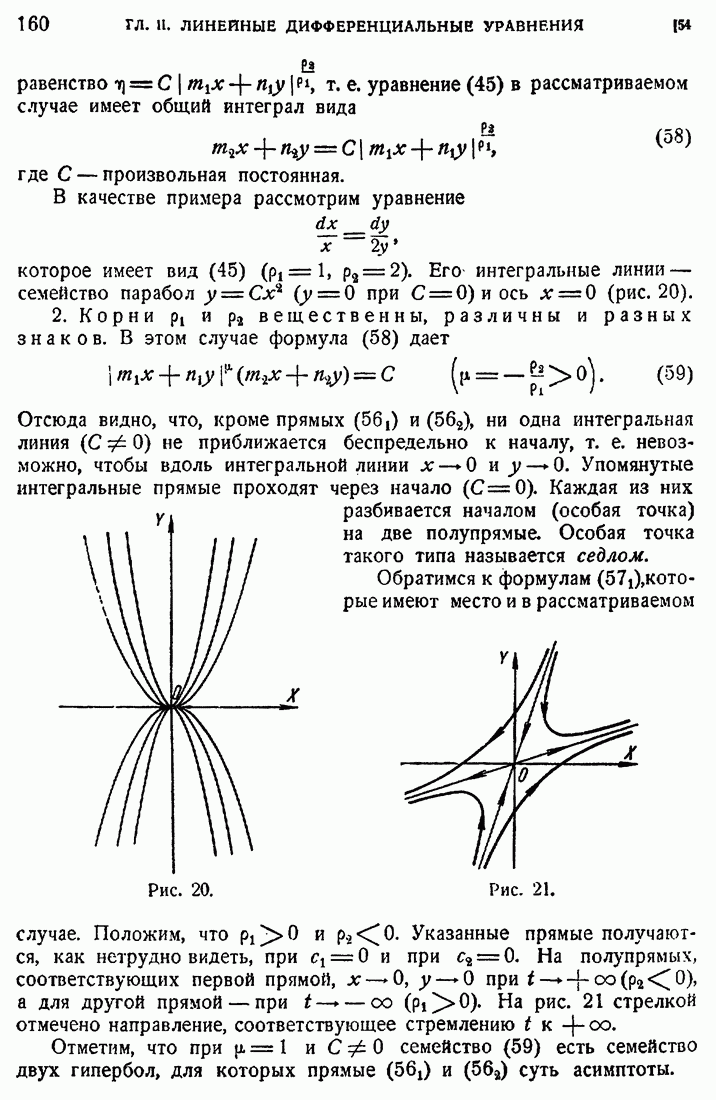
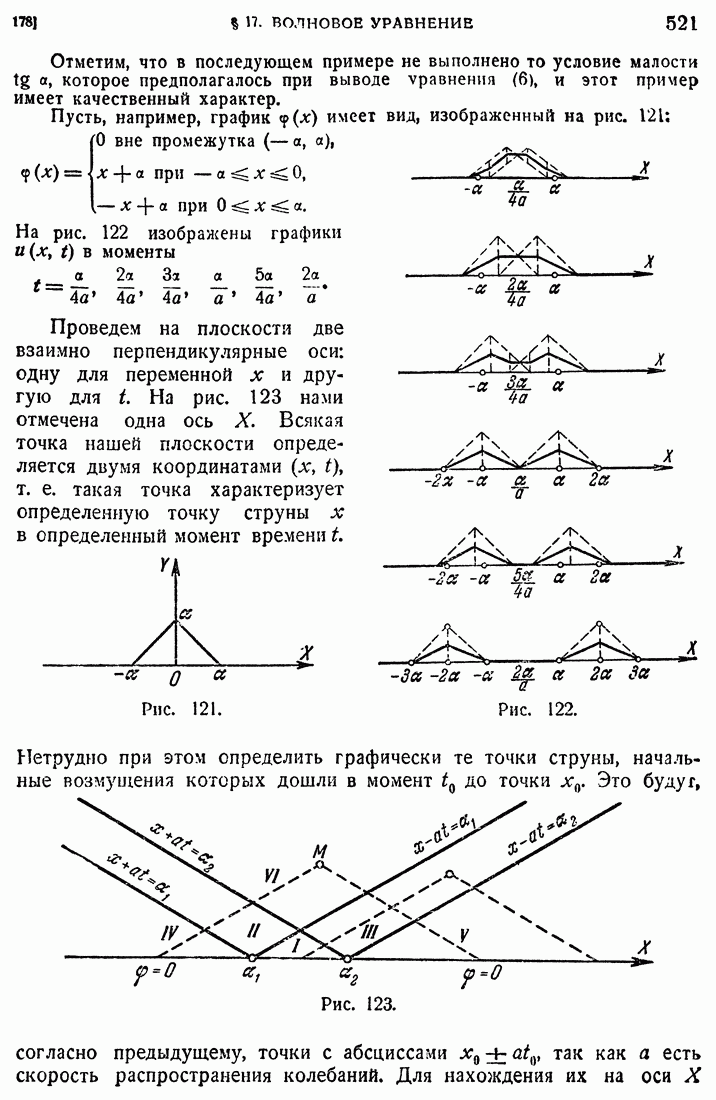
- 54. Особые точки дифференциальных уравнений первого порядка.
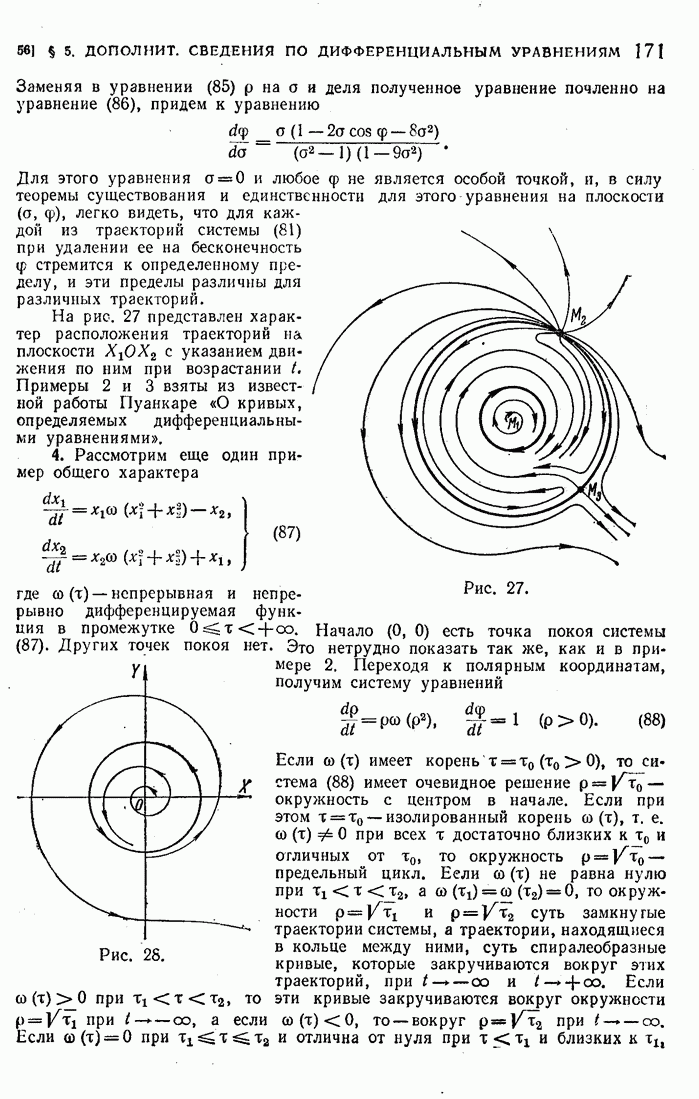
- 55. Автономные системы.
- 56. Примеры.
- ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 6. КРАТНЫЕ ИНТЕГРАЛЫ
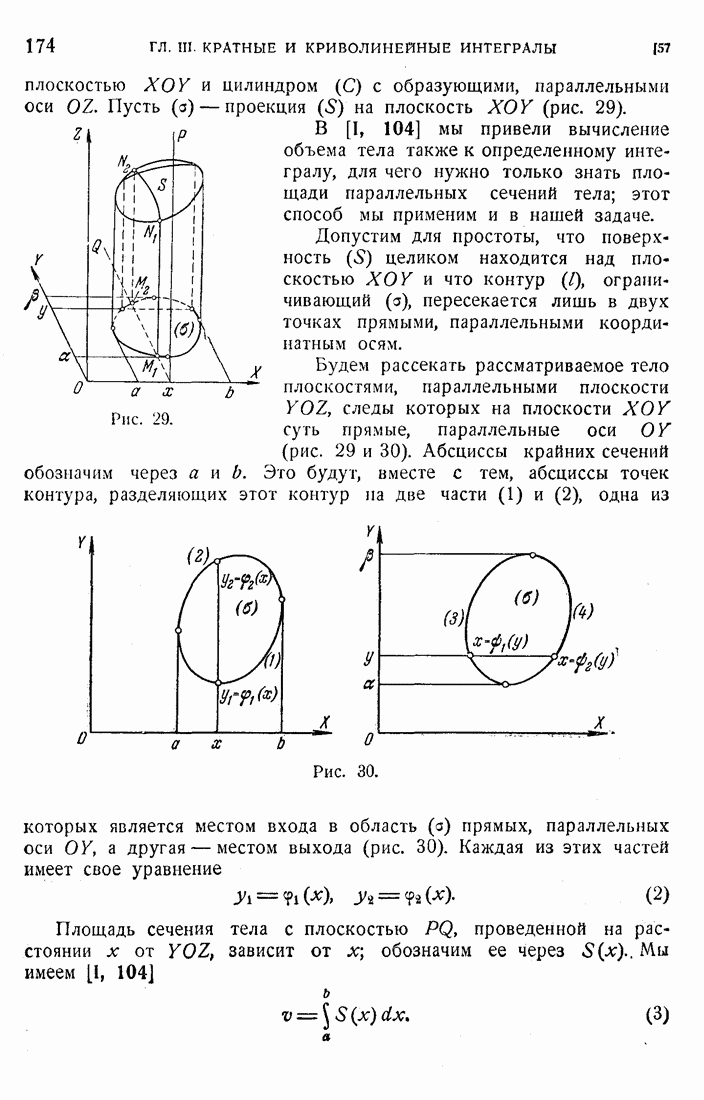
- 58. Двукратный интеграл.
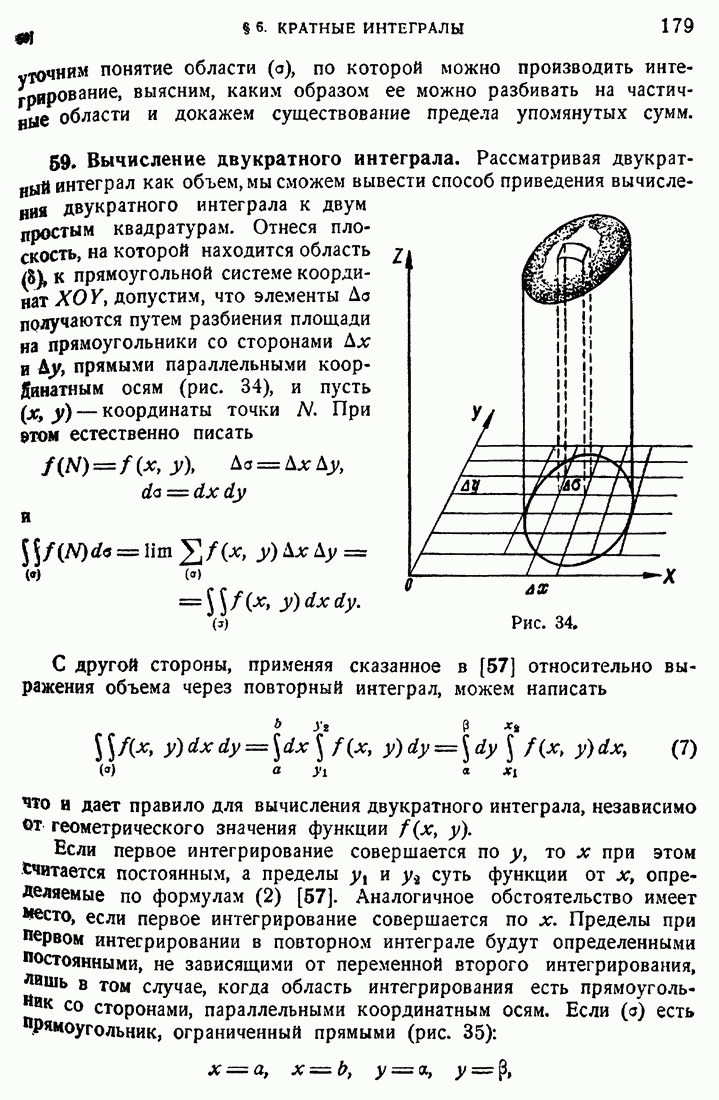
- 59. Вычисление двукратного интеграла.
- 60. Криволинейные координаты.
- 61. Трехкратный интеграл
- 62. Цилиндрические и сферические координаты.
- 63. Криволинейные координаты в пространстве.
- 64. Основные свойства кратных интегралов.
- 65. Площадь поверхности.
- 66. Интегралы по поверхности и формула Остроградского.
- 67. Интегралы по определенной стороне поверхности.
- 68. Моменты.
- § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- 69. Определение криволинейного интеграла.
- 70. Работа силового поля. Примеры.
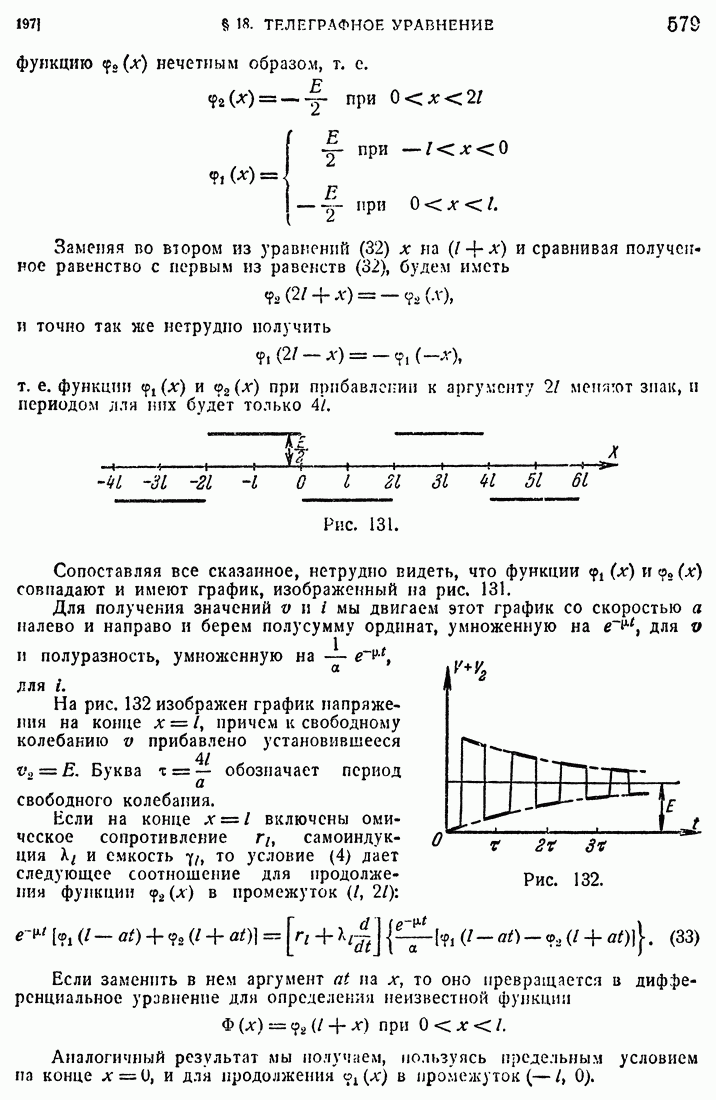
- 71. Площадь и криволинейный интеграл.
- 72. Формула Грина
- 73. Формула Стокса.
- 74. Независимость криволинейного интеграла от пути на плоскости.
- 75. Случай многосвязной области.
- 76. Независимость криволинейного интеграла от пути в пространстве.
- 77. Установившееся течение жидкости.
- 78. Интегрирующий множитель.
- 79. Уравнение в полных дифференциалах для случая трех переменных.
- 80. Замена переменных в двойном интеграле.
- § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 81. Интегрирование под знаком интеграла.
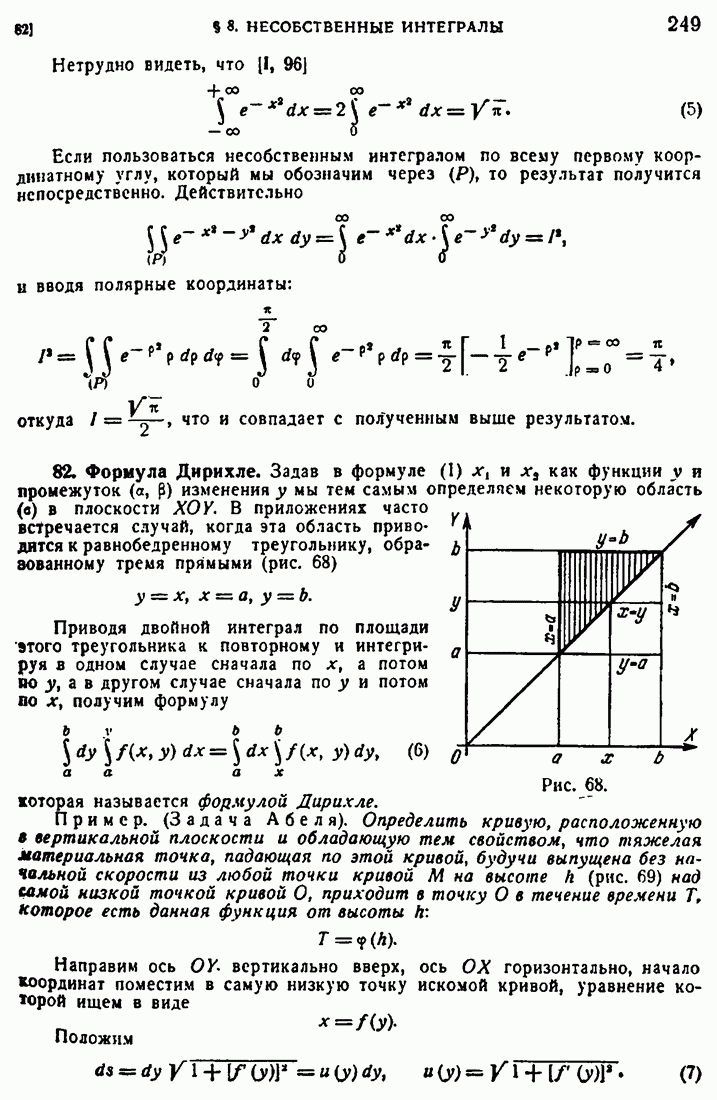
- 82. Формула Дирихле.
- 83. Дифференцирование под знаком интеграла
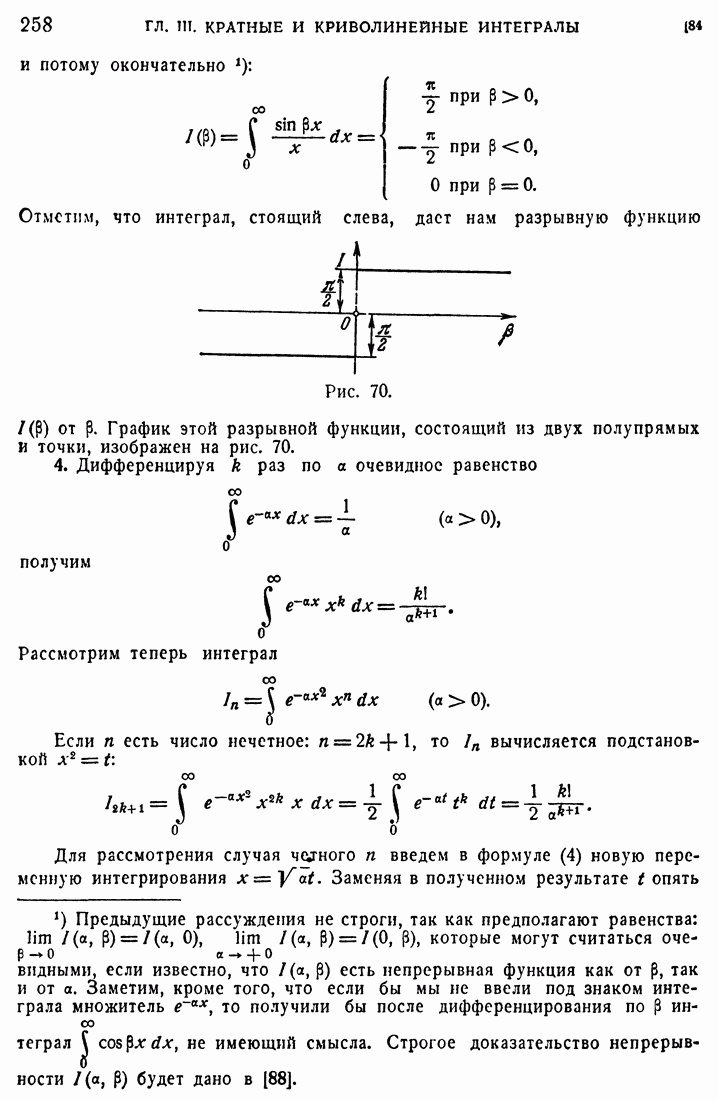
- 84. Примеры.
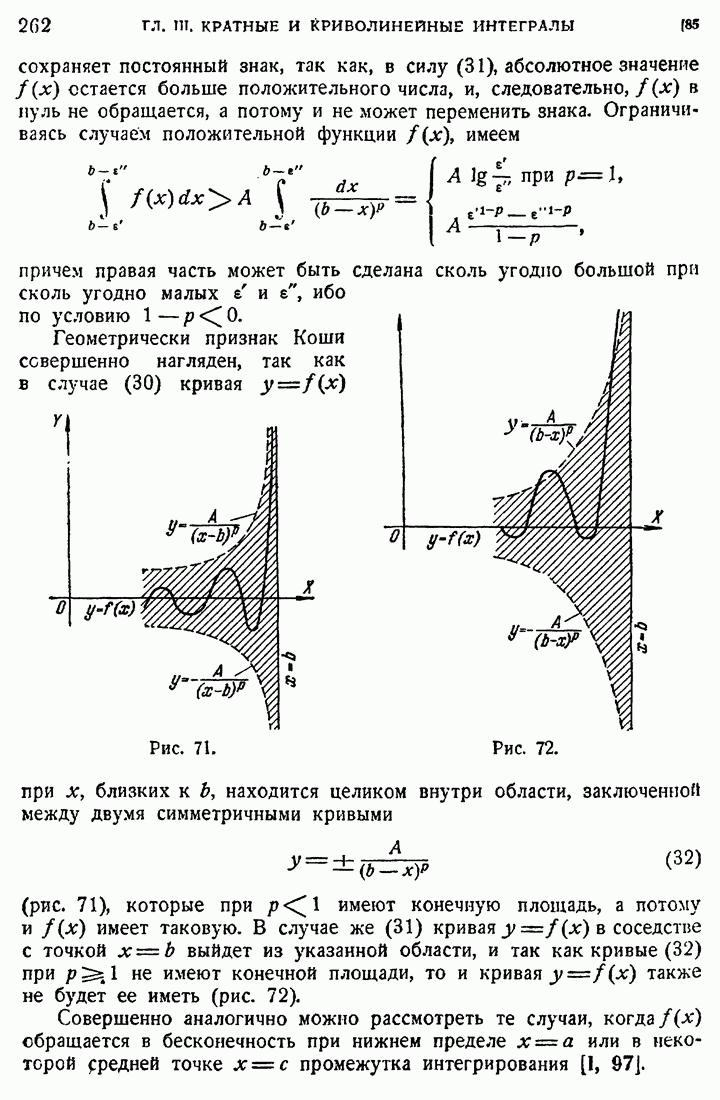
- 85. Несобственные интегралы.
- 86. Неабсолютно сходящиеся интегралы.
- 87. Равномерно сходящиеся интегралы.
- 88. Примеры.
- 89. Несобственные кратные интегралы.
- 90. Примеры.
- § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ
- 92. Основные теоремы.
- 93. Счетные множества. Действия над точечными множествами.
- 94. Мера Жордана.
- 95. Квадрируемые множества.
- 96. Независимость от выбора осей.
- 97. Случай любого числа измерений.
- 98. Интегрируемые функции.
- 99. Вычисление двойного интеграла.
- 100. n-кратные интегралы.
- 101. Примеры.
- 102. Внешняя мера Лебега.
- 103. Измеримые множества.
- 104. Измеримые функции.
- 105. Дополнительные сведения.
- 106. Интеграл Лебега.
- 107. Свойства интеграла Лебега.
- 108. Интегралы от неограниченных функций.
- 109. Предельный переход под знаком интеграла.
- 110. Теорема Фубини.
- 111. Интегралы по множеству бесконечной меры.
- ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ
- 112. Сложение и вычитание векторов.
- 113. Умножение вектора на скаляр. Компланарность векторов.
- 114. Разложение вектора по трем некомпланарным векторам.
- 115. Скалярное произведение.
- 116. Векторное произведение.
- 117. Соотношения между скалярным к векторным произведениями.
- 118. Скорости точек вращающегося твердого тела; момент вектора.
- § 11 ТЕОРИЯ ПОЛЯ
- 119. Дифференцирование вектора
- 120. Скалярное поле и его градиент.
- 121. Векторное поле; расходимость и вихрь.
- 122. Потенциальное и соленоидальное поля.
- 123. Направленный элемент поверхности.
- 124. Некоторые формулы векторного анализа.
- 125. Движение твердого тела и малая деформация.
- 126. Уравнение непрерывности.
- 127. Уравнения гидродинамики идеальной жидкости.
- 128. Уравнения распространения звука.
- 129. Уравнение теплопроводности.
- 130. Уравнения Максвелла.
- 131. Выражение оператора Лапласа в ортогональных координатах.
- 132. Операция дифференцирования для случая переменного поля.
- ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 133. Плоская кривая, ее кривизна и эволюта.
- 134. Эвольвента.
- 135. Естественное уравнение кривой.
- 136. Основные элементы кривой в пространстве.
- 137. Формулы Френе.
- 138. Соприкасающаяся плоскость.
- 139. Винтовые линии.
- 140. Поле единичных векторов.
- § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 141. Параметрические уравнения поверхности.
- 142. Первая дифференциальная форма Гаусса.
- 143. Вторая дифференциальная форма Гаусса.
- 144. О кривизне линий, начерченных на поверхности.
- 145. Индикатриса Дюпена и формула Эйлера.
- 146. Определение главных радиусов кривизны и главных направлений.
- 147. Линии кривизны.
- 148. Теорема Дюпена.
- 149. Примеры.
- 150. Гауссова кривизна.
- 151. Вариация элемента площади и средняя кривизна.
- 152. Огибающая семейства поверхностей и кривых.
- 153. Развертывающиеся поверхности.
- ГЛАВА VI. РЯДЫ ФУРЬЕ
- 154. Ортогональность тригонометрических функций.
- 155. Теорема Дирихле.
- 156. Примеры.
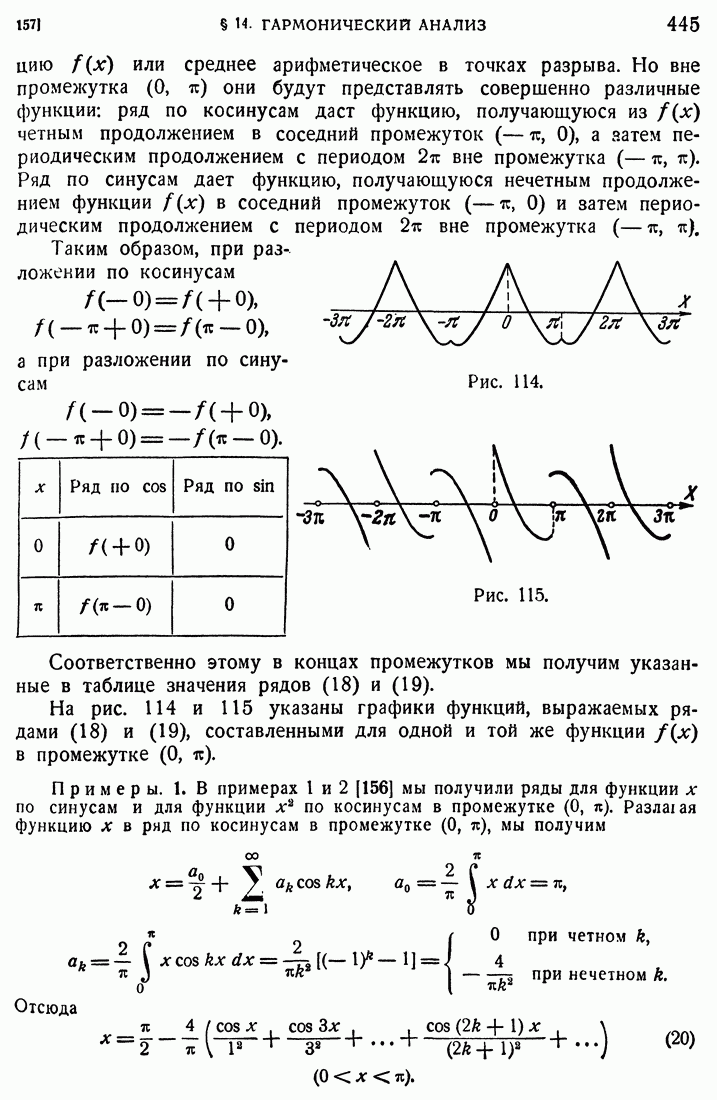
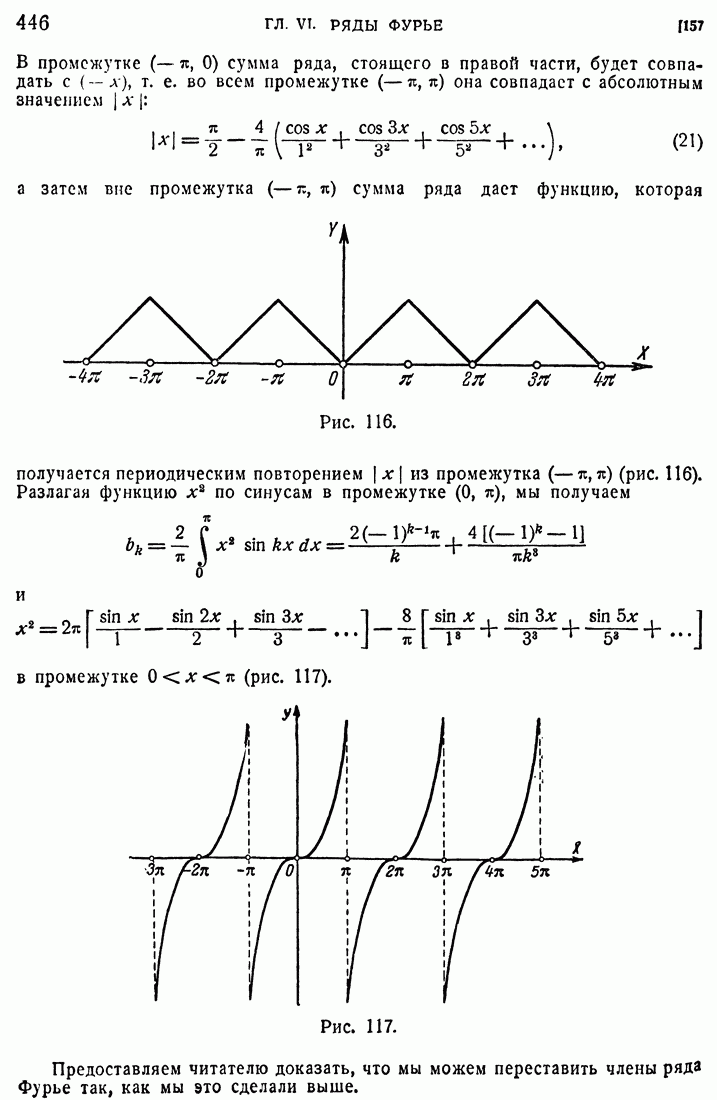
- 157. Разложение в промежутке (0, п).
- 158. Периодические функции периода 2l.
- 159. Средняя квадратичная погрешность.
- 160. Общие ортогональные системы функций.
- 161. Класс L2
- 162. Сходимость в среднем.
- 163. Ортонормированные системы в L2.
- § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ
- 164. Разложение в ряд Фурье.
- 165. Вторая теорема о среднем.
- 166. Интеграл Дирихле.
- 167. Теорема Дирихле.
- 168. Приближение к непрерывной функции полиномами.
- 169. Формула замкнутости.
- 170. Характер сходимости рядов Фурье.
- 171. Улучшение сходимости рядов Фурье.
- 172. Пример.
- § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ
- 173. Формула Фурье.
- 174. Ряды Фурье в комплексной форме.
- 176. Кратные ряды Фурье.
- ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- 176. Уравнение колебаний струны.
- 177. Решение Даламбера.
- 178. Частные случаи.
- 179. Ограниченная струна.
- 180. Способ Фурье.
- 181. Гармоники и стоячие волны.
- 182. Вынужденные колебания.
- 183. Сосредоточенная сила.
- 184. Формула Пуассона.
- 185. Цилиндрические волны.
- 186. Случай n-мерного пространства.
- 187. Неоднородное волновое уравнение.
- 188. Точечный источник.
- 189. Поперечные колебания мембран.
- 190. Прямоугольная мембрана.
- 191. Круглая мембрана.
- 192. Теорема единственности.
- 193. Применение интеграла Фурье.
- § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
- 195. Установившиеся процессы.
- 196. Устанавливающиеся процессы.
- 197. Примеры.
- 198. Обобщенное уравнение колебаний струны.
- 199. Неограниченная цепь в общем случае.
- 200. Способ Фурье для ограниченной цепи.
- 201. Обобщенное волновое уравнение.
- § 19. УРАВНЕНИЕ ЛАПЛАСА
- 202. Гармонические функции.
- 203. Формула Грина.
- 204. Основные свойства гармонических функций.
- 205. Решение задачи Дирихле для круга.
- 206. Интеграл Пуассона.
- 207. Задача Дирихле для сферы.
- 208. Функция Грина.
- 209. Случай полупространства.
- 210. Потенциал объемных масс.
- 211. Уравнение Пуассона.
- 212. Формула Кирхгофа.
- § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
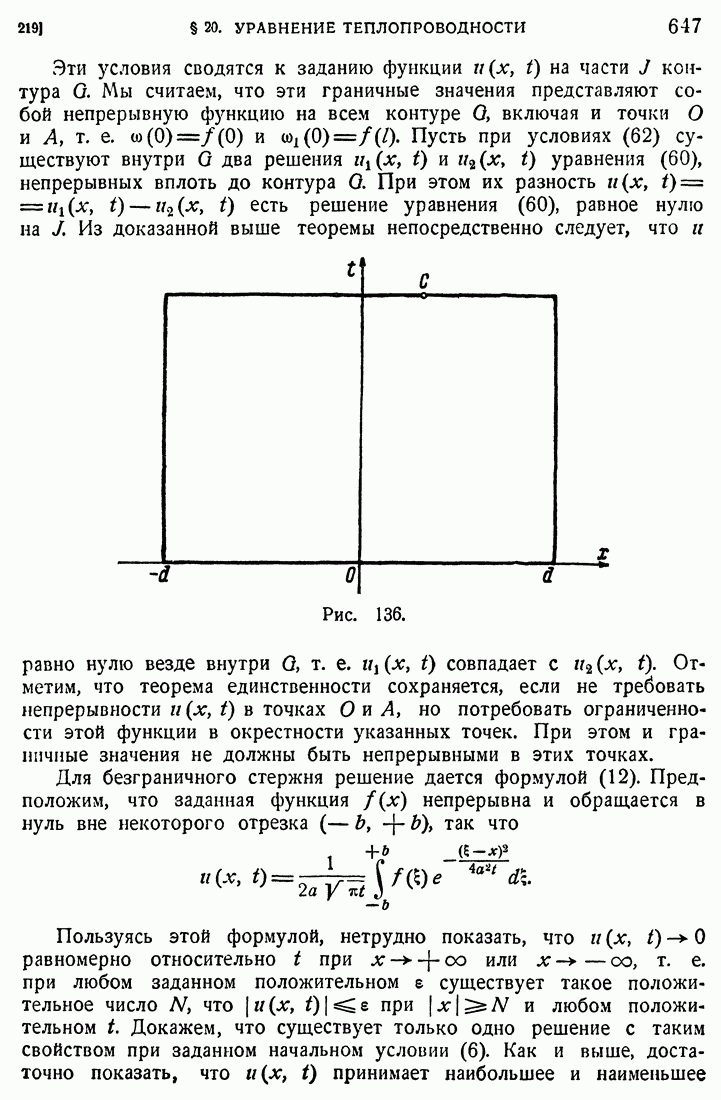
- 214. Неограниченный стержень.
- 215. Стержень, ограниченный с одного конца.
- 216. Стержень, ограниченный с обоих концов.
- 217. Дополнительные замечания.
- 218. Случай сферы.
- 219. Теорема единственности.