| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
90. Примеры.
1. Рассмотрим интеграл 

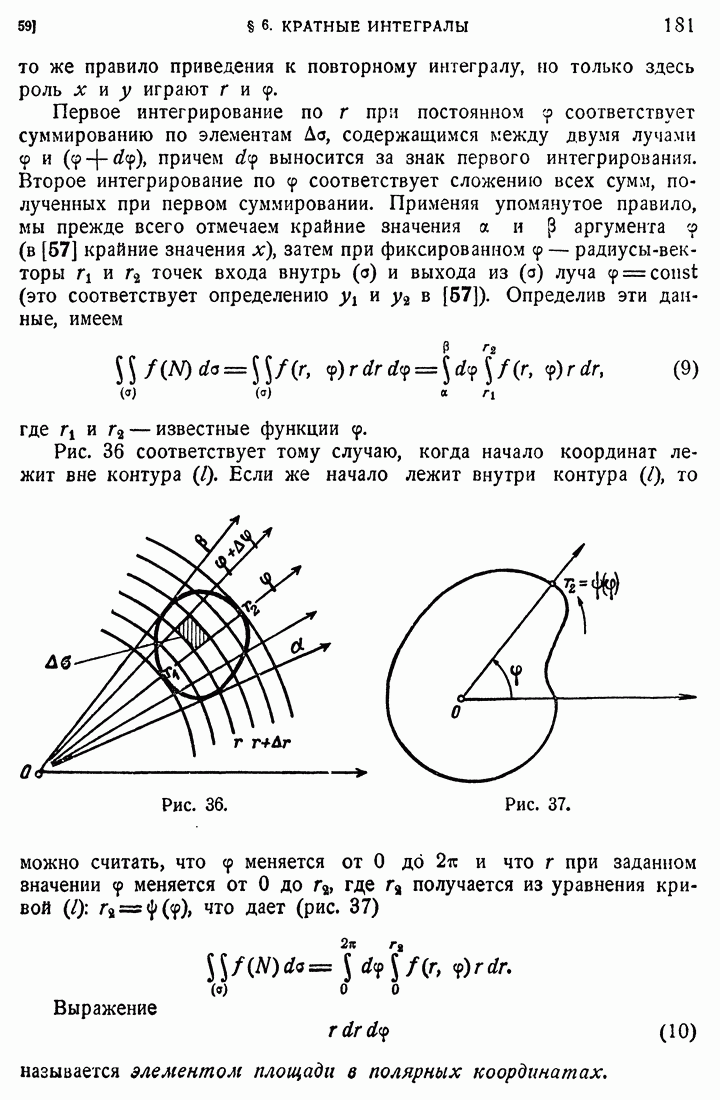
где  плоскость. Вводя полярные координаты и интегрируя по кругу
плоскость. Вводя полярные координаты и интегрируя по кругу  с центром в начале и радиусом R, получим
с центром в начале и радиусом R, получим

Если  то при беспредельном возрастании R правая часть беспредельно возрастает, и интеграл расходится. Если
то при беспредельном возрастании R правая часть беспредельно возрастает, и интеграл расходится. Если  то правая часть имеет конечный предел
то правая часть имеет конечный предел  т. е. интеграл сходится и равен
т. е. интеграл сходится и равен  . В последнем
. В последнем
случае сходимость можно доказать, пользуясь достаточным условием, указанным в предыдущем номере. При  интеграл расходится.
интеграл расходится.
2. Рассмотрим интеграл

где  есть квадрат, ограниченный прямыми;
есть квадрат, ограниченный прямыми;  Вдоль стороны
Вдоль стороны  подынтегральная функция обращается в бесконечность. Выключаем эту сторону узенькой вертикальной полоской, т. е. интегрируем по прямоугольнику
подынтегральная функция обращается в бесконечность. Выключаем эту сторону узенькой вертикальной полоской, т. е. интегрируем по прямоугольнику  ограниченному прямыми:
ограниченному прямыми: 

И при  будем
будем  предел, равный единице, т. е. наш интеграл сходится и равен единице.
предел, равный единице, т. е. наш интеграл сходится и равен единице.

Рис. 74.
3. Притяжение, оказываемое массой на точку, расположенную она или внутри нее (рис. 74). Пусть масса притягиваемой точки  есть единица. Разобьем притягивающее тело
есть единица. Разобьем притягивающее тело  на элементы массы
на элементы массы  и в каждом из них возьмем точку
и в каждом из них возьмем точку  Обозначив через
Обозначив через  расстояние СМ, мы получаем для величины притяжения точки С элементом
расстояние СМ, мы получаем для величины притяжения точки С элементом  приближенное выражение (сосредоточив всю массу
приближенное выражение (сосредоточив всю массу  в точке М)
в точке М)

причем постоянную тяготения мы считаем равной единице. Так как указанная сила притяжения имеет направление отрезка СМ, то проекции этого элементарного притяжения на координатные оси будут:

Проекции же полного притяжения будут иметь приближенные выражения

Обозначив через  плотность массы в точке М, мы приближенно имеем
плотность массы в точке М, мы приближенно имеем

и окончательно, увеличивая число элементов и уменьшая беспредельно каждый из них:

Обращаем внимание на то, что в написанных интегралах переменными интегрирования являются координаты  переменной точки М
переменной точки М
области (v), и плотность  является функцией этих переменных. Координаты
является функцией этих переменных. Координаты  точки С входят под знак интеграла как непосредственно в числители, так и через посредство
точки С входят под знак интеграла как непосредственно в числители, так и через посредство

и являются параметрами, так что величины  и Z суть функции
и Z суть функции  .
.
Если точка С находится вне притягивающей массы, величина  никогда не обращается в нуль, и мы будем иметь дело с обыкновенными интегралами. Если же точка С попадает внутрь массы, то подынтегральные функции в выражениях (66) обращаются в бесконечность при совпадении переменной точки интегрировании
никогда не обращается в нуль, и мы будем иметь дело с обыкновенными интегралами. Если же точка С попадает внутрь массы, то подынтегральные функции в выражениях (66) обращаются в бесконечность при совпадении переменной точки интегрировании  , и мы имеем дело с несобственными интегралами. Они, однако, наверно имеют смысл, если мы будем считать, что
, и мы имеем дело с несобственными интегралами. Они, однако, наверно имеют смысл, если мы будем считать, что  есть непрерывная функция, ибо, назвав через
есть непрерывная функция, ибо, назвав через  верхнюю границу значений функции
верхнюю границу значений функции  мы получим
мы получим

число  предыдущего правила в данном случае равно
предыдущего правила в данном случае равно 
Тем более будет иметь смысл и интеграл

выражающий потенциал рассматриваемой массы в точке С (С этим понятием мы познакомимся подробнее ниже.)
4. Мы имеем очевидные формулы

а потому интегралы (66) можно переписать в виде:

т. е. эти интегралы получаются путем дифференцирования интеграла (68) по  под знаком интеграла. Дифференцирование производится по координатам точки
под знаком интеграла. Дифференцирование производится по координатам точки  , в которой подынтегральная функция терпит разрыв, и рассматриваемый случай не подходит иод тот случай, для которого были установлены выше [87] теоремы, касающиеся непрерывности и возможности дифференцирования под знаком интеграла. Дальше мы увидим, что при условии непрерывности
, в которой подынтегральная функция терпит разрыв, и рассматриваемый случай не подходит иод тот случай, для которого были установлены выше [87] теоремы, касающиеся непрерывности и возможности дифференцирования под знаком интеграла. Дальше мы увидим, что при условии непрерывности  интегралы
интегралы  суть непрерывные функции
суть непрерывные функции  во всем пространстве,
во всем пространстве,  - непрерывная функция с непрерывными частными производными первого порядка, и эти производные могут быть получены дифференцированием интеграла (68) под знаком интеграла, т. е.
- непрерывная функция с непрерывными частными производными первого порядка, и эти производные могут быть получены дифференцированием интеграла (68) под знаком интеграла, т. е.

Дифференцируя потенциал U второй раз по  под знаком интеграла
под знаком интеграла
и помня, что  не зависит от
не зависит от  , получим
, получим

Эти формулы справедливы только в том случае, если точка  находится вне притягивающих масс, т. е. вне
находится вне притягивающих масс, т. е. вне  . При этом все интегралы — собственные. Если же С внутри
. При этом все интегралы — собственные. Если же С внутри  , то двукратное дифференцирование
, то двукратное дифференцирование  даст, как нетрудно проверить непосредственным дифференцированием:
даст, как нетрудно проверить непосредственным дифференцированием:

и к интегралам (69) не будет уже применим признак сходимости из (90], т. е. если С внутри  , то вторые производные от потенциала U нельзя определять, два раза дифференцируя под знаком интеграла.
, то вторые производные от потенциала U нельзя определять, два раза дифференцируя под знаком интеграла.

Рис. 75.
Складывая равенства (70), будем иметь

и, следовательно, складывая равенства (69), справедливые, если С вне  получим уравнение
получим уравнение

Итак, потенциал объемных масс  удовлетворяет уравнению (71) в точках
удовлетворяет уравнению (71) в точках  , находящихся вне этих масс. В дальнейшем мы выясним, как надо изменить это уравнение, если точка С находится внутри масс.
, находящихся вне этих масс. В дальнейшем мы выясним, как надо изменить это уравнение, если точка С находится внутри масс.
5. Рассмотрим случай однородного шара радиуса а  постоянно). Направим ось OZ но прямой ОС, где
постоянно). Направим ось OZ но прямой ОС, где  — центр шара (рис. 75), и введем сферические координаты
— центр шара (рис. 75), и введем сферические координаты  :
:

Но очевидно

Мы выполним сперва интегрирование по  :
:

Введем вместо 0 переменную  , причем
, причем  и считаются постоянными. Здесь придется различать два случая: если
и считаются постоянными. Здесь придется различать два случая: если  , то при постоянных
, то при постоянных  и при изменении 0 от 0 до
и при изменении 0 от 0 до  величина
величина  меняется от
меняется от  до
до  . Если же
. Если же  , то
, то  меняется от
меняется от  до
до  (рис. 76). Сверх того, в силу (73) при постоянных
(рис. 76). Сверх того, в силу (73) при постоянных  :
:

Итак, оказывается

Подставляя это в (72), мы должны различить два случая:
1) Точка С находится вне сферы или на ее поверхности; тогда и в промежутке (0, а) все значения  в этом случае мы имеем
в этом случае мы имеем

где m есть полная масса шара.
2) Точка С находится внутри сферы (рис. 76); здесь промежуток (0, а) нужно разбить на два:  , и мы получим
, и мы получим

при z = a, т. е. когда точка находится на поверхности шара, обе формулы (74) и (75) дают одинаковую величину для U, что доказывает непрерывность функции U. Переходим к вычислению притяжения. В силу симметрии, оно должно быть направлено по оси  так что нужно вычислить только
так что нужно вычислить только


Рис. 76.
Когда точка С находится вне шара, мы пользуемся формулой (74):

когда же точка С находится внутри шара, применяем формулу (75):

При  обе формулы (57) и (58) совпадают, что доказывает непрерывность притяжения Z.
обе формулы (57) и (58) совпадают, что доказывает непрерывность притяжения Z.
Формулы (74), (76), (77) показывают, что потенциал и притяжение однородного шара в точке вне шара можно получить, сосредоточив всю
массу шара в его центре. Притяжение же в точке внутри шара пропорционально расстоянию притягиваемой точки от центра шара.
Для простоты вычислений мы выбрали оси координат специальным образом, направив ось  в точку С, так что в предыдущих формулах z есть расстояние точки С до центра сферы. При любом расположении координатных осей с началом в центре сферы надо заменить z на
в точку С, так что в предыдущих формулах z есть расстояние точки С до центра сферы. При любом расположении координатных осей с началом в центре сферы надо заменить z на  где
где  как всегда, координаты точки С. Формулы (74) и (75) дадут
как всегда, координаты точки С. Формулы (74) и (75) дадут

Первое из выражений для U очевидно удовлетворяет уравнению (71). Дифференцируй второе выражение дна раза по х, у и z, получим

Как мы увидим в дальнейшем, это уравнение оказывается справедливым Я для любого объема  с переменной плотностью, если С находится внутри
с переменной плотностью, если С находится внутри 
6. Положим, что притягивающие массы распределены по поверхности (S) с поверхностной плотностью  которая является функцией переменной точки М поверхности (S). Обозначая, как и выше, через
которая является функцией переменной точки М поверхности (S). Обозначая, как и выше, через  притягиваемую точку с массой единица и через
притягиваемую точку с массой единица и через  расстояние
расстояние  получим для потенциала 0 выражение
получим для потенциала 0 выражение

и для проекций притяжения

Потенциал (79) называется обычно потенциалом простого слоя. Выше мы рассматривали тот случай, когда С находится не на (S) (внутри или вне  ), так что все интегралы собственные. При этом потенциал (79) удовлетворяет, как и в примере 4, уравнению (71).
), так что все интегралы собственные. При этом потенциал (79) удовлетворяет, как и в примере 4, уравнению (71).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮ
- ГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Определение решения по начальному условию. Теорема существования и единственности.
- 3. Уравнения с отделяющимися переменными.
- 4. Примеры.
- 5. Однородное уравнение.
- 6. Линейные уравнения и уравнение Бернулли.
- 7. Способ Эйлера—Коши.
- 8. Применение степенных рядов.
- 9. Общий интеграл и особое решение.
- 10. Уравнения, не решенные относительно у’.
- 11. Уравнение Клеро.
- 12. Уравнение Лагранжа.
- 13. Огибающие семейства кривых и особые решения.
- 14. Изогональные траектории.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ И СИСТЕМЫ УРАВНЕНИЙ
- 16. Графические способы интегрирования дифференциального уравнения второго порядка.
- 17. Уравнение у^(n)=f(x).
- 18. Понижение порядка дифференциального уравнения.
- 19. Системы обыкновенных дифференциальных уравнений.
- 20. Примеры.
- 21. Системы уравнений и уравнения высших порядков.
- 22. Линейные уравнения с частными производными.
- 23. Геометрическая интерпретация.
- 24. Примеры.
- ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 25. Линейные однородные уравнения второго порядка.
- 26. Линейные неоднородные уравнения второго порядка.
- 27. Линейные уравнения высших порядков.
- 28. Однородные уравнения второго порядка с постоянными коэффициентами.
- 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- 30. Частные случаи.
- 31. Корни решений и колеблющиеся решения
- 32. Линейные уравнения высших порядков с постоянными коэффициентами.
- 33. Линейные уравнения и колебательные явления.
- 34. Собственные и вынужденные колебания.
- 35. Синусоидальная внешняя сила и резонанс.
- 36. Предельные задачи.
- 37. Примеры.
- 38. Символический метод.
- 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами.
- 40. Линейные неоднородные уравнения с постоянными коэффициентами.
- 41. Пример.
- 42 Уравнение Эйлера.
- 43. Системы линейных уравнений с постоянными коэффициентами.
- 44. Примеры
- § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
- 45. Интегрирование линейного уравнения с помощью степенного ряда
- 46. Примеры.
- 47. Разложение решения в обобщенный степенной ряд.
- 48. Уравнение Бесселя
- 49. Уравнения, приводящиеся к уравнению Бесселя
- § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 50. Метод последовательных приближений для линейных уравнений.
- 51. Случай нелинейного уравнения.
- 52. Дополнения к теореме существования и единственности.
- 53. Сходимость метода Эйлера — Коши.
- 54. Особые точки дифференциальных уравнений первого порядка.
- 55. Автономные системы.
- 56. Примеры.
- ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 6. КРАТНЫЕ ИНТЕГРАЛЫ
- 58. Двукратный интеграл.
- 59. Вычисление двукратного интеграла.
- 60. Криволинейные координаты.
- 61. Трехкратный интеграл
- 62. Цилиндрические и сферические координаты.
- 63. Криволинейные координаты в пространстве.
- 64. Основные свойства кратных интегралов.
- 65. Площадь поверхности.
- 66. Интегралы по поверхности и формула Остроградского.
- 67. Интегралы по определенной стороне поверхности.
- 68. Моменты.
- § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- 69. Определение криволинейного интеграла.
- 70. Работа силового поля. Примеры.
- 71. Площадь и криволинейный интеграл.
- 72. Формула Грина
- 73. Формула Стокса.
- 74. Независимость криволинейного интеграла от пути на плоскости.
- 75. Случай многосвязной области.
- 76. Независимость криволинейного интеграла от пути в пространстве.
- 77. Установившееся течение жидкости.
- 78. Интегрирующий множитель.
- 79. Уравнение в полных дифференциалах для случая трех переменных.
- 80. Замена переменных в двойном интеграле.
- § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 81. Интегрирование под знаком интеграла.
- 82. Формула Дирихле.
- 83. Дифференцирование под знаком интеграла
- 84. Примеры.
- 85. Несобственные интегралы.
- 86. Неабсолютно сходящиеся интегралы.
- 87. Равномерно сходящиеся интегралы.
- 88. Примеры.
- 89. Несобственные кратные интегралы.
- 90. Примеры.
- § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ
- 92. Основные теоремы.
- 93. Счетные множества. Действия над точечными множествами.
- 94. Мера Жордана.
- 95. Квадрируемые множества.
- 96. Независимость от выбора осей.
- 97. Случай любого числа измерений.
- 98. Интегрируемые функции.
- 99. Вычисление двойного интеграла.
- 100. n-кратные интегралы.
- 101. Примеры.
- 102. Внешняя мера Лебега.
- 103. Измеримые множества.
- 104. Измеримые функции.
- 105. Дополнительные сведения.
- 106. Интеграл Лебега.
- 107. Свойства интеграла Лебега.
- 108. Интегралы от неограниченных функций.
- 109. Предельный переход под знаком интеграла.
- 110. Теорема Фубини.
- 111. Интегралы по множеству бесконечной меры.
- ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ
- 112. Сложение и вычитание векторов.
- 113. Умножение вектора на скаляр. Компланарность векторов.
- 114. Разложение вектора по трем некомпланарным векторам.
- 115. Скалярное произведение.
- 116. Векторное произведение.
- 117. Соотношения между скалярным к векторным произведениями.
- 118. Скорости точек вращающегося твердого тела; момент вектора.
- § 11 ТЕОРИЯ ПОЛЯ
- 119. Дифференцирование вектора
- 120. Скалярное поле и его градиент.
- 121. Векторное поле; расходимость и вихрь.
- 122. Потенциальное и соленоидальное поля.
- 123. Направленный элемент поверхности.
- 124. Некоторые формулы векторного анализа.
- 125. Движение твердого тела и малая деформация.
- 126. Уравнение непрерывности.
- 127. Уравнения гидродинамики идеальной жидкости.
- 128. Уравнения распространения звука.
- 129. Уравнение теплопроводности.
- 130. Уравнения Максвелла.
- 131. Выражение оператора Лапласа в ортогональных координатах.
- 132. Операция дифференцирования для случая переменного поля.
- ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 133. Плоская кривая, ее кривизна и эволюта.
- 134. Эвольвента.
- 135. Естественное уравнение кривой.
- 136. Основные элементы кривой в пространстве.
- 137. Формулы Френе.
- 138. Соприкасающаяся плоскость.
- 139. Винтовые линии.
- 140. Поле единичных векторов.
- § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 141. Параметрические уравнения поверхности.
- 142. Первая дифференциальная форма Гаусса.
- 143. Вторая дифференциальная форма Гаусса.
- 144. О кривизне линий, начерченных на поверхности.
- 145. Индикатриса Дюпена и формула Эйлера.
- 146. Определение главных радиусов кривизны и главных направлений.
- 147. Линии кривизны.
- 148. Теорема Дюпена.
- 149. Примеры.
- 150. Гауссова кривизна.
- 151. Вариация элемента площади и средняя кривизна.
- 152. Огибающая семейства поверхностей и кривых.
- 153. Развертывающиеся поверхности.
- ГЛАВА VI. РЯДЫ ФУРЬЕ
- 154. Ортогональность тригонометрических функций.
- 155. Теорема Дирихле.
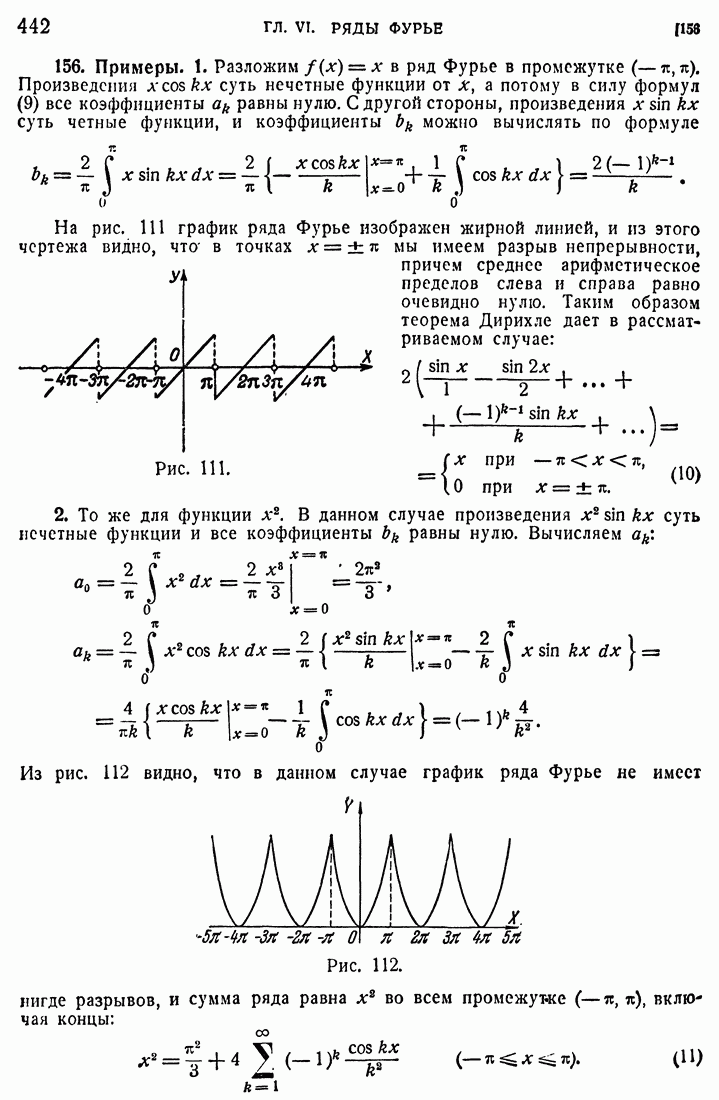
- 156. Примеры.
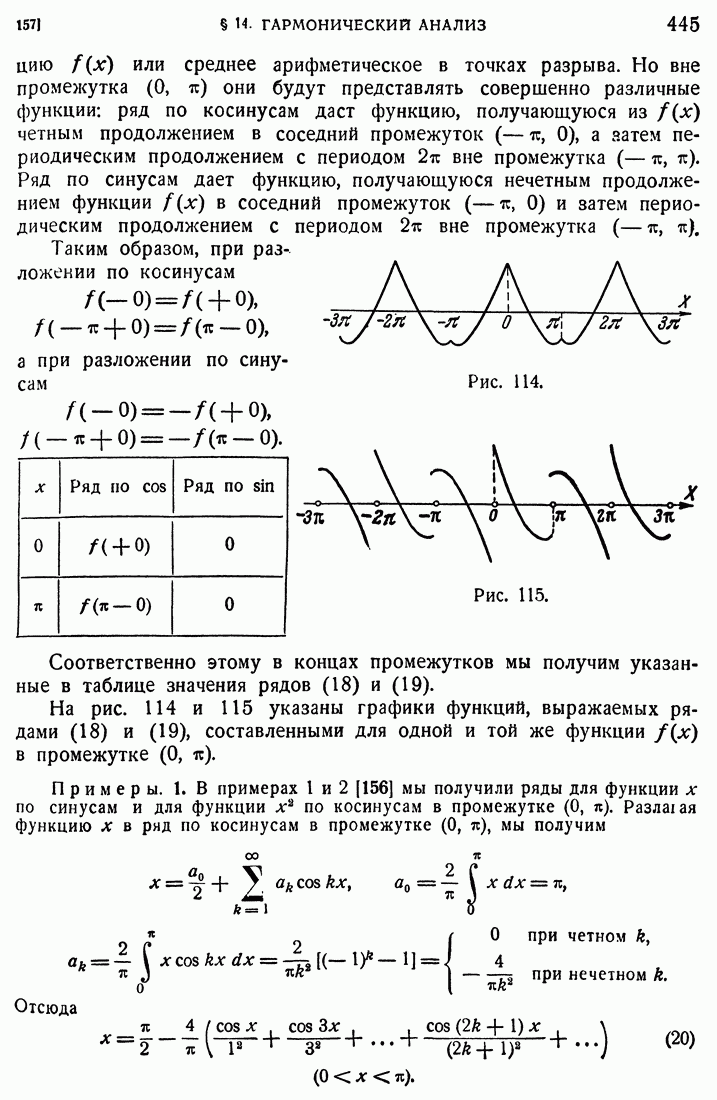
- 157. Разложение в промежутке (0, п).
- 158. Периодические функции периода 2l.
- 159. Средняя квадратичная погрешность.
- 160. Общие ортогональные системы функций.
- 161. Класс L2
- 162. Сходимость в среднем.
- 163. Ортонормированные системы в L2.
- § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ
- 164. Разложение в ряд Фурье.
- 165. Вторая теорема о среднем.
- 166. Интеграл Дирихле.
- 167. Теорема Дирихле.
- 168. Приближение к непрерывной функции полиномами.
- 169. Формула замкнутости.
- 170. Характер сходимости рядов Фурье.
- 171. Улучшение сходимости рядов Фурье.
- 172. Пример.
- § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ
- 173. Формула Фурье.
- 174. Ряды Фурье в комплексной форме.
- 176. Кратные ряды Фурье.
- ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- 176. Уравнение колебаний струны.
- 177. Решение Даламбера.
- 178. Частные случаи.
- 179. Ограниченная струна.
- 180. Способ Фурье.
- 181. Гармоники и стоячие волны.
- 182. Вынужденные колебания.
- 183. Сосредоточенная сила.
- 184. Формула Пуассона.
- 185. Цилиндрические волны.
- 186. Случай n-мерного пространства.
- 187. Неоднородное волновое уравнение.
- 188. Точечный источник.
- 189. Поперечные колебания мембран.
- 190. Прямоугольная мембрана.
- 191. Круглая мембрана.
- 192. Теорема единственности.
- 193. Применение интеграла Фурье.
- § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
- 195. Установившиеся процессы.
- 196. Устанавливающиеся процессы.
- 197. Примеры.
- 198. Обобщенное уравнение колебаний струны.
- 199. Неограниченная цепь в общем случае.
- 200. Способ Фурье для ограниченной цепи.
- 201. Обобщенное волновое уравнение.
- § 19. УРАВНЕНИЕ ЛАПЛАСА
- 202. Гармонические функции.
- 203. Формула Грина.
- 204. Основные свойства гармонических функций.
- 205. Решение задачи Дирихле для круга.
- 206. Интеграл Пуассона.
- 207. Задача Дирихле для сферы.
- 208. Функция Грина.
- 209. Случай полупространства.
- 210. Потенциал объемных масс.
- 211. Уравнение Пуассона.
- 212. Формула Кирхгофа.
- § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
- 214. Неограниченный стержень.
- 215. Стержень, ограниченный с одного конца.
- 216. Стержень, ограниченный с обоих концов.
- 217. Дополнительные замечания.
- 218. Случай сферы.
- 219. Теорема единственности.