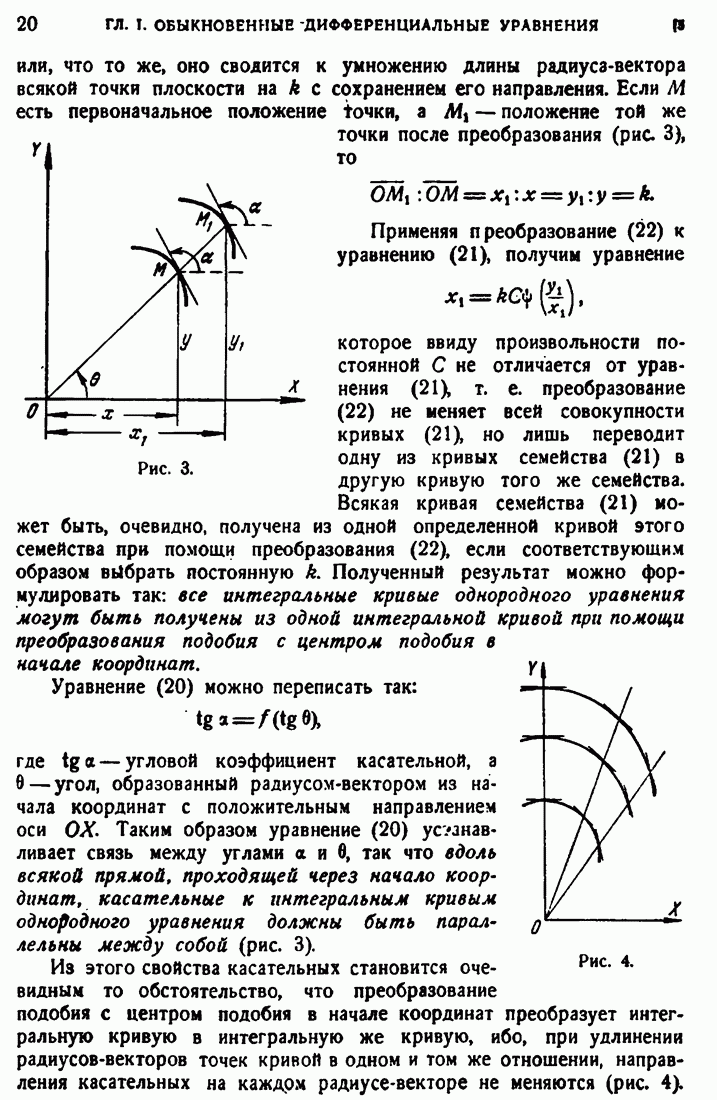
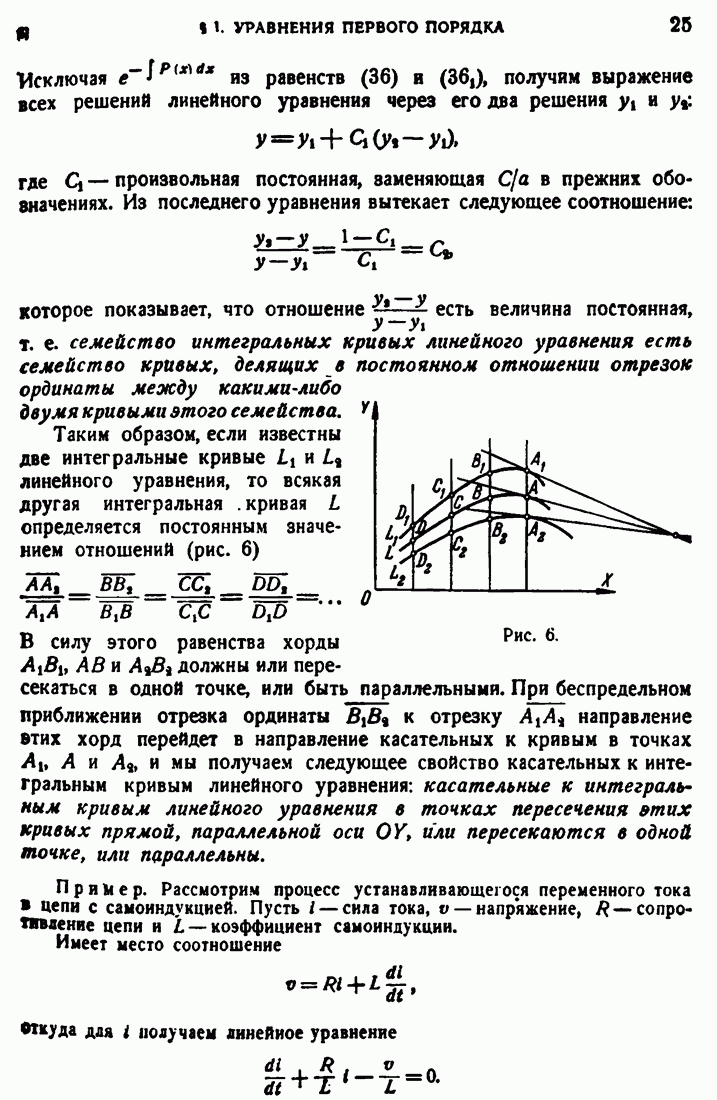
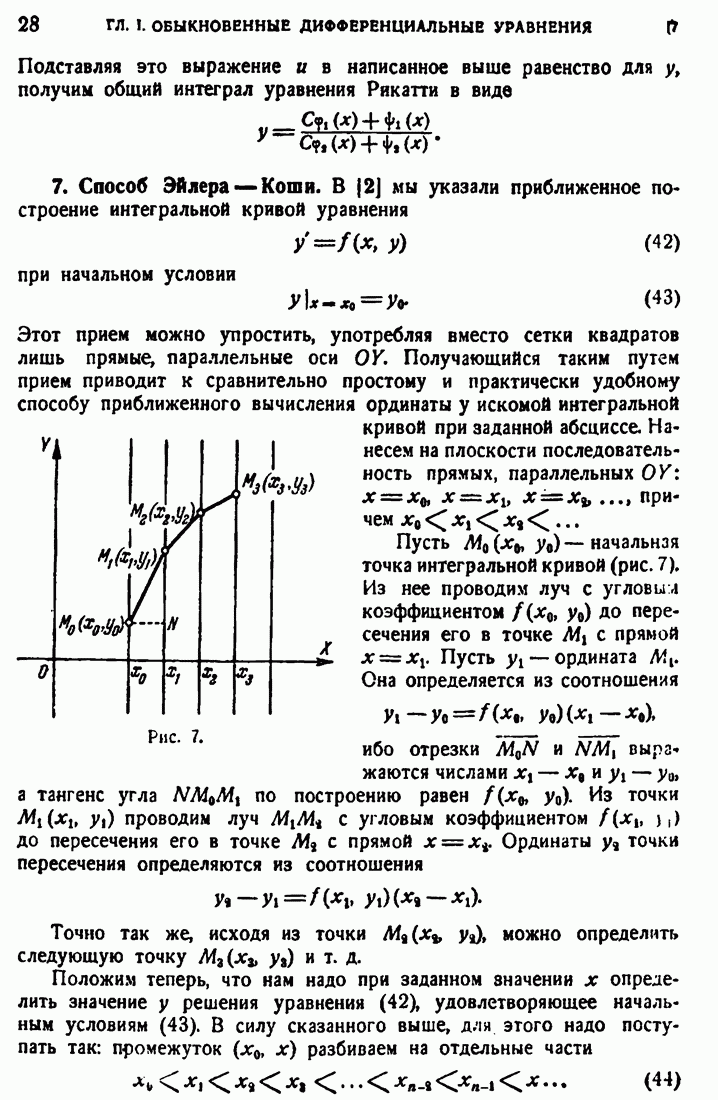
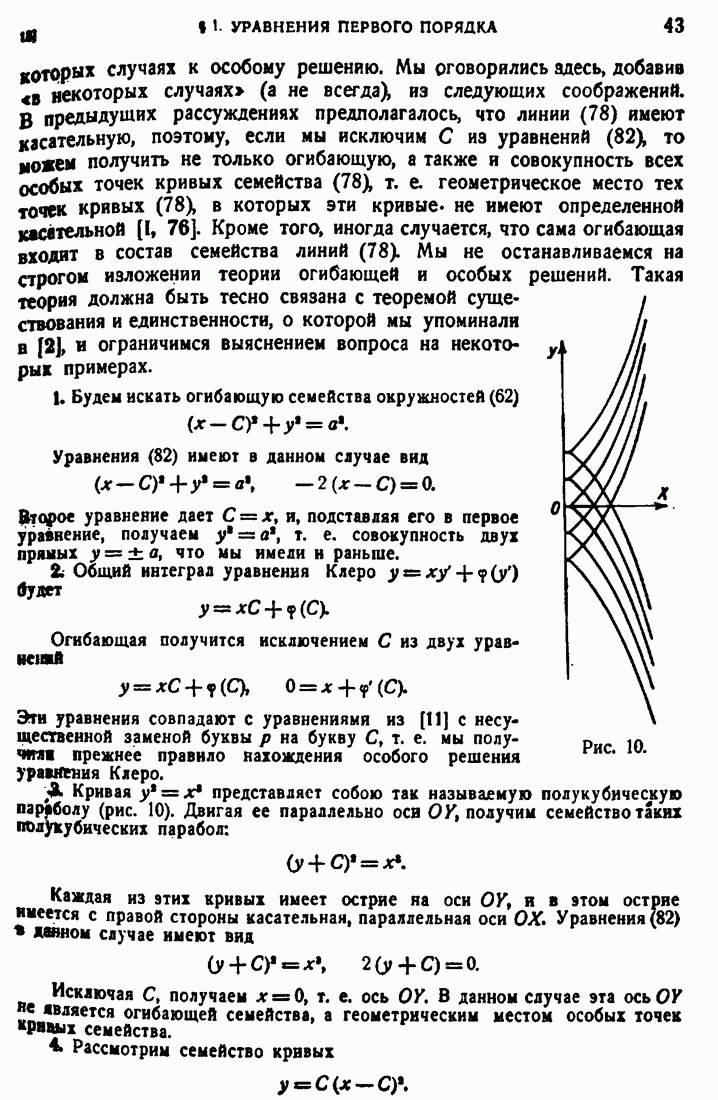
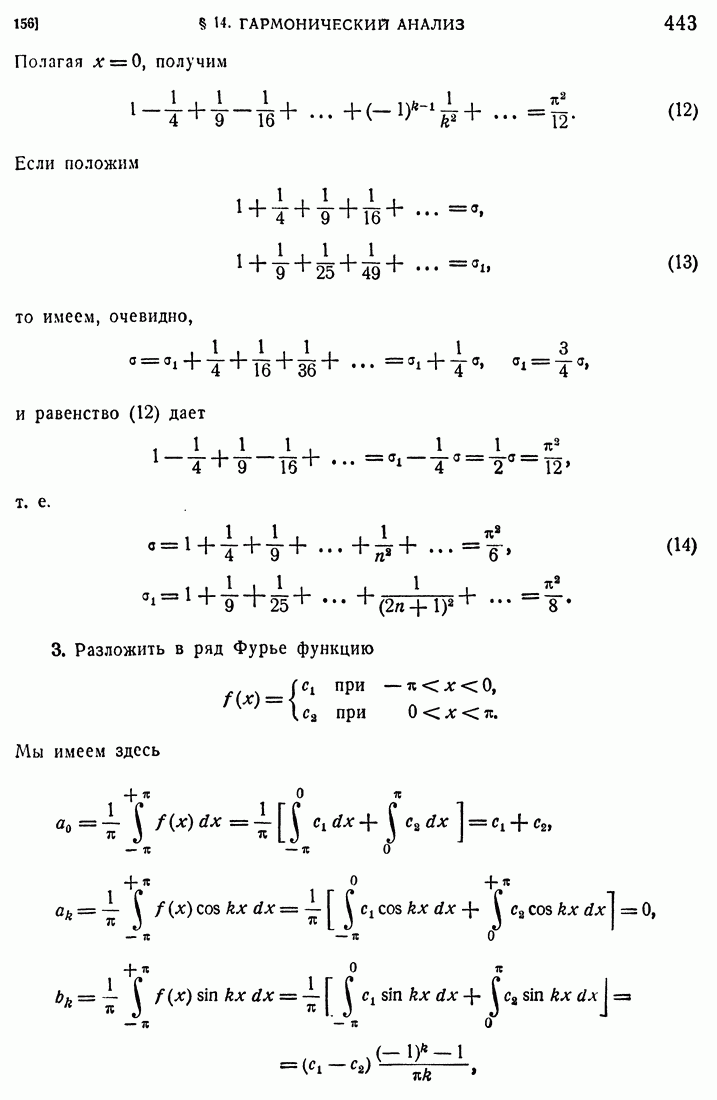| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
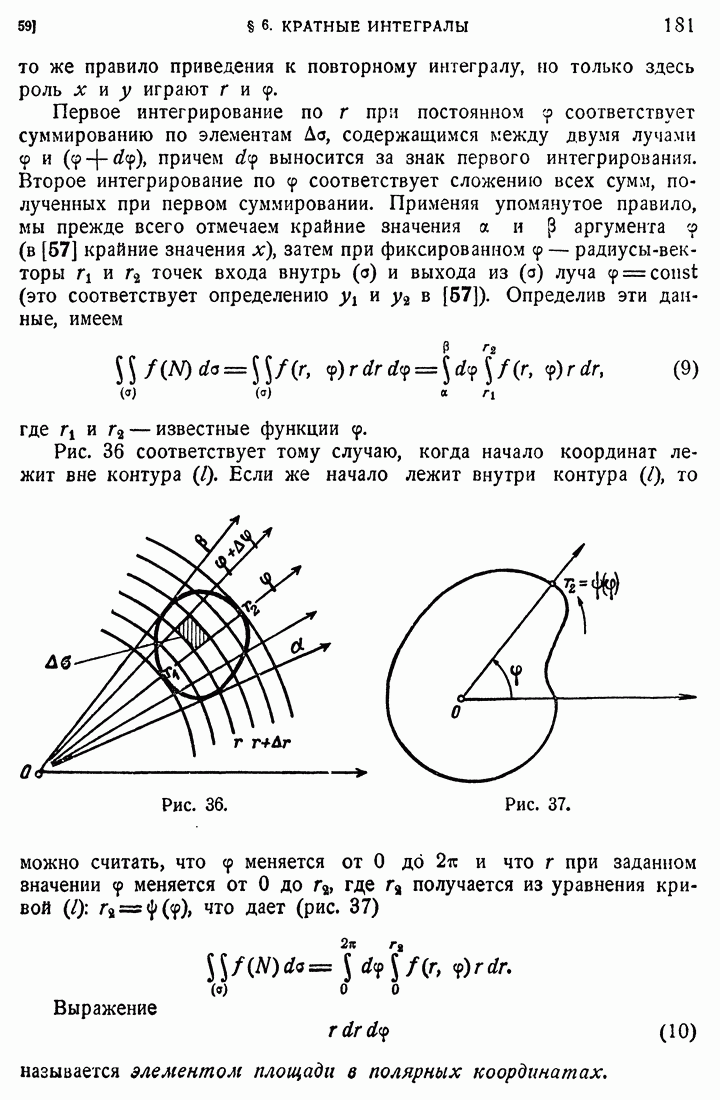
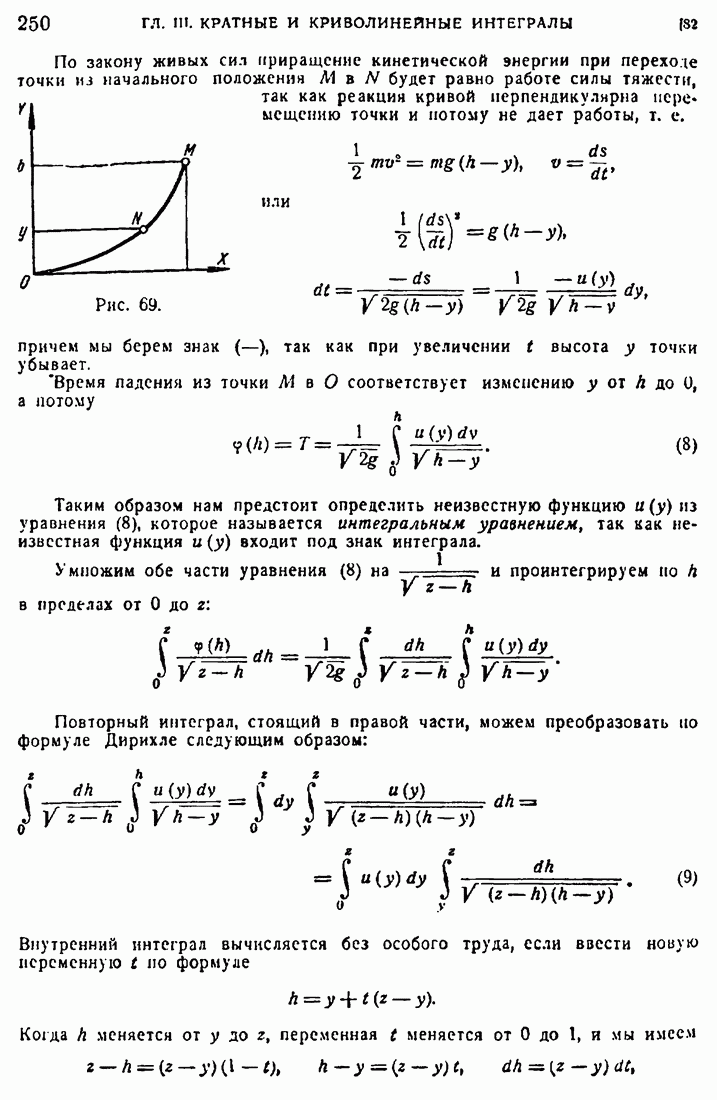
75. Случай многосвязной области.
Доказательство того, что условие (27) является необходимым и достаточным для того, чтобы криволинейный интеграл

не зависел от пути, существенным образом основано на следующих двух обстоятельствах:
1) Функции Р и Q и их частные производные первого порядка непрерывны в рассматриваемой области (D) изменения 
2) Если в области (D) начерчен какой-либо замкнутый контур  , то вся часть плоскости, заключенная внутри
, то вся часть плоскости, заключенная внутри  , принадлежит той области, где выполнены условия непрерывности и условие (27).
, принадлежит той области, где выполнены условия непрерывности и условие (27).
Первое условие важно потому, что упомянутые в нем функции входят под знак интеграла при доказательстве. Второе существенно для применения формулы Грина, т. е. для преобразования криволинейного интеграла к двукратному. Оно равносильно тому, что всякий замкнутый контур, начерченный в области, может быть непрерывным сужением приведен к точке, не выходя из области, или проще говоря, это условие равносильно тому, что область не имеет дыр.

Рис. 64.
Положим теперь, что функции Р и Q непрерывны со своими производными и условие (27) выполнено в некоторой области, имеющей две дыры (рис. 64). Если в такой области взять замкнутый контур  внутри которого нет дыр, то к такому контуру и области, им ограниченной, приложима формула Грина (18), и в силу условия (27) интеграл по такому замкнутому контуру
внутри которого нет дыр, то к такому контуру и области, им ограниченной, приложима формула Грина (18), и в силу условия (27) интеграл по такому замкнутому контуру  будет нуль. Возьмем теперь замкнутый контур (4), обходящий вокруг дыры
будет нуль. Возьмем теперь замкнутый контур (4), обходящий вокруг дыры  Здесь формула (18) неприменима, и интеграл (28) по
Здесь формула (18) неприменима, и интеграл (28) по  вообще говоря, окажется отличным от нуля. Покажем, что величина этого интеграла не зависит от вида контура
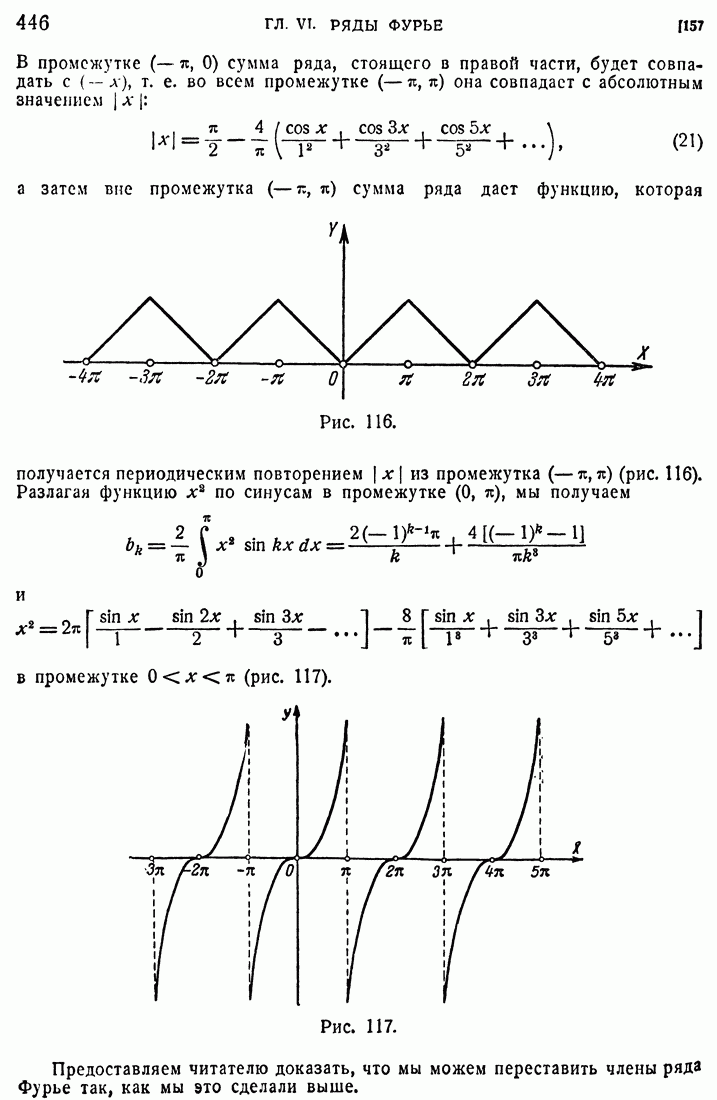
вообще говоря, окажется отличным от нуля. Покажем, что величина этого интеграла не зависит от вида контура  и важно лишь, что этот
и важно лишь, что этот
контур обходит вокруг одной дыры (I). Возьмем два контура  обходящих вокруг (I). Нам надо показать, что величины интеграла (28) по
обходящих вокруг (I). Нам надо показать, что величины интеграла (28) по  одинаковы. Проведем вспомогательный контур
одинаковы. Проведем вспомогательный контур  соединяющий
соединяющий  Кривые
Кривые  совместно являются контуром области, уже не имеющей дыр, причем этот контур должен обходиться в направлении, указанном стрелкой. К этому контуру, следовательно, приложима формула (18), и, в силу (27), интеграл по этому контуру будет нуль:
совместно являются контуром области, уже не имеющей дыр, причем этот контур должен обходиться в направлении, указанном стрелкой. К этому контуру, следовательно, приложима формула (18), и, в силу (27), интеграл по этому контуру будет нуль:

При этом интегралы по  взятые в противоположных направлениях, сокращаются, интегрирование по
взятые в противоположных направлениях, сокращаются, интегрирование по  надо производить по часовой стрелке и по
надо производить по часовой стрелке и по  против часовой стрелки. Меняя направление интегрирования по (4) и знак при интеграле, что не меняет результата, получим
против часовой стрелки. Меняя направление интегрирования по (4) и знак при интеграле, что не меняет результата, получим

или окончательно

т. е. действительно интегралы по  взятые оба, как всегда, против часовой стрелки, одинаковы по величине. Таким образом дыре (I) соответствует определенная постоянная
взятые оба, как всегда, против часовой стрелки, одинаковы по величине. Таким образом дыре (I) соответствует определенная постоянная  равная величине интеграла (28), взятого по любому замкнутому контуру, обходящему вокруг (I). Точно так же дыре (11) соответствует другая постоянная
равная величине интеграла (28), взятого по любому замкнутому контуру, обходящему вокруг (I). Точно так же дыре (11) соответствует другая постоянная  .
.
Если в области (D) проведем два разреза  от дыр к внешнему контуру (рис. 65), то получится новая область, не имеющая уже внутри дыр, и, в силу (27), в этой области можно построить однозначную функцию
от дыр к внешнему контуру (рис. 65), то получится новая область, не имеющая уже внутри дыр, и, в силу (27), в этой области можно построить однозначную функцию

но, в силу предыдущего, значения этой функции на противоположных краях разреза  отличаются на постоянную а на
отличаются на постоянную а на  постоянную
постоянную  Если уничтожить разрезы и вернуться к исходной области (D), то в ней функция
Если уничтожить разрезы и вернуться к исходной области (D), то в ней функция  будет многозначной. Обход вокруг дыр будет придавать этой функции слагаемые
будет многозначной. Обход вокруг дыр будет придавать этой функции слагаемые  т. е. функция
т. е. функция  будет
будет

Рис. 65.
содержать неопределенное слагаемое вида  , где
, где  — любые целые числа. Все наши рассуждения очевидно годятся для любого числа дыр в области, причем дыры могут быть и точечными, т. е. состоять из одной лишь точки. Число дыр, увеличенное на единицу, называется обычно степенью связности области (D), а сама область с дырами — многосвязной областью. Числа
— любые целые числа. Все наши рассуждения очевидно годятся для любого числа дыр в области, причем дыры могут быть и точечными, т. е. состоять из одной лишь точки. Число дыр, увеличенное на единицу, называется обычно степенью связности области (D), а сама область с дырами — многосвязной областью. Числа  и называются циркуляциями выражения
и называются циркуляциями выражения  или циклическими постоянными функции
или циклическими постоянными функции 
Пример. Рассмотрим функцию

определенную в области (D), ограниченной двумя концентрическими окружностями с центром в начале координат. Определим Р и Q но формулам

Эти функции непрерывны в (D) со своими производными, и, как нетрудно проверить, удовлетворяют соотношению (27). Рассмотрим криволинейный интеграл

и возьмем его по окружности  с центром в начале и некоторым радиусом
с центром в начале и некоторым радиусом  . Подставляя
. Подставляя  получим
получим

В данном случае область (D) имеет одну дыру, и циклическая постоянная  Функция
Функция  является полярным углом
является полярным углом

и при обходе вокруг дыры приобретает слагаемое  Заметим, что радиус внутренней окружности можно считать нулем, т. е. можно считать дыру точечной. Дело сведется к исключению точки
Заметим, что радиус внутренней окружности можно считать нулем, т. е. можно считать дыру точечной. Дело сведется к исключению точки  . В этой точке функции Р и 0 (37) принимают неопределенную форму
. В этой точке функции Р и 0 (37) принимают неопределенную форму  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮ
- ГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Определение решения по начальному условию. Теорема существования и единственности.
- 3. Уравнения с отделяющимися переменными.
- 4. Примеры.
- 5. Однородное уравнение.
- 6. Линейные уравнения и уравнение Бернулли.
- 7. Способ Эйлера—Коши.
- 8. Применение степенных рядов.
- 9. Общий интеграл и особое решение.
- 10. Уравнения, не решенные относительно у’.
- 11. Уравнение Клеро.
- 12. Уравнение Лагранжа.
- 13. Огибающие семейства кривых и особые решения.
- 14. Изогональные траектории.
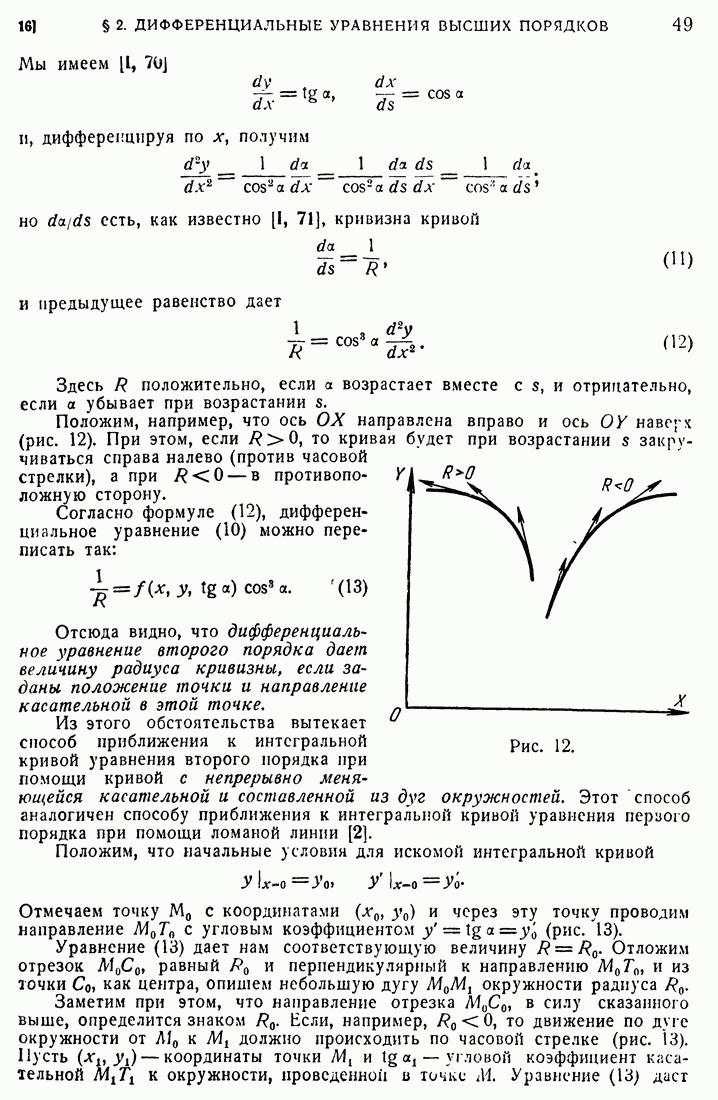
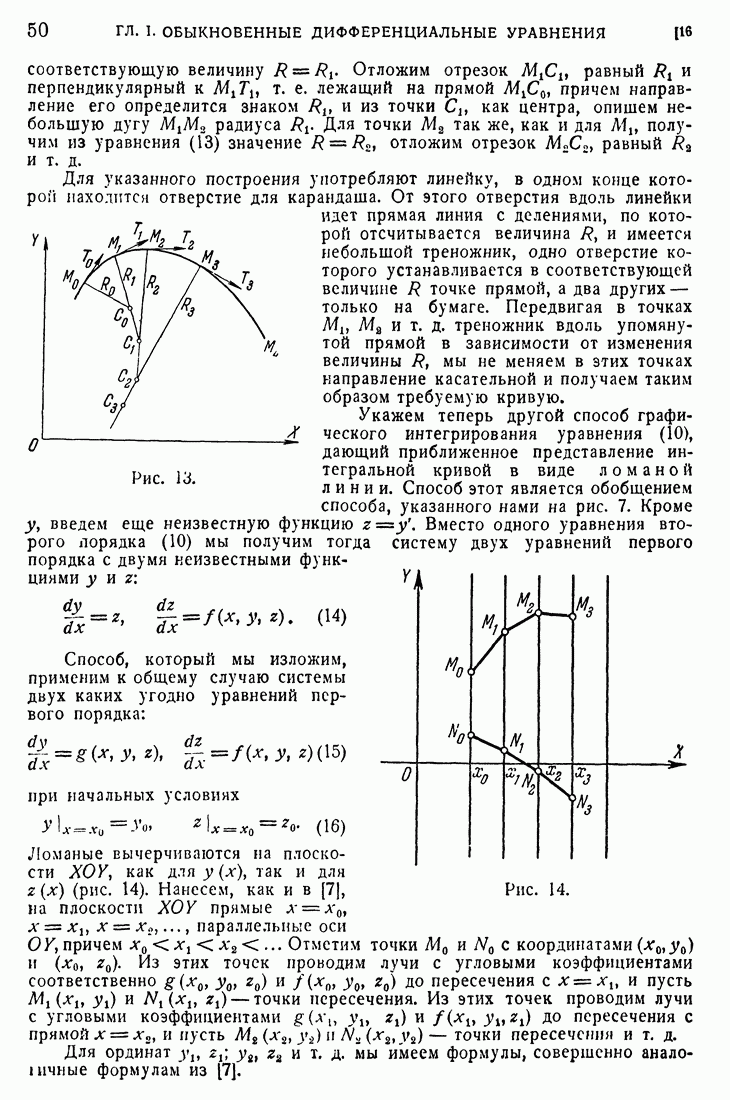
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ И СИСТЕМЫ УРАВНЕНИЙ
- 16. Графические способы интегрирования дифференциального уравнения второго порядка.
- 17. Уравнение у^(n)=f(x).
- 18. Понижение порядка дифференциального уравнения.
- 19. Системы обыкновенных дифференциальных уравнений.
- 20. Примеры.
- 21. Системы уравнений и уравнения высших порядков.
- 22. Линейные уравнения с частными производными.
- 23. Геометрическая интерпретация.
- 24. Примеры.
- ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 25. Линейные однородные уравнения второго порядка.
- 26. Линейные неоднородные уравнения второго порядка.
- 27. Линейные уравнения высших порядков.
- 28. Однородные уравнения второго порядка с постоянными коэффициентами.
- 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- 30. Частные случаи.
- 31. Корни решений и колеблющиеся решения
- 32. Линейные уравнения высших порядков с постоянными коэффициентами.
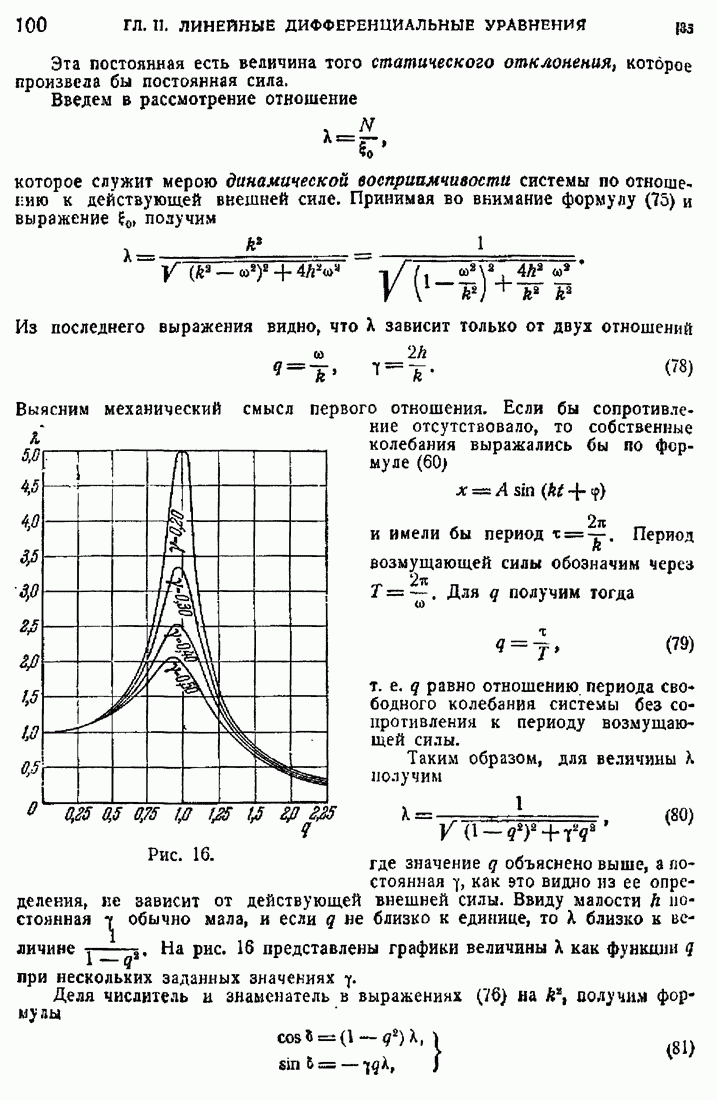
- 33. Линейные уравнения и колебательные явления.
- 34. Собственные и вынужденные колебания.
- 35. Синусоидальная внешняя сила и резонанс.
- 36. Предельные задачи.
- 37. Примеры.
- 38. Символический метод.
- 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами.
- 40. Линейные неоднородные уравнения с постоянными коэффициентами.
- 41. Пример.
- 42 Уравнение Эйлера.
- 43. Системы линейных уравнений с постоянными коэффициентами.
- 44. Примеры
- § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
- 45. Интегрирование линейного уравнения с помощью степенного ряда
- 46. Примеры.
- 47. Разложение решения в обобщенный степенной ряд.
- 48. Уравнение Бесселя
- 49. Уравнения, приводящиеся к уравнению Бесселя
- § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
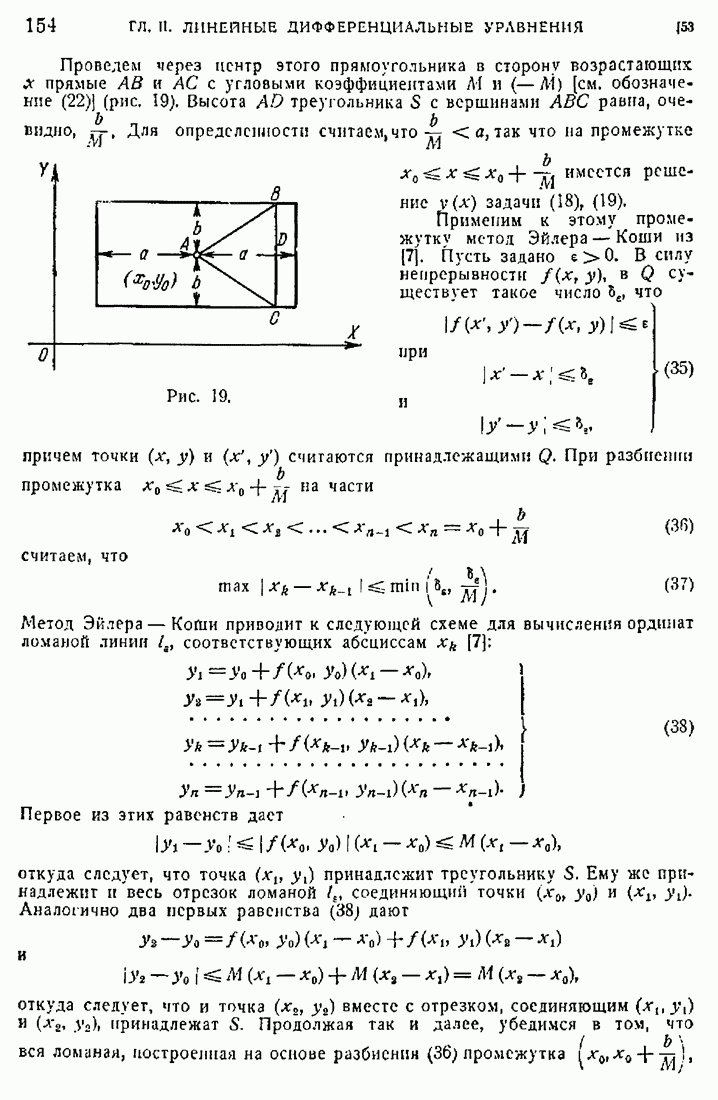
- 50. Метод последовательных приближений для линейных уравнений.
- 51. Случай нелинейного уравнения.
- 52. Дополнения к теореме существования и единственности.
- 53. Сходимость метода Эйлера — Коши.
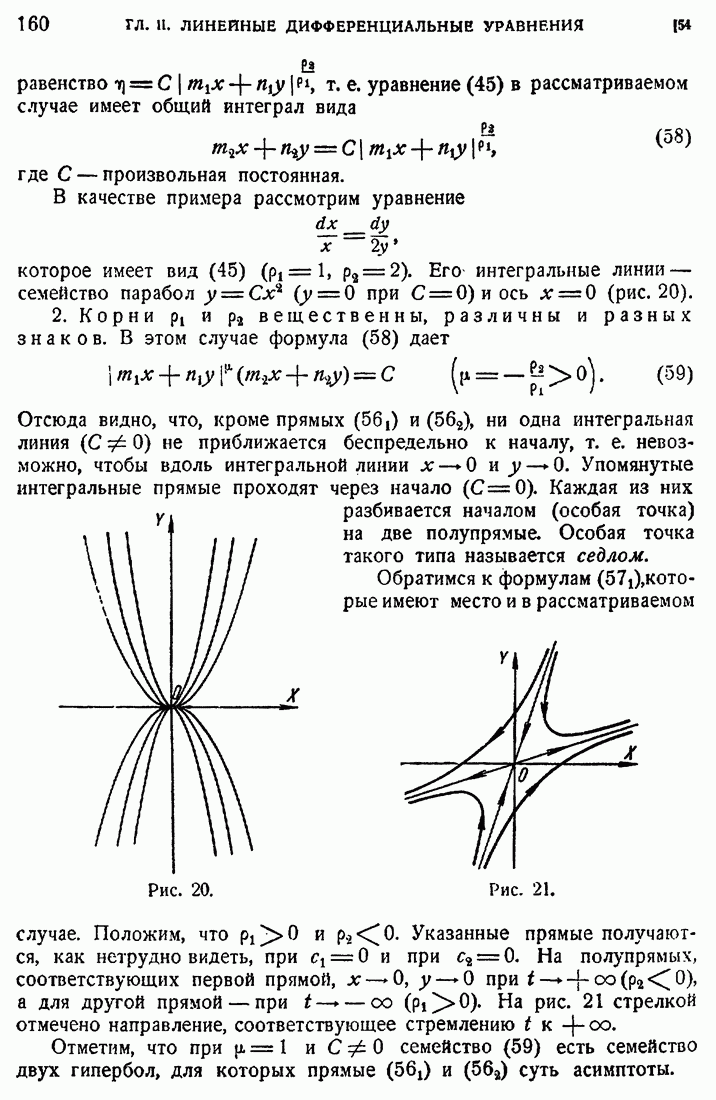
- 54. Особые точки дифференциальных уравнений первого порядка.
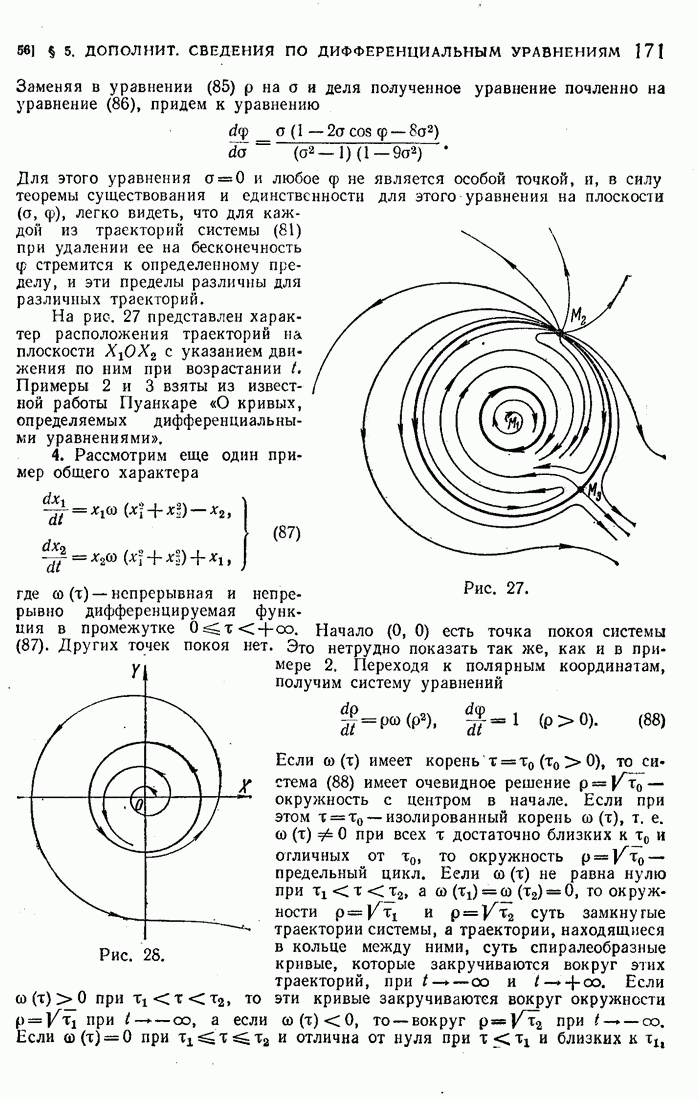
- 55. Автономные системы.
- 56. Примеры.
- ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 6. КРАТНЫЕ ИНТЕГРАЛЫ
- 58. Двукратный интеграл.
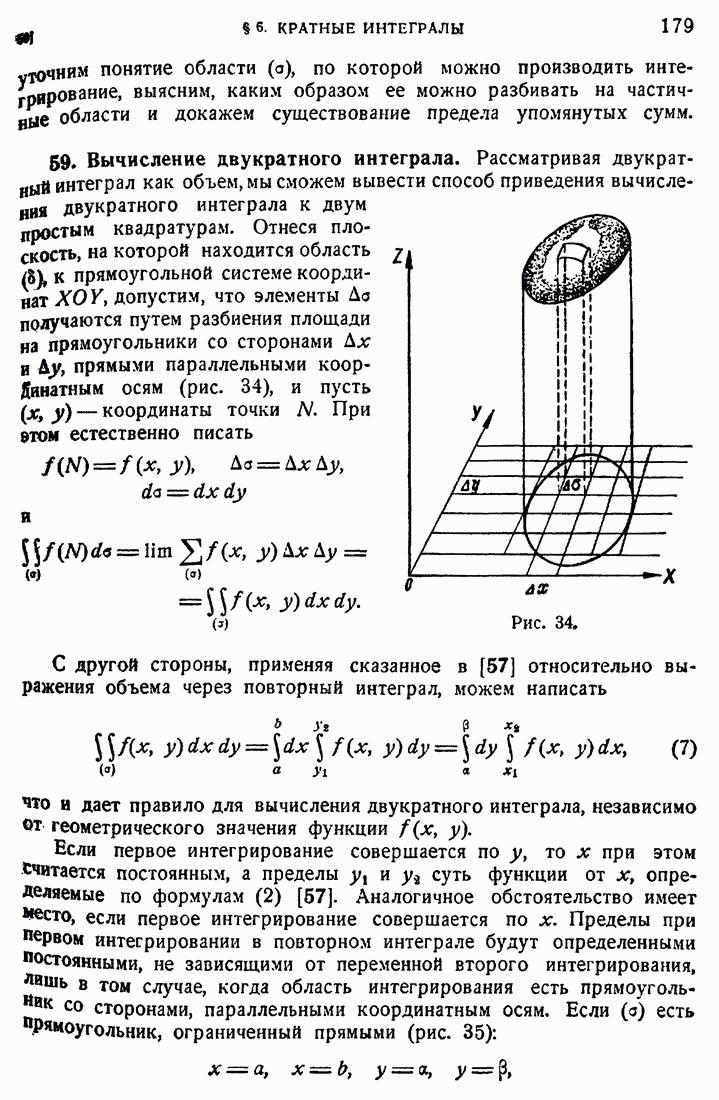
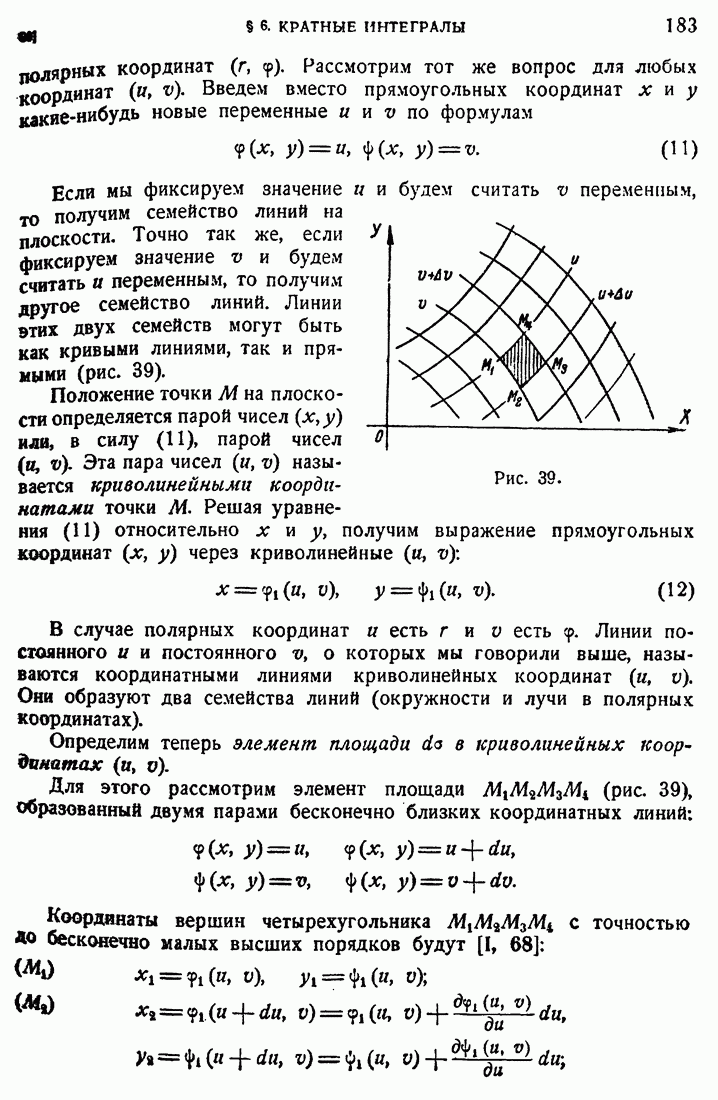
- 59. Вычисление двукратного интеграла.
- 60. Криволинейные координаты.
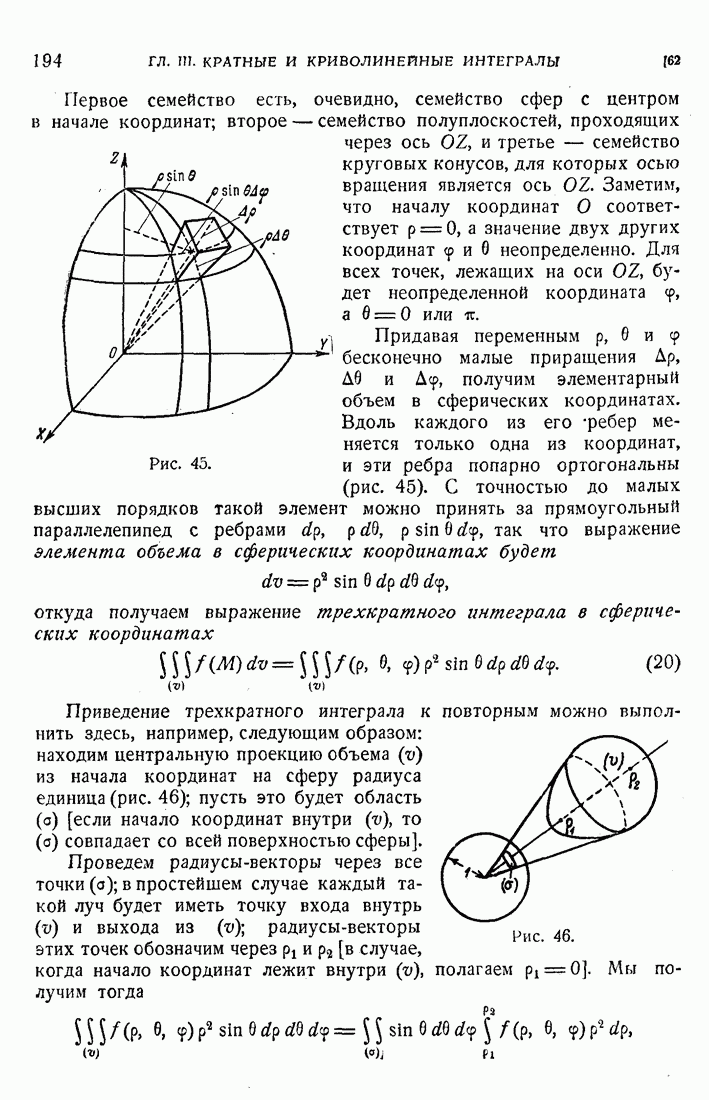
- 61. Трехкратный интеграл
- 62. Цилиндрические и сферические координаты.
- 63. Криволинейные координаты в пространстве.
- 64. Основные свойства кратных интегралов.
- 65. Площадь поверхности.
- 66. Интегралы по поверхности и формула Остроградского.
- 67. Интегралы по определенной стороне поверхности.
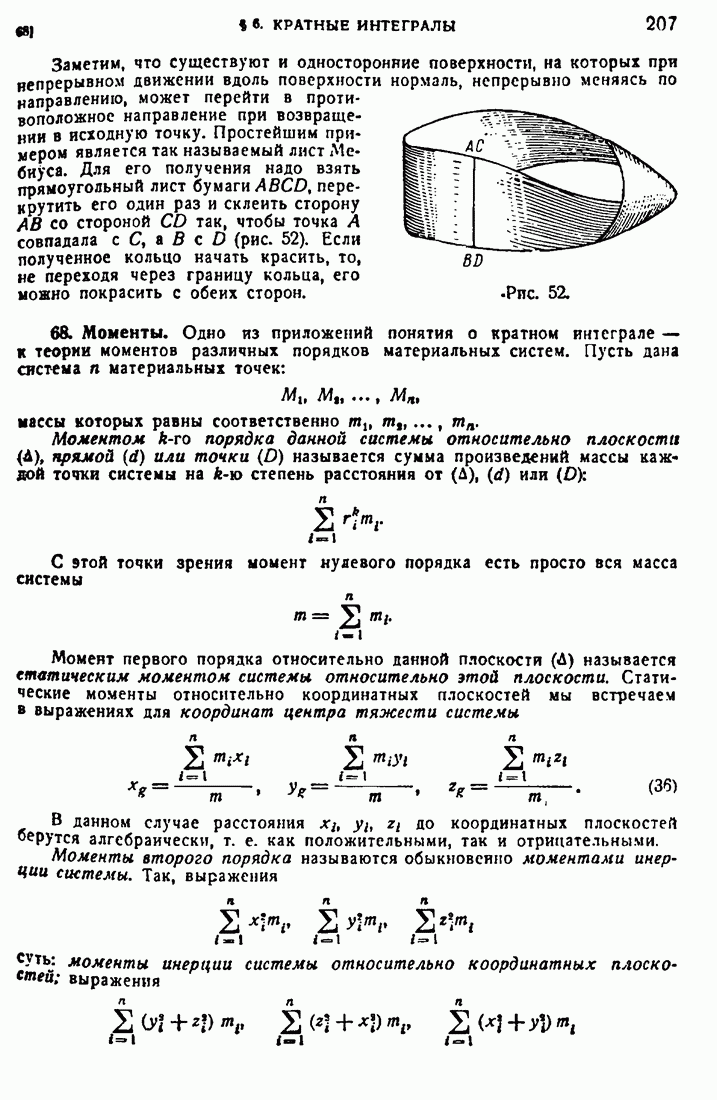
- 68. Моменты.
- § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- 69. Определение криволинейного интеграла.
- 70. Работа силового поля. Примеры.
- 71. Площадь и криволинейный интеграл.
- 72. Формула Грина
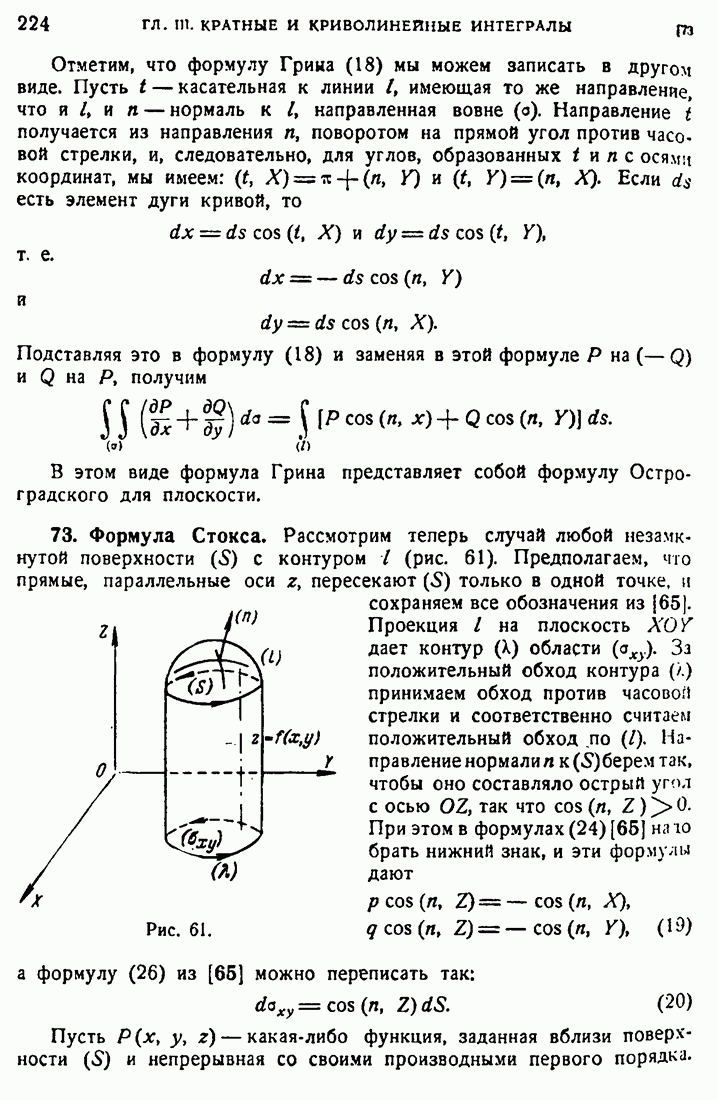
- 73. Формула Стокса.
- 74. Независимость криволинейного интеграла от пути на плоскости.
- 75. Случай многосвязной области.
- 76. Независимость криволинейного интеграла от пути в пространстве.
- 77. Установившееся течение жидкости.
- 78. Интегрирующий множитель.
- 79. Уравнение в полных дифференциалах для случая трех переменных.
- 80. Замена переменных в двойном интеграле.
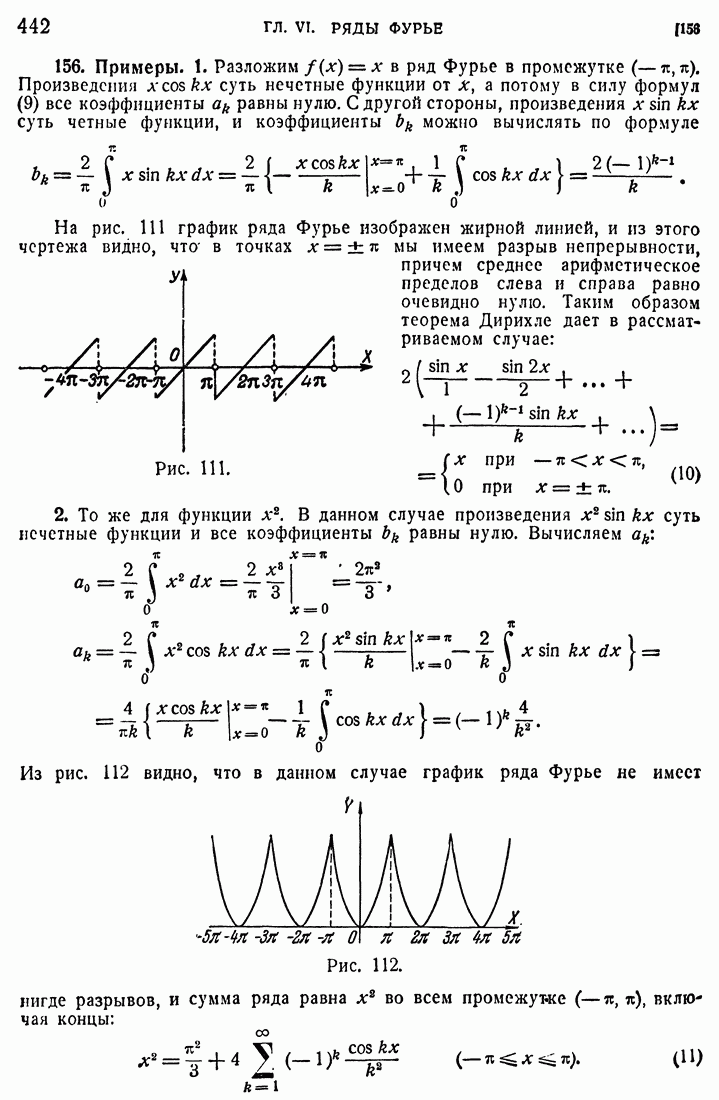
- § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 81. Интегрирование под знаком интеграла.
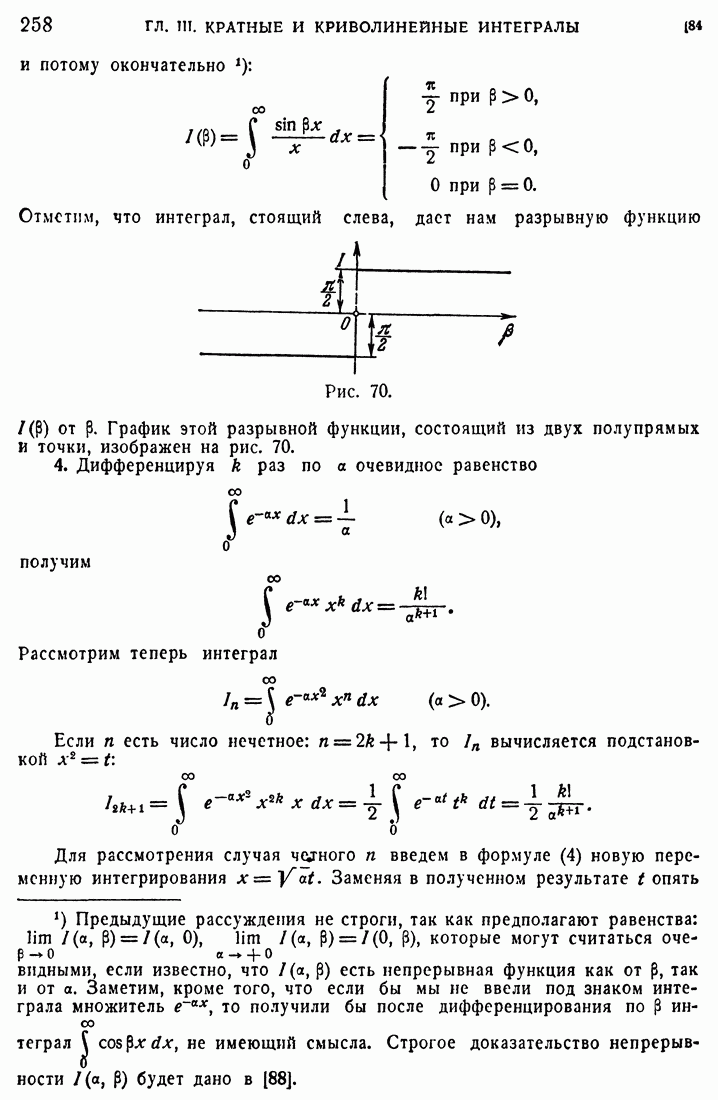
- 82. Формула Дирихле.
- 83. Дифференцирование под знаком интеграла
- 84. Примеры.
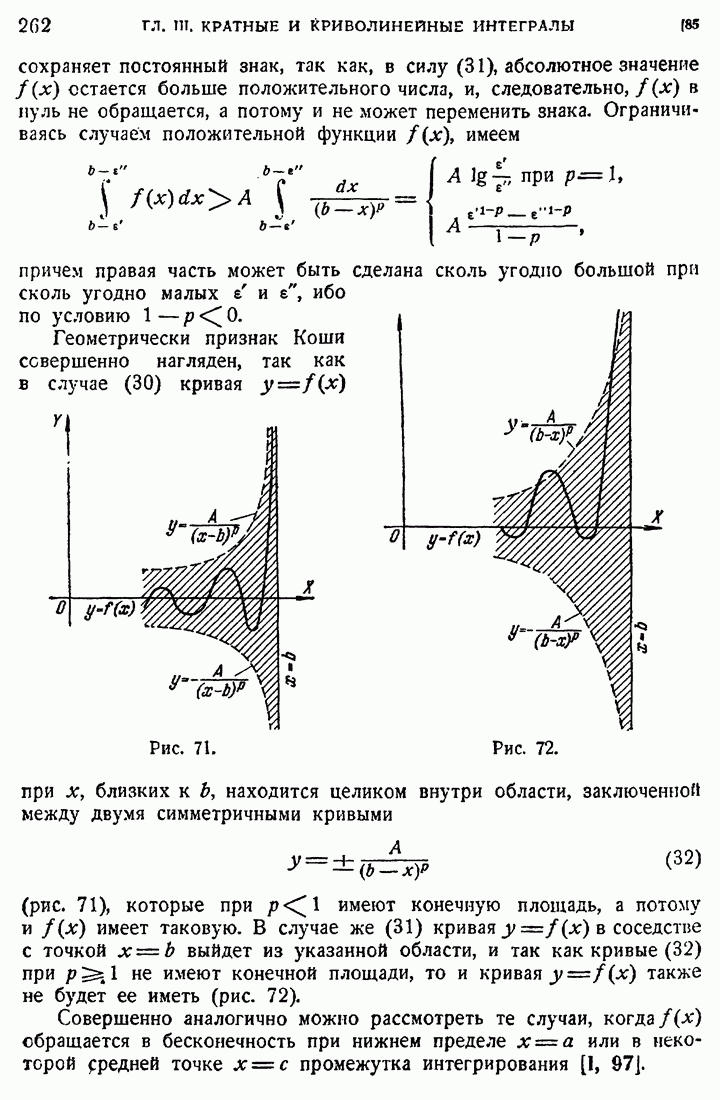
- 85. Несобственные интегралы.
- 86. Неабсолютно сходящиеся интегралы.
- 87. Равномерно сходящиеся интегралы.
- 88. Примеры.
- 89. Несобственные кратные интегралы.
- 90. Примеры.
- § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ
- 92. Основные теоремы.
- 93. Счетные множества. Действия над точечными множествами.
- 94. Мера Жордана.
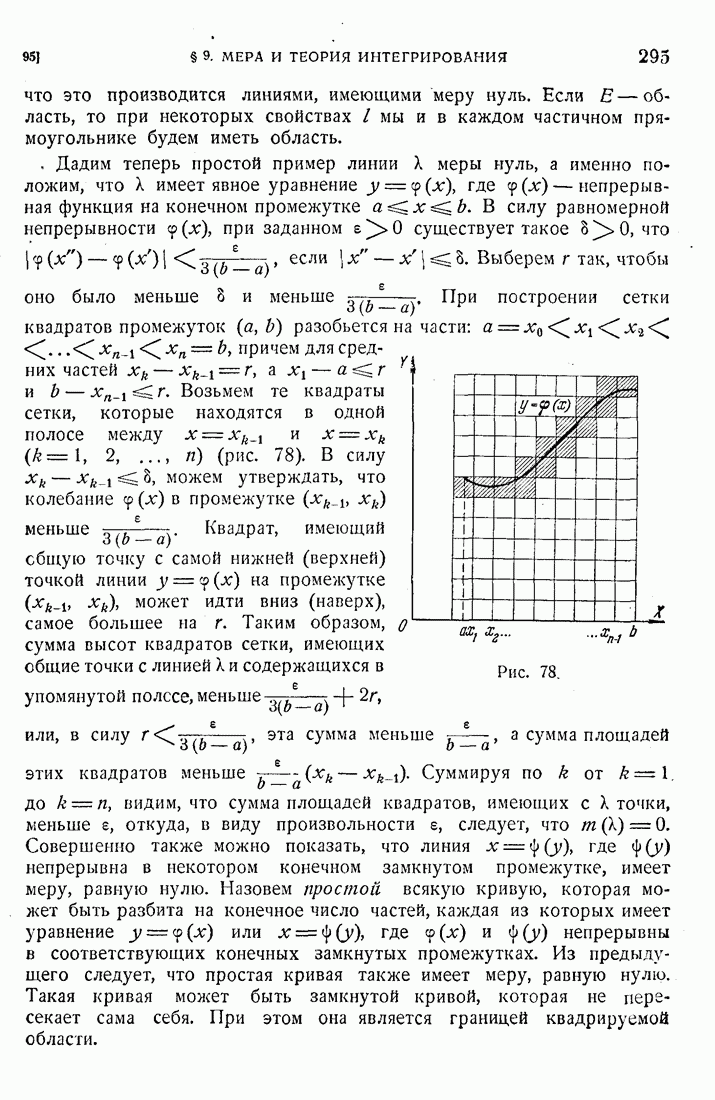
- 95. Квадрируемые множества.
- 96. Независимость от выбора осей.
- 97. Случай любого числа измерений.
- 98. Интегрируемые функции.
- 99. Вычисление двойного интеграла.
- 100. n-кратные интегралы.
- 101. Примеры.
- 102. Внешняя мера Лебега.
- 103. Измеримые множества.
- 104. Измеримые функции.
- 105. Дополнительные сведения.
- 106. Интеграл Лебега.
- 107. Свойства интеграла Лебега.
- 108. Интегралы от неограниченных функций.
- 109. Предельный переход под знаком интеграла.
- 110. Теорема Фубини.
- 111. Интегралы по множеству бесконечной меры.
- ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ
- 112. Сложение и вычитание векторов.
- 113. Умножение вектора на скаляр. Компланарность векторов.
- 114. Разложение вектора по трем некомпланарным векторам.
- 115. Скалярное произведение.
- 116. Векторное произведение.
- 117. Соотношения между скалярным к векторным произведениями.
- 118. Скорости точек вращающегося твердого тела; момент вектора.
- § 11 ТЕОРИЯ ПОЛЯ
- 119. Дифференцирование вектора
- 120. Скалярное поле и его градиент.
- 121. Векторное поле; расходимость и вихрь.
- 122. Потенциальное и соленоидальное поля.
- 123. Направленный элемент поверхности.
- 124. Некоторые формулы векторного анализа.
- 125. Движение твердого тела и малая деформация.
- 126. Уравнение непрерывности.
- 127. Уравнения гидродинамики идеальной жидкости.
- 128. Уравнения распространения звука.
- 129. Уравнение теплопроводности.
- 130. Уравнения Максвелла.
- 131. Выражение оператора Лапласа в ортогональных координатах.
- 132. Операция дифференцирования для случая переменного поля.
- ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 133. Плоская кривая, ее кривизна и эволюта.
- 134. Эвольвента.
- 135. Естественное уравнение кривой.
- 136. Основные элементы кривой в пространстве.
- 137. Формулы Френе.
- 138. Соприкасающаяся плоскость.
- 139. Винтовые линии.
- 140. Поле единичных векторов.
- § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 141. Параметрические уравнения поверхности.
- 142. Первая дифференциальная форма Гаусса.
- 143. Вторая дифференциальная форма Гаусса.
- 144. О кривизне линий, начерченных на поверхности.
- 145. Индикатриса Дюпена и формула Эйлера.
- 146. Определение главных радиусов кривизны и главных направлений.
- 147. Линии кривизны.
- 148. Теорема Дюпена.
- 149. Примеры.
- 150. Гауссова кривизна.
- 151. Вариация элемента площади и средняя кривизна.
- 152. Огибающая семейства поверхностей и кривых.
- 153. Развертывающиеся поверхности.
- ГЛАВА VI. РЯДЫ ФУРЬЕ
- 154. Ортогональность тригонометрических функций.
- 155. Теорема Дирихле.
- 156. Примеры.
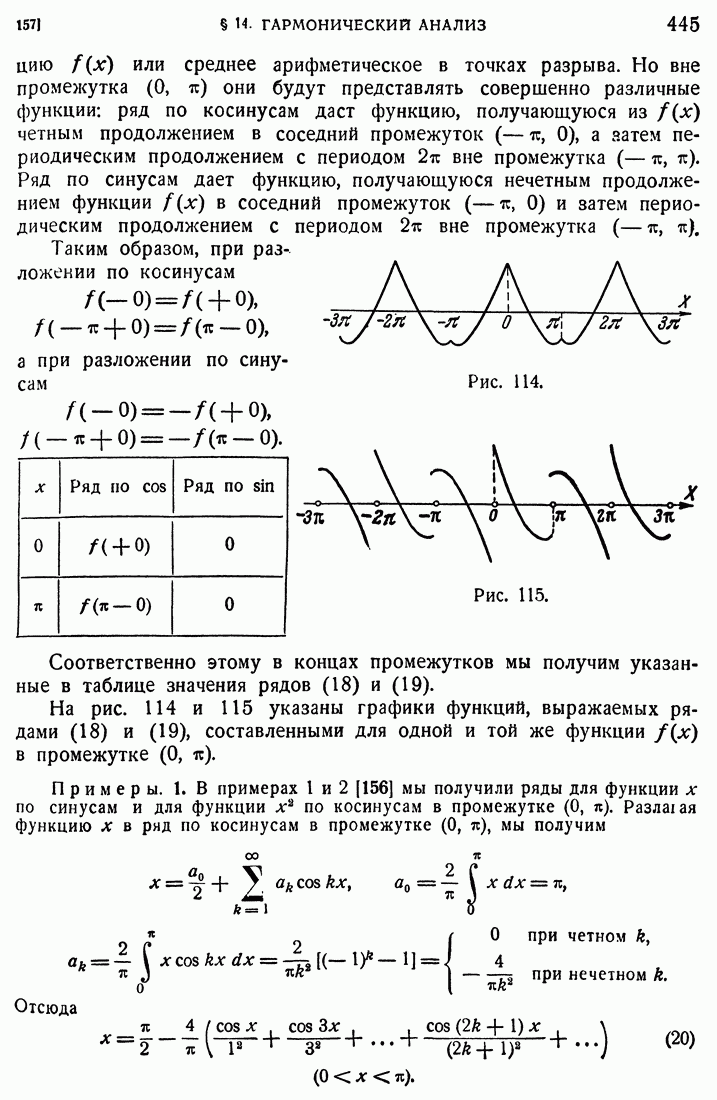
- 157. Разложение в промежутке (0, п).
- 158. Периодические функции периода 2l.
- 159. Средняя квадратичная погрешность.
- 160. Общие ортогональные системы функций.
- 161. Класс L2
- 162. Сходимость в среднем.
- 163. Ортонормированные системы в L2.
- § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ
- 164. Разложение в ряд Фурье.
- 165. Вторая теорема о среднем.
- 166. Интеграл Дирихле.
- 167. Теорема Дирихле.
- 168. Приближение к непрерывной функции полиномами.
- 169. Формула замкнутости.
- 170. Характер сходимости рядов Фурье.
- 171. Улучшение сходимости рядов Фурье.
- 172. Пример.
- § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ
- 173. Формула Фурье.
- 174. Ряды Фурье в комплексной форме.
- 176. Кратные ряды Фурье.
- ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- 176. Уравнение колебаний струны.
- 177. Решение Даламбера.
- 178. Частные случаи.
- 179. Ограниченная струна.
- 180. Способ Фурье.
- 181. Гармоники и стоячие волны.
- 182. Вынужденные колебания.
- 183. Сосредоточенная сила.
- 184. Формула Пуассона.
- 185. Цилиндрические волны.
- 186. Случай n-мерного пространства.
- 187. Неоднородное волновое уравнение.
- 188. Точечный источник.
- 189. Поперечные колебания мембран.
- 190. Прямоугольная мембрана.
- 191. Круглая мембрана.
- 192. Теорема единственности.
- 193. Применение интеграла Фурье.
- § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
- 195. Установившиеся процессы.
- 196. Устанавливающиеся процессы.
- 197. Примеры.
- 198. Обобщенное уравнение колебаний струны.
- 199. Неограниченная цепь в общем случае.
- 200. Способ Фурье для ограниченной цепи.
- 201. Обобщенное волновое уравнение.
- § 19. УРАВНЕНИЕ ЛАПЛАСА
- 202. Гармонические функции.
- 203. Формула Грина.
- 204. Основные свойства гармонических функций.
- 205. Решение задачи Дирихле для круга.
- 206. Интеграл Пуассона.
- 207. Задача Дирихле для сферы.
- 208. Функция Грина.
- 209. Случай полупространства.
- 210. Потенциал объемных масс.
- 211. Уравнение Пуассона.
- 212. Формула Кирхгофа.
- § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
- 214. Неограниченный стержень.
- 215. Стержень, ограниченный с одного конца.
- 216. Стержень, ограниченный с обоих концов.
- 217. Дополнительные замечания.
- 218. Случай сферы.
- 219. Теорема единственности.