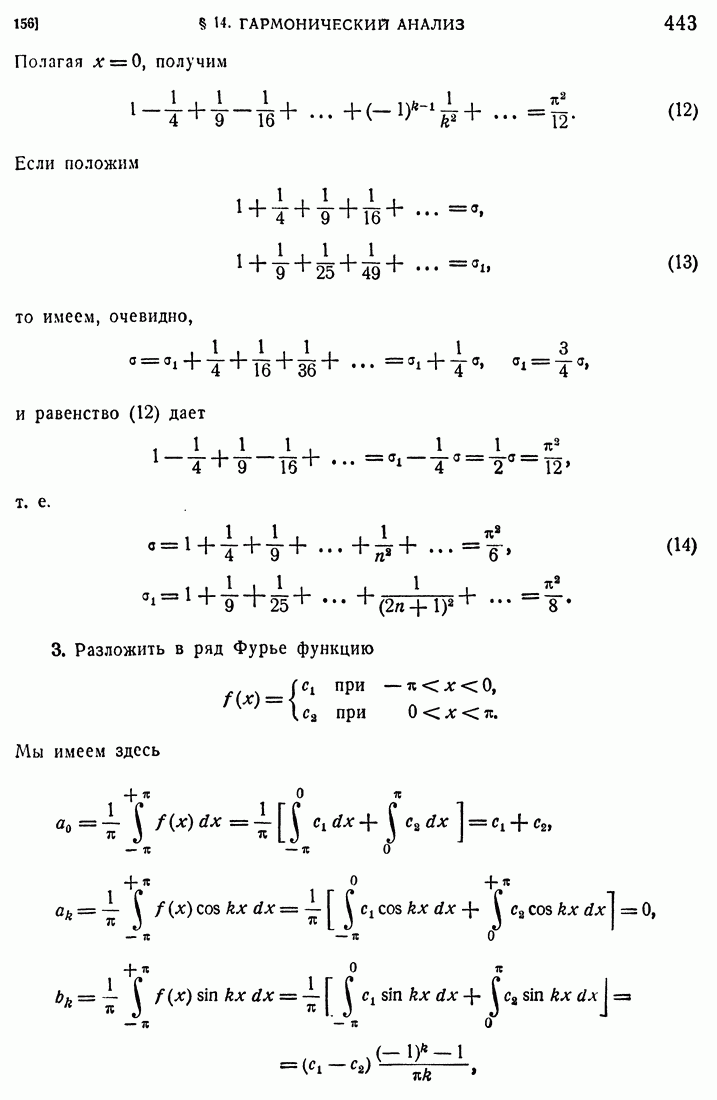| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
64. Основные свойства кратных интегралов.
Раньше мы доказывали свойства определенного интеграла, пользуясь его определением, как предела сумм [I, 94]. Совершенно так же можно доказать и основные свойства кратных интегралов. Для простоты мы все функции будем считать непрерывными, так что интегралы от них безусловно имеют смысл.
I. Постоянный множитель можно выносить за знак интеграла, и интеграл от конечной суммы функций равен сумме интегралов от слагаемых:

II. Если область  разложена на конечное число частей [например на две части
разложена на конечное число частей [например на две части  , то интеграл по всей области равен сумме интегралов по всем частям:
, то интеграл по всей области равен сумме интегралов по всем частям:

III. Если  в области
в области  , то
, то

В частности [I, 94]:

IV. Если  сохраняет знак в области (а), то имеет место теорема о среднем, выражающаяся формулой
сохраняет знак в области (а), то имеет место теорема о среднем, выражающаяся формулой

где  - некоторая точка, лежащая внутри области (а).
- некоторая точка, лежащая внутри области (а).
В частности, при  получаем
получаем

где  — площадь области
— площадь области  .
.
Аналогичные свойства имеют место и для трехкратного интеграла. Заметим, что при определении двукратного и трехкратного интеграла как предела суммы считается всегда, что область интегрирования конечна и подынтегральная функция  во всяком случае ограничена, т. е. существует такое положительное число А, что
во всяком случае ограничена, т. е. существует такое положительное число А, что  во всех точках N области интегрирования. Если эти условия не выполнены, то интеграл может существовать как несобственный интеграл аналогично тому, как это имело место для простого определенного интеграла [I, 97 и 98]. Мы займемся несобственными кратными интегралами в § 8.
во всех точках N области интегрирования. Если эти условия не выполнены, то интеграл может существовать как несобственный интеграл аналогично тому, как это имело место для простого определенного интеграла [I, 97 и 98]. Мы займемся несобственными кратными интегралами в § 8.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮ
- ГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Определение решения по начальному условию. Теорема существования и единственности.
- 3. Уравнения с отделяющимися переменными.
- 4. Примеры.
- 5. Однородное уравнение.
- 6. Линейные уравнения и уравнение Бернулли.
- 7. Способ Эйлера—Коши.
- 8. Применение степенных рядов.
- 9. Общий интеграл и особое решение.
- 10. Уравнения, не решенные относительно у’.
- 11. Уравнение Клеро.
- 12. Уравнение Лагранжа.
- 13. Огибающие семейства кривых и особые решения.
- 14. Изогональные траектории.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ И СИСТЕМЫ УРАВНЕНИЙ
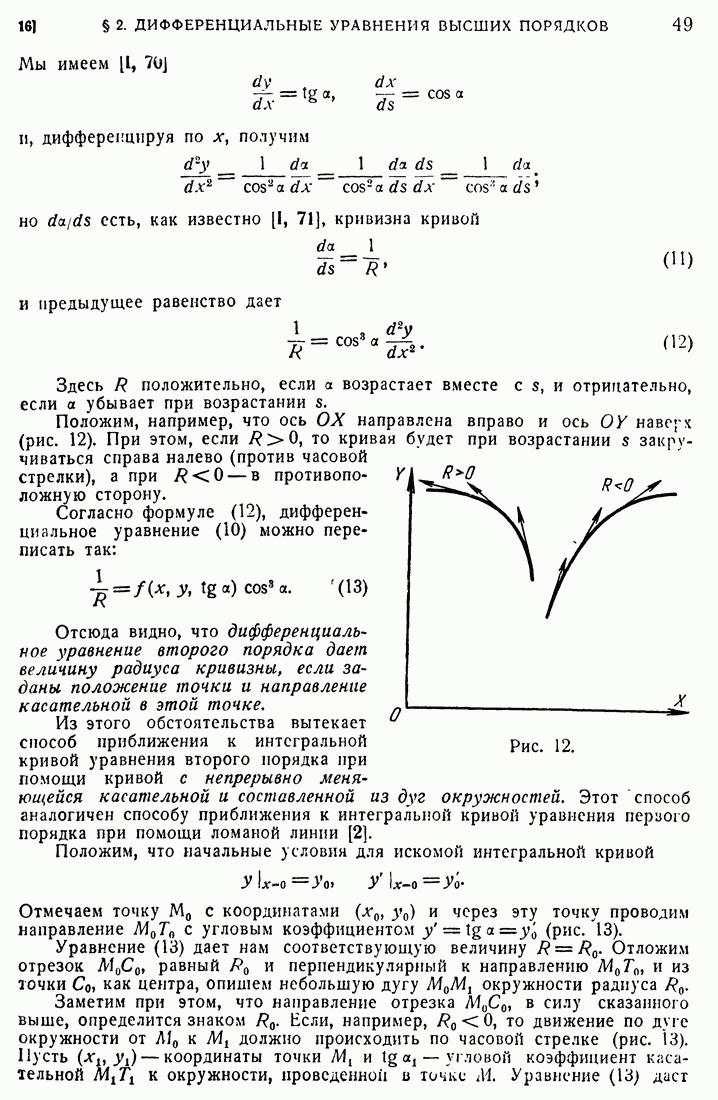
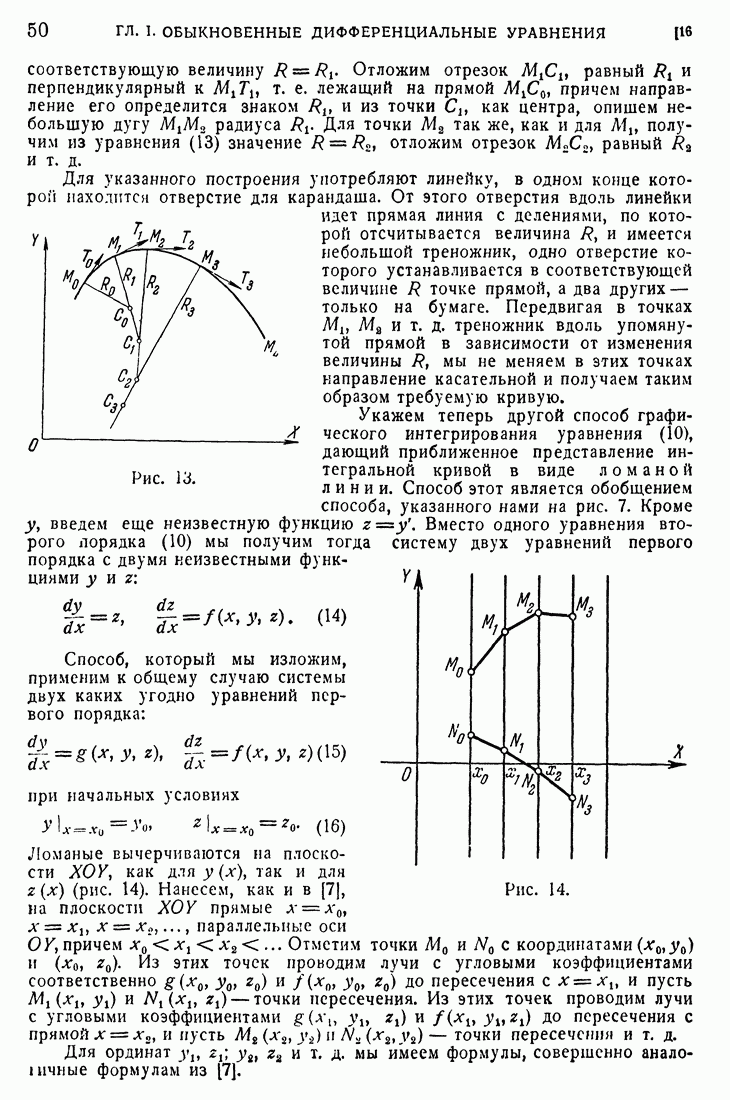
- 16. Графические способы интегрирования дифференциального уравнения второго порядка.
- 17. Уравнение у^(n)=f(x).
- 18. Понижение порядка дифференциального уравнения.
- 19. Системы обыкновенных дифференциальных уравнений.
- 20. Примеры.
- 21. Системы уравнений и уравнения высших порядков.
- 22. Линейные уравнения с частными производными.
- 23. Геометрическая интерпретация.
- 24. Примеры.
- ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 25. Линейные однородные уравнения второго порядка.
- 26. Линейные неоднородные уравнения второго порядка.
- 27. Линейные уравнения высших порядков.
- 28. Однородные уравнения второго порядка с постоянными коэффициентами.
- 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- 30. Частные случаи.
- 31. Корни решений и колеблющиеся решения
- 32. Линейные уравнения высших порядков с постоянными коэффициентами.
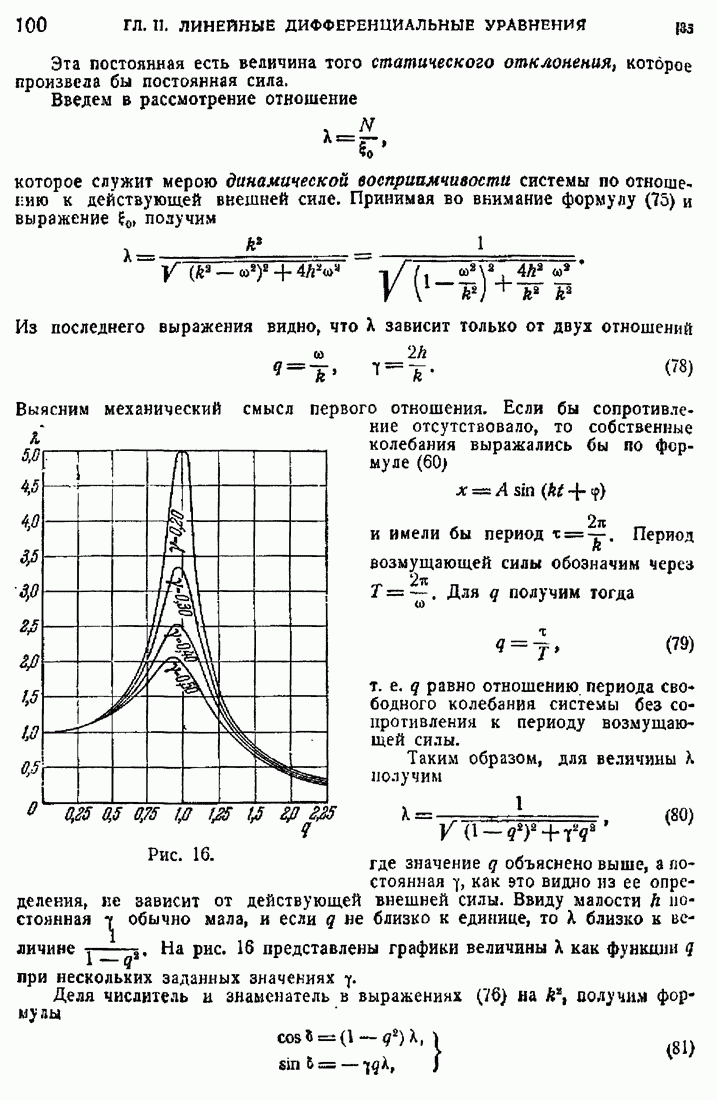
- 33. Линейные уравнения и колебательные явления.
- 34. Собственные и вынужденные колебания.
- 35. Синусоидальная внешняя сила и резонанс.
- 36. Предельные задачи.
- 37. Примеры.
- 38. Символический метод.
- 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами.
- 40. Линейные неоднородные уравнения с постоянными коэффициентами.
- 41. Пример.
- 42 Уравнение Эйлера.
- 43. Системы линейных уравнений с постоянными коэффициентами.
- 44. Примеры
- § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
- 45. Интегрирование линейного уравнения с помощью степенного ряда
- 46. Примеры.
- 47. Разложение решения в обобщенный степенной ряд.
- 48. Уравнение Бесселя
- 49. Уравнения, приводящиеся к уравнению Бесселя
- § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 50. Метод последовательных приближений для линейных уравнений.
- 51. Случай нелинейного уравнения.
- 52. Дополнения к теореме существования и единственности.
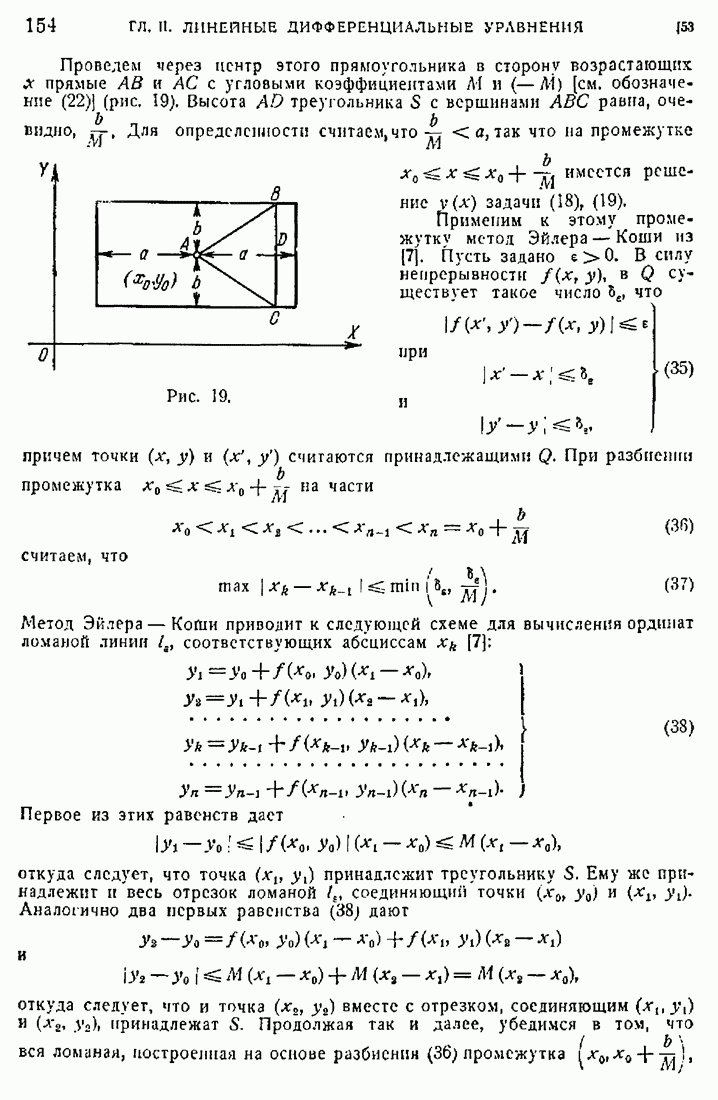
- 53. Сходимость метода Эйлера — Коши.
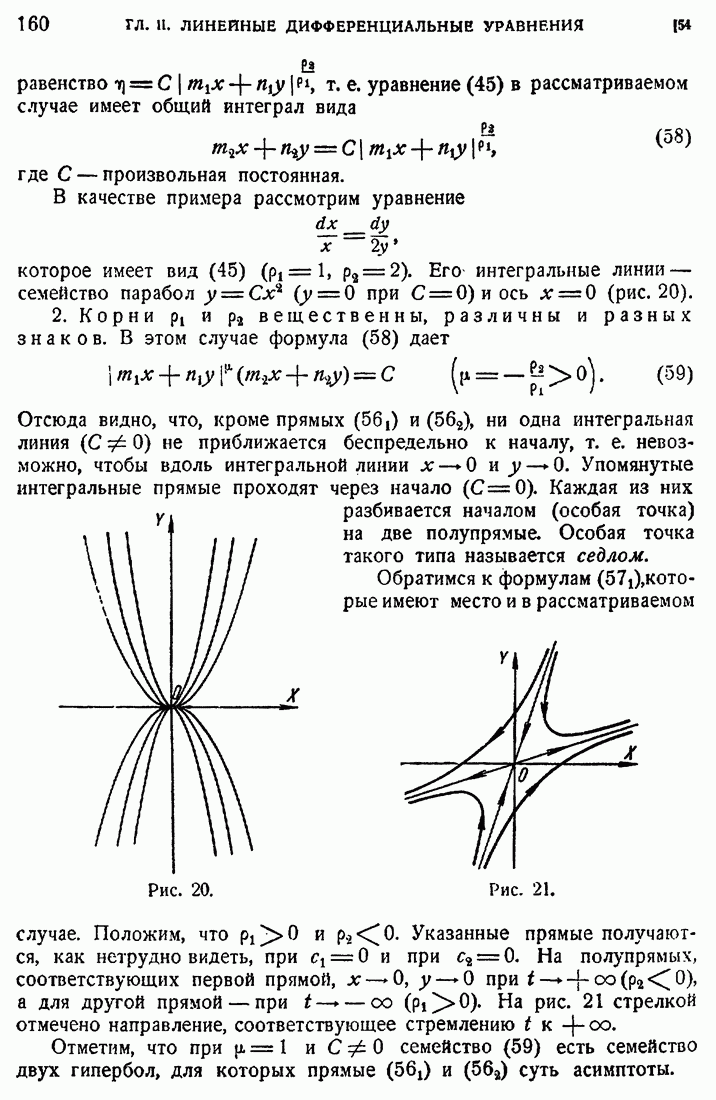
- 54. Особые точки дифференциальных уравнений первого порядка.
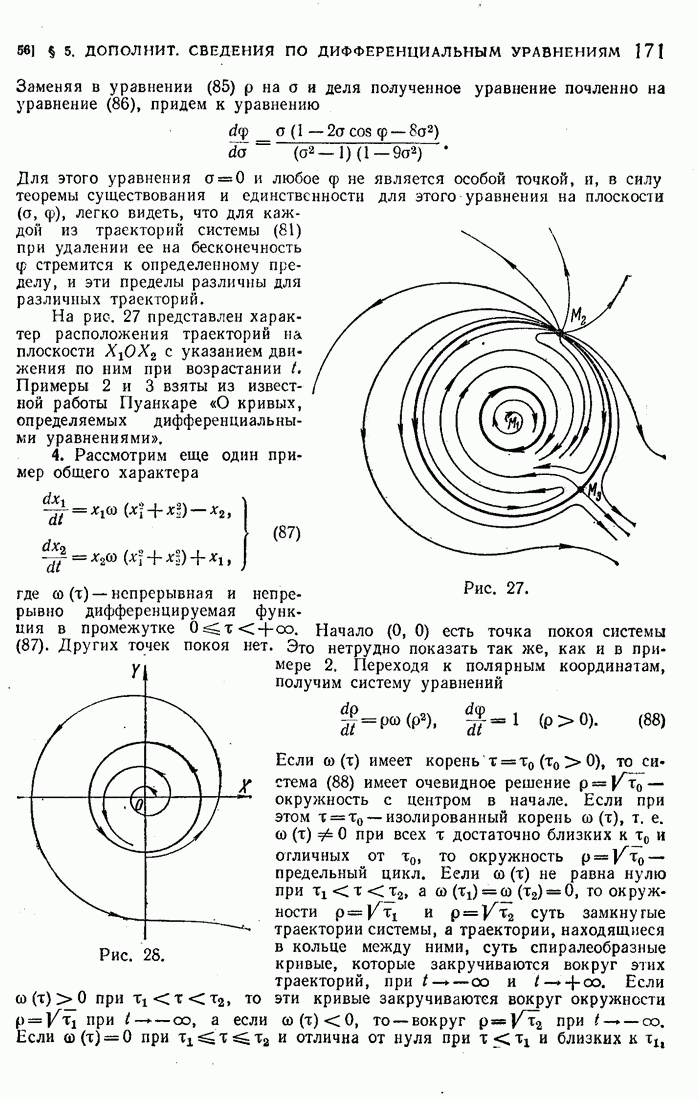
- 55. Автономные системы.
- 56. Примеры.
- ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 6. КРАТНЫЕ ИНТЕГРАЛЫ
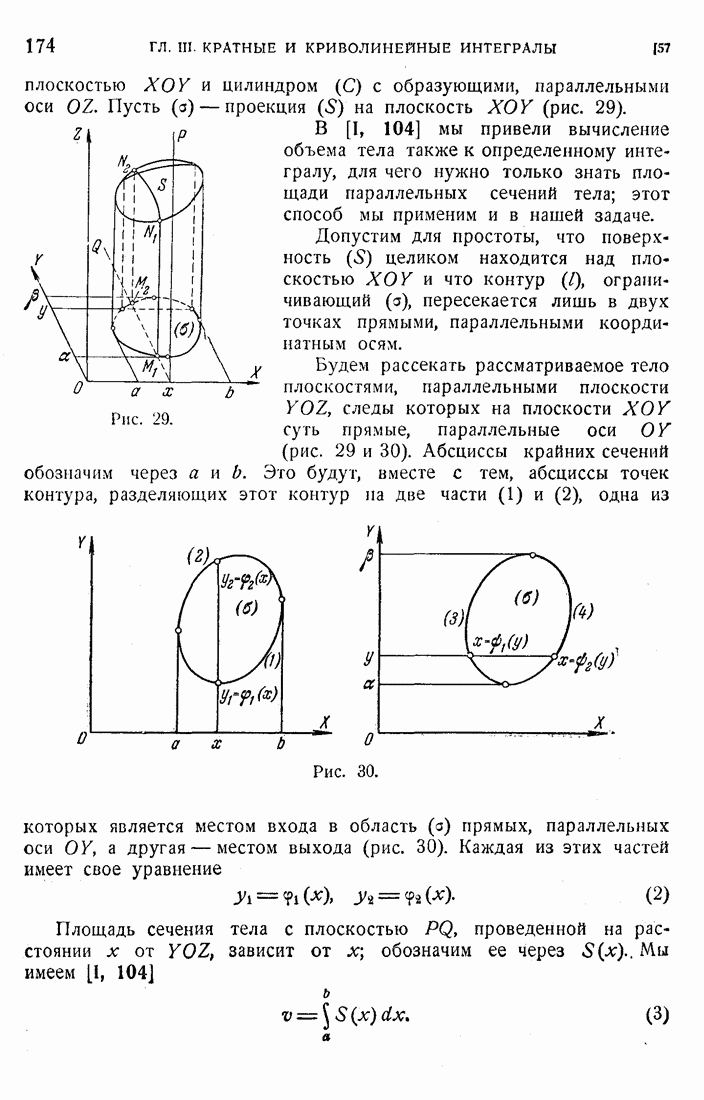
- 58. Двукратный интеграл.
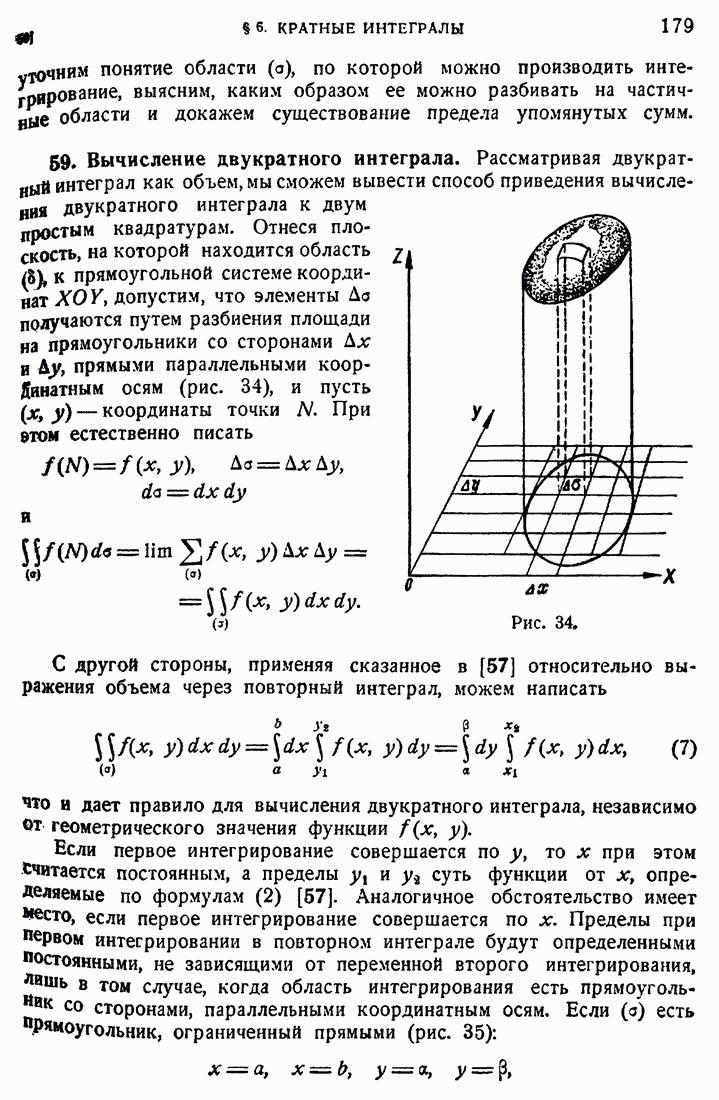
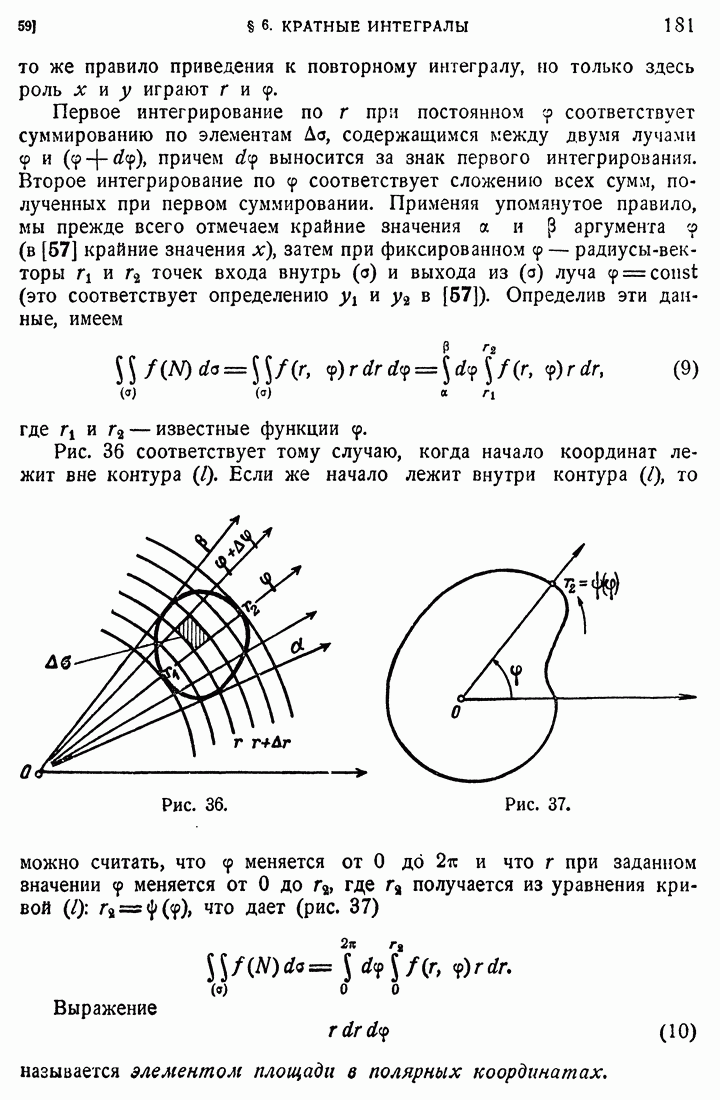
- 59. Вычисление двукратного интеграла.
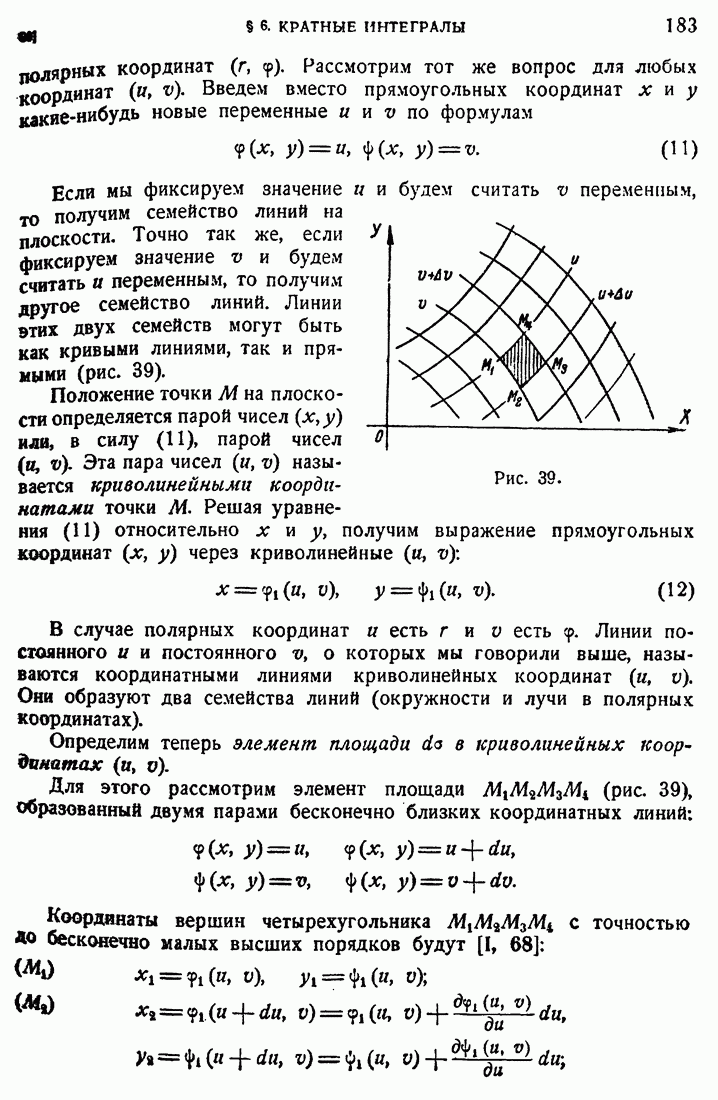
- 60. Криволинейные координаты.
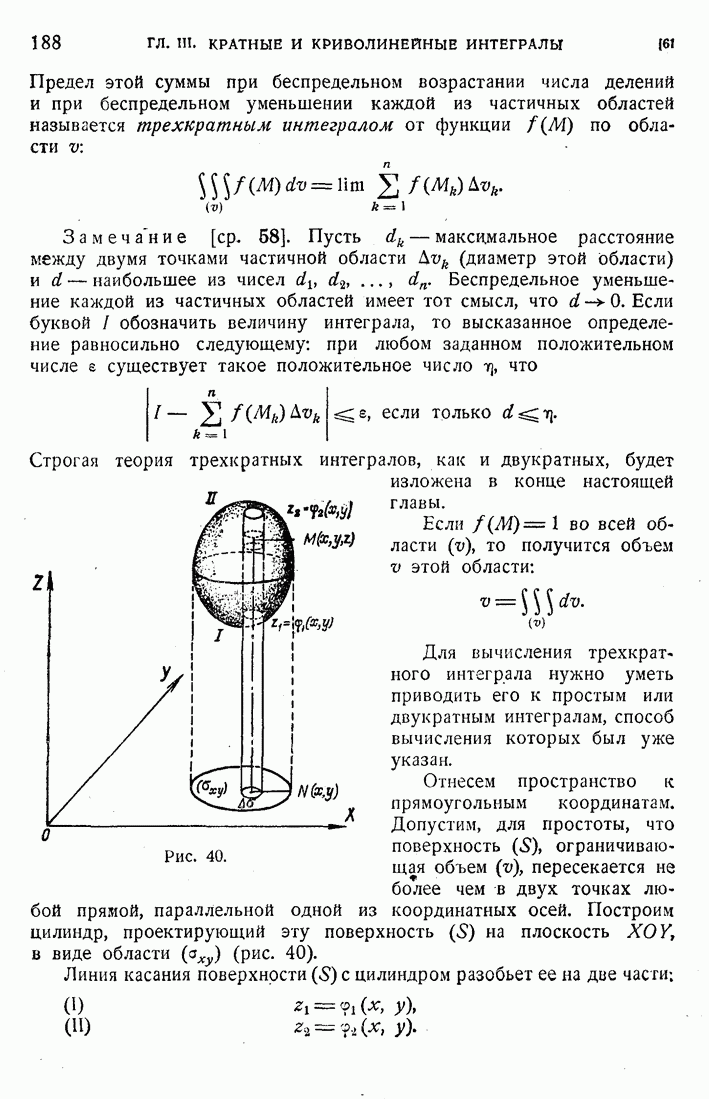
- 61. Трехкратный интеграл
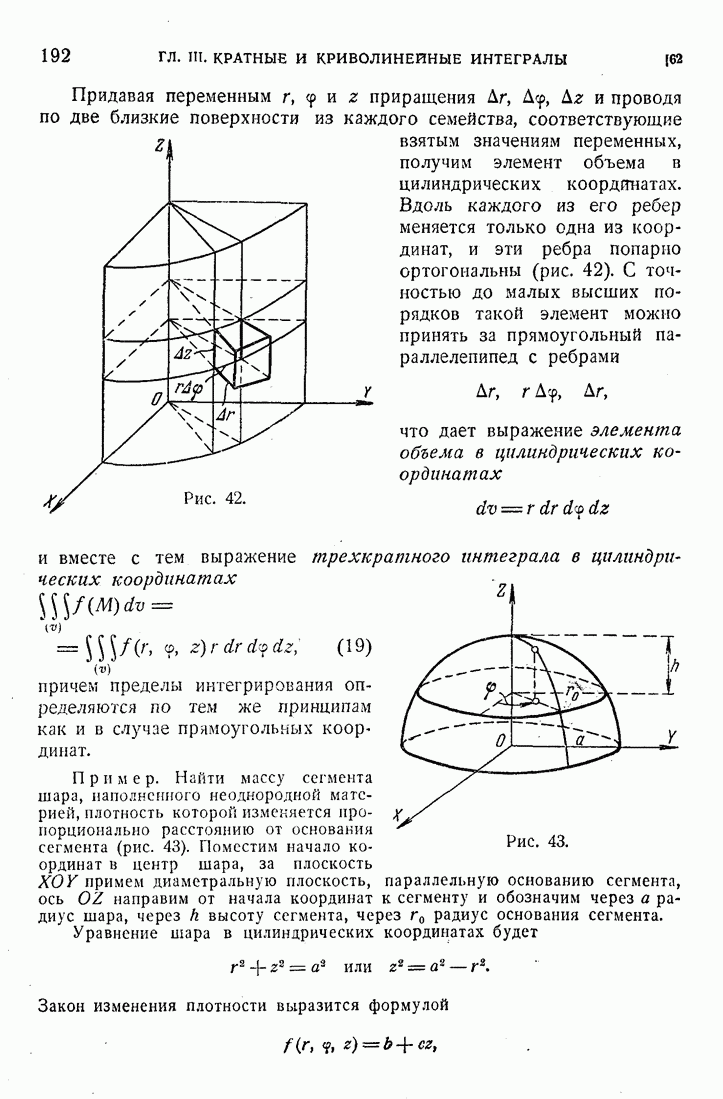
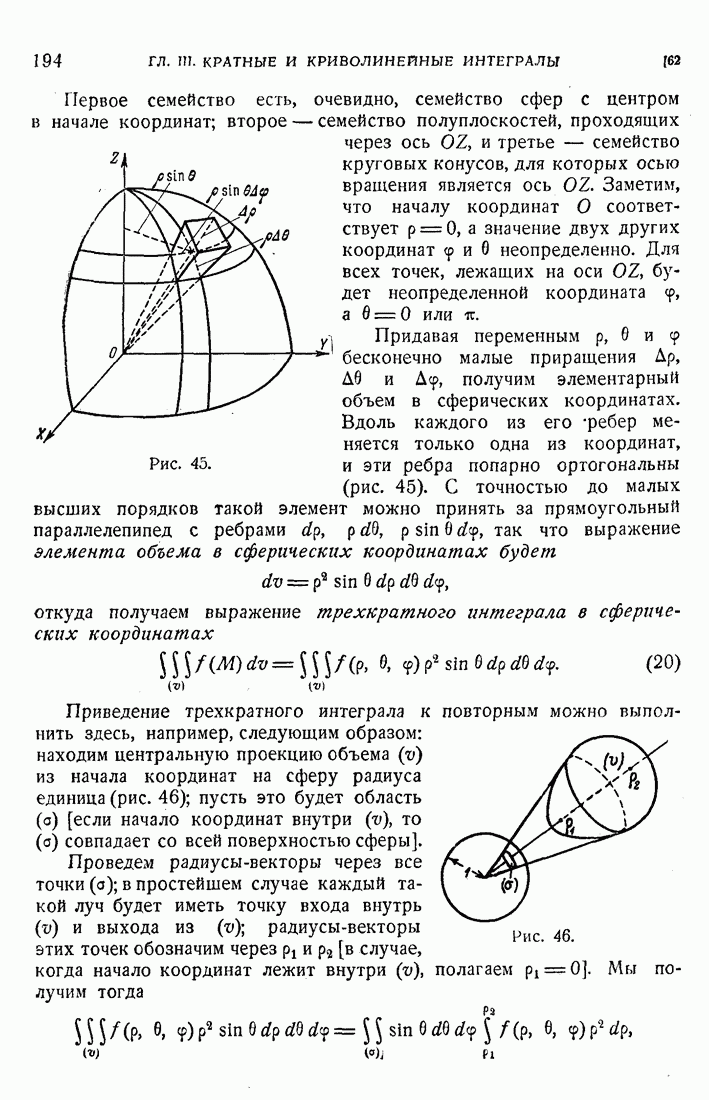
- 62. Цилиндрические и сферические координаты.
- 63. Криволинейные координаты в пространстве.
- 64. Основные свойства кратных интегралов.
- 65. Площадь поверхности.
- 66. Интегралы по поверхности и формула Остроградского.
- 67. Интегралы по определенной стороне поверхности.
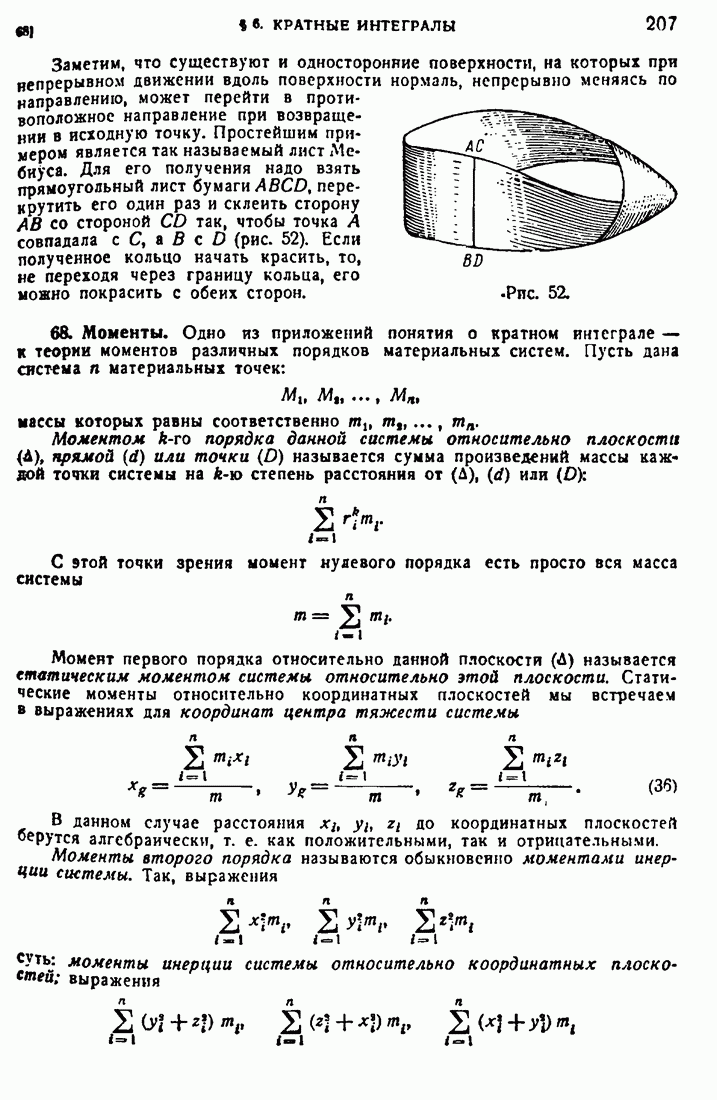
- 68. Моменты.
- § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- 69. Определение криволинейного интеграла.
- 70. Работа силового поля. Примеры.
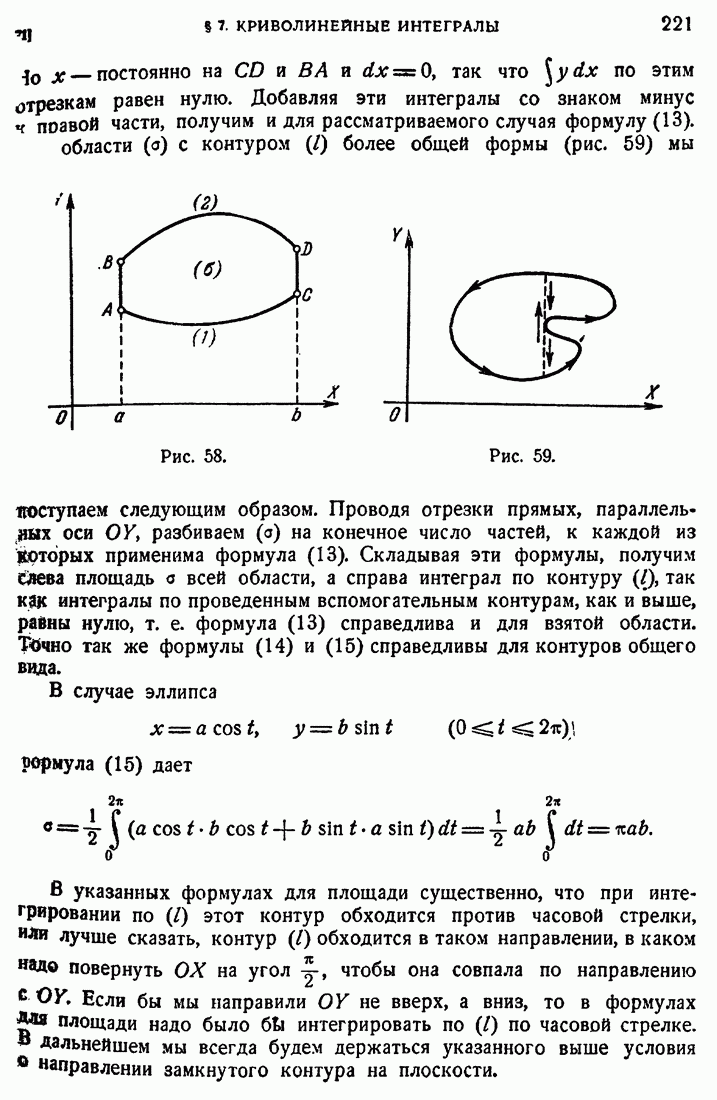
- 71. Площадь и криволинейный интеграл.
- 72. Формула Грина
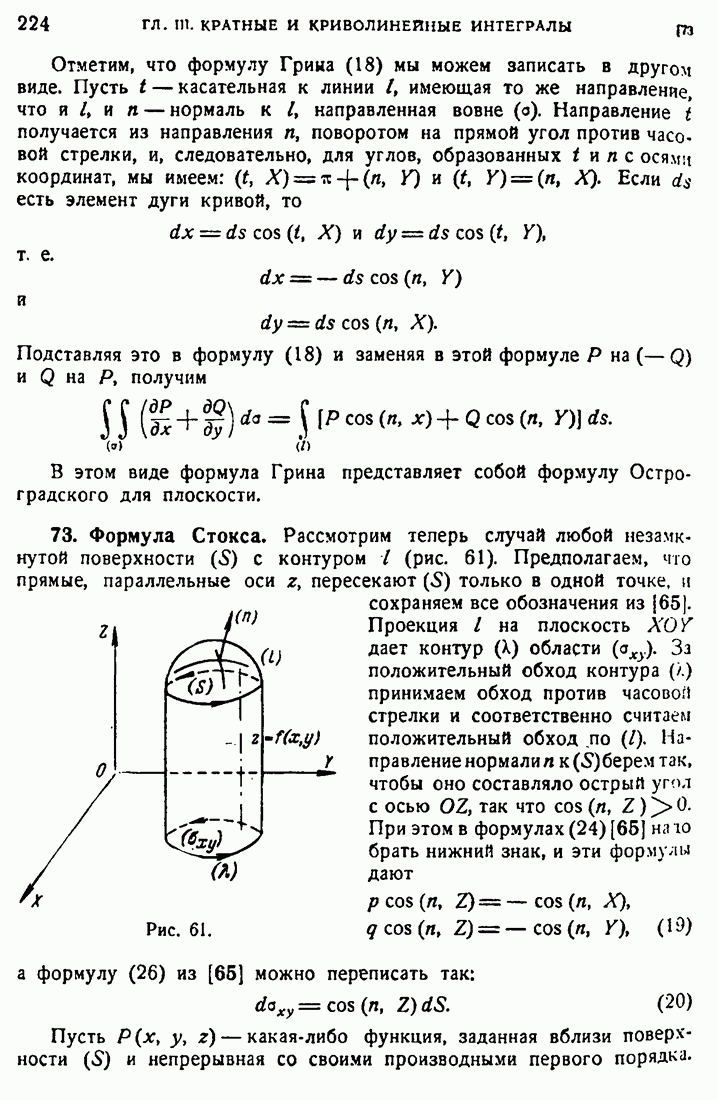
- 73. Формула Стокса.
- 74. Независимость криволинейного интеграла от пути на плоскости.
- 75. Случай многосвязной области.
- 76. Независимость криволинейного интеграла от пути в пространстве.
- 77. Установившееся течение жидкости.
- 78. Интегрирующий множитель.
- 79. Уравнение в полных дифференциалах для случая трех переменных.
- 80. Замена переменных в двойном интеграле.
- § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 81. Интегрирование под знаком интеграла.
- 82. Формула Дирихле.
- 83. Дифференцирование под знаком интеграла
- 84. Примеры.
- 85. Несобственные интегралы.
- 86. Неабсолютно сходящиеся интегралы.
- 87. Равномерно сходящиеся интегралы.
- 88. Примеры.
- 89. Несобственные кратные интегралы.
- 90. Примеры.
- § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ
- 92. Основные теоремы.
- 93. Счетные множества. Действия над точечными множествами.
- 94. Мера Жордана.
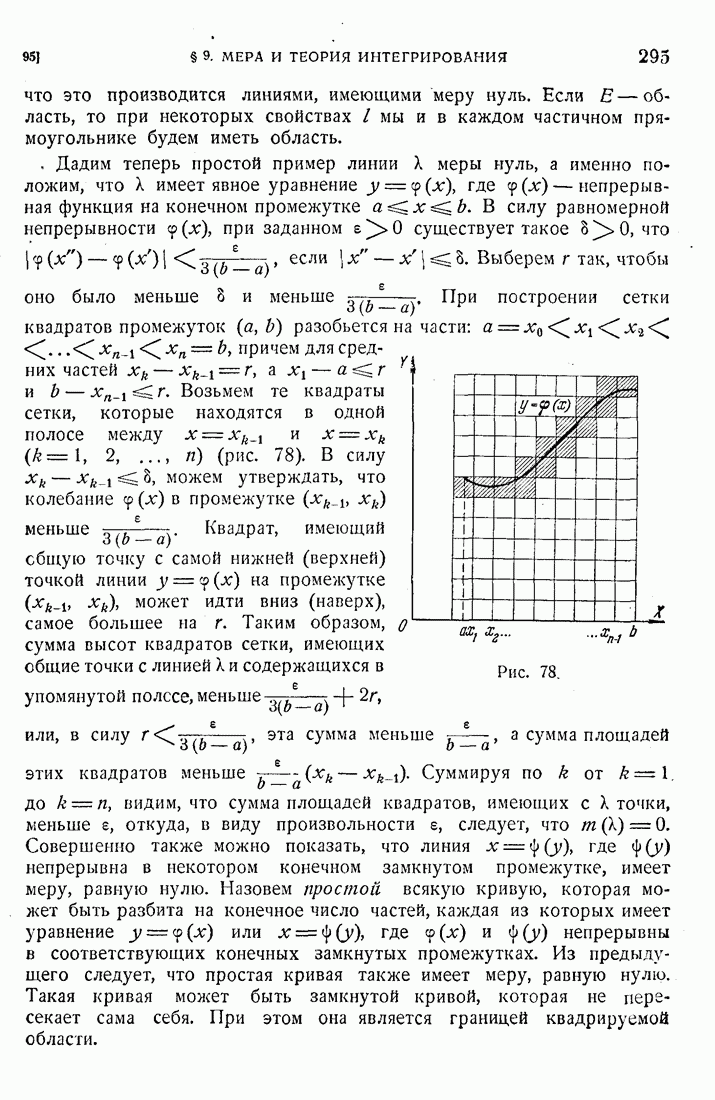
- 95. Квадрируемые множества.
- 96. Независимость от выбора осей.
- 97. Случай любого числа измерений.
- 98. Интегрируемые функции.
- 99. Вычисление двойного интеграла.
- 100. n-кратные интегралы.
- 101. Примеры.
- 102. Внешняя мера Лебега.
- 103. Измеримые множества.
- 104. Измеримые функции.
- 105. Дополнительные сведения.
- 106. Интеграл Лебега.
- 107. Свойства интеграла Лебега.
- 108. Интегралы от неограниченных функций.
- 109. Предельный переход под знаком интеграла.
- 110. Теорема Фубини.
- 111. Интегралы по множеству бесконечной меры.
- ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ
- 112. Сложение и вычитание векторов.
- 113. Умножение вектора на скаляр. Компланарность векторов.
- 114. Разложение вектора по трем некомпланарным векторам.
- 115. Скалярное произведение.
- 116. Векторное произведение.
- 117. Соотношения между скалярным к векторным произведениями.
- 118. Скорости точек вращающегося твердого тела; момент вектора.
- § 11 ТЕОРИЯ ПОЛЯ
- 119. Дифференцирование вектора
- 120. Скалярное поле и его градиент.
- 121. Векторное поле; расходимость и вихрь.
- 122. Потенциальное и соленоидальное поля.
- 123. Направленный элемент поверхности.
- 124. Некоторые формулы векторного анализа.
- 125. Движение твердого тела и малая деформация.
- 126. Уравнение непрерывности.
- 127. Уравнения гидродинамики идеальной жидкости.
- 128. Уравнения распространения звука.
- 129. Уравнение теплопроводности.
- 130. Уравнения Максвелла.
- 131. Выражение оператора Лапласа в ортогональных координатах.
- 132. Операция дифференцирования для случая переменного поля.
- ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 133. Плоская кривая, ее кривизна и эволюта.
- 134. Эвольвента.
- 135. Естественное уравнение кривой.
- 136. Основные элементы кривой в пространстве.
- 137. Формулы Френе.
- 138. Соприкасающаяся плоскость.
- 139. Винтовые линии.
- 140. Поле единичных векторов.
- § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 141. Параметрические уравнения поверхности.
- 142. Первая дифференциальная форма Гаусса.
- 143. Вторая дифференциальная форма Гаусса.
- 144. О кривизне линий, начерченных на поверхности.
- 145. Индикатриса Дюпена и формула Эйлера.
- 146. Определение главных радиусов кривизны и главных направлений.
- 147. Линии кривизны.
- 148. Теорема Дюпена.
- 149. Примеры.
- 150. Гауссова кривизна.
- 151. Вариация элемента площади и средняя кривизна.
- 152. Огибающая семейства поверхностей и кривых.
- 153. Развертывающиеся поверхности.
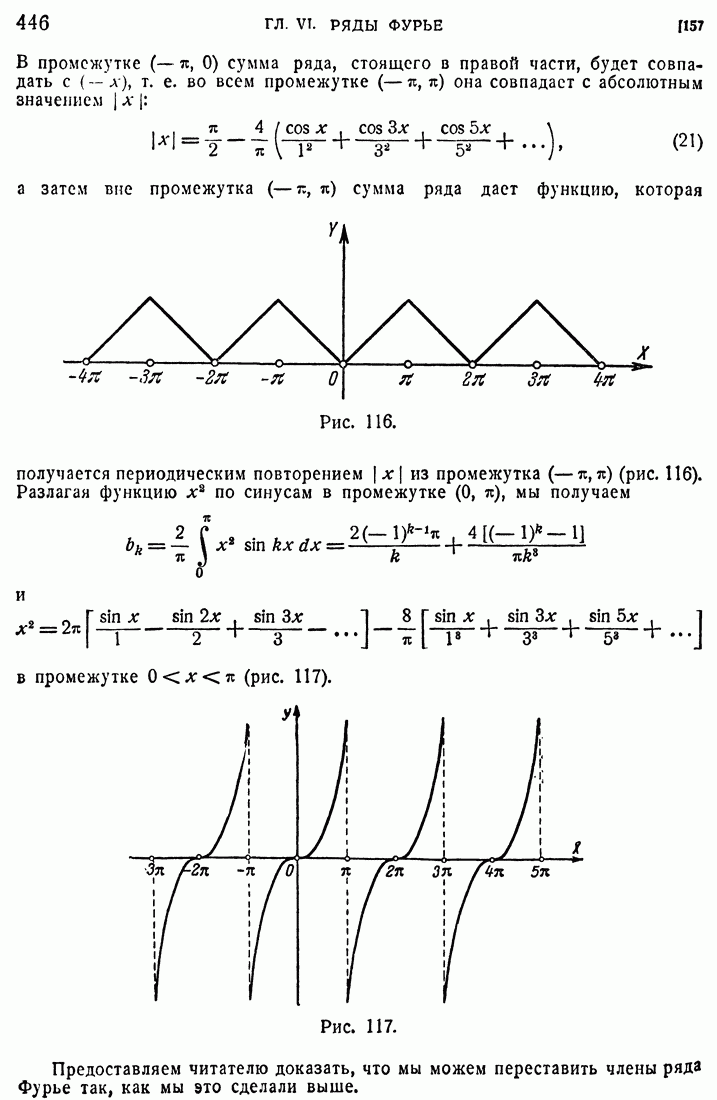
- ГЛАВА VI. РЯДЫ ФУРЬЕ
- 154. Ортогональность тригонометрических функций.
- 155. Теорема Дирихле.
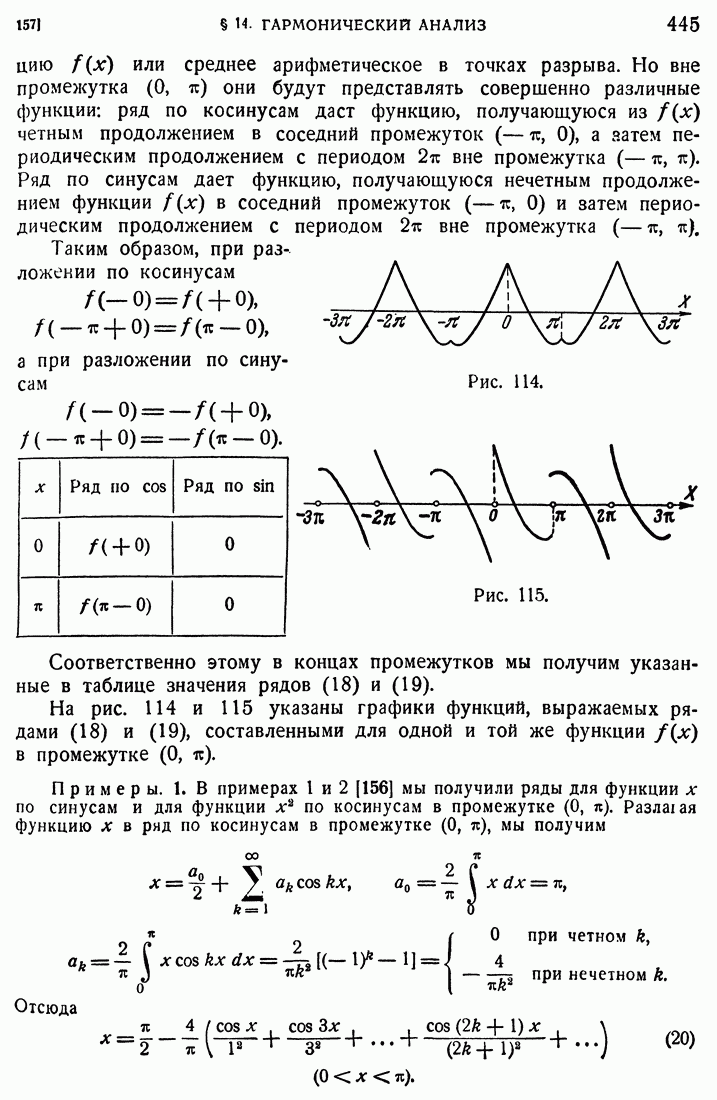
- 156. Примеры.
- 157. Разложение в промежутке (0, п).
- 158. Периодические функции периода 2l.
- 159. Средняя квадратичная погрешность.
- 160. Общие ортогональные системы функций.
- 161. Класс L2
- 162. Сходимость в среднем.
- 163. Ортонормированные системы в L2.
- § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ
- 164. Разложение в ряд Фурье.
- 165. Вторая теорема о среднем.
- 166. Интеграл Дирихле.
- 167. Теорема Дирихле.
- 168. Приближение к непрерывной функции полиномами.
- 169. Формула замкнутости.
- 170. Характер сходимости рядов Фурье.
- 171. Улучшение сходимости рядов Фурье.
- 172. Пример.
- § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ
- 173. Формула Фурье.
- 174. Ряды Фурье в комплексной форме.
- 176. Кратные ряды Фурье.
- ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- 176. Уравнение колебаний струны.
- 177. Решение Даламбера.
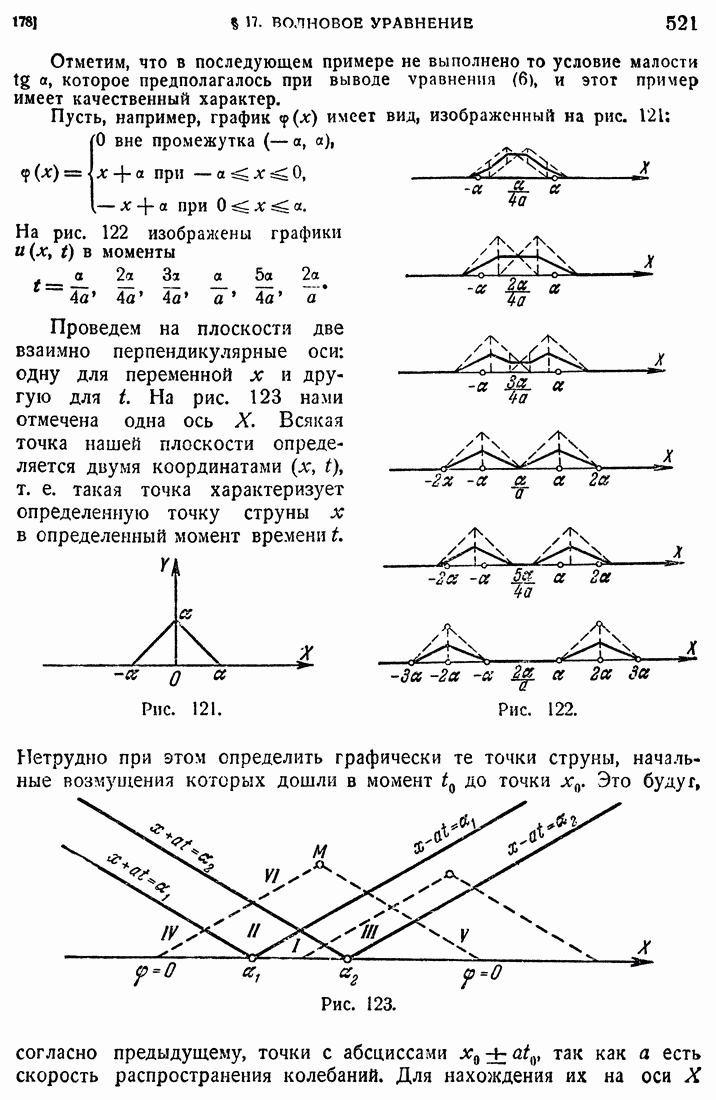
- 178. Частные случаи.
- 179. Ограниченная струна.
- 180. Способ Фурье.
- 181. Гармоники и стоячие волны.
- 182. Вынужденные колебания.
- 183. Сосредоточенная сила.
- 184. Формула Пуассона.
- 185. Цилиндрические волны.
- 186. Случай n-мерного пространства.
- 187. Неоднородное волновое уравнение.
- 188. Точечный источник.
- 189. Поперечные колебания мембран.
- 190. Прямоугольная мембрана.
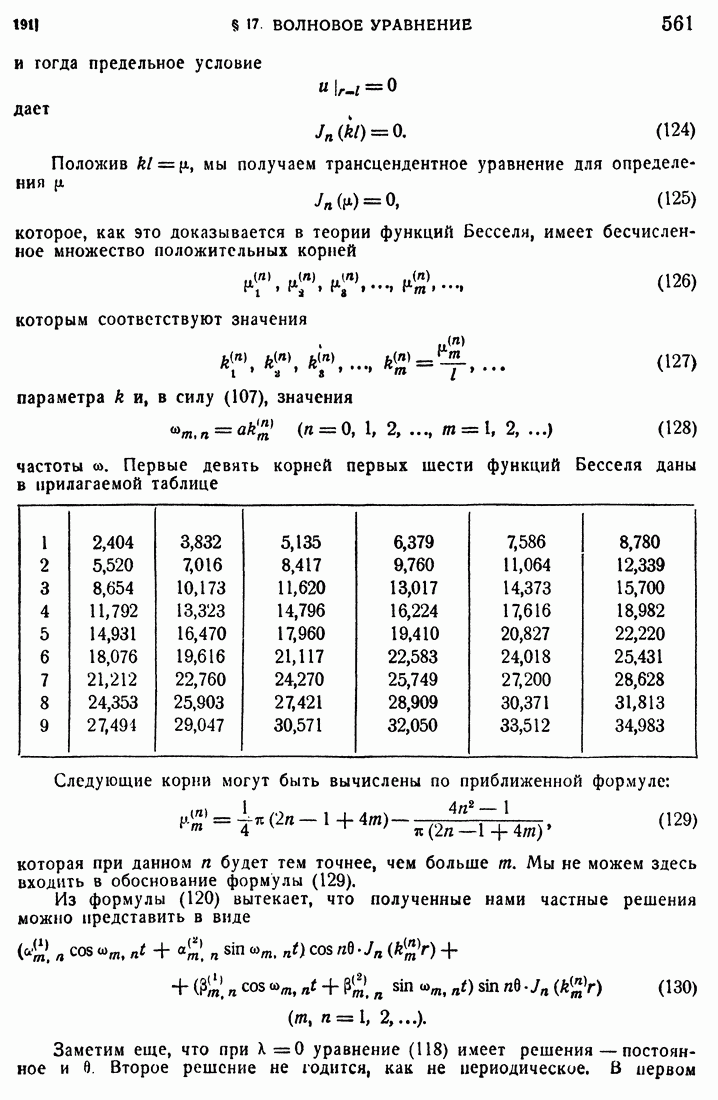
- 191. Круглая мембрана.
- 192. Теорема единственности.
- 193. Применение интеграла Фурье.
- § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
- 195. Установившиеся процессы.
- 196. Устанавливающиеся процессы.
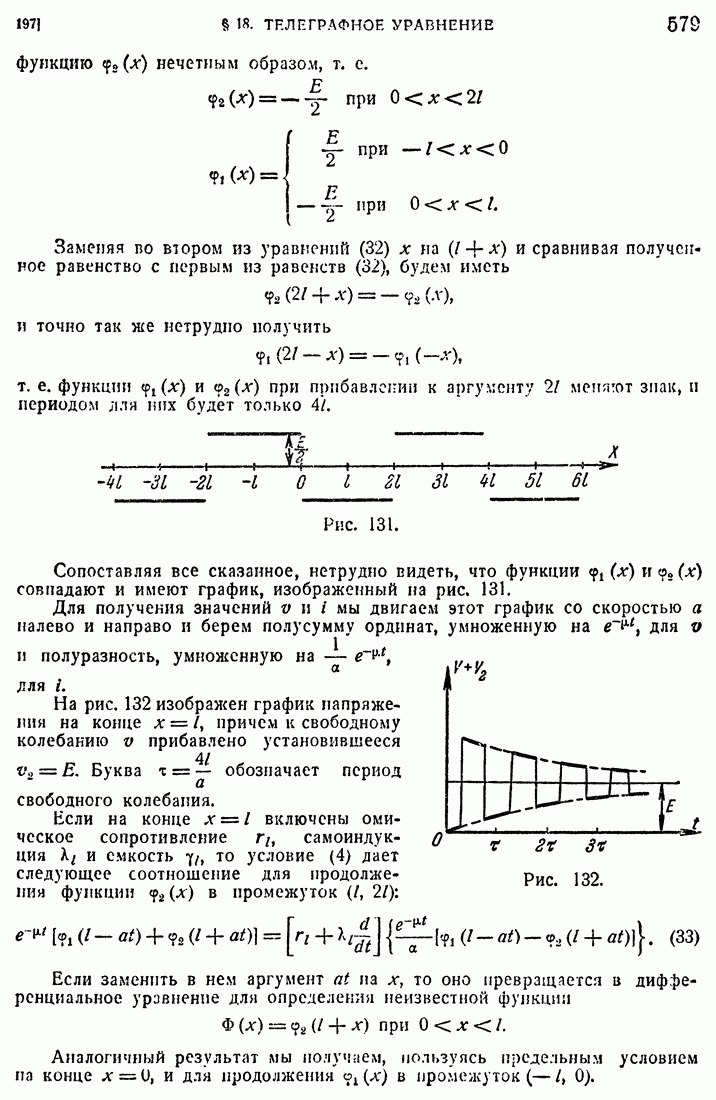
- 197. Примеры.
- 198. Обобщенное уравнение колебаний струны.
- 199. Неограниченная цепь в общем случае.
- 200. Способ Фурье для ограниченной цепи.
- 201. Обобщенное волновое уравнение.
- § 19. УРАВНЕНИЕ ЛАПЛАСА
- 202. Гармонические функции.
- 203. Формула Грина.
- 204. Основные свойства гармонических функций.
- 205. Решение задачи Дирихле для круга.
- 206. Интеграл Пуассона.
- 207. Задача Дирихле для сферы.
- 208. Функция Грина.
- 209. Случай полупространства.
- 210. Потенциал объемных масс.
- 211. Уравнение Пуассона.
- 212. Формула Кирхгофа.
- § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
- 214. Неограниченный стержень.
- 215. Стержень, ограниченный с одного конца.
- 216. Стержень, ограниченный с обоих концов.
- 217. Дополнительные замечания.
- 218. Случай сферы.
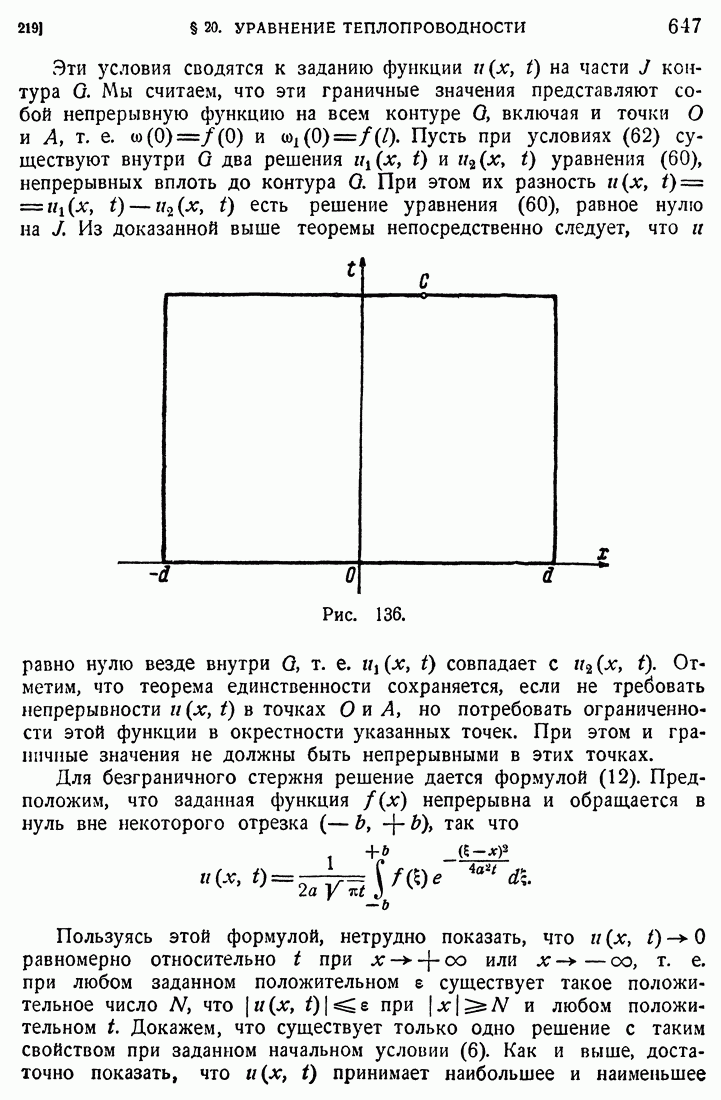
- 219. Теорема единственности.