| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ОТВЕТЫ И УКАЗАНИЯ
ГЛАВА 1
1.1. В плоскости а через точку О проведите прямую  параллельную прямой а, и докажите, что с, совпадает с прямой с.
параллельную прямой а, и докажите, что с, совпадает с прямой с.
1.3. Выберите одну из диагоналей и докажите, что каждая из оставшихся диагоналей пересекает ее в середине.
1.4. Все утверждения доказываются из равенства треугольников. Они обобщаются для любой правильной « -угольной пирамиды.
-угольной пирамиды.
1.5. Достаточно доказать, что этой плоскостью делится пополам линейный угол этого двугранного угла. Утверждение обобщается для любой правильной  -угольной пирамиды.
-угольной пирамиды.
1.20. Для вычисления PQ используйте два раза теорему косинусов.
1.21. Нарисуете линейные углы этих двугранных углов и треугольники, в которых эти линейные углы являются углами треугольников. Обобщается на правильную  -угольную пирамиду.
-угольную пирамиду.
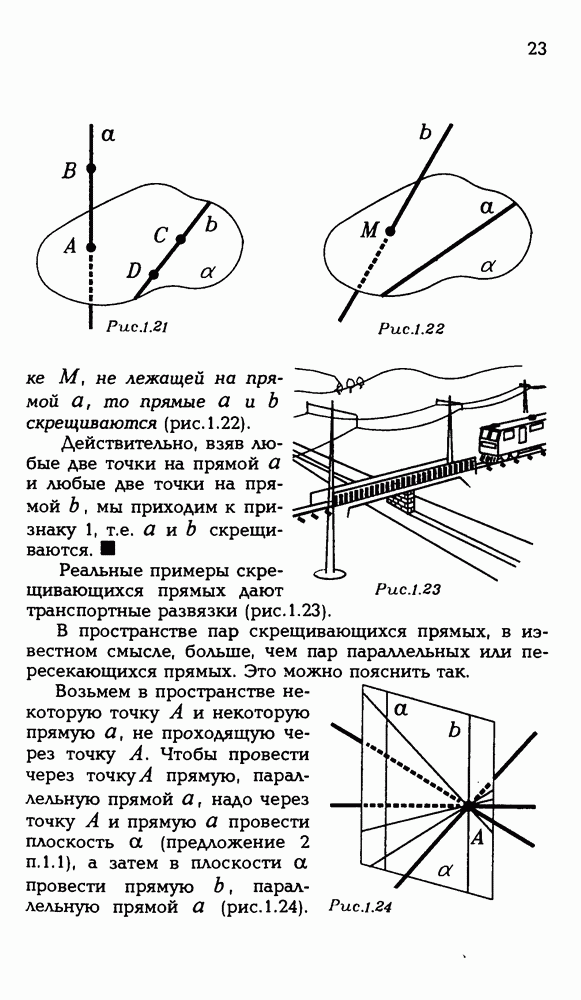
1.23-1.24. Попробуйте дать ответ, ничего не рисуя. Попытайтесь увидеть такую плоскость, которая содержит одну из данных прямых и пересекает другую. Тогда эти прямые скрещиваются или пересекаются.
1.25. Под граничными значениями понимаются (здесь и далее) наибольшее и наименьшее значения. Попытайтесь увидеть такие положения точки К, при которых расстояние КС становится наибольшим или наименьшим. Для этого можно представить себе треугольник АВК, вращающийся вокруг АВ. Оба гранчных значения для КС достигаются, когда точка К оказывается в плоскости ABC. При доказательстве используется теорема косинусов.
1.26. Необходимо рассмотреть два случая. В первом случае оценивается расстояние между известными ребрами. Во втором случае оценивается расстояние между ребром известным и ребром неизвестным. В каждом случае это расстояние выражается как функция от  где
где  длина неизвестного ребра. Полученная функция исследуется на наибольшее и наименьшее значения, при этом важно понимать, в каких границах лежит сама величина
длина неизвестного ребра. Полученная функция исследуется на наибольшее и наименьшее значения, при этом важно понимать, в каких границах лежит сама величина 
1.27. В равнобедренном треугольнике  основание А В постоянно, поэтому при движении точки X, надо проследить
основание А В постоянно, поэтому при движении точки X, надо проследить
только за изменением его высоты, проведенной из X на АВ.
1.28. Может.
1.29. а), б) Можно в любой, в) Можно в некоторой, г) Нет.
1.30. Рассмотрите отрезок KL как сторону треугольника KXL, где  середина АВ. Воспользуйтесь неравенством треугольника и свойством его средней линии.
середина АВ. Воспользуйтесь неравенством треугольника и свойством его средней линии.
1.31. Рассмотрите тетраэдр ABCD, считая все его ребра известными. Воспользуйтесь формулой для медианы треугольника, в котором известны все его стороны.
1.34. Достаточно измерить расстояние до самолета три раза через равные промежутки времени.
1.38. Используйте результат задачи 1.35а.
1.39. Рассмотрите правильную треугольную пирамиду, вершина которой находится в конце данной диагонали куба, а основание которой  треугольник с вершинами в рассматриваемых концах ребер. Затем используйте результат задачи 1.35а.
треугольник с вершинами в рассматриваемых концах ребер. Затем используйте результат задачи 1.35а.
1.42. Произвольную точку внутри острого угла между плоскостями спроектируйте на каждую из данных плоскостей и на прямую их пересечения. Соедините проекцию на прямую с проекциями на плоскости. Используя теорему о трех перпендикулярах, получите нужный результат.
1.43. "Положите" треугольник ВСХ на плоскость ВСА так, чтобы точки X и А оказались с одной стороны от ВС. Задача становится планиметрической.
1.44. Проведите высоту пирамиды и используйте результат задачи 1.43.
1.45. Проведите плоскость, перпендикулярную данной прямой в данной точке. Докажите теперь, что все данные перпендикуляры лежат в этой плоскости.
1.46. Через точку на ребре двугранного угла проведите плоскость, перпендикулярную этому ребру. Она пересекает двугранный угол по линейному углу, а биссектор  по биссектрисе этого линейного угла. Задача становится планиметрической. Не забудьте, что в таких задачах доказываются два взаимно обратных утверждения.
по биссектрисе этого линейного угла. Задача становится планиметрической. Не забудьте, что в таких задачах доказываются два взаимно обратных утверждения.
1.47. Данная точка получается в результате пересечения трех разумно выбранных вами биссекторов двугранных углов данного многогранника.
1.68. Обозначьте все отрезки на рисунке. Задачу решает использование теоремы Пифагора и теоремы косинусов.
1.69. В более трудной задаче г) введите дополнительный параметр — ребро основания. Через величину бокового ребра и ребра основания можно выразить величину данного угла. Но
тогда решается и обратная задача — выразить ребро основания через боковое ребро и данный двугранный угол. А найти высоту пирамиды, зная ребро основания и боковое ребро — это задача пункта а).
1.70-1.72. Наиболее трудные из зтих задач решаются с помощью введения дополнительного линейного параметра, как это было указано в задаче 1.69.
1.74. Не больше двух.
1.75. Сведите эту задачу к планиметрической.
1.76. Проведите высоту тетраэдра из точки Р. Она будет высотой во всех треугольниках PXY, являющихся нужными нам сечениями тетраэдра. Поэтому осталось оценить границы для величины XY в треугольнике ABC. Задача стала планиметрической.
1.77. Решая задачу б), обратите внимание на случай, когда все плоские углы при вершине Р — тупые.
1.78. Все такие прямые пересекаются в одной и той же точке. Результат обобщается на случай правильной  -угольной пирамиды, если данные точки — центры окружностей, описанных около ее граней.
-угольной пирамиды, если данные точки — центры окружностей, описанных около ее граней.
1.79. Проведите плоскость через данную точку, перпендикулярную прямой пересечения любых двух данных плоскостей, и докажите, что все проведенные перпендикуляры лежат в этой плоскости.
1.80. Из любых трех.
1.81. Можно.
1.90. Достаточно трех равных и сравнительно (с шестом) длинных тросов.
1.91. Чтобы увеличить площадь куска колбасы.
1.92. Проведите плоскость через эти параллельные прямые и задача станет планиметрической.
1.93. Используйте транзитивность параллельности прямых в пространстве (если  то
то  ).
).
1.94. Поскольку требуется доказать равносильность двух утверждений, постольку надо доказывать два взаимно обратных предложения: 1) если плоскости параллельны, то и перпендикуляры к ним параллельны (или совпадают); 2) если перпендикуляры к двум плоскостям параллельны, то и плоскости параллельны.
1.95. Эти задачи быстро решаются, если через данную прямую удачно провести плоскость, после чего ситуация становится планиметрической.
1.97. Проведите через другую прямую пару плоскостей, соответственно параллельных данным плоскостям. Задача свелась к задаче 1.93.
1.98. Проведите доказательство методом от противного. Для получения противоречия используйте транзитивность параллельности прямых в пространстве.
1.100. Докажите методом от противного. Для получения противоречия используйте задачу 1.93.
1.101. Используйте понятие угла между скрещивающимися прямыми.
1.109. Длины этих отрезков вычисляются после того, как сами отрезки оказываются гипотенузами некоторых прямоугольных треугольников.
1.110. Все расстояния находятся после того, как правильно нарисованы соответствующие перпендикуляры.
1.111-1.112. Для нахождения угла необходимо, чтобы на рисунке появился угол как пара лучей с общей вершиной. В эту пару лучей обычно входит один из данных лучей, тогда другой луч пары сонаправлен с другим из данных лучей. Например, для решения задачи 1.111а проведем из вершины А луч, сонаправленный с лучом СС, — получим луч AAV после чего ответ ясен. Иногда пара лучей имеет вершину в хорошо выбранной точке. Например, в задаче 1.112д такой точкой является точка В.
1.114. В этой задаче прежде всего надо понять, что может быть несколько случаев расположения параллелограмма относительно плоскости. Проще всего, если он весь находится с одной стороны от плоскости. Задача решается благодаря такому соображению: если известны расстояния до плоскости двух концов некоторого отрезка, то легко найти расстояние до нее от середины этого отрезка. В нашей задаче таким отрезком является одна из диагоналей параллелограмма.
1.115. Попробуйте получить результат по аналогии с планиметрией, заменив в условии плоскость на прямую.
1.116. Сначала выполните аналогичную планиметрическую задачу.
1.117. В задачах а) и б) сначала решите задачу в той плоскости, где лежат эти прямые, а затем "выходите в пространство". В задаче в) идите по аналогии с планиметрией. В задаче г) проведите одну плоскость через данную прямую и найдите фигуру в этой плоскости, а затем рассмотрите все множество таких плоскостей.
1.118. а) Треугольник, б) Точка, в — г) Отрезок.
1.119. Полуплоскость.
1.120. Проведите через Р прямую, параллельную AD, и рассмотрите треугольник, частью которого является сечение.
1.121. Ребро призмы и отрезок, соединяющий середины скрещивающихся диагоналей.
1.122. Спроектируйте на плоскость треугольника точки К и L. Сравните между собой радиусы описанной и вписанной окружностей для треугольника.
1.123. Прежде всего эти сечения имеет смысл построить. Они будут треугольниками.
1.124. Здесь могут быть логически разные случаи: в вершине А сходятся: 1) три острых угла ромбов; 2) два острых угла и один тупой; 3) один острый угол и два тупых; 4) три тупых угла. Все случаи можно свести к первому.
1.125. а), в) Нет. б) Да.
1.136. Посмотрите на их расположение.
1.137. Возможны разные ответы.
ГЛАВА 2
2.1. В задаче возможны 2 случая расположения сфер.
2.2. Выразите одну из величин через другую и радиус сферы. Проанализируйте полученные формулы.
2.3. а), б) Сведите к планиметрии, в) Окружность.
2.4. Докажите методом от противного.
2.5. Докажите методом от противного.
2.6. Рассмотрите 3 величины: радиус шара, радиус сечения и расстояние от центра шара до сечения. Установите связь между ними. Проанализируйте полученную формулу.
2.7. Через центр сферы, общую точку окружностей и их центры проведите плоскости. Докажите, что они совпадают.
2.14. Радиус сферы, проведенный в любую точку шестидесятой параллели, составляет с экваториальной плоскостью угол 60°
2.15. а) Центр сферы проектируется в центр окружности, описанной около треугольника, вершинами которого являются данные точки, б) Центр сферы проектируется в центр окружности, вписанной в данный треугольник.
2.16. Спроектируйте данную конфигурацию на плоскость, проходящую через центр шара и перпендикулярную данной прямой. Задача свелась к планиметрической.

2.24. Нарисуйте такое множество точек сначала на плоскости. Полученную фигуру повращайте вокруг данного отрезка.
2.27. Наибольшее значение угла достигается тогда, когда общая прямая касательных плоскостей перпендикулярна данной плоскости. Наименьшее значение угла достигается тогда, когда эта прямая параллельна данной плоскости.
2.28. а) Его центр лежит в плоскости, проведенной через центр данного шара перпендикулярно прямой пересечения данных плоскостей. Наибольшего такого шара нет. б) Посмотрите в угол комнаты.
2.29. Докажите, что для каждой точки первого сечения найдется симметричная (центрально, зеркально) точка во втором сечении. И наоборот (Хотя это и кажется странным).
2.30. а) Возможны два случая, б) Сведите задачу к планиметрической.
2.31. а), б) Можно, в) Нельзя.
2.32. а), б) Можно, в) Нельзя.
2.33. Возможны два случая.

2.54. Для каждого населенного пункта считаются известными его координаты на Земле.
2.55. Используйте равноудаленность точек биссекторной плоскости от граней двугранного угла.
2.56. Возьмите на этом луче точку, удаленную от вершины трехгранного угла на 1. Спроектируйте ее на все ребра трехгранного угла.
2.60. Используйте результат задачи 2.56.
2.61. Главный инструмент для работы здесь  теоремы косинусов и синусов для трехгранного угла. При этом должно быть понятно, что трехгранный угол полностью определяется своими плоскими углами, а потому в нем можно найти все однозначно заданные элементы.
теоремы косинусов и синусов для трехгранного угла. При этом должно быть понятно, что трехгранный угол полностью определяется своими плоскими углами, а потому в нем можно найти все однозначно заданные элементы.
2.62. Так как данная точка равноудалена от двух граней трехгранного угла, то она лежит на биссекторе соответствующего двугранного угла. Далее можно использовать результаты задачи 2.61.
2.63. Из условия следует, что в этом трехгранном угле все плоские углы равны. Далее, раз точка равноудалена от всех граней, то она лежит на луче, образующем равные углы с ребрами трехгранного угла и выходящем из вершины данного угла. Для ответа на вопрос задачи потребуется ввести самим как данные некие линейные и угловые величины, например, расстояние от данной точки до вершины считать равным а, а двугранные углы трехгранного угла положить равными 
2.66. Отложите от его вершины О три равных отрезка ОА, О В и ОС и спроектируйте точку О на плоскость 
2.67. а), б) Проведите через вершину трехгранного угла лучи, перпендикулярные плоскости каждой его грани. Рассмотрите углы между данной прямой и этими лучами и перейдите затем к углам между этой прямой и гранью трехгранного угла.
в) Используйте два раза теорему косинусов (или ее следствие) в двух трехгранных углах: данном и образованном двумя ребрами данного трехгранного угла и лучом данной прямой.
2.68. Задача сводится к сравнению двух углов, которые луч ОХ (О — вершина угла, X — взятая точка) составляет с ребрами и гранями трехгранного угла.

2.70. Для начала у него есть пара равных двугранных углов.
2.71. Из задачи 2.70 следует, что у него равны все двугранные углы.
2.80. а) Рассмотрите осевое сечение цилиндра, б) Рассмотрите диаметральное сечение сферы.
2.81. Рассмотрите диаметральное сечение сферы.
2.82. Рассмотрите осевое сечение такого цилиндра.
2.89. Это сечение является прямоугольником.
2.90. Спроектируйте эту конфигурацию на плоскость основания цилиндра.
2.91. Рассмотрите сечение этой конфигурации плоскостью, проходящей через ось цилиндра.
2.96. а) Когда АВ пересекает ось цилиндра, б) Дальше всего, когда параллелен оси.
2.97. Рассмотрите сечение этой конфигурации плоскостью, проходящей через ось цилиндра.
2.98. Сведите эту задачу к планиметрической.
2.99. Считайте цилиндр бесконечно длинным. Проведите плоскость через центр шара перпендикулярно оси цилиндра.
2.100. а) Рассмотрите множество общих точек прямой пересечения опорной плоскости с плоскостью основания цилиндра и основания цилиндра.
2.101. Рассмотрите плоскость, проходящую через основания обоих цилиндров, и прямую ее пересечения с опорной плоскостью. Сошлитесь на предыдущую задачу.
2.102. Выясните, какие возможны случаи взаимного расположения цилиндров. В каждом из них сведите задачу к планиметрической.
2.103. Поэкспериментируйте на карандашах или ручках.
2.109. Сначала установите, какое он займет положение внутри футляра.
2.110. Бочку катят так, что пол все время касается цилиндрической поверхности. Как перевести бочку в такое положение!
2.111. Сведите эту задачу к планиметрической.
2.112. Сведите эту задачу к планиметрической.
2.113. Найдите точку, равноудаленную от всех вершин.
2.114. Найдите точку, равноудаленную от оснований и боковых граней призмы.
2.115. Для доказательства равенства многоугольников достаточно доказать равенство их соответственных сторон и углов. Обратите внимание на то, что перпендикулярное сечение призмы не обязано принадлежать призме.
2.117. Задачу решает рассмотрение двух прямоугольных треугольников.
2.123. б) Боковое ребро параллельно противоположной грани, в) Расстояние от вершины до противоположного ребра основания, которому эта вершина не принадлежит, находится как высота в треугольнике, вершинами которого являются данная вершина призмы и две вершины другого основания призмы. г) Сводится к в).
2.124. Обратите внимание на то, какова проекция луча  на плоскость ABC. Используйте соотношения в трехгранном угле. Установите форму грани
на плоскость ABC. Используйте соотношения в трехгранном угле. Установите форму грани 
2.125. Определите положение центра этой сферы.
2.127. Везде ответ положительный.
2.129. а) Рассмотрите случаи треугольного и четырехугольного сечений. Не забудьте, что грани призмы являются ее сечениями, б) Кроме боковой грани, в которой лежит диагональ, ее сечениями являются треугольники. Основанием у всех этих треугольников является данная диагональ, поэтому на ребрах призмы надо искать точки наиболее (наименее) удаленные от прямой, на которой лежит данная диагональ, в) Имеется ввиду следующее. Если призма обозначена  и сечение проводится через вершину С, то оно идет параллельно
и сечение проводится через вершину С, то оно идет параллельно  Есть одна тонкость, — в частности, одно из таких сечений проходит через
Есть одна тонкость, — в частности, одно из таких сечений проходит через 
2.130. Такие сечения могуг проходить как через ребро длиной 2, так и через ребро длиной 1.
2.131. "Делают" призму так — от углов квадрата "отрезают" равные квадратные уголки, а затем сгибают оставшуюся часть листа, "скрепляя" между собой стороны уголков.
2.132. Обратите внимание на то, что отрезок, лежащий в грани, можно причислить к тем, которые ей параллельны. Сам этот отрезок можно построить, проведя через одну из переменных точек на диагонали, например  сечение, параллельное грани
сечение, параллельное грани 
2.133. Пусть  — данный параллелепипед,
— данный параллелепипед,  — два данных его сечения. Проведите плоскость
— два данных его сечения. Проведите плоскость  и сведите задачу к планиметрической.
и сведите задачу к планиметрической.
2.134. В задачах а) и в) используйте соотношение между ребрами прямоугольного параллелепипеда и его диагональю; в задачах б) и г) используйте зависимость между косинусами углов, которые диагональ прямоугольного параллелепипеда составляет с его ребрами (возможно и чисто "наглядное" решение).
2.147. Искомые пути ищите на развертках.
2.149. Рассмотрите осевое сечение конуса.
2.150. Рассмотрите осевое сечение конуса.
2.151. Рассмотрите сечение сферы, проходящее через ее центр — для описанного около сферы конуса; рассмотрите осевое сечение конуса — для вписанной сферы.
2.157. Проведя осевое сечение усеченного конуса, сведите задачу к планиметрической.
2.158. Проведя осевое сечение конуса, сведите задачу к планиметрической.
2.159. Примите образующую поверхности конуса равной 1. Пусть данные углы —а и  . Выразите через а и элементы прямоугольного треугольника, один катет которого — высота конуса, а другой — высота из вершины конуса в проведенном сечении. А само сечение выберите таким, чтобы оно пересекало основание конуса по хорде, параллельной диаметру основания конуса, в выбранном осевом сечении.
. Выразите через а и элементы прямоугольного треугольника, один катет которого — высота конуса, а другой — высота из вершины конуса в проведенном сечении. А само сечение выберите таким, чтобы оно пересекало основание конуса по хорде, параллельной диаметру основания конуса, в выбранном осевом сечении.
2.160. Сведите задачу к планиметрической.
2.161. Так как сфера задана (радиусом), то однозначно характеризуют вписанный в нее конус его высота или образующая поверхности (но не радиус основания!). Далее сведите задачу к планиметрической.
2.164. Нет.
2.165. В конусе — нет, в усеченном конусе — да.
2.166. Рассмотрите всевозможные треугольные сечения конуса.
2.167. Рассмотрите конусы двух видов: те у кого в осевом сечении тупоугольный треугольник и прочие.
2.168. Сведите задачу к планиметрии.
2.169. Обратите внимание на то, что конус, о котором говорится в условии задачи, не фиксирован. Поэтому введите еще один параметр этого конуса, который может меняться. Затем сведите задачу к планиметрической.
2.170. Решение аналогично решению задачи 2.100.
2.171. Выберите осевое сечение и сечение, проходящее через две его образующие, такие, чтобы они пересекали основание конуса по параллельным отрезкам. Примите, что образующая конуса равна 1. Выразите через  плоские углы трехгранного угла, вершина которого находится в точке пересечения плоскостей основания конуса и двух проведенных опорных плоскостей. Используйте соотношения в трехгранном угле.
плоские углы трехгранного угла, вершина которого находится в точке пересечения плоскостей основания конуса и двух проведенных опорных плоскостей. Используйте соотношения в трехгранном угле.
2.172. Центры таких шаров лежат в одной плоскости. Рассмотрите сечение данной конфигурации этой плоскостью.
2.173. Три конуса, лежащие на плоскости так, как сказано в условии, образуют "жесткую" конструкцию. Иначе говоря, можно однозначно найти угол в осевом сечении каждого из них. Но тогда однозначно фиксируется углубление между ними. Остается выяснить, войдет ли в него конус с тем же осевым сечением и той же образующей (или высотой, или радиусом основания), что и данные.
2.185. Сведите задачу к планиметрии.
2.186. а) Коническая поверхность, б) Надо понять, что такое "1 оборот конуса". Затем сведите к планиметрии.
2.188. Рассмотрите тетраэдр, одна вершина которого находится в вершине данной пирамиды, другая вершина является центром основания данной правильной пирамиды, а еще две — являются соседними вершинами основания данной правильной пирамиды. Только в задаче е) может понадобиться еще один такой же тетраэдр, соседний с первым.
2.189. В задачах а) и в) центр искомой сферы лежит на высоте пирамиды или ее продолжении. Осталось узнать — где именно. В задаче б) рассмотрите биссекторы трех двугранных углов данного тетраэдра.
2.195. Рассмотрите тетраэдр, о котором уже говорилось в задаче 2.188. Учтите, что мы считаем число  известным, а потому известен угол в основании этого тетраэдра, вершина которого находится в центре основания данной правильной пирамиды.
известным, а потому известен угол в основании этого тетраэдра, вершина которого находится в центре основания данной правильной пирамиды.
В задаче б) можно использовать результаты, полученные для сферы, описанной около конуса. В задаче ж) можно использовать теорему косинусов для трехгранного угла. В задаче з) искомый угол можно найти как угол между перпендикулярами к этим граням, проведенным из центра основания данной правильной пирамиды.
2.196. Рассмотрите данную усеченную пирамиду как часть полной пирамиды. Затем перейдите к рассмотрению тетраэдра, о котором говорилось в задаче 2.188. Используйте подобие.
2.197. а), г) Используйте подобие, в) Такое сечение не обязательно будет треугольником.
2.198. д) Плоскость такого сечения может пересекать пирамиду только по ребру.
2.199. а), в) Установите положение проекции РА на плоскость ABC. б) Воспользуйтесь известной формулой для угла между прямыми, одна из которых лежит на плоскости, а другая ее пересекает, г), д) Воспользуйтесь теоремой косинусов для трехгранного угла.
2.200. а) То же, что в задаче 2.199, б). б)Рассмотрите трехгранный угол с вершиной Р и ребрами PD, РА, PC. в) Найдите угол между AD и перпендикуляром к плоскости DPC, проведенным к ней из вершины В. г), д) Найдите угол между перпендикулярами к этим плоскостям, проведенными из точки В.
2.204. От 1 до 4.
2.205. Эти значения не достигаются.
2.206. Когда оно проходит еще через сторону основания пирамиды или через диагональ этого основания.
2.207. Наименьшее значение диагонали достигается в параллелепипеде, основанием которого является квадрат.
2.208. Возможны два вида сечений  треугольное и четырехугольное.
треугольное и четырехугольное.
2.209. Проведите 2 таких отрезка. Найдите треугольник, в котором они лежат. Затем найдите отношение, в котором два проведенных отрезка делят друг друга. Далее, рассмотрите другие пары отрезков, причем в качестве первого отрезка пары возьмите один и тот же отрезок  тот, который был в первой паре проведенных отрезков.
тот, который был в первой паре проведенных отрезков.
2.210. Да
2.211. Возможны разные формы сечения: четырехугольник, треугольник или ребро основания.
2.256. а) Да. б) Не обязательно.
ГЛАВА 3
3.7. Для фигур вращения достаточно рассмотреть плоские фигуры, от вращения которых получаются данные неплоские фигуры, и, тем самым, свести задачу к планиметрии.
3.8. а) Сфера, б) Шар без сферы.

3.10. а) Не всегда, б) Не всегда, в) Нет.
3.11. а) Да. б) Да. в) Нет.
3.12. а), б), в) Да.

3.14. а) Если не точка, б), г), д), е) Не всегда, в) Да.
3.15. Сначала докажите, что она содержит сторону ВС треугольника ABC (А, В, С — данные точки). Затем возьмите любую точку X треугольника и проведите отрезок, одним концом которого является А, другой конец лежит на ВС и проходит через X.
3.16. Проведите сечение сферы через эти три точки.
3.17. а) Внутренней, б) Данных для однозначного ответа мало.
3.18. Рассмотрите сечение шара диаметральной плоскостью, проходящей через точку X.
3.21. Проведите сечение сферы плоскостью, проходящей через грань многогранника.
3.37. Возможны два вида сечений. Полезно увидеть этот многогранник как часть призмы.
3.38. Рассмотрите развертку этого тетраэдра.
3.40. а) Любое число частей.
3.41. б) Куб, к одной из граней которого пристроена четырехугольная пирамида, основание которой совпадает с гранью. Пирамида достаточно высокая.

3.43. Тот же пример, что и в задаче 3.41, б).
3.44. б) Куб с фиксированной пирамидой, построенной как в задаче 3.41, б), в) "Отрежьте" от куба подходящий уголок.
3.46. Рассмотрите всевозможные развертки.
3.47. Разберитесь, что происходит с любой правильной пирамидой, у которой "срезан" уголок от вершины основания.
3.48. В выпуклом многограннике каждое ребро принадлежит двум и только двум граням.

3.52. Для правильного тетраэдра и гексаэдра (куба) такой точкой является центр описанной сферы. Для октаэдра и икосаэдра существование такой точки доказывается легче, если рассмотреть их вершины на поверхности куба. Для додекаэдра вопрос решается из соображений двойственности.
3.56. а) Используйте тот факт, что  б), в) Используйте параллельность плоскостей АВР и CDQ. г) Используйте параллельность этих плоскостей.
б), в) Используйте параллельность плоскостей АВР и CDQ. г) Используйте параллельность этих плоскостей.
3.59. При каждом положении точки N отрезок NP будет наибольшим, когда Р совпадает с А (или  ). Отрезок MN будет наибольшим, когда N совпадает с В.
). Отрезок MN будет наибольшим, когда N совпадает с В.
3.60. Докажите, что эти 4 точки К, L, М, N лежат в одной плоскости. Установите вид четырехугольника KLNM.
3.61. Ищите такую точку на высоте правильного тетраэдра.
3.75. Сведите задачу к планиметрической.
ГЛАВА 4
4.4. Сначала найдите объем вылившейся воды.
4.6. Смените основание куба.
4.9.-4.10. Рассмотрите сечение данной конфигурации плоскостью, проходящей через ось цилиндра.
4.11. Считайте, что размеры куска картона известны.
4.12. Рассмотрите сечение данной конфигурации плоскостью, проходящей через диаметр полушара и две вершины основания призмы. Можно также достроить данную конфигурацию до призмы, вписанной в шар.
4.13. Углы диагонали с гранями можно заменить углами диагонали с ребрами, перпендикулярными этим граням.
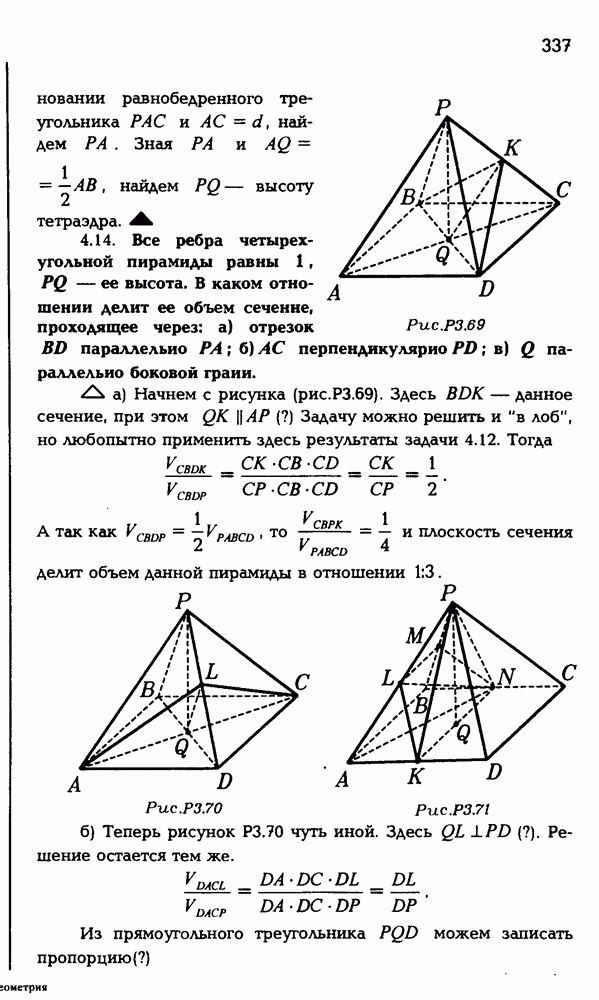
4.14. а), б). Кроме обычного решения, когда переменными считаются ребра призмы, попробуйте решить задачу, когда переменными считаются углы, которые диагональ образует с ребрами.
4.15. Эта призма должна быть вписанной.
4.16. а), б). Возможны различные случаи.
4.17. То же, что и в задаче 4.16.
4.18. Не поленитесь потратить время на хороший рисунок.
4.19. а) Нет. б) Да.
4.35. Докажите, что  где S — площадь основания призмы, Н — ее высота.
где S — площадь основания призмы, Н — ее высота.
4.40. а) Вспомните, куда в таком случае проектируется ребро AAV и затем воспользуйтесь соотношениями в трехгранном угле.
4.41. б) Найдите ту вершину параллелепипеда, в которой сходятся только острые углы ромбов.
4.44. Сделайте хороший планиметрический рисунок фигуры, которая вращается, и установите, какая получается пространственная фигура при вращении каждой стороны нарисованного плоскостью многоугольника.
4.45. д) Используя соотношения в трехгранном угле, найдите угол в боковой грани, прилежащей к ребру основания пирамиды.
4.46. г) Вершина пирамиды проектируется в центр квадрата.
4.47. Можно воспользоваться теоремой о параллельном сечении пирамиды и связать ее с отношением объемов подобных пирамид.
4.48. е) Разбейте тетраэдр на два тетраэдра, проведя сечение через ВС, перпендикулярное РА.
4.49. а) Вершина тетраэдра проектируется в центр окружности, описанной около основания, б) Рассмотрите тетраэдр как часть параллелепипеда, заданного этими ребрами и этими углами.
4.50. Установите, куда проектируется вершина пирамиды.
4.53. в) 1:3. г) 1:1. д) Найдите, в каком отношении сечение делит ребро  .
.
4.57. а) Отношение радиуса к высоте равно -Л.
4.58. а) Такого нет.
4.60. а) Конуса с наименьшим объемом нет. б), в) Конуса с наибольшим объемом нет.
4.61. Рассмотрите сечение пирамиды плоскостью, проходящей через боковое ребро и высоту пирамиды.
4.62. Задача сводится к планиметрической, ибо высота у конуса и тетраэдра одна и та же.
4.64. Проверьте, в каждую ли из этих пирамид можно вписать шар. Если да, то ищите его радиус по формуле  — радиус шара, V и S — объем и площадь поверхности пирамиды). Если нет, то ищите наибольший шар среди шаров, касающихся основания и двух противоположных граней.
— радиус шара, V и S — объем и площадь поверхности пирамиды). Если нет, то ищите наибольший шар среди шаров, касающихся основания и двух противоположных граней.
4.65. Окружность верхнего основания цилиндра касается каждой боковой грани в точке, лежащей на апофеме пирамиды. Рассмотрите сечение данной конфигурации плоскостью, проходящей через апофемы противоположных граней.
4.66. Рассмотрите осевое сечение конуса.
4.67. а) Параллелепипед необходим прямоугольный, б), в) Высоты этих пирамид лежат на диаметре шара. Рассмотрите сечение, проходящее через высоту и боковое ребро, г) Ось призмы лежит на диаметре шара, д), е) Оси этих тел лежат на диаметре шара. Рассмотрите осевые сечения.
4.68. Этот многогранник является тетраэдром.
4.69. Объем каждого из них составляет 0,25 объема всего тетраэдра.
4.70. Разбейте многогранник на пирамиды с вершиной во взятой точке, основаниями которых являются грани многогранника. Дальше работайте с объемами.
4.71. Примите за основание пирамиды ту грань, которая содержит угол  . Далее используйте соотношения в трехгранном угле. Учтите, что угол а может быть трех разных видов.
. Далее используйте соотношения в трехгранном угле. Учтите, что угол а может быть трех разных видов.
4.72. Многоугольники, полученные на гранях, могут быть разного вида.
4.73. а) Проведите плоскость через АВ, перпендикулярную 
4.118. Рассмотрите ее как разность площадей боковых поверхностей двух конусов.
4.123. Используйте формулу для вычисления площади боковой поверхности, в которой есть периметр перпендикулярного сечения.
4.124. Попытайтесь использовать в подходящем случае формулу  , где S — площадь боковой поверхности,
, где S — площадь боковой поверхности,  — площадь основания,
— площадь основания,  — угол между плоскостью боковой грани и плоскостью основания.
— угол между плоскостью боковой грани и плоскостью основания.
4.131. Используйте (по возможности) формулу  где R — искомый радиус, V и S — объем и площадь поверхности многогранника, описанного около данного шара.
где R — искомый радиус, V и S — объем и площадь поверхности многогранника, описанного около данного шара.
4.137. Поверхности с наибольшей площадью нет.
4.138. Наибольших нет.
4.139. а), в) Наибольшей нет. б), г) Наименьшего нет.
4.142. Наибольших нет.
4.144. Указание то же, что и к задаче 4.124.
4.145. Из площади сферы вычитаются площади четырех сферических сегментов.
4.146. Возможны два положения такого конуса.
ГЛАВА 5

Для у и z выражения аналогичные.
5.6. Применить формулу для расстояния между точками.
5.7. Найти длины сторон  и воспользоваться теоремой косинусов.
и воспользоваться теоремой косинусов.
5.8. а) Найти расстояние до точки  б), в), г) Спроектировать эти точки на координатные оси и плоскости и найти расстояние от них до этих проекций.
б), в), г) Спроектировать эти точки на координатные оси и плоскости и найти расстояние от них до этих проекций.
5.10. б), в) Воспользоваться результатами задачи 5.1.
5.13. Выясните, как расположен отрезок KL относительно плоскости ABC, и сведите задачу к планиметрической, спроектировав KL на эту плоскость.
5.14. а) Воспользуйтесь задачей 5.1 а. б) Следует задать четыре вершины, не лежащие на одной грани. Рассмотрите различные случаи.
5.15. Сначала найти координаты вершины  решив систему уравнений
решив систему уравнений  , а затем найти точку
, а затем найти точку  решив систему
решив систему 
5.18. Рассуждайте по аналогии с решением задачи 5.3 (из задач с решениями). При  нет решений, при
нет решений, при  — единственное, при
— единственное, при  — бесконечное множество.
— бесконечное множество.
5.25. г) Найти координаты центра  решив систему уравнений
решив систему уравнений  Найдите сначала центр этой сферы, используя касание сферы и плоскости
Найдите сначала центр этой сферы, используя касание сферы и плоскости  Центры этих сфер имеют координаты
Центры этих сфер имеют координаты 
Нарисуйте систему координат и данную сферу и вы увидите решение,  Проведите плоскость
Проведите плоскость  и сведите задачу к планиметрической.
и сведите задачу к планиметрической.
5.30. б) Радиус сферы равен 1; в) Три сферы, радиусами 3, 4, 5. г) Спроектируйте центр на координатные оси. Сферы должны проходить через эти проекции.
5.32. а)-в) Центром сферы может быть любая точка, равноудаленная от заданных точек. В случаях а), б) эти точки образуют
плоскость, в случае в) — прямую, в случае г) — такой сферы нет.
5.33. Введите координаты, выбрав за начало одну из вершин куба и направив оси по ребрам куба. Сделайте рисунок и ответьте на последний вопрос без вычислений.
5.34. Сделайте рисунок.
5.38. Сначала ищем точку В на прямой MN, используя условие,  а затем ищем точку С на прямой
а затем ищем точку С на прямой  используя условие
используя условие 
5.39. Вычислить площадь основания призмы, найти ее высоту и отложить от точки  вектор, перпендикулярный основанию призмы и равный по модулю ее высоте. Два решения.
вектор, перпендикулярный основанию призмы и равный по модулю ее высоте. Два решения.
5.51. Введите систему координат с началом в точке D и осями 
5.52. а) Нет. б) Нет. в) Да.
5.53. Шар с центром О и радиусом 2.
5.54. Аналогичную фигуру.
5.55. Вспомните неравенство треугольника.
5.58. а) 
5.66. а)  б, в) Найдите зависимость между углами, которые образует вектор с координатными плоскостями и осями координат; г)
б, в) Найдите зависимость между углами, которые образует вектор с координатными плоскостями и осями координат; г)  coscp 3).
coscp 3).
5.72. Выразите радиус-векторы этих точек, идущие из точки D, через векторы  и сравните эти выражения с разложением вектора DB, по этим же векторам.
и сравните эти выражения с разложением вектора DB, по этим же векторам.
5.78. Введите координаты с началом А и осями АВ, АС, AD.
5.84. Сделайте рисунок,  . Выразите векторы ВК и LM через векторы DA,
. Выразите векторы ВК и LM через векторы DA, 
5.85. а-д) Непосредственно по определению, е, ж) Разложите векторы  и
и  по тройке векторов, идущих по ребрам куба из его вершины.
по тройке векторов, идущих по ребрам куба из его вершины.
5.86. Разложите векторы по тройке ребер куба, идущих из одной вершины.
5.87. Получите равенство  возведите его в скалярный квадрат и воспользуйтесь результатами задачи 5.9 из задач с решениями.
возведите его в скалярный квадрат и воспользуйтесь результатами задачи 5.9 из задач с решениями.
5.88. Разложите вектор диагонали по векторам ребер и возведите в скалярный квадрат.
5.89. Выразите векторы этих отрезков через векторы ребер куба и возведите в скалярный квадрат.
5.90. Выразите вектор XY через РА, РВ, PC и примените скалярное умножение.
5.91. Решите систему 
5.104. В уравнении  две из переменных положить равными нулю и найти третью координату.
две из переменных положить равными нулю и найти третью координату.
5.105. Если векторы нормалей этих плоскостей неколлинеарны, то плоскости пересекаются.
5.106-5.107. Определить вектор нормали и воспользоваться результатами 
5.108. Угол между плоскостями равен углу между их нормалями.
5.109. Полупространство.
5.111. Отдельно рассмотрите случаи, когда равен нулю свободный член уравнения и когда обращается в нуль один из коэффициентов при переменных 
5.112. а) Не могут, б) Могут в тех случаях, когда эта плоскость координатная.  в плоскости
в плоскости  в плоскости
в плоскости  в плоскости
в плоскости 
ГЛАВА 6
6.6. Пусть Р — исходный многогранник, Q — его образ, F — их пересечение, G — их объединение. Следует найти объем того из многогранников F и G, который находится проще, а объем второго из них находится из соотношения:

6.7. Вычисляются объемы и площади поверхности следующих тел: а) цилиндра, б) тела, состоящего из двух конусов и цилиндра между ними; в) двух конусов; г) усеченного конуса, из которого удален усеченный конус.
6.8. Может.
6.11. Сведите задачу к планиметрической.
6.12. Попробуйте построить опровергающие примеры.
6.14. Катет, вокруг которого вращается треугольник, равен 
6.15. Если основание равно 
6.16. Да, можно.
6.18. а) Да. б) Да. в) Да. г) Нет. д) Нет. е) Нет. ж) Да. з) Да. и) Да. к) Нет.  Нет. м) Нет. н) Нет.
Нет. м) Нет. н) Нет.
6.19. Могут совпадать все четыре, например, у куба.
6.37. Сделайте хороший чертеж и попробуйте в каждом случае перенос, который сблизит рассматриваемые объекты. Но можно применить и векторы.
6.38. Постройте сечение, проходящее через точку К, а затем осуществите его перенос на вектор КА. И сразу увидите, что площадь сечения равна — 
6.40. Осуществите перенос одного конуса на вектор, идущий из центра его основания в центр основания другого конуса, и вы увидите, что не всегда найдутся такие сечения.
6.41. В первом случае не верно, а во втором — верно.
6.42. а) Всегда, б) Если соответствующей симметрией обладают пары их оснований, в) Если соответствующей симметрией обладают их основание и вершины.
6.43. Любыми, если ось поворота проходит через центр шара.
6.44. Соответствующая осевая симметрия в пространстве и будет таким поворотом.
6.45. Постройте опровергающий пример.
6.46. В отношении  .
.
6.50. Произведите поворот в пространстве вокруг биссектрисы на 180.
6.51. Да, можно.
6.52. Будет.
6.53. Будет. Обратное неверно.
6.54. Не всегда.
6.55. Поищите опровергающий пример.
6.56. Вспомните о правильных пирамидах.
6.61. а) Да. б) Нет. в) Нет. г) Да. д) Да. е) Нет. ж) Нет.
6.62. а) Нет. б) Да. в) Да. г) Да. д) Нет. е) Да. ж) Нет.
6.63. Во всех случаях поворотом и зеркальным поворотом, который может оказаться зеркальной или центральной симметриями.
6.64. а) Поворотом, переносом, центральной симметрией, б), ж) Винтом и зеркальным поворотом, в), е), и) Поворотом и зеркальной симметрией, г) Осевой симметрией и зеркальным поворотом, д) Осевой и зеркальной симметриями, з) Поворотом и зеркальным поворотом, к) Поворотом и зеркальной симметрией. При симметриях обе фигуры переходят друг в друга.
6.65. Для всех случаев имеются поворот и зеркальный поворот, совмещающие фигуры. Поворот иногда сводится к осевой симметрии  , а зеркальный поворот — к зеркальной симметрии
, а зеркальный поворот — к зеркальной симметрии  . Симметрии совмещают друг с другом обе фигуры.
. Симметрии совмещают друг с другом обе фигуры.
6.67. а) Если РА ВС, то двумя зеркальными симметриями и осевой симметрией, которая является их композицией, б) К движениям, указанным в п. а), добавляется зеркальный поворот, самосовмещающий квадратное сечение тетраэдра РАВС. в) Такой тетраэдр был рассмотрен при решении задачи 6.14 из задач с решениями (рис. Р 3.101). Он имеет три оси симметрии.
6.68. Если шары не равны, то поворотами вокруг линии центров и зеркальными симметриями. Если шары равны, то добавляется еще центральная симметрия.
6.69. Выясните, каким четырехугольником является основание пирамиды.

6.78. а, б) Возможны все случаи взаимного расположения прямых, в) Совпадают, параллельны или пересекаются.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
- 1.5. Взаимное расположение двух прямых в пространстве.
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
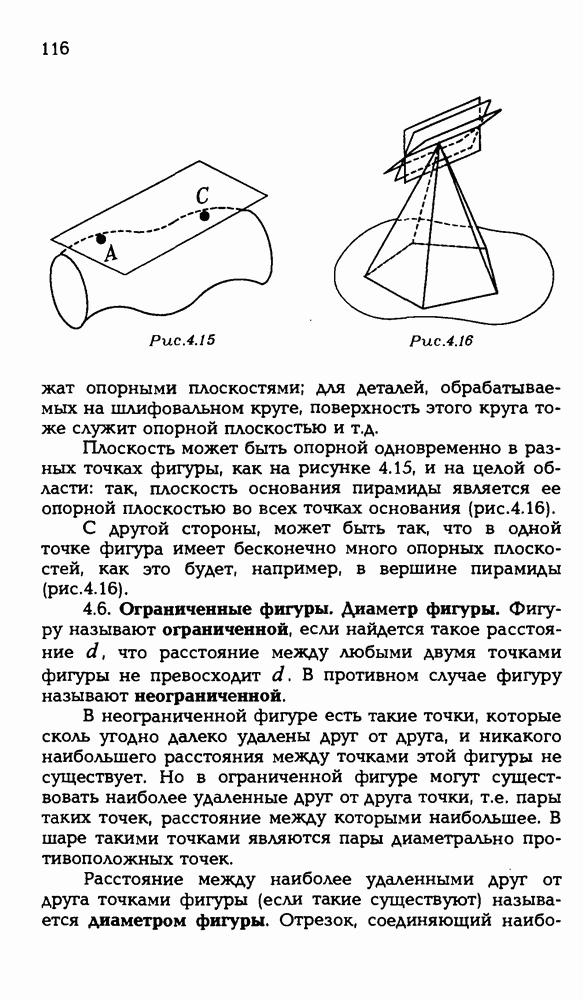
- 4.5. Опорная плоскость.
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
- § 6. ЦИЛИНДР
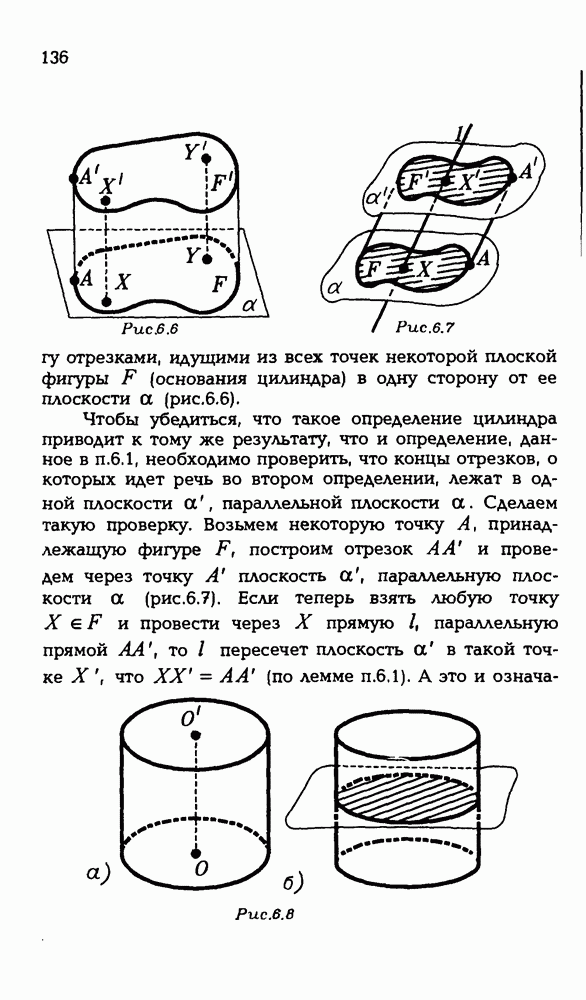
- 6.2. Другой подход к определению цилиндра.
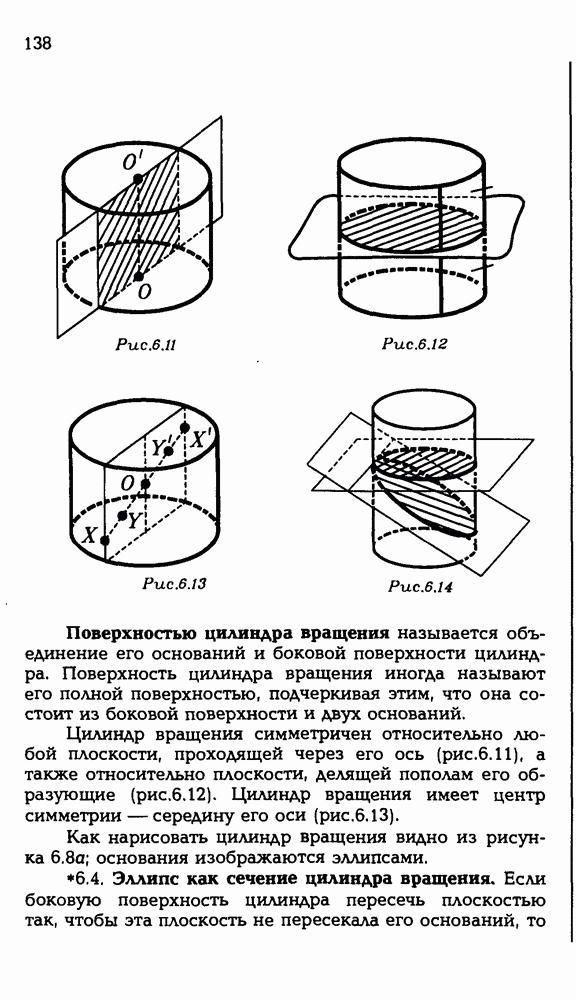
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
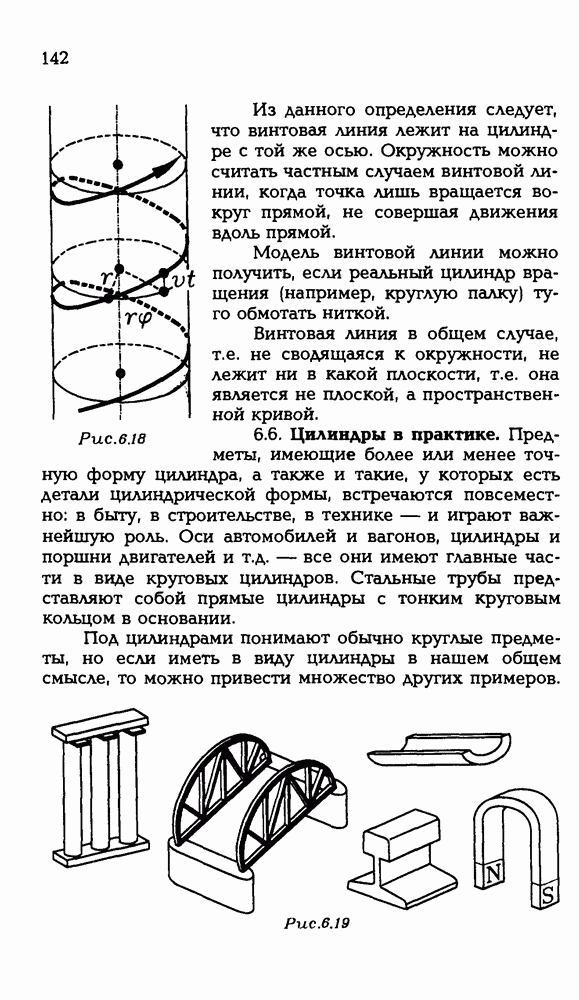
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
- 7.4. Симметрия параллелепипеда.
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
- § 8. КОНУС
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
- 8.4. Усеченный конус.
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
- 11.6. Развертка выпуклого многогранника.
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ