| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАДАЧИ К §4
Дополняем теорию
2.1. Две сферы имеют единственную общую точку. Установите зависимость между их радиусами и расстоянием между их центрами.
2.2. Докажите, что в одном и том же шаре: а) равные хорды равноудалены от центра (и обратно): б) чем больше хорда, тем ближе она к центру (и обратно); в) чем больше хорда, тем больше угол, под которым она видна из центра (и обратно).
2.3. Из одной точки сферы выходят равные хорды, а) Докажите, что они образуют равные углы с диаметром, выходящим из той же точки, б) Проверьте обратное утверждение, в) Какую фигуру образуют концы этих хорд, не совпадающие с данной точкой?
2.4. В шаре с центром О провели сечение с центром А. Докажите, что прямая ОА перпендикулярна плоскости сечения.
2.5. Докажите, что центр шара лежит на: а) прямой, перпендикулярной любому его круговому сечению и проходящей через его центр; б) прямой, проходящей через центры двух его круговых сечений, лежащих в параллельных плоскостях.
2.6. Докажите, что в одном и том же шаре: а) равные сечения равноудалены от центра (и обратно); б) чем больше сечение, тем ближе оно к центру (и обратно).
2.7. На сфере проведены две окружности, имеющие единственную общую точку. Докажите, что центр сферы, центры обеих окружностей и общая точка лежат в одной плоскости.
Рисуем
2.8. Нарисуйте шар. Нарисуйте шар, центрально-симметричный данному относительно: а) точки, лежащей вне шара;
б) точки, лежащей на его сфере; в) середины радиуса. Нарисуйте пересечение этих двух шаров (если оно не пусто).
2.9. Нарисуйте шар. Нарисуйте шар, зеркально-симметричный данному относительно плоскости: а) не пересекающей шар; б) касательной к шару; в) пересекающей шар. Нарисуйте пересечение этих двух шаров (если оно не пусто).
2.10. Нарисуйте шар. Нарисуйте его хорду, не лежащую в его экваториальной плоскости, а затем нарисуйте хорду: а) симметричную данной относительно центра шара; б) симметричную данной относительно экваториальной плоскости;
в) симметричную данной относительно плоскости большого круга, причем этот большой круг пересекает данную хорду.
2.11. Нарисуйте фигуру, которая получается в результате вращения круга вокруг прямой, проходящей: а) мимо него;
б) через точку на его окружности; в) внутри него, но не через центр.
2.12. Нарисуйте фигуру, которая получается в результате вращения кругового сегмента вокруг прямой, проходящей: а) через его хорду; б) параллельно его хорде; в) перпендикулярно его хорде; г) пересекающей его хорду в ее конце.
2.13. Нарисуйте фигуру, которая получается в результате вращения кругового сектора вокруг прямой, проходящей:
а) через его крайний радиус; б) через его средний радиус;
в) перпендикулярно его среднему радиусу и через центр круга;
г) через центр круга и в его плоскости.
Планируем
2.14. Как найти длину шестидесятой параллели на Земле?
2.15. а) На сфере данного радиуса даны три точки. Расстояния между этими точками известны. Как найти расстояние от центра сферы до плоскости, проходящей через эти точки?
б) Каждая сторона треугольника с данными сторонами имеет с шаром единственную общую точку. Как найти расстояние от центра сферы до плоскости треугольника?
2.16. Через одну прямую проведены к шару две касательные плоскости. Известен радиус шара и расстояние между точками касания шара с этими плоскостями. Как найти угол между этими плоскостями? Как найти расстояние от шара до общей прямой этих плоскостей?
Представляем
2.17. В пространстве зафиксирована точка. Какая фигура образована всеми точками такими, что: 
2.18. Рассмотрим на сфере фиксированную сетку меридианов и параллелей, а) Сколько меридианов проходит через данную точку сферы? б) Сколько параллелей проходит через данную точку сферы? в) Сколько общих точек имеют два меридиана? г) Через каждую ли точку на сфере проходит меридиан? Параллель? д) Как расположены плоскости: двух меридианов; двух параллелей; меридиана и параллели? е) Может ли длина параллели равняться длине меридиана? Быть больше длины меридиана? ж) Для каждой ли параллели есть параллель с той же длиной? с меньшей длиной?
2.19. На сколько частей разбивают сферу» а) две окружности, расположенные на ней; б) три окружности, расположенные на ней; в) плоскости граней тетраэдра, находящегося внутри
нее; г) плоскости граней треугольной призмы, находящейся внутри нее?
2.20. Сколько равных сечений шара можно провести через; а) данную точку шара; б) данную хорду шара?
2.21. На сфере дана точка. Сколько можно провести через нее: а) больших окружностей; б) окружностей данного радиуса, лежащих на сфере? Решите те же задачи, если будут даны две точки на сфере.
2.22. Шар касается плоскости. Эта фигура проектируется на плоскость, проходящую через радиус шара, проведенный в точку касания. Как выглядит проекция?
2.23. Две плоскости касаются шара. Эта фигура проектируется на плоскость, проходящую через радиусы, проведенные в точки касания. Как выглядит эта проекция, если две данные плоскости: а) параллельны; б) пересекаются?
2.24. Какой фигурой является множество точек пространства, из которых данный отрезок виден под данным углом?
2.25. Два шара имеют общую часть, отличную от точки. Является ли она: а) центрально-симметричной; б) зеркально симметричной? Обладает ли такими свойствами объединение таких шаров?
2.26. Какие элементы симметрии имеет: а) полушар; б) четверть шара; в) шаровой сегмент (часть шара между секущей его плоскостью и сферой); г) шаровой пояс (часть шара между двумя пересекающими его параллельными плоскостями); д) часть шара, отсеченная от него двумя перпендикулярными плоскостями, не проходящими через его центр?
Оцениваем
2.27. Шар лежит на плоскости. К нему проведены две касательные плоскости, образующие между собой данный угол и составляющие с данной плоскостью равные углы. В каком положении эти равные углы имеют наибольшее значение? А наименьшее?
2.28. а) Данный шар касается двух перпендикулярных плоскостей. Как расположен наименьший шар, касающийся данного шара и данных плоскостей? А наибольший? б) Решите аналогичную задачу, если плоскостей три.
Сделаем
2.29. Докажите, что два равных и параллельных сечения одного и того же шара: а) центрально-симметричны; б) зеркально симметричны.
Исследуем
2.30. В шаре данного радиуса провели два сечения данных радиусов, а) Как найти расстояние между ними, если эти сечения параллельны? б) Как найти расстояние от центра до их общего отрезка, если они пересекаются?
2.31. Шар пересекает две перпендикулярные плоскости. Известны радиусы получающихся при этом кругов. Можно ли найти радиус шара, если известные круги: а) имеют единственную общую точку; б) имеют общую хорду данной длины; в) находятся на известном расстоянии между собой?
2.32. В шаре радиусом R провели два сечения радиусом  , плоскости которых пересекаются под углом
, плоскости которых пересекаются под углом  Можно ли установить связь между
Можно ли установить связь между  если эти сечения: а) имеют единственную общую точку; б) имеют общую хорду данной длины; в) находятся на известном расстоянии между собой?
если эти сечения: а) имеют единственную общую точку; б) имеют общую хорду данной длины; в) находятся на известном расстоянии между собой?
2.33. На сфере, радиус которой равен 2, расположены три окружности радиуса 1, каждая из которых касается трех других. Как найти радиус окружности, которая расположена на этой сфере и касается каждой из данных окружностей?
Поступаем в ВУЗ
2.34. В шаре проведен диаметр АВ и две равные хорды AM и AN, каждая под углом а к диаметру. Найдите угол между хордами, если отрезок MN виден из центра шара под углом 
Ответ: 
2.35. Отрезок АВ единичной длины, являющийся хордой сферы радиуса 1, расположен под углом — к диаметру  этой сферы. Расстояние от конца С диаметра до ближайшего к нему конца А хорды равно
этой сферы. Расстояние от конца С диаметра до ближайшего к нему конца А хорды равно  Определите величину отрезка
Определите величину отрезка 
Ответ: 1.
2.36. Отрезки  концы которых лежат на сфере радиуса 10, попарно перпендикулярны и пересекаются в точке М. Длина отрезка АА, равна 12, длина отрезка
концы которых лежат на сфере радиуса 10, попарно перпендикулярны и пересекаются в точке М. Длина отрезка АА, равна 12, длина отрезка  равна 18. Найдите расстояние от центра сферы до точки М, если известно, что отношение длины отрезка СМ к длине отрезка
равна 18. Найдите расстояние от центра сферы до точки М, если известно, что отношение длины отрезка СМ к длине отрезка  равно
равно 
Ответ: 
2.37. Три хорды шара, исходящие из одной его точки на его поверхности, равны А, углы между хордами равны 60°. Найдите радиус шара.
Ответ: 
2.38. В шаре радиуса R хорда АВ равна R. Пусть точки С и D лежат на поверхности шара и угол АС В прямой, а угол ADB равен  Найдите угол между плоскостями АС В и
Найдите угол между плоскостями АС В и 
Ответ:  .
.
2.39. Через касательную к шару радиуса R проведены две плоскости под углом  друг к другу. Найдите радиусы сечений шара этими плоскостями, если известно, что они относятся как
друг к другу. Найдите радиусы сечений шара этими плоскостями, если известно, что они относятся как 
Ответ: радиус большего сечения равен 
2.40. Три параллельные прямые касаются в точках А, В и С сферы радиуса 4 с центром в точке О. Найдите угол ВАС, если известно, что площадь треугольника ОВС равна 4, а площадь треугольника ABC больше 16.
Ответ:  .
.
2.41. В плоскости Р дан равнобедренный треугольник ABC такой, что  . Шар радиуса
. Шар радиуса  касается плоскости Р в точке В. Две скрещивающиеся прямые проходят через точки А и С и касаются шара. Угол между каждой из этих прямых и плоскостью Р равен а . Найдите расстояние между этими прямыми.
касается плоскости Р в точке В. Две скрещивающиеся прямые проходят через точки А и С и касаются шара. Угол между каждой из этих прямых и плоскостью Р равен а . Найдите расстояние между этими прямыми.
Ответ: 
2.42. Основанием тетраэдра ABCD является треугольник  в котором
в котором  Длины ребер
Длины ребер  равны между собой. Сфера радиуса 1 касается ребер
равны между собой. Сфера радиуса 1 касается ребер
AD, BD, продолжения ребра CD за точку D и плоскости ABC. Найдите величину отрезка касательной, проведенной из точки А к сфере.
Ответ:  .
.
2.43. Отрезок PQ параллелен плоскости, в которой лежит прямоугольник KLMN, причем  Все стороны прямоугольника KLMN и отрезки КР, LP, NQ, MQ, PQ касаются некоторого шара. Найдите радиус этого шара.
Все стороны прямоугольника KLMN и отрезки КР, LP, NQ, MQ, PQ касаются некоторого шара. Найдите радиус этого шара.
Ответ: 
2.44. Сфера касается ребер AS, BS, ВС и АС тетраэдра SABC в точках К, L, М и N соответственно. Найдите длину отрезка KL, если 
Ответ: 9.
2.45. Две касающиеся сферы вписаны в двугранный угол величиной  . Пусть А — точка касания первой сферы с первой гранью, В — точка касания второй сферы со второй гранью. Найдите отношение
. Пусть А — точка касания первой сферы с первой гранью, В — точка касания второй сферы со второй гранью. Найдите отношение  если К и L — точки пересечения отрезка АВ с первой и второй сферами соответственно.
если К и L — точки пересечения отрезка АВ с первой и второй сферами соответственно.
Ответ: 
2.46. Два равных шара касаются друг друга и граней двугранного угла  . Пусть А — точка касания одного шара с одной гранью угла,
. Пусть А — точка касания одного шара с одной гранью угла,  точка касания другого шара с другой гранью угла. В каком отношении отрезок В делится сферами?
точка касания другого шара с другой гранью угла. В каком отношении отрезок В делится сферами?
Ответ: 
2.47. Три шара попарно касаются друг друга и некоторой плоскости. Точки касания шаров с плоскостью образуют прямоугольный треугольник с катетом, равным 3, и противоположным углом  Определите радиусы данных шаров.
Определите радиусы данных шаров.
Ответ: 
2.48. Три шара касаются плоскости треугольника со сторонами а, b и с в его вершинах и попарно касаются друг друга. Найдите радиусы шаров.
Ответ: 
2.49. Шар радиуса R и окружность радиуса  имеют общий центр О. Точка А расположена так, что
имеют общий центр О. Точка А расположена так, что  и множество точек данной окружности, которые можно соединить с А прямой, не пересекающейся с шаром, есть дуга, соответствующая центральному углу а. Найдите угол между ОА и плоскостью, содержащей данную окружность.
и множество точек данной окружности, которые можно соединить с А прямой, не пересекающейся с шаром, есть дуга, соответствующая центральному углу а. Найдите угол между ОА и плоскостью, содержащей данную окружность.
Ответ: 
Переключаемся
2.50. Муравей ползет по сфере. Сначала он прополз по меридиану вниз, затем по параллели направо, затем по меридиану вверх. Длина каждого участка пути одна и та же. Может ли он оказаться там, где он был с самого начала?
2.51. Можно ли циркулем постоянного раствора проводить окружности разных радиусов?
2.52. Придумайте свой способ вычисления радиуса реального шара.
2.53. Маленькие шарики чуть отличаются между собой по диаметру. Предложите устройство для их быстрой сортировки по размерам.
2.54. Как измерить расстояние по земле между двумя населенными пунктами, если они находятся на: а) одном меридиане; б) одной параллели?
ЗАДАЧИ К § 5
Дополняем теорию
2.55. Докажите, что три биссекторные плоскости трехгранного угла пересекаются по одной прямой.
2.56. В трехгранном угле все углы при вершине — прямые. Из его вершины выходит луч. Пусть  — углы, которые он составляет с ребрами трехгранного угла. Докажите, что
— углы, которые он составляет с ребрами трехгранного угла. Докажите, что 
Рисуем
2.57. Нарисуйте невыпуклый трехгранный угол.
2.58. Нарисуйте трехгранный угол. Нарисуйте трехгранный угол, центрально-симметричный данному относительно: а) вершины; б) точки внутри его ребра; в) точки внутри его
грани; г) точки внутри него. В случае г) нарисуйте пересечение и объединение исходного и полученного углов.
2.59. Нарисуйте трехгранный угол. Нарисуйте трехгранный угол, зеркально-симметричный данному относительно плоскости его грани.
Планируем
2.60. В трехгранном угле все плоские углы прямые. Известны два угла, которые составляет с двумя его ребрами луч, выходящий из вершины угла и проходящий внутри него. Как найти угол между этим лучом и третьим ребром?
2.61. Пусть известны три плоских угла трехгранного утла. Как вычислить: а) угол между его ребром и плоскостью противоположной грани; б) расстояние от некоторой точки ребра до плоскости противоположной грани; в) угол между ребром и лучом в противоположной грани, выходящим из вершины трехгранного угла; г) угол между ребром и лучом, выходящим из вершины трехгранного угла, если известно, какие углы он составляет с другими ребрами этого утла?
2.62. Каждый угол трехгранного угла равен  . Внутри угла расположена точка, удаленная от двух граней на расстояние а, а от третьей — на расстояние 2а Как найти расстояние от зтой точки до вершины угла?
. Внутри угла расположена точка, удаленная от двух граней на расстояние а, а от третьей — на расстояние 2а Как найти расстояние от зтой точки до вершины угла?
2.63. Пусть все двугранные углы трехгранного угла равны. Некоторая точка, лежащая внутри него, удалена от его вершины на данное расстояние и равноудалена от всех граней. Как найти расстояние от нее до его граней?
Представляем
2.64. Сколько трехгранных углов образуется при попарном пересечении трех плоскостей, имеющих общую точку?
2.65. Укажите элементы симметрии трехгранного угла, в котором: а) все плоские углы прямые; б) все плоские углы равны между собой; в) два плоских угла равны.
Оцениваем
2.66. Докажите, что сумма плоских углов выпуклого трехгранного утла меньше  .
.
Сделаем
2.67. Плоские углы трехгранного угла равны. Через его вершину проведена прямая, составляющая равные углы с его ребрами, а) Докажите, что она составляет равные углы с его гранями, б) Проверьте утверждение, обратное а). Пусть плоский угол трехгранного угла равен  . Найдите углы, которые эта прямая составляет с ребрами и гранями трехгранного угла.
. Найдите углы, которые эта прямая составляет с ребрами и гранями трехгранного угла.
2.68. В трехгранном угле, плоские углы которого равны, находится точка, равноудаленная от его граней. Докажите, что она равноудалена от его ребер. Докажите обратное.
Исследуем
2.69. Верно ли, что каждый двугранный угол трехгранного угла меньше суммы двух его других двугранных углов?
2.70. Какими свойствами обладает трехгранный угол, в котором два плоских угла равны?
2.71. Какими свойствами обладает трехгранный угол, в котором три плоских угла равны?
Поступаем в ВУЗ
2.72. Трехгранный угол образован тремя плоскостями а,  Две плоскости
Две плоскости  перпендикулярны плоскости
перпендикулярны плоскости  между собой они образуют угол
между собой они образуют угол  . Сфера S касается плоскости
. Сфера S касается плоскости  и пересекает плоскости
и пересекает плоскости  по окружностям радиуса R. Расстояние центра сферы от вершины трехгранного угла равно 1. Определите радиус сферы
по окружностям радиуса R. Расстояние центра сферы от вершины трехгранного угла равно 1. Определите радиус сферы 
Ответ: 
2.73. Один из двугранных углов трехгранного угла равен А; прилежащие к данному двугранному углу плоские углы равны а и  Найдите третий плоский угол.
Найдите третий плоский угол.
Ответ: 
2.74. В трехгранном угле каждый из плоских углов при вершине равен а. Как удалена от его вершины точка, которая находится внутри угла на расстоянии а от каждой грани?
Ответ: 
2.75. Все плоские углы трехгранного угла SPQR (S — вершина) — прямые. На грани PQS взята точка А на расстоянии 12 от ребра QS и на расстоянии 5 от ребра  Из некоторой точки Т, расположенной внутри трехгранного угла SPQR, в точку А направлен луч света. Он образует угол
Из некоторой точки Т, расположенной внутри трехгранного угла SPQR, в точку А направлен луч света. Он образует угол  с ребром
с ребром  и угол
и угол  с ребром
с ребром  Луч зеркально отражается от граней угла SPQR сначала в точке А, затем в точке В, затем в точке С. Найдите длину отрезка ВС.
Луч зеркально отражается от граней угла SPQR сначала в точке А, затем в точке В, затем в точке С. Найдите длину отрезка ВС.
Ответ: 14.
2.76. У трехгранного угла  угол между гранями ОАВ и ОВС прямой, а величина каждого
угол между гранями ОАВ и ОВС прямой, а величина каждого  остальных двугранных углов равна
остальных двугранных углов равна  Найдите величину плоского угла А ОС.
Найдите величину плоского угла А ОС.
Ответ: 
2.77. Дан трехгранный угол с вершиной О, у которого величина каждого из плоских углов равна  . Плоскость а пересекает ребра этого трехгранного угла в точках А, В, С, причем
. Плоскость а пересекает ребра этого трехгранного угла в точках А, В, С, причем  а отрезок ОС короче отрезка ОА. Известно, что величина двугранного угла между плоскостью а и гранью ОАВ равна Р. Два шара расположены по разные стороны от плоскости так, что каждый шар касается всех граней трехгранного угла и плоскости а. Найдите: а) величину угла между прямой, проходящей через центры шаров, и плоскостью грани ОАВ; б) отношение радиусов указанных шаров.
а отрезок ОС короче отрезка ОА. Известно, что величина двугранного угла между плоскостью а и гранью ОАВ равна Р. Два шара расположены по разные стороны от плоскости так, что каждый шар касается всех граней трехгранного угла и плоскости а. Найдите: а) величину угла между прямой, проходящей через центры шаров, и плоскостью грани ОАВ; б) отношение радиусов указанных шаров.
Ответ: 
2.78. Каждый из двугранных углов трехгранного угла равен а. Как удалена от его вершины точка, которая находится внутри угла на расстоянии а от каждого ребра?
Ответ:  .
.
ЗАДАЧИ К § 6
Дополняем теорию
2.79. Докажите, что сечение цилиндра плоскостью, параллельной его оси и проходящей через внутреннюю точку его основания, является прямоугольником.
2.80. Докажите, что: а) около цилиндра можно описать сферу; б) в сферу можно вписать цилиндр.
2.81. Докажите, что около сферы можно описать цилиндр.
2.82. Докажите, что в цилиндр можно вписать сферу, если образующая цилиндра равна диаметру его основания.
Рисуем
2.83. Нарисуйте цилиндр. Нарисуйте его сечение: а) проходящее через ось; б) параллельное оси; в) перпендикулярное оси; г) какого-либо другого вида.
2.84. Нарисуйте цилиндр. Нарисуйте плоскость, опорную к нему и проходящую через: а) образующую; б) основание; в) как-нибудь иначе.
2.85. Нарисуйте множество точек: а) удаленных от данной прямой на данное расстояние; б) удаленных от данного отрезка на данное расстояние; в) удаленных от каждой из двух параллельных прямых на одно и то же расстояние.
2.86. Нарисуйте фигуру, которая получается в результате вращения прямоугольника вокруг прямой, проходящей: а) через его сторону; б) через его среднюю линию; в) мимо него и параллельно его стороне.
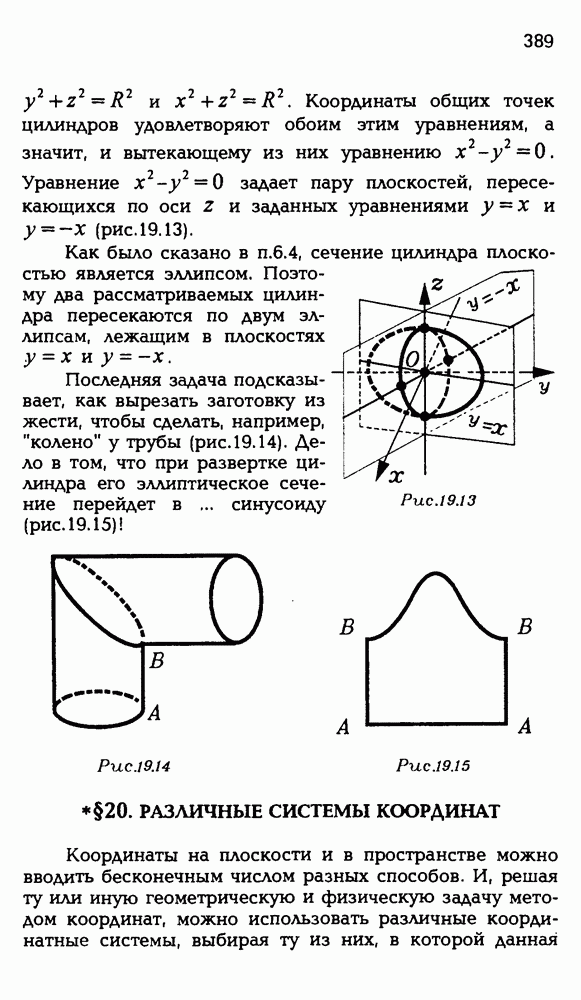
2.87. Нарисуйте фигуру, получающуюся при пересечении двух равных, тонких и достаточно длинных цилиндров, оси которых пересекаются под прямым углом.
2.88. а) В сферу вписан цилиндр. Нарисуйте осевое сечение зтой фигуры, б) Около сферы описан цилиндр. Нарисуйте осевое сечение этой фигуры.
Планируем
2.89. В цилиндре с радиусом основания R и высотой Н проводится сечеиие на расстоянии х от оси цилиндра. Как выразить его площадь как функцию от х?
2.90. Две пересекающиеся плоскости, опорные к цилиндру радиуса R, проходят через его образующие. Как иайти расстояние от прямой пересечения этих плоскостей до цилиндра?
2.91. В данную сферу вписан цилиндр с известными размерами. Как найти расстояние от центра сферы до поверхности цилиндра?
Представляем
2.92. Какие элементы симметрии есть у цилиндра?
2.93. На какое наибольшее число частей можно разрезать цилиндр плоскими разрезами, если разрезов: а) 2; б) 3; в) 4?
2.94. Как плоским разрезом разбить цилиндр на две равные части?
2.95. Какой фигурой является проекция цилиндра на плоскость: а) параллельную его оси; б) перпендикулярную его оси; в) пересекающую его ось?
Оцениваем
2.96. Точка А находится на окружности одного из оснований цилиндра, а точка В — на окружности другого основания, а) При каком положении прямая АВ составляет с плоскостью основания наименьший угол? б) В каком положении отрезок АВ ближе всего к оси цилиндра? А дальше всего?
2.97. В шаре радиусом R находится цилиндр с наибольшим по площади осевым сечением. Как он расположен?
2.98. Рассмотрим всевозможные цилиндры с диагональю осевого сечения 1. Каковы наибольший из шаров, содержащих такой цилиндр, и наименьший?
2.99. Цилиндр радиуса R касается плоскости по некоторой образующей и, не пересекаясь с ним, этой же плоскости касается шар радиуса  . Расстояние от оси цилиндра до центра шара равно а В каком положении находится минимально возможный шар, который касался бы одновременно цилиндра, плоскости и заданного шара?
. Расстояние от оси цилиндра до центра шара равно а В каком положении находится минимально возможный шар, который касался бы одновременно цилиндра, плоскости и заданного шара?
Сделаем
2.100. Пусть плоскость, опорная к цилиндру, проходит через образующую его поверхности. Докажите, что она: а) проходит через прямую, опорную к его основанию; б) перпендикулярна плоскости осевого сечения цилиндра, проходящего через эту образующую.
2.101. Два цилиндра имеют единственную общую образующую на поверхности каждого из них. Через эту образующую проведена плоскость, опорная к одному из цилиндров. Докажите, что она будет опорной и к другому из них.
Исследуем
2.102. Два равных цилиндра, размеры которых известны, лежат на данной плоскости (то есть каждый из них имеет с ней общее основание или общую образующую на поверхности). Цилиндры имеют единственную общую точку. Можете ли Вы найти расстояние между осями этих цилиндров?
2.103. Сможете ли Вы расположить пять равных цилиндров так, чтобы каждый имел единственную общую точку с каждым из остальных? А шесть таких же цилиндров?
Поступаем в ВУЗ
2.104. В цилиндре высота равна диаметру основания. Под углом а к плоскости основания проведена прямая, соединяющая некоторую точку окружности нижнего основания с некоторой точкой окружности верхнего основания. Найдите расстояние между зтой прямой и осью цилиндра, если радиус основания равен 
Ответ: 
2.105. Сторона основания ABC правильной призмы  равна 1, а каждое из боковых ребер имеет длину
равна 1, а каждое из боковых ребер имеет длину  . Цилиндр расположен так, что точка А. и середина М ребра СС, лежат на его боковой поверхности, а ось цилиндра параллельна прямой
. Цилиндр расположен так, что точка А. и середина М ребра СС, лежат на его боковой поверхности, а ось цилиндра параллельна прямой  и отстоит от нее на расстоянии 0,25. Определите радиус цилиндра.
и отстоит от нее на расстоянии 0,25. Определите радиус цилиндра.
Ответ: 
2.106. Внутри цилиндра, высота которого равна  , лежат три равных шара радиуса
, лежат три равных шара радиуса  так, что каждый шар касается двух других шаров и боковой поверхности цилиндра, причем два шара касаются нижнего основания цилиндра, а третий шар касается верхнего основания цилиндра. Найдите радиус основания цилиндра.
так, что каждый шар касается двух других шаров и боковой поверхности цилиндра, причем два шара касаются нижнего основания цилиндра, а третий шар касается верхнего основания цилиндра. Найдите радиус основания цилиндра.
Ответ: 
2.107. На плоскость положены два цилиндра, радиусы которых  цилиндры примыкают друг к другу по образующей. На них положены два других касающихся по образующей цилиндра с радиусами R и осями, перпендикулярными осям первых двух цилиндров. Найдите радиус шара, касающегося всех четырех цилиндров.
цилиндры примыкают друг к другу по образующей. На них положены два других касающихся по образующей цилиндра с радиусами R и осями, перпендикулярными осям первых двух цилиндров. Найдите радиус шара, касающегося всех четырех цилиндров.
Ответ: 
2.108. На плоскости лежат два шара с радиусами  и цилиндр с радиусом
и цилиндр с радиусом  Шары касаются друг друга и боковой поверхности цилиндра. Цилиндр касается плоскости по своей образующей. Найдите радиус шара, большего, чем данные, касающегося обоих данных шаров, цилиндра и плоскости.
Шары касаются друг друга и боковой поверхности цилиндра. Цилиндр касается плоскости по своей образующей. Найдите радиус шара, большего, чем данные, касающегося обоих данных шаров, цилиндра и плоскости.
Ответ: 
Переключаемся
2.109. Как найти длину самого длинного предмета, который уместится в цилиндрическом футляре?
2.110. Для вычисления площади поверхности испарения горючего в цилиндрических цистернах, расположенных горизонтально, в справочниках предлагается использовать такую формулу:  , где d — диаметр основания цистерны,
, где d — диаметр основания цистерны,  — ее длина. Всегда ли целесообразно применять эту формулу?
— ее длина. Всегда ли целесообразно применять эту формулу?
2.111. Два шарика от настольного тенниса укладывают в цилиндрический футляр. При каком условии это возможно?
2.112. Внутри полого цилиндра должна вращаться прямоугольная рамка. Ось вращения перпендикулярна оси цилиндра и проходит через его середину. При каком условии это возможно?
ЗАДАЧИ К § 7
Дополняем теорию
2.113. Докажите, что можно описать сферу около: а) правильной призмы; б) прямоугольного параллелепипеда.
2.114. Докажите, что в прямую призму можно вписать сферу, если ее высота равна диаметру окружности, вписанной в ее основание.
2.115. Докажите, что перпендикулярные сечения призмы равны между собой. (Перпендикулярное сечение призмы — это многоугольник, который получается при пересечении призмы или ее продолжения плоскостью, перпендикулярной ее образующей).
2.116. Докажите, что в прямой призме: а) плоскости боковых граней перпендикулярны основанию; б) высота равна боковому ребру; в) ее перпендикулярное сечение равно основанию.
2.117. Докажите, что квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Рисуем
2.118. Нарисуйте правильную треугольную призму и: а) плоскость ее симметрии, параллельную основанию; б) другие плоскости симметрии; в) ось поворотной симметрии,
2.119. Нарисуйте параллелепипед» имеющий: а) одну плоскость симметрии; б) две плоскости симметрии; в) три плоскости симметрии; г) одну ось поворотной симметрии; д) две оси поворотной симметрии; е) три оси поворотной симметрии. Решите аналогичную задачу для треугольной призмы.
2.120. 1) В треугольной призме  вершина
вершина  проектируется в центр треугольника ABC и все ее ребра равны. Нарисуйте: а) высоты этой призмы из вершин Си
проектируется в центр треугольника ABC и все ее ребра равны. Нарисуйте: а) высоты этой призмы из вершин Си  перпендикулярное сечение этой призмы, проходящее через точку
перпендикулярное сечение этой призмы, проходящее через точку  проекцию вершины
проекцию вершины  на плоскость грани
на плоскость грани  ;
;
г) проекции верхней грани и всей призмы на плоскость 
д) проекцию верхнего основания на плоскость ВХВС .
2) Сделайте аналогичные рисунки в треугольной призме  у которой в основании находится равносторонний треугольник, грань
у которой в основании находится равносторонний треугольник, грань  является квадратом, а две другие в точках А и С имеют острые углы.
является квадратом, а две другие в точках А и С имеют острые углы.
2.121. В параллелепипеде  все грани ромбы.
все грани ромбы.
Острые углы этих ромбов, равные  сходятся в вершине А. Нарисуйте: а) высоты этого параллелепипеда из вершии
сходятся в вершине А. Нарисуйте: а) высоты этого параллелепипеда из вершии  и С; б) перпендикулярные сечения, проходящие через точки
и С; б) перпендикулярные сечения, проходящие через точки  ; в) проекции верхнего основания и всего параллелепипеда на плоскость
; в) проекции верхнего основания и всего параллелепипеда на плоскость  .
.
2.122. Нарисуйте прямоугольный параллелепипед. Нарисуйте ему симметричный относительно диагональной плоскости. Нарисуйте объединение исходного и полученного параллелепипедов.
Планируем
2.123. В правильной треугольной призме ребро основания равно 1, а боковое ребро равио 2. Как вычислить: а) расстояние между боковыми ребрами; б) расстояние между боковым ребром и плоскостью противоположной грани; в) расстояние от вершины одного из оснований до ребра в другом основании, которое не лежит с этой вершиной в одной грани; г) площадь сечения, проходящего через ребро основания и вершину другого основания, не лежащую с этим ребром в одной грани?
2.124. В треугольной призме  все ребра равны и
все ребра равны и  Как вычислить угол между: а) боковым ребром и основанием; б) прямой
Как вычислить угол между: а) боковым ребром и основанием; б) прямой  и плоскостью
и плоскостью  боковыми гранями и основанием; г) боковыми гранями; д) боковым ребром и скрещивающимся ребром основания?
боковыми гранями и основанием; г) боковыми гранями; д) боковым ребром и скрещивающимся ребром основания?
2.125. Как найти радиус сферы, описанной около: а) куба с ребром 1; б) прямоугольного параллелепипеда с ребрами а, b, с; в) правильной треугольной призмы с ребром 1?
Представляем
2.126. а) У призмы 10 вершин. Сколько у нее ребер и граней? б) У призмы 12 ребер. Сколько у нее вершин и граней? в) У призмы 13 граней. Сколько у нее вершин и ребер?
2.127. Можно ли одной плоскостью разбить правильную треугольную призму на: а) две правильные треугольные призмы; б) две треугольные призмы, среди которых нет правильных; в) треугольную и четырехугольную призму; г) две равные призмы; д) два многогранника, не являющиеся призмами?
2.128. Как одним плоским разрезом разбить прямоугольный параллелепипед на: а) два прямоугольных параллелепипеда; б) две прямых треугольных призмы; в) две четырехугольных призмы, не являющихся параллелепипедами; г) два равных прямоугольных параллелепипеда?
Оцениваем
2.129. В правильной треугольной призме с ребром 1 проводится сечение через: а) ребро основания; б) диагональ боковой грани; в) вершину основания параллельно противоположному ребру. В каждом случае установите, в каком положении площадь такого сечения достигает граничных значений.
2.130. Высота прямой призмы равна 2, в ее основании — прямоугольник со сторонами 1 и 2. Через ребро основания проведено сечение. В каком положении оно имеет наибольшую площадь?
2.131. Из квадратного листа со стороной 1 делают правильную четырехугольную призму без одного из оснований. Какая из таких призм имеет наибольшую диагональ?
2.132. В правильной треугольной призме  все ребра имеют длину а Рассматриваются отрезки с концами на диагоналях
все ребра имеют длину а Рассматриваются отрезки с концами на диагоналях  параллельные плоскости
параллельные плоскости  . Какой из них имеет наименьшую длину?
. Какой из них имеет наименьшую длину?
Сделаем
2.133. В параллелепипеде проведены параллельные сечения, каждое из которых проходит через три его вершины, не лежащие в одной грани. Докажите, что они делят пересекающую их диагональ параллелепипеда на три равные части.
Исследуем
2.134. Существует ли такой прямоугольный параллелепипед, в котором: а) диагональ в два раза длиннее самого длинного ребра; б) диагональ составляет с ребрами, выходящими из
той же вершины три заданных угла; в) диагональ в два раза длиннее самой длинной диагонали грани; г) диагональ составляет с диагоналями граней, выходящими из той же вершины, три заданных угла?
Поступаем в ВУЗ
2.135. Сторона основания правильной треугольной призмы  равна а, точки О и О, являются центрами оснований
равна а, точки О и О, являются центрами оснований  соответственно. Длина ортогональной проекции отрезка
соответственно. Длина ортогональной проекции отрезка  на прямую
на прямую  равна
равна  . Определите высоту призмы.
. Определите высоту призмы.
Ответ: 
2.136. В основании прямой треугольной призмы  лежит правильный треугольник ABC со стороной
лежит правильный треугольник ABC со стороной  боковые ребра имеют длину
боковые ребра имеют длину  Пусть К — точка пересечения диагоналей ВСХ и
Пусть К — точка пересечения диагоналей ВСХ и  боковой грани
боковой грани  Сфера, центр которой принадлежит призме, касается граней
Сфера, центр которой принадлежит призме, касается граней  и прямой
и прямой  Найдите радиус сферы.
Найдите радиус сферы.
Ответ: 0,75.
2.137. В основании прямой треугольной призмы  лежит правильный треугольник ABC со стороной 4. Прямые
лежит правильный треугольник ABC со стороной 4. Прямые  и САХ перпендикулярны. Найдите высоту призмы.
и САХ перпендикулярны. Найдите высоту призмы.
Ответ: 
2.138. На диагоналях  и
и  боковых граней треугольной призмы
боковых граней треугольной призмы  расположены соответственно точки D и Е так, что
расположены соответственно точки D и Е так, что  . Определите отношение DE к ВС.
. Определите отношение DE к ВС.
Ответ: 
2.139. Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда наклонены к плоскости основания под углами  . Найдите угол между этими диагоналями.
. Найдите угол между этими диагоналями.
Ответ:  .
.
2.140. Одна из вершин верхнего прямоугольного основания наклонного параллелепипеда проектируется ортогонально в центр его нижнего основания. Сечение, проведенное через эту вершину и параллельные диагонали оснований, имеет площадь два раза большую площади основания. Острый угол при вершине сечения равен  . Найдите отношение сторон основания.
. Найдите отношение сторон основания.
Ответ: 
прямоугольный параллелепипед  в основании которого лежит квадрат со стороной 3, боковые ребра имеют длину 5. Равносторонний треугольник расположен так, что одна его вершина находится в точке С , а две другие расположены на прямых
в основании которого лежит квадрат со стороной 3, боковые ребра имеют длину 5. Равносторонний треугольник расположен так, что одна его вершина находится в точке С , а две другие расположены на прямых  и
и  соответственно. Найдите длину медианы этого треугольника.
соответственно. Найдите длину медианы этого треугольника.
Ответ: 
2.142. Основанием ABCD прямой призмы  служит ромб со стороной а и острым углом
служит ромб со стороной а и острым углом  а высота призмы равна И. Найти расстояние от вершины
а высота призмы равна И. Найти расстояние от вершины  до диагонали
до диагонали 
Ответ: 
2.143. В параллелепипеде все грани — равные ромбы с острыми углами а. Найдите отношение площадей диагональных сечений параллелепипеда.
Ответ: 
2.144. Основанием призмы является квадрат со стороной длины а, а боковые ребра наклонены к плоскости основания под углом а, причем проекция одного из них содержит диагональ квадрата. Из вершины квадрата, для которой проходящее через нее ребро и диагональ квадрата образуют острый угол, параллельно другой диагонали проведена секущая плоскость под углом Р к плоскости основания. Найдите площадь сечения в предположении, что сечение не пересекает верхнее основание.
Ответ: 
2.145. Докажите, что если все диагонали параллелепипеда равны, то он прямоугольный.
2.146. На диагоналях АВ, и ВС, граней параллелепипеда  взяты точки М и N так, что отрезки MN и
взяты точки М и N так, что отрезки MN и  параллельны. Найдите отношение длин этих отрезков.
параллельны. Найдите отношение длин этих отрезков.
Ответ: 
Переключаемся
2.147. 1) Из центра одного основания правильной треугольной призмы в центр другого основания ползет жук. Каков его кратчайший путь по поверхности призмы?
2) Решите аналогичную задачу для правильной четырехугольной призмы.
2.148. Можете ли вы вычислить длину диагонали спичечного коробка, ничего на нем не измеряя?
ЗАДАЧИ К § 8
Дополняем теорию
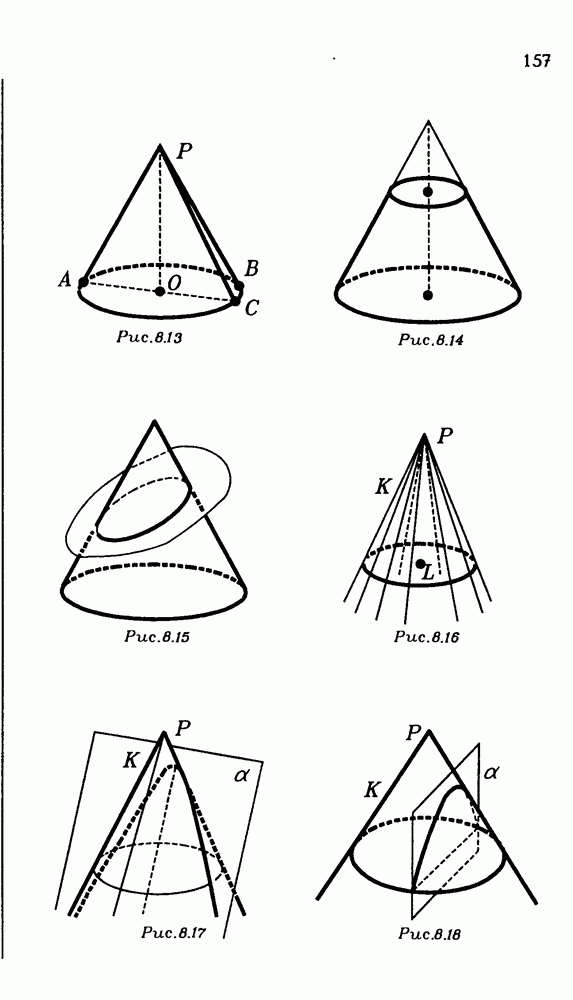
2.149. В конусе радиусом R и высотой Н проводится сечение, параллельное основанию. Выразите как функцию от  площадь этого сечения, где
площадь этого сечения, где  — расстояние от вершины конуса до этого сечения.
— расстояние от вершины конуса до этого сечения.
2.150. Говорят, что конус вписан в сферу (а сфера описана около конуса), если его вершина и окружность основания лежат на сфере. Докажите, что около конуса можно описать сферу.
2.151. Говорят, что конус описан около сферы (а сфера вписана в конус), если есть такая сфера, которая лежит в конусе, касается основания, а с боковой поверхностью конуса имеет общую окружность. Докажите, что около сферы можно описать конус, а в конус можно вписать сферу.
Рисуем
2.151. Нарисуйте опорную плоскость к конусу, проходящую через: а) его образующую; б) его основание; в) ровно одну точку основания; г) вершину.
2.153. Нарисуйте конус. Нарисуйте конус: а) центрально симметричный данному относительно вершины; б) зеркально симметричный данному относительно плоскости основания; в) зеркально симметричный данному относительно плоскости,
параллельной основанию и пересекающей его ось. Нарисуйте объединение исходного и полученного конусов.
2.154. Равносторонний треугольник вращается вокруг: а) высоты; б) стороны; в) прямой, параллельной высоте и проходящей через вершину. Нарисуйте получившуюся фигуру вращения.
2.155. Квадрат вращается вокруг: а) диагонали; б) прямой, параллельной диагонали и проходящей через вершину. Нарисуйте получившуюся фигуру вращения.
2.156. Ромб вращается вокруг: а) стороны; б) прямой, перпендикулярной стороне и проходящей через вершину ромба. Нарисуйте получившуюся фигуру вращения.
Планируем
2.157. Пусть  — радиусы оснований усеченного конуса, L — его образующая. Как найти его высоту?
— радиусы оснований усеченного конуса, L — его образующая. Как найти его высоту?
2.158. В конусе радиусом R и высотой Н провели два сечения, параллельные основанию. Их площади S и s. Как найти расстояние между этими сечениями?
2.159. Через вершину конуса проведено сечение. Пусть известен угол в осевом сечении конуса при его вершине и угол между образующими конуса, принадлежащими этому сечению. Как найти угол, который данное сечение составляет с плоскостью основания?
2.160. Как найти радиус шара, вписанного в конус?
2.161. В данную сферу вписан конус, размеры которого известны.
Представляем
2.162. Как проходит в конусе его сечение, являющееся: а) кругом; б) треугольником; в) какой-нибудь другой фигурой?
2.163. На сколько частей можно разделить конус: а) двумя плоскостями; б) тремя плоскостями?
2.164. В каждом ли конусе существует сечение, параллельное основанию, площадь которого равна площади осевого сечения?
2.165. Может ли в конусе находиться отрезок, более длинный, чем диаметр основания и образующая? А в усеченном конусе?
Оцениваем
2.166. В каком положении образующие конуса образуют между собой наибольший угол?
2.167. Дан конус. Какое положение имеет то его сечение, проходящее через вершину, которое имеет наибольшую площадь?
2.168. Дан шар. а) Как расположен такой вписанный в него конус, который имеет наибольшее по площади осевое сечение? А наименьшее  Решите аналогичную задачу про конус, описанный около данного шара.
Решите аналогичную задачу про конус, описанный около данного шара.
2.169. Образующая поверхности конуса равна 1. Как расположен: а) наибольший описанный около него шар; б) наименьший описанный около него шар; в) наибольший вписанный в него шар; г) наименьший вписанный в него шар 
Сделаем
2.170. Через образующую конуса проведена плоскость, опорная к нему. Докажите, что она: а) проходит через прямую, опорную к его основанию; б) перпендикулярна осевому сечению конуса, проходящему через ту же образующую.
2.171. Угол при вершине осевого сечения конуса равен а . Угол между двумя его образующими равен (3. Через эти образующие проводятся опорные плоскости к этому конусу. Как найти угол между: а) этими плоскостями; б) прямой пересечения этих плоскостей и плоскостью основания конуса?
2.172. Конус известных размеров стоит основанием на плоскости. Этой плоскости и боковой поверхности данного конуса касаются шары известного радиуса. Кроме того, каждые два соседних шара касаются между собой. Как подсчитать число таких шаров?
Исследуем
2.173. Три равных конуса лежат на плоскости и каждые два имеют общую образующую. Можно ли в образовавшееся углубление вложить такой же конус 
Поступаем в ВУЗ
2.174. В прямом круговом конусе с вершиной S угол между высотой SO и образующей решен  . На плоскости основания вне конуса выбрешы две точки А и В так, что прямые SA и SB взаимно перпендикулярны и образуют с высотой SO углы, соответственно равные а и
. На плоскости основания вне конуса выбрешы две точки А и В так, что прямые SA и SB взаимно перпендикулярны и образуют с высотой SO углы, соответственно равные а и  . Вычислите угол между образующими, по которым боковая поверхность конуса пересекает треугольники OSA и
. Вычислите угол между образующими, по которым боковая поверхность конуса пересекает треугольники OSA и 
Ответ: 
2.175. В прямом круговом конусе с вершиной S угол между образующими SA и SB равен а, а угол между их проекциями на плоскость основания равен  . Вычислите угол между биссектрисами углов OSA и OSB, где точка О является центром круга, служащего основанием конуса.
. Вычислите угол между биссектрисами углов OSA и OSB, где точка О является центром круга, служащего основанием конуса.
Ответ: 
2.176. Радиус основания конуса равен R, а образующая наклонена к плоскости основания под углом а. В этом конусе через его вершину проведена плоскость под углом  . Определите площадь проведенного сечения.
. Определите площадь проведенного сечения.
Ответ: 
2.177. Найдите центральный угол развертки боковой поверхности конуса, если угол при вершине его осевого сечения равен а.
Ответ: 
2.178. В конусе высота равна диаметру основания. Через некоторую образующую конуса проведена плоскость, касательная к боковой поверхности конуса, и в этой плоскости через вершину конуса проведена прямая под углом а к образующей. Найдите угол, который составляет проведенная прямая с плоскостью основания.
Ответ: 
2.179. Дан угол а а осевого сечения конуса с вершиной S и образующей длины 1. Через точку А, взятую на основании конуса, проведена плоскость Р, которая перпендикулярна к образующей SA. Через вершину конуса проведена плоскость  Эта плоскость перпендикулярна плоскости осевого сечения конуса, проходящего через
Эта плоскость перпендикулярна плоскости осевого сечения конуса, проходящего через  и составляет с образующей SA конуса угол
и составляет с образующей SA конуса угол  Плоскость Q рассекает конус по двум образующим. Пусть продолжения этих образующих пересекают плоскость Р в точках С, и
Плоскость Q рассекает конус по двум образующим. Пусть продолжения этих образующих пересекают плоскость Р в точках С, и  Найдите длину отрезка
Найдите длину отрезка 
Ответ: 
2.180. Угол между образующей конуса и его высотой равен а. Найдите угол  между двумя образующими этого конуса, если известно, что плоскости, касающиеся конуса по этим образующим, взаимно перпендикулярны.
между двумя образующими этого конуса, если известно, что плоскости, касающиеся конуса по этим образующим, взаимно перпендикулярны.
Ответ: 
2.181. Два конуса, осевое сечение каждого из которых является равносторонним треугольником со стороной а, лежат на горизонтальной плоскости, касаясь друг друга, имея общую вершину. На какой высоте над плоскостью находится точка касания оснований этих конусов?
Ответ: 
2.182. Три одинаковых конуса, радиусы оснований которых равны  и составляют 0,75 их высоты, расположены по одну сторону от плоскости Р, а их основания лежат в этой плоскости. Окружности оснований каждых двух из этих конусов касаются. Найти радиус шара, лежащего между конусами и касающегося как плоскости Р, так и всех трех конусов.
и составляют 0,75 их высоты, расположены по одну сторону от плоскости Р, а их основания лежат в этой плоскости. Окружности оснований каждых двух из этих конусов касаются. Найти радиус шара, лежащего между конусами и касающегося как плоскости Р, так и всех трех конусов.
Ответ: 
2.183. На плоскости лежат три равных конуса с общей вершиной. Каждый из них касается двух рядом лежащих. Найдите угол при вершине осевого сечения одного из этих конусов.
Ответ: 
2.184. На плоскости уложены  равных конусов, имеющих общую вершину в точке, лежащей на этой плоскости. Каждый конус касается двух других конусов. Найдите угол при вершине в осевом сечении конуса.
равных конусов, имеющих общую вершину в точке, лежащей на этой плоскости. Каждый конус касается двух других конусов. Найдите угол при вершине в осевом сечении конуса.
Ответ: 
Переключаемся
2.185. Как найти длину самого длинного предмета, который можно уместить в футляре, имеющем форму: а) конуса; б) усеченного конуса?
2.186. Закрепив вершину, конус покатили по плоскости, а) Какая получается фигура от движения оси? б) Пусть размеры
конуса известны. Как вычислить путь, который проделает центр основания конуса за один оборот конуса?
2.187. Вот цитата из Пушкина: "Читал я где-то, Что царь однажды воинам своим Велел снести земли по горсти в кучу, И гордый холм возвысился — и царь Мог с вышины с весельем озирать И дол, покрытый белыми шатрами, И море, где бежали корабли." Могло ли такое быть на самом деле?
ЗАДАЧИ К § 9
Дополняем теорию
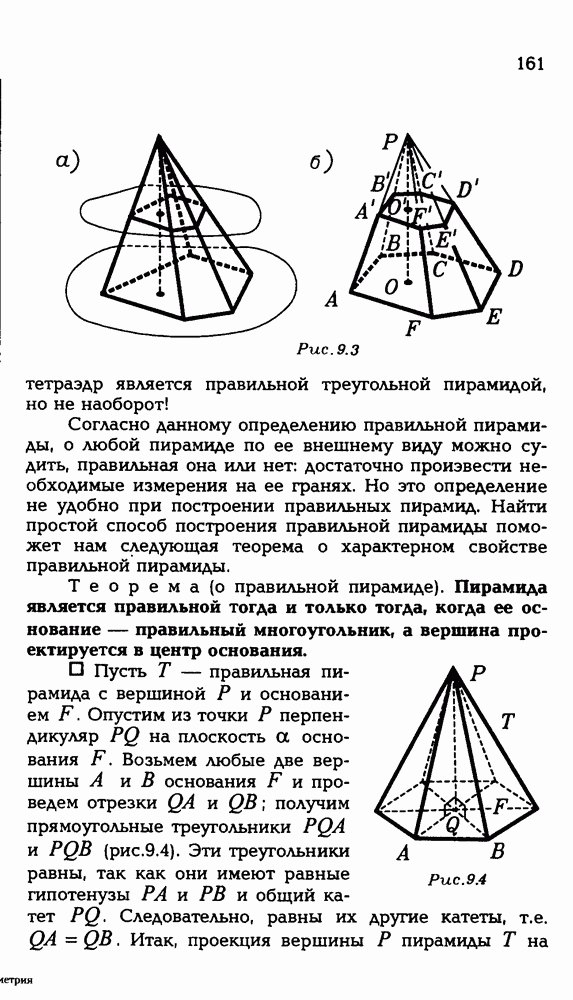
2.188. Докажите, что в правильной пирамиде: а) проекция высоты на боковую грань лежит на высоте грани (апофеме пирамиды); б) проекция высоты на ребро основания — середина этого ребра; в) каждая точка высоты равноудалена от боковых ребер, вершин основания, ребер основания, боковых граней; г) угол между боковым ребром и плоскостью основания один и тот же для всех ребер пирамиды; д) угол между боковой гранью и плоскостью основания для всех боковых граней один и тот же; е) все углы между соседними боковыми гранями равны.
2.189. Докажите, что: а) около правильной пирамиды можно описать сферу; б) около тетраэдра можно описать сферу; в) в правильную пирамиду можно вписать сферу.
Рисуем
2.190. Нарисуйте проекцию правильной треугольной пирамиды на плоскость: а) основания; б) проходящую через боковое ребро и апофему; в) боковой грани.
2.191. Нарисуйте проекцию правильной четырехугольной пирамиды на плоскость: а) основания; б) проходящую через апофемы, лежащие в противоположных гранях; в) боковой грани; г) проходящую через два противоположных боковых ребра.
2.192. Нарисуйте правильную усеченную пирамиду: а) треугольную; б) четырехугольную.
2.193. Нарисуйте правильную треугольную пирамиду. Нарисуйте затем пирамиду: а) центрально симметричную данной относительно середины ее высоты; б) зеркально симметричную данной относительно плоскости, параллельной основанию и проходящей через середину высоты; в) полученную в результате поворота вокруг высоты на угол 60. В каждом случае нарисуйте объединение исходной и полученной пирамиды.
2.194. Нарисуйте правильную четырехугольную пирамиду. Нарисуйте затем пирамиду: а) центрально симметричную данной относительно середины ее высоты; б) зеркально симметричную
данной относительно плоскости, параллельной основанию и проходящей через середину высоты; в) полученную в результате поворота вокруг высоты на угол  . В каждом случае нарисуйте объединение исходной и полученной пирамиды.
. В каждом случае нарисуйте объединение исходной и полученной пирамиды.
Планируем
2.195. В правильной  -угольной пирамиде известны сторона основания и плоский угол при вершине. Как найти: а) высоту пирамиды; б) радиус описанной сферы; в) радиус вписанной сферы; г) угол между боковым ребром и плоскостью основания; д) угол между апофемой и плоскостью основания; е) угол между боковой гранью и основанием; ж) угол между соседними боковыми гранями; з) угол между гранями, идущими через одну?
-угольной пирамиде известны сторона основания и плоский угол при вершине. Как найти: а) высоту пирамиды; б) радиус описанной сферы; в) радиус вписанной сферы; г) угол между боковым ребром и плоскостью основания; д) угол между апофемой и плоскостью основания; е) угол между боковой гранью и основанием; ж) угол между соседними боковыми гранями; з) угол между гранями, идущими через одну?
2.196. В правильной « -угольной усеченной пирамиде известны стороны оснований и боковое ребро. Как вычислить высоту пирамиды?
-угольной усеченной пирамиде известны стороны оснований и боковое ребро. Как вычислить высоту пирамиды?
2.197. В правильной треугольной пирамиде известны сторона основания и высота. Как вычислить площадь сечения, проходящего: а) параллельно основанию через середину высоты; б) через боковое ребро и высоту; в) через сторону основания перпендикулярно боковому ребру; г) через центр основания параллельно боковой грани; д) через середины четырех ребер?
2.198. В правильной четырехугольной пирамиде известны сторона основания и высота. Как вычислить площадь сечения, проходящего через: а) середину бокового ребра параллельно основанию; б) диагональ основания перпендикулярно боковому ребру; в) диагональ основания параллельно боковому ребру; г) центр основания параллельно боковой грани; д) ребро основания перпендикулярно боковой грани?
2.199. В тетраэдре РАВС основанием является правильный треугольник.  , другие боковые грани составляют с основанием угол
, другие боковые грани составляют с основанием угол  Как вычислить угол между а) прямыми РА и ВС, б) прямыми РВ и
Как вычислить угол между а) прямыми РА и ВС, б) прямыми РВ и  прямой РА и плоскостью ABC, г) плоскостями РАВ и РАС; д) плоскостями РАС и PBCi
прямой РА и плоскостью ABC, г) плоскостями РАВ и РАС; д) плоскостями РАС и PBCi
2.200. Основанием пирамиды PABCD является квадрат ABCD. РВ  Как вычислить угол между: а) прямыми PD и
Как вычислить угол между: а) прямыми PD и  прямой PD и плоскостью АРС; в) прямой AD и плоскостью DPC; г) плоскостями РАВ и PCD; д) плоскостями PAD и
прямой PD и плоскостью АРС; в) прямой AD и плоскостью DPC; г) плоскостями РАВ и PCD; д) плоскостями PAD и 
Представляем
2.201. Как разрезать тетраэдр на: а) два тетраэдра; б) усеченную пирамиду и пирамиду; в) треугольную пирамиду и четырехугольную пирамиду; г) два многогранника, не являющихся пирамидами; д) призму и две пирамиды?
2.202. Как разрезать четырехугольную пирамиду на: а) два тетраэдра; б) две четырехугольные пирамиды; в) пирамиду и усеченную пирамиду; г) четырехугольную пирамиду и многогранник, не являющийся пирамидой; д) два многогранника, не являющихся пирамидами?
2.203. Какие элементы симметрии можно найти в правильной усеченной пирамиде?
2.204. Основанием пирамиды является квадрат. Сколько ее граней могут быть прямоугольными треугольниками?
Оцениваем
2.205. В какой правильной треугольной пирамиде достигает граничных значений двугранный угол между соседними боковыми гранями? Обобщите полученный результат.
2.206. В основании пирамиды лежит прямоугольник. Все ее боковые грани — прямоугольные треугольники. Через ее наибольшее ребро проводится переменное сечение. Когда его площадь достигает граничных значений?
2.207. В правильную четырехугольную пирамиду со стороной основания и высотой, равными 1, вписан прямоугольный параллелепипед, основание которого расположено в плоскости основания пирамиды, а вершины противоположной грани — на боковой поверхности пирамиды. Площадь основания параллелепипеда равна  . В каком положении диагональ параллепипеда имеет наименьшее значение? А наибольшее?
. В каком положении диагональ параллепипеда имеет наименьшее значение? А наибольшее?
2.208. Сторона основания правильной треугольной пирамиды имеет длину а , боковое ребро — длину b. Сечение пирамиды проводится плоскостью, параллельной ребру основания и боковому ребру . Какое из них имеет наибольшую площадь?
Сделаем
2.209. В тетраэдре проведены отрезки, соединяющие его вершины с точками пересечения медиан противоположных граней. Докажите, что эти отрезки имеют общую точку. В каком отношении они делятся этой точкой?
Исследуем
2.210. В основании пирамиды — квадрат. Вершина пирамиды проектируется в центр основания, а два боковых ребра равны а и b. Можно ли найти другие боковые ребра пирамиды?
2.211. В правильной четырехугольной пирамиде через сторону основания проведена плоскость, перпендикулярная к противоположной грани. Как вычислить площадь сечения, если сторона основания равна а и двугранный угол при основании равен а.
Поступаем в ВУЗ
2.212. Основанием тетраэдра РАВС является треугольник  с углом
с углом  и острым углом 30. Боковые ребра тетраэдра наклонены к плоскости основания под углом
и острым углом 30. Боковые ребра тетраэдра наклонены к плоскости основания под углом  высота тетраэдра равна
высота тетраэдра равна  . Найдите площадь сечения тетраэдра плоскостью, проходящей через точку С параллельно АВ и делящей грань ASB на части равной площади.
. Найдите площадь сечения тетраэдра плоскостью, проходящей через точку С параллельно АВ и делящей грань ASB на части равной площади.
Ответ: 
2.213. В основании тетраэдра РАВС лежит правильный треугольник  а все боковые грани имеют равные площади. Ребро РА равно 2 см, ребро РВ равно
а все боковые грани имеют равные площади. Ребро РА равно 2 см, ребро РВ равно  см. Через вершину В перпендикулярно к ребру PC проведено сечение тетраэдра. Найдите площадь этого сечения.
см. Через вершину В перпендикулярно к ребру PC проведено сечение тетраэдра. Найдите площадь этого сечения.
Ответ: 
2.214. Все грани тетраэдра — равные равнобедренные треугольники. Высота тетраэдра совпадает с высотой одной из ее боковых граней. Найдите высоту тетраэдра, если расстояние между наибольшими боковыми ребрами равно 1.
Ответ:  .
.
2.215. В тетраэдре боковые ребра взаимно перпендикулярны и равны а, b, с. Высота тетраэдра, опущенная из вершины на основание, равна п. Докажите, что — 
2.216. В тетраэдре РАВС суммы трех плоских углов при каждой вершине А, В, С равны и . Найдите расстояние между скрещивающимися ребрами РА и ВС, если 
Ответ: 
2.217. Дан тетраэдр ABCD. Докажите, что его ребра AD и ВС перпендикулярны в том и только в том случае, когда выполняется равенство: 
2.218. Основанием тетраэдра SABC является равносторонний треугольник ABC, длина стороны которого равна  Боковое ребро SC перпендикулярно к плоскости основания и имеет длину 2. Найдите величину угла и расстояние между скрещивающимися прямыми, одна из которых проходит через точку S и середину ребра ВС, а другая проходит через точку С и середину АВ.
Боковое ребро SC перпендикулярно к плоскости основания и имеет длину 2. Найдите величину угла и расстояние между скрещивающимися прямыми, одна из которых проходит через точку S и середину ребра ВС, а другая проходит через точку С и середину АВ.
Ответ: 
2.219. Докажите, что треугольная пирамида является правильной, если: а) шар касается трех сторон основания в их серединах, а середины боковых ребер лежат на поверхности шара; б) шар касается всех боковых граней пирамиды в точках пересечения их медиан; в) шар касается боковых граней треугольной пирамиды в точках пересечения их высот, а сумма плоских углов при каждой вершине одна и та же; г) шар касается всех боковых граней в центрах описанных около них окружностей и все плоские углы при вершине равны; д) шар касается всех боковых граней в центрах вписанных в них окружностей. (Каждая из задач  ) предлагалась на вступительном экзамене как часть некоторой другой задачи).
) предлагалась на вступительном экзамене как часть некоторой другой задачи).
2.220. В основании тетраэдра лежит правильный треугольник со стороной а. Одна из его граней перпендикулярна плоскости основания. Она является равнобедренным треугольником с боковой стороной b ( ). Найдите площадь того сечения тетраэдра, которое является квадратом.
). Найдите площадь того сечения тетраэдра, которое является квадратом.
Ответ: 
2.221. В тетраэдре KLMN плоские углы LKN и MKN при вершине равны 45° и  соответственно. Угол между гранями LKM и MKN равен 90°. Определите плоский угол
соответственно. Угол между гранями LKM и MKN равен 90°. Определите плоский угол 
Ответ: 120°.
2.222. Все высоты тетраэдра EFGH, грани которого являются остроугольными треугольниками, равны между собой. Известно, что  Найдите длину ребра
Найдите длину ребра 
Ответ: 
2.223. Боковые ребра тетраэдра взаимно перпендикулярны. Высота тетраэдра равна И. Найдите радиус сферы, описанной около тетраэдра.
Ответ: 
2.224. Основанием тетраэдра служит равнобедренный треугольник, равные стороны которого имеют каждая длину b. Боковые грани тетраэдра, проходящие через эти стороны, перпендикулярны к плоскости основания и образуют между собой угол а . Угол между третьей боковой гранью и плоскостью основания равен также а. Определите радиус шара, вписанного в тетраэдр.
Ответ: 
2.225. В тетраэдре РАВС плоские углы при вершине Р — прямые. Докажите, что вершина Р, точка G пересечения медиан основания и центр О описанного около тетраэдра шара принадлежат одной прямой.
2.226. В тетраэдре РАВС боковое ребро PC равно ребру АВ и наклонено к плоскости основания ABC под углом 
Вершины А, В, С и середины боковых ребер тетраэдра расположены на сфере радиуса 1. Докажите, что центр этой сферы лежит на ребре АВ и найдите высоту тетраэдра.
Ответ: 
2.227. Шар радиуса  касается всех ребер тетраэдра. Центр шара лежит внутри тетраэдра на его высоте на расстоянии
касается всех ребер тетраэдра. Центр шара лежит внутри тетраэдра на его высоте на расстоянии  от вершины. Докажите, что тетраэдр является правильной пирамидой. Найдите ее высоту.
от вершины. Докажите, что тетраэдр является правильной пирамидой. Найдите ее высоту.
Ответ: — 
2.228. В основании тетраэдра лежит прямоугольный треугольник. Вершины основания и середины его боковых ребер лежат на одной сфере. Докажите, что углы наклона боковых ребер к основанию равны между собой. Найдите углы наклона
боковых граней тетраэдра к плоскости основания, если катеты основания равны а и b, а высота тетраэдра равна  .
.
Ответ:  .
.
2.229. Дан тетраэдр ABCD. Скрещивающиеся ребра АС и BD, AD и ВС перпендикулярны, ребра АВ и CD равны, все ребра касаются шара радиуса  . Найдите площадь грани
. Найдите площадь грани 
Ответ: 
2.230. В тетраэдре, ребро которого равно  высота служит диаметром шара. Найдите длину линии пересечения поверхности тетраэдра и шара.
высота служит диаметром шара. Найдите длину линии пересечения поверхности тетраэдра и шара.
Ответ: 
2.231. В тетраэдре РАВС грани РАС и ABC перпендикулярны и являются равными равнобедренными треугольниками  угол РАС равен —
угол РАС равен —  Найдите высоту конуса, окружность основания которого проходит через точки А, В и С, а боковая поверхность — через точку Р.
Найдите высоту конуса, окружность основания которого проходит через точки А, В и С, а боковая поверхность — через точку Р.
Ответ: 
2.232. В тетраэдре ABCD двугранные углы при ребрах АВ и BD прямые,  . Вершина конуса совпадает с одной из вершин тетраэдра, окружность основания конуса вписана в одну из граней. Найдите угол в осевом сечении конуса.
. Вершина конуса совпадает с одной из вершин тетраэдра, окружность основания конуса вписана в одну из граней. Найдите угол в осевом сечении конуса.
Ответ: 
2.233. Дана правильная треугольная пирамида DABC (D — вершина, ABC — основание). Известно, что  Пирамиду пересекает плоскость, параллельная ребрам AD и ВС и отстоящая на расстоянии d от ребра
Пирамиду пересекает плоскость, параллельная ребрам AD и ВС и отстоящая на расстоянии d от ребра  Найдите площадь сечения пирамиды этой плоскостью.
Найдите площадь сечения пирамиды этой плоскостью.
Ответ: 
2.234. В правильной треугольной пирамиде SABC, высота в которой в два раза больше стороны основания, на боковых ребрах SB и SC взяты точки М и N так, что MN параллельна
ВС. Через прямую MN проходят плоскости  Плоскость а перпендикулярна плоскости грани SBC и содержит точку А, плоскость
Плоскость а перпендикулярна плоскости грани SBC и содержит точку А, плоскость  проходит через середину бокового ребра SA. Найдите отношение площадей сечений пирамиды плоскостями
проходит через середину бокового ребра SA. Найдите отношение площадей сечений пирамиды плоскостями 
Ответ: 
2.235. В правильной треугольной пирамиде со стороной основания, равной а, углы между ребрами при ее вершине равны  . Определите площадь сечения, проведенного через сторону основания перпендикулярно противоположному боковому ребру.
. Определите площадь сечения, проведенного через сторону основания перпендикулярно противоположному боковому ребру.
Ответ:  .
.
2.236. В правильной треугольной пирамиде ABCD сторона основания ABC равна b , а высота пирамиды равна  . Сфера, вписанная в пирамиду, касается грани ACD в точке К. Найдите площадь сечения пирамиды плоскостью, проходящей через точку К и ребро АВ.
. Сфера, вписанная в пирамиду, касается грани ACD в точке К. Найдите площадь сечения пирамиды плоскостью, проходящей через точку К и ребро АВ.
Ответ: 
2.237. В правильную треугольную пирамиду РАВС вписан шар единичного радиуса; двугранный угол при ребре основания равен 60°. Докажите, что существует единственная плоскость, пересекающая ребра АВ и ВС в некоторых точках М и N таких, что  касающаяся шара в точке, удаленной на равные расстояния от точек М и N, пересекающая продолжение высоты пирамиды РК за точку К в некоторой точке D. Найдите длину отрезка
касающаяся шара в точке, удаленной на равные расстояния от точек М и N, пересекающая продолжение высоты пирамиды РК за точку К в некоторой точке D. Найдите длину отрезка 
Ответ: 9.
2.238. Шарик лежит на основании правильной треугольной пирамиды, касаясь основания в его центре. Плоскость, проведенная через вершину пирамиды и середины двух сторон основания, касается этого шарика. Найдите радиус шарика, если высота пирамиды равна Н, сторона основания пирамиды равна а.
Ответ: 
2.239. Сфера вписана в правильную треугольную пирамиду SABC, а также вписана в правильную треугольную призму  у которой
у которой  а боковое ребро ККХ лежит на прямой АВ. Найдите радиус сферы, если известно, что прямая SC параллельна плоскости
а боковое ребро ККХ лежит на прямой АВ. Найдите радиус сферы, если известно, что прямая SC параллельна плоскости 
Ответ: 
2.240. В правильной четырехугольной пирамиде PABCD угол между боковым ребром РА и плоскостью основания ABCD равен углу между ребром РА и плоскостью грани РВС. Определите этот угол.
Ответ:  .
.
2.241. Длина стороны основания правильной четырехугольной пирамиды равна а, длина апофемы пирамиды равна 1,5а. Ортогональной проекцией пирамиды на плоскость, перпендикулярную одной из боковых граней, является равнобедренная трапеция. Найдите площадь этой трапеции.
Ответ: 
2.242. В правильной четырехугольной пирамиде плоский угол при вершине равен  . Докажите, что один из двугранных углов этой пирамиды вдвое меньше другого.
. Докажите, что один из двугранных углов этой пирамиды вдвое меньше другого.
2.243. Дана правильная четырехугольная пирамида PABCD, у которой все ребра равны а. Через вершину А основания проведена плоскость, параллельная диагонали BD и образующая с плоскостью основания угол 30°. Найдите площадь сечения.
Ответ: 
2.244. В шар вписана пирамида, боковые ребра которой равны с. Основание ее — прямоугольник, стороны которого
стягивают дуги  в сечениях шара плоскостями боковых граней. Определите радиус описанного шара.
в сечениях шара плоскостями боковых граней. Определите радиус описанного шара.
Ответ: 
2.245. Сторона основания правильной треугольной пирамиды равна а, боковое ребро пирамиды равно b. Найдите радиус сферы, касающейся всех ребер пирамиды.
Ответ:  .
.
2.246. Центр сферы, описанной около правильной четырехугольной пирамиды, находится на расстоянии а от боковой грани и на расстоянии b от бокового ребра. Найдите радиус сферы.
Ответ: 
2.247. Центр шара, вписанного в правильную четырехугольную пирамиду, находится на расстоянии  от бокового ребра и на расстоянии
от бокового ребра и на расстоянии  от стороны основания. Найдите радиус шара.
от стороны основания. Найдите радиус шара.
Ответ: 
2.248. В правильной четырехугольной пирамиде PABCD сторона основания ABCD равна b, а высота пирамиды равна  Сфера, вписанная в эту пирамиду, касается боковой грани PAD в точке К. Найдите площадь сечения пирамиды плоскостью, проходящей через точку К и ребро АВ.
Сфера, вписанная в эту пирамиду, касается боковой грани PAD в точке К. Найдите площадь сечения пирамиды плоскостью, проходящей через точку К и ребро АВ.
Ответ: 
2.249. В четырехугольной пирамиде ABCDE основание ABCD — параллелограмм, а грани ADE и ВСЕ — прямоугольные треугольники. Ребро ВС перпендикулярно медиане ЕР грани CDE и  Сечением пирамиды плоскостью является равнобокая трапеция GKHL, вершины которой G, К, Н, L лежат соответственно на ребрах АЕ, BE, СЕ, DE, причем
Сечением пирамиды плоскостью является равнобокая трапеция GKHL, вершины которой G, К, Н, L лежат соответственно на ребрах АЕ, BE, СЕ, DE, причем  и
и  . Найдите отношение площади трапеции GKHL к площади грани
. Найдите отношение площади трапеции GKHL к площади грани 
Ответ: 
2.250. В основании пирамиды находится ромб. Шар касается боковых граней пирамиды в точках, лежащих на сторонах основания пирамиды. Докажите, что прямая, соединяющая вершину пирамиды с центром шара, проходит через точку пересечения диагоналей ромба.
2.251. В правильной пятиугольной пирамиде задан двугранный угол  при боковом ребре. Найдите плоский угол при вершине боковой грани.
при боковом ребре. Найдите плоский угол при вершине боковой грани.
Ответ: 
2.252. В правильной шестиугольной пирамиде сторона основания равна а, а высота равна А. Вычислите площадь сечения, проходящего через середины двух несмежных и непараллельных сторон основания и середину высоты пирамиды.
Ответ: 
2.253. В правильной шестиугольной пирамиде вписанная сфера проходит через центр описанной. Во сколько раз радиус описанной сферы больше радиуса вписанной?
Ответ: 
2.254. В правильной четырехугольной усеченной пирамиде  нижнее основание — квадрат ABCD со стороной 3, верхнее основание
нижнее основание — квадрат ABCD со стороной 3, верхнее основание  — квадрат со стороной 1, боковые ребра имеют длину 3. Точка М — середина ребра
— квадрат со стороной 1, боковые ребра имеют длину 3. Точка М — середина ребра  . Через точку М проходит прямая, пересекающая прямые
. Через точку М проходит прямая, пересекающая прямые  и ВС в точках
и ВС в точках  Найдите длину отрезка
Найдите длину отрезка 
Ответ: 
Переключаемся
2.255. Высоту пирамиды Хеопса Фалес нашел по ее тени. А вы смогли бы это сделать?
2.256. а) Из одной точки и в разных направлениях полетели четыре вороны. В некоторый момент времени они оказались в одной плоскости. Повторится ли еще такая ситуация? б) В другой раз эти же вороны вылетели из одной точки по четырем направлениям со скоростями 1, 2, 3, 4 соответственно. Окажутся ли они в какой нибудь момент времени в одной плоскости?
2.257. В одном задачнике по геометрии было написано, что не существует четырехугольной пирамиды, у которой противоположные грани перпендикулярны основанию. Опровергните это утверждение.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
- 1.5. Взаимное расположение двух прямых в пространстве.
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
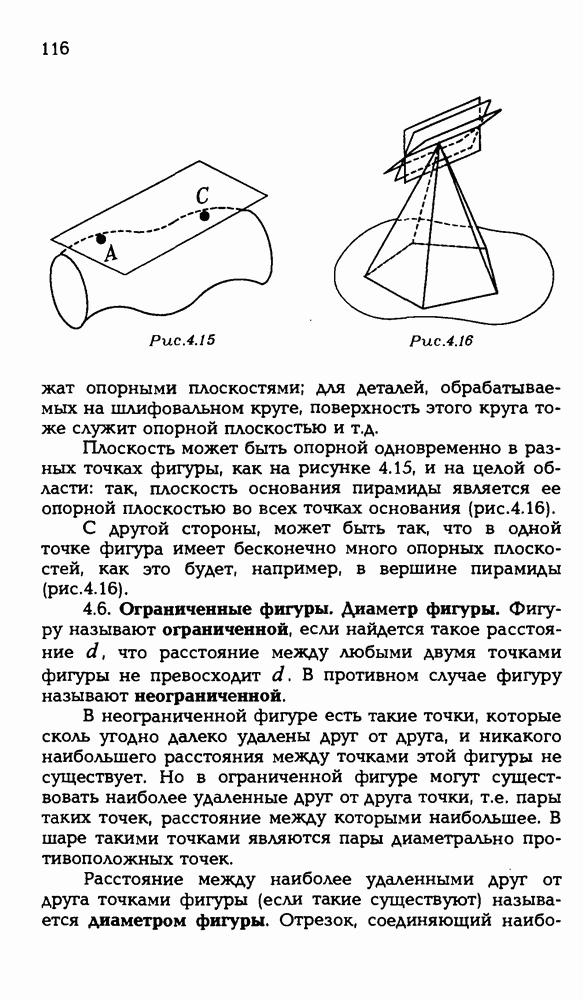
- 4.5. Опорная плоскость.
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
- § 6. ЦИЛИНДР
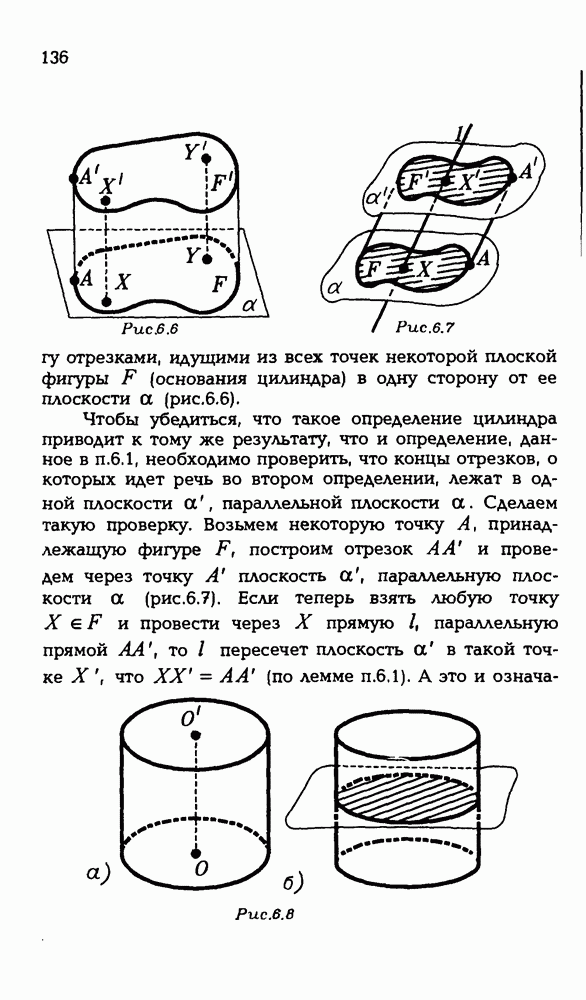
- 6.2. Другой подход к определению цилиндра.
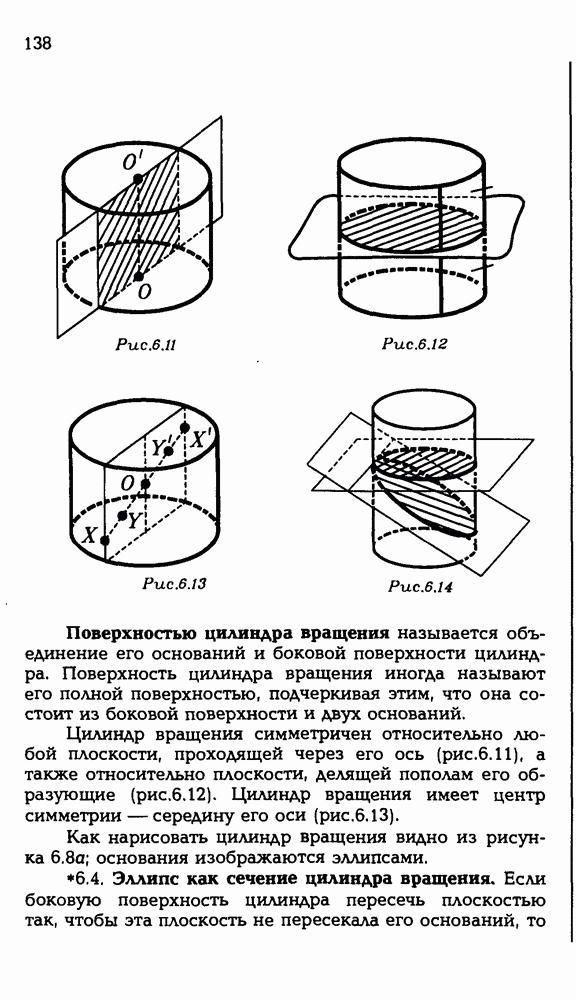
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
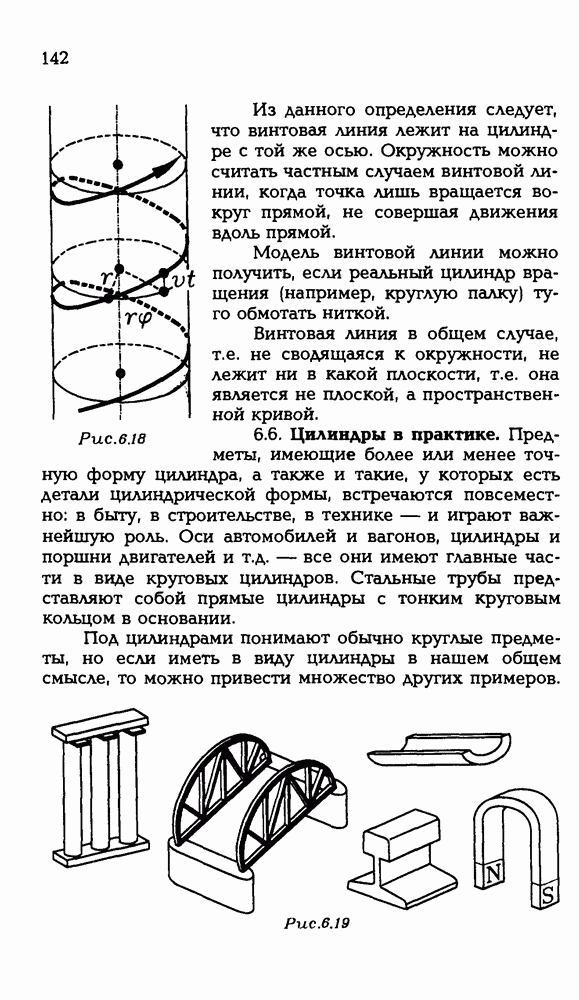
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
- 7.4. Симметрия параллелепипеда.
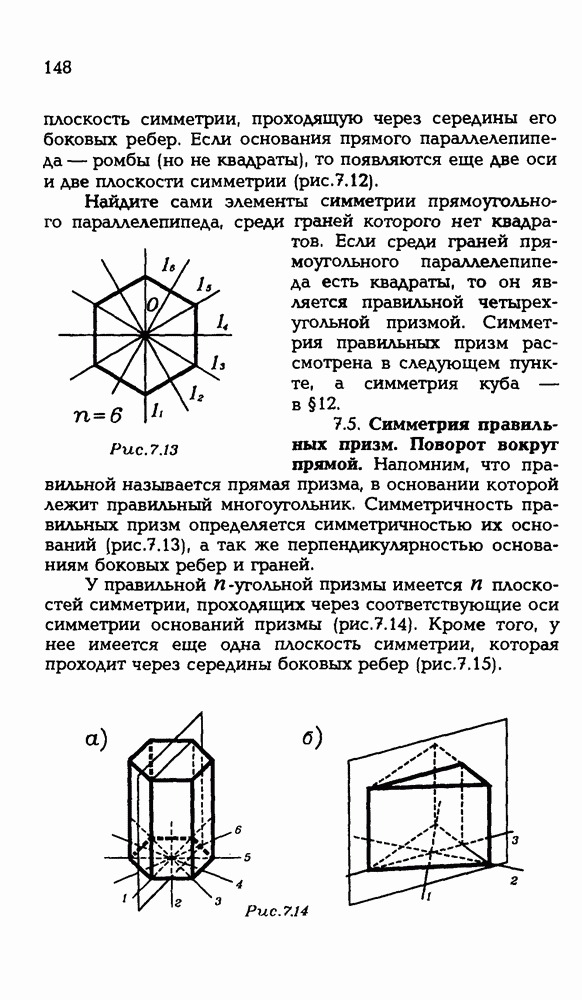
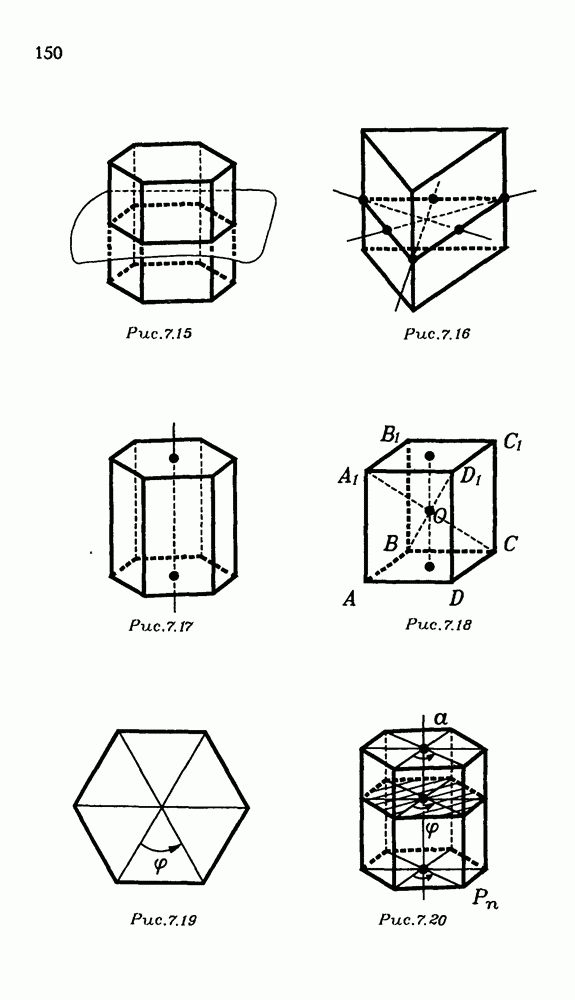
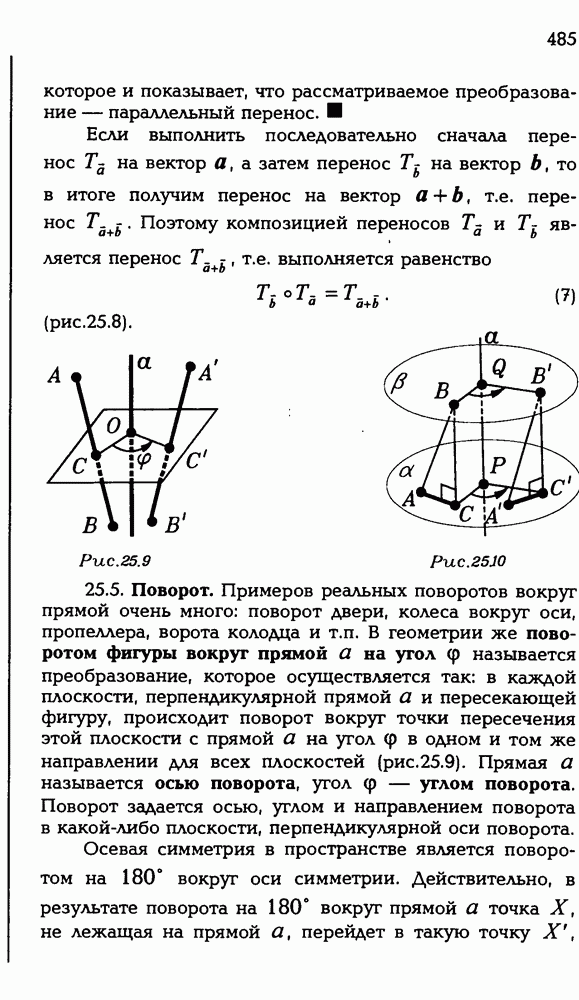
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
- § 8. КОНУС
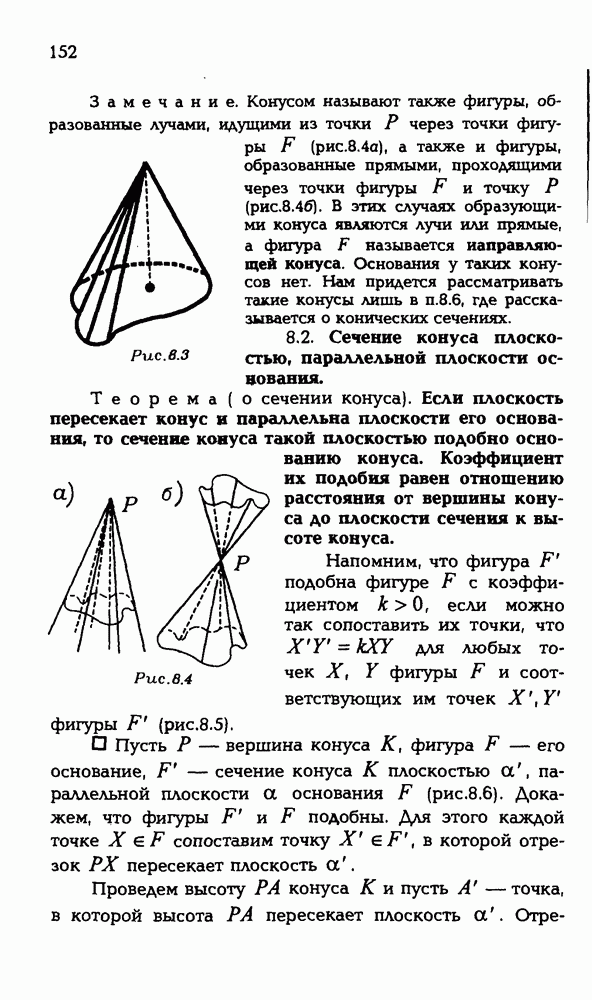
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
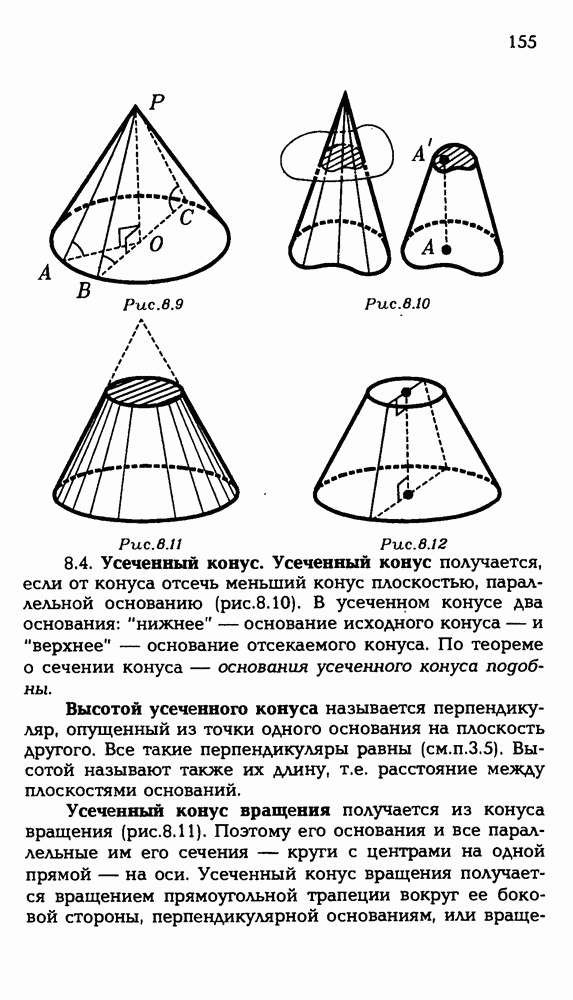
- 8.4. Усеченный конус.
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
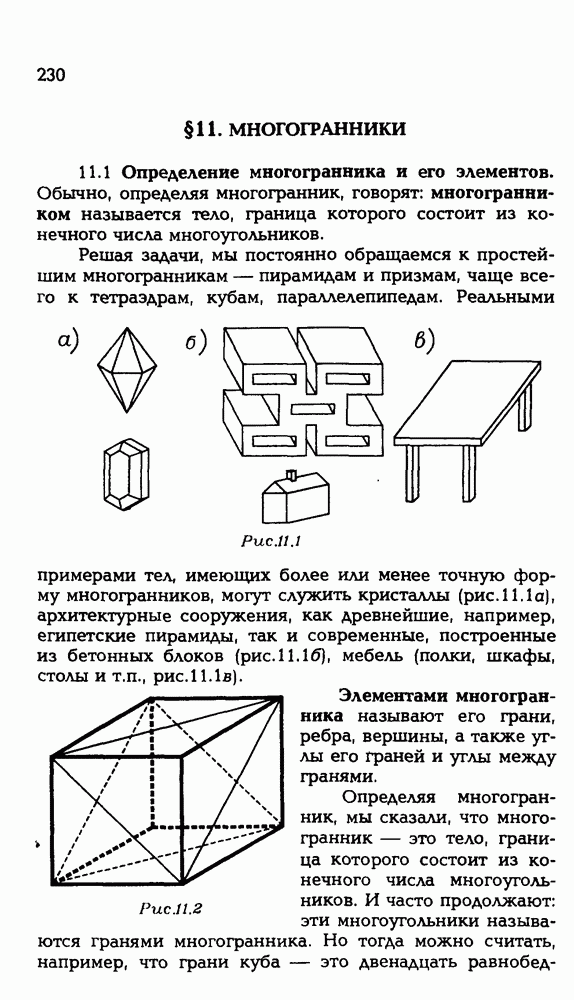
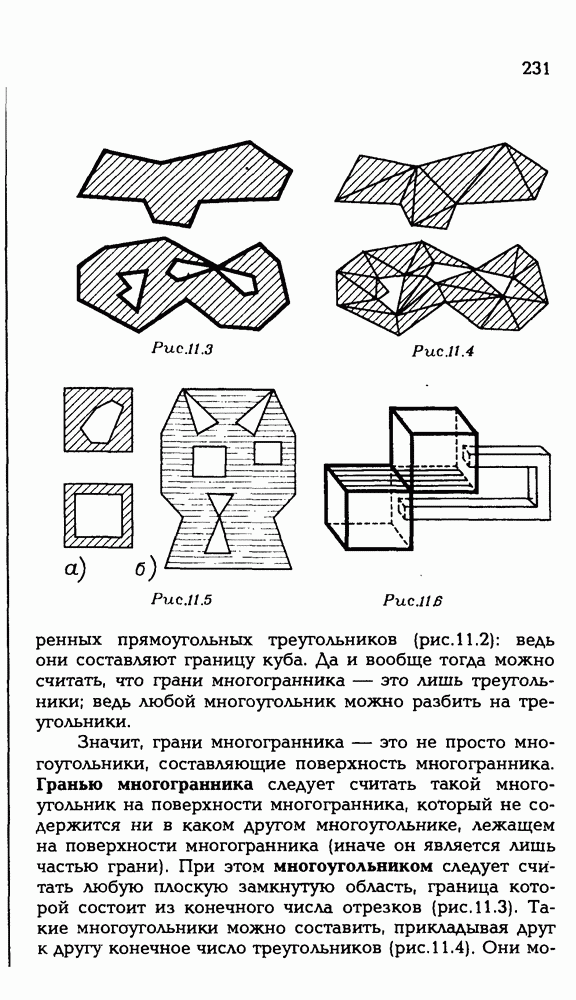
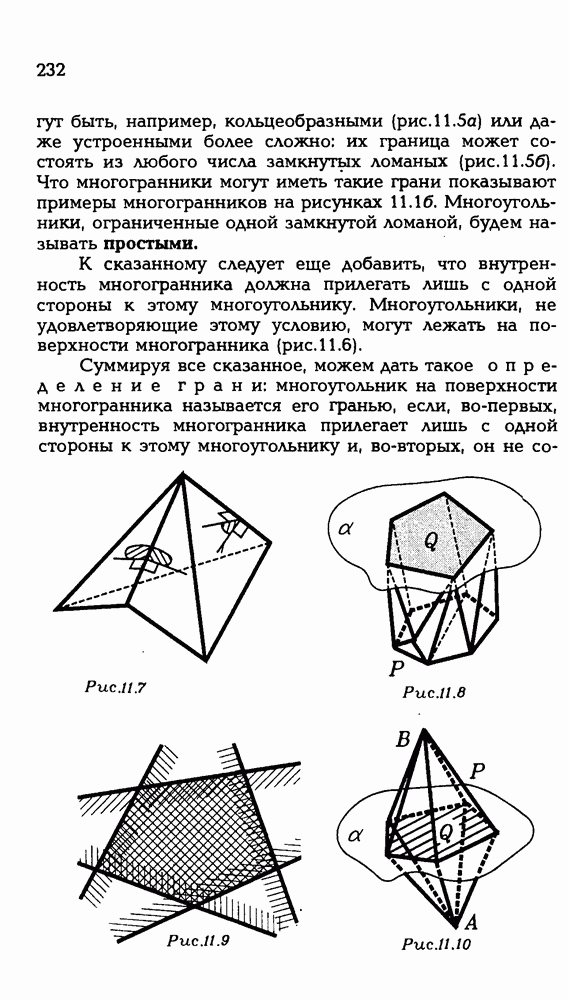
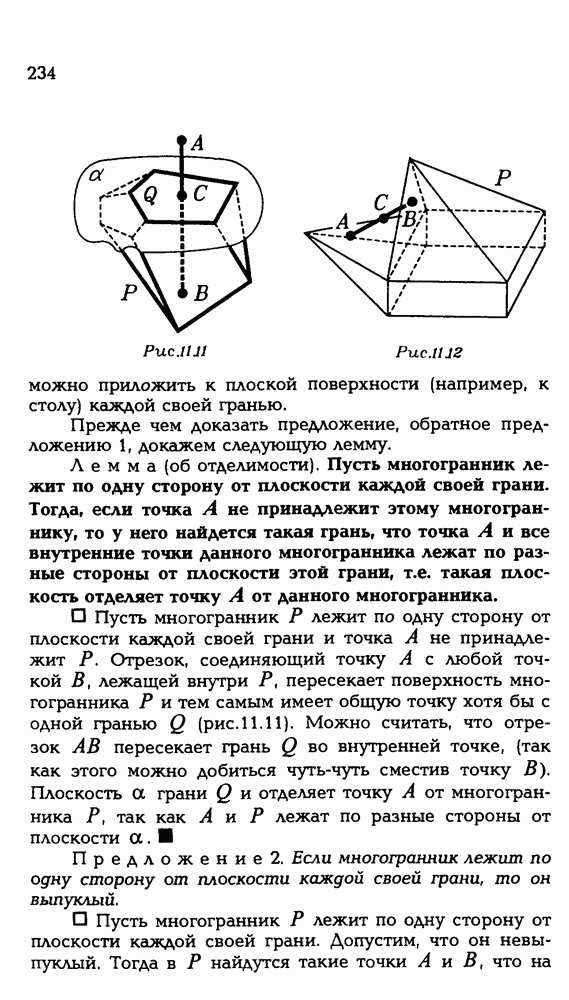
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
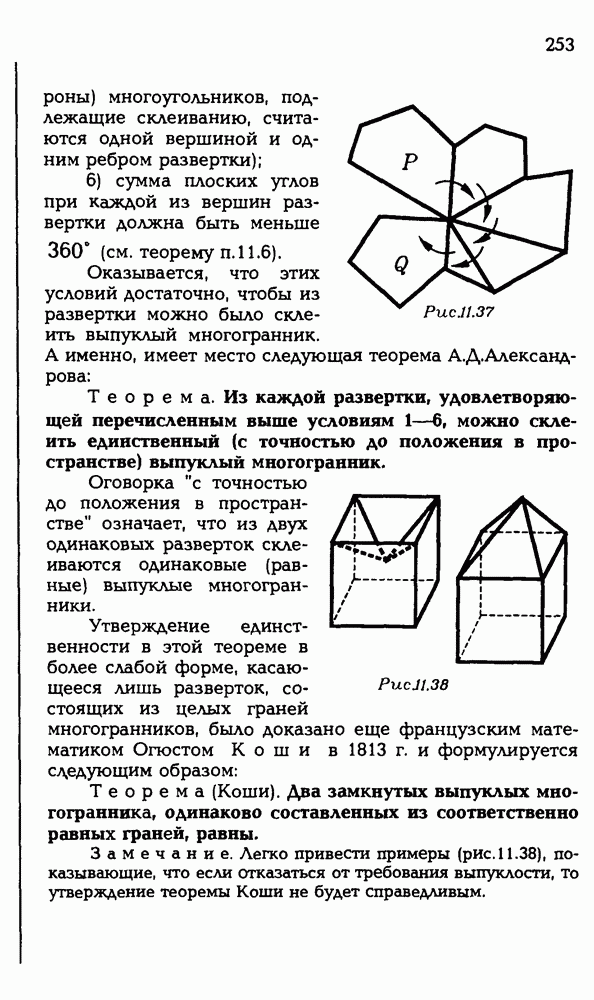
- 11.6. Развертка выпуклого многогранника.
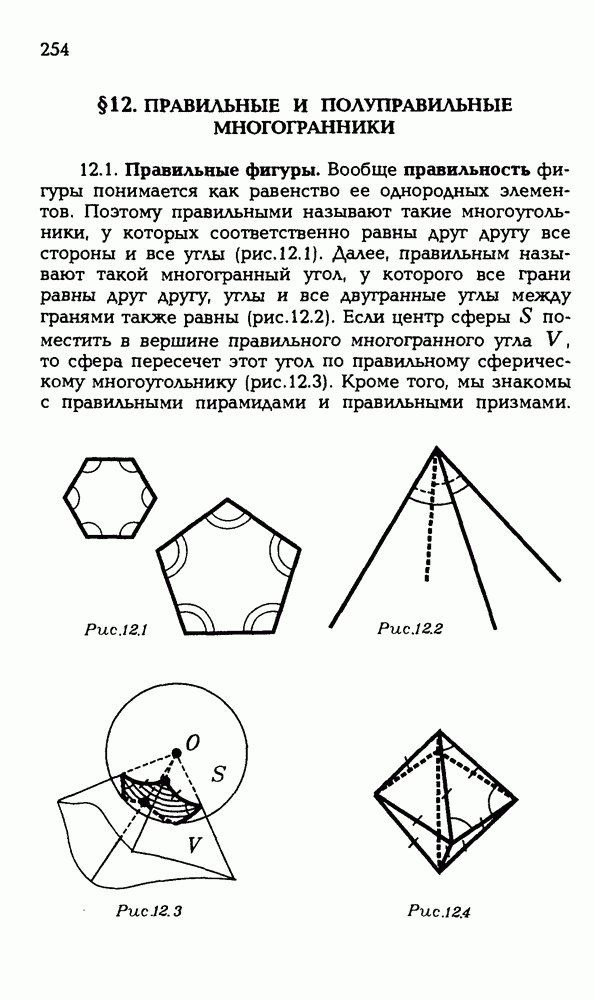
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
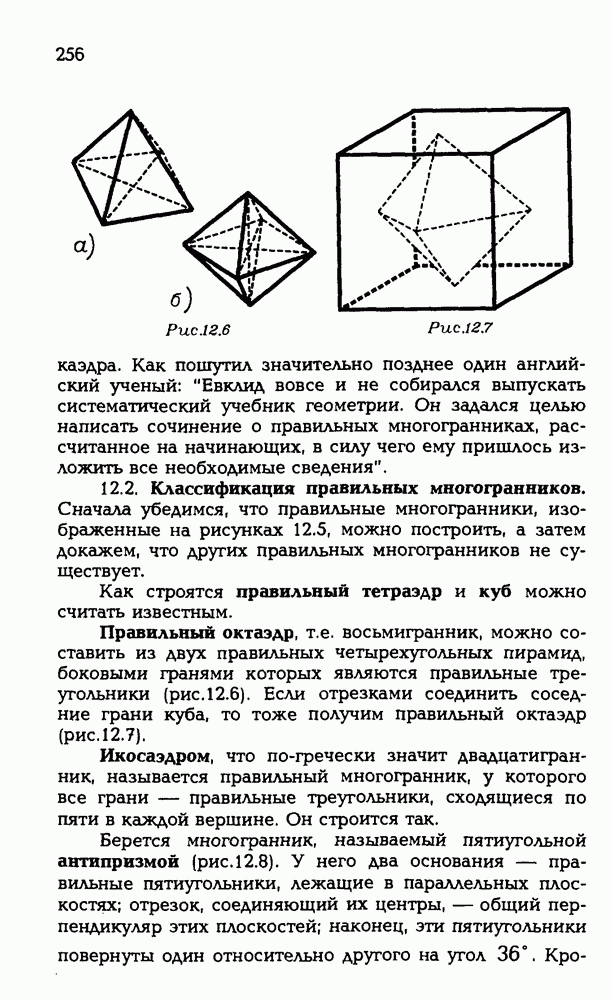
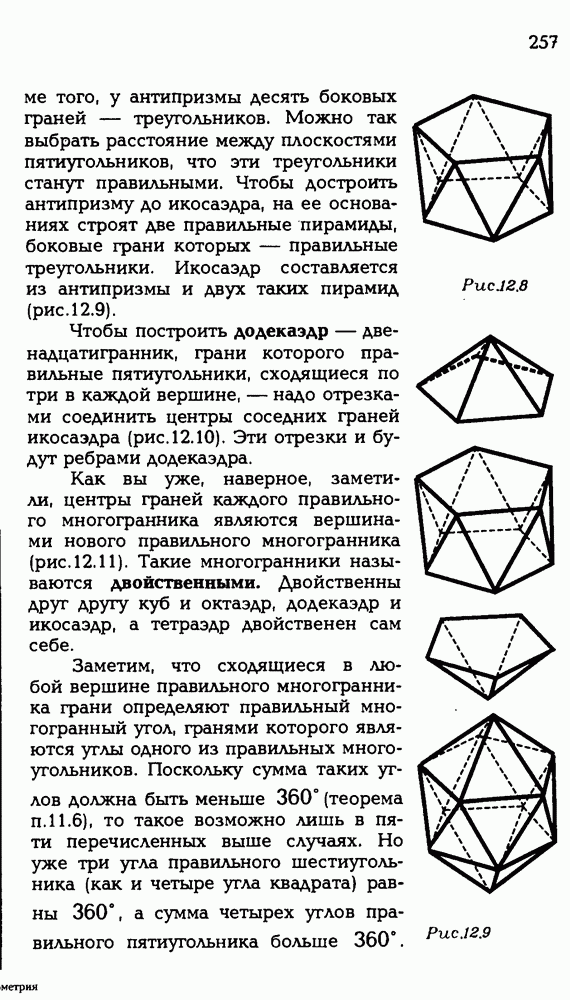
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ