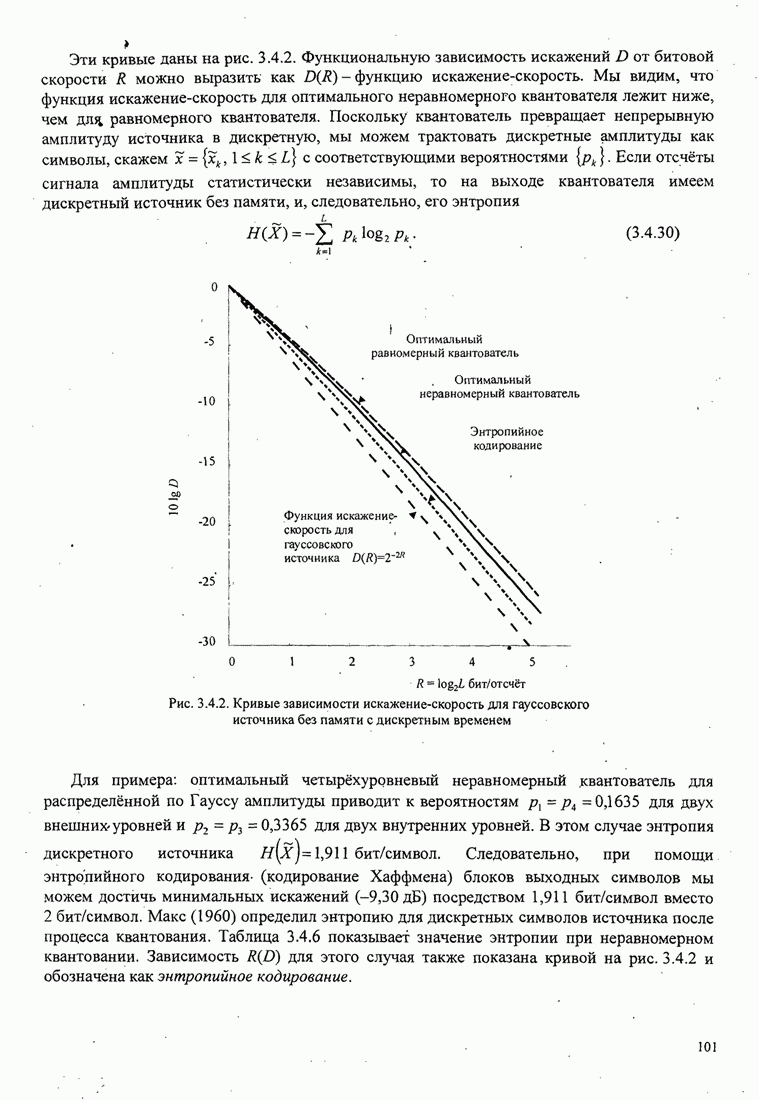
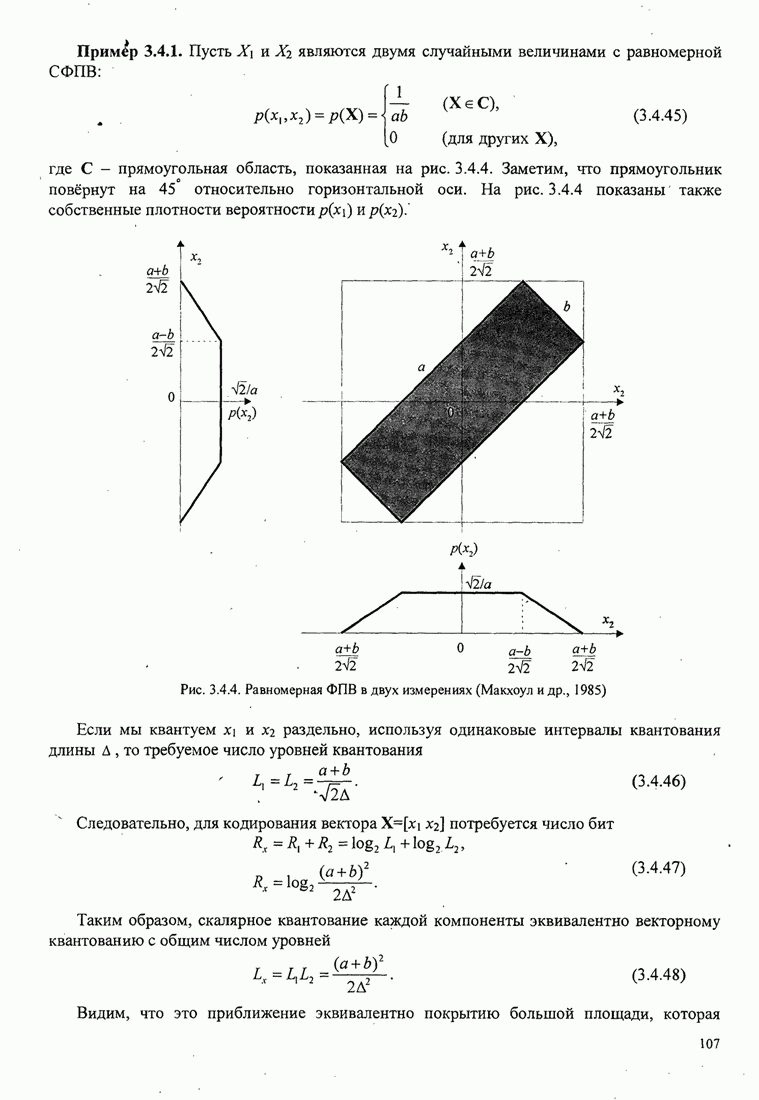
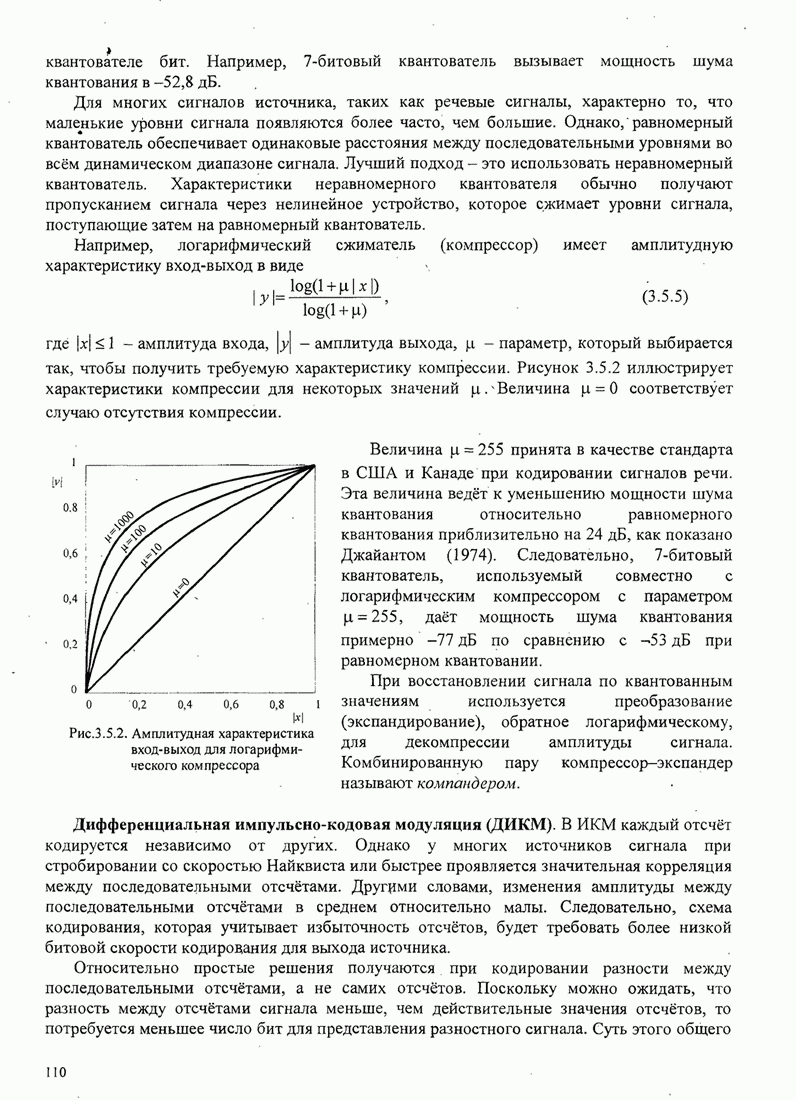
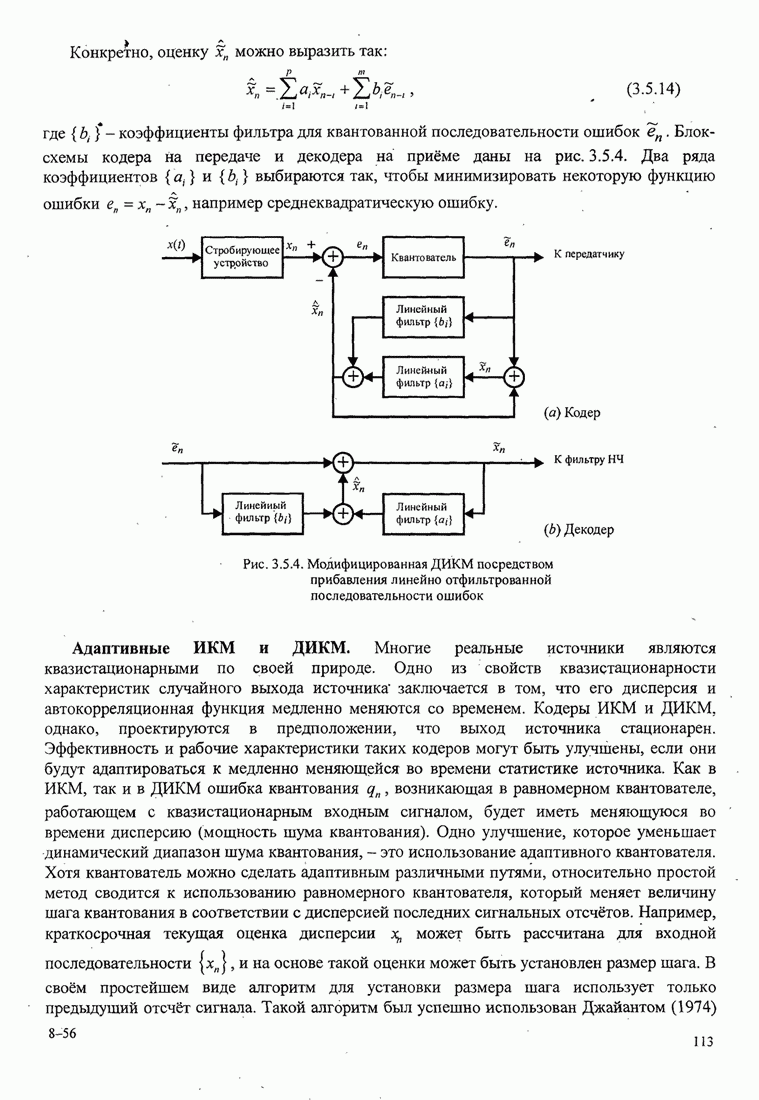
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
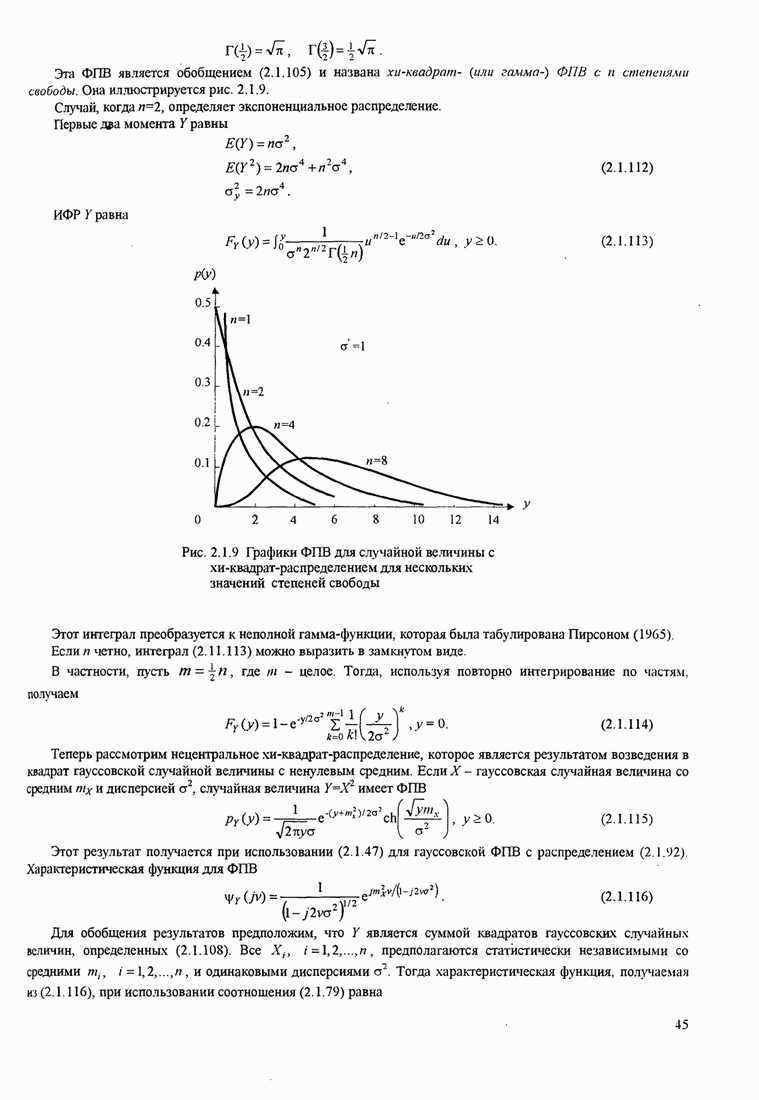
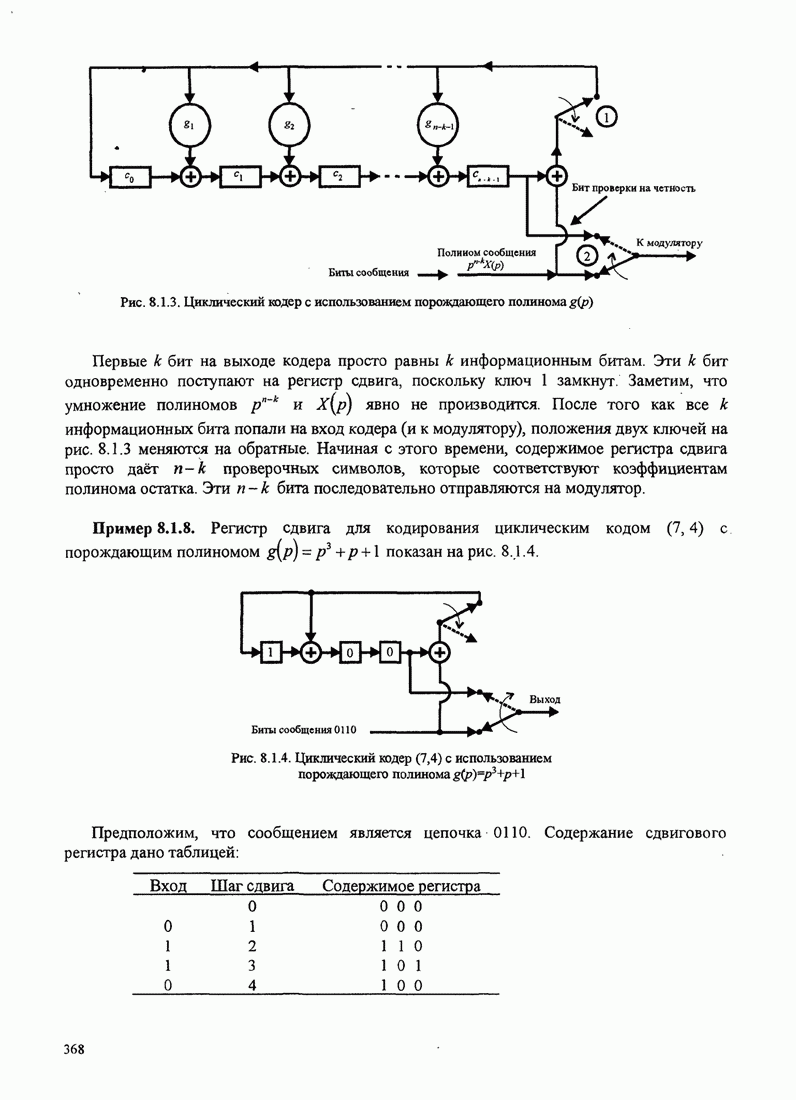
7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
Рассмотрим ансамбль из ![]() кодовых слов,
образованных из
кодовых слов,
образованных из ![]() -мерных
двоичных кодовых слов вида
-мерных
двоичных кодовых слов вида
![]() (7.2.1)
(7.2.1)
где ![]() или 1. Каждый символ
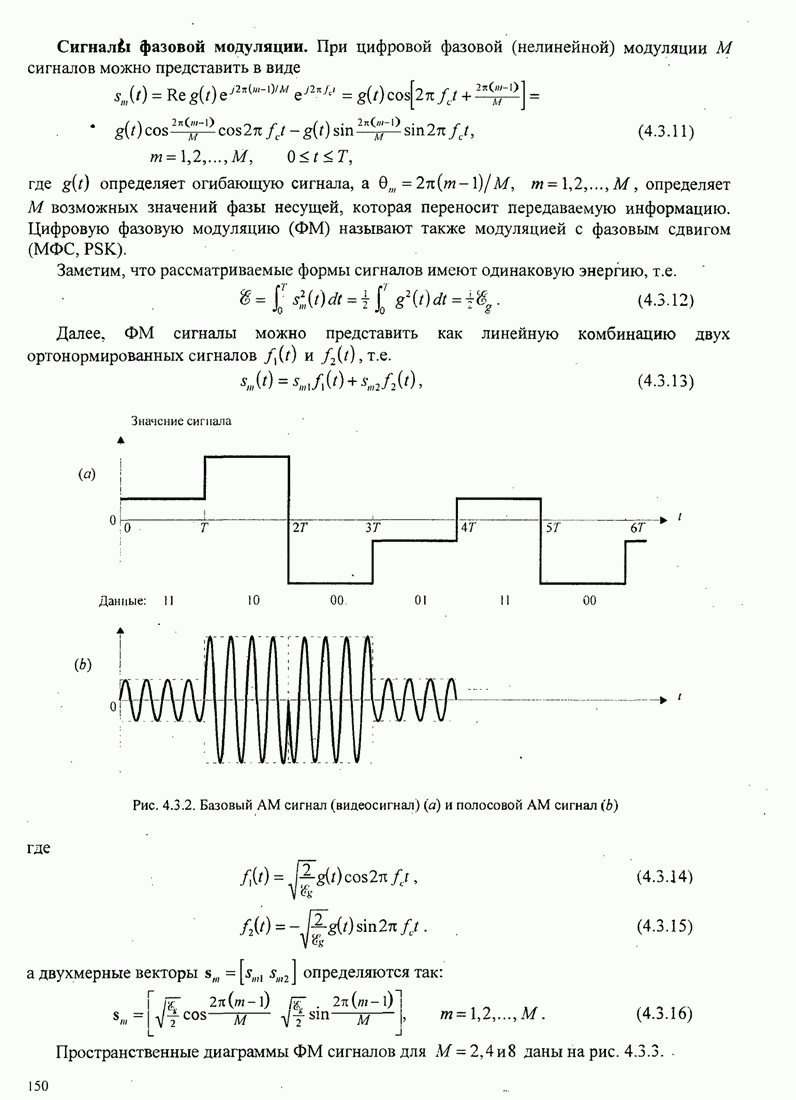
кодового слова отображается двоичным ФМ сигналом, так что сигналы,
соответствующие кодовому слову
или 1. Каждый символ
кодового слова отображается двоичным ФМ сигналом, так что сигналы,
соответствующие кодовому слову ![]() , можно выразить так:
, можно выразить так:
 (7.2.2)
(7.2.2)
где
 (7.2.3)
(7.2.3)
и ![]() - энергия на кодовый
символ. Таким образом, сигналы
- энергия на кодовый
символ. Таким образом, сигналы ![]() эквивалентны
эквивалентны ![]() -мерным векторам
-мерным векторам
![]() (7.2.4)
(7.2.4)
которые соответствуют вершинам гиперкуба
в ![]() -мерном
пространстве.
-мерном
пространстве.
Теперь предположим, что информационная
скорость на входе кодера равна ![]() бит/с и мы кодируем
блоки из
бит/с и мы кодируем
блоки из ![]() бит на определенном временном
интервале
бит на определенном временном
интервале ![]() посредством одного из
посредством одного из ![]() сигналов.
Следовательно,
сигналов.
Следовательно, ![]() и требуется
и требуется ![]() сигналов.
Удобно определить параметр
сигналов.
Удобно определить параметр ![]() следующим образом:
следующим образом:
![]() (7.2.5)
(7.2.5)
Таким образом, ![]() -
это размерность пространства сигналов.
-
это размерность пространства сигналов.
Гиперкуб имеет ![]() вершин, из которых
вершин, из которых![]() могут быть использованы для передачи информации. Если
мы навяжем условие
могут быть использованы для передачи информации. Если
мы навяжем условие ![]() , то часть вершин, которые мы
используем как сигнальные точки, равна
, то часть вершин, которые мы
используем как сигнальные точки, равна
![]() (7.2.6)
(7.2.6)
Ясно,
если ![]() , имеем
, имеем ![]() , когда
, когда ![]() .
.
Вопрос, который мы хотим ставить,
следующий. Можно ли выбрать подмножество ![]() вершин из
вершин из ![]() имеющихся
в распоряжении вершин так, чтобы вероятность ошибки
имеющихся
в распоряжении вершин так, чтобы вероятность ошибки ![]() при
при ![]() или,
что эквивалентно, когда
или,
что эквивалентно, когда ![]() ? Поскольку часть
? Поскольку часть ![]() используемых
вершин приближается к нулю, когда
используемых
вершин приближается к нулю, когда ![]() возможно выбрать
возможно выбрать ![]() сигналов, имеющих
минимальное расстояние, которое увеличивается, когда
сигналов, имеющих
минимальное расстояние, которое увеличивается, когда ![]() и, следовательно,
и, следовательно, ![]() .
.
Вместо того, чтобы пытаться найти простой ансамбль из ![]() кодовых
сигналов, для которых мы рассчитаем вероятность ошибки, рассмотрим ансамбль из
кодовых
сигналов, для которых мы рассчитаем вероятность ошибки, рассмотрим ансамбль из![]() различных путей,
по которым мы можем выбрать
различных путей,
по которым мы можем выбрать ![]() вершин из
вершин из
![]() имеющихся
в распоряжении вершин гиперкуба. С каждым из
имеющихся
в распоряжении вершин гиперкуба. С каждым из ![]() выборов мы можем связать
систему связи, содержащей модулятор, канал и демодулятор, которые оптимальны
для выбранного набора из
выборов мы можем связать
систему связи, содержащей модулятор, канал и демодулятор, которые оптимальны
для выбранного набора из ![]() сигналов.
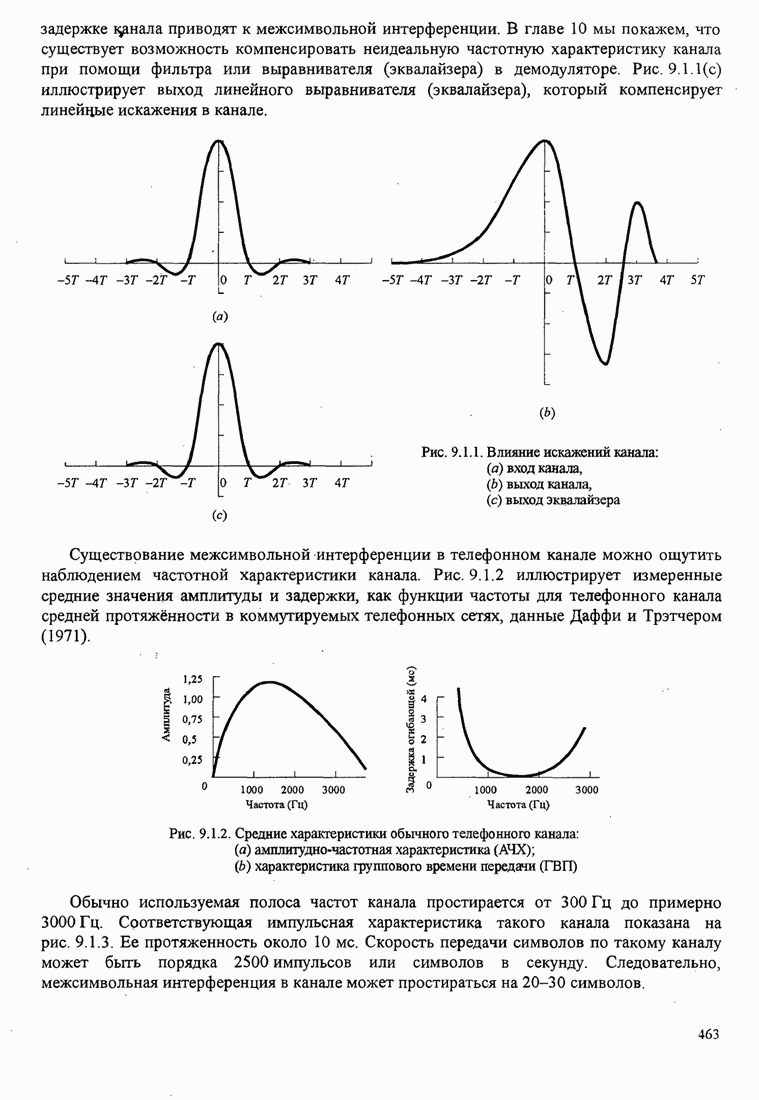
Таким образом, имеется
сигналов.
Таким образом, имеется ![]() систем связи, одна для каждого выбора
систем связи, одна для каждого выбора ![]() кодовых
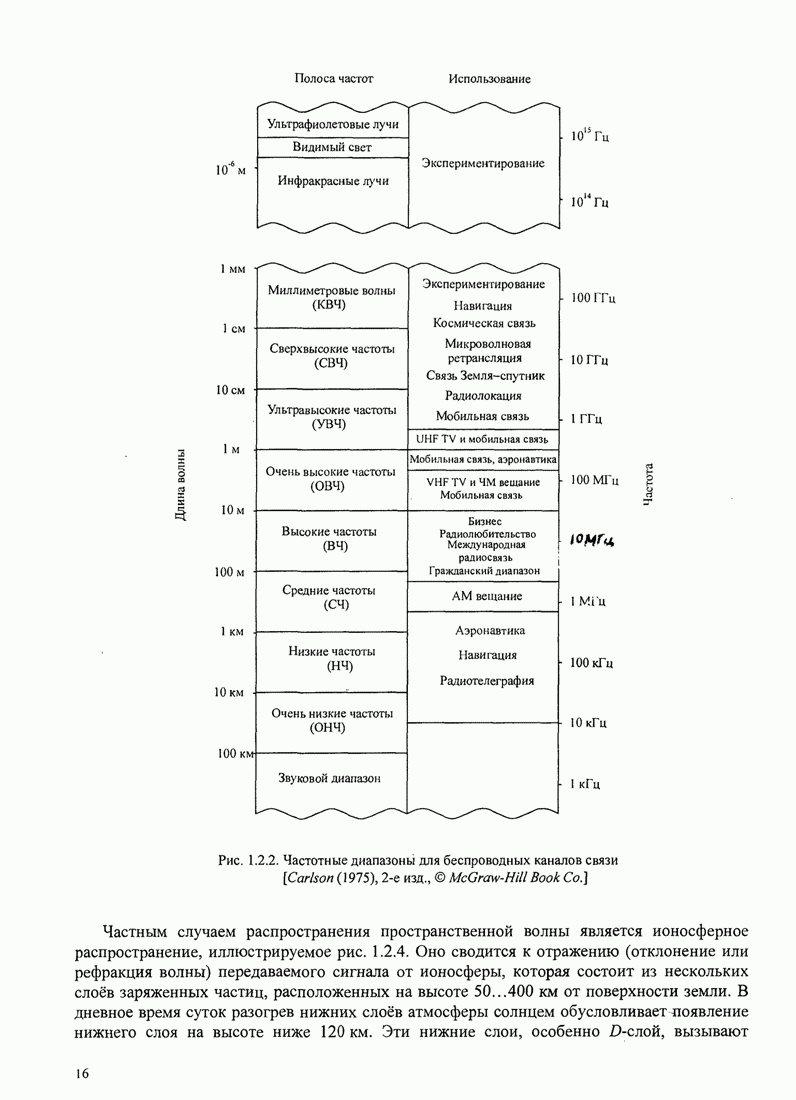
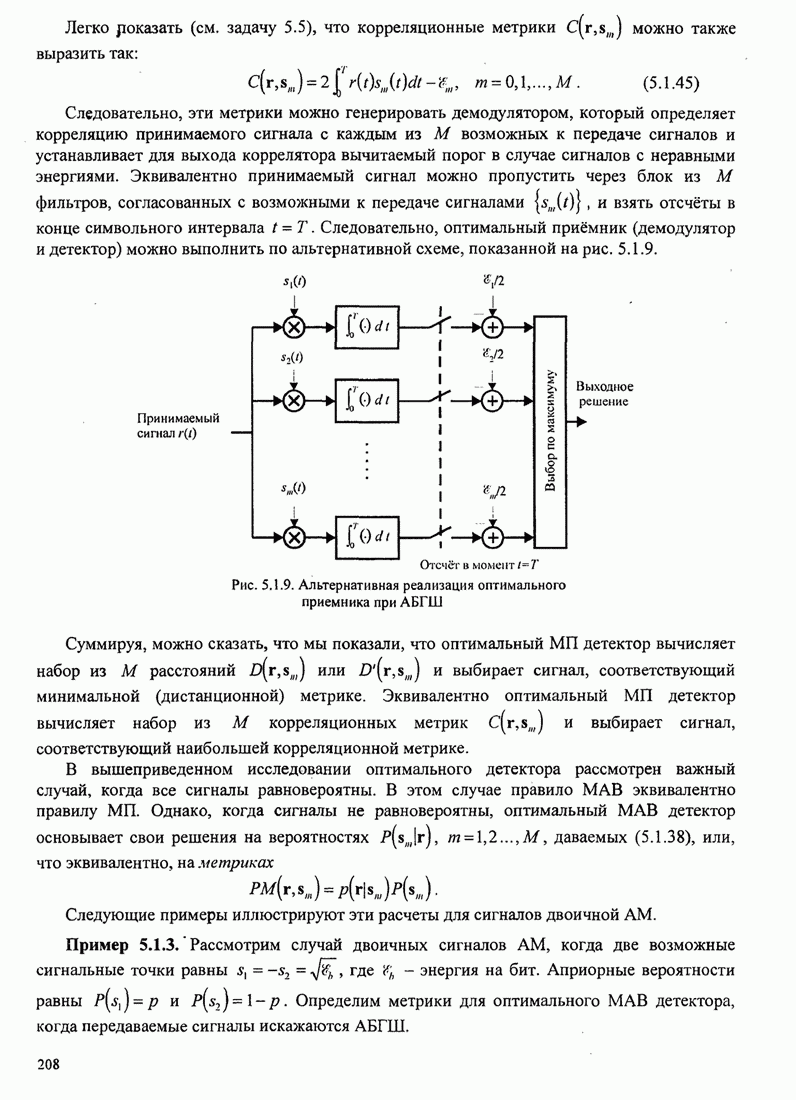
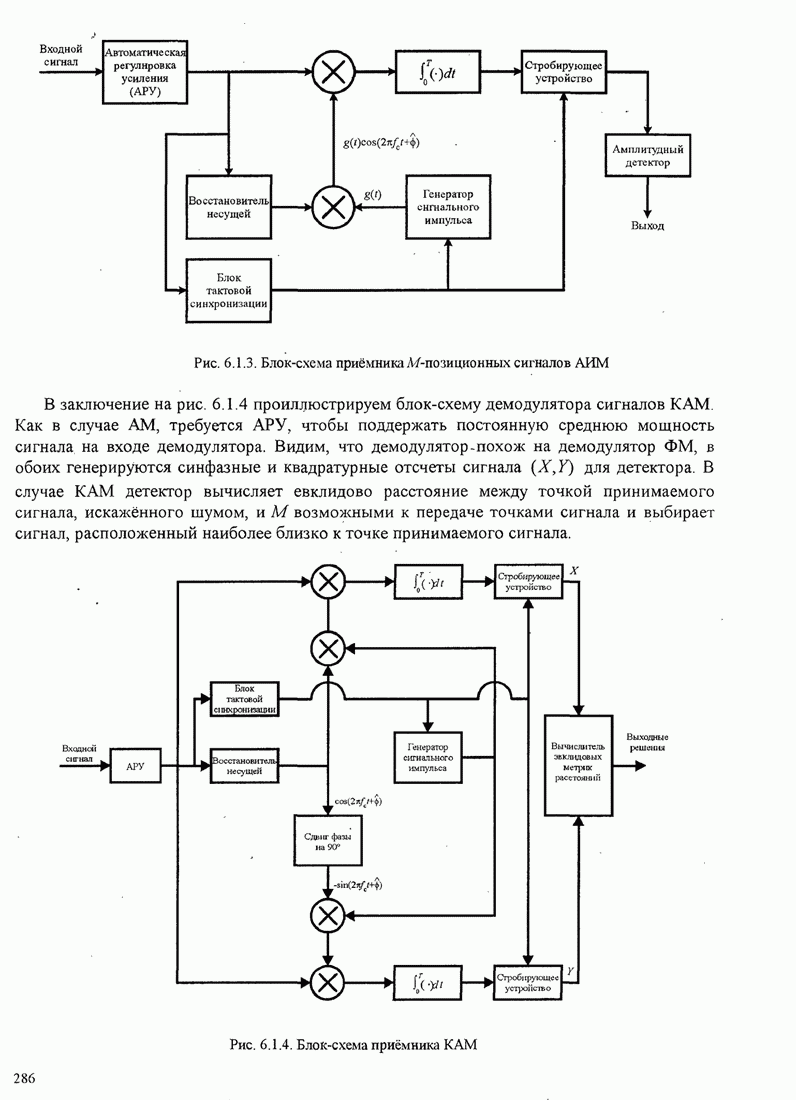
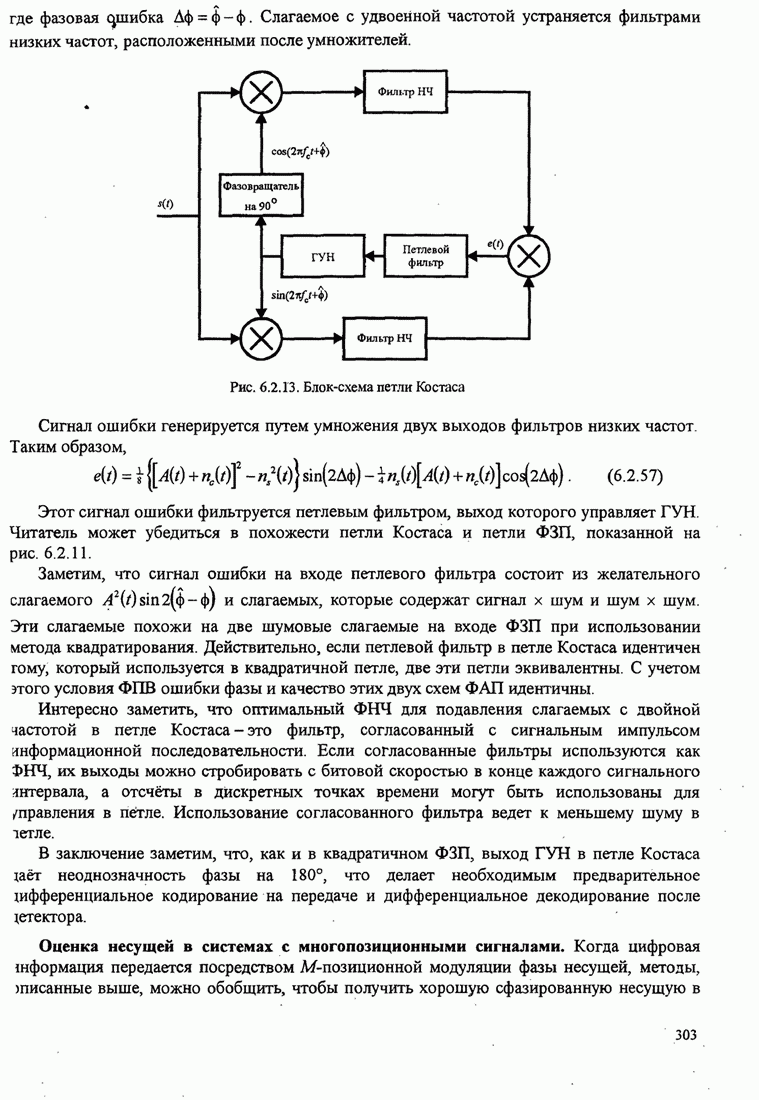
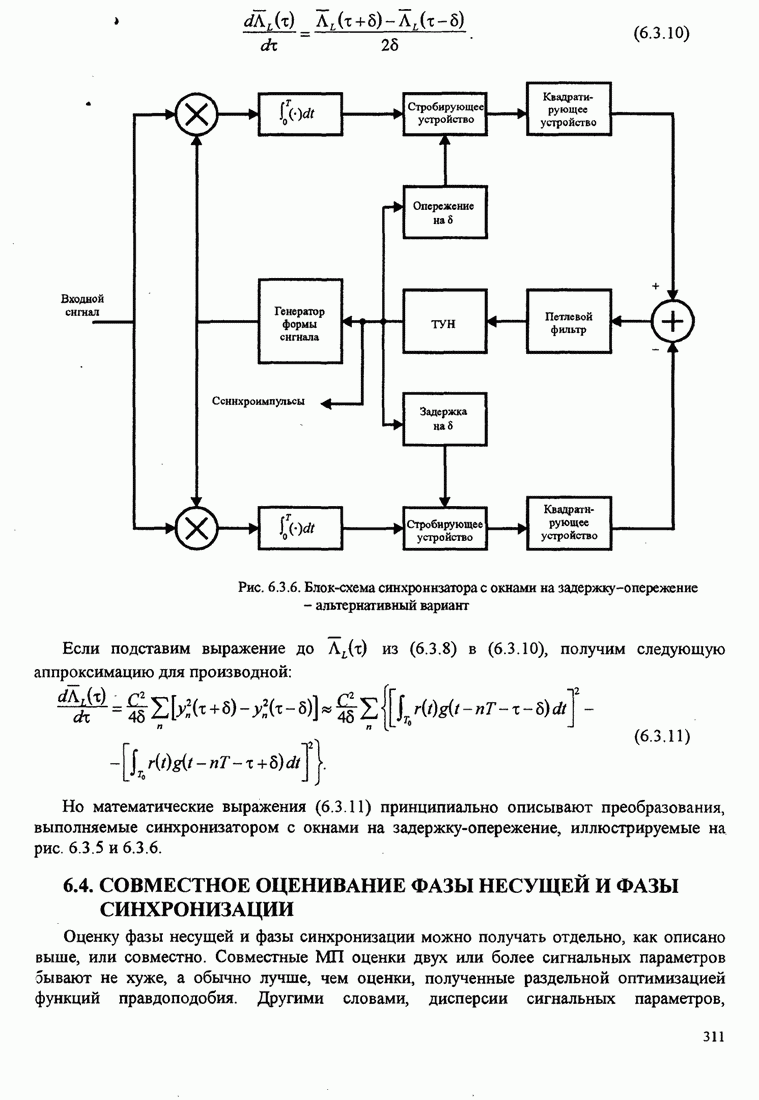
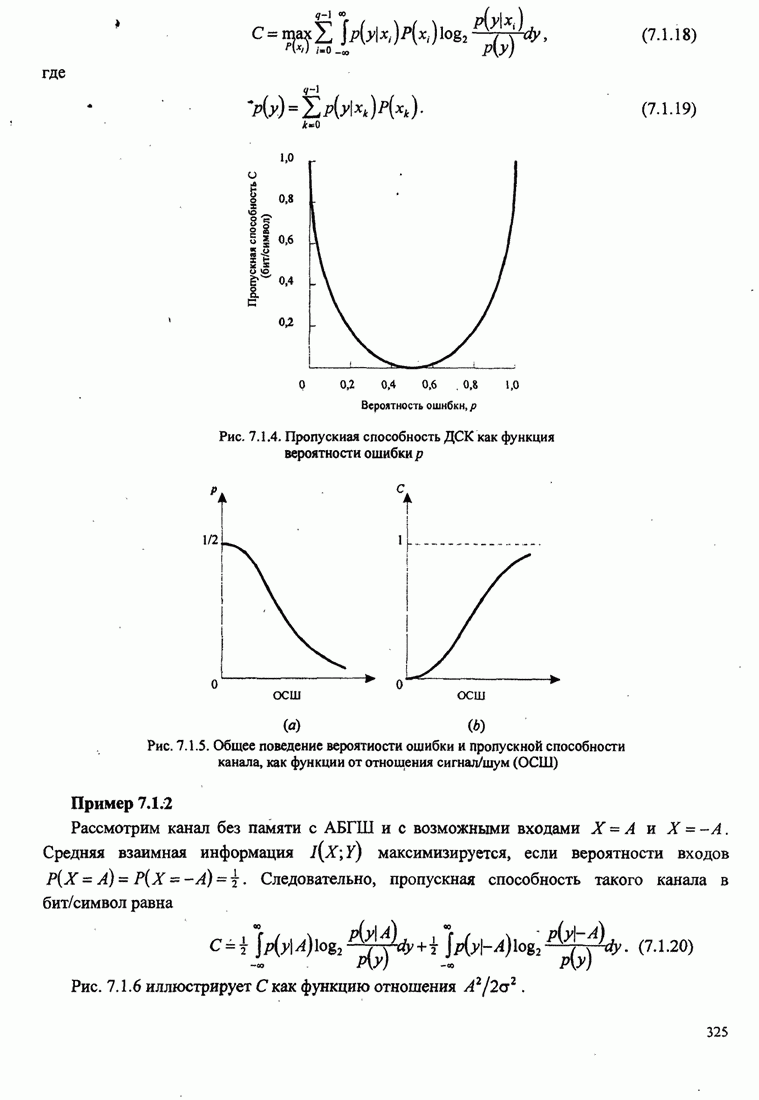
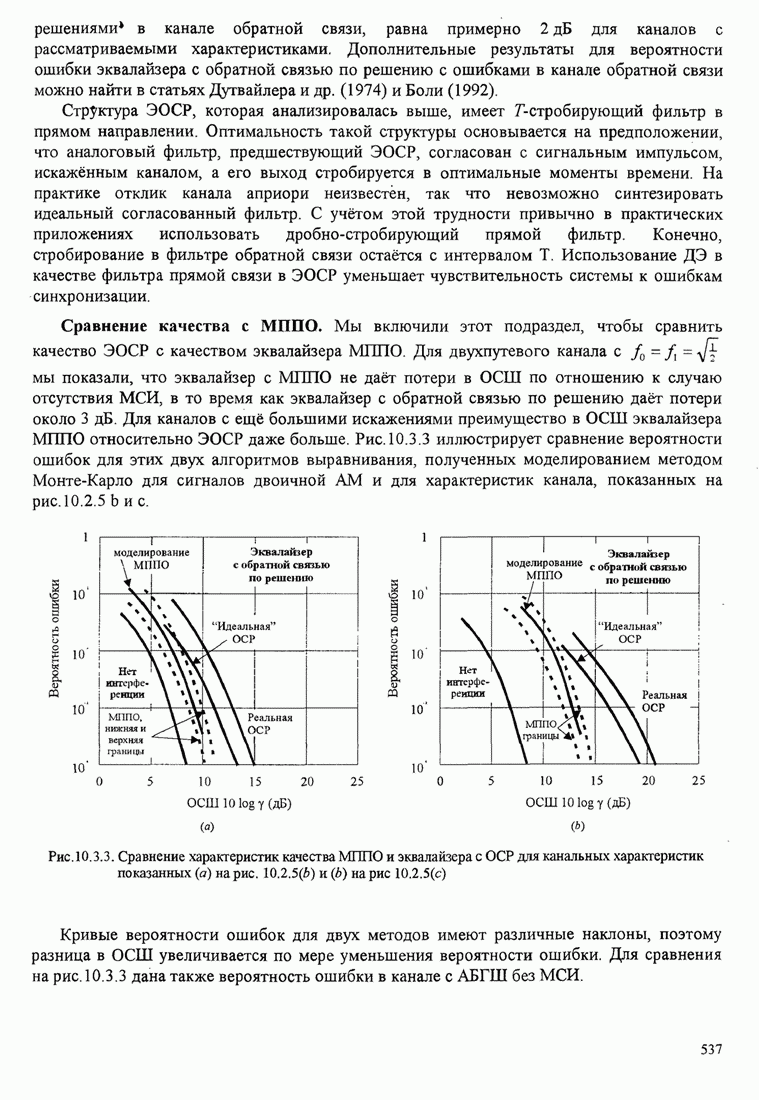
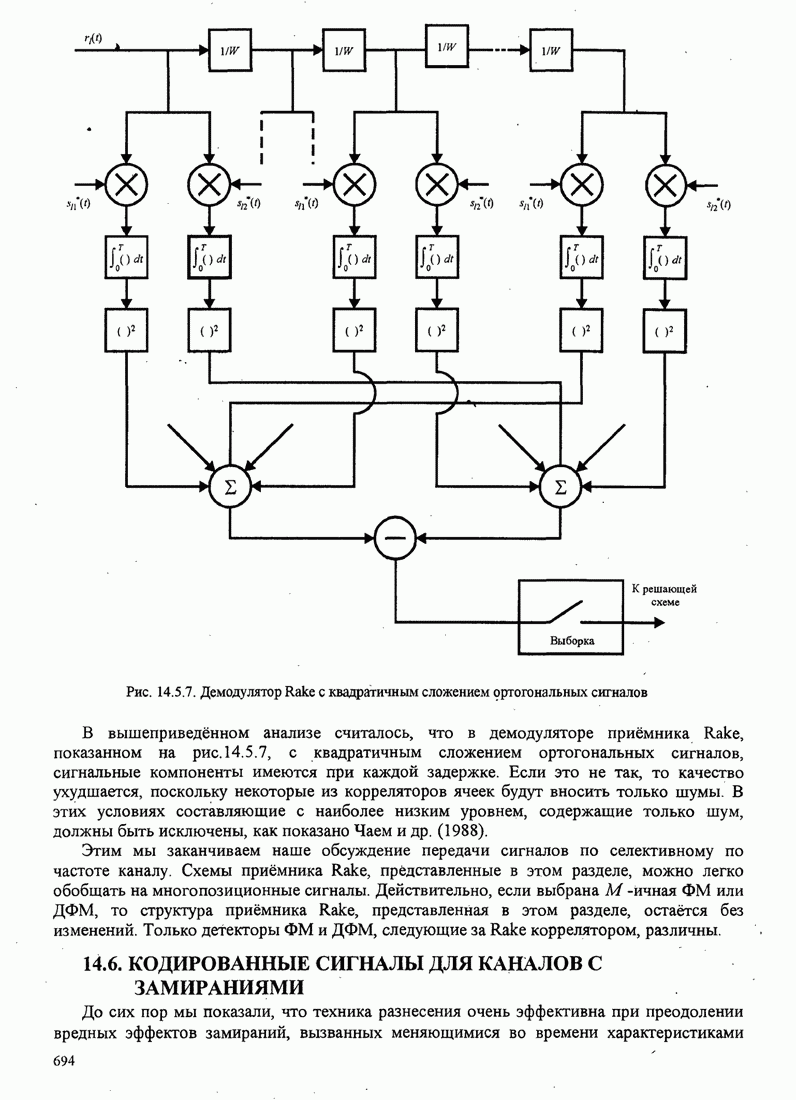
сигналов, как показано на рис. 7.2.1. Каждая система связи характеризуется
своей вероятностью ошибки.
кодовых
сигналов, как показано на рис. 7.2.1. Каждая система связи характеризуется
своей вероятностью ошибки.

Рис. 7.2.1. Ансамбль ![]() систем связи. Каждая система выбирает
одну из
систем связи. Каждая система выбирает
одну из ![]() возможных
последовательностей из
возможных
последовательностей из ![]() сигналов
сигналов
Предположим, что наш выбор ![]() кодовых
сигналов основан на случайном выборе из множества
кодовых
сигналов основан на случайном выборе из множества ![]() возможных
ансамблей кодов. Таким образом, случайный выбор
возможных
ансамблей кодов. Таким образом, случайный выбор ![]() -го кода, обозначенного
-го кода, обозначенного ![]() , происходит с
вероятностью
, происходит с
вероятностью
![]() (7.2.7)
(7.2.7)
и соответствующую условную вероятность
ошибки для этого выбора кодовых сигналов обозначим ![]() . Тогда средняя вероятность
ошибки по всему набору кодов
. Тогда средняя вероятность
ошибки по всему набору кодов
 (7.2.8)
(7.2.8)
где верхняя черта над ![]() означает
усреднение по ансамблю кодов.
означает
усреднение по ансамблю кодов.
Ясно,
что некоторые выборы кодов приведут к большим вероятностям ошибки. Например,
код, который сопоставит все ![]()
![]() -битовых последовательностей одну и ту
же вершину гиперкуба приведет к очень большой вероятности ошибки. В таком
случае
-битовых последовательностей одну и ту
же вершину гиперкуба приведет к очень большой вероятности ошибки. В таком
случае ![]() .
Однако будут так же выборы кодов, для которых
.
Однако будут так же выборы кодов, для которых ![]() . Следовательно, если мы получим
верхнюю границу для
. Следовательно, если мы получим
верхнюю границу для ![]() , эта граница
будет так же справедлива для тех кодов, для которых
, эта граница
будет так же справедлива для тех кодов, для которых ![]() . Далее, если
. Далее, если
![]() при
при
![]() , тогда
мы можем делать заключение, что для этих кодов
, тогда
мы можем делать заключение, что для этих кодов ![]() , когда
, когда ![]() .
.
Для
того, чтобы определить верхнюю границу для ![]() , рассмотрим
передачу
, рассмотрим
передачу ![]() -битового
сообщения
-битового
сообщения ![]() , где
, где ![]() или 1 для
или 1 для ![]() . Условная вероятность ошибки,
усредненная по ансамблям кодов, равна
. Условная вероятность ошибки,
усредненная по ансамблям кодов, равна
![]() , (7.2.9)
, (7.2.9)
где ![]() -
условная вероятность ошибки
-
условная вероятность ошибки ![]() -битового сообщения
-битового сообщения ![]() , которое передается
посредством кода
, которое передается
посредством кода ![]() .
Для
.
Для ![]() -го
кода вероятность ошибки
-го
кода вероятность ошибки ![]() имеет верхнюю границу
имеет верхнюю границу
 (7.2.10)
(7.2.10)
где![]() -
вероятность ошибки для двоичной системы связи, которая использует сигнальные
векторы
-
вероятность ошибки для двоичной системы связи, которая использует сигнальные
векторы ![]() и
и![]() для передачи одного из двух равновероятных
для передачи одного из двух равновероятных ![]() -битовых сообщений. Таким образом,
-битовых сообщений. Таким образом,
 (7.2.11)
(7.2.11)
Меняя порядок суммирования в (7.2.11), получаем
 (7.2.12)
(7.2.12)
где![]() представляет
среднюю по ансамблю вероятность
представляет
среднюю по ансамблю вероятность ![]() полученную усреднением по
полученную усреднением по ![]() кодам или по
кодам или по ![]() системам связи.
системам связи.
Для канала с АБГШ вероятность ошибки
двоичной системы ![]() равна
равна
 ,
(7.2.13)
,
(7.2.13)
где
![]() . Если
. Если ![]() и
и ![]() отличаются
по
отличаются
по ![]() координатам, то
координатам, то
 (7.2.14)
(7.2.14)
Следовательно,
 (7.2.15)
(7.2.15)
Теперь мы можем усреднить ![]() по
ансамблю кодов. Поскольку все коды равновероятны, сигнальный вектор
по
ансамблю кодов. Поскольку все коды равновероятны, сигнальный вектор ![]() с равной
вероятностью может соответствовать любой из
с равной
вероятностью может соответствовать любой из ![]() возможных
вершин гиперкуба, и это имеет место статистически независимо от соответствия
любой вершины сигнальному вектору
возможных
вершин гиперкуба, и это имеет место статистически независимо от соответствия
любой вершины сигнальному вектору![]() .
Следовательно,
.
Следовательно, ![]() и
и ![]() независимо
для всех
независимо
для всех ![]() .Как следствие, вероятность того, что
.Как следствие, вероятность того, что ![]() и
и ![]() различаются в
различаются в ![]() позициях,
равна
позициях,
равна
 (7.2.16)
(7.2.16)
Таким образом, математическое ожидание ![]() по
ансамблю кодов можно выразить так:
по
ансамблю кодов можно выразить так:
 . (7.2.17)
. (7.2.17)
Результат (7.2.17) можно упростить, если
воспользоваться верхней границей для ![]() -функции
-функции

Таким образом
 . (7.2.18)
. (7.2.18)
Мы видим, что правая часть (7.2.18) не
зависит от индексов ![]() и
и ![]() .
Следовательно, если мы подставим границу (7.2.18) в (7.2.12), то получим
.
Следовательно, если мы подставим границу (7.2.18) в (7.2.12), то получим
 .
.
Наконец, безусловную среднюю вероятность
ошибки ![]() получим усреднением
получим усреднением ![]() по всем
по всем ![]() -битовым информационным
последовательностям. Таким образом,
-битовым информационным
последовательностям. Таким образом,
 (7.2.19)
(7.2.19)
Этот
результат можно выразить в более удобной форме, прежде всего определив параметр
![]() , который
называется предельной скоростью и имеет размерность бит/измерение
, который
называется предельной скоростью и имеет размерность бит/измерение
![]() (7.2.20)
(7.2.20)
Тогда (7.2.19) можно записать в виде
![]() (7.2.21)
(7.2.21)
Поскольку
![]() , то
(7.2.21) можно выразить так
, то
(7.2.21) можно выразить так
![]() (7.2.22)
(7.2.22)
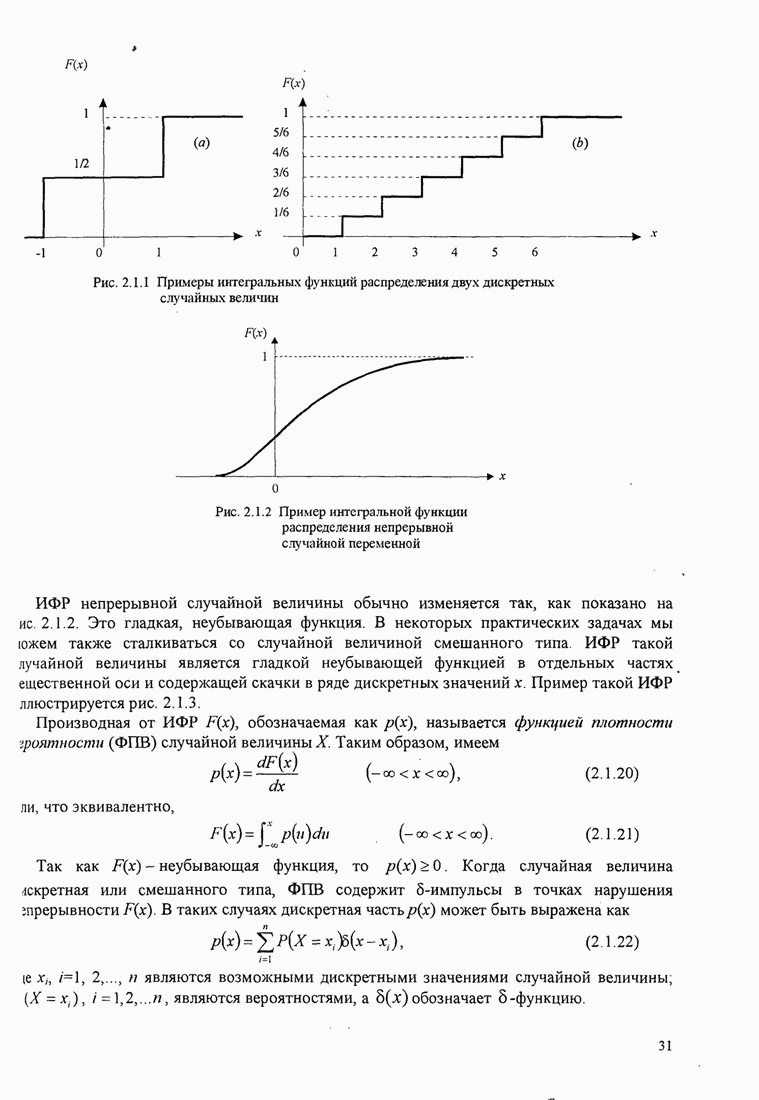
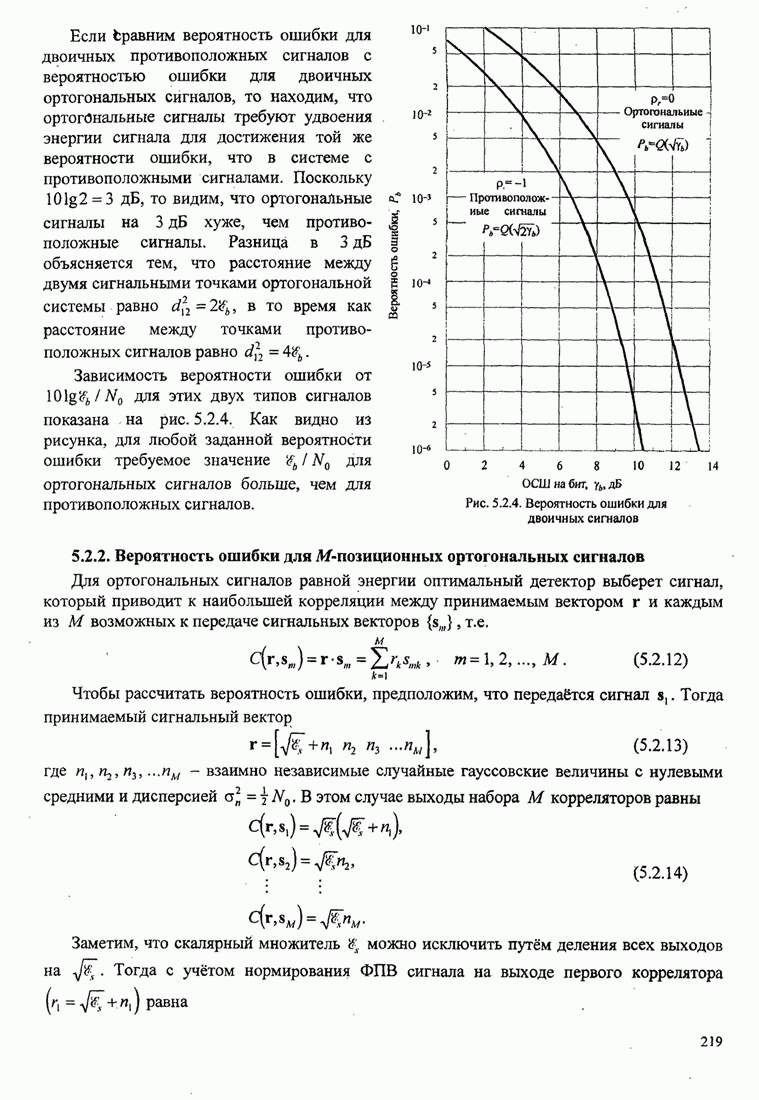
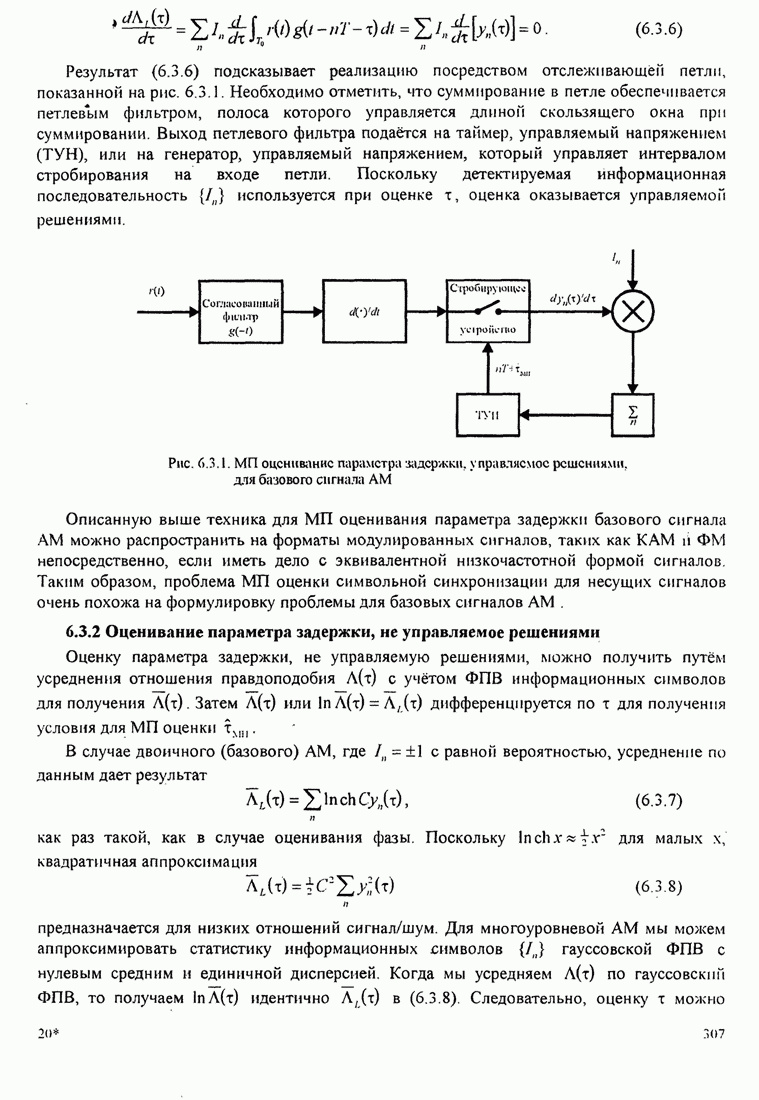
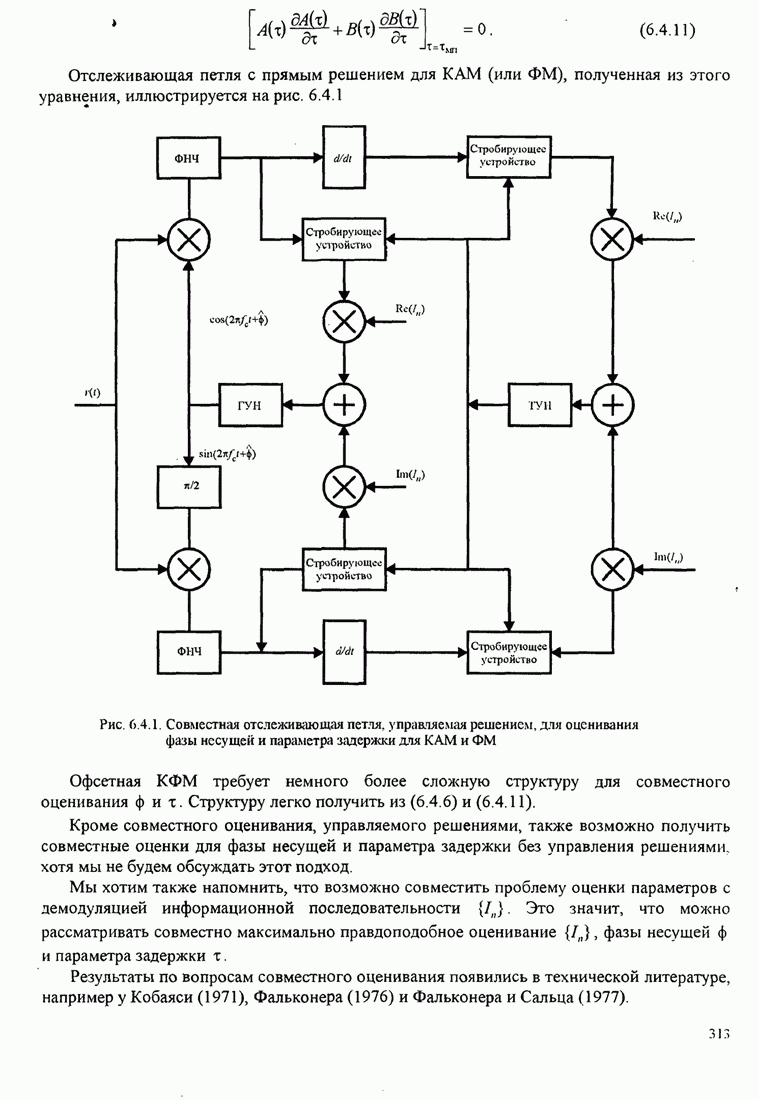
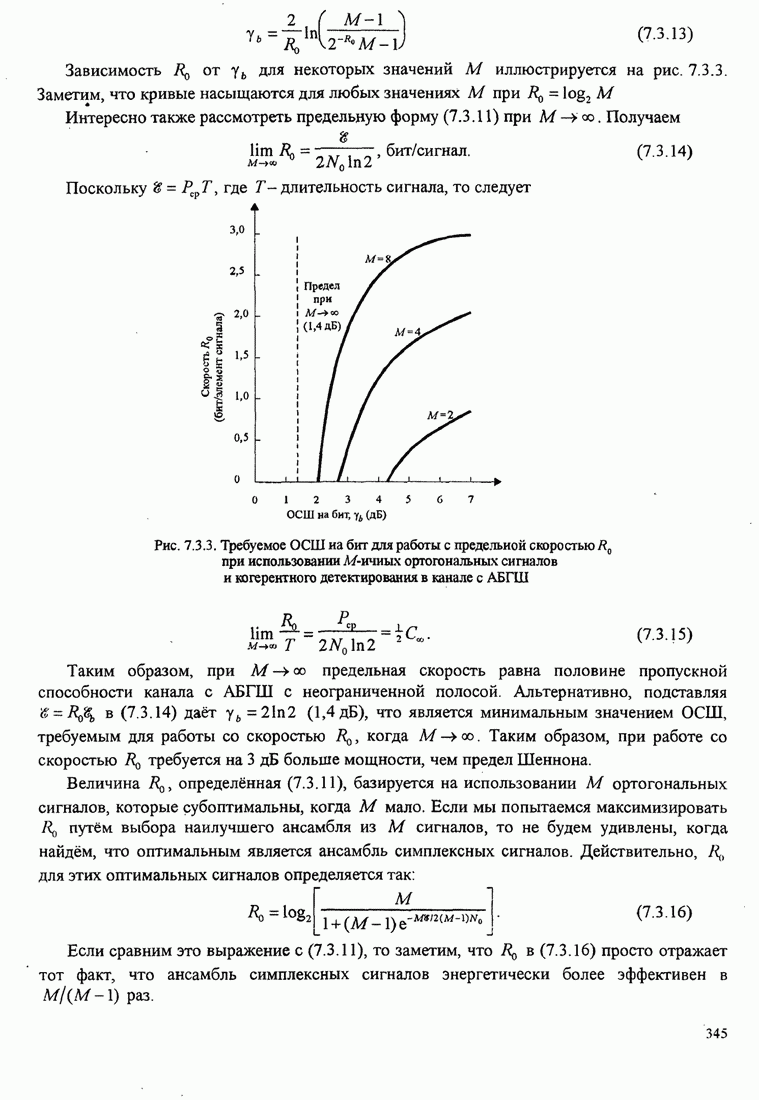
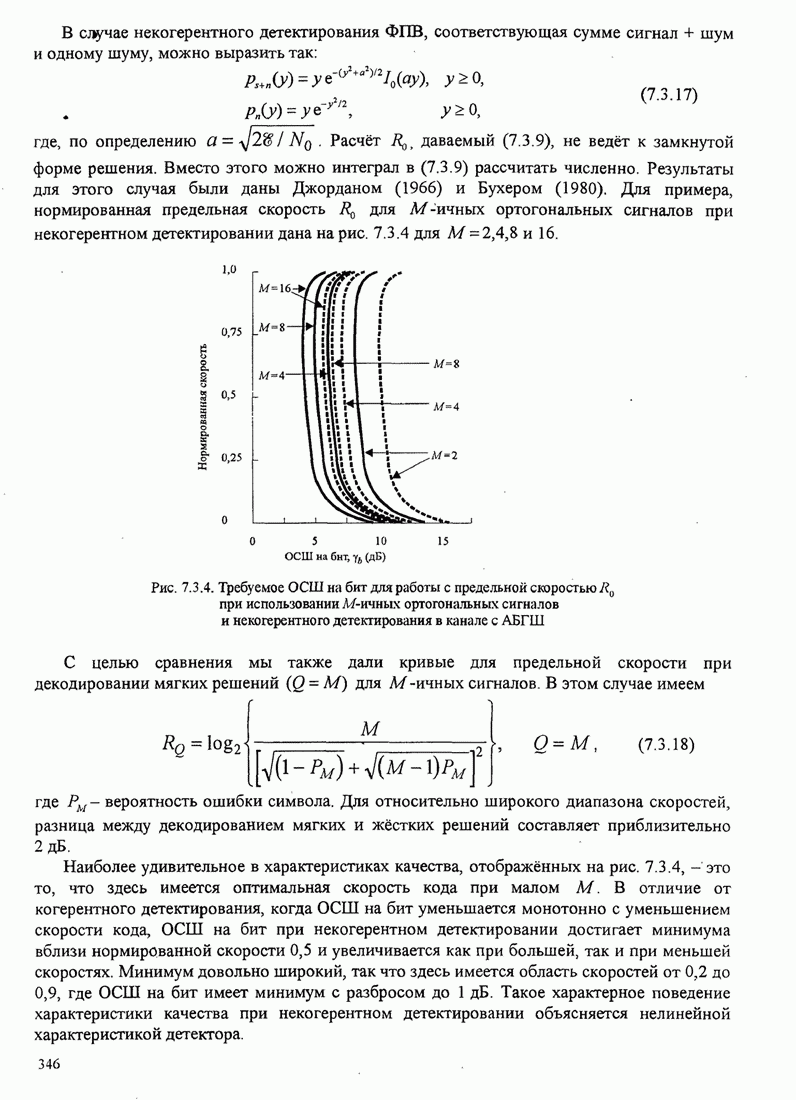
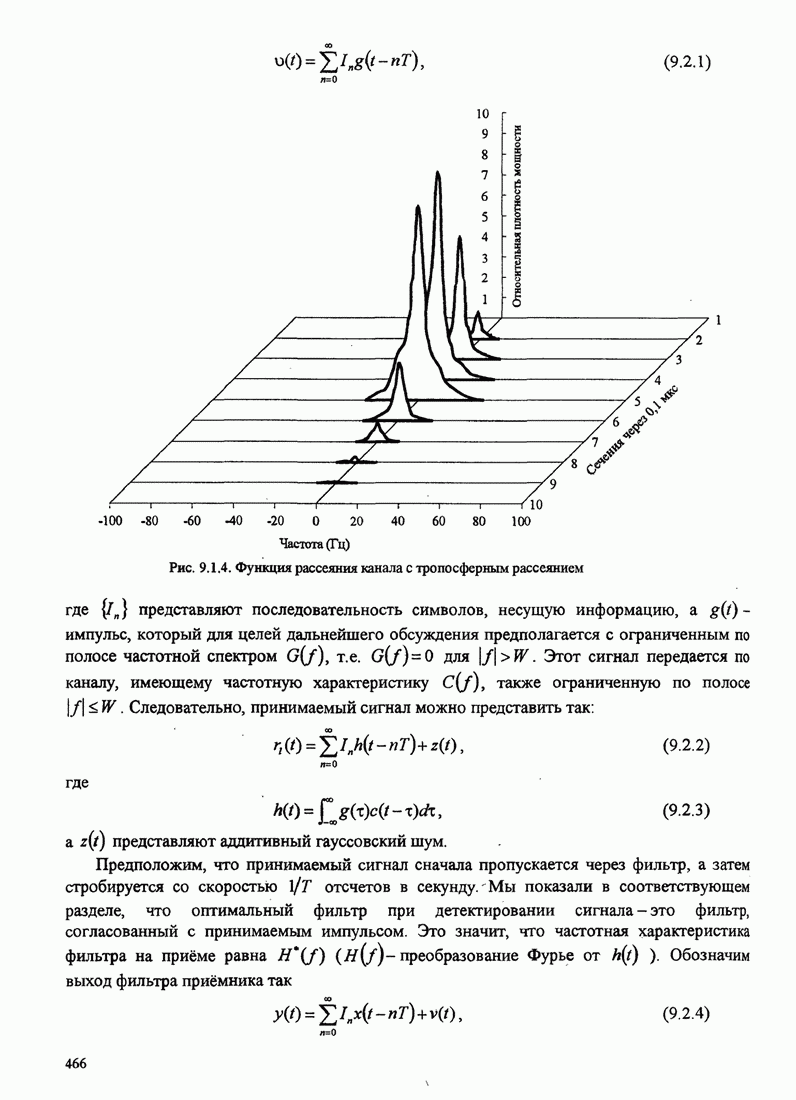
Зависимость
параметра ![]() как функции от
как функции от ![]() показана
на рис. 7.2.2.
показана
на рис. 7.2.2.
Видно,
что ![]() .
Следовательно,
.
Следовательно, ![]() ,
, ![]() , если
информационная скорость
, если
информационная скорость![]() .
.
Альтернативно (7.2.21) можно выразить так:
![]() (7.2.23)
(7.2.23)
Отношение
![]() также имеет размерность бит/измерение и может быть
определено так:
также имеет размерность бит/измерение и может быть
определено так:
![]() (7.2.24)
(7.2.24)
Таким
образом, ![]() - это скорость кода, и
- это скорость кода, и
![]() (7.2.25)
(7.2.25)

Рис. 7.2.2. Предельная скорость передачи ![]() как
функция ОСШ на измерение в децибелах
как
функция ОСШ на измерение в децибелах
Мы
замечаем, что, когда ![]() , средняя
вероятность ошибки
, средняя
вероятность ошибки ![]() , когда длина кодового блока
, когда длина кодового блока![]() . Поскольку среднюю
величину вероятности ошибки можно сделать произвольно малой при
. Поскольку среднюю
величину вероятности ошибки можно сделать произвольно малой при ![]() , отсюда следует,
что существуют коды в ансамбле
, отсюда следует,
что существуют коды в ансамбле ![]() кодов,
которые имеют вероятность ошибки не больше, чем
кодов,
которые имеют вероятность ошибки не больше, чем ![]() .
.
Из
определения средней вероятности ошибки, данного выше, мы заключаем, что хорошие
коды существуют. Хотя мы нормально не можем выбрать коды случайно, интересно
рассмотреть вопрос о том, может ли случайно выбранный код быть хорошим.
Действительно, можно легко показать, что в ансамбле имеется много хороших
кодов. Сначала заметим, что![]() - это средняя
по ансамблю вероятность ошибки, полученная усреднением по всем кодам и что все
отдельные вероятности, очевидно, положительные величины. Если код выбран
случайно, вероятность того, что его вероятность ошибки
- это средняя
по ансамблю вероятность ошибки, полученная усреднением по всем кодам и что все
отдельные вероятности, очевидно, положительные величины. Если код выбран
случайно, вероятность того, что его вероятность ошибки
![]() , меньше, чем
, меньше, чем ![]() . Следовательно, не больше, чем 10
процентов кодов имеет вероятность ошибки, которая превосходит
. Следовательно, не больше, чем 10
процентов кодов имеет вероятность ошибки, которая превосходит ![]() , и не больше, чем
1 процент кодов имеют вероятность ошибки, которая превосходит
, и не больше, чем
1 процент кодов имеют вероятность ошибки, которая превосходит ![]() .
.
Мы
хотим подчеркнуть, что коды с вероятностью ошибки, превосходящей ![]() ,
не является обязательно плохими кодами. Например, предположим, что среднюю
вероятность ошибки
,
не является обязательно плохими кодами. Например, предположим, что среднюю
вероятность ошибки ![]() можно получить,
используя коды с размерностью
можно получить,
используя коды с размерностью ![]() , когда
, когда ![]() .
Тогда, если мы выберем код с вероятностью ошибки
.
Тогда, если мы выберем код с вероятностью ошибки![]() , мы можем скомпенсировать это
увеличение вероятности ошибки увеличением длины кода
, мы можем скомпенсировать это
увеличение вероятности ошибки увеличением длины кода ![]() от
от ![]() до
до ![]() . Таким образом, скромным
увеличением размерности мы имеем код с
. Таким образом, скромным
увеличением размерности мы имеем код с ![]() . Суммируя
скажем, хороших кодов в изобилии и, следовательно, их можно легко найти даже
случайным выбором.
. Суммируя
скажем, хороших кодов в изобилии и, следовательно, их можно легко найти даже
случайным выбором.
Также
интересно выразить среднюю вероятность ошибки в (7.2.25) через ОСШ на бит ![]() . Чтобы это
сделать, выразим энергию кодового сигнала так:
. Чтобы это
сделать, выразим энергию кодового сигнала так:
![]() . (7.2.26)
. (7.2.26)
Следовательно,
![]() . Также
заметим, что
. Также
заметим, что ![]() .
Таким образом, (7.2.25)
.
Таким образом, (7.2.25)
можно выразить так:
![]() (7.2.27)
(7.2.27)
где ![]() -
параметр, определяющей нормирование ОСШ и равный
-
параметр, определяющей нормирование ОСШ и равный
![]() . (7.2.28)
. (7.2.28)
Теперь заметим, что ![]() , когда
, когда ![]() при
условии, что ОСШ на бит
при
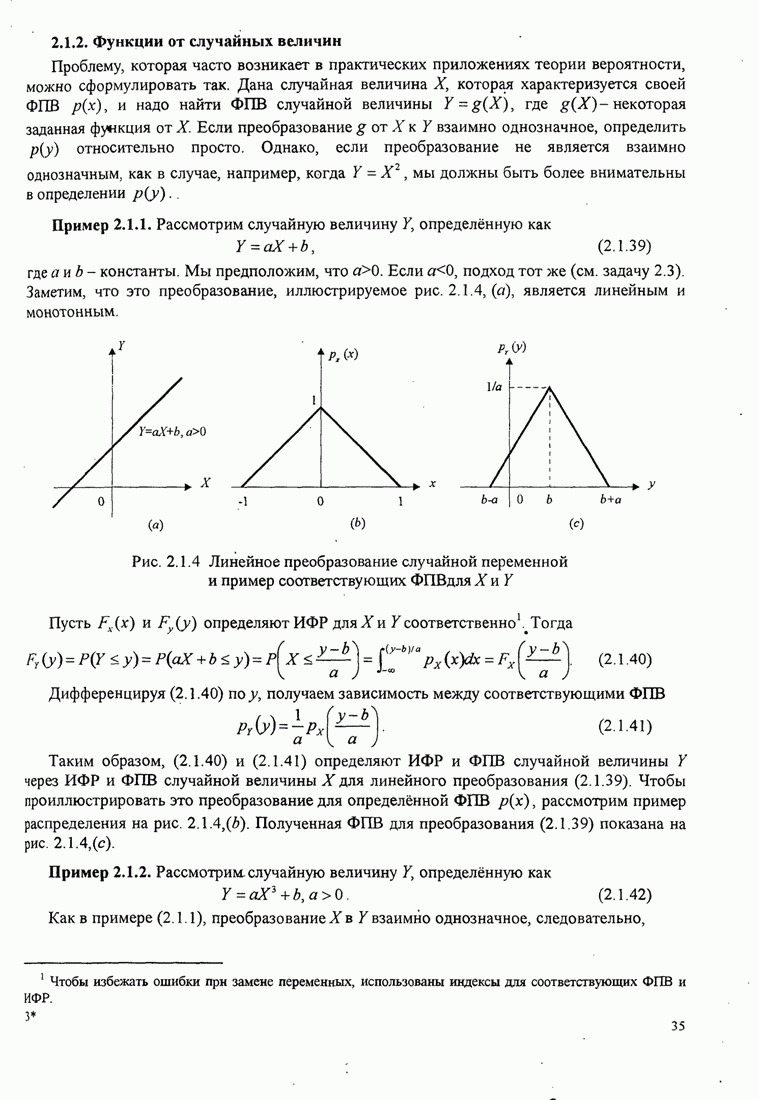
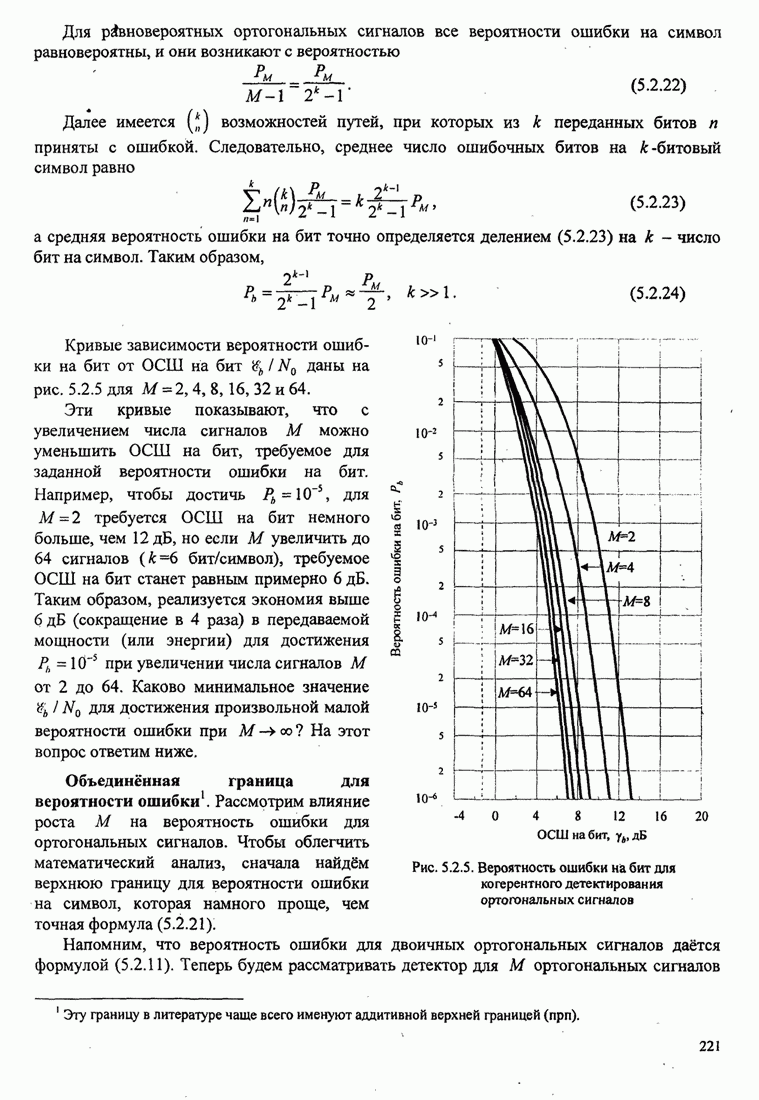
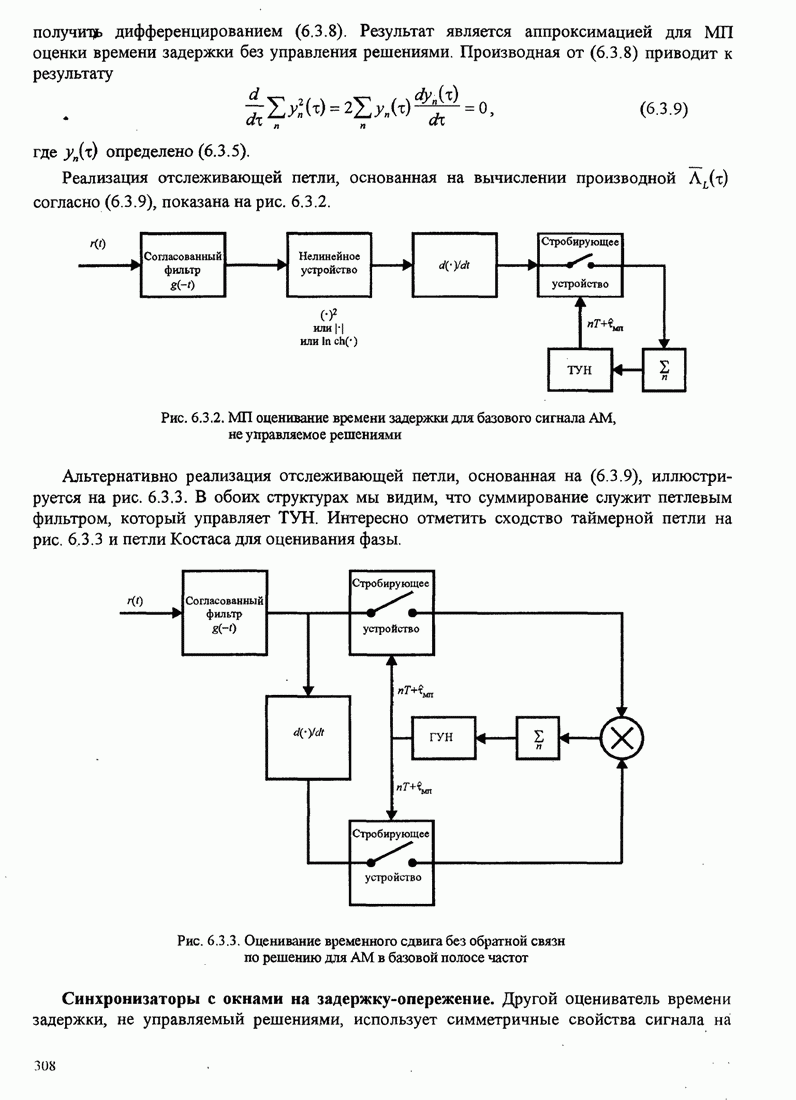
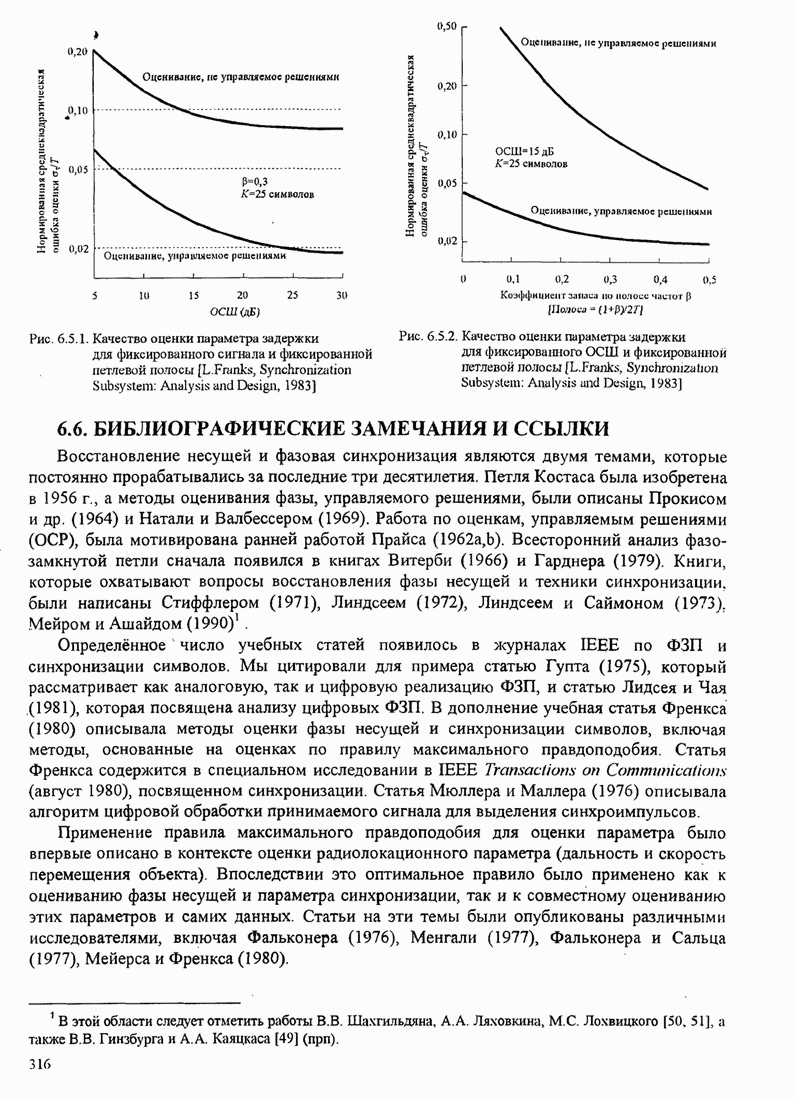
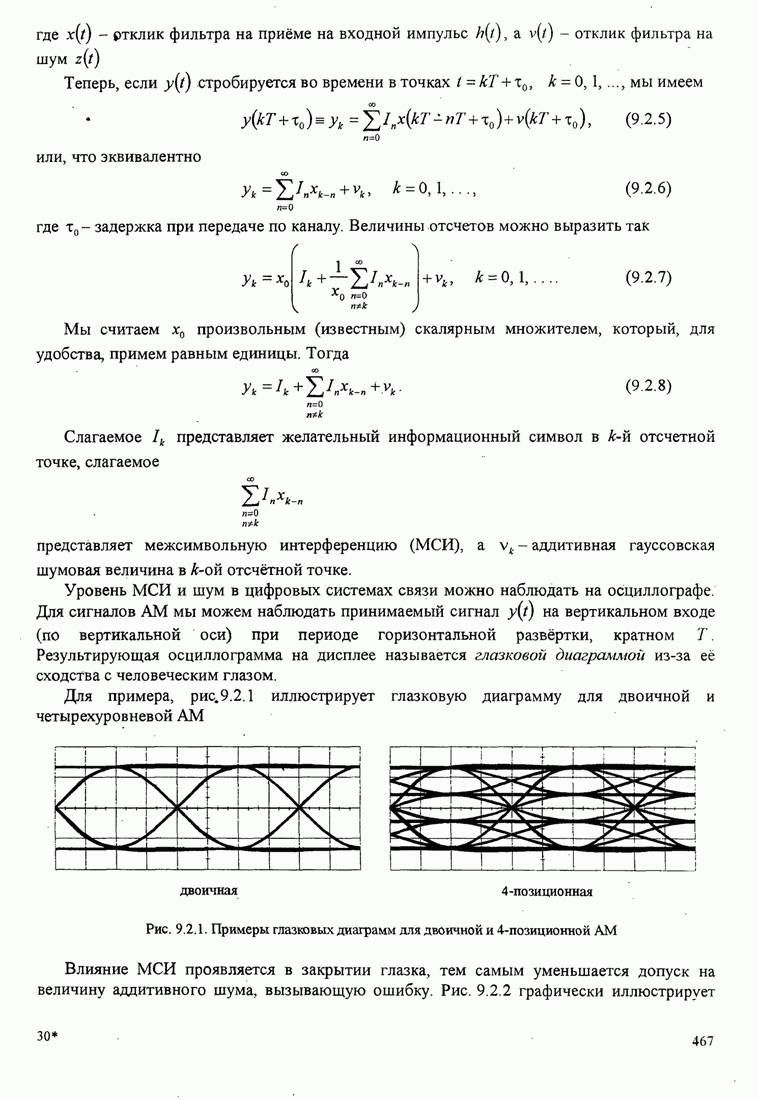
условии, что ОСШ на бит ![]() . Зависимость
. Зависимость ![]() от
от ![]() показана
на рис. 7.2.3.
показана
на рис. 7.2.3.

Pис. 7.2.3. Нижняя граница для ОСШ на бит для двоичных противоположных сигналов
Заметим, что когда ![]() ,
,![]() Следовательно, вероятность ошибки для
Следовательно, вероятность ошибки для
![]() двоичных
кодовых сигналов эквивалентна вероятности ошибки, полученной из объединенной
границы для
двоичных
кодовых сигналов эквивалентна вероятности ошибки, полученной из объединенной
границы для ![]() -ичных
ортогональных сигналов, предполагая, что размерность кодового сигнала
достаточно велика, так что
-ичных
ортогональных сигналов, предполагая, что размерность кодового сигнала
достаточно велика, так что![]() .
.
Параметр размерности ![]() который мы ввели в (7.2.5),
пропорционален полосе канала, требуемой для передачи сигналов. Напомним, что
согласно теореме отсчетов, сигнал с полосой
который мы ввели в (7.2.5),
пропорционален полосе канала, требуемой для передачи сигналов. Напомним, что
согласно теореме отсчетов, сигнал с полосой ![]() можно
представить отсчётами, взятыми со скоростью
можно
представить отсчётами, взятыми со скоростью ![]() отсчётов/с. Таким образом,
на временном интервале
отсчётов/с. Таким образом,
на временном интервале ![]() имеется
имеется ![]() отсчётов
или, что эквивалентно, имеем
отсчётов
или, что эквивалентно, имеем ![]() степеней свободы
(размерность). Следовательно,
степеней свободы
(размерность). Следовательно, ![]() можно приравнять
можно приравнять ![]() .
.
В заключение заметим, что двоичные
кодовые сигналы, рассмотренные в этом разделе, используются, когда ОСШ на
измерение мало, например,![]() . Однако, когда
. Однако, когда![]() , величина
, величина ![]() асимптотически
приближается к 1 бит/измерение. Поскольку скорость кода ограничена так, что она
меньше
асимптотически
приближается к 1 бит/измерение. Поскольку скорость кода ограничена так, что она
меньше![]() ,
то двоичные кодовые сигналы получаются неэффективными при
,
то двоичные кодовые сигналы получаются неэффективными при ![]() . В этом случае мы можем использовать
недвоичные кодовые сигналы для того, чтобы достичь увеличение числа бит на
измерение. Например, многоуровневый кодовый ансамбль можно синтезировать из
недвоичных кодов путем отражения каждого кодового элемента в один из возможных
уровней (как в AM). Такие коды
. В этом случае мы можем использовать
недвоичные кодовые сигналы для того, чтобы достичь увеличение числа бит на
измерение. Например, многоуровневый кодовый ансамбль можно синтезировать из
недвоичных кодов путем отражения каждого кодового элемента в один из возможных
уровней (как в AM). Такие коды
рассматриваются ниже.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
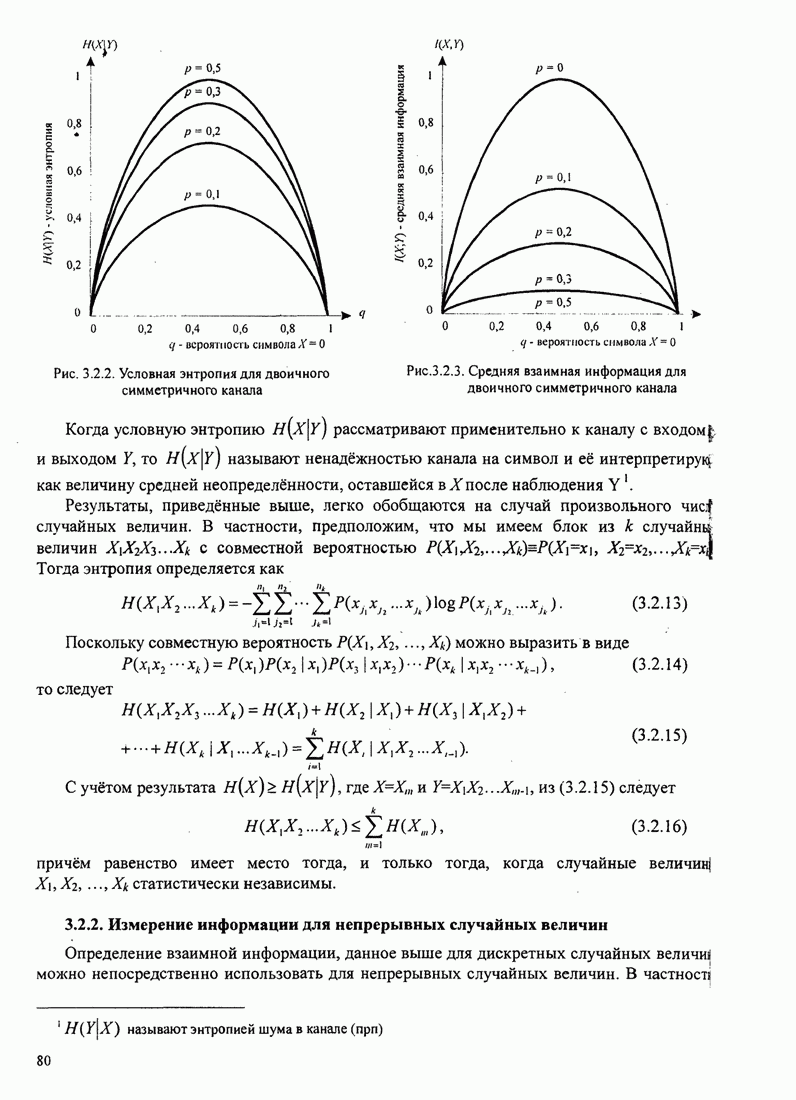
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
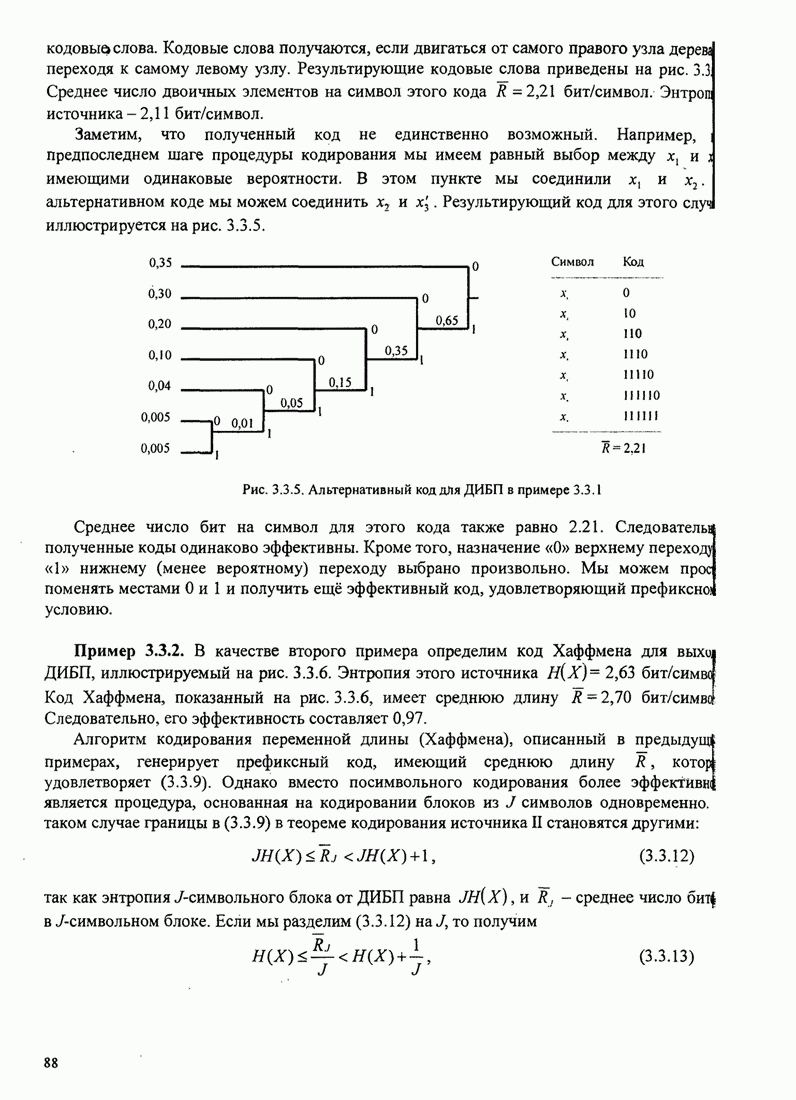
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
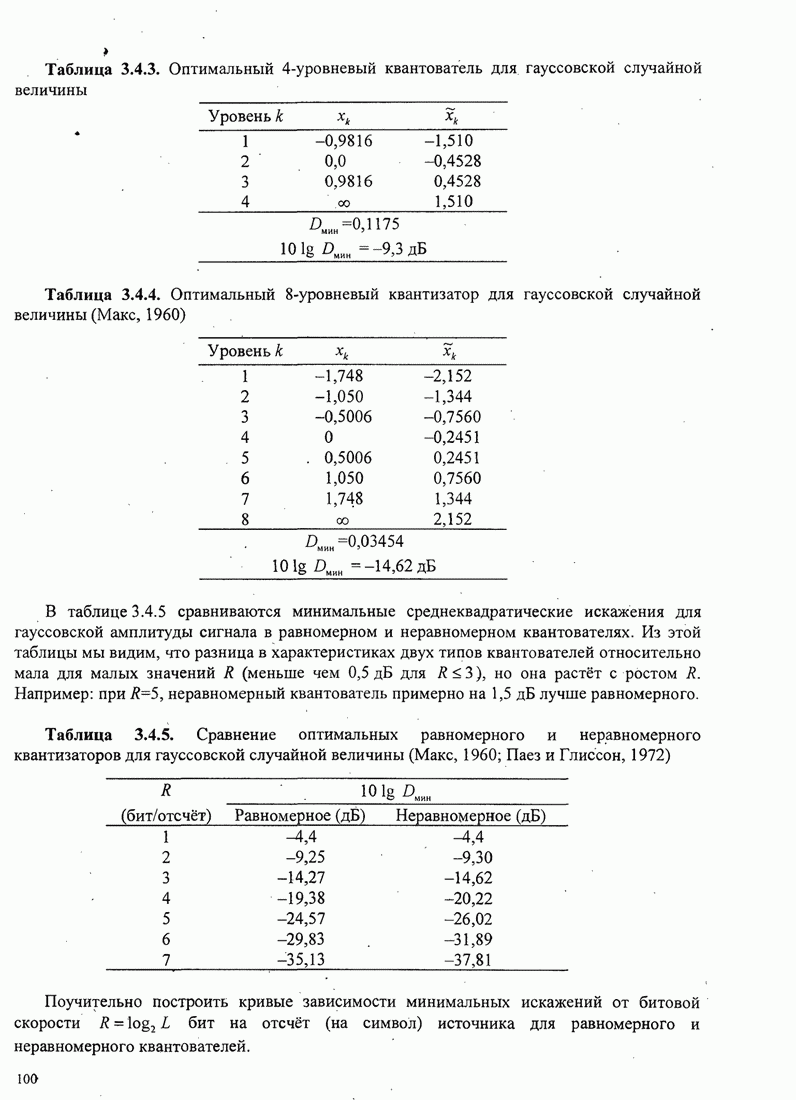
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
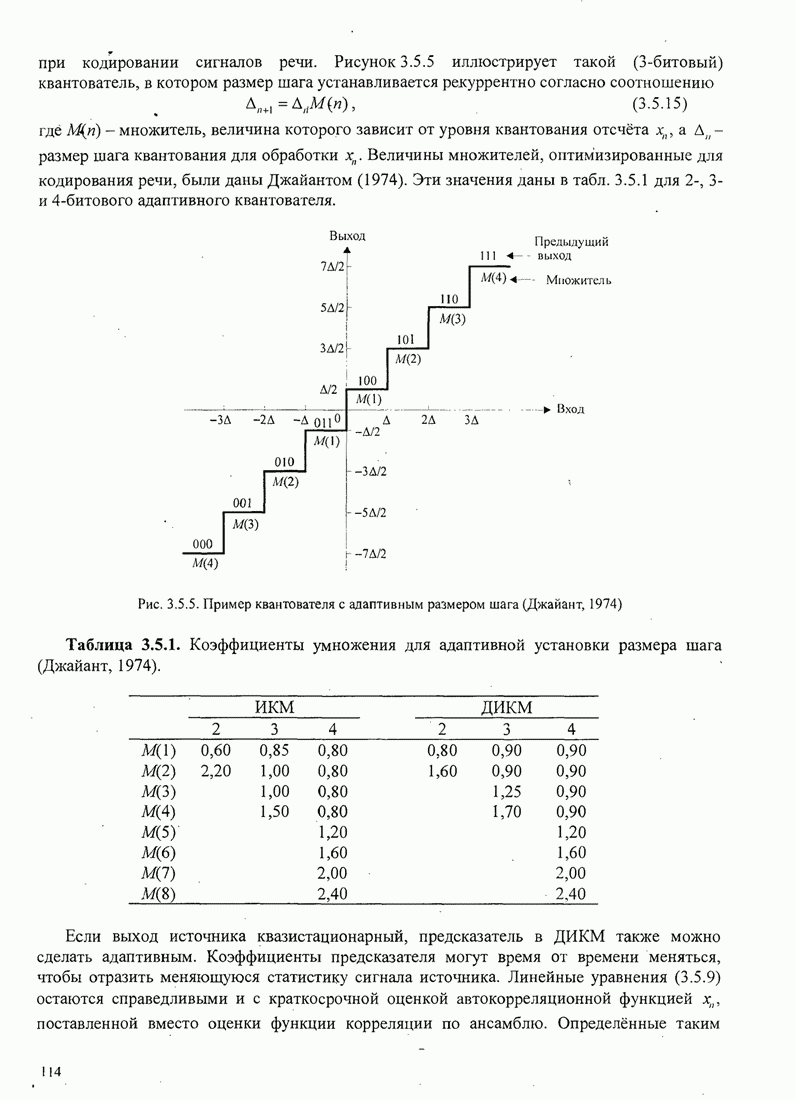
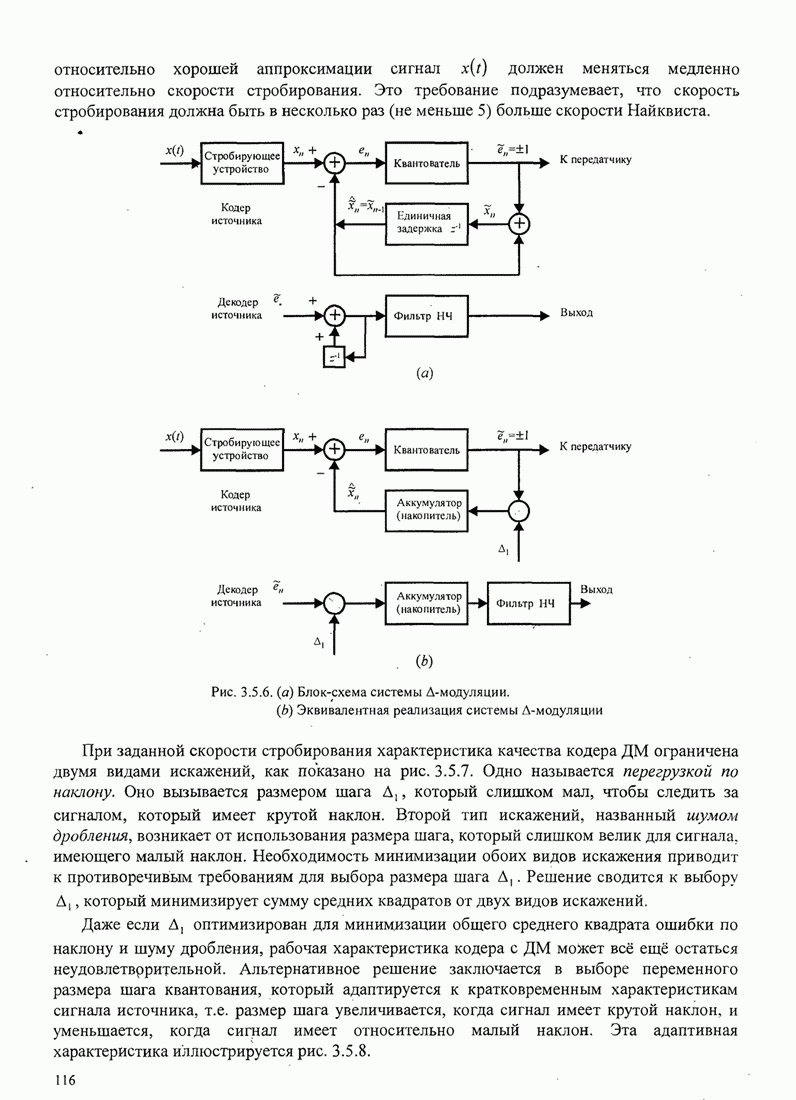
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
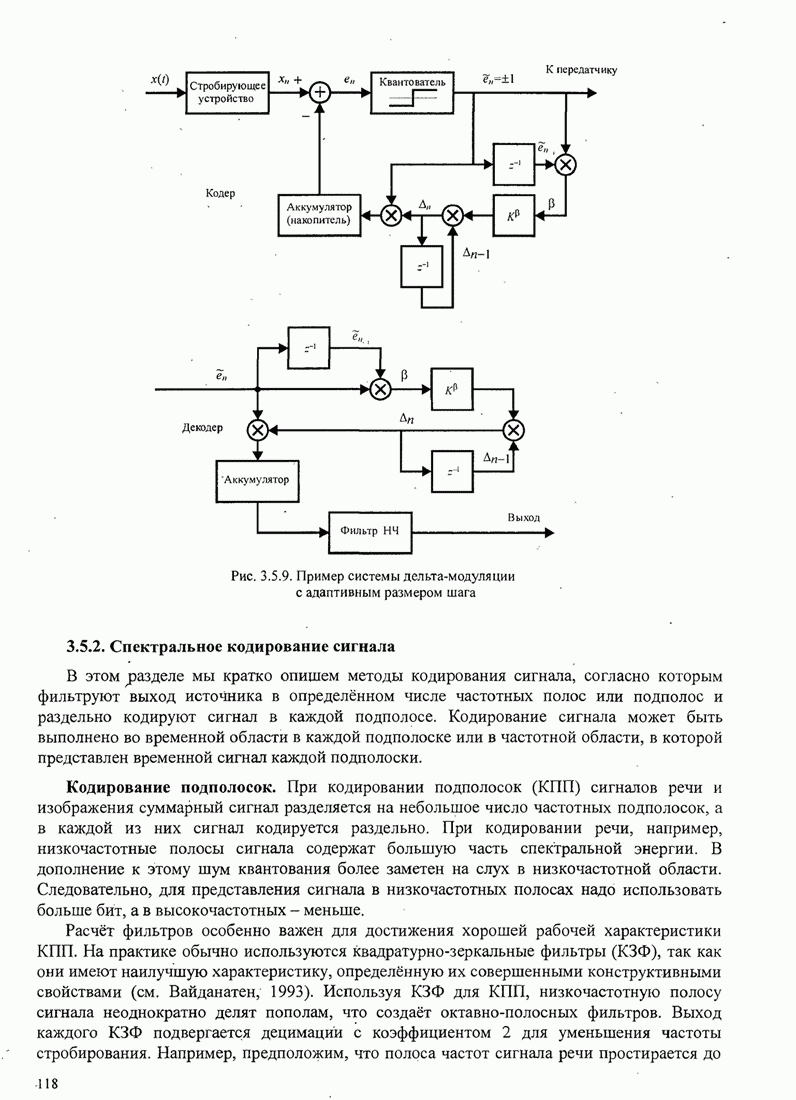
- 3.5.2. Спектральное кодирование сигнала
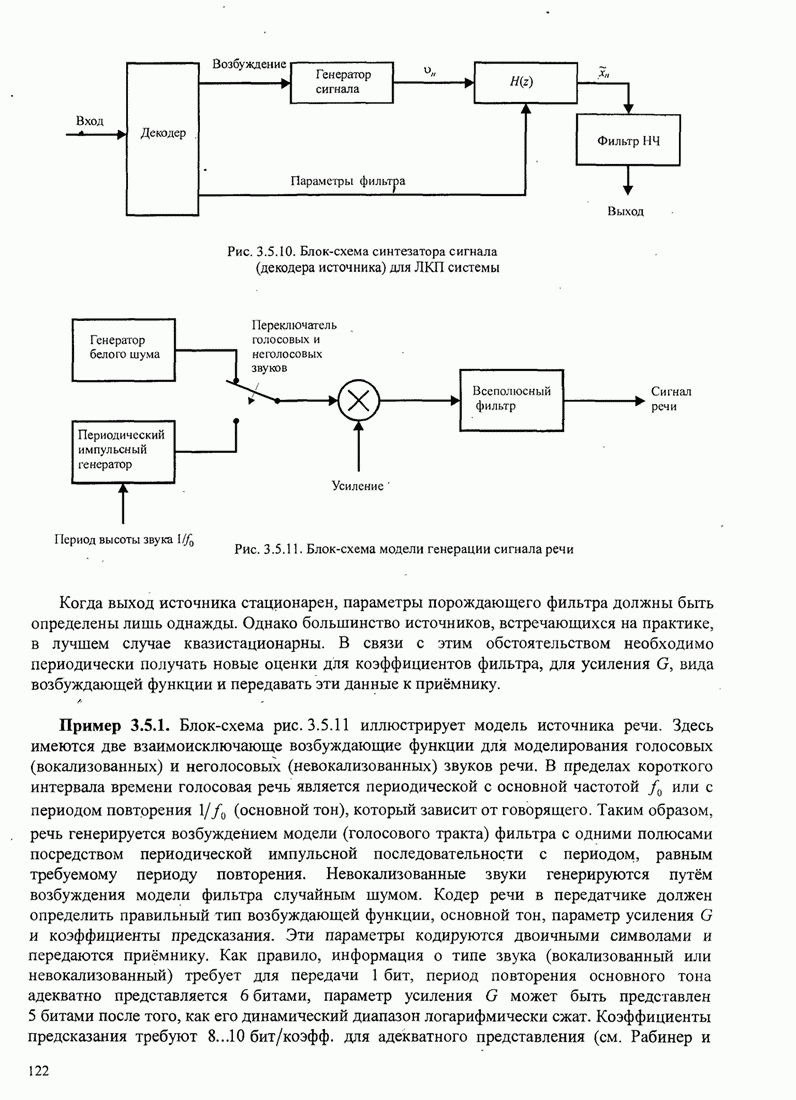
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
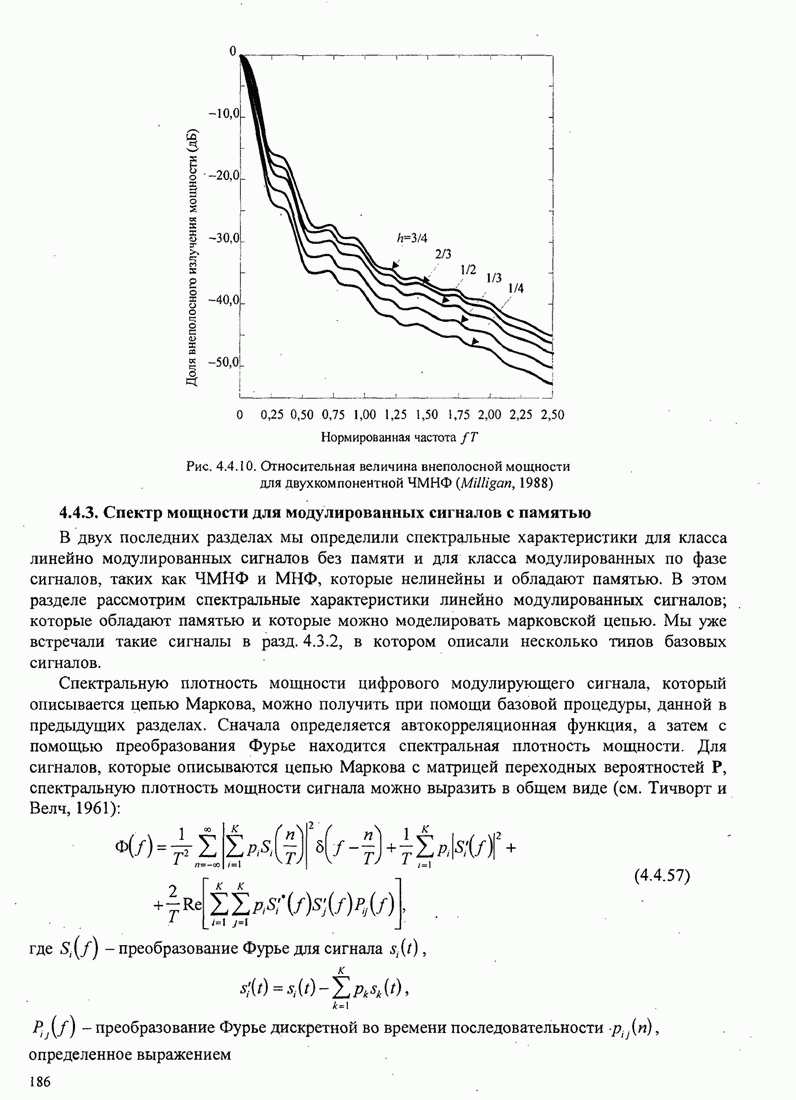
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
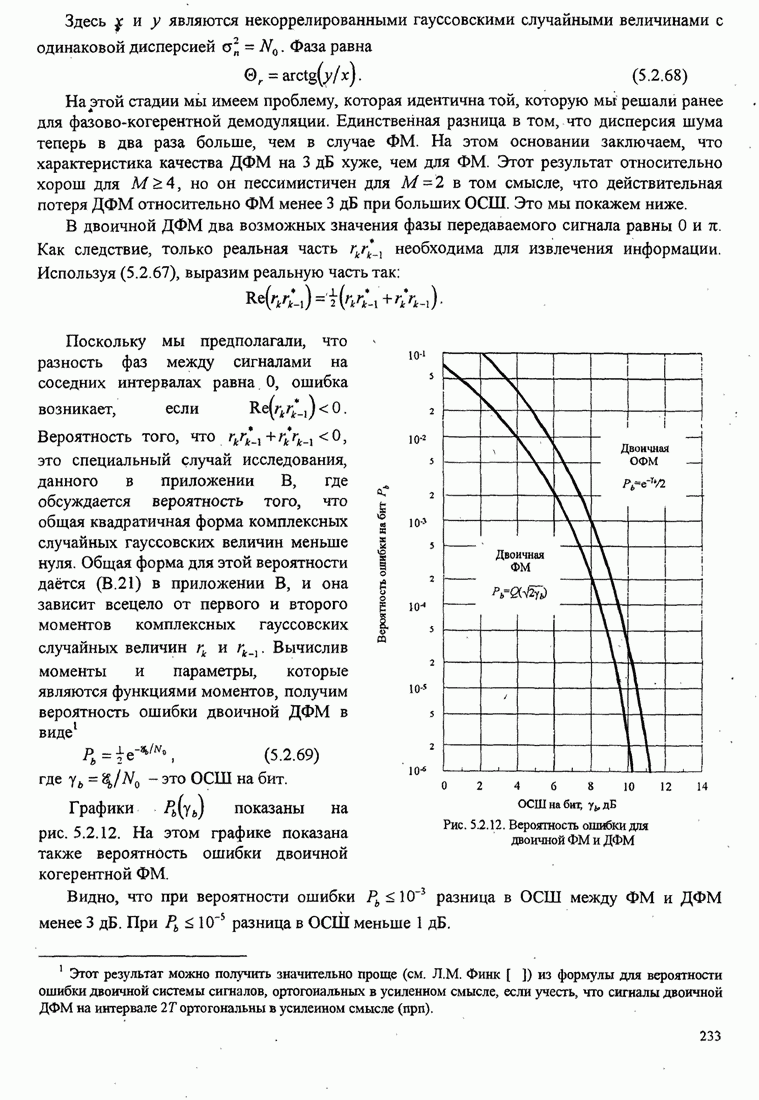
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
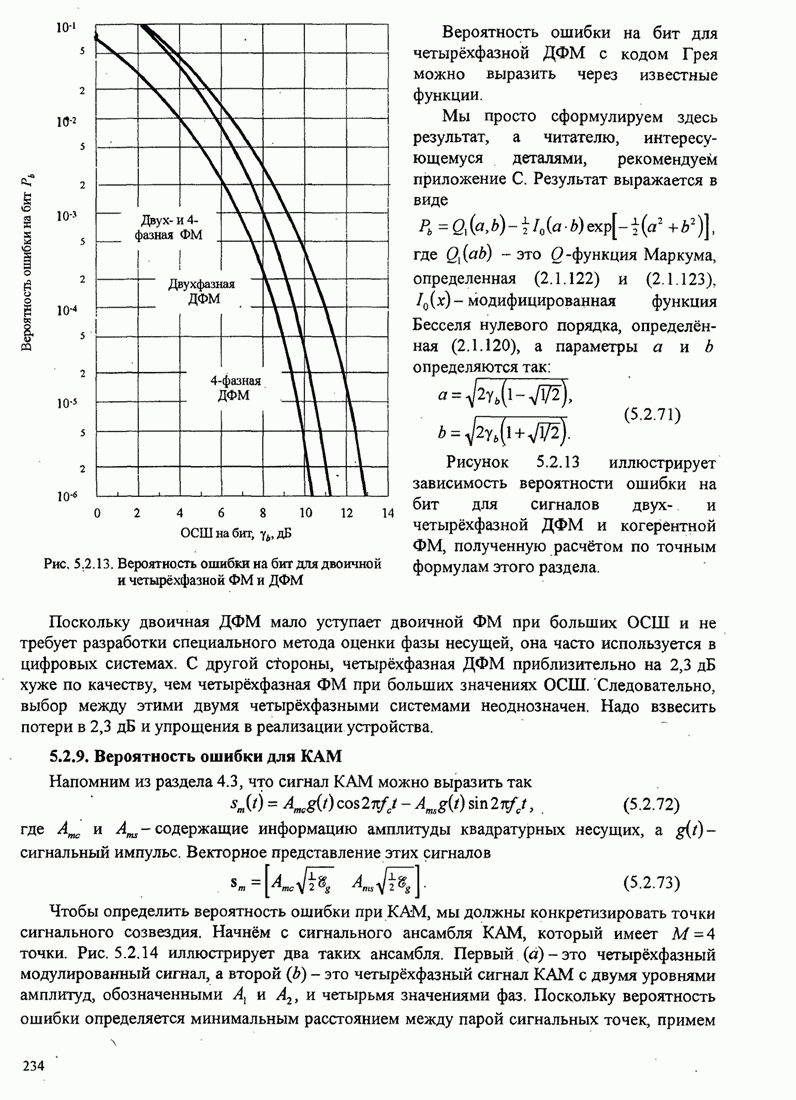
- 5.2.9. Вероятность ошибки для КАМ
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
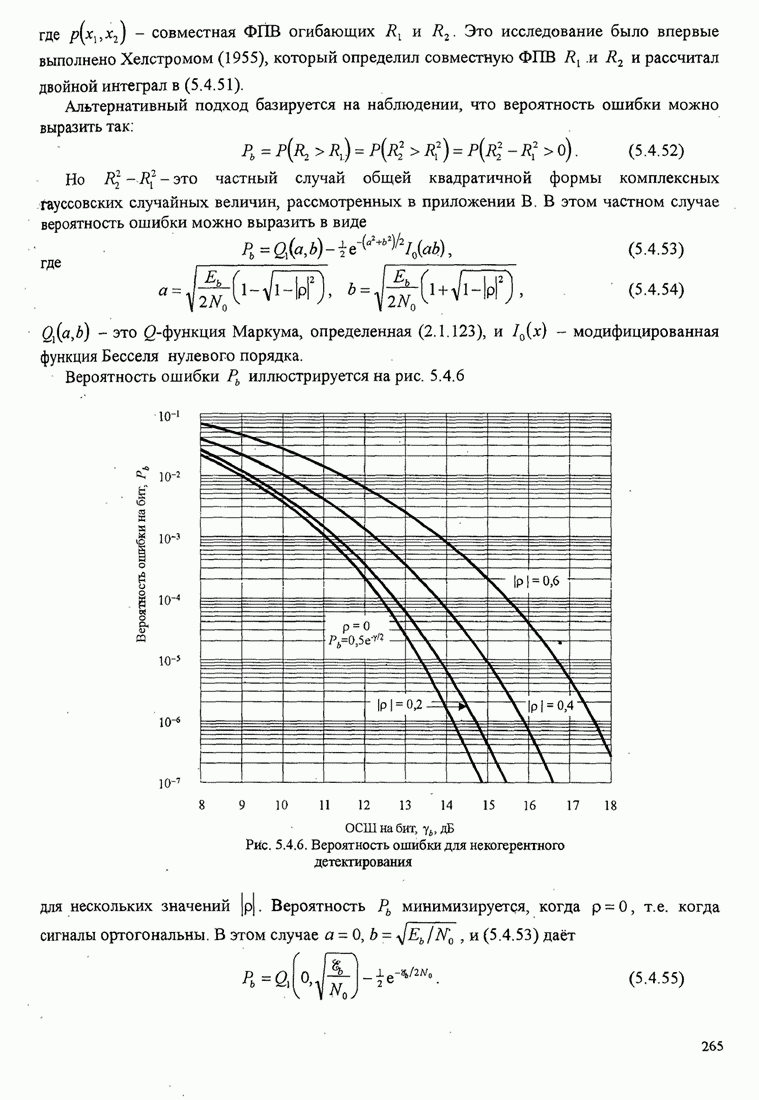
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
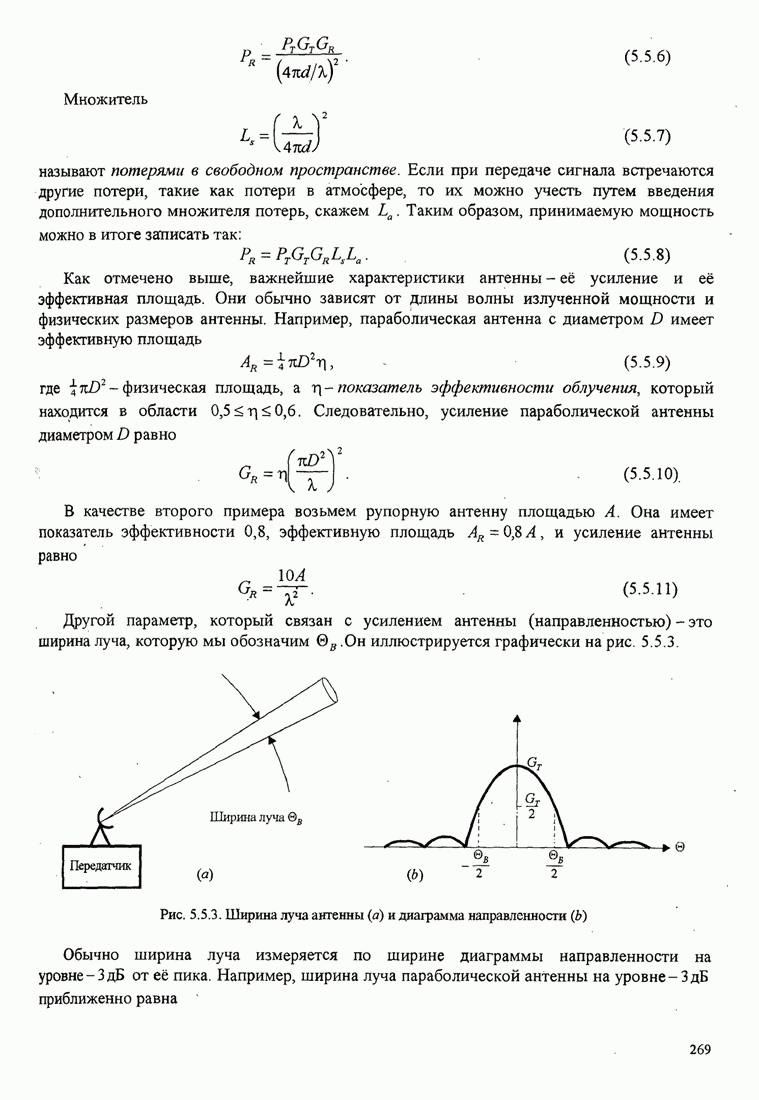
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
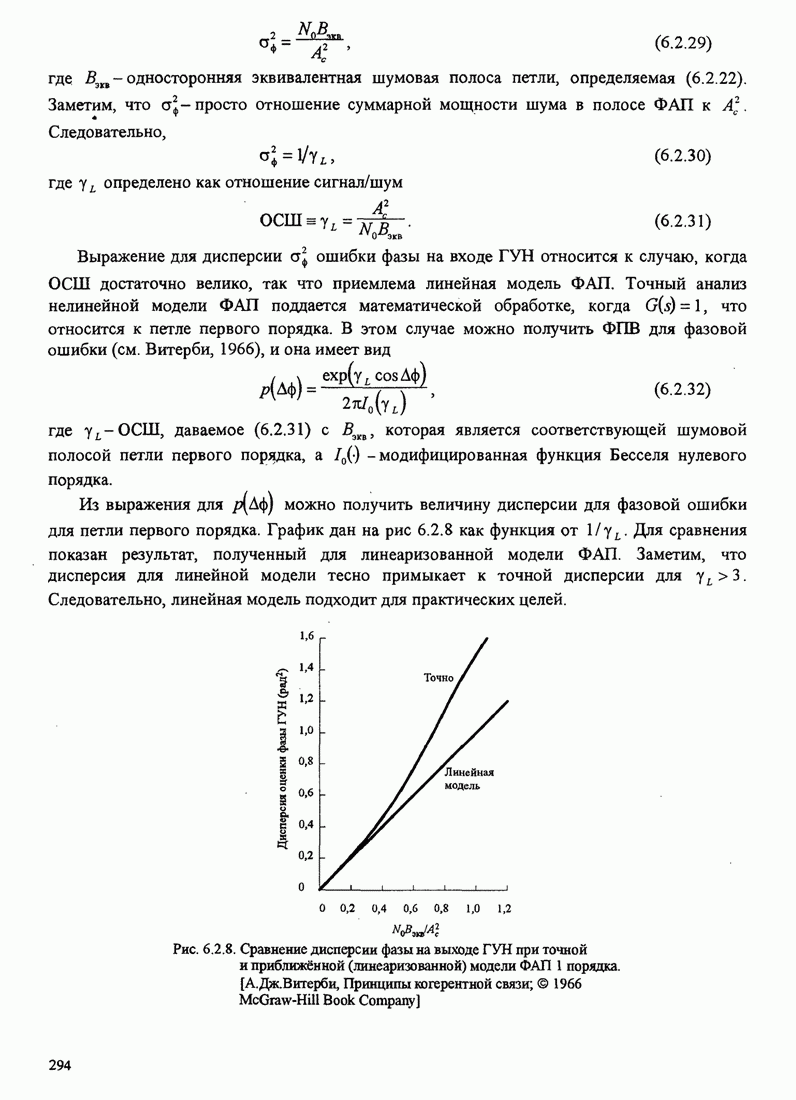
- 6.2.3. Влияние аддитивного шума на оценку фазы
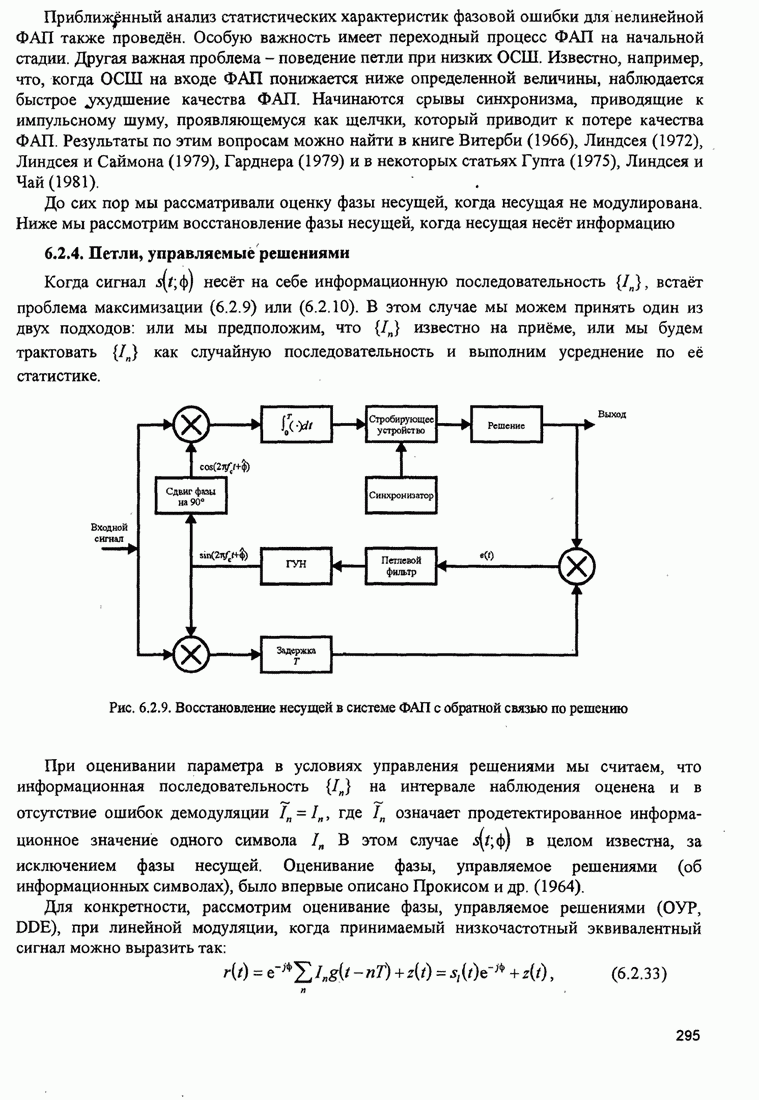
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
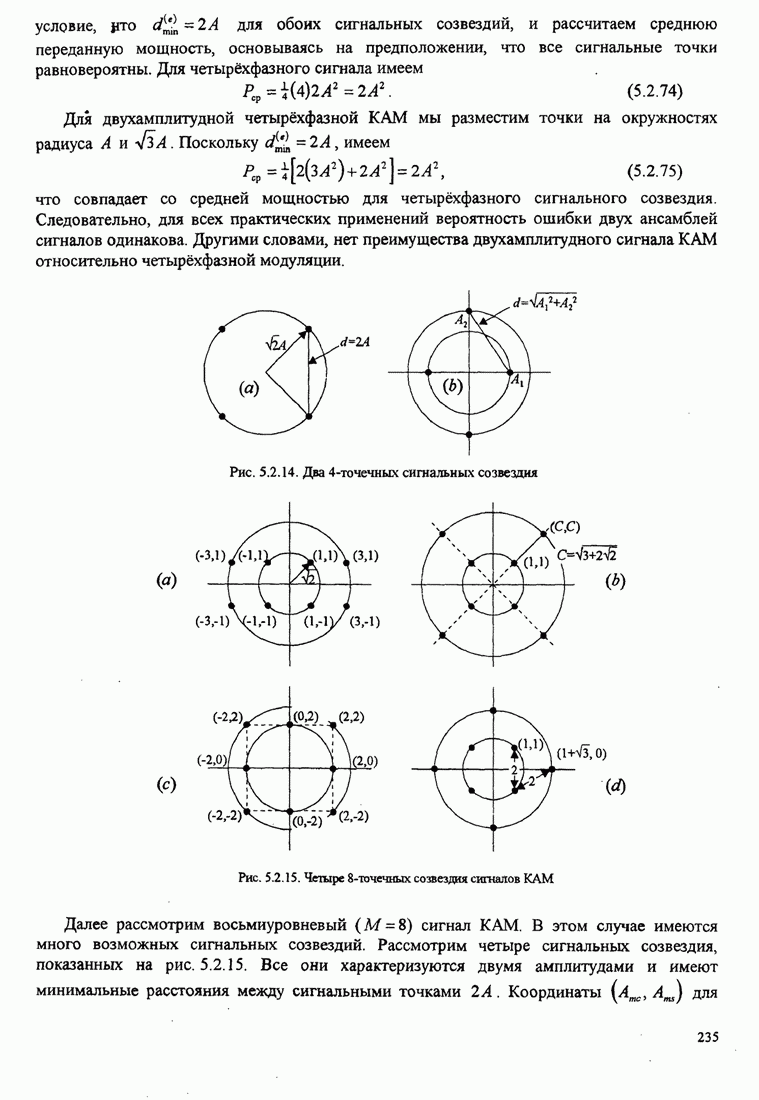
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
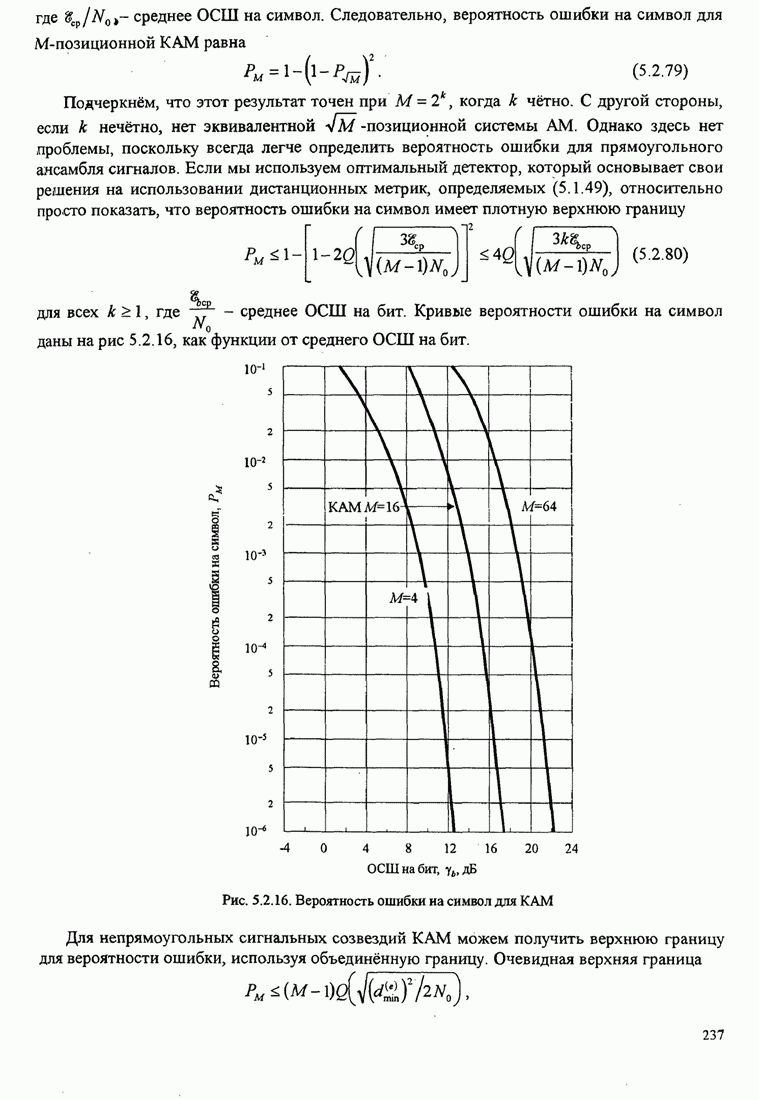
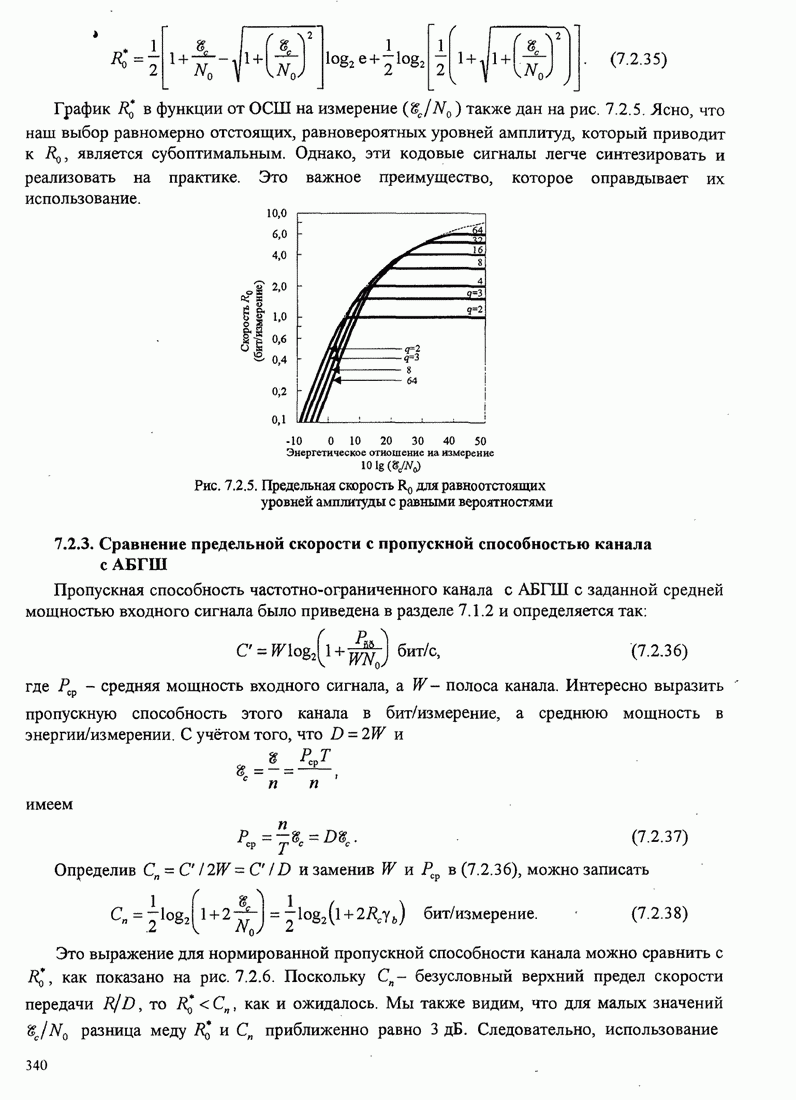
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
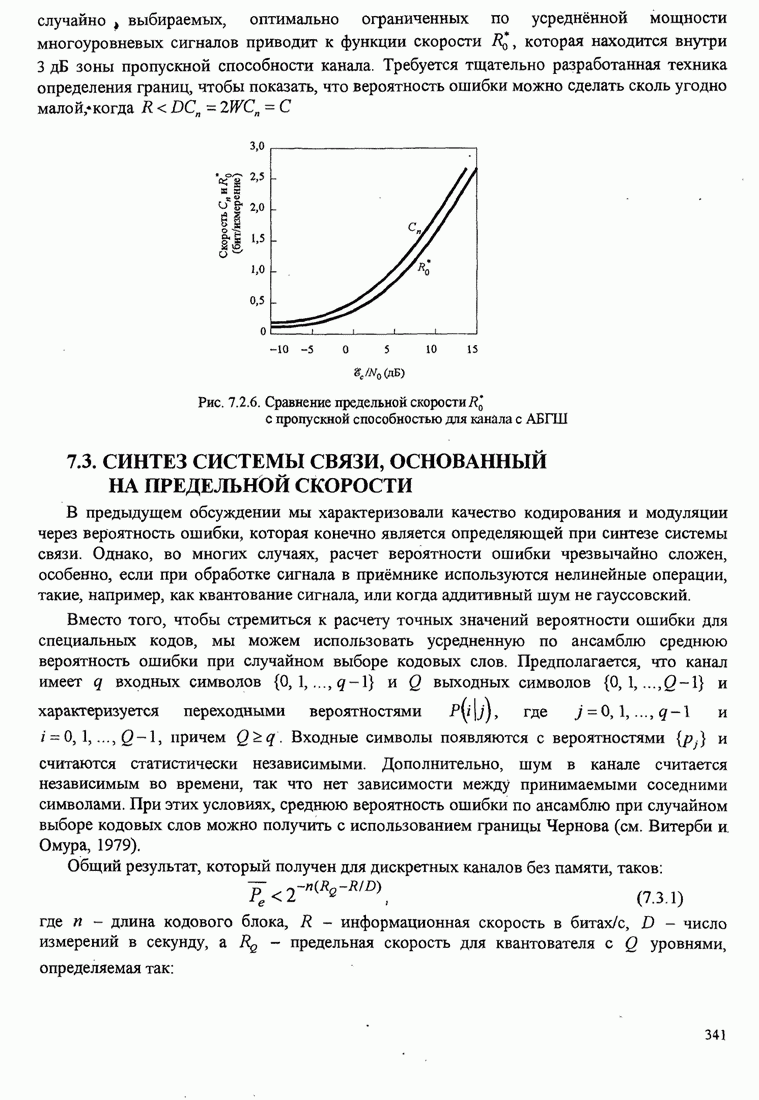
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
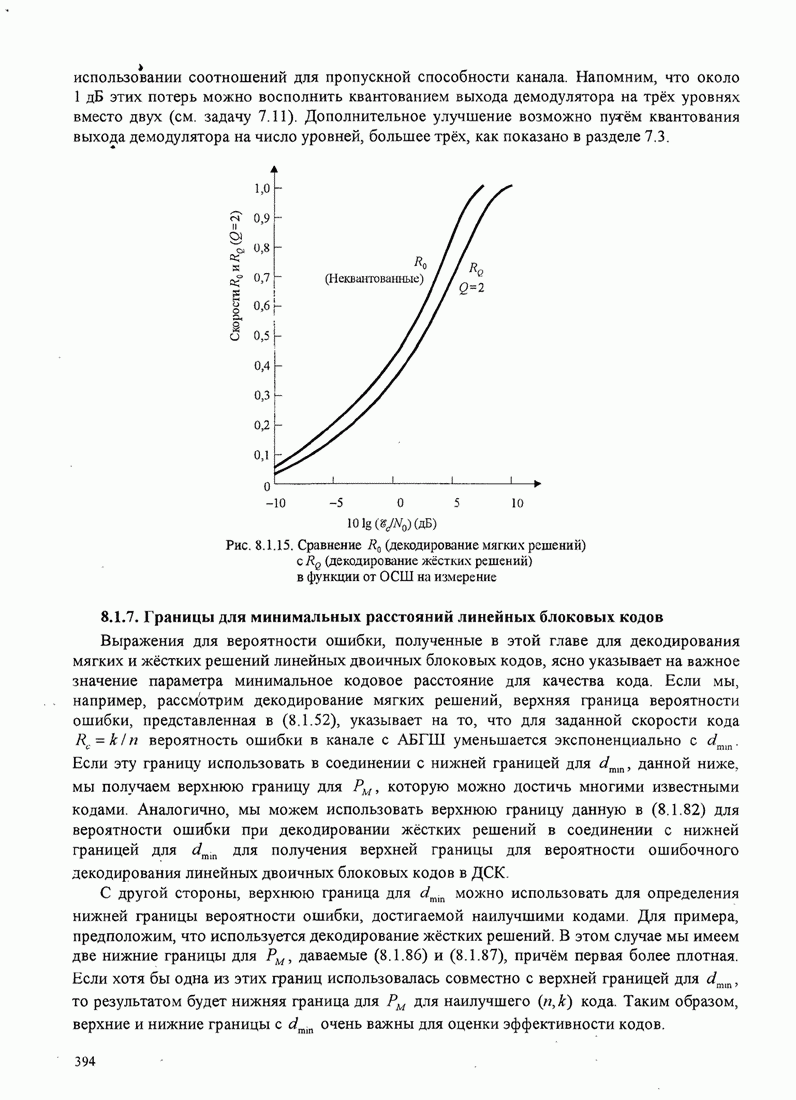
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
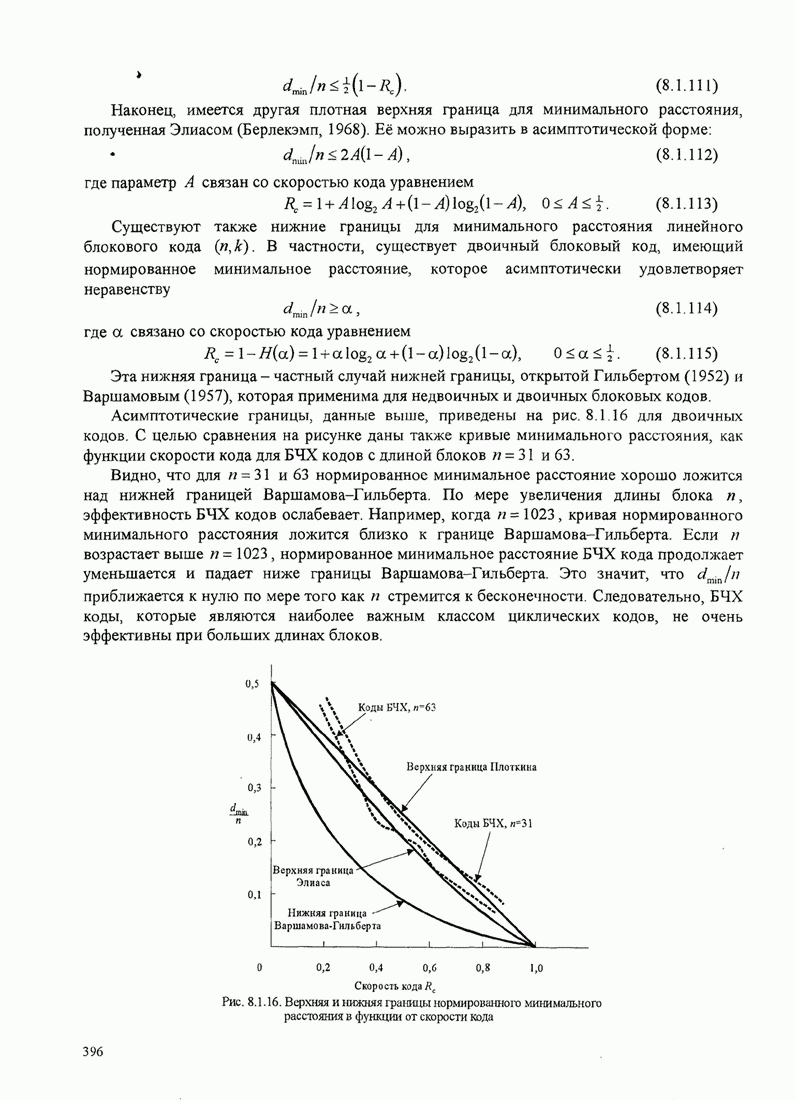
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
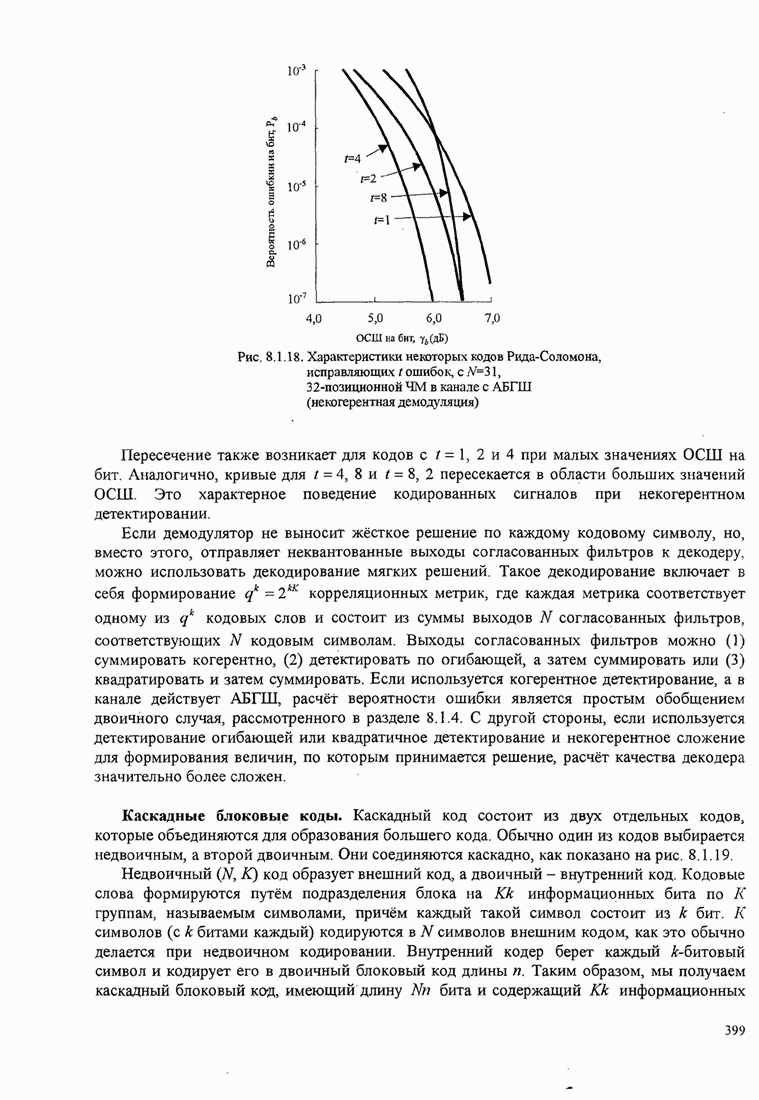
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
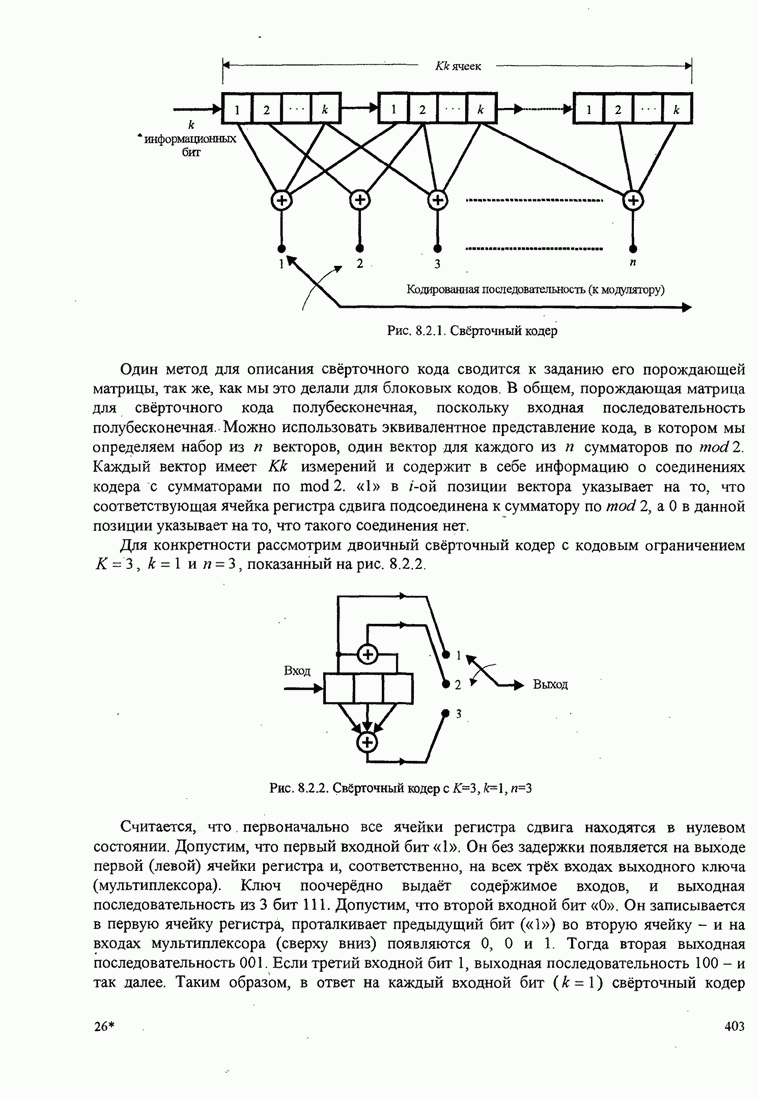
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
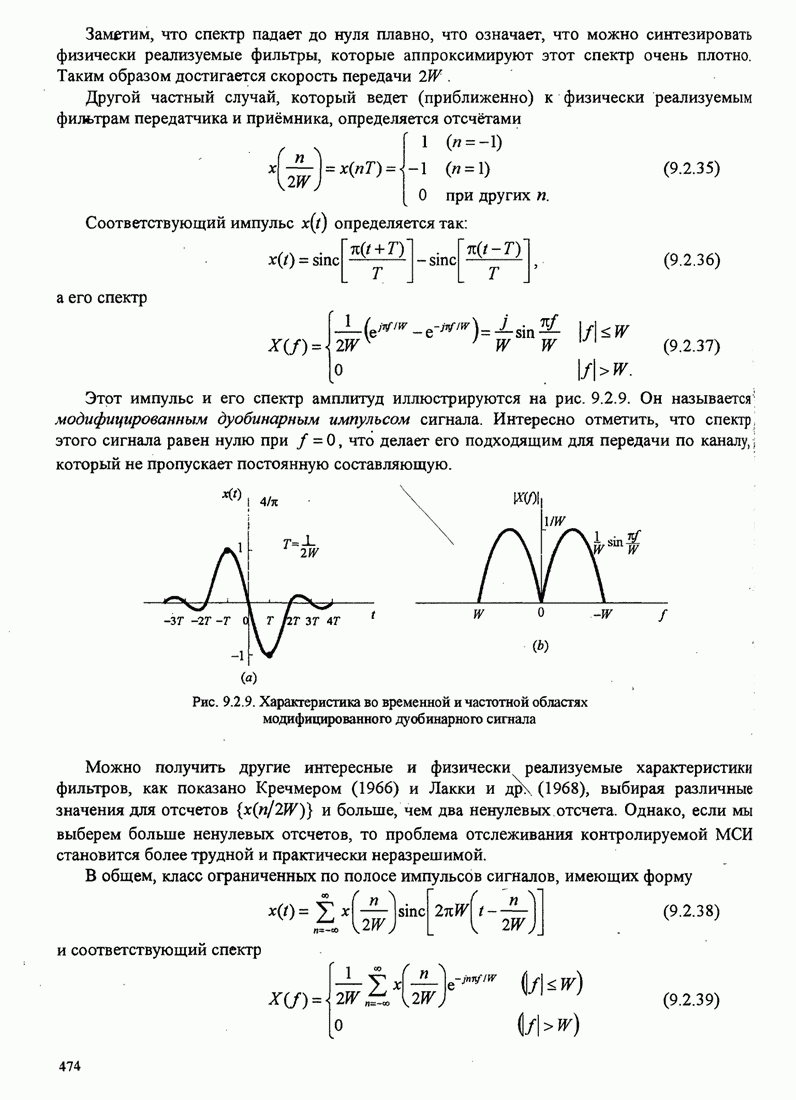
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
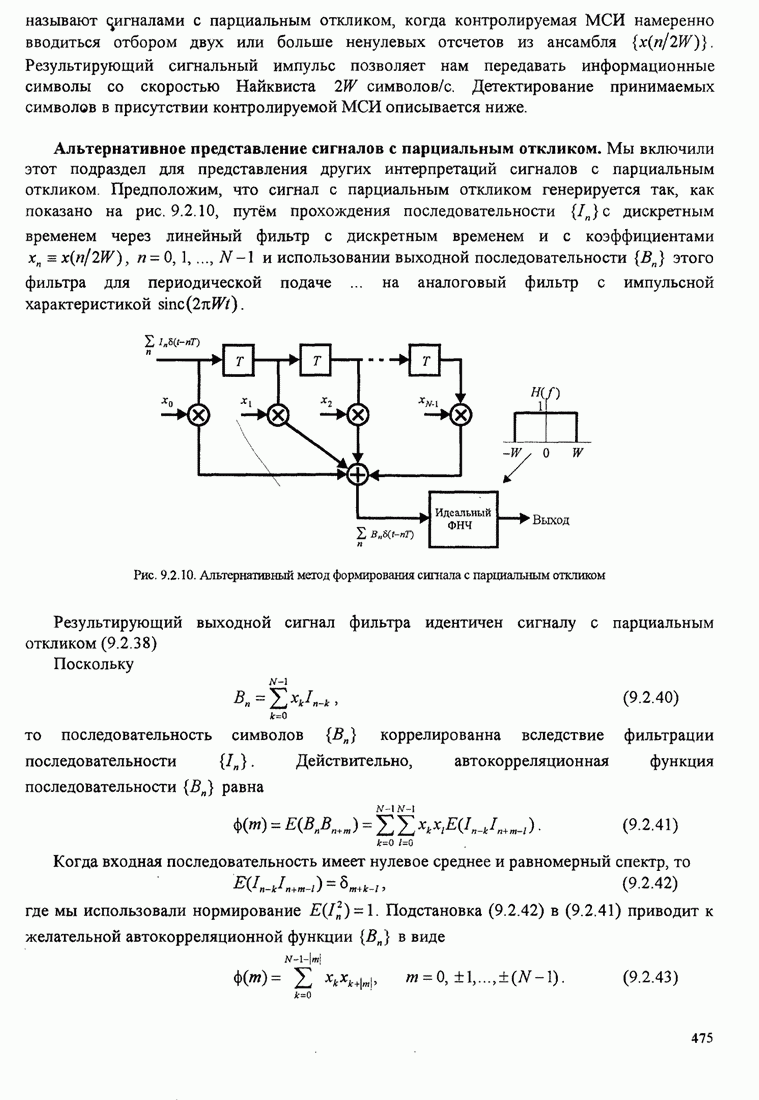
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
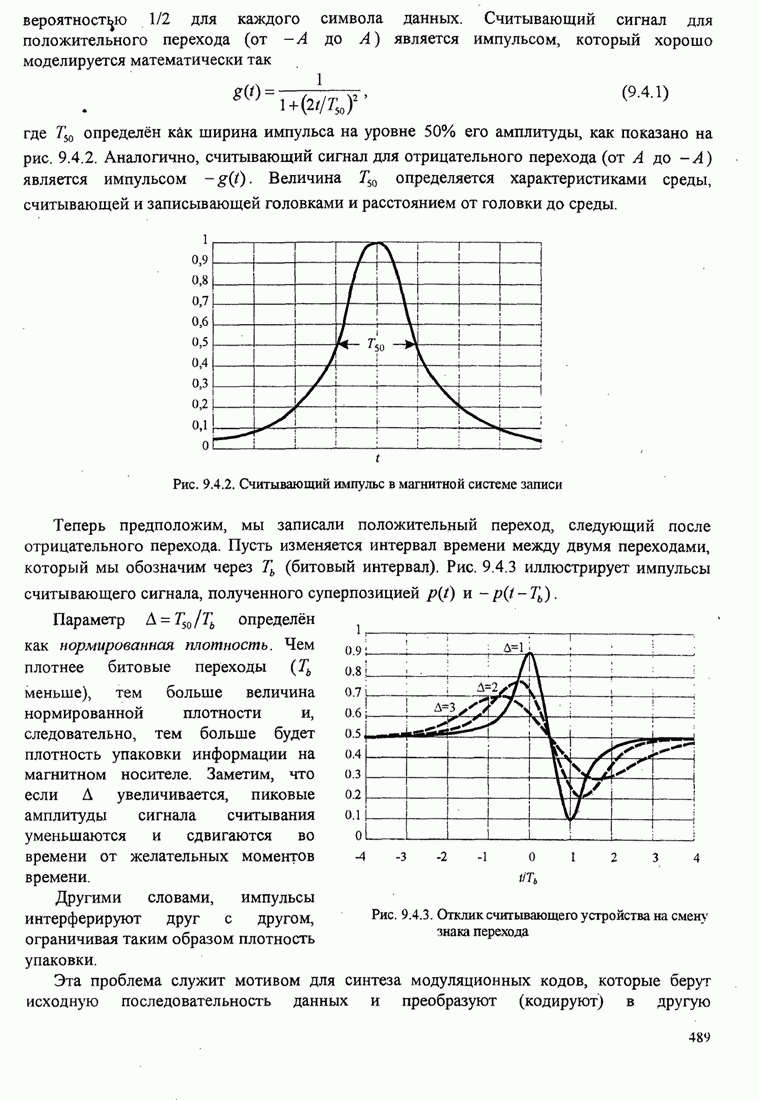
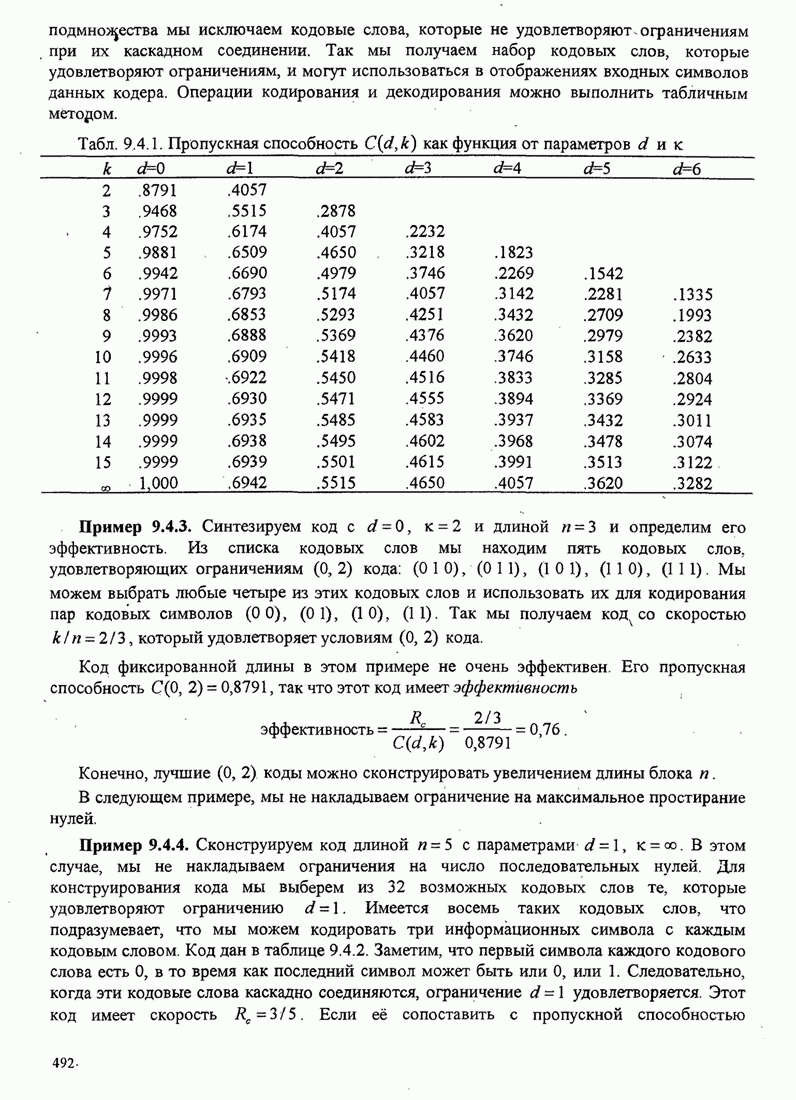
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
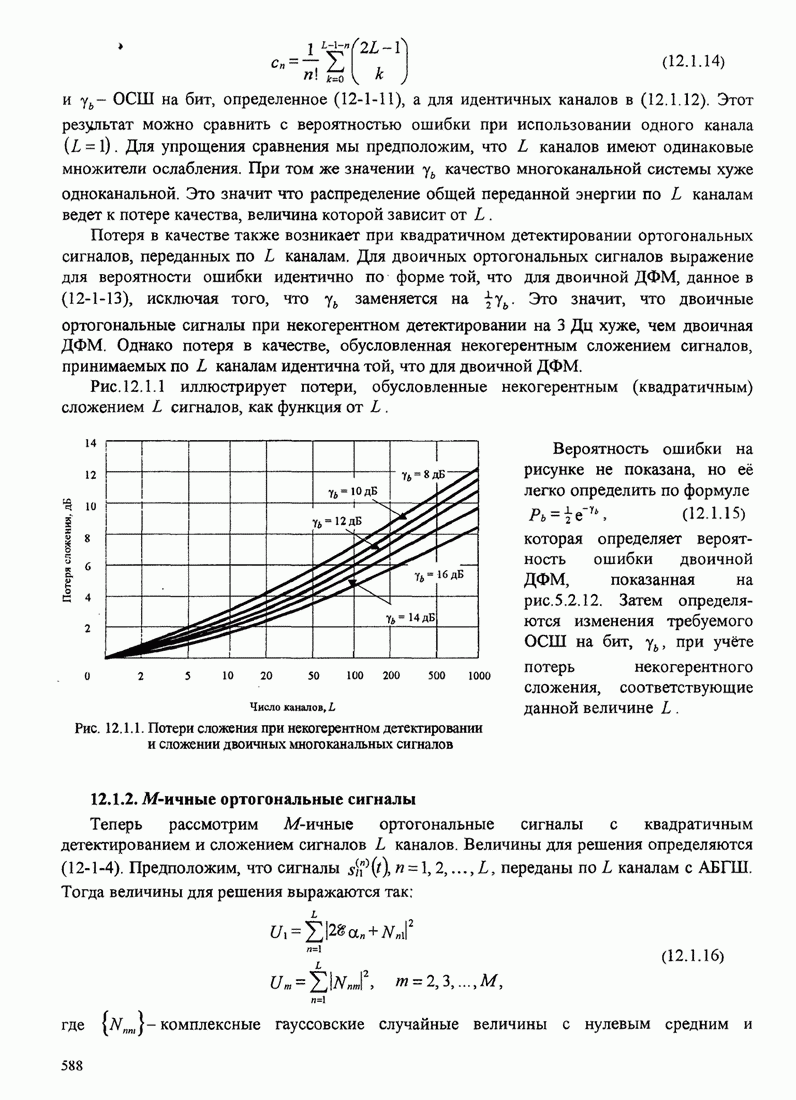
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
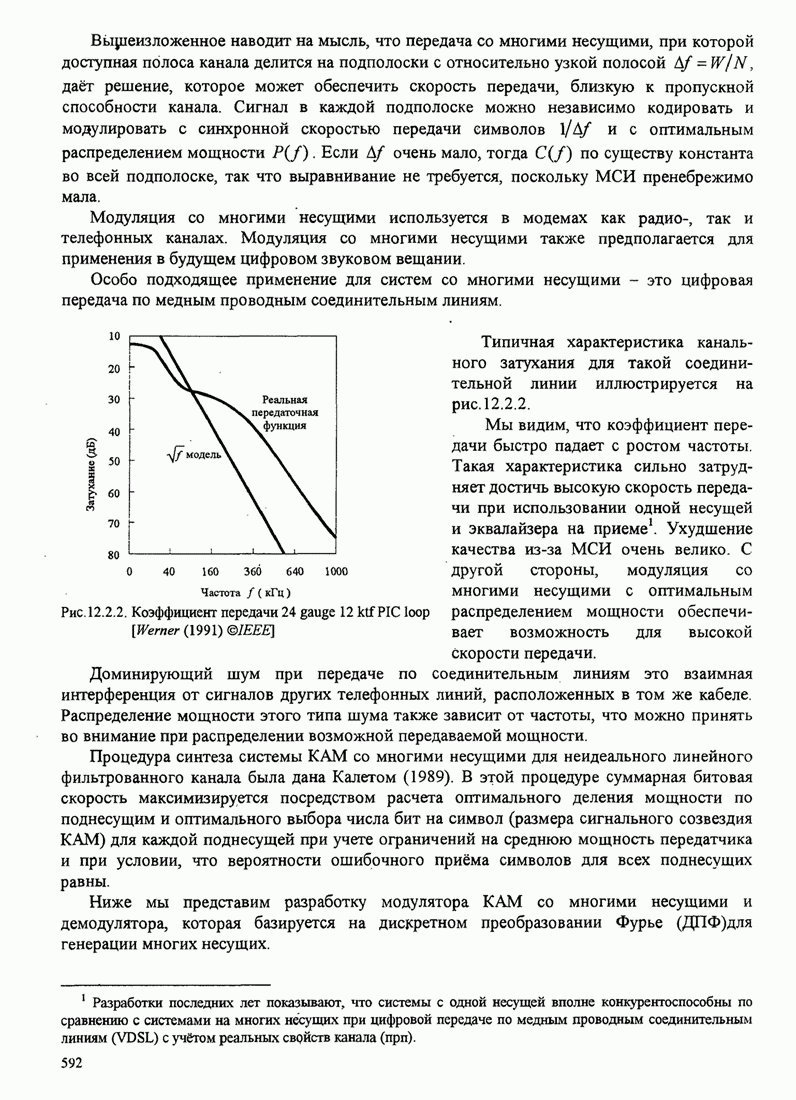
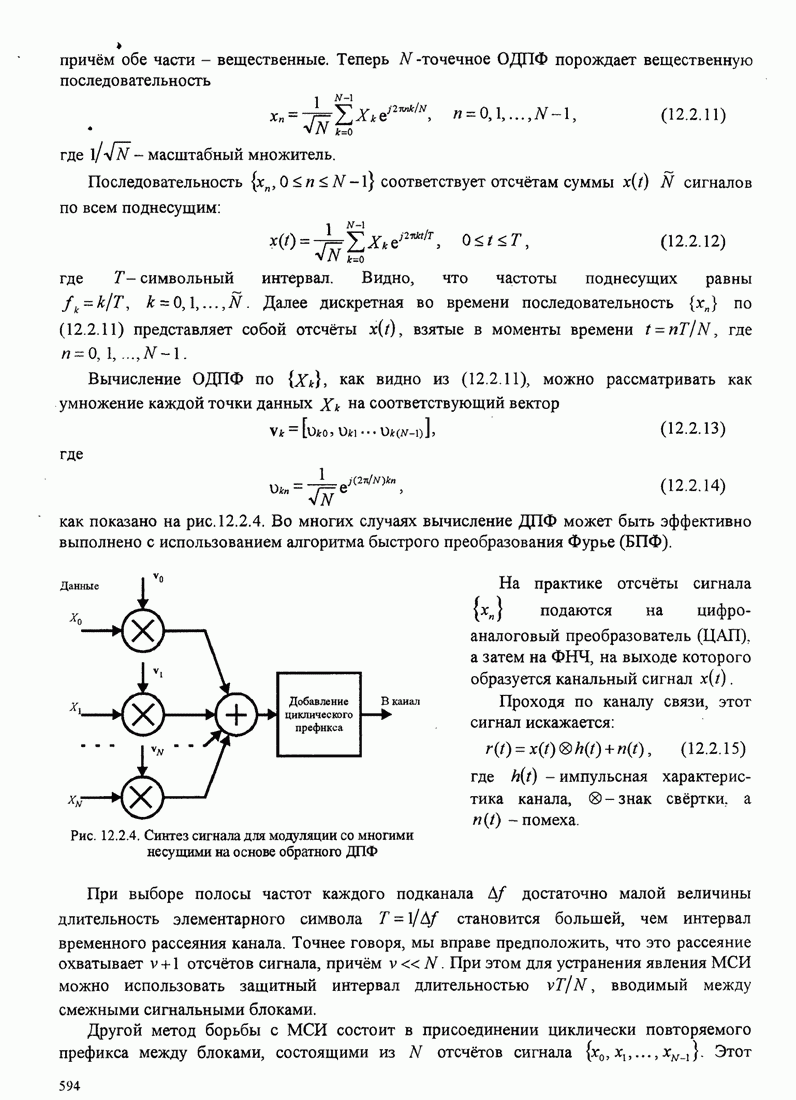
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
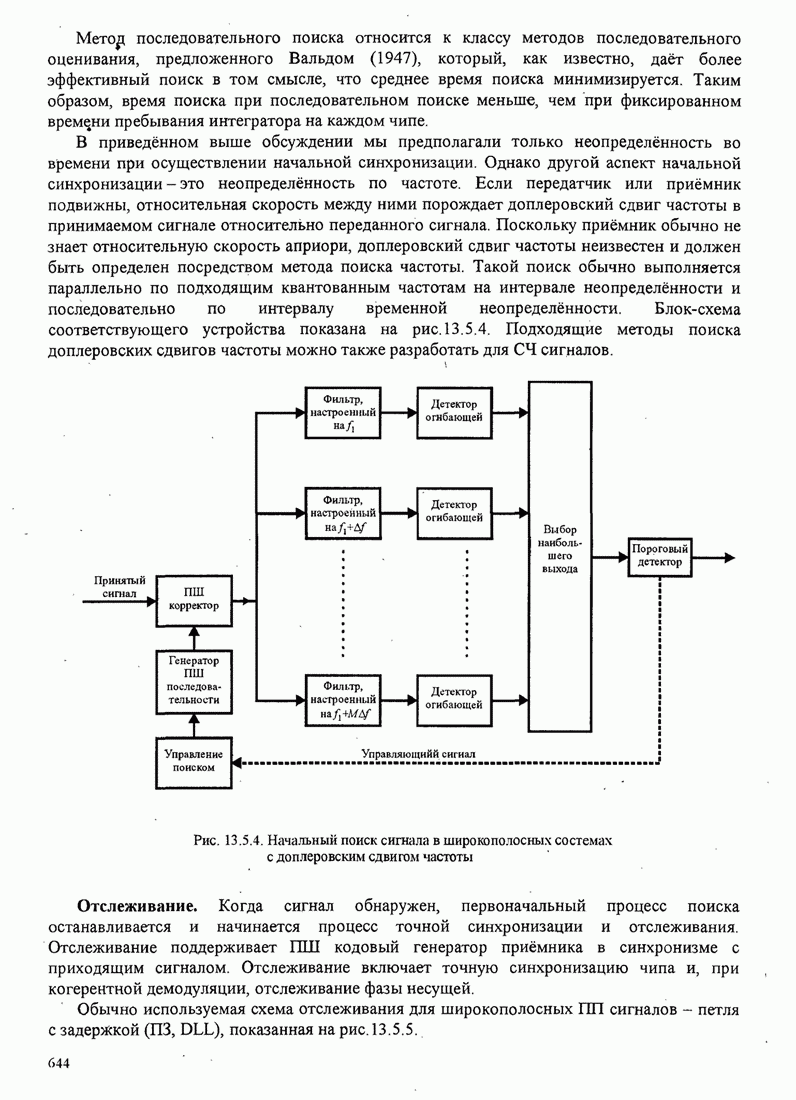
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
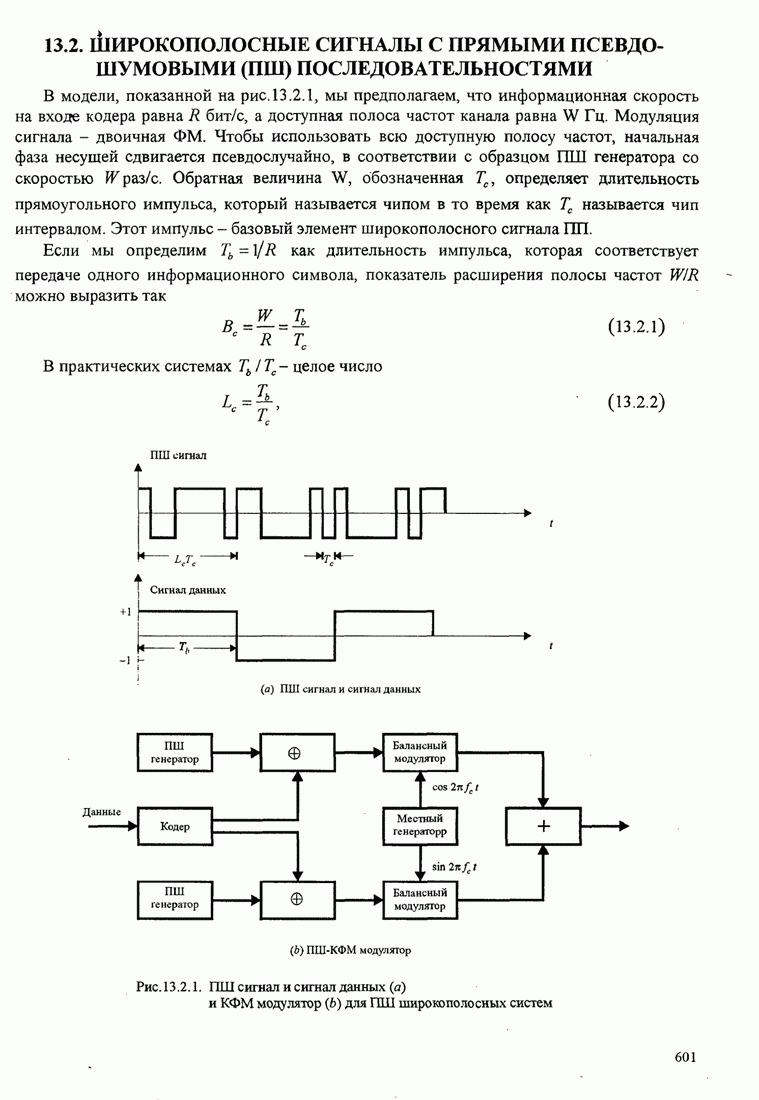
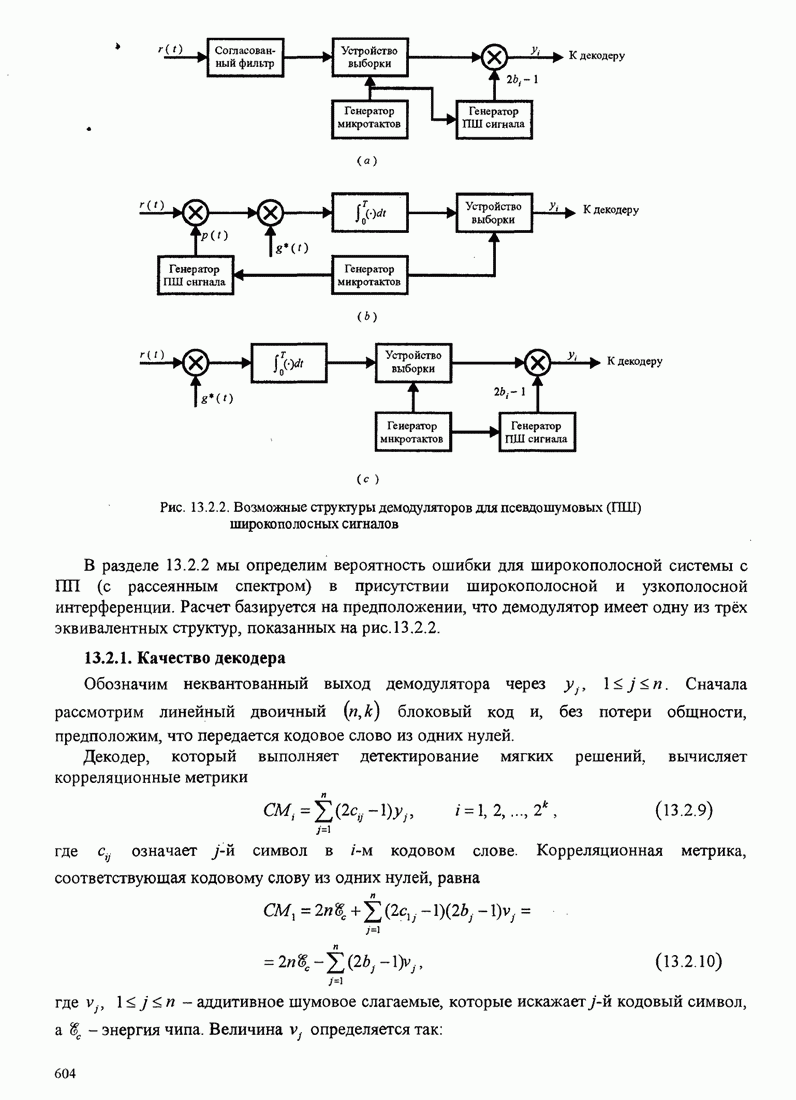
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
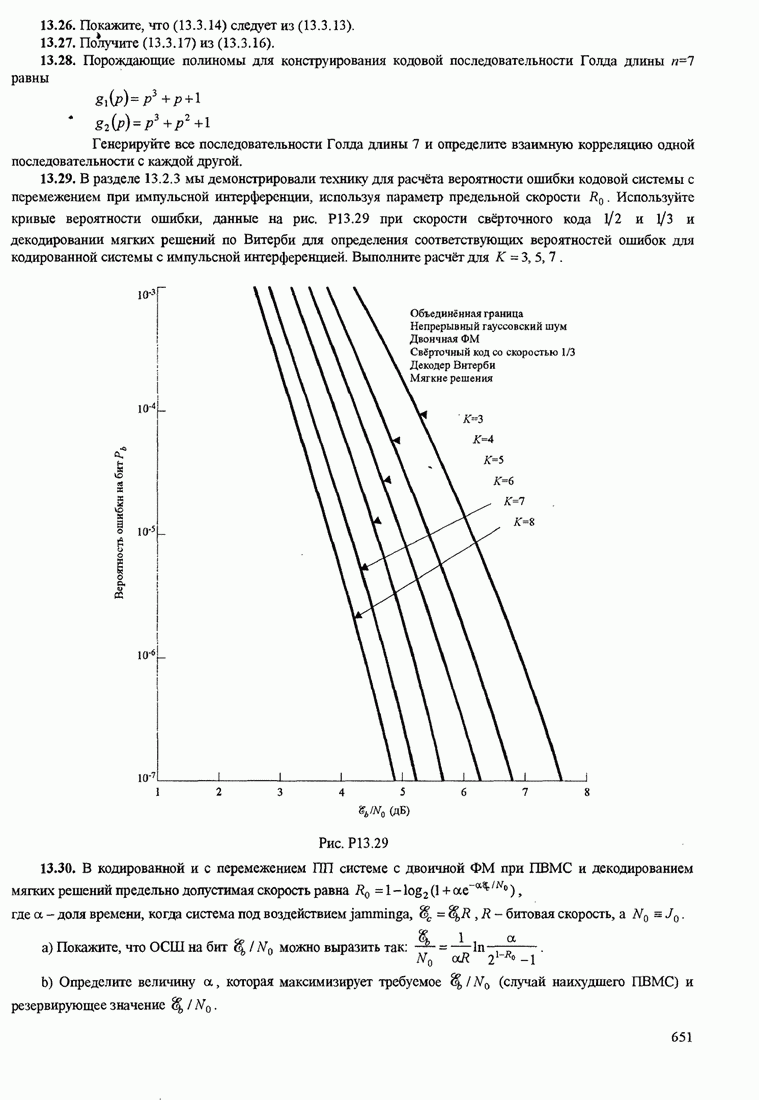
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
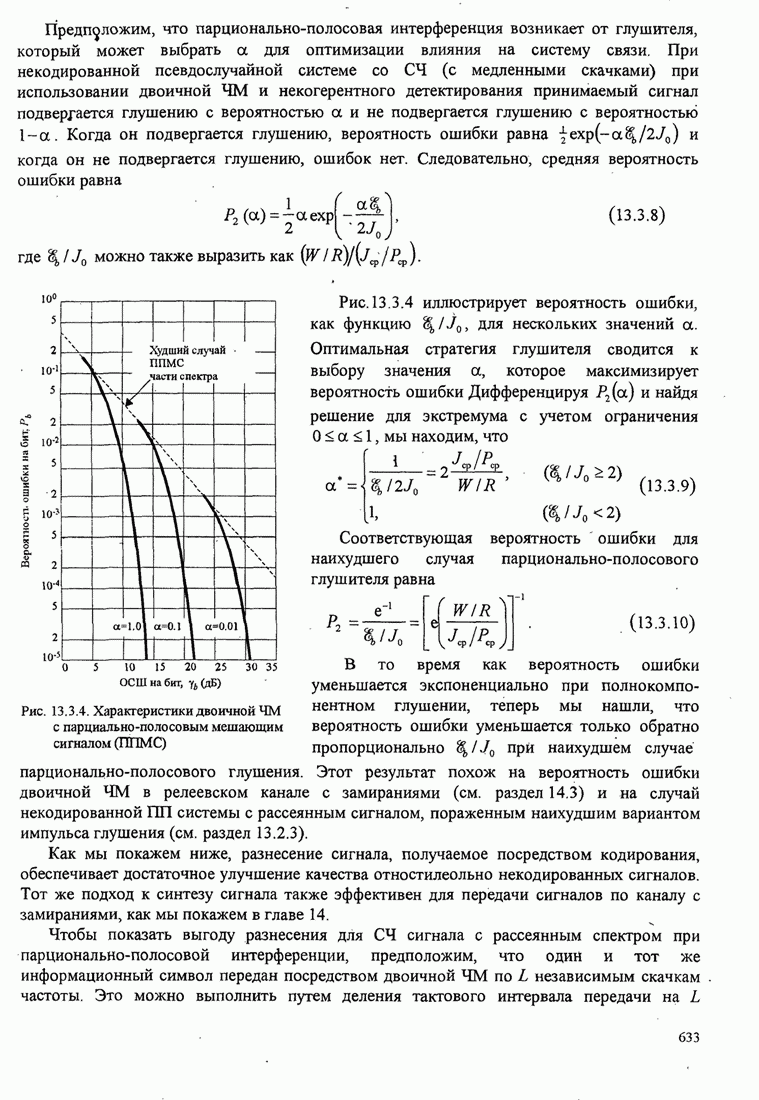
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
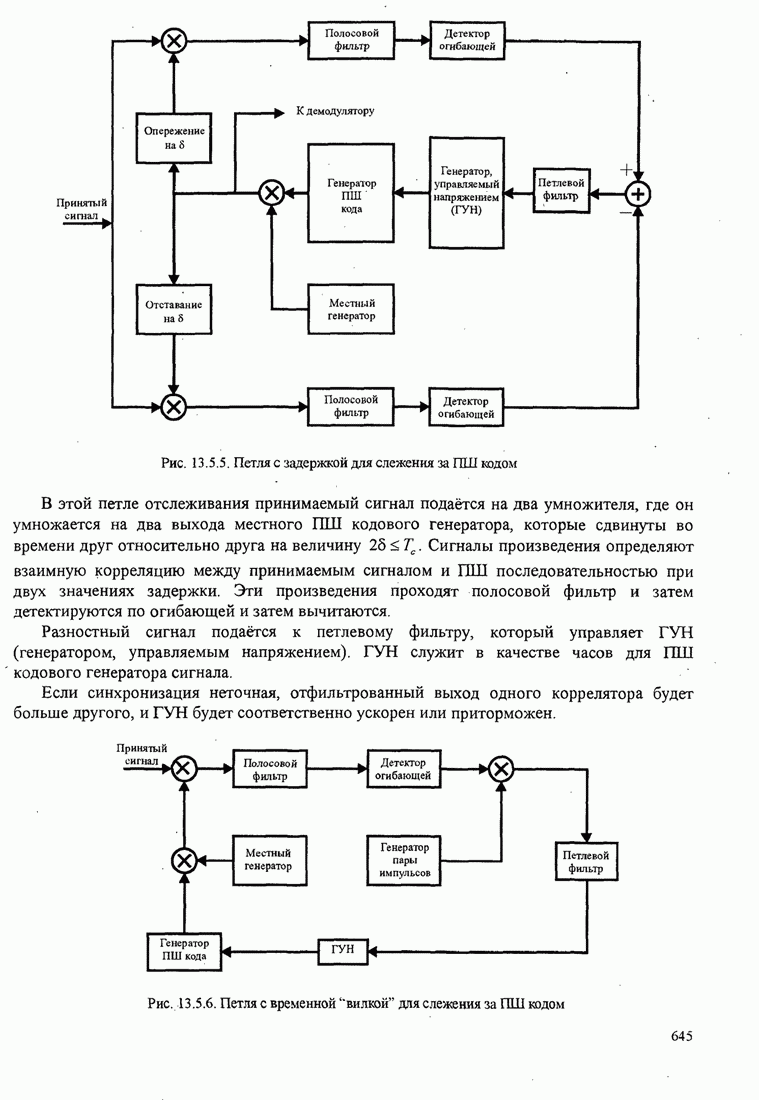
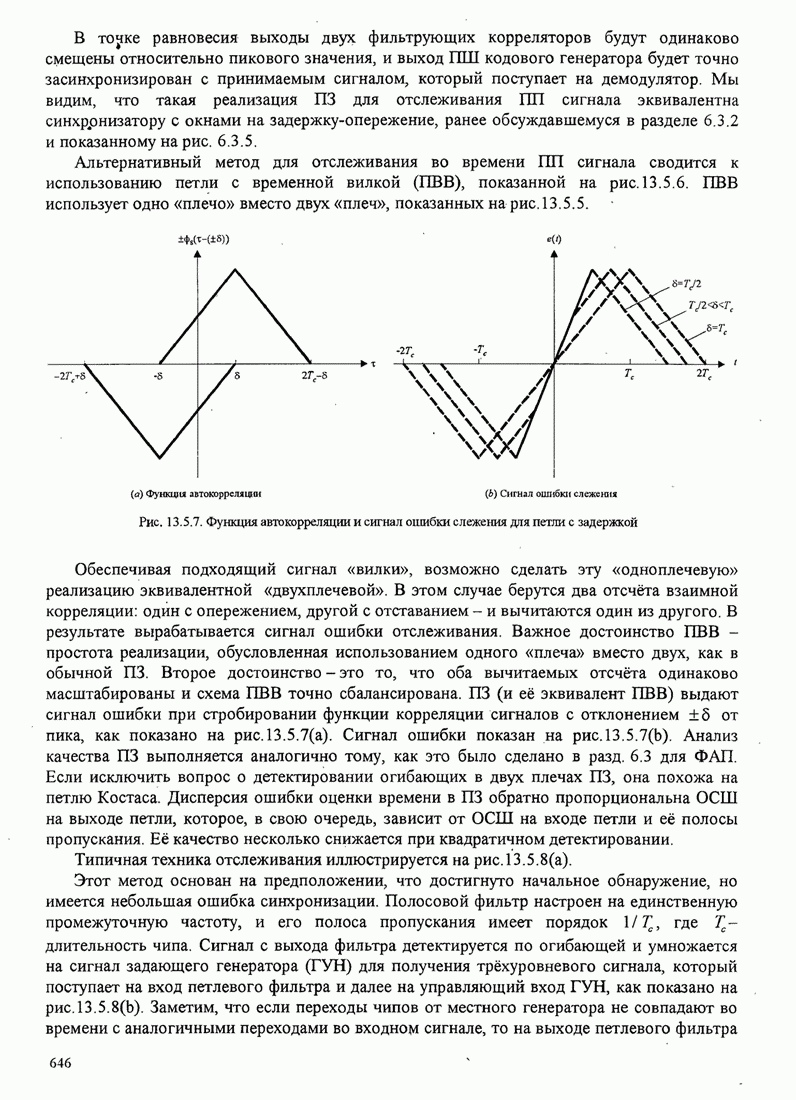
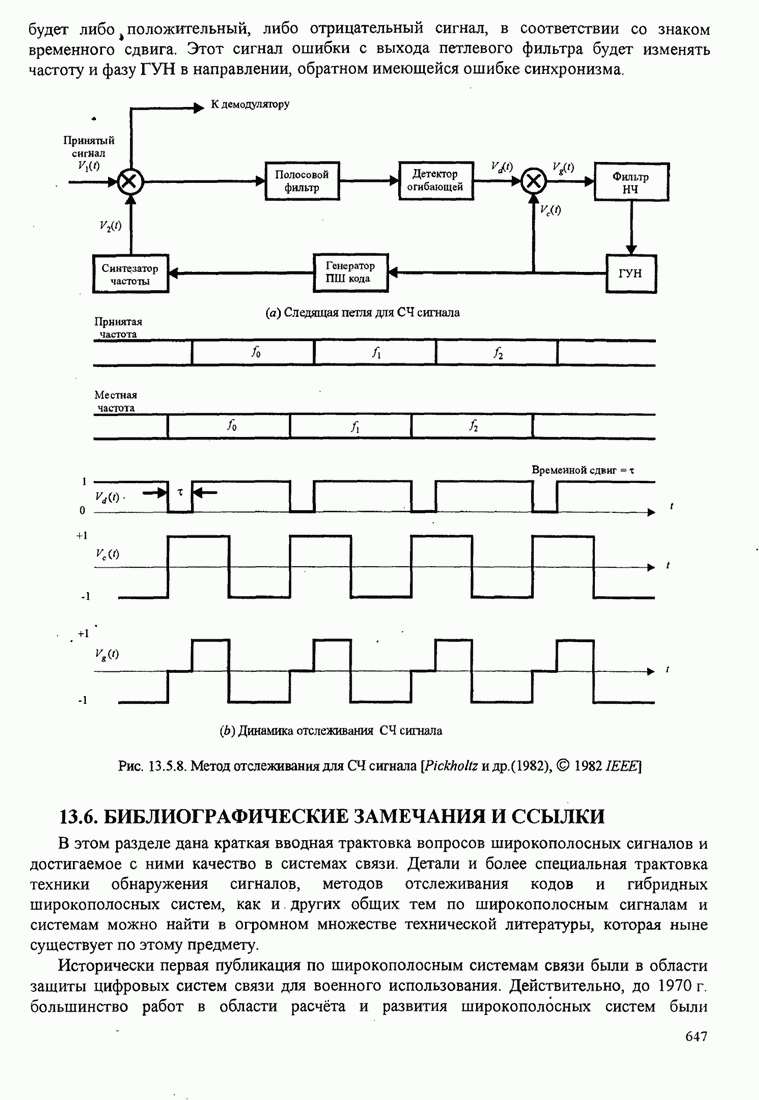
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
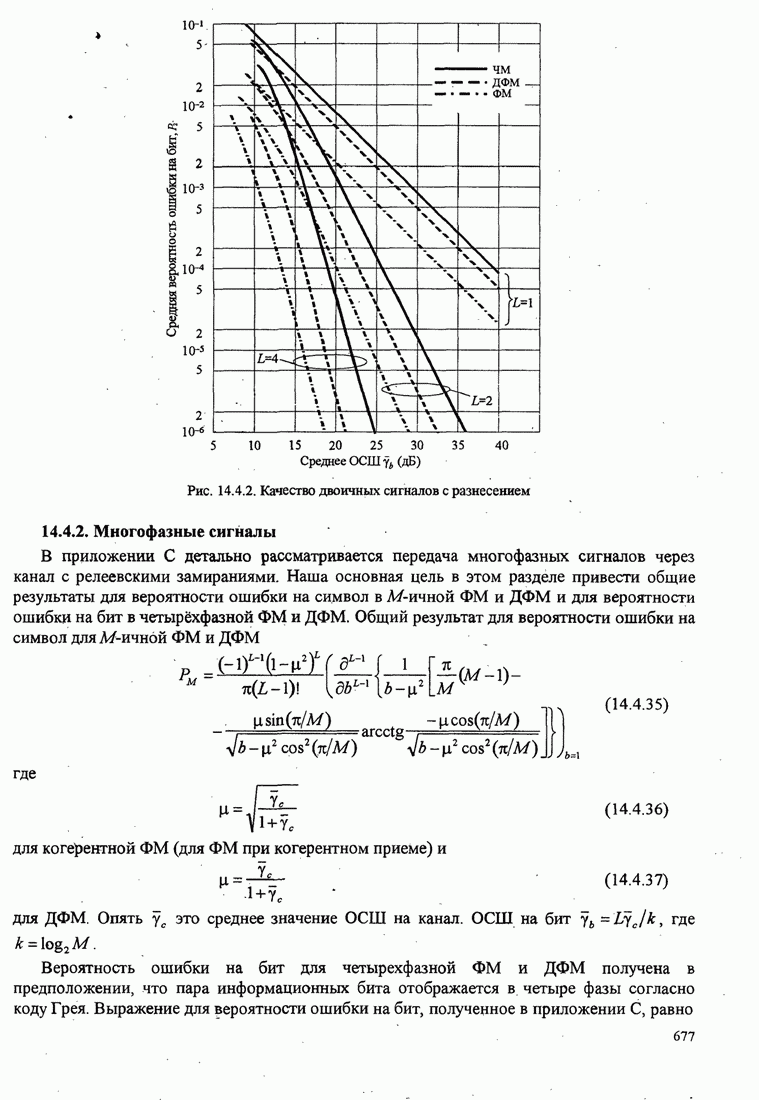
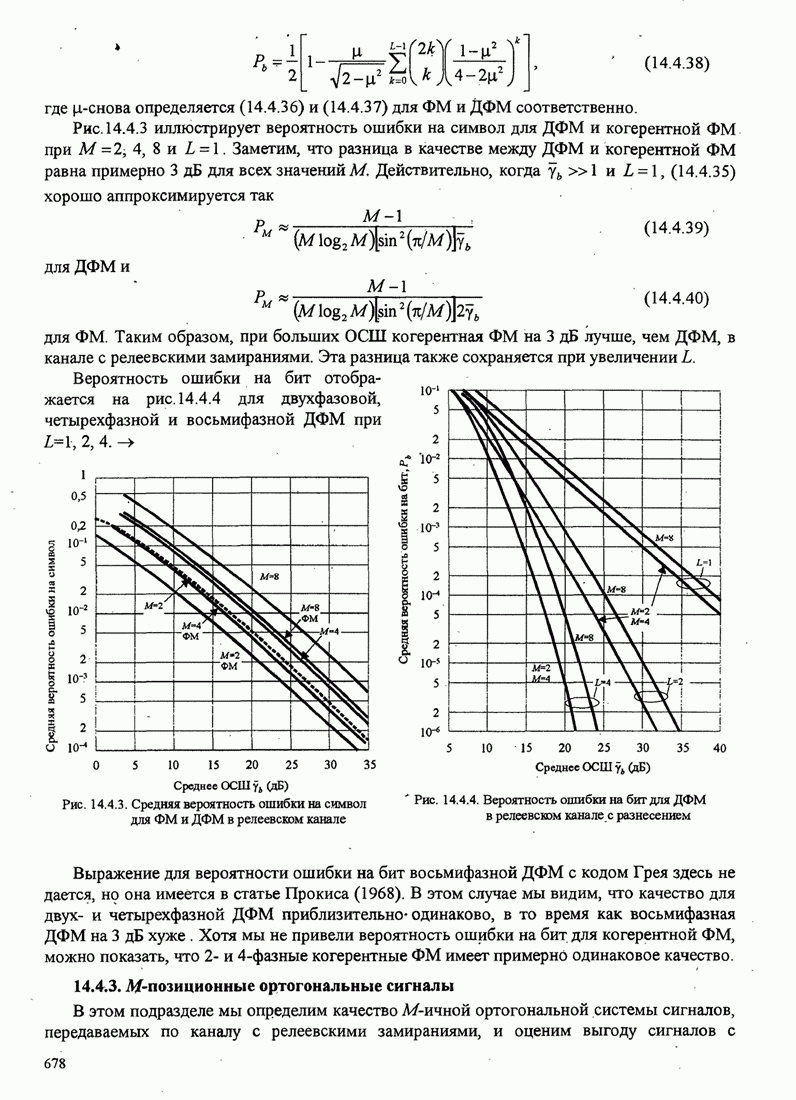
- 14.4.2. Многофазные сигналы
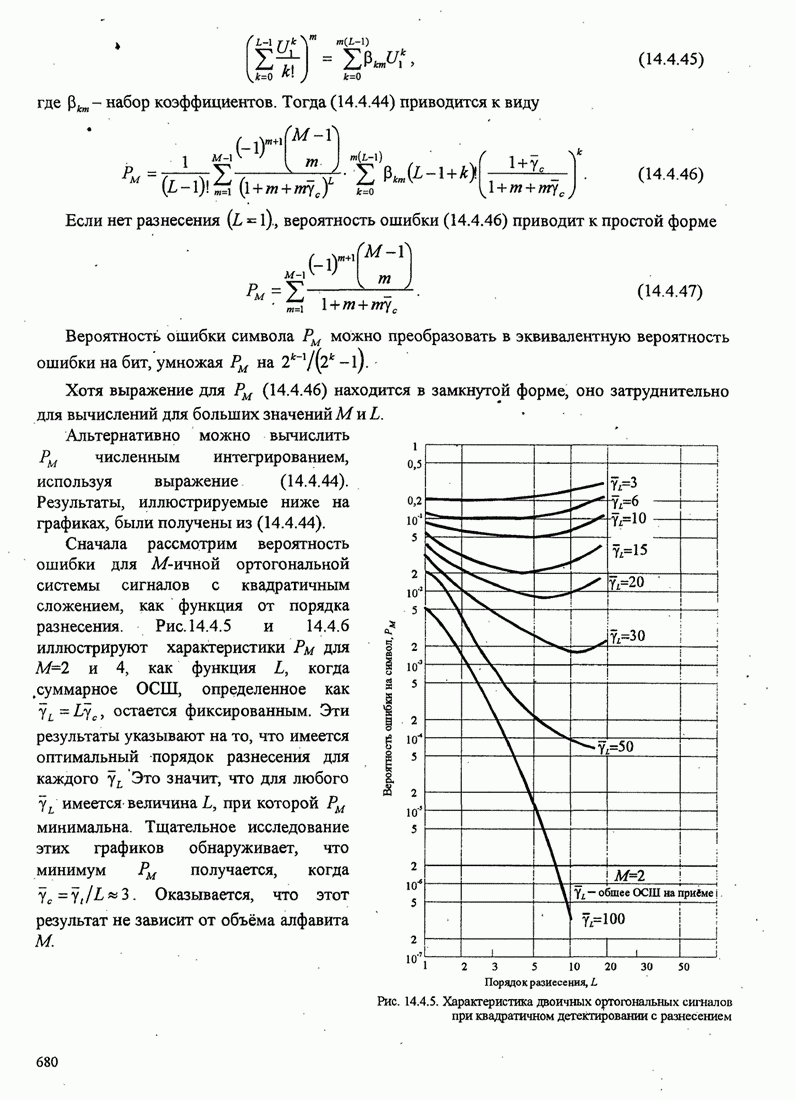
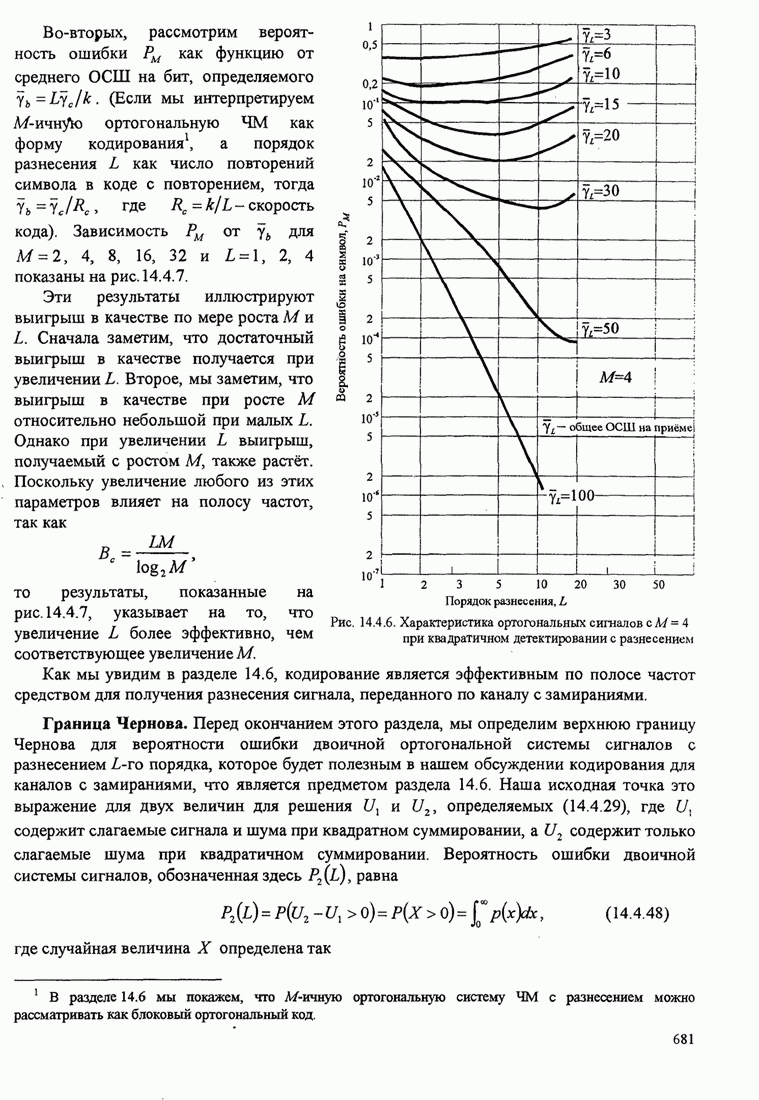
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
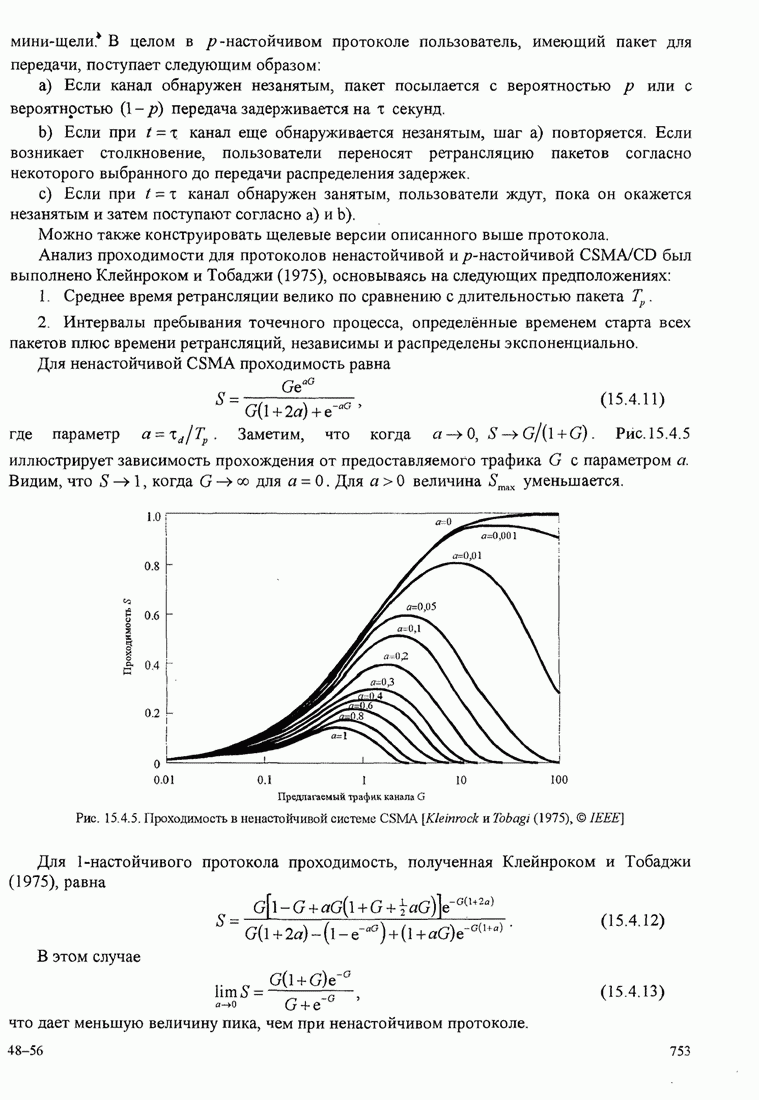
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)