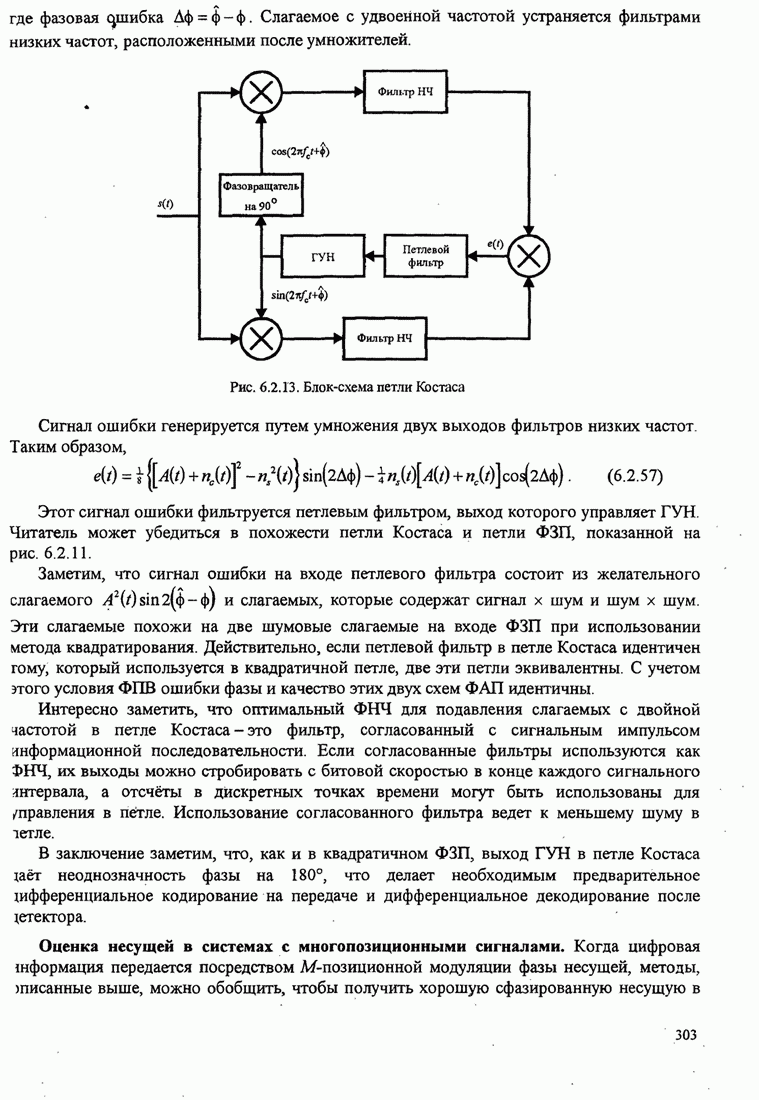
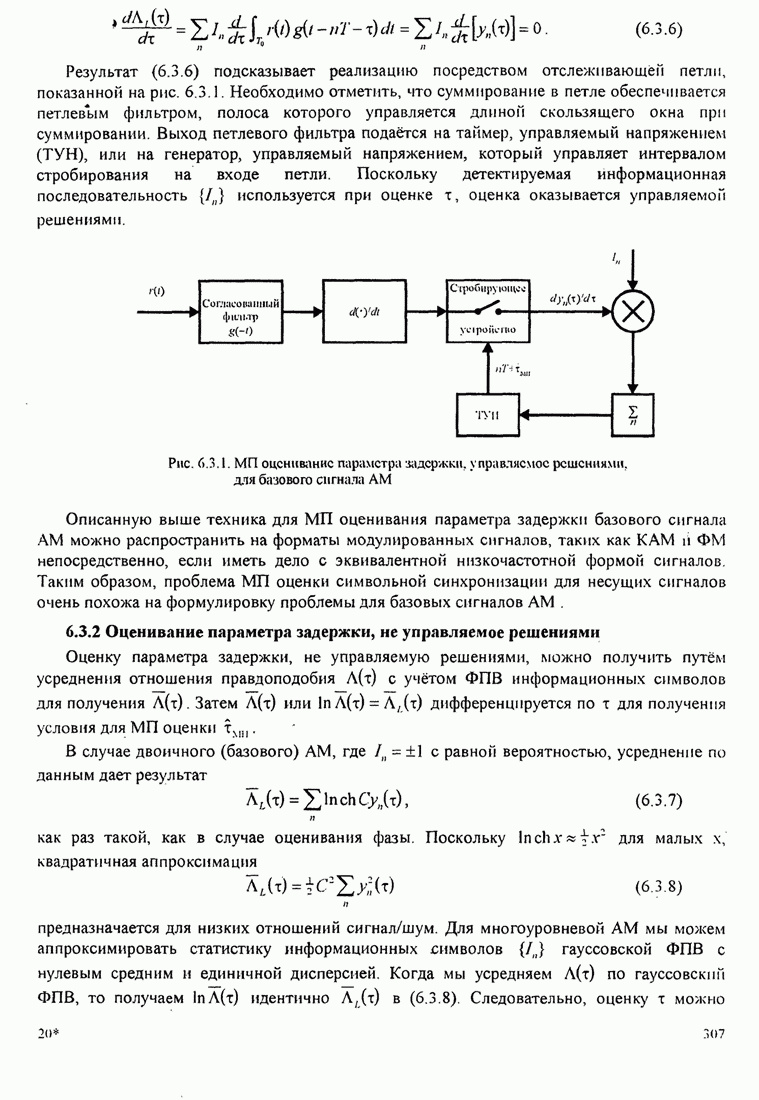
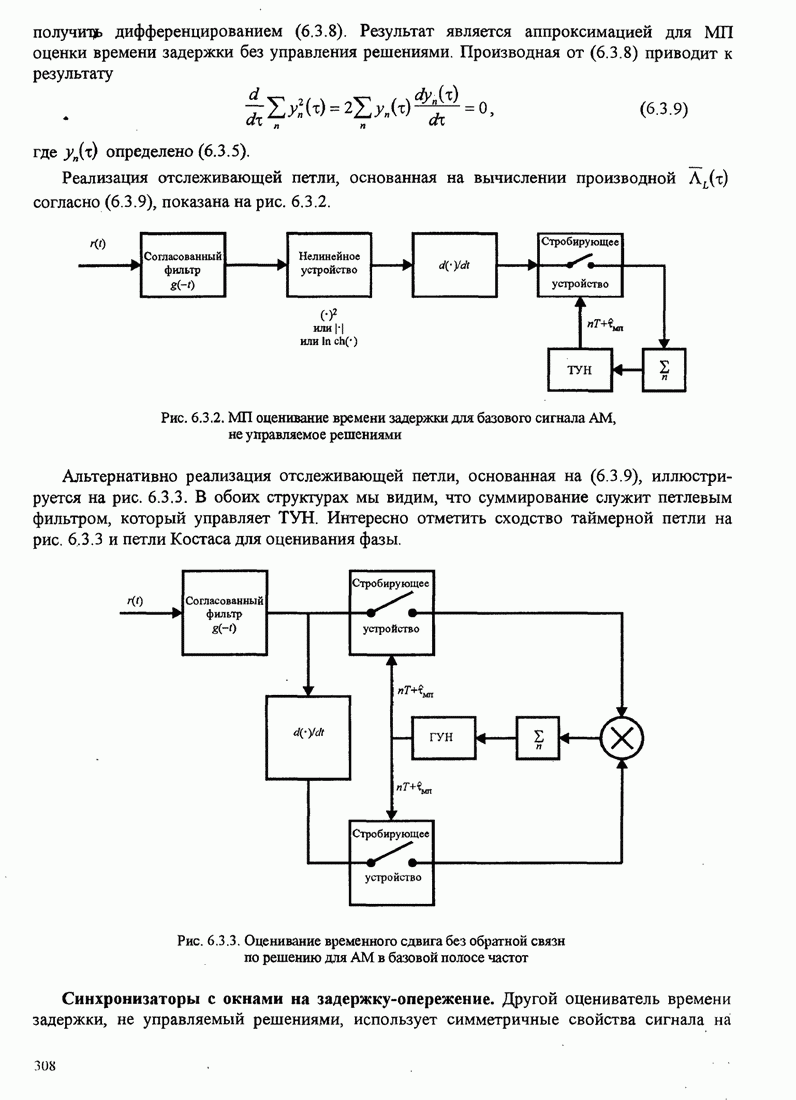
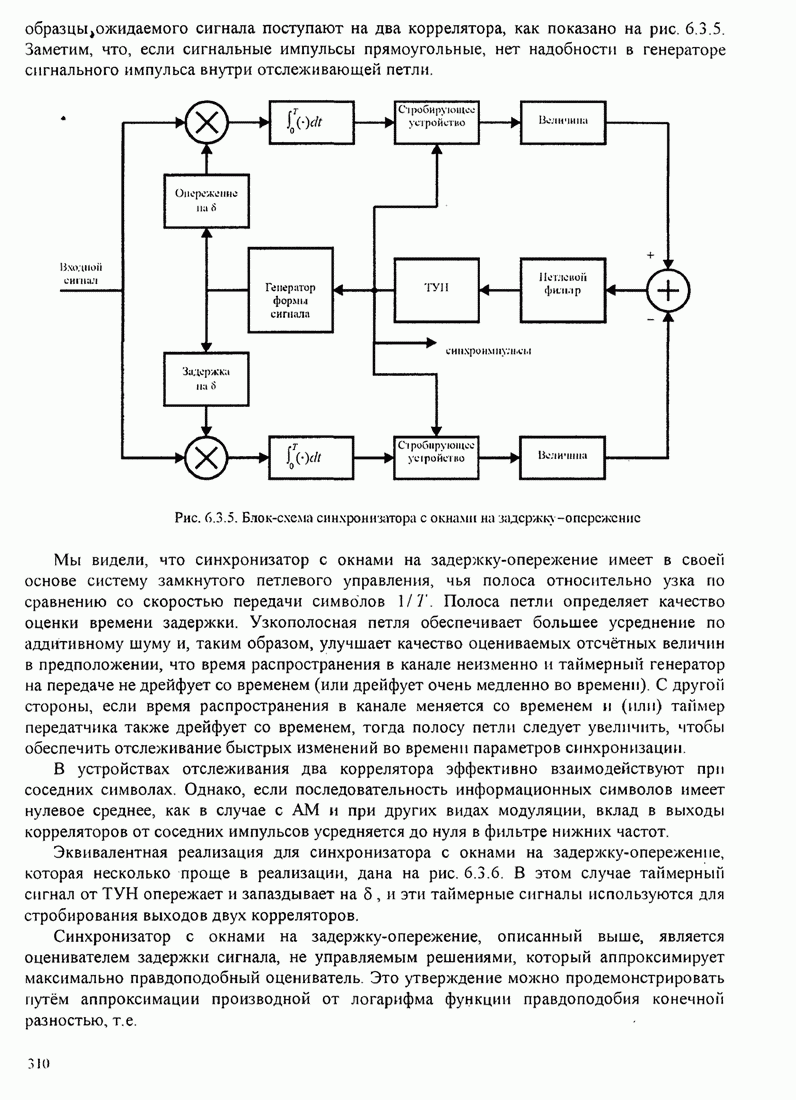
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3.1. Кодирование для дискретных источников без памяти
Предположим,
что ДИБП выдает буквы или символы каждые ![]() секунд. Каждый символ выбирается из
конечного алфавита
секунд. Каждый символ выбирается из
конечного алфавита ![]() ,
, ![]() , с вероятностью
, с вероятностью ![]() ,
, ![]() . Энтропия ДИБП в битах на
символ
. Энтропия ДИБП в битах на
символ
![]() , (3.3.1)
, (3.3.1)
причем
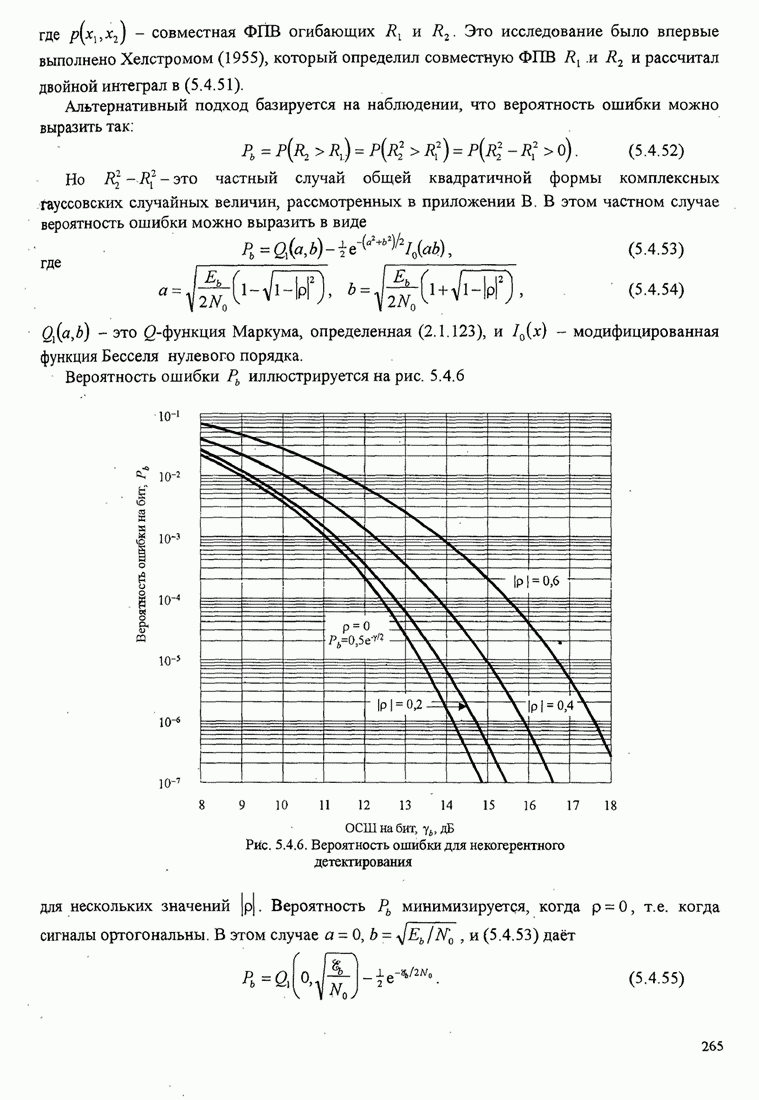
равенство имеет место, если все символы равновероятны. ![]() определяет среднее число бит
на символ источника, а производительность источника в битах определяется как
определяет среднее число бит
на символ источника, а производительность источника в битах определяется как ![]() .
.
Кодовые
слова фиксированной длины. Сначала рассмотрим схему блокового
кодирования, которая сопоставляет уникальный ряд из ![]() двоичных символов с каждым
символом источника. Поскольку имеется
двоичных символов с каждым
символом источника. Поскольку имеется ![]() возможных символов источника, то числа
двоичных символов кодера на один символ источника при уникальном кодировании
возможных символов источника, то числа
двоичных символов кодера на один символ источника при уникальном кодировании
![]() , (3.3.2)
, (3.3.2)
когда
![]() равно
целой степени основания 2, и
равно
целой степени основания 2, и
![]() , (3.3.3)
, (3.3.3)
когда
![]() не равно
целой степени основания 2.
не равно
целой степени основания 2.
Здесь
![]() означает
наибольшее целое, меньшее, чем
означает
наибольшее целое, меньшее, чем ![]() .
.
![]() будем называть скоростью кодирования.
Она определяет число символов кодера на один символ источника. Поскольку
будем называть скоростью кодирования.
Она определяет число символов кодера на один символ источника. Поскольку ![]() , то
, то ![]() .
.
Эффективность кодирования для ДИБП
определяется отношением ![]() . Видим, что
если
. Видим, что
если ![]() равнo степени числа 2
и символы источника равновероятны, то
равнo степени числа 2
и символы источника равновероятны, то ![]() . Следовательно, код фиксированной
длины с
. Следовательно, код фиксированной
длины с ![]() двоичными
символами на символ источника в данном случае обеспечивает стопроцентную
эффективность. Однако, если
двоичными
символами на символ источника в данном случае обеспечивает стопроцентную
эффективность. Однако, если ![]() не равно степени 2, но символы
источника всё ещё равновероятны,
не равно степени 2, но символы
источника всё ещё равновероятны, ![]() отличается от
отличается от ![]() самое большее на один бит на
символ. Если
самое большее на один бит на
символ. Если ![]() ,
эффективность такой схемы кодирования высока. С другой стороны, если
,
эффективность такой схемы кодирования высока. С другой стороны, если ![]() мало, эффективность
кода с фиксированной длиной можно увеличить путем кодирования
последовательности из
мало, эффективность
кода с фиксированной длиной можно увеличить путем кодирования
последовательности из ![]() символов источника за время
символов источника за время ![]() . Чтобы выполнить
такое кодирование, мы должны выбрать
. Чтобы выполнить
такое кодирование, мы должны выбрать ![]() уникальных кодовых слов. Используя
кодовую последовательность из
уникальных кодовых слов. Используя
кодовую последовательность из ![]() двоичных символов, мы можем образовать
двоичных символов, мы можем образовать
![]() возможных
кодовых слов. Число
возможных
кодовых слов. Число ![]() должно быть выбрано так, чтобы
должно быть выбрано так, чтобы
![]() .
.
Следовательно,
требуется минимальное целое значение для ![]() , равное
, равное
![]() . (3.3.4)
. (3.3.4)
Теперь
среднее число символов кода на символ источника ![]() , и, таким образом, неэффективность кодирования
сокращается примерно в
, и, таким образом, неэффективность кодирования
сокращается примерно в ![]() раз по сравнению с посимвольным
кодированием, описанным выше. Взяв
раз по сравнению с посимвольным
кодированием, описанным выше. Взяв ![]() достаточно большим, можно делать
эффективность процедуры кодирования, измеренную отношением
достаточно большим, можно делать
эффективность процедуры кодирования, измеренную отношением ![]() , как годно близкой к
единице. Методы кодирования, описанные выше, не приводят к искажениям, так как
кодирование символов источника или блоков таких символов в кодовые слова
выполняется однозначно (уникально). Такие типы кодов названы бесшумными.
, как годно близкой к
единице. Методы кодирования, описанные выше, не приводят к искажениям, так как
кодирование символов источника или блоков таких символов в кодовые слова
выполняется однозначно (уникально). Такие типы кодов названы бесшумными.
Теперь предположим, что мы пытаемся
уменьшить скорость кодирования ![]() путем смягчения условия однозначности
процесса кодирования. Например, предположим, что только доля
путем смягчения условия однозначности
процесса кодирования. Например, предположим, что только доля ![]() блоков символов
источника кодируется однозначно. Конкретно, выберем
блоков символов
источника кодируется однозначно. Конкретно, выберем ![]() наиболее вероятных
наиболее вероятных ![]() -символьных блоков и
будем кодировать каждый из них однозначно, в то время как оставшиеся
-символьных блоков и
будем кодировать каждый из них однозначно, в то время как оставшиеся ![]() блоков длины
блоков длины ![]() будем представлять
одним оставшимся кодовым словом. Эта процедура кодирования вызовет ошибку декодирования
каждый раз, когда источник выдаст такой маловероятный блок. Пусть
будем представлять
одним оставшимся кодовым словом. Эта процедура кодирования вызовет ошибку декодирования
каждый раз, когда источник выдаст такой маловероятный блок. Пусть ![]() означает
вероятность такой ошибки. Отталкиваясь от этой процедуры кодирования, Шеннон
(1948) доказал следующую теорему кодирования источника.
означает
вероятность такой ошибки. Отталкиваясь от этой процедуры кодирования, Шеннон
(1948) доказал следующую теорему кодирования источника.
Теорема
кодирования источника I. Пусть ![]() - это ансамбль символов ДИБП с конечной
энтропией
- это ансамбль символов ДИБП с конечной
энтропией ![]() .
Блоки из
.
Блоки из ![]() символов
источника кодируются в двоичные кодовые слова длиной
символов
источника кодируются в двоичные кодовые слова длиной ![]() . Для
любого
. Для
любого ![]() вероятность
вероятность
![]() ошибки
декодирования можно сделать сколь угодно малой, если
ошибки
декодирования можно сделать сколь угодно малой, если
![]() (3.3.5)
(3.3.5)
![]() достаточно велико.
достаточно велико.
Наоборот, если
![]() , (3.3.6)
, (3.3.6)
тогда
![]() сколь
угодно близка к 1 при достаточно больших
сколь
угодно близка к 1 при достаточно больших ![]() .
.
Исходя
из этой теоремы мы видим, что среднее число бит на символ источника требуемое
для кодирования выхода ДИБП с произвольно малой вероятностью ошибки
декодирования, ограничено снизу энтропией источника ![]() . С другой стороны, если
. С другой стороны, если ![]() , вероятность ошибки
декодирования приближается к 100%, если
, вероятность ошибки
декодирования приближается к 100%, если ![]() произвольно увеличивать.
произвольно увеличивать.
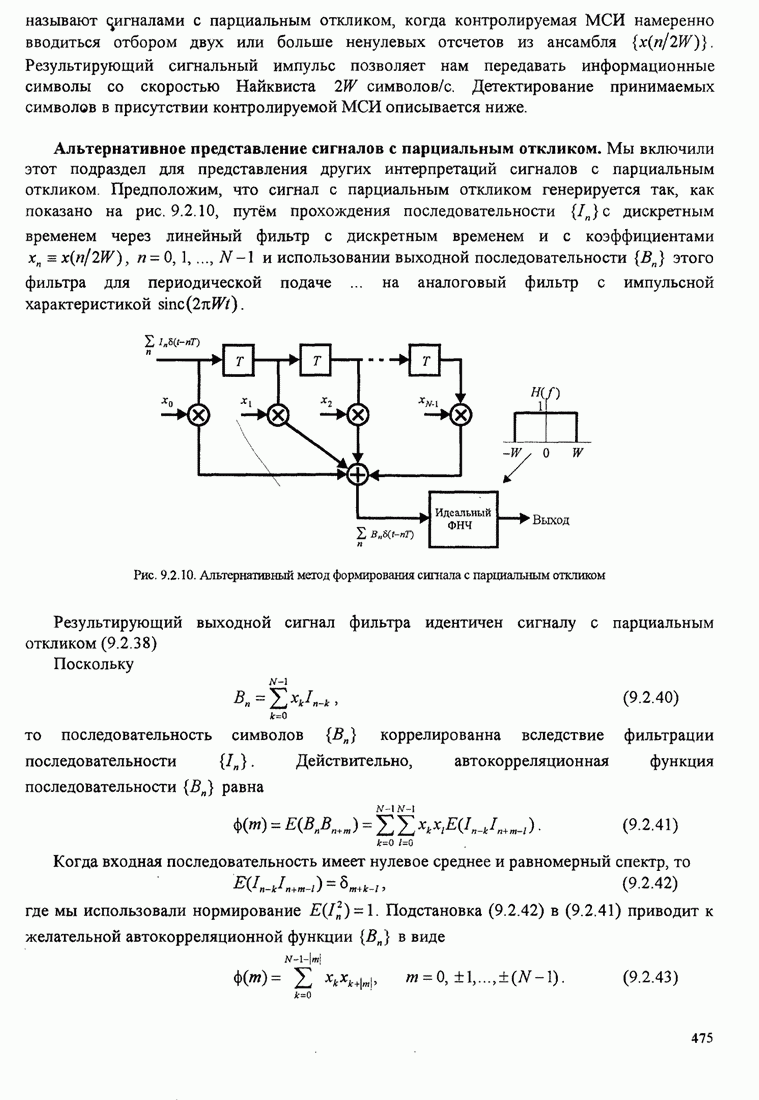
Кодовые слова переменной длины. Если символы источника неравновероятны, более эффективный метод кодирования сводится к использованию кодовых слов переменной длины. Примером такого кодирования является код Морзе, который восходит к девятнадцатому веку. В коде Морзе символам, возникающим более часто, сопоставляются более короткие кодовые слова, а символам, возникающим менее часто, сопоставляются более длинные кодовые слова. Следуя этой общей идее, мы можем учесть вероятность различных символов источника при выборе кодовых слов. Проблема в том, чтобы предложить метод выбора кодовых слов для символов источника. Этот метод кодирования назван энтропийным кодированием.
Таблица 3.3.1. Коды переменной длины
|
Символ |
|
Код I |
Код II |
Код III |
|
|
1/2 |
1 |
0 |
0 |
|
|
1/4 |
00 |
10 |
01 |
|
|
1/8 |
01 |
110 |
011 |
|
|
1/8 |
10 |
111 |
111 |
Для
примера предположим, что выходные символы ДИБП ![]() ,
,![]() ,
,![]() ,
,![]() соответствующими вероятностями
соответствующими вероятностями ![]() ,
, ![]() ,
, ![]() кодируются так как
показано в табл. 3.3.1. Код I имеет переменную длину и имеет принципиальный
недостаток. Чтобы увидеть этот недостаток, предположим, что мы приняли
последовательность 001001... Ясно, что 00 декодируется как
кодируются так как
показано в табл. 3.3.1. Код I имеет переменную длину и имеет принципиальный
недостаток. Чтобы увидеть этот недостаток, предположим, что мы приняли
последовательность 001001... Ясно, что 00 декодируется как ![]() . Однако последующие четыре
бита декодируются неоднозначно. Они могут декодироваться или как
. Однако последующие четыре
бита декодируются неоднозначно. Они могут декодироваться или как ![]() , или как
, или как ![]() . Возможно,
неоднозначность может быть разрешена путем ожидания последующих битов, но такое
декодирование крайне нежелательно. Мы должны рассмотреть только коды, которые
допускают немедленное декодирование, т.е. без задержки в декодере.
. Возможно,
неоднозначность может быть разрешена путем ожидания последующих битов, но такое
декодирование крайне нежелательно. Мы должны рассмотреть только коды, которые
допускают немедленное декодирование, т.е. без задержки в декодере.
Код
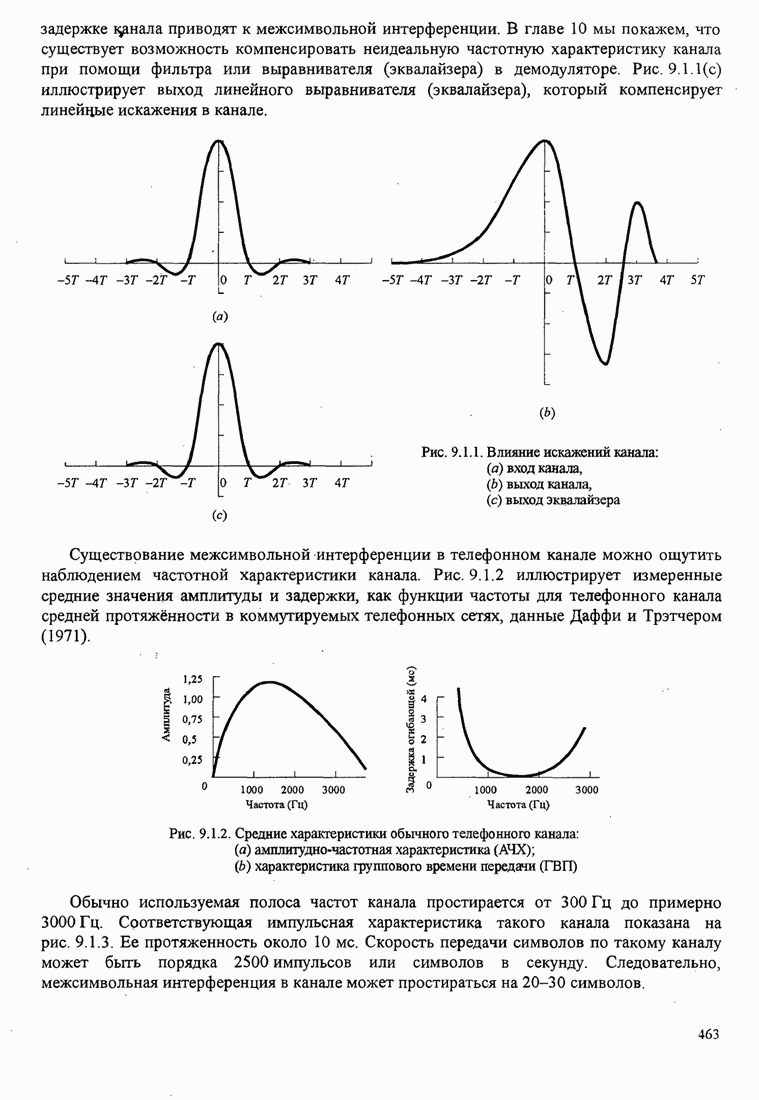
II в табл. 3.3.1 обеспечивает однозначное и немедленное декодирование. Удобно
представлять кодовые слова этого кода графически как узлы на дереве, как
показано на рис. 3.3.1. Видно, что 0 указывает на окончание кодового слова в
первых трех кодовых словах. Эта характеристика вместе с тем обстоятельством,
что ни одно кодовое слово не содержит более трех двоичных символов, что делает этот
код немедленно декодируемым. Заметим, что ни одно кодовое слово этого кода не
является префиксом (началом) другого кодового слова. В общем,
префиксное условие кода требует, чтобы
для данного кодового слова ![]() длины
длины ![]() с элементами
с элементами ![]() не существовало других
кодовых слов длинны
не существовало других
кодовых слов длинны ![]() с элементами
с элементами ![]() для
для ![]() .
.

Рис. 3.3.1. Кодовое дерево для кода II в табл.3.3.1

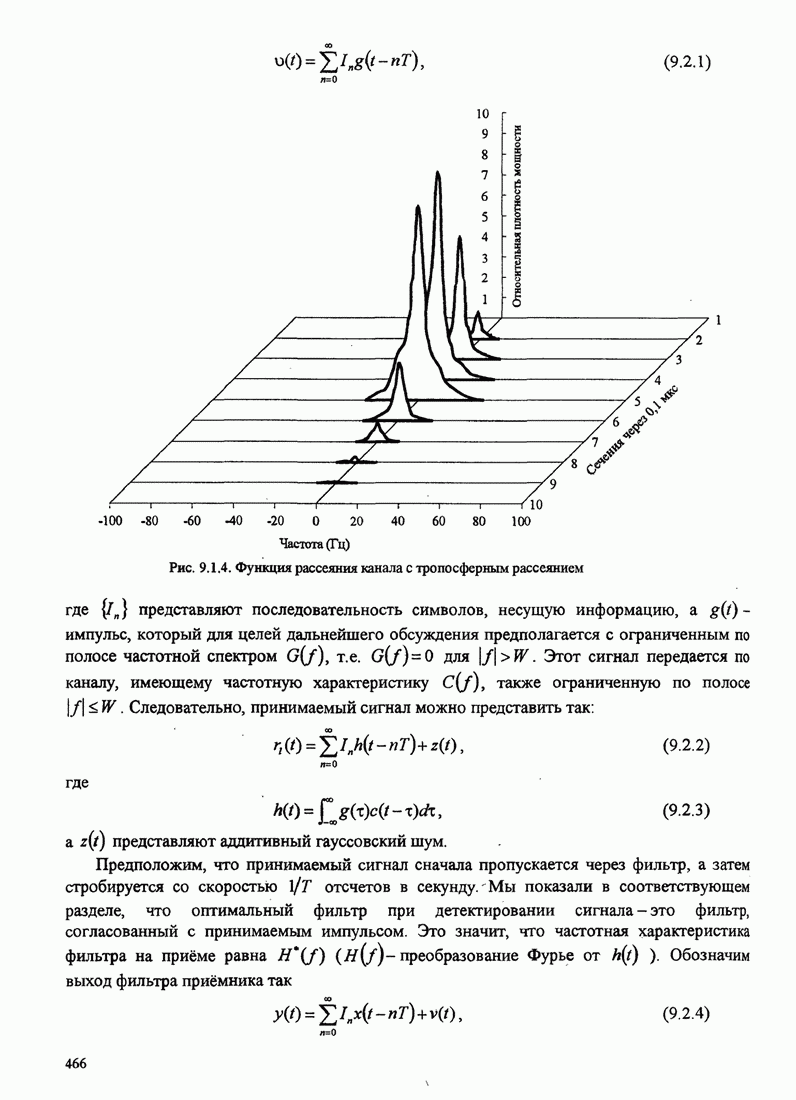
Рис. 3.3.2. Кодовое дерево для кода III в табл.3.3.1
Другими
словами, нет кодовых слов длины ![]() , которые совпадают с первыми
, которые совпадают с первыми ![]() двоичными символами
другого кодового слова длины
двоичными символами
другого кодового слова длины ![]() . Это
свойство делает кодовые слова немедленно декодируемыми.
. Это
свойство делает кодовые слова немедленно декодируемыми.
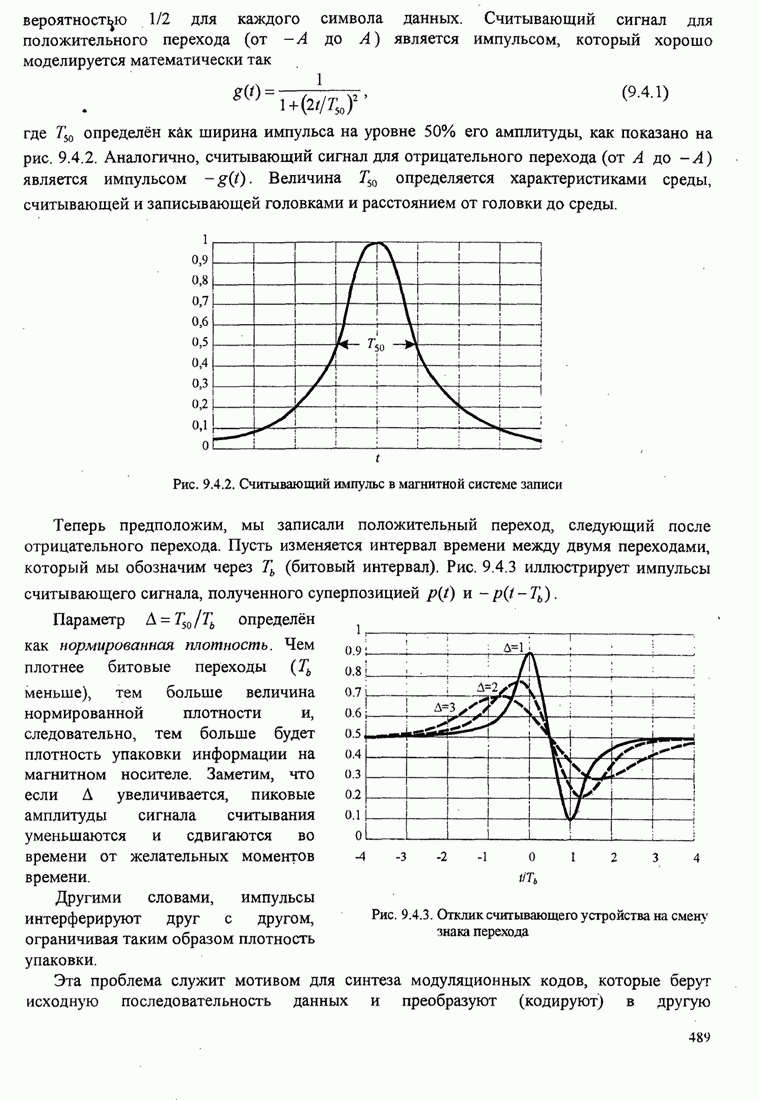
Код III из табл. 3.3.1 имеет кодовое дерево, показанное на рис. 3.3.2. Видим, что в этом случае имеет место однозначное декодирование, однако требующее задержки.
Ясно, что этот код не удовлетворяет префиксному условию.
Наша главная цель – создать систематическую процедуру для конструирования однозначных декодирующих кодов переменной длины, эффективных в том смысле, что среднее число бит на один символ источника, определяемое соотношением
![]() , (3.3.7)
, (3.3.7)
было бы минимальным. Условие существования кода переменной длины, которое удовлетворяет префиксному условию, дается неравенством Крафта.
Неравенство
Крафта.
Необходимым и достаточным условием существования двоичного кода с кодовыми
символами длины ![]() ,
удовлетворяющего условию префиксности, является
,
удовлетворяющего условию префиксности, является
![]() . (3.3.8)
. (3.3.8)
Сначала
мы докажем, что (3.3.8) является достаточным условием для существования префиксного
кода. Чтобы построить такой код, мы начнем с полного двоичного дерева порядка ![]() , которое имеет
, которое имеет ![]() конечных узлов,
причем от каждого узла порядка
конечных узлов,
причем от каждого узла порядка ![]() «растут» по два узла порядка
«растут» по два узла порядка ![]() ,
, ![]() .
.
Выберем
некоторый узел порядка в качестве первого кодового слова ![]() . Этот выбор устраняет
. Этот выбор устраняет ![]() конечных узлов
(т.е. долю
конечных узлов
(т.е. долю ![]() от
от
![]() конечных
узлов). От остающихся доступных узлов порядка
конечных
узлов). От остающихся доступных узлов порядка ![]() мы выбираем один узел для второго
кодового слова
мы выбираем один узел для второго
кодового слова ![]() .
Этот выбор устраняет
.
Этот выбор устраняет ![]() конечных узлов (т.е. долю
конечных узлов (т.е. долю ![]() от
от ![]() конечных узлов).
Этот процесс продолжается, пока последнее кодовое слово не определено в
конечном узле
конечных узлов).
Этот процесс продолжается, пока последнее кодовое слово не определено в
конечном узле ![]() .
Следовательно, в узле порядка
.
Следовательно, в узле порядка ![]() доля числа отсечённых конечных узлов
доля числа отсечённых конечных узлов
![]() .
.
Всегда
имеется узел порядка ![]() , который может быть выбран для
следующего слова. Таким образом, мы создали кодовое дерево, которое встроено в
полное дерево из
, который может быть выбран для
следующего слова. Таким образом, мы создали кодовое дерево, которое встроено в
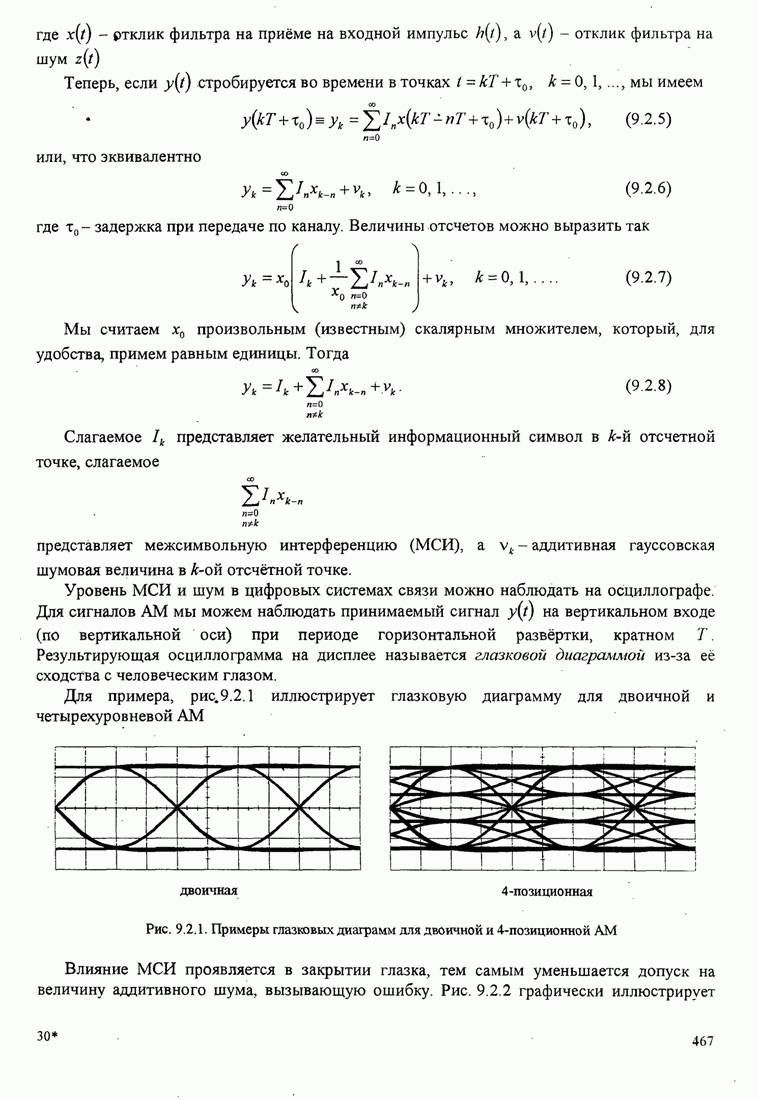
полное дерево из ![]() узлов,
как иллюстрируется на рис. 3.3.3, для дерева, имеющего 16 конечных узлов, и
источника, состоящего из пяти символов, отображаемых кодовыми словами длиной
узлов,
как иллюстрируется на рис. 3.3.3, для дерева, имеющего 16 конечных узлов, и
источника, состоящего из пяти символов, отображаемых кодовыми словами длиной ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

Рис. 3.3.3. Конструирование двоичного дерева, встроенного в полное дерево
Чтобы
доказать, что (3.3.8) является необходимым условием, мы заметим, что в дереве
порядка ![]() ,
число конечных узлов, отсечённых от общего числа
,
число конечных узлов, отсечённых от общего числа ![]() конечных узлов равно
конечных узлов равно
![]() . Следовательно,
. Следовательно, ![]() ,
,
и доказательство (3.3.8) закончено. Неравенство Крафта можно использовать для доказательства следующей теоремы кодирования источника (без шумов), которое применяется к кодам, удовлетворяющим префиксному условию.
Теорема
кодирования источника II. Пусть ![]() - ансамбль символов двоичного
источника без памяти с конечной энтропией
- ансамбль символов двоичного
источника без памяти с конечной энтропией ![]() и выходными символами
и выходными символами ![]() ,
, ![]() с соответствующими
вероятностями выбора
с соответствующими
вероятностями выбора ![]() ,
, ![]() . Существует возможность создать код,
который удовлетворяет префиксному условию и имеет среднюю длину
. Существует возможность создать код,
который удовлетворяет префиксному условию и имеет среднюю длину ![]() , которое
удовлетворяет неравенству
, которое
удовлетворяет неравенству
![]() . (3.3.9)
. (3.3.9)
Чтобы
установить нижнюю границу в (3.3.9), обратим внимание на то, что для кодовых
слов, которые имеют длину ![]() ,
, ![]() , разность
, разность ![]() может быть выражена в виде
может быть выражена в виде
![]() . (3.3.10)
. (3.3.10)
Используя
неравенство ![]() ,
из (3.3.10) находим
,
из (3.3.10) находим
 ,
,
где
последнее неравенство следует из неравенства Крафта. Равенство имеет место,
если только если ![]() для
для
![]() .
.
Верхняя
граница в (3.3.9) может быть установлена при предположении что ![]() ,
, ![]() - целые числа,
выбираемые из условия
- целые числа,
выбираемые из условия ![]() . Но если
. Но если ![]() просуммированы по
просуммированы по ![]() , получаем неравенство
Крафта, для которого демонстрировали, что там существует код, удовлетворяющий
префиксному условию другой стороны, если мы берем логарифм
, получаем неравенство
Крафта, для которого демонстрировали, что там существует код, удовлетворяющий
префиксному условию другой стороны, если мы берем логарифм ![]() , получаем
, получаем
![]()
или, что эквивалентно,
![]() . (3.3.11)
. (3.3.11)
Если
умножить обе части неравенства (3.3.11) на ![]() и просуммировать по
и просуммировать по ![]() , получаем
желательную верхнюю границу, данную в (3.3.9). Это завершает доказательство
(3.3.9).
, получаем
желательную верхнюю границу, данную в (3.3.9). Это завершает доказательство
(3.3.9).
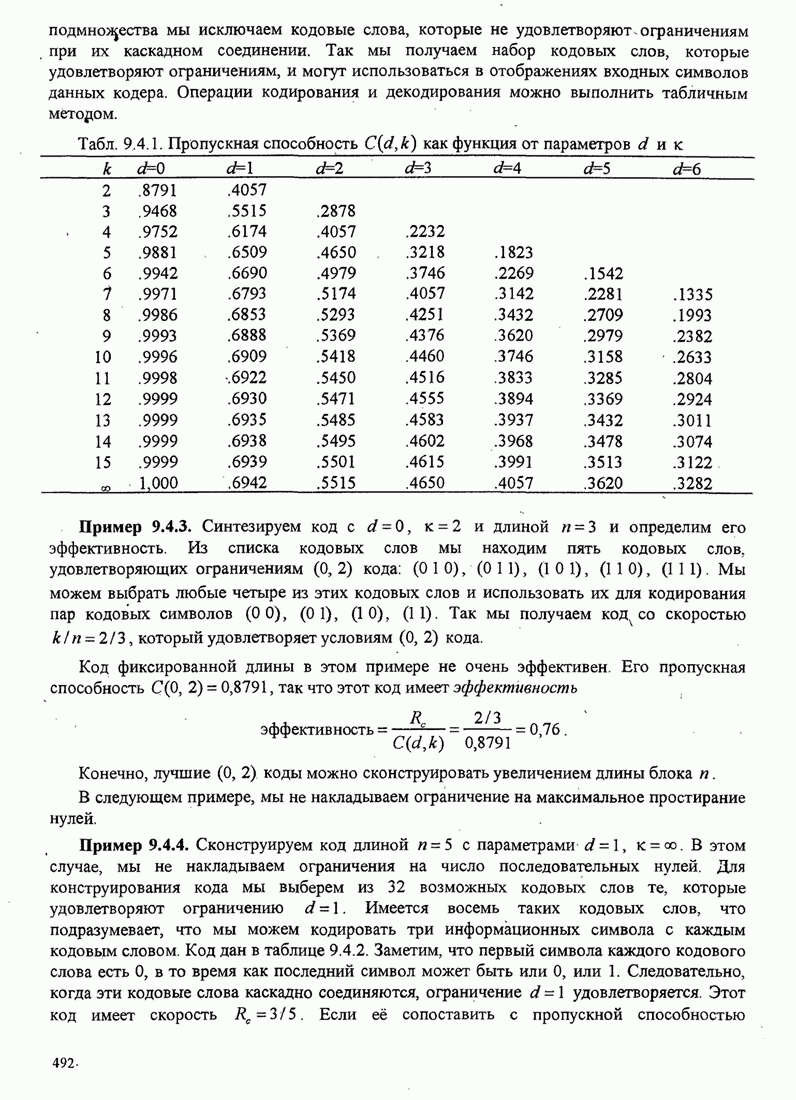
Мы установили, что коды переменной длины, которые удовлетворяют префиксному условию, - это эффективные коды для любого дискретного источника без памяти (ДИБП) с символами, имеющими различную априорную вероятность. Опишем теперь алгоритм для построения таких кодов.
Алгоритм
кодирования Хаффмена.
Хаффмен (1952) разработал алгоритм кодирования переменной длины, основанный на
знании априорных вероятностей символов ![]() ,
, ![]() . Этот алгоритм оптимален в том смысле,
что среднее число двоичных символов, требуемых для представления исходных
символов, минимально. Получаемые кодовые слова удовлетворяют префиксному
условию, определенному выше, что позволяет уникально и мгновенно декодировать
полученную последовательность. Мы проиллюстрируем этот алгоритм кодирования
посредством двух примеров.
. Этот алгоритм оптимален в том смысле,
что среднее число двоичных символов, требуемых для представления исходных
символов, минимально. Получаемые кодовые слова удовлетворяют префиксному
условию, определенному выше, что позволяет уникально и мгновенно декодировать
полученную последовательность. Мы проиллюстрируем этот алгоритм кодирования
посредством двух примеров.
Пример
3.3.1.
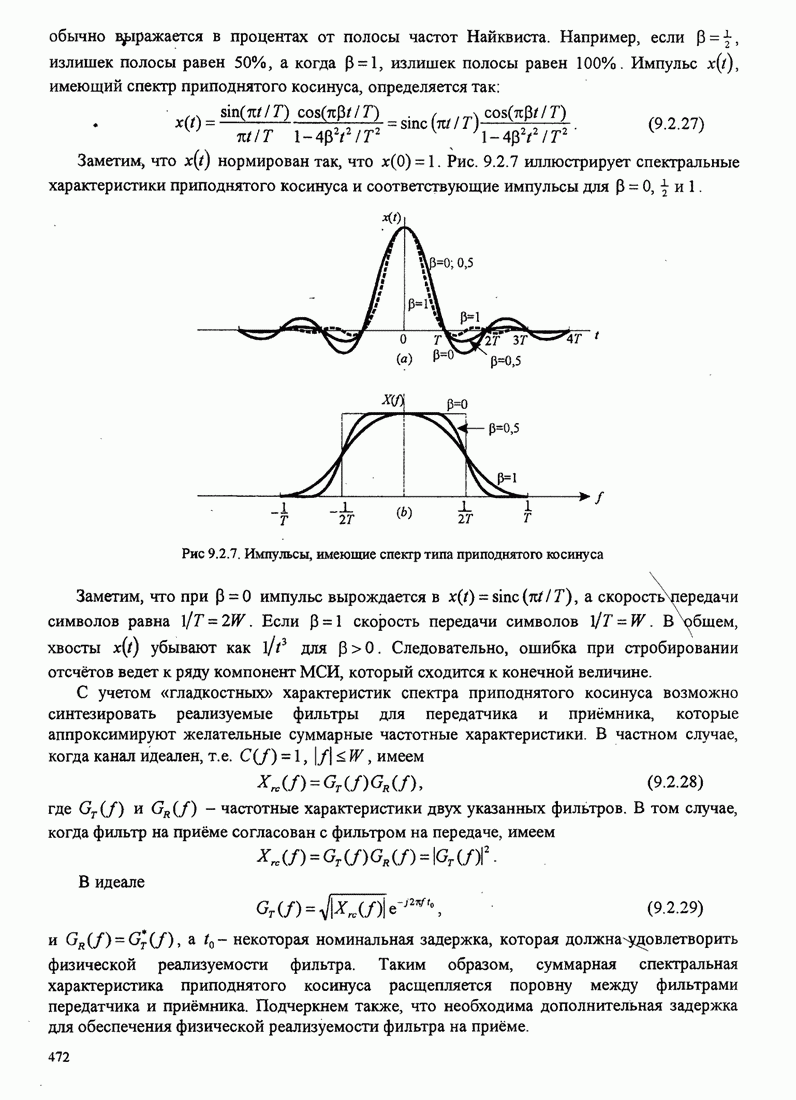
Рассмотрим ДИБГТ с семью возможными символами ![]() , имеющими вероятности выбора,
иллюстрируемые рис. 3.3.4.
, имеющими вероятности выбора,
иллюстрируемые рис. 3.3.4.

Рис. 3.3.4. Пример кодирования ДИБП кодом переменной длины
Мы
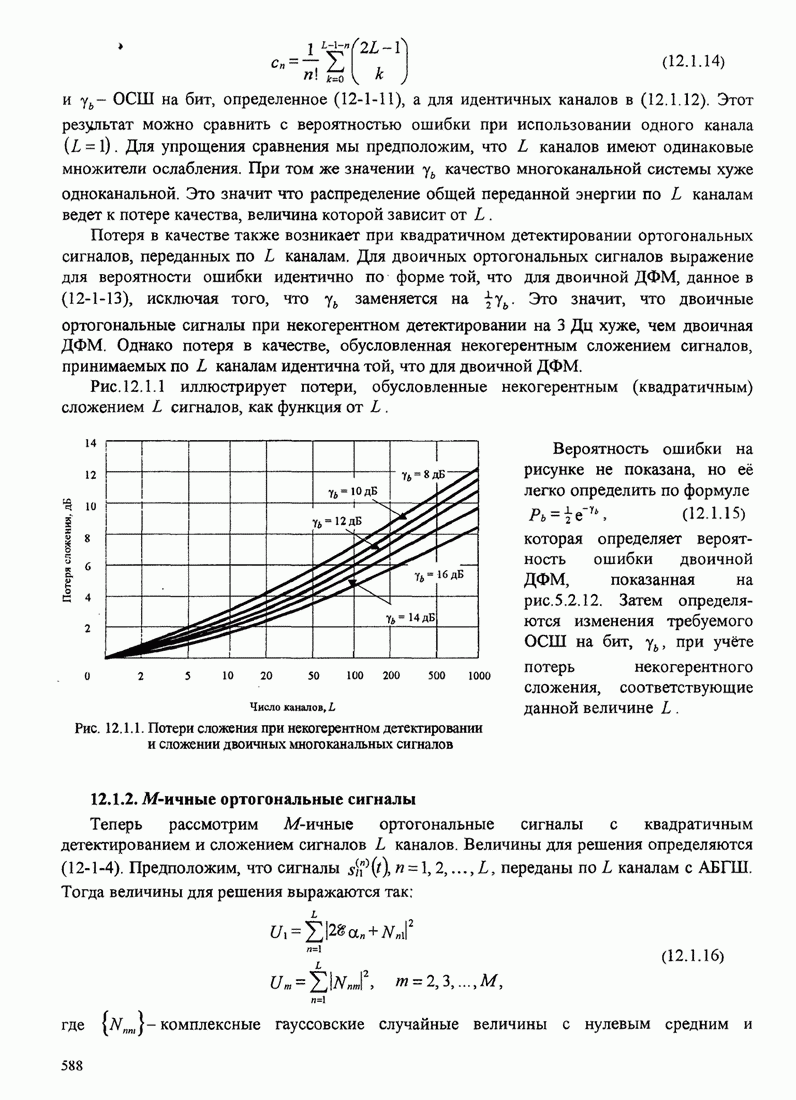
упорядочили символы источника в порядке убывания вероятностей, т.е. ![]() . Процесс
кодирования начинаем с двух наименее вероятных символов
. Процесс
кодирования начинаем с двух наименее вероятных символов ![]() и
и ![]() . Эти два символа объединяем,
как показано на рис. 3.3.4, причем верхнему ветвлению присваиваем «0», а
нижнему - «1». Вероятности этих двух ветвей складываются, и общему узлу
присваивается суммарная вероятность, равная в данном случае 0,01. Теперь мы имеем
исходные символы плюс новый символ, обозначим его
. Эти два символа объединяем,
как показано на рис. 3.3.4, причем верхнему ветвлению присваиваем «0», а
нижнему - «1». Вероятности этих двух ветвей складываются, и общему узлу
присваивается суммарная вероятность, равная в данном случае 0,01. Теперь мы имеем
исходные символы плюс новый символ, обозначим его ![]() , полученный объединением
, полученный объединением ![]() и
и ![]() . На следующем шаге
снова объединяются два наименее вероятных символа из набора
. На следующем шаге
снова объединяются два наименее вероятных символа из набора ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . Это
. Это ![]() и
и ![]() которые имеют объединенную
вероятность 0,05. Переходу от
которые имеют объединенную
вероятность 0,05. Переходу от ![]() присваиваем «0», а переходу от
присваиваем «0», а переходу от ![]() - «1». Эта
процедура продолжается, пока мы не исчерпаем все возможные символы источника.
Результат – кодовое дерево с ветвями, которые содержат требуемые кодовые слова.
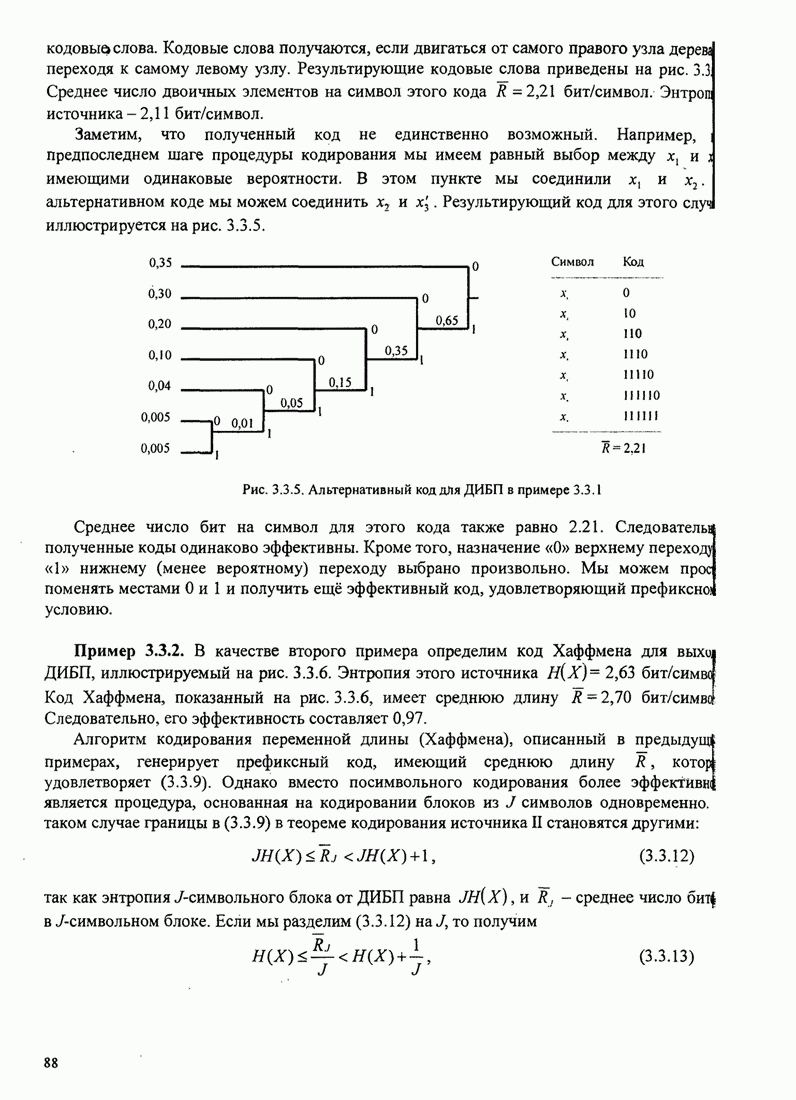
Кодовые слова получаются, если двигаться от самого правого узла дерева переходя
к самому левому узлу. Результирующие кодовые слова приведены на рис. 3.3
Среднее число двоичных элементов на символ этого кода
- «1». Эта
процедура продолжается, пока мы не исчерпаем все возможные символы источника.
Результат – кодовое дерево с ветвями, которые содержат требуемые кодовые слова.
Кодовые слова получаются, если двигаться от самого правого узла дерева переходя
к самому левому узлу. Результирующие кодовые слова приведены на рис. 3.3
Среднее число двоичных элементов на символ этого кода ![]() бит/символ. Энтропия
источника – 2,11 бит/символ.
бит/символ. Энтропия
источника – 2,11 бит/символ.
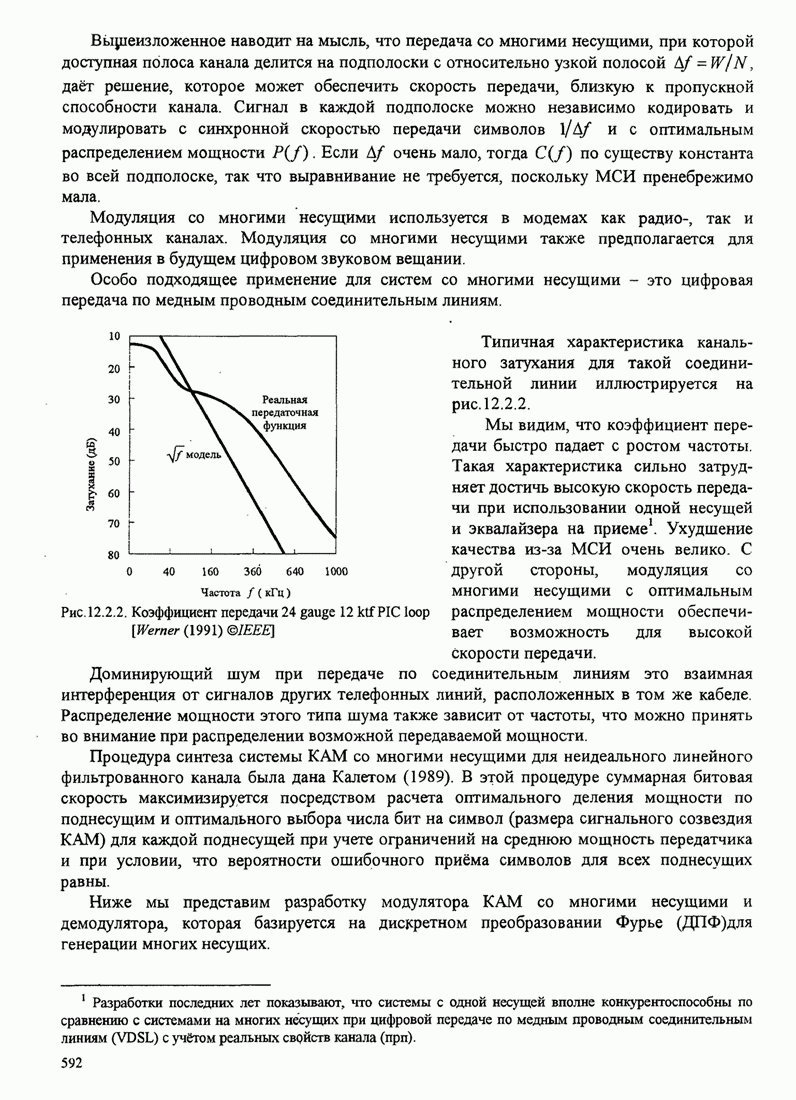
Заметим,
что полученный код не единственно возможный. Например, на предпоследнем шаге
процедуры кодирования мы имеем равный выбор между ![]() , и
, и ![]() имеющими одинаковые вероятности. В
этом пункте мы соединили
имеющими одинаковые вероятности. В
этом пункте мы соединили ![]() и
и ![]() . В альтернативном коде мы можем
соединить
. В альтернативном коде мы можем
соединить ![]() и
и
![]() .
Результирующий код для этого случая иллюстрируется на рис. 3.3.5.
.
Результирующий код для этого случая иллюстрируется на рис. 3.3.5.

Рис. 3.3.5. Альтернативный код для ДИБП в примере 3.3.1
Среднее число бит на символ для этого кода также равно 2.21. Следовательно, полученные коды одинаково эффективны. Кроме того, назначение «0» верхнему переходу и «1» нижнему (менее вероятному) переходу выбрано произвольно. Мы можем просто поменять местами 0 и 1 и получить ещё эффективный код, удовлетворяющий префиксному условию.
Пример
3.3.2.
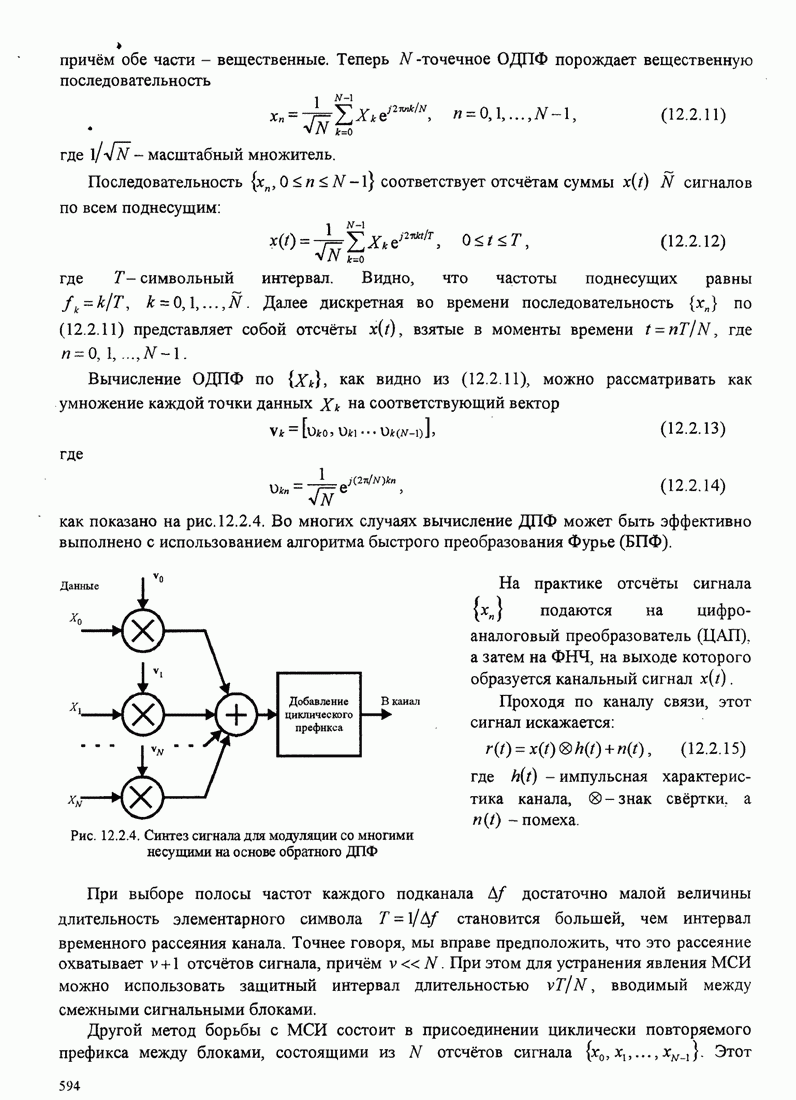
В качестве второго примера определим код Хаффмена для выхода ДИБП,
иллюстрируемый на рис. 3.3.6. Энтропия этого источника ![]() бит/символ. Код Хаффмена,
показанный на рис. 3.3.6, имеет среднюю длину
бит/символ. Код Хаффмена,
показанный на рис. 3.3.6, имеет среднюю длину ![]() бит/символ. Следовательно, его
эффективность составляет 0,97.
бит/символ. Следовательно, его
эффективность составляет 0,97.
Алгоритм
кодирования переменной длины (Хаффмена), описанный в предыдущих примерах,
генерирует префиксный код, имеющий среднюю длину ![]() , который удовлетворяет (3.3.9). Однако
вместо посимвольного кодирования более эффективной является процедура,
основанная на кодировании блоков из
, который удовлетворяет (3.3.9). Однако
вместо посимвольного кодирования более эффективной является процедура,
основанная на кодировании блоков из ![]() символов одновременно, таком случае
границы в (3.3.9) в теореме кодирования источника II становятся другими:
символов одновременно, таком случае
границы в (3.3.9) в теореме кодирования источника II становятся другими:
![]() , (3.3.12)
, (3.3.12)
так
как энтропия ![]() -символьного
блока от ДИБП равна
-символьного
блока от ДИБП равна ![]() , и
, и ![]() - среднее число бит в
- среднее число бит в ![]() -символьном блоке.
Если мы разделим (3.3.12) на
-символьном блоке.
Если мы разделим (3.3.12) на ![]() , то получим
, то получим
![]() , (3.3.13)
, (3.3.13)
где
![]() - среднее
число битов на исходный символ. Следовательно,
- среднее
число битов на исходный символ. Следовательно, ![]() можно сделать как угодно близким к
можно сделать как угодно близким к ![]() , выбирая
, выбирая ![]() достаточно большим.
достаточно большим.

Рис. 3.3.6. Код Хаффмена для примера 3.3.2
Пример
3.3.3.
Выход ДИБП состоит из символов и ![]() ,
,![]() и
и ![]() с вероятностями 0,45, 0,35 и 0,20
соответственно. Энтропия этого источника
с вероятностями 0,45, 0,35 и 0,20
соответственно. Энтропия этого источника ![]() бит/символ. Код Хаффмена для этого
источника, данный в табл. 3.3.2, требует
бит/символ. Код Хаффмена для этого
источника, данный в табл. 3.3.2, требует ![]() бит/символ и приводят к эффективности
97,9%, Если посредством алгоритма Хаффмена символы закодированы парами,
результирующий код выглядит так, как показано в табл. 3.3.3. Энтропия источника
для пар символов
бит/символ и приводят к эффективности
97,9%, Если посредством алгоритма Хаффмена символы закодированы парами,
результирующий код выглядит так, как показано в табл. 3.3.3. Энтропия источника
для пар символов ![]() бит/пара
символов. С другой стороны, код Хаффмена требует
бит/пара
символов. С другой стороны, код Хаффмена требует ![]() бит/пара символов. Таким образом,
эффективность кодирования увеличилась до
бит/пара символов. Таким образом,
эффективность кодирования увеличилась до ![]() (до 99,0 %).
(до 99,0 %).
Таблица 3.3.2. Код Хаффмена для примера 3.3.3
|
Символ |
Вероятность |
Собственная информация |
Код |
|
|
0,45 |
1,156 |
1 |
|
|
0,35 |
1,520 |
00 |
|
|
0,20 |
2,33 |
01 |
|
|
|||
|
|
|||
|
Эффективность 97,9 % |
|||
Итак,
мы продемонстрировали, что эффективное кодирование для ДИБП может быть
выполнено на посимвольной основе, если использовать неравномерный код,
основанный на алгоритме Хаффмена. Кроме того, эффективность процедуры
кодирования увеличивается при кодировании блоков из ![]() символов одновременно. Таким
образом, выход ДИБП с энтропией
символов одновременно. Таким
образом, выход ДИБП с энтропией ![]() может быть закодирован неравномерным
кодом со средним числом битов на исходный символ, которое может быть сделано
как угодно близким к
может быть закодирован неравномерным
кодом со средним числом битов на исходный символ, которое может быть сделано
как угодно близким к ![]() .
.
Таблица 3.3.3. Код Хаффмена для кодирования пар символов
|
Пара символов |
Вероятность |
Собственная информация |
Код |
|
|
0,2025 |
2,312 |
10 |
|
|
0,1575 |
2,676 |
001 |
|
|
0,1575 |
2,676 |
010 |
|
|
0,1225 |
3,039 |
011 |
|
|
0,09 |
3,486 |
111 |
|
|
0,09 |
3,486 |
0000 |
|
|
0,07 |
3,486 |
0001 |
|
|
0,07 |
3,850 |
1100 |
|
|
0,04 |
4,660 |
1101 |
|
|
|||
|
|
|||
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
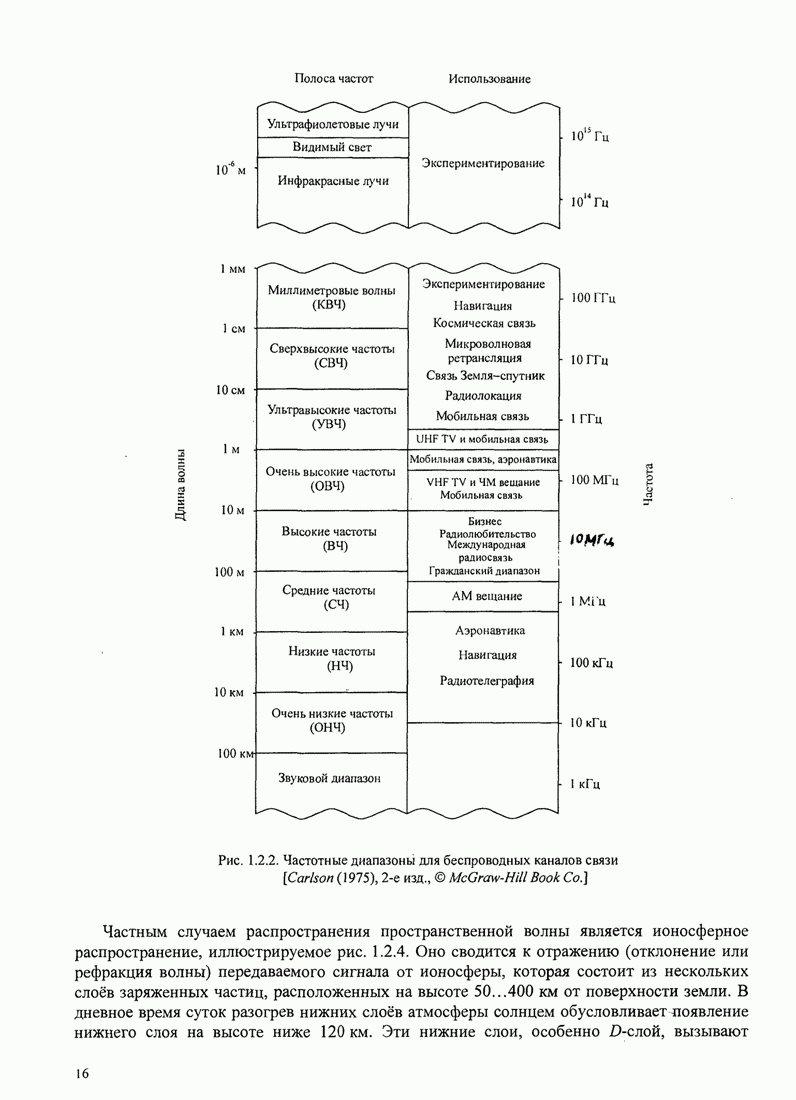
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
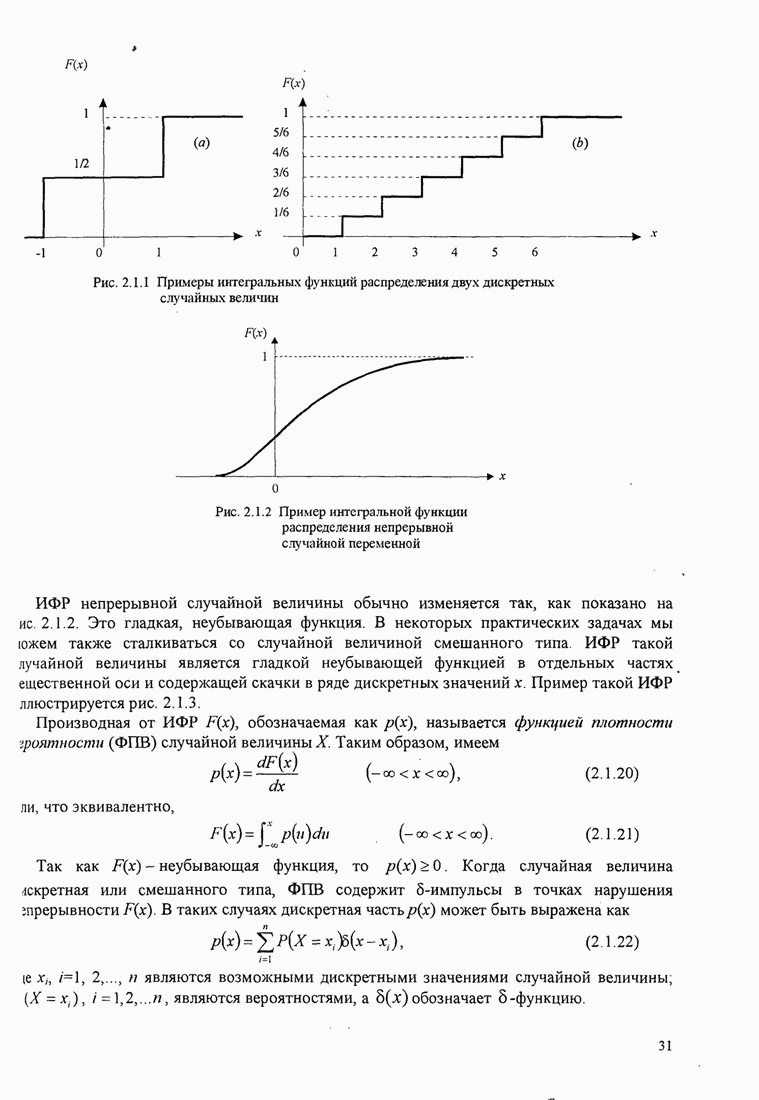
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
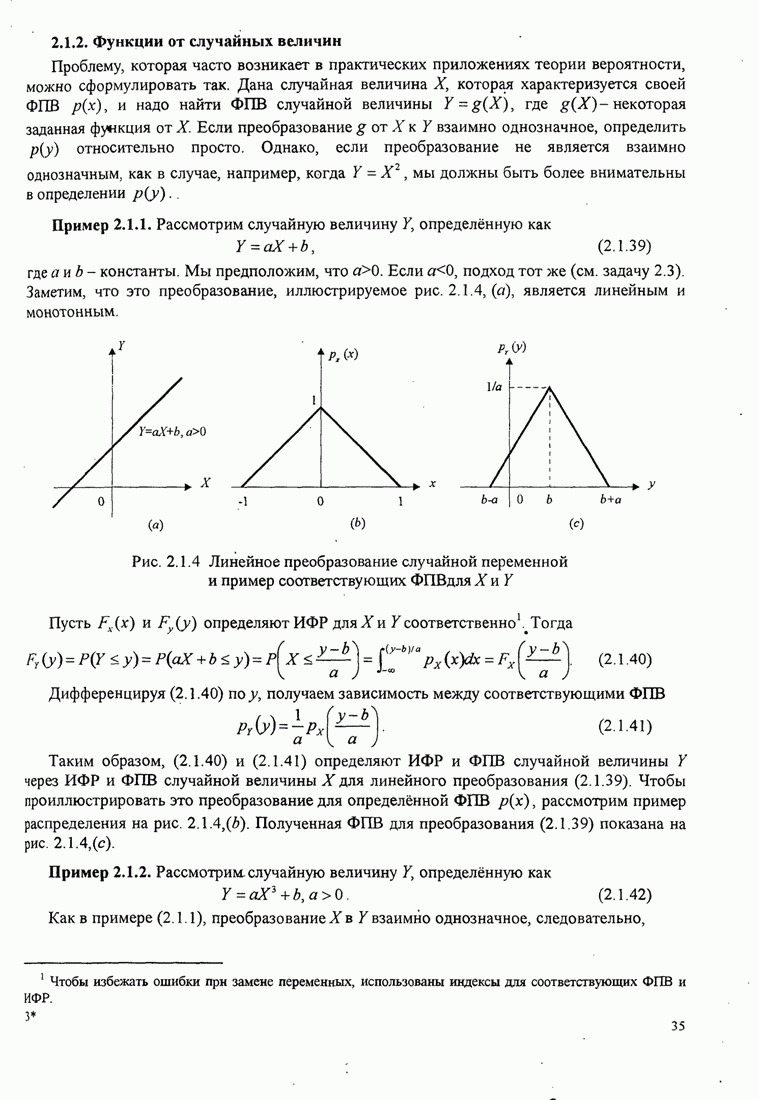
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
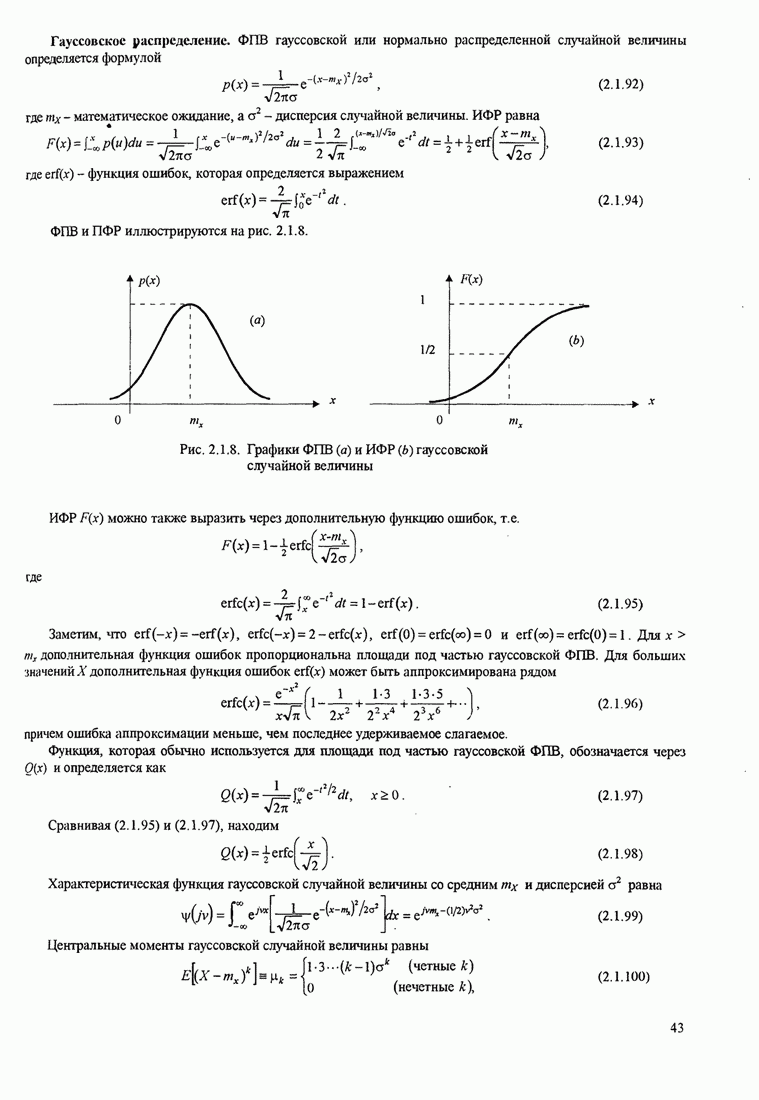
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
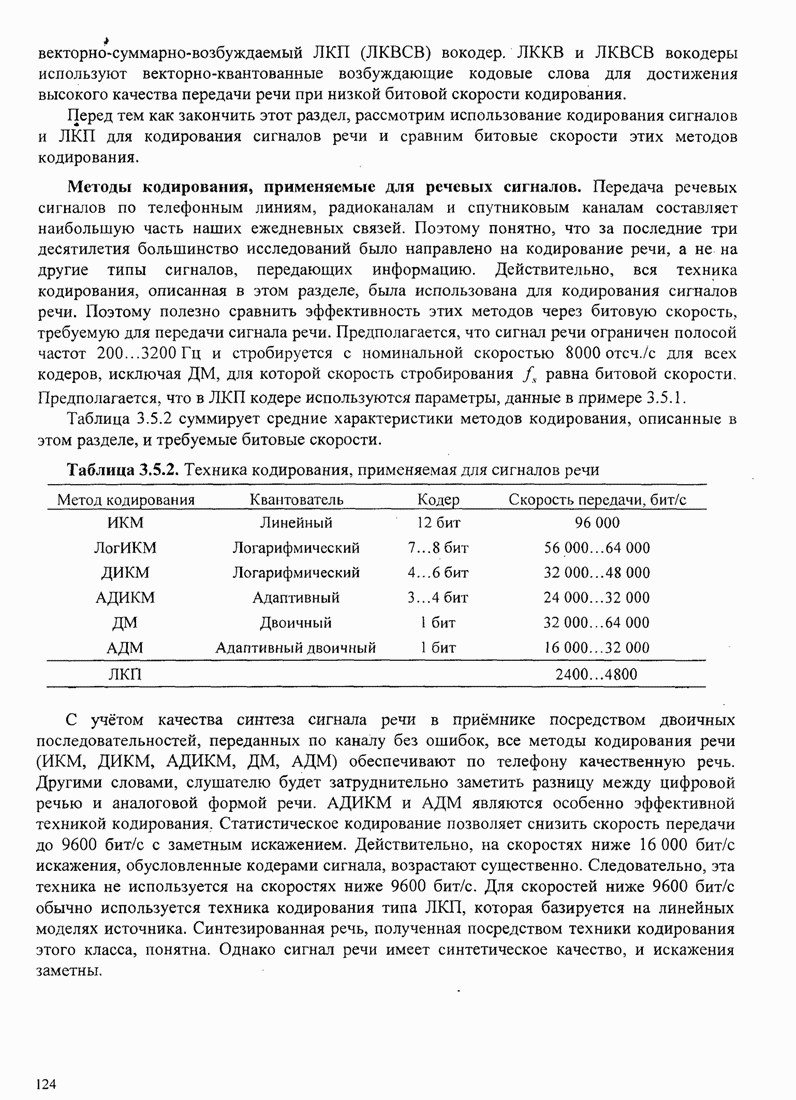
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
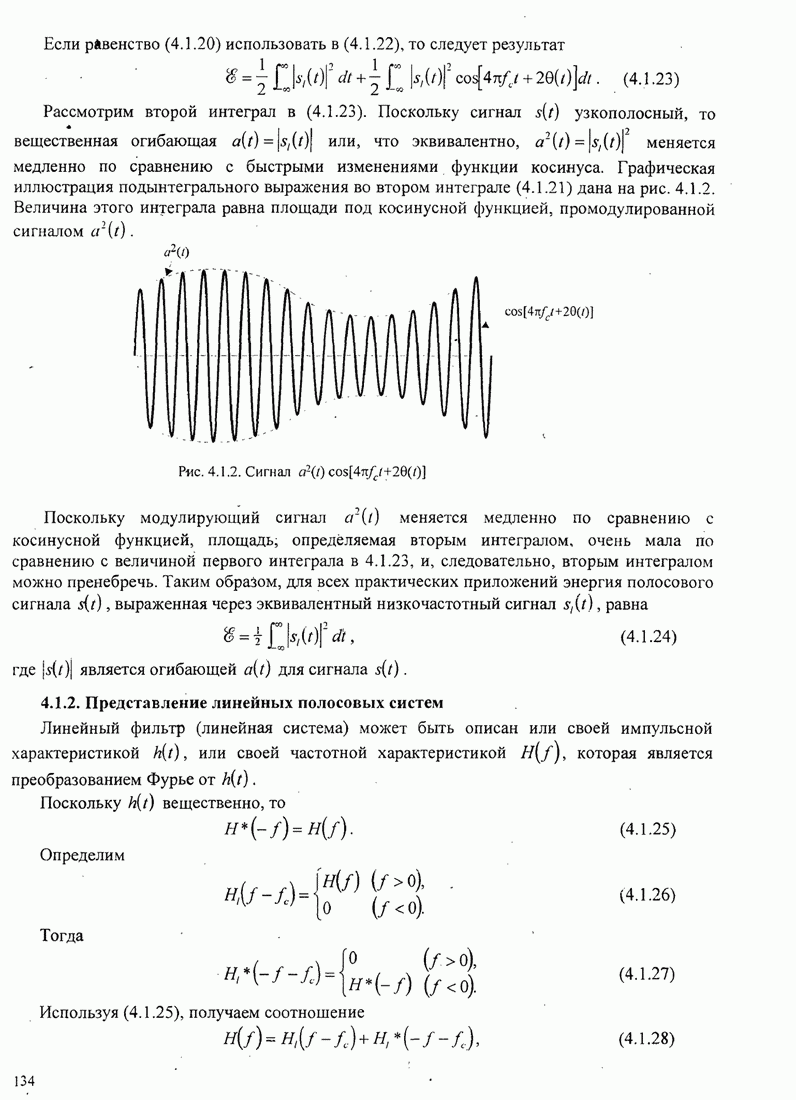
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
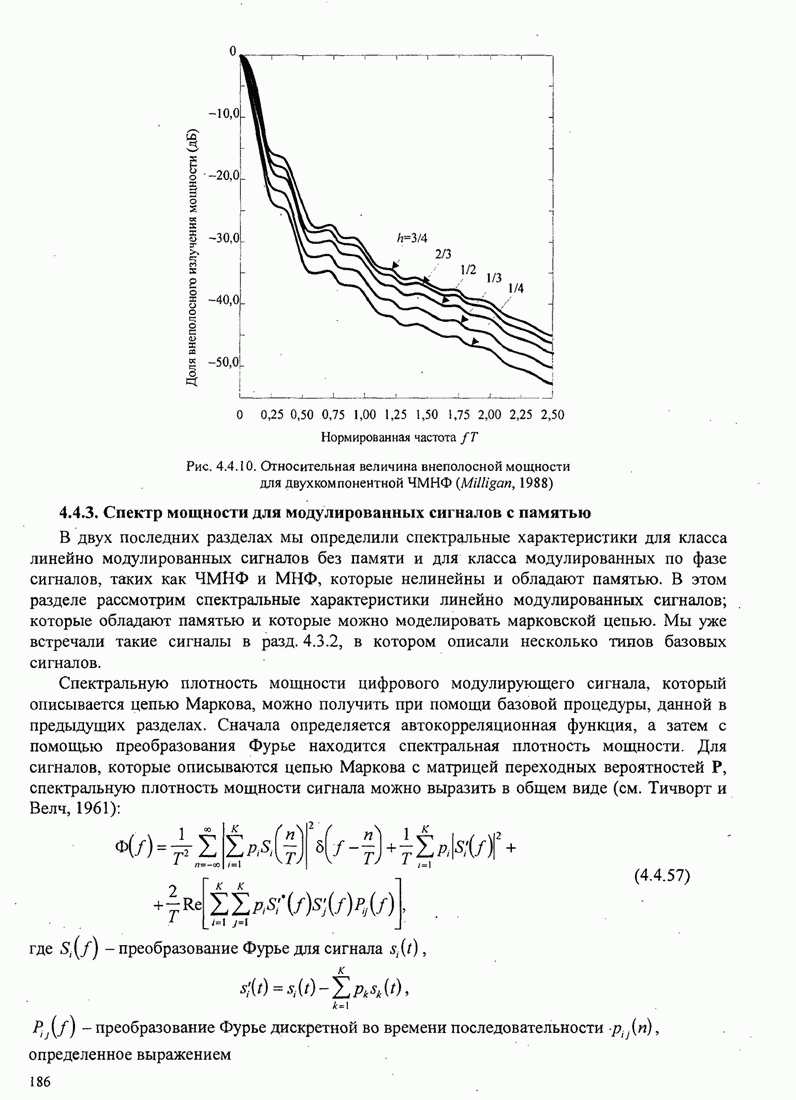
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
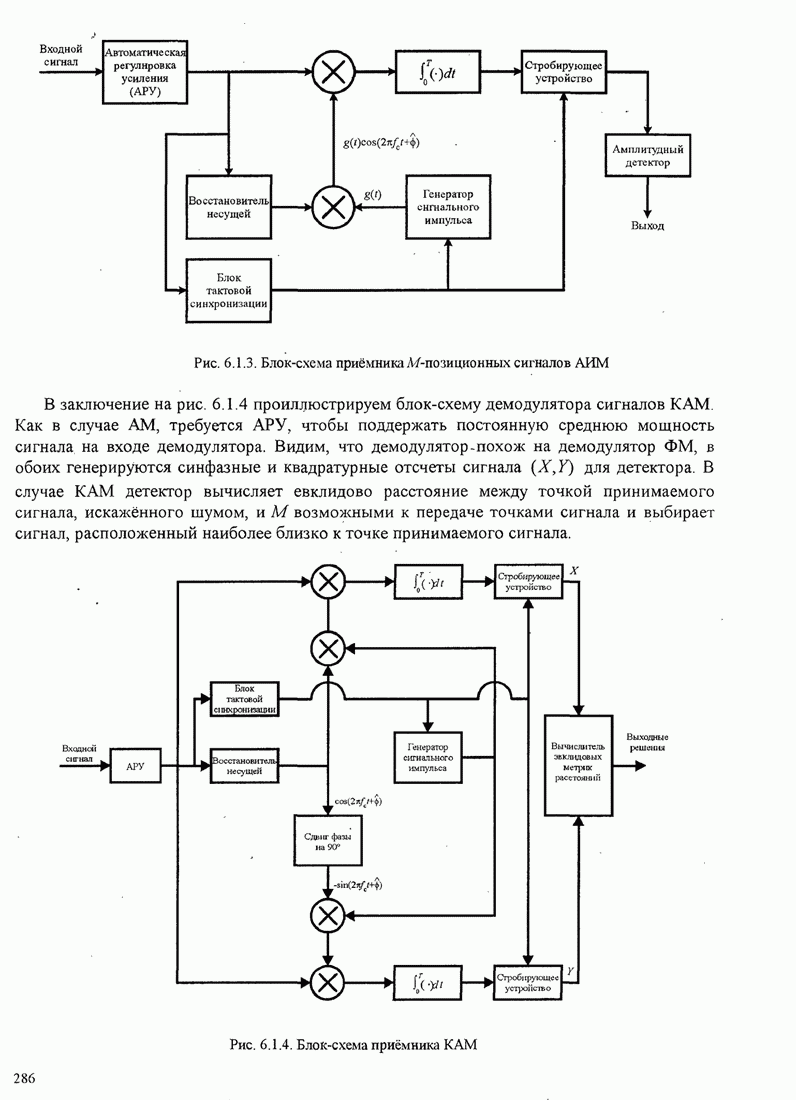
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
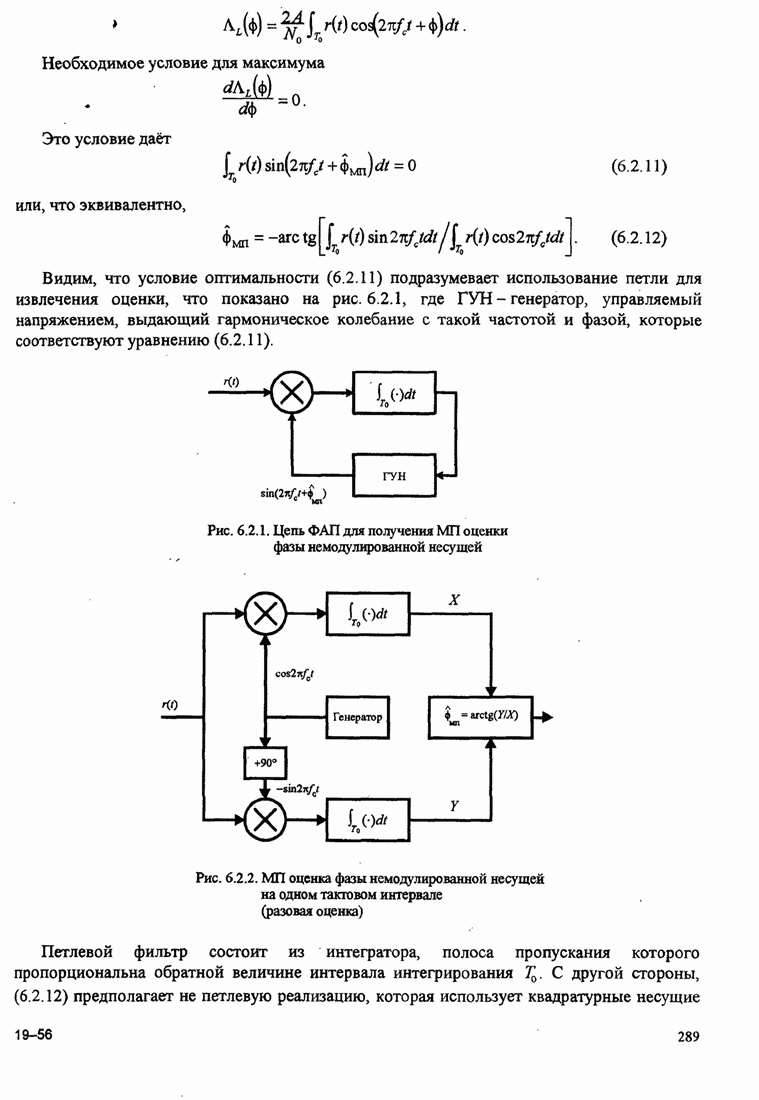
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
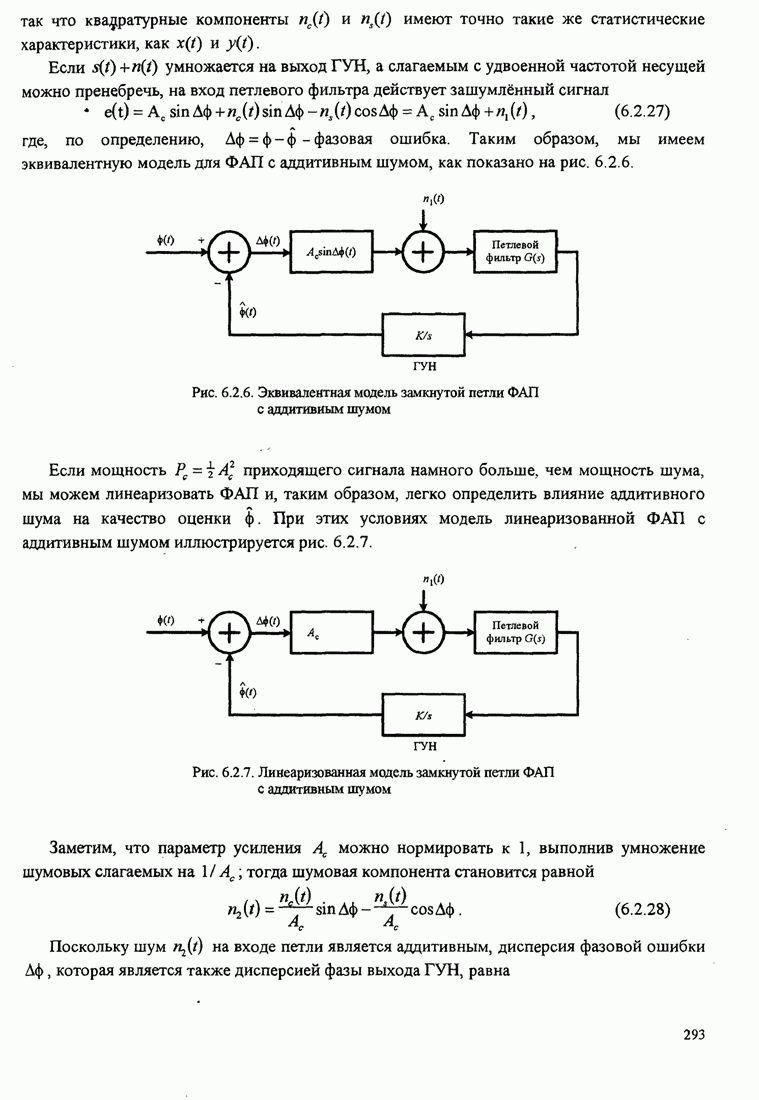
- 6.2.2. Модели замкнутой ФАП
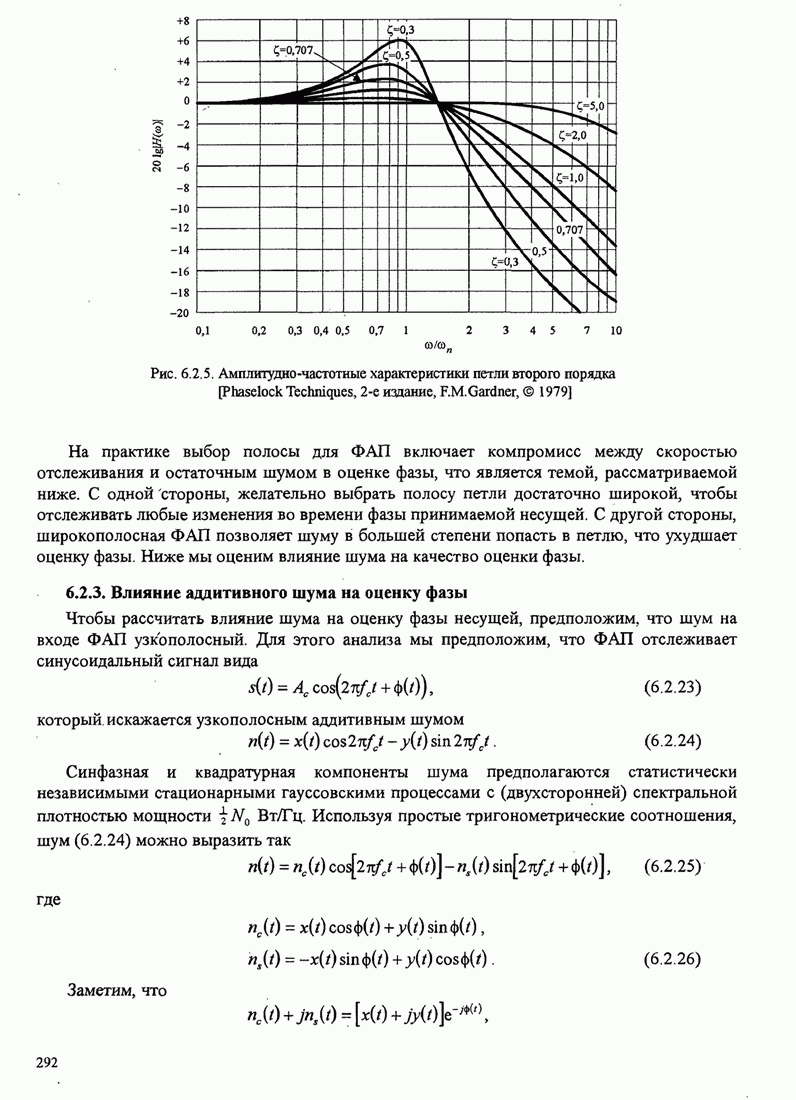
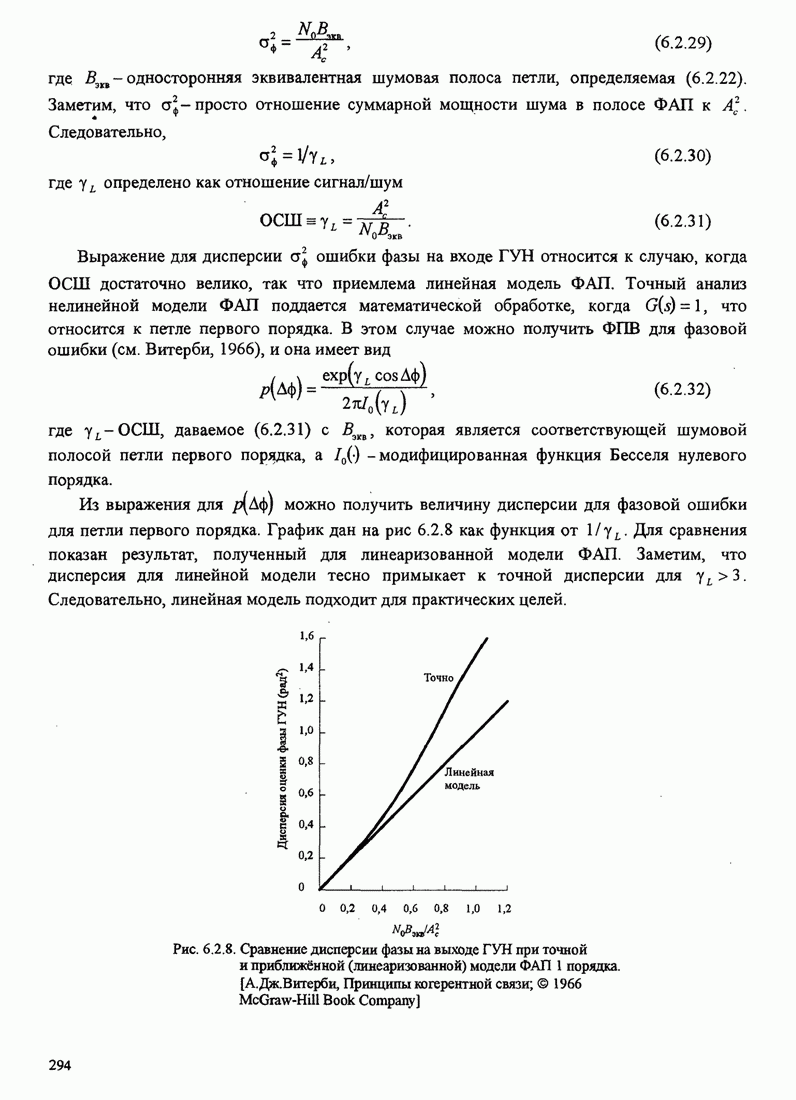
- 6.2.3. Влияние аддитивного шума на оценку фазы
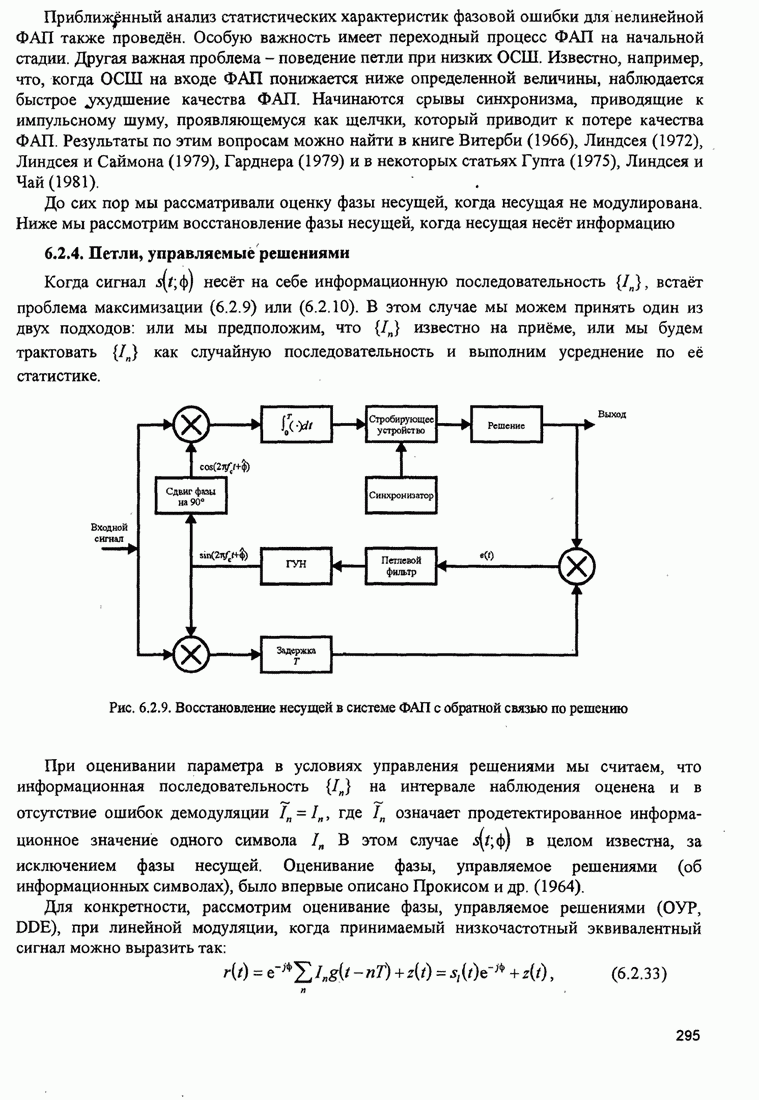
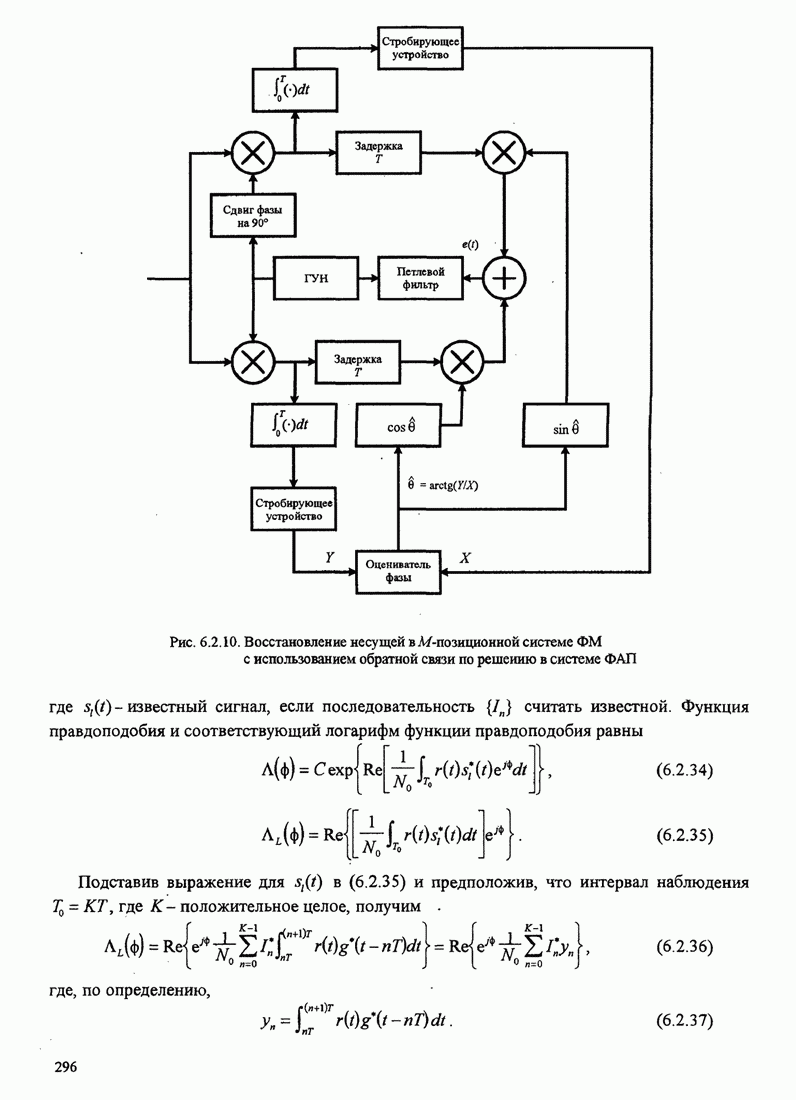
- 6.2.4. Петли, управляемые решениями
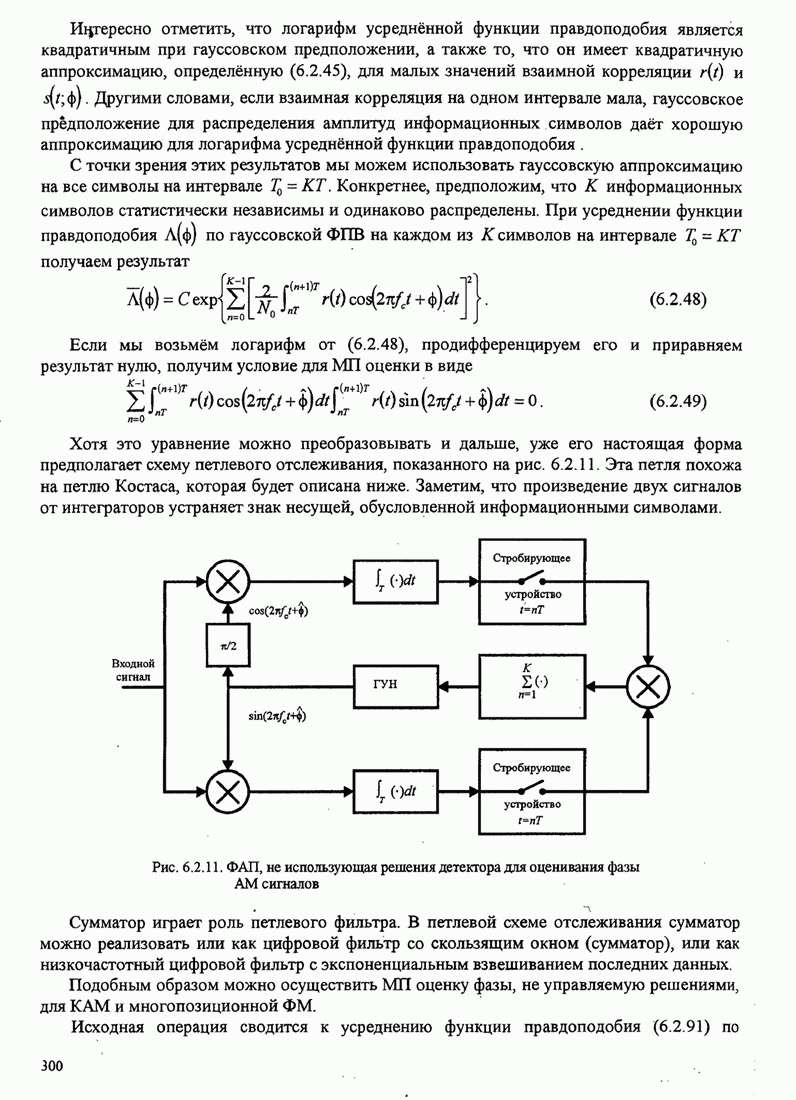
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
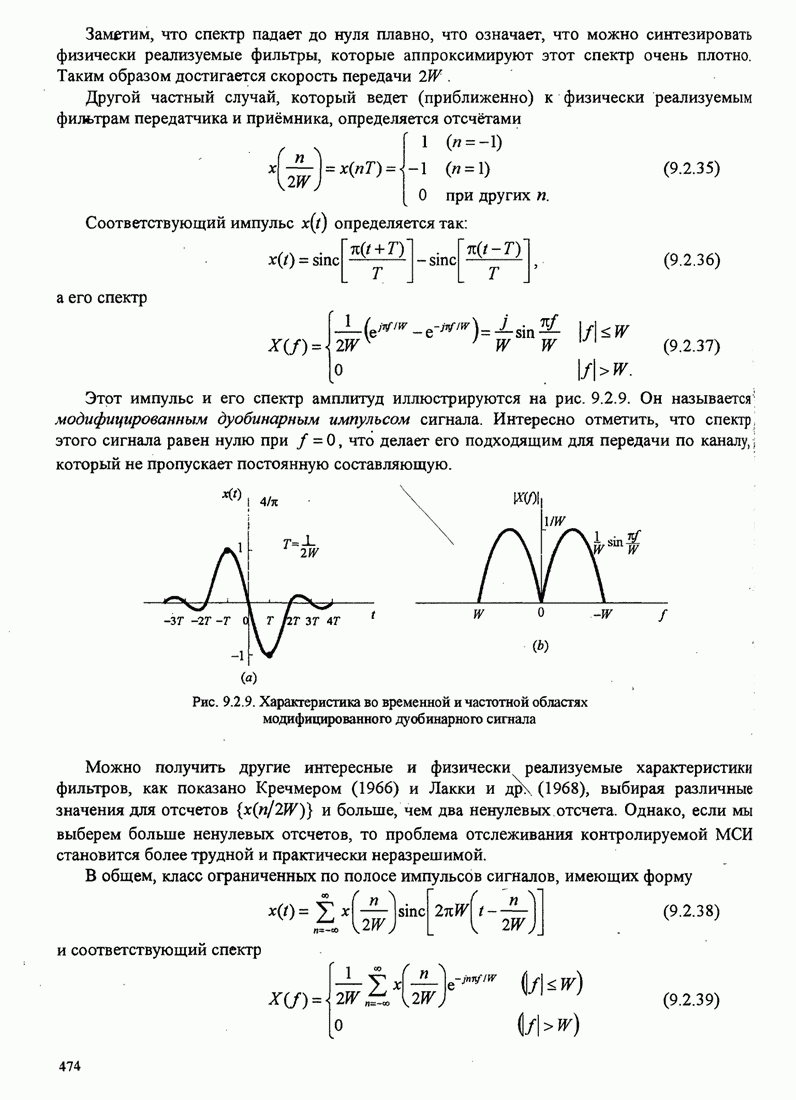
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
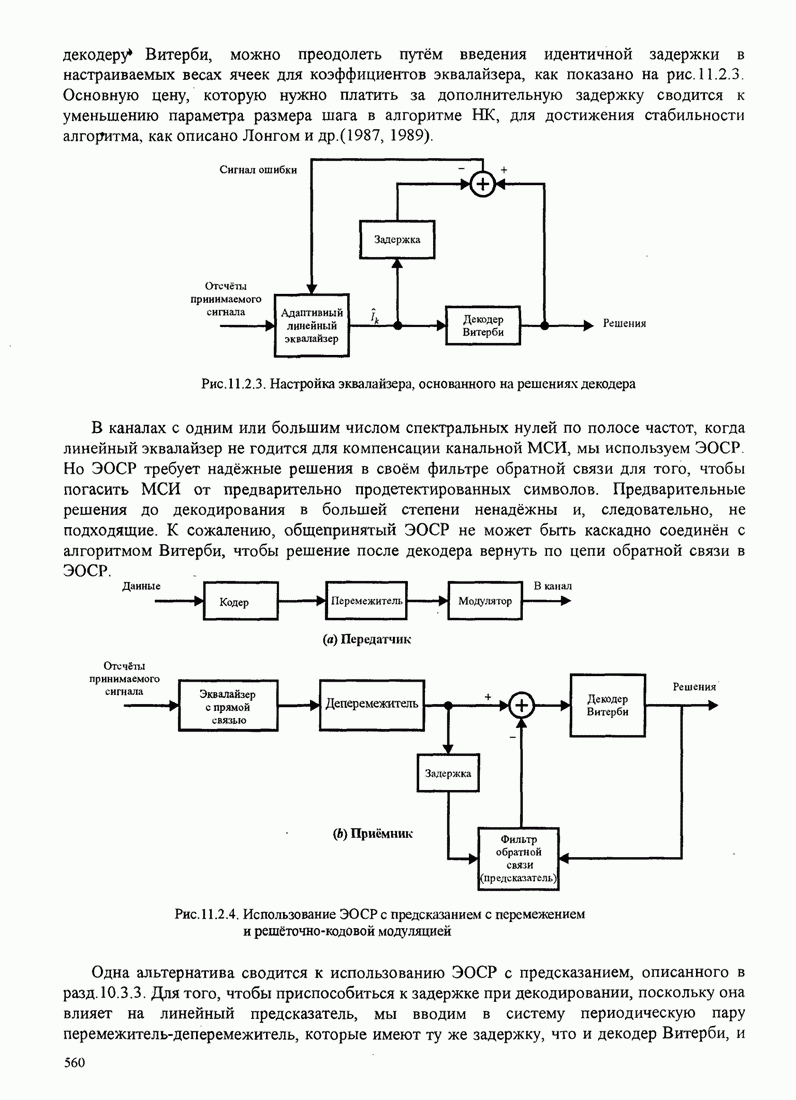
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
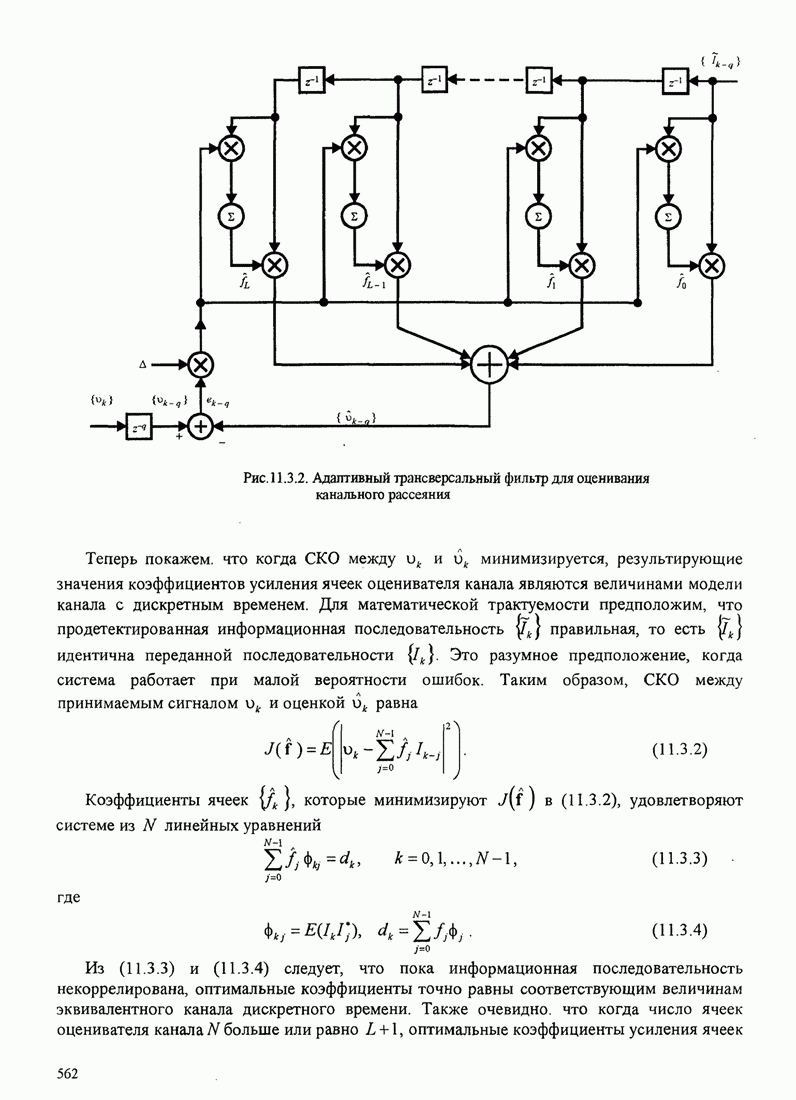
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
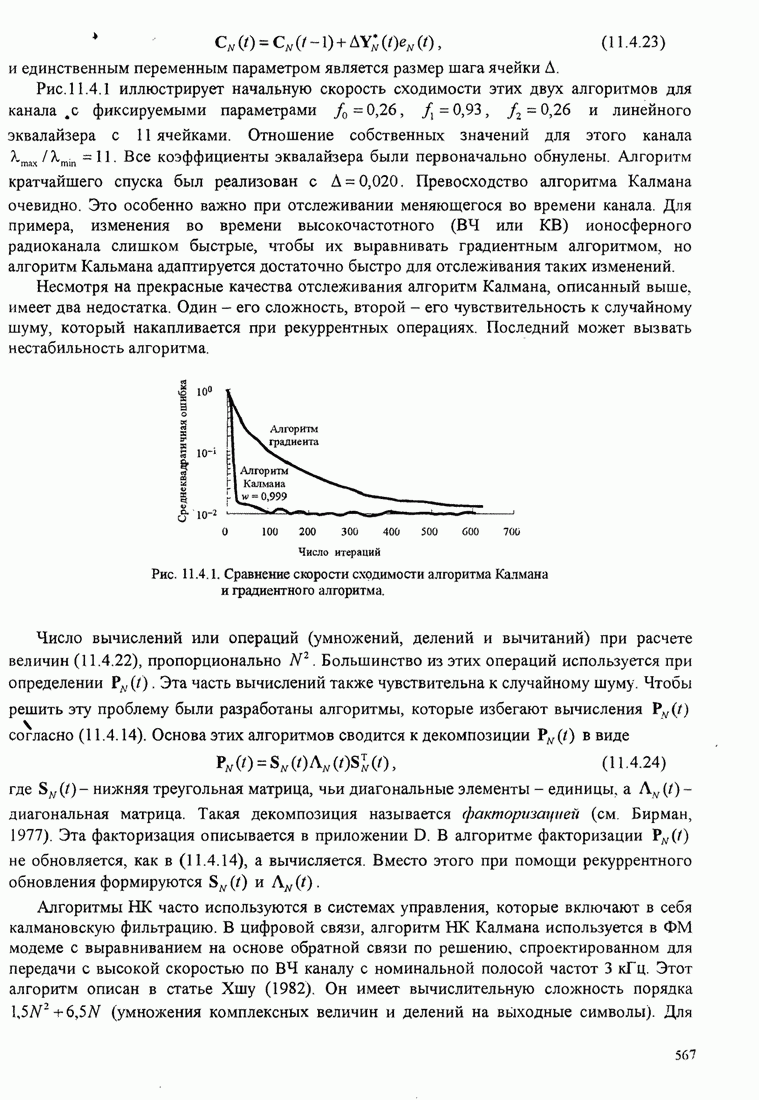
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
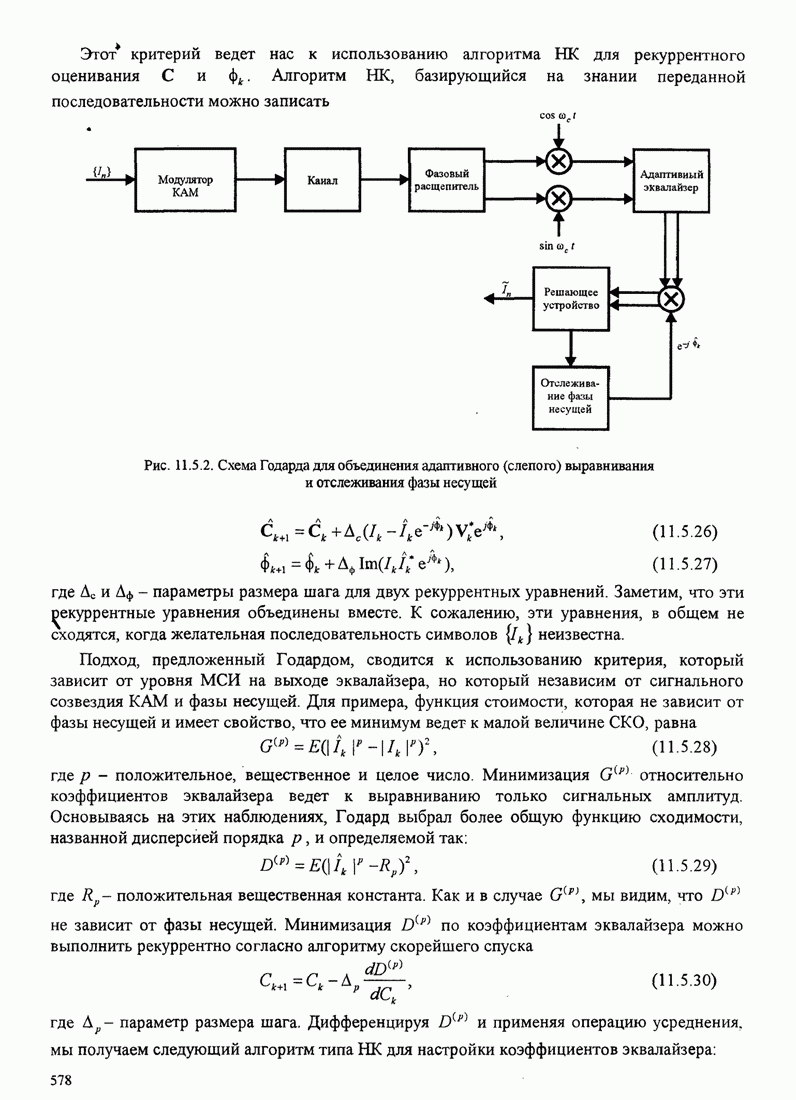
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
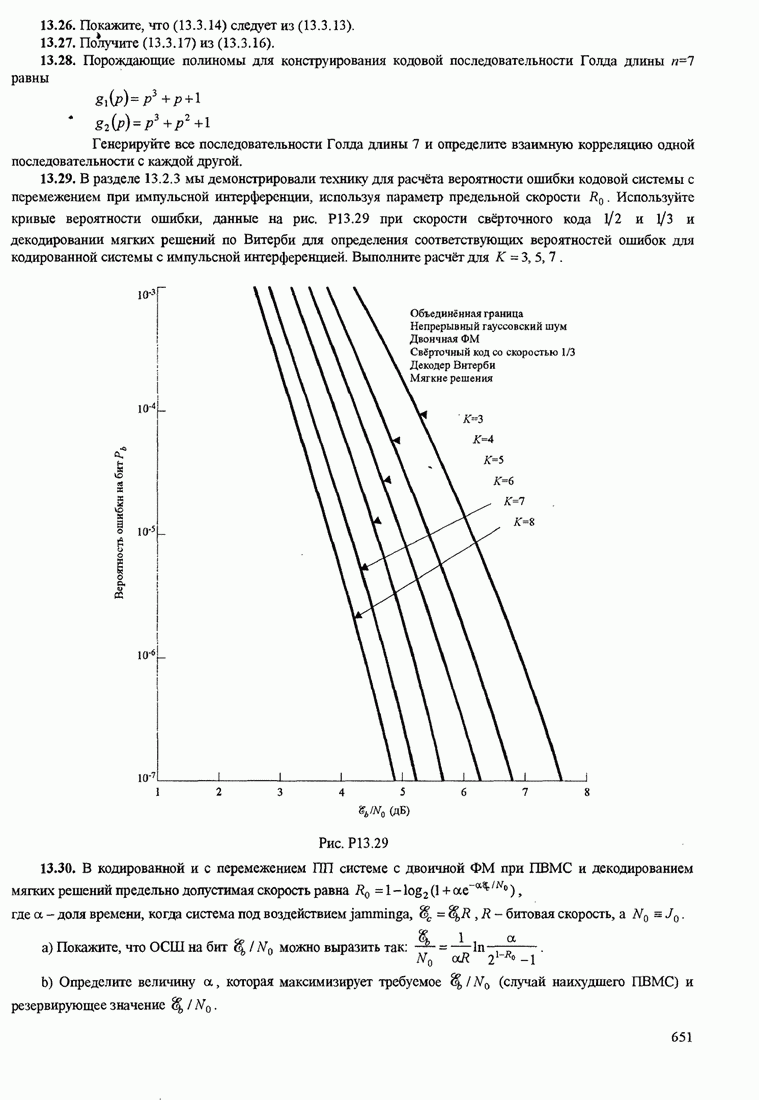
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
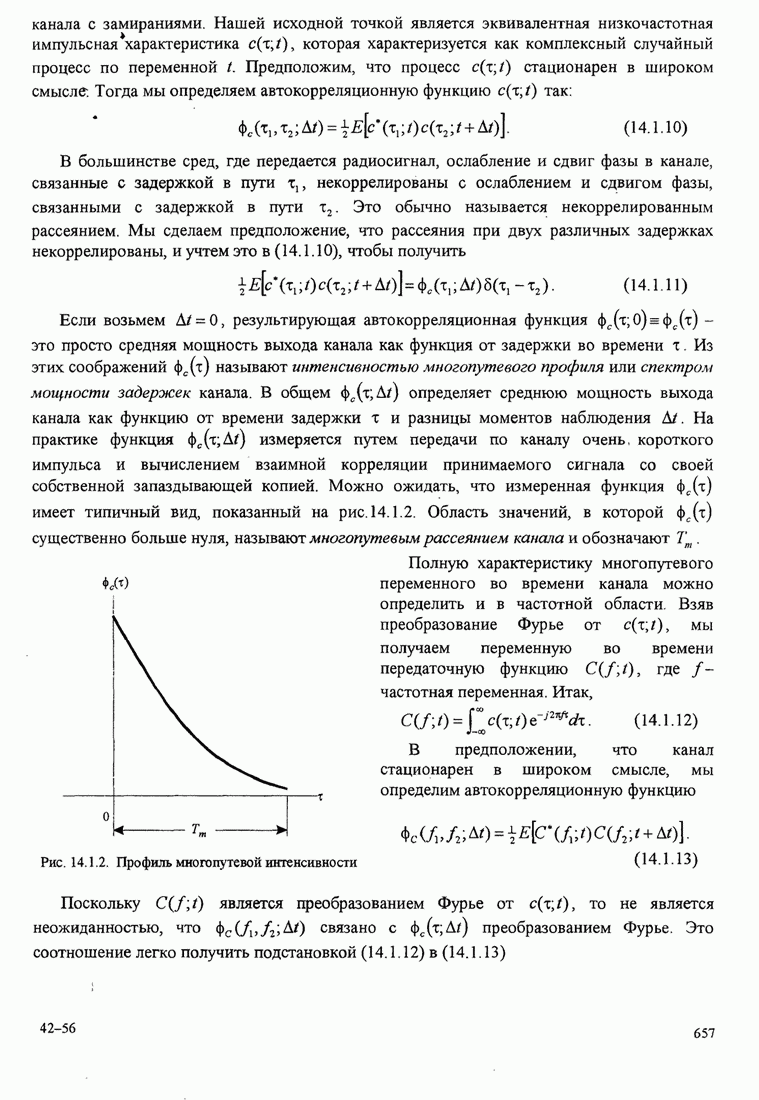
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
- 14.4.2. Многофазные сигналы
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)