| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
Следует отметить, что самая ранняя форма электрической связи, а именно телеграфная связь, была системой цифровой связи. Электрический телеграф был разработан Сэмюлем Морзе и демонстрировался в 1837 г. Морзе изобрел двоичный код переменной длины, в котором буквы английского алфавита представлены последовательностью точек и тире (кодовые слова). В этом коде часто встречающиеся буквы представлены короткими кодовыми словами, в то время как буквы, встречающиеся менее часто, - более короткими кодовыми словами. Таким образом, код Морзе был предшественником методов кодирования источников кодом переменной длины, описанных в гл.3.
Почти 40 годами позже, в 1875 г., Эмиль Бодо изобрёл код для телеграфной связи, в котором каждая буква кодировалась двоичным кодом фиксированной длины 5. В коде Бодо элементы двоичного кода имеют равную длину и именуются посылкой и паузой.
Хотя Морзе принадлежит первая электрическая система цифровой связи (телеграфная связь), начало того, что мы теперь считаем современной теорией цифровой связи, следует из работ Найквиста (1924), исследовавшего проблему определения максимальной скорости передачи, которую можно обеспечить по телеграфному каналу данной ширины полосы частот без межсимвольной интерференции (МСИ). Он сформулировал модель телеграфной системы, в которой передаваемый сигнал имеет общую форму
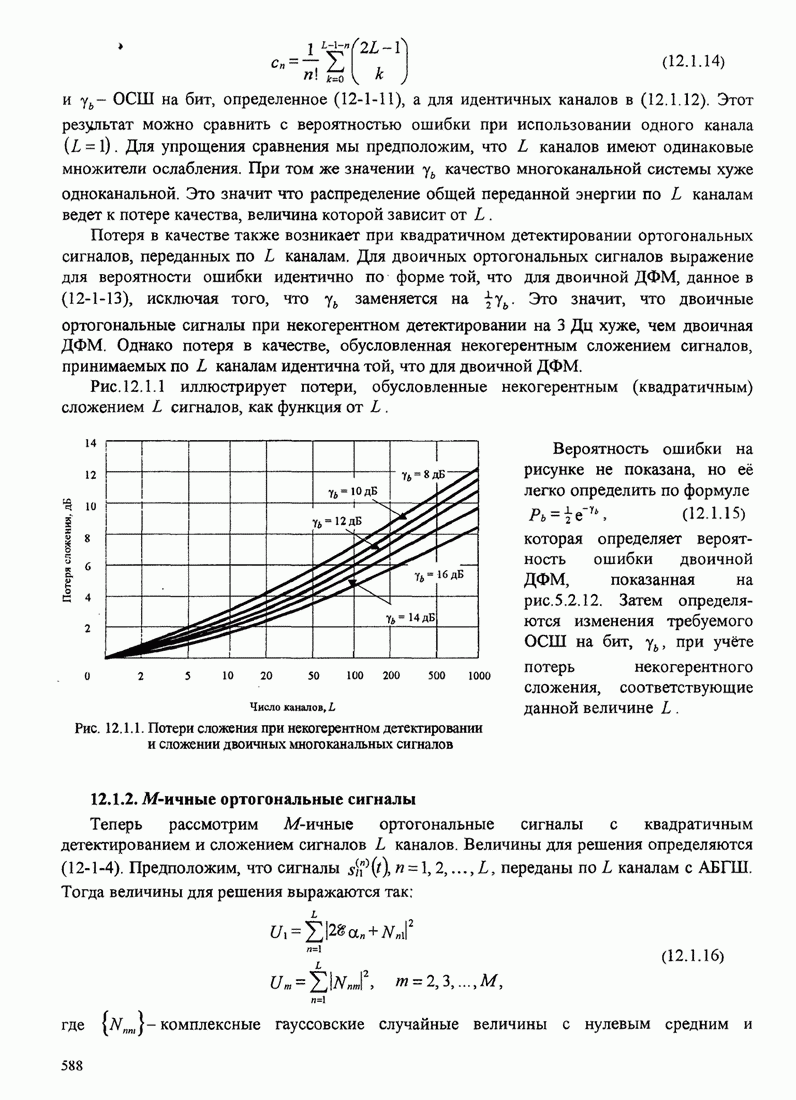
![]() , (1.4.1)
, (1.4.1)
где ![]() - базовая форма импульса (несущей);
- базовая форма импульса (несущей); ![]() - последовательность
данных в двоичном коде
- последовательность
данных в двоичном коде ![]() , передаваемых со скоростью 1/Т бит/с.
, передаваемых со скоростью 1/Т бит/с.
Найквист пытался определить
оптимальную форму импульса ![]() с ограниченной полосой
с ограниченной полосой ![]() Гц и максимизировать
скорость передачи данных в предположении, что импульс не вызывает МСИ в точках
отсчёта
Гц и максимизировать
скорость передачи данных в предположении, что импульс не вызывает МСИ в точках
отсчёта ![]() ,
,
![]() . Эти исследования привели его к заключению, что
максимальная скорость передачи равна
. Эти исследования привели его к заключению, что
максимальная скорость передачи равна ![]() отсч./с. Эту скорость теперь называют
скоростью Найквиста. Более того, эту скорость передачи можно достичь при
использовании импульса
отсч./с. Эту скорость теперь называют
скоростью Найквиста. Более того, эту скорость передачи можно достичь при
использовании импульса ![]() . Эта форма импульса допускает восстановление данных
без межсимвольных помех в выборочные моменты времени. Результат Найквиста
эквивалентен версии теоремы отсчётов для сигналов с ограниченной. полосой,
который был позже точно сформулирован Шенноном (1948). Теорема отсчётов гласит,
что сигнал с шириной полосы частот
. Эта форма импульса допускает восстановление данных
без межсимвольных помех в выборочные моменты времени. Результат Найквиста
эквивалентен версии теоремы отсчётов для сигналов с ограниченной. полосой,
который был позже точно сформулирован Шенноном (1948). Теорема отсчётов гласит,
что сигнал с шириной полосы частот ![]() может быть восстановлен по его
отсчётам, взятым со скоростью Найквиста
может быть восстановлен по его
отсчётам, взятым со скоростью Найквиста ![]() путем использования интерполяционной
формулы
путем использования интерполяционной
формулы
![]() . (1.4.2)
. (1.4.2)
В продолжение работы Найквиста
Хартли (1928) рассмотрел вопрос о количестве данных, которые могут быть
переданы надежно по каналу с ограниченной полосой частот, когда для последовательной
передачи данных используются импульсы со многими амплитудными уровнями. С
учетом шума и другой интерференции Хартли показал, что приемник может надежно
оценивать амплитуду принятого сигнала с некоторой точностью ![]() . Это исследование
привело Хартли к заключению, что имеется максимальная скорость передачи данных
по каналу с ограниченной полосой частот, зависящая от максимальной амплитуды
сигнала
. Это исследование
привело Хартли к заключению, что имеется максимальная скорость передачи данных
по каналу с ограниченной полосой частот, зависящая от максимальной амплитуды
сигнала ![]() (фиксированной
максимальной мощности) и величины
(фиксированной
максимальной мощности) и величины ![]() .
.
Другим значительным вкладом в
развитие теории связи была работа Винера (1942), который рассмотрел проблему
оценивания полезного сигнала ![]() на фоне аддитивного шума
на фоне аддитивного шума ![]() , исходя из наблюдения
принимаемого сигнала
, исходя из наблюдения
принимаемого сигнала ![]() . Эта проблема возникает при демодуляции
сигналов. Винер определил линейный фильтр, выход которого является лучшей
среднеквадратической аппроксимацией полезного сигнала
. Эта проблема возникает при демодуляции
сигналов. Винер определил линейный фильтр, выход которого является лучшей
среднеквадратической аппроксимацией полезного сигнала ![]() . Полученный фильтр назван оптимальным
линейным (винеровским) фильтром.
. Полученный фильтр назван оптимальным
линейным (винеровским) фильтром.
Результаты Хартли и Найквиста по
максимальной скорости передачи цифровой информации были предшественниками работ
Шеннона (1948), который установил математические основы передачи информации по
каналам связи и нашел фундаментальные ограничения для систем цифровой связи. В
своей пионерской работе Шеннон сформулировал основную проблему надежной
передачи информации в терминах статистической теории связи, используя
вероятностные модели для информационных источников и каналов связи. Применяя
вероятностный подход, он нашёл универсальную логарифмическую меру для
количества информации источника. Он также показал, что существует некоторый
предельный показатель, характеризующий скорость передачи информации по каналу
связи, зависящий от величины мощности передатчика, ширины полосы и
интенсивности аддитивного шума, названный им пропускной способностью канала.
Например, в случае аддитивного белого (с равномерным спектром) гауссовского
шума идеальный частотно-ограниченный канал с шириной полосы ![]() имеет пропускную способность
имеет пропускную способность ![]() , бит/с, которая определяется
формулой
, бит/с, которая определяется
формулой
 , (1.4.3)
, (1.4.3)
где ![]() - средняя мощность сигнала, а
- средняя мощность сигнала, а ![]() - спектральная
плотность мощности аддитивного шума. Значение параметра пропускной способности
канала
- спектральная
плотность мощности аддитивного шума. Значение параметра пропускной способности
канала ![]() состоит в том, что если информационная скорость
(производительность) источника
состоит в том, что если информационная скорость
(производительность) источника ![]() меньше, чем
меньше, чем ![]() , то теоретически возможно обеспечить надёжную (свободную от ошибок)
передачу через канал соответствующим кодированием. С другой стороны, если
, то теоретически возможно обеспечить надёжную (свободную от ошибок)
передачу через канал соответствующим кодированием. С другой стороны, если ![]() , то надежная
передача невозможна, независимо от способов обработки сигнала на передаче и
приеме. Таким образом, Шеннон установил основные ограничения передачи
информации и породил новое направление, которое теперь называется теорией информации.
, то надежная
передача невозможна, независимо от способов обработки сигнала на передаче и
приеме. Таким образом, Шеннон установил основные ограничения передачи
информации и породил новое направление, которое теперь называется теорией информации.
Другой важный вклад в области цифровой связи - это работа Котельникова (1947), который провел тщательный анализ различных систем цифровой связи, основанный на геометрическом представлении. Исследование Котельникова было позже развито Возенкрафтом и Джекобсом (1965).
Вслед публикациям Шеннона появилась классическая работа Хемминга (1950) по кодам с обнаружением и с исправлением ошибок, которые противодействуют вредному влиянию канального шума. Работа Хемминга стимулировала многих исследователей, которые в последующие годы открыли ряд новых и мощных кодов, многие из которых сегодня внедрены в современные системы связи.
Увеличение спроса на передачу данных в течение последних 3-4 десятков лет и развитие более сложных интегральных схем вело к созданию эффективных и надежных систем цифровой связи. В свете этих достижений оригинальные результаты Шеннона и обобщение его результатов по максимальным ограничениям на передачу информации по каналу и по достижимым характеристикам качества служили маяком при разработке любых проектов систем связи. Теоретические пределы, полученные Шенноном и другими исследователями, способствовали развитию теории информации и служат конечной целью в продолжающихся усилиях по разработке более эффективных систем цифровой связи.
За ранними работами Шеннона, Котельникова и Хемминга появилось много новых достижений в области цифровой связи. Некоторые из наиболее заметных достижений следующие:
· разработка новых блоковых кодов Маллером (1954), Ридом (1954) Ридом и Соломоном (1960), Боузом и Рой-Чоудхури (1960) и Гоппом (1970-1971);
· разработка каскадных кодов Форни (1966);
· разработка эффективных в вычислительном отношении БЧХ кодов, например, алгоритма Берлекампа-Месси (см. Чейн, 1964; Берлекамп, 1968);
· разработка сверточных кодов и алгоритмов декодирования Возенкрафтом и Рейффеном (1961), Фано (1963), Зигангировым (1966), Елинеком (1969), Форни (1970, 1972) и Витерби (1967, 1971);
· разработка решетчато-кодированной модуляции Унгербоеком (1982), Форни и др. (1984), Ваем (1987) и др.;
· разработка эффективных алгоритмов кодирования источника для сжатия данных, таких как алгоритм Зива и Лемпела (1977, 1978) и Линда и др. (1980).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
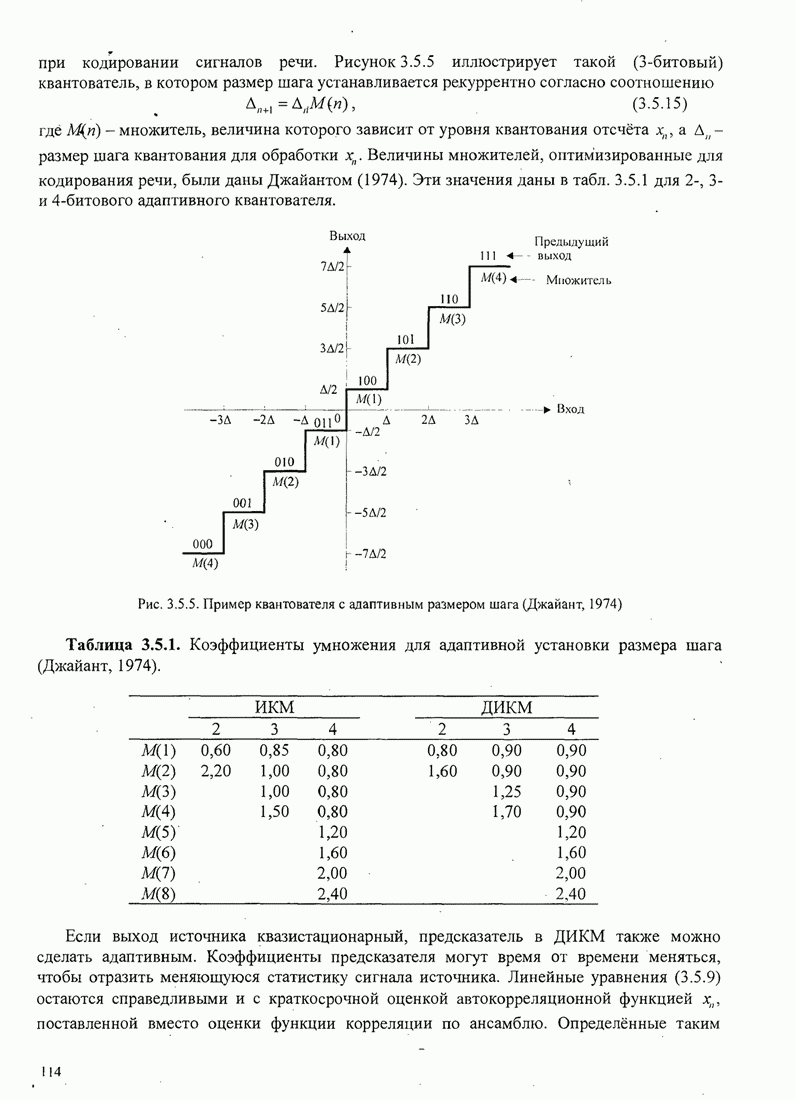
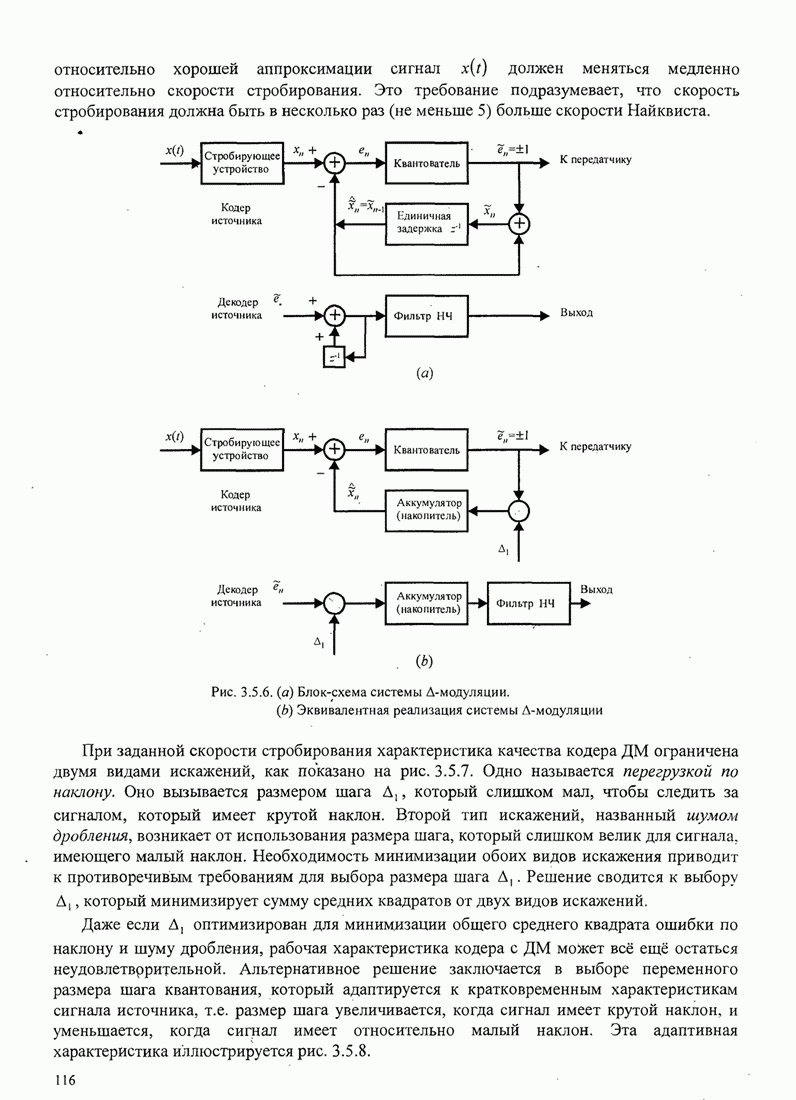
- 3.5.1. Временное сигнальное кодирование
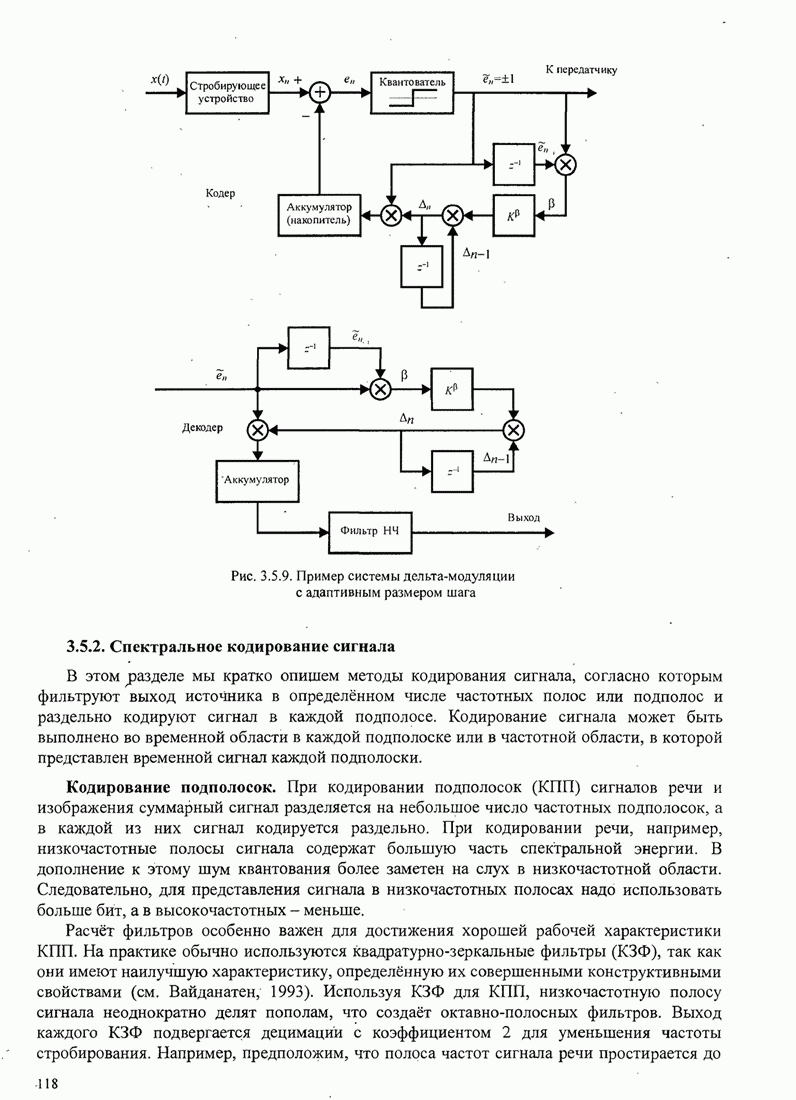
- 3.5.2. Спектральное кодирование сигнала
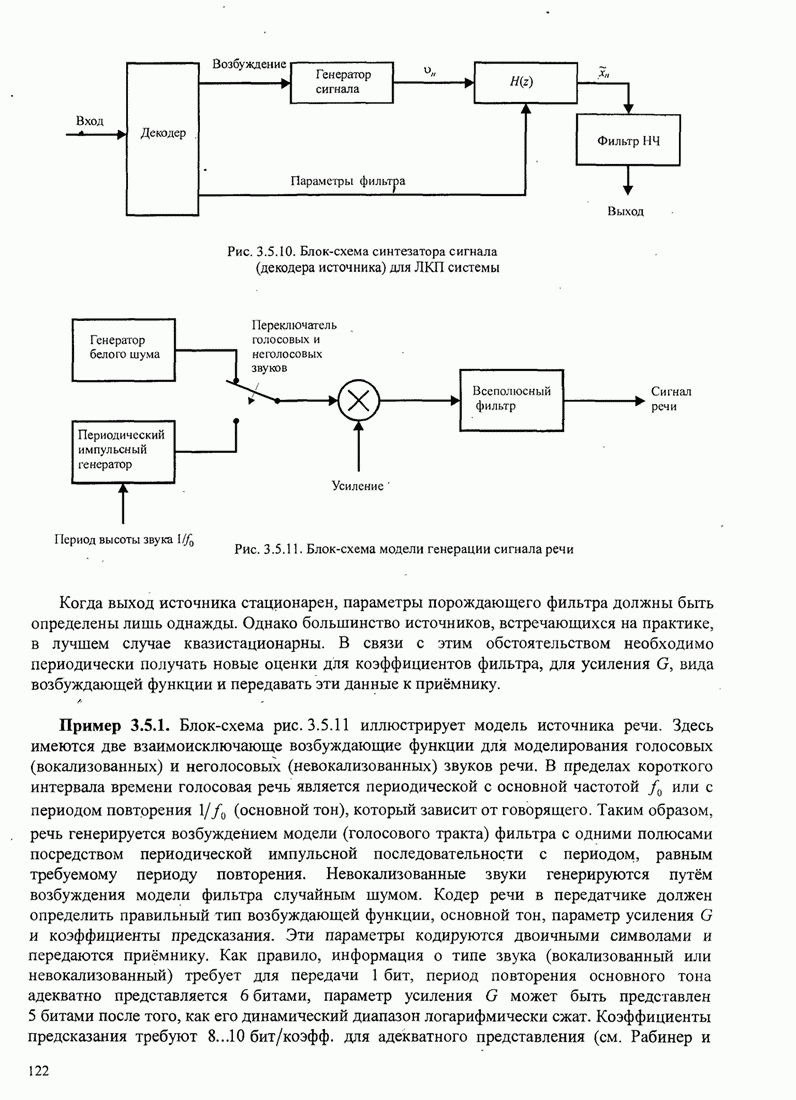
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
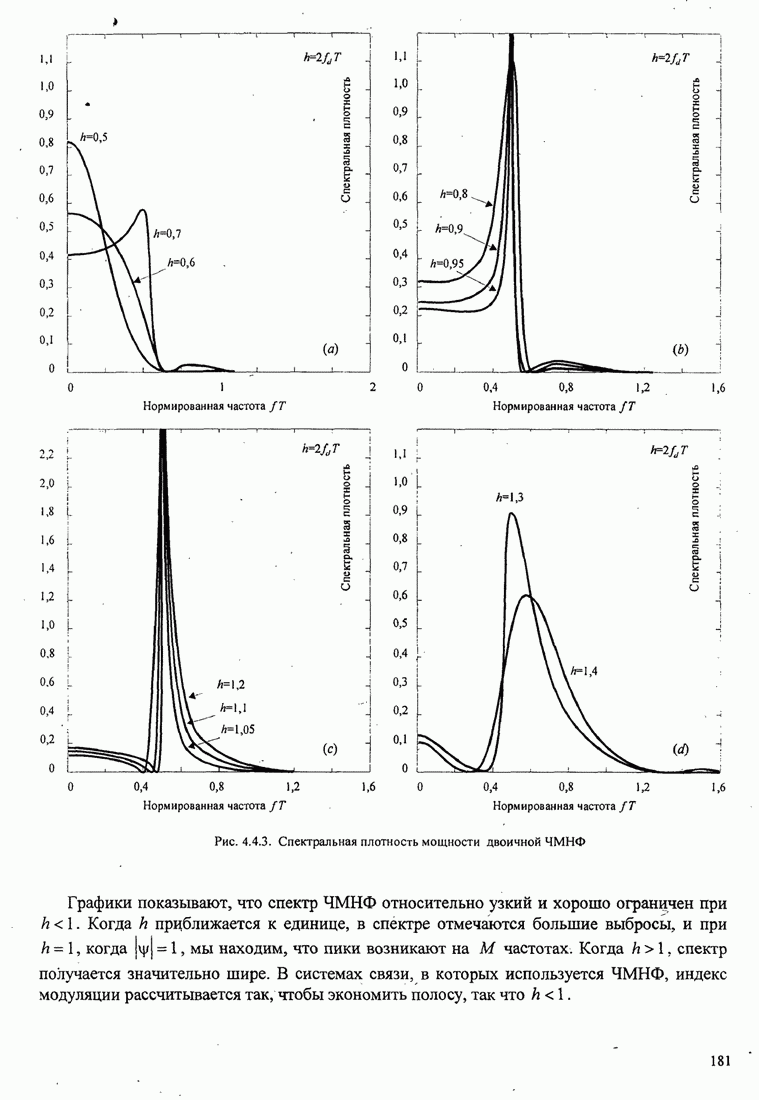
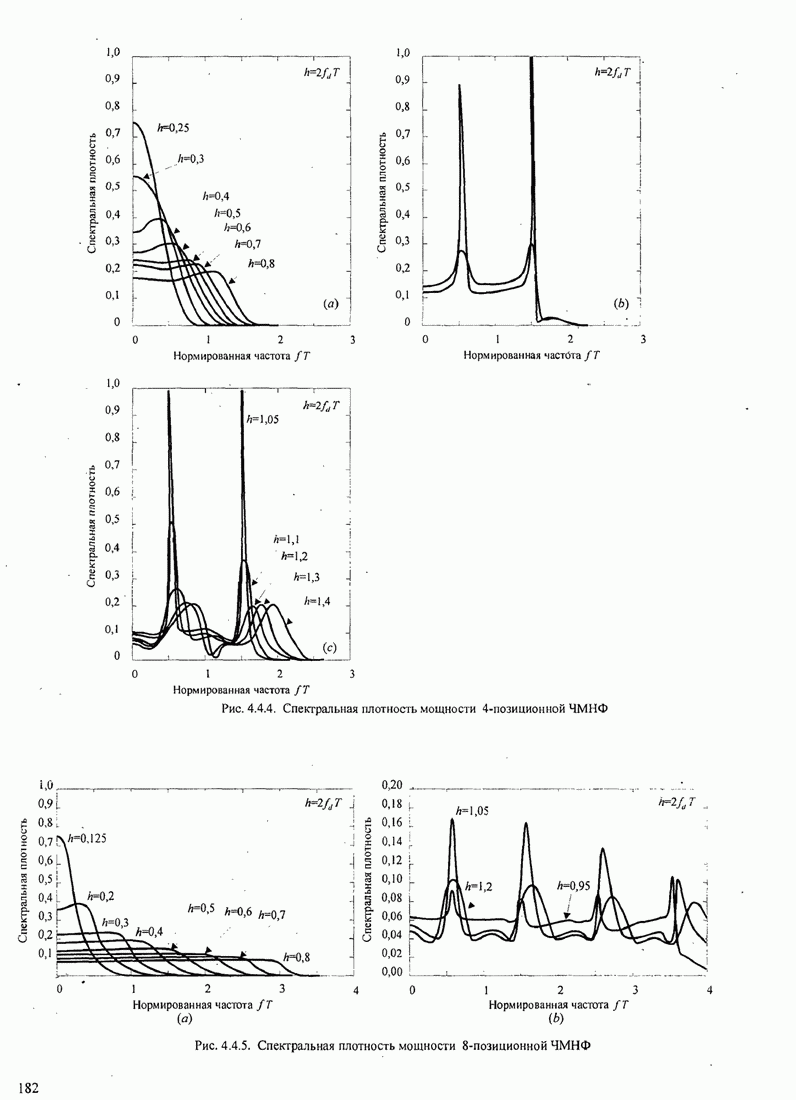
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
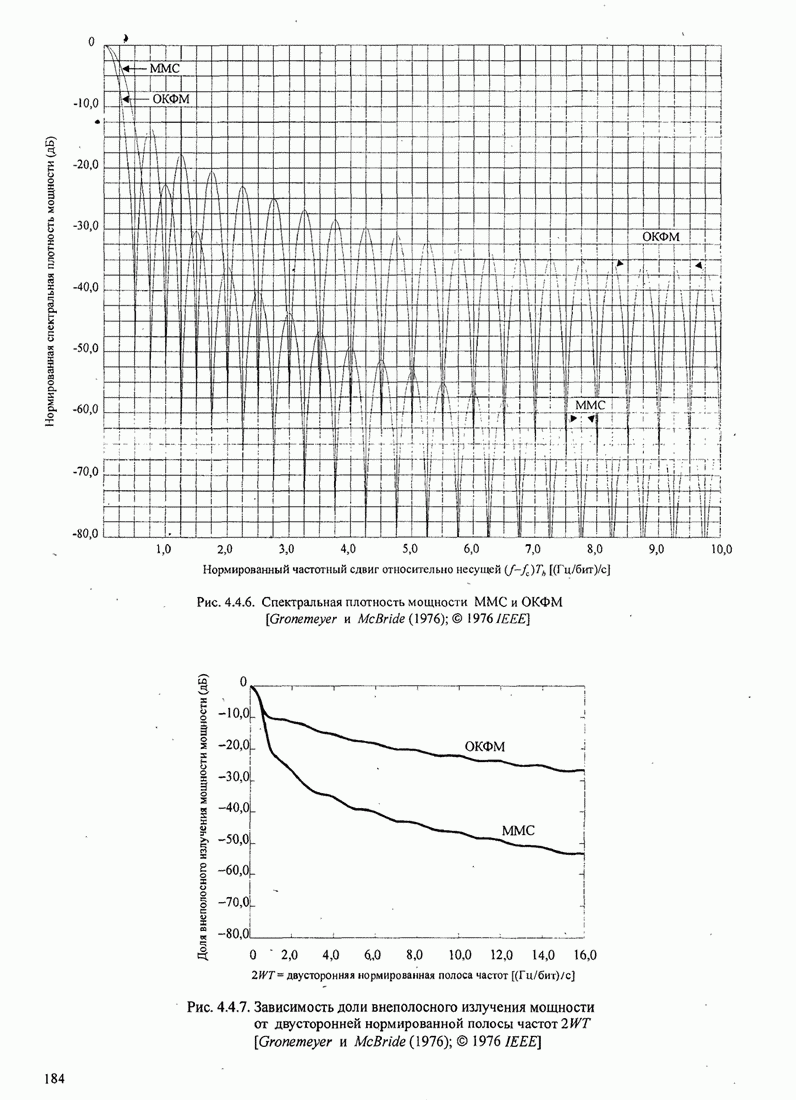
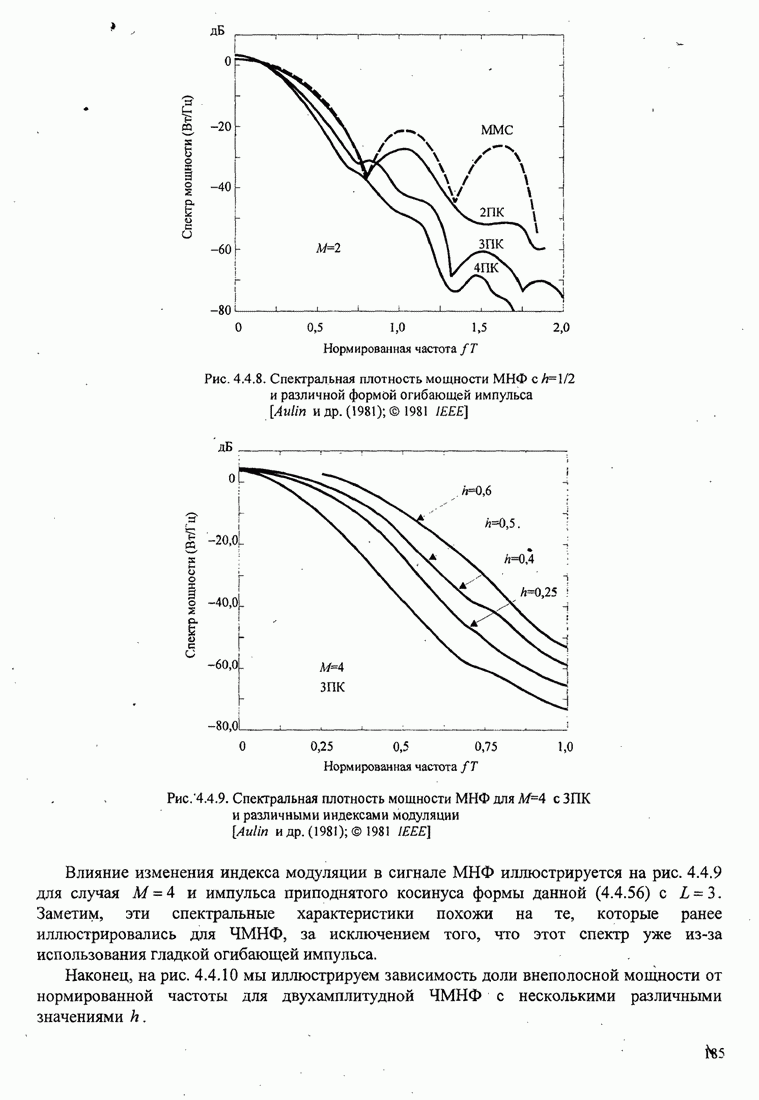
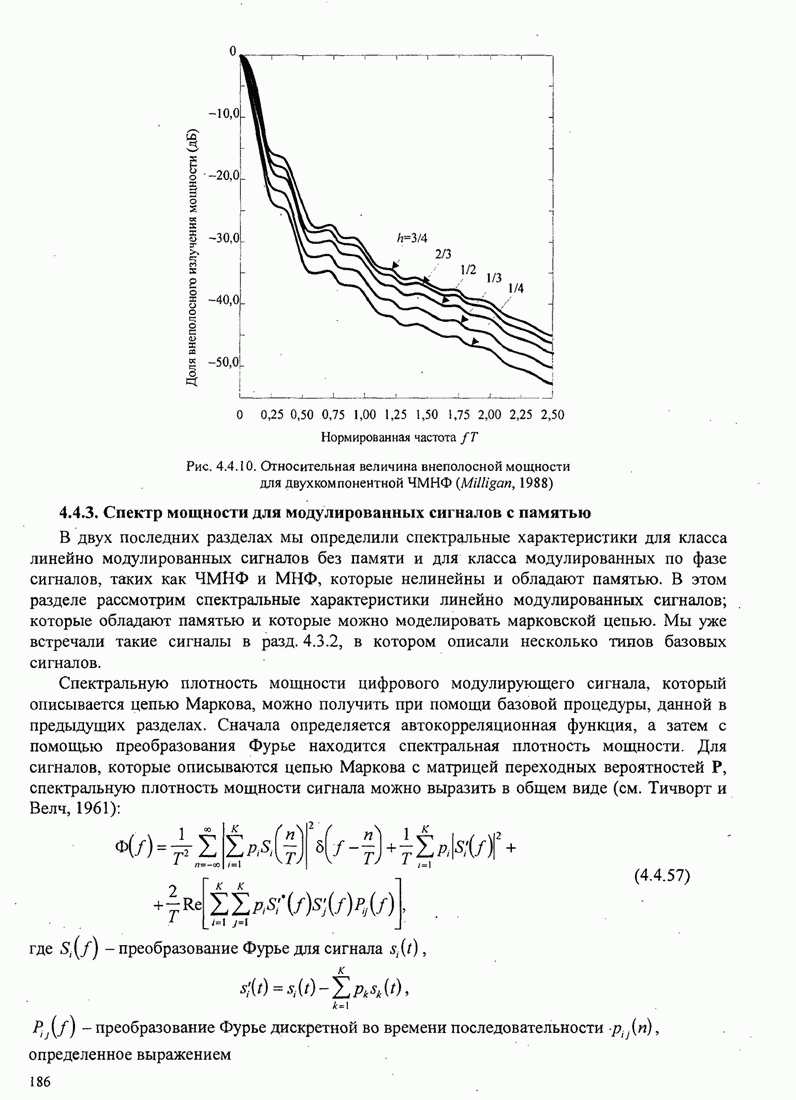
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
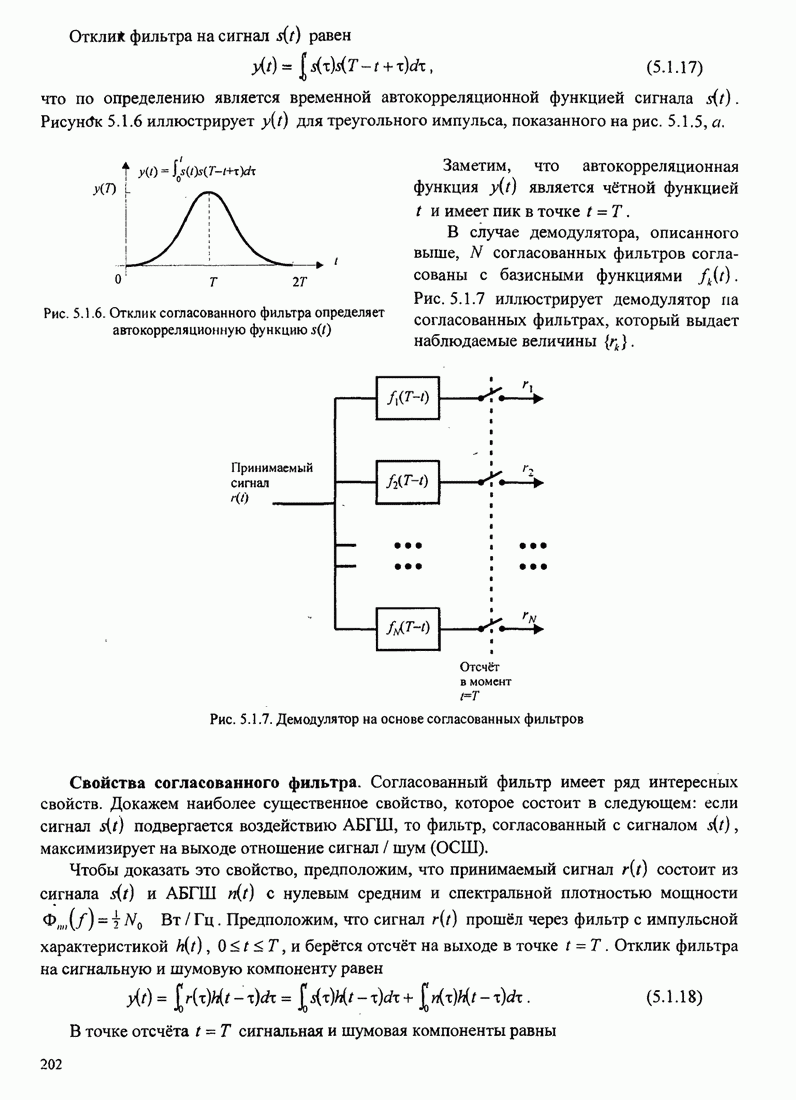
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
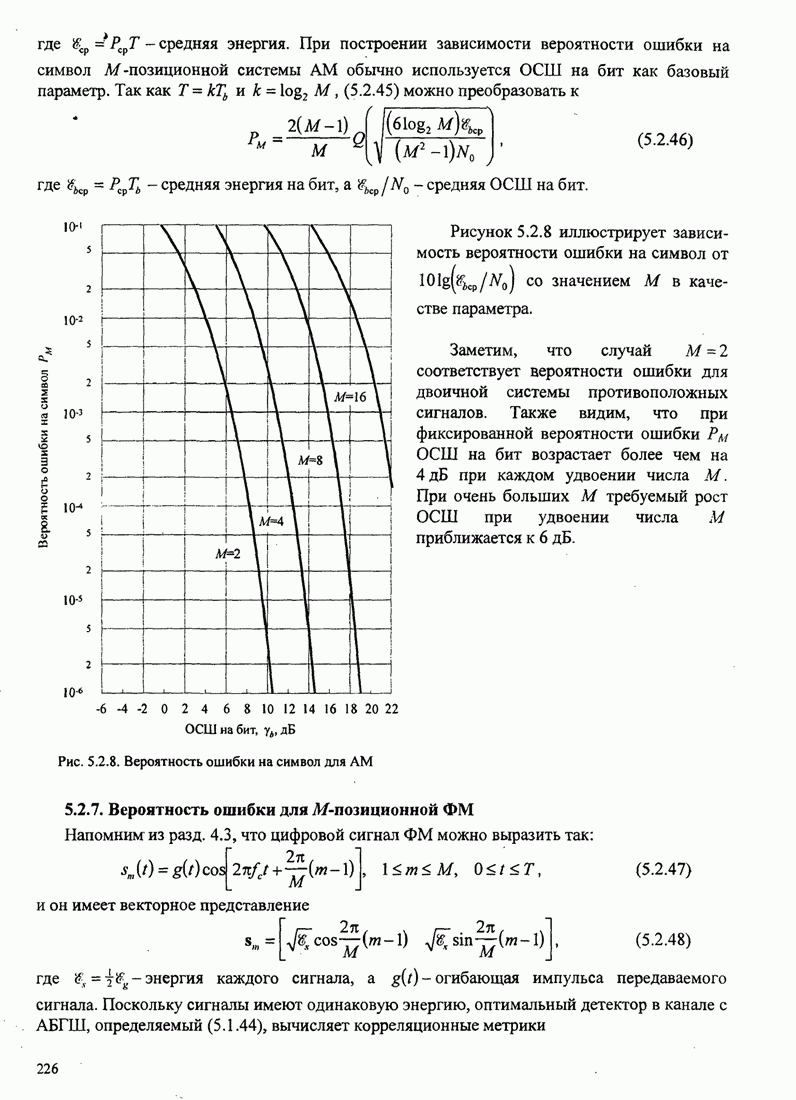
- 5.2.6. Вероятность ошибки для М-позиционной AM
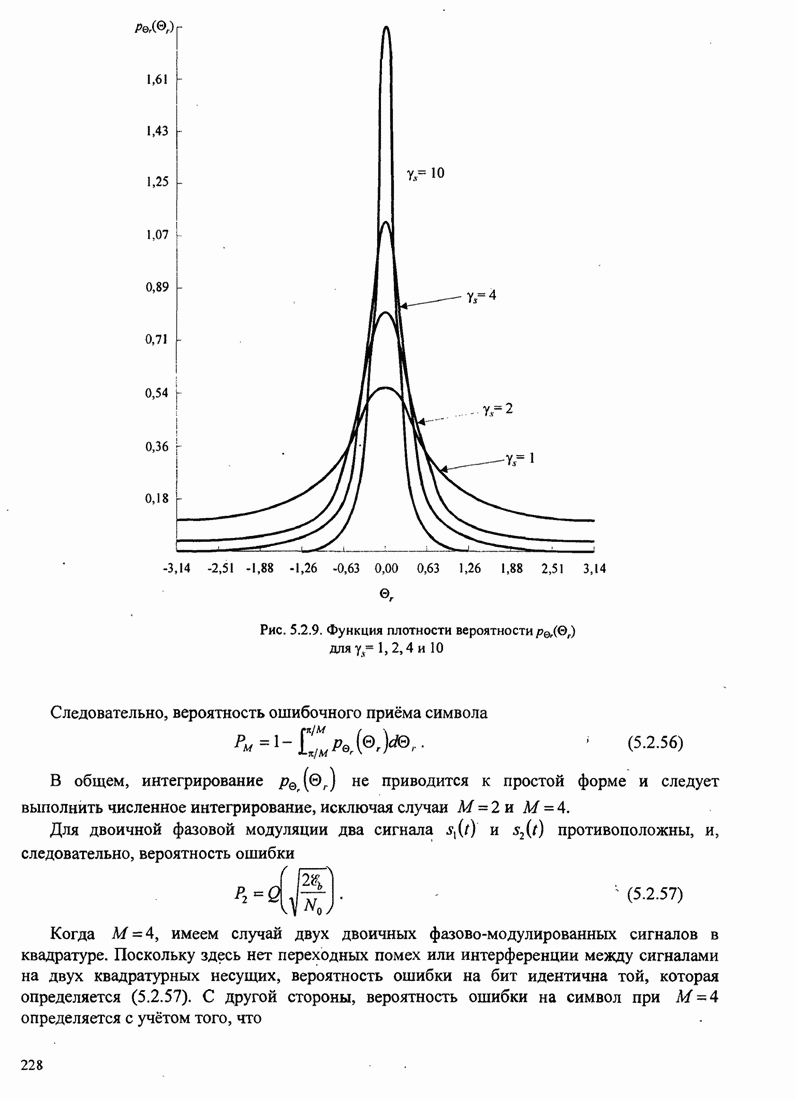
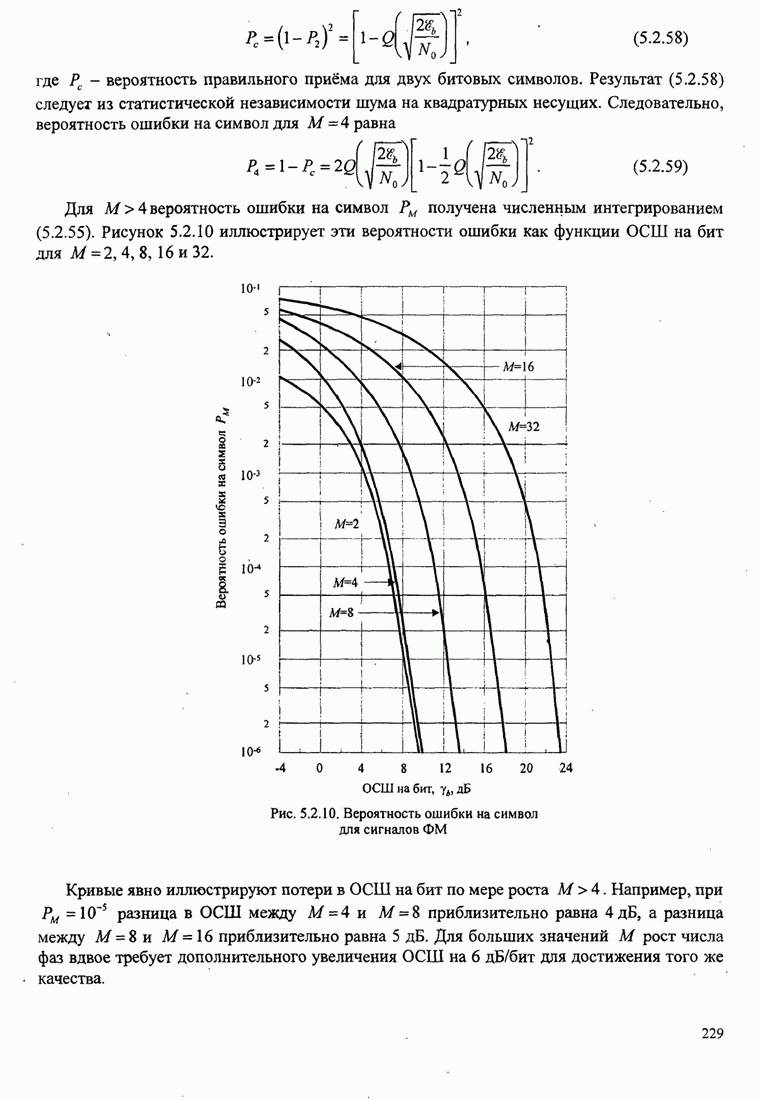
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
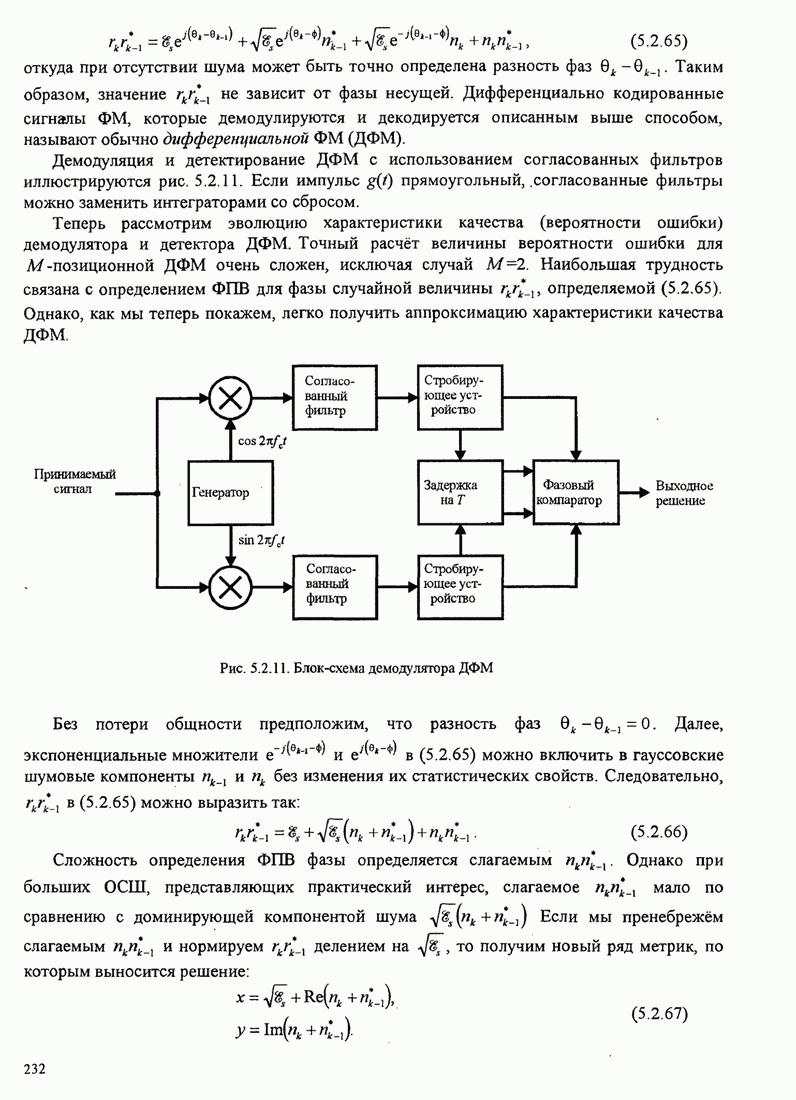
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
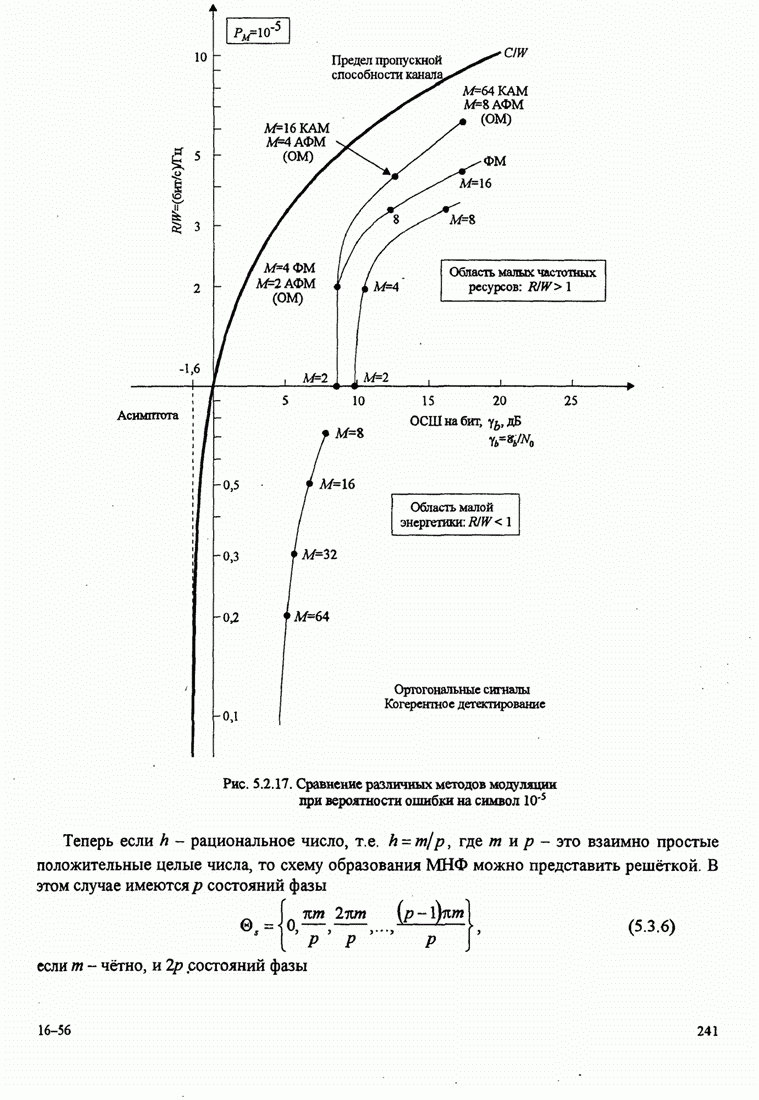
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
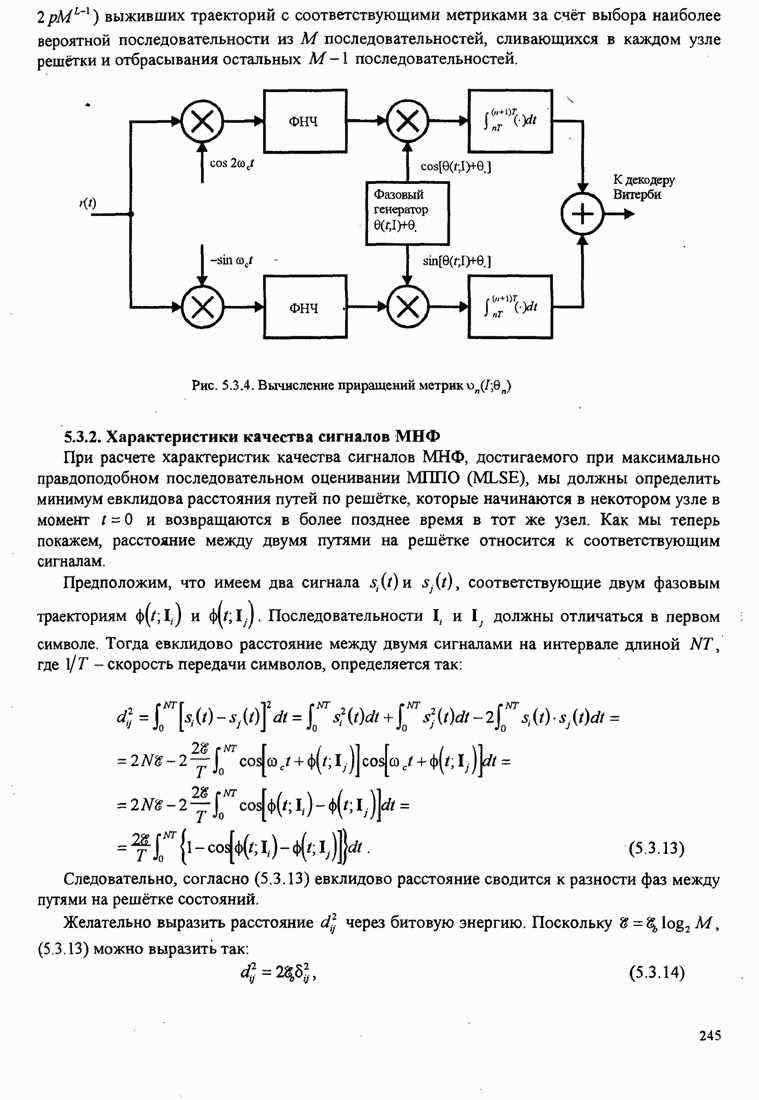
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
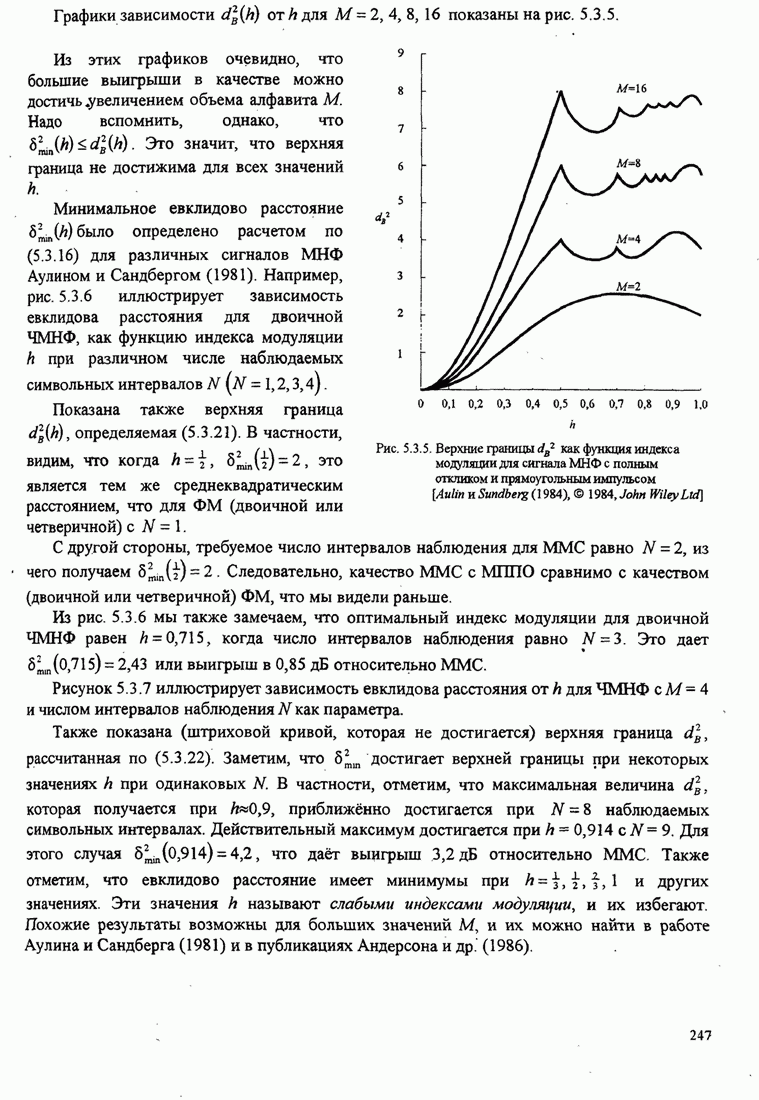
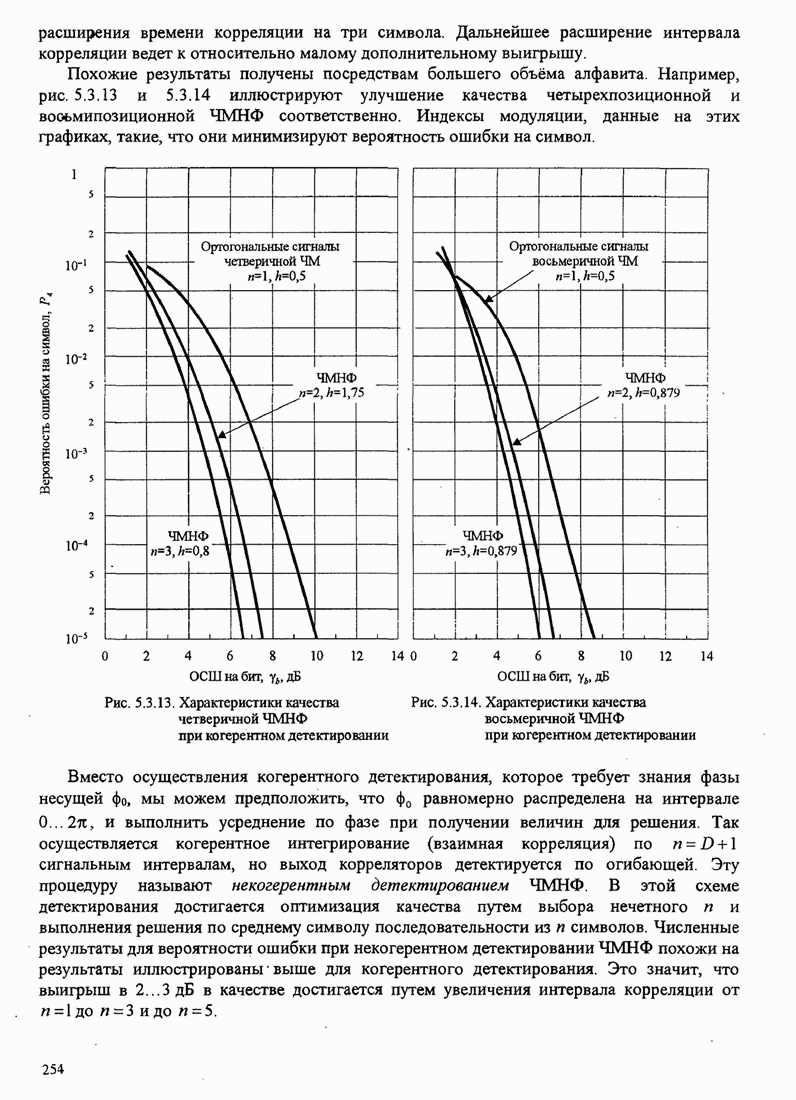
- 5.3.2. Характеристики качества сигналов МНФ
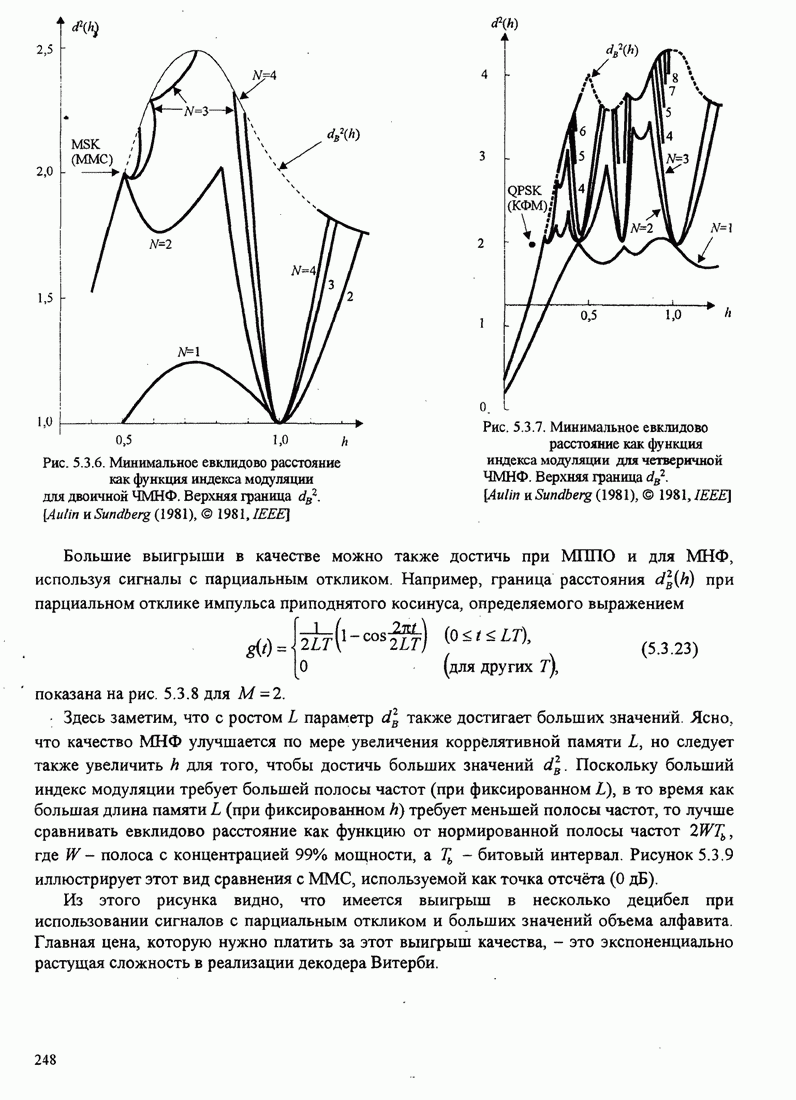
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
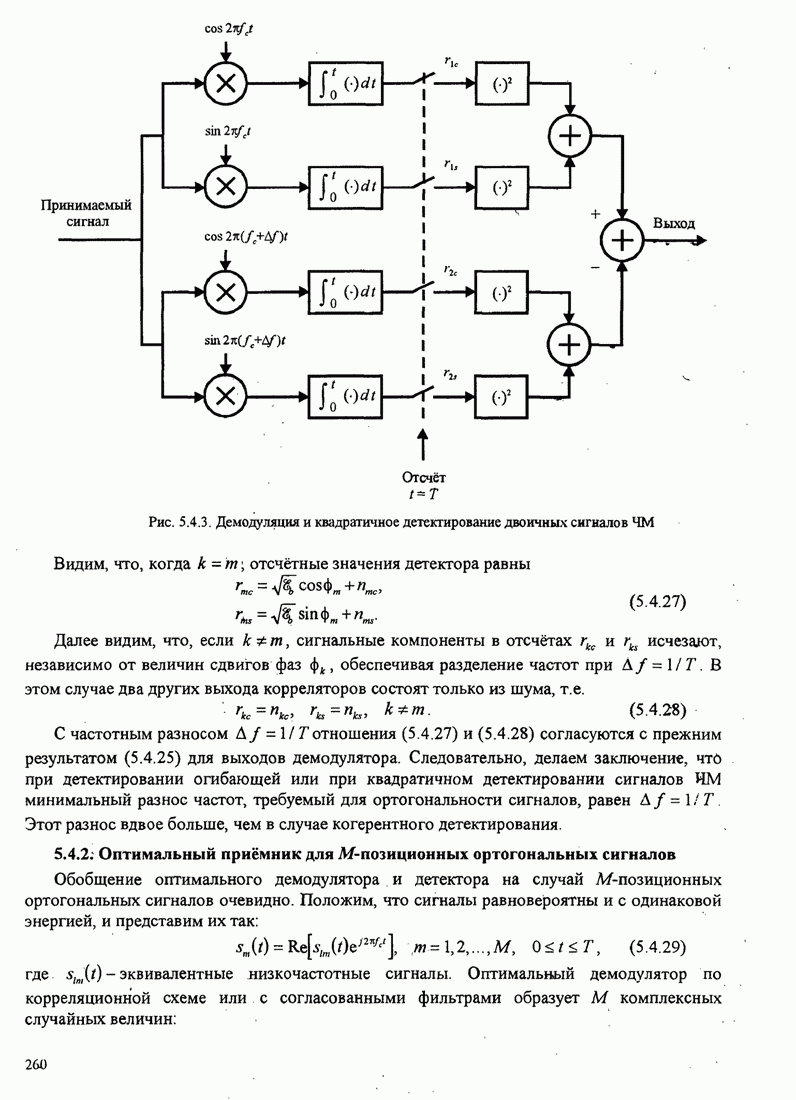
- 5.4.1. Оптимальный приёмник двоичных сигналов
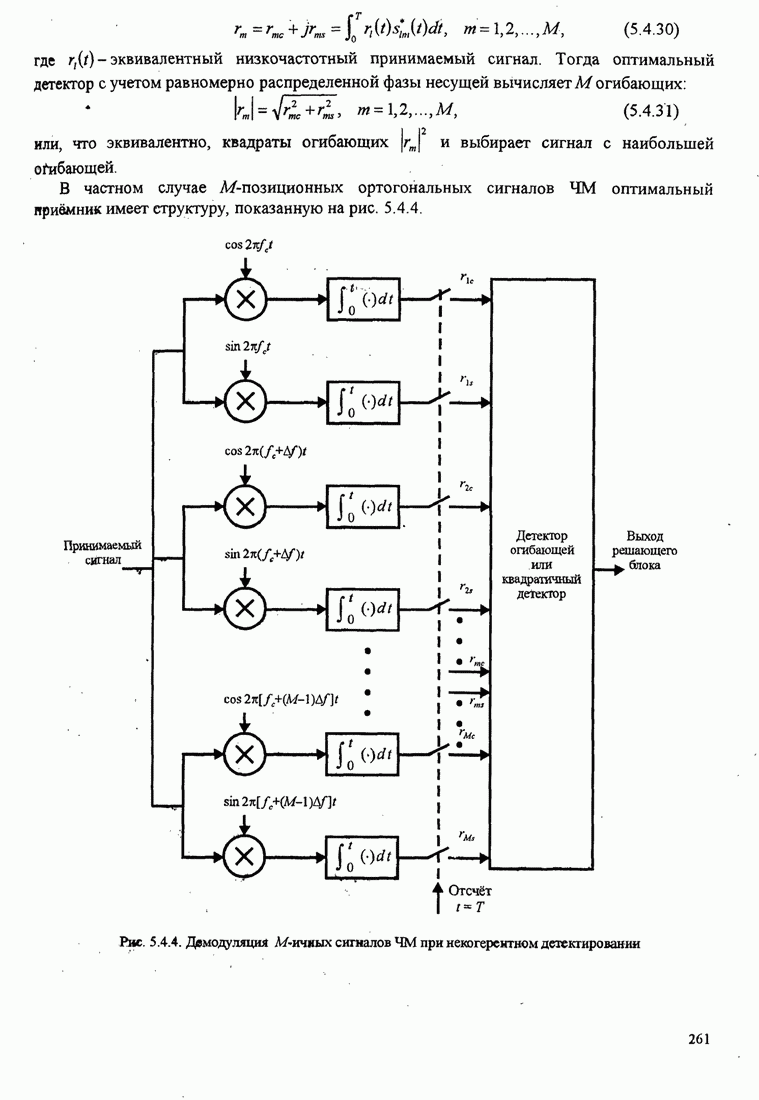
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
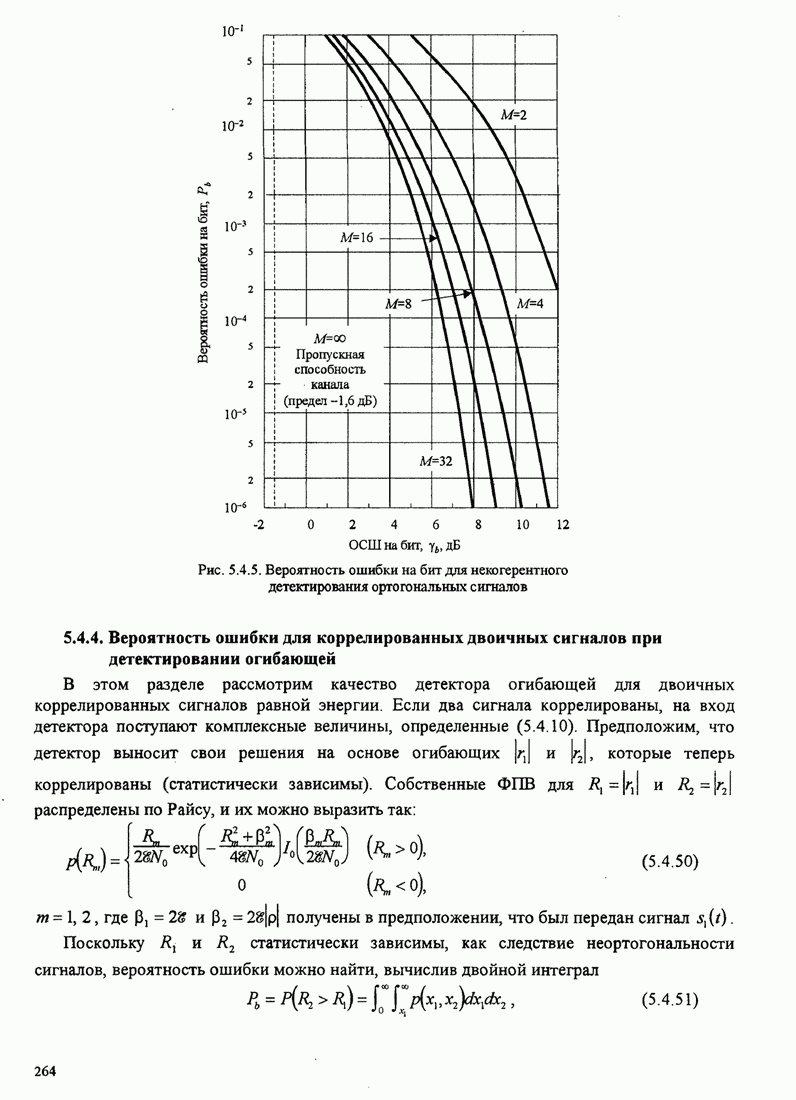
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
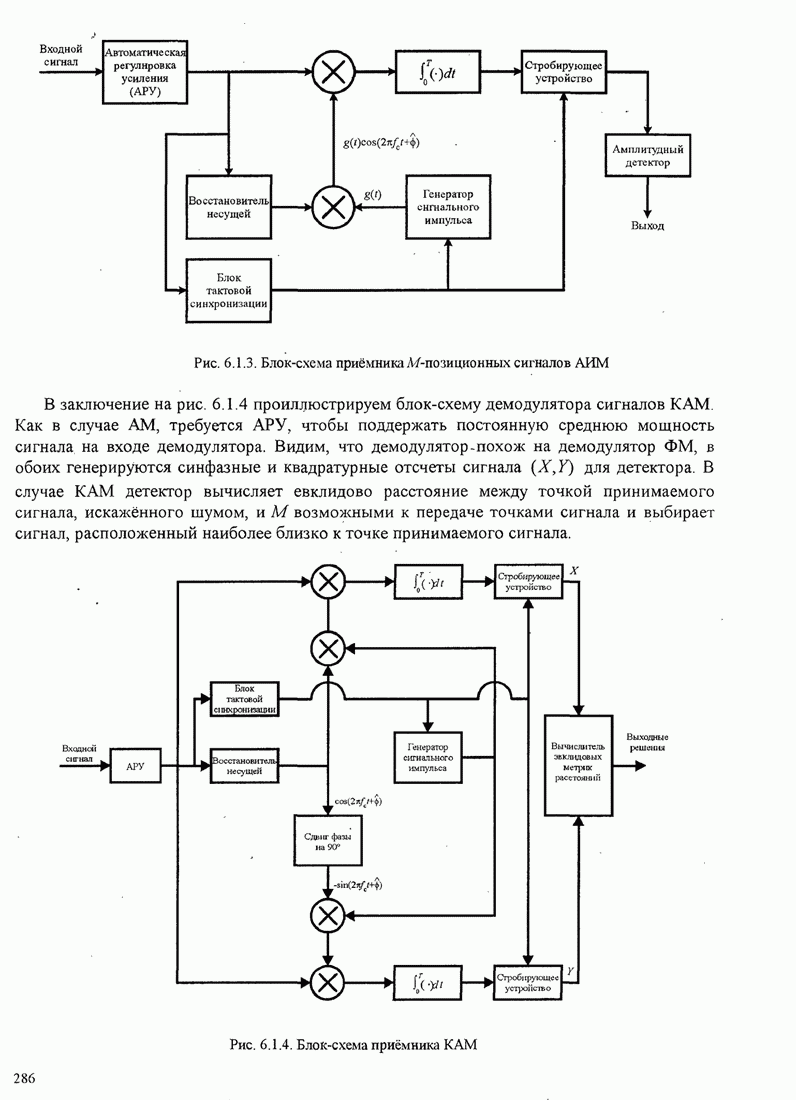
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
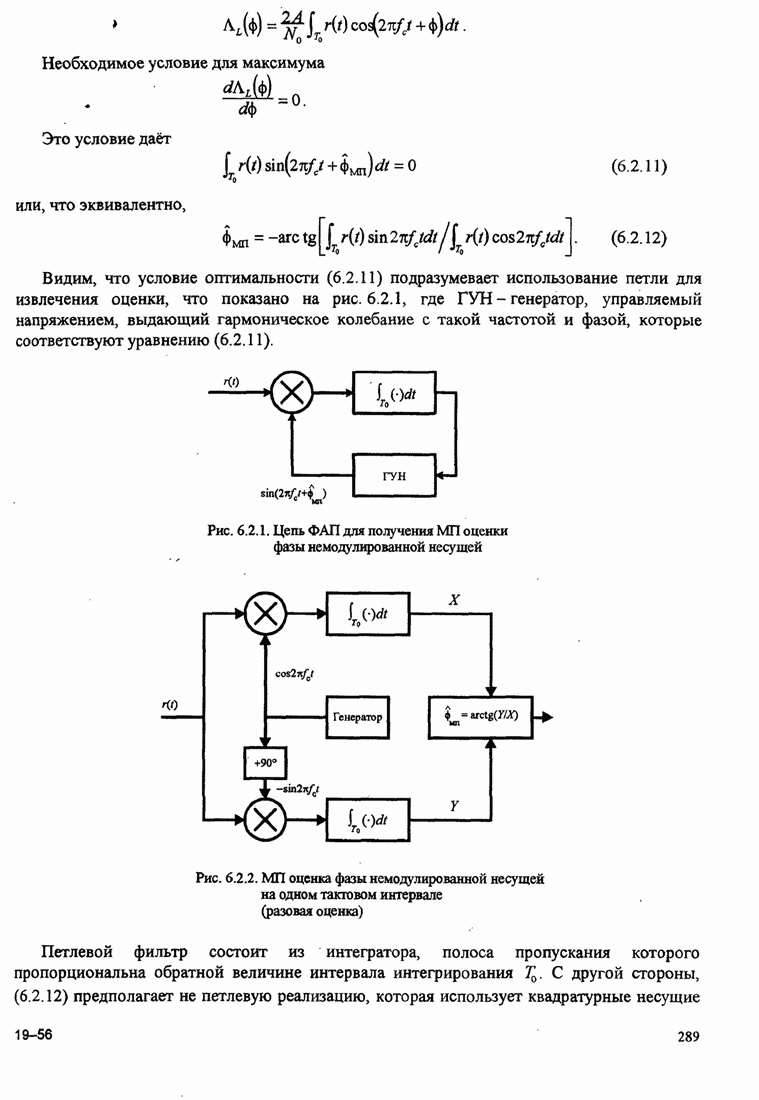
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
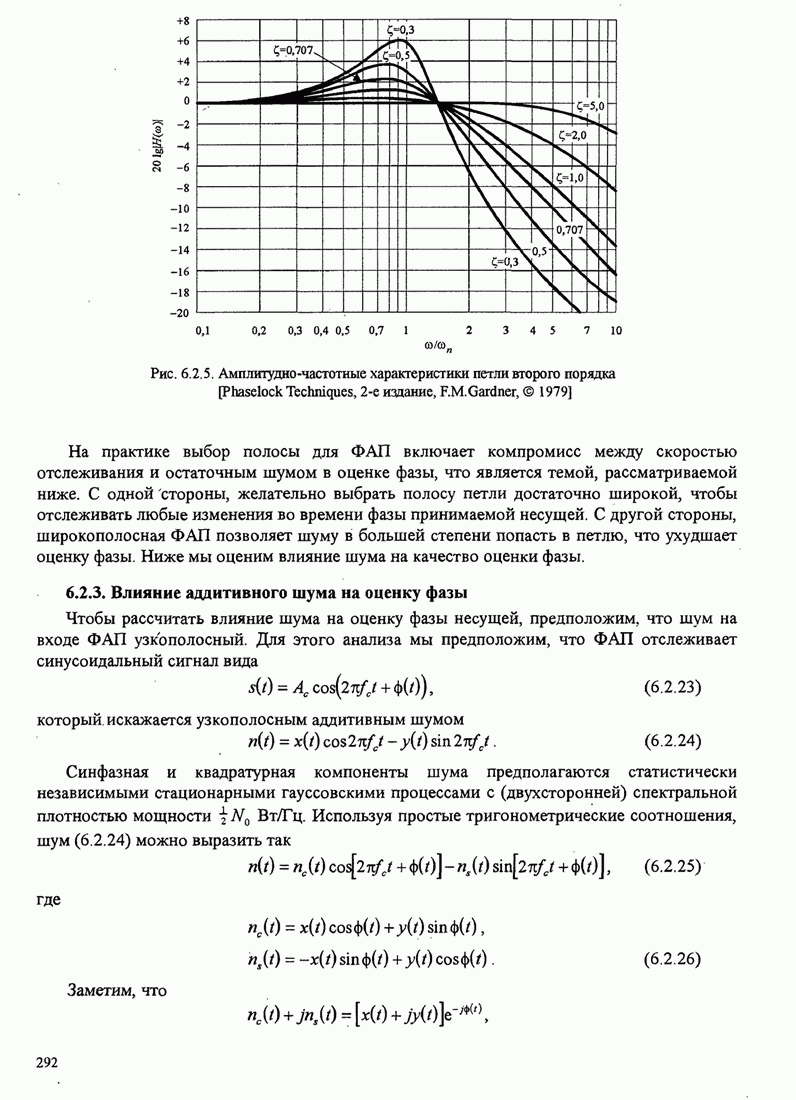
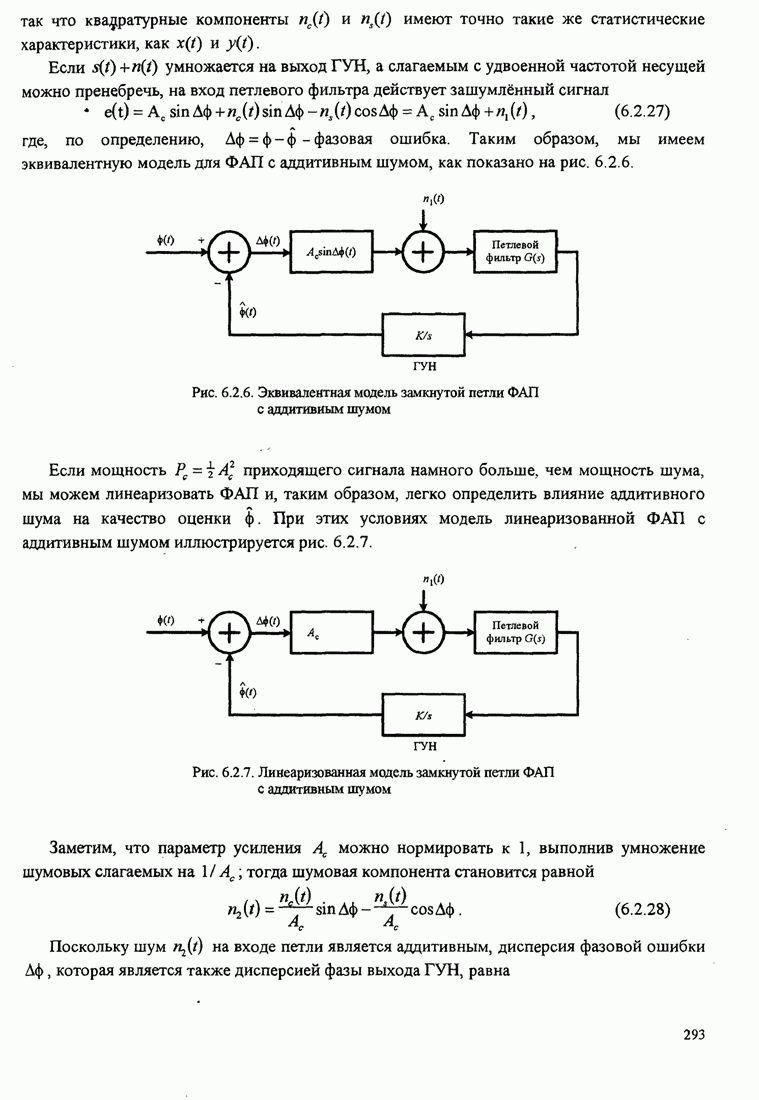
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
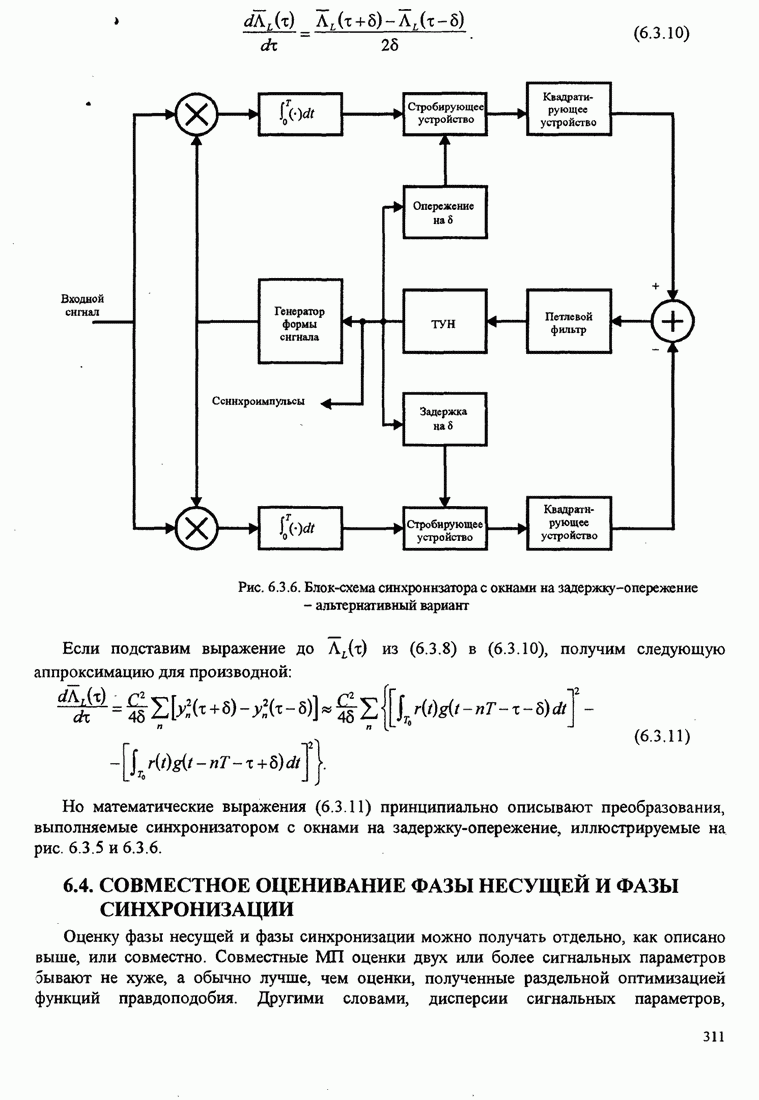
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
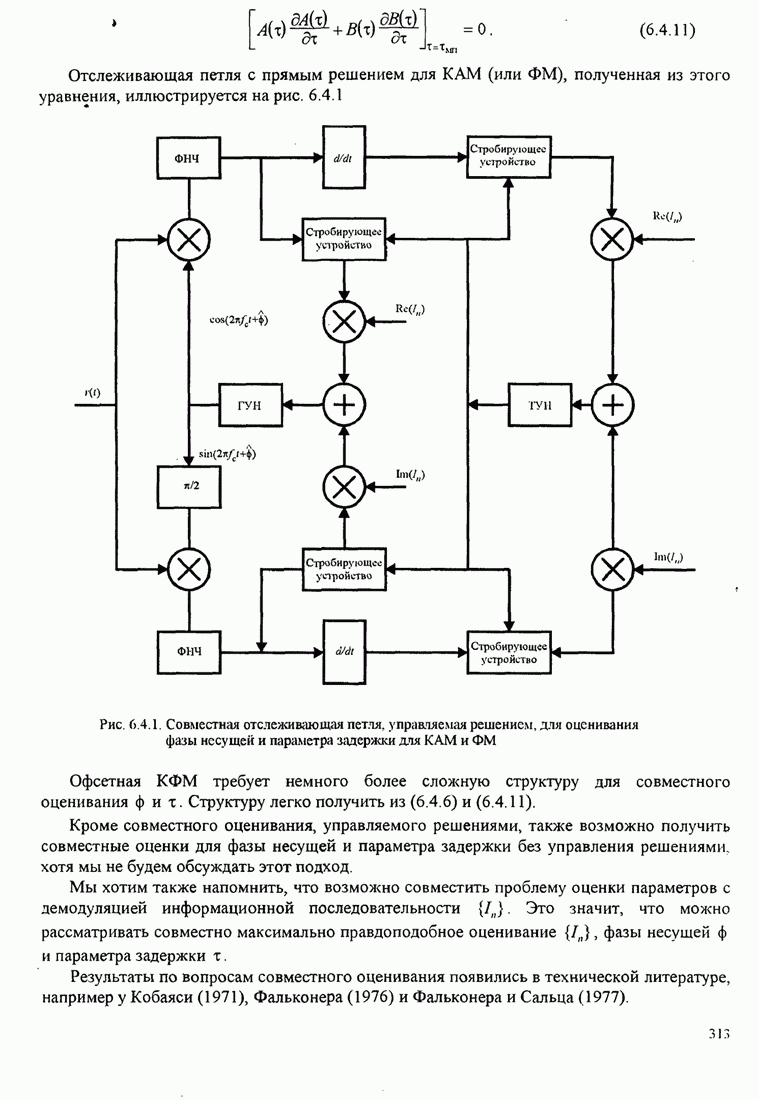
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
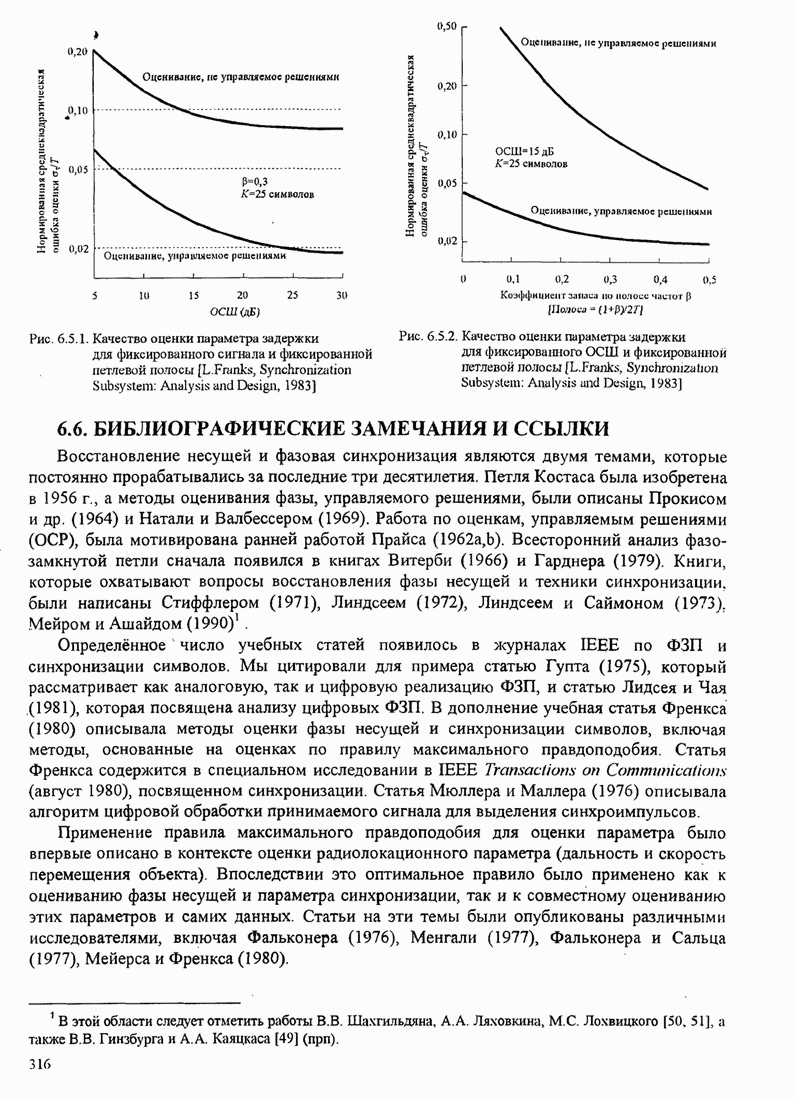
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
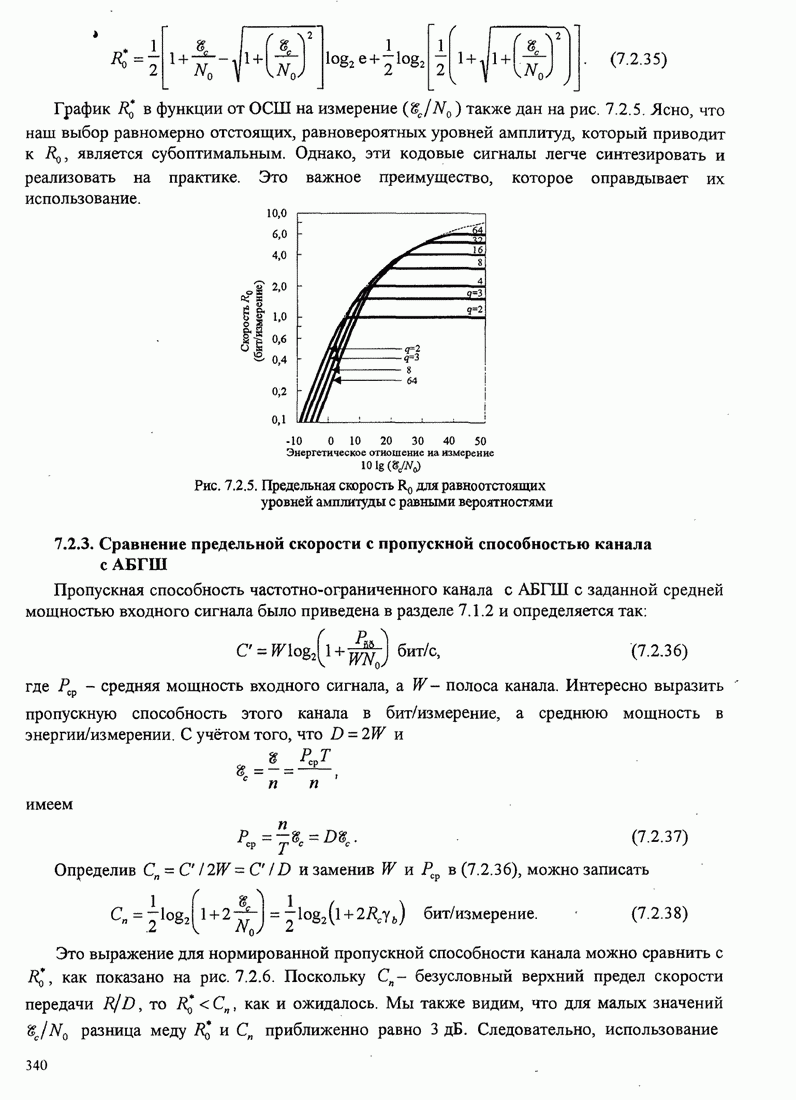
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
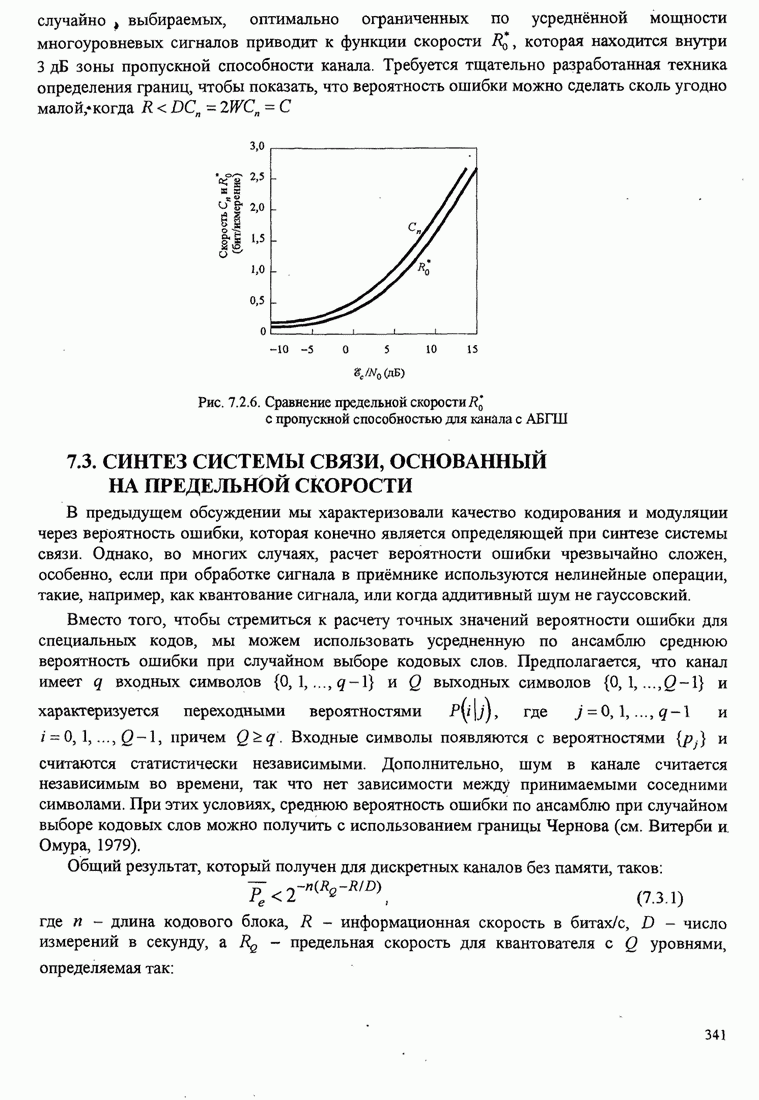
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
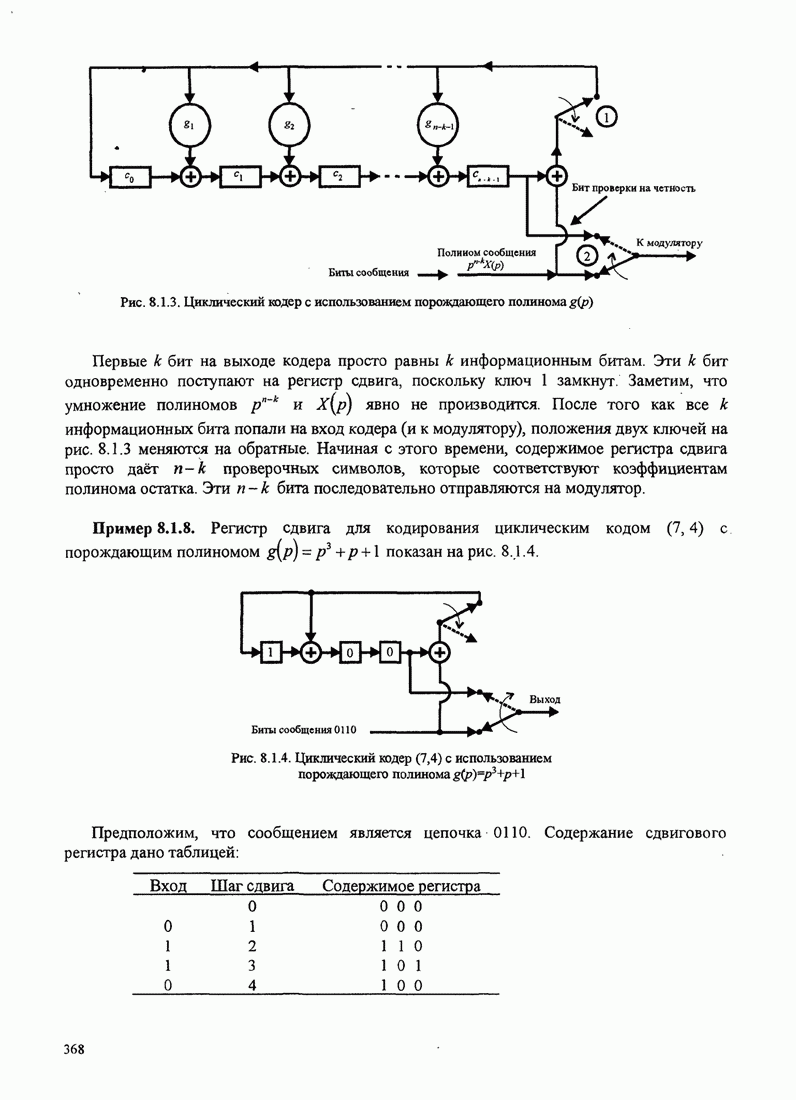
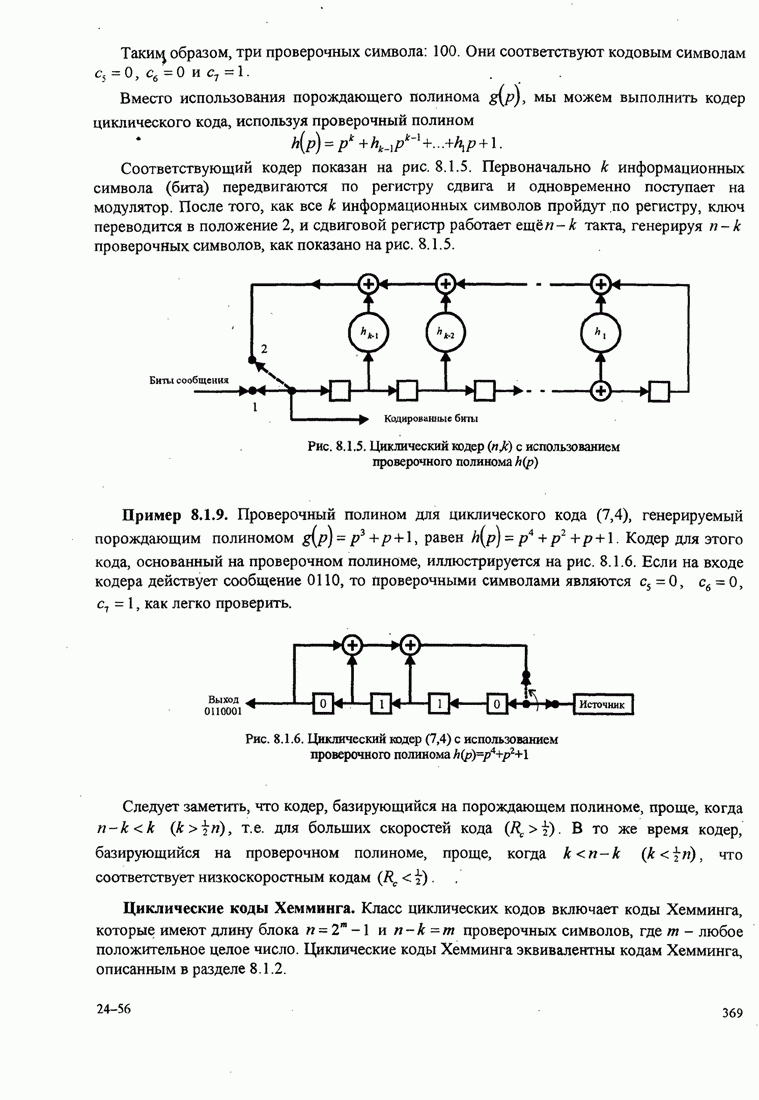
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
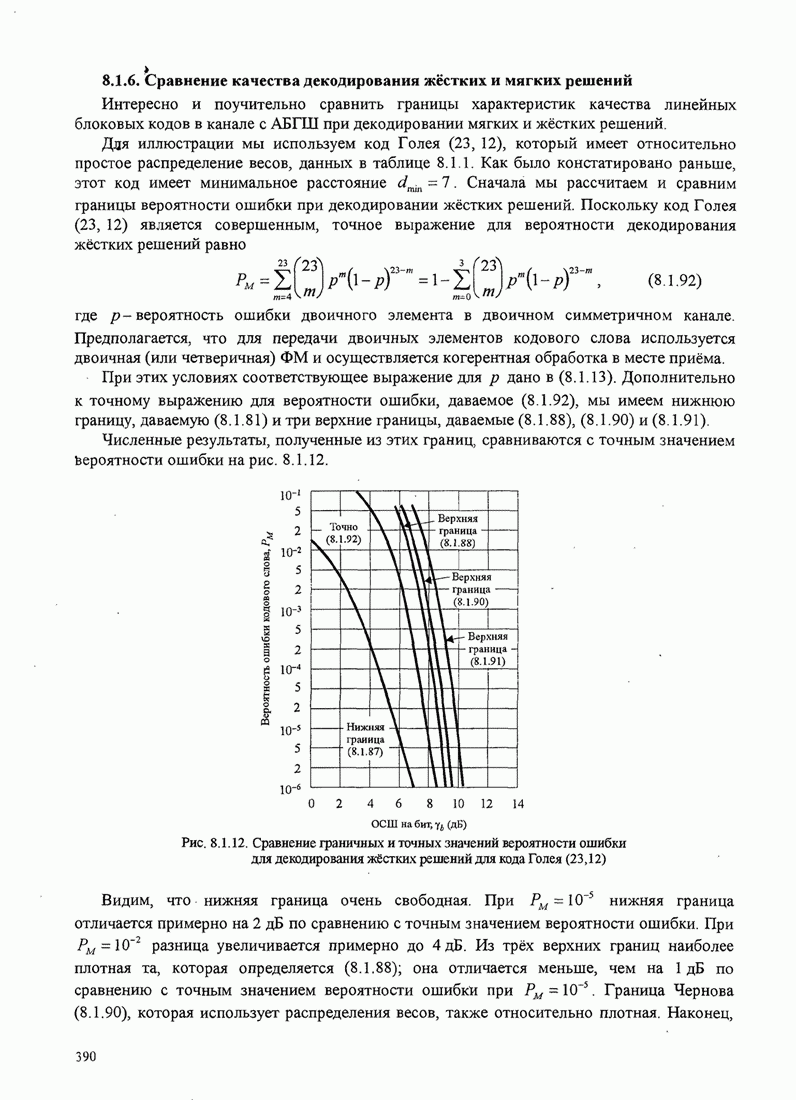
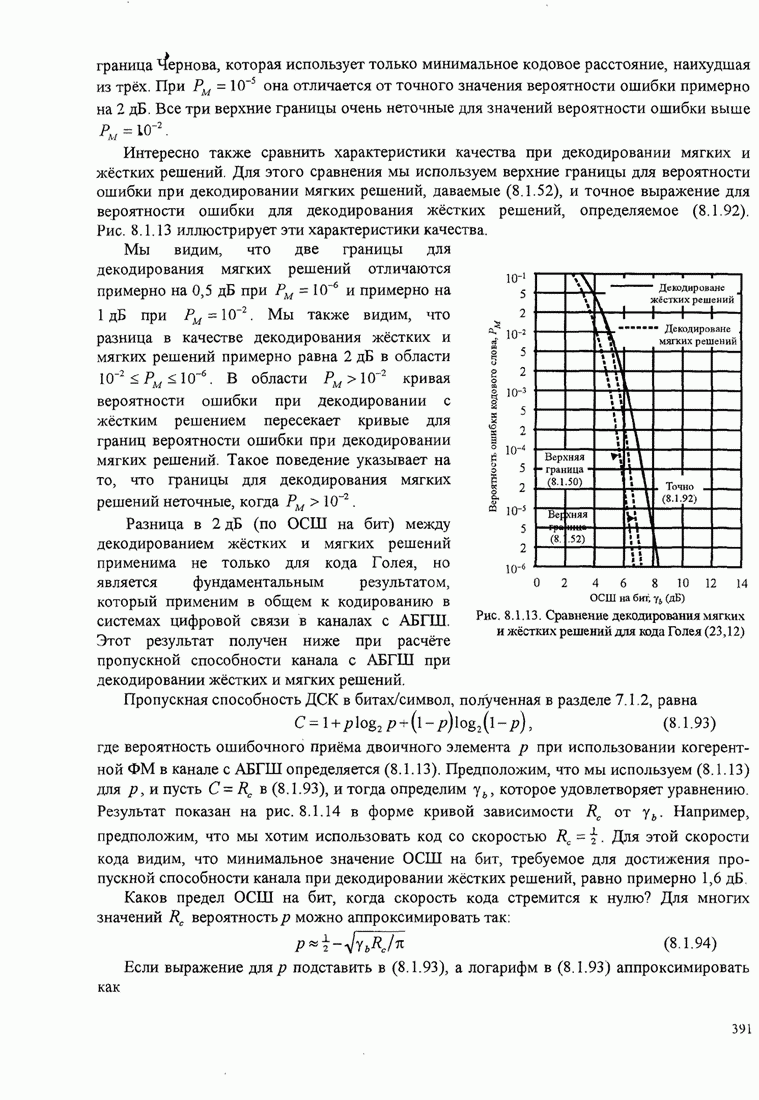
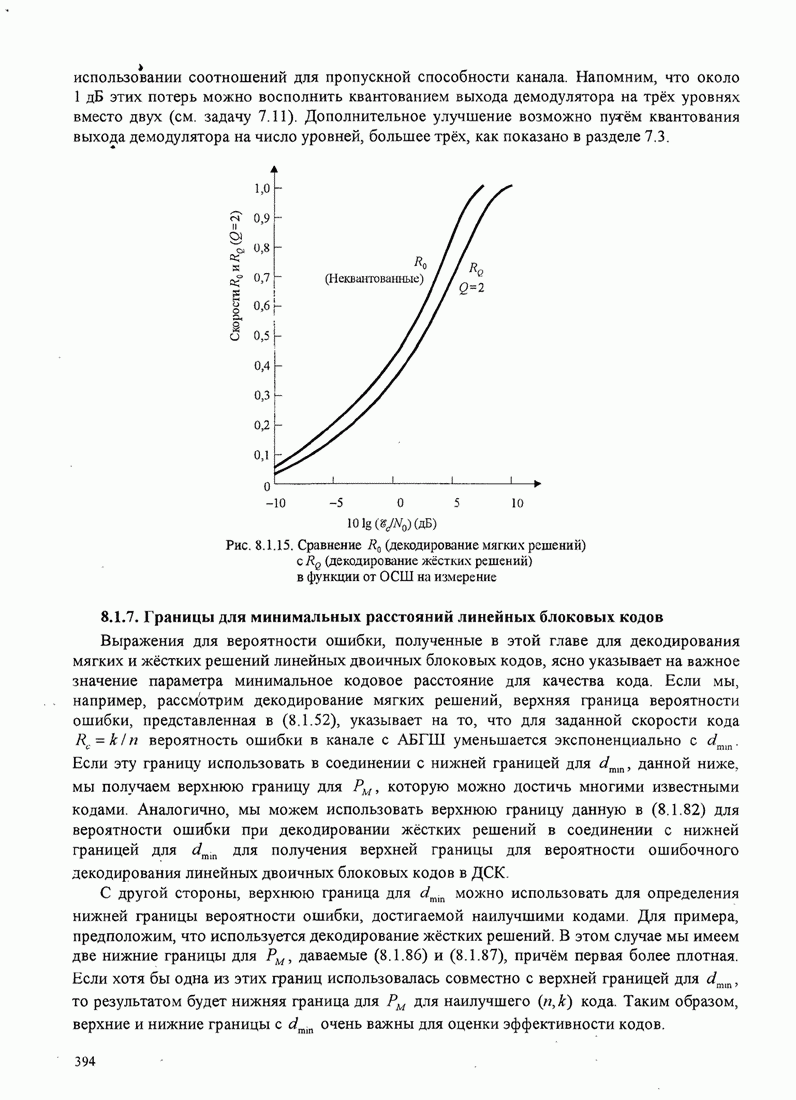
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
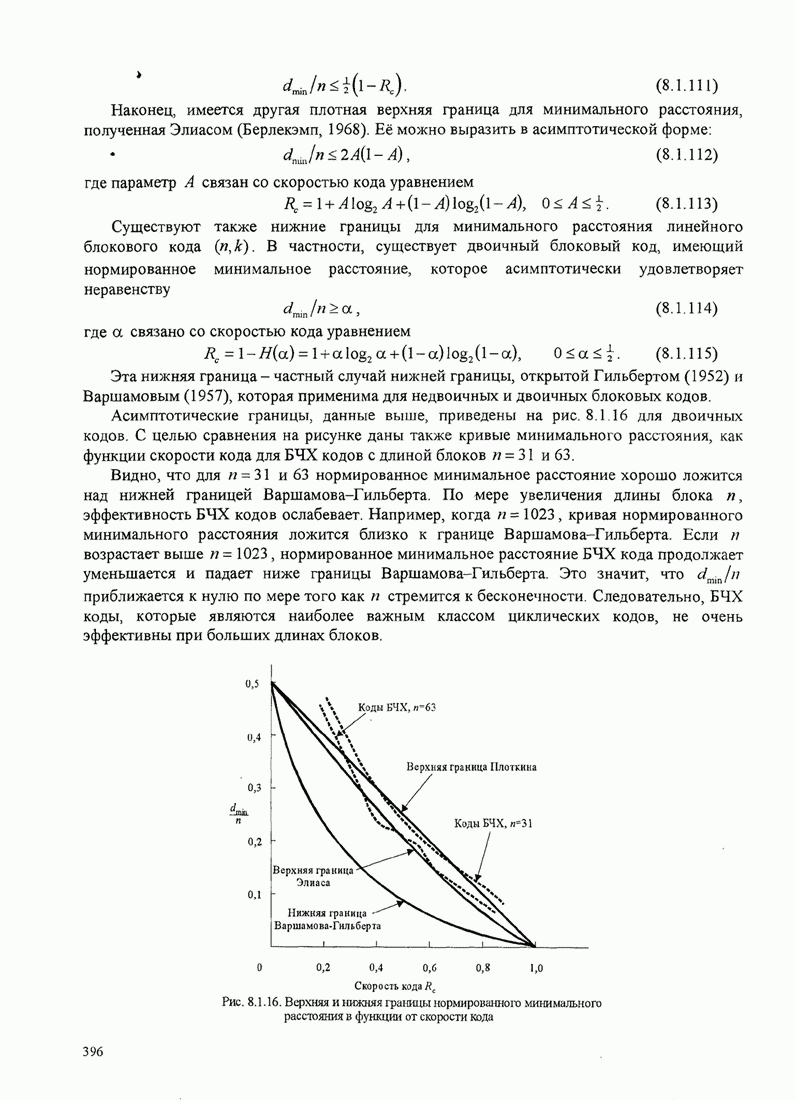
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
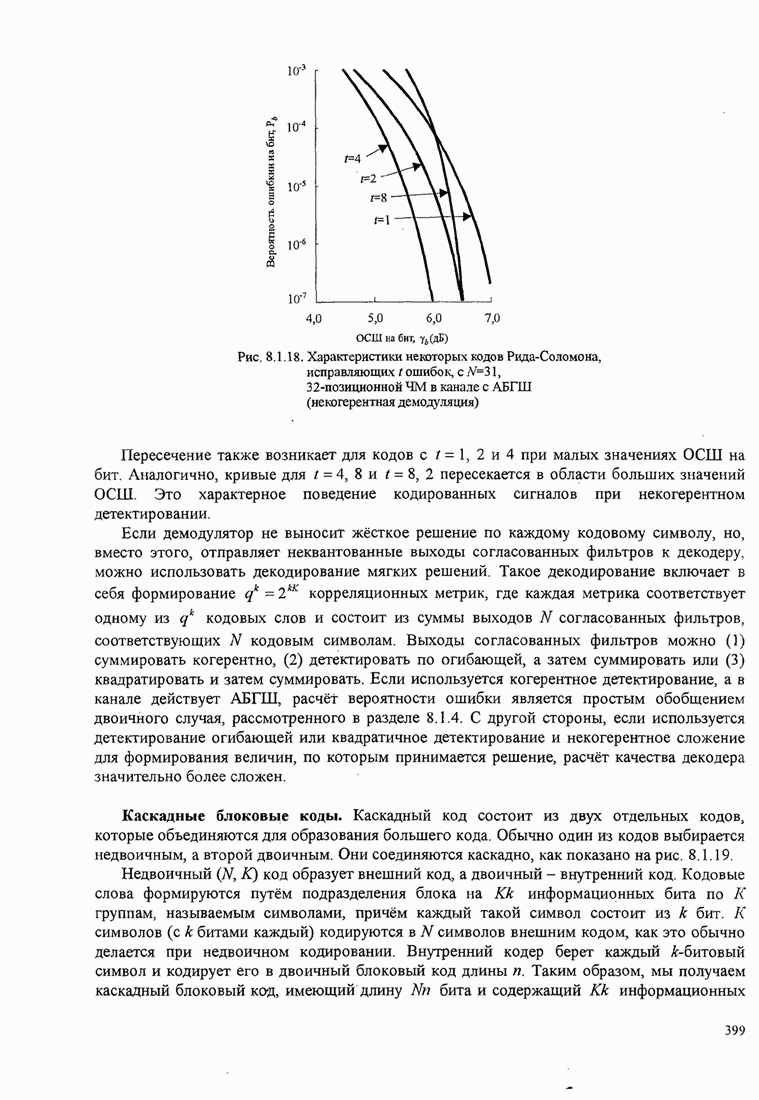
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
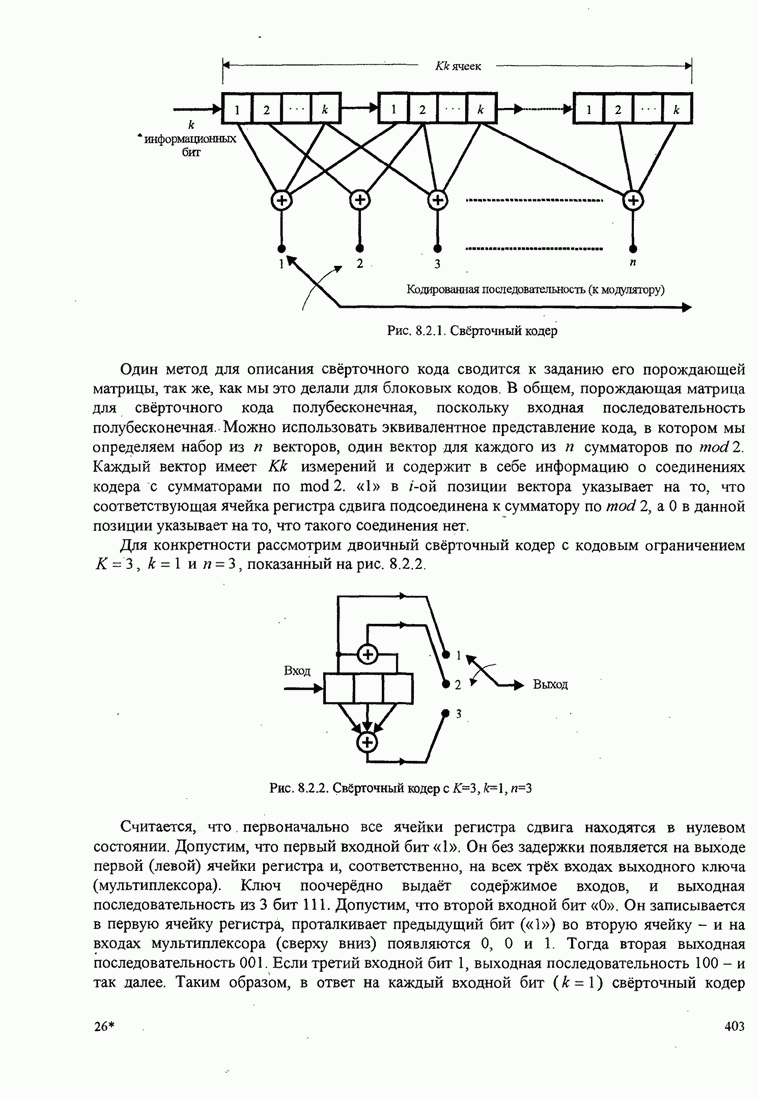
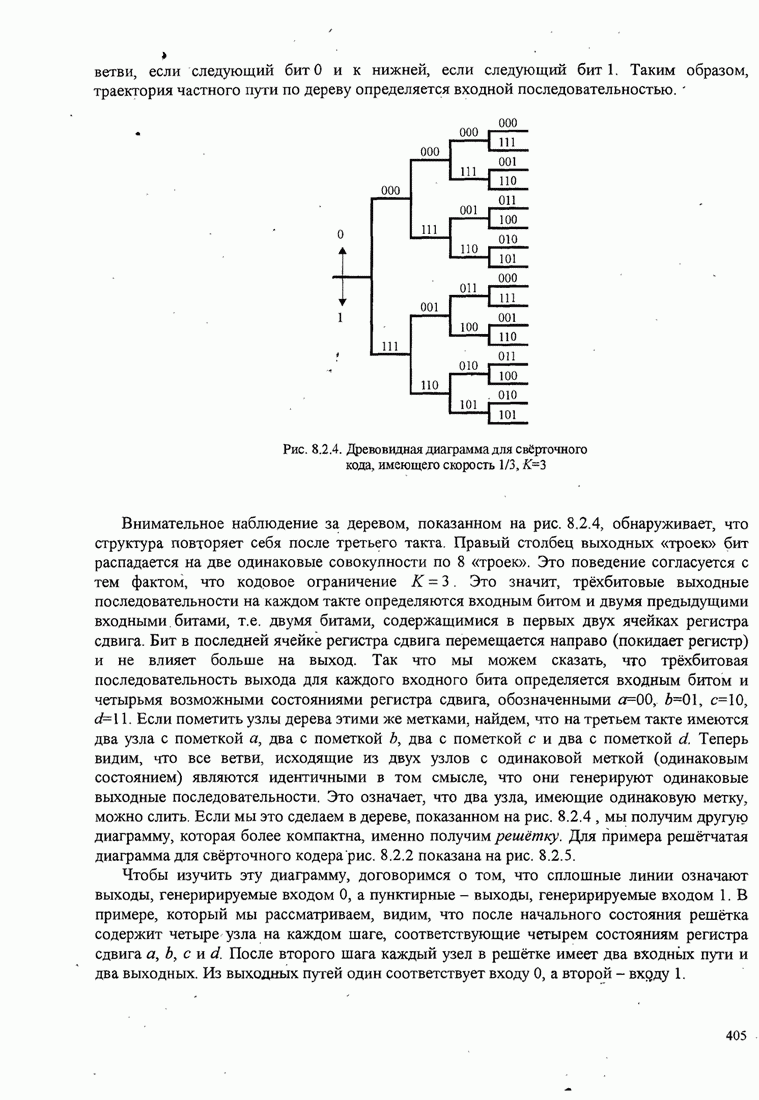
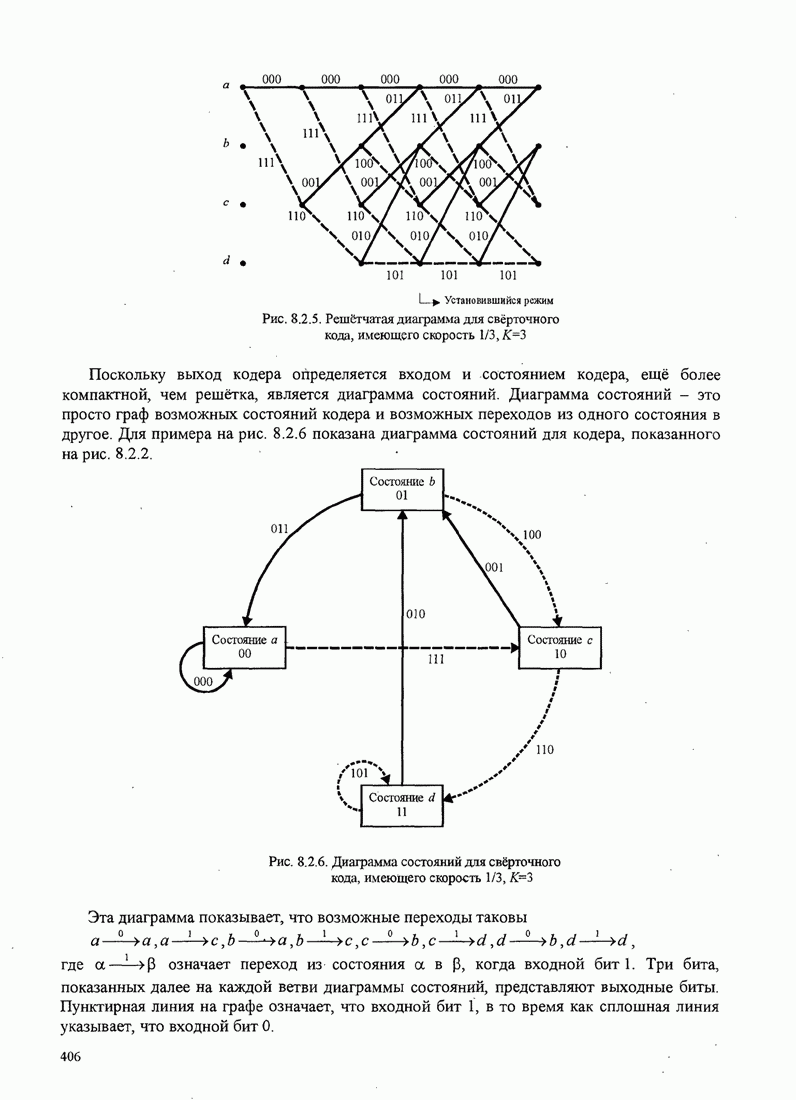
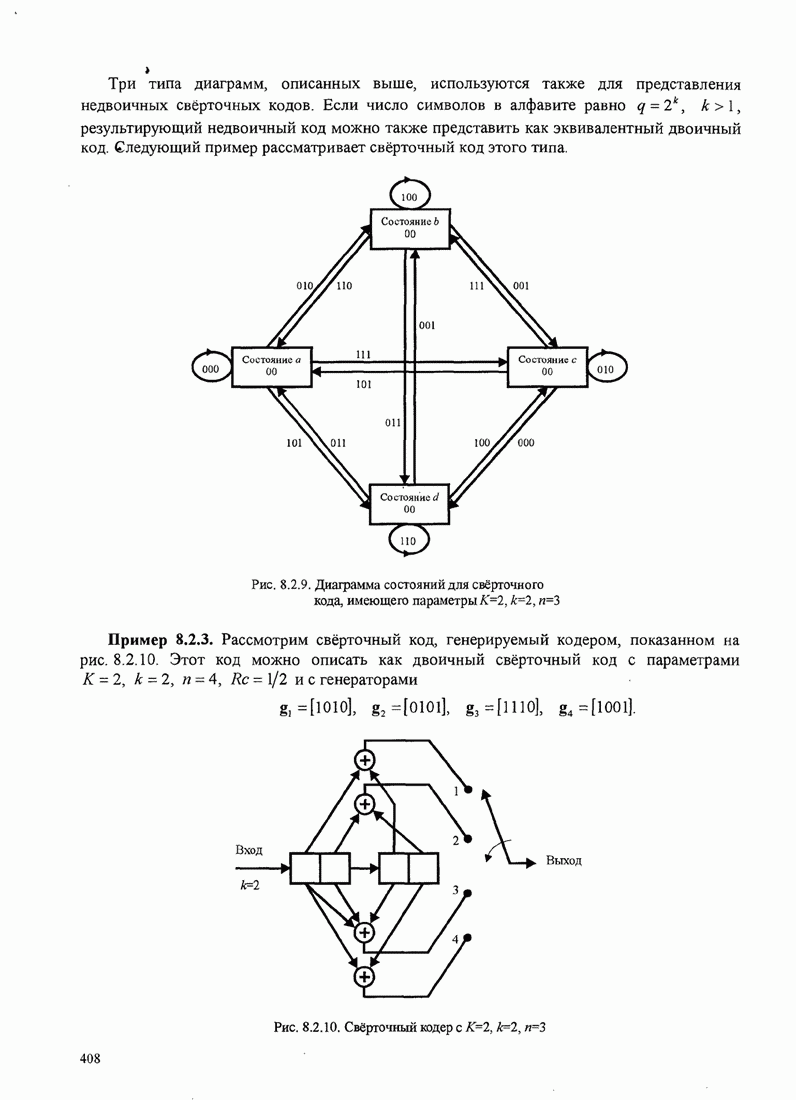
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
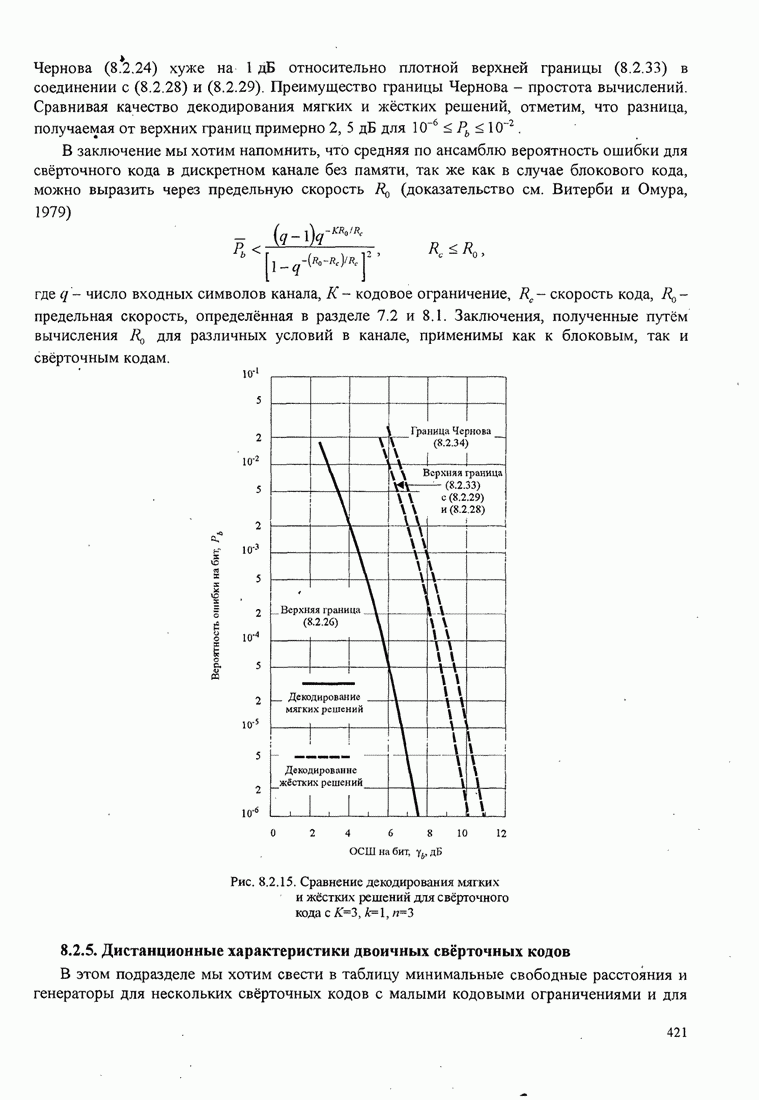
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
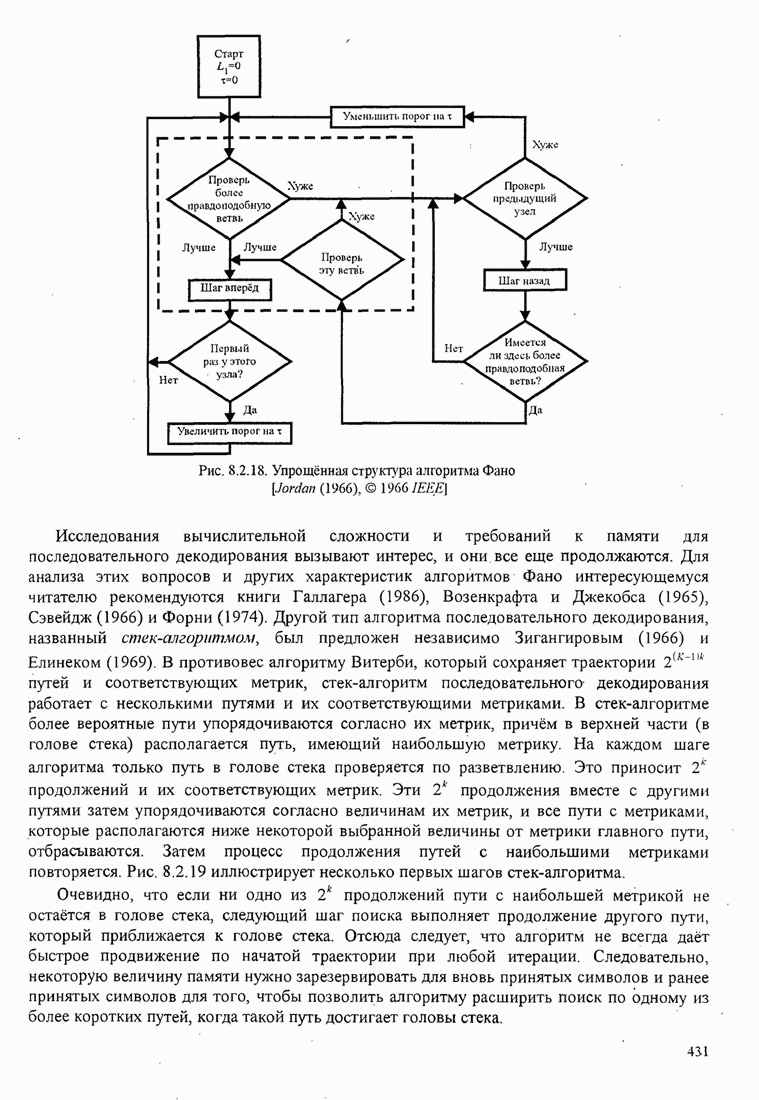
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
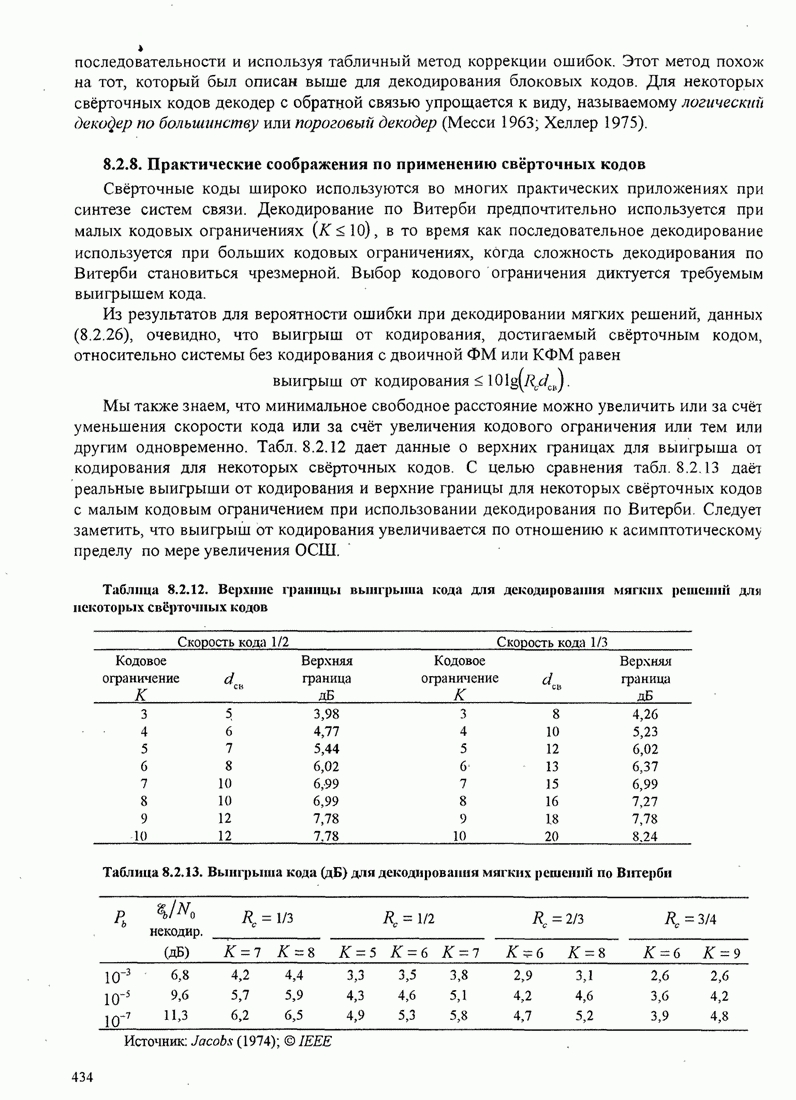
- 8.2.8. Практические соображения по применению свёрточных кодов
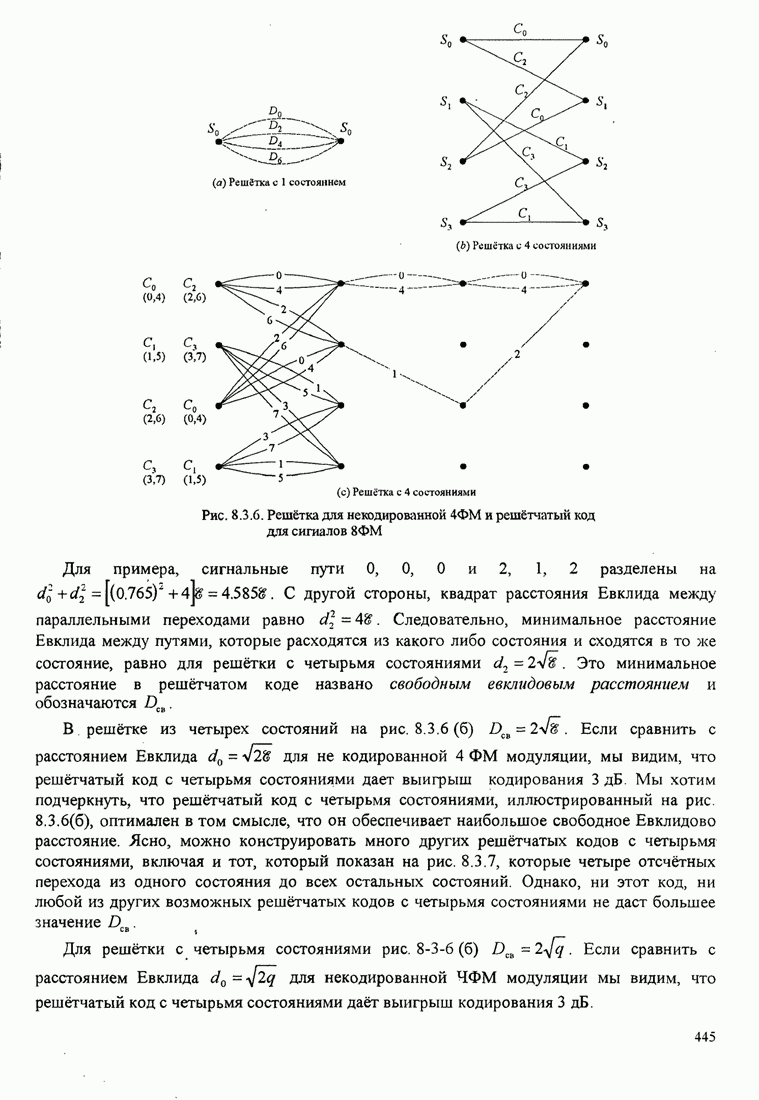
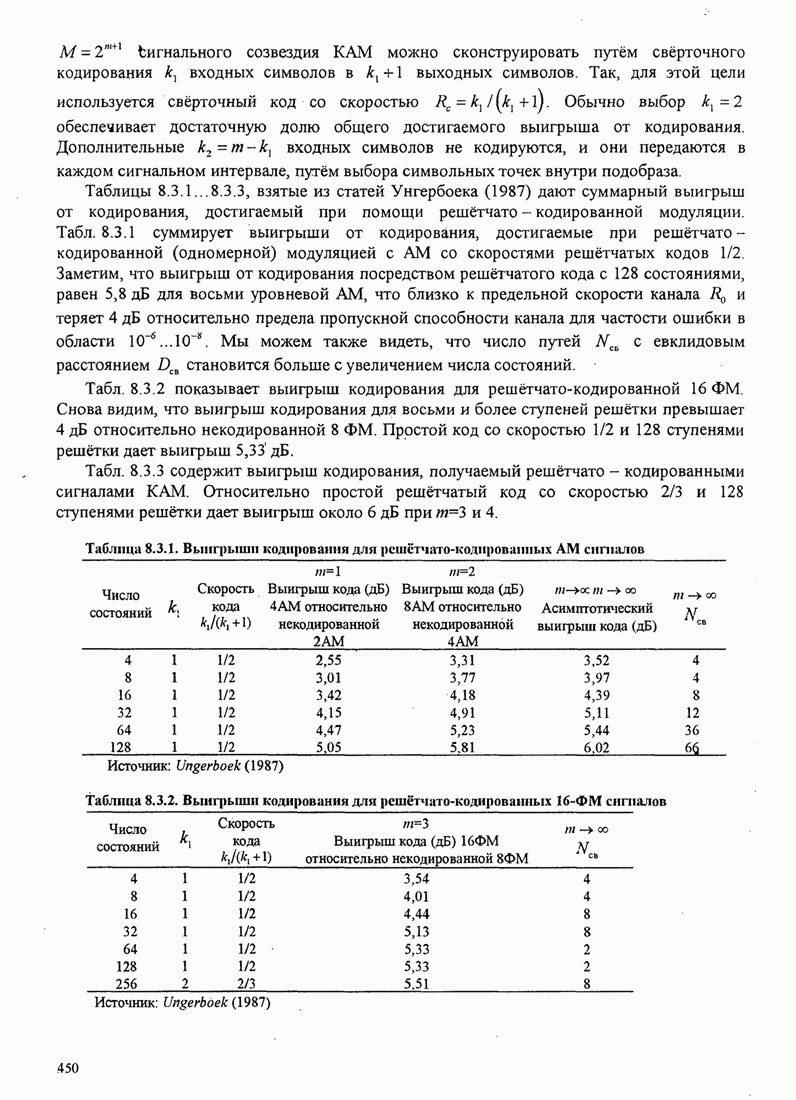
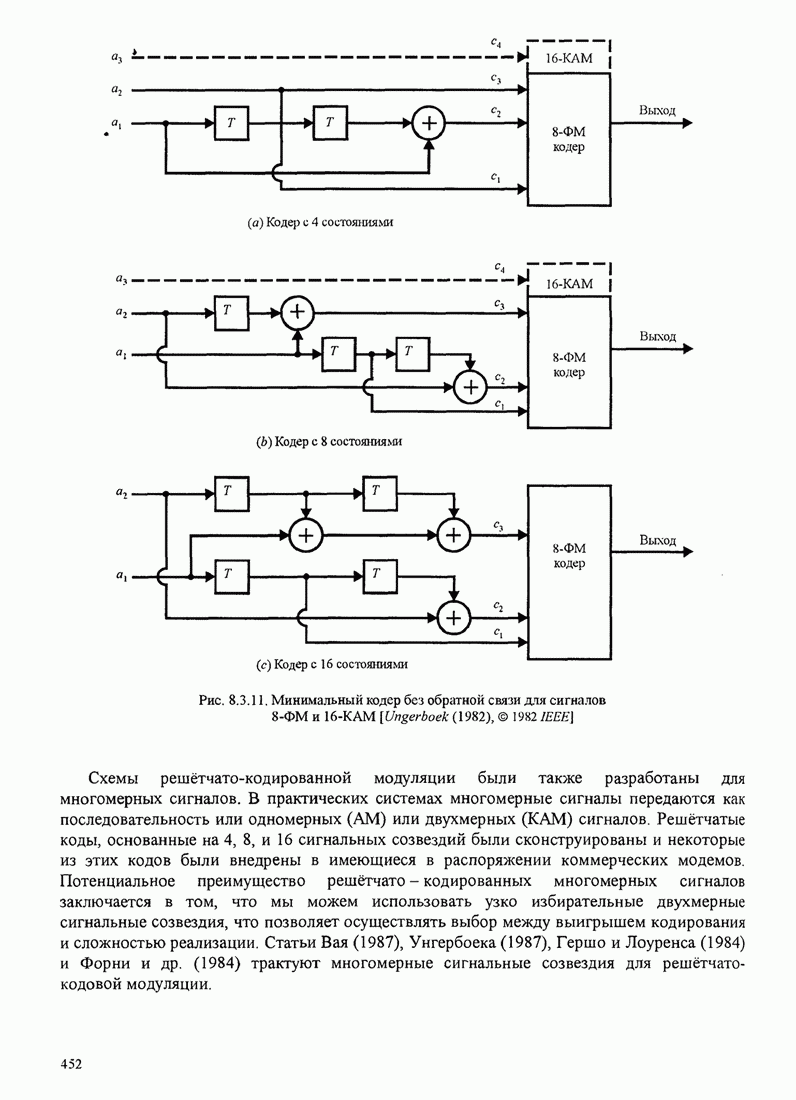
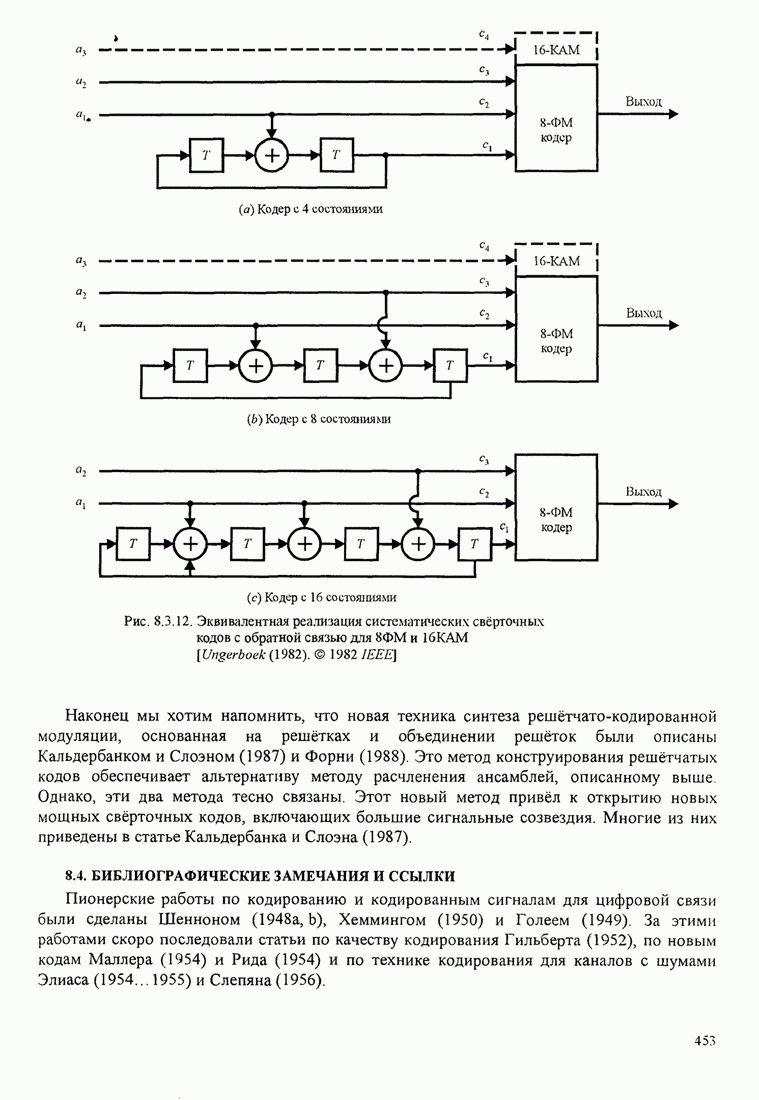
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
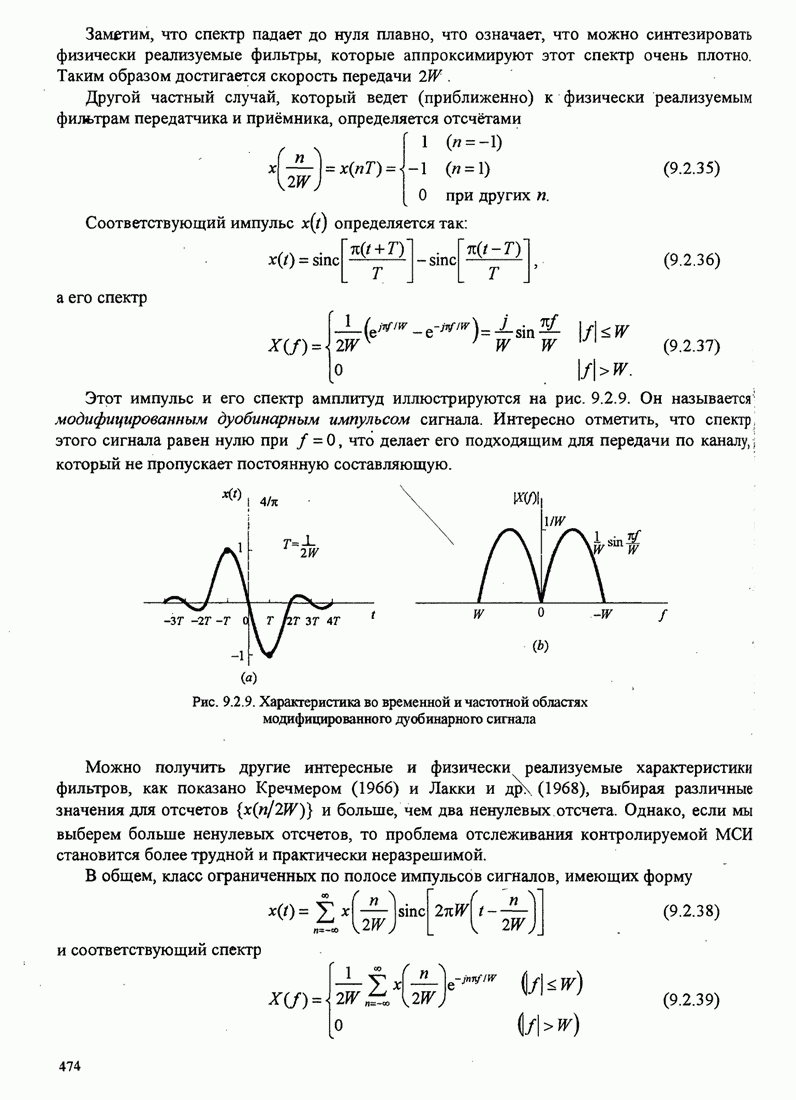
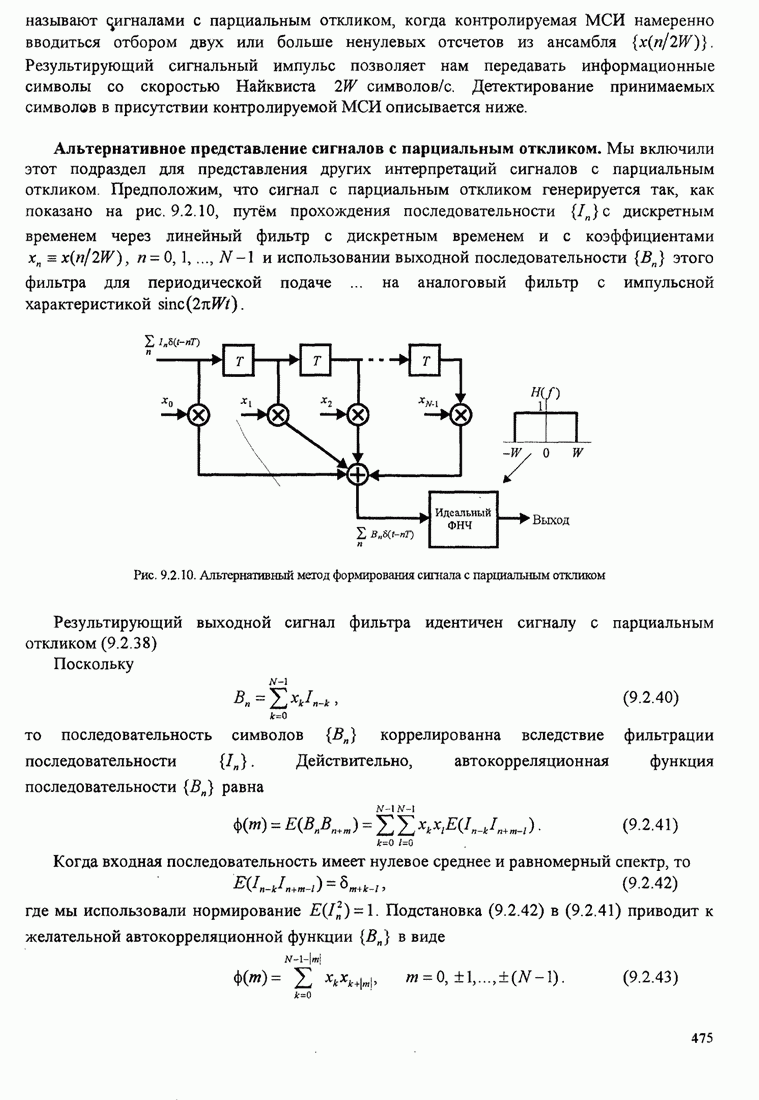
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
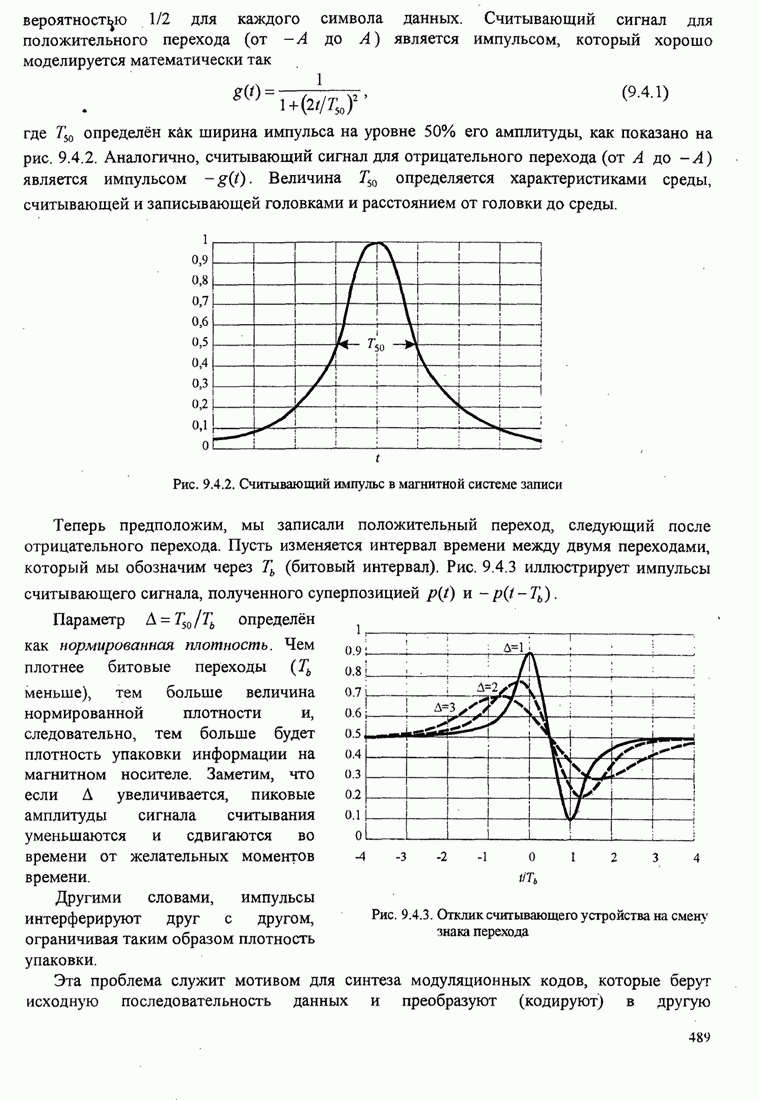
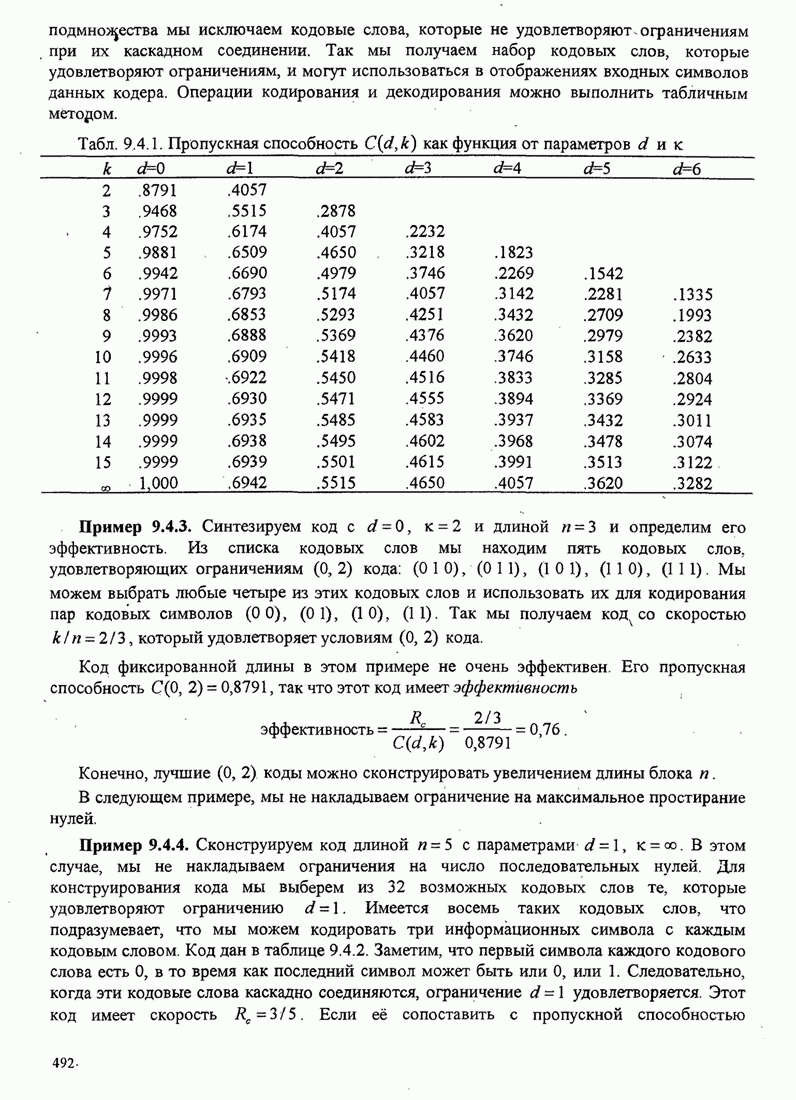
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
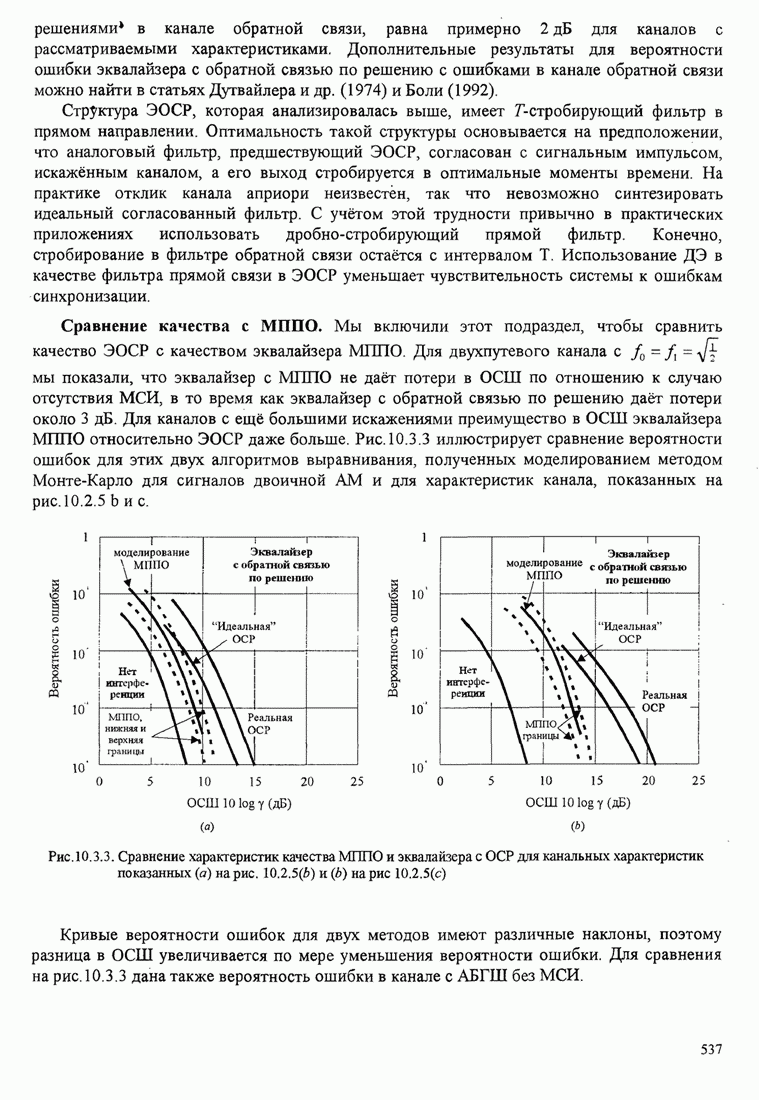
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
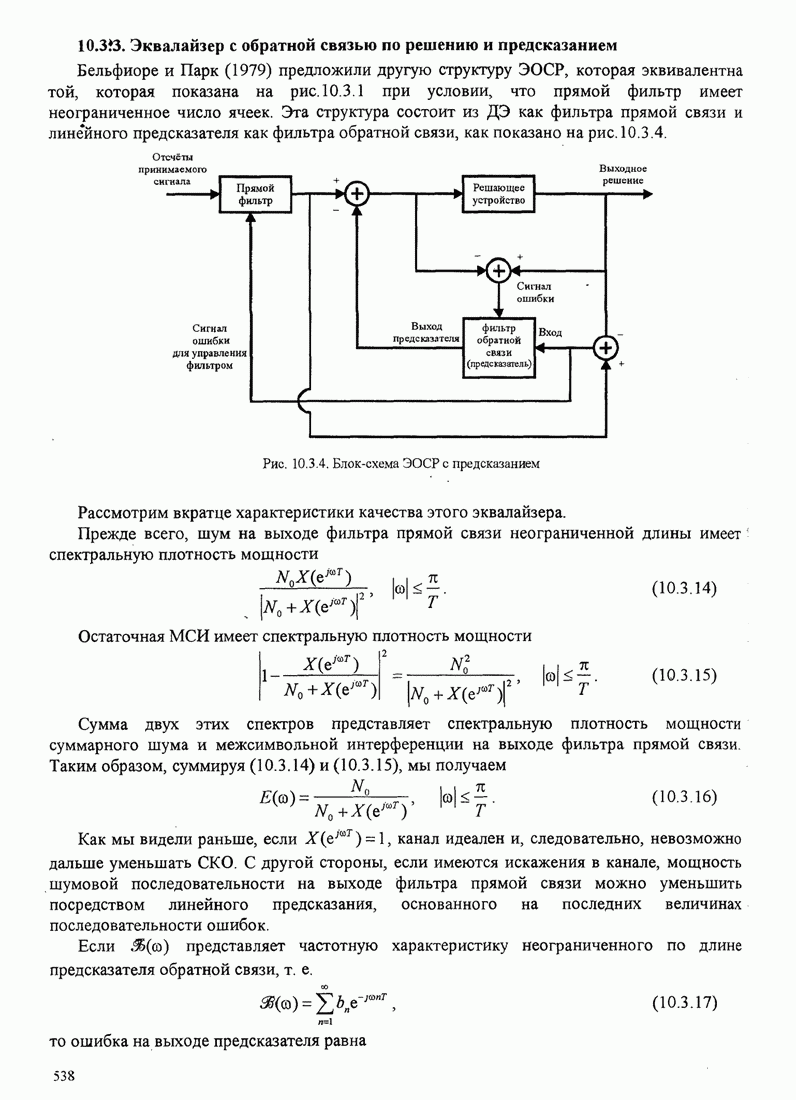
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
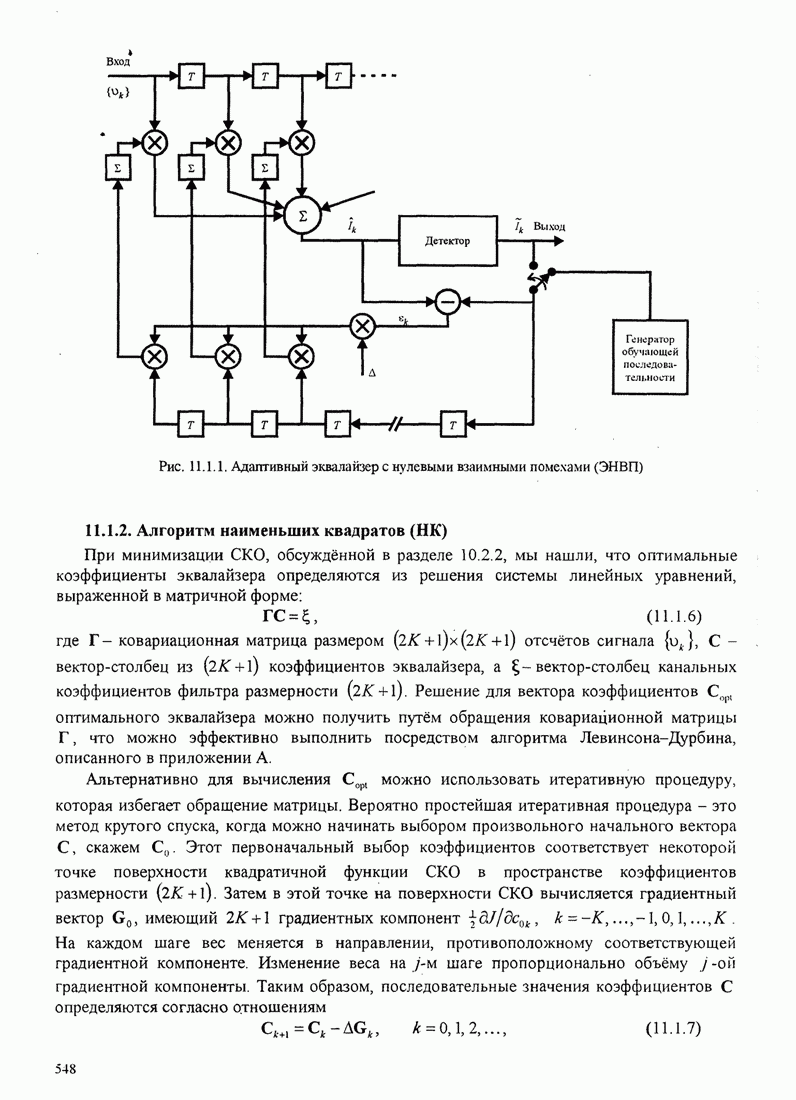
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
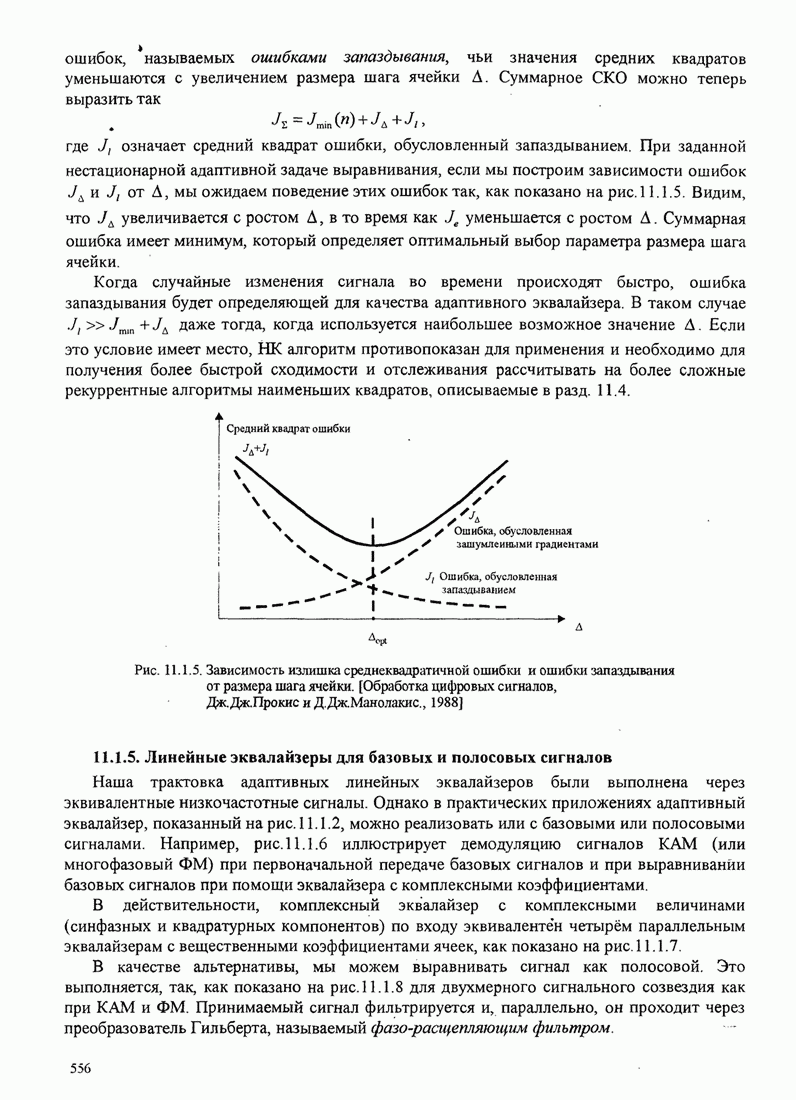
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
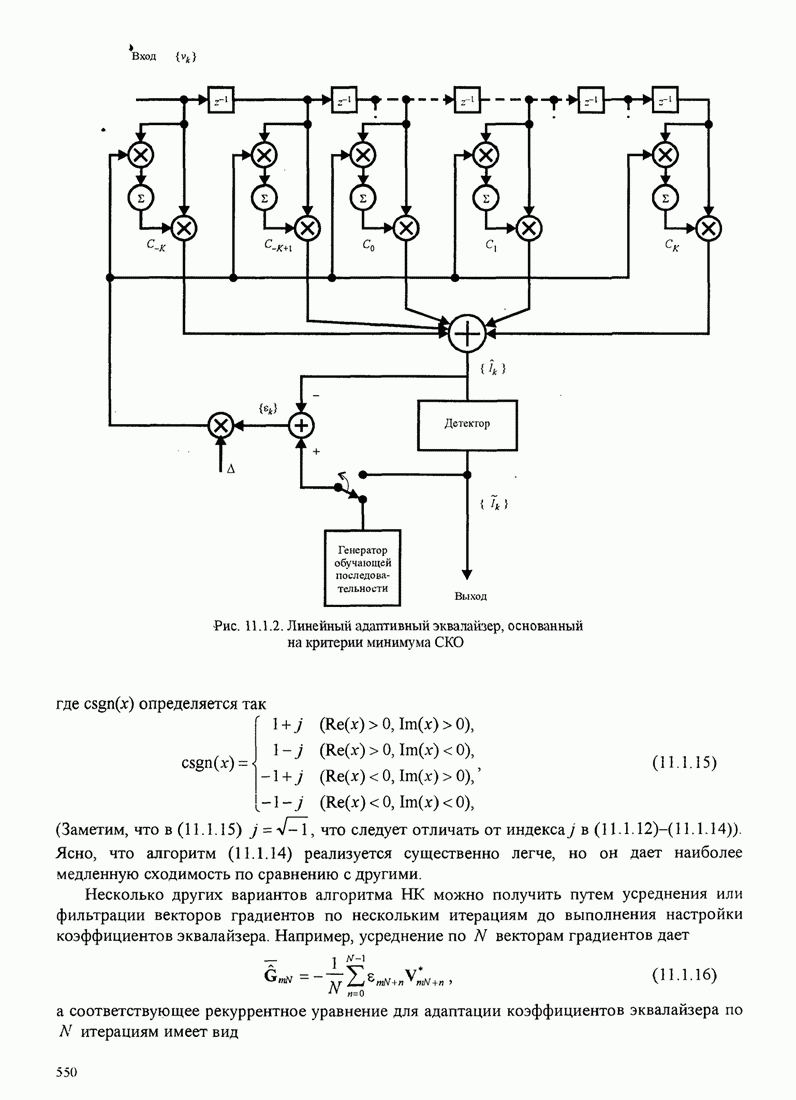
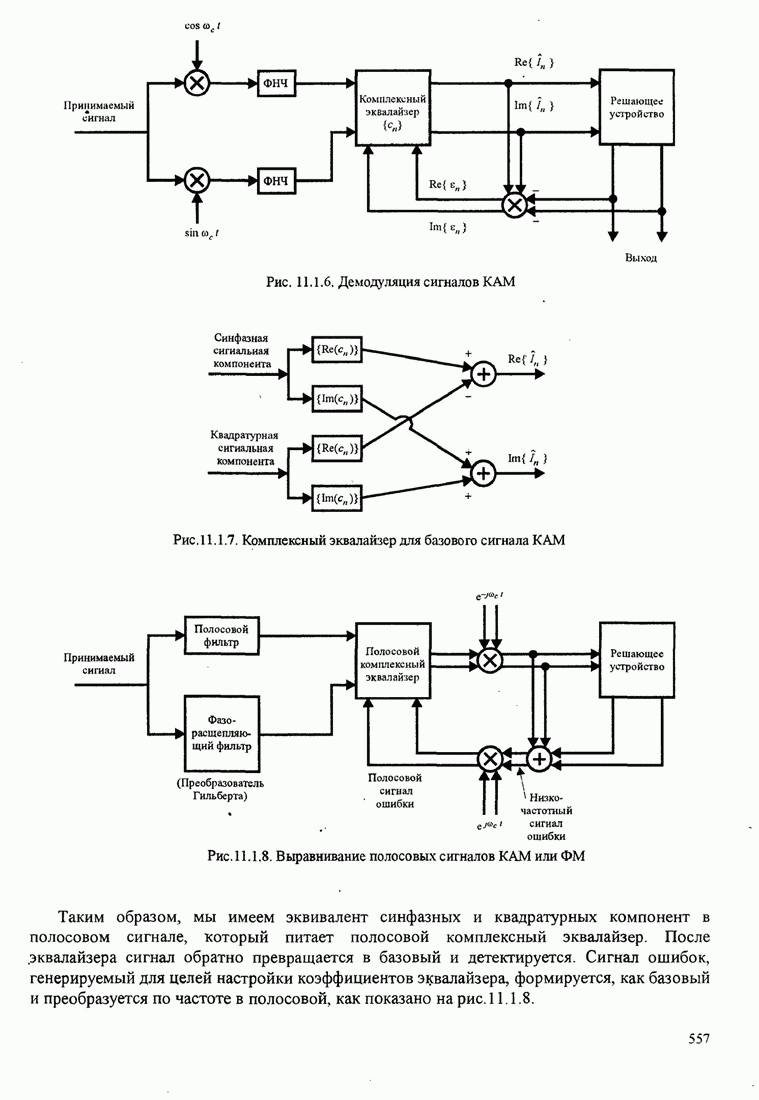
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
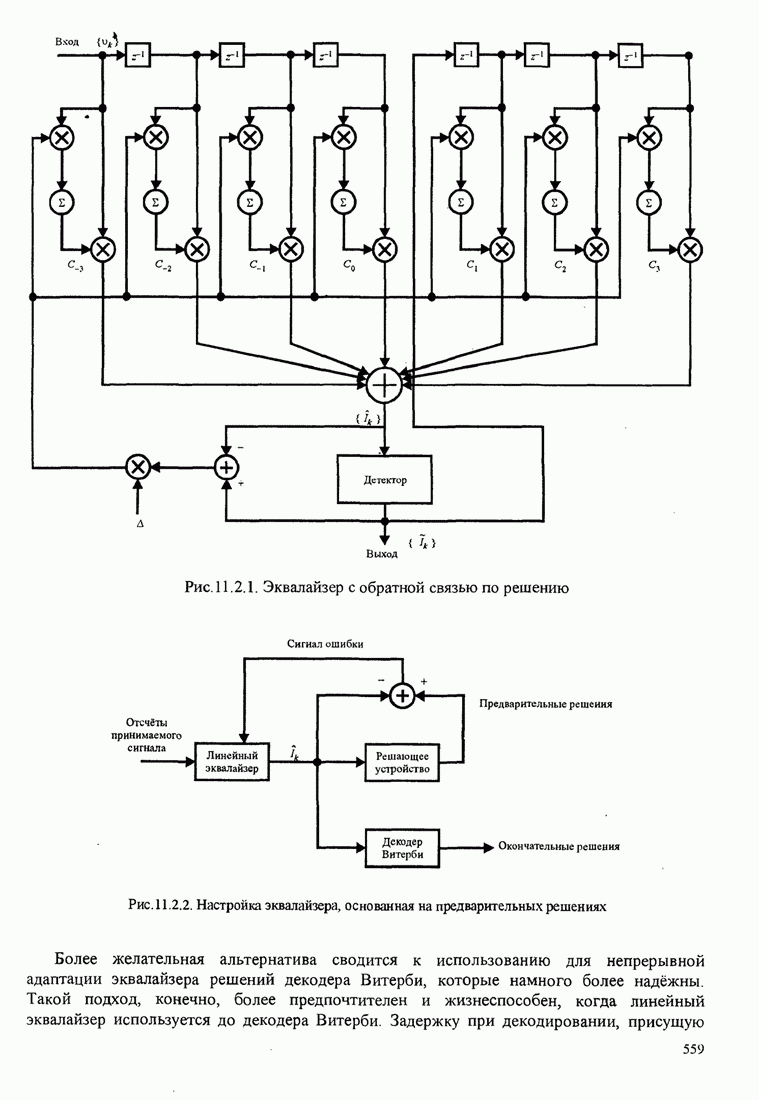
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
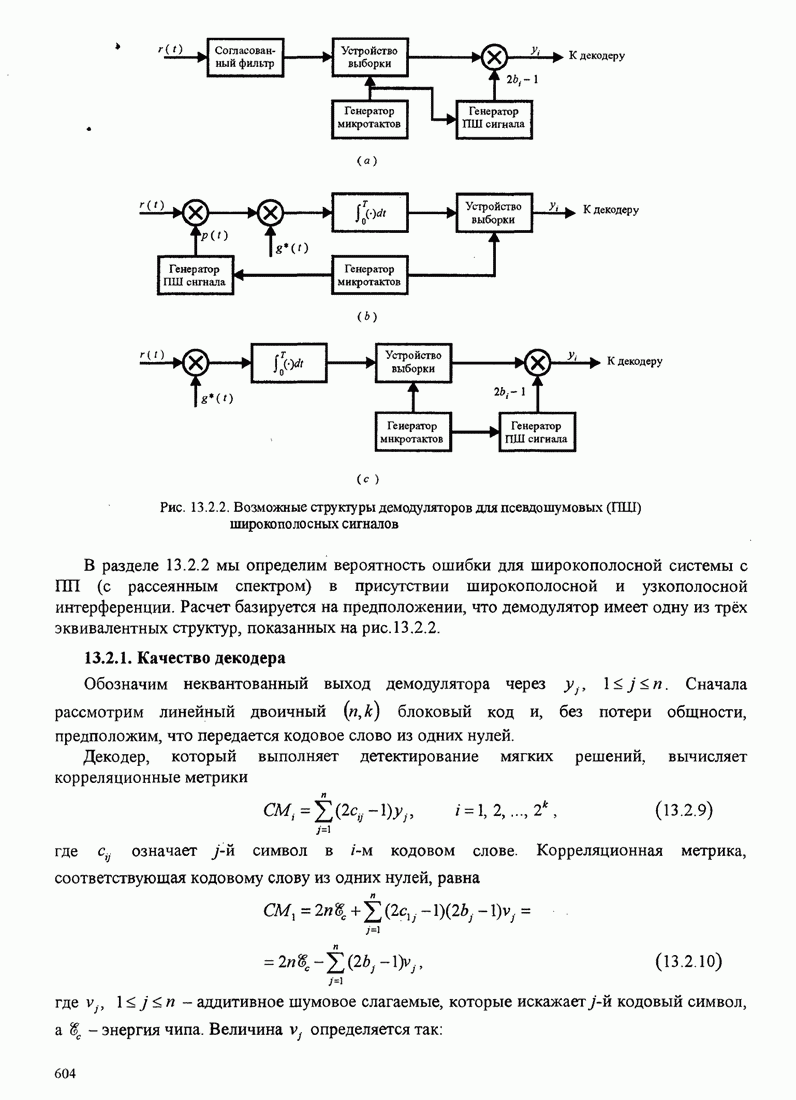
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
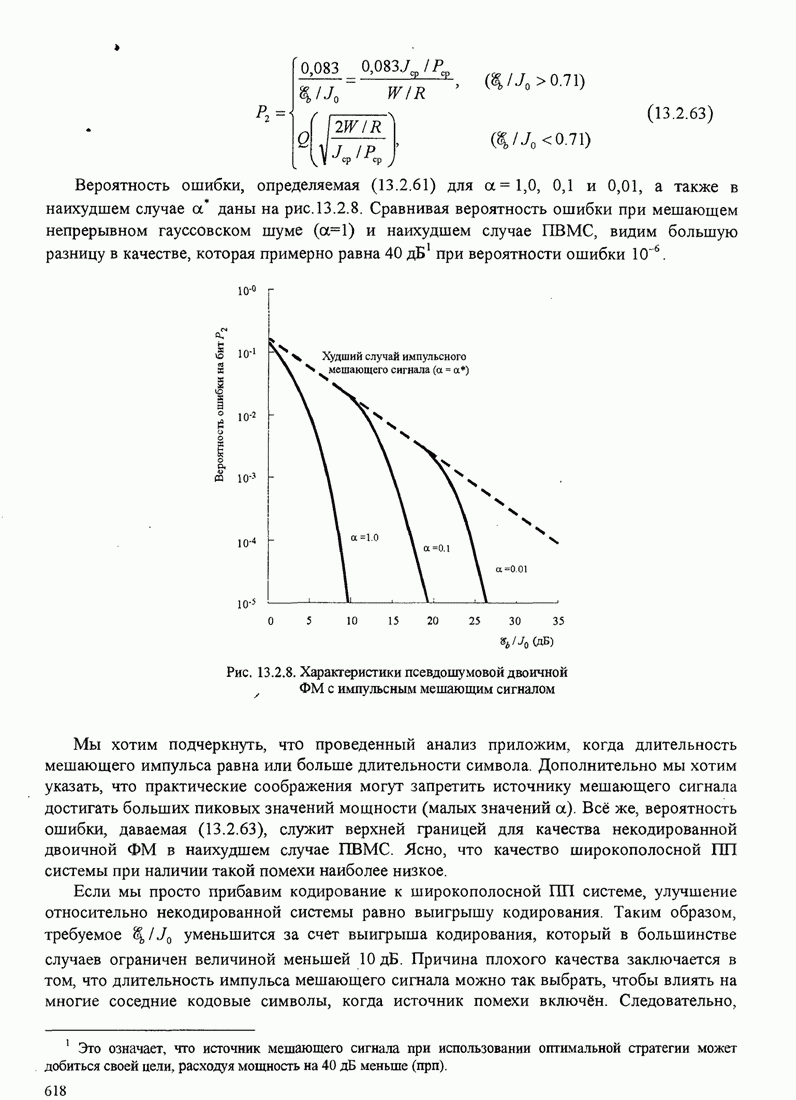
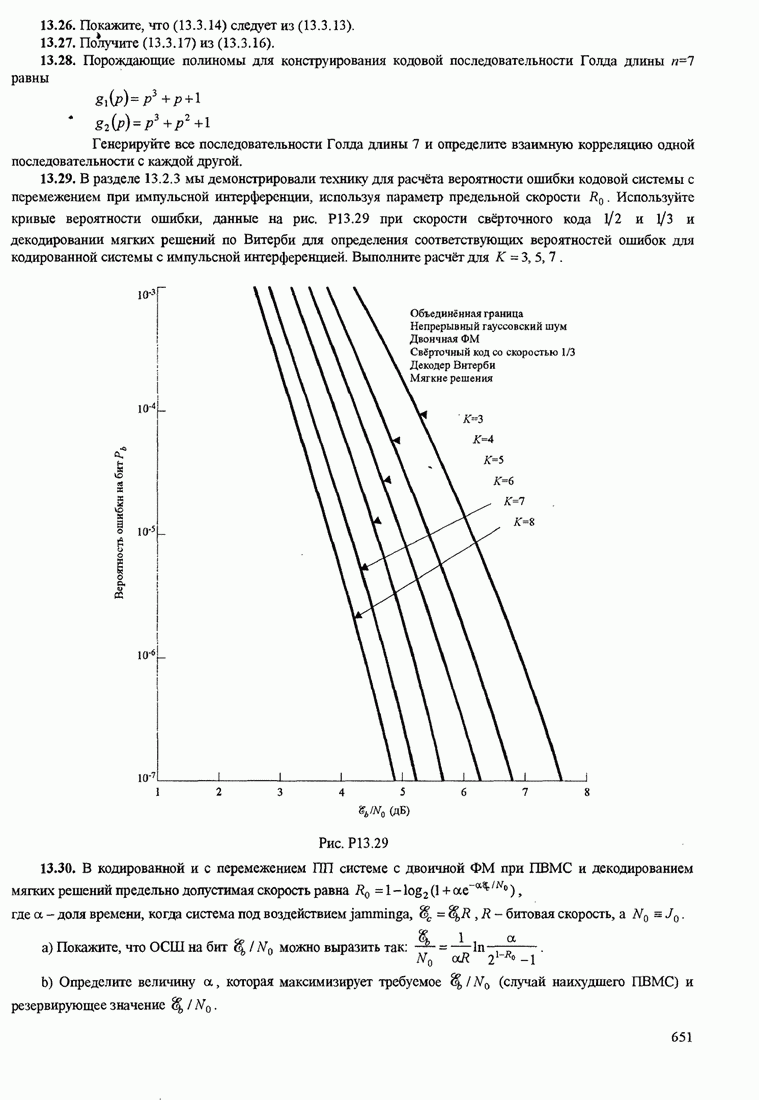
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
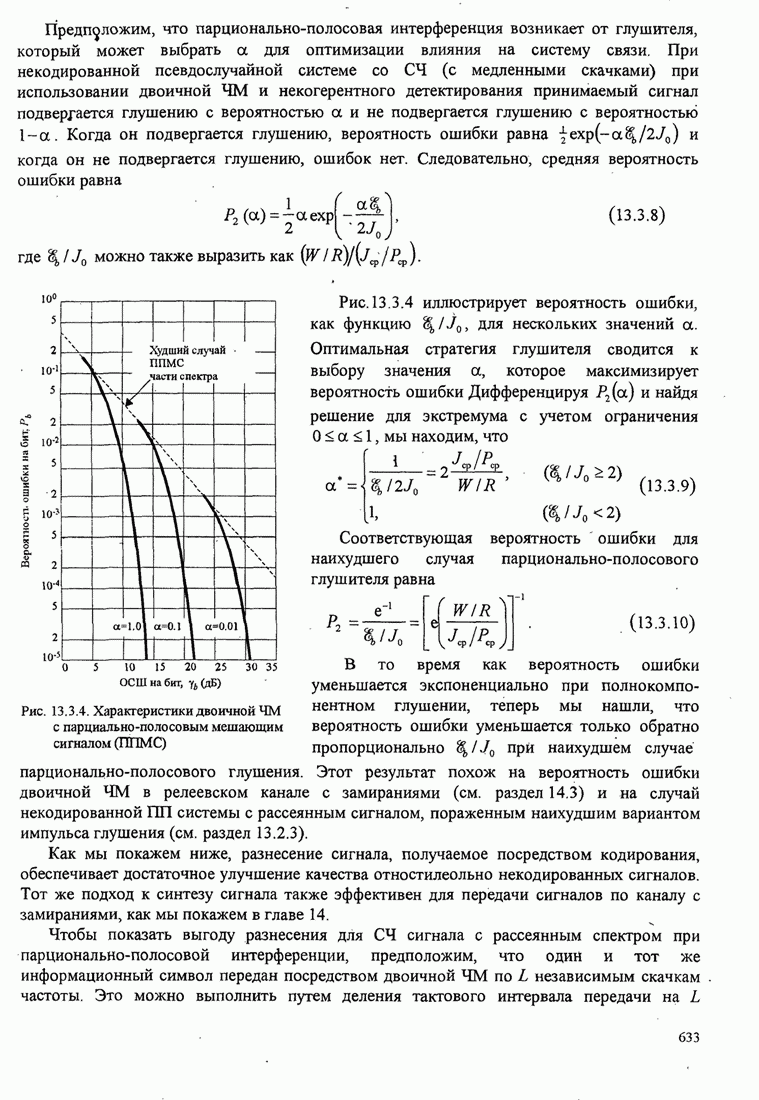
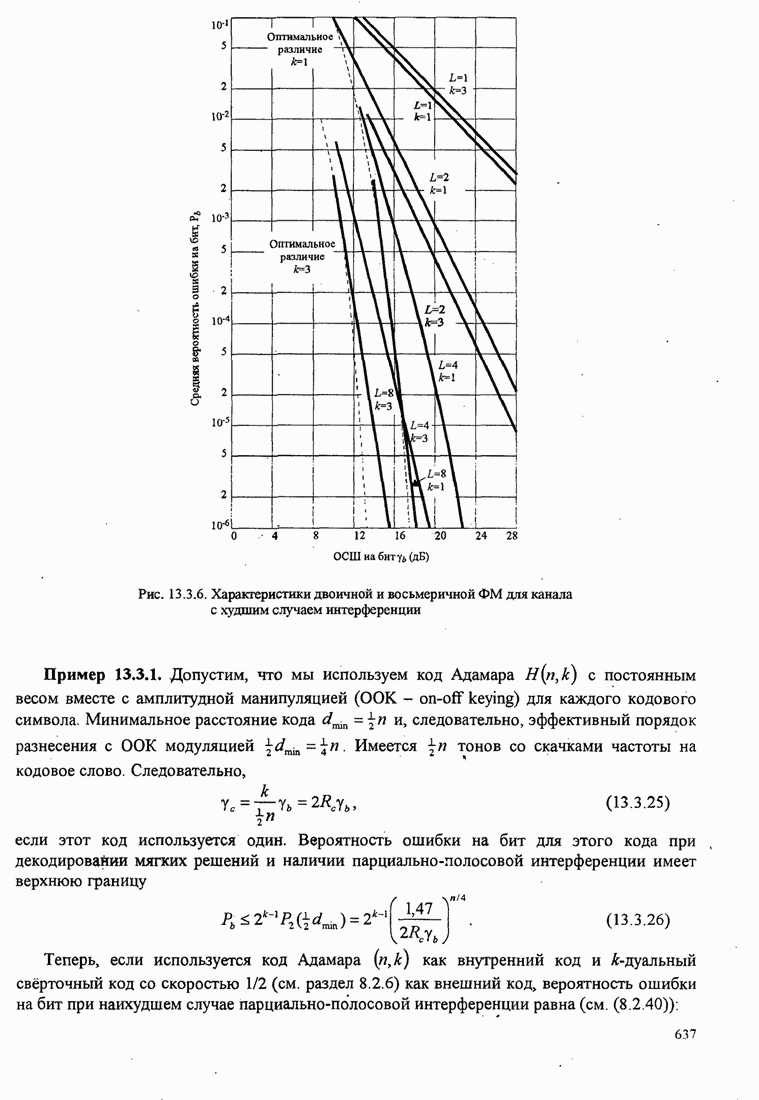
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
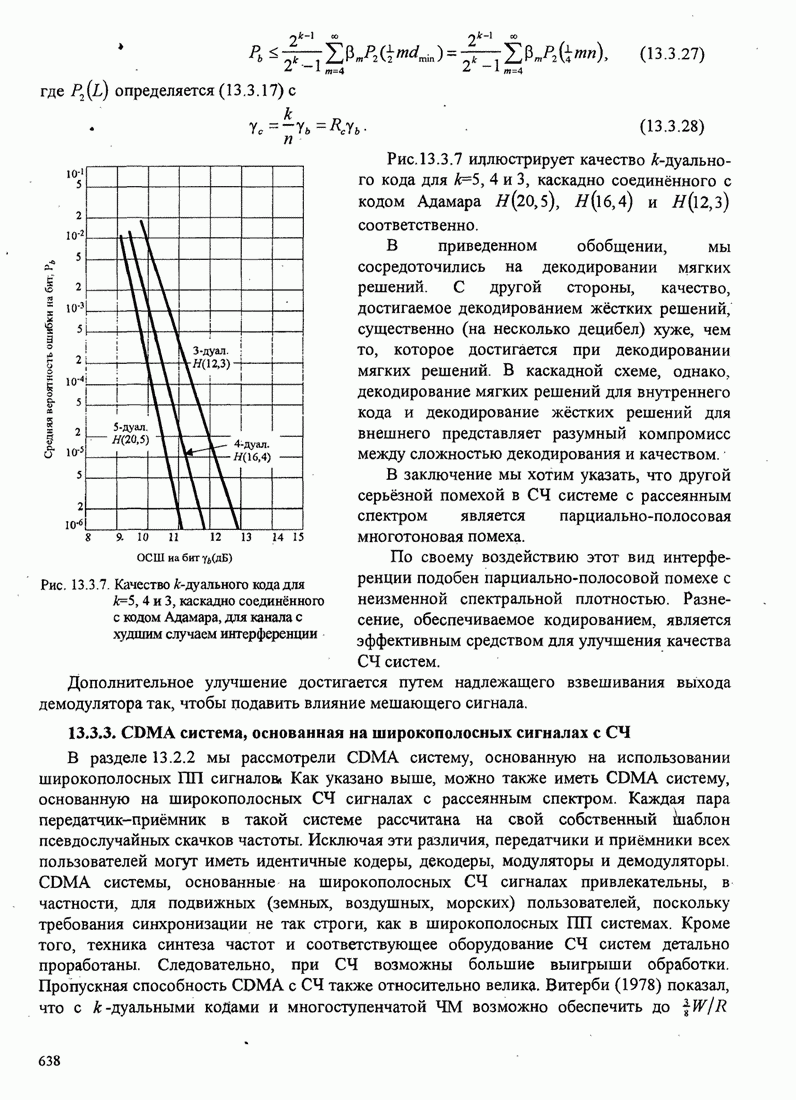
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
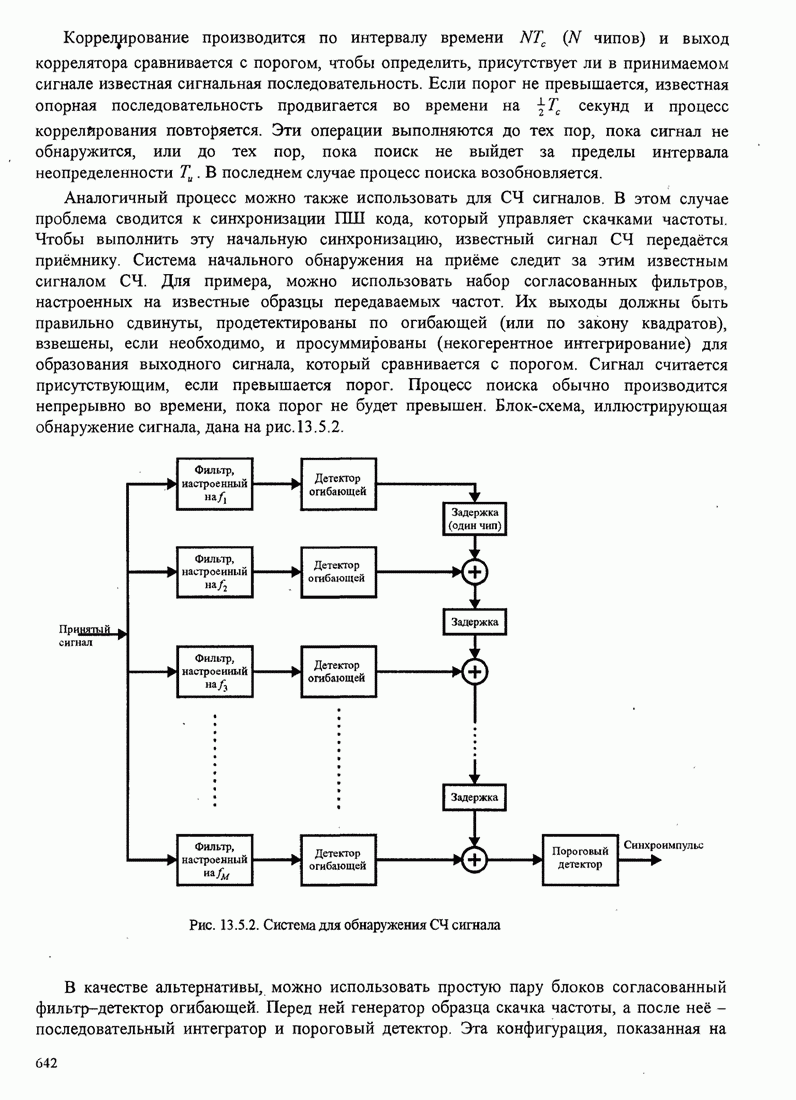
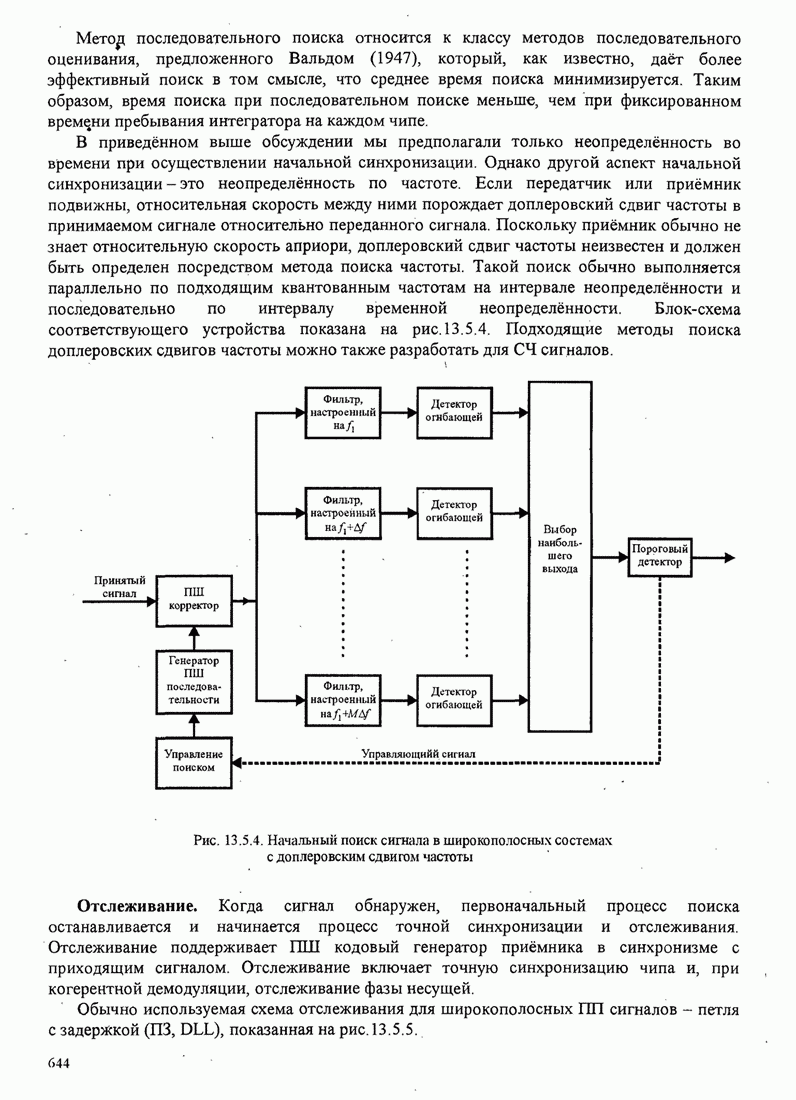
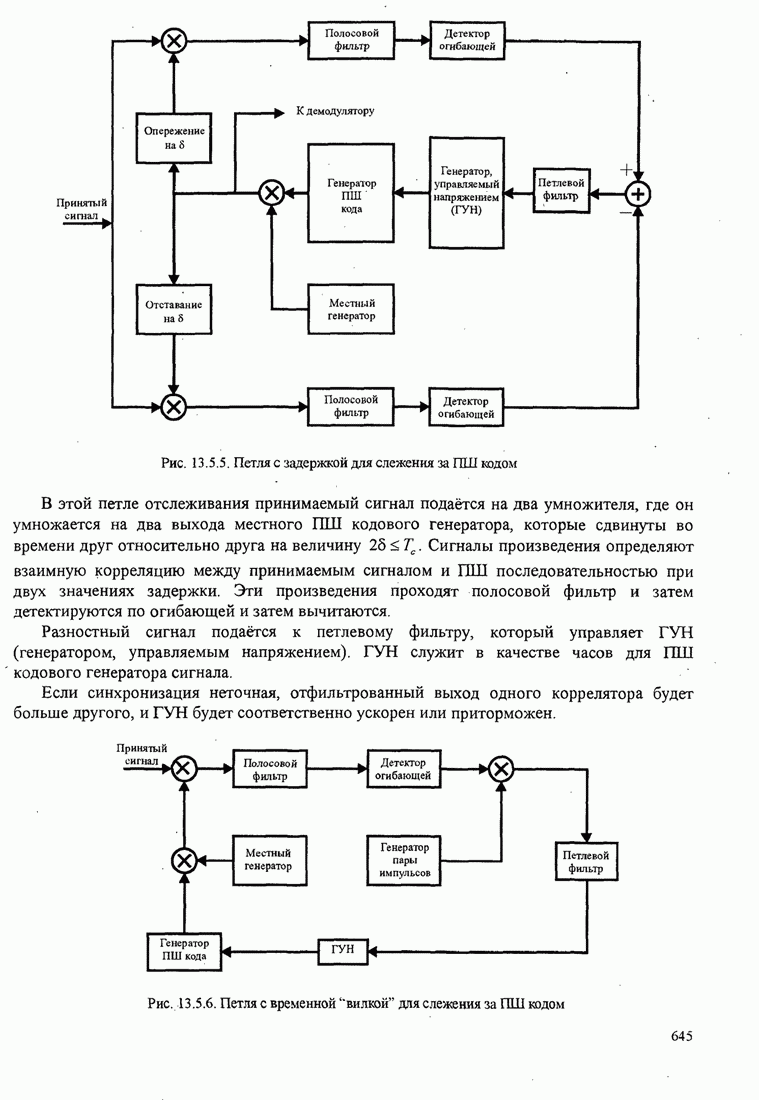
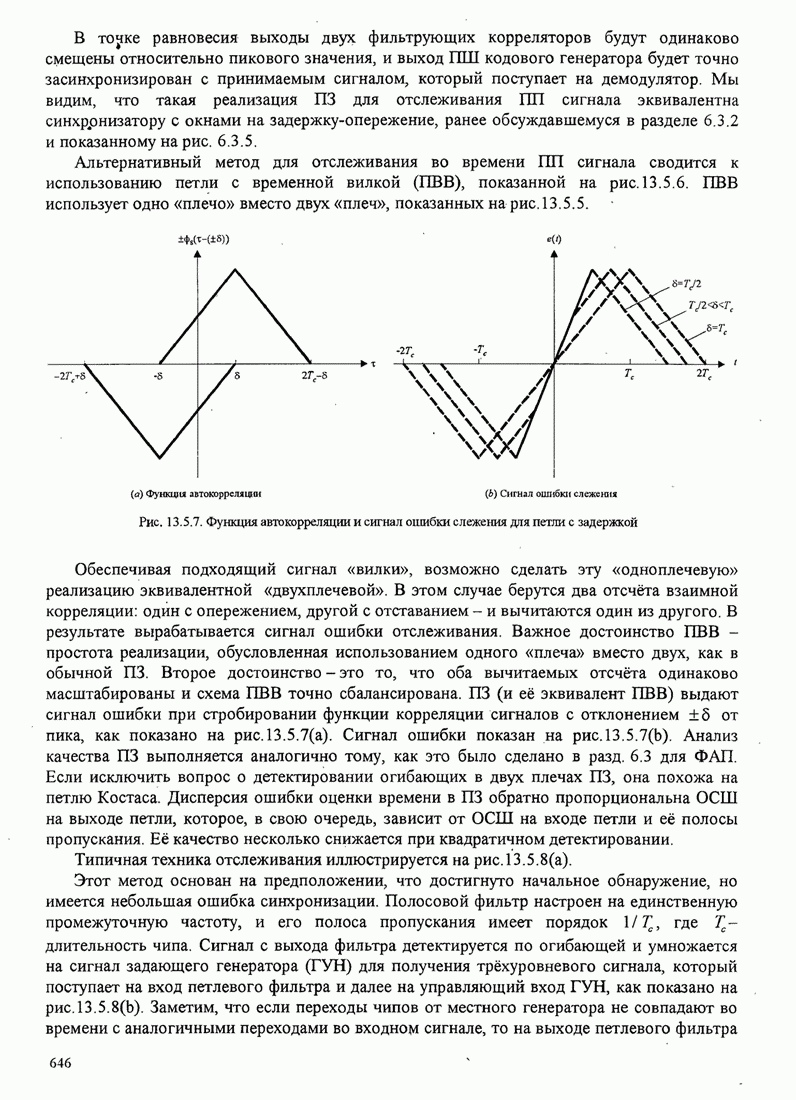
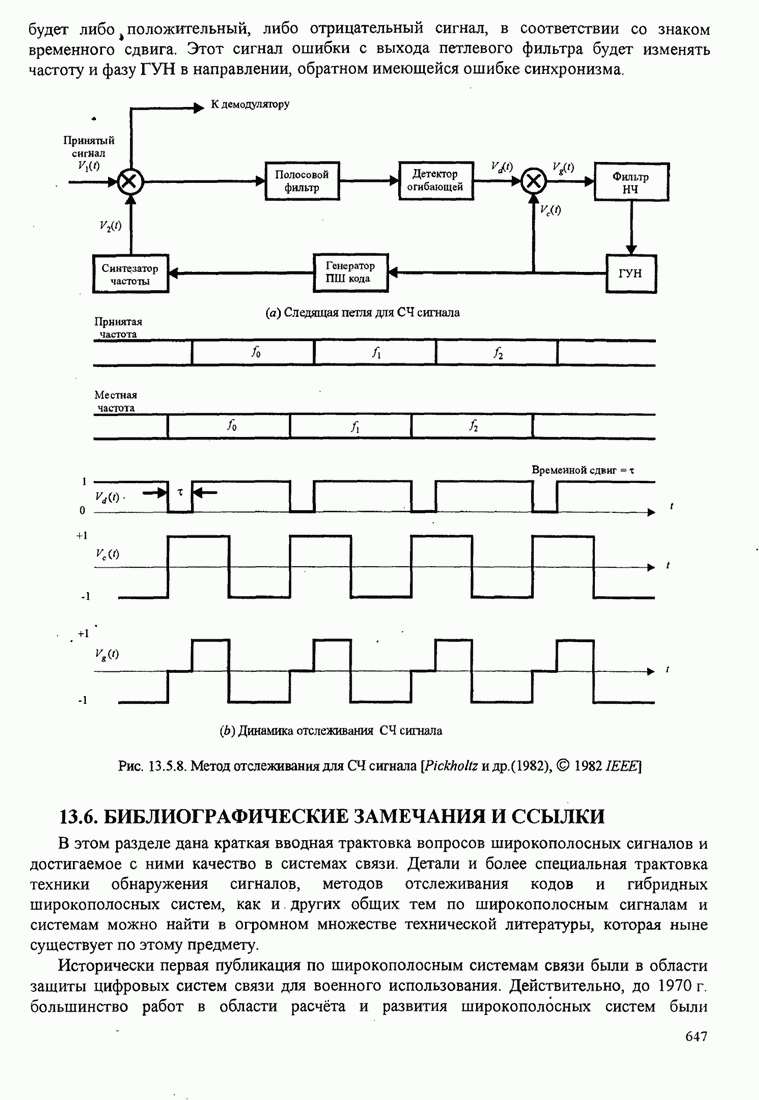
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
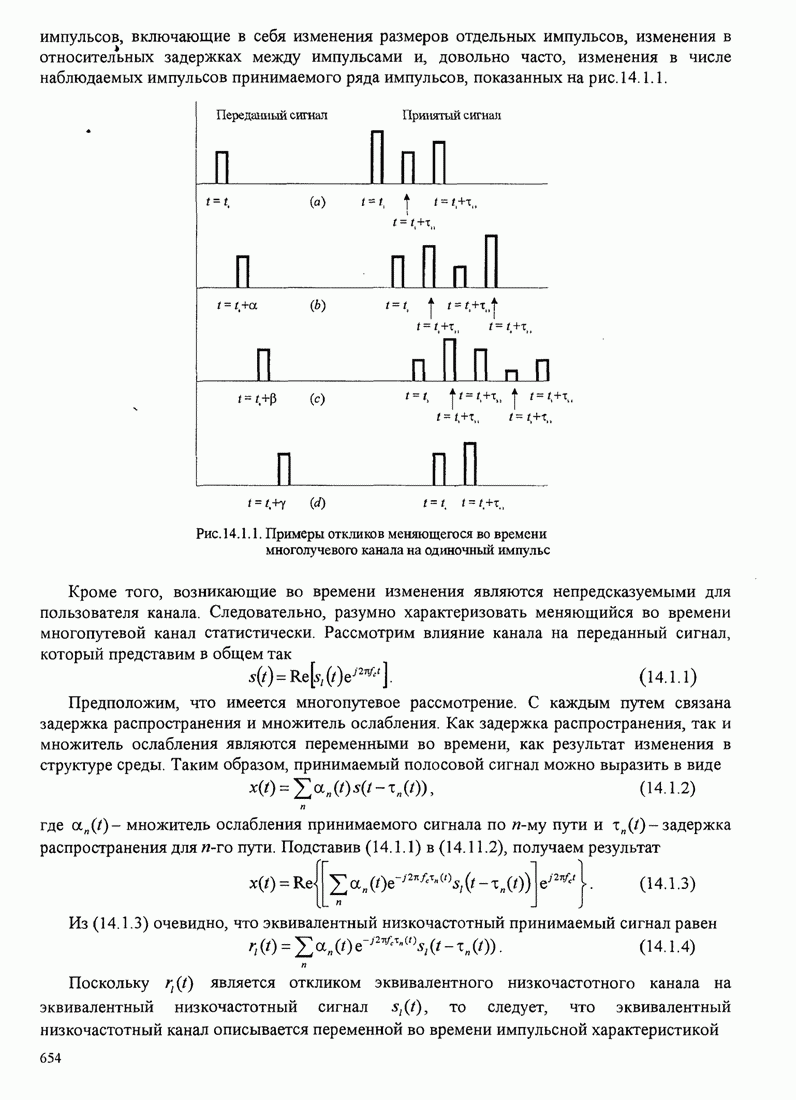
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
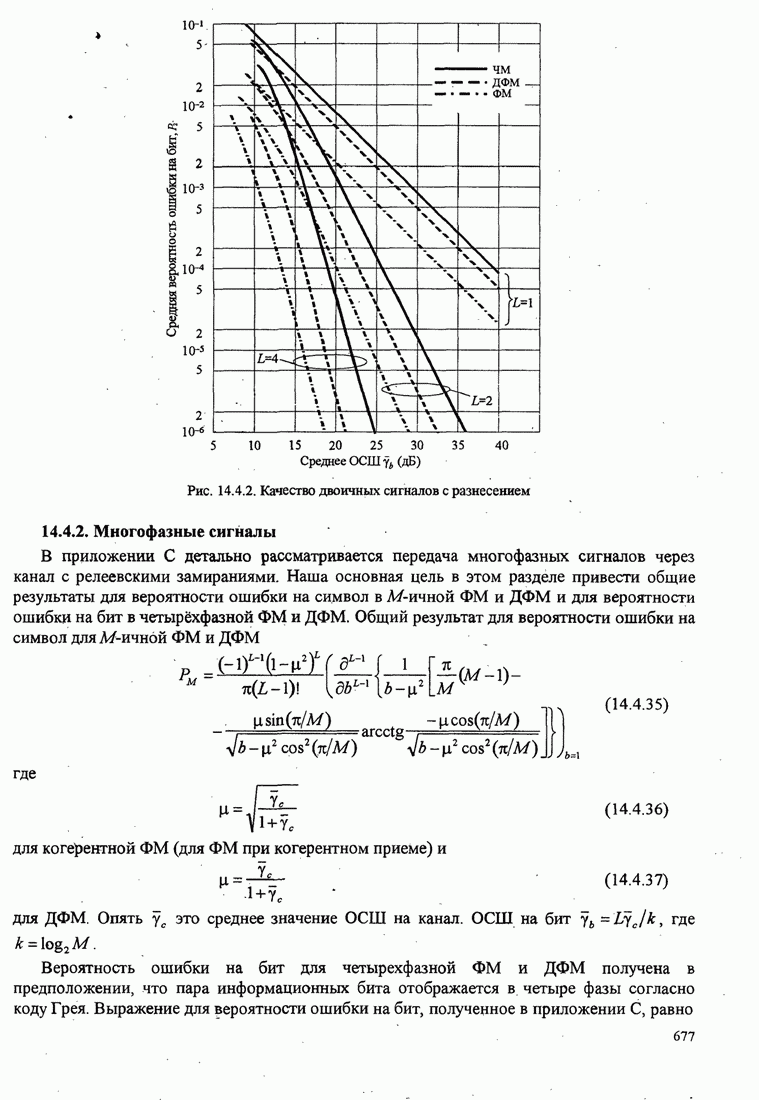
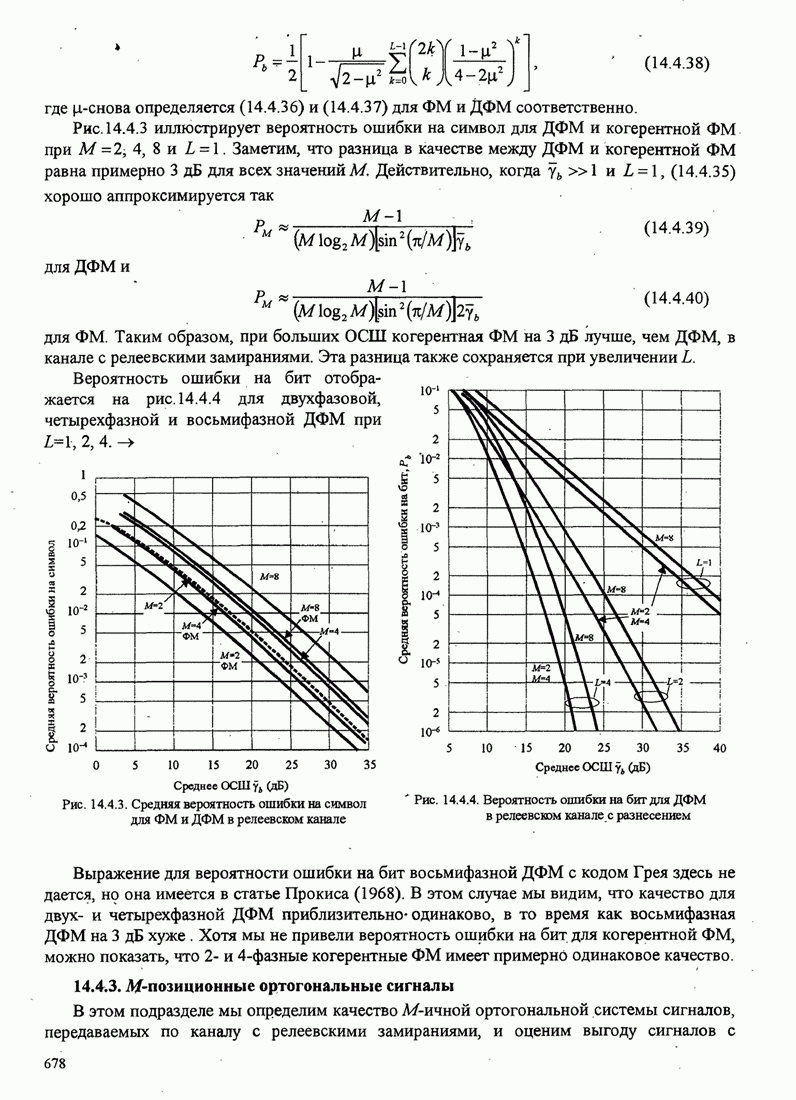
- 14.4.2. Многофазные сигналы
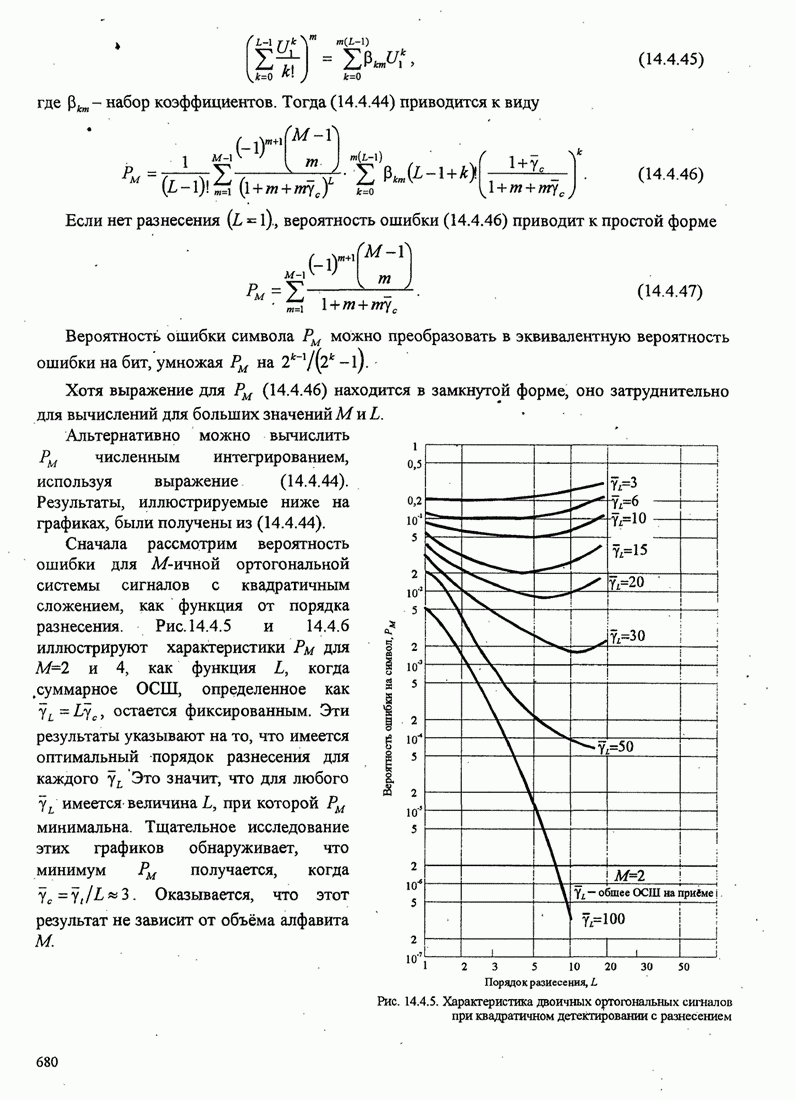
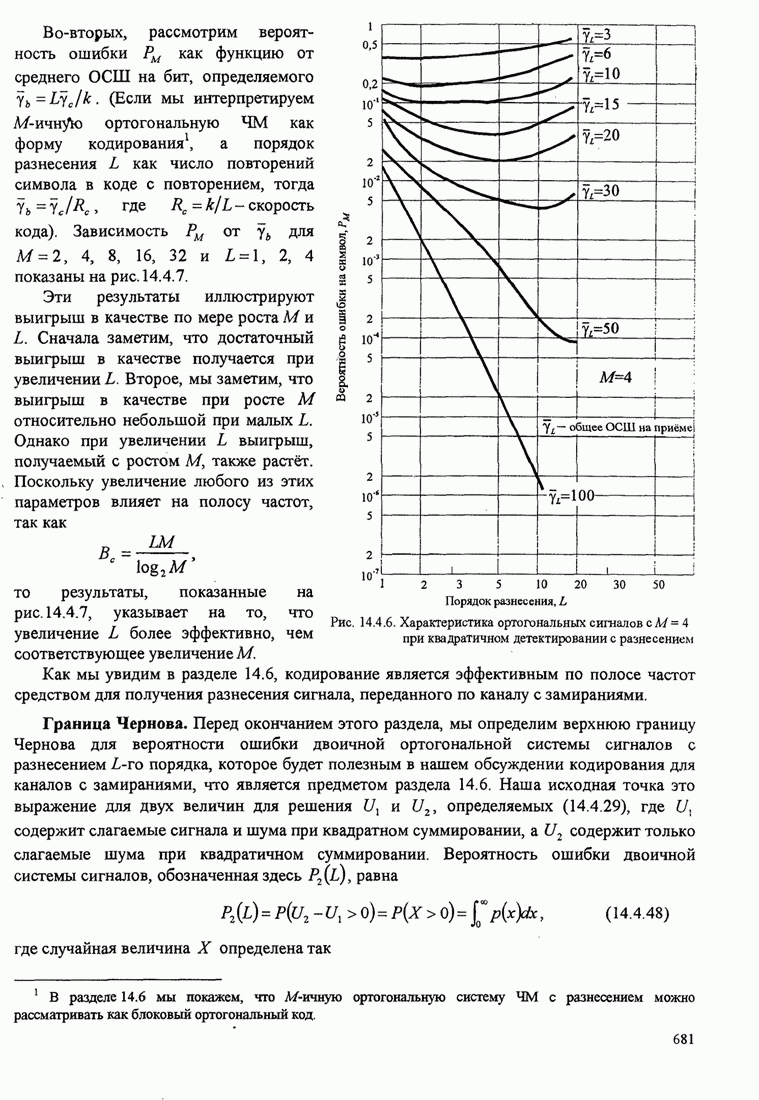
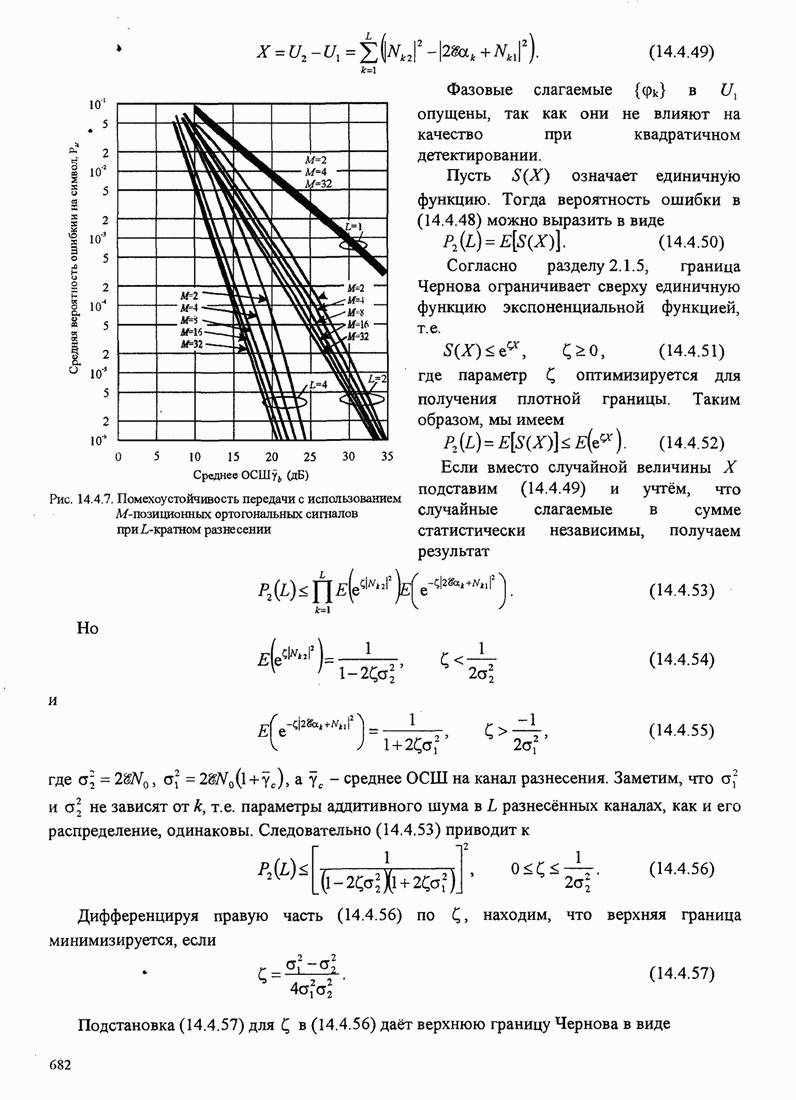
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
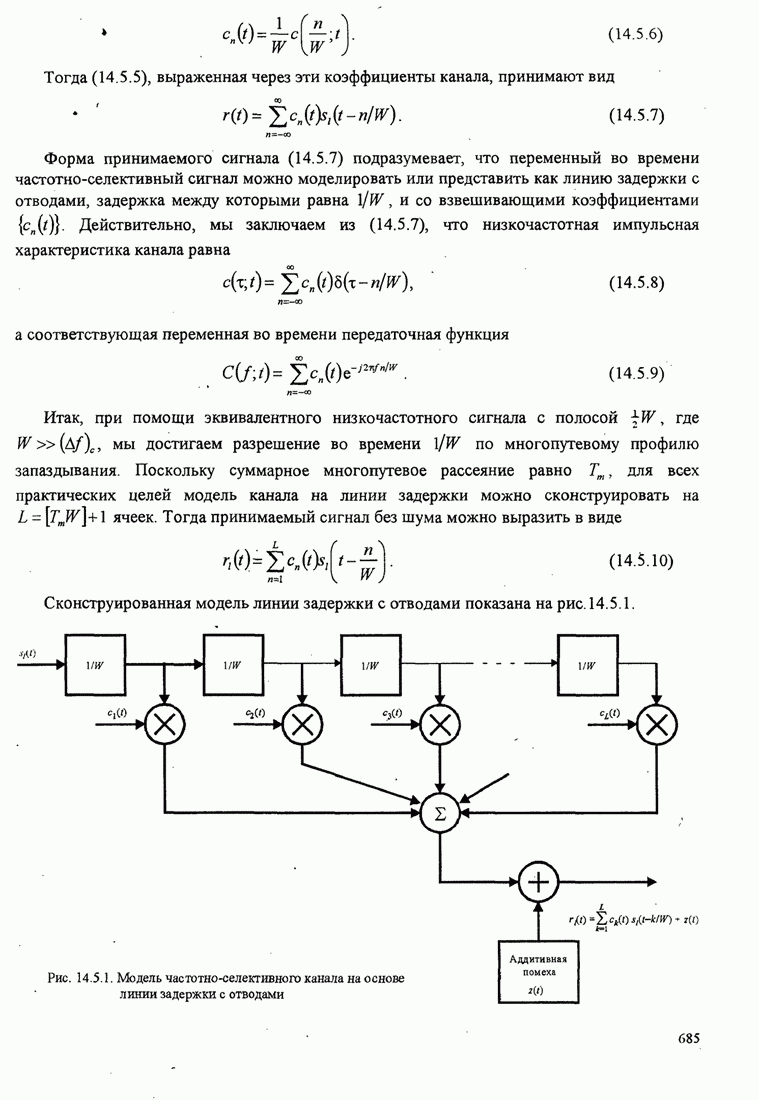
- 14.5.1. Модель канала в виде линии задержки с отводами
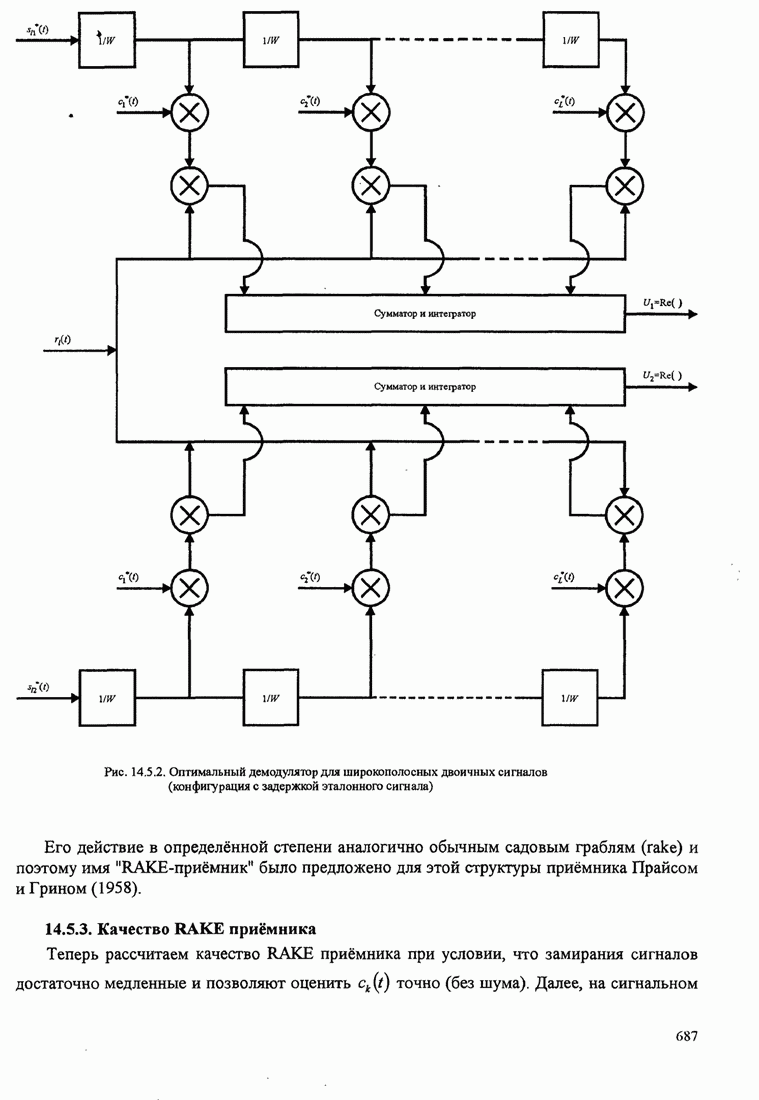
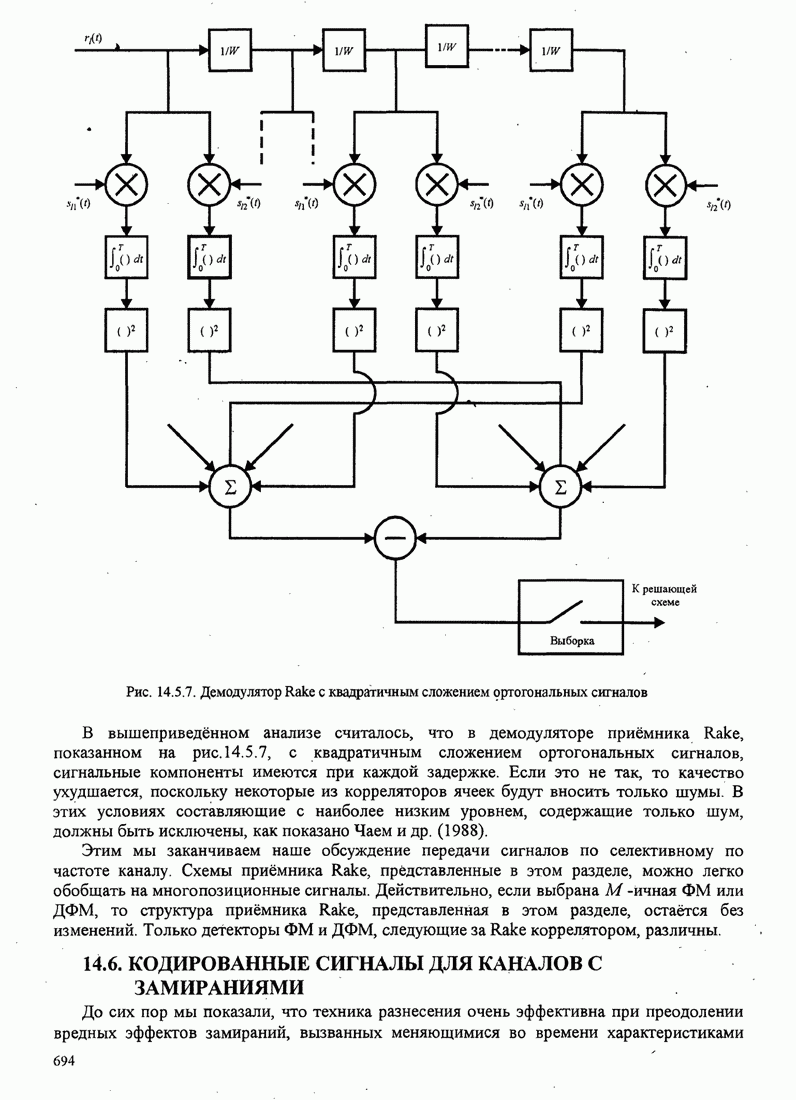
- 14.5.2. RAKE демодулятор
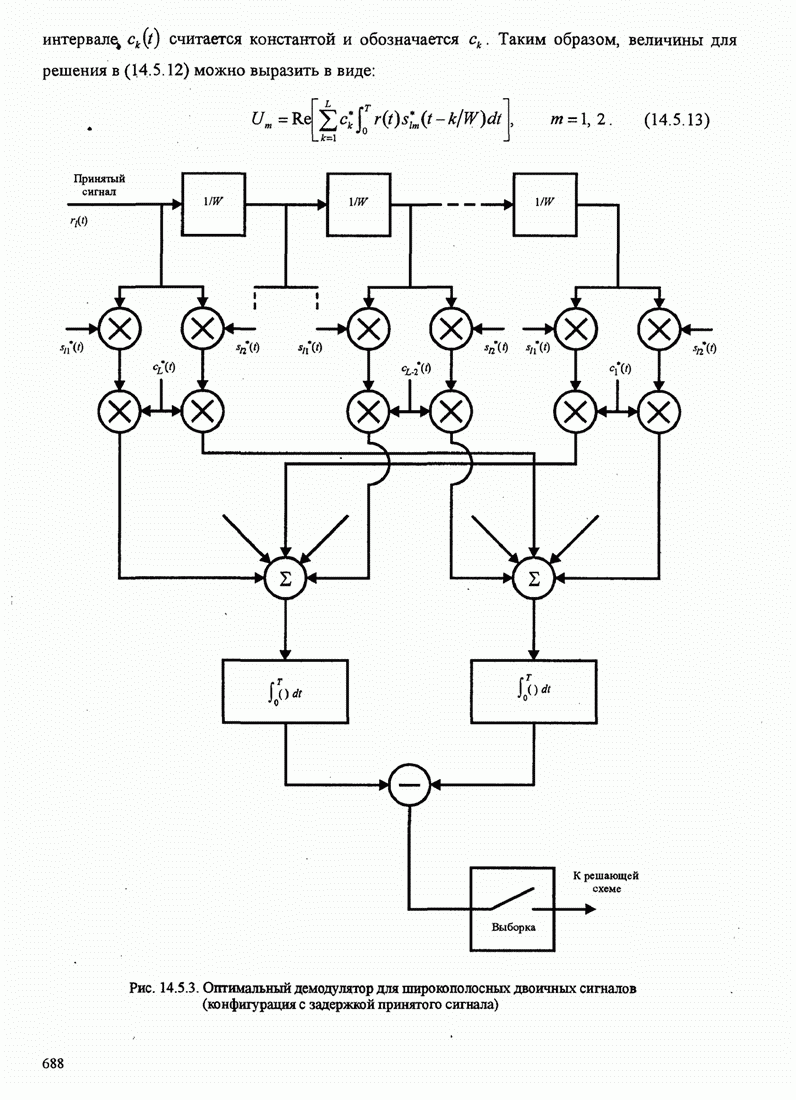
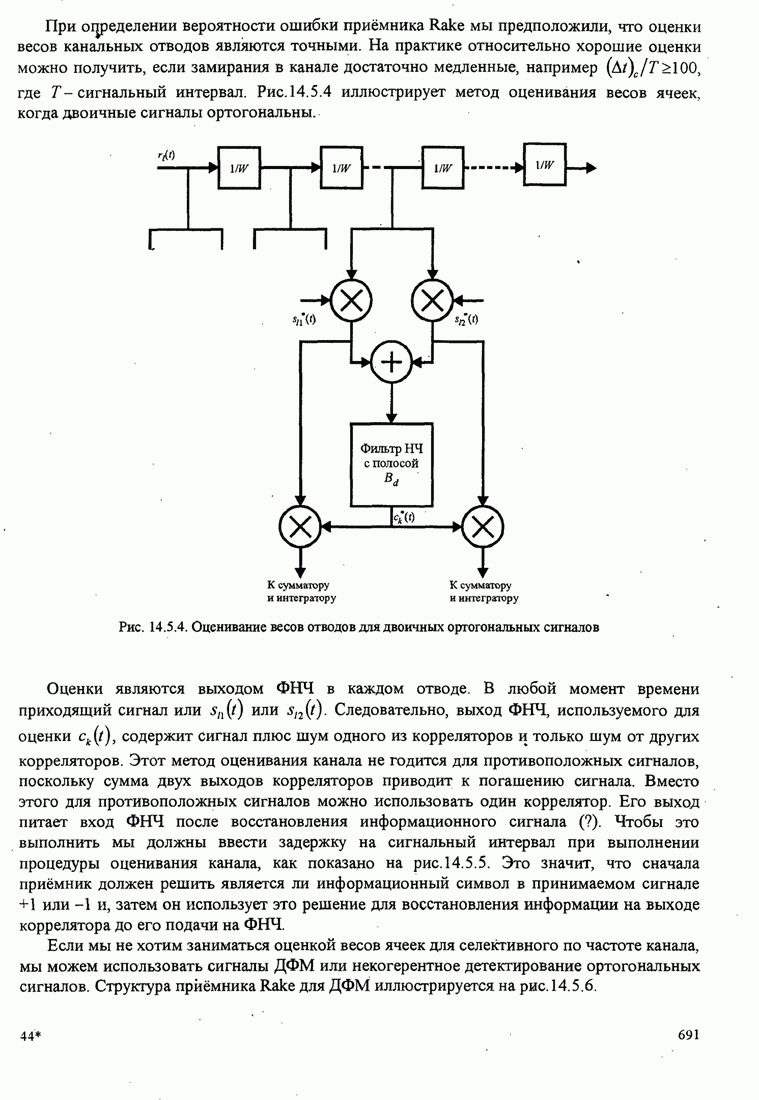
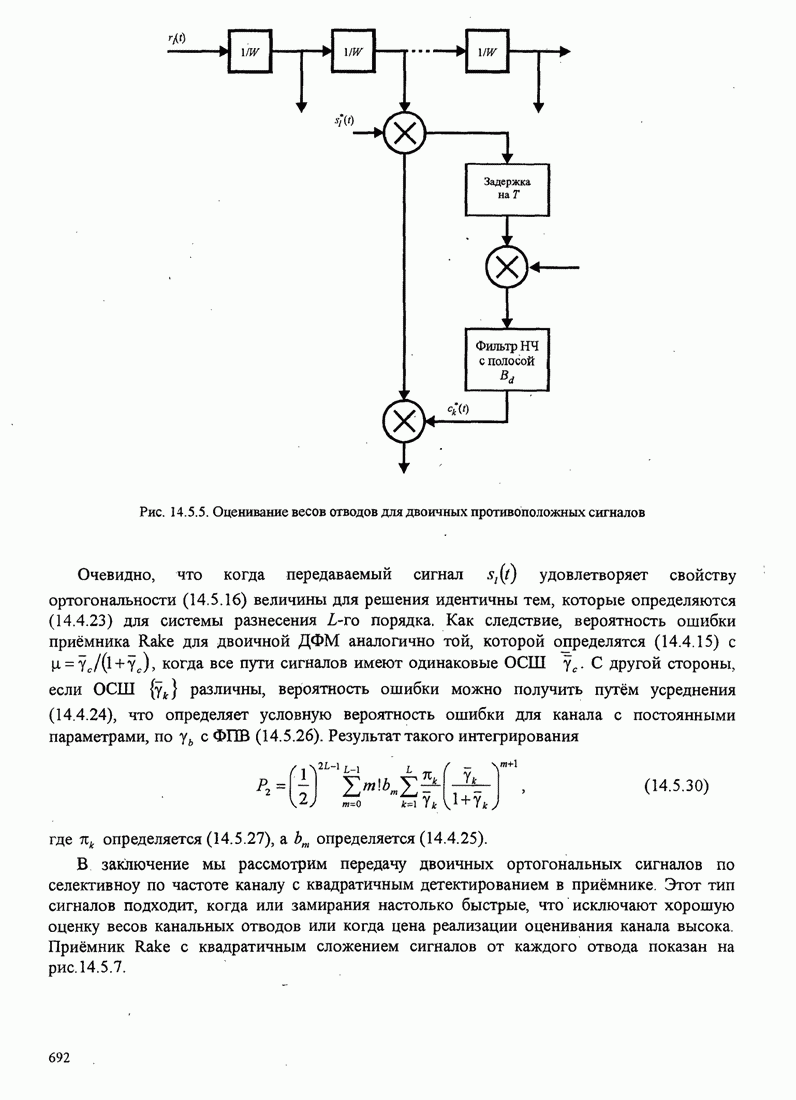
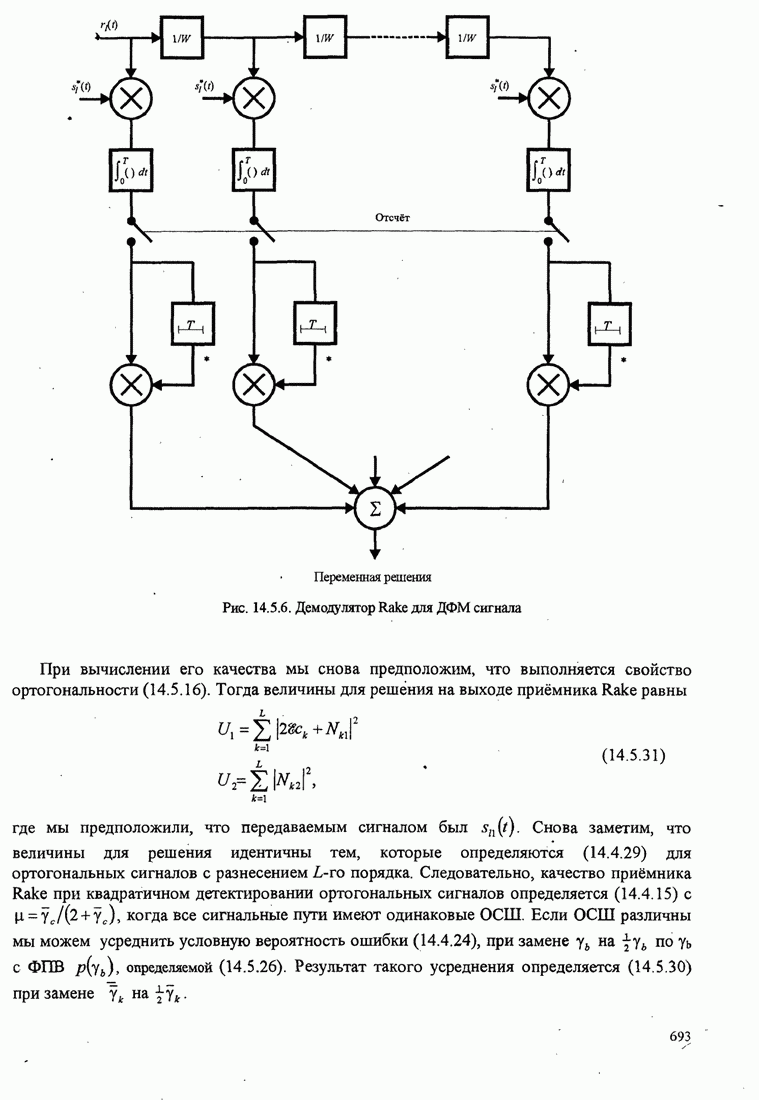
- 14.5.3. Качество RAKE приемника
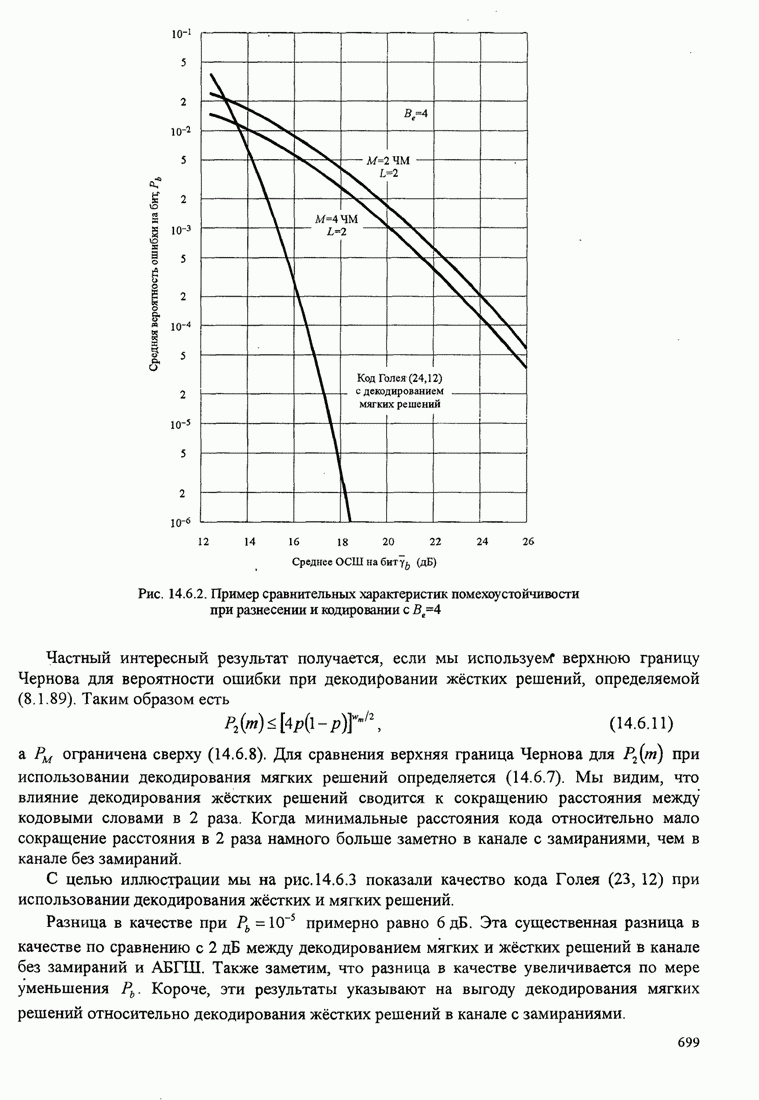
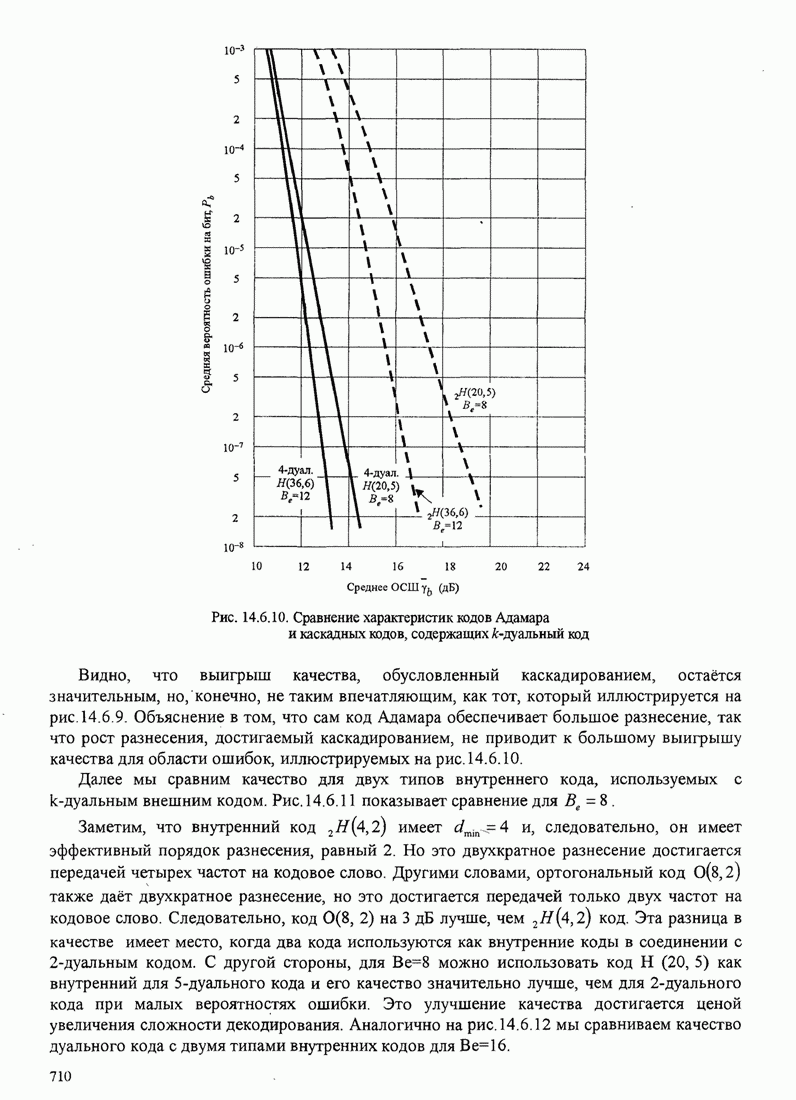
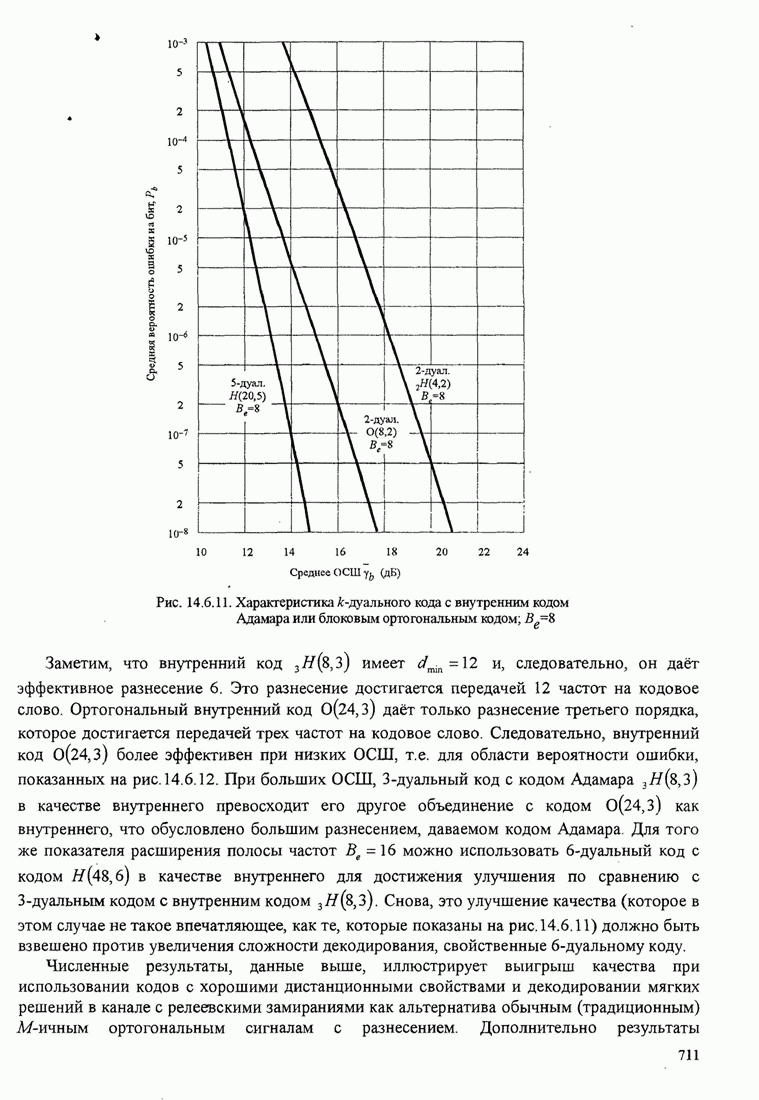
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
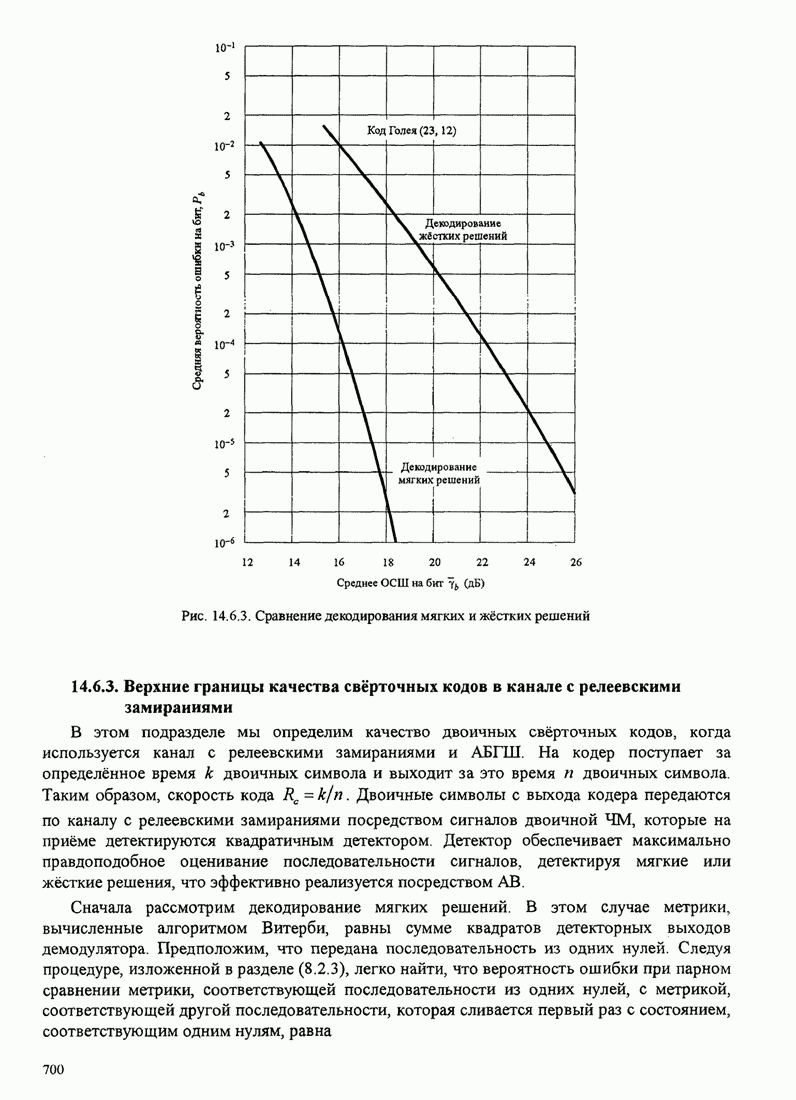
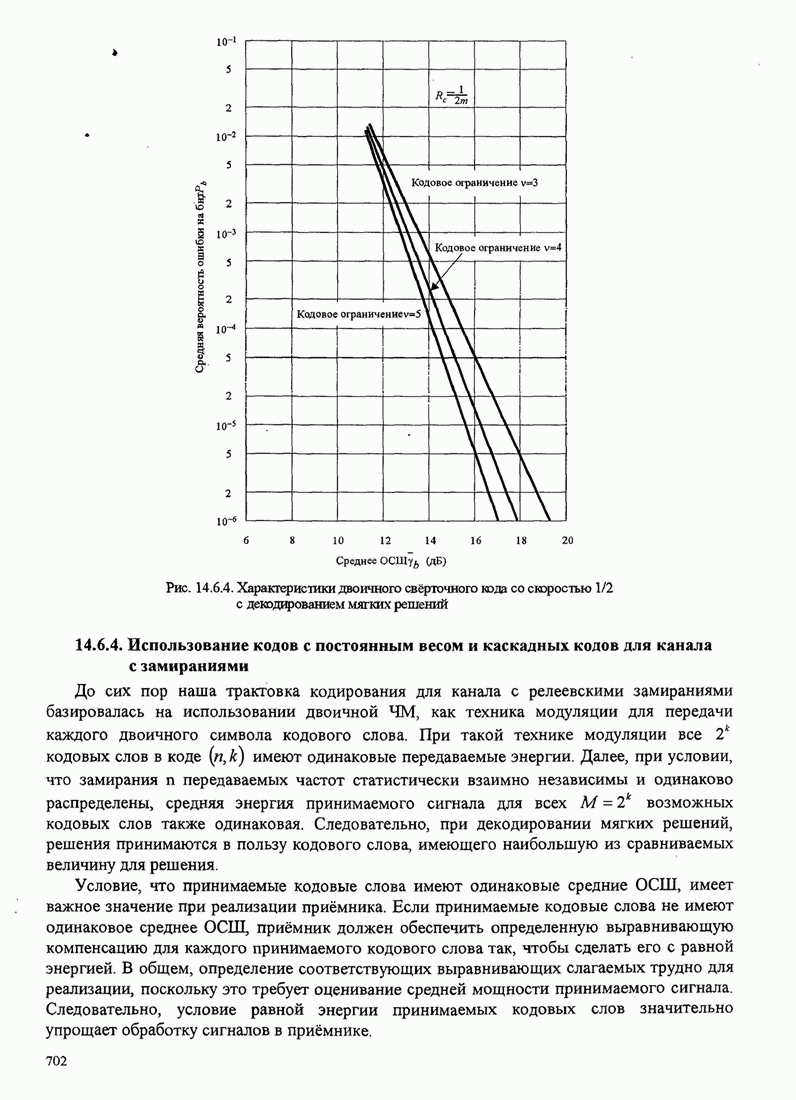
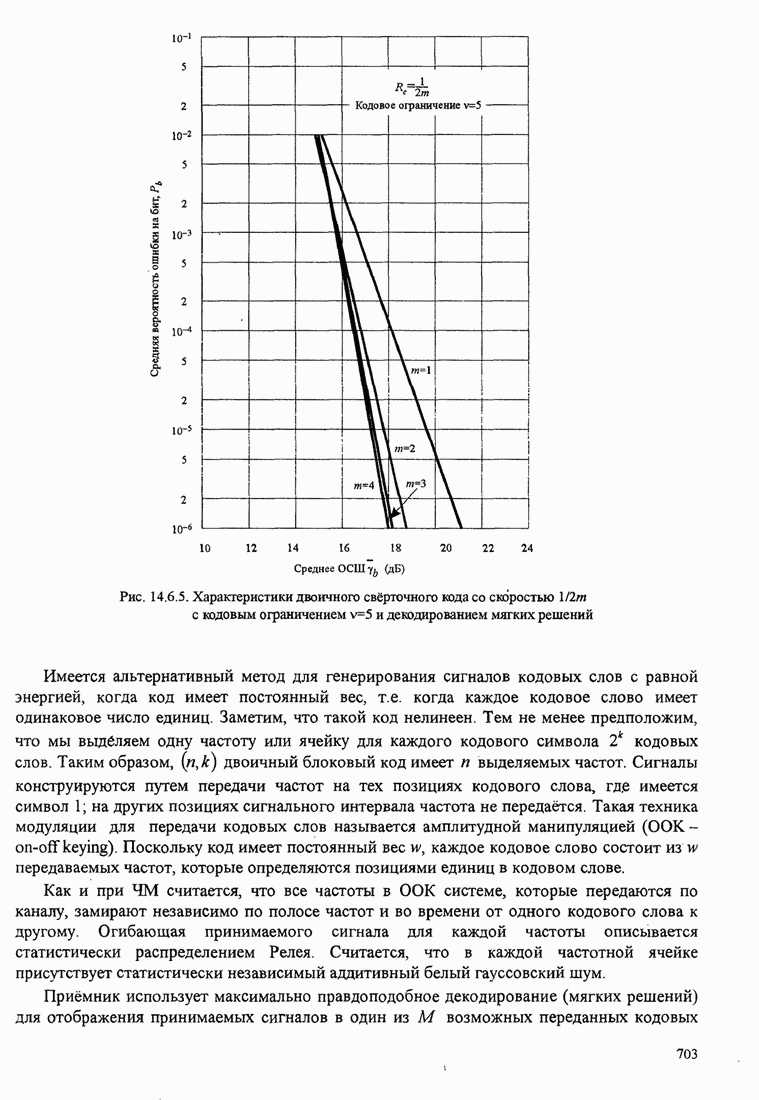
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
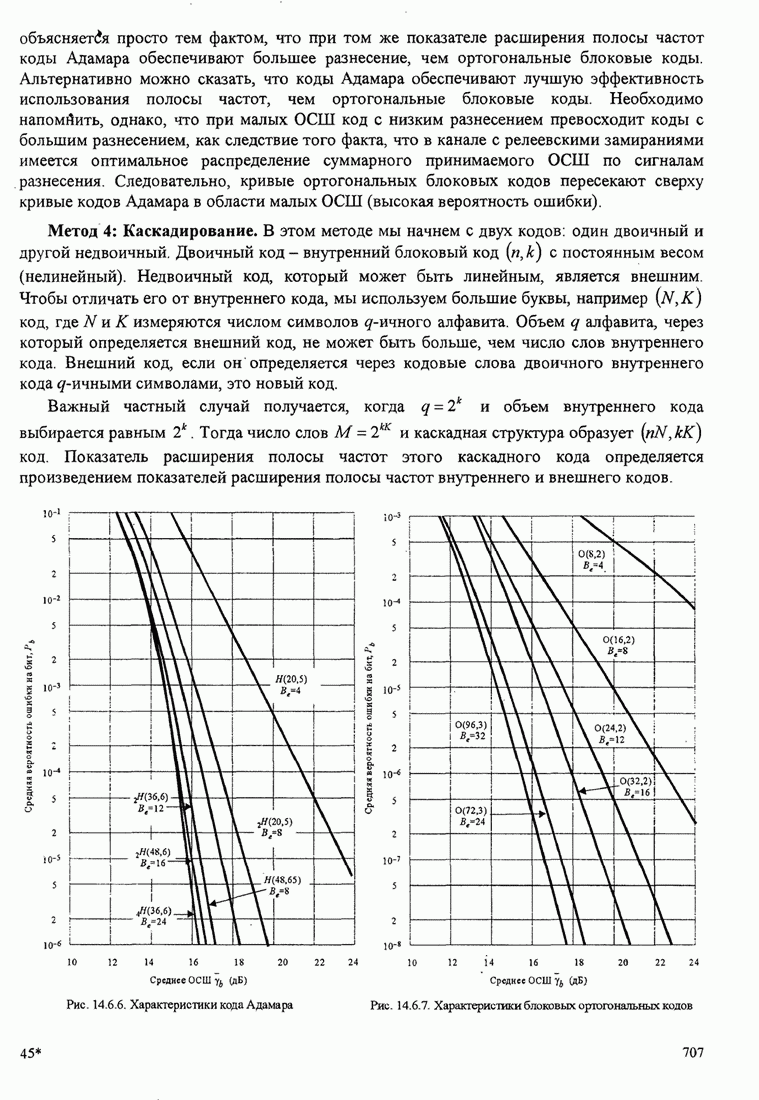
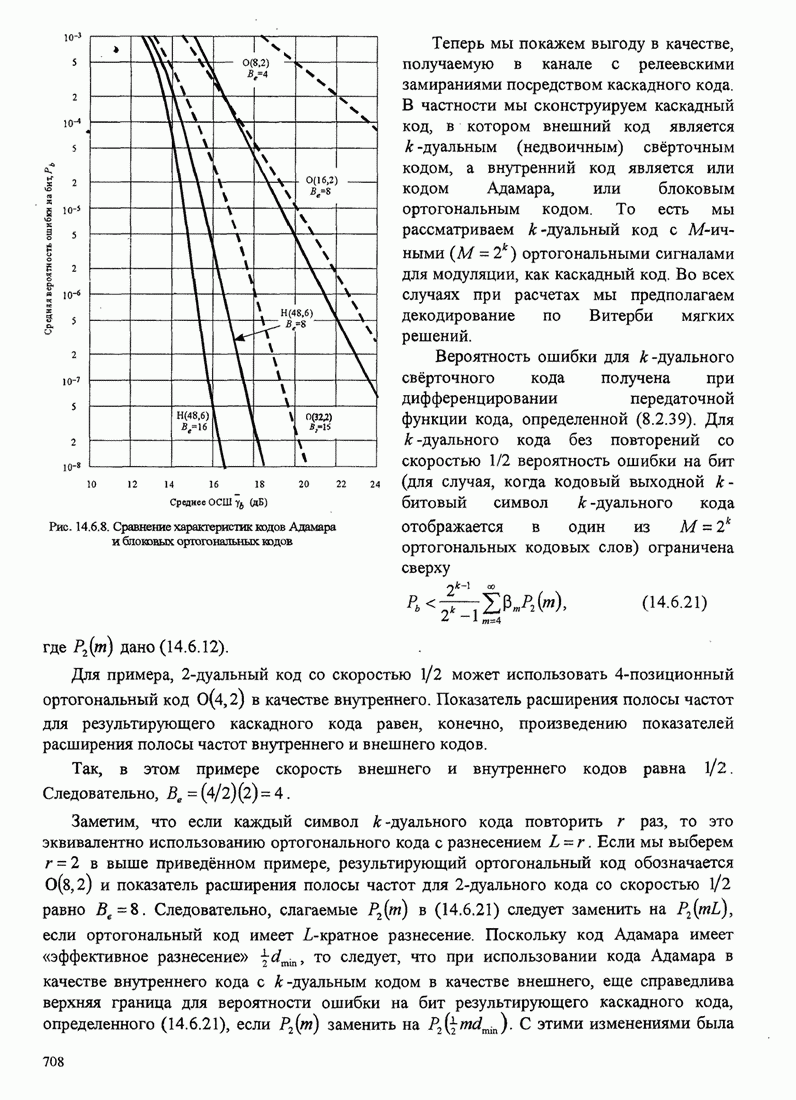
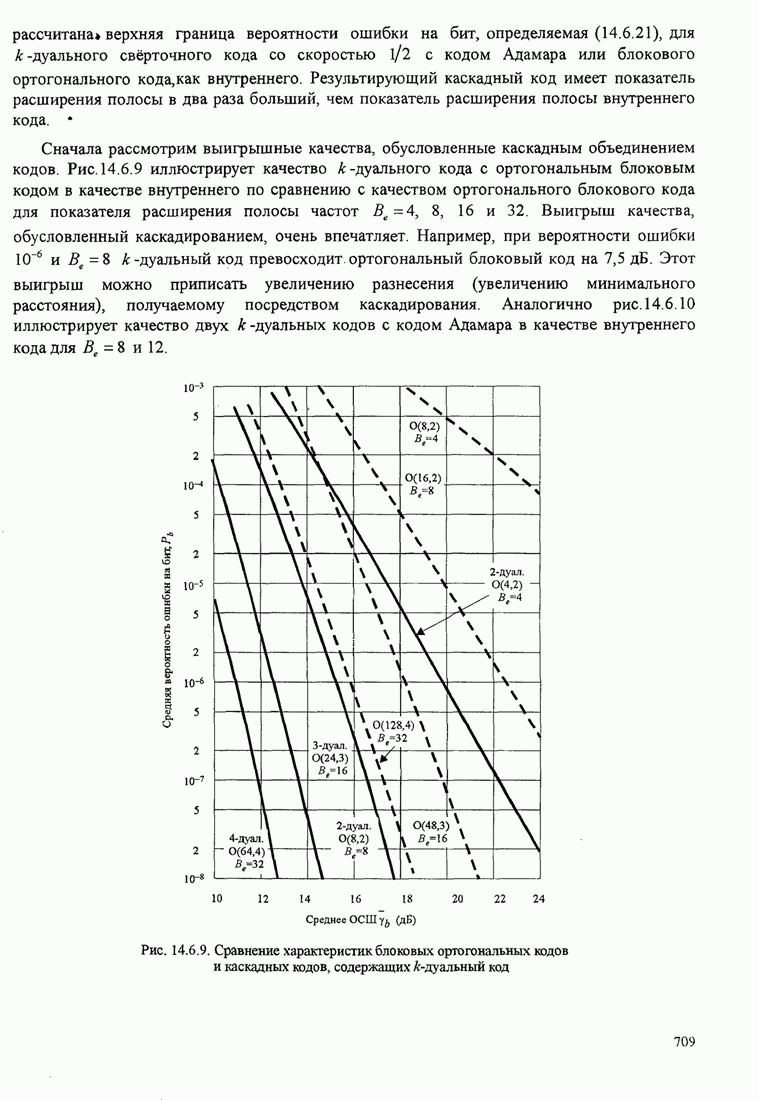
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
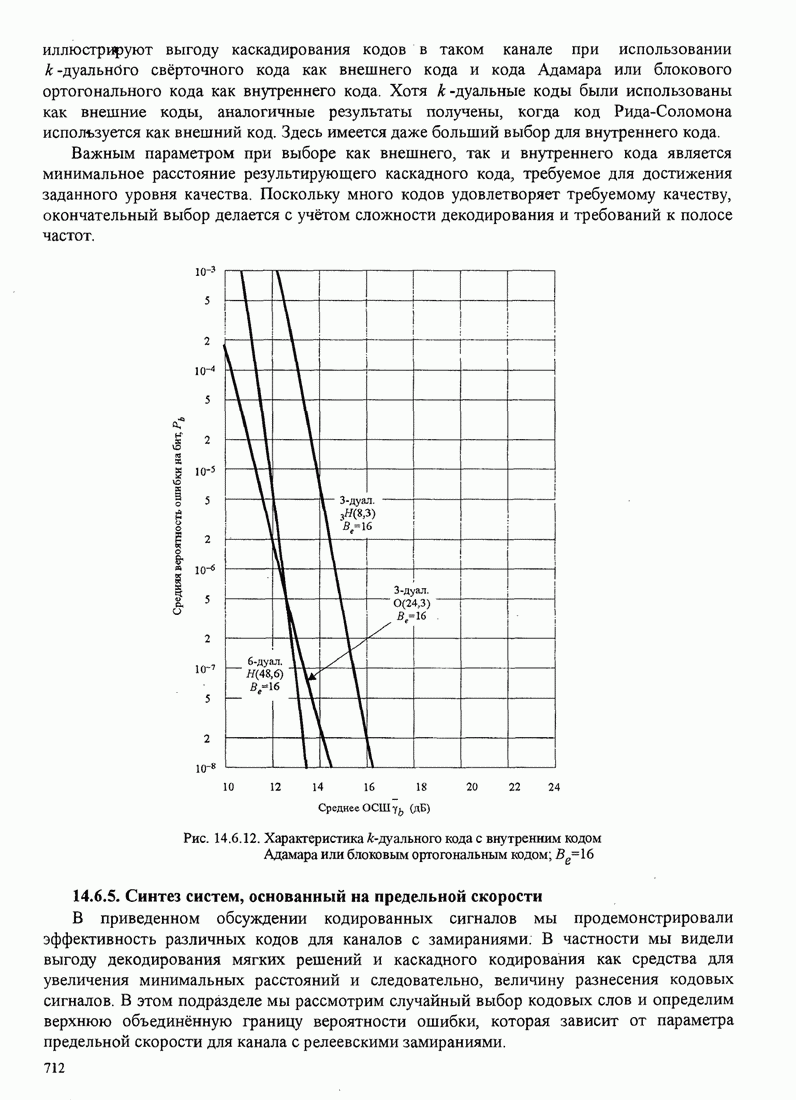
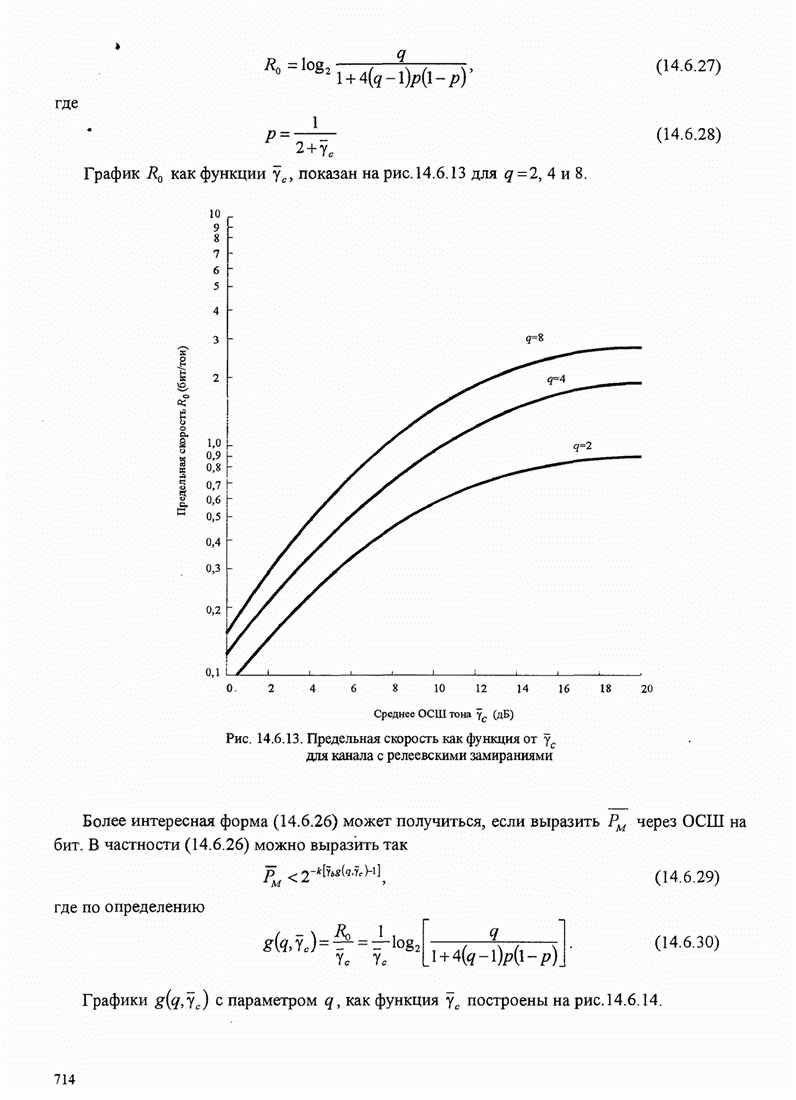
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
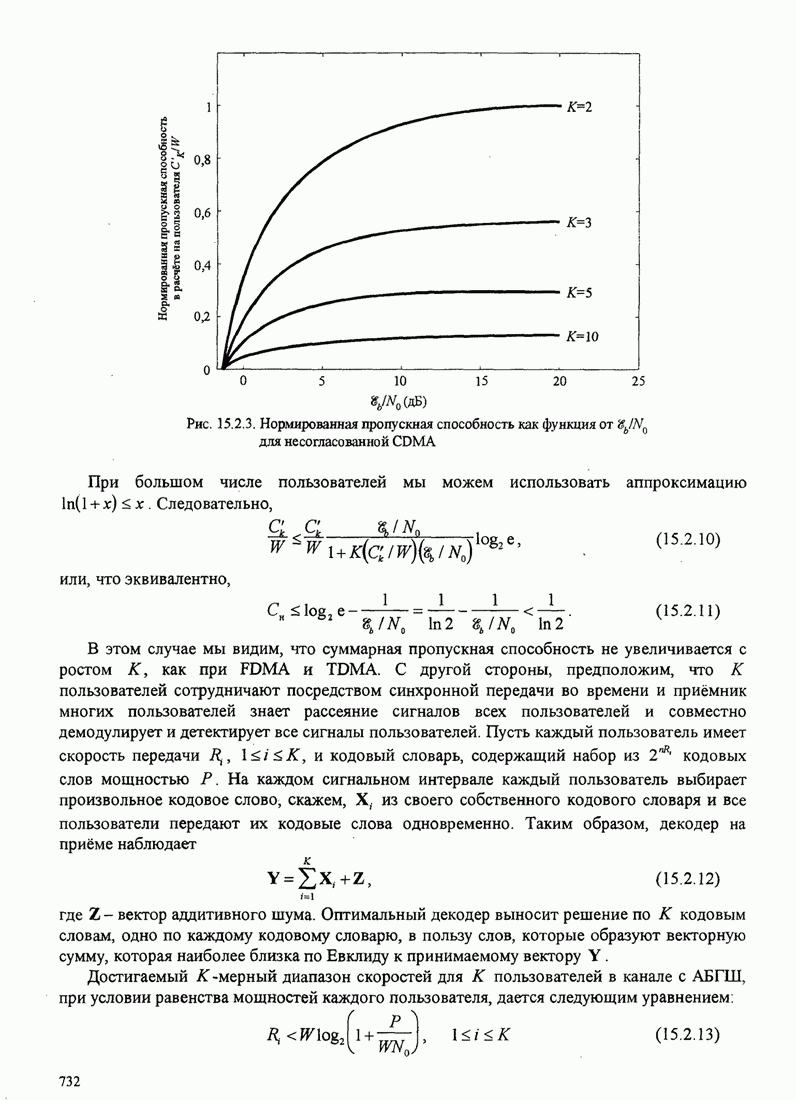
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
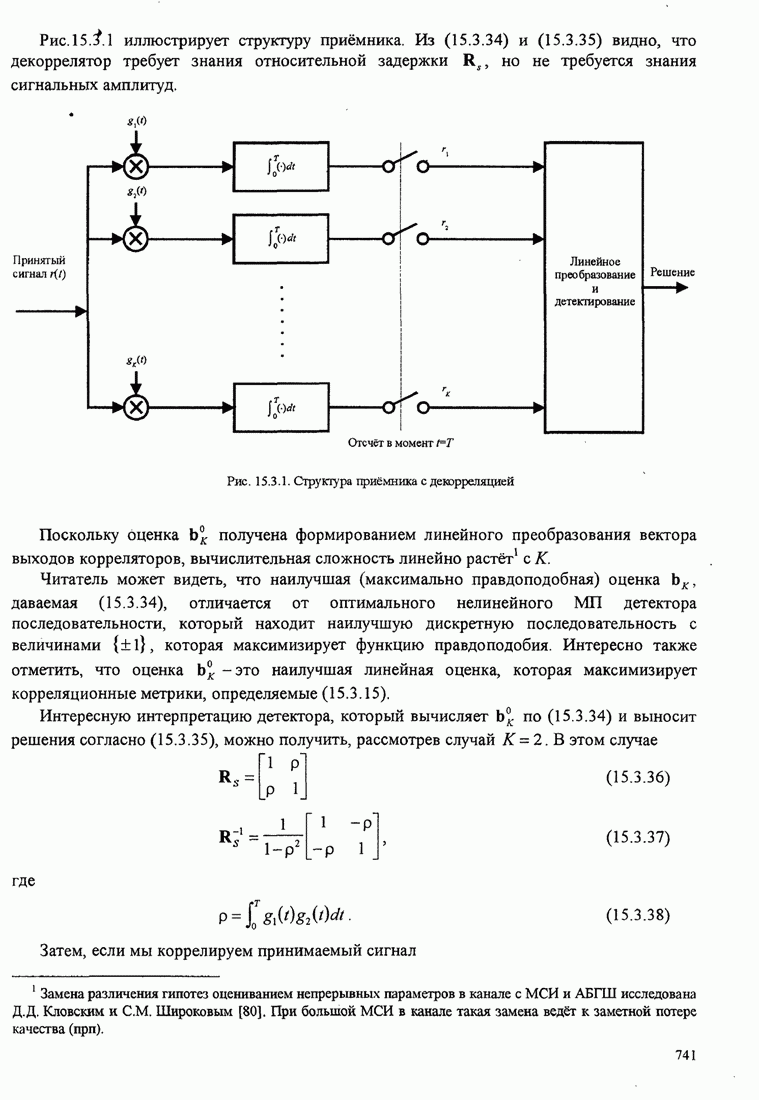
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
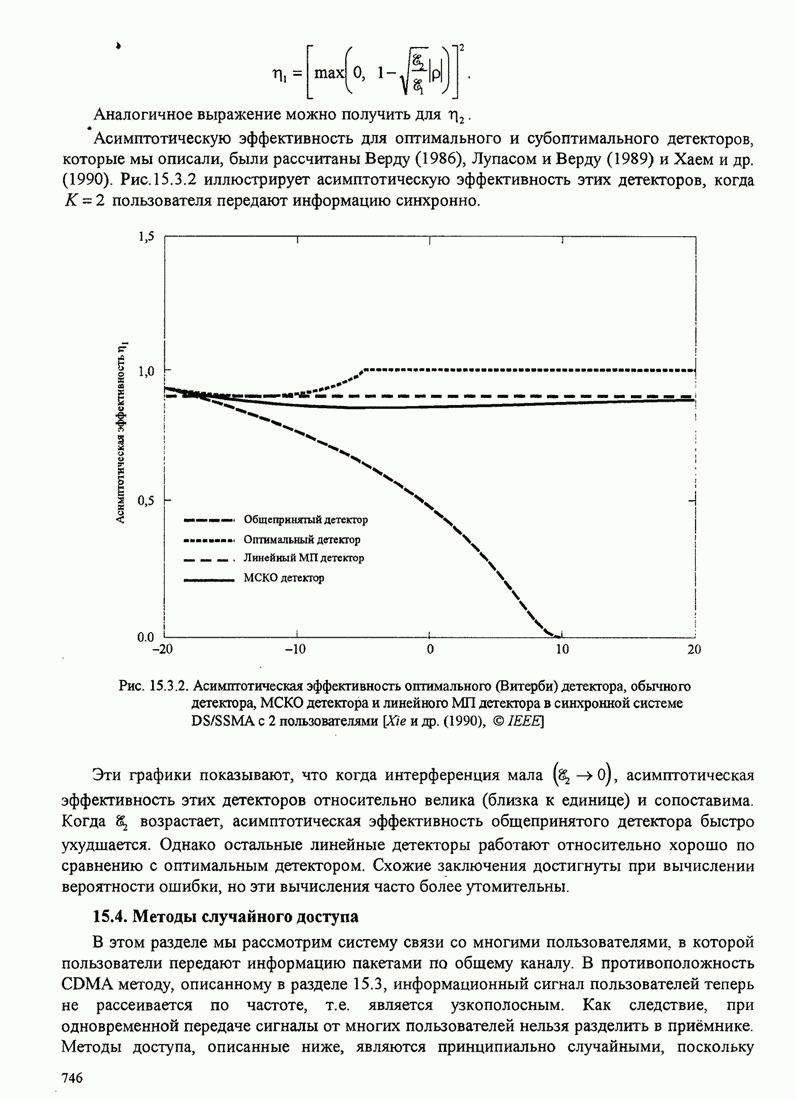
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
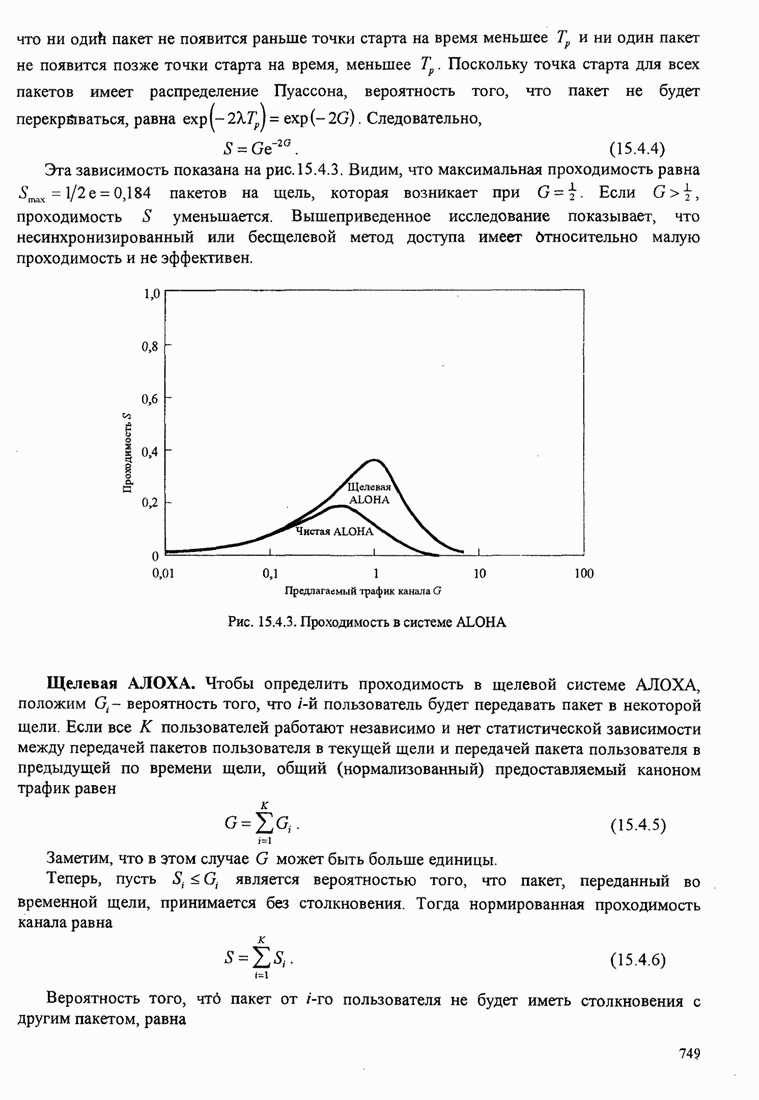
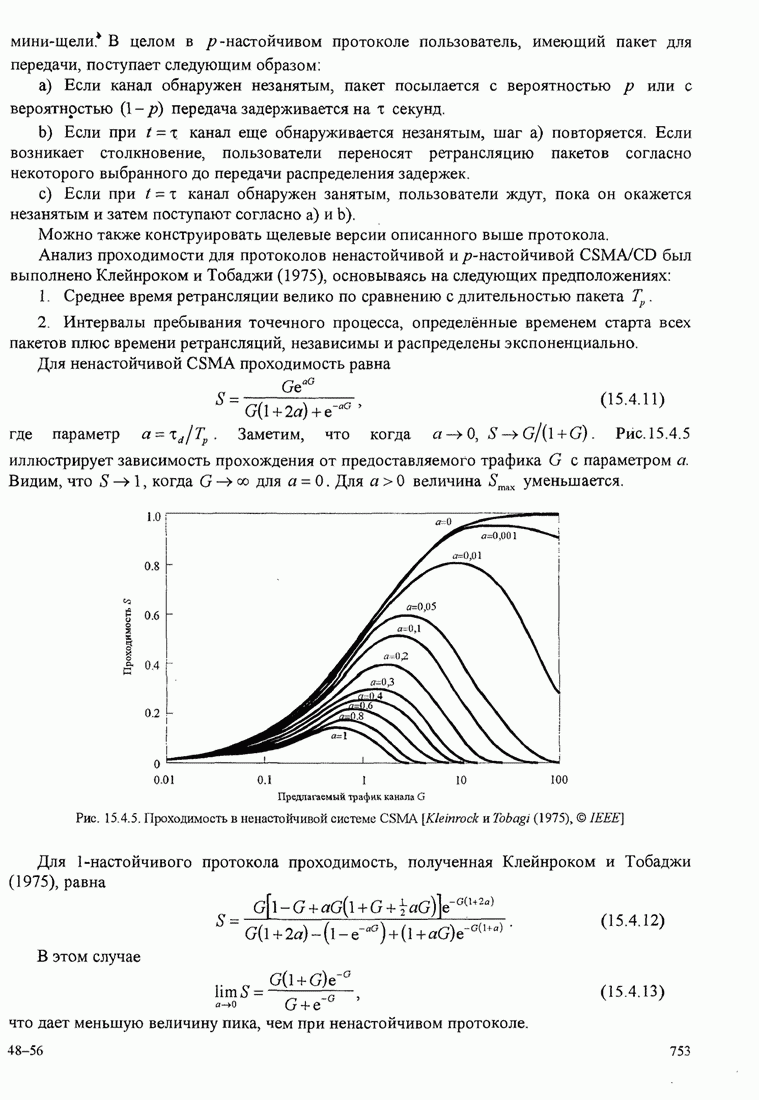
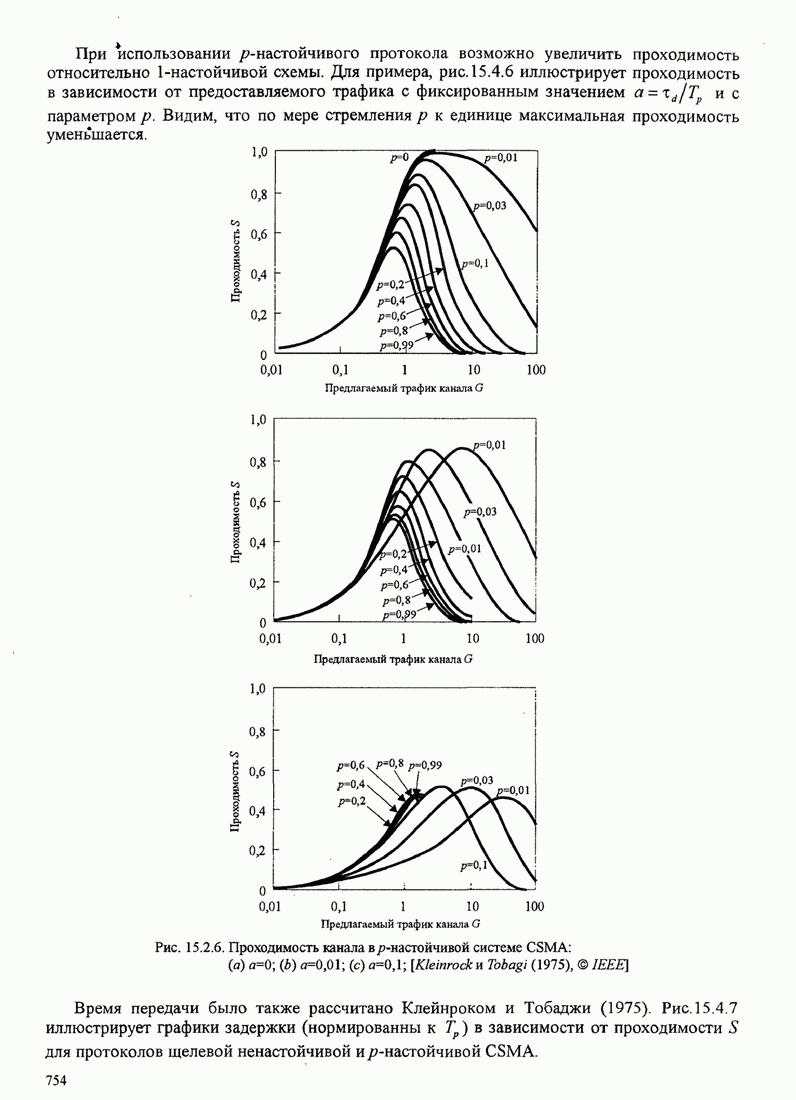
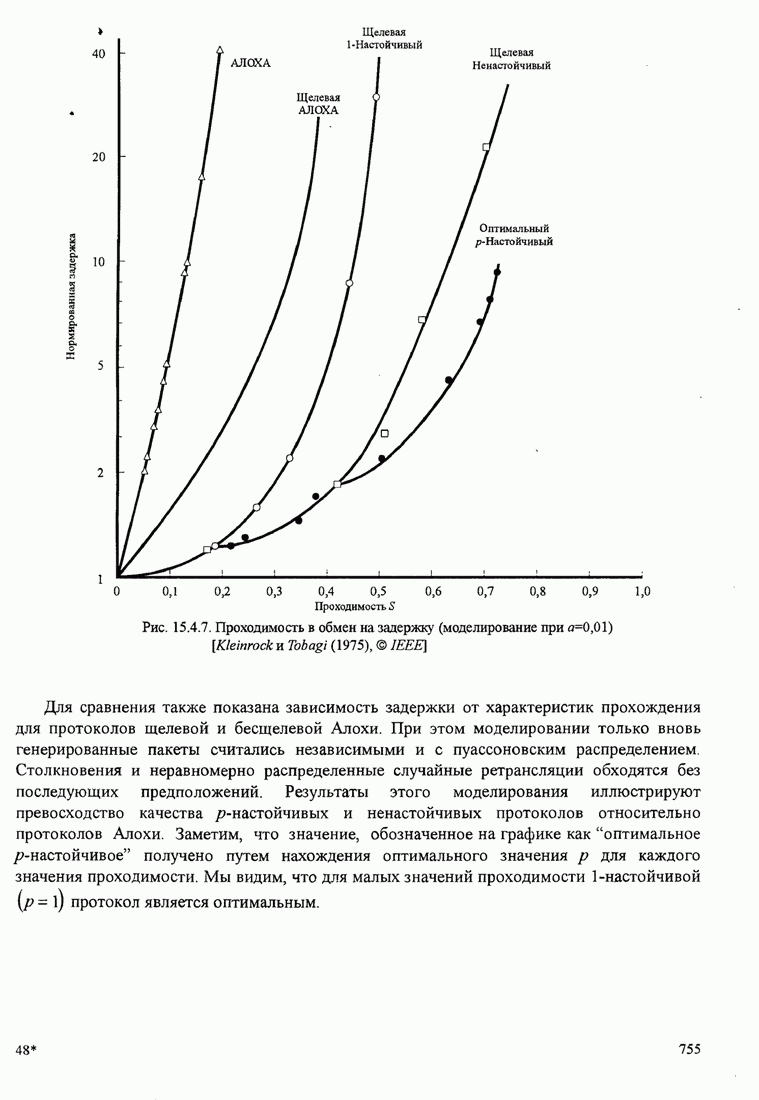
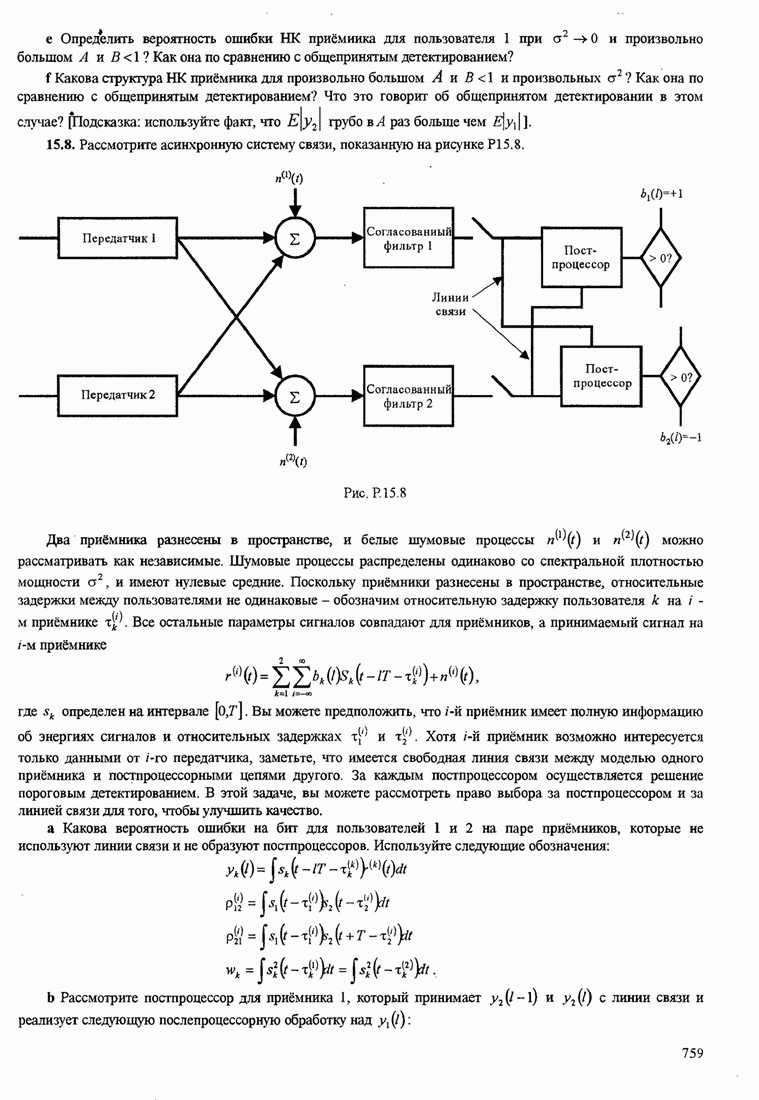
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)