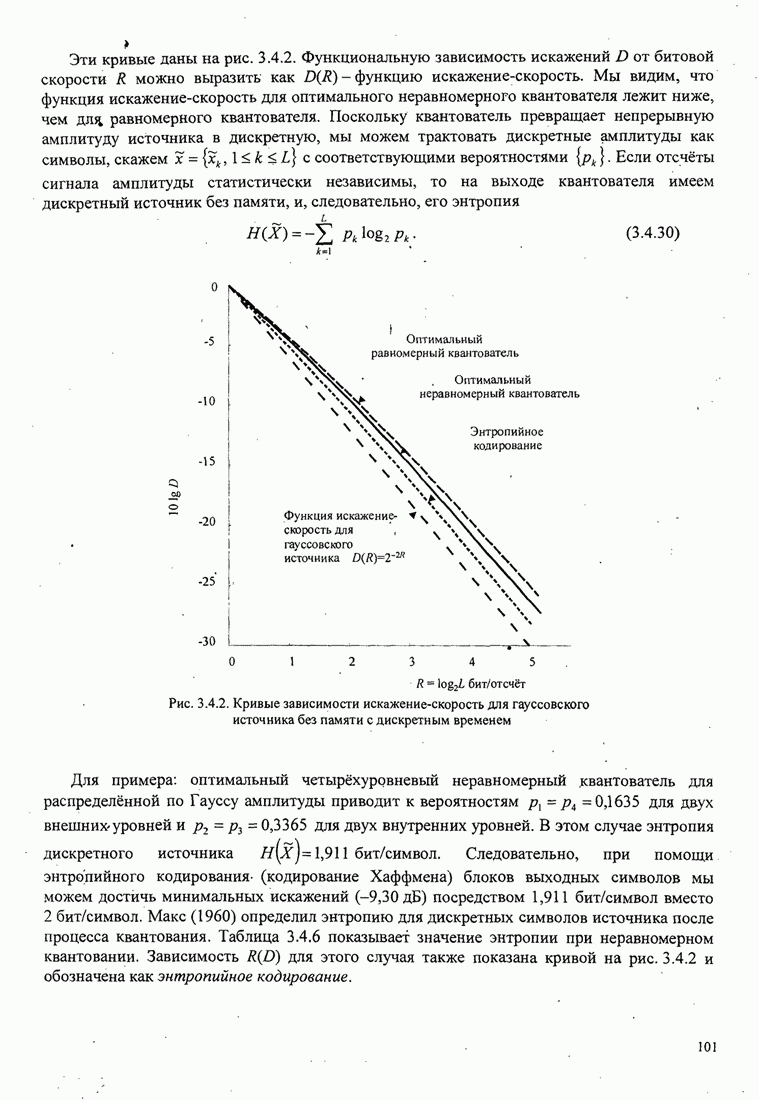
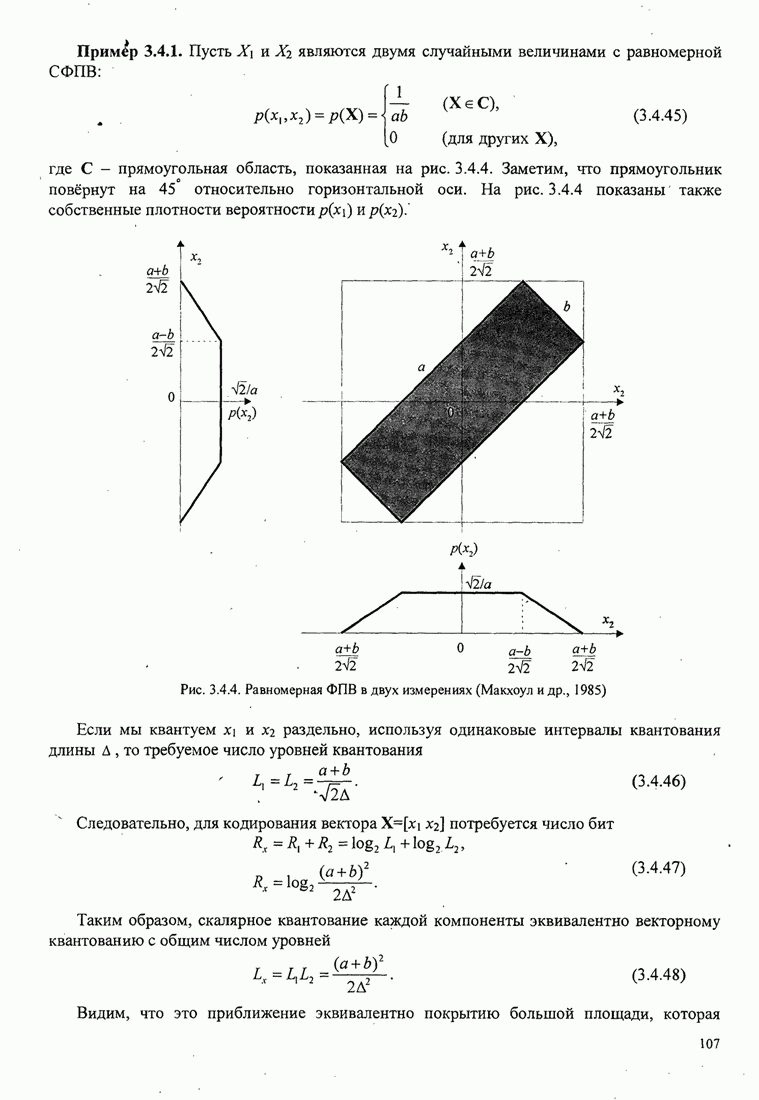
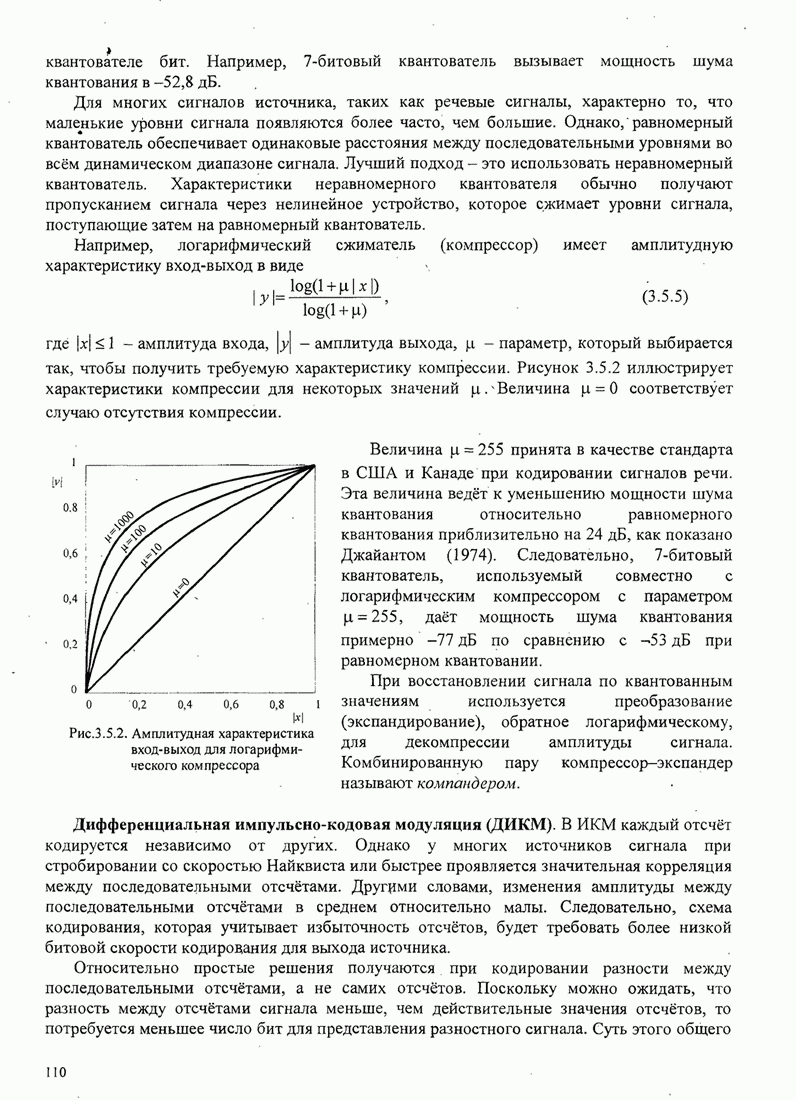
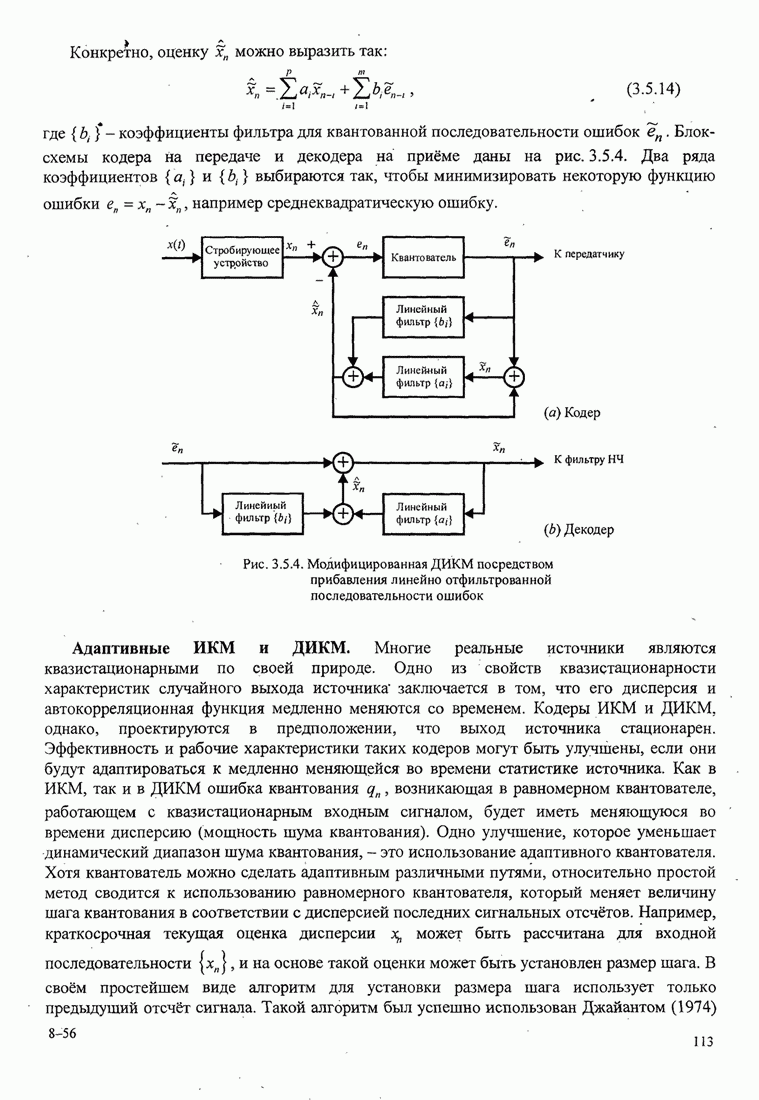
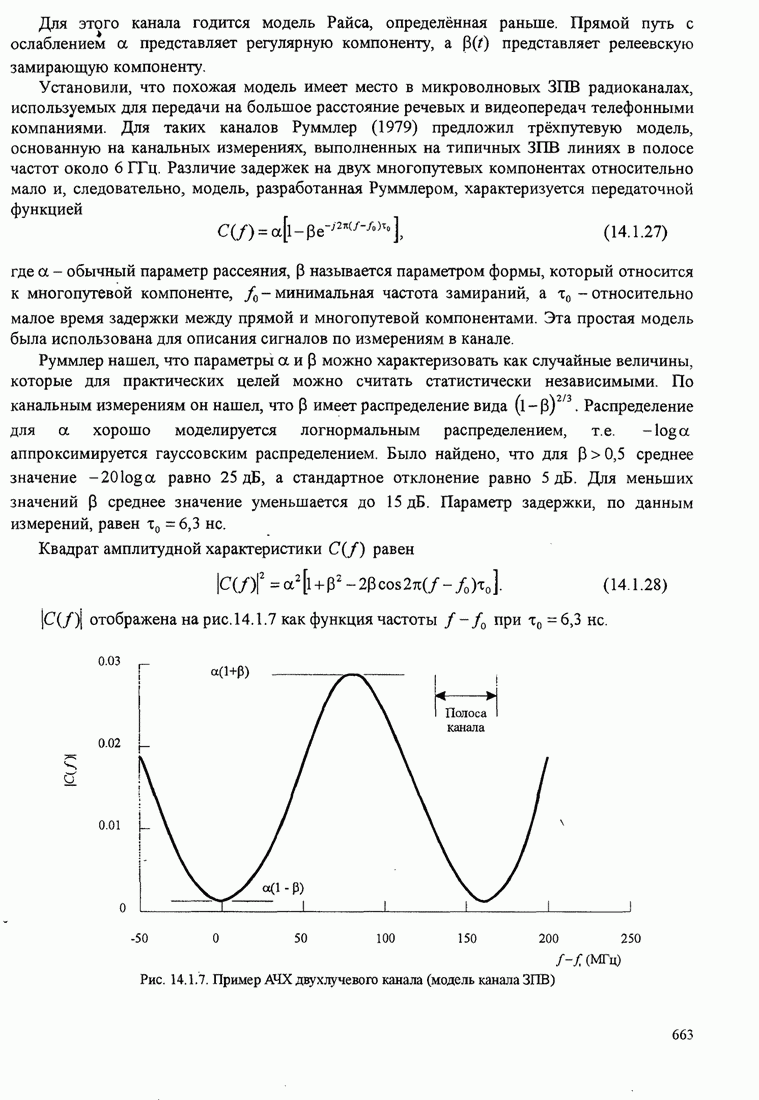
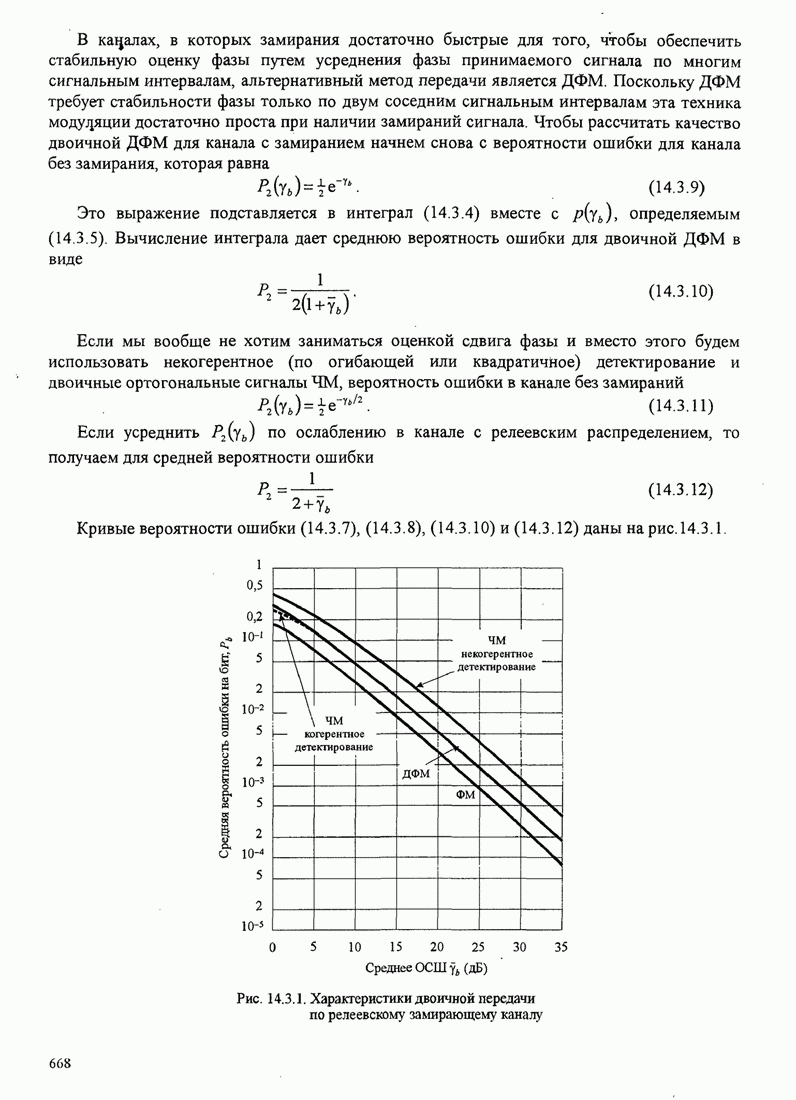
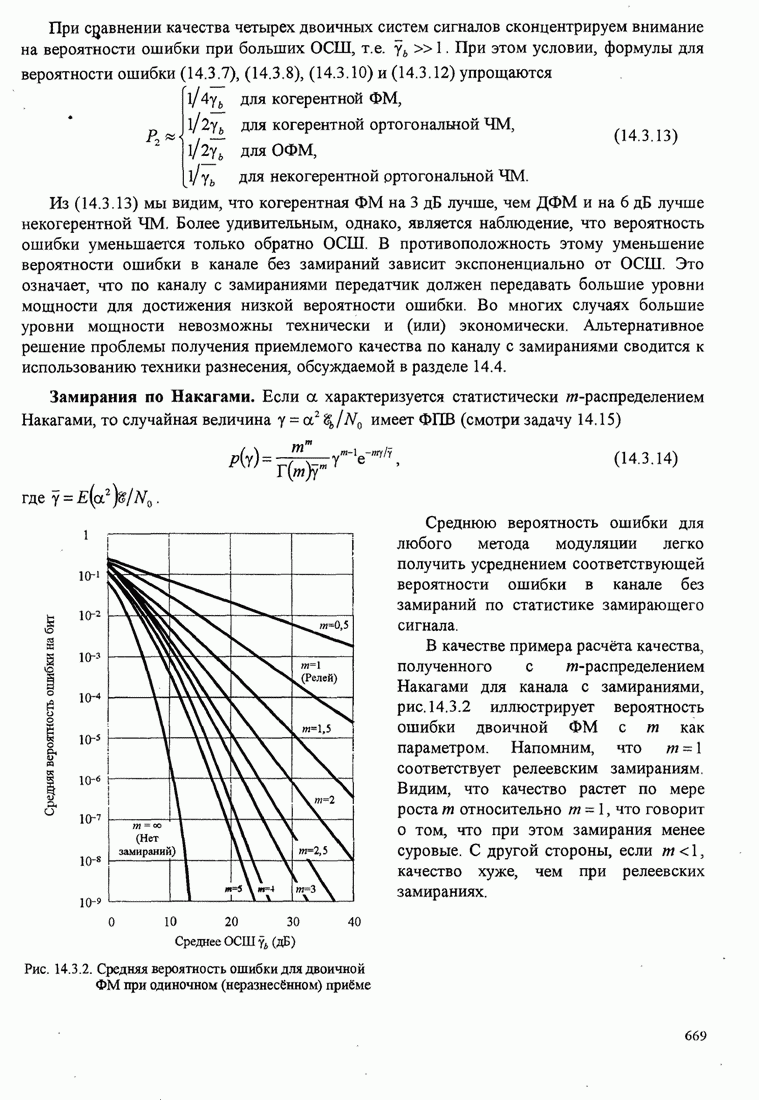
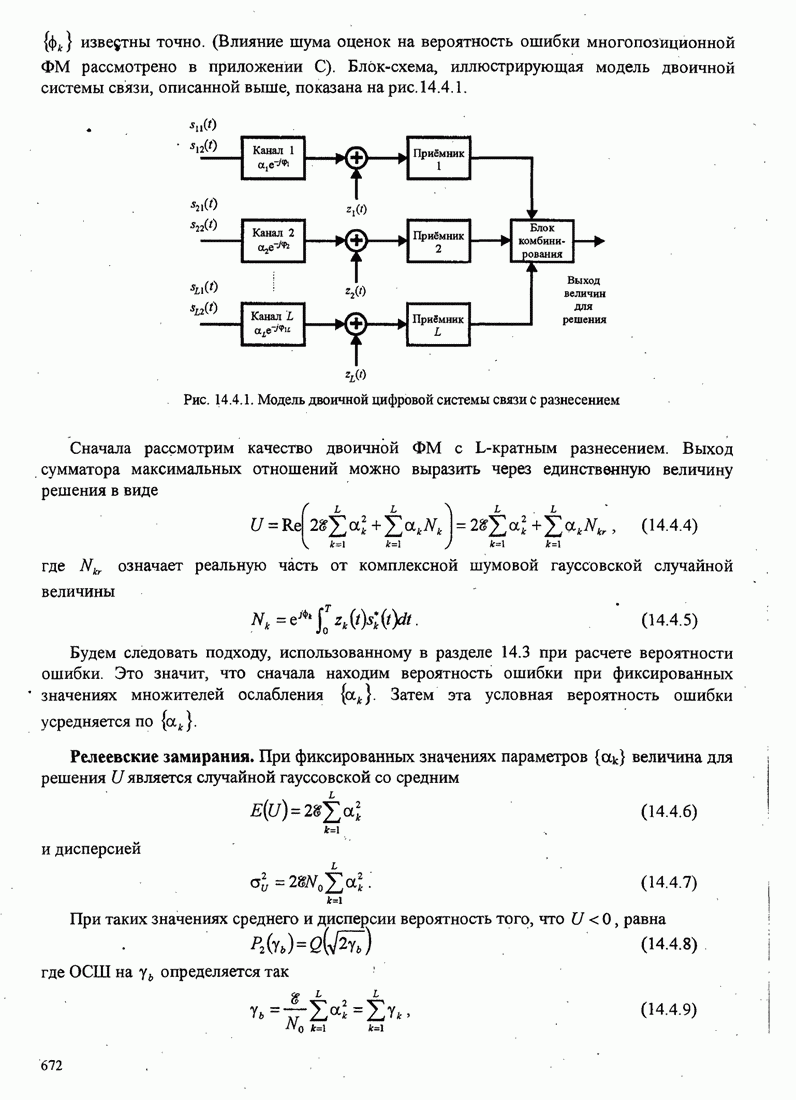
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
11.1.2. Алгоритм наименьших квадратов (НК)
При минимизации СКО, обсуждённой в разделе 10.2.2, мы нашли, что оптимальные коэффициенты эквалайзера определяются из решения системы линейных уравнений, выраженной в матричной форме:
![]()
где ![]() - ковариационная матрица размером
- ковариационная матрица размером ![]() отсчетов сигнала
отсчетов сигнала ![]() ,
, ![]() - вектор-столбец из
- вектор-столбец из
![]() коэффициентов
эквалайзера, а
коэффициентов
эквалайзера, а ![]() -
вектор-столбец канальных коэффициентов фильтра размерности
-
вектор-столбец канальных коэффициентов фильтра размерности ![]() . Решение для вектора
коэффициентов
. Решение для вектора
коэффициентов ![]() оптимального
эквалайзера можно получить путём обращения ковариационной матрицы
оптимального
эквалайзера можно получить путём обращения ковариационной матрицы ![]() , что можно
эффективно выполнить посредством алгоритма Левинсона-Дурбина, описанного в
приложении А.
, что можно
эффективно выполнить посредством алгоритма Левинсона-Дурбина, описанного в
приложении А.
Альтернативно для вычисления ![]() можно использовать
итеративную процедуру, которая избегает обращения матрицы. Вероятно простейшая
итеративная процедура – это метод крутого спуска, когда можно начинать выбором
произвольного начального вектора
можно использовать
итеративную процедуру, которая избегает обращения матрицы. Вероятно простейшая
итеративная процедура – это метод крутого спуска, когда можно начинать выбором
произвольного начального вектора ![]() , скажем
, скажем ![]() . Этот первоначальный выбор
коэффициентов соответствует некоторой точке поверхности квадратичной функции
СКО в пространстве коэффициентов размерности
. Этот первоначальный выбор
коэффициентов соответствует некоторой точке поверхности квадратичной функции
СКО в пространстве коэффициентов размерности ![]() . Затем в этой точке на поверхности
СКО вычисляется градиентный вектор
. Затем в этой точке на поверхности
СКО вычисляется градиентный вектор ![]() , имеющий
, имеющий ![]() градиентных компонент
градиентных компонент ![]() ,
, ![]() . На каждом шаге
вес меняется в направлении, противоположному соответствующей градиентной
компоненте. Изменение веса на
. На каждом шаге
вес меняется в направлении, противоположному соответствующей градиентной
компоненте. Изменение веса на ![]() -м шаге пропорционально объему
-м шаге пропорционально объему ![]() -ой градиентной
компоненты. Таким образом, последовательные значения коэффициентов
-ой градиентной
компоненты. Таким образом, последовательные значения коэффициентов ![]() определяются
согласно отношениям
определяются
согласно отношениям
![]()
а вектор градиента ![]() равен
равен
![]()
Вектор ![]() представляет набор коэффициентов
представляет набор коэффициентов ![]() -й итерации,
-й итерации, ![]() является сигналом
ошибки на
является сигналом
ошибки на ![]() -й
итерации.
-й
итерации. ![]() -
вектор отсчетов принимаемого сигнала, по которым делаются оценки
-
вектор отсчетов принимаемого сигнала, по которым делаются оценки ![]() , т.е.
, т.е. ![]() , а
, а ![]() - положительное
число, выбираемое достаточно малым для того, чтобы обеспечить сходимость
итеративной процедуры. Если минимум СКО достигнут на некотором шаге
- положительное
число, выбираемое достаточно малым для того, чтобы обеспечить сходимость
итеративной процедуры. Если минимум СКО достигнут на некотором шаге ![]() , тогда
, тогда ![]() , так что
дальнейшие изменения у шаговых весов не происходят. В общем случае, при методе
кратчайшего спуска точное значение
, так что
дальнейшие изменения у шаговых весов не происходят. В общем случае, при методе
кратчайшего спуска точное значение ![]() нельзя получить при
конечных величинах
нельзя получить при
конечных величинах ![]() . Однако, к нему можно как угодно
приблизиться при некотором конечном значении
. Однако, к нему можно как угодно
приблизиться при некотором конечном значении ![]() .
.
Принципиальная трудность метода
кратчайшего спуска для определения оптимальных шаговых весов – это отсутствие
знания вектора градиента ![]() , который зависит как от ковариационной
матрицы
, который зависит как от ковариационной
матрицы ![]() ,
так и от вектора
,
так и от вектора ![]() взаимных
корреляций. В свою очередь, эти величины зависят от коэффициентов
взаимных
корреляций. В свою очередь, эти величины зависят от коэффициентов ![]() эквивалентной
модели канала с дискретным временем и от ковариаций информационной
последовательности и аддитивного шума. Все эти величины могут быть, в общем,
неизвестны на приёме. Чтобы преодолеть эти трудности, можно использовать
оценку вектора градиентов. Это значит, что алгоритм настройки коэффициентов
шаговых весов можно выразить в форме
эквивалентной
модели канала с дискретным временем и от ковариаций информационной
последовательности и аддитивного шума. Все эти величины могут быть, в общем,
неизвестны на приёме. Чтобы преодолеть эти трудности, можно использовать
оценку вектора градиентов. Это значит, что алгоритм настройки коэффициентов
шаговых весов можно выразить в форме
![]()
где ![]() означает оценку вектора градиентов
означает оценку вектора градиентов ![]() , а
, а ![]() означает оценку
вектора коэффициента
означает оценку
вектора коэффициента ![]() .
.
Из (11.1.8) мы замечаем, что ![]() равно обратной
величине математического ожидания
равно обратной
величине математического ожидания ![]() , следовательно, оценка
, следовательно, оценка ![]() равна
равна
![]()
Поскольку ![]() , оценка
, оценка ![]() является несмещенной оценкой
правильного вектора градиента
является несмещенной оценкой
правильного вектора градиента ![]() . Подстановка (11.1.10) в (11.1.9)
даёт алгоритм
. Подстановка (11.1.10) в (11.1.9)
даёт алгоритм
![]()
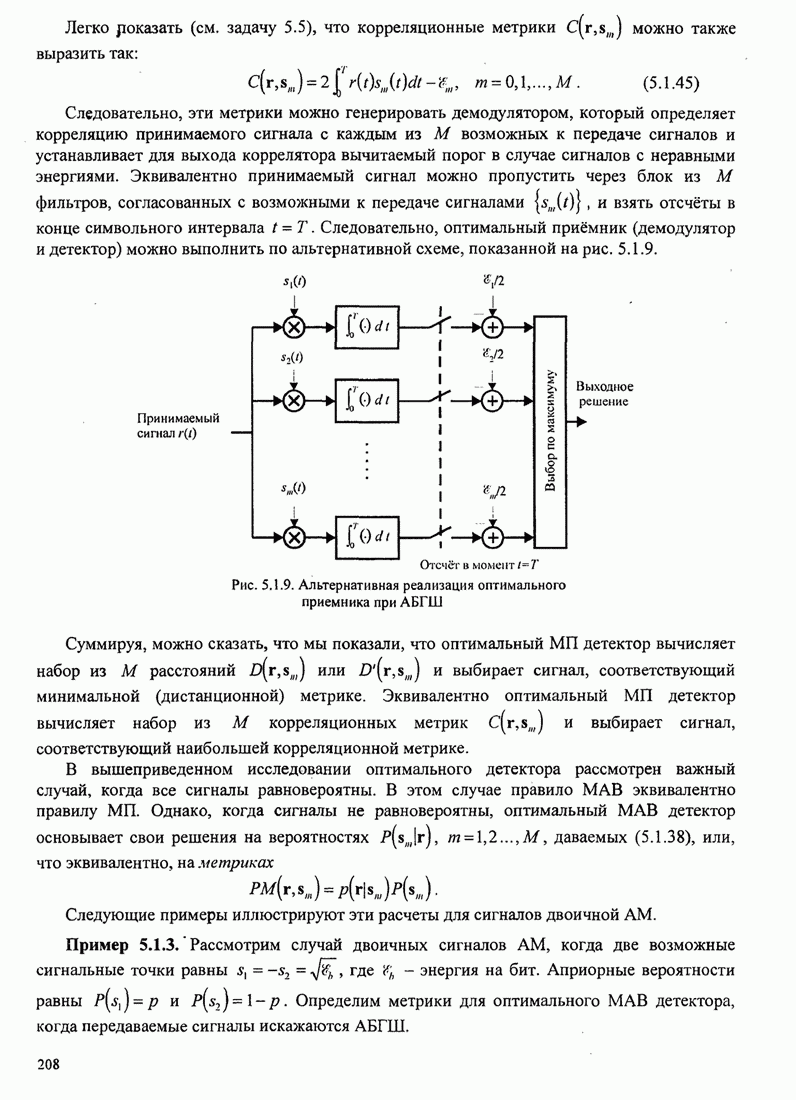
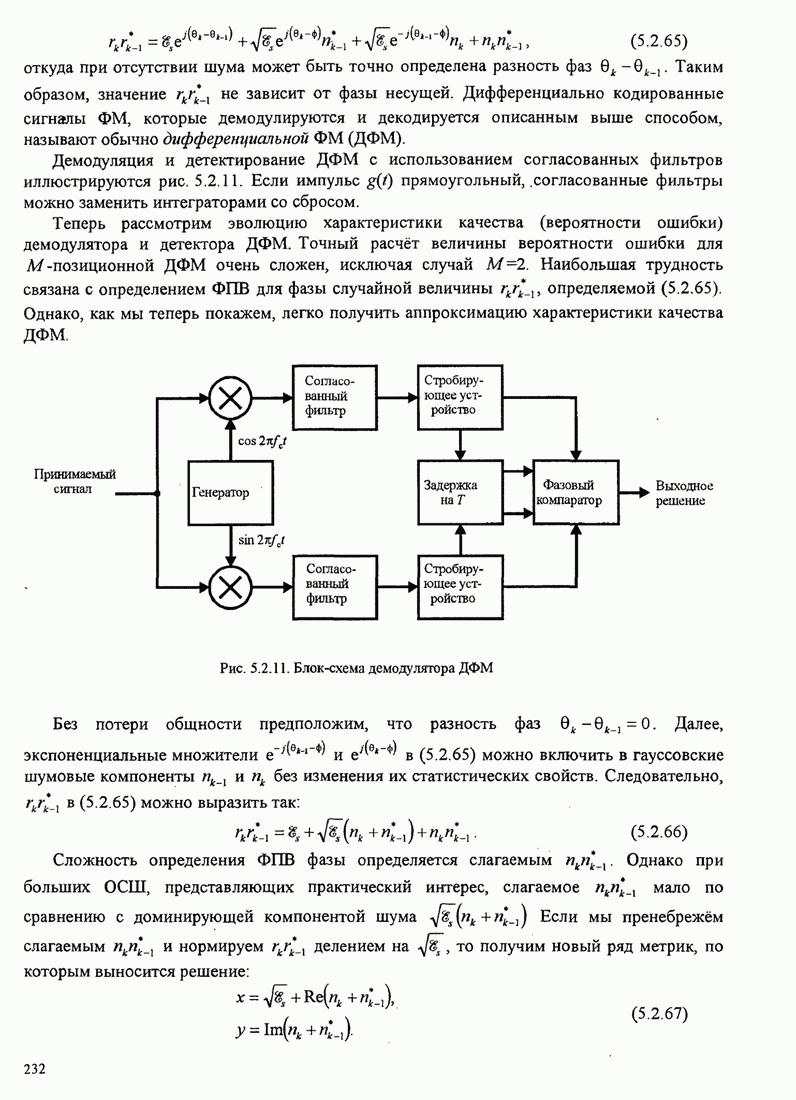
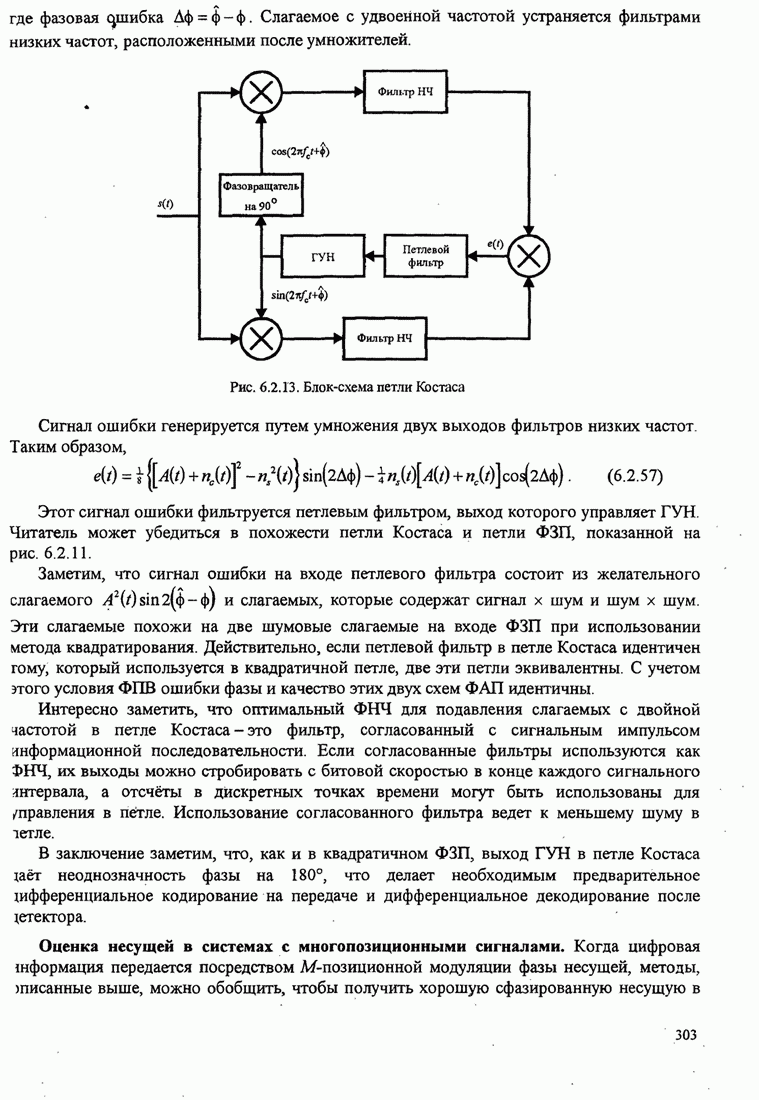
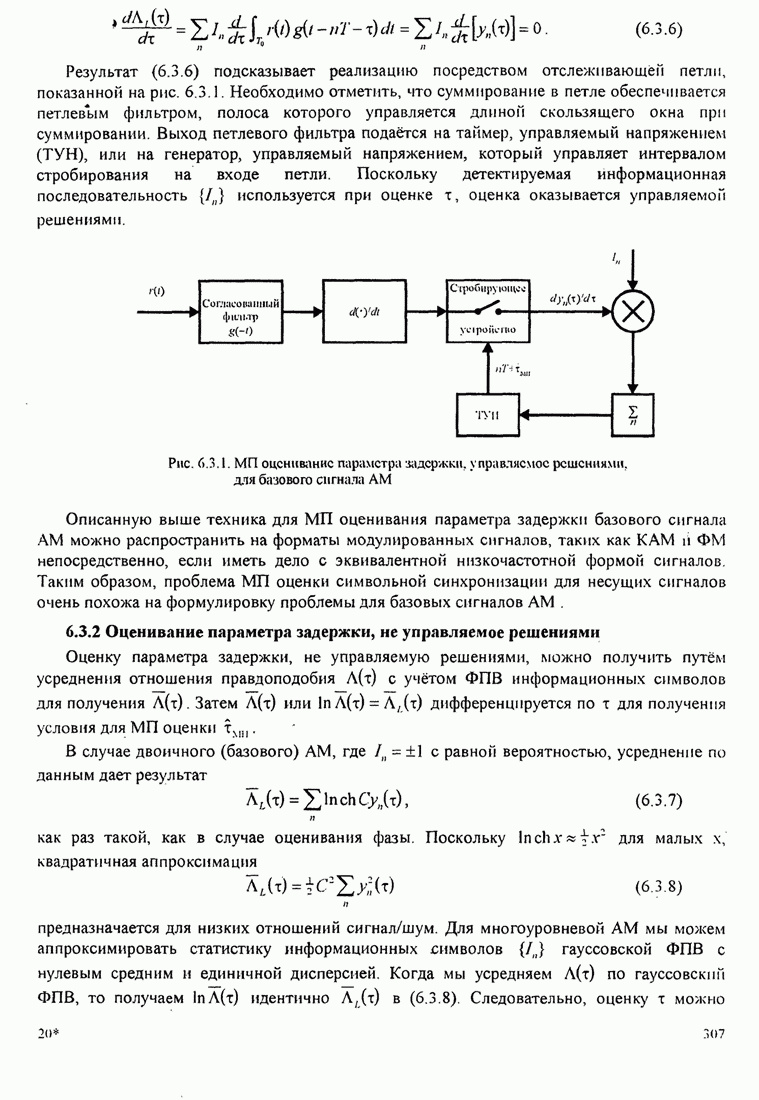
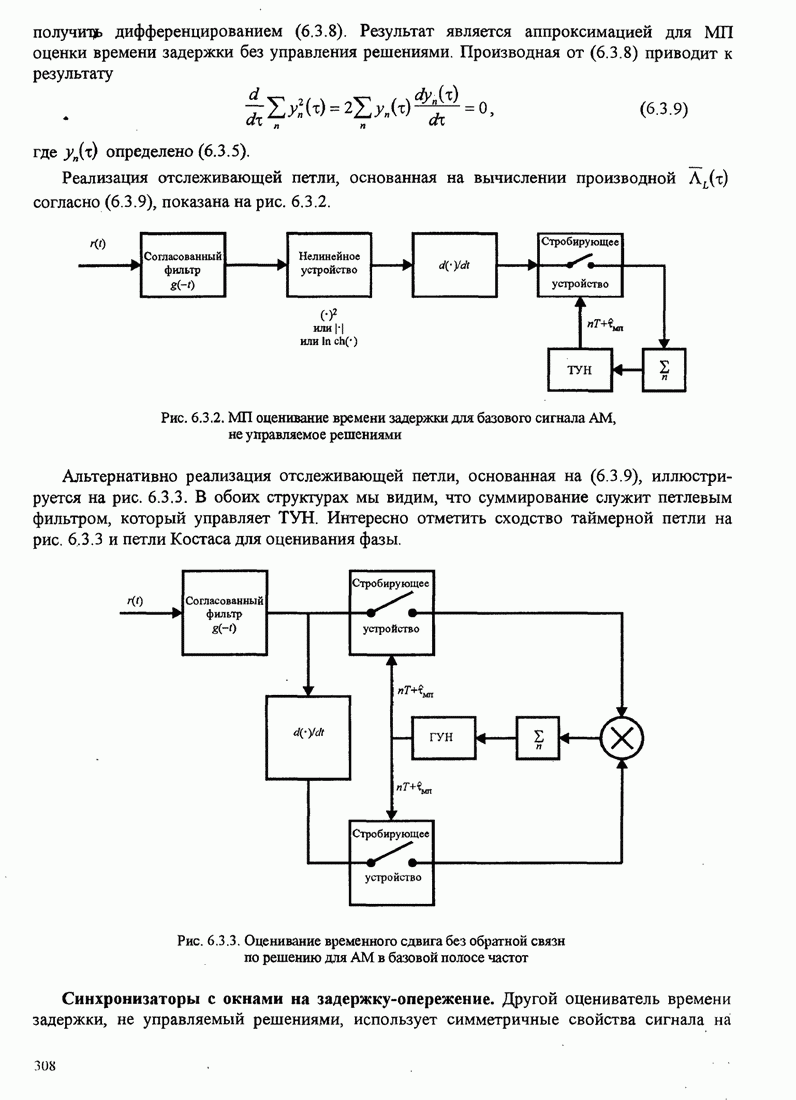
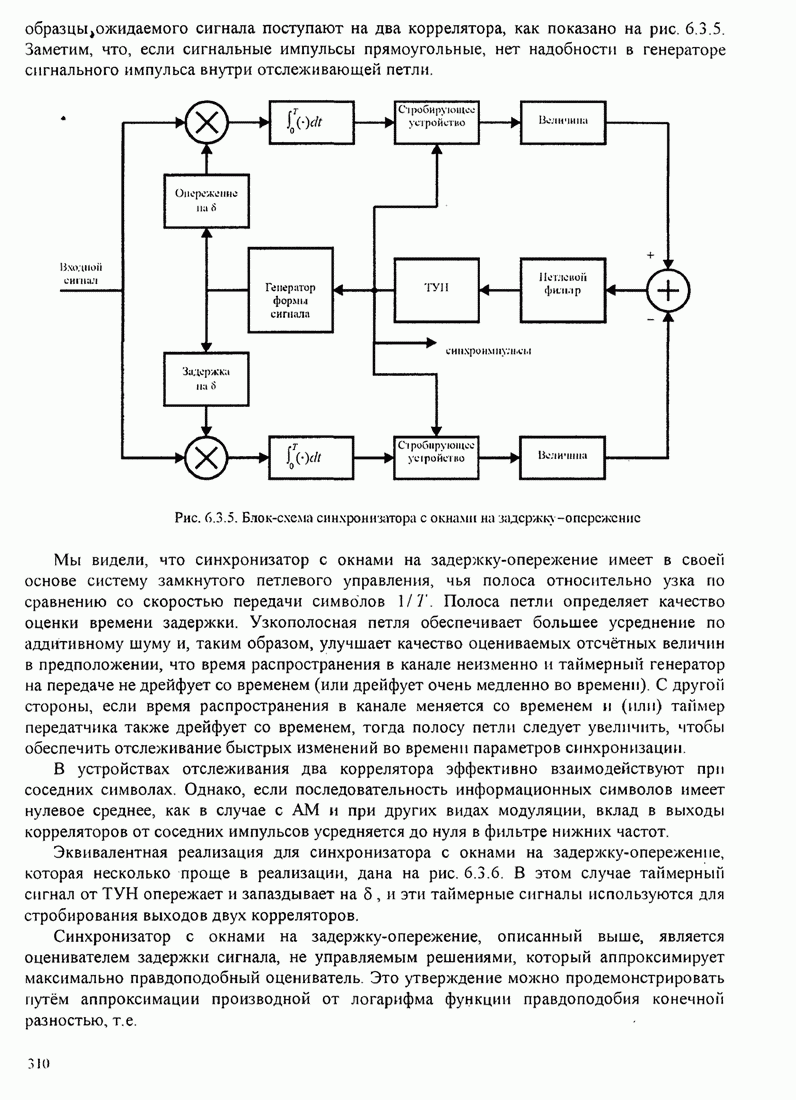
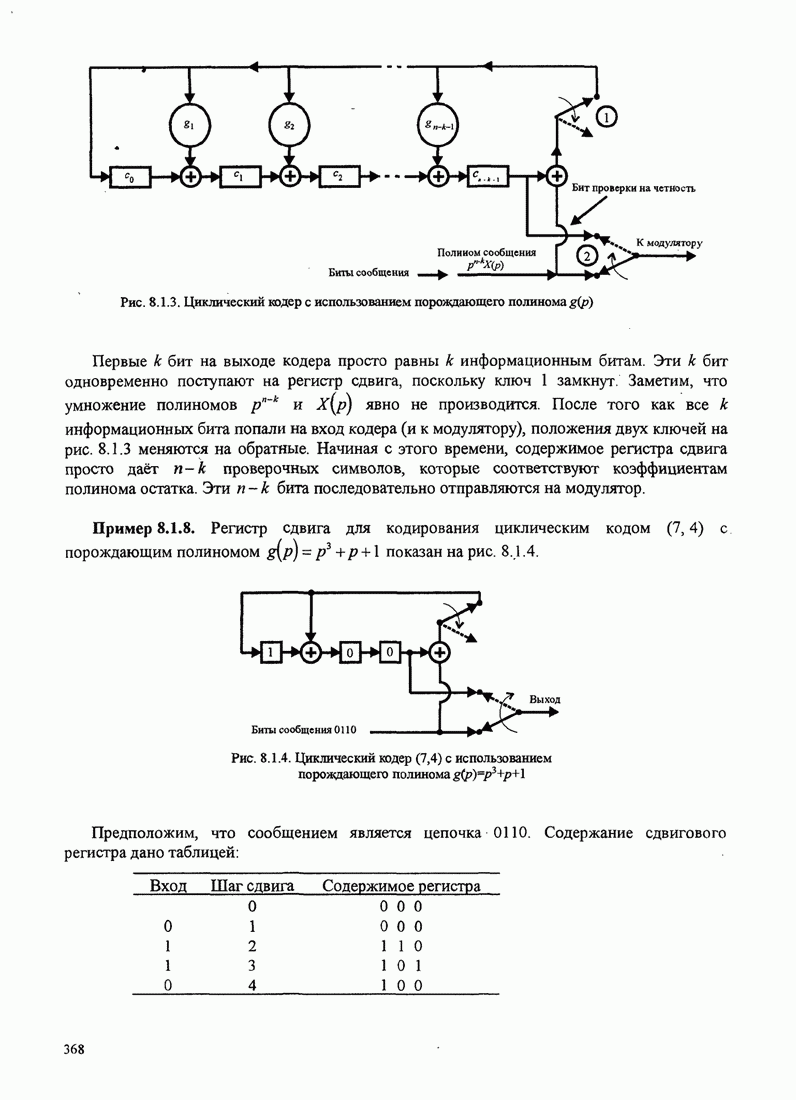
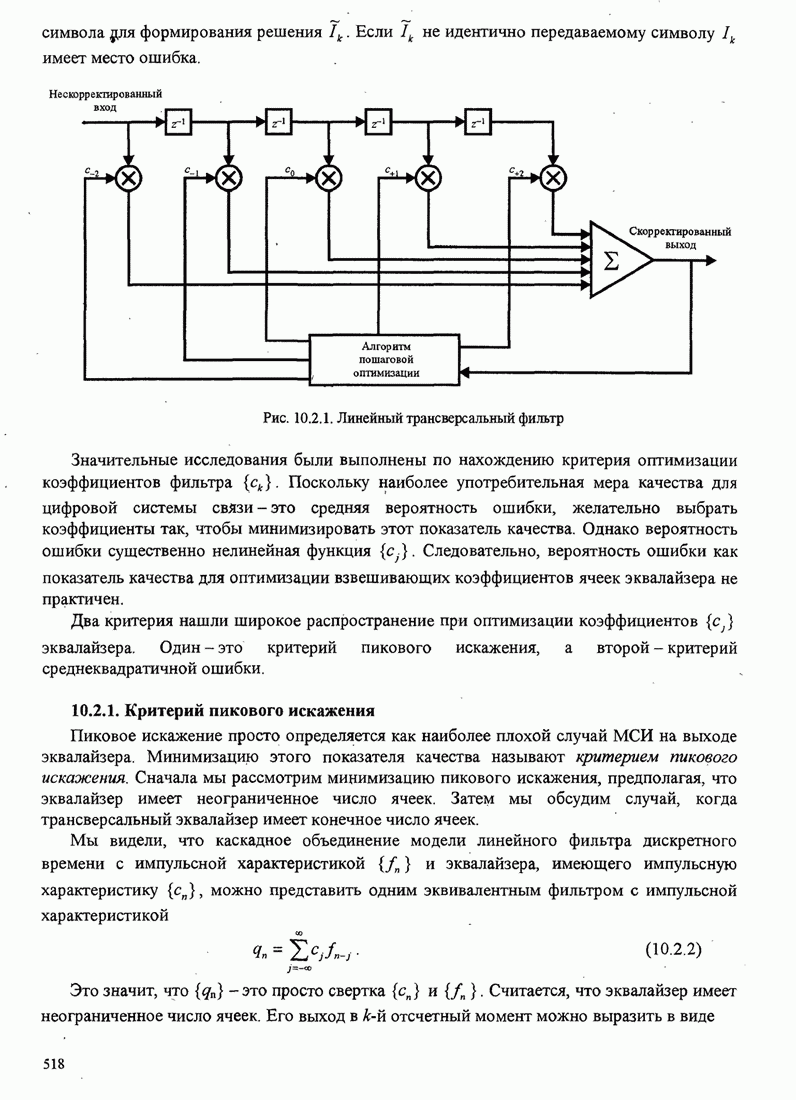
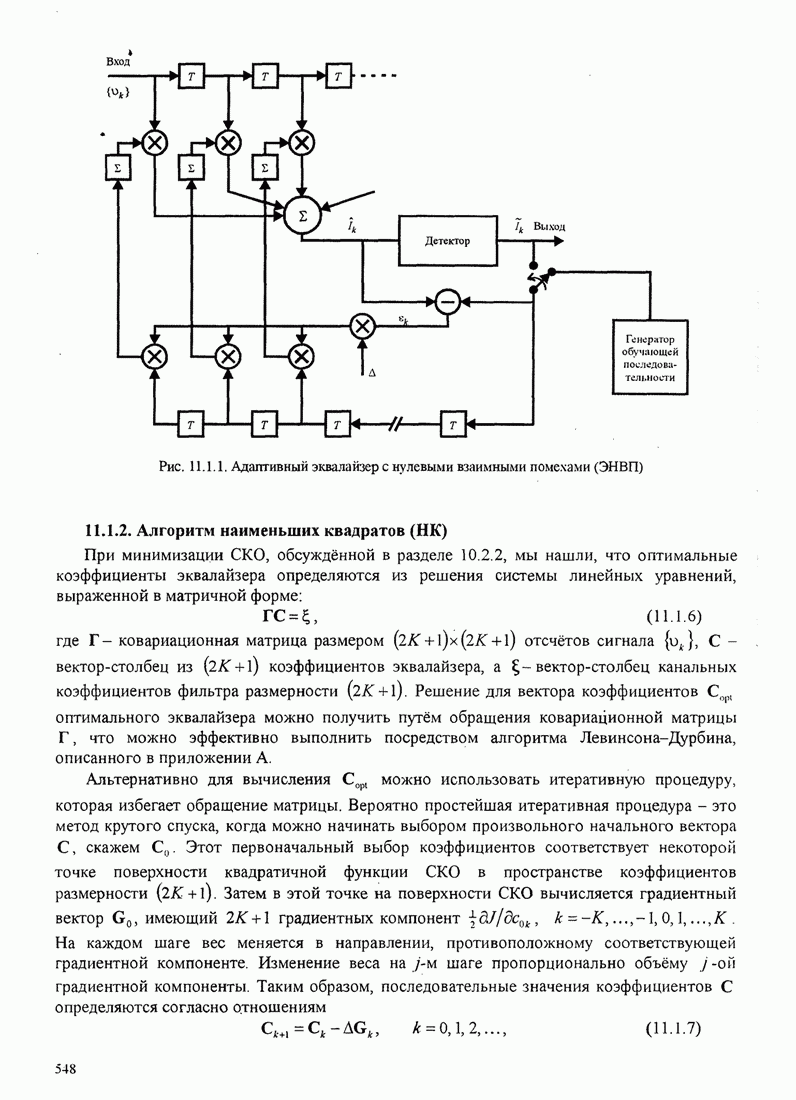
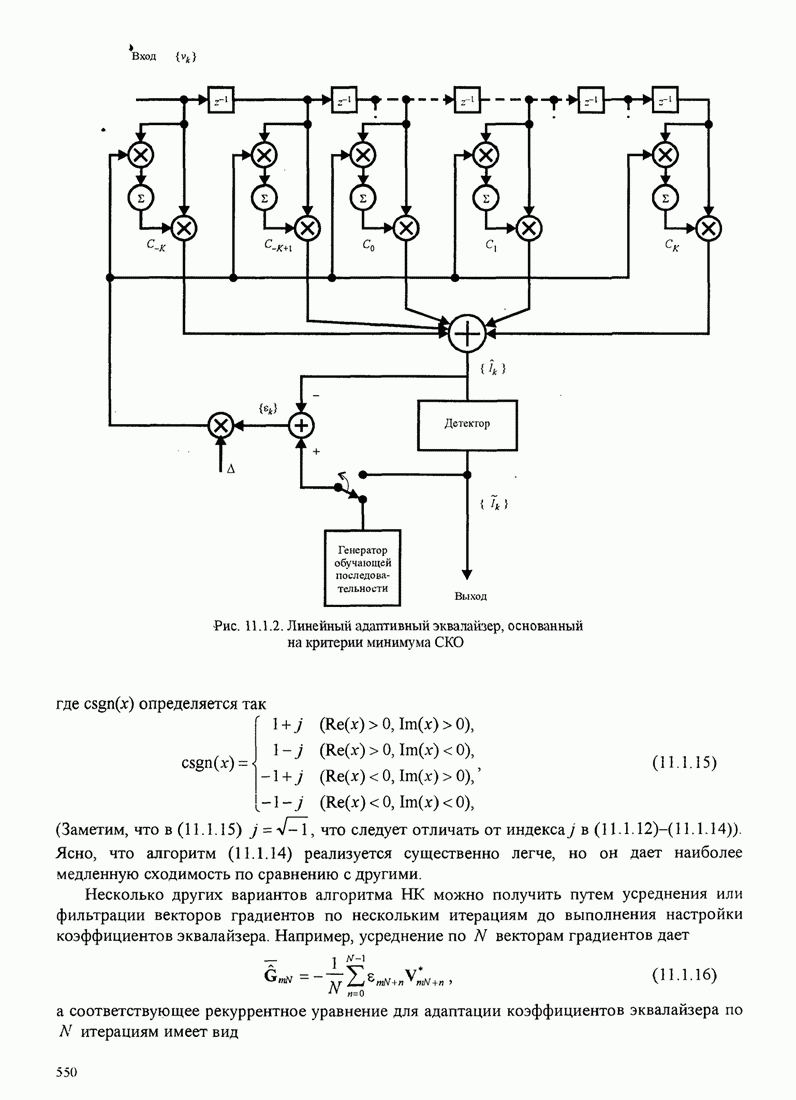
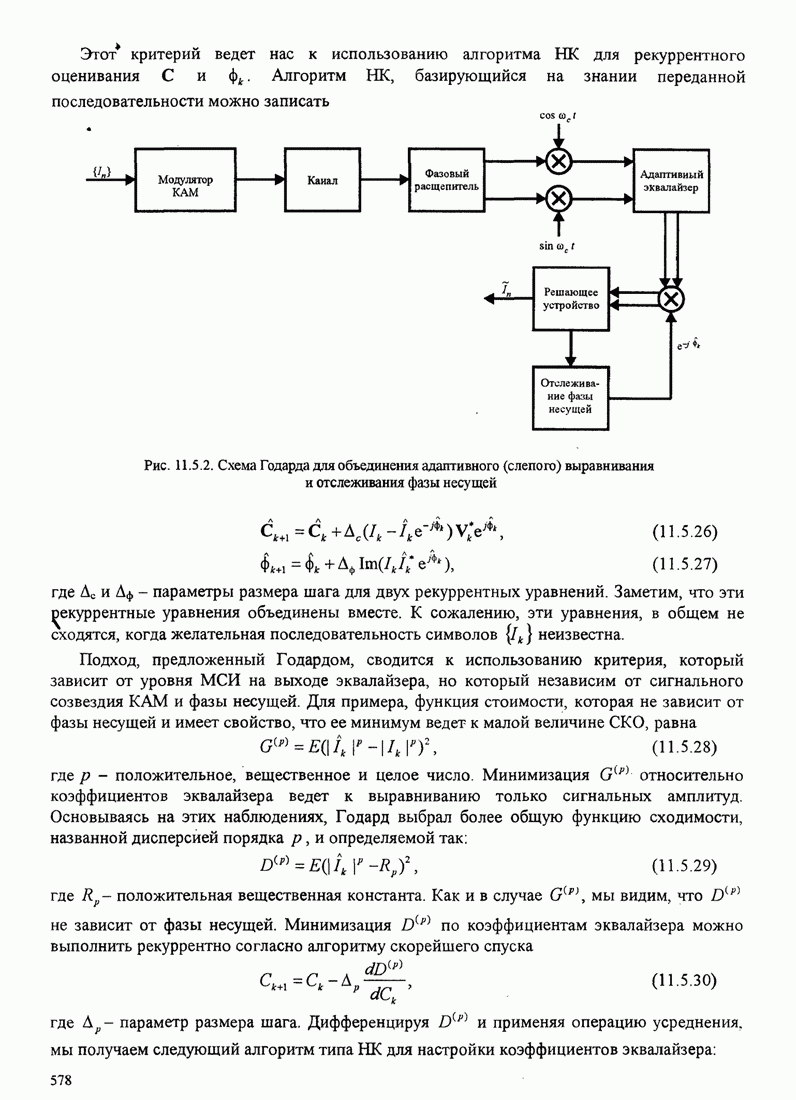
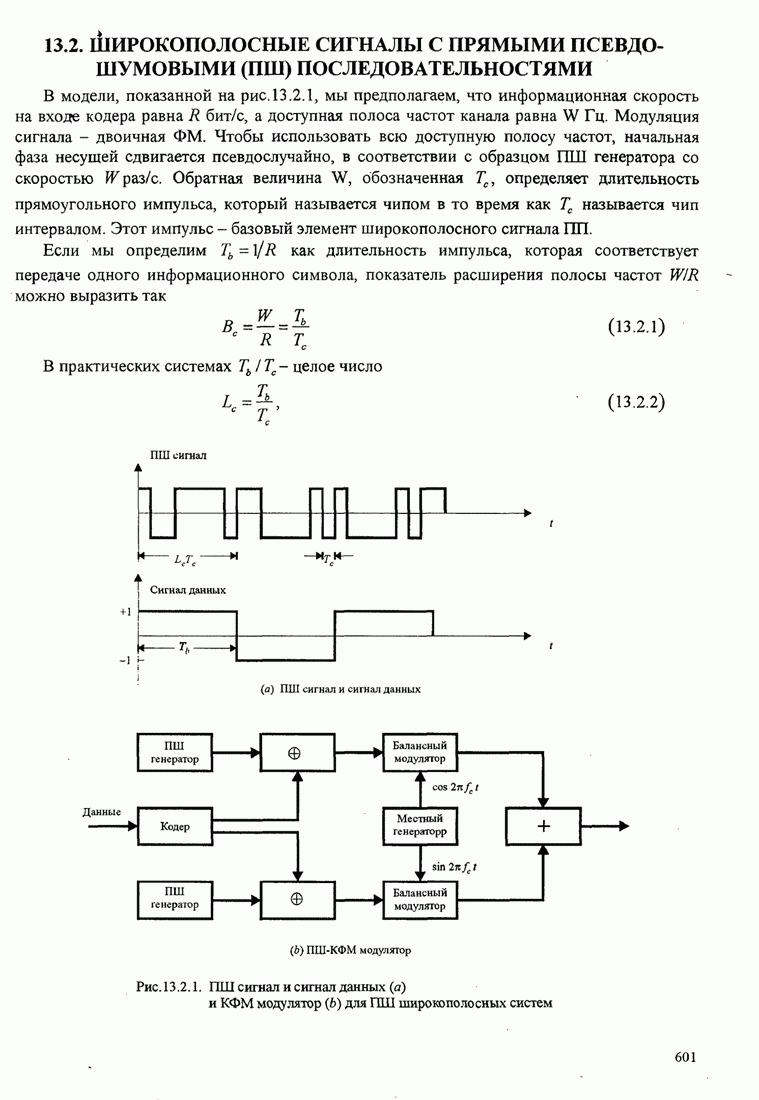
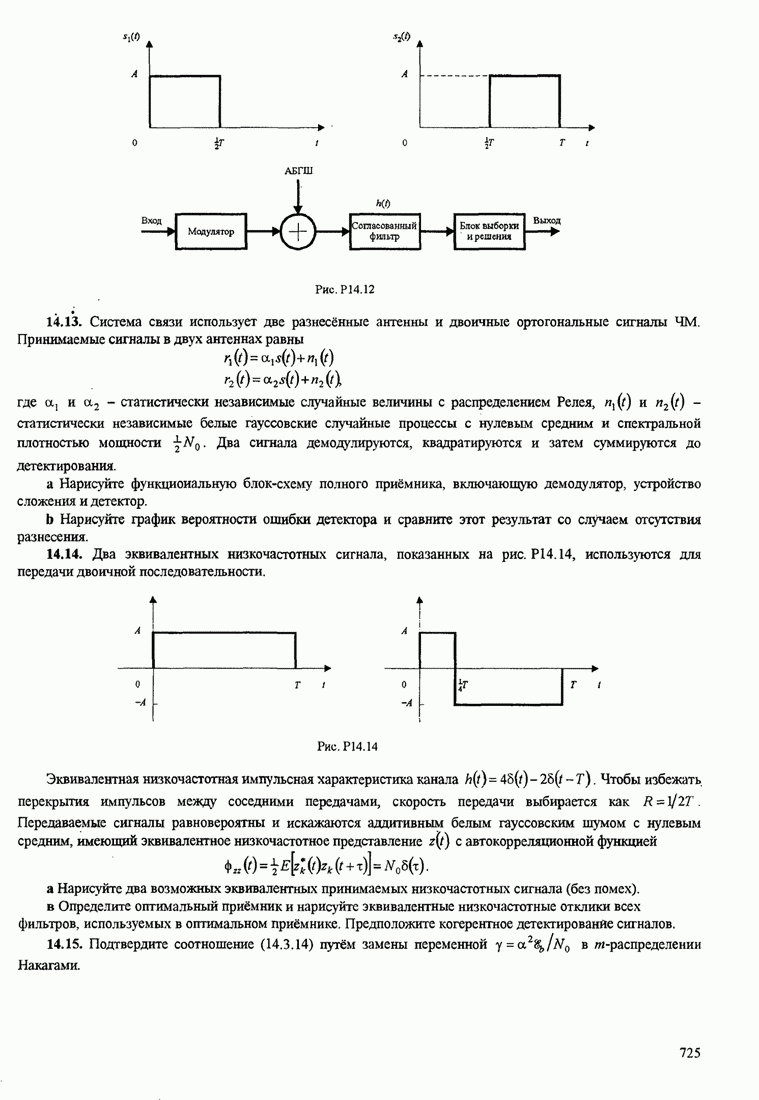
Это базовый алгоритм НК (наименьших квадратов) для рекуррентной настройки коэффициентов шаговых весов эквалайзера, впервые предложенный Уидроу и Хоффом (1960). Он иллюстрируется в эквалайзере, показанном на рис.11.1.2.
Базовый алгоритм (11.1.11) и некоторые
из его возможных вариантов были внедрены во многих коммерческих адаптивных
эквалайзерах, которые используются в высокоскоростных модемах. Три варианта
базового алгоритма были получены путем использования только информации о знаке,
содержащейся в сигнале ошибки ![]() и (или) в компонентах
и (или) в компонентах ![]() . Таким образом,
три возможных варианта алгоритма определяются так
. Таким образом,
три возможных варианта алгоритма определяются так
![]()
![]()
![]()
где ![]() определяется так
определяется так

(Заметим, что в (11.1.15) ![]() , что следует
отличать от индекса
, что следует
отличать от индекса ![]() в (11.1.12)-(11.1.14)). Ясно, что
алгоритм (11.1.14) реализуется существенно легче, но он дает наиболее медленную
сходимость по сравнению с другими.
в (11.1.12)-(11.1.14)). Ясно, что
алгоритм (11.1.14) реализуется существенно легче, но он дает наиболее медленную
сходимость по сравнению с другими.

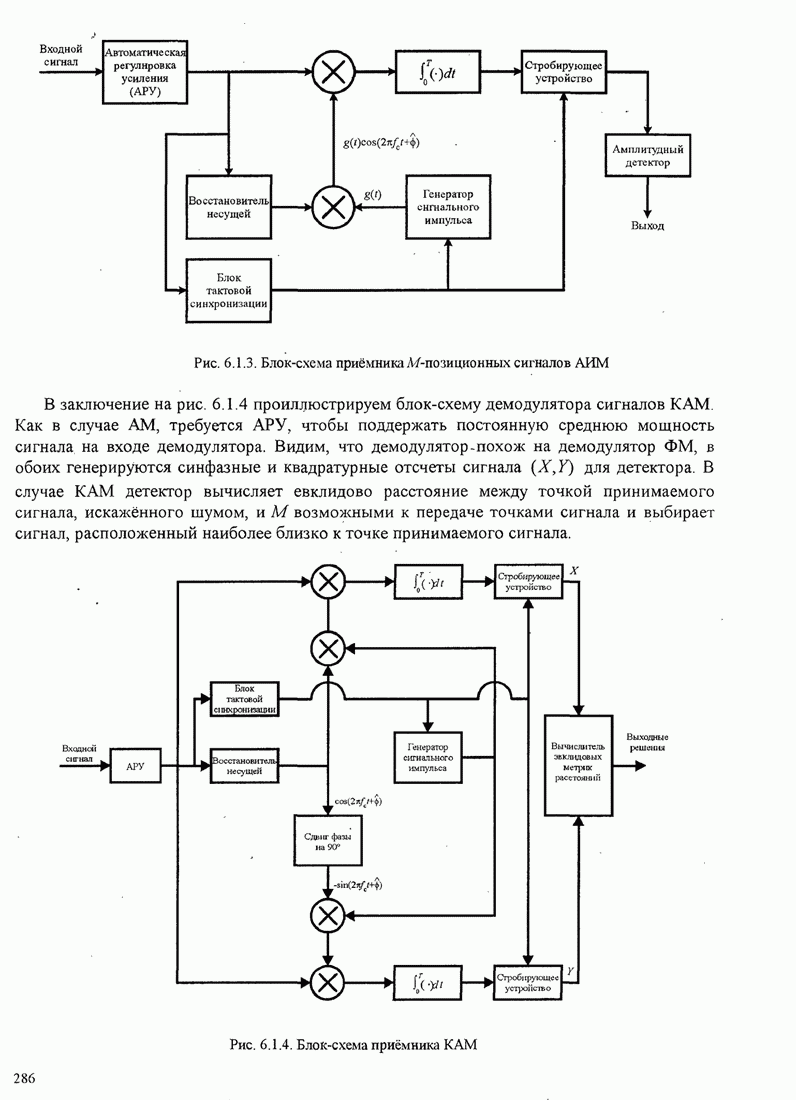
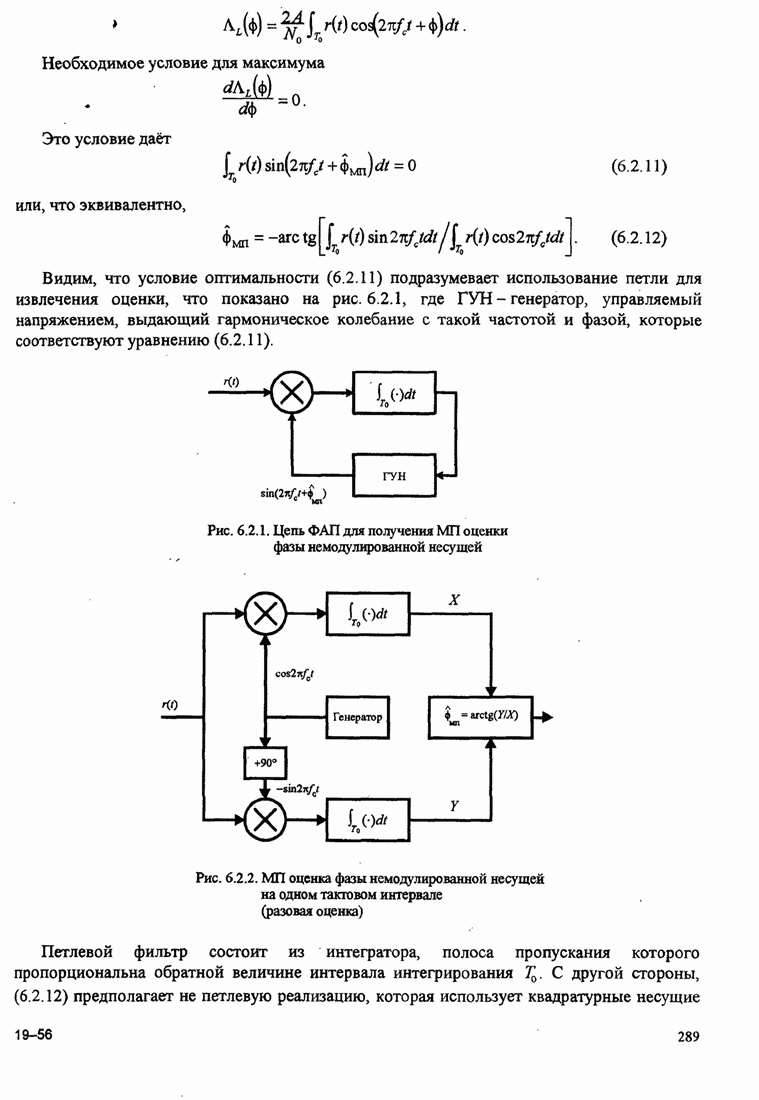
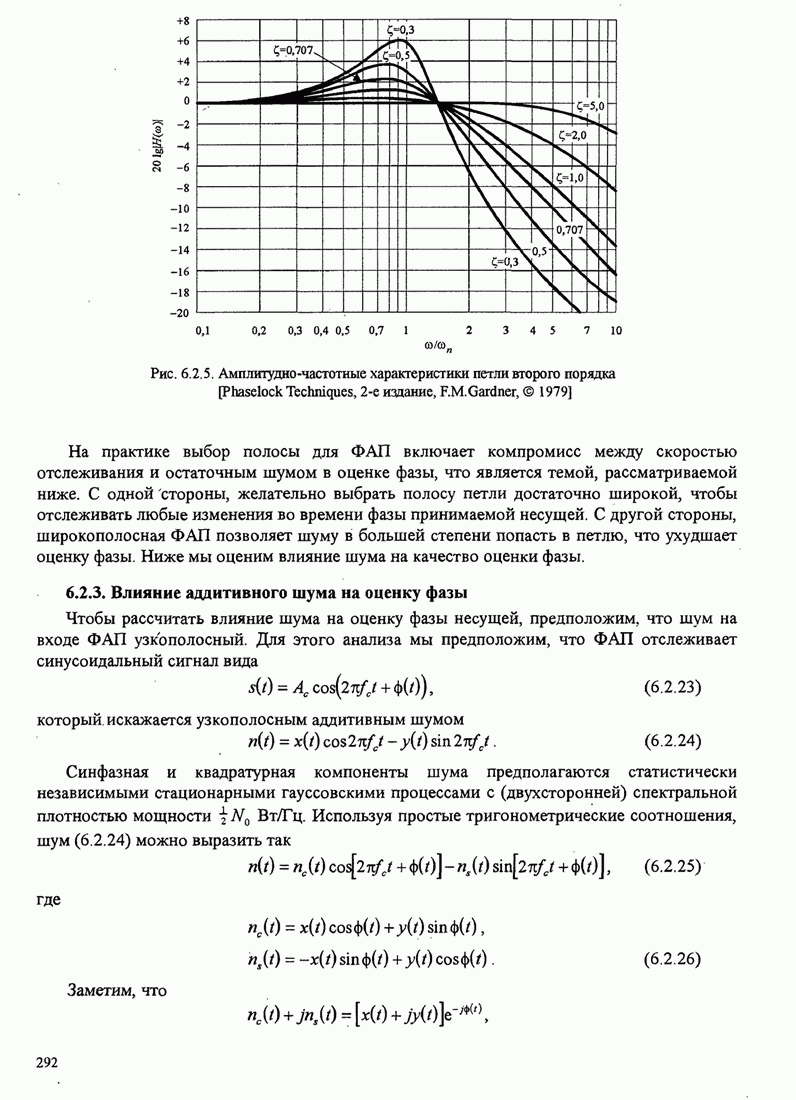
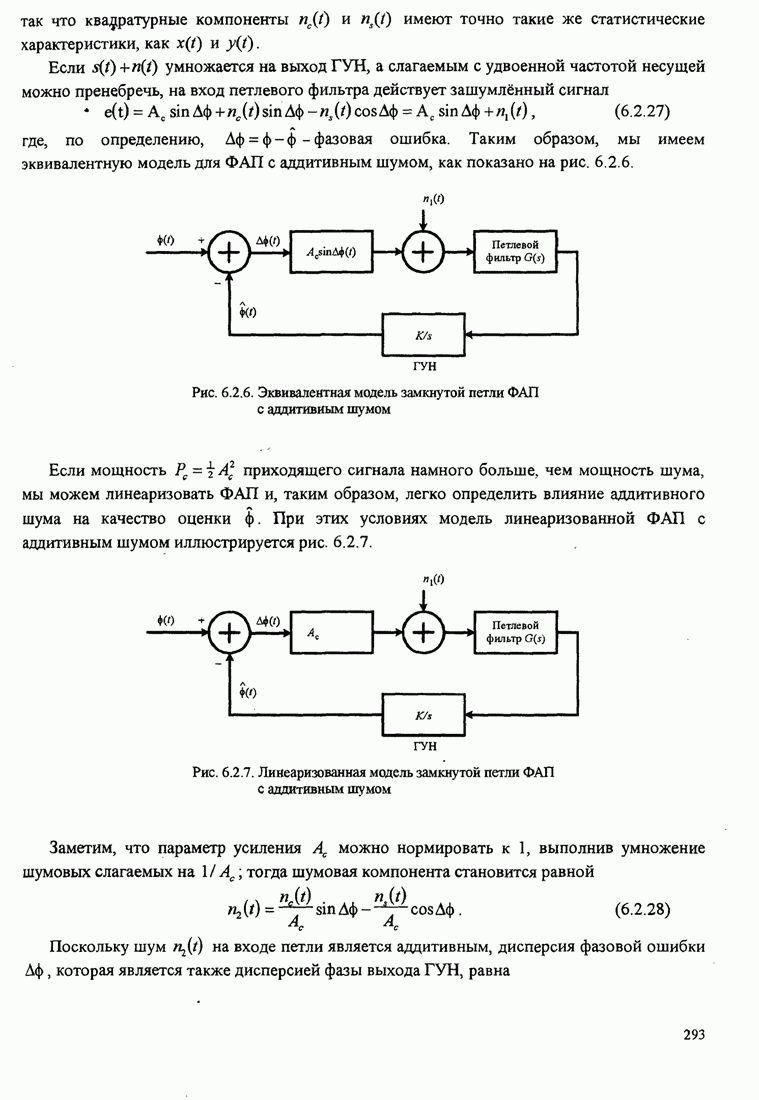
Рис. 11.1.2. Линейный адаптивный эквалайзер, основанный на критерии минимума СКО
Несколько других вариантов алгоритма НК
можно получить путем усреднения или фильтрации векторов градиентов по
нескольким итерациям до выполнения настройки коэффициентов эквалайзера.
Например, усреднение по ![]() векторам градиентов даёт
векторам градиентов даёт
![]()
а соответствующее рекуррентное уравнение
для адаптации коэффициентов эквалайзера по ![]() итерациями имеет вид
итерациями имеет вид
![]()
Действительно, операция усреднения согласно (11.1.16) уменьшает шум в оценке вектора градиентов, как показано Гарднером (1987).
Альтернативный подход сводится к фильтрации шумовых составляющих градиента с помощью низкочастотного фильтра и использованию выхода фильтра как оценки вектора градиента. Например, простой низкочастотный фильтр для шумовых градиентов даёт выход
![]()
где выбор ![]() определяет полосу пропускания
низкочастотного фильтра. Если
определяет полосу пропускания
низкочастотного фильтра. Если ![]() близко к единице, полоса фильтра мала
и эффективное усреднение осуществляется по многим векторам градиентов. С другой
стороны, если
близко к единице, полоса фильтра мала
и эффективное усреднение осуществляется по многим векторам градиентов. С другой
стороны, если ![]() мало,
низкочастотный фильтр имеет большую полосу и, следовательно, он обеспечивает
малое усреднение по векторам градиентов. С фильтрацией векторов градиентов по
(11.1.18) вместе
мало,
низкочастотный фильтр имеет большую полосу и, следовательно, он обеспечивает
малое усреднение по векторам градиентов. С фильтрацией векторов градиентов по
(11.1.18) вместе ![]() мы
получаем алгоритм НК с фильтрацией градиентов, определяемой так
мы
получаем алгоритм НК с фильтрацией градиентов, определяемой так
![]()
В вышеприведенном обслуживании было предположено, что приёмник имеет знание о переданной информационной последовательности при формировании сигналов ошибки между желательным символом и его оценкой. Такое знание можно получить в течение короткого периода обучения, когда к приемнику для первоначальной настройке шаговых весов передается известная информационная последовательность.
На практике часто в качестве обучающей
последовательности выбирается периодическая псевдослучайная последовательность,
такая как последовательность регистра максимальной длины с периодом ![]() , равным длине
(памяти) эквалайзера
, равным длине
(памяти) эквалайзера ![]() . В этом случае, градиент обычно
усредняется по длине последовательности как указанно в (11.1.6), а эквалайзер
настраивается на каждом периоде согласно (11.1..17). Практическая схема для
непрерывной настройки весов отводов может быть или основана на управлении
решениями, когда решения (оценки) по информационным символам предполагаются
правильными и используются вместо
. В этом случае, градиент обычно
усредняется по длине последовательности как указанно в (11.1.6), а эквалайзер
настраивается на каждом периоде согласно (11.1..17). Практическая схема для
непрерывной настройки весов отводов может быть или основана на управлении
решениями, когда решения (оценки) по информационным символам предполагаются
правильными и используются вместо ![]() при формировании сигнала ошибки
при формировании сигнала ошибки ![]() , или такая, в
которой известная псевдослучайная испытательная последовательность вставляется
в информационный сигнал (путём суммирования или перемежения во времени), а веса
отводов настраиваются путем сравнения принимаемых испытательных символов с
известными переданными сигналами. При использовании операционной модели с
управлением решениями сигнал ошибки оказывается равным
, или такая, в
которой известная псевдослучайная испытательная последовательность вставляется
в информационный сигнал (путём суммирования или перемежения во времени), а веса
отводов настраиваются путем сравнения принимаемых испытательных символов с
известными переданными сигналами. При использовании операционной модели с
управлением решениями сигнал ошибки оказывается равным ![]() , где
, где ![]() - это решение приемника,
основанное на оценке
- это решение приемника,
основанное на оценке ![]() . До тех пор, пока приёмник работает с
малыми вероятностями ошибок, редкие ошибки будут иметь несущественное влияние
на сходимость алгоритма.
. До тех пор, пока приёмник работает с
малыми вероятностями ошибок, редкие ошибки будут иметь несущественное влияние
на сходимость алгоритма.
Если характеристики канала меняются, эти
изменения отражаются в коэффициентах ![]() эквивалентной модели канала с
дискретным временем. Они также отражаются в сигнале ошибки
эквивалентной модели канала с
дискретным временем. Они также отражаются в сигнале ошибки ![]() , поскольку он зависит от
, поскольку он зависит от ![]() . Таким образом,
шаговые веса будут меняться согласно (11.1.11), отражая изменения в канале.
Простое изменение в шаговых весах возникает, если меняется статистика шума или
информационной последовательности. Таким образом, эквалайзер оказывается
адаптивным.
. Таким образом,
шаговые веса будут меняться согласно (11.1.11), отражая изменения в канале.
Простое изменение в шаговых весах возникает, если меняется статистика шума или
информационной последовательности. Таким образом, эквалайзер оказывается
адаптивным.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
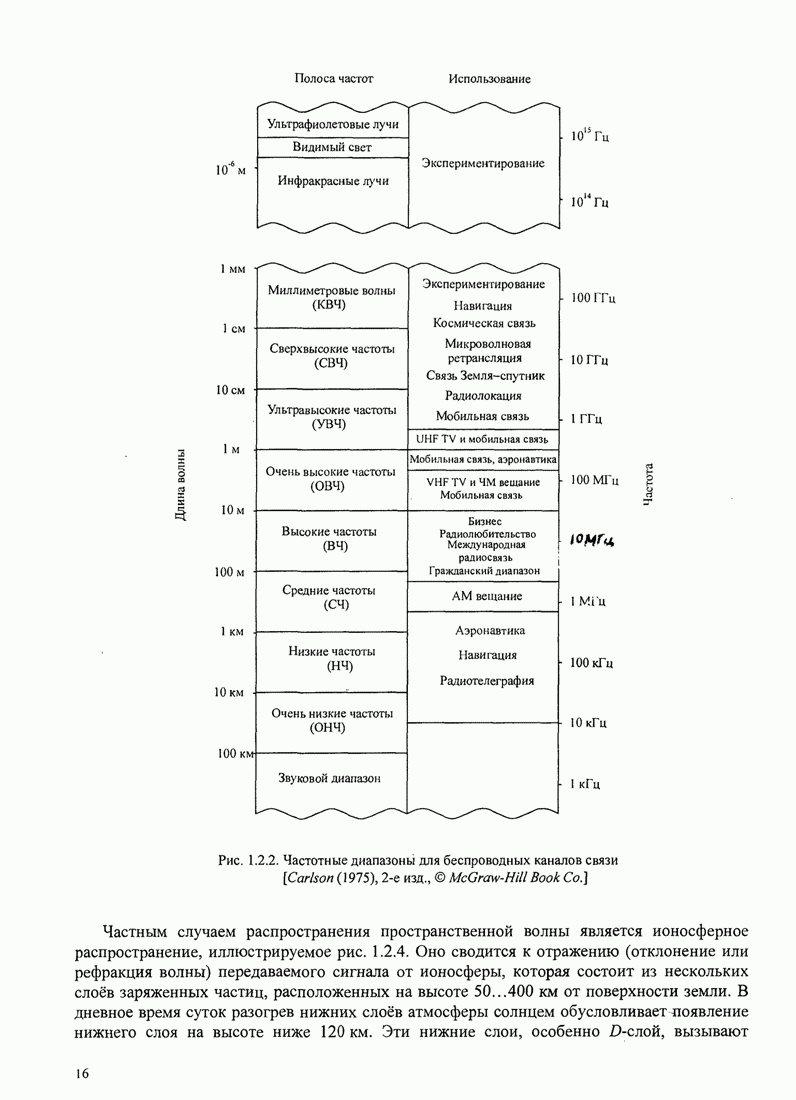
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
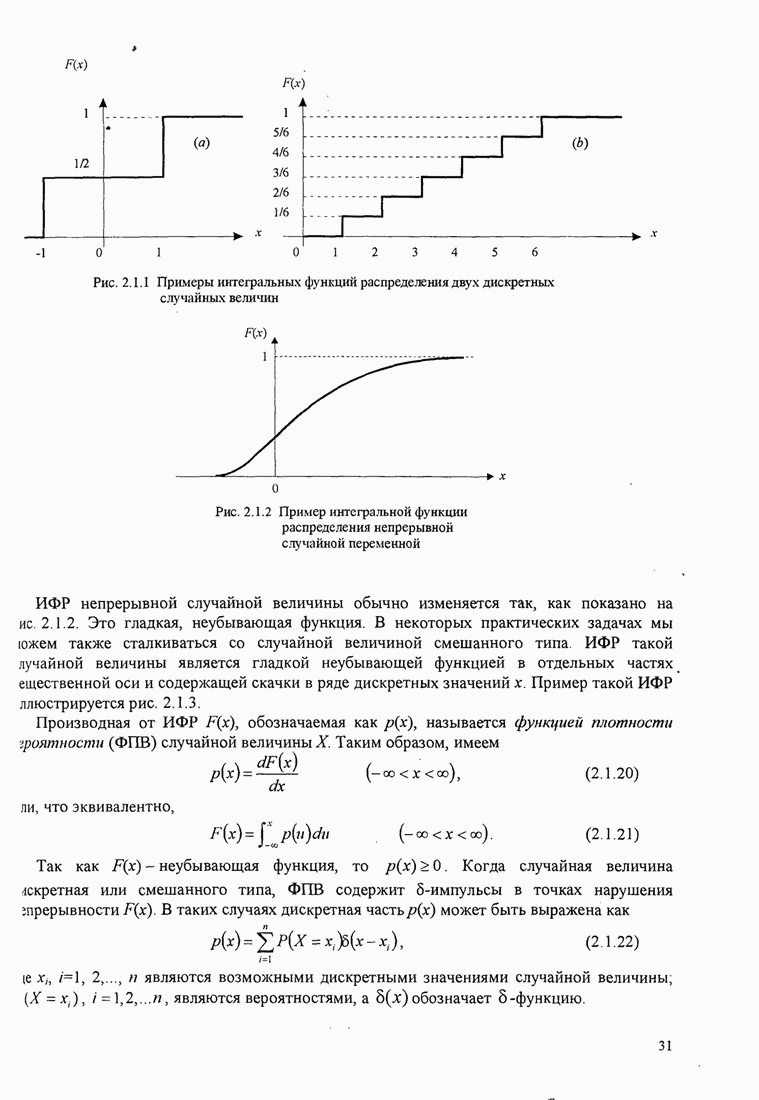
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
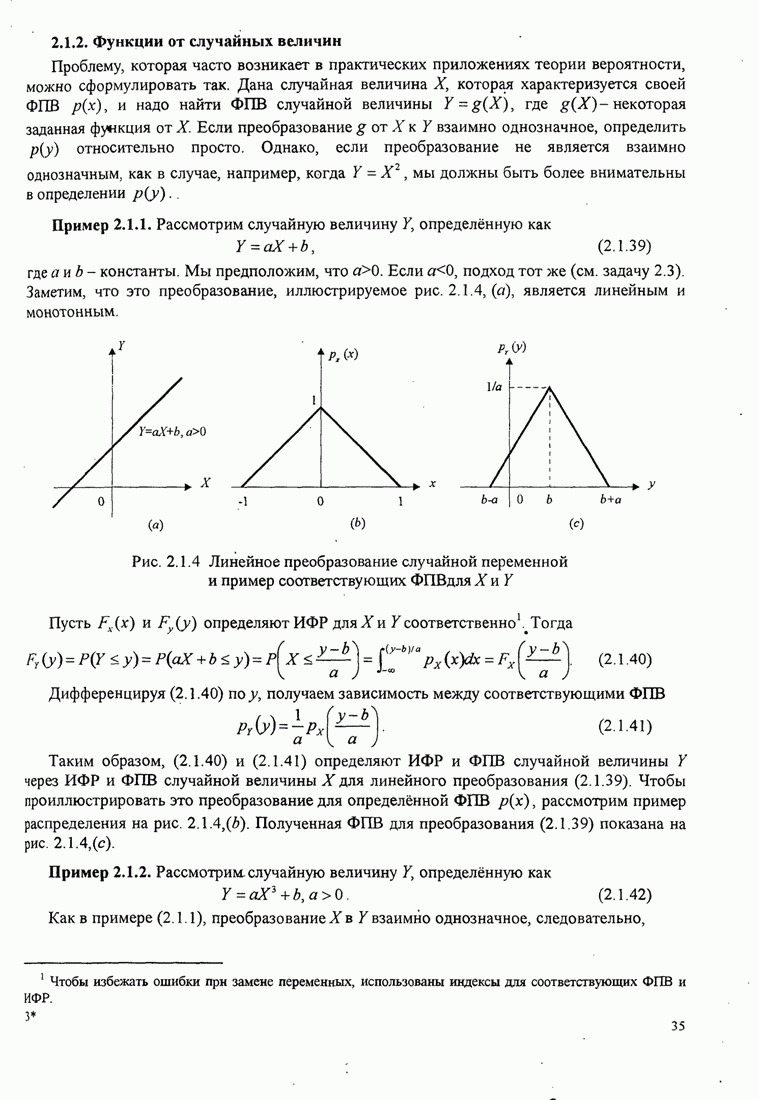
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
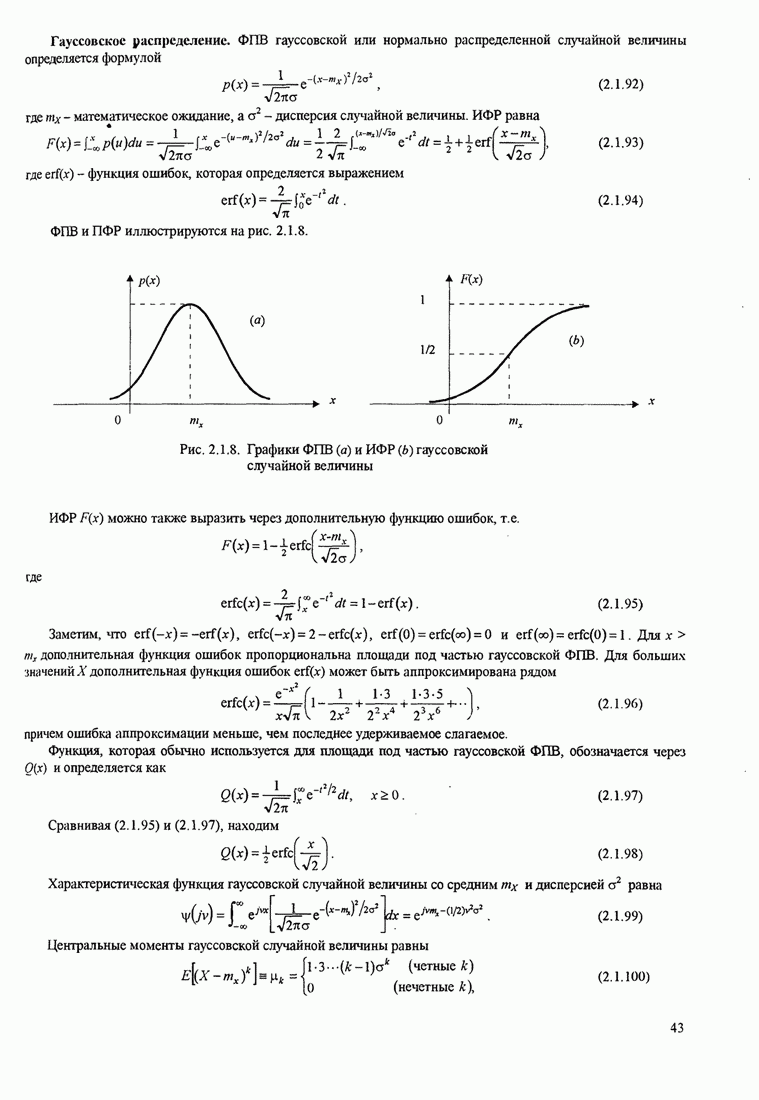
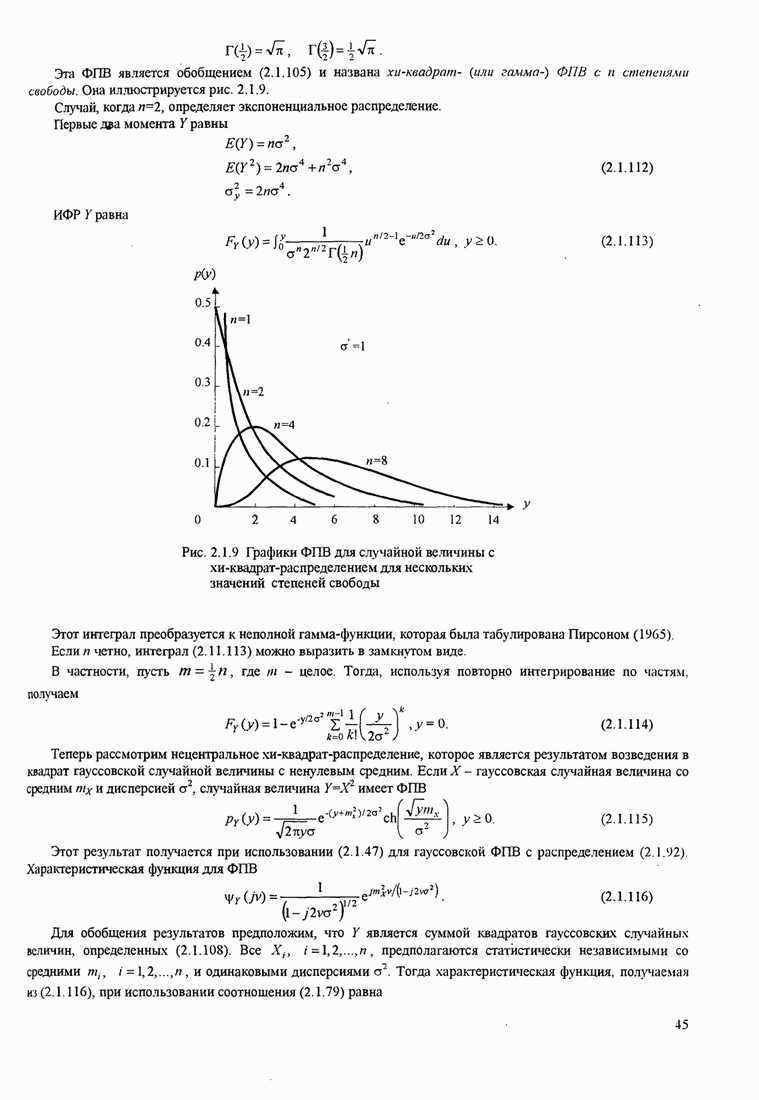
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
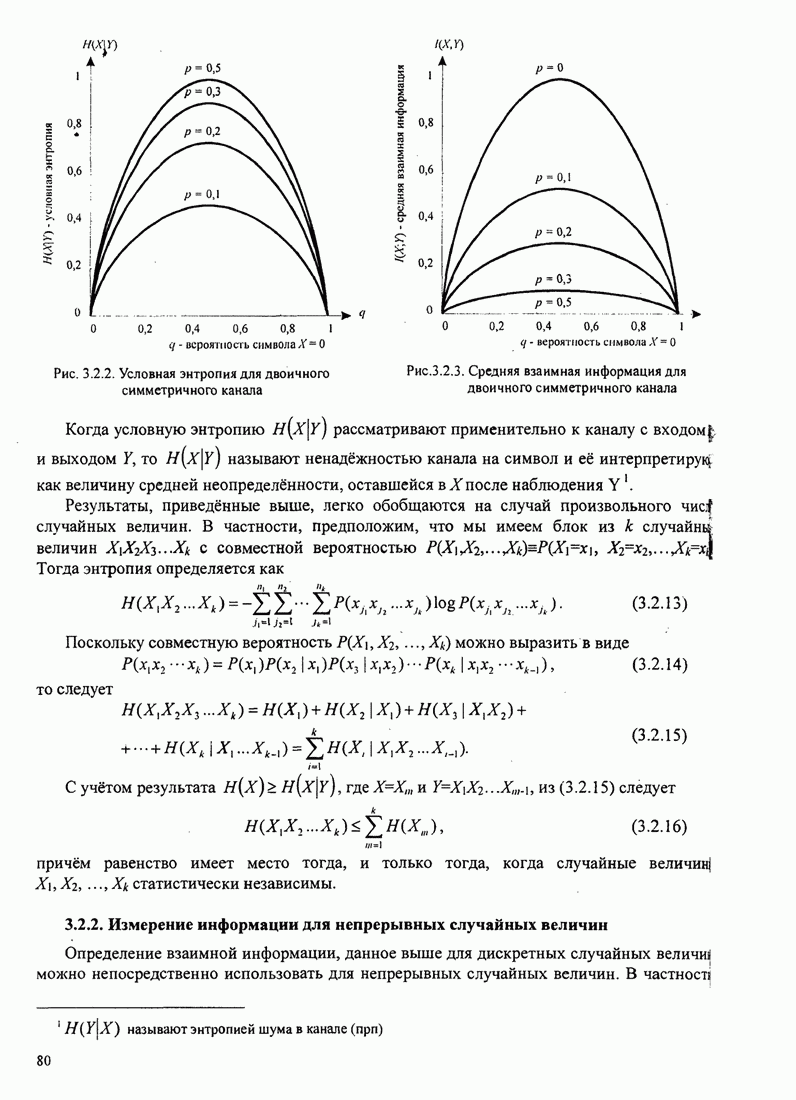
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
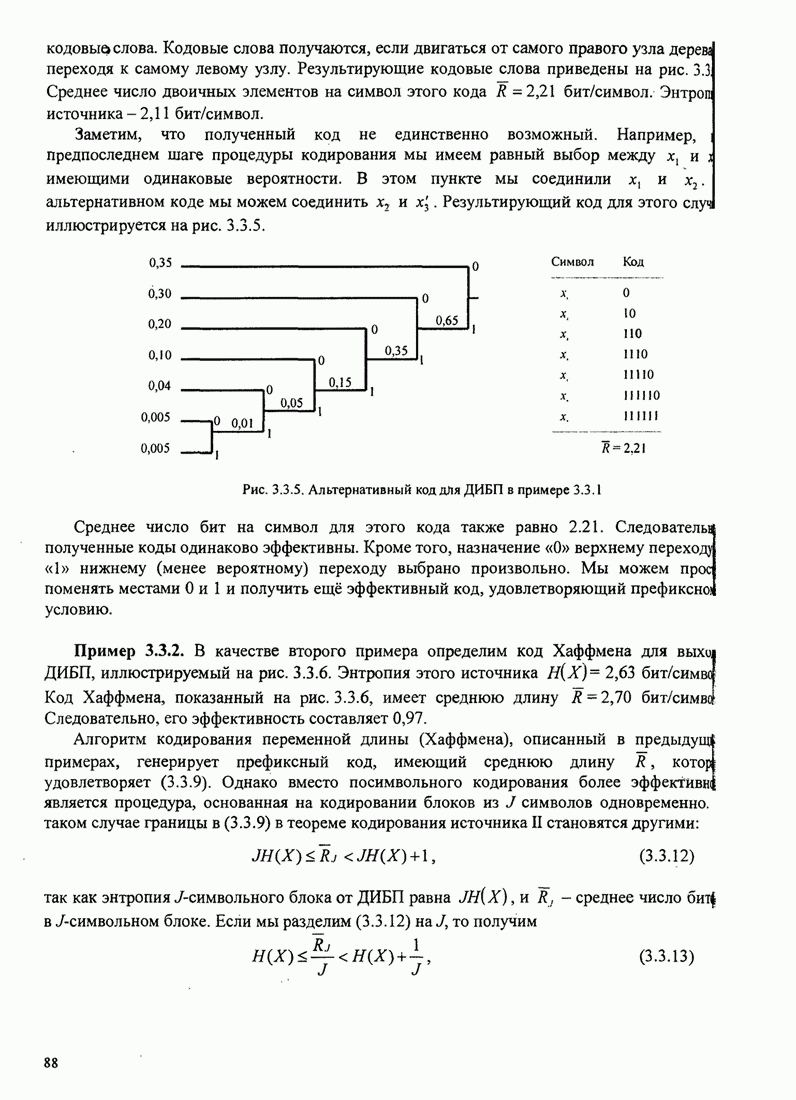
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
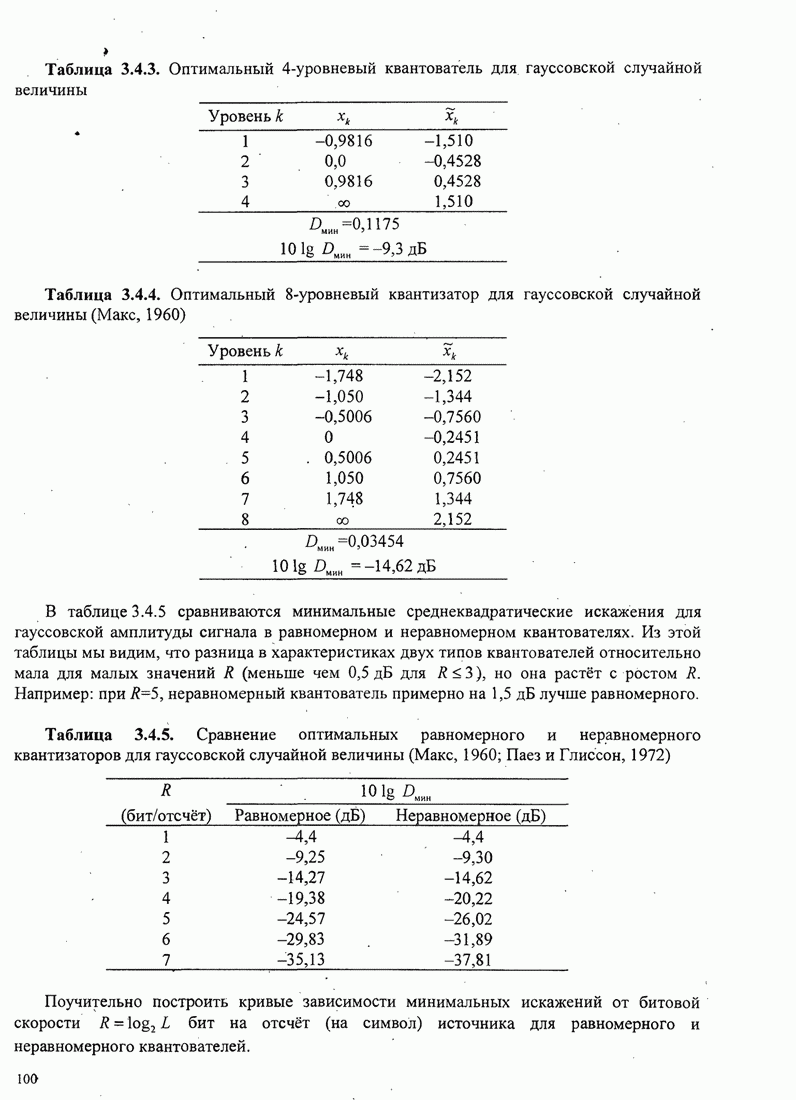
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
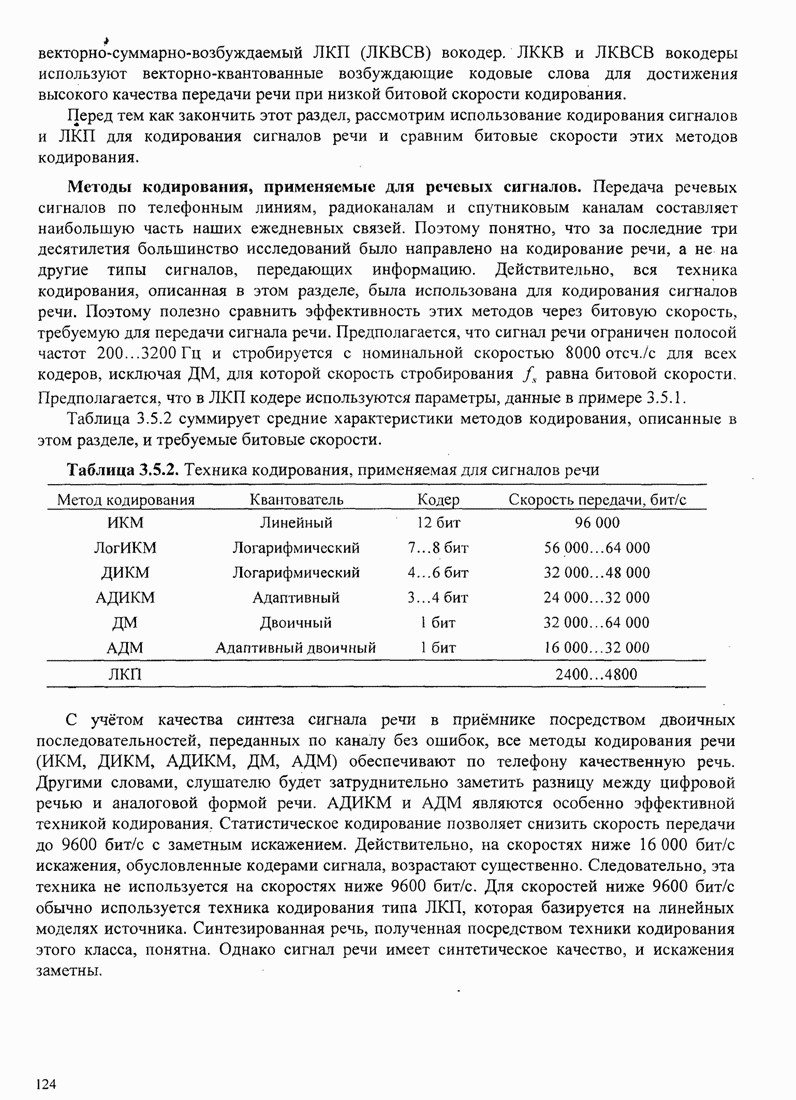
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
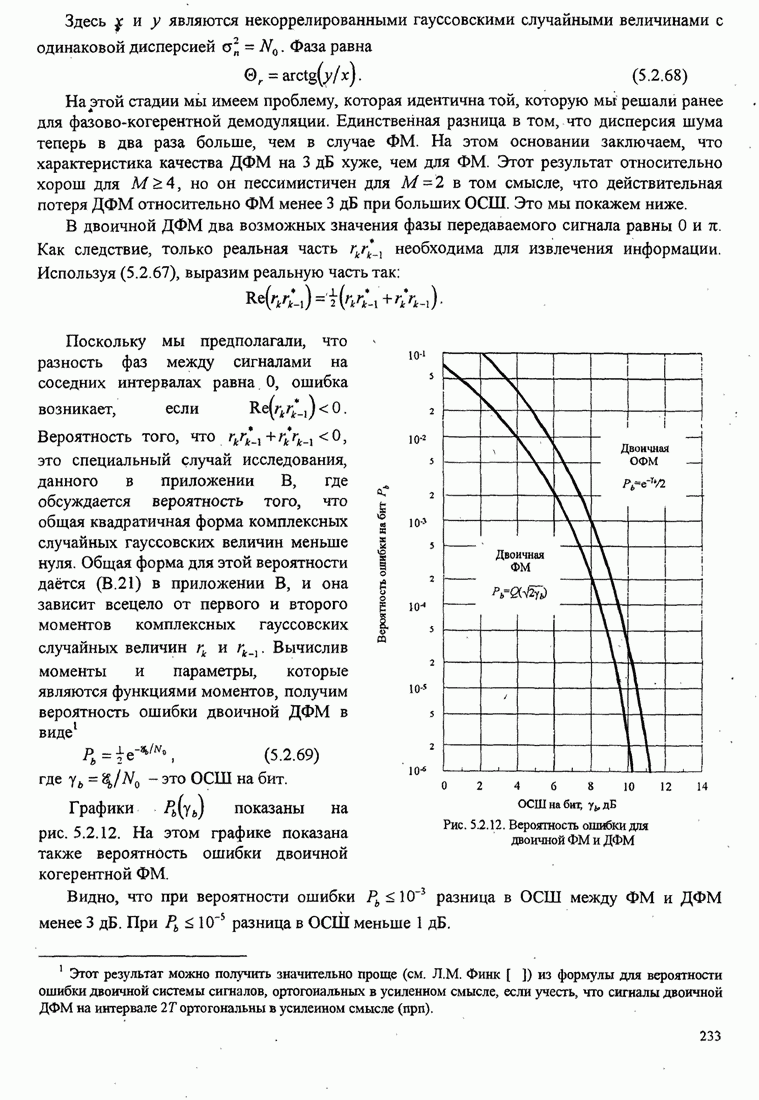
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
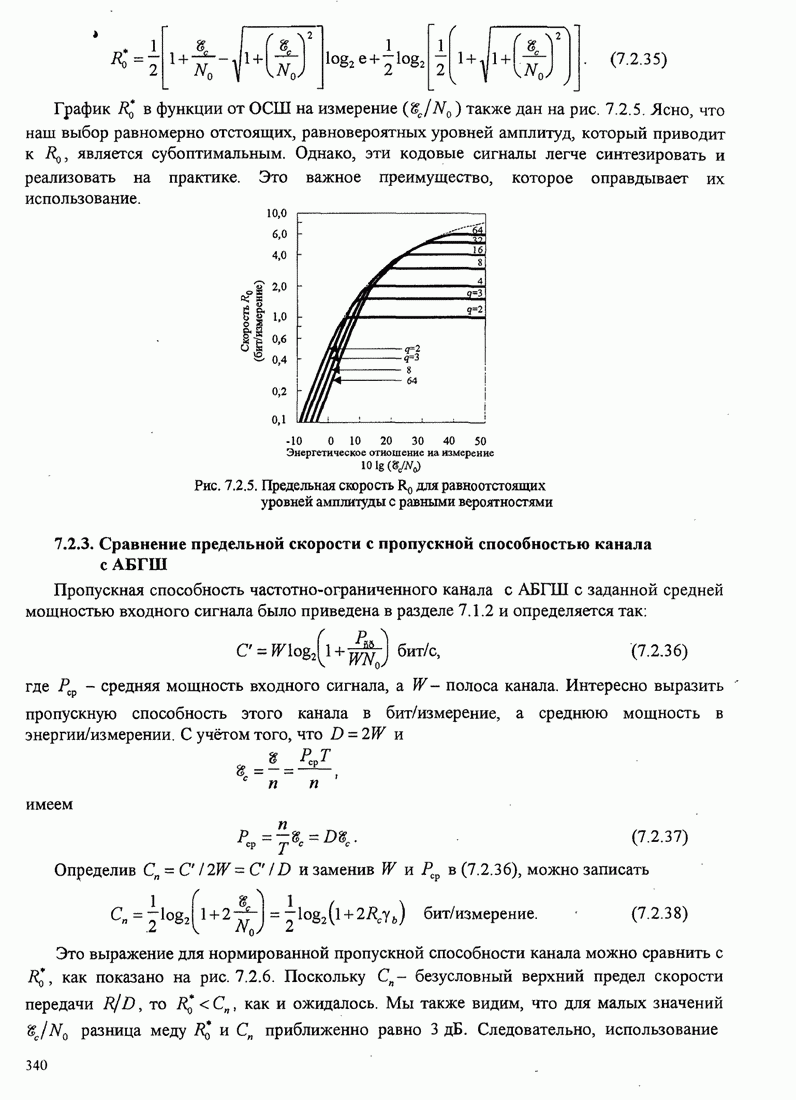
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
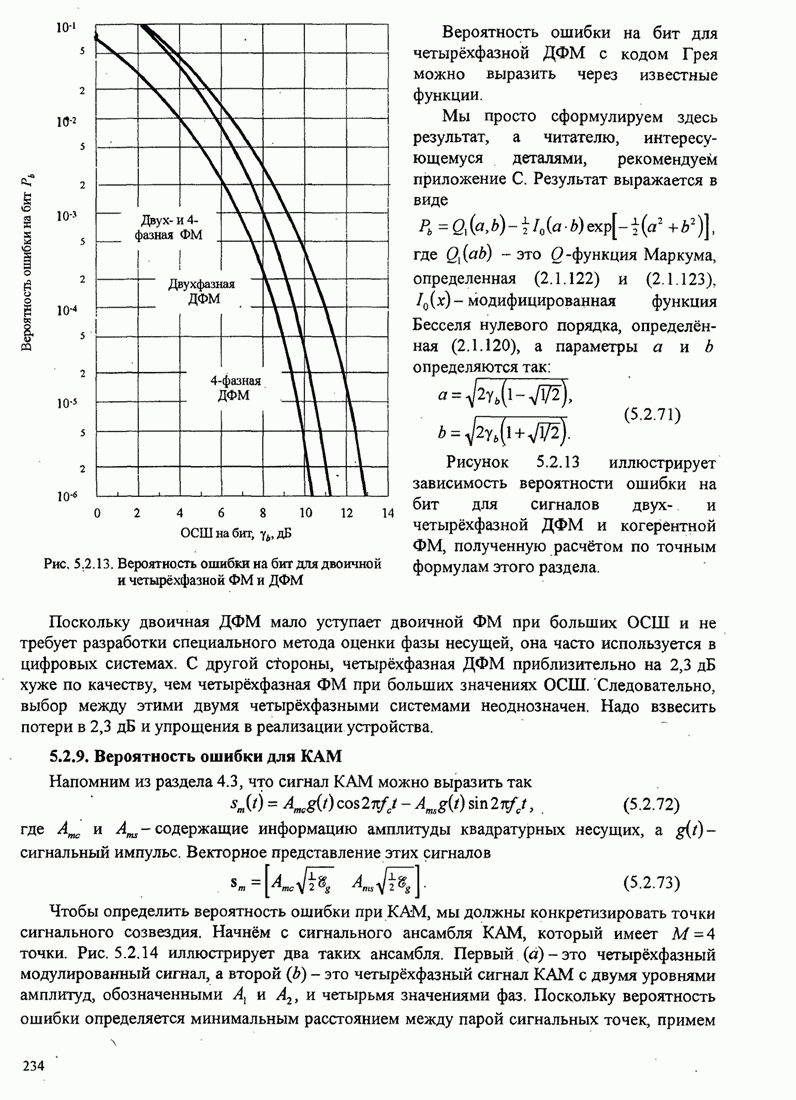
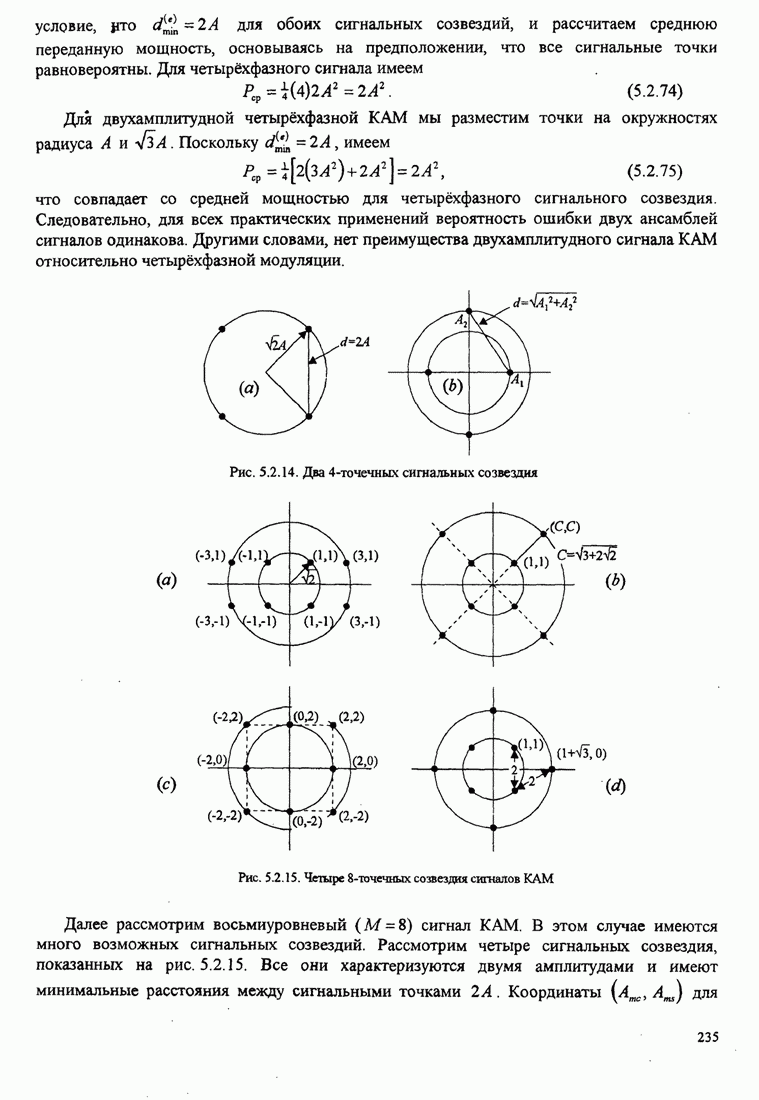
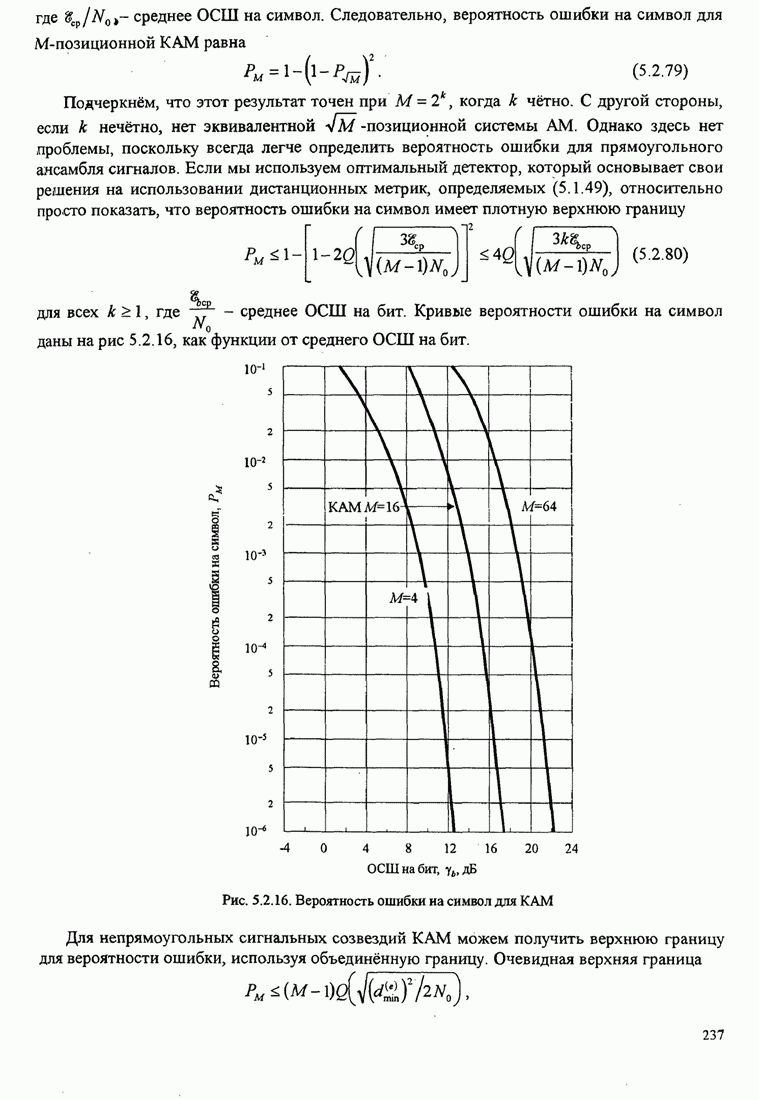
- 5.2.9. Вероятность ошибки для КАМ
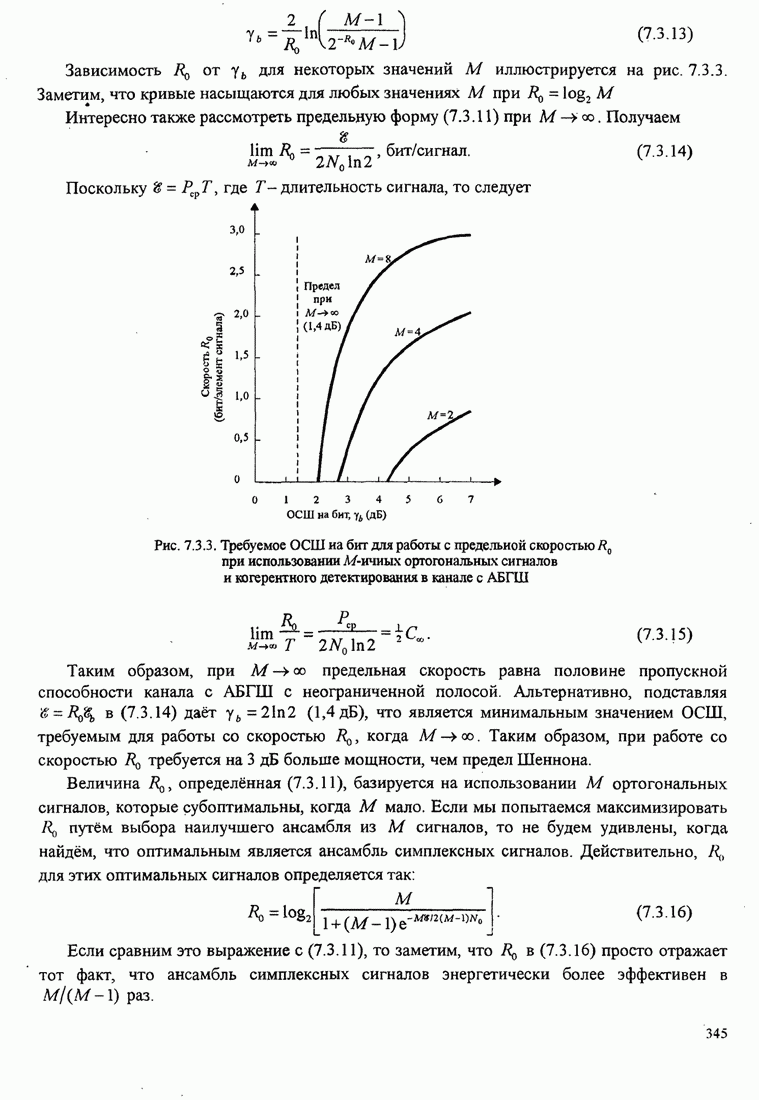
- 5.2.10. Сравнение цифровых методов модуляции
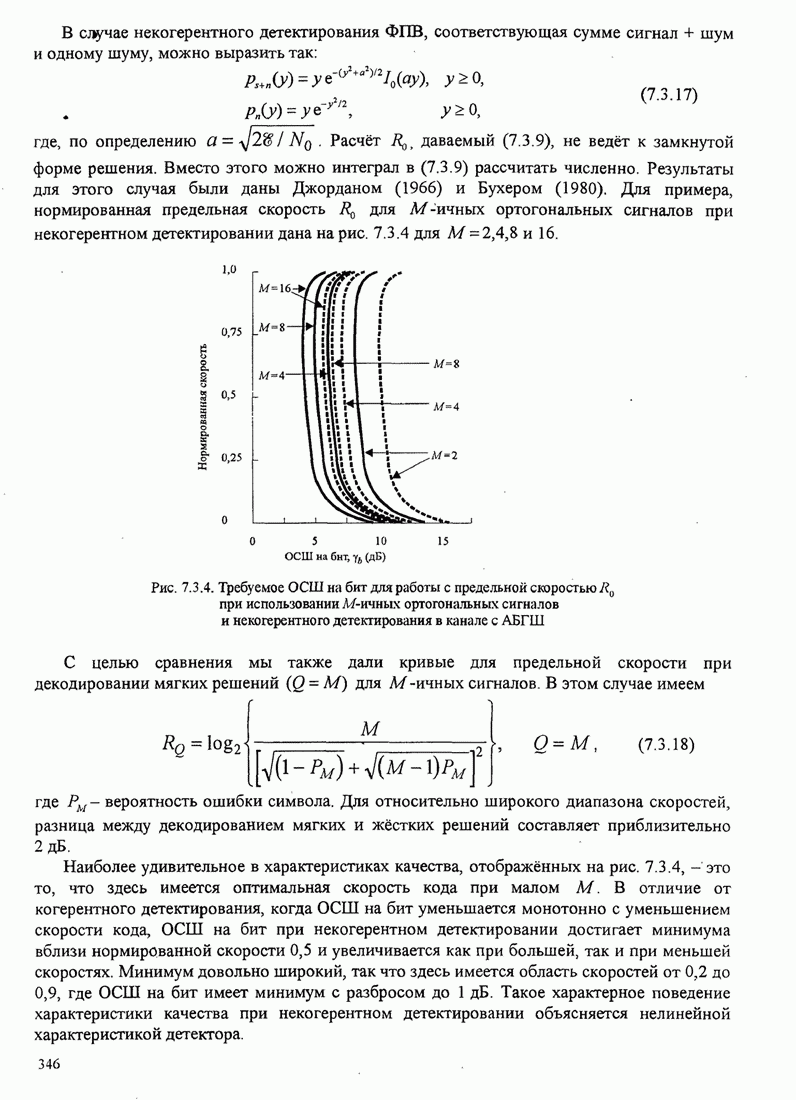
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
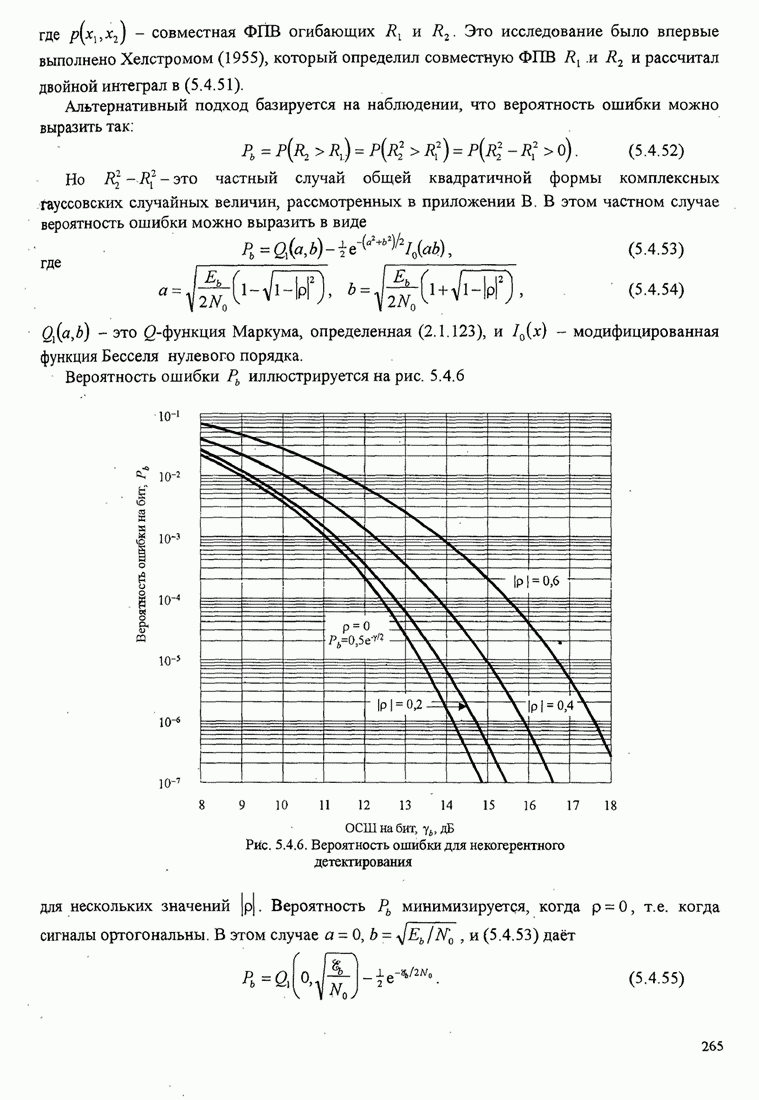
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
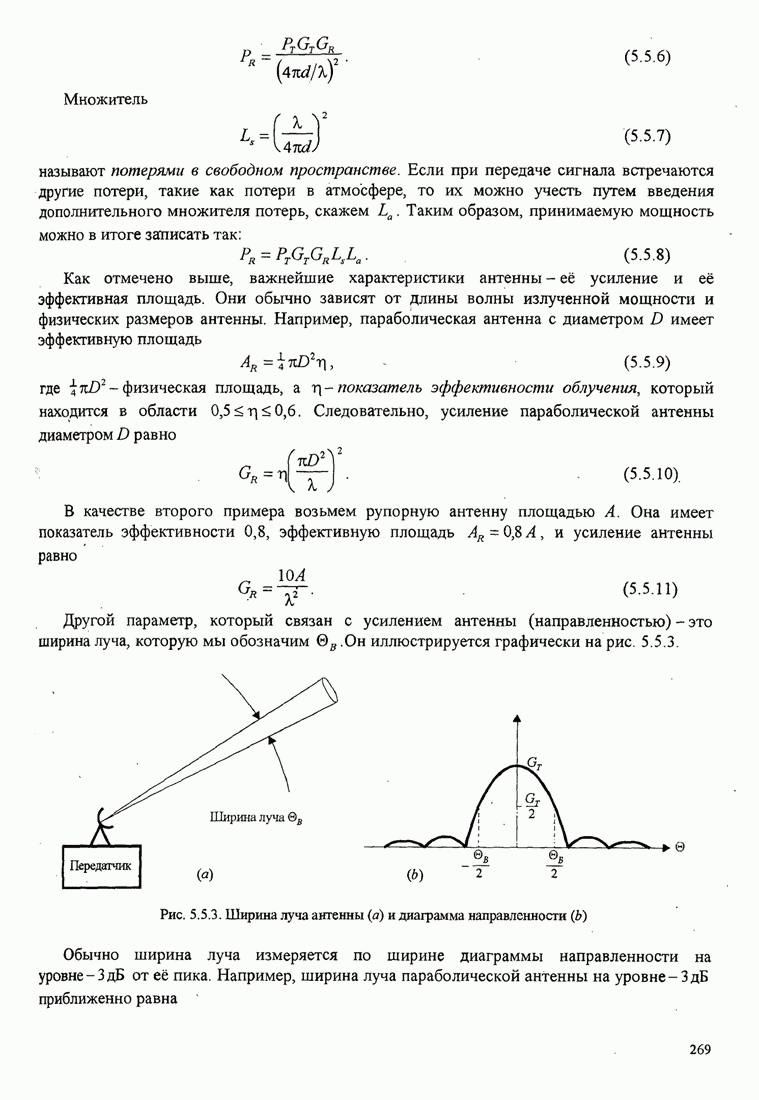
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
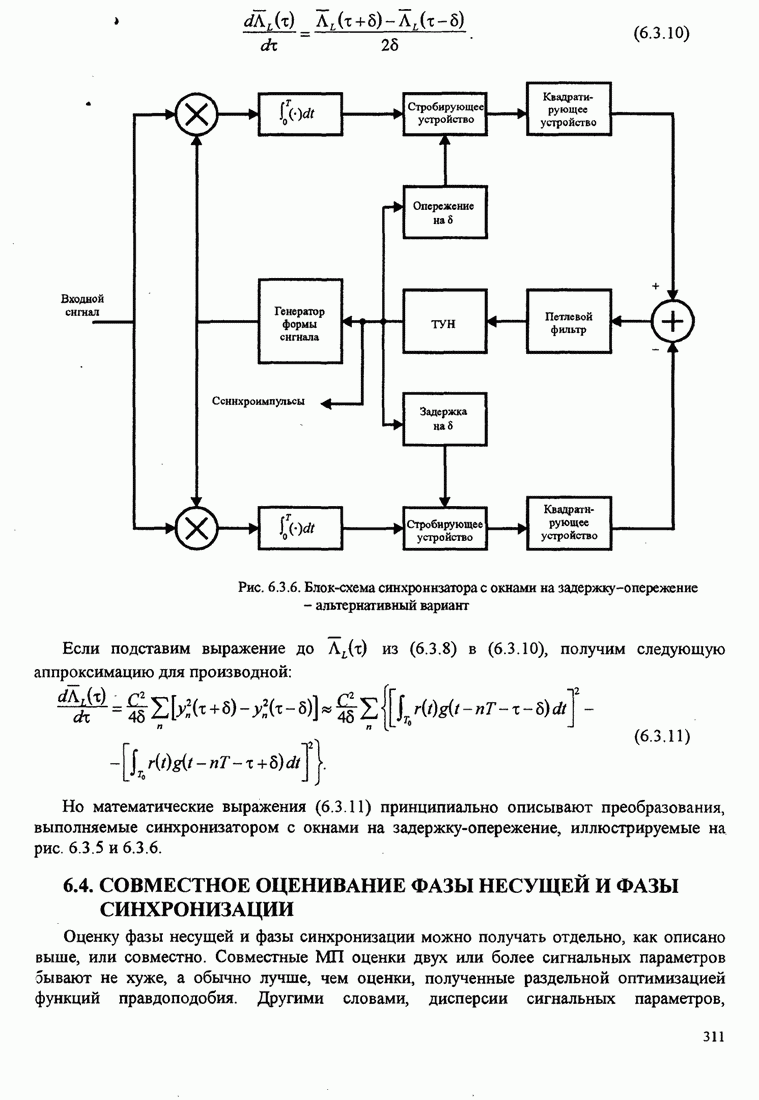
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
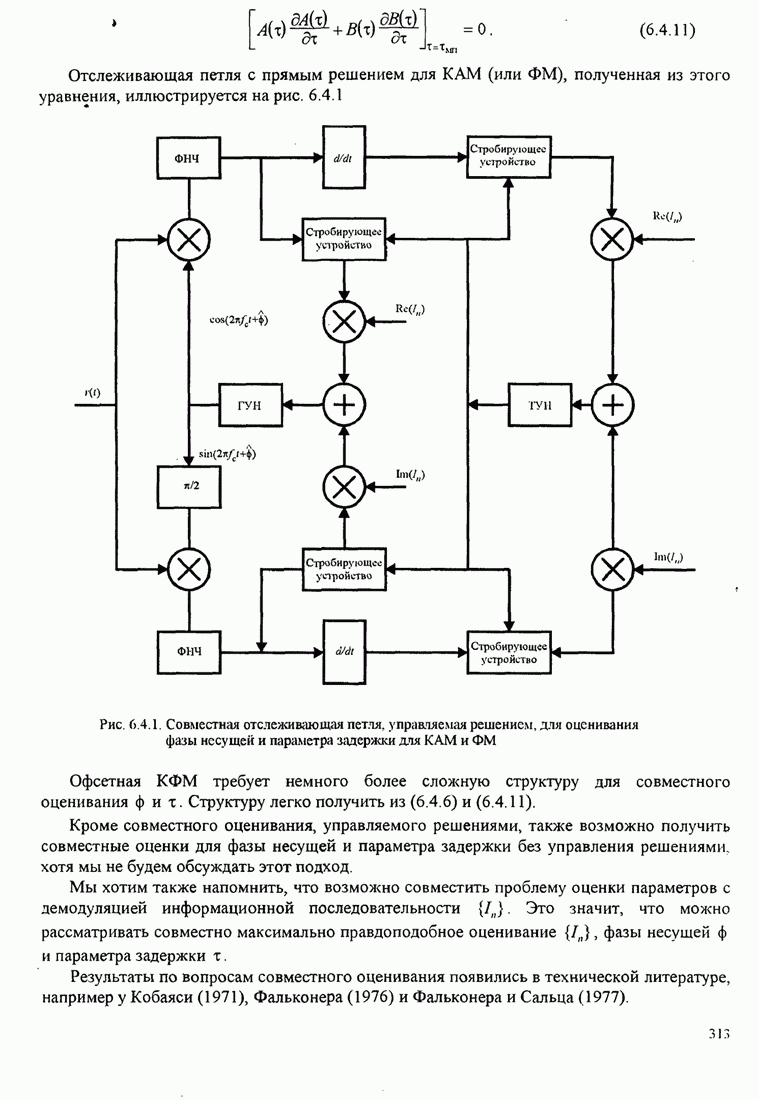
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
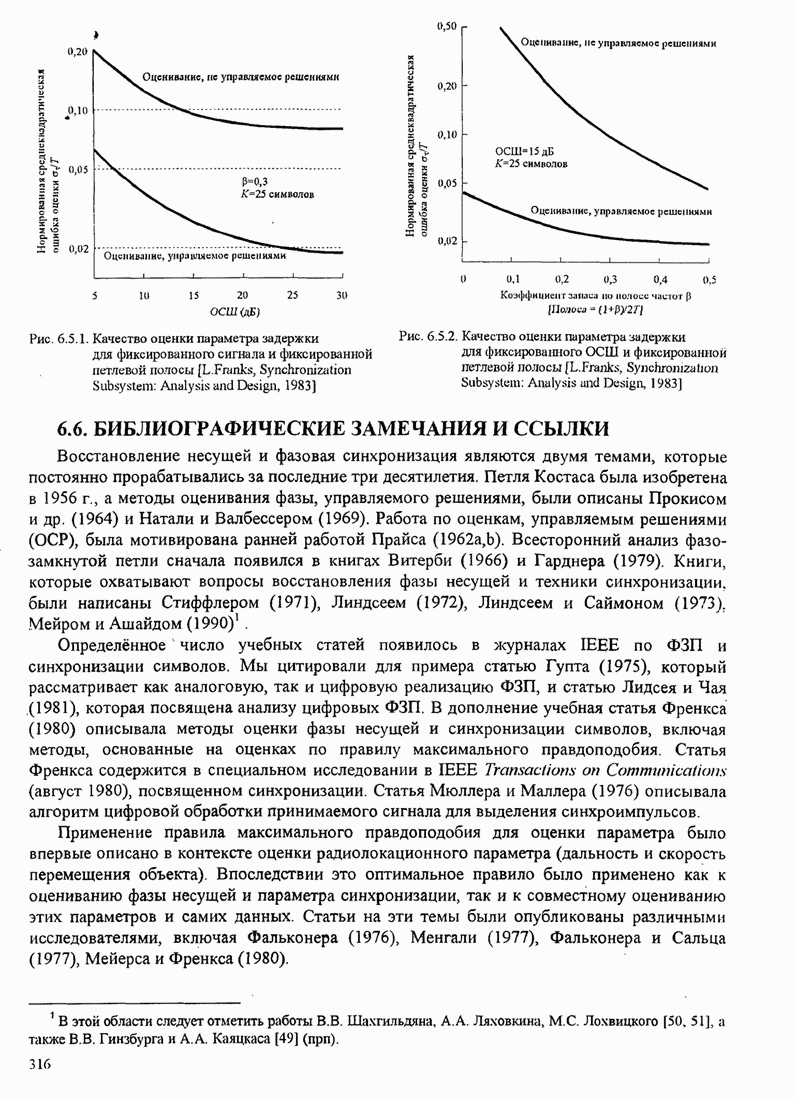
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
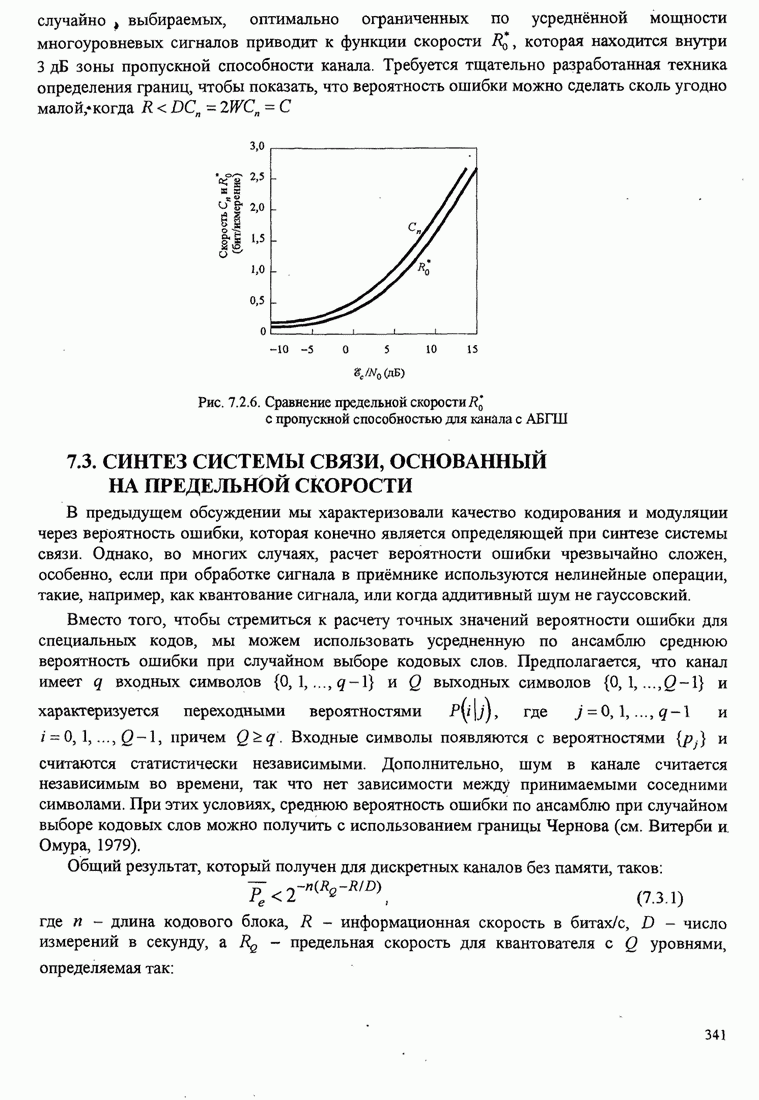
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
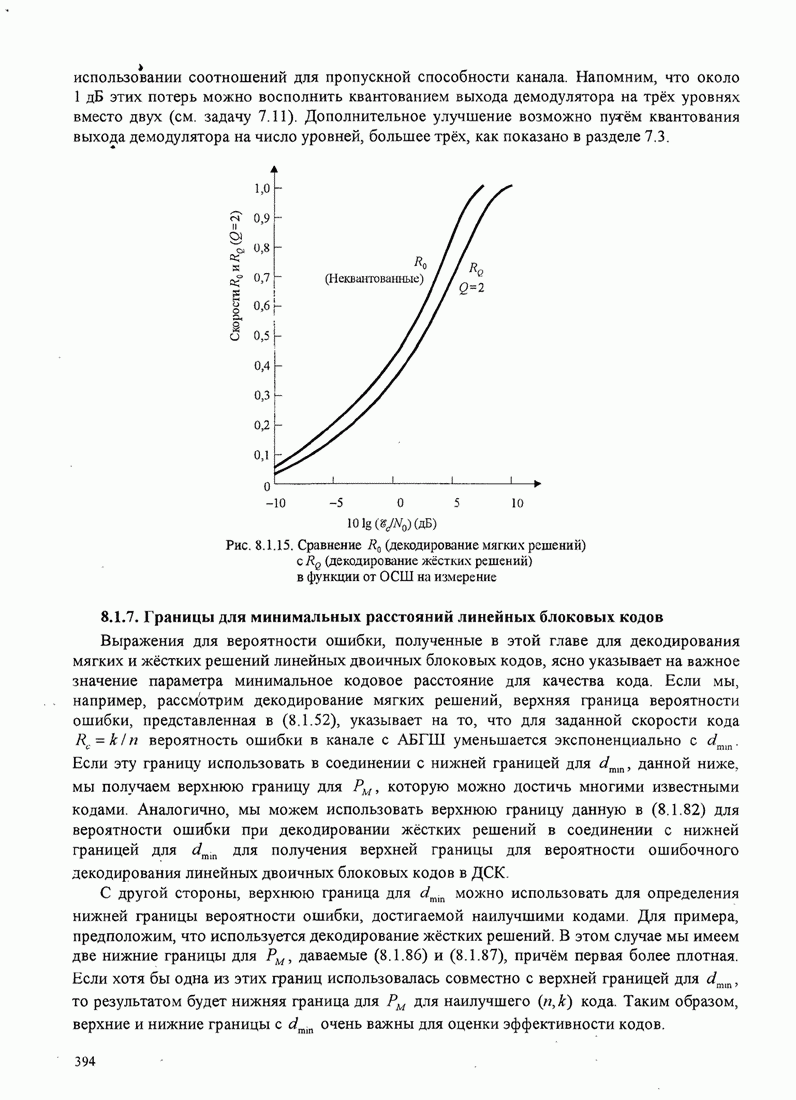
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
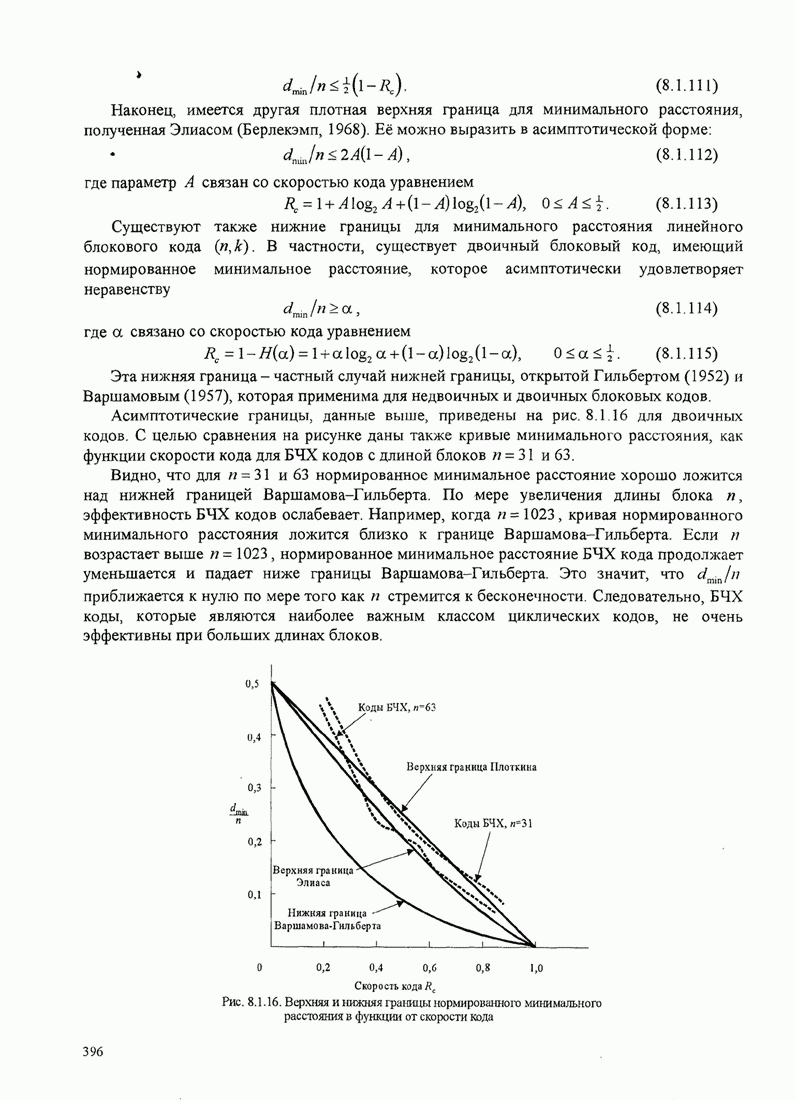
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
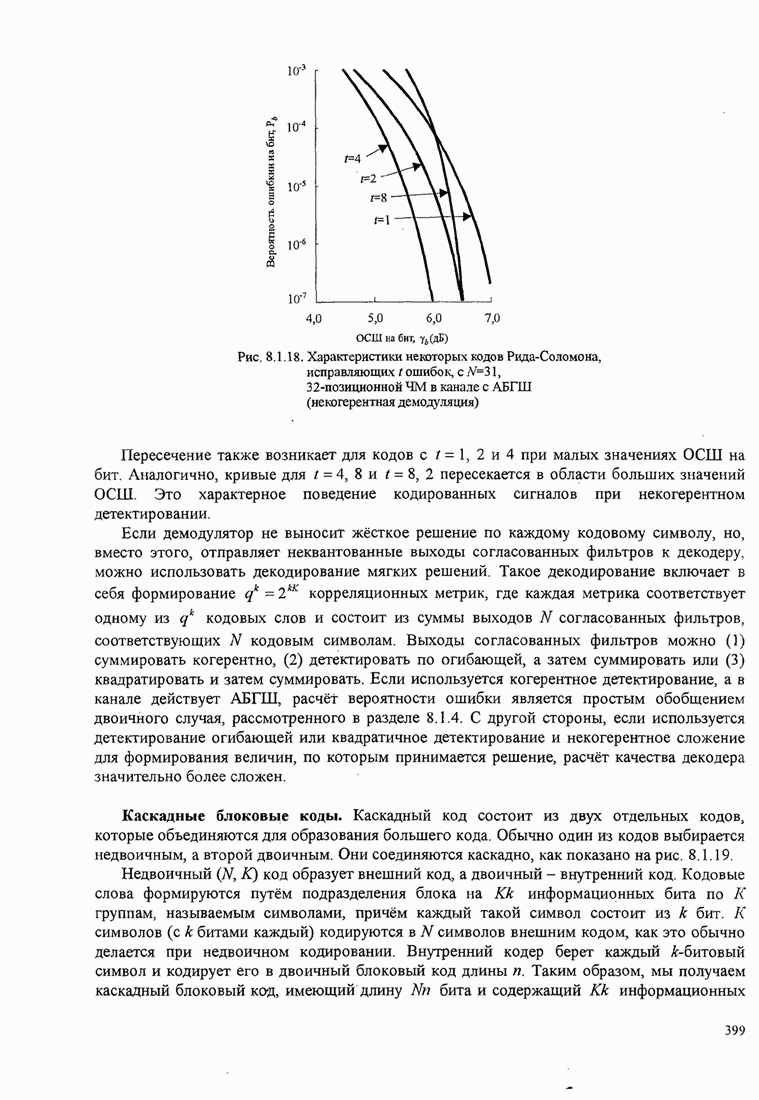
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
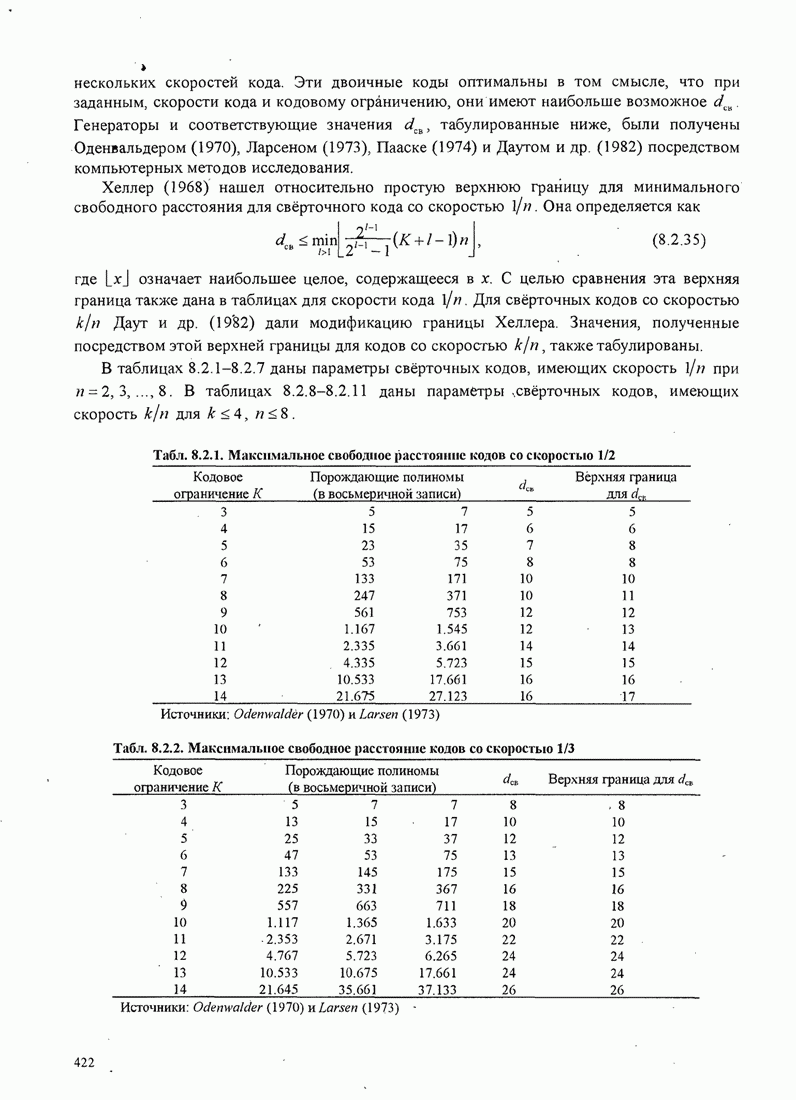
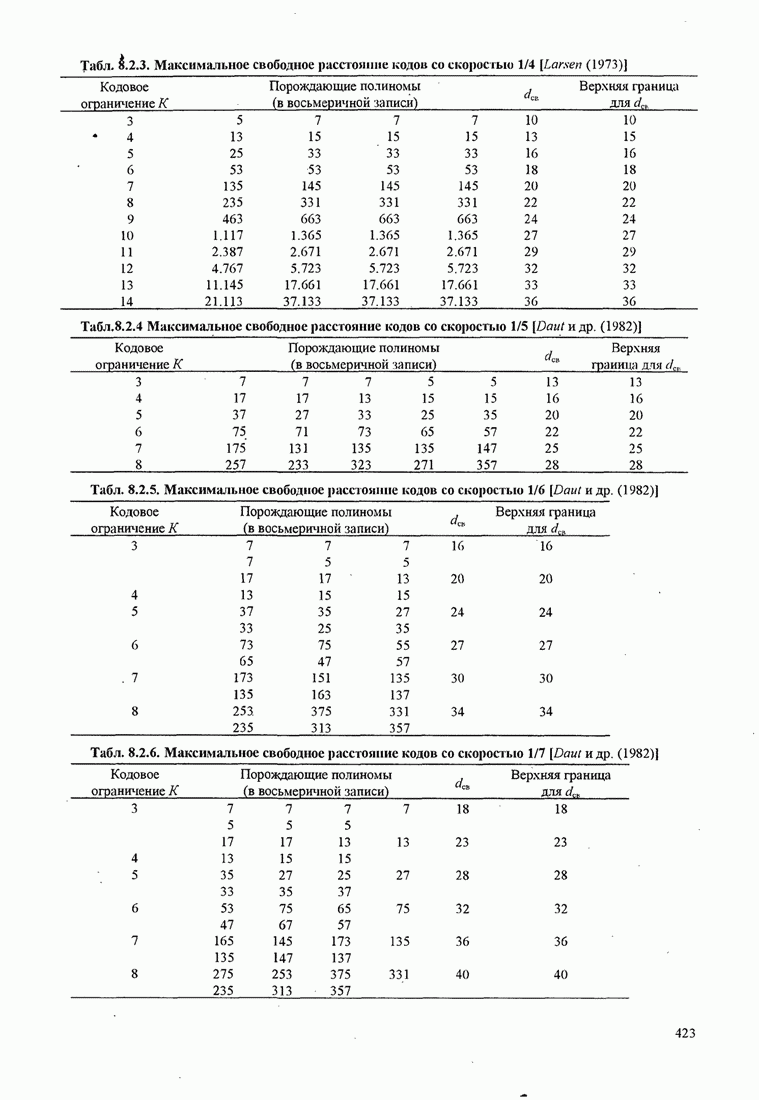
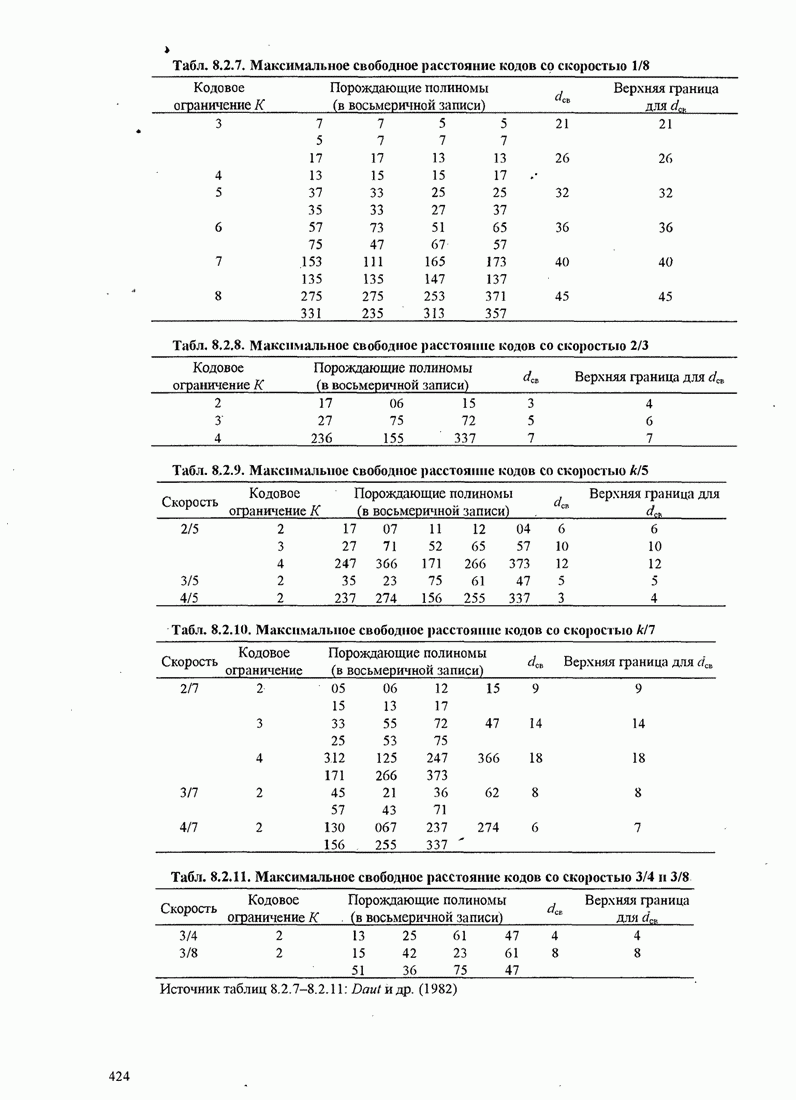
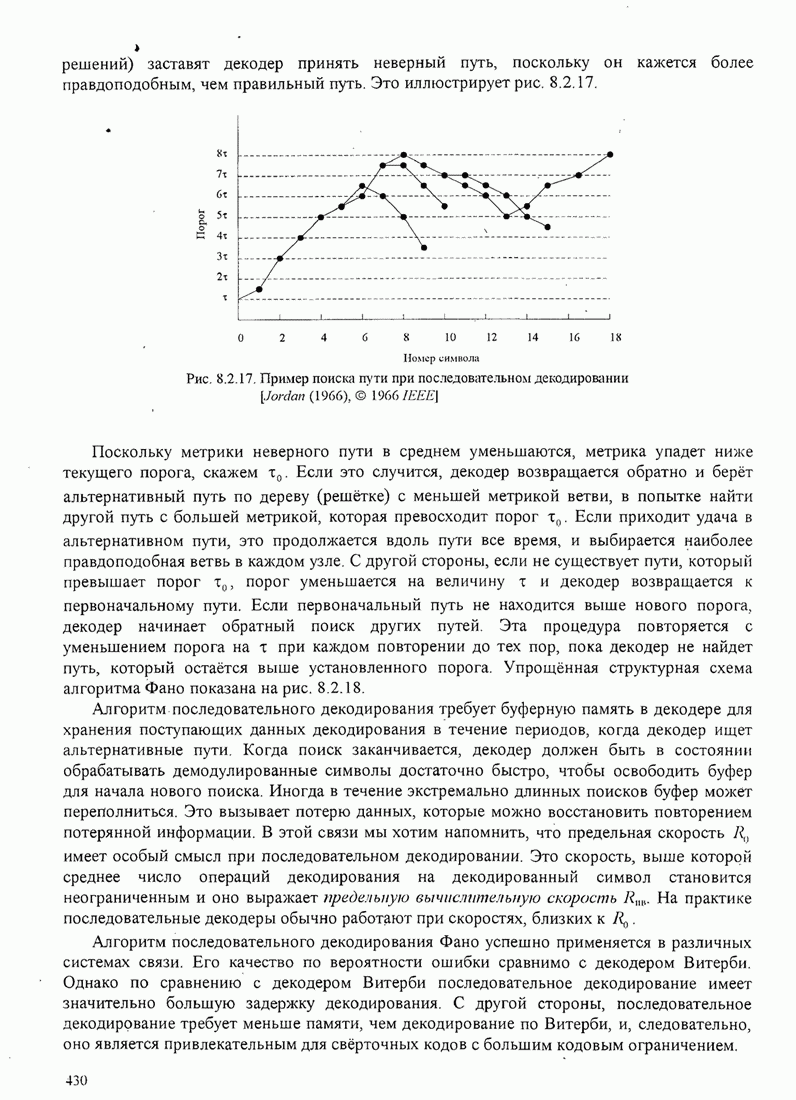
- 8.2. СВЁРТОЧНЫЕ КОДЫ
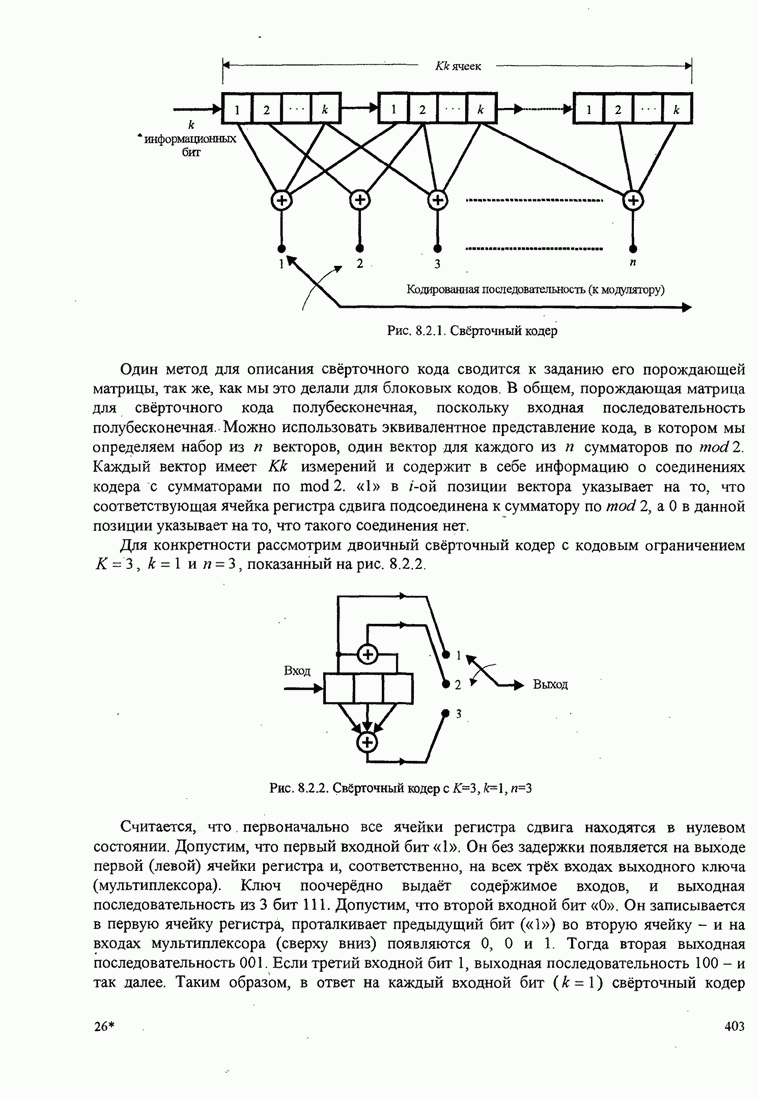
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
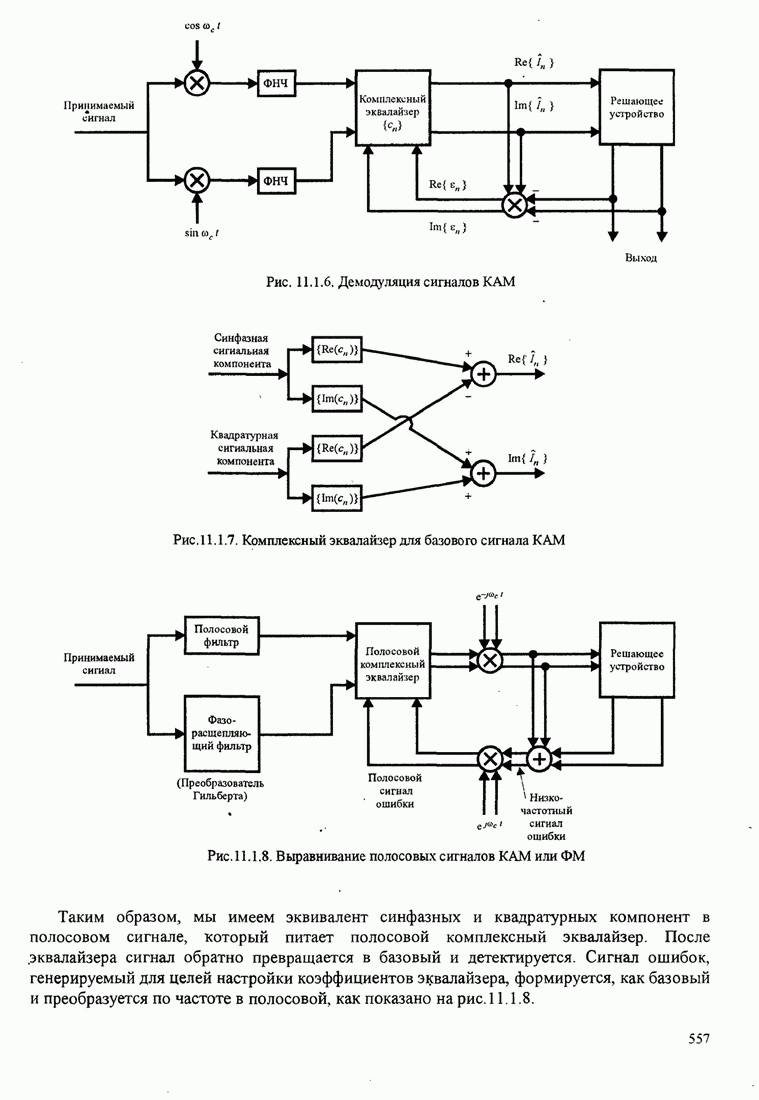
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
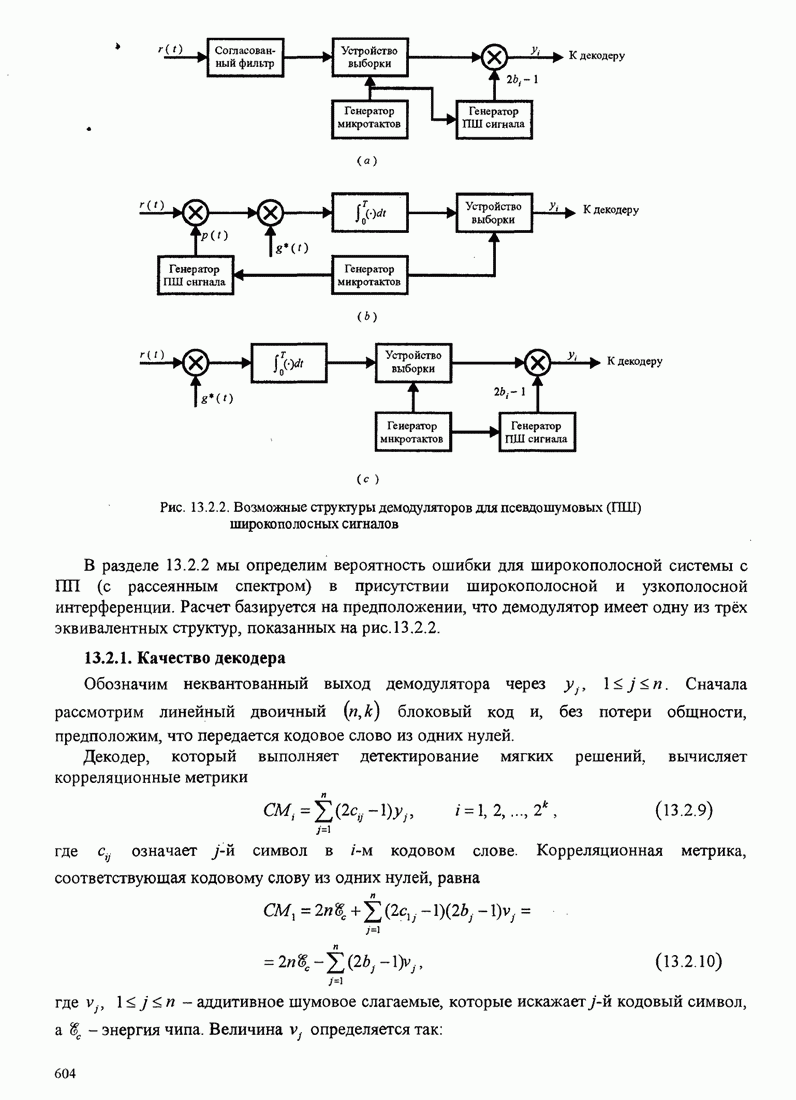
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
- 14.4.2. Многофазные сигналы
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)