| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
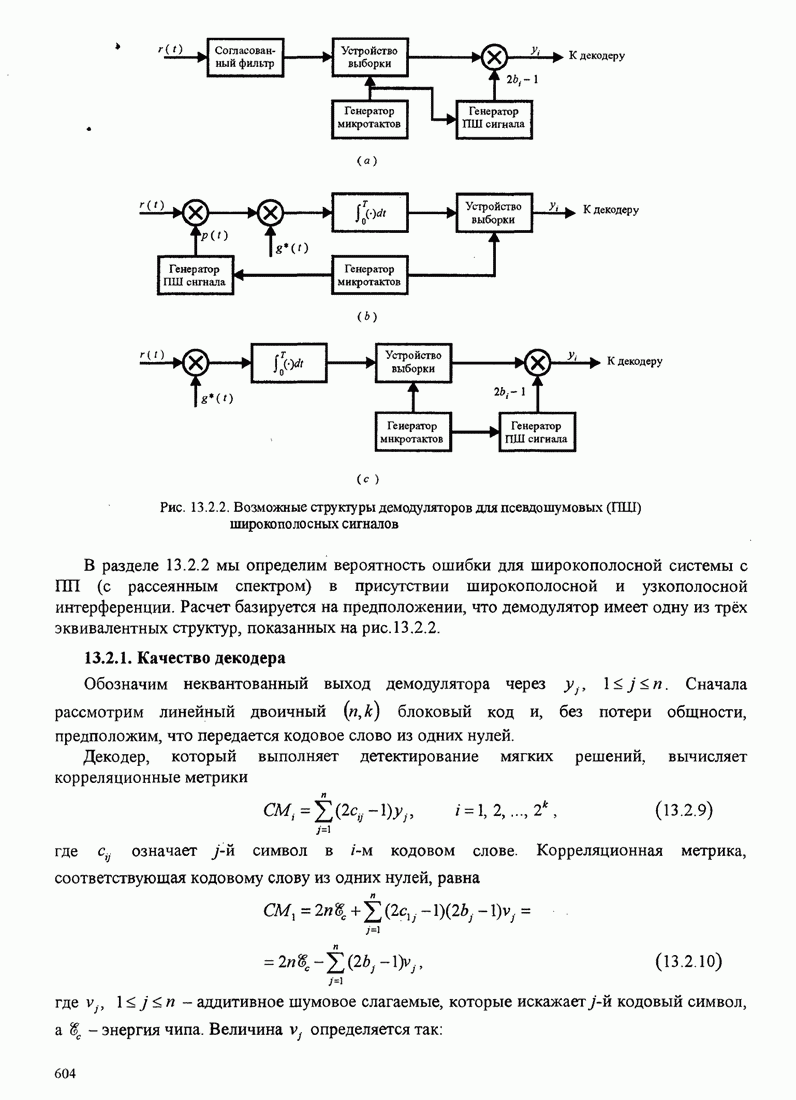
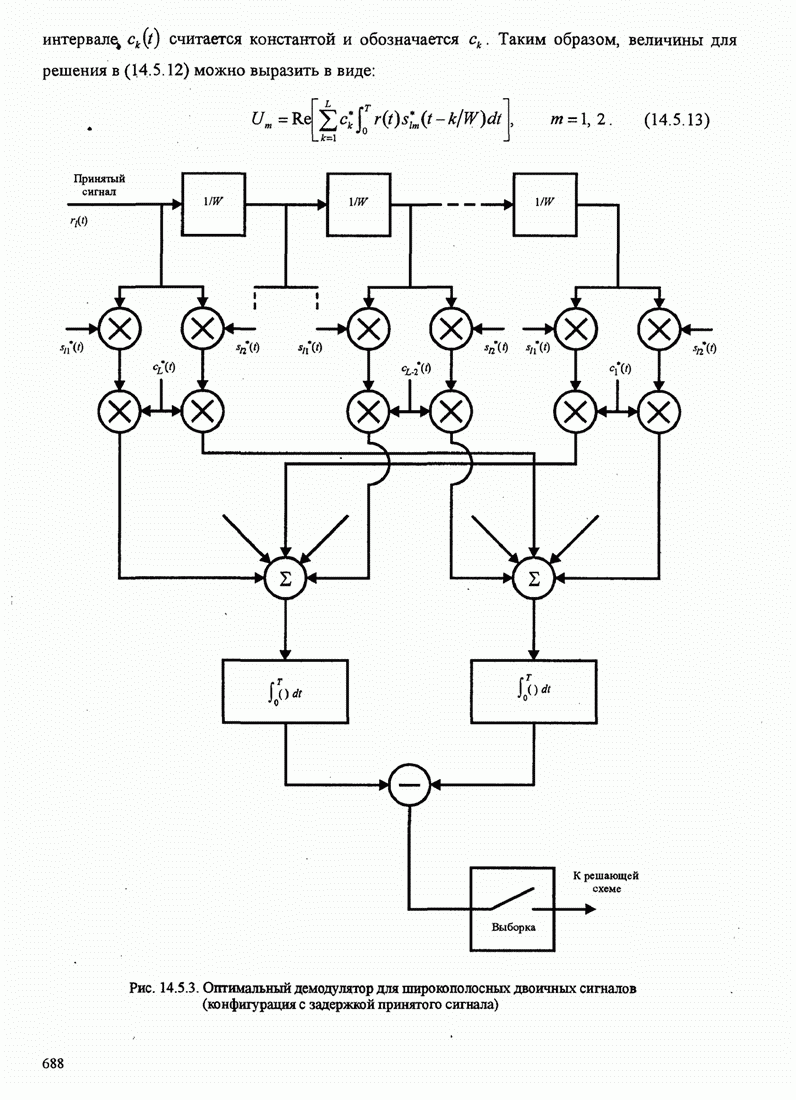
15.3.2. Оптимальный приёмник
Оптимальный
приёмник определяется как приемник, который выбирает наиболее правдоподобную последовательность
символов ![]() по
принимаемому сигналу
по
принимаемому сигналу ![]() , наблюдаемому на интервале
, наблюдаемому на интервале ![]() . Сначала мы
рассмотрим случай синхронной передачи; позже мы рассмотрим асинхронную
передачу.
. Сначала мы
рассмотрим случай синхронной передачи; позже мы рассмотрим асинхронную
передачу.
Синхронная
передача. При синхронной передаче каждый пользователь производит точно один
символ на сигнальном интервале рассматриваемого пользователя. При белом
гауссовском шуме в канале достаточно рассмотреть принимаемый сигнал на одном
сигнальном интервале, ![]() и определять оптимальный
приемник. Таким образом
и определять оптимальный
приемник. Таким образом ![]() можно выразить так
можно выразить так
![]() , (15.3.9)
, (15.3.9)
Оптимальный максимально правдоподобный приёмник вычисляет функцию правдоподобия
 (15.3.10)
(15.3.10)
и выбирает информационную
последовательность ![]() , которая минимизирует
, которая минимизирует ![]() . Если мы раскроем
интеграл в 15.3.10, то получим
. Если мы раскроем
интеграл в 15.3.10, то получим
 (15.3.11)
(15.3.11)
Видим, что
интеграл от ![]() является
общим для всех возможных последовательностей
является
общим для всех возможных последовательностей ![]() и он не влияет в определении
того, какая последовательность передана. Следовательно его можно упустить.
Слагаемое
и он не влияет в определении
того, какая последовательность передана. Следовательно его можно упустить.
Слагаемое
![]() (15.3.12)
(15.3.12)
представляет
собой взаимную корреляцию принимаемого сигнала с каждым из ![]() адресными
последовательностями. Вместо взаимных корреляторов мы можем использовать
согласованные фильтры. Наконец интеграл, включающий
адресными
последовательностями. Вместо взаимных корреляторов мы можем использовать
согласованные фильтры. Наконец интеграл, включающий ![]() и
и ![]() даёт
даёт
![]() .
(15.3.13)
.
(15.3.13)
Следовательно, (15.3.11) можно выразить в форме корреляционных метрик
 , (15.3.14)
, (15.3.14)
Эти корреляционные метрики можно также выразить в векторной форме
![]() ,
(15.3.15)
,
(15.3.15)
где
![]() ,
,
и ![]() - матрица
корреляции с элементами
- матрица
корреляции с элементами ![]() . Видно, что оптимальный
детектор должен знать энергии принимаемых сигналов для расчёта корреляционных
метрик.
. Видно, что оптимальный
детектор должен знать энергии принимаемых сигналов для расчёта корреляционных
метрик.
Имеется ![]() возможных выборов
символов в информационных последовательностях
возможных выборов
символов в информационных последовательностях ![]() пользователей. Оптимальный детектор
вычисляет корреляционные метрики для каждой возможной последовательности и
выбирает последовательность, которая имеет наибольшую корреляционную метрику.
Видно, что оптимальный детектор имеет сложность, которая растёт экспоненциально
с числом пользователей
пользователей. Оптимальный детектор
вычисляет корреляционные метрики для каждой возможной последовательности и
выбирает последовательность, которая имеет наибольшую корреляционную метрику.
Видно, что оптимальный детектор имеет сложность, которая растёт экспоненциально
с числом пользователей ![]() .
.
В целом
оптимальный приёмник при синхронной передаче символов состоит из банка из ![]() корреляторов или
согласованных фильтров, за ними детектор, который вычисляет
корреляторов или
согласованных фильтров, за ними детектор, который вычисляет ![]() корреляционных метрик,
определяемых (15.3.15), соответствующих
корреляционных метрик,
определяемых (15.3.15), соответствующих ![]() возможным передаваемым информационным
последовательностям. Затем детектор выбирает последовательность,
соответствующую, наибольшей корреляционной метрике.
возможным передаваемым информационным
последовательностям. Затем детектор выбирает последовательность,
соответствующую, наибольшей корреляционной метрике.
Асинхронная
передача. В этом случае имеются точно два соседних символа от каждого
пользователя, которые перекрывают символ на сигнальном интервале
рассматриваемого пользователя. Мы предполагаем, что приёмник знает энергии
принимаемых символов ![]() для
для ![]() пользователей и задержки
передачи
пользователей и задержки
передачи ![]() .
Ясно, что эти параметры должны быть измерены на приёме или переданы приёмнику
как сторонняя информация от пользователей посредством некоторого сигнала
управления.
.
Ясно, что эти параметры должны быть измерены на приёме или переданы приёмнику
как сторонняя информация от пользователей посредством некоторого сигнала
управления.
Оптимальный максимально правдоподобный приёмник вычисляет функцию правдоподобия
 (15.3.16)
(15.3.16)
где b представляет последовательность данных от ![]() пользователей.
Интеграл от
пользователей.
Интеграл от ![]() можно
упустить поскольку он общий для всех возможных последовательностей. Интеграл
можно
упустить поскольку он общий для всех возможных последовательностей. Интеграл
![]() (15.3.17)
(15.3.17)
представляет
выход коррелятора или согласованного фильтра для ![]() -го пользователя на каждом сигнальном
интервале. Наконец, интеграл
-го пользователя на каждом сигнальном
интервале. Наконец, интеграл
![]() (15.3.18)
(15.3.18)
можно легко
разложить на слагаемые, включающие взаимную корреляцию ![]() , для
, для ![]() и
и ![]() для
для ![]() . Следовательно, мы видим
что функция правдоподобия можно выразить через слагаемые корреляционных метрик,
которые включают выходы
. Следовательно, мы видим
что функция правдоподобия можно выразить через слагаемые корреляционных метрик,
которые включают выходы ![]()
![]() корреляторов или согласованных
фильтров - один для каждой из
корреляторов или согласованных
фильтров - один для каждой из ![]() адресных последовательностей.
Используя векторные обозначения, можно показать, что выходы
адресных последовательностей.
Используя векторные обозначения, можно показать, что выходы ![]() корреляторов или
согласованных фильтров -
корреляторов или
согласованных фильтров - ![]() можно выразить в форме
можно выразить в форме
![]() (15.3.19)
(15.3.19)
где по определению
 (15.3.20)
(15.3.20)
 (15.3.21)
(15.3.21)
 (15.3.22)
(15.3.22)
 , (15.3.23)
, (15.3.23)
a ![]() - матрица размером
- матрица размером ![]() с элементами
с элементами
![]() (15.3.24)
(15.3.24)
Векторы
гауссовского шума ![]() имеют нулевые средние и
автокорреляционную матрицу
имеют нулевые средние и
автокорреляционную матрицу
![]() (15.3.25)
(15.3.25)
Заметим, что
вектор ![]() ,
определённый (15.3.19), образует достаточную статистику для оценивания
передаваемых символов
,
определённый (15.3.19), образует достаточную статистику для оценивания
передаваемых символов ![]() .
.
Если мы хотим
проследить схему обработки то оптимальный МП детектор должен вычислить ![]() корреляционных
метрик и выбрать
корреляционных
метрик и выбрать ![]() последовательностей
длины
последовательностей
длины ![]() , которые
соответствуют наибольшей корреляционной метрике. Ясно, что такой подход слишком
сложен в вычислительном отношении, чтобы быть реализуемом на практике, особенно,
когда
, которые
соответствуют наибольшей корреляционной метрике. Ясно, что такой подход слишком
сложен в вычислительном отношении, чтобы быть реализуемом на практике, особенно,
когда ![]() и
и ![]() велико. Альтернативный
подход - МП оценивание последовательностей, использующее алгоритм Витерби.
Чтобы сконструировать детектор последовательного типа, мы должны использовать
то обстоятельство, что каждый передаваемый символ перекрывается с
велико. Альтернативный
подход - МП оценивание последовательностей, использующее алгоритм Витерби.
Чтобы сконструировать детектор последовательного типа, мы должны использовать
то обстоятельство, что каждый передаваемый символ перекрывается с ![]() символами. Таким
образом, получается существенное уменьшение вычислительной сложности с учётом
параметра длины блока
символами. Таким
образом, получается существенное уменьшение вычислительной сложности с учётом
параметра длины блока ![]() , но экспоненциальная зависимость от
, но экспоненциальная зависимость от
![]() остается.
остается.
Важно, что
оптимальный МП приёмник, использующий алгоритм Витерби, предполагает такую
большую вычислительную сложность, что его использование на практике ограничено
системами связи, в которых число пользователей крайне мало, например ![]() . Для больших
значений
. Для больших
значений ![]() следует
рассматривать детектор последовательного типа, который схож или
последовательному детектированию, или стек алгоритмам, описанным в гл. 8. Ниже
мы рассмотрим некоторые субоптимальные детекторы, сложность которых растёт
линейно с
следует
рассматривать детектор последовательного типа, который схож или
последовательному детектированию, или стек алгоритмам, описанным в гл. 8. Ниже
мы рассмотрим некоторые субоптимальные детекторы, сложность которых растёт
линейно с ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
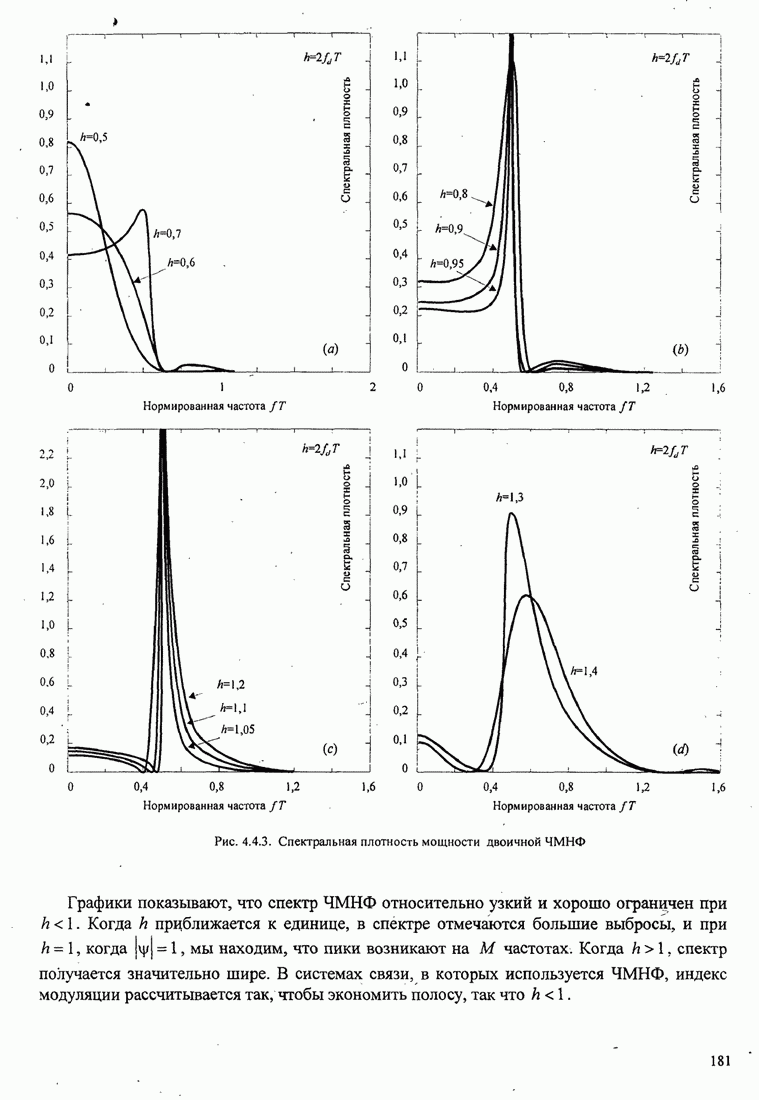
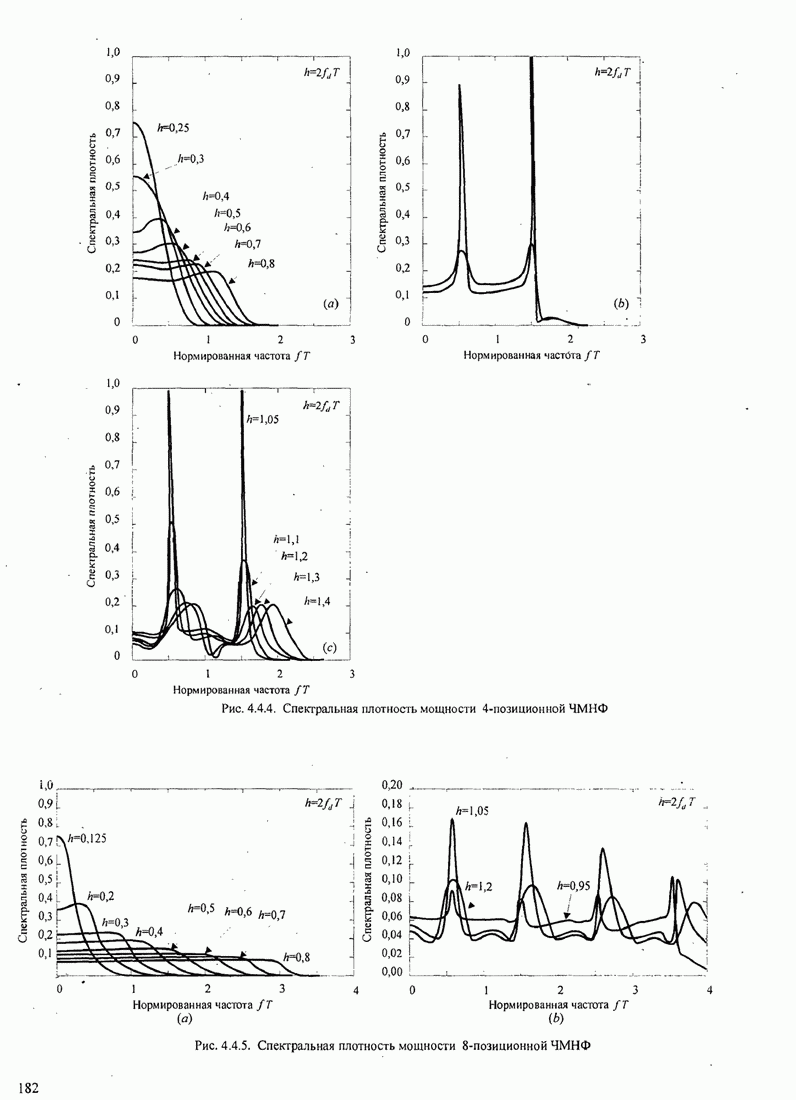
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
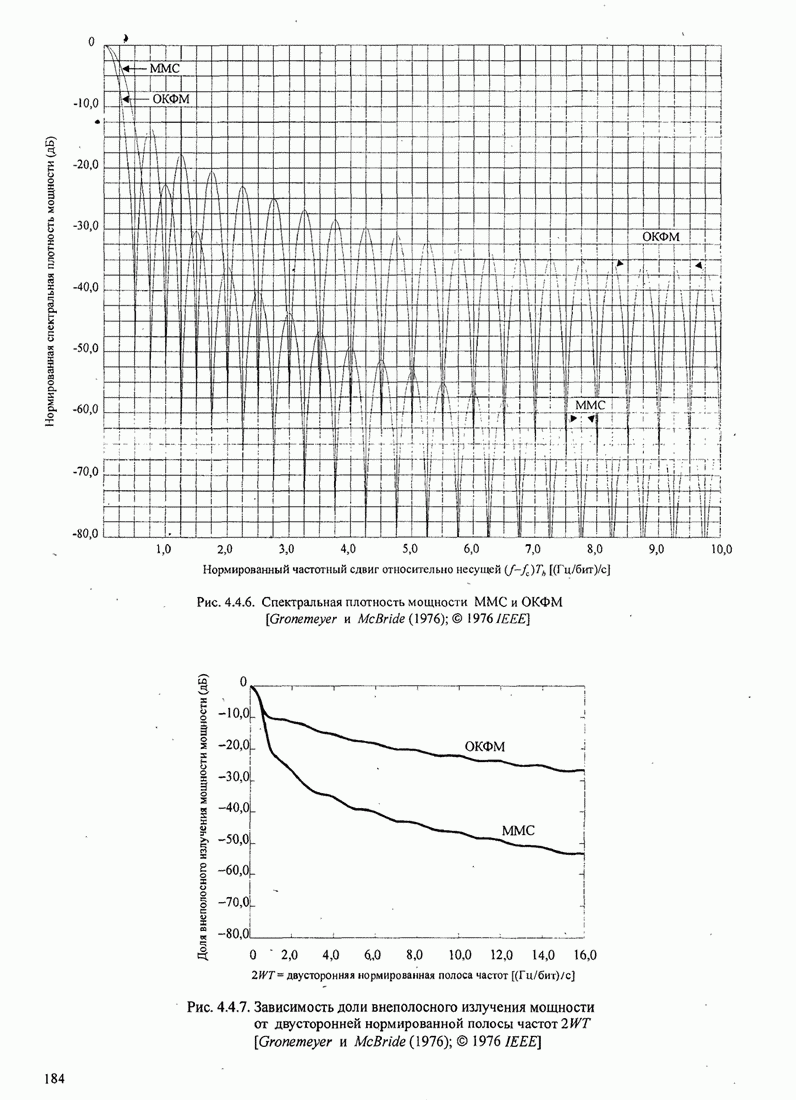
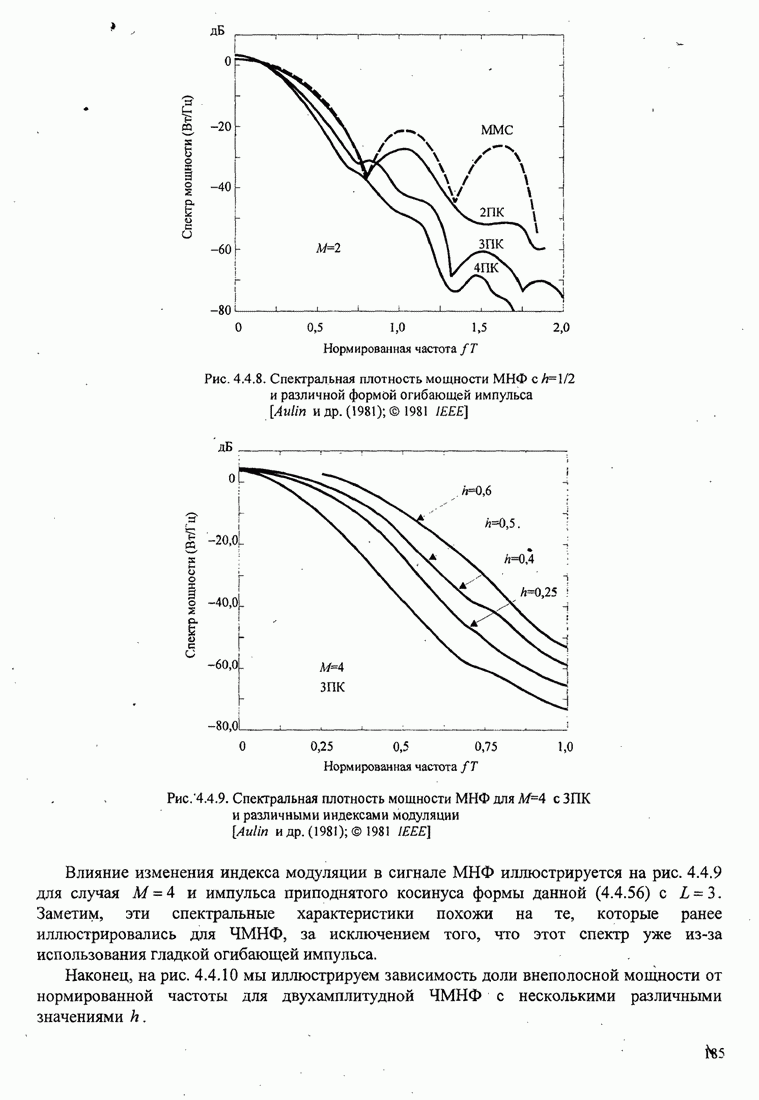
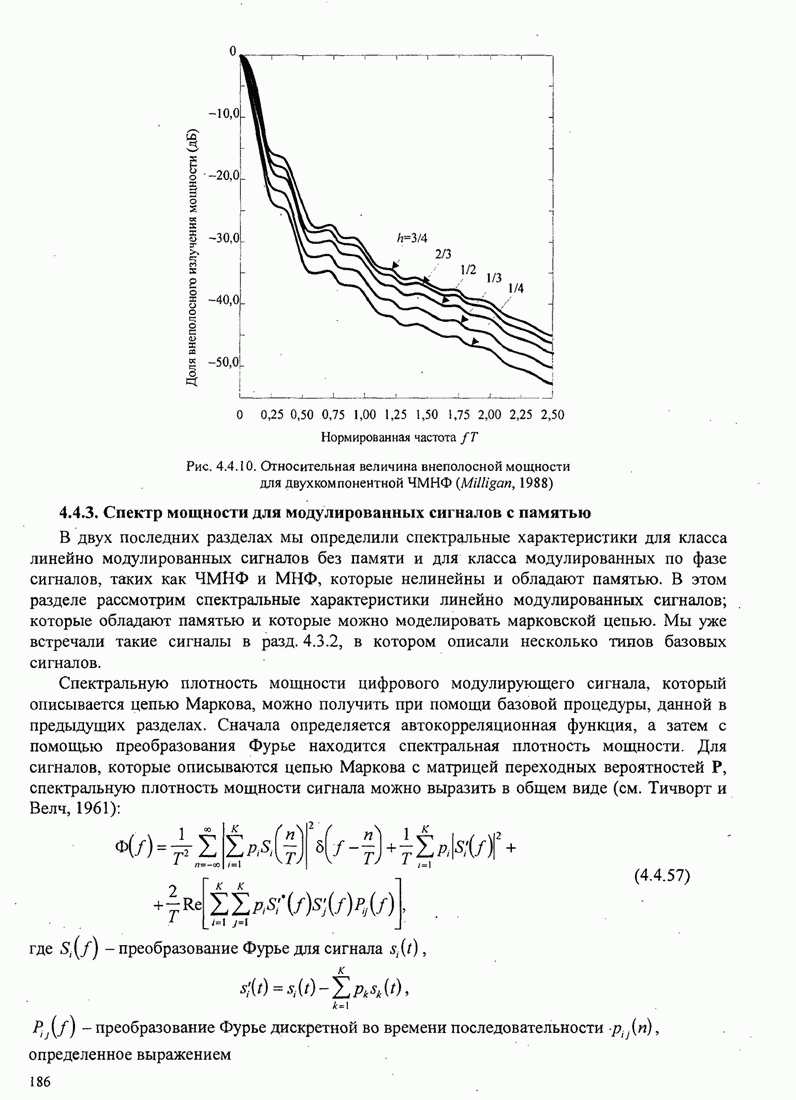
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
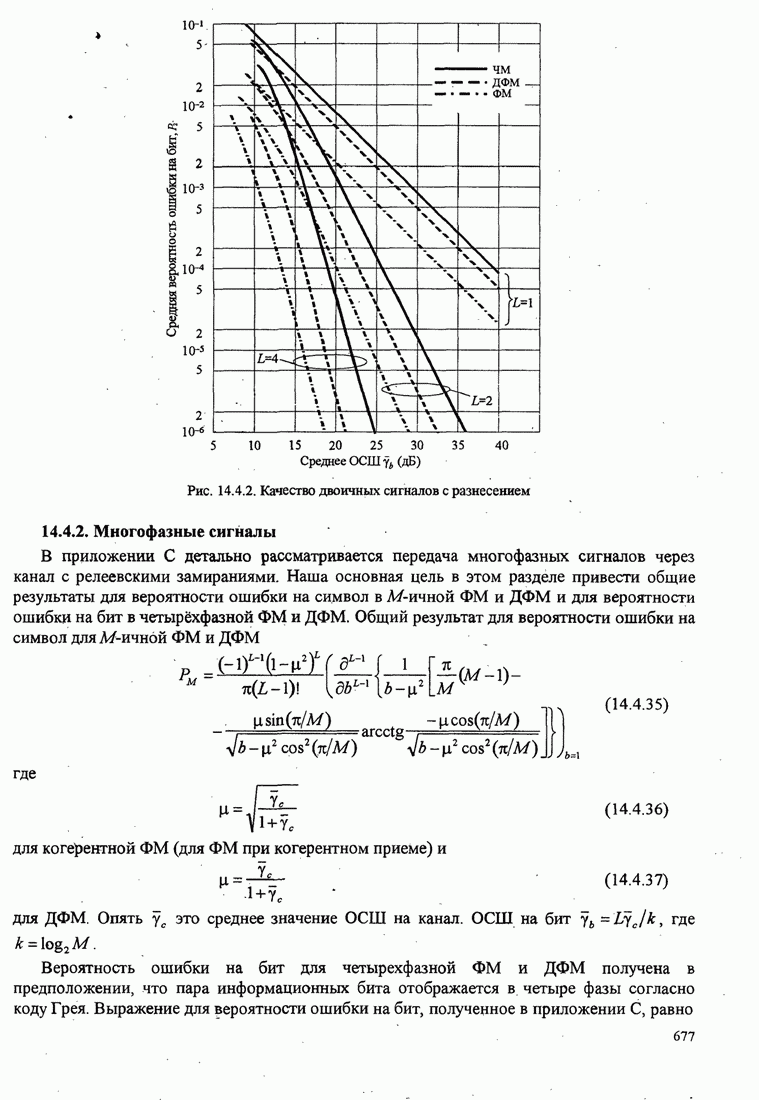
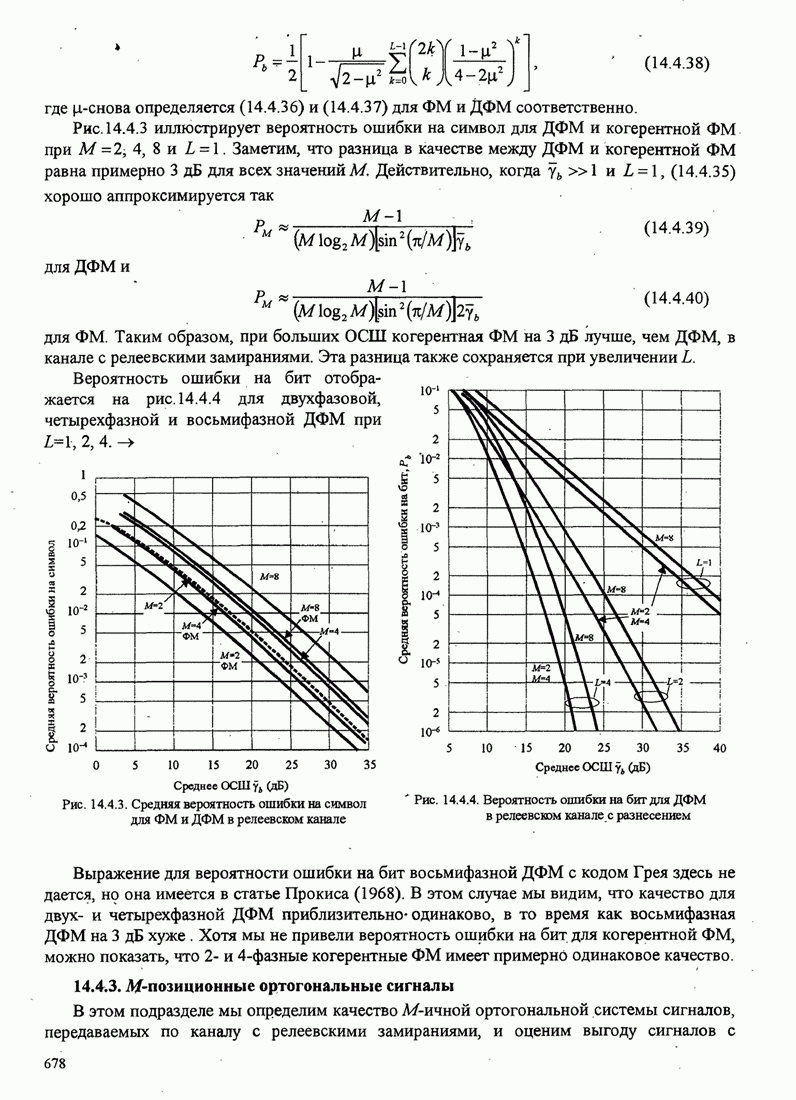
- 14.4.2. Многофазные сигналы
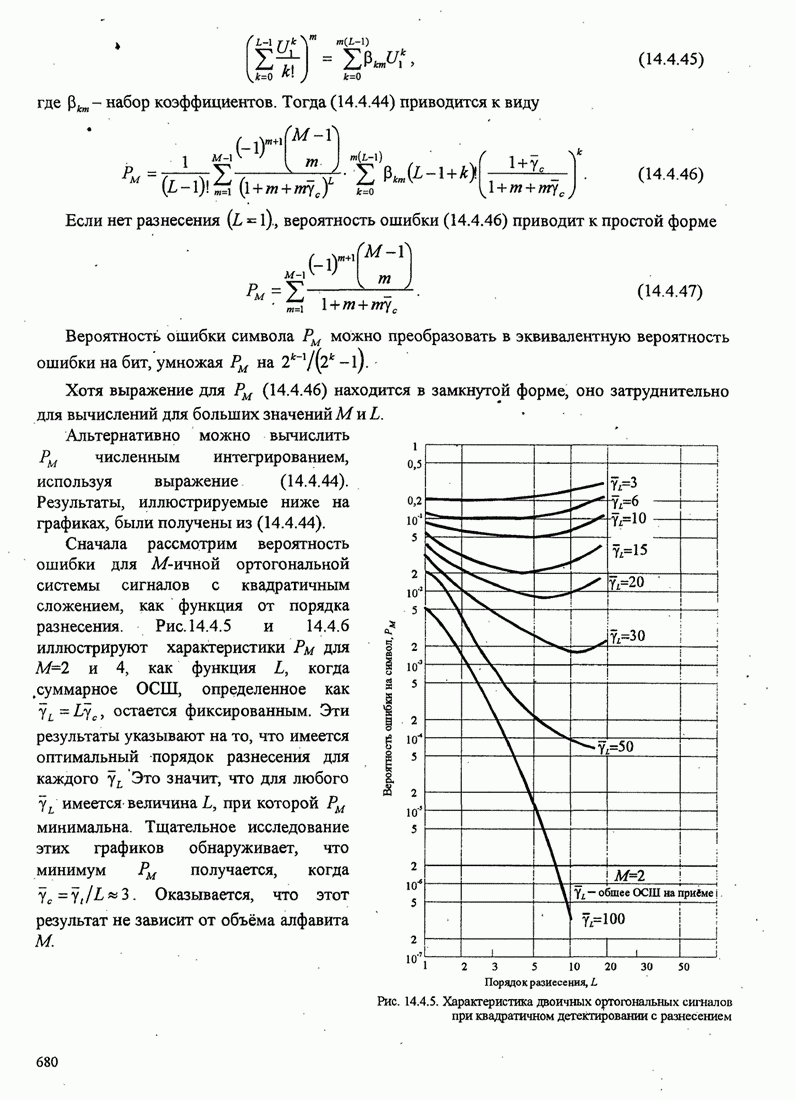
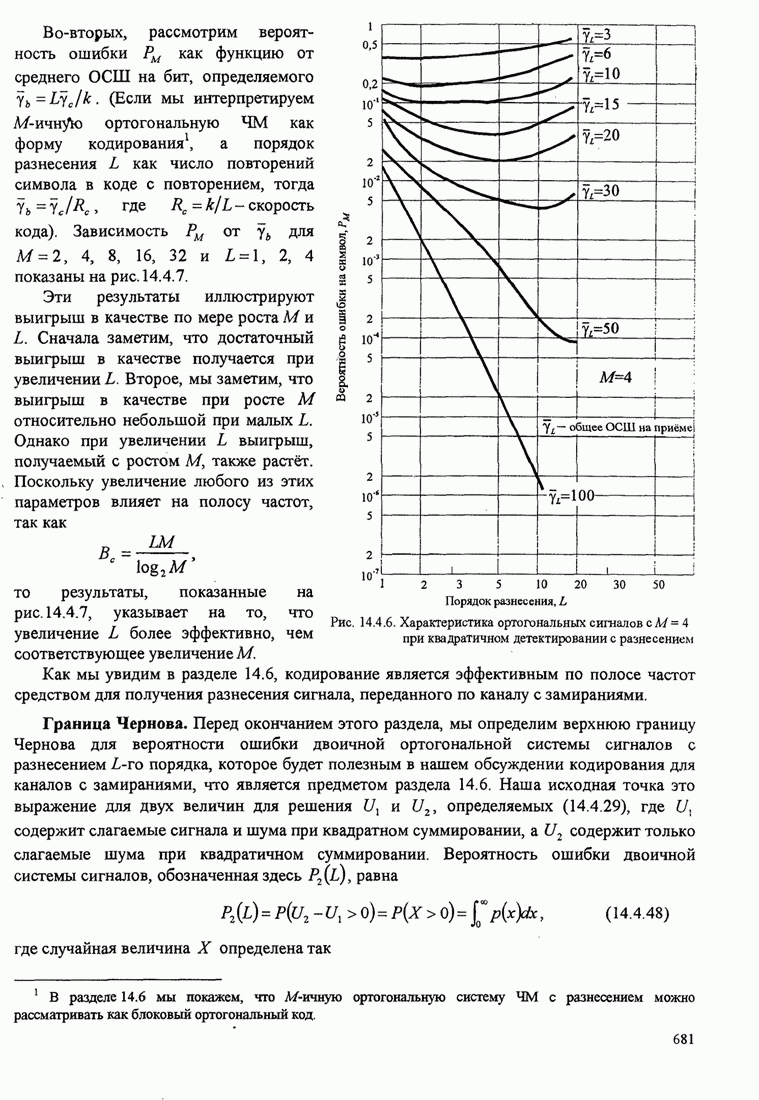
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)