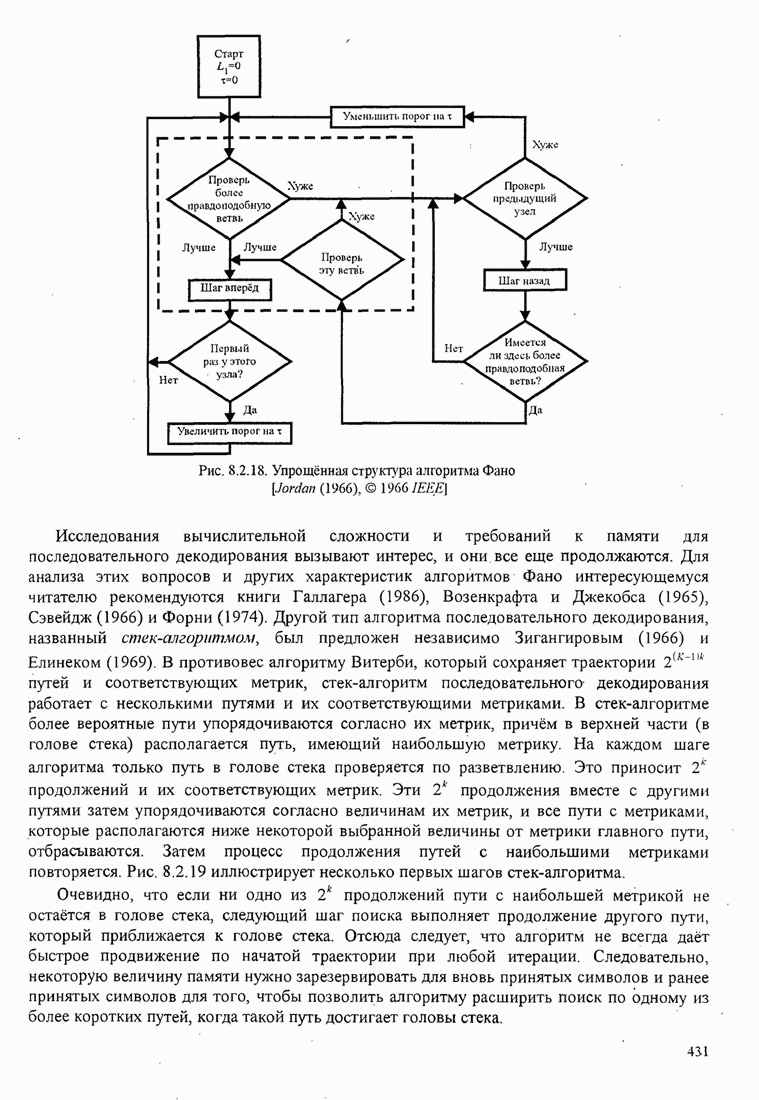
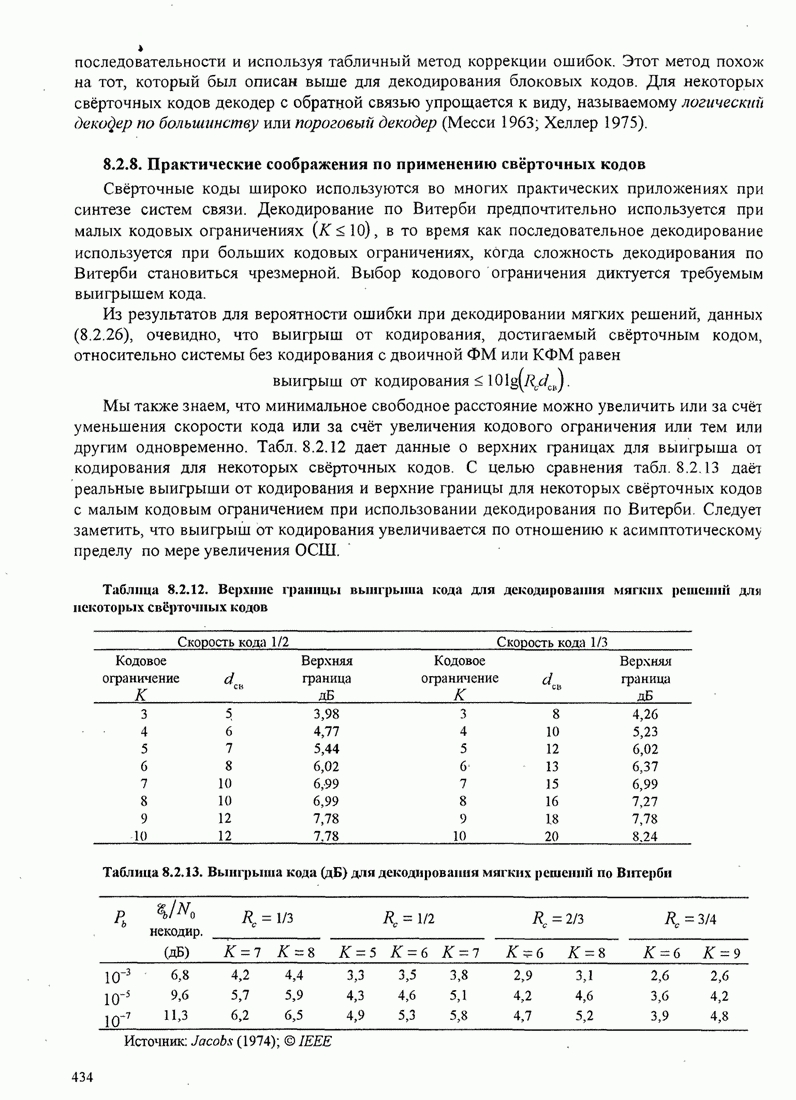
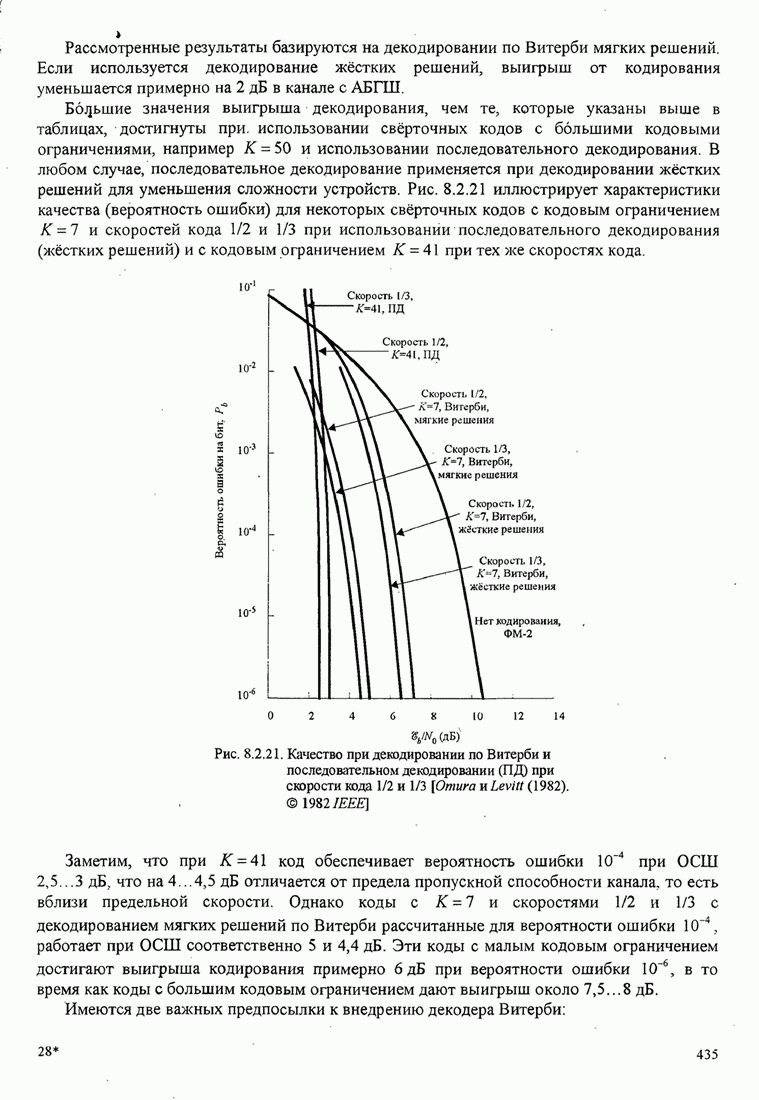
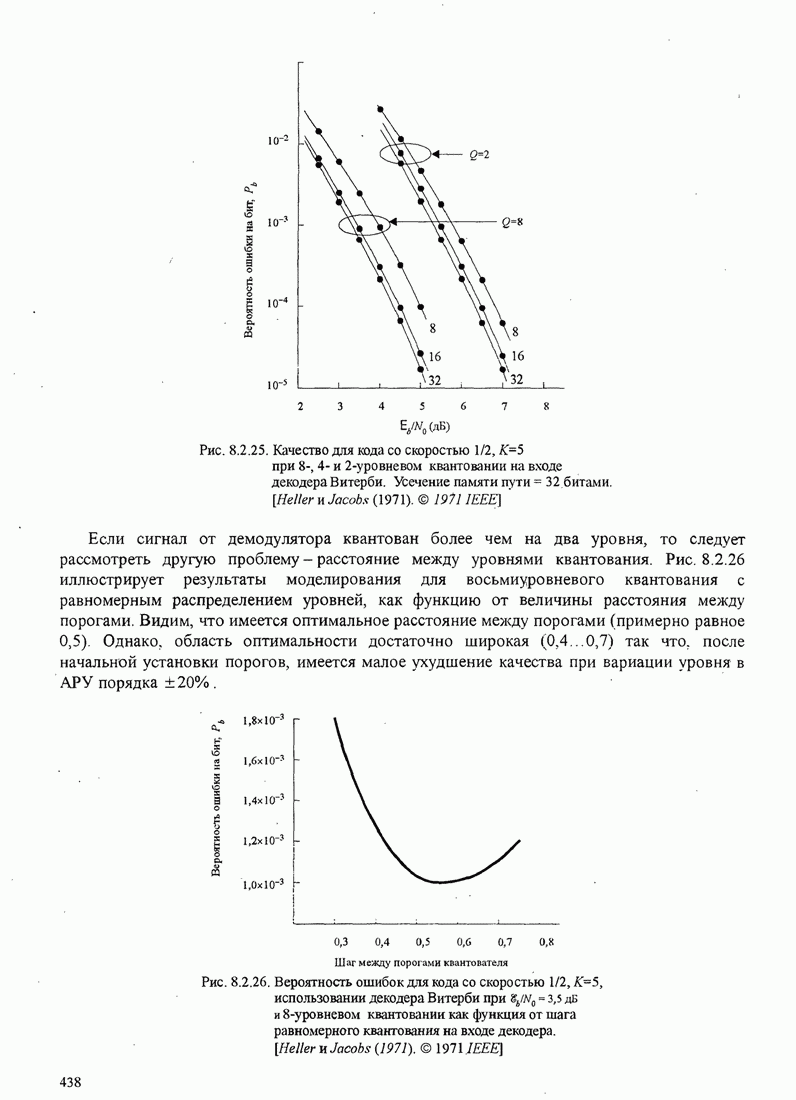
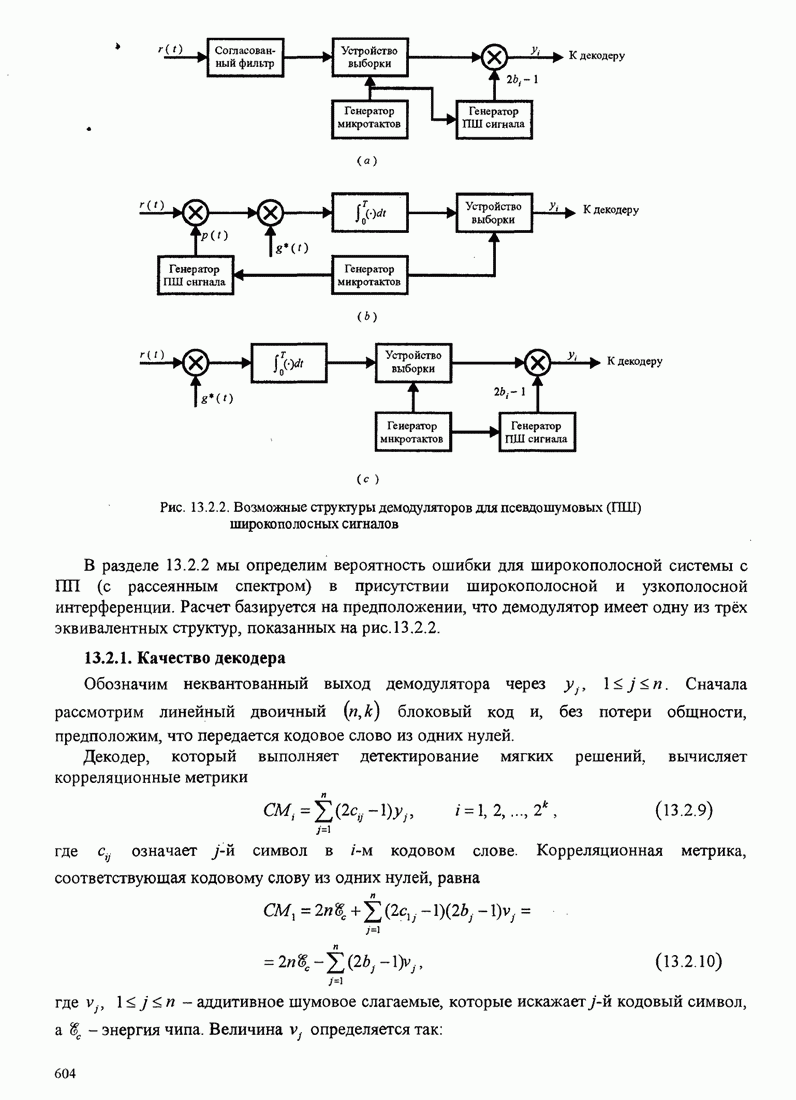
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
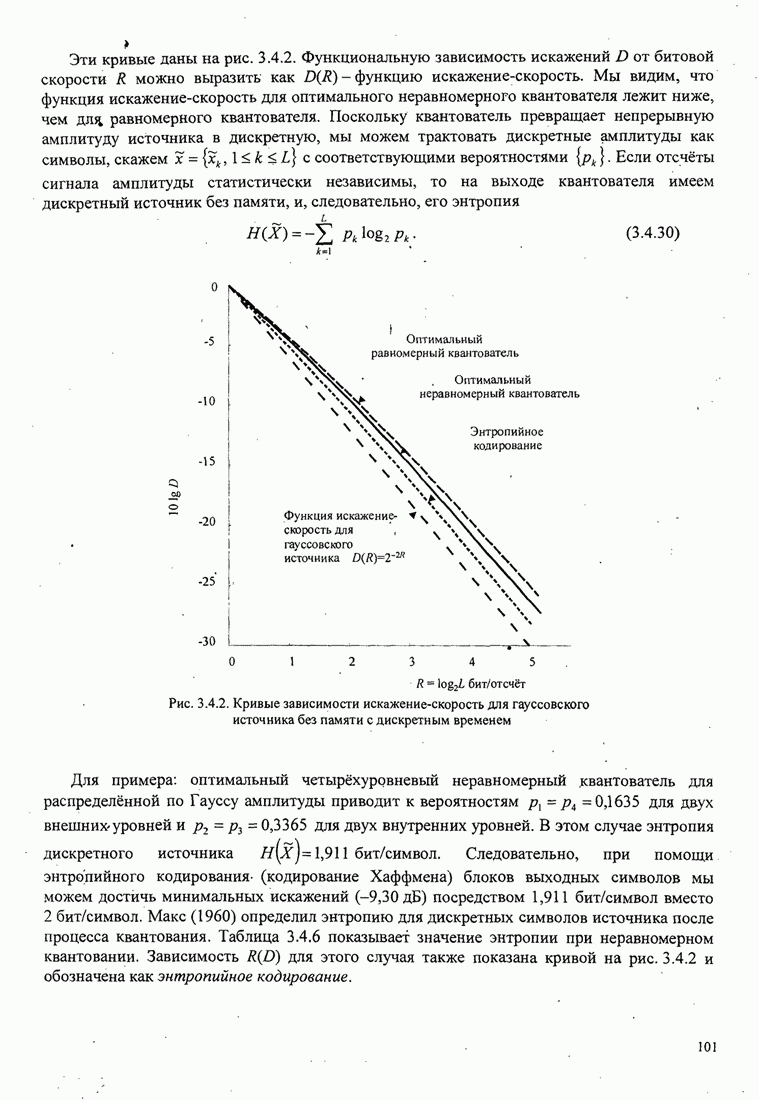
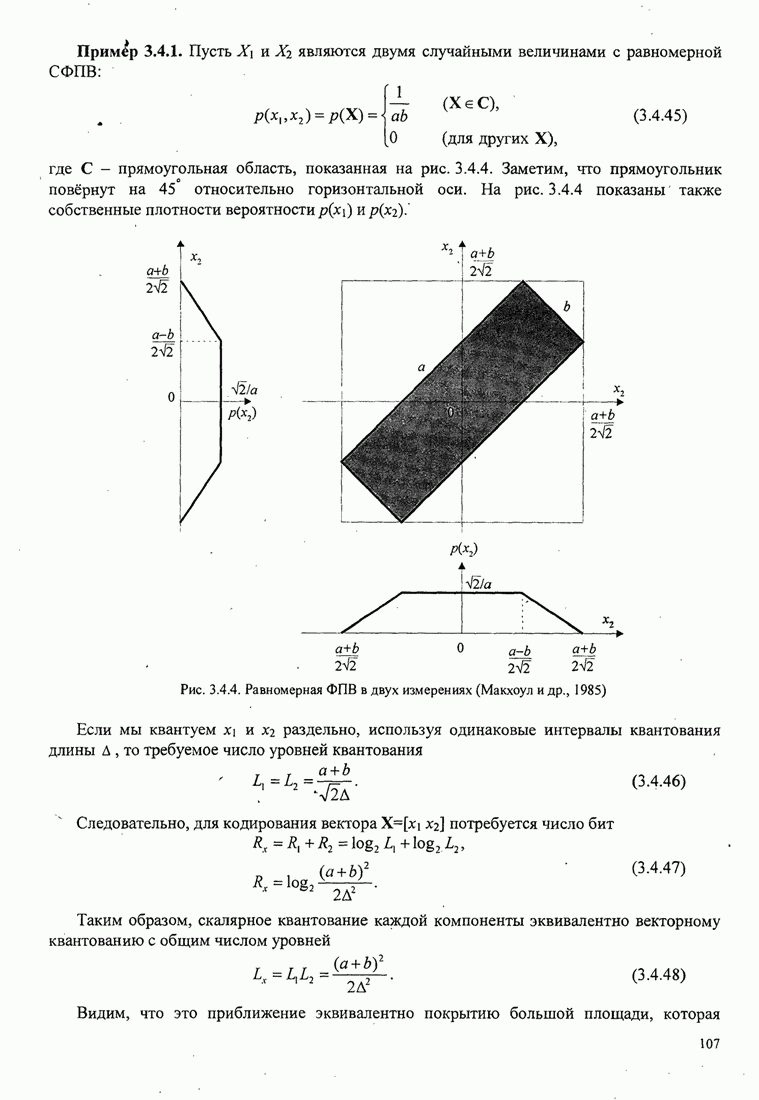
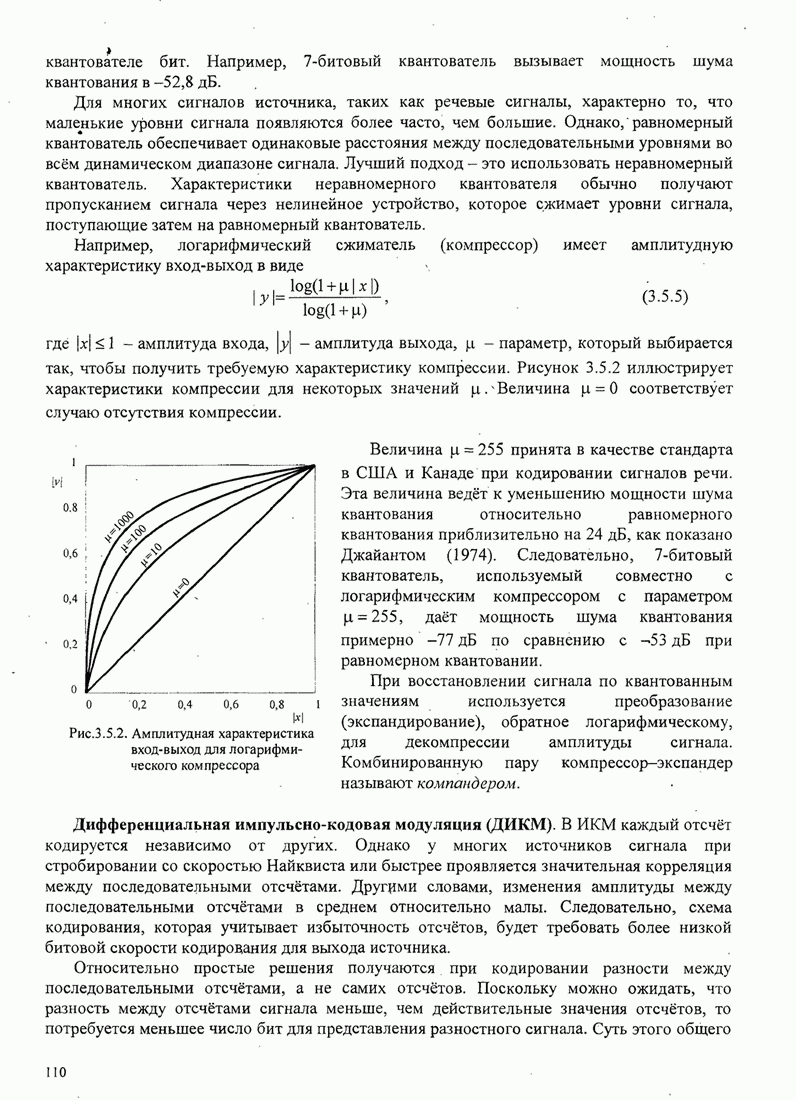
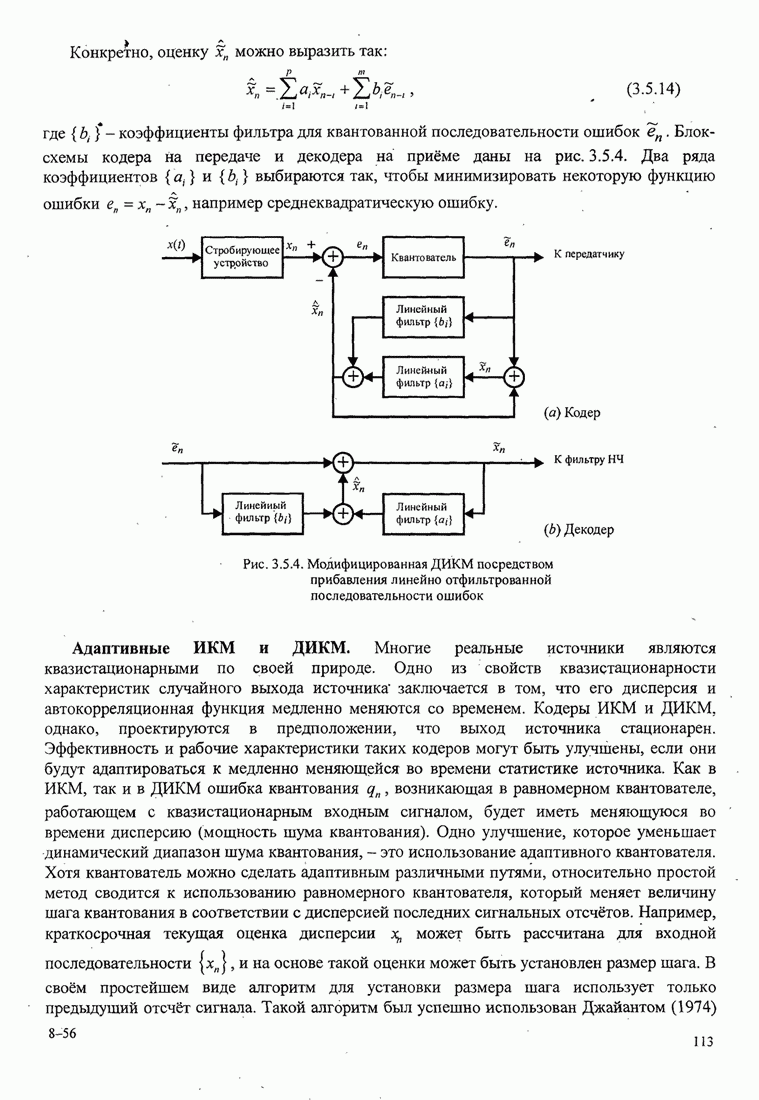
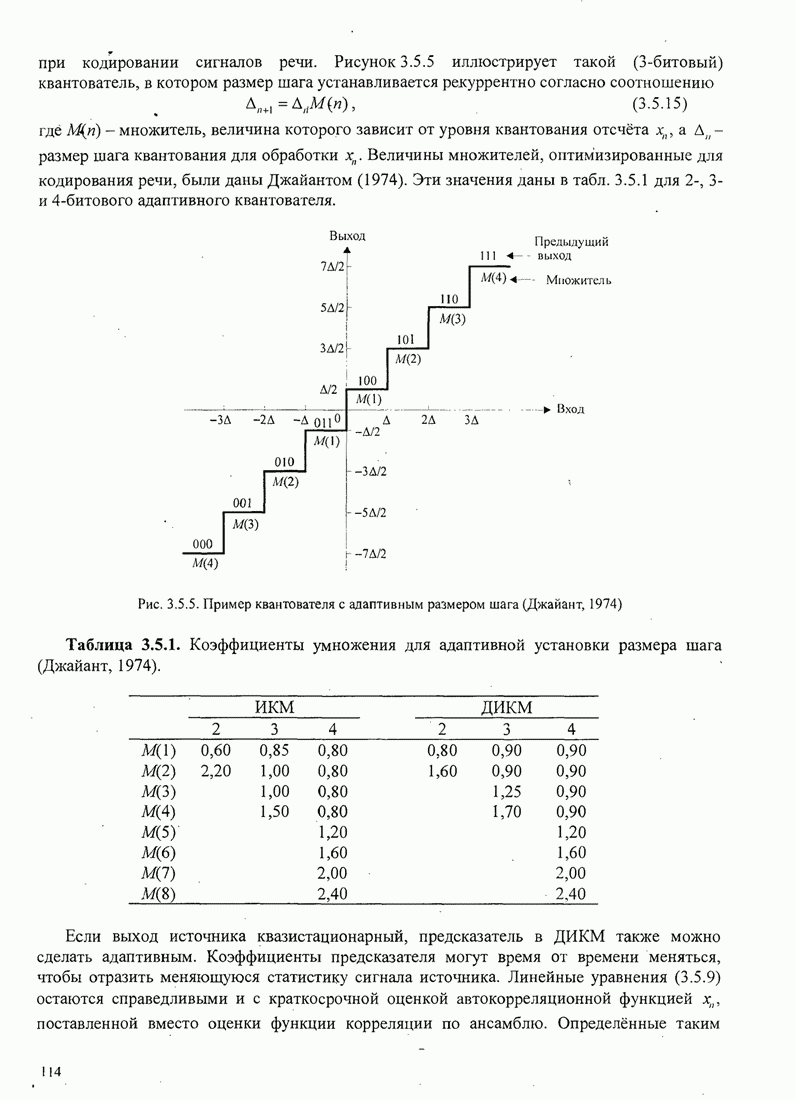
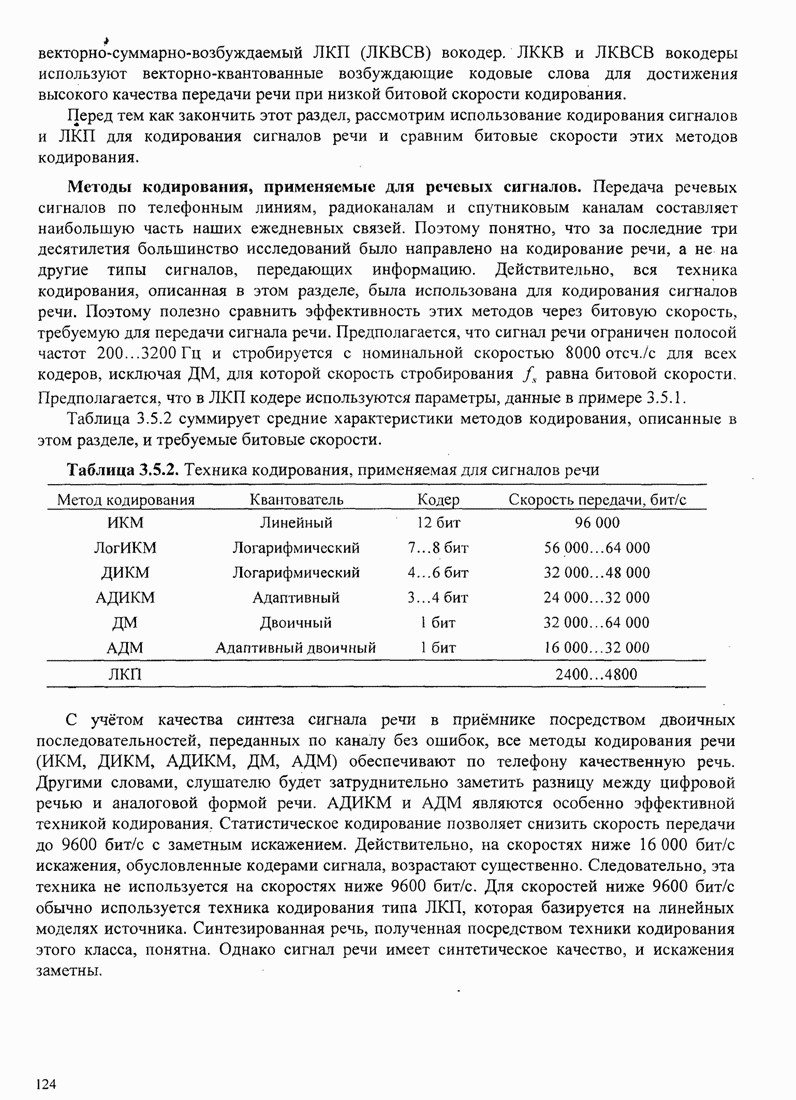
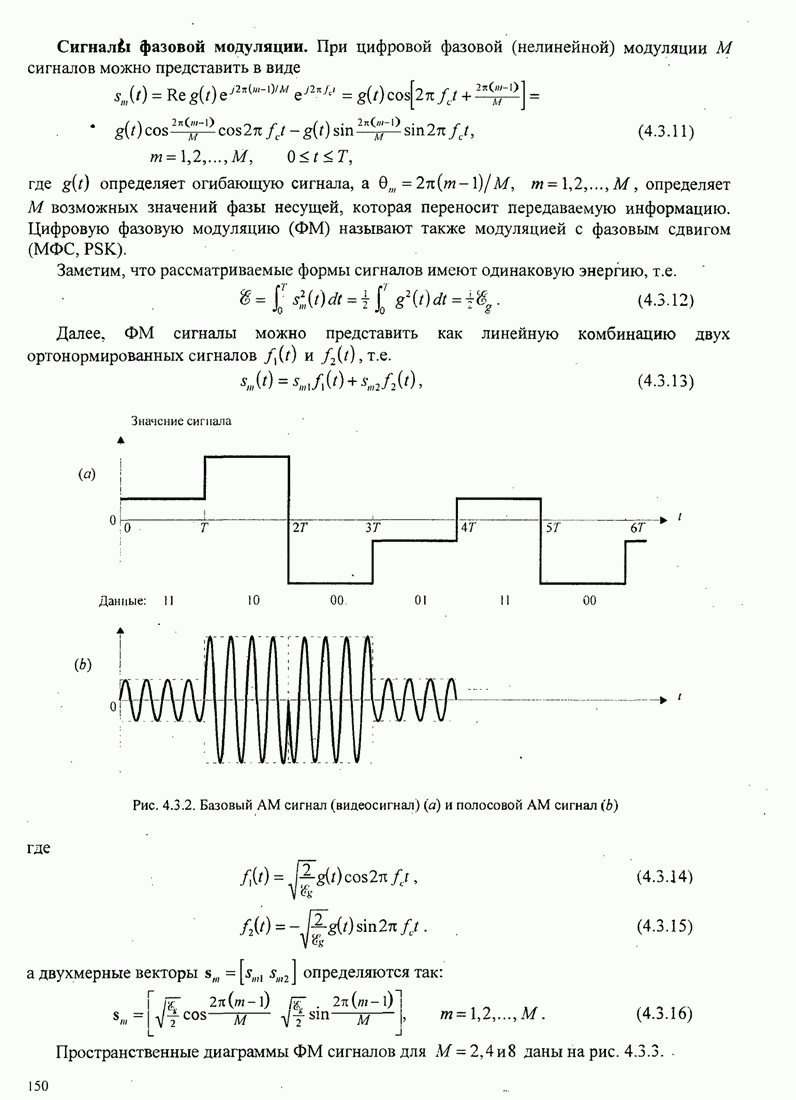
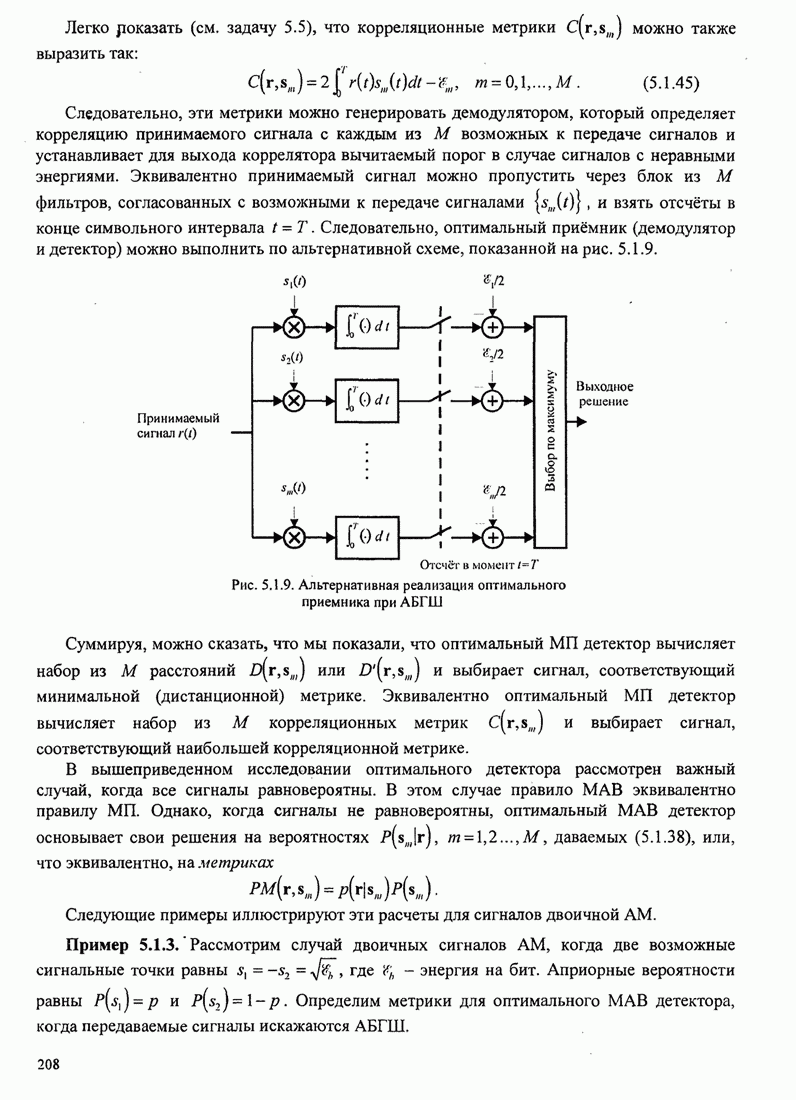
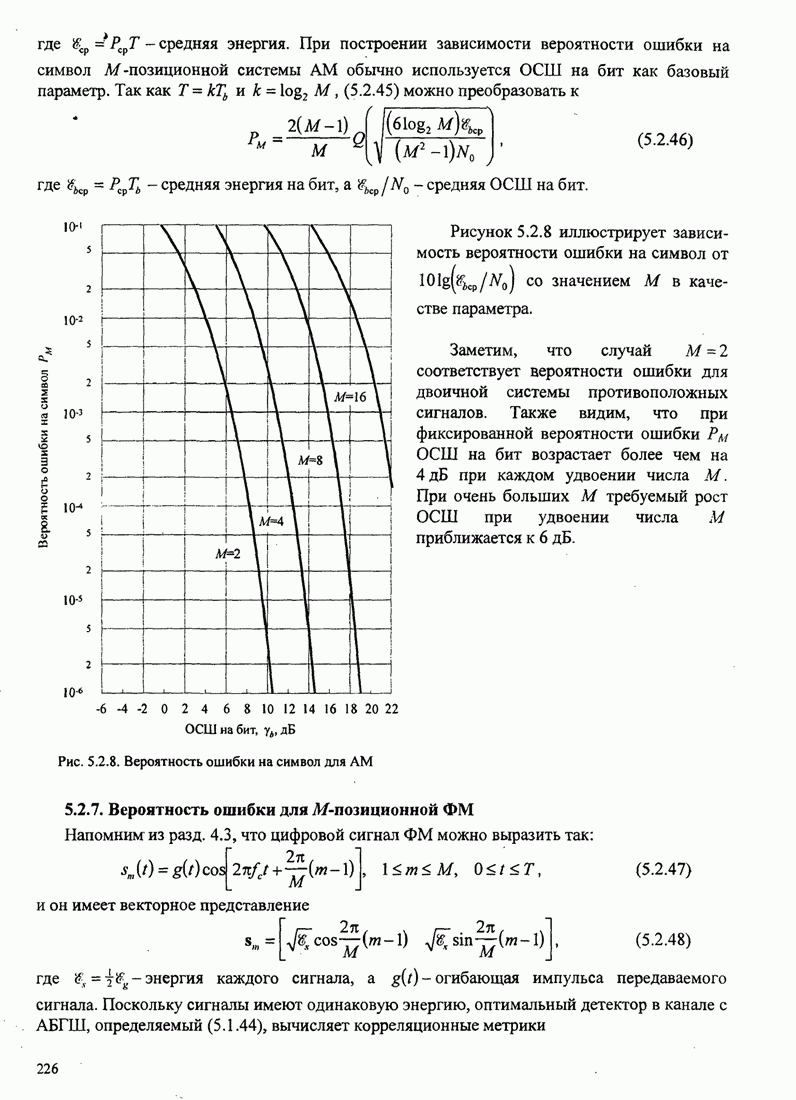
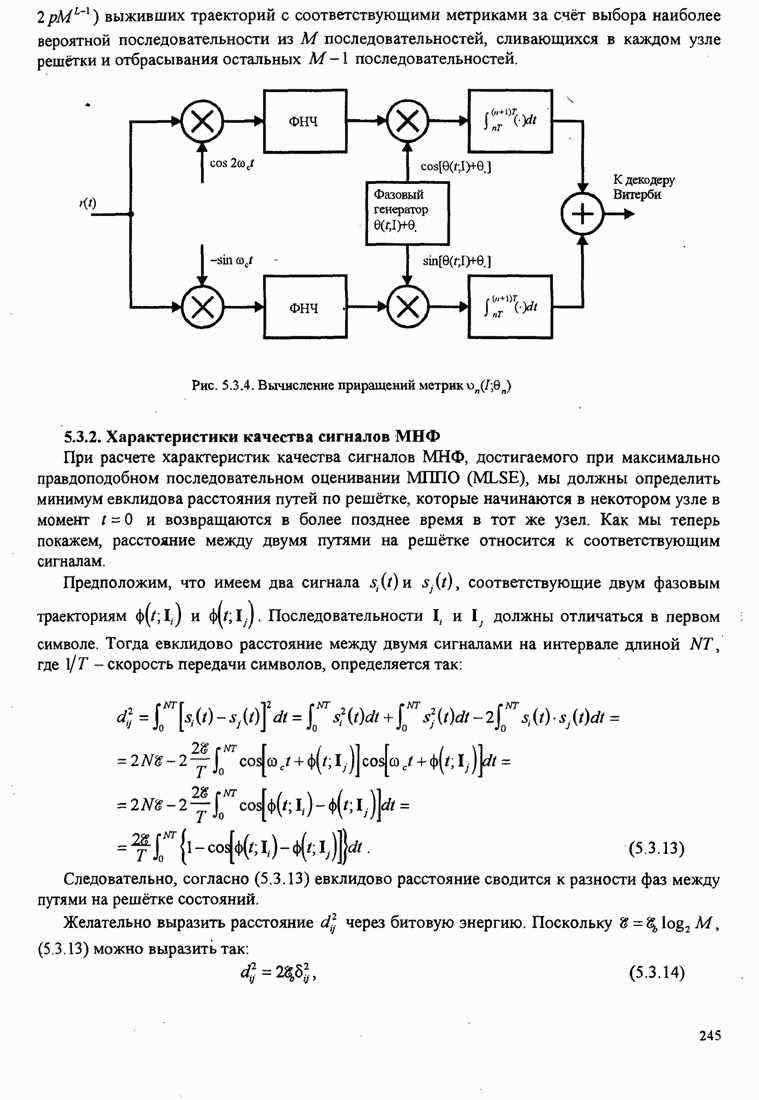
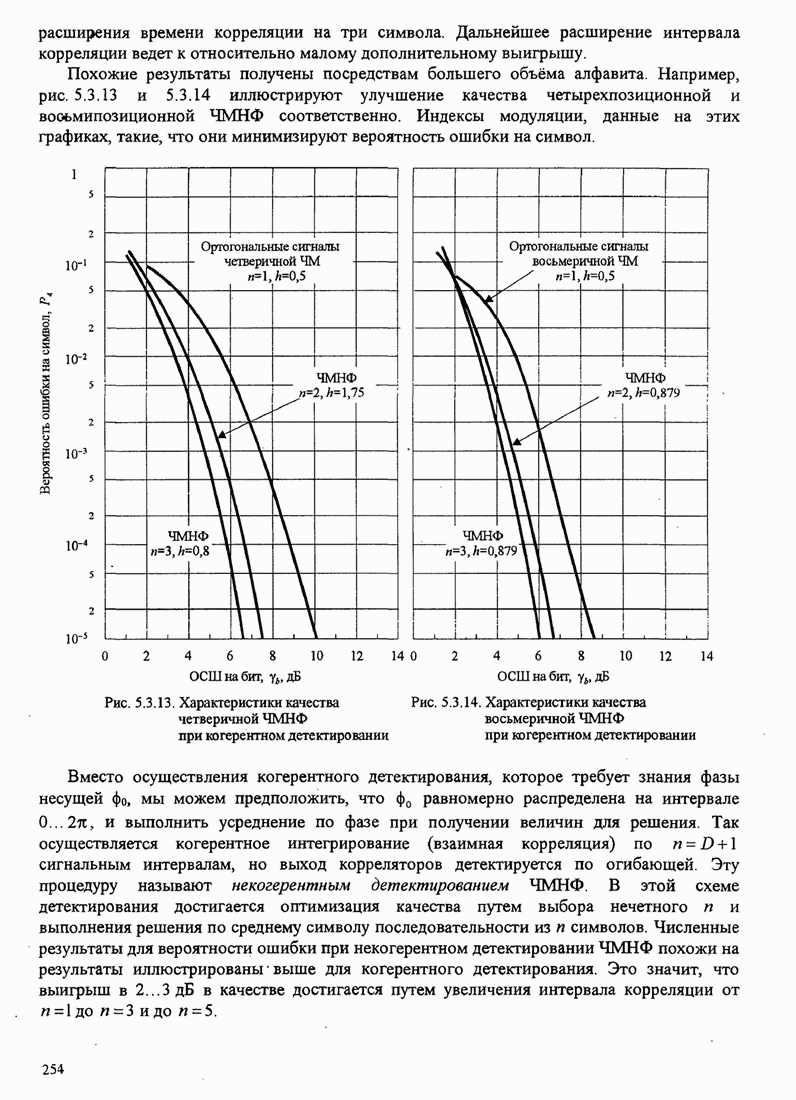
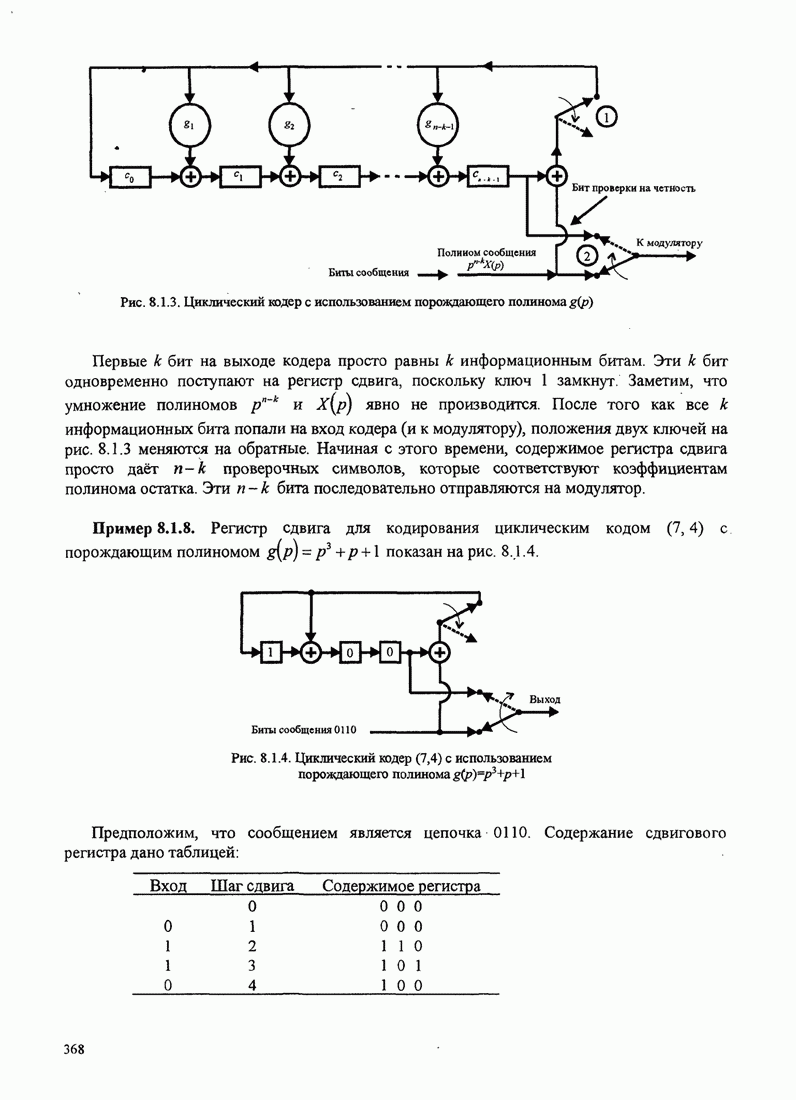
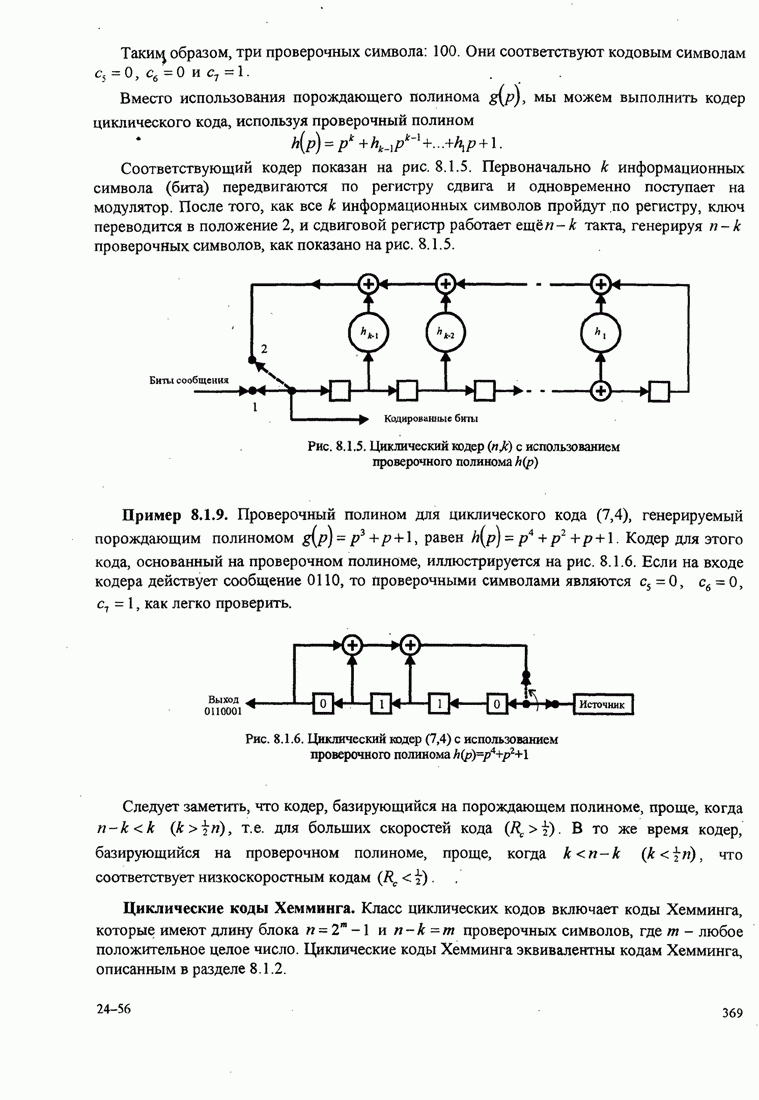
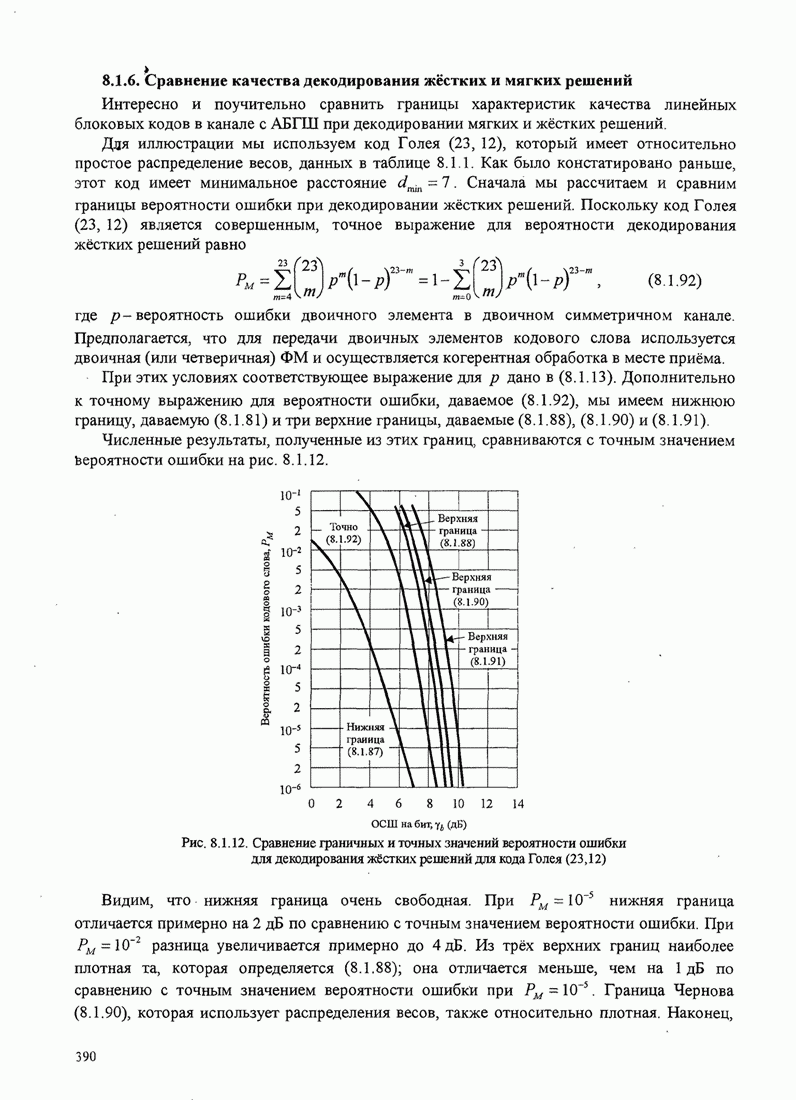
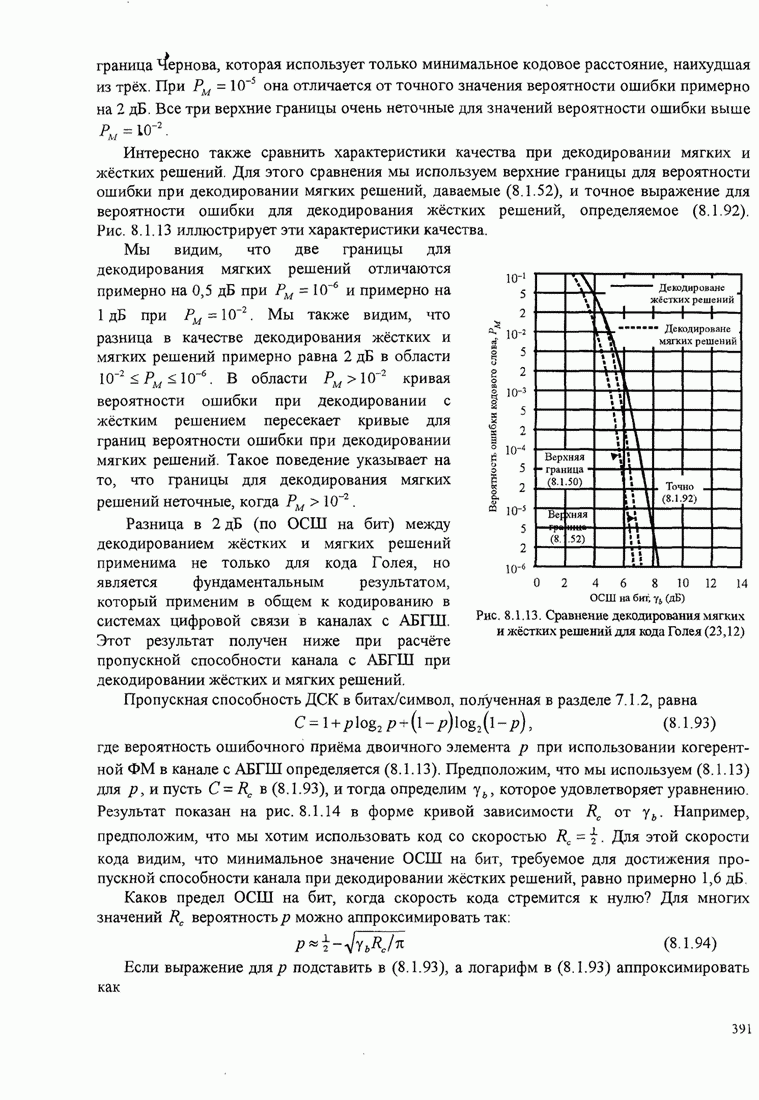
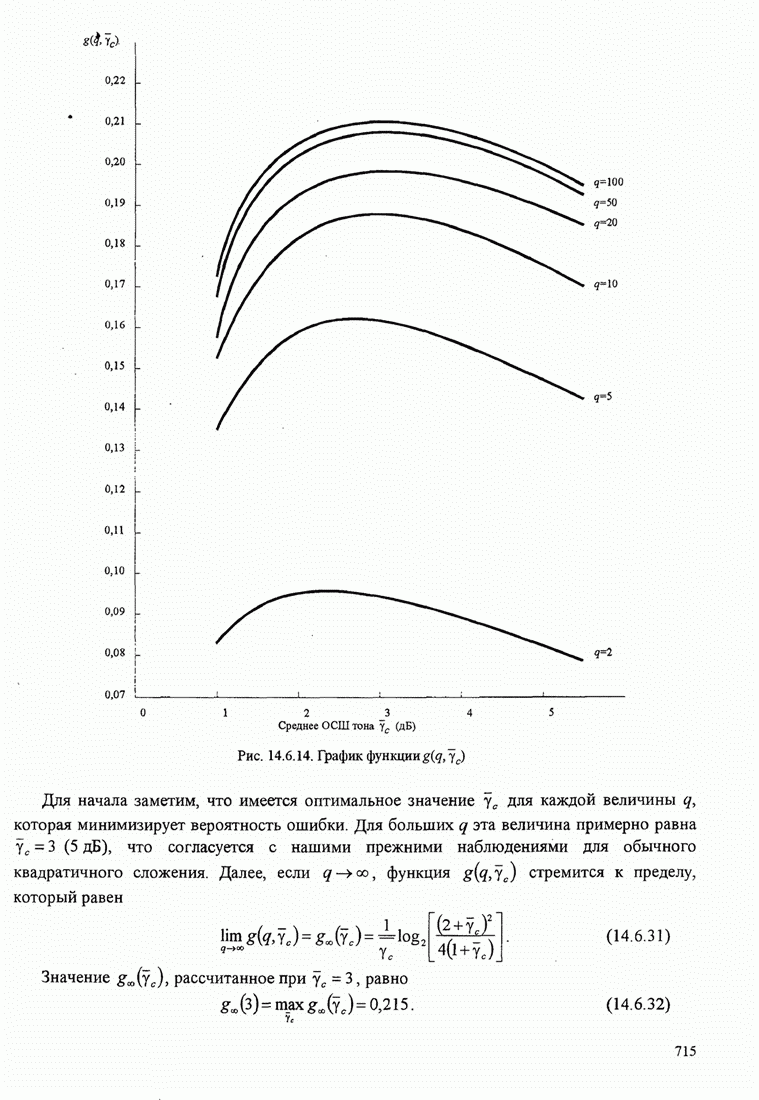
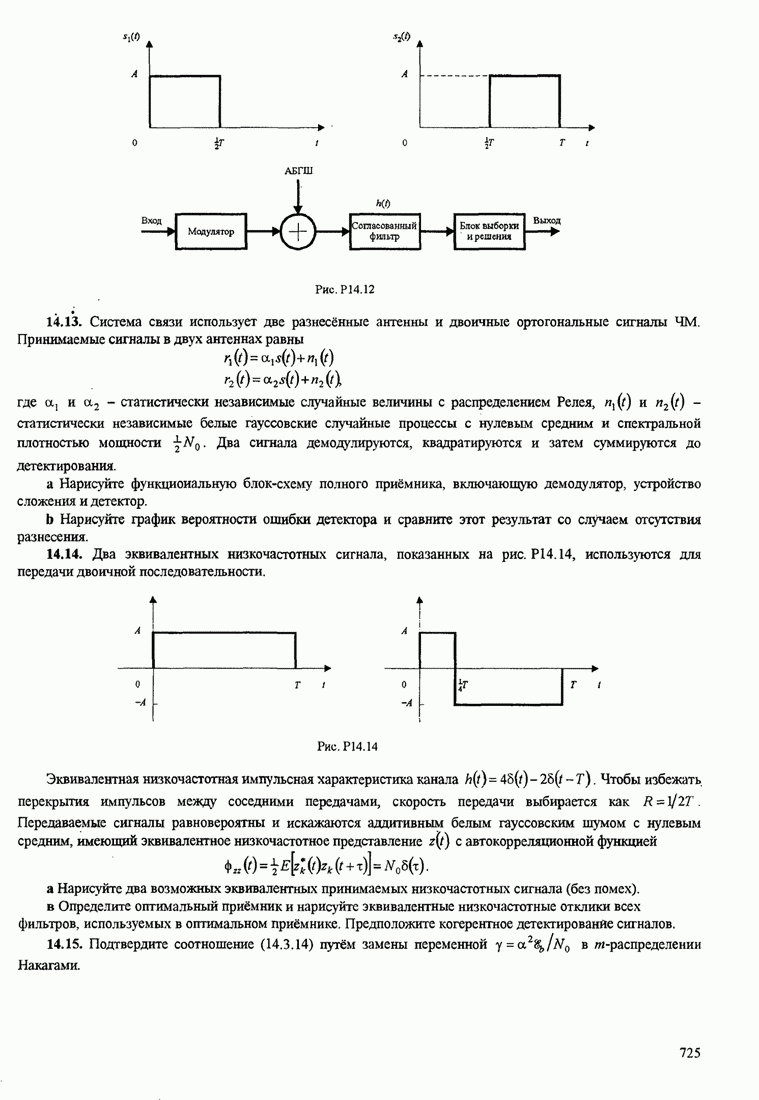
5.3.2. Характеристики качества сигналов МНФ
При расчете характеристик качества сигналов МНФ, достигаемого при
максимально правдоподобном последовательном оценивании МППО (MLSE), мы должны
определить минимум евклидова расстояния путей по решётке, которые начинаются в
некотором узле в момент ![]() и возвращаются в более позднее время в
тот же узел. Как мы теперь покажем, расстояние между двумя путями на решётке
относится к соответствующим сигналам.
и возвращаются в более позднее время в
тот же узел. Как мы теперь покажем, расстояние между двумя путями на решётке
относится к соответствующим сигналам.
Предположим, что имеем два сигнала ![]() и
и ![]() , соответствующие двум фазовым траекториям
, соответствующие двум фазовым траекториям
![]() и
и ![]() . Последовательности
. Последовательности
![]() и
и ![]() должны отличаться в
первом символе. Тогда евклидово расстояние между двумя сигналами на интервале
длиной
должны отличаться в
первом символе. Тогда евклидово расстояние между двумя сигналами на интервале
длиной ![]() ,
где
,
где ![]() -
скорость передачи символов, определяется так:
-
скорость передачи символов, определяется так:
 (5.3.13)
(5.3.13)
Следовательно, согласно (5.3.13) евклидово расстояние сводится к разности фаз между путями на решётке состояний.
Желательно выразить расстояние ![]() через битовую энергию. Поскольку
через битовую энергию. Поскольку ![]() , (5.3.13)
можно выразить так:
, (5.3.13)
можно выразить так:
![]() (5.3.14)
(5.3.14)
где ![]() определено
как
определено
как
![]() (5.3.15)
(5.3.15)
Далee видим, что ![]() так что, обозначив
так что, обозначив ![]() , (5.3.15) можно
переписать в виде
, (5.3.15) можно
переписать в виде
![]() (5.3.16)
(5.3.16)
где любой элемент из ![]() может принять значения
может принять значения ![]() , кроме
, кроме ![]() , которое
не может быть равным 0.
, которое
не может быть равным 0.
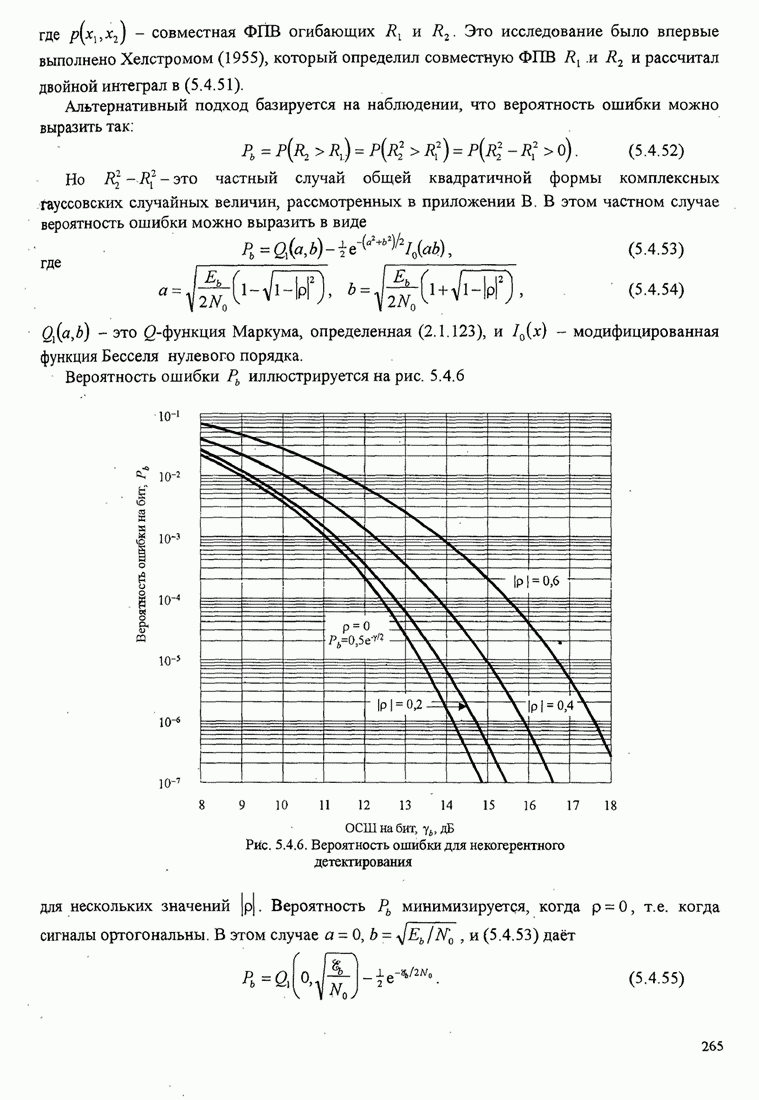
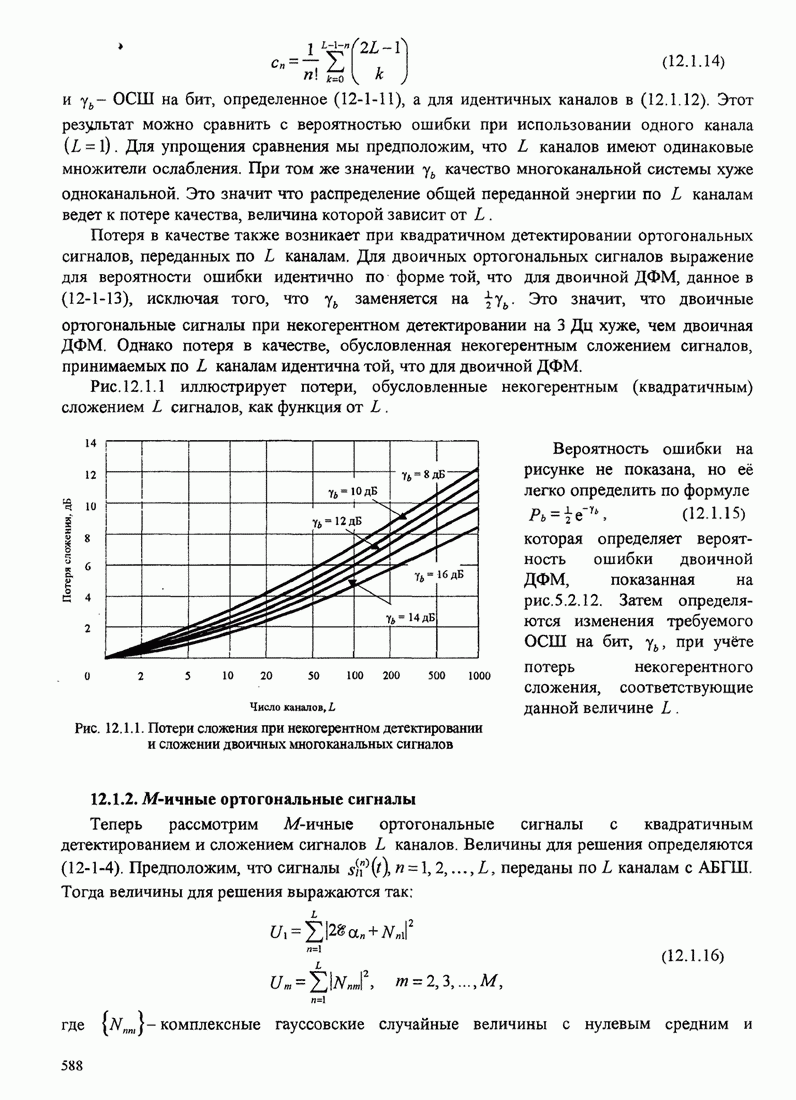
Вероятность ошибки МНФ определяется слагаемым ![]() , соответствующим
минимальному евклидову расстоянию, и ее можно выразить так:
, соответствующим
минимальному евклидову расстоянию, и ее можно выразить так:
 (5.3.17)
(5.3.17)
где
![]() (5.3.18)
(5.3.18)
Заметим, что для обычной двоичной ФМ без памяти ![]() и
и ![]() . Следовательно, (5.3.17)
согласуется с нашим прежним результатом.
. Следовательно, (5.3.17)
согласуется с нашим прежним результатом.
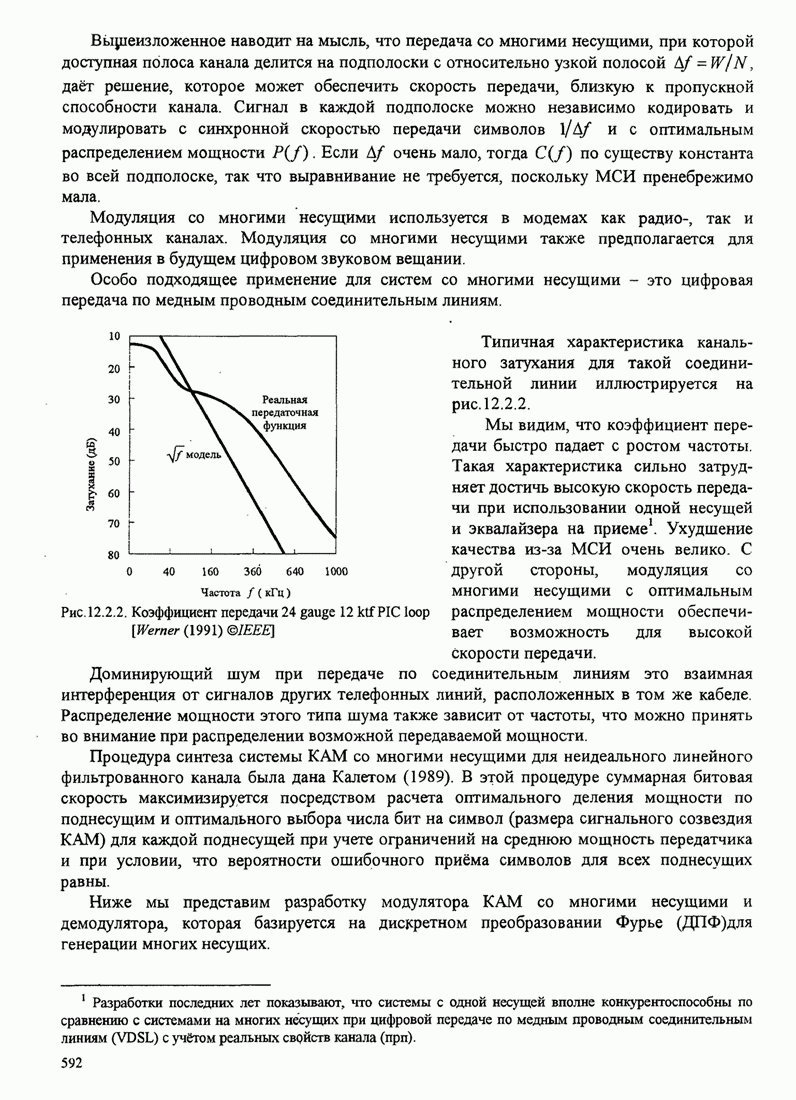
Поскольку ![]() характеризует качество МНФ с МППО, мы
можем исследовать влияние на
характеризует качество МНФ с МППО, мы
можем исследовать влияние на ![]() изменения объёма алфавита
изменения объёма алфавита ![]() , индекса
модуляции
, индекса
модуляции ![]() и
длительности переданного импульса в системе МНФ с парциальным откликом.
и
длительности переданного импульса в системе МНФ с парциальным откликом.
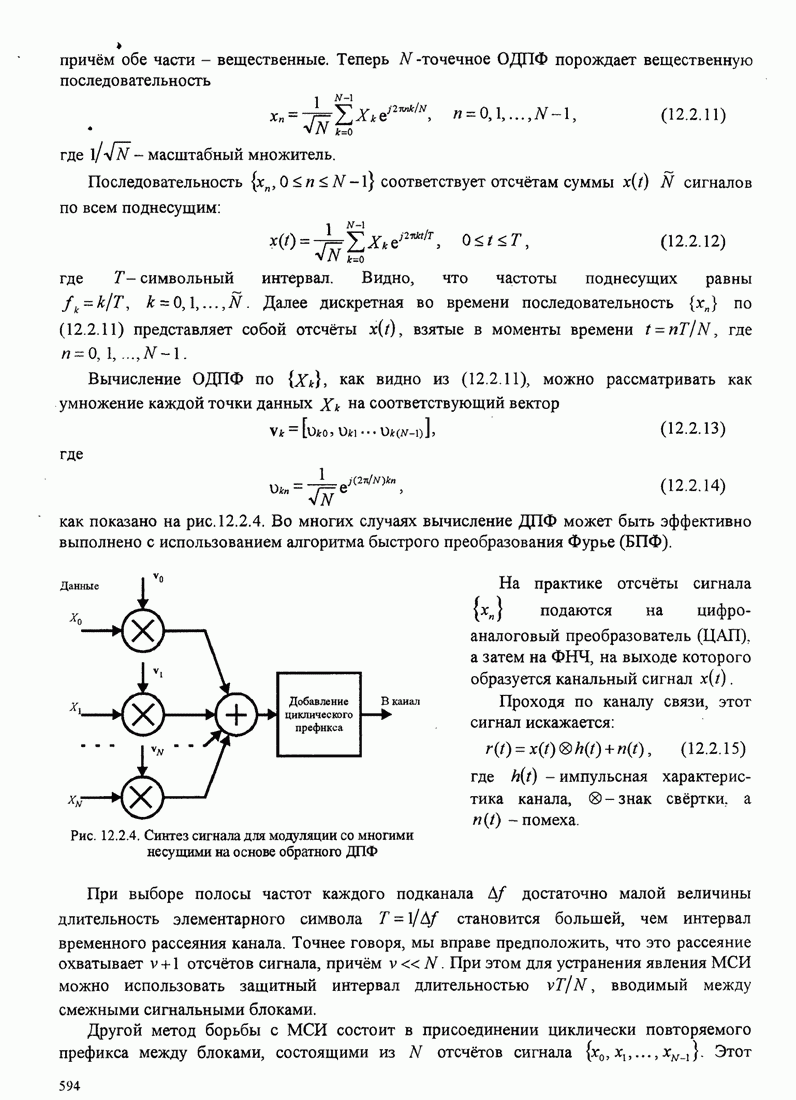
Прежде всего рассмотрим МНФ с полным откликом ![]() . Если возьмем
сначала
. Если возьмем
сначала ![]() ,
то заметим, что последовательности
,
то заметим, что последовательности
 (5.3.19)
(5.3.19)
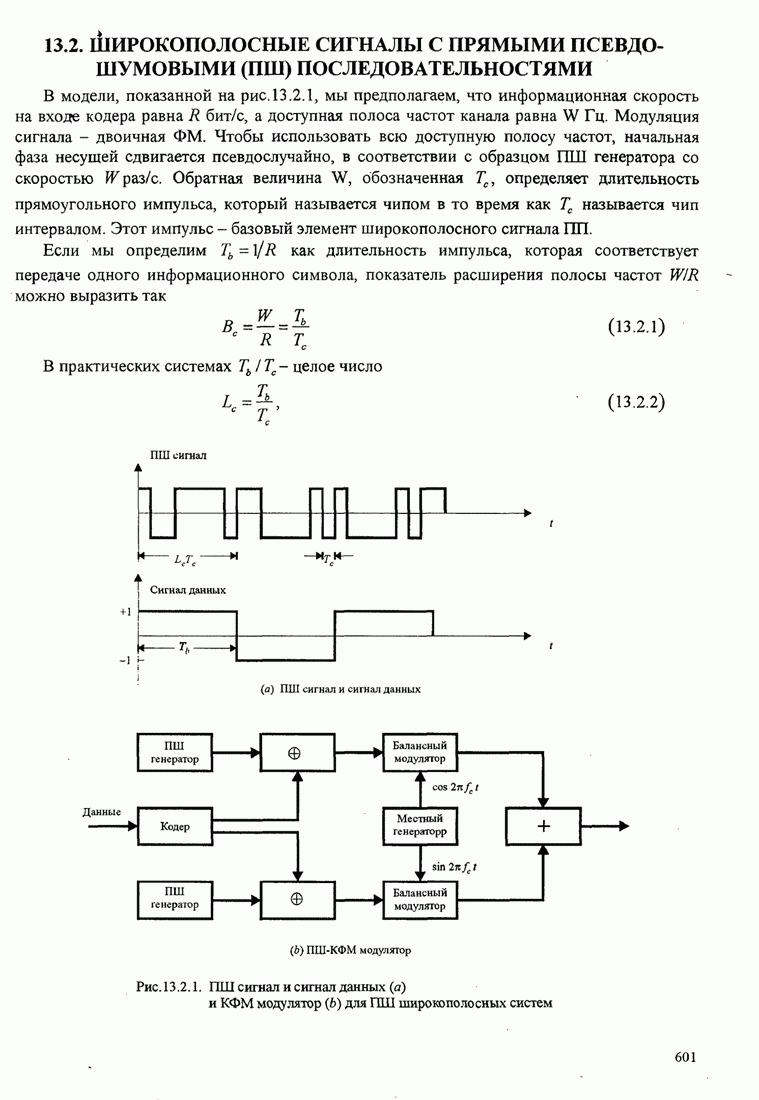
которые отличаются при ![]() и совпадают при
и совпадают при ![]() , приводят к двум
фазовым траекториям, которые сливаются после второго символа. Это соответствует
разностной последовательности
, приводят к двум
фазовым траекториям, которые сливаются после второго символа. Это соответствует
разностной последовательности
![]() (5.3.20)
(5.3.20)
Евклидово расстояние для этих последовательностей легко вычислить из (5.3.16),
а затем найти верхнюю границу для ![]() . Эта верхняя граница для
. Эта верхняя граница для ![]() равна
равна
![]() (5.3.21)
(5.3.21)
Например, когда ![]() , что ведет к ММС, имеем d2B
, что ведет к ММС, имеем d2B![]() , так что
, так что
![]() .
.
Для ![]() и
при полном отклике МНФ также можно легко увидеть, что фазовые траектории
сливаются при
и
при полном отклике МНФ также можно легко увидеть, что фазовые траектории
сливаются при ![]() .
Следовательно, верхнюю границу
.
Следовательно, верхнюю границу ![]() можно получить, рассматривая
последовательности разностей фаз
можно получить, рассматривая
последовательности разностей фаз ![]() , где
, где
![]()
Эти последовательности дают верхнюю границу
![]() (5.3.22)
(5.3.22)
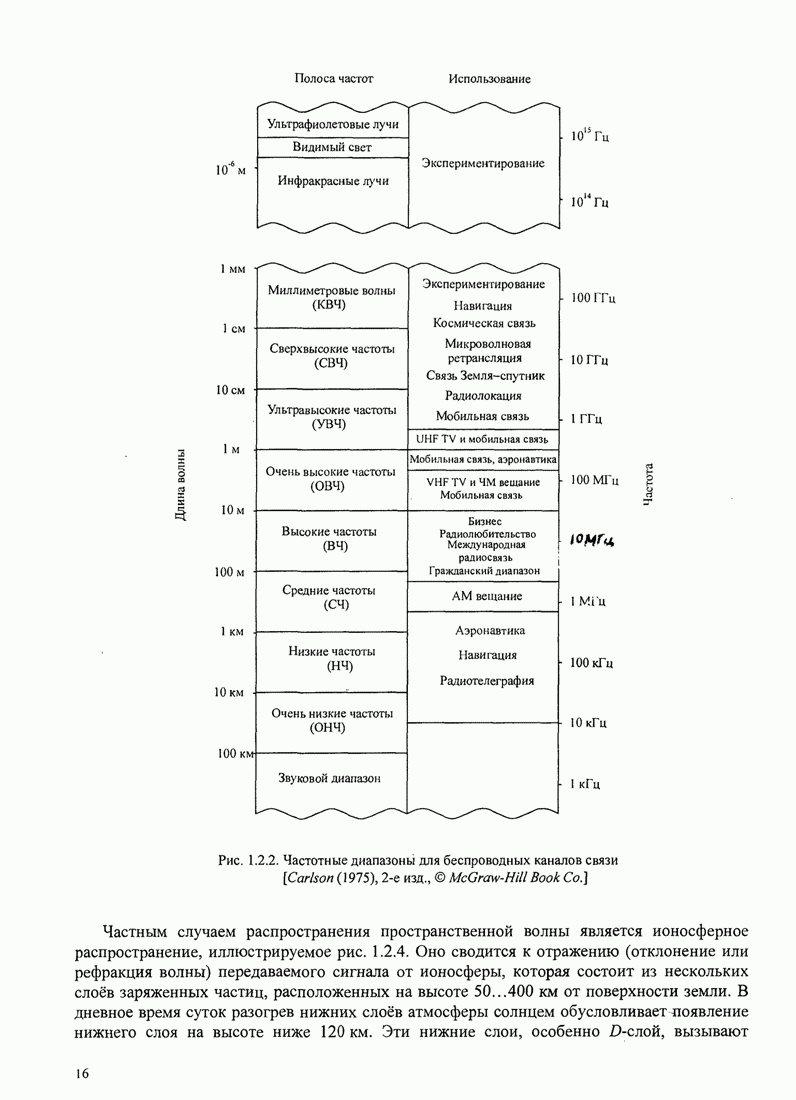
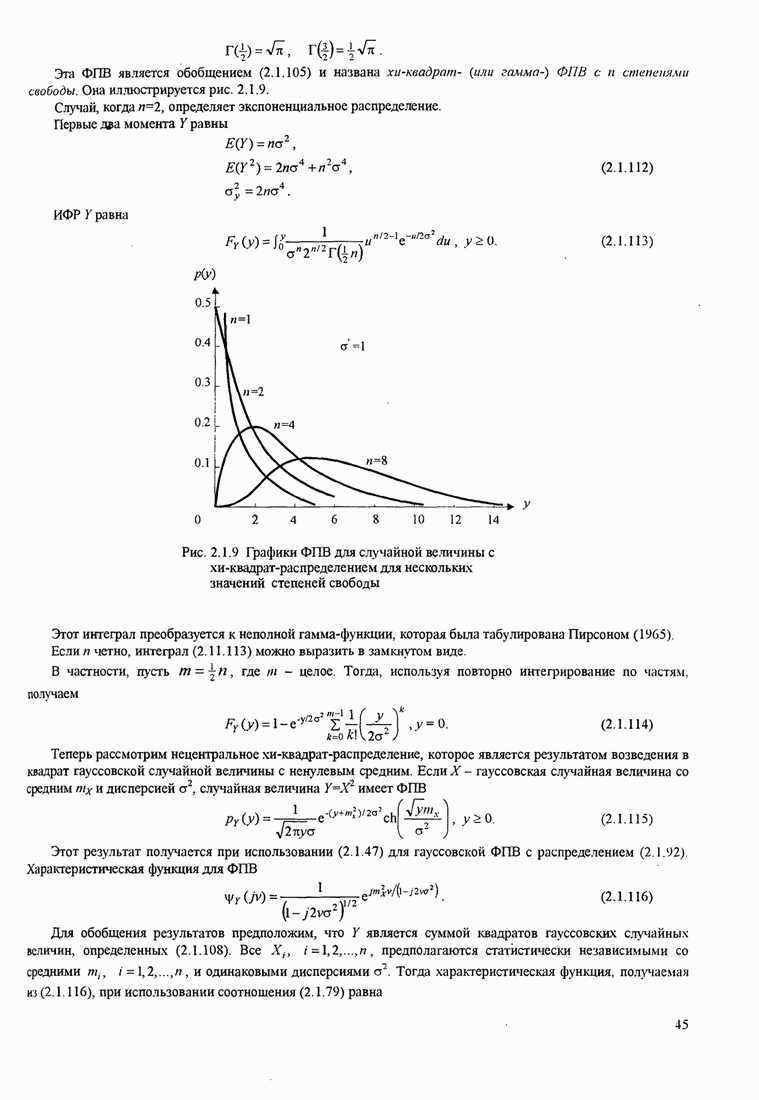
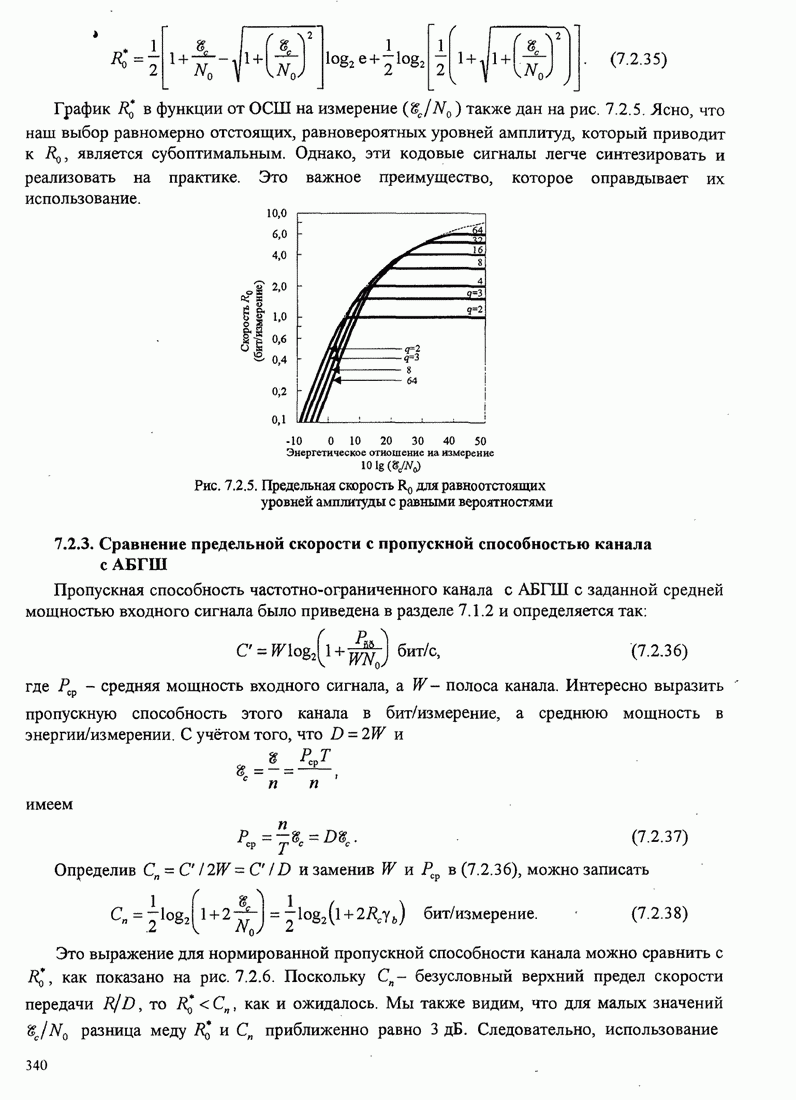
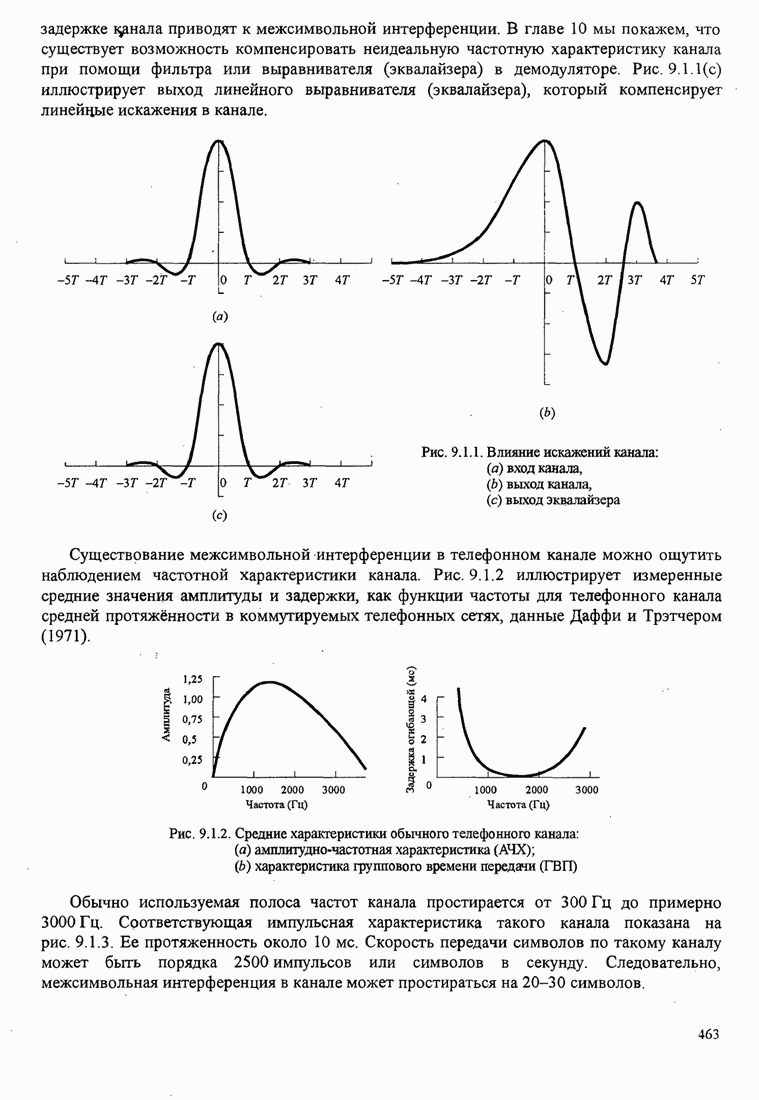
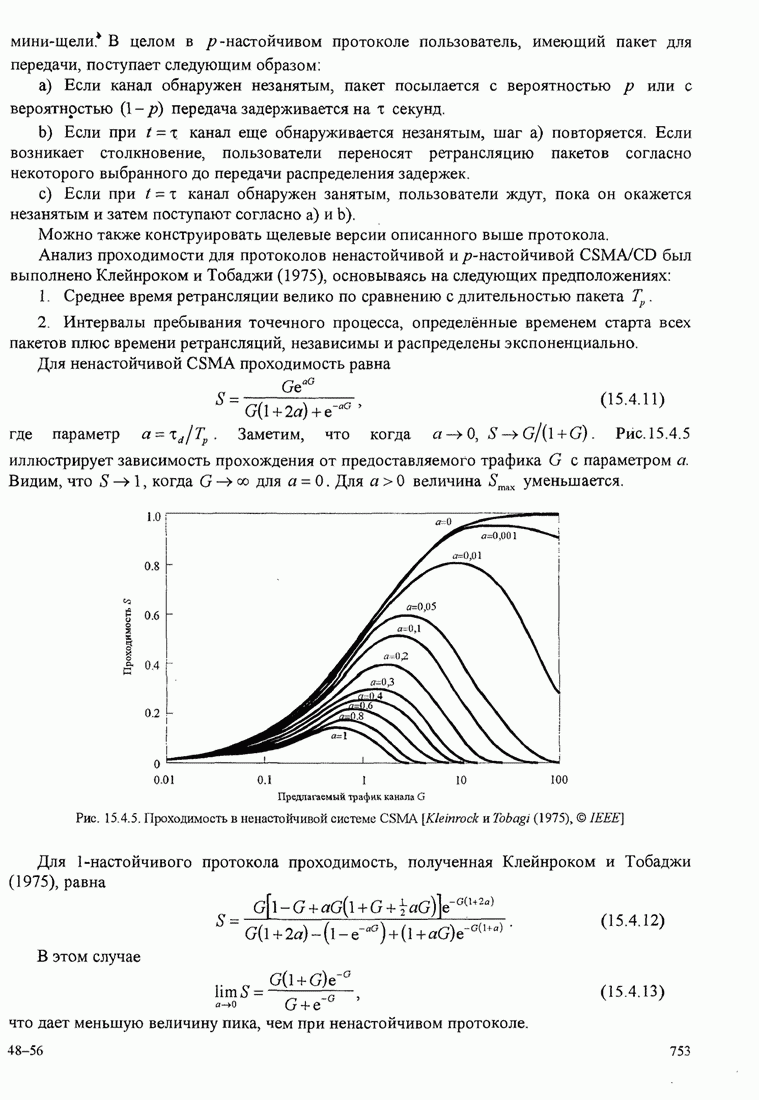
Графики зависимости ![]() от
от ![]() для
для ![]() показаны на рис. 5.3.5.
показаны на рис. 5.3.5.

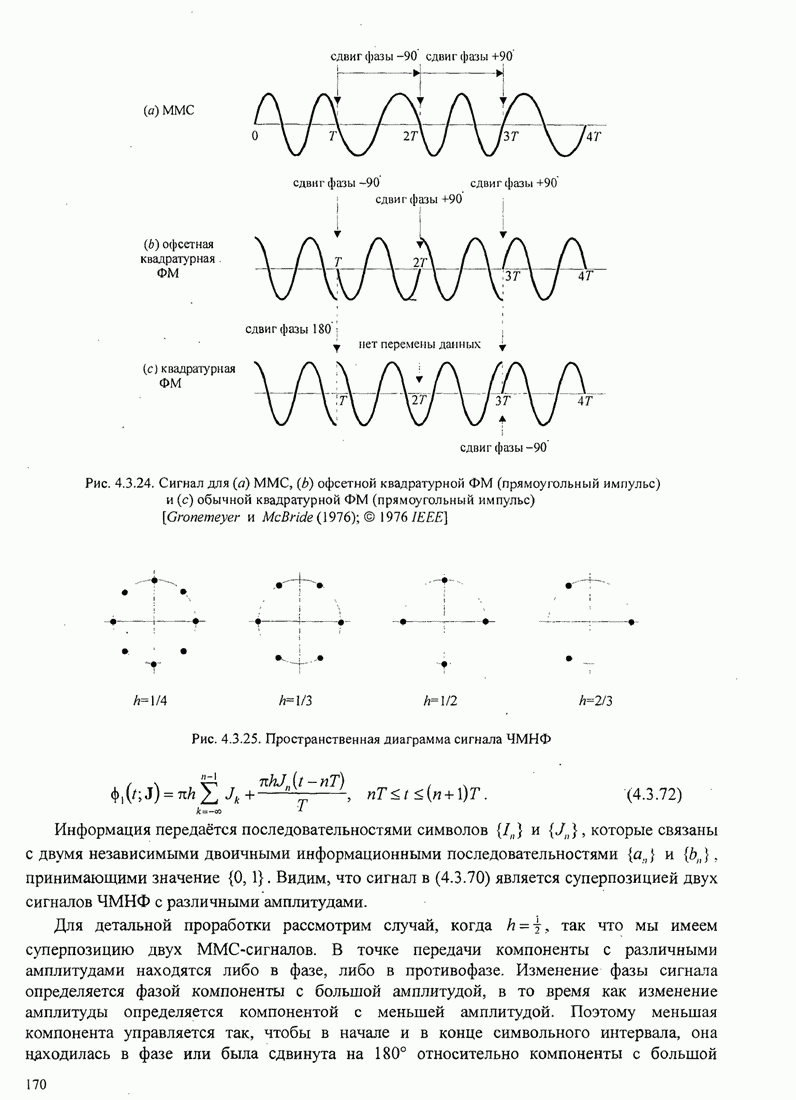
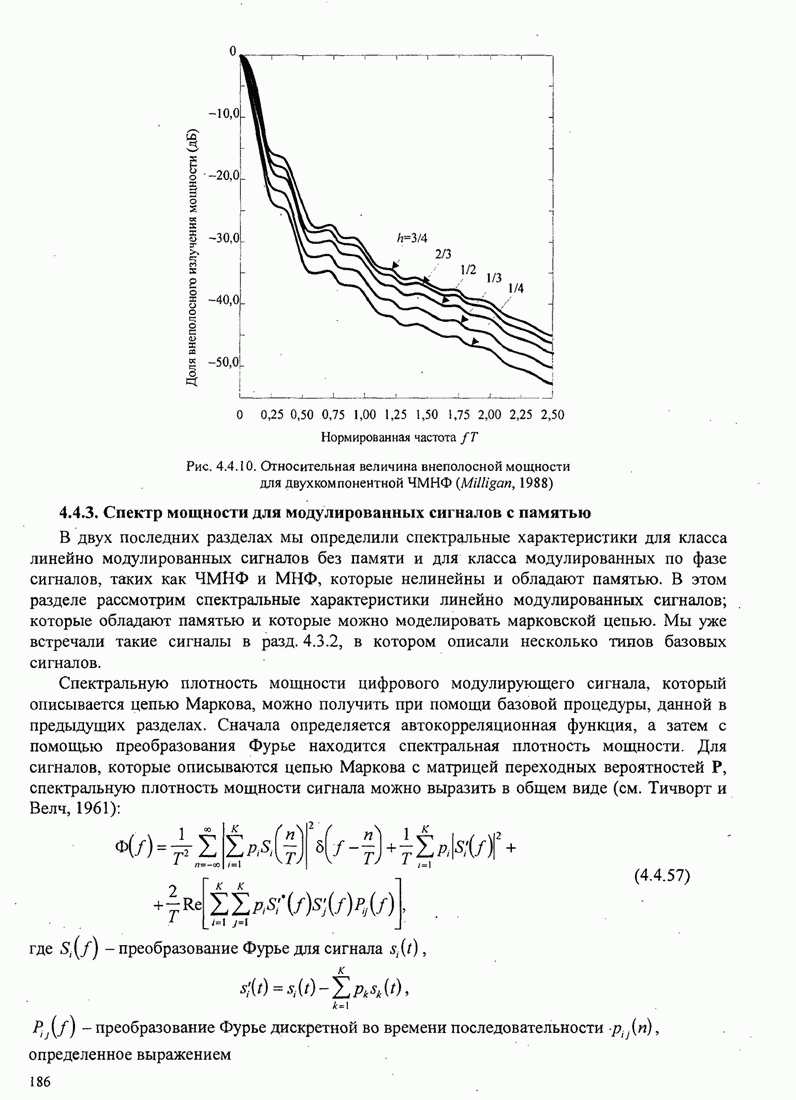
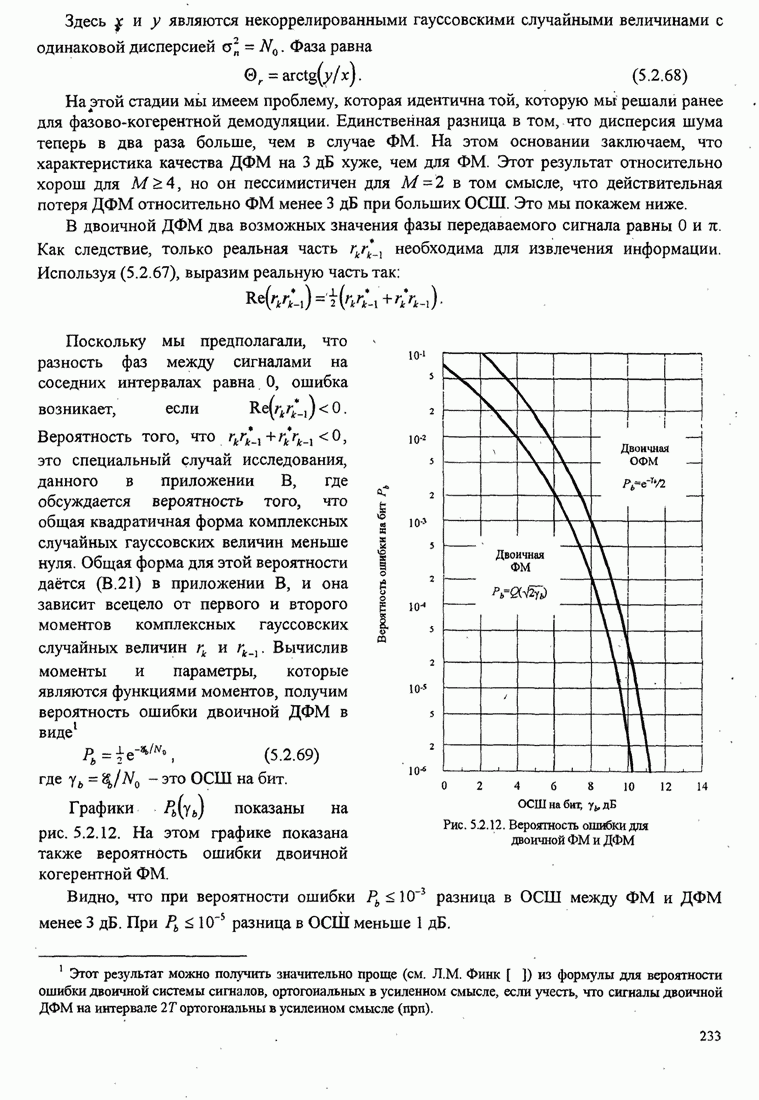
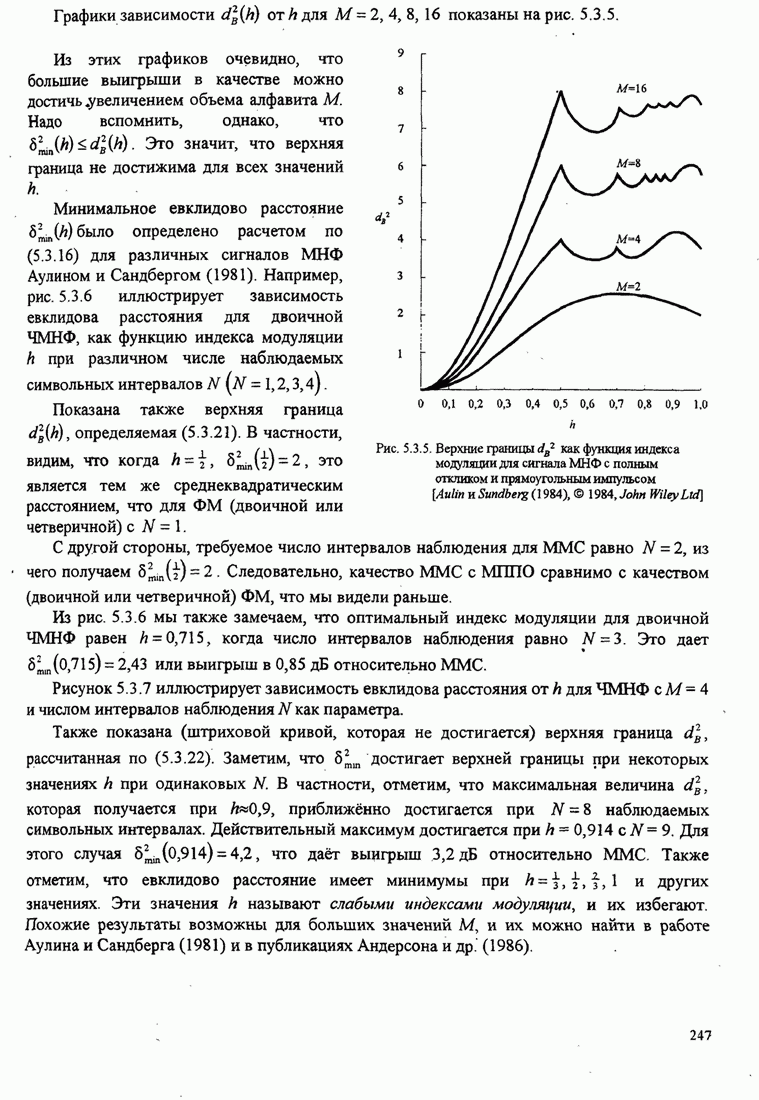
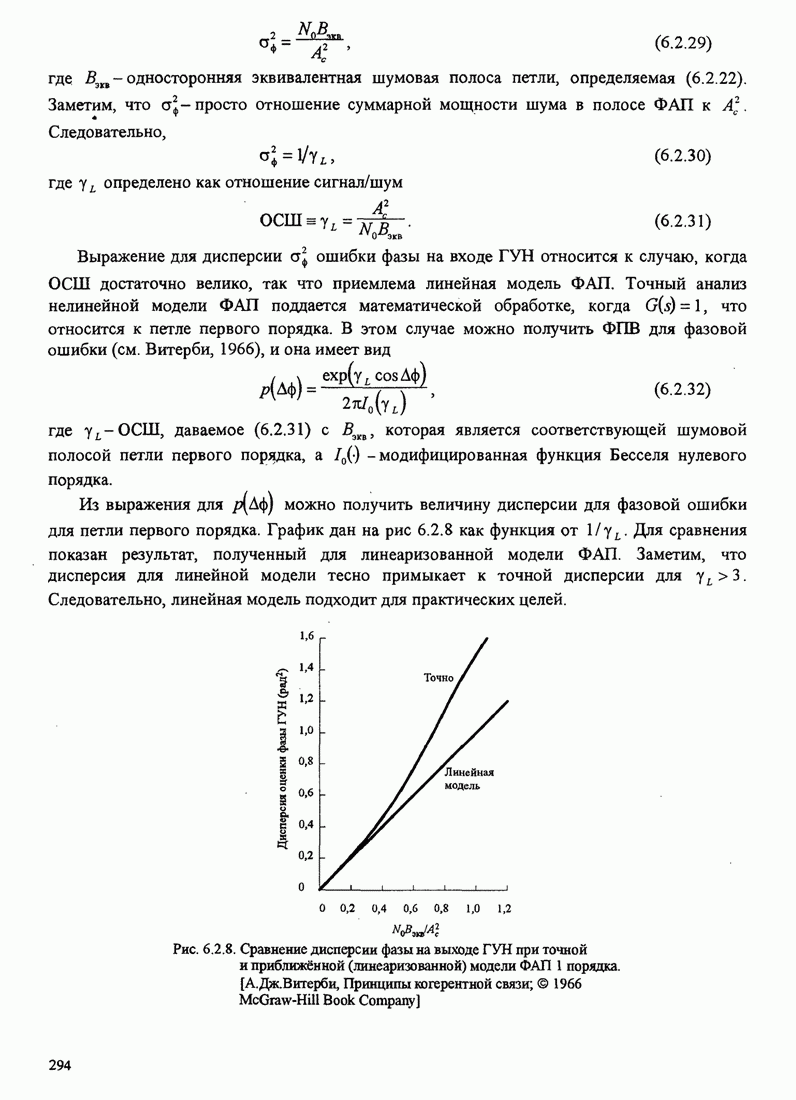
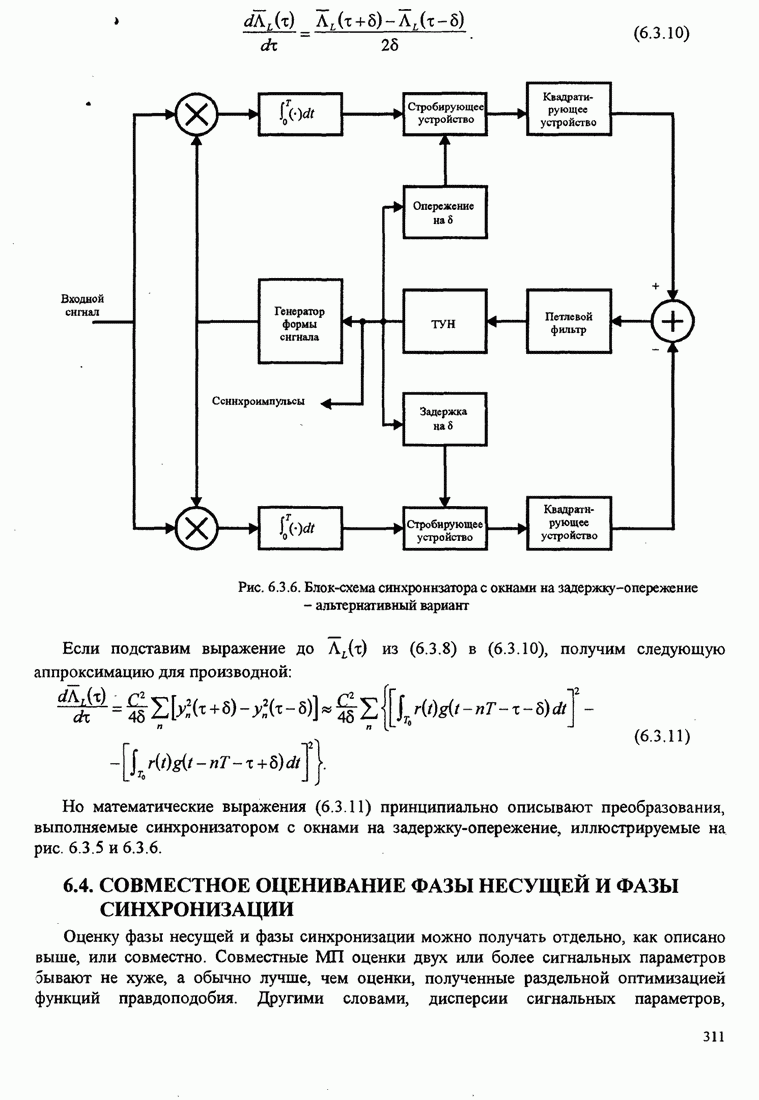
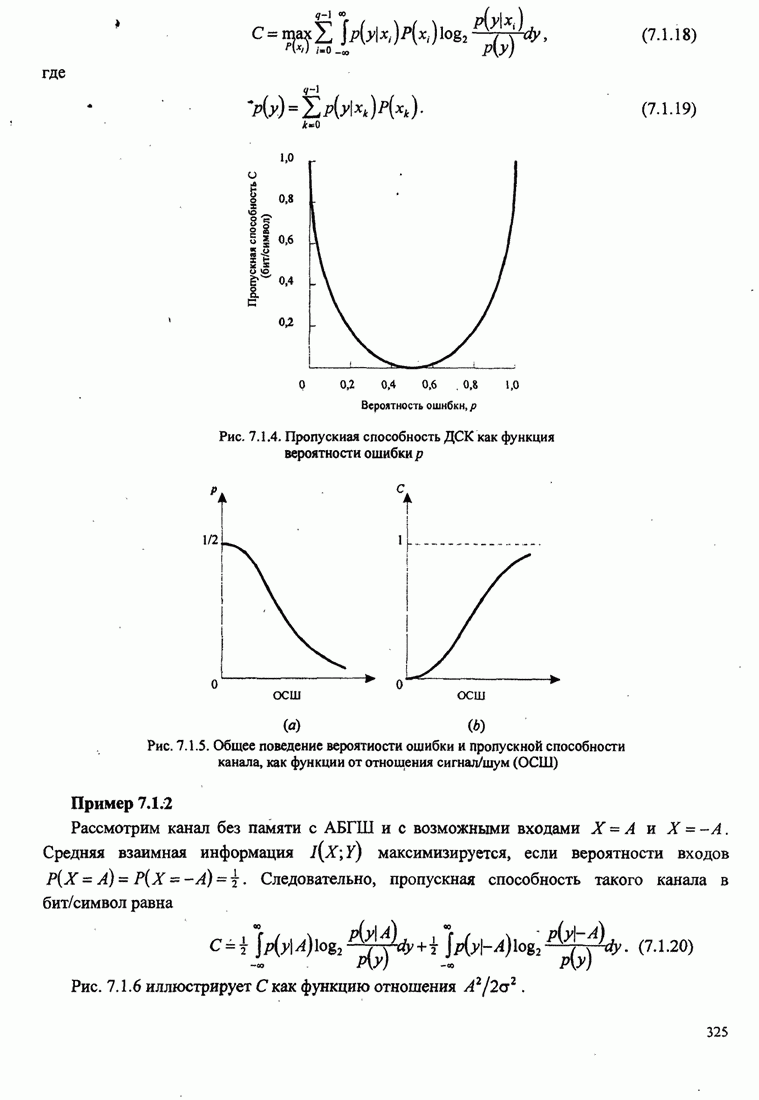
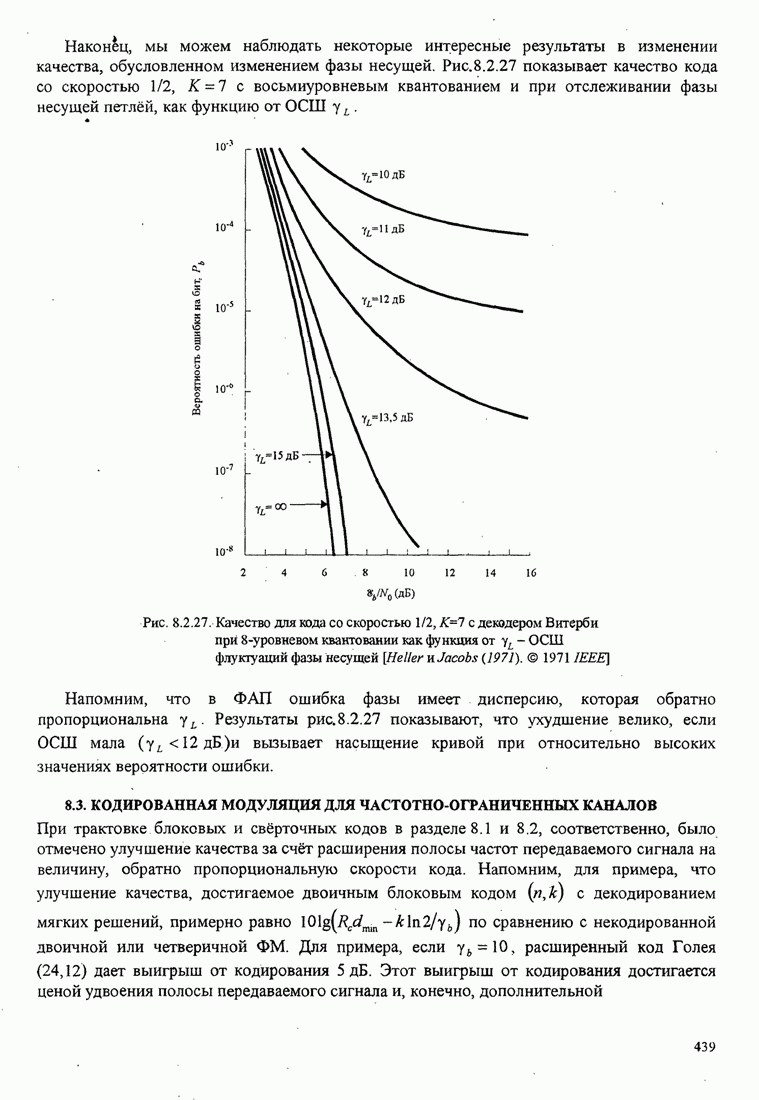
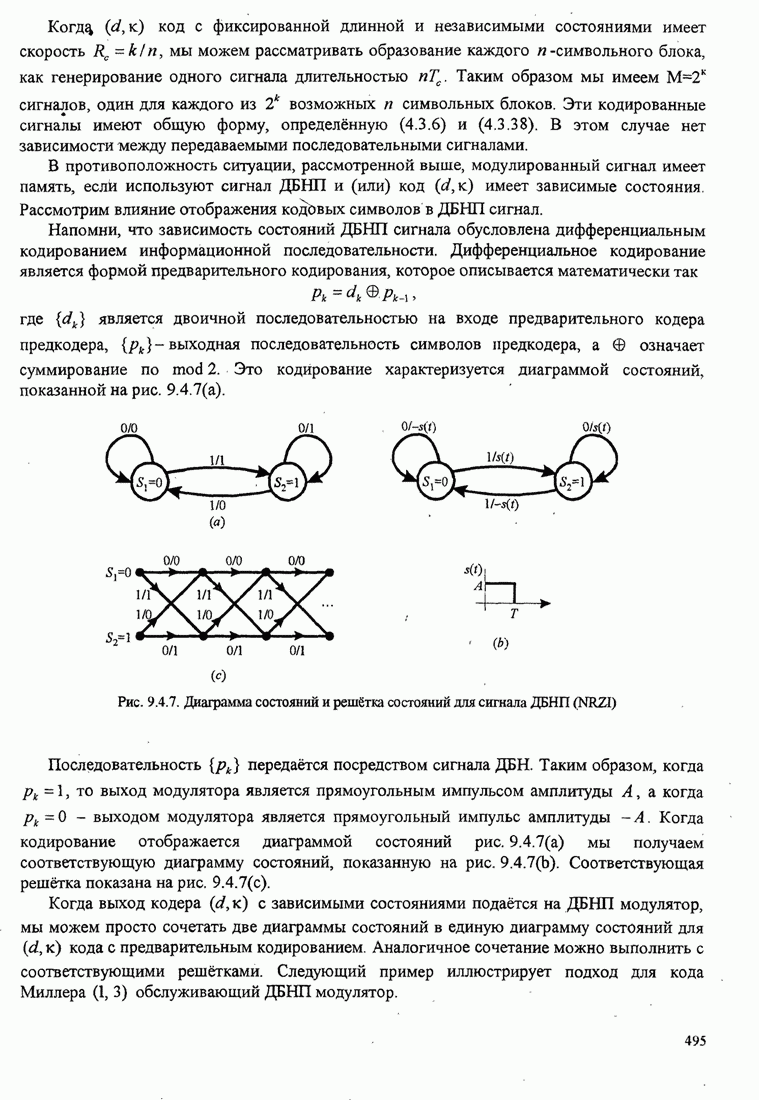
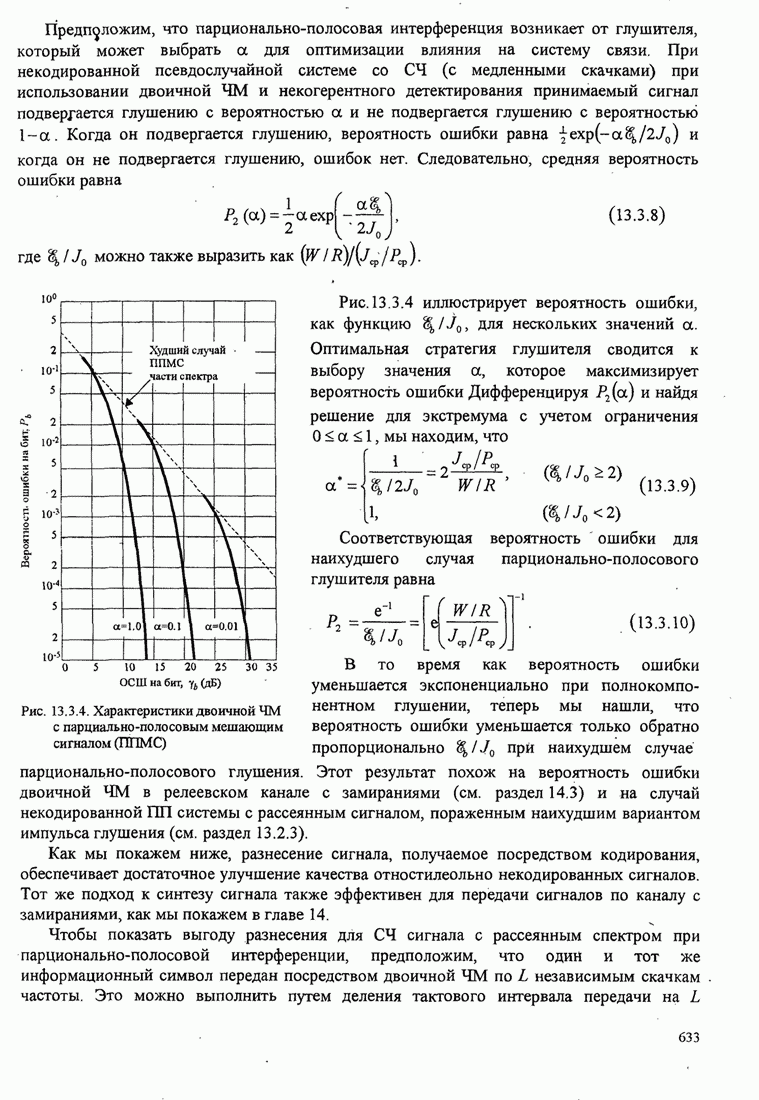
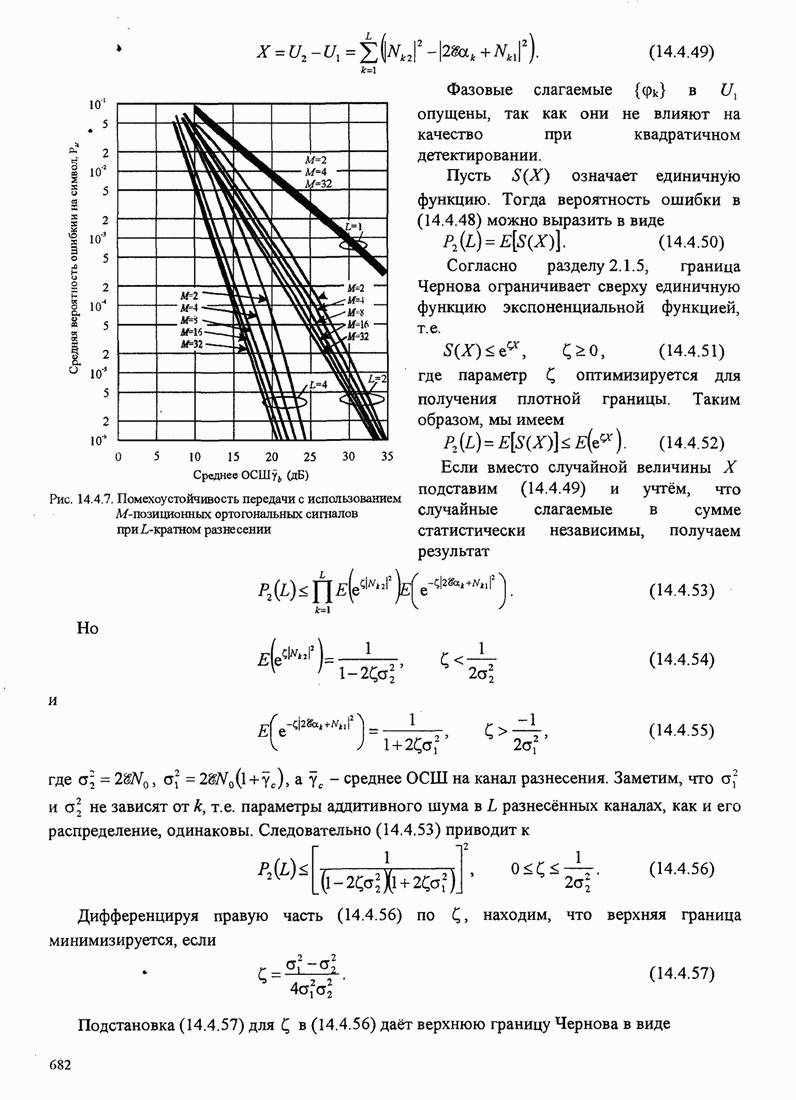
Рис.5.3.5. Верхние границы ![]() как функция индекса модуляции для
сигнала МНФ с полным откликом и прямоугольным импульсом
как функция индекса модуляции для
сигнала МНФ с полным откликом и прямоугольным импульсом
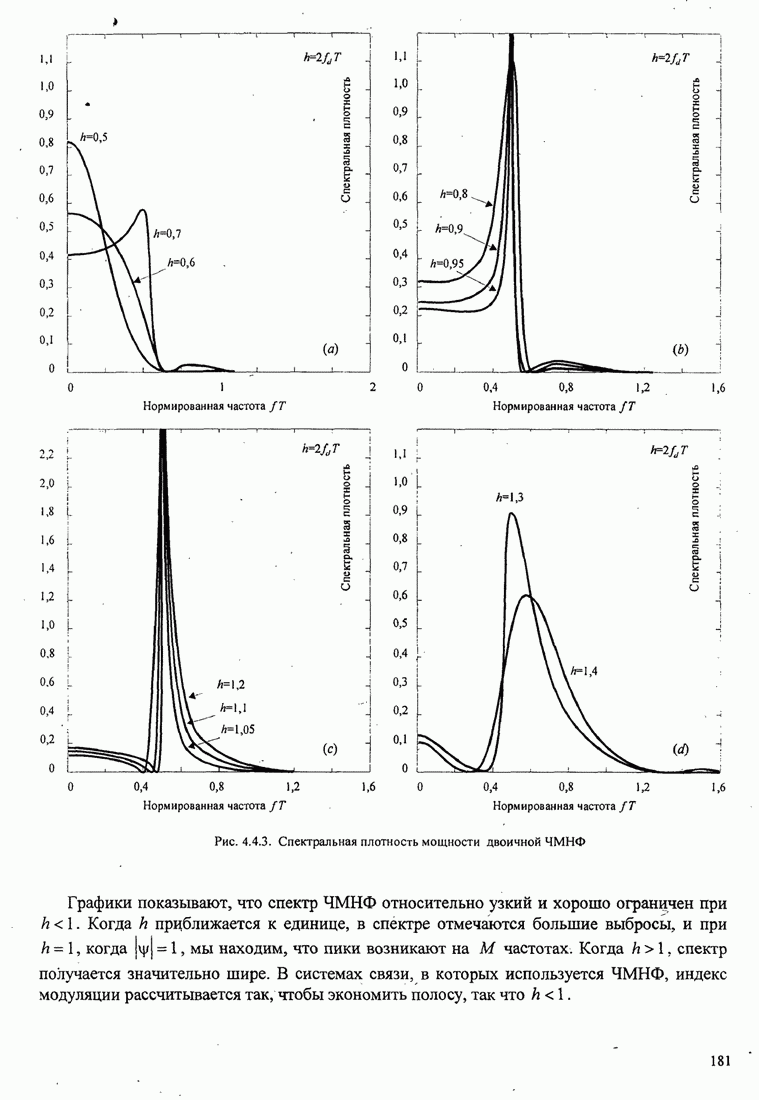
Из этих графиков очевидно, что большие выигрыши в качестве можно
достичь «увеличением объема алфавита ![]() . Надо вспомнить, однако,
что
. Надо вспомнить, однако,
что ![]() .
Это значит, что верхняя граница не достижима для всех значений
.
Это значит, что верхняя граница не достижима для всех значений ![]() .
.
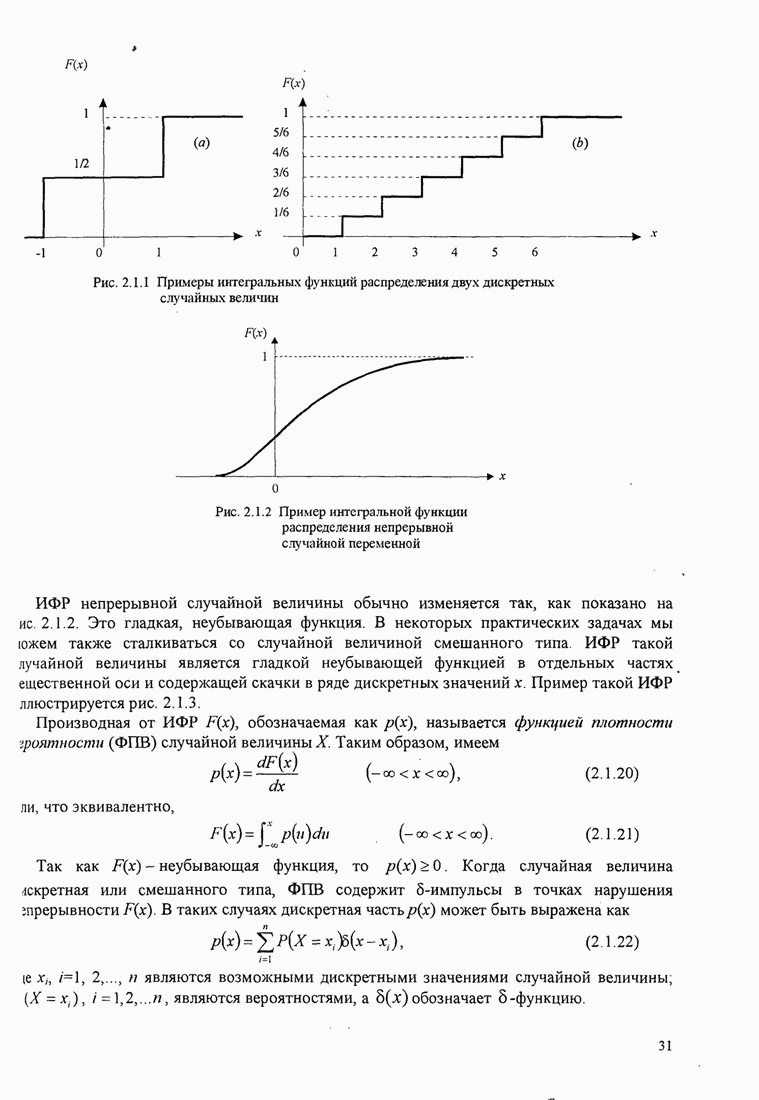
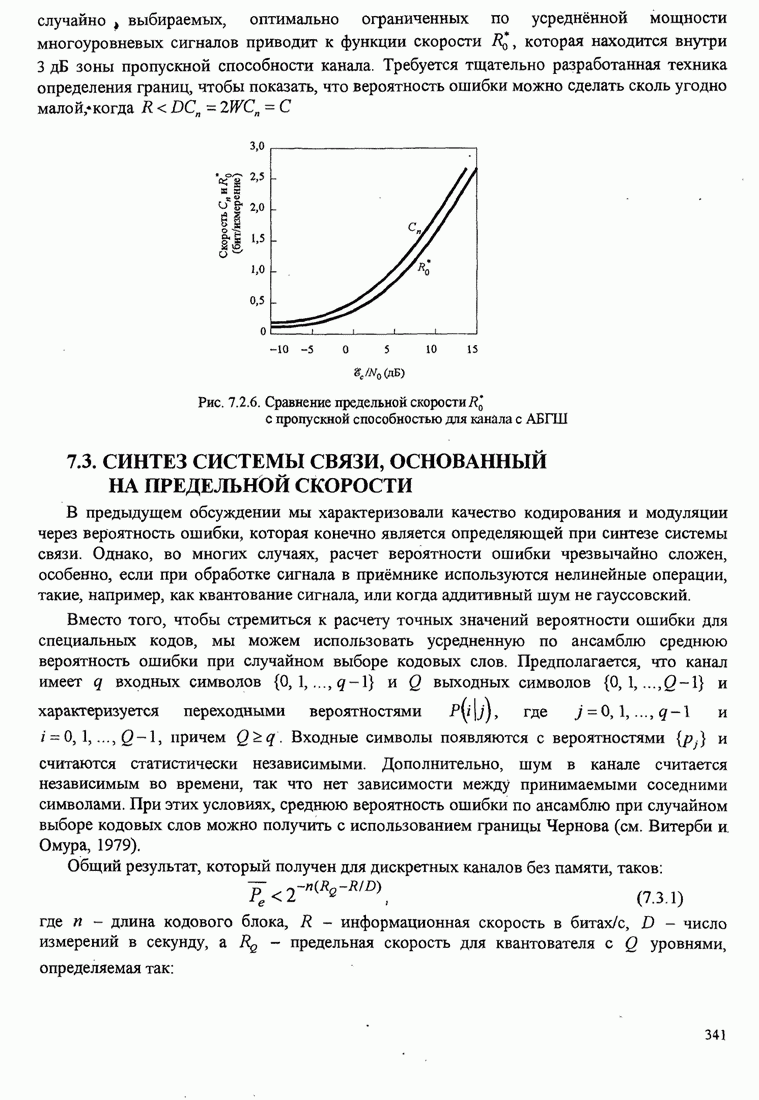
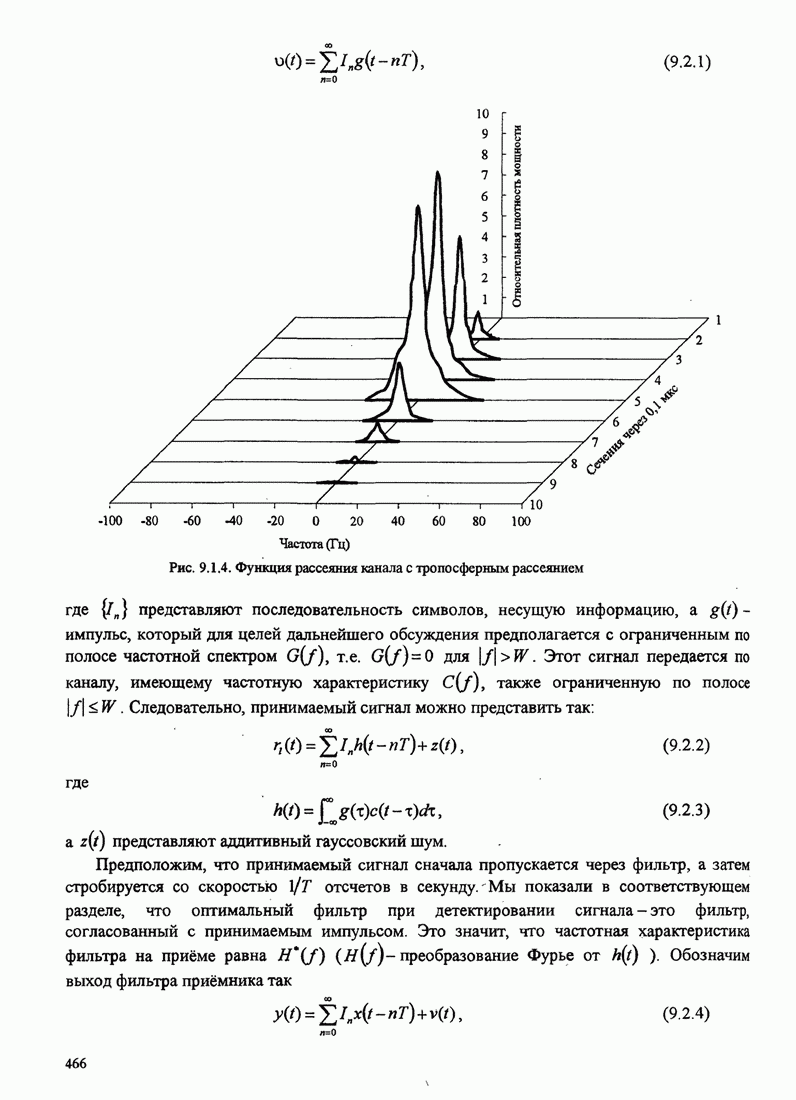
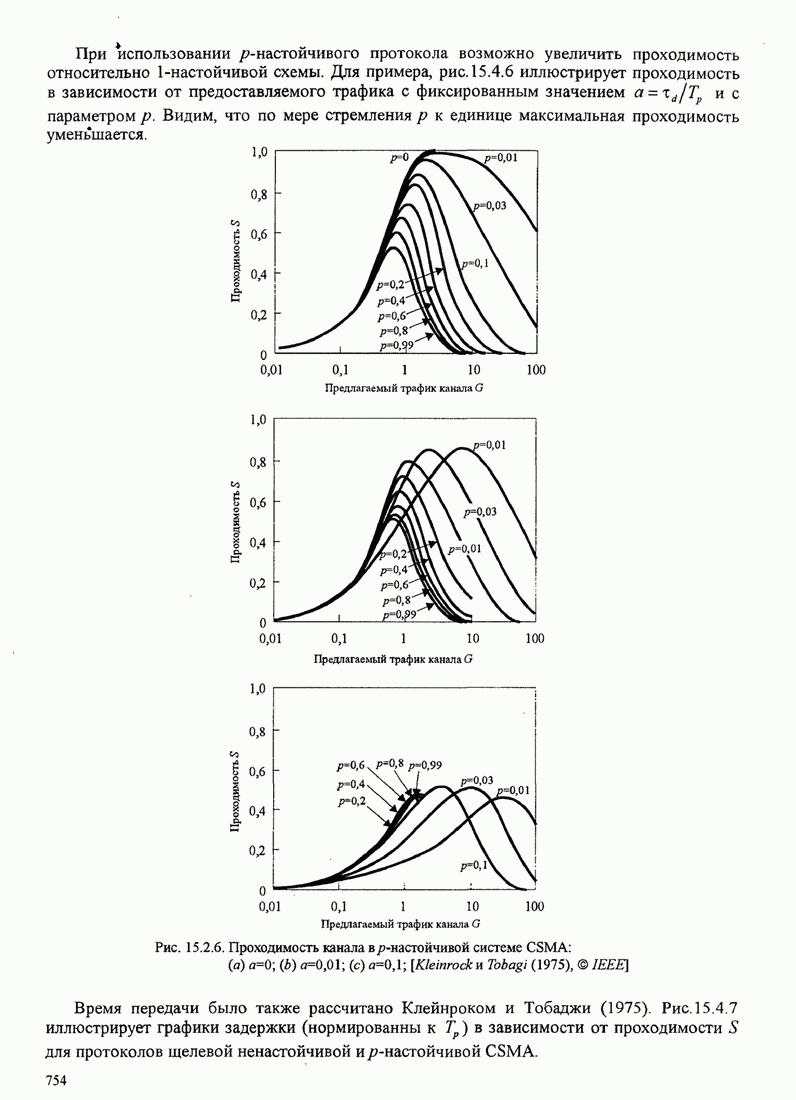
Минимальное евклидово расстояние ![]() было определено расчетом по (5.3.16)
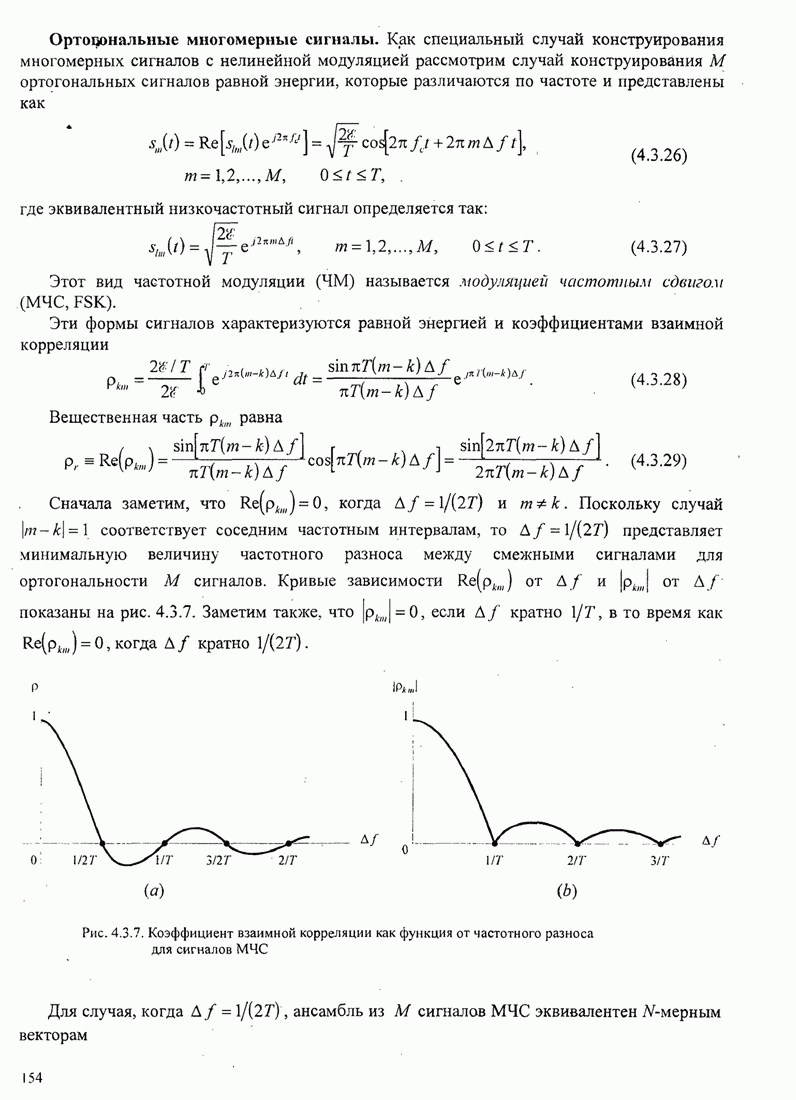
для различных сигналов МНФ Аулином и Сандбергом (1981). Например, рис. 5.3.6
иллюстрирует зависимость евклидова расстояния для двоичной ЧМНФ, как функцию индекса
модуляции
было определено расчетом по (5.3.16)
для различных сигналов МНФ Аулином и Сандбергом (1981). Например, рис. 5.3.6
иллюстрирует зависимость евклидова расстояния для двоичной ЧМНФ, как функцию индекса
модуляции ![]() при
различном числе наблюдаемых символьных интервалов
при
различном числе наблюдаемых символьных интервалов ![]() .
.
Показана также верхняя граница ![]() , определяемая (5.3.21). В
частности, видим, что когда
, определяемая (5.3.21). В
частности, видим, что когда ![]() , это является тем же
среднеквадратическим расстоянием, что для ФМ (двоичной или четверичной) с
, это является тем же
среднеквадратическим расстоянием, что для ФМ (двоичной или четверичной) с ![]() .
.
С другой стороны, требуемое число интервалов наблюдения для ММС равно ![]() , из чего
получаем
, из чего
получаем ![]() .
Следовательно, качество ММС с МППО сравнимо с качеством (двоичной или
четверичной) ФМ, что мы видели раньше.
.
Следовательно, качество ММС с МППО сравнимо с качеством (двоичной или
четверичной) ФМ, что мы видели раньше.
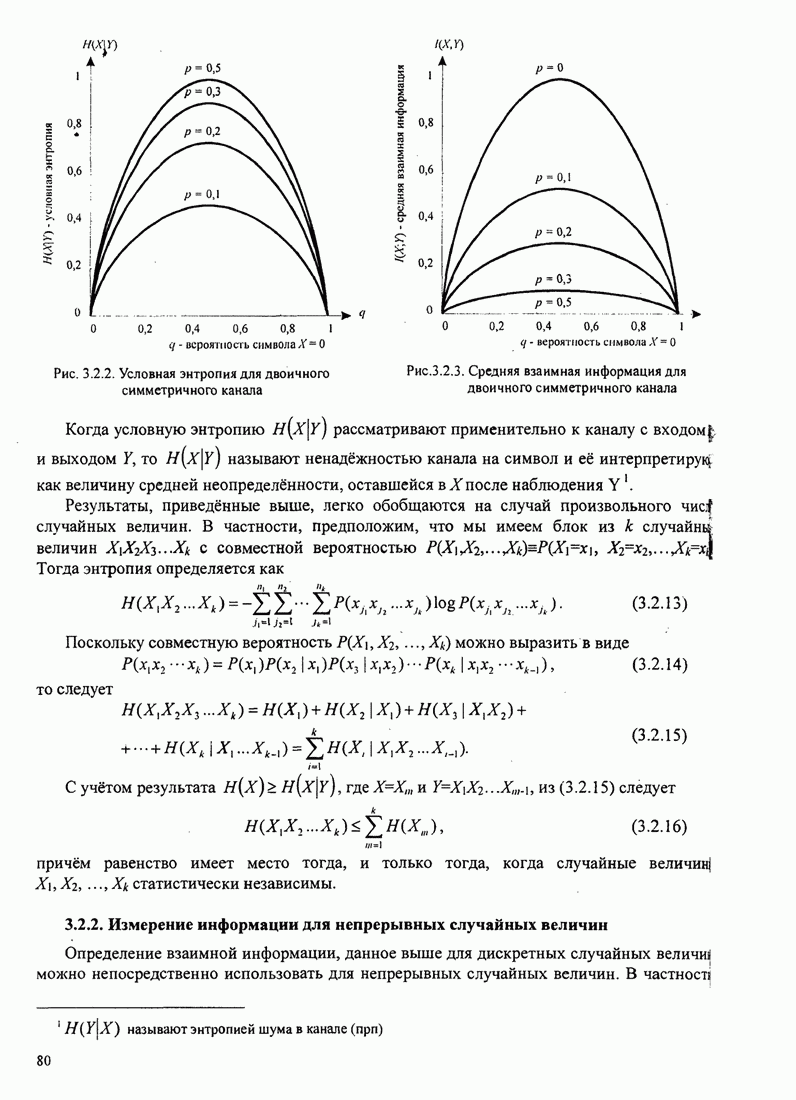
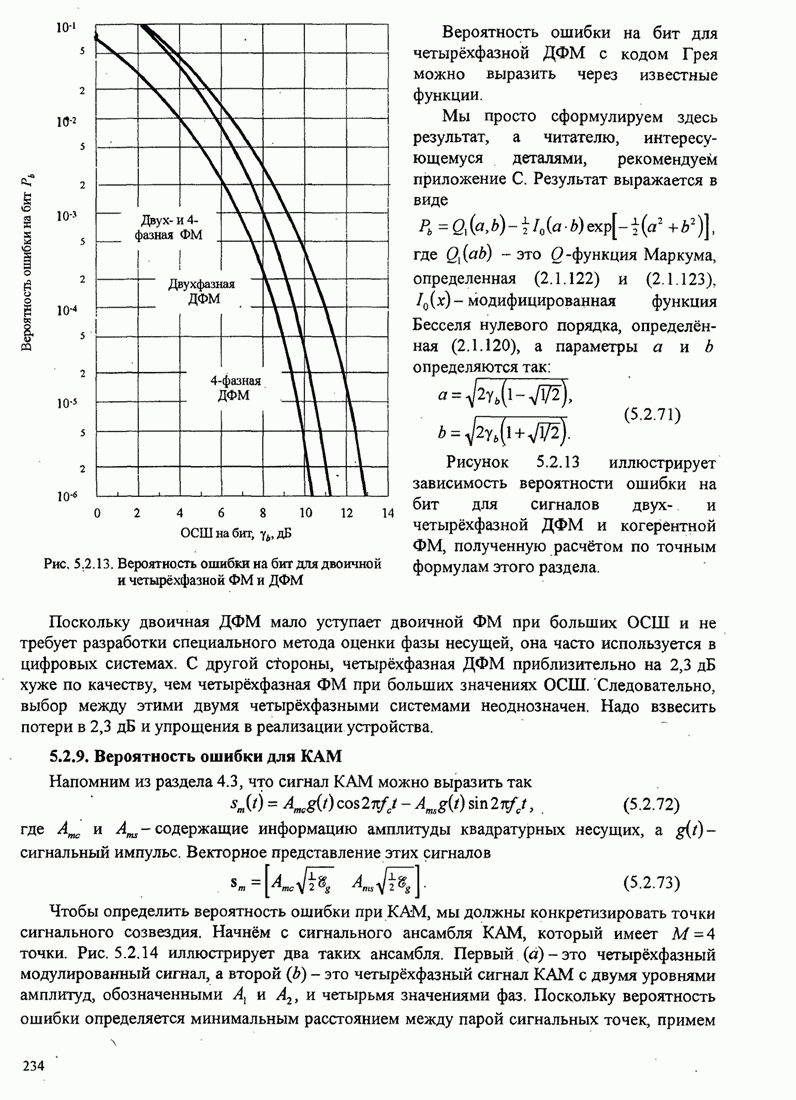
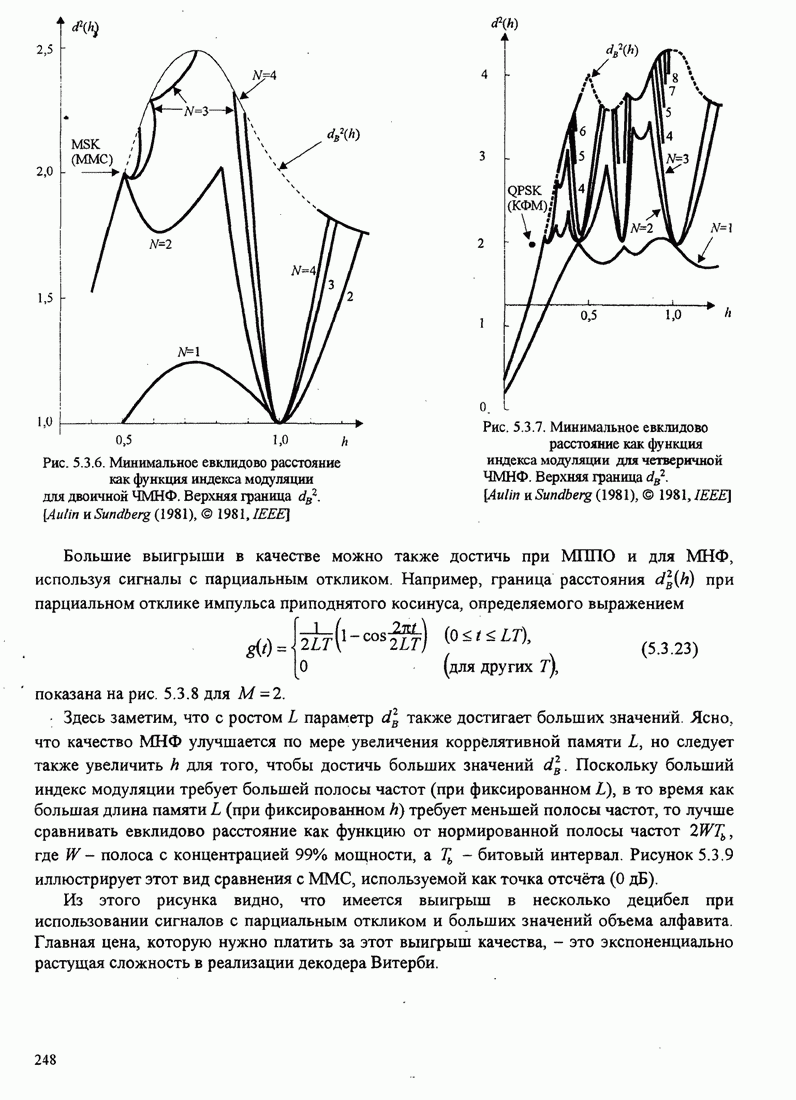
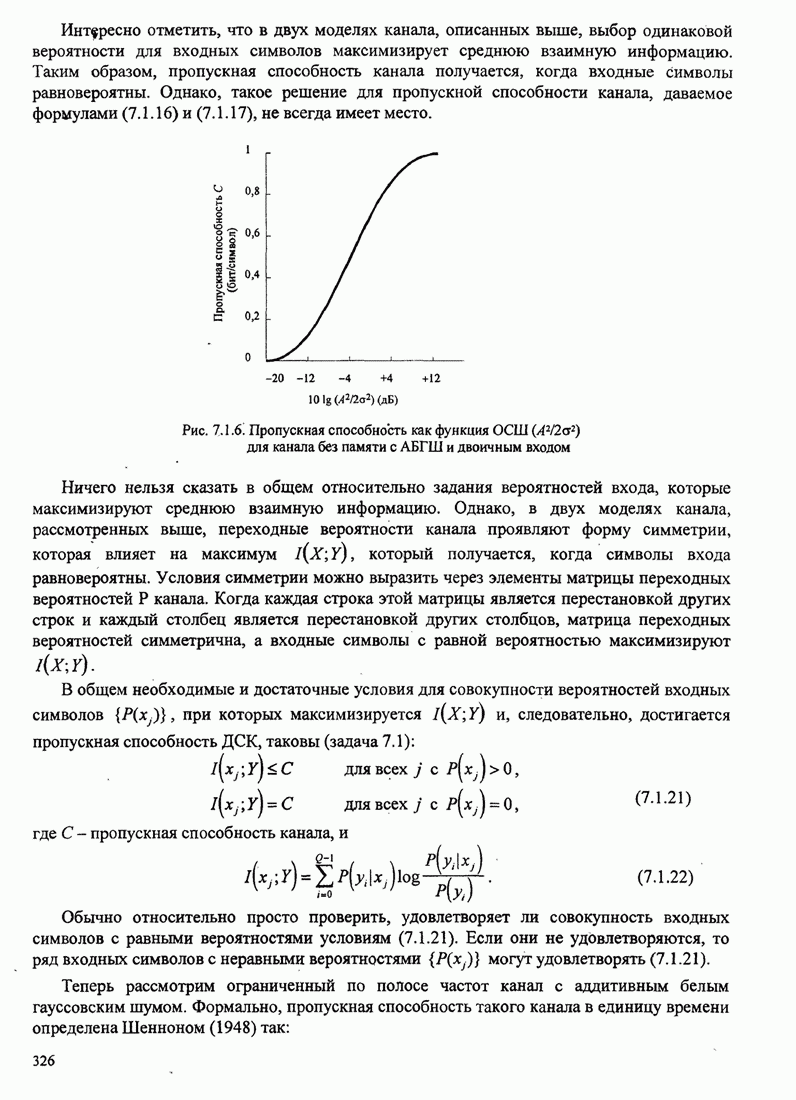
Из рис. 5.3.6 мы также замечаем, что оптимальный индекс модуляции для
двоичной ЧМНФ равен ![]() , когда число интервалов
наблюдения равно
, когда число интервалов
наблюдения равно ![]() .
Это дает
.
Это дает ![]() или
выигрыш в 0,85 дБ относительно ММС.
или
выигрыш в 0,85 дБ относительно ММС.
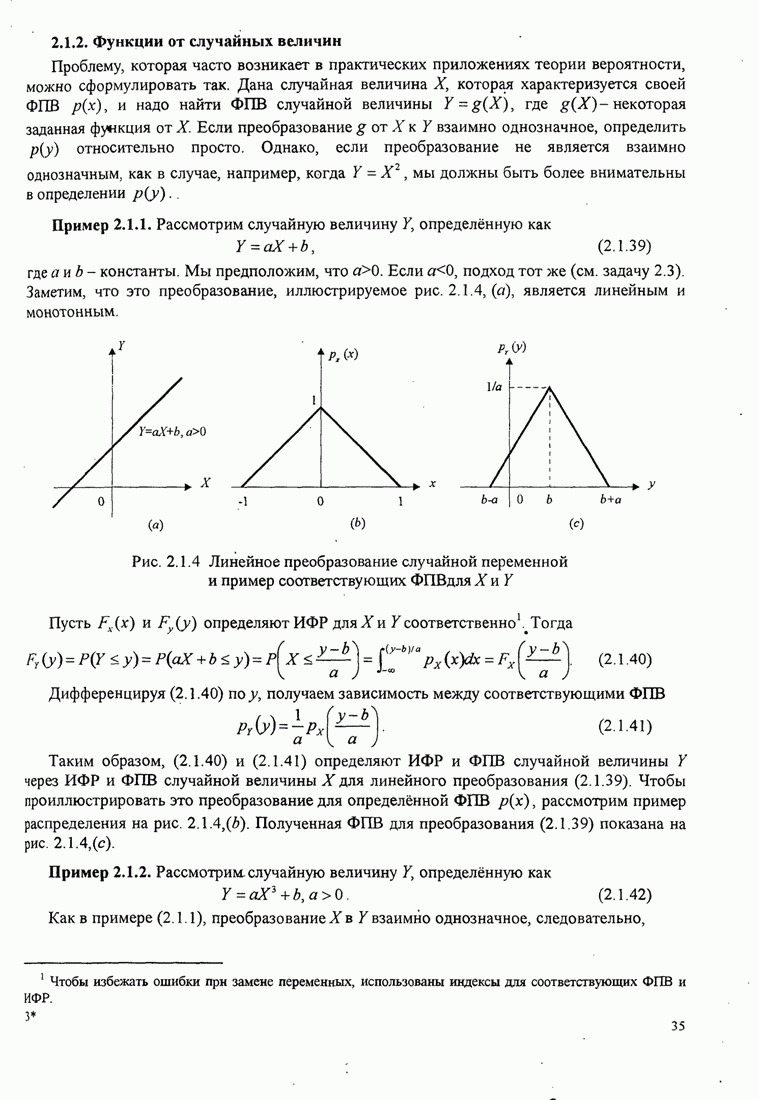
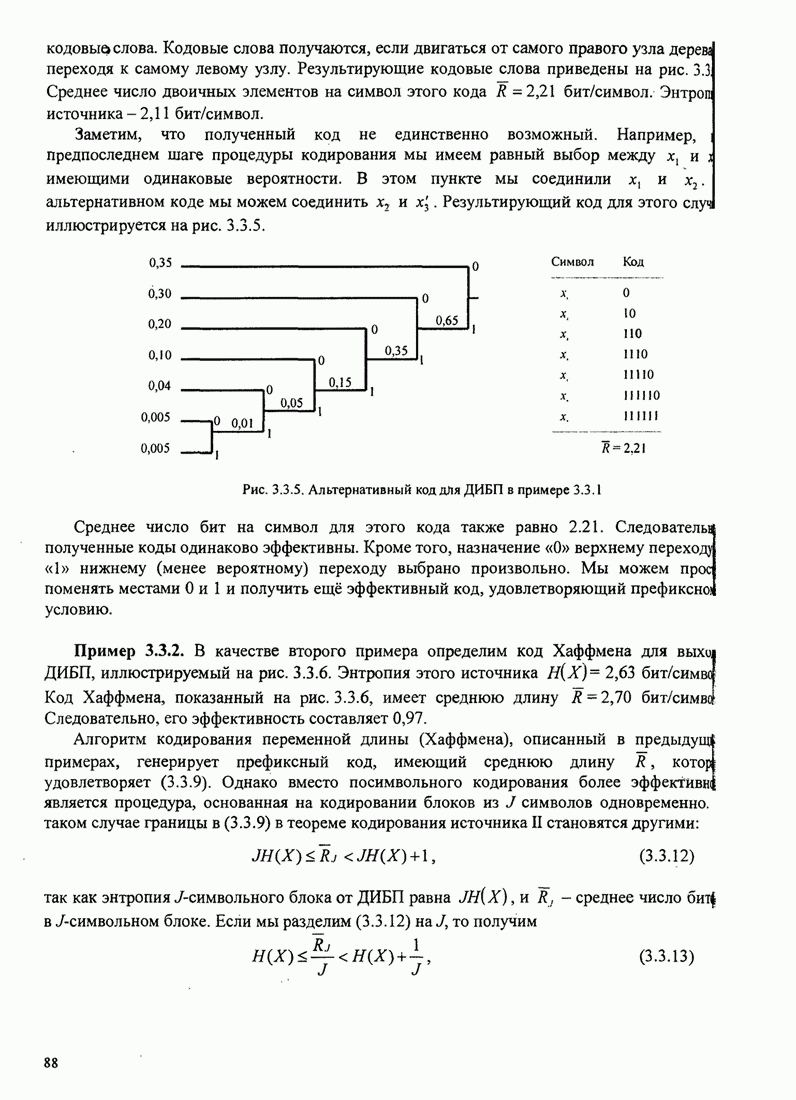
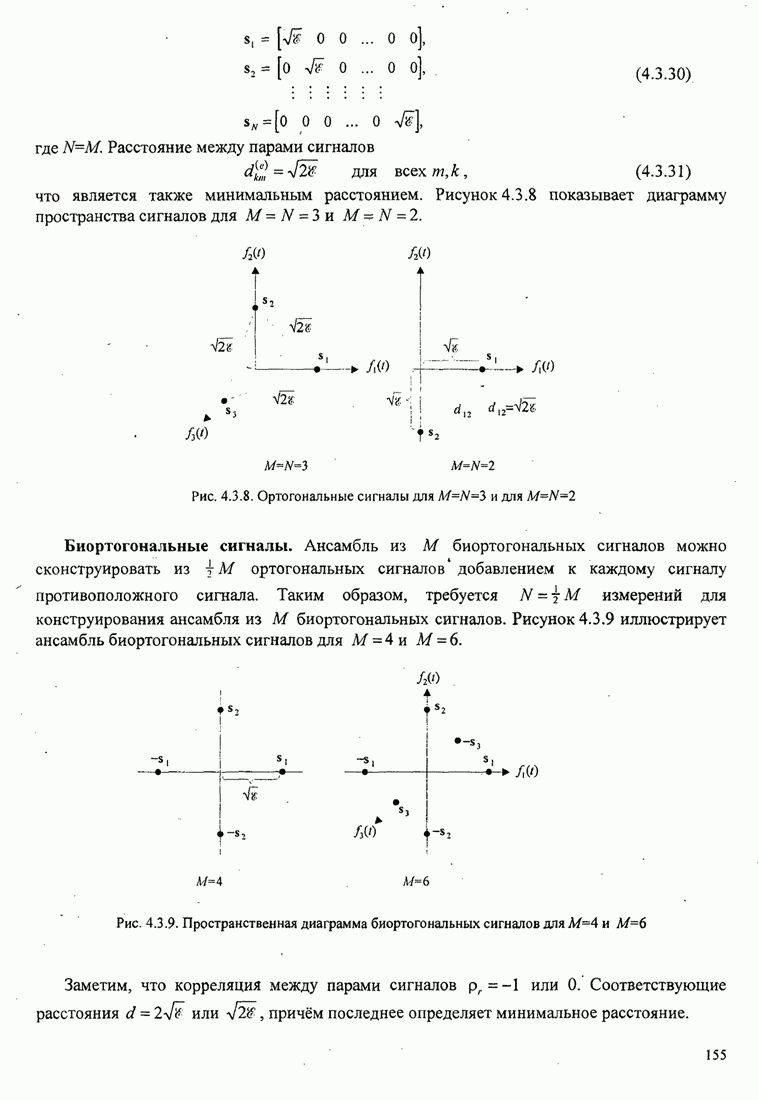
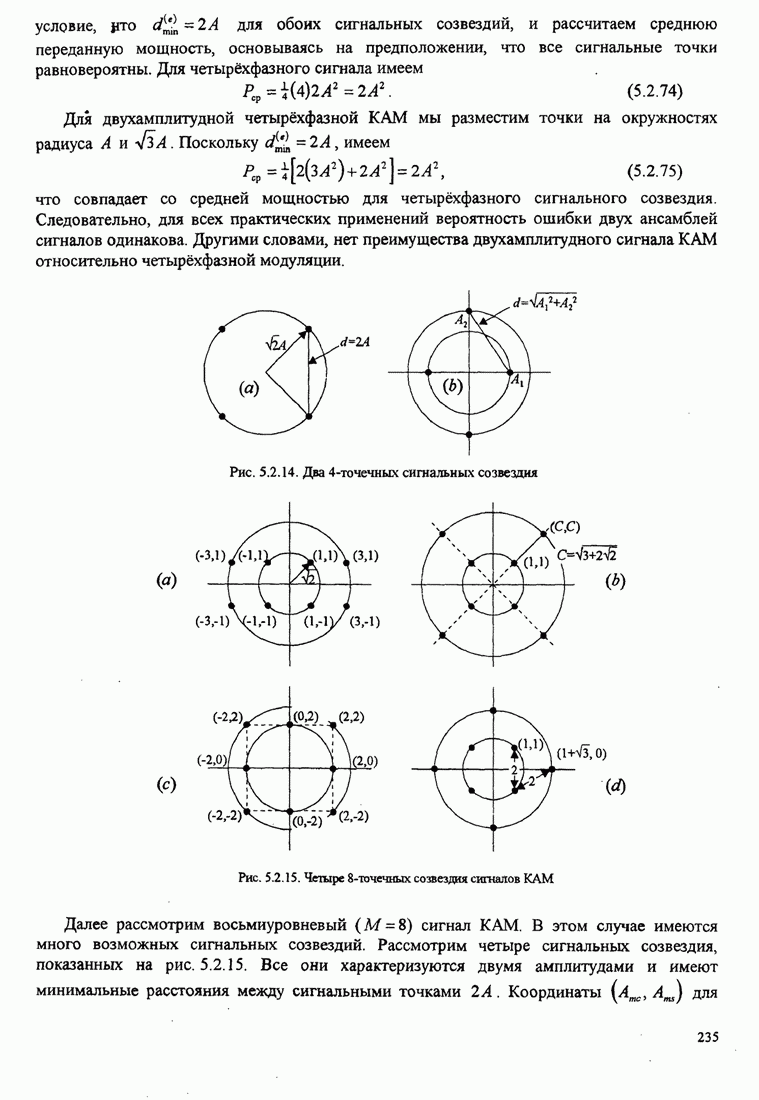
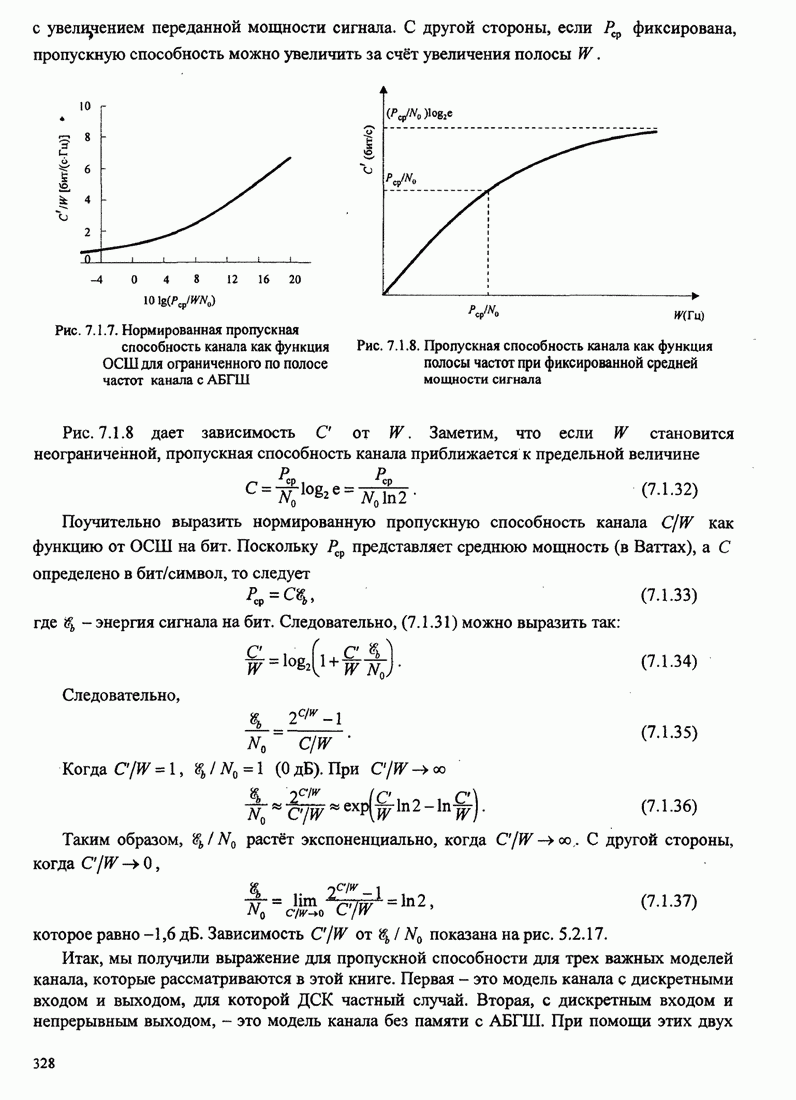
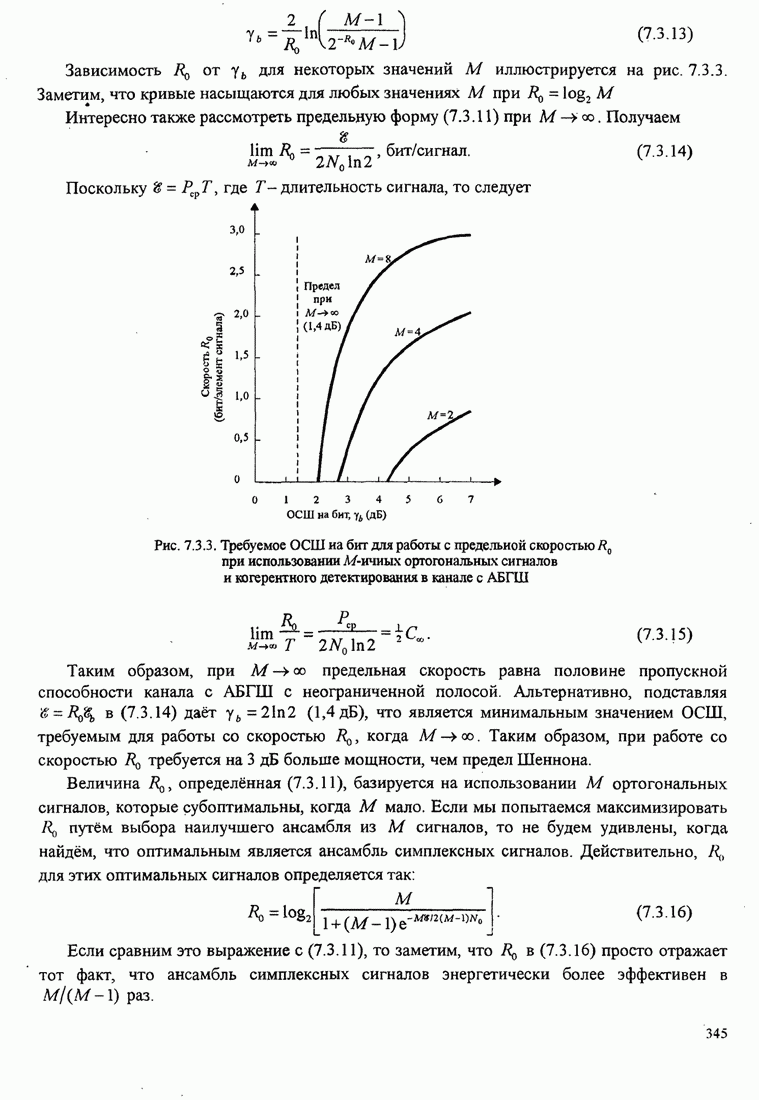
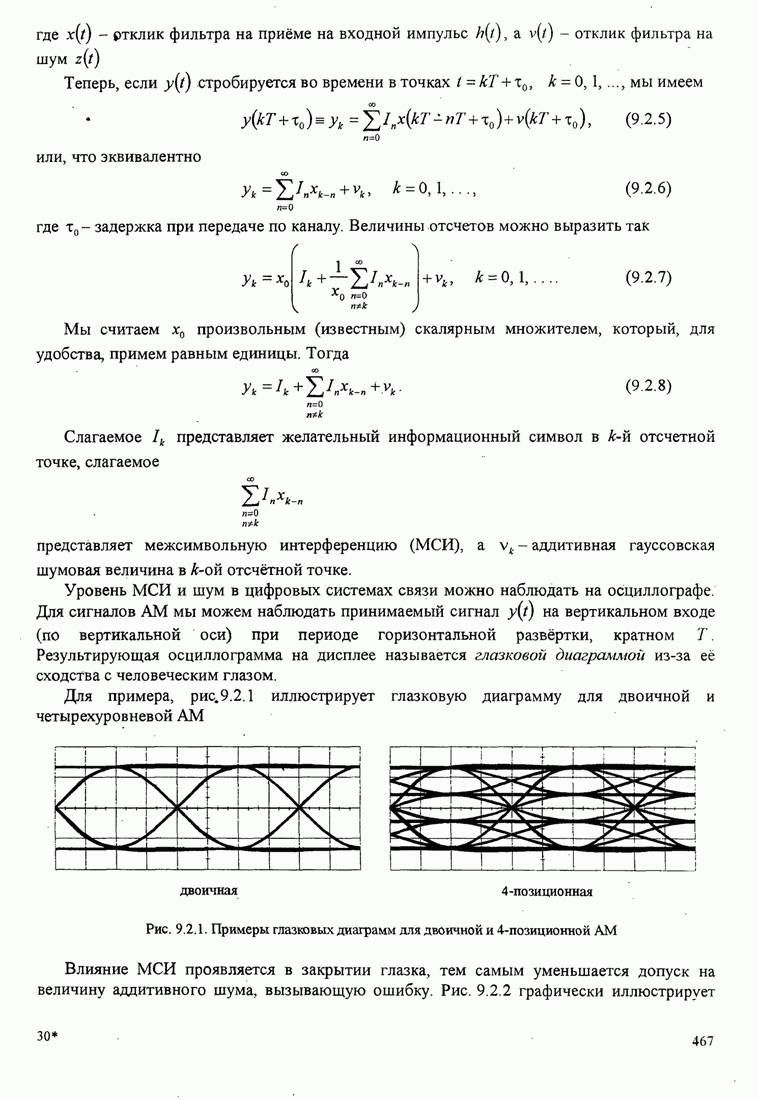
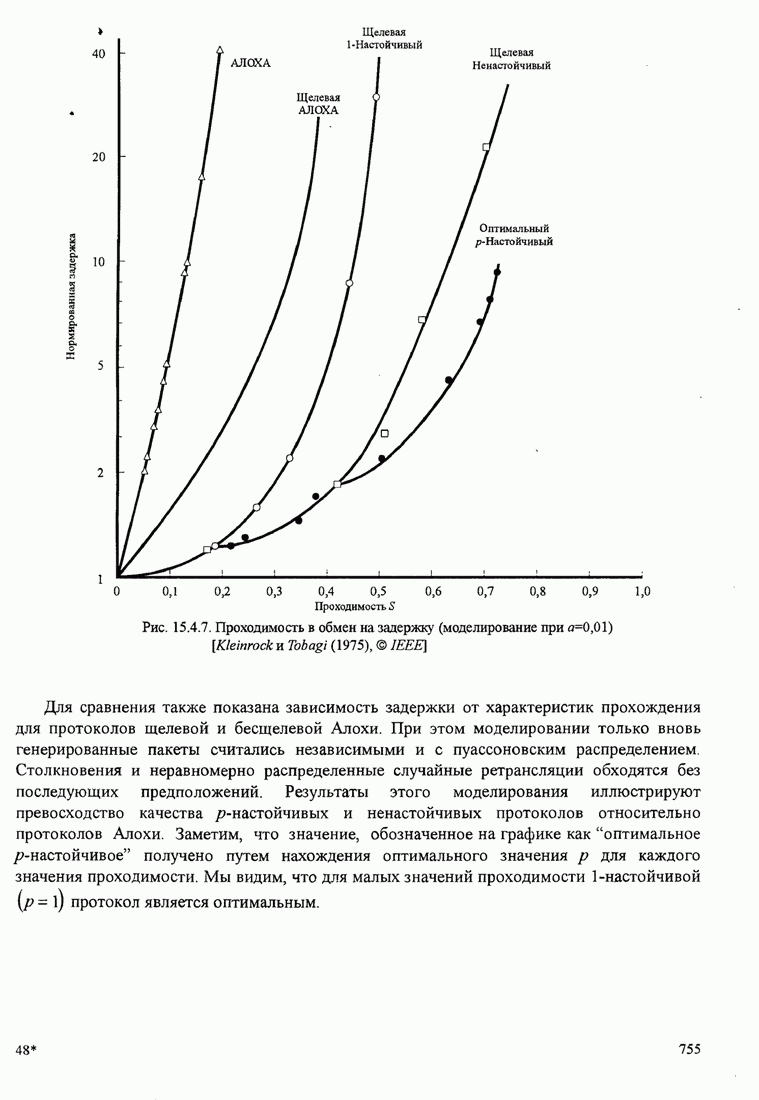
Рисунок 5.3.7 иллюстрирует зависимость евклидова расстояния от ![]() для ЧМНФ
с
для ЧМНФ
с ![]() и
числом интервалов наблюдения
и
числом интервалов наблюдения ![]() как параметра.
как параметра.
Также показана (штриховой кривой, которая не достигается) верхняя
граница ![]() ,
рассчитанная по (5.3.22). Заметим, что
,
рассчитанная по (5.3.22). Заметим, что ![]() достигает верхней границы при
некоторых значениях
достигает верхней границы при
некоторых значениях ![]() при одинаковых
при одинаковых ![]() . В
частности, отметим, что максимальная величина
. В
частности, отметим, что максимальная величина ![]() , которая получается при
, которая получается при ![]() , приближённо
достигается при
, приближённо
достигается при ![]() наблюдаемых
символьных интервалах. Действительный максимум достигается при
наблюдаемых
символьных интервалах. Действительный максимум достигается при ![]() с
с ![]() . Для этого случая
. Для этого случая ![]() , что
даёт выигрыш 3,2 дБ относительно ММС. Также отметим, что евклидово расстояние
имеет минимумы при
, что
даёт выигрыш 3,2 дБ относительно ММС. Также отметим, что евклидово расстояние
имеет минимумы при ![]() и других значениях. Эти
значения
и других значениях. Эти
значения ![]() называют
слабыми индексами модуляции, и их избегают. Похожие результаты возможны для больших
значений
называют
слабыми индексами модуляции, и их избегают. Похожие результаты возможны для больших
значений ![]() ,
и их можно найти в работе Аулина и Сандберга (1981) и в публикациях Андерсона и
др. (1986).
,
и их можно найти в работе Аулина и Сандберга (1981) и в публикациях Андерсона и
др. (1986).

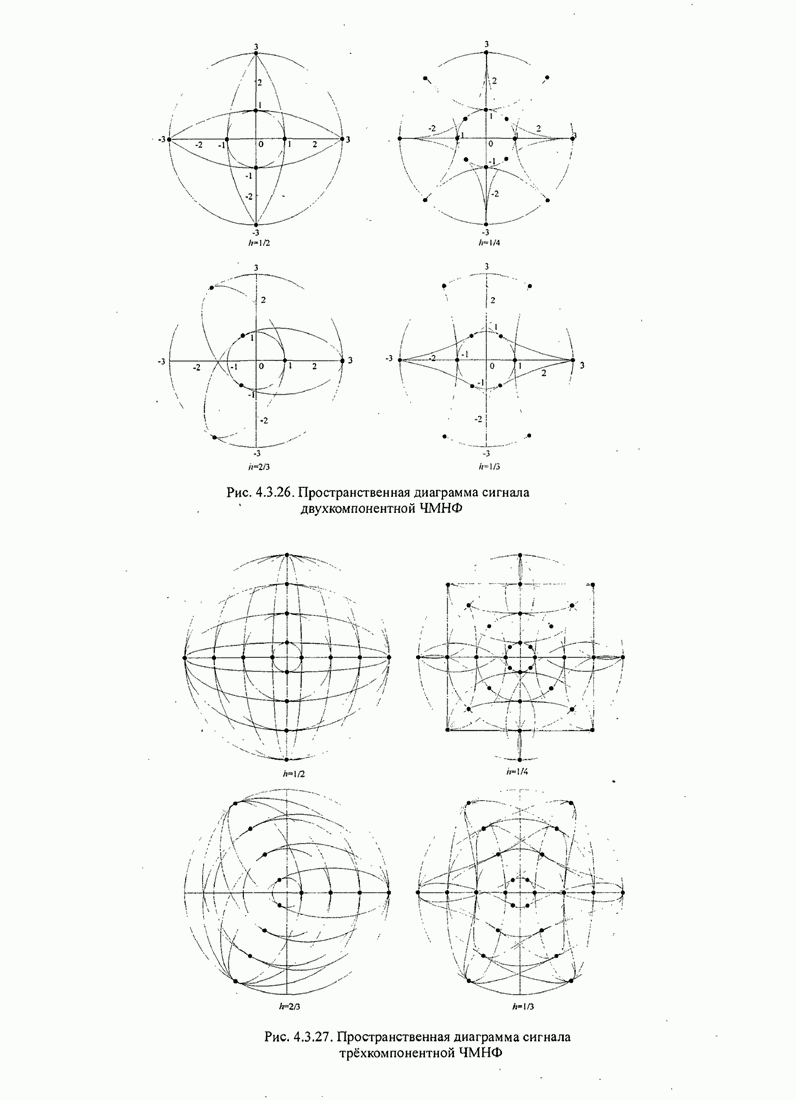
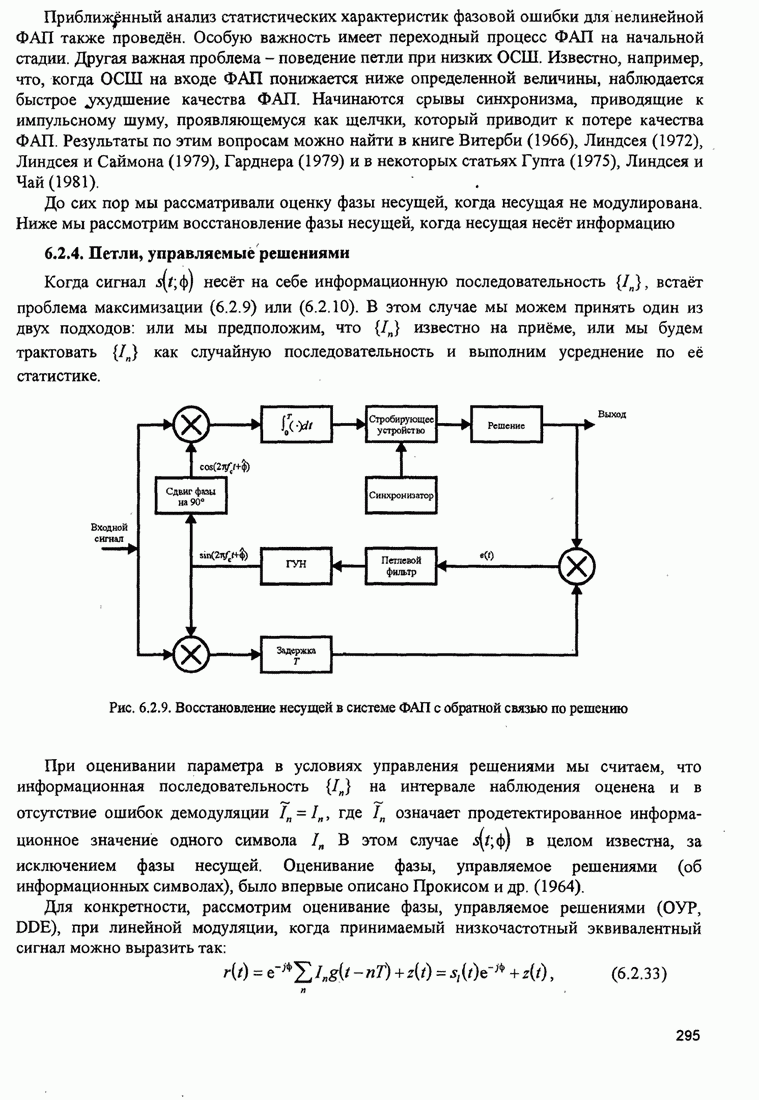
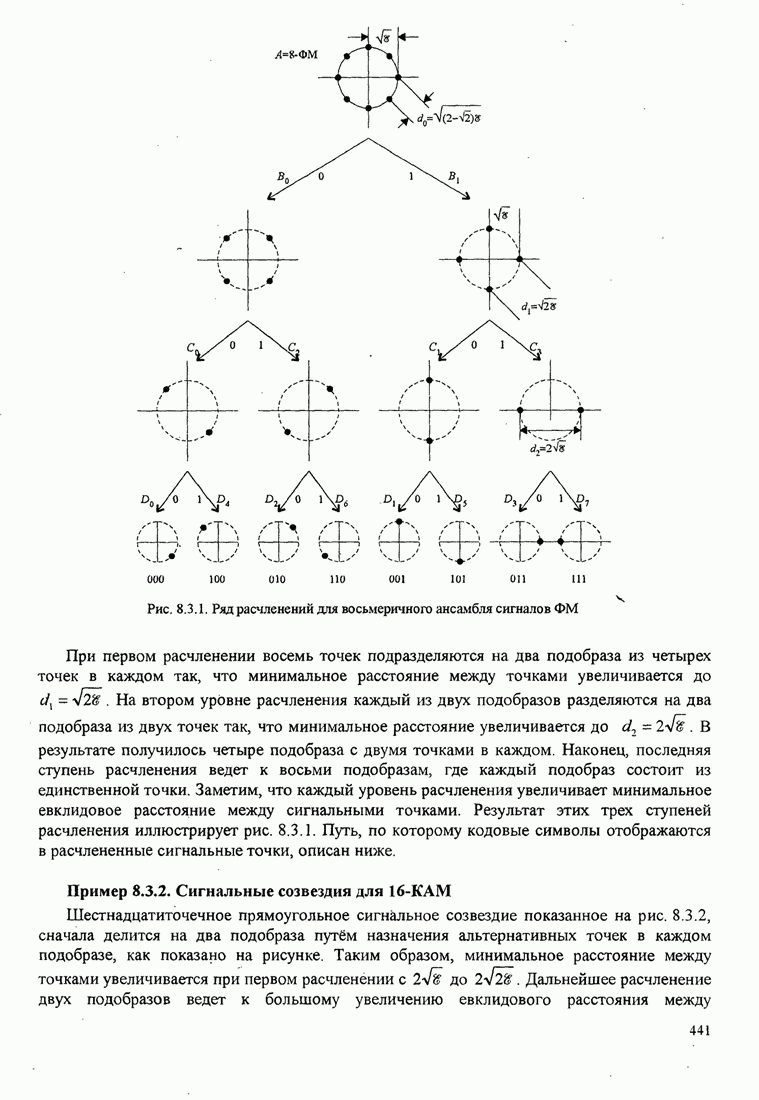
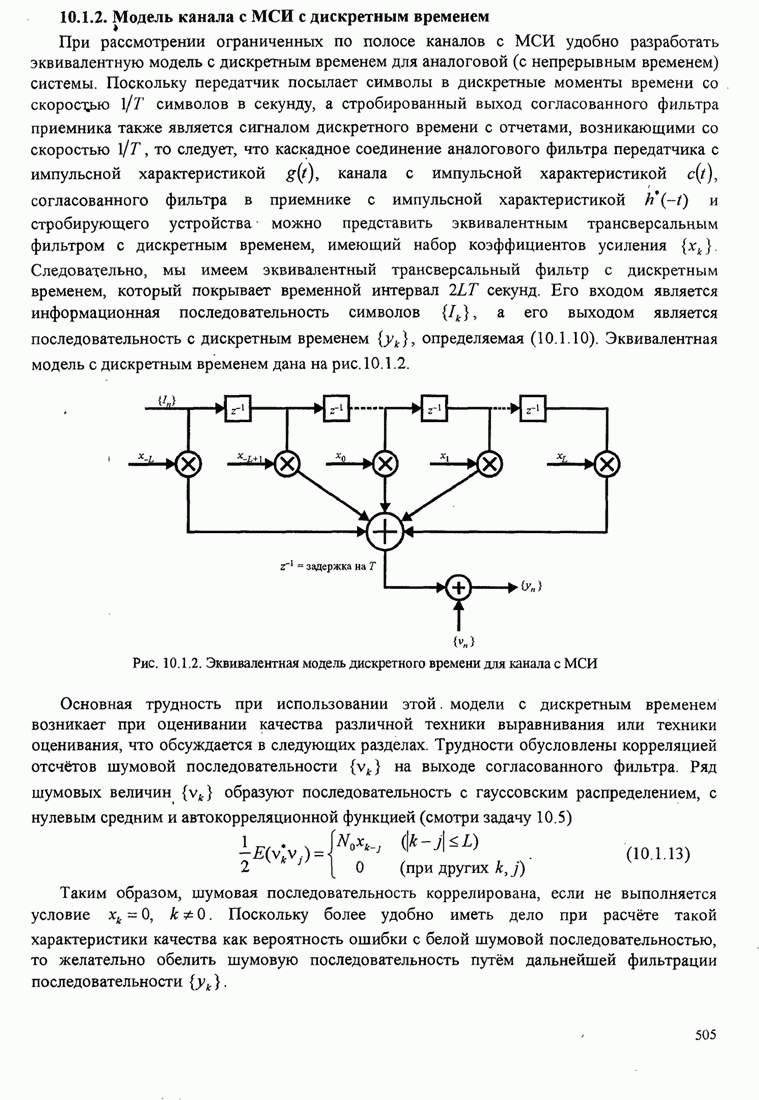
Рис.5.3.6. Минимальное евклидово расстояние как функция
индекса модуляции для двоичной ЧМНФ. Верхняя граница ![]() .
.

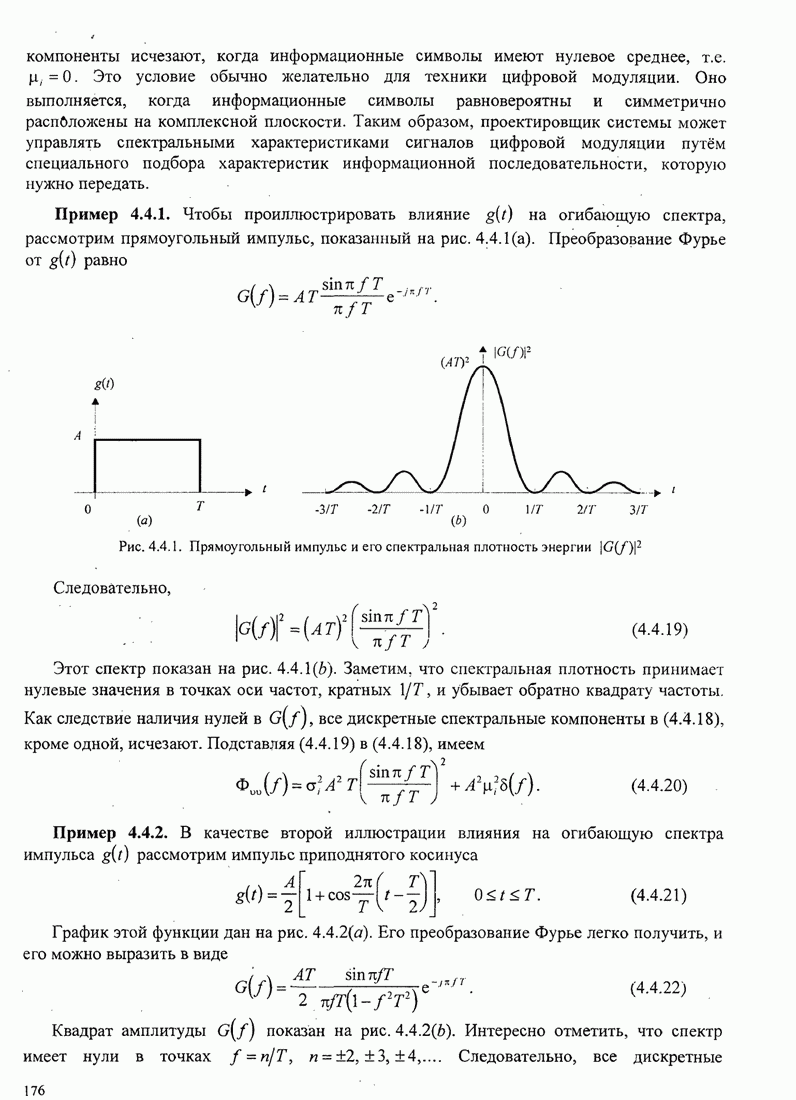
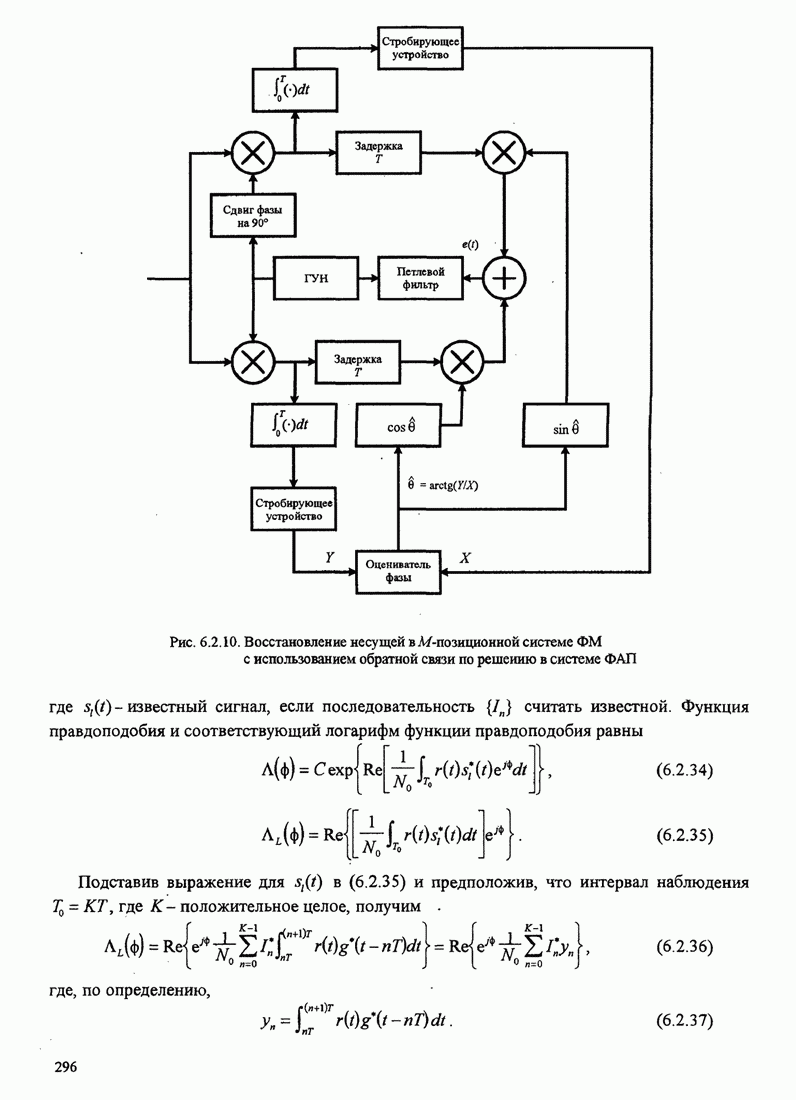
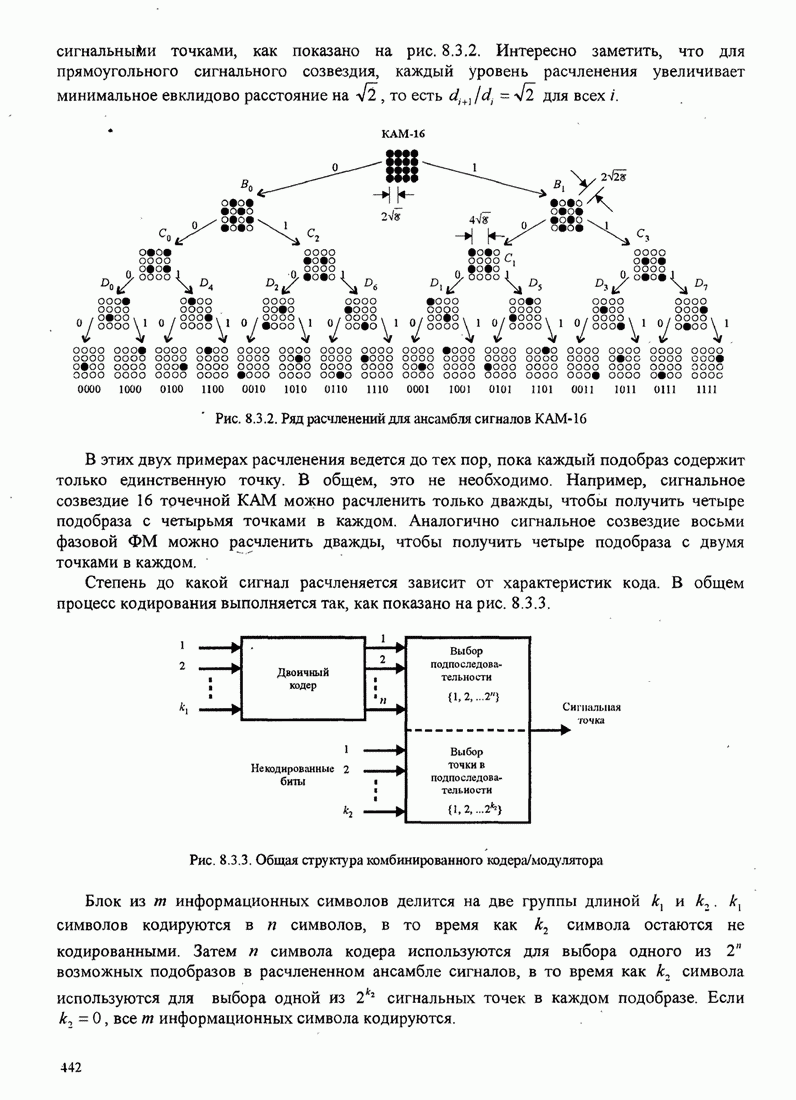
Рис.5.3.7. Минимальное евклидово расстояние как функция
индекса модуляции для четверичной ЧМНФ. Верхняя граница ![]() .
.
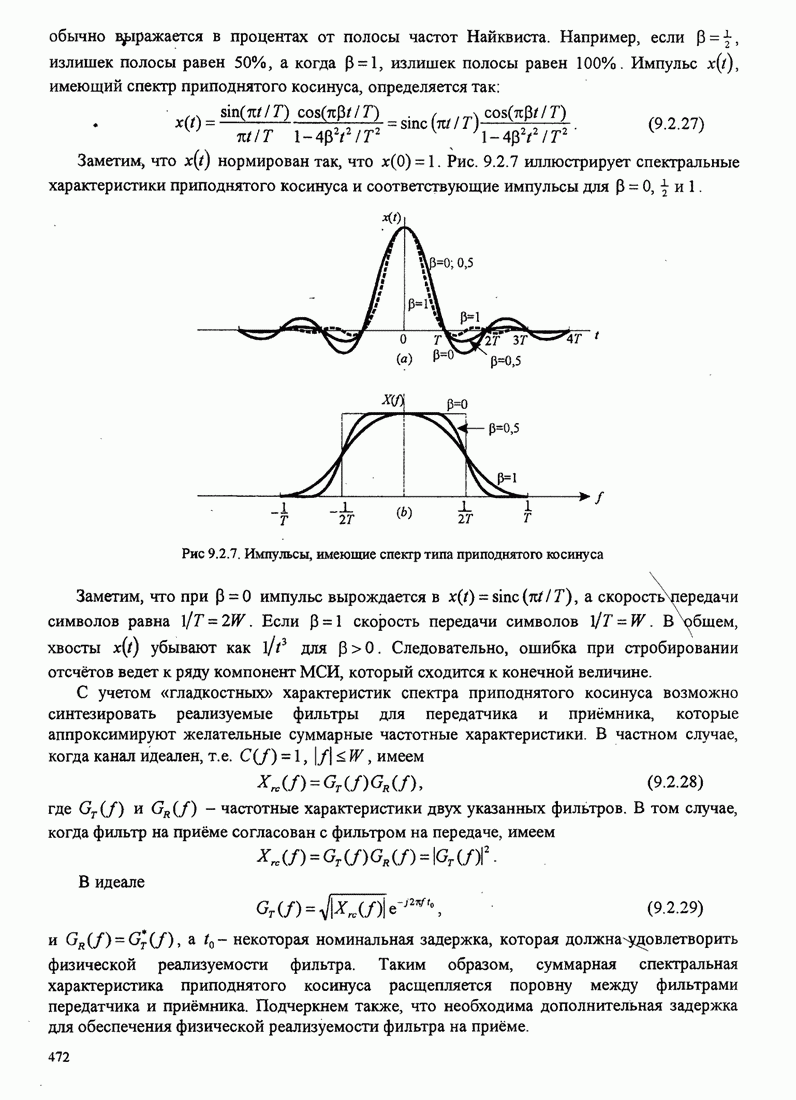
Большие выигрыши в качестве можно также достичь при МППО и для МНФ,
используя сигналы с парциальным откликом. Например, граница расстояния ![]() при
парциальном отклике импульса приподнятого косинуса, определяемого выражением
при
парциальном отклике импульса приподнятого косинуса, определяемого выражением
 (5.3.23)
(5.3.23)
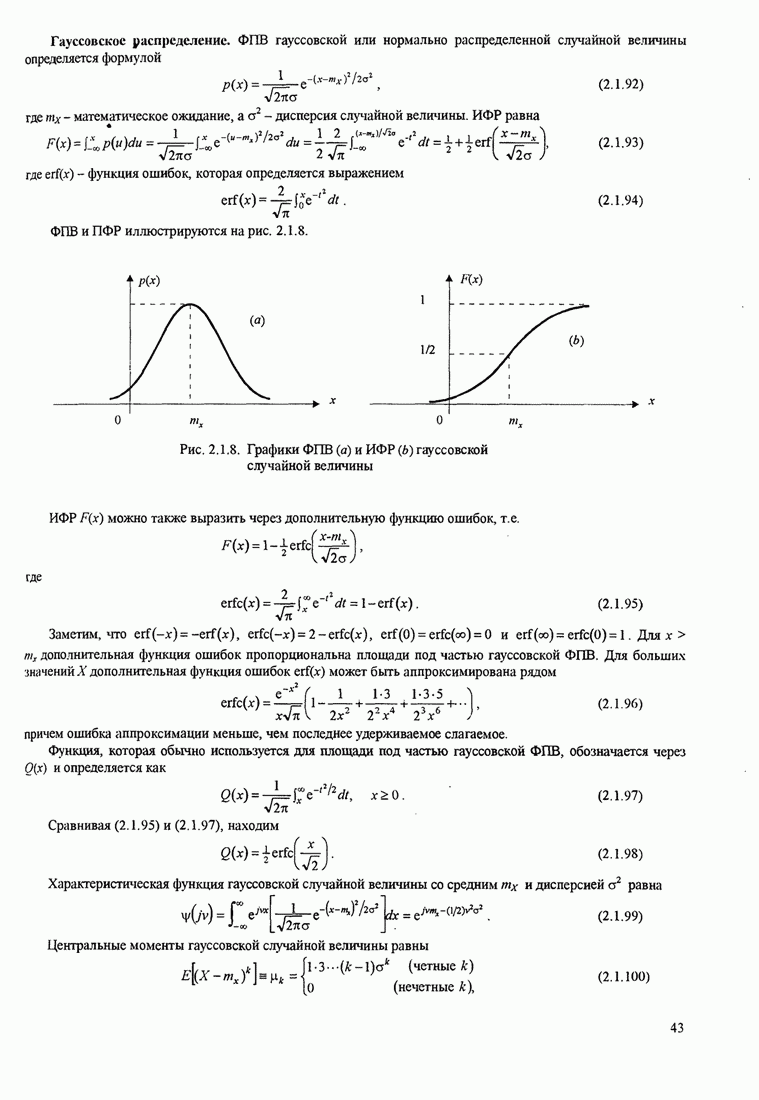
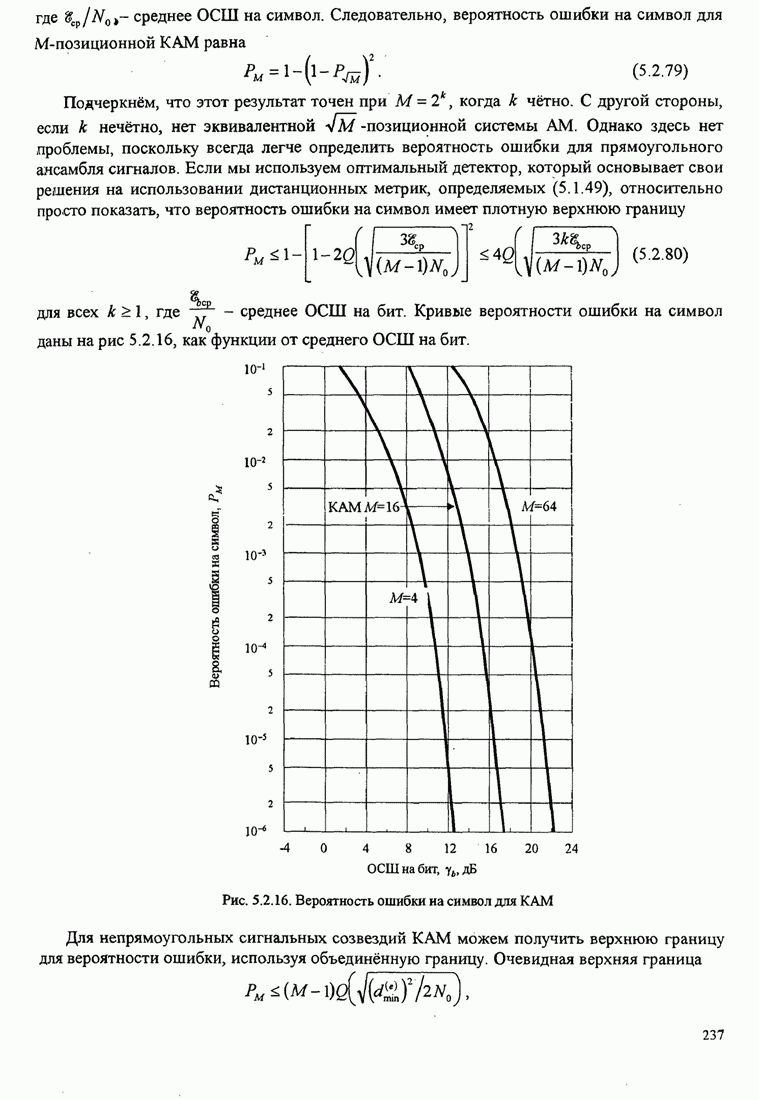
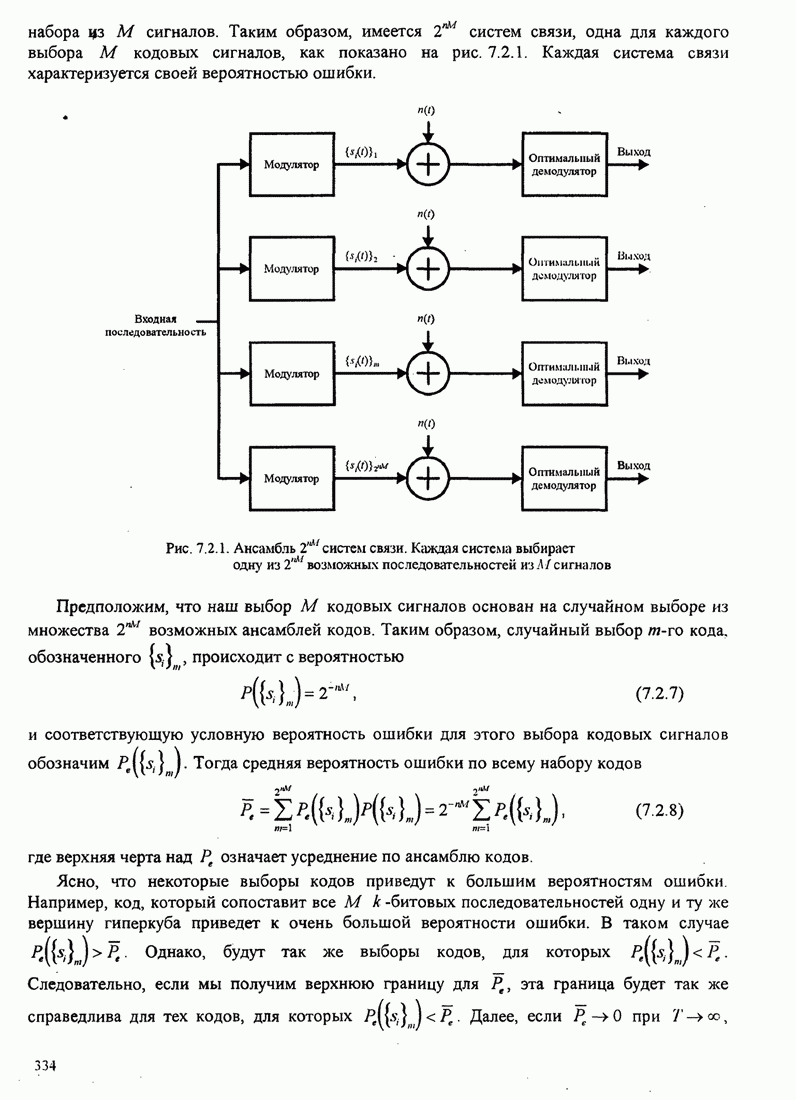
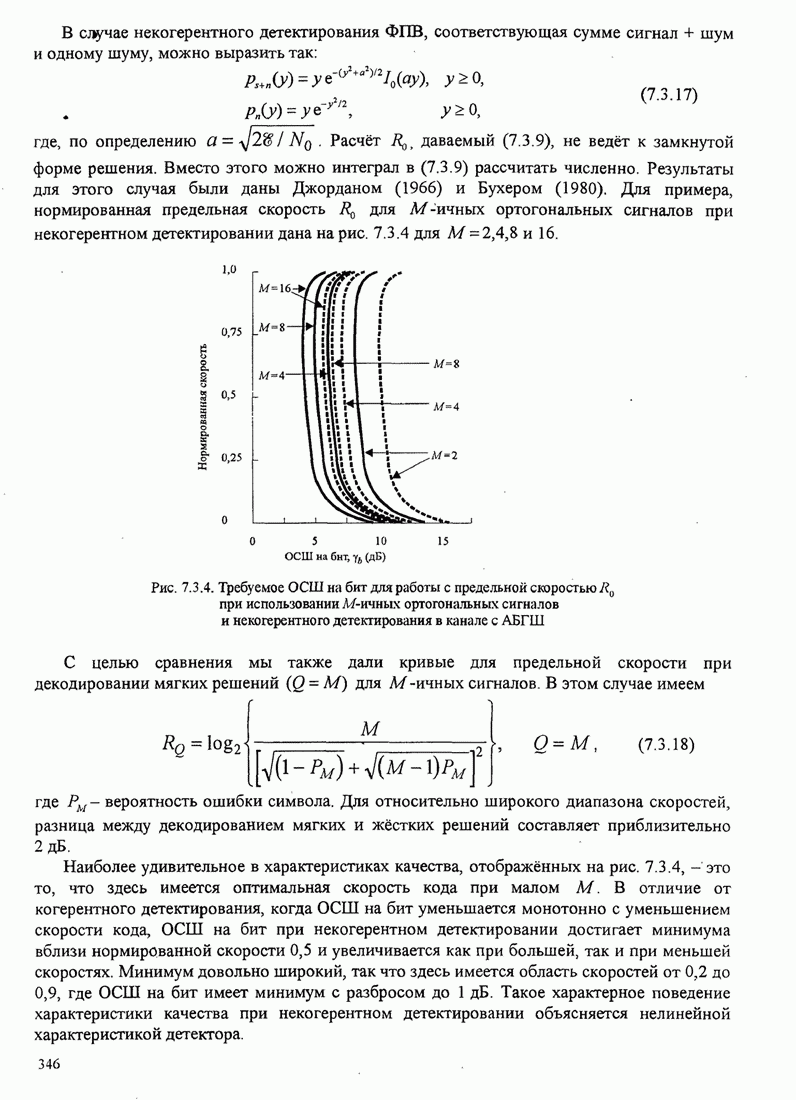
показана на рис. 5.3.8 для ![]() .
.
Здесь заметим, что с ростом ![]() параметр
параметр ![]() также достигает
больших значений. Ясно, что качество МНФ улучшается по мере увеличения
коррелятивной памяти
также достигает
больших значений. Ясно, что качество МНФ улучшается по мере увеличения
коррелятивной памяти ![]() , но следует также увеличить
, но следует также увеличить
![]() для того,
чтобы достичь больших значений
для того,
чтобы достичь больших значений ![]() . Поскольку больший индекс
модуляции требует большей полосы частот (при фиксированном
. Поскольку больший индекс
модуляции требует большей полосы частот (при фиксированном ![]() ), в то время как большая
длина памяти
), в то время как большая
длина памяти ![]() (при
фиксированном
(при
фиксированном ![]() )
требует меньшей полосы частот, то лучше сравнивать евклидово расстояние как
функцию от нормированной полосы частот
)
требует меньшей полосы частот, то лучше сравнивать евклидово расстояние как
функцию от нормированной полосы частот ![]() где
где ![]() - полоса с концентрацией
99% мощности, а
- полоса с концентрацией
99% мощности, а ![]() -
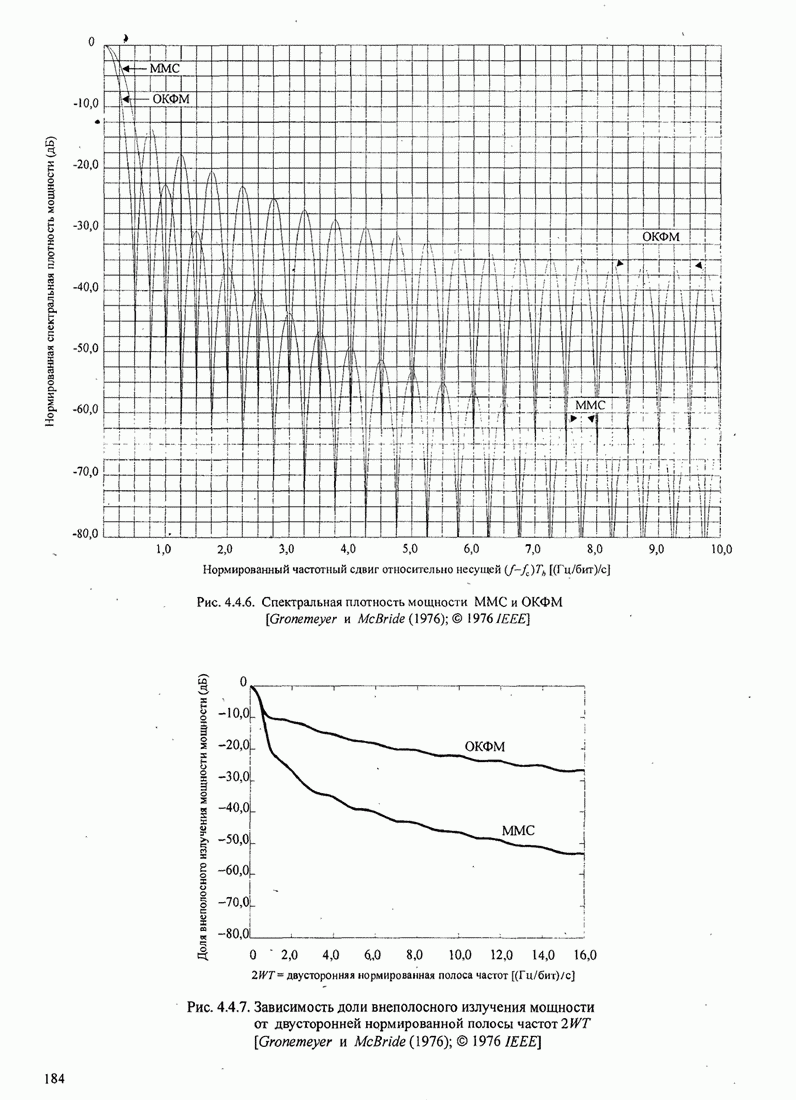
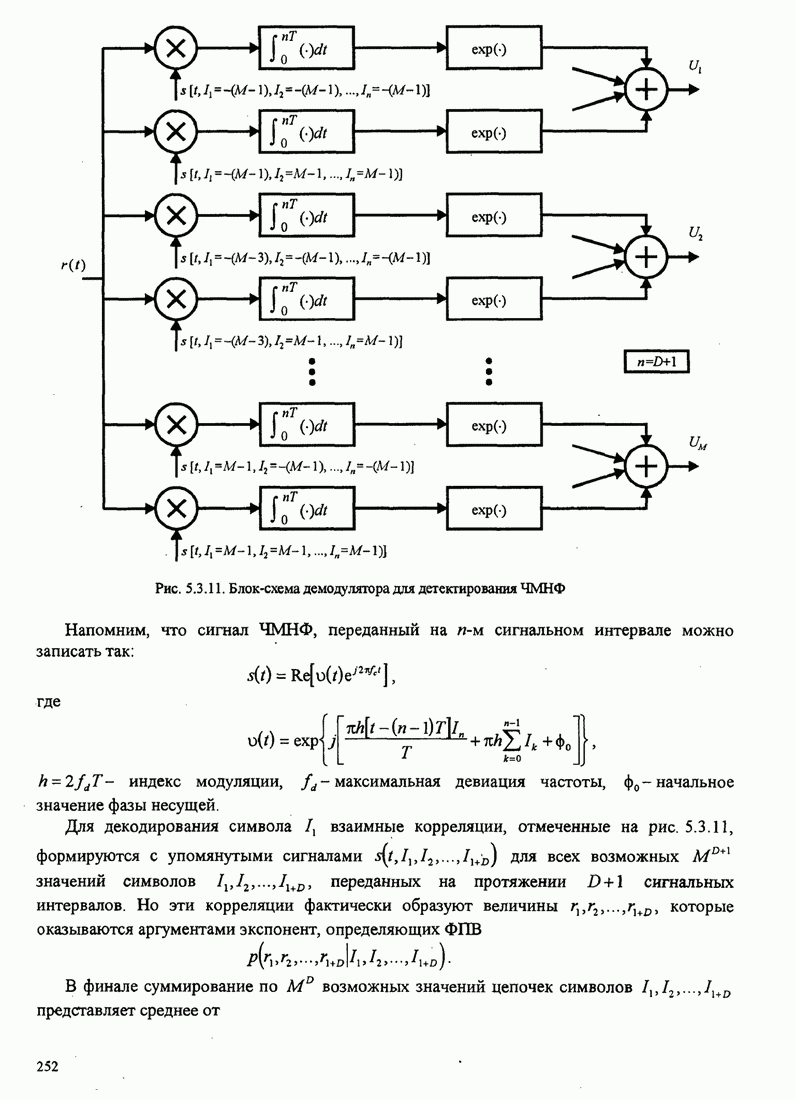
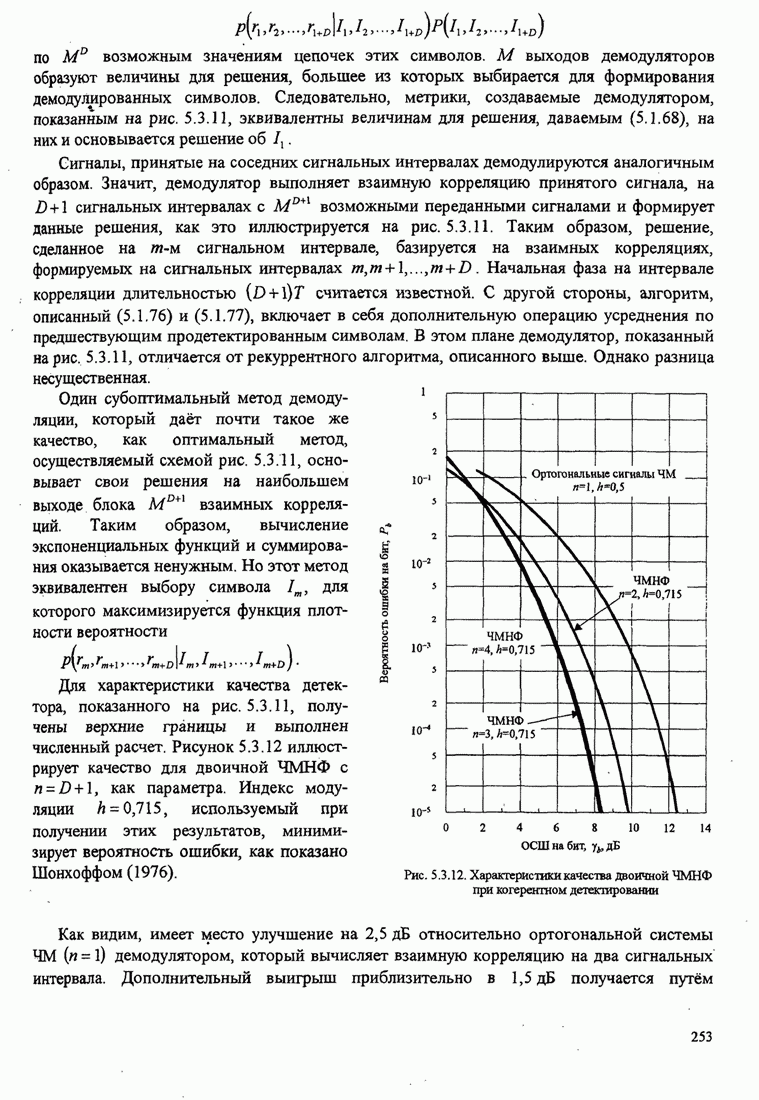
битовый интервал. Рисунок 5.3.9 иллюстрирует этот вид сравнения с ММС,
используемой как точка отсчёта (0 дБ).
-
битовый интервал. Рисунок 5.3.9 иллюстрирует этот вид сравнения с ММС,
используемой как точка отсчёта (0 дБ).

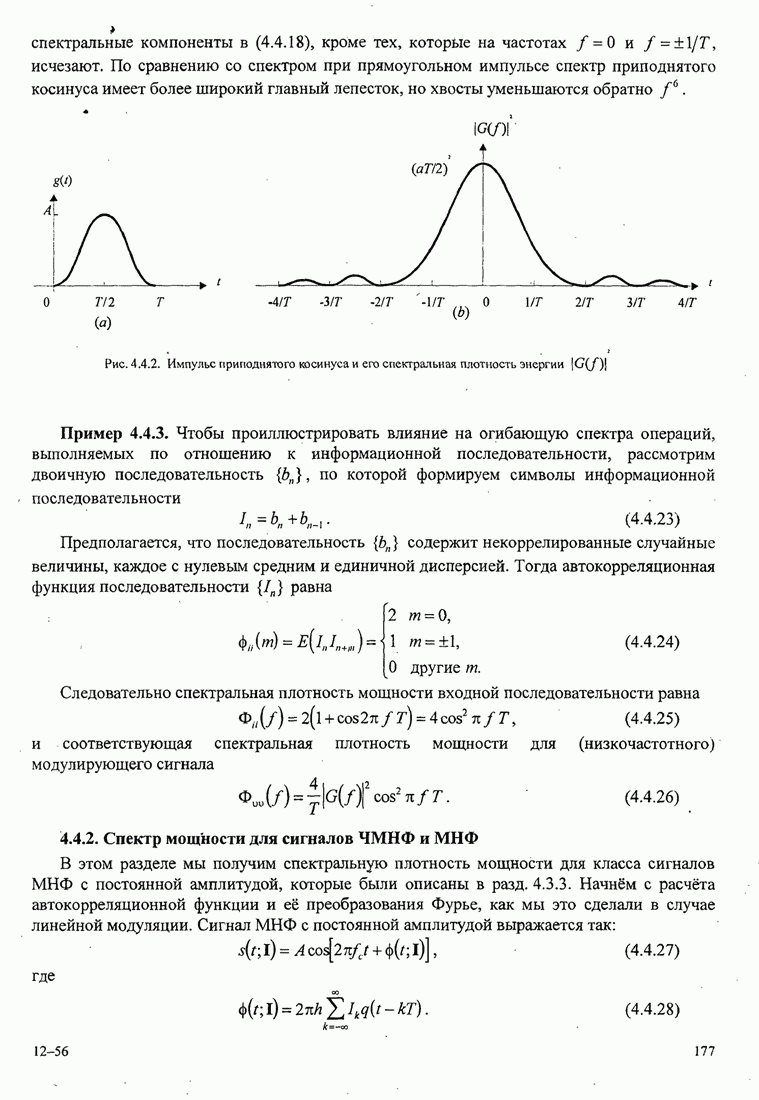
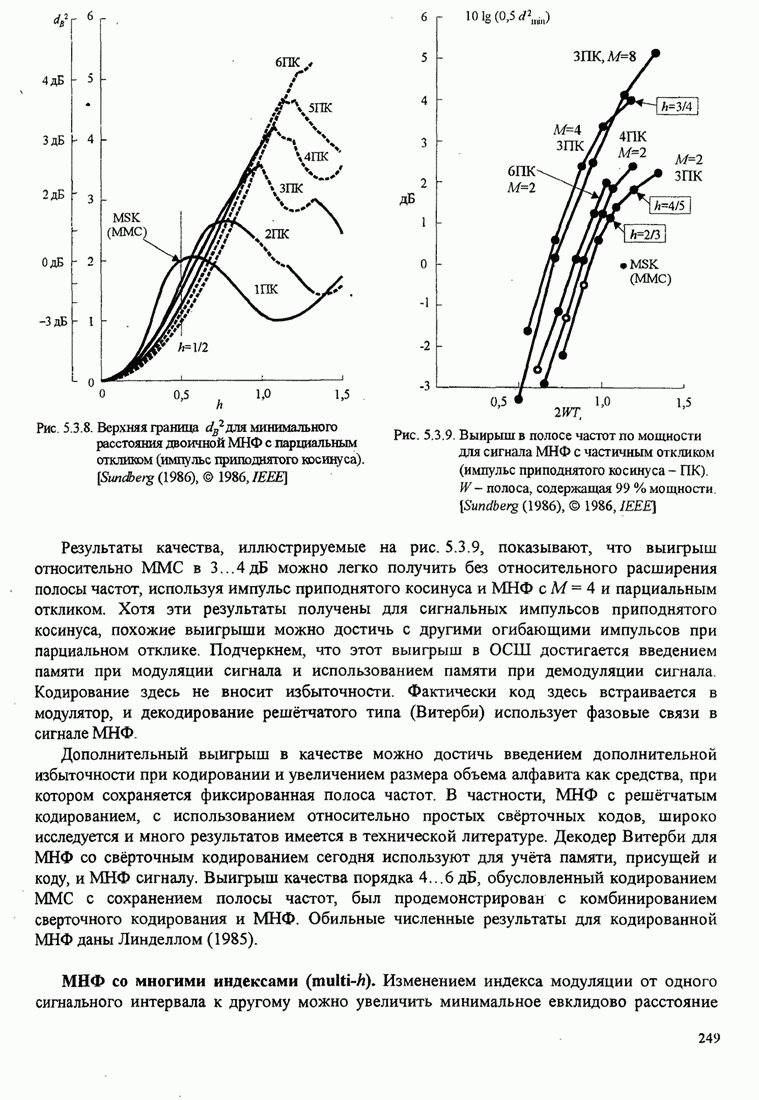
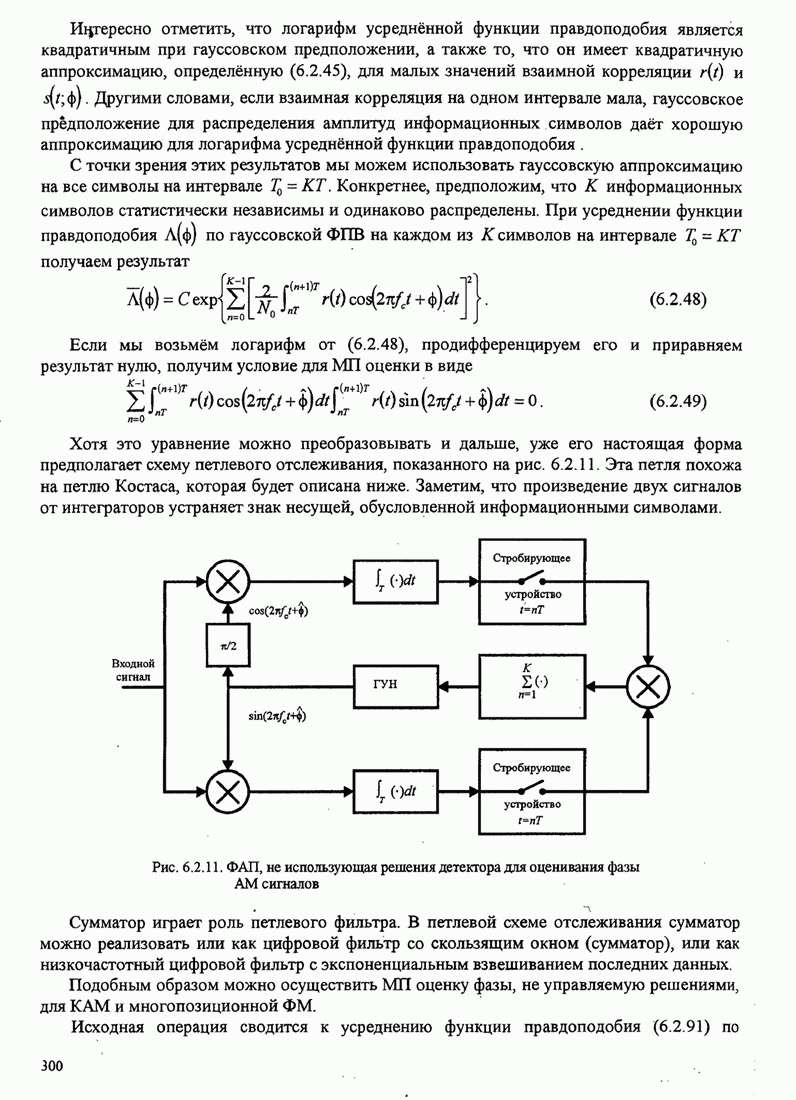
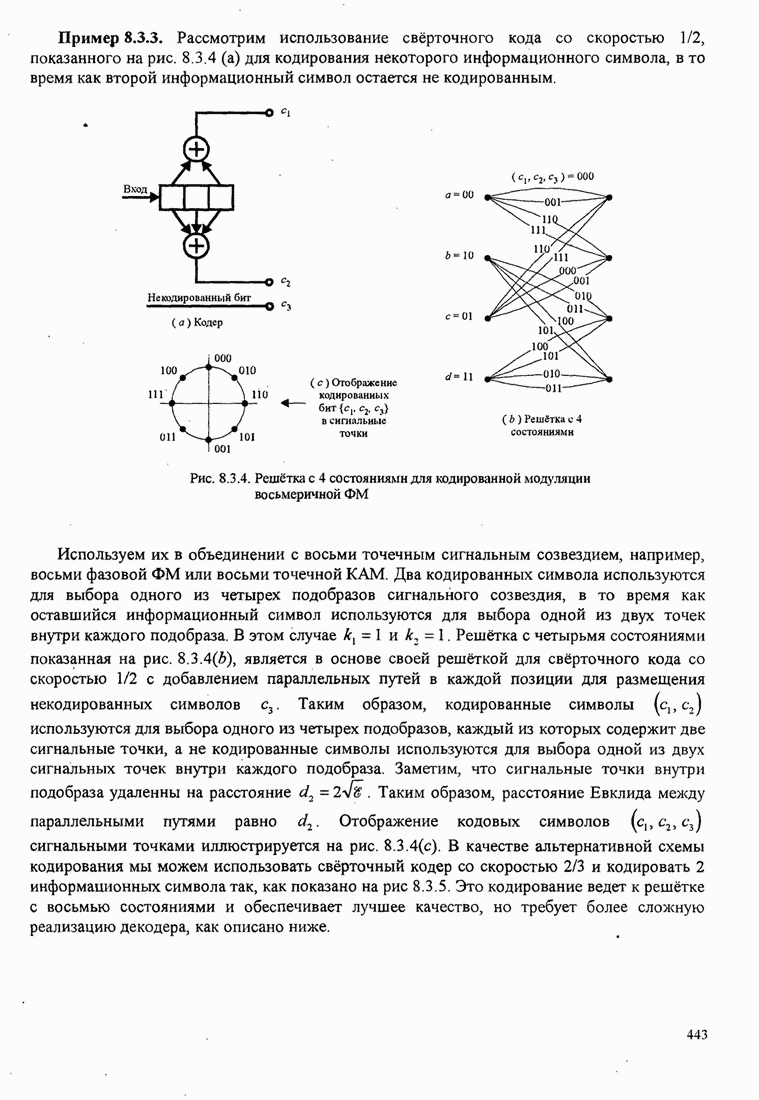
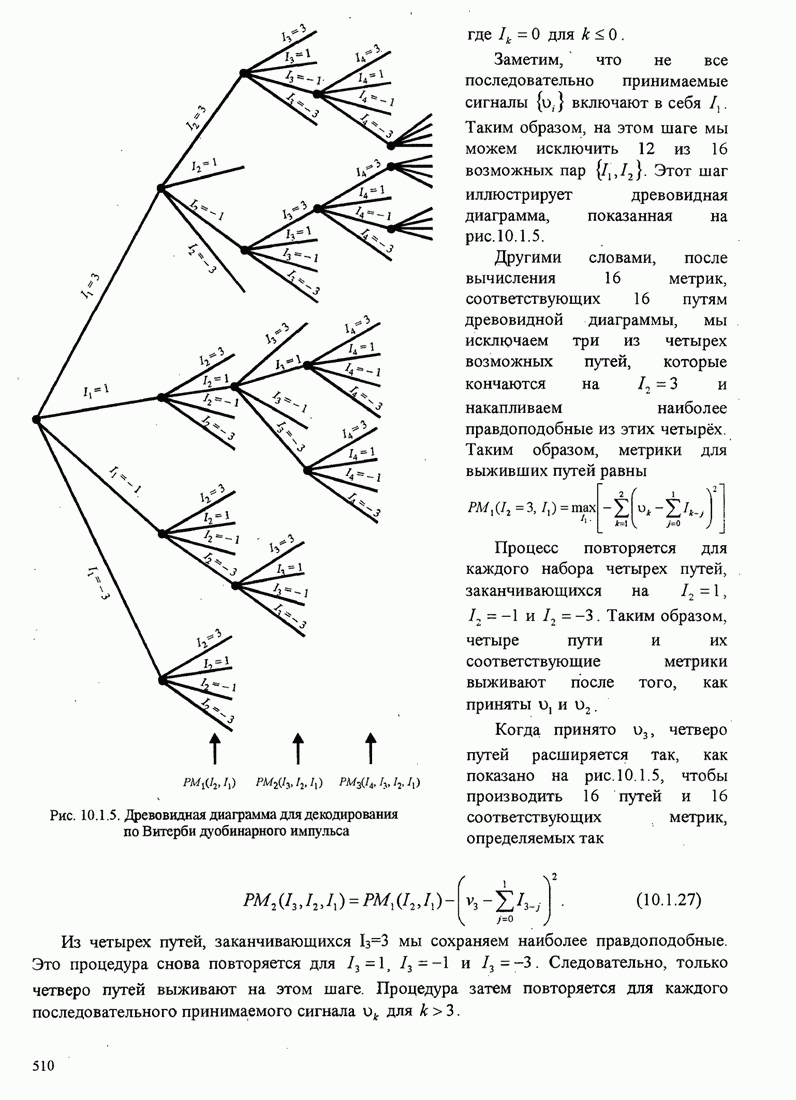
Рис.5.3.8. Верхняя граница ![]() для минимального расстояния двоичной
МНФ с парциальным откликом (импульс приподнятого косинуса).
для минимального расстояния двоичной
МНФ с парциальным откликом (импульс приподнятого косинуса).

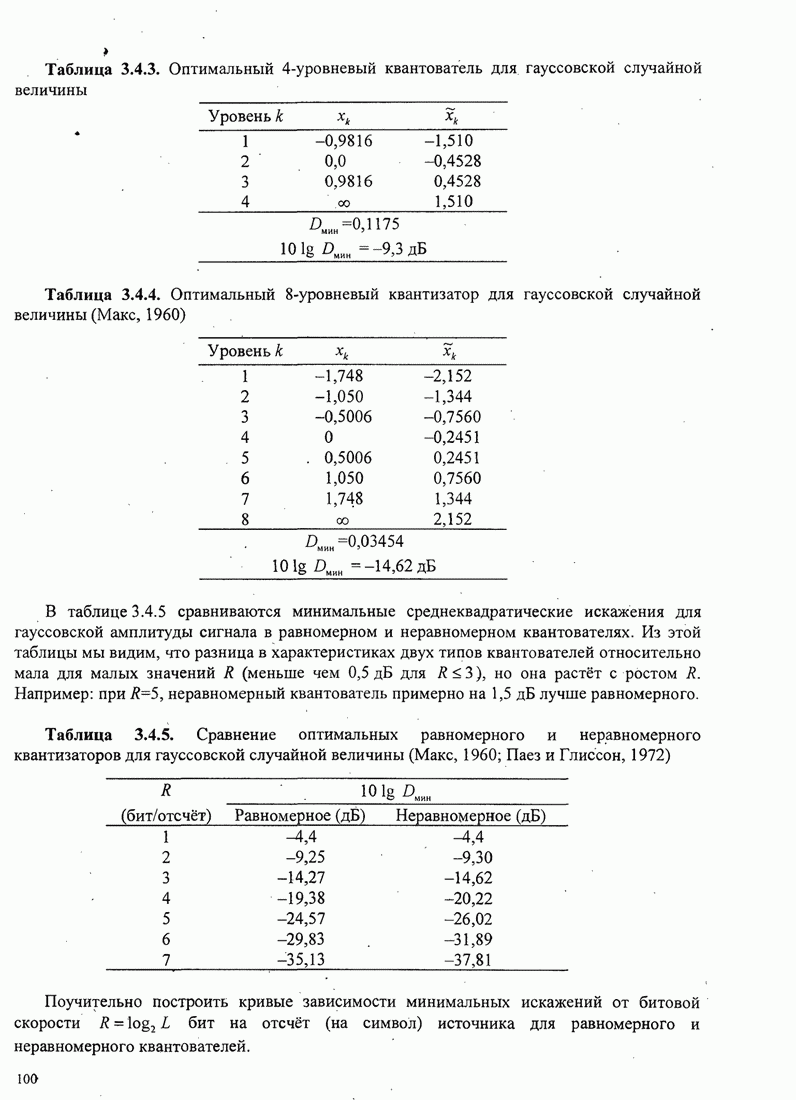
Рис.5.3.9. Выигрыш в полосе частот по мощности для сигнала
МНФ с частичным откликом (импульс приподнятого косинуса – ПК). ![]() – полоса,
содержащая 99% мощности.
– полоса,
содержащая 99% мощности.
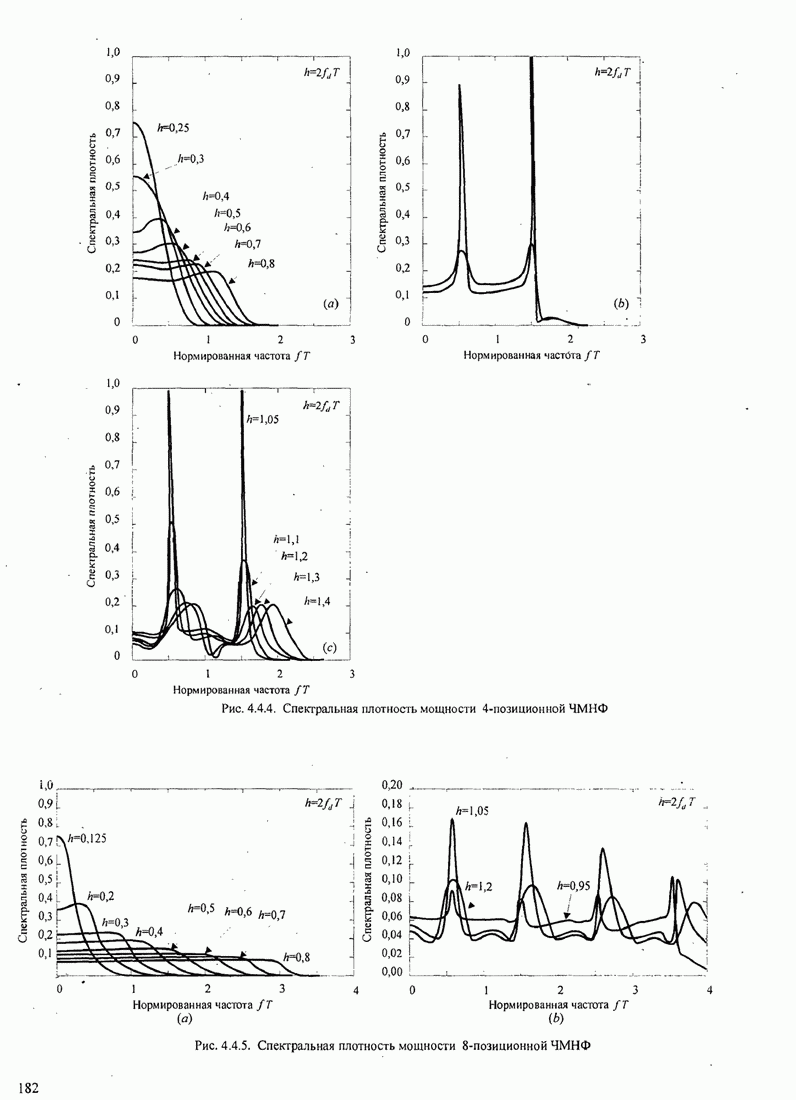
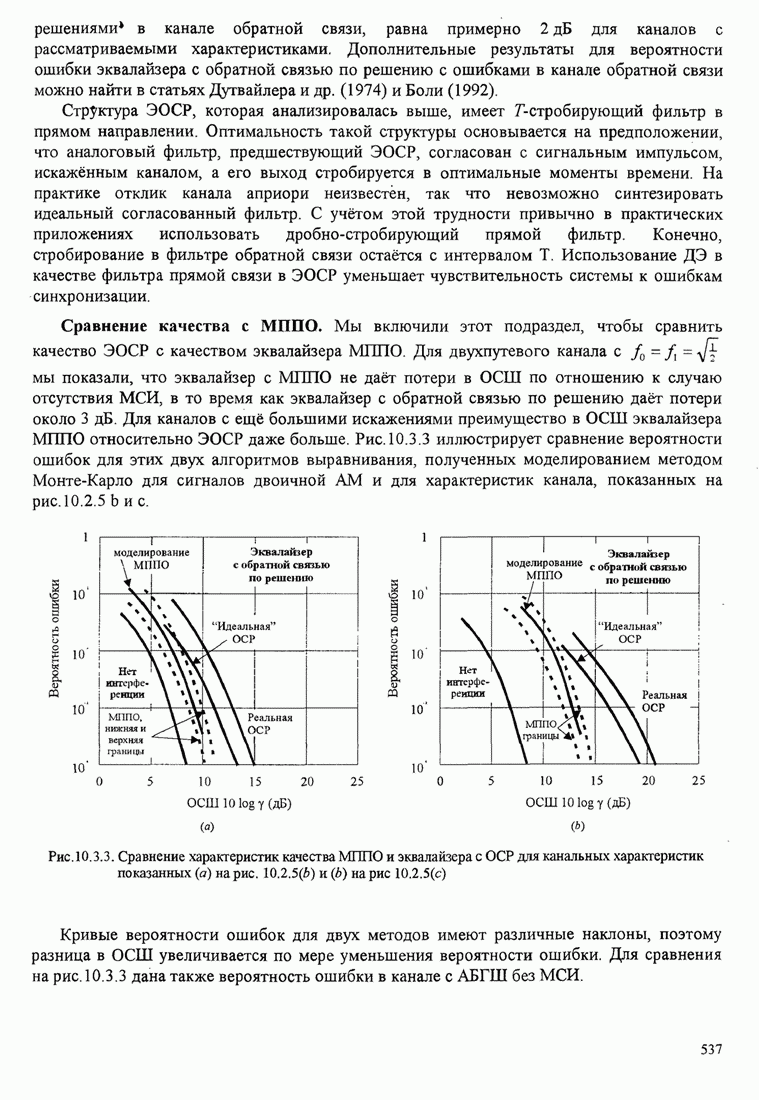
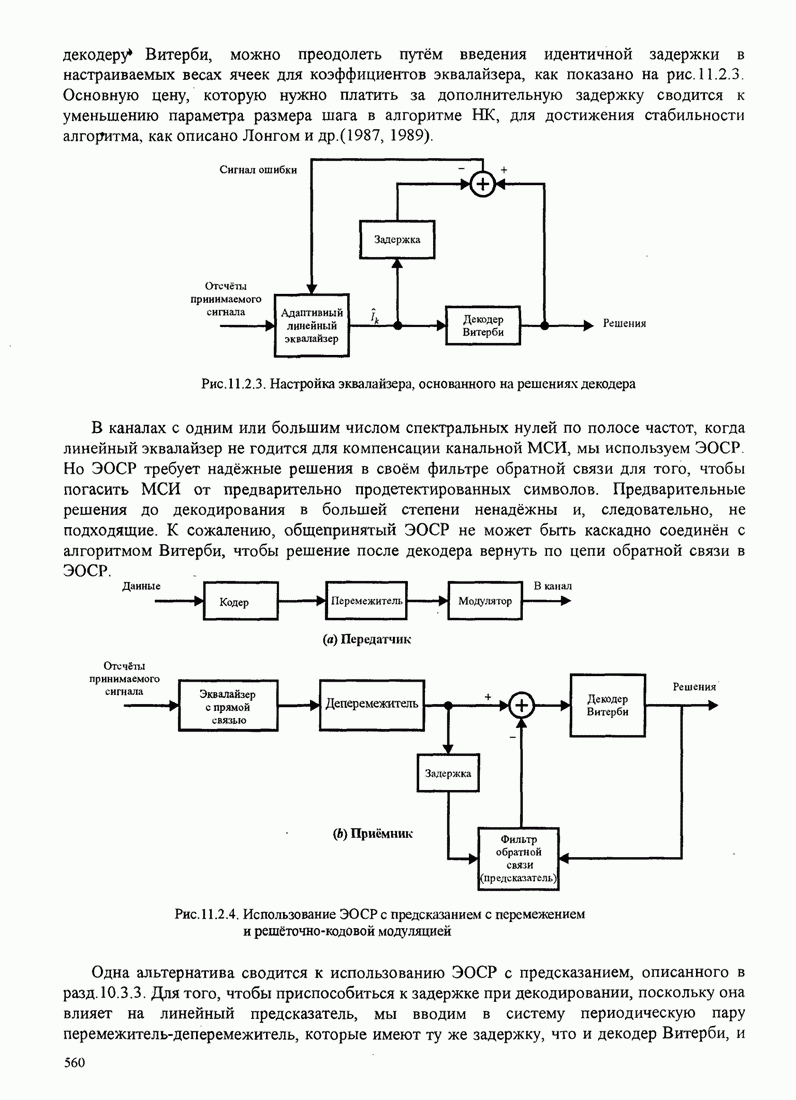
Из этого рисунка видно, что имеется выигрыш в несколько децибел при использовании сигналов с парциальным откликом и больших значений объема алфавита. Главная цена, которую можно платить за этот выигрыш качества, - это экспоненциально растущая сложность в реализации декодера Витерби.
Результаты качества, иллюстрируемые на рис. 5.3.9, показывают, что
выигрыш относительно ММС в 3...4дБ можно легко получить без относительного
расширения полосы частот, используя импульс приподнятого косинуса и МНФ с ![]() и
парциальным откликом. Хотя эти результаты получены для сигнальных импульсов
приподнятого косинуса, похожие выигрыши можно достичь с другими огибающими
импульсов при парциальном отклике. Подчеркнем, что этот выигрыш в ОСШ достигается
введением памяти при модуляции сигнала и использованием памяти при демодуляции
сигнала. Кодирование здесь не вносит избыточности. Фактически код здесь
встраивается в модулятор, и декодирование решётчатого типа (Витерби) использует
фазовые связи в сигнале МНФ.
и
парциальным откликом. Хотя эти результаты получены для сигнальных импульсов
приподнятого косинуса, похожие выигрыши можно достичь с другими огибающими
импульсов при парциальном отклике. Подчеркнем, что этот выигрыш в ОСШ достигается
введением памяти при модуляции сигнала и использованием памяти при демодуляции
сигнала. Кодирование здесь не вносит избыточности. Фактически код здесь
встраивается в модулятор, и декодирование решётчатого типа (Витерби) использует
фазовые связи в сигнале МНФ.
Дополнительный выигрыш в качестве можно достичь введением дополнительной избыточности при кодировании и увеличением размера объема алфавита как средства, при котором сохраняется фиксированная полоса частот. В частности, МНФ с решётчатым кодированием, с использованием относительно простых свёрточных кодов, широко исследуется и много результатов имеется в технической литературе. Декодер Витерби для МНФ со свёрточным кодированием сегодня используют для учёта памяти, присущей и коду, и МНФ сигналу. Выигрыш качества порядка 4...6 дБ, обусловленный кодированием ММС с сохранением полосы частот, был продемонстрирован с комбинированием сверточного кодирования и МНФ. Обильные численные результаты для кодированной МНФ даны Линделлом (1985).
МНФ со многими индексами (multi-h). Изменением индекса модуляции от одного сигнального
интервала к другому можно увеличить минимальное евклидово расстояние ![]() между парами
фазовых траекторий и таким образом улучшить выигрыш качества относительно МНФ с
фиксированным индексом
между парами
фазовых траекторий и таким образом улучшить выигрыш качества относительно МНФ с
фиксированным индексом ![]() . Обычно МНФ со многими индексами
. Обычно МНФ со многими индексами ![]() использует фиксированное число
использует фиксированное число ![]() индексов модуляции, которые меняются циклически в
соседних сигнальных интервалах. Таким образом, фаза сигнала меняется
кусочно-линейно.
индексов модуляции, которые меняются циклически в
соседних сигнальных интервалах. Таким образом, фаза сигнала меняется
кусочно-линейно.
Существенный выигрыш в ОСШ достигается использованием только небольшого
количества различных значений ![]() . Например, для МНФ с полным откликом
. Например, для МНФ с полным откликом ![]() и
и ![]() можно получить выигрыш в 3 дБ относительно двоичной
или четверичной ФМ. При увеличении
можно получить выигрыш в 3 дБ относительно двоичной
или четверичной ФМ. При увеличении ![]() до
до ![]() можно получить выигрыш в 4,5 дБ
относительно ФМ. Выигрыш качества можно также увеличить с увеличением объема
сигнального алфавита. Таблица 5.3.1 показывает выигрыш качества, достигаемый
при
можно получить выигрыш в 4,5 дБ
относительно ФМ. Выигрыш качества можно также увеличить с увеличением объема
сигнального алфавита. Таблица 5.3.1 показывает выигрыш качества, достигаемый
при ![]() для различных значений
для различных значений ![]() .
.
Таблица 5.3.1. Максимальные
значения верхней границы ![]() для линейной МНФ с переменным индексом
для линейной МНФ с переменным индексом
|
|
|
|
Выигрыш относительно ММС, дБ |
|
|
|
|
|
|
2 |
1 |
2,43 |
0,85 |
0,715 |
|
|
|
0,715 |
|
2 |
2 |
4,0 |
3,0 |
0,5 |
0,5 |
|
|
0,5 |
|
2 |
3 |
4,88 |
3,87 |
0,620 |
0,686 |
0,714 |
|
0,673 |
|
2 |
4 |
5,69 |
4,54 |
0,73 |
0,55 |
0,73 |
|
0,64 |
|
4 |
1 |
4,23 |
3,25 |
0,914 |
|
|
|
0,914 |
|
4 |
2 |
6,54 |
5,15 |
0,772 |
0,772 |
|
|
0,772 |
|
4 |
3 |
7,65 |
5,83 |
0,795 |
0,795 |
0,795 |
|
0,795 |
|
8 |
1 |
6,14 |
4,87 |
0,964 |
|
|
|
0,964 |
|
8 |
2 |
7,50 |
5,74 |
0,883 |
0,883 |
|
|
0,883 |
|
8 |
3 |
8,40 |
6,23 |
0,879 |
0,879 |
0,879 |
|
0,879 |
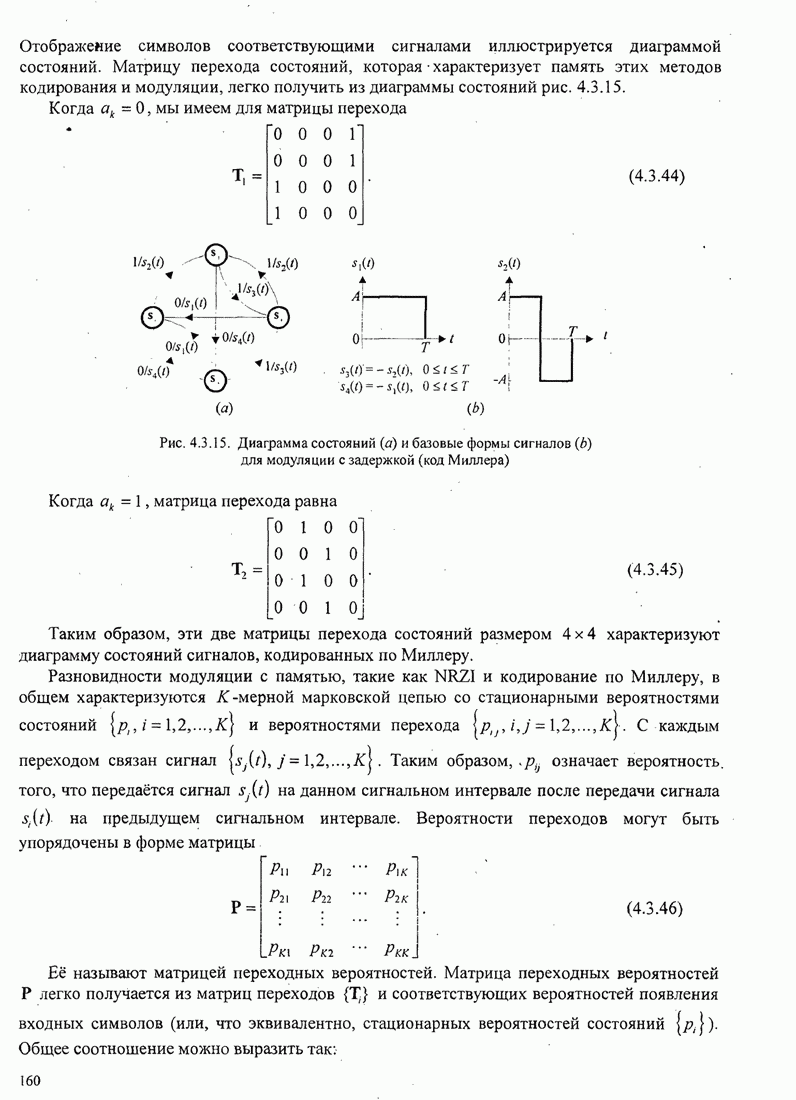
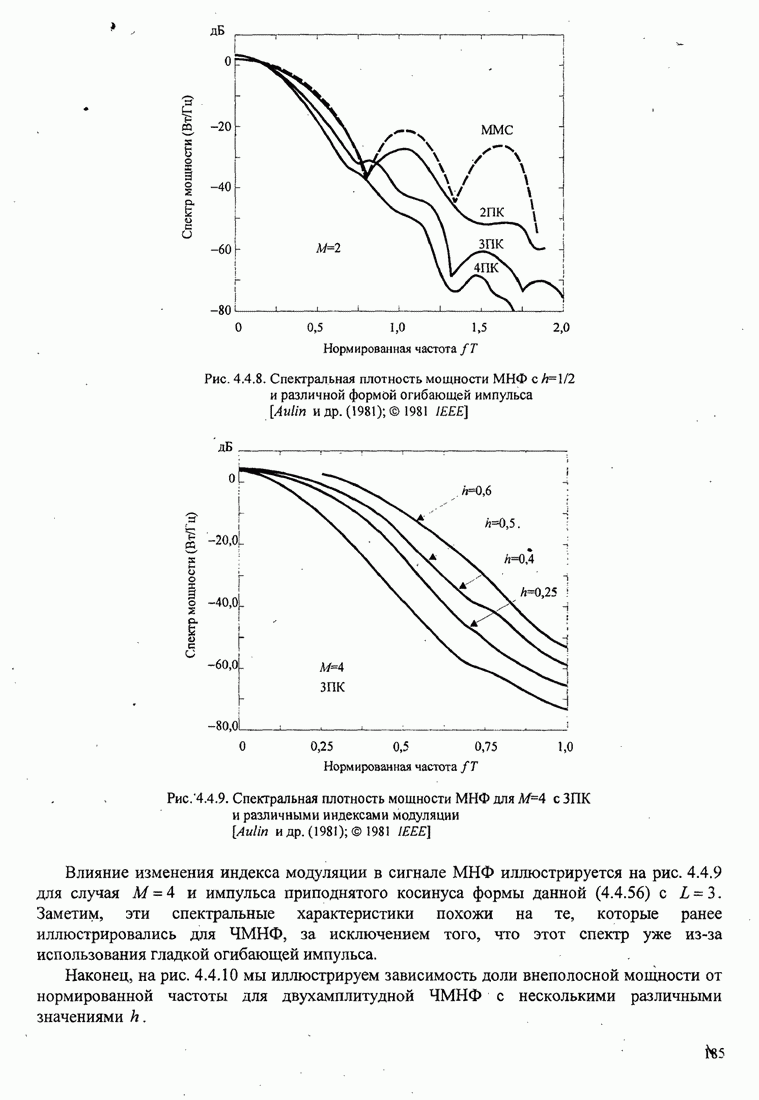
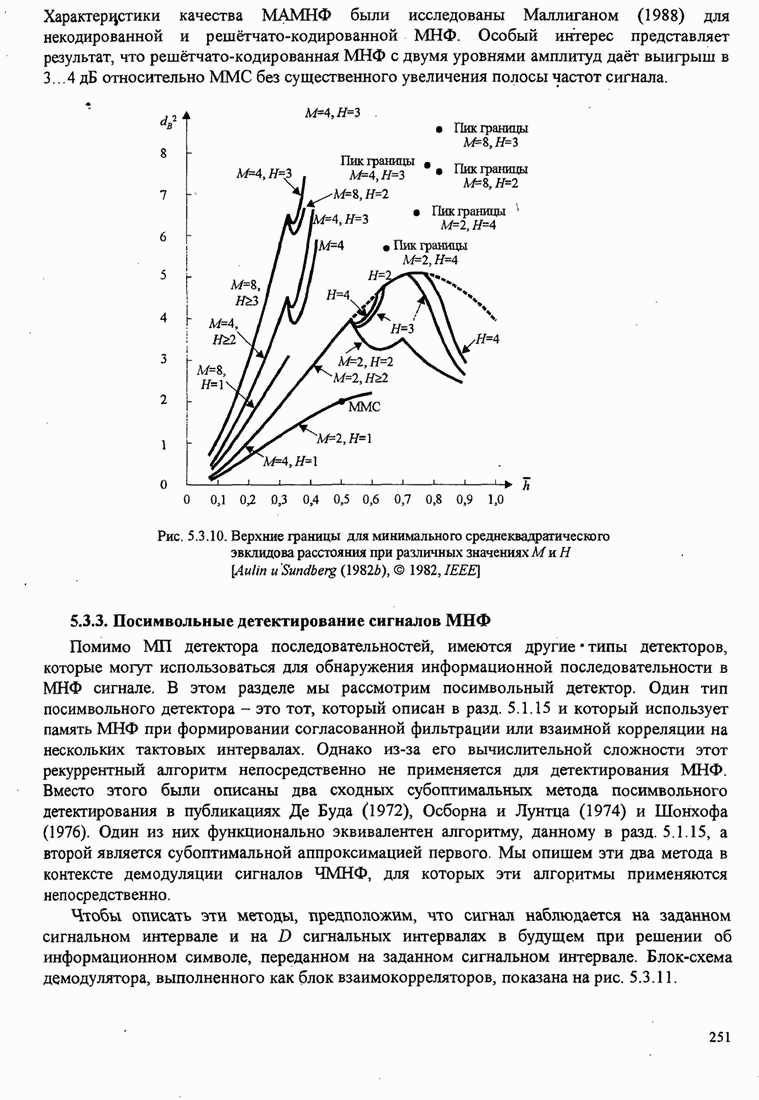
На рис. 5.3.10 показана верхняя граница
минимального евклидова расстояния для нескольких величин ![]() и
и ![]() . По оси абсцисс отложено среднее значение
. По оси абсцисс отложено среднее значение ![]() . Отметим, что основной выигрыш в качестве получается,
когда
. Отметим, что основной выигрыш в качестве получается,
когда ![]() увеличивается от
увеличивается от ![]() до
до ![]() . Для
. Для ![]() дополнительный выигрыш относительно мал для малых
величин
дополнительный выигрыш относительно мал для малых
величин ![]() . С другой стороны, существенный выигрыш качества
достигается увеличением объема алфавита
. С другой стороны, существенный выигрыш качества
достигается увеличением объема алфавита ![]() .
.
Результаты, показанные выше, имеют
место для МНФ с полным откликом. Наверняка существует польза от МНФ со многими
индексами ![]() при парциальном отклике в попытке дальнейшего
улучшения качества. Можно предвидеть, что такие схемы обеспечат дополнительный
выигрыш качества, но имеющиеся численные результаты для МНФ со многими
индексами
при парциальном отклике в попытке дальнейшего
улучшения качества. Можно предвидеть, что такие схемы обеспечат дополнительный
выигрыш качества, но имеющиеся численные результаты для МНФ со многими
индексами ![]() и парциальным откликом ограничены. Интересующемуся
читателю рекомендуется статья Аулина и Сандберга (1982).
и парциальным откликом ограничены. Интересующемуся
читателю рекомендуется статья Аулина и Сандберга (1982).
Многоамплитудная МНФ. Многоамплитудная МНФ (МАМНФ) является по существу схемой комбинирования амплитудной и фазовой модуляции, которая позволяет увеличить сигнальный алфавит относительно МНФ до другой размерности и таким образом достичь большей скорости передачи данных в частотно-ограниченном канале. Одновременно комбинирование AM с МНФ приводит к эффективной по полосе частот технике модуляции. Мы уже наблюдали спектральные характеристики МАМНФ в разд. 4.3.
Характеристики качества МАМНФ были исследованы Маллиганом (1988) для некодированной и решётчато-кодированной МНФ. Особый интерес представляет результат, что решётчато-кодированная МНФ с двумя уровнями амплитуд даёт выигрыш в 3...4 дБ относительно ММС без существенного увеличения полосы частот сигнала.

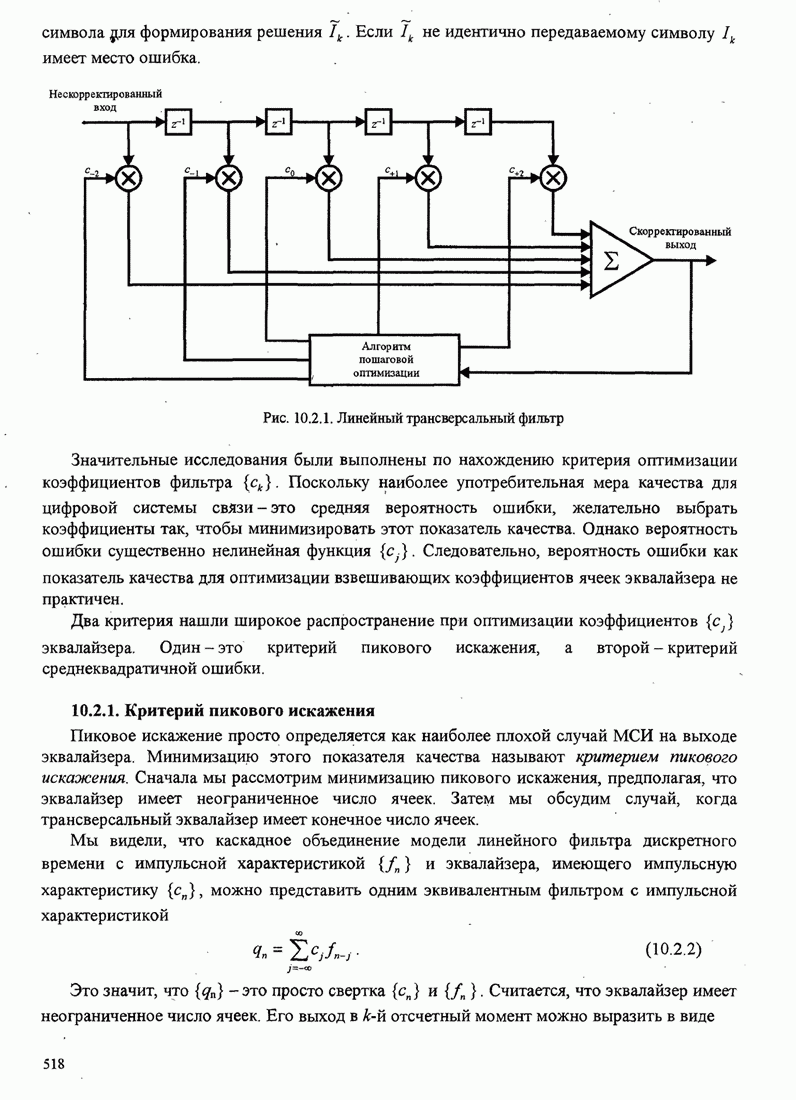
Рис.5.3.10. Верхние границы
для минимального среднеквадратического эвклидова расстояния при различных
значениях ![]() и
и
![]()
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
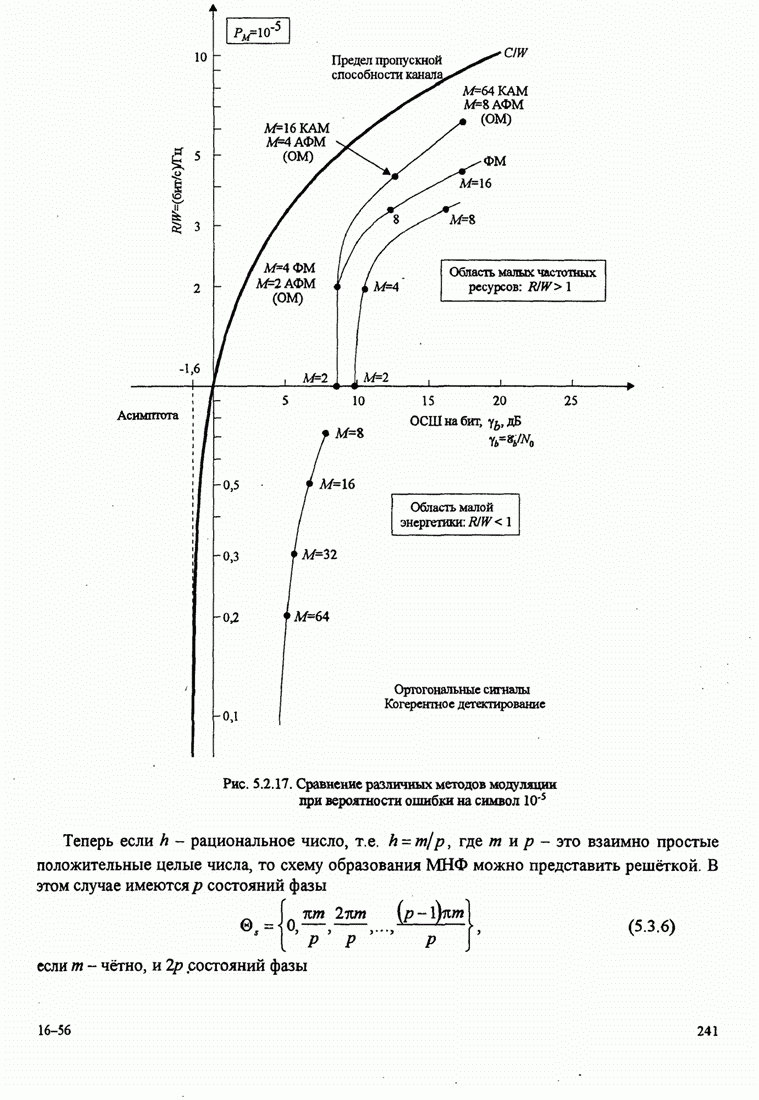
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
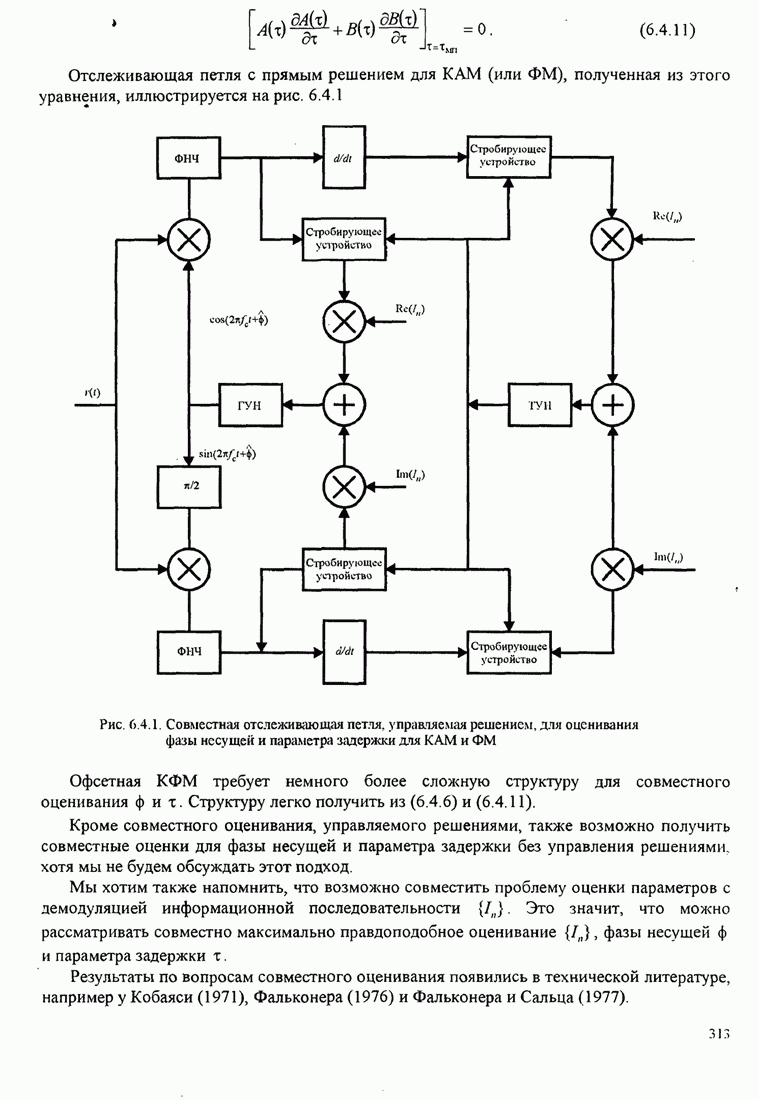
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
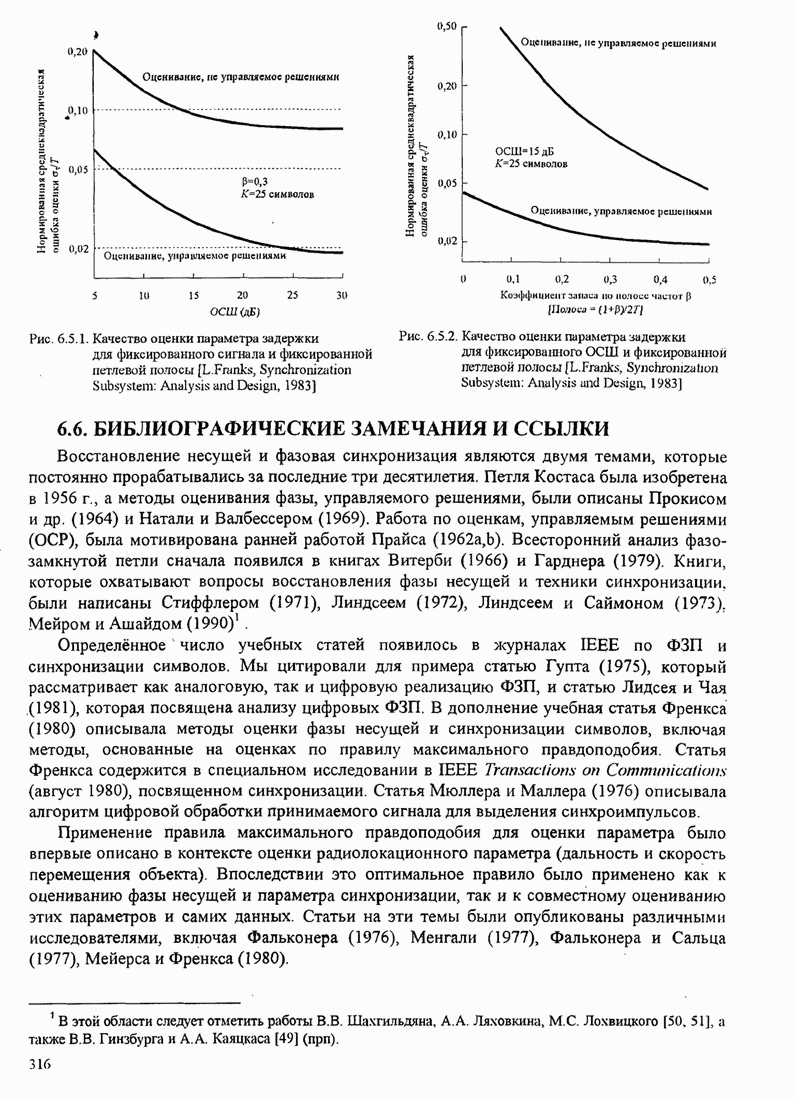
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
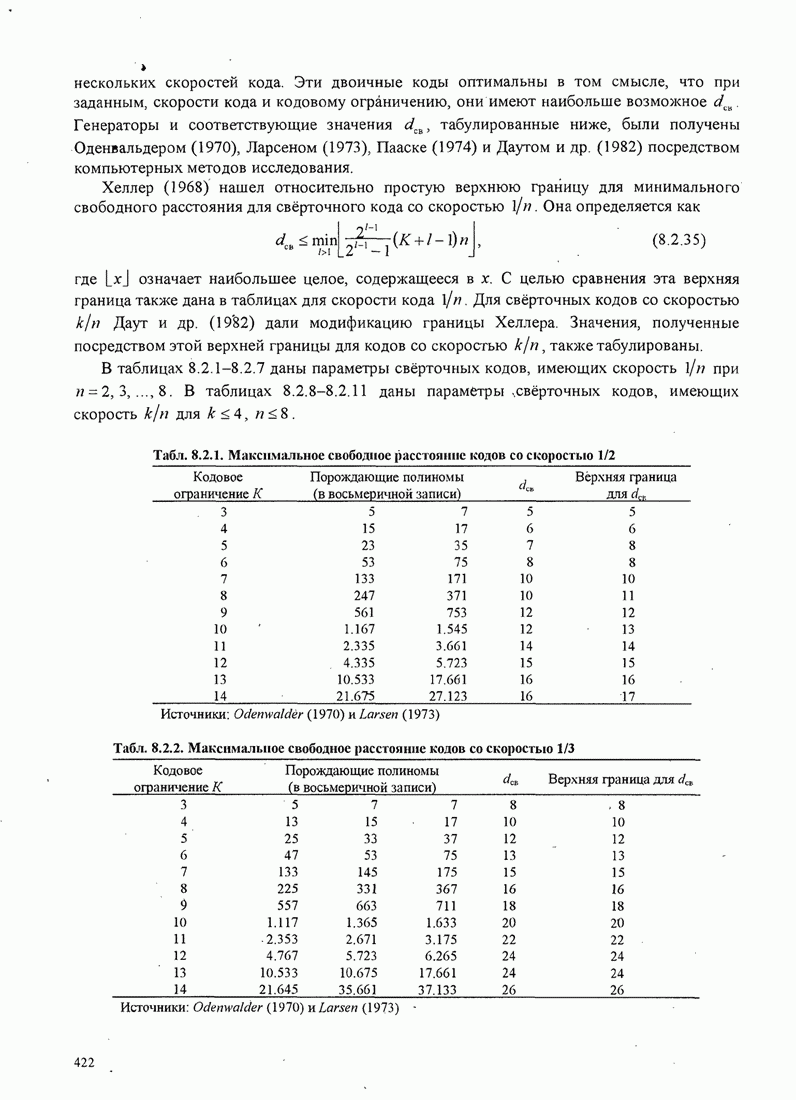
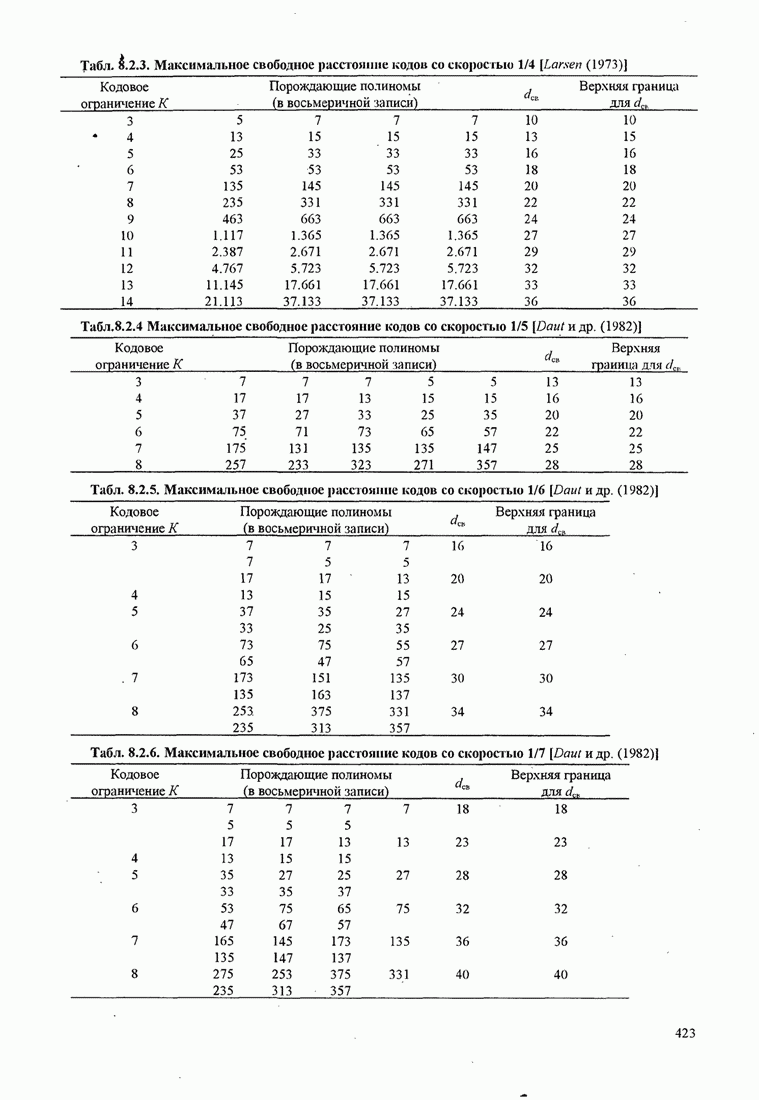
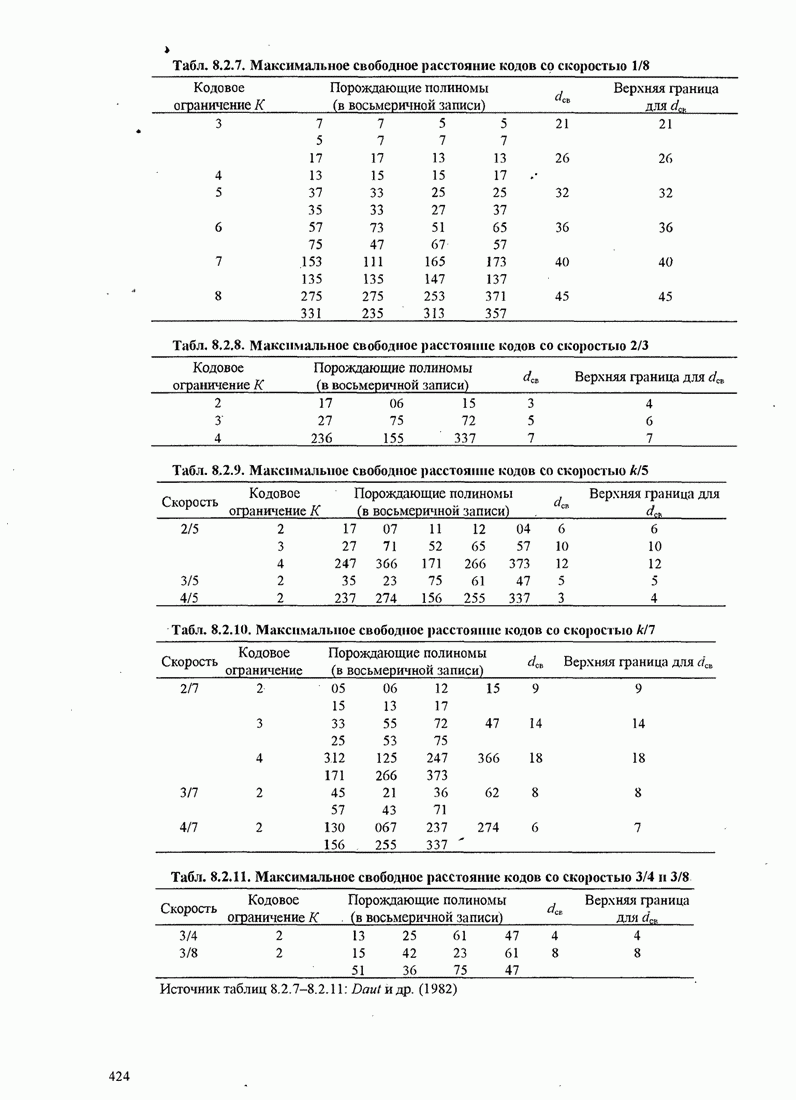
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
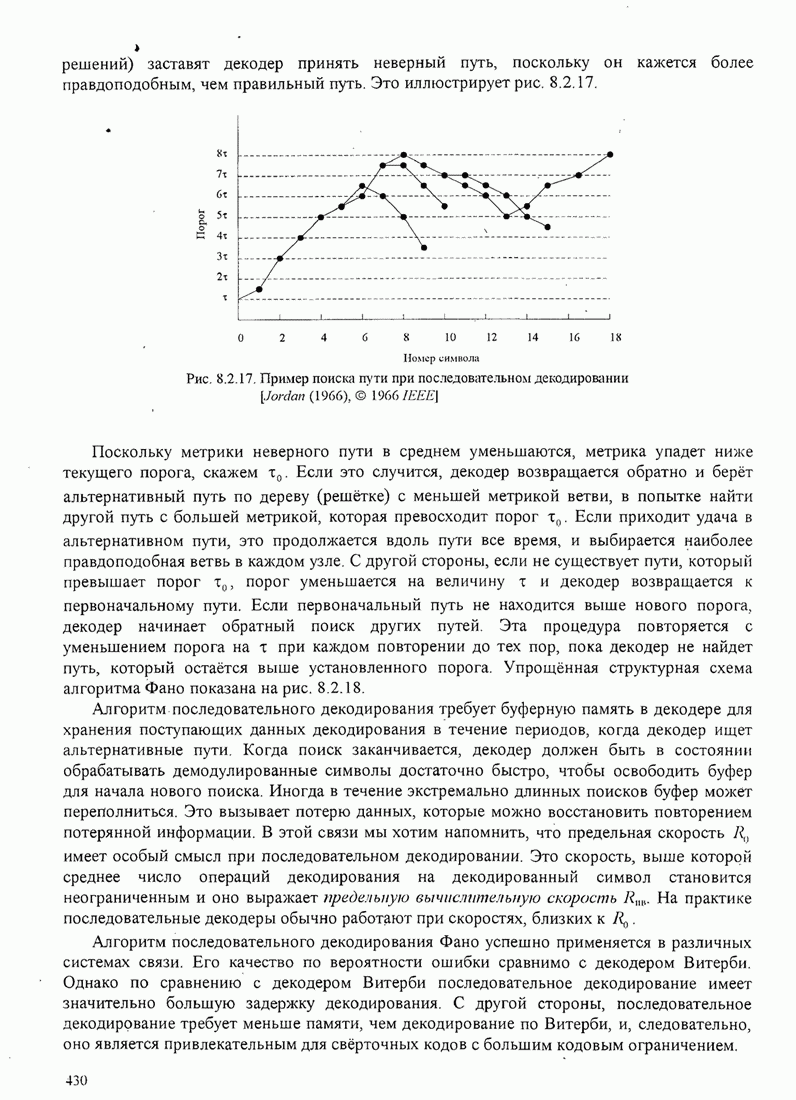
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
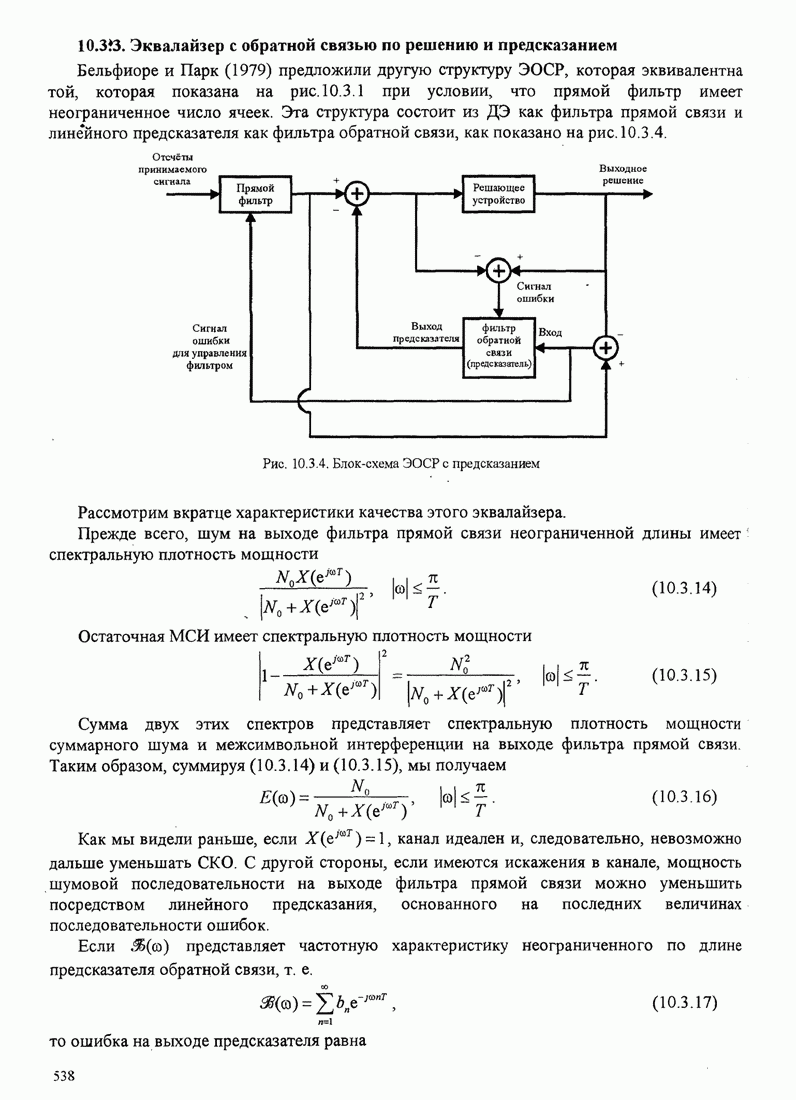
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
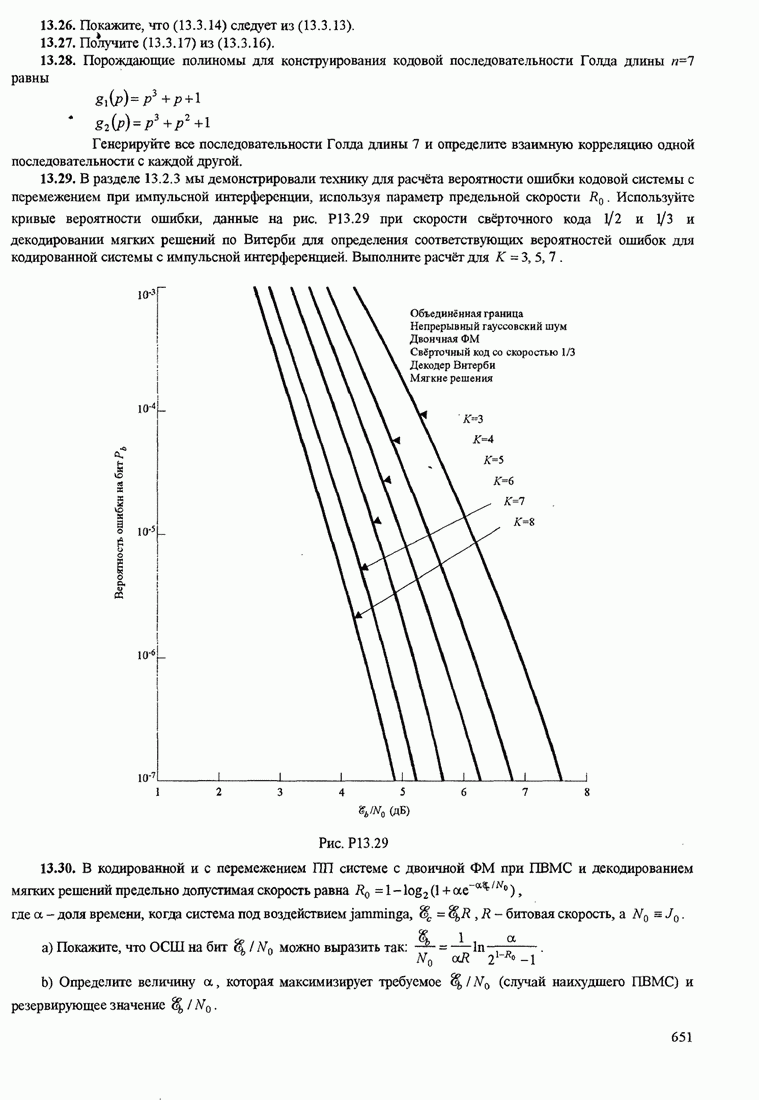
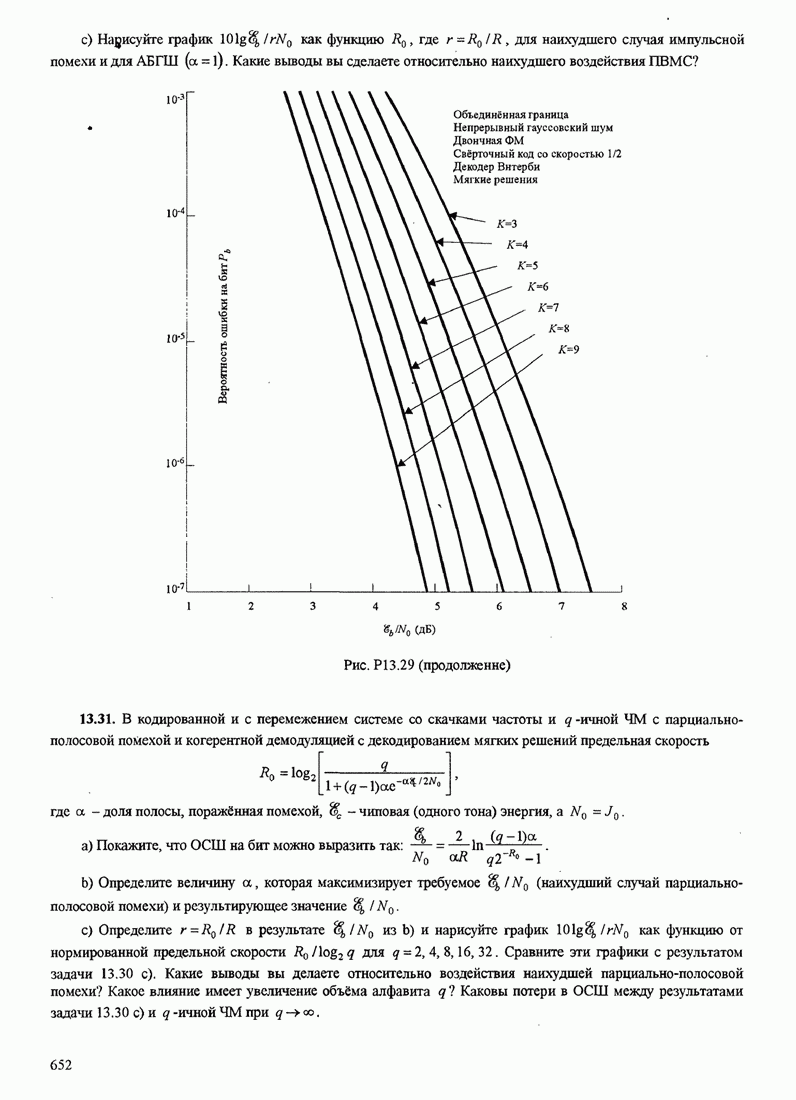
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
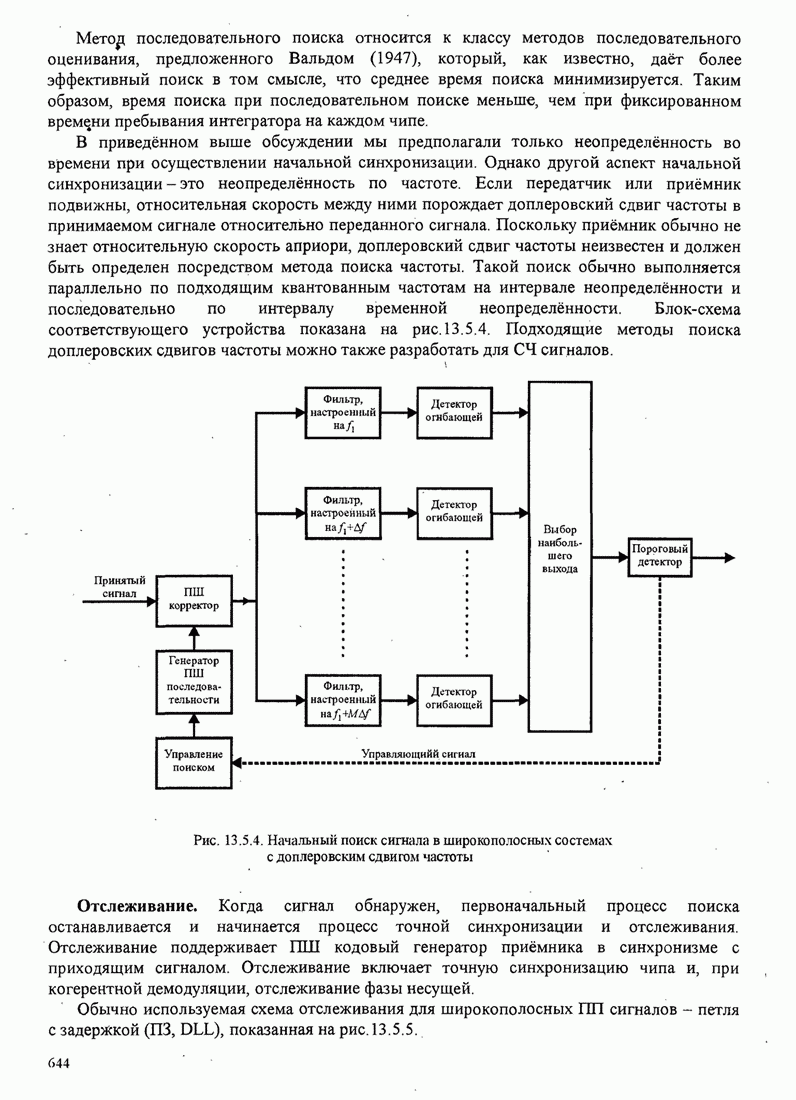
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
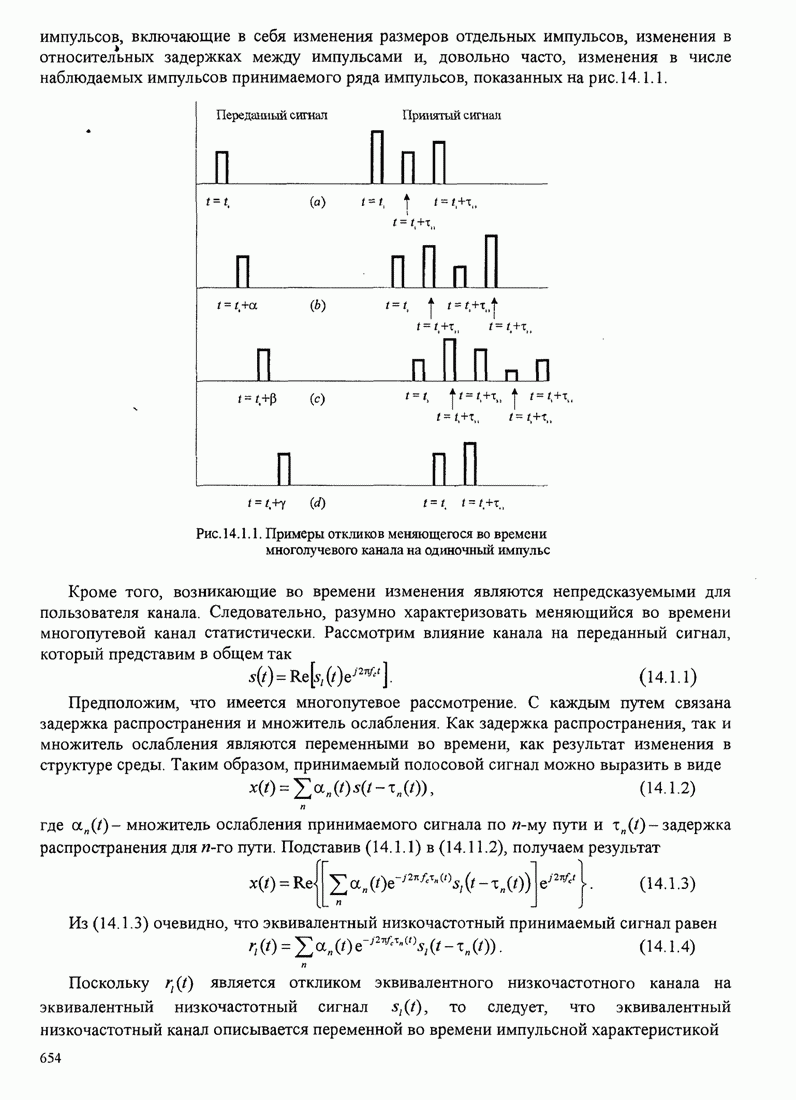
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
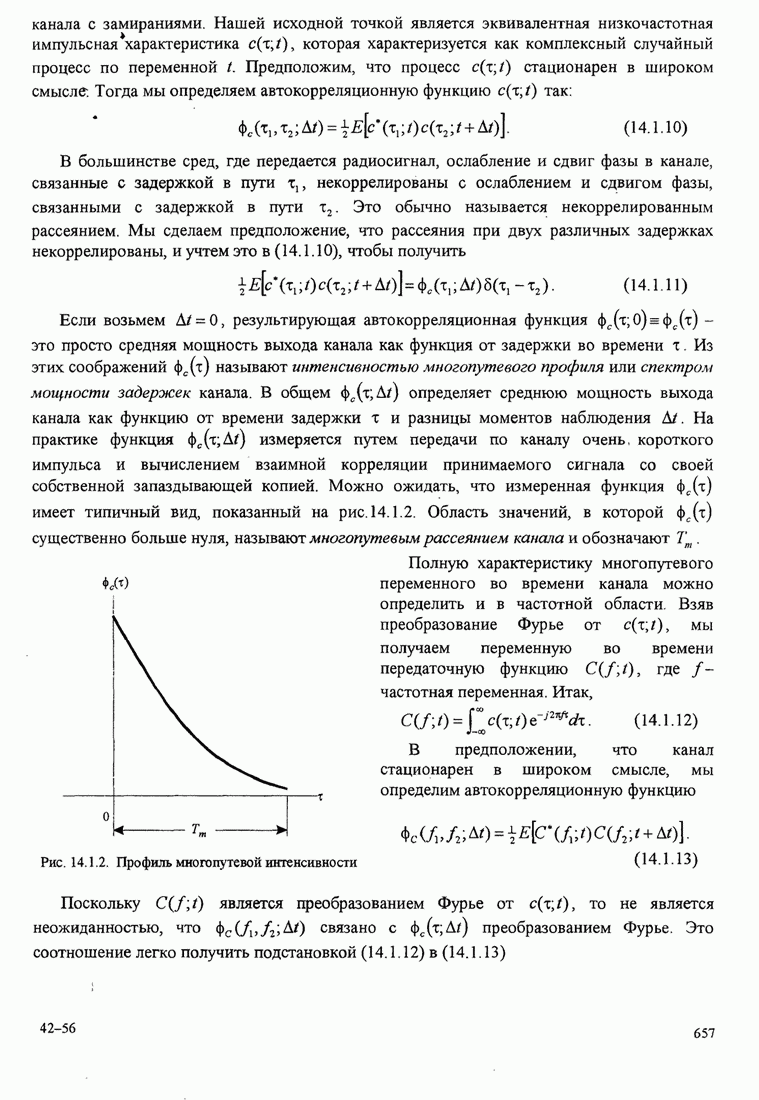
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
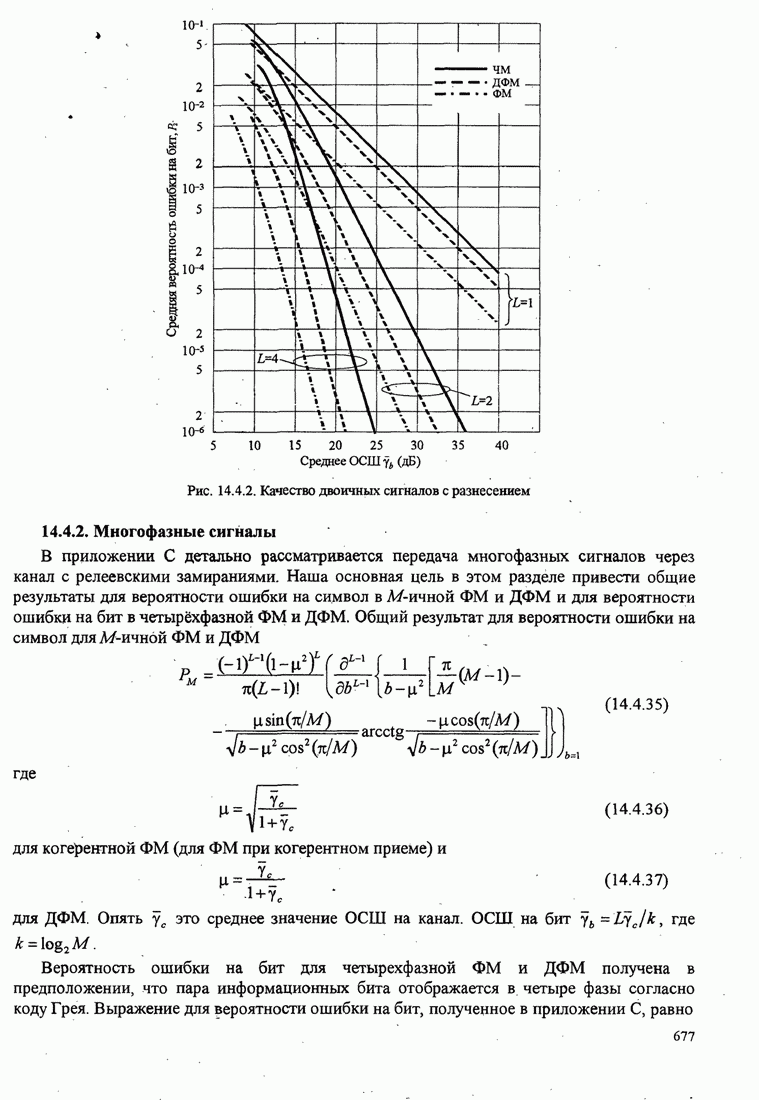
- 14.4.2. Многофазные сигналы
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
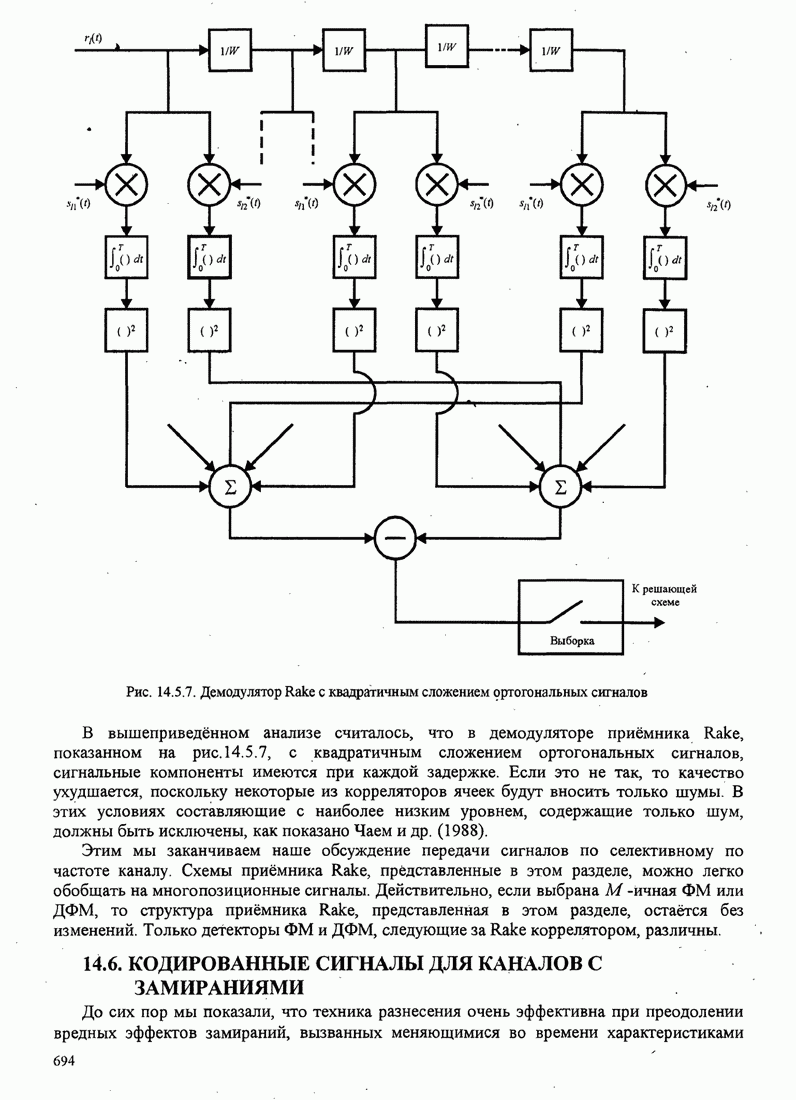
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
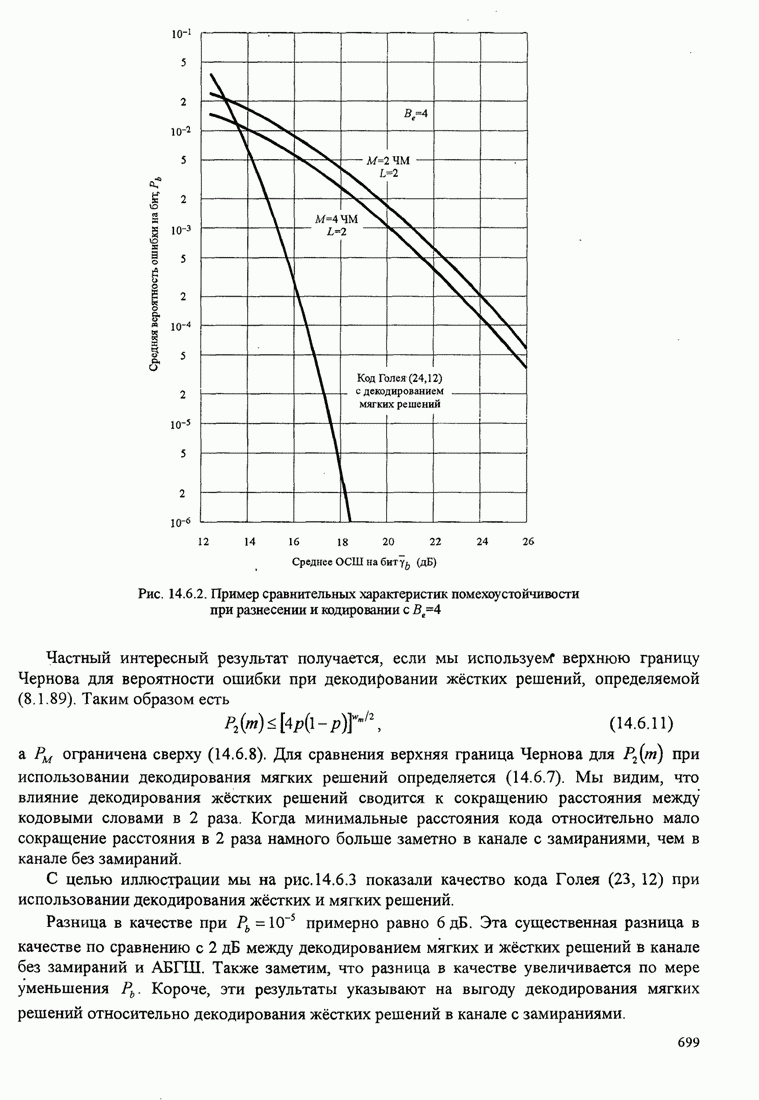
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
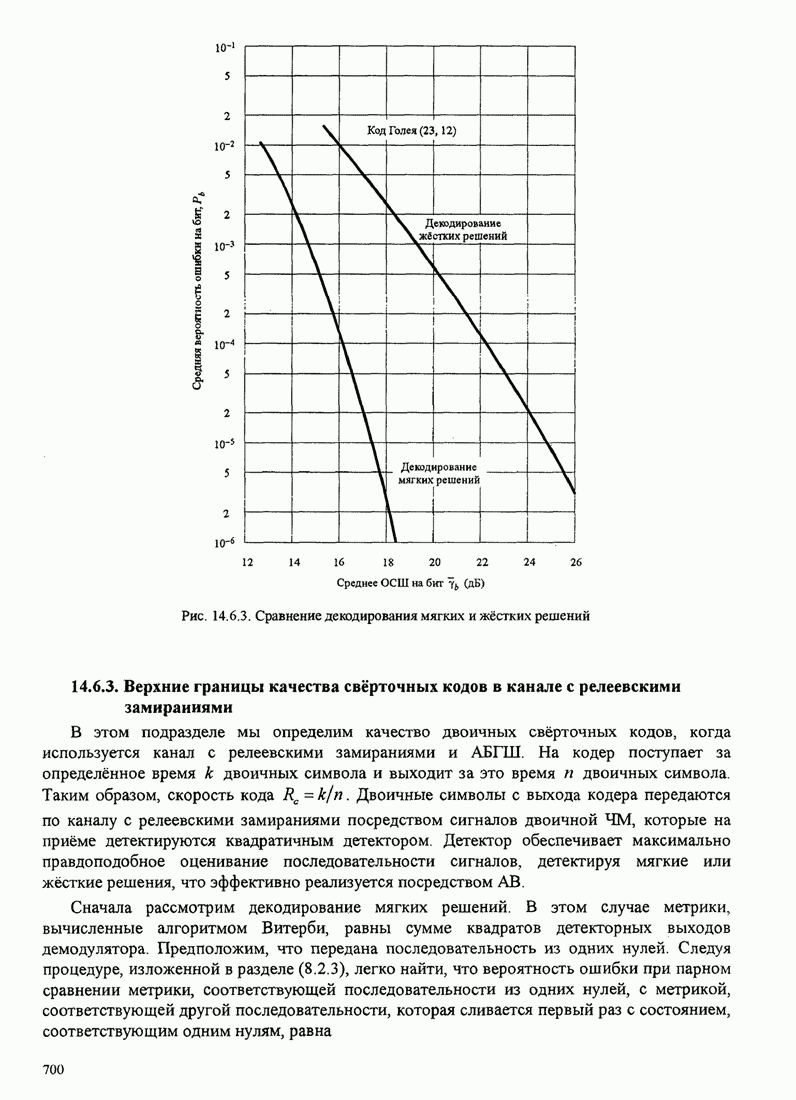
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
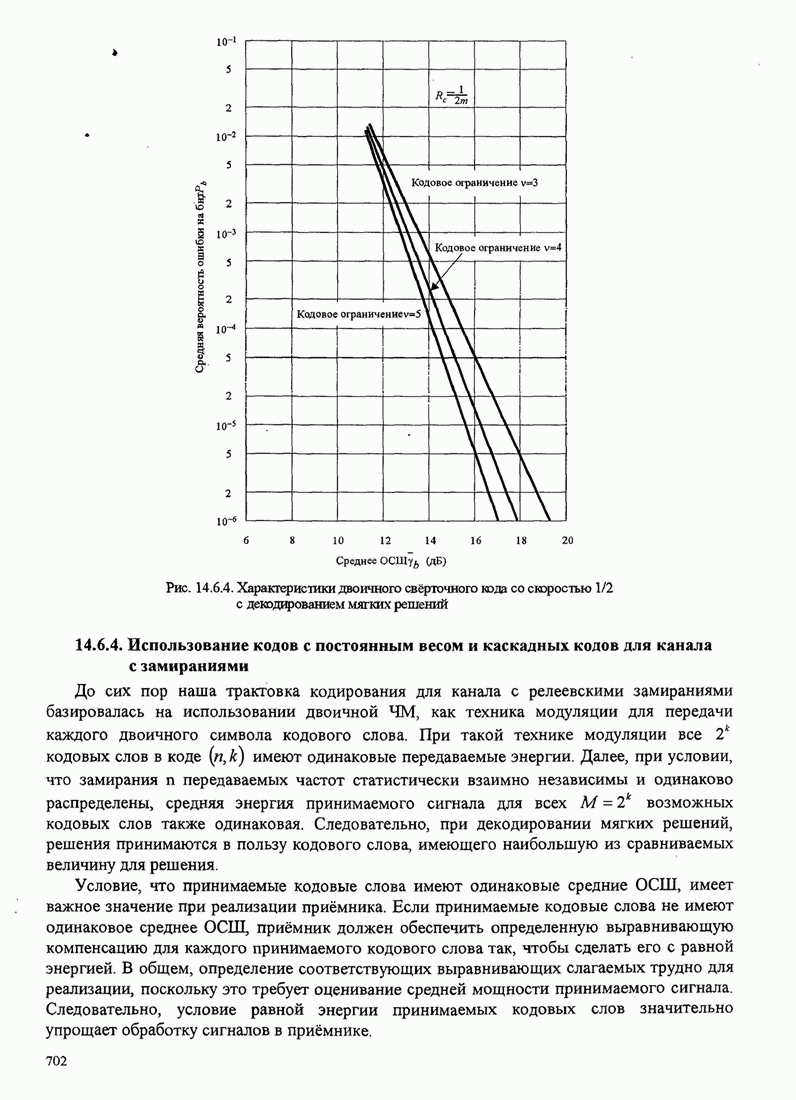
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)