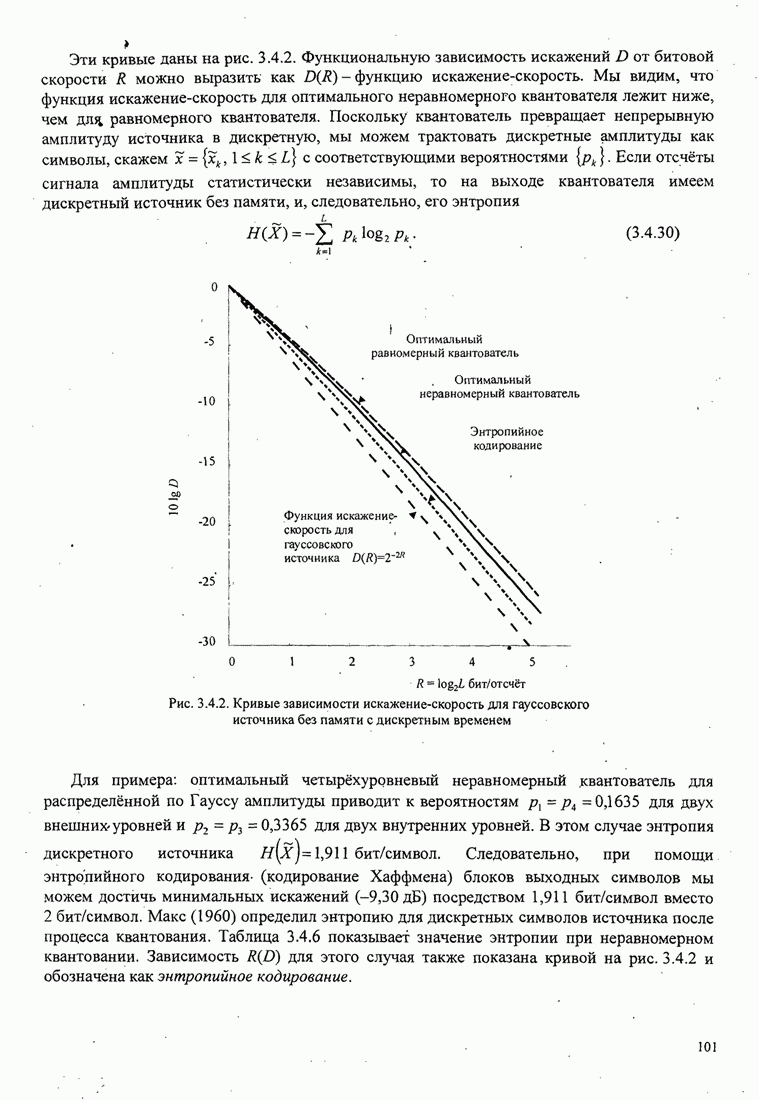
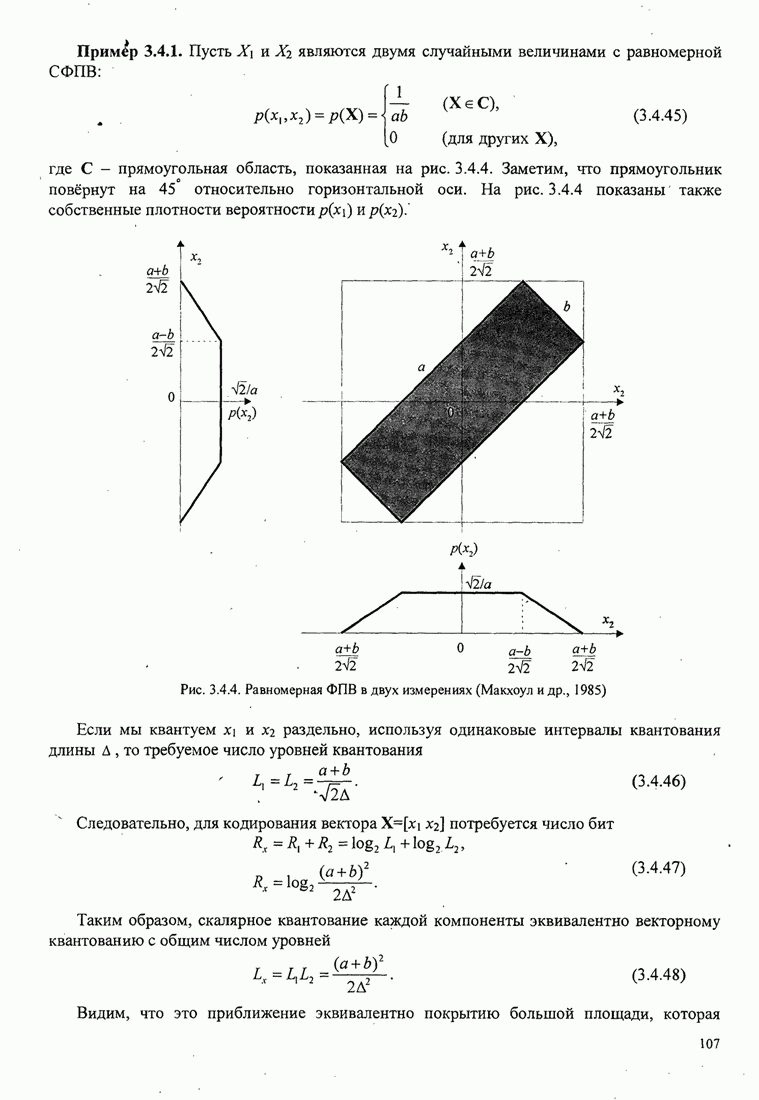
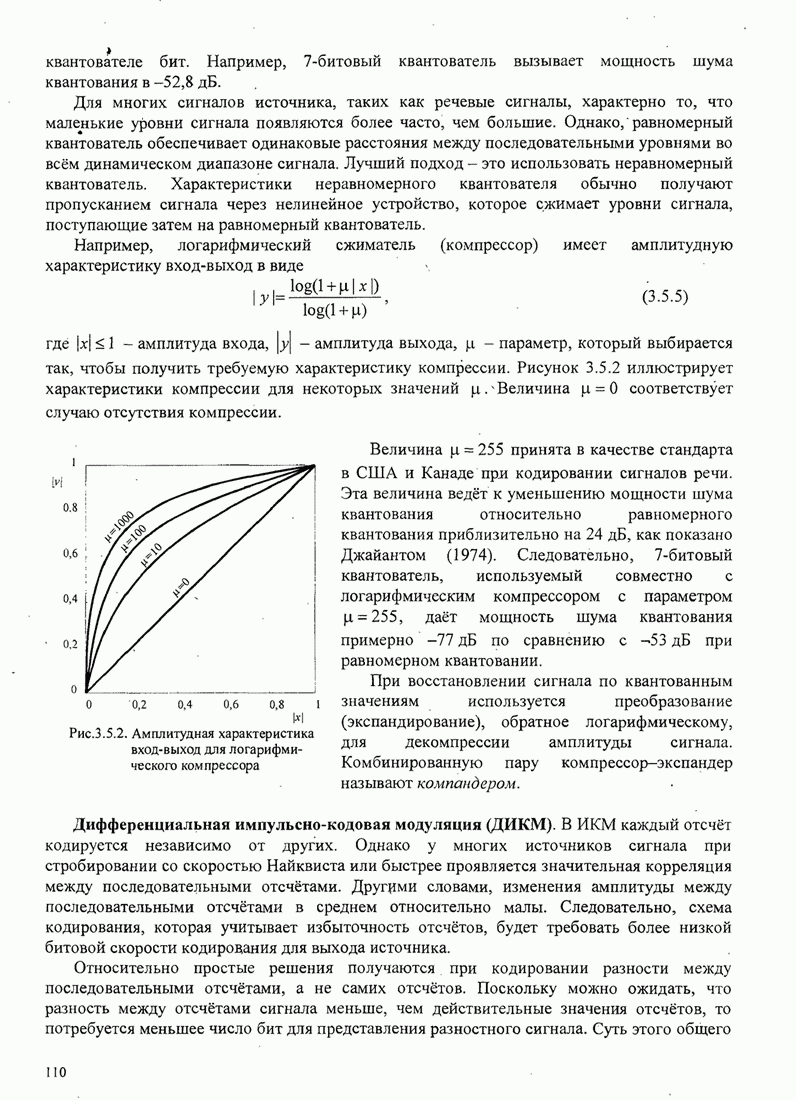
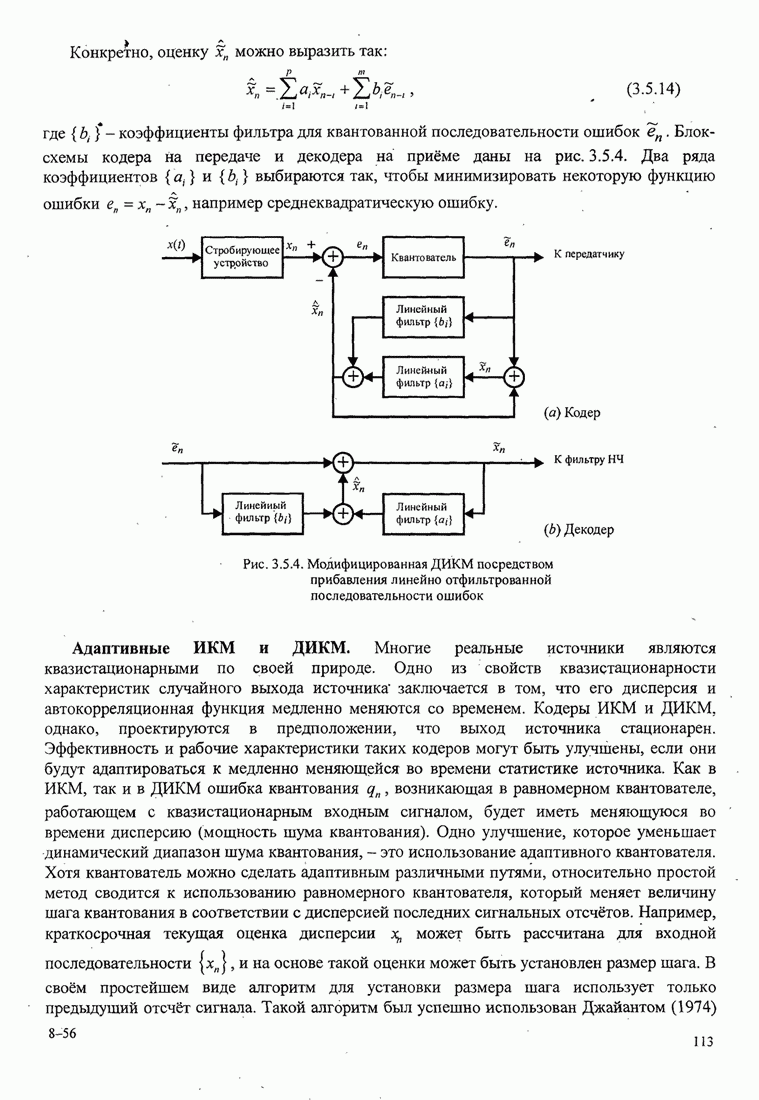
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
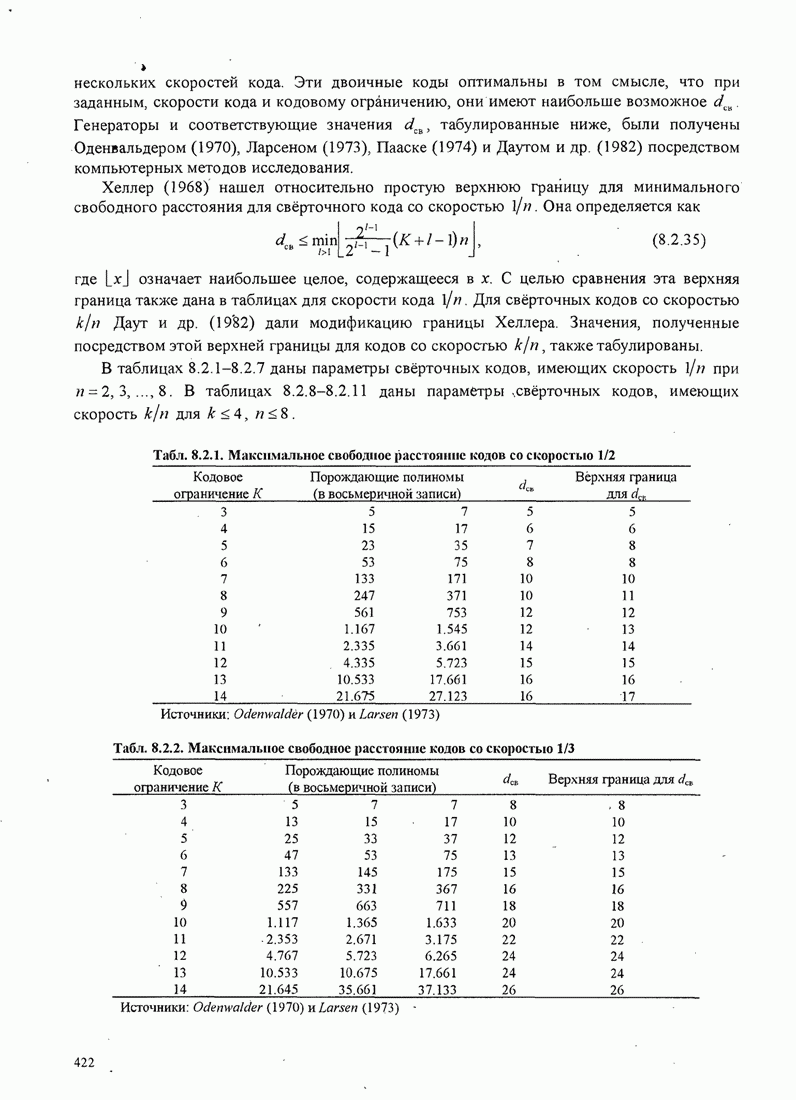
8.2.7. Другие алгоритмы декодирования свёрточных кодов
Алгоритм Витерби,
описанный в разделе 8.2.2, это оптимальный алгоритм декодирования для
свёрточных кодов. Однако он требует вычисления ![]() метрик каждого узла решётки и
хранения
метрик каждого узла решётки и
хранения ![]() метрик
и
метрик
и ![]() выживших
последовательностей, каждая из них имеет длину около
выживших
последовательностей, каждая из них имеет длину около ![]() бит. Вычислительное время и
память для хранения, требуемого для реализации алгоритма Витерби, делают его
практически неприемлемым для свёрточных кодов с большим кодовым ограничением.
бит. Вычислительное время и
память для хранения, требуемого для реализации алгоритма Витерби, делают его
практически неприемлемым для свёрточных кодов с большим кодовым ограничением.
Еще до открытия оптимального алгоритма Витерби, были придуманы другие алгоритмы для декодирования свёрточных кодов. Самым ранним был алгоритм последовательного декодирования, впервые предложенный Возенкрафтом и впоследствии модифицированный Фано (1963).
Последовательный алгоритм декодирования Фано ищет наиболее правдоподобный путь по дереву или решётке путём проверки каждый раз одного пути. Приращение, добавляемое к метрике вдоль ветви пропорционально вероятности принимаемого сигнала для этой ветви, как в алгоритме Витерби, за исключением того, что к метрике каждой ветви добавляется отрицательная константа. Величина этой константы выбирается так, что метрика правильного пути будет в среднем увеличиваться, в то время как метрика для любого неправильного пути в среднем будет уменьшаться. Путём сравнения метрики претендующего пути с меняющимся (увеличивающимся) порогом алгоритм Фано обнаруживает и отвергает неправильные пути.
Для большей конкретности рассмотрим канал без памяти.
Метрика для ![]() -го пути по дереву
или решётке от первой ветви до
-го пути по дереву
или решётке от первой ветви до ![]() -й ветви можно выразить так
-й ветви можно выразить так
 , (8.2.42)
, (8.2.42)
где
 . (8.2.43)
. (8.2.43)
В (8.2.43) ![]() - выходная
последовательность демодулятора,
- выходная
последовательность демодулятора, ![]() означает условную ФПВ
означает условную ФПВ ![]() при условии
кодового бита
при условии
кодового бита ![]() (
(![]() -й бит в
-й бит в ![]() -й ветви
-й ветви ![]() -гo пути), а
-гo пути), а ![]() - положительная
константа.
- положительная
константа. ![]() выбирается,
как сказано выше, так, что неправильные пути будут иметь уменьшающиеся метрики,
в то время как правильный путь в среднем увеличивает метрику. Заметим, что член
выбирается,
как сказано выше, так, что неправильные пути будут иметь уменьшающиеся метрики,
в то время как правильный путь в среднем увеличивает метрику. Заметим, что член
![]() в
знаменателе не зависит от кодовой последовательности и, следовательно, может
быть включен в постоянную.
в
знаменателе не зависит от кодовой последовательности и, следовательно, может
быть включен в постоянную.
Метрика, определённая
(8.2.43), в общем применима при декодировании как жёстких, так и мягких
решений. Однако она может быть особенно упрощена, когда используется
декодирование жёстких решений. В частном случае, если мы имеем ДСК с переходной
вероятностью ошибки ![]() , метрика для каждого принятого
символа, согласующаяся с формулой (8.2.43), определяется так
, метрика для каждого принятого
символа, согласующаяся с формулой (8.2.43), определяется так
 (8.2.44)
(8.2.44)
где ![]() - выходы жёстких решений демодулятора;
- выходы жёстких решений демодулятора;
![]() -
- ![]() -й кодовый символ в
-й кодовый символ в
![]() -й ветви
-й ветви ![]() -го пути дерева;
-го пути дерева; ![]() - скорость кода.
- скорость кода.
Заметим, что эти метрики
требуют хотя бы приближённого знания вероятности ошибки ![]() .
.
Пример 8.2.6. Предположим, что для
передачи информации по ДСК с вероятностью ошибки ![]() используется двоичный свёрточный код
со скоростью
используется двоичный свёрточный код
со скоростью ![]() .
Вычисление согласно (8.2.44) дает
.
Вычисление согласно (8.2.44) дает
 (8.2.45)
(8.2.45)
Для упрощения расчётов метрики (8.2.45) можно нормировать. Они хорошо аппроксимируются так:
 (8.2.46)
(8.2.46)
Поскольку скорость кода равна 1/3, то кодер имеет три выходных символа на каждый входной символ. Тогда метрики ветвей, согласующиеся с (8.2.46), равны
![]()
или, что эквивалентно,
![]() , (8.2.47)
, (8.2.47)
где ![]() — хеммингово расстояние
трёх принятых бит от трёх битов на ветви.
— хеммингово расстояние
трёх принятых бит от трёх битов на ветви.
Таким образом, метрики ![]() просто связаны с
расстоянием Хемминга между принимаемыми символами и кодовыми символами
просто связаны с
расстоянием Хемминга между принимаемыми символами и кодовыми символами ![]() -й ветви
-й ветви ![]() -го пути.
-го пути.
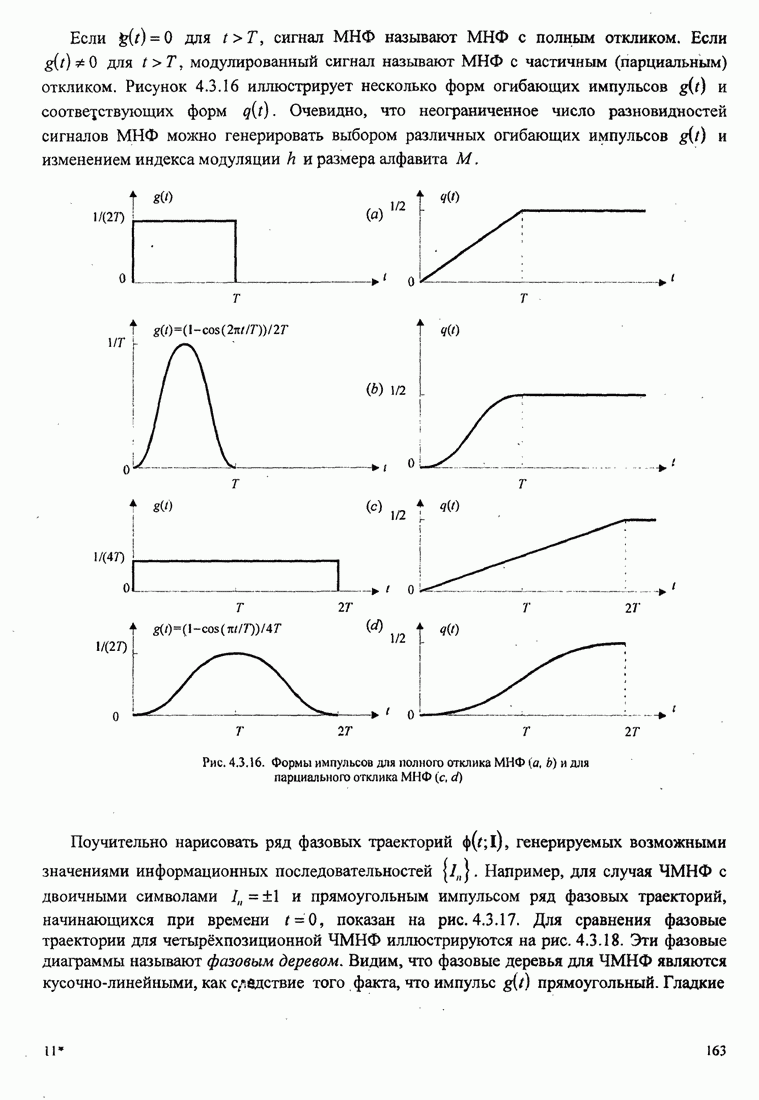
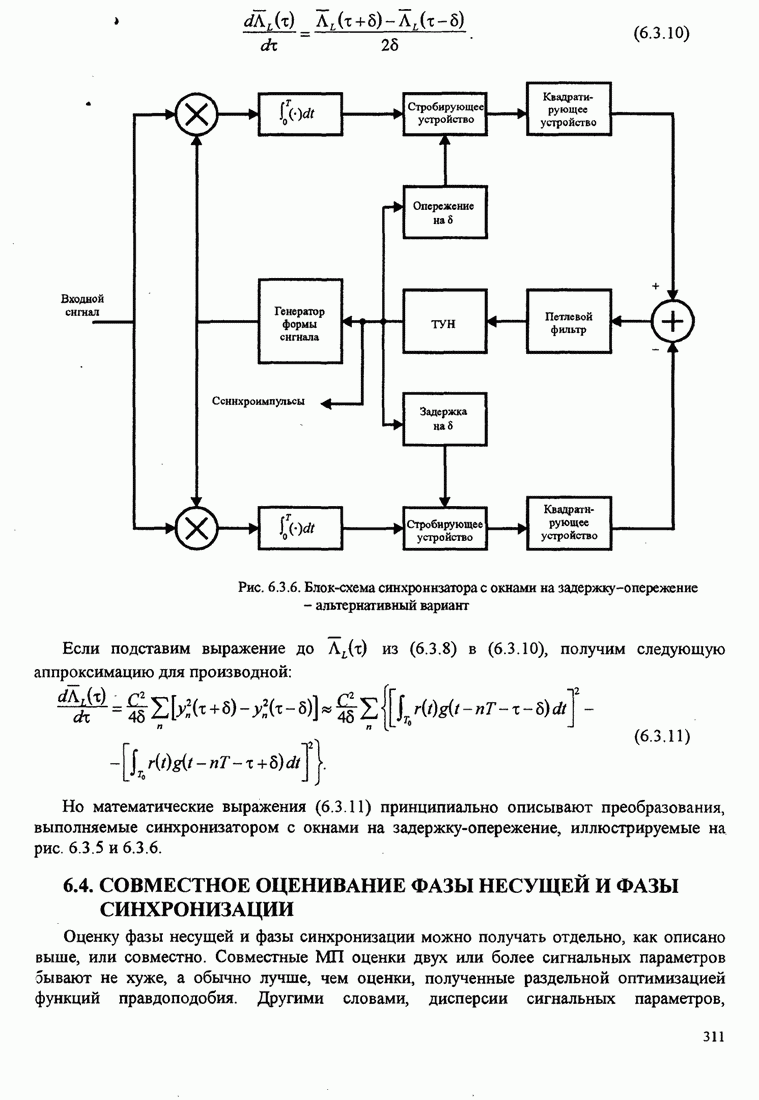
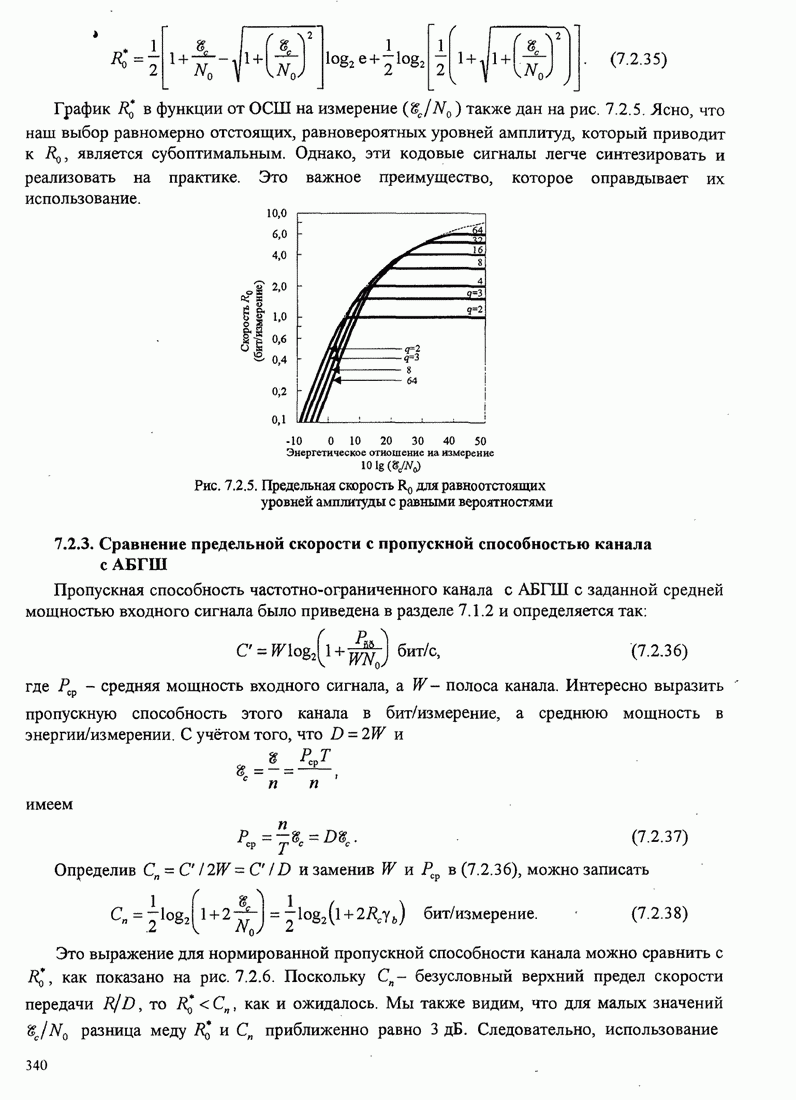
Первоначально декодер
можно заставить выбирать правильную траекторию путём передачи известной цепочки
данных. Тогда он продвигается вперед от узла к узлу, выбирая наиболее вероятную
(с большей метрикой) ветвь в каждом узле и увеличивая порог так, что его
изменение никогда не больше, чем некоторая заранее выбранная величина, скажем, ![]() . Теперь
предположим, что аддитивный шум (при декодировании мягких решений) или ошибки
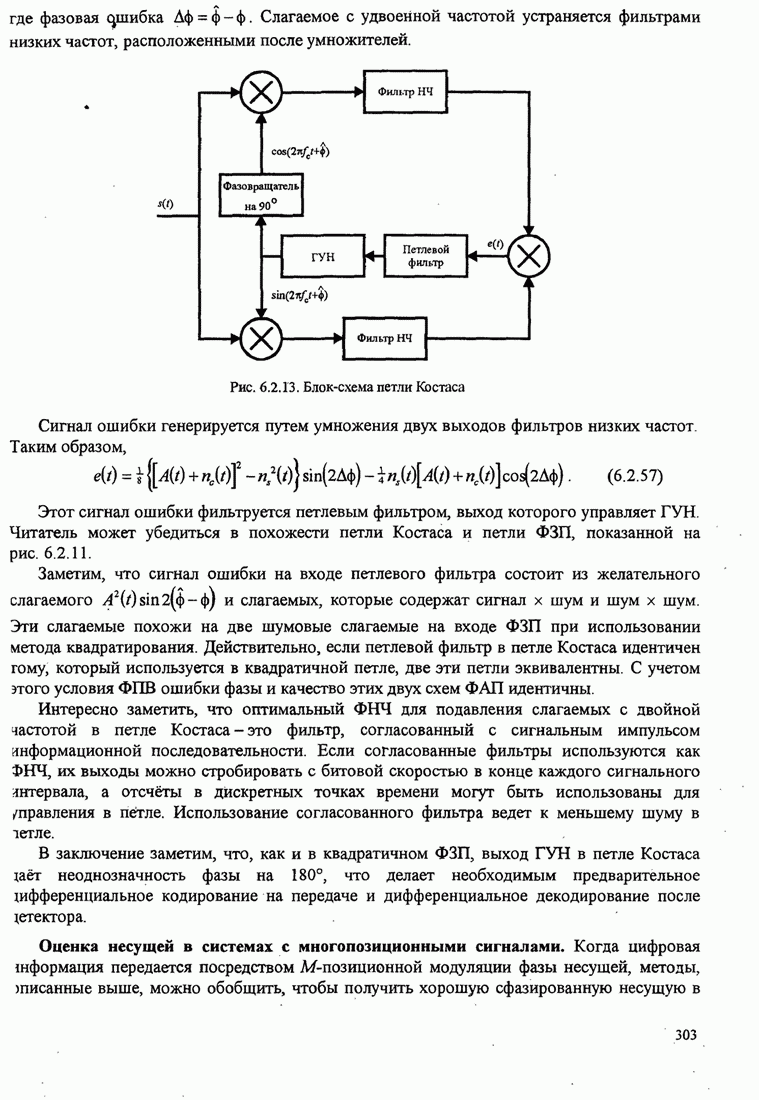
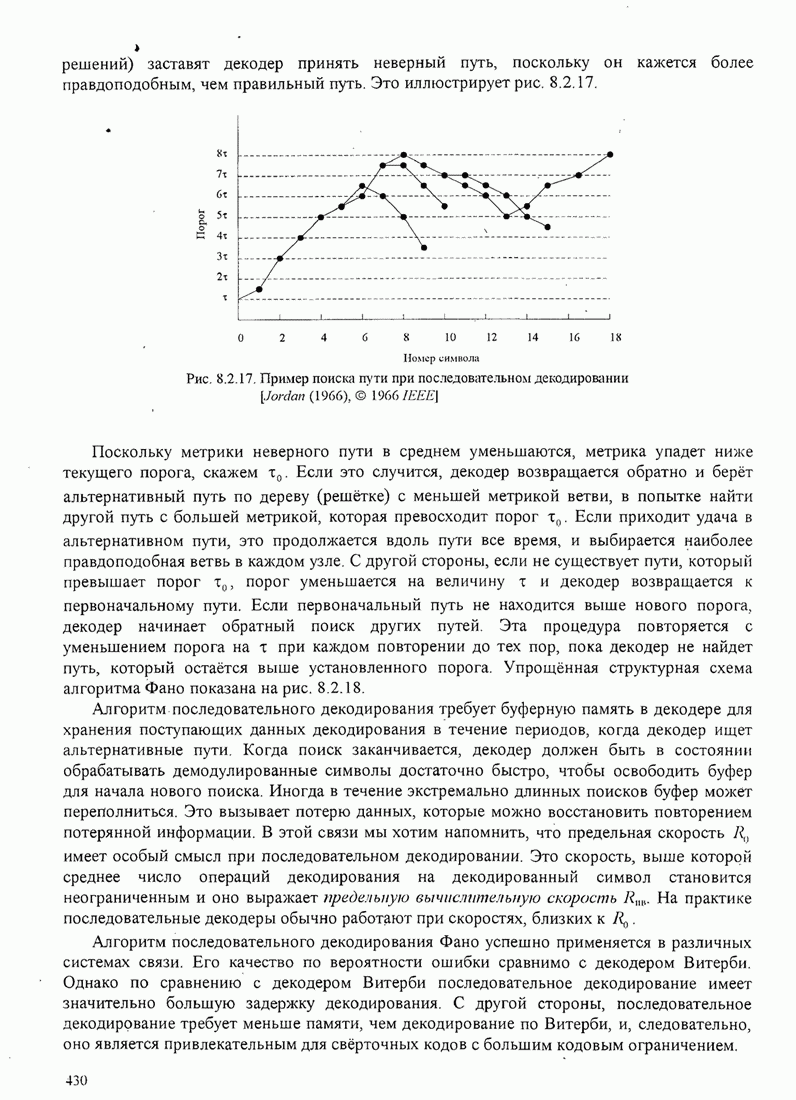
демодуляции, возникающие из-за шума в канале (при декодировании жёстких решений) заставят декодер принять неверный путь,
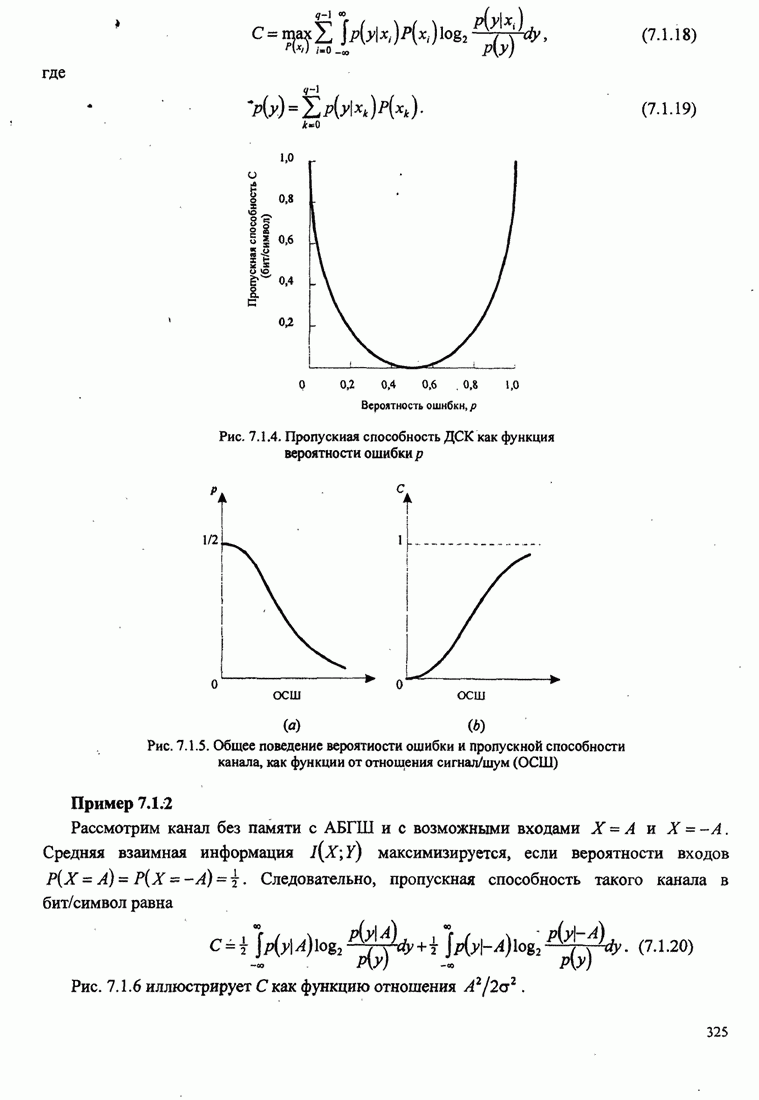
поскольку он кажется более правдоподобным, чем правильный путь. Это
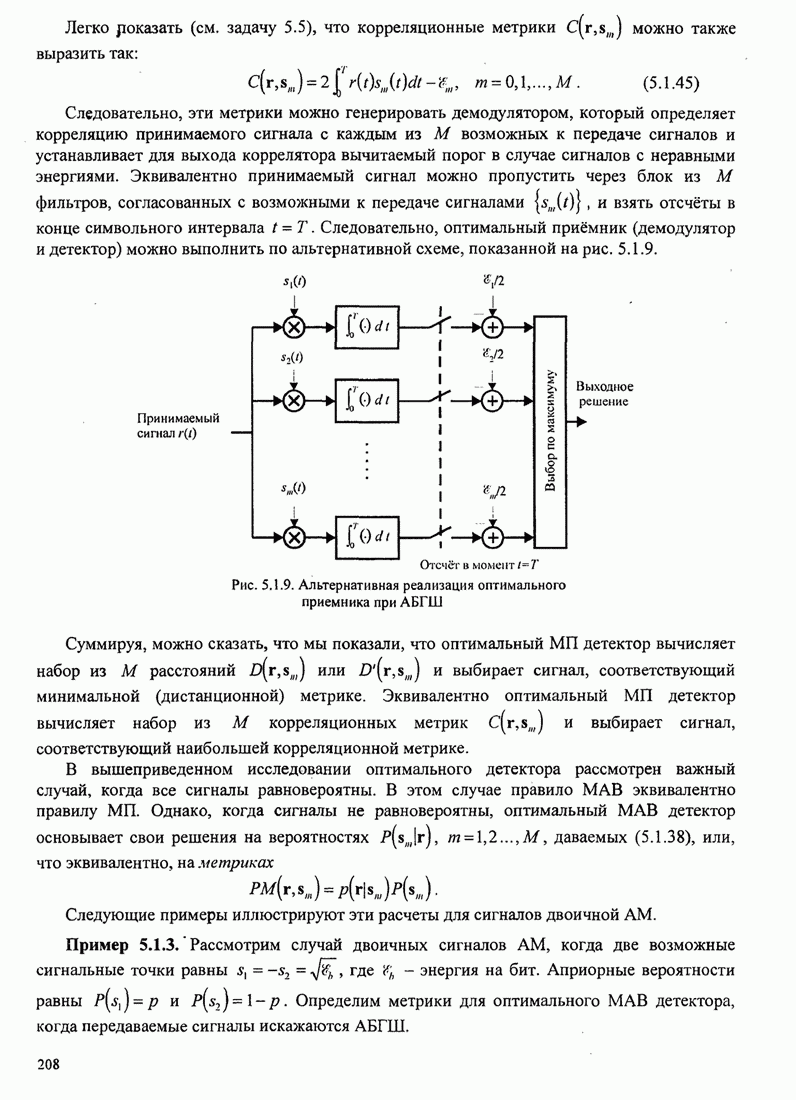
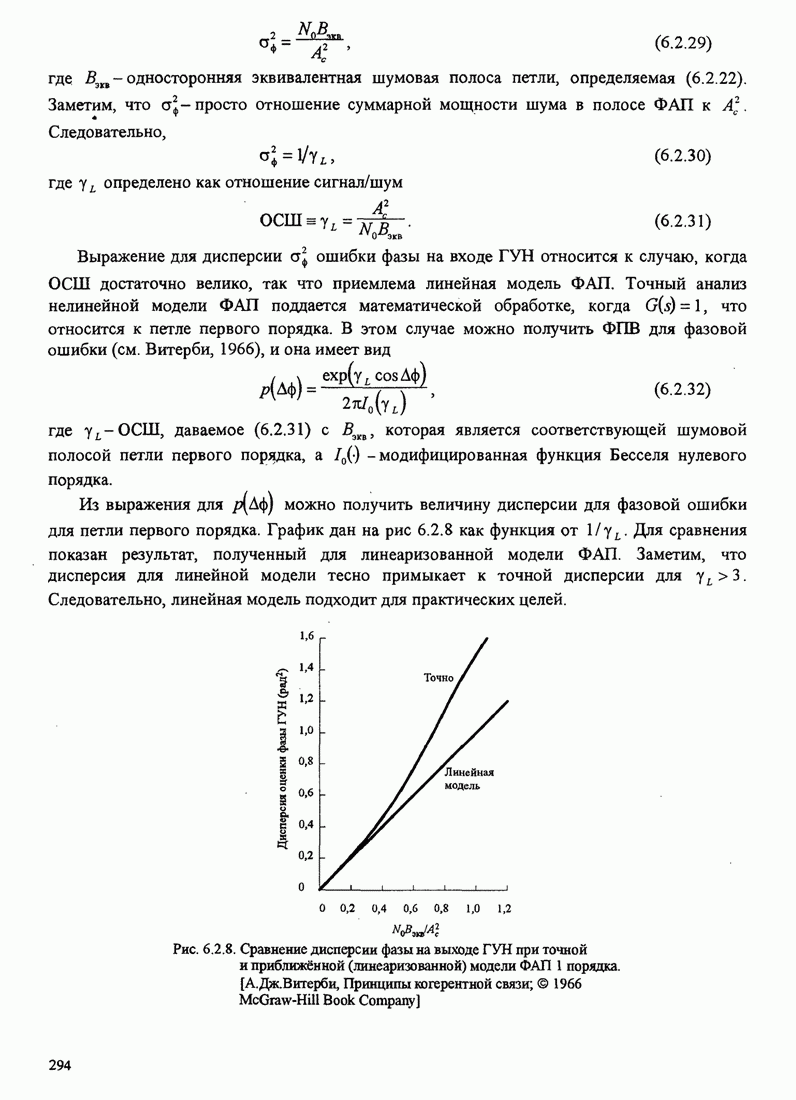
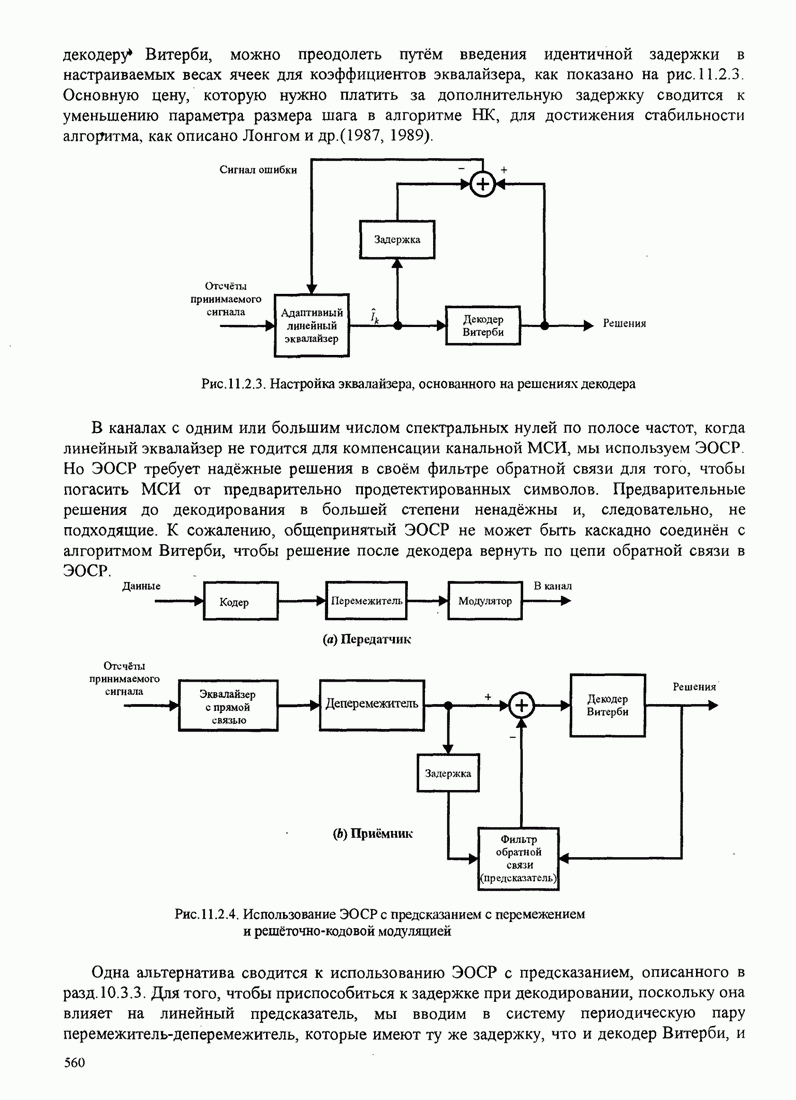
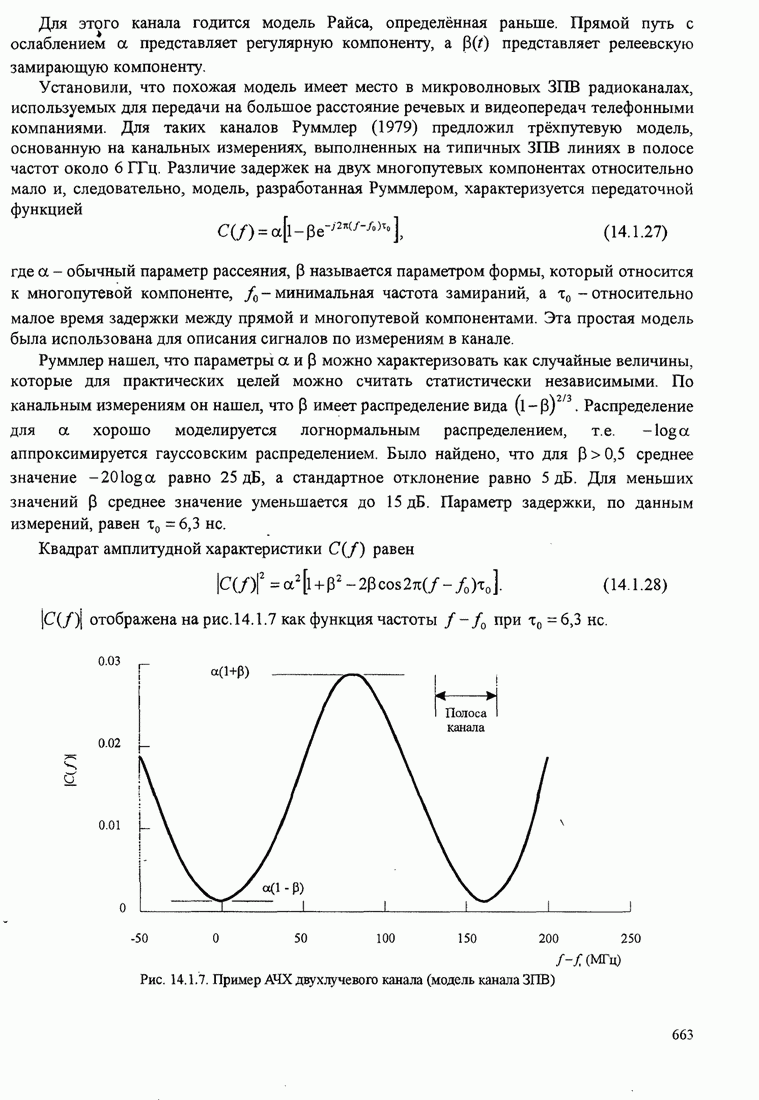
иллюстрирует рис. 8.2.17.
. Теперь
предположим, что аддитивный шум (при декодировании мягких решений) или ошибки
демодуляции, возникающие из-за шума в канале (при декодировании жёстких решений) заставят декодер принять неверный путь,
поскольку он кажется более правдоподобным, чем правильный путь. Это
иллюстрирует рис. 8.2.17.

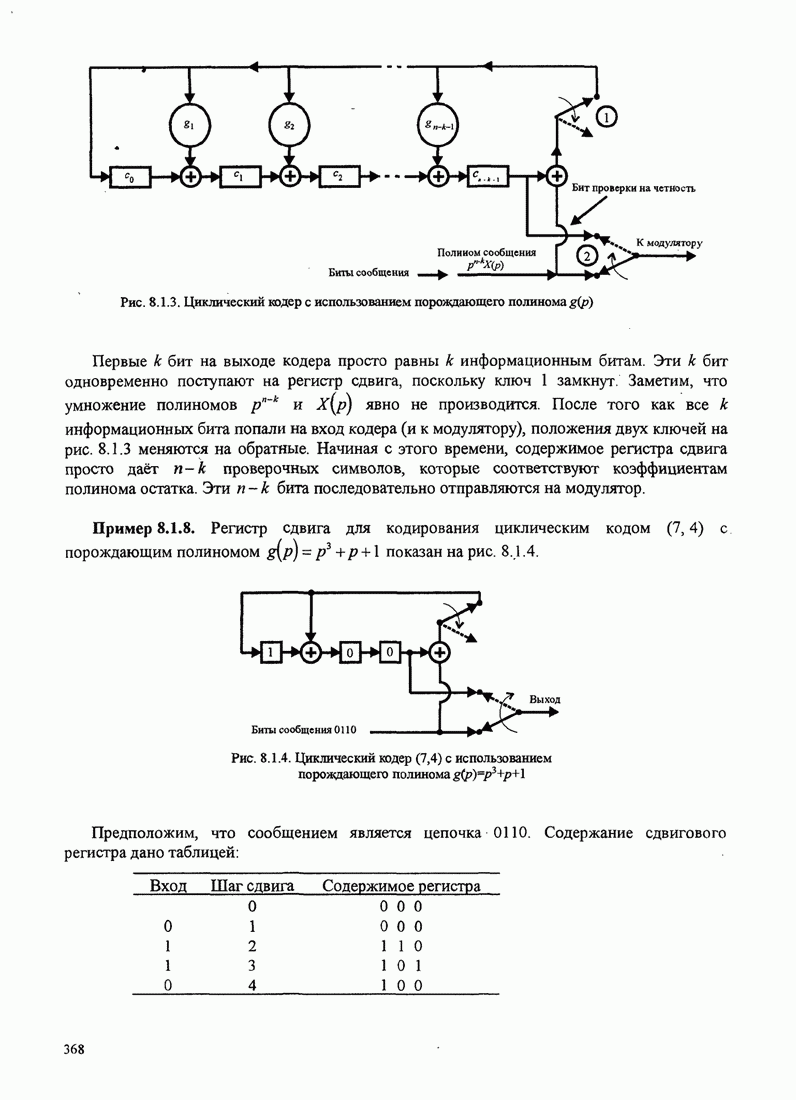
Рис. 8.2.17. Пример поиска пути при последовательном декодировании [Jordan (1966), © 1966 IЕЕЕ]
Поскольку метрики
неверного пути в среднем уменьшаются, метрика упадет ниже текущего порога,
скажем ![]() .
Если это случится, декодер возвращается обратно и берёт альтернативный путь по
дереву (решётке) с меньшей метрикой ветви, в попытке найти другой путь с
большей метрикой, которая превосходит порог
.
Если это случится, декодер возвращается обратно и берёт альтернативный путь по
дереву (решётке) с меньшей метрикой ветви, в попытке найти другой путь с
большей метрикой, которая превосходит порог ![]() . Если приходит удача в альтернативном
пути, это продолжается вдоль пути все время, и выбирается наиболее правдоподобная
ветвь в каждом узле. С другой стороны, если не существует пути, который
превышает порог
. Если приходит удача в альтернативном
пути, это продолжается вдоль пути все время, и выбирается наиболее правдоподобная
ветвь в каждом узле. С другой стороны, если не существует пути, который
превышает порог ![]() ,
порог уменьшается на величину
,
порог уменьшается на величину ![]() и декодер возвращается к
первоначальному пути. Если первоначальный путь не находится выше нового порога,
декодер начинает обратный поиск других путей. Эта процедура повторяется с
уменьшением порога на
и декодер возвращается к
первоначальному пути. Если первоначальный путь не находится выше нового порога,
декодер начинает обратный поиск других путей. Эта процедура повторяется с
уменьшением порога на ![]() при каждом повторении до тех пор,
пока декодер не найдет путь, который остаётся выше установленного порога.
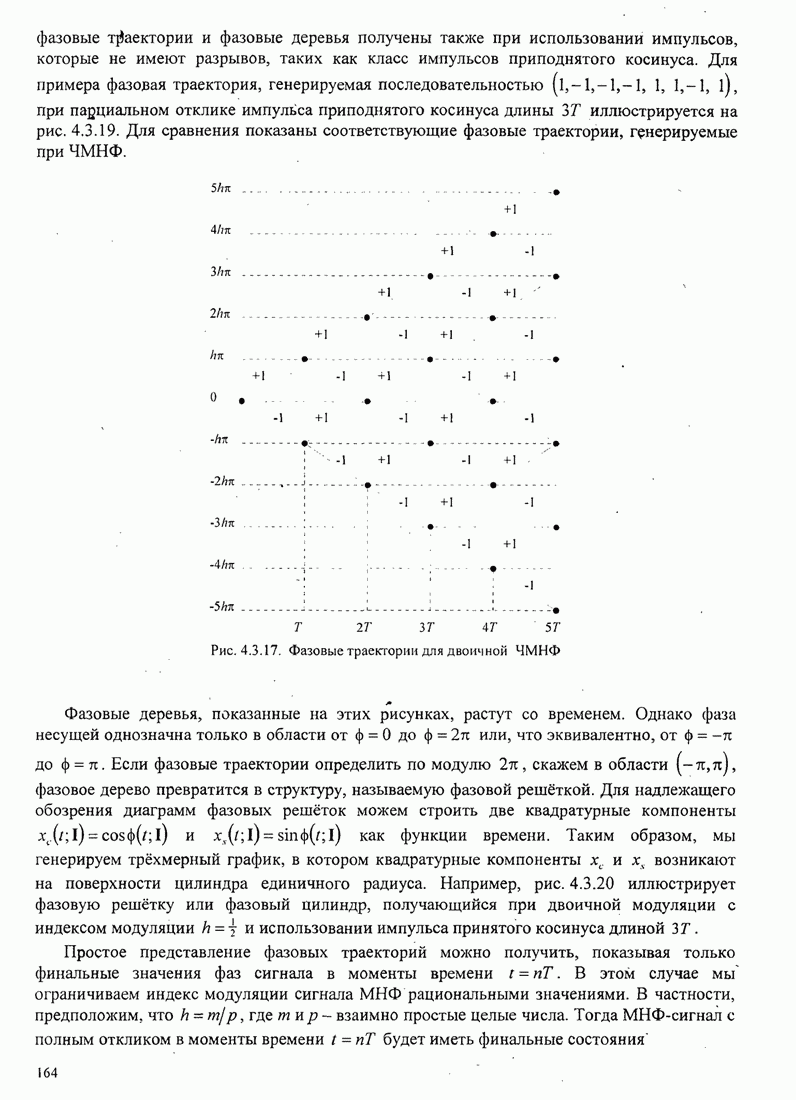
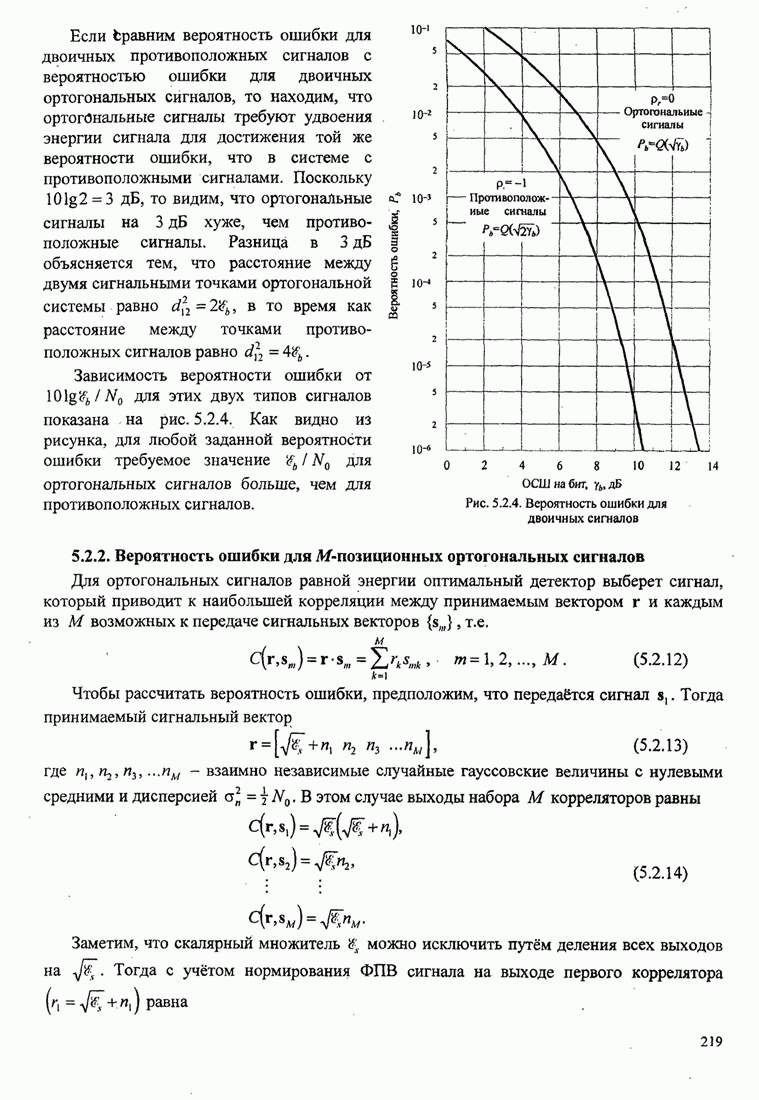
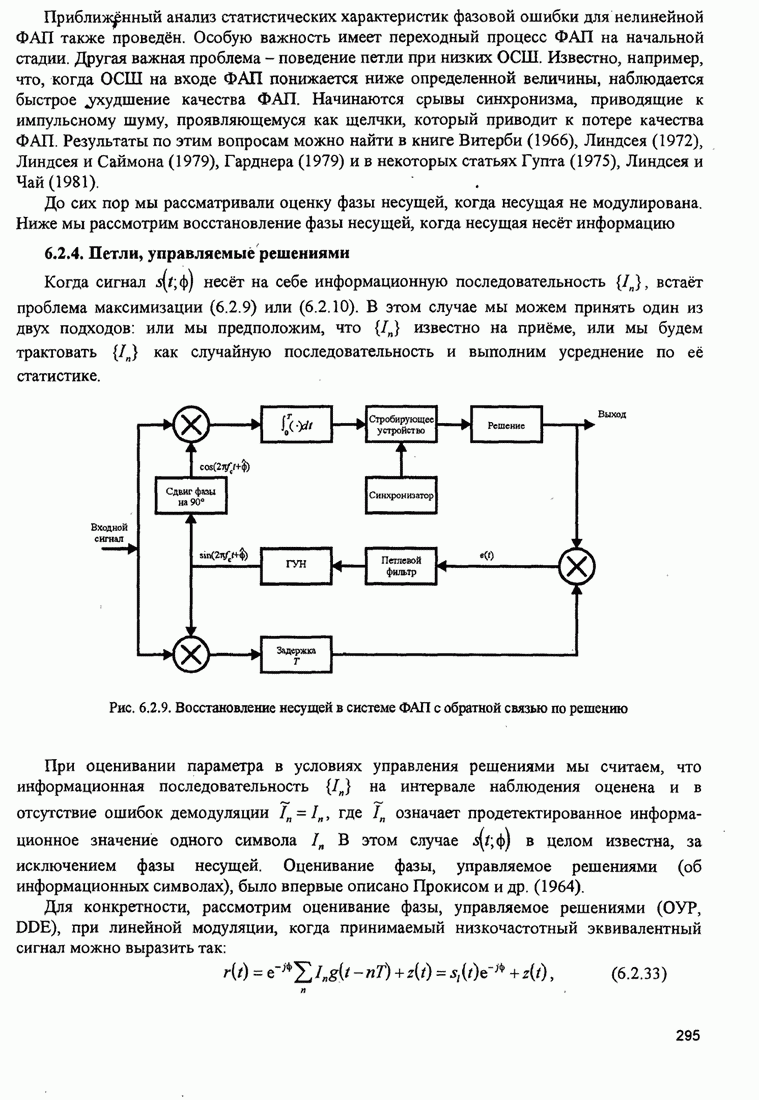
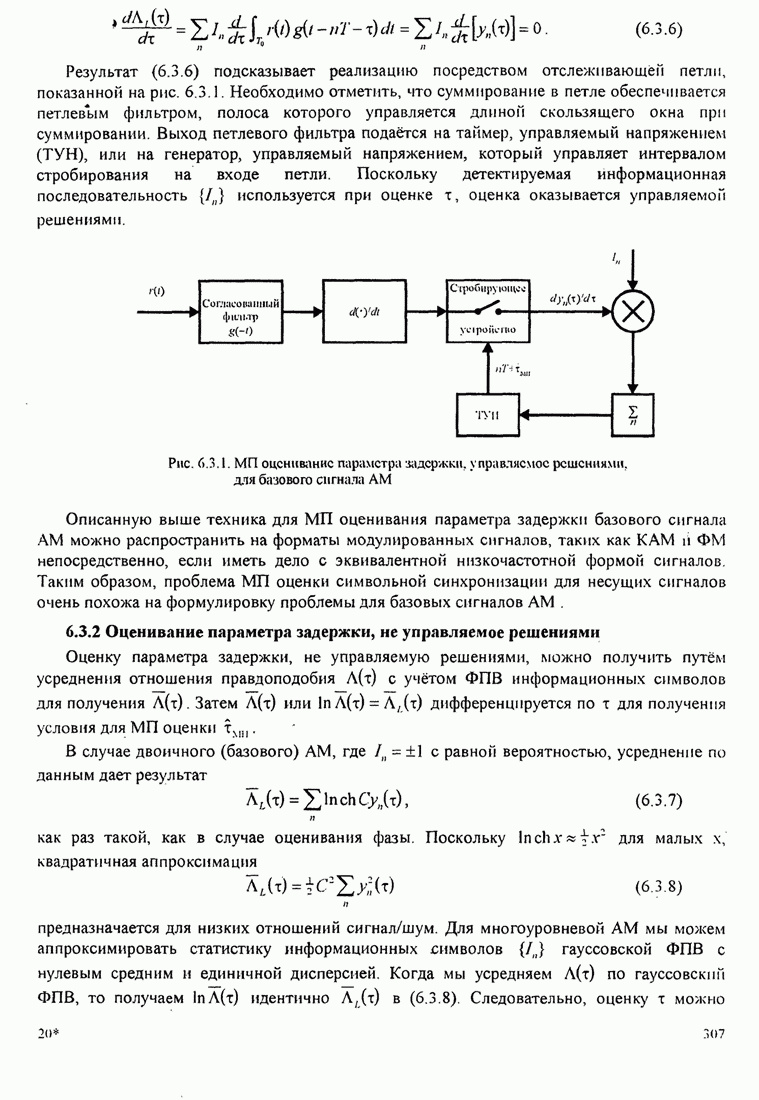
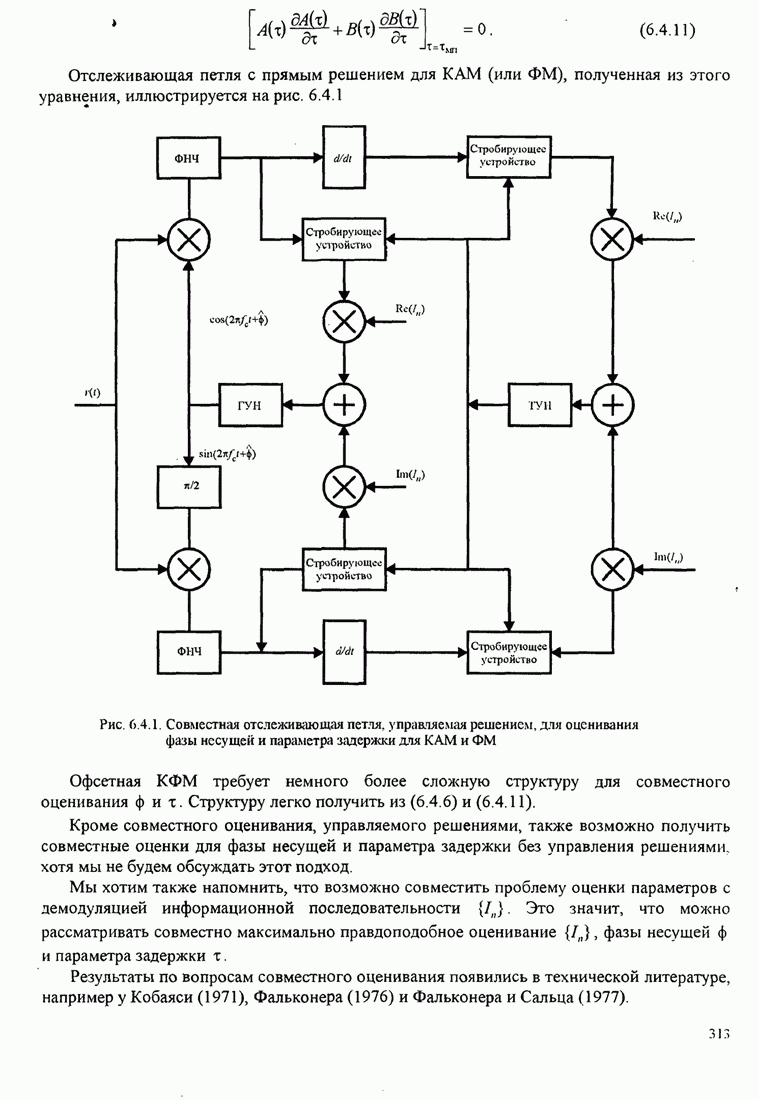
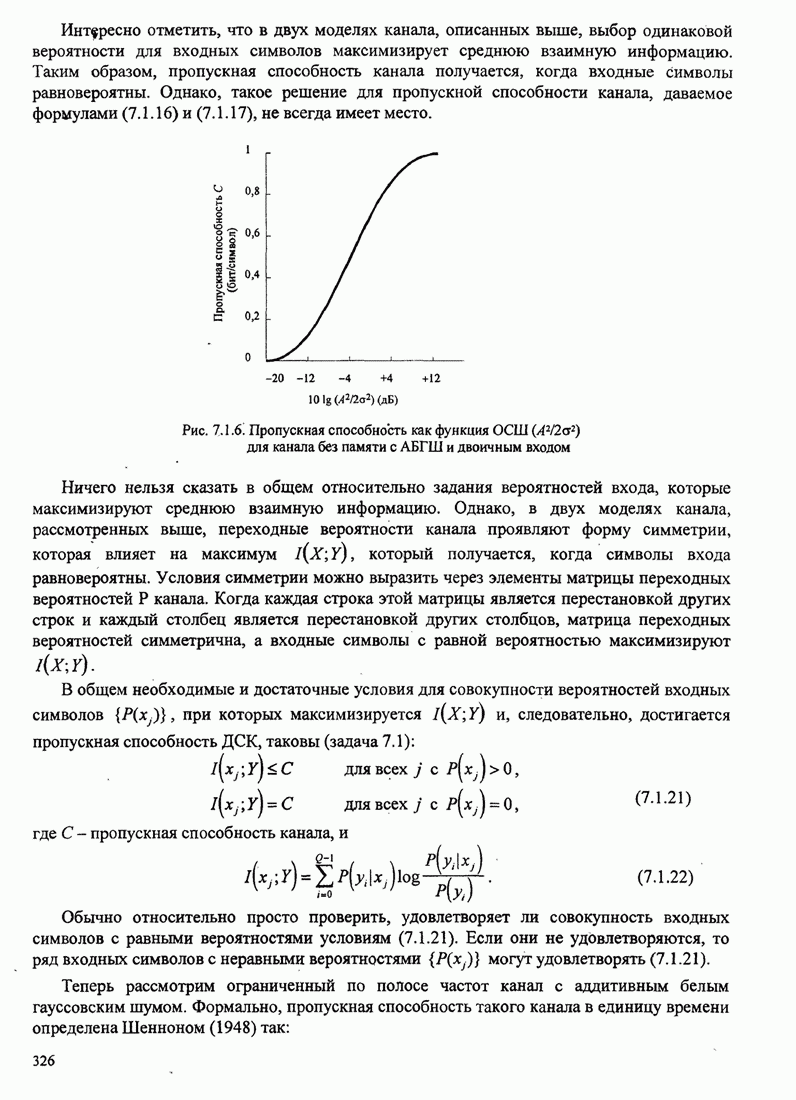
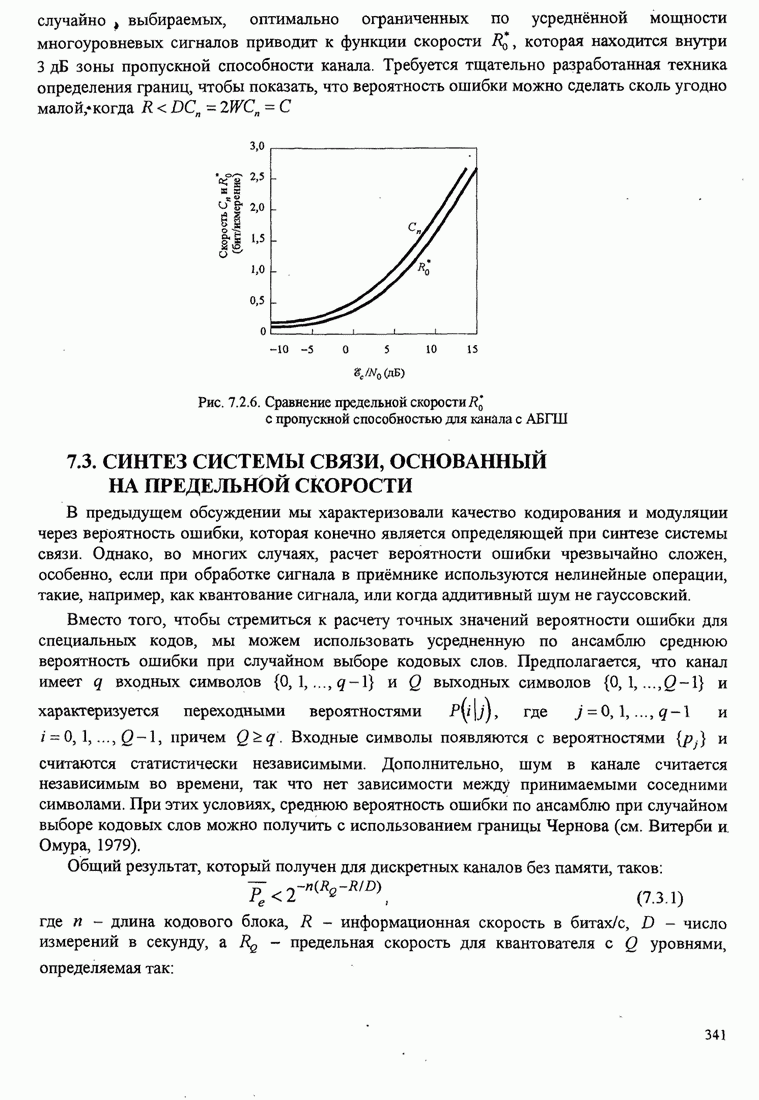
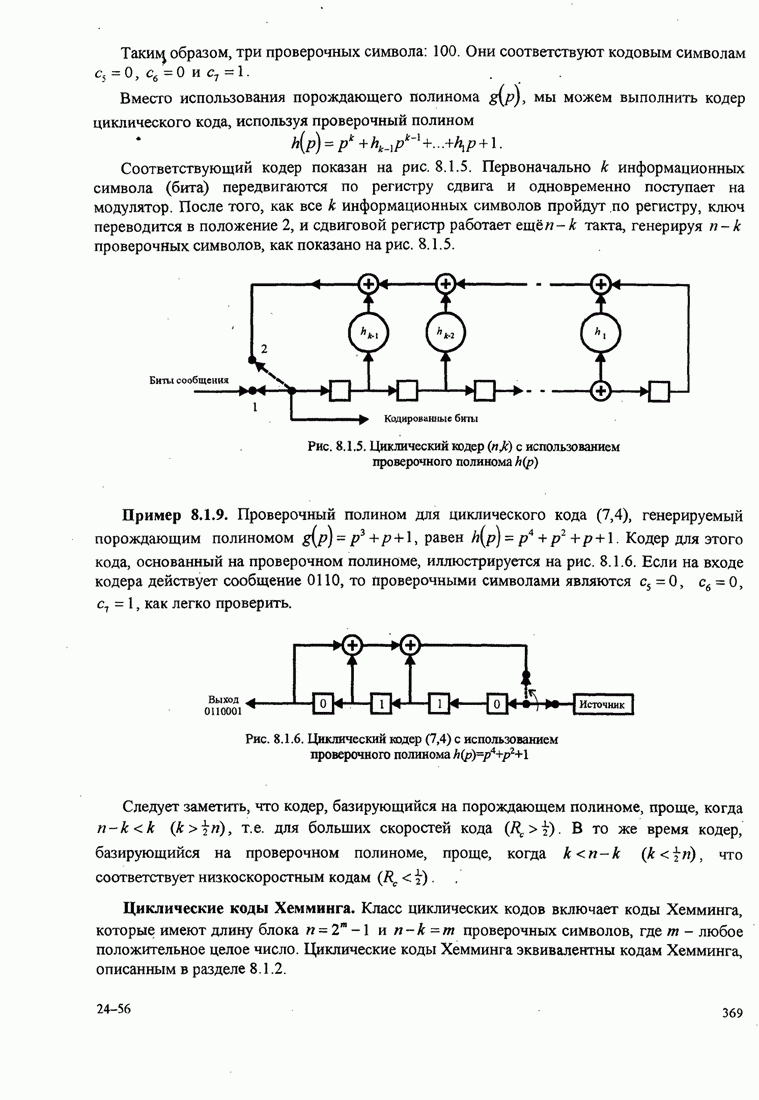
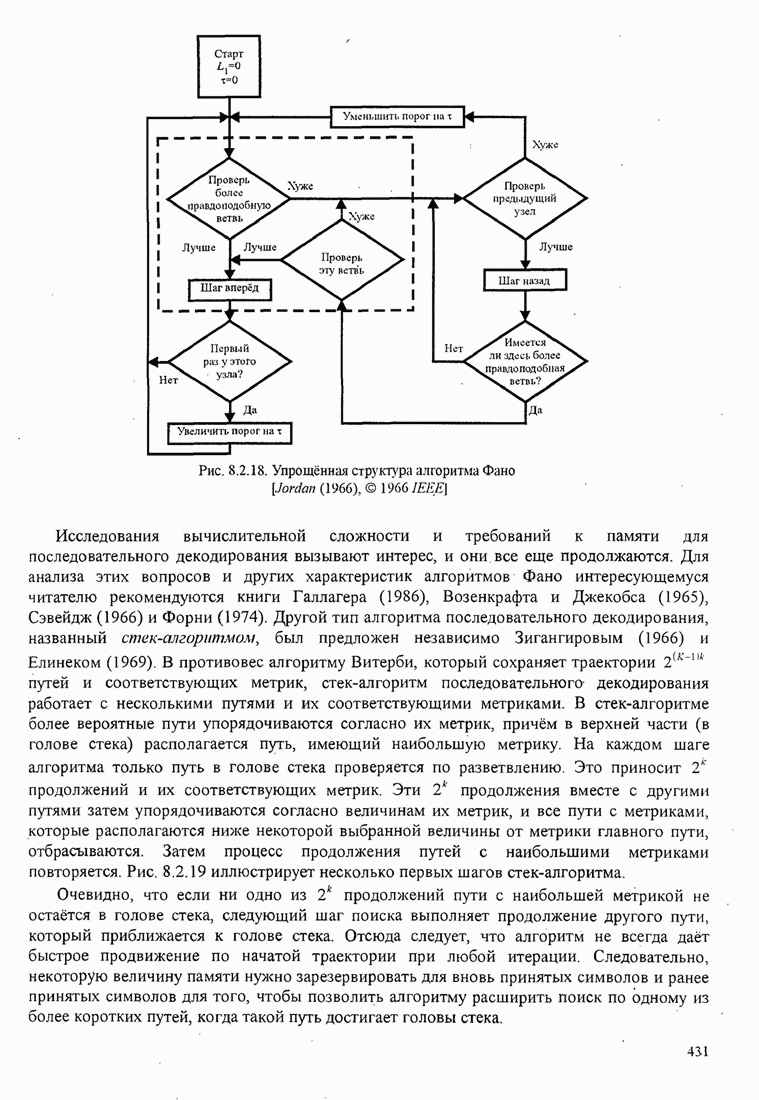
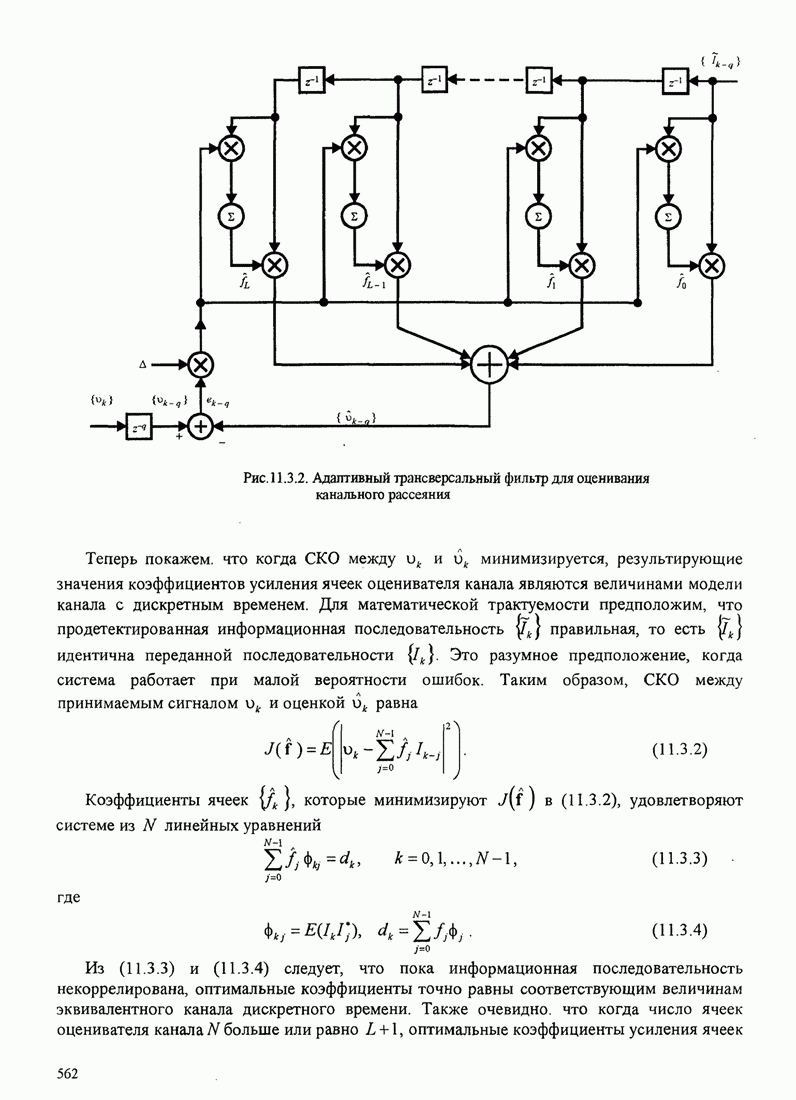
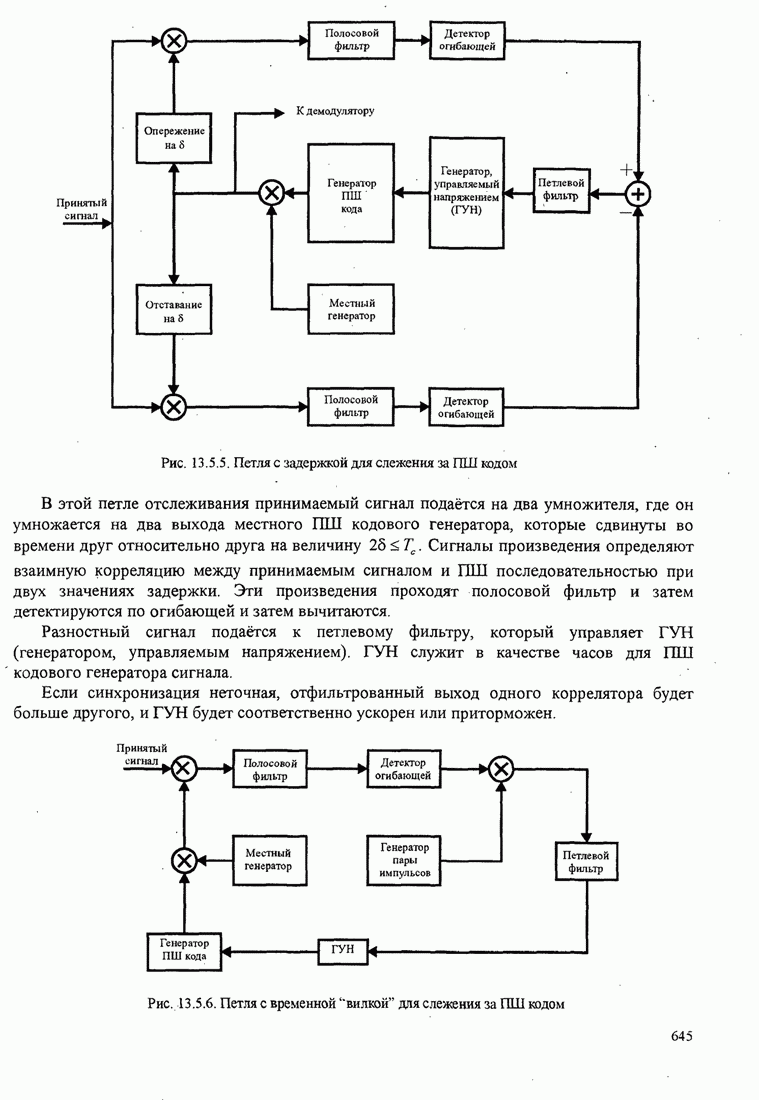
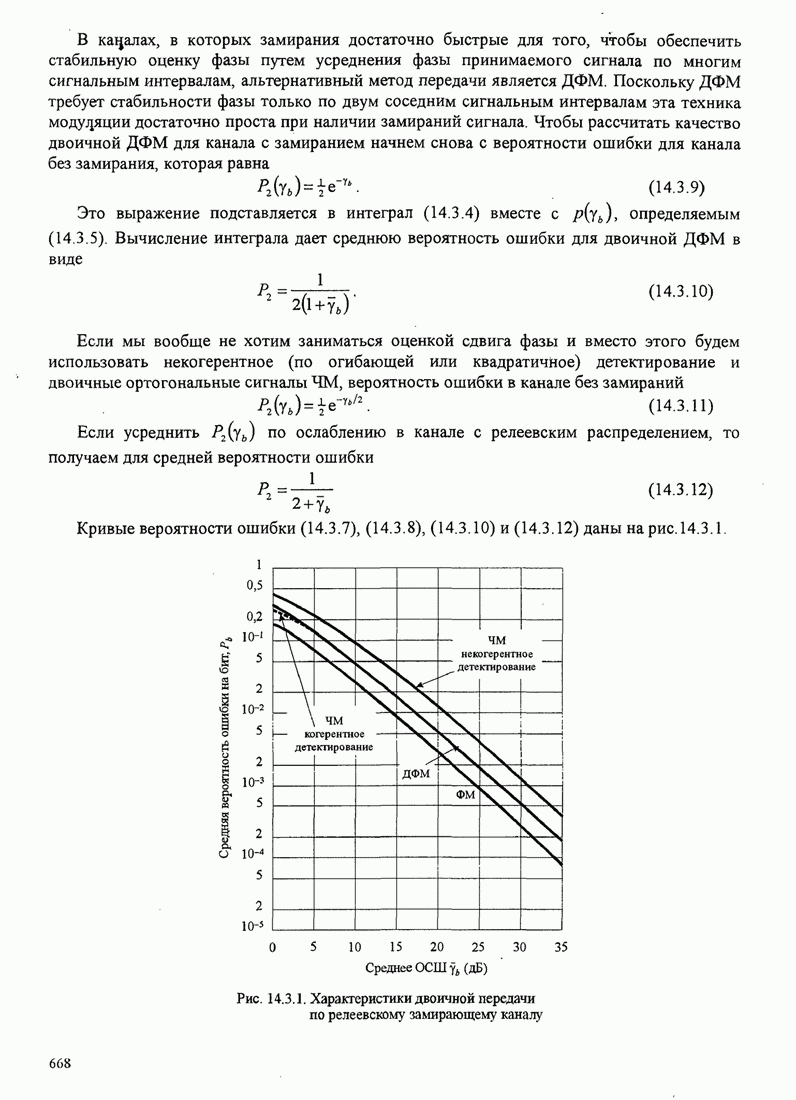
Упрощённая структурная схема алгоритма Фано показана на рис. 8.2.18.
при каждом повторении до тех пор,
пока декодер не найдет путь, который остаётся выше установленного порога.
Упрощённая структурная схема алгоритма Фано показана на рис. 8.2.18.
Алгоритм
последовательного декодирования требует буферную память в декодере для хранения
поступающих данных декодирования в течение периодов, когда декодер ищет
альтернативные пути. Когда поиск заканчивается, декодер должен быть в состоянии
обрабатывать демодулированные символы достаточно быстро, чтобы освободить буфер
для начала нового поиска. Иногда в течение экстремально длинных поисков буфер
может переполниться. Это вызывает потерю данных, которые можно восстановить
повторением потерянной информации. В этой связи мы хотим напомнить, что
предельная скорость ![]() имеет особый смысл при
последовательном декодировании. Это скорость, выше которой среднее число операций
декодирования на декодированный символ становится неограниченным и оно выражает
предельную вычислительную скорость
имеет особый смысл при
последовательном декодировании. Это скорость, выше которой среднее число операций
декодирования на декодированный символ становится неограниченным и оно выражает
предельную вычислительную скорость ![]() . На практике последовательные
декодеры обычно работают при скоростях, близких к
. На практике последовательные
декодеры обычно работают при скоростях, близких к ![]() .
.
Алгоритм последовательного декодирования Фано успешно применяется в различных системах связи. Его качество по вероятности ошибки сравнимо с декодером Витерби. Однако по сравнению с декодером Витерби последовательное декодирование имеет значительно большую задержку декодирования. С другой стороны, последовательное декодирование требует меньше памяти, чем декодирование по Витерби, и, следовательно, оно является привлекательным для свёрточных кодов с большим кодовым ограничением.

Рис. 8.2.18. Упрощённая структура алгоритма Фано [Jordan (1966), © 1966 IЕЕЕ]
Исследования
вычислительной сложности и требований к памяти для последовательного
декодирования вызывают интерес, и они все еще продолжаются. Для анализа этих
вопросов и других характеристик алгоритмов Фано интересующемуся читателю
рекомендуются книги Галлагера (1986), Возенкрафта и Джекобса (1965), Сэвейдж
(1966) и Форни (1974). Другой тип алгоритма последовательного декодирования,
названный стек-алгоритмом, был предложен независимо Зигангировым
(1966) и Елинеком (1969). В противовес алгоритму Витерби, который сохраняет
траектории ![]() путей
и соответствующих метрик, стек-алгоритм последовательного декодирования
работает с несколькими путями и их соответствующими метриками. В стек-алгоритме
более вероятные пути упорядочиваются согласно их метрик, причём в верхней части
(в голове стека) располагается путь, имеющий наибольшую метрику. На каждом шаге
алгоритма только путь в голове стека проверяется по разветвлению. Это приносит
путей
и соответствующих метрик, стек-алгоритм последовательного декодирования
работает с несколькими путями и их соответствующими метриками. В стек-алгоритме
более вероятные пути упорядочиваются согласно их метрик, причём в верхней части
(в голове стека) располагается путь, имеющий наибольшую метрику. На каждом шаге
алгоритма только путь в голове стека проверяется по разветвлению. Это приносит ![]() продолжений и их
соответствующих метрик. Эти
продолжений и их
соответствующих метрик. Эти ![]() продолжения вместе с другими путями
затем упорядочиваются согласно величинам их метрик, и все пути с метриками,
которые располагаются ниже некоторой выбранной величины от метрики главного
пути, отбрасываются. Затем процесс продолжения путей с наибольшими метриками
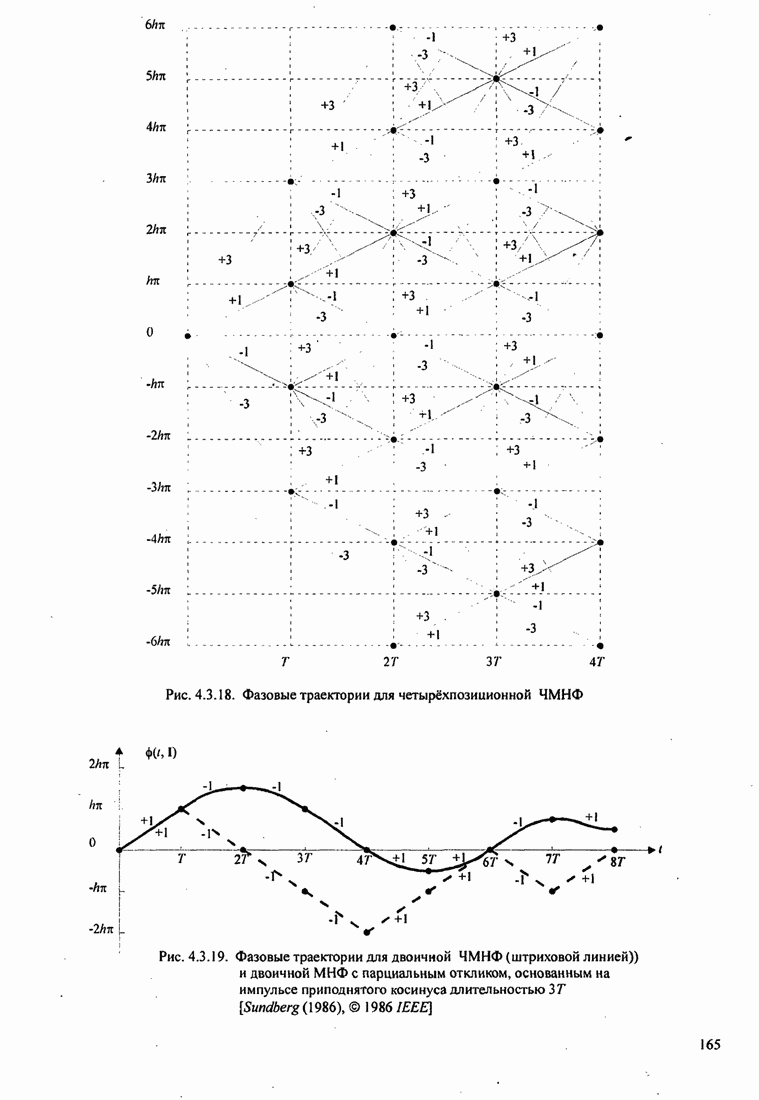
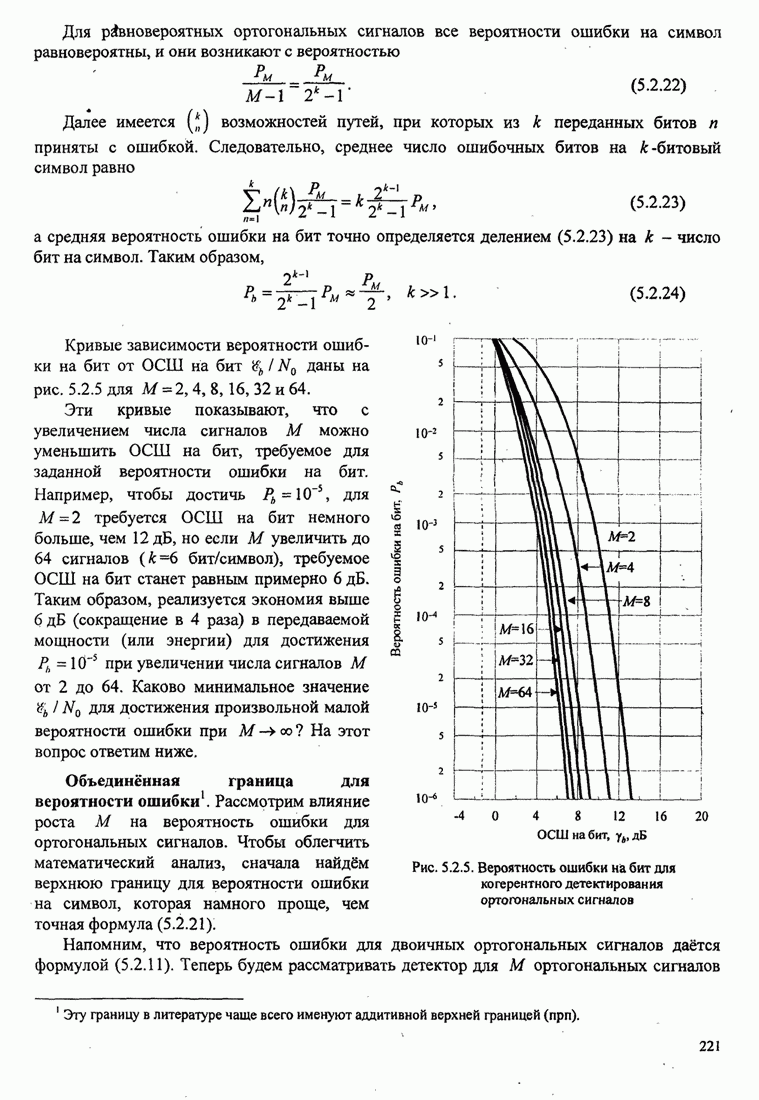
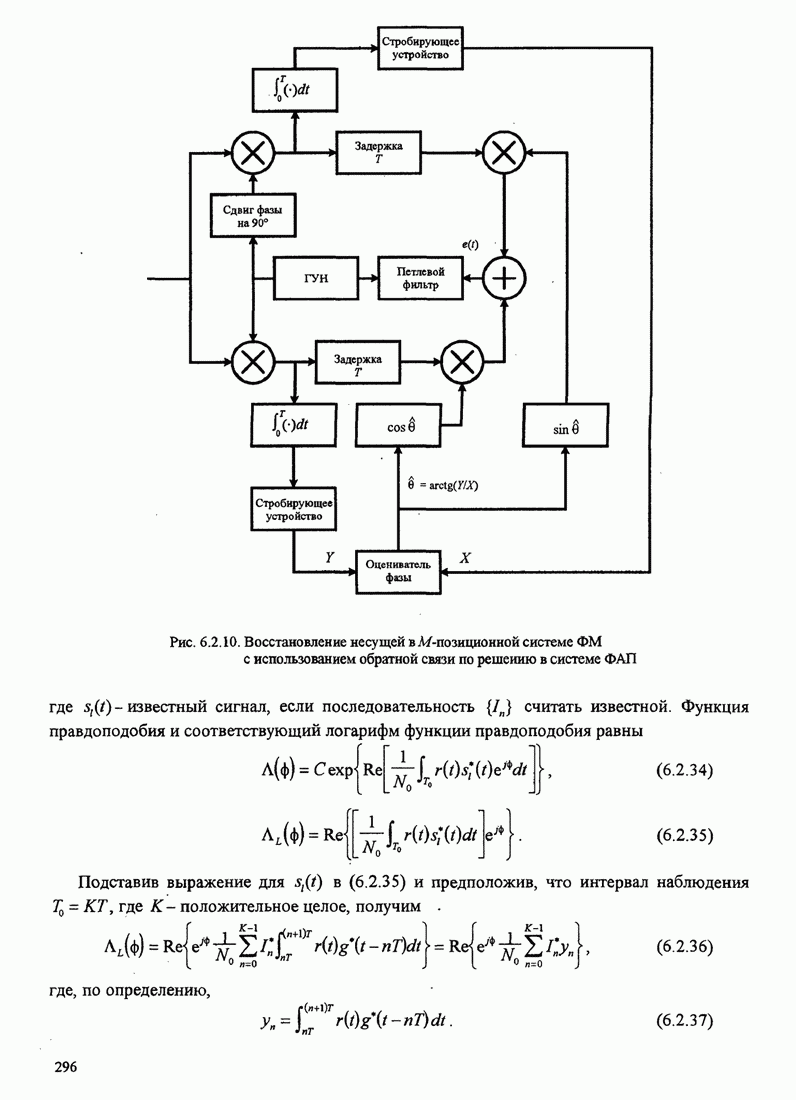
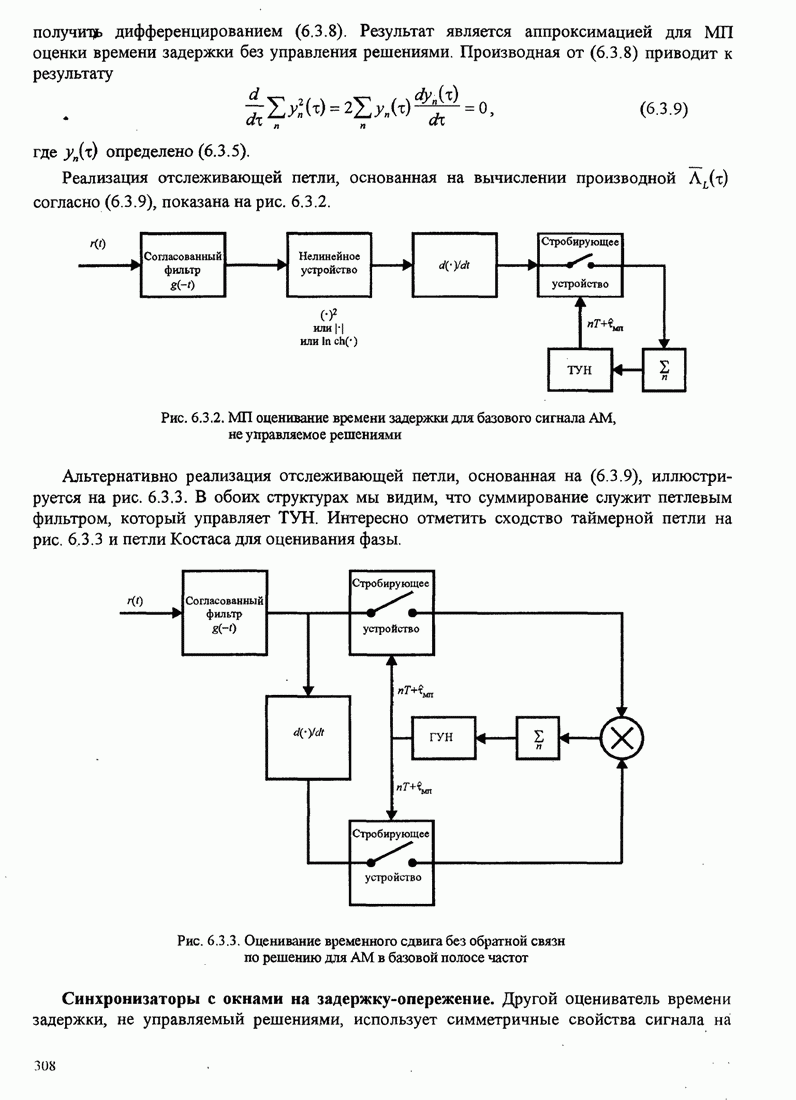
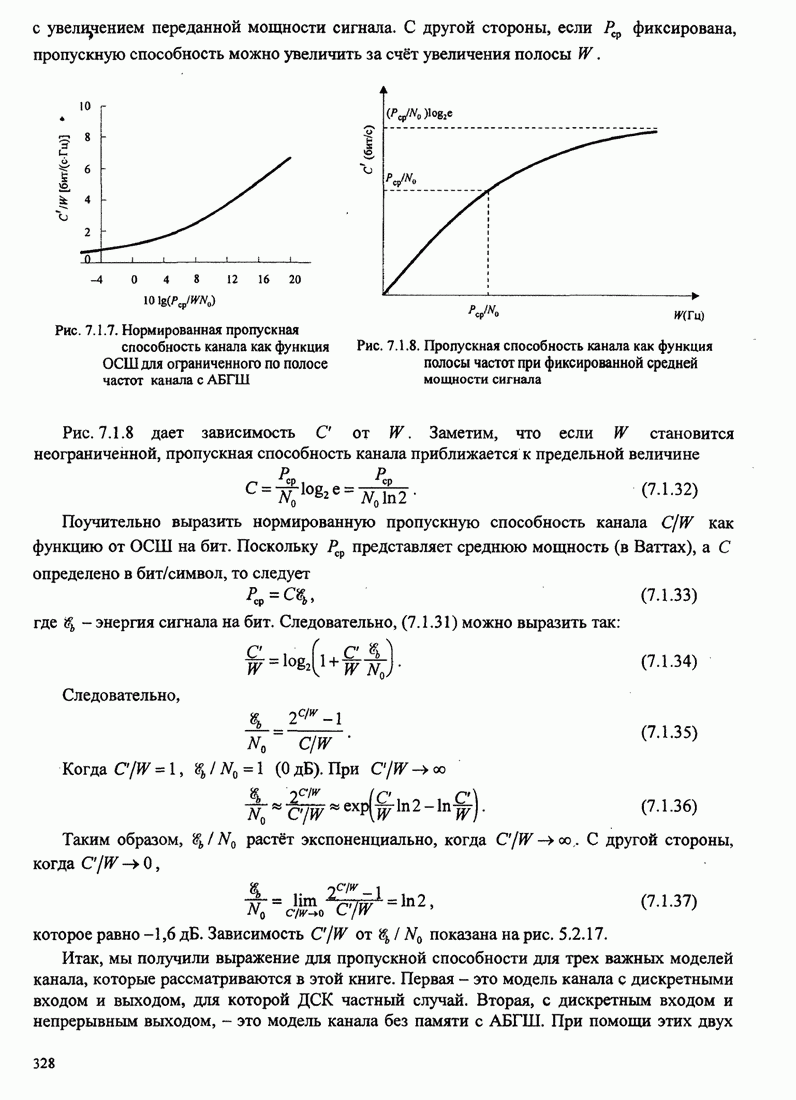
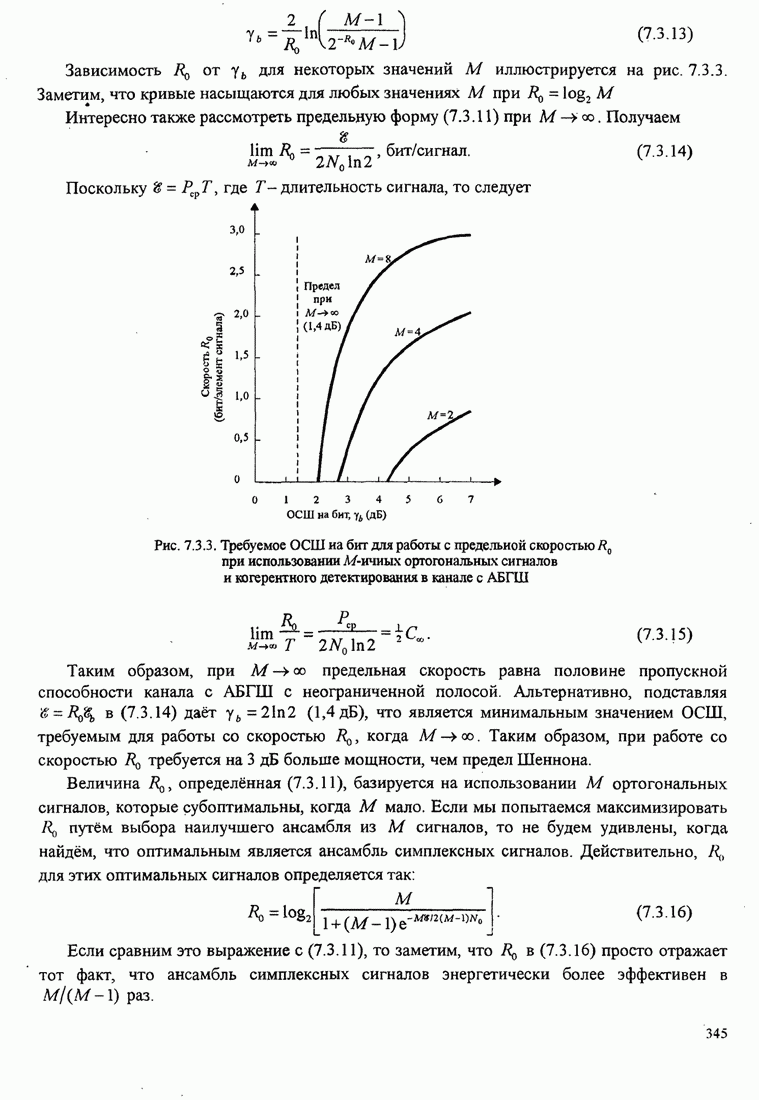
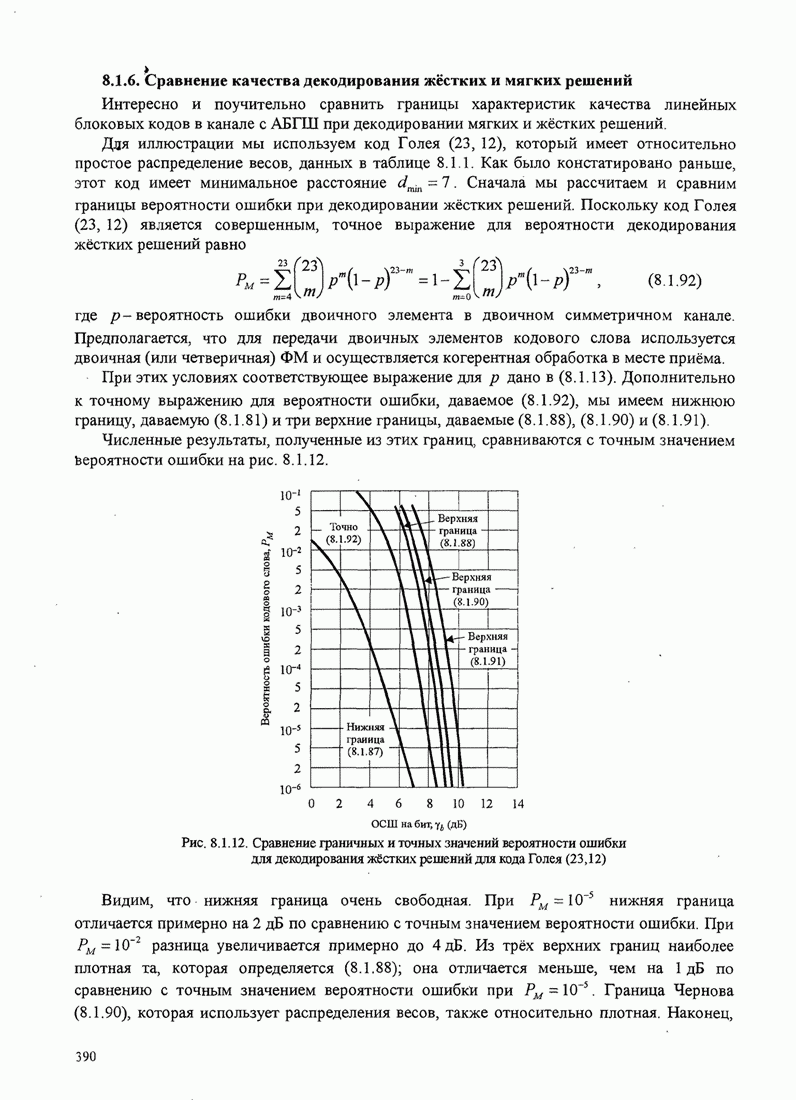
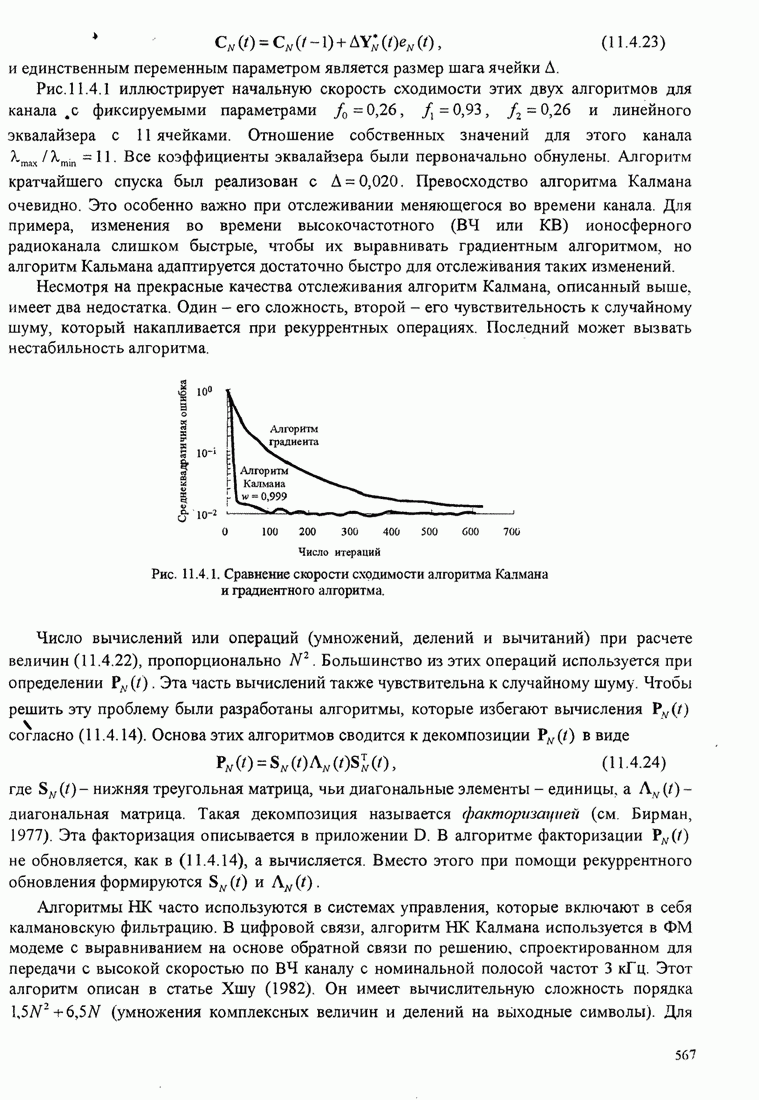
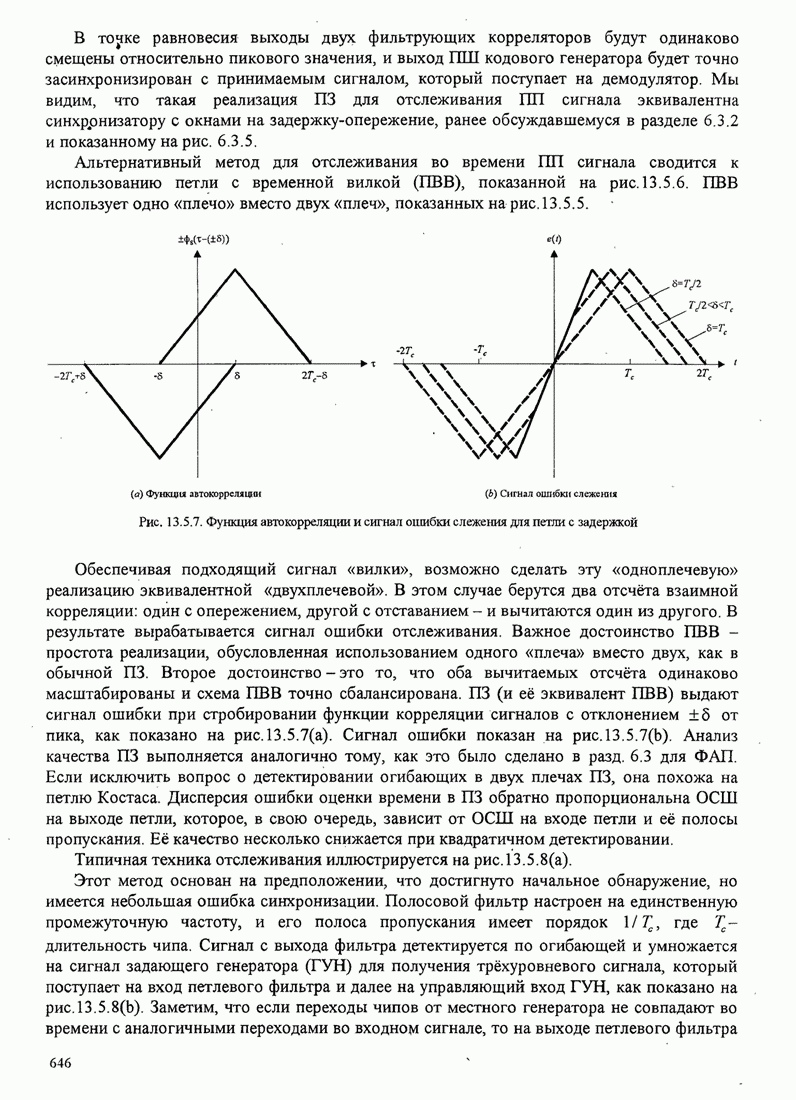
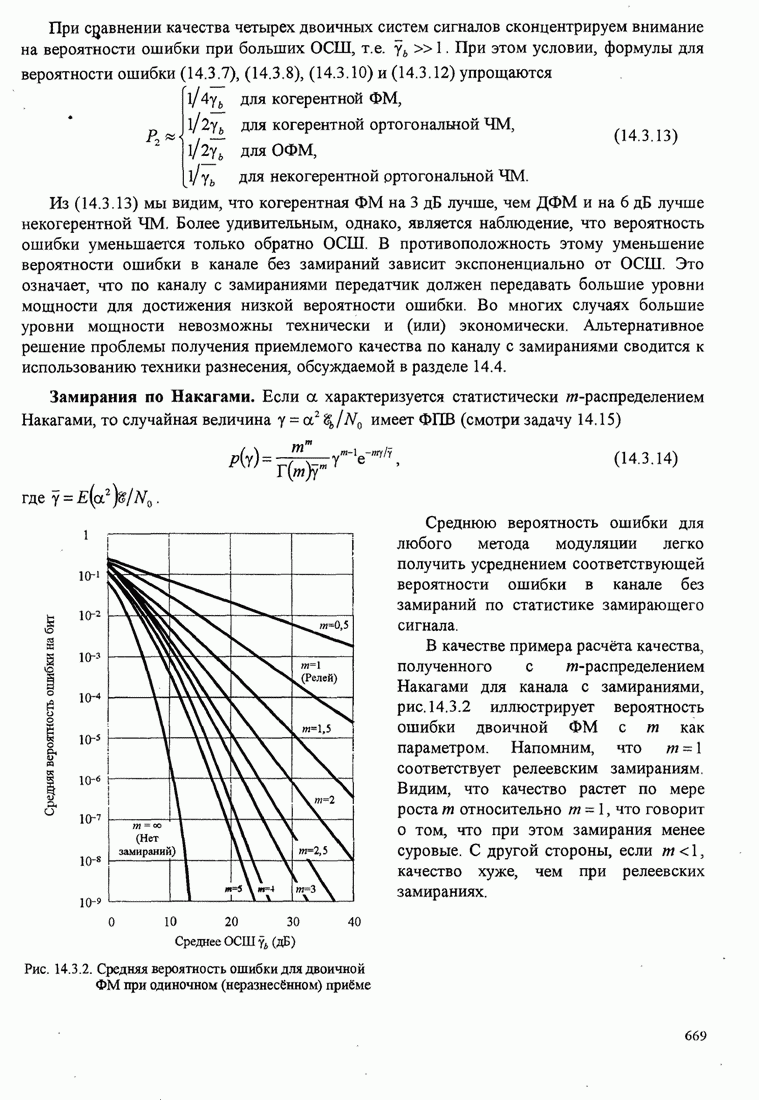
повторяется. Рис. 8.2.19 иллюстрирует несколько первых шагов стек-алгоритма.
продолжения вместе с другими путями
затем упорядочиваются согласно величинам их метрик, и все пути с метриками,
которые располагаются ниже некоторой выбранной величины от метрики главного
пути, отбрасываются. Затем процесс продолжения путей с наибольшими метриками
повторяется. Рис. 8.2.19 иллюстрирует несколько первых шагов стек-алгоритма.
Очевидно, что если ни
одно из ![]() продолжений
пути с наибольшей метрикой не остаётся в голове стека, следующий шаг поиска
выполняет продолжение другого пути, который приближается к голове стека. Отсюда
следует, что алгоритм не всегда даёт быстрое продвижение по начатой траектории
при любой итерации. Следовательно, некоторую величину памяти нужно
зарезервировать для вновь принятых символов и ранее принятых символов для того,
чтобы позволить алгоритму расширить поиск по одному из более коротких путей,
когда такой путь достигает головы стека.
продолжений
пути с наибольшей метрикой не остаётся в голове стека, следующий шаг поиска
выполняет продолжение другого пути, который приближается к голове стека. Отсюда
следует, что алгоритм не всегда даёт быстрое продвижение по начатой траектории
при любой итерации. Следовательно, некоторую величину памяти нужно
зарезервировать для вновь принятых символов и ранее принятых символов для того,
чтобы позволить алгоритму расширить поиск по одному из более коротких путей,
когда такой путь достигает головы стека.

Стек с накопленными метриками путей
|
Шаг
|
Шаг
|
Шаг
|
Шаг
|
Шаг
|
Шаг
|
|
-1 |
-2 |
-2 |
-2 |
-2 |
-3 |
|
-2 |
-2 |
-3 |
-3 |
-3 |
-3 |
|
|
-3 |
-3 |
-3 |
-3 |
-3 |
|
|
|
-4 |
-3 |
-4 |
-4 |
|
|
|
|
-5 |
-5 |
-4 |
|
|
|
|
|
-8 |
-5 |
|
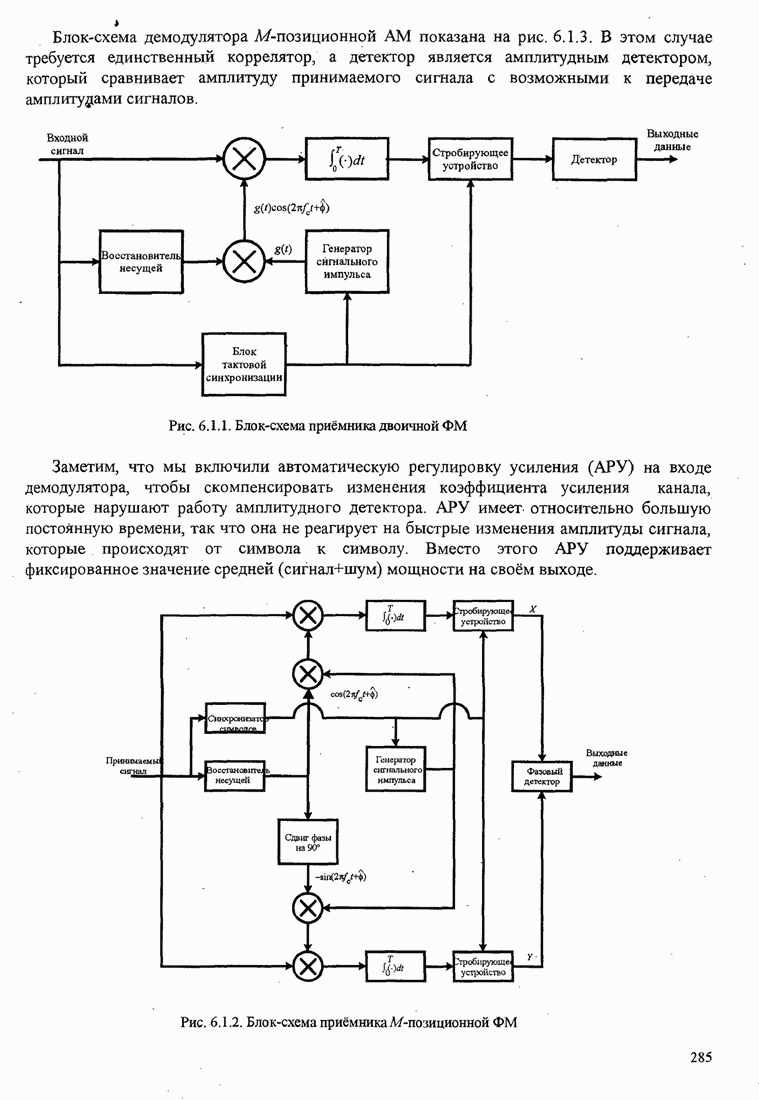
|
|
|
|
|
-8 |
Рис. 8.2.19. Пример работы стек-алгоритма для декодирования свёрточного кода со скоростью 1/3
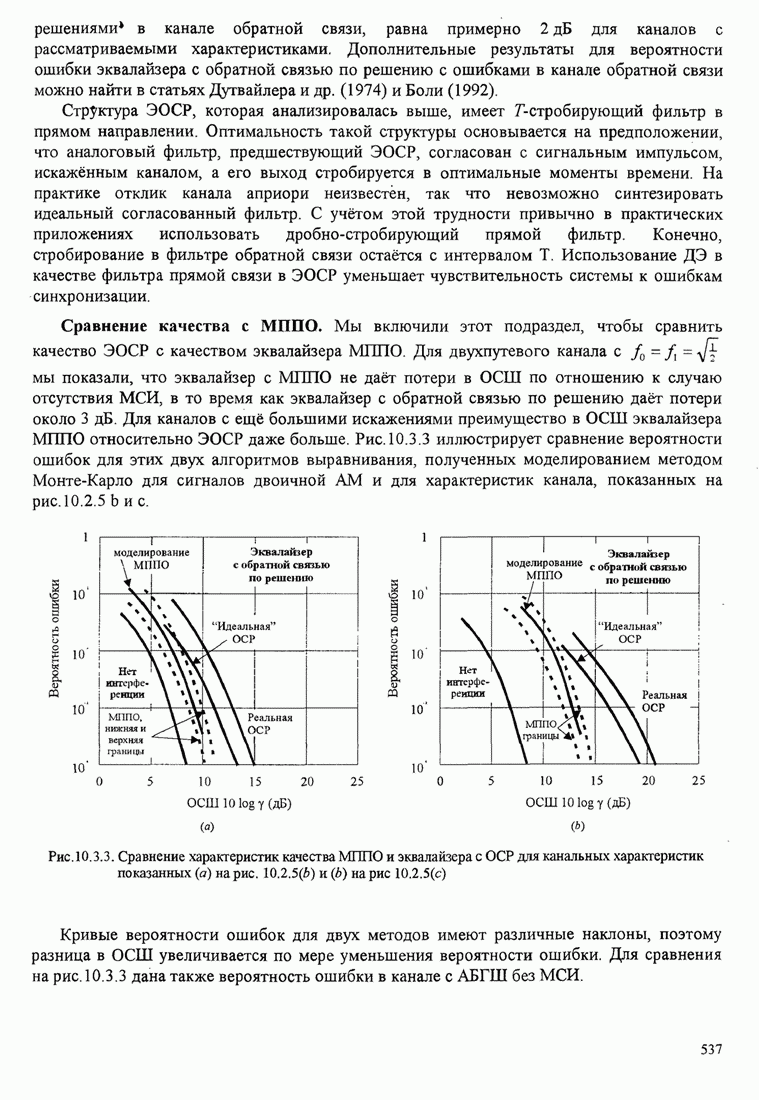
Из сравнения стек-алгоритма с алгоритмом Витерби следует, что стек-алгоритм требует малого числа сравнений метрик, но его вычислительная экономия в большой степени снижается за счёт вычислений, требуемых для упорядочивания стека после каждой итерации. По сравнению с алгоритмом Фано, стек-алгоритм в вычислительном отношении проще, поскольку здесь нет возвращения по тому же пути, как это делает алгоритм Фано. С другой стороны, стек-алгоритм требует больше памяти, чем алгоритм Фано.
Третья альтернатива
оптимального декодера Витерби – это метод, названный декодированием с обратной
связью (Хеллер 1975), который был разработан для декодирования в ДСК
(декодирование жёстких решений). При декодировании с обратной связью декодер
делает жёсткое решение об информационном символе на ![]() -м шаге, основываясь на
метриках, вычисленных от
-м шаге, основываясь на
метриках, вычисленных от ![]() -го до
-го до ![]() -го шага, где
-го шага, где ![]() - выбранное целое число.
Таким образом, решение об информационном символе в пользу 0 или 1 зависит от
того, каково минимальное расстояние по Хеммингу для пути, который начинается на
- выбранное целое число.
Таким образом, решение об информационном символе в пользу 0 или 1 зависит от
того, каково минимальное расстояние по Хеммингу для пути, который начинается на
![]() -м шаге и
кончается на
-м шаге и
кончается на ![]() -м шаге и сколько содержится «0» или
«1» в ветви, исходящих от шага
-м шаге и сколько содержится «0» или
«1» в ветви, исходящих от шага ![]() . Решение выносится один раз об
информационном символе на
. Решение выносится один раз об
информационном символе на ![]() шаге, и только часть дерева, которая связана с этим символом,
сохраняется (половина путей, исходящих из
узла
шаге, и только часть дерева, которая связана с этим символом,
сохраняется (половина путей, исходящих из
узла ![]() ), а
остальные пути исключаются. Так осуществляется обратная связь в декодере.
Следующий шаг заключается в расширении части дерева, которая вышла до шага
), а
остальные пути исключаются. Так осуществляется обратная связь в декодере.
Следующий шаг заключается в расширении части дерева, которая вышла до шага ![]() и рассмотрении
путей от шага
и рассмотрении
путей от шага ![]() -го
до
-го
до ![]() -гo для принятия решения о
символе на шаге
-гo для принятия решения о
символе на шаге ![]() .
Так процедура повторяется на каждом шаге. Параметр
.
Так процедура повторяется на каждом шаге. Параметр ![]() - это просто число шагов по
дереву, которое декодер учитывает при вынесении жёсткого решения. Поскольку
большая величина
- это просто число шагов по
дереву, которое декодер учитывает при вынесении жёсткого решения. Поскольку
большая величина ![]() ведет
к большой величине памяти, желательно
ведет
к большой величине памяти, желательно ![]() выбрать как можно меньше. С другой
стороны,
выбрать как можно меньше. С другой
стороны, ![]() должно
быть достаточно большим, чтобы избежать существенного ухудшения качества. Чтобы
сбалансировать эти два противоречивых требования,
должно
быть достаточно большим, чтобы избежать существенного ухудшения качества. Чтобы
сбалансировать эти два противоречивых требования, ![]() обычно выбирается в области
обычно выбирается в области ![]() , где
, где ![]() - кодовое
ограничение. Заметим, что эта задержка при декодировании значительно меньше,
чем задержка при использовании алгоритма Витерби, которая обычно около
- кодовое
ограничение. Заметим, что эта задержка при декодировании значительно меньше,
чем задержка при использовании алгоритма Витерби, которая обычно около ![]() .
.
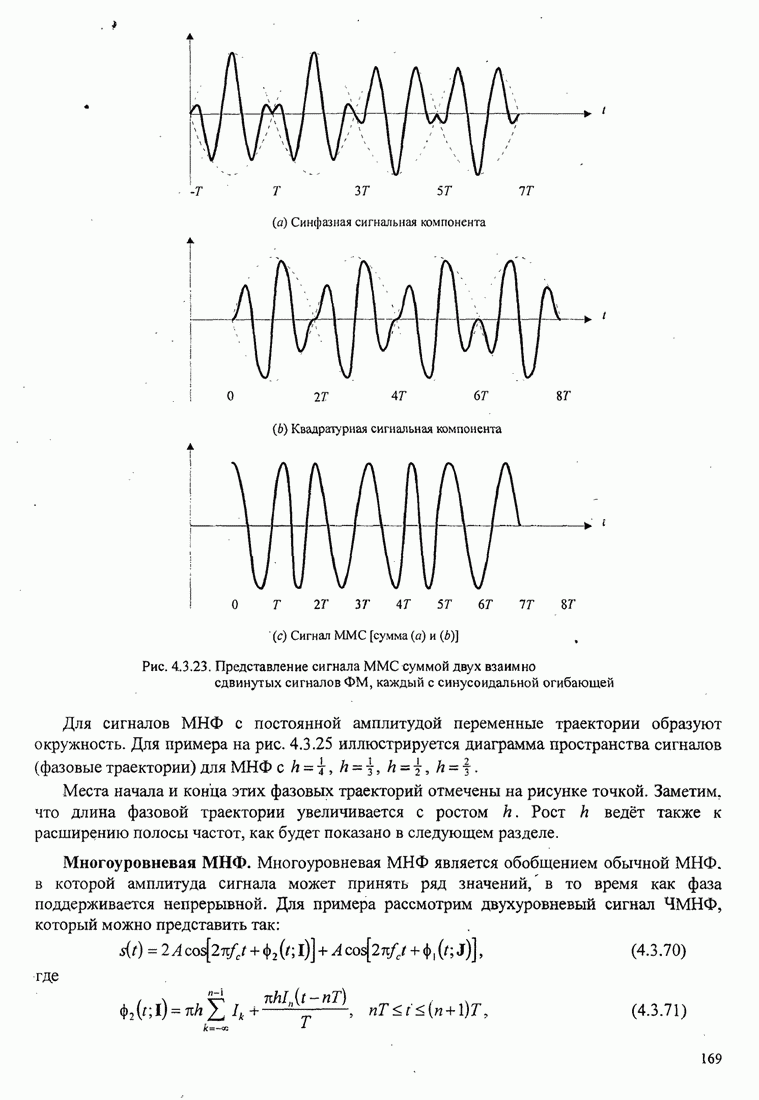
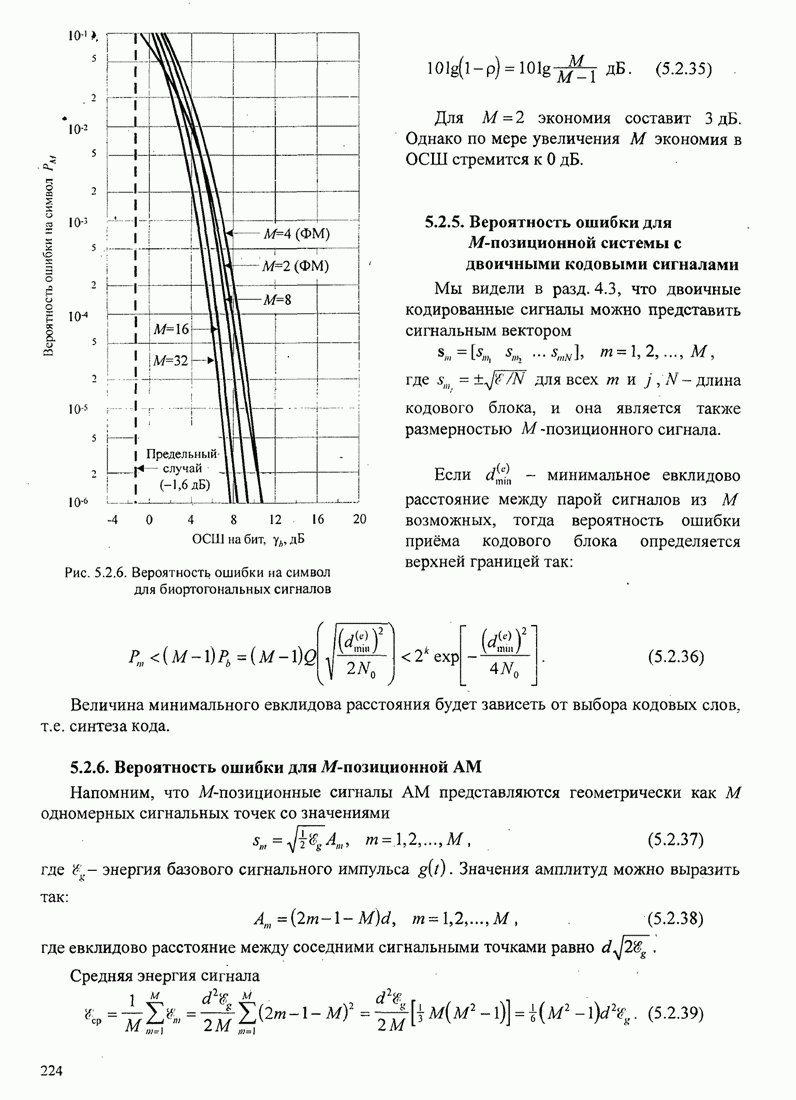
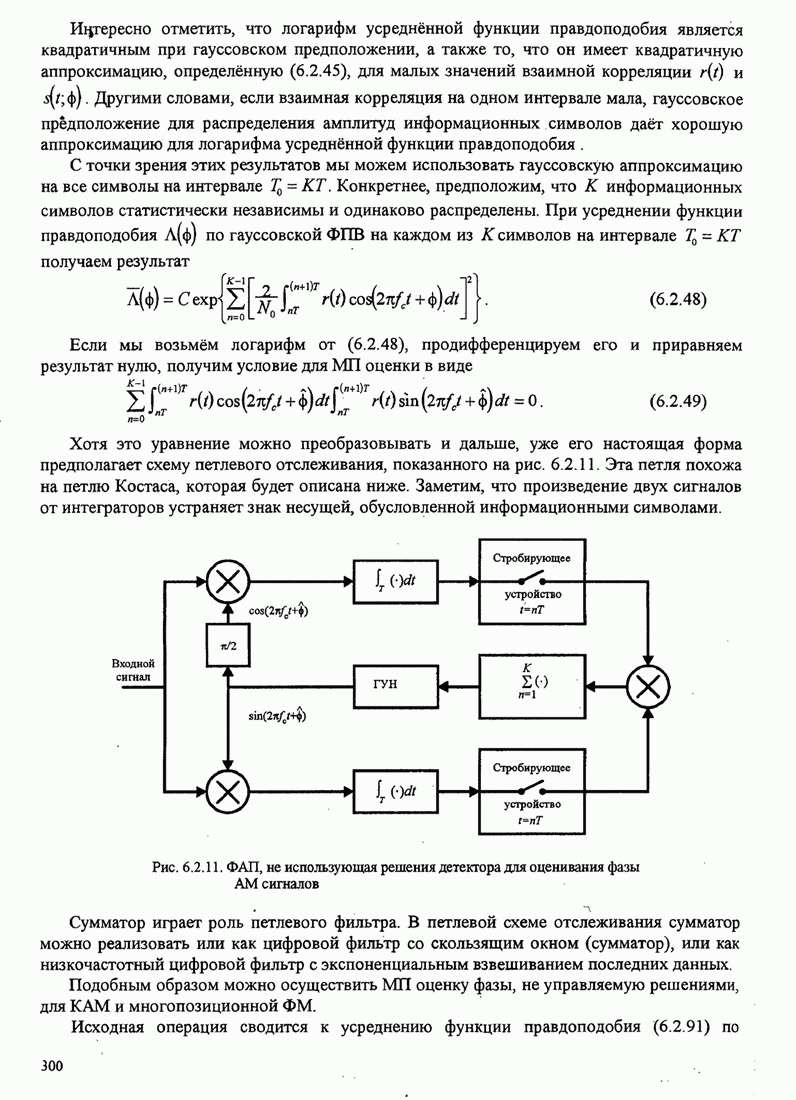
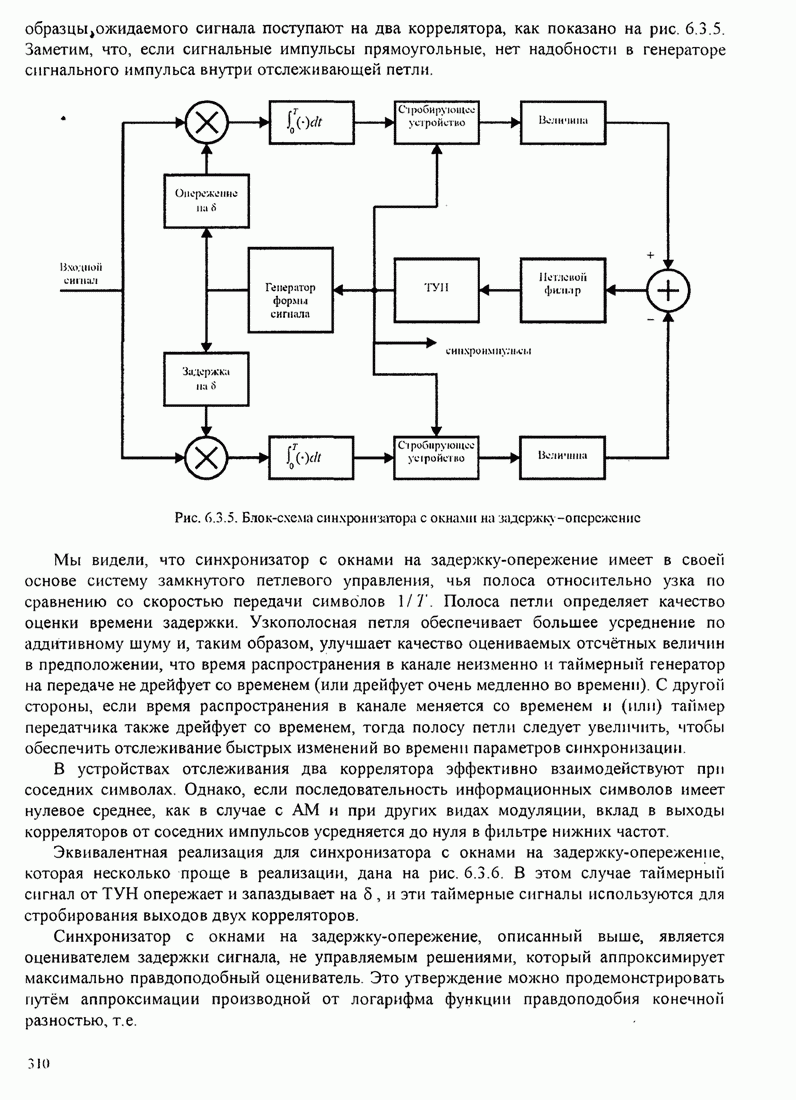
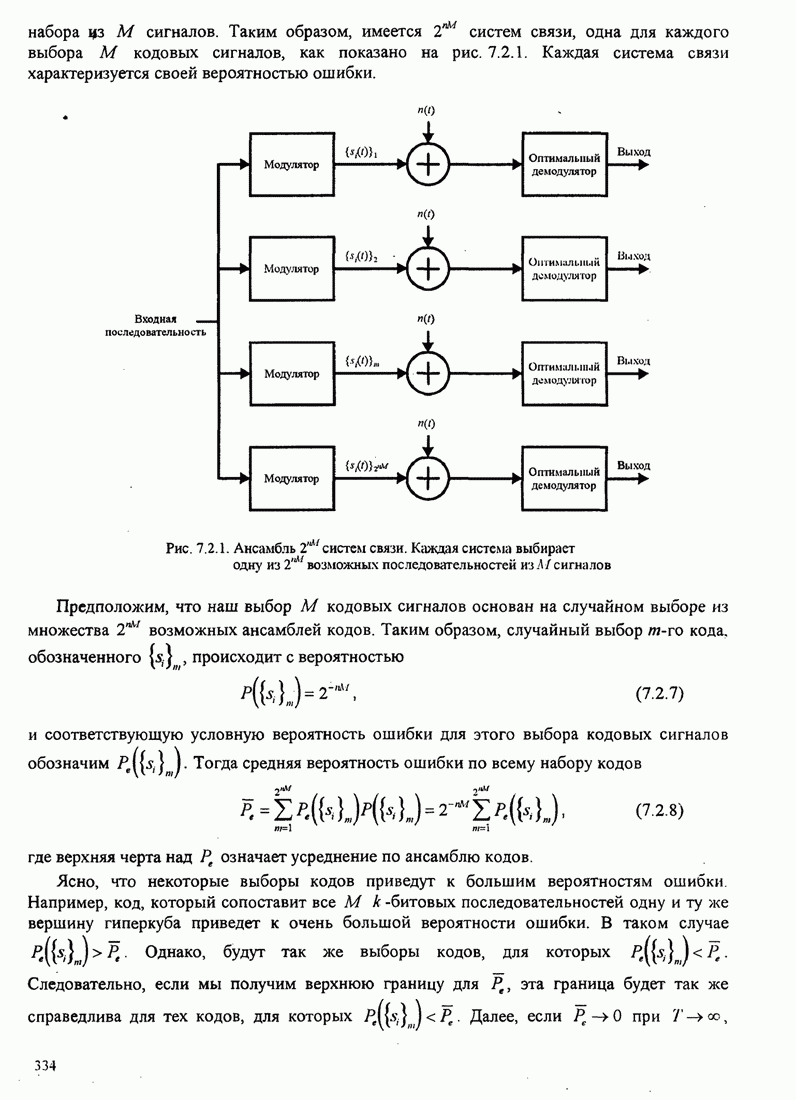
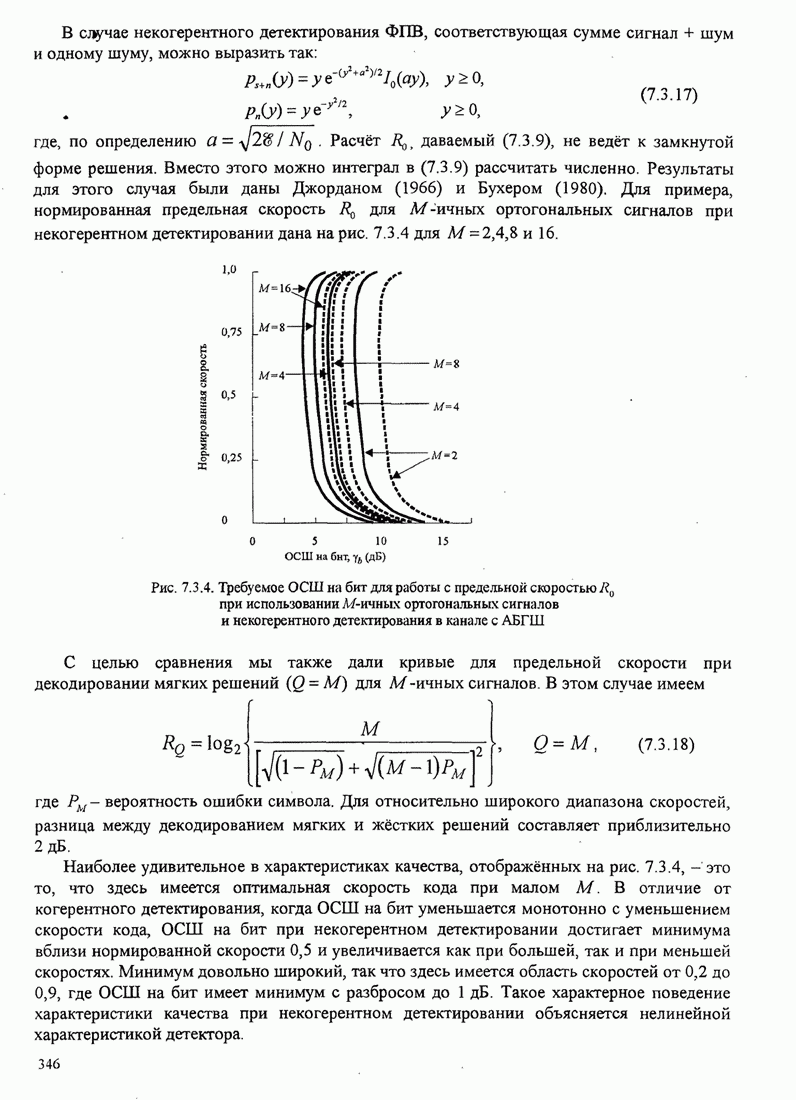
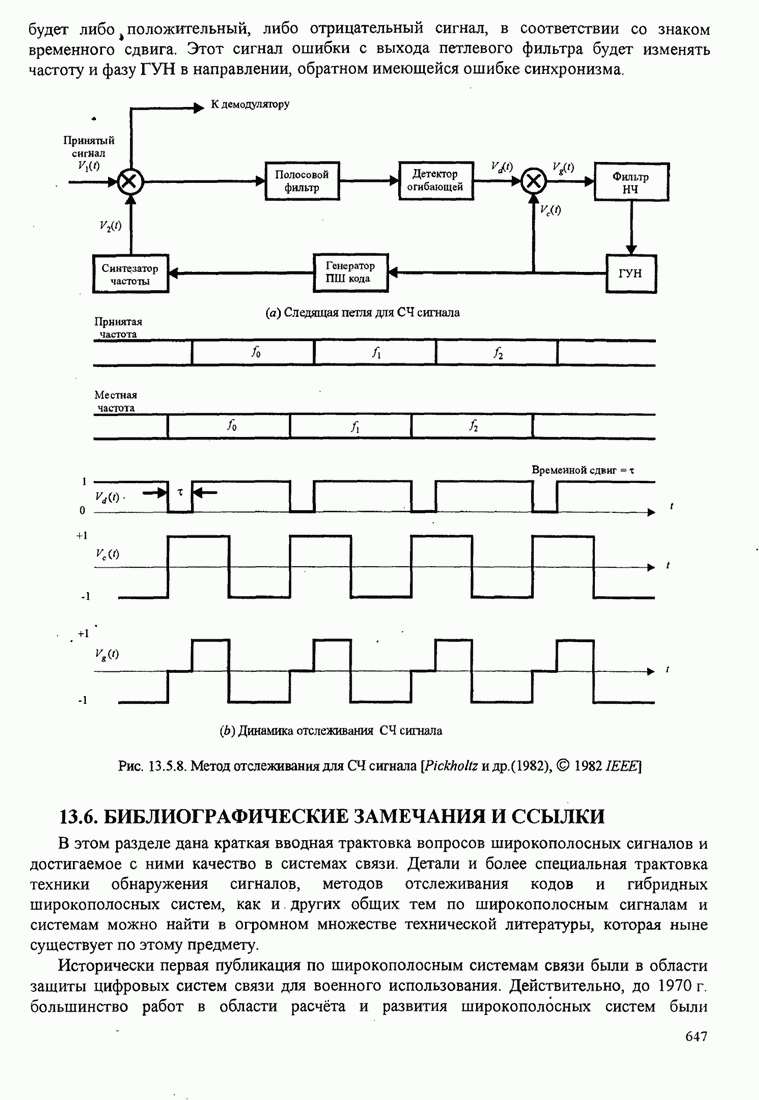
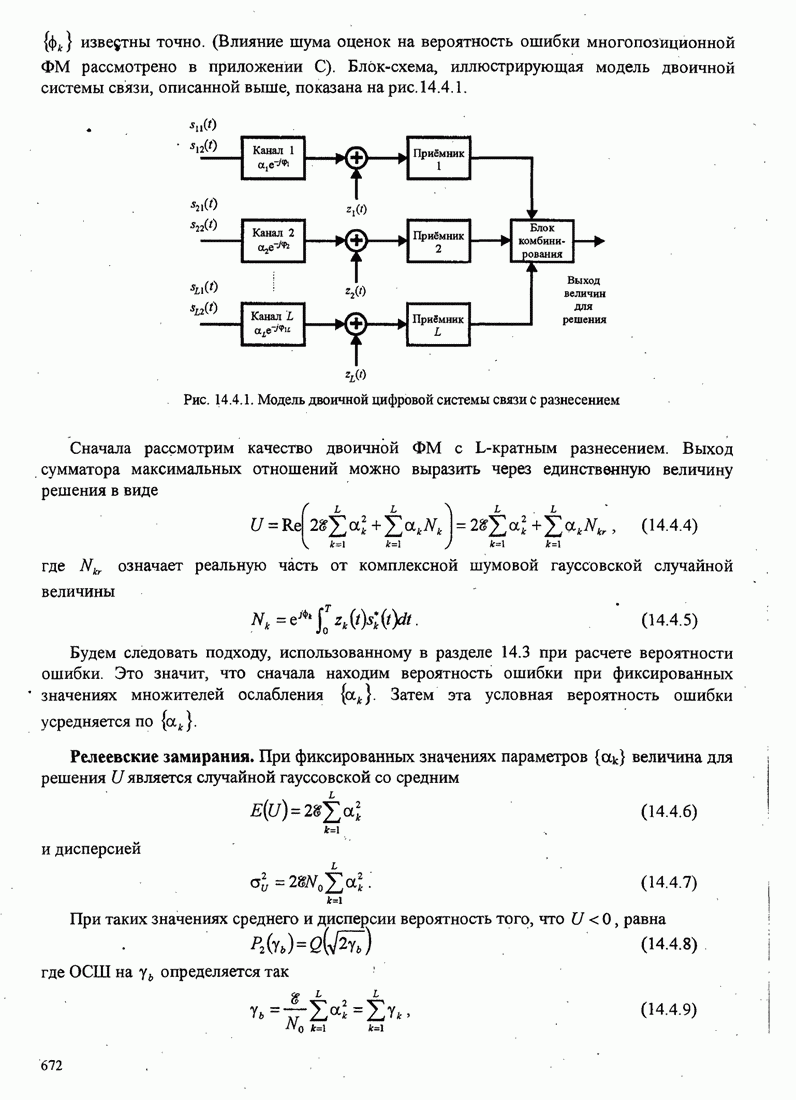
Пример 8.2.7. Рассмотрим использование
декодера с обратной связью для свёрточного кода со скоростью 1/3, показанного
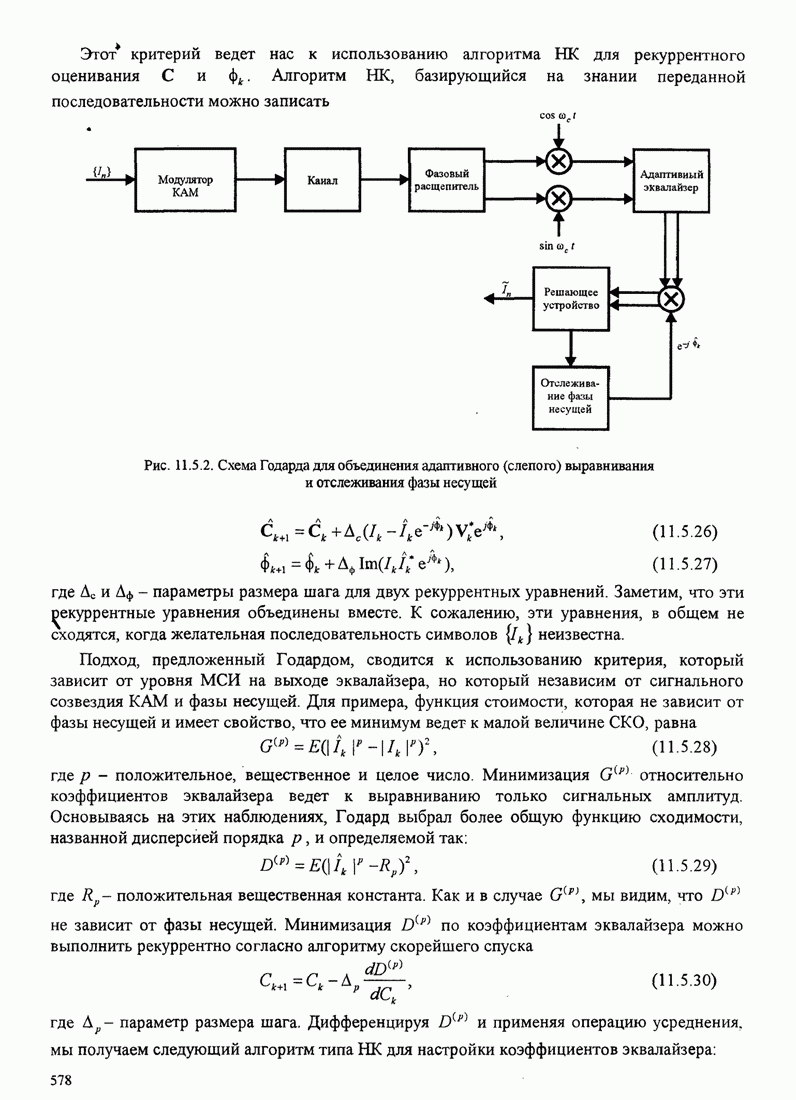
на рис. 8.2.2. Рис. 8.2.20 иллюстрирует древовидную диаграмму и операции
декодера с обратной связью при ![]() . Это значит, что при декодировании
символа ветви
. Это значит, что при декодировании
символа ветви ![]() ,
декодер рассматривает пути на ветвях
,
декодер рассматривает пути на ветвях ![]() и
и ![]() . Начиная с первой ветви, декодер
рассчитывает восемь метрик (расстояние Хемминга) и решает, что символ в первой
ветви является 0, если путь с минимальным расстоянием находится в верхней части
дерева и, что символ 1, если путь с минимальным расстоянием находится в нижней
части дерева. В этом примере принимаемая последовательность для первых трёх
ветвей полагается такой 101 111 110, поэтому путь с минимальным расстоянием
находится в верхней части дерева, следовательно, первый выход символа декодера
0.
. Начиная с первой ветви, декодер
рассчитывает восемь метрик (расстояние Хемминга) и решает, что символ в первой
ветви является 0, если путь с минимальным расстоянием находится в верхней части
дерева и, что символ 1, если путь с минимальным расстоянием находится в нижней
части дерева. В этом примере принимаемая последовательность для первых трёх
ветвей полагается такой 101 111 110, поэтому путь с минимальным расстоянием
находится в верхней части дерева, следовательно, первый выход символа декодера
0.
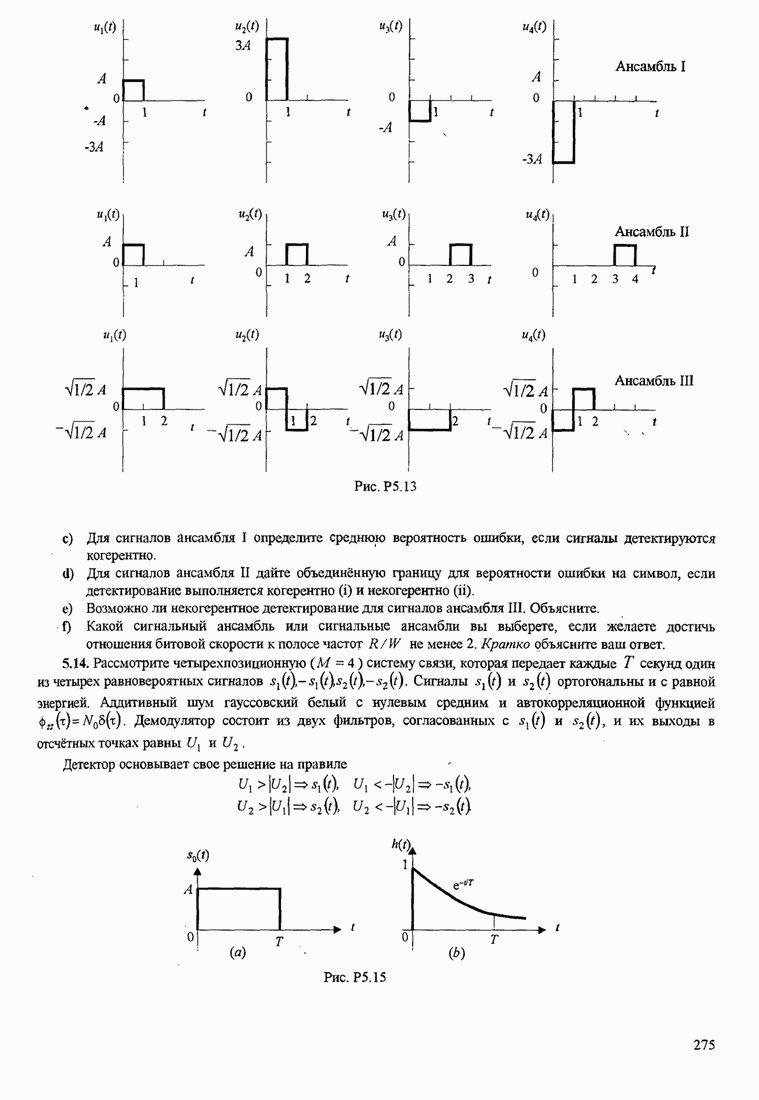
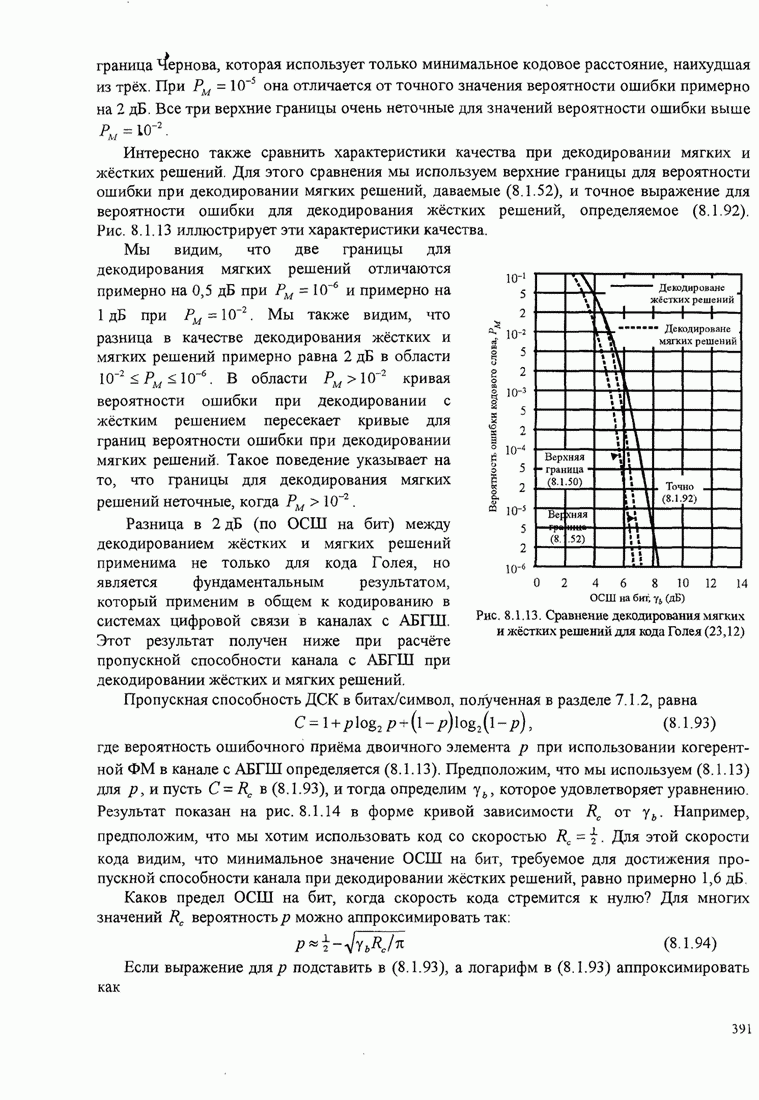
Следующие шаги сводятся к расширению верхней части дерева (той части дерева, которая выжила) на одну ветвь и к вычислению восьми метрик в ветвях 2, 3 и 4. Для предположения входной последовательности 111 110 011 путь с минимальным расстоянием находится в нижней части секции дерева, вычислившей после первого шага. Итак, второй выходной символ декодера 1. Третий шаг заключается в расширении этой нижней части дерева и повторении процедуры, описанной для двух первых шагов.

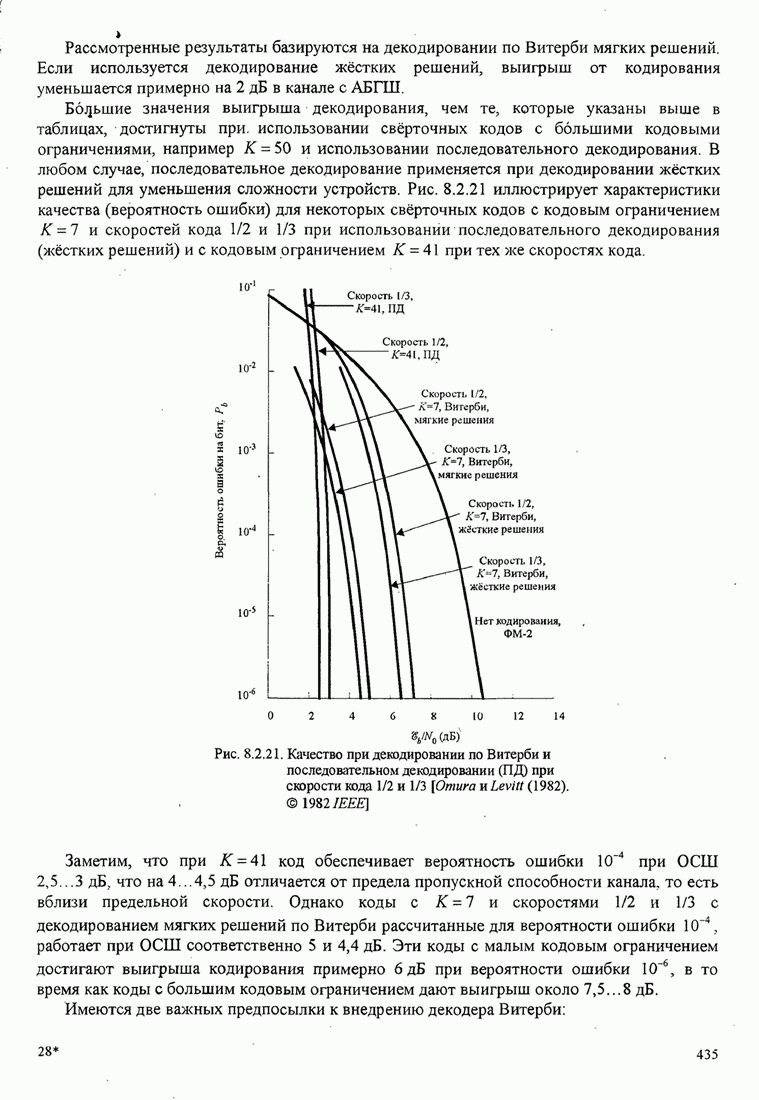
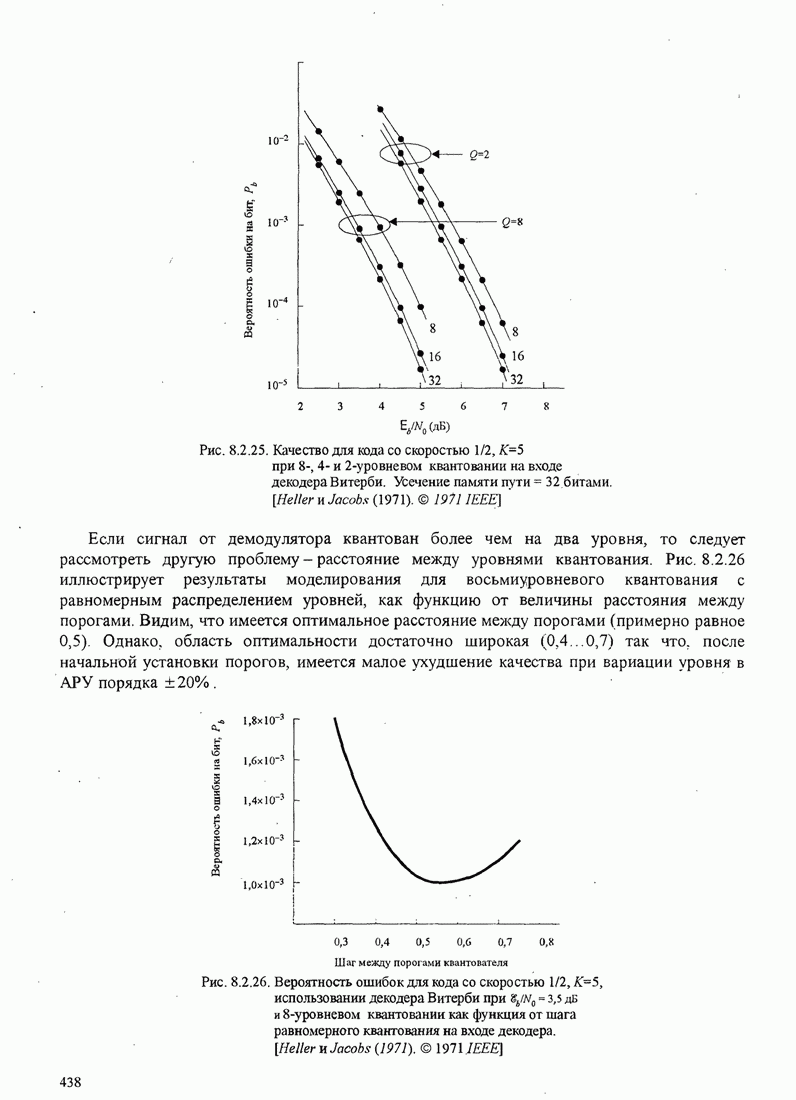
Рис. 8.2.20. Пример декодирования с обратной связью для свёрточного кода со скоростью 1/3
Вместо вычисления метрик описанным выше способом, декодер с обратной связью в ДСК можно эффективно реализовать путём вычисления синдрома по принимаемой последовательности и используя табличный метод коррекции ошибок. Этот метод похож на тот, который был описан выше для декодирования блоковых кодов. Для некоторых свёрточных кодов декодер с обратной связью упрощается к виду, называемому логический декодер по большинству или пороговый декодер (Месси 1963; Хеллер 1975).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
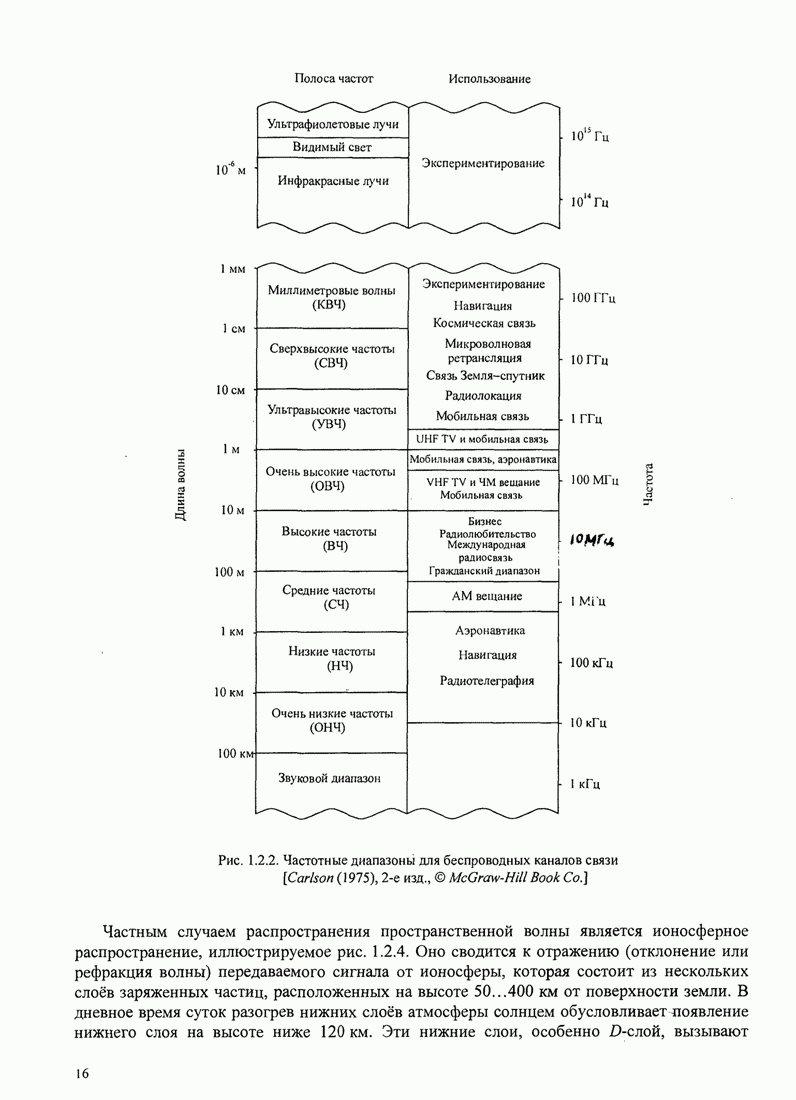
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
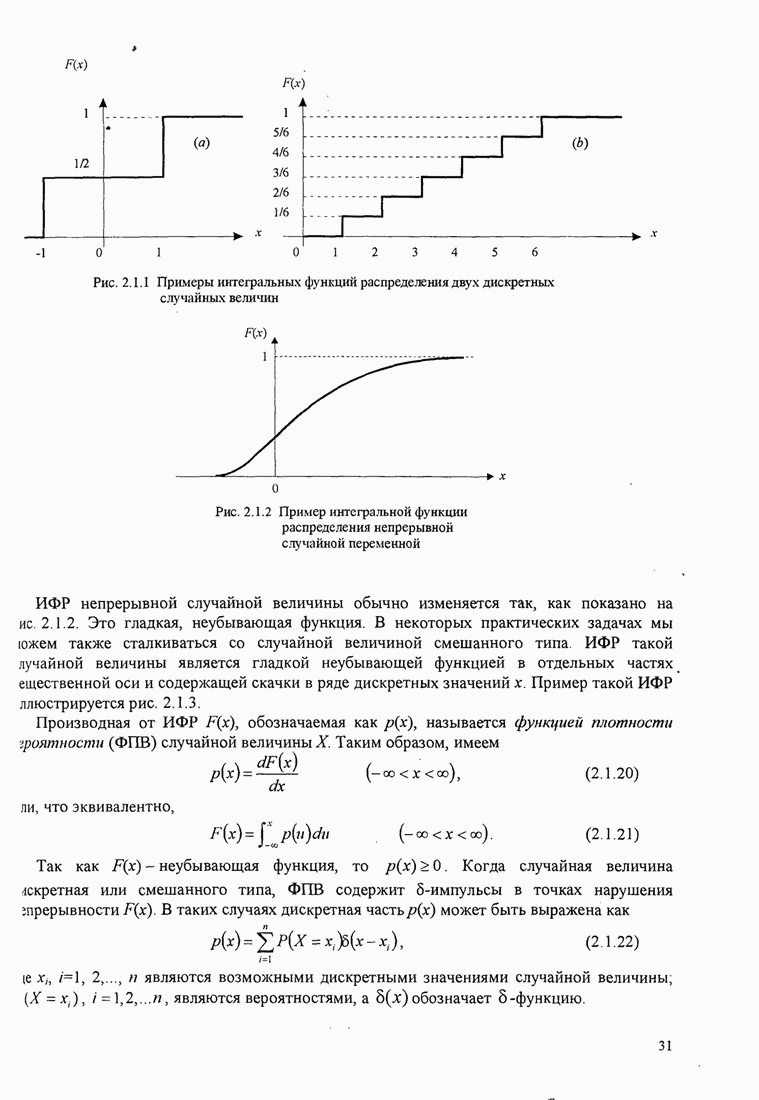
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
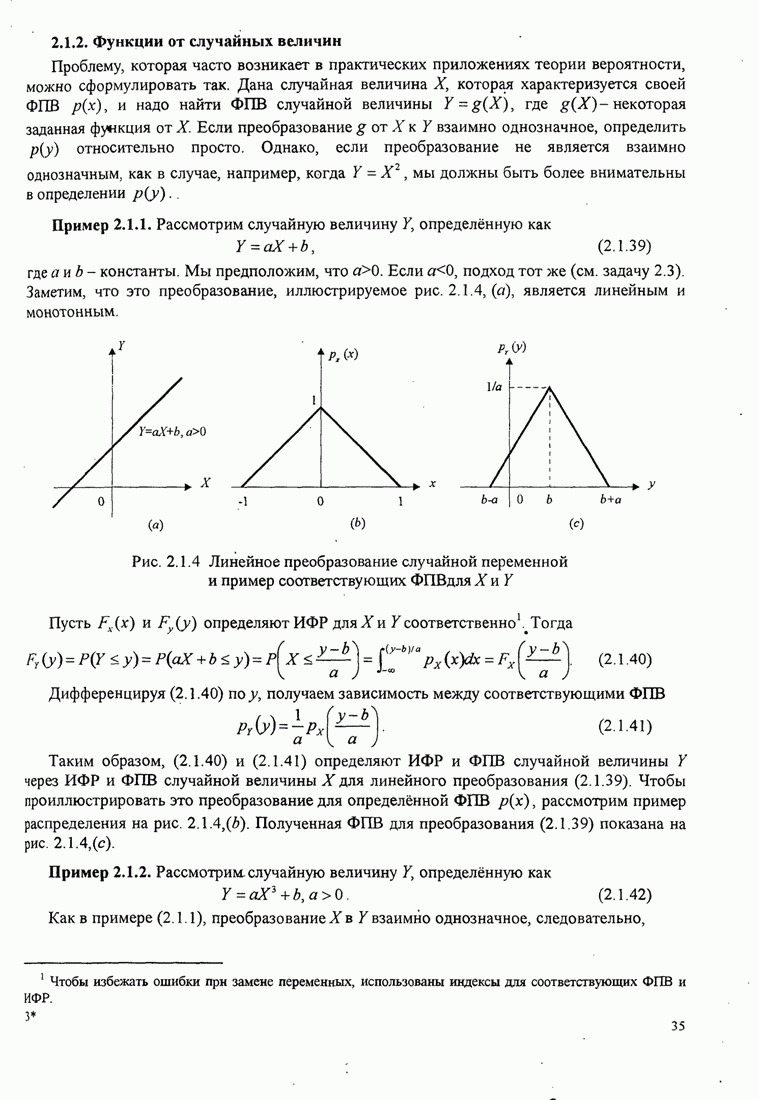
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
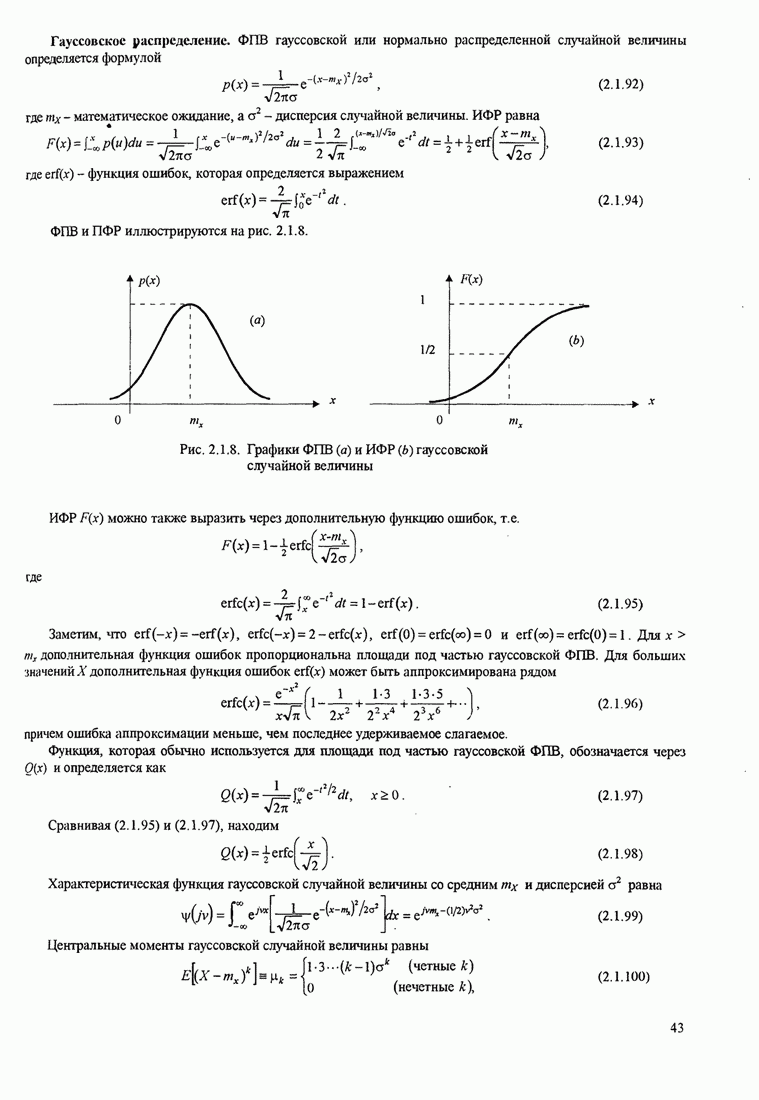
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
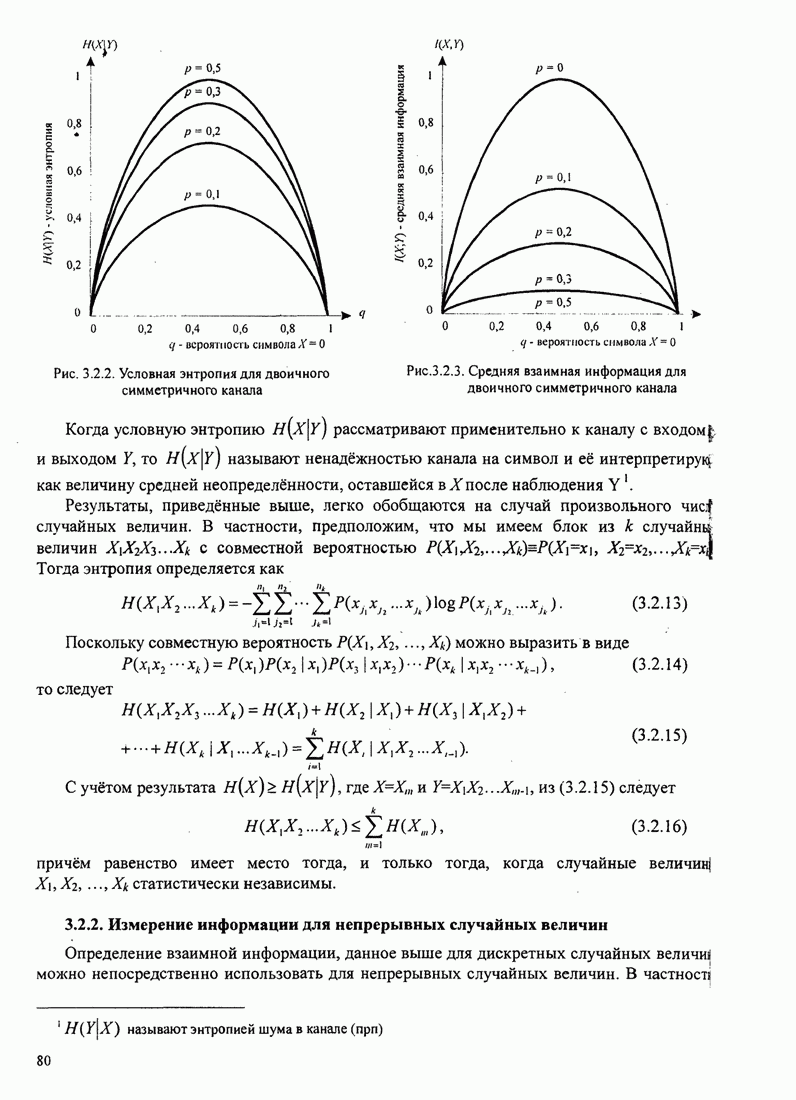
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
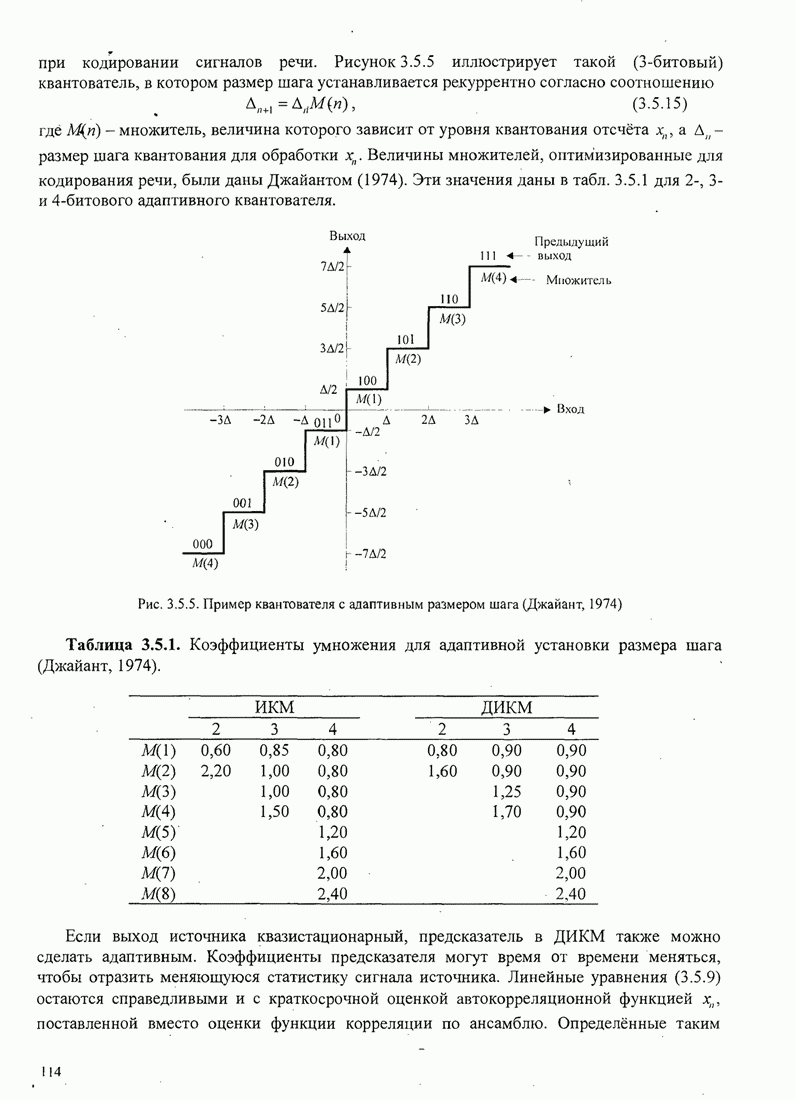
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
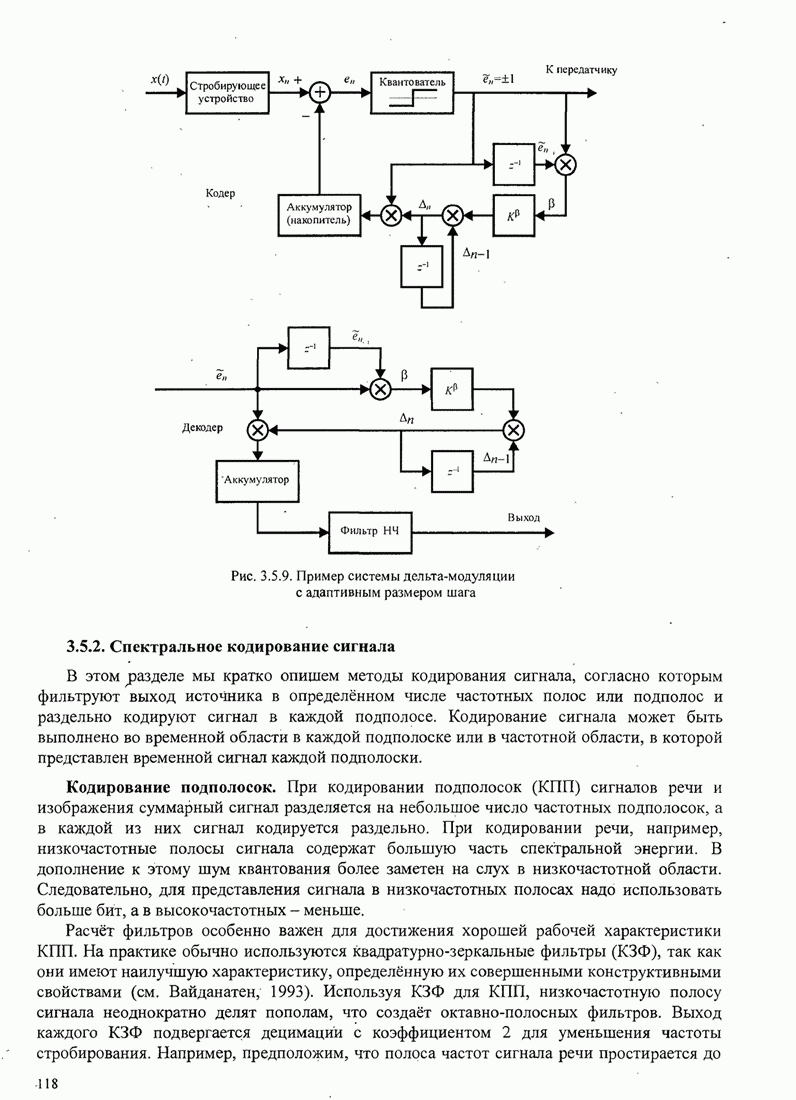
- 3.5.2. Спектральное кодирование сигнала
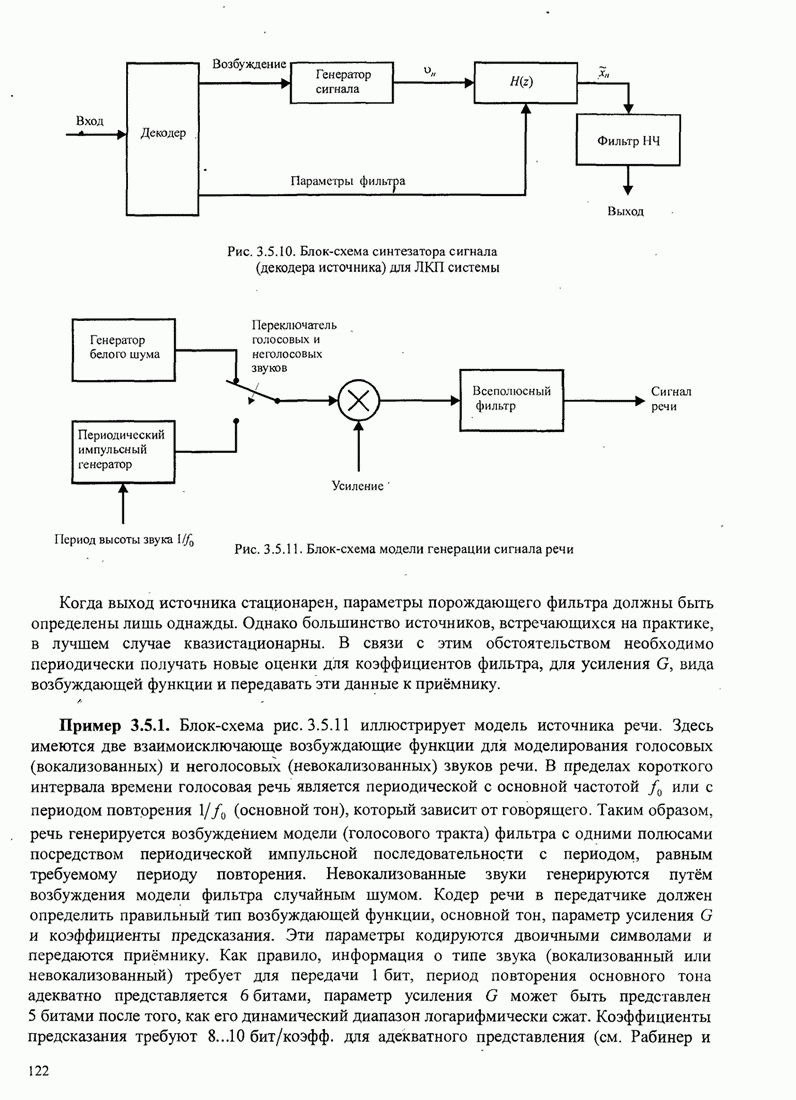
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
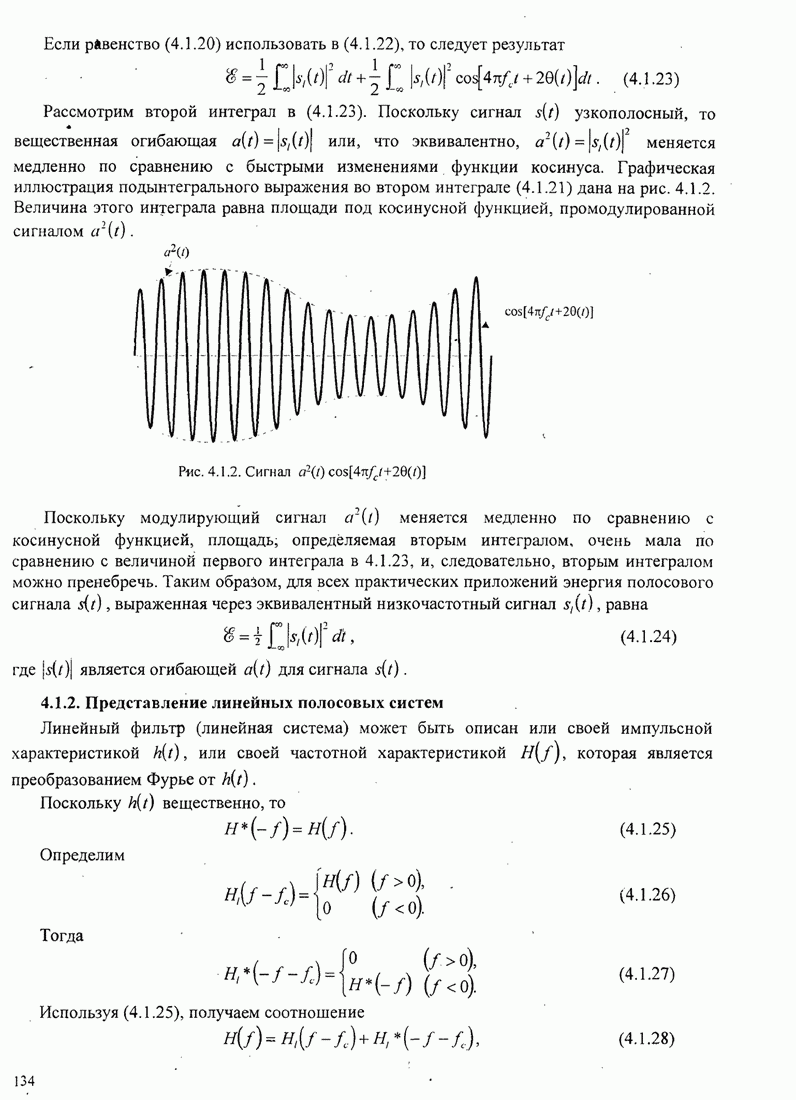
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
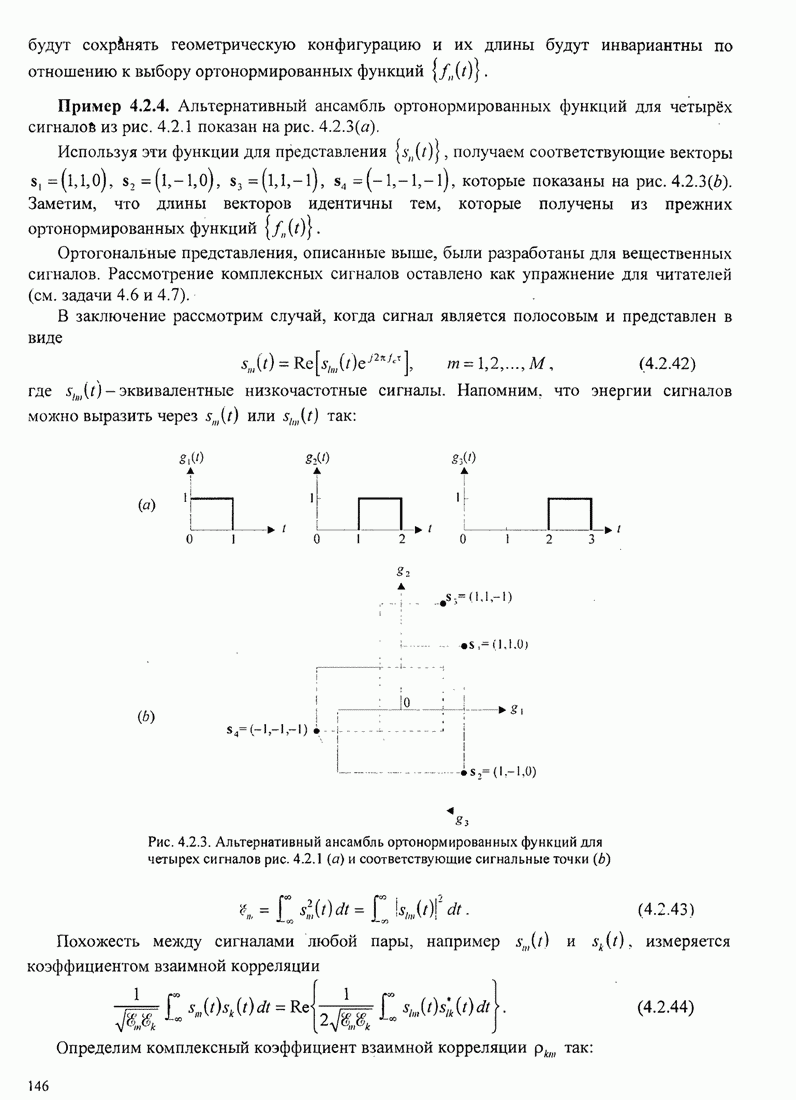
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
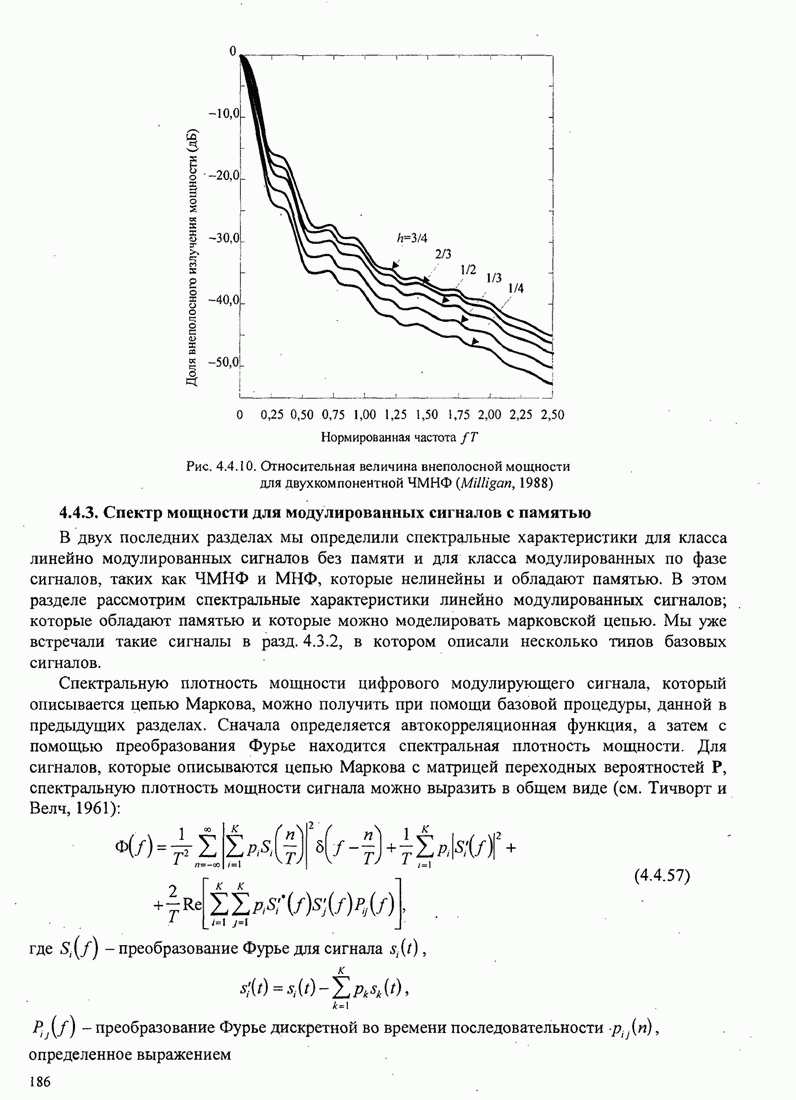
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
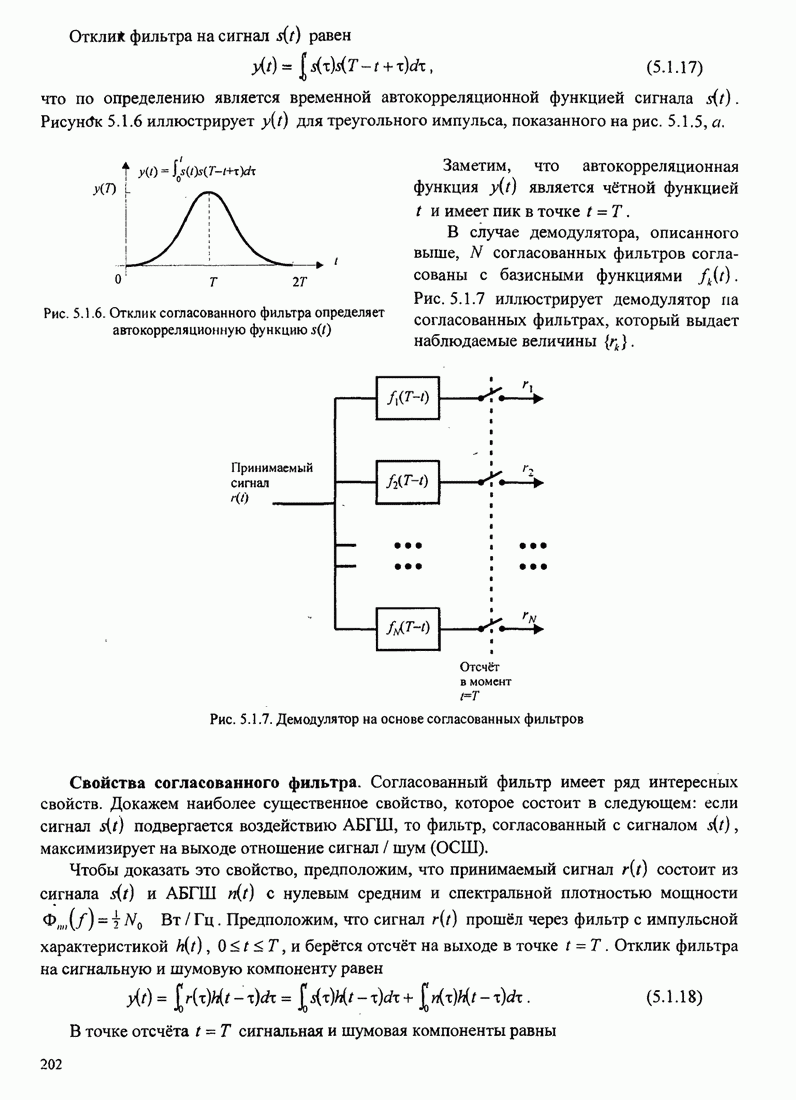
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
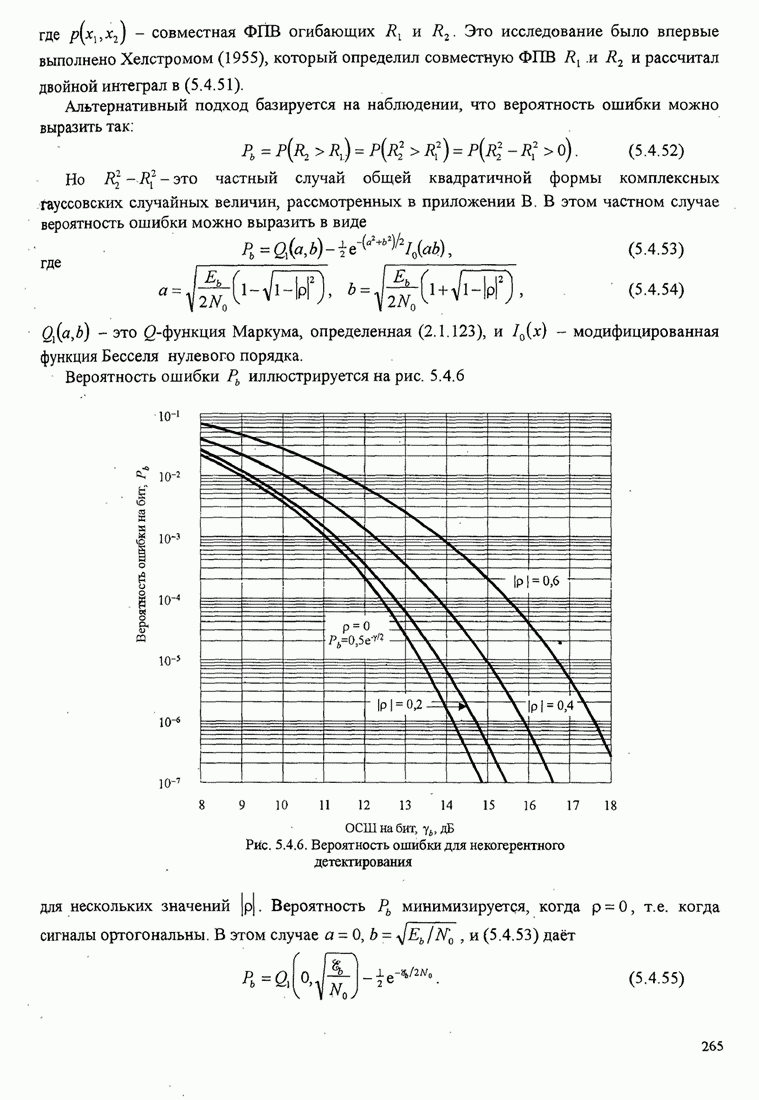
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
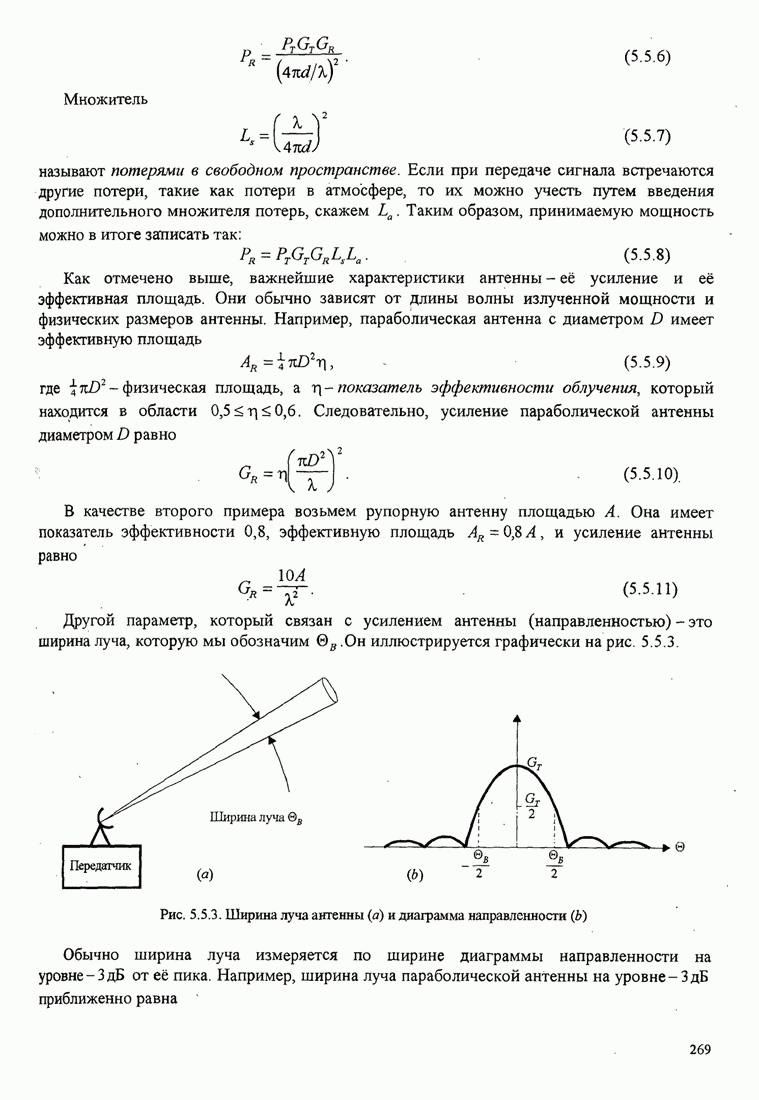
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
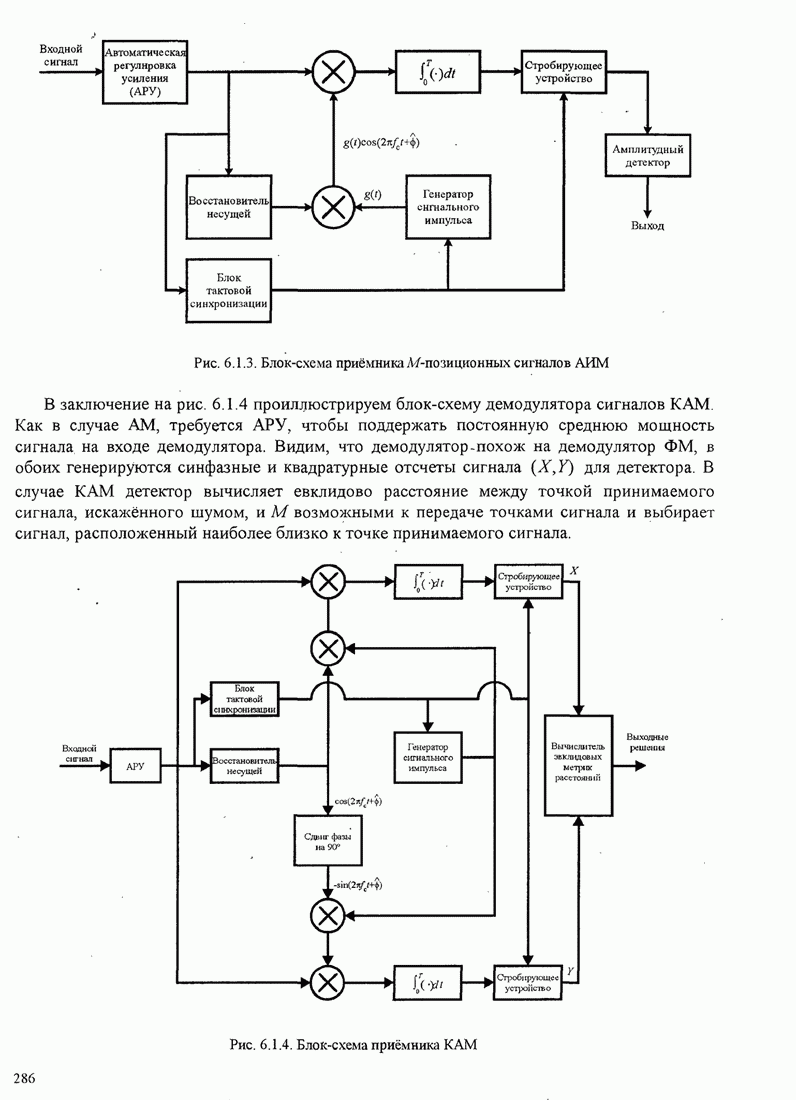
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
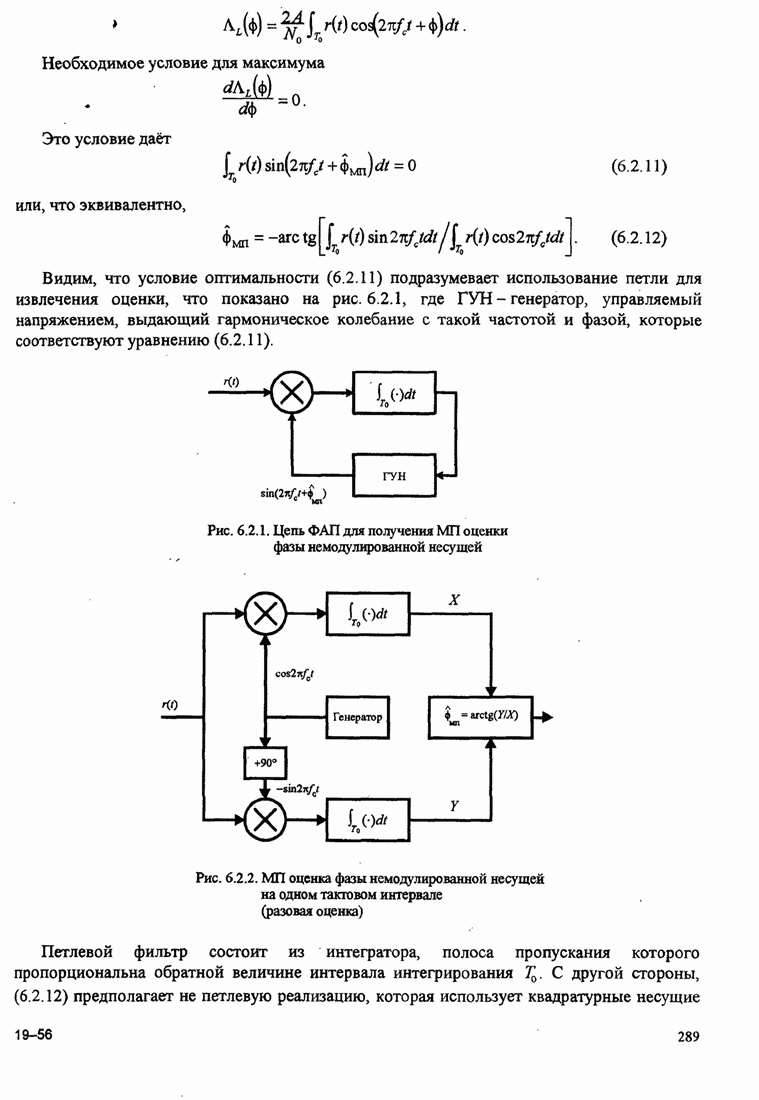
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
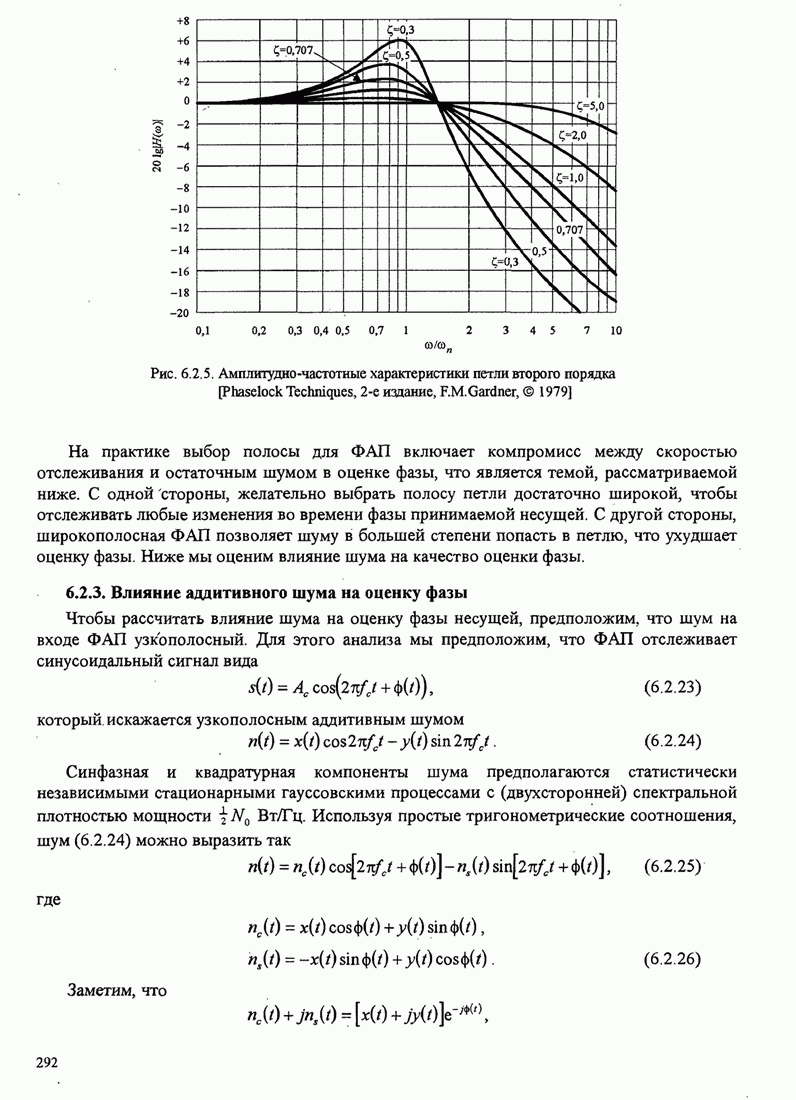
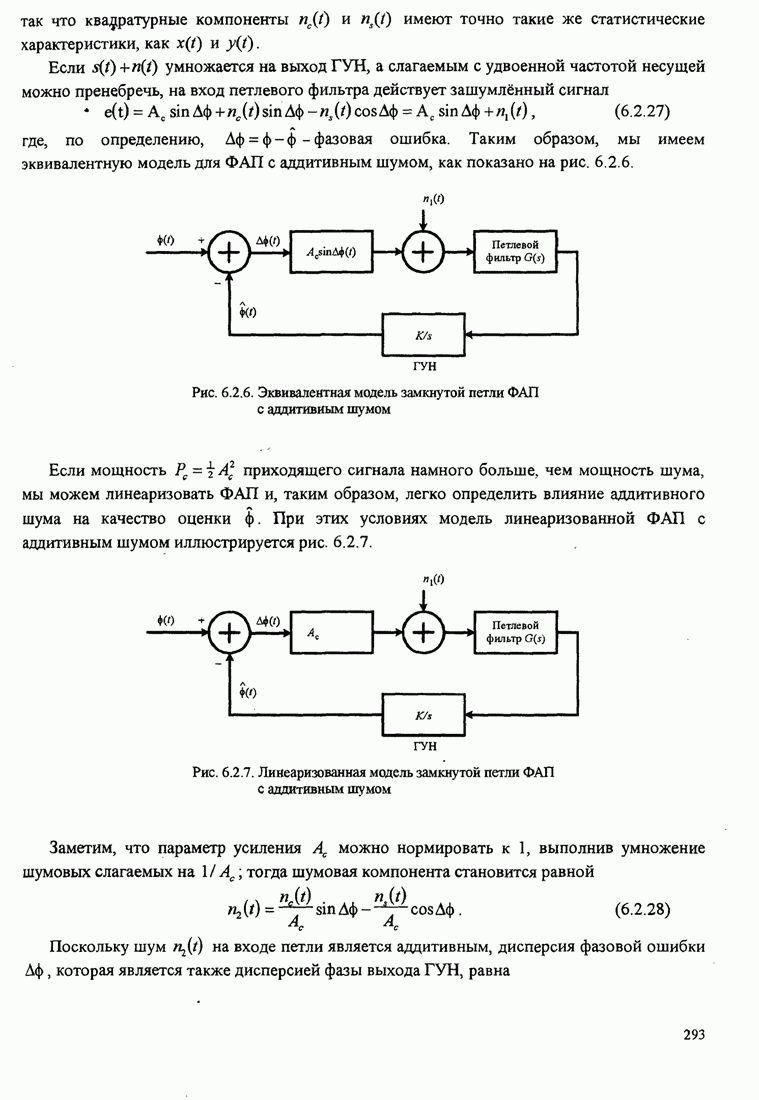
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
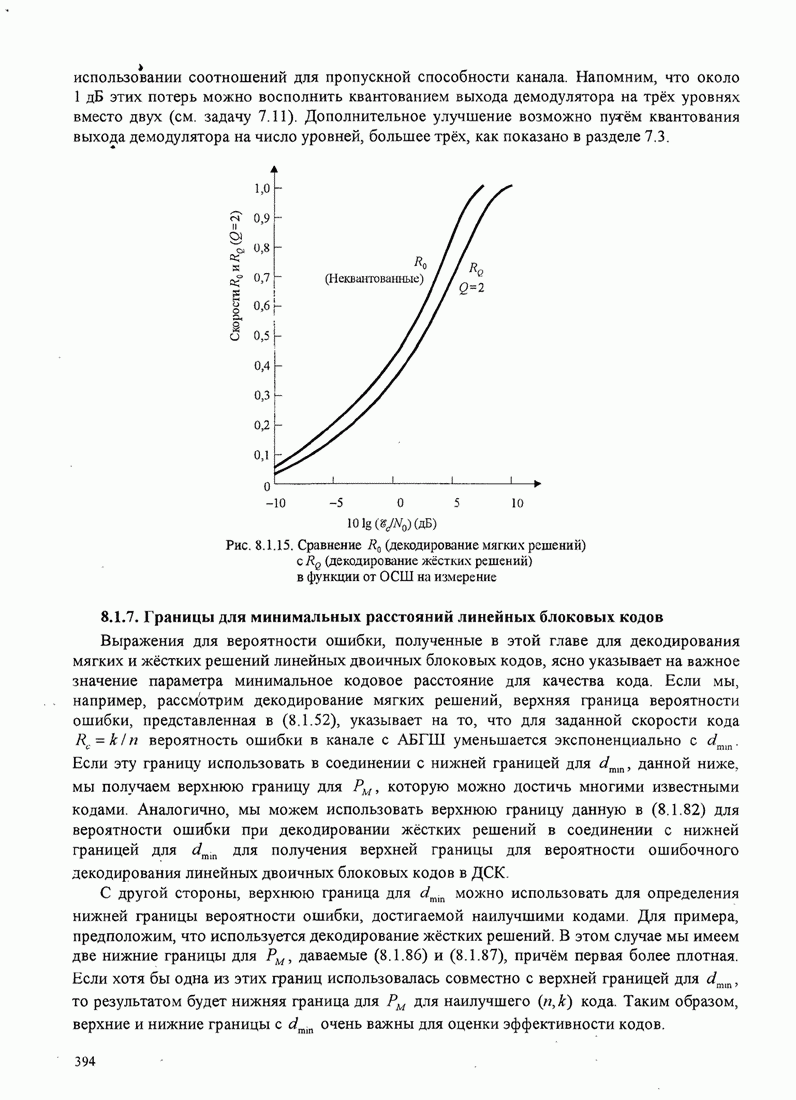
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
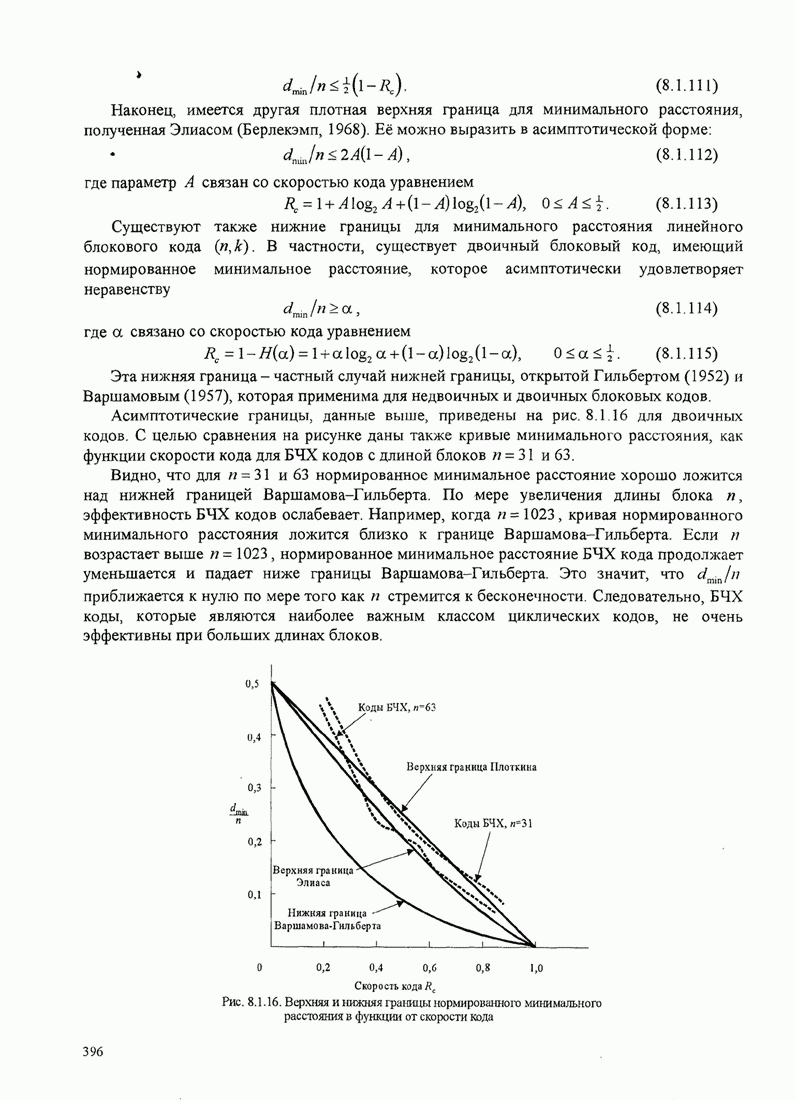
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
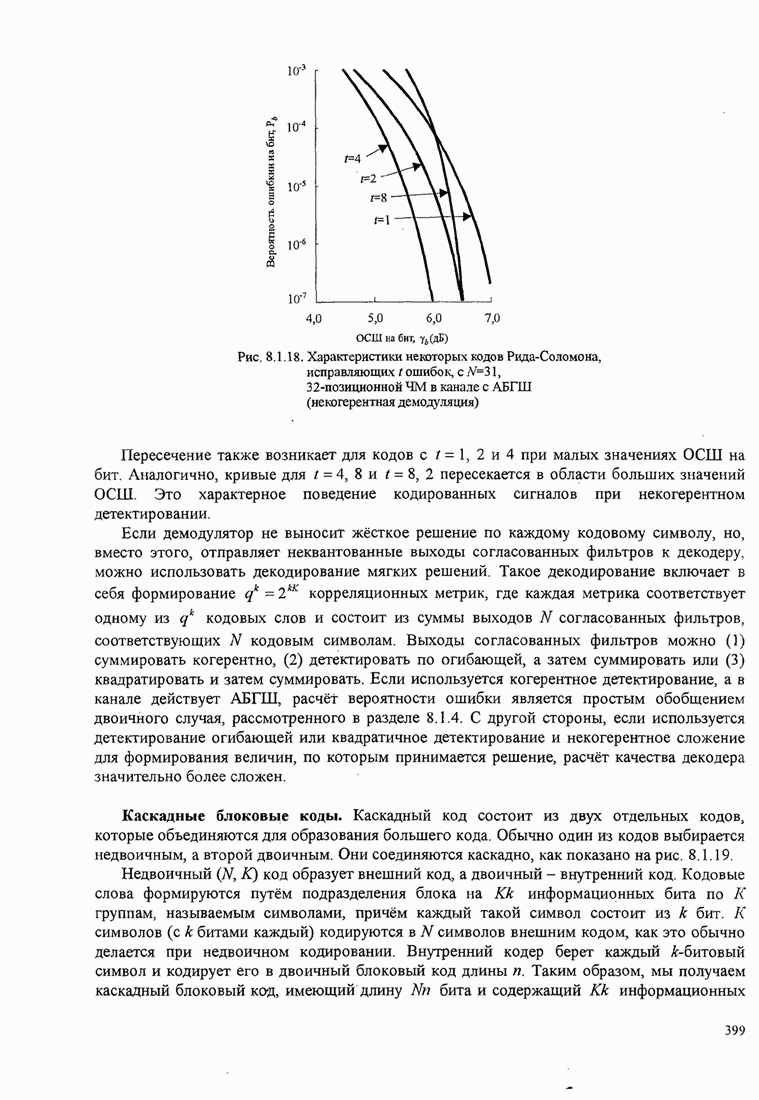
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
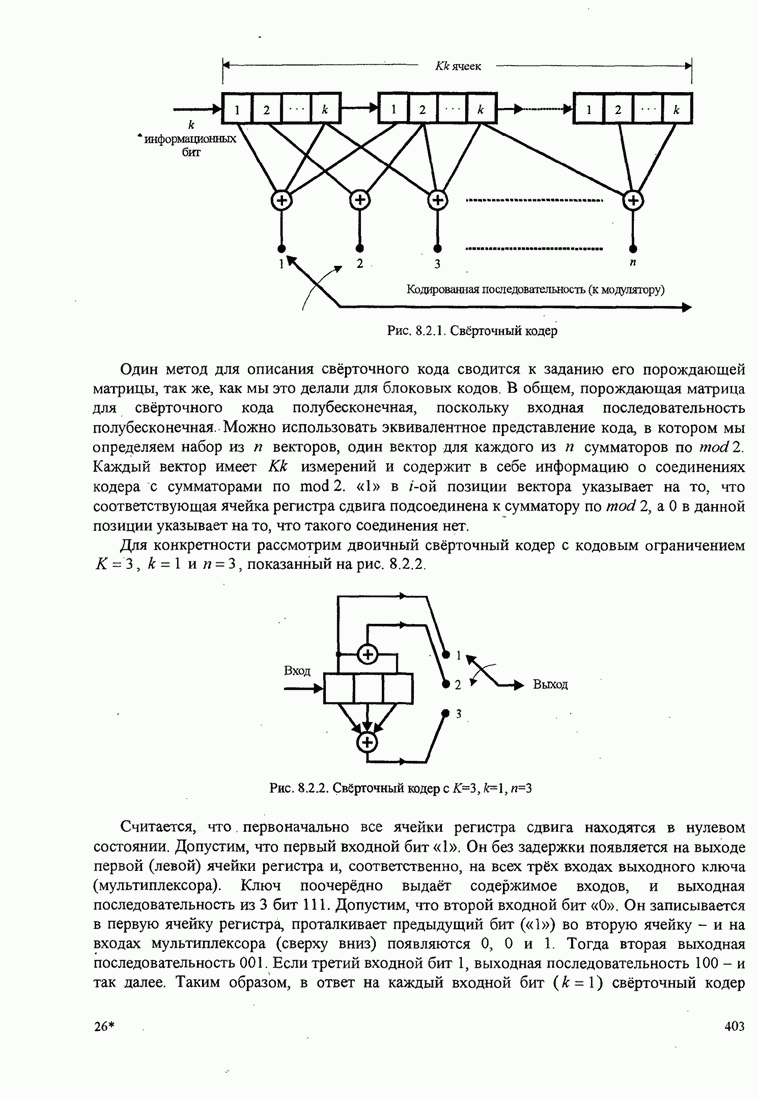
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
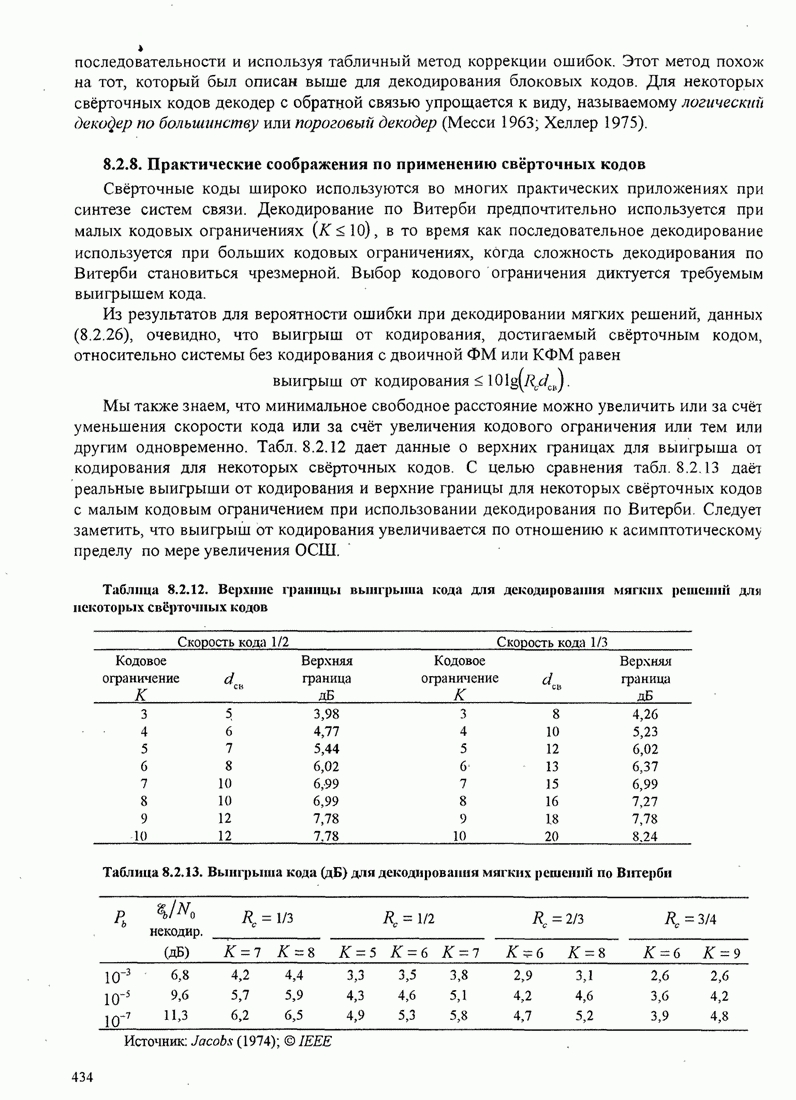
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
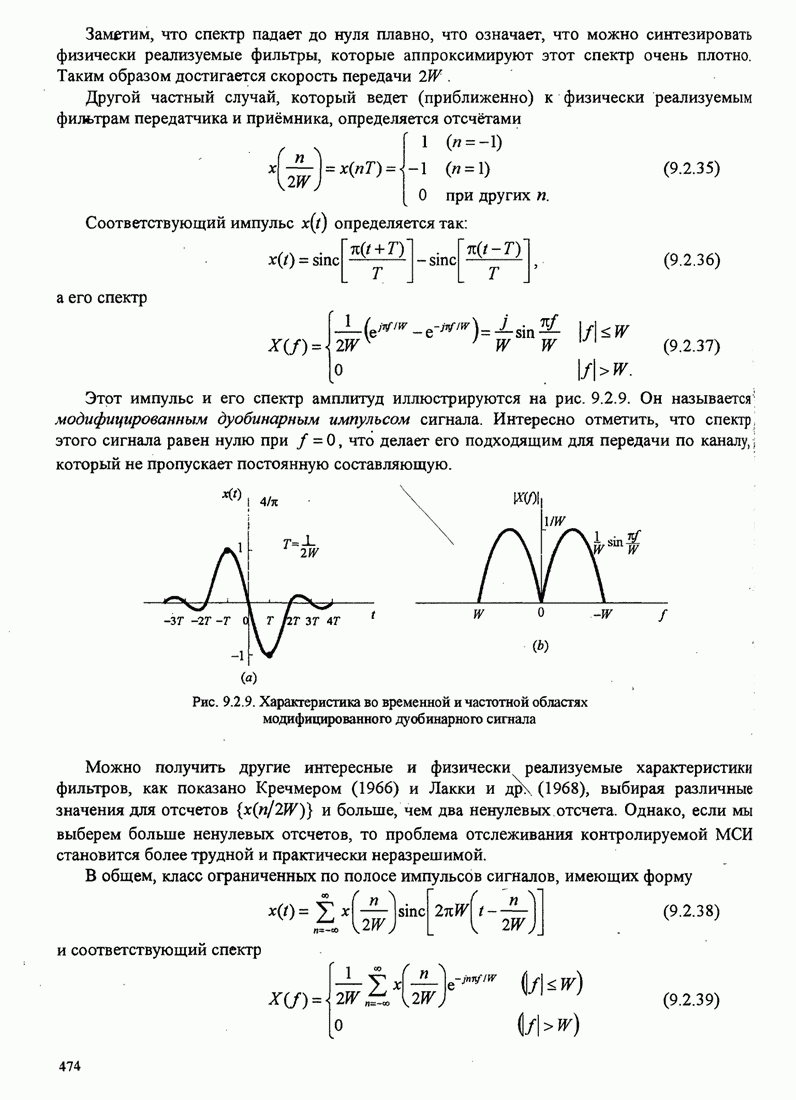
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
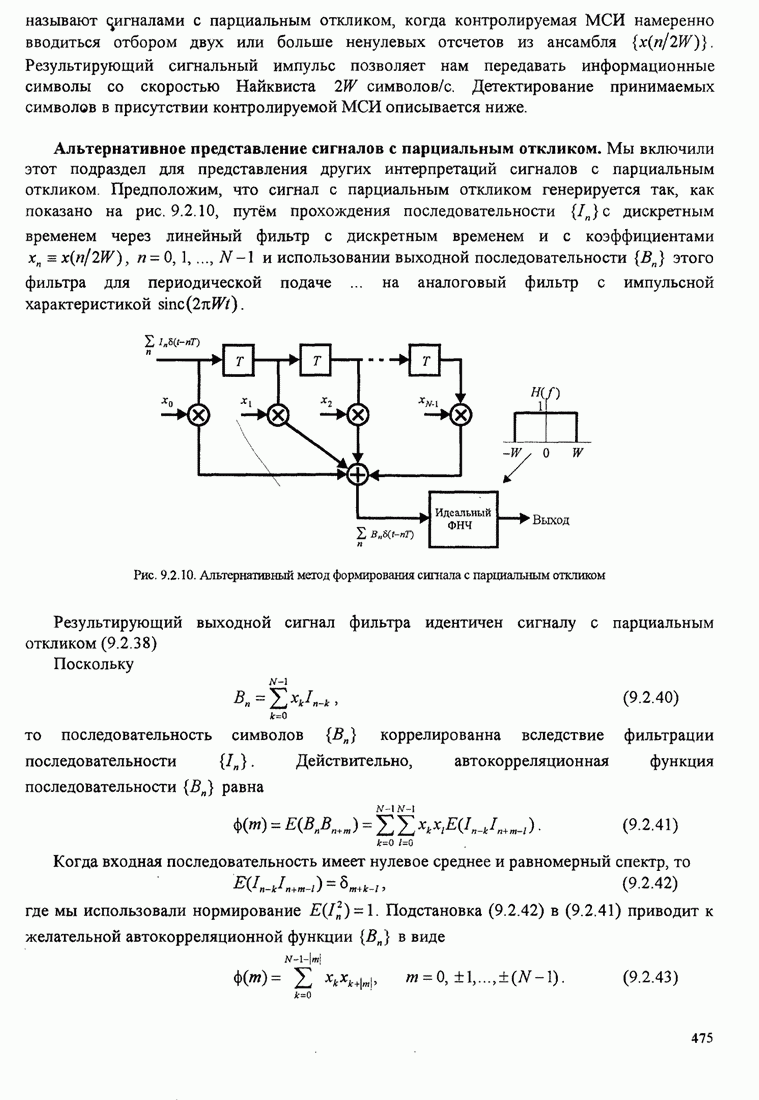
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
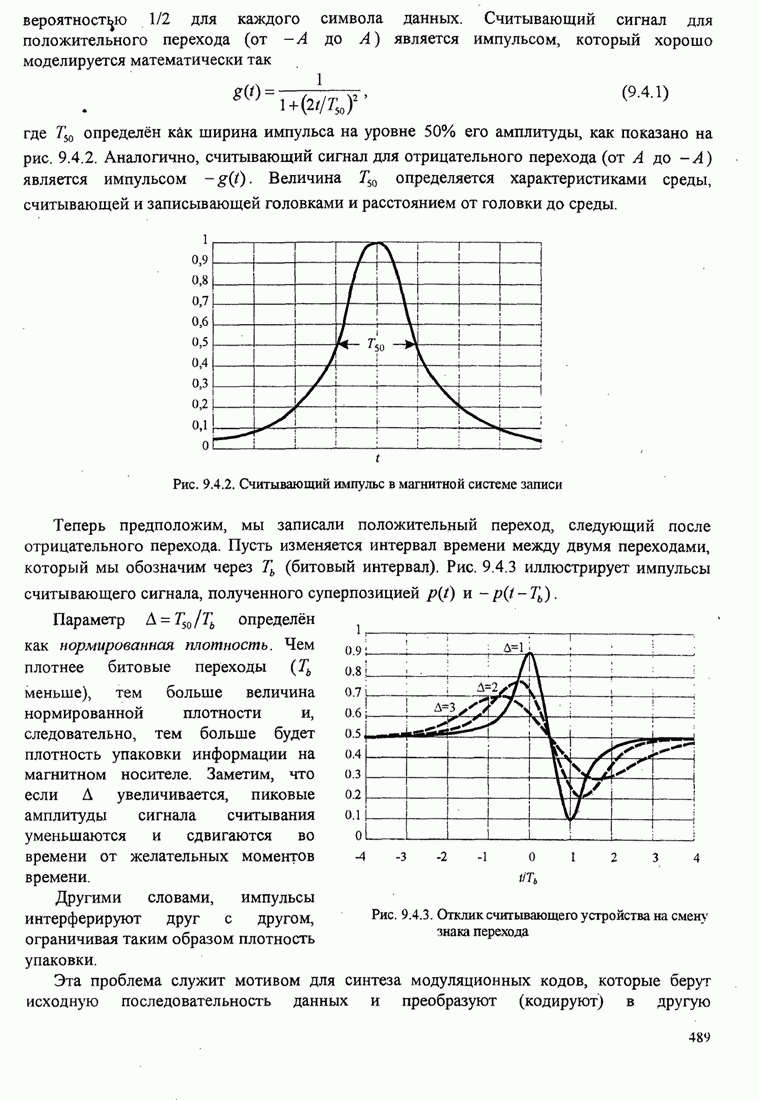
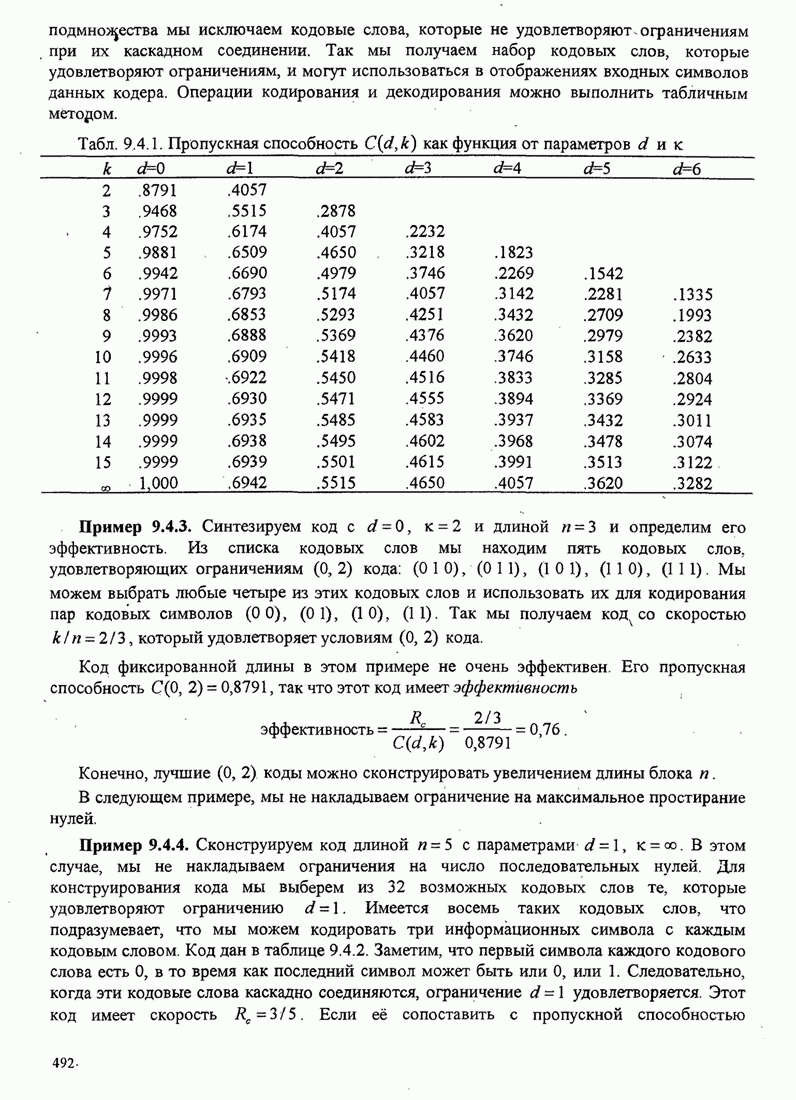
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
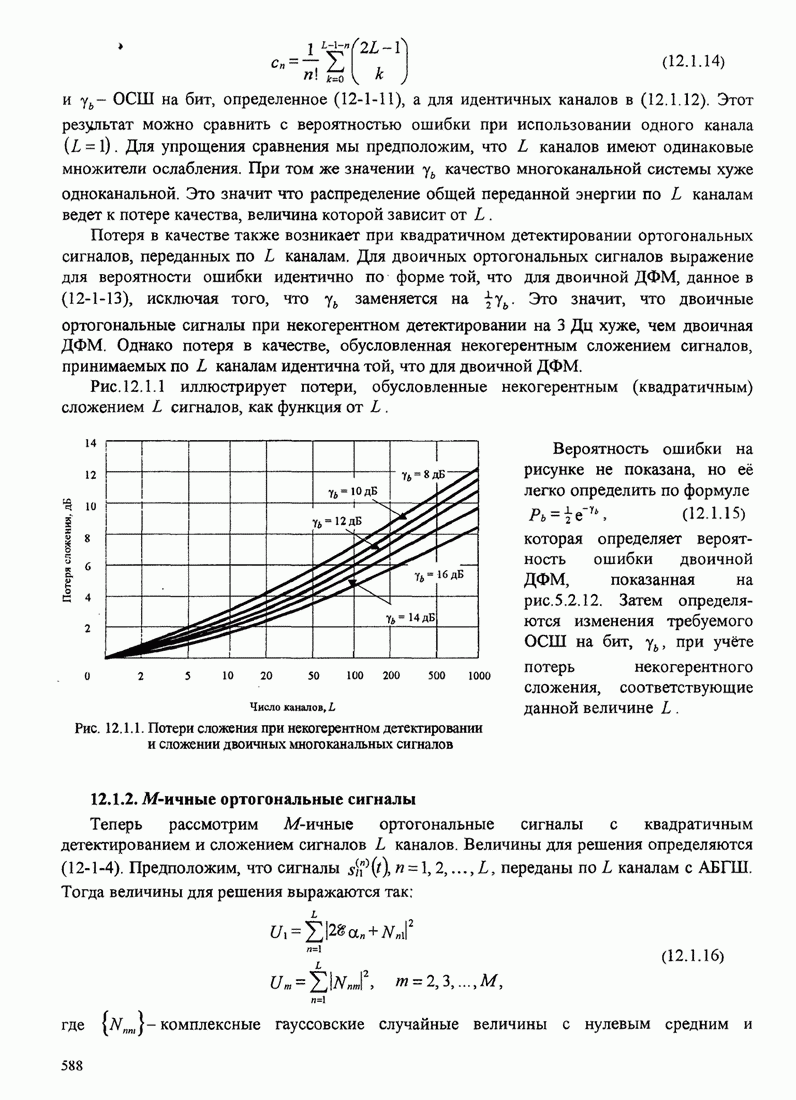
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
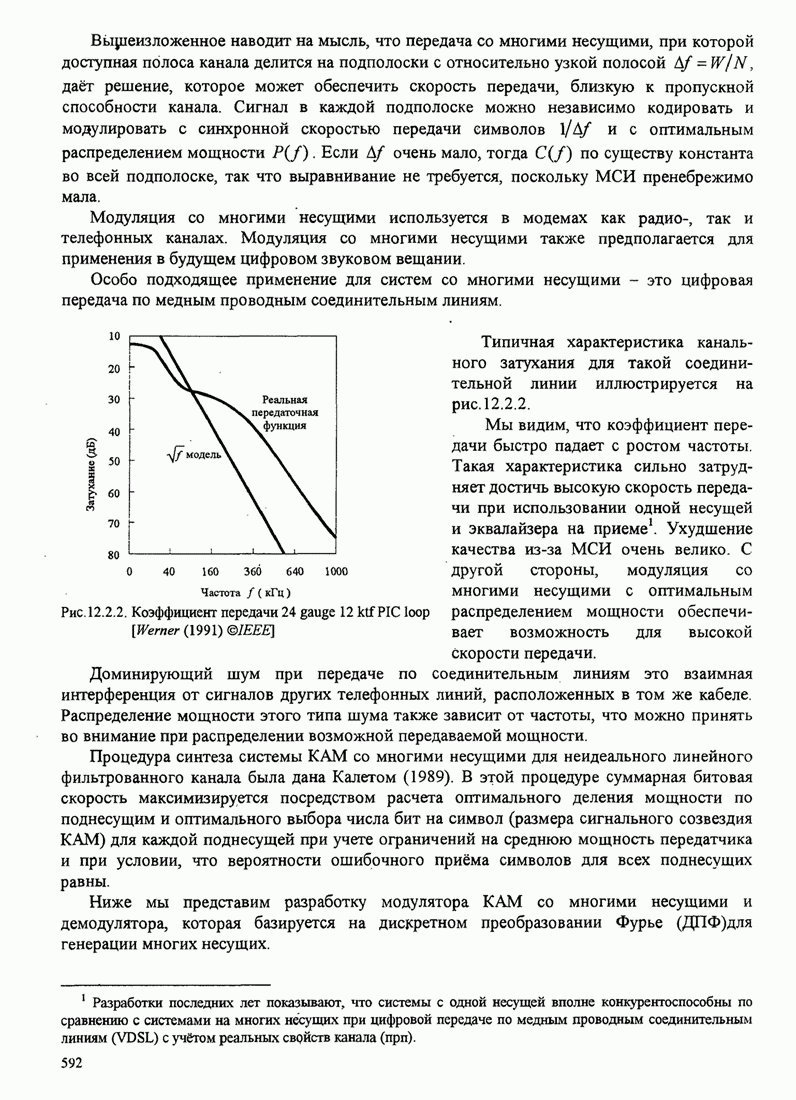
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
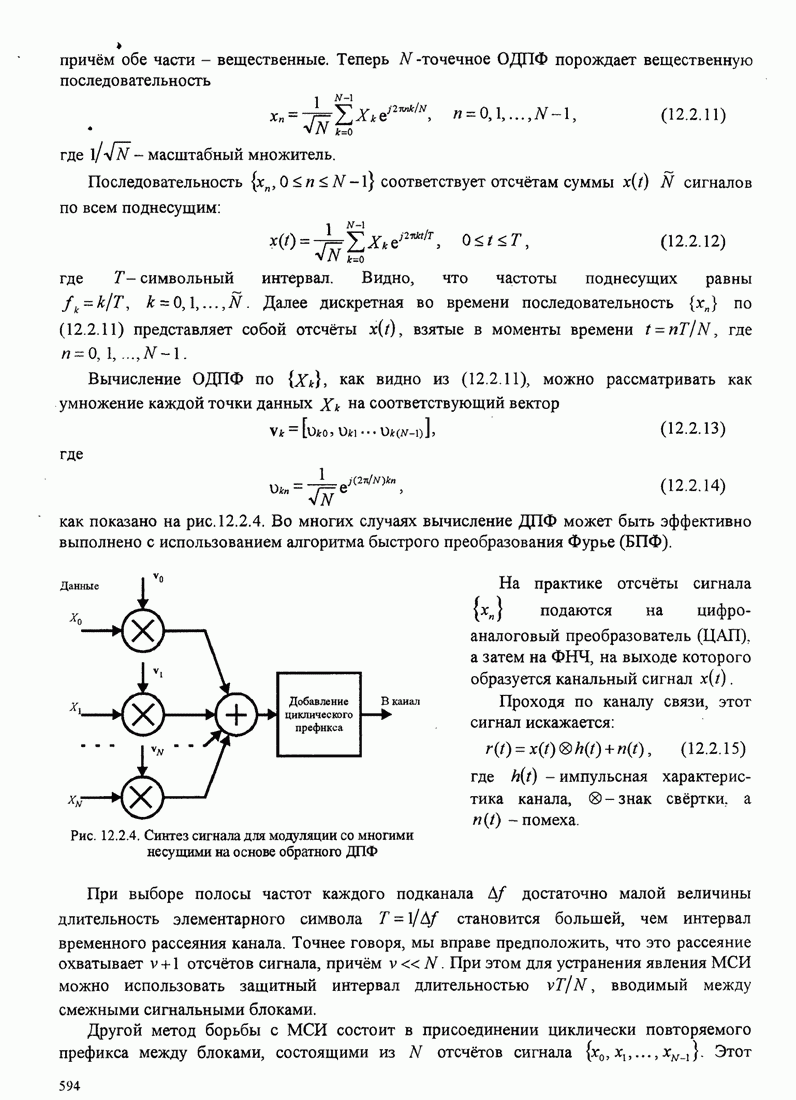
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
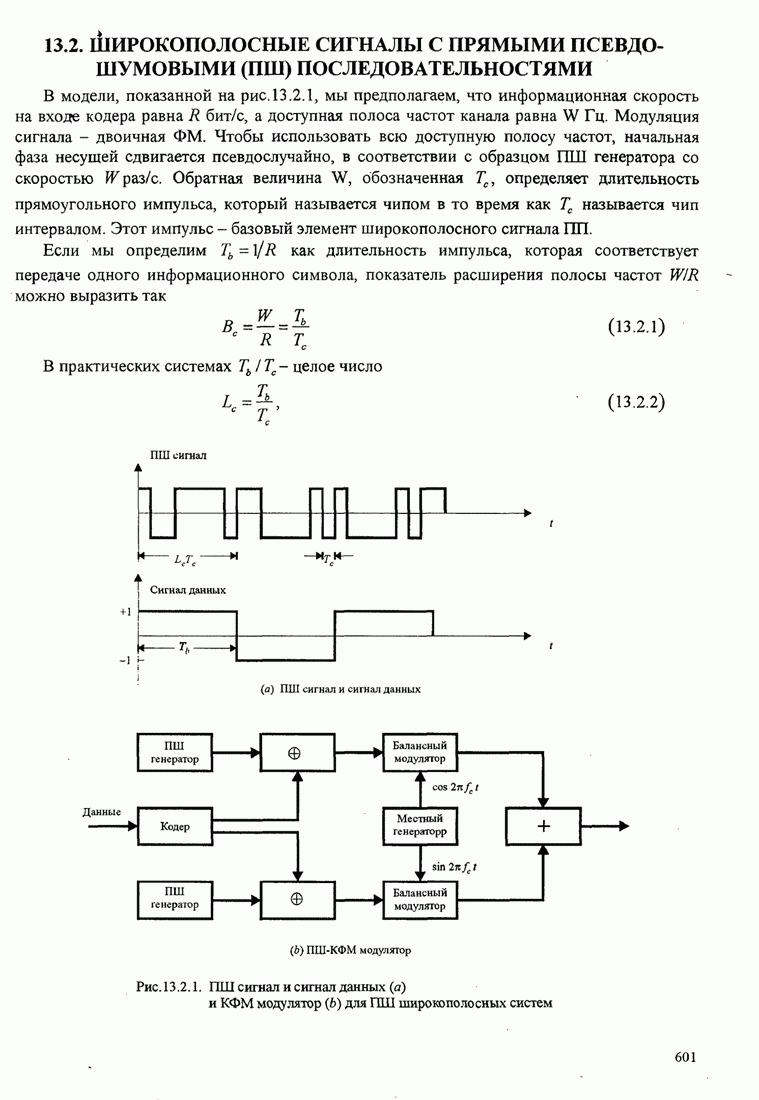
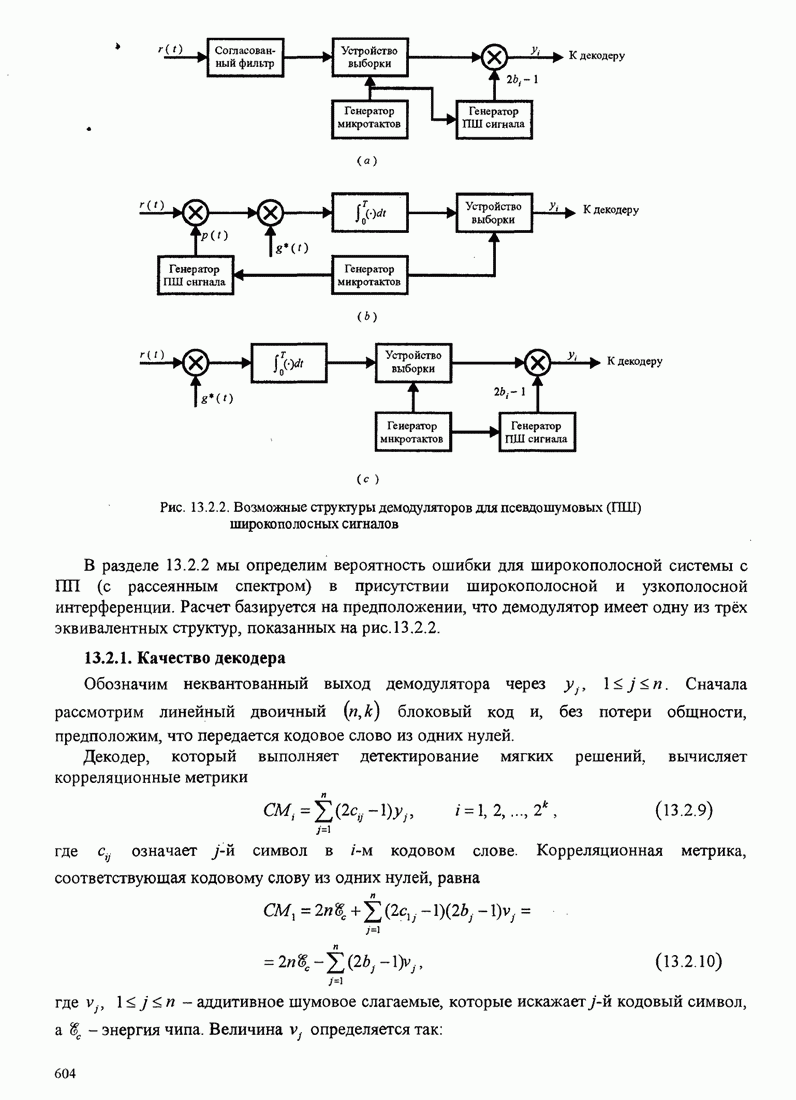
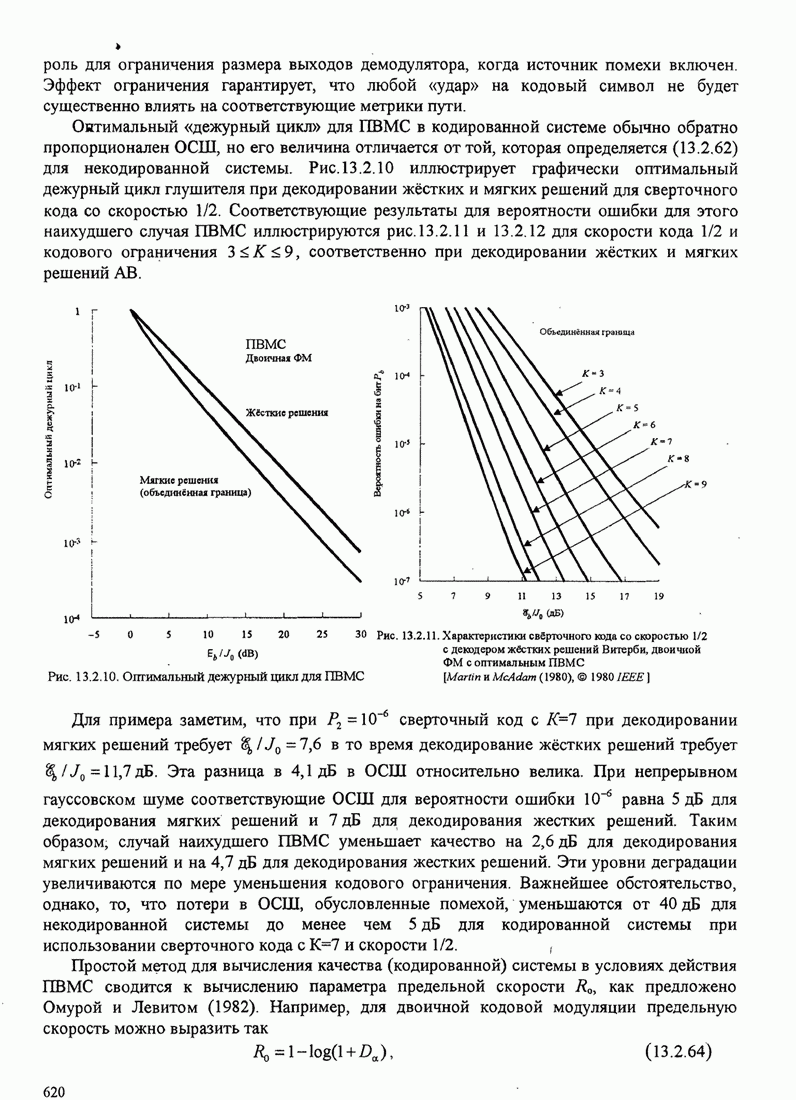
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
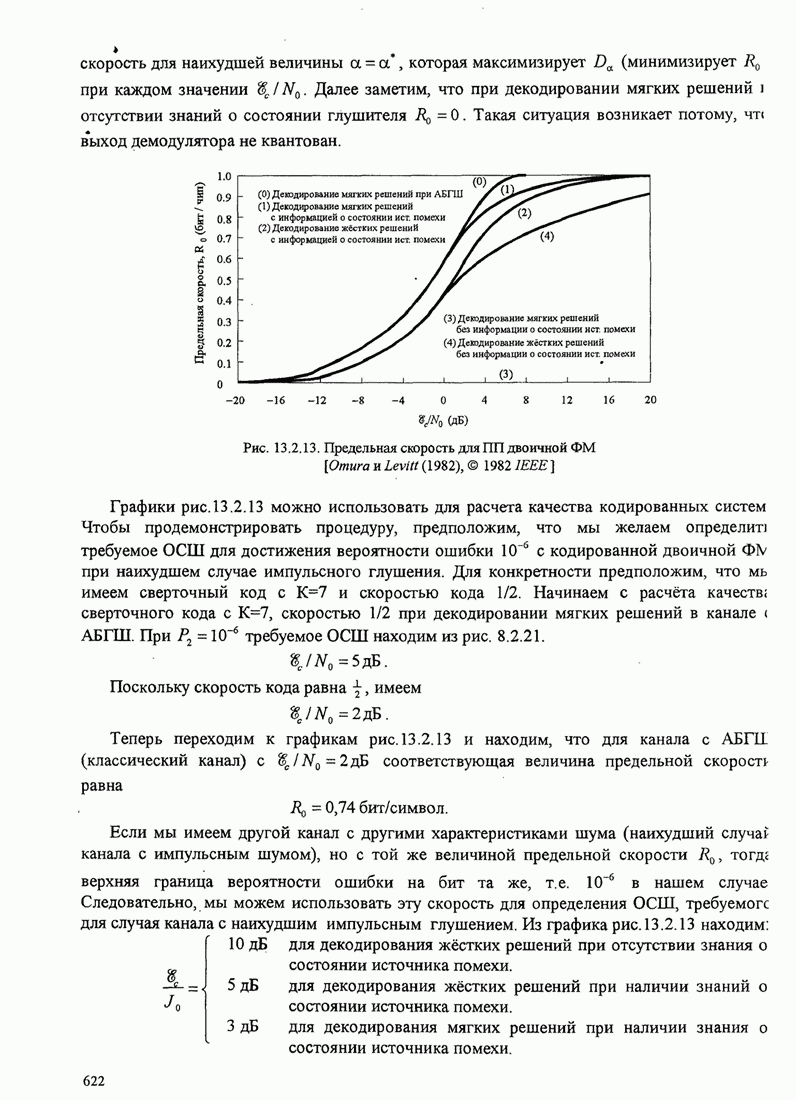
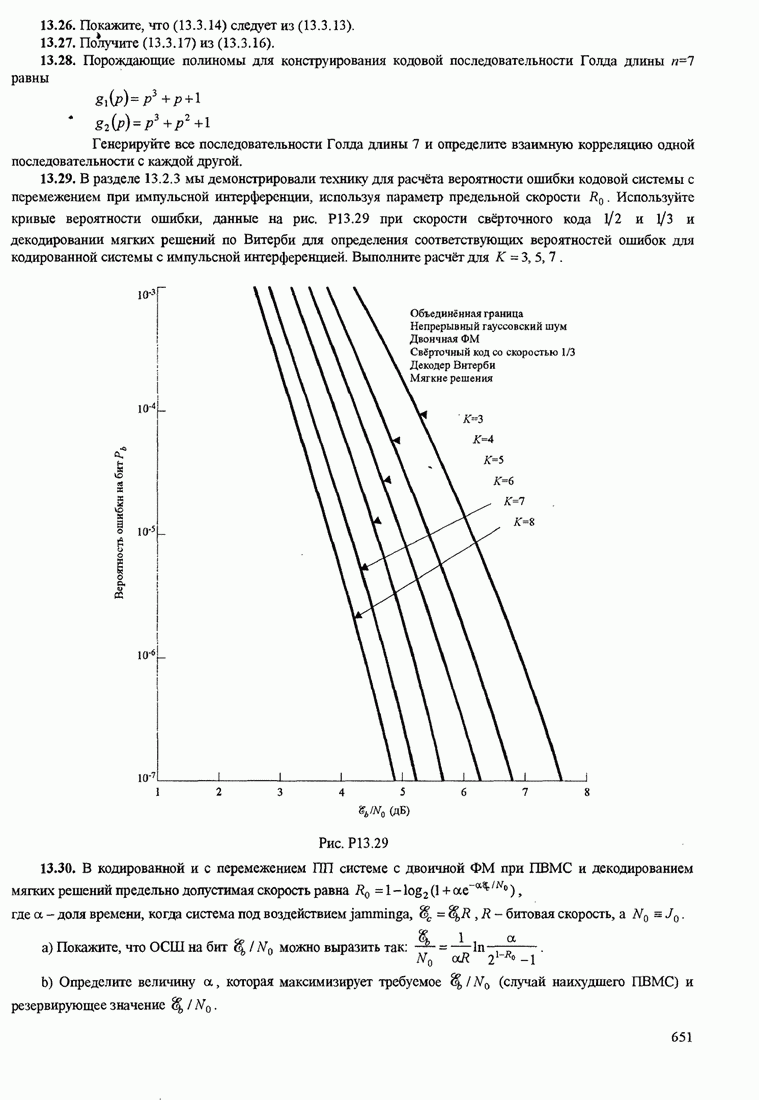
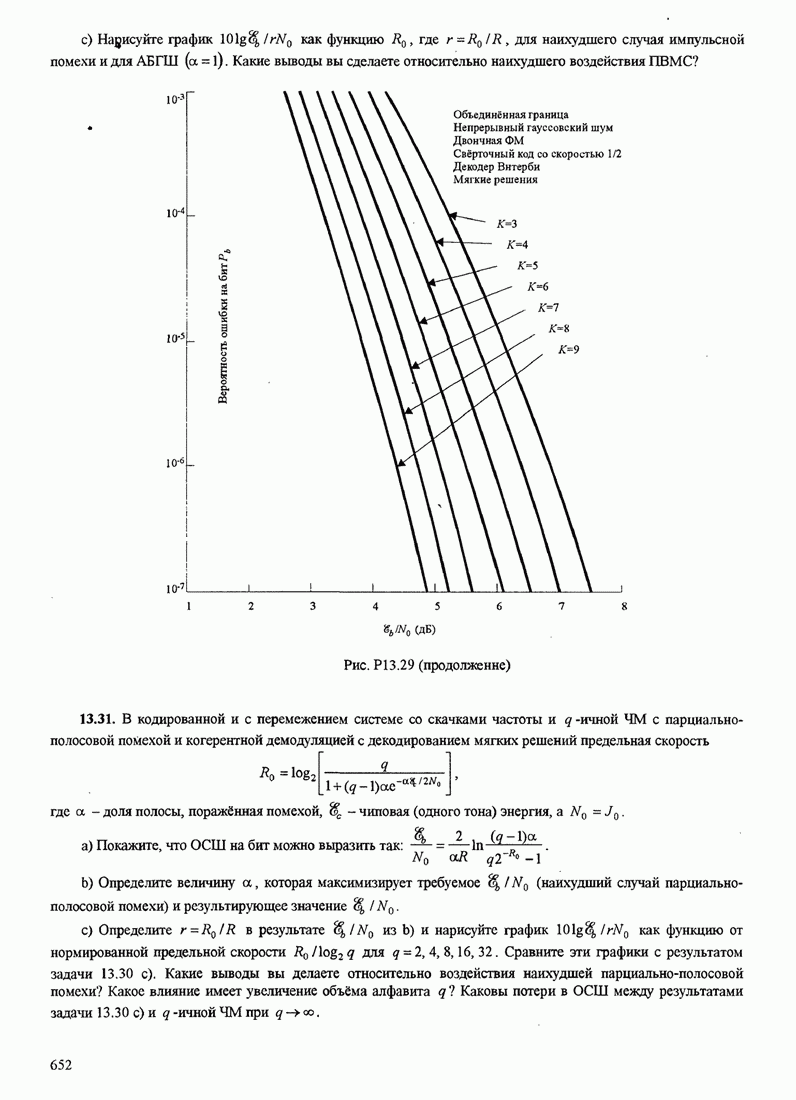
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
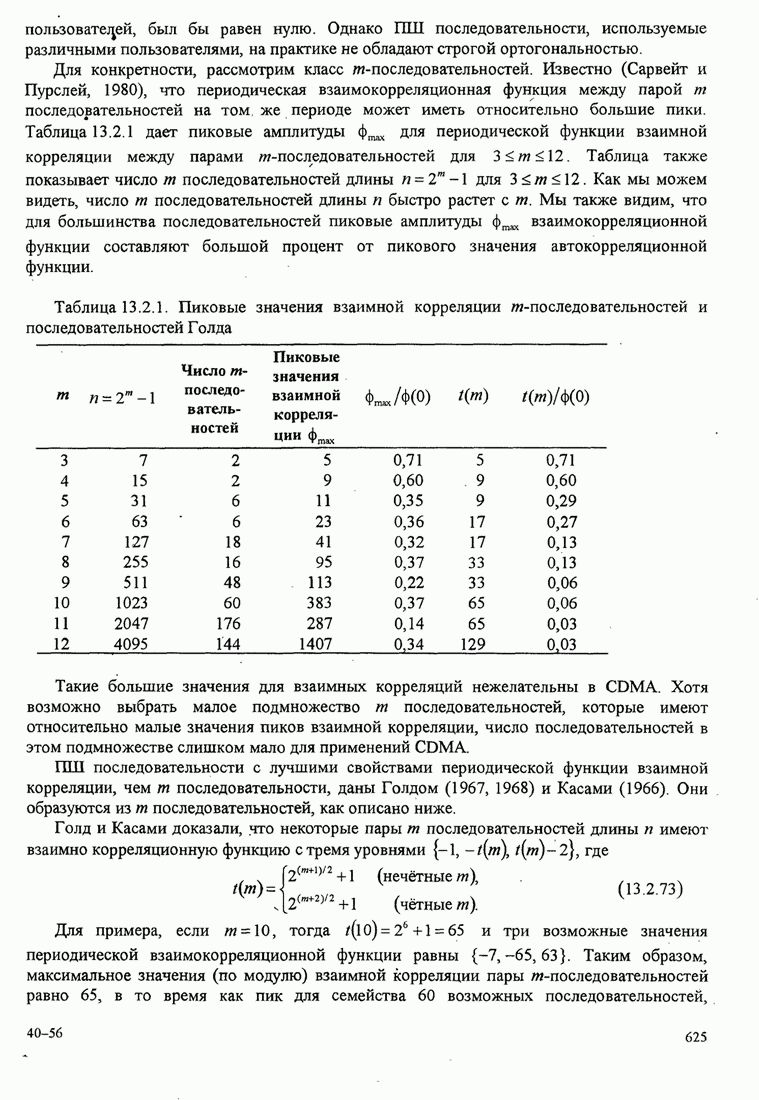
- 13.2.4. Генерирование ПШ последовательностей
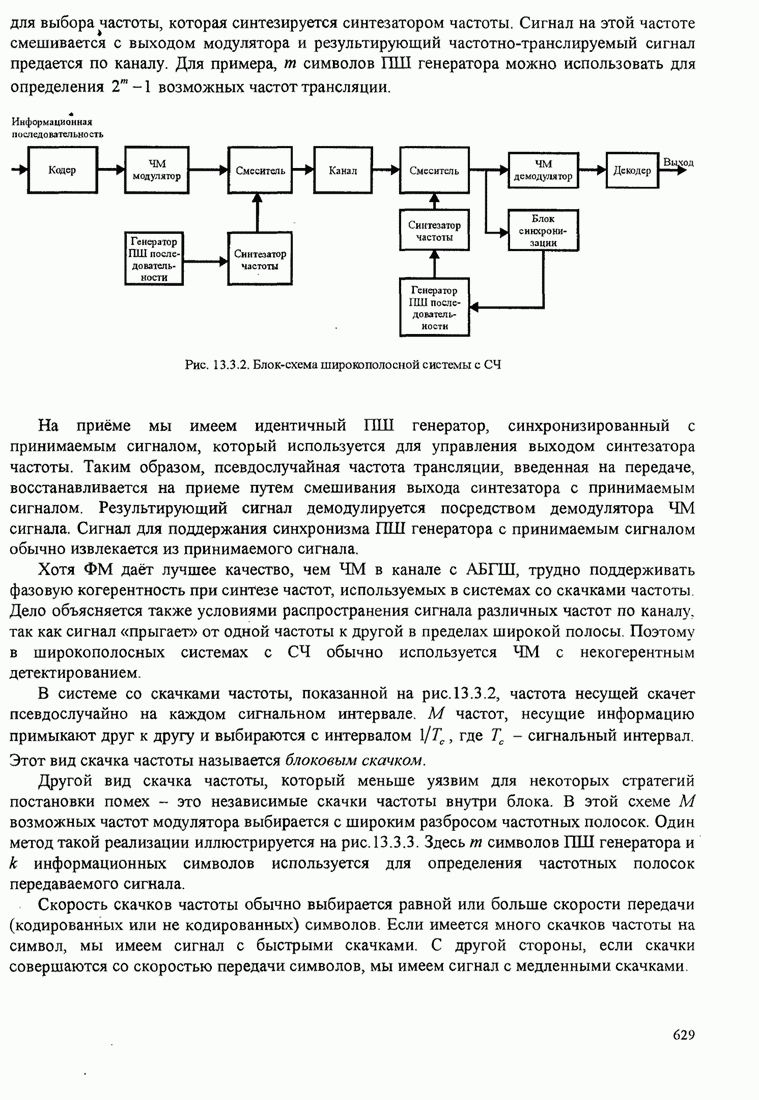
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
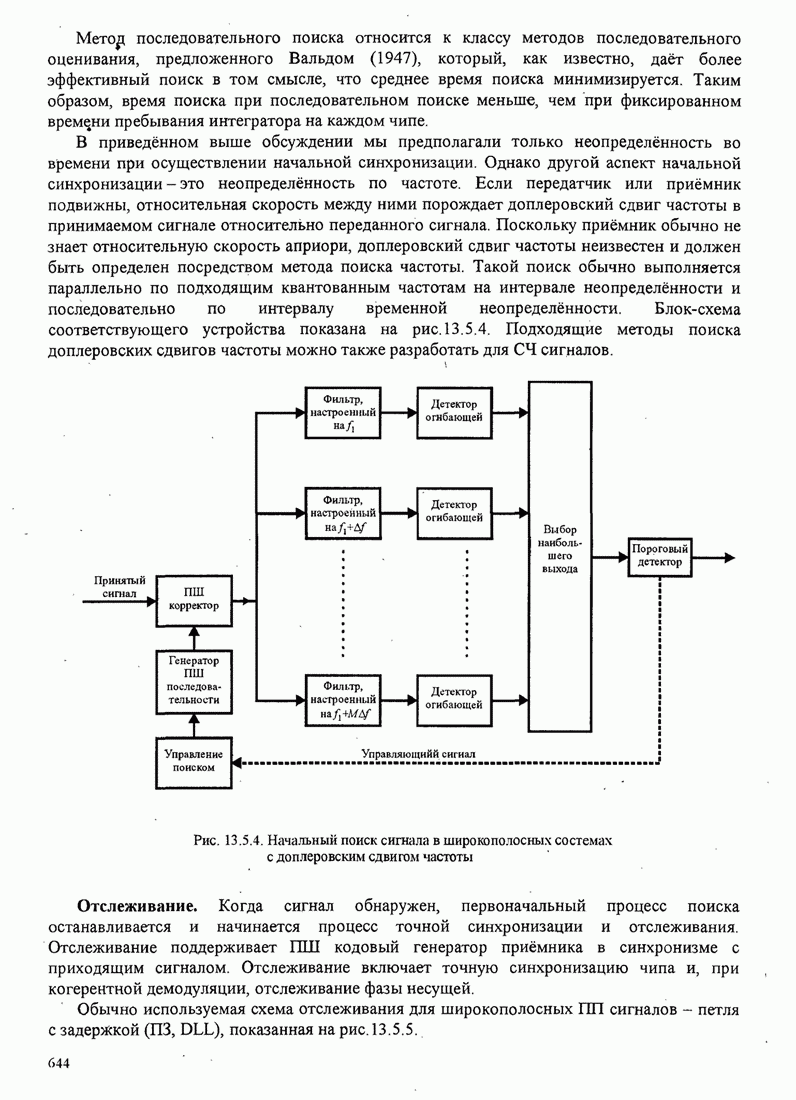
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
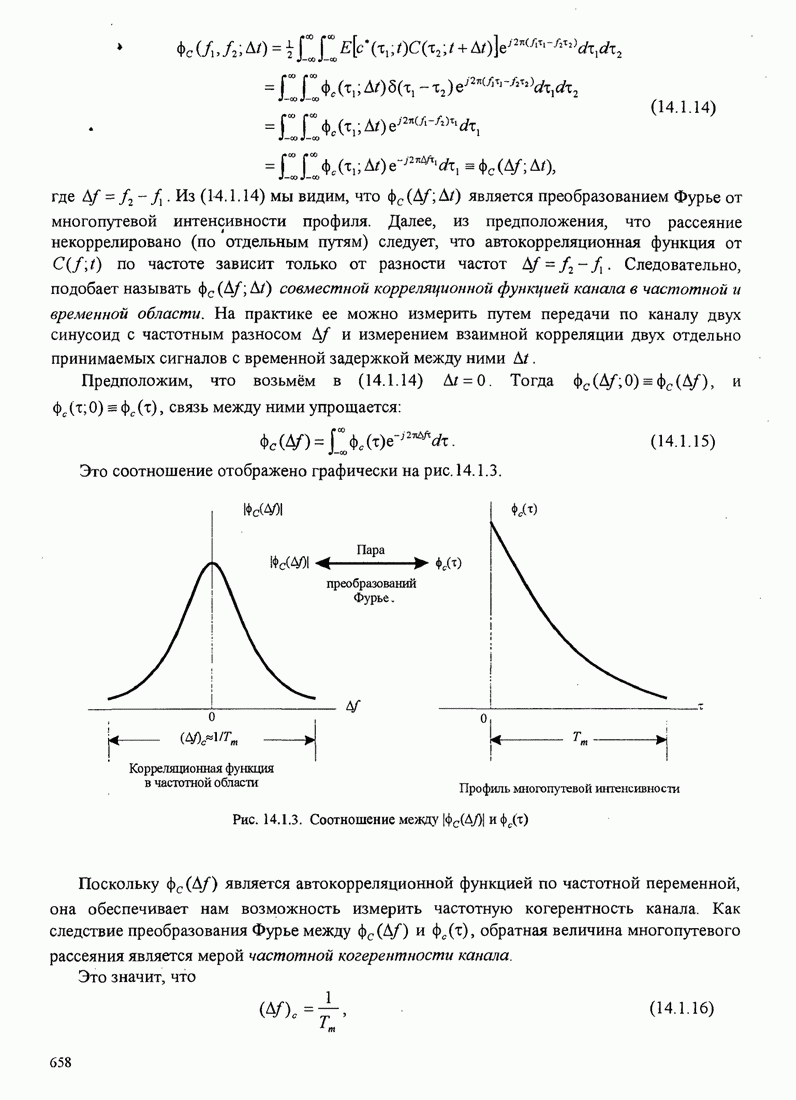
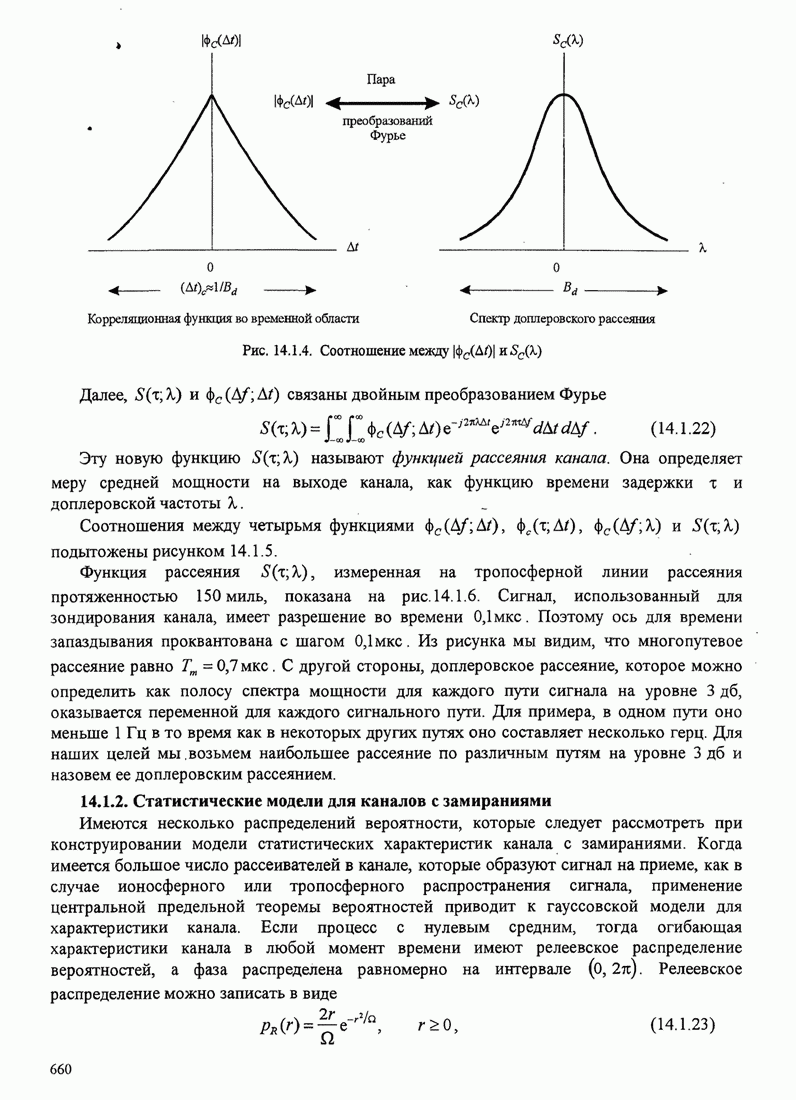
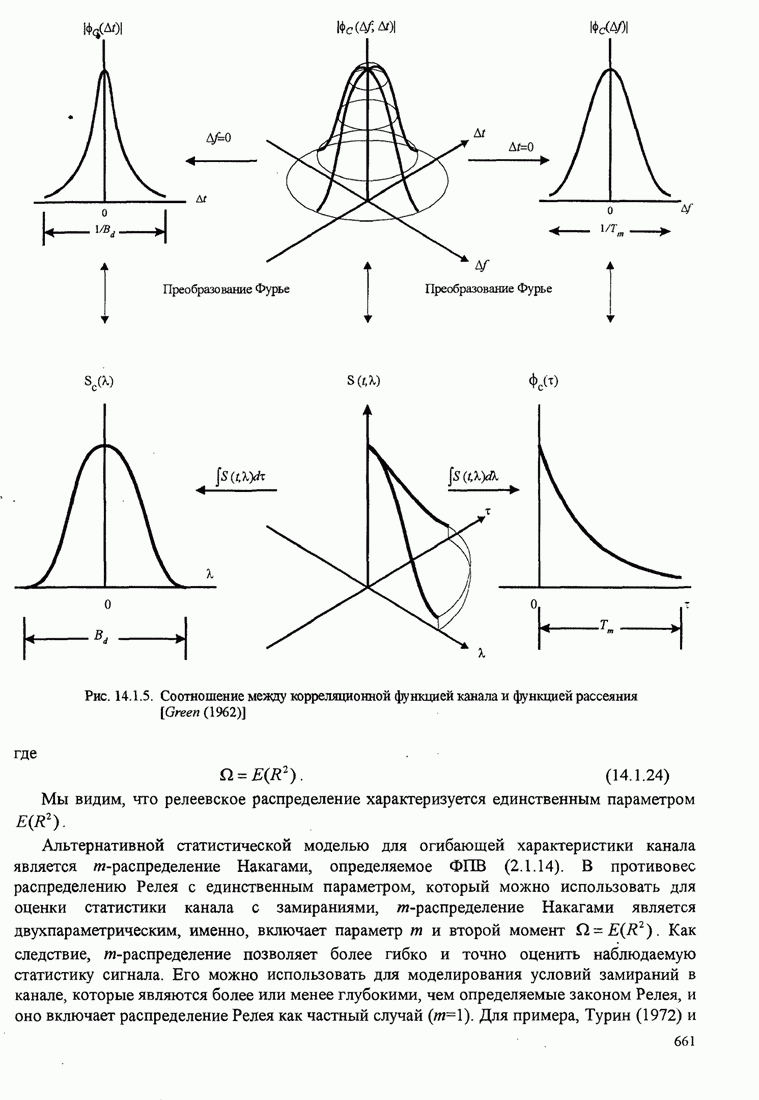
- 14.1.1. Корреляционная функция канала и спектр мощности
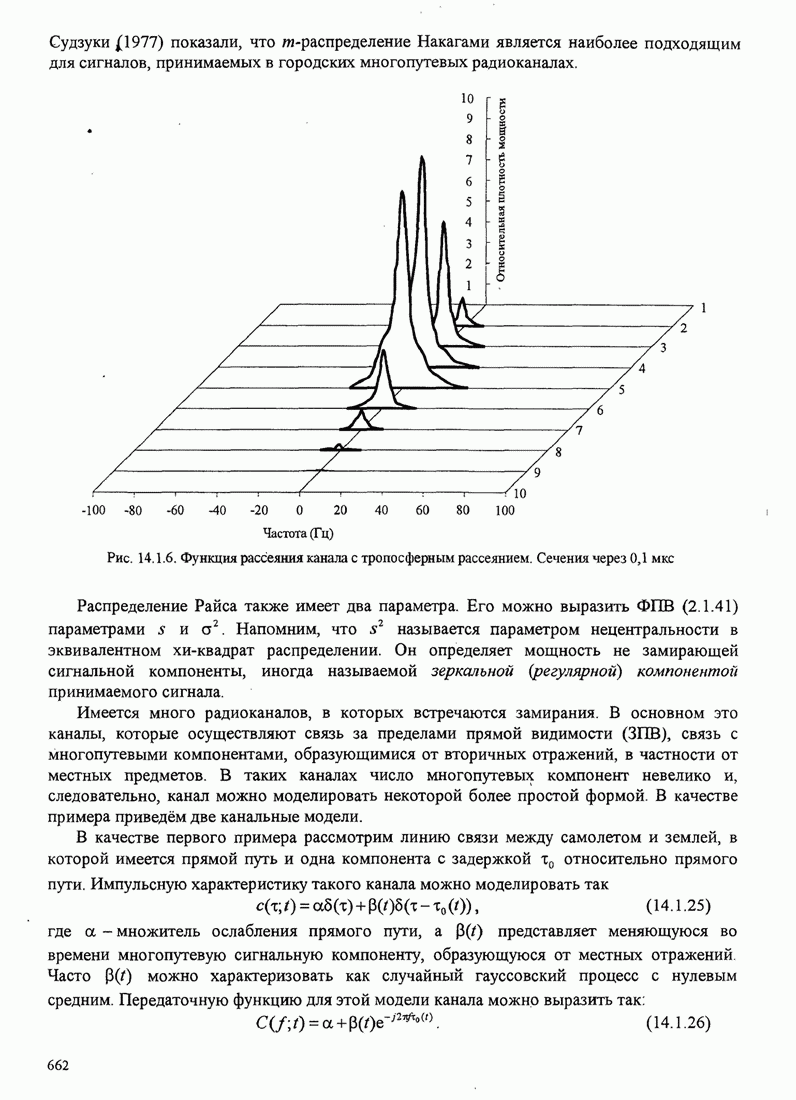
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
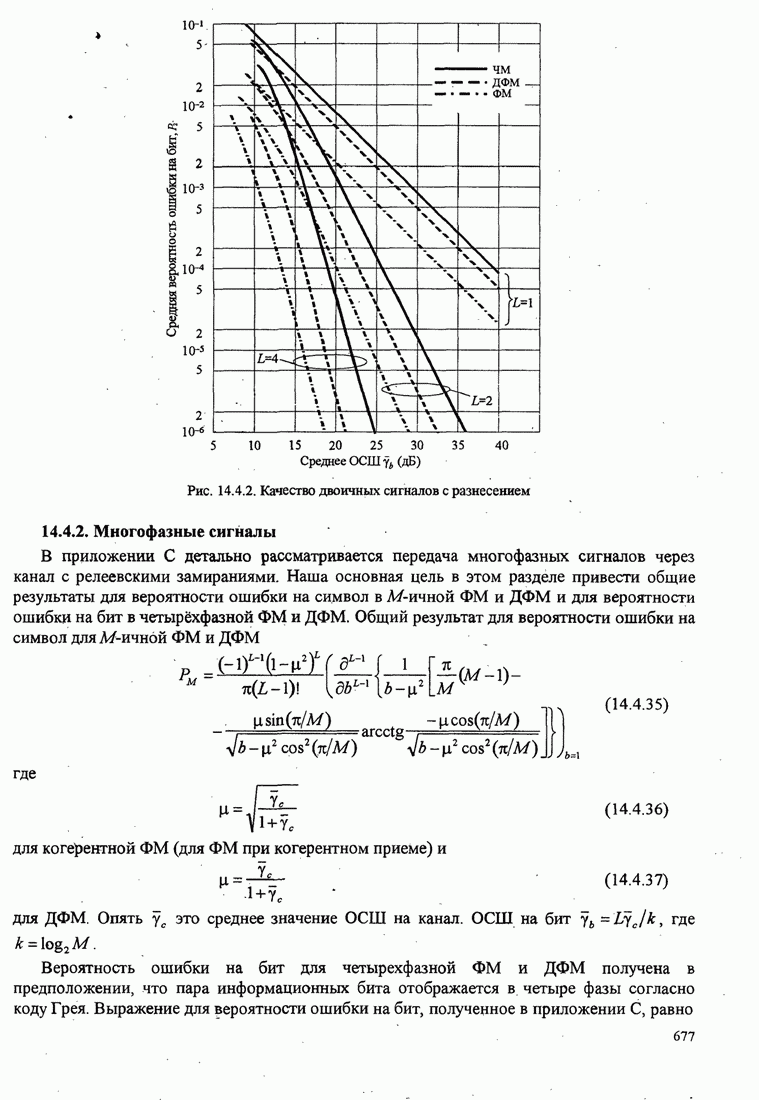
- 14.4.2. Многофазные сигналы
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
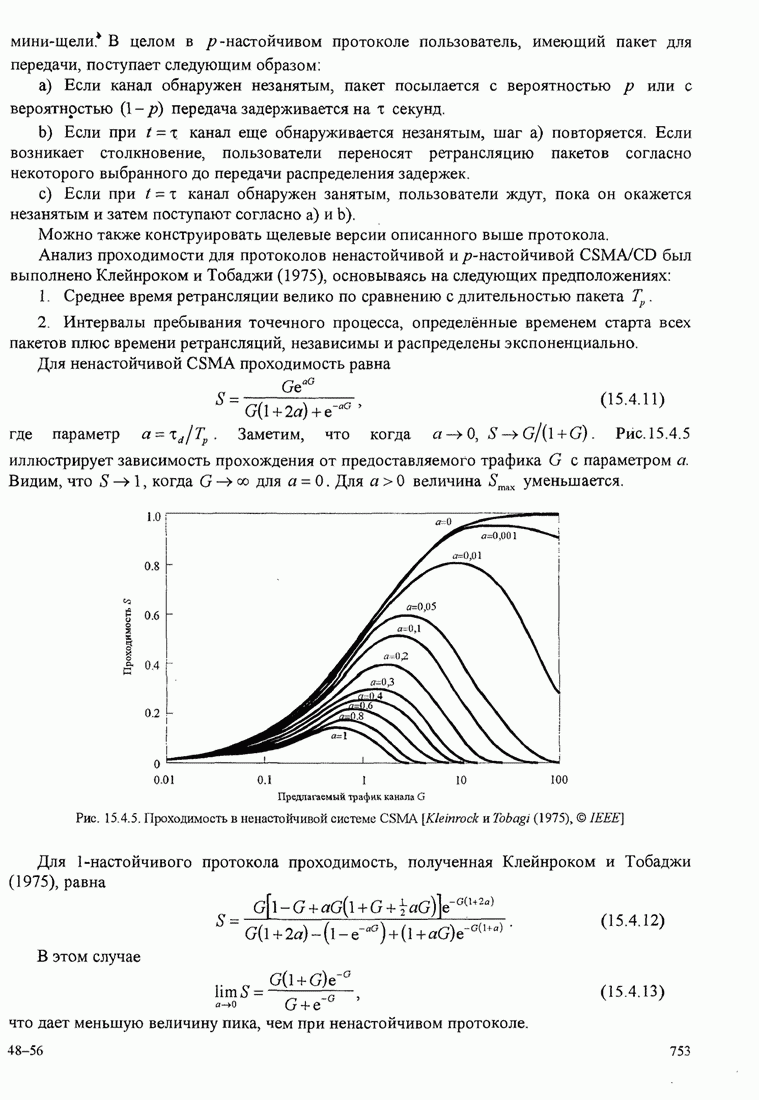
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)