| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
Рекуррентное по наименьшим квадратам
(РНК) оценивание ![]() можно
сформулировать следующим образом. Допустим, мы наблюдаем векторы
можно
сформулировать следующим образом. Допустим, мы наблюдаем векторы ![]() ,
, ![]() и желаем
определить вектор коэффициентов
и желаем
определить вектор коэффициентов ![]() эквалайзера (линейного или с обратной
связью по решению), который минимизирует усреднённые во времени взвешенные
квадраты ошибок
эквалайзера (линейного или с обратной
связью по решению), который минимизирует усреднённые во времени взвешенные
квадраты ошибок
![]()
где ошибки определяются так
![]()
а ![]() представляет взвешивающий множитель
представляет взвешивающий множитель ![]() . Таким образом, мы
ввели показательное взвешивание по последним данным, которое приемлемо, когда
характеристики канала меняются во времени. Минимизация
. Таким образом, мы
ввели показательное взвешивание по последним данным, которое приемлемо, когда
характеристики канала меняются во времени. Минимизация ![]() по вектору коэффициентов
по вектору коэффициентов ![]() ведет к системе
линейных уравнений
ведет к системе
линейных уравнений
![]()
где ![]() - матрица корреляций сигнала,
определенная так
- матрица корреляций сигнала,
определенная так
![]()
а ![]() - вектор взаимных корреляций
- вектор взаимных корреляций
![]()
Решение (11.4.6) равно
![]()
Матрица ![]() родственна матрице статистических
автокорреляций
родственна матрице статистических
автокорреляций ![]() ,
в то время как вектор
,
в то время как вектор ![]() родственен вектору
родственен вектору ![]() взаимных
корреляций, определенных раньше. Подчеркнём, однако, что
взаимных
корреляций, определенных раньше. Подчеркнём, однако, что ![]() не является тёплицевой
матрицей. Мы также хотим напомнить, что для малых значений
не является тёплицевой
матрицей. Мы также хотим напомнить, что для малых значений ![]() ,
, ![]() может быть плохо
обусловленной; следовательно, это обычно приводит к первоначальной добавке
матрицы
может быть плохо
обусловленной; следовательно, это обычно приводит к первоначальной добавке
матрицы ![]() к
к
![]() , где
, где ![]() - малая
положительная константа, а
- малая
положительная константа, а ![]() - единичная матрица. При
показательном взвешивании по последним данным влияние прибавления
- единичная матрица. При
показательном взвешивании по последним данным влияние прибавления ![]() ослабевает со
временем.
ослабевает со
временем.
Теперь предположим, что мы имеем решение
(11.4.9) для момента ![]() , то есть
, то есть ![]() , и мы желаем вычислить
, и мы желаем вычислить ![]() . Неэффективно и,
следовательно, непрактично решать систему
. Неэффективно и,
следовательно, непрактично решать систему ![]() линейных уравнений для каждой новой
сигнальной компоненты, которая принимается. Чтобы преодолеть эту трудность, мы
поступим так. Сначала
линейных уравнений для каждой новой
сигнальной компоненты, которая принимается. Чтобы преодолеть эту трудность, мы
поступим так. Сначала ![]() можно вычислить рекуррентно следующим
образом
можно вычислить рекуррентно следующим
образом
![]() (11.4.10)
(11.4.10)
Мы назовем формулу (11.4.10) обновляющее уравнение
для ![]() .
.
Поскольку
в (11.4.9) требуется обращение ![]() , используем соотношение для
обращенных матриц
, используем соотношение для
обращенных матриц
 (11.4.11)
(11.4.11)
Таким образом, ![]() можно вычислить рекуррентно
согласно (11.4.11).
можно вычислить рекуррентно
согласно (11.4.11).
Для удобства определим ![]() . Также удобно определить
. Также удобно определить
![]() -мерный
вектор, называемый вектор калмановского усиления, так
-мерный
вектор, называемый вектор калмановского усиления, так
![]() (11.4.12)
(11.4.12)
где ![]() является скаляром, определяемым так
является скаляром, определяемым так
![]() (11.4.13)
(11.4.13)
С этими определениями (11.4.11) приводится к виду
![]() (11.4.14)
(11.4.14)
Предположим, что мы умножаем обе части
(11.4.14) на ![]() .
Тогда
.
Тогда
 (11.4.15)
(11.4.15)
Следовательно, вектор калмановского усилия можно
также определить как ![]() .
.
Теперь используем соотношение для
обратных матриц для получения уравнения, определяющего ![]() по
по ![]() . Поскольку
. Поскольку
![]()
и
![]() (11.4.16)
(11.4.16)
имеем
 (11.4.17)
(11.4.17)
Заметим, что ![]() это выход эквалайзера в
момент
это выход эквалайзера в
момент ![]() ,
то есть
,
то есть
![]() (11.4.18)
(11.4.18)
и
![]() (11.4.19)
(11.4.19)
- это ошибка между желательным символом
и его оценкой. Таким образом, ![]() определяется рекуррентно согласно
отношению
определяется рекуррентно согласно
отношению
![]() (11.4.20)
(11.4.20)
Остаточный СКО, получаемый при такой оптимизации, равен
![]() (11.4.21)
(11.4.21)
Для суммирования предположим, что мы
имеем ![]() и
и ![]() . Когда принимается
новая сигнальная компонента имеем
. Когда принимается
новая сигнальная компонента имеем ![]() . Затем рекуррентные вычисления для
обновления
. Затем рекуррентные вычисления для
обновления ![]() и
и
![]() продолжаются
так:
продолжаются
так:
- вычисляется выход:
![]()
- вычисляется ошибка:
![]()
- вычисляется вектор калмановского усиления:

- вычисляется соотношение обратных матриц
![]()
- определяются коэффициенты
![]() (11.4.22)
(11.4.22)
Алгоритм, определяемый (11.4.22), назван
прямой формой РНК или алгоритмом Калмана. Он подходит, когда эквалайзер имеет
трансверсальную (прямая форма) структуру. Заметим, что коэффициенты эквалайзера
меняются со временем на величину, равной ошибки ![]() , уменьшенной на вектор усиления
Калмана
, уменьшенной на вектор усиления
Калмана ![]() .
Поскольку
.
Поскольку ![]() является
является
![]() -мерным
каждый коэффициент ячейки в действительности управляется одним из элементов
-мерным
каждый коэффициент ячейки в действительности управляется одним из элементов ![]() . Как следствие
получается быстрая сходимость. В противоположность этому, алгоритм кратчайшего
спуска, выраженный в новых обозначениях, определяется так
. Как следствие
получается быстрая сходимость. В противоположность этому, алгоритм кратчайшего
спуска, выраженный в новых обозначениях, определяется так
![]() (11.4.23)
(11.4.23)
и единственным переменным параметром
является размер шага ячейки ![]() .
.
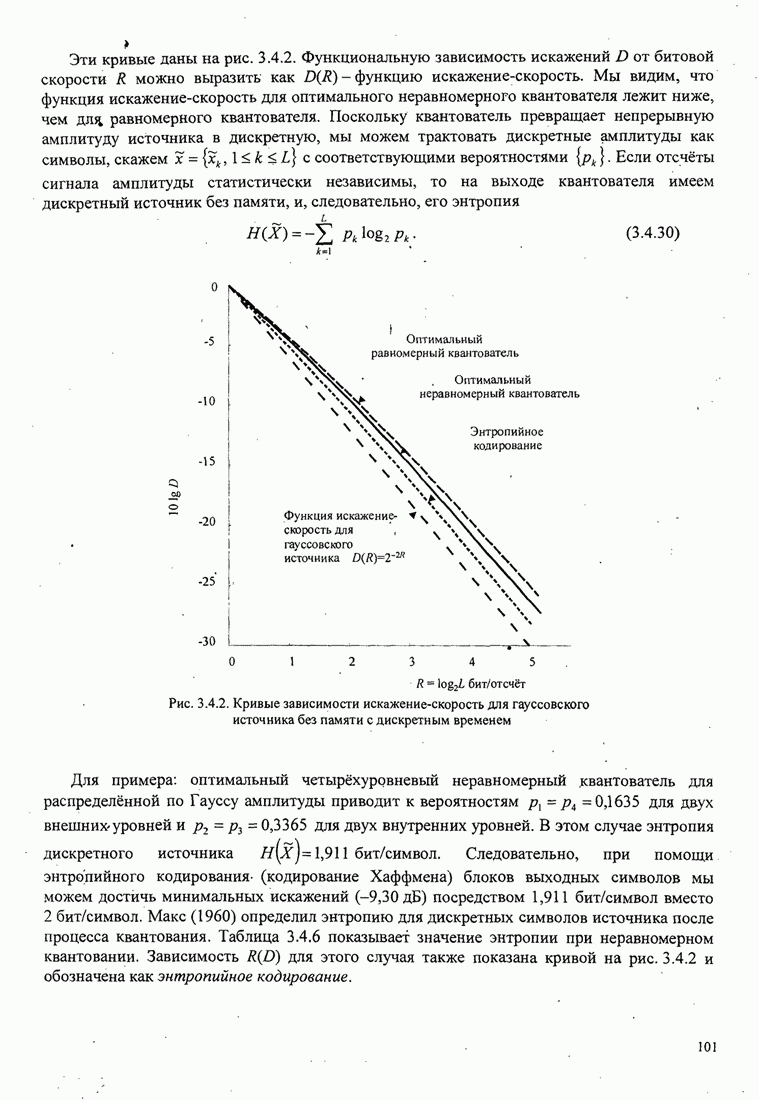
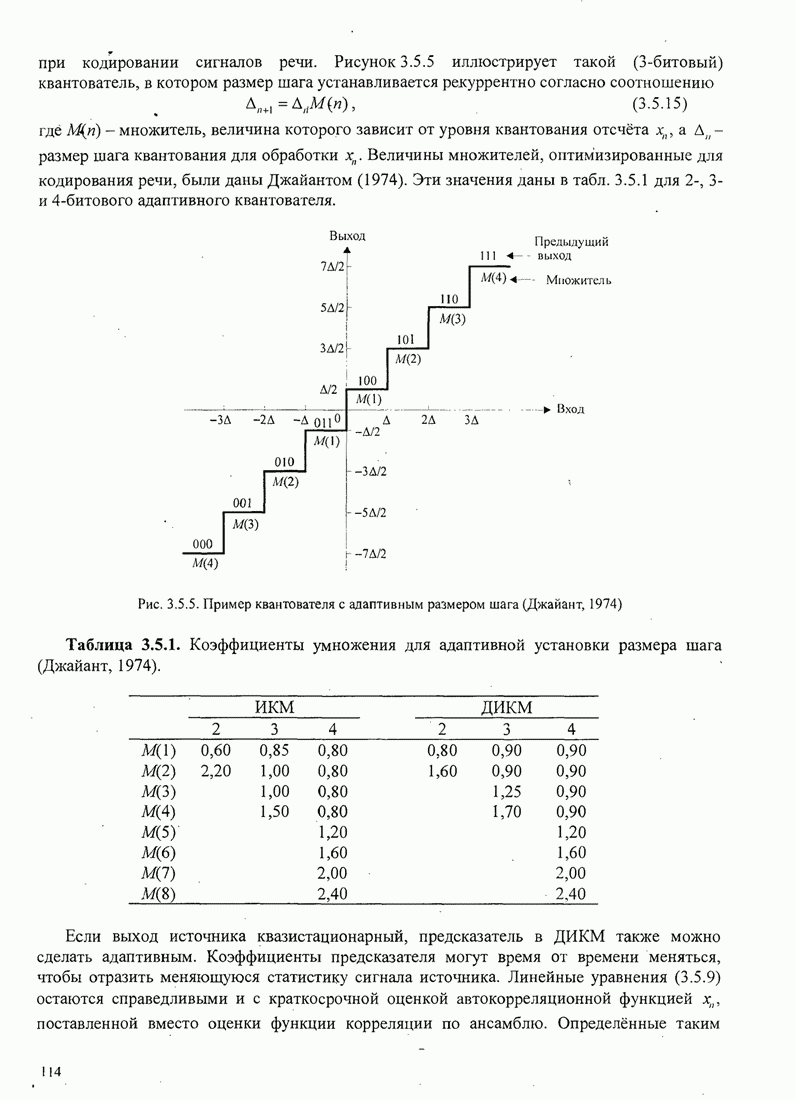
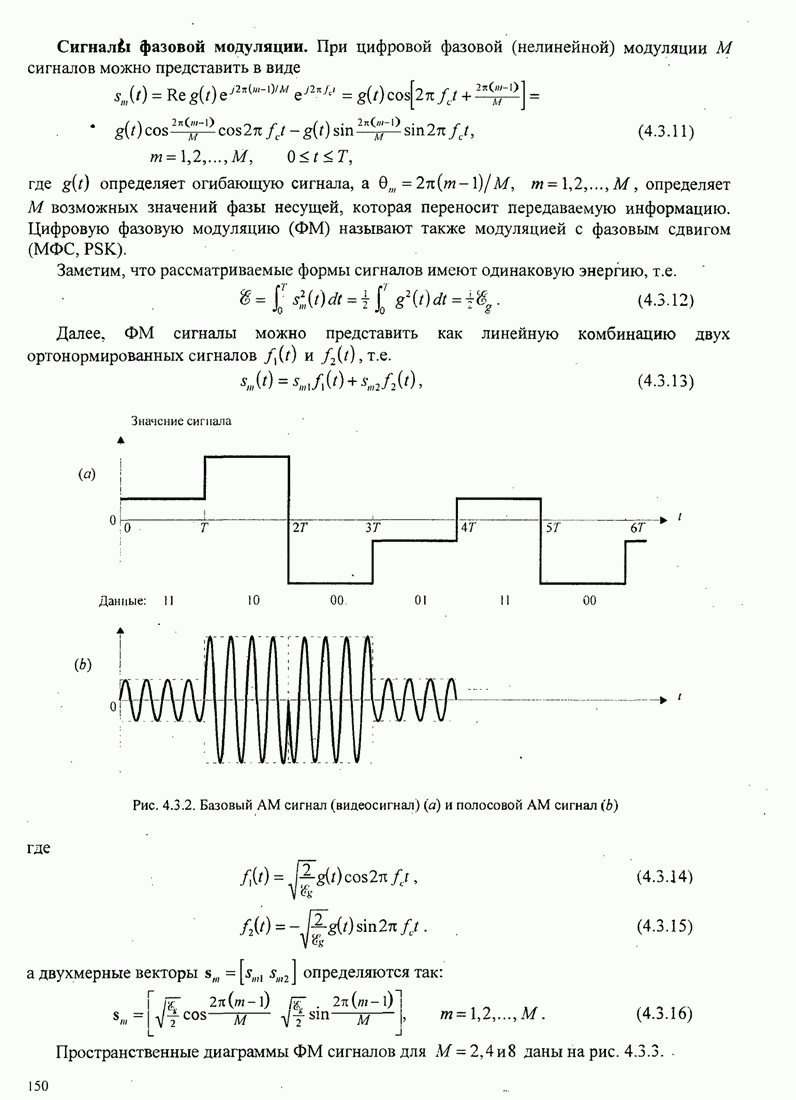
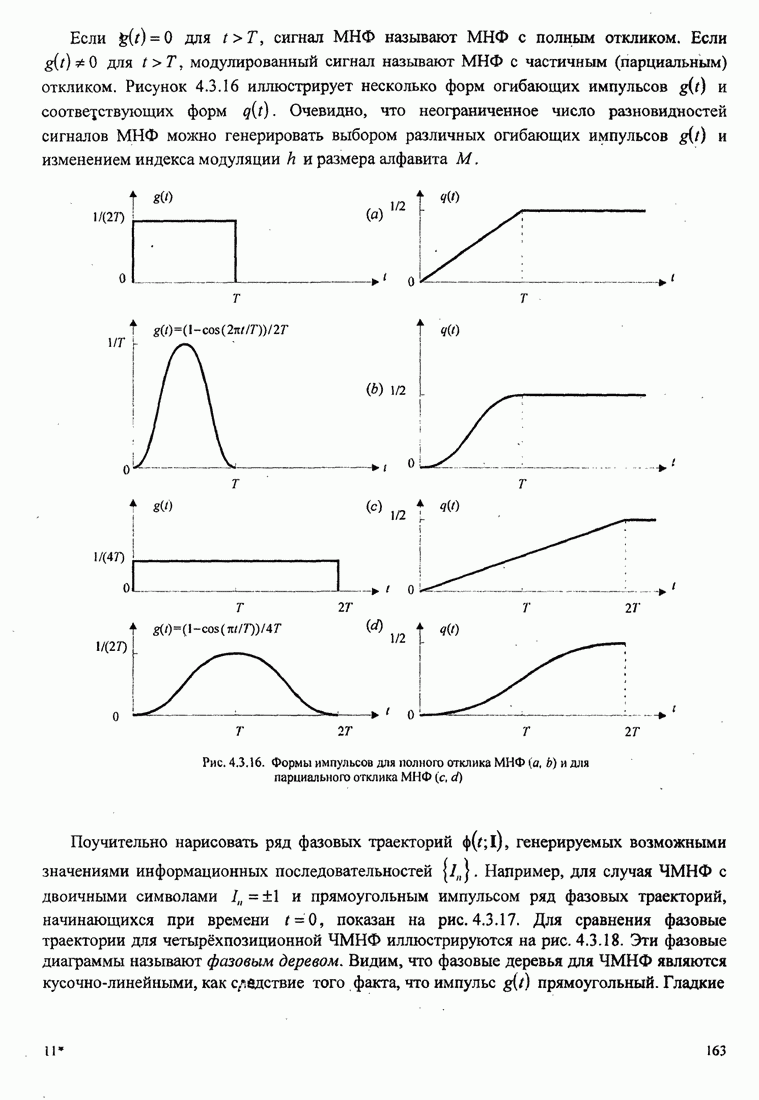
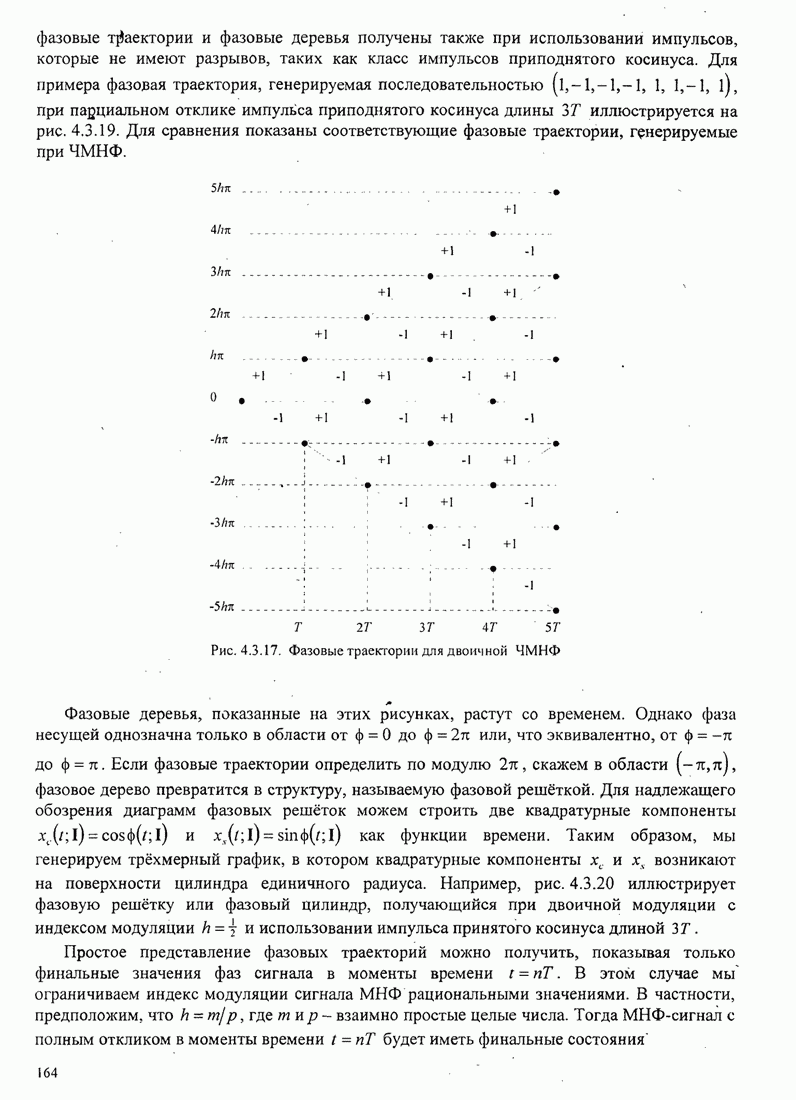
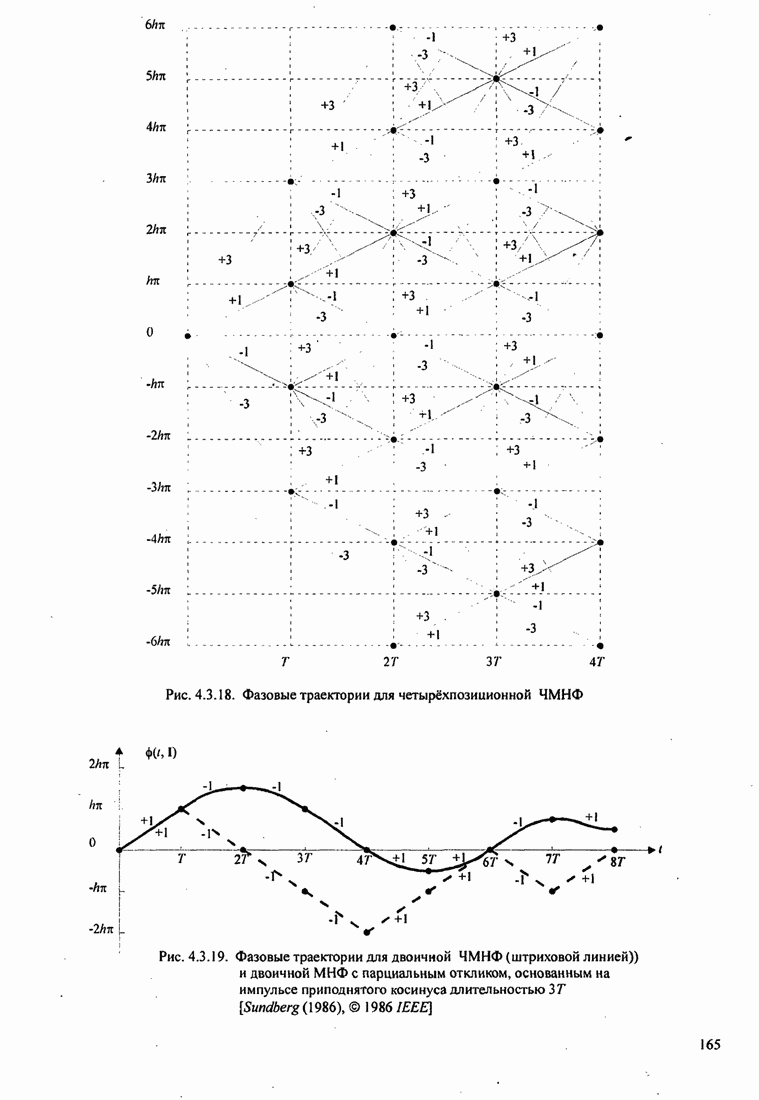
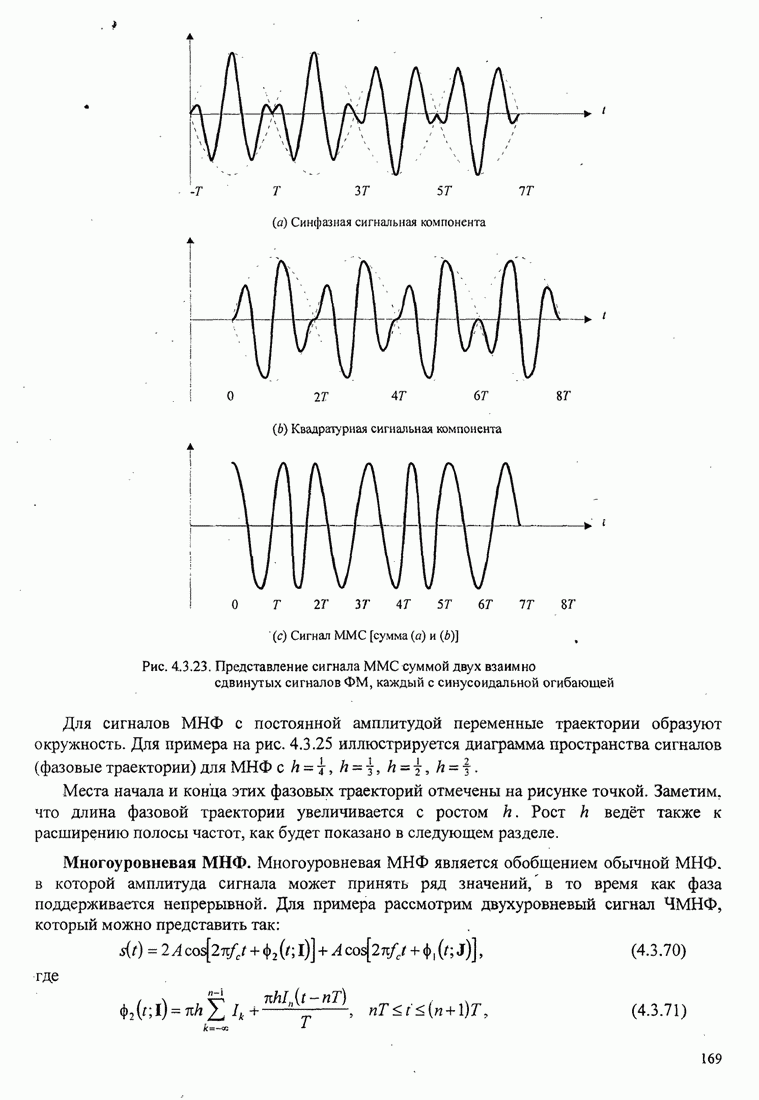
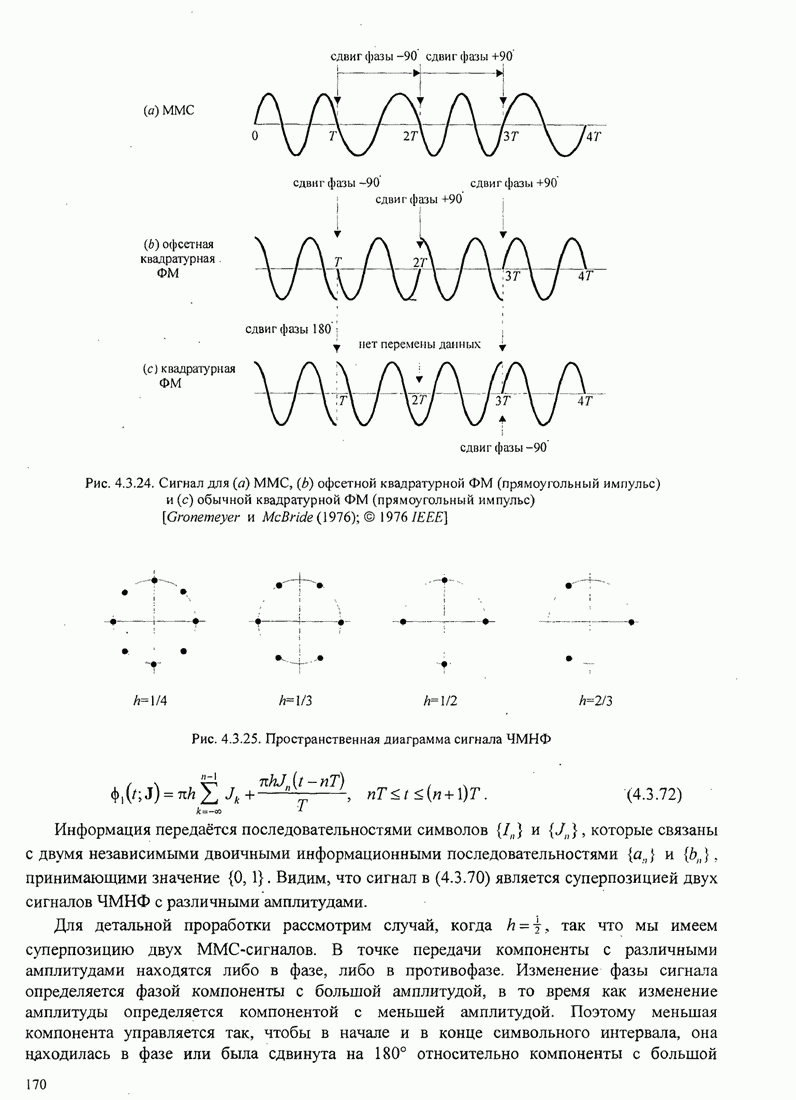
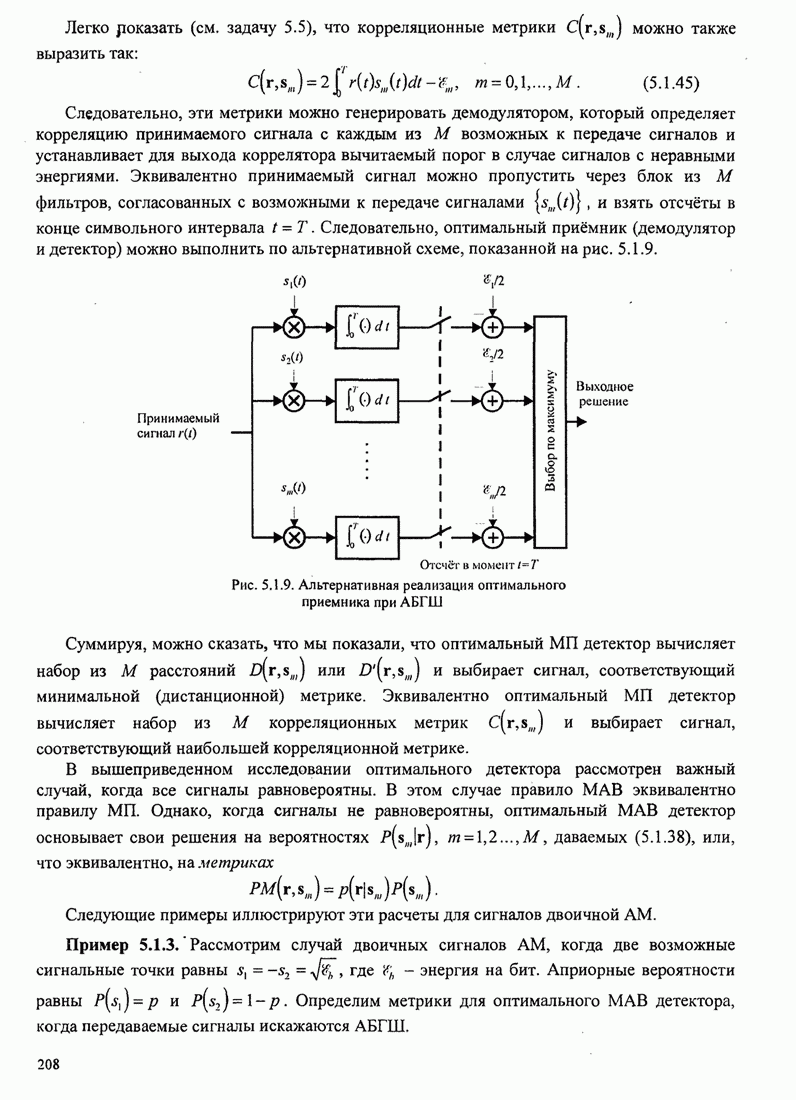
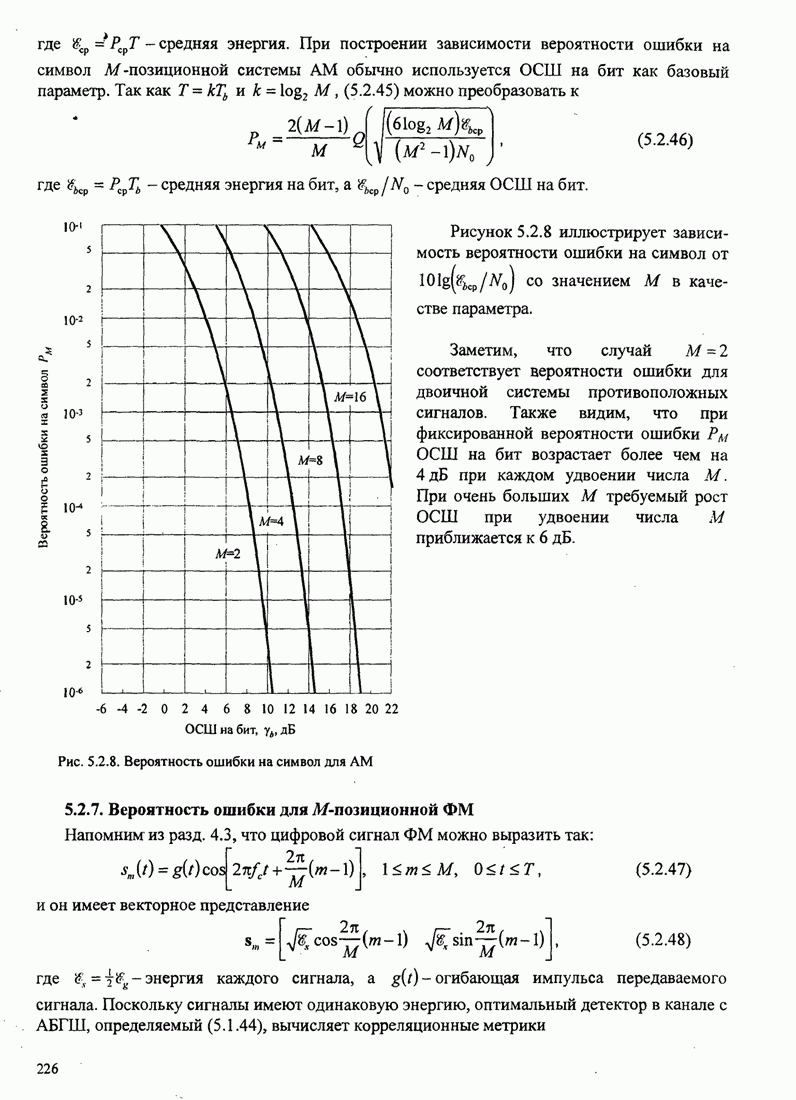
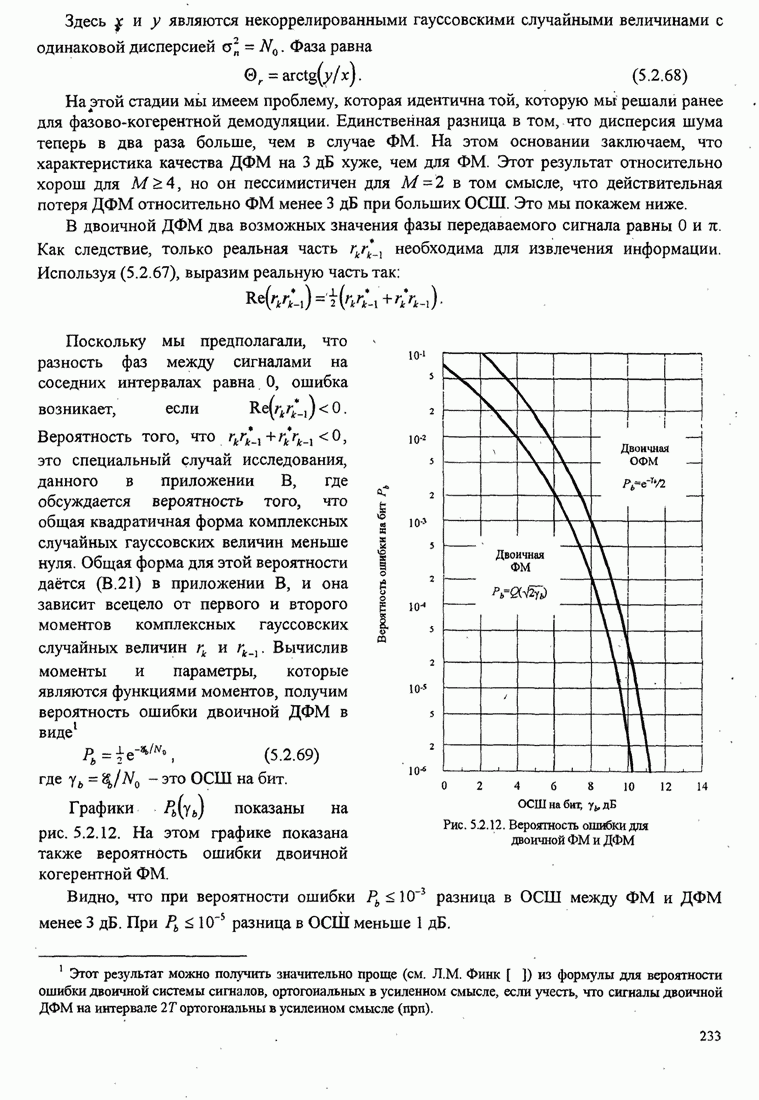
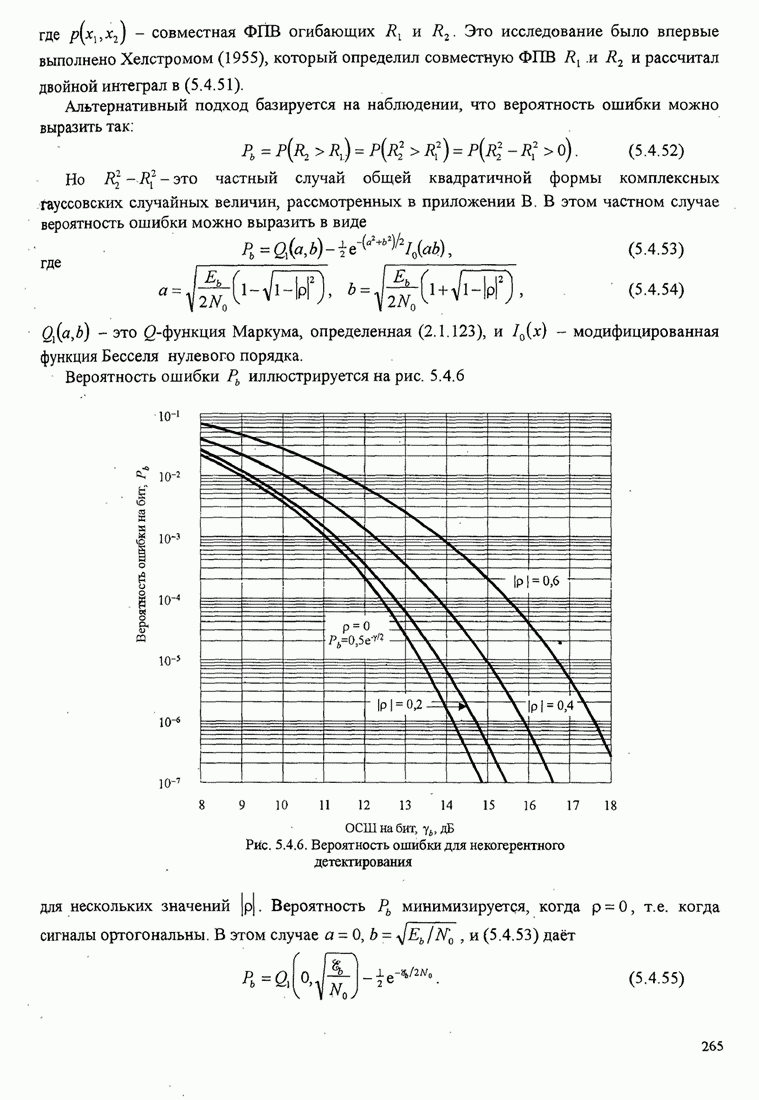
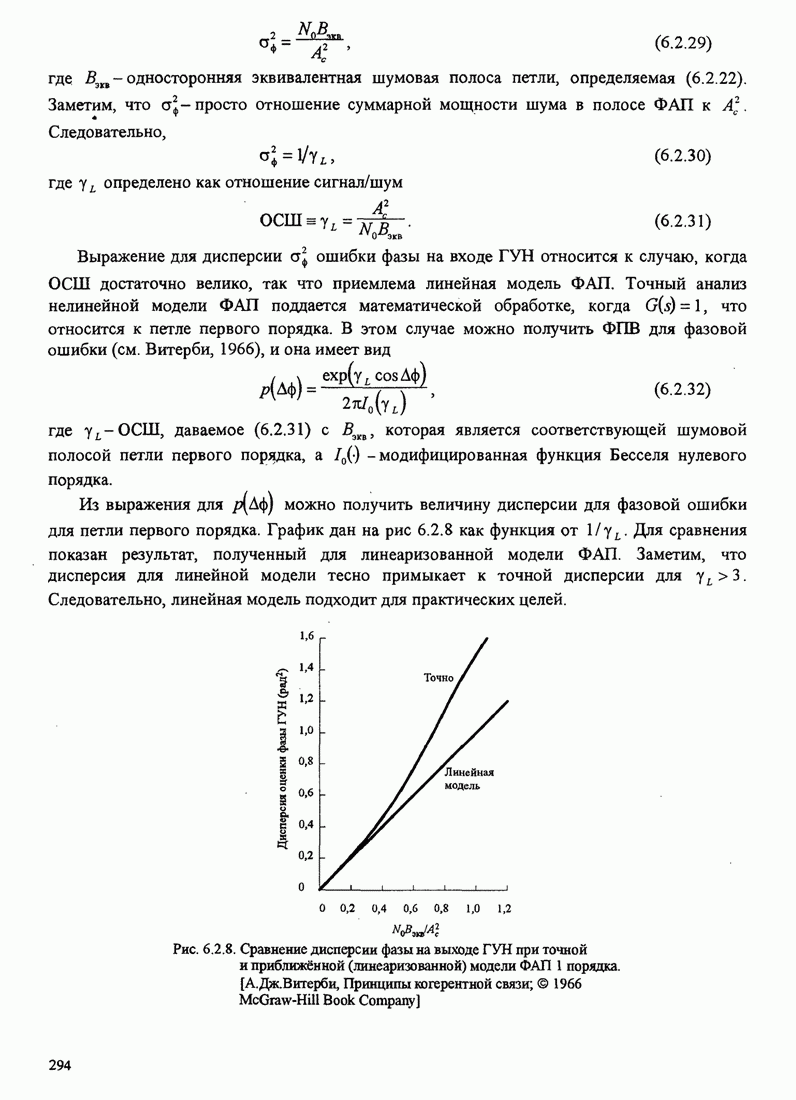
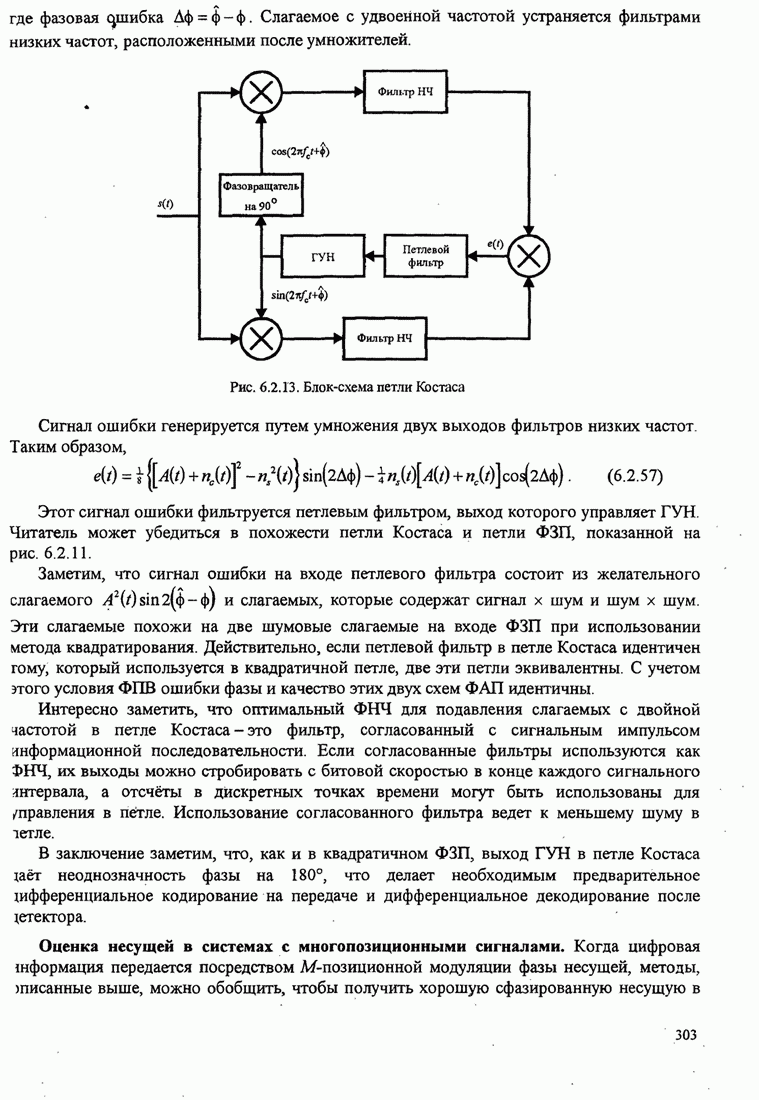
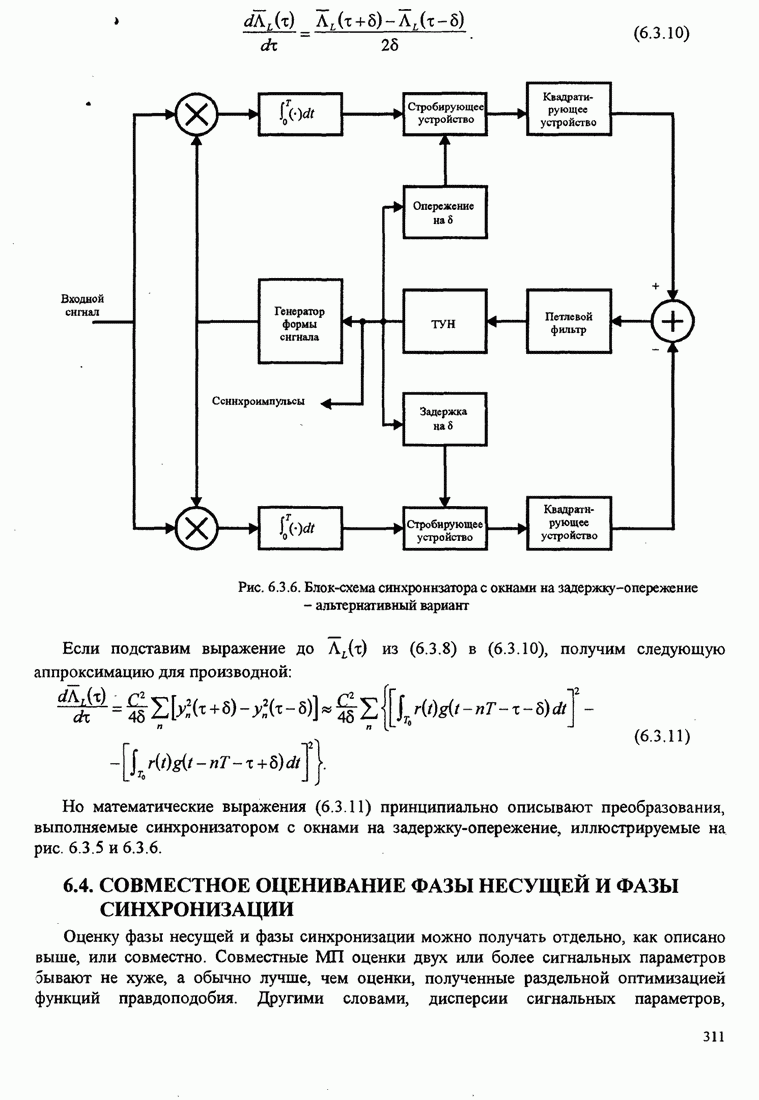
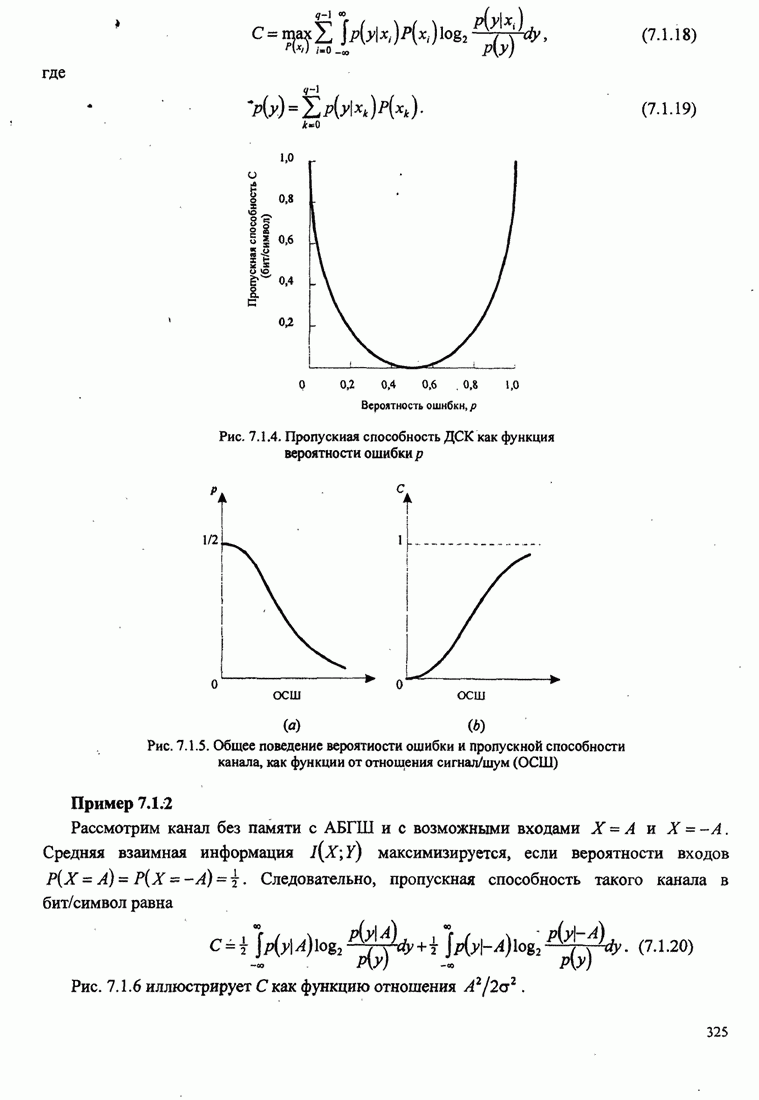
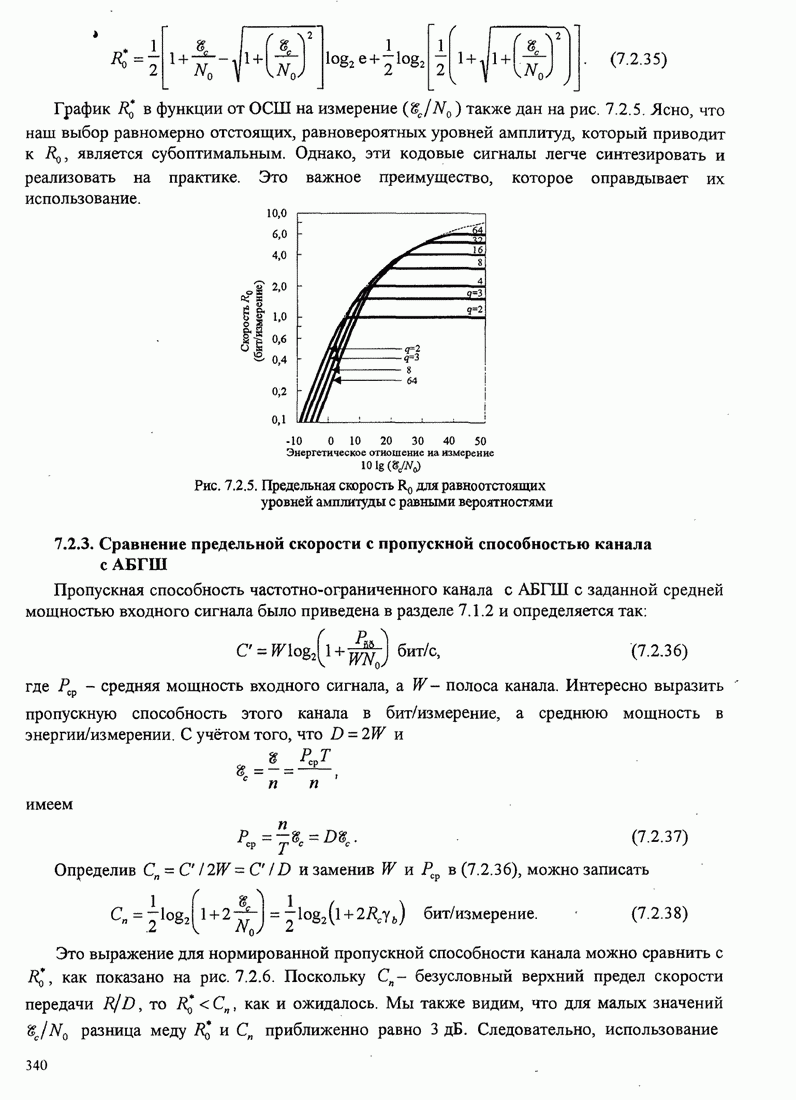
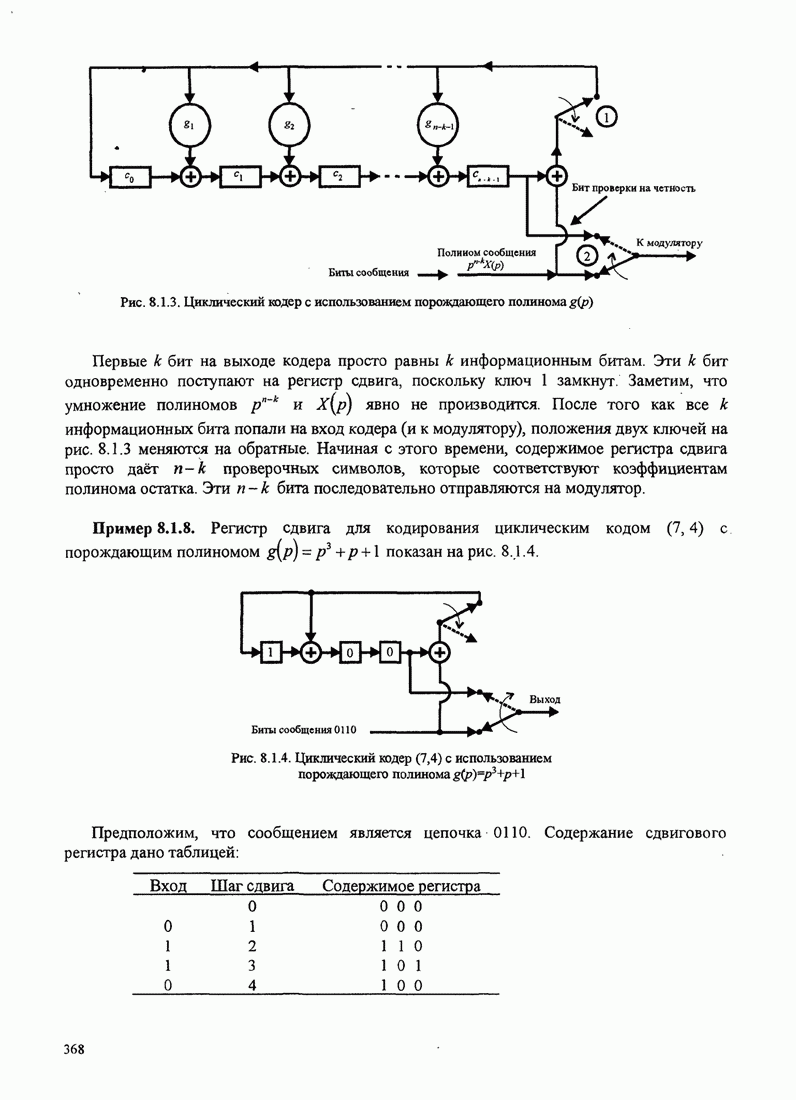
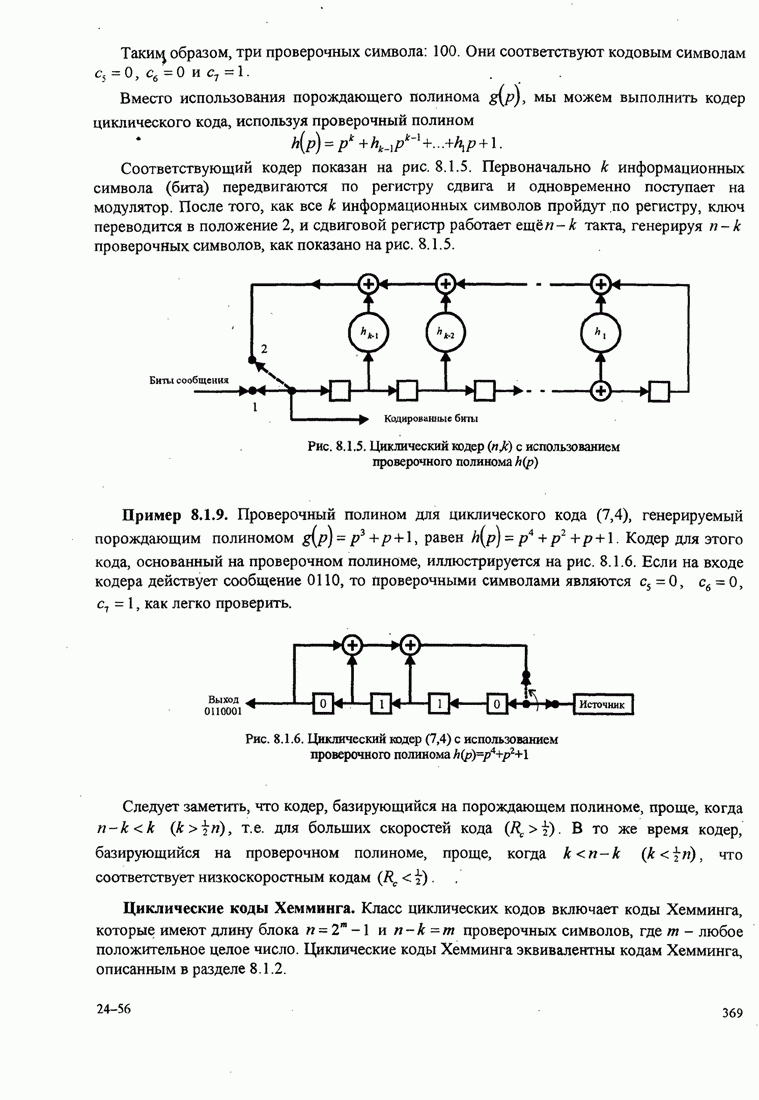
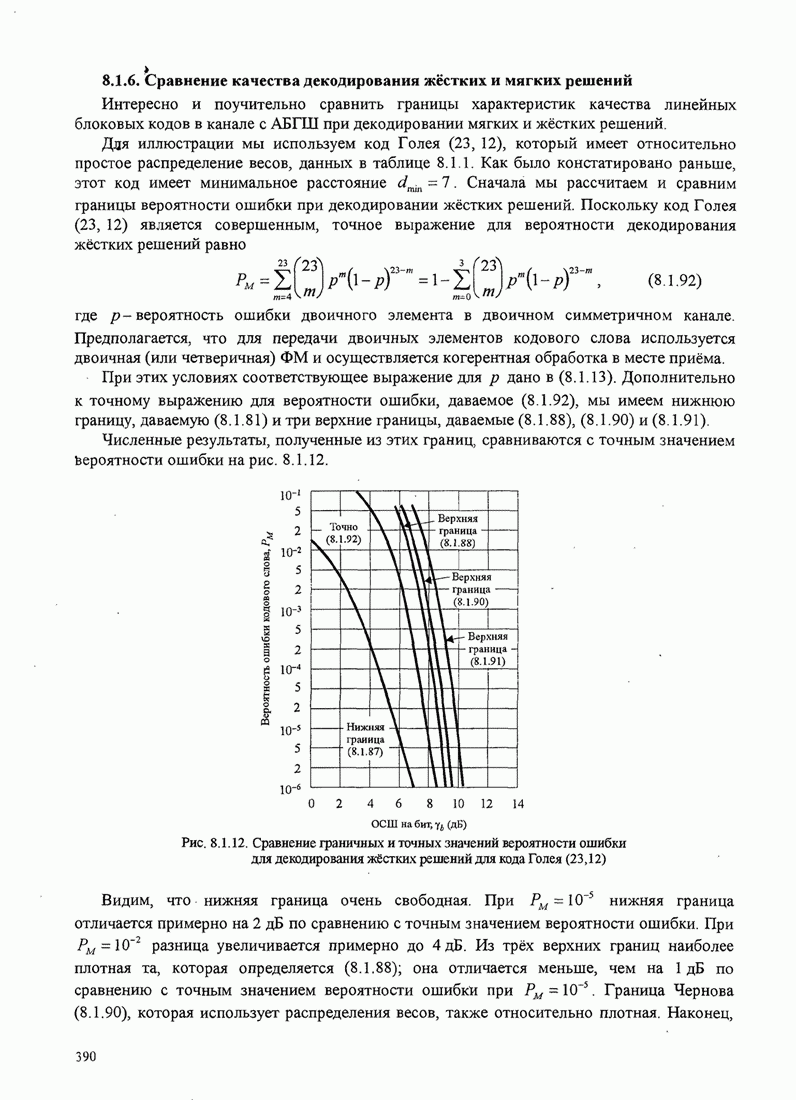
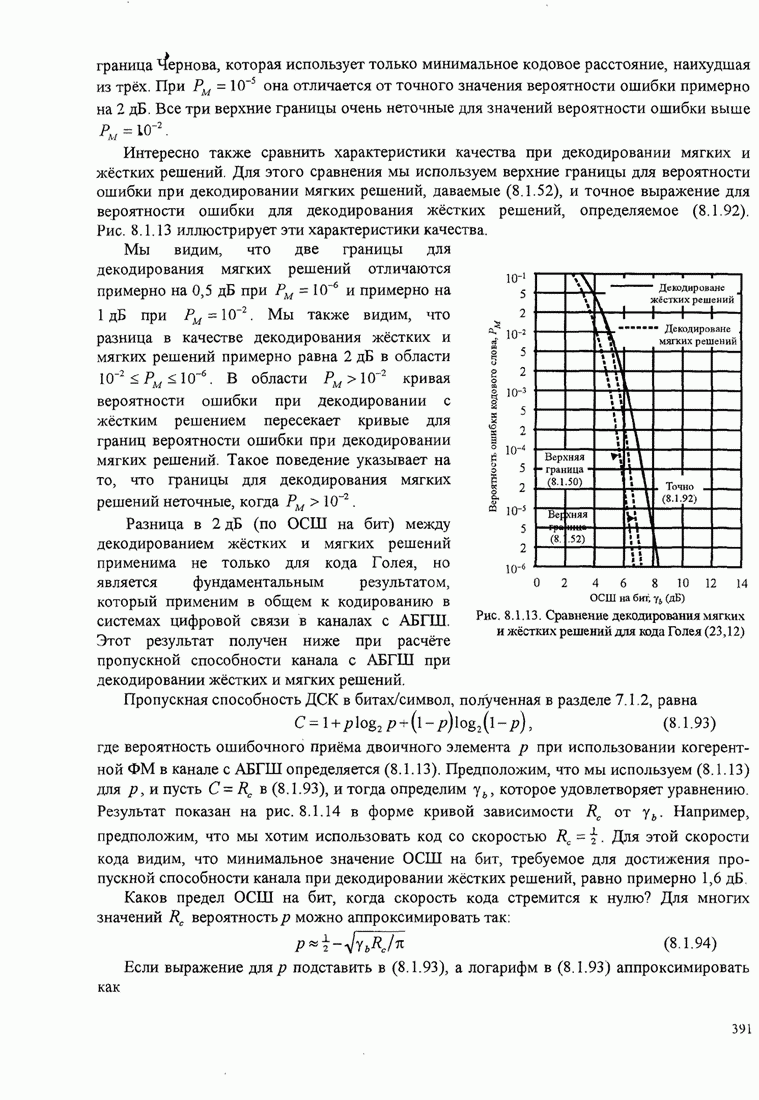
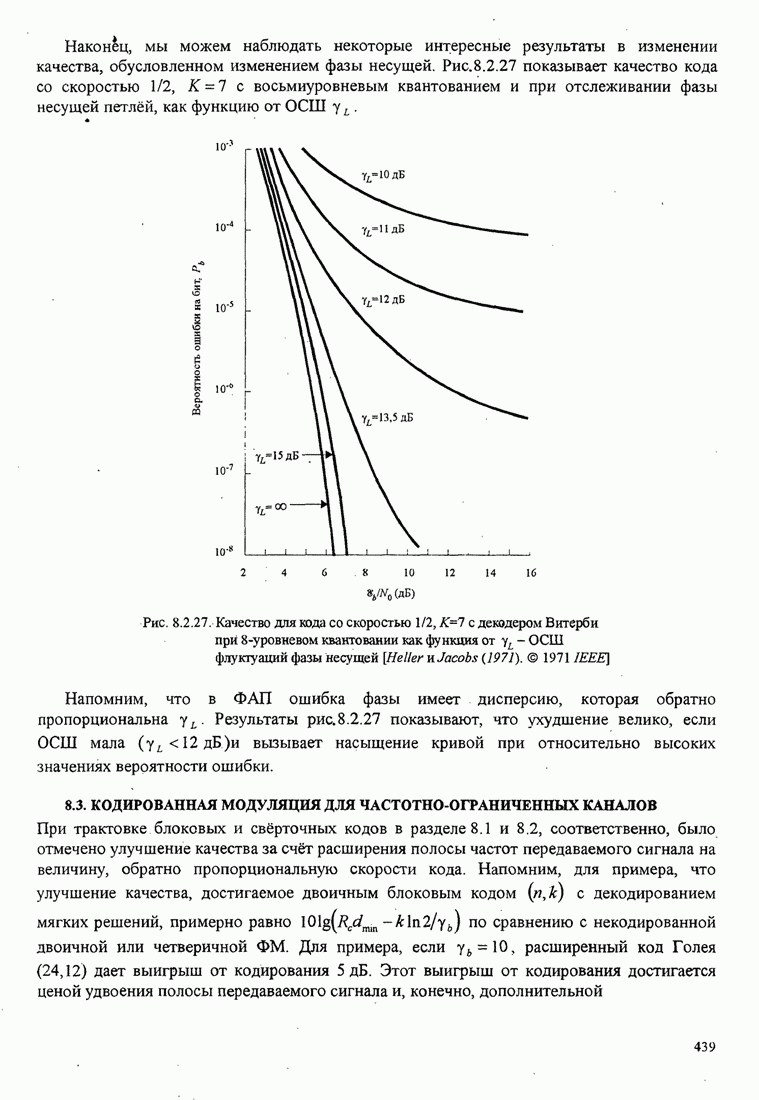
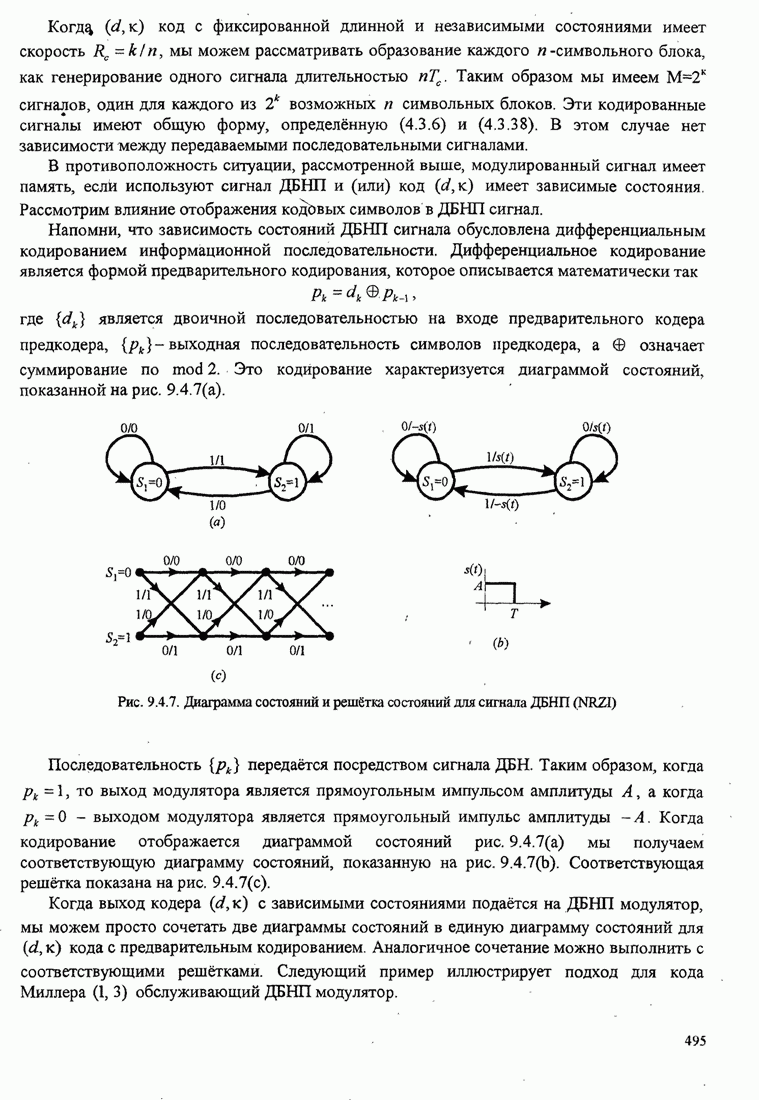
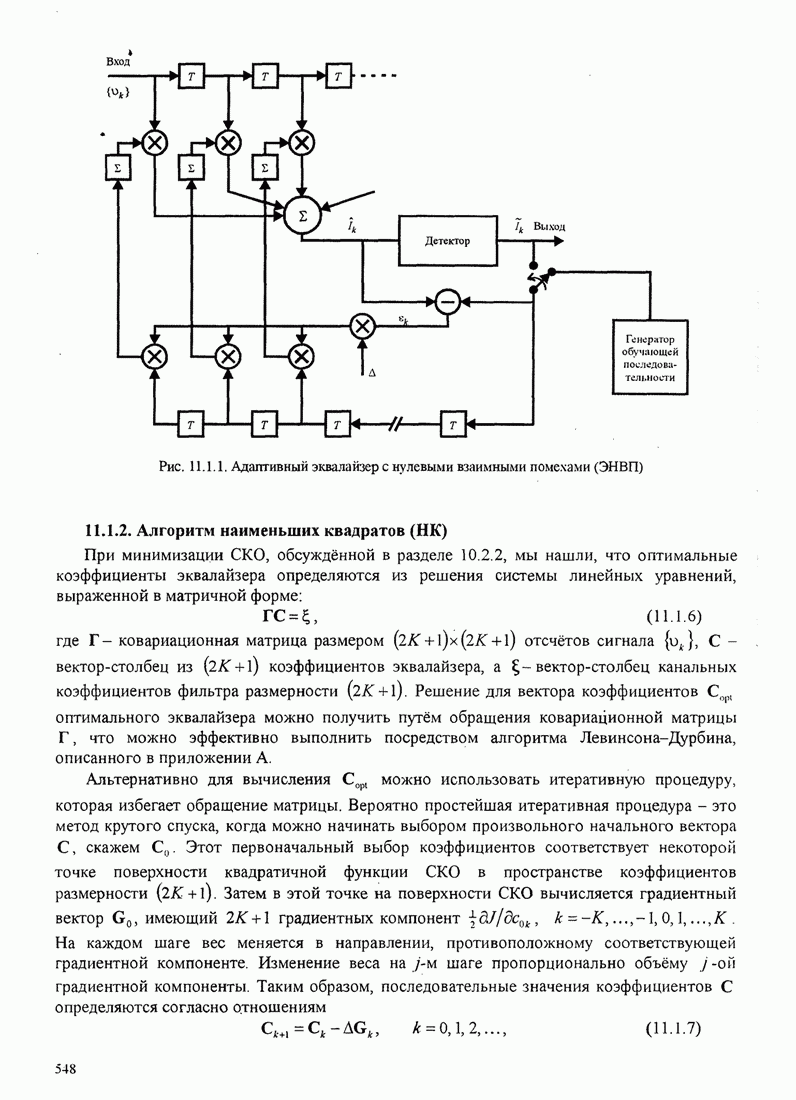
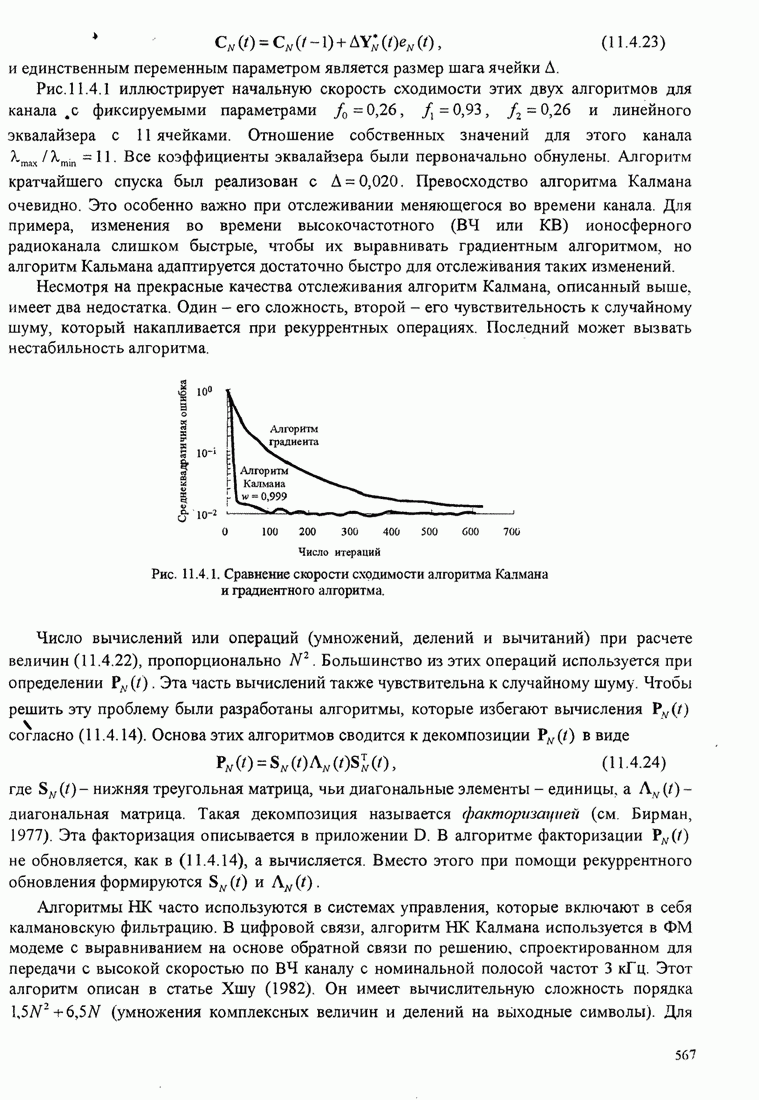
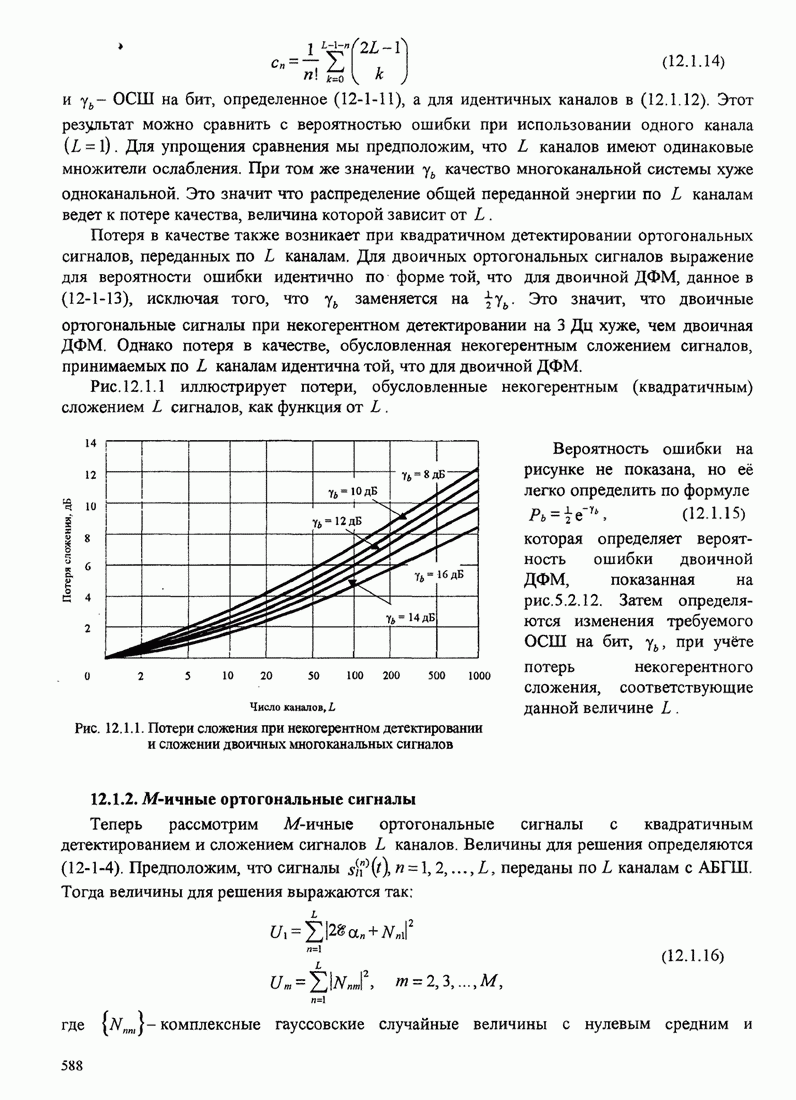
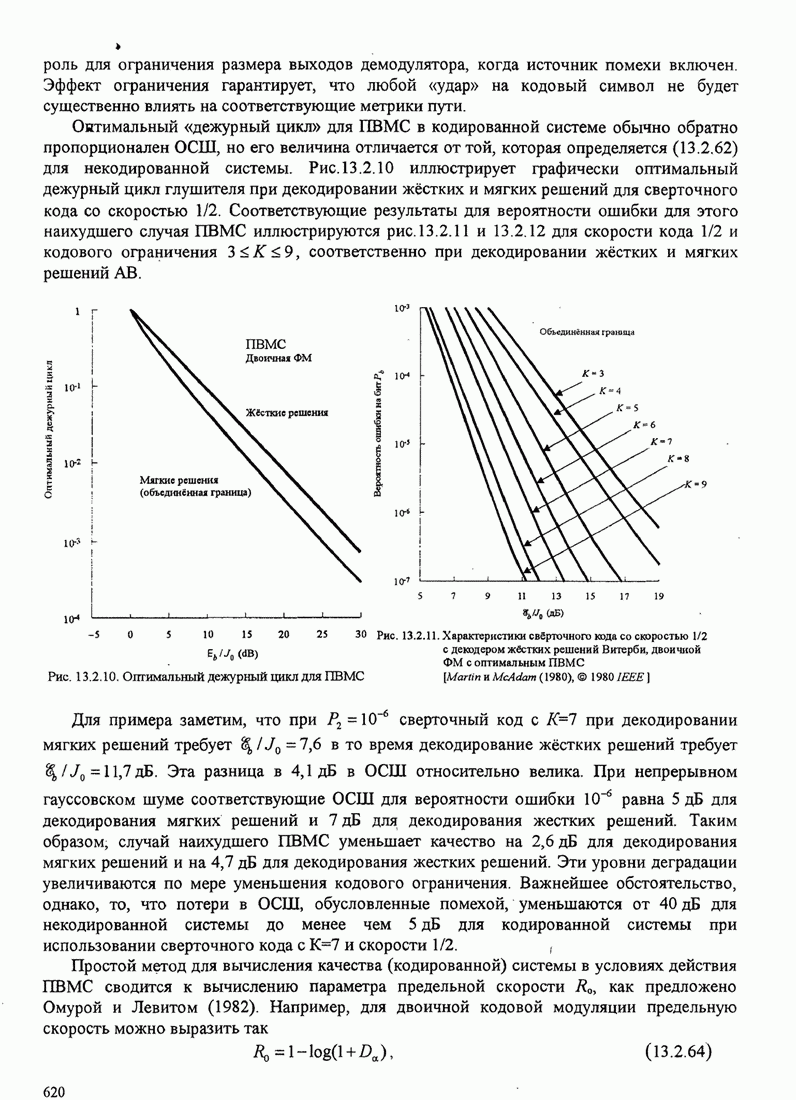
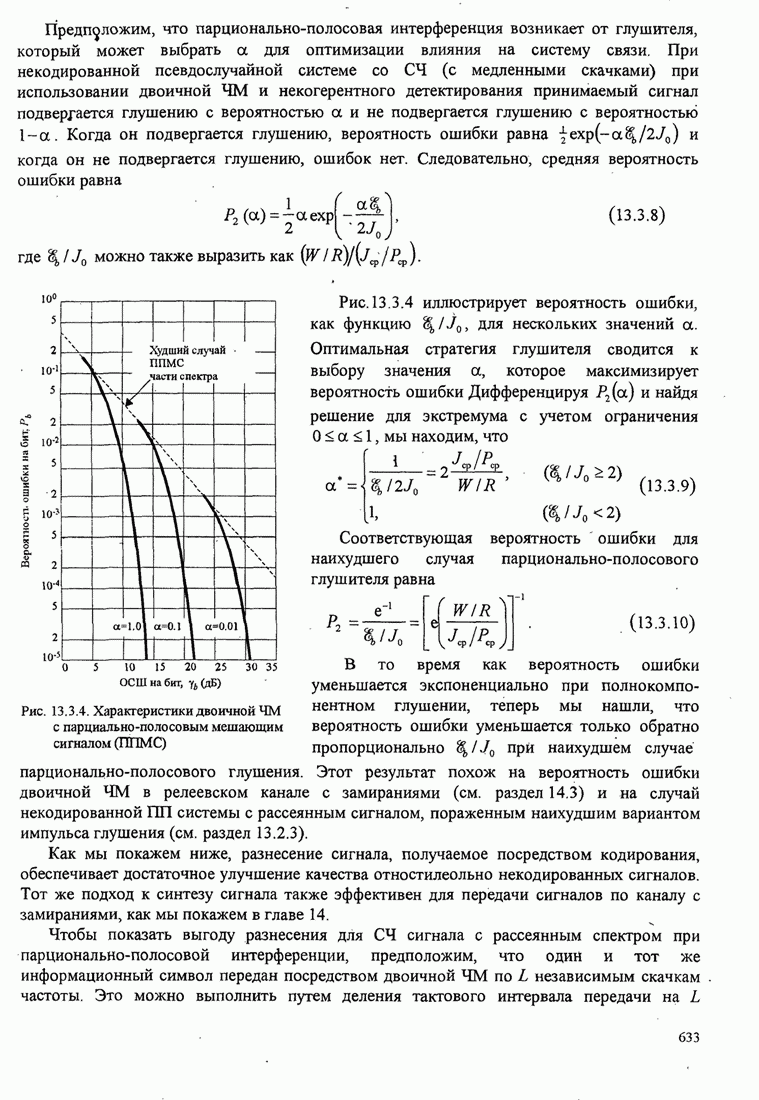
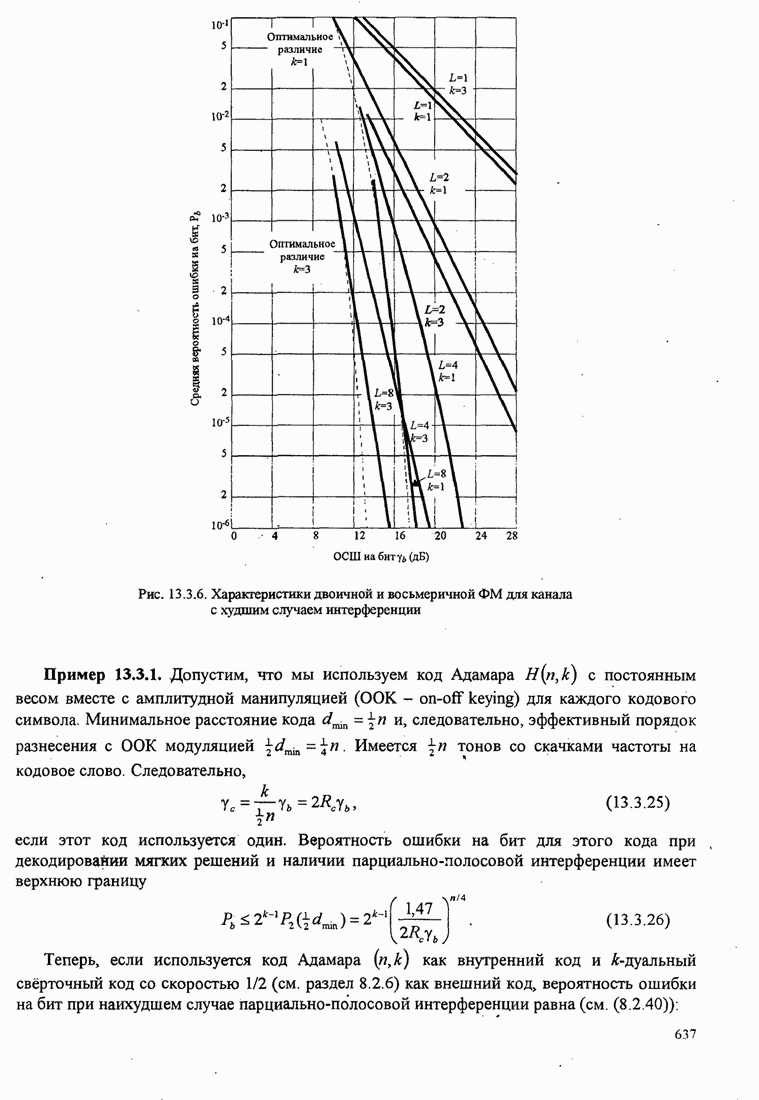
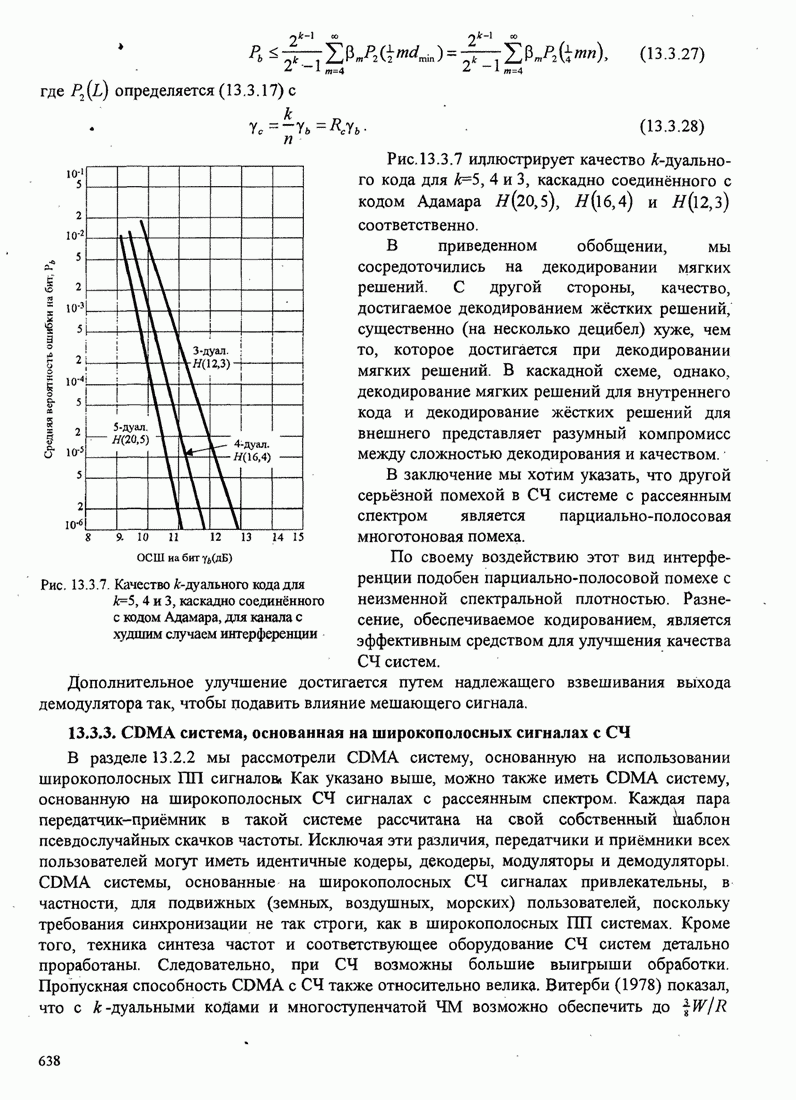
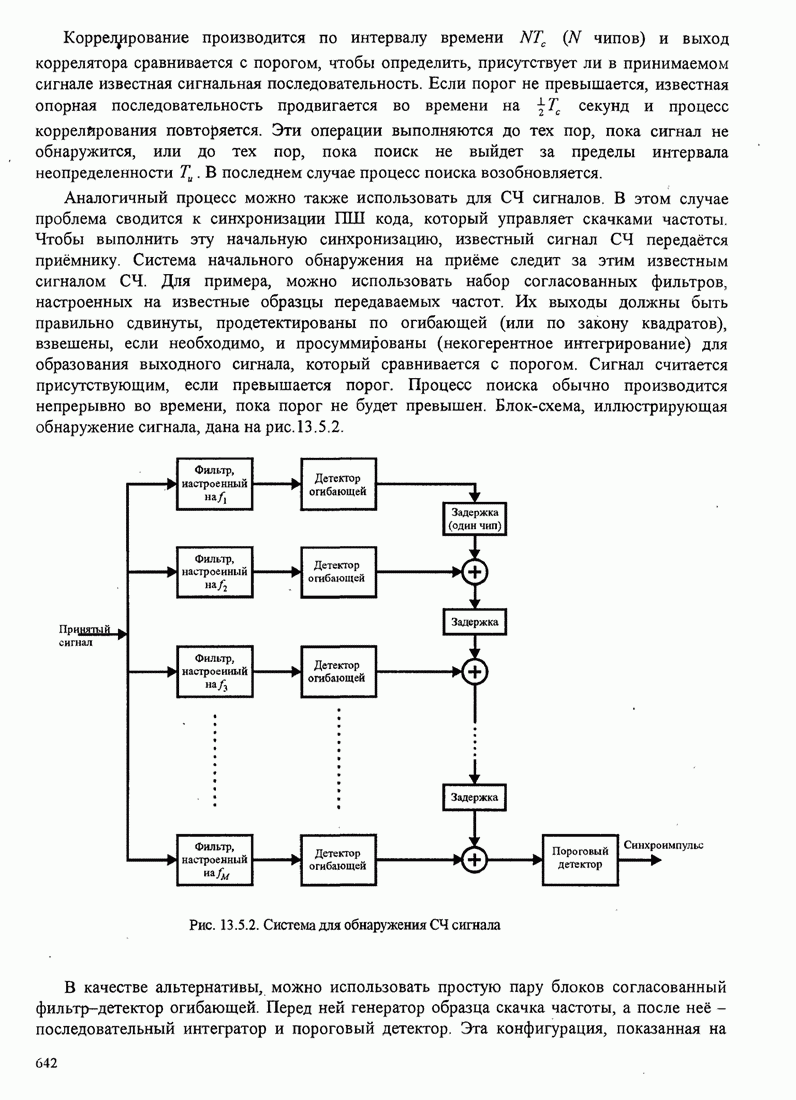
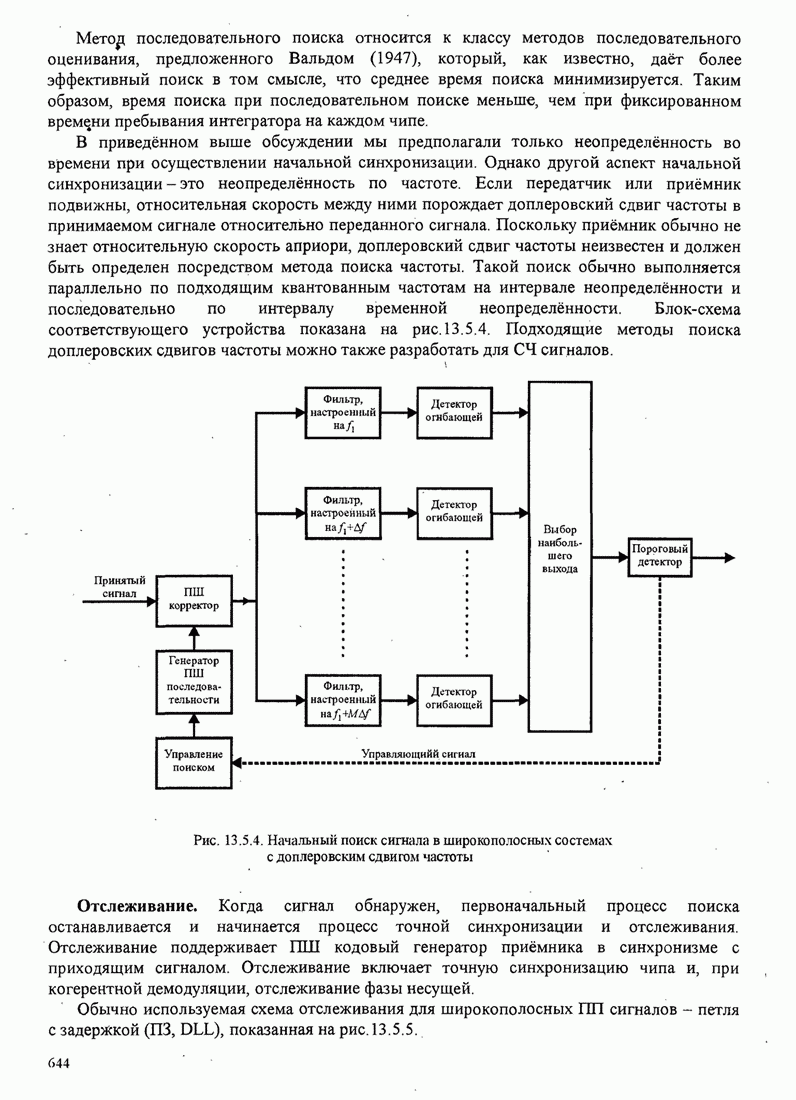
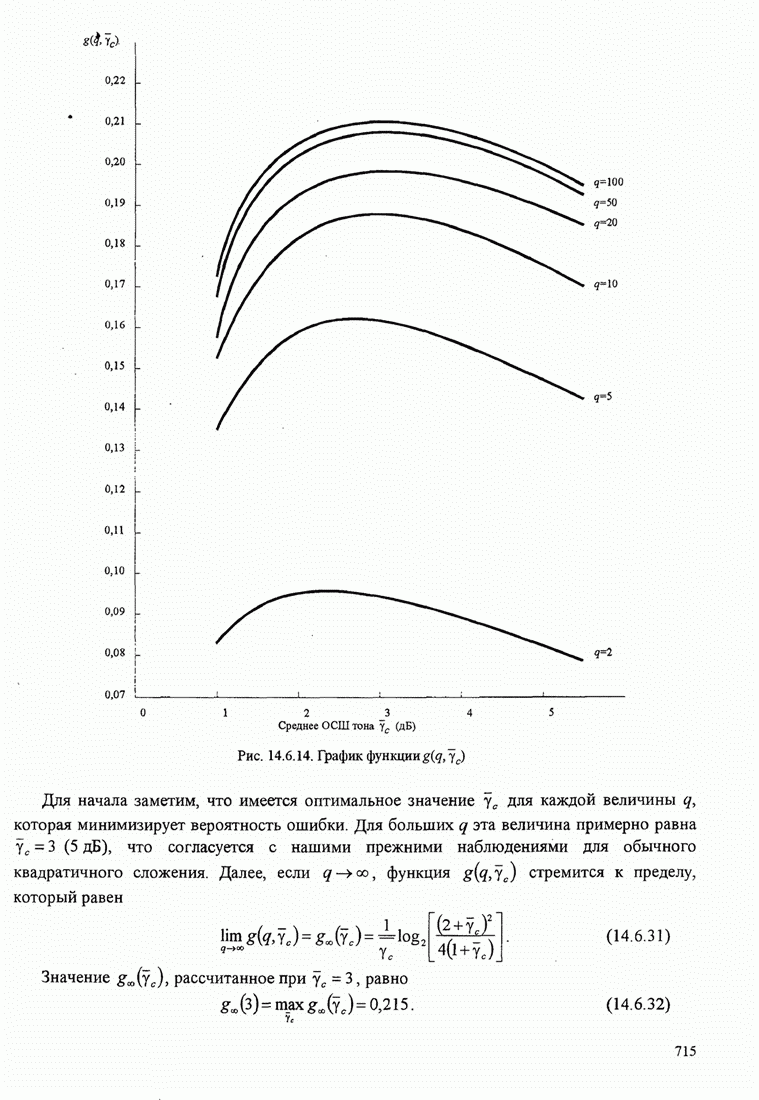
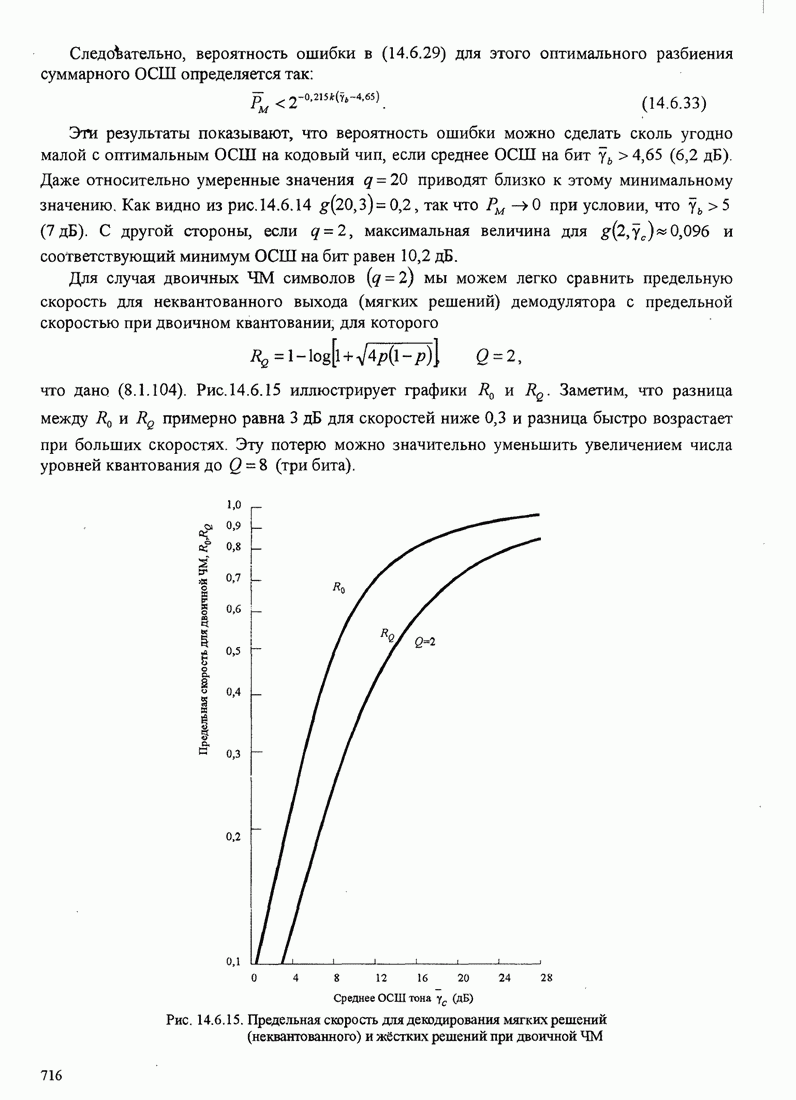
Рис.11.4.1 иллюстрирует начальную
скорость сходимости этих алгоритмов для канала с фиксируемыми параметрами ![]() ,
, ![]() ,
, ![]() и линейного
эквалайзера с 11 ячейками. Отношение собственных значений для этого канала
и линейного
эквалайзера с 11 ячейками. Отношение собственных значений для этого канала ![]() . Все коэффициенты
эквалайзера были первоначально обнулены. Алгоритм кратчайшего спуска был
реализован с
. Все коэффициенты
эквалайзера были первоначально обнулены. Алгоритм кратчайшего спуска был
реализован с ![]() .
Превосходство алгоритма Калмана очевидно. Это особенно важно при отслеживании
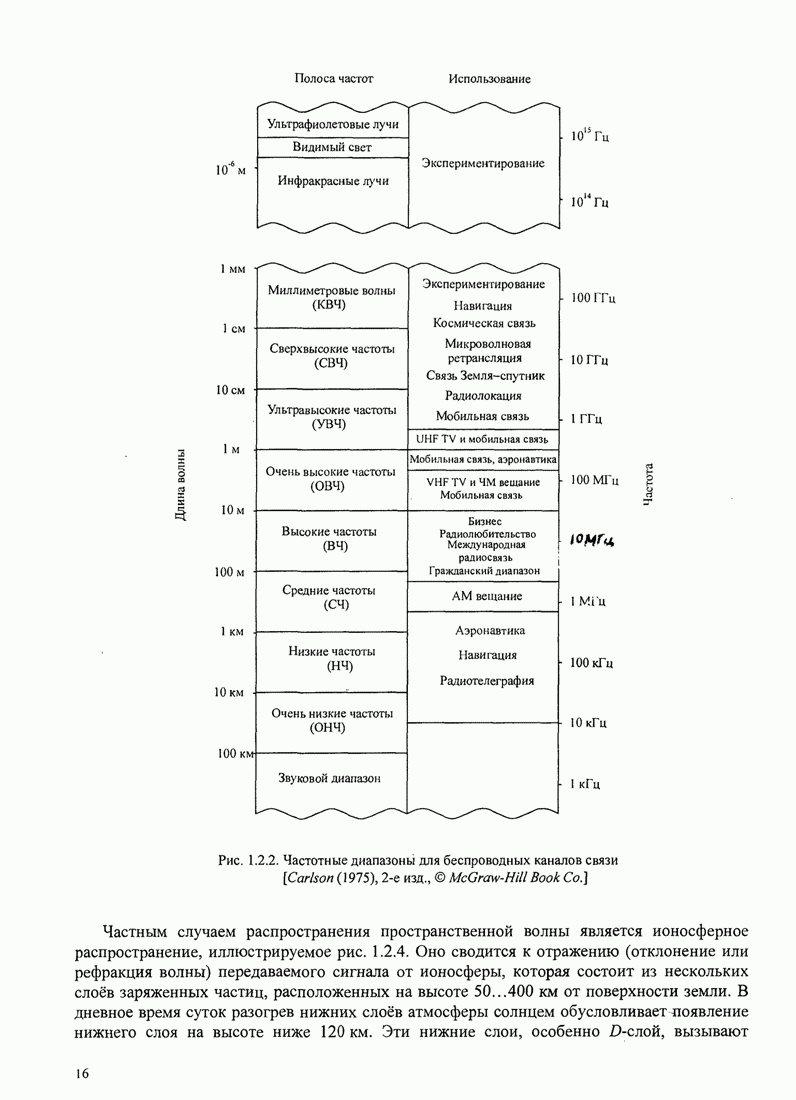
меняющегося во времени канала. Для примера, изменения во времени
высокочастотного (ВЧ или КВ) ионосферного радиоканала слишком быстрые, чтобы их
выравнивать градиентным алгоритмом, но алгоритм Калмана адаптируется достаточно
быстро для отслеживания таких изменений.
.
Превосходство алгоритма Калмана очевидно. Это особенно важно при отслеживании
меняющегося во времени канала. Для примера, изменения во времени
высокочастотного (ВЧ или КВ) ионосферного радиоканала слишком быстрые, чтобы их
выравнивать градиентным алгоритмом, но алгоритм Калмана адаптируется достаточно
быстро для отслеживания таких изменений.
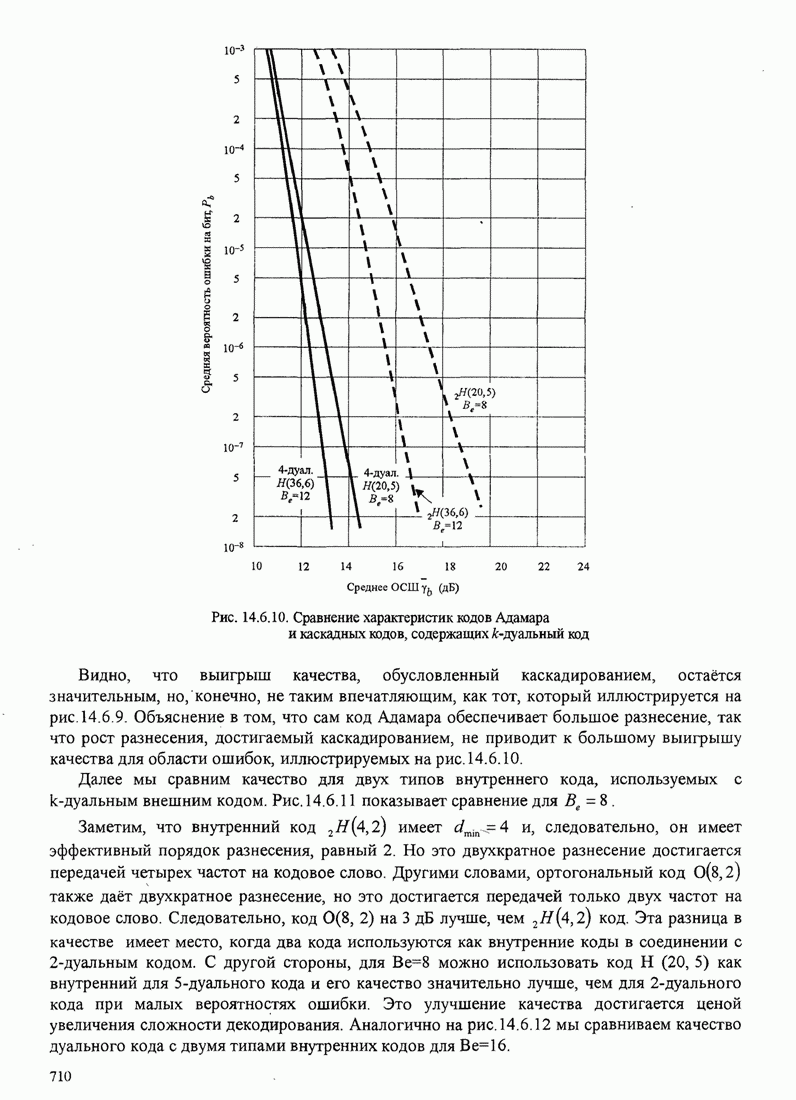
Несмотря на прекрасные качества отслеживания алгоритм Калмана, описанный выше, имеет два недостатка. Один – его сложность, второй – его чувствительность к случайному шуму, который накапливается при рекуррентных операциях. Последний может вызвать нестабильность алгоритма.

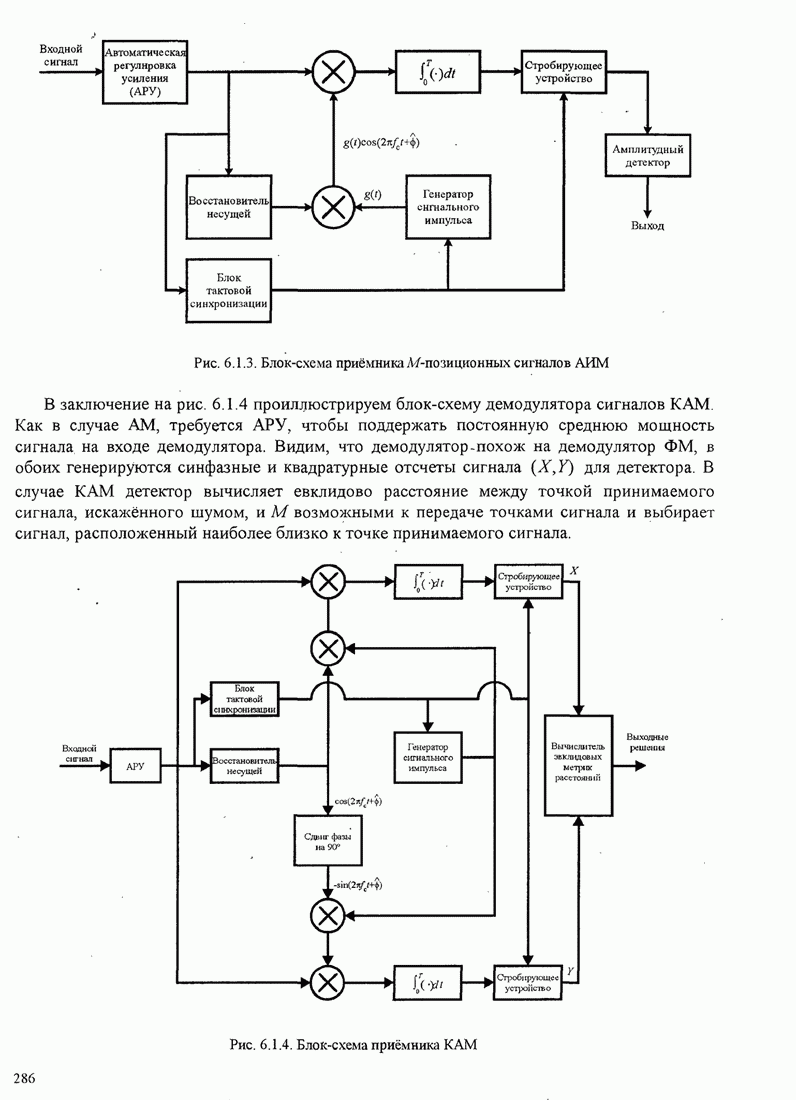
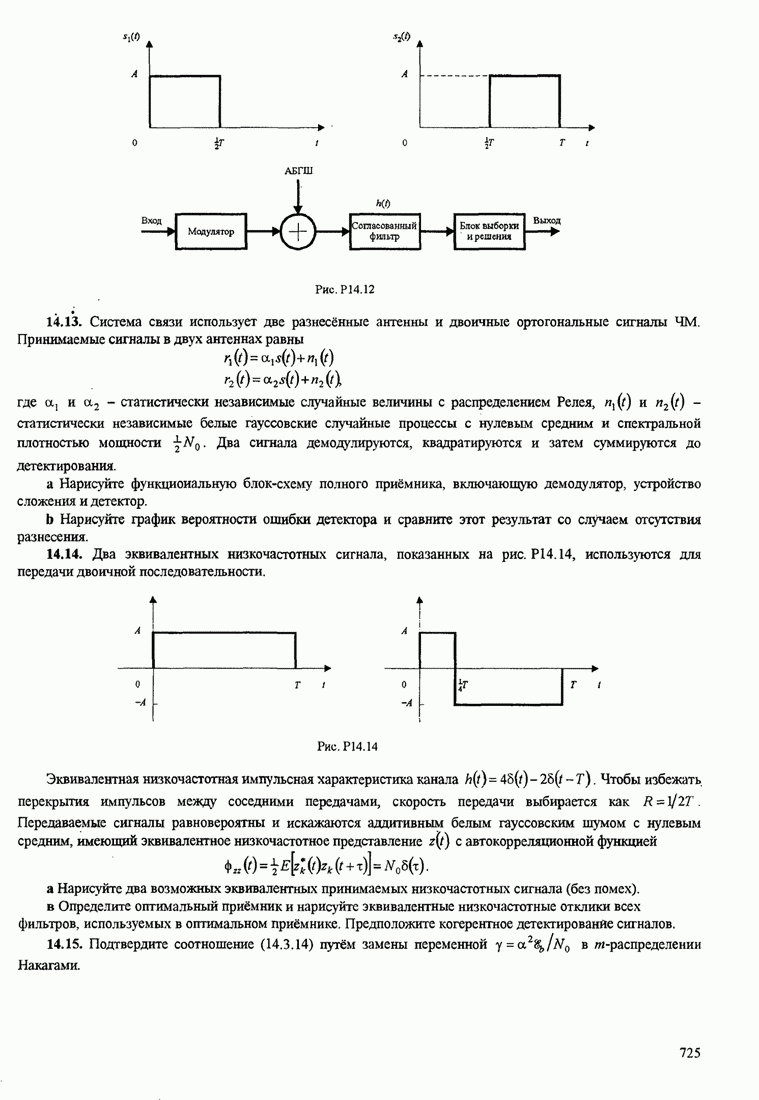
Рис. 11.4.1. Сравнение скорости сходимости алгоритма Калмана и градиентного алгоритма.
Число вычислений или операций
(умножений, делений и вычитаний) при расчете величин (11.4.22), пропорционально
![]() .
Большинство из этих операций используется при определении
.
Большинство из этих операций используется при определении ![]() . Эта часть вычислений также
чувствительна к случайному шуму. Чтобы решить эту проблему были разработаны
алгоритмы, которые избегают вычисления
. Эта часть вычислений также
чувствительна к случайному шуму. Чтобы решить эту проблему были разработаны
алгоритмы, которые избегают вычисления ![]() согласно (11.4.14). Основа этих
алгоритмов сводится к декомпозиции
согласно (11.4.14). Основа этих
алгоритмов сводится к декомпозиции ![]() в виде
в виде
![]() (11.4.24)
(11.4.24)
где ![]() - нижняя треугольная матрица, чьи
диагональные элементы – единицы, а
- нижняя треугольная матрица, чьи
диагональные элементы – единицы, а ![]() - диагональная матрица. Такая
декомпозиция называется факторизацией (см. Бирман, 1977). Эта
факторизация описывается в приложении D.
В алгоритме факторизации
- диагональная матрица. Такая
декомпозиция называется факторизацией (см. Бирман, 1977). Эта
факторизация описывается в приложении D.
В алгоритме факторизации ![]() не обновляется, как в (11.4.14), а
вычисляется. Вместо этого при помощи рекуррентного обновления формируется
не обновляется, как в (11.4.14), а
вычисляется. Вместо этого при помощи рекуррентного обновления формируется ![]() и
и ![]() .
.
Алгоритмы НК часто используются в
системах управления, которые включают в себя калмановскую фильтрацию. В
цифровой связи, алгоритм НК Калмана используется в ФМ модеме с выравниванием на
основе обратной связи по решению, спроектированном для передачи с высокой
скоростью по ВЧ каналу с номинальной полосой частот 3 кГц. Этот алгоритм описан
в статье Хшу (1982). Он имеет вычислительную сложность порядка ![]() (умножения
комплексных величин и делений на выходные символы). Для подробного ознакомления
с алгоритмами НК в последовательном оценивании читателю рекомендуется книга
Бирмана (1977).
(умножения
комплексных величин и делений на выходные символы). Для подробного ознакомления
с алгоритмами НК в последовательном оценивании читателю рекомендуется книга
Бирмана (1977).
Возможно также разработать РНК алгоритмы
с вычислительной сложностью, которая возрастает линейно с числом коэффициентов
эквалайзера ![]() .
Такие алгоритмы обычно называются быстрыми РНК алгоритмами, и они были
описаны статьях Караяниса и др. (1983), Чиффи и Кайлата (1989) и Слока и
Кайлата (1988).
.
Такие алгоритмы обычно называются быстрыми РНК алгоритмами, и они были
описаны статьях Караяниса и др. (1983), Чиффи и Кайлата (1989) и Слока и
Кайлата (1988).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
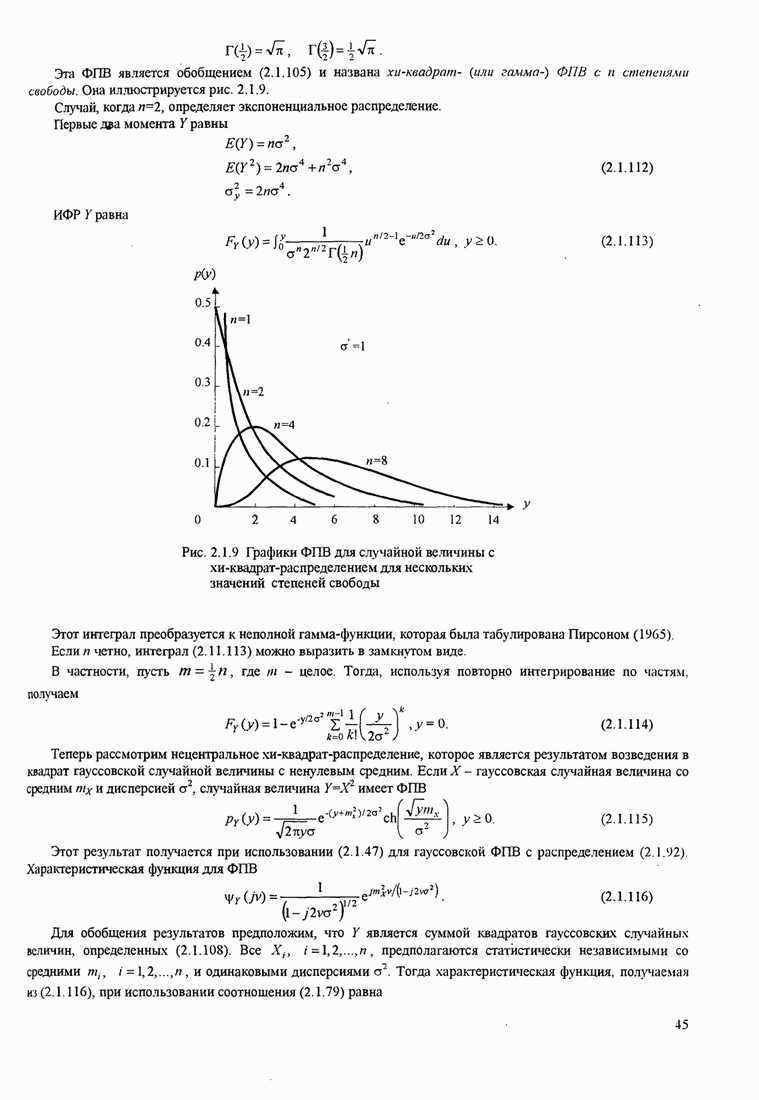
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
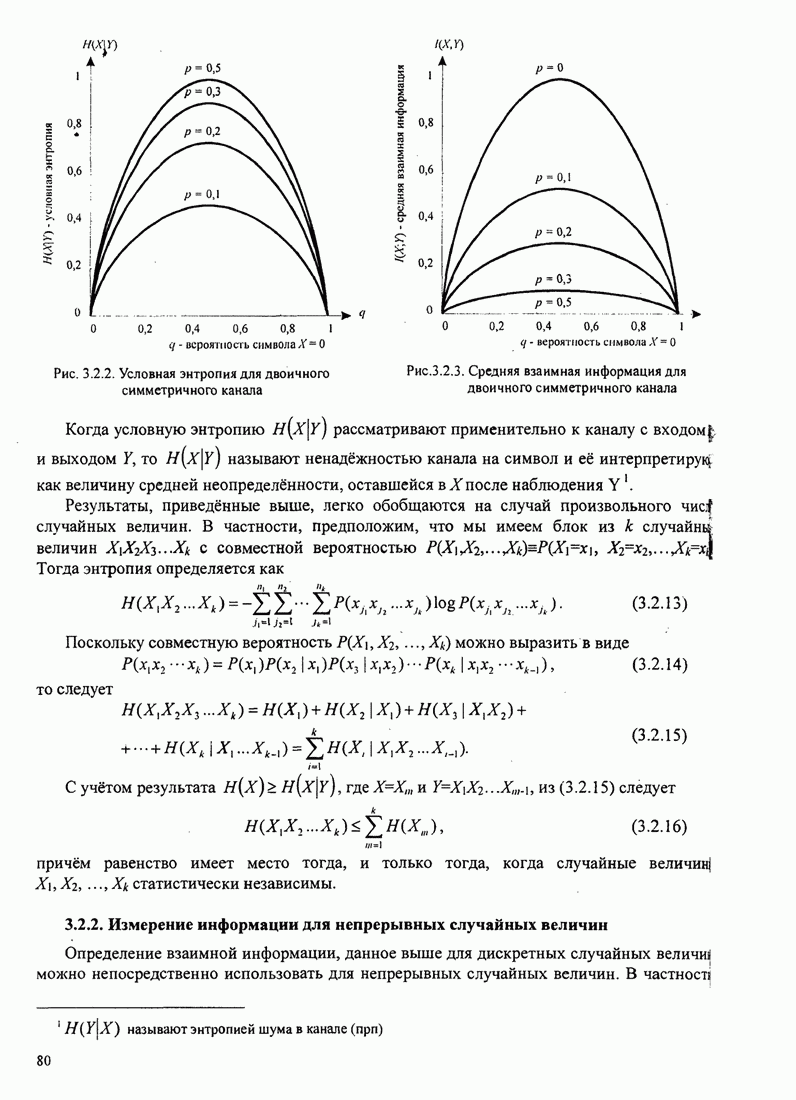
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
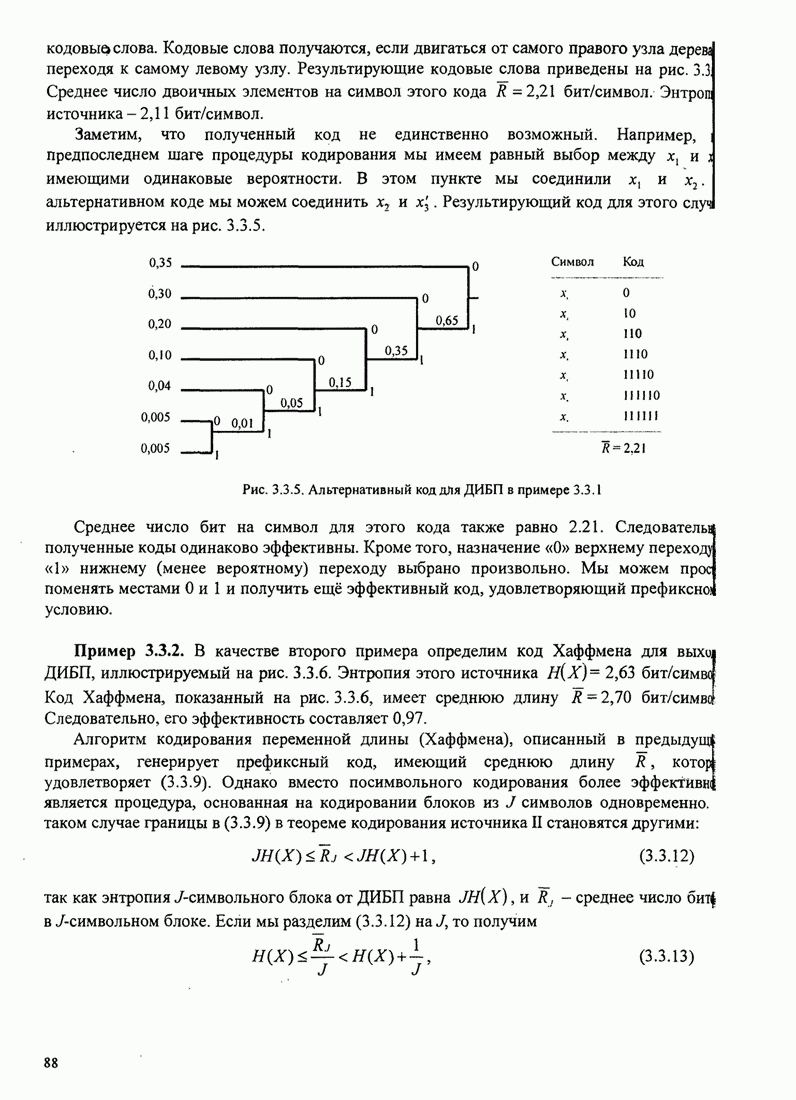
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
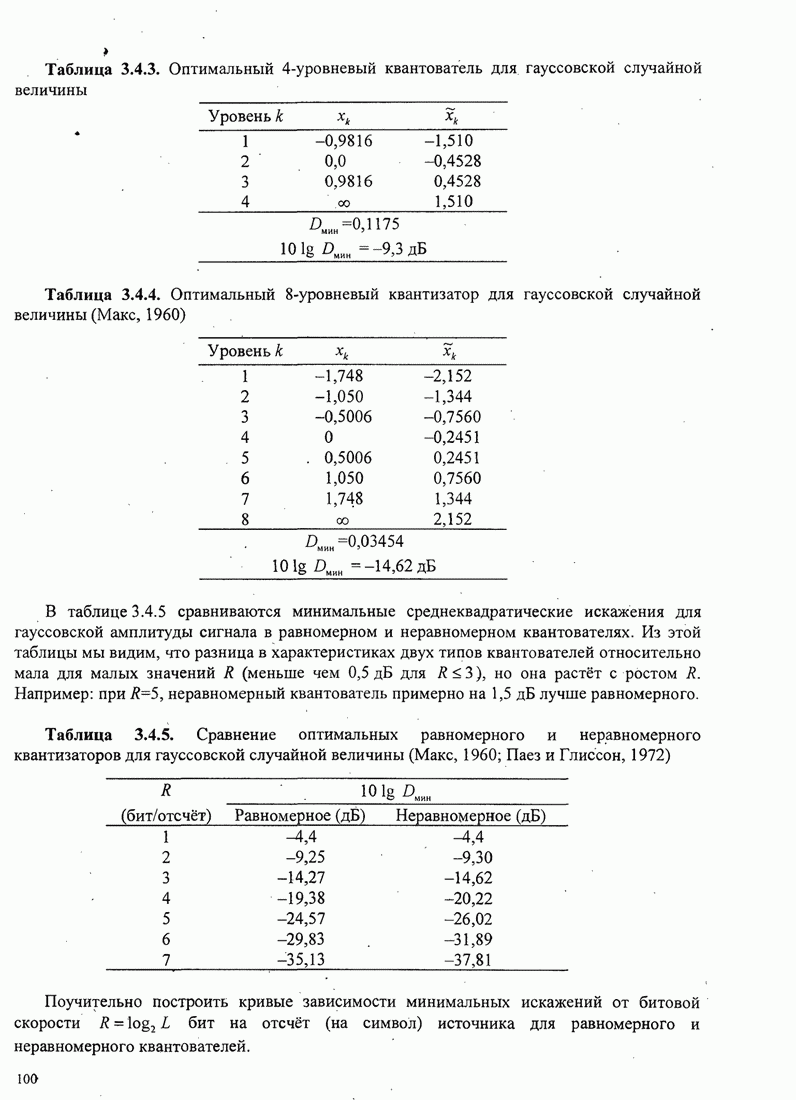
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
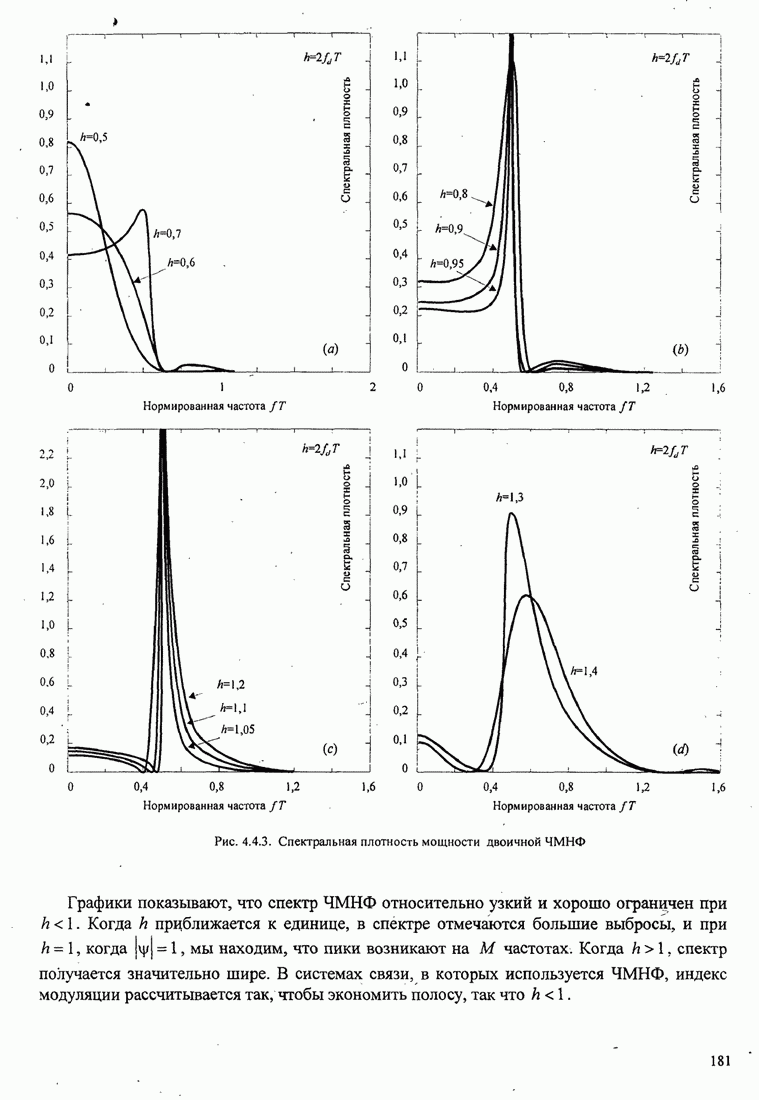
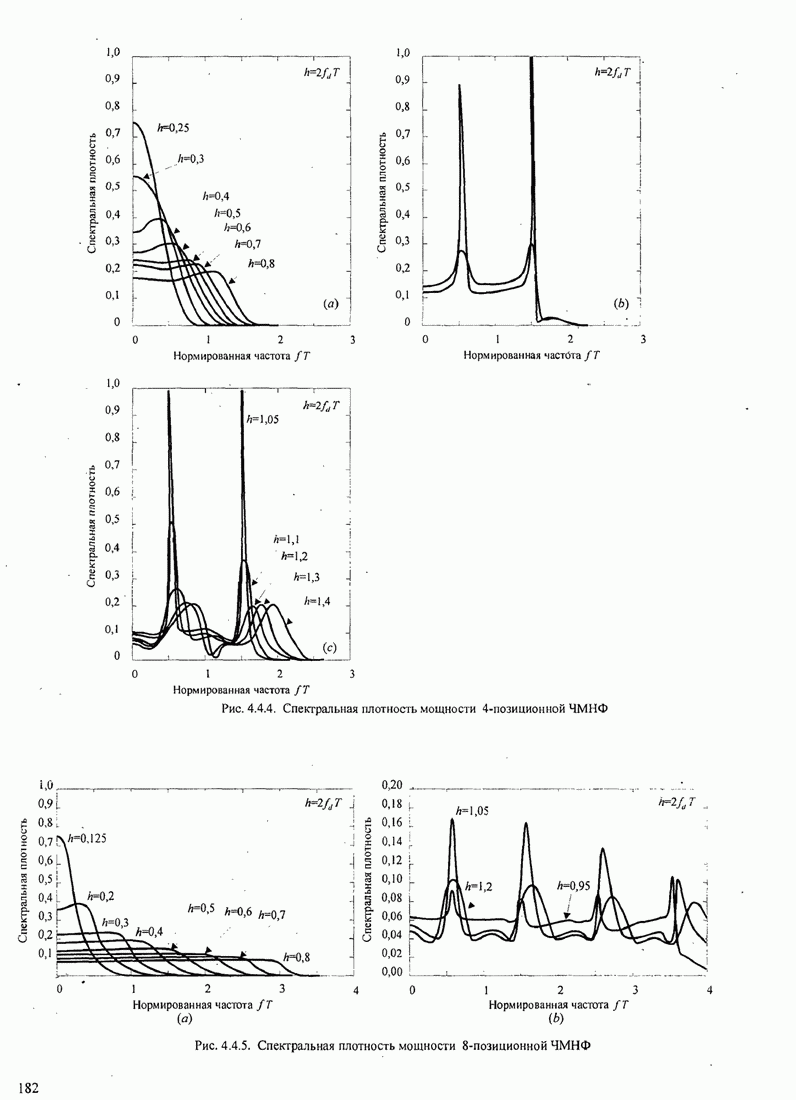
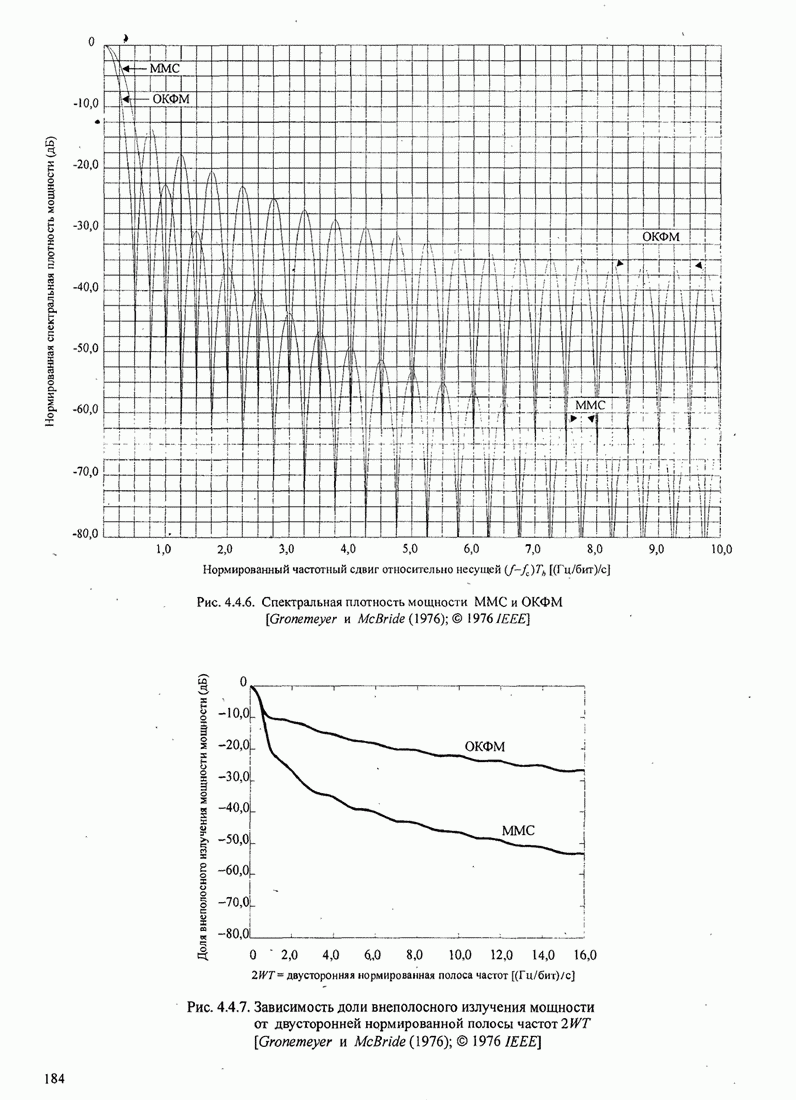
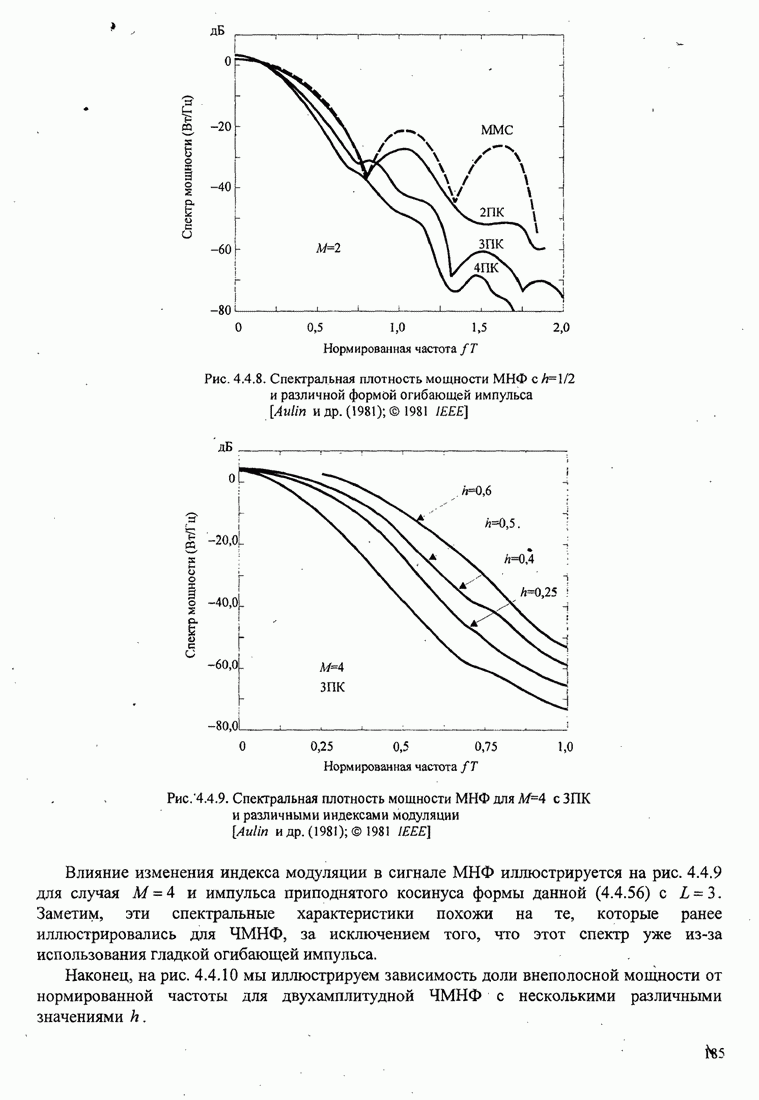
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
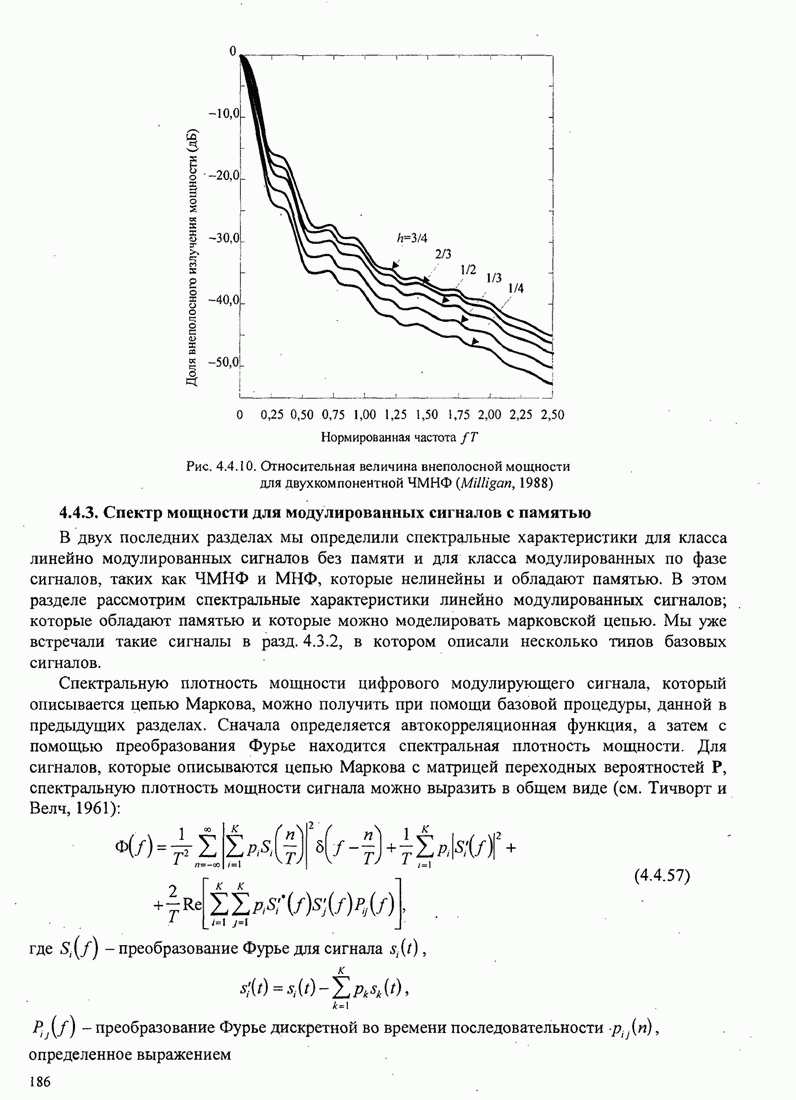
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
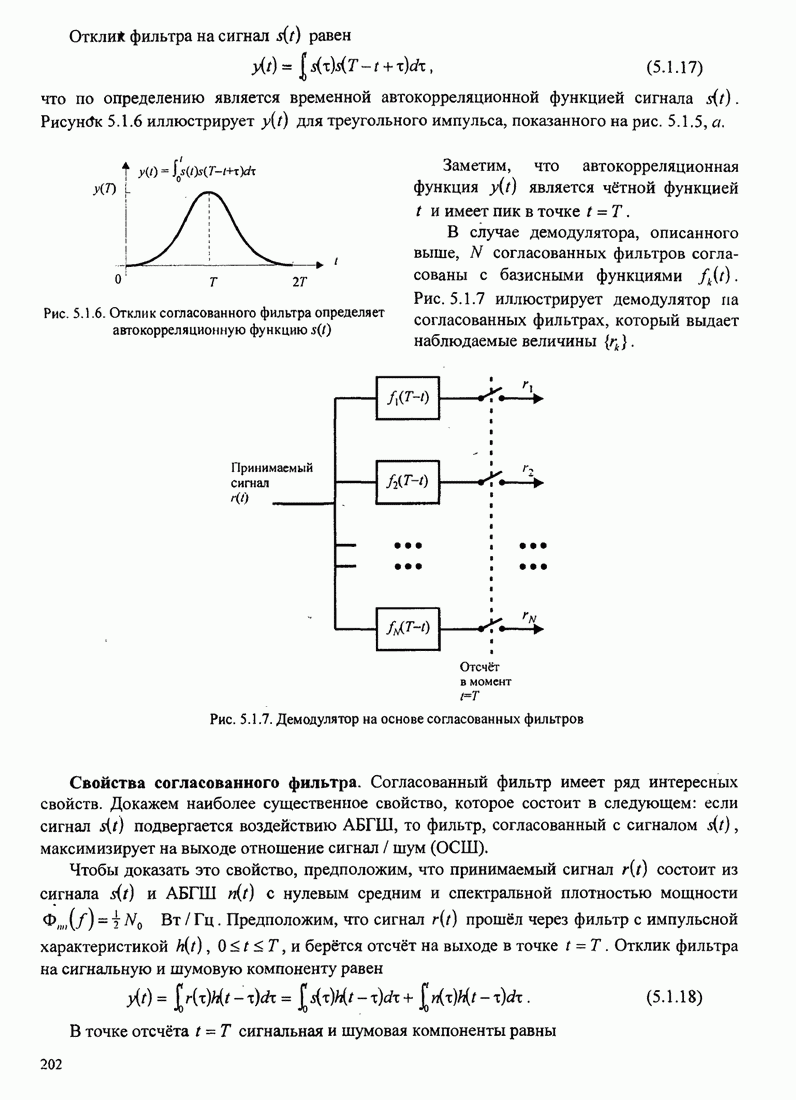
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
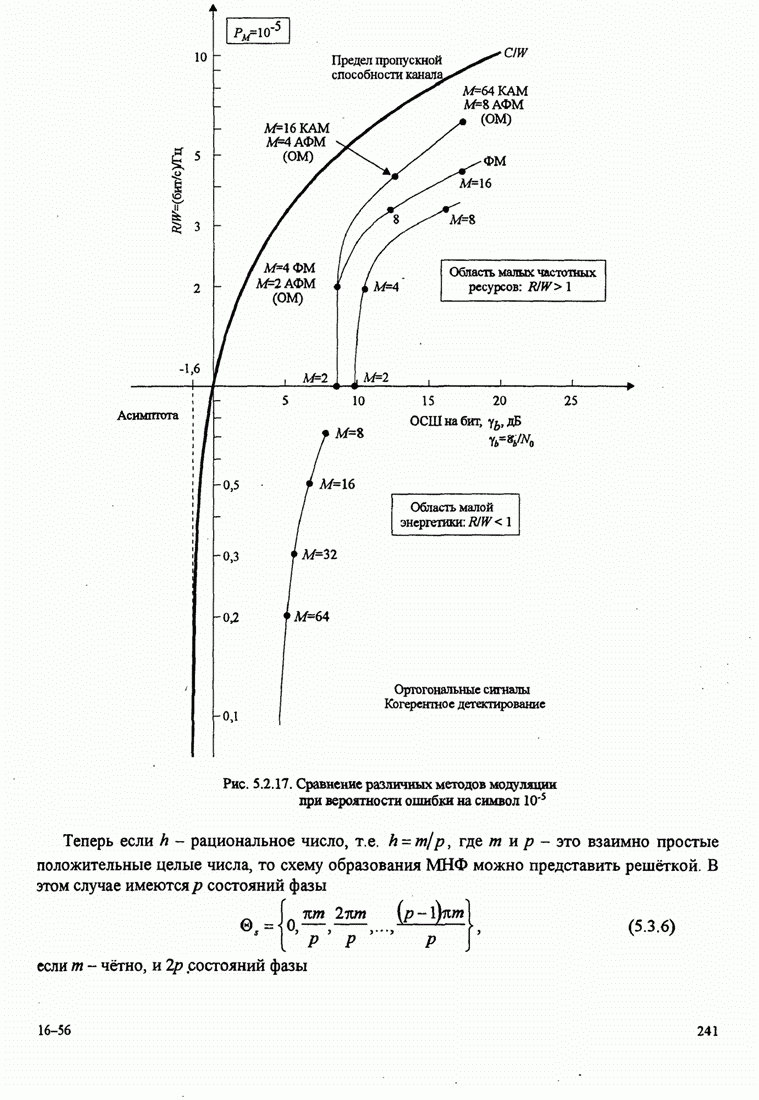
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
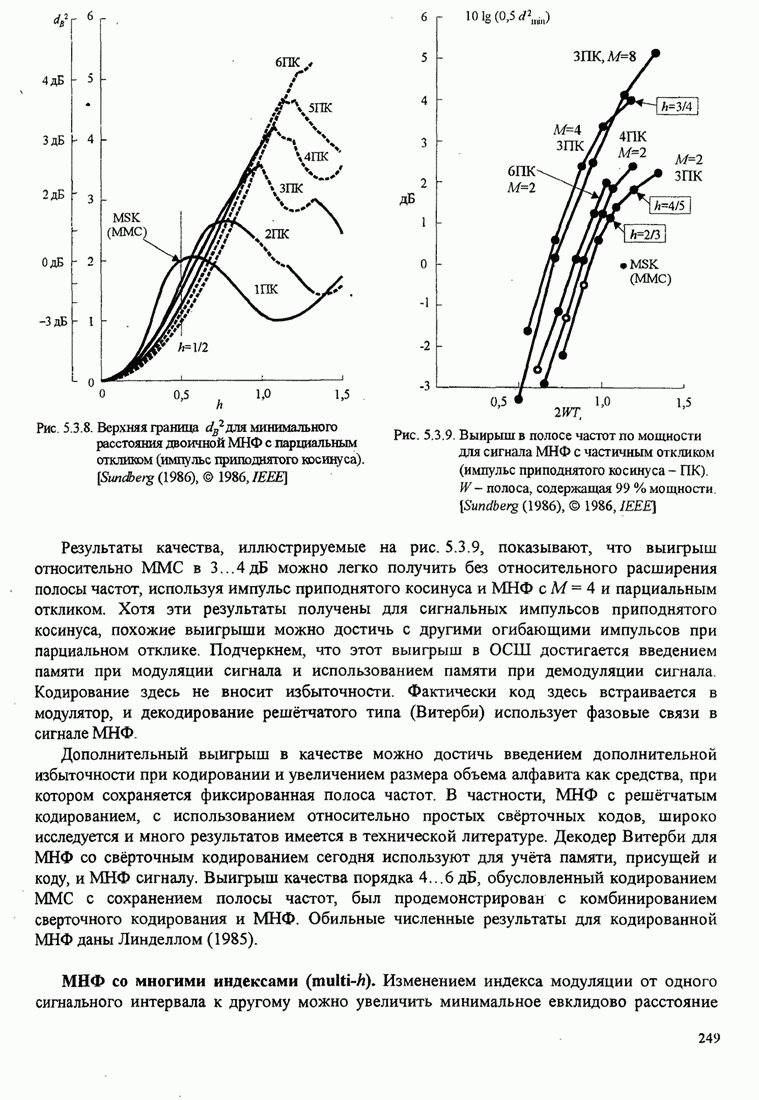
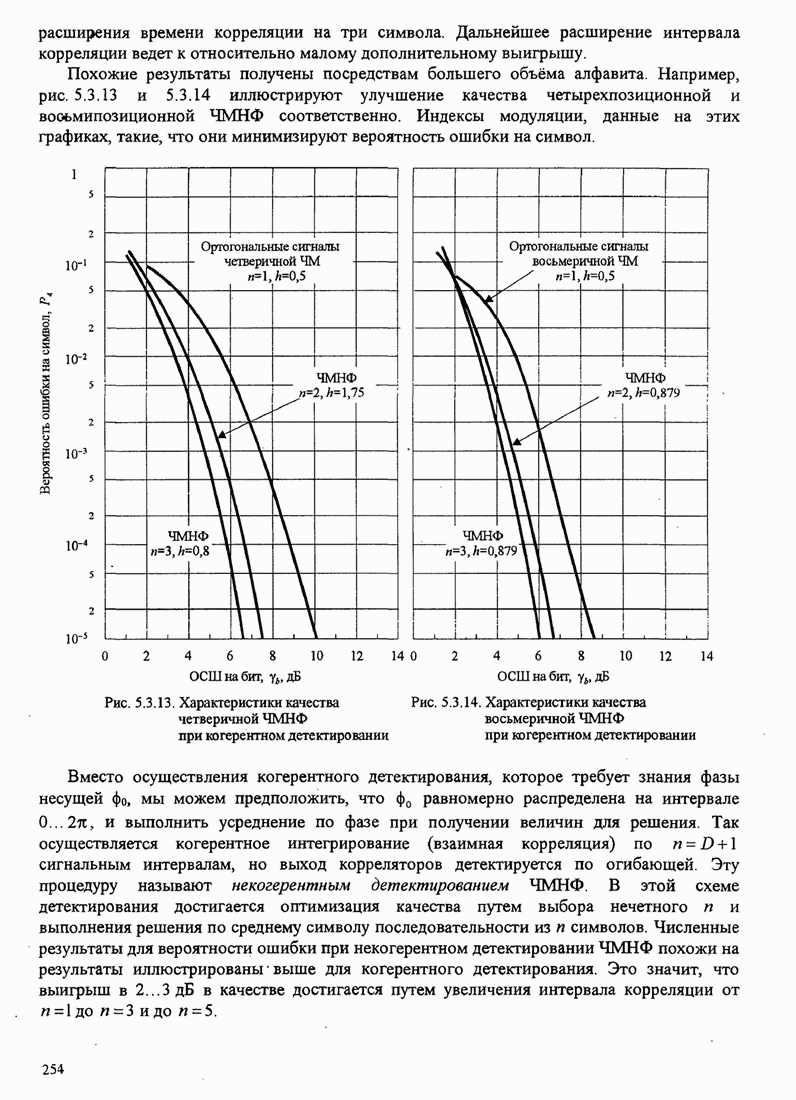
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
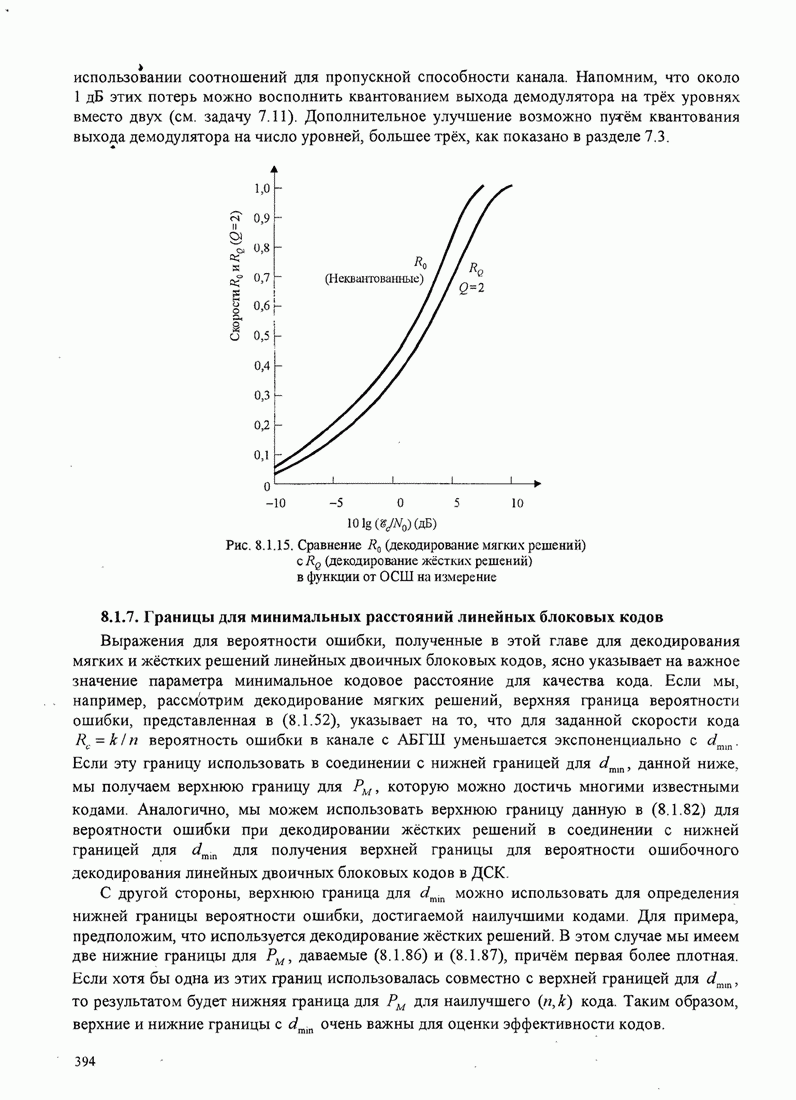
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
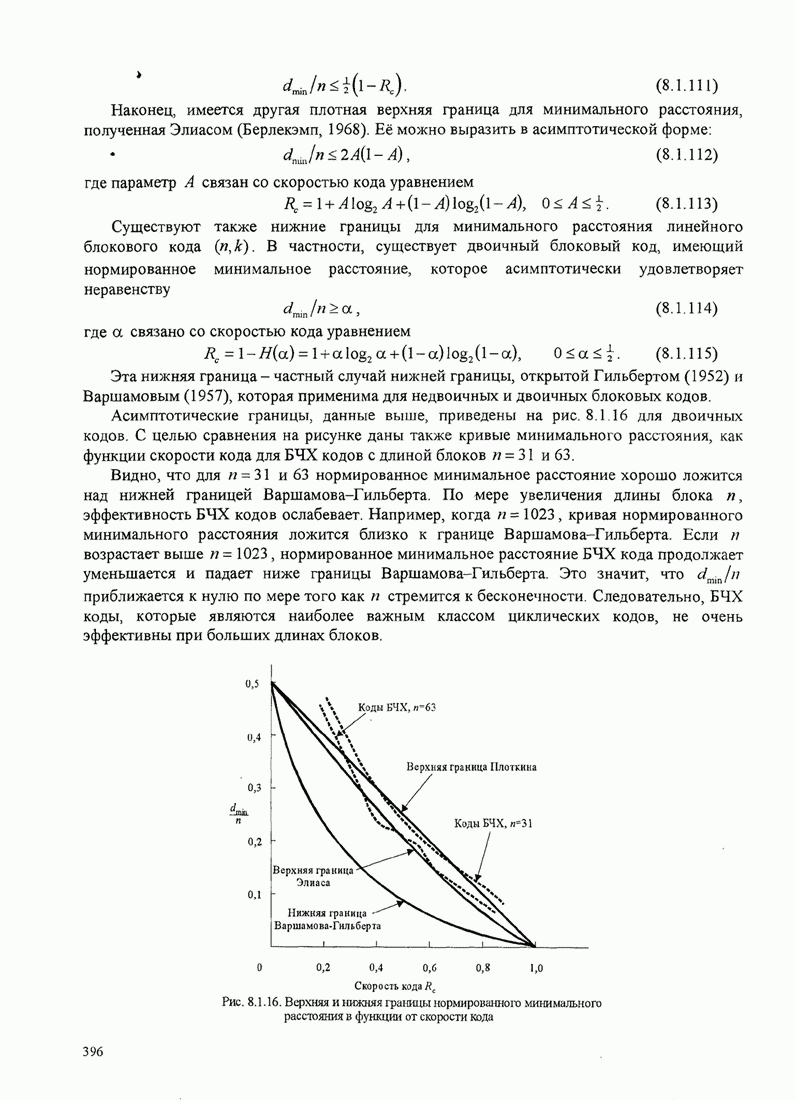
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
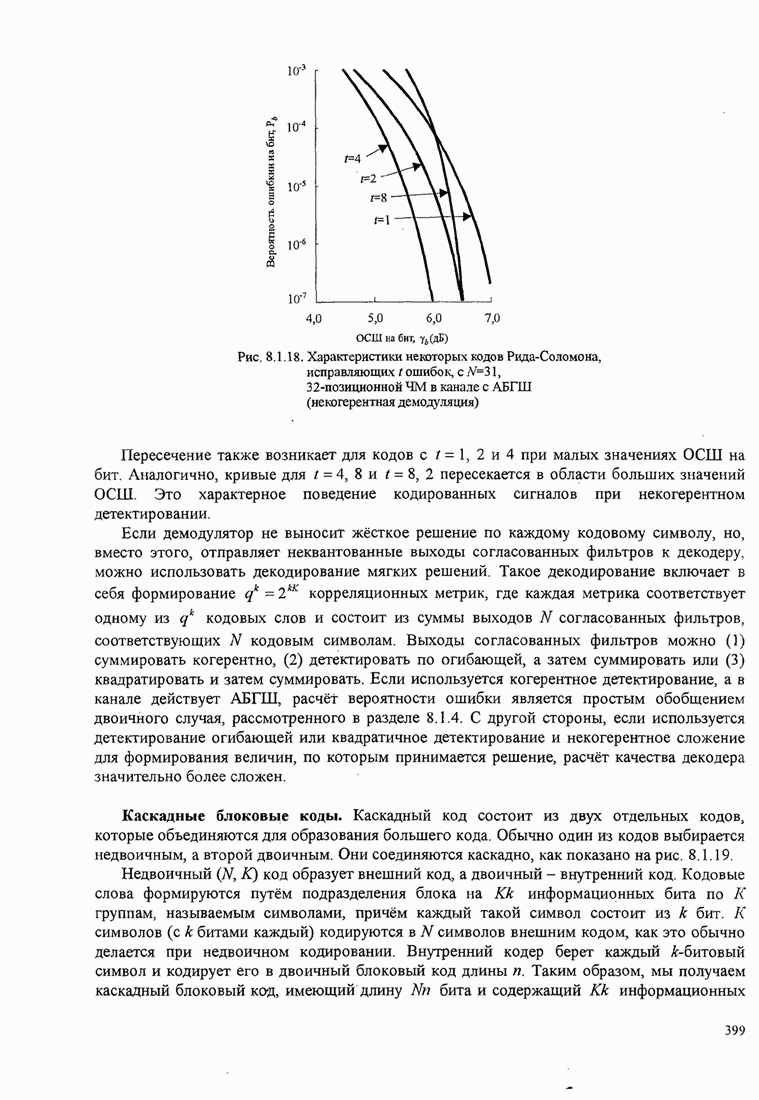
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
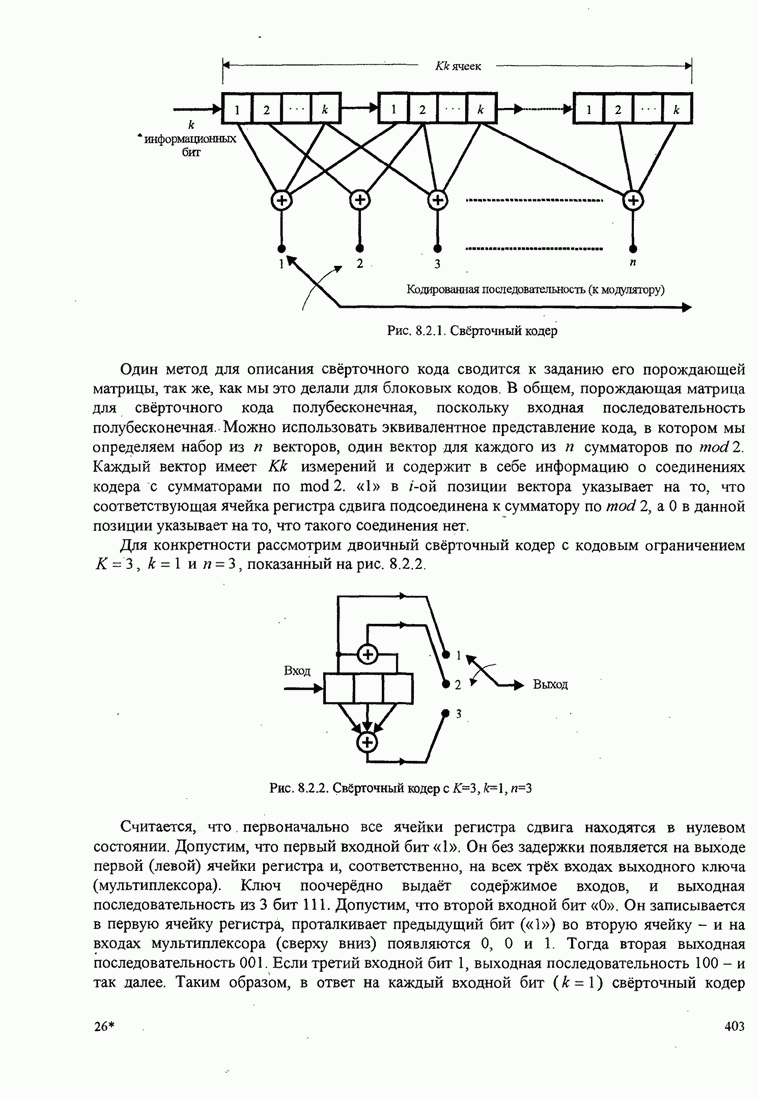
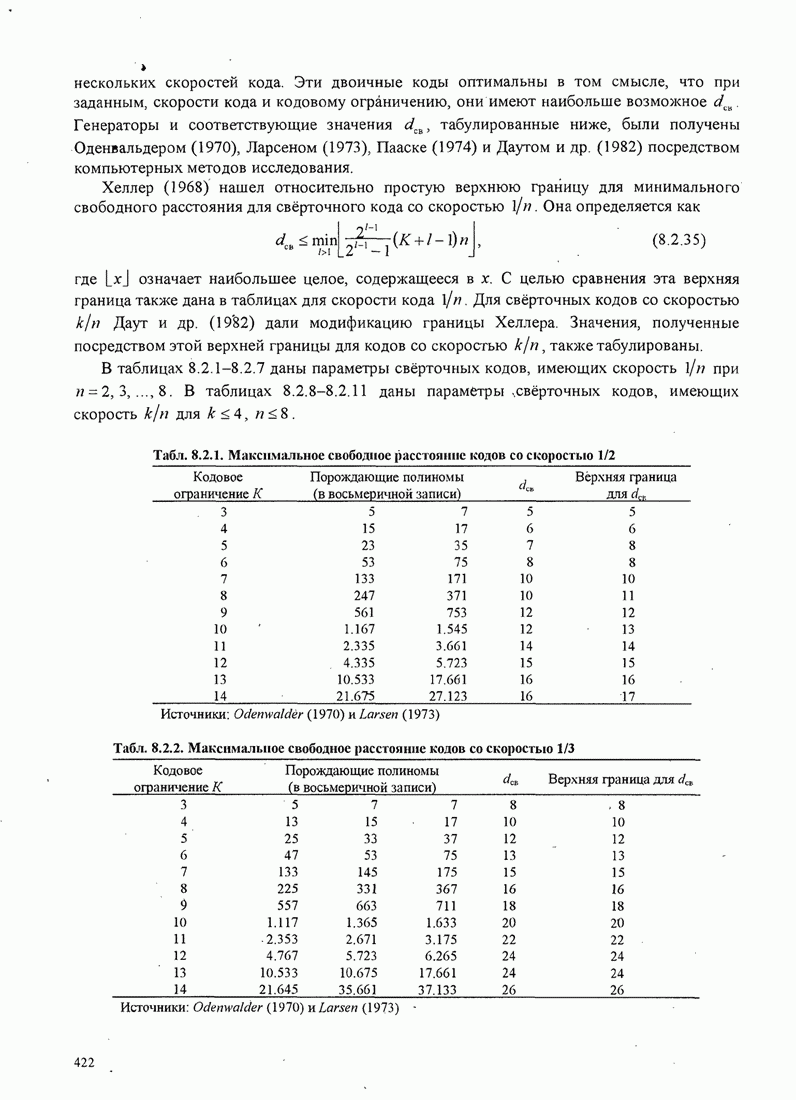
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
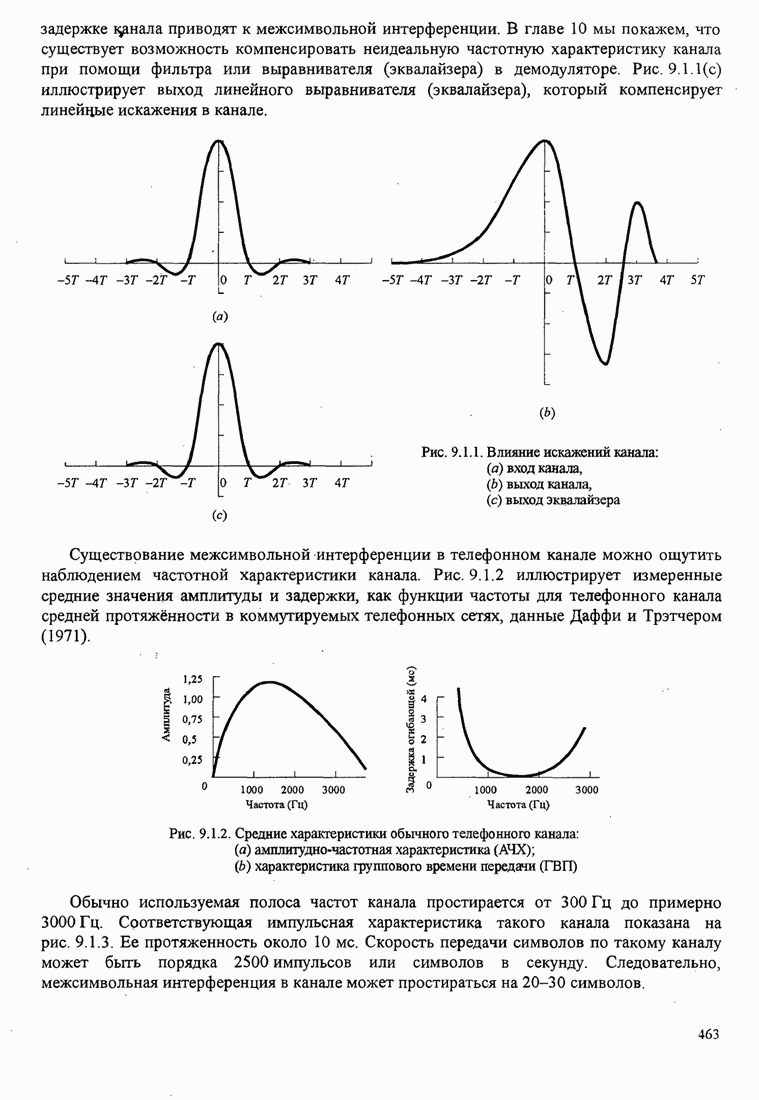
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
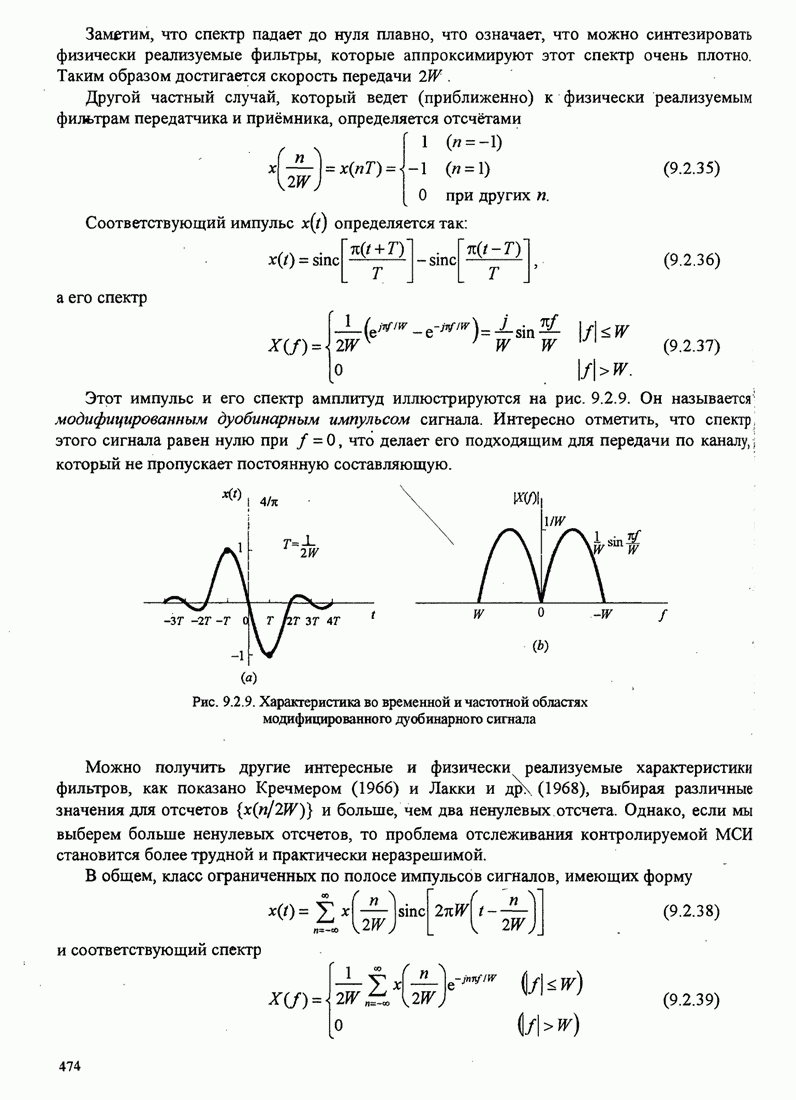
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
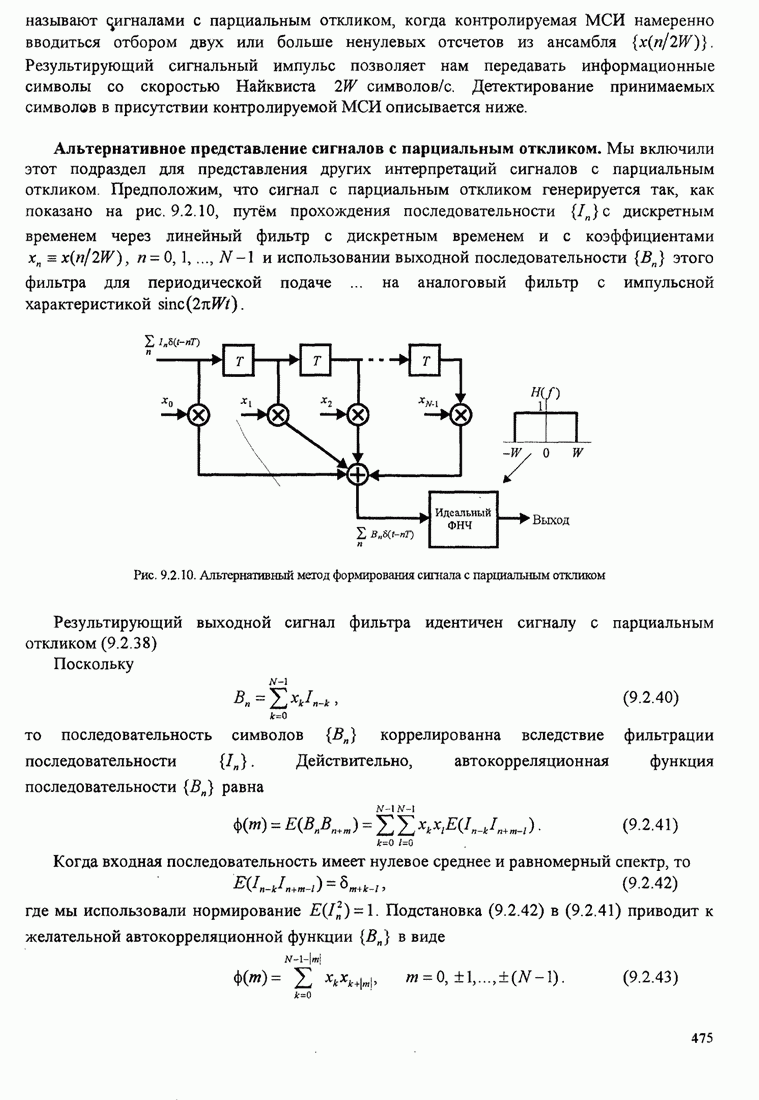
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
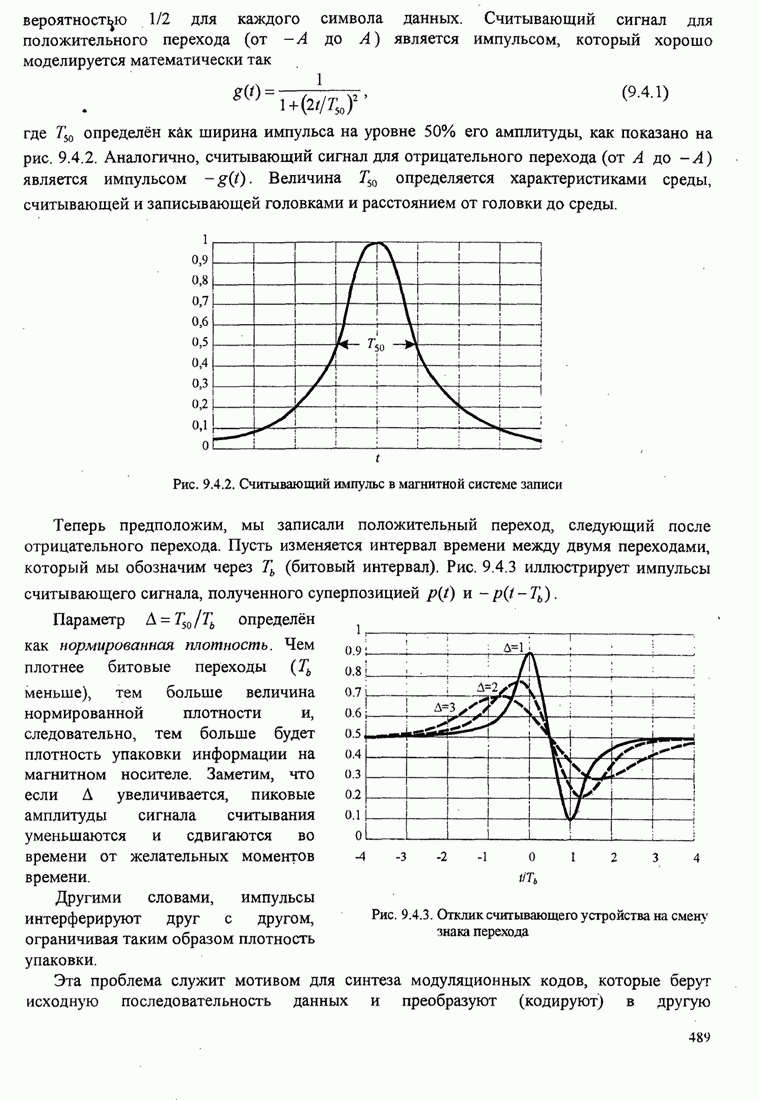
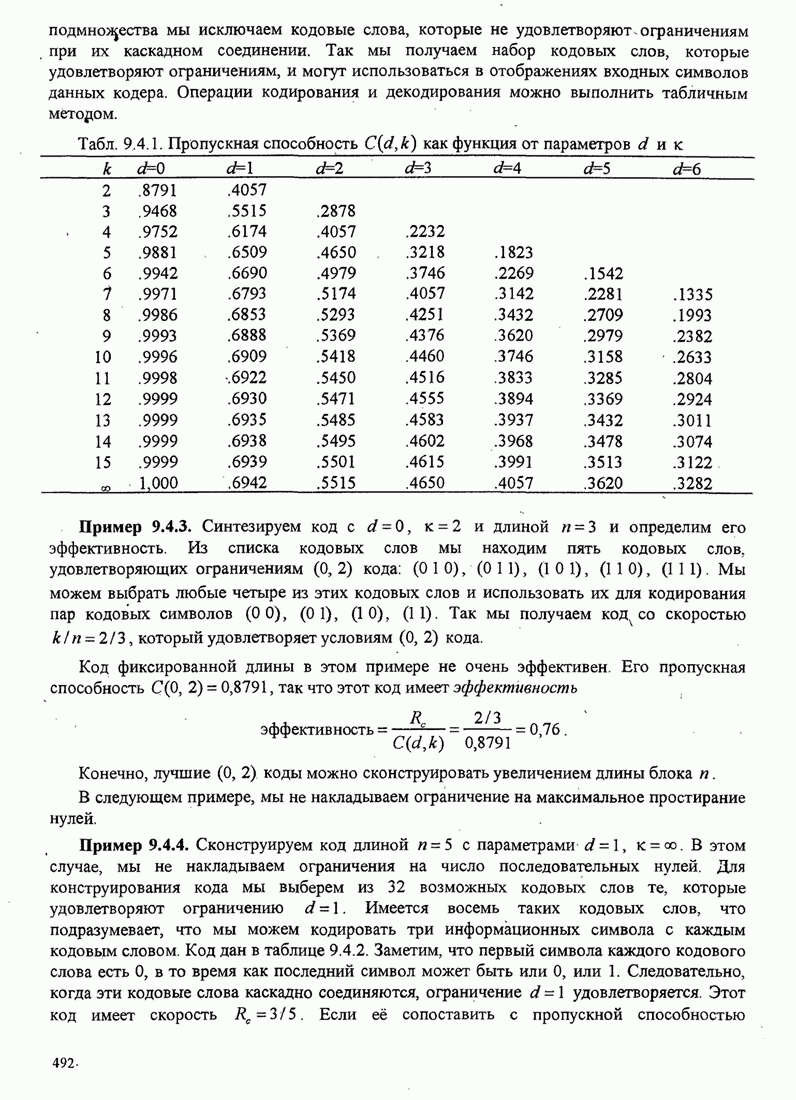
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
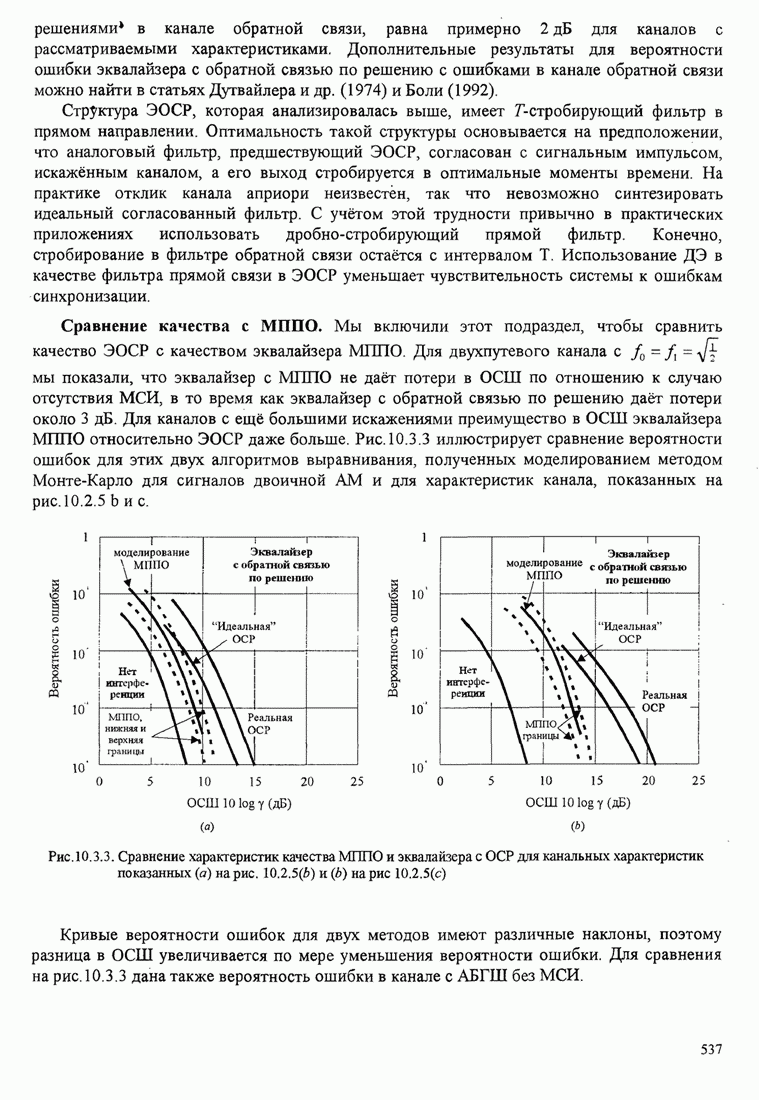
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
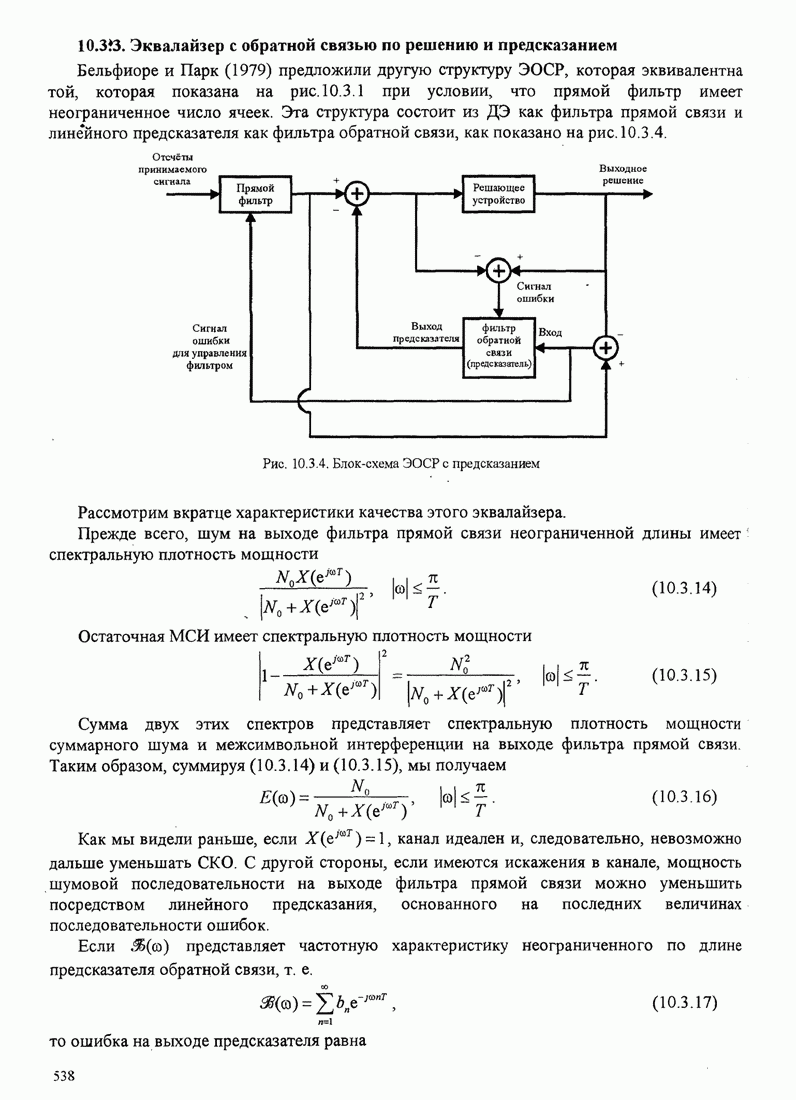
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
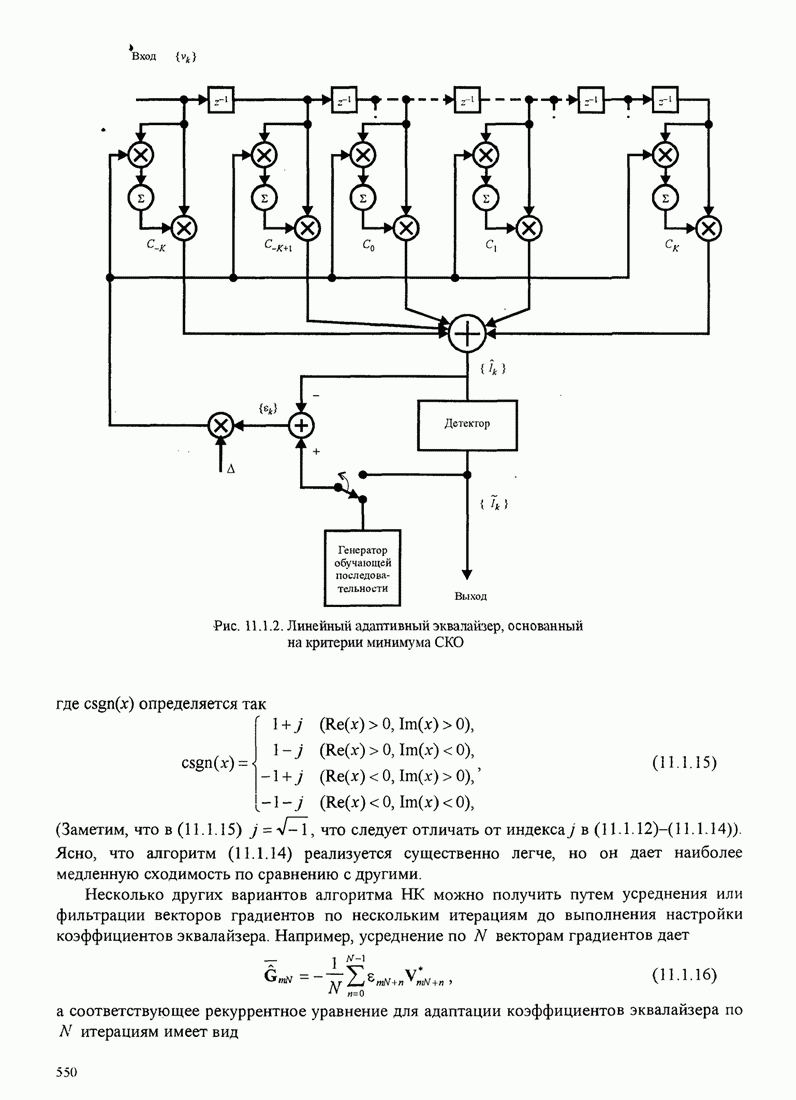
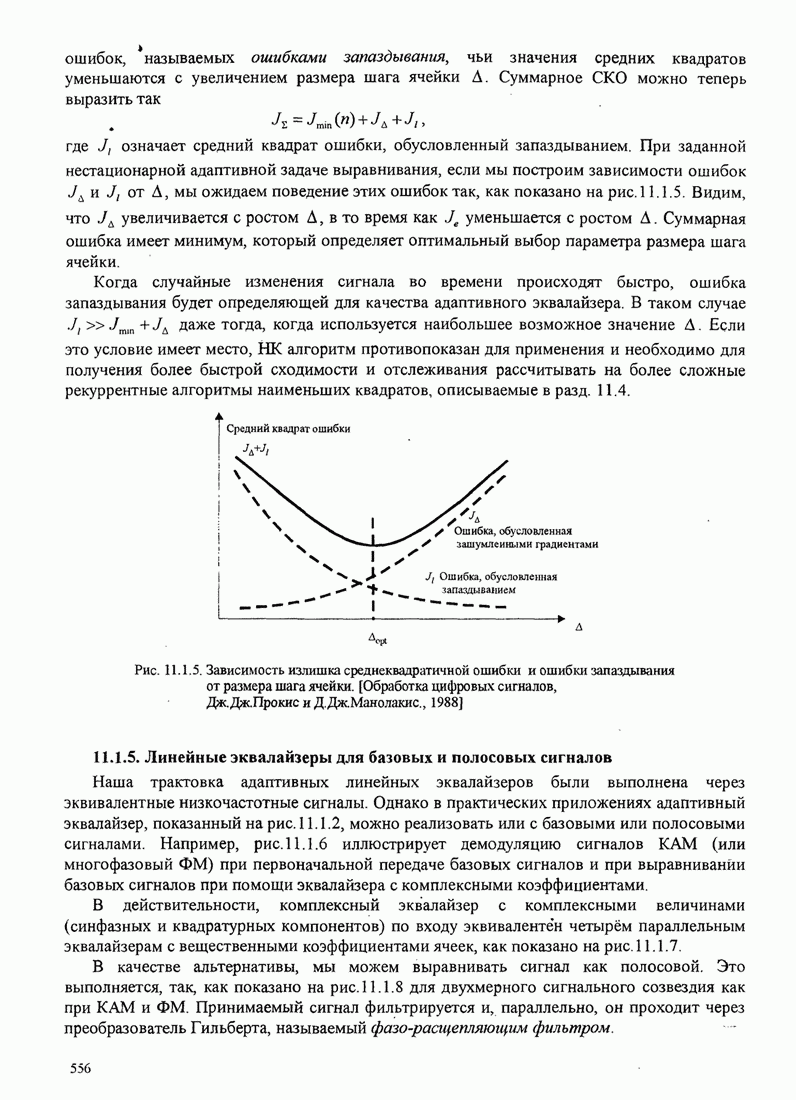
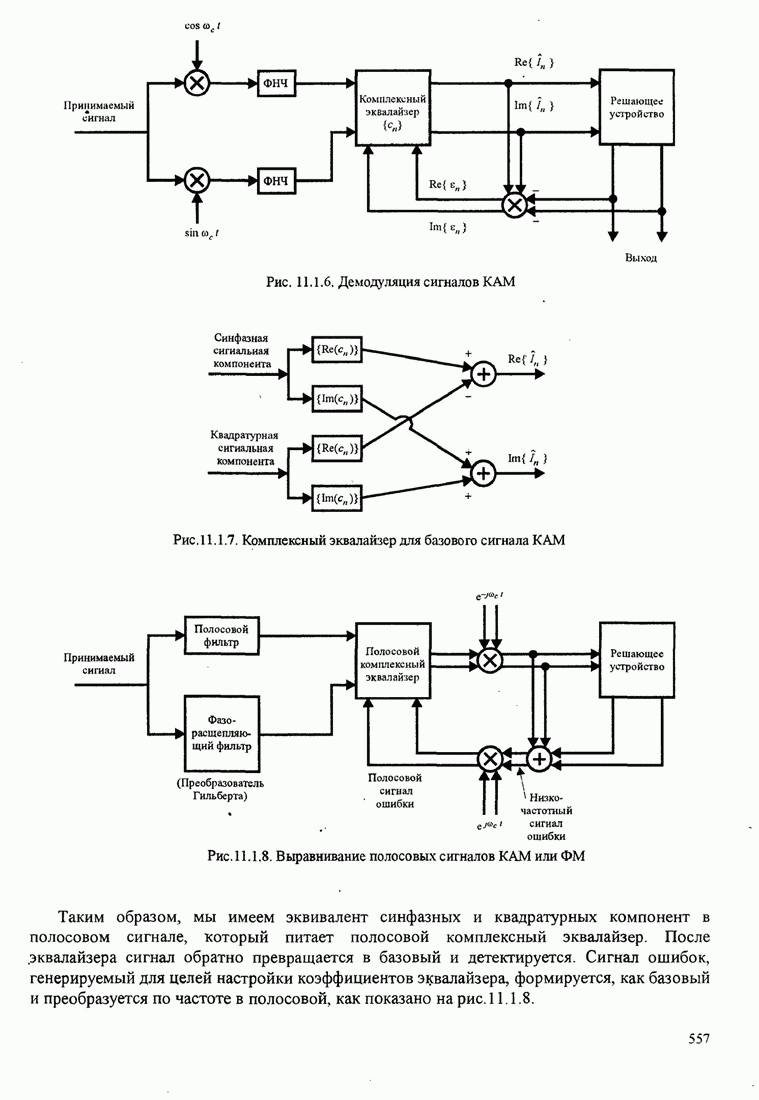
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
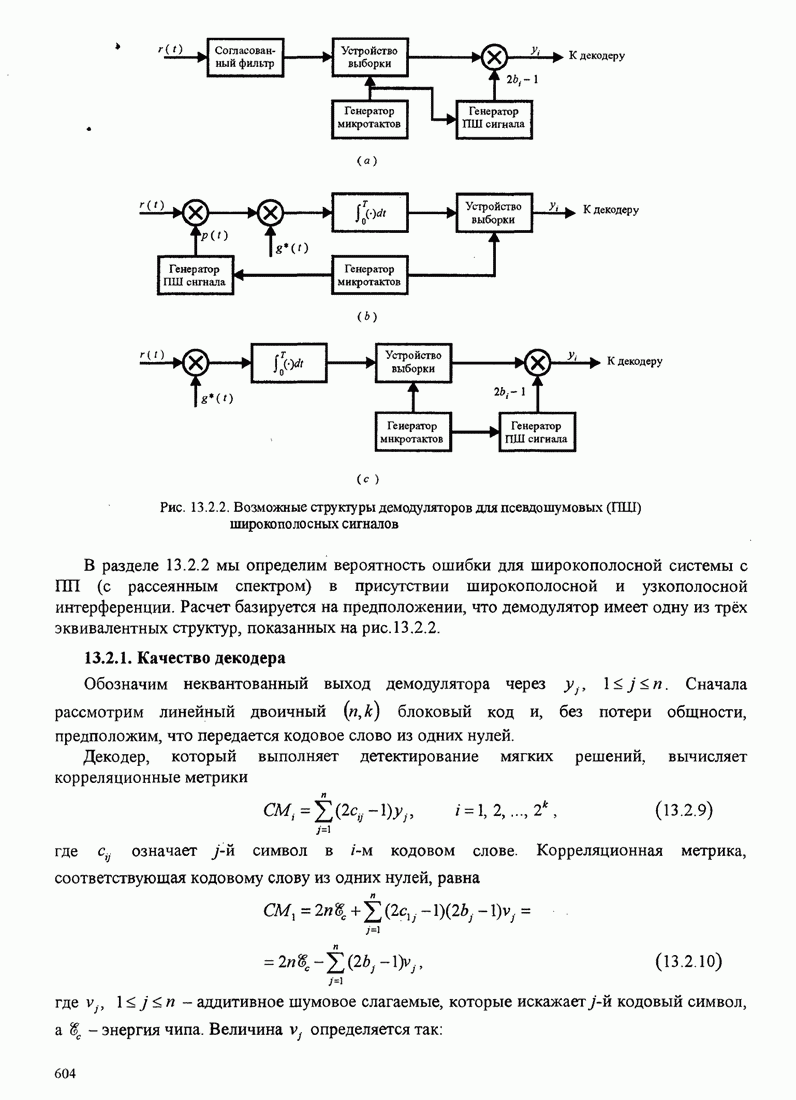
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
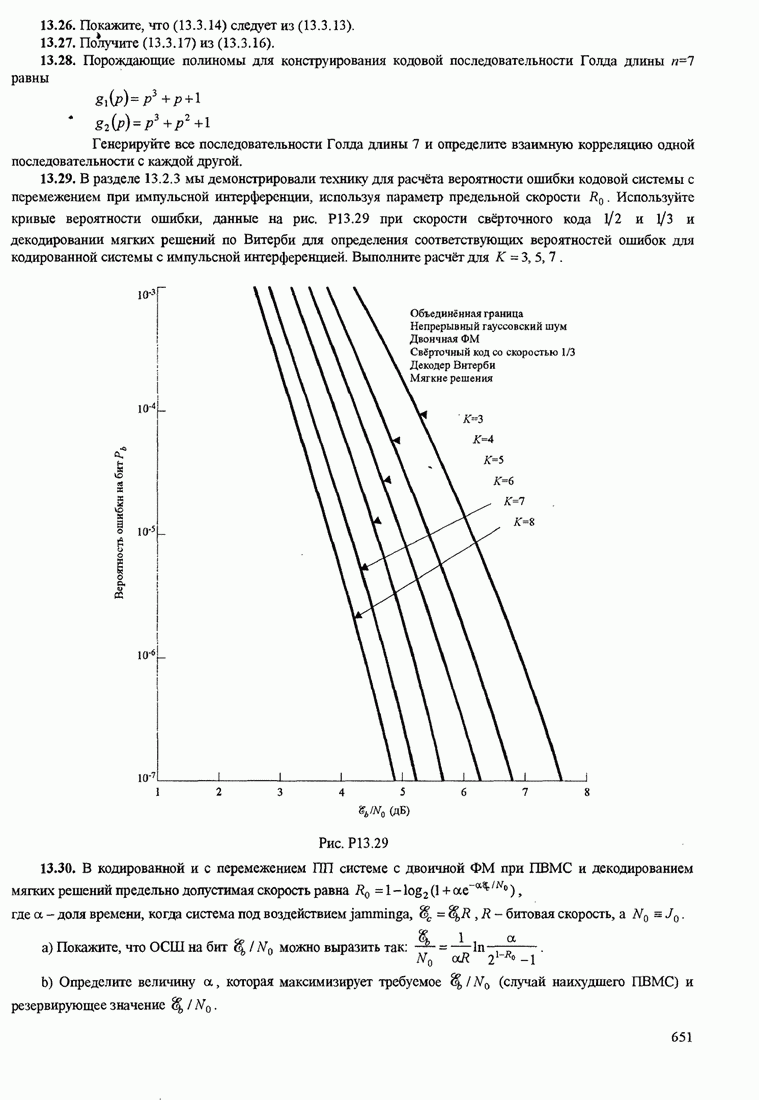
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
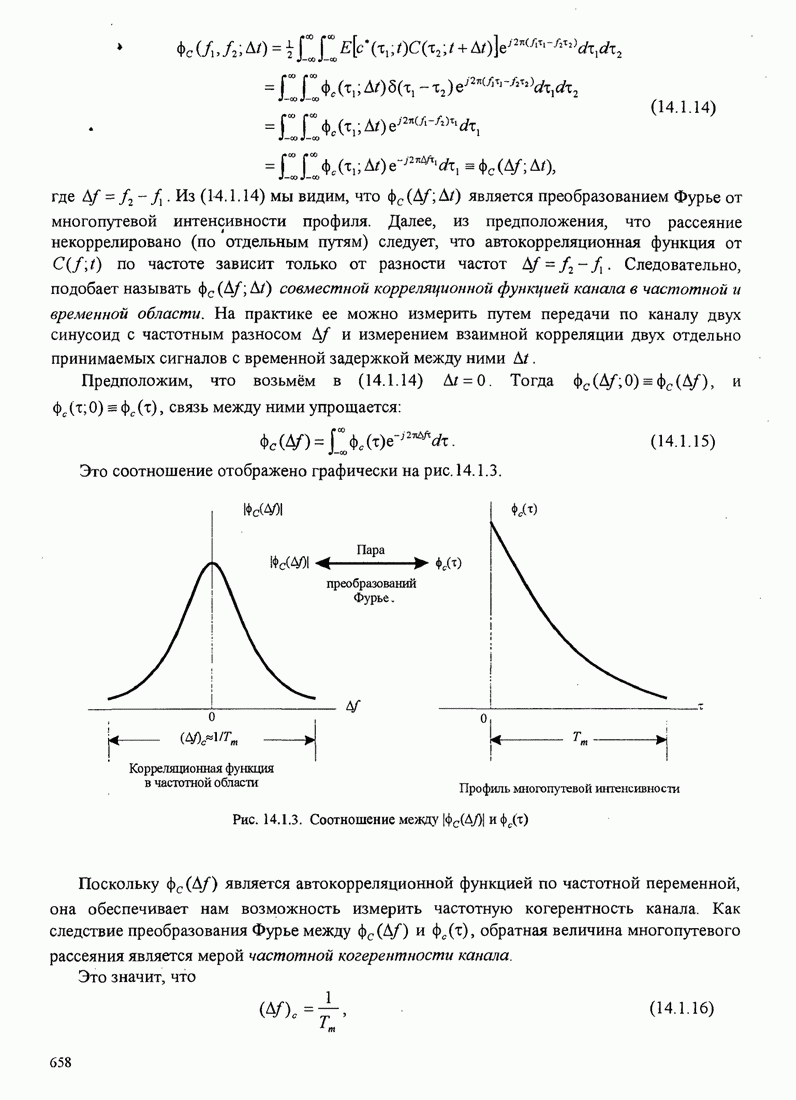
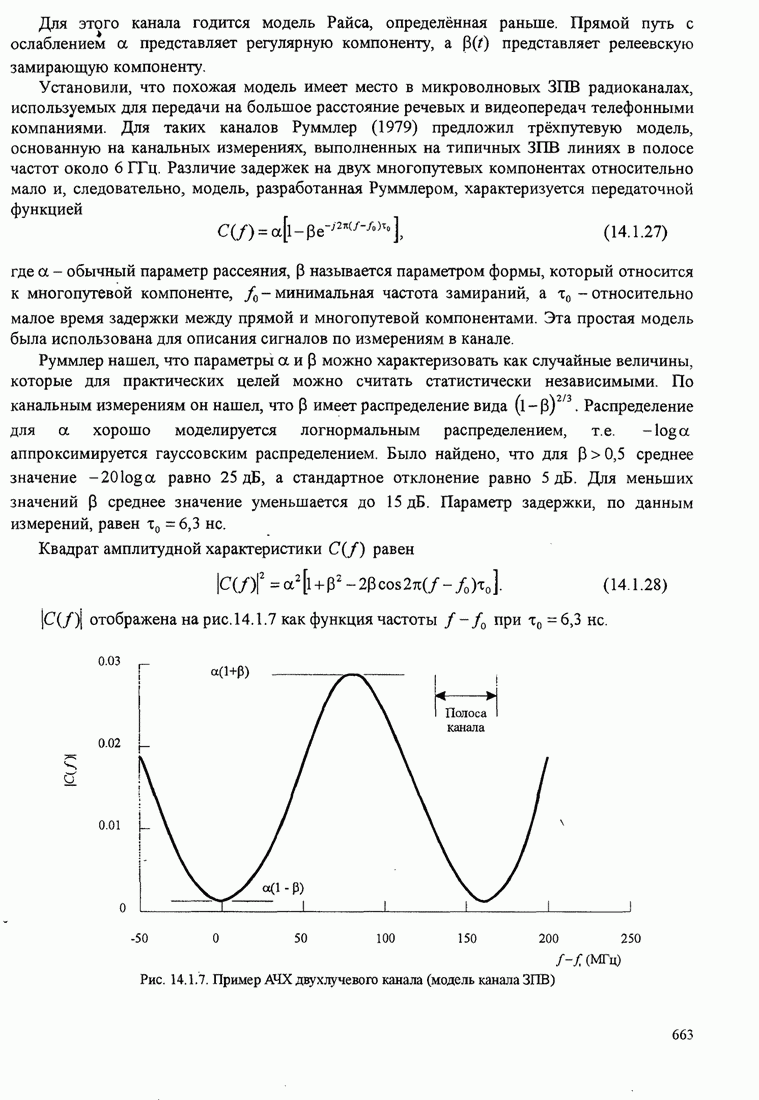
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
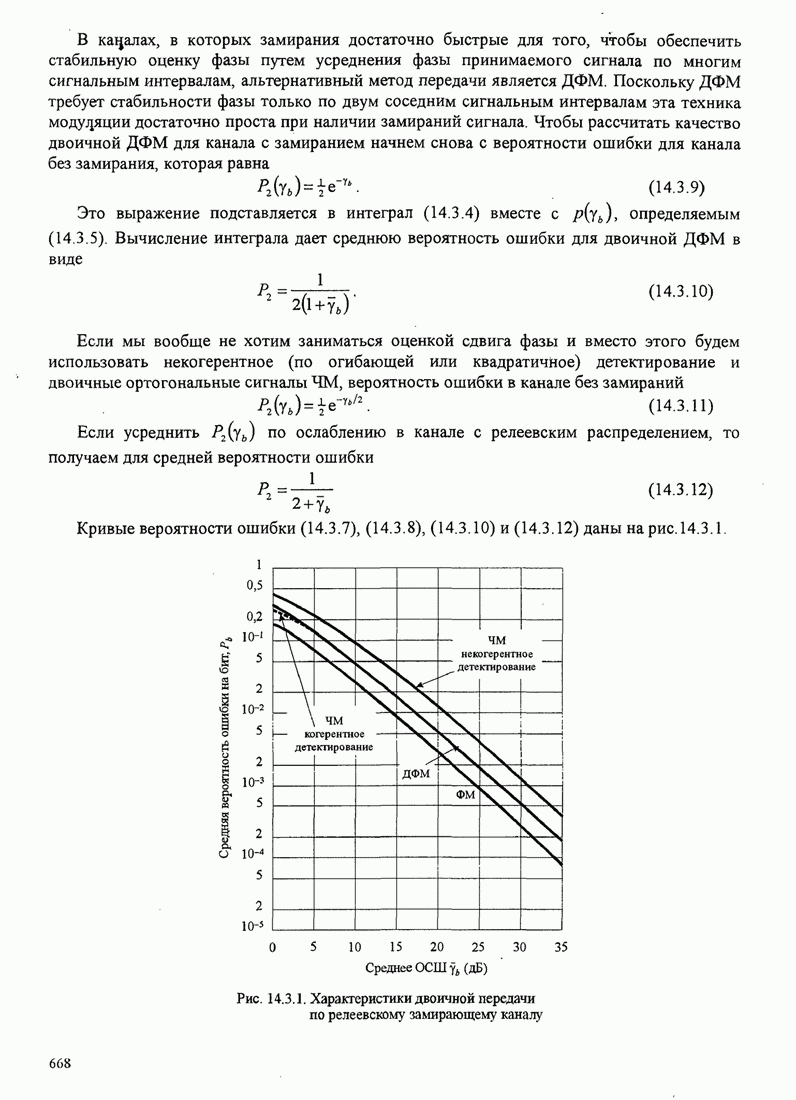
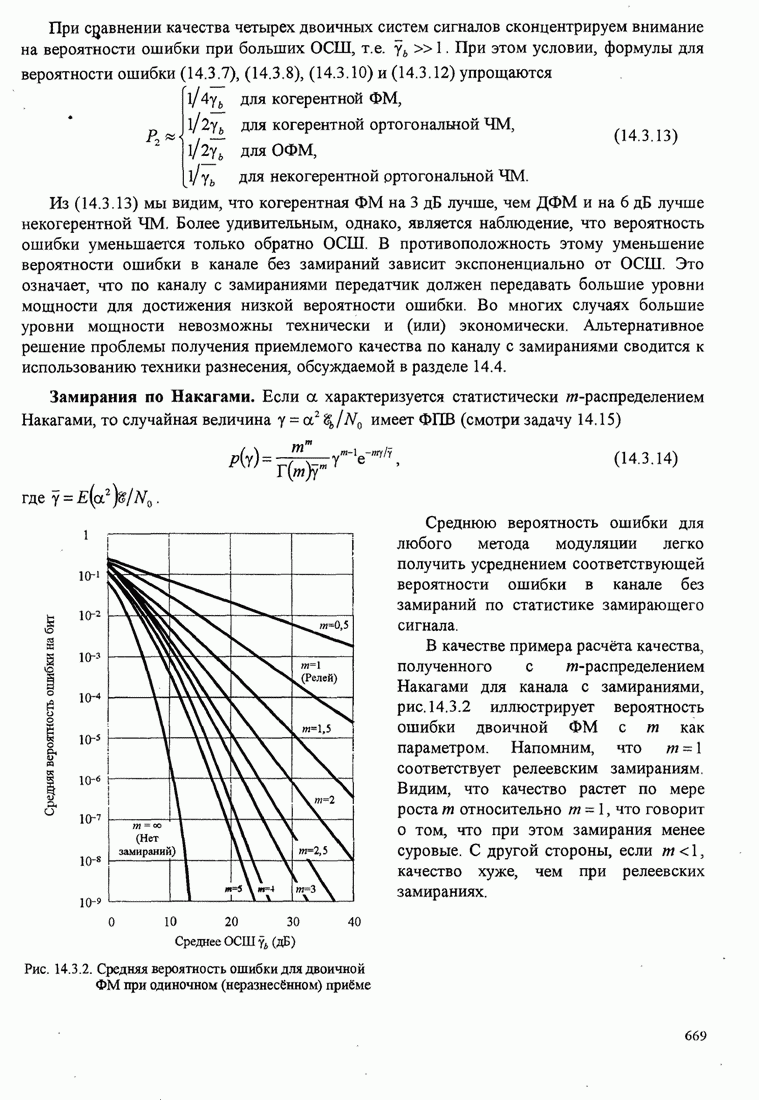
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
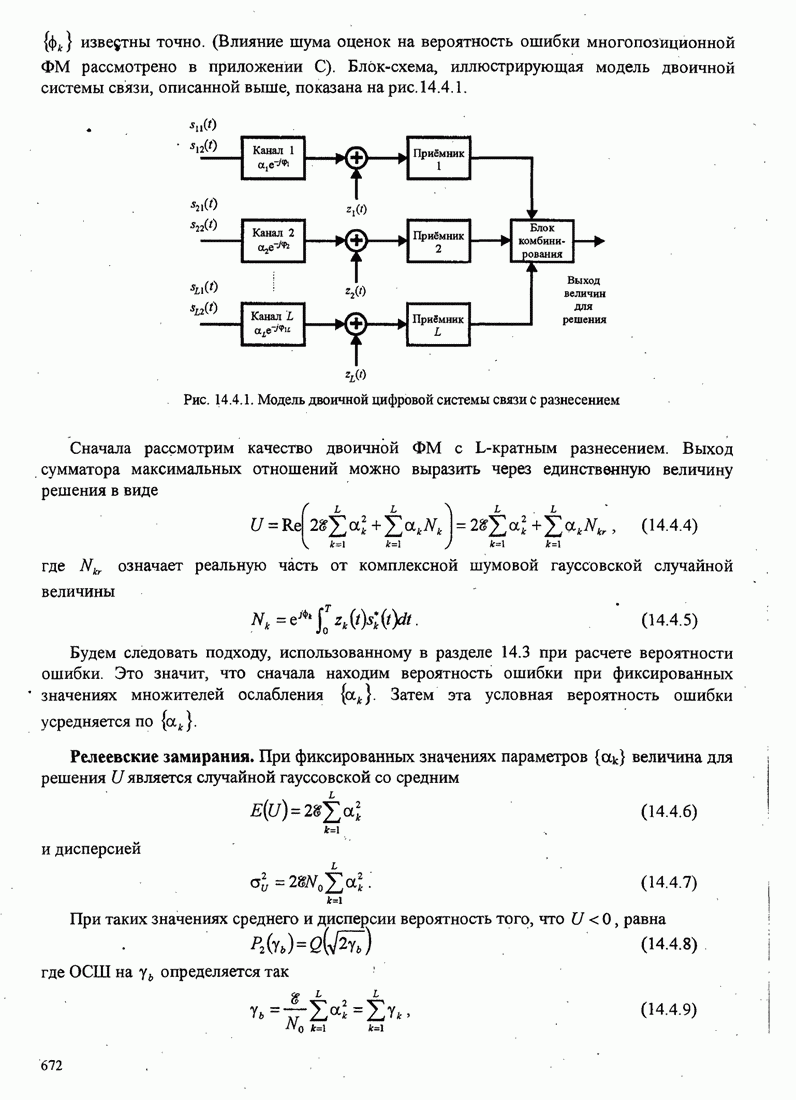
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
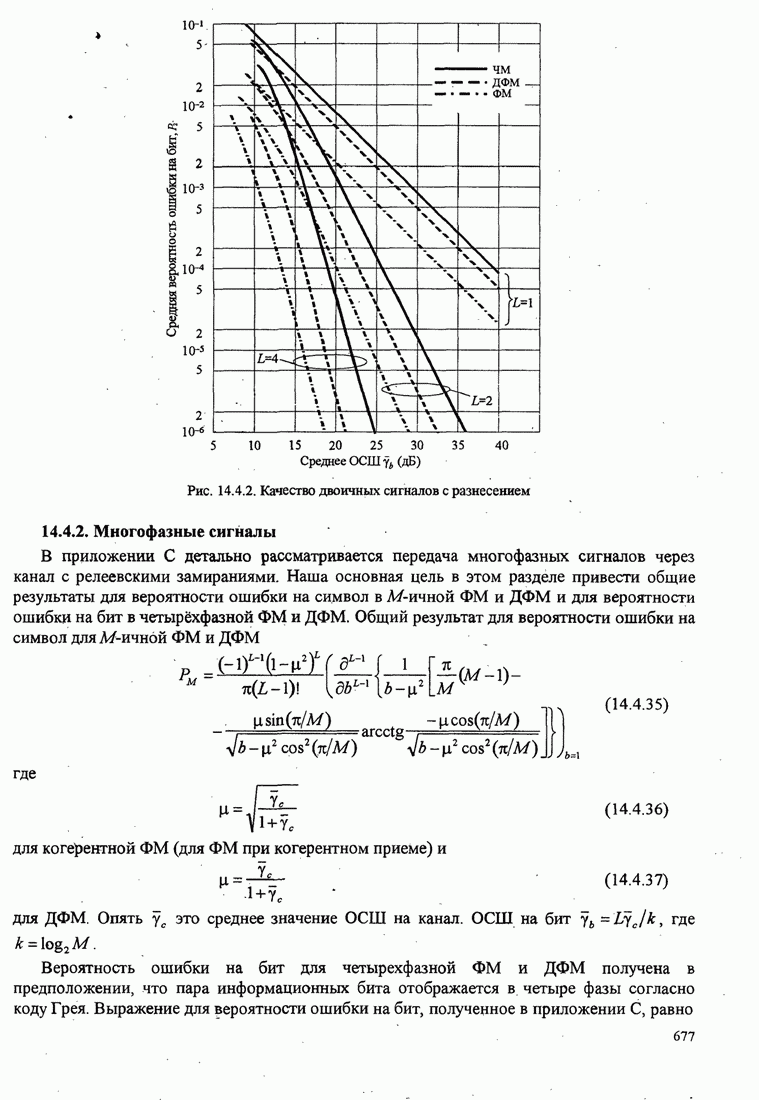
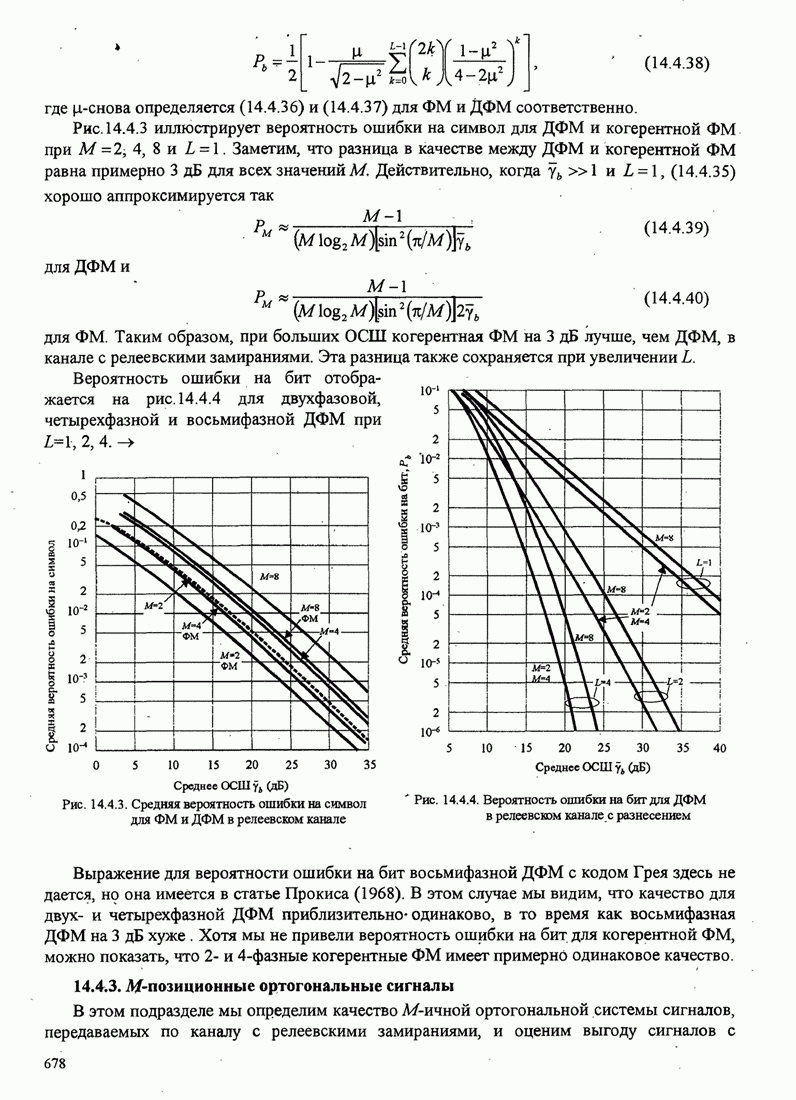
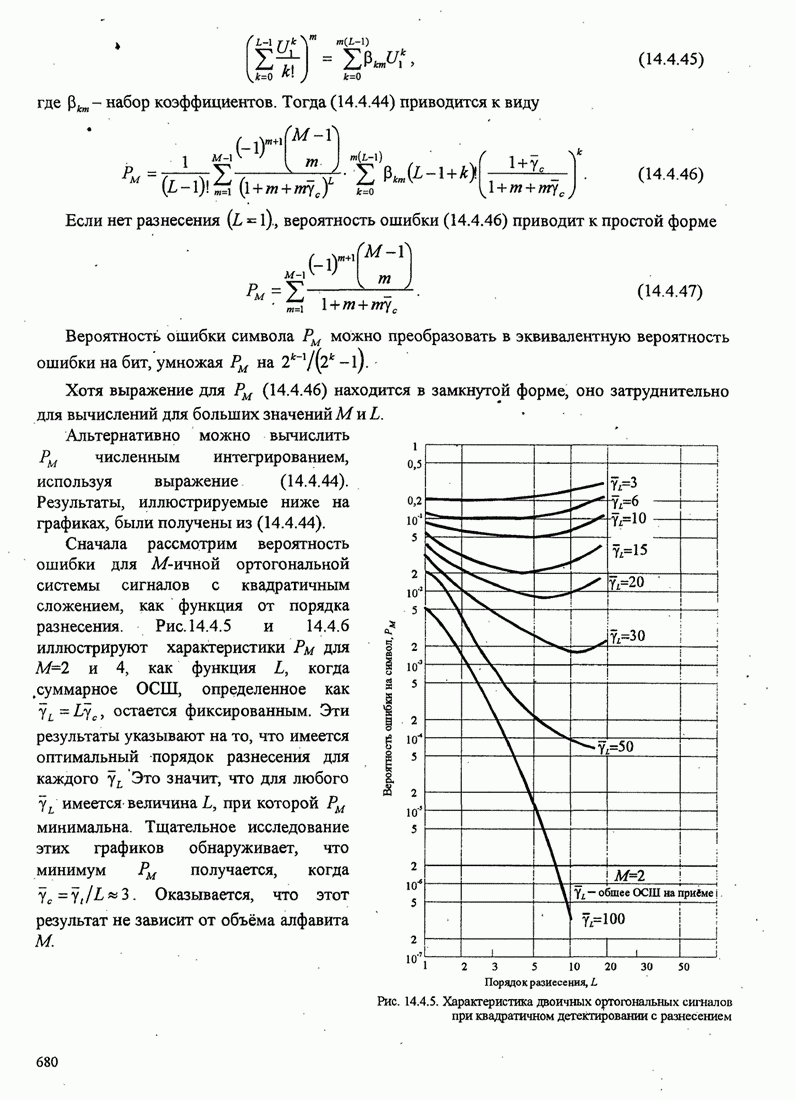
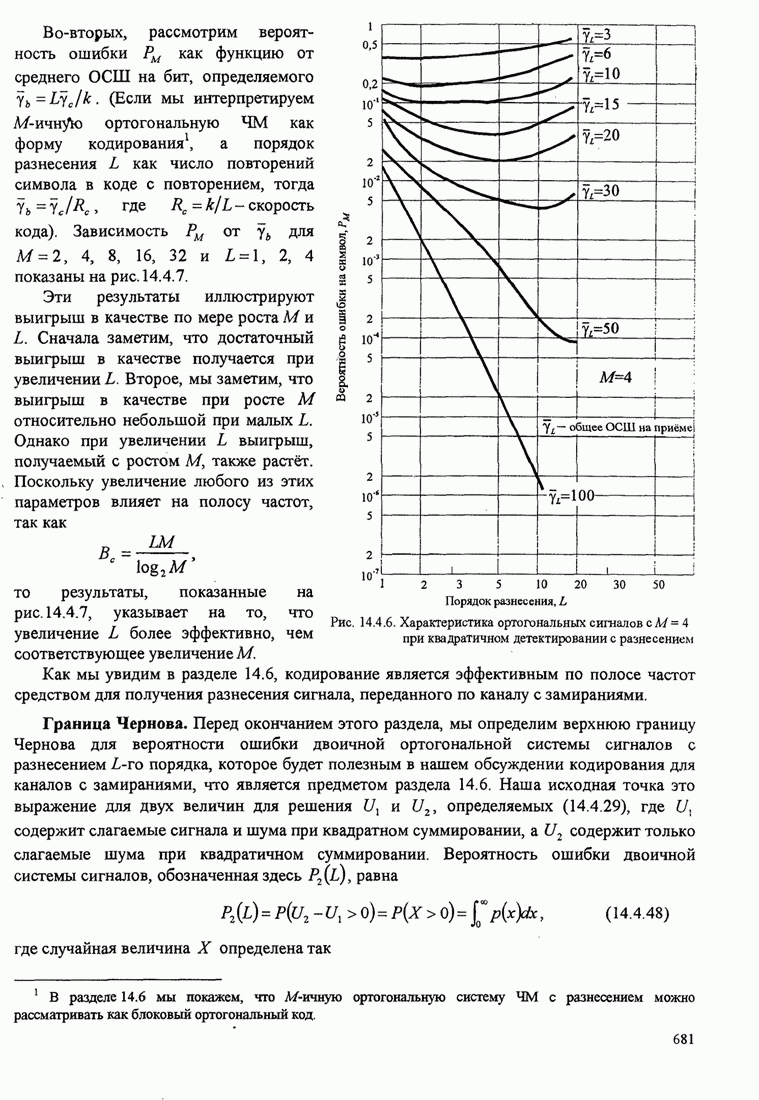
- 14.4.2. Многофазные сигналы
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
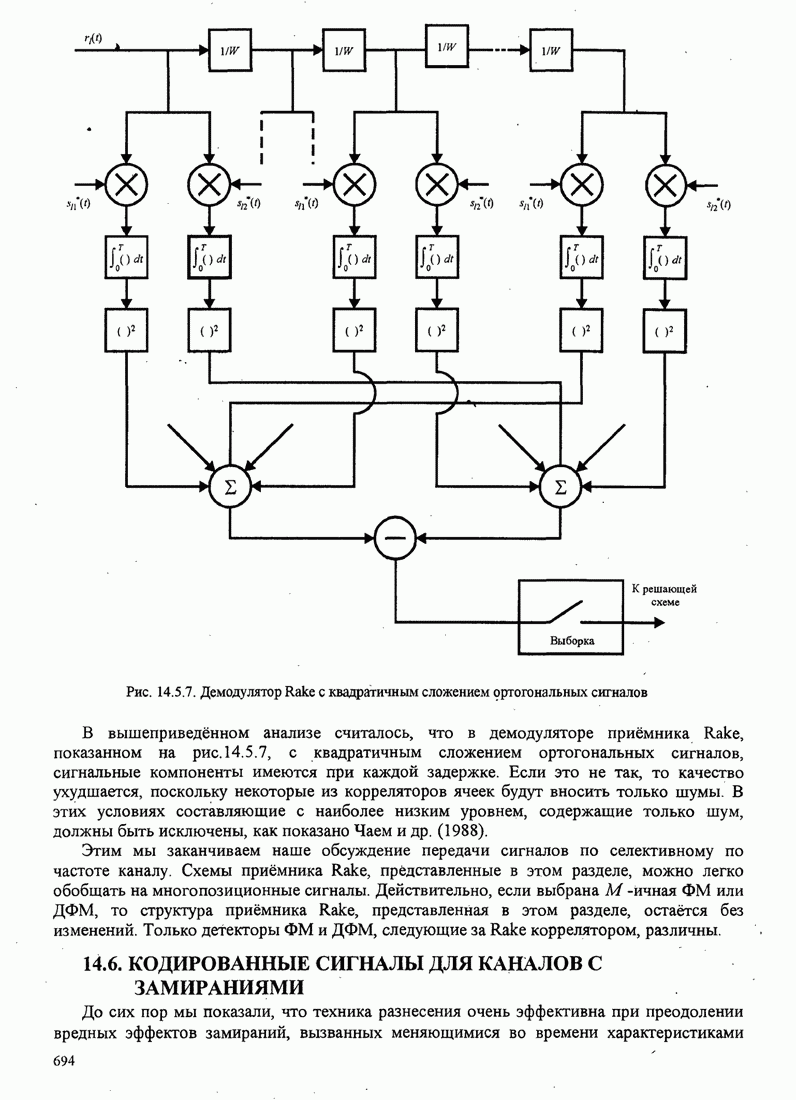
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
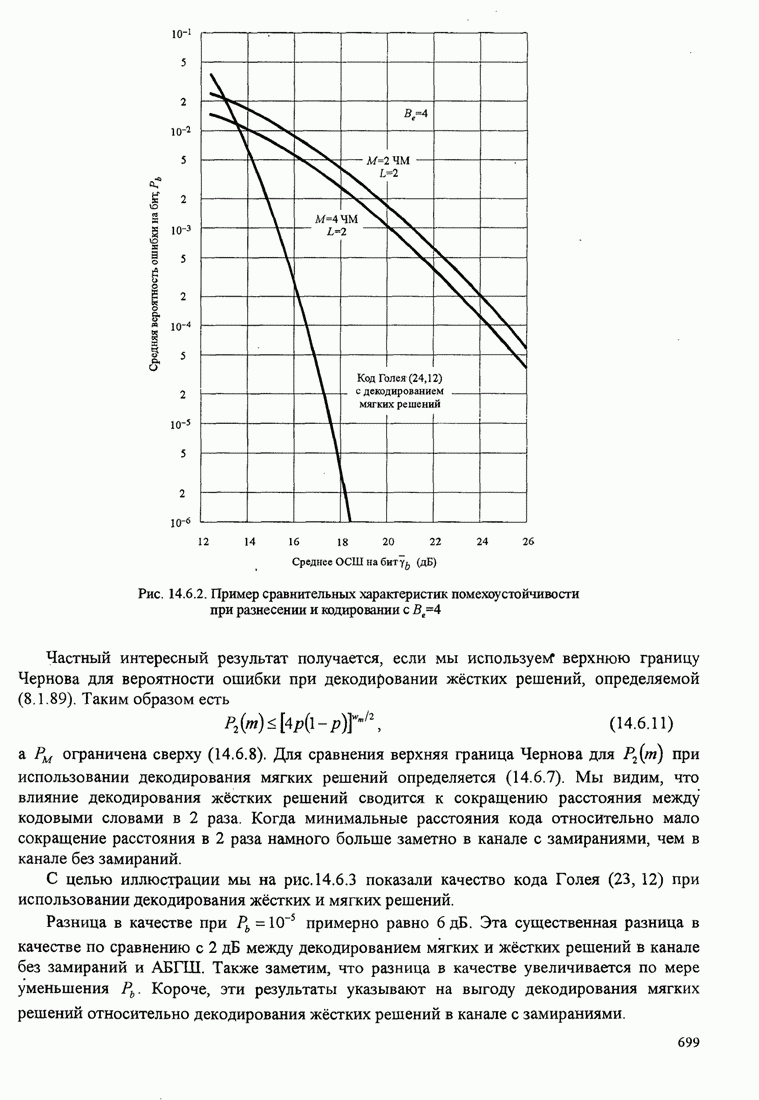
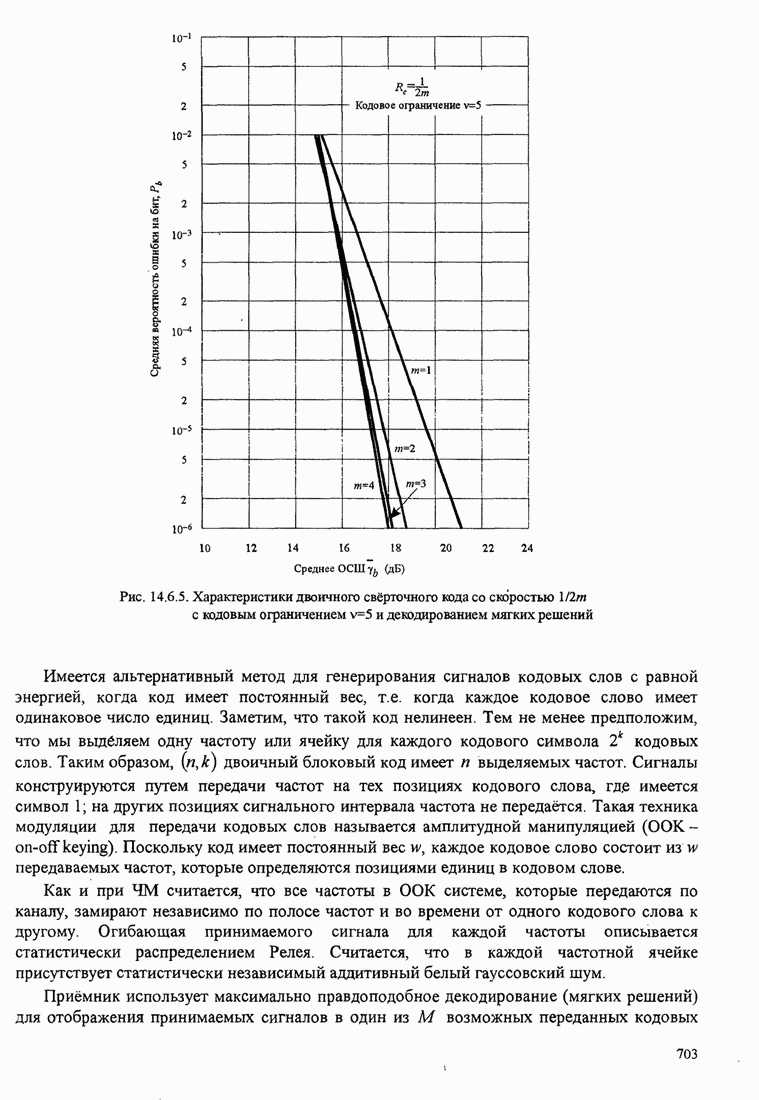
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
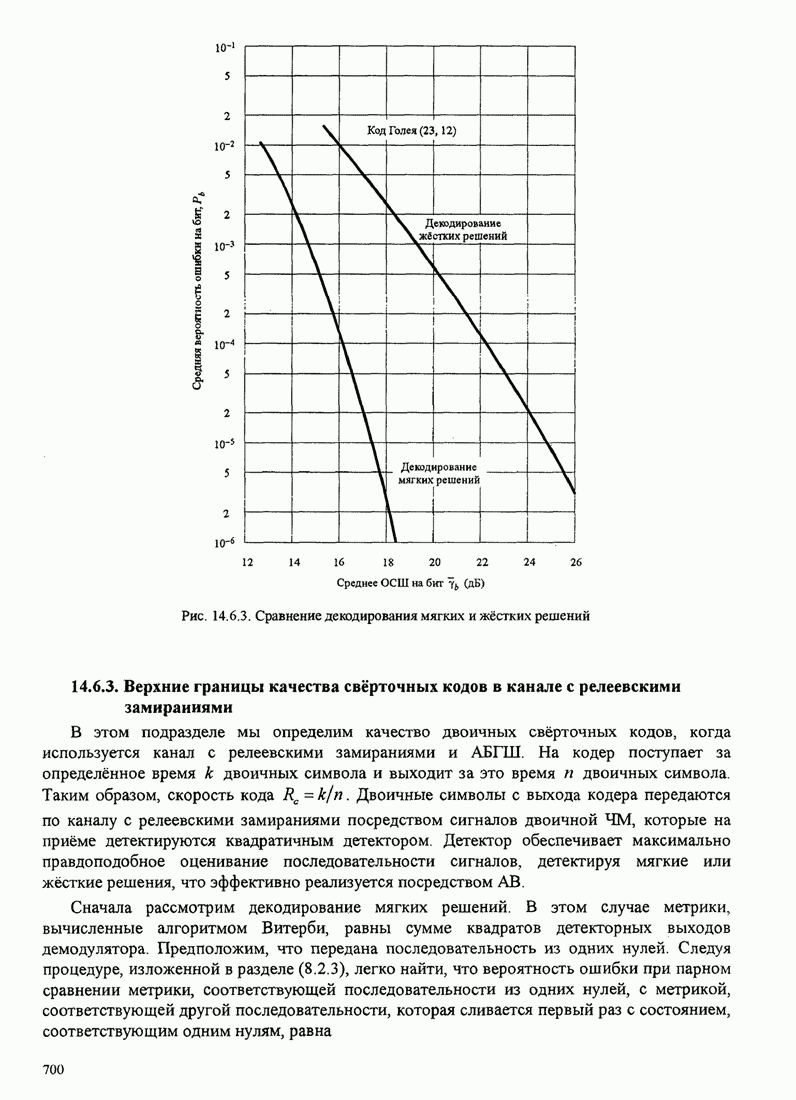
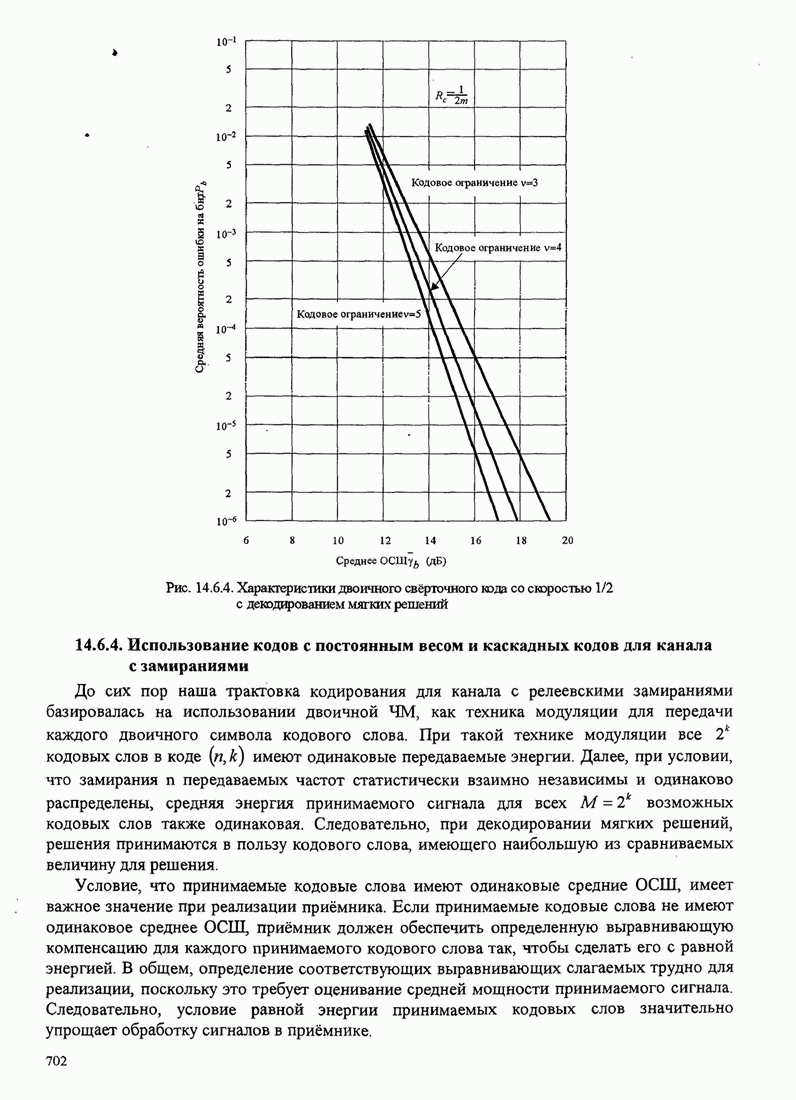
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
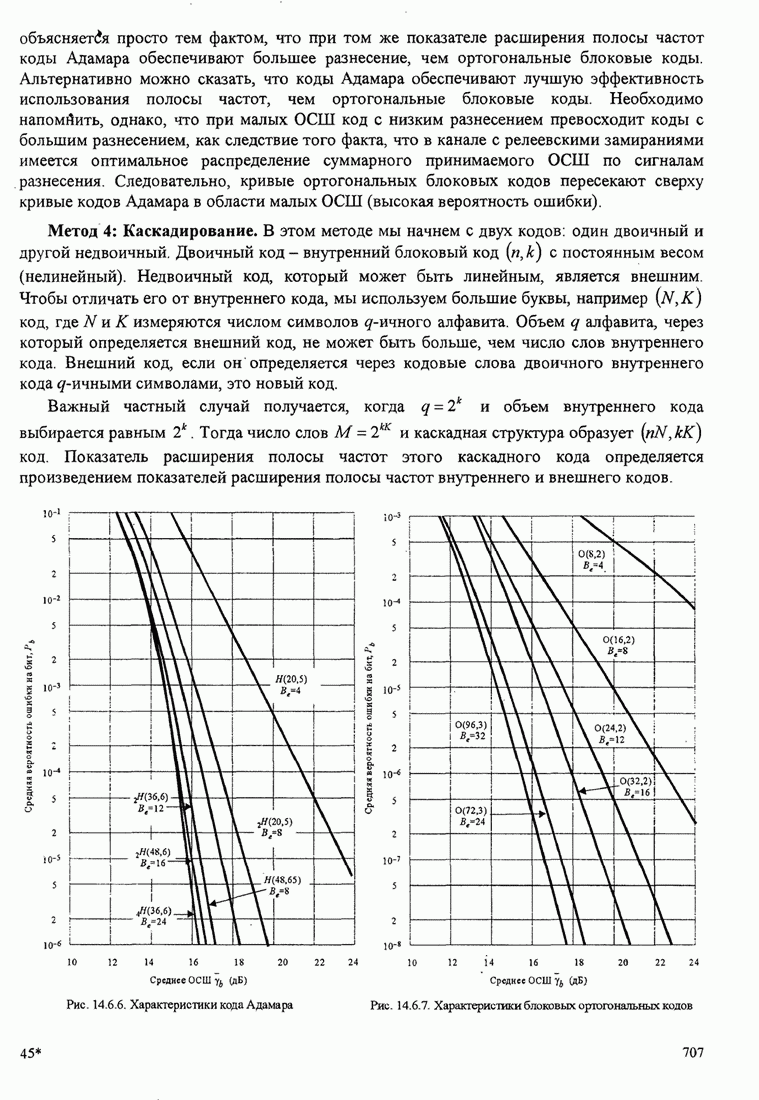
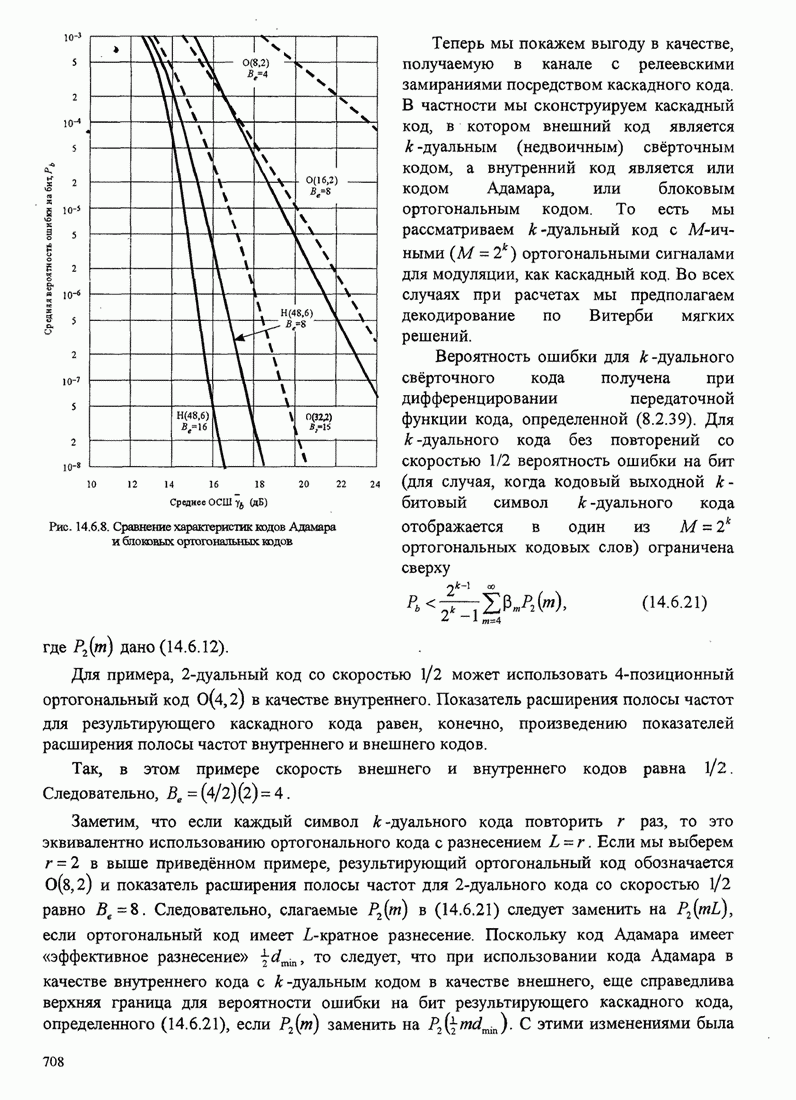
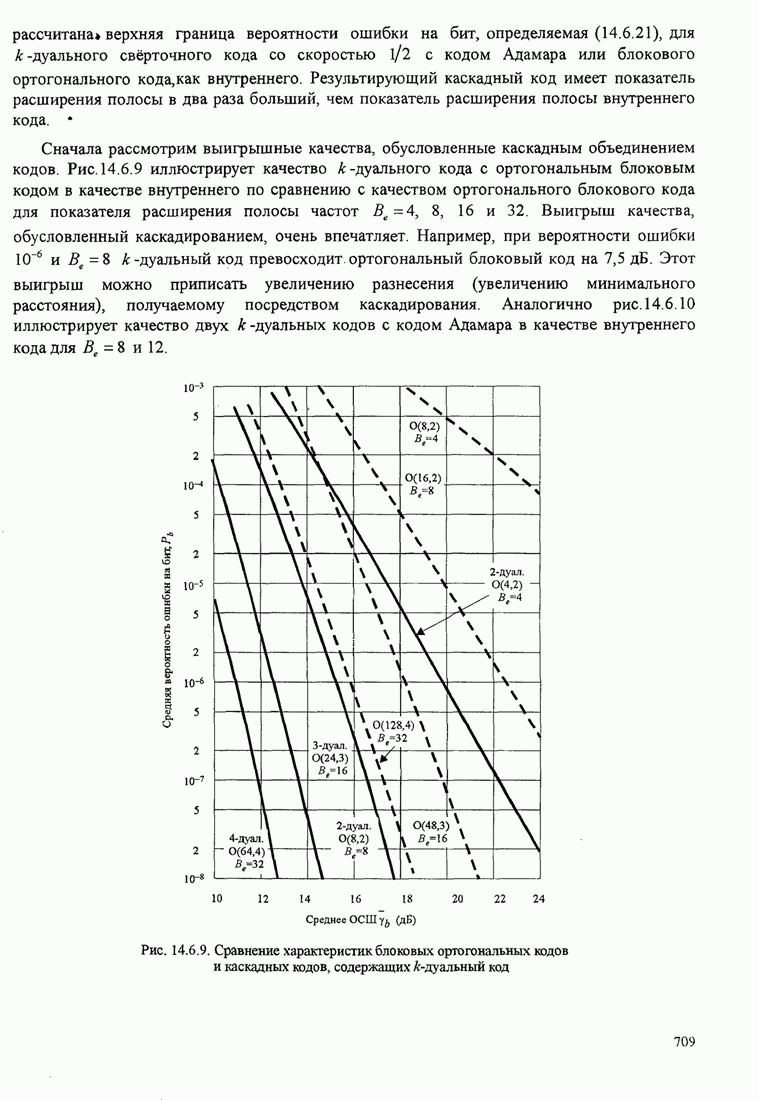
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
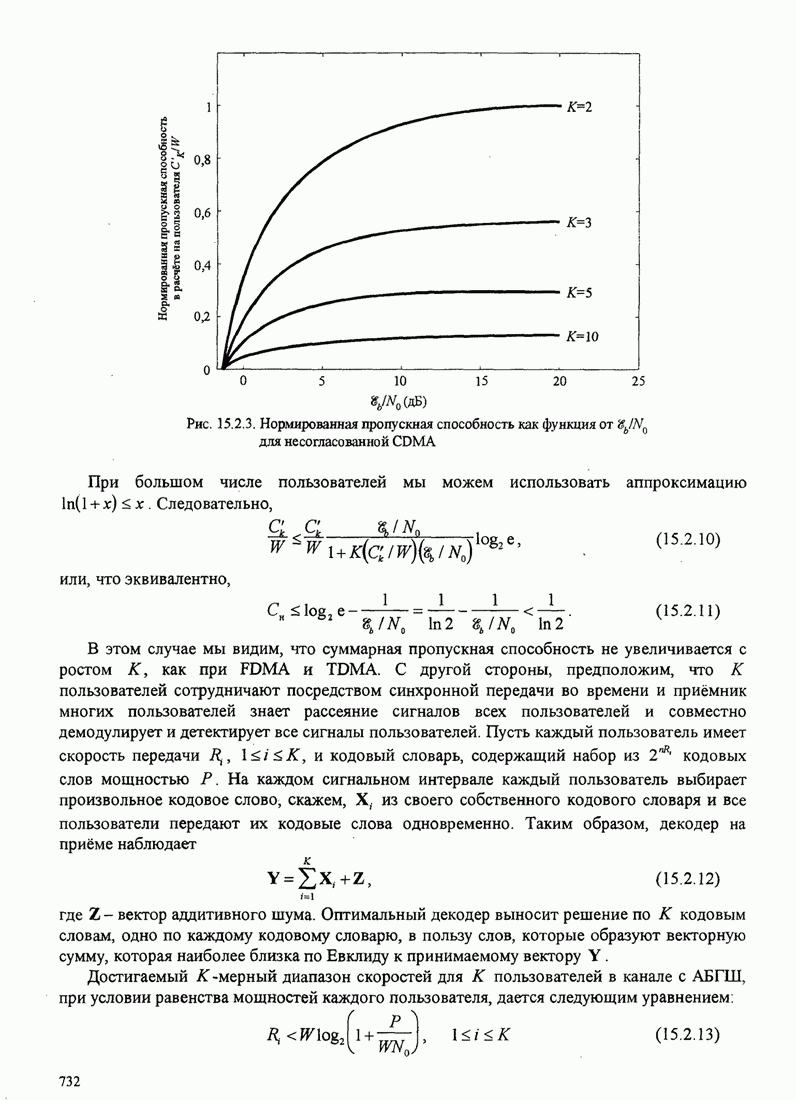
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
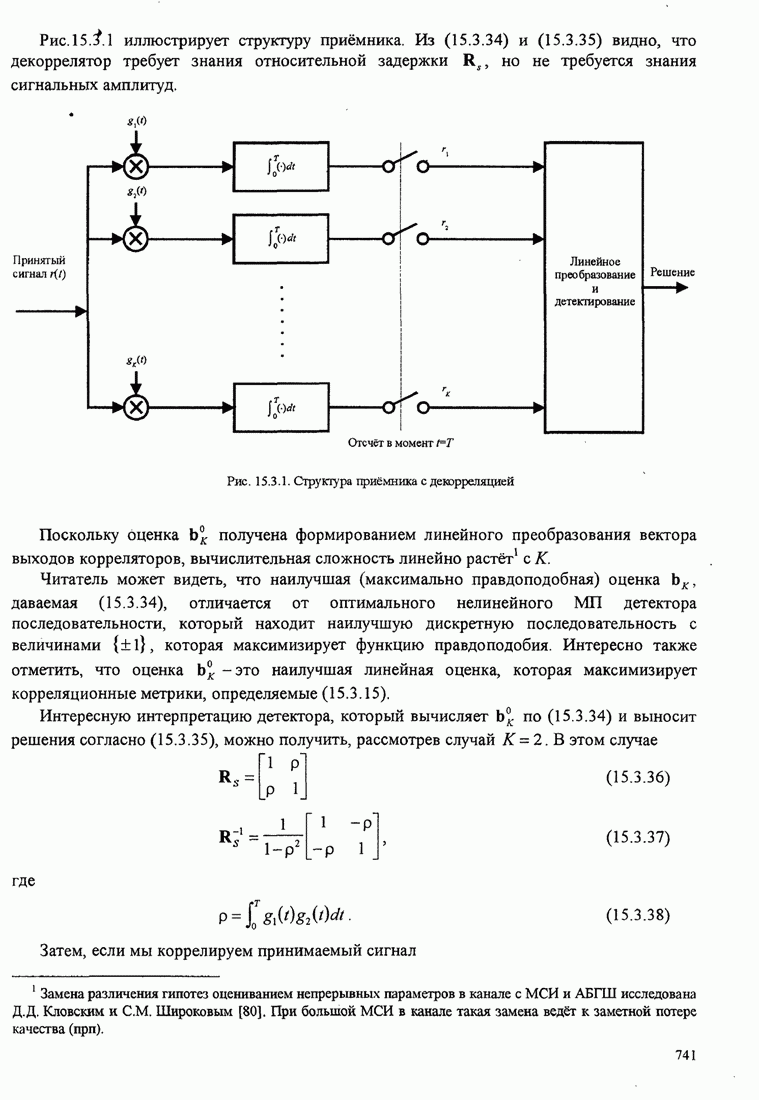
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
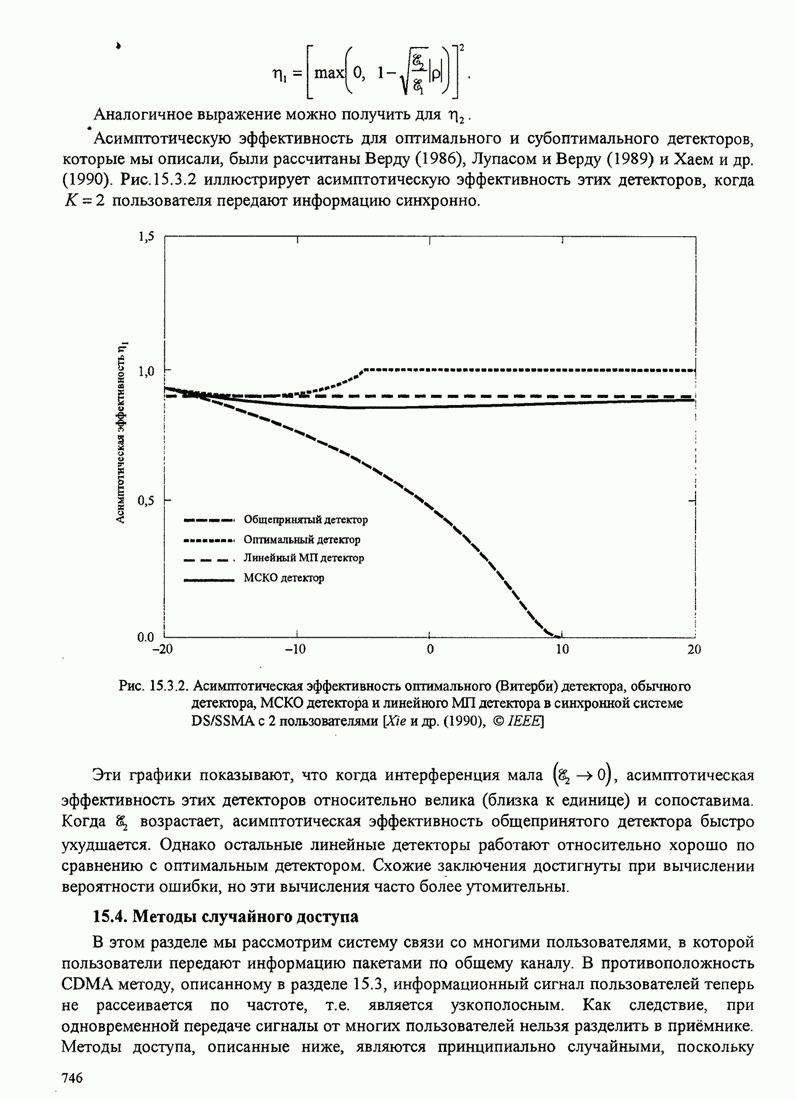
- 15.3.4. Характеристики качества детекторов
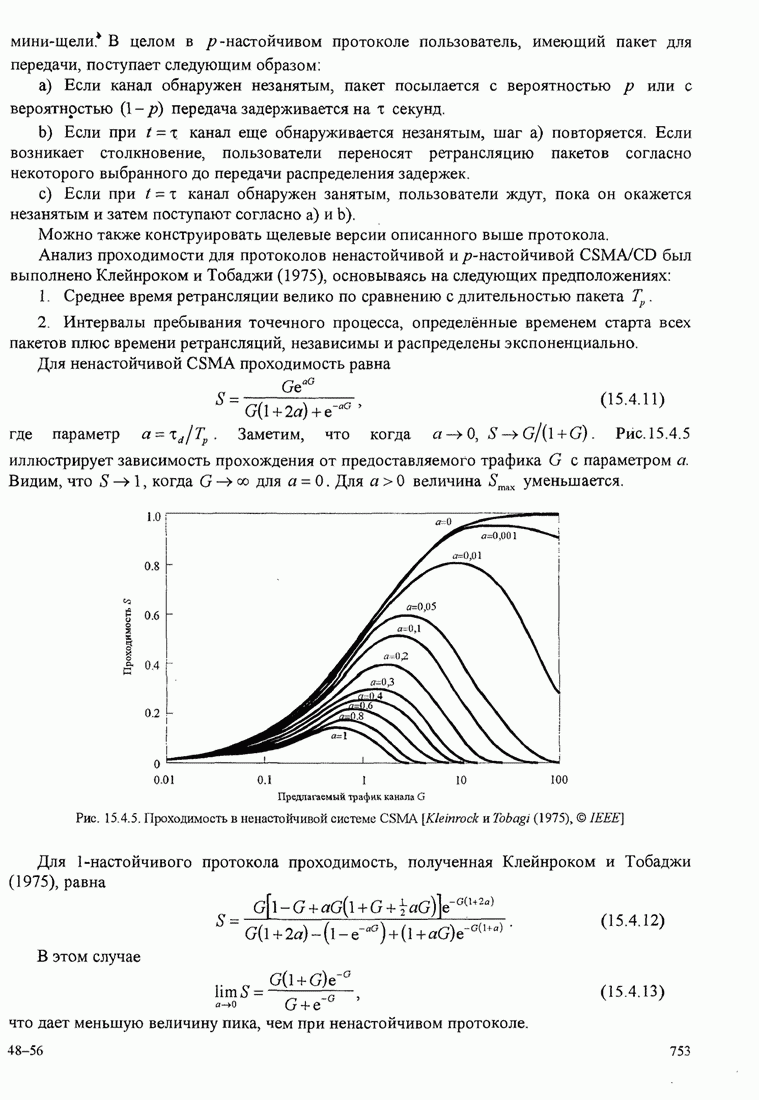
- 15.4. Методы случайного доступа
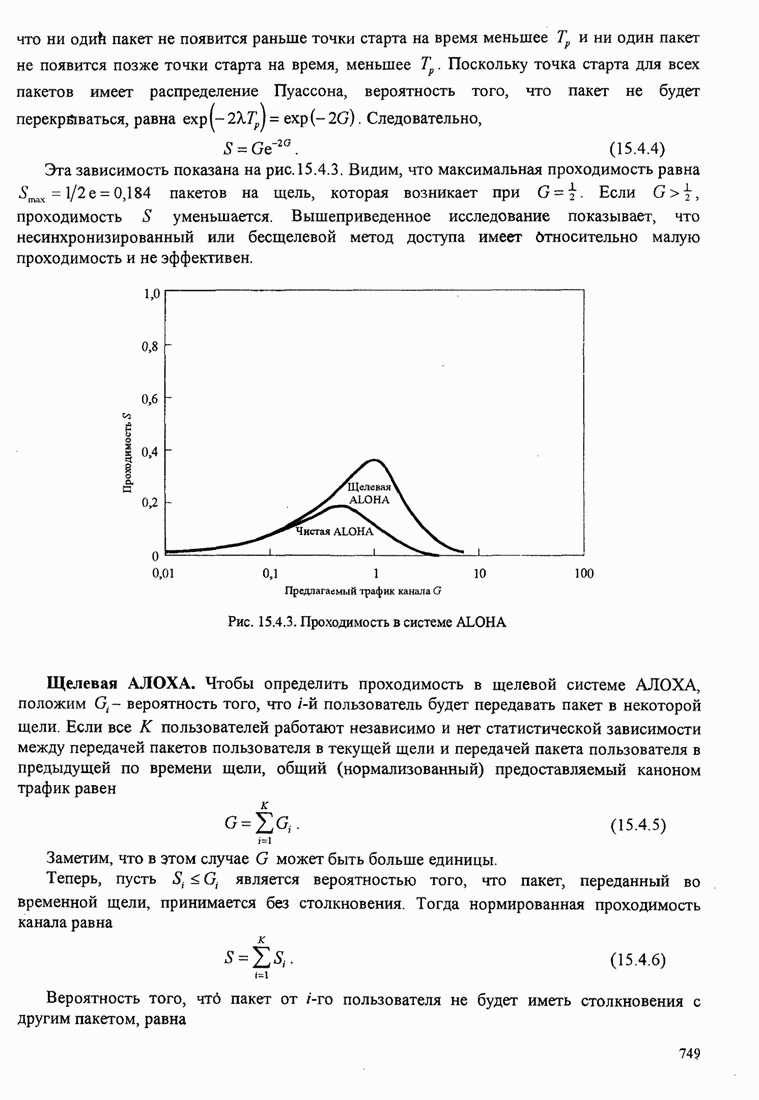
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)