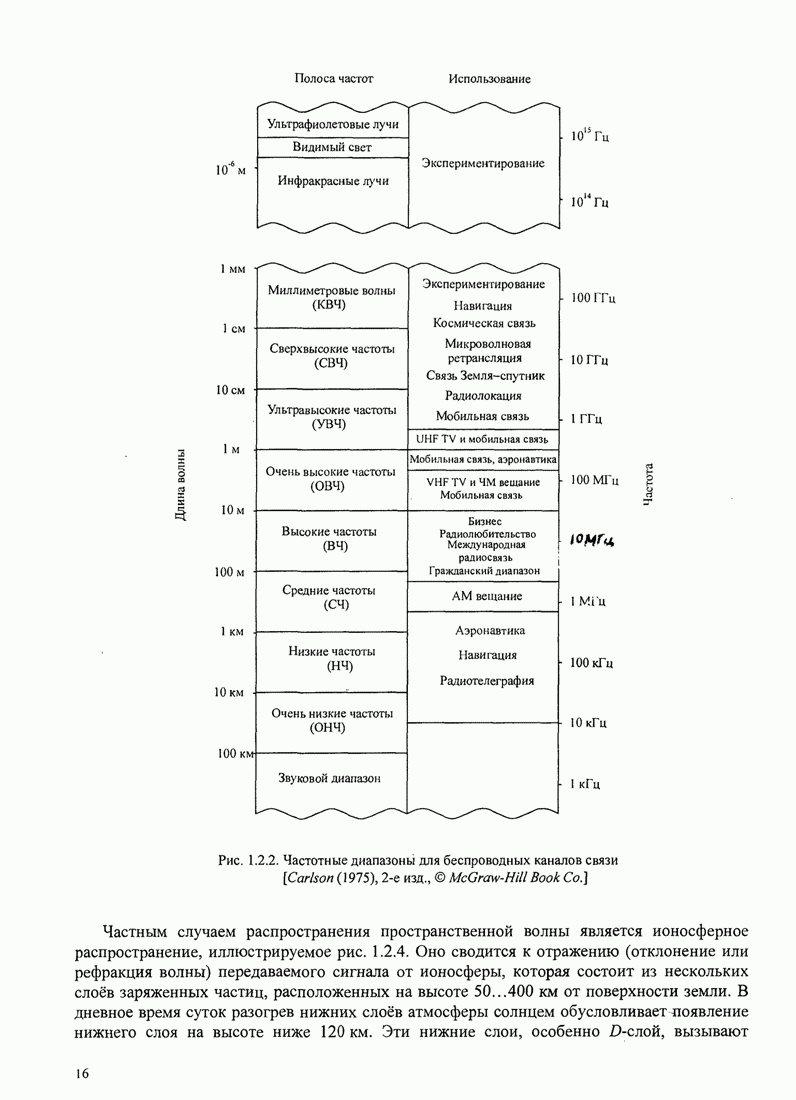
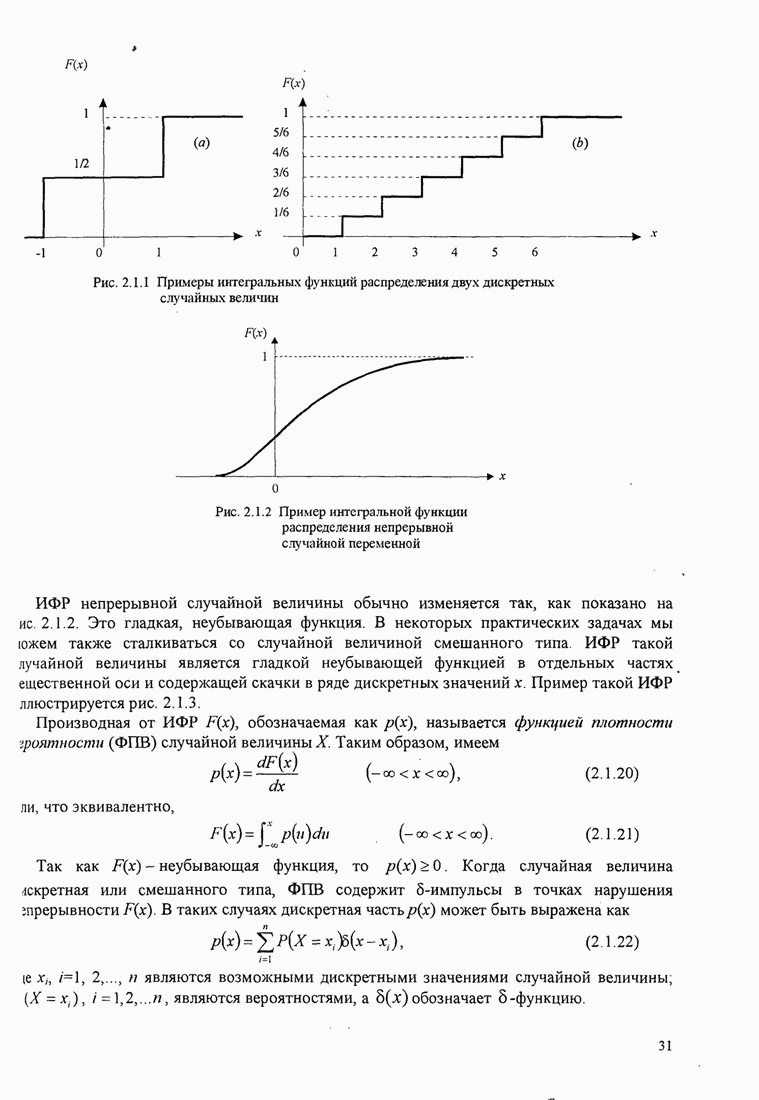
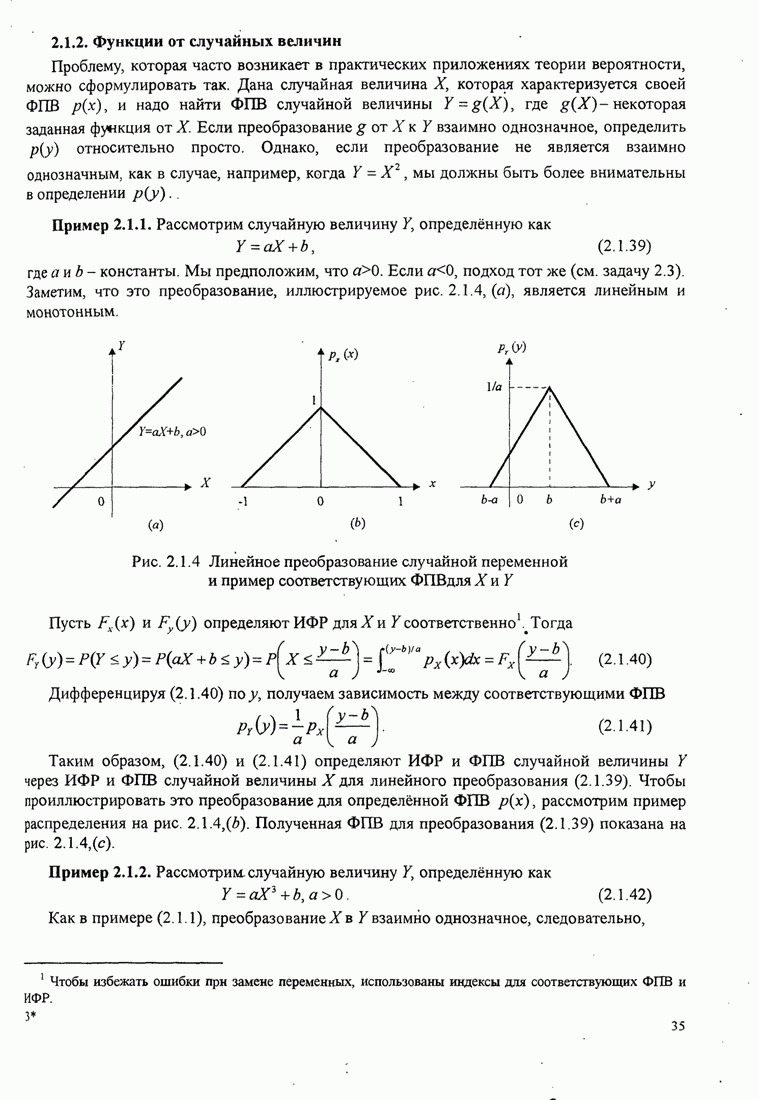
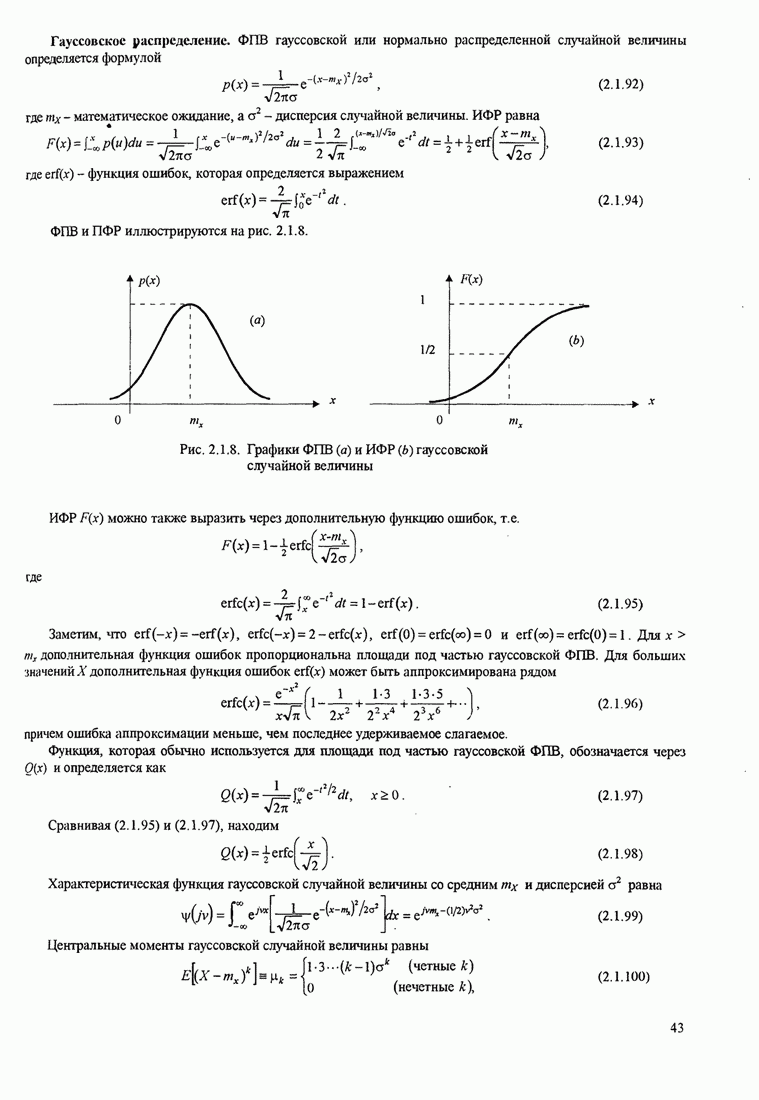
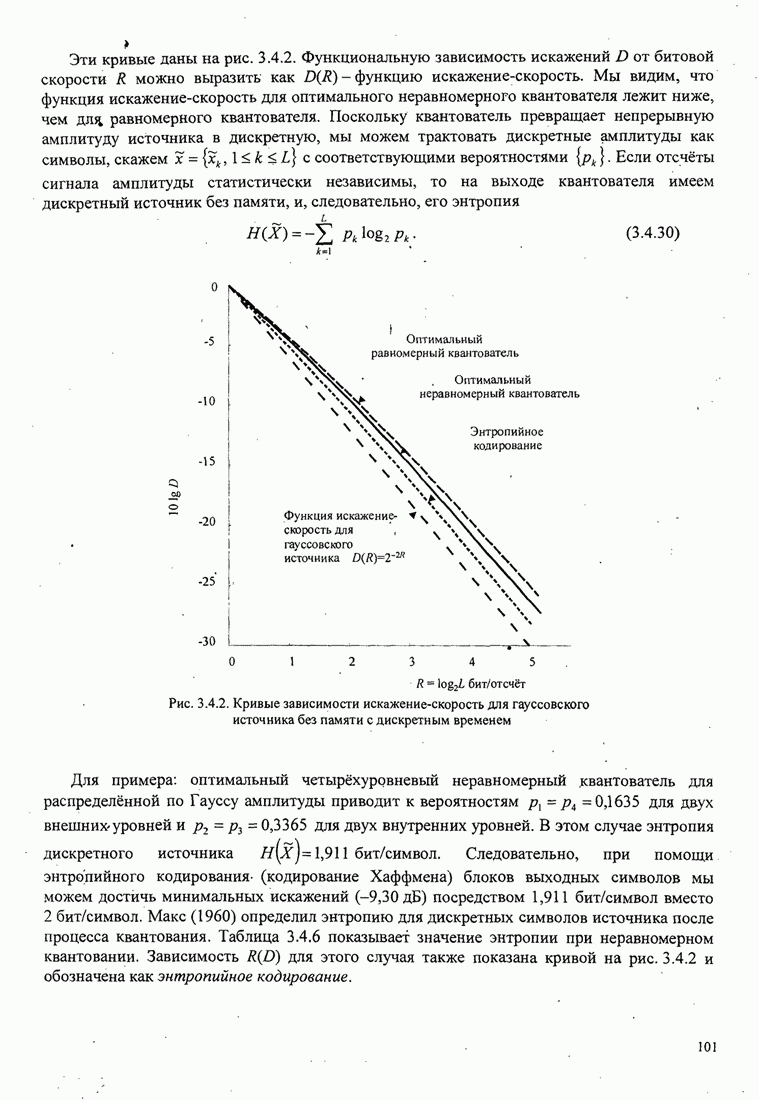
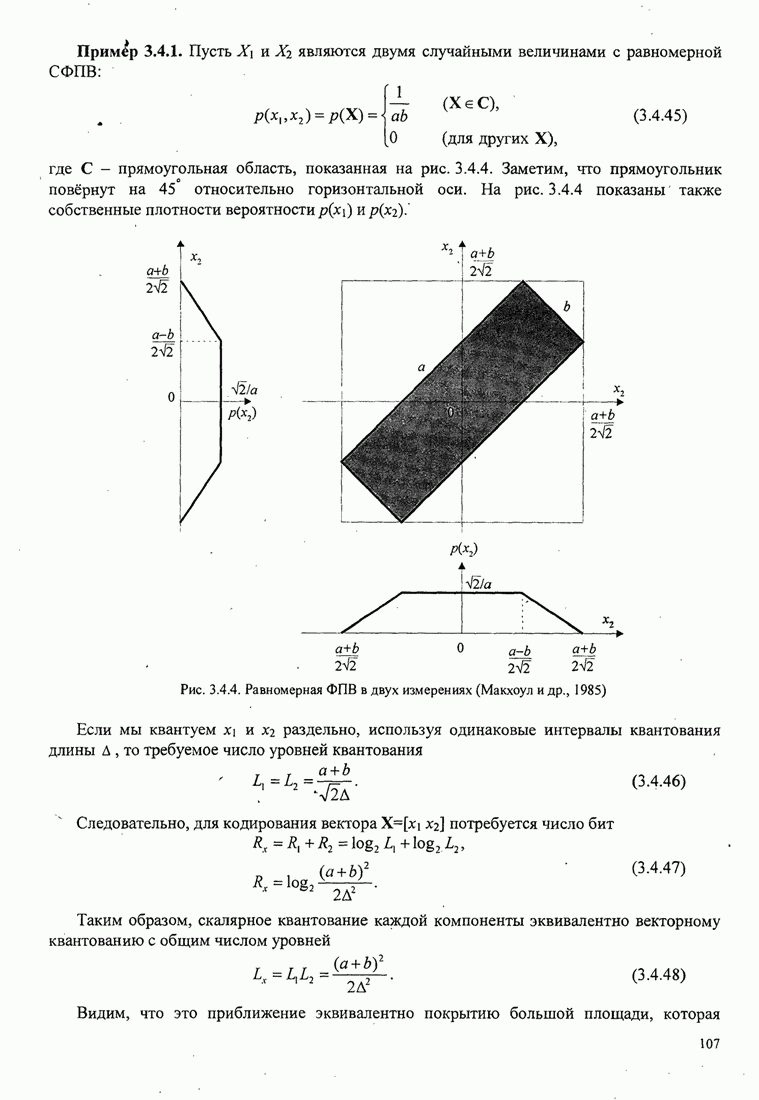
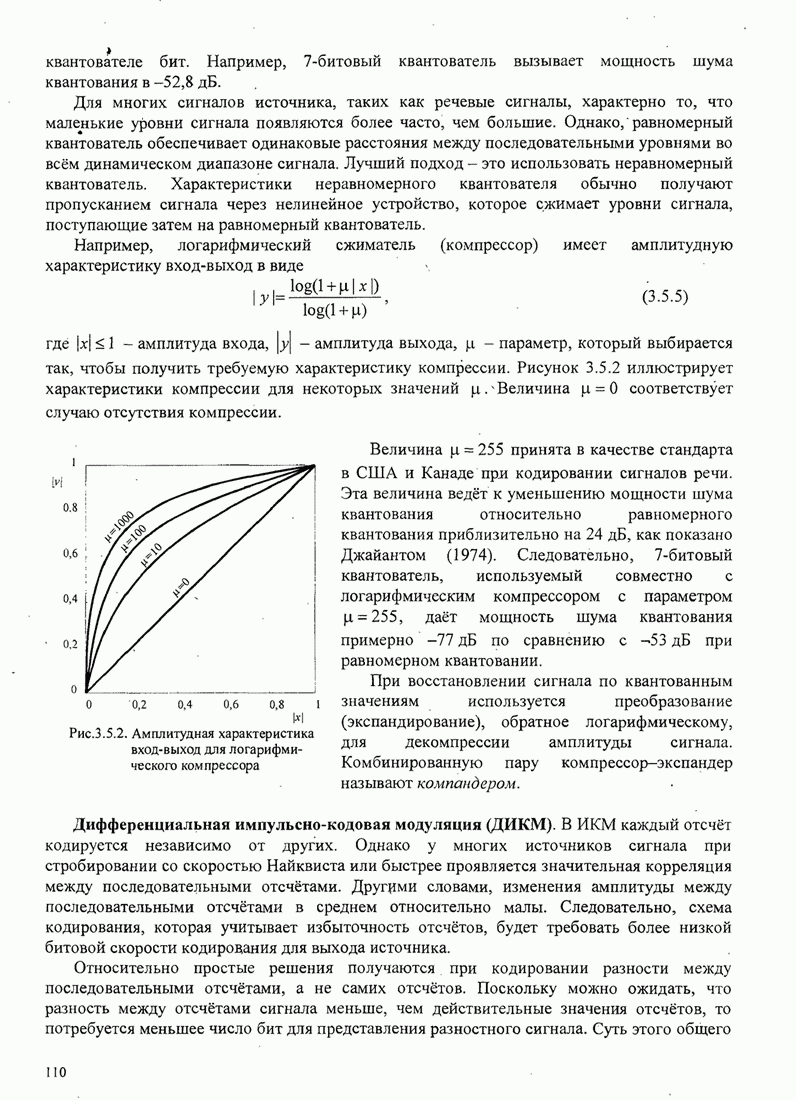
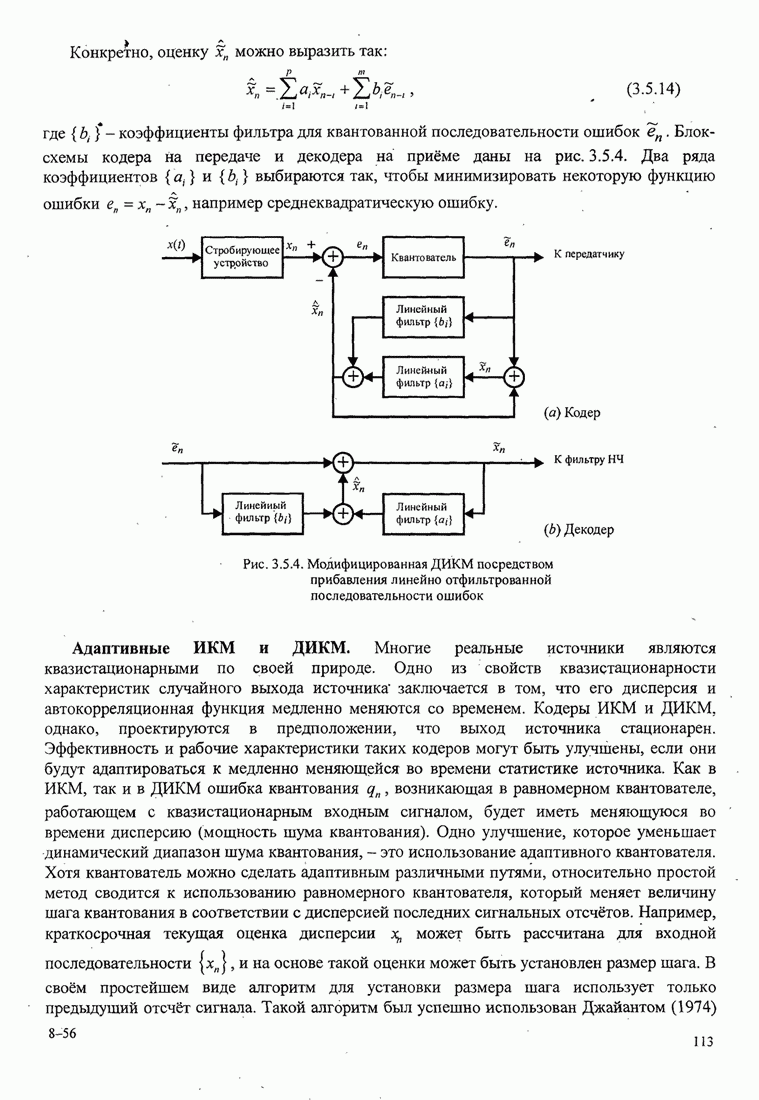
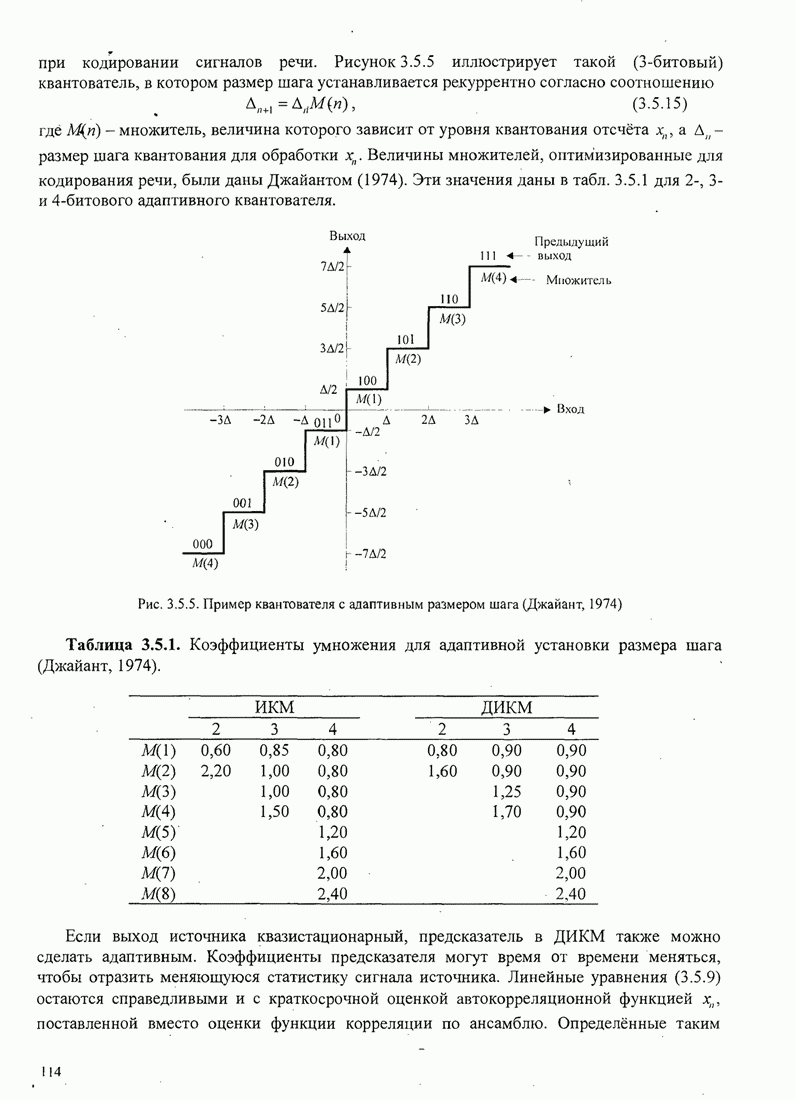
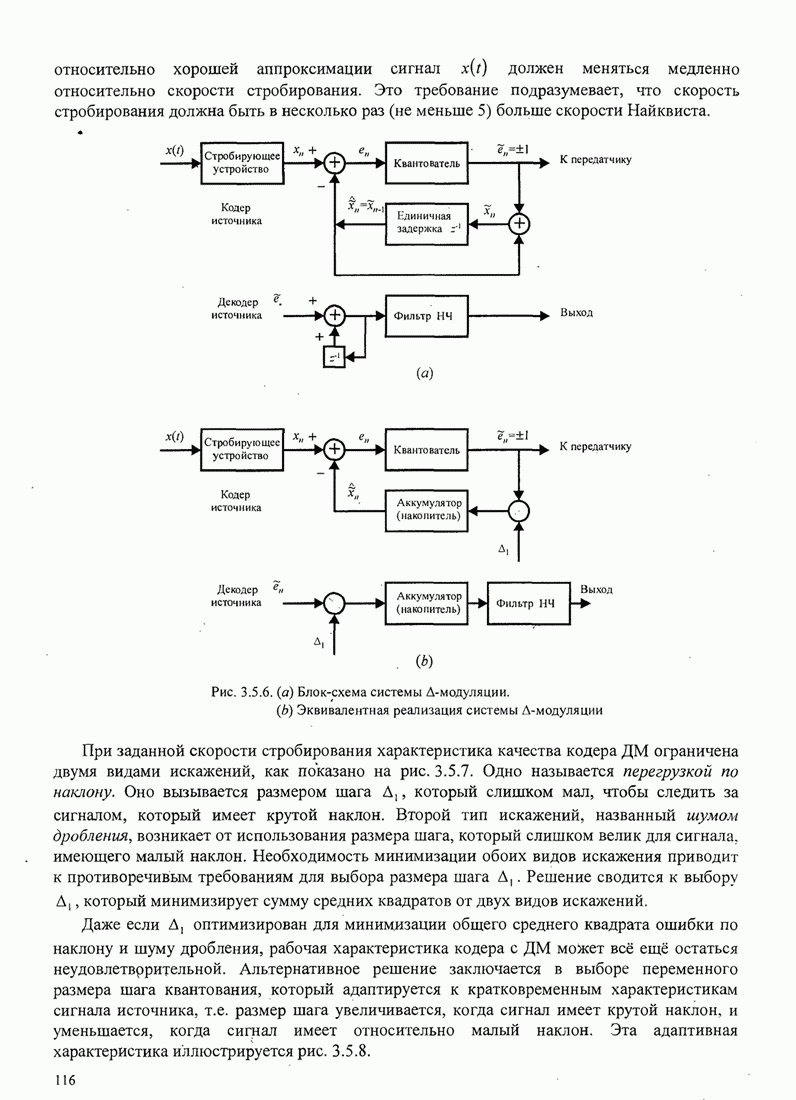
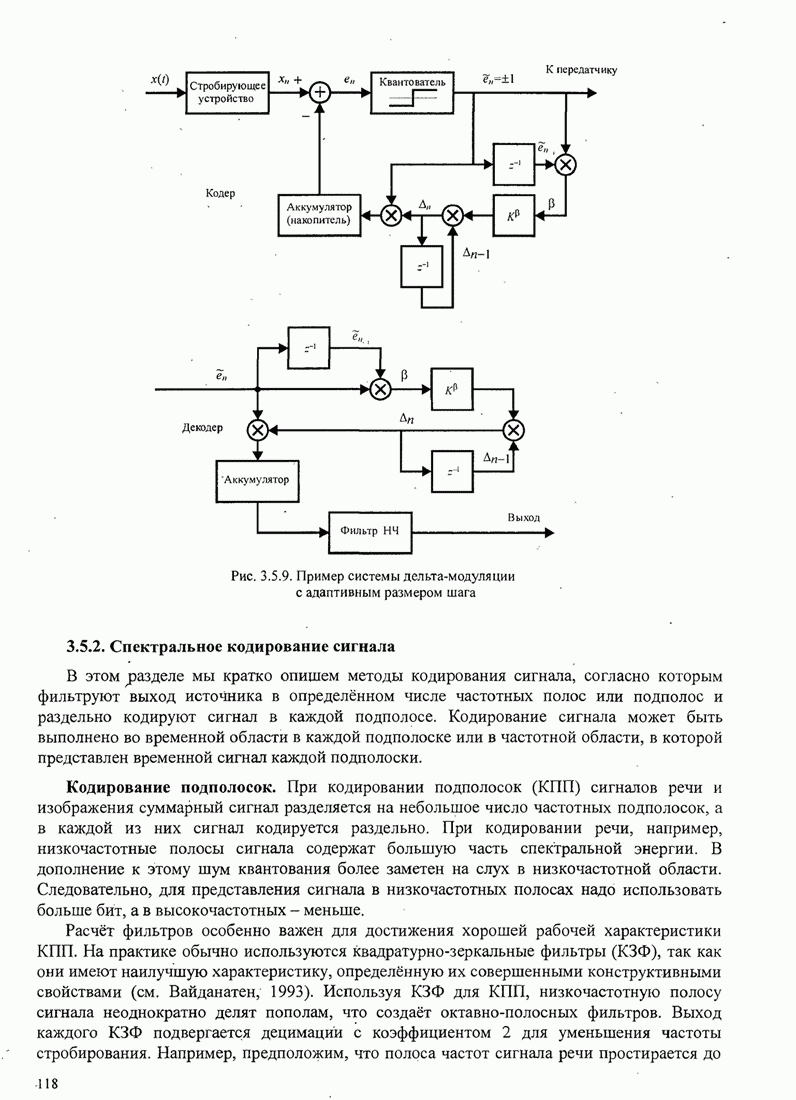
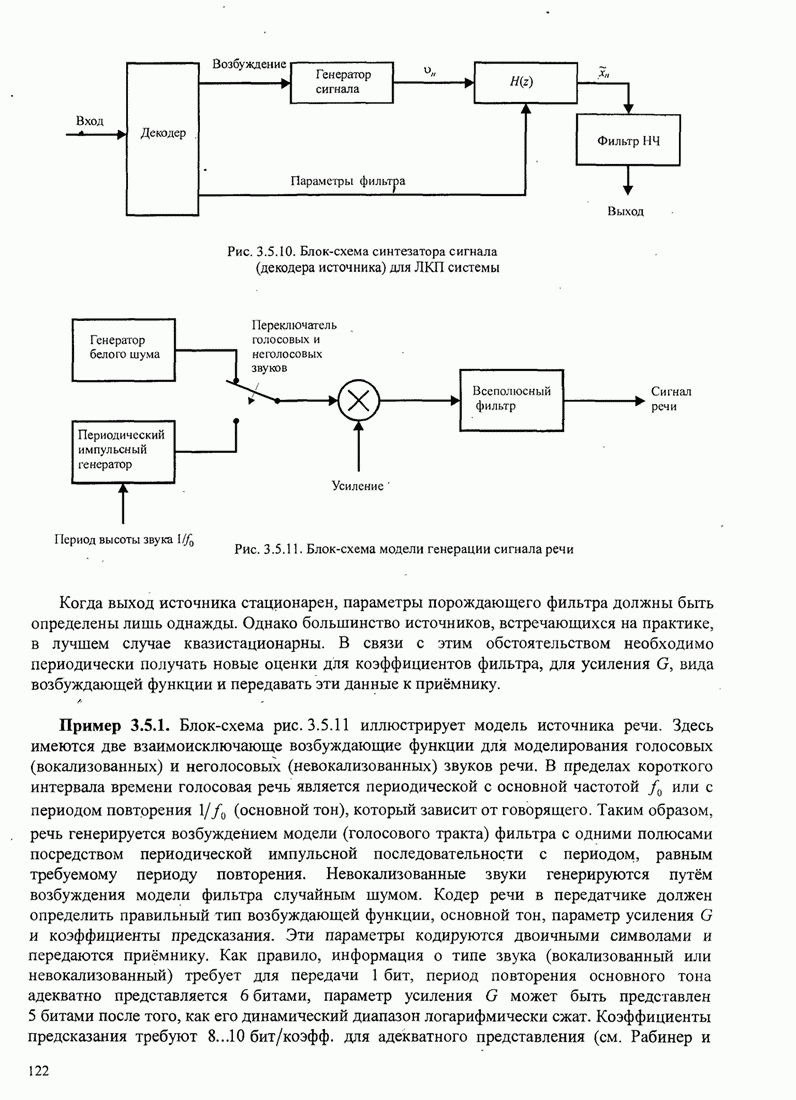
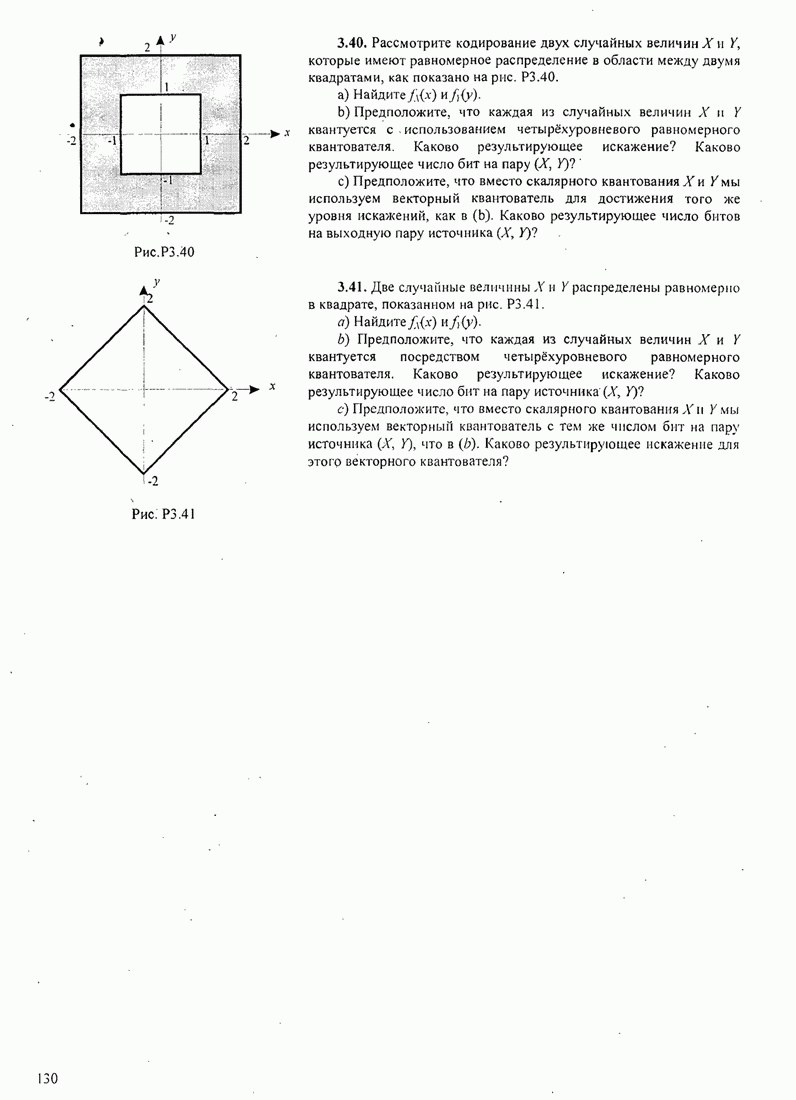
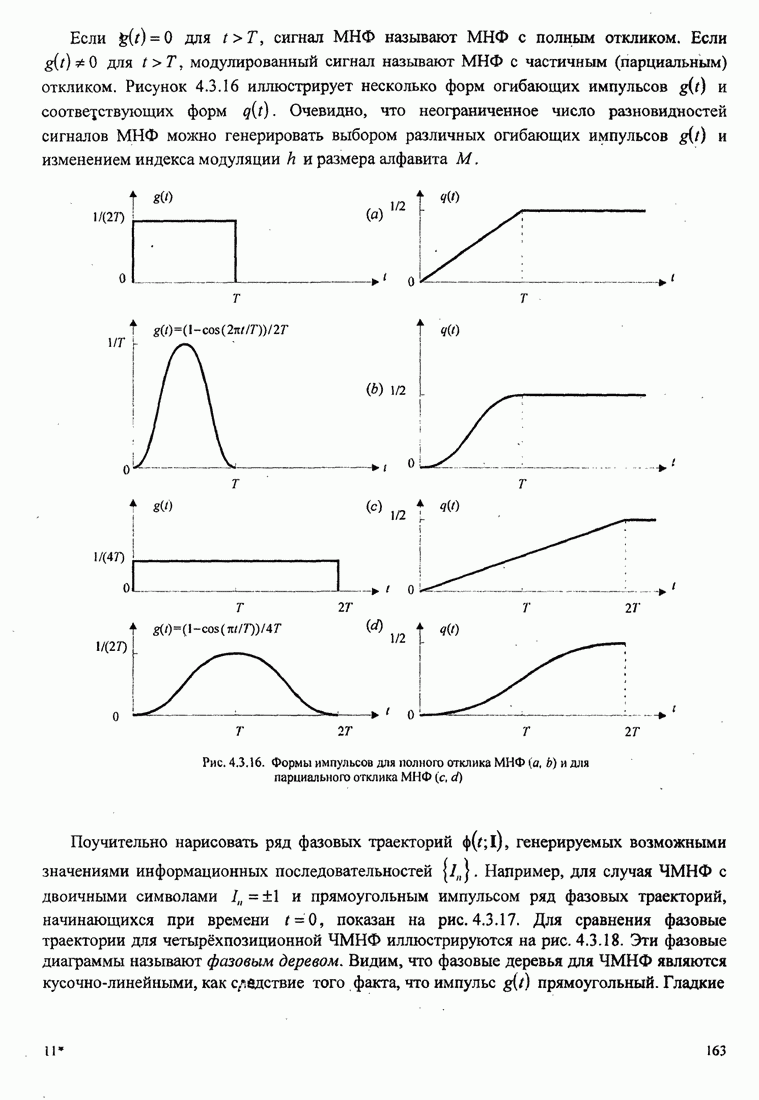
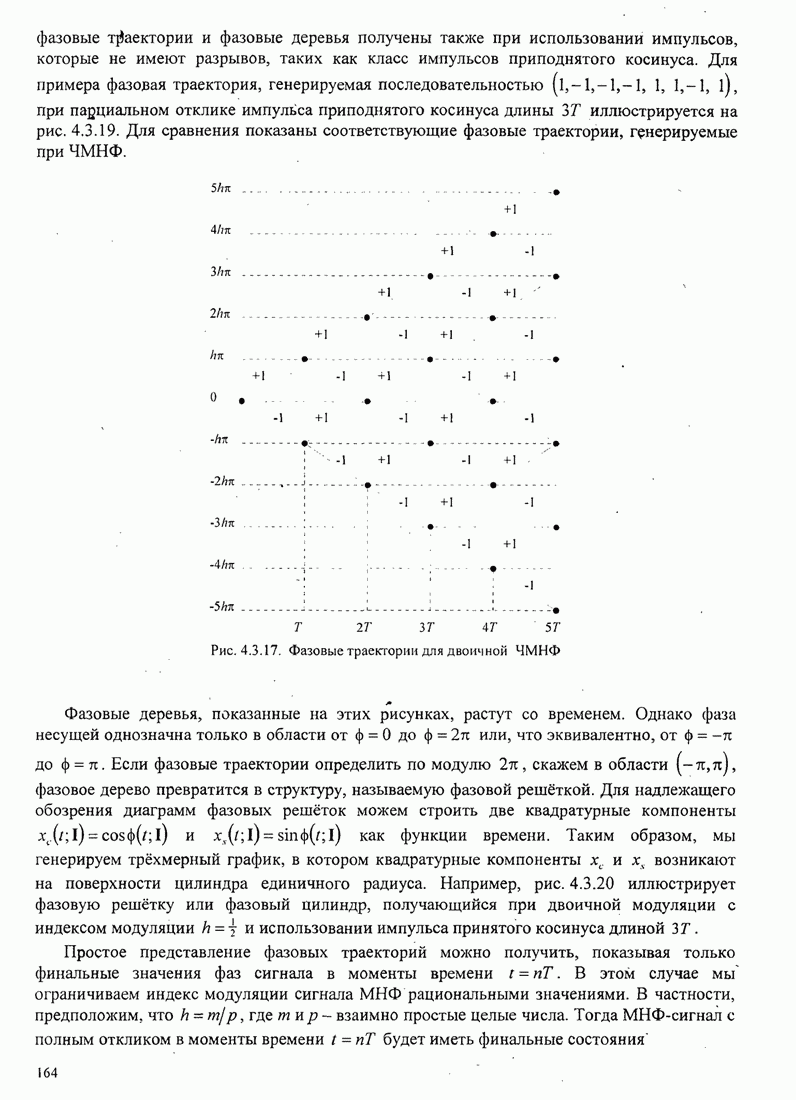
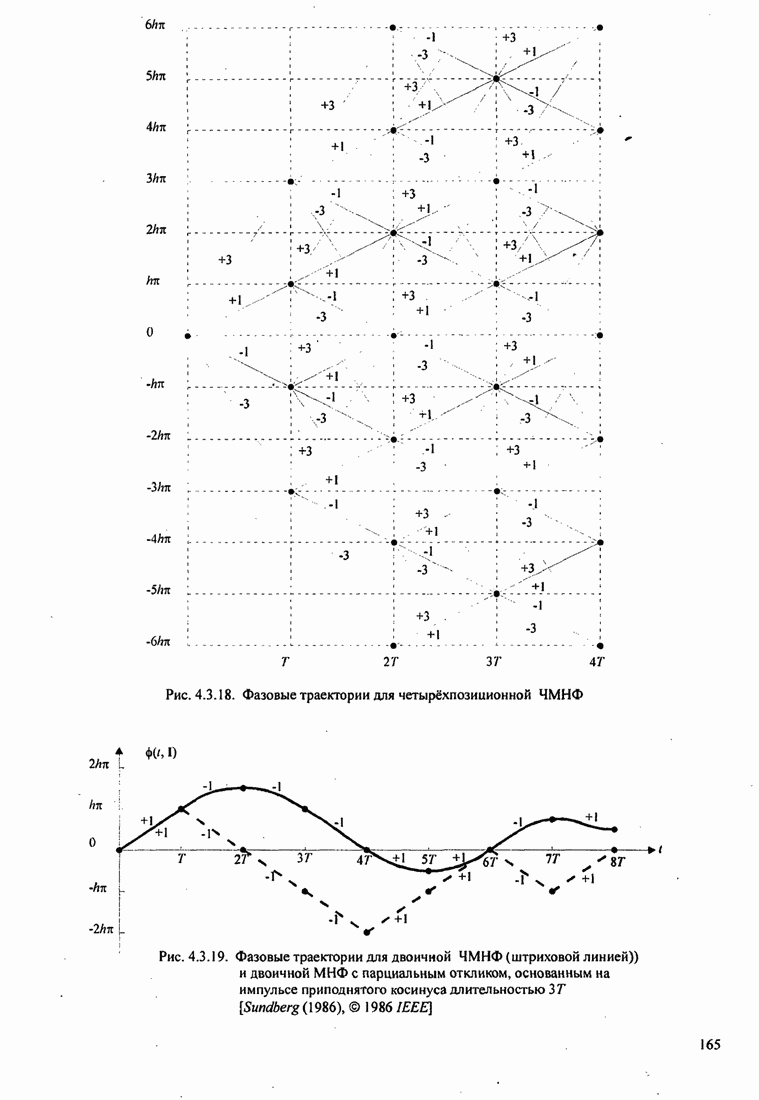
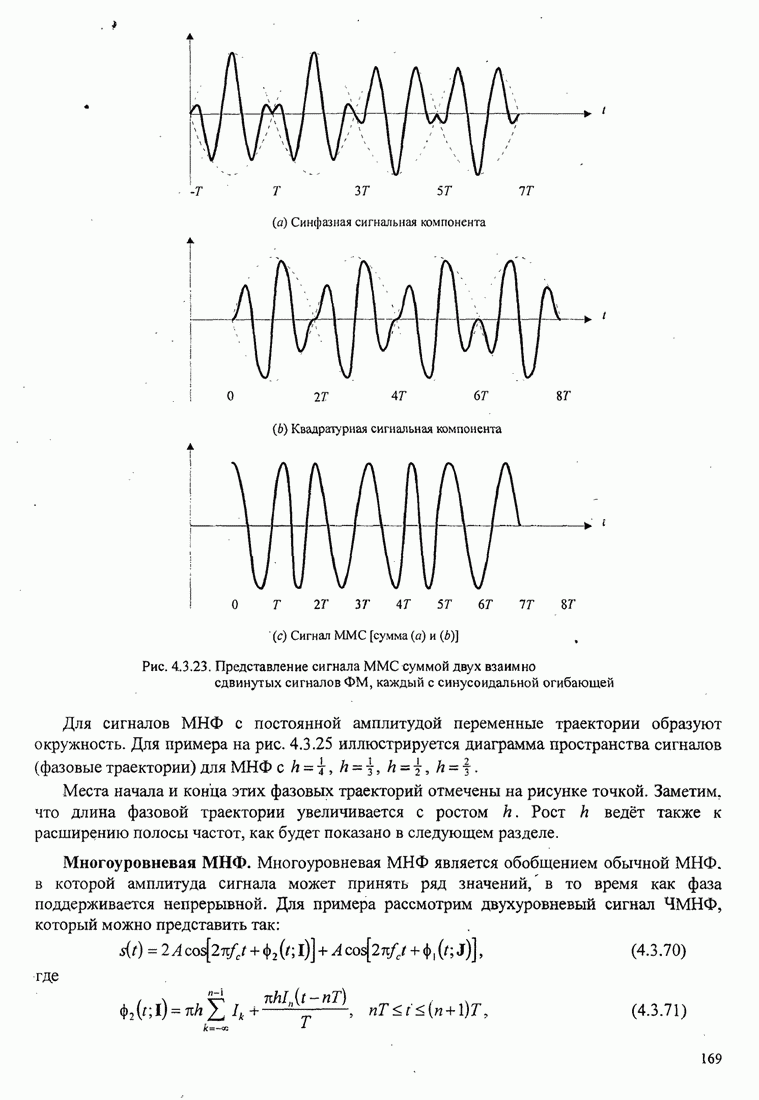
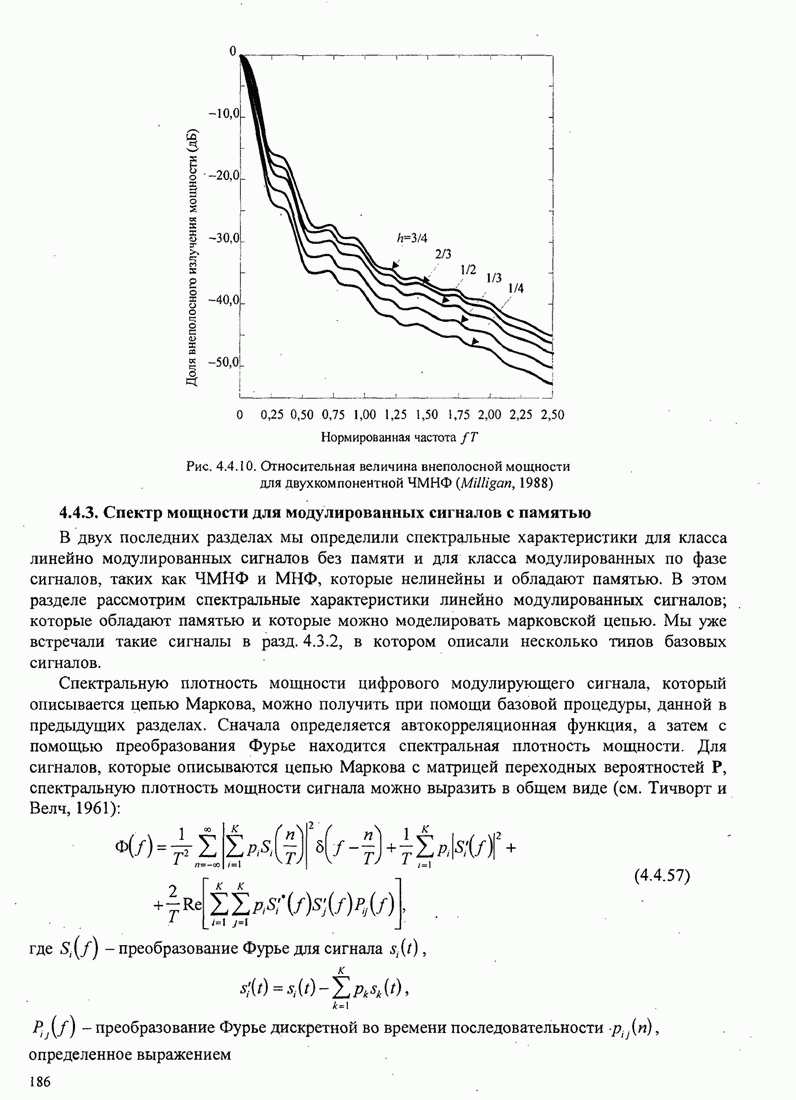
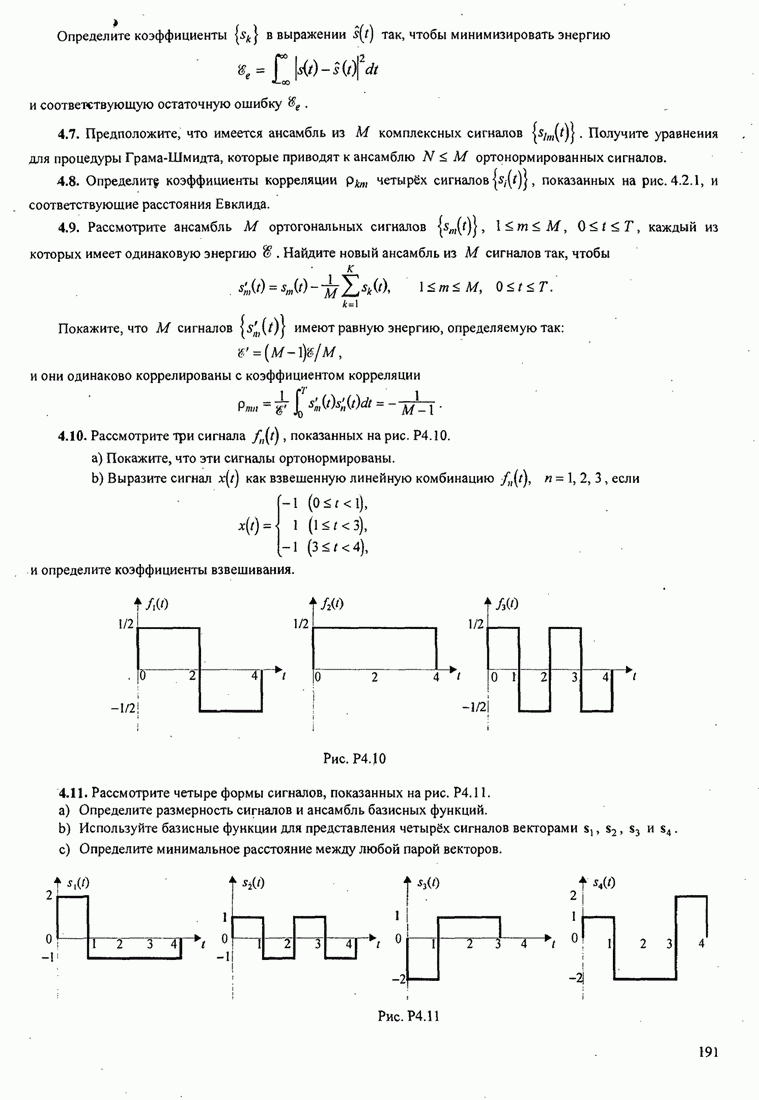
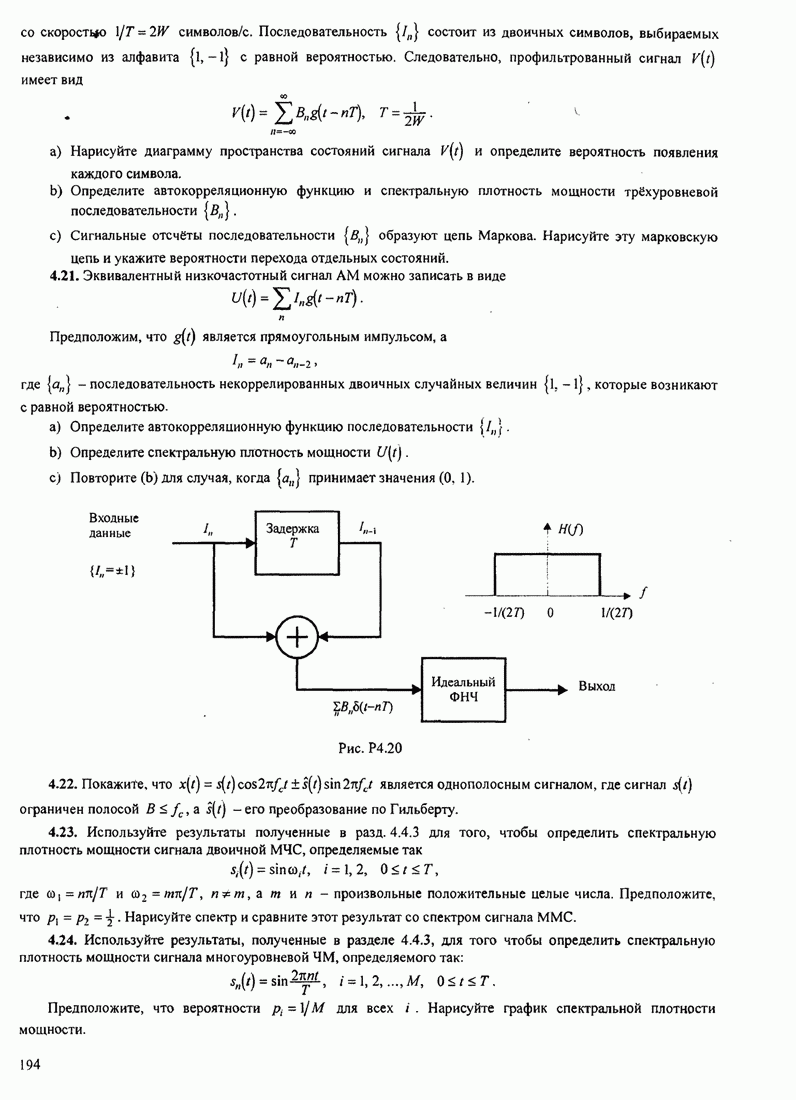
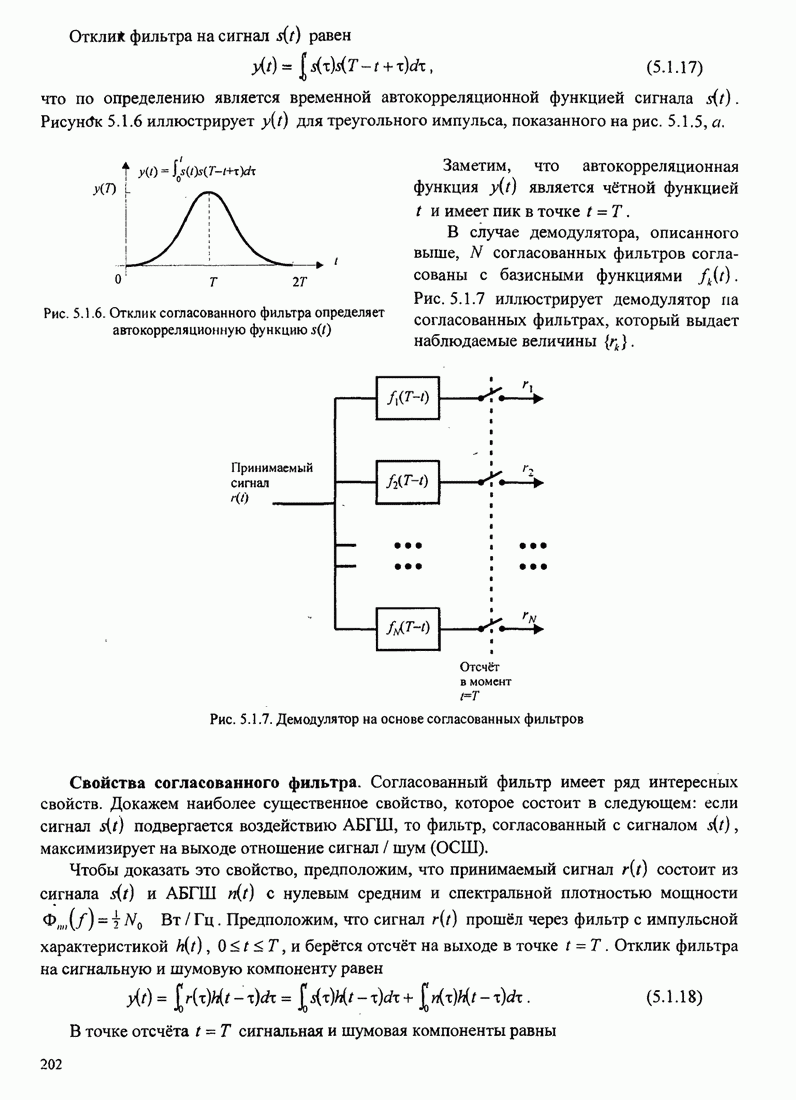
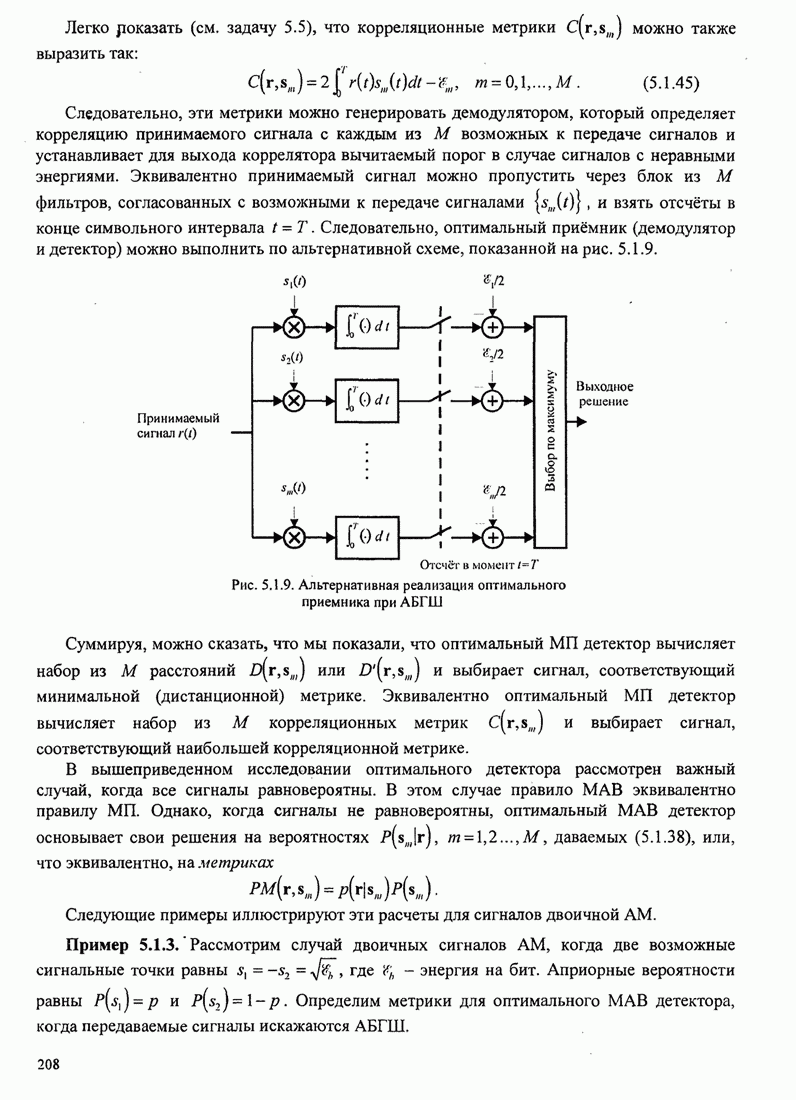
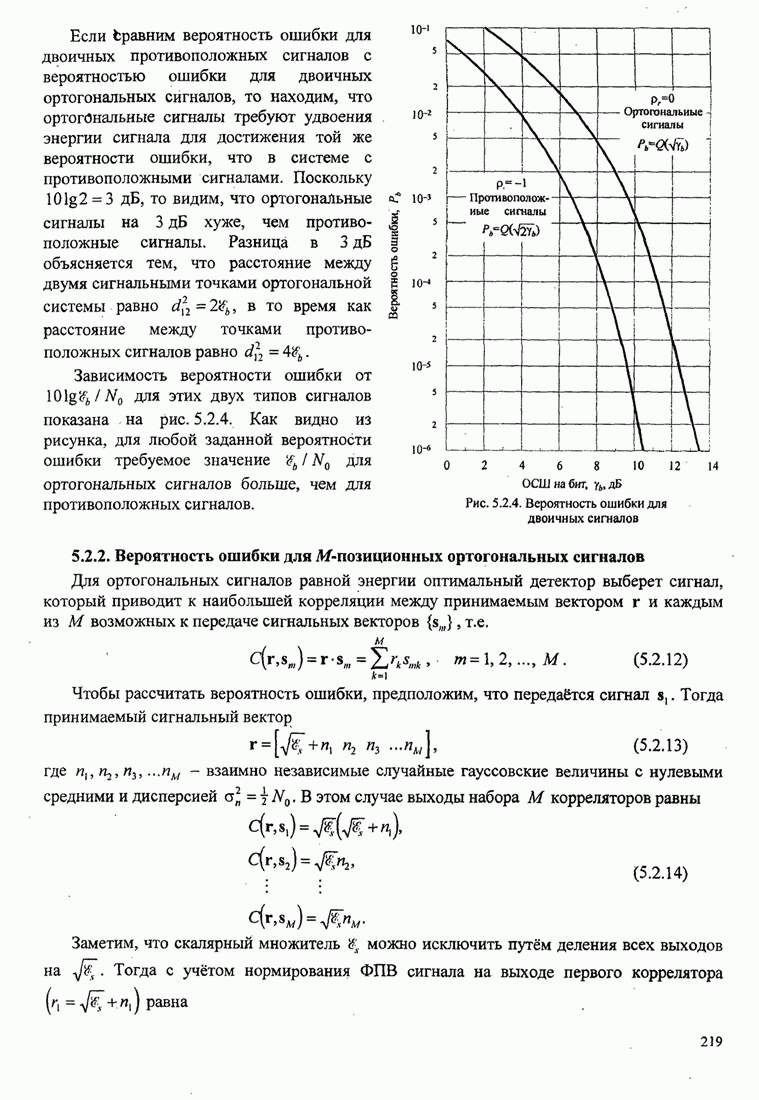
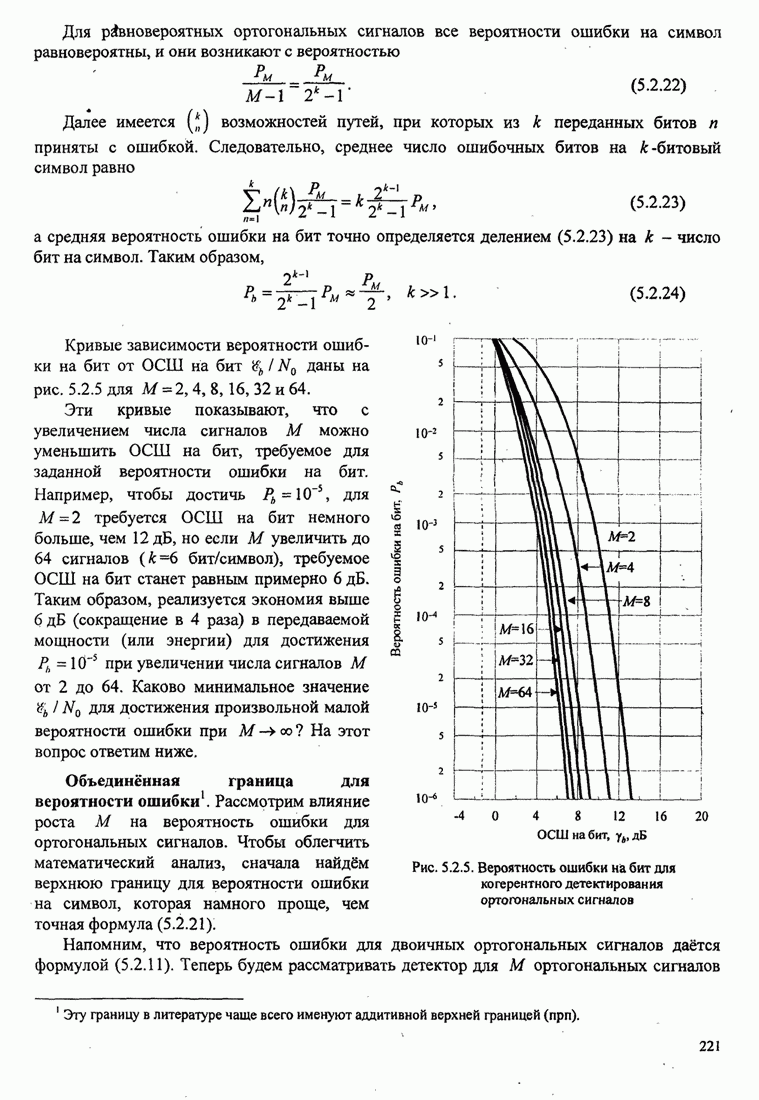
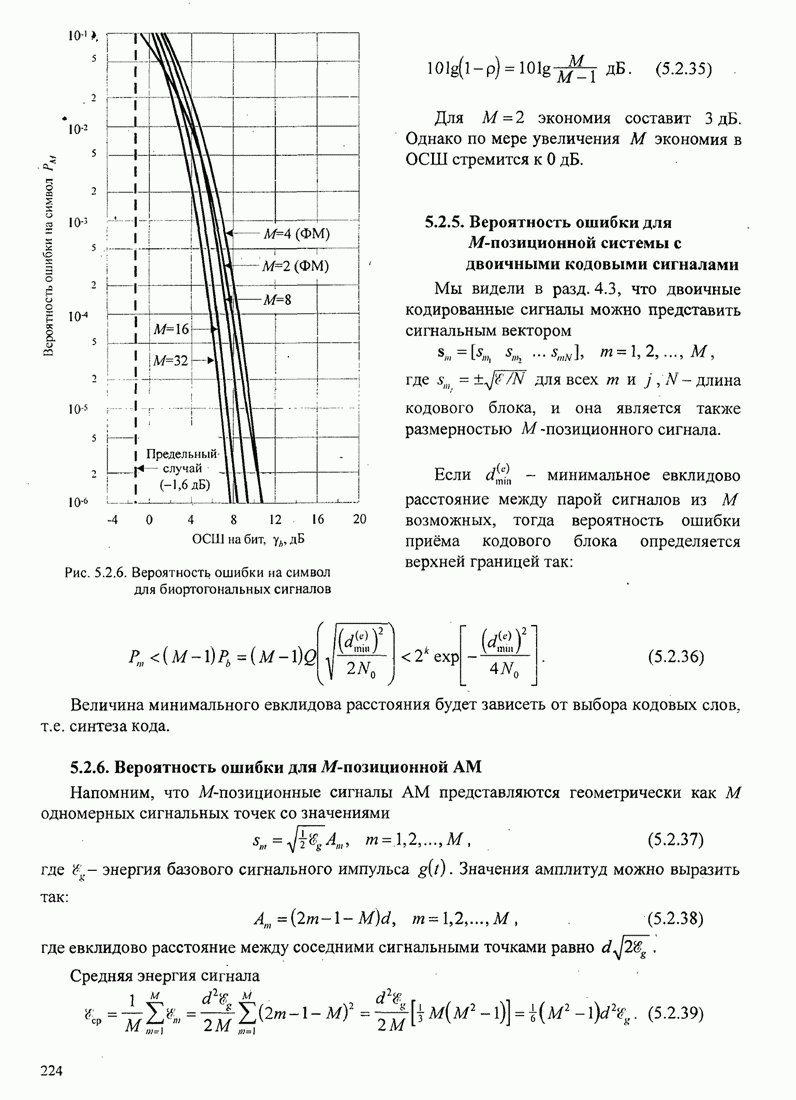
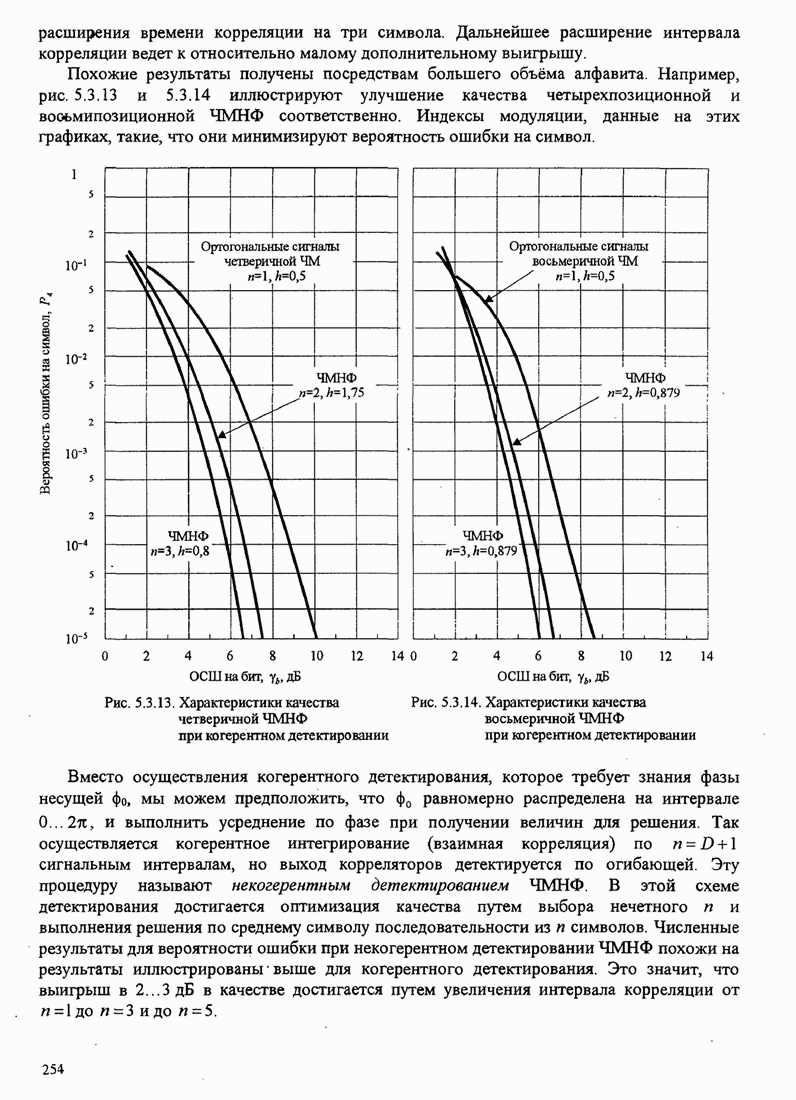
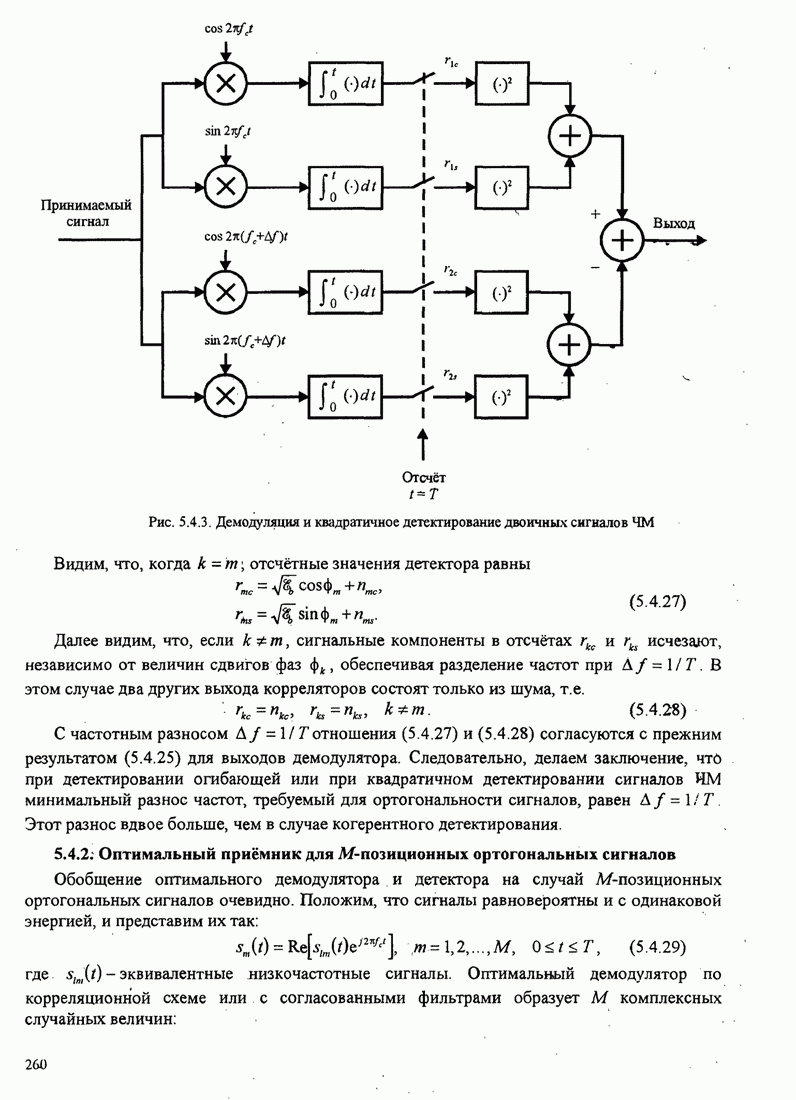
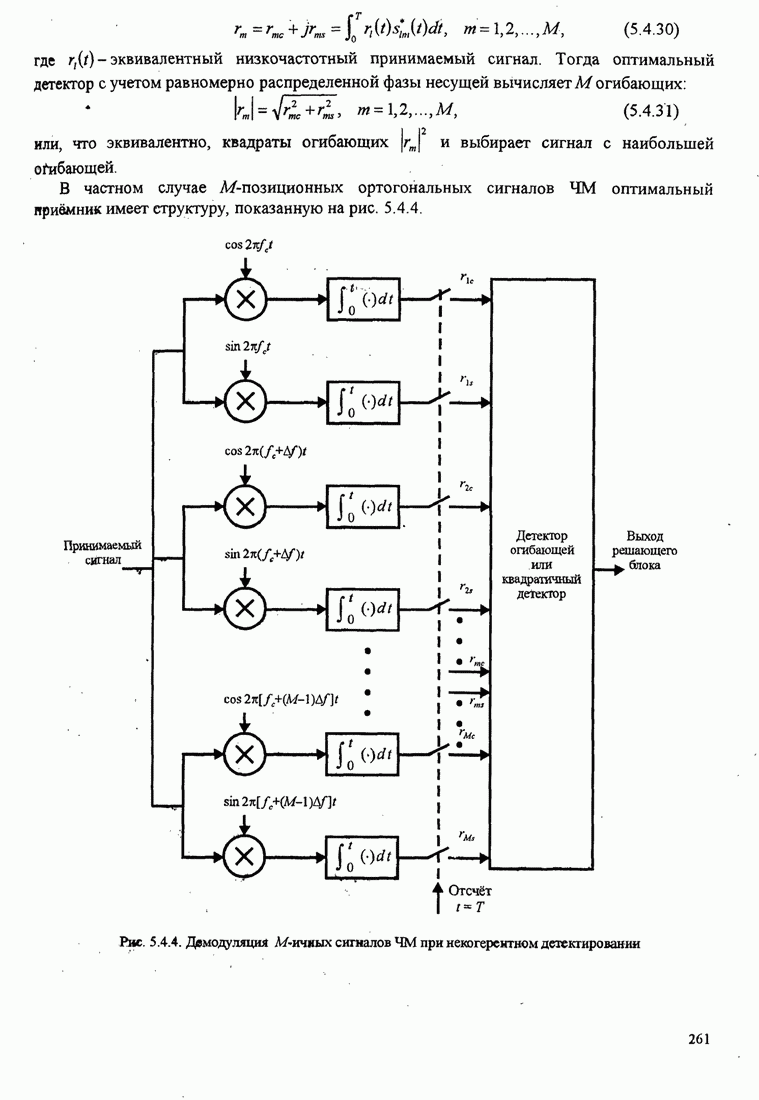
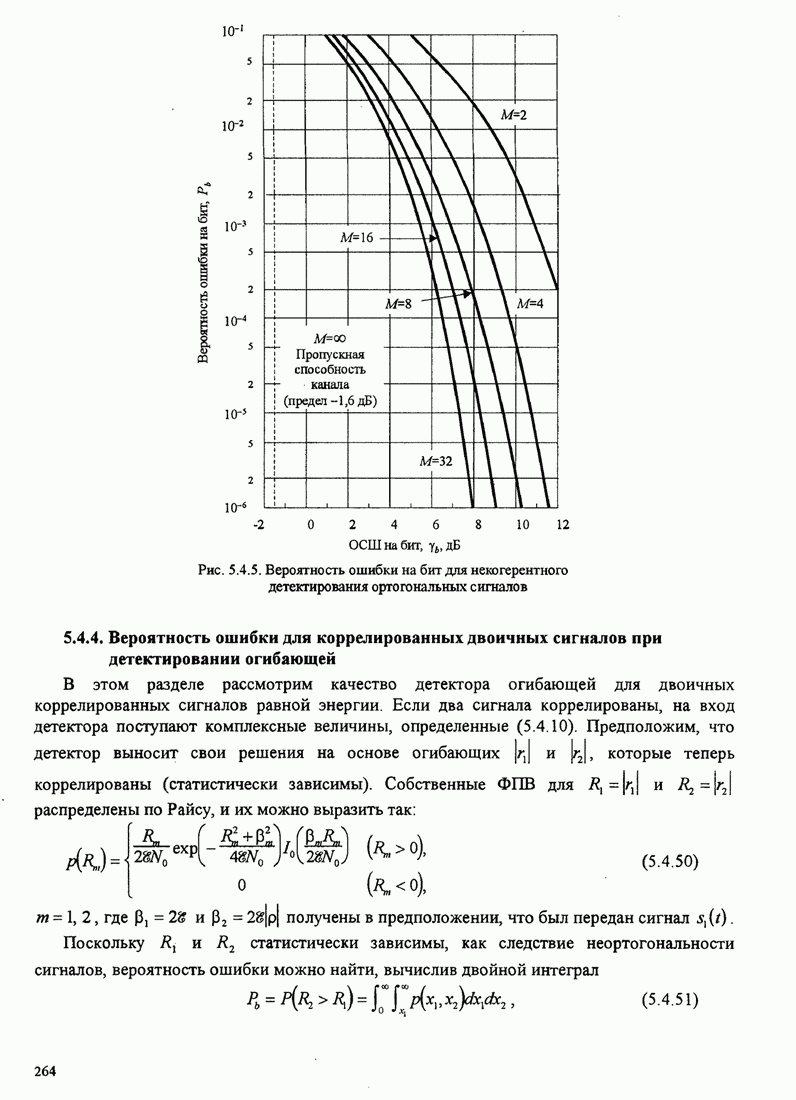
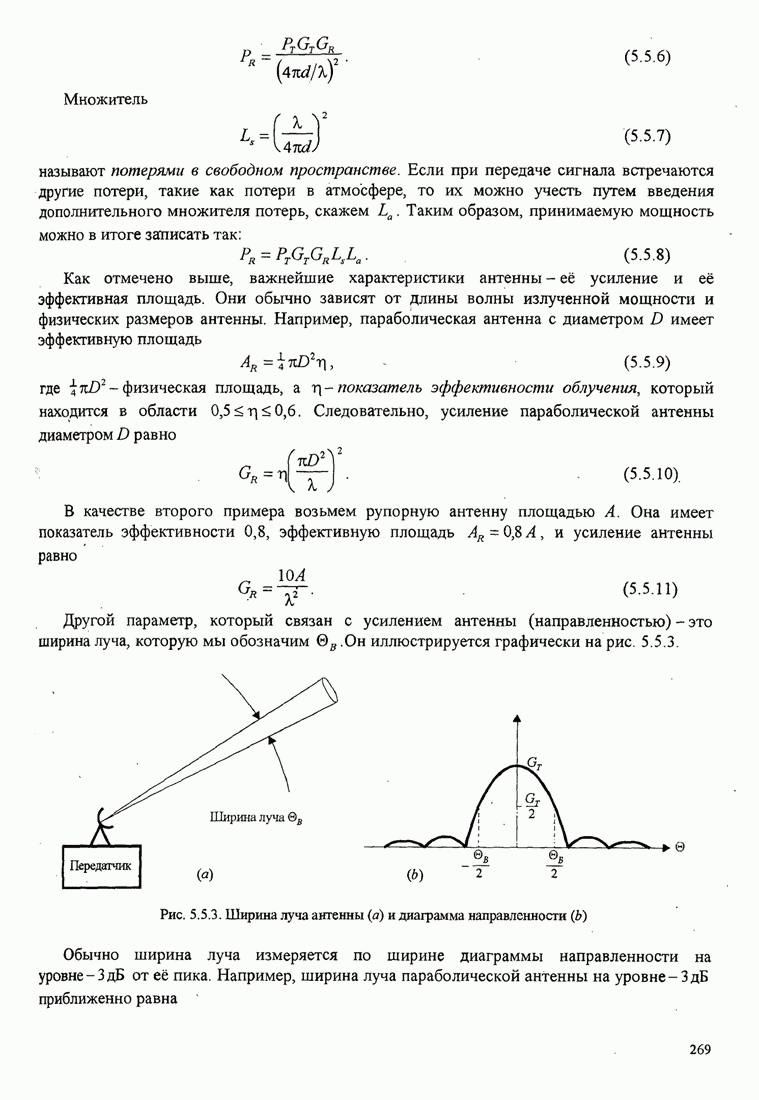
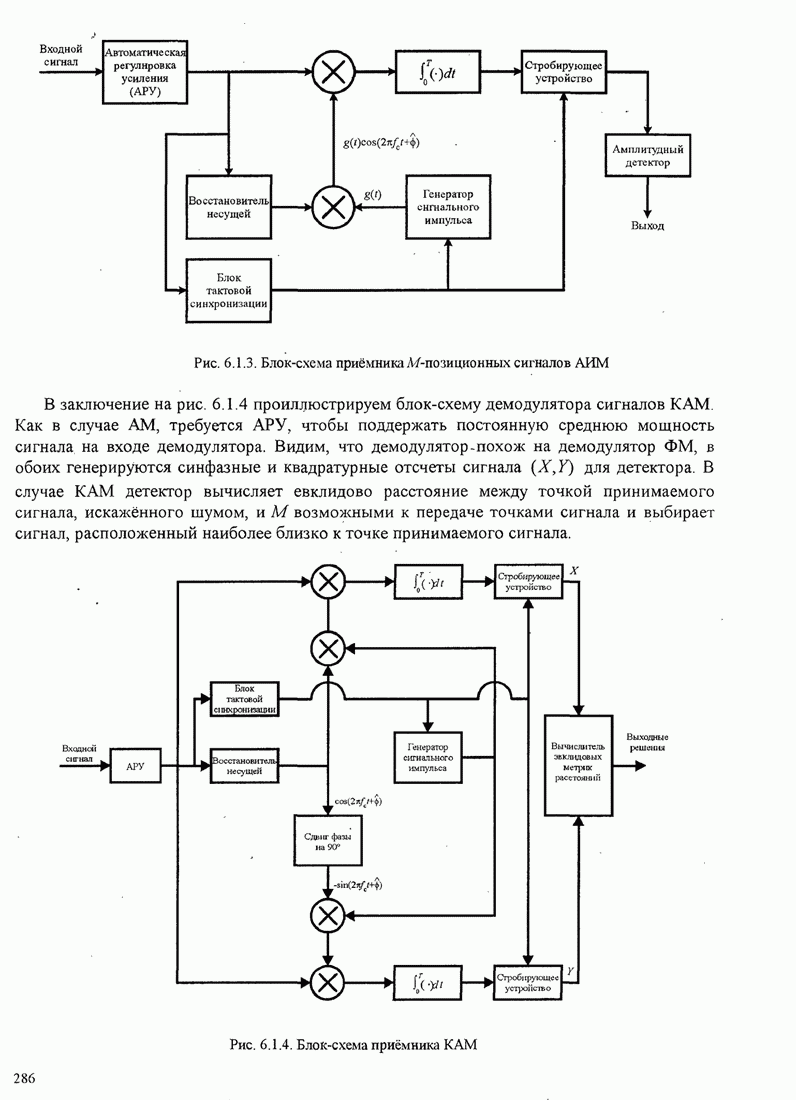
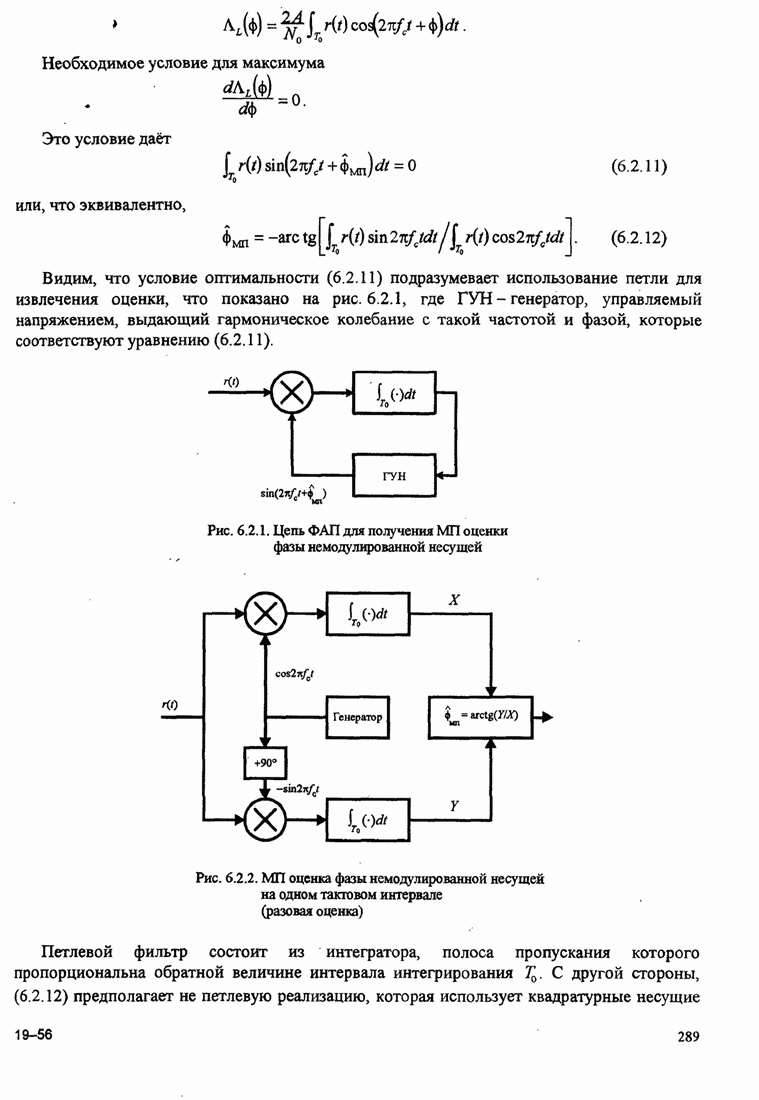
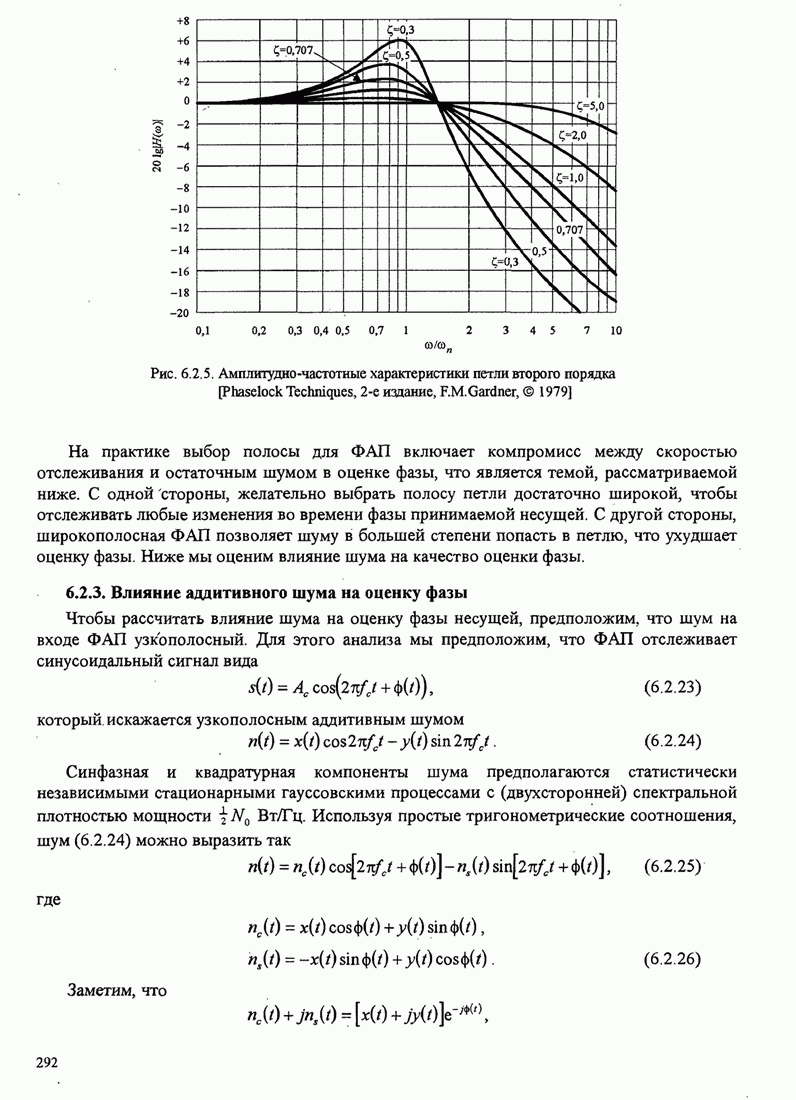
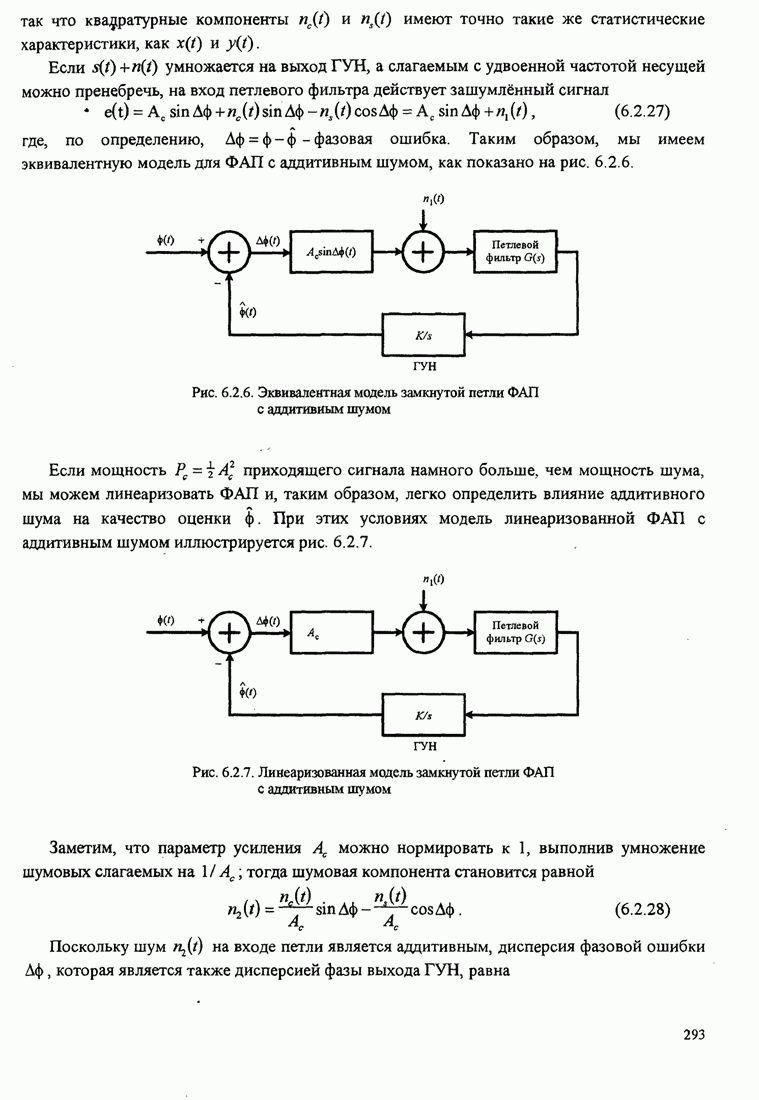
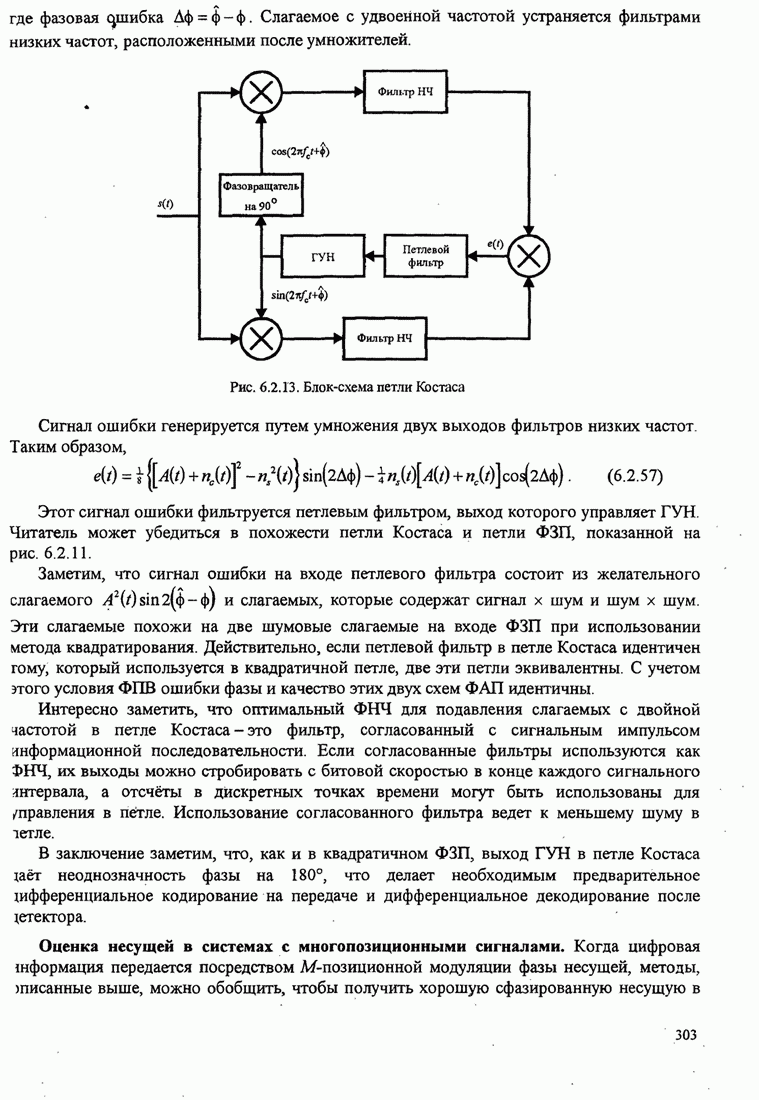
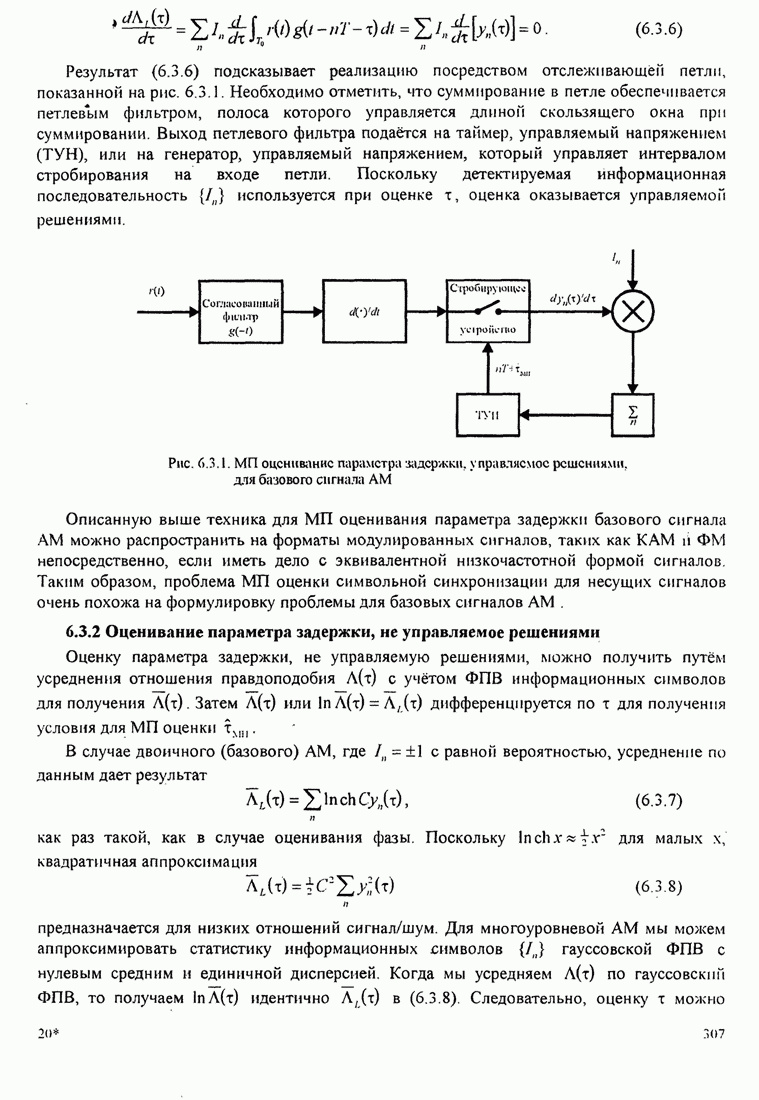
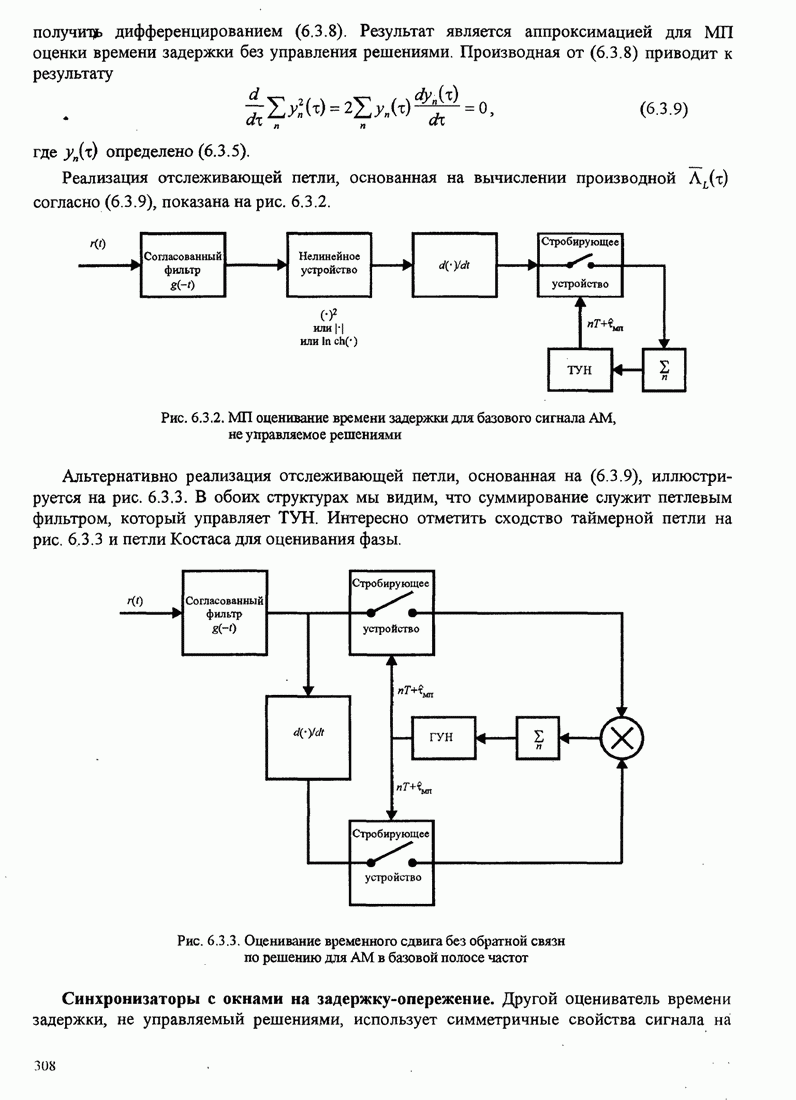
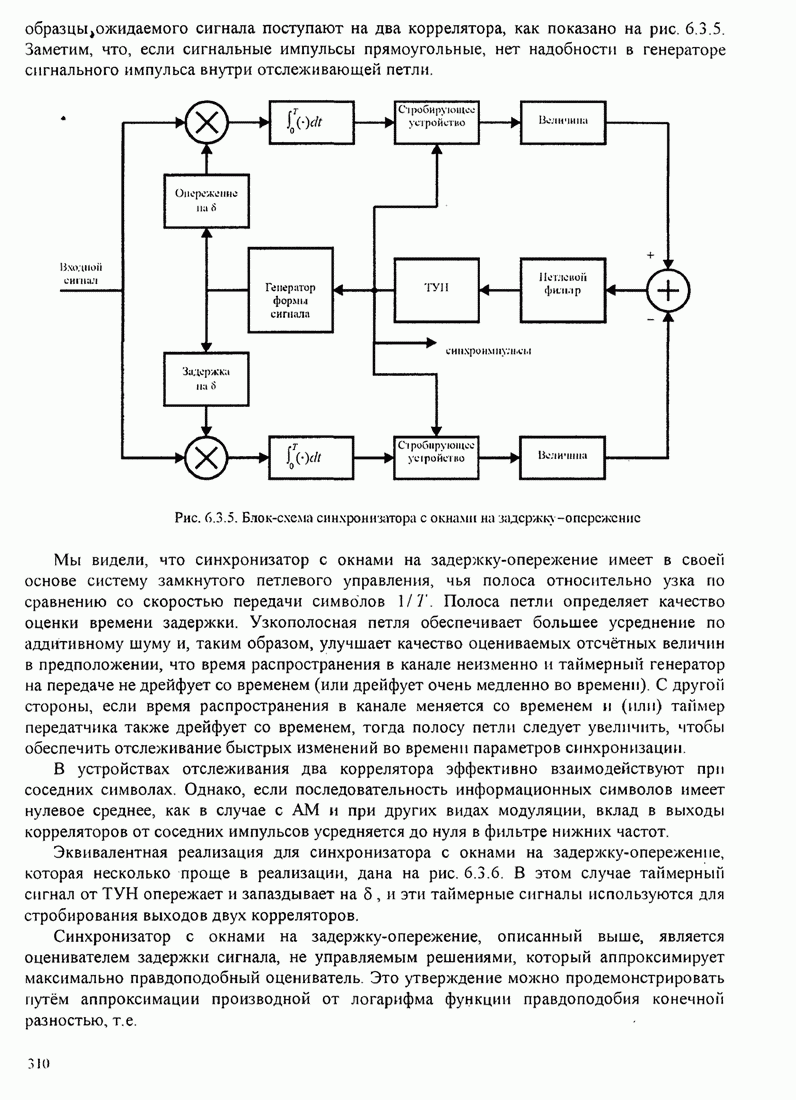
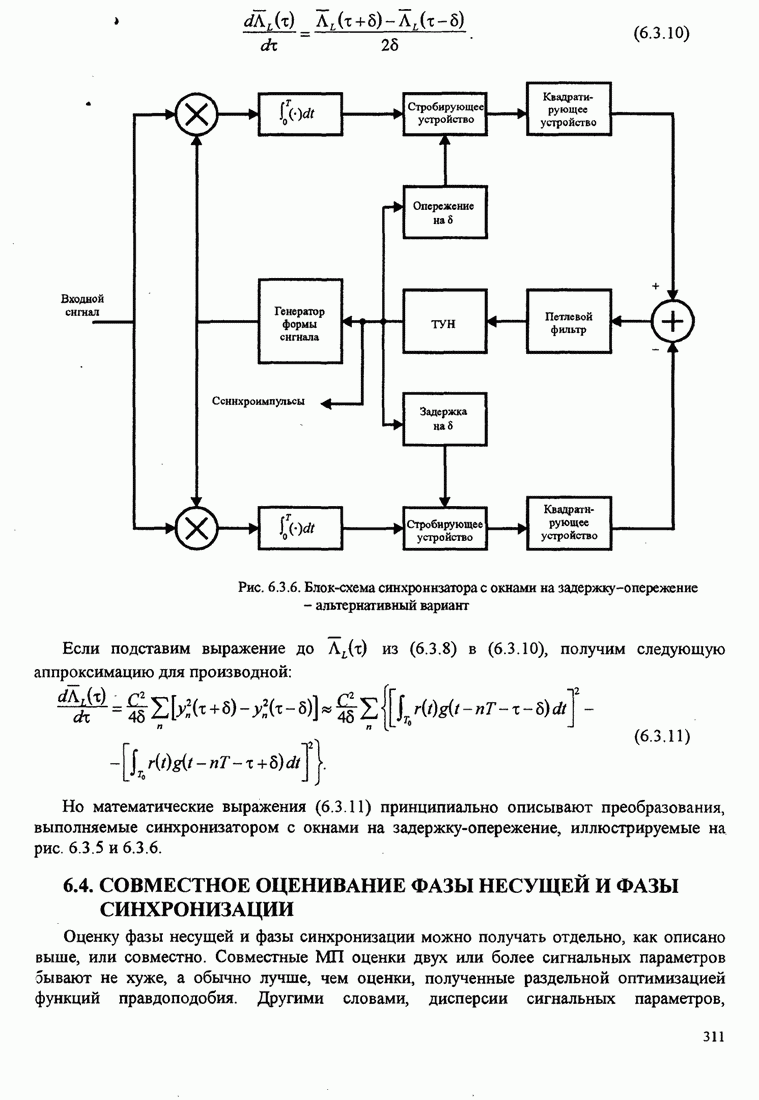
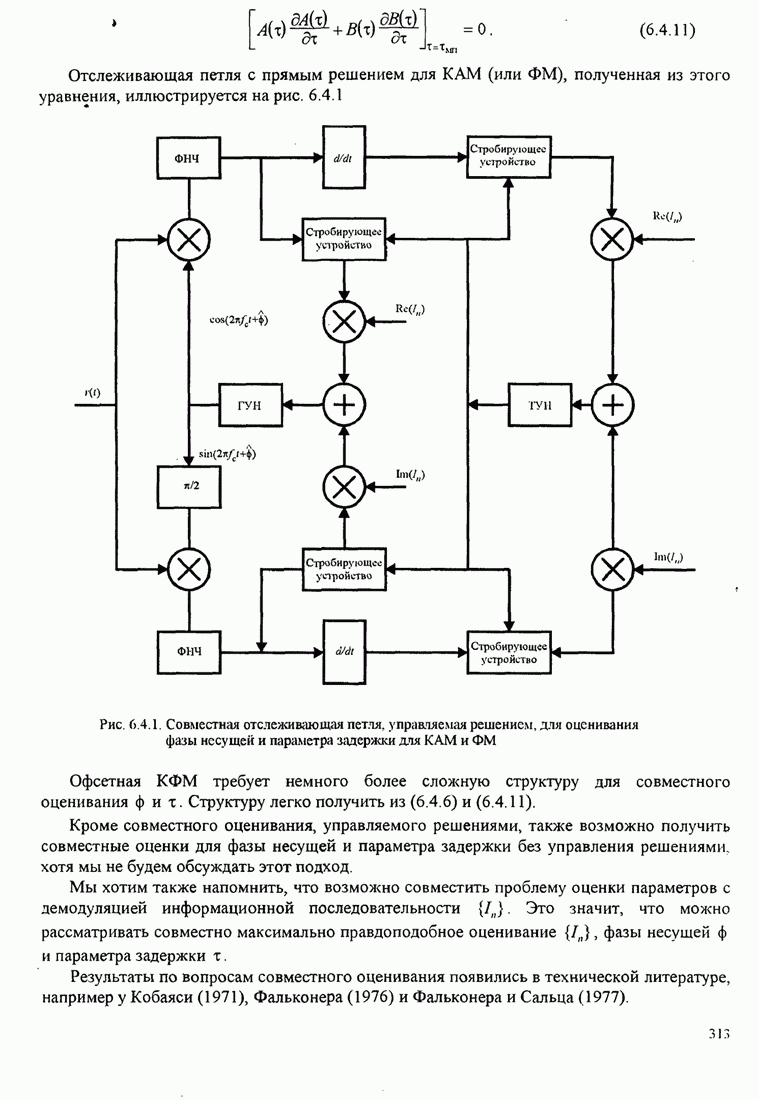
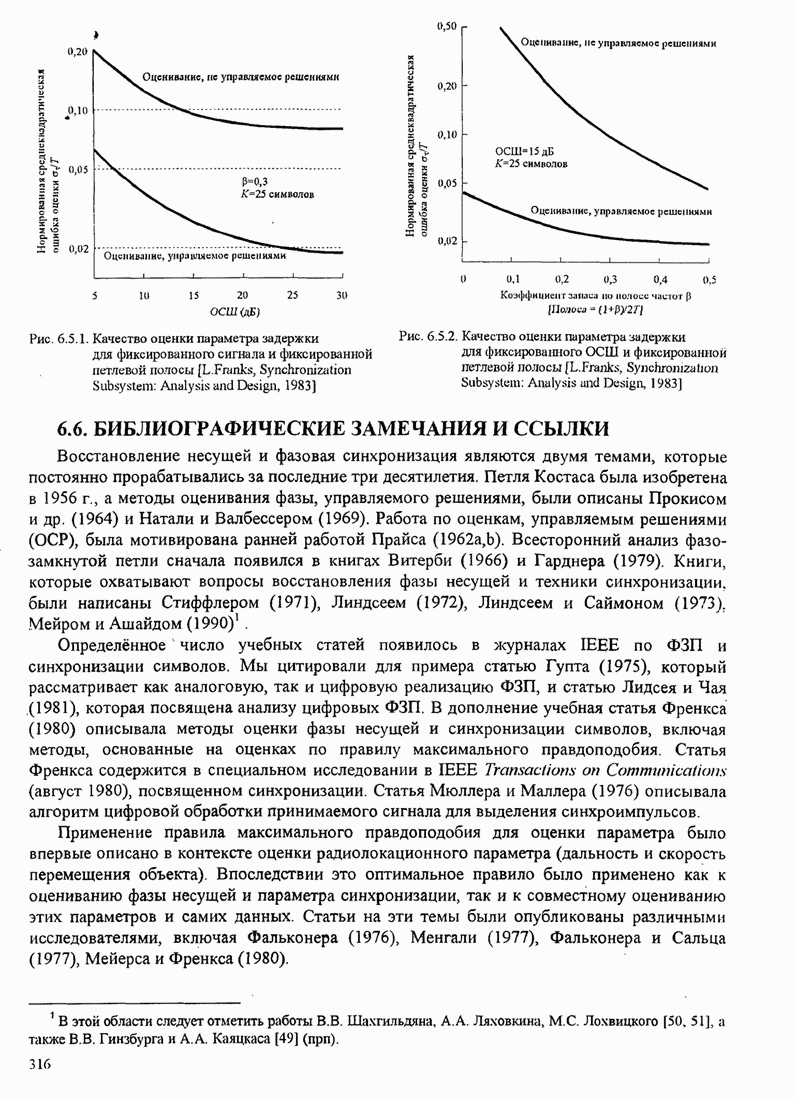
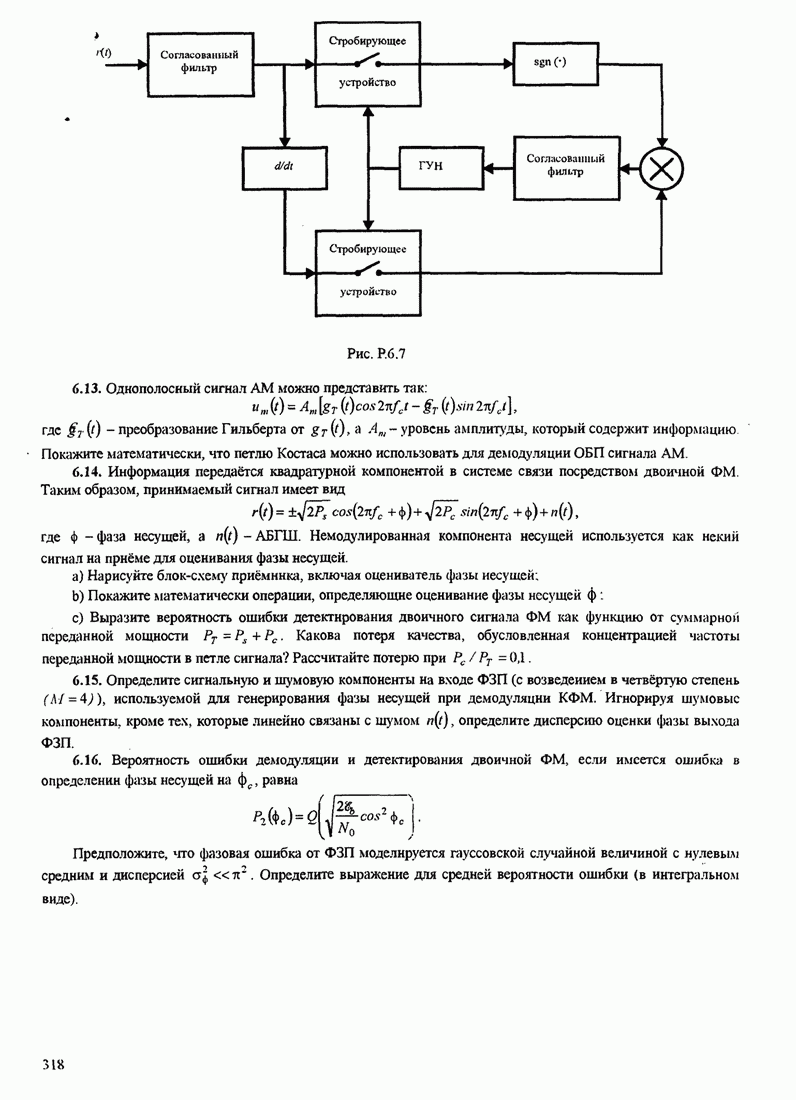
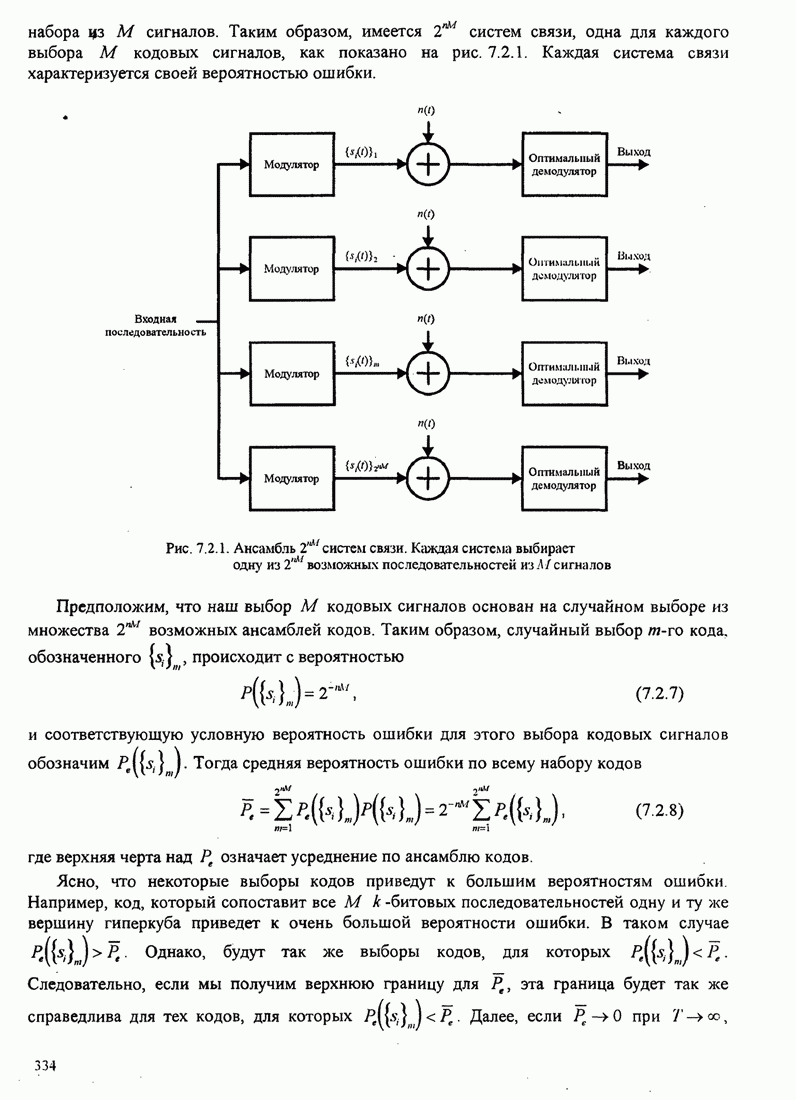
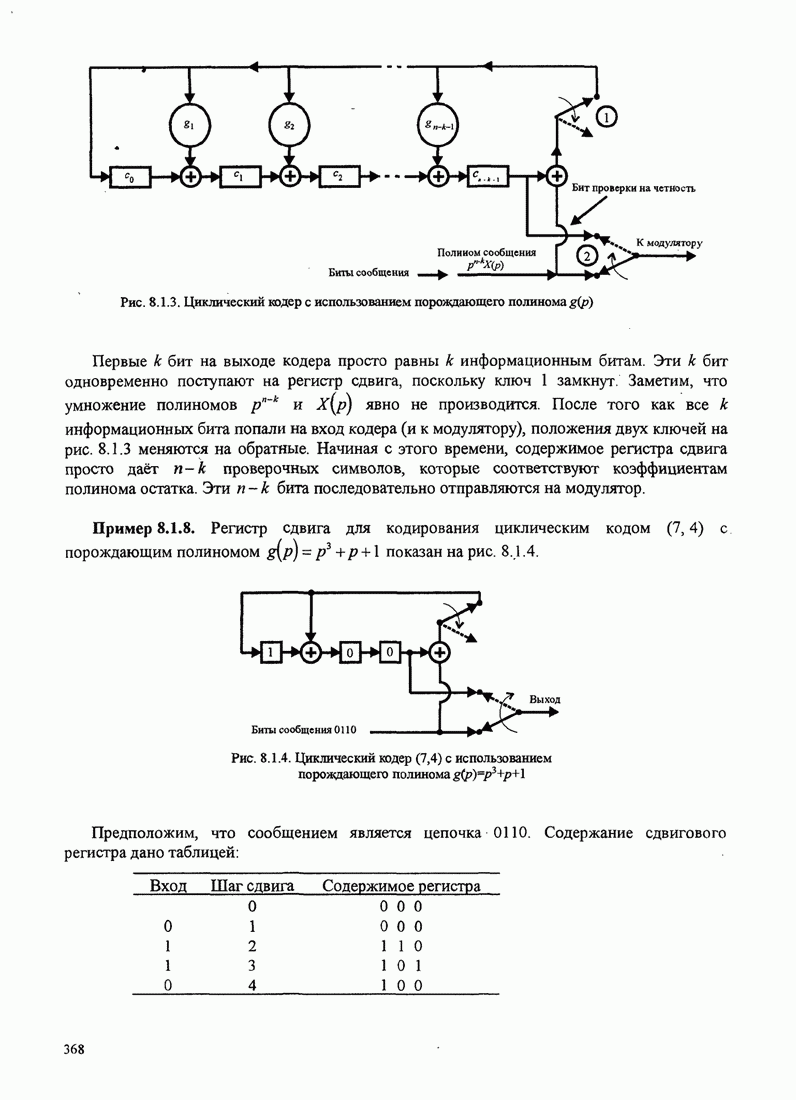
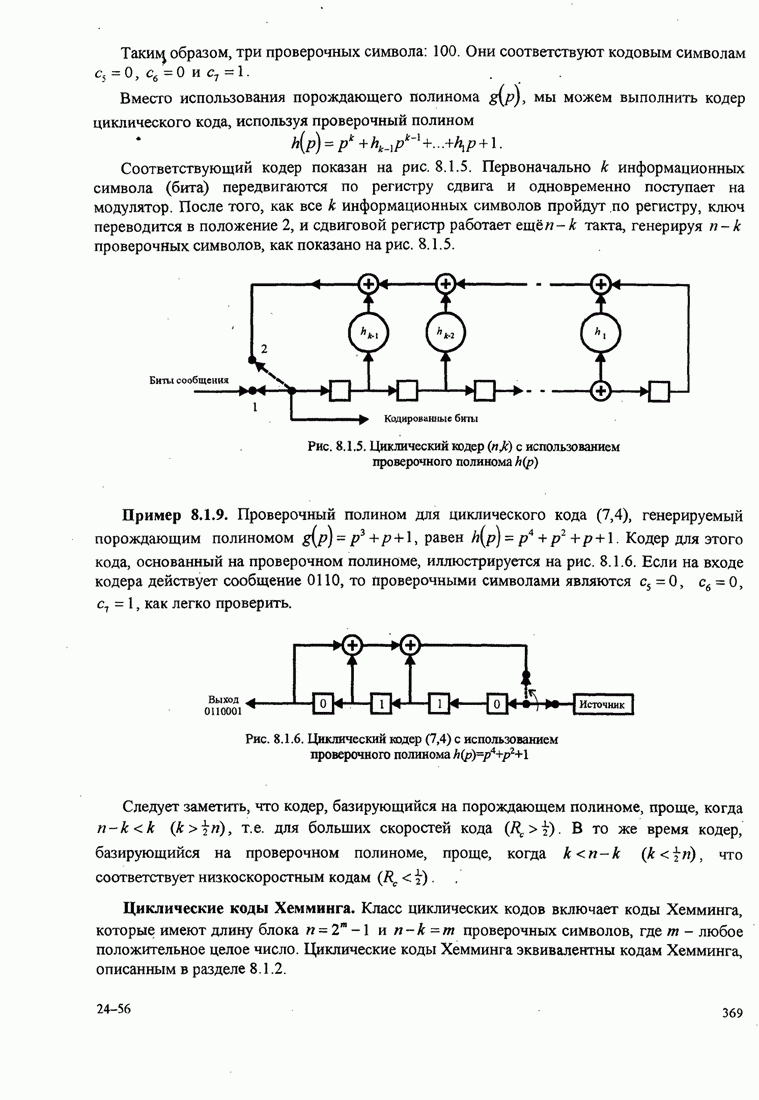
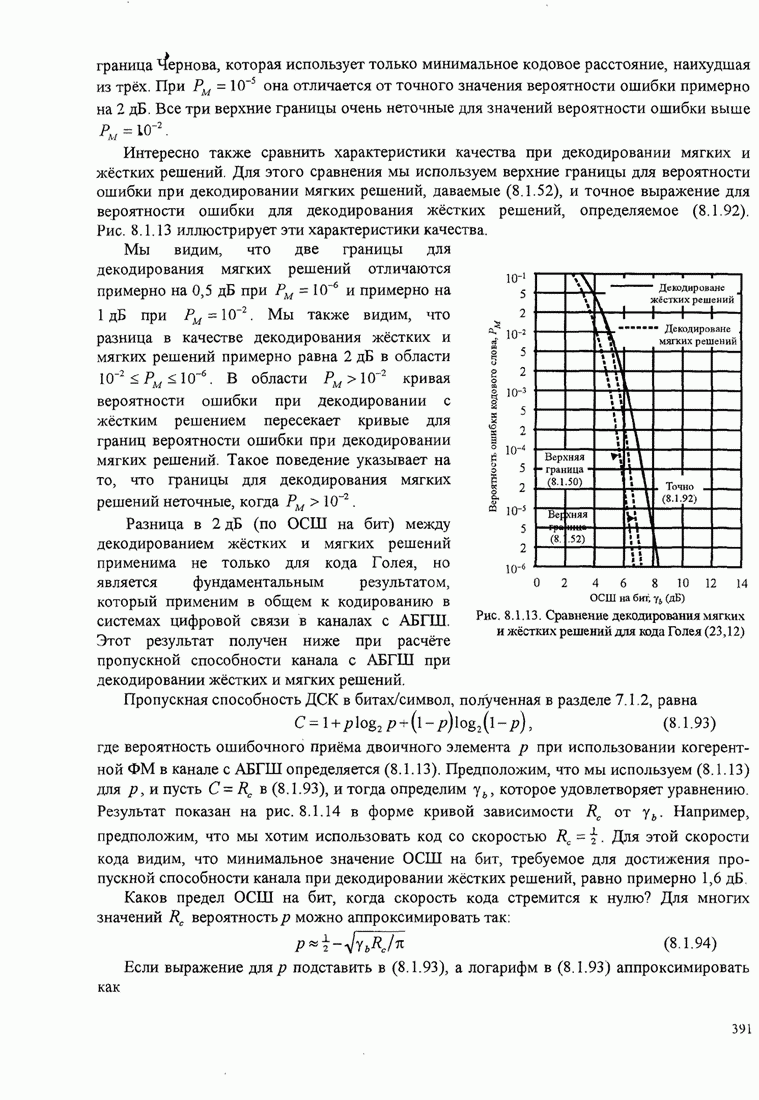
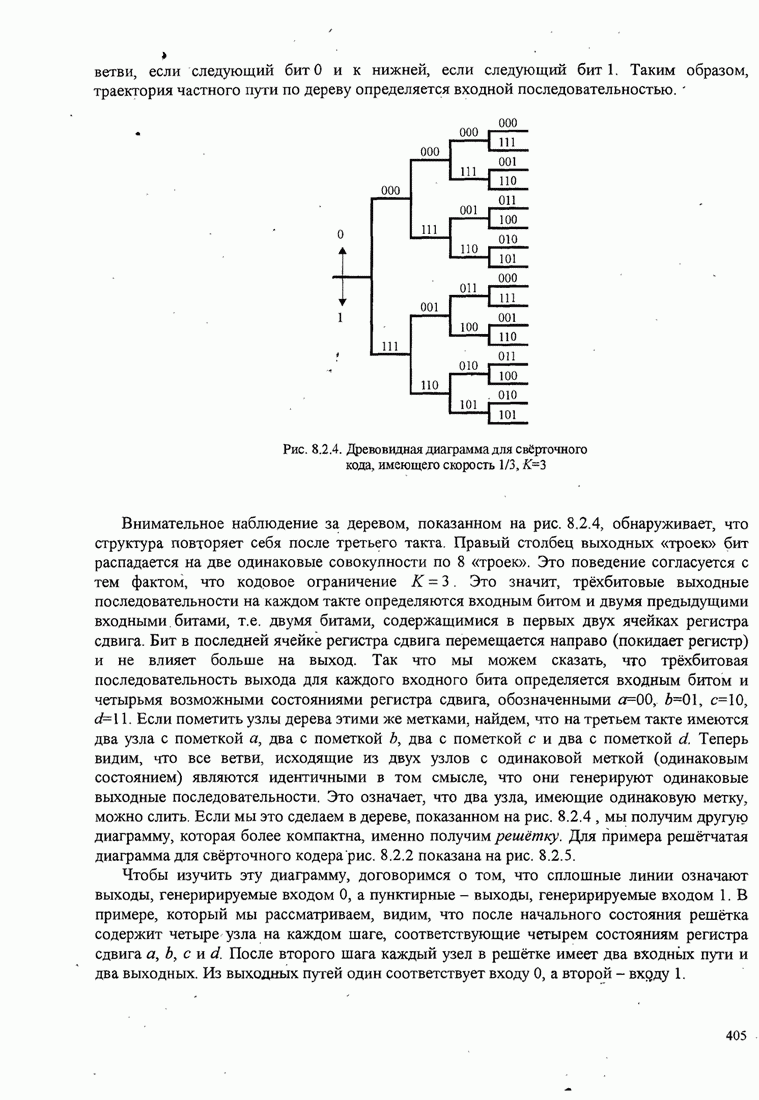
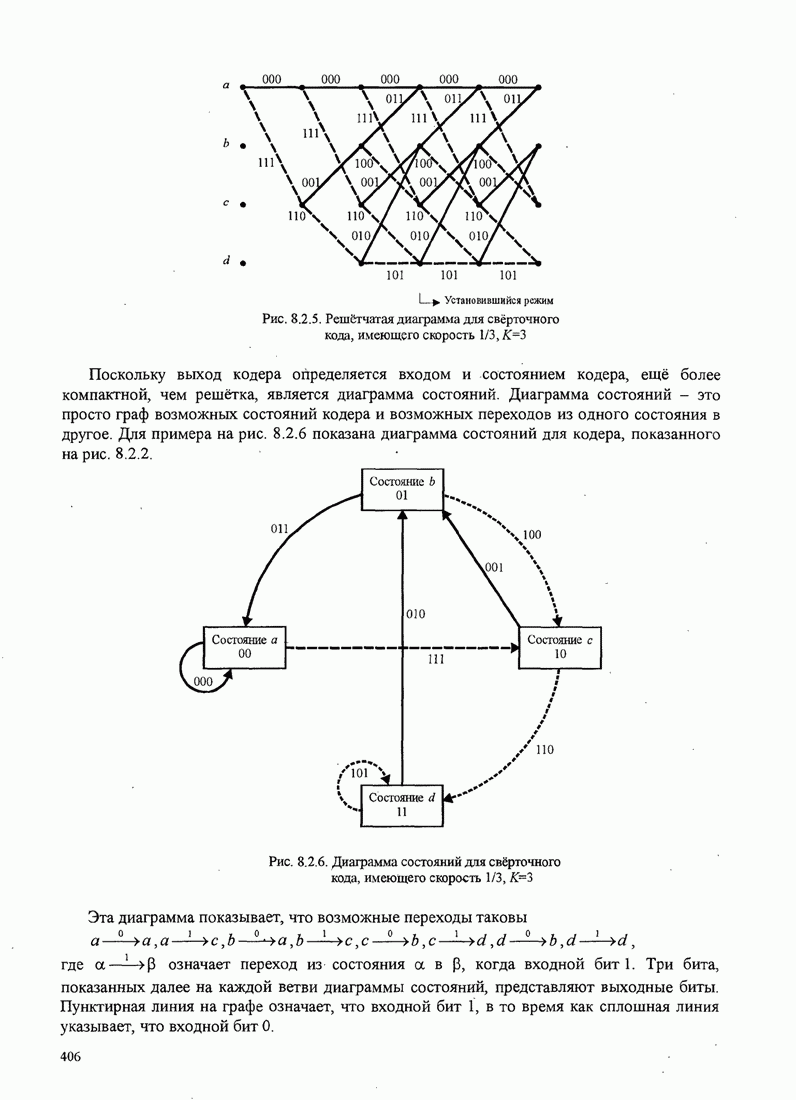
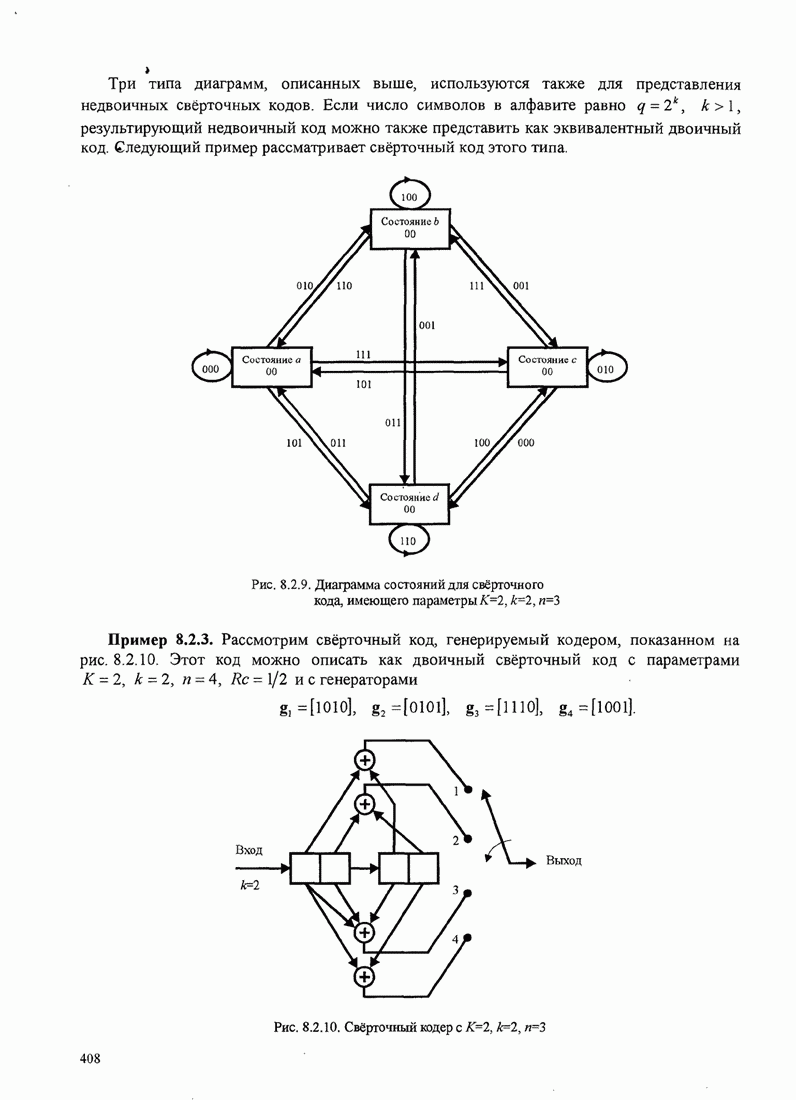
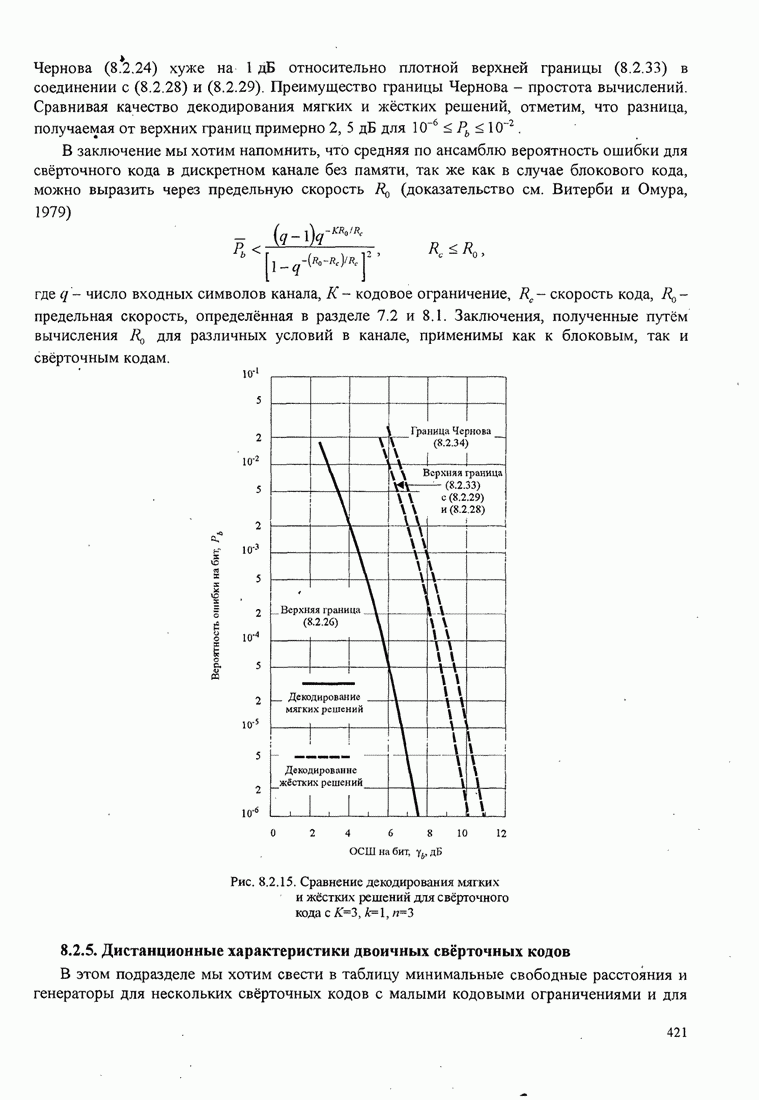
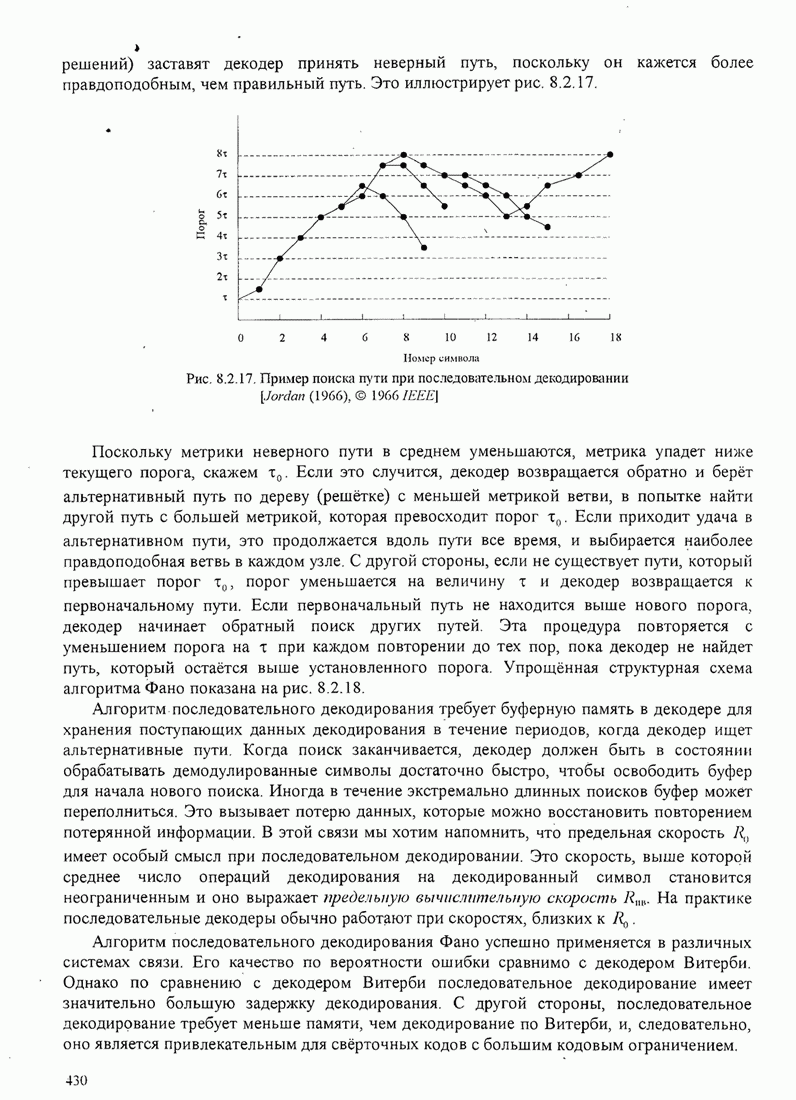
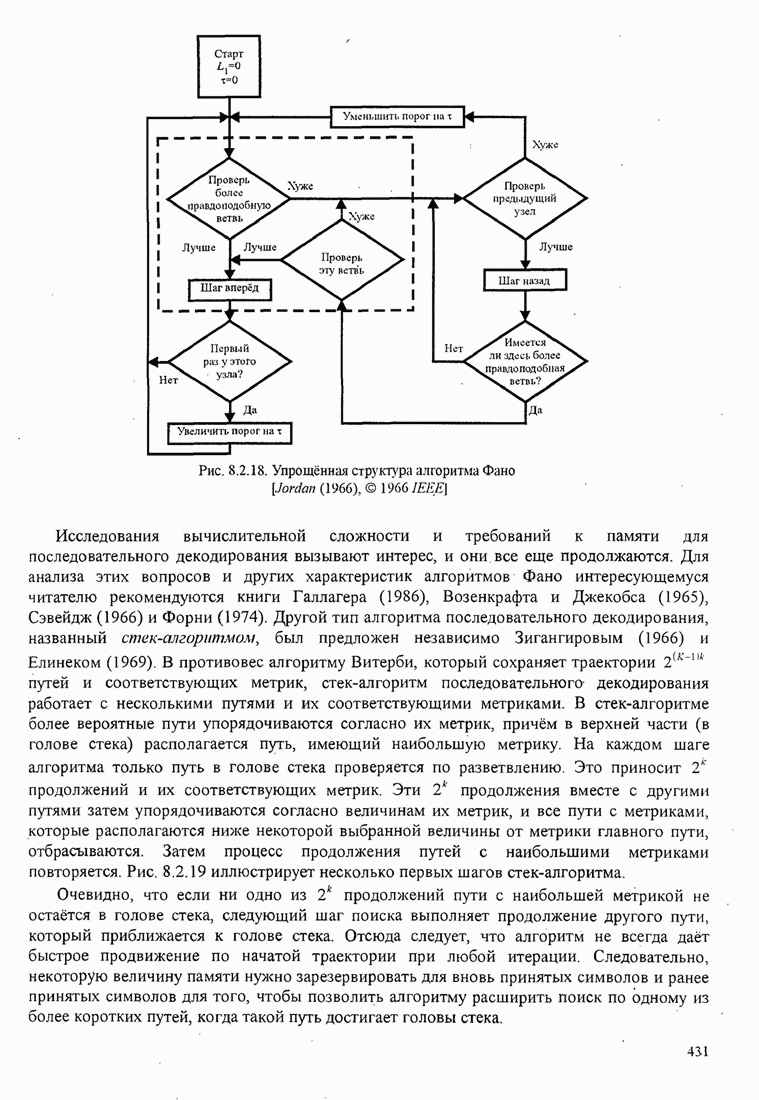
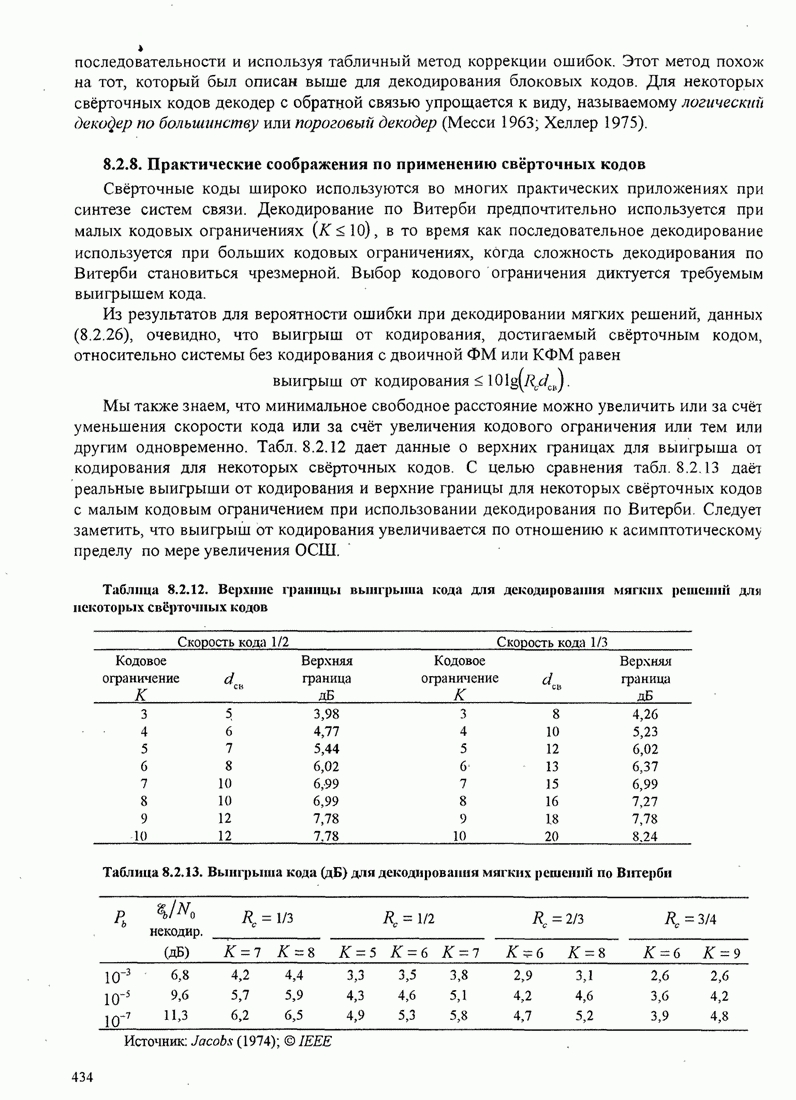
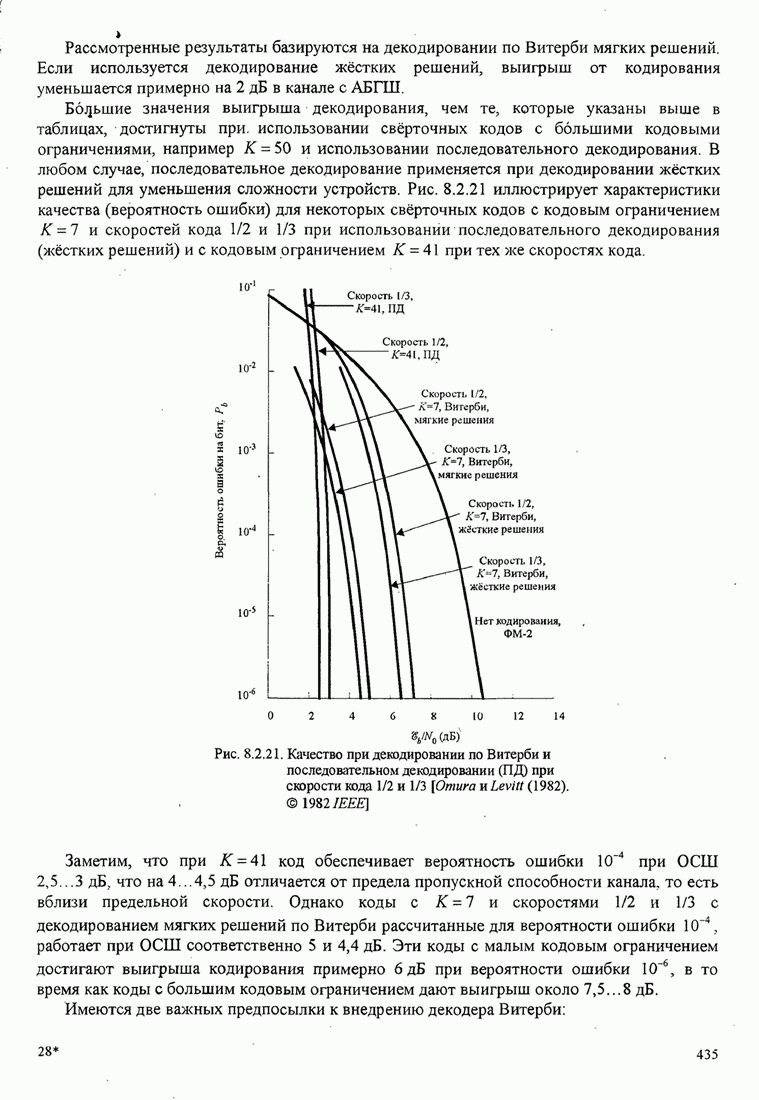
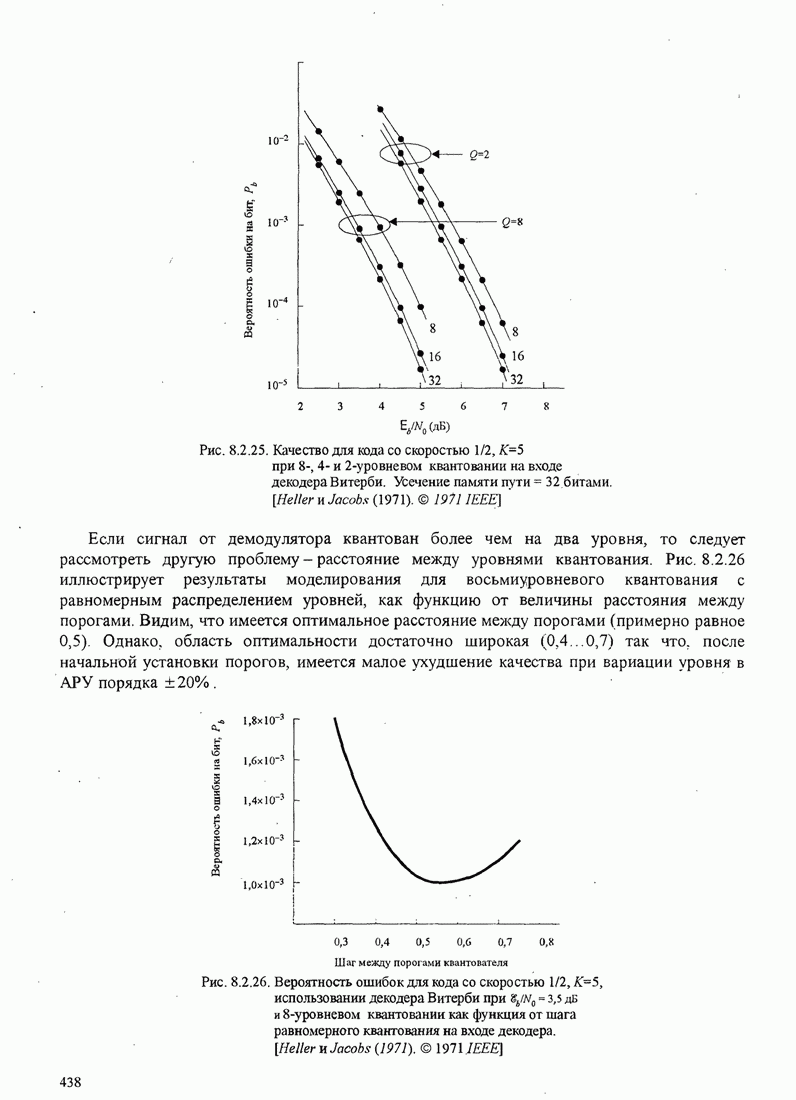
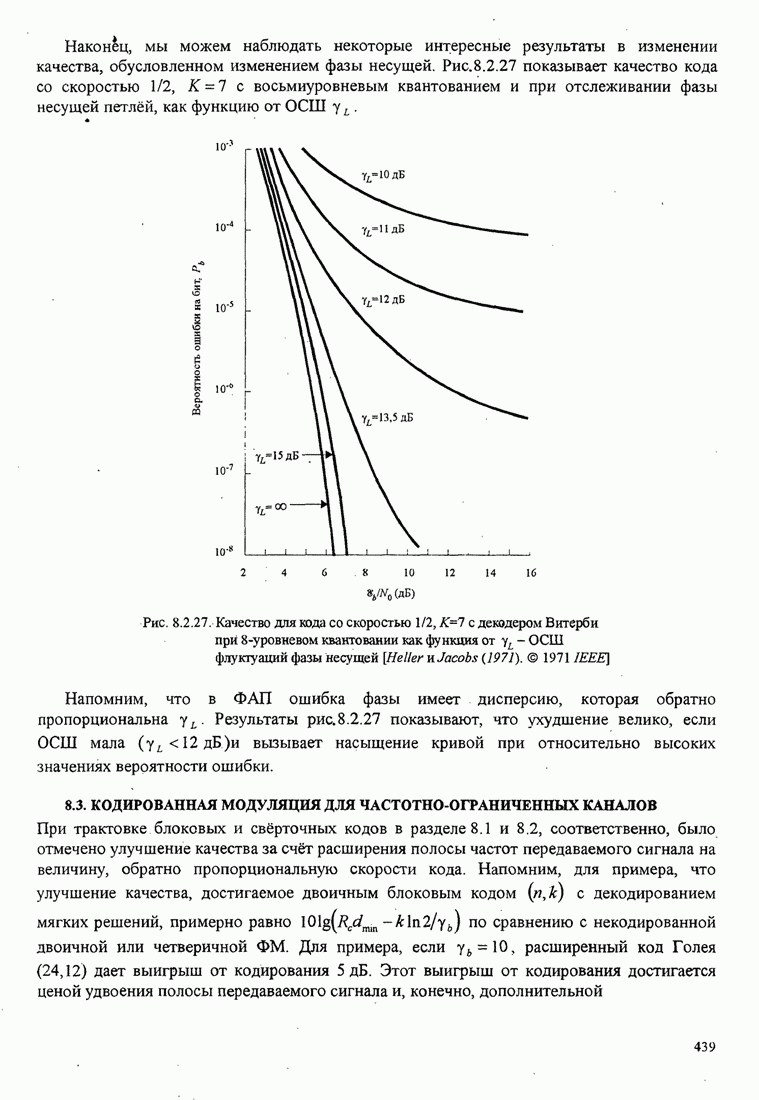
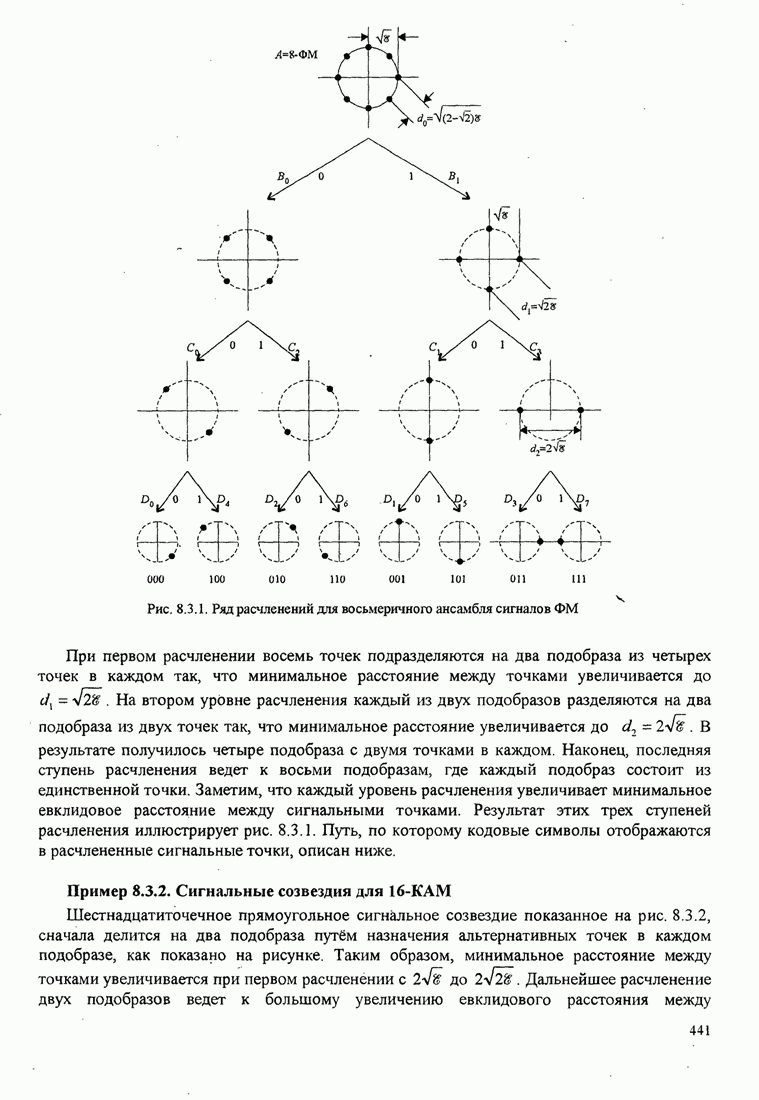
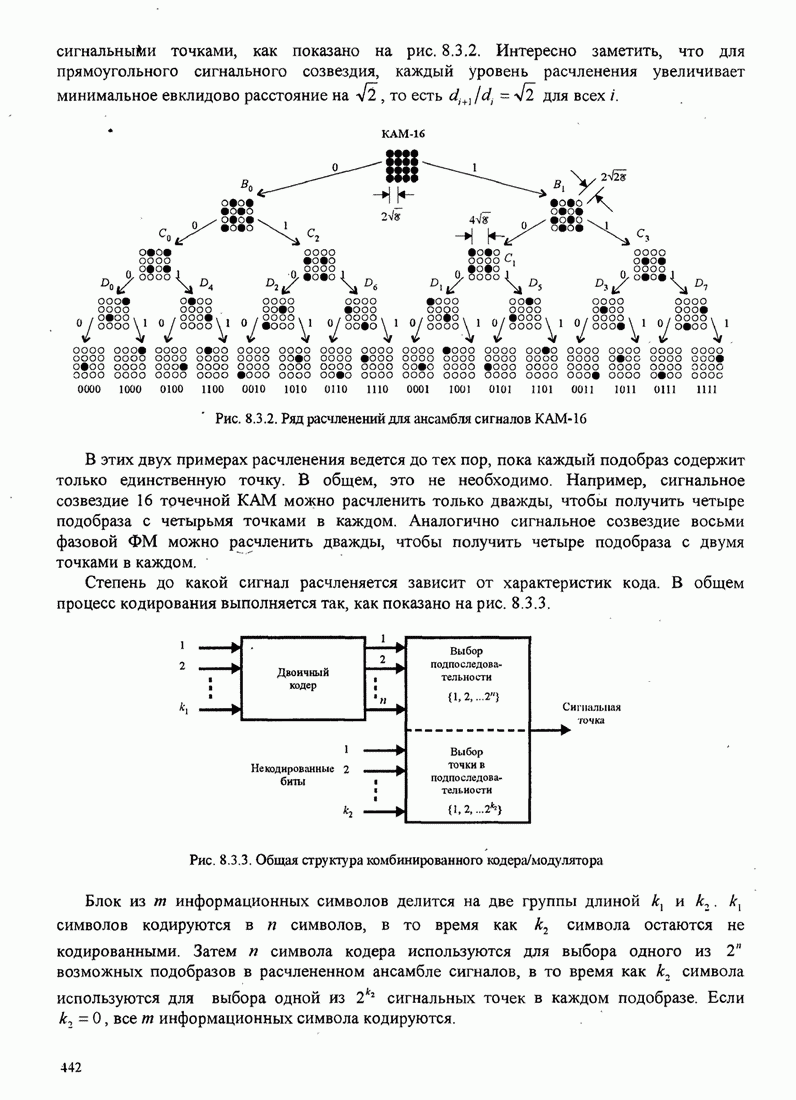
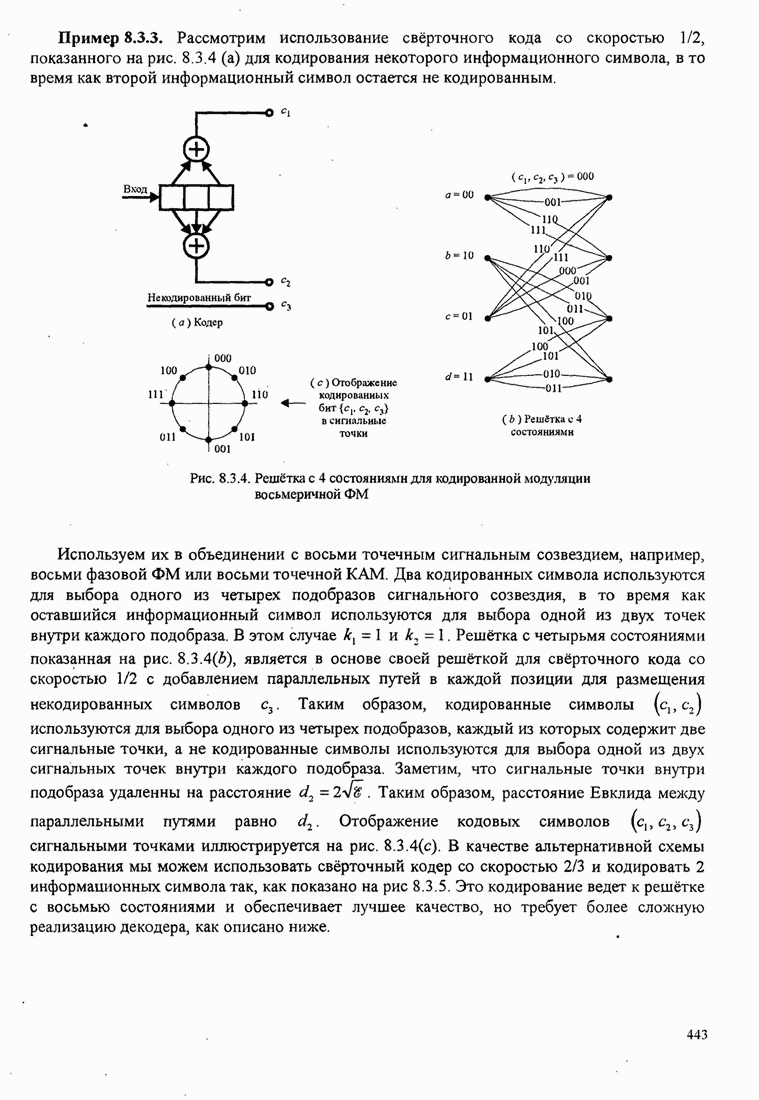
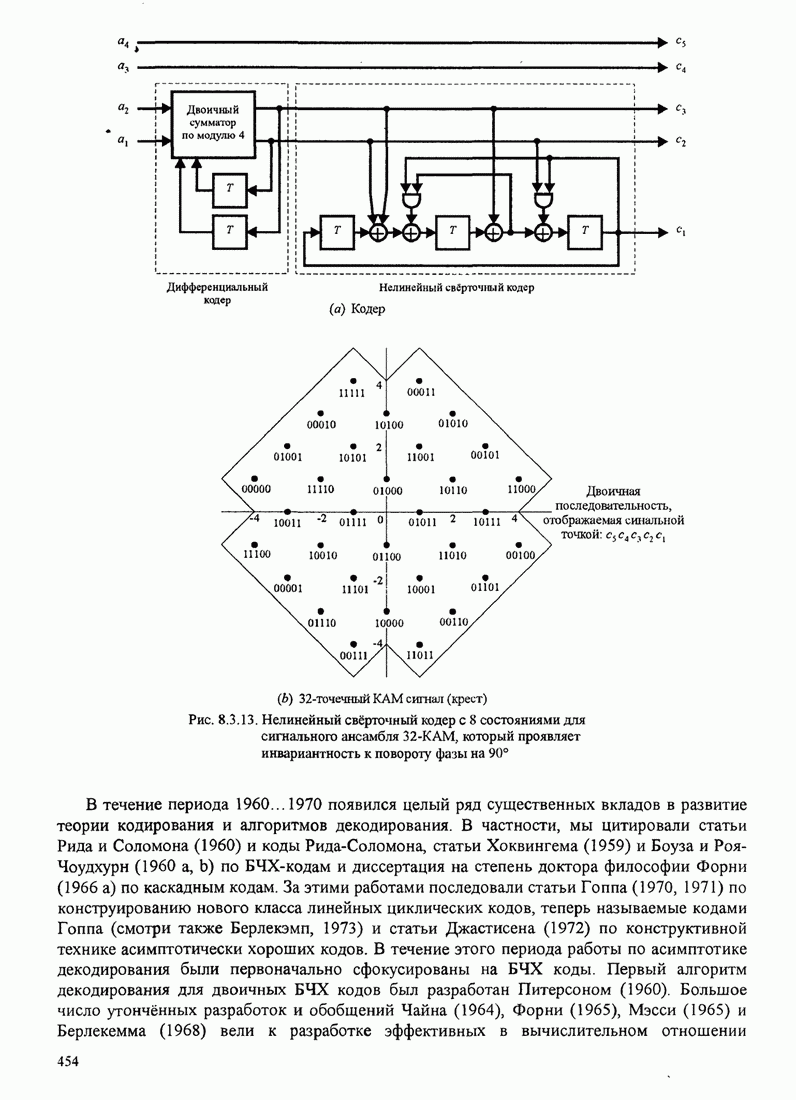
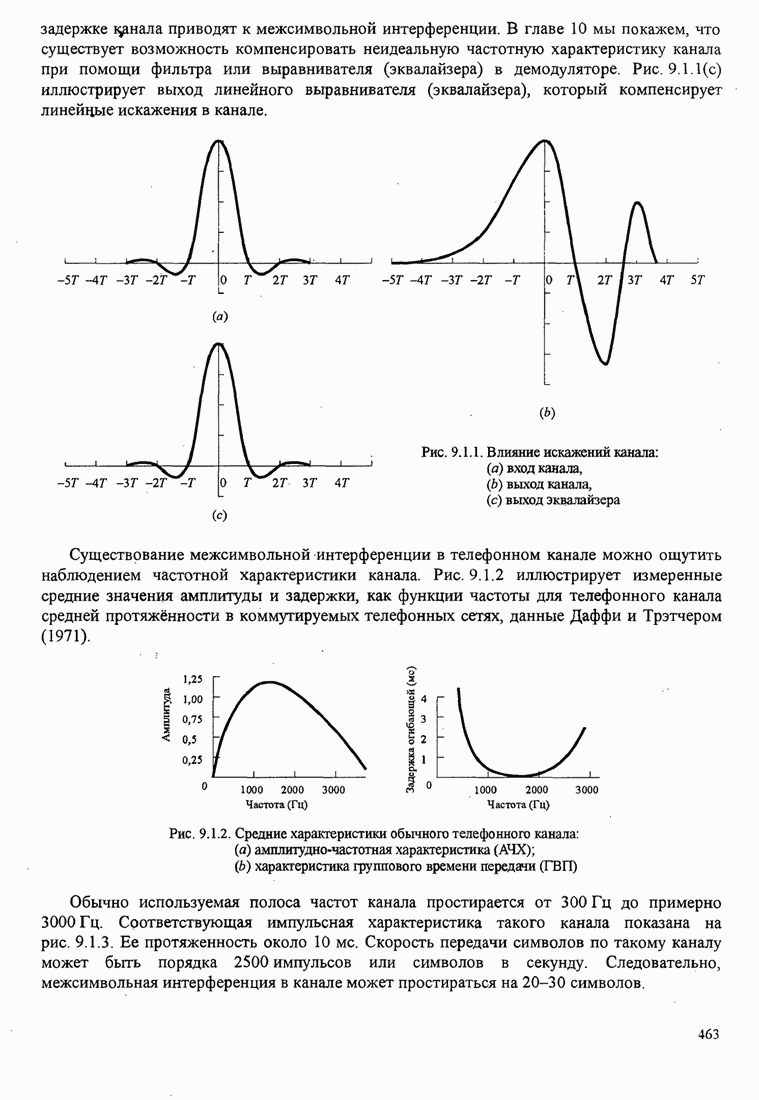
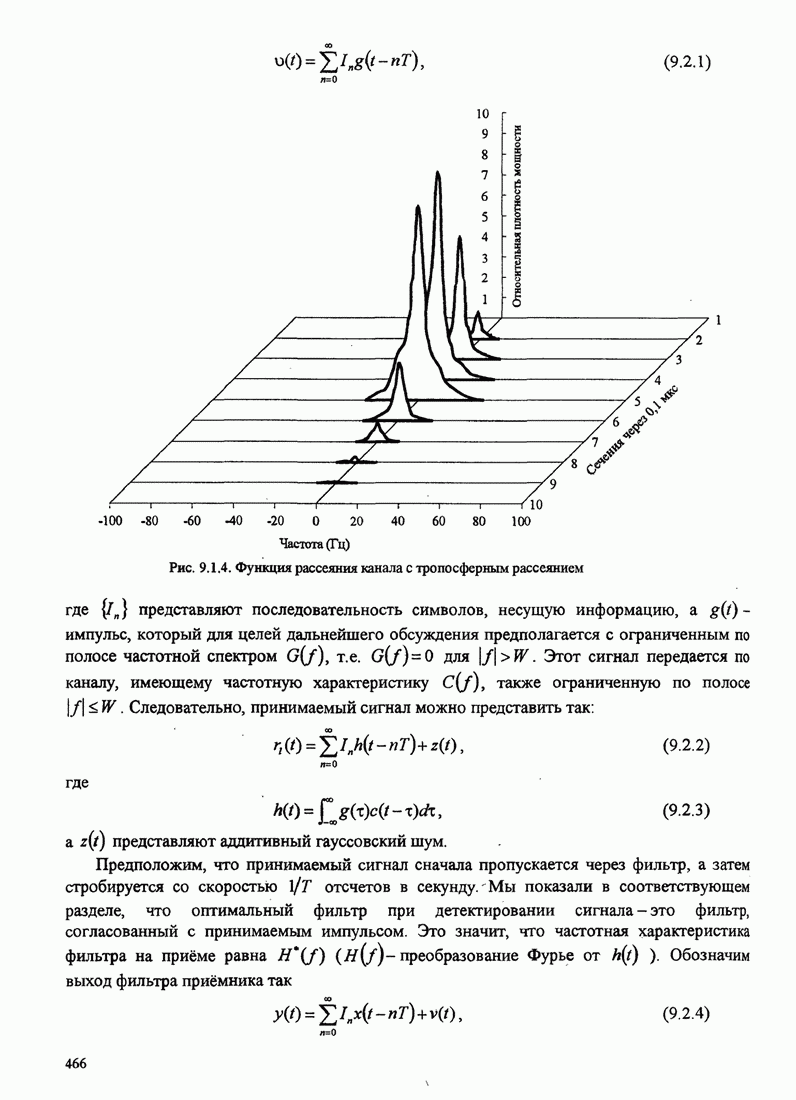
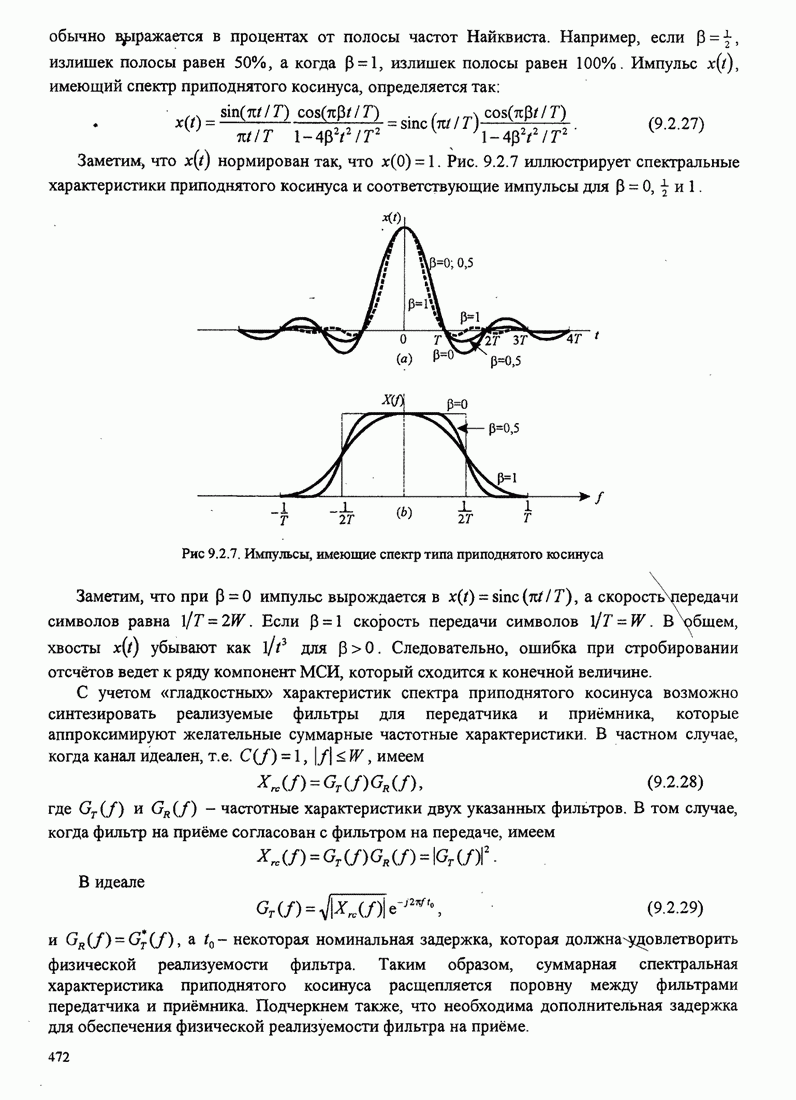
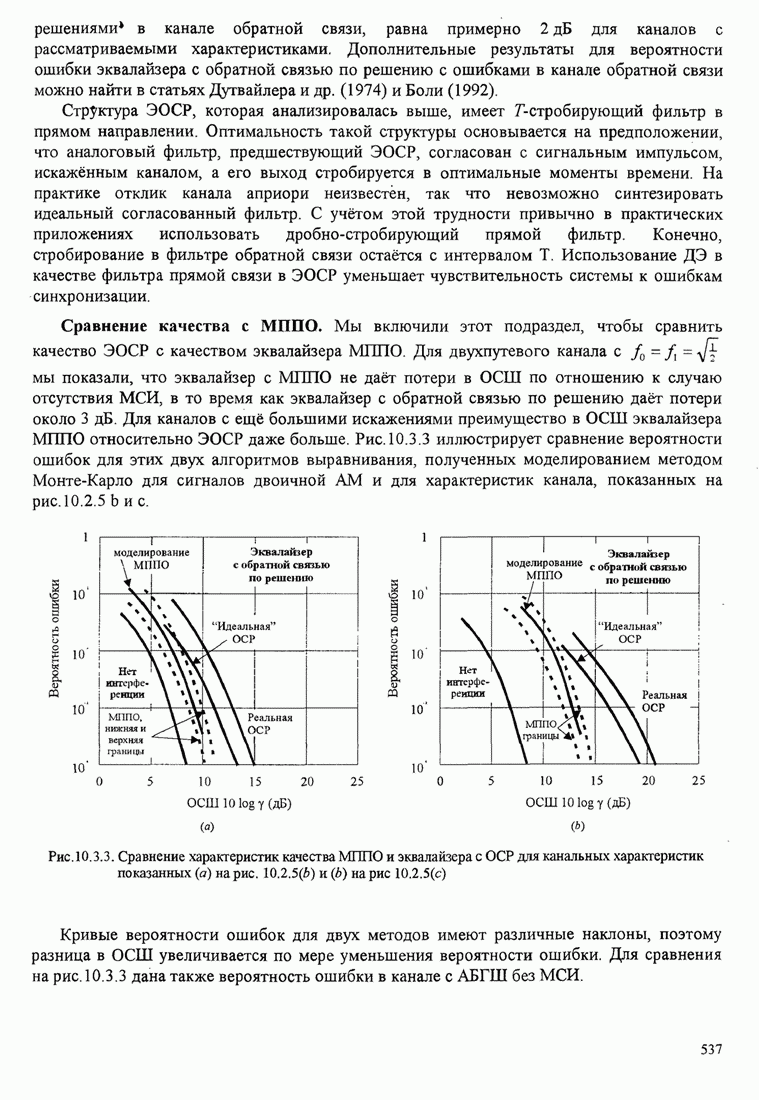
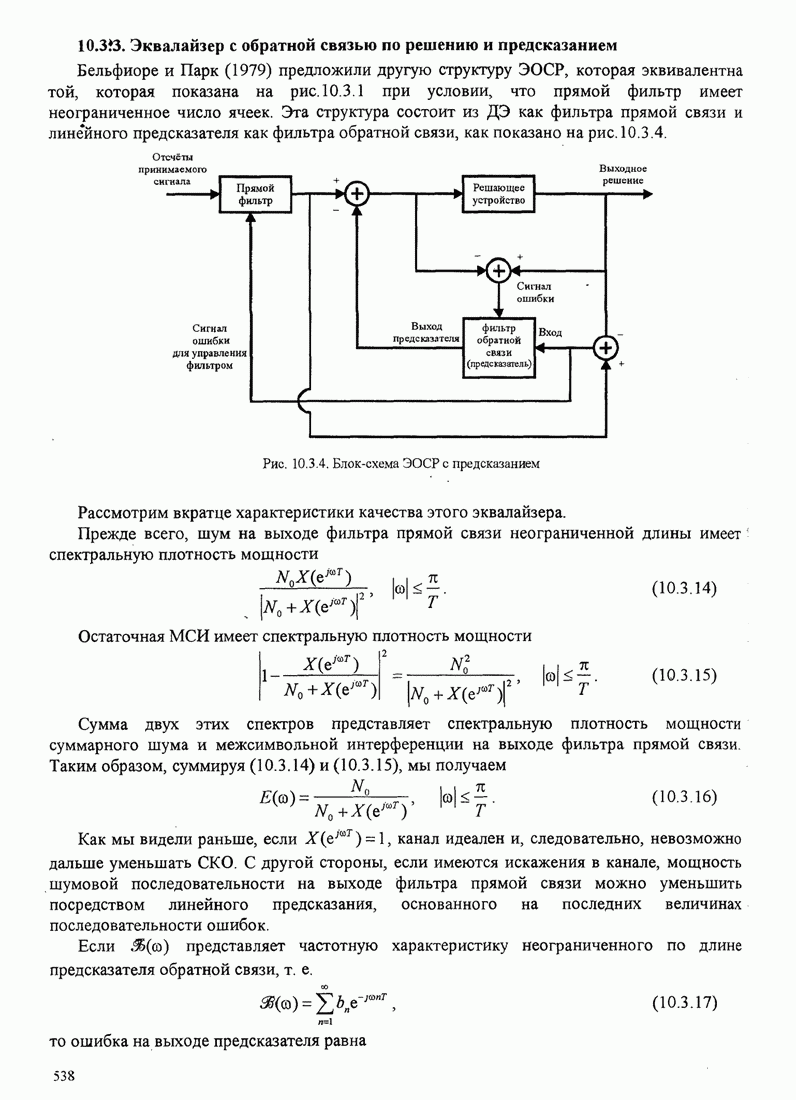
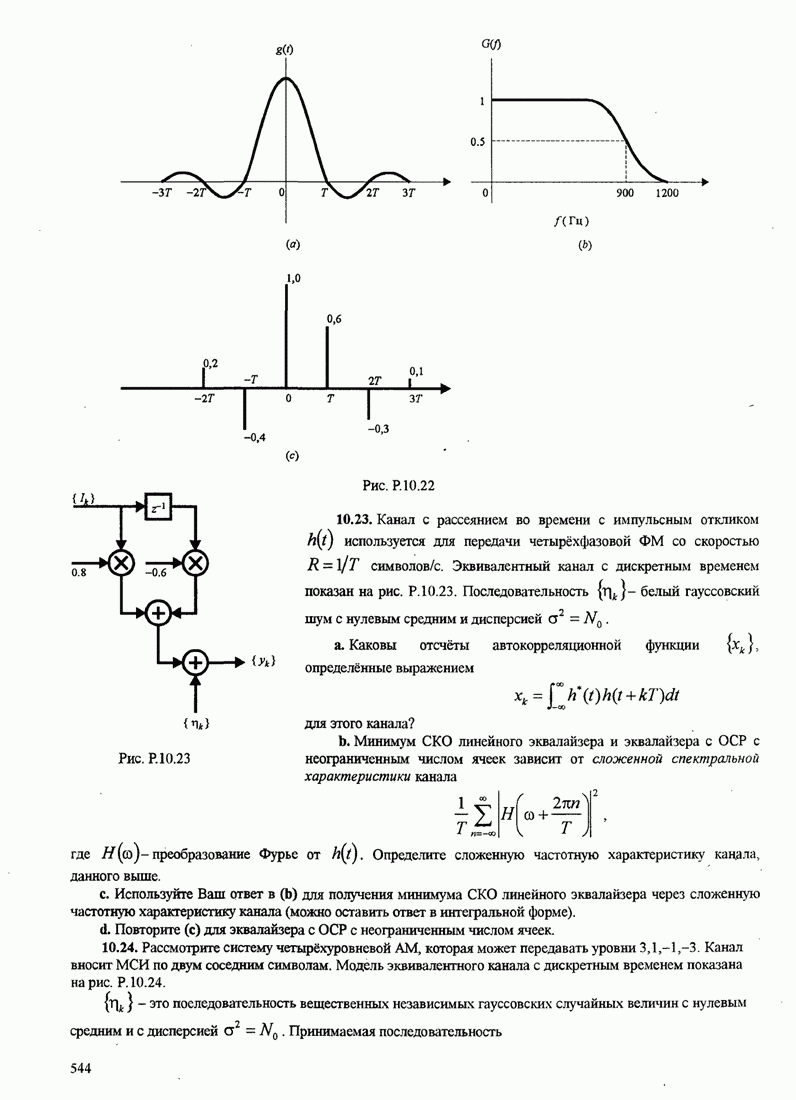
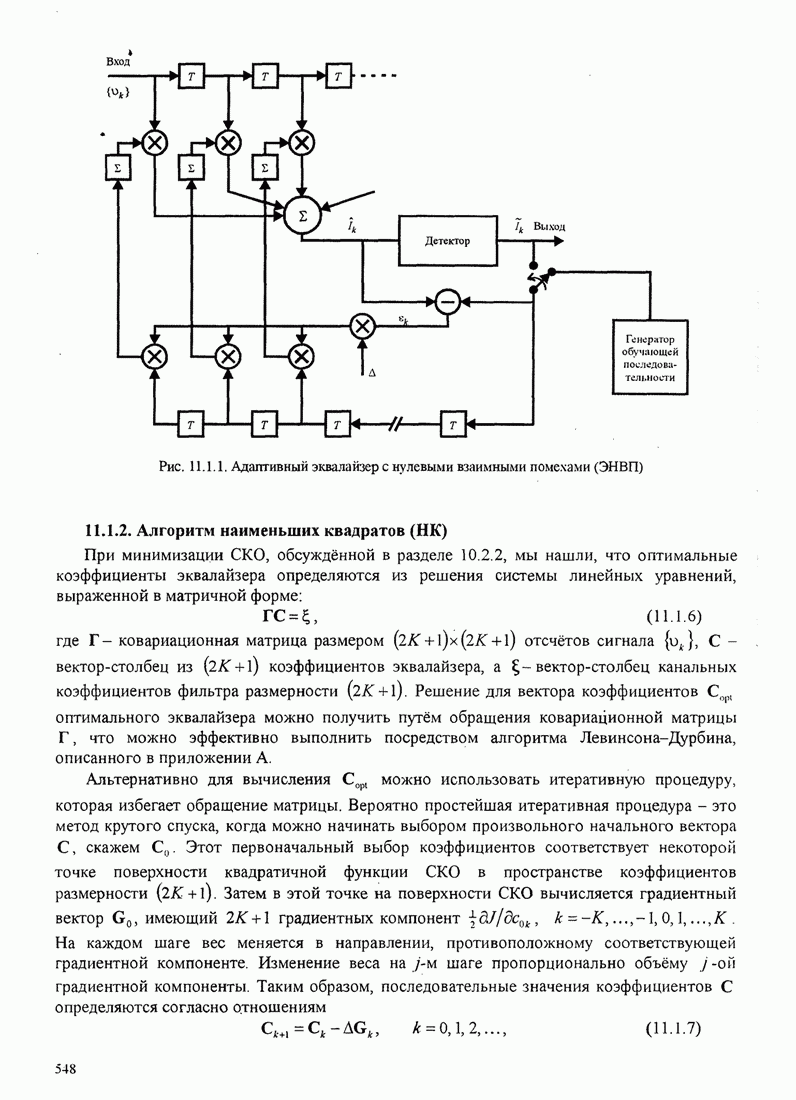
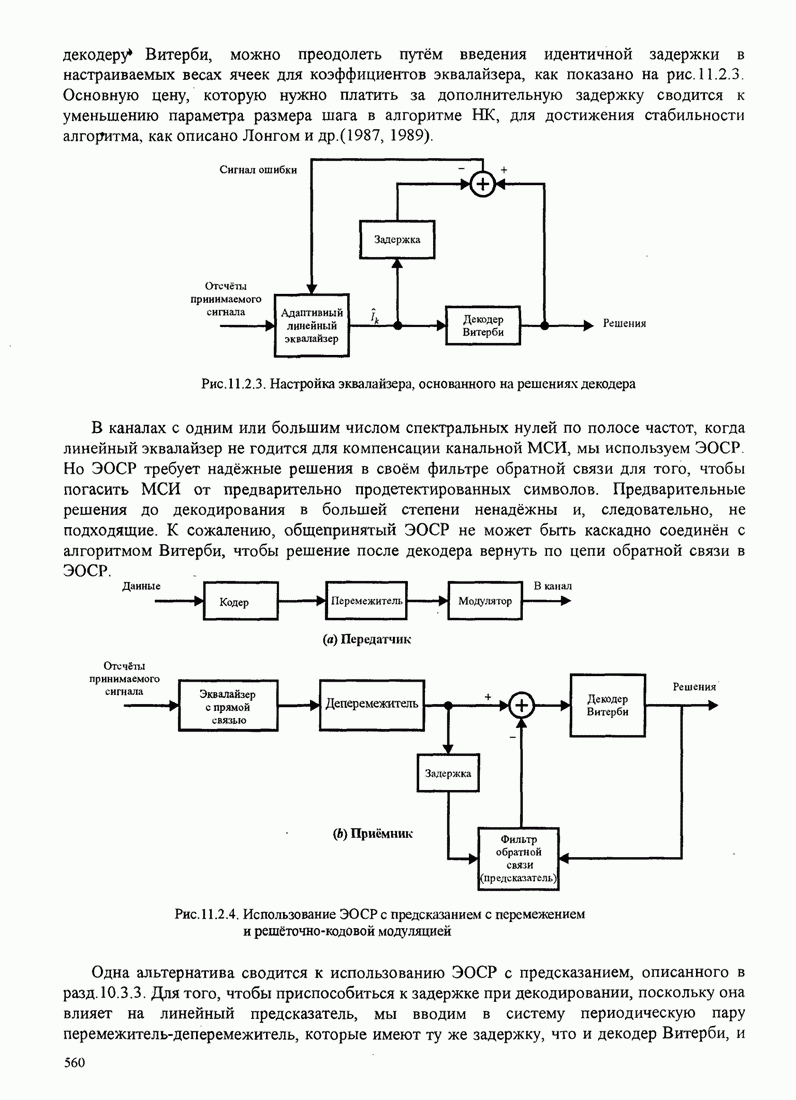
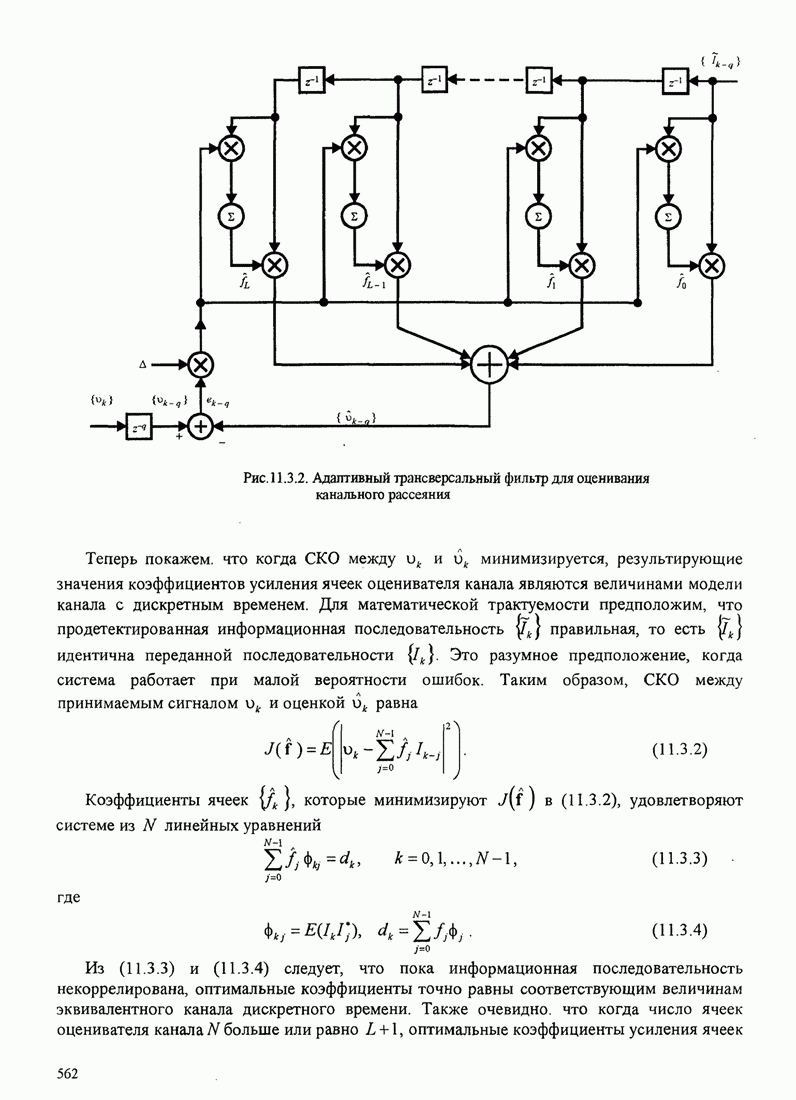
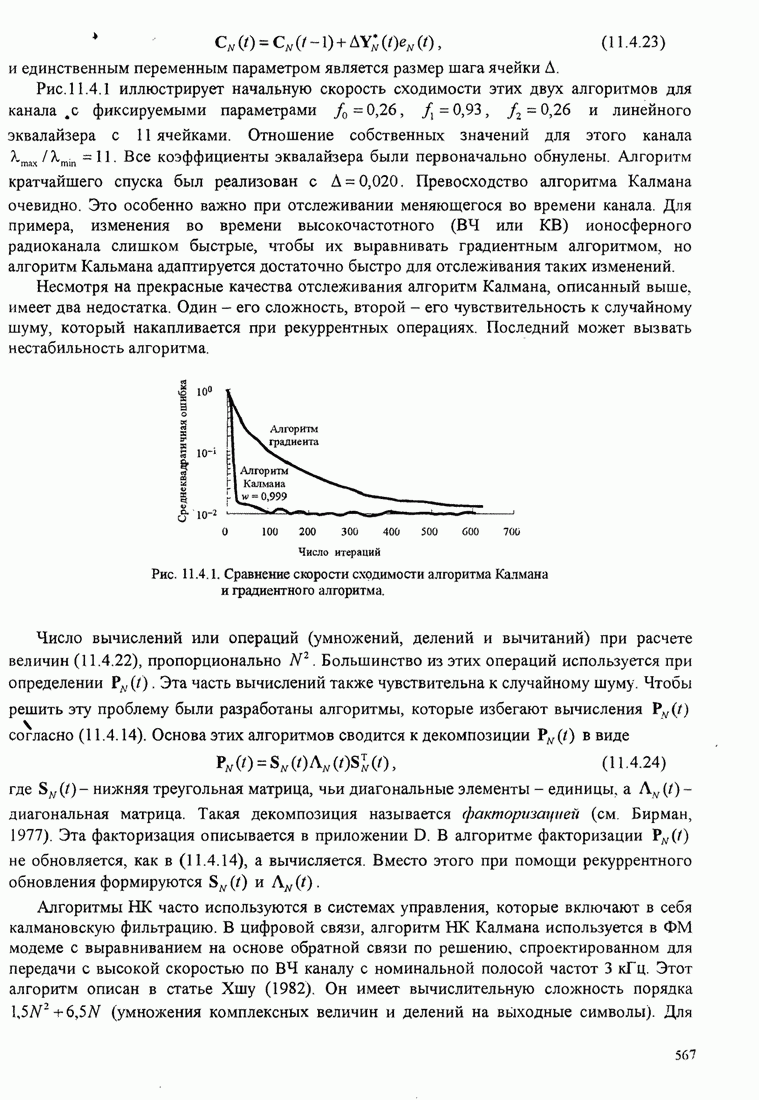
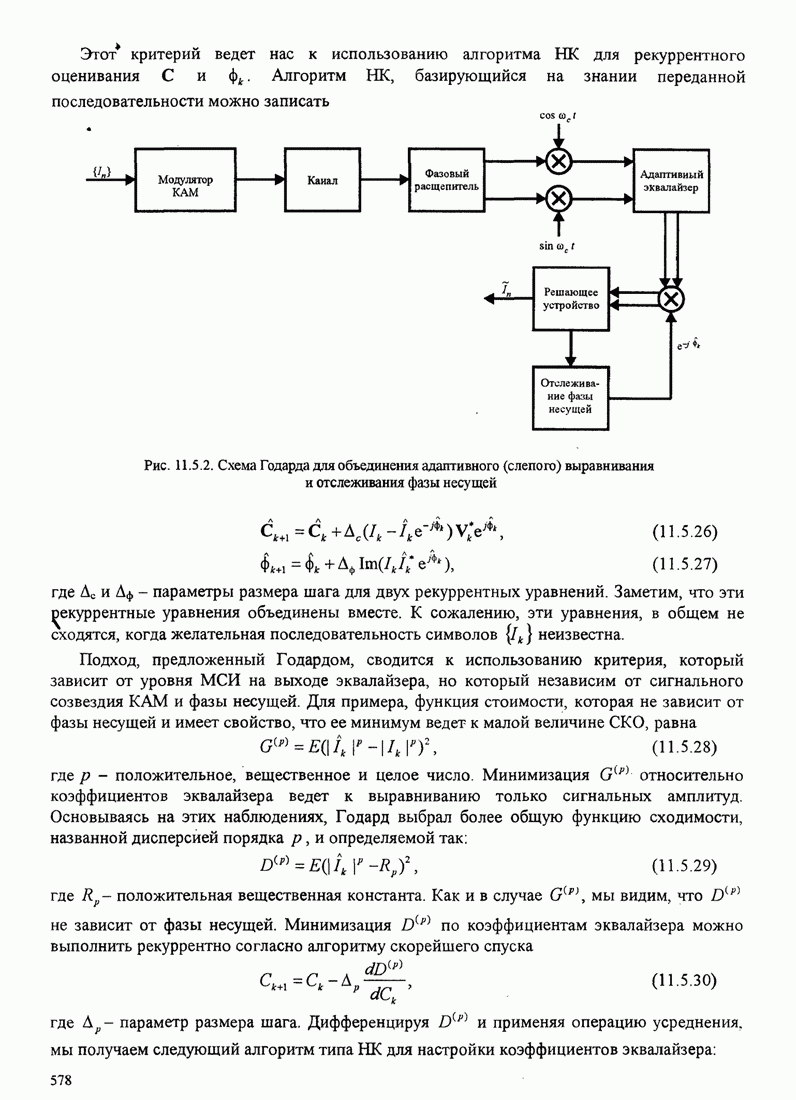
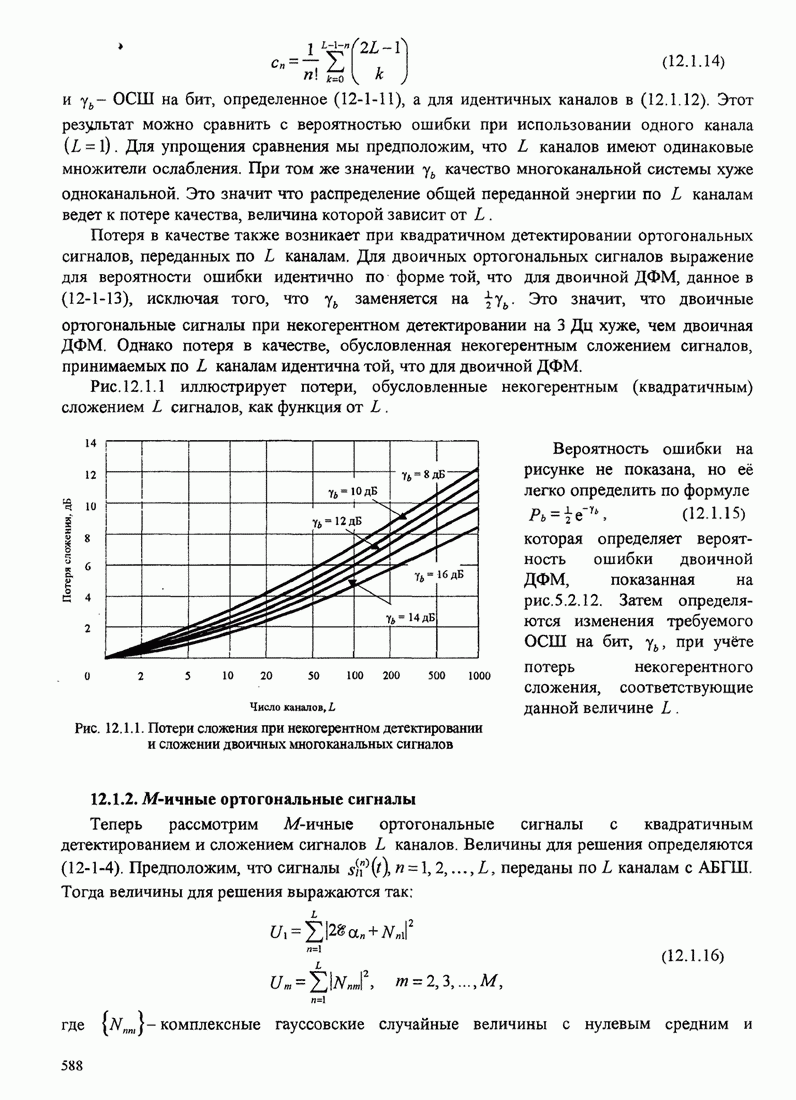
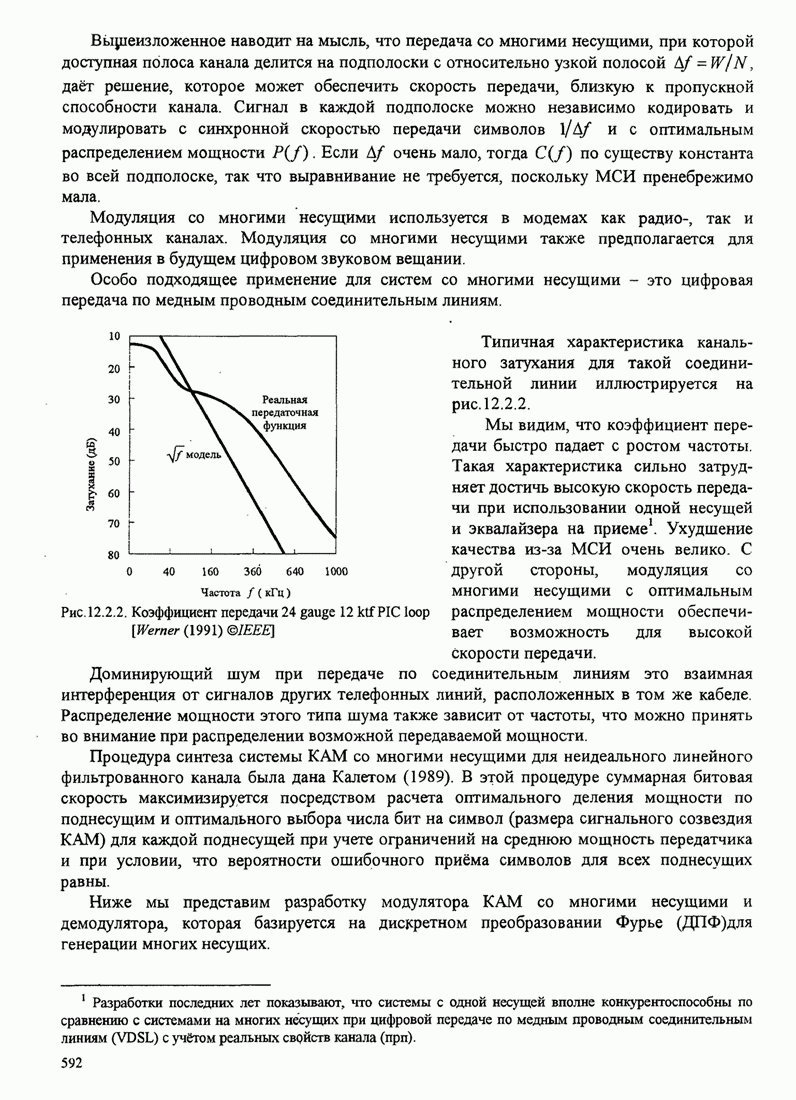
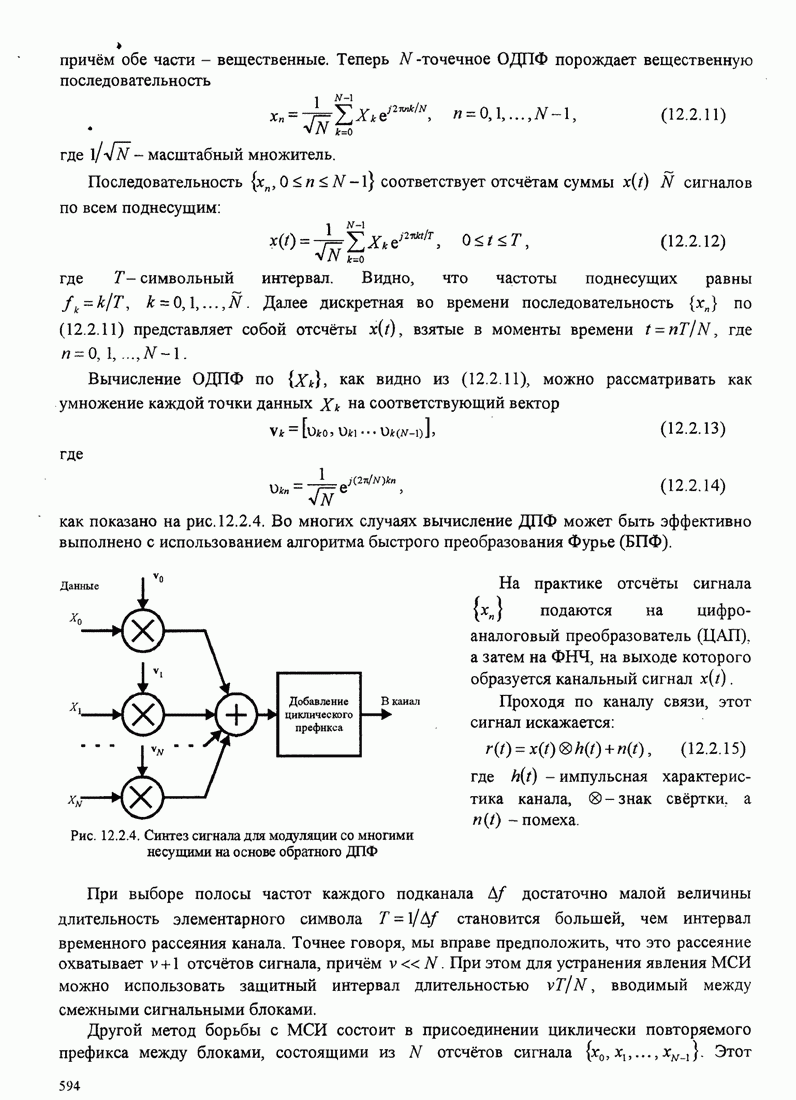
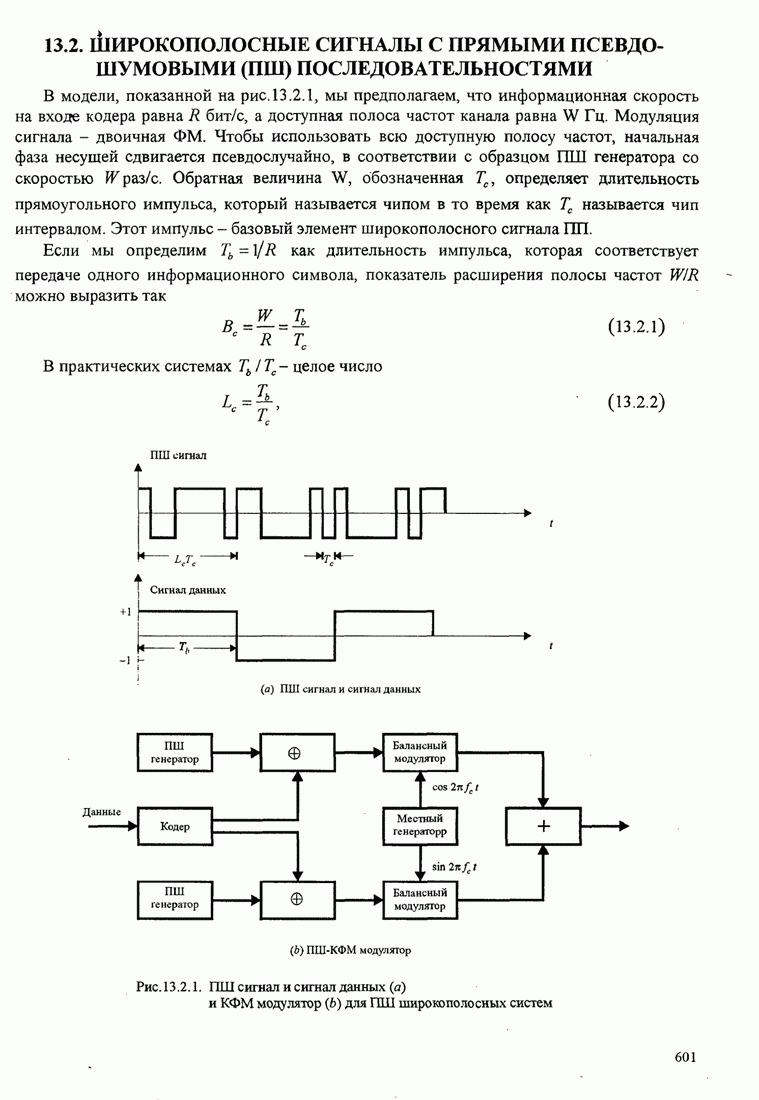
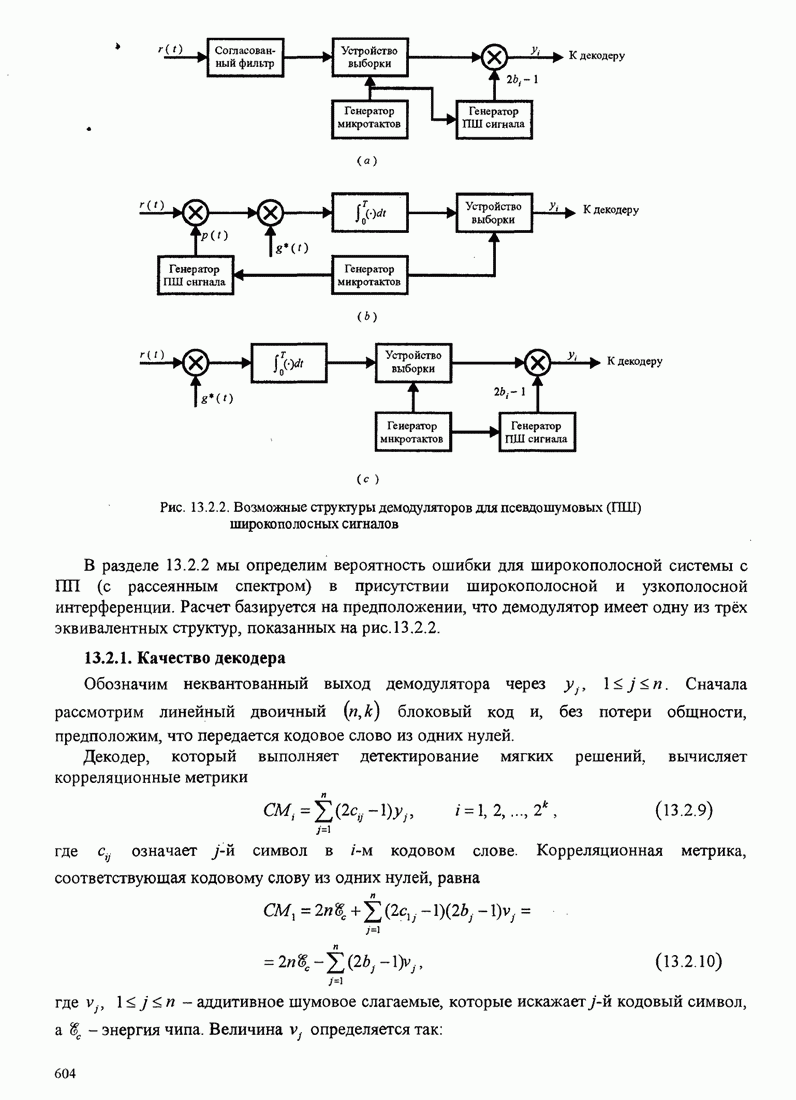
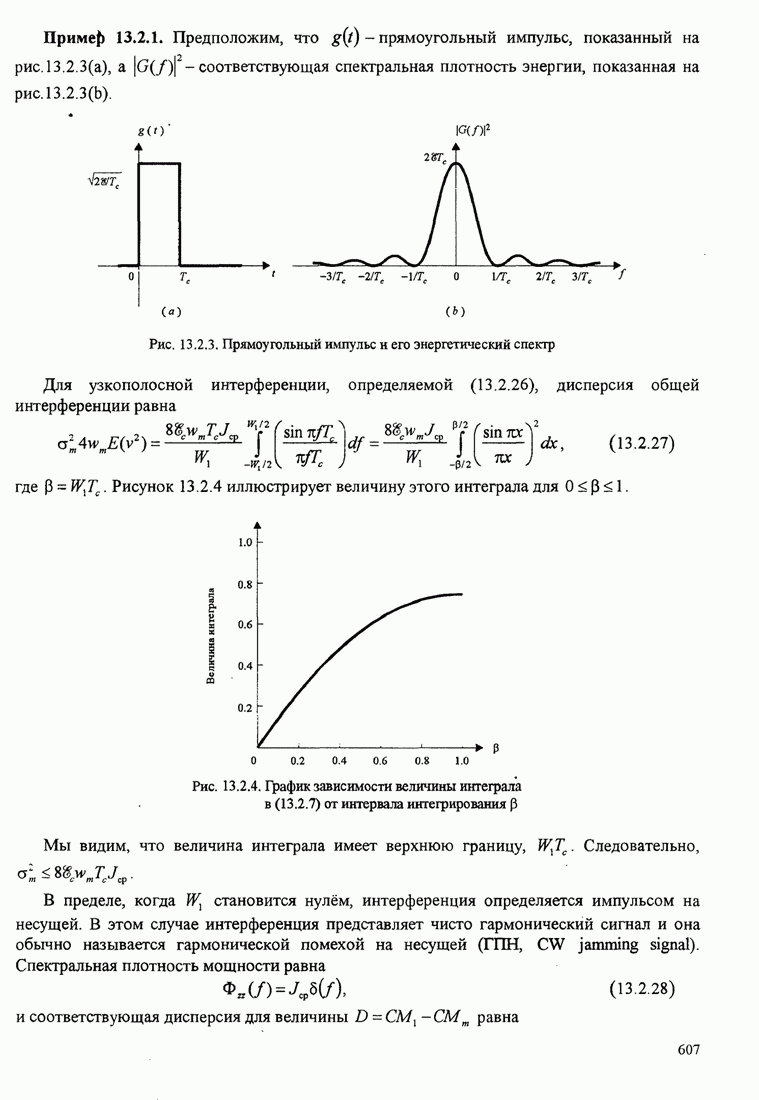
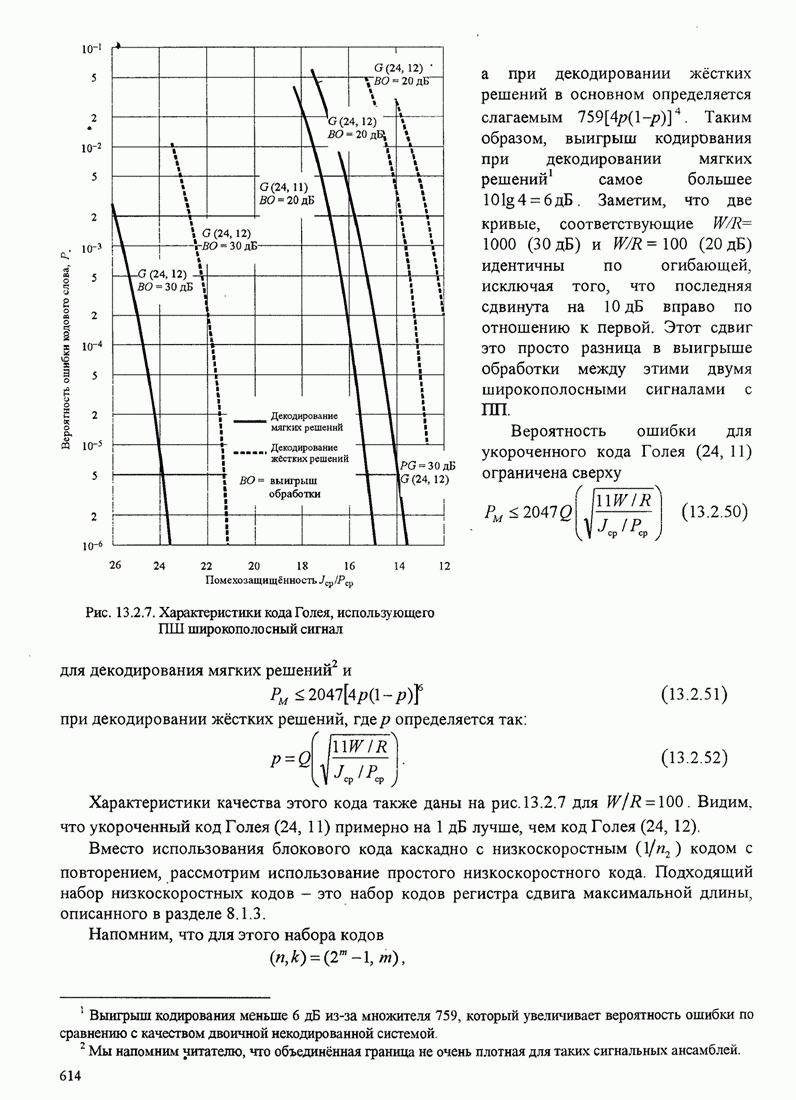
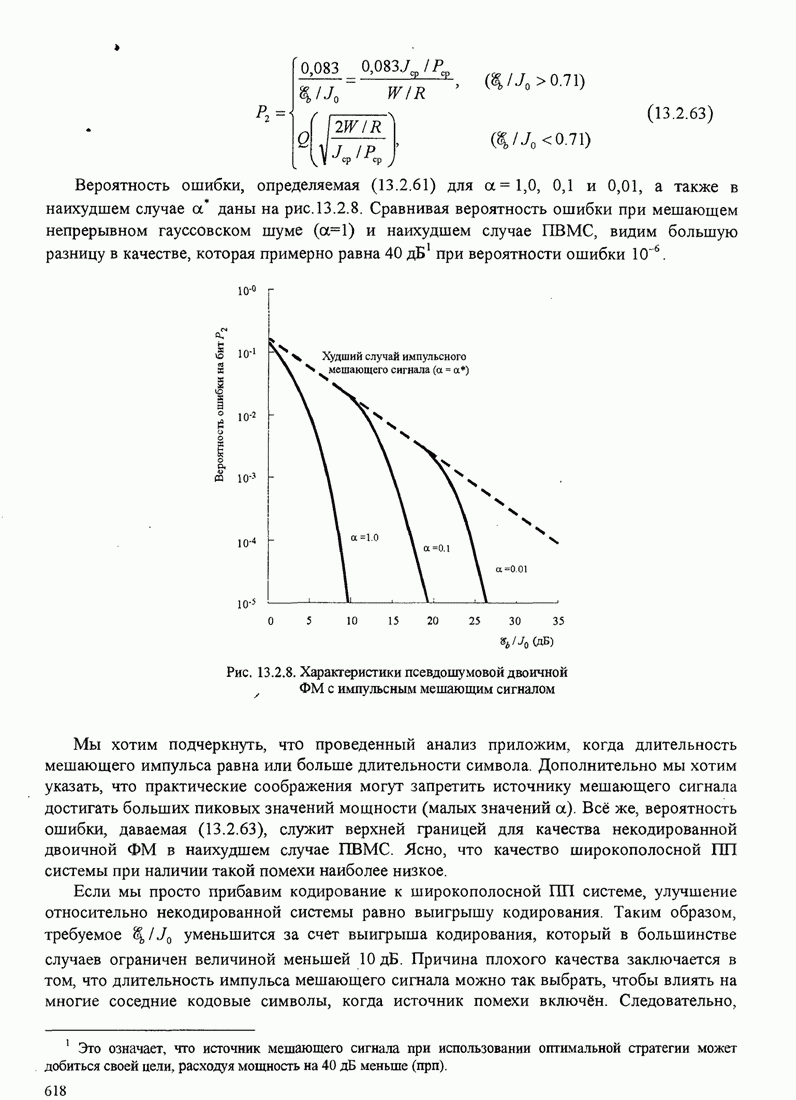
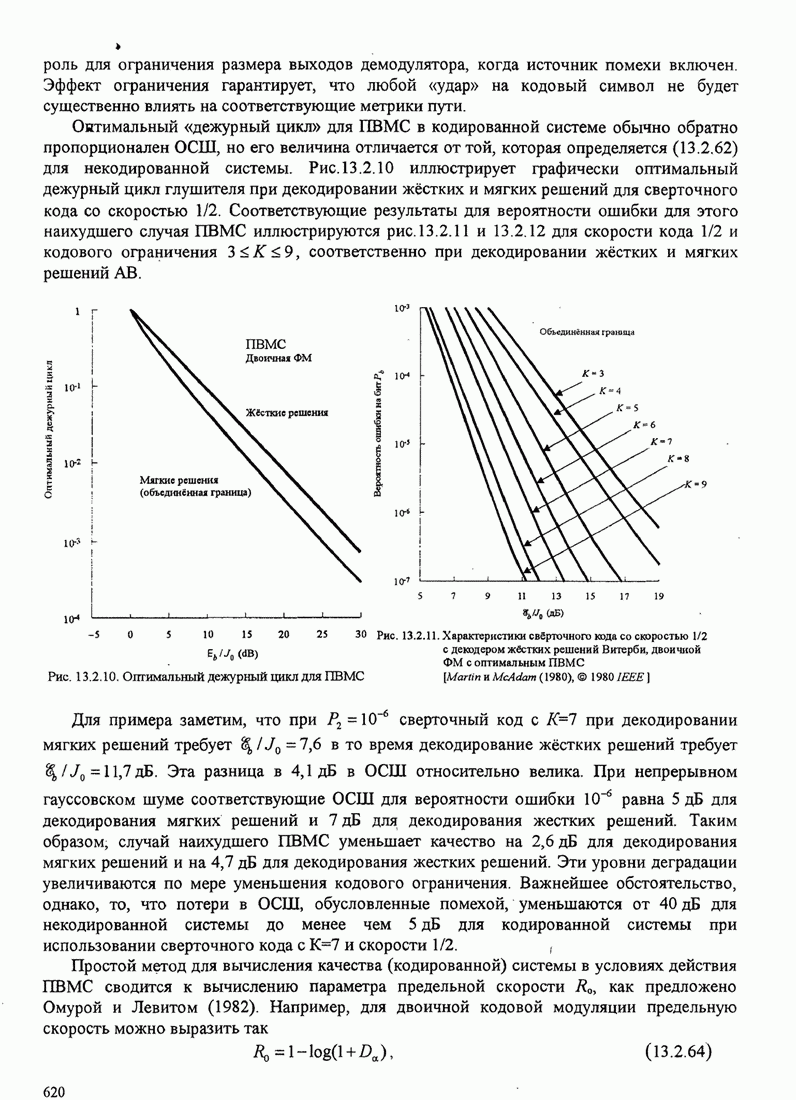
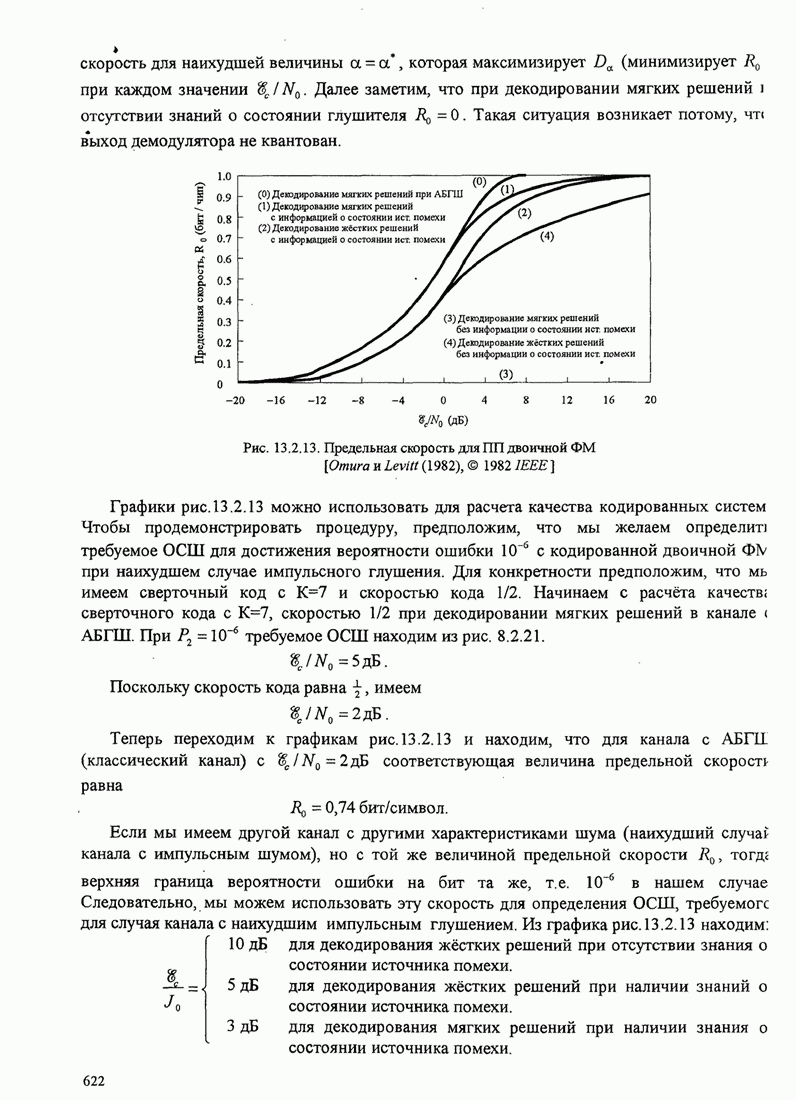
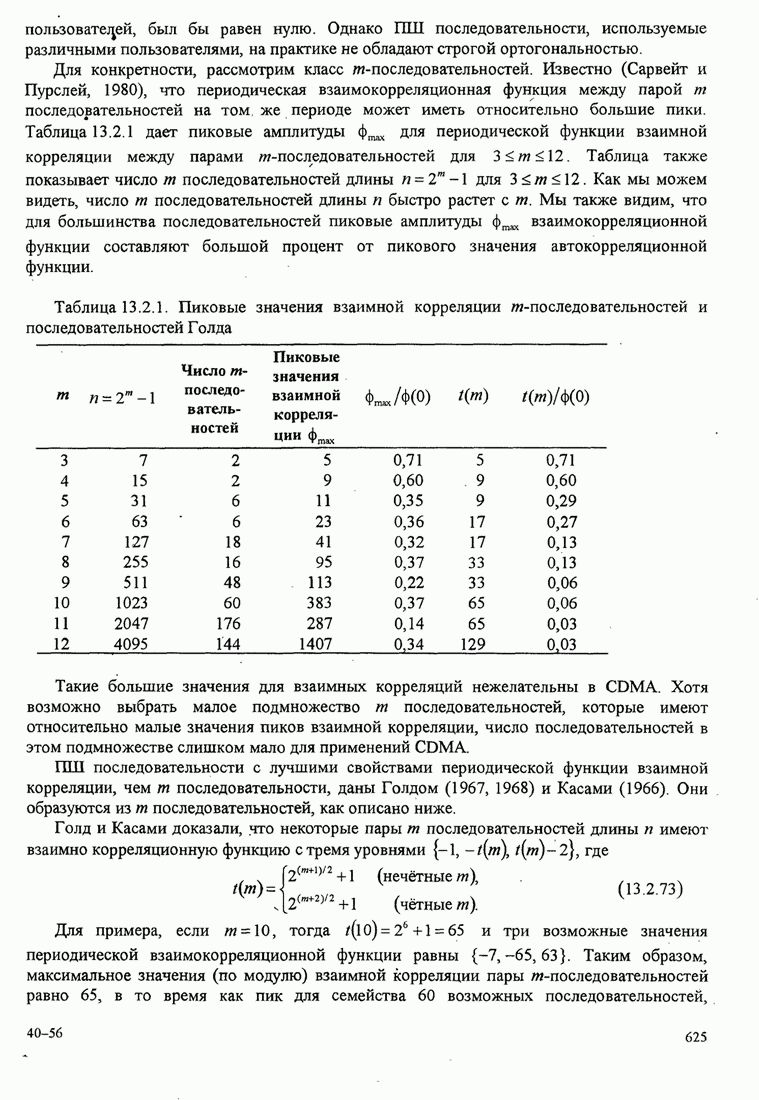
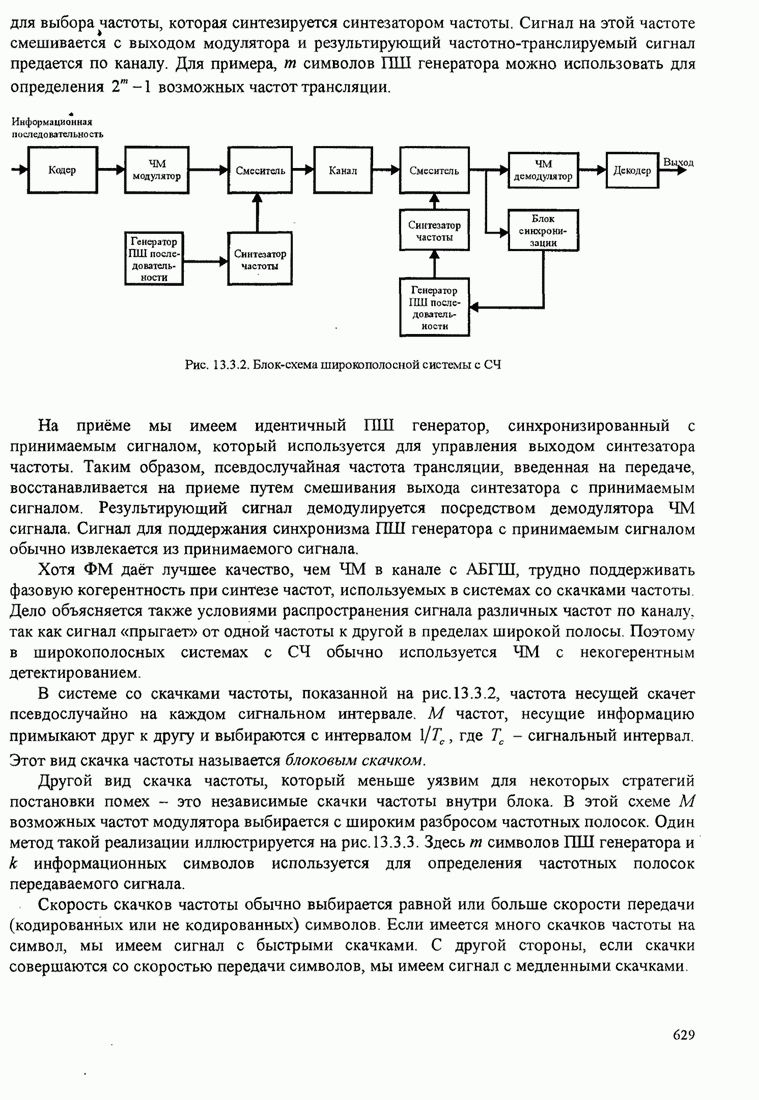
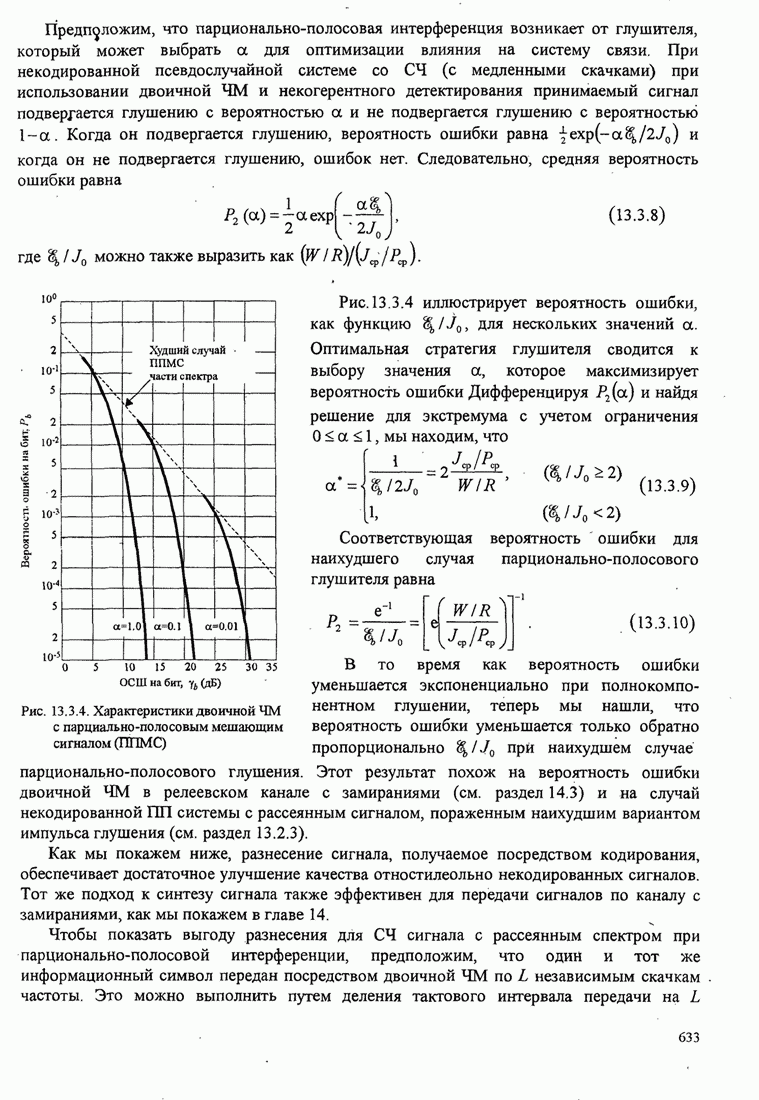
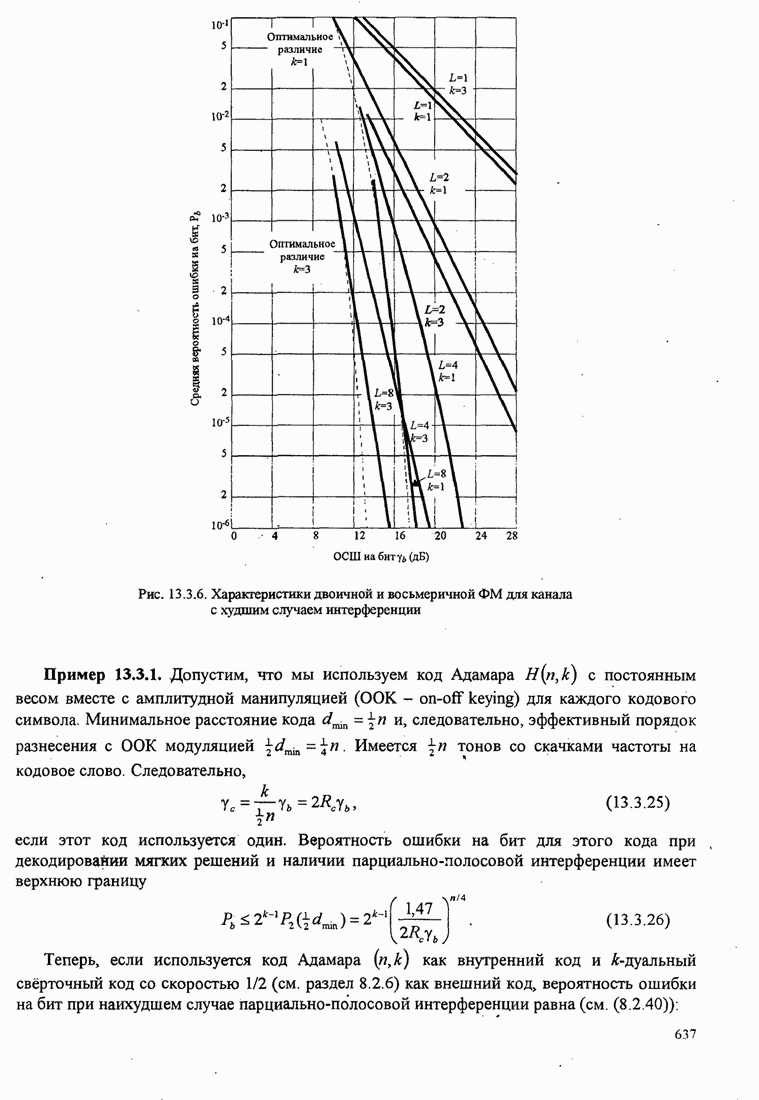
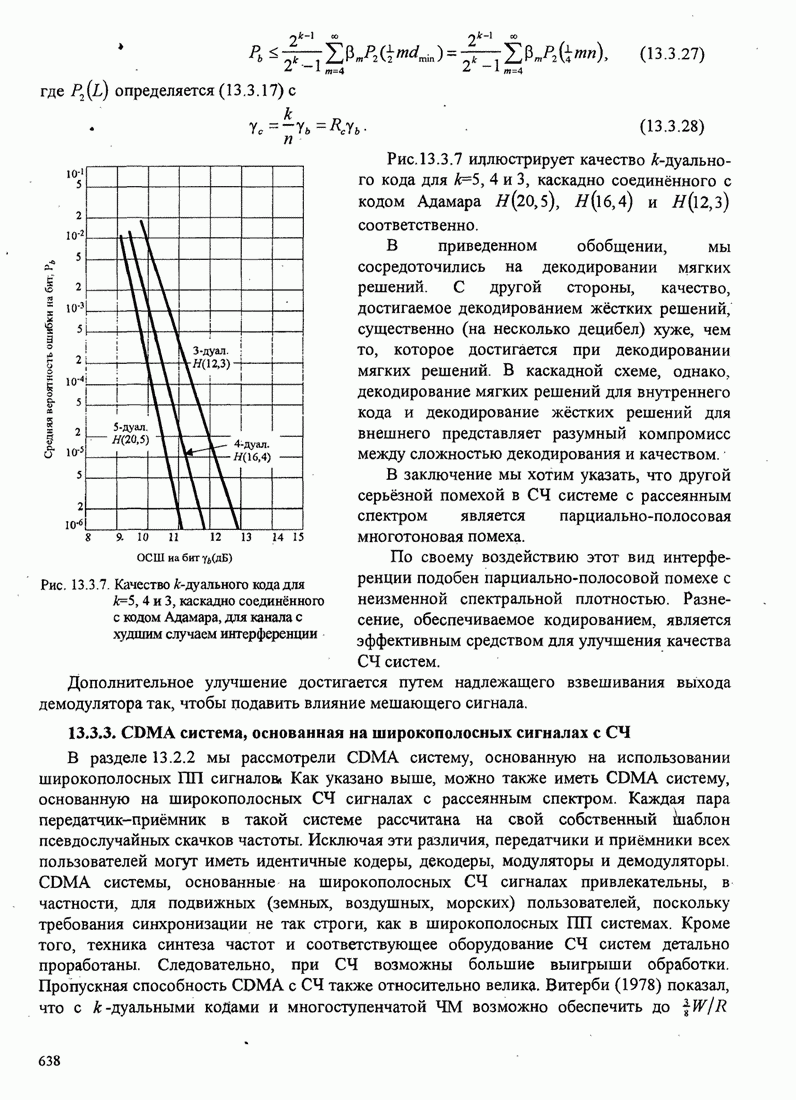
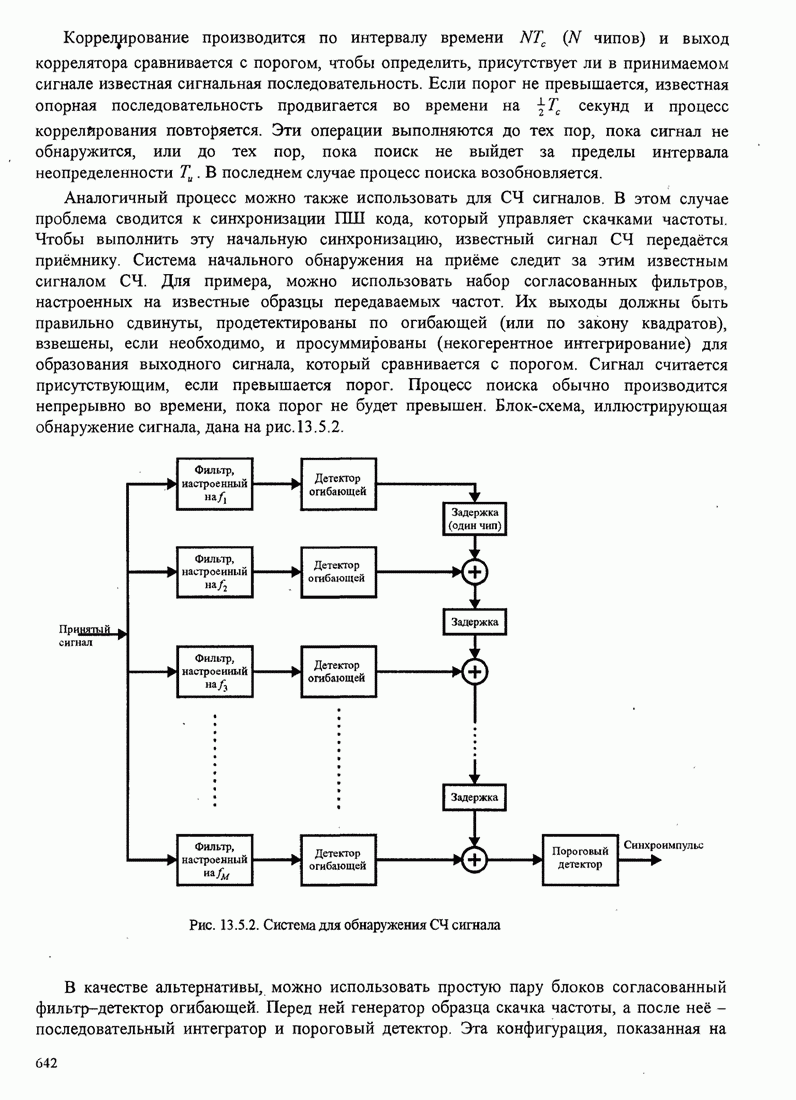
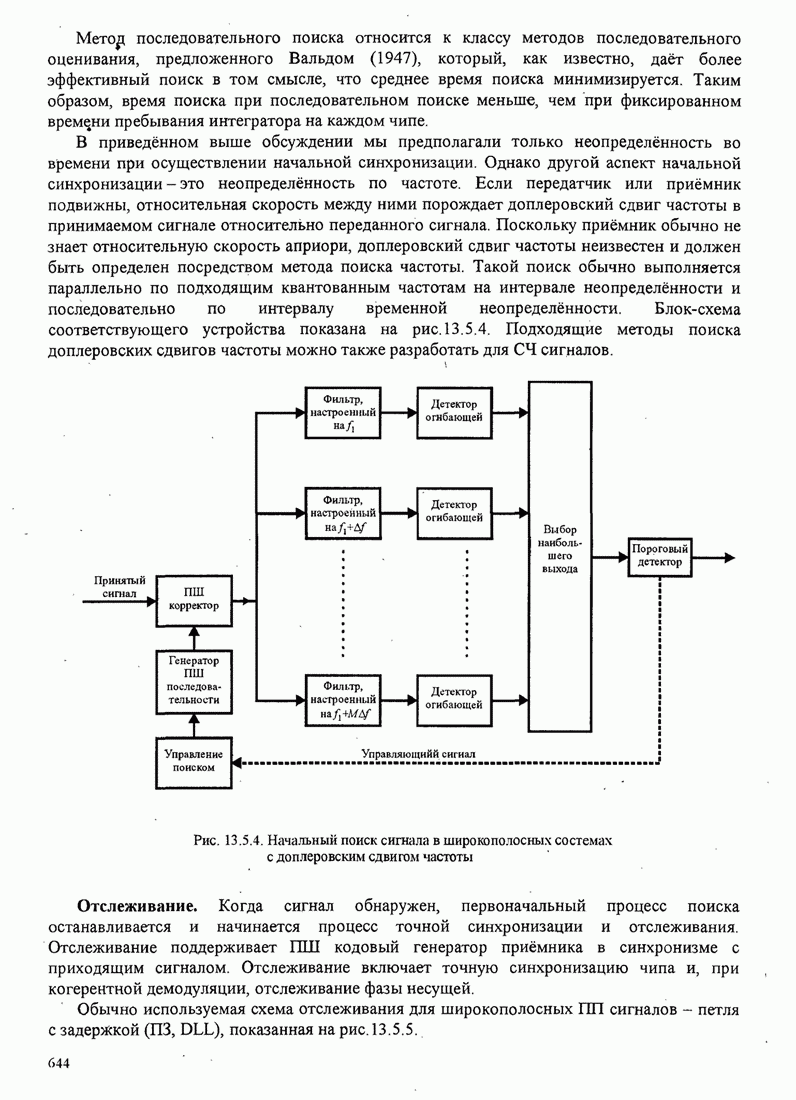
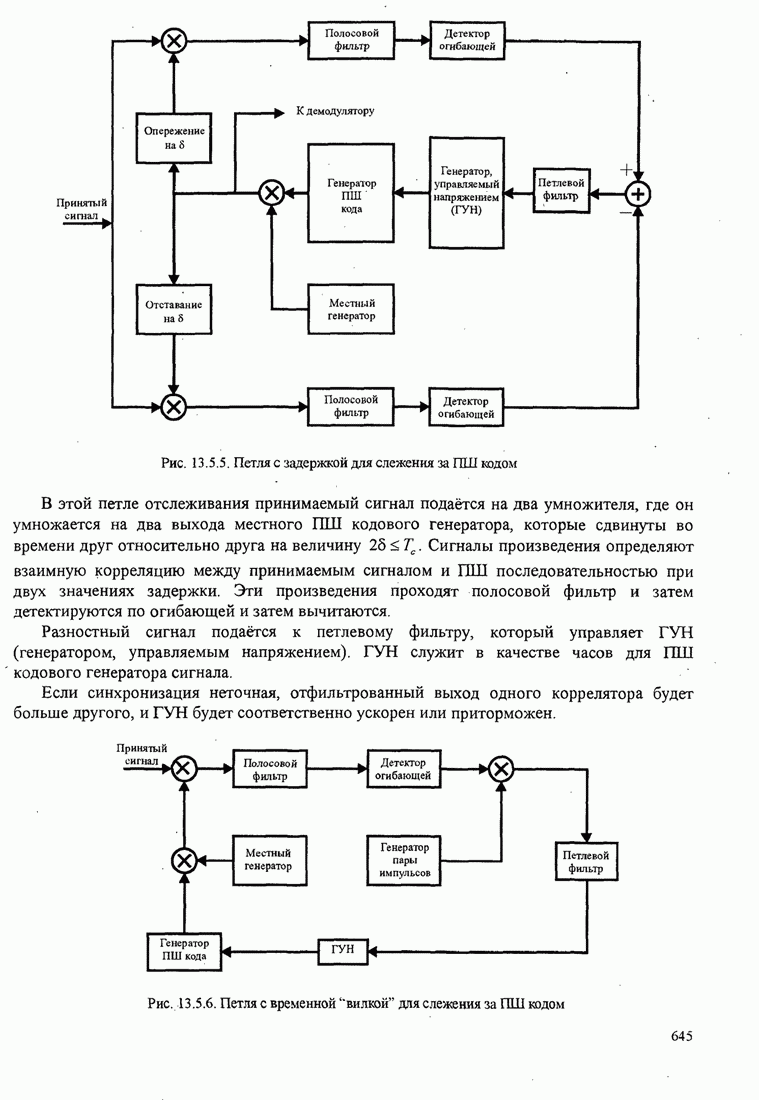
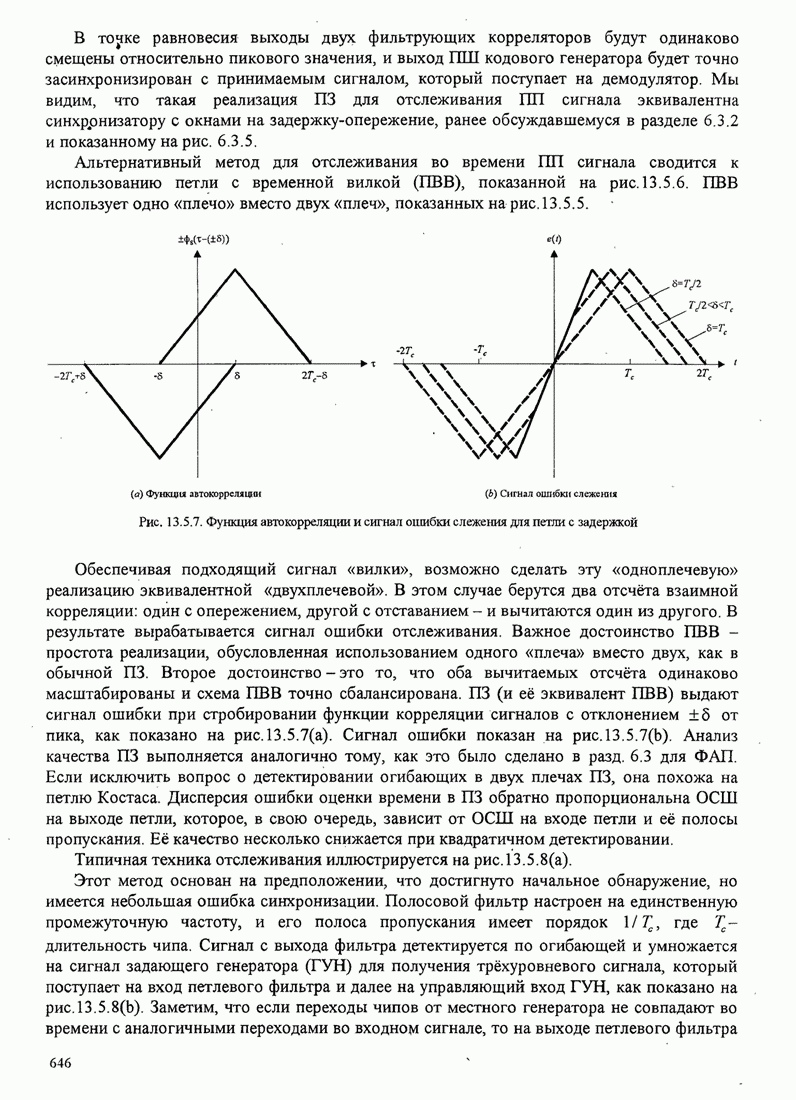
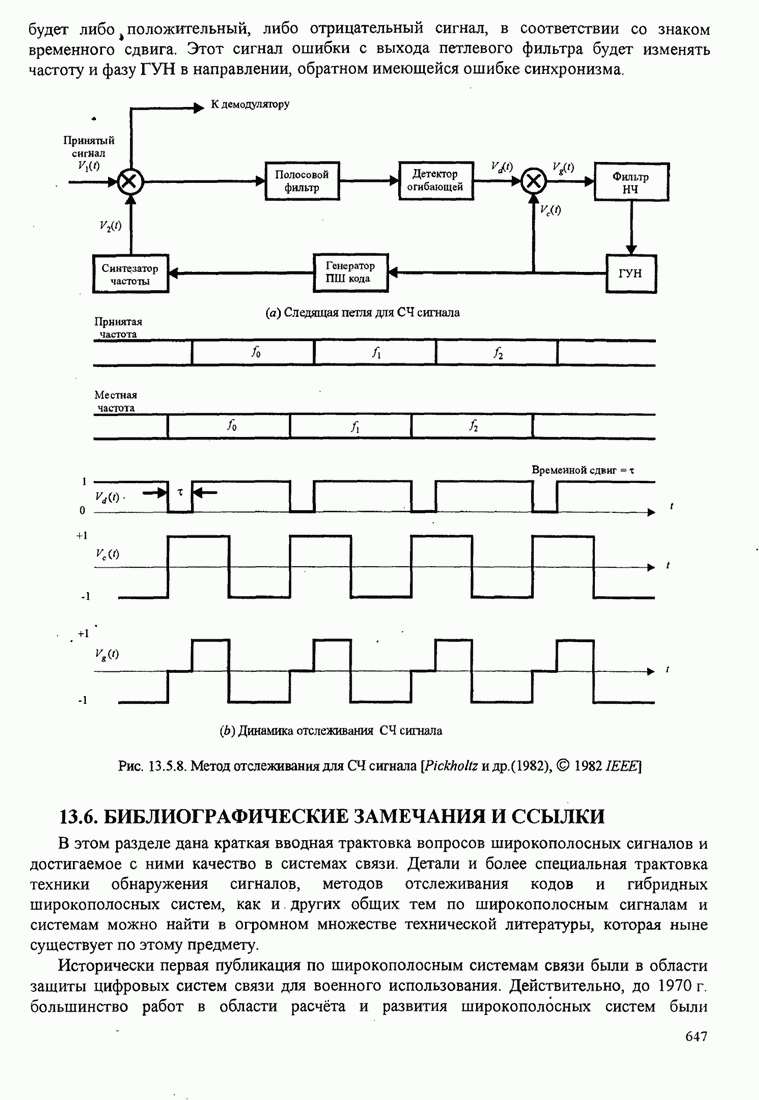
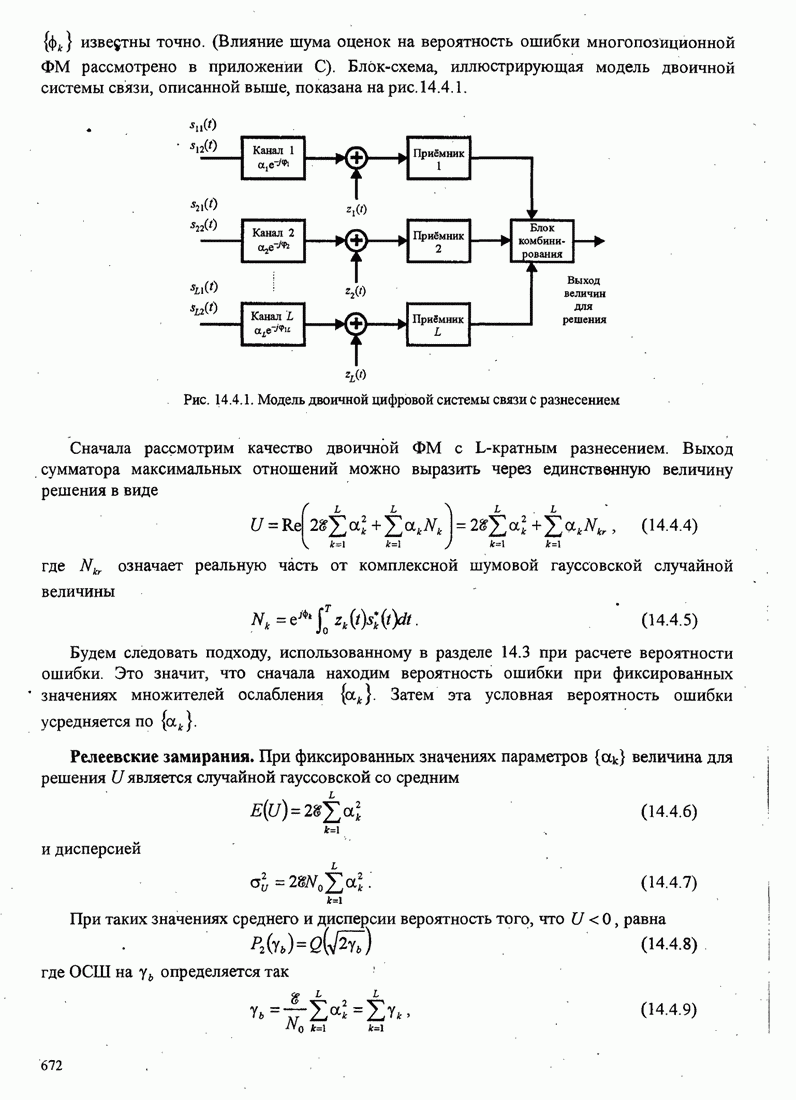
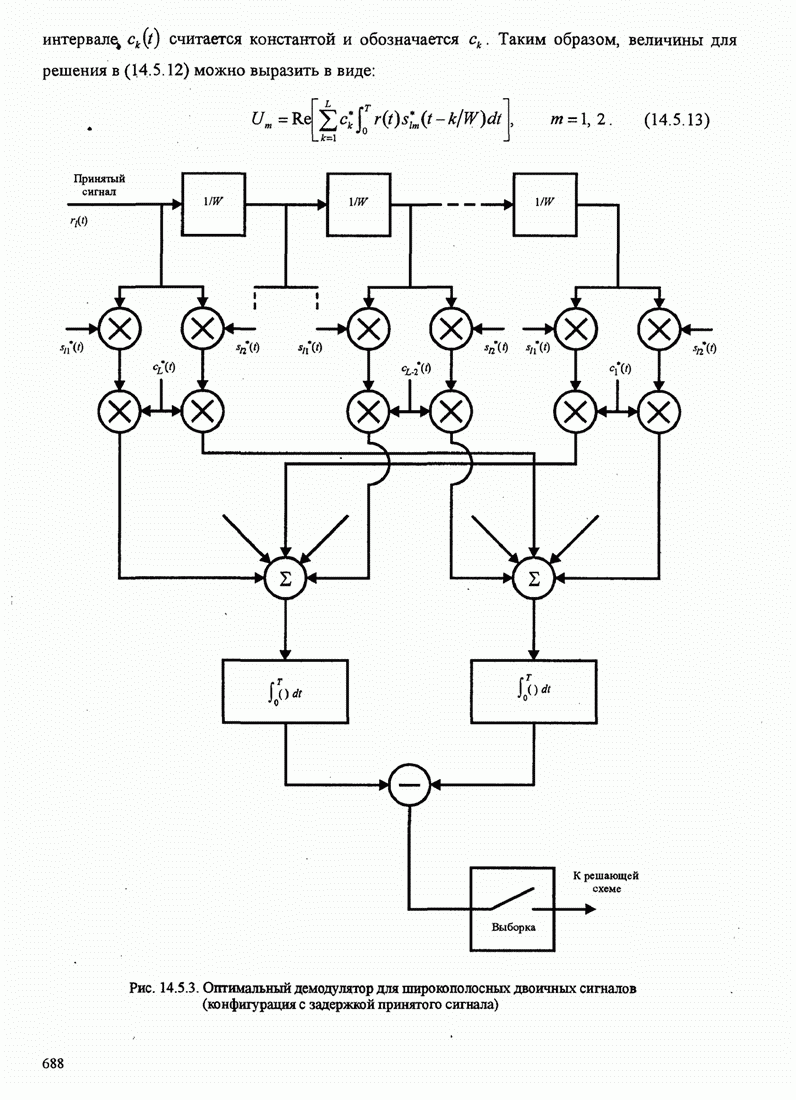
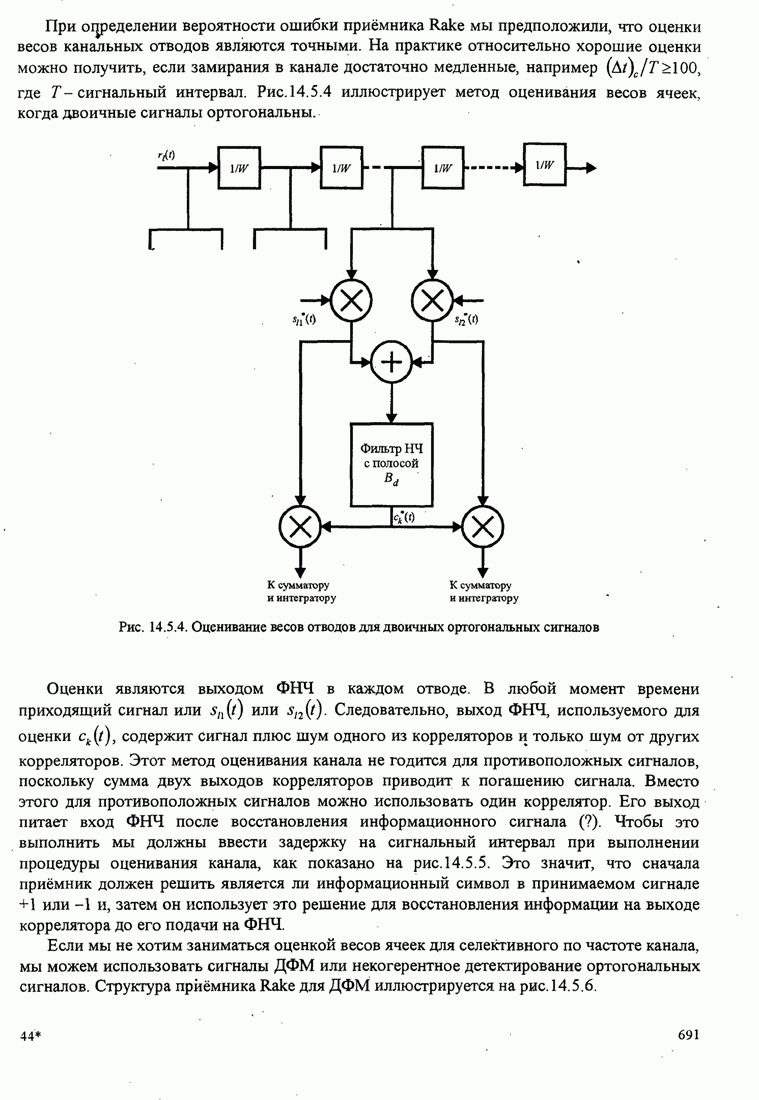
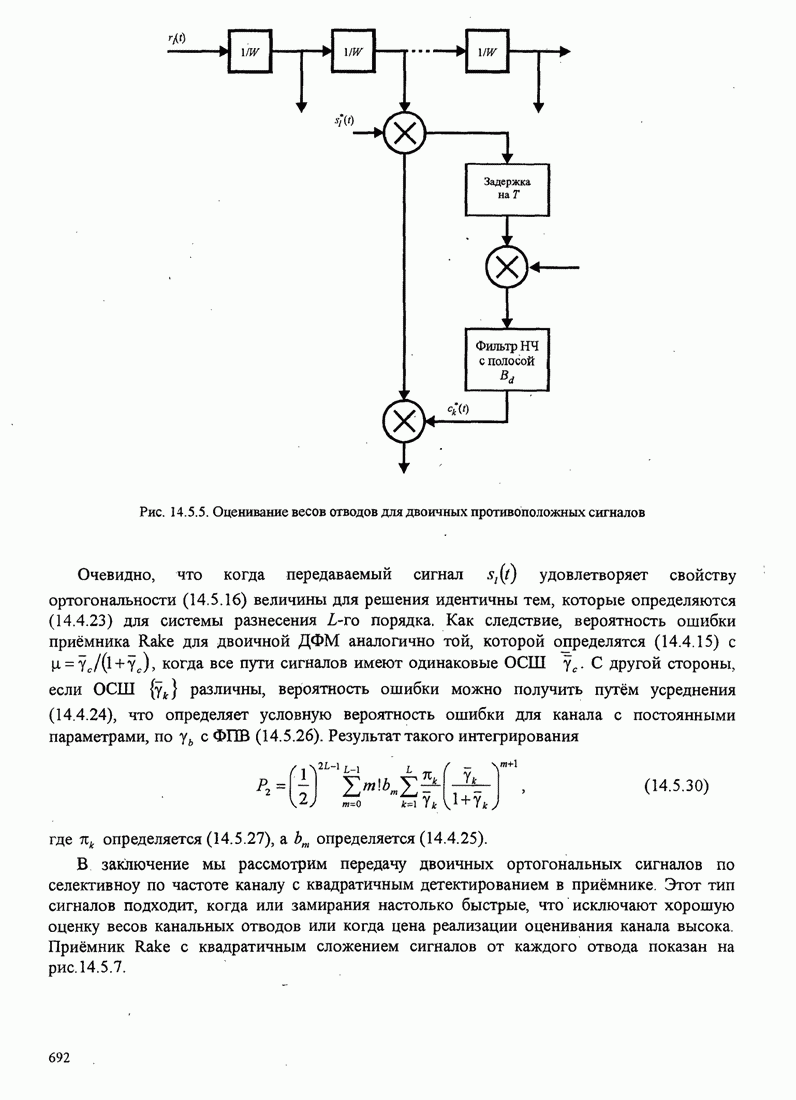
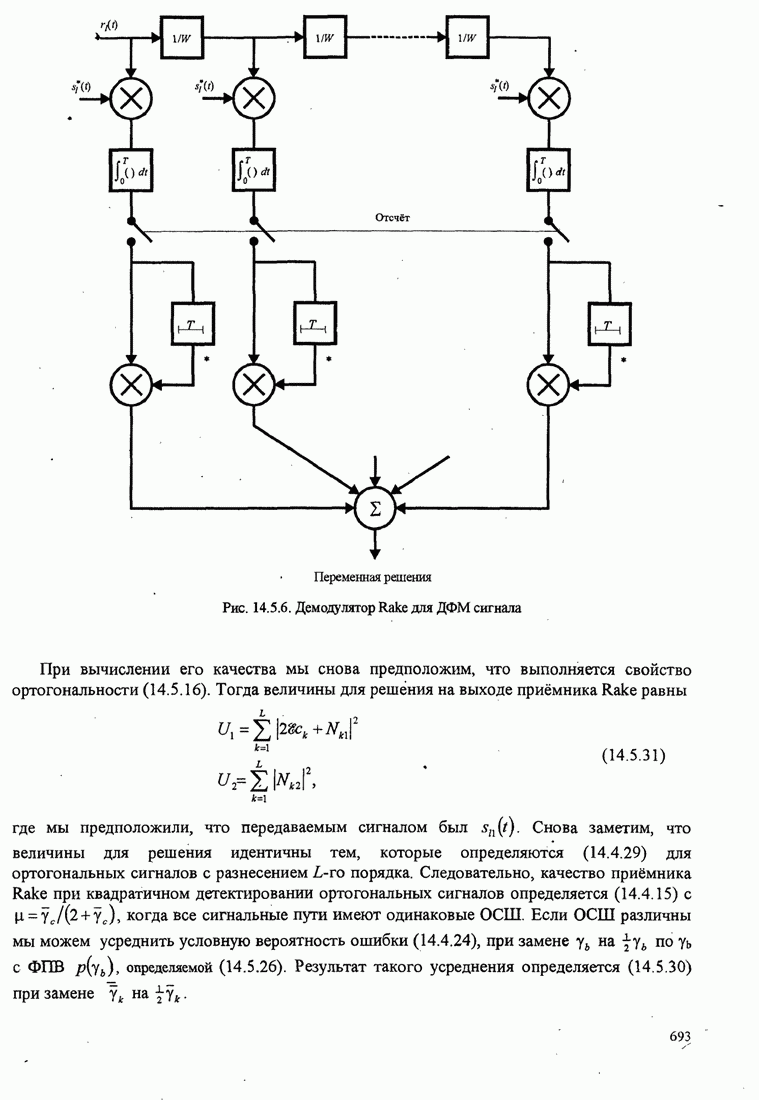
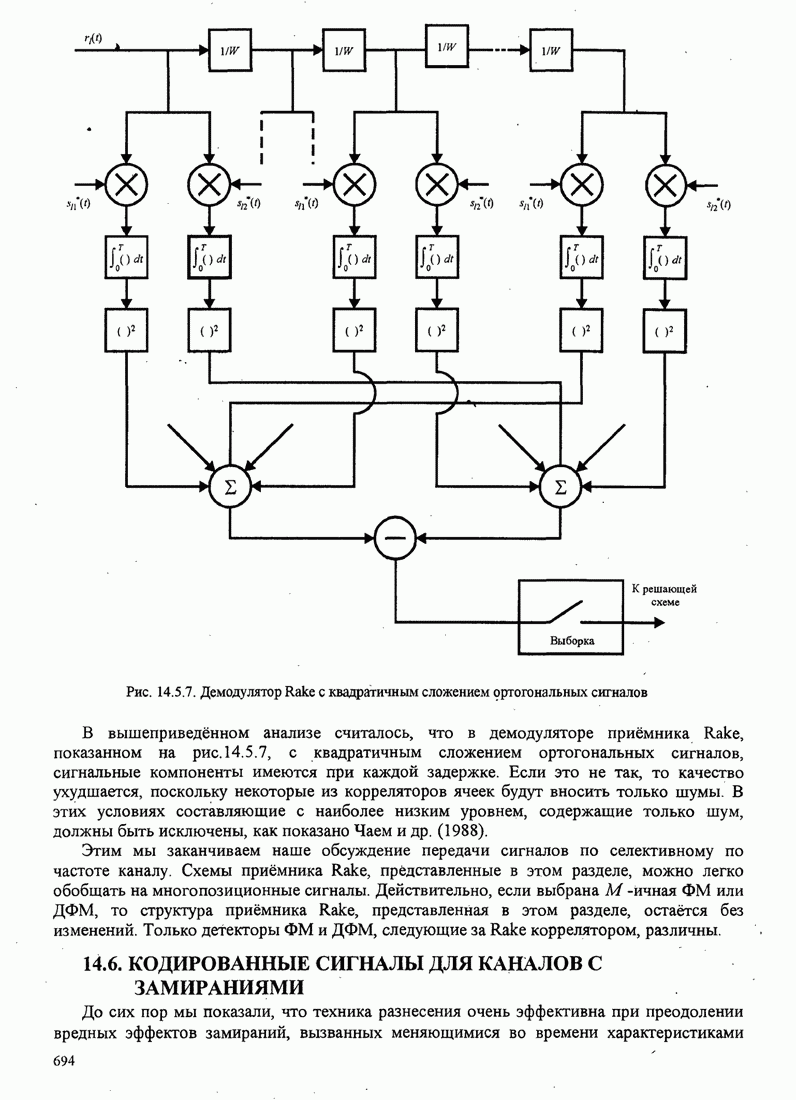
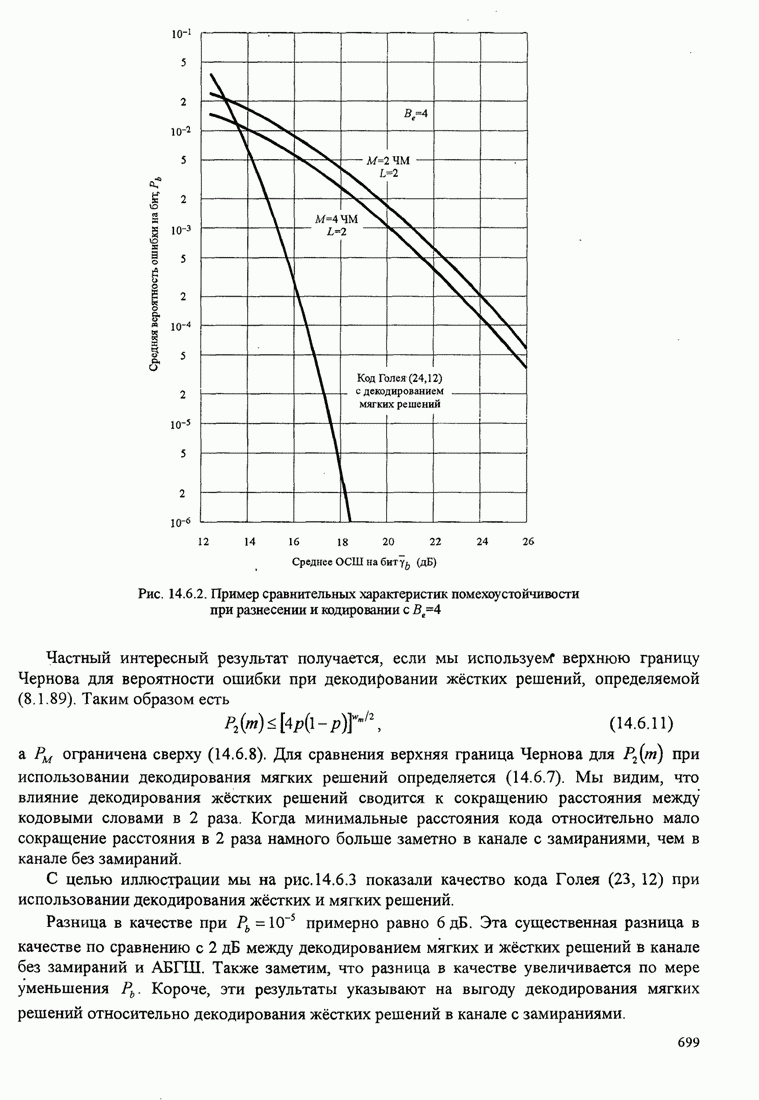
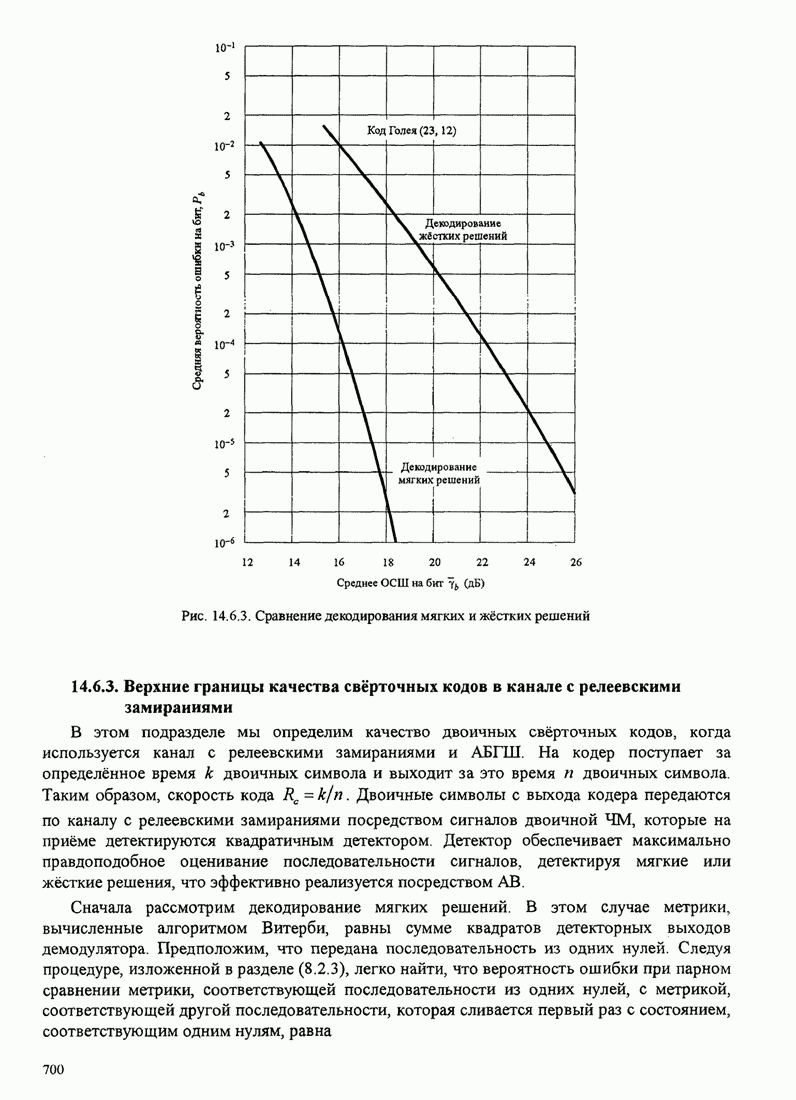
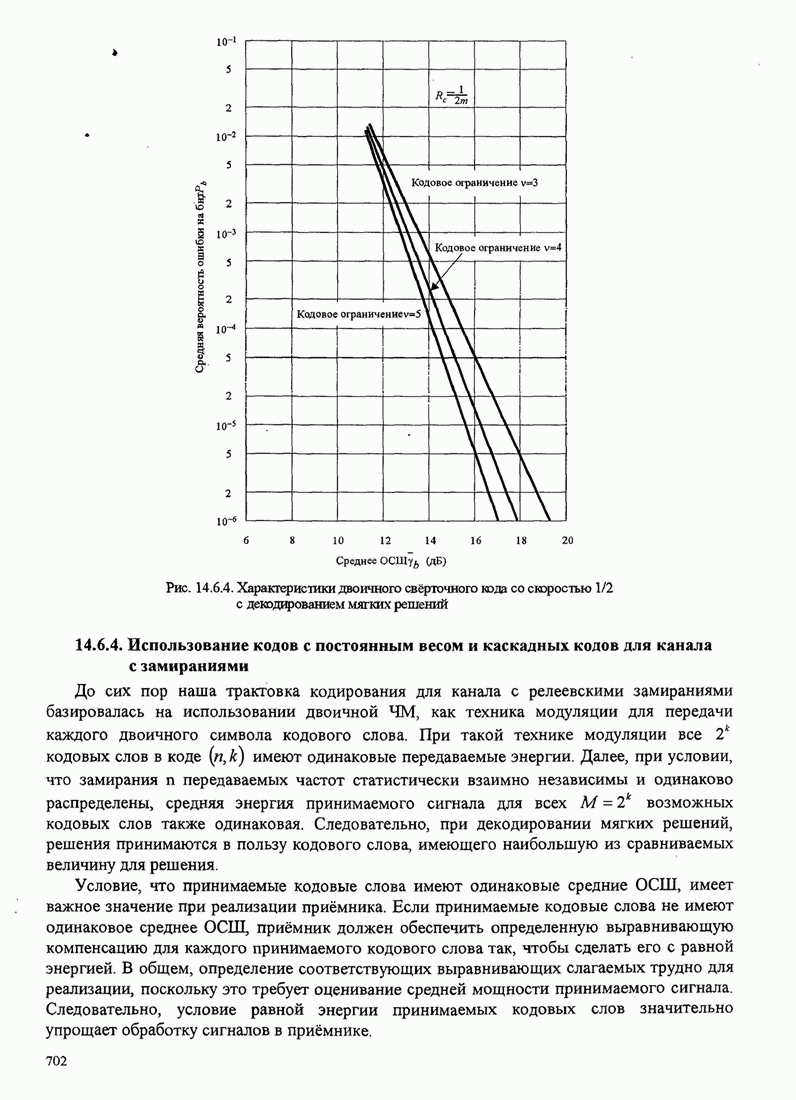
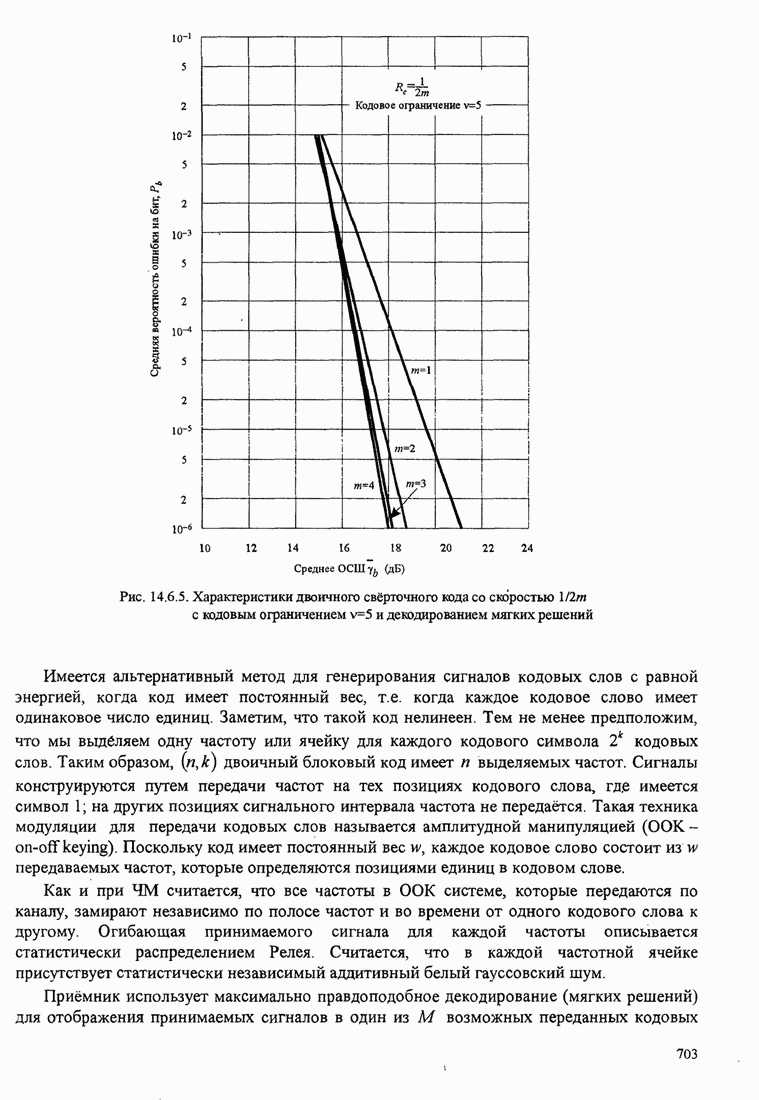
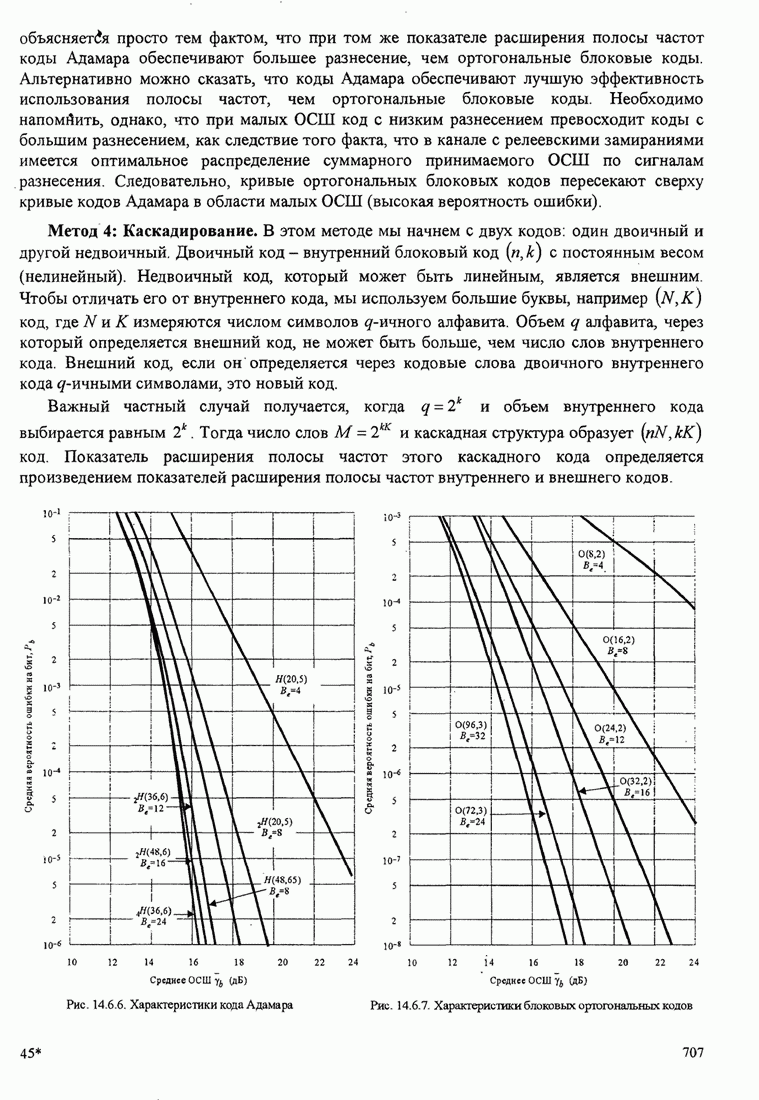
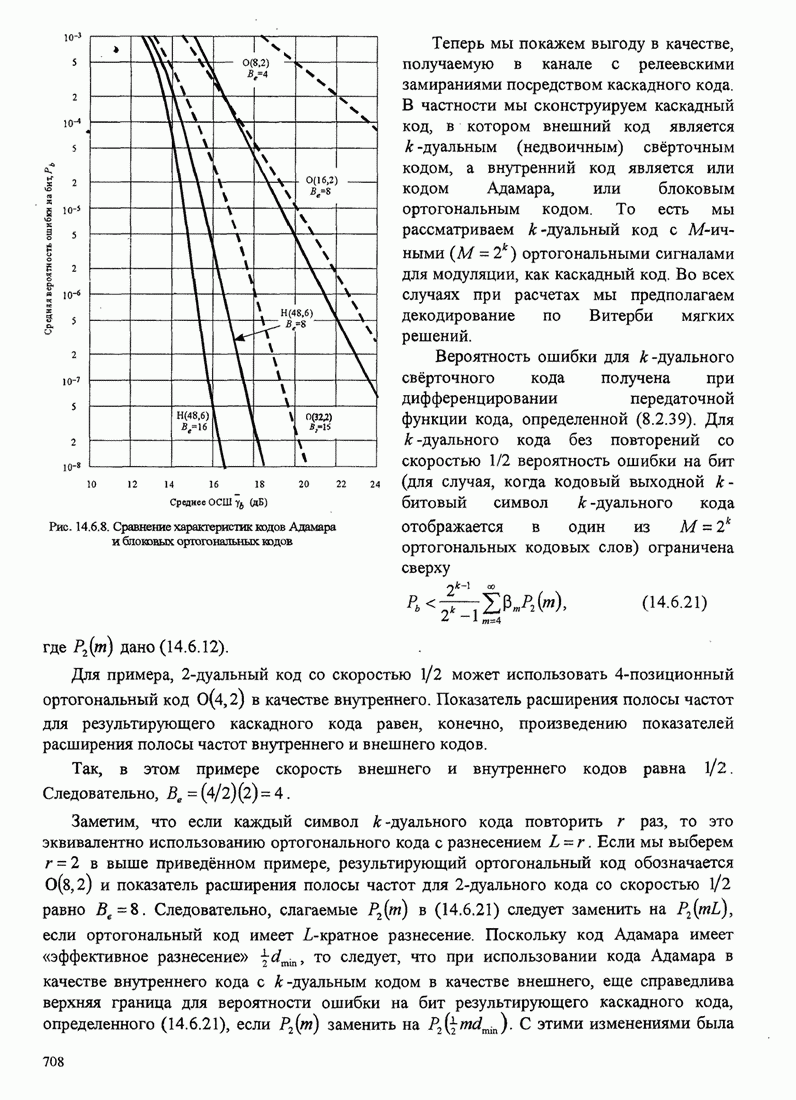
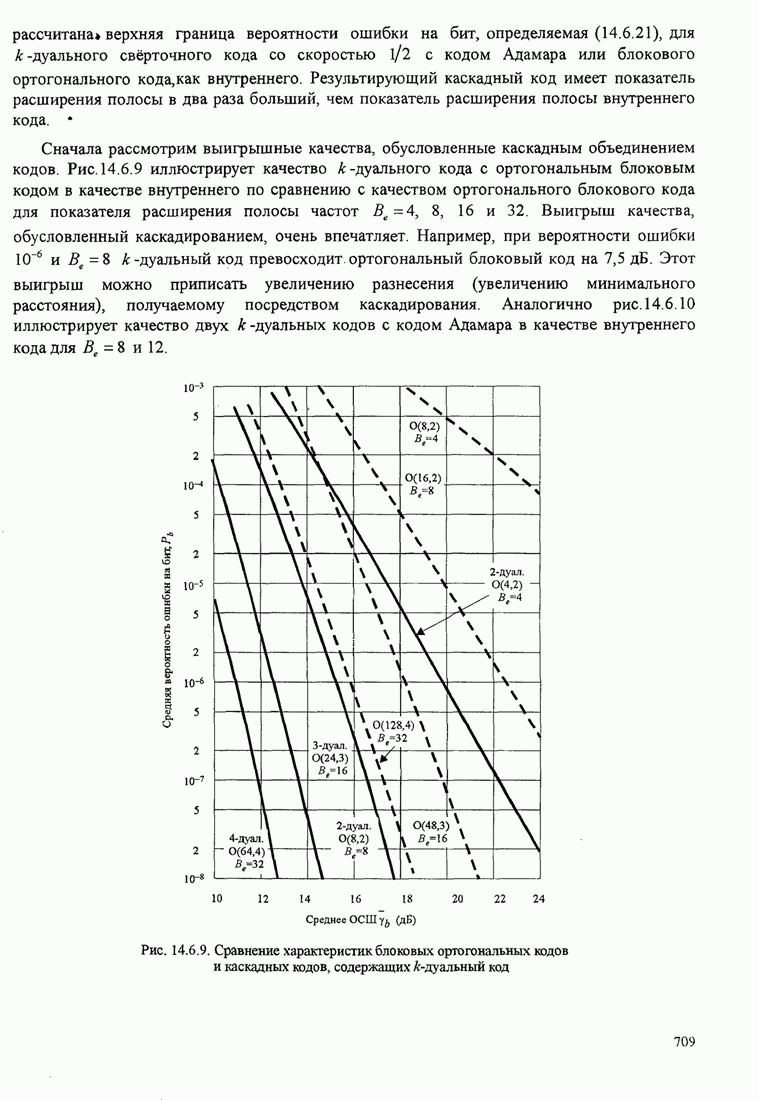
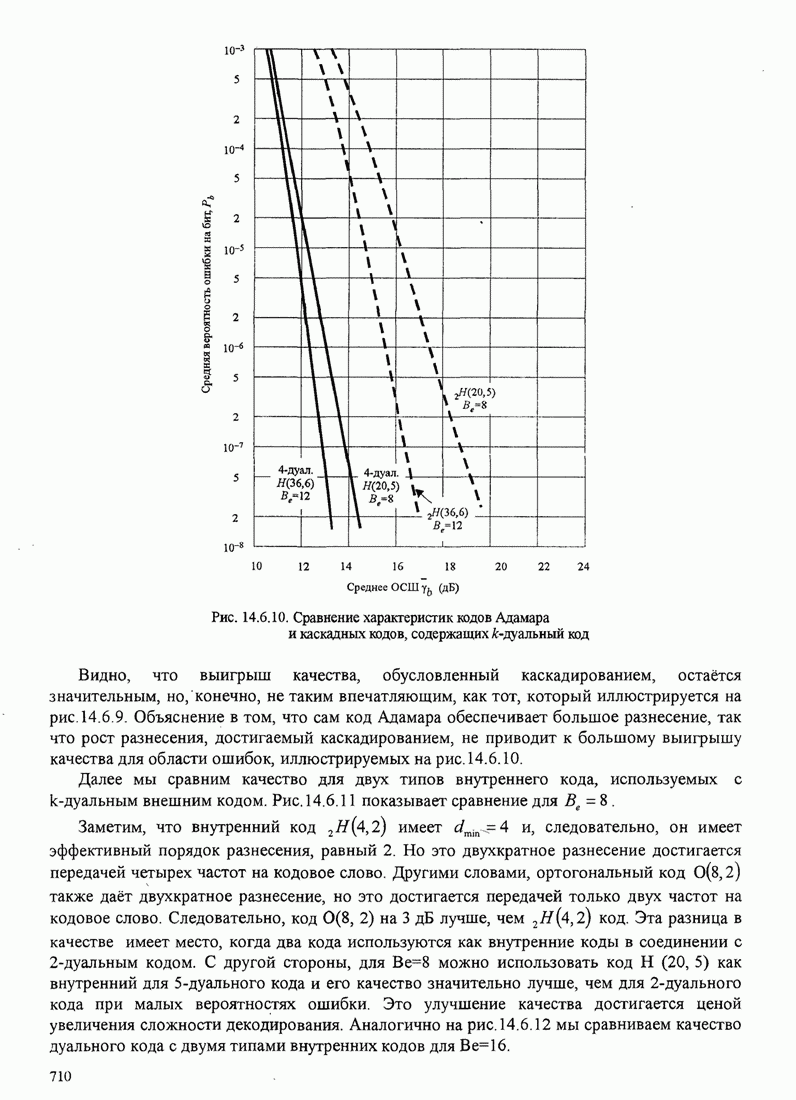
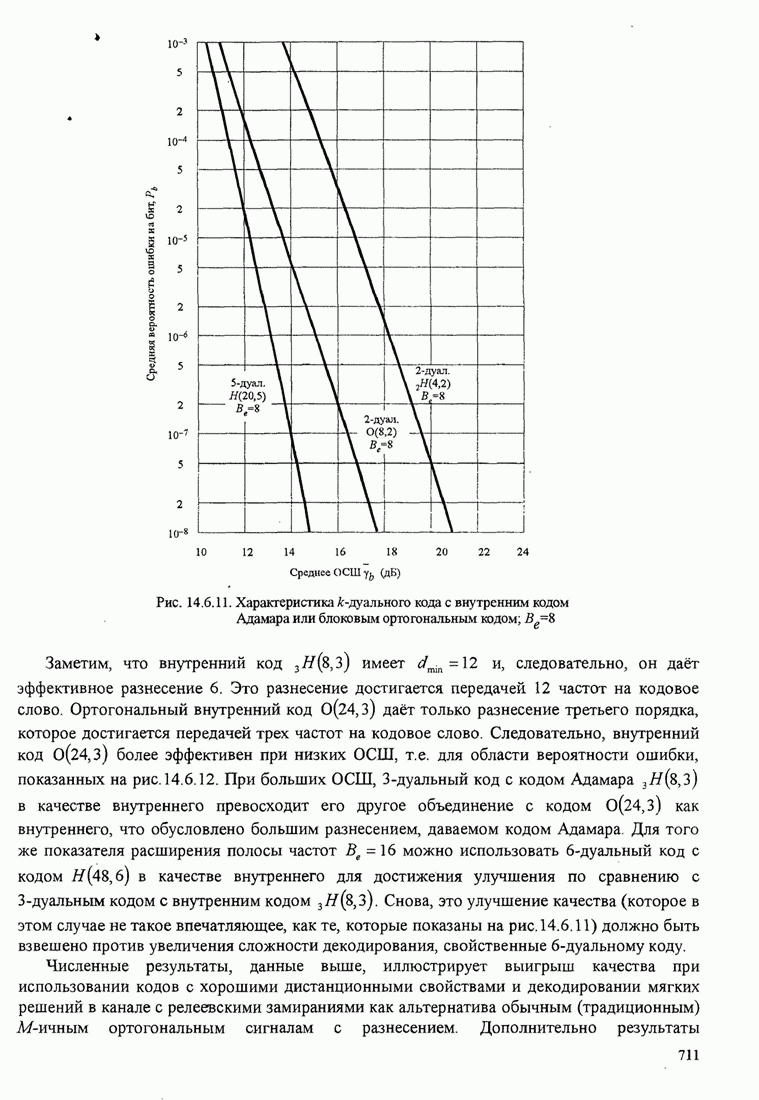
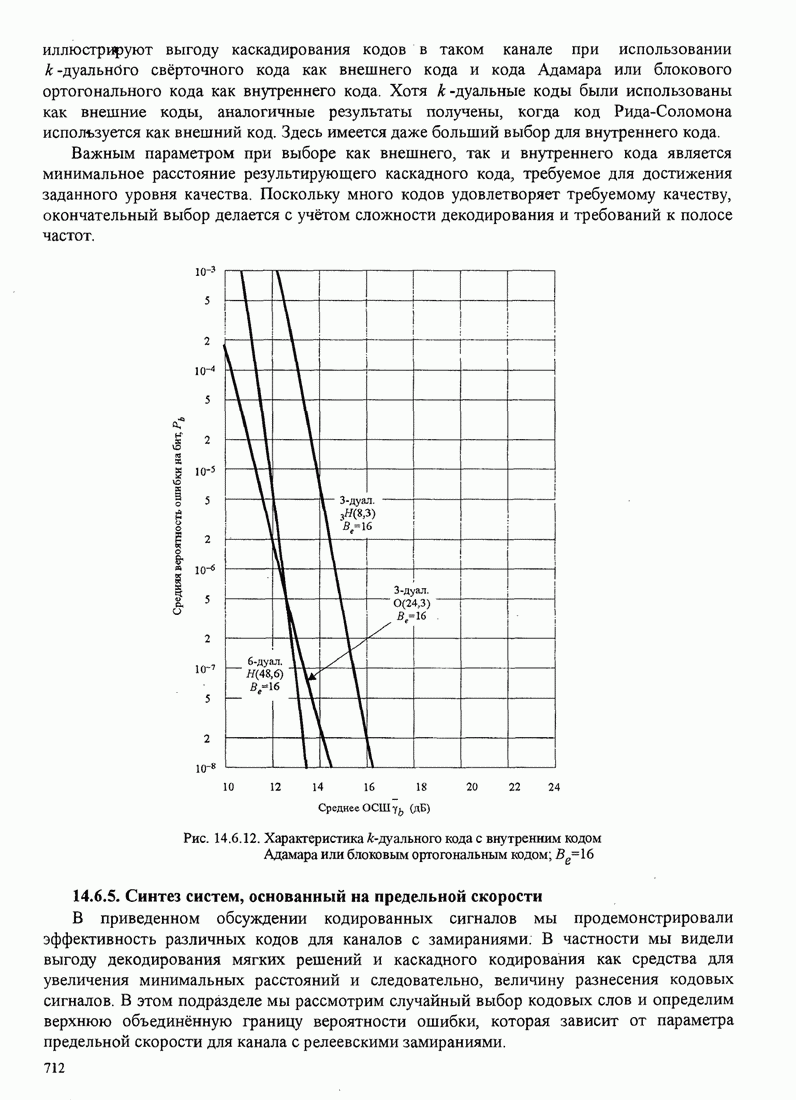
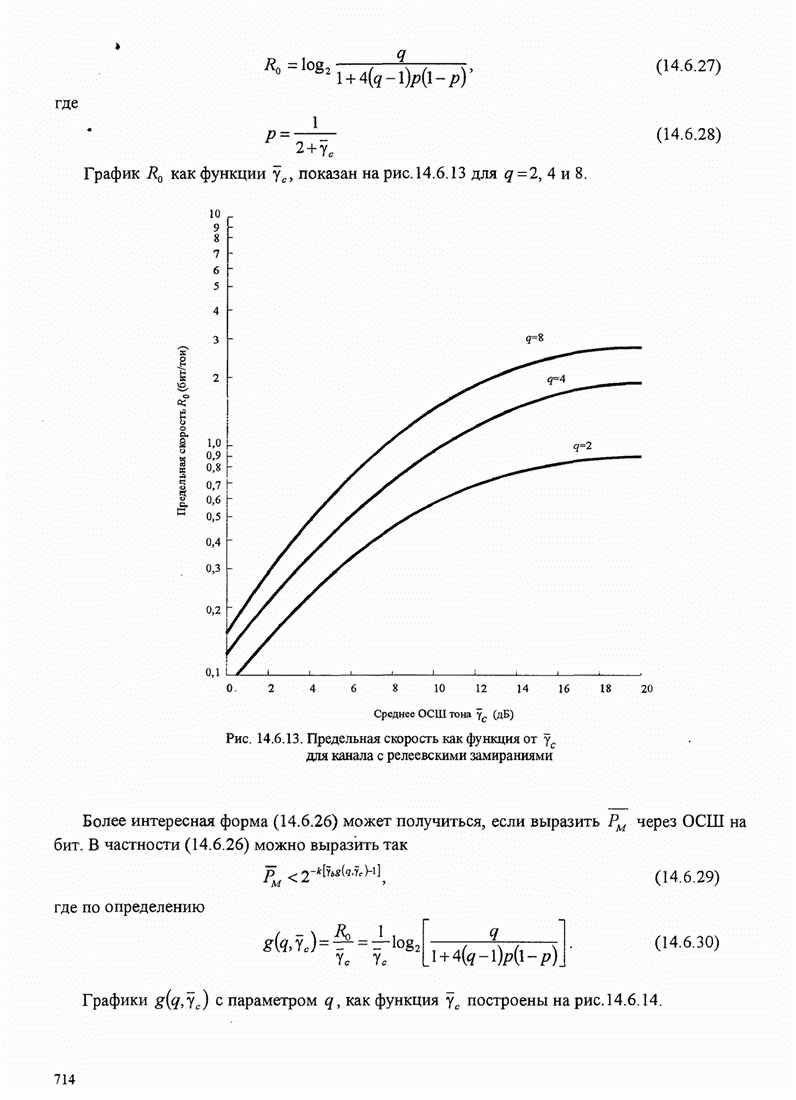
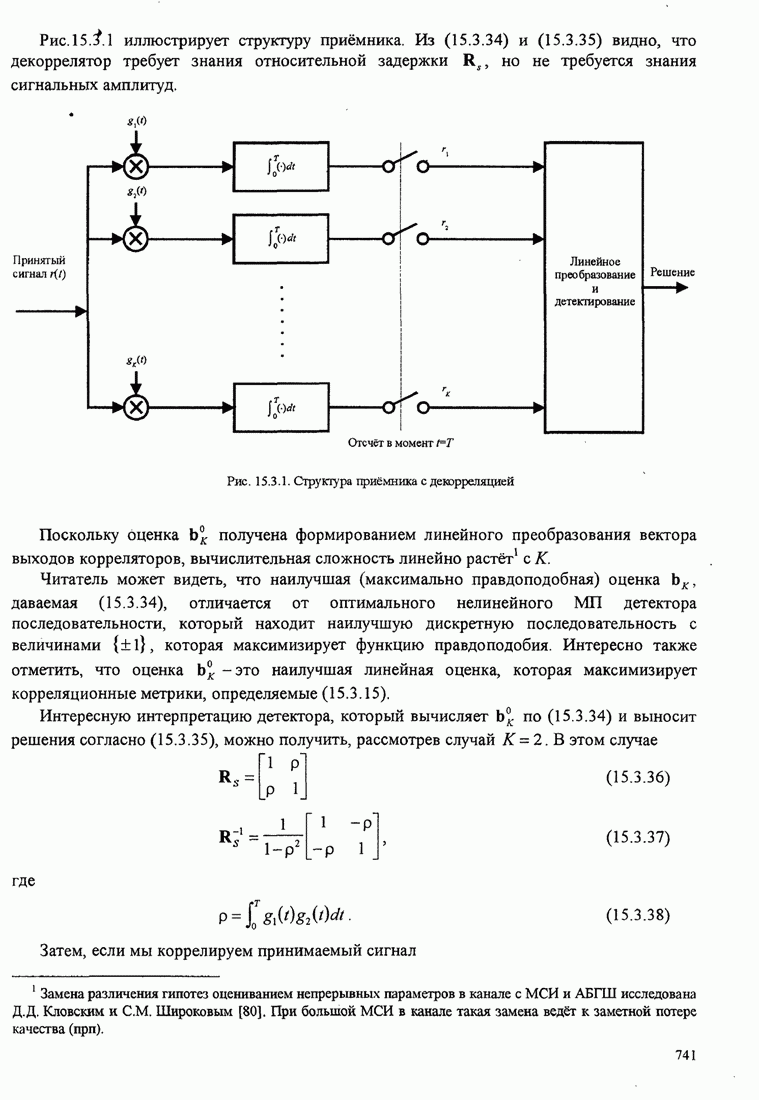
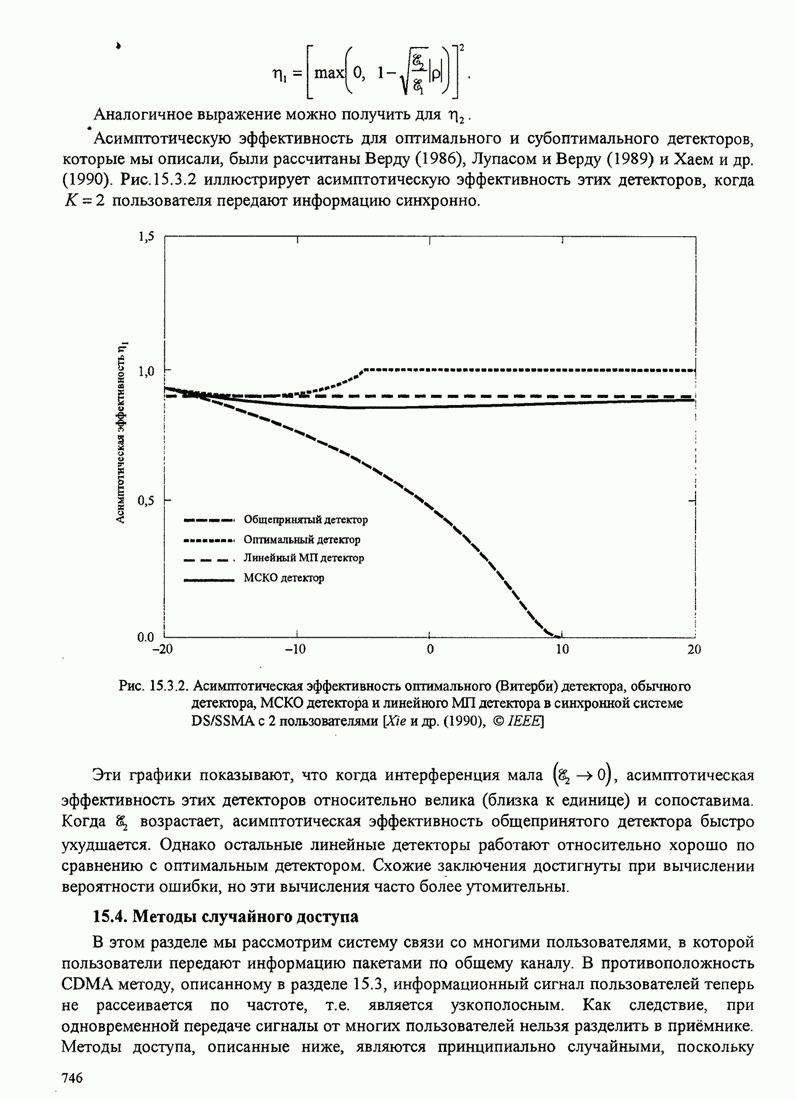
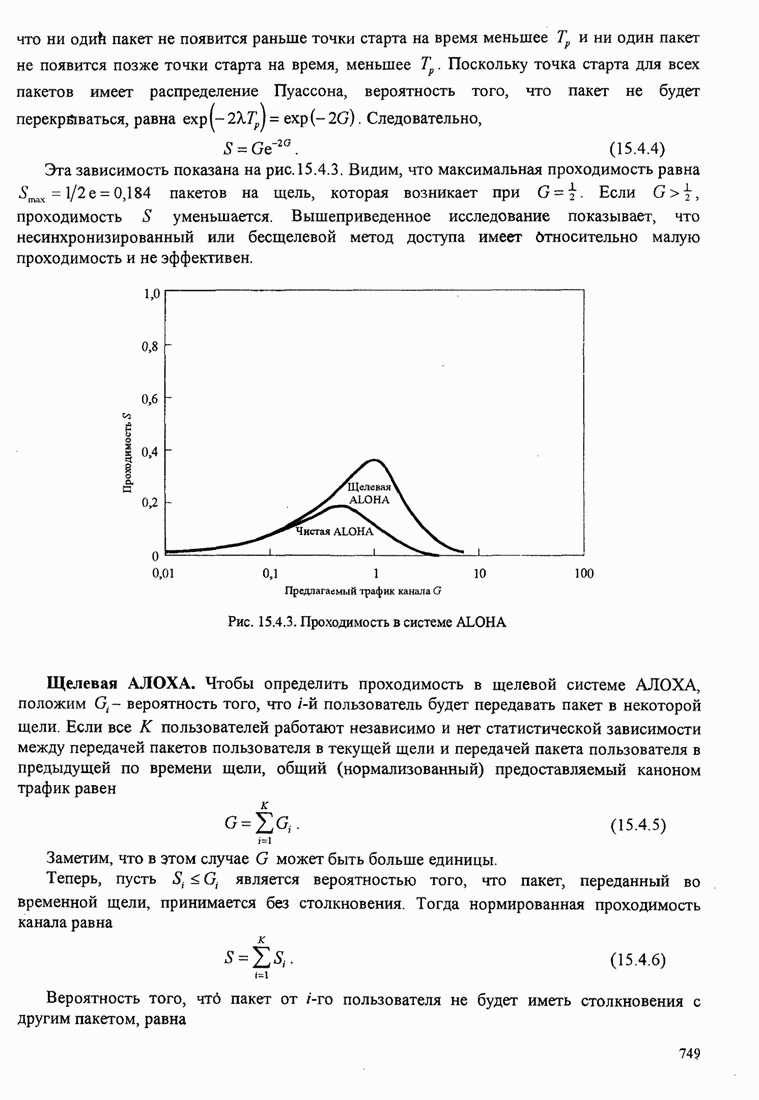
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
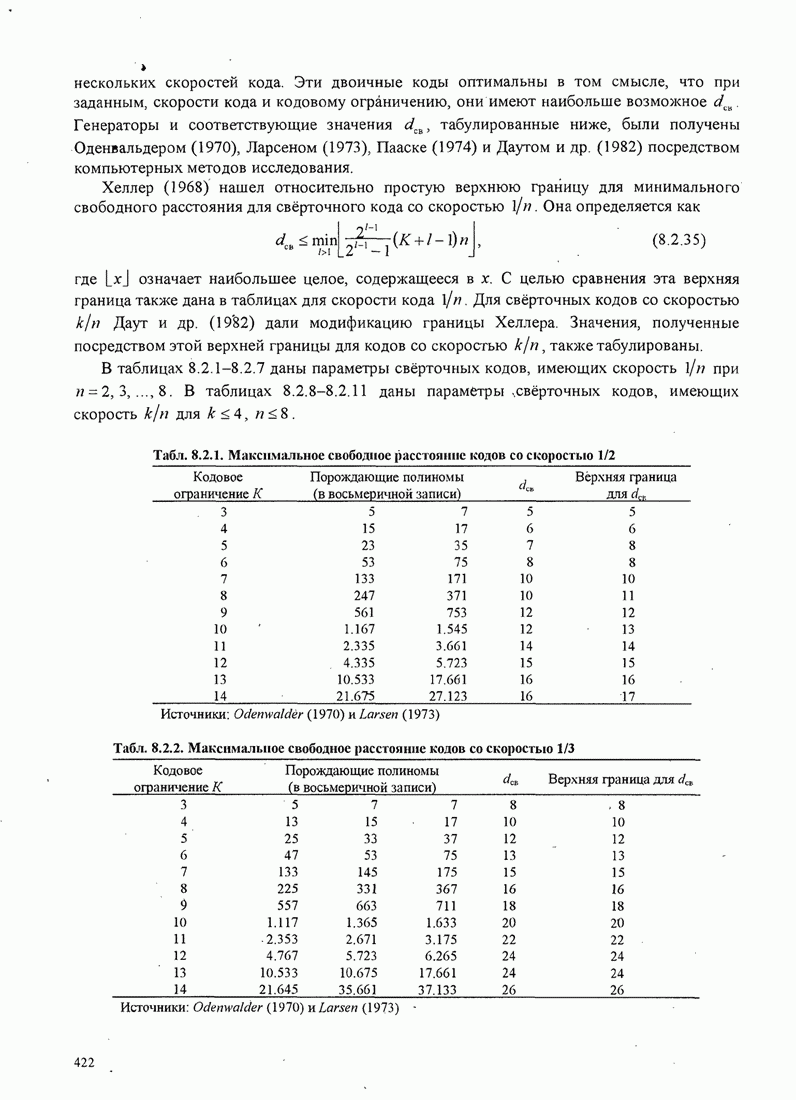
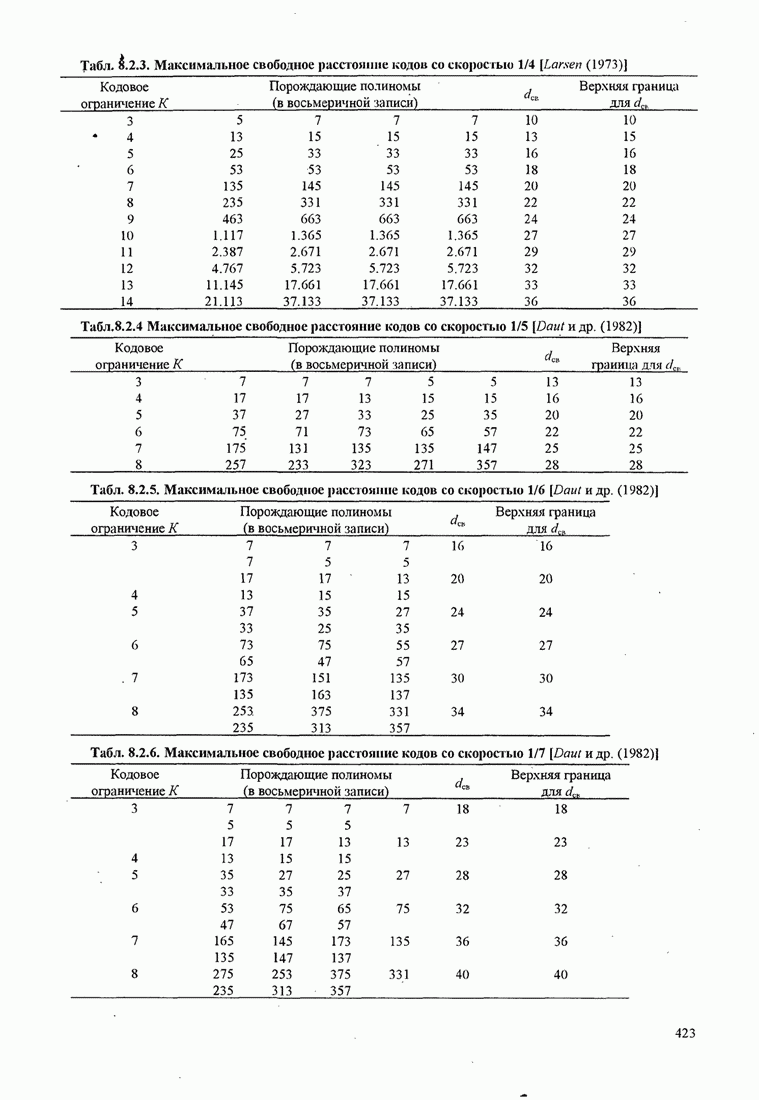
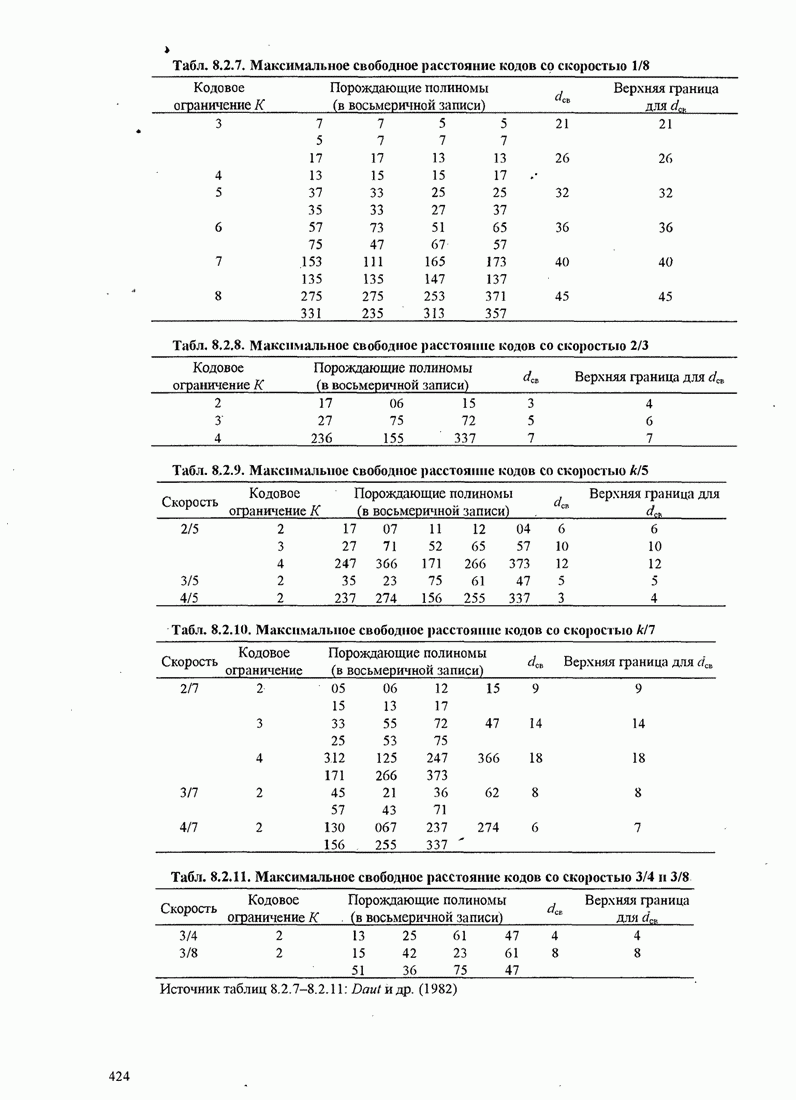
ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
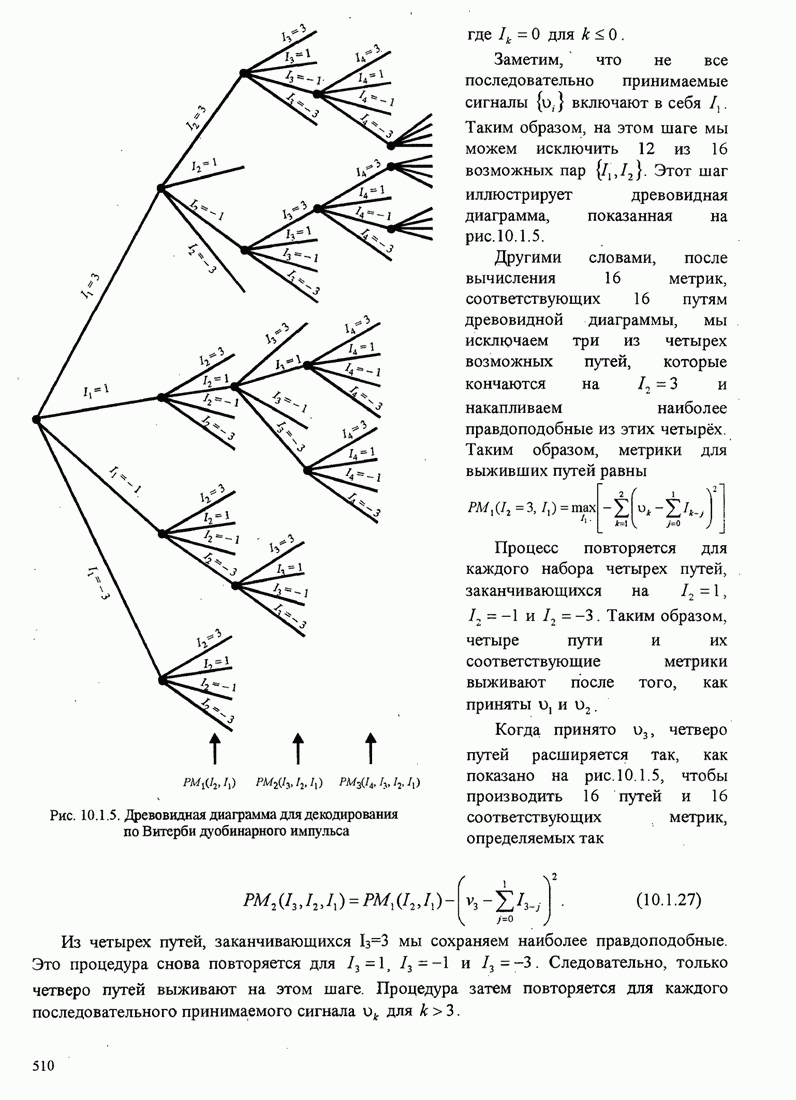
В этом приложении мы определим
вероятности ошибки для двух- и четырехфазовых сигналов при передачи по
неизменному во времени каналу с аддиивным белым гауссовским шумом при ![]() -кратном разнесении
и для
-кратном разнесении
и для ![]() -фазовых сигналов по каналу с
релеевскими замираниями и адаптивным белым гауссовским шумом с
-фазовых сигналов по каналу с
релеевскими замираниями и адаптивным белым гауссовским шумом с ![]() -кратным
разнесением. Оба канала искажают передаваемые сигналы путем введения
аддитивного белого гауссовского шума и случайного мультипликативного ослабления
и фазового сдвига в сигнале. Обработка сигнала в приемнике состоит из
нахождения взаимной корреляции сигнала в смеси с шумом, принимаемого в каждой
ветви разнесения, с опорным сигналом, получаемым или от предыдущего принятого
информационного сигнала, или от пилот-сигнала, и суммирования выходов всех
-кратным
разнесением. Оба канала искажают передаваемые сигналы путем введения
аддитивного белого гауссовского шума и случайного мультипликативного ослабления
и фазового сдвига в сигнале. Обработка сигнала в приемнике состоит из
нахождения взаимной корреляции сигнала в смеси с шумом, принимаемого в каждой
ветви разнесения, с опорным сигналом, получаемым или от предыдущего принятого
информационного сигнала, или от пилот-сигнала, и суммирования выходов всех ![]() каналов разнесения
для формирования величины для решения.
каналов разнесения
для формирования величины для решения.
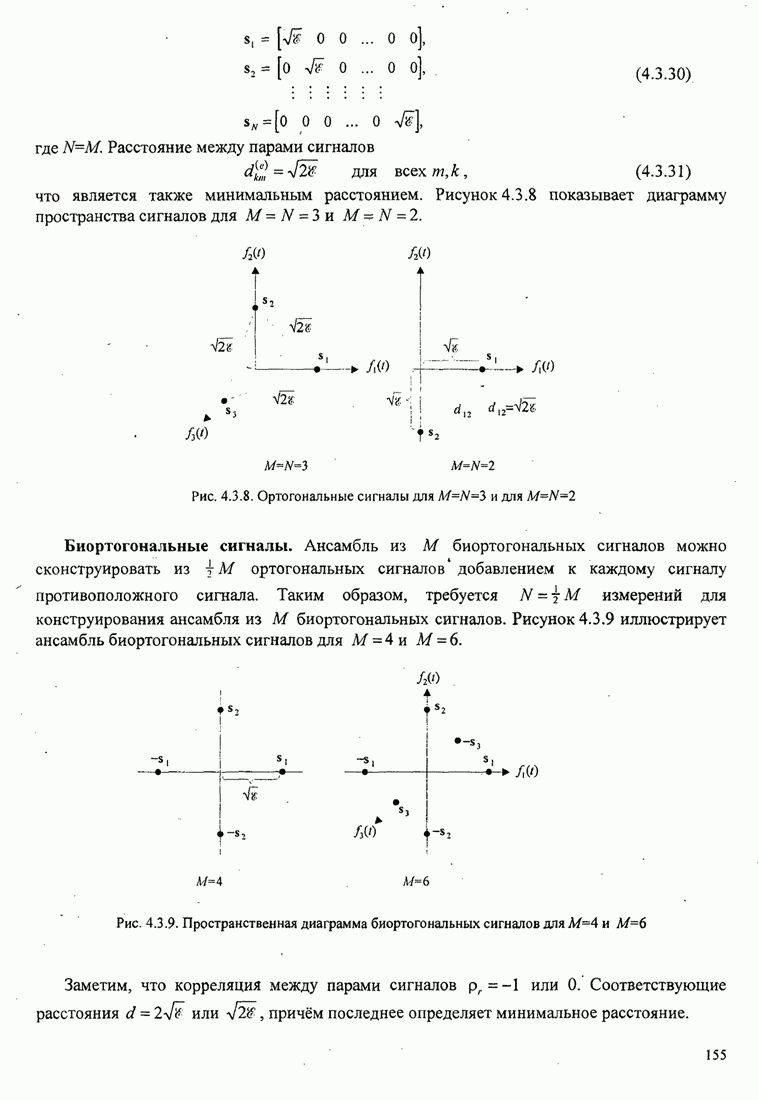
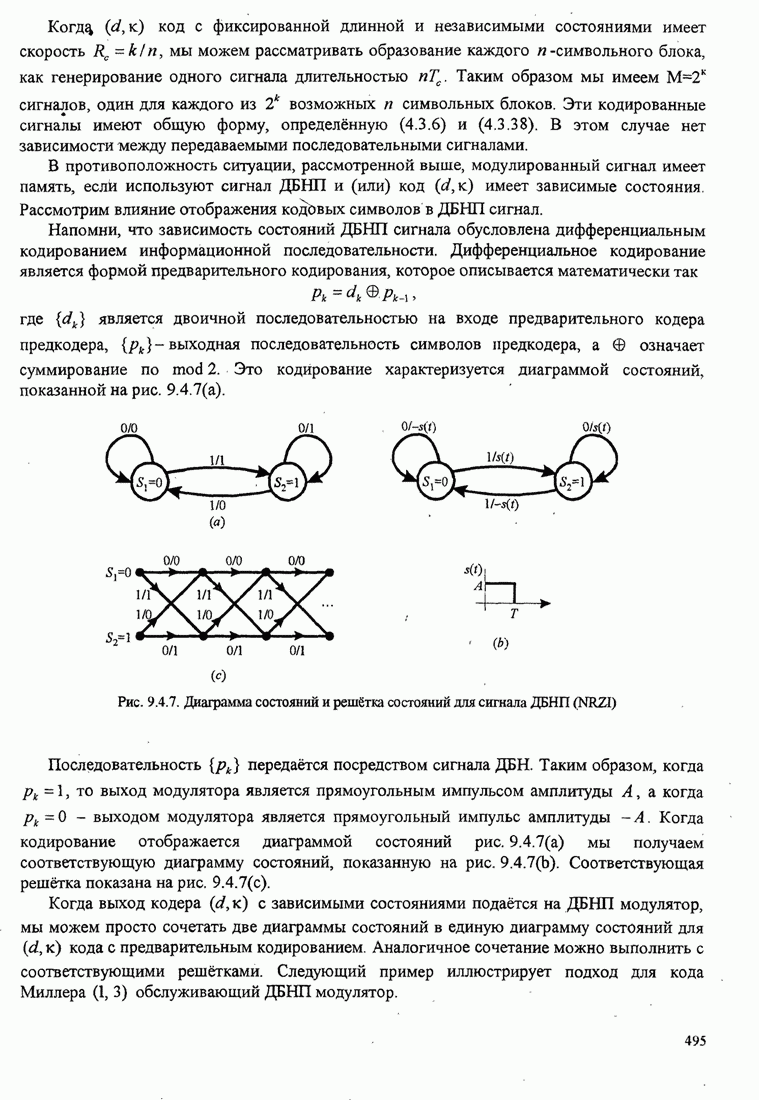
С.1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ СИСТЕМЫ СВЯЗИ С М-ФАЗОВЫМ СИГНАЛОМ
В общем случае ![]() -фазовой модуляции
передаваемый сигнал имеет вид:
-фазовой модуляции
передаваемый сигнал имеет вид:
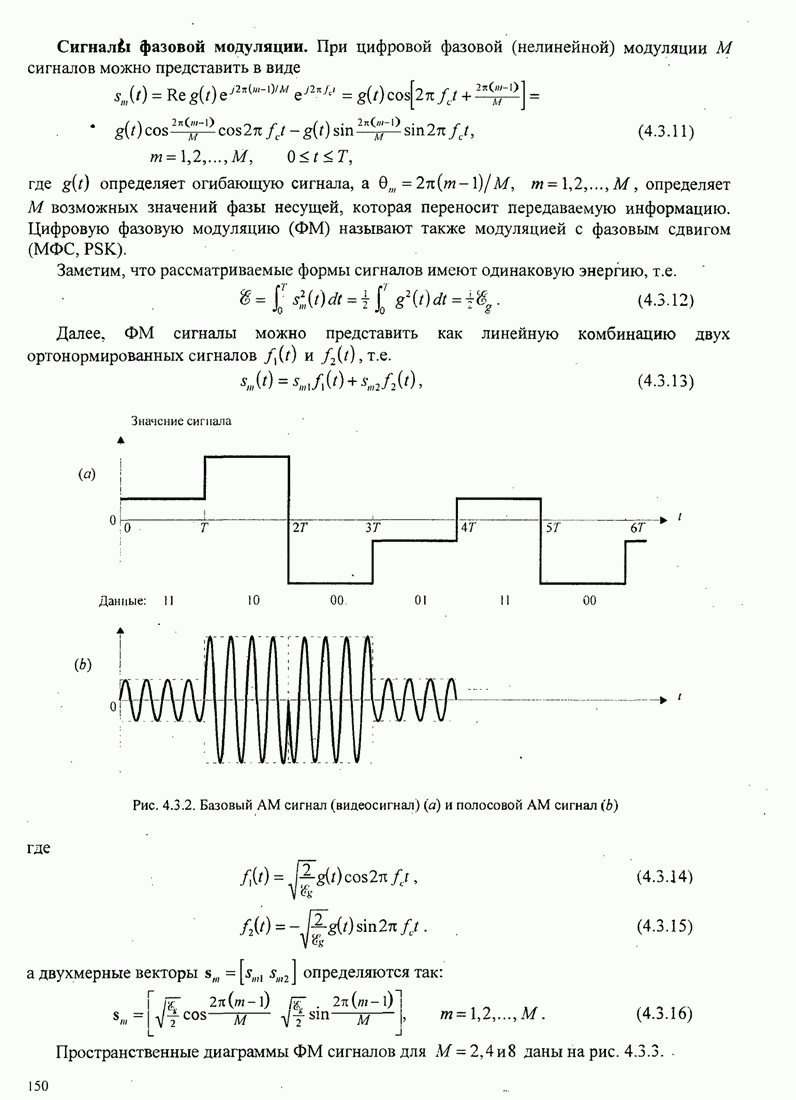
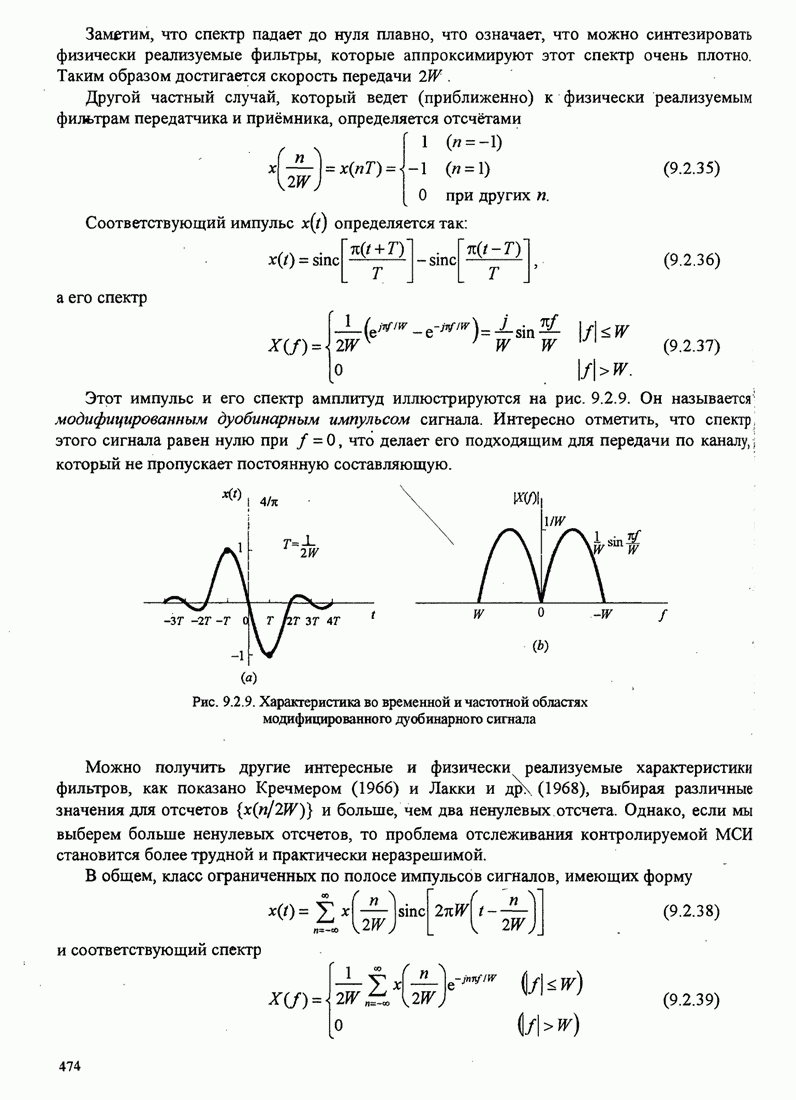
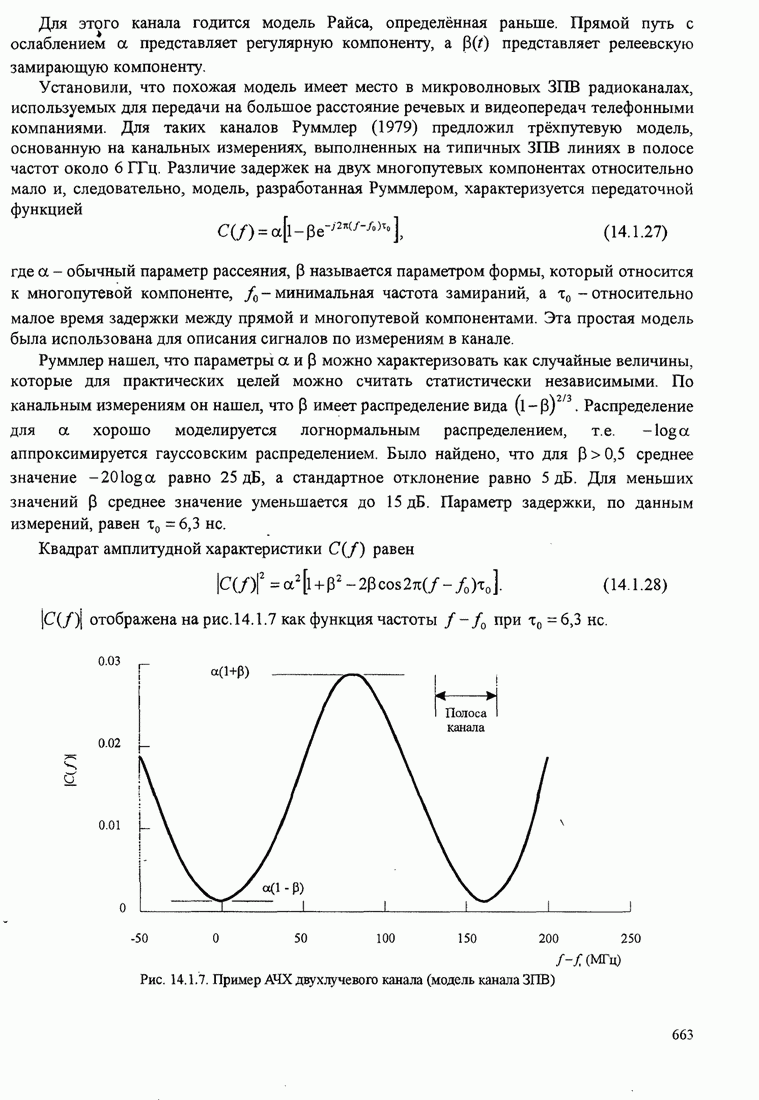
![]()
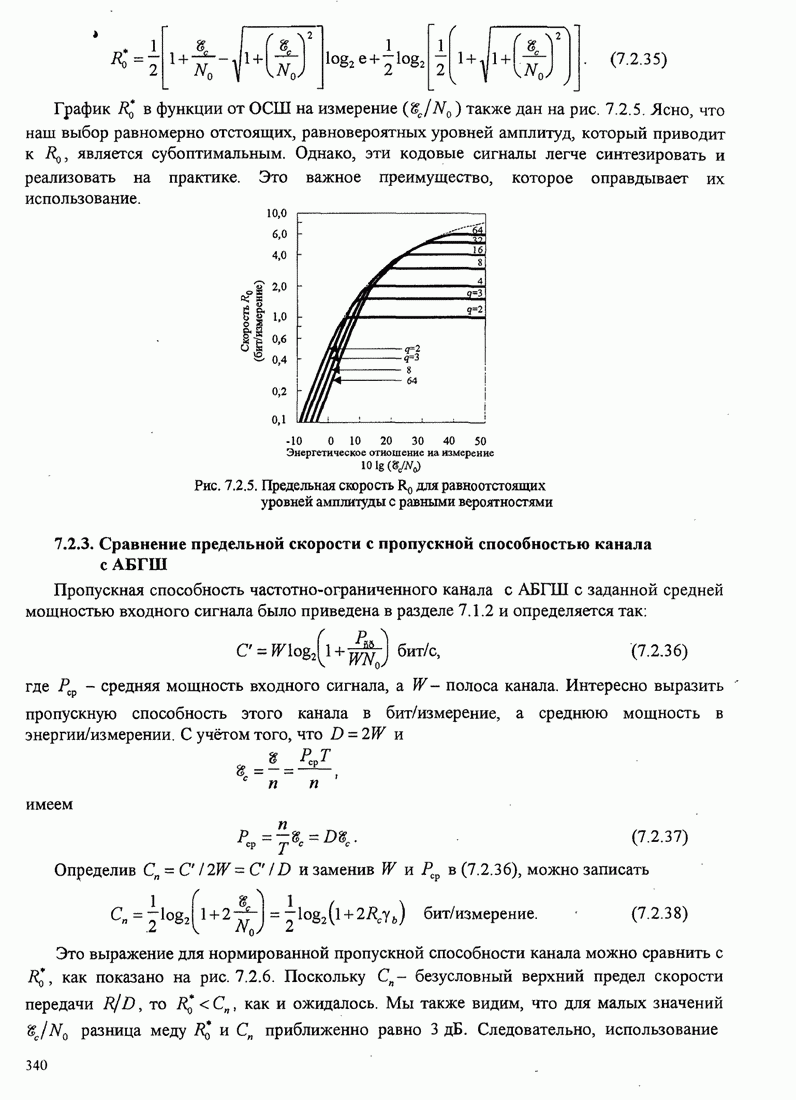
где
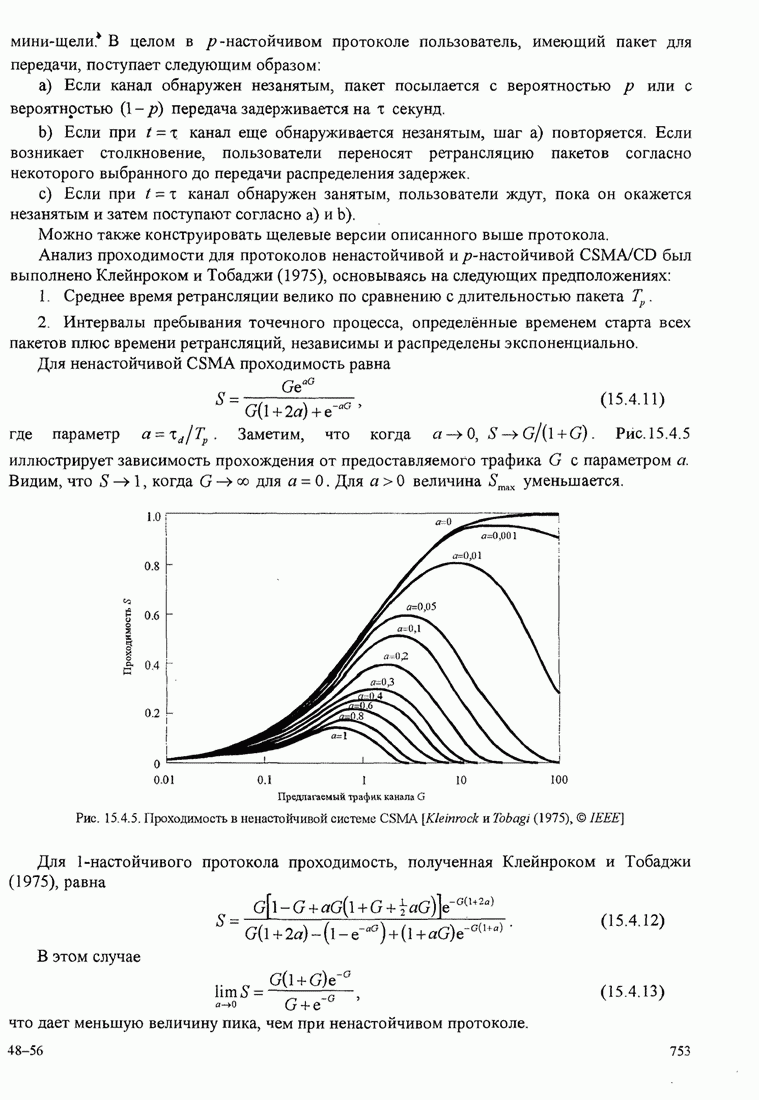
![]() (С.1)
(С.1)
а ![]() - длительность сигнального интервала.
- длительность сигнального интервала.
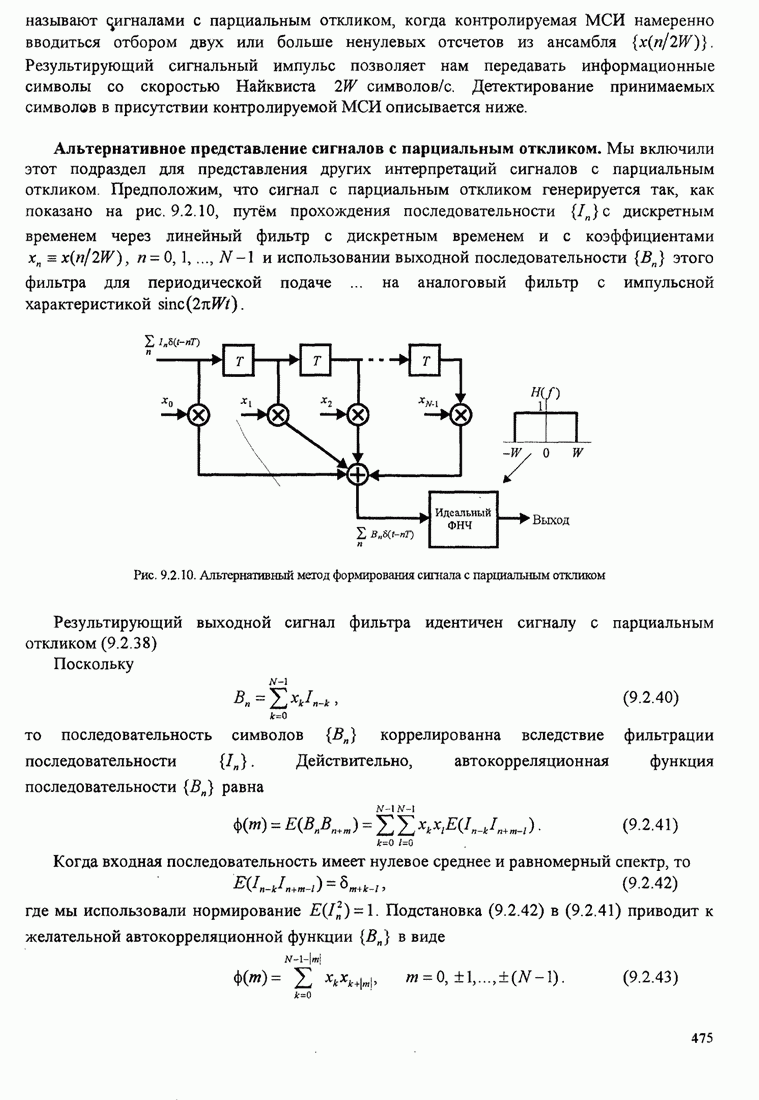
Рассмотрим случай, когда на
протяжении сигнального интервала передаётся один из ![]() сигналов по
сигналов по ![]() каналам.
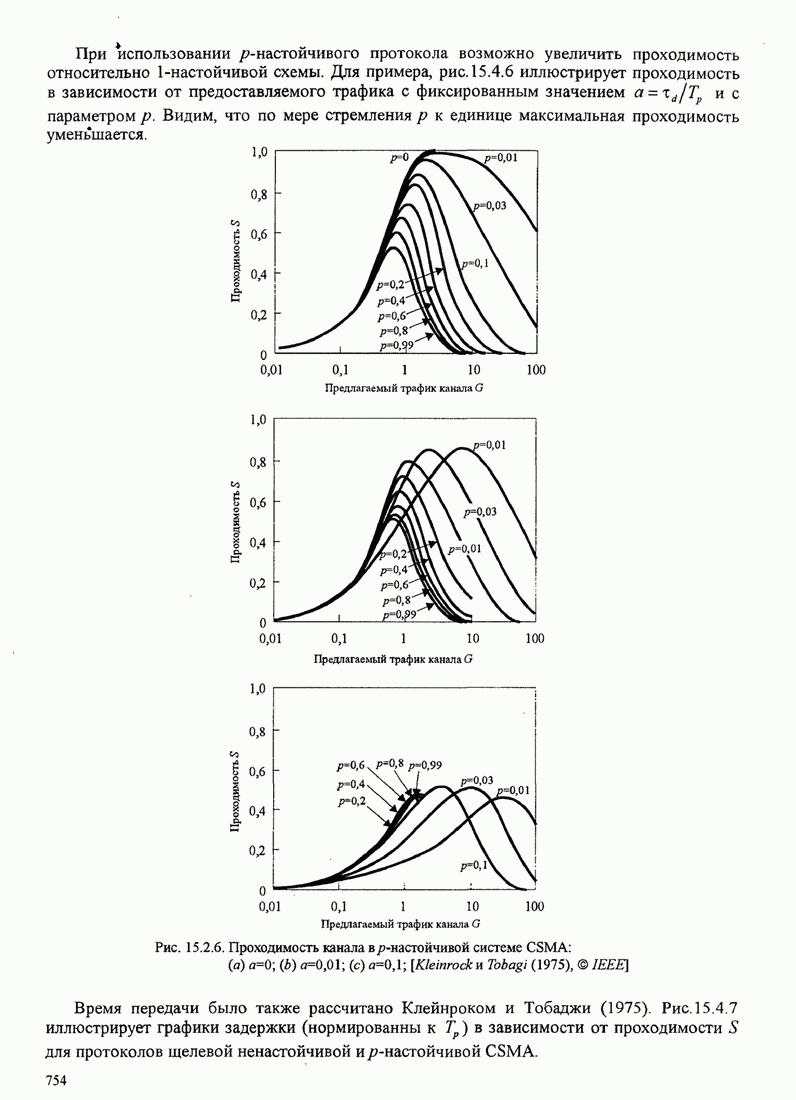
Предположим, что в каждом из каналов передаваемый сигнал искажается введением
мультипликативного ослабления и фазового сдвига, представленных комплексным
множителем
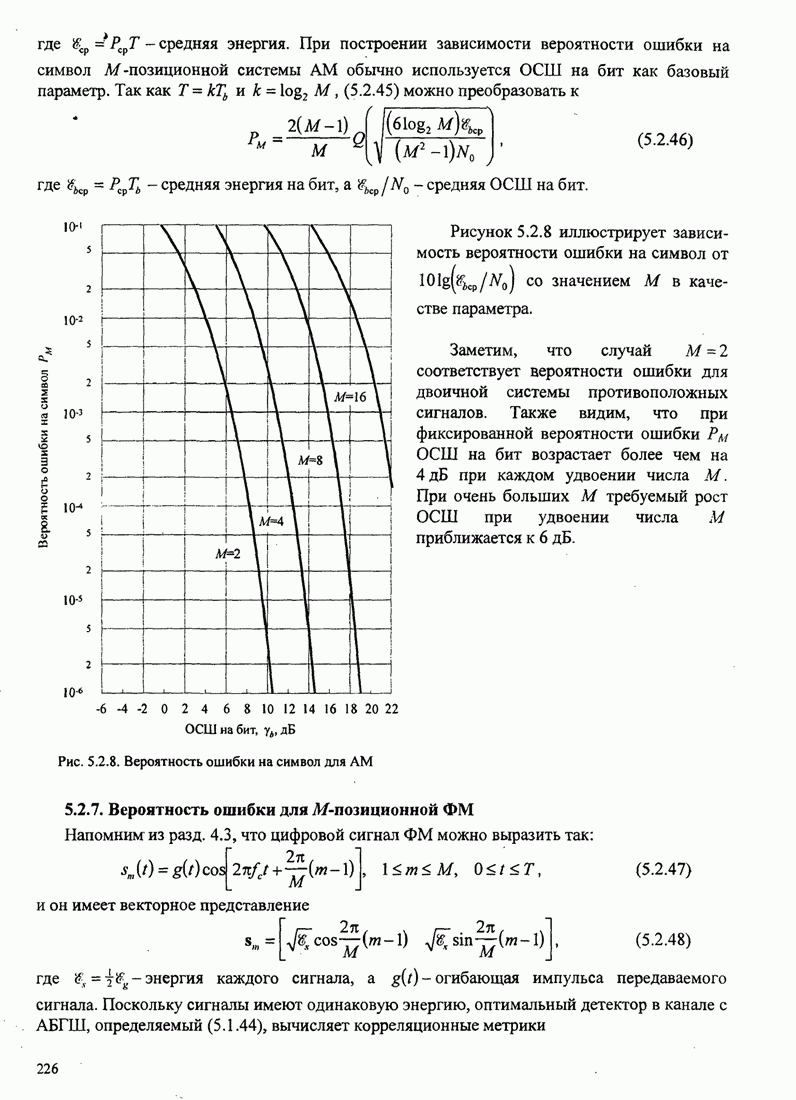
каналам.
Предположим, что в каждом из каналов передаваемый сигнал искажается введением
мультипликативного ослабления и фазового сдвига, представленных комплексным
множителем ![]() и
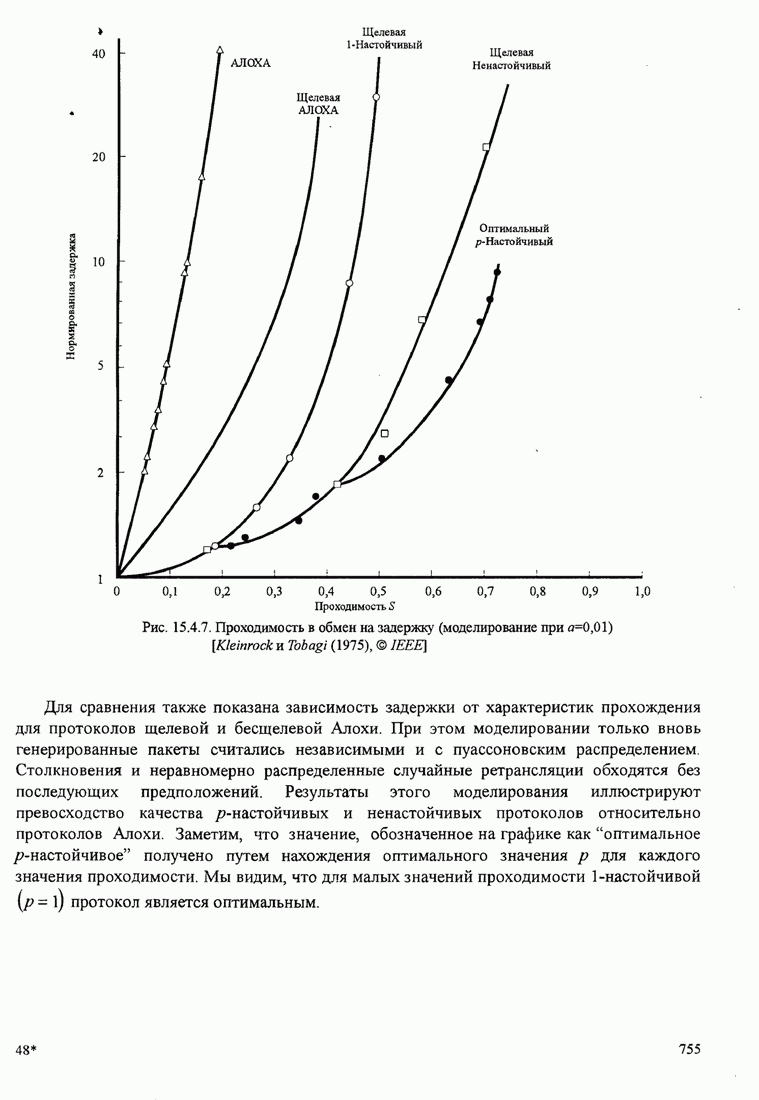
аддитивным шумом
и
аддитивным шумом ![]() . Так, если передаваемый сигнал
. Так, если передаваемый сигнал ![]() , то принимаемый сигнал в
, то принимаемый сигнал в ![]() -м канале
-м канале
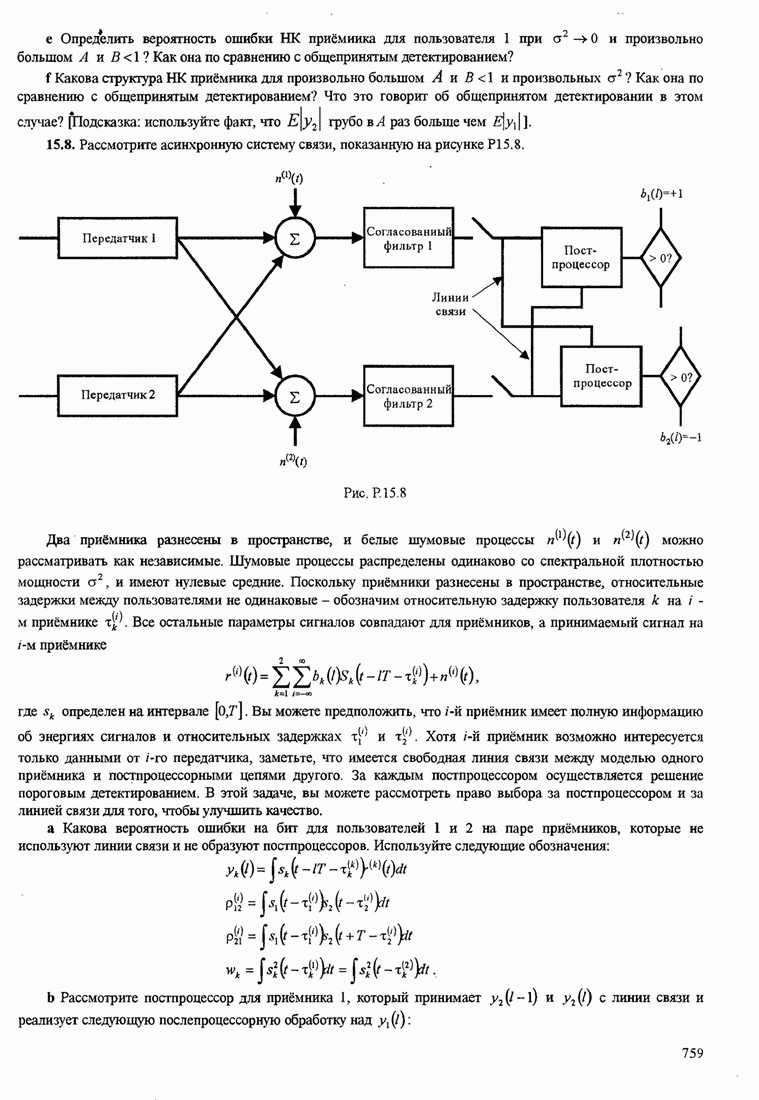
![]() (С.2)
(С.2)
Шум ![]() считается реализацией стационарного
белого гауссовского случайного процесса с нулевым средним и автокорреляционной
функцией
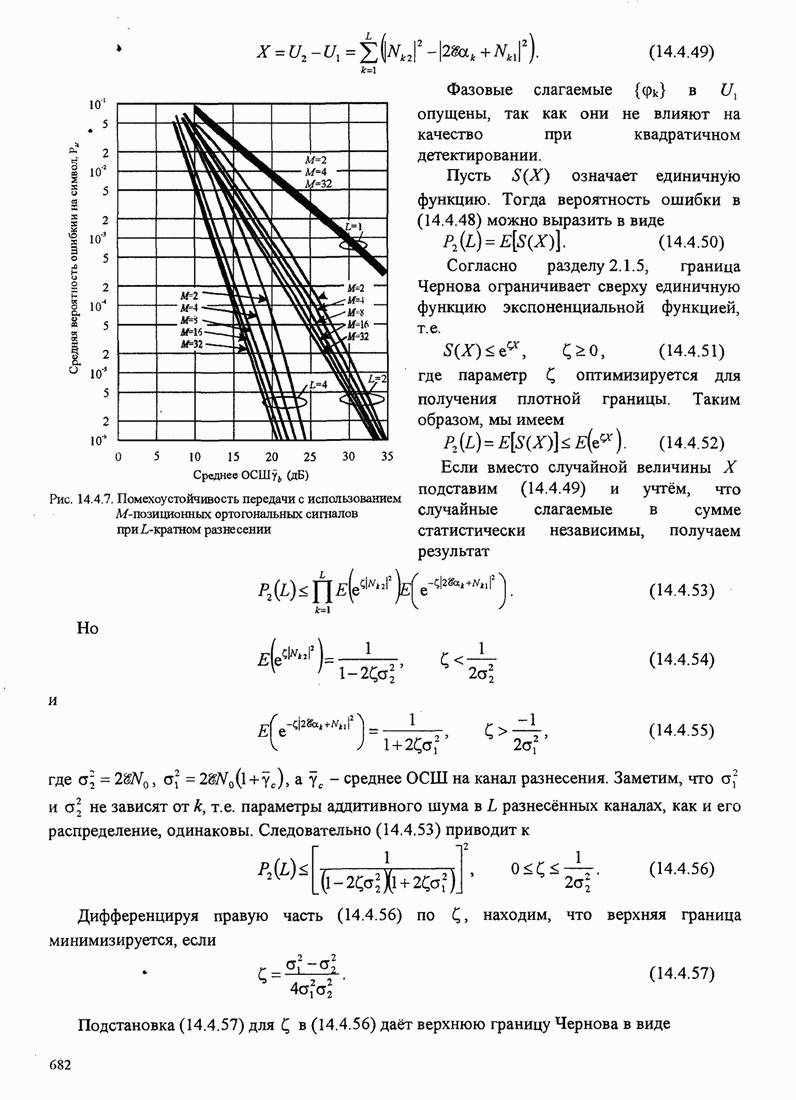
считается реализацией стационарного
белого гауссовского случайного процесса с нулевым средним и автокорреляционной
функцией ![]() ,
где
,
где ![]() - спектральная
плотность мощности шума.
- спектральная
плотность мощности шума.
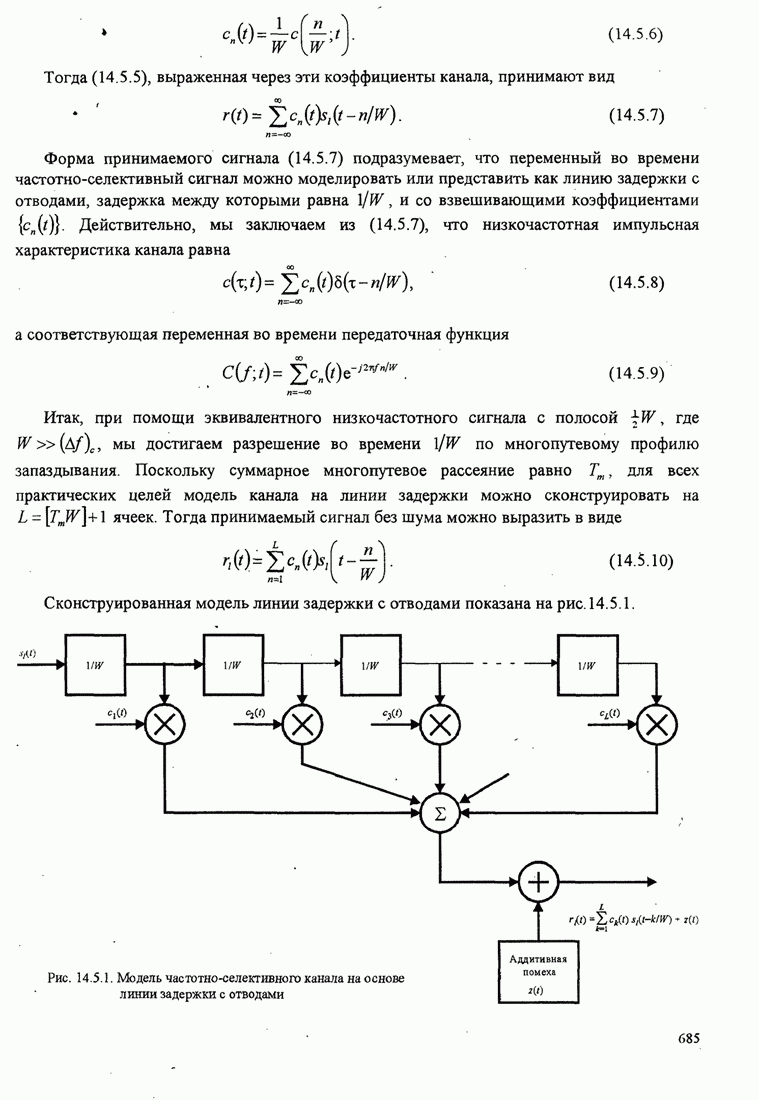
В демодуляторе ![]() пропускается через фильтр,
импульсная характеристика которого согласована с сигналом
пропускается через фильтр,
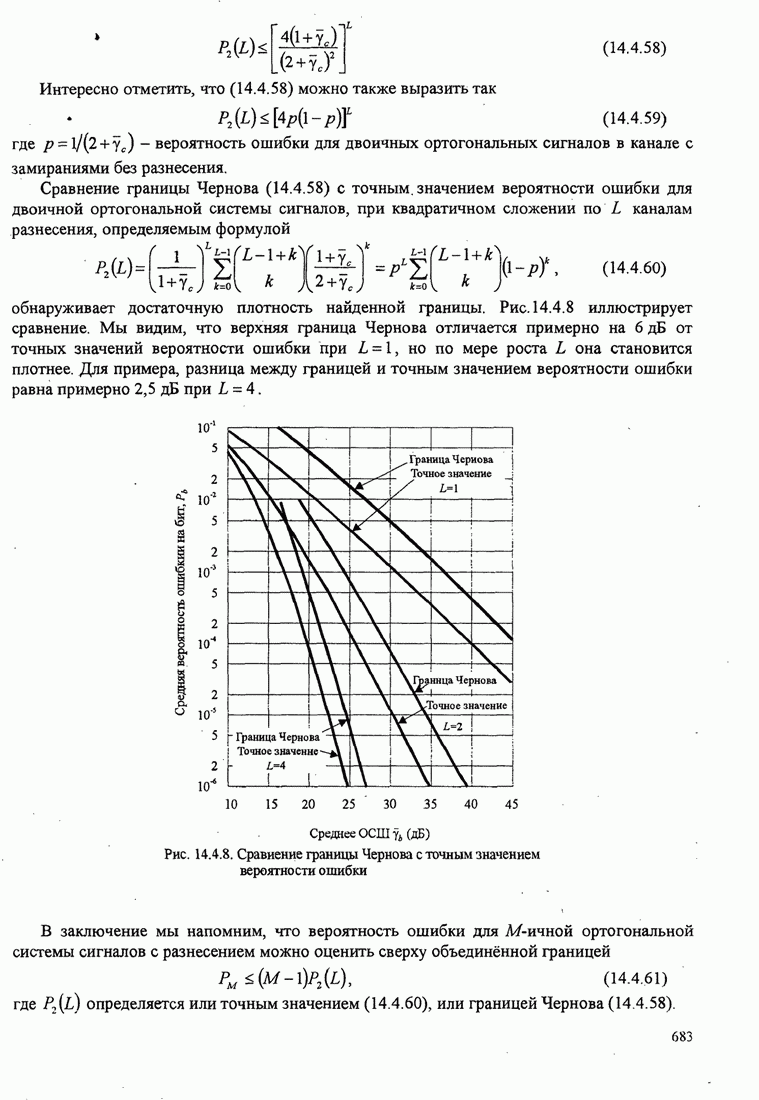
импульсная характеристика которого согласована с сигналом ![]() . Выход этого фильтра в момент стробирования
. Выход этого фильтра в момент стробирования ![]() обозначаем так;
обозначаем так;
![]() (СЗ)
(СЗ)
где ![]() - энергия переданного сигнала, a
- энергия переданного сигнала, a ![]() - отсчёт шума на выходе в
- отсчёт шума на выходе в ![]() -го фильтра. Для
того, чтобы демодулятор мог решить, какая из
-го фильтра. Для
того, чтобы демодулятор мог решить, какая из ![]() фаз передана по каналу на сигнальном
интервале
фаз передана по каналу на сигнальном
интервале ![]() ,
следует попытаться убрать фазовый сдвиг, введённый в каждом канале. На практике
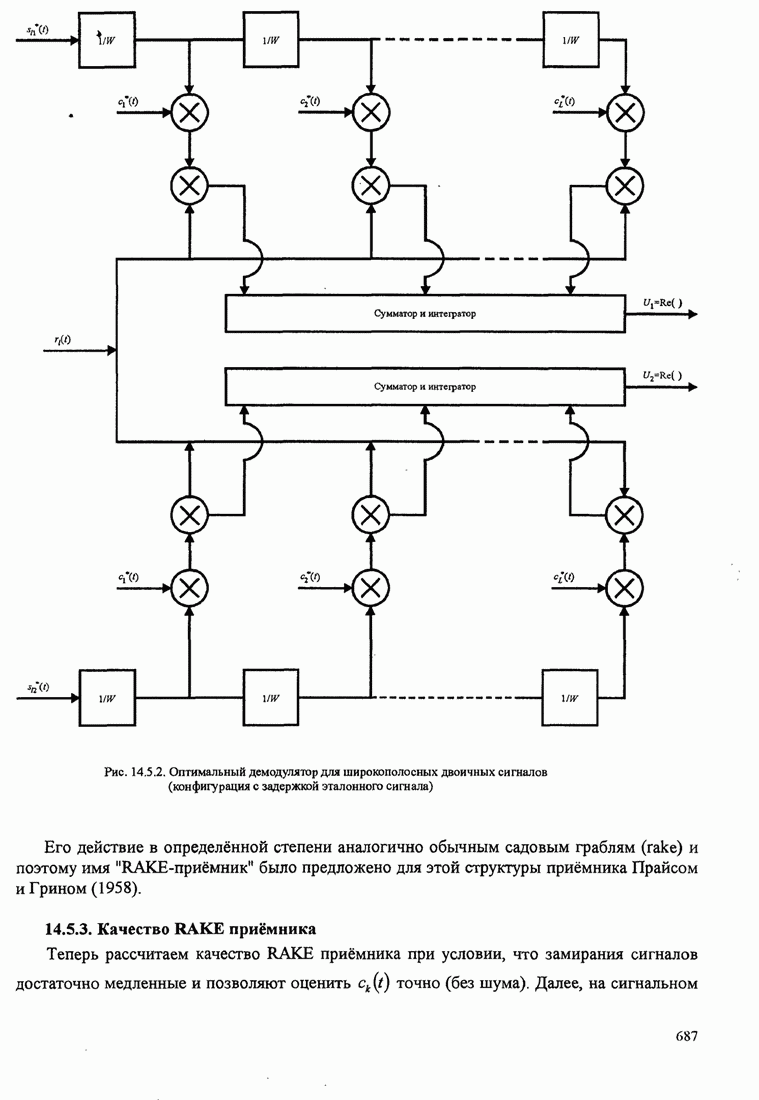
это осуществляется путем умножения выхода фильтра
,
следует попытаться убрать фазовый сдвиг, введённый в каждом канале. На практике
это осуществляется путем умножения выхода фильтра ![]() на комплексно сопряженную величину
оценки
на комплексно сопряженную величину
оценки ![]() канального
ослабления и фазового сдвига. Результатом является взвешенный и сдвинутый по
фазе выходной отсчет фильтра в
канального
ослабления и фазового сдвига. Результатом является взвешенный и сдвинутый по
фазе выходной отсчет фильтра в ![]() -м канале, который затем суммируется
со взвешенным и сдвинутым
по фазе выходными отсчетами остальных
-м канале, который затем суммируется
со взвешенным и сдвинутым
по фазе выходными отсчетами остальных ![]() канальных фильтров.
канальных фильтров.
Считается, что оценка ![]() ослабления и фазового сдвига в k-м канале определяется или от
передачи пилот-сигнала или путем снятия модуляции в информационном сигнале,
принятом на предыдущем сигнальном интервале. Как пример формирователя,
предположим, что пилот-сигнал, обозначенный
ослабления и фазового сдвига в k-м канале определяется или от
передачи пилот-сигнала или путем снятия модуляции в информационном сигнале,
принятом на предыдущем сигнальном интервале. Как пример формирователя,
предположим, что пилот-сигнал, обозначенный ![]() ,
, ![]() , передаётся по
, передаётся по ![]() -му каналу с целью измерения
ослабления и фазового сдвига в канале. Принимаемый сигнал равен
-му каналу с целью измерения
ослабления и фазового сдвига в канале. Принимаемый сигнал равен
![]() ,
,
где ![]() - отсчётная функция стационарного белого гауссовского
случайного процесса с нулевым средним и автокорреляционной функцией
- отсчётная функция стационарного белого гауссовского
случайного процесса с нулевым средним и автокорреляционной функцией ![]() . Этот сигнал плюс
шум пропускается через фильтр, согласованный с
. Этот сигнал плюс
шум пропускается через фильтр, согласованный с ![]() . Отсчёт выхода фильтра в момент
. Отсчёт выхода фильтра в момент ![]() содержит случайную переменную
содержит случайную переменную ![]() , где
, где ![]() - энергия пилот-сигнала,
которая считается одинаковой для всех каналов, a
- энергия пилот-сигнала,
которая считается одинаковой для всех каналов, a ![]() - отсчет аддитивного шума. Оценка
- отсчет аддитивного шума. Оценка ![]() получается путем
соответствующей нормировки
получается путем
соответствующей нормировки ![]() , то есть
, то есть ![]() .
.
С другой стороны, оценку ![]() можно получить из
информационного сигнала следующим образом. Если знать информационные
компоненты, содержащиеся в выходе согласованного фильтра, то оценку
можно получить из
информационного сигнала следующим образом. Если знать информационные
компоненты, содержащиеся в выходе согласованного фильтра, то оценку ![]() можно получить
соответствующей нормировкой этого выхода. Для примера, информационная
компонента выхода фильтра в (С.З) равна
можно получить
соответствующей нормировкой этого выхода. Для примера, информационная
компонента выхода фильтра в (С.З) равна ![]() и, следовательно, оценка
и, следовательно, оценка
![]()
где ![]() , а ФПВ
, а ФПВ ![]() аналогична ФПВ
аналогична ФПВ ![]() . Оценка, полученная от
информационного сигнала таким путём, иногда называется ясновидящей оценкой.
Хотя физически реализуемый приемник не может обладать таким «ясновидением», он
может аппроксимировать эту оценку путем использования временной задержки
сигнального интервала и получить путём обратной связи оценку переданной фазы на
предшествующем временном интервале.
. Оценка, полученная от
информационного сигнала таким путём, иногда называется ясновидящей оценкой.
Хотя физически реализуемый приемник не может обладать таким «ясновидением», он
может аппроксимировать эту оценку путем использования временной задержки
сигнального интервала и получить путём обратной связи оценку переданной фазы на
предшествующем временном интервале.
Получена ли оценка ![]() от пилот-сигнала
или от информационного сигнала, оценку можно улучшить путем расширения
временного интервала в ее формировании, чтобы включить несколько предыдущих
сигнальных интервалов способом, описанном Прайсом (1962а, b). Результатом расширения интервала
измерения является увеличение отношения сигнал-щум в оценке
от пилот-сигнала
или от информационного сигнала, оценку можно улучшить путем расширения
временного интервала в ее формировании, чтобы включить несколько предыдущих
сигнальных интервалов способом, описанном Прайсом (1962а, b). Результатом расширения интервала
измерения является увеличение отношения сигнал-щум в оценке ![]() . В общем случае, если
интервалы оценивания не ограничены, нормированная оценка по пилот-сигналу
. В общем случае, если
интервалы оценивания не ограничены, нормированная оценка по пилот-сигналу
![]() (C.4)
(C.4)
где ![]() - взвешивающее
коэффициенты для подоценок
- взвешивающее
коэффициенты для подоценок ![]() , полученных на
, полученных на ![]() -м предшествующем
сигнальном интервале, a
-м предшествующем
сигнальном интервале, a ![]() - отсчёт аддитивного гауссовского шума на выходе фильтра,
согласованного с
- отсчёт аддитивного гауссовского шума на выходе фильтра,
согласованного с ![]() на
на ![]() -м предшествующем сигнальном
интервале. Аналогично «ясновидящая» оценка, полученная из информационного
сигнала путем снятия модуляции, при неограниченном интервале обработки, равна
-м предшествующем сигнальном
интервале. Аналогично «ясновидящая» оценка, полученная из информационного
сигнала путем снятия модуляции, при неограниченном интервале обработки, равна
![]() (C.5)
(C.5)
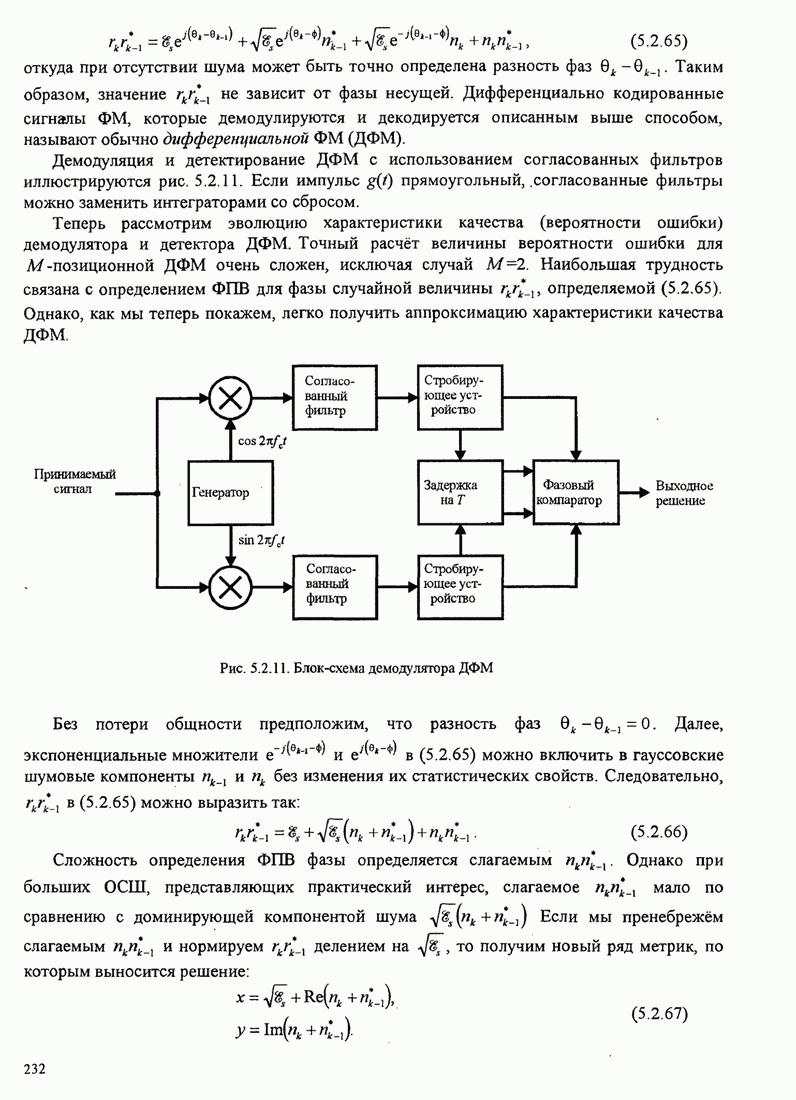
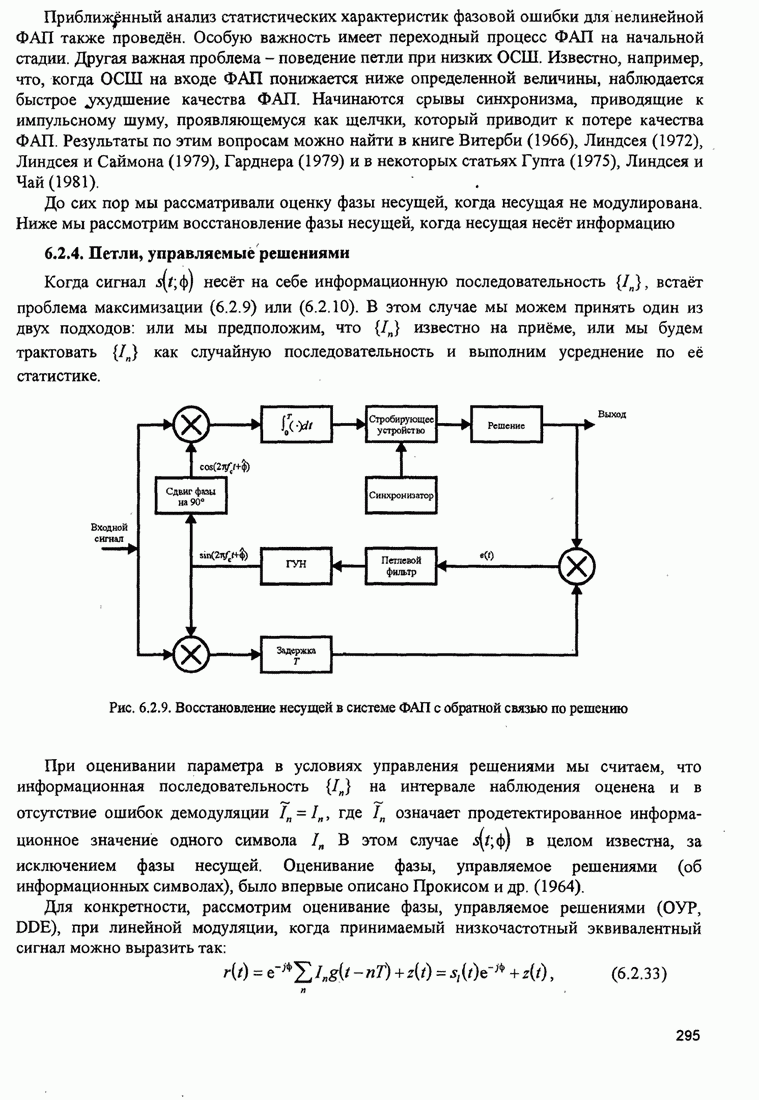
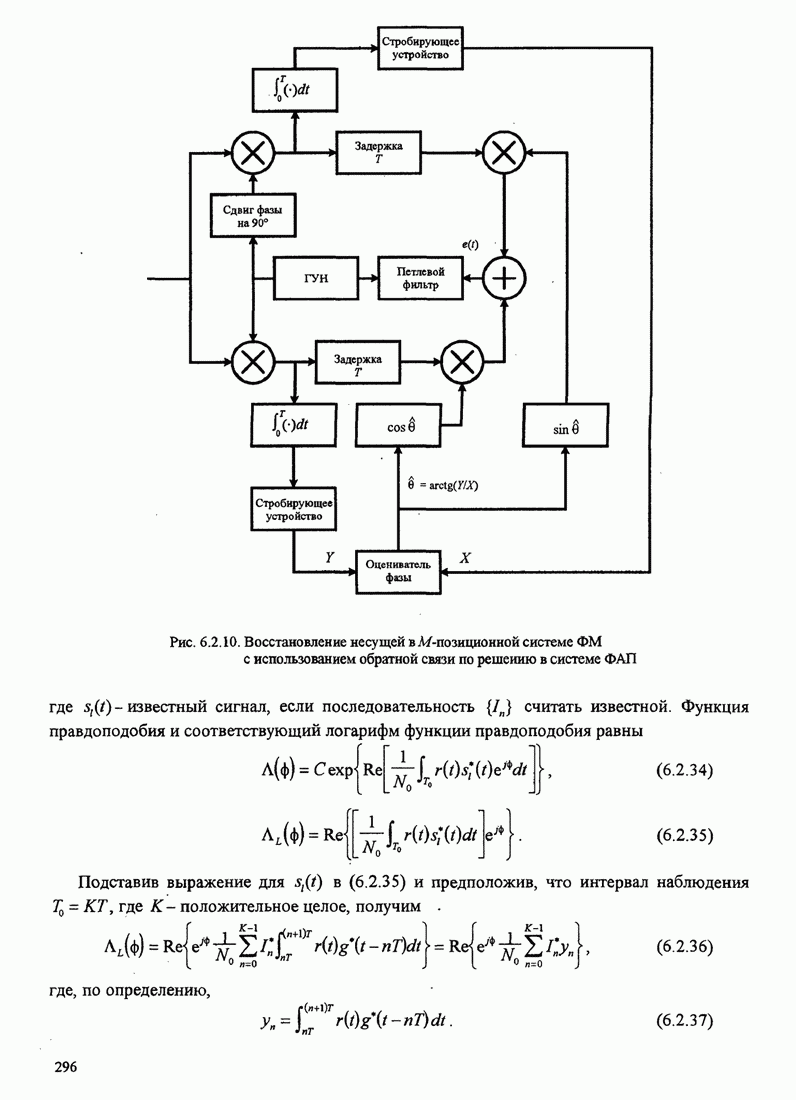
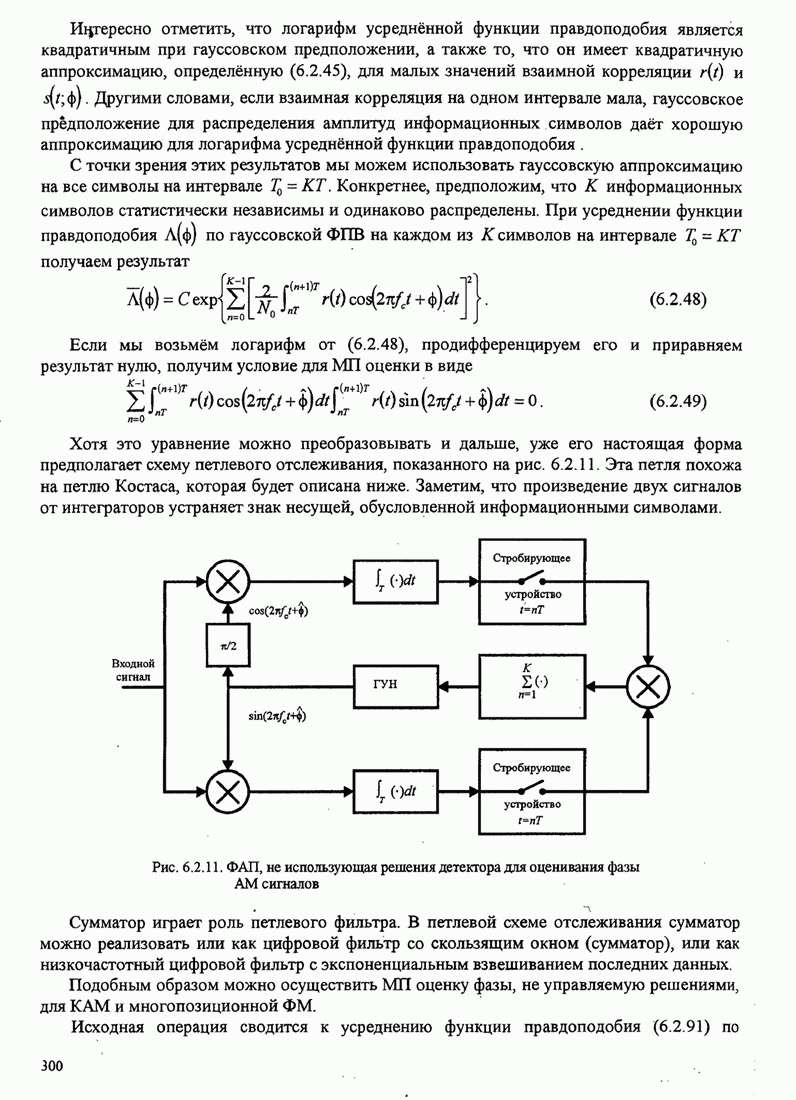
Как указывалось, демодулятор образует
произведение между ![]() и
и ![]() и суммирует его с аналогичными
произведениями остальных
и суммирует его с аналогичными
произведениями остальных ![]() каналов. В результате получаются случайные величины
каналов. В результате получаются случайные величины
![]() (C.6)
(C.6)
где, по определению, ![]() . Фаза z является величиной для решения. Она
равна
. Фаза z является величиной для решения. Она
равна
 (C.7)
(C.7)
С.2. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ И ФУКЦИЯ ВЕРОЯТНОСТИ ФАЗЫ
Будем исходить из предположения, что
фаза переданного сигнала равна нулю, то есть ![]() . При необходимости ФПВ для
. При необходимости ФПВ для ![]() при условии передачи фазы другого
переданного сигнала можно получить преобразованием
при условии передачи фазы другого
переданного сигнала можно получить преобразованием ![]() на угол
на угол ![]() . Мы также предполагаем, что
комплексные слагаемые
. Мы также предполагаем, что
комплексные слагаемые ![]() , характеризующие
, характеризующие ![]() каналов, статистически взаимно
независимые и одинаково распределенные гауссовские случайные величины с
нулевыми средними. Такая характеристика приемлема для каналов с медленными релеевскими
замираниями. Как следствие, случайные величины
каналов, статистически взаимно
независимые и одинаково распределенные гауссовские случайные величины с
нулевыми средними. Такая характеристика приемлема для каналов с медленными релеевскими
замираниями. Как следствие, случайные величины ![]() гауссовские, коррелированные
комплексные, с нулевыми средними и статистически независимые, но одинаково
распределённые с любой другой парой
гауссовские, коррелированные
комплексные, с нулевыми средними и статистически независимые, но одинаково
распределённые с любой другой парой ![]() .
.
Метод, который используется при
расчёте плотности вероятности ![]() , в общем случае разнесенного приема,
следующий. Во-первых, определяется характеристическая функция совместной
функции плотности вероятности
, в общем случае разнесенного приема,
следующий. Во-первых, определяется характеристическая функция совместной
функции плотности вероятности ![]() и
и ![]() , где
, где ![]() и
и ![]() - две компоненты, которые определяют величину для решения
- две компоненты, которые определяют величину для решения ![]() . Во-вторых,
выполняются двойное преобразование Фурье характеристической функции, что даст
. Во-вторых,
выполняются двойное преобразование Фурье характеристической функции, что даст
![]() . Затем преобразование
. Затем преобразование
![]() (С.8)
(С.8)
даст совместную ФПВ огибающей ![]() и фазы
и фазы ![]() . В заключение
интегрирование совместной ФПВ по случайной величине
. В заключение
интегрирование совместной ФПВ по случайной величине ![]() дает ФПВ для
дает ФПВ для ![]() .
.
Совместная характеристическая функция
случайных величин ![]() и
и ![]() , можно выразить в виде
, можно выразить в виде
 (C.9)
(C.9)
где, по определению,
 (C.10)
(C.10)
 .
.
Результат преобразования Фурье ![]() по величинам
по величинам ![]() даёт
даёт
 (C.11)
(C.11)
где ![]() - модифицированная функция Ханкеля
порядка
- модифицированная функция Ханкеля
порядка ![]() .
Затем преобразование случайных величин указанных в (С.8), дает совместную ФПВ
огибающей
.
Затем преобразование случайных величин указанных в (С.8), дает совместную ФПВ
огибающей ![]() и
фазы
и
фазы ![]() в
виде
в
виде
 (С.12)
(С.12)
Теперь интегрирование по величине ![]() даёт собственно
ФПВ фазы
даёт собственно
ФПВ фазы ![]() .
Мы вычислим интеграл для получения
.
Мы вычислим интеграл для получения ![]() в виде
в виде
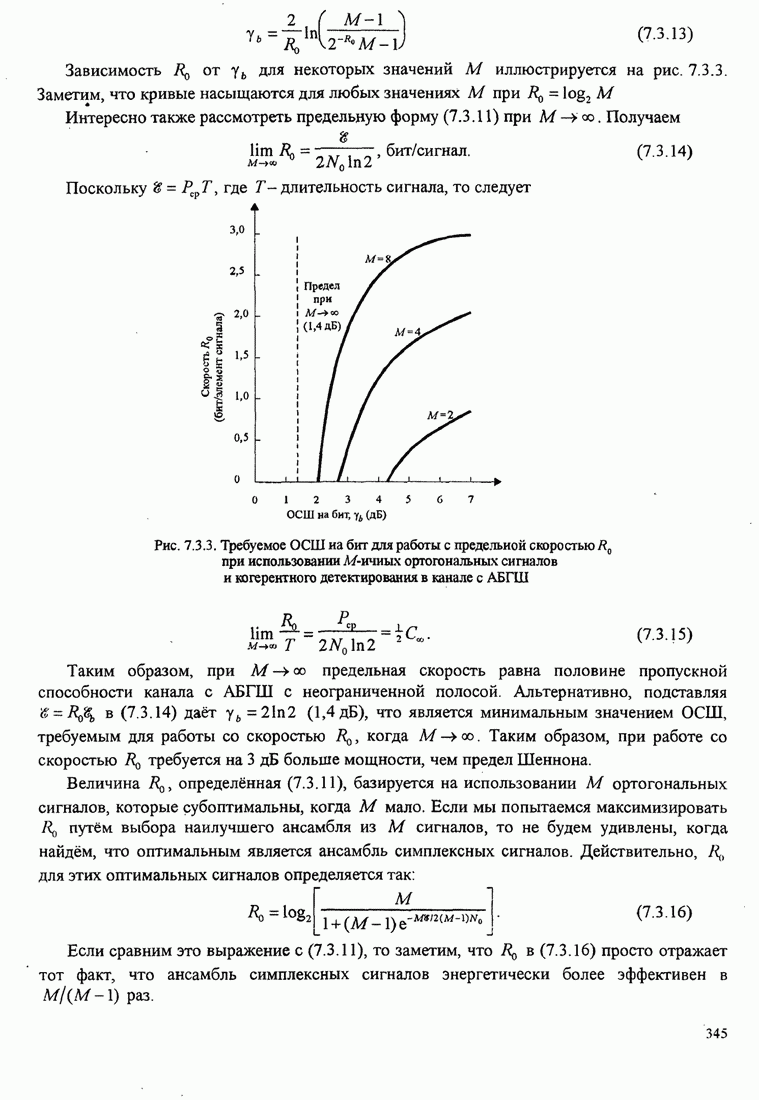
 (С.13)
(С.13)
В этом уравнении обозначение ![]() означает
означает ![]() -ю частную
производную функции
-ю частную
производную функции ![]() при
при ![]() .
.
С.З. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ КАНАЛОВ С МЕДЛЕННЫМИ РЕЛЕЕВСКИМИ ЗАМИРАНИЯМИ
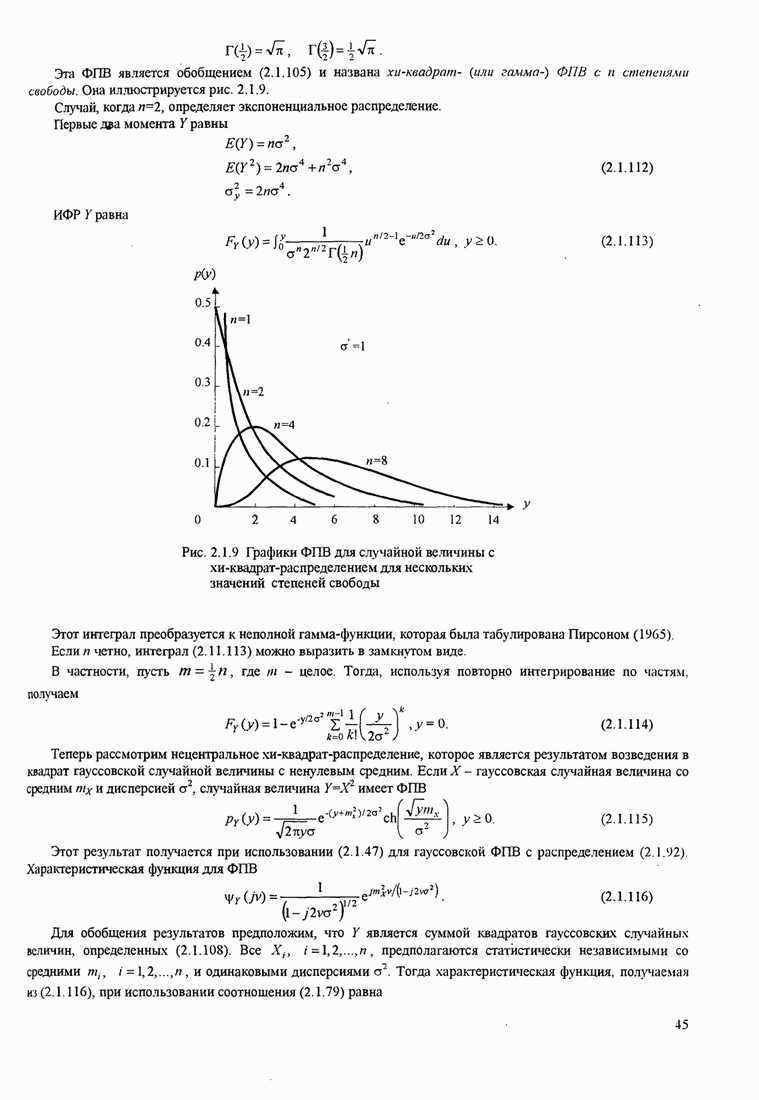
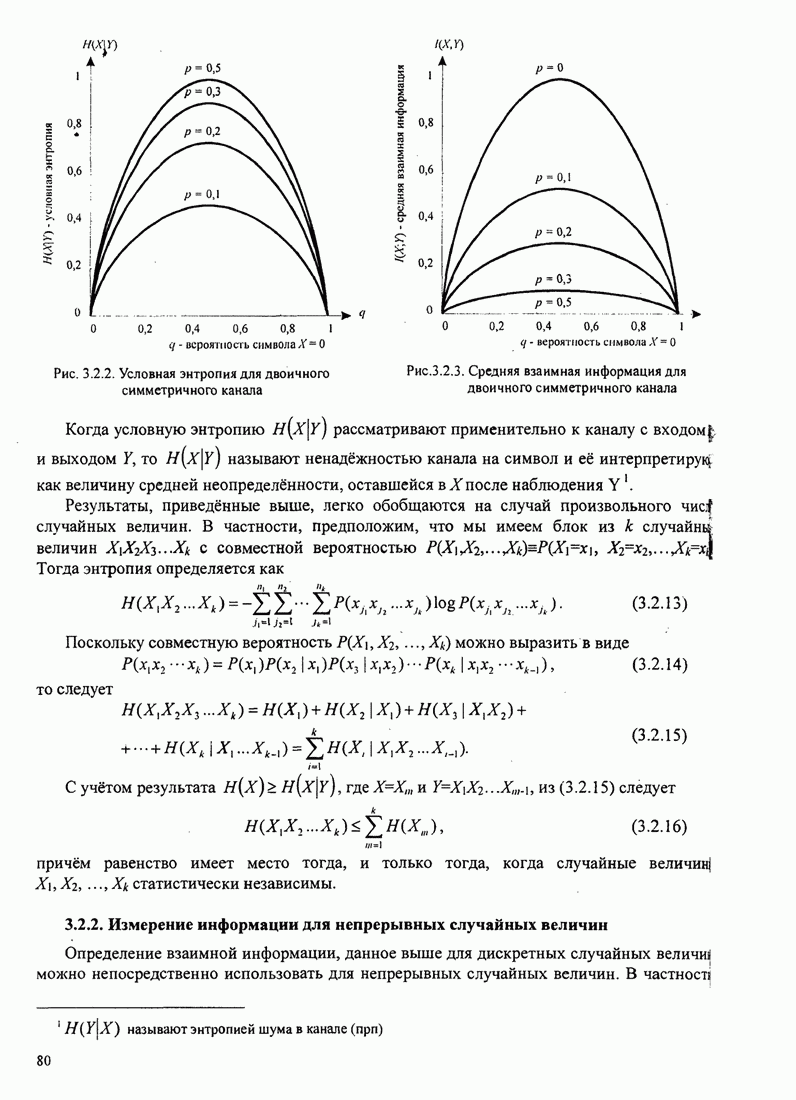
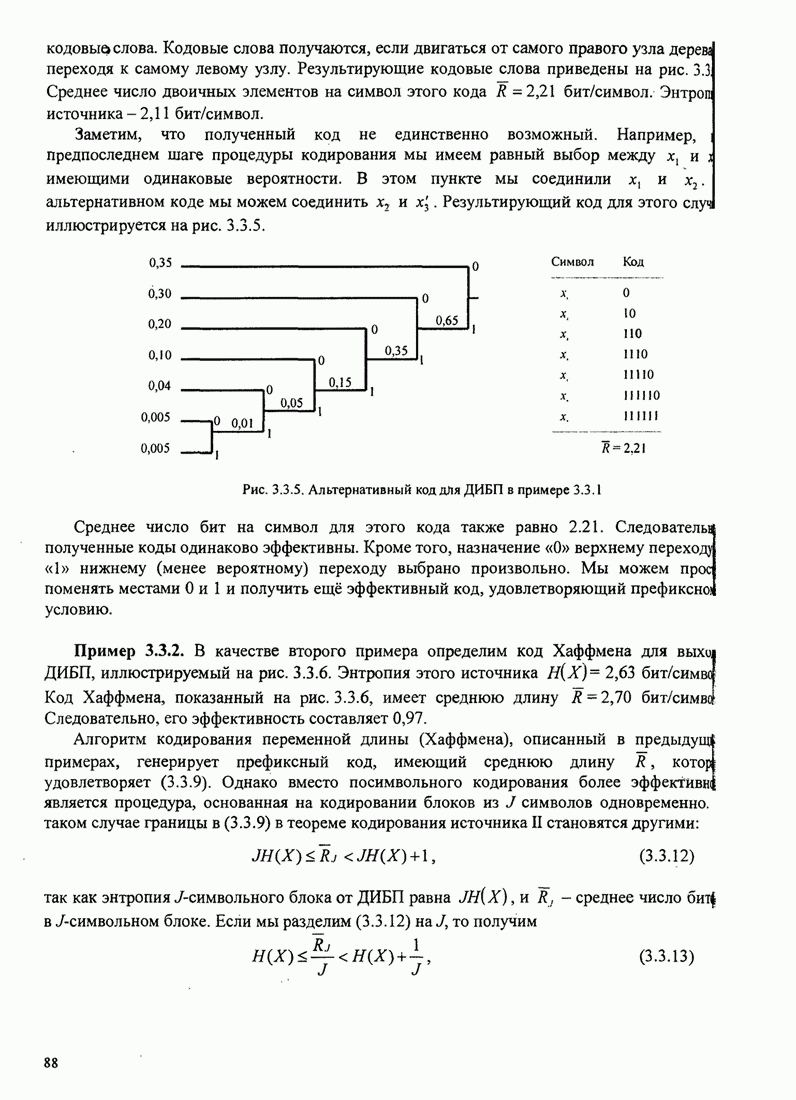
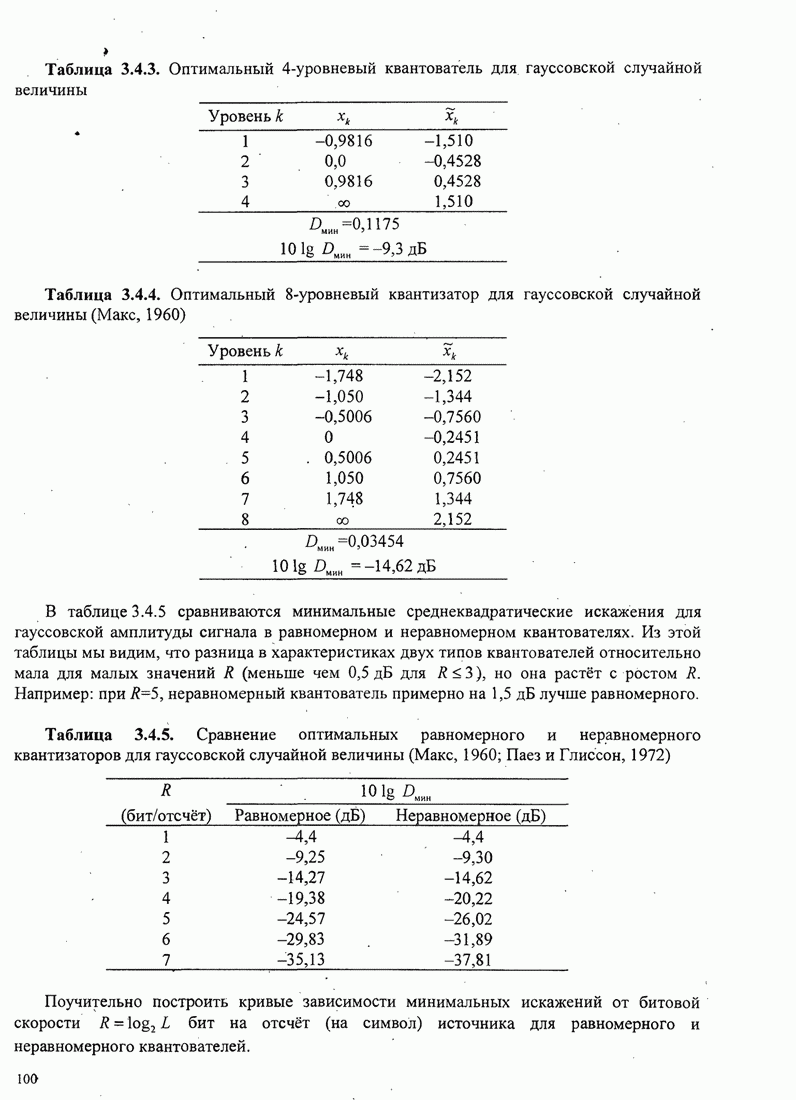
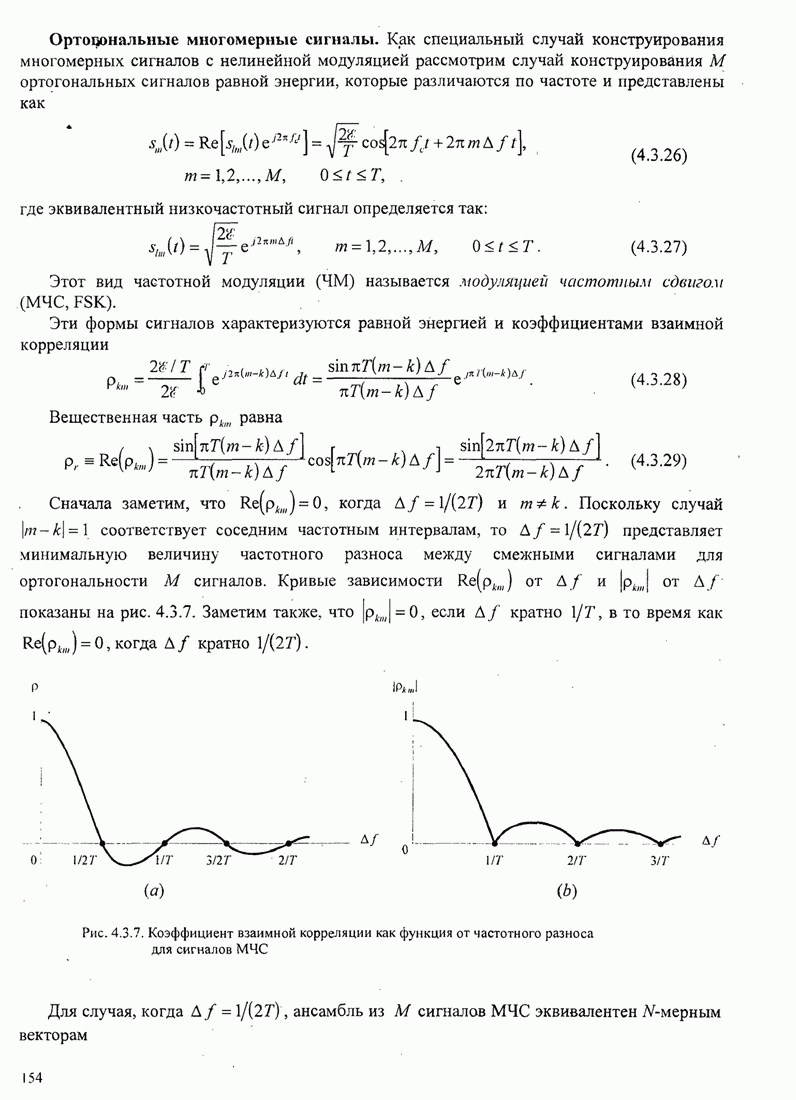
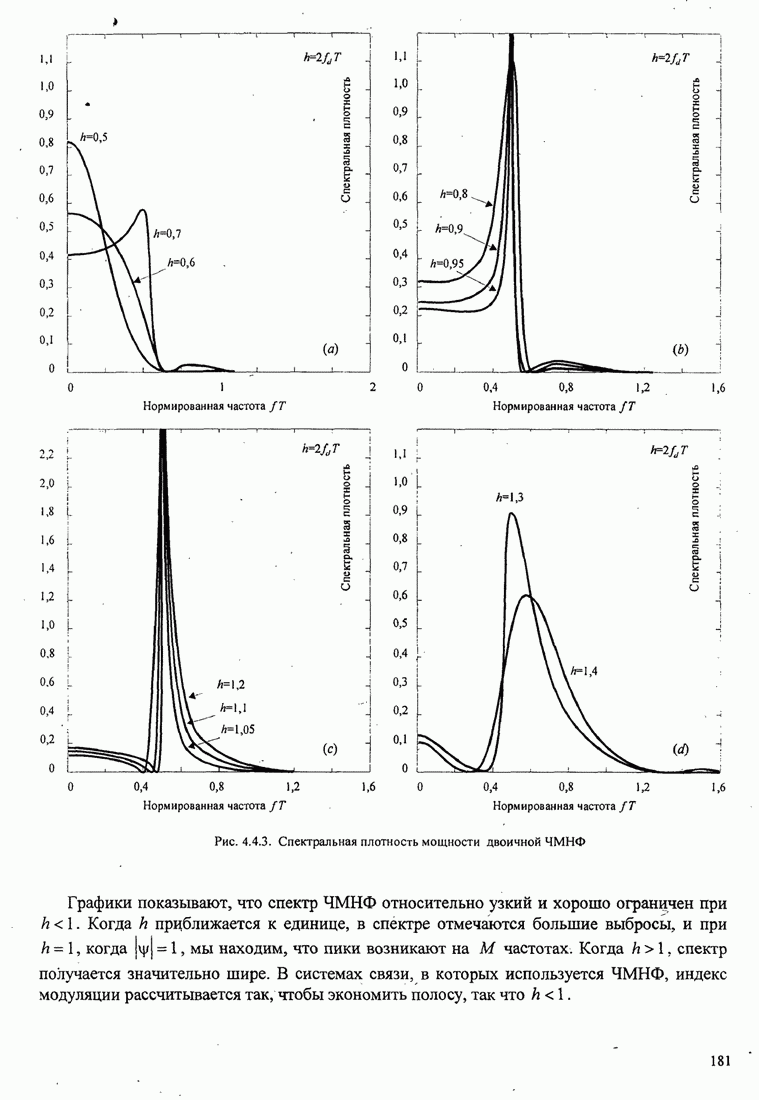
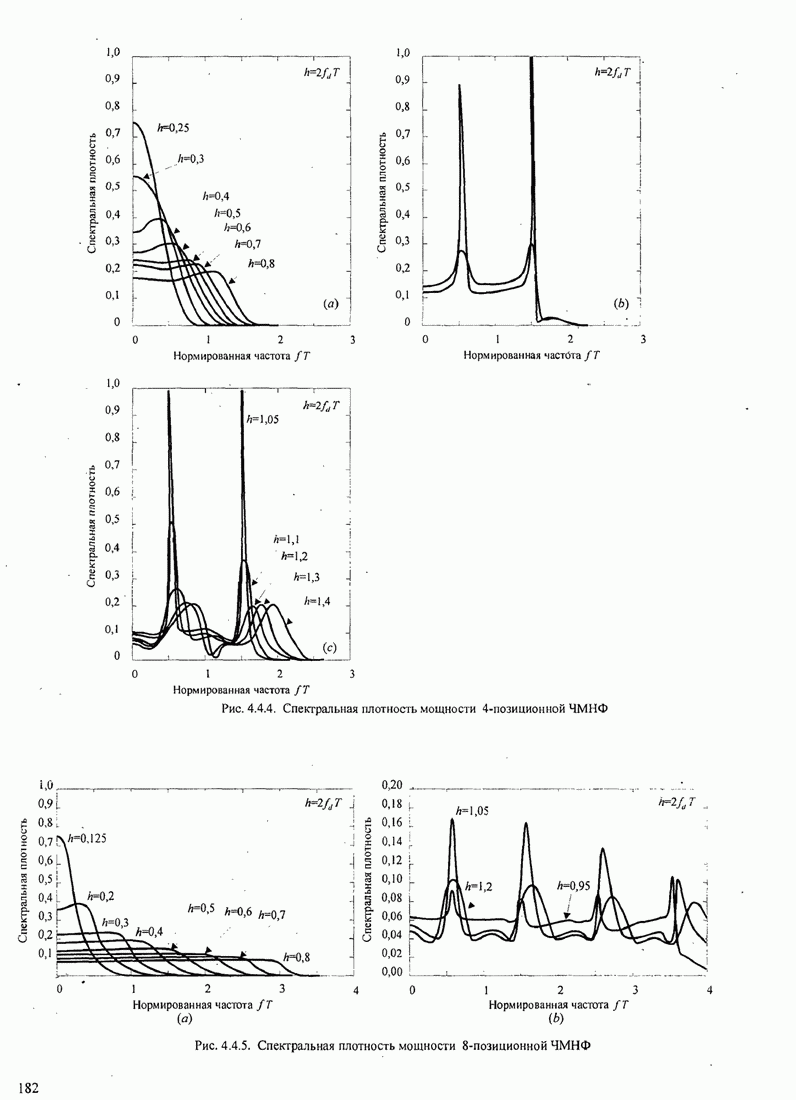
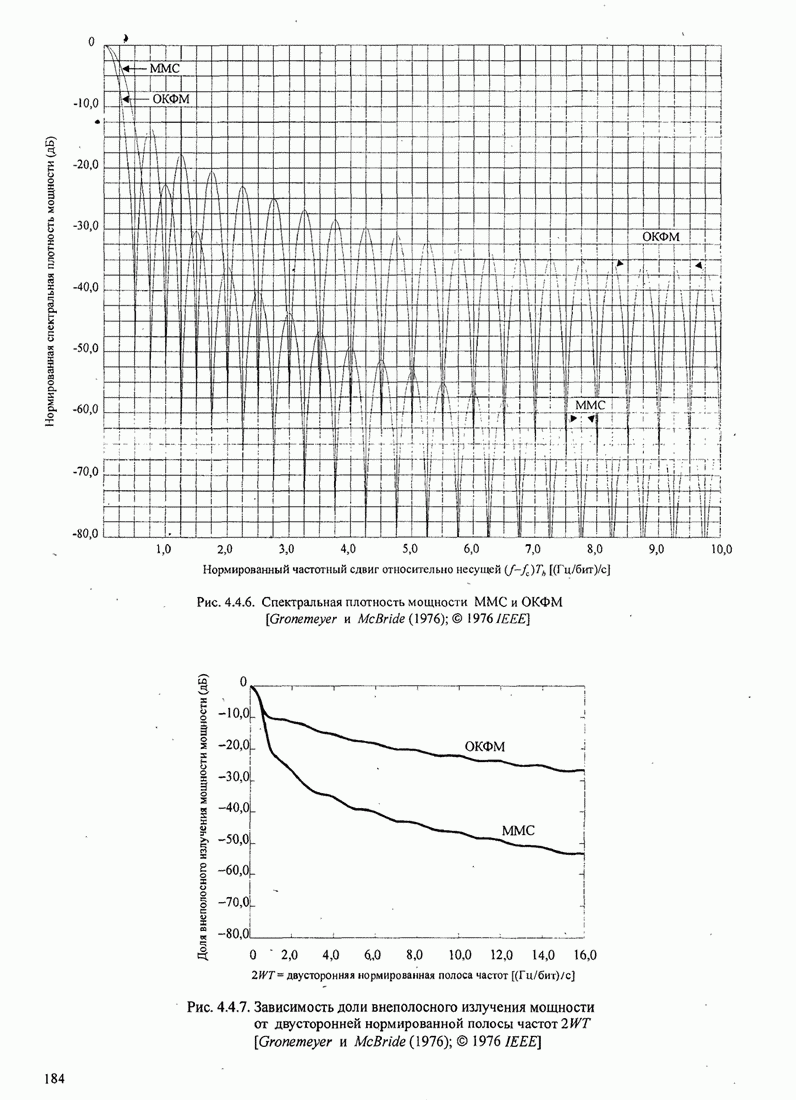
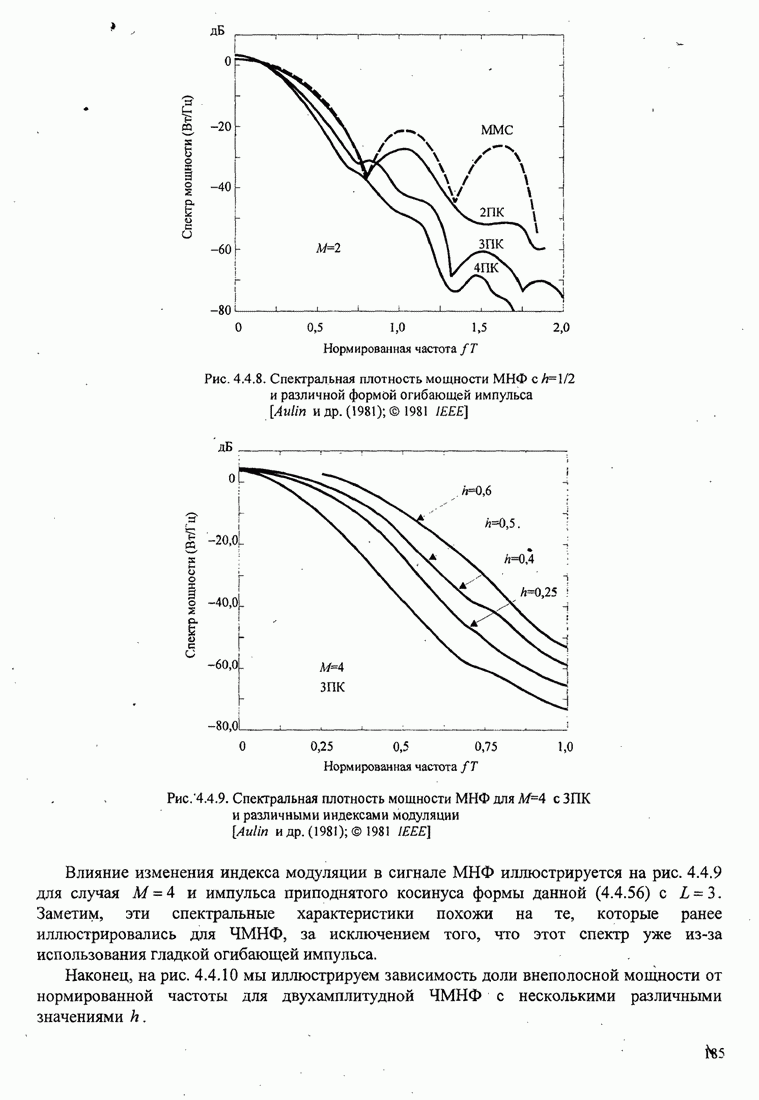
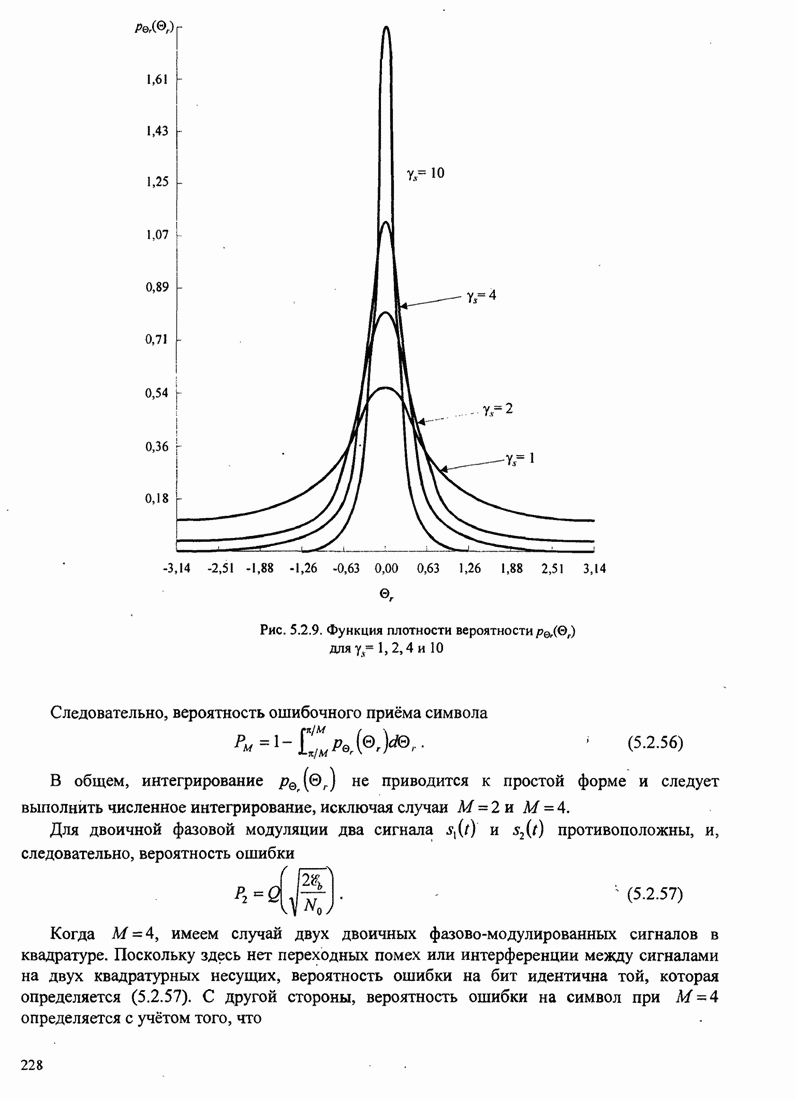
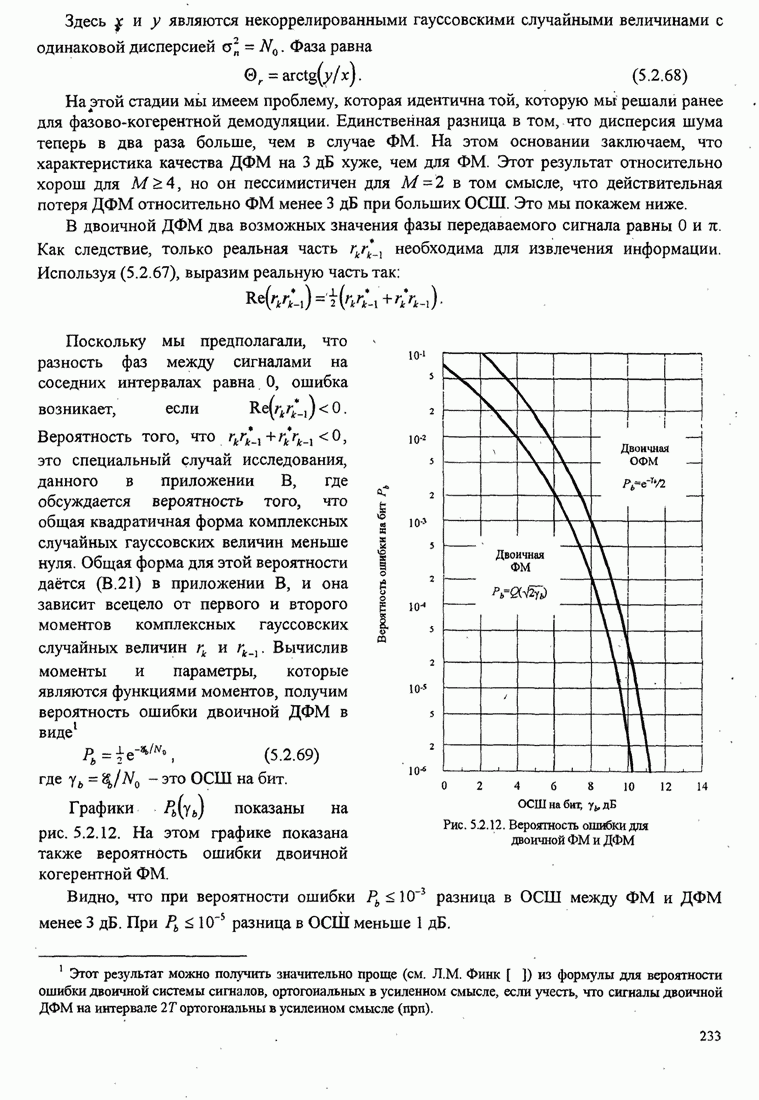
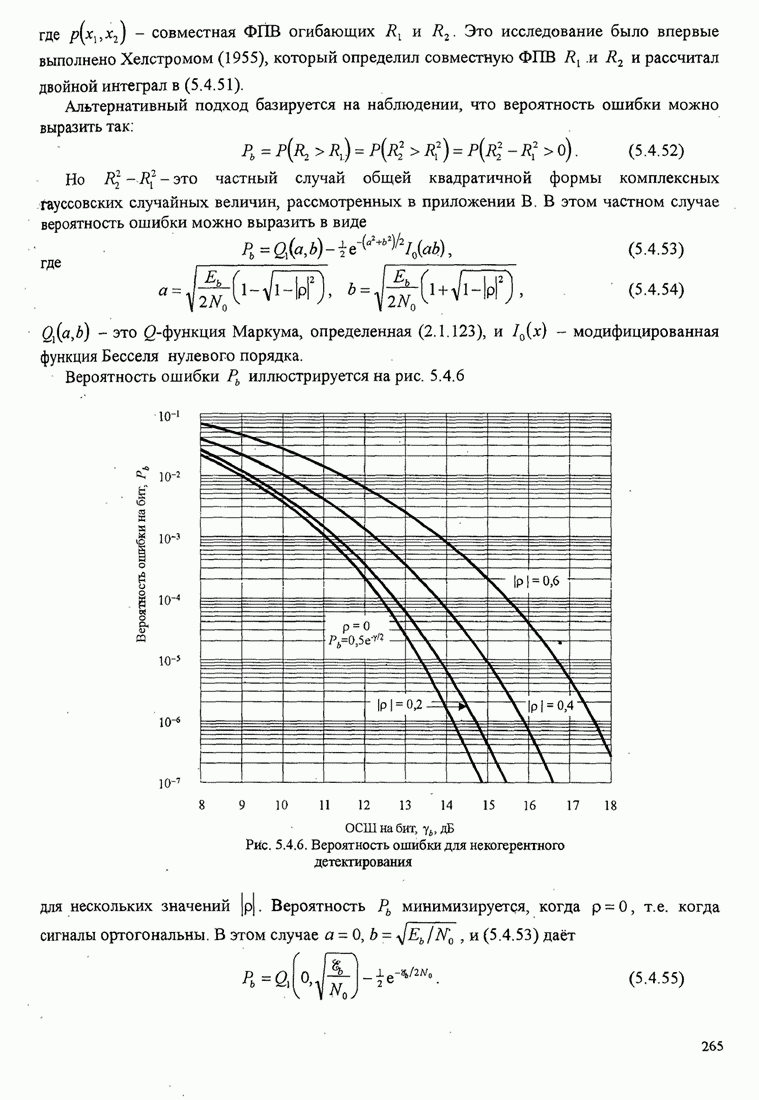
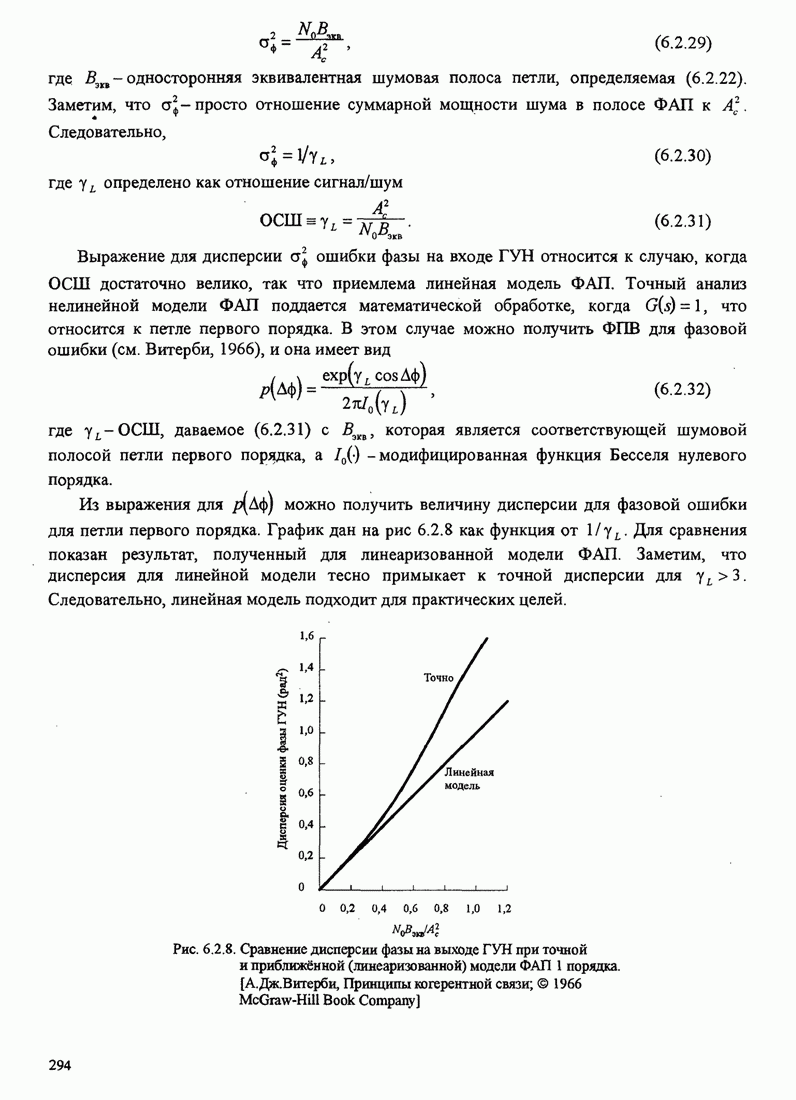
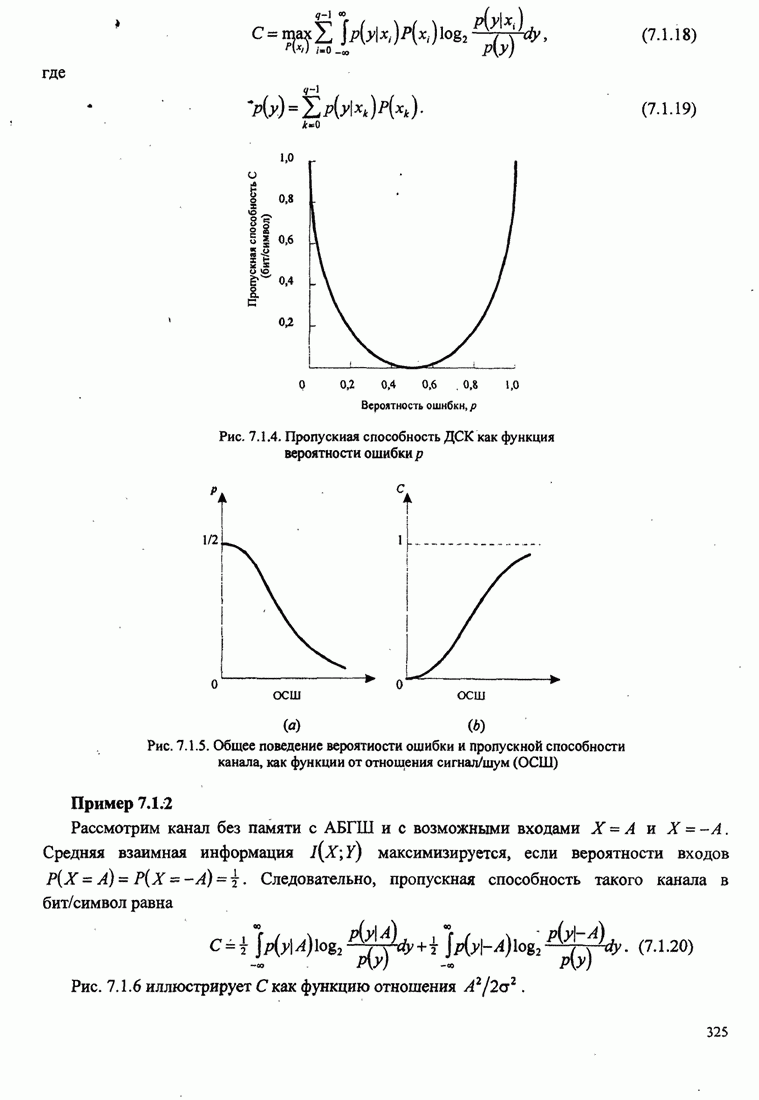
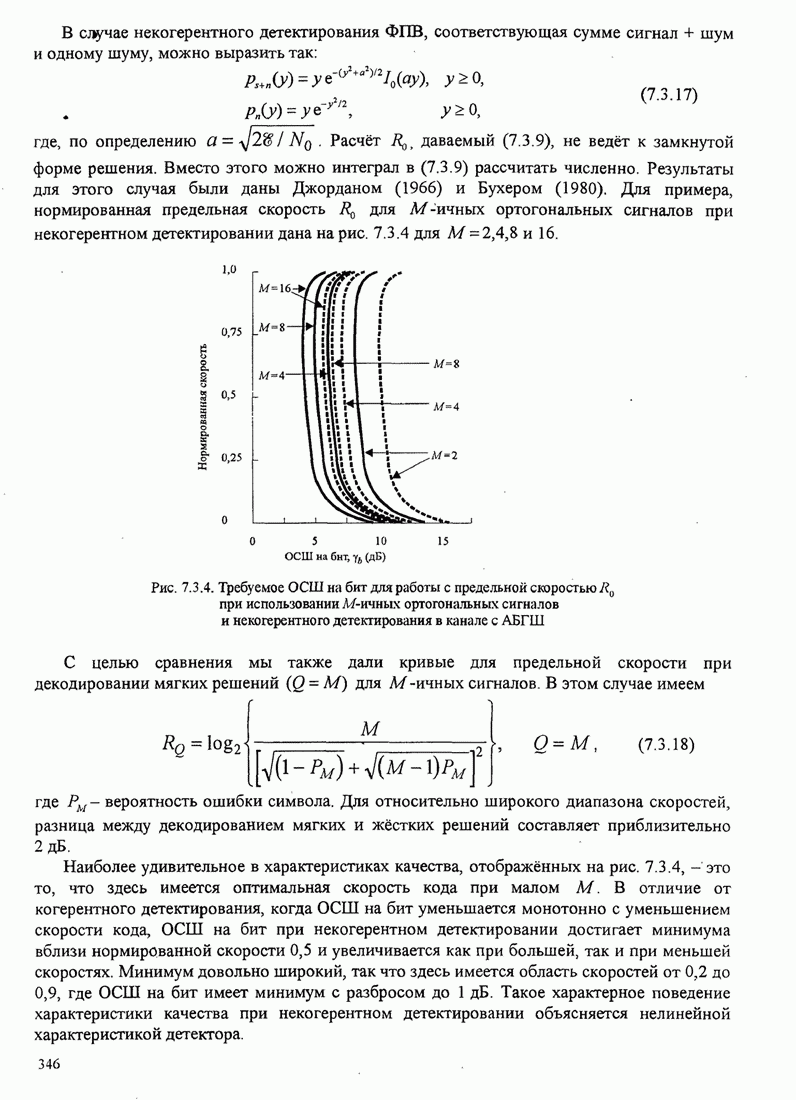
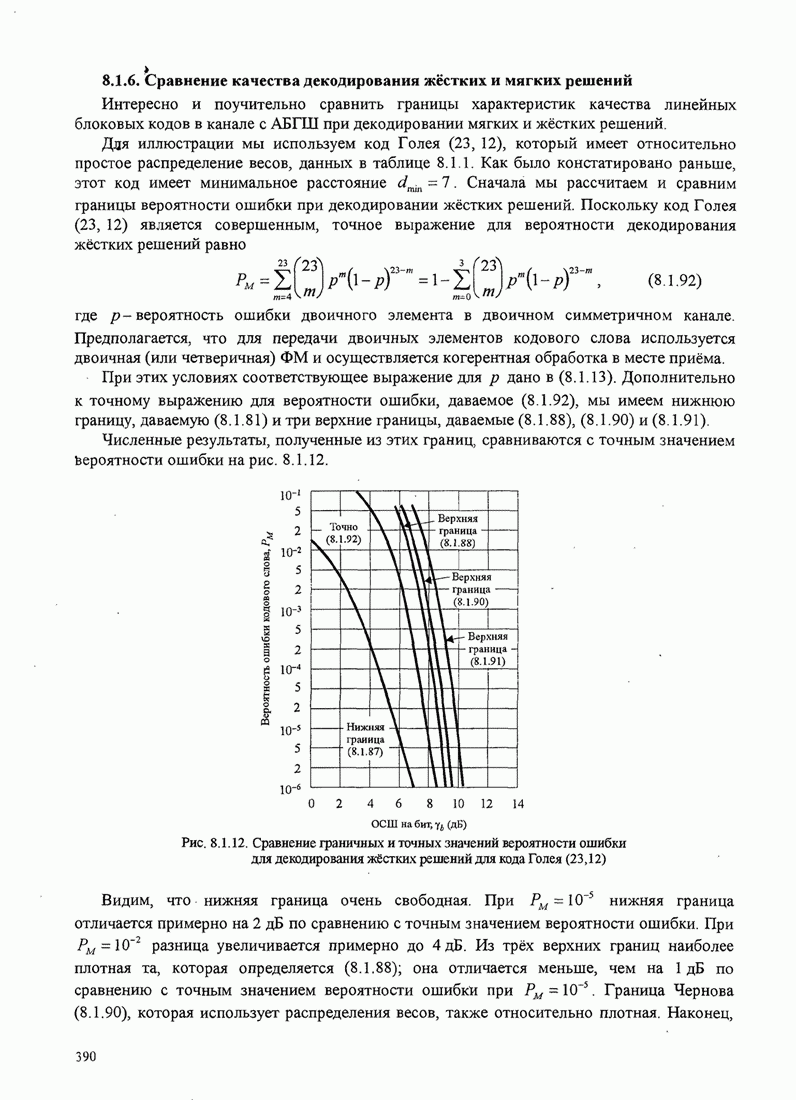
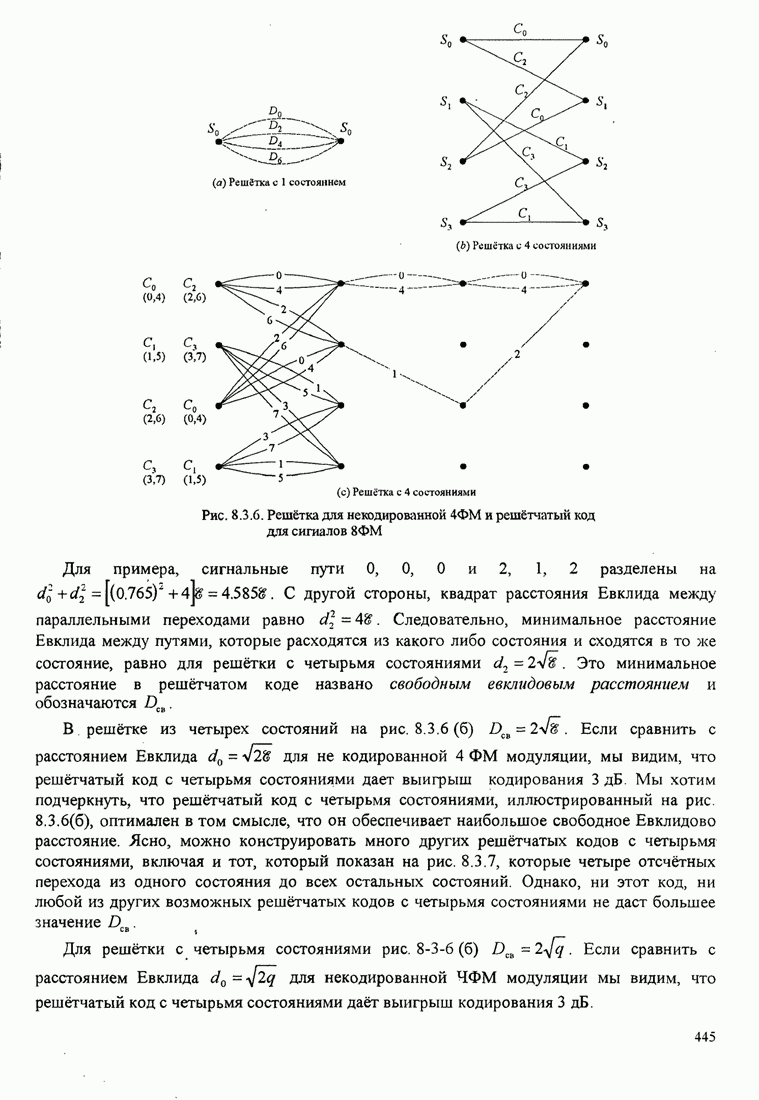
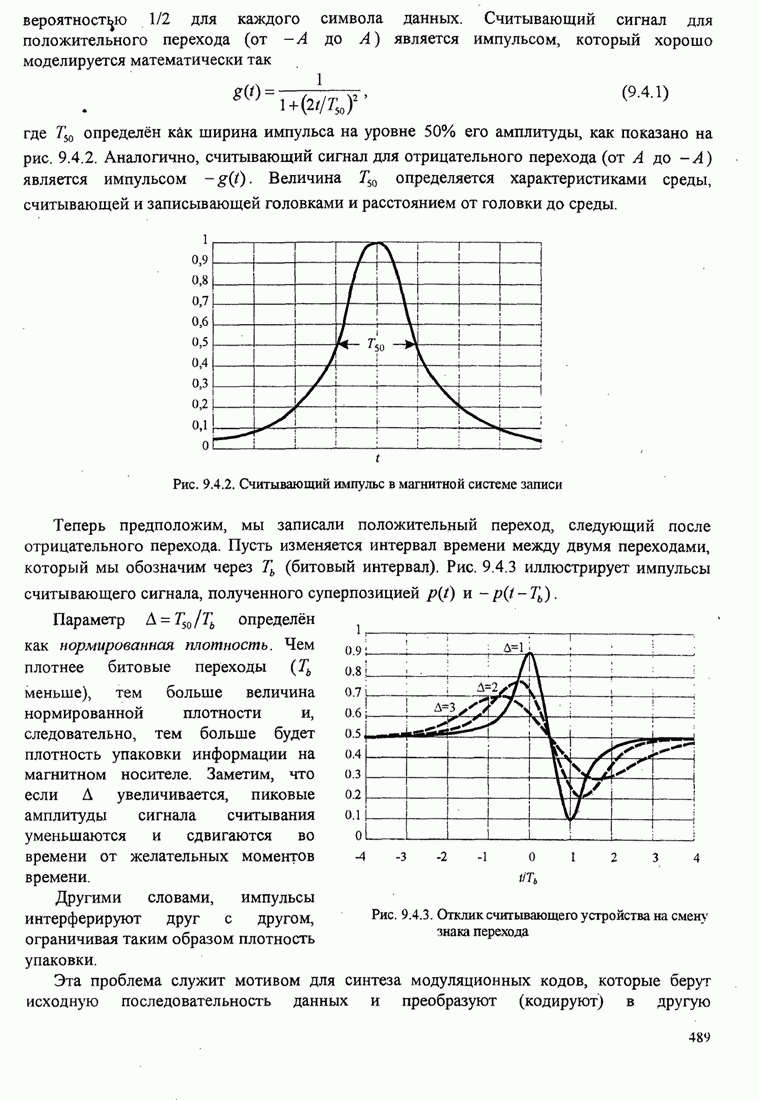
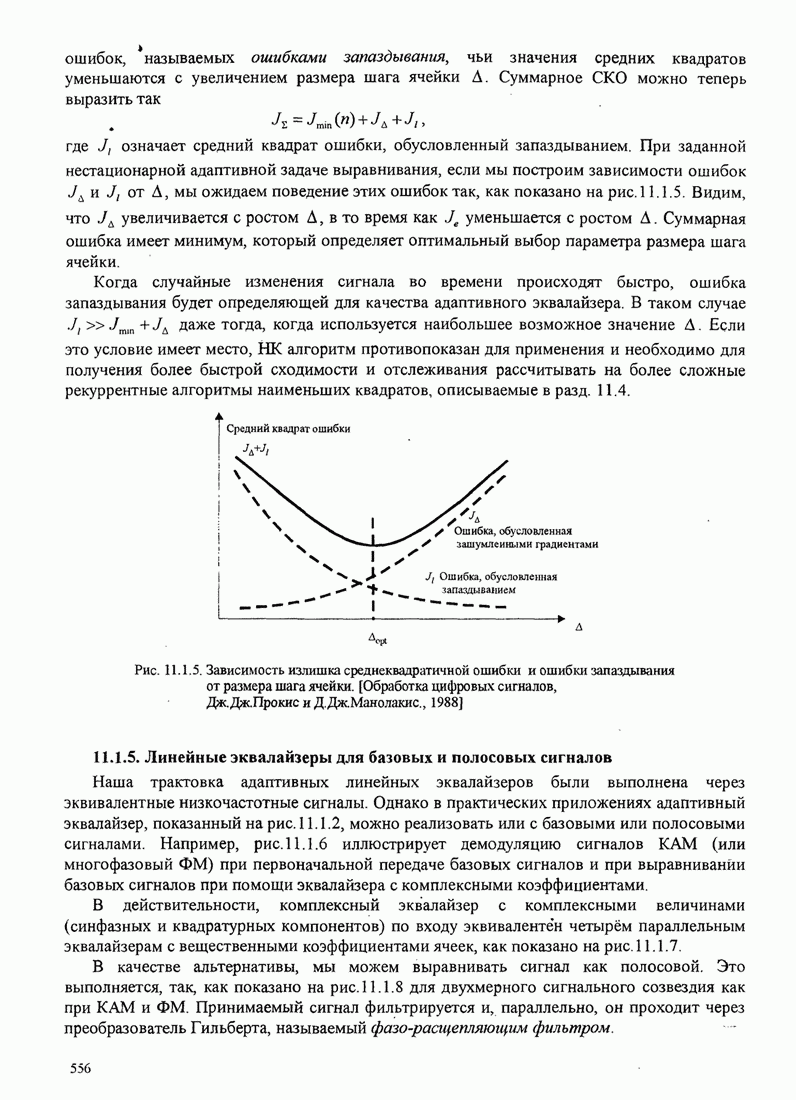
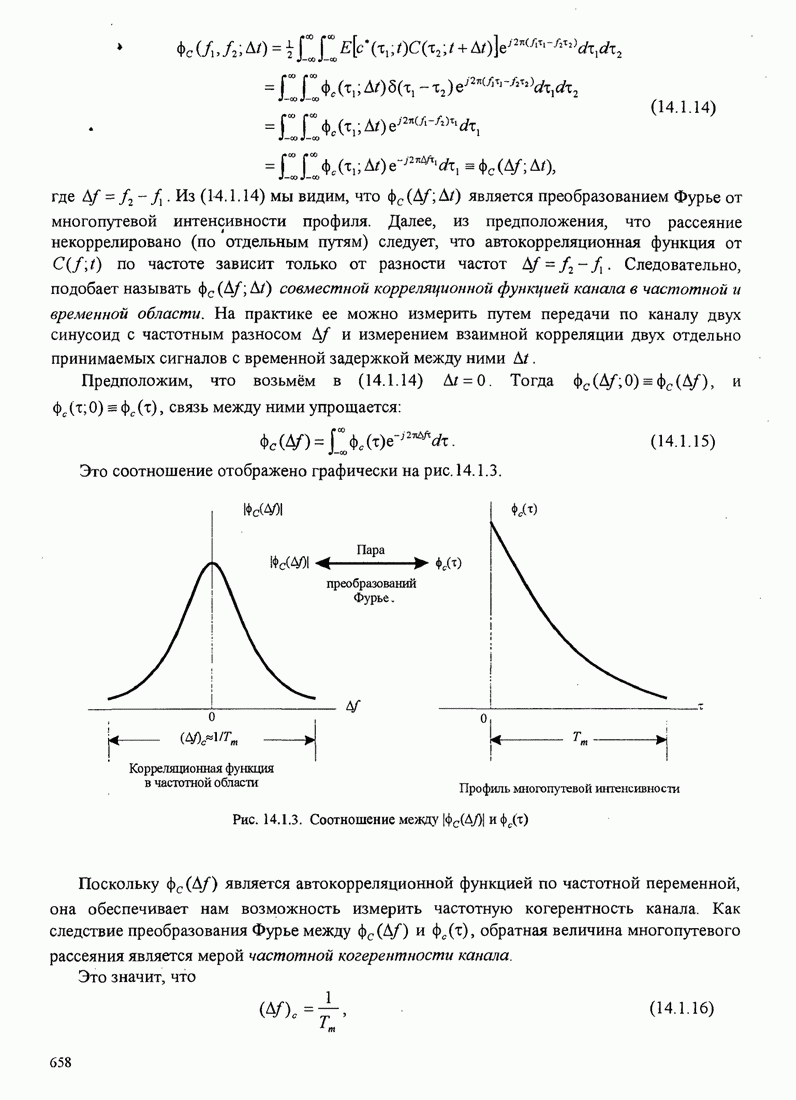
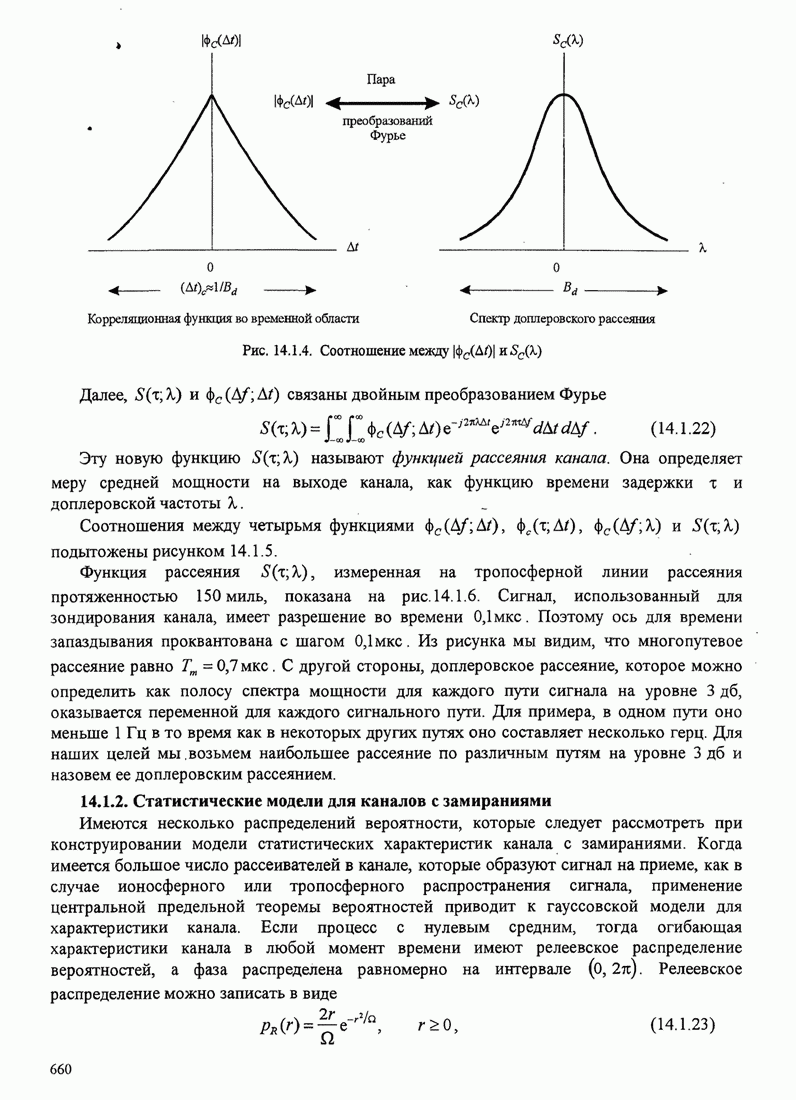
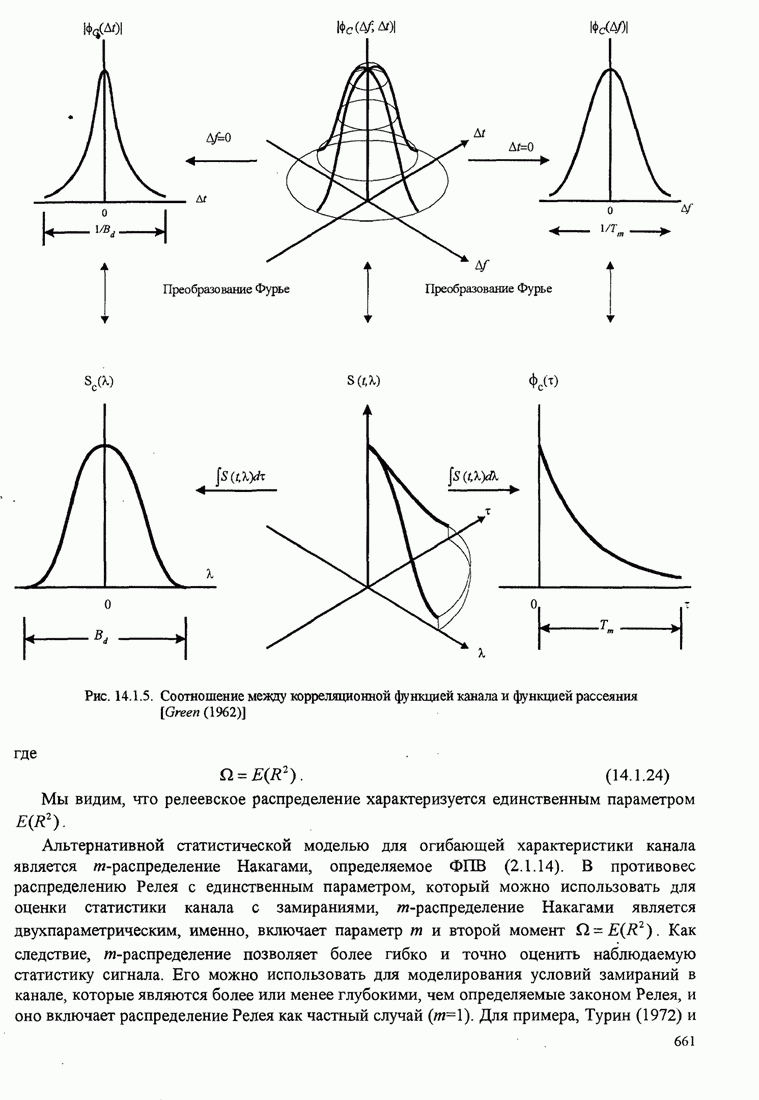
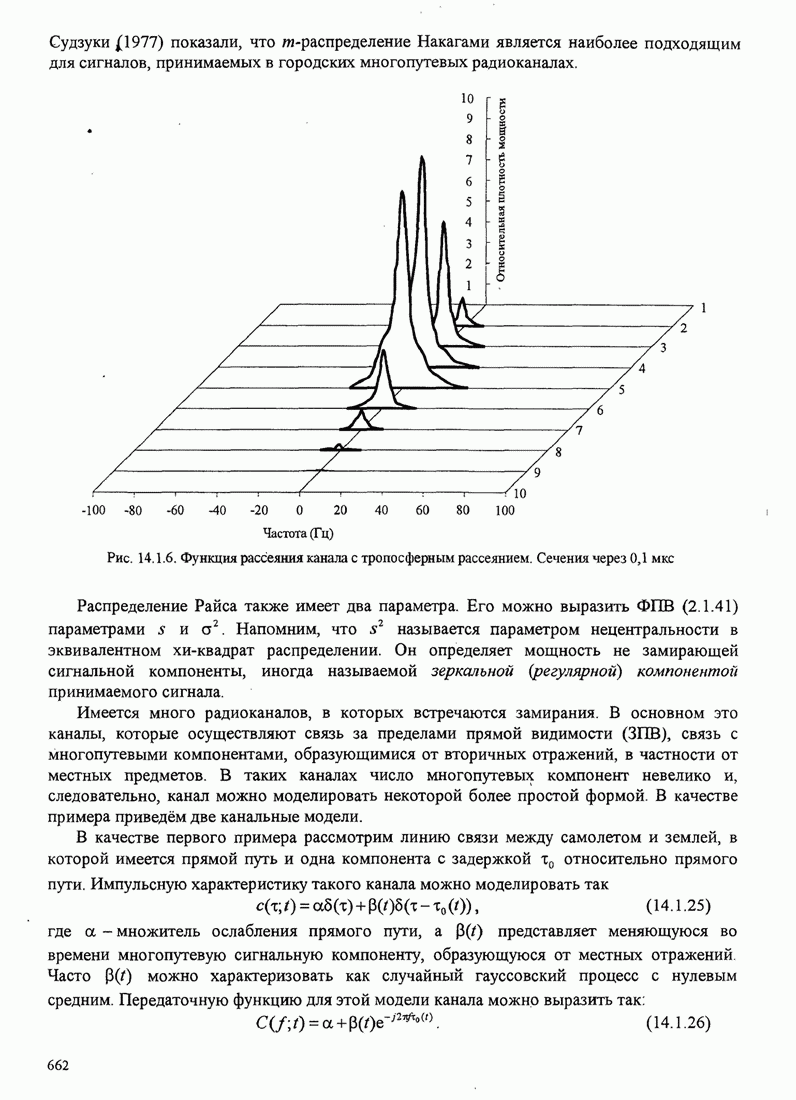
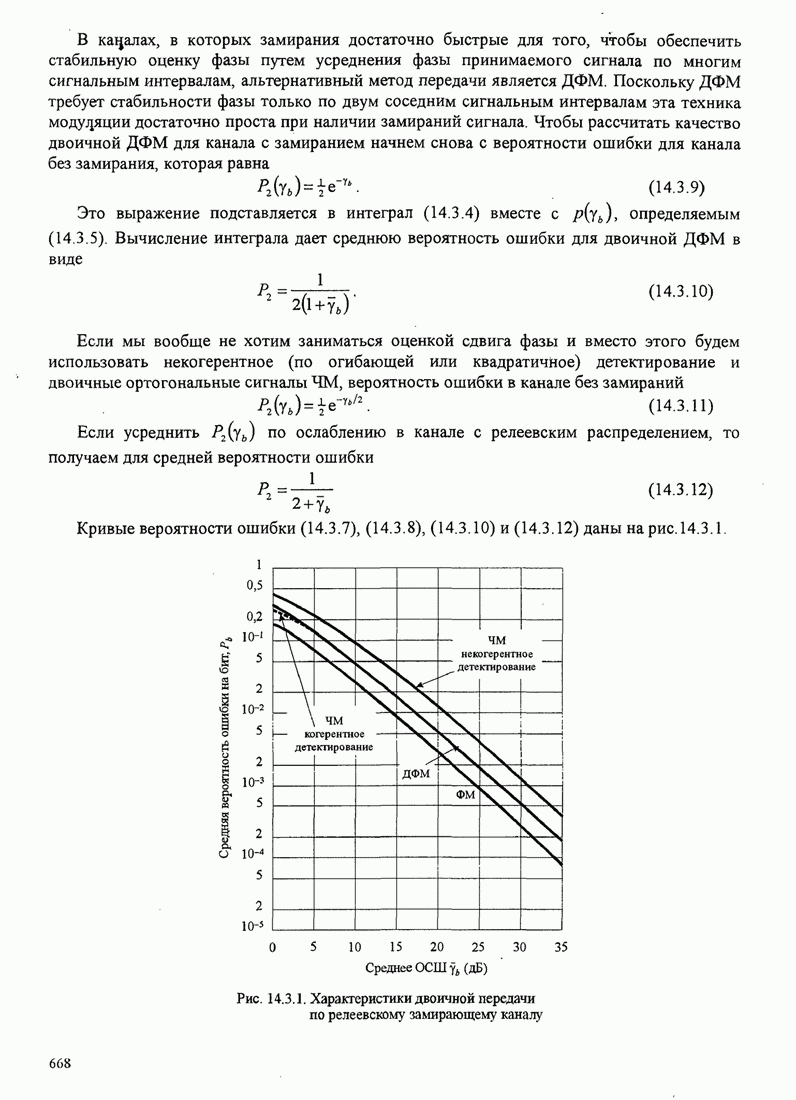
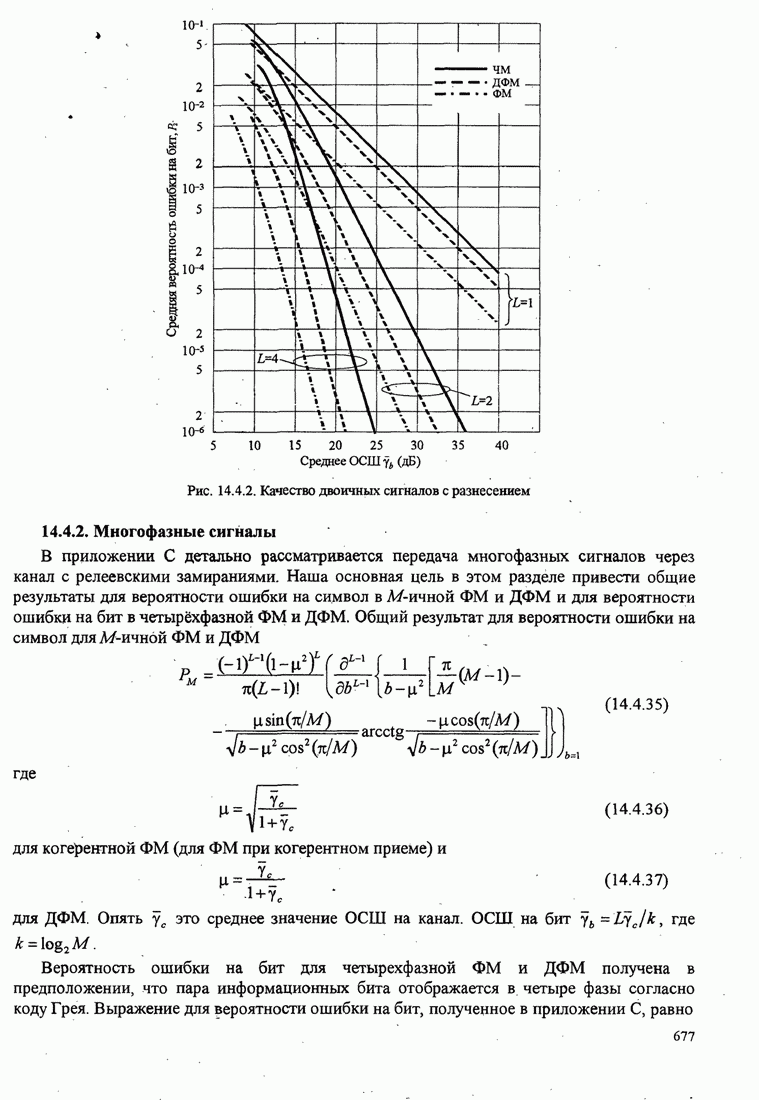
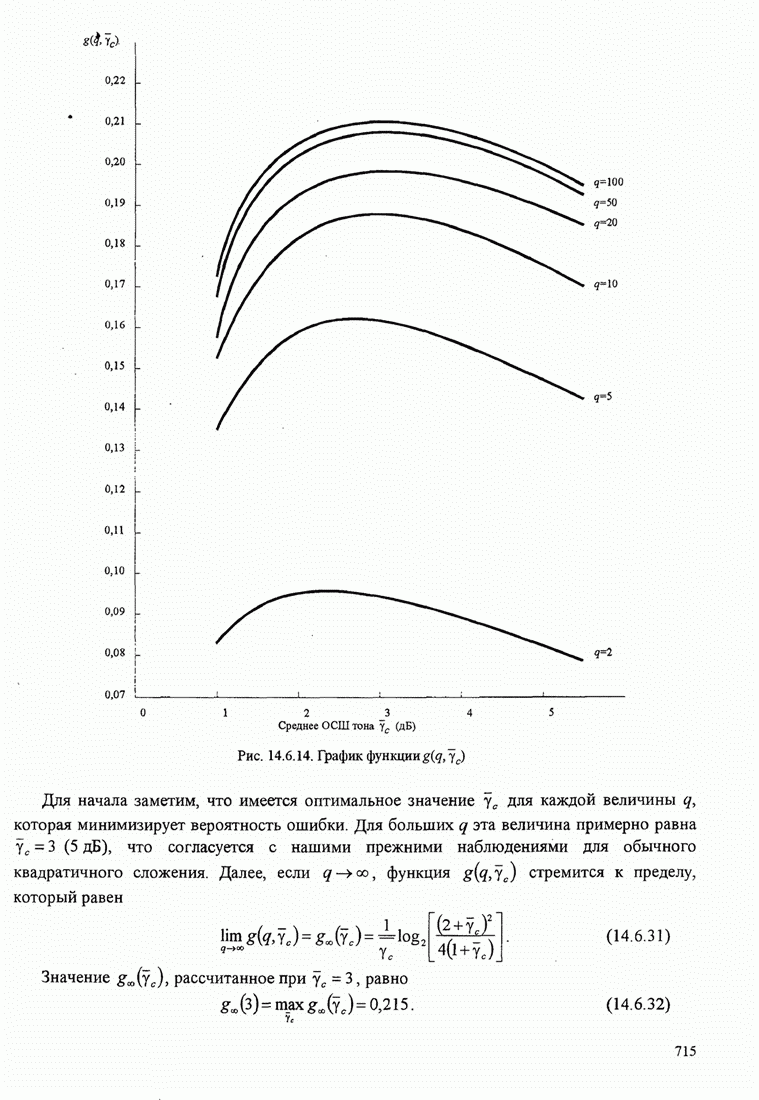
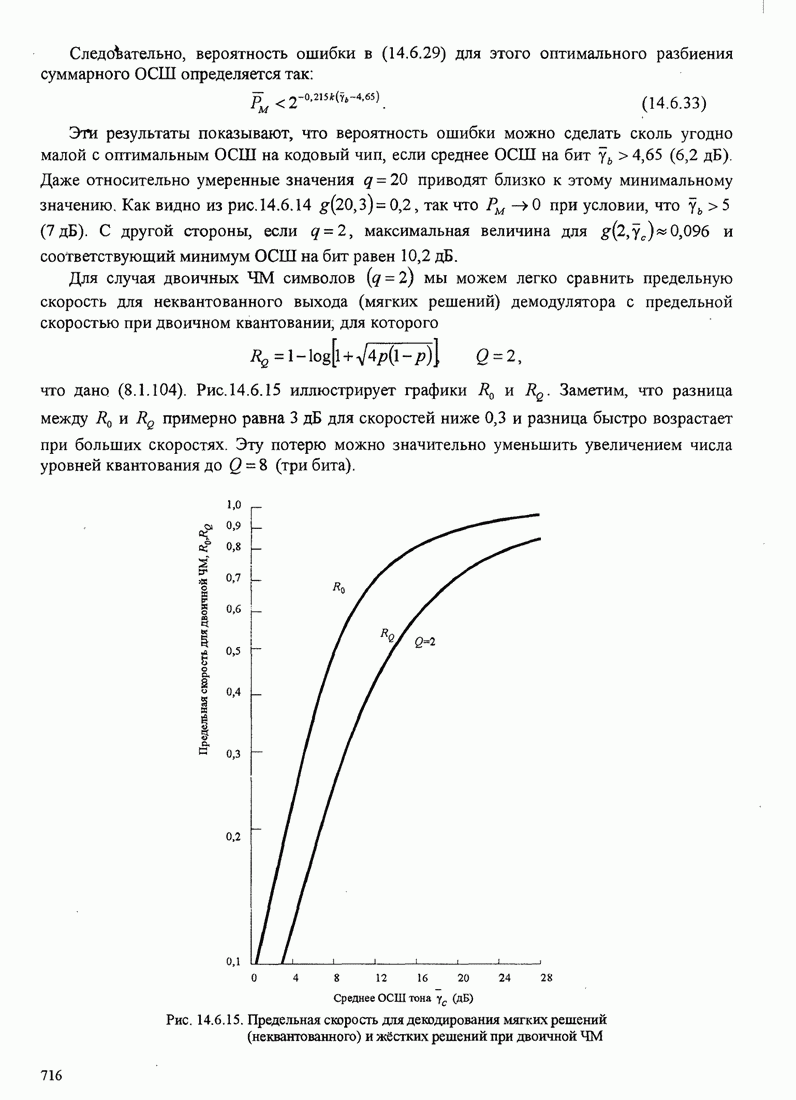
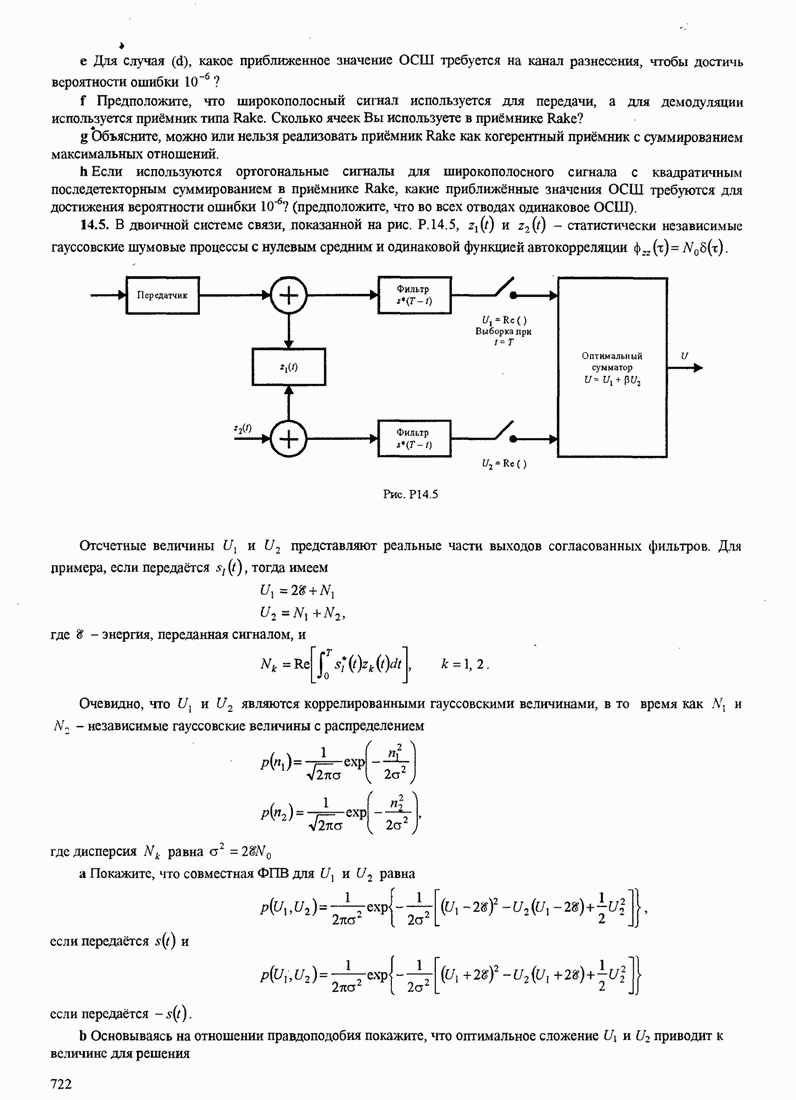
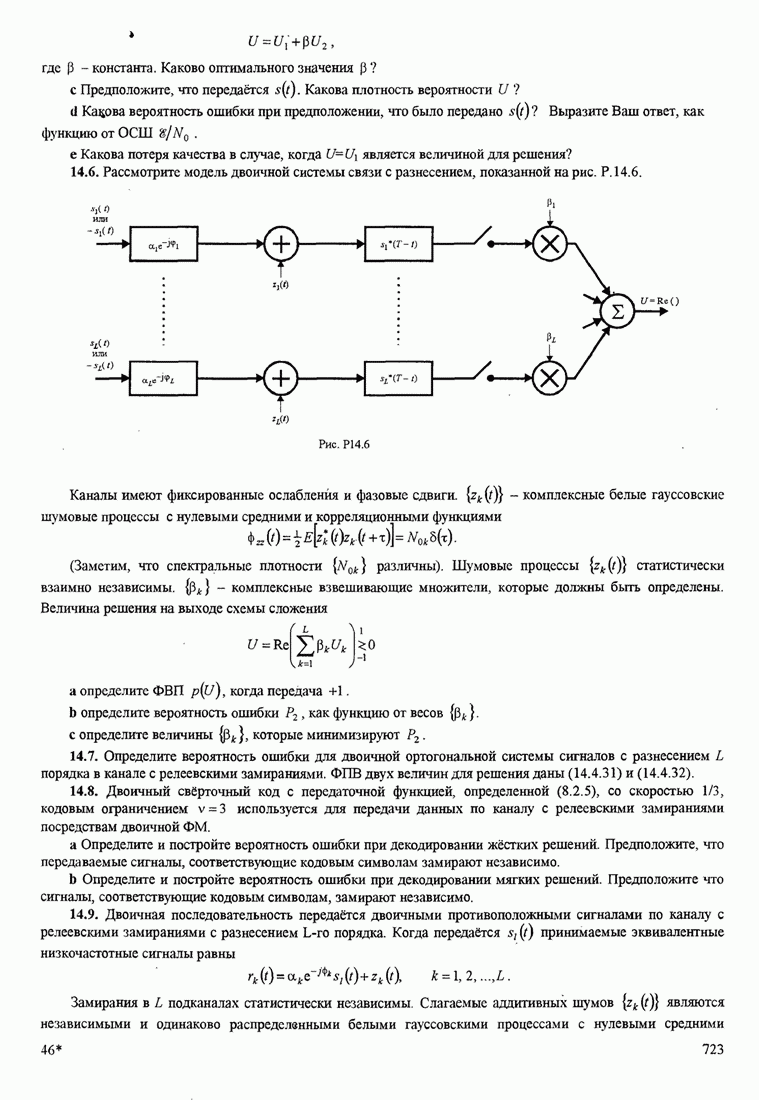
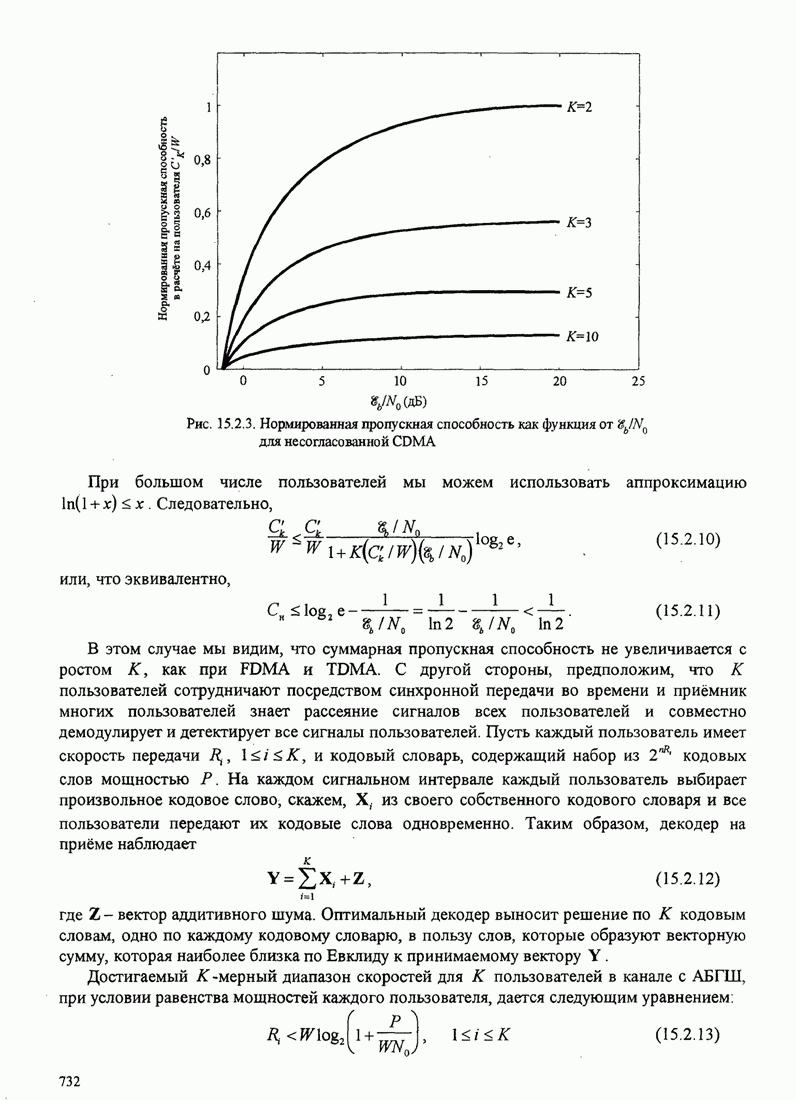
В этом разделе определяется вероятность характерных ошибок и вероятность ошибочного приема двоичных символов для M-фазных сигналов. Вероятности вычисляются через функцию плотности вероятности и функций распределения вероятностей 0.
Функция распределения вероятности фазы. Чтобы определить вероятность ошибки, мы должны вычислить определенный интеграл.
![]() ,
,
где ![]() и
и ![]() пределы интегрирования, a
пределы интегрирования, a ![]() определяется (С.13). Все последующие
вычисления выполняются для вещественных коэффициентов взаимной корреляции
определяется (С.13). Все последующие
вычисления выполняются для вещественных коэффициентов взаимной корреляции ![]() . Вещественность
. Вещественность
![]() означает,
что сигнал имеет симметричный спектр. Такая ситуация обычно встречается.
Поскольку комплексная величина
означает,
что сигнал имеет симметричный спектр. Такая ситуация обычно встречается.
Поскольку комплексная величина ![]() обуславливает сдвиг с в ФПВ
обуславливает сдвиг с в ФПВ ![]() , то есть
, то есть ![]() просто слагаемое
наклона, результаты, даваемые для вещественной
просто слагаемое
наклона, результаты, даваемые для вещественной ![]() можно тривиальным путем .изменить,
чтобы охватить более общий случай комплексного
можно тривиальным путем .изменить,
чтобы охватить более общий случай комплексного ![]() .
.
При интегрирования ![]() рассматривается только область
рассматривается только область ![]() , поскольку
, поскольку ![]() является четной функцией. Далее,
непрерывность интегрируемой функции и её производных и тот факт, что пределы
является четной функцией. Далее,
непрерывность интегрируемой функции и её производных и тот факт, что пределы ![]() и
и ![]() зависят от
зависят от ![]() позволяют менять
местами интегрирование и дифференцирование. Если это выполнить результирующая
интеграл можно вычислить совсем легко, и его молено выразить так:
позволяют менять
местами интегрирование и дифференцирование. Если это выполнить результирующая
интеграл можно вычислить совсем легко, и его молено выразить так:
 (С.14)
(С.14)
где по определению
 (С. 15)
(С. 15)
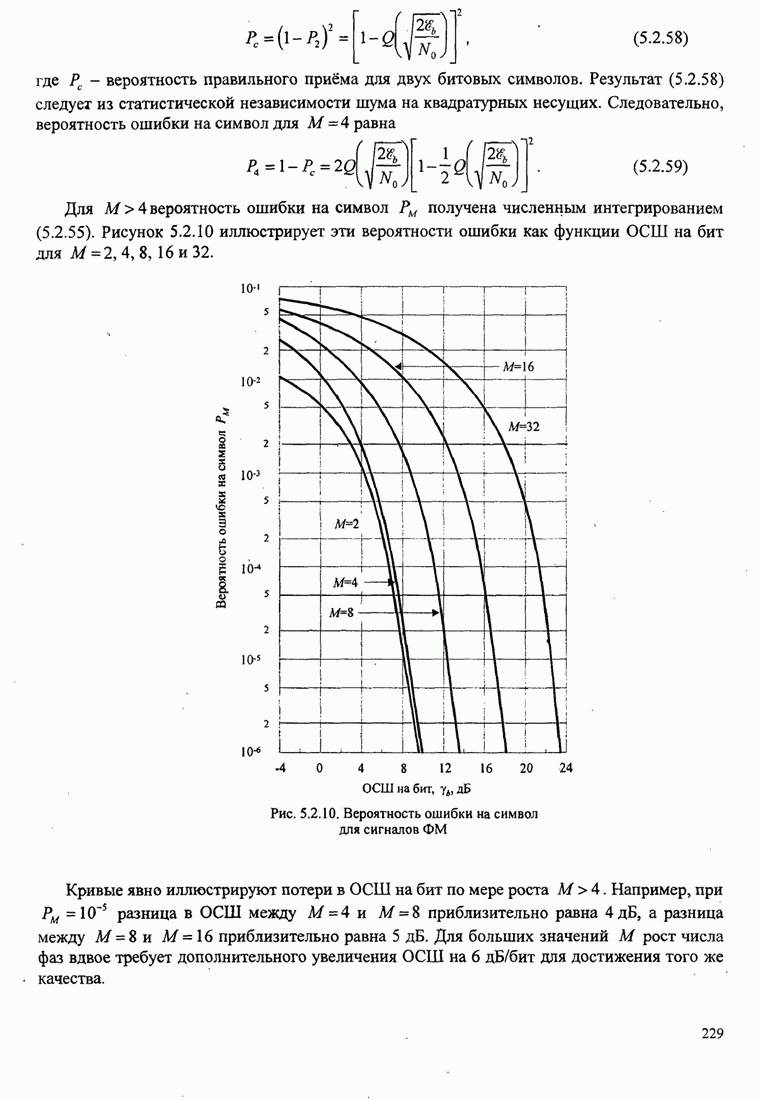
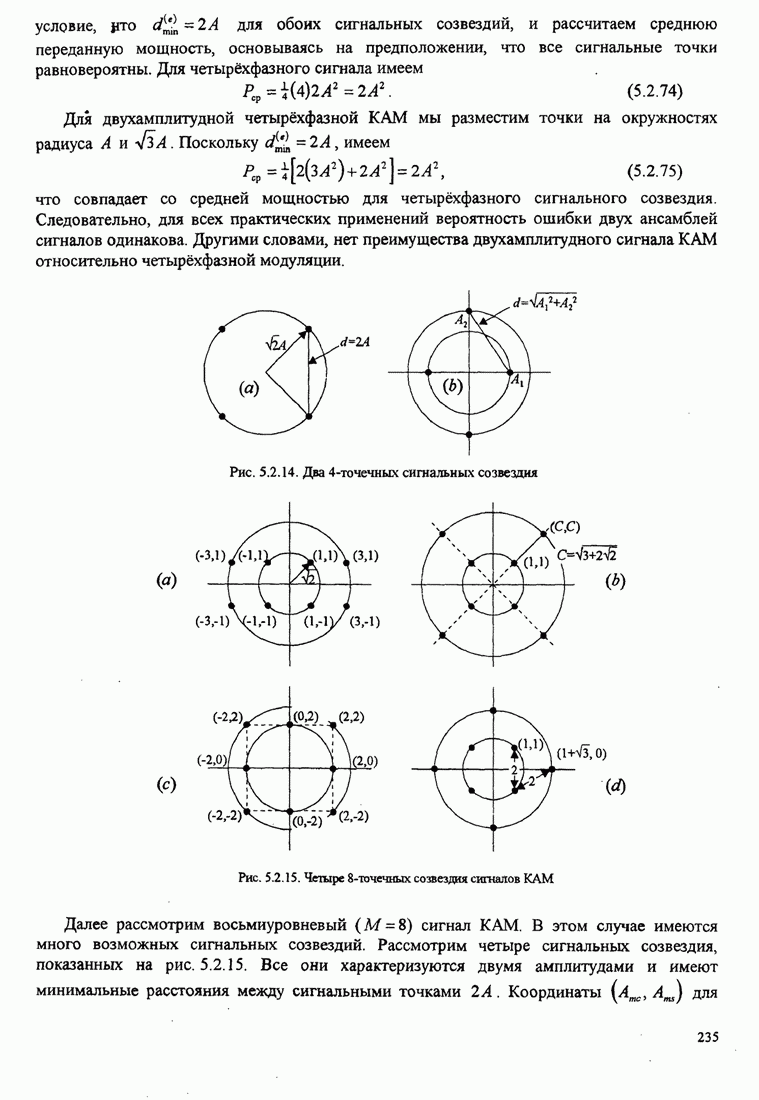
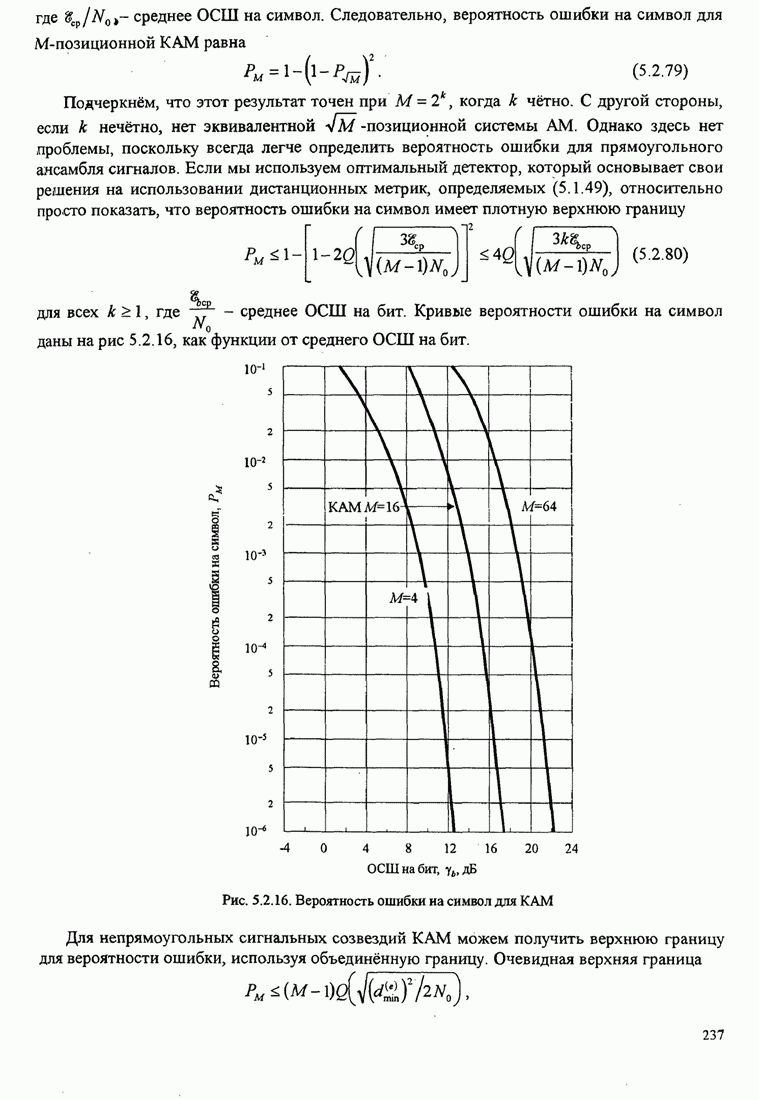
Вероятность ошибочного приёма символа. Вероятность ошибки символа для М-фазной системы сигналов равна
![]()
Если (С. 14) проинтегрировать в этих пределах, то результат равен
 (С.16)
(С.16)
Вероятность ошибки двоичных символов. Сначала рассмотрим двухфазовых
сигналов. В этом случае вероятность ошибки двоичных символов получается
интегрированием ФПВ ![]() в области
в области ![]() . Поскольку
. Поскольку ![]() - чётная функция, а сигналы априорно равновероятны, эту
вероятность молено выразить так:
- чётная функция, а сигналы априорно равновероятны, эту
вероятность молено выразить так:
![]()
Легко показать, что ![]() предполагает
предполагает ![]() и
и ![]() предполагает
предполагает ![]() . Таким образом.
. Таким образом.
 (С.17)
(С.17)
После выполнения дифференцирования,
указанного в (С.17) и вычисления результата при ![]() вероятность ошибки для двоичного
символа получается в виде
вероятность ошибки для двоичного
символа получается в виде
 (C.18)
(C.18)
Далее мы рассмотрим случай четырех
фазовых сигналов с использованием кода Грея для отображения пары двоичных
символов в определенную фазу. Снова предположив, что передаваемый сигнал ![]() становится ясно, что одиночная ошибка
совершается, когда принимаемая фаза
становится ясно, что одиночная ошибка
совершается, когда принимаемая фаза ![]() , а двойная ошибка совершается, когда
принимаемая фаза
, а двойная ошибка совершается, когда
принимаемая фаза ![]() .
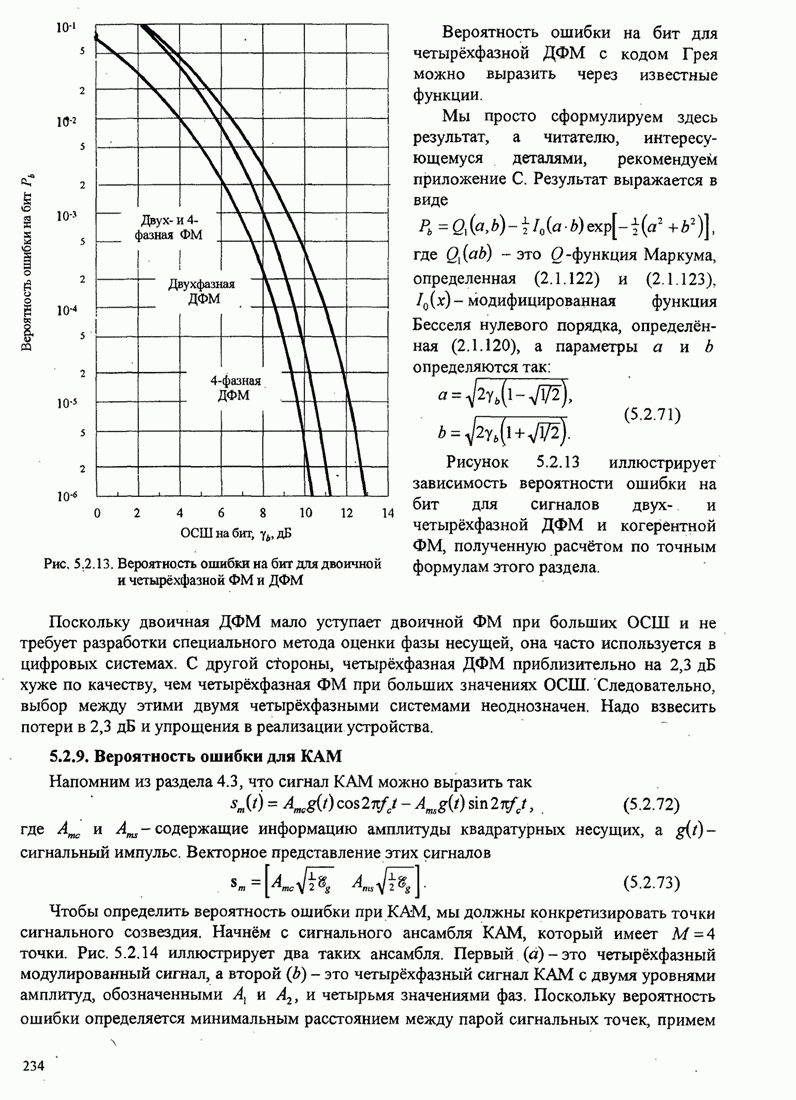
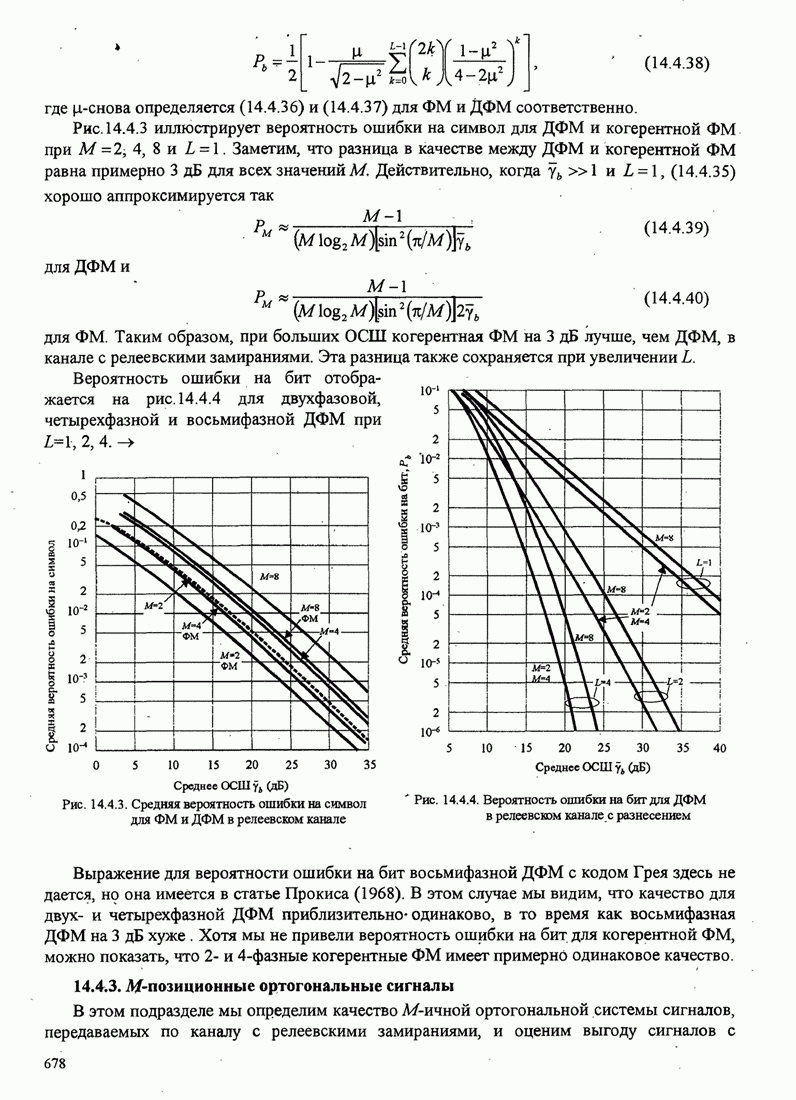
Это значит, что вероятность ошибки на бит для четырехфазовой системы символов
.
Это значит, что вероятность ошибки на бит для четырехфазовой системы символов
![]() (C.19)
(C.19)
Легко получить с учетом (С. 14) и (С, 19), что

Таким образом, окончательно для вероятности ошибки на бит для четырeхфазовых сигналов
 (C.20)
(C.20)
Заметим, что если ввести замену ![]() , выражение для
, выражение для
![]() можно
выразить через
можно
выразить через ![]() так:
так:
 (C.21)
(C.21)
Другими словами ![]() имеет тот же вид что
имеет тот же вид что ![]() , определяемое (С.18). Далее заметим,
что
, определяемое (С.18). Далее заметим,
что ![]() подобно
подобно ![]() можно интерпретировать как
коэффициент взаимной корреляции, так как при
можно интерпретировать как
коэффициент взаимной корреляции, так как при ![]() область определения
область определения ![]() . Этот простой факт
будет использован в разделе С.4.
. Этот простой факт
будет использован в разделе С.4.
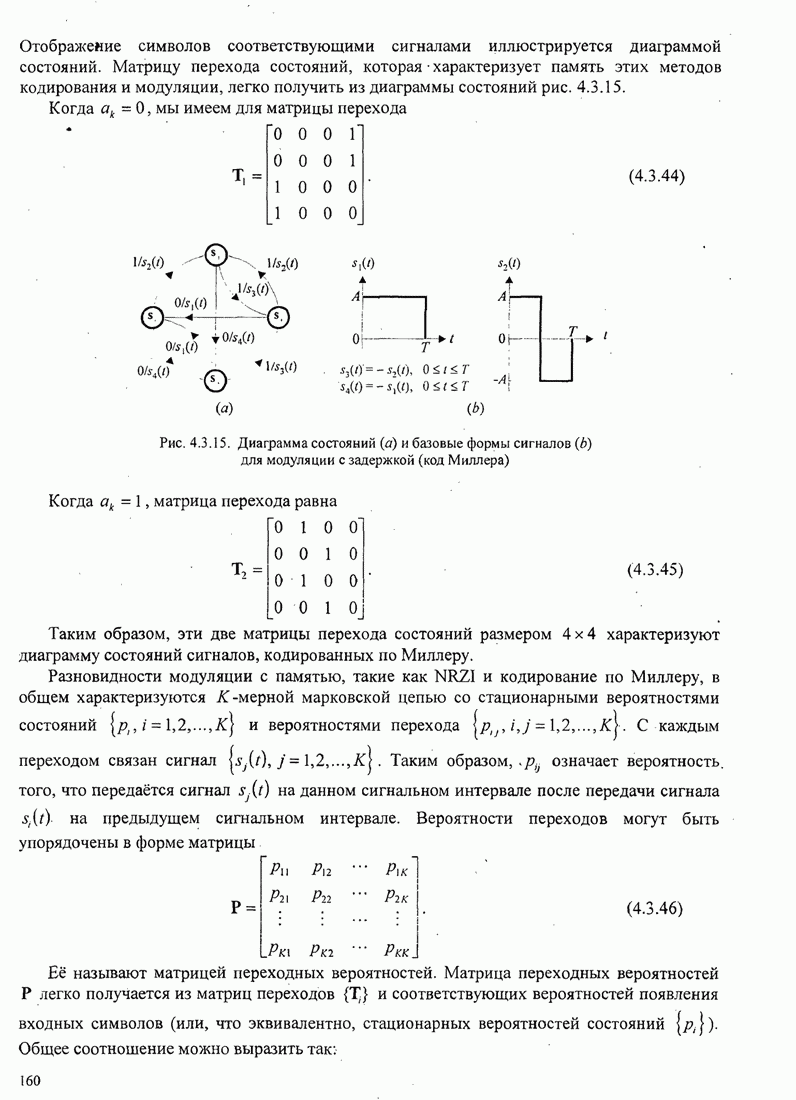
Вышеизложенная процедура получения
вероятности ошибки на бит для ![]() -фазовых сигналов с кодом Грея можно
использовать для получения результатов при
-фазовых сигналов с кодом Грея можно
использовать для получения результатов при ![]() и так далее, как показано Прокисом
(1968).
и так далее, как показано Прокисом
(1968).
Вычисление коэффициентов взаимной
корреляции.
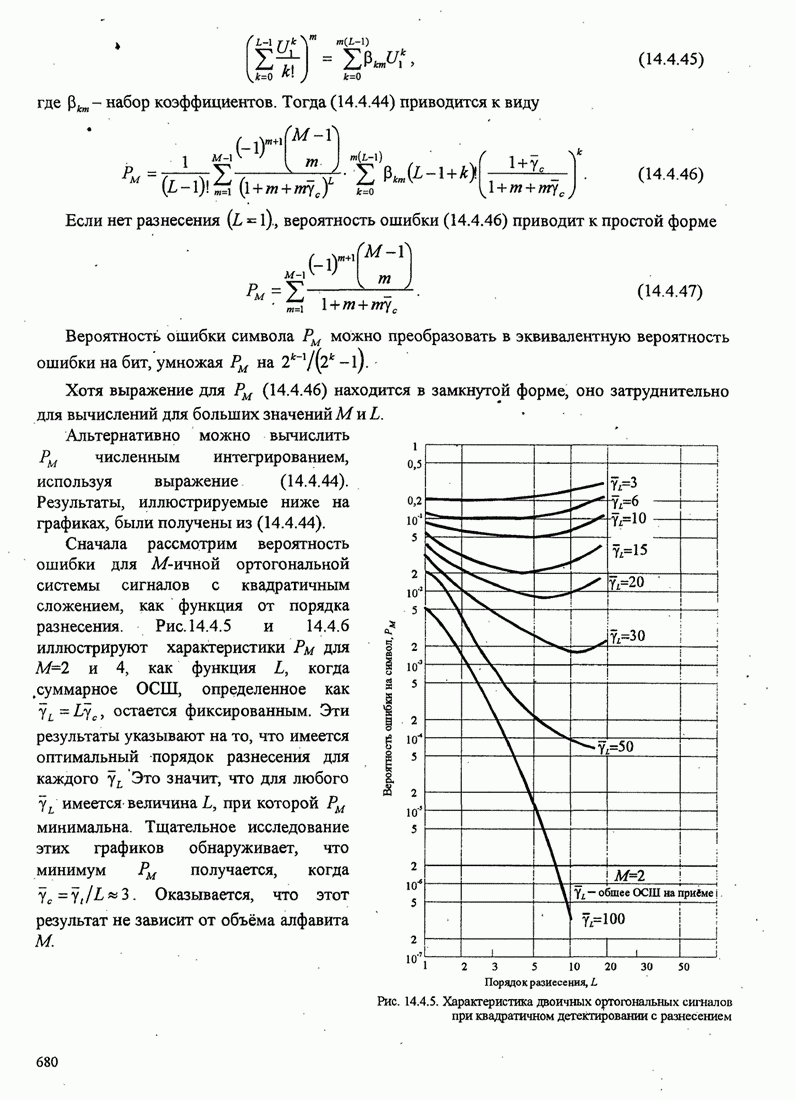
Выражение для вероятности ошибок данных выше зависит от единственного
параметра, именно, коэффициентов взаимной корреляции ![]() «ясновидящая» оценка дана
(С.5) а выход согласованного фильтра, когда передастся сигнал
«ясновидящая» оценка дана
(С.5) а выход согласованного фильтра, когда передастся сигнал ![]() равен
равен ![]() . Следовательно, коэффициент взаимной
корреляции равен
. Следовательно, коэффициент взаимной
корреляции равен
 , (С.22)
, (С.22)
где по определению
 ;
; ![]() (С.23)
(С.23)
Параметр ![]() представляет эффективное
число сигнальных интервалов, на которых формируется оценка, а
представляет эффективное
число сигнальных интервалов, на которых формируется оценка, а ![]() - это среднее ОСШ
на канале.
- это среднее ОСШ
на канале.
Для случая дифференциальной ФМ
взвешивающие коэффициенты раны ![]() для
для ![]() . Следовательно,
. Следовательно, ![]() и
и ![]() .
.
Когда ![]() , совершенная оценка равна
, совершенная оценка равна
 .
.
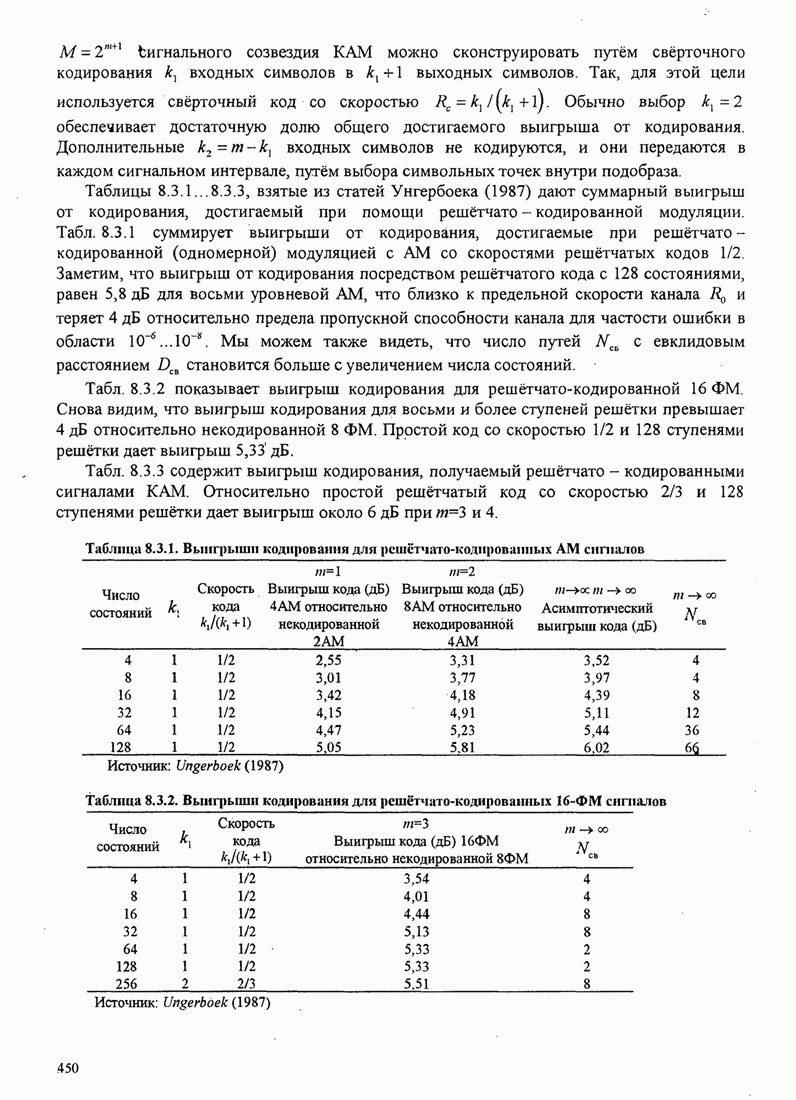
Таблица С.1. Канал с релеевскими замираниями
|
Тип оценки |
Коэффициент взаимном корреляции |
|
«ясновидящая» оценка |
|
|
Оценка по пилот-сигналу |
|
|
Дифференциальная ФМ |
|
|
Совершенная оценка |
|
Наконец, для случая оценки на основе пилот-сигнала, даваемой (С.4), коэффициент взаимной корреляции равен
 , (C.24)
, (C.24)
где по определению,
![]()
Величина ![]() , определенная выше,
приведена в таблице С.1.
, определенная выше,
приведена в таблице С.1.
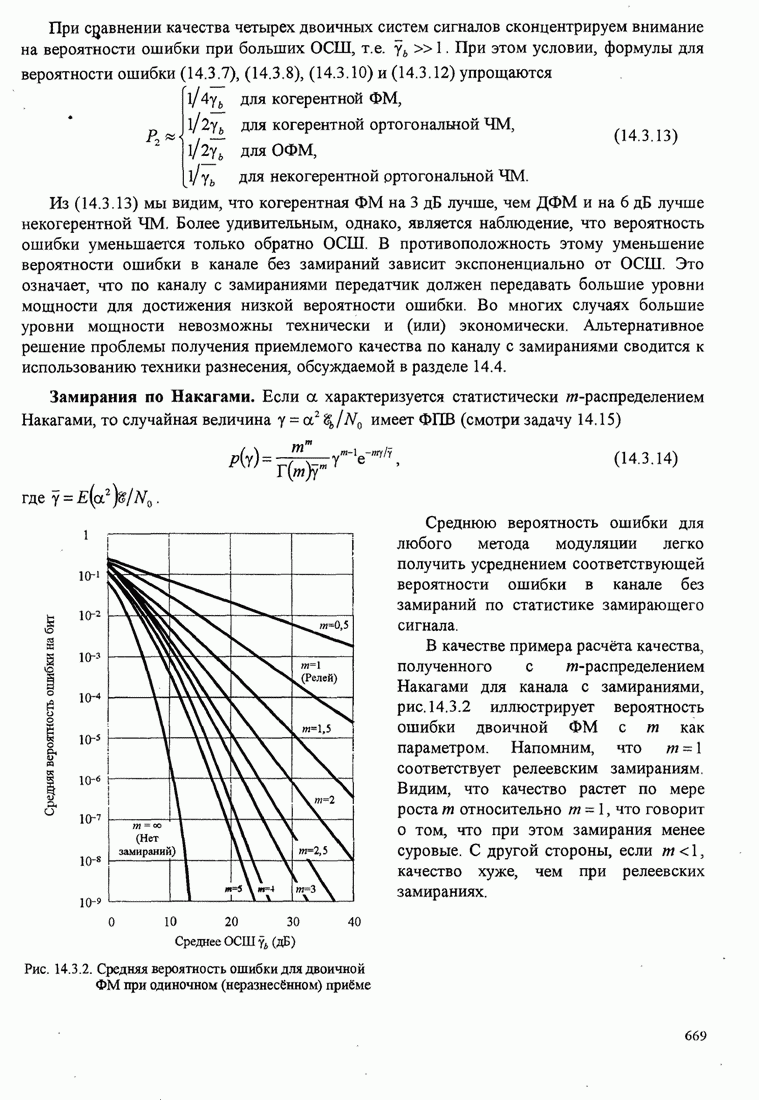
С.4. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ НЕИЗМЕННЫХ ВО ВРЕМЕНИ КАНАЛОВ И КАНАЛОВ С РАЙСОВСКИМИ ЗАМИРАНИЯМИ
В разделе С.2 комплексные
коэффициенты ослабления канала ![]() характеризовались как гауссовские
случайные величины с нулевым средним, что соответствует каналам с релеевскими
замираниями. В этом разделе коэффициенты ослабления канала
характеризовались как гауссовские
случайные величины с нулевым средним, что соответствует каналам с релеевскими
замираниями. В этом разделе коэффициенты ослабления канала ![]() предполагаются гауссовскими
случайными величинами с ненулевыми средними. Оценки коэффициентов ослабления
канала формируются демодулятором, и они используются так, как описано в разделе
С.1. Более того, величины для решения
предполагаются гауссовскими
случайными величинами с ненулевыми средними. Оценки коэффициентов ослабления
канала формируются демодулятором, и они используются так, как описано в разделе
С.1. Более того, величины для решения ![]() опять-таки определяются (С.2). Однако
в рассматриваемом случае гауссовские случайные величины
опять-таки определяются (С.2). Однако
в рассматриваемом случае гауссовские случайные величины ![]() и
и ![]() , которые определяют выходы согласных
фильтров и оценок, соответственно, для
, которые определяют выходы согласных
фильтров и оценок, соответственно, для ![]() -го канала, имеют ненулевые средние,
обозначаемые
-го канала, имеют ненулевые средние,
обозначаемые ![]() и
и ![]() . Далее, вторые моменты равны
. Далее, вторые моменты равны

а нормированная ковариация равна
 .
.
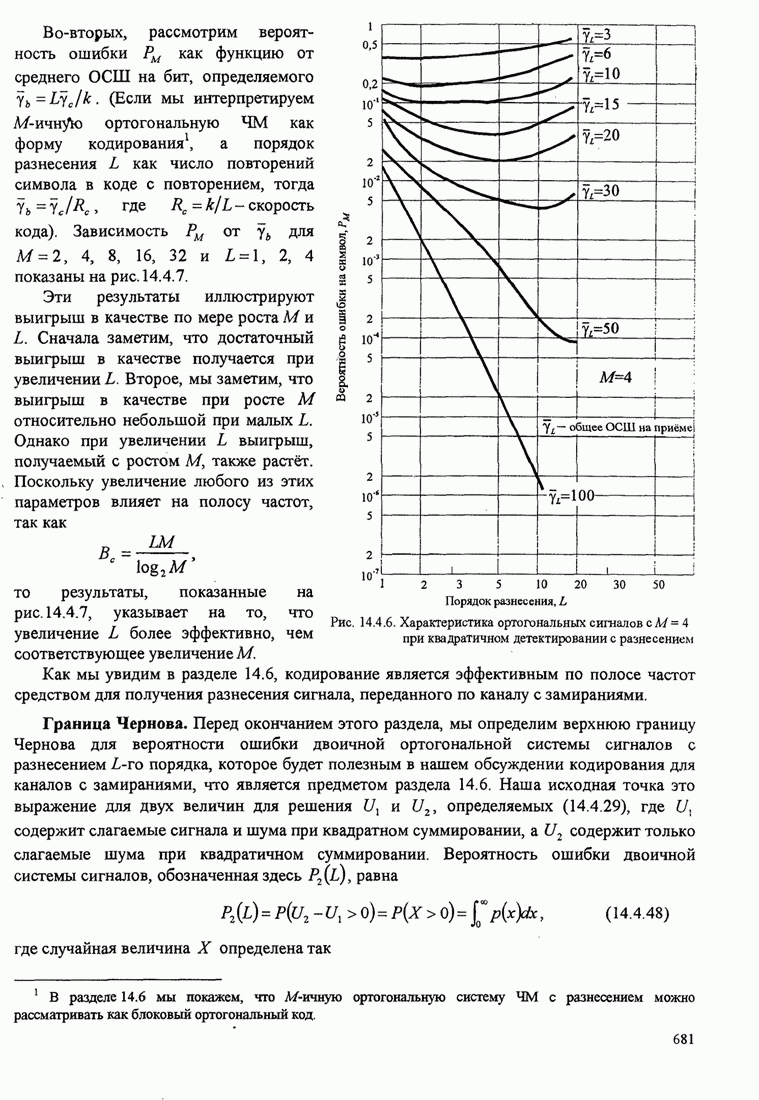
Для этой модели канала ниже даны
вероятности ошибка только для двух- и четырехфазовых сигналов. Мы интересуемся
частным случаем, когда флуктуирующие компоненты каждого из канальных ослаблений
![]() отсутствуют, так что каналы неизменны
во времени. Если дополнительно к неизменности во времени параметров канала шумы
оценки и выхода согласованного фильтра не коррелированны, то
отсутствуют, так что каналы неизменны
во времени. Если дополнительно к неизменности во времени параметров канала шумы
оценки и выхода согласованного фильтра не коррелированны, то ![]() .
.
В общем случае вероятность ошибки
передачи двухфазовых сигналов по статистически независимым ![]() каналам, характеризуемым
так, как описано выше, можно получить из результатов приложения В. В наиболее
общем виде выражение для вероятности ошибки двоичной системы символов
каналам, характеризуемым
так, как описано выше, можно получить из результатов приложения В. В наиболее
общем виде выражение для вероятности ошибки двоичной системы символов

![]() ,
,
где, по определению.

![]()
где ![]() - модифицированная функция Бесселя
первого ряда порядка
- модифицированная функция Бесселя
первого ряда порядка ![]() .
.
Определим константы а и b , когда канал неизменен во времени, ![]() , а оценка ослабления канала
и фазы даны в разделе С.1. Напомним, что когда передается
, а оценка ослабления канала
и фазы даны в разделе С.1. Напомним, что когда передается ![]() выход согласованного
фильтра
выход согласованного
фильтра ![]() ,
«ясновидящая» оценка дана (С.5). Следовательно, для этой оценки моменты равны
,
«ясновидящая» оценка дана (С.5). Следовательно, для этой оценки моменты равны ![]() где
где ![]() - энергия сигнал,
- энергия сигнал, ![]() - значение
спектральной плотности шума, a
- значение
спектральной плотности шума, a ![]() определено (С.23).
Подстановка этих моментов в (С.26) дает следующее выражение для
определено (С.23).
Подстановка этих моментов в (С.26) дает следующее выражение для ![]() и
и ![]()
![]() (С.27)
(С.27)
Этот результат первоначально полнен Прайсом (1962).
Вероятность ошибки для
дифференциальной ФМ можно получить, положив ![]() в (С.27).
в (С.27).
Далее рассмотрим оценку по пилот
сигналу, В этом случае оценка дается (С.4), а выход согласованного фильтра
снова ![]() . Если
вычислить моменты и их подставить в (С.26) получаются следующие выражения для
. Если
вычислить моменты и их подставить в (С.26) получаются следующие выражения для ![]() и
и ![]() :
:
 , (С.28)
, (С.28)
где
![]() .
.
Наконец, рассмотрим вероятность
ошибки при передаче четырехфазовой системы сигналов по неизменному во времени
каналу, при условии ![]() . Один из подходов, который можно
использовать для определения вероятности ошибки сводится к определению ФПВ 0 и
затем к ее интегрированию по соответствующей области значений
. Один из подходов, который можно
использовать для определения вероятности ошибки сводится к определению ФПВ 0 и
затем к ее интегрированию по соответствующей области значений ![]() . К сожалению,
такой подход математически трудно осуществить. Вместо этого можно использовать
простой, хотя и обходной метод, включающий преобразование Лапласа. Интеграл
(14.4.14), который связывает вероятность ошибки
. К сожалению,
такой подход математически трудно осуществить. Вместо этого можно использовать
простой, хотя и обходной метод, включающий преобразование Лапласа. Интеграл
(14.4.14), который связывает вероятность ошибки ![]() в канале с АБГШ с вероятностью ошибки
в канале с АБГШ с вероятностью ошибки
![]() в канале
с релеевскими замираниями, является преобразованием Лапласа. Поскольку
вероятность ошибки на бит
в канале
с релеевскими замираниями, является преобразованием Лапласа. Поскольку
вероятность ошибки на бит ![]() и
и ![]() для
канала с релеевским замираниями, определяемые (С.18) и (С.21) соответственно
имеет туже форму, но отличается только коэффициентом корреляции, то следует,
что вероятность ошибки на бит для неизмененного во времени канала также имеет
туже форму. Это значит, что (С.25) с
для
канала с релеевским замираниями, определяемые (С.18) и (С.21) соответственно
имеет туже форму, но отличается только коэффициентом корреляции, то следует,
что вероятность ошибки на бит для неизмененного во времени канала также имеет
туже форму. Это значит, что (С.25) с ![]() является также выражением для
вероятности ошибки на бит для четырех фазовой системы сигналов с
модифицированными параметрами а и b, отражающими разницу коэффициентов корреляции. Дальнейшие исследования
можно найти в статье Прокиса (1968). Выражение для
является также выражением для
вероятности ошибки на бит для четырех фазовой системы сигналов с
модифицированными параметрами а и b, отражающими разницу коэффициентов корреляции. Дальнейшие исследования
можно найти в статье Прокиса (1968). Выражение для ![]() и
и ![]() даны в таблице С.2.
даны в таблице С.2.
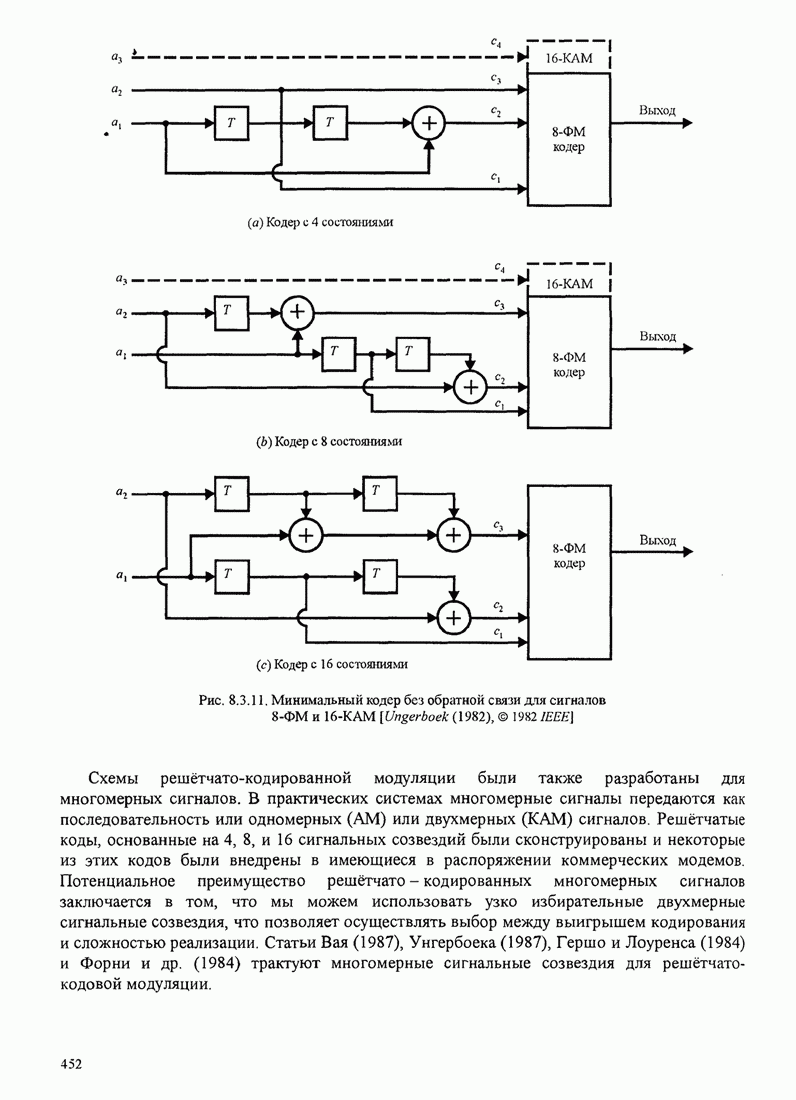
Таблица С.2. Канал, неизменный во времени
|
Тип оценки |
а |
b |
|
|
Двоичная ФМ |
|
|
«яновидящая» оценка |
|
|
|
Дифференциальная ФМ |
0 |
|
|
Оценка по пилот-сигналу |
|
|
|
|
4-позиционная ФМ |
|
|
«яновидящая» оценка |
|
|
|
Дифференциальная ФМ |
|
|
|
Оценка по пилот-сигналу |
|
|
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
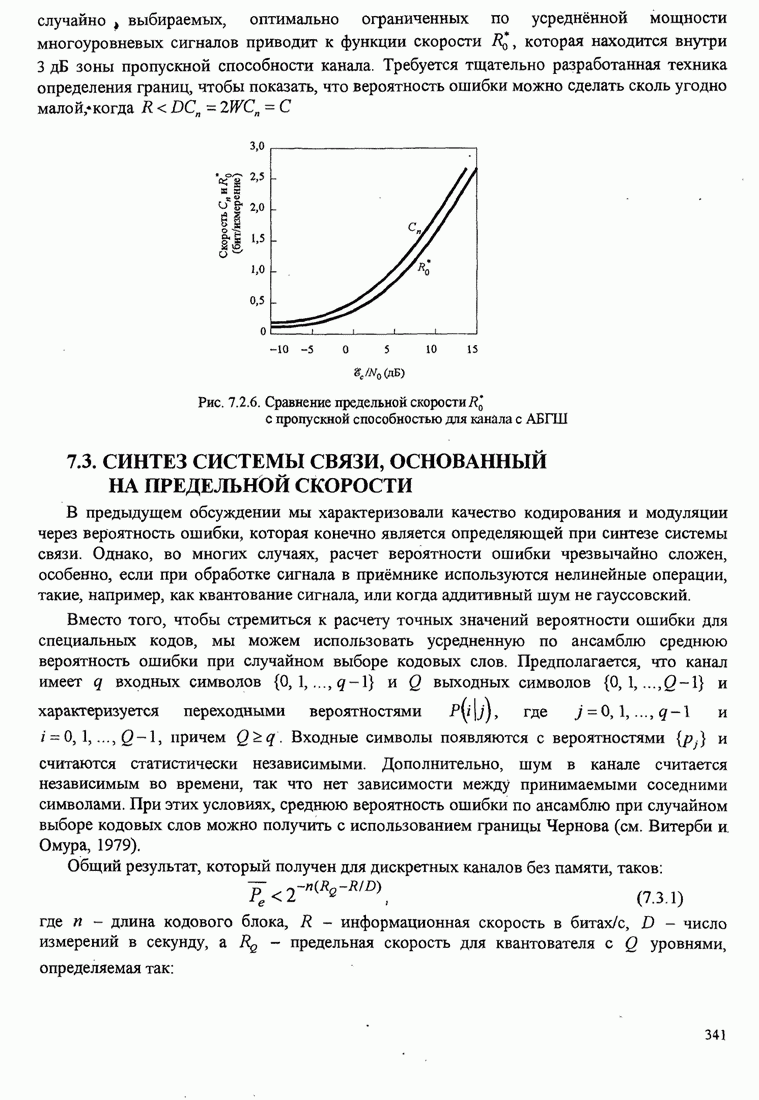
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
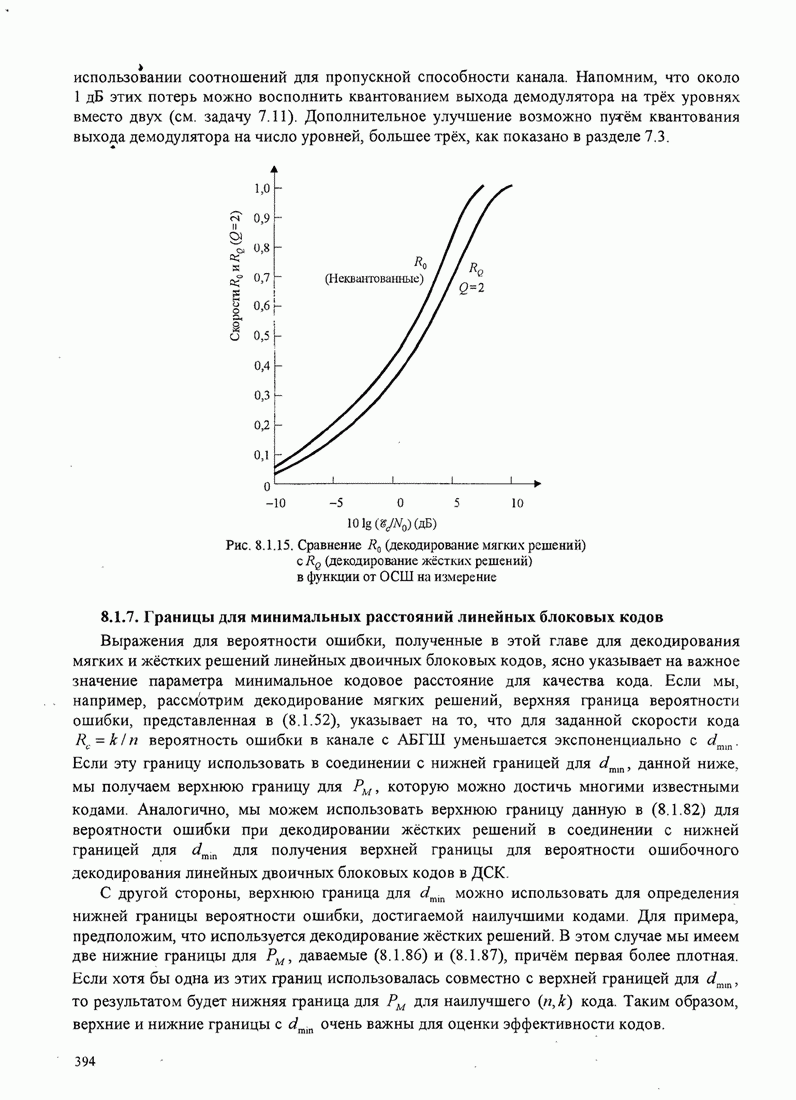
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
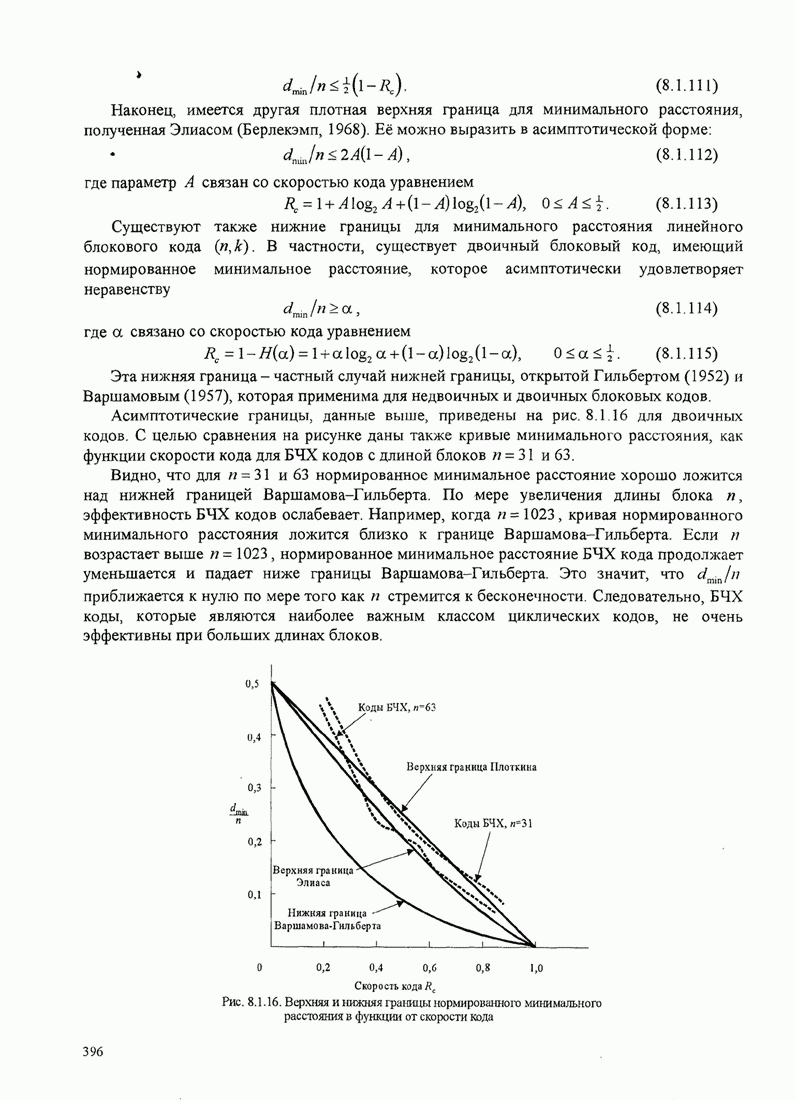
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
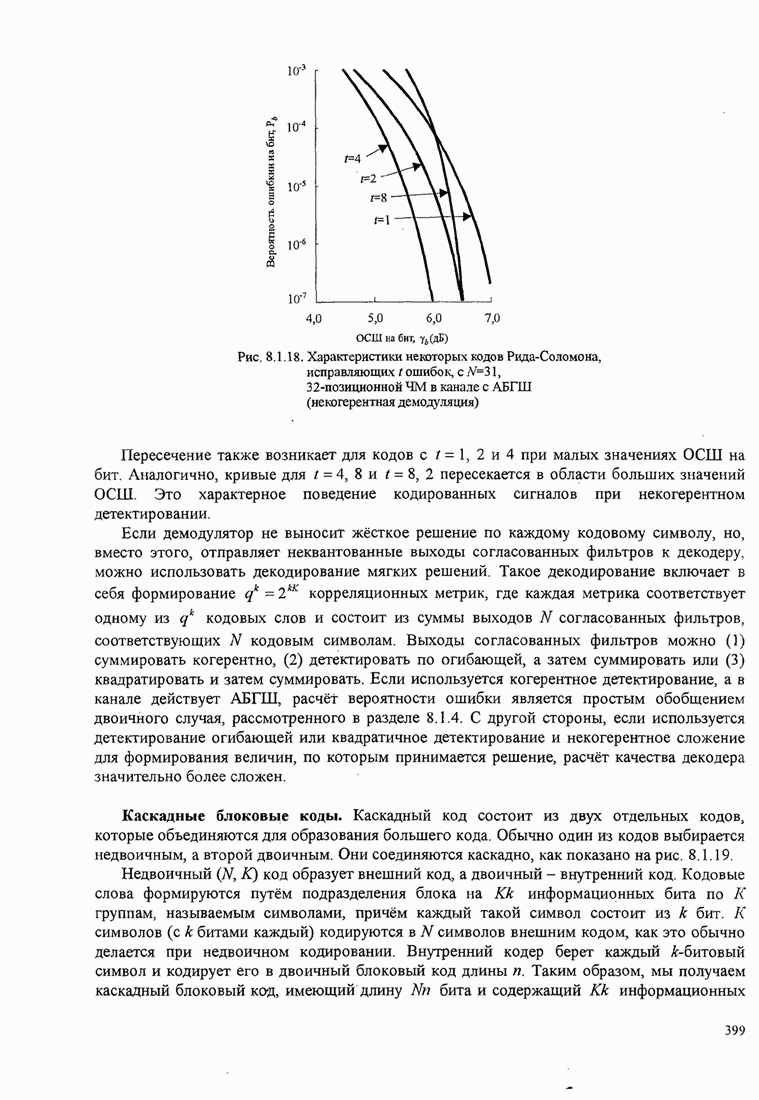
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
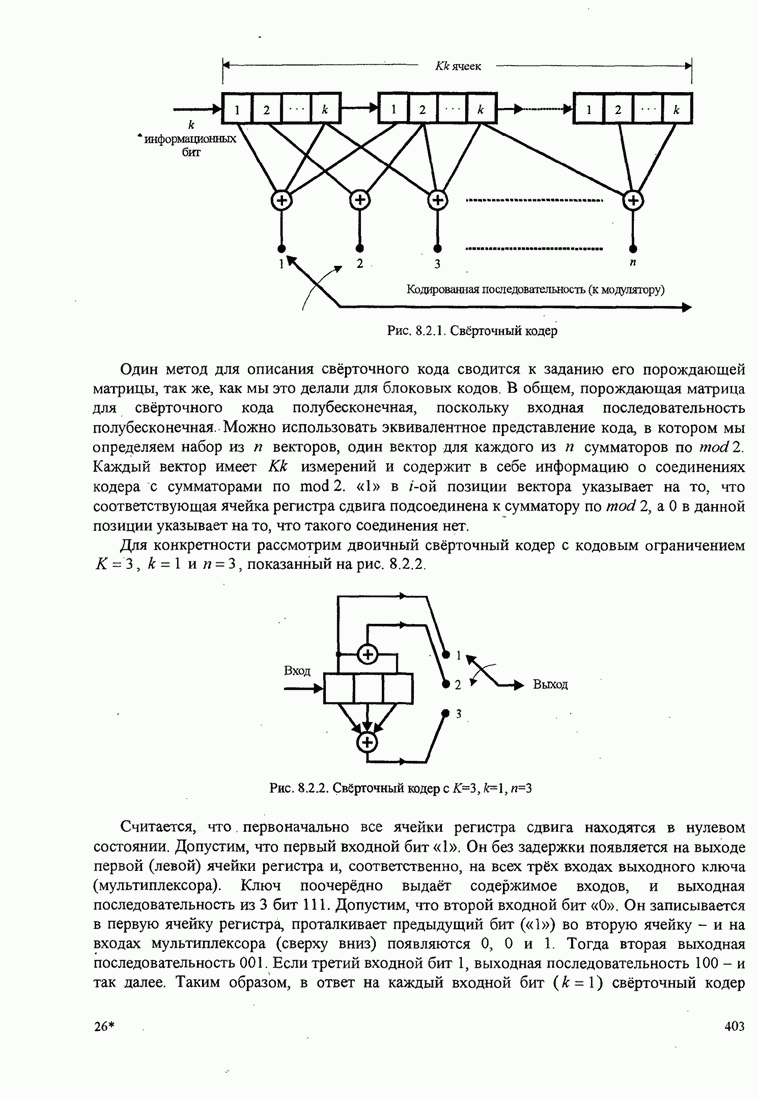
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
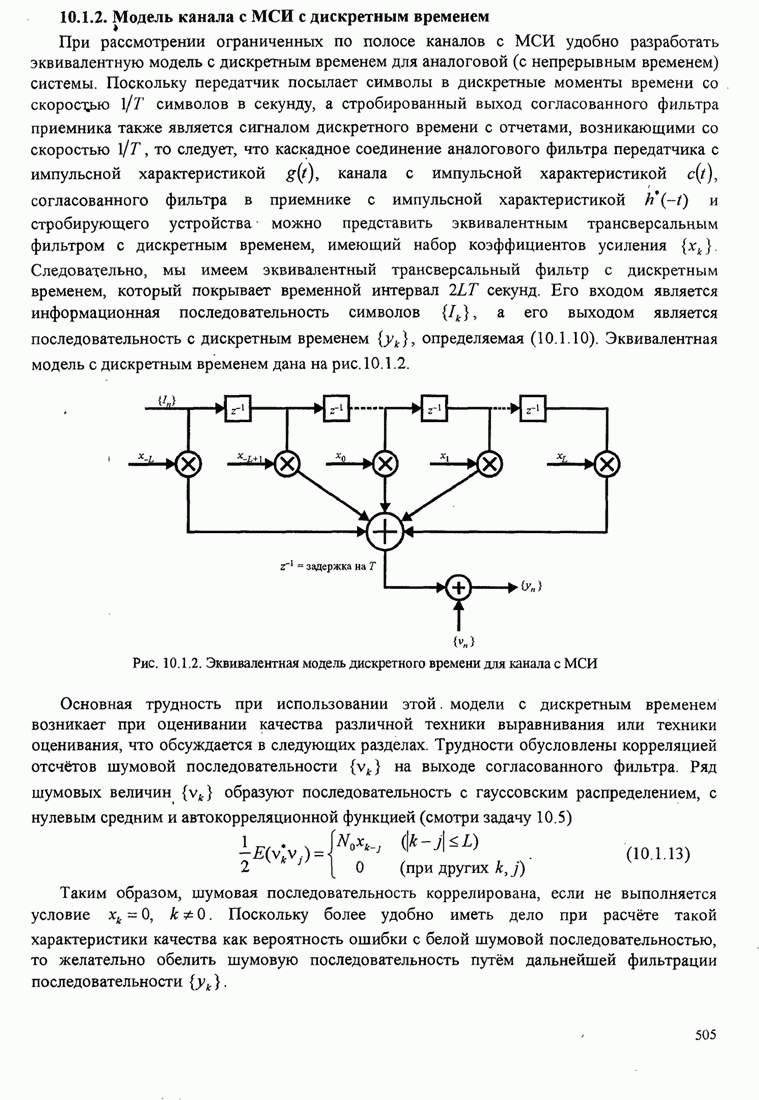
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
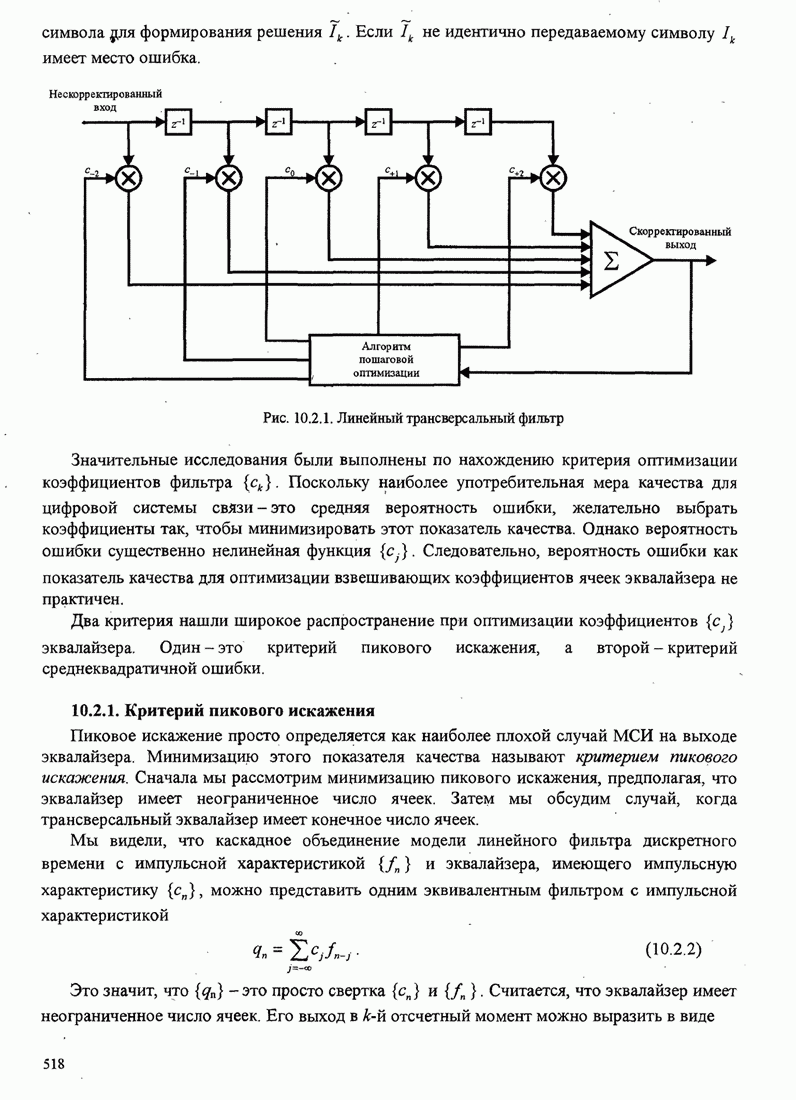
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
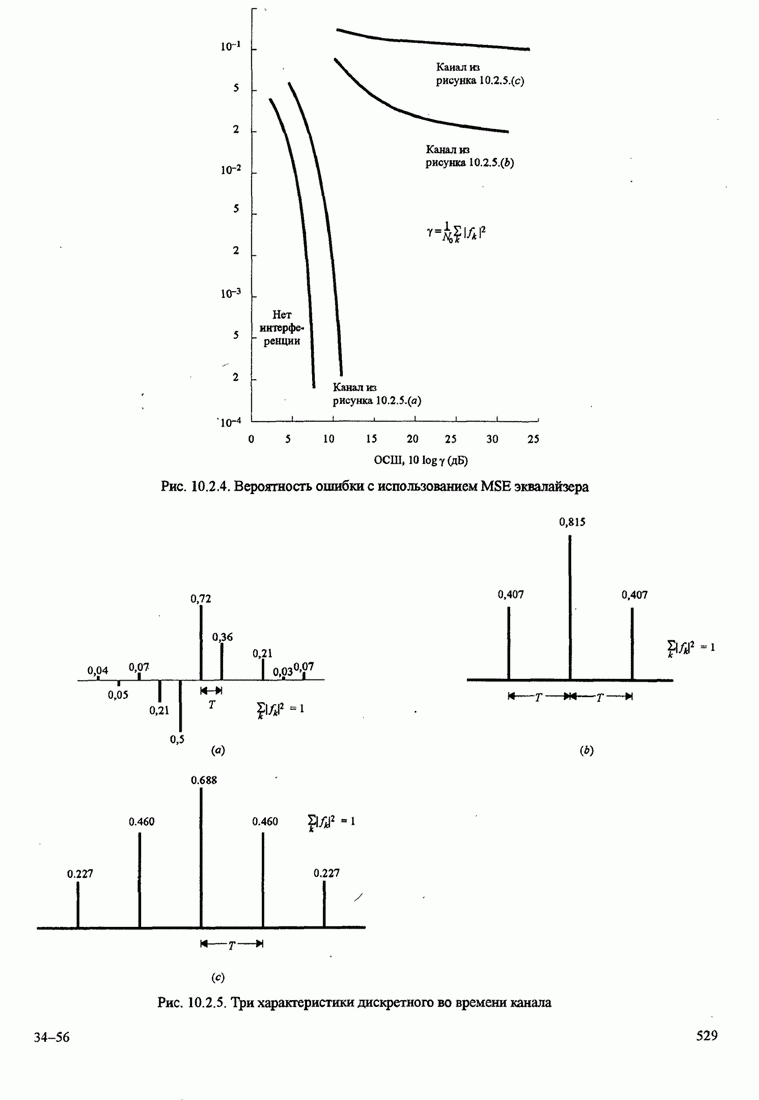
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
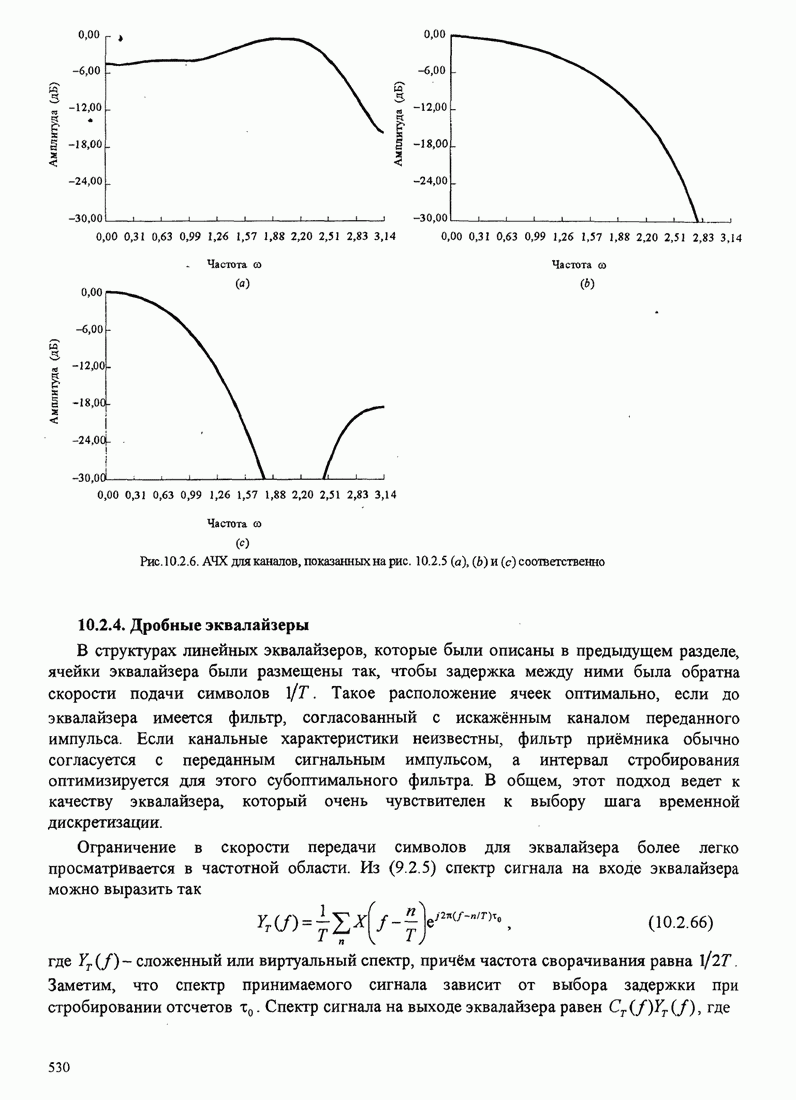
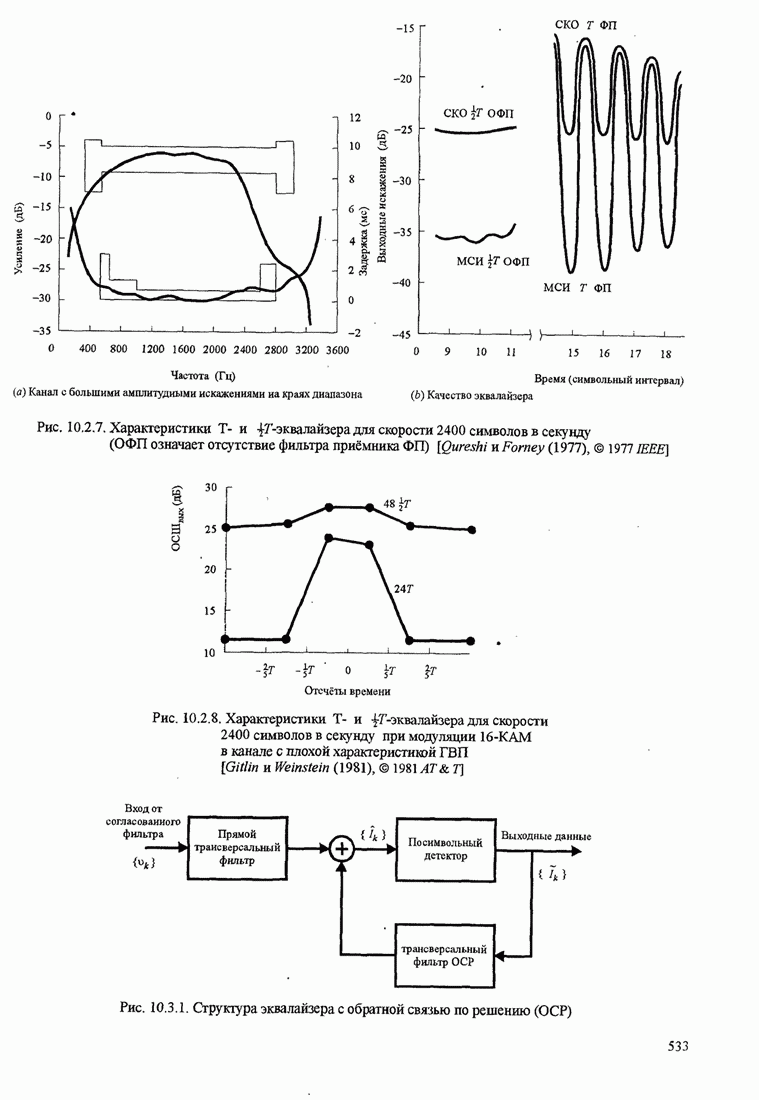
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
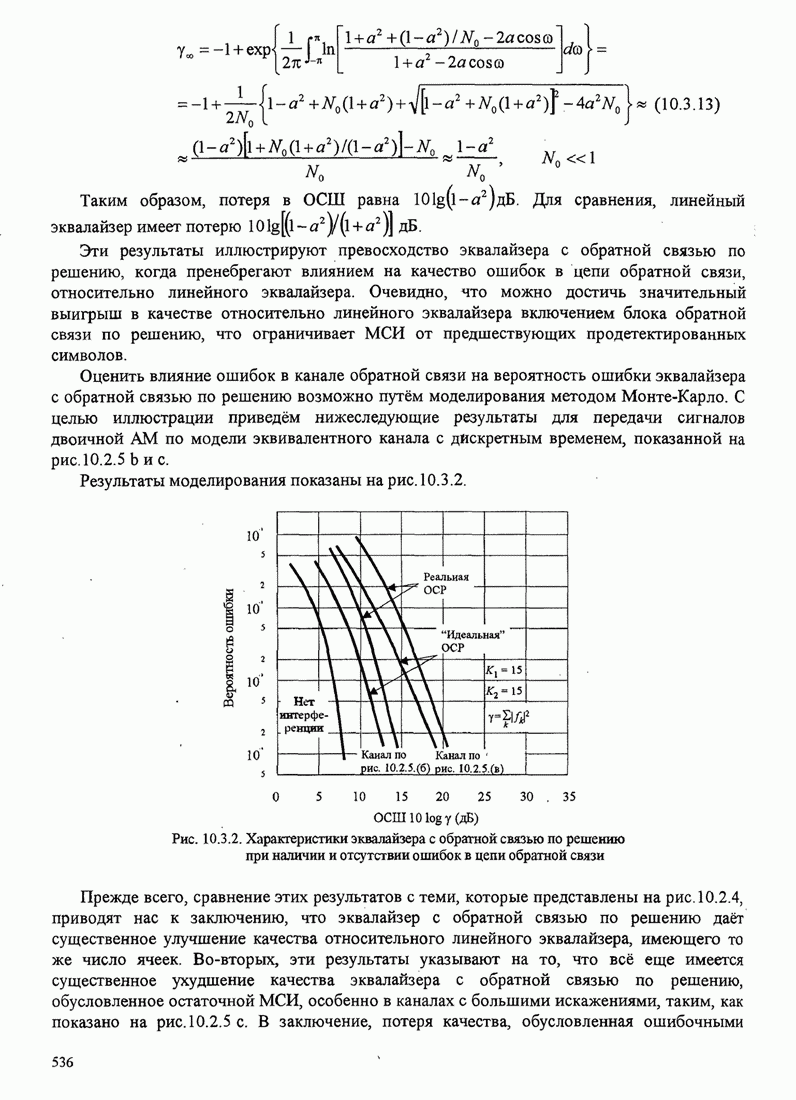
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
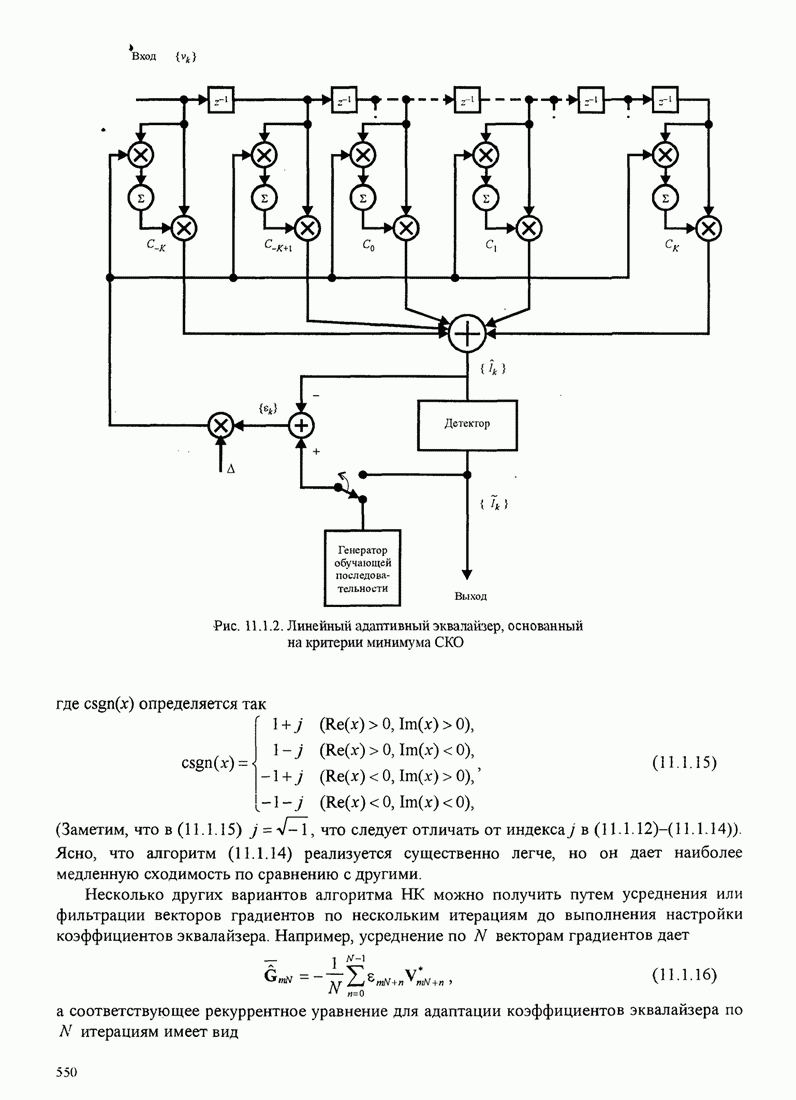
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
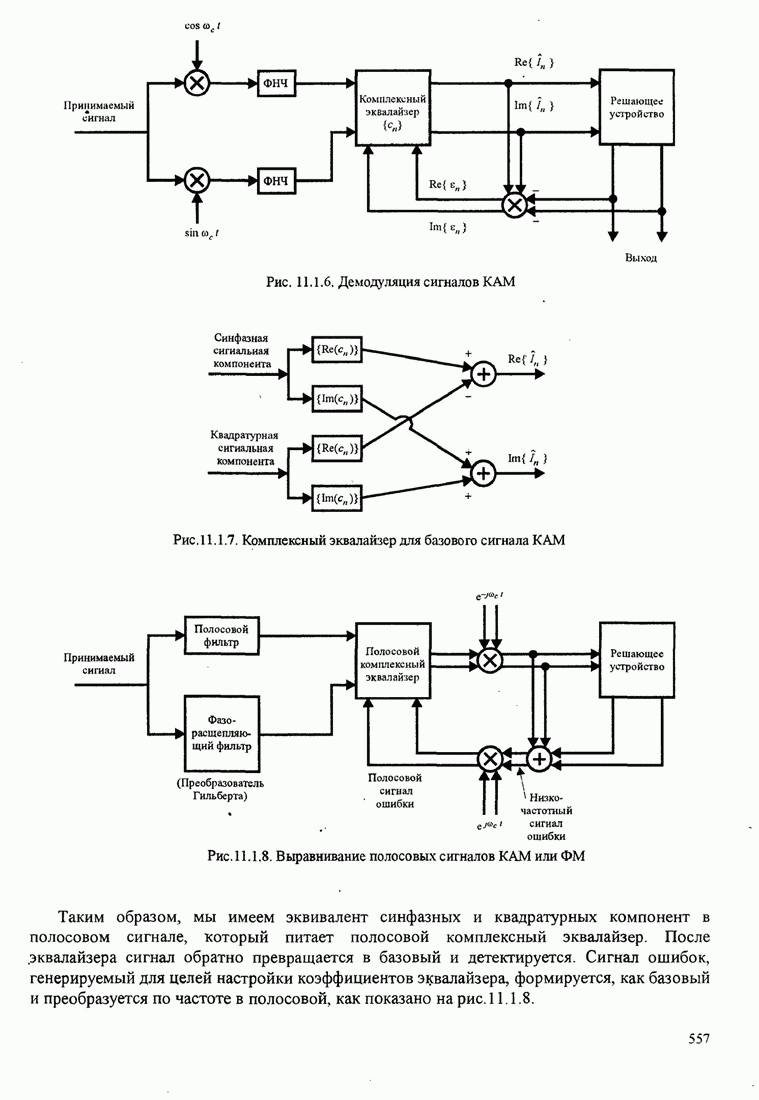
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
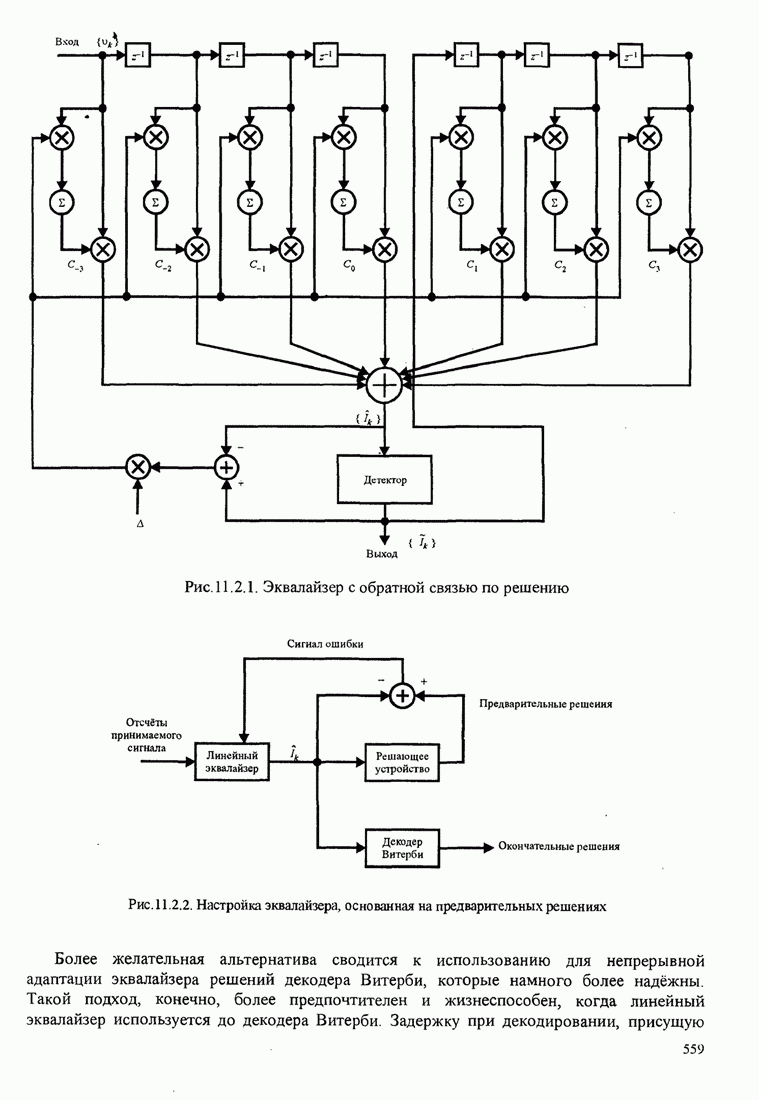
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
- 14.4.2. Многофазные сигналы
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)