| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
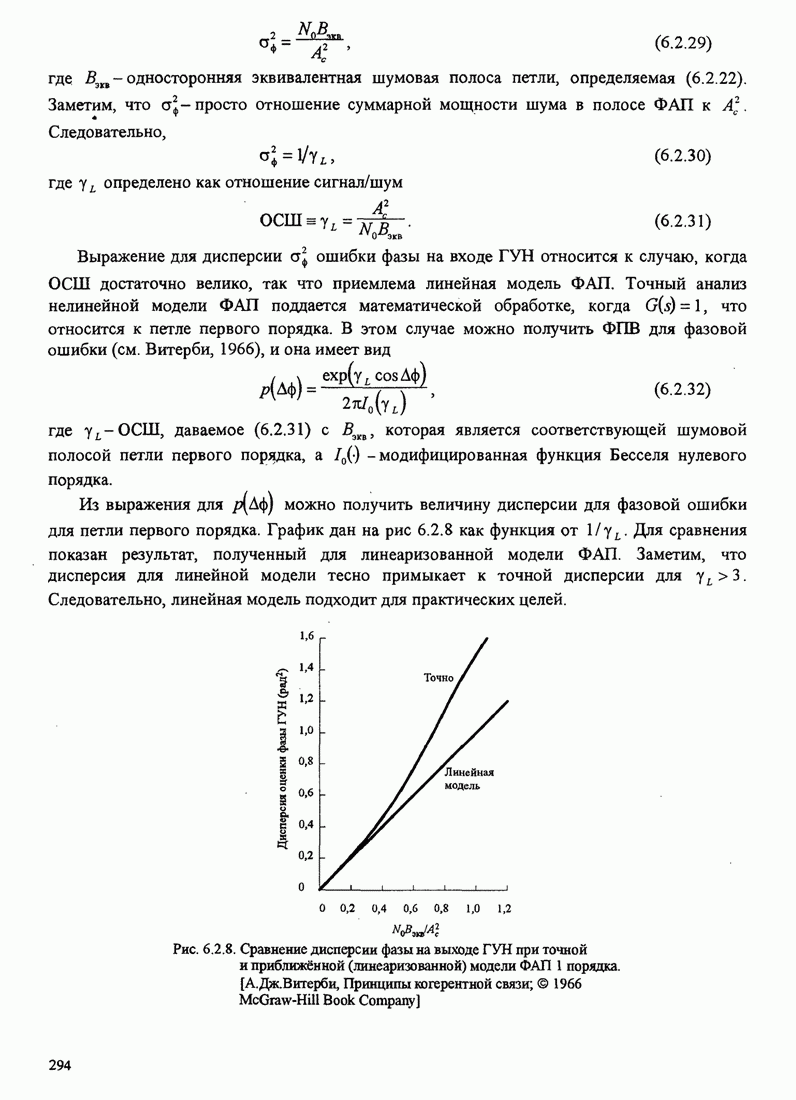
6.2.5. Петли, не управляемые решениями
Вместо использования схемы, управляемой решениями
для получения оценки фазы, можно трактовать данные как случайные величины и
просто усреднить ![]() по
этим случайным величинам до её максимизации. Чтобы выполнить такое усреднение,
можно использовать или действительную функцию распределения вероятностей
данных, если она известна, или можно предположить некоторое распределение
вероятностей, которое является подходящим приближением для правильного
распределения. Следующие примеры демонстрируют первый подход.
по
этим случайным величинам до её максимизации. Чтобы выполнить такое усреднение,
можно использовать или действительную функцию распределения вероятностей
данных, если она известна, или можно предположить некоторое распределение
вероятностей, которое является подходящим приближением для правильного
распределения. Следующие примеры демонстрируют первый подход.
Пример 6.2.2. Предположим, что сигнал
двоичной линейной модуляции ![]() является вещественным. Тогда на
сигнальном интервале мы можем написать
является вещественным. Тогда на
сигнальном интервале мы можем написать
![]()
где ![]() с равными вероятностями. Ясно, что
ФПВ для
с равными вероятностями. Ясно, что
ФПВ для ![]() равна
равна
![]() .
.
Теперь функция правдоподобия ![]() , определяемая (6.2.9),
является условной при заданном значении
, определяемая (6.2.9),
является условной при заданном значении ![]() , и её следует усреднять по этим двум
значениям. Таким образом,
, и её следует усреднять по этим двум
значениям. Таким образом,

а соответствующий логарифм функции правдоподобия
 (6.2.44)
(6.2.44)
Если продифференцируем ![]() и приравняем производную
нулю, получим МП оценку для фазы, не управляемую решениями (оценивание, не
управляемое решениями - ОНУР, NDDE). К сожалению, функциональное отношение в
(6.2.44) существенно нелинейно, и, следовательно, точное решение трудно получить.
С другой стороны, возможна аппроксимация. В частности,
и приравняем производную
нулю, получим МП оценку для фазы, не управляемую решениями (оценивание, не
управляемое решениями - ОНУР, NDDE). К сожалению, функциональное отношение в
(6.2.44) существенно нелинейно, и, следовательно, точное решение трудно получить.
С другой стороны, возможна аппроксимация. В частности,
 (6.2.45)
(6.2.45)
С этой аппроксимацией решение для ![]() получается в
трактуемом виде.
получается в
трактуемом виде.
В этом примере мы усреднили по двум возможным
значениям амплитуды информационных символов. Если информационные символы ![]() -позиционные, а
-позиционные, а ![]() велико, операция
усреднения содержит нелинейные функции высокого порядка от параметра, который
оценивается. В этом случае мы можем упростить проблему, предположив, что
амплитуды информационных символов являются непрерывными случайными величинами.
Например, мы можем предположить, что они подчиняются гауссовскому распределению
с нулевым средним. Следующие примеры иллюстрируют эту аппроксимацию и
результирующую форму для усредненной функции правдоподобия.
велико, операция
усреднения содержит нелинейные функции высокого порядка от параметра, который
оценивается. В этом случае мы можем упростить проблему, предположив, что
амплитуды информационных символов являются непрерывными случайными величинами.
Например, мы можем предположить, что они подчиняются гауссовскому распределению
с нулевым средним. Следующие примеры иллюстрируют эту аппроксимацию и
результирующую форму для усредненной функции правдоподобия.
Пример 6.2.3. Рассмотрим тот же сигнал, что
в примере 6.2.2, но теперь предположим, что амплитуда ![]() является гауссовской, с
нулевым средним и единичной дисперсией, т.е.
является гауссовской, с
нулевым средним и единичной дисперсией, т.е.
![]()
Если мы усредним ![]() по заданной ФПВ
по заданной ФПВ ![]() , получим для усреднённой
функции правдоподобия
, получим для усреднённой
функции правдоподобия
 (6.2.46)
(6.2.46)
и соответствующий логарифм усреднённой функции правдоподобия
 (6.2.47)
(6.2.47)
Теперь мы можем получить МП оценку для ![]() путём
дифференцирования
путём
дифференцирования ![]() и приравнивания результата нулю.
и приравнивания результата нулю.
Интересно отметить, что логарифм усреднённой
функции правдоподобия является квадратичным при гауссовском предположении, а
также то, что он имеет квадратичную аппроксимацию, определённую (6.2.45), для
малых значений взаимной корреляции ![]() и
и ![]() . Другими словами, если
взаимная корреляция на одном интервале мала, гауссовское предположение для
распределения амплитуд информационных символов даёт хорошую аппроксимацию для
логарифма усреднённой функции правдоподобия.
. Другими словами, если
взаимная корреляция на одном интервале мала, гауссовское предположение для
распределения амплитуд информационных символов даёт хорошую аппроксимацию для
логарифма усреднённой функции правдоподобия.
С точки зрения этих результатов мы можем
использовать гауссовскую аппроксимацию на все символы на интервале![]() .
Конкретнее, предположим, что
.
Конкретнее, предположим, что ![]() информационных символов статистически
независимы и одинаково распределены. При усреднении функции правдоподобия
информационных символов статистически
независимы и одинаково распределены. При усреднении функции правдоподобия ![]() по гауссовской ФПВ
на каждом из
по гауссовской ФПВ
на каждом из ![]() символов
на интервале
символов
на интервале ![]() получаем
результат
получаем
результат
 (6.2.48)
(6.2.48)
Если мы возьмём логарифм от (6.2.48), продифференцируем его и приравняем результат нулю, получим условие для МП оценки в виде
![]() (6.2.49)
(6.2.49)
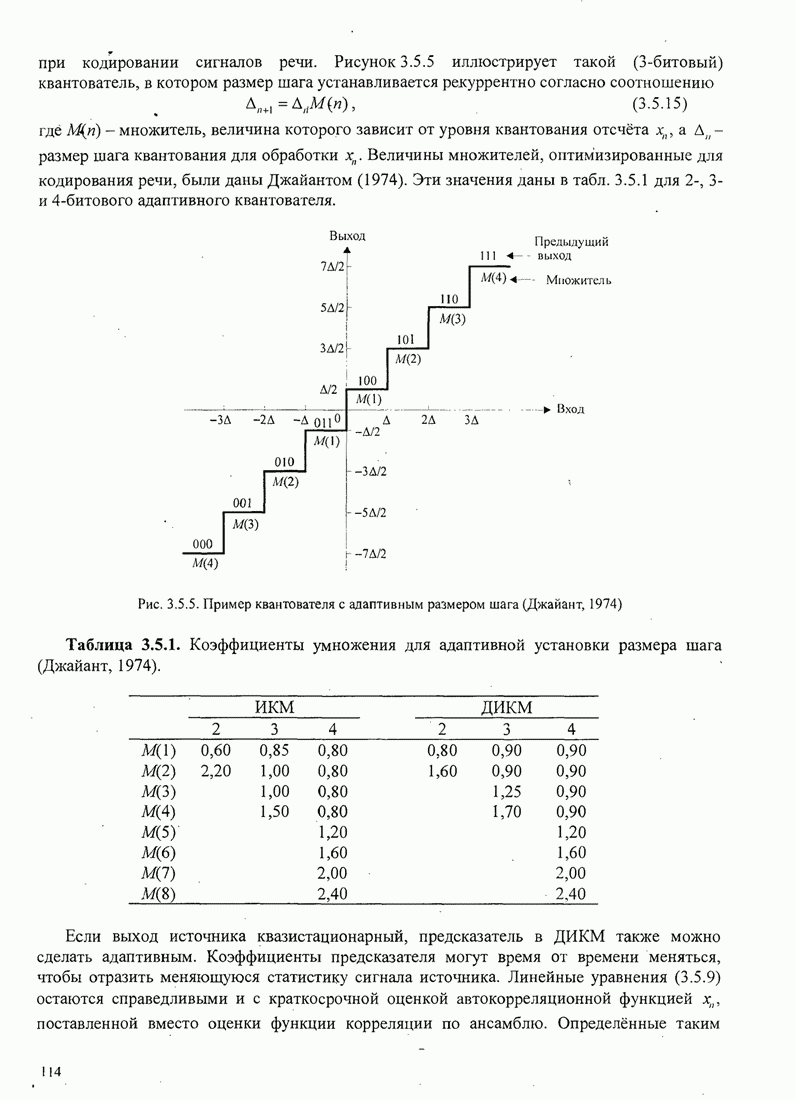
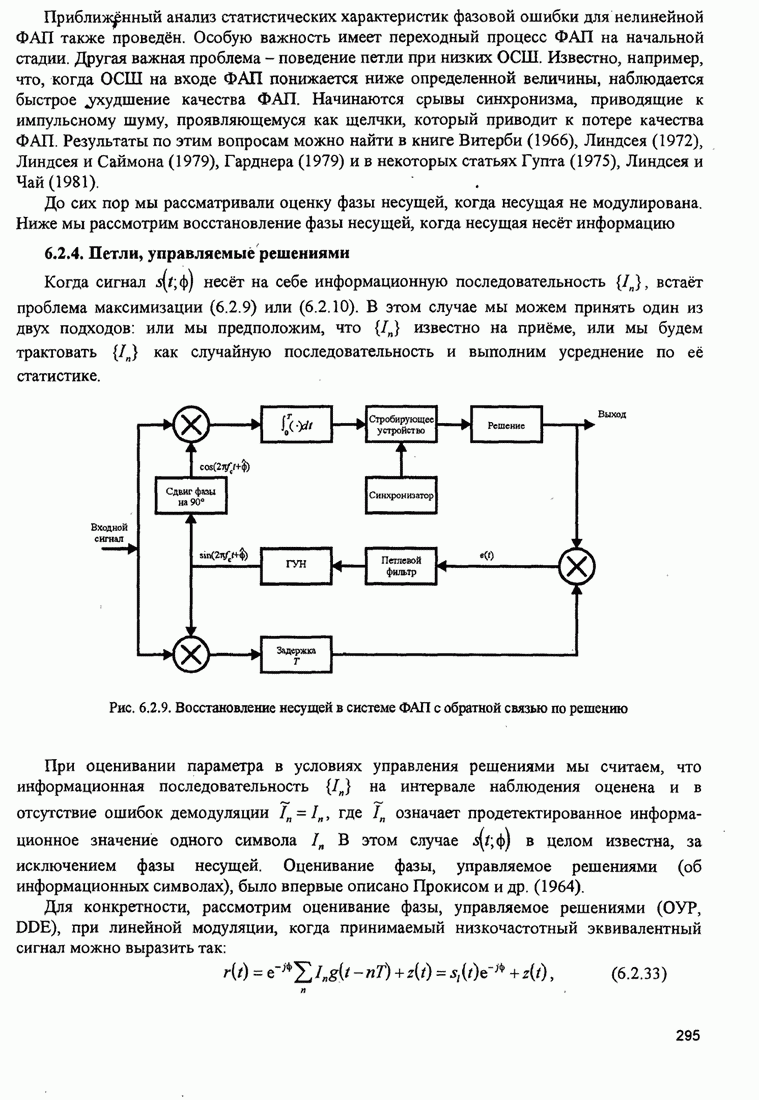
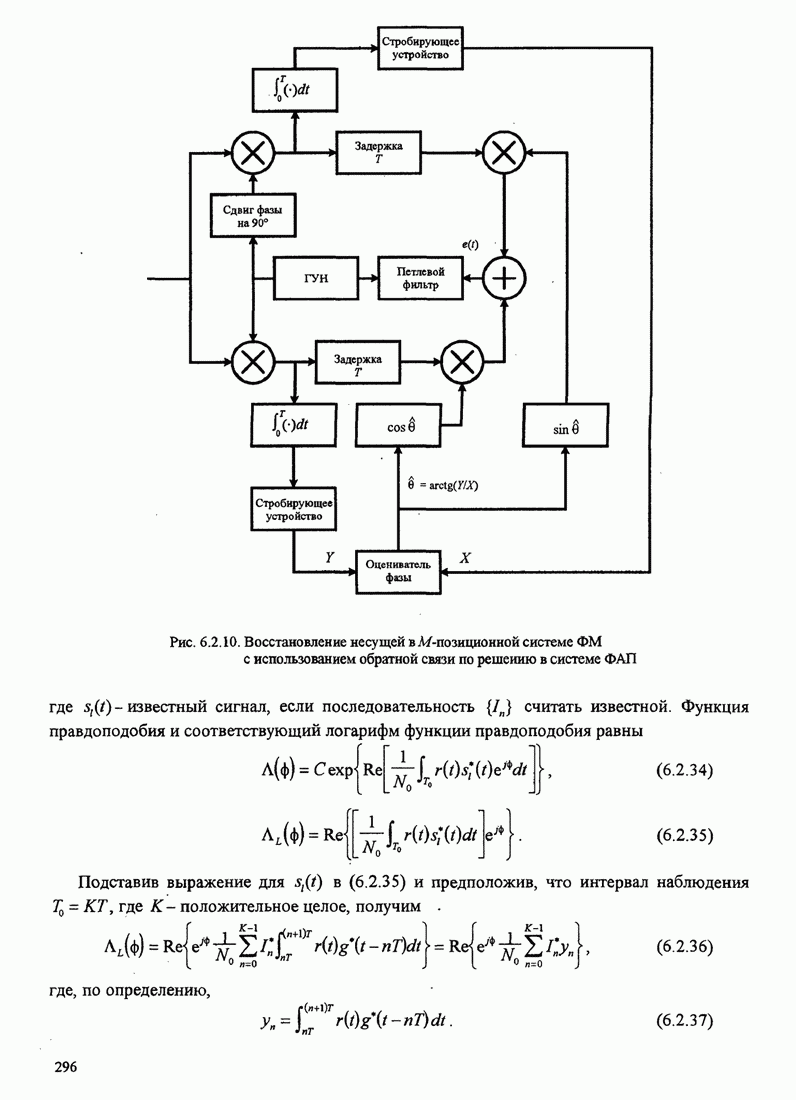
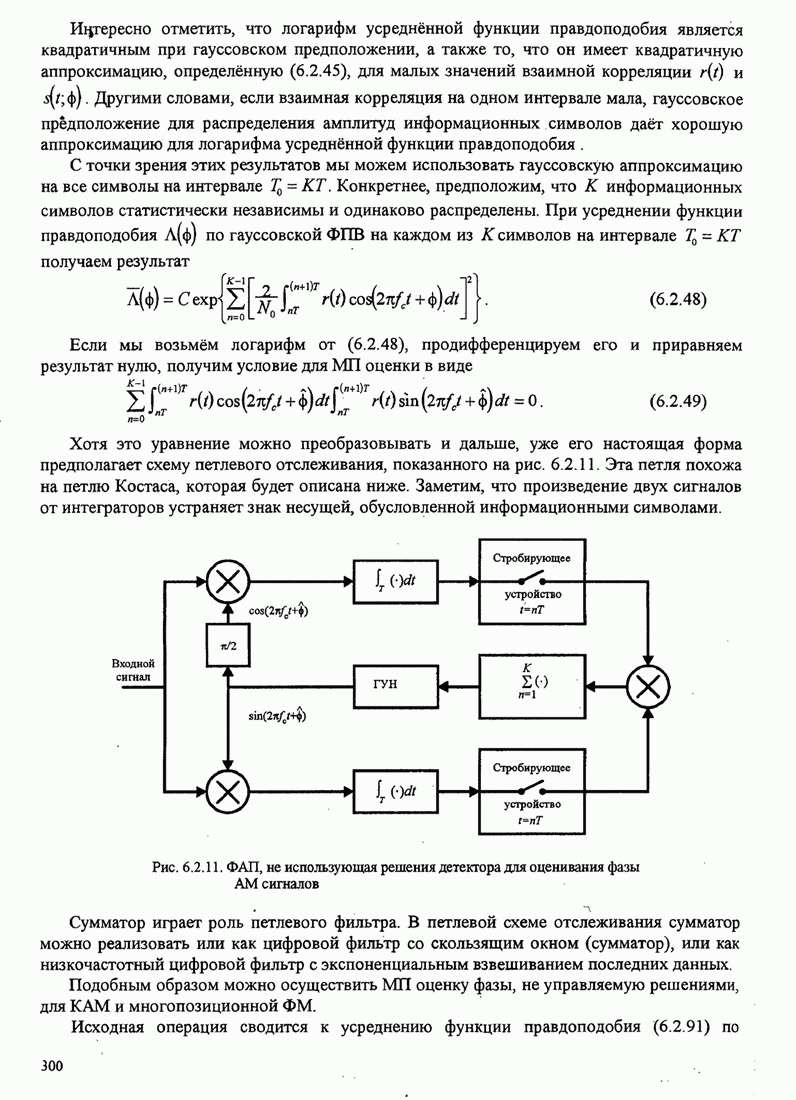
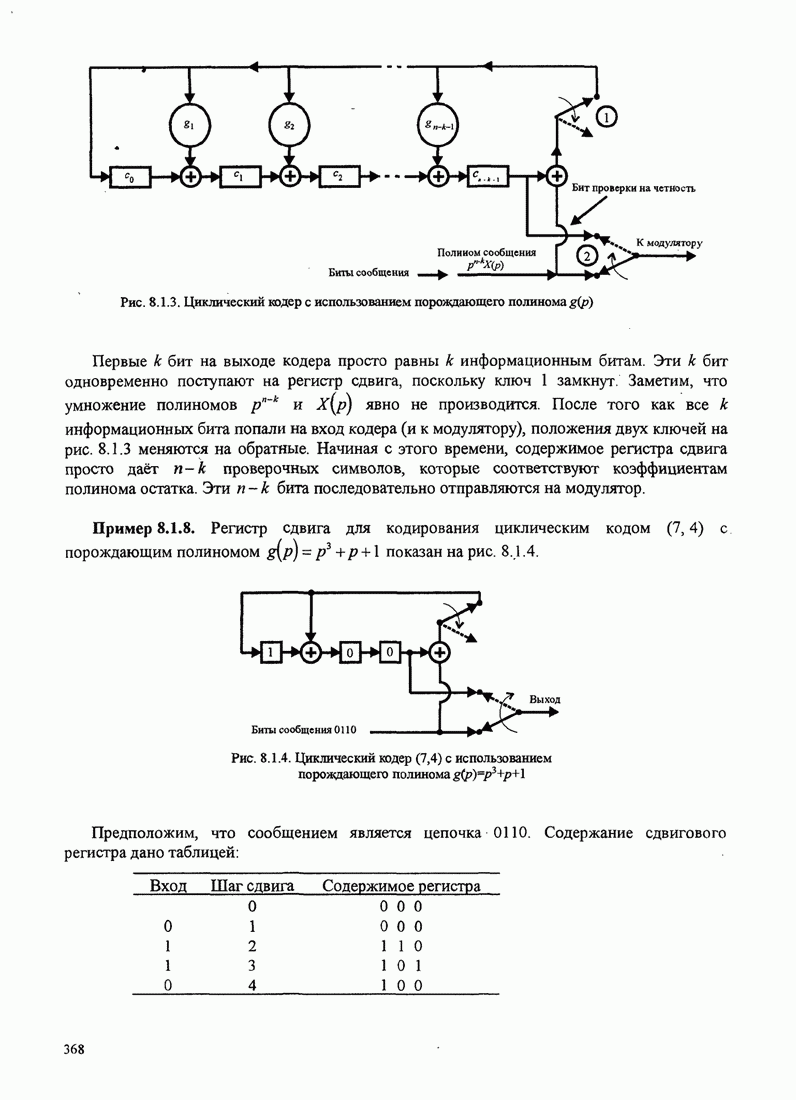
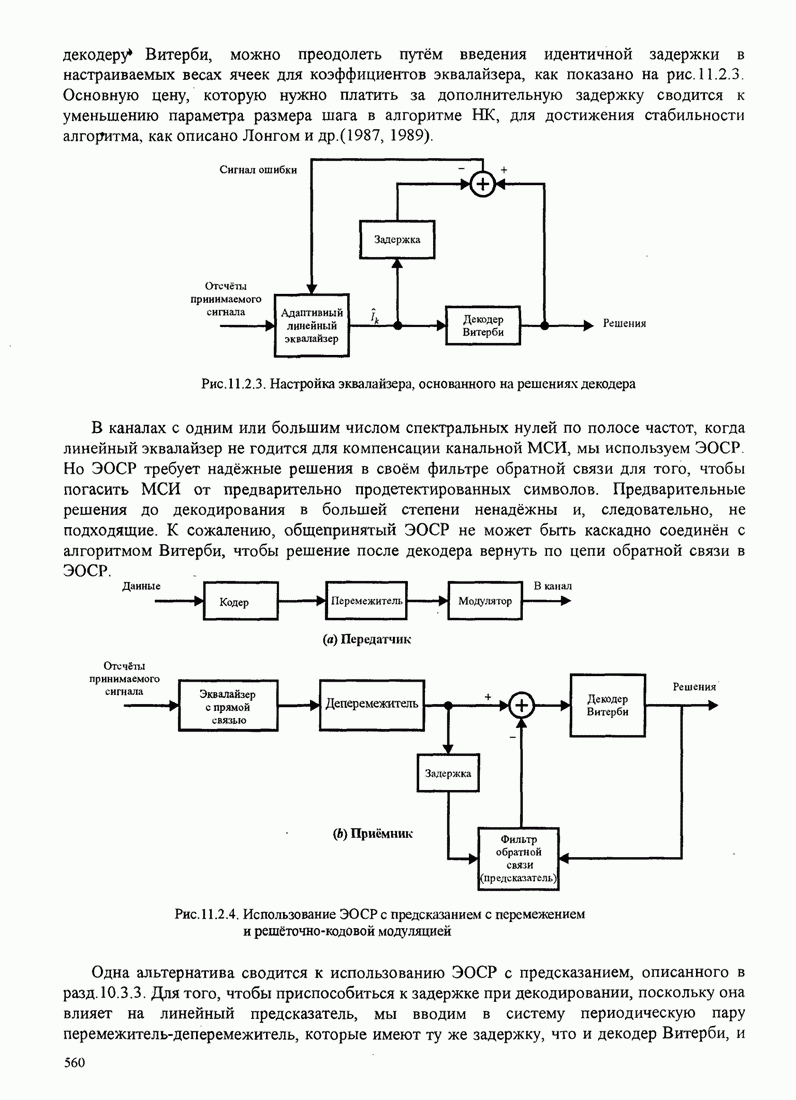
Хотя это уравнение можно преобразовывать и дальше, уже его настоящая форма предполагает схему петлевого отслеживания, показанного на рис. 6.2.11. Эта петля похожа на петлю Костаса, которая будет описана ниже. Заметим, что произведение двух сигналов от интеграторов устраняет знак несущей, обусловленной информационными символами

Рис. 6.2.11. ФАП, не использующая решения детектора для оценивания фазы АМ сигналов
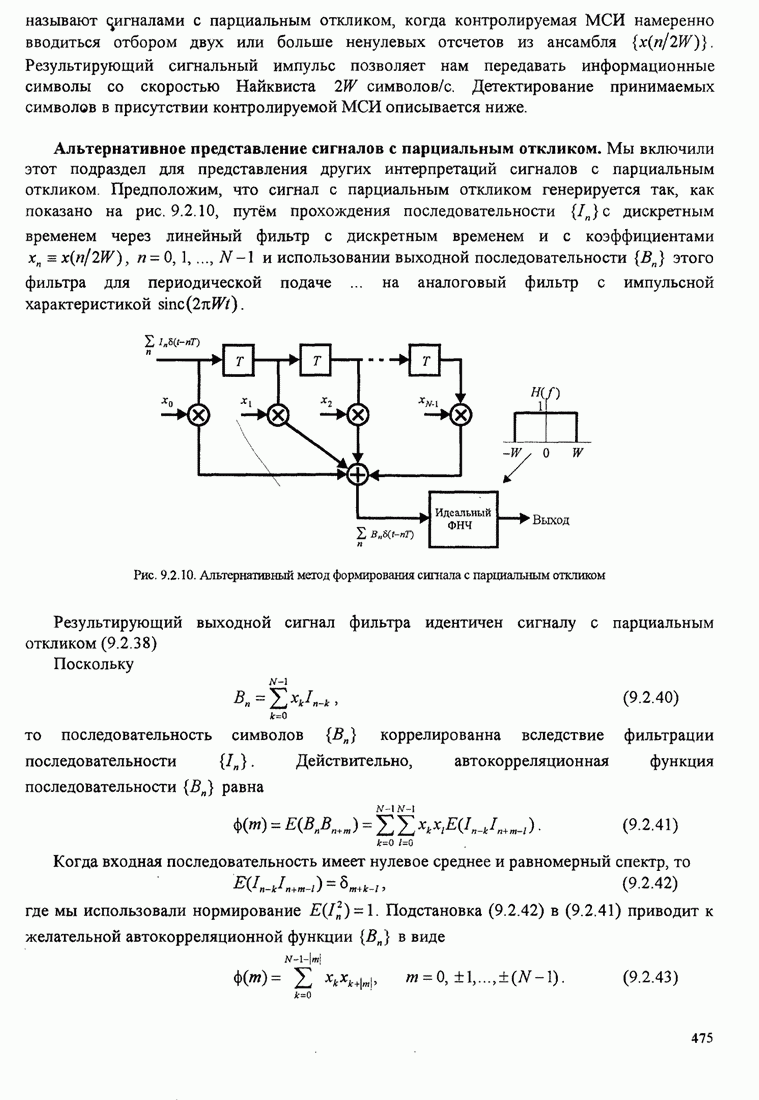
Сумматор играет роль петлевого фильтра. В петлевой схеме отслеживания сумматор можно реализовать или как цифровой фильтр со скользящим окном (сумматор), или как низкочастотный цифровой фильтр с экспоненциальным взвешиванием последних данных.
Подобным образом можно осуществить МП оценку фазы, не управляемую решениями, для КАМ и многопозиционной ФМ.
Исходная операция сводится к усреднению функции правдоподобия (6.2.91) по статистике параметров данных. Здесь снова мы можем использовать гауссовскую аппроксимацию (двухмерное гауссовское распределение для комплексных информационных символов) или усреднение по информационной последовательности.
Квадратичная петля. Квадратичная петля – это петля, не управляемая решениями, которая широко используется на практике для установления фазы несущей в двухполосной системе с подавленной несущей, такой как AM. Чтобы описать её работу, рассмотрим проблему оценивания фазы несущей сигнала цифровой AM в виде
![]() (6.2.50)
(6.2.50)
где ![]() несёт цифровую информацию. Заметим,
что
несёт цифровую информацию. Заметим,
что ![]() ,
когда сигнальные уровни распределены симметрично относительно нуля.
Следовательно, усреднённое значение
,
когда сигнальные уровни распределены симметрично относительно нуля.
Следовательно, усреднённое значение ![]() не может дать ни одной
фазокогерентной частотной компоненты, исключая несущую. Один из методов
восстановления несущей от принимаемого сигнала сводится к его квадратированию
и, следовательно, к генерированию частотной компоненты
не может дать ни одной
фазокогерентной частотной компоненты, исключая несущую. Один из методов
восстановления несущей от принимаемого сигнала сводится к его квадратированию
и, следовательно, к генерированию частотной компоненты![]() , которую можно использовать
для образования фазозамкнутой петли (ФЗП), настроенной на частоту
, которую можно использовать
для образования фазозамкнутой петли (ФЗП), настроенной на частоту ![]() . Этот метод
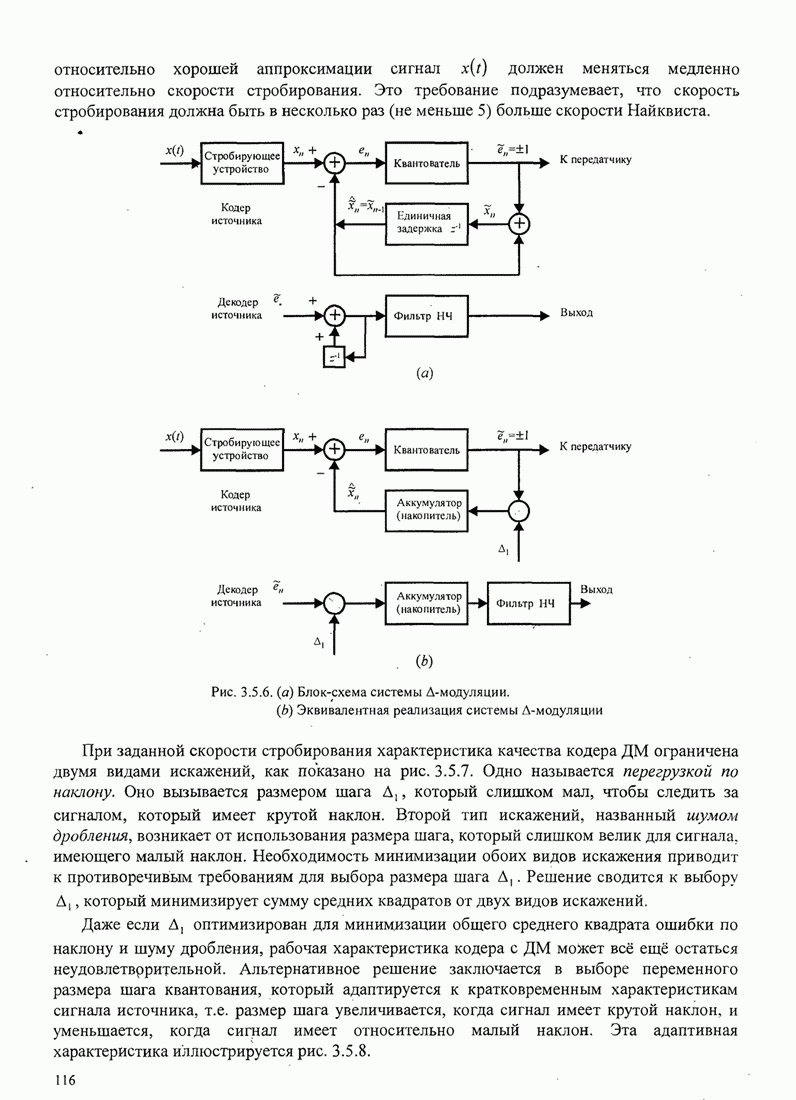
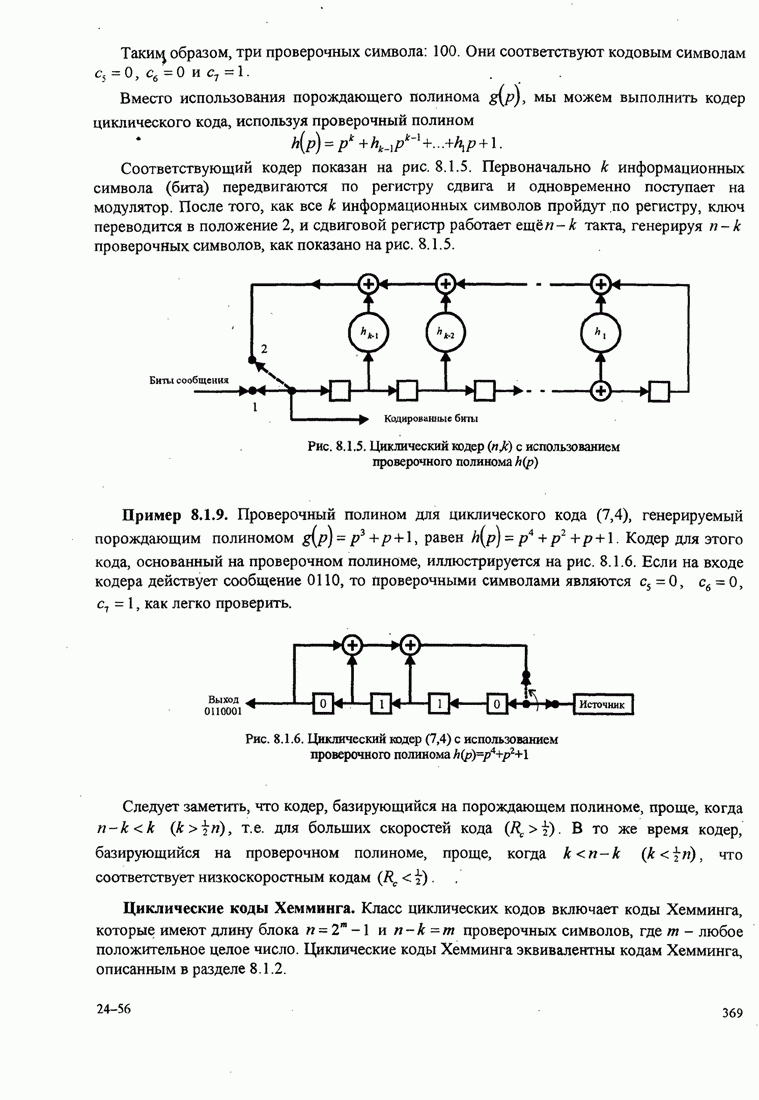
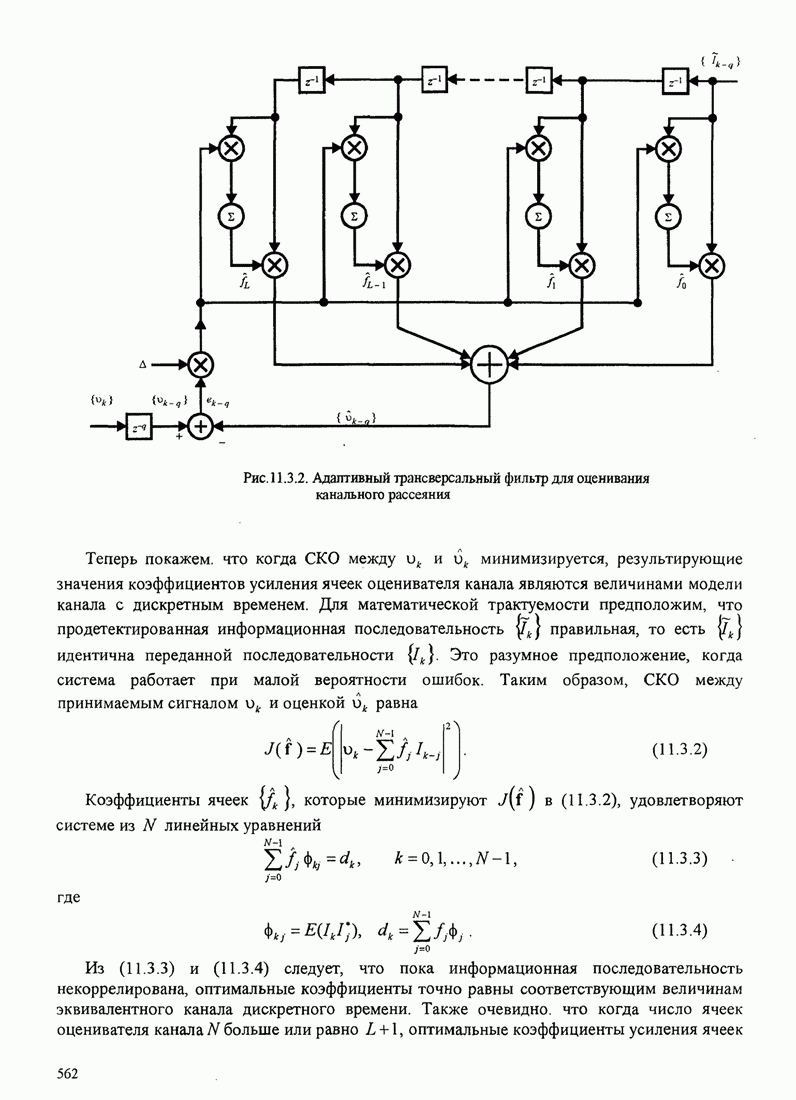
иллюстрируется блок-схемой, показанной на рис. 6.2.12.
. Этот метод
иллюстрируется блок-схемой, показанной на рис. 6.2.12.

Рис.6.2.12. Восстановление несущей с использованием квадратирующего устройства
Выход квадратичного устройства равен
![]() (6.2.51)
(6.2.51)
Поскольку модулированный сигнал является
циклостационарным случайным процессом, математическое ожидание от ![]() равно
равно
![]() (6.2.52)
(6.2.52)
Следовательно, имеется мощность на частоте ![]() .
.
Когда выход квадратирующего устройства проходит
через полосовой фильтр, настроенный на удвоенную частоту в (6.2.51),
среднее-значение на выходе фильтра – это синусоида с частотой ![]() , фазой
, фазой ![]() и амплитудой
и амплитудой ![]() , где
, где ![]() - усиление фильтра
на частоте
- усиление фильтра
на частоте ![]() .
Таким образом, квадратирующее устройство образует периодическую компоненту от
входного сигнала
.
Таким образом, квадратирующее устройство образует периодическую компоненту от
входного сигнала ![]() .
По существу, квадратирование уничтожает знак информации, содержащейся в
.
По существу, квадратирование уничтожает знак информации, содержащейся в ![]() и таким образом
приводит к фазокогерентндй частотной компоненте на удвоенной частоте несущей.
Фильтруемая компонента на частоте
и таким образом
приводит к фазокогерентндй частотной компоненте на удвоенной частоте несущей.
Фильтруемая компонента на частоте ![]() затем используется для управления
ФЗП.
затем используется для управления
ФЗП.
Операция квадратирования ведет к обогащению шума, что увеличивает уровень шумовой мощности на входе ФАП и ведёт к увеличению дисперсии фазовой ошибки.
Чтобы разобраться с этим вопросом, допустим, что на
вход квадратирующего звена поступает сигнал ![]() , где
, где ![]() определено (6.2.50), а
определено (6.2.50), а ![]() представляет
полосовой аддитивный гауссовский шумовой процесс. При квадратировании
представляет
полосовой аддитивный гауссовский шумовой процесс. При квадратировании ![]() получаем
получаем
![]() (6.2.53)
(6.2.53)
где ![]() - желательная сигнальная компонента,
а две остальные компоненты – это слагаемые
- желательная сигнальная компонента,
а две остальные компоненты – это слагаемые ![]() и
и ![]() . Вычислив автокорреляционную функцию
и спектральную плотность мощности этих двух шумовых компонент, можно легко
показать, что обе компоненты имеют спектральную плотность мощности в частотной
полосе, сосредоточенной вблизи
. Вычислив автокорреляционную функцию
и спектральную плотность мощности этих двух шумовых компонент, можно легко
показать, что обе компоненты имеют спектральную плотность мощности в частотной
полосе, сосредоточенной вблизи ![]() . Следовательно, полосовой фильтр с
полосой
. Следовательно, полосовой фильтр с
полосой ![]() ,
центрированной на частоте
,
центрированной на частоте ![]() , который создает желательные
синусоидальные компоненты сигнала, управляющие ФЗП, также пропускает шум,
обусловленный двумя слагаемыми. Поскольку полоса петли рассчитывается так,
чтобы быть существенно меньшей, чем полоса
, который создает желательные
синусоидальные компоненты сигнала, управляющие ФЗП, также пропускает шум,
обусловленный двумя слагаемыми. Поскольку полоса петли рассчитывается так,
чтобы быть существенно меньшей, чем полоса ![]() полосового фильтра, суммарный спектр
шума на входе ФЗП можно аппроксимировать константой на частотах внутри полосы
петли. Такая аппроксимация позволяет нам получить простое выражение для
дисперсии фазовой ошибки
полосового фильтра, суммарный спектр
шума на входе ФЗП можно аппроксимировать константой на частотах внутри полосы
петли. Такая аппроксимация позволяет нам получить простое выражение для
дисперсии фазовой ошибки
![]() (6.2.54)
(6.2.54)
где ![]() названа квадратичными потерями и
определяется так:
названа квадратичными потерями и
определяется так:
 (6.2.55)
(6.2.55)
Поскольку ![]() определяет увеличение дисперсии
фазовой ошибки, вызванной дополнительным шумом (слагаемым
определяет увеличение дисперсии
фазовой ошибки, вызванной дополнительным шумом (слагаемым ![]() ), обусловленным
квадратированием. Заметим для примера, что, когда
), обусловленным
квадратированием. Заметим для примера, что, когда ![]() , потери составляют 3 дБ.
, потери составляют 3 дБ.
В заключение заметим, что выход ГУН в схеме с
квадратированием необходимо делить по частоте на 2, чтобы генерировать
синхронную несущую для демодуляции сигнала. Надо подчеркнуть, что выход
делителя частоты характеризуется неоднозначностью фазы на ![]() относительно фазы
принимаемого сигнала. Из этих соображений двоичные данные следует
дифференциально кодировать до модуляции и дифференциально декодировать в
приёмнике.
относительно фазы
принимаемого сигнала. Из этих соображений двоичные данные следует
дифференциально кодировать до модуляции и дифференциально декодировать в
приёмнике.
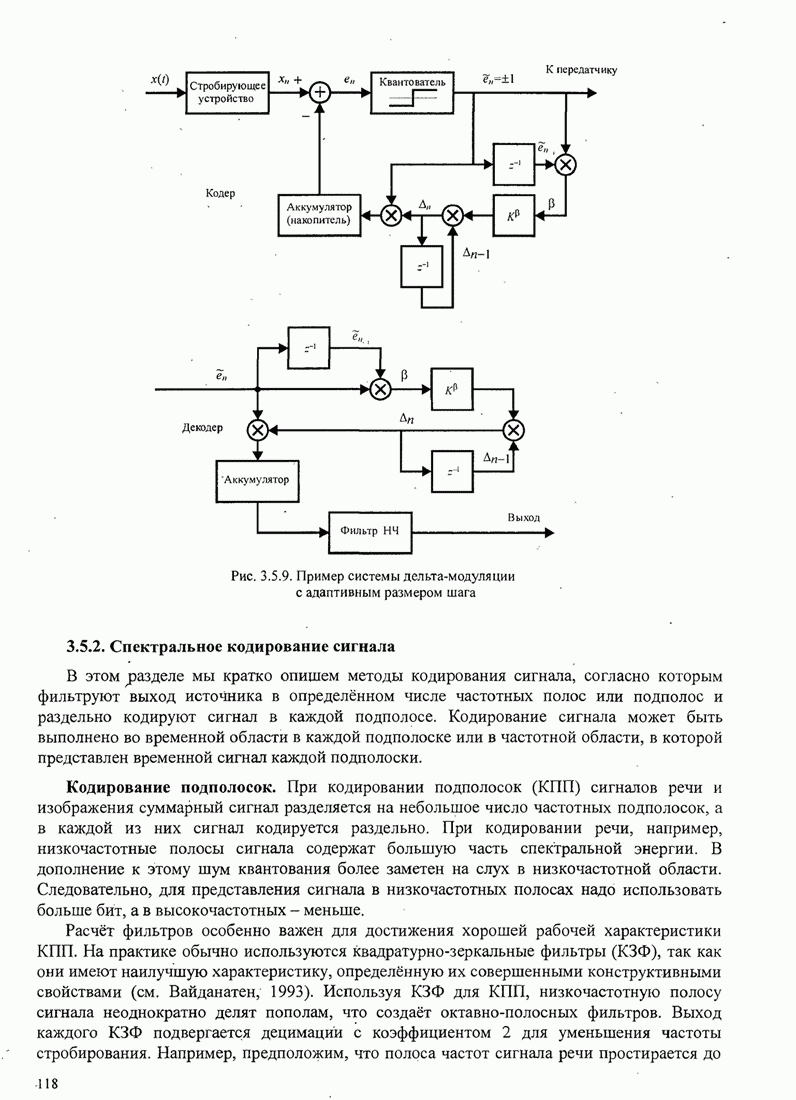
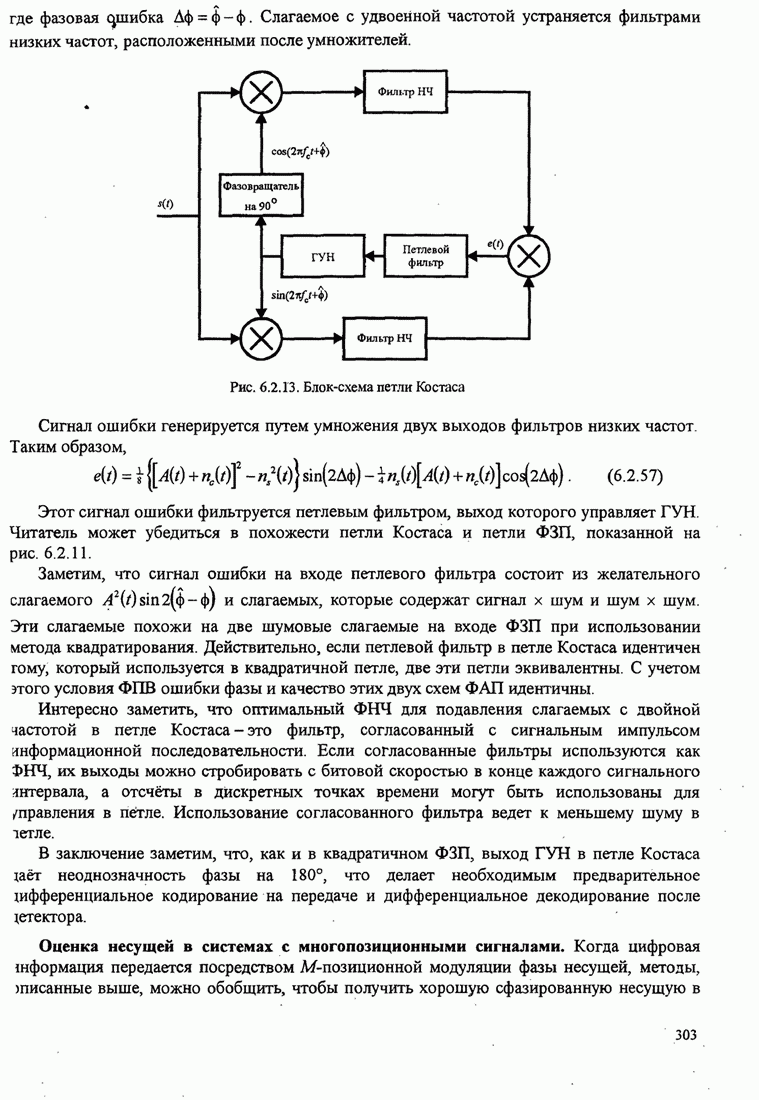
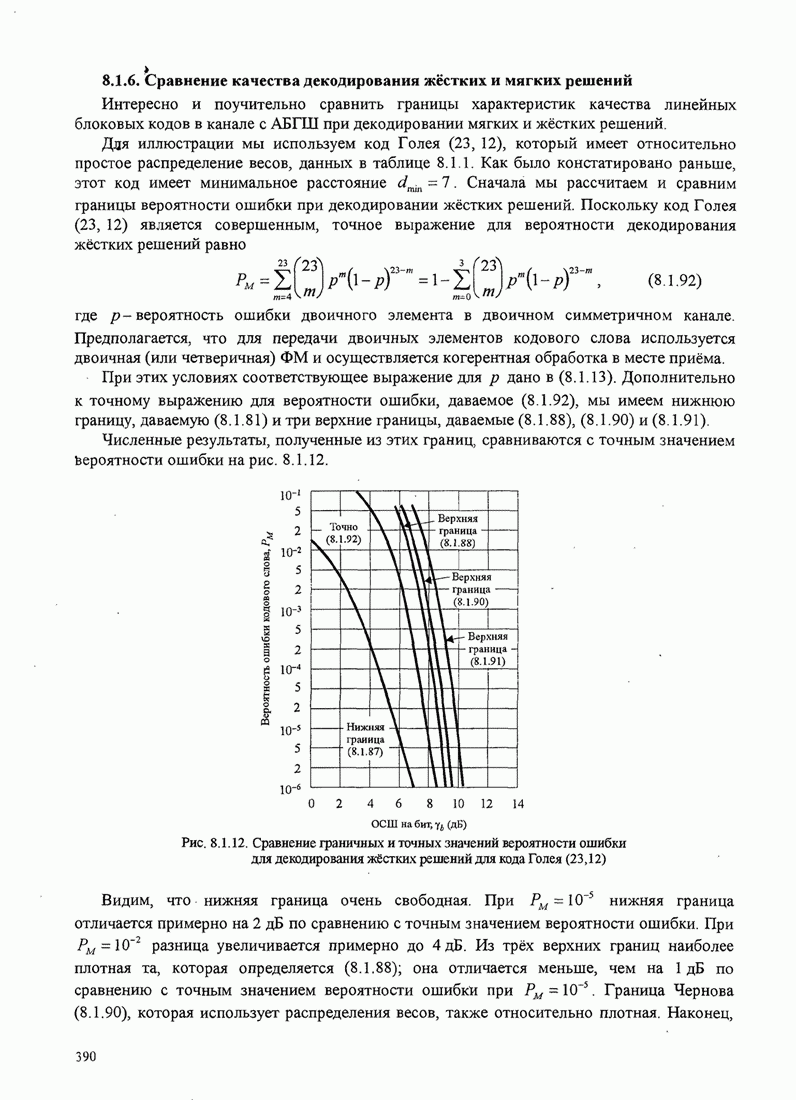
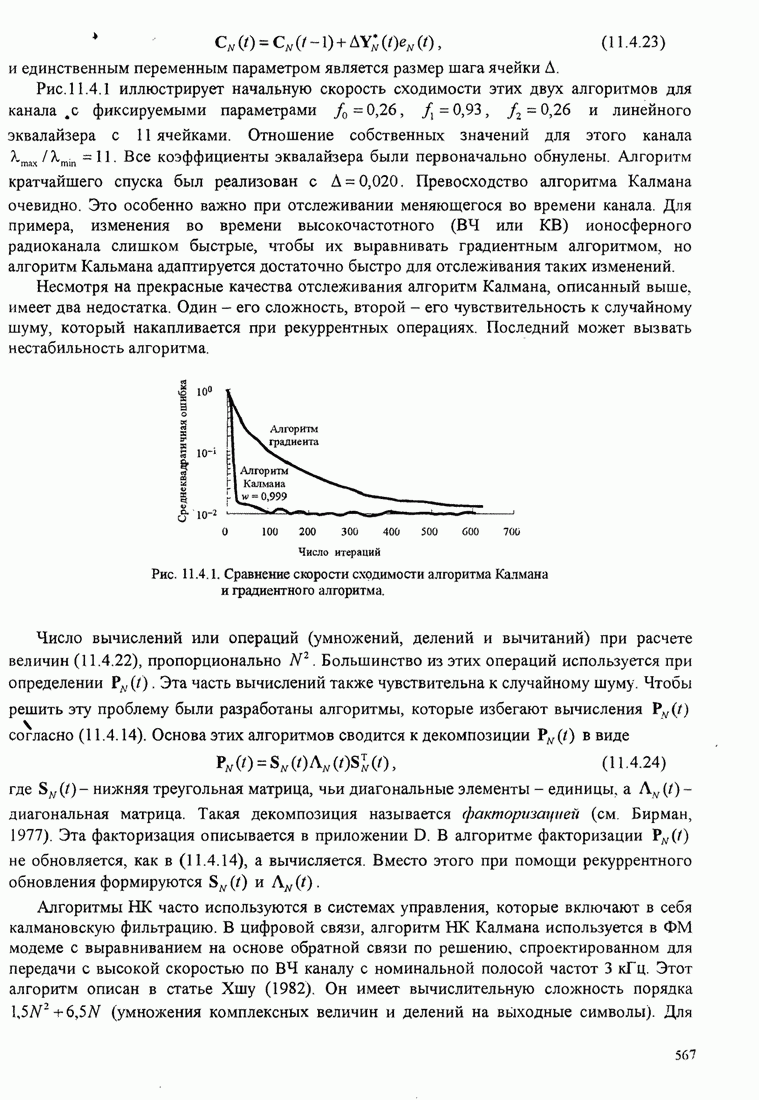
Петля Костаса. Другой метод восстановления фазированной несущей для двухполосной системы с подавленной несущей иллюстрируется рис. 6.2.13. Эта схема была предложена Костасом (1956) и называется петлей Костаса.
Принимаемый сигнал умножается на ![]() и
и ![]() , которые являются
выходами ГУН. Получаем два произведения:
, которые являются
выходами ГУН. Получаем два произведения:
 (6.2.56)
(6.2.56)
где фазовая ошибка ![]() . Слагаемое с удвоенной частотой
устраняется фильтрами низких частот, расположенными после умножителей.
. Слагаемое с удвоенной частотой
устраняется фильтрами низких частот, расположенными после умножителей.

Рис.6.2.13. Блок-схема петли Костаса.
Сигнал ошибки генерируется путем умножения двух выходов фильтров низких частот. Таким образом,
![]() (6.2.57)
(6.2.57)
Этот сигнал ошибки фильтруется петлевым фильтром, выход которого управляет ГУН. Читатель может убедиться в похожести петли Костаса и петли ФЗП, показанной на рис. 6.2.11.
Заметим, что сигнал ошибки на входе петлевого
фильтра состоит из желательного слагаемого ![]() и слагаемых, которые содержат
и слагаемых, которые содержат ![]() и
и ![]() . Эти слагаемые
похожи на две шумовые слагаемые на входе ФЗП при использовании метода
квадратирования. Действительно, если петлевой фильтр в петле Костаса идентичен
тому, который используется в квадратичной петле, две эти петли эквивалентны. С
учетом этого условия ФПВ ошибки фазы и качество этих двух схем ФАП идентичны.
. Эти слагаемые
похожи на две шумовые слагаемые на входе ФЗП при использовании метода
квадратирования. Действительно, если петлевой фильтр в петле Костаса идентичен
тому, который используется в квадратичной петле, две эти петли эквивалентны. С
учетом этого условия ФПВ ошибки фазы и качество этих двух схем ФАП идентичны.
Интересно заметить, что оптимальный ФНЧ для подавления слагаемых с двойной частотой в петле Костаса – это фильтр, согласованный с сигнальным импульсом информационной последовательности. Если согласованные фильтры используются как ФНЧ, их выходы можно стробировать с битовой скоростью в конце каждого сигнального интервала, а отсчёты в дискретных точках времени могут быть использованы для правления в петле. Использование согласованного фильтра ведет к меньшему шуму в петле.
В заключение заметим, что, как и в квадратичном
ФЗП, выход ГУН в петле Костаса а неоднозначность фазы на ![]() , что делает необходимым
предварительное дифференциальное кодирование на передаче и дифференциальное
декодирование после детектора.
, что делает необходимым
предварительное дифференциальное кодирование на передаче и дифференциальное
декодирование после детектора.
Оценка несущей в системах с многопозиционными
сигналами. Когда цифровая информация передается посредством ![]() -позиционной модуляции
фазы несущей, методы, описанные выше, можно обобщить, чтобы получить хорошую
сфазированную несущую в демодуляторе. Принимаемый
-позиционной модуляции
фазы несущей, методы, описанные выше, можно обобщить, чтобы получить хорошую
сфазированную несущую в демодуляторе. Принимаемый ![]() -фазный сигнал, исключая аддитивный
шум, можно выразить так:
-фазный сигнал, исключая аддитивный
шум, можно выразить так:
![]() (6.2.58)
(6.2.58)
где ![]() представляет информационную
компоненту фазы сигнала. Проблема восстановления несущей сводится к устранению
информационной компоненты фазы и, как следствие, получению немодулированной
несущей
представляет информационную
компоненту фазы сигнала. Проблема восстановления несущей сводится к устранению
информационной компоненты фазы и, как следствие, получению немодулированной
несущей ![]() .
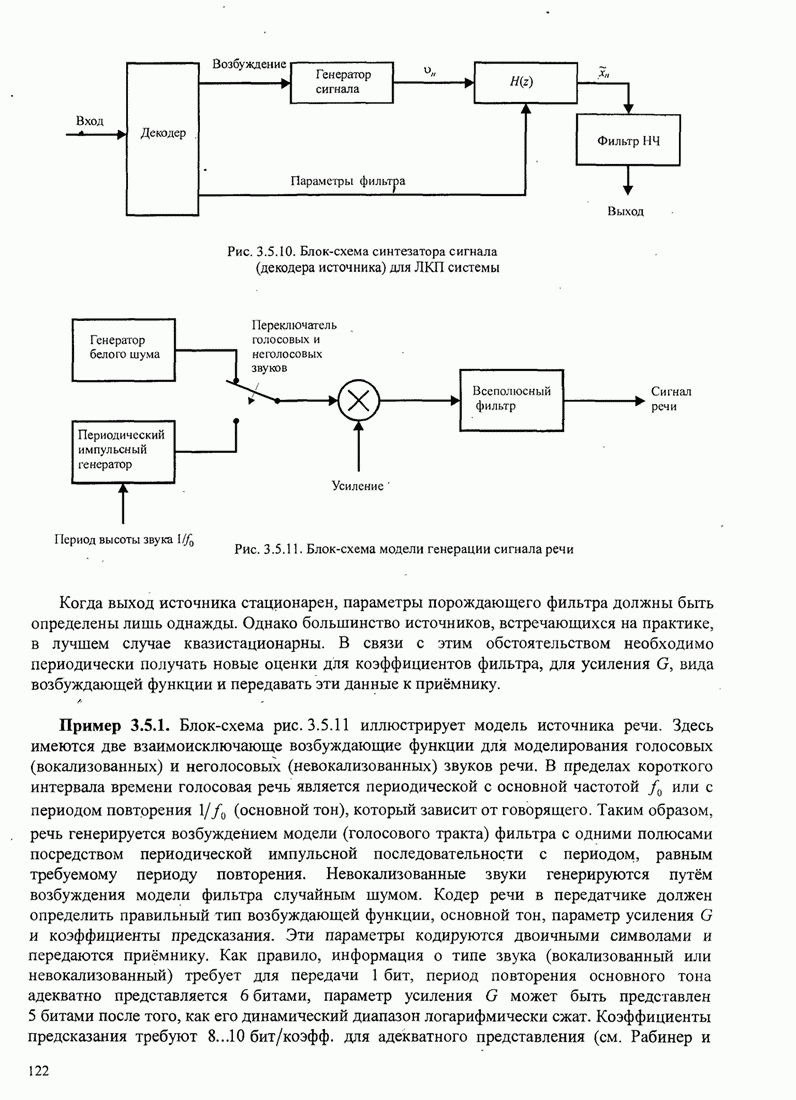
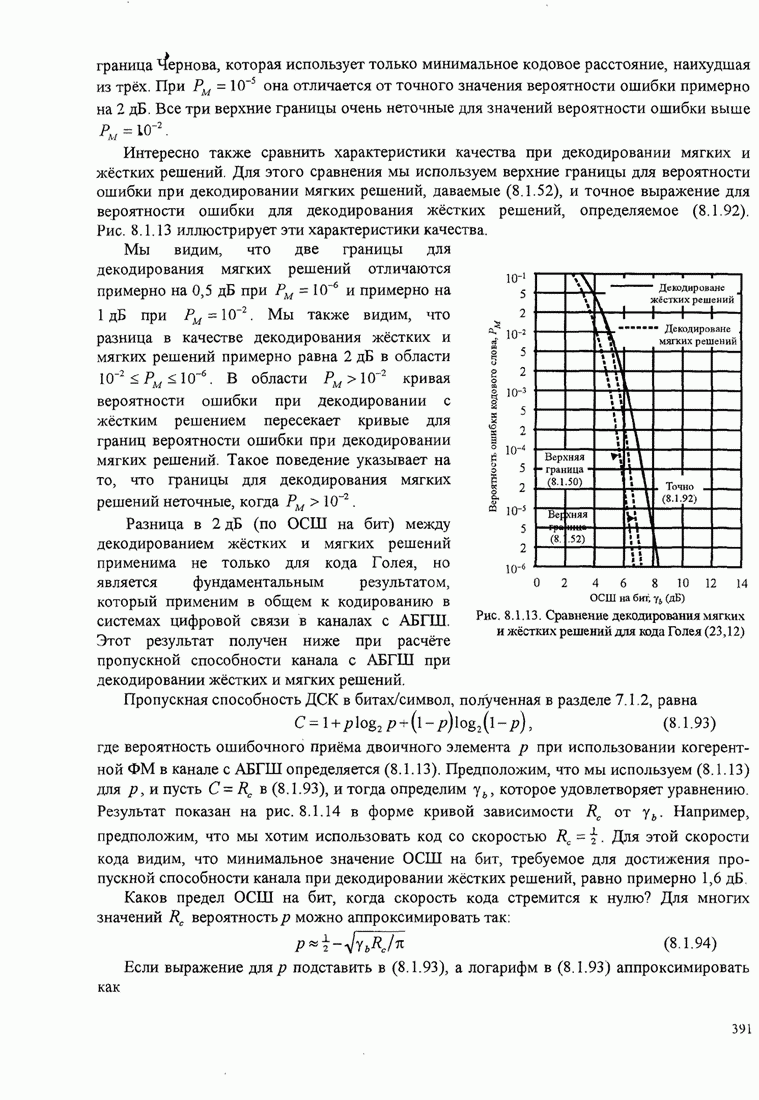
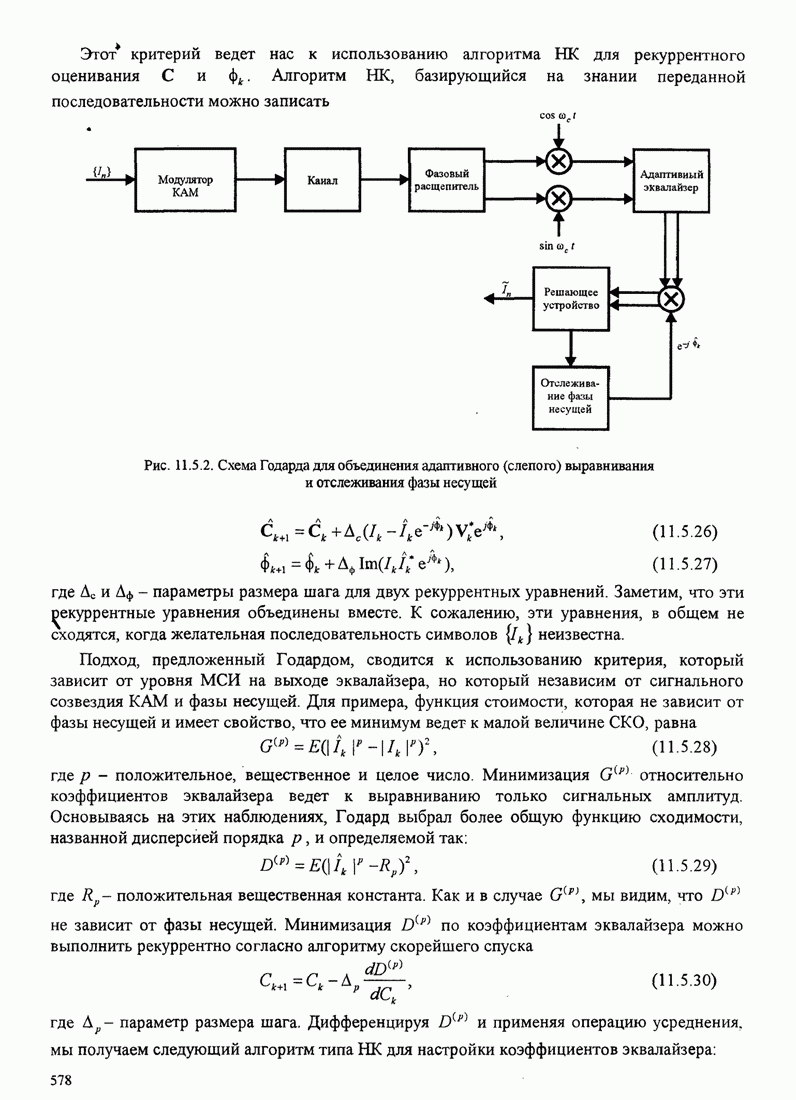
Один из методов, при помощи которого это можно сделать, иллюстрируется на рис.
6.2.14, который представляет обобщение петли с квадратированием. Сигнал
проходит через устройство возведения в
.
Один из методов, при помощи которого это можно сделать, иллюстрируется на рис.
6.2.14, который представляет обобщение петли с квадратированием. Сигнал
проходит через устройство возведения в ![]() -ю степень, которое генерирует
определённое число гармоник
-ю степень, которое генерирует
определённое число гармоник ![]() . Полосовой фильтр выбирает гармонику
. Полосовой фильтр выбирает гармонику ![]() для управления
ФЗП. Слагаемое информационной компоненты фазы сигнала
для управления
ФЗП. Слагаемое информационной компоненты фазы сигнала
![]()

Рис.6.2.14. Восстановление несущей с
использованием устройства возведения в ![]() -ю степень для
-ю степень для ![]() -позиционной ФМ
-позиционной ФМ
Таким образом, информация устранена. Выход ГУН – это
![]() ; этот выход
делится по частоте на
; этот выход
делится по частоте на ![]() для получения
для получения ![]() и сдвигается на
и сдвигается на ![]() для получения
для получения ![]() . Эта компонента
затем подаётся на демодулятор. Нетрудно показать, что имеется неоднозначность в
этих упомянутых синусоидах на
. Эта компонента
затем подаётся на демодулятор. Нетрудно показать, что имеется неоднозначность в
этих упомянутых синусоидах на ![]() , которую можно преодолеть
дифференциальным кодированием данных на передаче и дифференциальным
декодированием после демодуляции на приёме.
, которую можно преодолеть
дифференциальным кодированием данных на передаче и дифференциальным
декодированием после демодуляции на приёме.
Как в случае квадратичной ФЗП, полиномиальная ФЗП
работает в присутствии шума, возрастающего после прохождения через устройство
возведения в ![]() -ю
степень, которое даёт на выходе сигнал
-ю
степень, которое даёт на выходе сигнал ![]() .
.
Дисперсию фазовой ошибки в ФЗП, обусловленной аддитивным шумом, можно выразить в простой форме:
![]() (6.2.59)
(6.2.59)
где ![]() - петлевое ОСШ, а
- петлевое ОСШ, а ![]() - потери из-за
возведения в
- потери из-за
возведения в ![]() -ю
степень.
-ю
степень. ![]() рассчитали
Линдсей и Саймон (1979) для
рассчитали
Линдсей и Саймон (1979) для ![]() .
.
Другой метод восстановления несущей в ![]() -фазной ФМ
базируется на обобщении петли Костаса. Этот метод требует умножения
принимаемого сигнала на несущую с фазовым сдвигом вида
-фазной ФМ
базируется на обобщении петли Костаса. Этот метод требует умножения
принимаемого сигнала на несущую с фазовым сдвигом вида
![]()
низкочастотной фильтрации слагаемых произведения и затем перемножения выходов низкочастотных фильтров для генерирования сигнала ошибки. Сигнал ошибки возбуждает петлевой фильтр, который создаёт сигнал управления для ГУН. Этот метод относительно сложен для применения и, как следствие, обычно не используется на практике.
Сравнение петель, управляемых и не управляемых
решениями. Заметим, что фазозамкнутая петля с ОСР (ФЗПОСР, DFPLL)
отличается от петли Костаса только методом очищения ![]() с целью устранения
модуляции. В петле Костаса каждый из двух квадратурных сигналов, используемых
для очищения
с целью устранения
модуляции. В петле Костаса каждый из двух квадратурных сигналов, используемых
для очищения ![]() ,
поражается шумом. С другой стороны, квадратичная петля похожа на петлю Костела
шумовыми компонентами, влияющими на оценку
,
поражается шумом. С другой стороны, квадратичная петля похожа на петлю Костела
шумовыми компонентами, влияющими на оценку ![]() . Следовательно, ФЗПОСР
предпочтительнее по качеству по отношению как к петле Костаса, так и к
квадратичной петле, обеспечивая работу демодулятора при вероятности ошибки ниже
. Следовательно, ФЗПОСР
предпочтительнее по качеству по отношению как к петле Костаса, так и к
квадратичной петле, обеспечивая работу демодулятора при вероятности ошибки ниже
![]() , причём
редкие ошибки решения несущественно влияют на
, причём
редкие ошибки решения несущественно влияют на ![]() . Численные сравнения дисперсии
фазовых ошибок в петле Костаса относительно тех, которые имеют место в ФЗПОСР.
были выполнены Линдсеем и Саймоном (1973), и они показывает, что дисперсия в
ФЗПОСР в 4... 10 раз меньше для отношения сигнал/шум на бит около 0 дБ.
. Численные сравнения дисперсии
фазовых ошибок в петле Костаса относительно тех, которые имеют место в ФЗПОСР.
были выполнены Линдсеем и Саймоном (1973), и они показывает, что дисперсия в
ФЗПОСР в 4... 10 раз меньше для отношения сигнал/шум на бит около 0 дБ.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
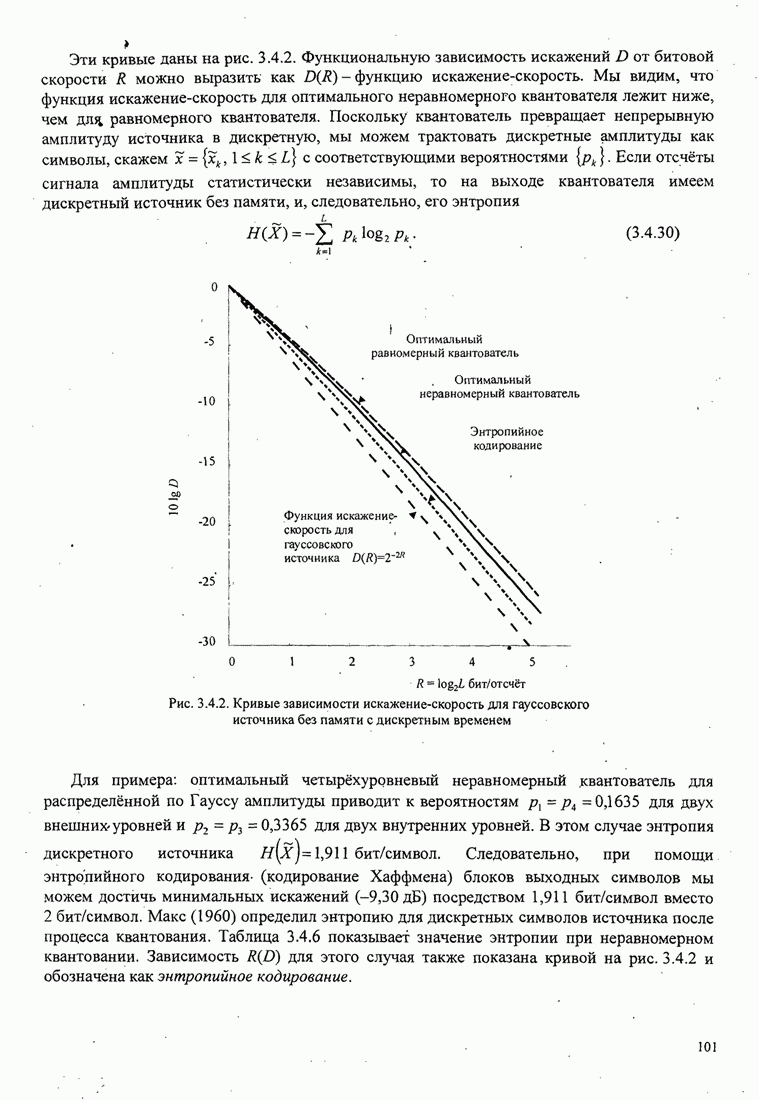
- 3.4.1. Функция скорость-искажение R(D)
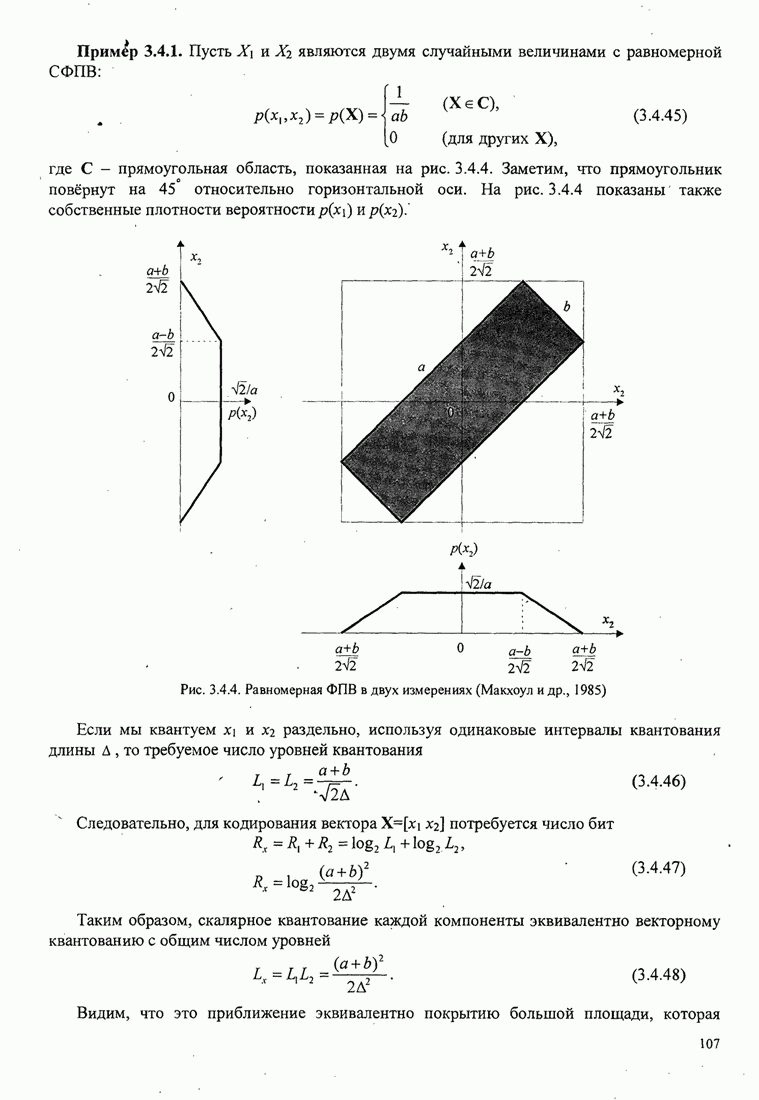
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
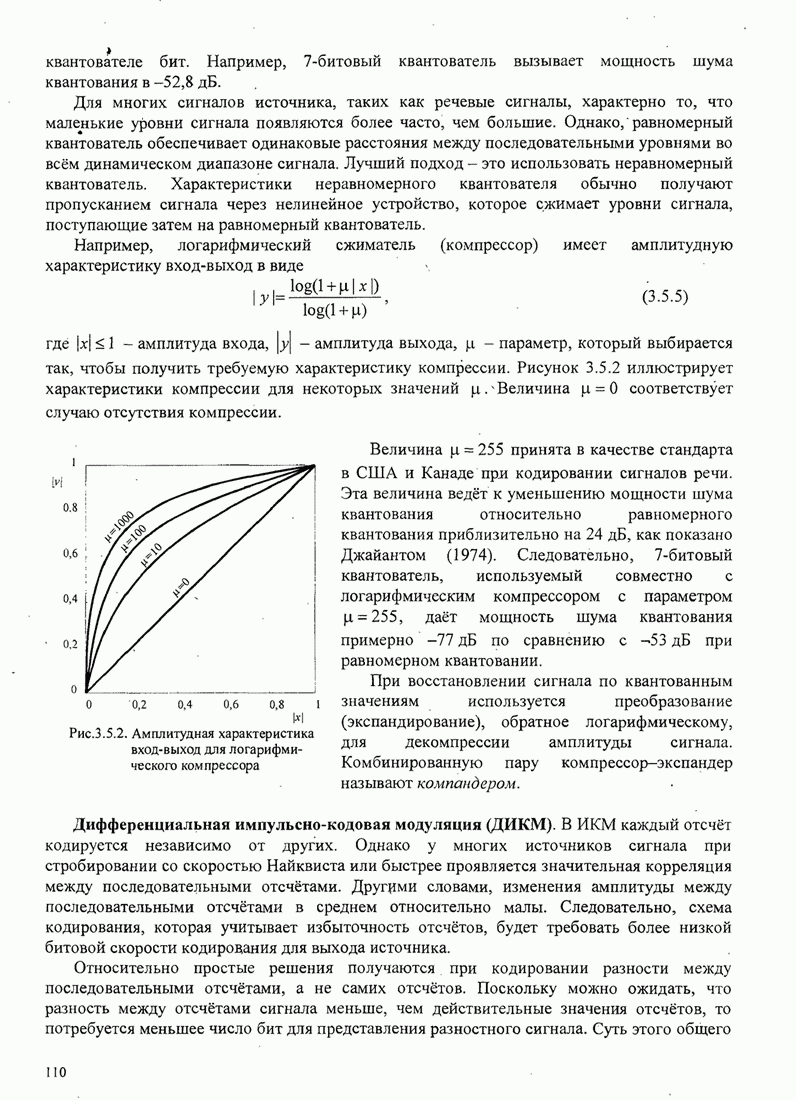
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
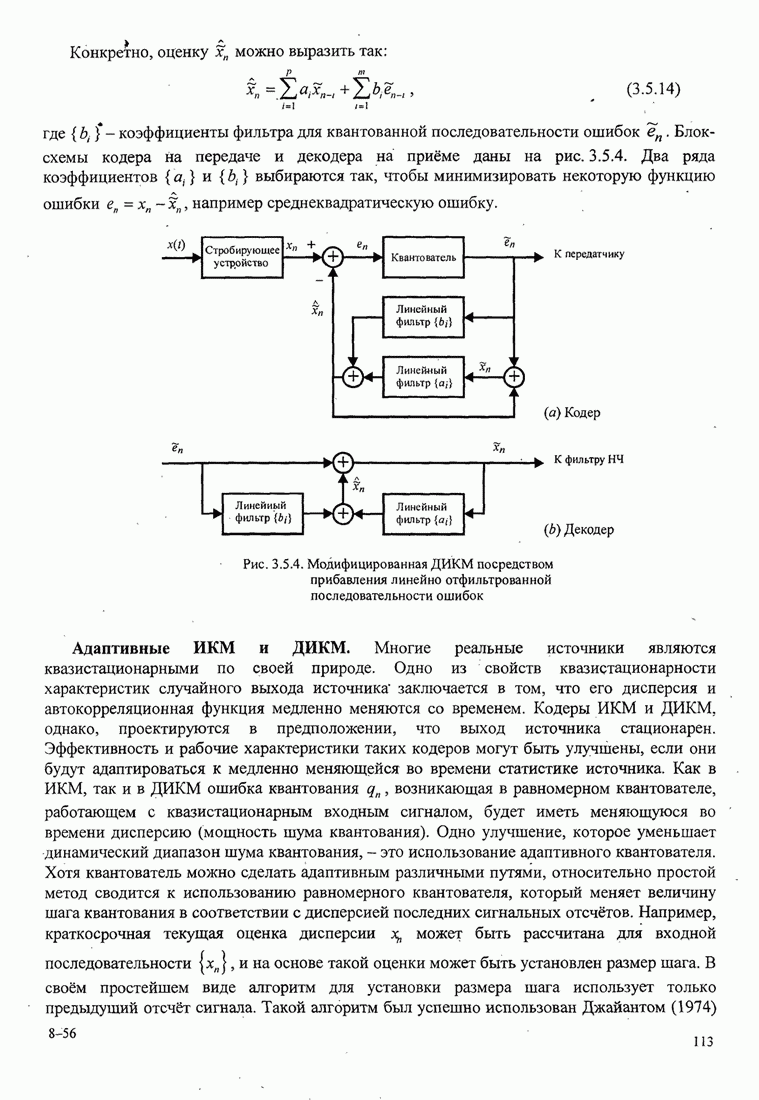
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
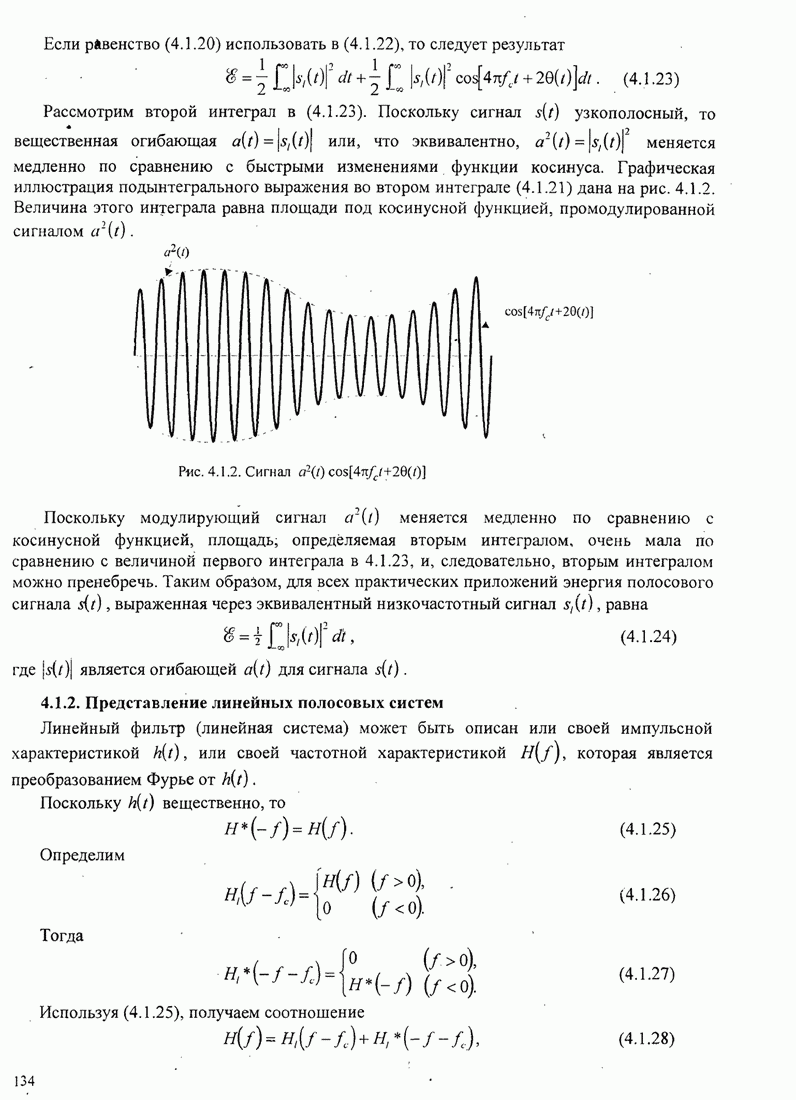
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
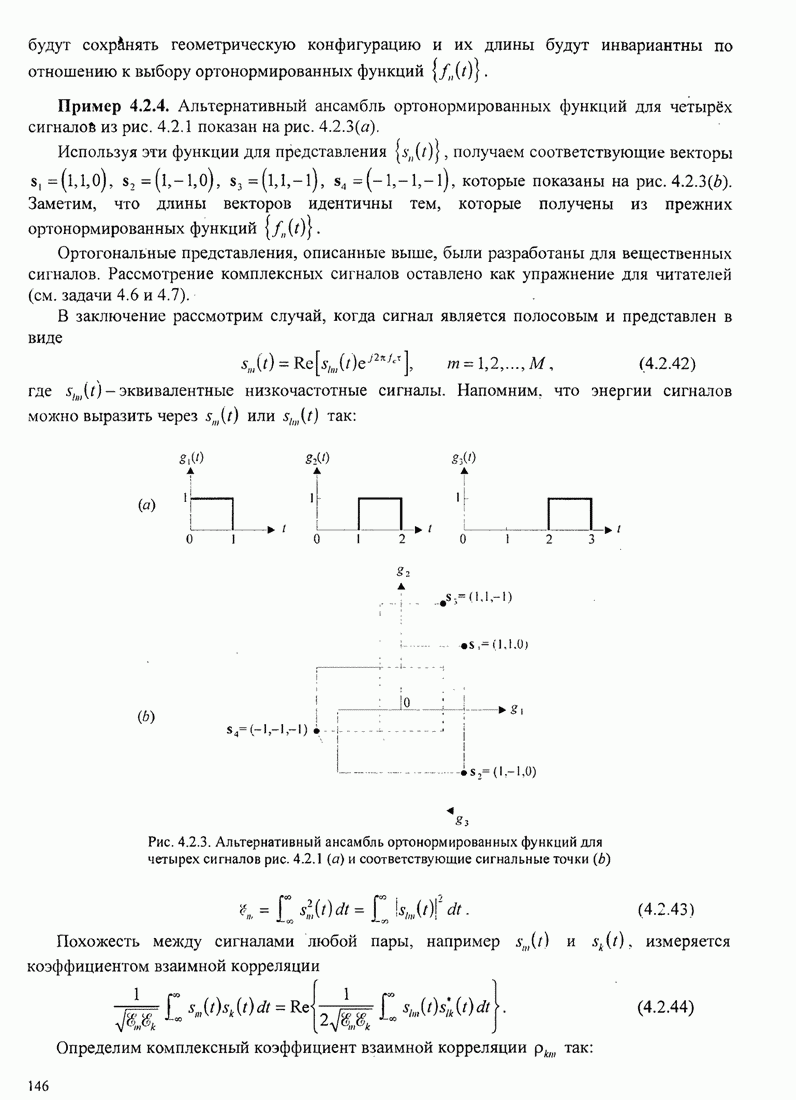
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
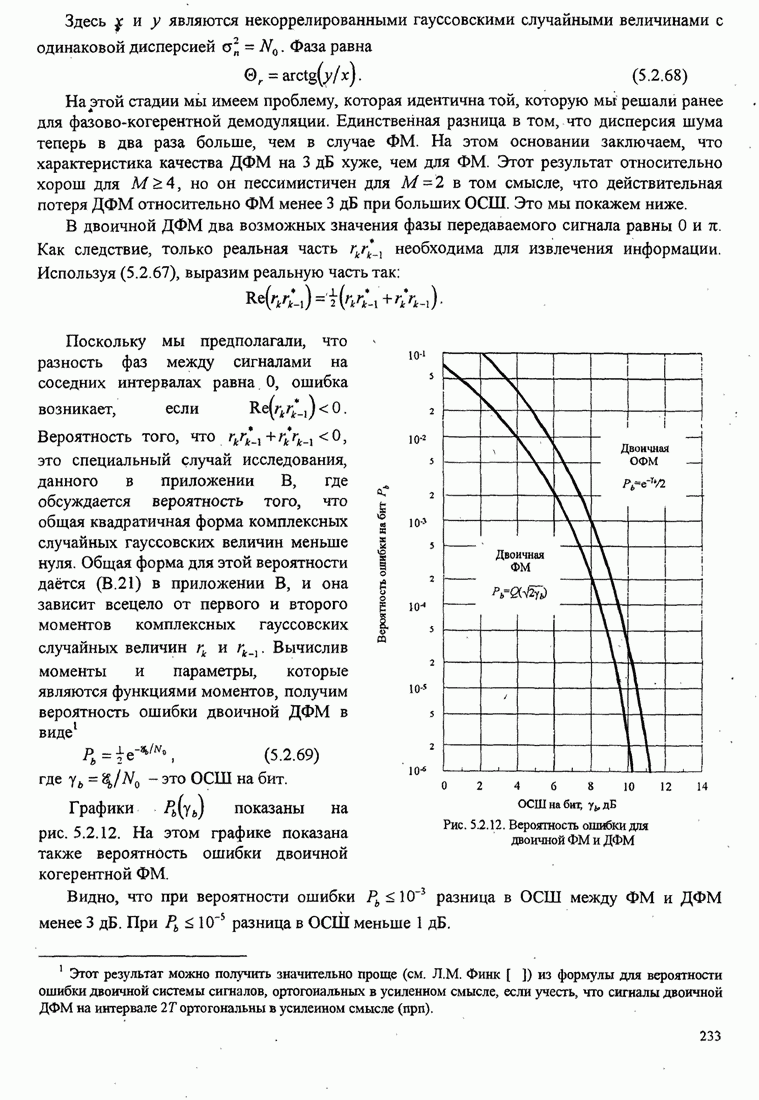
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
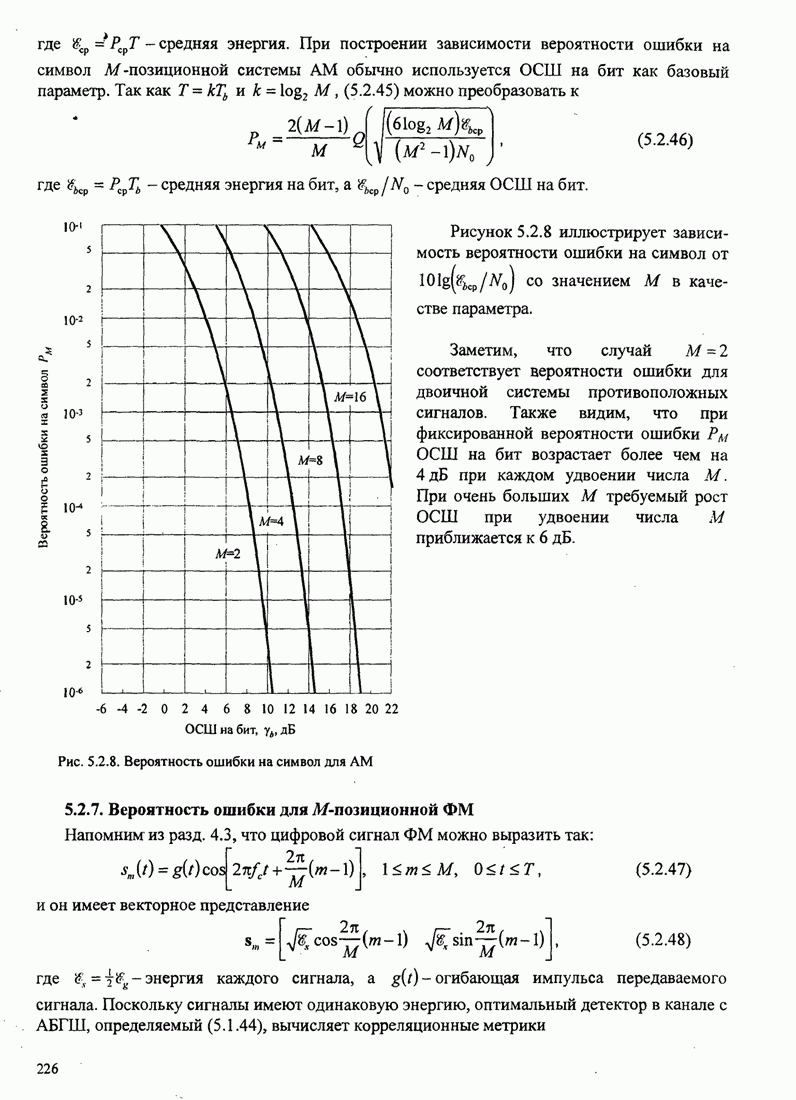
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
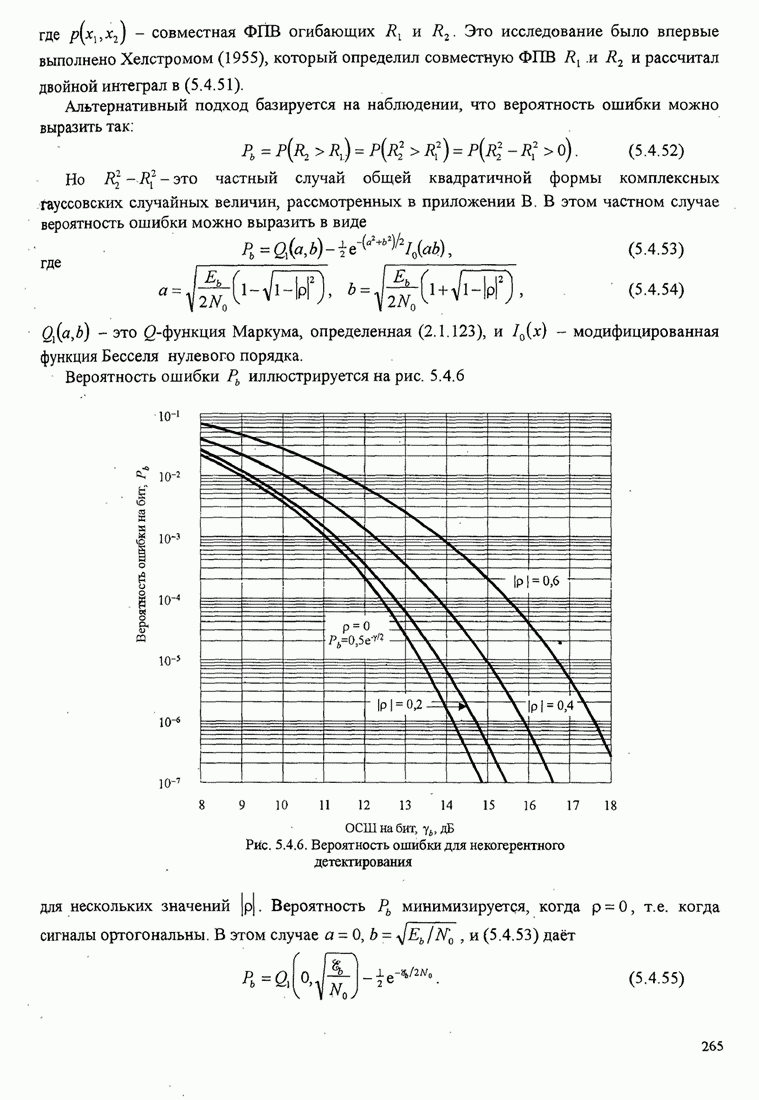
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
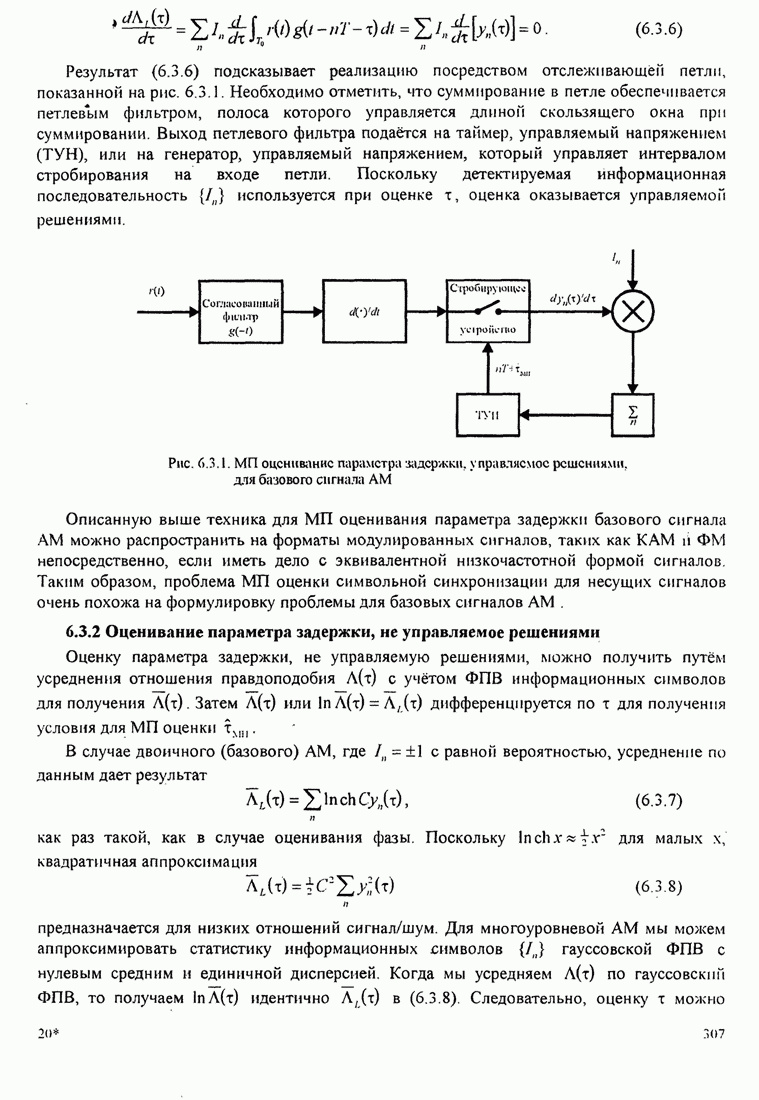
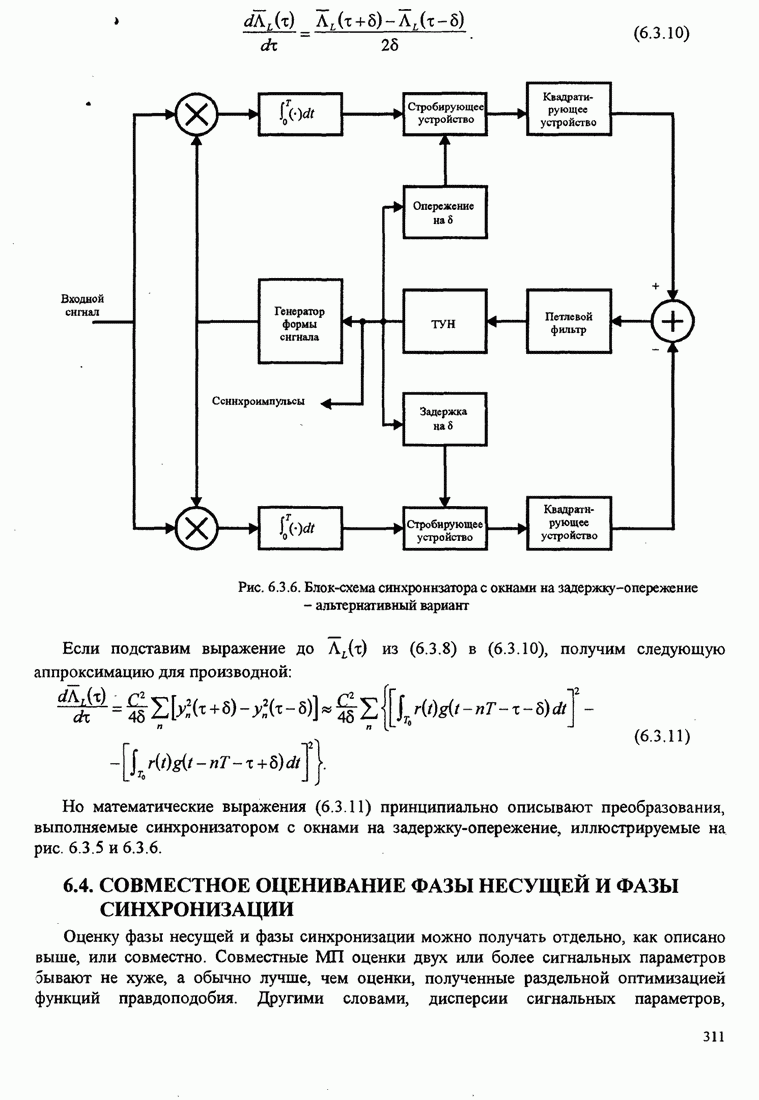
- 6.3.1. Максимально правдоподобная оценка параметра задержки
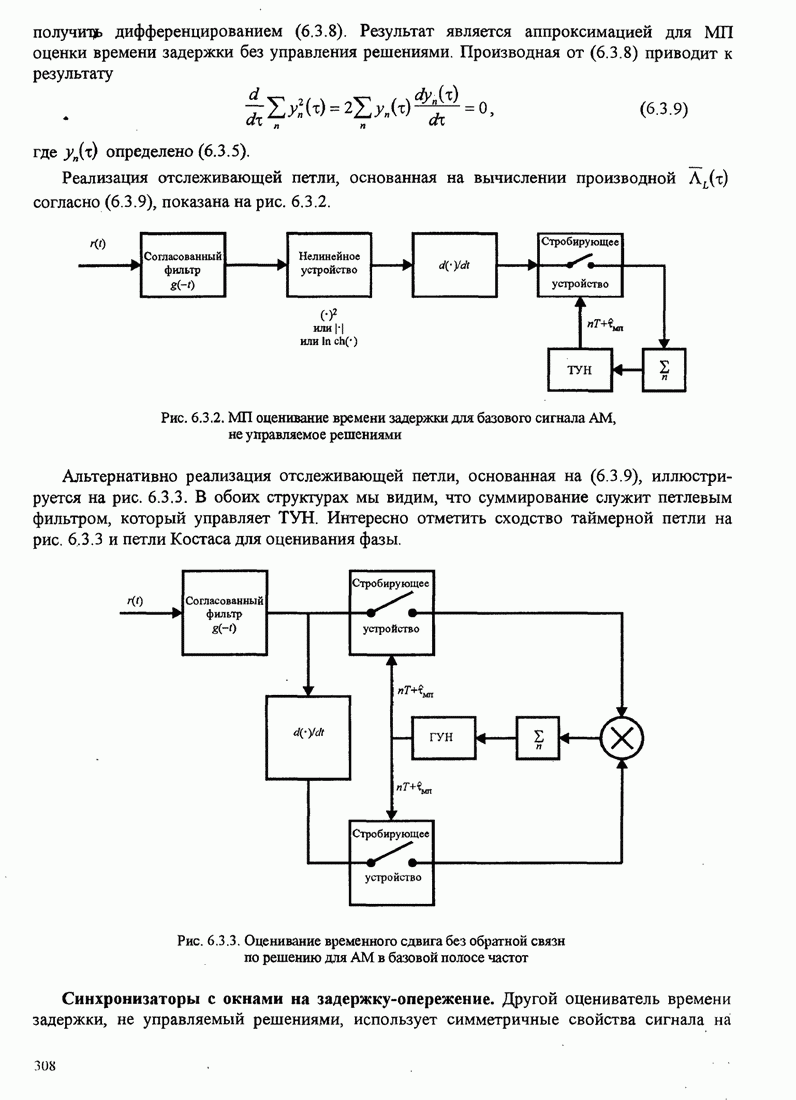
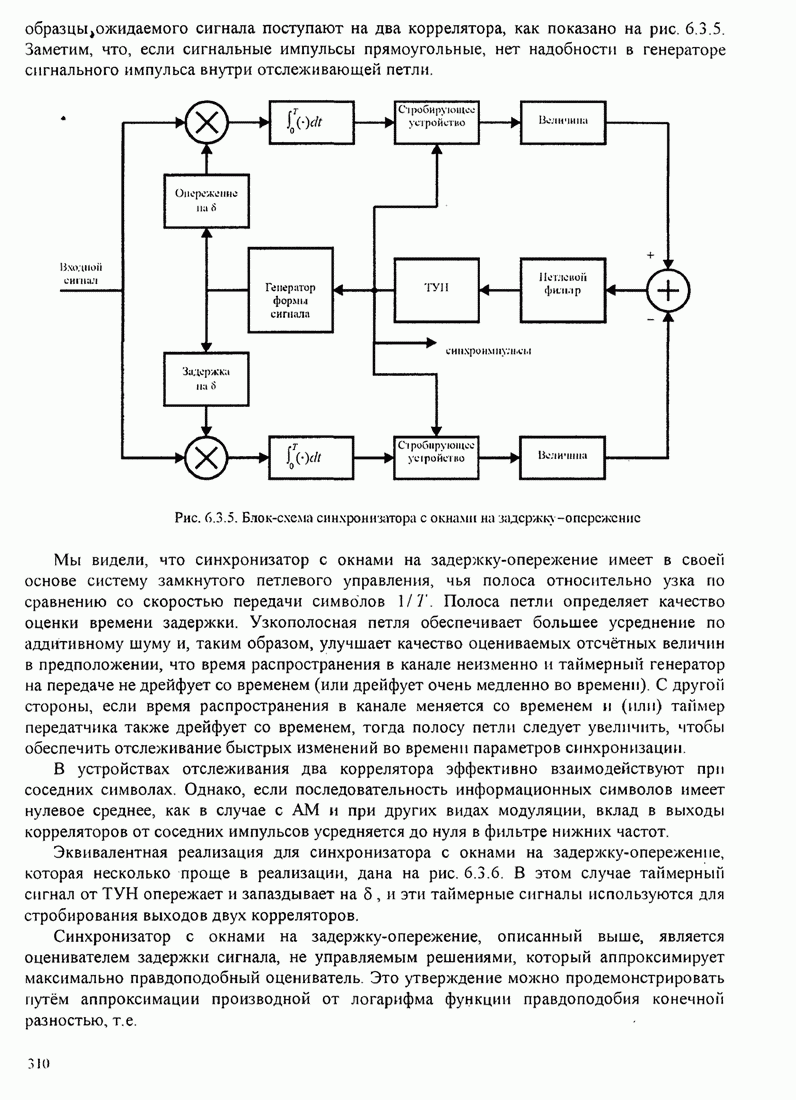
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
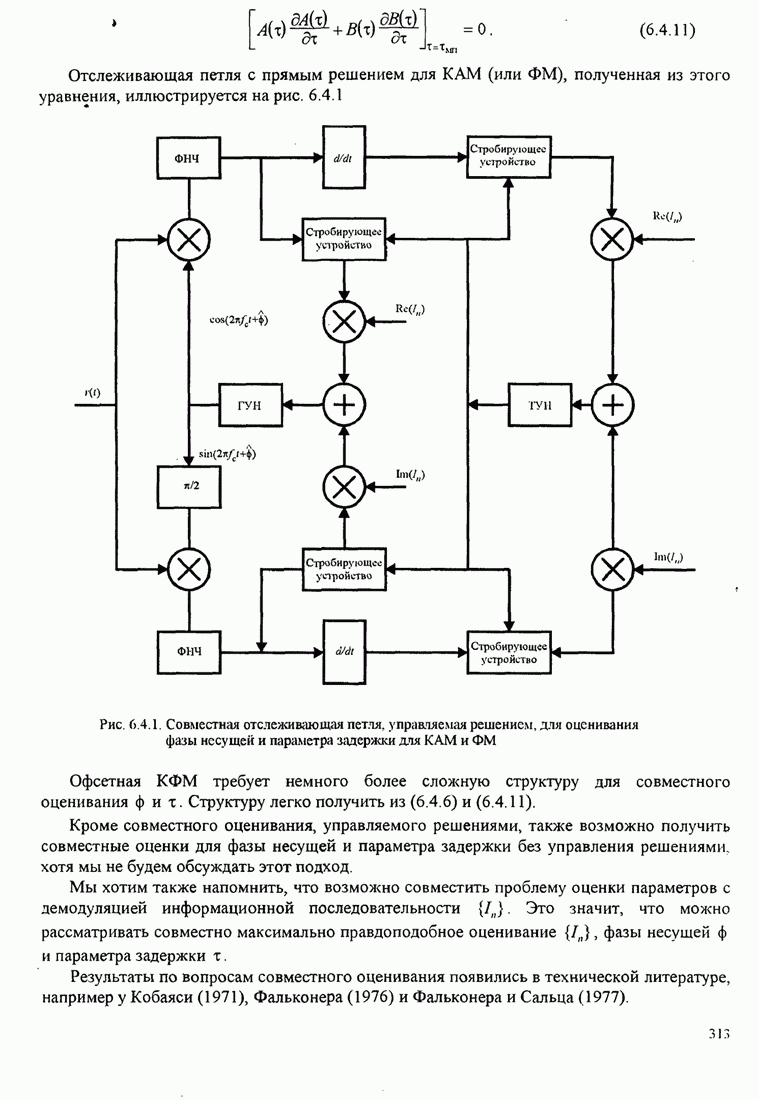
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
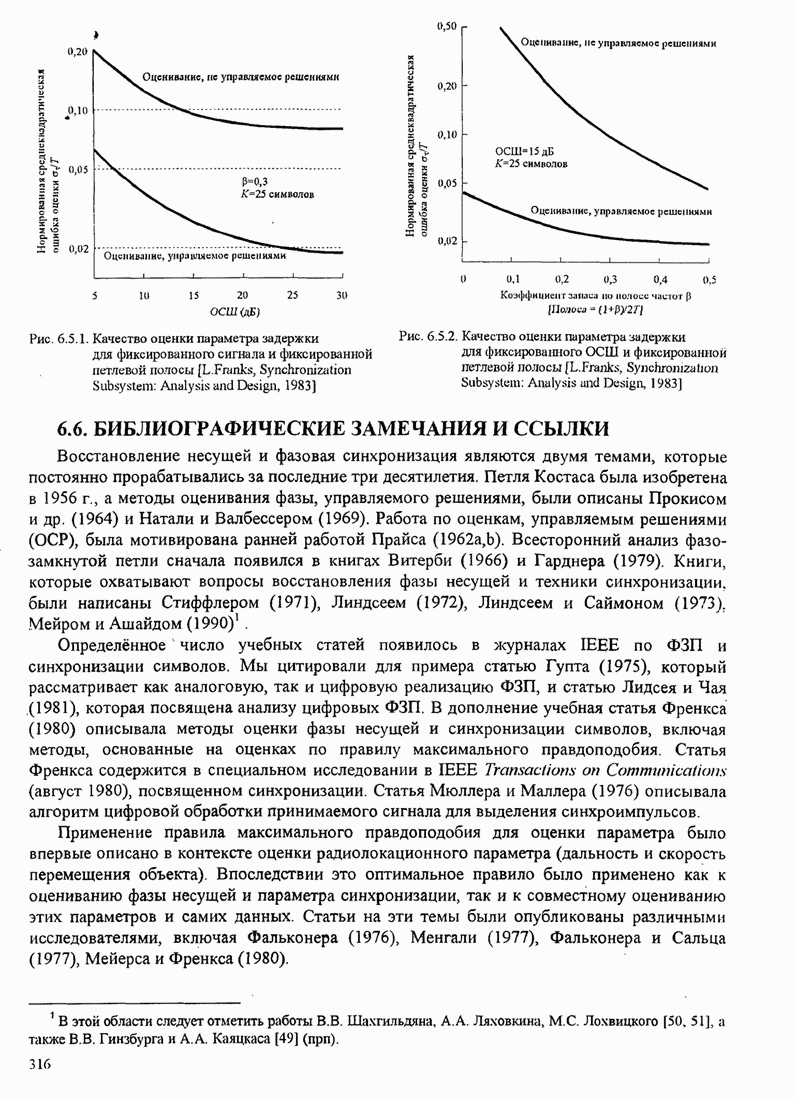
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
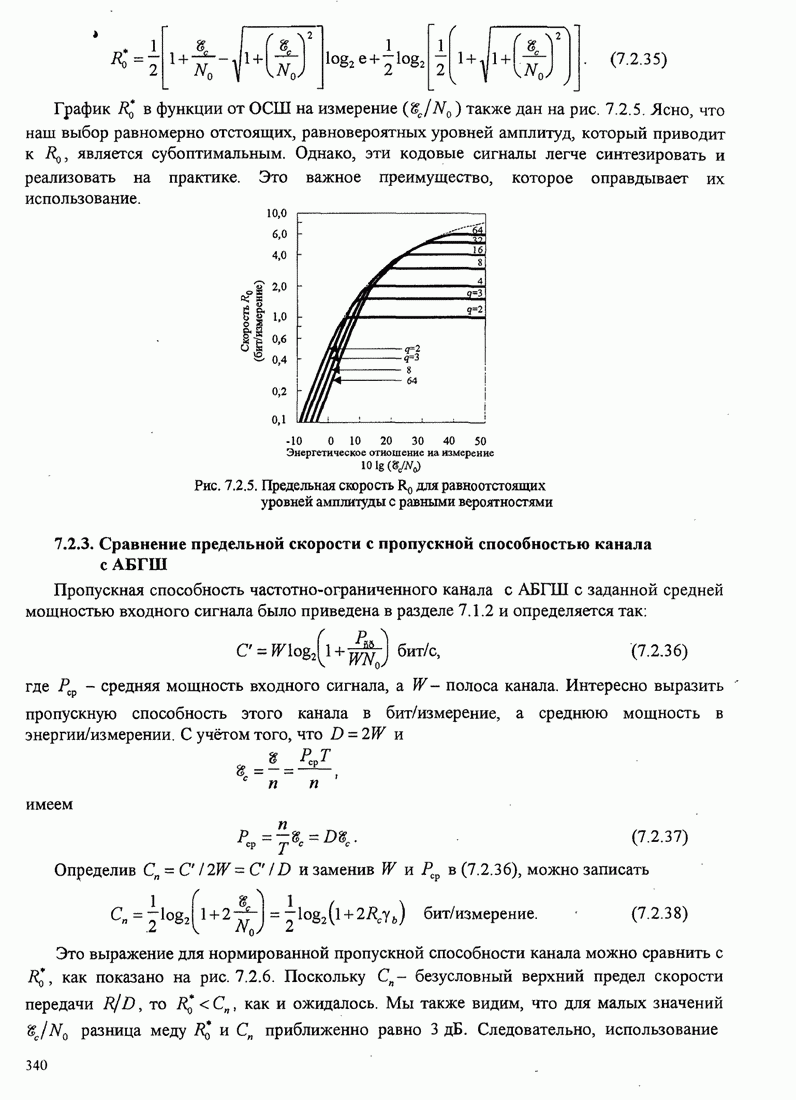
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
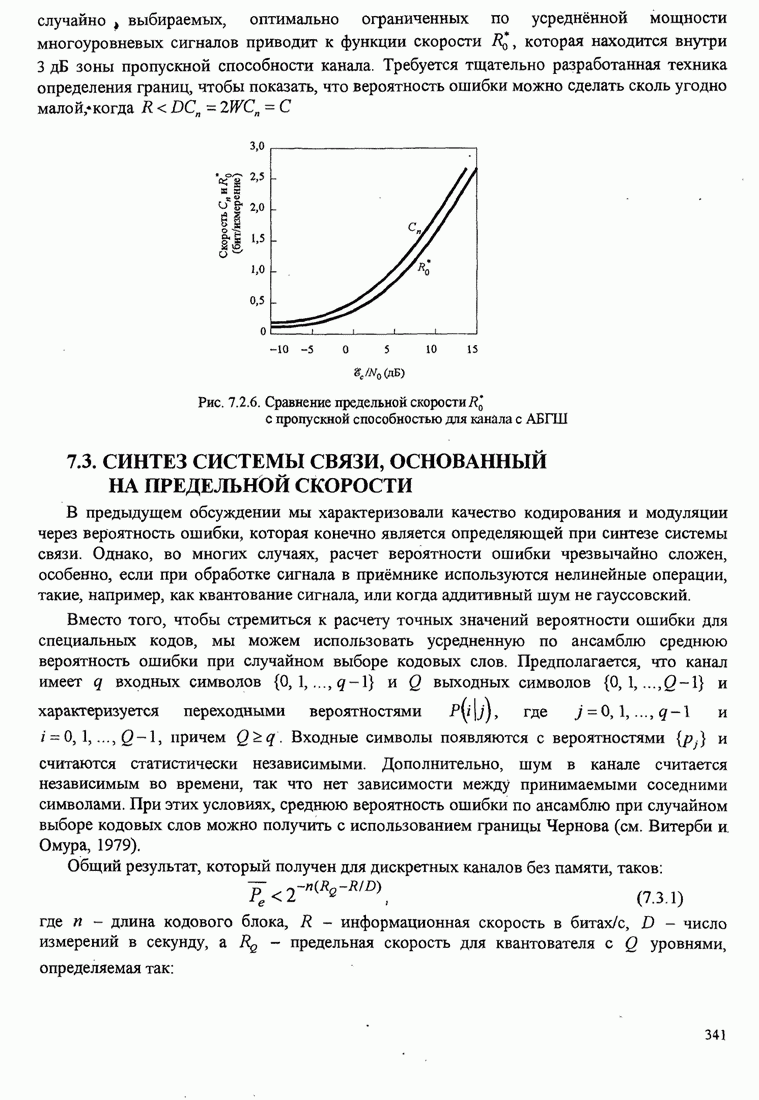
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
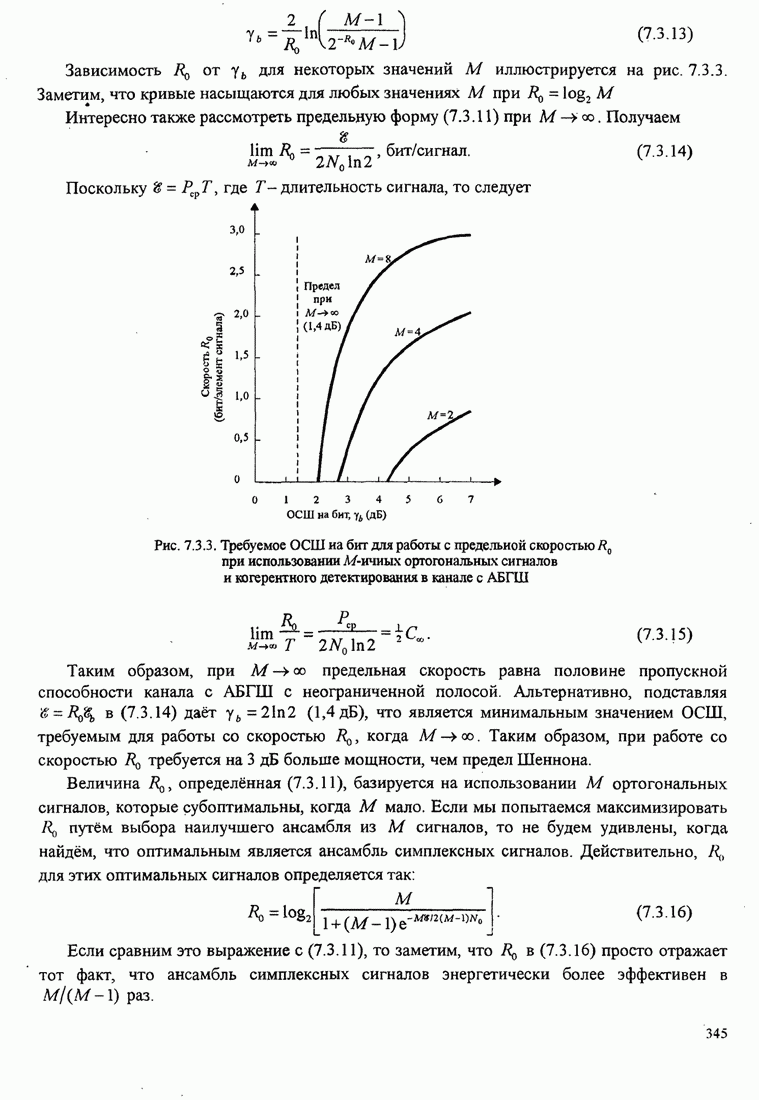
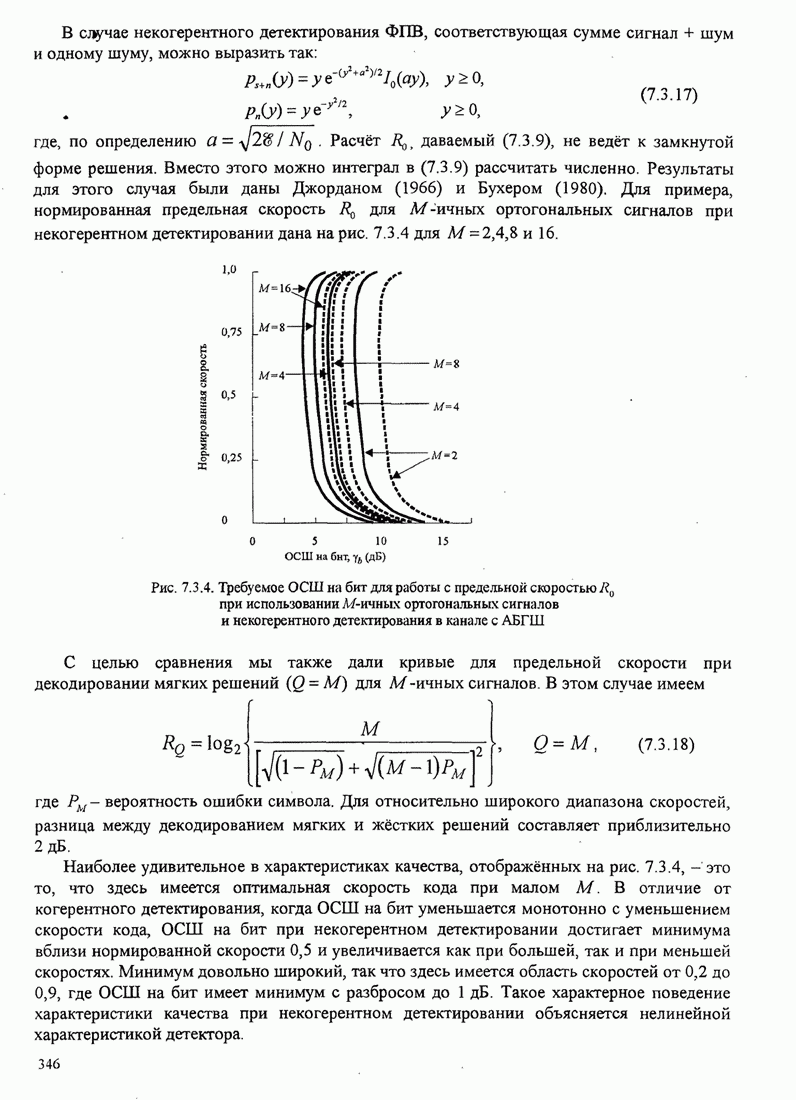
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
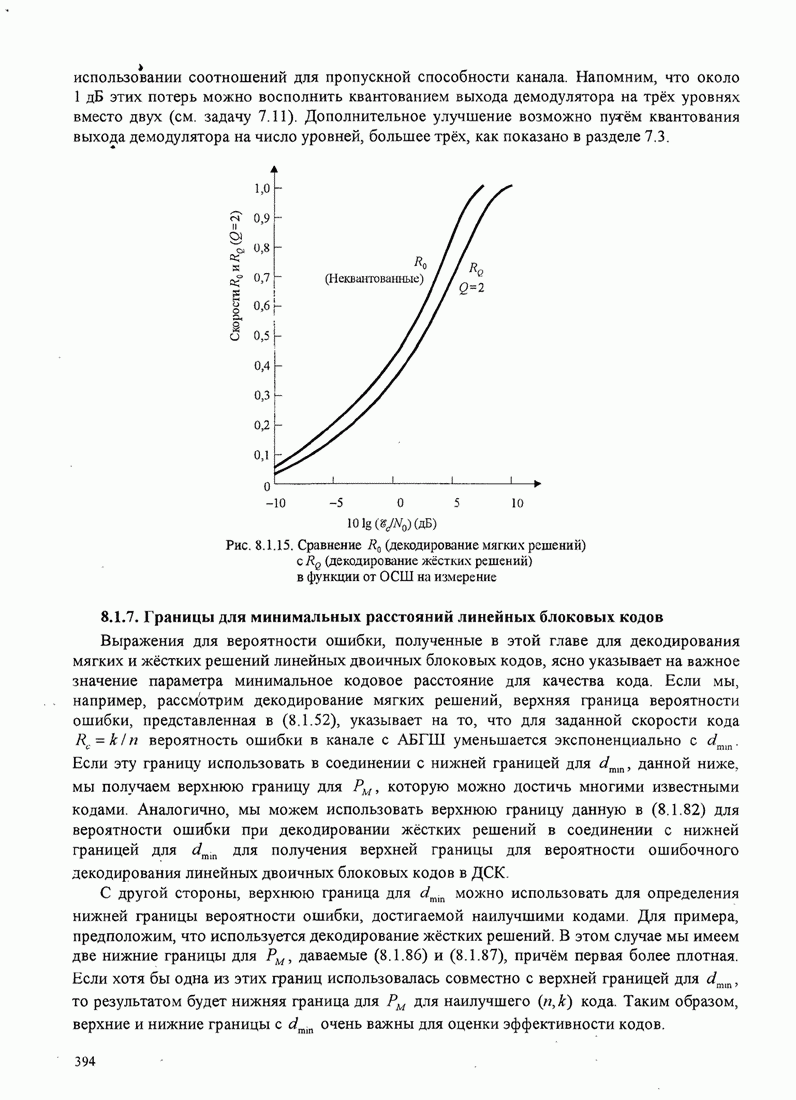
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
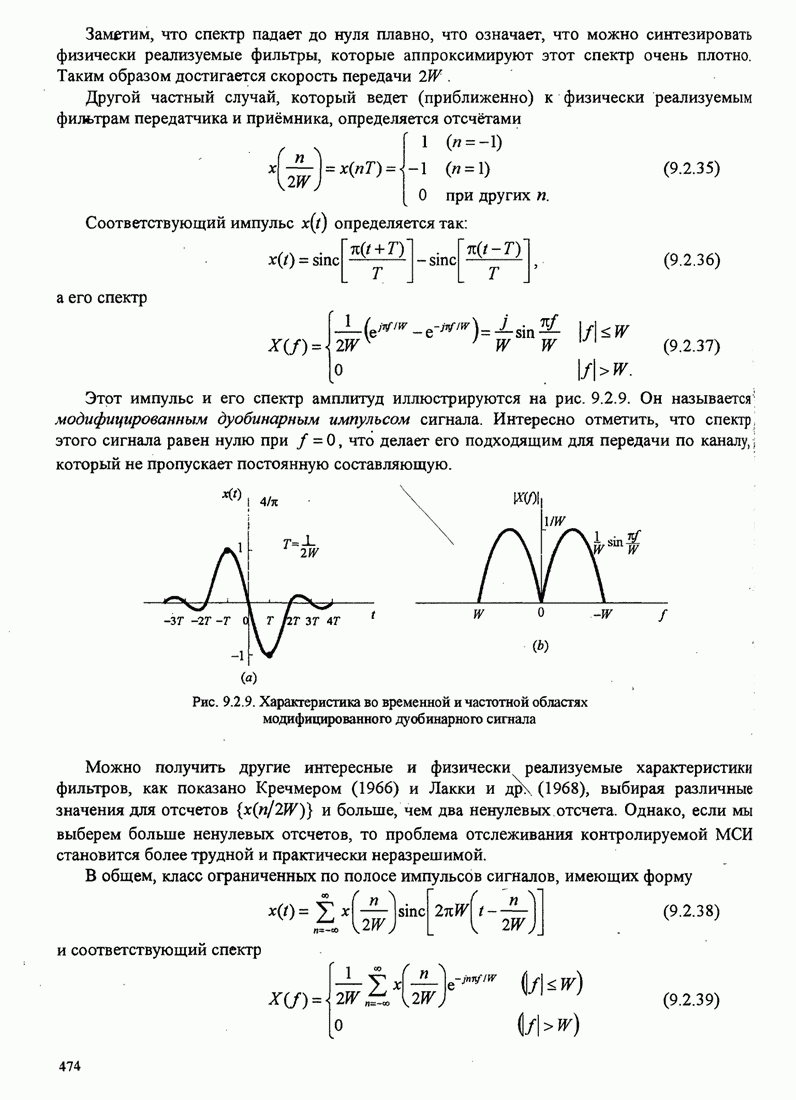
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
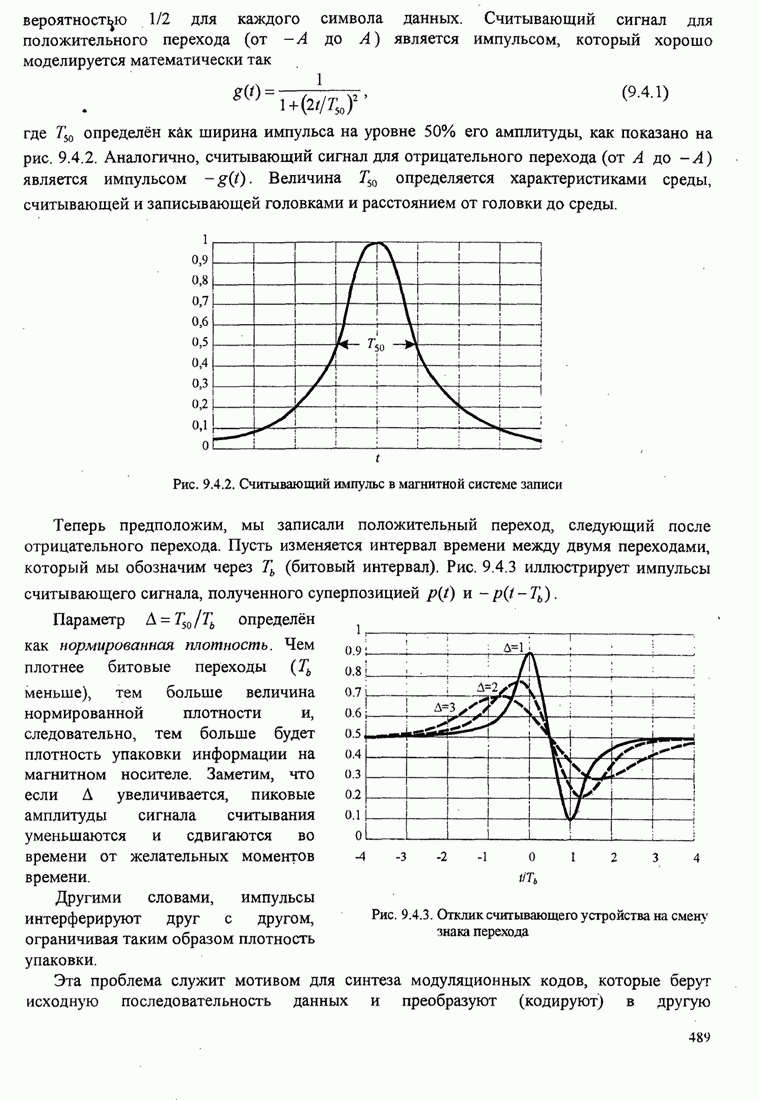
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
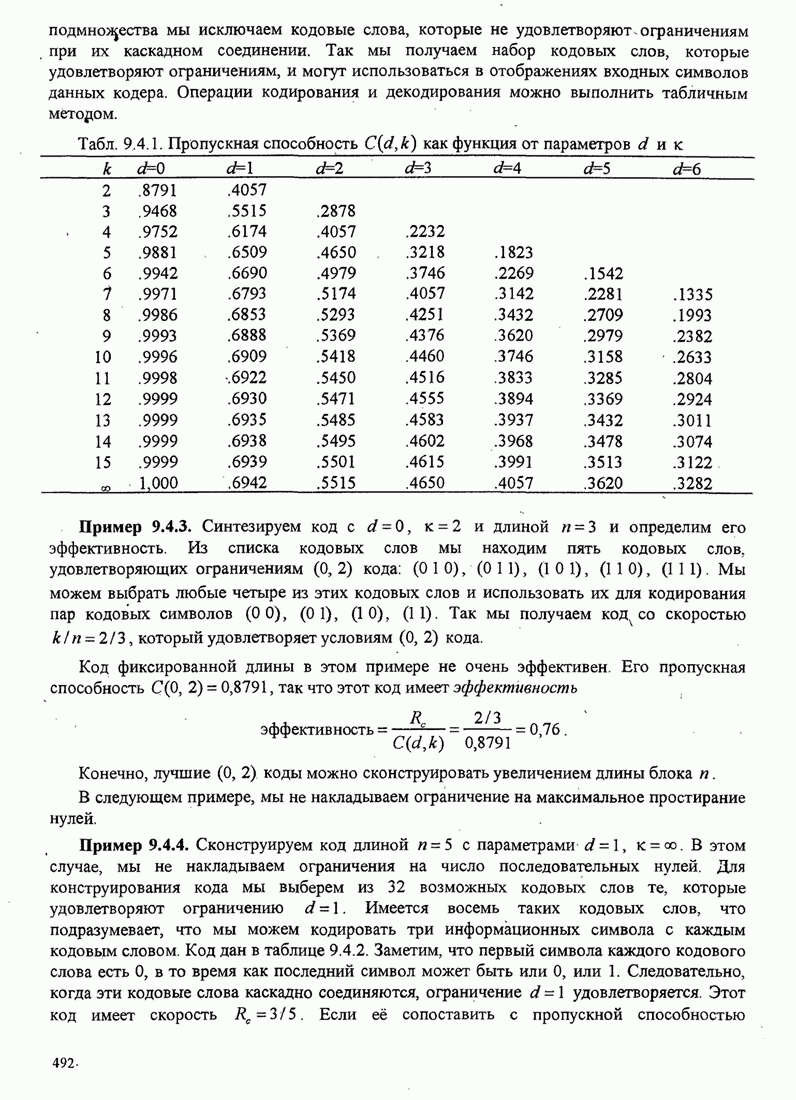
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
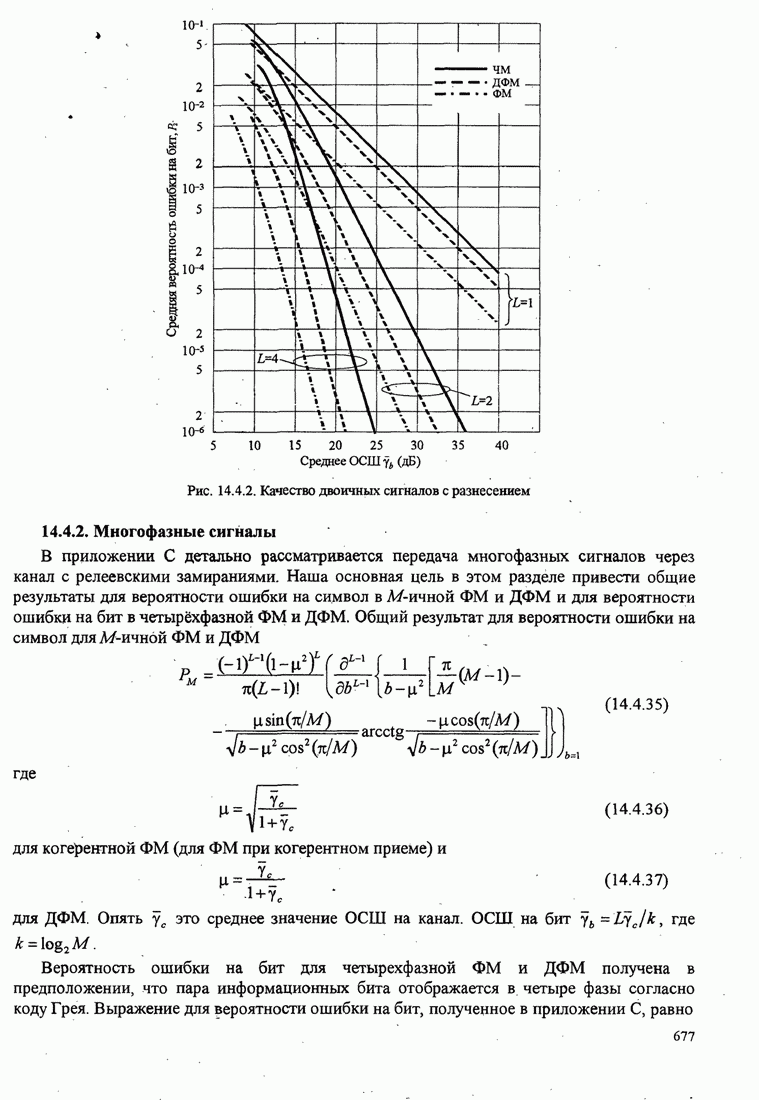
- 14.4.1. Двоичные сигналы
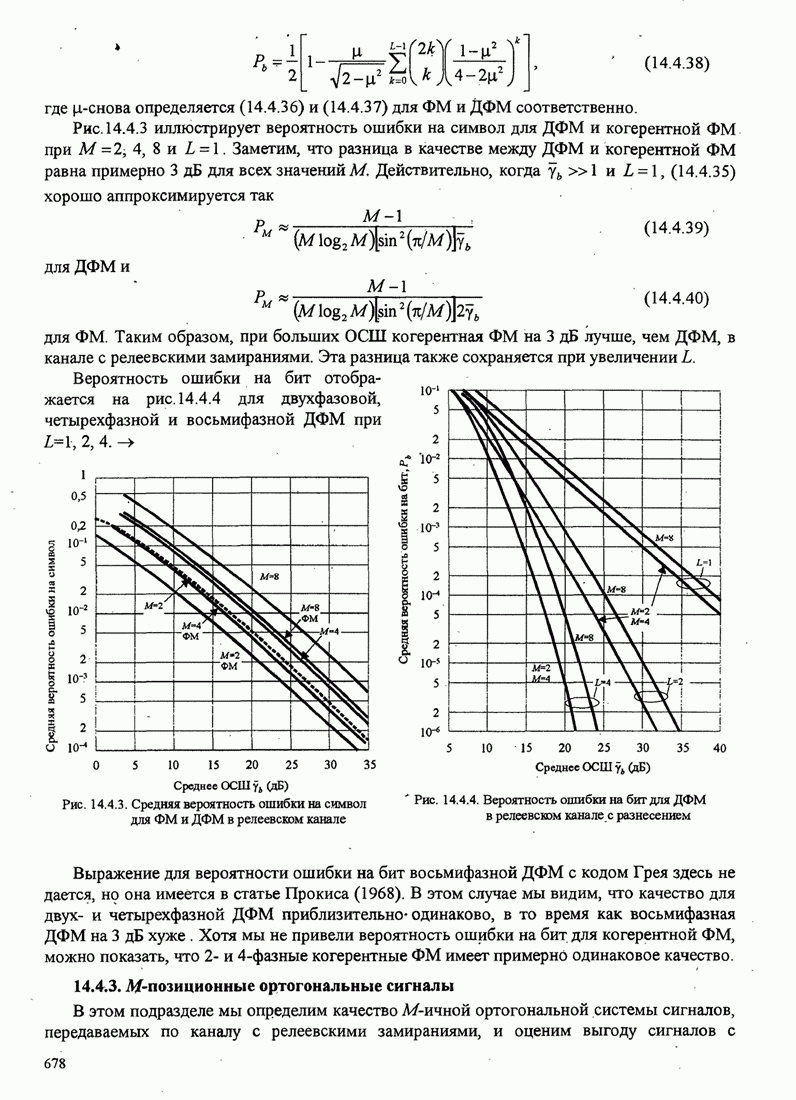
- 14.4.2. Многофазные сигналы
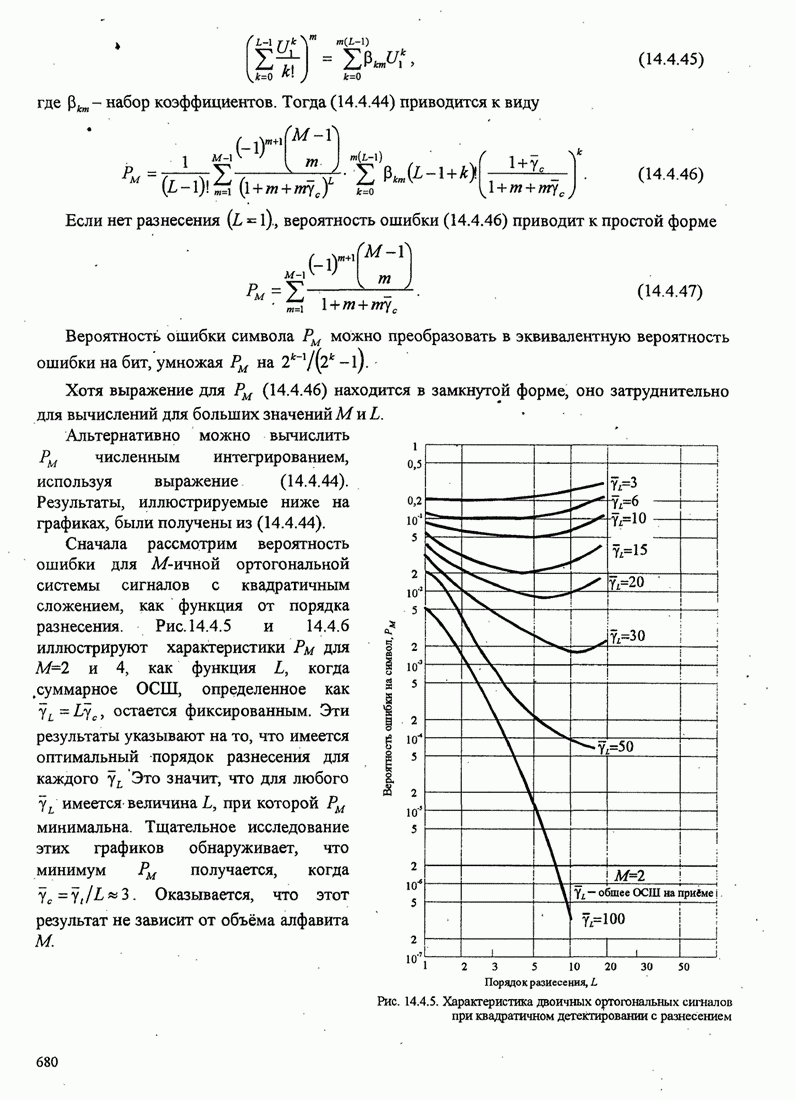
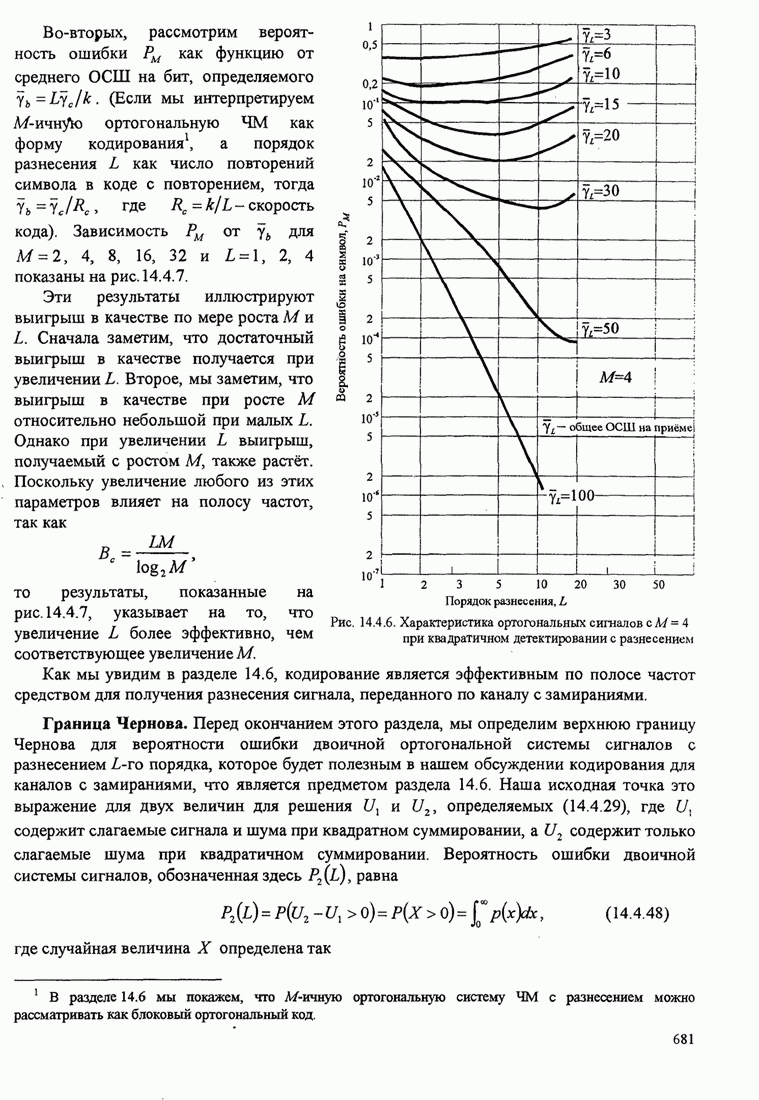
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)